UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID JUNIO 2008
|
|
|
- Teresa Lorena Maestre Agüero
- hace 5 años
- Vistas:
Transcripción
1 UNIVERSIDDES PÚBLICS DE L COMUNIDD DE MDRID JUNIO El mn pnt o opcion, B. El lumno bá lgi UN Y SÓLO UN ll olv lo cuto jcicio qu cont. No pmit l uó clculo con cpci pntción gáfic. PUNTUCIÓN: L clificción máim c jcicio inic n l ncbzminto l mimo. OPCIÓN Ejcicio. Clificción máim: punto. Do l itm cucion linl: pi:. ) ( punto). Dicuti l itm gún lo vlo l pámto. Rolvlo cuno l olución únic. b) ( punto). Dtmin p qué vlo o vlo l itm tin un olución n l qu.. El itm tá finio po l mtiz coficint () po l mpli. ( ). g g Si, g g n, l itm comptibl tmino, po lo tnto tui l tipo olución p lo vlo l pámto qu nuln l. : : : t ± Dicuión: i. Si ±: g g n. Sitm comptibl tmino. Solución únic. S pu olv po culqui métoo, unqu comino l métoo Cm. ii. Si : g <. g.. D lo mno olo l mno on, olo qu po tui l mno fomo po l ª ª column; g g < n. Sitm comptibl intmino. Infinit olucion. Sitm quivlnt: { ': S iii. Si : g <. g.. D lo mno olo l mno on, olo qu po tui l mno fomo po l ª ª column; g g. Sitm incomptibl.
2 b. H qu tui i p lo itm comptibl it un olución n l qu. -Sitm comptibl tmino: : : P it un olución n l qu qu l punto (, ). - Sitm comptibl intmino: P : S ': :. Eit un olución n l qu qu l punto (, ). Ejcicio. Clificción máim: punto. D l ct: z z z pi: ) (, punto). Dicuti l poición ltiv l o ct, gún lo, vlo l pámto. b) (, punto). Si, clcul l itnci mínim nt l o ct,.. L poición ltiv l o ct tui mint l ngo l mtiz fom po lo vcto icción mb ct, un gmnto fomo nt o punto, uno c ct, po lo tnto, ncio obtn un punto un vcto c un l ct, p lo cul tnfomn u cucion pmétic. λ ct λ (,,) λ : z z (,, ) z λ µ z z ct z zµ B (,, ) µ : z z (,,) z µ B b (,, ) (,, ) Rct no coplni, cuzn po no cotn k Rct cnt g Rt coplni : k Rct pll B Rct coincint El g g tui pti lo vlo l pámto qu nuln l tminnt l mtiz. : Poición ltiv i. Si :, g. L ct cuzn po no cotn. No tinn punto n común ii. Si :, g <., g. L ct on coplni.,, k,, L ct on cnt
3 b. S pu clcul o fom: i. Como ltu l pllpípo fomo po lo vcto, B. b B V h o { } B o,,,,,,,, Sutituno: B o ii. Como itnci un punto un plno. π Sino un punto π un plno pllo qu contin. z : z :,,,,,, B : π π π π Ejcicio. Clificción máim: punto. Etui lo iguint límit: ) ( punto). b) ( punto)..? L H L H b.
4 Sí < < Ejcicio. Clificción máim: punto. Obtn lo máimo mínimo ltivo, lo punto inflión l función: f () (Ln ()) ino Ln() l logitmo npino. Un función pnt tmo ltivo n lo punto on u pim iv co l gun itint co, con l iguint citio; i l gun iv poitiv á un mínimo, i l gun iv ngtiv á un máimo. Un función pnt punto inflión n lo punto on u gun iv co l tc iv itint co. f Ln Ln Ln Ln Ln f Ln ( Ln ) Ln Ln f Máimo mínimo ltivo: f : Ln Ln f Ln ( ) En l punto, : Ln ( Ln ) < l función pnt un máimo. Ln : : Ln : Ln : f : ( ) Ln En l punto f Ln, l función pnt un mínimo. () > : f ( Ln) Punto inflión: Ln f : : Ln : Ln : - Ln f ( ) : f Ln En l punto, l función pnt un punto inflión.
5 OPCIÓN B Ejcicio. Clificción máim: punto. D l iguint mtiz on n: n pi: ) (, punto). Clcul l tminnt l mtiz. b) (, punto). Clcul l tminnt l mtiz. c) ( punto). Clcul l tminnt l mtiz.. t { F F F } 9 b. F F F t 9 F F F 9 c. Siguino l l cunci pu infi qu: t n n... 9 Sgún t l: t Ejcicio. Clificción máim: punto. ) (, punto). P c vlo c >, clcul l á l gión cot compni nt l gáfic l función: f c c l j OX l ct,. b) (, punto). Hll l vlo c p l cul l á obtni n l pto ) mínim.. Si c >, f () > R. Tnino n cunt qu l función imp poitiv (t itu po ncim l j OX), l á n un intvlo á: c c c Á f c c c c c c c c c u c c c b. El á mínim obtin ivno l pión pcto c igulno co. c c c ( c ) c ( c c ) ( c) ( c ) c c c
6 c : : c : c ± c L compobción qu tt un á mínim hc con l gun iv. c c c c ( ) c c > P c l á mínim. P c l á máim. Ejcicio. Clificción máim: punto. Do lo punto (,, ), B(l,, ), C(,, ) D(l,, ), pi: ) (, punto). Dmot qu lo cuto punto no on coplnio. b) ( punto). Hll l cución l plno π tmino po lo punto, B C. c) (, punto). Hll l itnci l punto D l plno π.. Si cuto punto no on coplnio, nt llo hbá t vcto linlmnt inpnint, po tnto, l mtiz fom po to bá tn ngo. B b (,, ) (,, ) C c (,, ) (,, ) D,,,, < R tmin l ngo tui l tminnt l mtiz. 7 g Lo vcto on linlmnt inpnint, lo punto no coplnio b. El plno buco fom con o vcto ( B, C) (,,) (,, ) (,, ) un punto (). z π : B π C Dollno l tminnt po lo lmnto l ª fil onno obtin l cución gnl l plno. π z
7 c. L itnci D π clcul pticulizno l cución nomliz l plno n l coon D. 7 ( D π) Ejcicio. Clificción máim: punto. Do l plno π z l punto P(l,, ), pi: ) (, punto). Hll l cución l ct ppnicul l plno π qu p po l punto P. b) (, punto). Hll l punto Q intcción π. c) (, punto). Hll l punto R intcción π con l j OY. ) (, punto). Hll l á l tiángulo PQR.. L ct buc obtin con l vcto noml l plno como vcto icción l ct con l punto P. λ : P (,, ) n (,, ) π z λ λ b. El punto buco Q, ptnc po igul l ct l plno po tnto u coon cumpln l cucion mbo. S clcul utituno l cucion pmétic l ct n l cución gnl l plno, pj l pámto, con l vlo l pámto utituno n l cucion pmétic l ct ncuntn l coon l punto cot. π q q z q q λ q Q : : ( λ q ) ( λ q ) ( λ q ) q λ q z q λ q Opno onno pj l pámto. λ : λ Sutituno n l cucion pmétic obtinn l coon Q. q Q q z q : Q (,, ) c. S utitun l cucion pmétic l j OY n l cución l plno. OY R : µ : µ : µ : R (,, ) z z. El á un tiángulo finio po t punto obtin como plicción l móulo l poucto vctoil o vcto. Á ( PQR) PQ PR P(l,, ); Q (,, ); R (,, ) PQ PR (,, ) (,,) (,, ) (, 7, ) Á : PQ PR 7, ( PQR) PQ PR ( ) ( 9), 7 (,, 9)
SEPTIEMBRE 2001 INSTRUCCIONES:
 SEPTIEMBRE INSTRUCCIONES El mn psnt os opcions B; l lumno bá lgi un lls contst zonmnt los cuto jcicios qu const ich opción n h. min. OPCIÓN Ejcicio. Clificción máim puntos. Dtmin l cución ctsin l lug gomético
SEPTIEMBRE INSTRUCCIONES El mn psnt os opcions B; l lumno bá lgi un lls contst zonmnt los cuto jcicios qu const ich opción n h. min. OPCIÓN Ejcicio. Clificción máim puntos. Dtmin l cución ctsin l lug gomético
SEPTIEMBRE Tiempo: 90 minutos OPCIÓN A ( ) ( )
 SEPTIEMRE 5 INSTRUCCIONES El mn psn os opcions ; l lumno bá lgi un sólo un lls solv los cuo jcicios qu cons. No s pmi l uso clculos con cpci psnción gáfic. PUNTUCIÓN L clificción máim c jcicio s inic n
SEPTIEMRE 5 INSTRUCCIONES El mn psn os opcions ; l lumno bá lgi un sólo un lls solv los cuo jcicios qu cons. No s pmi l uso clculos con cpci psnción gáfic. PUNTUCIÓN L clificción máim c jcicio s inic n
[ ] ( ) ( ) [ ] [ ] [ ] [ ] ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2. Opción A 4 A. u 4
![[ ] ( ) ( ) [ ] [ ] [ ] [ ] ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2. Opción A 4 A. u 4 [ ] ( ) ( ) [ ] [ ] [ ] [ ] ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2. Opción A 4 A. u 4](/thumbs/88/115624296.jpg) IES Mditáno d Málg Solución Sptim 7 Jun Clo lono Ginontti Opción..- S qu l gáic d l unción () c l qu pc n l diujo - - - - - - - - ) Dtmin l unción [ punto] ) Clcul l á d l unción omd [ punto] [ ] [ ] [
IES Mditáno d Málg Solución Sptim 7 Jun Clo lono Ginontti Opción..- S qu l gáic d l unción () c l qu pc n l diujo - - - - - - - - ) Dtmin l unción [ punto] ) Clcul l á d l unción omd [ punto] [ ] [ ] [
Problema A.1. Obtener razonadamente, escribiendo todos los pasos del razonamiento utilizado: S, (2 puntos) y la matriz S -1, que es la
 José Aulio Pin Romo JULIO MII www.pin.s EXAMEN DE ELECTIVIDAD JULIO. MATEMÁTICA II OPCIÓN A Poblm A.. Obtn ondmnt scibindo todos los psos dl onminto utilido: ) El vlo dl dtminnt d l mti ( puntos) l mti
José Aulio Pin Romo JULIO MII www.pin.s EXAMEN DE ELECTIVIDAD JULIO. MATEMÁTICA II OPCIÓN A Poblm A.. Obtn ondmnt scibindo todos los psos dl onminto utilido: ) El vlo dl dtminnt d l mti ( puntos) l mti
+ + = = π 4 ( ) ( ) ( ) + +
 Moelo 8. Ejecicio B. Clificción máim: punto Do lo plno π π el punto B( ) e pie: c) (. punto) Hll el ángulo que fomn lo plno π π. c. El ángulo ente plno e clcul como ángulo ente u vectoe nomle meinte el
Moelo 8. Ejecicio B. Clificción máim: punto Do lo plno π π el punto B( ) e pie: c) (. punto) Hll el ángulo que fomn lo plno π π. c. El ángulo ente plno e clcul como ángulo ente u vectoe nomle meinte el
( ) ( ) ( ) ( ) BLOQUE A + = + IES Mediterráneo de Málaga Solución Junio 2012 Juan Carlos Alonso Gianonatti
 IES Mditáno d Málg Solución Junio Jun Clos Alonso Ginontti BLOQUE A CUESTIÓN A..- ) Discut l guint stm d cucions n unción dl pámto [ 5 puntos] ) Rsul l stm cundo s comptil [ punto] λ λ λ Solución 8 Con
IES Mditáno d Málg Solución Junio Jun Clos Alonso Ginontti BLOQUE A CUESTIÓN A..- ) Discut l guint stm d cucions n unción dl pámto [ 5 puntos] ) Rsul l stm cundo s comptil [ punto] λ λ λ Solución 8 Con
EJERCICIOS DE PUNTOS, RECTAS Y PLANOS PUNTOS
 EJERCICIOS DE PUNTOS, RECTAS Y PLANOS PUNTOS Ejecicio nº.- Repeent lo punto iguiente: A(, 5, ), B(,, ) C(,, ) Ejecicio nº.- Repeent lo punto iguiente: A(,, ), B(,, ) C(,, ) Ejecicio nº.- Repeent lo punto
EJERCICIOS DE PUNTOS, RECTAS Y PLANOS PUNTOS Ejecicio nº.- Repeent lo punto iguiente: A(, 5, ), B(,, ) C(,, ) Ejecicio nº.- Repeent lo punto iguiente: A(,, ), B(,, ) C(,, ) Ejecicio nº.- Repeent lo punto
( ) Peje=1 HP, Ve=120V, f=60hz, n=1650rpm, η=65%, fp=75% Sabemos que: 2
 Unividd Simón Bolív Dtmnto d Convión y Tnot d Engí Auto: Edudo Albánz. Cnt: 06-91 Pofo: J. M. All Máquin Eléctic II CT-11 Un moto d inducción monofáico d 1 HP, 10V, 60Hz, 1650m, 65% d ndiminto y 75% d
Unividd Simón Bolív Dtmnto d Convión y Tnot d Engí Auto: Edudo Albánz. Cnt: 06-91 Pofo: J. M. All Máquin Eléctic II CT-11 Un moto d inducción monofáico d 1 HP, 10V, 60Hz, 1650m, 65% d ndiminto y 75% d
= 001. ( ) t. 1 adja A = A 1
 UNIVERSIDDES PÚLICS DE L COMUNIDD DE MDRID PRUE DE CCESO LS ENSEÑNZS UNIVERSITRIS OICILES DE GRDO MODELO Cso / MTERI MTEMTICS II El lmno contstá los cto jcicios d n d ls dos opcions ( o ) q s l ocn. Nnc
UNIVERSIDDES PÚLICS DE L COMUNIDD DE MDRID PRUE DE CCESO LS ENSEÑNZS UNIVERSITRIS OICILES DE GRDO MODELO Cso / MTERI MTEMTICS II El lmno contstá los cto jcicios d n d ls dos opcions ( o ) q s l ocn. Nnc
Lím. = Lím. 1 e. x 1. x 0
 UNIVERSIDDES PÚLICS DE L COMUNIDD DE MDRID PRUE DE CCESO LS ENSEÑNZS UNIVERSITRIS OICILES DE GRDO MODELO Cuso / MTERI: MTEMTICS II El lumno consá los cuo jcicios d un d ls dos opcions ( o ) qu s l ofcn.
UNIVERSIDDES PÚLICS DE L COMUNIDD DE MDRID PRUE DE CCESO LS ENSEÑNZS UNIVERSITRIS OICILES DE GRDO MODELO Cuso / MTERI: MTEMTICS II El lumno consá los cuo jcicios d un d ls dos opcions ( o ) qu s l ofcn.
TRANSFORMACIONES GEOMÉTRICAS Proyectividad y homografía Homología y afinidad Inversión TEMA4. Objetivos y orientaciones metodológicas. 1.
 TRNSRMINES GEMÉTRIS Poyctivi y homogfí Homologí y fini Invsión TEM4 IUJ GEMÉTRI bjtivos y ointcions mtoológics Est Tm tin como objtivos intouci l lumno n los conocimintos poyctivi, homogfí, homologí, fini
TRNSRMINES GEMÉTRIS Poyctivi y homogfí Homologí y fini Invsión TEM4 IUJ GEMÉTRI bjtivos y ointcions mtoológics Est Tm tin como objtivos intouci l lumno n los conocimintos poyctivi, homogfí, homologí, fini
IES Mediterráneo de Málaga Solución Septiembre 2013 Juan Carlos Alonso Gianonatti OPCIÓN A. se pide
 IES Mditáno d Málg Solución Sptimb Jun los lonso Ginontti Ejcicio.- liicción máim puntos Dd l unción: 7 s pid ( 7 puntos Hll ls síntots d dich gic OPIÓN b ( 7 puntos Dtmin los intlos d cciminto dcciminto
IES Mditáno d Málg Solución Sptimb Jun los lonso Ginontti Ejcicio.- liicción máim puntos Dd l unción: 7 s pid ( 7 puntos Hll ls síntots d dich gic OPIÓN b ( 7 puntos Dtmin los intlos d cciminto dcciminto
Ejercicio 1. x a. Ejercicio 2.
 Sptim 5 - Opción A (Molo 6) Ejcicio. D un función f: R R s s qu f() y qu f (. () [ punto] Dtmin f. () [ 5 puntos] Clcul l á l ión limit po l áfic f, po l j sciss y po ls cts cucions - y. () Aplicno l Tom
Sptim 5 - Opción A (Molo 6) Ejcicio. D un función f: R R s s qu f() y qu f (. () [ punto] Dtmin f. () [ 5 puntos] Clcul l á l ión limit po l áfic f, po l j sciss y po ls cts cucions - y. () Aplicno l Tom
I.E.S. Mediterráneo de Málaga Modelo6_09_Soluciones Juan Carlos Alonso Gianonatti. Opción A. Ejercicio 1
 I.E.S. Mditáno d Málaga Modlo6_9_Solucions Juan Calos Alonso Gianonatti - Sa f:r R la función dfinida po f ( ) =+. Opción A Ejcicio 1 [ 7 puntos] Dtmina los intvalos d cciminto y dcciminto d f, así como
I.E.S. Mditáno d Málaga Modlo6_9_Solucions Juan Calos Alonso Gianonatti - Sa f:r R la función dfinida po f ( ) =+. Opción A Ejcicio 1 [ 7 puntos] Dtmina los intvalos d cciminto y dcciminto d f, así como
EJERCICIOS DE REPASO TODA LA MATERIA (Ficha 2)
 IES ÁFRIC º BCHILLERTO CCNN EJERCICIOS DE REPSO TOD L MTERI (Fich ) Ejecicio nº.- Un estdo comp biles de petóleo tes suministdoes dieentes que lo venden 7,8 y dóles el bil, espectivmente. L ctu totl sciende
IES ÁFRIC º BCHILLERTO CCNN EJERCICIOS DE REPSO TOD L MTERI (Fich ) Ejecicio nº.- Un estdo comp biles de petóleo tes suministdoes dieentes que lo venden 7,8 y dóles el bil, espectivmente. L ctu totl sciende
Matemáticas II Unidad 4 Geometría
 Mtemátic II Unidd Geometí UNIDAD EL ESPACIO AFÍN.- Demot que i do punto etán ddo epecto del item de efeenci fín cteino, entonce el vecto que lo une tiene po coodend l difeenci de l coodend de mbo punto
Mtemátic II Unidd Geometí UNIDAD EL ESPACIO AFÍN.- Demot que i do punto etán ddo epecto del item de efeenci fín cteino, entonce el vecto que lo une tiene po coodend l difeenci de l coodend de mbo punto
GUÍA III : FUERZAS ELECTROMAGNÉTICAS
 Sitma Elctomcánico, Guía III: Fuza Elctomagnética GUÍA III : FUERZAS EECROMAGÉICAS. El núclo d la figua tin una pmabilidad dl fio infinita y cción tanval d 9 [cm ]. El dvanado tin 5 [vulta] y una itncia
Sitma Elctomcánico, Guía III: Fuza Elctomagnética GUÍA III : FUERZAS EECROMAGÉICAS. El núclo d la figua tin una pmabilidad dl fio infinita y cción tanval d 9 [cm ]. El dvanado tin 5 [vulta] y una itncia
UNIVERSIDAD DE LA RIOJA JUNIO lim
 IES Mditrráno d Málg Emn Junio d Jun Crlos lonso Ginontti UNIVERSIDD DE L RIOJ JUNIO El lumno contstrá los jrcicios d un d ls dos propusts ( o ) qu s l ofrcn. Nunc dbrá contstr jrcicios d un propust jrcicios
IES Mditrráno d Málg Emn Junio d Jun Crlos lonso Ginontti UNIVERSIDD DE L RIOJ JUNIO El lumno contstrá los jrcicios d un d ls dos propusts ( o ) qu s l ofrcn. Nunc dbrá contstr jrcicios d un propust jrcicios
5.1. LA DERIVADA, DERIVADAS LATERALES. Observación: df sí existe y es finito lim x a
 Divd d ucio u vibl l 5 LA DERIVADA, DERIVADAS LATERALES Diició 5 S : lr lr u ució, Dom, dimo qu divbl d í it y iito lim D D y d Si divbl t tbjo umo l otcio, d d p dci l divd d Ejmplo: Sí lim lim 8 Obvció:
Divd d ucio u vibl l 5 LA DERIVADA, DERIVADAS LATERALES Diició 5 S : lr lr u ució, Dom, dimo qu divbl d í it y iito lim D D y d Si divbl t tbjo umo l otcio, d d p dci l divd d Ejmplo: Sí lim lim 8 Obvció:
OPERACIONES MATEMÁTICAS
 Cpítulo OPERACIONES MATEMÁTICAS OPERACIÓN MATEMÁTICA E un poo qu onit n l tnfoión un o á nti n ot ll ulto, jo it gl o oniion n l ul fin l opión. To opión táti pnt un gl finiión y un íolo qu l intifi llo
Cpítulo OPERACIONES MATEMÁTICAS OPERACIÓN MATEMÁTICA E un poo qu onit n l tnfoión un o á nti n ot ll ulto, jo it gl o oniion n l ul fin l opión. To opión táti pnt un gl finiión y un íolo qu l intifi llo
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE LA RIOJA JUNIO 2011 (GENERAL) (RESUELTOS por Antonio Menguiano) Tiempo máximo: 1 horas y 30 minutos
 IES CASTEAR BADAJOZ PRUEBA DE ACCESO (OGSE) UNIVERSIDAD DE A RIOJA JUNIO (GENERA) (RESUETOS po Antonio Mnguiano) MATEMÁTICAS II Timpo máimo: hoas y minutos El alumno contstaá a los jcicios d una d las
IES CASTEAR BADAJOZ PRUEBA DE ACCESO (OGSE) UNIVERSIDAD DE A RIOJA JUNIO (GENERA) (RESUETOS po Antonio Mnguiano) MATEMÁTICAS II Timpo máimo: hoas y minutos El alumno contstaá a los jcicios d una d las
EL ESPACIO AFÍN. Respecto del sistema de referencia, las coordenadas del punto A= a, a, a
 Geometí Anlític: El Espcio Afín Pofeso:Mí José Sánchez Queedo. EL ESPACIO AFÍN SISTEMA DE REFERENCIA EN EL ESPACIO AFÍN Un sistem de efeenci del espcio fín está compuesto po un punto fijo O del espcio
Geometí Anlític: El Espcio Afín Pofeso:Mí José Sánchez Queedo. EL ESPACIO AFÍN SISTEMA DE REFERENCIA EN EL ESPACIO AFÍN Un sistem de efeenci del espcio fín está compuesto po un punto fijo O del espcio
RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO EN POSICIÓN NORMAL
 Cpít ulo RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO EN POSICIÓN NORMAL Dfiniions Pvis: I. ÁNGULO EN POSICIÓN NORMAL Llmo tmién n posiión nóni o stán. Es quél ángulo tigonométio uo véti oini on l oign l sistm
Cpít ulo RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO EN POSICIÓN NORMAL Dfiniions Pvis: I. ÁNGULO EN POSICIÓN NORMAL Llmo tmién n posiión nóni o stán. Es quél ángulo tigonométio uo véti oini on l oign l sistm
IES CASTELAR BADAJOZ Examen Junio de 2011(General) Solución Antonio Mengiano Corbacho UNIVERSIDAD DE EXTREMADURA MATEMÁTICAS II
 IES CASTELAR BADAJOZ Emn Junio d (Gnrl) Antonio ngino Corbcho UNIVERSIDAD DE ETREADURA ATEÁTICAS II ATEÁTICAS II Timpo máimo: hor minutos Instruccions: El lumno lgirá un d ls dos opcions propusts Cd un
IES CASTELAR BADAJOZ Emn Junio d (Gnrl) Antonio ngino Corbcho UNIVERSIDAD DE ETREADURA ATEÁTICAS II ATEÁTICAS II Timpo máimo: hor minutos Instruccions: El lumno lgirá un d ls dos opcions propusts Cd un
Curso MATERIA: MATEMÁTICAS II (Fase general)
 Cuso 9- MTERI MTEMÁTICS II (Fse genel) INSTRUCCIONES GENERLES Y VLORCIÓN El lumno contest los cuto ejecicios de un de l dos opciones ( o B) que se le oecen. Nunc deeá contest unos ejecicios de un opción
Cuso 9- MTERI MTEMÁTICS II (Fse genel) INSTRUCCIONES GENERLES Y VLORCIÓN El lumno contest los cuto ejecicios de un de l dos opciones ( o B) que se le oecen. Nunc deeá contest unos ejecicios de un opción
I.E.S. Mediterráneo de Málaga Junio 2012 Juan Carlos Alonso Gianonatti PROPUESTA A
 I.E.S. Mditrráno d Málg Junio Jun Crlos lonso Ginontti PROPUEST.- ( punto) S f() un función positiv n l intrvlo [ ] sí ( ) f pr. Si l ár itd por f() l j d bciss (j O) ls rcts s igul clcul l ár dl rcinto
I.E.S. Mditrráno d Málg Junio Jun Crlos lonso Ginontti PROPUEST.- ( punto) S f() un función positiv n l intrvlo [ ] sí ( ) f pr. Si l ár itd por f() l j d bciss (j O) ls rcts s igul clcul l ár dl rcinto
Tomamos el menor formado por las dos primeras columnas y la primera y tercera filas. 1 1
 Blu I. Álg Mtmátis II Autvluión Págin D l mti M m m : ) Hll ls vls m u ls vts il M sn linlmnt innints. ) Estui l ng M sgún ls vls m. ) P m, lul l invs M. ) P u ls vts il M sn linlmnt innints, n (M ) tin
Blu I. Álg Mtmátis II Autvluión Págin D l mti M m m : ) Hll ls vls m u ls vts il M sn linlmnt innints. ) Estui l ng M sgún ls vls m. ) P m, lul l invs M. ) P u ls vts il M sn linlmnt innints, n (M ) tin
GEOMETRÍA 1º BACHILLERATO
 GEOMETRÍA º AHILLERATO ) Dmin c co l coo pi ) A() A =() hll () - = = - = = ) () A =(--) hll A A() - =- = - =- = ( ) A( ) c) (-) A =() hll A A() - = = + = =- ) S lo co li ( ) ( ) w ( ) hz l pción gáfic
GEOMETRÍA º AHILLERATO ) Dmin c co l coo pi ) A() A =() hll () - = = - = = ) () A =(--) hll A A() - =- = - =- = ( ) A( ) c) (-) A =() hll A A() - = = + = =- ) S lo co li ( ) ( ) w ( ) hz l pción gáfic
PRUEBA DE ACCESO A LA UNIVERSIDAD ENUNCIADO Y RESOLUCIÓN
 PRUEBA DE ACCESO A LA UNIVERSIDAD.6 ENUNCIADO Y RESOLUCIÓN Instucciones: )Dución: 1 ho y minutos. b) Tienes que elegi ente eliz únicmente los cuto ejecicios de l Opción A o eliz únicmente los cuto ejecicios
PRUEBA DE ACCESO A LA UNIVERSIDAD.6 ENUNCIADO Y RESOLUCIÓN Instucciones: )Dución: 1 ho y minutos. b) Tienes que elegi ente eliz únicmente los cuto ejecicios de l Opción A o eliz únicmente los cuto ejecicios
CAPITULO 6 INTEGRALES MULTIPLES
 CAPITULO Nusts lms cus cults pun compn l mvillos quitctu l muno mi l cuso c plnt vguno ún scln ts l conociminto ininito Chistoph Mlow. INTEGALES MULTIPLES.. Intgls ols... Cálculo un intgl ol n gions gnls...
CAPITULO Nusts lms cus cults pun compn l mvillos quitctu l muno mi l cuso c plnt vguno ún scln ts l conociminto ininito Chistoph Mlow. INTEGALES MULTIPLES.. Intgls ols... Cálculo un intgl ol n gions gnls...
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE GALICIA SEPTIEMBRE (RESUELTOS por Antonio Menguiano) Tiempo máximo: 1 horas y 30 minutos
 IES CSTELR DJOZ Mnguino PRUE DE CCESO (LOGSE) UNIVERSIDD DE GLICI SEPTIEMRE - (RESUELTOS por ntonio Mnguino) MTEMÁTICS II Timpo máimo: hors minutos El lumno db rspondr solmnt los jrcicios d un d ls opcions
IES CSTELR DJOZ Mnguino PRUE DE CCESO (LOGSE) UNIVERSIDD DE GLICI SEPTIEMRE - (RESUELTOS por ntonio Mnguino) MTEMÁTICS II Timpo máimo: hors minutos El lumno db rspondr solmnt los jrcicios d un d ls opcions
I.E.S. Mediterráneo de Málaga Junio 2010 Juan Carlos Alonso Gianonatti OPCIÓN A
 I.E.S. diáno álg Junio Jun Clo lono Ginoni OPCIÓN.- ) Pon un jplo i iéi on oo i niiéi on. ) S un i iéi on on () -. Clul onndo l pu l inn indo l i pu. ) Clul un i iéi ngo qu iiqu ) Un i iéi qull n qu l
I.E.S. diáno álg Junio Jun Clo lono Ginoni OPCIÓN.- ) Pon un jplo i iéi on oo i niiéi on. ) S un i iéi on on () -. Clul onndo l pu l inn indo l i pu. ) Clul un i iéi ngo qu iiqu ) Un i iéi qull n qu l
TEMA II: POSICIONES RELATIVAS ENTRE ELEMENTOS
 TEA II: POSICIONES RELATIVAS ENTRE ELEENTOS..D Ente dos ects Dos ects en el espcio pueden se: ) plels (sus poecciones homónims son plels) b) secntes (tienen un único punto en común) c) o cuse Ejemplo 4
TEA II: POSICIONES RELATIVAS ENTRE ELEENTOS..D Ente dos ects Dos ects en el espcio pueden se: ) plels (sus poecciones homónims son plels) b) secntes (tienen un único punto en común) c) o cuse Ejemplo 4
IES Mediterráneo de Málaga Solución Julio 2014 Juan Carlos Alonso Gianonatti. Opción A
 IE Mediteáneo de Málg olución Julio Jun Clos lonso Ginontti Opción Poblem.. Obtene ondmente escibiendo todos los psos del onmiento utilido que: El lo del deteminnte de l mti ( puntos l mti - que es l mti
IE Mediteáneo de Málg olución Julio Jun Clos lonso Ginontti Opción Poblem.. Obtene ondmente escibiendo todos los psos del onmiento utilido que: El lo del deteminnte de l mti ( puntos l mti - que es l mti
Metálico: teoría de bandas
 CP.: ELCES vn d Wl ( ) (Lnnd Jon) / q Iónico ( ) (Buckingm ) Covlnt ( ) D (Mo) Mtálico: toí d bnd - + - F + Enlc d hidógno Equm d ólido gún l tio d nlc Etuctu hgonl d Etuctu hgonl d hilo (nlc d hidógno)
CP.: ELCES vn d Wl ( ) (Lnnd Jon) / q Iónico ( ) (Buckingm ) Covlnt ( ) D (Mo) Mtálico: toí d bnd - + - F + Enlc d hidógno Equm d ólido gún l tio d nlc Etuctu hgonl d Etuctu hgonl d hilo (nlc d hidógno)
2. MÉTODO DE COEFICIENTES INDETERMINADOS.
 . MÉTODO DE COEFICIENTES INDETERMINADOS. E un étodo r hllr un olución rticulr d l cución linl colt [], u conit fundntlnt n intuir l for d un olución rticulr. No udn dr rgl n l co d cucion linl con coficint
. MÉTODO DE COEFICIENTES INDETERMINADOS. E un étodo r hllr un olución rticulr d l cución linl colt [], u conit fundntlnt n intuir l for d un olución rticulr. No udn dr rgl n l co d cucion linl con coficint
Modelo 4 de sobrantes de 2005 - Opción A
 Modelo de onte de - Opción A Ejecicio. 8 Se f : R R l función definid po f () () [ punto] Clcul lo punto de cote de l gáfic de f con lo eje coodendo. () [ punto] Hll l íntot de l gáfic de f. (c) [ punto]
Modelo de onte de - Opción A Ejecicio. 8 Se f : R R l función definid po f () () [ punto] Clcul lo punto de cote de l gáfic de f con lo eje coodendo. () [ punto] Hll l íntot de l gáfic de f. (c) [ punto]
TEMA 4: GEOMETRÍA: RECTAS Y PLANOS Para empezar:
 Ceno Concedo Pl Mde Mol nº 86- MADRID TEMA GEOMETRÍA RECTAS Y PLANOS P empe. Ddo lo puno A() B(8) hll ) L coodend de lo vecoe fijo AB BA b) Do puno C D le que CD e equipolene AB. c) El eemo F de un veco
Ceno Concedo Pl Mde Mol nº 86- MADRID TEMA GEOMETRÍA RECTAS Y PLANOS P empe. Ddo lo puno A() B(8) hll ) L coodend de lo vecoe fijo AB BA b) Do puno C D le que CD e equipolene AB. c) El eemo F de un veco
ECUACIONES DE LA RECTA
 RECTAS Y PLANOS EN EL ESPACIO ECUACIONES DE LA RECTA P hll l ecución de un ect en el espcio necesito: Dos puntos Un punto su vecto diecto Not: Nosotos utiliemos siempe un punto A(,, ) un vecto v (,b,c).
RECTAS Y PLANOS EN EL ESPACIO ECUACIONES DE LA RECTA P hll l ecución de un ect en el espcio necesito: Dos puntos Un punto su vecto diecto Not: Nosotos utiliemos siempe un punto A(,, ) un vecto v (,b,c).
IES Mediterráneo de Málaga Solución Junio 2004 Juan Carlos Alonso Gianonatti OPCIÓN A
 IES Mditrráno d Málg Solución Junio Jun rlos lonso Ginontti OPIÓN - undo l ño 8 Bthovn scrib su Primr Sinoní su dd s di vcs mor qu l dl jovncito Frn Schubrt Ps l timpo s Schubrt quin compon su célbr Sinoní
IES Mditrráno d Málg Solución Junio Jun rlos lonso Ginontti OPIÓN - undo l ño 8 Bthovn scrib su Primr Sinoní su dd s di vcs mor qu l dl jovncito Frn Schubrt Ps l timpo s Schubrt quin compon su célbr Sinoní
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE BALEARES JUNIO (RESUELTOS por Antonio Menguiano) Tiempo máximo: 1 horas y 30 minutos OPCIÓN A
 I.E.S. CSTELR DJOZ PRUE DE CCESO (LOGSE) UNIVERSIDD DE LERES JUNIO (RESUELTOS po nonio Mnguiano) MTEMÁTICS II Timpo máimo: hoas minuos Consa mana claa aonaa una las os opcions popusas. Caa cusión s punúa
I.E.S. CSTELR DJOZ PRUE DE CCESO (LOGSE) UNIVERSIDD DE LERES JUNIO (RESUELTOS po nonio Mnguiano) MTEMÁTICS II Timpo máimo: hoas minuos Consa mana claa aonaa una las os opcions popusas. Caa cusión s punúa
I.E.S. Mediterráneo de Málaga Junio 2015 Juan Carlos Alonso Gianonatti OPCIÓN A
 I.E.. Mdiáno d Málg Junio Jun Clo lono Ginoni OPCIÓN.- Conido l unción dinid n l inlo [ ]. Din l cución d l c ngn l cu qu pll l c qu p po lo puno P( Q(. ( puno..- Clcul l ingl indinid iguin d d ( puno.
I.E.. Mdiáno d Málg Junio Jun Clo lono Ginoni OPCIÓN.- Conido l unción dinid n l inlo [ ]. Din l cución d l c ngn l cu qu pll l c qu p po lo puno P( Q(. ( puno..- Clcul l ingl indinid iguin d d ( puno.
IES Mediterráneo de Málaga Solución Junio 2014 Juan Carlos Alonso Gianonatti BLOQUE A
 IES Mditrráno d Málg Solución Junio Jun Crlos lonso Ginontti BLOQUE CUESTIÓN.: Sbindo qu, clcul, sin dsrrollr ni utilir l rgl d Srrus, los siguints dtrminnts, indicndo n cd pso qué propidd d los dtrminnts
IES Mditrráno d Málg Solución Junio Jun Crlos lonso Ginontti BLOQUE CUESTIÓN.: Sbindo qu, clcul, sin dsrrollr ni utilir l rgl d Srrus, los siguints dtrminnts, indicndo n cd pso qué propidd d los dtrminnts
TEMAS 6 Y 7 GEOMETRÍA EN EL ESPACIO
 Tems Geometí en el espcio Mtemátics II º Bchilleto TEMAS Y GEOMETRÍA EN EL ESACIO ECUACIONES DE RECTAS Y LANOS EJERCICIO es plelo plno que contiene l ect Escibe l ecución del. s hll l ecución de un plno,
Tems Geometí en el espcio Mtemátics II º Bchilleto TEMAS Y GEOMETRÍA EN EL ESACIO ECUACIONES DE RECTAS Y LANOS EJERCICIO es plelo plno que contiene l ect Escibe l ecución del. s hll l ecución de un plno,
2. EL ÁTOMO DE HIDRÓGENO
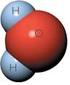 . EL ÁTOMO DE HIDRÓGENO. Dificultd d l toí d Boh ob l átomo d hidógno L toí d Boh ob l átomo d hidógno i bin fu un vnc, no contituyó un b tifctoi p xplic l compotminto d átomo má complo. Admá l intoducción
. EL ÁTOMO DE HIDRÓGENO. Dificultd d l toí d Boh ob l átomo d hidógno L toí d Boh ob l átomo d hidógno i bin fu un vnc, no contituyó un b tifctoi p xplic l compotminto d átomo má complo. Admá l intoducción
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE MURCIA JUNIO 2012 (GENERAL) MATEMÁTICAS II SOLUCIONES Tiempo máximo: 1 horas y 30 minutos ----------
 IES ASTELAR BADAJOZ A nguino PRUEBA DE AESO (LOGSE) UNIVERSIDAD DE URIA JUNIO (GENERAL) ATEÁTIAS II SOLUIONES Timpo máimo: hors minutos Osrvcions importnts: El lumno drá rspondr tods ls custions d un d
IES ASTELAR BADAJOZ A nguino PRUEBA DE AESO (LOGSE) UNIVERSIDAD DE URIA JUNIO (GENERAL) ATEÁTIAS II SOLUIONES Timpo máimo: hors minutos Osrvcions importnts: El lumno drá rspondr tods ls custions d un d
Ecuaciones de Poisson y Laplace
 Elctc y Mgntsmo / Elctostátc Dfncón Los conuctos n lctostátc. mpo un cg puntul. plccons l Ly Guss Intgls supposcón. Potncl lctostátco Dfncón Intptcón. Intgls supposcón. Ecucons Posson y Lplc. oncons Intfs.oncons
Elctc y Mgntsmo / Elctostátc Dfncón Los conuctos n lctostátc. mpo un cg puntul. plccons l Ly Guss Intgls supposcón. Potncl lctostátco Dfncón Intptcón. Intgls supposcón. Ecucons Posson y Lplc. oncons Intfs.oncons
José Antonio Galindo. CANTIGAS DE SANTA MARÍA de Alfonso X "el Sabio" 4 Cantigas Armonizadas para Coro mixto "a capella" SATB
 é Antni Glin ANIGA DE ANA MARÍA d Aln X "l i" 4 ng Amnizd xt " cll" A ROA DA ROA ANA MARÍA, RELA DO DÍA O QUE OLA IRGEN LEIXA AN GRAN ODER Ducin md 3' +1'15 (4') +2'45", 2'40" Edición i dl Aut Mdid, 2011
é Antni Glin ANIGA DE ANA MARÍA d Aln X "l i" 4 ng Amnizd xt " cll" A ROA DA ROA ANA MARÍA, RELA DO DÍA O QUE OLA IRGEN LEIXA AN GRAN ODER Ducin md 3' +1'15 (4') +2'45", 2'40" Edición i dl Aut Mdid, 2011
3A,,. Prueba que M es un subespacio
 .- Dtin os tis us X Y on tls qu: Y X Y X.- Estui l inpnni linl ls tis C.- Pu qu ls siguints tis son un s l spio vtoil ls tis us on.- S onsi l onjunto } R. Pu qu s un suspio vtoil.- Hll os tis us on os
.- Dtin os tis us X Y on tls qu: Y X Y X.- Estui l inpnni linl ls tis C.- Pu qu ls siguints tis son un s l spio vtoil ls tis us on.- S onsi l onjunto } R. Pu qu s un suspio vtoil.- Hll os tis us on os
OPCIÓN A. rg A = rg A* = n = 3 sistema compatible determinado.
 UNIVERSIDDES ÚBLICS DE L COUNIDD DE DRID RUEB DE CCESO LS ENSEÑNZS UNIVERSITRIS OFICILES DE GRDO Cuso -5 TERI: TEÁTICS II INSTRUCCIONES GENERLES Y VLORCIÓN Dsués l tntnt tos ls gunts, l luno á sog un ls
UNIVERSIDDES ÚBLICS DE L COUNIDD DE DRID RUEB DE CCESO LS ENSEÑNZS UNIVERSITRIS OFICILES DE GRDO Cuso -5 TERI: TEÁTICS II INSTRUCCIONES GENERLES Y VLORCIÓN Dsués l tntnt tos ls gunts, l luno á sog un ls
MATEMÁTICAS (II) JUNIO 2002
 MTEMÁTICS (II) JUNIO El emen present dos opciones, B. El lumno deberá elegir UN Y SÓLO UN de ells resolver los cutro ejercicios de que const. No se permite el usó de clculdors con cpcidd de representción
MTEMÁTICS (II) JUNIO El emen present dos opciones, B. El lumno deberá elegir UN Y SÓLO UN de ells resolver los cutro ejercicios de que const. No se permite el usó de clculdors con cpcidd de representción
( ) ( ) Calculando por separado cada termino de la igualdad e igualando, se calcula el valor del parámetro A.
 UNIVERSIDDES ÚBLICS DE L COMUNIDD DE MDRID RUEB DE CCESO LS ENSEÑNZS UNIVERSITRIS OFICILES DE GRDO Cuo - Setiebe MTERI: MTEMTICS II INSTRUCCIONES GENERLES Y VLORCION El luno contet lo cuto ejecicio de
UNIVERSIDDES ÚBLICS DE L COMUNIDD DE MDRID RUEB DE CCESO LS ENSEÑNZS UNIVERSITRIS OFICILES DE GRDO Cuo - Setiebe MTERI: MTEMTICS II INSTRUCCIONES GENERLES Y VLORCION El luno contet lo cuto ejecicio de
OPCIÓN A. Días de lectura Total de páginas Quijote Eva E D ED Marta E 5 D + 14 (E 5).( D + 14) Susana E 11 D + 44 (E 11).( D + 44)
 IES Mditrráno d Málg Solución Junio Jun Crlos lonso Ginontti OPCIÓN..- Ev Mrt Susn son trs jóvns migs qu s compromtn lr El Quijot st vrno. Cd un por sprdo n unción dl timpo dl qu dispon dcid lr un mismo
IES Mditrráno d Málg Solución Junio Jun Crlos lonso Ginontti OPCIÓN..- Ev Mrt Susn son trs jóvns migs qu s compromtn lr El Quijot st vrno. Cd un por sprdo n unción dl timpo dl qu dispon dcid lr un mismo
INTEGRALES MÚLTIPLES
 APITULO VI I. INTEGALE OBLE INTOUION INTEGALE MÚLTIPLE En l stuio intgls oinis f l función f s fini n un intvlo co [ ] p l cso stuimos ls intgls cuvilíns G c l función s fini so l cuv ho stuimos los intgls
APITULO VI I. INTEGALE OBLE INTOUION INTEGALE MÚLTIPLE En l stuio intgls oinis f l función f s fini n un intvlo co [ ] p l cso stuimos ls intgls cuvilíns G c l función s fini so l cuv ho stuimos los intgls
TALKINGISTEACHING.ORG
 l b T Tlk Wht c o my lo ock? Wht c olo you? Tlk, d, d ig with you child ight fom th tt. It build thi bi d pp thm fo ucc i chool d byod. Fo id, viit TALKINGISTEACHING.ORG Sh you tlk, d, ig momt t th ludomt!
l b T Tlk Wht c o my lo ock? Wht c olo you? Tlk, d, d ig with you child ight fom th tt. It build thi bi d pp thm fo ucc i chool d byod. Fo id, viit TALKINGISTEACHING.ORG Sh you tlk, d, ig momt t th ludomt!
Pruebas de Acceso a las Universidades de Castilla y León
 IES diáo d álg Jio J Clo loo Gioi P d cco l Uividd d Cill Ló TEÁTICS II To p lo lmo Nº pági INDICCIONES:.- OPTTIVIDD: El lmo dá cog d l do opcio pdido doll lo co jcicio l od q d..- CLCULDOR.- S pmiiá l
IES diáo d álg Jio J Clo loo Gioi P d cco l Uividd d Cill Ló TEÁTICS II To p lo lmo Nº pági INDICCIONES:.- OPTTIVIDD: El lmo dá cog d l do opcio pdido doll lo co jcicio l od q d..- CLCULDOR.- S pmiiá l
47. Contesta a les qüestions següents referents a l àtom d hidrogen.
 .6 Àtom d hidogn 7. Contst ls qüstions sgünts fnts l àtom d hidogn. n l ón l nom dls obitls cosponnts ls obitls qu s spcifiqun tvés dls nombs quàntics d l tul. b Assign cdscun d lls ls sus nombs quàntics
.6 Àtom d hidogn 7. Contst ls qüstions sgünts fnts l àtom d hidogn. n l ón l nom dls obitls cosponnts ls obitls qu s spcifiqun tvés dls nombs quàntics d l tul. b Assign cdscun d lls ls sus nombs quàntics
Tema 2: Antonio González Fernández Departamento de Física Aplicada III Universidad de Sevilla. Parte 6/7 Energía electrostática
 Tm : Pincipios d l lctostátic, Antonio Gon nzálz Fná ándz Antonio Gonzálz Fnándz Dptmnto d Físic Aplicd III nivsidd d Svill Pt 6/7 Engí lctostátic Engí, tbjo y clo: l pim pincipio i i d l tmodinámic i
Tm : Pincipios d l lctostátic, Antonio Gon nzálz Fná ándz Antonio Gonzálz Fnándz Dptmnto d Físic Aplicd III nivsidd d Svill Pt 6/7 Engí lctostátic Engí, tbjo y clo: l pim pincipio i i d l tmodinámic i
INSTRUCCIONES Y CRITERIOS GENERALES DE CALIFICACIÓN
 UNIVERSIDDES PÚBLICS DE L COUNIDD DE DRID PRUEB DE CCESO ESTUDIOS UNIVERSITRIOS (LOE) EEN ODELOCURSO - TEÁTICS PLICDS LS CIENCIS SOCILES II INSTRUCCIONES Y CRITERIOS GENERLES DE CLIFICCIÓN INSTRUCCIONES:
UNIVERSIDDES PÚBLICS DE L COUNIDD DE DRID PRUEB DE CCESO ESTUDIOS UNIVERSITRIOS (LOE) EEN ODELOCURSO - TEÁTICS PLICDS LS CIENCIS SOCILES II INSTRUCCIONES Y CRITERIOS GENERLES DE CLIFICCIÓN INSTRUCCIONES:
r,, R r exp exp 1 cos cos 1
 Como obtn función on y su ngí tvés cución Schöing. Rcomos qu función on s un cución mtmátic, qu cump citos quisitos, n cu s ncunt to infomción sistm, n st cso s tt infomción cion con ctón o núco. st función
Como obtn función on y su ngí tvés cución Schöing. Rcomos qu función on s un cución mtmátic, qu cump citos quisitos, n cu s ncunt to infomción sistm, n st cso s tt infomción cion con ctón o núco. st función
DEFORMACIONES. 1. Sean x, y, z la posición inicial de una partícula cuyo movimiento está descrito en un sistema lagrangiano por:
 Facltad d Cincias Epimntals Univsidad d Almía DEFORMACIONES. San,, la posición inicial d na patícla co moviminto stá dscito n n sistma lagangiano po: t X ( )( t Y ( )( + ( )( + ( )( + + Z Encnt: a) l vcto
Facltad d Cincias Epimntals Univsidad d Almía DEFORMACIONES. San,, la posición inicial d na patícla co moviminto stá dscito n n sistma lagangiano po: t X ( )( t Y ( )( + ( )( + ( )( + + Z Encnt: a) l vcto
Solución Tarea de Aproximaciones y errores de redondeo
 Métodos numéicos y álgb linl CB0085 Apoximcions y os d dondo T d Apoximcions y os d dondo. Clcul l o bsoluto y l o ltivo si p y p 2.78 dond p s l vlo clculdo. : vlo l vlo clculdo 2.78 o bsoluto : vlo clculdo
Métodos numéicos y álgb linl CB0085 Apoximcions y os d dondo T d Apoximcions y os d dondo. Clcul l o bsoluto y l o ltivo si p y p 2.78 dond p s l vlo clculdo. : vlo l vlo clculdo 2.78 o bsoluto : vlo clculdo
DERIVADAS. La derivada de una función f en el punto de abscisa x = a, se define como el siguiente límite, si existe:
 DERIVADAS.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pá. DERIVADAS Dinición d drivd. L drivd d un unción n l punto d bscis, s din como l siuint límit, si ist: lím A l drivd d un unción n un punto s l llm tmbién
DERIVADAS.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pá. DERIVADAS Dinición d drivd. L drivd d un unción n l punto d bscis, s din como l siuint límit, si ist: lím A l drivd d un unción n un punto s l llm tmbién
Solución de la ecuación de Schödinger para una partícula libre.
 Solución d l cución d Schöding un tícul lib. Vmos nliz l volución tmol d l función d ond d un tícul lib con un jmlo concto. Ptimos d l siguint condición inicil: (; ) ik dond y k son dos constnts ls. Lo
Solución d l cución d Schöding un tícul lib. Vmos nliz l volución tmol d l función d ond d un tícul lib con un jmlo concto. Ptimos d l siguint condición inicil: (; ) ik dond y k son dos constnts ls. Lo
LUGARES GEOMÉTRICOS Y ÁNGULOS
 REPASO Y APOYO OBJETIVO 1 LUGARES GEOMÉTRICOS Y ÁNGULOS Nombe: Cuso: Fec: Se llm lug geomético l conjunto de todos los puntos que cumplen un detemind popiedd geométic. EJEMPLO Cuál es el lug geomético
REPASO Y APOYO OBJETIVO 1 LUGARES GEOMÉTRICOS Y ÁNGULOS Nombe: Cuso: Fec: Se llm lug geomético l conjunto de todos los puntos que cumplen un detemind popiedd geométic. EJEMPLO Cuál es el lug geomético
RADIACIONES ÓPTICAS INCOHERENTES. Problemas resueltos
 RADIACIONS ÓPTICAS INCOHRNTS Poblms sultos ÍNDIC SÍMBOOS Y ABRVIATURAS... 7. CONCPTOS BÁSICOS... 9. VAUACIÓN D A XPOSICIÓN ABORA A RADIACIONS ÓPTICAS... 39 3. CONTRO Y RDUCCIÓN D A XPOSICIÓN A AS RADIACIONS
RADIACIONS ÓPTICAS INCOHRNTS Poblms sultos ÍNDIC SÍMBOOS Y ABRVIATURAS... 7. CONCPTOS BÁSICOS... 9. VAUACIÓN D A XPOSICIÓN ABORA A RADIACIONS ÓPTICAS... 39 3. CONTRO Y RDUCCIÓN D A XPOSICIÓN A AS RADIACIONS
Ecuaciones generales Modelo de Maxwell
 Elcticidad y Magntimo 9/ Ecuacion gnal Modlo d Maxwll Intoducción Funt d campo: Caga léctica. Coint léctica. Ecuación d continuidad. Dfinición dl campo lctomagnético. Ecuacion d Maxwll. Foma Intgal. Foma
Elcticidad y Magntimo 9/ Ecuacion gnal Modlo d Maxwll Intoducción Funt d campo: Caga léctica. Coint léctica. Ecuación d continuidad. Dfinición dl campo lctomagnético. Ecuacion d Maxwll. Foma Intgal. Foma
Derivadas: Teoría y ejercicios DERIVADAS. La derivada de una función f en el punto de abscisa x = a, se define como el siguiente límite, si existe:
 Drivds: Torí jrcicios Bcillrto DERIVADAS Dinición d drivd. L drivd d un unción n l punto d bscis =, s din como l siuint límit, si ist: lím A l drivd d un unción n un punto s l llm tmbién ts d vrición instntán.
Drivds: Torí jrcicios Bcillrto DERIVADAS Dinición d drivd. L drivd d un unción n l punto d bscis =, s din como l siuint límit, si ist: lím A l drivd d un unción n un punto s l llm tmbién ts d vrición instntán.
Por tanto,p(r) es la probabilidad de encontrar al electrón en esta envolvente.
 LAS FUNCIONES DE ONDA PARA EL HIDROGENO qq Ddo qu : U k dpnd solnt d l distnci dil nt l núclo y l lctón, lgunos d los stdos pitidos p st átoo pudn s psntdos dint funcions d ond qu solo dpndn d L s sipl
LAS FUNCIONES DE ONDA PARA EL HIDROGENO qq Ddo qu : U k dpnd solnt d l distnci dil nt l núclo y l lctón, lgunos d los stdos pitidos p st átoo pudn s psntdos dint funcions d ond qu solo dpndn d L s sipl
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID
 UNIVERSIDDES PÚBLICS DE L COMUNIDD DE MDRID PRUEB DE CCESO LS ENSEÑNZS UNIVERSITRIS OFICILES DE GRDO Curso -6 MTERI: MTEMÁTICS II INSTRUCCIONES GENERLES Y VLORCIÓN Dspués d lr tntmnt tods ls prgunts, l
UNIVERSIDDES PÚBLICS DE L COMUNIDD DE MDRID PRUEB DE CCESO LS ENSEÑNZS UNIVERSITRIS OFICILES DE GRDO Curso -6 MTERI: MTEMÁTICS II INSTRUCCIONES GENERLES Y VLORCIÓN Dspués d lr tntmnt tods ls prgunts, l
ESCUELA TÉCNICA SUPERIOR DE INGENIEROS DE TELECOMUNICACIÓN UNIVERSIDAD POLITÉCNICA DE VALENCIA
 SCULA ÉCNCA SUPROR D NGNROS D LCOMUNCACÓN UNRSDAD POLÉCNCA D ALNCA ANNAS 7-no-3 PROBLMA Una antna conocia po los aioaficionaos como W8JK, consta n su configuación más simpl os ipolos mu póimos longitu
SCULA ÉCNCA SUPROR D NGNROS D LCOMUNCACÓN UNRSDAD POLÉCNCA D ALNCA ANNAS 7-no-3 PROBLMA Una antna conocia po los aioaficionaos como W8JK, consta n su configuación más simpl os ipolos mu póimos longitu
Z = número atómico o número de protones del núcleo Z = 1 (H); 2 (He + ); 3 (Li 2+ ).
 CAPITULO. l átoo d idógo ) Atoo d idógo idogoid Z úo atóico o úo d poto dl úclo Z (H); (H + ); (Li + ). F q q / ε F q q / θ.6-9 cul.8 - u N u cul /( ε ) / φ V() -Z / ( u ) Hˆ Hˆ Hˆ + Ψ (, ) ψ ( )ψit( )
CAPITULO. l átoo d idógo ) Atoo d idógo idogoid Z úo atóico o úo d poto dl úclo Z (H); (H + ); (Li + ). F q q / ε F q q / θ.6-9 cul.8 - u N u cul /( ε ) / φ V() -Z / ( u ) Hˆ Hˆ Hˆ + Ψ (, ) ψ ( )ψit( )
Junio 2010 (Prueba General) JUNIO 2010 OPCIÓN A
 Junio 00 (Prueb Generl) JUNIO 00 OPCIÓN A.- ) Dds ls funciones f () = ln () y g() =, hllr el áre del recinto plno limitdo por ls rects =, = y ls gráfics de f () y g (). b) Dr un ejemplo de función continu
Junio 00 (Prueb Generl) JUNIO 00 OPCIÓN A.- ) Dds ls funciones f () = ln () y g() =, hllr el áre del recinto plno limitdo por ls rects =, = y ls gráfics de f () y g (). b) Dr un ejemplo de función continu
4πε. q r 2. q r C 2 2
 . ) A un distnci d. cm dl cnto d un sf conducto con cg cuyo dio s d. cm, l cmpo léctico s d 48 N/. uál s l cmpo léctico.6 cm dl cnto d l sf? ) A un distnci d. cm dl j d un cilindo conducto muy lgo con
. ) A un distnci d. cm dl cnto d un sf conducto con cg cuyo dio s d. cm, l cmpo léctico s d 48 N/. uál s l cmpo léctico.6 cm dl cnto d l sf? ) A un distnci d. cm dl j d un cilindo conducto muy lgo con
=-2.8 µc, se mantiene en una posición fija por medio de soportes aislantes. Se proyecta hacia q 1
 . n esfe etálic peueñ, con un cg net de -.8 µ, se ntiene en un posición fij po edio de sopotes islntes. Se poyect hci un segund esfe etálic peueñ, con un cg net de -7.8 µ y un s de.5 g. undo ls dos esfes
. n esfe etálic peueñ, con un cg net de -.8 µ, se ntiene en un posición fij po edio de sopotes islntes. Se poyect hci un segund esfe etálic peueñ, con un cg net de -7.8 µ y un s de.5 g. undo ls dos esfes
CONTINUIDAD Y DERIVABILIDAD DE FUNCIONES
 Colgio Mtr Slvtoris CONTINUIDAD Y DERIVABILIDAD DE FUNCIONES Ejrcicio nº.- Estudi l continuidd y l drivilidd d l guint unción: ) < < Continuidd: - Si y ) s continu, pus stá ormd por uncions continus. -
Colgio Mtr Slvtoris CONTINUIDAD Y DERIVABILIDAD DE FUNCIONES Ejrcicio nº.- Estudi l continuidd y l drivilidd d l guint unción: ) < < Continuidd: - Si y ) s continu, pus stá ormd por uncions continus. -
Problemas de difusión
 Probla d difuión PROBLEMA 1 Un acro contin 8,5 % n po d Ni n l cntro d un grano d F... y 8,8% n l líit dl grano. Si lo do punto tán parado 0 μ ual l flujo d átoo ntr to punto a 0 º?. a 0,65 n Ma Ni 58,71
Probla d difuión PROBLEMA 1 Un acro contin 8,5 % n po d Ni n l cntro d un grano d F... y 8,8% n l líit dl grano. Si lo do punto tán parado 0 μ ual l flujo d átoo ntr to punto a 0 º?. a 0,65 n Ma Ni 58,71
Hacia la universidad Geometría
 Hc l unvesdd Geomeí OPCIÓN A Solucono ) Clcul es vecoes que sen pependcules u ) peo que no sen plelos ene sí. b) Clcul un veco que se pependcul l ve u l pmeo que hs ddo como eemplo del pdo neo. ) Los vecoes
Hc l unvesdd Geomeí OPCIÓN A Solucono ) Clcul es vecoes que sen pependcules u ) peo que no sen plelos ene sí. b) Clcul un veco que se pependcul l ve u l pmeo que hs ddo como eemplo del pdo neo. ) Los vecoes
El punto (a, b) es un punto de la recta 2x + y = 8. Por tanto, 2a + b = 8; es decir, b = 8 2a.
 5 Dntro dl triángulo limitado por los js OX y OY y la rcta + y 8, s S inscrib un rctángulo d vértics (a, 0), (0, 0), (a, b) y (0, b). Dtrmina l punto (a, b) al qu corrspond l rctángulo d ára máima. 8 b
5 Dntro dl triángulo limitado por los js OX y OY y la rcta + y 8, s S inscrib un rctángulo d vértics (a, 0), (0, 0), (a, b) y (0, b). Dtrmina l punto (a, b) al qu corrspond l rctángulo d ára máima. 8 b
III. Campo eléctrico y conductores
 III. Cmpo léctico y conductos Método d ls imágns Gbil Cno Gómz, G 7/8 Dpto. Físic F Aplicd III (U. Svill) Cmpos Elctomgnéticos ticos Ingnio d Tlcomunicción Gbil Cno G Gómz, 7/8 Sistm cg puntul plno plno
III. Cmpo léctico y conductos Método d ls imágns Gbil Cno Gómz, G 7/8 Dpto. Físic F Aplicd III (U. Svill) Cmpos Elctomgnéticos ticos Ingnio d Tlcomunicción Gbil Cno G Gómz, 7/8 Sistm cg puntul plno plno
3.11 Trasformada de Laplace de una función periódica 246
 3. Trformd d plc d un función priódic 46 3. Trformd d plc d un función priódic Dfinición 3.. Un función f llmd priódic i y olo i, it un númro no nulo f tl qu impr y cundo té n l dominio d f, tmbién lo
3. Trformd d plc d un función priódic 46 3. Trformd d plc d un función priódic Dfinición 3.. Un función f llmd priódic i y olo i, it un númro no nulo f tl qu impr y cundo té n l dominio d f, tmbién lo
FORMACIÓN PROFESIONAL
 FOMCIÓN POFIONL DIÑO CUICUL N UNIDD TÉCNIC CUDO 1228 D GOTO D 1985 INTUCCIÓN 0329 D 1986 DOGÓ L INTUCCIÓN 217 D 1972 Oscar Gaboa Carrillo FOMCION POFIONL: POCO MDINT L CUL L PON: DQUI Y DOLL CONOCIMINTO,
FOMCIÓN POFIONL DIÑO CUICUL N UNIDD TÉCNIC CUDO 1228 D GOTO D 1985 INTUCCIÓN 0329 D 1986 DOGÓ L INTUCCIÓN 217 D 1972 Oscar Gaboa Carrillo FOMCION POFIONL: POCO MDINT L CUL L PON: DQUI Y DOLL CONOCIMINTO,
Curso Septiembre MATERIA: MATEMÁTICAS II (Fase general)
 Cuso - Sepiebe MTERI MTEMÁTICS II (Fse genel) INSTRUCCIONES GENERLES Y VLORCIÓN El luno cones los cuo ejecicios e un e l os opciones ( o B) que se le ofecen. Nunc ebeá cones unos ejecicios e un opción
Cuso - Sepiebe MTERI MTEMÁTICS II (Fse genel) INSTRUCCIONES GENERLES Y VLORCIÓN El luno cones los cuo ejecicios e un e l os opciones ( o B) que se le ofecen. Nunc ebeá cones unos ejecicios e un opción
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE MADRID JUNIO Tiempo máximo: 1 hora y 30 minutos OPCIÓN A
 IES STELR BDJOZ PRUEB DE ESO (LOGSE) UNIVERSIDD DE MDRID JUNIO MTEMÁTIS II Tiempo máimo: hor minutos El lumno contestrá los cutro ejercicios de un de ls dos opciones ( o B) que se le ofrecen Nunc deberá
IES STELR BDJOZ PRUEB DE ESO (LOGSE) UNIVERSIDD DE MDRID JUNIO MTEMÁTIS II Tiempo máimo: hor minutos El lumno contestrá los cutro ejercicios de un de ls dos opciones ( o B) que se le ofrecen Nunc deberá
Cálculo con vectores
 Unidd didáctic 1 Cálculo con vectoes 1.- Mgnitudes escles vectoiles. Son mgnitudes escles quells, como l ms, l tempetu, l enegí, etc., cuo vlo qued fijdo po un númeo (con su unidd coespondiente). Gáficmente
Unidd didáctic 1 Cálculo con vectoes 1.- Mgnitudes escles vectoiles. Son mgnitudes escles quells, como l ms, l tempetu, l enegí, etc., cuo vlo qued fijdo po un númeo (con su unidd coespondiente). Gáficmente
( 32 x )= 53 arcsen ( 32 x ) sen x +7 cos x 1 dx. x x. e 2 x +1 dx. 5x 7 dx. x sen x dx. x 4 x x 1 dx. x 2 dx. dxx. x x x dx. 1 x.
 IES Jun Clos I Mmáics II Cimpozulos Mdid * nálisis III: Ingls Ingls inmdis o csi inmdis: b d c d d d sn d f sn cos d g g d h d i d j d k cos bd l d m n d o d p q d C d sn d cos sn d cos d dcos sn d d d
IES Jun Clos I Mmáics II Cimpozulos Mdid * nálisis III: Ingls Ingls inmdis o csi inmdis: b d c d d d sn d f sn cos d g g d h d i d j d k cos bd l d m n d o d p q d C d sn d cos sn d cos d dcos sn d d d
OPCIÓN A. Colegio La Presentación Granada MATEMATICAS II. Examen de Matemáticas GLOBAL DE GEOMETRÍA
 Colegio L Pesentción Gnd OPCIÓN A 1- () [1 punto] Sen u y v dos vectoes otogonles y de módulo 1 Hll los vloes del pámeto p que lo vectoes u + v y u v fomen un ángulo 60º (b) [1 punto] Hll un vecto z de
Colegio L Pesentción Gnd OPCIÓN A 1- () [1 punto] Sen u y v dos vectoes otogonles y de módulo 1 Hll los vloes del pámeto p que lo vectoes u + v y u v fomen un ángulo 60º (b) [1 punto] Hll un vecto z de
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE EXTREMADURA JUNIO 2009. (RESUELTOS por Antonio Menguiano) Tiempo máximo: 1 hora y 30 minutos
 I.E.S. CSTELR BDJOZ PRUEB DE CCESO (LOGSE) UNIVERSIDD DE EXTREMDUR JUNIO 9 (RESUELTOS po ntonio Menguino) MTEMÁTICS II Tiempo máimo: ho minutos El lumno elegiá un de ls dos opciones popuests. Cd un de
I.E.S. CSTELR BDJOZ PRUEB DE CCESO (LOGSE) UNIVERSIDD DE EXTREMDUR JUNIO 9 (RESUELTOS po ntonio Menguino) MTEMÁTICS II Tiempo máimo: ho minutos El lumno elegiá un de ls dos opciones popuests. Cd un de
INSTITUTO TÉCNICO MARÍA INMACULADA 2011 FORMANDO LÍDERES ESTUDIANTILES PARA UN FUTURO MEJOR PLAN DE NIVELACIÓN GENERAL DE MATEMÁTICAS 8.
 INSTITUTO TÉCNICO MARÍA INMACULADA 0 FORMANDO LÍDERES ESTUDIANTILES PARA UN FUTURO MEJOR PLAN DE NIVELACIÓN GENERAL DE MATEMÁTICAS. 0 Resuelve ls siguientes situciones TALLER NÚMERO. Ubic cd entero su
INSTITUTO TÉCNICO MARÍA INMACULADA 0 FORMANDO LÍDERES ESTUDIANTILES PARA UN FUTURO MEJOR PLAN DE NIVELACIÓN GENERAL DE MATEMÁTICAS. 0 Resuelve ls siguientes situciones TALLER NÚMERO. Ubic cd entero su
Física. g u a y F R. Entonces : tg
 Físic g u y. Clcul l istnci el equiliio ente ls os esfes e l figu, e ms m, cgos con q coulomios, si se supone que el ángulo con l veticl es muy pequeño, y los hilos que los sujetn no tienen ms. SOLUCIÓN:
Físic g u y. Clcul l istnci el equiliio ente ls os esfes e l figu, e ms m, cgos con q coulomios, si se supone que el ángulo con l veticl es muy pequeño, y los hilos que los sujetn no tienen ms. SOLUCIÓN:
CONTROL 2 2ªEVAL 2ºBACH
 CONTROL ªEVAL ºACH INSTRUCCIONES Y CRITERIOS GENERALES DE CALIFICACIÓN La prueba conta de una opción, que incluye cuatro pregunta. Se podrá hacer uo de calculadora científica no programable. CALIFICACIÓN:
CONTROL ªEVAL ºACH INSTRUCCIONES Y CRITERIOS GENERALES DE CALIFICACIÓN La prueba conta de una opción, que incluye cuatro pregunta. Se podrá hacer uo de calculadora científica no programable. CALIFICACIÓN:
lím 1 si x=0 3) Halla la ecuación de la recta tangente a la gráfica de la siguiente función en el punto de abscisa π/2: sen x y = arc tg 1+cos x
 CURSO 4-5. de myo de 5. ) Clcul los siguientes ites: (+e ) / sen(/) ) Estudi l continuidd de l siguiente función: +e/ f() -e / si si ) Hll l ecución de l rect tngente l gráfic de l siguiente función en
CURSO 4-5. de myo de 5. ) Clcul los siguientes ites: (+e ) / sen(/) ) Estudi l continuidd de l siguiente función: +e/ f() -e / si si ) Hll l ecución de l rect tngente l gráfic de l siguiente función en
IES Mediterráneo de Málaga Solución Septiembre 2010 (Específico) Juan Carlos Alonso Gianonatti OPCIÓN A. 2, se pide determinar:
 IES Mdirráno d Málg Soluión Spimr (Espíio) Jun Crlos lonso Ginoni OPCIÓN E.- Dd l unión ( ), s pid drminr: ) El dominio, los punos d or on los js y ls sínos ( puno) ) Los inrvlos d rimino y drimino, y
IES Mdirráno d Málg Soluión Spimr (Espíio) Jun Crlos lonso Ginoni OPCIÓN E.- Dd l unión ( ), s pid drminr: ) El dominio, los punos d or on los js y ls sínos ( puno) ) Los inrvlos d rimino y drimino, y
CINEMÁTICA DE UNA PARTÍCULA
 Cpíulo IX CINEMÁTICA DE UNA PARTÍCULA 9.1 INTRODUCCIÓN L Cinemáic e ocup del movimieno de lo cuepo in conide l cu que oiginn dicho movimieno. E deci, eudiemo el movimieno de lo cuepo o pícul in conide
Cpíulo IX CINEMÁTICA DE UNA PARTÍCULA 9.1 INTRODUCCIÓN L Cinemáic e ocup del movimieno de lo cuepo in conide l cu que oiginn dicho movimieno. E deci, eudiemo el movimieno de lo cuepo o pícul in conide
5. Convergencia de integrales impropias. Las funciones Γ y Β de Euler.
 GRADO DE INGENIERÍA AEROESPACIAL. CURSO. Lcción. Intgals y aplicacions. 5. Convgncia d intgals impopias. Las funcions Γ y Β d Eul. La foma haitual d calcula una intgal impopia, po jmplo dl intgando, aplica
GRADO DE INGENIERÍA AEROESPACIAL. CURSO. Lcción. Intgals y aplicacions. 5. Convgncia d intgals impopias. Las funcions Γ y Β d Eul. La foma haitual d calcula una intgal impopia, po jmplo dl intgando, aplica
EXAMEN DE MATEMATICAS II. Apellidos: Nombre:
 EXAMEN DE MATEMATICAS II ª ENSAYO Apellidos: Nobe: Instucciones: Cuso: º Gupo: A Dí: CURSO 56 ) Dución: HORA y MINUTOS. b) Debes elegi ente eliz únicente los cuto ejecicios de l Opción A o bien únicente
EXAMEN DE MATEMATICAS II ª ENSAYO Apellidos: Nobe: Instucciones: Cuso: º Gupo: A Dí: CURSO 56 ) Dución: HORA y MINUTOS. b) Debes elegi ente eliz únicente los cuto ejecicios de l Opción A o bien únicente
Examen Reserva Septiembre2009
 Eamn Rsva ptimb009 1. La validz d los tsts hac fncia a: a) la quivalncia nt las puntuacions obsvadas y las vdadas, b) la adcuación d las infncias qu s hagan a pati d las puntuacions obsvadas al objtivo
Eamn Rsva ptimb009 1. La validz d los tsts hac fncia a: a) la quivalncia nt las puntuacions obsvadas y las vdadas, b) la adcuación d las infncias qu s hagan a pati d las puntuacions obsvadas al objtivo
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID
 UNIVERSIDDES ÚBLIS DE L OMUNIDD DE MDRID RUEB DE ESO ESTUDIOS UNIVERSITRIOS (LOGSE) JUNIO INSTRUIONES GENERLES Y VLORIÓN El lumo coeá lo cuo ejecicio e u e l o opcioe ( o B) que e le oece. Nuc ebeá coe
UNIVERSIDDES ÚBLIS DE L OMUNIDD DE MDRID RUEB DE ESO ESTUDIOS UNIVERSITRIOS (LOGSE) JUNIO INSTRUIONES GENERLES Y VLORIÓN El lumo coeá lo cuo ejecicio e u e l o opcioe ( o B) que e le oece. Nuc ebeá coe
Integrales impropias.
 IX / 8 UNIVERSIDAD SIMON BOLIVAR MA nro-mrzo d 4 Dprtmnto d Mtmátics Purs y Aplicds. Intgrls impropis. Ejrcicios sugridos pr : los tms d ls clss dl 4 y 9 d mrzo d 4. Tms : Otrs forms indtrminds. Intgrls
IX / 8 UNIVERSIDAD SIMON BOLIVAR MA nro-mrzo d 4 Dprtmnto d Mtmátics Purs y Aplicds. Intgrls impropis. Ejrcicios sugridos pr : los tms d ls clss dl 4 y 9 d mrzo d 4. Tms : Otrs forms indtrminds. Intgrls
Dadas las matrices: y. a) Hallar A 10. b) Hallar la matriz inversa de B. c) En el caso particular de k=0, halla B 10. (PAU Septiembre )
 Dds ls mtrices: ) Hllr A. b) Hllr l mtri invers de B. c) En el cso prticulr de k=, hll B. (PAU Septiembre 4-5) ) A = = A = = = O A 4 = A A= O A = O ; lo mismo A 5, A 6 por tnto A = b) B = = ; Es un mtri
Dds ls mtrices: ) Hllr A. b) Hllr l mtri invers de B. c) En el cso prticulr de k=, hll B. (PAU Septiembre 4-5) ) A = = A = = = O A 4 = A A= O A = O ; lo mismo A 5, A 6 por tnto A = b) B = = ; Es un mtri
