El algoritmo de Resolución
|
|
|
- Samuel Cáceres Domínguez
- hace 5 años
- Vistas:
Transcripción
1 El algoritmo de Resolución El algoritmo de resolución es casi idéntico al de lógica proposicional: Suponga que quiere demostrar que ϕ es consecuencia lógica de Σ. El método es el siguiente: Transforme las oraciones en Σ { ϕ} a forma normal prenex sin cuantificadores existenciales. Usando la equivalencia x (φ(x) ψ(x)) x φ(x) x ψ(x) transforme las fórmulas a un conjunto de cláusulas C = {C 1,..., C n } sin cuantificadores. Mientras C y existen C i, C j C, tales que la regla de resolución es aplicable: Aplique la regla de resolución a C i y C j generando C y haga C := C {C } Nuevamente, usamos Σ r ϕ para decir que la oración ϕ se puede demostrar por resolución a partir de Σ. Jorge Baier Aranda, PUC << Atrás 160
2 Ejemplos de Resolución Demuestre que = x (P (x) y P (y)) Primero transformamos la negación de la fórmula en un conjunto de cláusulas. 1. x (P (x) y P (y)) 2. x (P (x) y P (y)) 3. x (P (x) y P (y)) 4. x (P (x) y P (y)) 5. x y (P (x) P (y)) 6. x (P (x) P (f(x))) De la última fórmula, generamos el conjunto de cláusulas {P (x), P (f(x))} Antes de iniciar la resolución, es siempre conveniente renombrar las variables en las distintas cláusulas. Esto aumenta las posibilidades de encontrar unificadores para éstas. Jorge Baier Aranda, PUC << Atrás 161
3 Este renombramiento también se puede hacer antes de aplicar la regla de resolución. Partimos con el conjunto de cláusulas {P (x), P (f(y))} Basta una aplicación de la regla de resolución para encontrar que: P (x) con θ = {x/f(y)} P (f(y)) Veamos un ejemplo más complejo. Demuestre que { x y z (P (x, y) R(y, z)), x P (x, x)} r x y R(x, y) Las cláusulas son las siguientes: Jorge Baier Aranda, PUC << Atrás 162
4 1. P (x, y) R(y, f(x, y)) 2. P (z, z) 3. R(C, u) P (x, C) se obtiene de la resolución de 1 y 3 y finalmente se obtiene a partir de esta nueva cláusula y 2. Jorge Baier Aranda, PUC << Atrás 163
5 Propiedades de Resolución de Primer Orden Resolución de Primer Orden tiene las mismas propiedades esperadas de la resolución en lógica proposicional, es decir es correcta y completa. Jorge Baier Aranda, PUC << Atrás 164
6 Igualdad y Resolución La propiedad de igualdad es esencial para representar muchas teorías y muchos teoremas se pueden demostrar sólo gracias a que ésta existe. Ya hemos visto que para manejarla es necesario agregar axiomas adicionales. Dichos axiomas establecen las propiedades básicas que cumple la igualdad: Es refleja, simétrica y transitiva y Permite la sustitución de iguales por iguales. Por ejemplo, para demostrar teoremas de la teoría de grupos es esencial que podamos manejar la igualdad. Los siguientes son los axiomas de la teoría de grupos: Jorge Baier Aranda, PUC << Atrás 165
7 xyz x (y z) = (x y) z x x e = e x = x x (x i(x) = e i(x) x = e) (asociatividad) (identidad, e es elemento neutro) (existencia de un inverso) Un teorema de esta teoría es el siguiente: Si todo elemento es inverso de sí mismo, entonces el grupo es conmutativo. Es decir: x x x = e yz y z = z y Usando resolución por sí sola no podemos demostrar este teorema. Para demostrar un teorema usando igualdad tenemos 2 alternativas: Usar resolución estándar incorporando los axiomas de igualdad. Incorporar algún otro método al demostrador mecánico, para simplificar ciertas tareas. Jorge Baier Aranda, PUC << Atrás 166
8 Si elegimos la primera alternativa, deberemos incluir los siguientes axiomas de igualdad. x = x x = y y = x x = y y = z x = z Para cada predicado n-ario P y para cada j = 1,..., n agregamos: x j = x 0 P (x 1,..., x j,..., x n ) P (x 1,..., x 0,..., x n ) Para cada función n-aria P y para cada j = 1,..., n agregamos: x j = x 0 f(x 1,..., x j,..., x n ) = f(x 1,..., x 0,..., x n ) Jorge Baier Aranda, PUC << Atrás 167
9 Paramodulación Paramodulación es un método sencillo para incorporar la igualdad en demostraciones por resolución. En la práctica, no deberemos considerar los axiomas de transitividad, sustitución y simetría. Supongamos que se tienen las siguientes cláusulas: C 1 : P (A) C 2 : A = B Dado que se cumple una igualdad en C 2 podríamos aplicar una regla de sustitución para obtener P (B). En general, la regla de sustitución de la siguiente manera: Si una cláusula C 1 contiene un término t y una cláusula unitaria C 2 es t = s, entonces inferimos la cláusula que corresponda de sustituir s por t en C 1. Jorge Baier Aranda, PUC << Atrás 168
10 Paramodulación es una extensión de la regla que acabamos de mencionar. Si una expresión E 8 que contiene un término t, la llamaremos E[t]. De esta manera, la sustitución de t por s en la expresión E[t] la escribiremos como E[s]. De esta forma, la regla de paramodulación para cláusulas instanciadas (sin variables) está dada por la siguiente definición: Definición 24. [Regla de Paramodulación para Cláusulas Instanciadas] Sea def C 1 = L[t] C 1, con C 1 def cláusula. Si C 2 = t = s C 2, con C 2 una cláusula. Entonces inferimos la siguiente cláusula: 8 Una expresión puede ser un literal o una cláusula L[s] C 1 C 2 Jorge Baier Aranda, PUC << Atrás 169
11 Ejemplo: Consideremos las siguientes cláusulas, C 1 : P (A) Q(B) C 2 : A = B R(B) Usando paramodulación obtenemos la siguiente cláusula: P (B) Q(B) R(B) A partir del concepto de sustitución, también es posible definir la regla de paramodulación para cláusulas con variables. Definición 25. [Regla de Paramodulación de Primer Orden] Sean L[t], C 1 y C 2 cláusulas arbitrarias sin variables en común. A partir de las cláusulas C 1 : L[t] C 1 C 2 : r = s C 2 Jorge Baier Aranda, PUC << Atrás 170
12 Si t y r tienen un UMG θ, entonces, por paramodulación se obtiene C 1 : Lθ[sθ] C 1θ C 2θ Ejemplo: Demuestre a partir de C 1 : P (g(f(x))) Q(x) C 2 : f(g(b)) = A R(g(C)) Es posible generar, usando la regla de paramodulación, la cláusula: P (g(a)) Q(g(B)) R(g(C)) Ejercicio: demuestre el teorema de teoría de grupos enunciado al principio de esta sección usando resolución con la regla de paramodulación. Es posible demostrar que resolución+paramodulación es correcta y completa en el sentido que: Jorge Baier Aranda, PUC << Atrás 171
13 Σ 0 AX = = ϕ ssi Σ 0 { x (x = x)} r+p ϕ Donde el símbolo r+p se utiliza para denotar una demostración que usa resolución junto con la regla de paramodulación, y AX = son los axiomas de igualdad para el conjunto de oraciones Σ 0. Jorge Baier Aranda, PUC << Atrás 172
14 Cálculo de Secuentes y Primer Orden También es sencillo modificar el cálculo de secuentes para que maneje primer orden. En las siguientes reglas, c es una constante de Skolem y t un término arbitrario: Instanciación: Γ, A[x/t] Γ, x A Γ A[x/t], Γ x A, Skolemización: Γ, A[x/c] Γ, x A Γ A[x/c], Γ x A, Jorge Baier Aranda, PUC << Atrás 173
Tema 9: Resolución en lógica de primer orden
 de Tema 9: en lógica de no Dpto. Ciencias de la Computación Inteligencia Artificial Universidad de Sevilla Lógica Informática (Tecnologías Informáticas) Curso 2016 17 Contenido de no no Introducción Por
de Tema 9: en lógica de no Dpto. Ciencias de la Computación Inteligencia Artificial Universidad de Sevilla Lógica Informática (Tecnologías Informáticas) Curso 2016 17 Contenido de no no Introducción Por
Teorías. Una teoría acerca de una base de conocimiento Σ contendrá no sólo a Σ sino que a todo lo que se puede deducir de Σ.
 Teorías Qué es una teoría? Ya hemos usado antes la noción de base de conocimiento Este concepto se refiere a un conocimiento, representado a través de axiomas. Una teoría acerca de una base de conocimiento
Teorías Qué es una teoría? Ya hemos usado antes la noción de base de conocimiento Este concepto se refiere a un conocimiento, representado a través de axiomas. Una teoría acerca de una base de conocimiento
Demostraciones por resolución
 Demostraciones por resolución A lo largo del curso, hemos prometido insistentemente que hay métodos para mecanizar demostraciones En particular, queremos un método, dado una base de conocimiento Σ y una
Demostraciones por resolución A lo largo del curso, hemos prometido insistentemente que hay métodos para mecanizar demostraciones En particular, queremos un método, dado una base de conocimiento Σ y una
LÓGICA FORMAL TEORIAS DE PRIMER ORDEN. Sintaxis y semántica
 LÓGICA FORMAL TEORIAS DE PRIMER ORDEN Sintaxis y semántica Pedro López Departamento de Inteligencia Artificial Facultad de Informática Universidad Politécnica de Madrid Lenguajes de primer orden 1 La lógica
LÓGICA FORMAL TEORIAS DE PRIMER ORDEN Sintaxis y semántica Pedro López Departamento de Inteligencia Artificial Facultad de Informática Universidad Politécnica de Madrid Lenguajes de primer orden 1 La lógica
LÓGICA FORMAL TEORIAS DE PRIMER ORDEN. Axiomática
 LÓGICA FORMAL TEORIAS DE PRIMER ORDEN Francisco Bueno Pedro López Departamento de Inteligencia Artificial Facultad de Informática Universidad Politécnica de Madrid Teoría de Primer Orden 1 Formalmente,
LÓGICA FORMAL TEORIAS DE PRIMER ORDEN Francisco Bueno Pedro López Departamento de Inteligencia Artificial Facultad de Informática Universidad Politécnica de Madrid Teoría de Primer Orden 1 Formalmente,
Resolución Proposicional
 Resolución Proposicional IIC2213 IIC2213 Resolución Proposicional 1 / 19 Resolución proposicional Sabemos que Σ = ϕ si y sólo si Σ { ϕ} es inconsistente. Cómo verificamos si Σ { ϕ} es inconsistente? El
Resolución Proposicional IIC2213 IIC2213 Resolución Proposicional 1 / 19 Resolución proposicional Sabemos que Σ = ϕ si y sólo si Σ { ϕ} es inconsistente. Cómo verificamos si Σ { ϕ} es inconsistente? El
Eliminación de cuantificadores
 Eliminación de cuantificadores Teorema Si una teoría admite eliminación de cuantificadores, y existe un algoritmo que construye ϕ sc a partir de ϕ, entonces es decidible. Cómo se demuestra este teorema?
Eliminación de cuantificadores Teorema Si una teoría admite eliminación de cuantificadores, y existe un algoritmo que construye ϕ sc a partir de ϕ, entonces es decidible. Cómo se demuestra este teorema?
Conjuntos, relaciones y funciones Susana Puddu
 Susana Puddu 1. Repaso sobre la teoría de conjuntos. Denotaremos por IN al conjunto de los números naturales y por ZZ al de los enteros. Dados dos conjuntos A y B decimos que A está contenido en B o también
Susana Puddu 1. Repaso sobre la teoría de conjuntos. Denotaremos por IN al conjunto de los números naturales y por ZZ al de los enteros. Dados dos conjuntos A y B decimos que A está contenido en B o también
Tema 8: Teorema de Herbrand. Tableros en lógica de primer orden
 Tema 8:. en de primer orden Dpto. Ciencias de la Computación Inteligencia Artificial Universidad de Sevilla Lógica Informática (Tecnologías Informáticas) Curso 2016 17 Contenido Sea Γ un conjunto de fórmulas
Tema 8:. en de primer orden Dpto. Ciencias de la Computación Inteligencia Artificial Universidad de Sevilla Lógica Informática (Tecnologías Informáticas) Curso 2016 17 Contenido Sea Γ un conjunto de fórmulas
ALGEBRA y ALGEBRA LINEAL. Primer Semestre CAPITULO I LOGICA Y CONJUNTOS.
 ALGEBRA y ALGEBRA LINEAL 520142 Primer Semestre CAPITULO I LOGICA Y CONJUNTOS. DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas Universidad de Concepción 1 La lógica es
ALGEBRA y ALGEBRA LINEAL 520142 Primer Semestre CAPITULO I LOGICA Y CONJUNTOS. DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas Universidad de Concepción 1 La lógica es
1. Formas normales en lógica de proposiciones FORMAS NORMALES. Índice. César Ignacio García Osorio Definiciones. Lógica
 Lógica Índice FORMAS NORMALES César Ignacio García Osorio 1. Formas normales en lógica de proposiciones Gracias a las leyes asociativas los paréntesis en (F (G H)) oen((f G) H) pueden eliminarse, es decir,
Lógica Índice FORMAS NORMALES César Ignacio García Osorio 1. Formas normales en lógica de proposiciones Gracias a las leyes asociativas los paréntesis en (F (G H)) oen((f G) H) pueden eliminarse, es decir,
Coordinación de Matemática I (MAT021) 1 er Semestre de 2013 Semana 1: Lunes 11 Viernes 16 de Marzo. Contenidos
 Coordinación de Matemática I (MAT021) 1 er Semestre de 2013 Semana 1: Lunes 11 Viernes 16 de Marzo Complementos Contenidos Clase 1: Elementos de lógica: Conectivos, tablas de verdad, tautologías y contingencias.
Coordinación de Matemática I (MAT021) 1 er Semestre de 2013 Semana 1: Lunes 11 Viernes 16 de Marzo Complementos Contenidos Clase 1: Elementos de lógica: Conectivos, tablas de verdad, tautologías y contingencias.
Problemas de Decisión
 Problemas de Decisión La motivación de este capítulo puede estar dado por lo siguiente: Dado un conjunto Σ de fórmulas proposicionales en L(P ), existe un algoritmo general para determinar si Σ = ϕ Qué
Problemas de Decisión La motivación de este capítulo puede estar dado por lo siguiente: Dado un conjunto Σ de fórmulas proposicionales en L(P ), existe un algoritmo general para determinar si Σ = ϕ Qué
Lógica Primer Orden: Deducción (Natural)
 LÓGICA - 1º Grado en Ingeniería Informática Facultad de Informática Universidad Politécnica de Madrid Lógica Primer Orden: Deducción (Natural) Andrei Paun apaun@fi.upm.es http://web3.fi.upm.es/aulavirtual/
LÓGICA - 1º Grado en Ingeniería Informática Facultad de Informática Universidad Politécnica de Madrid Lógica Primer Orden: Deducción (Natural) Andrei Paun apaun@fi.upm.es http://web3.fi.upm.es/aulavirtual/
Introducción a la Complejidad Computacional
 Introducción a la Complejidad Computacional El análisis sobre decidibilidad que hemos hecho nos permite saber qué podemos hacer y qué no podemos hacer. Pero nada sabemos de qué tan difícil resolver los
Introducción a la Complejidad Computacional El análisis sobre decidibilidad que hemos hecho nos permite saber qué podemos hacer y qué no podemos hacer. Pero nada sabemos de qué tan difícil resolver los
Teorías decidibles. Definición. Ejercicio
 Teorías decidibles Definición Una teoría Σ sobre un vocabulario L es decidible si existe un algoritmo que, dada una L-oración ϕ, verificasiϕ Σ. Ejercicio Sea Ord k el siguiente conjunto de axiomas sobre
Teorías decidibles Definición Una teoría Σ sobre un vocabulario L es decidible si existe un algoritmo que, dada una L-oración ϕ, verificasiϕ Σ. Ejercicio Sea Ord k el siguiente conjunto de axiomas sobre
Completitud en Lógica de Predicados
 Completitud en de Predicados Predicados - Completitud 1 Corrección. Significa que las derivaciones expresan una consecuencia lógica. Establece una correspondencia tal que partiendo de nociones sintácticas
Completitud en de Predicados Predicados - Completitud 1 Corrección. Significa que las derivaciones expresan una consecuencia lógica. Establece una correspondencia tal que partiendo de nociones sintácticas
Conjuntos. Un conjunto es una colección de objetos. Si a es un objeto y R es un conjunto entonces por. a R. se entiende que a pertenece a R.
 Conjuntos Un conjunto es una colección de objetos. Si a es un objeto y R es un conjunto entonces por se entiende que a pertenece a R. a R Normalmente, podremos definir a un conjunto de dos maneras: Por
Conjuntos Un conjunto es una colección de objetos. Si a es un objeto y R es un conjunto entonces por se entiende que a pertenece a R. a R Normalmente, podremos definir a un conjunto de dos maneras: Por
Lógica Clásica de Predicados
 Lógica Clásica de Predicados Lógica Computacional Departamento de Matemática Aplicada Universidad de Málaga 10 de enero de 2008 Contenido 1 Sintaxis 2 Variables y Sustituciones 3 Significado y verdad 4
Lógica Clásica de Predicados Lógica Computacional Departamento de Matemática Aplicada Universidad de Málaga 10 de enero de 2008 Contenido 1 Sintaxis 2 Variables y Sustituciones 3 Significado y verdad 4
Forma Clausular. Forma Clausular
 Forma Clausular Formas Normales: Literal: fórmula atómica o negación de fórmula atómica Un literal se denota con l y su complementario con l C L = P binario, Q unario, f unaria l 1 =
Forma Clausular Formas Normales: Literal: fórmula atómica o negación de fórmula atómica Un literal se denota con l y su complementario con l C L = P binario, Q unario, f unaria l 1 =
Algebras booleanas. B2) Leyes Distributivas. Cada operación es distributiva con respecto a la otra:
 Algebras booleanas AXIOMAS DEL ALGEBRA DE BOOLE Sea B un conjunto en el cual se han definido dos operaciones binarias, + y * (En algunos casos se definen en términos de y respectivamente), y una operación
Algebras booleanas AXIOMAS DEL ALGEBRA DE BOOLE Sea B un conjunto en el cual se han definido dos operaciones binarias, + y * (En algunos casos se definen en términos de y respectivamente), y una operación
1. Resolución en lógica proposicional
 1. Resolución en lógica proposicional 1.1. Introducción 1.1.1. Pseudo-motivación Si tengo una fórmula de proposicional, puedo probar con fuerza bruta todas las valuaciones a ver si es satisfactible? Si
1. Resolución en lógica proposicional 1.1. Introducción 1.1.1. Pseudo-motivación Si tengo una fórmula de proposicional, puedo probar con fuerza bruta todas las valuaciones a ver si es satisfactible? Si
Clase Práctica 1 - Inducción estructural, conectivos adecuados y consecuencia - Viernes 23 de marzo de 2012
 Lógica y Computabilidad Primer Cuatrimestre 2012 Clase Práctica 1 - Inducción estructural, conectivos adecuados y consecuencia - Viernes 23 de marzo de 2012 Definición 1. Notaremos con Form al conjunto
Lógica y Computabilidad Primer Cuatrimestre 2012 Clase Práctica 1 - Inducción estructural, conectivos adecuados y consecuencia - Viernes 23 de marzo de 2012 Definición 1. Notaremos con Form al conjunto
Axiomas del Cálculo de Predicados
 Axiomas del Cálculo de Predicados Si bien el cálculo proposicional nos permitió analizar cierto tipo de razonamientos y resolver acertijos lógicos, su poder expresivo no es suficiente para comprobar la
Axiomas del Cálculo de Predicados Si bien el cálculo proposicional nos permitió analizar cierto tipo de razonamientos y resolver acertijos lógicos, su poder expresivo no es suficiente para comprobar la
Formas clausulares Teoría de Herbrand Algoritmo de Herbrand Semidecidibilidad. Teoría de Herbrand. Lógica Computacional
 Teoría de Herbrand Lógica Computacional Departamento de Matemática Aplicada Universidad de Málaga Curso 2005/2006 Contenido 1 Formas clausulares Refutación y formas clausulares 2 Teoría de Herbrand Universo
Teoría de Herbrand Lógica Computacional Departamento de Matemática Aplicada Universidad de Málaga Curso 2005/2006 Contenido 1 Formas clausulares Refutación y formas clausulares 2 Teoría de Herbrand Universo
DETERMINACIÓN DE UN CONJUNTO
 CONJUNTO UNIVERSAL U A Gráficamente, al conjunto universal se lo representa mediante un rectángulo. Cualquier otro conjunto A es representado por una región cerrada, dentro del rectángulo, A este tipo
CONJUNTO UNIVERSAL U A Gráficamente, al conjunto universal se lo representa mediante un rectángulo. Cualquier otro conjunto A es representado por una región cerrada, dentro del rectángulo, A este tipo
Tema 5: (Tecnologías Informáticas) Curso Dpto. Ciencias de la Computación Inteligencia Artificial Universidad de Sevilla
 Tema 5: Dpto. Ciencias de la Computación Inteligencia Artificial Universidad de Sevilla Lógica Informática (Tecnologías Informáticas) Curso 2017 18 en LPO no restringida Contenido en LPO no restringida
Tema 5: Dpto. Ciencias de la Computación Inteligencia Artificial Universidad de Sevilla Lógica Informática (Tecnologías Informáticas) Curso 2017 18 en LPO no restringida Contenido en LPO no restringida
ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- V V V V F F F V F F F V
 Resumen teoría Prof. Alcón ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- Tablas de Verdad: p q p q p p V V V V F V F F F V F V F F F F p q p q V V V V F V F V V F F F p q p q V V V V F F F V V F F V p q p q
Resumen teoría Prof. Alcón ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- Tablas de Verdad: p q p q p p V V V V F V F F F V F V F F F F p q p q V V V V F V F V V F F F p q p q V V V V F F F V V F F V p q p q
Minimización de Aútomatas Finitos
 Minimización de Aútomatas Finitos Supongamos que para un AFD M = (Q, Σ, δ, q 0, F ) definimos la siguiente relación R M : xr M y ssi δ(q 0, x) = δ(q 0, y) Claramente, podemos notar que esta relación es
Minimización de Aútomatas Finitos Supongamos que para un AFD M = (Q, Σ, δ, q 0, F ) definimos la siguiente relación R M : xr M y ssi δ(q 0, x) = δ(q 0, y) Claramente, podemos notar que esta relación es
Resolución en lógica de primer orden
 Resolución en lógica de primer orden Eduardo Bonelli Departamento de Computación, FCEyN, UBA 15 de mayo, 2006 Clase pasada Repasamos lógica proposicional Introdujimos el método de resolución para lógica
Resolución en lógica de primer orden Eduardo Bonelli Departamento de Computación, FCEyN, UBA 15 de mayo, 2006 Clase pasada Repasamos lógica proposicional Introdujimos el método de resolución para lógica
Lógica de Predicados de Primer Orden
 Lógica de Predicados de Primer Orden La lógica proposicional puede ser no apropiada para expresar ciertos tipos de conocimiento. Por ejemplo: Algunas manzanas son rojas Esta afirmación no se refiere específicamente
Lógica de Predicados de Primer Orden La lógica proposicional puede ser no apropiada para expresar ciertos tipos de conocimiento. Por ejemplo: Algunas manzanas son rojas Esta afirmación no se refiere específicamente
Axiomas y Teoremas APÉNDICE A. Teoremas del Cálculo Proposicional. Índice del Capítulo
 APÉNDICE A Axiomas y Teoremas Índice del Capítulo A.1. Teoremas del Cálculo Proposicional..................... 217 A.2. Teoremas del Cálculo de Predicados..................... 220 A.3. Cuantificación Existencial...........................
APÉNDICE A Axiomas y Teoremas Índice del Capítulo A.1. Teoremas del Cálculo Proposicional..................... 217 A.2. Teoremas del Cálculo de Predicados..................... 220 A.3. Cuantificación Existencial...........................
Eliminación de Símbolos Inútiles
 Eliminación de Símbolos Inútiles Veremos cómo eliminar los símbolos inútiles de una gramática. Lo haremos con dos algoritmos, que son definidos en la demostración de los siguientes lemas. Lema 1 Dada una
Eliminación de Símbolos Inútiles Veremos cómo eliminar los símbolos inútiles de una gramática. Lo haremos con dos algoritmos, que son definidos en la demostración de los siguientes lemas. Lema 1 Dada una
Semana02[1/23] Conjuntos. 9 de marzo de Conjuntos
![Semana02[1/23] Conjuntos. 9 de marzo de Conjuntos Semana02[1/23] Conjuntos. 9 de marzo de Conjuntos](/thumbs/53/31721818.jpg) Semana02[1/23] 9 de marzo de 2007 Introducción Semana02[2/23] La teoría de conjuntos gira en torno a la función proposicional x A. Los valores que hacen verdadera la función proposicional x A son aquellos
Semana02[1/23] 9 de marzo de 2007 Introducción Semana02[2/23] La teoría de conjuntos gira en torno a la función proposicional x A. Los valores que hacen verdadera la función proposicional x A son aquellos
IIC2213. IIC2213 Teorías 1 / 42
 Teorías IIC2213 IIC2213 Teorías 1 / 42 Qué es una teoría? Una teoría es un cúmulo de información. Debe estar libre de contradicciones. Debe ser cerrada con respecto a lo que se puede deducir de ella. Inicialmente
Teorías IIC2213 IIC2213 Teorías 1 / 42 Qué es una teoría? Una teoría es un cúmulo de información. Debe estar libre de contradicciones. Debe ser cerrada con respecto a lo que se puede deducir de ella. Inicialmente
Guía 4: Demostraciones en Cálculo Proposicional
 Introducción a los Algoritmos - 2do. cuatrimestre 2014 Guía 4: Demostraciones en Cálculo Proposicional Docentes: Walter Alini y Luciana Benotti. El objetivo principal de esta guía es lograr un buen entrenamiento
Introducción a los Algoritmos - 2do. cuatrimestre 2014 Guía 4: Demostraciones en Cálculo Proposicional Docentes: Walter Alini y Luciana Benotti. El objetivo principal de esta guía es lograr un buen entrenamiento
LÓGICA FORMAL TEORIAS DE PRIMER ORDEN. Teoremas. Departamento de Inteligencia Artificial Facultad de Informática Universidad Politécnica de Madrid
 LÓGICA FORMAL TEORIAS DE PRIMER ORDEN Pedro López Departamento de Inteligencia Artificial Facultad de Informática Universidad Politécnica de Madrid Fórmulas elementales 1 Teniendo en cuenta las definiciones:
LÓGICA FORMAL TEORIAS DE PRIMER ORDEN Pedro López Departamento de Inteligencia Artificial Facultad de Informática Universidad Politécnica de Madrid Fórmulas elementales 1 Teniendo en cuenta las definiciones:
LÓGICA FORMAL TEORIAS DE PRIMER ORDEN. Teoremas
 LÓGICA FORMAL TEORIAS DE PRIMER ORDEN Pedro López Departamento de Inteligencia Artificial Facultad de Informática Universidad Politécnica de Madrid Fórmulas elementales 1 Teniendo en cuenta las definiciones:
LÓGICA FORMAL TEORIAS DE PRIMER ORDEN Pedro López Departamento de Inteligencia Artificial Facultad de Informática Universidad Politécnica de Madrid Fórmulas elementales 1 Teniendo en cuenta las definiciones:
Capítulo 2 El Método de Resolución
 Capítulo 2 El Método de Resolución En este capítulo se realiza una descripción general del método de resolución, dado que el programa de razonamiento automático OTTER lo utiliza y prueba a través de refutación.
Capítulo 2 El Método de Resolución En este capítulo se realiza una descripción general del método de resolución, dado que el programa de razonamiento automático OTTER lo utiliza y prueba a través de refutación.
Anillos, módulos y álgebras de artin. Lic. Manuel Flores Galicia Dr. Octavio Mendoza Hernández
 Anillos, módulos y álgebras de artin Lic. Manuel Flores Galicia Dr. Octavio Mendoza Hernández ii Índice general Introducción vii 1. Nociones de conjuntos, funciones y categorías 1 1.1. Nociones de Lógica
Anillos, módulos y álgebras de artin Lic. Manuel Flores Galicia Dr. Octavio Mendoza Hernández ii Índice general Introducción vii 1. Nociones de conjuntos, funciones y categorías 1 1.1. Nociones de Lógica
Estructuras algebraicas. Departamento de Álgebra. Apuntes de teoría
 ESTRUCTURAS ALGEBRAICAS GRADO EN MATEMÁTICAS. CURSO 2015/2016 Apuntes de teoría Tema 1: Grupos y subgrupos. 1.1. Introducción Definición 1.1. Un grupo es un par (G, ), donde G es un conjunto no vacío,
ESTRUCTURAS ALGEBRAICAS GRADO EN MATEMÁTICAS. CURSO 2015/2016 Apuntes de teoría Tema 1: Grupos y subgrupos. 1.1. Introducción Definición 1.1. Un grupo es un par (G, ), donde G es un conjunto no vacío,
Tema 8: Formas normales.
 Lógica informática Curso 2003 04 Tema 8: Formas normales. Cláusulas José A. Alonso Jiménez Andrés Cordón Franco Dpto. de Ciencias de la Computación e Inteligencia Artificial Universidad de Sevilla LI 2003
Lógica informática Curso 2003 04 Tema 8: Formas normales. Cláusulas José A. Alonso Jiménez Andrés Cordón Franco Dpto. de Ciencias de la Computación e Inteligencia Artificial Universidad de Sevilla LI 2003
Lógica proposicional: Lectura única
 Lógica proposicional: Lectura única Una fórmula ϕ es atómica si ϕ = p, donde p P. Una fórmula ϕ es compuesta si no es atómica. - Si ϕ = ( α), entonces es un conectivo primario de ϕ y α es una subfórmula
Lógica proposicional: Lectura única Una fórmula ϕ es atómica si ϕ = p, donde p P. Una fórmula ϕ es compuesta si no es atómica. - Si ϕ = ( α), entonces es un conectivo primario de ϕ y α es una subfórmula
Capítulo 1: Fundamentos: Lógica y Demostraciones Clase 2: Lógica de Predicados y Métodos de Demostración
 Capítulo 1: Fundamentos: Lógica y Demostraciones Clase 2: Lógica de Predicados y Métodos de Demostración Matemática Discreta - CC3101 Profesor: Pablo Barceló P. Barceló Matemática Discreta - Cap. 1: Fundamentos:
Capítulo 1: Fundamentos: Lógica y Demostraciones Clase 2: Lógica de Predicados y Métodos de Demostración Matemática Discreta - CC3101 Profesor: Pablo Barceló P. Barceló Matemática Discreta - Cap. 1: Fundamentos:
Algunas Aplicaciones de LP
 Algunas Aplicaciones de LP Diversas son las aplicaciones directas de lógica proposicional. A continuación veremos cómo un problema de búsqueda (típico de aplicaciones de Inteligencia Artificial) se puede
Algunas Aplicaciones de LP Diversas son las aplicaciones directas de lógica proposicional. A continuación veremos cómo un problema de búsqueda (típico de aplicaciones de Inteligencia Artificial) se puede
Resumen de aritmética de Peano
 Resumen de aritmética de Peano UDELAR/FING/IMERL 16 de febrero de 2017 1. Fundamentos de la Aritmética de Peano. Axioma 1.1. Existe un conjunto al que denotamos N, un elemento 0 N y una función s : N N
Resumen de aritmética de Peano UDELAR/FING/IMERL 16 de febrero de 2017 1. Fundamentos de la Aritmética de Peano. Axioma 1.1. Existe un conjunto al que denotamos N, un elemento 0 N y una función s : N N
Imágenes y preimágenes de uniones e intersecciones de familias de conjuntos
 Imágenes y preimágenes de uniones e intersecciones de familias de conjuntos Objetivos. Demostrar las fórmulas principales para las imágenes y preimágenes de las uniones e intersecciones de familias de
Imágenes y preimágenes de uniones e intersecciones de familias de conjuntos Objetivos. Demostrar las fórmulas principales para las imágenes y preimágenes de las uniones e intersecciones de familias de
Definición 11.1 Sea f : A E F una aplicación r-veces diferenciable en un punto a A. o
 Capítulo 11 Teoremas de Taylor Una vez más nos disponemos a extender a las funciones de varias variables resultados ya conocidos para funciones de una variable, los teoremas de aproximación de Taylor.
Capítulo 11 Teoremas de Taylor Una vez más nos disponemos a extender a las funciones de varias variables resultados ya conocidos para funciones de una variable, los teoremas de aproximación de Taylor.
Tema 7: Formas normales: Formas prenex y de Skolem
 Tema 7: Formas normales: Formas prenex y de Skolem Dpto. Ciencias de la Computación Inteligencia Artificial Universidad de Sevilla Lógica Informática (Ingeniería del Software) Curso 2013 14 LI(IS), 2013
Tema 7: Formas normales: Formas prenex y de Skolem Dpto. Ciencias de la Computación Inteligencia Artificial Universidad de Sevilla Lógica Informática (Ingeniería del Software) Curso 2013 14 LI(IS), 2013
Ejemplo 66 Sea A = {los alumnos de este curso}, entonces podemos definir la siguiente relación el el conjunto A, dada por:
 Capítulo 3 Relaciones Definición 8 Sea A un conjunto no vacío. Se dice que R es una relación en A si y sólo si R A A. Ejemplo 65 Sea A = {a,b,c}, luego definimos los conjuntos: R 1 = {(a,a),(a,b),(b,c)},r
Capítulo 3 Relaciones Definición 8 Sea A un conjunto no vacío. Se dice que R es una relación en A si y sólo si R A A. Ejemplo 65 Sea A = {a,b,c}, luego definimos los conjuntos: R 1 = {(a,a),(a,b),(b,c)},r
b) Sea una relación de equivalencia en A y una operación en A. Decimos que y son compatibles si a b a c b c y c a c b para todo a, b, c A
 APENDICE Relaciones y Operaciones Compatibles 1 Definición: a) Sea A un conjunto y una relación entre elementos de A. Decimos que es una relación de equivalencia si es: i Reflexiva: a A, a a. ii Simétrica:
APENDICE Relaciones y Operaciones Compatibles 1 Definición: a) Sea A un conjunto y una relación entre elementos de A. Decimos que es una relación de equivalencia si es: i Reflexiva: a A, a a. ii Simétrica:
El sistema deductivo de Hilbert
 El sistema deductivo de Hilbert IIC2213 IIC2213 El sistema deductivo de Hilbert 1 / 17 Completidad de resolución proposicional Qué tenemos que agregar a nuestro sistema de deducción para que sea completo?
El sistema deductivo de Hilbert IIC2213 IIC2213 El sistema deductivo de Hilbert 1 / 17 Completidad de resolución proposicional Qué tenemos que agregar a nuestro sistema de deducción para que sea completo?
Lógica Proposicional. Significado de una Fórmula Proposicional
 Proposicional Semántica Semántica Proposicional - Significado de una Fórmula Proposicional El significado de una proposición está dado por su valor de verdad (o sea, si es Verdadera o Falsa) que se obtiene
Proposicional Semántica Semántica Proposicional - Significado de una Fórmula Proposicional El significado de una proposición está dado por su valor de verdad (o sea, si es Verdadera o Falsa) que se obtiene
LÓGICA DE PREDICADOS 5. IDENTIDAD Y FUNCIONES
 Juan Carlos León Universidad de Murcia LÓGICA DE PREDICADOS 5. IDENTIDAD Y FUNCIONES (PARTE 1) Esquema del tema 5.1. La noción lógica de identidad 5.2. Reglas de deducción natural para = 5.3. Cuantificadores
Juan Carlos León Universidad de Murcia LÓGICA DE PREDICADOS 5. IDENTIDAD Y FUNCIONES (PARTE 1) Esquema del tema 5.1. La noción lógica de identidad 5.2. Reglas de deducción natural para = 5.3. Cuantificadores
Terminaremos el capítulo con una breve referencia a la teoría de cardinales.
 TEMA 5. CARDINALES 241 Tema 5. Cardinales Terminaremos el capítulo con una breve referencia a la teoría de cardinales. Definición A.5.1. Diremos que el conjunto X tiene el mismo cardinal que el conjunto
TEMA 5. CARDINALES 241 Tema 5. Cardinales Terminaremos el capítulo con una breve referencia a la teoría de cardinales. Definición A.5.1. Diremos que el conjunto X tiene el mismo cardinal que el conjunto
Lógica Proposicional
 Proposicional Semántica Semántica Proposicional - Significado de una Fórmula Proposicional El significado de una proposición está dado por su valor de verdad (o sea, si es Verdadera o Falsa) que se obtiene
Proposicional Semántica Semántica Proposicional - Significado de una Fórmula Proposicional El significado de una proposición está dado por su valor de verdad (o sea, si es Verdadera o Falsa) que se obtiene
La clase de hoy. 22 de abril de 2017
 La clase de hoy 22 de abril de 2017 1. Satisfacibilidad 1.1. Vamos a extender ahora nuestra noción de verdad bajo una interpretación de enunciados a fórmulas. Por supuesto, el tema es cómo interpretar
La clase de hoy 22 de abril de 2017 1. Satisfacibilidad 1.1. Vamos a extender ahora nuestra noción de verdad bajo una interpretación de enunciados a fórmulas. Por supuesto, el tema es cómo interpretar
TEORÍA DE GRUPOS (Parte 1)
 TEORÍA DE GRUPOS (Parte 1 OPERACIONES BINARIAS Sea A un conjunto. Una relación de A A en A es una operación inaria (o ley de composición interna si es una función. La imagen del elemento (a, A A mediante
TEORÍA DE GRUPOS (Parte 1 OPERACIONES BINARIAS Sea A un conjunto. Una relación de A A en A es una operación inaria (o ley de composición interna si es una función. La imagen del elemento (a, A A mediante
Curso Extraordinario INTELIGENCIA ARTIFICIAL Y SISTEMAS EXPERTOS
 Curso Extraordinario INTELIGENCIA ARTIFICIAL Y SISTEMAS EXPERTOS Contenidos del Curso Introducción a la I.A. Cómo razonamos?. Algunas experiencias con el razonamiento automático El problema de representación
Curso Extraordinario INTELIGENCIA ARTIFICIAL Y SISTEMAS EXPERTOS Contenidos del Curso Introducción a la I.A. Cómo razonamos?. Algunas experiencias con el razonamiento automático El problema de representación
Tema de la clase: Lógica Matemática. Introducción
 Tema de la clase: Lógica Matemática Instructor: Marcos Villagra Clase # 01 Escriba: Sergio Mercado Fecha 30/10/2017 Introducción Una de las características principales que distinguen a las matemáticas
Tema de la clase: Lógica Matemática Instructor: Marcos Villagra Clase # 01 Escriba: Sergio Mercado Fecha 30/10/2017 Introducción Una de las características principales que distinguen a las matemáticas
Los Teoremas de Incompletitud de Gödel: Parte II: Coherencia y completitud
 Los Teoremas de Incompletitud de Gödel: Parte II: Coherencia y completitud Guillermo Morales Luna Departmento de Computación CINVESTAV-IPN gmorales@cs.cinvestav.mx 2-o Encuentro Nacional de Epistemología
Los Teoremas de Incompletitud de Gödel: Parte II: Coherencia y completitud Guillermo Morales Luna Departmento de Computación CINVESTAV-IPN gmorales@cs.cinvestav.mx 2-o Encuentro Nacional de Epistemología
Teorema de Compacidad
 Teorema de Compacidad Seminario de Teoría de Modelos - FCEyN - UBA 1 de septiembre de 2011 Teorema 1 (Compacidad). Una L-teoría T es satisfacible si y solo si todo subconjunto finito de T es satisfacible.
Teorema de Compacidad Seminario de Teoría de Modelos - FCEyN - UBA 1 de septiembre de 2011 Teorema 1 (Compacidad). Una L-teoría T es satisfacible si y solo si todo subconjunto finito de T es satisfacible.
Teoremas de Taylor. Capítulo 7
 Capítulo 7 Teoremas de Taylor Una vez más nos disponemos a extender a las funciones de varias variables resultados ya conocidos para funciones de una variable, los teoremas de aproximación de Taylor. Por
Capítulo 7 Teoremas de Taylor Una vez más nos disponemos a extender a las funciones de varias variables resultados ya conocidos para funciones de una variable, los teoremas de aproximación de Taylor. Por
Conjuntos. () April 4, / 32
 Conjuntos En general, un conjunto A se de ne seleccionando los elementos de un cierto conjunto U de referencia (o universal) que cumplen una determinada propiedad. () April 4, 2014 1 / 32 Conjuntos En
Conjuntos En general, un conjunto A se de ne seleccionando los elementos de un cierto conjunto U de referencia (o universal) que cumplen una determinada propiedad. () April 4, 2014 1 / 32 Conjuntos En
Estructuras algebraicas
 Semana 10[1/14] 26 de abril de 2007 Semana 10[2/14] Grupos Un grupo es un caso particular de una estructura algebraica. Veremos que esta noción rescata ampliamente las propiedades de estructuras tales
Semana 10[1/14] 26 de abril de 2007 Semana 10[2/14] Grupos Un grupo es un caso particular de una estructura algebraica. Veremos que esta noción rescata ampliamente las propiedades de estructuras tales
Matemáticas Discretas TC1003
 Matemáticas Discretas TC1003 Demostración Automática de Teoremas Departamento de Matemáticas / Centro de Sistema Inteligentes ITESM ATP Matemáticas Discretas - p. 1/30 En lo anterior, hemos visto cómo
Matemáticas Discretas TC1003 Demostración Automática de Teoremas Departamento de Matemáticas / Centro de Sistema Inteligentes ITESM ATP Matemáticas Discretas - p. 1/30 En lo anterior, hemos visto cómo
Lógica de predicados 3. Sintaxis. Juan Carlos León Universidad de Murcia
 Lógica de predicados 3. Sintaxis Juan Carlos León Universidad de Murcia Esquema del tema 3.1. Fórmulas bien formadas y funciones proposicionales 3.2. Alcance. Variables libres y ligadas 3.3. Teoremas 3.4.
Lógica de predicados 3. Sintaxis Juan Carlos León Universidad de Murcia Esquema del tema 3.1. Fórmulas bien formadas y funciones proposicionales 3.2. Alcance. Variables libres y ligadas 3.3. Teoremas 3.4.
Lógica de predicados 3. Sintaxis
 Lógica de predicados 3. Sintaxis Juan Carlos León Universidad de Murcia Esquema del tema 3.1. Fórmulas bien formadas y funciones proposicionales 3.2. Alcance. Variables libres y ligadas 3.3. Teoremas 3.4.
Lógica de predicados 3. Sintaxis Juan Carlos León Universidad de Murcia Esquema del tema 3.1. Fórmulas bien formadas y funciones proposicionales 3.2. Alcance. Variables libres y ligadas 3.3. Teoremas 3.4.
Capítulo 8 Sistemas completos de contectivos
 Capítulo 8 Sistemas completos de contectivos por G 3 Agosto 2014 Resumen Un conectivo de aridad n, es una función que asigna un valor de verdad a un conjunto de n proposiciones ordenadas. Mostramos que
Capítulo 8 Sistemas completos de contectivos por G 3 Agosto 2014 Resumen Un conectivo de aridad n, es una función que asigna un valor de verdad a un conjunto de n proposiciones ordenadas. Mostramos que
Compuertas Lógicas, Algebra Booleana
 Compuertas Lógicas, Algebra Booleana Representación de números negativos Herramientas para conversión y operaciones aritméticas Evaluación BIN DEC DEC Revisión Evaluación Compuertas lógicas Algebra Booleana
Compuertas Lógicas, Algebra Booleana Representación de números negativos Herramientas para conversión y operaciones aritméticas Evaluación BIN DEC DEC Revisión Evaluación Compuertas lógicas Algebra Booleana
PROGRAMA DE CURSO UNIDADES TEMÁTICAS. Unidades Docentes Cátedra Auxiliares Trabajo Personal
 PROGRAMA DE CURSO Código MA1101 Nombre del Curso Introducción al Álgebra Unidades Docentes Cátedra Auxiliares Trabajo Personal 10 3.0 2.0 5.0 Requisitos Requisitos específicos Carácter del curso Ingreso
PROGRAMA DE CURSO Código MA1101 Nombre del Curso Introducción al Álgebra Unidades Docentes Cátedra Auxiliares Trabajo Personal 10 3.0 2.0 5.0 Requisitos Requisitos específicos Carácter del curso Ingreso
Introducción al razonamiento automático con OTTER
 Introducción al razonamiento automático con OTTER José A. Alonso Jiménez Grupo de Lógica Computacional Dpto. de Ciencias de la Computación e Inteligencia Artificial Universidad de Sevilla Sevilla, 1 de
Introducción al razonamiento automático con OTTER José A. Alonso Jiménez Grupo de Lógica Computacional Dpto. de Ciencias de la Computación e Inteligencia Artificial Universidad de Sevilla Sevilla, 1 de
En general, un conjunto A se define seleccionando los elementos de un cierto conjunto U de referencia que cumplen una determinada propiedad.
 nidad 3: Conjuntos 3.1 Introducción Georg Cantor [1845-1918] formuló de manera individual la teoría de conjuntos a finales del siglo XIX y principios del XX. Su objetivo era el de formalizar las matemáticas
nidad 3: Conjuntos 3.1 Introducción Georg Cantor [1845-1918] formuló de manera individual la teoría de conjuntos a finales del siglo XIX y principios del XX. Su objetivo era el de formalizar las matemáticas
Tema 9: Modelos de Herbrand
 Lógica informática Curso 2003 04 Tema 9: Modelos de Herbrand José A. Alonso Jiménez Andrés Cordón Franco Dpto. de Ciencias de la Computación e Inteligencia Artificial Universidad de Sevilla LI 2003 04
Lógica informática Curso 2003 04 Tema 9: Modelos de Herbrand José A. Alonso Jiménez Andrés Cordón Franco Dpto. de Ciencias de la Computación e Inteligencia Artificial Universidad de Sevilla LI 2003 04
ÁLGEBRA I. Curso Grado en Matemáticas
 ÁLGEBRA I. Curso 2012-13 Grado en Matemáticas Relación 1: Lógica Proposicional y Teoría de Conjuntos 1. Establecer las siguientes tautologías: (a) A A A (b) A A A (c) A B B A (d) A B B A (e) (A B) C A
ÁLGEBRA I. Curso 2012-13 Grado en Matemáticas Relación 1: Lógica Proposicional y Teoría de Conjuntos 1. Establecer las siguientes tautologías: (a) A A A (b) A A A (c) A B B A (d) A B B A (e) (A B) C A
Estructuras algebraicas
 Semana 11[1/22] 4 de mayo de 2007 Anillos y cuerpos Semana 11[2/22] Anillos Comenzamos ahora el estudio de estructuras algebraicas que tengan definidas dos operaciones, y las clasificaremos en anillos
Semana 11[1/22] 4 de mayo de 2007 Anillos y cuerpos Semana 11[2/22] Anillos Comenzamos ahora el estudio de estructuras algebraicas que tengan definidas dos operaciones, y las clasificaremos en anillos
Qué es la lógica? Esfuerzos por modelar estas leyes del pensamiento humano. Han existido desde la antigüedad.
 Qué es la lógica? La definición del Diccionario General de la Lengua Española dice: Disciplina que estudia los principios formales del conocimiento humano, es decir, las formas y las leyes más generales
Qué es la lógica? La definición del Diccionario General de la Lengua Española dice: Disciplina que estudia los principios formales del conocimiento humano, es decir, las formas y las leyes más generales
APÉNDICE A. Axiomas y Teoremas. Índice del Capítulo
 APÉNDICE A Axiomas y Teoremas Índice del Capítulo A.1. Teoremas del Cálculo Proposicional..................... 219 A.2. Leyes Generales de la Cuantificación.................... 222 A.3. Teoremas del Cálculo
APÉNDICE A Axiomas y Teoremas Índice del Capítulo A.1. Teoremas del Cálculo Proposicional..................... 219 A.2. Leyes Generales de la Cuantificación.................... 222 A.3. Teoremas del Cálculo
Tema 3 Equivalencia. Formas normales.
 Tema 3 Equivalencia. Formas normales. Lógica Proposicional Antonio de J. Pérez Jiménez Departamento Ccia. Lógica Informática Antonio de J. Pérez Jiménez (Departamento Ccia.) Tema 3 Equivalencia. Formas
Tema 3 Equivalencia. Formas normales. Lógica Proposicional Antonio de J. Pérez Jiménez Departamento Ccia. Lógica Informática Antonio de J. Pérez Jiménez (Departamento Ccia.) Tema 3 Equivalencia. Formas
Lógica de predicados
 Matemática Discreta y Lógica 2 Lógica de predicados 1 Cuantificadores El lenguaje de la lógica proposicional que ya vimos, no es suficiente para representar todo el lenguaje matemático. Por ejemplo, la
Matemática Discreta y Lógica 2 Lógica de predicados 1 Cuantificadores El lenguaje de la lógica proposicional que ya vimos, no es suficiente para representar todo el lenguaje matemático. Por ejemplo, la
Álgebra Booleana. Suma Booleana. El término suma es 1 si al menos uno de sus literales son 1. El término suma es 0 solamente si cada literal es 0.
 Álgebra Booleana El álgebra de Boole son las matemáticas de los sistemas digitales. En el nivel de lógica digital de una computadora, lo que comúnmente se llama hardware y que está formado por los componentes
Álgebra Booleana El álgebra de Boole son las matemáticas de los sistemas digitales. En el nivel de lógica digital de una computadora, lo que comúnmente se llama hardware y que está formado por los componentes
Un elemento de un monoide se dice que es inversible si tiene elemento inverso.
 Tema 1: Semigrupos 1 Tema 1: Semigrupos 1. Semigrupos: Conceptos fundamentales. Recordemos que un sistema algebraico es un conjunto S con una o varias operaciones sobre él, siendo una operación ó ley de
Tema 1: Semigrupos 1 Tema 1: Semigrupos 1. Semigrupos: Conceptos fundamentales. Recordemos que un sistema algebraico es un conjunto S con una o varias operaciones sobre él, siendo una operación ó ley de
Capítulo 4: Conjuntos
 Capítulo 4: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2014 Olalla (Universidad de Sevilla) Capítulo 4: Conjuntos Septiembre de
Capítulo 4: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2014 Olalla (Universidad de Sevilla) Capítulo 4: Conjuntos Septiembre de
Tema 5: Teoría de la Demostración en Predicados
 Tema 5: Teoría de la Demostración en Predicados Resumen introducción lógica de predicados Resumen introducción lógica de predicados Conceptos: ahora para lógica de predicados de 1 er orden Estructura deductiva
Tema 5: Teoría de la Demostración en Predicados Resumen introducción lógica de predicados Resumen introducción lógica de predicados Conceptos: ahora para lógica de predicados de 1 er orden Estructura deductiva
Lógica Proposicional IIC2213. IIC2213 Lógica Proposicional 1/42
 Lógica Proposicional IIC2213 IIC2213 Lógica Proposicional 1/42 Por qué necesitamos la lógica? Necesitamos un lenguaje con una sintaxis precisa y una semántica bien definida. Queremos usar este lenguaje
Lógica Proposicional IIC2213 IIC2213 Lógica Proposicional 1/42 Por qué necesitamos la lógica? Necesitamos un lenguaje con una sintaxis precisa y una semántica bien definida. Queremos usar este lenguaje
Lógica informática ( )
 Lógica informática (2008 09) Tema 8: de Skolem y cláusulas José A. Alonso Jiménez María J. Hidalgo Doblado Grupo de Lógica Computacional Departamento de Ciencias de la Computación e I.A. Universidad de
Lógica informática (2008 09) Tema 8: de Skolem y cláusulas José A. Alonso Jiménez María J. Hidalgo Doblado Grupo de Lógica Computacional Departamento de Ciencias de la Computación e I.A. Universidad de
Lógica Proposicional IIC2213. IIC2213 Lógica Proposicional 1/42
 Lógica Proposicional IIC2213 IIC2213 Lógica Proposicional 1/42 Por qué necesitamos la lógica? Necesitamos un lenguaje con una sintaxis precisa y una semántica bien definida. Queremos usar este lenguaje
Lógica Proposicional IIC2213 IIC2213 Lógica Proposicional 1/42 Por qué necesitamos la lógica? Necesitamos un lenguaje con una sintaxis precisa y una semántica bien definida. Queremos usar este lenguaje
Tema 4: Lógicas Informática (Tecnologías Informáticas) Curso Dpto. Ciencias de la Computación Inteligencia Artificial Universidad de Sevilla
 Tema 4: Dpto. Ciencias de la Computación Inteligencia Artificial Universidad de Sevilla Lógicas Informática (Tecnologías Informáticas) Curso 2017 18 Contenido Presentaremos un algoritmo más para estudiar
Tema 4: Dpto. Ciencias de la Computación Inteligencia Artificial Universidad de Sevilla Lógicas Informática (Tecnologías Informáticas) Curso 2017 18 Contenido Presentaremos un algoritmo más para estudiar
Lógica informática ( )
 1 / 23 Lógica informática (2011 12) Tema 9: de Skolem y cláusulas José A. Alonso Jiménez Andrés Cordón Franco María J. Hidalgo Doblado Grupo de Lógica Computacional Departamento de Ciencias de la Computación
1 / 23 Lógica informática (2011 12) Tema 9: de Skolem y cláusulas José A. Alonso Jiménez Andrés Cordón Franco María J. Hidalgo Doblado Grupo de Lógica Computacional Departamento de Ciencias de la Computación
Relaciones. Estructuras Discretas. Relaciones. Relaciones en un Conjunto. Propiedades de Relaciones en A Reflexividad
 Estructuras Discretas Relaciones Definición: relación Relaciones Claudio Lobos, Jocelyn Simmonds clobos,jsimmond@inf.utfsm.cl Universidad Técnica Federico Santa María Estructuras Discretas INF 152 Sean
Estructuras Discretas Relaciones Definición: relación Relaciones Claudio Lobos, Jocelyn Simmonds clobos,jsimmond@inf.utfsm.cl Universidad Técnica Federico Santa María Estructuras Discretas INF 152 Sean
Introducción a la Lógica Proposicional Seminario de Matemáticas
 Introducción a la Lógica Proposicional Seminario de Matemáticas Julio Ariel Hurtado Alegría ahurtado@unicauca.edu.co 8 de mayo de 2015 Julio A. Hurtado A. Departamento de Sistemas 1 / 34 Agenda Motivación
Introducción a la Lógica Proposicional Seminario de Matemáticas Julio Ariel Hurtado Alegría ahurtado@unicauca.edu.co 8 de mayo de 2015 Julio A. Hurtado A. Departamento de Sistemas 1 / 34 Agenda Motivación
4.1 La prueba formal de la consistencia o de la inconsistencia 4.2 La prueba formal de la invalidez 4.3 La prueba formal de la validez
 4.- Métodos de razonamiento En este módulo hemos estudiado algunas estrategias que han sido desarrolladas con el fin de sistematizar el razonamiento lógico, es decir, la demostración formal de teoremas.
4.- Métodos de razonamiento En este módulo hemos estudiado algunas estrategias que han sido desarrolladas con el fin de sistematizar el razonamiento lógico, es decir, la demostración formal de teoremas.
Semana04[1/17] Funciones. 21 de marzo de Funciones
![Semana04[1/17] Funciones. 21 de marzo de Funciones Semana04[1/17] Funciones. 21 de marzo de Funciones](/thumbs/73/69418199.jpg) Semana04[1/17] 21 de marzo de 2007 Composición de funciones Semana04[2/17] Pensemos que tenemos tres conjuntos no vacíos A, B, C, y dos funciones, f : A B y g : B C, como en el siguiente diagrama: Figura:
Semana04[1/17] 21 de marzo de 2007 Composición de funciones Semana04[2/17] Pensemos que tenemos tres conjuntos no vacíos A, B, C, y dos funciones, f : A B y g : B C, como en el siguiente diagrama: Figura:
Universidad Central de Venezuela Facultad de Ciencias Escuela de Computación. Lecturas en Ciencias de la Computación ISSN
 Universidad Central de Venezuela Facultad de Ciencias Escuela de Computación Lecturas en Ciencias de la Computación ISSN 1316-6239 Relaciones Prof. Luis Manuel Hernández R. ND 2006-02 Centro de Cálculo
Universidad Central de Venezuela Facultad de Ciencias Escuela de Computación Lecturas en Ciencias de la Computación ISSN 1316-6239 Relaciones Prof. Luis Manuel Hernández R. ND 2006-02 Centro de Cálculo
Relaciones IIC1253. IIC1253 Relaciones 1 / 32
 Relaciones IIC1253 IIC1253 Relaciones 1 / 32 Relaciones binarias Dado: conjunto A R es una relación binaria sobre A si R A A. Para indicar que a,b A están relacionados a través de R usamos las notaciones:
Relaciones IIC1253 IIC1253 Relaciones 1 / 32 Relaciones binarias Dado: conjunto A R es una relación binaria sobre A si R A A. Para indicar que a,b A están relacionados a través de R usamos las notaciones:
Apuntes de Lógica Matemática I
 Apuntes de Lógica Matemática I Héctor Olvera Vital 1. Primeras definiciones Definición 1 Un alfabeto A es un conjunto de símbolos. Definición 2 Una expresión del alfabeto A es una sucesión finita de símbolos
Apuntes de Lógica Matemática I Héctor Olvera Vital 1. Primeras definiciones Definición 1 Un alfabeto A es un conjunto de símbolos. Definición 2 Una expresión del alfabeto A es una sucesión finita de símbolos
La trascendencia de e y π
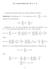 La trascendencia de e y π Comenzamos introduciendo unos convenios útiles de notación: Definición 1 Escribiremos h r = r!, de modo que si fz) = m c r z r C[z], entonces fh) representará fh) = m c r h r
La trascendencia de e y π Comenzamos introduciendo unos convenios útiles de notación: Definición 1 Escribiremos h r = r!, de modo que si fz) = m c r z r C[z], entonces fh) representará fh) = m c r h r
Sistema Axiomático para el Cálculo Proposicional
 Sistema Axiomático para el Cálculo Proposicional Lógica Matemática José de Jesús Lavalle Martínez 12 de julio de 2011 Resumen Este documento es una traducción de partes de la sección 1.4 AN AXIOM SYSTEM
Sistema Axiomático para el Cálculo Proposicional Lógica Matemática José de Jesús Lavalle Martínez 12 de julio de 2011 Resumen Este documento es una traducción de partes de la sección 1.4 AN AXIOM SYSTEM
