Aproximaciones y Error
|
|
|
- Margarita Núñez Quiroga
- hace 5 años
- Vistas:
Transcripción
1 Aproximaciones y Error Oldemar Rodríguez R. UCR 14 de septiembre de 2014 Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
2 Outline 1 Aritmética punto flotante 2 Problemas con la aritmética punto flotante 3 Algoritmos y convergencia 4 Origen del error Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
3 Punto flotante Definición Un número real x está en forma punto flotante si se escribe de la forma: 0.d 1 d 2 d k 10 n donde 0 d i 9, d 1 = 0, i = 1, 2,..., k. Ejemplo π = 0, Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
4 Punto flotante Definición Un número real x está en forma punto flotante si se escribe de la forma: 0.d 1 d 2 d k 10 n donde 0 d i 9, d 1 = 0, i = 1, 2,..., k. Ejemplo π = 0, Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
5 Observación Veamos: En análisis numérico todas las respuestas deben darse en notación punto flotante. Si x R, entonces x = 0.d 1 d 2 d n, pero el computador solo puede almacenar números en punto flotante debido a las limitaciones de memoria. Por lo tanto quedan 2 posibilidades: 1 Cortar x = f l(x) = 0.d 1 d 2 d k 10 n, i.e. cortar a partir del dígito k Redondear y Cortar Si d k+1 5 entonces sume 1 a d k y corte. Si no solamente corte. Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
6 Observación Veamos: En análisis numérico todas las respuestas deben darse en notación punto flotante. Si x R, entonces x = 0.d 1 d 2 d n, pero el computador solo puede almacenar números en punto flotante debido a las limitaciones de memoria. Por lo tanto quedan 2 posibilidades: 1 Cortar x = f l(x) = 0.d 1 d 2 d k 10 n, i.e. cortar a partir del dígito k Redondear y Cortar Si d k+1 5 entonces sume 1 a d k y corte. Si no solamente corte. Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
7 Observación Veamos: En análisis numérico todas las respuestas deben darse en notación punto flotante. Si x R, entonces x = 0.d 1 d 2 d n, pero el computador solo puede almacenar números en punto flotante debido a las limitaciones de memoria. Por lo tanto quedan 2 posibilidades: 1 Cortar x = f l(x) = 0.d 1 d 2 d k 10 n, i.e. cortar a partir del dígito k Redondear y Cortar Si d k+1 5 entonces sume 1 a d k y corte. Si no solamente corte. Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
8 Observación Veamos: En análisis numérico todas las respuestas deben darse en notación punto flotante. Si x R, entonces x = 0.d 1 d 2 d n, pero el computador solo puede almacenar números en punto flotante debido a las limitaciones de memoria. Por lo tanto quedan 2 posibilidades: 1 Cortar x = f l(x) = 0.d 1 d 2 d k 10 n, i.e. cortar a partir del dígito k Redondear y Cortar Si d k+1 5 entonces sume 1 a d k y corte. Si no solamente corte. Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
9 Observación Veamos: En análisis numérico todas las respuestas deben darse en notación punto flotante. Si x R, entonces x = 0.d 1 d 2 d n, pero el computador solo puede almacenar números en punto flotante debido a las limitaciones de memoria. Por lo tanto quedan 2 posibilidades: 1 Cortar x = f l(x) = 0.d 1 d 2 d k 10 n, i.e. cortar a partir del dígito k Redondear y Cortar Si d k+1 5 entonces sume 1 a d k y corte. Si no solamente corte. Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
10 Ejemplo π = 3, , con k = 5 tenemos: f l(π) = 0, (Cortando) f l(π) = 0, (Redondeando) Definición El error que resulta de reemplazar x por f l(x) se denomina: Error de Redondeo. Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
11 Ejemplo π = 3, , con k = 5 tenemos: f l(π) = 0, (Cortando) f l(π) = 0, (Redondeando) Definición El error que resulta de reemplazar x por f l(x) se denomina: Error de Redondeo. Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
12 Cómo medir, controlar, la propagación del error? Definición Si P es una aproximación de P se llama: Ejemplo Error absoluto = P P Error relativo = P P, si P = 0 P Si P = 0, y P = 0, entonces: P P = 0,1 10 1, P P P = 0, Pero si P = 0, y P = 0, entonces: P P = 0,1 10 3, P P P = 0, Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
13 Cómo medir, controlar, la propagación del error? Definición Si P es una aproximación de P se llama: Ejemplo Error absoluto = P P Error relativo = P P, si P = 0 P Si P = 0, y P = 0, entonces: P P = 0,1 10 1, P P P = 0, Pero si P = 0, y P = 0, entonces: P P = 0,1 10 3, P P P = 0, Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
14 Cómo medir, controlar, la propagación del error? Definición Si P es una aproximación de P se llama: Ejemplo Error absoluto = P P Error relativo = P P, si P = 0 P Si P = 0, y P = 0, entonces: P P = 0,1 10 1, P P P = 0, Pero si P = 0, y P = 0, entonces: P P = 0,1 10 3, P P P = 0, Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
15 Teorema Teorema Sea x R, x = 0, entonces: 1 Si f l(x) se obtiene usando k-dígitos de x cortando, entonces: x f l(x) x 10 k+1 2 Si f l(x) se obtiene usando k-dígitos de x redondeado, entonces: x f l(x) x 0,5 10 k+1 = 5 10 k Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
16 Teorema Teorema Sea x R, x = 0, entonces: 1 Si f l(x) se obtiene usando k-dígitos de x cortando, entonces: x f l(x) x 10 k+1 2 Si f l(x) se obtiene usando k-dígitos de x redondeado, entonces: x f l(x) x 0,5 10 k+1 = 5 10 k Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
17 Prueba Prueba 1 x f l(x) x = = = 0.d 1 d 2 10 n 0.d 1 d 2 d k 10 n 0.d 1 d 2 10 n 0.d k+1 d k+2 10 n k 0.d 1 d 2 10 n 0.d k+1 d k+2 0.d 1 d 2 10 k 1 0,1 10 k = 10 k+1 2 Ejercicio: por casos (1) d k+1 < 5, (2) d k+1 5 Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
18 Prueba Prueba 1 x f l(x) x = = = 0.d 1 d 2 10 n 0.d 1 d 2 d k 10 n 0.d 1 d 2 10 n 0.d k+1 d k+2 10 n k 0.d 1 d 2 10 n 0.d k+1 d k+2 0.d 1 d 2 10 k 1 0,1 10 k = 10 k+1 2 Ejercicio: por casos (1) d k+1 < 5, (2) d k+1 5 Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
19 Definición Se dice que un número P aproxima a P con t dígitos significativos si t N es el número más grande tal que: P P P < 5 10 t = 0,5 10 t+1 Ejemplo x = π = }{{} x = 22 = }{{} x x x = 0, < 0, por lo que x aproxima x con 4 dígitos significativos. Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
20 Definición Se dice que un número P aproxima a P con t dígitos significativos si t N es el número más grande tal que: P P P < 5 10 t = 0,5 10 t+1 Ejemplo x = π = }{{} x = 22 = }{{} x x x = 0, < 0, por lo que x aproxima x con 4 dígitos significativos. Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
21 Ejemplo Ejemplo Qué valores puede tomar x para aproximar 1000 con 4 dígitos significativos? x = 1000 = 0, , luego tenemos que: x < < x < ,5 < x < 1000,5 Note que x = 0, aproxima a x con 4 dígitos significativos, pero y = 0, no aproxima x con 4 dígitos significativos. Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
22 Ejemplo Ejemplo Qué valores puede tomar x para aproximar 1000 con 4 dígitos significativos? x = 1000 = 0, , luego tenemos que: x < < x < ,5 < x < 1000,5 Note que x = 0, aproxima a x con 4 dígitos significativos, pero y = 0, no aproxima x con 4 dígitos significativos. Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
23 Outline 1 Aritmética punto flotante 2 Problemas con la aritmética punto flotante 3 Algoritmos y convergencia 4 Origen del error Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
24 Posibles problemas con la aritmética punto flotante División: Si x = x + ε y se divide entre δ muy pequeño se tiene: x = x + ε = x δ δ δ + ε }{{} δ Nuevo error enorme Resta de dos número casi iguales: f l(x) = 0.d 1 d 2 d p α p+1 α p+2 α k 10 n f l(y) = 0.d 1 d 2 d p β p+1 β p+2 β k 10 n x y = f l(x) f l(y) = 0. γ p+1 γ p+2 γ k }{{} Podría ser basura 10 n p Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
25 Posibles problemas con la aritmética punto flotante División: Si x = x + ε y se divide entre δ muy pequeño se tiene: x = x + ε = x δ δ δ + ε }{{} δ Nuevo error enorme Resta de dos número casi iguales: f l(x) = 0.d 1 d 2 d p α p+1 α p+2 α k 10 n f l(y) = 0.d 1 d 2 d p β p+1 β p+2 β k 10 n x y = f l(x) f l(y) = 0. γ p+1 γ p+2 γ k }{{} Podría ser basura 10 n p Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
26 Notación: x = x x δ x = x x = x x x Teorema Si x = x 1 + x x n y x = x 1 + x x n con x i 0 entonces: n xi i=1 δ x max{δ x1, δ x2,..., δ xn } x Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
27 Notación: x = x x δ x = x x = x x x Teorema Si x = x 1 + x x n y x = x 1 + x x n con x i 0 entonces: n xi i=1 δ x max{δ x1, δ x2,..., δ xn } x Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
28 Prueba 1 x = x x = n i=1 x i n xi i=1 n x i xi = i=1 n xi i=1 2 Sabemos que δ x = x x x 1 + x2 + + xn x 1 + x x n, pero δ xi = x i x i x i = δ xi x i δ x x 1 δ x1 + x 2 δ x2 + + x n δ xn x 1 + x x n max{δ x 1, δ x2,..., δ xn } ( x 1 + x x n ) x 1 + x x n max{δ x1, δ x2,..., δ xn }, pues x i 0 i Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
29 Prueba 1 x = x x = n i=1 x i n xi i=1 n x i xi = i=1 n xi i=1 2 Sabemos que δ x = x x x 1 + x2 + + xn x 1 + x x n, pero δ xi = x i x i x i = δ xi x i δ x x 1 δ x1 + x 2 δ x2 + + x n δ xn x 1 + x x n max{δ x 1, δ x2,..., δ xn } ( x 1 + x x n ) x 1 + x x n max{δ x1, δ x2,..., δ xn }, pues x i 0 i Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
30 Observación: Se debe evitar la pérdida de dígitos significativos: Por ejemplo al evaluar: f (x) = 1 cos(x) con x cercano a 0 se producirá una pérdida de dígitos significativos. Esto se puede evitar racionalizando, como sigue: f (x) = 1 cos(x) = sin2 (x) 1 + cos(x) Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
31 Outline 1 Aritmética punto flotante 2 Problemas con la aritmética punto flotante 3 Algoritmos y convergencia 4 Origen del error Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
32 Qué es un algoritmo? Definición Un algoritmo es un procedimiento que describe, sin ninguna ambigüedad, una sucesión finita de pasos a realizar en orden específico, con el propósito de resolver un problema. Características: Finito Definido (no ambiguo) Entrada Salida Efectivo Eficiente Para representar las instrucciones utilizaremos pseudocódigo. Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
33 Qué es un algoritmo? Definición Un algoritmo es un procedimiento que describe, sin ninguna ambigüedad, una sucesión finita de pasos a realizar en orden específico, con el propósito de resolver un problema. Características: Finito Definido (no ambiguo) Entrada Salida Efectivo Eficiente Para representar las instrucciones utilizaremos pseudocódigo. Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
34 Ejemplo Para calcular k=a f (x, k) tenemos: Entrada: ε, f, a, x Salida: Valor aproximado de k=a f (x, k) 1: k a 2: s 0 3: T f (x, k) 4: while T < ε do 5: s s + t 6: t t ( f (x, k + 1)/ f (x, k)) 7: k k + 1 8: end while 9: return s Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
35 Algoritmos Estables Definición Un algoritmo se dice estable si pequeños cambios en la entrada producen pequeños cambio en la salida. En caso contrario, es decir, pequeños cambio en la entrada producen grandes cambios en la salida, entonces el algoritmo se dice inestable (caótico). Notación: E = Error inicial E n = Error luego de n pasos Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
36 Algoritmos Estables Definición Un algoritmo se dice estable si pequeños cambios en la entrada producen pequeños cambio en la salida. En caso contrario, es decir, pequeños cambio en la entrada producen grandes cambios en la salida, entonces el algoritmo se dice inestable (caótico). Notación: E = Error inicial E n = Error luego de n pasos Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
37 Definición Si E n = CnE, con C constante, entonces el crecimiento del error es lineal. Definición Si E n = K n E con K > 1, entonces el crecimiento del error es exponencial. Observación Crecimiento error lineal estable. Crecimiento error exponencial inestable. Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
38 Definición Si E n = CnE, con C constante, entonces el crecimiento del error es lineal. Definición Si E n = K n E con K > 1, entonces el crecimiento del error es exponencial. Observación Crecimiento error lineal estable. Crecimiento error exponencial inestable. Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
39 Definición Si E n = CnE, con C constante, entonces el crecimiento del error es lineal. Definición Si E n = K n E con K > 1, entonces el crecimiento del error es exponencial. Observación Crecimiento error lineal estable. Crecimiento error exponencial inestable. Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
40 Definición Sea {α n } n N una sucesión que converge a α, se dice que {α n } n N converge con una rapidez O(β n ), donde {β n } n N es otra sucesión (β n = 0 n) si: α n α β n < K para n suficientemente grande y K constante que no depende de n. Notación: α n = α + O(β n ) α n α con rapidez O(β n ) Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
41 Definición Sea {α n } n N una sucesión que converge a α, se dice que {α n } n N converge con una rapidez O(β n ), donde {β n } n N es otra sucesión (β n = 0 n) si: α n α β n < K para n suficientemente grande y K constante que no depende de n. Notación: α n = α + O(β n ) α n α con rapidez O(β n ) Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
42 Observación α n α β n < K Kβ n + α < α n < Kβ n + α Ejemplo Si α n = n + 3 n 3 entonces α n = 0 + O(1/n 2 ) pues: α n α n+3 β n = + 0 n 3 1 = n 3 + 3n 2 n 3 = n 4, si n n 2 es decir, que n + 3 n 3 converge a 0 tan rápido como 1 converge a 0. n2 Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
43 Observación α n α β n < K Kβ n + α < α n < Kβ n + α Ejemplo Si α n = n + 3 n 3 entonces α n = 0 + O(1/n 2 ) pues: α n α n+3 β n = + 0 n 3 1 = n 3 + 3n 2 n 3 = n 4, si n n 2 es decir, que n + 3 n 3 converge a 0 tan rápido como 1 converge a 0. n2 Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
44 Observación α n α β n < K Kβ n + α < α n < Kβ n + α Ejemplo Si α n = n + 3 n 3 entonces α n = 0 + O(1/n 2 ) pues: α n α n+3 β n = + 0 n 3 1 = n 3 + 3n 2 n 3 = n 4, si n n 2 es decir, que n + 3 n 3 converge a 0 tan rápido como 1 converge a 0. n2 Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
45 Ejemplo Si α n = sin(n) n entonces α n = 0 + O ( ) 1, cuando n. n Observación: Velocidad de convergencia de los ciclos 1 For[i=1, i++, i<=n,...] tiene una velocidad de convergencia O(N) 2 For[i=1, i++, i<=n, For[j=1, j++, j<=m,...]] tiene una velocidad de convergencia O(N 2 ) 3 For[i=1, i++, i<=n, For[j=1, j++, j<=m, For[k=1, k++, k<=l,...]]] tiene una velocidad de convergencia O(N 3 ) Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
46 Ejemplo Si α n = sin(n) n entonces α n = 0 + O ( ) 1, cuando n. n Observación: Velocidad de convergencia de los ciclos 1 For[i=1, i++, i<=n,...] tiene una velocidad de convergencia O(N) 2 For[i=1, i++, i<=n, For[j=1, j++, j<=m,...]] tiene una velocidad de convergencia O(N 2 ) 3 For[i=1, i++, i<=n, For[j=1, j++, j<=m, For[k=1, k++, k<=l,...]]] tiene una velocidad de convergencia O(N 3 ) Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
47 Ejemplo Si α n = sin(n) n entonces α n = 0 + O ( ) 1, cuando n. n Observación: Velocidad de convergencia de los ciclos 1 For[i=1, i++, i<=n,...] tiene una velocidad de convergencia O(N) 2 For[i=1, i++, i<=n, For[j=1, j++, j<=m,...]] tiene una velocidad de convergencia O(N 2 ) 3 For[i=1, i++, i<=n, For[j=1, j++, j<=m, For[k=1, k++, k<=l,...]]] tiene una velocidad de convergencia O(N 3 ) Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
48 Ejemplo Si α n = sin(n) n entonces α n = 0 + O ( ) 1, cuando n. n Observación: Velocidad de convergencia de los ciclos 1 For[i=1, i++, i<=n,...] tiene una velocidad de convergencia O(N) 2 For[i=1, i++, i<=n, For[j=1, j++, j<=m,...]] tiene una velocidad de convergencia O(N 2 ) 3 For[i=1, i++, i<=n, For[j=1, j++, j<=m, For[k=1, k++, k<=l,...]]] tiene una velocidad de convergencia O(N 3 ) Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
49 Outline 1 Aritmética punto flotante 2 Problemas con la aritmética punto flotante 3 Algoritmos y convergencia 4 Origen del error Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
50 Tipos de Error Existen dos tipos de error: El error en los datos y el error computacional: Definición Sea a R y sea ã una aproximación de a y f una función o procedimiento, entonces f (ã) f (a) se llama propagación del error o error propagado. Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
51 Tipos de Error Existen dos tipos de error: El error en los datos y el error computacional: Definición Sea a R y sea ã una aproximación de a y f una función o procedimiento, entonces f (ã) f (a) se llama propagación del error o error propagado. Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
52 Observación En la práctica muchas veces no es posible calcular f en forma exacta, sino que se usa una aproximación f. Definición f (ã) f (ã) se llama error computacional. Esto se ilustra en el siguiente gráfico: Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
53 Ejemplo Suponga que se desea calcular c en el siguiente triángulo: Supongamos que a tiene un error y usamos 100,1. Entonces el error se propaga como se muestra en la siguiente tabla: Expresión Exacto Aproximado Error relativo a ,1 0,1 % b a 1 0,9 10 % (b a) 2 1 0,81 19 % 4ab sin 2 ( γ 2 ) 3,0765 3,0796 0,1 % (b a) 2 + 4ab sin 2 ( γ 2 ) 4,0765 3,8896 4,6 % c 2,0190 1,9722 2,3 % Error relativo inicial 0,1 % Error relativo final 2,3 % Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
54 Ejemplo: Inestabilidad Numérica Suponga que se desea calcular z = 1,000 1,208 x en una computadora que solamente utiliza 4 dígitos, con x = 1,209. Algoritmo 1. Calcule primero y := 1,208 x y luego calcule z := 1,000 y Algoritmo 2. Calcule primero y := x 1,208 y luego calcule z := y x Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
55 Principio Básico: Si es posible, evite operaciones sensibles con operandos contaminados por la propagación del error. Ejemplo: Usualmente para calcular las raíces de una ecuación cuadrática se usa: x 1,2 = b ± b 2 4ac 2a Pero si b > 0 es mejor usar: y si b < 0 es mejor usar: x 1 = x 2 = 2c b b 2 4ac 2c b + b 2 4ac Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
56 Ejemplos de Inestabilidad Numérica Ejemplo Otros ejemplos que evitan problemas de cancelación cuando x = y son: x 2 y 2 (x y)(x + y) ( ) ( ) x y x + y sin(x) sin(y) 2 sin cos 2 2 } ( ) ln(x) ( ) ln(y) ln x 2 tanh 1 x y y x + y ( ) x y e x e y 2 sinh e x+y 2 2 Oldemar Rodríguez R. (UCR) Aproximaciones y Error 14 de septiembre de / 30
Asignatura : Análisis Numérico Grupo : ::Tarea 1::.
 .::Tarea 1::. Ejercicios Teóricos 1. Convertir los siguientes Números Binarios en forma decimal. (a) 11111110 dos (b) 1000000111 dos (c) 0.1010101 dos (d) 0.110110110 dos (e) 1.0110101 dos (f) 11.00100100001
.::Tarea 1::. Ejercicios Teóricos 1. Convertir los siguientes Números Binarios en forma decimal. (a) 11111110 dos (b) 1000000111 dos (c) 0.1010101 dos (d) 0.110110110 dos (e) 1.0110101 dos (f) 11.00100100001
Tema 1: Conceptos generales del Análisis Numérico
 Tema 1: Conceptos generales del Análisis Numérico Asignatura: Cálculo Numérico I 1er. curso Grado en Matemáticas Anna Doubova Dpto. EDAN, Universidad de Sevilla 5 de febrero de 2018 A. Doubova (Dpto. EDAN)
Tema 1: Conceptos generales del Análisis Numérico Asignatura: Cálculo Numérico I 1er. curso Grado en Matemáticas Anna Doubova Dpto. EDAN, Universidad de Sevilla 5 de febrero de 2018 A. Doubova (Dpto. EDAN)
Introducción al Cálculo Numérico
 Tema 1 Introducción al Cálculo Numérico 1.1 Introducción El Cálculo Numérico, o como también se le denomina, el Análisis numérico, es la rama de las Matemáticas que estudia los métodos numéricos de resolución
Tema 1 Introducción al Cálculo Numérico 1.1 Introducción El Cálculo Numérico, o como también se le denomina, el Análisis numérico, es la rama de las Matemáticas que estudia los métodos numéricos de resolución
Lección 7. Aritmética Computacional
 Lección 7. Aritmética Computacional MIGUEL ANGEL UH ZAPATA 1 Análisis Numérico I Facultad de Matemáticas, UADY Agosto 2014 1 Centro de Investigación en Matemáticas, Unidad Mérida. En esta lección analizaremos
Lección 7. Aritmética Computacional MIGUEL ANGEL UH ZAPATA 1 Análisis Numérico I Facultad de Matemáticas, UADY Agosto 2014 1 Centro de Investigación en Matemáticas, Unidad Mérida. En esta lección analizaremos
OCW-V.Muto Análisis de los errores Cap. II CAPITULO II. ANALISIS DE LOS ERRORES 1. ESQUEMA DE RESOLUCION NUMERICA DE UN PROBLEMA
 CAPITULO II. ANALISIS DE LOS ERRORES 1. ESQUEMA DE RESOLUCION NUMERICA DE UN PROBLEMA Si se desea resolver un problema físico B, lo primero que se suele hacer es traducirlo al lenguaje matemático para
CAPITULO II. ANALISIS DE LOS ERRORES 1. ESQUEMA DE RESOLUCION NUMERICA DE UN PROBLEMA Si se desea resolver un problema físico B, lo primero que se suele hacer es traducirlo al lenguaje matemático para
Computación Científica. Ciencias Computacionales INAOE Gustavo Rodríguez Gómez
 Ciencias Computacionales INAOE Gustavo Rodríguez Gómez Errores y Aritmética de Punto Flotante INAOE Ciencias Computacionales Objetivos Identificar las fuentes de error en la computación científica. Determinar
Ciencias Computacionales INAOE Gustavo Rodríguez Gómez Errores y Aritmética de Punto Flotante INAOE Ciencias Computacionales Objetivos Identificar las fuentes de error en la computación científica. Determinar
ERRORES. , siempre que p 0.
 ERRORES Indice 1. Errores 2. Clases de errores 3. Números en coma flotante 4. Aritmética del punto flotante 4.1. Errores 4.2. Operaciones en punto flotante 4.3. Problemas con operaciones en punto flotante
ERRORES Indice 1. Errores 2. Clases de errores 3. Números en coma flotante 4. Aritmética del punto flotante 4.1. Errores 4.2. Operaciones en punto flotante 4.3. Problemas con operaciones en punto flotante
01. A qué se denomina conjunto de punto flotante? Conjunto de números racionales utilizado para representar a los números reales.
 PREGUNTAS PARA ORIENTAR EL ESTUDIO DEL CAPITULO 1. Subtemas: 1.1. Representación de un número real en punto flotante y operaciones. 1.2. Underflow y Overflow. 01. A qué se denomina conjunto de punto flotante?
PREGUNTAS PARA ORIENTAR EL ESTUDIO DEL CAPITULO 1. Subtemas: 1.1. Representación de un número real en punto flotante y operaciones. 1.2. Underflow y Overflow. 01. A qué se denomina conjunto de punto flotante?
Representación Numérica. y Errores. Capítulo 1: Cálculo Numérico MA-33A. Gonzalo Hernández Oliva
 Universidad de Chile Departamento de Ingeniería Matemática Capítulo : Representación Numérica y Errores Cálculo Numérico MA-33A Gonzalo Hernández Oliva GHO RN y E MA-33A Representación Numérica y Errores
Universidad de Chile Departamento de Ingeniería Matemática Capítulo : Representación Numérica y Errores Cálculo Numérico MA-33A Gonzalo Hernández Oliva GHO RN y E MA-33A Representación Numérica y Errores
Tema 1: Conceptos generales del Análisis
 Tema 1: Conceptos generales del Análisis Numérico Cálculo Numérico I Anna Doubova y Blanca Climent Ezquerra Dpto. EDAN, Universidad de Sevilla 11 de febrero de 2018 A.Doubova y B. Climent Conceptos generales
Tema 1: Conceptos generales del Análisis Numérico Cálculo Numérico I Anna Doubova y Blanca Climent Ezquerra Dpto. EDAN, Universidad de Sevilla 11 de febrero de 2018 A.Doubova y B. Climent Conceptos generales
Programación y Métodos Numéricos Errores de de redondeo en en la la representación de de números reales: INTRODUCCIÓN Y MOTIVACIÓN
 Programación y Métodos Numéricos Errores de de redondeo en en la la representación de de números reales: INTRODUCCIÓN Y MOTIVACIÓN Carlos Conde LázaroL Arturo Hidalgo LópezL Alfredo López L Benito Febrero,
Programación y Métodos Numéricos Errores de de redondeo en en la la representación de de números reales: INTRODUCCIÓN Y MOTIVACIÓN Carlos Conde LázaroL Arturo Hidalgo LópezL Alfredo López L Benito Febrero,
σ * (.a 1 a 2... a t ) β * β e
 . ERRORES DE REDONDEO Y ESTABILIDAD Qué es un método numérico? Un método numérico es un procedimiento mediante el cual se obtiene, casi siempre de manera aproximada, la solución de ciertos problemas realizando
. ERRORES DE REDONDEO Y ESTABILIDAD Qué es un método numérico? Un método numérico es un procedimiento mediante el cual se obtiene, casi siempre de manera aproximada, la solución de ciertos problemas realizando
Aritmetica del Computador
 Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Métodos Computacionales Contenido Introducción 1 Introducción 2 3 Introducción al estudio de métodos computacionales Aproximación
Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Métodos Computacionales Contenido Introducción 1 Introducción 2 3 Introducción al estudio de métodos computacionales Aproximación
Tema 1 Preliminares. 1. Introducción. 2. Teoremas básicos. 3. Errores. 3.1 Fuentes usuales de error 3.2 Representación de números 3.
 Tema 1 Preliminares Índice 1. Introducción. Teoremas básicos 3. Errores 3.1 Fuentes usuales de error 3. Representación de números 3.3 Tipos de errores 4. Propagación del error 5. Condicionamiento y Estabilidad
Tema 1 Preliminares Índice 1. Introducción. Teoremas básicos 3. Errores 3.1 Fuentes usuales de error 3. Representación de números 3.3 Tipos de errores 4. Propagación del error 5. Condicionamiento y Estabilidad
Lección 6. Errores. MIGUEL ANGEL UH ZAPATA 1 Análisis Numérico I Facultad de Matemáticas, UADY. Agosto 2014
 Lección 6. Errores MIGUEL ANGEL UH ZAPATA 1 Análisis Numérico I Facultad de Matemáticas, UADY Agosto 2014 1 Centro de Investigación en Matemáticas, Unidad Mérida En esta lección conoceremos y analizaremos
Lección 6. Errores MIGUEL ANGEL UH ZAPATA 1 Análisis Numérico I Facultad de Matemáticas, UADY Agosto 2014 1 Centro de Investigación en Matemáticas, Unidad Mérida En esta lección conoceremos y analizaremos
APROXIMACIÓN NUMÉRICA Y ERRORES
 Análisis numérico APROXIMACIÓN NUMÉRICA Y ERRORES Antecedentes En 1947 se crea en la universidad de California el INSITITUTO DE ANÁLISIS NUMÉRICO. El análisis numérico es la rama de las matemáticas, cuyos
Análisis numérico APROXIMACIÓN NUMÉRICA Y ERRORES Antecedentes En 1947 se crea en la universidad de California el INSITITUTO DE ANÁLISIS NUMÉRICO. El análisis numérico es la rama de las matemáticas, cuyos
75.12 ANÁLISIS NUMÉRICO I GUÍA DE PROBLEMAS 1. ERRORES
 75.12 ANÁLISIS NUMÉRICO I FACULTAD DE INGENIERÍA UNIVERSIDAD DE BUENOS AIRES GUÍA DE PROBLEMAS 1. ERRORES 1. Calcular las siguientes expresiones, incluyendo sus cotas de error absoluto, donde x = 2,00,
75.12 ANÁLISIS NUMÉRICO I FACULTAD DE INGENIERÍA UNIVERSIDAD DE BUENOS AIRES GUÍA DE PROBLEMAS 1. ERRORES 1. Calcular las siguientes expresiones, incluyendo sus cotas de error absoluto, donde x = 2,00,
Definición 1.1 Dado un número x R su representación decimal en punto flotante es: Dados d k N, 0 d k 9 y d 1 0,
 CAPITULO 1 Introducción al análisis numérico 1.1 Notación en punto flotante Dado un número x R cómo es representado en una computadora? Es siempre de la misma forma, independientemente del tipo de instrumento
CAPITULO 1 Introducción al análisis numérico 1.1 Notación en punto flotante Dado un número x R cómo es representado en una computadora? Es siempre de la misma forma, independientemente del tipo de instrumento
MÓDULO DEL CAPITULO 1.
 MÓDULO DEL CAPITULO. Subtemas:.. Representación de un número real en punto flotante y operaciones..2. Underflow y Overflow. 0. A qué se denomina conjunto de punto flotante? Conjunto de números racionales
MÓDULO DEL CAPITULO. Subtemas:.. Representación de un número real en punto flotante y operaciones..2. Underflow y Overflow. 0. A qué se denomina conjunto de punto flotante? Conjunto de números racionales
Redondeo. Análisis Numérico Universidad Nacional Autónoma de México Facultad de Ciencias
 Análisis Numérico 2018 2 Universidad Nacional Autónoma de México Facultad de Ciencias Contenido 1 Redondeo 2 3 4 5 6 Error absoluto de redondeo y ULP Error relativo, ɛ Dígitos significativos Redondeo Sea
Análisis Numérico 2018 2 Universidad Nacional Autónoma de México Facultad de Ciencias Contenido 1 Redondeo 2 3 4 5 6 Error absoluto de redondeo y ULP Error relativo, ɛ Dígitos significativos Redondeo Sea
Los errores asociados a todo cálculo numérico tienen su origen en dos grandes factores:
 Errores El concepto de error es consustancial con el cálculo numérico. En todos los problemas es fundamental hacer un seguimiento de los errores cometidos a fin de poder estimar el grado de aproximación
Errores El concepto de error es consustancial con el cálculo numérico. En todos los problemas es fundamental hacer un seguimiento de los errores cometidos a fin de poder estimar el grado de aproximación
Tema 5: Resolución aproximada de ecuaciones
 Métodos Numéricos: Solución de los ejercicios Tema 5: Resolución aproximada de ecuaciones Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Abril
Métodos Numéricos: Solución de los ejercicios Tema 5: Resolución aproximada de ecuaciones Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Abril
Cálculo numérico. Sistemas de ecuaciones lineales.
 José Luis Morales http://allman.rhon.itam.mx/ jmorales Departamento de Matemáticas. ITAM. 2010. Las raíces de x 2 bx + c = 0. r = b ± b 2 4c 2 b = 3.6778, c = 0.0020798 r 1 = 3.67723441190... r 2 = 0.00056558809...
José Luis Morales http://allman.rhon.itam.mx/ jmorales Departamento de Matemáticas. ITAM. 2010. Las raíces de x 2 bx + c = 0. r = b ± b 2 4c 2 b = 3.6778, c = 0.0020798 r 1 = 3.67723441190... r 2 = 0.00056558809...
Métodos Numéricos: aproximación y error
 Métodos Numéricos: aproximación y error Eduardo P. Serrano Versión previa Feb 0. Problemas y métodos numéricos Un problema numérico es aquel cuya solución es un número finito de números reales. Ej: - Ecuaciones
Métodos Numéricos: aproximación y error Eduardo P. Serrano Versión previa Feb 0. Problemas y métodos numéricos Un problema numérico es aquel cuya solución es un número finito de números reales. Ej: - Ecuaciones
Métodos Numéricos. Grado en Ingeniería en Informática Tema 1 : Aritméticas de Precisión Finita
 Métodos Numéricos. Grado en Ingeniería en Informática Tema 1 : Aritméticas de Precisión Finita Luis Alvarez León Univ. de Las Palmas de G.C. Luis Alvarez León () Análisis Numérico Univ. de Las Palmas de
Métodos Numéricos. Grado en Ingeniería en Informática Tema 1 : Aritméticas de Precisión Finita Luis Alvarez León Univ. de Las Palmas de G.C. Luis Alvarez León () Análisis Numérico Univ. de Las Palmas de
Instituto de Matemática. Agosto de ) Encuentre experimentalmente los siguientes valores de su calculadora:
 Curso de Métodos Numéricos Instituto de Matemática Práctico 1: Errores Agosto de 2005 1) Encuentre experimentalmente los siguientes valores de su calculadora: (a) El valor ɛ mach definido como el minimo
Curso de Métodos Numéricos Instituto de Matemática Práctico 1: Errores Agosto de 2005 1) Encuentre experimentalmente los siguientes valores de su calculadora: (a) El valor ɛ mach definido como el minimo
Ecuaciones diferenciales y cálculo numérico
 Ecuaciones diferenciales y cálculo numérico Tema 6. Introducción al análisis cálculo numérico (Grado en Ingeniería de Tecnologías de Telecomunicación) EDCN-GITT (UGR) Tema 6 Versión 3-05-04 / 4 Tema 6.
Ecuaciones diferenciales y cálculo numérico Tema 6. Introducción al análisis cálculo numérico (Grado en Ingeniería de Tecnologías de Telecomunicación) EDCN-GITT (UGR) Tema 6 Versión 3-05-04 / 4 Tema 6.
1 Método de la bisección. 1.1 Teorema de Bolzano Teorema 1.1 (Bolzano) Contenido
 E.T.S. Minas: Métodos Matemáticos Resumen y ejemplos Tema 3: Solución aproximada de ecuaciones Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña
E.T.S. Minas: Métodos Matemáticos Resumen y ejemplos Tema 3: Solución aproximada de ecuaciones Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña
2 Obtener el término general de las siguientes sucesiones definidas por recurrencia: y0 = a > 0
 CÁLCULO NUMÉRICO I (Ejercicios Temas 1 y ) 1 Cuáles de los siguientes algoritmos son finitos? (a) Cálculo del producto de dos números enteros. (b) Cálculo de la división de dos números enteros. (c) Cálculo
CÁLCULO NUMÉRICO I (Ejercicios Temas 1 y ) 1 Cuáles de los siguientes algoritmos son finitos? (a) Cálculo del producto de dos números enteros. (b) Cálculo de la división de dos números enteros. (c) Cálculo
Relación de ejercicios 6
 Relación de ejercicios 6 Ecuaciones Diferenciales y Cálculo Numérico Grado en Ingeniería de Tecnologías de Telecomunicación Mayo de 2017 Ejercicio 6.1. 1. Construye, usando la base canónica del espacio
Relación de ejercicios 6 Ecuaciones Diferenciales y Cálculo Numérico Grado en Ingeniería de Tecnologías de Telecomunicación Mayo de 2017 Ejercicio 6.1. 1. Construye, usando la base canónica del espacio
E.T.S. Minas: Métodos Matemáticos Soluciones Tema 3 Resolución aproximada de ecuaciones
 E.T.S. Minas: Métodos Matemáticos Soluciones Tema 3 Resolución aproximada de ecuaciones Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Curso
E.T.S. Minas: Métodos Matemáticos Soluciones Tema 3 Resolución aproximada de ecuaciones Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Curso
Cálculo Numérico. Introducción a la teoría de errores. Cá álculo umérico Tema 0:
 Cálculo Numérico Tema 0: Problema Introducción a la teoría de errores Tipos de errores en un proceso numérico de resolución de un problema. Errores absoluto y relativo. Número de cifras exactas. Error
Cálculo Numérico Tema 0: Problema Introducción a la teoría de errores Tipos de errores en un proceso numérico de resolución de un problema. Errores absoluto y relativo. Número de cifras exactas. Error
E.T.S. Minas: Métodos Matemáticos Soluciones Tema 3: Resolución aproximada de ecuaciones
 E.T.S. Minas: Métodos Matemáticos Soluciones Tema 3: Resolución aproximada de ecuaciones Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Octubre
E.T.S. Minas: Métodos Matemáticos Soluciones Tema 3: Resolución aproximada de ecuaciones Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Octubre
7. Forma de Lagrange para el polinomio interpolador. 9. Forma de Newton para el polinomio interpolador
 E.T.S. Minas: Métodos Matemáticos Resumen y ejemplos Tema 2: Aproximación e interpolación Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Septiembre
E.T.S. Minas: Métodos Matemáticos Resumen y ejemplos Tema 2: Aproximación e interpolación Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Septiembre
Relación de ejercicios 5
 Relación de ejercicios 5 Ecuaciones Diferenciales y Cálculo Numérico Grado en Ingeniería de Tecnologías de Telecomunicación Mayo de 2017 Ejercicio 51 Halla un intervalo, para el cero más próximo al origen,
Relación de ejercicios 5 Ecuaciones Diferenciales y Cálculo Numérico Grado en Ingeniería de Tecnologías de Telecomunicación Mayo de 2017 Ejercicio 51 Halla un intervalo, para el cero más próximo al origen,
CÁLCULO NUMÉRICO I (Tema 2 - Relación 1)
 CÁLCULO NUMÉRICO I (Tema - Relación 1) 1 Cuáles de los siguientes algoritmos son finitos? a) Cálculo del producto de dos números enteros. b) Cálculo de la división de dos números enteros. c) Cálculo de
CÁLCULO NUMÉRICO I (Tema - Relación 1) 1 Cuáles de los siguientes algoritmos son finitos? a) Cálculo del producto de dos números enteros. b) Cálculo de la división de dos números enteros. c) Cálculo de
OCW-V.Muto El algoritmo de bisección Cap. VI CAPITULO VI. EL ALGORITMO DE BISECCION 1. INTRODUCCION Y METODO
 CAPITULO VI. EL ALGORITMO DE BISECCION 1. INTRODUCCION Y METODO En este capítulo comenzaremos a analizar uno de los problemas más básicos del análisis numérico: el problema de búsqueda de raíces. El problema
CAPITULO VI. EL ALGORITMO DE BISECCION 1. INTRODUCCION Y METODO En este capítulo comenzaremos a analizar uno de los problemas más básicos del análisis numérico: el problema de búsqueda de raíces. El problema
x (0) si f (x) = 2s 1, s > 1 d) f 3. Analizar la existencia de derivadas laterales y de derivada en a = 0, para las siguientes funciones:
 FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
Cálculo Numérico (0258) TEMA 6 SOLUCIÓN NUMÉRICA DE ECUACIONES DIFERENCIALES ORDINARIAS. Semestre
 Cálculo Numérico (58) Semestre - TEMA 6 SOLUCIÓN NUMÉRICA DE ECUACIONES DIFERENCIALES ORDINARIAS Semestre - Septiembre U.C.V. F.I.U.C.V. CÁLCULO NUMÉRICO (58) - TEMA 6 Las notas presentadas a continuación
Cálculo Numérico (58) Semestre - TEMA 6 SOLUCIÓN NUMÉRICA DE ECUACIONES DIFERENCIALES ORDINARIAS Semestre - Septiembre U.C.V. F.I.U.C.V. CÁLCULO NUMÉRICO (58) - TEMA 6 Las notas presentadas a continuación
FUNDAMENTOS DE LA TEORÍA DE ERRORES
 21 de Julio de 2014 FUNDAMENTOS DE LA TEORÍA DE ERRORES Departamento de Matemática Aplicada Facultad de Ingeniería Universidad Central de Venezuela Cálculo Numérico José Luis Quintero 1 Puntos a tratar
21 de Julio de 2014 FUNDAMENTOS DE LA TEORÍA DE ERRORES Departamento de Matemática Aplicada Facultad de Ingeniería Universidad Central de Venezuela Cálculo Numérico José Luis Quintero 1 Puntos a tratar
Introducción al análisis numérico
 Introducción al análisis numérico Javier Segura Universidad de Cantabria Cálculo Numérico I. Tema 1 Javier Segura (Universidad de Cantabria) Introducción al análisis numérico CNI 1 / 22 Contenidos: 1 Sistemas
Introducción al análisis numérico Javier Segura Universidad de Cantabria Cálculo Numérico I. Tema 1 Javier Segura (Universidad de Cantabria) Introducción al análisis numérico CNI 1 / 22 Contenidos: 1 Sistemas
UNIVERSIDAD DE EXTREMADURA Departamento de Matemáticas. Matemáticas. Manuel Fernández García-Hierro Badajoz, Febrero 2008
 UNIVERSIDAD DE EXTREMADURA Departamento de Matemáticas Matemáticas Manuel Fernández García-Hierro Badajoz, Febrero 2008 Capítulo X Integración numérica Introducción La integral definida I(f) = b a f(x)
UNIVERSIDAD DE EXTREMADURA Departamento de Matemáticas Matemáticas Manuel Fernández García-Hierro Badajoz, Febrero 2008 Capítulo X Integración numérica Introducción La integral definida I(f) = b a f(x)
Aritmética del Computador
 Facultad de Ingeniería Mecánica Universidad Nacional de Ingeniería Métodos Numéricos Contenido 1 Introducción 2 Teoria de Errores 3 Aritmetica del computador Introducción al estudio de métodos computacionales
Facultad de Ingeniería Mecánica Universidad Nacional de Ingeniería Métodos Numéricos Contenido 1 Introducción 2 Teoria de Errores 3 Aritmetica del computador Introducción al estudio de métodos computacionales
1) Determinar qué elección de h asegurará, a priori, que la solución numérica del P.C.: con el método de diferencias centrales, existe y es única.
 I. Resolución numérica de Problemas de Contorno en E.D.O.: Métodos en diferencias finitas 1) Determinar qué elección de h asegurará, a priori, que la solución numérica del P.C.: y (x) + 4 sen x y (x) 4
I. Resolución numérica de Problemas de Contorno en E.D.O.: Métodos en diferencias finitas 1) Determinar qué elección de h asegurará, a priori, que la solución numérica del P.C.: y (x) + 4 sen x y (x) 4
O bien si queremos calcular el error aproximado porcentual lo hacemos:
 En situaciones reales es común que no se conoce el valor verdadero del resultado: las mediciones dependen del instrumento y del procedimiento de medición; los métodos numéricos se aplican, cuando no se
En situaciones reales es común que no se conoce el valor verdadero del resultado: las mediciones dependen del instrumento y del procedimiento de medición; los métodos numéricos se aplican, cuando no se
CURSO DE METODOS NUMERICOS Año Académico Curso Tercero de Matemáticas EXAMEN FINAL FEBRERO
 Año Académico 2000-2001 Curso Tercero de Matemáticas EXAMEN FINAL FEBRERO 1. Dá el enunciado y demuestra el teorema de convergencia del método del punto fijo. (2 puntos) 2. Resuelve el siguiente sistema
Año Académico 2000-2001 Curso Tercero de Matemáticas EXAMEN FINAL FEBRERO 1. Dá el enunciado y demuestra el teorema de convergencia del método del punto fijo. (2 puntos) 2. Resuelve el siguiente sistema
Introducción al análisis numérico
 Introducción al análisis numérico Javier Segura Universidad de Cantabria Cálculo Numérico I. Tema 1 Javier Segura (Universidad de Cantabria) Introducción al análisis numérico CNI 1 / 25 Contenidos: 1 Sistemas
Introducción al análisis numérico Javier Segura Universidad de Cantabria Cálculo Numérico I. Tema 1 Javier Segura (Universidad de Cantabria) Introducción al análisis numérico CNI 1 / 25 Contenidos: 1 Sistemas
2. Representación de números 1
 2. Representación de números 1 Julio C. Carrillo E. Escuela de Matemáticas, UIS 2. Representación de números 2 1. Pérdida de significancia Usualmente se presenta una pérdida de significancia cuando se
2. Representación de números 1 Julio C. Carrillo E. Escuela de Matemáticas, UIS 2. Representación de números 2 1. Pérdida de significancia Usualmente se presenta una pérdida de significancia cuando se
(a) (0.5 puntos) Compruebe que esta ecuación tiene exactamente una solución en el intervalo
 UNIVERSIDAD DIEGO PORTALES. FACULTAD DE INGENIERÍA. INSTITUTO DE CIENCIAS BÁSICAS. Cálculo Numérico, Control 1. Semestre Otoño 007 Problema 1. Se desea encontrar una raíz de la función f(x) = cos (x) x.
UNIVERSIDAD DIEGO PORTALES. FACULTAD DE INGENIERÍA. INSTITUTO DE CIENCIAS BÁSICAS. Cálculo Numérico, Control 1. Semestre Otoño 007 Problema 1. Se desea encontrar una raíz de la función f(x) = cos (x) x.
Redondeo, Truncamiento, Método del Punto Fijo y MétodoBarranquilla, de bisección / 22
 Redondeo, Truncamiento, Método del Punto Fijo y Método de bisección. Jeinny Peralta 1 Barranquilla, 2017 Redondeo, Truncamiento, Método del Punto Fijo y MétodoBarranquilla, de bisección. 2017 1 / 22 Números
Redondeo, Truncamiento, Método del Punto Fijo y Método de bisección. Jeinny Peralta 1 Barranquilla, 2017 Redondeo, Truncamiento, Método del Punto Fijo y MétodoBarranquilla, de bisección. 2017 1 / 22 Números
1.4.3 Errores de redondeo y la aritmética finita de las computadoras
 1.4.3 Errores de redondeo y la aritmética finita de las computadoras Como la computadora sólo puede almacenar un número fijo de cifras significativas, y cantidades como π, e, 3, 2 no pueden ser expresadas
1.4.3 Errores de redondeo y la aritmética finita de las computadoras Como la computadora sólo puede almacenar un número fijo de cifras significativas, y cantidades como π, e, 3, 2 no pueden ser expresadas
CALCULO NUMERICO (MB535) PRIMERA PRACTICA CALIFICADA (PARTE A)
 UNIVERSIDAD NACIONAL DE INGENIERIA Ciclo :005- FACULTAD DE INGENIERIA MECANICA AREA ACADEMICA DE CIENCIAS BASICAS INDICACIONES CALCULO NUMERICO (MB535) PRIMERA PRACTICA CALIFICADA (PARTE A) 1. Resolver
UNIVERSIDAD NACIONAL DE INGENIERIA Ciclo :005- FACULTAD DE INGENIERIA MECANICA AREA ACADEMICA DE CIENCIAS BASICAS INDICACIONES CALCULO NUMERICO (MB535) PRIMERA PRACTICA CALIFICADA (PARTE A) 1. Resolver
3 RAÍCES REALES DE ECUACIONES NO-LINEALES. 3.1 Método de la bisección
 3 RAÍCES REALES DE ECUACIONES NO-LINEALES Sea f: R R. Dada la ecuación f(x) = 0, se debe encontrar un valor real r tal que f(r) = 0. Entonces r es una raíz real de la ecuación Si no es posible obtener
3 RAÍCES REALES DE ECUACIONES NO-LINEALES Sea f: R R. Dada la ecuación f(x) = 0, se debe encontrar un valor real r tal que f(r) = 0. Entonces r es una raíz real de la ecuación Si no es posible obtener
TEMA 1 LOS NÚMEROS REALES
 TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES.-LA RECTA REAL Los NÚMEROS RACIONALES: Se caracterizan porque pueden expresarse: En forma de fracción, es decir, como cociente b a de dos números enteros:
TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES.-LA RECTA REAL Los NÚMEROS RACIONALES: Se caracterizan porque pueden expresarse: En forma de fracción, es decir, como cociente b a de dos números enteros:
Teoria de Errores. Mg. Hermes Pantoja Carhuavilca. Métodos Computacionales. Universidad Nacional Mayor de San Marcos Facultad de Ingenieria Industrial
 Pantoja Carhuavilca Métodos Computacionales Agenda al estudio de métodos computacionales 3 Aproximación y Errores Los cálculos númericos inevitablemente conducen a errores Estos son de dos clases principales:
Pantoja Carhuavilca Métodos Computacionales Agenda al estudio de métodos computacionales 3 Aproximación y Errores Los cálculos númericos inevitablemente conducen a errores Estos son de dos clases principales:
MÉTODOS NUMÉRICOS PARA INGENIERÍA ERROR GUIÓN PARA EL TEMA CONCEPTOS BÁSICOS
 ERROR GUIÓN PARA EL TEMA CONCEPTOS BÁSICOS REPASO de conceptos de dígito significativo y de orden, para números en notación decimal. Para señalar la diferencia entre el concepto de dígito significativo
ERROR GUIÓN PARA EL TEMA CONCEPTOS BÁSICOS REPASO de conceptos de dígito significativo y de orden, para números en notación decimal. Para señalar la diferencia entre el concepto de dígito significativo
Teoria de Errores. Hermes Pantoja Carhuavilca. Facultad de Ingeniería Mecanica Universidad Nacional de Ingeniería. Hermes Pantoja Carhuavilca 1 de 31
 Hermes Pantoja Carhuavilca Facultad de Ingeniería Mecanica Universidad Nacional de Ingeniería Métodos Numérico Hermes Pantoja Carhuavilca 1 de 31 CONTENIDO Introducción Hermes Pantoja Carhuavilca 2 de
Hermes Pantoja Carhuavilca Facultad de Ingeniería Mecanica Universidad Nacional de Ingeniería Métodos Numérico Hermes Pantoja Carhuavilca 1 de 31 CONTENIDO Introducción Hermes Pantoja Carhuavilca 2 de
Aritmética finita y análisis de error
 Aritmética finita y análisis de error Escuela de Ingeniería Informática de Oviedo (Dpto. de Matemáticas-UniOvi) Computación Numérica Aritmética finita y análisis de error 1 / 38 Contenidos 1 Almacenamiento
Aritmética finita y análisis de error Escuela de Ingeniería Informática de Oviedo (Dpto. de Matemáticas-UniOvi) Computación Numérica Aritmética finita y análisis de error 1 / 38 Contenidos 1 Almacenamiento
Representación de números
 Representación de números MAT-251 Dr. CIMAT A.C. e-mail: alram@cimat.mx web: http://www.cimat.mx/~alram/met_num/ Dr. Salvador Botello Rionda CIMAT A.C. e-mail: botello@cimat.mx Aritmética de cómputadora
Representación de números MAT-251 Dr. CIMAT A.C. e-mail: alram@cimat.mx web: http://www.cimat.mx/~alram/met_num/ Dr. Salvador Botello Rionda CIMAT A.C. e-mail: botello@cimat.mx Aritmética de cómputadora
OCW-V.Muto Aritmética del computador Cap. IV CAPITULO IV. ARITMETICA DEL COMPUTADOR 1. REPRESENTACION DE LOS NUMEROS
 CAPITULO IV. ARITMETICA DEL COMPUTADOR 1. REPRESENTACION DE LOS NUMEROS Cuando se usa una calculadora o una computadora digital para realizar cálculos numéricos, se debe considerar un error inevitable,
CAPITULO IV. ARITMETICA DEL COMPUTADOR 1. REPRESENTACION DE LOS NUMEROS Cuando se usa una calculadora o una computadora digital para realizar cálculos numéricos, se debe considerar un error inevitable,
Interpolación y aproximaciones polinómicas
 This is page i Printer: Opaque this Interpolación y aproximaciones polinómicas Oldemar Rodríguez Rojas Octubre 008 ii This is page iii Printer: Opaque this Contents 1 Interpolación y aproximaciones polinómicas
This is page i Printer: Opaque this Interpolación y aproximaciones polinómicas Oldemar Rodríguez Rojas Octubre 008 ii This is page iii Printer: Opaque this Contents 1 Interpolación y aproximaciones polinómicas
Cursada Segundo Cuatrimestre 2017 Guía de Trabajos Prácticos Nro. 2
 Temas: Programación en MATLAB: Sentencias, expresiones y variables. Estructuras de control. Operadores relacionales y lógicos. Programación de funciones. Aritmética finita: Representación de números en
Temas: Programación en MATLAB: Sentencias, expresiones y variables. Estructuras de control. Operadores relacionales y lógicos. Programación de funciones. Aritmética finita: Representación de números en
TEMA 1 LOS NÚMEROS REALES
 TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES.-LA RECTA REAL Los NÚMEROS RACIONALES: Se caracterizan porque pueden expresarse: En forma de fracción, es decir, como cociente b a de dos números enteros:
TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES.-LA RECTA REAL Los NÚMEROS RACIONALES: Se caracterizan porque pueden expresarse: En forma de fracción, es decir, como cociente b a de dos números enteros:
Errores por la representación de punto flotante y propagación de errores
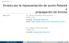 Clase No. 2: Errores por la representación de punto flotante y propagación de errores MAT 251 Dr. Alonso Ramírez Manzanares CIMAT, A.C. e-mail: alram@ cimat.mx web: http://www.cimat.mx/ alram/met_num/
Clase No. 2: Errores por la representación de punto flotante y propagación de errores MAT 251 Dr. Alonso Ramírez Manzanares CIMAT, A.C. e-mail: alram@ cimat.mx web: http://www.cimat.mx/ alram/met_num/
EXAMEN PARCIAL DE METODOS NUMERICOS (MB536)
 EXAMEN PARCIAL DE METODOS NUMERICOS (MB536) SOLO SE PERMITE EL USO DE UNA HOJA DE FORMULARIO Y CALCULADORA ESCRIBA CLARAMENTE SUS PROCEDIMIENTOS PROHIBIDO EL USO DE CELULARES U OTROS EQUIPOS DE COMUNICACION
EXAMEN PARCIAL DE METODOS NUMERICOS (MB536) SOLO SE PERMITE EL USO DE UNA HOJA DE FORMULARIO Y CALCULADORA ESCRIBA CLARAMENTE SUS PROCEDIMIENTOS PROHIBIDO EL USO DE CELULARES U OTROS EQUIPOS DE COMUNICACION
2 Ecuaciones Algebraicas y Trascendentes
 2 Ecuaciones Algebraicas y Trascendentes 2.1 Introducción Las sucesiones asintóticas son una herramienta usada en el análisis de las soluciones de problemas que surgen en la Teoría de Perturbaciones. En
2 Ecuaciones Algebraicas y Trascendentes 2.1 Introducción Las sucesiones asintóticas son una herramienta usada en el análisis de las soluciones de problemas que surgen en la Teoría de Perturbaciones. En
2. Representación de números 1
 2. Representación de números 1 Julio C. Carrillo E. Escuela de Matemáticas, UIS 2. Representación de números 2 1. Representación de punto flotante normalizada La notación científica es un tipo de representación
2. Representación de números 1 Julio C. Carrillo E. Escuela de Matemáticas, UIS 2. Representación de números 2 1. Representación de punto flotante normalizada La notación científica es un tipo de representación
Universidad Técnica Federico Santa María Departamento de Matemática Preinforme 2 Laboratorio Mat 270 Análisis Numérico Entrega 4 al 8 junio de 2018
 Universidad Técnica Federico Santa María Departamento de Matemática Preinforme 2 Laboratorio Mat 270 Análisis Numérico Entrega 4 al 8 junio de 2018 Utilice el instructivo para presentar preinformes publicado
Universidad Técnica Federico Santa María Departamento de Matemática Preinforme 2 Laboratorio Mat 270 Análisis Numérico Entrega 4 al 8 junio de 2018 Utilice el instructivo para presentar preinformes publicado
1. INTRODUCCIÓN A LA COMPUTACIÓN NUMÉRICA: Segunda parte: Teoría de Errores
 1. INTRODUCCIÓN A LA COMPUTACIÓN NUMÉRICA: Segunda parte: Teoría de Errores Jorge Eduardo Ortiz Triviño jeortizt@unal.edu.co http://www.docentes.unal.edu.co/jeortizt/ Objetivos de la sección Exponer los
1. INTRODUCCIÓN A LA COMPUTACIÓN NUMÉRICA: Segunda parte: Teoría de Errores Jorge Eduardo Ortiz Triviño jeortizt@unal.edu.co http://www.docentes.unal.edu.co/jeortizt/ Objetivos de la sección Exponer los
Métodos Numéricos: Ejercicios Tema 5: Resolución aproximada de ecuaciones
 Métodos Numéricos: Ejercicios Tema 5: Resolución aproximada de ecuaciones Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Abril 2008, versión
Métodos Numéricos: Ejercicios Tema 5: Resolución aproximada de ecuaciones Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Abril 2008, versión
METODO DE LA BISECCIÓN Si f : a, b es continua con f a f b 0,el procedimiento de la
 METODO DE LA BISECCIÓN Si f : a, b es continua con f a f b,el procedimiento de la bisección genera una sucesión (s n ) n convergente siendo s n a n b n ytal 2 que si lim s n s se cumple que f s y n s n
METODO DE LA BISECCIÓN Si f : a, b es continua con f a f b,el procedimiento de la bisección genera una sucesión (s n ) n convergente siendo s n a n b n ytal 2 que si lim s n s se cumple que f s y n s n
Resolución de Ecuaciones No Lineales
 Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Métodos Computacionales Contenido 1 Introducción Introducción 2 Localización de Raíces Localización de Raíces 3 Métodos Iterativos
Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Métodos Computacionales Contenido 1 Introducción Introducción 2 Localización de Raíces Localización de Raíces 3 Métodos Iterativos
Al considerar varios polígonos regulares inscritos resulta: perímetro del cuadrado < π. perímetro del 96 gono < π
 AMPLIACIÓN DE MATEMÁTICAS INTRODUCCIÓN Método Constructivo: Conjunto de instrucciones que permiten calcular la solución de un problema, bien en un número finito de pasos, bien en un proceso de paso al
AMPLIACIÓN DE MATEMÁTICAS INTRODUCCIÓN Método Constructivo: Conjunto de instrucciones que permiten calcular la solución de un problema, bien en un número finito de pasos, bien en un proceso de paso al
INTERPOLACIÓN: Error en la la interpolación polinómica de Lagrange
 INTERPOLACIÓN: Error en la la interpolación polinómica de Lagrange Arturo Hidalgo LópezL Alfredo López L Benito Carlos Conde LázaroL Marzo, 007 Departamento de Matemática Aplicada y Métodos Informáticos
INTERPOLACIÓN: Error en la la interpolación polinómica de Lagrange Arturo Hidalgo LópezL Alfredo López L Benito Carlos Conde LázaroL Marzo, 007 Departamento de Matemática Aplicada y Métodos Informáticos
Consistencia, Estabilidad y Convergencia
 Consistencia, Estabilidad y Convergencia 1. étodos a un paso Para aproximar la solución x = x(t) del problema de valores iniciales (PVI) x = f(t, x) a t b x(a) = α consideramos el método numérico a un
Consistencia, Estabilidad y Convergencia 1. étodos a un paso Para aproximar la solución x = x(t) del problema de valores iniciales (PVI) x = f(t, x) a t b x(a) = α consideramos el método numérico a un
Problemas. Hoja 1. Escriba el algoritmo para N = 4 y calcule el número de operaciones que realiza.
 Dpto. de Matemáticas. CÁLCULO NUMÉRICO. Curso 12/13 Problemas. Hoja 1 Problema 1. El método o algoritmo de Horner para evaluar en x 0 el polinomio P (x) = a 0 + a 1 x + + a N x N consiste formalmente en
Dpto. de Matemáticas. CÁLCULO NUMÉRICO. Curso 12/13 Problemas. Hoja 1 Problema 1. El método o algoritmo de Horner para evaluar en x 0 el polinomio P (x) = a 0 + a 1 x + + a N x N consiste formalmente en
MÉTODOS NUMÉRICOS. Curso o. B Resolución de ecuaciones I (ecuaciones generales f (x) = 0)
 MÉTODOS NUMÉRICOS. Curso 06-07. 1 o. B Resolución de ecuaciones I (ecuaciones generales f (x = 0 1. Utiliza el método de bisección para calcular con una precisión de 10 las soluciones de x 3 7x + 14x 6
MÉTODOS NUMÉRICOS. Curso 06-07. 1 o. B Resolución de ecuaciones I (ecuaciones generales f (x = 0 1. Utiliza el método de bisección para calcular con una precisión de 10 las soluciones de x 3 7x + 14x 6
Análisis Matemático. Convocatoria de enero Prueba Global. Evaluación Continua
 Apellidos y nombre: Análisis Matemático. Convocatoria de enero. 9--26. Prueba Global. Evaluación Continua Instrucciones: No abandonar el examen durante los primeros 3 minutos. Tiempo para esta parte del
Apellidos y nombre: Análisis Matemático. Convocatoria de enero. 9--26. Prueba Global. Evaluación Continua Instrucciones: No abandonar el examen durante los primeros 3 minutos. Tiempo para esta parte del
Observación: El método de Euler, es el método de Taylor de orden 1.
 METODO DE TAYLOR TEOREMA DE TAYLOR DE ORDEN N Sea y(t) una función tal que sea n veces continuamente diferenciable en el intervalo [a,b] y existe y (N+1) existe en [a, b] Para todo t k + [a, b] abrá un
METODO DE TAYLOR TEOREMA DE TAYLOR DE ORDEN N Sea y(t) una función tal que sea n veces continuamente diferenciable en el intervalo [a,b] y existe y (N+1) existe en [a, b] Para todo t k + [a, b] abrá un
La interpolación polinomial en el análisis de métodos iterativos
 Notas La interpolación polinomial en el análisis de métodos iterativos Resumen La solución de ecuaciones no lineales es de extrema importancia en la ingeniería y ciencias. Los métodos que se estudian para
Notas La interpolación polinomial en el análisis de métodos iterativos Resumen La solución de ecuaciones no lineales es de extrema importancia en la ingeniería y ciencias. Los métodos que se estudian para
Métodos Numéricos: Solución de los ejercicios Tema 3: Integración Numérica
 Métodos Numéricos: Solución de los ejercicios Tema : Integración Numérica Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Febrero 8, versión.4
Métodos Numéricos: Solución de los ejercicios Tema : Integración Numérica Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Febrero 8, versión.4
Propagación de Errores en Expresiones Aritméticas
 Teoría de Errores Contenido Propagación de Errores en Expresiones Aritméticas Error Absoluto Error Relativo Errores de Redondeo Errores de Truncamiento Notación de Punto Flotante Notación de Punto Flotante
Teoría de Errores Contenido Propagación de Errores en Expresiones Aritméticas Error Absoluto Error Relativo Errores de Redondeo Errores de Truncamiento Notación de Punto Flotante Notación de Punto Flotante
Sistemas de ecuaciones no lineales
 Práctica 6 Sistemas de ecuaciones no lineales En esta práctica revisaremos algunos métodos básicos para la resolución numérica de sistemas de ecuaciones no lineales 61 Método iterativo del punto fijo Partimos
Práctica 6 Sistemas de ecuaciones no lineales En esta práctica revisaremos algunos métodos básicos para la resolución numérica de sistemas de ecuaciones no lineales 61 Método iterativo del punto fijo Partimos
1. Cuáles de los siguientes algoritmos son finitos?
 . Cuáles de los siguientes algoritmos son finitos? a Cálculo del producto de dos números enteros. b Cálculo de la división de dos números enteros. c Cálculo de la raíz cuadrada de un número natural. d
. Cuáles de los siguientes algoritmos son finitos? a Cálculo del producto de dos números enteros. b Cálculo de la división de dos números enteros. c Cálculo de la raíz cuadrada de un número natural. d
1. Cuáles de los siguientes algoritmos son finitos?
 . Cuáles de los siguientes algoritmos son finitos? a Cálculo del producto de dos números enteros. b Cálculo de la división de dos números enteros. c Cálculo de la raíz cuadrada de un número natural. d
. Cuáles de los siguientes algoritmos son finitos? a Cálculo del producto de dos números enteros. b Cálculo de la división de dos números enteros. c Cálculo de la raíz cuadrada de un número natural. d
Ceros de Funciones: Multivariable
 Ceros de Funciones: Multivariable Prof. Marlliny Monsalve 1 1 Postgrado en Ciencias de la Computación Universidad Central de Venezuela Análisis Numérico May 19, 2015 Prof. Monsalve (UCV) Ceros Multivariable
Ceros de Funciones: Multivariable Prof. Marlliny Monsalve 1 1 Postgrado en Ciencias de la Computación Universidad Central de Venezuela Análisis Numérico May 19, 2015 Prof. Monsalve (UCV) Ceros Multivariable
1 El Análisis Numérico.
 Dr. M. Palacios Primavera 1999-2001 1.I Introducción al Cálculo Numérico. 1 El Análisis Numérico. El Análisis Numérico es la parte de las Matemáticas que se encarga de diseñar métodos para aproximar de
Dr. M. Palacios Primavera 1999-2001 1.I Introducción al Cálculo Numérico. 1 El Análisis Numérico. El Análisis Numérico es la parte de las Matemáticas que se encarga de diseñar métodos para aproximar de
a) Plantear un sistema de ecuaciones para calcular los coeficientes de f y resolverlo usando la descomposición LU de la matriz del sistema.
 E.T.S. de Álgebra Numérica 30 de junio de 2006 Se quiere encontrar una función de la forma f(x) = ax 3 + bx + c que pase por los puntos (1, 4), ( 2, 23) y (2, 21). a) Plantear un sistema de ecuaciones
E.T.S. de Álgebra Numérica 30 de junio de 2006 Se quiere encontrar una función de la forma f(x) = ax 3 + bx + c que pase por los puntos (1, 4), ( 2, 23) y (2, 21). a) Plantear un sistema de ecuaciones
Formulación de Galerkin El método de los elementos finitos
 Clase No. 28: MAT 251 Formulación de Galerkin El método de los elementos finitos Dr. Alonso Ramírez Manzanares Depto. de Matemáticas Univ. de Guanajuato e-mail: alram@ cimat.mx web: http://www.cimat.mx/
Clase No. 28: MAT 251 Formulación de Galerkin El método de los elementos finitos Dr. Alonso Ramírez Manzanares Depto. de Matemáticas Univ. de Guanajuato e-mail: alram@ cimat.mx web: http://www.cimat.mx/
Método de diferencias finitas para ecuaciones diferenciales parciales elípticas. (Parte II)
 Método de diferencias finitas para ecuaciones diferenciales parciales elípticas (Parte II) Métodos numéricos para sistemas lineales Solución numérica de EDPs requiere resolver sistemas de ecuaciones lineales
Método de diferencias finitas para ecuaciones diferenciales parciales elípticas (Parte II) Métodos numéricos para sistemas lineales Solución numérica de EDPs requiere resolver sistemas de ecuaciones lineales
Propagación de errores
 Clase No. 2: MAT 251 Propagación de errores Dr. Alonso Ramírez Manzanares Depto. de Matemáticas Univ. de Guanajuato e-mail: alram@ cimat.mx web: http://www.cimat.mx/ alram/met_num/ Dr. Joaquín Peña Acevedo
Clase No. 2: MAT 251 Propagación de errores Dr. Alonso Ramírez Manzanares Depto. de Matemáticas Univ. de Guanajuato e-mail: alram@ cimat.mx web: http://www.cimat.mx/ alram/met_num/ Dr. Joaquín Peña Acevedo
Matemáticas Empresariales I. Funciones y concepto de ĺımite
 Matemáticas Empresariales I Lección 3 Funciones y concepto de ĺımite Manuel León Navarro Colegio Universitario Cardenal Cisneros M. León Matemáticas Empresariales I 1 / 22 Concepto de función Función de
Matemáticas Empresariales I Lección 3 Funciones y concepto de ĺımite Manuel León Navarro Colegio Universitario Cardenal Cisneros M. León Matemáticas Empresariales I 1 / 22 Concepto de función Función de
Álgebra Lineal Ma1010
 Álgebra Lineal Ma1010 Métodos Iterativos para Resolver Sistemas Lineales Departamento de Matemáticas ITESM Métodos Iterativos para Resolver Sistemas Lineales Álgebra Lineal - p. 1/30 En esta lectura veremos
Álgebra Lineal Ma1010 Métodos Iterativos para Resolver Sistemas Lineales Departamento de Matemáticas ITESM Métodos Iterativos para Resolver Sistemas Lineales Álgebra Lineal - p. 1/30 En esta lectura veremos
TALLERES DE METODOS NUMERICOS SOLUCION NUMERICA DE ECUACIONES NO LINEALES
 TALLERES DE METODOS NUMERICOS SOLUCION NUMERICA DE ECUACIONES NO LINEALES. Usar un procedimiento iterativo para calcular una aproimación a la menor raíz positiva de la ecuación : sen π = 0 Calcular tres
TALLERES DE METODOS NUMERICOS SOLUCION NUMERICA DE ECUACIONES NO LINEALES. Usar un procedimiento iterativo para calcular una aproimación a la menor raíz positiva de la ecuación : sen π = 0 Calcular tres
Métodos de factorización para resolver sistemas de ecuaciones lineales. 22 de agosto, 2012
 Cálculo numérico Métodos de factorización para resolver sistemas de ecuaciones lineales 22 de agosto, 2012 1 Factorización LU Considera el siguiente ejemplo de factorización LU de una matriz en un sistema
Cálculo numérico Métodos de factorización para resolver sistemas de ecuaciones lineales 22 de agosto, 2012 1 Factorización LU Considera el siguiente ejemplo de factorización LU de una matriz en un sistema
Parte 1: Errores de redondeo. 1. Calcule el error absoluto y el error relativo en las aproximaciones de p mediante p para:
 Universidad de Antioquia Facultad de Ciencias Exactas y Naturales Departamento de Matemáticas Seccional Caucasia Taller N o de Análisis Numérico 16 de febrero de 010 Nota: El taller consta de 5 partes
Universidad de Antioquia Facultad de Ciencias Exactas y Naturales Departamento de Matemáticas Seccional Caucasia Taller N o de Análisis Numérico 16 de febrero de 010 Nota: El taller consta de 5 partes
Derivación de funciones reales de una variable
 Derivación de funciones reales de una variable Derivada de una función en un punto. Interpretación física y geométrica Aproximación de raíces: Método de Newton Raphson Derivabilidad Cálculo de derivadas
Derivación de funciones reales de una variable Derivada de una función en un punto. Interpretación física y geométrica Aproximación de raíces: Método de Newton Raphson Derivabilidad Cálculo de derivadas
