PROBABILIDADES Y ESTADÍSTICA (C) Práctica 3
|
|
|
- Elena María Ángeles Cordero Cuenca
- hace 5 años
- Vistas:
Transcripción
1 PROBABILIDADES Y ESTADÍSTICA (C) Práctica 3 1. Sea X una v.a. con función de densidad ½ 0.75 (1 x f X (x) = 2 ) 1 x 1 0 en otro caso. a) Verificar que f X es realmente una función de densidad. b) Calcular: P (X >0) P ( 0.5 <X<0.5) P ( X > 0.25) 2. Sea X una v.a. continua con función de distribución 0 si x<0 x F X (x) = 3 si 0 x<2 θ 1 si 2 x a) Cuál es el valor de θ? b) Calcular, usando F X (x), P (X 1) P (0.5 X 1) P (0.5 <X 1 X <1) c) Hallar la mediana μ de esta distribución. d) Encontrar la función de densidad f X (x). 3. Consideremos una v.a. X con función de densidad donde α ( 1, 1). f X (x) = (1 + αx) 2 I ( 1,1) (x) a) Hallar la función de distribución acumulada de X. b) Calcular E (X) y V (X). c) Calcular la mediana y los cuartiles de esta distribución. 4. Consideremos una v.a. Y con función de densidad 1 25 y 0 y<5 f Y (y) = y 5 y<10 0 en otro caso. 12
2 a) Calcular la función de distribución de Y. b) Calcular E (Y ) y V (Y ). c) Calcular E (1/Y ). QuéconclusiónsacarespectoalarelaciónentreE(1/Y ) y 1/E (Y ). 5. La función de densidad de la v.a. X es: f(x) =(a + bx 2 ) I (0,1) (x) a) Hallar los valores de a y b sabiendo que E(X) =0.6. b) Calcular la función de distribución acumulada de X. 6. Sean f(x) y g(x) funciones de densidad. Demostrar que, si α (0, 1), entonces αf(x)+(1 α) g(x) es una función de densidad. Cuál es el valor esperado de la nueva distribución?. 7. Se eligen n puntos al azar en el intervalo [0, 1] de forma independiente (con distribución uniforme). Sea X = Cantidad de puntos que caen en el intervalo [0,p](0 < p < 1). Qué distribución tiene X? 8. Sea Z una v.a. con distribución N(0, 1). Calcular: a) P (0 Z 2) b) P ( Z 2.5) c) P (Z 1.37) d) c tal que P (Z <c)=0.98 e) c tal que P ( Z c) =0.90 f) el valor z α para α =0.1, 0.05, 0.025, Sea X una v.a. con distribución N(5, 0.25). Calcular: a) P (4.75 X 5.50) b) P ( X > 5.25) c) c tal que P ( X 5 c) =0.90 d) el 90-percentil de X. 10. Se supone que en cierta población humana, el índice cefálico I (anchura del cráneo expresada como porcentaje de la longitud) es una v.a. con distribución N (μ, σ 2 ). Si hay un 58% de individuos con I 75, un38%con75 <I 80 yun4%coni 80, hallar la función de densidad de I ycalcularp (78 I 82). 13
3 11. La biblioteca de una facultad dispone de una red de computadoras al alcance de los estudiantes. El porcentaje de tiempo que un usuario destina a búsqueda bibliográfica es una variable aleatoria T con función de densidad f T (t) =c (100 t) I [0,100] (t) a) Hallar el valor de la constante c b) Supóngase que de acuerdo con el porcentaje de tiempo destinado a la búsqueda bibliográfica el usuario es clasificado en una de cuatro categorías: 1 si T<25%, 2 si 25% T<50%, 3 si 50% T<75% y 4 si T>75%. Hallar la distribución de la categoría asignada a un usuario. 12. El diámetro D (expresado en dm) del tronco de cierta especie de árboles es una variable aleatoria con función de densidad f D (x) =kxi (0,10) (x). a) Hallar el valor de la constante k. b) Cuál es la probabilidad de que el diámetro de un árbol de esa especie elegido al azar mida entre 4 y 6 dm? c) Idem b) sabiendo que el diámetro mide más de 5 dm. d) En un área del bosque hay 3 árboles de esa especie. Calcular la probabilidad de queexactamente2deellostenganeldiámetroentre4y6dm. e) Cuántos árboles habría que muestrear en el bosque para que la probabilidad de encontraralmenosunocuyodiámetromidaentre4y6dm,seamayoroigual que 0.99? 13. Dos fábricas de tomates en lata (A y B) abastecen a una gran cadena de supermercados en una proporción de 40% y 60% respectivamente. El peso en gramos de las latas tiene distribución normal. En el caso de las latas producidas por la fábrica A el valor esperado es 250 gramos y el desvío standard 4 gramos y en el caso de las producidas por la fábrica B la mediana es 249 gramos y el desvío standard 5 gramos. a) Hallar la probabilidad de que el peso de una lata elegida al azar entre las producidas por la fábrica A sea mayor que 248 gramos. b) Hallar la probabilidad de que una lata elegida al azar de la producción total sea mayor que 248 gramos. c) Si el peso de una lata elegida al azar de la producción total es mayor que 248 gramos, Cuál es la probabilidad de que provenga de la fábrica A?. 14. La porción de memoria ocupada en un servidor de un sistema de terminales en red es una variable aleatoria continua X que toma valores entre 0 (sin carga) y 1 (carga completa). La densidad de X está dada por f X (x) =4x 3 si 0 <x<1 14
4 a) Halle la mediana de la porción ocupada de memoria. b) Deduzca la densidad de la variable que mide la porción de memoria que falta ocupar, es decir Z =1 X. 15. El tiempo de caída de un sistema se define como la fracción de tiempo que el sistema no está operativo debido a una falla del hardware o del software. Supongamos que T = tiempo de caída de un sistema en horas es una variable aleatoria con función de densidad dada por te t2 2 I (0, ) (t) a) Deduzca la función de distribución acumulada de T. b) Cuando el sistema está caído por más de una hora, todos los archivos de trabajo abiertos en el momento de la caída se pierden. Si un usuario está trabajando en un archivo mientras el sistema cae, cuál es la probabilidad de que el archivo no se pierda? c) Supongamosquealcaerelsistema,eltiempoquetardaunusuarioenrecuperar su trabajo es una función creciente del tiempo de caída, digamos T 2. Deduzca la función de densidad de T La vida útil (en meses) de un componente electrónico es una v.a. V con distribución E (λ), talquep (V >20) = a) Hallar E(V ) y Var(V ). b) Hallar la probabilidad de que la vida útil de uno de estos componentes sea mayor que 10 meses. c) Si se sabe que uno de estos componentes dura más de 20 meses, cuál es la probabilidad de que dure más de 30 meses? Comparar con (b). d) Si se sabe que uno de estos componentes dura más de t meses, cuál es la probabilidad de que dure más de t + s meses (t >0, s>0)? 17. Las tareas llegan a una cola de un sistema de computación con un solo servidor de acuerdo con un proceso de Poisson de parámetro λ =4tareas por minuto. Llamemos a dicho proceso X t.seat el tiempo de espera hasta que llegue la primera tarea medido en minutos. Calcule la probabilidad de que a lo sumo haya que esperar 15 segundos hasta que arribe la primera tarea. 18. Un sistema consta de 5 componentes electrónicos como los del Ejercicio 16, conectados en serie. Al fallar uno cualquiera de éstos, automáticamente se desconecta el sistema. Se supone que los tiempos de vida de los componentes son independientes. Es decir, si se definen los eventos A i = {el i-ésimo componente dura por lo menos hasta el instante t}, con i =1,..., 5, estos eventos son independientes. Sea X elmomentoenelcualelsistemasedesconecta. 15
5 a) Escribir el evento {X t} en función de los A i. b) Usar la independencia de los A i para calcular P (X t). c) Hallar las funciones de distribución y de densidad de X. A qué familia pertenece esta distribución? 19. Sea X una v.a. con función de densidad Γ (α, λ): f (x; α, λ) = λα Γ (α) xα 1 e λx I [0, ) (x), con α>0,λ>0. a) Hallar E(X) y V (X). (Nota: Usar que Γ (α) =(α 1) Γ (α 1) para α>0.) b) Probar que si X Γ (α, λ) y c>0 entonces cx Γ (α, λ/c). 20. Sea X una v.a. con distribución U(0, 1). Hallar las funciones de distribución y de densidad de las siguientes variables aleatorias. a) cx + d b) X α, siendo α un número real positivo c) lnx d) 1 ln(1 X), siendo λ>0. λ 21. Sea Z una v.a. con distribución normal standard. Pruebe que Z 2 Γ(1/2, 1/2). (Esta distribución recibe el nombre de χ 2 con un grado de libertad). (Nota: Γ (1/2) = π.) 22. Sea X una v.a. con función de distribución E(2). Sedefine Y =[X]+1(donde [ ] es la parte entera). Probar que Y G (1 e 2 ). 23. Sea X una variable aleatoria continua que mide el tiempo de duración de cierto sistema. Se define la función tasa de falla r(t) como el límite (cuando t 0)delaprobabilidad de que el sistema falle en el intervalo(t, t+ t) dado que a tiempo t estaba funcionando, sobre la longitud del intervalo ( t). (a) Probar que r(t) = f X(t) 1 F X (t) (b) Probar que si X E(λ) entonces r(t) =λ para todo t. (c) Probar que si X 0 y r(t) =λ para todo t entonces X E(λ). Esta es una de las razones que justifican la utilización de la distribución exponencial para modelar este tipo de fenómenos. 16
6 24. Generación de números al azar (a) Usando el Ejercicio 20 parte a), generar, a partir de una muestra aleatoria de variables con distribución U(0, 1), unamuestraaleatoriadevariables con distribución U(3, 8). (b) Usando el Ejercicio 20 parte d), generar, a partir de una muestra aleatoria de variables con distribución U(0, 1), unamuestraaleatoriadevariables con distribución exponencial de parámetro 10. (c) Generar, a partir de una muestra aleatoria de variables con distribución U(0, 1), una muestra aleatoria de variables con la siguiente distribución uniforme discreta: p X (k) = si k =0, 1,..., 99. (d) Generar, a partir de una muestra aleatoria de variables con distribución U(0, 1), una muestra aleatoria de variables con distribución Bi(1, 1/3). (e) Generar, a partir de una muestra aleatoria de variables con distribución U(0, 1), una muestra aleatoria de variables con distribución de Poisson de parámetro Verifique las expresiones de las funciones generadoras de momentos dadas en la siguiente tabla, indicando para qué valores de t está definida cada una de ellas: Bi(n, p) [pe t +(1 p)] n P (λ) e λ(et 1) N(μ, σ 2 ) e σ2 t 2 2 +μt E(λ) λ λ t U(a, b) Γ(α, λ) e tb e ta t(b a) λ λ t α 17
PROBABILIDADES Y ESTADÍSTICA (C) Práctica 3 P (X > 0) P ( 0,5 < X < 0,5) P ( X > 0,25) 1 si 2 x P (X 1) P (0,5 X 1) P (0,5 < X 1 X < 1)
 PROBABILIDADES Y ESTADÍSTICA (C) Práctica 3 1. Sea X una v.a. con función de densidad { 0,75 (1 x f X (x) = 2 ) 1 x 1 0 en otro caso. a) Verificar que f X es realmente una función de densidad. b) Calcular:
PROBABILIDADES Y ESTADÍSTICA (C) Práctica 3 1. Sea X una v.a. con función de densidad { 0,75 (1 x f X (x) = 2 ) 1 x 1 0 en otro caso. a) Verificar que f X es realmente una función de densidad. b) Calcular:
0 en otro caso. P (X > 0) P ( 0.5 < X < 0.5) P ( X > 0.25) x 3 si 0 x < 2. 1 si 2 x P(X 1) P(0.5 X 1) P(0.5 < X 1 X < 1) f X (x) = (1+αx) 2
 PROBABILIDADES Y ESTADÍSTICA (C) Práctica 3 1. Sea X una v.a. con función de densidad { 0.75(1 x f X (x) = 2 ) 1 x 1 0 en otro caso. a) Verificar que f X es realmente una función de densidad. b) Calcular:
PROBABILIDADES Y ESTADÍSTICA (C) Práctica 3 1. Sea X una v.a. con función de densidad { 0.75(1 x f X (x) = 2 ) 1 x 1 0 en otro caso. a) Verificar que f X es realmente una función de densidad. b) Calcular:
PROBABILIDADES Y ESTADÍSTICA (C) PRÁCTICA 3. ..,, f 0,75(1 -x2) -l<x<l fy (X) < [O en otro caso. P(X > 0) P(-0,5 < X < 0,5) P( X > 0,25) ' 0
 PROBABILIDADES Y ESTADÍSTICA (C) PRÁCTICA 3. Sea X una v.a. con función de densidad..,, f 0,75(1 -x2) -l
PROBABILIDADES Y ESTADÍSTICA (C) PRÁCTICA 3. Sea X una v.a. con función de densidad..,, f 0,75(1 -x2) -l
PROBABILIDADES Trabajo Práctico 5. 0 si x<0. x3 si 0 x<2 1 si x 2
 PROBABILIDADES Trabajo Práctico 5 1. Sea X una variable aleatoria con función de distribución acumulada a) Calcular, usando F X, P (X 1) P (0.5 X 1) P (X >1.5) b) Hallar la mediana de esta distribución.
PROBABILIDADES Trabajo Práctico 5 1. Sea X una variable aleatoria con función de distribución acumulada a) Calcular, usando F X, P (X 1) P (0.5 X 1) P (X >1.5) b) Hallar la mediana de esta distribución.
0 si x<0. si 1 x<2 1 si x 2. si 4 x 6 1 si x>6. 1 e x si x 0
 Probabilidades y Estadística (M) Práctica 3 2 cuatrimestre 2004 Variables Aleatorias. Sea X una v.a. con función de distribución (a) F X (x) = 0 si x< 3 4 si 3 x< 3 4 si x
Probabilidades y Estadística (M) Práctica 3 2 cuatrimestre 2004 Variables Aleatorias. Sea X una v.a. con función de distribución (a) F X (x) = 0 si x< 3 4 si 3 x< 3 4 si x
Matemática 3 Curso 2013
 Matemática 3 Curso 2013 Práctica 3: Variables aleatorias discretas. Funciones de distribución Binomial, Geométrica, Hipergeométrica, Poisson. 1) Dadas las siguientes funciones, determinar cuales son funciones
Matemática 3 Curso 2013 Práctica 3: Variables aleatorias discretas. Funciones de distribución Binomial, Geométrica, Hipergeométrica, Poisson. 1) Dadas las siguientes funciones, determinar cuales son funciones
Transformaciones y esperanza
 Capítulo 3 Transformaciones y esperanza 3.1. Introducción Por lo general estamos en condiciones de modelar un fenómeno en términos de una variable aleatoria X cuya función de distribución acumulada es
Capítulo 3 Transformaciones y esperanza 3.1. Introducción Por lo general estamos en condiciones de modelar un fenómeno en términos de una variable aleatoria X cuya función de distribución acumulada es
F (x, y) = no es la función de distribución acumulada de ningún vector aleatorio. b) Mostrar que. { (1 e x )(1 e y ) si x 0, y 0
 Probabilidades y Estadística (M) Práctica 5 1 o cuatrimestre 2014 Vectores aleatorios 1. a) Demostrar que la función F (x, y) = 1 e x y si x 0, y 0 0 en caso contrario no es la función de distribución
Probabilidades y Estadística (M) Práctica 5 1 o cuatrimestre 2014 Vectores aleatorios 1. a) Demostrar que la función F (x, y) = 1 e x y si x 0, y 0 0 en caso contrario no es la función de distribución
ESTADÍSTICA I. A continuación se presentan los Modelos Probabilísticos Continuos más importantes.
 1 ESTADÍSTICA I Capítulo 6: MODELOS PROBABILÍSTICOS CONTINUOS. Contenido: Distribución Uniforme Continua. Distribución Triangular. Distribución Normal. Distribuciones Gamma, Exponencial, Erlang y Chi Cuadrado.
1 ESTADÍSTICA I Capítulo 6: MODELOS PROBABILÍSTICOS CONTINUOS. Contenido: Distribución Uniforme Continua. Distribución Triangular. Distribución Normal. Distribuciones Gamma, Exponencial, Erlang y Chi Cuadrado.
Relación de Problemas. Tema 5
 Relación de Problemas. Tema 5. Supongamos que tenemos una muestra aleatoria simple de tamaño n de una v.a. X que sigue una distribución geométrica con función de probabilidad P (X = k) = p( p) k Calcular
Relación de Problemas. Tema 5. Supongamos que tenemos una muestra aleatoria simple de tamaño n de una v.a. X que sigue una distribución geométrica con función de probabilidad P (X = k) = p( p) k Calcular
Variables aleatorias continuas
 Variables aleatorias continuas VARIABLE ALEATORIA UNIFORME Definición Se dice que una variable X tiene una distribución uniforme en el intervalo [a;b] si la fdp de X es: 1 si a x b f(x)= b-a 0 en otro
Variables aleatorias continuas VARIABLE ALEATORIA UNIFORME Definición Se dice que una variable X tiene una distribución uniforme en el intervalo [a;b] si la fdp de X es: 1 si a x b f(x)= b-a 0 en otro
Cálculo de Probabilidades II Preguntas Tema 2
 Cálculo de Probabilidades II Preguntas Tema 2 1. Demuestre que la suma de n v.a. Bernuolli(p) independientes tiene una distribución Binomial con parametros (n, p). 2. Se dice que una v.a tiene una distribución
Cálculo de Probabilidades II Preguntas Tema 2 1. Demuestre que la suma de n v.a. Bernuolli(p) independientes tiene una distribución Binomial con parametros (n, p). 2. Se dice que una v.a tiene una distribución
1. Sea (X, Y ) un vector aleatorio con función de densidad conjunta. 0 en otro caso.
 18 PROBABILIDADES Y ESTADÍSTICA (C) Práctica 4 1. Sea (X, Y ) un vector aleatorio con función de densidad conjunta { k (x f XY (x, y) = 2 + y 2 ) 20 x 30, 20 y 30 0 en otro caso. a) Cuál es el valor de
18 PROBABILIDADES Y ESTADÍSTICA (C) Práctica 4 1. Sea (X, Y ) un vector aleatorio con función de densidad conjunta { k (x f XY (x, y) = 2 + y 2 ) 20 x 30, 20 y 30 0 en otro caso. a) Cuál es el valor de
UNIVERSIDAD DE ATACAMA FACULTAD DE INGENIERÍA / DEPARTAMENTO DE MATEMÁTICA
 UNIVERSIDAD DE ATACAMA FACULTAD DE INGENIERÍA / DEPARTAMENTO DE MATEMÁTICA ESTADÍSTICA Y PROBABILIDADES GUÍA 3: VARIABLES ALEATORIAS Y ESTIMACIÓN Profesor: Hugo S. Salinas Segundo Semestre 2010 1. Una
UNIVERSIDAD DE ATACAMA FACULTAD DE INGENIERÍA / DEPARTAMENTO DE MATEMÁTICA ESTADÍSTICA Y PROBABILIDADES GUÍA 3: VARIABLES ALEATORIAS Y ESTIMACIÓN Profesor: Hugo S. Salinas Segundo Semestre 2010 1. Una
no es función de distribución de un vector aleatorio (b) Mostrar que:
 Probabilidades y Estadística (M) Práctica 4 2 cuatrimestre 2004 Vectores aleatorios e independencia de variables 1. (a) Demostrar que la función 1 e x y si x 0 e y 0 F (x, y) = 0 sino no es función de
Probabilidades y Estadística (M) Práctica 4 2 cuatrimestre 2004 Vectores aleatorios e independencia de variables 1. (a) Demostrar que la función 1 e x y si x 0 e y 0 F (x, y) = 0 sino no es función de
Variables Aleatorias y Distribución de Probabilidades
 Variables Aleatorias y Distribución de Probabilidades Julio Deride Silva Área de Matemática Facultad de Ciencias Químicas y Farmcéuticas Universidad de Chile 27 de mayo de 2011 Tabla de Contenidos Variables
Variables Aleatorias y Distribución de Probabilidades Julio Deride Silva Área de Matemática Facultad de Ciencias Químicas y Farmcéuticas Universidad de Chile 27 de mayo de 2011 Tabla de Contenidos Variables
Cálculo de Probabilidades y Estadística. Segunda prueba. 1
 08231. Cálculo de Probabilidades y Estadística. Segunda prueba. 1 Problema 1. Se eligen tres puntos A, B y C, al azar e independientemente, sobre una circunferencia. Determinar la distribución del valor
08231. Cálculo de Probabilidades y Estadística. Segunda prueba. 1 Problema 1. Se eligen tres puntos A, B y C, al azar e independientemente, sobre una circunferencia. Determinar la distribución del valor
UNIVERSIDAD DE ATACAMA
 UNIVERSIDAD DE ATACAMA FACULTAD DE INGENIERÍA / DEPARTAMENTO DE MATEMÁTICA ESTADÍSTICA Y PROBABILIDAD GUÍA DE TRABAJO 3 Profesor: Hugo S. Salinas. Primer Semestre 2010 1. Sea X 1,..., X n una muestra aleatoria
UNIVERSIDAD DE ATACAMA FACULTAD DE INGENIERÍA / DEPARTAMENTO DE MATEMÁTICA ESTADÍSTICA Y PROBABILIDAD GUÍA DE TRABAJO 3 Profesor: Hugo S. Salinas. Primer Semestre 2010 1. Sea X 1,..., X n una muestra aleatoria
INGENIERO EN COMPUTACIÓN DISTRIBUCIONES DE PROBABILIDAD CONTINUA ELABORÓ: M. EN C. LUIS ENRIQUE KU MOO FECHA: AGOSTO DE 2017
 UNIVERSIDAD AUTÓNOMA DEL ESTADO DE MÉXICO CENTRO UNIVERSITARIO UAEM ZUMPANGO INGENIERO EN COMPUTACIÓN DISTRIBUCIONES DE PROBABILIDAD CONTINUA ELABORÓ: M. EN C. LUIS ENRIQUE KU MOO FECHA: AGOSTO DE 2017
UNIVERSIDAD AUTÓNOMA DEL ESTADO DE MÉXICO CENTRO UNIVERSITARIO UAEM ZUMPANGO INGENIERO EN COMPUTACIÓN DISTRIBUCIONES DE PROBABILIDAD CONTINUA ELABORÓ: M. EN C. LUIS ENRIQUE KU MOO FECHA: AGOSTO DE 2017
PROBABILIDADES Y ESTADÍSTICA (C) Práctica 4. a) Hallar las funciones de probabilidad marginal de X ydey : p X (x) y p Y (y) respectivamente.
 PROBABILIDADES Y ESTADÍSTICA (C) Práctica 4 1. En la siguiente tabla se presenta la función de probabilidad conjunta del vector aleatorio discreto (X, Y ): Y \ X 1 2 3 4 1 0.10 0.05 0.02 0.02 2 0.05 0.20
PROBABILIDADES Y ESTADÍSTICA (C) Práctica 4 1. En la siguiente tabla se presenta la función de probabilidad conjunta del vector aleatorio discreto (X, Y ): Y \ X 1 2 3 4 1 0.10 0.05 0.02 0.02 2 0.05 0.20
Cálculo de probabilidad. Tema 3: Variables aleatorias continuas
 Cálculo de probabilidad Tema 3: Variables aleatorias continuas Guión Guión 3.1. La función de densidad de probabilidad Definición 3.1 Sea P una medida de probabilidad en un espacio muestral Ω. Se dice
Cálculo de probabilidad Tema 3: Variables aleatorias continuas Guión Guión 3.1. La función de densidad de probabilidad Definición 3.1 Sea P una medida de probabilidad en un espacio muestral Ω. Se dice
Ejercicios para auto evaluación Variables continuas y Teorema de Límite Central
 Ejercicios para auto evaluación Variables continuas y Teorema de Límite Central Enero 2008. Sea f(u) = ce u, u R. Determine el valor de c para que f sea una función de densidad de probabilidad y calcule
Ejercicios para auto evaluación Variables continuas y Teorema de Límite Central Enero 2008. Sea f(u) = ce u, u R. Determine el valor de c para que f sea una función de densidad de probabilidad y calcule
Y \ X
 18 PROBABILIDADES Y ESTADÍSTICA (C) Práctica 4 1. En la siguiente tabla se presenta la función de probabilidad conjunta del vector aleatorio discreto (X, Y ): Y \ X 1 2 3 4 1 0.10 0.05 0.02 0.02 2 0.05
18 PROBABILIDADES Y ESTADÍSTICA (C) Práctica 4 1. En la siguiente tabla se presenta la función de probabilidad conjunta del vector aleatorio discreto (X, Y ): Y \ X 1 2 3 4 1 0.10 0.05 0.02 0.02 2 0.05
FORMULARIO DE DISTRIBUCIONES DE PROBABILIDAD
 FORMULARIO DE DISTRIBUCIONES DE PROBABILIDAD Jorge M. Galbiati pág. DISTRIBUCION BINOMIAL 2 DISTRIBUCION POISSON 4 DISTRIBUCION HIPERGEOMETRICA 5 DISTRIBUCION GEOMETRICA 7 DISTRIBUCION NORMAL 8 DISTRIBUCION
FORMULARIO DE DISTRIBUCIONES DE PROBABILIDAD Jorge M. Galbiati pág. DISTRIBUCION BINOMIAL 2 DISTRIBUCION POISSON 4 DISTRIBUCION HIPERGEOMETRICA 5 DISTRIBUCION GEOMETRICA 7 DISTRIBUCION NORMAL 8 DISTRIBUCION
CO3121: Problemario Marzo 2005.
 CO3121: Problemario Marzo 2005. 1. Sea f(u) = ce u, u R. Si f es una función de densidad de probabilidad, cuál es el valor de c?. 2. Sea X una v.a. con función de densidad f(x) = 2x, 0 < x < 1. Encuentre
CO3121: Problemario Marzo 2005. 1. Sea f(u) = ce u, u R. Si f es una función de densidad de probabilidad, cuál es el valor de c?. 2. Sea X una v.a. con función de densidad f(x) = 2x, 0 < x < 1. Encuentre
VARIABLES ALEATORIAS CONTINUAS
 VARIABLES ALEATORIAS CONTINUAS M. en C. Juan Carlos Gutiérrez Matus Instituto Politécnico Nacional Primavera 2004 IPN UPIICSA c 2004 Juan C. Gutiérrez Matus Definición de una V.A.C. Definición de una V.A.C.
VARIABLES ALEATORIAS CONTINUAS M. en C. Juan Carlos Gutiérrez Matus Instituto Politécnico Nacional Primavera 2004 IPN UPIICSA c 2004 Juan C. Gutiérrez Matus Definición de una V.A.C. Definición de una V.A.C.
Estimación por intervalos
 Capítulo 9 Estimación por intervalos 9.1. Introducción En este capítulo se desarrolla la estimación por intervalos donde el proceso de inferencia se realiza de la forma θ C, donde C = Cx) es un conjunto
Capítulo 9 Estimación por intervalos 9.1. Introducción En este capítulo se desarrolla la estimación por intervalos donde el proceso de inferencia se realiza de la forma θ C, donde C = Cx) es un conjunto
Unidad 3. Probabilidad. Javier Santibáñez (IIMAS, UNAM) Inferencia Estadística Semestre / 22
 Unidad 3. Probabilidad Javier Santibáñez (IIMAS, UNAM) Inferencia Estadística Semestre 2018-1 1 / 22 Espacios de probabilidad El modelo matemático para estudiar la probabilidad se conoce como espacio de
Unidad 3. Probabilidad Javier Santibáñez (IIMAS, UNAM) Inferencia Estadística Semestre 2018-1 1 / 22 Espacios de probabilidad El modelo matemático para estudiar la probabilidad se conoce como espacio de
Curso de Probabilidad y Estadística
 Curso de Probabilidad y Estadística Distribuciones de Probabilidad Dr. José Antonio Camarena Ibarrola camarena@umich.mx Universidad Michoacana de San Nicolás de Hidalgo Facultad de Ingeniería Eléctrica
Curso de Probabilidad y Estadística Distribuciones de Probabilidad Dr. José Antonio Camarena Ibarrola camarena@umich.mx Universidad Michoacana de San Nicolás de Hidalgo Facultad de Ingeniería Eléctrica
Familias de distribuciones
 Capítulo 2 Familias de distribuciones 2.1. Introducción Las distribuciones estadísticas son usadas para modelar poblaciones a través de un miembro de una familia de distribuciones. Cada familia se encuentra
Capítulo 2 Familias de distribuciones 2.1. Introducción Las distribuciones estadísticas son usadas para modelar poblaciones a través de un miembro de una familia de distribuciones. Cada familia se encuentra
1. Una variable aleatoria X sigue una distribución binomial con parámetros m = 3 y p =0.2.
 Ejercicios y Problemas. Capítulo III 1. Una variable aleatoria X sigue una distribución binomial con parámetros m = 3 y p =0.2. (a) Calcular P (X = 0), P (X = 1), P (X = 2), P (X = 3), utilizando la función
Ejercicios y Problemas. Capítulo III 1. Una variable aleatoria X sigue una distribución binomial con parámetros m = 3 y p =0.2. (a) Calcular P (X = 0), P (X = 1), P (X = 2), P (X = 3), utilizando la función
Probabilidad y Estadística Segundo del grado en Telecomunicaciones, UAM, Examen de la convocatoria extraordinaria,
 Probabilidad y Estadística Segundo del grado en Telecomunicaciones, UAM, 2014-2015 Examen de la convocatoria extraordinaria, 22-6-2015 Nombre y apellidos.......................................................................
Probabilidad y Estadística Segundo del grado en Telecomunicaciones, UAM, 2014-2015 Examen de la convocatoria extraordinaria, 22-6-2015 Nombre y apellidos.......................................................................
PROBABILIDADES (TELE-00031)
 PROBABILIDADES (TELE-0003) Tema. Variable aleatoria en una dimensión Abril 06. La unción de probabilidad de la variable aleatoria discreta N viene dada por N n p (n) = K.r, n = 0,,.... Calcule el valor
PROBABILIDADES (TELE-0003) Tema. Variable aleatoria en una dimensión Abril 06. La unción de probabilidad de la variable aleatoria discreta N viene dada por N n p (n) = K.r, n = 0,,.... Calcule el valor
Algunas Distribuciones Continuas de Probabilidad. UCR ECCI CI-1352 Probabilidad y Estadística Prof. M.Sc. Kryscia Daviana Ramírez Benavides
 Algunas Distribuciones Continuas de Probabilidad UCR ECCI CI-1352 Probabilidad y Estadística Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción El comportamiento de una variable aleatoria queda
Algunas Distribuciones Continuas de Probabilidad UCR ECCI CI-1352 Probabilidad y Estadística Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción El comportamiento de una variable aleatoria queda
Hoja de Problemas Tema 3 (Variables aleatorias multidimensionales)
 Depto. de Matemáticas Estadística (Ing. de Telecom.) Curso 2004-2005 Hoja de Problemas Tema 3 (Variables aleatorias multidimensionales) 1. Consideremos dos variables aleatorias independientes X 1 y X 2,
Depto. de Matemáticas Estadística (Ing. de Telecom.) Curso 2004-2005 Hoja de Problemas Tema 3 (Variables aleatorias multidimensionales) 1. Consideremos dos variables aleatorias independientes X 1 y X 2,
5 Variables aleatorias contínuas
 5 Variables aleatorias contínuas Una variable aleatoria continua puede tomar cualquier valor en un intervalo de números reales.. Función de densidad. La función de densidad de una variable aleatoria continua
5 Variables aleatorias contínuas Una variable aleatoria continua puede tomar cualquier valor en un intervalo de números reales.. Función de densidad. La función de densidad de una variable aleatoria continua
ETSI de Topografía, Geodesia y Cartografía
 Distribuciones (discretas y continuas) EVALUACIÓN CONTINUA (Tipo I) 14-XII-11 1. Una prueba del examen de Estadística consiste en un cuestionario de 10 preguntas con tres posibles respuestas, solamente
Distribuciones (discretas y continuas) EVALUACIÓN CONTINUA (Tipo I) 14-XII-11 1. Una prueba del examen de Estadística consiste en un cuestionario de 10 preguntas con tres posibles respuestas, solamente
Variables aleatorias continuas y Teorema Central del Limite
 Variables aleatorias continuas y Teorema Central del Limite FaMAF 17 de marzo, 2015 Variables aleatorias continuas Definición Una variable aleatoria X se dice (absolutamente continua) si existe f : R R
Variables aleatorias continuas y Teorema Central del Limite FaMAF 17 de marzo, 2015 Variables aleatorias continuas Definición Una variable aleatoria X se dice (absolutamente continua) si existe f : R R
ESTADÍSTICA Y ANÁLISIS DE DATOS. Práctica del Tema 5. Variable aleatoria (en R y R 2 )
 ESTADÍSTICA Y ANÁLISIS DE DATOS Práctica del Tema 5. Variable aleatoria (en R y R ). Se considera un dado regular y se define la v.a. X: puntuación obtenida en un lanzamiento cualquiera de dicho dado.
ESTADÍSTICA Y ANÁLISIS DE DATOS Práctica del Tema 5. Variable aleatoria (en R y R ). Se considera un dado regular y se define la v.a. X: puntuación obtenida en un lanzamiento cualquiera de dicho dado.
Generalidades 1. Sea X una variable aleatoria continua con función densidad dada por
 Generalidades 1. Sea X una variable aleatoria continua con función dendad dada por kt f ( t ) = 0 1 t en otro caso Determine a) el valor de la constante k b) E(X) y V(X) c) la función de distribución acumulada
Generalidades 1. Sea X una variable aleatoria continua con función dendad dada por kt f ( t ) = 0 1 t en otro caso Determine a) el valor de la constante k b) E(X) y V(X) c) la función de distribución acumulada
Relación de Problemas. Variables Aleatorias
 Relación de Problemas. Variables Aleatorias 1. Un experimento consiste en lanzar cuatro monedas al aire. Calcular la función de probabilidad y la función de distribución de las siguientes variables aleatorias:
Relación de Problemas. Variables Aleatorias 1. Un experimento consiste en lanzar cuatro monedas al aire. Calcular la función de probabilidad y la función de distribución de las siguientes variables aleatorias:
Cálculo de Probabilidades II Preguntas Tema 1
 Cálculo de Probabilidades II Preguntas Tema 1 1. Suponga que un experimento consiste en lanzar un par de dados, Sea X El número máximo de los puntos obtenidos y Y Suma de los puntos obtenidos. Obtenga
Cálculo de Probabilidades II Preguntas Tema 1 1. Suponga que un experimento consiste en lanzar un par de dados, Sea X El número máximo de los puntos obtenidos y Y Suma de los puntos obtenidos. Obtenga
I. Distribuciones discretas
 Probabilidades y Estadística (M) Funciones de densidad o probabilidad puntual, esperanzas, varianzas y funciones características de las variables aleatorias más frecuentes I. Distribuciones discretas Distribución
Probabilidades y Estadística (M) Funciones de densidad o probabilidad puntual, esperanzas, varianzas y funciones características de las variables aleatorias más frecuentes I. Distribuciones discretas Distribución
Pérdida Esperada. Pérdida Esperada (PE): Valor esperado de pérdida por riesgo crediticio en un horizonte de tiempo determinado.
 Pérdida Esperada Uno de los objetivos de este estudio es construir una función de pérdidas para el portafolio de la cartera de préstamos que ofrece la entidad G&T Continental, basados en el comportamiento
Pérdida Esperada Uno de los objetivos de este estudio es construir una función de pérdidas para el portafolio de la cartera de préstamos que ofrece la entidad G&T Continental, basados en el comportamiento
Modelos Básicos de Distribuciones Discretas y Continuas
 Modelos de Distribuciones Discretas y Continuas 1/27 Modelos Básicos de Distribuciones Discretas y Continuas Departamento de Estadística e Investigación Operativa Universidad de Sevilla Contenidos Modelos
Modelos de Distribuciones Discretas y Continuas 1/27 Modelos Básicos de Distribuciones Discretas y Continuas Departamento de Estadística e Investigación Operativa Universidad de Sevilla Contenidos Modelos
6.3. Distribuciones continuas
 144 Bioestadística: Métodos y Aplicaciones Solución: Si consideramos la v.a. X que contabiliza el número de personas que padecen la enfermedad, es claro que sigue un modelo binomial, pero que puede ser
144 Bioestadística: Métodos y Aplicaciones Solución: Si consideramos la v.a. X que contabiliza el número de personas que padecen la enfermedad, es claro que sigue un modelo binomial, pero que puede ser
TEMA 2.- VARIABLES ALEATORIAS UNIDIMENSIONALES.- CURSO 17/18
 TEMA 2.- VARIABLES ALEATORIAS UNIDIMENSIONALES.- CURSO 17/18 2.1. Concepto de variable aleatoria. Tipos de variables aleatorias: discretas y continuas. 2.2. Variables aleatorias discretas. Diagrama de
TEMA 2.- VARIABLES ALEATORIAS UNIDIMENSIONALES.- CURSO 17/18 2.1. Concepto de variable aleatoria. Tipos de variables aleatorias: discretas y continuas. 2.2. Variables aleatorias discretas. Diagrama de
Variables aleatorias continuas, TCL y Esperanza Condicional
 Variables aleatorias continuas, TCL y Esperanza Condicional FaMAF 17 de marzo, 2011 1 / 37 Poisson P(λ) Número de éxitos en una cantidad grande de ensayos independientes Rango: {0, 1, 2,... } = {0} N Función
Variables aleatorias continuas, TCL y Esperanza Condicional FaMAF 17 de marzo, 2011 1 / 37 Poisson P(λ) Número de éxitos en una cantidad grande de ensayos independientes Rango: {0, 1, 2,... } = {0} N Función
Tema 6 Algunas distribuciones importantes Hugo S. Salinas
 Algunas distribuciones importantes Hugo S. Salinas 1 Distribución binomial Se han estudiado numerosas distribuciones de probabilidad que modelan características asociadas a fenómenos que se presentan frecuentemente
Algunas distribuciones importantes Hugo S. Salinas 1 Distribución binomial Se han estudiado numerosas distribuciones de probabilidad que modelan características asociadas a fenómenos que se presentan frecuentemente
Probabilidad para una V.A. Continua. P( a X b) = f ( x)
 Tema 4: Variables Aleatorias Contínuas Prof. Heriberto Figueroa S. Capítulo 4 Variables Aleatorias Continuas y sus Distribuciones de Probabilidad 4.1. Variables Aleatorias Continuas Una variable aleatoria
Tema 4: Variables Aleatorias Contínuas Prof. Heriberto Figueroa S. Capítulo 4 Variables Aleatorias Continuas y sus Distribuciones de Probabilidad 4.1. Variables Aleatorias Continuas Una variable aleatoria
Tablas de Probabilidades
 Tablas de Probabilidades Ernesto Barrios Zamudio José Ángel García Pérez José Matuk Villazón Departamento Académico de Estadística Instituto Tecnológico Autónomo de México Mayo 2016 Versión 1.00 1 Barrios
Tablas de Probabilidades Ernesto Barrios Zamudio José Ángel García Pérez José Matuk Villazón Departamento Académico de Estadística Instituto Tecnológico Autónomo de México Mayo 2016 Versión 1.00 1 Barrios
MODELOS DE SIMULACIÓN ESTADÍSTICOS CLASE 4: DISTRIBUCIÓN t, CHI-CUADRADA y EXPONENCIAL PROFESOR: OSCAR SAAVEDRA ANDRÉS DURANGO.
 DISTRIBUCIÓN t Con frecuencia intentamos estimar la media de una población cuando se desconoce la varianza, en estos casos utilizamos la distribución de t de Student. Si el tamaño de la muestra es suficientemente
DISTRIBUCIÓN t Con frecuencia intentamos estimar la media de una población cuando se desconoce la varianza, en estos casos utilizamos la distribución de t de Student. Si el tamaño de la muestra es suficientemente
Hoja 4 Variables aleatorias multidimensionales
 Hoja 4 Variables aleatorias multidimensionales 1.- Estudiar si F (x, y) = 1, si x + 2y 1, 0, si x + 2y < 1, es una función de distribución en IR 2. 2.- Dada la variable aleatoria 2-dimensional (X, Y )
Hoja 4 Variables aleatorias multidimensionales 1.- Estudiar si F (x, y) = 1, si x + 2y 1, 0, si x + 2y < 1, es una función de distribución en IR 2. 2.- Dada la variable aleatoria 2-dimensional (X, Y )
EJERCICIOS VARIABLES ALEATORIAS
 EJERCICIOS VARIABLES ALEATORIAS 1.- Tenemos dos urnas, en la urna A hay 5 bolas blancas y 4 rojas y en la B hay 6 blancas y 3 rojas. Se sacan, sin reemplazamiento, dos bolas de cada urna. Sea X el nº de
EJERCICIOS VARIABLES ALEATORIAS 1.- Tenemos dos urnas, en la urna A hay 5 bolas blancas y 4 rojas y en la B hay 6 blancas y 3 rojas. Se sacan, sin reemplazamiento, dos bolas de cada urna. Sea X el nº de
Grado en Ciencias Ambientales. Matemáticas. Curso 11/12
 Grado en Ciencias Ambientales. Matemáticas. Curso 11/12 Problemas Tema 1. Espacios Vectoriales. 1 Repaso de Estructuras Algebraicas 1.1. Construye explícitamente el conjunto A B, siendo A = {1, 2, 3},
Grado en Ciencias Ambientales. Matemáticas. Curso 11/12 Problemas Tema 1. Espacios Vectoriales. 1 Repaso de Estructuras Algebraicas 1.1. Construye explícitamente el conjunto A B, siendo A = {1, 2, 3},
Unidad 3. Probabilidad
 Unidad 3. Probabilidad Javier Santibáñez 17 de agosto de 2018 1. Introducción Definición 1. La probabilidad es una medida subjetiva del grado de creencia que se tiene acerca de que algo desconocido sea
Unidad 3. Probabilidad Javier Santibáñez 17 de agosto de 2018 1. Introducción Definición 1. La probabilidad es una medida subjetiva del grado de creencia que se tiene acerca de que algo desconocido sea
Selección de distribuciones de probabilidad
 Selección de distribuciones de probabilidad Georgina Flesia FaMAF 3 de mayo, 2012 Análisis estadístico de datos simulados Los sistemas reales tienen fuentes de aleatoriedad: Tipo de sistema Fabricación
Selección de distribuciones de probabilidad Georgina Flesia FaMAF 3 de mayo, 2012 Análisis estadístico de datos simulados Los sistemas reales tienen fuentes de aleatoriedad: Tipo de sistema Fabricación
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2015-coincidente) Selectividad-Opción A Tiempo: 90 minutos 5 7 C = 1 5
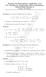 Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2015-coincidente) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (2 puntos) Considérense las matrices ( ) ( ) ( ) 1 2 3 2 5 7 A =,
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2015-coincidente) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (2 puntos) Considérense las matrices ( ) ( ) ( ) 1 2 3 2 5 7 A =,
Distribuciones unidimensionales continuas
 Estadística II Universidad de Salamanca Curso 2011/2012 Outline 1 Distribución uniforme continua 2 Estándar 3 Distribución χ 2 de Pearson 4 Distribución uniforme continua Definición Es una variable continua
Estadística II Universidad de Salamanca Curso 2011/2012 Outline 1 Distribución uniforme continua 2 Estándar 3 Distribución χ 2 de Pearson 4 Distribución uniforme continua Definición Es una variable continua
Dagoberto Salgado Horta Variables aleatorias y distribuciones de probabilidad - 1 TALLER VARIABLES ALEATORIAS Y DISTRIBUCIONES DE PROBABILIDAD
 Dagoberto Salgado Horta Variables aleatorias y distribuciones de probabilidad - 1 TALLER VARIABLES ALEATORIAS Y DISTRIBUCIONES DE PROBABILIDAD 1. Sea X la variable aleatoria nivel de colesterol, en mg/dl,
Dagoberto Salgado Horta Variables aleatorias y distribuciones de probabilidad - 1 TALLER VARIABLES ALEATORIAS Y DISTRIBUCIONES DE PROBABILIDAD 1. Sea X la variable aleatoria nivel de colesterol, en mg/dl,
Algunas distribuciones teóricas continuas
 Algunas distribuciones teóricas continuas Dr. Pastore, Juan Ignacio Profesor Adjunto. Algunas Distribuciones Estadísticas Teóricas Distribución Continuas: a) Distribución Uniforme b) Distribución de Exponencial
Algunas distribuciones teóricas continuas Dr. Pastore, Juan Ignacio Profesor Adjunto. Algunas Distribuciones Estadísticas Teóricas Distribución Continuas: a) Distribución Uniforme b) Distribución de Exponencial
Estadística. Tema 2. Variables Aleatorias Funciones de distribución y probabilidad Ejemplos distribuciones discretas y continuas
 Estadística Tema 2 Variables Aleatorias 21 Funciones de distribución y probabilidad 22 Ejemplos distribuciones discretas y continuas 23 Distribuciones conjuntas y marginales 24 Ejemplos distribuciones
Estadística Tema 2 Variables Aleatorias 21 Funciones de distribución y probabilidad 22 Ejemplos distribuciones discretas y continuas 23 Distribuciones conjuntas y marginales 24 Ejemplos distribuciones
5 Variables aleatorias contínuas
 5 Variables aleatorias contínuas Año 202 Una variable aleatoria continua puede tomar cualquier valor en un intervalo de números reales.. Función de densidad. La función de densidad de una variable aleatoria
5 Variables aleatorias contínuas Año 202 Una variable aleatoria continua puede tomar cualquier valor en un intervalo de números reales.. Función de densidad. La función de densidad de una variable aleatoria
Tema 3:Introducción a las variables aleatorias PROBLEMAS PROPUESTOS. 2. La función de densidad de la variable aleatoria X viene dada por la expresión
 Tema :Introducción a las variables aleatorias PROBLEMAS PROPUESTOS. Puede ser la función de densidad de una variable aleatoria continua mayor que uno en algún punto? Sí. La función de densidad de la variable
Tema :Introducción a las variables aleatorias PROBLEMAS PROPUESTOS. Puede ser la función de densidad de una variable aleatoria continua mayor que uno en algún punto? Sí. La función de densidad de la variable
El momento k-ésimo para una variable aleatoria discreta respecto del origen, es. n = esperanza matemática de X
 Momentos El momento k-ésimo para una variable aleatoria discreta respecto del origen, es E(x) n = i = 1 k i ( ) x.p x El primer momento centrado en el origen (k=1) es la esperanza matemática de X También
Momentos El momento k-ésimo para una variable aleatoria discreta respecto del origen, es E(x) n = i = 1 k i ( ) x.p x El primer momento centrado en el origen (k=1) es la esperanza matemática de X También
TALLER DISTRIBUCIONES DE PROBABILIDAD Y VARIABLES ALEATORIAS
 TALLER DISTRIBUCIONES DE PROBABILIDAD Y VARIABLES ALEATORIAS 1. Sea X la variable aleatoria nivel de colesterol, en mg/dl, de los varones de 40 años. Escribir los siguientes sucesos, con notación abreviada,
TALLER DISTRIBUCIONES DE PROBABILIDAD Y VARIABLES ALEATORIAS 1. Sea X la variable aleatoria nivel de colesterol, en mg/dl, de los varones de 40 años. Escribir los siguientes sucesos, con notación abreviada,
Tema 5 Algunas distribuciones importantes
 Algunas distribuciones importantes 1 Modelo Bernoulli Distribución Bernoulli Se llama experimento de Bernoulli a un experimento con las siguientes características: 1. Se realiza un experimento con dos
Algunas distribuciones importantes 1 Modelo Bernoulli Distribución Bernoulli Se llama experimento de Bernoulli a un experimento con las siguientes características: 1. Se realiza un experimento con dos
Tema 6: Modelos de probabilidad.
 Estadística 60 Tema 6: Modelos de probabilidad. 6.1 Modelos discretos. (a) Distribución uniforme discreta: La variable aleatoria X tiene una distribución uniforme discreta de parámetro n,que denoteramos
Estadística 60 Tema 6: Modelos de probabilidad. 6.1 Modelos discretos. (a) Distribución uniforme discreta: La variable aleatoria X tiene una distribución uniforme discreta de parámetro n,que denoteramos
Modelos de distribuciones discretas y continuas
 Ignacio Cascos Fernández Departamento de Estadística Universidad Carlos III de Madrid Modelos de distribuciones discretas y continuas Estadística I curso 2008 2009 1. Distribuciones discretas Aquellas
Ignacio Cascos Fernández Departamento de Estadística Universidad Carlos III de Madrid Modelos de distribuciones discretas y continuas Estadística I curso 2008 2009 1. Distribuciones discretas Aquellas
Procesos de Poisson. 21 de marzo, FaMAF 1 / 25
 Procesos de Poisson FaMAF 21 de marzo, 2013 1 / 25 Distribución exponencial Definición Una v.a. X con función de densidad dada por f λ (x) = λ e λx, x > 0, para cierto λ > 0 se dice una v.a. exponencial
Procesos de Poisson FaMAF 21 de marzo, 2013 1 / 25 Distribución exponencial Definición Una v.a. X con función de densidad dada por f λ (x) = λ e λx, x > 0, para cierto λ > 0 se dice una v.a. exponencial
PRUEBA DE BONDAD DE AJUSTE O PRUEBA CHI - CUADRADO
 O PRUEBA CHI - CUADRADO Hasta ahora se han mencionado formas de probar lo que se puede llamar hipótesis paramétricas con relación a una variable aleatoria, o sea que se ha supuesto que se conoce la ley
O PRUEBA CHI - CUADRADO Hasta ahora se han mencionado formas de probar lo que se puede llamar hipótesis paramétricas con relación a una variable aleatoria, o sea que se ha supuesto que se conoce la ley
Generación de variables aleatorias continuas Método de rechazo
 Generación de variables aleatorias continuas Método de rechazo Georgina Flesia FaMAF 18 de abril, 2013 Método de Aceptación y Rechazo Repaso Se desea simular una v. a. X discreta, con probabilidad de masa
Generación de variables aleatorias continuas Método de rechazo Georgina Flesia FaMAF 18 de abril, 2013 Método de Aceptación y Rechazo Repaso Se desea simular una v. a. X discreta, con probabilidad de masa
ESTADÍSTICA (Química) PRÁCTICA 4 Sumas de variables aleatorias
 ESTADÍSTICA (Química) PRÁCTICA 4 Sumas de variables aleatorias 1. Se realizan mediciones independientes del volumen inicial y final en una bureta. Supongamos que las mediciones inicial y final siguen el
ESTADÍSTICA (Química) PRÁCTICA 4 Sumas de variables aleatorias 1. Se realizan mediciones independientes del volumen inicial y final en una bureta. Supongamos que las mediciones inicial y final siguen el
PROBABILIDAD Relación de problemas 3: Variables aleatorias continuas
 PROBABILIDAD Relación de problemas 3: Variables aleatorias continuas 1. Un autobús pasa por una cierta parada cada 8 minutos. Si un usuario llega a la parada, el tiempo que debe esperar es una variable
PROBABILIDAD Relación de problemas 3: Variables aleatorias continuas 1. Un autobús pasa por una cierta parada cada 8 minutos. Si un usuario llega a la parada, el tiempo que debe esperar es una variable
Introducción al Tema 8. Tema 6. Variables aleatorias unidimensionales Distribución. Características: media, varianza, etc. Transformaciones.
 Introducción al Tema 8 1 Tema 6. Variables aleatorias unidimensionales Distribución. Características: media, varianza, etc. Transformaciones. V.A. de uso frecuente Tema 7. Modelos probabiĺısticos discretos
Introducción al Tema 8 1 Tema 6. Variables aleatorias unidimensionales Distribución. Características: media, varianza, etc. Transformaciones. V.A. de uso frecuente Tema 7. Modelos probabiĺısticos discretos
Part VI. Distribuciones notables. Estadística I. Mario Francisco. Principales distribuciones unidimensionales. discretas. Principales distribuciones
 Part VI notables El proceso de Bernoulli En cada observación se clasifica el elemento de la población en una de las dos posibles categorías, correspondientes a la ocurrencia o no de un suceso. Llamaremos
Part VI notables El proceso de Bernoulli En cada observación se clasifica el elemento de la población en una de las dos posibles categorías, correspondientes a la ocurrencia o no de un suceso. Llamaremos
El momento de orden n de una variable aleatoria X es el valor esperado de X elevado a la n, es decir,
 1 CLASES DE ESTADÍSTICA II CLASE 4) MOMENTOS. FUNCIÓN GENERATRIZ DE MOMENTOS CONJUNTA. El concepto de Momentos ya se conocía en el análisis de una variable aleatoria y es bueno recordarlo ahora para generalizarlo
1 CLASES DE ESTADÍSTICA II CLASE 4) MOMENTOS. FUNCIÓN GENERATRIZ DE MOMENTOS CONJUNTA. El concepto de Momentos ya se conocía en el análisis de una variable aleatoria y es bueno recordarlo ahora para generalizarlo
a) Definir un espacio muestral S apropiado para este experimento. b) Consideremos la variable aleatoria
 7 PROBABILIDADES Y ESTADÍSTICA (C) Práctica 2 1. Se eligen tres autos al azar y cada uno es clasificado N si tiene motor naftero o D si tiene motor diesel (por ejemplo, un resultado posible sería N N D).
7 PROBABILIDADES Y ESTADÍSTICA (C) Práctica 2 1. Se eligen tres autos al azar y cada uno es clasificado N si tiene motor naftero o D si tiene motor diesel (por ejemplo, un resultado posible sería N N D).
Introducción a los Procesos de Poisson *
 Introducción a los Procesos de Poisson * Victor M. Pérez Abreu C. Departamento de Probabilidad y Estadística, CIMAT David Reynoso Valle Licenciatura en Matemáticas, DEMAT, Universidad de Guanajuato 22
Introducción a los Procesos de Poisson * Victor M. Pérez Abreu C. Departamento de Probabilidad y Estadística, CIMAT David Reynoso Valle Licenciatura en Matemáticas, DEMAT, Universidad de Guanajuato 22
Generación de variables aleatorias continuas Método de la transformada inversa
 Generación de variables aleatorias continuas Método de la transformada inversa Georgina Flesia FaMAF 17 de abril, 2012 Generación de v.a. discretas Existen diversos métodos para generar v.a. discretas:
Generación de variables aleatorias continuas Método de la transformada inversa Georgina Flesia FaMAF 17 de abril, 2012 Generación de v.a. discretas Existen diversos métodos para generar v.a. discretas:
Variables aleatorias
 Ejemplo: Suponga que un restaurant ofrecerá una comida gratis al primer cliente que llegue que cumpla años ese día. Cuánto tiene que esperar el restaurant para que la primera persona cumpliendo años aparezca?
Ejemplo: Suponga que un restaurant ofrecerá una comida gratis al primer cliente que llegue que cumpla años ese día. Cuánto tiene que esperar el restaurant para que la primera persona cumpliendo años aparezca?
1. Teoría de probabilidad
 Disclaimer: Este apunte no es autocontenido y fue pensado como un repaso de los conceptos, no para aprenderlos de aquí directamente 1 Teoría de probabilidad Definición 1 (espacio muestral) Un espacio muestral
Disclaimer: Este apunte no es autocontenido y fue pensado como un repaso de los conceptos, no para aprenderlos de aquí directamente 1 Teoría de probabilidad Definición 1 (espacio muestral) Un espacio muestral
JUEGO DE BASKETBALL. Repaso de Distribuciones de Probabilidad Discretas y Continuas
 JUEGO DE BASKETBALL Repaso de Distribuciones de Probabilidad Discretas y Continuas PREGUNTA #1 Qué es una variable aleatoria uniforme discreta? Cómo es su distribución? Qué es una variable aleatoria uniforme
JUEGO DE BASKETBALL Repaso de Distribuciones de Probabilidad Discretas y Continuas PREGUNTA #1 Qué es una variable aleatoria uniforme discreta? Cómo es su distribución? Qué es una variable aleatoria uniforme
Profesores: M. Guerrero - J. Pérez - C. Olivares - J. Rozas 09 de julio de Examen Probabilidad y Estadísticas
 09 de julio de 013 Examen Probabilidad y Estadísticas 1) Una cadena de tiendas de pintura produce y vende pinturas de látex y esmaltes. Con base en las ventas de largo plazo, la probabilidad de que un
09 de julio de 013 Examen Probabilidad y Estadísticas 1) Una cadena de tiendas de pintura produce y vende pinturas de látex y esmaltes. Con base en las ventas de largo plazo, la probabilidad de que un
PROBABILIDADES Y ESTADÍSTICA (C) PRÁCTICA 4
 PROBABILIDADES Y ESTADÍSTICA (C) PRÁCTICA 4 1. Sea (X,Y) un vector aleatorio con función de densidad conjunta i*,, í k(x2 + y2) 20
PROBABILIDADES Y ESTADÍSTICA (C) PRÁCTICA 4 1. Sea (X,Y) un vector aleatorio con función de densidad conjunta i*,, í k(x2 + y2) 20
Generación de variables aleatorias continuas
 Generación de variables aleatorias continuas Se dice que una variable aleatoria X es continua, o más propiamente, absolutamente continua, si existe f : R R tal que F (x) := P (X x) = x f(t) dt. Al igual
Generación de variables aleatorias continuas Se dice que una variable aleatoria X es continua, o más propiamente, absolutamente continua, si existe f : R R tal que F (x) := P (X x) = x f(t) dt. Al igual
Definición 1 (Probabilidad Condicional) Observación 1 Se puede aplicar la definición también a variables discretas o continuas.
 CAPÍTULO 1: ALGUNAS REGLAS DE PROBABILIDAD Para leer Lee: Capítulo 1 Definición 1 (Probabilidad Condicional) Para dos sucesos A y B, P (A B) P (A B) P (B) Observación 1 Se puede aplicar la definición también
CAPÍTULO 1: ALGUNAS REGLAS DE PROBABILIDAD Para leer Lee: Capítulo 1 Definición 1 (Probabilidad Condicional) Para dos sucesos A y B, P (A B) P (A B) P (B) Observación 1 Se puede aplicar la definición también
TEMA 6. Distribuciones
 TEMA 6. Distribuciones Alicia Nieto Reyes BIOESTADÍSTICA Alicia Nieto Reyes (BIOESTADÍSTICA) TEMA 6. Distribuciones 1 / 16 Probabilidad= Distribución= Distribución de Probabilidad Cuando queremos conocer
TEMA 6. Distribuciones Alicia Nieto Reyes BIOESTADÍSTICA Alicia Nieto Reyes (BIOESTADÍSTICA) TEMA 6. Distribuciones 1 / 16 Probabilidad= Distribución= Distribución de Probabilidad Cuando queremos conocer
8 Resolución de algunos ejemplos y ejercicios del tema 8.
 INTRODUCCIÓN A LA ESTADÍSTICA. GRUPO 71 LADE. 29 8 Resolución de algunos ejemplos y ejercicios del tema 8. 8.1 Ejemplos. Ejemplo 49 Supongamos que el tiempo que tarda en dar respuesta a un enfermo el personal
INTRODUCCIÓN A LA ESTADÍSTICA. GRUPO 71 LADE. 29 8 Resolución de algunos ejemplos y ejercicios del tema 8. 8.1 Ejemplos. Ejemplo 49 Supongamos que el tiempo que tarda en dar respuesta a un enfermo el personal
Departamento de Matemática Aplicada a las T.I.C. SOLUCIONES
 Departamento de Matemática Aplicada a las T.I.C. ASIGNATURA: ESTADÍSTICA Y PROCESOS ESTOCÁSTICOS EAMEN FINAL Otoño 25-6 FECHA: 5 de Enero de 26 Fecha publicación notas: 22 de Enero de 26 Fecha revisión
Departamento de Matemática Aplicada a las T.I.C. ASIGNATURA: ESTADÍSTICA Y PROCESOS ESTOCÁSTICOS EAMEN FINAL Otoño 25-6 FECHA: 5 de Enero de 26 Fecha publicación notas: 22 de Enero de 26 Fecha revisión
Modelo de Probabilidad
 Capítulo 1 Modelo de Probabilidad 1.1 Definiciones y Resultados Básicos Sea Ω un conjunto arbitrario. Definición 1.1 Una familia no vacía F de subconjuntos de Ω es llamada una σ-álgebra de subconjuntos
Capítulo 1 Modelo de Probabilidad 1.1 Definiciones y Resultados Básicos Sea Ω un conjunto arbitrario. Definición 1.1 Una familia no vacía F de subconjuntos de Ω es llamada una σ-álgebra de subconjuntos
PROBLEMAS DE ESTADISTICA
 ESTADÍSTICA, CURSO 2008 2009 1 PROBLEMAS DE ESTADISTICA 2. DISTRIBUCIONES DE PROBABILIDAD 2 1. Una urna contiene 6 bolas blancas, 4 rojas y 2 azules. Si se extraen 3 bolas sucesivamente sin reemplazamiento,
ESTADÍSTICA, CURSO 2008 2009 1 PROBLEMAS DE ESTADISTICA 2. DISTRIBUCIONES DE PROBABILIDAD 2 1. Una urna contiene 6 bolas blancas, 4 rojas y 2 azules. Si se extraen 3 bolas sucesivamente sin reemplazamiento,
Var E E x f x dx E. E[aX + b] = b + a E[X] Var[aX + b] = a Var[X] 83) Mendel pg158 Sea la función de densidad de una variable aleatoria continua
![Var E E x f x dx E. E[aX + b] = b + a E[X] Var[aX + b] = a Var[X] 83) Mendel pg158 Sea la función de densidad de una variable aleatoria continua Var E E x f x dx E. E[aX + b] = b + a E[X] Var[aX + b] = a Var[X] 83) Mendel pg158 Sea la función de densidad de una variable aleatoria continua](/thumbs/86/94758077.jpg) 1.1 Continuas 1.1.1 Genéricas Transformaciones: Probabilidades: E F(x) = P( x) df(x) = M f( xdx ) = 1 dx = x f x dx [] [] = ( []) = ( []) [ ] Var E E x f x dx E E[a + b] = b + a E[] Var[a + b] = a Var[]
1.1 Continuas 1.1.1 Genéricas Transformaciones: Probabilidades: E F(x) = P( x) df(x) = M f( xdx ) = 1 dx = x f x dx [] [] = ( []) = ( []) [ ] Var E E x f x dx E E[a + b] = b + a E[] Var[a + b] = a Var[]
Folleto de Estadísticas. Teoría del 1er Parcial
 Folleto de Estadísticas Teoría del 1er Parcial 2012 Población objetivo: Es un conjunto bien definido de elementos sobre los que se desea hacer algún tipo de investigación o medida. Unidades de investigación:
Folleto de Estadísticas Teoría del 1er Parcial 2012 Población objetivo: Es un conjunto bien definido de elementos sobre los que se desea hacer algún tipo de investigación o medida. Unidades de investigación:
Definición Una hipótesis es una afirmación acerca de un parámetro.
 Capítulo 8 Prueba de hipótesis Existen dos áreas de interés en el proceso de inferencia estadística: la estimación puntual y las pruebas de hipótesis. En este capítulo se presentan algunos métodos para
Capítulo 8 Prueba de hipótesis Existen dos áreas de interés en el proceso de inferencia estadística: la estimación puntual y las pruebas de hipótesis. En este capítulo se presentan algunos métodos para
