Ingeniería en Informática
|
|
|
- Vicente Aranda Castilla
- hace 7 años
- Vistas:
Transcripción
1 Ingeniería en Informática Criptografía 7 de septiembre de 2007 APELLIDOS: En el siguiente test cada respuesta correcta aporta 2 3 resta 1 6 puntos. NOMBRE: puntos, mientras que cada respuesta fallida 1. La función resumen MD5 ha quedado en entredicho y se considera no resistente a colisiones fuertes. Por otro lado, SHA1 todavía se considera una función resumen segura. Consideremos las siguientes composiciones: SHA1 MD5(X) y MD5 SHA1(X) son funciones resúmenes resistentes a colisiones fuertes. SHA1 MD5(X) no es resistente a colisiones fuertes. MD5 SHA1(X) no es unidireccional. SHA1 MD5(X) no es una función resumen. 2. Sea α un elemento primitivo de Z p. Elegir la respuesta correcta. α i mod p es un elemento primitivo para cualquier 0 < i < p 1. α i mod p sólo es un elemento primitivo para i = 1. α i mod p es un elemento primitivo para 0 < i < p 1 con mcd(i, p 1) 1. α i mod p es un elemento primitivo para 0 < i < p 1 con mcd(i, p 1) = Sea X = x 1... x n una secuencia de bits donde cada x i es un bloque de 64-bits (1 i n). X se va a cifrar usando DES del siguiente modo: z 0 = IV z i = DES(z i 1, k), y i = x i z i donde k es una clave para DES y IV un bloque inicial de 64 bits. Y = y 0 y 1... y n denota la secuencia obtenida mediante el cifrado. Supongamos que en la transmisión del bloque j-ésimo, y j, (0 < j < n) se ha producido algunos errores (algunos 1 s se han cambiado por 0 s y/o viceversa) entonces en el descifrado de Y por parte del receptor se obtiene la secuencia X = x 1... x n: Hay un sólo bloque que no se descifra correctamente (x j x j ), el resto de los bloques se descifran correctamente (x i = x i, i j). Hay exactamente dos bloques que no se descifran correctamente (x j x j y x j+1 x j+1 ). Todos los bloques a partir del j-ésimo no se descifran correctamente (x i x i, j i n). 4. De las siguientes posibilidades para n, señalar cuál es la más apropiada de entre todas para formar una buena clave pública RSA (n, 35): En un criptosistema de ElGamal de clave pública (p, α, α a ) un intruso intercepta el mensaje cifrado (n, k), e identifica n como α 3. En estas circunstancias: El intruso puede descifrar el mensaje, aun cuando no puede saber el valor de a, con sólo calcular el inverso i de (α a ) 3 en Z p y realizar k i (mod p). El intruso puede descifrar cualquier mensaje enviado con este criptosistema, toda vez que puede calcular el valor a de la clave privada. El intruso no puede descifrar ningún mensaje (ni siquiera el que ha interceptado), toda vez que no puede resolver el problema del logaritmo discreto.
2 6. Trabajando en Z 27 (x i Z 27 ) se cifra un texto x = x 1 x l del siguiente modo : x se divide en n bloques de 6 elementos, efectuando un relleno del último bloque si fuera necesario, x = X 1... X n Y i = X i K + b con K = y b = (4, 4, 4, 4, 4) Retorna y = Y 1... Y n (y es el cifrado de x). Se trata de un cifrado por sustitución monoalfabética. Se trata de un cifrado por sustitución polialfabética (Vigenère). Se trata de un cifrado por transposición. Se trata de un cifrado por una composición de sustitución y transposición. 7. En una empresa todos los usuarios usan el número 3 como su exponente de cifrado en RSA. Indique cuál es el riesgo cuando alguien envía el mismo mensaje a varios miembros de la empresa: Ninguno, porque cada uno usa un módulo diferente. Usando el Teorema de Euler se podrían obtener las claves privadas ya que 3 es muy pequeño. Interceptando el cifrado de un mensaje enviado a 3 destinatarios y usando el Teorema Chino del Resto, es muy probable que un atacante pueda encontrar el mensaje en claro. 8. Benito tiene como clave pública RSA n = y e = Óscar ha descubierto que la clave privada de Benito es d = 2207 y la usa para factorizar n: Usando que d y e son inversos en φ(n) y de ahí calcular φ(n). Utilizando un ataque de fuerza bruta para calcular φ(n). No está bien planteado ya que no es un primo fuerte. 9. Para aumentar la seguridad de un cifrado AES un usuario divide su mensaje en bloques de 8 bits y cifra cada uno de ellos. Indique la respuesta correcta: Es igual de seguro que si se utilizan bloques más grandes, su seguridad es la de AES. Es muy inseguro ya que bastaría un análisis de frecuencias sobre los 2 8 posibles mensajes cifrados. Es más seguro ya que aumenta la confusión.
3 10. Benito tiene como clave pública RSA n = 33, e = 3 y clave privada d. Supongamos que es computacionalmente imposible el cálculo de la clave privada d a partir de la pública (n, d). Entonces la firma del mensaje se realizará como: 10 3 mod 33 = d mod 33 = 10. Sería 10 d mod 33 = 10, pero no es una firma fiable ya que cualquiera podría realizarla si observa que x no se cifra. 11. Usando un alfabeto de 64 caracteres, el cifrado afín x 8x + 1 no es adecuado, principalmente por el siguiente motivo: Hay mensajes en claro que dan lugar al mismo mensaje cifrado. Hay mensajes que no se pueden cifrar. La función de descifrado está bien definida. 12. Alicia y Benito desean acordar una clave común usando el sistema de Diffie-Hellman usando como primo p = 72 y generador g = 7. Si Alicia elige el exponente 12 y Benito el 5, cuál es la clave que intercambian? Alicia (A) y Benito (B) usan el siguiente protocolo con el cual ambos verifican que conocen una clave secreta común k, usando una función resumen h: A envía a B el valor h(h(k)). B calcula h(h(k)) y comprueba que coincide con lo recibido. B envía h(k) a A. A calcula h(k) y comprueba que coincide con lo recibido. Si las dos comprobaciones han sido correctas, entonces ambos conocen el valor de k. Indique cuál es la afirmación correcta: Es un método válido y tan seguro como lo sea la función resumen utilizada. Es innecesario que A envíe h(h(k)), bastaría con enviar h(k). No es seguro porque cualquiera de los dos puede ser suplantado. 14. En un intento por aumentar la seguridad, un usuario que usa el alfabeto de 64 caracteres utiliza un doble cifrado XOR. Usando consecutivamente dos claves que él cree haber obtenido de forma aleatoria: la clave (A, B, C, D, E, F ) y la clave (,,, A D, B E, C F ). (Ayuda: X = X para todo carácter X del alfabeto). Indicar cuál es la respuesta más correcta: La seguridad ha aumentado, aunque el resultado sigue siendo un XOR de la misma longitud. El resultado no es un,criptosistema XOR. La seguridad ha disminuido; el resultado equivale a un XOR de longitud 3.
4 15. Un usuario de RSA ha elegido como clave pública n = 15 y e = 2 quiere cifrar los mensajes 15, 31. Al hacerlo e intentar descifrar encuentra problemas. Indique cuál es el motivo: Ha elegido un módulo demasiado pequeño y además el exponente no es primo. Ha elegido un módulo demasiado pequeño y además el exponente no tiene inverso en φ(n). Con otro exponente, por ejemplo e = 3 no hubiera tenido problemas, ya que tiene inverso en φ(n). Observaciones Alfabeto de 64 caracteres: a b c d e f g h i j k l m n ñ o p q r s t u v w x y z Ç ( ) { } < > = * / % &, ;. :?!
5 Ingeniería en Informática Criptografía 7 de Septiembre de 2007 APELLIDOS: En el siguiente test cada respuesta correcta aporta 2 3 resta 1 6 puntos. NOMBRE: puntos, mientras que cada respuesta fallida 1. La función resumen MD5 ha quedado en entredicho y se considera no resistente a colisiones fuertes. Por otro lado, SHA1 todavía se considera una función resumen segura. Consideremos las siguientes composiciones: SHA1 MD5(X) y MD5 SHA1(X) son funciones resúmenes resistentes a colisiones fuertes. X SHA1 MD5(X) no es resistente a colisiones fuertes. MD5 SHA1(X) no es unidireccional. SHA1 MD5(X) no es una función resumen. Solución Al no ser MD5 resistente a colisiones fuertes, significa que podemos encontrar parejas (X, X ) donde MD5(X) = MD5(X ). Y por tanto, SHA1 MD5(X) = SHA1 MD5(X ). 2. Sea α un elemento primitivo de Z p. Elegir la respuesta correcta. α i mod p es un elemento primitivo para cualquier 0 < i < p 1. α i mod p sólo es un elemento primitivo para i = 1. α i mod p es un elemento primitivo para 0 < i < p 1 con mcd(i, p 1) 1. X α i mod p es un elemento primitivo para 0 < i < p 1 con mcd(i, p 1) = 1. Solución. Por ser α un elemento primitivo se tiene que Z p = {α i : 0 i p 2} donde α p 1 = 1. Apliquemos el test para detectar los elementos primitivos. Se tiene que p 1 = q s qsj j. (α i ) (p 1)/q l = (α i(p 1)/q l ) Si mcd(i, p 1) = 1 se tiene que el exponente i(p 1)/q l no es divisible por p 1 para cualquier 1 l j, entonces existe 0 < r < p 1 tal que (este r es el resto de dividir el exponente por p 1) (α i(p 1)/q l ) = α r α c (p 1) = α r 1 mod p q l. 3. Sea X = x 1... x n una secuencia de bits donde cada x i es un bloque de 64-bits (1 i n). X se va a cifrar usando DES del siguiente modo: z 0 = IV, z i = DES(z i 1, k), y i = x i z i donde k es una clave para DES y IV un bloque inicial de 64 bits. Y = y 0 y 1... y n denota la secuencia obtenida mediante el cifrado. Supongamos que en la transmisión del bloque j-ésimo, y j, (0 < j < n) se ha producido algunos errores (algunos 1 s se han cambiado por 0 s y/o viceversa) entonces en el descifrado de Y por parte del receptor se obtiene la secuencia X = x 1... x n: X Hay un sólo bloque que no se descifra correctamente (x j x j ), el resto de los bloques se descifran correctamente (x i = x i, i j). Hay exactamente dos bloques que no se descifran correctamente (x j x j y x j+1 x j+1 ). Todos los bloques a partir del j-ésimo no se descifran correctamente (x i x i, j i n). Solución.
6 Es fácil ver que el descifrado viene dado por z 0 = IV, z i = DES(z i 1, k), x i = y i z i Teniendo en cuenta esta fórmula que y j interviene sólo en x j. 4. De las siguientes posibilidades para n, señalar cuál es la más apropiada de entre todas para formar una buena clave pública RSA (n, 35): X Solución. La opción segunda no es válida, pues se puede factorizar por el método de Fermat. La tercera opción no es buena, porque el mínimo común múltiplo de p 1 y q 1 es muy pequeño, lo que provoca que haya muchos exponentes que descifran. La cuarta no es compatible con e = 35, toda vez que 35 no es primo con φ(n). 5. En un criptosistema de ElGamal de clave pública (p, α, α a ) un intruso intercepta el mensaje cifrado (n, k), e identifica n como α 3. En estas circunstancias: X El intruso puede descifrar el mensaje, aun cuando no puede saber el valor de a, con sólo calcular el inverso i de (α a ) 3 en Z p y realizar k i (mod p). El intruso puede descifrar cualquier mensaje enviado con este criptosistema, toda vez que puede calcular el valor a de la clave privada. El intruso no puede descifrar ningún mensaje (ni siquiera el que ha interceptado), toda vez que no puede resolver el problema del logaritmo discreto. Solución. Efectivamente, si la máscara utilizada ha sido n = α 3, para descifrar el mensaje enviado basta proceder haciendo k ((α a ) 3 ) 1, operaciones todas que puede hacer el intruso sin necesidad de conocer a (recuérdese que α a es público). 6. Trabajando en Z 27 (x i Z 27 ) se cifra un texto x = x 1 x l del siguiente modo : x se divide en n bloques de 6 elementos, efectuando un relleno del último bloque si fuera necesario, x = X 1... X n Y i = X i K + b con K = y b = (4, 4, 4, 4, 4, 4) Retorna y = Y 1... Y n (y es el cifrado de x). Se trata de un cifrado por sustitución monoalfabética. Se trata de un cifrado por sustitución polialfabética. Se trata de un cifrado por transposición. X Se trata de un cifrado por una composición de sustitución y transposición. Solución. Es claro que el producto X i K lo que hace es permutar los bits de X i y al sumar 4 módulo 27 a todos los caracteres se trata de un desplazamiento (sustitución). 7. En una empresa todos los usuarios usan el número 3 como su exponente de cifrado en RSA. Indique cuál es el riesgo cuando alguien envía el mismo mensaje a varios miembros de la empresa:
7 Ninguno, porque cada uno usa un módulo diferente. Usando el Teorema de Euler se podrían obtener las claves privadas ya que 3 es muy pequeño. X Interceptando el cifrado de un mensaje enviado a 3 destinatarios y usando el Teorema Chino del Resto, es muy probable que un atacante pueda encontrar el mensaje en claro. Solución. Si las claves públicas de los 3 destinatarios son respectivamente; (n 1, 3), (n 2, 3) y (n 3, 3) y los tres mensajes cifrados son y 1, y 2 e y 3 entonces el atacante resolvería el sistema α y 1 mod n 1 α y 2 mod n 2 α y 3 mod n 3 como es muy probable que los n i sean primos entre si dos a dos, entonces por el Teorema Chino del Resto, el sistema tiene una única solución 0 < α < n 1 n 2 n 3. Entonces el mensaje en claro x sería la raíz cúbica entera de α. 8. Benito tiene como clave pública RSA n = y e = Óscar ha descubierto que la clave privada de Benito es d = 2207 y la usa para factorizar n: X Usando que d y e son inversos en φ(n) y de ahí calcular φ(n). Utilizando un ataque de fuerza bruta para calcular φ(n). No está bien planteado ya que no es un primo fuerte. Solución. Óscar sabe que d e 1 mod φ(n) con lo que d e 1 = k φ(n) lo que puede proporcionar el valor de φ(n) y con él factorizar n. 9. Para aumentar la seguridad de un cifrado AES un usuario divide su mensaje en bloques de 8 bits y cifra cada uno de ellos. Indique la respuesta correcta: Es igual de seguro que si se utilizan bloques más grandes, su seguridad es la de AES. X Es muy inseguro ya que bastaría un análisis de frecuencias sobre los 2 8 posibles mensajes cifrados. Es más seguro ya que aumenta la confusión. solución El resultado equivale a un criptosistema de sustitución con un alfabeto de 2 8 = 256 caracteres que puede ser roto con el ataque basado en el de análisis de frecuencias. 10. Benito tiene como clave pública RSA n = 33, e = 3 y clave privada d. Supongamos que es computacionalmente imposible el cálculo de la clave privada d a partir de la pública (n, d). Entonces la firma del mensaje se realizará como: 10 3 mod 33 = d mod 33 = 10. X Sería 10 d mod 33 = 10, pero no es una firma fiable ya que cualquiera podría realizarla si observa que x no se cifra. Solución. El cálculo de la firma se hace con la clave privada y sería 10 d mod 33. Como 10 3 mod 33 = 10 entonces 10 d mod 33 = 10 (10 es un mensaje que no se cifra). Un atacante que lo observara podría suplantar a Benito firmando este mensaje por él.
8 11. Usando un alfabeto de 64 caracteres, el cifrado afín x 8x + 1 no es adecuado, principalmente por el siguiente motivo: X Hay mensajes en claro que dan lugar al mismo mensaje cifrado. Hay mensajes que no se pueden cifrar. La función de descifrado está bien definida. Solución. Al ser 8 no invertible en Z 64, no se podrá definir la función de descifrado y habrá varios mensajes que se cifren en el mismo. Por ejemplo, 1 9, Alicia y Benito desean acordar una clave común usando el sistema de Diffie-Hellman usando como primo p = 72 y generador g = 7. Si Alicia elige el exponente 12 y Benito el 5, cuál es la clave que intercambian? X Solución. esquema: Hemos seguido la misma notación que en los apuntes, el protocolo sigue el siguiente Alicia envía a Benito: g xa mod p = 7 5 mod 71 = 51. Benito envía a Alicia: g x b mod p = 7 12 mod 71 = 4. Benito calcula: 51 x b mod p = mod 71 = 30. Alicia calcula: 4 5 mod p = 4 5 mod 71 = Alicia (A) y Benito (B) usan el siguiente protocolo con el cual ambos verifican que conocen una clave secreta común k, usando una función resumen h: A envía a B el valor h(h(k)). B calcula h(h(k)) y comprueba que coincide con lo recibido. B envía h(k) a A. A calcula h(k) y comprueba que coincide con lo recibido. Si las dos comprobaciones han sido correctas, entonces ambos conocen el valor de k. Indique cuál es la afirmación correcta: X Es un método válido y tan seguro como lo sea la función resumen utilizada. Es innecesario que A envíe h(h(k)), bastaría con enviar h(k). No es seguro porque cualquiera de los dos puede ser suplantado. Solución Ninguno que no conozca k puede calcular h(k) ni h(h(k)). Más aún h(h(k)) no da información sobre h(k). El sistema es tan seguro como h. 14. En un intento por aumentar la seguridad, un usuario que usa el alfabeto de 64 caracteres utiliza un doble cifrado XOR. Usando consecutivamente dos claves que él cree haber obtenido de forma aleatoria: la clave (A, B, C, D, E, F ) y la clave (,,, A D, B E, C F ). (Ayuda: X = X para todo carácter X del alfabeto). Indicar cuál es la respuesta más correcta: La seguridad ha aumentado, aunque el resultado sigue siendo un XOR de la misma longitud. El resultado no es un,criptosistema XOR. X La seguridad ha disminuido; el resultado equivale a un XOR de longitud 3.
9 Solución. El efecto del doble cifrado es: (A, B, C, D, E, F ) (,,, A D, B E, C F ) = (A, B, C, D A D, E B E, F C F ) = (A, B, C, A, B, C) que resulta equivalente a un cifrado de sustitución con una clave de longitud Un usuario de RSA ha elegido como clave pública n = 15 y e = 2 quiere cifrar los mensajes 15, 31. Al hacerlo e intentar descifrar encuentra problemas. Indique cuál es el motivo: Ha elegido un módulo demasiado pequeño y además el exponente no es primo. X Ha elegido un módulo demasiado pequeño y además el exponente no tiene inverso en φ(n). Con otro exponente, por ejemplo e = 3 no hubiera tenido problemas, ya que tiene inverso en φ(n). Solución. El mensaje 15 es 0 en Z 15 con lo que su cifrado es 0. Por otro lado, el mensaje 31 es 1 en Z 15 con lo que su cifrado sería 1. Por tanto, el descifrado daría siempre 0 y 1, respectivamente, no 15 y 31. Esto ocurre independiente del exponente e. Además, hay otro problema ya que e = 2 no es primo con φ(15) = 8 con lo que no existe el exponente, d, de descifrado (d = e 1 mod φ(15)). Observaciones Alfabeto de 64 caracteres: a b c d e f g h i j k l m n ñ o p q r s t u v w x y z Ç ( ) { } < > = * / % &, ;. :?!
05. Criptografía de clave pública
 05. Criptografía de clave pública Criptografía 5º Curso de Ingeniería Informática Escuela Técnica Superior de Ingeniería Informática Universidad de Sevilla Contenido Cifrado con clave pública Ventajas
05. Criptografía de clave pública Criptografía 5º Curso de Ingeniería Informática Escuela Técnica Superior de Ingeniería Informática Universidad de Sevilla Contenido Cifrado con clave pública Ventajas
Ingeniería en Informática
 Ingeniería en Informática Criptografía curso 2008/09 Boletín 1. Fundamentos de la Criptografía 1. Se tiene el criptograma C que es el cifrado de un texto en castellano, C = MUNLP HJRRT OP QRT UUUUU LMUNR
Ingeniería en Informática Criptografía curso 2008/09 Boletín 1. Fundamentos de la Criptografía 1. Se tiene el criptograma C que es el cifrado de un texto en castellano, C = MUNLP HJRRT OP QRT UUUUU LMUNR
Lección 3: Sistemas de Cifra con Clave Pública
 Lección 3: Sistemas de Cifra con Pública Gonzalo Álvarez Marañón [email protected] Consejo Superior de Investigaciones Científicas Científico Titular Los tipos de criptografía Criptografía Simétrica
Lección 3: Sistemas de Cifra con Pública Gonzalo Álvarez Marañón [email protected] Consejo Superior de Investigaciones Científicas Científico Titular Los tipos de criptografía Criptografía Simétrica
Criptografía de clave pública
 Modelo de comunicación cifrada Texto Base ------------- ------ Cifrado Cifra ---------- ---------- ------ Descifrado Texto Base ------------- ---------- Intruso Terminología Texto base (B, P): mensaje
Modelo de comunicación cifrada Texto Base ------------- ------ Cifrado Cifra ---------- ---------- ------ Descifrado Texto Base ------------- ---------- Intruso Terminología Texto base (B, P): mensaje
Dígitos de control. Test de Primalidad Algoritmo para calcular a r mod n Criptografía. Aritmética Modular. personal.us.es/lcamacho. Luisa M.
 personal.us.es/lcamacho 1 NIF ISBN 2 3 4 Sistema RSA NIF NIF ISBN La letra del NIF se obtiene reduciendo el número del DNI módulo 23 y aplicando al resultado la siguiente tabla 0 T 6 Y 12 N 18 H 1 R 7
personal.us.es/lcamacho 1 NIF ISBN 2 3 4 Sistema RSA NIF NIF ISBN La letra del NIF se obtiene reduciendo el número del DNI módulo 23 y aplicando al resultado la siguiente tabla 0 T 6 Y 12 N 18 H 1 R 7
Sistemas criptográficos modernos
 Sistemas criptográficos modernos Servicios de seguridad: protocolos criptográficos Confidencialidad Autenticación del usuario Integridad del mensaje Distribución de claves Compartición de secretos Pruebas
Sistemas criptográficos modernos Servicios de seguridad: protocolos criptográficos Confidencialidad Autenticación del usuario Integridad del mensaje Distribución de claves Compartición de secretos Pruebas
APLICACIONES DE LA ARITMÉTICA MODULAR
 APLICACIONES DE LA ARITMÉTICA MODULAR Funciones de dispersión Números pseudoaleatorios Computación con números grandes Dígitos de control Criptografía Arte FUNCIONES DE DISPERSIÓN Hashing Functions Se
APLICACIONES DE LA ARITMÉTICA MODULAR Funciones de dispersión Números pseudoaleatorios Computación con números grandes Dígitos de control Criptografía Arte FUNCIONES DE DISPERSIÓN Hashing Functions Se
Seguridad Informática
 Seguridad Informática Fundamentos Matemáticos de la Criptografía Ramón Hermoso y Matteo Vasirani Universidad Rey Juan Carlos Índice 1 Divisibilidad 2 Artimética modular 3 Grupos 4 El problema del logaritmo
Seguridad Informática Fundamentos Matemáticos de la Criptografía Ramón Hermoso y Matteo Vasirani Universidad Rey Juan Carlos Índice 1 Divisibilidad 2 Artimética modular 3 Grupos 4 El problema del logaritmo
Criptografía Susana Puddu
 Susana Puddu Supongamos que Juan quiere enviar un mensaje a Pedro de forma tal que únicamente Pedro sea capaz de entender su contenido. Una manera ingenua de hacer esto es reemplazar cada letra, signo
Susana Puddu Supongamos que Juan quiere enviar un mensaje a Pedro de forma tal que únicamente Pedro sea capaz de entender su contenido. Una manera ingenua de hacer esto es reemplazar cada letra, signo
Clave Pública. Criptografía-ULL
 Clave Pública Clave Pública UsuarioA Cifrado E B Mensaje cifrado C Mensaje cifrado C Descifrado D B Usuario B Clave Pública de B Clave Privada de B Mensaje original M Mensaje original M Clave Pública Clave
Clave Pública Clave Pública UsuarioA Cifrado E B Mensaje cifrado C Mensaje cifrado C Descifrado D B Usuario B Clave Pública de B Clave Privada de B Mensaje original M Mensaje original M Clave Pública Clave
Escuela Técnica Superior de Ingeniería Informática Ingeniería en Informática CRIPTOGRAFÍA
 Escuela Técnica Superior de Ingeniería Informática Ingeniería en Informática CRIPTOGRAFÍA 6 de septiembre de 2002 Ejercicio 1[3 ptos] Consideramos el criptosistema siguiente: Cada usuario elige dos enteros
Escuela Técnica Superior de Ingeniería Informática Ingeniería en Informática CRIPTOGRAFÍA 6 de septiembre de 2002 Ejercicio 1[3 ptos] Consideramos el criptosistema siguiente: Cada usuario elige dos enteros
- Firma digital y cifrado de mensajes. Luis Villalta Márquez
 - Firma digital y cifrado de mensajes. Luis Villalta Márquez No hay nada más fácil que leer los correos de otras personas, ya que viajan desnudos por la Red. Valga la siguiente analogía. Un correo electrónico
- Firma digital y cifrado de mensajes. Luis Villalta Márquez No hay nada más fácil que leer los correos de otras personas, ya que viajan desnudos por la Red. Valga la siguiente analogía. Un correo electrónico
Algoritmos de cifrado
 11 de junio de 2015 Estructuración 1 Conceptos generales 2 3 4 5 El problema de la Criptografía tux@linux# Internet -----BEGIN PGP MESSAGE----- Version: GnuPG v1.4.10 (GNU/Linux) FcelCIKc+xEzuVo1Wbg5v91kEGDaXHhjJ1
11 de junio de 2015 Estructuración 1 Conceptos generales 2 3 4 5 El problema de la Criptografía tux@linux# Internet -----BEGIN PGP MESSAGE----- Version: GnuPG v1.4.10 (GNU/Linux) FcelCIKc+xEzuVo1Wbg5v91kEGDaXHhjJ1
Aritmética Modular MATEMÁTICA DISCRETA I. F. Informática. UPM. MATEMÁTICA DISCRETA I () Aritmética Modular F. Informática.
 Aritmética Modular MATEMÁTICA DISCRETA I F. Informática. UPM MATEMÁTICA DISCRETA I () Aritmética Modular F. Informática. UPM 1 / 30 La relación de congruencia La relación de congruencia Definición Dado
Aritmética Modular MATEMÁTICA DISCRETA I F. Informática. UPM MATEMÁTICA DISCRETA I () Aritmética Modular F. Informática. UPM 1 / 30 La relación de congruencia La relación de congruencia Definición Dado
Criptografía Simétrica / Asimétrica. La mejor forma de que la información este segura es que no exista, que no se guarden los datos, Martin Hellman
 Criptografía Simétrica / Asimétrica La mejor forma de que la información este segura es que no exista, que no se guarden los datos, Martin Hellman Criptografía Moderna. Claude Shannon (1948). Whitfield
Criptografía Simétrica / Asimétrica La mejor forma de que la información este segura es que no exista, que no se guarden los datos, Martin Hellman Criptografía Moderna. Claude Shannon (1948). Whitfield
Seguridad Informática
 Seguridad Informática Introducción a la Criptografía Ramón Hermoso y Matteo Vasirani Universidad Rey Juan Carlos Índice 1 Terminología e historia 2 Primitivas criptográficas 3 Nociones de criptoanálisis
Seguridad Informática Introducción a la Criptografía Ramón Hermoso y Matteo Vasirani Universidad Rey Juan Carlos Índice 1 Terminología e historia 2 Primitivas criptográficas 3 Nociones de criptoanálisis
Criptografía moderna La era de la criptografía moderna comienza con Claude Shannon, considerado el padre de la criptografía matemática 1.
 6.5 Criptografía 6.5.1. Criptografía clásica En la década de los setenta, ante la perspectiva de crecimiento de las redes de telecomunicaciones, las grandes empresas como IBM, iniciaron la realización
6.5 Criptografía 6.5.1. Criptografía clásica En la década de los setenta, ante la perspectiva de crecimiento de las redes de telecomunicaciones, las grandes empresas como IBM, iniciaron la realización
Sistemas basados en la Teoría de Números
 Criptografía de clave pública Sistemas basados en la Teoría de Números Departamento de Sistemas Informáticos y Computación DSIC - UPV http://www.dsic.upv.es p.1/20 Criptografía de clave pública Sistemas
Criptografía de clave pública Sistemas basados en la Teoría de Números Departamento de Sistemas Informáticos y Computación DSIC - UPV http://www.dsic.upv.es p.1/20 Criptografía de clave pública Sistemas
Sistema criptográfico de llave publica RSA. Análisis y diseño de algoritmos Jose F. Torres M.
 Sistema criptográfico de llave publica RSA Análisis y diseño de algoritmos Jose F. Torres M. Introducción Un mensaje puede cifrarse mediante la aplicación de una regla que transforme el texto en claro
Sistema criptográfico de llave publica RSA Análisis y diseño de algoritmos Jose F. Torres M. Introducción Un mensaje puede cifrarse mediante la aplicación de una regla que transforme el texto en claro
Criptografía asimétrica o de clave pública
 Criptografía asimétrica o de clave pública F. J. Martínez Zaldívar Departamento de Comunicaciones ETSI Telecomunicación Universidad Politécnica de Valencia Comunicación de Datos II Índice 1 Introducción
Criptografía asimétrica o de clave pública F. J. Martínez Zaldívar Departamento de Comunicaciones ETSI Telecomunicación Universidad Politécnica de Valencia Comunicación de Datos II Índice 1 Introducción
Matemáticas Discretas. Tema 2. Introducción a la teoría de núm
 Matemáticas Discretas. Tema Departamento de Ciencias Computacionales. Universidad Autónoma del Estado de Morelos. October 3, 2016 Tabla de contenidos. 1 Del temario. 2 Contenido del subtema 2.3 Criptografía
Matemáticas Discretas. Tema Departamento de Ciencias Computacionales. Universidad Autónoma del Estado de Morelos. October 3, 2016 Tabla de contenidos. 1 Del temario. 2 Contenido del subtema 2.3 Criptografía
CRIPTOGRAFÍA 5º CURSO DE INGENIERÍA INFORMÁTICA
 CRIPTOGRAFÍA 5º CURSO DE INGENIERÍA INFORMÁTICA Aplicaciones E.T.S.I. Informática Universidad de Sevilla Curso 2007/2008 SOBRE DIGITAL RSA Problema: Cómo intercambiar gran volumen de información cifrada
CRIPTOGRAFÍA 5º CURSO DE INGENIERÍA INFORMÁTICA Aplicaciones E.T.S.I. Informática Universidad de Sevilla Curso 2007/2008 SOBRE DIGITAL RSA Problema: Cómo intercambiar gran volumen de información cifrada
jra Taller de Criptografía Aplicada, CyberCamp 2017, Santander, 3/12/17 Página 1
 Taller de Criptografía Aplicada CyberCamp 2017. Domingo 3 de diciembre de 2017, 10:00 a 12:00 horas Dr. Jorge Ramió Aguirre 1. Ejercicios prácticos con AES (AESphere - OpenSSL) 1.1. Cifrado AES 128 en
Taller de Criptografía Aplicada CyberCamp 2017. Domingo 3 de diciembre de 2017, 10:00 a 12:00 horas Dr. Jorge Ramió Aguirre 1. Ejercicios prácticos con AES (AESphere - OpenSSL) 1.1. Cifrado AES 128 en
Redes de comunicación
 UNIVERSIDAD AMERICANA Redes de comunicación Unidad III- Criptografía: Sistemas Asimétricos Recopilación de teoría referente a la materia Ing. Luis Müller 2011 Esta es una recopilación de la teoría referente
UNIVERSIDAD AMERICANA Redes de comunicación Unidad III- Criptografía: Sistemas Asimétricos Recopilación de teoría referente a la materia Ing. Luis Müller 2011 Esta es una recopilación de la teoría referente
Criptografía. 1 a parte : Confidencialidad en las transmisiones. Curso 2013/14. Gestión Informática Empresarial
 ASI - Criptografía : Confidencialidad,1 Criptografía 1 a parte : Confidencialidad en las transmisiones Curso 2013/14 Grado Asignatura Gestión Informática Empresarial Auditoría y Seguridad Informática Profesores
ASI - Criptografía : Confidencialidad,1 Criptografía 1 a parte : Confidencialidad en las transmisiones Curso 2013/14 Grado Asignatura Gestión Informática Empresarial Auditoría y Seguridad Informática Profesores
Sistemas de claves públicas y privadas
 Sistemas de claves públicas y privadas Noemí P. Kisbye Resumen La criptografía consiste en transformar un texto claro en otro texto cifrado, de modo que este último sea ilegible a menos que se conozca
Sistemas de claves públicas y privadas Noemí P. Kisbye Resumen La criptografía consiste en transformar un texto claro en otro texto cifrado, de modo que este último sea ilegible a menos que se conozca
Criptografía. Diplomado- TI (2) Criptografía. Diplomado-TI (2) 9 de enero de 2012
 9 de enero de 2012 Simetrías y Asimetrías Para generar una transmisión segura de datos, debemos contar con un canal que sea seguro, esto es debemos emplear técnicas de forma que los datos que se envían
9 de enero de 2012 Simetrías y Asimetrías Para generar una transmisión segura de datos, debemos contar con un canal que sea seguro, esto es debemos emplear técnicas de forma que los datos que se envían
Matemáticas para proteger la Información
 ! Matemáticas para proteger la Información Ángel Martín del Rey Departamento de Matemática Aplicada Universidad de Salamanca [email protected] Bachillerato de Inves1gación, I.E.S. Vaguada de la Palma, 18
! Matemáticas para proteger la Información Ángel Martín del Rey Departamento de Matemática Aplicada Universidad de Salamanca [email protected] Bachillerato de Inves1gación, I.E.S. Vaguada de la Palma, 18
CRYPT4YOU TABLA DE CONTENIDOS DOCUMENTO ANEXO A LA LECCIÓN 3 DEL CURSO "EL ALGORITMO RSA" EJERCICIOS Y PRÁCTICAS PROPUESTOS Y RESUELTOS
 CRYPT4YOU DOCUMENTO ANEXO A LA LECCIÓN 3 DEL CURSO "EL ALGORITMO RSA" EJERCICIOS Y PRÁCTICAS PROPUESTOS Y RESUELTOS Autor: Dr. Jorge Ramió Aguirre Fecha de publicación: 12 de abril de 2012 http://www.criptored.upm.es/crypt4you/temas/rsa/leccion3/leccion03.html
CRYPT4YOU DOCUMENTO ANEXO A LA LECCIÓN 3 DEL CURSO "EL ALGORITMO RSA" EJERCICIOS Y PRÁCTICAS PROPUESTOS Y RESUELTOS Autor: Dr. Jorge Ramió Aguirre Fecha de publicación: 12 de abril de 2012 http://www.criptored.upm.es/crypt4you/temas/rsa/leccion3/leccion03.html
Capítulo 8 Seguridad en redes
 Capítulo 8 Seguridad en redes Estas clases son de Kurose y Ross Gracias a Kurose y Ross que pusieron este material libre La traducción y adaptación es de Alejandra Stolk para la materia Redes de Computadoras
Capítulo 8 Seguridad en redes Estas clases son de Kurose y Ross Gracias a Kurose y Ross que pusieron este material libre La traducción y adaptación es de Alejandra Stolk para la materia Redes de Computadoras
1. Introducción Cifrado de Hill RSA ElGamal Firma DSA Test de Miller-Rabin...
 Índice 1. Introducción 3 2. Técnicas criptográficas 5 2.1. Cifrado de Hill..................................... 8 2.2. RSA........................................... 16 2.3. ElGamal.........................................
Índice 1. Introducción 3 2. Técnicas criptográficas 5 2.1. Cifrado de Hill..................................... 8 2.2. RSA........................................... 16 2.3. ElGamal.........................................
Asignatura: Horas: Total (horas): Obligatoria Teóricas 3.0 Semana 3.0 Optativa X Prácticas Semanas 48.0 de elección
 UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE INGENIERÍA PROGRAMA DE ESTUDIO Aprobado por el Consejo Técnico de la Facultad de Ingeniería en su sesión ordinaria del 15 de octubre de 2008 CRIPTOGRAFÍA
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE INGENIERÍA PROGRAMA DE ESTUDIO Aprobado por el Consejo Técnico de la Facultad de Ingeniería en su sesión ordinaria del 15 de octubre de 2008 CRIPTOGRAFÍA
Características y uso. Recordando. La criptografia define una función de
 Introducción Criptografía Simétrica Características y uso Lámina 1 Recordando La criptografia define una función de transformación de un mensaje con base a un elemento base o llave, para obtener un nuevo
Introducción Criptografía Simétrica Características y uso Lámina 1 Recordando La criptografia define una función de transformación de un mensaje con base a un elemento base o llave, para obtener un nuevo
Un Poco de Historia Criptografía, Criptografía Clásica
 CRIPTOGRAFÍA Un Poco de Historia Criptografía, según el diccionario de la real Academia de la Lengua Española: -Arte de escribir con clave secreta o de un modo enigmático. Del griego kryptos, que significa
CRIPTOGRAFÍA Un Poco de Historia Criptografía, según el diccionario de la real Academia de la Lengua Española: -Arte de escribir con clave secreta o de un modo enigmático. Del griego kryptos, que significa
Nombre del documento: Programa de Estudio de asignatura de Especialidad
 1.- DATOS DE LA ASIGNATURA Nombre de la asignatura: Criptografía Carrera: Ingeniería en Sistemas Computacionales Clave de la asignatura: SIF-1202 SATCA: 3-2-5 2.- PRESENTACIÓN Caracterización de la asignatura.
1.- DATOS DE LA ASIGNATURA Nombre de la asignatura: Criptografía Carrera: Ingeniería en Sistemas Computacionales Clave de la asignatura: SIF-1202 SATCA: 3-2-5 2.- PRESENTACIÓN Caracterización de la asignatura.
ARITMÉTICA II. Adolfo Quirós. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS Curso
 ARITMÉTICA II COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS Curso 2012-2013 LO QUE TENÍAMOS PENDIENTE DEL OTRO DÍA Hay más números reales que números racionales? Números complejos? Números
ARITMÉTICA II COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS Curso 2012-2013 LO QUE TENÍAMOS PENDIENTE DEL OTRO DÍA Hay más números reales que números racionales? Números complejos? Números
Seguridad en Redes. Dr. Arturo Redondo Galván 1
 Seguridad en Redes 1 UNIDAD III CRIPTOGRAFÍA Y AUTENTICACIÓN 2 OBJETIVO: Identificar los elementos de seguridad y el ciclo de vida de las operaciones y las políticas de seguridad. 3 INTRODUCCIÓN (1/3)
Seguridad en Redes 1 UNIDAD III CRIPTOGRAFÍA Y AUTENTICACIÓN 2 OBJETIVO: Identificar los elementos de seguridad y el ciclo de vida de las operaciones y las políticas de seguridad. 3 INTRODUCCIÓN (1/3)
Cuadernos de Laboratorio de Criptografía jra - Entrega nº 3 - Vigenère: cifrado, descifrado y criptoanálisis 1
 Proyecto CLCript Cuadernos de Laboratorio de Criptografía. Entrega nº 3. Ultima actualización 03/07/18 Autor: Dr. Jorge Ramió Aguirre (@criptored) Prácticas con el algoritmo de Vigenère: cifrado, descifrado
Proyecto CLCript Cuadernos de Laboratorio de Criptografía. Entrega nº 3. Ultima actualización 03/07/18 Autor: Dr. Jorge Ramió Aguirre (@criptored) Prácticas con el algoritmo de Vigenère: cifrado, descifrado
CRYPT4YOU TABLA DE CONTENIDOS DOCUMENTO ANEXO A LA LECCIÓN 1 DEL CURSO "EL ALGORITMO RSA" EJERCICIOS Y PRÁCTICAS PROPUESTOS Y RESUELTOS
 CRYPT4YOU DOCUMENTO ANEXO A LA LECCIÓN 1 DEL CURSO "EL ALGORITMO RSA" EJERCICIOS Y PRÁCTICAS PROPUESTOS Y RESUELTOS Autor: Dr. Jorge Ramió Aguirre Fecha de publicación: 15 de marzo de 2012 Fecha de actualización:
CRYPT4YOU DOCUMENTO ANEXO A LA LECCIÓN 1 DEL CURSO "EL ALGORITMO RSA" EJERCICIOS Y PRÁCTICAS PROPUESTOS Y RESUELTOS Autor: Dr. Jorge Ramió Aguirre Fecha de publicación: 15 de marzo de 2012 Fecha de actualización:
Matemáticas Discretas 2 - Taller 2 Aritmética modular G. Padilla
 Matemáticas Discretas 2 - Taller 2 Aritmética modular G Padilla 1 EQUIVALENCIAS Y RELACIONES DE ORDEN (1) Decide cuáles de las siguientes relaciones son equivalencias En caso afirmativo, halla el conjunto
Matemáticas Discretas 2 - Taller 2 Aritmética modular G Padilla 1 EQUIVALENCIAS Y RELACIONES DE ORDEN (1) Decide cuáles de las siguientes relaciones son equivalencias En caso afirmativo, halla el conjunto
CLCript Cuadernos de Laboratorio de Criptografía jra - Entrega nº 9 Matemáticas discretas en criptografía Página 1
 Proyecto CLCript Cuadernos de Laboratorio de Criptografía. Entrega nº 9 Última actualización 24/10/18 Autor: Dr. Jorge Ramió Aguirre (@criptored) Prácticas con el software SAMCript: Matemáticas discretas
Proyecto CLCript Cuadernos de Laboratorio de Criptografía. Entrega nº 9 Última actualización 24/10/18 Autor: Dr. Jorge Ramió Aguirre (@criptored) Prácticas con el software SAMCript: Matemáticas discretas
Seguridad Informática
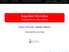 Seguridad Informática Criptografía de clave pública Ramón Hermoso y Matteo Vasirani Universidad Rey Juan Carlos Índice 1 Introducción 2 Clave pública 3 Intercambio de claves (Diffie-Hellman) 4 Cifrado
Seguridad Informática Criptografía de clave pública Ramón Hermoso y Matteo Vasirani Universidad Rey Juan Carlos Índice 1 Introducción 2 Clave pública 3 Intercambio de claves (Diffie-Hellman) 4 Cifrado
Criptografía de clave pública Sistemas basados en el problema de la mochila
 de la la La Criptografía de clave pública Sistemas basados de la DSIC - UPV (DSIC - UPV) de la 1 / 21 Contenidos del tema de la la La 1 Características de los sistemas de clave pública Principios para
de la la La Criptografía de clave pública Sistemas basados de la DSIC - UPV (DSIC - UPV) de la 1 / 21 Contenidos del tema de la la La 1 Características de los sistemas de clave pública Principios para
Síntesis y análisis de criptosistemas asimétricos
 Síntesis y análisis de criptosistemas asimétricos Prof. Dr. Javier Areitio Bertolín Director del Grupo de En el presente artículo se aborda el Investigación Redes y análisis y síntesis de una tecnología
Síntesis y análisis de criptosistemas asimétricos Prof. Dr. Javier Areitio Bertolín Director del Grupo de En el presente artículo se aborda el Investigación Redes y análisis y síntesis de una tecnología
Sistemas de Cifra en Flujo
 Sistemas de Cifra en Flujo Cifrador de flujo básico Siguiendo la propuesta de cifrador hecha en 1917 por Vernam, los cifradores de flujo (clave secreta) usan: Una cifra basada en la función XOR. Una secuencia
Sistemas de Cifra en Flujo Cifrador de flujo básico Siguiendo la propuesta de cifrador hecha en 1917 por Vernam, los cifradores de flujo (clave secreta) usan: Una cifra basada en la función XOR. Una secuencia
Comprueba tu trabajo: Cuadernos de Laboratorio de Criptografía jra - Entrega nº 7 Ataque por paradoja de cumpleaños a RSA: Parte 1 Página 1
 Proyecto CLCript Cuadernos de Laboratorio de Criptografía. Entrega nº 7 Última actualización 18/07/18 Autor: Dr. Jorge Ramió Aguirre (@criptored) Prácticas con el algoritmo RSA: ataque por paradoja del
Proyecto CLCript Cuadernos de Laboratorio de Criptografía. Entrega nº 7 Última actualización 18/07/18 Autor: Dr. Jorge Ramió Aguirre (@criptored) Prácticas con el algoritmo RSA: ataque por paradoja del
CRIPTOGRAFÍA APLICADA
 CRIPTOGRAFÍA APLICADA Duración del examen: 2 ½ horas. Consta de dos ejercicios y se usa el software safedes y genrsa que puedes encontrar en Google. El documento de examen lo tiene el alumno en su ordenador
CRIPTOGRAFÍA APLICADA Duración del examen: 2 ½ horas. Consta de dos ejercicios y se usa el software safedes y genrsa que puedes encontrar en Google. El documento de examen lo tiene el alumno en su ordenador
Tecnologías Grid Seguridad en entornos grid
 Tecnologías Grid Seguridad en entornos grid Master en Sistemas y Servicios Informáticos para Internet Universidad de Oviedo Seguridad en entornos grid Introducción Introducción Objetivos Coordinar la seguridad
Tecnologías Grid Seguridad en entornos grid Master en Sistemas y Servicios Informáticos para Internet Universidad de Oviedo Seguridad en entornos grid Introducción Introducción Objetivos Coordinar la seguridad
Algoritmos de cifrado Definir el problema con este tipo de cifrado
 Criptografía Temario Criptografía de llave secreta (simétrica) Algoritmos de cifrado Definir el problema con este tipo de cifrado Criptografía de llave pública (asimétrica) Algoritmos de cifrado Definir
Criptografía Temario Criptografía de llave secreta (simétrica) Algoritmos de cifrado Definir el problema con este tipo de cifrado Criptografía de llave pública (asimétrica) Algoritmos de cifrado Definir
UD 3:Implantación de técnicas de seguridad remoto. Seguridad perimetral
 UD 3:Implantación de técnicas de seguridad remoto Seguridad perimetral TAREA 4: VPN Acceso Remoto a) Simulación VPN de acceso Remoto usando Packet Tracer. La misión de esta práctica es simular una VPN
UD 3:Implantación de técnicas de seguridad remoto Seguridad perimetral TAREA 4: VPN Acceso Remoto a) Simulación VPN de acceso Remoto usando Packet Tracer. La misión de esta práctica es simular una VPN
Criptografía sobre curvas eĺıpticas
 Criptografía sobre curvas eĺıpticas José Galaviz Casas Departamento de Matemáticas, Facultad de Ciencias, Universidad Nacional Autónoma de México. José Galaviz Casas (Facultad de Ciencias, UNAM) Criptografía
Criptografía sobre curvas eĺıpticas José Galaviz Casas Departamento de Matemáticas, Facultad de Ciencias, Universidad Nacional Autónoma de México. José Galaviz Casas (Facultad de Ciencias, UNAM) Criptografía
Una Introducción Matemática a la Criptografía (para mis alumnos de Álgebra I)
 Una Introducción Matemática a la Criptografía (para mis alumnos de Álgebra I) Pablo De Nápoli [email protected] Una Introducción Matemática a la Criptografía(para mis alumnos de Álgebra I) p. 1 Qué es
Una Introducción Matemática a la Criptografía (para mis alumnos de Álgebra I) Pablo De Nápoli [email protected] Una Introducción Matemática a la Criptografía(para mis alumnos de Álgebra I) p. 1 Qué es
Capítulo 8 Seguridad en Redes Generalidades y Principios. Basado en: Computer Networking: A Top Down Approach, Jim Kurose, Keith Ross Addison-Wesley
 Capítulo 8 Seguridad en Redes Generalidades y Principios Basado en: Computer Networking: A Top Down Approach, Jim Kurose, Keith Ross Addison-Wesley Capítulo 8 contenidos 8.1 Qué es la seguridad en la red?
Capítulo 8 Seguridad en Redes Generalidades y Principios Basado en: Computer Networking: A Top Down Approach, Jim Kurose, Keith Ross Addison-Wesley Capítulo 8 contenidos 8.1 Qué es la seguridad en la red?
Criptografía Hash para Firma Electrónica. Dr. Luis A. Lizama Pérez
 Criptografía Hash para Firma Electrónica Dr. Luis A. Lizama Pérez Firma Electrónica Función Hash Firma de Una Sola Vez (OTS) Cadena Hash + S/Key HMAC Protocolo básico de Firma Electrónica Hash Conclusiones
Criptografía Hash para Firma Electrónica Dr. Luis A. Lizama Pérez Firma Electrónica Función Hash Firma de Una Sola Vez (OTS) Cadena Hash + S/Key HMAC Protocolo básico de Firma Electrónica Hash Conclusiones
Introducción a la Matemática Discreta
 Introducción a la Matemática Discreta Aritmética Modular Luisa María Camacho Camacho Introd. a la Matemática Discreta 1 / 39 Introducción a la Matemática Discreta Temario Tema 1. Teoría de Conjuntos. Tema
Introducción a la Matemática Discreta Aritmética Modular Luisa María Camacho Camacho Introd. a la Matemática Discreta 1 / 39 Introducción a la Matemática Discreta Temario Tema 1. Teoría de Conjuntos. Tema
Capítulo 13 Cifrado Asimétrico con Mochilas
 Capítulo 13 Cifrado Asimétrico con Mochilas Seguridad Informática y Criptografía Ultima actualización del archivo: 01/03/06 Este archivo tiene: 30 diapositivas v 4.1 Material Docente de Libre Distribución
Capítulo 13 Cifrado Asimétrico con Mochilas Seguridad Informática y Criptografía Ultima actualización del archivo: 01/03/06 Este archivo tiene: 30 diapositivas v 4.1 Material Docente de Libre Distribución
Criptografía de clave pública. El sistema RSA
 Criptografía de clave pública. El sistema RSA Estímulo del Talento Matemático Real Academia de Ciencias 20 de mayo de 2006 Intercambio de claves En 1976, Diffie y Hellman presentaron un sistema de intercambio
Criptografía de clave pública. El sistema RSA Estímulo del Talento Matemático Real Academia de Ciencias 20 de mayo de 2006 Intercambio de claves En 1976, Diffie y Hellman presentaron un sistema de intercambio
El sistema RSA. Estímulo del Talento Matemático. Real Academia de Ciencias
 El sistema RSA Estímulo del Talento Matemático Real Academia de Ciencias 30 de julio de 2003 1. Criptografíadeclave... pública? Recordemos, de la primera sesión: Qué es la criptografía? En qué consiste
El sistema RSA Estímulo del Talento Matemático Real Academia de Ciencias 30 de julio de 2003 1. Criptografíadeclave... pública? Recordemos, de la primera sesión: Qué es la criptografía? En qué consiste
Introducción a la Criptografía Cuántica
 Introducción a la Criptografía Cuántica Alfonsa García, Francisco García 1 y Jesús García 1 1 Grupo de investigación en Información y Computación Cuántica (GIICC) Introducción a la criptografía cuántica
Introducción a la Criptografía Cuántica Alfonsa García, Francisco García 1 y Jesús García 1 1 Grupo de investigación en Información y Computación Cuántica (GIICC) Introducción a la criptografía cuántica
CRIPTOGRAFÍA SIMÉTRICA Y ASIMÉTRICA
 CRIPTOGRAFÍA SIMÉTRICA Y ASIMÉTRICA Para generar una transmisión segura de datos, debemos contar con un canal que sea seguro, esto es debemos emplear técnicas de forma que los datos que se envían de una
CRIPTOGRAFÍA SIMÉTRICA Y ASIMÉTRICA Para generar una transmisión segura de datos, debemos contar con un canal que sea seguro, esto es debemos emplear técnicas de forma que los datos que se envían de una
VÍDEO intypedia014es LECCIÓN 14: FUNCIONES UNIDIRECCIONALES Y HASH. AUTOR: Dr. Hugo Krawczyk. IBM, Estados Unidos
 VÍDEO intypedia014es LECCIÓN 14: FUNCIONES UNIDIRECCIONALES Y HASH AUTOR: Dr. Hugo Krawczyk IBM, Estados Unidos Hola, bienvenidos a intypedia. Hoy vamos a estudiar el interesante mundo de las funciones
VÍDEO intypedia014es LECCIÓN 14: FUNCIONES UNIDIRECCIONALES Y HASH AUTOR: Dr. Hugo Krawczyk IBM, Estados Unidos Hola, bienvenidos a intypedia. Hoy vamos a estudiar el interesante mundo de las funciones
Tema 10 Seguridad y criptografía
 Tema 10 Seguridad y criptografía Febrero, 2011 Jorge Juan Chico , Julián Viejo Cortés Departamento de Tecnología Electrónica Universidad de Sevilla Usted es libre
Tema 10 Seguridad y criptografía Febrero, 2011 Jorge Juan Chico , Julián Viejo Cortés Departamento de Tecnología Electrónica Universidad de Sevilla Usted es libre
ESTUDIO SOBRE LA COMPLEMENTARIEDAD DEL PAR DE CLAVES RSA Y USO DE HERRAMIENTAS DE ACCESO PÚBLICO
 ESTUDIO SOBRE LA COMPLEMENTARIEDAD DEL PAR DE CLAVES RSA Y USO DE HERRAMIENTAS DE ACCESO PÚBLICO En el criptosistema asimétrico RSA el cálculo del par de claves (pública/privada) se basa en funciones aritméticas
ESTUDIO SOBRE LA COMPLEMENTARIEDAD DEL PAR DE CLAVES RSA Y USO DE HERRAMIENTAS DE ACCESO PÚBLICO En el criptosistema asimétrico RSA el cálculo del par de claves (pública/privada) se basa en funciones aritméticas
Criptografía: Matemáticas para proteger la información
 ! Criptografía: Matemáticas para proteger la información Ángel Martín del Rey Departamento de Matemática Aplicada Universidad de Salamanca [email protected] 16 de diciembre de 2015 Bachillerato de Investigación
! Criptografía: Matemáticas para proteger la información Ángel Martín del Rey Departamento de Matemática Aplicada Universidad de Salamanca [email protected] 16 de diciembre de 2015 Bachillerato de Investigación
Prácticas Seguras de Criptografía en Aplicaciones WEB Henry Sánchez
 Prácticas Seguras de Criptografía en Aplicaciones WEB Henry Sánchez @_g05u_ AGENDA QUIEN SOY? Security Leader en INZAFE PERU S.A., 7 años de experiencia en TI, 5 años de experiencia profesional en seguridad
Prácticas Seguras de Criptografía en Aplicaciones WEB Henry Sánchez @_g05u_ AGENDA QUIEN SOY? Security Leader en INZAFE PERU S.A., 7 años de experiencia en TI, 5 años de experiencia profesional en seguridad
Algoritmo de Dixon Ataque de Wiener
 Algoritmo de Dixon Ataque de Wiener México 2011 1 Criba cuadrática 2 Ataque de Wiener Algoritmo de Dixon Factorización Supongamos que nuestra base de primos B := {p 1,...,p b } consiste de los primeros
Algoritmo de Dixon Ataque de Wiener México 2011 1 Criba cuadrática 2 Ataque de Wiener Algoritmo de Dixon Factorización Supongamos que nuestra base de primos B := {p 1,...,p b } consiste de los primeros
Seguridad y criptografía
 Seguridad y criptografía Jorge Juan Chico , Julián Viejo Cortés . 2011, 2014 Departamento de Tecnología Electrónica Universidad de Sevilla Usted es libre de copiar,
Seguridad y criptografía Jorge Juan Chico , Julián Viejo Cortés . 2011, 2014 Departamento de Tecnología Electrónica Universidad de Sevilla Usted es libre de copiar,
MÓDULO 2 NIVEL AVANZADO Las fuentes de información institucional Unidad didáctica 5: La seguridad en las operaciones telemáticas
 MÓDULO 2 NIVEL AVANZADO Las fuentes de información institucional E. La seguridad en las operaciones telemáticas La firma digital La firma electrónica es un sistema electrónico de acreditación que permite
MÓDULO 2 NIVEL AVANZADO Las fuentes de información institucional E. La seguridad en las operaciones telemáticas La firma digital La firma electrónica es un sistema electrónico de acreditación que permite
6.4 Criptología Elementos de la criptología
 6.4 Criptología 6.4.1. Elementos de la criptología La criptología actual está basada en el estudio de aspectos matemáticos y computacionales, además del contexto social y económico de todos los servicios
6.4 Criptología 6.4.1. Elementos de la criptología La criptología actual está basada en el estudio de aspectos matemáticos y computacionales, además del contexto social y económico de todos los servicios
Matemáticas aplicadas a la criptografía
 Matemáticas aplicadas a la criptografía Unidad II - Teoría de Números Dr. Luis J. Dominguez Perez Universidad Don Bosco Abril 23, 2013 Contenido de la sección 1 Divisibilidad y Euclides Congruencias Factorización
Matemáticas aplicadas a la criptografía Unidad II - Teoría de Números Dr. Luis J. Dominguez Perez Universidad Don Bosco Abril 23, 2013 Contenido de la sección 1 Divisibilidad y Euclides Congruencias Factorización
TEMA 3: SERVICIO SSH
 TEMA 3: SERVICIO SSH QUE ES SSH? Sucesor de telnet Problemas de seguridad Permite conexiones seguras a través de redes inseguras Da soporte seguro a cualquier protocolo que funcionen sobre TCP VENTAJAS
TEMA 3: SERVICIO SSH QUE ES SSH? Sucesor de telnet Problemas de seguridad Permite conexiones seguras a través de redes inseguras Da soporte seguro a cualquier protocolo que funcionen sobre TCP VENTAJAS
T E M A. Algoritmos de criptografía simétrica. [2.1] Cómo estudiar este tema? [2.2] Cifradores de bloque. [2.3] Cifradores de flujo
![T E M A. Algoritmos de criptografía simétrica. [2.1] Cómo estudiar este tema? [2.2] Cifradores de bloque. [2.3] Cifradores de flujo T E M A. Algoritmos de criptografía simétrica. [2.1] Cómo estudiar este tema? [2.2] Cifradores de bloque. [2.3] Cifradores de flujo](/thumbs/54/33552196.jpg) Algoritmos de criptografía simétrica [2.1] Cómo estudiar este tema? [2.2] Cifradores de bloque [2.3] Cifradores de flujo [2.4] Funciones resumen T E M A 2 Esquema Algoritmos de criptografía simétrica Cifrado
Algoritmos de criptografía simétrica [2.1] Cómo estudiar este tema? [2.2] Cifradores de bloque [2.3] Cifradores de flujo [2.4] Funciones resumen T E M A 2 Esquema Algoritmos de criptografía simétrica Cifrado
Introducción a la Matemática Discreta. Grado en Ingeniería Informática. Informática de Computadores. 22 de Diciembre de Grupo 3.
 Introducción a la Matemática Discreta. Grado en Ingeniería Informática. Informática de Computadores. 22 de Diciembre de 2014. Grupo 3. Nombre: Ejercicio 1 (1.5 puntos) a) Hallar una fórmula explícita para
Introducción a la Matemática Discreta. Grado en Ingeniería Informática. Informática de Computadores. 22 de Diciembre de 2014. Grupo 3. Nombre: Ejercicio 1 (1.5 puntos) a) Hallar una fórmula explícita para
Taller de Talento Matemático. Congruencias
 Taller de Talento Matemático http://www.unizar.es/ttm [email protected] Congruencias (5 de noviembre de 2004) Alberto Elduque Departamento de Matemáticas. Universidad de Zaragoza. [email protected] Hoy vamos
Taller de Talento Matemático http://www.unizar.es/ttm [email protected] Congruencias (5 de noviembre de 2004) Alberto Elduque Departamento de Matemáticas. Universidad de Zaragoza. [email protected] Hoy vamos
Explicación del Cifrado en Bloques Simétrico DES
 Explicación del Cifrado en Bloques Simétrico DES 1. Introducción 2. Descripción del algoritmo DES 3. Algoritmo de Cifrado 4. Generación de la subclave Ki 5. Función f(r i-1, K i ) 6. Suma L i R i 7. Permutación
Explicación del Cifrado en Bloques Simétrico DES 1. Introducción 2. Descripción del algoritmo DES 3. Algoritmo de Cifrado 4. Generación de la subclave Ki 5. Función f(r i-1, K i ) 6. Suma L i R i 7. Permutación
CAPITULO 1 INTRODUCCIÓN A LA CRIPTOGRAFÍA
 CAPITULO 1 INTRODUCCIÓN A LA CRIPTOGRAFÍA Cuando se realiza cualquier tipo de transacción comercial en Internet, como por ejemplo, comprar una entrada para un espectáculo, revisar el estado de cuenta en
CAPITULO 1 INTRODUCCIÓN A LA CRIPTOGRAFÍA Cuando se realiza cualquier tipo de transacción comercial en Internet, como por ejemplo, comprar una entrada para un espectáculo, revisar el estado de cuenta en
VÍDEO intypedia002es LECCIÓN 2: SISTEMAS DE CIFRA CON CLAVE SECRETA. AUTOR: Fausto Montoya Vitini
 VÍDEO intypedia002es LECCIÓN 2: SISTEMAS DE CIFRA CON CLAVE SECRETA AUTOR: Fausto Montoya Vitini Consejo Superior de Investigaciones Científicas, Madrid, España Hola, bienvenidos a intypedia. La lección
VÍDEO intypedia002es LECCIÓN 2: SISTEMAS DE CIFRA CON CLAVE SECRETA AUTOR: Fausto Montoya Vitini Consejo Superior de Investigaciones Científicas, Madrid, España Hola, bienvenidos a intypedia. La lección
10 CRIPTOGRAFÍA, PROTECCIÓN DE DATOS Y APLICACIONES c RA-MA
 ÍNDICE PRÓLOGO................................................... 27 CAPÍTULO 1. INTRODUCCIÓN A LA CRIPTOGRAFÍA.. 29 1.1. IDEAS BÁSICAS Y CONCEPTOS GENERALES....... 29 1.2. SUSTITUCIÓN Y TRANSPOSICIÓN.............
ÍNDICE PRÓLOGO................................................... 27 CAPÍTULO 1. INTRODUCCIÓN A LA CRIPTOGRAFÍA.. 29 1.1. IDEAS BÁSICAS Y CONCEPTOS GENERALES....... 29 1.2. SUSTITUCIÓN Y TRANSPOSICIÓN.............
