UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO
|
|
|
- María José del Río Ortíz
- hace 7 años
- Vistas:
Transcripción
1 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MODELO CURSO MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES Y CRITERIOS GENERALES DE CALIFICACIÓN INSTRUCCIONES: El alumno deberá elegir una de las dos opciones A o B que figuran en el presente examen y contestar razonadamente a los cinco ejercicios de los que consta la opción elegida. Para la realización de esta prueba se puede utilizar calculadora científica, siempre que no disponga de capacidad de representación gráfica o de cálculo simbólico. CALIFICACIÓN: La puntuación máxima de cada ejercicio es de 2 puntos. TIEMPO: Una hora y treinta minutos. OPCIÓN A Problema 1.- (Calificación máxima: 2 puntos) Discútase el sistema siguiente en función del parámetro a R : x y = a x +az = 0 2x y +a 2 z = 1. Problema 2.- (Calificación máxima: 2 puntos) Dada la función real de variable real f (x) = 3x2 5 x + 1 a) Hállense sus asíntotas horizontales, verticales y oblícuas. b) Hállense los puntos de corte de la gráfica de f con los ejes de coordenadas y sus intervalos de crecimiento y decrecimiento. Problema 3.- (Calificación máxima: 2 puntos) x 2 3x 5 si x 1 Dada la función real de variable real f (x) = x 2 si x > 1. a) Estúdiese la continuidad de la función en R. b) Calcúlese 2 0 f (x) dx. Problema 4.- (Calificación máxima: 2 puntos) Tres máquinas A, B y C fabrican tornillos del mismo tipo. La probabilidad de que un tornillo fabricado en la máquina A sea defectuoso es 0, 01, de que lo sea uno fabricado en B es 0, 02 y de que lo sea si ha sido manufacturado en C es 0, 03. En una caja se mezclan 120 tornillos: 15 de la máquina A, 30 de la B y 75 de la C. a) Calcúlese la probabilidad de que un tornillo elegido al azar no sea defectuoso. b) Elegido un tornillo al azar resulta defectuoso. Cuál es la probabilidad de que haya sido fabricado por la máquina B? Problema 5.- (Calificación máxima: 2 puntos) El peso en gramos del contenido de las cajas de cereales de una cierta marca se puede aproximar por una variable aleatoria con distribución normal de media µ desconocida y desviación típica igual a 5 gramos. Se toma una muestra de tamaño 144. a) Calcúlese la probabilidad de que el valor absoluto de la diferencia entre la media de la muestra y µ sea menor de 1 gramo. b) Si la media muestral obtenida es igual a 499, 5 gramos, determínese un intervalo de confianza con un nivel del 90 % para el peso medio de ese tipo de cajas de cereales.
2 OPCIÓN B Problema 1.- (Calificación máxima: 2 puntos) a) Determínense los valores de a y b para que la función objetivo F(x, y) = 3x + y alcance su valor máximo en el punto (6, 3) de la región factible definida por x 0 y 0 x + ay 3 2x + y b. b) Represéntese la región factible para esos valores y calcúlense las coordenadas de todos sus vértices. Problema 2.- (Calificación ( ) máxima: 2 puntos) 2 3 Sea la matriz A =. 1 2 a) Obténgase A b) Hállese la matriz B tal que A B = ( ) Problema 3.- (Calificación máxima: 2 puntos) El coste de fabricación de una serie de hornos microondas viene dado por la función C(x) = x x , donde x representa el número de hornos fabricados. Supongamos que cada horno se vende por 490 euros. a) Determínese la función de beneficios. b) Cuántos microondas deben fabricarse y venderse para que los beneficios sean máximos? Cuál es el importe de esos beneficios máximos? Problema 4.- (Calificación máxima: 2 puntos) Sean A y B dos sucesos aleatorios tales que P(A) = 1 2 P(B) = 3 4 P(A B) = 2 3. a) Determínese si son compatibles o incompatibles los sucesos A y B. b) Determínese si son dependientes o independientes los sucesos A y B. Nota: S denota al suceso complementario del suceso S. Problema 5.- (Calificación máxima: 2 puntos) La altura de los árboles de una determinada comarca se puede aproximar por una variable aleatoria con distribución normal de media desconocida y varianza 25 cm. Se toma una muestra aleatoria simple y, para un nivel de confianza del 95 %, se construye un intervalo de confianza para la media poblacional cuya amplitud es de 2, 45 cm. a) Determínese el tamaño de la muestra seleccionada. b) Determínese el límite superior y el inferior del intervalo de confianza si la altura media para la muestra seleccionada fue de 170 cm.
3 ÁREAS BAJO LA DISTRIBUCIÓN DE PROBABILIDAD NORMAL ESTÁNDAR Los valores en la tabla representan el área bajo la curva normal hasta un valor positivo de z. z,00,01,02,03,04,05,06,07,08,09 0,0 0,5000 0,5040 0,5080 0,5120 0,5160 0,5199 0,5239 0,5279 0,5319 0,5359 0,1 0,5398 0,5438 0,5478 0,5517 0,5557 0,5596 0,5636 0,5675 0,5714 0,5753 0,2 0,5793 0,5832 0,5871 0,5910 0,5948 0,5987 0,6026 0,6064 0,6103 0,6141 0,3 0,6179 0,6217 0,6255 0,6293 0,6331 0,6368 0,6406 0,6443 0,6480 0,6517 0,4 0,6554 0,6591 0,6628 0,6664 0,6700 0,6736 0,6772 0,6808 0,6844 0,6879 0,5 0,6915 0,6950 0,6985 0,7019 0,7054 0,7088 0,7123 0,7157 0,7190 0,7224 0,6 0,7257 0,7291 0,7324 0,7357 0,7389 0,7422 0,7454 0,7486 0,7517 0,7549 0,7 0,7580 0,7611 0,7642 0,7673 0,7703 0,7734 0,7764 0,7794 0,7823 0,7652 0,8 0,7881 0,7910 0,7939 0,7967 0,7995 0,8023 0,8051 0,8078 0,8106 0,8133 0,9 0,8159 0,8186 0,8212 0,8238 0,8264 0,8289 0,8315 0,8340 0,8365 0,8389 1,0 0,8413 0,8438 0,8461 0,8485 0,8508 0,8531 0,8554 0,8577 0,8599 0,8621 1,1 0,8643 0,8665 0,8686 0,8708 0,8729 0,8749 0,8770 0,8790 0,8810 0,8930 1,2 0,8849 0,8869 0,8888 0,8907 0,8925 0,8944 0,8962 0,8980 0,8997 0,9015 1,3 0,9032 0,9049 0,9066 0,9082 0,9099 0,9115 0,9131 0,9147 0,9162 0,9177 1,4 0,9192 0,9207 0,9222 0,9236 0,9251 0,9265 0,9279 0,9292 0,9306 0,9319 1,5 0,9332 0,9345 0,9357 0,9370 0,9382 0,9394 0,9406 0,9418 0,9429 0,9441 1,6 0,9452 0,9463 0,9474 0,9484 0,9495 0,9505 0,9515 0,9525 0,9535 0,9545 1,7 0,9554 0,9561 0,9573 0,9582 0,9591 0,9599 0,9608 0,9616 0,9625 0,9633 1,8 0,9641 0,9649 0,9656 0,9664 0,9671 0,9678 0,9686 0,9693 0,9699 0,9706 1,9 0,9713 0,9719 0,9726 0,9732 0,9738 0,9744 0,9750 0,9756 0,9761 0,9767 2,0 0,9772 0,9778 0,9783 0,9788 0,9793 0,9798 0,9803 0,9808 0,9812 0,9817 2,1 0,9821 0,9826 0,9830 0,9834 0,9838 0,9842 0,9846 0,9850 0,9854 0,9857 2,2 0,9861 0,9864 0,9868 0,9871 0,9875 0,9878 0,9881 0,9884 0,9887 0,9890 2,3 0,9893 0,9896 0,9898 0,9901 0,9901 0,9906 0,9909 0,9911 0,9913 0,9916 2,4 0,9918 0,9920 0,9922 0,9925 0,9927 0,9929 0,9931 0,9932 0,9934 0,9936 2,5 0,9938 0,9940 0,9941 0,9943 0,9945 0,9946 0,9948 0,9949 0,9951 0,9952 2,6 0,9953 0,9954 0,9956 0,9957 0,9959 0,9960 0,9961 0,9962 0,9963 0,9964 2,7 0,9965 0,9966 0,9967 0,9968 0,9969 0,9970 0,9971 0,9972 0,9973 0,9974 2,8 0,9974 0,9975 0,9976 0,9977 0,9977 0,9978 0,9979 0,9979 0,9980 0,9981 2,9 0,9981 0,9982 0,9982 0,9983 0,9984 0,9984 0,9985 0,9985 0,9986 0,9986 3,0 0,9987 0,9987 0,9987 0,9988 0,9988 0,9989 0,9989 0,9989 0,9990 0,9990
4 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II. MODELO PAU CRITERIOS ESPECÍFICOS DE CORRECCIÓN Y CALIFICACIÓN ATENCIÓN: La calificación debe hacerse en múltiplos de OPCIÓN A Ejercicio 1. (Puntuación máxima: 2 puntos). Obtención de los valores críticos Discusión del sistema 0,50 para cada caso (0,50x2) Total ejercicio 1 Ejercicio 2. (Puntuación máxima: 2 puntos). Apartado (a) Cálculo correcto de asíntotas verticales Cálculo correcto de asíntotas horizontales Cálculo correcto de asíntotas oblícuas Apartado (b) Cálculo correcto de los cortes con los ejes Cálculo correcto de la derivada Cálculo correcto de los intervalos de crec. Y decrec. Total ejercicio 2 Ejercicio 3. (Puntuación máxima: 2 puntos). Apartado (a) Cálculo correcto de límites laterales en x=1 (0,25 cada uno) Estudio correcto de la continuidad (en x=1 y en R-{1}) Apartado (b) Planteamiento correcto de la integral Cálculo correcto de la integral definida Total ejercicio 3 Ejercicio 4. (Puntuación máxima: 2 puntos). Apartado (a) Planteamiento correcto Cálculo correcto de la probabilidad pedida Apartado (b) Planteamiento correcto Cálculo correcto de la probabilidad pedida Total ejercicio 4 Ejercicio 5. (Puntuación máxima: 2 puntos). Apartado (a) Planteamiento correcto Cálculo correcto de la probabilidad pedida Apartado (b) Cálculo correcto del punto crítico z α/2 Expresión correcta de la fórmula del intervalo de confianza Obtención correcta del intervalo de confianza Total ejercicio 5 NOTA: La resolución de ejercicios por cualquier otro procedimiento correcto, diferente al propuesto por los coordinadores, ha de valorarse con los criterios convenientemente adaptados
5 OPCIÓN B Ejercicio 1. (Puntuación máxima: 2 puntos). Apartado (a) Planteamiento correcto Determinación correcta de a y b Apartado (b) Repr. correcta de la región para los valores hallados en (a) Determ. correcta de los vértices para los valores hallados en (a) Total ejercicio 1 Ejercicio 2. (Puntuación máxima: 2 puntos). Apartado (a) Cálculo correcto de la potencia pedida Apartado (b) Cálculo correcto de la matriz inversa de A Cálculo correcto de B Total ejercicio 2 Ejercicio 3. (Puntuación máxima: 2 puntos). Apartado (a) Determinación correcta de la función de beneficios Apartado (b) Determinación del número de hornos que se deben vender Cálculo del beneficio máximo Total ejercicio 3 Ejercicio 4. (Puntuación máxima: 2 puntos). Apartado (a) Planteamiento y respuesta correctos Apartado (b) Planteamiento y respuesta correctos Total ejercicio 4 Ejercicio 5. (Puntuación máxima: 2 puntos). Apartado (a) Planteamiento correcto Cálculo correcto del punto crítico z α/2 Cálculo correcto del tamaño muestral Apartado (b) Expresión correcta de la fórmula del intervalo de confianza Obtención correcta del intervalo de confianza Total ejercicio 5 NOTA: La resolución de ejercicios por cualquier otro procedimiento correcto, diferente al propuesto por los coordinadores, ha de valorarse con los criterios convenientemente adaptados
6 Principales conceptos que se tendrán en cuenta en la elaboración de la Prueba de Acceso a las Enseñanzas Universitarias Oficiales de Grado correspondientes a la materia Matemáticas Aplicadas a las Ciencias Sociales II Curso Álgebra. Utilización de matrices como forma de representación de situaciones de contexto real. Transposición, suma, producto de matrices y producto de matrices por números reales. Concepto de inversa de una matriz. Obtención de la inversa de matrices de órdenes dos y tres. Determinantes de órdenes dos y tres. Resolución de ecuaciones y sistemas de ecuaciones matriciales sencillos. Regla de Cramer. Discusión y resolución de sistemas de ecuaciones lineales con dos o tres incógnitas y un parámetro. Resolución de problemas con enunciados relativos a las ciencias sociales y a la economía que pueden resolverse mediante el planteamiento de sistemas de ecuaciones lineales con dos o tres incógnitas. Interpretación y resolución gráfica de inecuaciones y sistemas de inecuaciones lineales con dos incógnitas. Iniciación a la programación lineal bidimensional. Región factible. Solución óptima. Aplicación de la programación lineal a la resolución de problemas de contexto real con dos variables. Interpretación de la solución obtenida. 2.- Análisis. Límite y continuidad de una función en un punto. Límites laterales. Ramas infinitas. Continuidad de funciones definidas a trozos. Determinación de asíntotas de funciones racionales. Derivada de una función en un punto. Interpretación geométrica. Relación entre continuidad y derivabilidad. Derivación de funciones polinómicas, exponenciales y logarítmicas. Reglas de derivación: sumas, productos y cocientes. Composición de funciones polinómicas, exponenciales y logarítmicas. Aplicaciones: Cálculo de la tasa de variación instantánea, ritmo de crecimiento, coste marginal, etc. Obtención de la ecuación de la recta tangente a una curva en un punto de la misma.
7 Obtención de extremos relativos, puntos de inflexión e intervalos de crecimiento y decrecimiento de una función. Resolución de problemas de optimización. Estudio y representación gráfica de funciones polinómicas, racionales, exponenciales y logarítmicas sencillas a partir de sus propiedades globales y locales. Integrales indefinidas. Propiedades elementales. Cálculo de integrales indefinidas inmediatas o reducibles a inmediatas. Integrales definidas de funciones polinómicas, exponenciales y racionales inmediatas mediante la aplicación de la regla de Barrow. Aplicación de la integral definida al cálculo de áreas planas. 3.- Probabilidad y Estadística. Experimentos aleatorios. Concepto de espacio muestral y de suceso elemental. Operaciones con sucesos. Leyes de De Morgan. Definición de probabilidad. Probabilidad de la unión, intersección, diferencia de sucesos y suceso contrario. Regla de Laplace de asignación de probabilidades. Probabilidad condicionada. Teorema del Producto, Teorema de la Probabilidad Total y Teorema de Bayes. Concepto de población y muestra. Muestreo. Parámetros poblacionales y estadísticos muestrales. Distribuciones de probabilidad de las medias muestrales. Caso normal. Intervalo de confianza para la media de una distribución normal de desviación típica conocida. Tamaño muestral mínimo
Examen de Matemáticas Aplicadas a las CC. Sociales II (Modelo 2013) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Modelo 2013) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (2 puntos) Discútase el sistema siguiente en función del parámetro a R: x y = a x+
Examen de Matemáticas Aplicadas a las CC. Sociales II (Modelo 2013) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (2 puntos) Discútase el sistema siguiente en función del parámetro a R: x y = a x+
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MODELO DE EXAMEN CURSO 2013-2014 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MODELO DE EXAMEN CURSO 2013-2014 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES
Examen de Matemáticas Aplicadas a las CC. Sociales II (Modelo 2013) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Modelo 2013) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (2 puntos) Discútase el sistema siguiente en función del parámetro a R: x y = a x+
Examen de Matemáticas Aplicadas a las CC. Sociales II (Modelo 2013) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (2 puntos) Discútase el sistema siguiente en función del parámetro a R: x y = a x+
MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES Y CRITERIOS GENERALES DE CALIFICACIÓN
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MODELO DE EXAMEN CURSO 2014-2015 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MODELO DE EXAMEN CURSO 2014-2015 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES Y CRITERIOS
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES Y CRITERIOS
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID EVALUACIÓN PARA EL ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2018-2019 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II Modelo
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID EVALUACIÓN PARA EL ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2018-2019 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II Modelo
OPCIÓN A. dependiente del parámetro real a.
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID EVALUACIÓN PARA EL ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2017-2018 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II MODELO
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID EVALUACIÓN PARA EL ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2017-2018 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II MODELO
MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II
 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II CRITERIOS ESPECÍFICOS DE CORRECCIÓN Y CALIFICACIÓN ATENCIÓN: La calificación debe hacerse en múltiplos de 0,25 puntos OPCIÓN A Ejercicio 1. (Puntuación
MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II CRITERIOS ESPECÍFICOS DE CORRECCIÓN Y CALIFICACIÓN ATENCIÓN: La calificación debe hacerse en múltiplos de 0,25 puntos OPCIÓN A Ejercicio 1. (Puntuación
14.1. Modelo Opción A
 14.1. Modelo 213 - Opción A Problema 14.1.1 2 puntos Discútase el sistema siguiente en función del parámetro a R: x y = a x+ az = 2x y+ a 2 z = 1 1 1 a 1 a 2 1 a 2 1 ; A = aa 1 = = a =, a = 1 Si a y a
14.1. Modelo 213 - Opción A Problema 14.1.1 2 puntos Discútase el sistema siguiente en función del parámetro a R: x y = a x+ az = 2x y+ a 2 z = 1 1 1 a 1 a 2 1 a 2 1 ; A = aa 1 = = a =, a = 1 Si a y a
x + 3y 3 2x y 4 2x + y 24
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2012-2013 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2012-2013 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2012-2013 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2012-2013 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2015-2016 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2015-2016 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
MATERIA: MATEMÁTICAS APLICACADAS A LAS CIENCIAS SOCIALES
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBAS DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) MODELO DE EXAMEN (Curso 2002-2003) MATERIA: MATEMÁTICAS APLICACADAS A LAS CIENCIAS SOCIALES INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBAS DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) MODELO DE EXAMEN (Curso 2002-2003) MATERIA: MATEMÁTICAS APLICACADAS A LAS CIENCIAS SOCIALES INSTRUCCIONES
Modelo EvAU Matemáticas Aplicadas A Las Ciencias Sociales II Modelos y Exámenes Prueba EvAU Modelo y Solución EvAU 2018
 Modelo EvAU 2018 Matemáticas Aplicadas A Las Ciencias Sociales II Modelos y Exámenes Prueba EvAU Modelo y Solución EvAU 2018 Serie Selectividad / EvAU Curso 2017/18 General Común Títulos de la Serie Selectividad
Modelo EvAU 2018 Matemáticas Aplicadas A Las Ciencias Sociales II Modelos y Exámenes Prueba EvAU Modelo y Solución EvAU 2018 Serie Selectividad / EvAU Curso 2017/18 General Común Títulos de la Serie Selectividad
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2012-2013 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2012-2013 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2014-2015 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2014-2015 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO 2 Curso 2014-2015 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO 2 Curso 2014-2015 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
OPCIÓN A. dependiente del parámetro real a.
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID EVALUACIÓN PARA EL ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2017-2018 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II MODELO
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID EVALUACIÓN PARA EL ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2017-2018 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II MODELO
x 2y z = 2 2x az = 2 y +az = 2
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID EVALUACIÓN PARA EL ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2016-2017 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID EVALUACIÓN PARA EL ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2016-2017 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
OPCIÓN A Ejercicio 1. (Calificación máxima: 2 puntos) 1 0 y B = Sean las matrices A = 2 1
 OPCIÓN A Ejercicio 1. (Calificación máxima: 2 puntos) Sean las matrices A = 2 1 1 0 y B = 3 1 0 2 1 2 1 0 a) Calcúlese (A t B) 1, donde A t denota a la traspuesta de la matriz A. ( x b) Resuélvase la ecuación
OPCIÓN A Ejercicio 1. (Calificación máxima: 2 puntos) Sean las matrices A = 2 1 1 0 y B = 3 1 0 2 1 2 1 0 a) Calcúlese (A t B) 1, donde A t denota a la traspuesta de la matriz A. ( x b) Resuélvase la ecuación
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2012) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2012) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (3 puntos) Un pintor dispone de dos tipos de pintura para realizar su trabajo.
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2012) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (3 puntos) Un pintor dispone de dos tipos de pintura para realizar su trabajo.
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID EVALUACIÓN PARA EL ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2017-2018 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID EVALUACIÓN PARA EL ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2017-2018 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID EVALUACIÓN PARA EL ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2017-2018 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID EVALUACIÓN PARA EL ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2017-2018 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2015-2016 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2015-2016 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
OPCIÓN A. x 2 2x si x < 1,
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID EVALUACIÓN PARA EL ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2016-2017 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID EVALUACIÓN PARA EL ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2016-2017 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2012) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 01) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (3 puntos) Un pintor dispone de dos tipos de pintura para realizar su trabajo.
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 01) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (3 puntos) Un pintor dispone de dos tipos de pintura para realizar su trabajo.
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID EVALUACIÓN PARA EL ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2016-2017 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID EVALUACIÓN PARA EL ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2016-2017 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
OPCIÓN A B = A 1 B C 1 B A X = C
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2014-2015 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2014-2015 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
OPCIÓN A m. y B =
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID EVALUACIÓN PARA EL ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2017-2018 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID EVALUACIÓN PARA EL ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2017-2018 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2014-2015 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2014-2015 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2014-2015 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2014-2015 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES I Y II CONTENIDOS BACHILLERATO
 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES I Y II CONTENIDOS BACHILLERATO BLOQUE 1. PROCESOS, MÉTODOS Y ACTITUDES EN MATEMÁTICAS Los contenidos de este bloque se desarrollan de forma simultánea al resto
MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES I Y II CONTENIDOS BACHILLERATO BLOQUE 1. PROCESOS, MÉTODOS Y ACTITUDES EN MATEMÁTICAS Los contenidos de este bloque se desarrollan de forma simultánea al resto
DEPARTAMENTO DE MATEMÁTICAS PLAN DE TRABAJO PARA LA CONVOCATORIA DE SEPTIEMBRE º BACHILLERATO DE CIENCIAS SOCIALES.
 DEPARTAMENTO DE MATEMÁTICAS PLAN DE TRABAJO PARA LA CONVOCATORIA DE SEPTIEMBRE 2017 UNIDAD 1.-Matrices. Conceptos: 2º BACHILLERATO DE CIENCIAS SOCIALES. Tipos de matrices. Tipos de matrices cuadradas.
DEPARTAMENTO DE MATEMÁTICAS PLAN DE TRABAJO PARA LA CONVOCATORIA DE SEPTIEMBRE 2017 UNIDAD 1.-Matrices. Conceptos: 2º BACHILLERATO DE CIENCIAS SOCIALES. Tipos de matrices. Tipos de matrices cuadradas.
MATEMÁTICAS DE 2º BACHILLER APLICADAS A LAS CIENCIAS SOCIALES
 MATEMÁTICAS DE 2º BACHILLER APLICADAS A LAS CIENCIAS SOCIALES BLOQUE DE ÁLGEBRA Editorial SM TEMA 1: MATRICES Concepto de matriz Dimensión de una matriz Tipos de Matrices: o Matriz fila o Matriz columna
MATEMÁTICAS DE 2º BACHILLER APLICADAS A LAS CIENCIAS SOCIALES BLOQUE DE ÁLGEBRA Editorial SM TEMA 1: MATRICES Concepto de matriz Dimensión de una matriz Tipos de Matrices: o Matriz fila o Matriz columna
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2016) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2016) Selectividad-Opción A Tiempo: 90 minutos k 1 0 Problema 1 (2 puntos) Se considera la matriz A = 7 k k 1 1 k a) Estudíese para qué
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2016) Selectividad-Opción A Tiempo: 90 minutos k 1 0 Problema 1 (2 puntos) Se considera la matriz A = 7 k k 1 1 k a) Estudíese para qué
Examen de Matemáticas Aplicadas a las CC. Sociales II (Junio 2012) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Junio 2012) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (3 puntos) Se considera el sistema lineal de ecuaciones, dependiente del parámetro
Examen de Matemáticas Aplicadas a las CC. Sociales II (Junio 2012) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (3 puntos) Se considera el sistema lineal de ecuaciones, dependiente del parámetro
UNIVERSIDAD COMPLUTENSE DE MADRID
 TIEMPO: INSTRUCCIONES GENERALES Y VALORACIÓN Una hora y treinta minutos. INSTRUCCIONES: El examen presenta dos opciones A y B; el alumno deberá elegir una de ellas y contestar razonadamente a los cuatro
TIEMPO: INSTRUCCIONES GENERALES Y VALORACIÓN Una hora y treinta minutos. INSTRUCCIONES: El examen presenta dos opciones A y B; el alumno deberá elegir una de ellas y contestar razonadamente a los cuatro
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2013) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II Septiembre 2013 Selectividad-Opción A Tiempo: 90 minutos Problema 1 2 puntos Se consideran las matrices A = 3 8. 3 5 0 2 3 0 y B = a Calcúlese la matriz
Examen de Matemáticas Aplicadas a las CC. Sociales II Septiembre 2013 Selectividad-Opción A Tiempo: 90 minutos Problema 1 2 puntos Se consideran las matrices A = 3 8. 3 5 0 2 3 0 y B = a Calcúlese la matriz
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2013) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2013) Selectividad-Opción A Tiempo: 90 minutos 0 2 Problema 1 (2 puntos) Se consideran las matrices A y B 3 0 3 8. 3 5 a) Calcúlese la
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2013) Selectividad-Opción A Tiempo: 90 minutos 0 2 Problema 1 (2 puntos) Se consideran las matrices A y B 3 0 3 8. 3 5 a) Calcúlese la
MATEMÁTICAS APLICADAS A LAS CCSS II (2º BACHILLERATO)
 MATEMÁTICAS APLICADAS A LAS CCSS II (2º BACHILLERATO) 1.1.1 Contenidos y temporalización. Matemáticas Aplicadas a las Ciencias Sociales II 1.1.1.1 Bloque 1. Álgebra (Total : 40 sesiones) Matrices y determinantes
MATEMÁTICAS APLICADAS A LAS CCSS II (2º BACHILLERATO) 1.1.1 Contenidos y temporalización. Matemáticas Aplicadas a las Ciencias Sociales II 1.1.1.1 Bloque 1. Álgebra (Total : 40 sesiones) Matrices y determinantes
Examen de Matemáticas Aplicadas a las CC. Sociales II (Junio 2011) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Junio 011) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (3 puntos) Se considera el sistema lineal de ecuaciones dependiente del parámetro real
Examen de Matemáticas Aplicadas a las CC. Sociales II (Junio 011) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (3 puntos) Se considera el sistema lineal de ecuaciones dependiente del parámetro real
MATEMÁTICAS 2º BACHILLERATO
 MATEMÁTICAS 2º BACHILLERATO MATRICES 1. Matrices y tipos de matrices 2. Operaciones con matrices 3. Producto de matrices 4. Matriz traspuesta 5. Matriz inversa 6. Rango de matrices DETERMINANTES 7. Determinantes
MATEMÁTICAS 2º BACHILLERATO MATRICES 1. Matrices y tipos de matrices 2. Operaciones con matrices 3. Producto de matrices 4. Matriz traspuesta 5. Matriz inversa 6. Rango de matrices DETERMINANTES 7. Determinantes
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2015) Selectividad-Opción A Tiempo: 90 minutos. 1 3 y B = 1 2
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 205) Selectividad-Opción A Tiempo: 90 minutos Problema (2 puntos) Se consideran las matrices 3 A = 6 2 3 y B = 2 a) Calcúlese A 5 e indíquese
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 205) Selectividad-Opción A Tiempo: 90 minutos Problema (2 puntos) Se consideran las matrices 3 A = 6 2 3 y B = 2 a) Calcúlese A 5 e indíquese
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2015) Selectividad-Opción A Tiempo: 90 minutos. 1 3 y B = 1 2
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 205) Selectividad-Opción A Tiempo: 90 minutos Problema (2 puntos) Se consideran las matrices 3 A = 6 2 3 y B = 2 a) Calcúlese A 5 e indíquese
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 205) Selectividad-Opción A Tiempo: 90 minutos Problema (2 puntos) Se consideran las matrices 3 A = 6 2 3 y B = 2 a) Calcúlese A 5 e indíquese
Examen de Matemáticas Aplicadas a las CC. Sociales II (Modelo 2015) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Modelo 2015) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (2 puntos) Una empresa láctea se plantea la producción de dos nuevas bebidas A y
Examen de Matemáticas Aplicadas a las CC. Sociales II (Modelo 2015) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (2 puntos) Una empresa láctea se plantea la producción de dos nuevas bebidas A y
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2017) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2017) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (2 puntos) Se considera el sistema lineal de ecuaciones dependiente del parámetro
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2017) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (2 puntos) Se considera el sistema lineal de ecuaciones dependiente del parámetro
ORIENTACIONES PARA LA MATERIA DE MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II. EBAU 2018
 ORIENTACIONES PARA LA MATERIA DE MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II. EBAU 2018 Criterios de evaluación Criterios específicos NÚMEROS Y ÁLGEBRA Matrices 1. Conocer el concepto de matriz y
ORIENTACIONES PARA LA MATERIA DE MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II. EBAU 2018 Criterios de evaluación Criterios específicos NÚMEROS Y ÁLGEBRA Matrices 1. Conocer el concepto de matriz y
OPCIÓN B. Ejercicio 1. (Calificación máxima: 2 puntos) Considérese la matriz
 OPCIÓN B Ejercicio 1. (Calificación máxima: 2 puntos) Considérese la matriz A = 1 0 0 0. 0 1 a) Calcúlese (A A t ) 200. b) Calcúlese (A A t 3I) 1. Nota: A t denota a la traspuesta de la matriz A. I es
OPCIÓN B Ejercicio 1. (Calificación máxima: 2 puntos) Considérese la matriz A = 1 0 0 0. 0 1 a) Calcúlese (A A t ) 200. b) Calcúlese (A A t 3I) 1. Nota: A t denota a la traspuesta de la matriz A. I es
Examen de Matemáticas Aplicadas a las CC. Sociales II (Modelo 2012) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Modelo 2012) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (3 puntos) Se considera el siguiente sistema lineal de ecuaciones dependiente del
Examen de Matemáticas Aplicadas a las CC. Sociales II (Modelo 2012) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (3 puntos) Se considera el siguiente sistema lineal de ecuaciones dependiente del
Examen de Matemáticas Aplicadas a las CC. Sociales II (Junio 2013) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Junio 203) Selectividad-Opción A Tiempo: 90 minutos 3 2 0 Problema (2 puntos) Dada la matriz A = 0. a) Calcúlese A x b) Resuélvase el sistema de ecuaciones
Examen de Matemáticas Aplicadas a las CC. Sociales II (Junio 203) Selectividad-Opción A Tiempo: 90 minutos 3 2 0 Problema (2 puntos) Dada la matriz A = 0. a) Calcúlese A x b) Resuélvase el sistema de ecuaciones
SISTEMA DE ECUACIONES LINEALES
 MATRICES 1. MATRICES Y TIPOS DE MATRICES 2. OPERACIONES CON MATRICES 3. PRODUCTO DE MATRICES 4. MATRIZ TRASPUESTA 5. MATRIZ INVERSA 6. RANGO DE MATRICES DETERMINANTES 7. DETERMINANTES DE ORDEN 2 Y 3 8.
MATRICES 1. MATRICES Y TIPOS DE MATRICES 2. OPERACIONES CON MATRICES 3. PRODUCTO DE MATRICES 4. MATRIZ TRASPUESTA 5. MATRIZ INVERSA 6. RANGO DE MATRICES DETERMINANTES 7. DETERMINANTES DE ORDEN 2 Y 3 8.
MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II DISTRITO ÚNICO DE ANDALUCÍA
 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II DISTRITO ÚNICO DE ANDALUCÍA CONTENIDOS Y OBJETIVOS MÍNIMOS PARA EL CURSO 2007/08. 1. INTRODUCCIÓN A LOS CONTENIDOS. ( Decreto 208/2002. B.O.J.A. de 20.08.02
MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II DISTRITO ÚNICO DE ANDALUCÍA CONTENIDOS Y OBJETIVOS MÍNIMOS PARA EL CURSO 2007/08. 1. INTRODUCCIÓN A LOS CONTENIDOS. ( Decreto 208/2002. B.O.J.A. de 20.08.02
14.3. Junio Opción A
 4.3. Junio 23 - Opción A Problema 4.3. (2 puntos) Dada la matriz A = a) Calcúlese A b) Resuélvase el sistema de ecuaciones dado por A 3 2 x y z =. a) A = 2 2 2 3 3 2 b) AX = B = X = A B = 2 2 2 3 3 2 =
4.3. Junio 23 - Opción A Problema 4.3. (2 puntos) Dada la matriz A = a) Calcúlese A b) Resuélvase el sistema de ecuaciones dado por A 3 2 x y z =. a) A = 2 2 2 3 3 2 b) AX = B = X = A B = 2 2 2 3 3 2 =
MATEMÁTICAS 2º DE BACHILLERATO
 MATRICES 1. Matrices y tipos de matrices 2. Operaciones con matrices 3. Producto de matrices 4. Matriz traspuesta 5. Matriz inversa 6. Rango de matrices DETERMINANTES 7. Determinantes de orden 2 y 3 8.
MATRICES 1. Matrices y tipos de matrices 2. Operaciones con matrices 3. Producto de matrices 4. Matriz traspuesta 5. Matriz inversa 6. Rango de matrices DETERMINANTES 7. Determinantes de orden 2 y 3 8.
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID. PRUEBAS DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) MODELO DE EXAMEN (Curso )
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBAS DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) MODELO DE EXAMEN (Curso 00-003) MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN INSTRUCCIONES:
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBAS DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) MODELO DE EXAMEN (Curso 00-003) MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN INSTRUCCIONES:
Examen de Matemáticas Aplicadas a las CC. Sociales II-Coincidente (Junio 2017) Selectividad-Opción A Tiempo: 90 minutos 2 3 A = , y B = 3 5 1
 Examen de Matemáticas Aplicadas a las CC. Sociales II-Coincidente (Junio 217) Selectividad-Opción A Tiempo: 9 minutos Problema 1 (2 puntos) Considérense las matrices ( ) ( ) 1 2 2 A =, y B = 5 1 1 4 a)
Examen de Matemáticas Aplicadas a las CC. Sociales II-Coincidente (Junio 217) Selectividad-Opción A Tiempo: 9 minutos Problema 1 (2 puntos) Considérense las matrices ( ) ( ) 1 2 2 A =, y B = 5 1 1 4 a)
UNIVERSIDAD AUTÓNOMA DE MADRID PRUEBA DE ACCESO A LA UNIVERSIDAD PARA MAYORES DE 25 AÑOS Convocatoria 2017
 INSTRUCCIONES GENERALES Y VALORACIÓN INSTRUCCIONES: Escoja entre una de las dos opciones A o B. Lea con atención y detenimiento los enunciados de las cuestiones y responda de manera razonada a los puntos
INSTRUCCIONES GENERALES Y VALORACIÓN INSTRUCCIONES: Escoja entre una de las dos opciones A o B. Lea con atención y detenimiento los enunciados de las cuestiones y responda de manera razonada a los puntos
CONTENIDOS MÍNIMOS Y ESTÁNDARES DE APRENDIZAJE EVALUABLES IMPRESCINDIBLES PARA SUPERAR LA MATERIA
 DEPARTAMENTO DE MATEMÁTICAS Área: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II Curso: 2º Bach CCSS CONTENIDOS MÍNIMOS Y ESTÁNDARES DE APRENDIZAJE EVALUABLES IMPRESCINDIBLES PARA SUPERAR LA MATERIA
DEPARTAMENTO DE MATEMÁTICAS Área: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II Curso: 2º Bach CCSS CONTENIDOS MÍNIMOS Y ESTÁNDARES DE APRENDIZAJE EVALUABLES IMPRESCINDIBLES PARA SUPERAR LA MATERIA
OBJETIVOS, CONTENIDOS y CRITERIOS DE EVALUACIÓN. COMPETENCIAS.
 OBJETIVOS, CONTENIDOS y CRITERIOS DE EVALUACIÓN. COMPETENCIAS. BLOQUE I: ÁLGEBRA UNIDAD 1: SISTEMAS de ECUACIONES LINEALES. MÉTODO de GAUSS Recordar la resolución de ecuaciones lineales con una o varias
OBJETIVOS, CONTENIDOS y CRITERIOS DE EVALUACIÓN. COMPETENCIAS. BLOQUE I: ÁLGEBRA UNIDAD 1: SISTEMAS de ECUACIONES LINEALES. MÉTODO de GAUSS Recordar la resolución de ecuaciones lineales con una o varias
OPCIÓN A. Restricciones. i. El club de fútbol dispone de un máximo de 2 millones de euros para fichajes de futbolistas españoles y extranjeros
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) JUNIO MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II Fase de modalidad INSTRUCCIONES: El alumno deberá
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) JUNIO MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II Fase de modalidad INSTRUCCIONES: El alumno deberá
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2013)(coincidentes) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II Septiembre 013coincidentes Selectividad-Opción A Tiempo: 90 minutos Problema 1 puntos Hemos ido tres días seguidos al bar de la Universidad. El primer
Examen de Matemáticas Aplicadas a las CC. Sociales II Septiembre 013coincidentes Selectividad-Opción A Tiempo: 90 minutos Problema 1 puntos Hemos ido tres días seguidos al bar de la Universidad. El primer
Examen de Matemáticas Aplicadas a las CC. Sociales II (Junio 2017) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Junio 07) Selectividad-Opción A Tiempo: 90 minutos Problema ( puntos) Considérense las matrices k A = y B = 0 k 0 0 3 a) Discútase para qué valores
Examen de Matemáticas Aplicadas a las CC. Sociales II (Junio 07) Selectividad-Opción A Tiempo: 90 minutos Problema ( puntos) Considérense las matrices k A = y B = 0 k 0 0 3 a) Discútase para qué valores
RECOMENDACIONES Y ORIENTACIONES PARA LA MATERIA DE MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II (CURSO )
 RECOMENDACIONES Y ORIENTACIONES PARA LA MATERIA DE MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II (CURSO 01-013) MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II ÍNDICE 1. Contenidos. Criterios de evaluación.1.
RECOMENDACIONES Y ORIENTACIONES PARA LA MATERIA DE MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II (CURSO 01-013) MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II ÍNDICE 1. Contenidos. Criterios de evaluación.1.
Examen de Matemáticas Aplicadas a las CC. Sociales II (Modelo 2018) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Modelo 208) Selectividad-Opción A Tiempo: 90 minutos 0 a a Problema (2 puntos) Se considera la matriz A = a 0 a a a 0 a) Determínese para qué valores
Examen de Matemáticas Aplicadas a las CC. Sociales II (Modelo 208) Selectividad-Opción A Tiempo: 90 minutos 0 a a Problema (2 puntos) Se considera la matriz A = a 0 a a a 0 a) Determínese para qué valores
Matemáticas Aplicadas a las Ciencias Sociales. Coordinadora: Mª Carmen García Llamas
 Matemáticas Aplicadas a las Ciencias Sociales Coordinadora: Mª Carmen García Llamas E-mail: mgarcia@cee.uned.es Contenidos Se distribuyen en cuatro bloques 1. Procesos, métodos y actitudes en matemáticas
Matemáticas Aplicadas a las Ciencias Sociales Coordinadora: Mª Carmen García Llamas E-mail: mgarcia@cee.uned.es Contenidos Se distribuyen en cuatro bloques 1. Procesos, métodos y actitudes en matemáticas
1. PROGRAMACION 2º CURSO BACHILLERATO CCSS
 1. PROGRAMACION 2º CURSO BACHILLERATO CCSS Esta programación incluye las indicaciones del Armonizador de la Universidad de Zaragoza 1.1. CONTENIDOS Se estructuran en tres grandes bloques: BLOQUE 1: ÁLGEBRA
1. PROGRAMACION 2º CURSO BACHILLERATO CCSS Esta programación incluye las indicaciones del Armonizador de la Universidad de Zaragoza 1.1. CONTENIDOS Se estructuran en tres grandes bloques: BLOQUE 1: ÁLGEBRA
GUÍA ESTUDIO MATEMÁTICAS II
 I. ÁLGEBRA GUÍA ESTUDIO MATEMÁTICAS II 1. Matrices a. Definición. Tipos. b. Operaciones con matrices: suma de matrices y multiplicación de una matriz por un número. Estructura vectorial de matrices. c.
I. ÁLGEBRA GUÍA ESTUDIO MATEMÁTICAS II 1. Matrices a. Definición. Tipos. b. Operaciones con matrices: suma de matrices y multiplicación de una matriz por un número. Estructura vectorial de matrices. c.
Matemáticas Aplicadas a las Ciencias Sociales
 Matemáticas Aplicadas a las Ciencias Sociales Coordinadora: Mª Carmen García Llamas E-mail: mgarcia@cee.uned.es Real Decreto-ley 5/2016, de 9 de diciembre, de medidas urgentes para la ampliación del calendario
Matemáticas Aplicadas a las Ciencias Sociales Coordinadora: Mª Carmen García Llamas E-mail: mgarcia@cee.uned.es Real Decreto-ley 5/2016, de 9 de diciembre, de medidas urgentes para la ampliación del calendario
SEGUNDO DE BACHILLERATO MATEMÁTICAS II
 SEGUNDO DE BACHILLERATO MATEMÁTICAS II La asignatura Matemáticas II, de segundo de bachillerato, en una materia troncal de acuerdo con el Real Decreto 1105/2104, de 26 de diciembre, (BOE 3-I- 2015), por
SEGUNDO DE BACHILLERATO MATEMÁTICAS II La asignatura Matemáticas II, de segundo de bachillerato, en una materia troncal de acuerdo con el Real Decreto 1105/2104, de 26 de diciembre, (BOE 3-I- 2015), por
RECOMENDACIONES Y ORIENTACIONES PARA LA MATERIA DE MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II (CURSO )
 RECOMENDACIONES Y ORIENTACIONES PARA LA MATERIA DE MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II (CURSO 2015-2016) MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II ÍNDICE 1. Contenidos 2. Criterios
RECOMENDACIONES Y ORIENTACIONES PARA LA MATERIA DE MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II (CURSO 2015-2016) MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II ÍNDICE 1. Contenidos 2. Criterios
OBJETIVOS DE LAS MATEMÁTICAS APLICADAS A LAS CIENCIAS
 2º BACHILLERATO DE CIENCIAS SOCIALES OBJETIVOS DE LAS MATEMÁTICAS APLICADAS A LAS CIENCIAS SICIALES II CONTENIDOS DE LAS MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II CRITERIOS DE EVALUACIÓN DE LAS
2º BACHILLERATO DE CIENCIAS SOCIALES OBJETIVOS DE LAS MATEMÁTICAS APLICADAS A LAS CIENCIAS SICIALES II CONTENIDOS DE LAS MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II CRITERIOS DE EVALUACIÓN DE LAS
MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES I Y II CONTENIDOS BACHILLERATO
 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES I Y II CONTENIDOS BACHILLERATO BLOQUE 1. PROCESOS, MÉTODOS Y ACTITUDES EN MATEMÁTICAS Los contenidos de este bloque se desarrollan de forma simultánea al resto
MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES I Y II CONTENIDOS BACHILLERATO BLOQUE 1. PROCESOS, MÉTODOS Y ACTITUDES EN MATEMÁTICAS Los contenidos de este bloque se desarrollan de forma simultánea al resto
Curso 2º de bachillerato de humanidades y ciencias sociales Matemáticas Aplicadas a las Ciencias Socia
 Curso 2º de bachillerato de humanidades y ciencias sociales Matemáticas Aplicadas a las Ciencias Sociales II Tema 1 MATRICES? Concepto de matriz? Tipos de matrices? Operaciones con matrices? Rango de una
Curso 2º de bachillerato de humanidades y ciencias sociales Matemáticas Aplicadas a las Ciencias Sociales II Tema 1 MATRICES? Concepto de matriz? Tipos de matrices? Operaciones con matrices? Rango de una
MATEMÁTICAS APLICADAS A CCSS II
 MATEMÁTICAS APLICADAS A CCSS II CONTENIDOS TEMA 1: Matrices, determinantes y sistemas. Concepto de matriz o tabla. Operaciones con matrices. Matriz identidad. Matriz inversa. Determinantes de orden 2 y
MATEMÁTICAS APLICADAS A CCSS II CONTENIDOS TEMA 1: Matrices, determinantes y sistemas. Concepto de matriz o tabla. Operaciones con matrices. Matriz identidad. Matriz inversa. Determinantes de orden 2 y
RECOMENDACIONES Y ORIENTACIONES PARA LA MATERIA DE MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II (CURSO )
 RECOMENDACIONES Y ORIENTACIONES PARA LA MATERIA DE MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II (CURSO 2014-2015) MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II ÍNDICE 1. Contenidos 2. Criterios
RECOMENDACIONES Y ORIENTACIONES PARA LA MATERIA DE MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II (CURSO 2014-2015) MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II ÍNDICE 1. Contenidos 2. Criterios
Examen de Matemáticas Aplicadas a las CC. Sociales II-Coincidente (Septiembre 2017) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II-Coincidente (Septiembre 207) Selectividad-Opción A Tiempo: 90 minutos a + a Problema (2 puntos) Se considera la matriz A = a a a 0 a a) Estúdiese para
Examen de Matemáticas Aplicadas a las CC. Sociales II-Coincidente (Septiembre 207) Selectividad-Opción A Tiempo: 90 minutos a + a Problema (2 puntos) Se considera la matriz A = a a a 0 a a) Estúdiese para
MATEMÁTICAS I.TEMARIO. Prueba de Evaluación para el Acceso a la Universidad Mayores de 25 años 1. MATRICES Y DETERMINANTES
 I.TEMARIO. 1. MATRICES Y DETERMINANTES Operaciones con matrices Cálculo de determinantes Matriz inversa Rango de una matriz Ecuaciones con matrices 2. SISTEMAS DE ECUACIONES LINEALES Regla de Cramer Sistemas
I.TEMARIO. 1. MATRICES Y DETERMINANTES Operaciones con matrices Cálculo de determinantes Matriz inversa Rango de una matriz Ecuaciones con matrices 2. SISTEMAS DE ECUACIONES LINEALES Regla de Cramer Sistemas
DESARROLLO DE LAS UNIDADES DIDÁCTICAS MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II
 DESARROLLO DE LAS UNIDADES DIDÁCTICAS MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II Según REAL DECRETO 1467/2007, de 2 de noviembre, por el que se establece la estructura del bachillerato y se fijan
DESARROLLO DE LAS UNIDADES DIDÁCTICAS MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II Según REAL DECRETO 1467/2007, de 2 de noviembre, por el que se establece la estructura del bachillerato y se fijan
( ) ( ) ( ) ( ) ( ) ( )
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBADE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso - (JUNIO) MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBADE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso - (JUNIO) MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
Examen de Matemáticas Aplicadas a las CC. Sociales II (Modelo 2019) Selectividad-Opción A Tiempo: 90 minutos
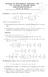 Examen de Matemáticas Aplicadas a las CC. Sociales II (Modelo 9) Selectividad-Opción A Tiempo: 9 minutos Problema ( puntos) Se consideran lan matrices 3 5 A = 3 6 y B = 3 3 m donde m es un parámetro real.
Examen de Matemáticas Aplicadas a las CC. Sociales II (Modelo 9) Selectividad-Opción A Tiempo: 9 minutos Problema ( puntos) Se consideran lan matrices 3 5 A = 3 6 y B = 3 3 m donde m es un parámetro real.
Examen de Matemáticas Aplicadas a las CC. Sociales II (Junio 2015) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Junio 2015) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (2 puntos) Se considera el sistema de ecuaciones dependiente del parámetro real a:
Examen de Matemáticas Aplicadas a las CC. Sociales II (Junio 2015) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (2 puntos) Se considera el sistema de ecuaciones dependiente del parámetro real a:
Examen de Matemáticas Aplicadas a las CC. Sociales II (Coincidente-Junio 2012) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Coincidente-Junio 1) Selectividad-Opción A Tiempo: 9 minutos Problema 1 (3 puntos) Dadas las matrices A = x y z y B = 1, se pide: 1 1 3 1 k, X = 1.
Examen de Matemáticas Aplicadas a las CC. Sociales II (Coincidente-Junio 1) Selectividad-Opción A Tiempo: 9 minutos Problema 1 (3 puntos) Dadas las matrices A = x y z y B = 1, se pide: 1 1 3 1 k, X = 1.
Matemáticas. Si un error simple ha llevado a un problema más sencillo se disminuirá la puntuación.
 UNIVERSIDAD POLITÉCNICA DE CARTAGENA PRUEBAS DE ACCESO A LA UNIVERSIDAD DE LOS MAYORES DE 25 AÑOS CONVOCATORIA 2014 CRITERIOS DE EVALUACIÓN Matemáticas GENERALES: El examen constará de dos opciones (dos
UNIVERSIDAD POLITÉCNICA DE CARTAGENA PRUEBAS DE ACCESO A LA UNIVERSIDAD DE LOS MAYORES DE 25 AÑOS CONVOCATORIA 2014 CRITERIOS DE EVALUACIÓN Matemáticas GENERALES: El examen constará de dos opciones (dos
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2015-coincidente) Selectividad-Opción A Tiempo: 90 minutos 5 7 C = 1 5
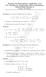 Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2015-coincidente) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (2 puntos) Considérense las matrices ( ) ( ) ( ) 1 2 3 2 5 7 A =,
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2015-coincidente) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (2 puntos) Considérense las matrices ( ) ( ) ( ) 1 2 3 2 5 7 A =,
UNIVERSIDAD COMPLUTENSE DE MADRID
 Principales conceptos que se tendrán en cuenta en la elaboración de las pruebas de Acceso a la Universidad para los estudiantes provenientes del Bachillerato LOGSE de la materia "Matemáticas II" ÁLGEBRA
Principales conceptos que se tendrán en cuenta en la elaboración de las pruebas de Acceso a la Universidad para los estudiantes provenientes del Bachillerato LOGSE de la materia "Matemáticas II" ÁLGEBRA
EVAU Matemáticas Aplicadas a las Ciencias Sociales. Reunión con los centros (6 de noviembre de 2018)
 EVAU 2019 Matemáticas Aplicadas a las Ciencias Sociales Reunión con los centros (6 de noviembre de 2018) Fechas propuestas para las pruebas: (no definitivas) Convocatoria junio: 4, 5 y 6 de junio; 7 de
EVAU 2019 Matemáticas Aplicadas a las Ciencias Sociales Reunión con los centros (6 de noviembre de 2018) Fechas propuestas para las pruebas: (no definitivas) Convocatoria junio: 4, 5 y 6 de junio; 7 de
18 Experimentos aleatorios. Sucesos y espacio muestral. Frecuencia y probabilidad de un suceso.
 PRIMER CURSO DE E.S.O Criterios de calificación: 80% exámenes, 10% actividades, 10% actitud y trabajo 1 Números naturales. 2 Potencias de exponente natural. Raíces cuadradas exactas. 3 Divisibilidad. Concepto
PRIMER CURSO DE E.S.O Criterios de calificación: 80% exámenes, 10% actividades, 10% actitud y trabajo 1 Números naturales. 2 Potencias de exponente natural. Raíces cuadradas exactas. 3 Divisibilidad. Concepto
MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II
 CONOCIMIENTOS MÍNIMOS MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II CONTENIDOS DESTREZAS Álgebra Sistemas lineales Matrices, operaciones con matrices. Rango de una matriz Propiedades y cálculo de determinantes
CONOCIMIENTOS MÍNIMOS MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II CONTENIDOS DESTREZAS Álgebra Sistemas lineales Matrices, operaciones con matrices. Rango de una matriz Propiedades y cálculo de determinantes
Examen de Matemáticas Aplicadas a las CC. Sociales II (Junio 2015-coincidente) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Junio 015-coincidente) Selectividad-Opción A Tiempo: 90 minutos Problema 1 ( puntos) Se considera el sistema de ecuaciones dependiente del parámetro
Examen de Matemáticas Aplicadas a las CC. Sociales II (Junio 015-coincidente) Selectividad-Opción A Tiempo: 90 minutos Problema 1 ( puntos) Se considera el sistema de ecuaciones dependiente del parámetro
Unidad 1: Sistemas de ecuaciones. Método de Gauss
 CRITERIOS DE EVALUACIÓN Y EXIGIBLES. MATEMÁTICAS CCSS II Unidad 1: Sistemas de ecuaciones. Método de Gauss Sistemas de ecuaciones lineales - Sistemas equivalentes. - Transformaciones que mantienen la equivalencia.
CRITERIOS DE EVALUACIÓN Y EXIGIBLES. MATEMÁTICAS CCSS II Unidad 1: Sistemas de ecuaciones. Método de Gauss Sistemas de ecuaciones lineales - Sistemas equivalentes. - Transformaciones que mantienen la equivalencia.
Dpto. de Matemáticas IES Las Breñas CONTENIDOS MÍNIMOS del ÁREA DE MATEMÁTICAS Septiembre 2.016
 Dpto. de Matemáticas IES Las Breñas CONTENIDOS MÍNIMOS del ÁREA DE MATEMÁTICAS Septiembre 2.016 4º ESO OPCIÓN A U1: Estadística. Estadística. Nociones generales - Individuo, población, muestra, caracteres,
Dpto. de Matemáticas IES Las Breñas CONTENIDOS MÍNIMOS del ÁREA DE MATEMÁTICAS Septiembre 2.016 4º ESO OPCIÓN A U1: Estadística. Estadística. Nociones generales - Individuo, población, muestra, caracteres,
IES EMILIO CASTELAR Curso 2016/2017
 IES EMILIO CASTELAR Curso 2016/2017 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II - 2º BTO Índice IES EMILIO CASTELAR Curso 2016/2017...1 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II - 2º BTO...1
IES EMILIO CASTELAR Curso 2016/2017 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II - 2º BTO Índice IES EMILIO CASTELAR Curso 2016/2017...1 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II - 2º BTO...1
Examen de Matemáticas Aplicadas a las CC. Sociales II (Modelo 2016) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Modelo 2016) Selectividad-Opción A Tiempo: 90 minutos 1 3 1 Problema 1 (2 puntos) Considérese la matriz A = a 0 8 1 a 6 a) Determínese para qué valores
Examen de Matemáticas Aplicadas a las CC. Sociales II (Modelo 2016) Selectividad-Opción A Tiempo: 90 minutos 1 3 1 Problema 1 (2 puntos) Considérese la matriz A = a 0 8 1 a 6 a) Determínese para qué valores
