Completa con letra de imprenta
|
|
|
- Silvia Naranjo Díaz
- hace 7 años
- Vistas:
Transcripción
1 XX OLIMPÍADA MATEMÁTICA ÑANDÚ CERTAMEN ESCOLAR PRIMER NIVEL Completa con letra de imprenta En cada problema señala la única respuesta correcta. 1. En la escuela I hay 460 alumnos; en la escuela II hay 400 alumnos; en la escuela III hay 200 alumnos y en la escuela IV, 1020 alumnos. La cantidad de alumnos que suman entre las cuatro escuelas es a) 2080 b) 208 c) 1162 d) Aldo tiene 5 años menos que su hermano Dante. Entre los dos suman 29 años, entonces a) Dante tiene 15 años b) Dante tiene 12 años c) Aldo tiene 12 años d) Aldo tiene 17 años 3. ABCD es un rectángulo, AB = 2 BC; BC = 4 cm. El perímetro de ABCD es a) 24 cm b) 8 cm c) 16 cm d)32 cm 4. El número de cuadrados que hay en esta figura es a) 12 b) 18 c) 20 d) 0 5. El rectángulo, de 120 cm de perímetro se partió en 3 cuadrados iguales. El lado de cada cuadrado mide D A C B a) 60 cm b) 15 cm c) 12 cm d) 45 cm - 6. Si cambio mi billete de $ 100 en monedas de 50 centavos, me dan a) 2 monedas b) 20 monedas c) 2000 monedas d) 200 monedas 7. Pedro escribe la siguiente lista de números: 2; 5; 8; 11;... En el séptimo lugar Pedro escribió el número a) 14 b) 20 c) 17 d) 23 -
2 (continuación) CERTAMEN ESCOLAR PRIMER NIVEL 8. La figura se armó con 2 triángulos equiláteros de 21 cm de perímetro. El perímetro de la figura es a) 12 cm b) 42cm c) 18 cm d) 28 cm 9. Desde el hall al living se puede entrar por 3 puertas distintas. Entre el living y el jardín hay dos puertas. Mía acaba de llegar y quiere ir al jardín. Lo puede hacer de a) 5 maneras b) 6 maneras c) 3 maneras d) 2 maneras 10. Juan fue de su casa a la ciudad Bella en 3 días, recorriendo, el primer día 120 km; el segundo día, el doble que el primer día y el tercer día 310 km. La distancia entre su casa y la ciudad Bella es de a) 490 km b) 430 km c) 550 km d) 670 km
3 XX OLIMPÍADA MATEMÁTICA ÑANDÚ CERTAMEN ESCOLAR SEGUNDO NIVEL Completa con letra de imprenta En cada problema señala la única respuesta correcta. 1. Si escribo todos los números pares entre 2 y 80, escribo el 4 a) 13 veces b) 15 veces c) 41 veces d) 12 veces 2. Marcos pagó con diez billetes de $100 y le devolvieron un billete de $50, tres billetes de $10 y cuatro billetes de $2. Marcos había gastado a) $ 932 b) $ 912 c) $ 12 d) $ Se tienen un cuadrado C de 6 cm de lado y un rectángulo R de lados 3 cm y 12 cm, entonces a) Perímetro de C = perímetro de R = 36 cm b) Perímetro de R = 15 cm c) Perímetro de R = 30 cm d) Perímetro de C = 28 cm El número de cuadriláteros que hay en la figura es a) 30 b) 8 c) 29 d) Un tercio de la mitad de 36 es a) 12 b) 18 c) 3 d) ABCD es un rectángulo, AB = 2 BC y BC = 4 cm. Entonces, el área de ABCD es a) 24 cm b) 16 cm 2 c) 32 cm 2 d) 24 cm Utilizando los colores: azul, verde, rojo y negro, se quiere pintar cada casilla de un color. Cada color se debe usar una vez. Esto se puede hacer de a) 24 maneras b) 12 maneras c) 1 manera d) 4 maneras Si en un triángulo isósceles hay un ángulo de 120º, los otros dos miden a) 120º y 30º b) 40º y 20º c) 35º y 25º d) 30º y 30º
4 (continuación) CERTAMEN ESCOLAR SEGUNDO NIVEL 9. Los números capicúas de exactamente tres cifras son a) 81 b) 90 c) 100 d) Valentina arma con botones estos triángulos primero segundo tercero Para armar el quinto triángulo usará a) 15 botones b) 20 botones c) 21 botones d) 28 botones
5 XX OLIMPÍADA MATEMÁTICA ÑANDÚ CERTAMEN ESCOLAR TERCER NIVEL Completa con letra de imprenta En cada problema señala la única respuesta correcta. 1. Usando rojo, verde y azul, se quiere pintar cada casilla de un color. Cada color se debe usar al menos una vez y casillas vecinas deben ser de distinto color. Esto se puede hacer de a) 6 maneras b) 18 maneras c) 12 maneras d) 81 maneras El 20 % de 100 es a) la quinta parte de 100 b) la décima parte de 100 c) la vigésima parte de 100 d) los dos quintos de En un triángulo isósceles rectángulo, los ángulos miden a) 60º; 60º y 60º b) 90º; 60º y 30º c) 90º; 60º y 60º d) 90º; 45º y 45º Usando palillos iguales, Juan arma estos cuadrados primero segundo tercero Para armar el quinto cuadrado utilizará a) 60 palillos b) 40 palillos c) 25 palillos d) 96 palillos Dos chicos y cuatro chicas comen una pizza. Cada chica come un cuarto de pizza. Los chicos parten lo que sobra en partes iguales. Cada chico come a) un cuarto de pizza b) un sexto de pizza c) un octavo de pizza d) media pizza ABCD es un rectángulo BC mide 6 cm y AB = 3 BC. El área de ABCD es a) 12 cm 2 b) 108 cm 2 c) 48 cm 2 d) 24 cm Los números capicúas de exactamente tres cifras, múltiplos de 3, son a) 10 b) 27 c) 30 d) 90 --
6 (continuación) CERTAMEN ESCOLAR TERCER NIVEL 8. Ana y José son los padres de Pablo. Entre los tres suman 77 años. Entre Ana y Pablo suman 45 años. Entre José y Pablo suman 47 años. Las edades de Ana, José y Pablo son, respectivamente a) y 15 b) y 15 c) y 17 d) y La longitud de una circunferencia de 10 cm de radio es a) 314 cm b) 3,14 cm c) 62,8 cm d) 628 cm En la figura se ven a) 9 triángulos b) 10 triángulos c) 12 triángulos d) 13 triángulos --
XXII OLIMPÍADA MATEMÁTICA ÑANDÚ PRIMER NIVEL APELLIDO NOMBRES. En cada problema señala la única respuesta correcta.
 XXII OLIMPÍ MTEMÁTI ÑNÚ ERTMEN ESOLR PRIMER NIVEL ompleta con letra de imprenta En cada problema señala la única respuesta correcta. 1. En el turno tarde hay 35 alumnos en primer grado, 37 alumnos en segundo
XXII OLIMPÍ MTEMÁTI ÑNÚ ERTMEN ESOLR PRIMER NIVEL ompleta con letra de imprenta En cada problema señala la única respuesta correcta. 1. En el turno tarde hay 35 alumnos en primer grado, 37 alumnos en segundo
a) Las mediatrices de un triángulo se cortan en un punto llamado... b) Las bisectrices de un triángulo se cortan en un punto llamado...
 Geometría Plana 3º E.S.O. PARTE TEÓRICA 1.- Define para un triángulo los siguientes conceptos: Mediatriz: Bisectriz: Mediana: Altura: 2.- Completa las siguientes frases: a) Las mediatrices de un triángulo
Geometría Plana 3º E.S.O. PARTE TEÓRICA 1.- Define para un triángulo los siguientes conceptos: Mediatriz: Bisectriz: Mediana: Altura: 2.- Completa las siguientes frases: a) Las mediatrices de un triángulo
Completa con letra de imprenta
 XXIII OLIMPÍAA MATEMÁTIA ÑANÚ ERTAMEN ESOLAR PRIMER NIVEL ompleta con letra de imprenta En cada problema señala la única respuesta correcta. 1. En la biblioteca hay: 6 mesas con 4 sillas cada una, 4 mesas
XXIII OLIMPÍAA MATEMÁTIA ÑANÚ ERTAMEN ESOLAR PRIMER NIVEL ompleta con letra de imprenta En cada problema señala la única respuesta correcta. 1. En la biblioteca hay: 6 mesas con 4 sillas cada una, 4 mesas
TORNEOS GEOMÉTRICOS 2018 Segunda Ronda. Primer Nivel - 5º Año de Escolaridad. Apellido Nombres. Calle..N Piso.Dpto..CP.. Localidad.Provincia.
 TORNEOS GEOMÉTRICOS 2018 Segunda Ronda Primer Nivel - 5º Año de Escolaridad Apellido Nombres. DNI.. Tu Escuela. Tu Domicilio Calle..N Piso.Dpto..CP.. Localidad.Provincia. Lee con atención: 1- Es posible
TORNEOS GEOMÉTRICOS 2018 Segunda Ronda Primer Nivel - 5º Año de Escolaridad Apellido Nombres. DNI.. Tu Escuela. Tu Domicilio Calle..N Piso.Dpto..CP.. Localidad.Provincia. Lee con atención: 1- Es posible
13Soluciones a los ejercicios y problemas PÁGINA 250
 PÁGINA 50 Pág. 1 Á REAS Y PERÍMETROS DE FIGURAS SENCILLAS Halla el área y el perímetro de las figuras coloreadas de los siguientes ejercicios: 1 a) b) 5 dm 4 cm cm 5 cm 8 cm a) 5 5 dm b) 8 8 cm P 5 4 0
PÁGINA 50 Pág. 1 Á REAS Y PERÍMETROS DE FIGURAS SENCILLAS Halla el área y el perímetro de las figuras coloreadas de los siguientes ejercicios: 1 a) b) 5 dm 4 cm cm 5 cm 8 cm a) 5 5 dm b) 8 8 cm P 5 4 0
NOMBRE Y APELLIDOS: debe medir el tercero para que ese triángulo sea un triángulo rectángulo?
 FICHA REFUERZO TEMA 8: TEOREMA DE PITAGORAS. SEMEJANZA. CURSO: 2 FECHA: NOMBRE Y APELLIDOS: Ejercicio nº 1.-Los dos lados menores de un triángulo miden 8 cm y 15 cm. Cuánto debe medir el tercero para que
FICHA REFUERZO TEMA 8: TEOREMA DE PITAGORAS. SEMEJANZA. CURSO: 2 FECHA: NOMBRE Y APELLIDOS: Ejercicio nº 1.-Los dos lados menores de un triángulo miden 8 cm y 15 cm. Cuánto debe medir el tercero para que
TORNEOS GEOMÉTRICOS 2016 Segunda Ronda. Primer Nivel - 5º Año de Escolaridad. Apellido Nombres.. DNI Tu Escuela. Localidad Provincia
 TORNEOS GEOMÉTRICOS 2016 Segunda Ronda Primer Nivel - 5º Año de Escolaridad justificar tus respuestas. hacerla cada participante. 1. Halla la suma de los ángulos marcados en el cuadrilátero inscripto en
TORNEOS GEOMÉTRICOS 2016 Segunda Ronda Primer Nivel - 5º Año de Escolaridad justificar tus respuestas. hacerla cada participante. 1. Halla la suma de los ángulos marcados en el cuadrilátero inscripto en
OLIMPÍADA JUVENIL DE MATEMÁTICA 2015 CANGURO MATEMÁTICO PRIMER AÑO
 OLIMPÍADA JUVENIL DE MATEMÁTICA 2015 CANGURO MATEMÁTICO PRIMER AÑO RESPONDE LA PRUEBA EN LA HOJA DE RESPUESTA ANEXA 1. Qué figura tiene sombreada exactamente la mitad de su área? 2. Mi sombrilla tiene
OLIMPÍADA JUVENIL DE MATEMÁTICA 2015 CANGURO MATEMÁTICO PRIMER AÑO RESPONDE LA PRUEBA EN LA HOJA DE RESPUESTA ANEXA 1. Qué figura tiene sombreada exactamente la mitad de su área? 2. Mi sombrilla tiene
Á REAS Y PERÍMETROS DE FIGURAS SENCILLAS
 Pág. 1 Á REAS Y PERÍMETROS DE FIGURAS SENCILLAS Halla el área y el perímetro de las figuras coloreadas de los siguientes ejercicios: 1 a) b) 5 dm 4 cm 2 cm 5 cm 8 cm 2 a) b) 5 m 8 m 17 m 15 m 3 a) b) 5
Pág. 1 Á REAS Y PERÍMETROS DE FIGURAS SENCILLAS Halla el área y el perímetro de las figuras coloreadas de los siguientes ejercicios: 1 a) b) 5 dm 4 cm 2 cm 5 cm 8 cm 2 a) b) 5 m 8 m 17 m 15 m 3 a) b) 5
TORNEOS GEOMÉTRICOS 2016 Primera Ronda. Primer Nivel - 5º Año de Escolaridad. Apellido Nombres.. DNI Tu Escuela. Localidad Provincia
 Primer Nivel - 5º Año de Escolaridad 1- En el triángulo rectángulo ABC cuyo ángulo en C mide 48º se trazan la bisectrices de los ángulos B y C, que se cortan en O. Calcula la medida de los ángulos del
Primer Nivel - 5º Año de Escolaridad 1- En el triángulo rectángulo ABC cuyo ángulo en C mide 48º se trazan la bisectrices de los ángulos B y C, que se cortan en O. Calcula la medida de los ángulos del
Primer Nivel. Solución: Por los valores de los lados del triángulo, éste debe ser un triángulo rectángulo, y en consecuencia su área es (3 4 ) 6
 Primer Nivel Problema 1- Los lados de un cuadrado de área 4cm se han dividido en cuatro partes iguales. Halla el área del cuadrado sombreado. Solución: Trazando los segmentos adicionales indicados en la
Primer Nivel Problema 1- Los lados de un cuadrado de área 4cm se han dividido en cuatro partes iguales. Halla el área del cuadrado sombreado. Solución: Trazando los segmentos adicionales indicados en la
EJERCICIOS PENDIENTES 3º E.S.O. GEOMETRÍA
 3º E.S.O. GEOMETRÍA ) Halla la medida del ángulo Âen el triángulo de la figura. ) En un triángulo isósceles, el ángulo desigual mide 6º 4. Calcula el valor de los otros dos ángulos. 3) Halla la medida
3º E.S.O. GEOMETRÍA ) Halla la medida del ángulo Âen el triángulo de la figura. ) En un triángulo isósceles, el ángulo desigual mide 6º 4. Calcula el valor de los otros dos ángulos. 3) Halla la medida
TORNEOS GEOMÉTRICOS Segunda Ronda. Primer Nivel - 5º Año de Escolaridad. Apellido Nombres. DNI Tu Escuela. Localidad Provincia
 TORNEOS GEOMÉTRICOS 2017. Segunda Ronda Primer Nivel - 5º Año de Escolaridad Apellido Nombres DNI Tu Escuela. Tu domicilio: Calle. Nº Piso Dpto C.P... Localidad Provincia Lee con atención: 1- Es posible
TORNEOS GEOMÉTRICOS 2017. Segunda Ronda Primer Nivel - 5º Año de Escolaridad Apellido Nombres DNI Tu Escuela. Tu domicilio: Calle. Nº Piso Dpto C.P... Localidad Provincia Lee con atención: 1- Es posible
MATEMÁTICA-PRIMER AÑO REVISIÓN INTEGRADORA. A) Reproduce la siguiente figura, luego trace las bisectrices de los ángulos ACD y BCD.
 Universidad de Buenos Aires Instituto Libre de Segunda Enseñanza MATEMÁTICA-PRIMER AÑO REVISIÓN INTEGRADORA Construcciones con regla no graduada y compás A) Reproduce la siguiente figura, luego trace las
Universidad de Buenos Aires Instituto Libre de Segunda Enseñanza MATEMÁTICA-PRIMER AÑO REVISIÓN INTEGRADORA Construcciones con regla no graduada y compás A) Reproduce la siguiente figura, luego trace las
CANGURO MATEMÁTICO 2014 TERCERO DE SECUNDARIA
 CANGURO MATEMÁTICO 2014 TERCERO DE SECUNDARIA INDICACIONES Las marcas en la hoja de respuestas se deben realizar, únicamente, con LÁPIZ. Escriba su apellido paterno, apellido materno y nombres con letras
CANGURO MATEMÁTICO 2014 TERCERO DE SECUNDARIA INDICACIONES Las marcas en la hoja de respuestas se deben realizar, únicamente, con LÁPIZ. Escriba su apellido paterno, apellido materno y nombres con letras
( ) ( ) SOLUCIONES MINIMOS 2º ESO TEMA 5 ECUACIONES. IES CINCO VILLAS TEMA 5 2º ESO Página 1. b) = 3. Ejercicio nº 1.- a) 4. b) 2x.
 SOLUCIONES MINIMOS 2º ESO TEMA 5 ECUACIONES Ejercicio nº 1.- Indica cuál de los siguientes valores es solución de la ecuación x + 6 =. a) 4 b) 2 c) 4 c) 4 a) + 5 = 2 b) 3 + 5x = x 1 a) + 5 = 2 = 2 5 x
SOLUCIONES MINIMOS 2º ESO TEMA 5 ECUACIONES Ejercicio nº 1.- Indica cuál de los siguientes valores es solución de la ecuación x + 6 =. a) 4 b) 2 c) 4 c) 4 a) + 5 = 2 b) 3 + 5x = x 1 a) + 5 = 2 = 2 5 x
Problema 1 Problema 2 Problema 3 Problema 4 Problema 5
 QUINTO GRADO Yo rompí un papel en 10 pedazos. Mi hermano tomó algunos de ellos y los rompió a su vez en 10 pedazos -cada uno-. Si al final quedaron 46 pedazos, Cuántos pedazos rompió mi hermanito? Mary
QUINTO GRADO Yo rompí un papel en 10 pedazos. Mi hermano tomó algunos de ellos y los rompió a su vez en 10 pedazos -cada uno-. Si al final quedaron 46 pedazos, Cuántos pedazos rompió mi hermanito? Mary
NIVEL 1 (6.º y 7.º grado)
 NIVEL 1 (6.º y 7.º grado) 26.ª OLIMPIADA NACIONAL JUVENIL DE MATEMÁTICA Nombre y Apellido:.............................................. Colegio:.......................... Grado/Curso:............ E-mail:..............
NIVEL 1 (6.º y 7.º grado) 26.ª OLIMPIADA NACIONAL JUVENIL DE MATEMÁTICA Nombre y Apellido:.............................................. Colegio:.......................... Grado/Curso:............ E-mail:..............
MATEMÁTICAS EJERCICIOS DE RECUPERACIÓN 2º ESO
 MATEMÁTICAS EJERCICIOS DE RECUPERACIÓN º ESO TEMA 06 - ECUACIONES DE PRIMER Y SEGUNDO GRADO 1º. De las siguientes expresiones, identifica las que sean ecuaciones o identidades. a) x - 5 = x - 1 x + 8 b)
MATEMÁTICAS EJERCICIOS DE RECUPERACIÓN º ESO TEMA 06 - ECUACIONES DE PRIMER Y SEGUNDO GRADO 1º. De las siguientes expresiones, identifica las que sean ecuaciones o identidades. a) x - 5 = x - 1 x + 8 b)
ÁNGULOS: (triángulos - cuadriláteros)
 1 ÁNGULOS: (triángulos - cuadriláteros) 1. - Transforma en grados, minutos y segundos: a) 15.910" b) 27.673" c) 78.385" d) 38.890" e) 21.930" f) 35.627" g) 50.420" h) 43.692" i) 22.475" j) 95.486" k) 9.999"
1 ÁNGULOS: (triángulos - cuadriláteros) 1. - Transforma en grados, minutos y segundos: a) 15.910" b) 27.673" c) 78.385" d) 38.890" e) 21.930" f) 35.627" g) 50.420" h) 43.692" i) 22.475" j) 95.486" k) 9.999"
Geometría. 1 a.- Qué diferencia hay entre una recta y una semirrecta?, y entre una semirrecta y un segmento?
 Geometría 1 a.- Qué diferencia hay entre una recta y una semirrecta?, y entre una semirrecta y un segmento? 2 a.- Qué originan dos puntos en una recta?. Cuántas rectas pasan por dos puntos?, y por un punto?
Geometría 1 a.- Qué diferencia hay entre una recta y una semirrecta?, y entre una semirrecta y un segmento? 2 a.- Qué originan dos puntos en una recta?. Cuántas rectas pasan por dos puntos?, y por un punto?
XXII OLIMPIADA NACIONAL DE MATEMÁTICA PRIMERA RONDA COLEGIAL - MAYO DE NIVEL 1
 Primera Ronda Nivel 1 XXII OLIMPIADA NACIONAL DE MATEMÁTICA PRIMERA RONDA COLEGIAL - MAYO DE 2010 - NIVEL 1 Nombre y Apellido:................................. Grado:....... Sección:...... Puntaje:..........
Primera Ronda Nivel 1 XXII OLIMPIADA NACIONAL DE MATEMÁTICA PRIMERA RONDA COLEGIAL - MAYO DE 2010 - NIVEL 1 Nombre y Apellido:................................. Grado:....... Sección:...... Puntaje:..........
MATEMÁTICA-PRIMER AÑO REVISIÓN INTEGRADORA. A) Reproduce la siguiente figura, luego trace las bisectrices de los ángulos ACD y BCD.
 Universidad de Buenos Aires Instituto Libre de Segunda Enseñanza MATEMÁTICA-PRIMER AÑO REVISIÓN INTEGRADORA Construcciones con regla no graduada y compás A) Reproduce la siguiente figura, luego trace las
Universidad de Buenos Aires Instituto Libre de Segunda Enseñanza MATEMÁTICA-PRIMER AÑO REVISIÓN INTEGRADORA Construcciones con regla no graduada y compás A) Reproduce la siguiente figura, luego trace las
Nombre del alumno: Profesora Noelia Freita Colegio Pablo Neruda
 Nombre del alumno: Profesora Noelia Freita Colegio Pablo Neruda Pasos para la resolución de un problema 1 Instancia Final de la Olimpíada Nacional de Matemática 2013 Nivel I A (4to. Año Escolar) PROBLEMA
Nombre del alumno: Profesora Noelia Freita Colegio Pablo Neruda Pasos para la resolución de un problema 1 Instancia Final de la Olimpíada Nacional de Matemática 2013 Nivel I A (4to. Año Escolar) PROBLEMA
Tema 6: Ecuaciones de primer y segundo grado x x
 Matemáticas º ESO Ejercicios Tema Bloque II: Álgebra Tema : Ecuaciones de primer y segundo grado. A) Resuelve las siguientes ecuaciones de primer grado:.- 0.-.- 8.- 9.- ( ) ( ).- ( ) ( ) ( ) 8.- ( ) (
Matemáticas º ESO Ejercicios Tema Bloque II: Álgebra Tema : Ecuaciones de primer y segundo grado. A) Resuelve las siguientes ecuaciones de primer grado:.- 0.-.- 8.- 9.- ( ) ( ).- ( ) ( ) ( ) 8.- ( ) (
a) 12 = b) 45 = c) 54 a) 2 = 2 c) 9 c) 9 = 9 Tema 2 - Hoja 2: Raíz de un número
 Tema - Hoja : Raíz de un número Expresa como producto de un número entero y un radical los siguientes radicales: a) a) = = = = = = Expresa en forma de raíz las siguientes potencias de exponente fraccionario:
Tema - Hoja : Raíz de un número Expresa como producto de un número entero y un radical los siguientes radicales: a) a) = = = = = = Expresa en forma de raíz las siguientes potencias de exponente fraccionario:
2. El menor número que se le debe sumar a 2553 para que desaparezca el dígito 5 es: a) 550 c) 150 e) 50 b) 510 d) 110 f) n.d.l.a.
 XIV OLIMPIADA NACIONAL DE MATEMÁTICA SEGUNDA RONDA COLEGIAL - DE AGOSTO DE 00 - NIVEL Nombre y Apellido:... Curso/Grado:...Sección:... Puntaje:... Tienes 80 minutos para resolver los problemas. Escribe
XIV OLIMPIADA NACIONAL DE MATEMÁTICA SEGUNDA RONDA COLEGIAL - DE AGOSTO DE 00 - NIVEL Nombre y Apellido:... Curso/Grado:...Sección:... Puntaje:... Tienes 80 minutos para resolver los problemas. Escribe
XV OLIMPIADA NACIONAL DE MATEMÁTICA SEGUNDA RONDA COLEGIAL - 1 DE AGOSTO DE NIVEL 1
 SEGUNDA RONDA COLEGIAL - DE AGOSTO DE 00 - NIVEL Nombre y Apellido:................................. Grado:....... Sección:...... Puntaje:.......... Los dibujos correspondientes a problemas de Geometría,
SEGUNDA RONDA COLEGIAL - DE AGOSTO DE 00 - NIVEL Nombre y Apellido:................................. Grado:....... Sección:...... Puntaje:.......... Los dibujos correspondientes a problemas de Geometría,
TORNEOS GEOMÉTRICOS 2016 Primera Ronda. Primer Nivel - 5º Año de Escolaridad
 TORNEOS GEOMÉTRICOS 2016 Primera Ronda Primer Nivel - 5º Año de Escolaridad 1- En el triángulo rectángulo ABC cuyo ángulo en C mide 48º se trazan la bisectrices de los ángulos B y C, que se cortan en O.
TORNEOS GEOMÉTRICOS 2016 Primera Ronda Primer Nivel - 5º Año de Escolaridad 1- En el triángulo rectángulo ABC cuyo ángulo en C mide 48º se trazan la bisectrices de los ángulos B y C, que se cortan en O.
PRUEBA REGIONAL SÉPTIMO GRADO 2005
 PRUEBA REGIONAL SÉPTIMO GRADO 2005 1.- Iván cobra en un banco un cheque por Bs. 270.000 y le pide al cajero que le entregue cierta cantidad de billetes de Bs. 1000, 20 veces esa cantidad de billetes en
PRUEBA REGIONAL SÉPTIMO GRADO 2005 1.- Iván cobra en un banco un cheque por Bs. 270.000 y le pide al cajero que le entregue cierta cantidad de billetes de Bs. 1000, 20 veces esa cantidad de billetes en
Soluciones Nota nº 2. Problemas propuestos 1. El segmento AC es una diagonal del cuadrado ABCD. Reconstruir el cuadrado.
 Soluciones Nota nº 2 Problemas propuestos 1. El segmento AC es una diagonal del cuadrado ABCD. Reconstruir el cuadrado. Si el segmento AC fuera una diagonal del rectángulo ABCD, que no es cuadrado, es
Soluciones Nota nº 2 Problemas propuestos 1. El segmento AC es una diagonal del cuadrado ABCD. Reconstruir el cuadrado. Si el segmento AC fuera una diagonal del rectángulo ABCD, que no es cuadrado, es
TALLER DE POLÍGONOS Y CÍRCULOS (Areas y Perímetros)
 3 TALLER DE POLÍGONOS Y CÍRCULOS (Areas y Perímetros) Ejemplo 1: Un rectángulo tiene 60 m de área y 3m de perimetro. Hallar sus dimensiones.. Ejemplo : La base de un rectángulo es el triple de su altura
3 TALLER DE POLÍGONOS Y CÍRCULOS (Areas y Perímetros) Ejemplo 1: Un rectángulo tiene 60 m de área y 3m de perimetro. Hallar sus dimensiones.. Ejemplo : La base de un rectángulo es el triple de su altura
LECCIÓN 8 5 PROBLEMAS RESUELTOS. Cuál de los siguientes es un triángulo rectángulo?
 LECCIÓN 8 5 PROBLEMAS RESUELTOS Problema 1. Cuál de los siguientes es un triángulo rectángulo? A. B. C. D. E. Solución. Este ejercicio es para recordar los diversos tipos de triángulos que debemos conocer.
LECCIÓN 8 5 PROBLEMAS RESUELTOS Problema 1. Cuál de los siguientes es un triángulo rectángulo? A. B. C. D. E. Solución. Este ejercicio es para recordar los diversos tipos de triángulos que debemos conocer.
CANGURO MATEMÁTICO 2015 PRIMERO DE SECUNDARIA
 CANGURO MATEMÁTICO 2015 PRIMERO DE SECUNDARIA INDICACIONES Las marcas en la hoja de respuestas se deben realizar, únicamente, con LÁPIZ. Escriba su apellido paterno, apellido materno y nombres con letras
CANGURO MATEMÁTICO 2015 PRIMERO DE SECUNDARIA INDICACIONES Las marcas en la hoja de respuestas se deben realizar, únicamente, con LÁPIZ. Escriba su apellido paterno, apellido materno y nombres con letras
SEGUNDA OLIMPIADA ESTATAL DE MATEMÁTICAS
 PROBLEMAS PROPUESTOS PARA LA ETAPA DE ZONA TERCER GRADO 1. Cuánto mide el área sombreada A entre el área sombreada B en la siguiente figura? Para referenciar las argumentaciones se le inscriben letras
PROBLEMAS PROPUESTOS PARA LA ETAPA DE ZONA TERCER GRADO 1. Cuánto mide el área sombreada A entre el área sombreada B en la siguiente figura? Para referenciar las argumentaciones se le inscriben letras
Segundo Nivel 209. Siempre moviéndonos en el sentido de las flechas, de cuántas maneras podemos ir de A hasta P? F
 Problemas de Graciela errarini y Julia Seveso 4 de mayo 109. La figura está formada por dos triángulos iguales y un rectángulo. l perímetro de es 70 cm. l perímetro del triángulo es 60 cm. = 4 y = 3. uál
Problemas de Graciela errarini y Julia Seveso 4 de mayo 109. La figura está formada por dos triángulos iguales y un rectángulo. l perímetro de es 70 cm. l perímetro del triángulo es 60 cm. = 4 y = 3. uál
FORMULARIO (ÁREAS DE FIGURAS PLANAS)
 FORMULARIO (ÁREAS DE FIGURAS PLANAS) Rectángulo Triángulo Paralelogramo Cuadrado Cuadrilátero cuyos lados forman ángulos de 90º. Es la porción de plano limitada por tres segmentos de recta. Cuadrilátero
FORMULARIO (ÁREAS DE FIGURAS PLANAS) Rectángulo Triángulo Paralelogramo Cuadrado Cuadrilátero cuyos lados forman ángulos de 90º. Es la porción de plano limitada por tres segmentos de recta. Cuadrilátero
Problemas y ejercicios de áreas de polígonos
 Problemas y ejercicios de áreas de polígonos 1Un campo rectangular tiene 170 m de base y 28 m de altura. Calcular: 1Las hectáreas que tiene. 2El precio del campo si el metro cuadrado cuesta 15. 2 Calcula
Problemas y ejercicios de áreas de polígonos 1Un campo rectangular tiene 170 m de base y 28 m de altura. Calcular: 1Las hectáreas que tiene. 2El precio del campo si el metro cuadrado cuesta 15. 2 Calcula
Clasifi cación de polígonos
 Clasifi cación de polígonos Cuándo un polígono es regular? Marca la opción correcta. Sus ángulos son iguales. Sus lados son iguales. Sus lados y sus ángulos son iguales. Sus diagonales son iguales. Escribe
Clasifi cación de polígonos Cuándo un polígono es regular? Marca la opción correcta. Sus ángulos son iguales. Sus lados son iguales. Sus lados y sus ángulos son iguales. Sus diagonales son iguales. Escribe
DEPARTAMENTO DE MATEMATICAS
 1.- Halla la suma de los ángulos interiores de los siguientes polígonos convexos. a) Cuadrilátero b) Heptágono c) Octógono 2.- Halla la medida de los ángulos interiores de: a) Un octógono regular. b) Un
1.- Halla la suma de los ángulos interiores de los siguientes polígonos convexos. a) Cuadrilátero b) Heptágono c) Octógono 2.- Halla la medida de los ángulos interiores de: a) Un octógono regular. b) Un
Unidad 7 Figuras planas. Polígonos
 Polígonos 1.- Halla la suma de los ángulos interiores de los siguientes polígonos convexos. a) Cuadrilátero b) Heptágono c) Octógono.- Halla la medida de los ángulos interiores de: a) Un octógono regular.
Polígonos 1.- Halla la suma de los ángulos interiores de los siguientes polígonos convexos. a) Cuadrilátero b) Heptágono c) Octógono.- Halla la medida de los ángulos interiores de: a) Un octógono regular.
Problemas Perímetro. ACes un arco de circunferencia de BM OA. de Graciela Ferrarini y Julia Seveso
 Problemas de Graciela Ferrarini y Julia Seveso 1 de agosto XX-120 Primer nivel n la figura: es un rectángulo de 32 cm de perímetro = 6 cm = es un triángulo de 24 cm de perímetro uál es la longitud del
Problemas de Graciela Ferrarini y Julia Seveso 1 de agosto XX-120 Primer nivel n la figura: es un rectángulo de 32 cm de perímetro = 6 cm = es un triángulo de 24 cm de perímetro uál es la longitud del
PROYECTO # 2 SISTEMAS DE ECUACIONES CON LOS 4 MÉTODOS
 PROYECTO # 2 SISTEMAS DE ECUACIONES CON LOS 4 MÉTODOS Matemáticas 2 Secundaria 5 Bimestre Prof. Héctor Lagunes Espinosa FECHA DE ENTREGA: 29 DE MAYO DEL 2015 Nombre: - Grado y Grupo: Nota: Escribe todos
PROYECTO # 2 SISTEMAS DE ECUACIONES CON LOS 4 MÉTODOS Matemáticas 2 Secundaria 5 Bimestre Prof. Héctor Lagunes Espinosa FECHA DE ENTREGA: 29 DE MAYO DEL 2015 Nombre: - Grado y Grupo: Nota: Escribe todos
OLIMPÍADA JUVENIL DE MATEMÁTICA 2010 CANGURO MATEMÁTICO PRUEBA PRELIMINAR TERCER AÑO
 OLIMPÍADA JUVENIL DE MATEMÁTICA 2010 CANGURO MATEMÁTICO PRUEBA PRELIMINAR TERCER AÑO RESPONDE LA PRUEBA EN LA HOJA DE RESPUESTA ANEXA 1. El perímetro de la figura es igual a: A 3a+4b; B 3a+8b; C 6a+4b;
OLIMPÍADA JUVENIL DE MATEMÁTICA 2010 CANGURO MATEMÁTICO PRUEBA PRELIMINAR TERCER AÑO RESPONDE LA PRUEBA EN LA HOJA DE RESPUESTA ANEXA 1. El perímetro de la figura es igual a: A 3a+4b; B 3a+8b; C 6a+4b;
8. POLÍGONOS Y FIGURAS CIRCULARES
 8. POLÍGONOS Y FIGURAS CIRCULARES 1. Los ángulos del triángulo ABC de la siguiente gura miden: m A = 60 o, m B = 100 o. Prolongando AB tal que BD = BC, los ángulos del triángulo CBD miden: a) B 80 o, C
8. POLÍGONOS Y FIGURAS CIRCULARES 1. Los ángulos del triángulo ABC de la siguiente gura miden: m A = 60 o, m B = 100 o. Prolongando AB tal que BD = BC, los ángulos del triángulo CBD miden: a) B 80 o, C
Soluciones Primer Nivel - 5º Año de Escolaridad
 Primer Nivel - 5º Año de Escolaridad Problema 1. La diagonal del cuadrado mide cm. El cuadrado se descompone en cuatro triángulos rectángulos cuyos catetos miden 1cm. Las áreas de estos triángulos miden
Primer Nivel - 5º Año de Escolaridad Problema 1. La diagonal del cuadrado mide cm. El cuadrado se descompone en cuatro triángulos rectángulos cuyos catetos miden 1cm. Las áreas de estos triángulos miden
SOLUCIONES PRIMER NIVEL
 SOLUCIONES PRIMER NIVEL 1. Los cuatro polígonos de la figura son regulares. Halla los valores de los tres ángulos, de vértice A limitados por dos lados de los polígonos dados, indicados en la figura. Solución:
SOLUCIONES PRIMER NIVEL 1. Los cuatro polígonos de la figura son regulares. Halla los valores de los tres ángulos, de vértice A limitados por dos lados de los polígonos dados, indicados en la figura. Solución:
XX OLIMPIADA NACIONAL DE MATEMÁTICA TERCERA RONDA REGIONAL - 6 DE SETIEMBRE DE NIVEL 1. Nombre y Apellido:... Puntaje:...
 TERCERA RONDA REGIONAL - 6 DE SETIEMBRE DE 2008 - NIVEL 1 Nombre y Apellido:................................. Puntaje:.................... Colegio:................................... Grado:...........
TERCERA RONDA REGIONAL - 6 DE SETIEMBRE DE 2008 - NIVEL 1 Nombre y Apellido:................................. Puntaje:.................... Colegio:................................... Grado:...........
Nombre y Apellido:... Puntaje:... Colegio:... Grado:... Teléfono (L B):... Celular: Número de Cédula de Identidad:...
 XXII OLIMPIADA NACIONAL DE MATEMÁTICA RONDA REGIONAL 14 DE AGOSTO DE 2010 - NIVEL 1 PEGÁ TU STICKER AQUÍ Nombre y Apellido:............................................ Puntaje:......... Colegio:.......................................................
XXII OLIMPIADA NACIONAL DE MATEMÁTICA RONDA REGIONAL 14 DE AGOSTO DE 2010 - NIVEL 1 PEGÁ TU STICKER AQUÍ Nombre y Apellido:............................................ Puntaje:......... Colegio:.......................................................
NIVEL 1 (6.º y 7.º grado)
 NIVEL 1 (6.º y 7.º grado) 25.ª OLIMPIADA NACIONAL JUVENIL DE MATEMÁTICA 3ª RONDA ZONAL - 29 de junio de 2013 Nombre y Apellido:.............................................. Colegio:..........................
NIVEL 1 (6.º y 7.º grado) 25.ª OLIMPIADA NACIONAL JUVENIL DE MATEMÁTICA 3ª RONDA ZONAL - 29 de junio de 2013 Nombre y Apellido:.............................................. Colegio:..........................
OLIMPÍADA NACIONAL RONDA FINAL. 1er. NIVEL
 OLIMPÍADA NACIONAL 001 - RONDA FINAL 1er. NIVEL Problema 1 Laura tenía un jardín rectangular de 8m de ancho y 10m de largo. Si aumentó metros el ancho de su jardín y m el largo, en cuánto aumentó la superficie
OLIMPÍADA NACIONAL 001 - RONDA FINAL 1er. NIVEL Problema 1 Laura tenía un jardín rectangular de 8m de ancho y 10m de largo. Si aumentó metros el ancho de su jardín y m el largo, en cuánto aumentó la superficie
XXVII CONCURSO PUIG ADAM DE RESOLUCIÓN DE PROBLEMAS Facultad de Matemáticas U.C.M. Madrid, 13 de junio de 2009
 Madrid, 13 de junio de 009 NIVEL I (3º de E.S.O.) Primera parte (1 hora 30 minutos) Problema 1. Los tres apartados de este problema están encadenados. La respuesta de cada uno es un dato para el siguiente.
Madrid, 13 de junio de 009 NIVEL I (3º de E.S.O.) Primera parte (1 hora 30 minutos) Problema 1. Los tres apartados de este problema están encadenados. La respuesta de cada uno es un dato para el siguiente.
Cuadriláteros - Áreas cuadrangulares
 3A Cuadriláteros - Áreas cuadrangulares EJERCICIOS PROPUESTOS 1. En un rombo de lado 6 cm, uno de sus ángulos mide 60º. Calcula la longitud de la diagonal menor. A. 6 cm C. 4 cm B. 5 cm D. 3 cm. En un
3A Cuadriláteros - Áreas cuadrangulares EJERCICIOS PROPUESTOS 1. En un rombo de lado 6 cm, uno de sus ángulos mide 60º. Calcula la longitud de la diagonal menor. A. 6 cm C. 4 cm B. 5 cm D. 3 cm. En un
Tema 9: Teoremas de Thales y Pitágoras.
 Matemáticas Ejercicios Tema 9 2º ESO Bloque IV: Geometría Tema 9: Teoremas de Thales y Pitágoras. 1.- Calcula los valores de x e y. 2.- Calcula la longitud x MN 3.- Explica por qué dos triángulos rectángulos
Matemáticas Ejercicios Tema 9 2º ESO Bloque IV: Geometría Tema 9: Teoremas de Thales y Pitágoras. 1.- Calcula los valores de x e y. 2.- Calcula la longitud x MN 3.- Explica por qué dos triángulos rectángulos
OLIMPÍADA JUVENIL DE MATEMÁTICA 2016 CANGURO MATEMÁTICO PRIMER AÑO
 OLIMPÍADA JUVENIL DE MATEMÁTICA 2016 CANGURO MATEMÁTICO PRIMER AÑO RESPONDE LA PRUEBA EN LA HOJA DE RESPUESTA ANEXA 1. Cuál de las siguientes señales de tránsito tiene un mayor número de ejes de simetría?
OLIMPÍADA JUVENIL DE MATEMÁTICA 2016 CANGURO MATEMÁTICO PRIMER AÑO RESPONDE LA PRUEBA EN LA HOJA DE RESPUESTA ANEXA 1. Cuál de las siguientes señales de tránsito tiene un mayor número de ejes de simetría?
TAREAS SEMANA 22 al 26 de enero B1MESTRE 3
 COLEGIO AGUILA CICLO ESCOLAR 2017-2018 SECUNDARIA TAREAS SEMANA 22 al 26 de enero 2018. B1MESTRE 3 Materia: MATEMÁTICAS 3A,3B,3C y 2D PROFRA: EMMA LAURA MELÉNDEZ AGUNDIS. N FECHA DE ENTREGA 1 Lunes 22
COLEGIO AGUILA CICLO ESCOLAR 2017-2018 SECUNDARIA TAREAS SEMANA 22 al 26 de enero 2018. B1MESTRE 3 Materia: MATEMÁTICAS 3A,3B,3C y 2D PROFRA: EMMA LAURA MELÉNDEZ AGUNDIS. N FECHA DE ENTREGA 1 Lunes 22
SEGUNDA ELIMINATORIA NACIONAL
 XXIX OLIMPIADA COSTARRICENSE DE MATEMÁTICA MEP - UNA - UCR - MICITT - UNED - TEC SEGUNDA ELIMINATORIA NACIONAL (7 ) 2017 Estimado estudiante: La Comisión Organizadora de las Olimpiadas Costarricenses de
XXIX OLIMPIADA COSTARRICENSE DE MATEMÁTICA MEP - UNA - UCR - MICITT - UNED - TEC SEGUNDA ELIMINATORIA NACIONAL (7 ) 2017 Estimado estudiante: La Comisión Organizadora de las Olimpiadas Costarricenses de
Examen Eliminatorio Estatal de la Olimpiada Mexicana de Matemáticas 2010.
 Examen Eliminatorio Estatal de la Olimpiada Mexicana de Matemáticas 2010. Instrucciones: En la hoja de las respuestas marca la respuesta que creas correcta. Si marcas más de una respuesta en alguna pregunta
Examen Eliminatorio Estatal de la Olimpiada Mexicana de Matemáticas 2010. Instrucciones: En la hoja de las respuestas marca la respuesta que creas correcta. Si marcas más de una respuesta en alguna pregunta
OLIMPÍADA JUVENIL DE MATEMÁTICA 2014 CANGURO MATEMÁTICO TERCER AÑO
 OLIMPÍADA JUVENIL DE MATEMÁTICA 2014 CANGURO MATEMÁTICO TERCER AÑO RESPONDE LA PRUEBA EN LA HOJA DE RESPUESTA ANEXA 1. Cuál es el resultado de 2014 2014 : 2014 2014? A 1; B 0; C 2013; D 2014; E 4028. 2.
OLIMPÍADA JUVENIL DE MATEMÁTICA 2014 CANGURO MATEMÁTICO TERCER AÑO RESPONDE LA PRUEBA EN LA HOJA DE RESPUESTA ANEXA 1. Cuál es el resultado de 2014 2014 : 2014 2014? A 1; B 0; C 2013; D 2014; E 4028. 2.
25.º OLIMPIADA NACIONAL JUVENIL DE MATEMÁTICA CUARTA RONDA DEPARTAMENTAL NIVEL 1 17 de agosto de 2013
 CUARTA RONDA DEPARTAMENTAL NIVEL 1 Nombre y Apellido:............................................... Colegio:............................. Grado/Curso:...... Sección:..... Ciudad:................................
CUARTA RONDA DEPARTAMENTAL NIVEL 1 Nombre y Apellido:............................................... Colegio:............................. Grado/Curso:...... Sección:..... Ciudad:................................
Junior (1ro. y 2do. Año)
 CANGURO MATEMÁTICO 2003 Junior (1ro. y 2do. Año) Nivel Junior (1ro. y 2do. Año) Día 22 de marzo de 2003. Tiempo : 1 hora y 15 minutos No se permite el uso de calculadoras. Hay una única respuesta correcta
CANGURO MATEMÁTICO 2003 Junior (1ro. y 2do. Año) Nivel Junior (1ro. y 2do. Año) Día 22 de marzo de 2003. Tiempo : 1 hora y 15 minutos No se permite el uso de calculadoras. Hay una única respuesta correcta
Problema 1 En la Figura 2 de la gráfica hay 3 ángulos. Cuántos ángulos hay en la Figura 3? A) 3 D) 6 B) 4 E) 7 C) 5 F) n. d. l. a.
 PRIMERA RONDA COLEGIAL NIVEL 1 Nombre y Apellido:............................................ Puntaje: Grado/Curso....... Sección:...... Los dibujos correspondientes a los problemas de Geometría, no están
PRIMERA RONDA COLEGIAL NIVEL 1 Nombre y Apellido:............................................ Puntaje: Grado/Curso....... Sección:...... Los dibujos correspondientes a los problemas de Geometría, no están
RELACIÓN DE EJERCICIOS DE GEOMETRÍA PLANA
 RELACIÓN DE EJERCICIOS DE GEOMETRÍA PLANA 1. Halla el perímetro y el área de las siguientes figuras: 2. Entre las dos diagonales de un rombo suman 100 cm, siendo la menor 20 cm más corta que la mayor.
RELACIÓN DE EJERCICIOS DE GEOMETRÍA PLANA 1. Halla el perímetro y el área de las siguientes figuras: 2. Entre las dos diagonales de un rombo suman 100 cm, siendo la menor 20 cm más corta que la mayor.
Soluciones Primer Nivel
 Soluciones Primer Nivel Torneos Geométricos 2017 2º Ronda 1. En un papel cuadriculado con cuadrados de un centímetro de lado, se ha dibujado un cuadrilátero con vértices en los nodos del mismo (vértices
Soluciones Primer Nivel Torneos Geométricos 2017 2º Ronda 1. En un papel cuadriculado con cuadrados de un centímetro de lado, se ha dibujado un cuadrilátero con vértices en los nodos del mismo (vértices
OLIMPÍADA JUVENIL DE MATEMÁTICA 2010 CANGURO MATEMÁTICO PRUEBA PRELIMINAR QUINTO AÑO
 OLIMPÍADA JUVENIL DE MATEMÁTICA 2010 CANGURO MATEMÁTICO PRUEBA PRELIMINAR QUINTO AÑO RESPONDE LA PRUEBA EN LA HOJA DE RESPUESTA ANEXA 1. Examinando la figura se puede concluir que 1+3+5+7 = 4 4. Cuál es
OLIMPÍADA JUVENIL DE MATEMÁTICA 2010 CANGURO MATEMÁTICO PRUEBA PRELIMINAR QUINTO AÑO RESPONDE LA PRUEBA EN LA HOJA DE RESPUESTA ANEXA 1. Examinando la figura se puede concluir que 1+3+5+7 = 4 4. Cuál es
TEMARIO PARA EL EXAMEN DE RECUPERACIÓN 4TO AÑO SECUNDARIA 2013
 TEMARIO PARA EL EXAMEN DE RECUPERACIÓN 4TO AÑO SECUNDARIA 2013 1.- FUNCIONES: Dominio y rango, función real de variable real, operaciones con funciones, composición de funciones. 2.- ÁNGULOS: congruencia
TEMARIO PARA EL EXAMEN DE RECUPERACIÓN 4TO AÑO SECUNDARIA 2013 1.- FUNCIONES: Dominio y rango, función real de variable real, operaciones con funciones, composición de funciones. 2.- ÁNGULOS: congruencia
1. Con el dígito a se forman el número de dos dígitos a 3 y los números de tres dígitos 3aa y a 34. Si se sabe que 281, calcular el valor de a.
 PRIMER NIVEL CERTAMEN ZONAL XXIX OLIMPÍADA MATEMÁTICA ARGENTINA APELLIDO: NOMBRES: DNI: ESCUELA: LOCALIDAD Y PROVINCIA: ESCRIBIR EN LA HOJA DE SOLUCIONES LOS CÁLCULOS Y RAZONAMIENTOS QUE JUSTIFICAN LAS
PRIMER NIVEL CERTAMEN ZONAL XXIX OLIMPÍADA MATEMÁTICA ARGENTINA APELLIDO: NOMBRES: DNI: ESCUELA: LOCALIDAD Y PROVINCIA: ESCRIBIR EN LA HOJA DE SOLUCIONES LOS CÁLCULOS Y RAZONAMIENTOS QUE JUSTIFICAN LAS
4. Resolver un triángulo rectángulo e isósceles en el que la hipotenusa tiene 9 pies de longitud.
 7 CAPÍTULO SIETE Ejercicios propuestos 7.5 Triángulos 1. Construya de ser posible los siguientes triángulos ABC. En caso de que existan, determine sus cuatro puntos característicos empleando regla y compás.
7 CAPÍTULO SIETE Ejercicios propuestos 7.5 Triángulos 1. Construya de ser posible los siguientes triángulos ABC. En caso de que existan, determine sus cuatro puntos característicos empleando regla y compás.
Definiciones I. Definiciones II
 Definiciones I Una ecuación es una igualdad algebraica que se verifica únicamente para un conjunto determinado de valores de las variables o indeterminadas que forman la ecuación. Esta igualdad es una
Definiciones I Una ecuación es una igualdad algebraica que se verifica únicamente para un conjunto determinado de valores de las variables o indeterminadas que forman la ecuación. Esta igualdad es una
Colegio Fernando de Aragón Departamento de matemática Prof. Sergio Moreno SEMEJANZA N 15 NOMBRE: II FECHA: / /201
 Colegio Fernando de Aragón Departamento de matemática Prof. Sergio Moreno N lista: SEMEJANZA N 15 NOMBRE: II FECHA: / /201 ALTERNATIVAS Cómo se puede saber si los polígonos ABCD y A B C D (figura 1) son
Colegio Fernando de Aragón Departamento de matemática Prof. Sergio Moreno N lista: SEMEJANZA N 15 NOMBRE: II FECHA: / /201 ALTERNATIVAS Cómo se puede saber si los polígonos ABCD y A B C D (figura 1) son
Examen de Matemáticas (1º E.S.O) UNIDAD 13: ÁREAS Y PERÍMETROS. Grupo: 1ºB Fecha: 11/06/2009
 I.E.S SAN JOSÉ (CORTEGANA) DEPARTAMENTO DE MATEMÁTICAS Examen de Matemáticas (1º E.S.O) UNIDAD 13: ÁREAS Y PERÍMETROS Nombre y Apellidos: Grupo: 1ºB Fecha: 11/06/009 CALIFICACIÓN: Ejercicio nº 1.- Calcula
I.E.S SAN JOSÉ (CORTEGANA) DEPARTAMENTO DE MATEMÁTICAS Examen de Matemáticas (1º E.S.O) UNIDAD 13: ÁREAS Y PERÍMETROS Nombre y Apellidos: Grupo: 1ºB Fecha: 11/06/009 CALIFICACIÓN: Ejercicio nº 1.- Calcula
27.- La diferencia entre el lado de un triangulo equilátero y su altura es 12 cm. Cuanto mide el perímetro del triangulo?
 EJERCICIOS 1.- Calcular la altura a la hipotenusa de un triángulo rectángulo cuyos catetos miden 6 y 8 cm. 5 2.- En un triángulo rectángulo, un cateto mide 15 cm., y la proyección del otro sobre la hipotenusa
EJERCICIOS 1.- Calcular la altura a la hipotenusa de un triángulo rectángulo cuyos catetos miden 6 y 8 cm. 5 2.- En un triángulo rectángulo, un cateto mide 15 cm., y la proyección del otro sobre la hipotenusa
El abuelo quiere repartir entre sus nietos, Martín y Juan, $264. A Juan le da $15 cada semana;
 Problemas Semanales 4 de marzo XXII-101 El abuelo quiere repartir entre sus nietos, Martín y Juan, $264. Juan le da $15 cada semana; a Martín le da $18 cada semana. espués de cuántas semanas habrá repartido
Problemas Semanales 4 de marzo XXII-101 El abuelo quiere repartir entre sus nietos, Martín y Juan, $264. Juan le da $15 cada semana; a Martín le da $18 cada semana. espués de cuántas semanas habrá repartido
VIII Concurso Intercentros de Matemáticas de la Comunidad de Madrid
 PRUE POR EQUIPOS 1º y º de E.S.O. (45 minutos) 1.- Pedro y Juan eligen ocho números de los nueve que hay escritos en este diagrama, cuatro cada uno; así pues hay un número que no elige ninguno. Pedro observa
PRUE POR EQUIPOS 1º y º de E.S.O. (45 minutos) 1.- Pedro y Juan eligen ocho números de los nueve que hay escritos en este diagrama, cuatro cada uno; así pues hay un número que no elige ninguno. Pedro observa
ÁNGULOS. 2. En el triángulo ABC, el ángulo B se obtiene aumentando en 50% el ángulo A o también reduciendo en 25% el ángulo C. Cuál es la medida de B?
 ENTRENAMIENTO COMPETENCIA COTORRA 2015 GEOMETRÍA (PROBLEMAS INTRODUCTORIOS) IIS AMIR MADRID GARZÓN Enero / 2015 ÁNGULOS 1. Cuántos ángulos hay en la siguiente figura? a) 13 b) 14 c) 21 d) 18 2. En el triángulo
ENTRENAMIENTO COMPETENCIA COTORRA 2015 GEOMETRÍA (PROBLEMAS INTRODUCTORIOS) IIS AMIR MADRID GARZÓN Enero / 2015 ÁNGULOS 1. Cuántos ángulos hay en la siguiente figura? a) 13 b) 14 c) 21 d) 18 2. En el triángulo
VI CONCURSO DE PRIMAVERA DE LA RIOJA
 VI CONCURSO DE PRIMAVERA DE LA RIOJA 2ª FASE Día 24 de Abril de 2.004 NIVEL I (5º Y 6º DE PRIMARIA) Lee detenidamente las instrucciones!!! Escribe ahora los siguientes datos: Apellidos Nombre Año de nacimiento
VI CONCURSO DE PRIMAVERA DE LA RIOJA 2ª FASE Día 24 de Abril de 2.004 NIVEL I (5º Y 6º DE PRIMARIA) Lee detenidamente las instrucciones!!! Escribe ahora los siguientes datos: Apellidos Nombre Año de nacimiento
PRUEBA DE CUARTO GRADO.
 PRUEBA DE CUARTO GRADO. Francisco tiene 10 cajas y 44 monedas. Quiere poner las monedas en las cajas repartiéndolas de modo que cada caja contenga un número distinto de monedas. Puede hacerlo? Si puede,
PRUEBA DE CUARTO GRADO. Francisco tiene 10 cajas y 44 monedas. Quiere poner las monedas en las cajas repartiéndolas de modo que cada caja contenga un número distinto de monedas. Puede hacerlo? Si puede,
XXI OLIMPIADA NACIONAL DE MATEMÁTICA
 TERCERA RONDA REGIONAL - 22 DE AGOSTO DE 2009 - NIVEL 1 Nombre y Apellido:................................. Puntaje:.................... Colegio:................................... Grado:........... Sección:..........
TERCERA RONDA REGIONAL - 22 DE AGOSTO DE 2009 - NIVEL 1 Nombre y Apellido:................................. Puntaje:.................... Colegio:................................... Grado:........... Sección:..........
OLIMPÍADA JUVENIL DE MATEMÁTICA 2014 CANGURO MATEMÁTICO QUINTO AÑO
 OLIMPÍADA JUVENIL DE MATEMÁTICA 2014 CANGURO MATEMÁTICO QUINTO AÑO RESPONDE LA PRUEBA EN LA HOJA DE RESPUESTA ANEXA 1. La prueba Canguro se aplica el tercer jueves del mes de marzo, cada año. Cuál es el
OLIMPÍADA JUVENIL DE MATEMÁTICA 2014 CANGURO MATEMÁTICO QUINTO AÑO RESPONDE LA PRUEBA EN LA HOJA DE RESPUESTA ANEXA 1. La prueba Canguro se aplica el tercer jueves del mes de marzo, cada año. Cuál es el
OLIMPÍADA JUVENIL DE MATEMÁTICA 2014 CANGURO MATEMÁTICO CUARTO AÑO
 OLIMPÍADA JUVENIL DE MATEMÁTICA 2014 CANGURO MATEMÁTICO CUARTO AÑO RESPONDE LA PRUEBA EN LA HOJA DE RESPUESTA ANEXA 1. La prueba Canguro se aplica el tercer jueves del mes de marzo, cada año. Cuál es el
OLIMPÍADA JUVENIL DE MATEMÁTICA 2014 CANGURO MATEMÁTICO CUARTO AÑO RESPONDE LA PRUEBA EN LA HOJA DE RESPUESTA ANEXA 1. La prueba Canguro se aplica el tercer jueves del mes de marzo, cada año. Cuál es el
2ª.- Halla el valor de Xˆ, Yˆ, Z ˆ, en los siguientes polígonos regulares:
 TRABAJO DE RECUPERACIÓN DE GEOMETRÍA de 3º ESO 1ª.- Calcula el valor de Xˆ, Yˆ, Z ˆ, en los siguientes polígonos regulares: a) b) 2ª.- Halla el valor de Xˆ, Yˆ, Z ˆ, en los siguientes polígonos regulares:
TRABAJO DE RECUPERACIÓN DE GEOMETRÍA de 3º ESO 1ª.- Calcula el valor de Xˆ, Yˆ, Z ˆ, en los siguientes polígonos regulares: a) b) 2ª.- Halla el valor de Xˆ, Yˆ, Z ˆ, en los siguientes polígonos regulares:
Matemáticas 3º E.S.O. 2014/15
 Matemáticas 3º E.S.O. 2014/15 TEMA 5: Figuras planas Ficha número 16 1.- Calcula la altura del siguiente triángulo: (Sol: 12,12 cm) 2.- En un triángulo isósceles la altura sobre el lado desigual mide 50
Matemáticas 3º E.S.O. 2014/15 TEMA 5: Figuras planas Ficha número 16 1.- Calcula la altura del siguiente triángulo: (Sol: 12,12 cm) 2.- En un triángulo isósceles la altura sobre el lado desigual mide 50
MEDIDAS DE LONGITUDES Y SUPERFICIES_ADAPT (6ºEP)
 Adaptación Unidad 11 _La longitud y la superficie. Página 1 LA LONGITUD. Copia en tu cuaderno y aprende. Adaptación Unidad 11 _La longitud y la superficie. Página 2 1. Copia y completa: metros (m) centímetros
Adaptación Unidad 11 _La longitud y la superficie. Página 1 LA LONGITUD. Copia en tu cuaderno y aprende. Adaptación Unidad 11 _La longitud y la superficie. Página 2 1. Copia y completa: metros (m) centímetros
MATEMÁTICAS 1º ESO. Operaciones con números enteros y fraccionarios, potencias y raíces
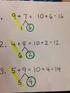 COLEGIO MARÍA INMACULADA - CARCAIXENT DEPARTAMENTO DE MATEMÁTICAS MATEMÁTICAS 1º ESO Operaciones con números enteros y fraccionarios, potencias y raíces 1. Realiza las siguientes operaciones: 2. Realiza
COLEGIO MARÍA INMACULADA - CARCAIXENT DEPARTAMENTO DE MATEMÁTICAS MATEMÁTICAS 1º ESO Operaciones con números enteros y fraccionarios, potencias y raíces 1. Realiza las siguientes operaciones: 2. Realiza
OLIMPÍADA JUVENIL DE MATEMÁTICA 2017 CANGURO MATEMÁTICO QUINTO AÑO
 OLIMPÍADA JUVENIL DE MATEMÁTICA 2017 CANGURO MATEMÁTICO QUINTO AÑO RESPONDE LA PRUEBA EN LA HOJA DE RESPUESTA ANEXA 1. En este diagrama cada número es la suma de los dos números que están debajo de él.
OLIMPÍADA JUVENIL DE MATEMÁTICA 2017 CANGURO MATEMÁTICO QUINTO AÑO RESPONDE LA PRUEBA EN LA HOJA DE RESPUESTA ANEXA 1. En este diagrama cada número es la suma de los dos números que están debajo de él.
INSTITUTO DE FORMACIÓN DOCENTE DE CANELONES REPARTIDO Nº 6. 3) Calcular la diagonal de un cuadrado de 7 cm de lado.
 REPARTIDO Nº 6 1) Calcular la hipotenusa de un triángulo rectángulo sabiendo que los catetos miden 6 cm y 8 cm respectivamente. 2) Si la hipotenusa de un triángulo rectángulo mide 13 cm y uno de sus catetos
REPARTIDO Nº 6 1) Calcular la hipotenusa de un triángulo rectángulo sabiendo que los catetos miden 6 cm y 8 cm respectivamente. 2) Si la hipotenusa de un triángulo rectángulo mide 13 cm y uno de sus catetos
La carrera geométrica
 La carrera geométrica Materiales: el tablero 1, un personaje por cada jugador y un dado. 1. Cada jugador ubica su ficha en la salida. 2. Por turno, cada jugador tira el dado y mueve su ficha tantos casilleros
La carrera geométrica Materiales: el tablero 1, un personaje por cada jugador y un dado. 1. Cada jugador ubica su ficha en la salida. 2. Por turno, cada jugador tira el dado y mueve su ficha tantos casilleros
LOS POLÍGONOS (I): TRIÁNGULOS
 Apellidos: Curso: Grupo: Nombre: Fecha: LOS POLÍGONOS (I): TRIÁNGULOS El triángulo es un polígono que tiene 3 lados, 3 vértices y 3 ángulos. Los tres ángulos de un triángulo siempre suman 180. 1. Relaciona:
Apellidos: Curso: Grupo: Nombre: Fecha: LOS POLÍGONOS (I): TRIÁNGULOS El triángulo es un polígono que tiene 3 lados, 3 vértices y 3 ángulos. Los tres ángulos de un triángulo siempre suman 180. 1. Relaciona:
CUADERNO DEL ALUMNO/A
 CUADERNO DEL ALUMNO/A PRUEBA DE EVALUACIÓN INICIAL DE MATEMÁTICAS. 6º CURSO EDUCACIÓN PRIMARIA Evaluación Inicial de Matemáticas 6º Curso 1.- LECTURA Y ESCRITURA DE NÚMEROS NATURALES. Completa con cifras
CUADERNO DEL ALUMNO/A PRUEBA DE EVALUACIÓN INICIAL DE MATEMÁTICAS. 6º CURSO EDUCACIÓN PRIMARIA Evaluación Inicial de Matemáticas 6º Curso 1.- LECTURA Y ESCRITURA DE NÚMEROS NATURALES. Completa con cifras
CUADERNILLO RECUPERACIÓN DE PENDIENTES
 Cuadernillo de recuperación. ª Evaluación Curso 017/018 CUADERNILLO RECUPERACIÓN DE PENDIENTES CURSO 017/018 MATEMÁTICAS ORIENTADAS A LAS ENSEÑANZAS APLICADAS 3º E.S.O. ª EVALUACIÓN Los ejercicios deben
Cuadernillo de recuperación. ª Evaluación Curso 017/018 CUADERNILLO RECUPERACIÓN DE PENDIENTES CURSO 017/018 MATEMÁTICAS ORIENTADAS A LAS ENSEÑANZAS APLICADAS 3º E.S.O. ª EVALUACIÓN Los ejercicios deben
Hoja de problemas nº 5. Progresiones Aritméticas y Geométricas
 Hoja de problemas nº 5 Progresiones Aritméticas y Geométricas 1. Calcula el término que ocupa el lugar 100 de una progresión aritmética cuyo primer término es igual a 4 y la diferencia es 5. 2. El décimo
Hoja de problemas nº 5 Progresiones Aritméticas y Geométricas 1. Calcula el término que ocupa el lugar 100 de una progresión aritmética cuyo primer término es igual a 4 y la diferencia es 5. 2. El décimo
ARITMÉTICA 1. Cómo se leen los siguientes números?
 TAREA PARA EL VERANO NIVEL de 1º ESO Preparando el siguiente curso y con el fin de repasar y profundizar en algunos conocimientos y adquirir algunas destrezas, este alumno tiene que hacer durante el verano
TAREA PARA EL VERANO NIVEL de 1º ESO Preparando el siguiente curso y con el fin de repasar y profundizar en algunos conocimientos y adquirir algunas destrezas, este alumno tiene que hacer durante el verano
ARITMÉTICA 1. Cómo se leen los siguientes números?
 TAREA PARA EL VERANO NIVEL de 1º ESO Preparando el siguiente curso y con el fin de repasar y profundizar en algunos conocimientos y adquirir algunas destrezas, este alumno tiene que hacer durante el verano
TAREA PARA EL VERANO NIVEL de 1º ESO Preparando el siguiente curso y con el fin de repasar y profundizar en algunos conocimientos y adquirir algunas destrezas, este alumno tiene que hacer durante el verano
Taller especial de capacitación de los profesores del 4º Ciclo
 Taller especial de capacitación de los profesores del 4º Ciclo Este taller fue preparado para satisfacer la inquietud de los docentes que solicitaron más capacitación Olimpiada Akâ Porâ Olimpiada Nacional
Taller especial de capacitación de los profesores del 4º Ciclo Este taller fue preparado para satisfacer la inquietud de los docentes que solicitaron más capacitación Olimpiada Akâ Porâ Olimpiada Nacional
PSU Matemática NM-4 Guía 14: Ángulos y Triángulos
 1 Centro Educacional San Carlos de Aragón. Dpto. Matemática. Prof. Ximena Gallegos H. PSU Matemática NM- Guía 1: Ángulos y Triángulos Nombre: Curso: Fecha: - Contenido: Geometría. Aprendizaje Esperado:
1 Centro Educacional San Carlos de Aragón. Dpto. Matemática. Prof. Ximena Gallegos H. PSU Matemática NM- Guía 1: Ángulos y Triángulos Nombre: Curso: Fecha: - Contenido: Geometría. Aprendizaje Esperado:
