Medidas de tendencia Central
|
|
|
- Gloria Cárdenas Ríos
- hace 10 años
- Vistas:
Transcripción
1 Medidas de tendencia Central 7.1 Media Media para un conjunto de datos no agrupados Este parámetro lo usamos con tanta cotidianidad que nos será muy familiar, aunque también aprenderemos algunas propiedades y mostraremos un teorema sumamente importante. Si tenemos el siguiente conjunto de datos y deseamos encontrar un valor que represente a todo el conjunto, seguramente lo primero que vendrá a nuestra mente es sumar todos los valores y dividirlos entre el número total de datos. 13 Ejemplo: Número de alumnados en la clase de Educación Física. 10, 9, 8, 10, 9, 9, 10, 9, 10, 9 Este valor, promedio aritmético, es conocido como la media y es una de las medidas de tendencia central ya que representa un valor con respeto a toda la información. Ejemplo para el cálculo de la media. Sean los siguientes valores las calificaciones de la asignatura de Educación Física de estudiantes de primer año: Sumando los valores de las 30 calificaciones y dividiéndolas entre los 30 datos obtendremos:
2 Por lo que la media de las calificaciones obtenidas por el grupo considerado es igual a 8. Para datos agrupados la expresión de la media cambia ligeramente, como se muestra a continuación Media para un conjunto de datos agrupados. La media para datos agrupados es la siguiente: Donde es el total de datos, m es el número total de clase y es la frecuencia de datos. La definición es claramente entendida como una extensión de la definición que dimos para datos no agrupados, ya que es lógico suponer que datos que se repiten con una frecuencia pueden simplificar la suma por supuesto que los índices de la segunda suma con respecto a la primera corren con respecto a menor número, es decir, con respecto al número de agrupamientos m. Ejemplo: Goles anotados por el Querétaro durante la temporada. Sean los siguientes datos 1, 1, 2, 2, 4, 4, 5, 2, 3, 2, 3, 4, 1, 2, 1. La media para dichos datos es aproximadamente igual a Para la obtención de la media cuando las frecuencias están sujetas a la elección de clase bajo los métodos mostrados, se realiza de igual manera, la única diferencia existe en determinar el valor como el punto medio de cada estatura, veamos el siguiente ejemplo: Tabla de frecuencias reportadas por un equipo de baloncesto con respecto a la estatura de los jugadores. 7.2 Moda Moda para datos agrupados La moda es la medida que se relaciona con la frecuencia con la que se representa el dato o los datos con mayor incidencia, por lo que se considera la posibilidad de que exista más de un moda para un conjunto de datos. La notación más frecuente es la siguiente: Moda y esta medida se puede aparecer tanto para datos cualitativos como cuantitativos. Se dice que cuando un conjunto de datos tiene una moda la muestra es unimodal, cuando tiene dos modas bimodal, cuando la muestra contiene mas de un dato repetido se dice que es multimodal y un último caso es cuando ningún dato tiene una frecuencia, en dicho caso se dice que la muestra es amodal. Ejemplos:
3 1.- Determinar la moda del siguiente conjunto de datos: a) 1,2,3,3,4,5,6,7,7,3,1,9,3 2.- La moda de este conjunto de datos es igual a 3 y se considera unimodal: b) 1,2,3,4,4,5,2,1,3,4,2,-3,4,6,3,3 3.- Las modas de este conjunto de datos son 3 y 4 ya que ambas tienen la mas alta frecuencia, por lo que la muestra es binomial. c) 1,2,3,4,5,6,7,8,9 4.- La muestra no contiene ningún dato repetido por lo que se considera que la muestra es a modal. Gráficamente eso se puede reflejar mediante el análisis de un histograma de frecuencias Moda para datos agrupados Para determinar la moda para datos agrupados en clases de igual tamaño su cálculo se puede realizar de la siguiente forma: Donde: Aunque la expresión se ve un poco diferente en realidad se trata de una misma ecuación. Ejemplo: Tabla de frecuencias reportadas por un equipo de baloncesto con respecto a la estatura de los jugadores.
4 7.3 Mediana Mediana para datos no agrupados La mediana de un conjunto finito es aquel valor que divide al conjunto en dos partes iguales, de forma que el número de valores mayor o igual a la mediana es igual al número de valores menores o igual a estos. Su aplicación se ve limitada ya que solo considérale orden jerárquico de los datos y no alguna propiedad propia de los datos, como es en el caso de la media. A continuación se muestran los criterios para construir la mediana. Se puede construir los siguientes criterios: Lo primero que se requiere es ordenar los datos en de forma ascendente o descendente, cualquiera de los dos criterios conduce al mismo resultado. Sean ordenados los datos en orden ascendente. Si el número de valores es impar, la mediana es el valor medio, el cual corresponde al dato. Cuando el número de valores en el conjunto es par, no existe un solo valor Medio, si no que existen dos valores medios, en tal caso, la mediana es el promedio de los valores, es decir, la mediana es numéricamente igual. Podemos describir algunas propiedades para la mediana: 1.- Es única. 2.- Es simple. 3.- Los valores extremos no tienen efectos importantes sobre la mediana, lo que si ocurre con la media. 13 Ejemplo: Dados los siguiente datos: 1,2,3,4,0,1,4,3,1,1,1,1,2,1,3 para la obtención de la mediana se deberán de ordenar. Tomemos el criterio de orden ascendente con lo que tendremos: 0,1,1,1,1,1,1,1,2,2,3,3,3,4,4 Por otro lado el número de datos es igual a 15 datos, siendo el número de datos impar se elige el dato que se encuentra a la mitad, una vez ordenados los datos, en este caso es 1.
5 7.3.2 La mediana para datos agrupados. La extensión para el cálculo de la mediana en el caso de datos agrupados es realizada a continuación: Donde: Md = Mediana. Li = Limite inferior o frontera o inferior de donde se encuentra la mediana, la forma de calcularlo es a través de encontrar la posición. En ocasiones en el intervalo donde se encuentra la mediana de conoce como intervalo mediano. n= Número de observaciones o frecuencia total. F acum. = frecuencia acumulada anterior al intervalo mediano F mediana = Frecuencia del intervalo mediano. A= Amplitud del intervalo en el que se encuentra la mediana. Geométricamente la mediana se encuentra en el valor X que divide al histograma en dos partes de áreas iguales. 13 FORMULARIO Medidas de tendencia central Para datos no Agrupados
6 Para datos Agrupados Donde: es la medida muestral. x es cada uno de los datos (no agrupados) o la marca de clase (agrupados) f es la frecuencia absoluta de cada Clase n es el número de datos (tamaño de la muestra) Para datos agrupados. Donde: es la mediana de la muestra. n es el número total de los elementos de la distribución F es la suma de todas las frecuencias de clase anteriores a la clase mediana f m es la frecuencia de la clase mediana (que contiene el dato intermedio) w es el ancho de intervalo de clase. L m es el limite inferior del intervalo de clase mediano. Para datos agrupados Donde: es la moda de la muestra L mo es el limite inferior de la clase modal. d 1 es la frecuencia de la clase modal menos la frecuencia de la anterior d 2 es la frecuencia de la clase modal menos la frecuencia de la clase siguiente w 2 es el ancho del intervalo de la clase modal MEDIDAS DE DISPERSIÓN 17 Existe otro tipo de medidas que indican la tendencia de los datos a dispersarse respecto al valor central. Algunas de las medidas de dispersión más usuales son: a) Rango, amplitud o recorrido (R) b) Desviación estándar (S, muestral; s, poblacional ). c) Varianza (S², s² ) d) Desviación media (DM). e) Coeficiente de Variación (C. V.) 7.4 Rango Es la diferencia entre el dato mayor y el dato menor. 7.5 Desviación estándar. R= X máx. - Xmín. La desviación estándar o desviación tipo se define como la raíz cuadrada de los cuadrados de las desviaciones de los valores de la variable respecto a su media. 17
7 7.6 Varianza. Es el cuadrado de la desviación estándar. EJEMPLO: Hallar la desviación estándar y la varianza de la siguiente serie de datos. 10, 18, 15, 12, 3,6,5,7 SOLUCION: EJEMPLO: Hallar la desviación estándar y la varianza para la siguiente distribución de frecuencias.
8 7.7 Desviación media. S 2 = 43.4 Se conoce también como promedio de desviación. Para una serie de N valores se Puede calcular a través de la siguiente expresión: = Valor absoluto de las desviaciones de los x valores, respecto de la media. Y para datos agrupados se tiene: EJEMPLO: Hallar la desviación media de: 4,6,12,16,22.
9 EJEMPLO: Hallar la desviación media en la siguiente distribución de frecuencias.17 SOLUCION: 7.8 Coeficiente de Variación. Es la relación que existe entre la S y la X, expresada en términos de porcentaje y se expresa: EJEMPLO: Hallar el coeficiente de variación de una serie de datos cuya S= 2 y X = 16. SOLUCION:
10 FORMULARIO Medidas de dispersión Rango = valor de la observación más alta valor de la observación más pequeña Rango = valor del límite inferior de la 1er clase valor del límite superior de la última clase. Para datos no agrupados. Para datos agrupados. Donde: (agrupados) s2 es la varianza de la muestra x es cada uno de los datos (no agrupados) o la marca de clase es la media muestral f es la frecuencia absoluta de cada clase n es el número total de datos (tamaño de la muestra) Para datos no agrupados. Para datos agrupados. Donde: s es la desviación estándar de la muestra x es cada uno de los datos (no agrupados) o la marca de clase (agrupados) es la media muestral f es la frecuencia absoluta de cada clase n es el número total de datos (tamaño de la muestra)
11 Donde: c.v. es el coeficiente de variación de la muestra s es la desviación estándar de la muestra es la media muestral
1. MEDIDAS DE TENDENCIA CENTRAL
 1. MEDIDAS DE TENDENCIA CENTRAL Lo importante en una tendencia central es calcular un valor central que actúe como resumen numérico para representar al conjunto de datos. Estos valores son las medidas
1. MEDIDAS DE TENDENCIA CENTRAL Lo importante en una tendencia central es calcular un valor central que actúe como resumen numérico para representar al conjunto de datos. Estos valores son las medidas
Ejercicio de estadística para 3º de la ESO
 Ejercicio de estadística para 3º de la ESO Unibelia La estadística es una disciplina técnica que se apoya en las matemáticas y que tiene como objetivo la interpretación de la realidad de una población
Ejercicio de estadística para 3º de la ESO Unibelia La estadística es una disciplina técnica que se apoya en las matemáticas y que tiene como objetivo la interpretación de la realidad de una población
MEDIDAS DE DISPERSIÓN EMPLEANDO EXCEL
 MEDIDAS DE DISPERSIÓN EMPLEANDO EXCEL Las medias de tendencia central o posición nos indican donde se sitúa un dato dentro de una distribución de datos. Las medidas de dispersión, variabilidad o variación
MEDIDAS DE DISPERSIÓN EMPLEANDO EXCEL Las medias de tendencia central o posición nos indican donde se sitúa un dato dentro de una distribución de datos. Las medidas de dispersión, variabilidad o variación
Estadística. Conceptos de Estadística. Un individuo o unidad estadística es cada uno de los elementos que componen la población.
 Estadística La Estadística trata del recuento, ordenación y clasificación de los datos obtenidos por las observaciones, para poder hacer comparaciones y sacar conclusiones. Un estudio estadístico consta
Estadística La Estadística trata del recuento, ordenación y clasificación de los datos obtenidos por las observaciones, para poder hacer comparaciones y sacar conclusiones. Un estudio estadístico consta
Medidas de tendencia central o de posición: situación de los valores alrededor
 Tema 10: Medidas de posición y dispersión Una vez agrupados los datos en distribuciones de frecuencias, se calculan unos valores que sintetizan la información. Estudiaremos dos grandes secciones: Medidas
Tema 10: Medidas de posición y dispersión Una vez agrupados los datos en distribuciones de frecuencias, se calculan unos valores que sintetizan la información. Estudiaremos dos grandes secciones: Medidas
ANÁLISIS DESCRIPTIVO CON SPSS
 ESCUELA SUPERIOR DE INFORMÁTICA Prácticas de Estadística ANÁLISIS DESCRIPTIVO CON SPSS 1.- INTRODUCCIÓN Existen dos procedimientos básicos que permiten describir las propiedades de las distribuciones:
ESCUELA SUPERIOR DE INFORMÁTICA Prácticas de Estadística ANÁLISIS DESCRIPTIVO CON SPSS 1.- INTRODUCCIÓN Existen dos procedimientos básicos que permiten describir las propiedades de las distribuciones:
UNIDAD 4: MEDIDAS DE TENDENCIA CENTRAL
 UNIDAD 4: MEDIDAS DE TENDENCIA CENTRAL Objetivo terminal: Calcular e interpretar medidas de tendencia central para un conjunto de datos estadísticos. Objetivos específicos: 1. Mencionar las características
UNIDAD 4: MEDIDAS DE TENDENCIA CENTRAL Objetivo terminal: Calcular e interpretar medidas de tendencia central para un conjunto de datos estadísticos. Objetivos específicos: 1. Mencionar las características
Estadística con Excel Informática 4º ESO ESTADÍSTICA CON EXCEL
 1. Introducción ESTADÍSTICA CO EXCEL La estadística es la rama de las matemáticas que se dedica al análisis e interpretación de series de datos, generando unos resultados que se utilizan básicamente en
1. Introducción ESTADÍSTICA CO EXCEL La estadística es la rama de las matemáticas que se dedica al análisis e interpretación de series de datos, generando unos resultados que se utilizan básicamente en
Media vs mediana vs moda Cual medida de tendencia central es mas adecuada? MEDIA conveniencias:
 Iniciar con las interpretaciones de las medidas MEDIA VS MEDIANA VS MODA CUAL ES LA MEDIDA ADECUADA TAREA MEDIA PONDERADA Actividad de Medidas de Localización Problema 1. El problema de las tasas de delito.
Iniciar con las interpretaciones de las medidas MEDIA VS MEDIANA VS MODA CUAL ES LA MEDIDA ADECUADA TAREA MEDIA PONDERADA Actividad de Medidas de Localización Problema 1. El problema de las tasas de delito.
Población, muestra y variable estadística
 Población, muestra y variable estadística La estadística es la parte de las Matemáticas que estudia cómo recopilar y resumir gran cantidad de información para extraer conclusiones. La población de un estudio
Población, muestra y variable estadística La estadística es la parte de las Matemáticas que estudia cómo recopilar y resumir gran cantidad de información para extraer conclusiones. La población de un estudio
INSTITUCION EDUCATIVA LUIS PATRON ROSANO DOCUMENTO PARA ESTUDIAR LOGROS PENDIENTES DE ESTADISTICA DE 10º
 INSTITUCION EDUCATIVA LUIS PATRON ROSANO DOCUMENTO PARA ESTUDIAR LOGROS PENDIENTES DE ESTADISTICA DE 10º DEFINICIÓN DE PARÁMETRO ESTADÍSTICO Un parámetro estadístico es un número que se obtiene a partir
INSTITUCION EDUCATIVA LUIS PATRON ROSANO DOCUMENTO PARA ESTUDIAR LOGROS PENDIENTES DE ESTADISTICA DE 10º DEFINICIÓN DE PARÁMETRO ESTADÍSTICO Un parámetro estadístico es un número que se obtiene a partir
ESTADÍSTICA SEMANA 4
 ESTADÍSTICA SEMANA 4 ÍNDICE MEDIDAS DE DISPERSIÓN... 3 APRENDIZAJES ESPERADOS... 3 DEfinición de Medida de dispersión... 3 Rango o Recorrido... 3 Varianza Muestral (S 2 )... 3 CÁLCULO DE LA VARIANZA...
ESTADÍSTICA SEMANA 4 ÍNDICE MEDIDAS DE DISPERSIÓN... 3 APRENDIZAJES ESPERADOS... 3 DEfinición de Medida de dispersión... 3 Rango o Recorrido... 3 Varianza Muestral (S 2 )... 3 CÁLCULO DE LA VARIANZA...
UNIDAD III MEDIDAS DE TENDENCIA CENTRAL
 UNIDAD III MEDIDAS DE TENDENCIA CENTRAL ISC. Claudia García Pérez 1 PRESENTACIÓN La representación gráfica de los datos permite realizar una descripción visual de manera general de los datos obtenidos
UNIDAD III MEDIDAS DE TENDENCIA CENTRAL ISC. Claudia García Pérez 1 PRESENTACIÓN La representación gráfica de los datos permite realizar una descripción visual de manera general de los datos obtenidos
Socioestadística I Análisis estadístico en Sociología
 Análisis estadístico en Sociología Capítulo 3 CARACTERÍSTICAS DE LAS DISTRIBUCIOES DE FRECUECIAS 1. CARACTERÍSTICAS DE UA DISTRIBUCIÓ UIVARIATE Hasta ahora hemos utilizado representaciones gráficas para
Análisis estadístico en Sociología Capítulo 3 CARACTERÍSTICAS DE LAS DISTRIBUCIOES DE FRECUECIAS 1. CARACTERÍSTICAS DE UA DISTRIBUCIÓ UIVARIATE Hasta ahora hemos utilizado representaciones gráficas para
MEDIDAS DE TENDENCIA CENTRAL Y DISPERSIÓN
 MEDIDAS DE TENDENCIA CENTRAL Y DISPERSIÓN Suponga que le pedimos a un grupo de estudiantes de la asignatura de estadística que registren su peso en kilogramos. Con los datos del peso de los estudiantes
MEDIDAS DE TENDENCIA CENTRAL Y DISPERSIÓN Suponga que le pedimos a un grupo de estudiantes de la asignatura de estadística que registren su peso en kilogramos. Con los datos del peso de los estudiantes
Aplicaciones de Estadística Descriptiva
 Aplicaciones de Estadística Descriptiva Contenidos de la presentación Funciones estadísticas en Excel. Gráficos. El módulo de análisis de datos y las tablas dinámicas de Excel. Información Intentaremos
Aplicaciones de Estadística Descriptiva Contenidos de la presentación Funciones estadísticas en Excel. Gráficos. El módulo de análisis de datos y las tablas dinámicas de Excel. Información Intentaremos
Tema 3. Medidas de tendencia central. 3.1. Introducción. Contenido
 Tema 3 Medidas de tendencia central Contenido 31 Introducción 1 32 Media aritmética 2 33 Media ponderada 3 34 Media geométrica 4 35 Mediana 5 351 Cálculo de la mediana para datos agrupados 5 36 Moda 6
Tema 3 Medidas de tendencia central Contenido 31 Introducción 1 32 Media aritmética 2 33 Media ponderada 3 34 Media geométrica 4 35 Mediana 5 351 Cálculo de la mediana para datos agrupados 5 36 Moda 6
Tema 2 Estadística Descriptiva
 Estadística Descriptiva 1 Tipo de Variables 2 Tipo de variables La base de datos anterior contiene la información de 2700 individuos con 8 variables. Los datos provienen de una encuesta nacional realizada
Estadística Descriptiva 1 Tipo de Variables 2 Tipo de variables La base de datos anterior contiene la información de 2700 individuos con 8 variables. Los datos provienen de una encuesta nacional realizada
Clase 2: Estadística
 Clase 2: Estadística Los datos Todo conjunto de datos tiene al menos dos características principales: CENTRO Y DISPERSIÓN Los gráficos de barra, histogramas, de puntos, entre otros, nos dan cierta idea
Clase 2: Estadística Los datos Todo conjunto de datos tiene al menos dos características principales: CENTRO Y DISPERSIÓN Los gráficos de barra, histogramas, de puntos, entre otros, nos dan cierta idea
14 ESTADÍSTICA UNIDIMENSIONAL
 1 ESTADÍSTICA UNIDIMENSIONAL EJERCICIOS PROPUESTOS 1.1 Clasifica los siguientes caracteres estadísticos. a) Número de canastas encestadas en un partido de baloncesto. b) Canal de televisión preferido por
1 ESTADÍSTICA UNIDIMENSIONAL EJERCICIOS PROPUESTOS 1.1 Clasifica los siguientes caracteres estadísticos. a) Número de canastas encestadas en un partido de baloncesto. b) Canal de televisión preferido por
MEDIDAS DE TENDENCIA CENTRAL
 CAPÍTULO 14 MEDIDAS DE TENDENCIA CENTRAL A veces, de los datos recolectados ya organizados en alguna de las formas vistas en capítulos anteriores, se desea encontrar una especie de punto central en función
CAPÍTULO 14 MEDIDAS DE TENDENCIA CENTRAL A veces, de los datos recolectados ya organizados en alguna de las formas vistas en capítulos anteriores, se desea encontrar una especie de punto central en función
Se podría entender como una matriz de filas y columnas. Cada combinación de fila y columna se denomina celda. Por ejemplo la celda A1, B33, Z68.
 Departamento de Economía Aplicada: UDI de Estadística. Universidad Autónoma de Madrid Notas sobre el manejo de Excel para el análisis descriptivo y exploratorio de datos. (Descriptiva) 1 1 Introducción
Departamento de Economía Aplicada: UDI de Estadística. Universidad Autónoma de Madrid Notas sobre el manejo de Excel para el análisis descriptivo y exploratorio de datos. (Descriptiva) 1 1 Introducción
1 Comida Favorita.Cualitativa. 2 Profesión que te gusta.cualitativa. 3 Número de goles marcados por tu equipo favorito en la última
 1.-Indica que variables son cualitativas y cuales cuantitativas: 1 Comida Favorita.Cualitativa. 2 Profesión que te gusta.cualitativa. 3 Número de goles marcados por tu equipo favorito en la última temporada.cuantitativa.
1.-Indica que variables son cualitativas y cuales cuantitativas: 1 Comida Favorita.Cualitativa. 2 Profesión que te gusta.cualitativa. 3 Número de goles marcados por tu equipo favorito en la última temporada.cuantitativa.
Parámetros y estadísticos
 Parámetros y estadísticos «Parámetro»: Es una cantidad numérica calculada sobre una población y resume los valores que esta toma en algún atributo Intenta resumir toda la información que hay en la población
Parámetros y estadísticos «Parámetro»: Es una cantidad numérica calculada sobre una población y resume los valores que esta toma en algún atributo Intenta resumir toda la información que hay en la población
15 PARÁMETROS ESTADÍSTICOS
 EJERCICIOS PROPUESTOS 1.1 El número de libros leídos por los miembros de un círculo de lectores en un mes se resume en esta tabla. N. o de libros leídos x i N. o de personas f i 1 1 3 18 11 7 7 1 Halla
EJERCICIOS PROPUESTOS 1.1 El número de libros leídos por los miembros de un círculo de lectores en un mes se resume en esta tabla. N. o de libros leídos x i N. o de personas f i 1 1 3 18 11 7 7 1 Halla
ESTIMACIÓN. puntual y por intervalo
 ESTIMACIÓN puntual y por intervalo ( ) Podemos conocer el comportamiento del ser humano? Podemos usar la información contenida en la muestra para tratar de adivinar algún aspecto de la población bajo estudio
ESTIMACIÓN puntual y por intervalo ( ) Podemos conocer el comportamiento del ser humano? Podemos usar la información contenida en la muestra para tratar de adivinar algún aspecto de la población bajo estudio
Eduardo Kido 26-Mayo-2004 ANÁLISIS DE DATOS
 ANÁLISIS DE DATOS Hoy día vamos a hablar de algunas medidas de resumen de datos: cómo resumir cuando tenemos una serie de datos numéricos, generalmente en variables intervalares. Cuando nosotros tenemos
ANÁLISIS DE DATOS Hoy día vamos a hablar de algunas medidas de resumen de datos: cómo resumir cuando tenemos una serie de datos numéricos, generalmente en variables intervalares. Cuando nosotros tenemos
Clase 2: Estadística
 Clase 2: Estadística Los datos Todo conjunto de datos tiene al menos dos características principales: CENTRO Y DISPERSIÓN Los gráficos de barra, histogramas, de puntos, entre otros, nos dan cierta idea
Clase 2: Estadística Los datos Todo conjunto de datos tiene al menos dos características principales: CENTRO Y DISPERSIÓN Los gráficos de barra, histogramas, de puntos, entre otros, nos dan cierta idea
ESTADÍSTICA APLICADA A LA INVESTIGACIÓN EN SALUD Medidas de Tendencia Central y Dispersión
 Descargado desde www.medwave.cl el 13 Junio 2011 por iriabeth villanueva Medwave. Año XI, No. 3, Marzo 2011. ESTADÍSTICA APLICADA A LA INVESTIGACIÓN EN SALUD Medidas de Tendencia Central y Dispersión Autor:
Descargado desde www.medwave.cl el 13 Junio 2011 por iriabeth villanueva Medwave. Año XI, No. 3, Marzo 2011. ESTADÍSTICA APLICADA A LA INVESTIGACIÓN EN SALUD Medidas de Tendencia Central y Dispersión Autor:
Estimación. Intervalos de Confianza para la Media y para las Proporciones
 Estimación. Intervalos de Confianza para la Media y para las Proporciones Algunas secciones han sido tomadas de: Apuntes de Estadística Inferencial Instituto Tecnológico de Chiuhuahua Estimación El objetivo
Estimación. Intervalos de Confianza para la Media y para las Proporciones Algunas secciones han sido tomadas de: Apuntes de Estadística Inferencial Instituto Tecnológico de Chiuhuahua Estimación El objetivo
Medidas de la tendencia central y las gráficas de caja
 LECCIÓN CONDENSADA 2.1 Medidas de la tendencia central y las gráficas de caja En esta lección Encontrarás e interpretarás la media, la mediana, y la moda para unos conjuntos de datos Crearás e interpretarás
LECCIÓN CONDENSADA 2.1 Medidas de la tendencia central y las gráficas de caja En esta lección Encontrarás e interpretarás la media, la mediana, y la moda para unos conjuntos de datos Crearás e interpretarás
SENA: CENTRO BIOTECNOLOGIA INDUSTRIAL PROGRAMA DE FORMACIÓN: TECNOLOGO GESTION LOGISTICA
 Por población o universo se entiende como un conjunto de medidas, cuando estas son aplicadas a una característica cuantitativa, o como el recuento de todas las unidades que presentan una característica
Por población o universo se entiende como un conjunto de medidas, cuando estas son aplicadas a una característica cuantitativa, o como el recuento de todas las unidades que presentan una característica
CONTENIDOS MÍNIMOS BLOQUE III: ÁLGEBRA
 CONTENIDOS MÍNIMOS BLOQUE III: ÁLGEBRA Interpolación de términos en una sucesión. Cálculo del término general de sucesiones muy sencillas. Distinción entre progresiones aritméticas y geométricas. Interpolación
CONTENIDOS MÍNIMOS BLOQUE III: ÁLGEBRA Interpolación de términos en una sucesión. Cálculo del término general de sucesiones muy sencillas. Distinción entre progresiones aritméticas y geométricas. Interpolación
REPASO CONCEPTOS BÁSICOS DE ESTADÍSTICA. DISTRIBUCIÓN NORMAL.
 REPASO COCEPTOS BÁSICOS DE ESTADÍSTICA. DISTRIBUCIÓ ORMAL. Éste es un breve repaso de conceptos básicos de estadística que se han visto en cursos anteriores y que son imprescindibles antes de acometer
REPASO COCEPTOS BÁSICOS DE ESTADÍSTICA. DISTRIBUCIÓ ORMAL. Éste es un breve repaso de conceptos básicos de estadística que se han visto en cursos anteriores y que son imprescindibles antes de acometer
Capítulo 10. Análisis descriptivo: Los procedimientos Frecuencias y Descriptivos
 Capítulo 10 Análisis descriptivo: Los procedimientos Frecuencias y Descriptivos Al analizar datos, lo primero que conviene hacer con una variable es, generalmente, formarse una idea lo más exacta posible
Capítulo 10 Análisis descriptivo: Los procedimientos Frecuencias y Descriptivos Al analizar datos, lo primero que conviene hacer con una variable es, generalmente, formarse una idea lo más exacta posible
Análisis estadístico con Microsoft Excel
 Análisis estadístico con Microsoft Excel Microsoft Excel ofrece un conjunto de herramientas para el análisis de los datos (denominado Herramientas para análisis) con el que podrá ahorrar pasos en el desarrollo
Análisis estadístico con Microsoft Excel Microsoft Excel ofrece un conjunto de herramientas para el análisis de los datos (denominado Herramientas para análisis) con el que podrá ahorrar pasos en el desarrollo
Síntesis Numérica de una Variable
 Relación de problemas 2 Síntesis Numérica de una Variable Estadística 1. En siete momentos del día se observa el número de clientes que hay en un negocio, anotando: 2, 5, 2, 7, 3, 4, 9. Calcular e interpretar
Relación de problemas 2 Síntesis Numérica de una Variable Estadística 1. En siete momentos del día se observa el número de clientes que hay en un negocio, anotando: 2, 5, 2, 7, 3, 4, 9. Calcular e interpretar
1.1. Introducción y conceptos básicos
 Tema 1 Variables estadísticas Contenido 1.1. Introducción y conceptos básicos.................. 1 1.2. Tipos de variables estadísticas................... 2 1.3. Distribuciones de frecuencias....................
Tema 1 Variables estadísticas Contenido 1.1. Introducción y conceptos básicos.................. 1 1.2. Tipos de variables estadísticas................... 2 1.3. Distribuciones de frecuencias....................
Departamento de Economía Aplicada I ESCUELA UNIVERSITARIA DE ESTUDIOS EMPRESARIALES DIPLOMATURA EN CIENCIAS EMPRESARIALES ESTADÍSTICA
 ESCUELA UIVERSITARIA DE ESTUDIOS EMPRESARIALES DIPLOMATURA E CIECIAS EMPRESARIALES ESTADÍSTICA Ejercicios Resueltos AÁLISIS ESTADÍSTICO DE DOS VARIABLES Y RE- GRESIÓ LIEAL SIMPLE Curso 6-7 Curso 6-7 1)
ESCUELA UIVERSITARIA DE ESTUDIOS EMPRESARIALES DIPLOMATURA E CIECIAS EMPRESARIALES ESTADÍSTICA Ejercicios Resueltos AÁLISIS ESTADÍSTICO DE DOS VARIABLES Y RE- GRESIÓ LIEAL SIMPLE Curso 6-7 Curso 6-7 1)
1 VARIABLES ESTADÍSTICAS UNIDIMENSIONALES
 1 VARIABLES ESTADÍSTICAS UNIDIMENSIONALES 1 La tabla siguiente refleja la distribución por cursos de los alumnos matriculados en un Instituto: Curso n i 1º de ESO 56 2º de ESO 90 3º de ESO 120 4º de ESO
1 VARIABLES ESTADÍSTICAS UNIDIMENSIONALES 1 La tabla siguiente refleja la distribución por cursos de los alumnos matriculados en un Instituto: Curso n i 1º de ESO 56 2º de ESO 90 3º de ESO 120 4º de ESO
2 Resolución de algunos ejemplos y ejercicios del tema 2.
 INTRODUCCIÓN A LA ESTADÍSTICA. GRUPO 71 LADE. 8 2 Resolución de algunos ejemplos y ejercicios del tema 2. 2.1 Ejemplos. Ejemplo 13 La siguiente tabla de frecuencias absolutas corresponde a 200 observaciones
INTRODUCCIÓN A LA ESTADÍSTICA. GRUPO 71 LADE. 8 2 Resolución de algunos ejemplos y ejercicios del tema 2. 2.1 Ejemplos. Ejemplo 13 La siguiente tabla de frecuencias absolutas corresponde a 200 observaciones
Tema 3: Variables aleatorias y vectores aleatorios bidimensionales
 Estadística 38 Tema 3: Variables aleatorias y vectores aleatorios bidimensionales El concepto de variable aleatoria surge de la necesidad de hacer más manejables matemáticamente los resultados de los experimentos
Estadística 38 Tema 3: Variables aleatorias y vectores aleatorios bidimensionales El concepto de variable aleatoria surge de la necesidad de hacer más manejables matemáticamente los resultados de los experimentos
Otras medidas descriptivas usuales
 Tema 7 Otras medidas descriptivas usuales Contenido 7.1. Introducción............................. 1 7.2. Medidas robustas.......................... 2 7.2.1. Media recortada....................... 2 7.2.2.
Tema 7 Otras medidas descriptivas usuales Contenido 7.1. Introducción............................. 1 7.2. Medidas robustas.......................... 2 7.2.1. Media recortada....................... 2 7.2.2.
33 El interés compuesto y la amortización de préstamos.
 33 El interés compuesto y la amortización de préstamos. 33.0 El interés compuesto. 33.0.0 Concepto. 33.0.02 Valor actualizado de un capital. 33.0.03 Tiempo equivalente. 33.02 Amortización de préstamos.
33 El interés compuesto y la amortización de préstamos. 33.0 El interés compuesto. 33.0.0 Concepto. 33.0.02 Valor actualizado de un capital. 33.0.03 Tiempo equivalente. 33.02 Amortización de préstamos.
Explicación de la tarea 3 Felipe Guerra
 Explicación de la tarea 3 Felipe Guerra 1. Una ruleta legal tiene los números del 1 al 15. Este problema corresponde a una variable aleatoria discreta. La lectura de la semana menciona lo siguiente: La
Explicación de la tarea 3 Felipe Guerra 1. Una ruleta legal tiene los números del 1 al 15. Este problema corresponde a una variable aleatoria discreta. La lectura de la semana menciona lo siguiente: La
Tema 10. Estimación Puntual.
 Tema 10. Estimación Puntual. Presentación y Objetivos. 1. Comprender el concepto de estimador y su distribución. 2. Conocer y saber aplicar el método de los momentos y el de máxima verosimilitud para obtener
Tema 10. Estimación Puntual. Presentación y Objetivos. 1. Comprender el concepto de estimador y su distribución. 2. Conocer y saber aplicar el método de los momentos y el de máxima verosimilitud para obtener
x 10000 y 8000 x + y 15000 a) La región factible asociada a las restricciones anteriores es la siguiente: Pedro Castro Ortega lasmatematicas.
 Pruebas de Acceso a Enseñanzas Universitarias Oficiales de Grado (PAEG) Matemáticas aplicadas a las Ciencias Sociales II - Septiembre 2012 - Propuesta A 1. Queremos realizar una inversión en dos tipos
Pruebas de Acceso a Enseñanzas Universitarias Oficiales de Grado (PAEG) Matemáticas aplicadas a las Ciencias Sociales II - Septiembre 2012 - Propuesta A 1. Queremos realizar una inversión en dos tipos
Gráficas de caja. El borde derecho de la caja es el tercer cuartil, Q 3, que es la mediana de los valores que están por encima de la mediana.
 LECCIÓN CONDENSADA 2.1 Gráficas de caja En esta lección crearás e interpretarás las gráficas de caja para conjuntos de datos usarás el rango intercuartil (IQR) para identificar valores extremos potenciales
LECCIÓN CONDENSADA 2.1 Gráficas de caja En esta lección crearás e interpretarás las gráficas de caja para conjuntos de datos usarás el rango intercuartil (IQR) para identificar valores extremos potenciales
Estadística Descriptiva
 Estadística Descriptiva 1. El porcentaje de algodón en una tela utilizada para elaborar camisas para hombre se presenta en la siguiente tabla. Calcular los estadísticos más importantes y realícese el histograma
Estadística Descriptiva 1. El porcentaje de algodón en una tela utilizada para elaborar camisas para hombre se presenta en la siguiente tabla. Calcular los estadísticos más importantes y realícese el histograma
Ecuaciones de primer grado con dos incógnitas
 Ecuaciones de primer grado con dos incógnitas Si decimos: "las edades de mis padres suman 120 años", podemos expresar esta frase algebraicamente de la siguiente forma: Entonces, Denominamos x a la edad
Ecuaciones de primer grado con dos incógnitas Si decimos: "las edades de mis padres suman 120 años", podemos expresar esta frase algebraicamente de la siguiente forma: Entonces, Denominamos x a la edad
PRÁCTICA No. 1 ESTADÍSTICA DESCRIPTIVA PARTE I
 PRÁCTICA No. 1 ESTADÍSTICA DESCRIPTIVA PARTE I Objetivos: Al finalizar esta práctica, el alumno podrá utilizar de manera más eficiente diversas funciones de Excel que le faciliten el cálculo de los principales
PRÁCTICA No. 1 ESTADÍSTICA DESCRIPTIVA PARTE I Objetivos: Al finalizar esta práctica, el alumno podrá utilizar de manera más eficiente diversas funciones de Excel que le faciliten el cálculo de los principales
BASES Y DIMENSIÓN. Propiedades de las bases. Ejemplos de bases.
 BASES Y DIMENSIÓN Definición: Base. Se llama base de un espacio (o subespacio) vectorial a un sistema generador de dicho espacio o subespacio, que sea a la vez linealmente independiente. β Propiedades
BASES Y DIMENSIÓN Definición: Base. Se llama base de un espacio (o subespacio) vectorial a un sistema generador de dicho espacio o subespacio, que sea a la vez linealmente independiente. β Propiedades
Tema 3. Espacios vectoriales
 Tema 3. Espacios vectoriales Estructura del tema. Definición y propiedades. Ejemplos. Dependencia e independencia lineal. Conceptos de base y dimensión. Coordenadas Subespacios vectoriales. 0.1. Definición
Tema 3. Espacios vectoriales Estructura del tema. Definición y propiedades. Ejemplos. Dependencia e independencia lineal. Conceptos de base y dimensión. Coordenadas Subespacios vectoriales. 0.1. Definición
Tema 4 : Tabulación de datos
 Tema 4 : Tabulación de datos La tabulación consiste en presentar los datos estadísticos en forma de tablas o cuadros. --Partes de una tabla TITULO de la tabla, que debe ser preciso y conciso CONTENIDO,
Tema 4 : Tabulación de datos La tabulación consiste en presentar los datos estadísticos en forma de tablas o cuadros. --Partes de una tabla TITULO de la tabla, que debe ser preciso y conciso CONTENIDO,
LECCION 1ª Introducción a la Estadística Descriptiva
 LECCION 1ª Introducción a la Estadística Descriptiva La estadística descriptiva es una ciencia que analiza series de datos (por ejemplo, edad de una población, altura de los estudiantes de una escuela,
LECCION 1ª Introducción a la Estadística Descriptiva La estadística descriptiva es una ciencia que analiza series de datos (por ejemplo, edad de una población, altura de los estudiantes de una escuela,
Estadística: conceptos básicos y definiciones.
 Estadística: conceptos básicos y definiciones. 1 Conceptos básicos 2 Conceptos básicos cont. 3 Conceptos básicos cont. 4 Conceptos básicos cont. 5 Conceptos básicos cont. 6 Definición de Estadística La
Estadística: conceptos básicos y definiciones. 1 Conceptos básicos 2 Conceptos básicos cont. 3 Conceptos básicos cont. 4 Conceptos básicos cont. 5 Conceptos básicos cont. 6 Definición de Estadística La
Imagen de Rosaura Ochoa con licencia Creative Commons
 Imagen de Rosaura Ochoa con licencia Creative Commons Durante el primer tema hemos aprendido a elaborar una encuesta. Una vez elaborada la encuesta necesitamos escoger a los individuos a los que se la
Imagen de Rosaura Ochoa con licencia Creative Commons Durante el primer tema hemos aprendido a elaborar una encuesta. Una vez elaborada la encuesta necesitamos escoger a los individuos a los que se la
La Lección de Hoy es Distancia entre dos puntos. El cuál es la expectativa para el aprendizaje del estudiante CGT.5.G.1
 La Lección de Hoy es Distancia entre dos puntos El cuál es la expectativa para el aprendizaje del estudiante CGT.5.G.1 La formula de la distancia dada a dos pares es: d= (x 2 -x 1 ) 2 + (y 2 -y 1 ) 2 De
La Lección de Hoy es Distancia entre dos puntos El cuál es la expectativa para el aprendizaje del estudiante CGT.5.G.1 La formula de la distancia dada a dos pares es: d= (x 2 -x 1 ) 2 + (y 2 -y 1 ) 2 De
Raíces cuadradas y radicales
 Raíces cuadradas y radicales Raíz cuadrada - la raíz cuadrada de x, donde x, es igual a c (donde c si c 2 = x. Se usa la notación para representar la raíz cuadrada principal de x. Al símbolo se le llama
Raíces cuadradas y radicales Raíz cuadrada - la raíz cuadrada de x, donde x, es igual a c (donde c si c 2 = x. Se usa la notación para representar la raíz cuadrada principal de x. Al símbolo se le llama
Módulo 9 Sistema matemático y operaciones binarias
 Módulo 9 Sistema matemático y operaciones binarias OBJETIVO: Identificar los conjuntos de números naturales, enteros, racionales e irracionales; resolver una operación binaria, representar un número racional
Módulo 9 Sistema matemático y operaciones binarias OBJETIVO: Identificar los conjuntos de números naturales, enteros, racionales e irracionales; resolver una operación binaria, representar un número racional
Asignatura: Econometría. Conceptos MUY Básicos de Estadística
 Asignatura: Econometría Conceptos MUY Básicos de Estadística Ejemplo: encuesta alumnos matriculados en la UMH Estudio: Estamos interesados en conocer el nivel de renta y otras características de los estudiantes
Asignatura: Econometría Conceptos MUY Básicos de Estadística Ejemplo: encuesta alumnos matriculados en la UMH Estudio: Estamos interesados en conocer el nivel de renta y otras características de los estudiantes
Las técnicas muestrales, los métodos prospectivos y el diseño de estadísticas en desarrollo local
 21 Las técnicas muestrales, los métodos prospectivos y el diseño de estadísticas en desarrollo local Victoria Jiménez González Introducción La Estadística es considerada actualmente una herramienta indispensable
21 Las técnicas muestrales, los métodos prospectivos y el diseño de estadísticas en desarrollo local Victoria Jiménez González Introducción La Estadística es considerada actualmente una herramienta indispensable
Media: x = OBJETIVOS CONTENIDOS PROCEDIMIENTOS. Estadística. Población y muestra.
 86 _ 089-008.qxd //0 :6 Página 89 Estadística INTRODUCCIÓN La presencia de la Estadística es habitual en multitud de contextos de la vida real: encuestas electorales, sondeos de opinión, etc. La importancia
86 _ 089-008.qxd //0 :6 Página 89 Estadística INTRODUCCIÓN La presencia de la Estadística es habitual en multitud de contextos de la vida real: encuestas electorales, sondeos de opinión, etc. La importancia
HUMANIDADES Y CIENCIAS SOCIALES BLOQUE III ESTADÍSTICA Y PROBABILIDAD
 HUMANIDADES Y CIENCIAS SOCIALES BLOQUE III ESTADÍSTICA Y PROBABILIDAD π π PROYECTO EDITORIAL Equipo de Educación Secundaria de Ediciones SM AUTORES José Ramón Vizmanos Joaquín Hernández Fernando Alcaide
HUMANIDADES Y CIENCIAS SOCIALES BLOQUE III ESTADÍSTICA Y PROBABILIDAD π π PROYECTO EDITORIAL Equipo de Educación Secundaria de Ediciones SM AUTORES José Ramón Vizmanos Joaquín Hernández Fernando Alcaide
ESTADÍSTICA DESCRIPTIVA CON MINITAB
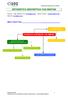 ESTADÍSTICA DESCRIPTIVA CON MINITAB Autores: Angel Alejandro Juan ([email protected]), Maximo Sedano ([email protected]), Alicia Vila ([email protected]). MAPA CONCEPTUAL DEFINICIÓN DE POBLACIÓN Y MUESTRA ESTADÍSTICA
ESTADÍSTICA DESCRIPTIVA CON MINITAB Autores: Angel Alejandro Juan ([email protected]), Maximo Sedano ([email protected]), Alicia Vila ([email protected]). MAPA CONCEPTUAL DEFINICIÓN DE POBLACIÓN Y MUESTRA ESTADÍSTICA
www.fundibeq.org Además se recomienda su uso como herramienta de trabajo dentro de las actividades habituales de planificación y control.
 ESTUDIOS DE CAPACIDAD POTENCIAL DE CALIDAD 1.- INTRODUCCIÓN Este documento proporciona las pautas para la realización e interpretación de una de las herramientas fundamentales para el control y la planificación
ESTUDIOS DE CAPACIDAD POTENCIAL DE CALIDAD 1.- INTRODUCCIÓN Este documento proporciona las pautas para la realización e interpretación de una de las herramientas fundamentales para el control y la planificación
2. Seleccionar Insertar función:
 Estadística I Curso 2014/2015 Guión de la Práctica 1 Introducción a la Estadística con Excel; Estadística Descriptiva En el siguiente guión vamos a ver cómo realizar Estadística Descriptiva con el software
Estadística I Curso 2014/2015 Guión de la Práctica 1 Introducción a la Estadística con Excel; Estadística Descriptiva En el siguiente guión vamos a ver cómo realizar Estadística Descriptiva con el software
Tema 2. Espacios Vectoriales. 2.1. Introducción
 Tema 2 Espacios Vectoriales 2.1. Introducción Estamos habituados en diferentes cursos a trabajar con el concepto de vector. Concretamente sabemos que un vector es un segmento orientado caracterizado por
Tema 2 Espacios Vectoriales 2.1. Introducción Estamos habituados en diferentes cursos a trabajar con el concepto de vector. Concretamente sabemos que un vector es un segmento orientado caracterizado por
CAPÍTULO VI PREPARACIÓN DEL MODELO EN ALGOR. En este capítulo, se hablará acerca de los pasos a seguir para poder realizar el análisis de
 CAPÍTULO VI PREPARACIÓN DEL MODELO EN ALGOR. En este capítulo, se hablará acerca de los pasos a seguir para poder realizar el análisis de cualquier modelo en el software Algor. La preparación de un modelo,
CAPÍTULO VI PREPARACIÓN DEL MODELO EN ALGOR. En este capítulo, se hablará acerca de los pasos a seguir para poder realizar el análisis de cualquier modelo en el software Algor. La preparación de un modelo,
CALIDAD página: 1 JOSÉ MANUEL DOMENECH ROLDÁN PROFESOR DE ECONOMÍA Y ADMINISTRACIÓN DE EMPRESA
 CALIDAD página: 1 HISTOGRAMA QUÉ ES EL HISTOGRAMA? El histograma es una herramienta útil para resumir y analizar datos. Por su naturaleza gráfica, puede ayudar a identificar e interpretar pautas que son
CALIDAD página: 1 HISTOGRAMA QUÉ ES EL HISTOGRAMA? El histograma es una herramienta útil para resumir y analizar datos. Por su naturaleza gráfica, puede ayudar a identificar e interpretar pautas que son
17.- PARABRISAS RESOLUCIÓN
 17.- PARABRISAS La sección de control de calidad de una fábrica de parabrisas elige, aleatoriamente, una muestra de 100 parabrisas producidos por una determinada máquina y registra la longitud de los parabrisas
17.- PARABRISAS La sección de control de calidad de una fábrica de parabrisas elige, aleatoriamente, una muestra de 100 parabrisas producidos por una determinada máquina y registra la longitud de los parabrisas
2. Aritmética modular Ejercicios resueltos
 2. Aritmética modular Ejercicios resueltos Ejercicio 2.1 Probar, mediante congruencias, que 3 2n+5 + 2 4n+1 es divisible por 7 cualquiera que sea el entero n 1. Trabajando módulo 7 se tiene que 3 2n+5
2. Aritmética modular Ejercicios resueltos Ejercicio 2.1 Probar, mediante congruencias, que 3 2n+5 + 2 4n+1 es divisible por 7 cualquiera que sea el entero n 1. Trabajando módulo 7 se tiene que 3 2n+5
CUESTIONES DE AUTOEVALUACIÓN (TEMA 1)
 CUESTIONES DE AUTOEVALUACIÓN (TEMA 1) Cuestiones de Verdadero/Falso 1. Un estadístico es una característica de una población. 2. Un parámetro es una característica de una población. 3. Las variables discretas
CUESTIONES DE AUTOEVALUACIÓN (TEMA 1) Cuestiones de Verdadero/Falso 1. Un estadístico es una característica de una población. 2. Un parámetro es una característica de una población. 3. Las variables discretas
Programa para el Mejoramiento de la Enseñanza de la Matemática en ANEP Proyecto: Análisis, Reflexión y Producción. Fracciones
 Fracciones. Las fracciones y los números Racionales Las fracciones se utilizan cotidianamente en contextos relacionados con la medida, el reparto o como forma de relacionar dos cantidades. Tenemos entonces
Fracciones. Las fracciones y los números Racionales Las fracciones se utilizan cotidianamente en contextos relacionados con la medida, el reparto o como forma de relacionar dos cantidades. Tenemos entonces
Tema 9 Estadística Matemáticas B 4º E.S.O. 1 TABLAS DE FRECUENCIAS Y REPRESENTACIONES GRÁFICAS EN VARIABLES DISCRETAS
 Tema 9 Estadística Matemáticas B º E.S.O. TEMA 9 ESTADÍSTICA TABLAS DE FRECUENCIAS Y REPRESENTACIONES GRÁFICAS EN VARIABLES DISCRETAS EJERCICIO : En un grupo de personas hemos preguntado por el número
Tema 9 Estadística Matemáticas B º E.S.O. TEMA 9 ESTADÍSTICA TABLAS DE FRECUENCIAS Y REPRESENTACIONES GRÁFICAS EN VARIABLES DISCRETAS EJERCICIO : En un grupo de personas hemos preguntado por el número
UNIDAD II MEDIDAS DE TENDENCIA CENTRAL. Otras Medidas de tendencia central
 UNIDAD II MEDIDAS DE TENDENCIA CENTRAL Otras Medidas de tendencia central INTRODUCCIÓN La media, mediana y moda son las medidas de tendencia central más importantes, de mayor aplicación y más fáciles de
UNIDAD II MEDIDAS DE TENDENCIA CENTRAL Otras Medidas de tendencia central INTRODUCCIÓN La media, mediana y moda son las medidas de tendencia central más importantes, de mayor aplicación y más fáciles de
PROCEDIMIENTOS DE EVALUACIÓN Y CRITERIOS DE CALIFICACION.
 PROCEDIMIENTOS DE EVALUACIÓN Y CRITERIOS DE CALIFICACION. A) EN LA ESO En 1º de ESO se comenzará la evaluación realizando a principio de curso una prueba inicial para ver el nivel de conocimientos que
PROCEDIMIENTOS DE EVALUACIÓN Y CRITERIOS DE CALIFICACION. A) EN LA ESO En 1º de ESO se comenzará la evaluación realizando a principio de curso una prueba inicial para ver el nivel de conocimientos que
EJERCICIOS RESUELTOS SOBRE ERRORES DE REDONDEO
 EJERCICIOS RESUELTOS SOBRE ERRORES DE REDONDEO 1º) Considérese un número estrictamente positivo del sistema de números máquina F(s+1, m, M, 10). Supongamos que tal número es: z = 0.d 1 d...d s 10 e Responde
EJERCICIOS RESUELTOS SOBRE ERRORES DE REDONDEO 1º) Considérese un número estrictamente positivo del sistema de números máquina F(s+1, m, M, 10). Supongamos que tal número es: z = 0.d 1 d...d s 10 e Responde
Tema 1: Test de Distribuciones de Probabilidad
 Tema 1: Test de Distribuciones de Probabilidad 1.- Una compañía de seguros tiene 1000 asegurados en el ramo de accidentes. Si la el modelo mejor para el número de siniestros en un año es: a) Normal (5;,3).
Tema 1: Test de Distribuciones de Probabilidad 1.- Una compañía de seguros tiene 1000 asegurados en el ramo de accidentes. Si la el modelo mejor para el número de siniestros en un año es: a) Normal (5;,3).
ANÁLISIS DE VARIANZA EMPLEANDO EXCEL y WINSTATS
 ANÁLISIS DE VARIANZA EMPLEANDO EXCEL y WINSTATS 1) INTRODUCCIÓN El análisis de varianza es una técnica que se puede utilizar para decidir si las medias de dos o más poblaciones son iguales. La prueba se
ANÁLISIS DE VARIANZA EMPLEANDO EXCEL y WINSTATS 1) INTRODUCCIÓN El análisis de varianza es una técnica que se puede utilizar para decidir si las medias de dos o más poblaciones son iguales. La prueba se
Inferencia Estadística
 EYP14 Estadística para Construcción Civil 1 Inferencia Estadística El campo de la inferencia estadística está formado por los métodos utilizados para tomar decisiones o para obtener conclusiones sobre
EYP14 Estadística para Construcción Civil 1 Inferencia Estadística El campo de la inferencia estadística está formado por los métodos utilizados para tomar decisiones o para obtener conclusiones sobre
Las bebidas Alcohólicas
 Las bebidas Alcohólicas Hecho por: - Elisa Gutiérrez - Guillermo Rivas-plata - Rodrigo Pumares - Beatriz Sánchez 1 Índice 1- Introducción... 3 2- Objetivos... 3 3- Preguntas de la encuesta... 4 4- Encuesta...
Las bebidas Alcohólicas Hecho por: - Elisa Gutiérrez - Guillermo Rivas-plata - Rodrigo Pumares - Beatriz Sánchez 1 Índice 1- Introducción... 3 2- Objetivos... 3 3- Preguntas de la encuesta... 4 4- Encuesta...
Práctica 2 ESTADÍSTICA DESCRIPTIVA
 Práctica 2. Estadística descriptiva 1 Práctica 2 ESTADÍSTICA DESCRIPTIVA Objetivos: En esta práctica utilizaremos el paquete SPSS para calcular estadísticos descriptivos de una muestra. Se representarán
Práctica 2. Estadística descriptiva 1 Práctica 2 ESTADÍSTICA DESCRIPTIVA Objetivos: En esta práctica utilizaremos el paquete SPSS para calcular estadísticos descriptivos de una muestra. Se representarán
Estadística descriptiva con Excel (Cálculo de medidas)
 Universidad Pedagógica Experimental Libertador Instituto Pedagógico de Miranda José Manuel Siso Martínez Departamento de Ciencias Naturales y Matemáticas Cátedra: Estadística aplicada a la educación Estadística
Universidad Pedagógica Experimental Libertador Instituto Pedagógico de Miranda José Manuel Siso Martínez Departamento de Ciencias Naturales y Matemáticas Cátedra: Estadística aplicada a la educación Estadística
ESTADÍSTICA APLICADA A LA INVESTIGACIÓN EN SALUD Construcción de una Base de Datos
 Descargado desde www.medwave.cl el 13 Junio 2011 por iriabeth villanueva Medwave. Año XI, No. 2, Febrero 2011. ESTADÍSTICA APLICADA A LA INVESTIGACIÓN EN SALUD Construcción de una Base de Datos Autor:
Descargado desde www.medwave.cl el 13 Junio 2011 por iriabeth villanueva Medwave. Año XI, No. 2, Febrero 2011. ESTADÍSTICA APLICADA A LA INVESTIGACIÓN EN SALUD Construcción de una Base de Datos Autor:
Análisis de datos estadísticos usando Ms. Excel
 Análisis de datos estadísticos usando Ms. Excel Fundamentos de informática Ing. Patricia Mores - Dra. Sonia Benz 2010 Qué es el análisis estadístico? Es extraer o deducir de un conjunto de datos resultados
Análisis de datos estadísticos usando Ms. Excel Fundamentos de informática Ing. Patricia Mores - Dra. Sonia Benz 2010 Qué es el análisis estadístico? Es extraer o deducir de un conjunto de datos resultados
Métodos Iterativos para Resolver Sistemas Lineales
 Métodos Iterativos para Resolver Sistemas Lineales Departamento de Matemáticas, CCIR/ITESM 17 de julio de 2009 Índice 3.1. Introducción............................................... 1 3.2. Objetivos................................................
Métodos Iterativos para Resolver Sistemas Lineales Departamento de Matemáticas, CCIR/ITESM 17 de julio de 2009 Índice 3.1. Introducción............................................... 1 3.2. Objetivos................................................
Representaciones Gráficas
 Representaciones Gráficas Gráficos para variables cualitativas Los gráficos más usuales para representar variables de tipo nominal son los siguientes: Diagramas de barras: Se representa en el eje de ordenadas
Representaciones Gráficas Gráficos para variables cualitativas Los gráficos más usuales para representar variables de tipo nominal son los siguientes: Diagramas de barras: Se representa en el eje de ordenadas
A estas alturas de nuestros conocimientos vamos a establecer dos reglas muy prácticas de cómo sumar dos números reales:
 ADICIÓN Y RESTA DE NUMEROS REALES ADICIÓN L a adición o suma de números reales se representa mediante el símbolo más (+) y es considerada una operación binaria porque se aplica a una pareja de números,
ADICIÓN Y RESTA DE NUMEROS REALES ADICIÓN L a adición o suma de números reales se representa mediante el símbolo más (+) y es considerada una operación binaria porque se aplica a una pareja de números,
5.1.1 Sumadores con anticipación de Acarreo. g i = a i b i. c i = c i-1 p i + g i s i = p i + c i-1. c 0 = g 0 + c -1 p 0
 5.1.1 Sumadores con anticipación de Acarreo. El sumador paralelo de n bits que se ha mostrado hasta ahora, tiene un nivel de retardo de 2*n puertas, pues necesita 2*n etapas de puertas lógicas para que
5.1.1 Sumadores con anticipación de Acarreo. El sumador paralelo de n bits que se ha mostrado hasta ahora, tiene un nivel de retardo de 2*n puertas, pues necesita 2*n etapas de puertas lógicas para que
Tema 9: Estadística Descriptiva. Distribuciones estadísticas. Representaciones
 Tema 9: Estadística Descriptiva Distribuciones estadísticas Representaciones gráficas 1 Conceptos fundamentales La Estadística es el conjunto de métodos necesarios para recoger, clasificar, representar
Tema 9: Estadística Descriptiva Distribuciones estadísticas Representaciones gráficas 1 Conceptos fundamentales La Estadística es el conjunto de métodos necesarios para recoger, clasificar, representar
Matemáticas I: Hoja 3 Espacios vectoriales y subespacios vectoriales
 Matemáticas I: Hoa 3 Espacios vectoriales y subespacios vectoriales Eercicio 1. Demostrar que los vectores v 1, v 2, v 3, v 4 expresados en la base canónica forman una base. Dar las coordenadas del vector
Matemáticas I: Hoa 3 Espacios vectoriales y subespacios vectoriales Eercicio 1. Demostrar que los vectores v 1, v 2, v 3, v 4 expresados en la base canónica forman una base. Dar las coordenadas del vector
MÉTODOS DE ELIMINACIÓN Son tres los métodos de eliminación más utilizados: Método de igualación, de sustitución y de suma o resta.
 ECUACIONES SIMULTÁNEAS DE PRIMER GRADO CON DOS INCÓGNITAS. Dos o más ecuaciones con dos incógnitas son simultáneas cuando satisfacen iguales valores de las incógnitas. Para resolver ecuaciones de esta
ECUACIONES SIMULTÁNEAS DE PRIMER GRADO CON DOS INCÓGNITAS. Dos o más ecuaciones con dos incógnitas son simultáneas cuando satisfacen iguales valores de las incógnitas. Para resolver ecuaciones de esta
no descompone no descompone no descompone
 Problema 1. Sea I n el conjunto de los n primeros números naturales impares. Por ejemplo: I 3 = {1, 3, 5, I 6 = {1, 3, 5, 7, 9, 11, etc. Para qué números n el conjunto I n se puede descomponer en dos partes
Problema 1. Sea I n el conjunto de los n primeros números naturales impares. Por ejemplo: I 3 = {1, 3, 5, I 6 = {1, 3, 5, 7, 9, 11, etc. Para qué números n el conjunto I n se puede descomponer en dos partes
Contenido: CARTAS DE CONTROL. Cartas de control C Cartas de control U Cartas de control P Cartas de control NP DIAGRAMA DE PARETTO HISTOGRAMAS
 Contenido: CARTAS DE CONTROL Cartas de control C Cartas de control U Cartas de control P Cartas de control NP DIAGRAMA DE PARETTO HISTOGRAMAS TEST DE MEDIANAS CEL: 72488950 1 Antes de querer utilizar cualquier
Contenido: CARTAS DE CONTROL Cartas de control C Cartas de control U Cartas de control P Cartas de control NP DIAGRAMA DE PARETTO HISTOGRAMAS TEST DE MEDIANAS CEL: 72488950 1 Antes de querer utilizar cualquier
Cualquier número de cualquier base se puede representar mediante la siguiente ecuación polinómica:
 SISTEMAS DE NUMERACIÓN Los números se pueden representar en distintos sistemas de numeración que se diferencian entre si por su base. Así el sistema de numeración decimal es de base 10, el binario de base
SISTEMAS DE NUMERACIÓN Los números se pueden representar en distintos sistemas de numeración que se diferencian entre si por su base. Así el sistema de numeración decimal es de base 10, el binario de base
HERRAMIENTAS DE APOYO PARA LA IMPLEMENTACIÓN DE LA GESTIÓN POR PROCESOS EN EL MARCO DE LA POLÍTICA NACIONAL DE MODERNIZACIÓN DE LA GESTIÓN PÚBLICA
 HERRAMIENTAS DE APOYO PARA LA IMPLEMENTACIÓN DE LA GESTIÓN POR PROCESOS EN EL MARCO DE LA POLÍTICA NACIONAL DE MODERNIZACIÓN DE LA GESTIÓN PÚBLICA Documento elaborado por la de la Presidencia del Consejo
HERRAMIENTAS DE APOYO PARA LA IMPLEMENTACIÓN DE LA GESTIÓN POR PROCESOS EN EL MARCO DE LA POLÍTICA NACIONAL DE MODERNIZACIÓN DE LA GESTIÓN PÚBLICA Documento elaborado por la de la Presidencia del Consejo
REGRESION simple. Correlación Lineal:
 REGRESION simple Correlación Lineal: Dadas dos variable numéricas continuas X e Y, decimos que están correlacionadas si entre ambas variables hay cierta relación, de modo que puede predecirse (aproximadamente)
REGRESION simple Correlación Lineal: Dadas dos variable numéricas continuas X e Y, decimos que están correlacionadas si entre ambas variables hay cierta relación, de modo que puede predecirse (aproximadamente)
Aproximación local. Plano tangente. Derivadas parciales.
 Univ. de Alcalá de Henares Ingeniería de Telecomunicación Cálculo. Segundo parcial. Curso 004-005 Aproximación local. Plano tangente. Derivadas parciales. 1. Plano tangente 1.1. El problema de la aproximación
Univ. de Alcalá de Henares Ingeniería de Telecomunicación Cálculo. Segundo parcial. Curso 004-005 Aproximación local. Plano tangente. Derivadas parciales. 1. Plano tangente 1.1. El problema de la aproximación
Divisibilidad y números primos
 Divisibilidad y números primos Divisibilidad En muchos problemas es necesario saber si el reparto de varios elementos en diferentes grupos se puede hacer equitativamente, es decir, si el número de elementos
Divisibilidad y números primos Divisibilidad En muchos problemas es necesario saber si el reparto de varios elementos en diferentes grupos se puede hacer equitativamente, es decir, si el número de elementos
