RESISTENCIA AL IMPACTO
|
|
|
- Purificación María Pilar Hernández Paz
- hace 9 años
- Vistas:
Transcripción
1 ESISTENCIA AL IMPACTO En solados de tránsito no exclusivamente peatonal, asociados habitualmente a actividad comercial (grandes superficies) o industrial, los pavimentos suelen estar sometidos a impactos por caída de objetos. Un ensayo que evalúe el comportamiento de la baldosa cerámica frente a esa agresión mecánica, manifestada como fisuras e incluso escamaduras, nos dará información sobre su durabilidad bajo esas condiciones. La norma EN 44 establece esta característica como opcional para el fabricante. Se mide a través del coeficiente de restitución, magnitud adimensional que nos indica la energía perdida en el rebote de una esfera de acero sobre la superficie de la baldosa, ya adherida a una losa de hormigón, que, descontando la energía perdida en el rozamiento con el aire y la deformación de la bola de acero, hay que atribuirla a la deformación de la superficie de la baldosa. El Anexo P (informativo) de la norma EN 44 aconseja un valor mínimo de 0,55 para las baldosas destinadas a suelos de bajas exigencias mecánicas. Los ingleses recomiendan valores de 0,70 para baldosas destinadas a suelos de exigencias mecánicas medias y de 0,85 en suelos de altas exigencias. Los franceses tienen dos ensayos particulares (impacto ligero y pesado) para baldosas GL y UGL respectivamente. La medida de la resistencia al impacto en ISO El ensayo relaciona la resistencia al impacto con el coeficiente de restitución, definido a su vez como cociente entre la velocidad de partida (rebote) tras el impacto y la velocidad de la esfera en el momento de impactar. Despreciando rozamientos y la propia deformación de la esfera, y aplicando la ecuación de la Cinemática que nos expresa la conversión de la energía potencial [esfera a m de altura de la superficie de la baldosa] en cinética en el momento del impacto, deducimos la definición del coeficiente de restitución como raíz cuadrada de la altura alcanzada por la bola en el rebote, que es como se mide en el ensayo (o midiendo el tiempo entre dos rebotes consecutivos). Las condiciones del ensayo son: Colocar con adhesivo la baldosa sobre una placa de hormigón maduro Tras el endurecimiento del adhesivo, dejar caer una bola de acero de 9 mm de diámetro desde m de altura Contar el tiempo transcurrido entre el primer impacto sobre la baldosa y el segundo impacto y calcular mediante una fórmula la altura alcanzada en el rebote. Con ella calcular el coeficiente de restitución.
2 Lanzador de bola Fisuras de tipo hertziano sobre la superficie esmaltada de la baldosa tras un impacto. El coeficiente de restitución (sin dimensiones) se suele representar con la letra e (por ejemplo, e=0,65). El resultado del ensayo debe informar de los efectos sobre la superficie de la baldosa: Un coeficiente de restitución cercano a nos indica que apenas se ha perdido energía en la baldosa y, en consecuencia, no se habrá producido deterioro [al ser un material rígido, la deformación será cuanto menos la generación de microfisuras] Un coeficiente de restitución por debajo de 0,5 nos indica que más de la mitad de la energía en el rebote se ha perdido en la deformación de la superficie de la baldosa. El impacto ligero y pesado en el Cuaderno 355 del CSTB de Francia El Cuaderno 355 (Enero 005) del Centro Científico y Técnico de la Construcción, CSTB (Francia) establece sendos ensayos de resistencia mecánica al impacto para baldosas cerámicas esmaltadas (Anexo 7) y no esmaltadas (Anexo 6), con la denominación respectiva de resistencia al impacto ligero y al impacto pesado. eproducimos aquí las condiciones de ambos ensayos por si Vd. tiene curiosidad de comparar las exigencias francesas respecto al ensayo de ISO
3 CHOQUE PESADO (Anexo 6) EQUIPOS Y MATEIALES ASOCIADOS. Un lecho de arena capaz de albergar una losa de 40x40 cm Un soporte vertical equipado con un electroimán capaz de sujetar la bola antes de su caída y que pueda ser desplazado verticalmente sobre el soporte. Una bola de acero pulido de 50 g. POBETAS. En la medida de lo posible deben someterse a ensayo tres baldosas enteras, que son fijadas sobre una losa de hormigón, el conjunto constituye una probeta. TES probetas al menos deben sufrir el ensayo. EALIZACION DEL ENSAYO. Al acabar el secado, la probeta se coloca sobre el lecho de arena de forma que la superficie de las baldosas sea horizontal pudiendo realizarse el ensayo: dejar caer la bola verticalmente (agarrar la bola inmediatamente después del rebote a fin de evitar que recaiga sobre la baldosa) desde una altura de 80 cm de forma que el punto de impacto se sitúe en un círculo de cm de diámetro en torno al centro de la probeta. Nota: Teniendo en cuenta la influencia que puede tener el tiempo de secado sobre el resultado del ensayo, a menudo es útil preparar un doble juego de probetas, el segundo puede utilizarse en caso de que el ensayo, después de los 7 días (de secado) no sea satisfactorio. CHOQUE LIGEO (Anexo 7) EQUIPOS Y MATEIALES ASOCIADOS. Un soporte rígido capaz de sostener una losa de 40x40 cm Un soporte vertical equipado con un electroimán capaz de sujetar la bola antes de su caída y que pueda ser desplazado verticalmente sobre el soporte. Una bola de acero pulido de 50 g. POBETAS. TES piezas de dimensiones de 75x75mm deben ser recortadas a partir de tres baldosas distintas. Llegado el caso, las baldosas de dimensiones inferiores a 75 mm pueden ser utilizadas. Las piezas son pegadas sobre una losa de hormigón, el conjunto constituye una probeta. Las tres probetas deben sufrir el ensayo. EALIZACION DEL ENSAYO. Al acabar el secado, la probeta se coloca sobre el soporte rígido de forma que la superficie de las baldosas sea horizontal y perpendicular al soporte sobre el cual se desplaza el electroimán pudiendo realizarse el ensayo: dejar caer la bola verticalmente (agarrar la bola inmediatamente después del rebote a fin de evitar que recaiga sobre la baldosa) desde una altura de m de forma que el punto de impacto se sitúe en un circulo de cm de diámetro en tomo al centro de la probeta. Nota: Teniendo en cuenta la influencia que puede tener el tiempo de secado sobre el resultado del ensayo, a menudo es útil preparar un doble juego de probetas, el segundo puede utilizarse en caso de que el ensayo, después de las 48 horas (de secado) no sea satisfactorio. 3
4 MEDIDA DEL IMPACTO LIGEO SOBE BALDOSAS ESMALTADAS (GL) Caída de una bola de acero de 50 g desde una altura de m sobre una maqueta, constituida por una placa de hormigón de 40 x 40 cm sobre la que se han adherido tres probetas de 75x75 mm cortadas de tres baldosas diferentes, colocadas con junta abierta. Los resultados obtenidos se clasifican en los siguientes niveles: NIVEL DESCIPCIÓN DEL DETEIOO 0 Ningún deterioro apreciable a la vista en la superficie de la baldosa Línea o trazas circulares alrededor del impacto Ni fisuras radiales ni desprendimiento de material (escamaduras) Fisuras radiales de longitud l 5 mm Sin desprendimiento de material Fisuras radiales de longitud 5 < l 0 mm 3 Sin desprendimiento de material Fisuras radiales de longitud l > 0 mm 4 Sin desprendimiento de material 5 Desprendimiento de material en forma de escamas Nota: Para la clasificación del nivel, al menos dos probetas deben presentar el máximo deterioro observado Cómo se obtiene el coeficiente de restitución Ya se ha definido el coeficiente de restitución como una magnitud que nos da información de la cantidad de energía perdida en el choque elástico entre una bola de acero y la superficie vista de una baldosa cerámica GL o UGL. Siendo aproximadamente constantes las energías perdidas por rozamiento con el aire y por la ligera deformación de la bola de acero, se deduce que la energía Aperdida@ por la bola en el primer rebote se ha transferido al sistema baldosa/material de agarre/placa de hormigón, alternando su estructura y provocando una onda de choque. Para deducir esa energía transferida se recurre a la Física, en base a principios elementales de la Mecánica. Tomando como referencia el plano de la baldosa, toda la energía potencial de la bola de acero situada a m de altura sobre ese plano teórico se transformará en energía cinética, medida por la velocidad de la bola en el momento de impactar contra la baldosa, energía perdida en el rozamiento con el aire y energía transferida al impacto elástico entre los dos cuerpos, según se describe en la figura adjunta. Si consideramos despreciable el rozamiento con el aire respecto a la energía perdida en el choque tendremos: 4
5 Momento inicial antes de soltar la bola: Sólo energía potencial E p =mgh donde: m es la masa de la bola g la aceleración de la gravedad (9,8 m/s ) h la altura inicial ( m) En el momento del impacto sobre el plano de la baldosa toda la energía potencial se habrá transformado en cinética (hemos despreciado el rozamiento con el aire) E =mgh = mv p donde v es la velocidad de la bola en el momento del impacto v = mgh =gh v= gh m Esta energía cinética se transformará en el primer rebote en: Energía potencial en la posición E p =mgh Energía transferida a los cuerpos en el impacto Si designamos por v la velocidad inicial de la bola en el rebote, tras el impacto, la energía cinética de la bola tras el impacto será: E C = mv que, despreciando una vez más el rozamiento con el aire, se transformará otra vez en energía potencial en el punto más alto de la trayectoria, en cuyo instante y posición (h ) su velocidad será nula e iniciará el descenso hacia el segundo impacto con la baldosa cerámica. Así pues: mgh mv = mgh v = =gh v gh m = Si definimos el coeficiente de restitución como una magnitud adimensional que nos mide la pérdida de energía en el impacto, será el cociente entre la energía cinética de la bola de acero tras el impacto (momento inicial del rebote) [mv ] y la energía cinética antes del mismo [mv ]; es decir: Coeficiente de restitución e= mv = mv v v = gh gh = h h Así, siendo que h = m, midiendo h y expresándolo en metros, tendríamos directamente el coeficiente de restitución. Por ejemplo, si el rebote sobre una baldosa de gres porcelánico (BI a UGL) lisa alcanza una altura de 7 cm, el coeficiente de restitución sería e = 0,7 m / m = 0,7. 5
6 Sin embargo, el método de ensayo contemplado en la norma ISO :998 define el coeficiente de restitución como el cociente entre las velocidades después del impacto y antes del mismo ((no como el cociente de sus cuadrados!), con lo que: c= v v = gh gh = h h En consecuencia, en el ejemplo anterior nos saldrá un e = 0,7 = 0,85 A nivel práctico, es más sencillo medir el tiempo entre el primer impacto y el segundo, tras el primer rebote. En este caso, debemos echar mano de las ecuaciones de la Cinemática: h = gt ya que en lo alto del rebote (posición ) la velocidad de la bola es cero y donde t es la mitad del tiempo transcurrido entre los dos impactos que conforman el primer rebote. Si medimos ese tiempo entre los dos primeros impactos consecutivos con un automatismo que, mediante la percepción del sonido de los impactos, active y desactive, un cronómetro tendremos: h = gt x9,8x T = 9,8 T =,6T (m) =,6T (cm) 8 Según la fórmula propuesta en el método de ensayo contemplado en ISO :998, el coeficiente de restitución tienen las siguientes expresiones: e= h h =,6T h y si consideramos que h = m e = h =,6T =,xt siendo T el tiempo transcurrido entre los dos primeros impactos. El coeficiente de restitución se mantiene entre dos valores teóricos extremos: e = 0 supondría que no hay choque elástico, que la bola queda incrustada en la baldosa cerámica y que toda la energía que tenía cuando estaba situada a m de altura respecto al plano definido por la superficie de la baldosa (energía potencial) se ha transformado en: Energía empleada en vencer el rozamiento con el aire; es decir, energía disipada Energía empleada en modificar la estructura del cuerpo cerámico y la bola de acero e = supondría que toda la energía potencial inicial se ha transformado en energía cinética tras el impacto, sin pérdidas por el rozamiento con el aire ni con el choque. 6
7 En consecuencia, cuanto más nos acerquemos al valor e = más seguridad tendremos de que la baldosa cerámica impactada apenas habrá sufrido deformación con el choque. Según los trabajos de investigación del Centro Cerámico Británico, se obtienen coeficientes de restitución de 0,9-0,93 con bolas de acero de 3/4 de pulgada de diámetro (aprox. 9 mm Ø), sobre baldosas BI a UGL de grosores entre 8 y 6,5 mm. Con bolas de 3,5 mm Ø se obtienen coeficientes de restitución de 0,76-0,8 para el mismo tipo de baldosas. En cualquier caso, el examen visual tras el impacto es determinante para asegurar el buen comportamiento en el tiempo de la baldosa cerámica. Cualquier microfisuración superficial (incluso las fisuras no contempladas en la norma) supone el deterioro irreversible del pavimento. Es más realista la consideración del impacto pesado según NF-UPEC, ya diseñado para baldosas no esmaltadas (UGL), con la caída de una bola de 50 g desde una altura de 80 cm sobre una maqueta embaldosada de 40x40 cm. En la clasificación UPEC de locales se recomiendan baldosas P 4S allá donde exista riesgo fundado de impactos. Hasta aquí hablamos siempre de impactos no punzantes, pues el choque de objetos punzantes (con cantos vivos) sobre la superficie de la baldosa siempre producirán incisiones y escamaduras, como consecuencia de la misma naturaleza del cuerpo cerámico ( los materiales cerámicos son frágiles!). Otra cosa es que esa incisión o escamadura sea perceptible por el ojo humano. Comentarios La medida del coeficiente de restitución y la clasificación de los resultados del ensayo según el deterioro superficial (fisuras y desprendimientos de material) nos aproxima al comportamiento de la baldosa cerámica frente a impactos. Es una característica que debiera contemplarse cuando el destino de la baldosa es un pavimento de la Arquitectura de Pública Concurrencia y, en general, todos los solados con exigencias especiales de resistencia mecánica. En destinos de ámbito residencial privado debieran discriminarse los solados con riesgo (exteriores, zaguanes y cocinas) de los restantes. En el extremo opuesto, los solados con especial riesgo de la edificación industrial y comercial debieran resolverse con baldosas no vidriadas y que superen el ensayo del impacto pesado [Anexo 6 del Cuaderno 355 del CSTB], que reciban además el código P 4S de la clasificación francesa UPEC. 7
Examen de Física-1, 1 Ingeniería Química Examen final. Septiembre de 2014 Problemas (Dos puntos por problema).
 Examen de Física-1, 1 Ingeniería Química Examen final. Septiembre de 014 Problemas (Dos puntos por problema). Problema 1 (Primer parcial): Un cuerpo de masa 10 g se desliza bajando por un plano inclinado
Examen de Física-1, 1 Ingeniería Química Examen final. Septiembre de 014 Problemas (Dos puntos por problema). Problema 1 (Primer parcial): Un cuerpo de masa 10 g se desliza bajando por un plano inclinado
Ejercicio nº 1 Deducir la ecuación del movimiento asociado a la gráfica. Ejercicio nº 2 Deducir la ecuación del movimiento asociado a la gráfica.
 1(9) Ejercicio nº 1 Deducir la ecuación del movimiento asociado a la gráfica. X(m) 4 2 4 6 8 t(s) -4 Ejercicio nº 2 Deducir la ecuación del movimiento asociado a la gráfica. X(m) 3 1 2 3 t(s) -3 Ejercicio
1(9) Ejercicio nº 1 Deducir la ecuación del movimiento asociado a la gráfica. X(m) 4 2 4 6 8 t(s) -4 Ejercicio nº 2 Deducir la ecuación del movimiento asociado a la gráfica. X(m) 3 1 2 3 t(s) -3 Ejercicio
CANTABRIA / JUNIO 02. LOGSE / FÍSICA / EXAMEN COMPLETO
 CANTABRIA / JUNIO 0. LOGSE / FÍSICA / EXAMEN COMPLETO El alumno elegirá tres de las cinco cuestiones propuestas, así como sólo una de las dos opciones de problemas CUESTIONES ( puntos cada una) A. Se considera
CANTABRIA / JUNIO 0. LOGSE / FÍSICA / EXAMEN COMPLETO El alumno elegirá tres de las cinco cuestiones propuestas, así como sólo una de las dos opciones de problemas CUESTIONES ( puntos cada una) A. Se considera
Trabajo y Energía 30º. Viento
 Física y Química TEM 7 º de achillerato Trabajo y Energía.- Un barco y su tripulación se desplazan de una isla hasta otra que dista Km en línea recta. Sabiendo que la fuerza del viento sobre las velas
Física y Química TEM 7 º de achillerato Trabajo y Energía.- Un barco y su tripulación se desplazan de una isla hasta otra que dista Km en línea recta. Sabiendo que la fuerza del viento sobre las velas
CONTESTAR: 1 ó 2; 3 ó 4; 6 ó 7; 8 ó 9 ó 10; 5 ó 11
 NOMBRE APELLIDOS FÍSICA y QUÍMICA 1º DE BACHILLERATO NA 1DA GLOBAL 1ª EVALUACIÓN 015-16 CONTESTAR: 1 ó ; 3 ó 4; 6 ó 7; 8 ó 9 ó 10; 5 ó 11 1- Sobre un cuerpo cuya masa es m = 5,0 kg, actúan una fuerza hacia
NOMBRE APELLIDOS FÍSICA y QUÍMICA 1º DE BACHILLERATO NA 1DA GLOBAL 1ª EVALUACIÓN 015-16 CONTESTAR: 1 ó ; 3 ó 4; 6 ó 7; 8 ó 9 ó 10; 5 ó 11 1- Sobre un cuerpo cuya masa es m = 5,0 kg, actúan una fuerza hacia
MOVIMIENTO ARMÓNICO SIMPLE
 MOVIMIENTO ARMÓNICO SIMPLE Junio 2016. Pregunta 2A.- Un bloque de 2 kg de masa, que descansa sobre una superficie horizontal, está unido a un extremo de un muelle de masa despreciable y constante elástica
MOVIMIENTO ARMÓNICO SIMPLE Junio 2016. Pregunta 2A.- Un bloque de 2 kg de masa, que descansa sobre una superficie horizontal, está unido a un extremo de un muelle de masa despreciable y constante elástica
EJERCICIOS DE MOMENTO LINEAL, IMPULSO Y COLISIONES
 SEXTO TALLER DE REPASO 2015-01 EJERCICIOS DE MOMENTO LINEAL, IMPULSO Y COLISIONES 1. Dos carros, A y B, se empujan, uno hacia el otro. Inicialmente B está en reposo, mientras que A se mueve hacia la derecha
SEXTO TALLER DE REPASO 2015-01 EJERCICIOS DE MOMENTO LINEAL, IMPULSO Y COLISIONES 1. Dos carros, A y B, se empujan, uno hacia el otro. Inicialmente B está en reposo, mientras que A se mueve hacia la derecha
Movimiento armónico simple Modelo A. Pregunta 2.- Un bloque de masa m = 0,2 kg está unido al extremo libre de un muelle horizontal de
 Movimiento armónico simple 1.- 2015-Modelo A. Pregunta 2.- Un bloque de masa m = 0,2 kg está unido al extremo libre de un muelle horizontal de constante elástica k = 2 N m -1 que se encuentra fijo a una
Movimiento armónico simple 1.- 2015-Modelo A. Pregunta 2.- Un bloque de masa m = 0,2 kg está unido al extremo libre de un muelle horizontal de constante elástica k = 2 N m -1 que se encuentra fijo a una
Trabajo y Energía II. = [Joule]
![Trabajo y Energía II. = [Joule] Trabajo y Energía II. = [Joule]](/thumbs/68/58368678.jpg) U R S O: FÍSIA MENIÓN MATERIAL: FM-1 Trabajo y Energía II ENERGÍA INÉTIA: Un cuerpo, por el sólo hecho de estar en movimiento, tiene energía cinética ( E ). La energía cinética de un cuerpo que se está
U R S O: FÍSIA MENIÓN MATERIAL: FM-1 Trabajo y Energía II ENERGÍA INÉTIA: Un cuerpo, por el sólo hecho de estar en movimiento, tiene energía cinética ( E ). La energía cinética de un cuerpo que se está
Problemas de Física I DINAMICA DE SISTEMAS DE PARTICULAS. (1 er Q.:prob impares, 2 ndo Q.:prob pares)
 Problemas de Física I DINAMICA DE SISTEMAS DE PARTICULAS (1 er Q.:prob impares, 2 ndo Q.:prob pares) 1. (T) Una placa circular homogénea de radio r tiene un orificio circular cortado en ella de radio r/2
Problemas de Física I DINAMICA DE SISTEMAS DE PARTICULAS (1 er Q.:prob impares, 2 ndo Q.:prob pares) 1. (T) Una placa circular homogénea de radio r tiene un orificio circular cortado en ella de radio r/2
En la actualidad, se dispone de un método de ensayo representativo de la potencial agresión química que pueden sufrir las baldosas cerámicas:
 RESISTENCIA QUÍMICA Todas las baldosas cerámicas están sometidas a la agresión química, consecuencia de operaciones de limpieza, contaminación ambiental en exteriores y vertidos de productos en suelos.
RESISTENCIA QUÍMICA Todas las baldosas cerámicas están sometidas a la agresión química, consecuencia de operaciones de limpieza, contaminación ambiental en exteriores y vertidos de productos en suelos.
TEMA 9. MOVIMIENTO ARMÓNICO SIMPLE
 TEMA 9. MOVIMIENTO ARMÓNICO SIMPLE Un movimiento periódico es aquel que describe una partícula cuando las variables posición, velocidad y aceleración de su movimiento toman los mismos valores después de
TEMA 9. MOVIMIENTO ARMÓNICO SIMPLE Un movimiento periódico es aquel que describe una partícula cuando las variables posición, velocidad y aceleración de su movimiento toman los mismos valores después de
Ejercicios Física PAU Comunidad de Madrid Enunciados Revisado 25 noviembre 2014
 2015-Modelo A. Pregunta 2.- Un bloque de masa m = 0,2 kg está unido al extremo libre de un muelle horizontal de constante elástica k = 2 N m -1 que se encuentra fijo a una pared. Si en el instante inicial
2015-Modelo A. Pregunta 2.- Un bloque de masa m = 0,2 kg está unido al extremo libre de un muelle horizontal de constante elástica k = 2 N m -1 que se encuentra fijo a una pared. Si en el instante inicial
fig. 1 sobre un objeto, es igual al cambio en su energía cinética, y esto se representa mediante la siguiente ecuación
 C U R S O: FÍSICA MENCIÓN MATERIAL: FM-14 ENERGÍA II ENERGÍA CINÉTICA, POTENCIAL GRAVITATORIA Y MECÁNICA Aunque no existe una definición formal de energía, a este nivel la podemos entender simplemente
C U R S O: FÍSICA MENCIÓN MATERIAL: FM-14 ENERGÍA II ENERGÍA CINÉTICA, POTENCIAL GRAVITATORIA Y MECÁNICA Aunque no existe una definición formal de energía, a este nivel la podemos entender simplemente
RSEF.-Olimpiada de Física Fase local.-principado de Asturias.-Cuestiones OLIMPIADA DE FÍSICA 2014 FASE LOCAL PRINCIPADO DE ASTURIAS
 OLIMPIADA DE FÍSICA 2014 FASE LOCAL PRINCIPADO DE ASTURIAS CUESTIONES (40 puntos). Se marcará con una cruz la casilla que se considere acertada (sólo hay una) en la hoja de respuestas (no en el cuestionario).
OLIMPIADA DE FÍSICA 2014 FASE LOCAL PRINCIPADO DE ASTURIAS CUESTIONES (40 puntos). Se marcará con una cruz la casilla que se considere acertada (sólo hay una) en la hoja de respuestas (no en el cuestionario).
TALLER DE MOMENTO LINEAL, IMPULSO Y COLISIONES MOMENTO LINEAL E IMPULSO
 TALLER DE MOMENTO LINEAL, IMPULSO Y COLISIONES MOMENTO LINEAL E IMPULSO 1. Una bola de boliche de 7 kg se mueve en línea recta a 3 m/s. Qué tan rápido debe moverse una bola de ping-pong de 2.45 gr. en
TALLER DE MOMENTO LINEAL, IMPULSO Y COLISIONES MOMENTO LINEAL E IMPULSO 1. Una bola de boliche de 7 kg se mueve en línea recta a 3 m/s. Qué tan rápido debe moverse una bola de ping-pong de 2.45 gr. en
ACADEMIA CENTRO DE APOYO AL ESTUDIO MOVIMIENTO VIBRATORIO.
 MOVIMIENTO VIBRATORIO. Movimiento vibratorio armónico simple 1. Explica como varía la energía mecánica de un oscilador lineal si: a) Se duplica la amplitud. b) Se duplica la frecuencia. c) Se duplica la
MOVIMIENTO VIBRATORIO. Movimiento vibratorio armónico simple 1. Explica como varía la energía mecánica de un oscilador lineal si: a) Se duplica la amplitud. b) Se duplica la frecuencia. c) Se duplica la
Física para Ciencias: Trabajo y Energía
 Física para Ciencias: Trabajo y Energía Dictado por: Profesor Aldo Valcarce 1 er semestre 2014 Trabajo (W) En la Física la palabra trabajo se le da un significado muy específico: El trabajo (W) efectuado
Física para Ciencias: Trabajo y Energía Dictado por: Profesor Aldo Valcarce 1 er semestre 2014 Trabajo (W) En la Física la palabra trabajo se le da un significado muy específico: El trabajo (W) efectuado
Momento Lineal y Choques. Repaso. Problemas.
 Momento Lineal y Choques. Repaso. Problemas. Resumen: Momentum lineal.. El momentum lineal p de una partícula da masa m que se mueve con una velocidad v.unidad de momentum en el sistema SI: kg m/s. Momentum
Momento Lineal y Choques. Repaso. Problemas. Resumen: Momentum lineal.. El momentum lineal p de una partícula da masa m que se mueve con una velocidad v.unidad de momentum en el sistema SI: kg m/s. Momentum
Problemas propuestos y resueltos energía mecánica Elaborado por: Profesora Pilar Cristina Barrera Silva
 Problemas propuestos y resueltos energía mecánica Elaborado por: Profesora Pilar Cristina Barrera Silva Serway, física, volumen 1, tercera edición. Un niño se desliza desdeel reposo, por una resbaladilla
Problemas propuestos y resueltos energía mecánica Elaborado por: Profesora Pilar Cristina Barrera Silva Serway, física, volumen 1, tercera edición. Un niño se desliza desdeel reposo, por una resbaladilla
1- Una masa de 2 kg y otra de 200 kg tienen el mismo momento lineal, 40 kg m/s. Determina la energía cinética de cada una.
 PROBLEMAS MOMENTO LINEAL Y ENERGÍA 1- Una masa de 2 kg y otra de 200 kg tienen el mismo momento lineal, 40 kg m/s. Determina la energía cinética de cada una. Resp: 400 J / 4 J 2- Una fuerza de 1 N actúa
PROBLEMAS MOMENTO LINEAL Y ENERGÍA 1- Una masa de 2 kg y otra de 200 kg tienen el mismo momento lineal, 40 kg m/s. Determina la energía cinética de cada una. Resp: 400 J / 4 J 2- Una fuerza de 1 N actúa
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE FÍSICA
 ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE FÍSICA PRIMERA EVALUACIÓN DE FÍSICA A DICIEMBRE 10 DE 2014 SOLUCIÓN TEMA 1 (8 puntos) Una persona corre
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE FÍSICA PRIMERA EVALUACIÓN DE FÍSICA A DICIEMBRE 10 DE 2014 SOLUCIÓN TEMA 1 (8 puntos) Una persona corre
Movimiento parabólico
 Movimiento parabólico INTRODUCCIÓN Para saber experimentalmente si el movimiento de un objeto es parabólico se necesita medir sus coordenadas x e y. Un procedimiento es utilizar la fotografía estroboscópica
Movimiento parabólico INTRODUCCIÓN Para saber experimentalmente si el movimiento de un objeto es parabólico se necesita medir sus coordenadas x e y. Un procedimiento es utilizar la fotografía estroboscópica
MÉTODOS DEL TRABAJO Y LA ENERGÍA, Y DEL IMPULSO Y LA CANTIDAD DE MOVIMIENTO
 Serie de ejercicios de Cinemática y Dinámica MÉTODOS DEL TRJO Y L ENERGÍ, Y DEL IMPULSO Y L CNTIDD DE MOVIMIENTO 1. Calcular el trabajo que realiza cada una de las fuerzas externas que actúa sobre el cuerpo
Serie de ejercicios de Cinemática y Dinámica MÉTODOS DEL TRJO Y L ENERGÍ, Y DEL IMPULSO Y L CNTIDD DE MOVIMIENTO 1. Calcular el trabajo que realiza cada una de las fuerzas externas que actúa sobre el cuerpo
9 MECANICA Y FLUIDOS: Colisiones
 9 MECANICA Y FLUIDOS: Colisiones CONTENIDOS Conservación de cantidad de movimiento y de la energía. Colisiones elásticas e inelásticas. Coeficiente de restitución. Trabajo de Fuerzas conservativas y no
9 MECANICA Y FLUIDOS: Colisiones CONTENIDOS Conservación de cantidad de movimiento y de la energía. Colisiones elásticas e inelásticas. Coeficiente de restitución. Trabajo de Fuerzas conservativas y no
2 o Bachillerato. Conceptos básicos
 Física 2 o Bachillerato Conceptos básicos Movimiento. Cambio de posición de un cuerpo respecto de un punto que se toma como referencia. Cinemática. Parte de la Física que estudia el movimiento de los cuerpos
Física 2 o Bachillerato Conceptos básicos Movimiento. Cambio de posición de un cuerpo respecto de un punto que se toma como referencia. Cinemática. Parte de la Física que estudia el movimiento de los cuerpos
INSTITUCIÓN EDUCATIVA GENERAL SANTANDER FÍSICA GRADO DÉCIMO MATERIAL DE APOYO CAÍDA LIBRE Y TIRO VERTICAL
 1 INSTITUCIÓN EDUCATIVA GENERAL SANTANDER FÍSICA GRADO DÉCIMO MATERIAL DE APOYO CAÍDA LIBRE Y TIRO VERTICAL CONCEPTOS FUNDAMENTALES LÍNEA VERTICAL Es aquella línea recta, radial a un planeta. MOVIMIENTO
1 INSTITUCIÓN EDUCATIVA GENERAL SANTANDER FÍSICA GRADO DÉCIMO MATERIAL DE APOYO CAÍDA LIBRE Y TIRO VERTICAL CONCEPTOS FUNDAMENTALES LÍNEA VERTICAL Es aquella línea recta, radial a un planeta. MOVIMIENTO
Ejercicios Física PAU Comunidad de Madrid Enunciados Revisado 18 septiembre 2012.
 2013-Modelo A. Pregunta 2.- Un objeto está unido a un muelle horizontal de constante elástica 2 10 4 Nm -1. Despreciando el rozamiento: a) Qué masa ha de tener el objeto si se desea que oscile con una
2013-Modelo A. Pregunta 2.- Un objeto está unido a un muelle horizontal de constante elástica 2 10 4 Nm -1. Despreciando el rozamiento: a) Qué masa ha de tener el objeto si se desea que oscile con una
CINEMÁTICA. El periodo de un péndulo sólo depende de la longitud de la cuerda ( l ) y la aceleración de la gravedad ( g ).
 CINEMÁTICA Es la rama de la mecánica que estudia el movimiento de los cuerpos sin tomar en cuenta las causas. Distancia: es una magnitud escalar que mide la separación entre dos cuerpos o entre dos lugares.
CINEMÁTICA Es la rama de la mecánica que estudia el movimiento de los cuerpos sin tomar en cuenta las causas. Distancia: es una magnitud escalar que mide la separación entre dos cuerpos o entre dos lugares.
6 Energía, trabajo y potencia
 6 Energía, trabajo y potencia ACTIVIDADES Actividades DELdel INTERIOR interior DE LAde UNIDAD la unidad. Se arrastra una mesa de 0 kg por el suelo a lo largo de 5 m. Qué trabajo realiza el peso? El trabajo
6 Energía, trabajo y potencia ACTIVIDADES Actividades DELdel INTERIOR interior DE LAde UNIDAD la unidad. Se arrastra una mesa de 0 kg por el suelo a lo largo de 5 m. Qué trabajo realiza el peso? El trabajo
MOVIMIENTO BIDIMENSIONAL
 MOVIMIENTO BIDIMENSIONAL EXPERIENCIA N 03 Nota Galileo Galilei (1564-1542) Calificado como Padre de la Cinemática, que a partir del movimiento del proyectil se eplica la velocidad de escape que deben alcanzar
MOVIMIENTO BIDIMENSIONAL EXPERIENCIA N 03 Nota Galileo Galilei (1564-1542) Calificado como Padre de la Cinemática, que a partir del movimiento del proyectil se eplica la velocidad de escape que deben alcanzar
Problemas. Laboratorio. Física moderna 09/11/07 DEPARTAMENTO DE FÍSICA E QUÍMICA. Nombre:
 Física moderna 9/11/7 DEPARTAMENTO DE FÍSICA E QUÍMICA Problemas Nombre: 1. Un muelle de constante k =, 1 3 N/m está apoyado en una superficie horizontal sin rozamiento. A 1, m hay un bucle vertical de
Física moderna 9/11/7 DEPARTAMENTO DE FÍSICA E QUÍMICA Problemas Nombre: 1. Un muelle de constante k =, 1 3 N/m está apoyado en una superficie horizontal sin rozamiento. A 1, m hay un bucle vertical de
4-. Sean u = (2, 0, -1, 3), v = (5, 4, 7, -2), w = (6, 2, 0, 9). Determine el vector x que satisface a: 2u v + x = 7x + w.
 EJERCICIOS VECTORES. 1-. Calcule la dirección de los siguientes vectores: a) v = (2, 2) d) v = (-3, -3) b) v = (-2 3, 2) e) v = (6, -6) c) v = (2, 2 3 ) f) v = (0,3) 3-. Para los siguientes vectores encuentre
EJERCICIOS VECTORES. 1-. Calcule la dirección de los siguientes vectores: a) v = (2, 2) d) v = (-3, -3) b) v = (-2 3, 2) e) v = (6, -6) c) v = (2, 2 3 ) f) v = (0,3) 3-. Para los siguientes vectores encuentre
Problemas de Movimiento vibratorio. MAS 2º de bachillerato. Física
 Problemas de Movimiento vibratorio. MAS º de bachillerato. Física 1. Un muelle se deforma 10 cm cuando se cuelga de él una masa de kg. Se separa otros 10 cm de la posición de equilibrio y se deja en libertad.
Problemas de Movimiento vibratorio. MAS º de bachillerato. Física 1. Un muelle se deforma 10 cm cuando se cuelga de él una masa de kg. Se separa otros 10 cm de la posición de equilibrio y se deja en libertad.
GUÍA DE ESTUDIO PARA EXAMEN SEGUNDO PARCIAL CICLO ESCOLAR FÍSICA I GRUPOS 2 I, 2 II Y 2 III PROFESOR: BENJAMÍN HERNÁNDEZ ARELLANO.
 GUÍA DE ESTUDIO PARA EXAMEN SEGUNDO PARCIAL CICLO ESCOLAR 2014-2015 FÍSICA I GRUPOS 2 I, 2 II Y 2 III PROFESOR: BENJAMÍN HERNÁNDEZ ARELLANO. A. Instrucción. En los espacios en blanco, escribe la palabra
GUÍA DE ESTUDIO PARA EXAMEN SEGUNDO PARCIAL CICLO ESCOLAR 2014-2015 FÍSICA I GRUPOS 2 I, 2 II Y 2 III PROFESOR: BENJAMÍN HERNÁNDEZ ARELLANO. A. Instrucción. En los espacios en blanco, escribe la palabra
2.- Cuánto valen el potencial y la intensidad del campo gravitatorio creado por la Tierra en un punto de su superficie?
 PROBLEMAS 1.- Con una órbita de 8000 Km de radio gira alrededor de la Tierra un satélite de 500 Kg de masa. Determina: a) su momento angular b) su energía cinética c) su energía potencial d) su energía
PROBLEMAS 1.- Con una órbita de 8000 Km de radio gira alrededor de la Tierra un satélite de 500 Kg de masa. Determina: a) su momento angular b) su energía cinética c) su energía potencial d) su energía
TEMA 2. Dinámica, Trabajo, Energía y Presión
 TEMA 2. Dinámica, Trabajo, Energía y Presión 1. Objeto de la dinámica Dinámica es la parte de la mecánica que estudia el movimiento atendiendo a las causas que lo producen. Estas causas son las fuerzas.
TEMA 2. Dinámica, Trabajo, Energía y Presión 1. Objeto de la dinámica Dinámica es la parte de la mecánica que estudia el movimiento atendiendo a las causas que lo producen. Estas causas son las fuerzas.
CINEMÁTICA II. ) cuerpos de diferentes masas desde la misma altura, llegarán al suelo con la misma velocidad y en el mismo instante.
 C U R S O: FÍSICA COMÚN MATERIAL: FC-3 CINEMÁTICA II CAÍDA LIBRE En cinemática, la caída libre es un movimiento dónde solamente influye la gravedad. En este movimiento se desprecia el rozamiento del cuerpo
C U R S O: FÍSICA COMÚN MATERIAL: FC-3 CINEMÁTICA II CAÍDA LIBRE En cinemática, la caída libre es un movimiento dónde solamente influye la gravedad. En este movimiento se desprecia el rozamiento del cuerpo
Movimiento armónico simple
 Movimiento armónico simple Cuestiones (99-R) Una partícula describa un movimiento armónico simple de amplitud A y frecuencia f. a) Represente gráficamente la posición y la velocidad de la partícula en
Movimiento armónico simple Cuestiones (99-R) Una partícula describa un movimiento armónico simple de amplitud A y frecuencia f. a) Represente gráficamente la posición y la velocidad de la partícula en
LABORATORIO 1: MEDICIONES BASICAS
 UNIVERSIDAD DON BOSCO DEPARTAMENTO DE CIENCIAS BASICA LABORATORIO DE FISICA ASIGNATURA: FISICA TECNICA I. OBJETIVO GENERAL LABORATORIO : MEDICIONES BASICAS Realizar mediciones de objetos utilizando diferentes
UNIVERSIDAD DON BOSCO DEPARTAMENTO DE CIENCIAS BASICA LABORATORIO DE FISICA ASIGNATURA: FISICA TECNICA I. OBJETIVO GENERAL LABORATORIO : MEDICIONES BASICAS Realizar mediciones de objetos utilizando diferentes
EL CHOQUE. v 1 N 2 N 1. Antes del choque P 2 P 1 F 21 F 12. Choque. v 2. Después del choque
 EL CHOQUE Una masa de 400 g se desliza sobre una superficie horizontal sin rozamiento con una velocidad de m/s y, choca con otra de 600 g inicialmente en reposo. a) Si el choque es central y elástico,
EL CHOQUE Una masa de 400 g se desliza sobre una superficie horizontal sin rozamiento con una velocidad de m/s y, choca con otra de 600 g inicialmente en reposo. a) Si el choque es central y elástico,
Selección Instituto Balseiro Problema 1. x 8m
 Problema 1 4m 7m x 8m Dos postes verticales, de 4 y 7 m de altura, se encuentran a una distancia de 8 m uno del otro. Se desea conectar sus extremos superiores con un cable, que además debe tocar el suelo
Problema 1 4m 7m x 8m Dos postes verticales, de 4 y 7 m de altura, se encuentran a una distancia de 8 m uno del otro. Se desea conectar sus extremos superiores con un cable, que además debe tocar el suelo
UNIDAD 9: TRABAJO Y ENERGÍA MECÁNICA 1. Trabajo mecánico
 UNIDAD 9: TRABAJO Y ENERGÍA MECÁNICA 1. Trabajo mecánico a) Indica en los siguientes casos si se realiza o no trabajo mecánico: Un cuerpo en caída libre (fuerza de gravedad Un cuerpo apoyado en una meda
UNIDAD 9: TRABAJO Y ENERGÍA MECÁNICA 1. Trabajo mecánico a) Indica en los siguientes casos si se realiza o no trabajo mecánico: Un cuerpo en caída libre (fuerza de gravedad Un cuerpo apoyado en una meda
Balance de energía en un diafragma
 Balance de energía en un diafragma Objetivos de la práctica! Estudiar el perfil de presiones que se produce a lo largo de una tubería en la que se encuentra instalado un diafragma.! Determinar el coeficiente
Balance de energía en un diafragma Objetivos de la práctica! Estudiar el perfil de presiones que se produce a lo largo de una tubería en la que se encuentra instalado un diafragma.! Determinar el coeficiente
PRÁCTICA PARA TRIMESTRAL 2011 DÉCIMO AÑO. Tema: Análisis dimensional. Cinemática del Movimiento en dos dimensiones. Lanzamiento de proyectiles.
 PRÁCTICA PARA TRIMESTRAL 2011 DÉCIMO AÑO Tema: Análisis dimensional. Cinemática del Movimiento en dos dimensiones. Lanzamiento de proyectiles. Resuelva los siguientes problemas y establezca sus propios
PRÁCTICA PARA TRIMESTRAL 2011 DÉCIMO AÑO Tema: Análisis dimensional. Cinemática del Movimiento en dos dimensiones. Lanzamiento de proyectiles. Resuelva los siguientes problemas y establezca sus propios
ALGUNOS EJERCICIOS RESUELTOS DE TRABAJO Y ENERGÍA (TEMA 9)
 I..S. Padre Manjón. Dpto de ísica y Química. ísica y Química º Bachillerato LGUS JCICIS SULTS D TBJ Y GÍ (TM 9) Un bloque de 5 kg se desliza por una superficie horizontal lisa con una velocidad de 4 m/s
I..S. Padre Manjón. Dpto de ísica y Química. ísica y Química º Bachillerato LGUS JCICIS SULTS D TBJ Y GÍ (TM 9) Un bloque de 5 kg se desliza por una superficie horizontal lisa con una velocidad de 4 m/s
TALLER DE TRABAJO Y ENERGÍA
 TALLER DE TRABAJO Y ENERGÍA EJERCICIOS DE TRABAJO 1. Un bloque de 9kg es empujado mediante una fuerza de 150N paralela a la superficie, durante un trayecto de 26m. Si el coeficiente de fricción entre la
TALLER DE TRABAJO Y ENERGÍA EJERCICIOS DE TRABAJO 1. Un bloque de 9kg es empujado mediante una fuerza de 150N paralela a la superficie, durante un trayecto de 26m. Si el coeficiente de fricción entre la
Física Cinemática velocidad v = x/t (1) Movimiento rectilíneo uniforme (M.R.U.) velocidad es constante
 Física Cinemática La cinemática se ocupa de la descripción del movimiento sin tener en cuenta sus causas. La velocidad (la tasa de variación de la posición) se define como la razón entre el espacio recorrido
Física Cinemática La cinemática se ocupa de la descripción del movimiento sin tener en cuenta sus causas. La velocidad (la tasa de variación de la posición) se define como la razón entre el espacio recorrido
PAU CASTILLA Y LEON JUNIO Y SEPTIEMBRE M.A.S. ONDAS José Mª Martín Hernández
 MAS Estudio dinámico y cinemático 1. (90-J11) Una pequeña plataforma horizontal sufre un movimiento armónico simple en sentido vertical, de 3 cm de amplitud y cuya frecuencia aumenta progresivamente. Sobre
MAS Estudio dinámico y cinemático 1. (90-J11) Una pequeña plataforma horizontal sufre un movimiento armónico simple en sentido vertical, de 3 cm de amplitud y cuya frecuencia aumenta progresivamente. Sobre
g planeta = g tierra / 2 = 4 9 m/s 2 v planeta = 11 2 / 2 = 5 6 km/s
 PAU MADRID JUNIO 2003 Cuestión 1.- Suponiendo un planeta esférico que tiene un radio la mitad del radio terrestre e igual densidad que la tierra, calcule: a) La aceleración de la gravedad en la superficie
PAU MADRID JUNIO 2003 Cuestión 1.- Suponiendo un planeta esférico que tiene un radio la mitad del radio terrestre e igual densidad que la tierra, calcule: a) La aceleración de la gravedad en la superficie
METODOS DE ENERGIA Problema #1 Problema #2 PROBLEMA #3
 METODOS DE ENERGIA Problema #1 El mecanismo mostrado se utiliza para probar la resistencia de un bloque al impacto, lanzándolo desde un extremo al otro. El resorte de la izquierda se comprime hasta que
METODOS DE ENERGIA Problema #1 El mecanismo mostrado se utiliza para probar la resistencia de un bloque al impacto, lanzándolo desde un extremo al otro. El resorte de la izquierda se comprime hasta que
Guía Nº I Experimentación CAIDA LIBRE
 OBJETIVO Liceo Juan XXIII, Villa Alemana Departamento de Ciencias Prof. David Valenzuela Guía Nº I Experimentación Cinemática MRUA CAIDA LIBRE W³.fisic.jimdo.com Investigar la influencia de la masa en
OBJETIVO Liceo Juan XXIII, Villa Alemana Departamento de Ciencias Prof. David Valenzuela Guía Nº I Experimentación Cinemática MRUA CAIDA LIBRE W³.fisic.jimdo.com Investigar la influencia de la masa en
FQ1B. FUERZAS CONSERVATIVAS Y NO CONSERVATIVAS. CONSERVACIÓN DE LA ENERGÍA
 FQ1B. FUERZAS CONSERVATIVAS Y NO CONSERVATIVAS. CONSERVACIÓN DE LA ENERGÍA Fuerzas conservativas El trabajo realizado por las fuerzas conservativas solo depende de la posición inicial y final del cuerpo
FQ1B. FUERZAS CONSERVATIVAS Y NO CONSERVATIVAS. CONSERVACIÓN DE LA ENERGÍA Fuerzas conservativas El trabajo realizado por las fuerzas conservativas solo depende de la posición inicial y final del cuerpo
MOVIMIENTO OSCILATORIO O VIBRATORIO
 MOVIMIENTO OSCILATORIO O VIBRATORIO 1. Movimiento armónico simple (MAS). 2. Ecuaciones del MAS. 3. Dinámica del MAS. 4. Energía del MAS. 5. El oscilador armónico. 6. El péndulo simple. Física 2º bachillerato
MOVIMIENTO OSCILATORIO O VIBRATORIO 1. Movimiento armónico simple (MAS). 2. Ecuaciones del MAS. 3. Dinámica del MAS. 4. Energía del MAS. 5. El oscilador armónico. 6. El péndulo simple. Física 2º bachillerato
Guia N 6 - Primer cuatrimestre de 2007 Sólidos rígidos planos. Energía potencial y mecánica.
 æ Mecánica CLásica Guia N 6 - Primer cuatrimestre de 2007 Sólidos rígidos planos. Energía potencial y mecánica. Problema 1: Dos barras delgadas uniformes de longitudes iguales, l=0.5 m, una de 4 kg y la
æ Mecánica CLásica Guia N 6 - Primer cuatrimestre de 2007 Sólidos rígidos planos. Energía potencial y mecánica. Problema 1: Dos barras delgadas uniformes de longitudes iguales, l=0.5 m, una de 4 kg y la
Centro de Estudios de Bachillerato 4/1 Maestro Moisés Sáenz Garza Segundo Examen Parcial. Temas Selectos de Física I. Grupo: Fecha: Firma:
 Centro de Estudios de Bachillerato 4/1 Maestro Moisés Sáenz Garza Segundo Examen Parcial Temas Selectos de Física I Atividades para preparar Portafolio de evidencias Elaboro: Enrique Galindo Chávez. Nombre:
Centro de Estudios de Bachillerato 4/1 Maestro Moisés Sáenz Garza Segundo Examen Parcial Temas Selectos de Física I Atividades para preparar Portafolio de evidencias Elaboro: Enrique Galindo Chávez. Nombre:
a) La trayectoria 4 b) La trayectoria 3 c) La trayectoria 2 d) La trayectoria 1
 ESCUELA SUPERIOR POLITECNICA DEL LITORAL Instituto de Ciencias Físicas SEGUNDA EVALUACIÓN CURSO NIVEL CERO B VERSIÓN 1 Nombre: Curso:.. 29 de Agosto de 2012 CADA PROBLEMA TIENE UN VALOR DE 2.8 PUNTOS.
ESCUELA SUPERIOR POLITECNICA DEL LITORAL Instituto de Ciencias Físicas SEGUNDA EVALUACIÓN CURSO NIVEL CERO B VERSIÓN 1 Nombre: Curso:.. 29 de Agosto de 2012 CADA PROBLEMA TIENE UN VALOR DE 2.8 PUNTOS.
OLIMPIADA DE FÍSICA. FASE LOCAL UNIVERSIDAD DE JAÉN 15 DE MARZO CUESTIONES
 PRIMERA CUESTIÓN 15 DE MARZO 013. CUESTIONES En una montaña rusa, como la de la figura, la vagoneta arranca sin velocidad inicial de O, desciende por la pista indicada, y tras superar el punto E se frena
PRIMERA CUESTIÓN 15 DE MARZO 013. CUESTIONES En una montaña rusa, como la de la figura, la vagoneta arranca sin velocidad inicial de O, desciende por la pista indicada, y tras superar el punto E se frena
Medición de la aceleración de la gravedad mediante plano inclinado
 Medición de la aceleración de la gravedad mediante plano inclinado Segunda parte Lopez, Johanna Giselle ([email protected]) Martinez Roldan, Antu ([email protected]) Viglezzi, Ramiro ([email protected])
Medición de la aceleración de la gravedad mediante plano inclinado Segunda parte Lopez, Johanna Giselle ([email protected]) Martinez Roldan, Antu ([email protected]) Viglezzi, Ramiro ([email protected])
MOVIMIENTO ARMÓNICO SIMPLE.
 MOVIMIENTO ARMÓNICO SIMPLE. JUNIO 1997. 1.- Un cuerpo de masa m = 10 kg describe un movimiento armónico simple de amplitud A = 30 mm y con un periodo de T = 4 s. Calcula la energía cinética máxima de dicho
MOVIMIENTO ARMÓNICO SIMPLE. JUNIO 1997. 1.- Un cuerpo de masa m = 10 kg describe un movimiento armónico simple de amplitud A = 30 mm y con un periodo de T = 4 s. Calcula la energía cinética máxima de dicho
LA ENERGÍA E. Cabe preguntarse entonces: toda fuerza actuando sobre un cuerpo realiza trabajo sobre él?
 LA ENERGÍA E l concepto de energía es uno de los más importantes del mundo de la ciencia. En nuestra vida diaria, el termino energía tiene que ver con el costo del combustible para transporte y calefacción,
LA ENERGÍA E l concepto de energía es uno de los más importantes del mundo de la ciencia. En nuestra vida diaria, el termino energía tiene que ver con el costo del combustible para transporte y calefacción,
Caída libre con velocidad límite
 Caída libre con velocidad límite Introducción Un cuerpo de densidad elevada cuando se deja caer libremente cerca de la superficie terrestre con el aire en calma y para distancias relativamente pequeñas
Caída libre con velocidad límite Introducción Un cuerpo de densidad elevada cuando se deja caer libremente cerca de la superficie terrestre con el aire en calma y para distancias relativamente pequeñas
NOTA CALI/ORDEN/PRES ORTOGRAFÍA PUNTUACIÓN EXPRESIÓN NOTA FINAL
 1. Conteste razonadamente a las siguientes preguntas: a) Puede asociarse una energía potencial a una fuerza de rozamiento? b) Qué tiene más sentido físico, la energía potencial en un punto o la variación
1. Conteste razonadamente a las siguientes preguntas: a) Puede asociarse una energía potencial a una fuerza de rozamiento? b) Qué tiene más sentido físico, la energía potencial en un punto o la variación
2 Fuerzas cotidianas. Unidad 4. Fuerzas en la naturaleza. ESO Física y Química 3 Actividades de los epígrafes. Página 114
 Actividades de los epígrafes Fuerzas cotidianas ágina 114 13. Identifica las fuerzas que actúan sobre cada cuerpo de la imagen. En la siguiente imagen se representan las fuerzas que actúan sobre cada cuerpo:
Actividades de los epígrafes Fuerzas cotidianas ágina 114 13. Identifica las fuerzas que actúan sobre cada cuerpo de la imagen. En la siguiente imagen se representan las fuerzas que actúan sobre cada cuerpo:
Examen de Física-1, 1 Ingeniería Química Examen final. Enero de 2017 Problemas (Dos puntos por problema).
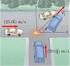
 Examen de Física-1, 1 Ingeniería Química Examen final. Enero de 017 Problemas (Dos puntos por problema). Problema 1: Un barco enemigo está en el lado este de una isla montañosa como se muestra en la figura.
Examen de Física-1, 1 Ingeniería Química Examen final. Enero de 017 Problemas (Dos puntos por problema). Problema 1: Un barco enemigo está en el lado este de una isla montañosa como se muestra en la figura.
Movimientos vibratorio y ondulatorio.-
 Movimientos vibratorio y ondulatorio.- 1. Una onda armónica, en un hilo tiene una amplitud de 0,015 m. una longitud de onda de 2,4 m. y una velocidad de 3,5 m/s. Determine: a) El período, la frecuencia
Movimientos vibratorio y ondulatorio.- 1. Una onda armónica, en un hilo tiene una amplitud de 0,015 m. una longitud de onda de 2,4 m. y una velocidad de 3,5 m/s. Determine: a) El período, la frecuencia
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE FÍSICA
 ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE FÍSICA SEGUNDA EVALUACIÓN DE FÍSICA A FEBRERO 18 DE 2015 SOLUCIÓN Analice las siguientes preguntas
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE FÍSICA SEGUNDA EVALUACIÓN DE FÍSICA A FEBRERO 18 DE 2015 SOLUCIÓN Analice las siguientes preguntas
2.004 MODELISMO, DINÁMICA Y CONTROL II Primavera Boletín de problemas 3
 2.004 MODELISMO, DINÁMICA Y CONTROL II Primavera 2003 Boletín de problemas 3 Problema 1 Las dos masas a la derecha del dibujo están ligeramente separadas e inicialmente en reposo. La masa de la izquierda
2.004 MODELISMO, DINÁMICA Y CONTROL II Primavera 2003 Boletín de problemas 3 Problema 1 Las dos masas a la derecha del dibujo están ligeramente separadas e inicialmente en reposo. La masa de la izquierda
COLISIONES EN DOS DIMENSIONES
 Objetivo COLISIONES EN DOS DIMENSIONES Estudiar las leyes de conservación del momento lineal y la energía mecánica en colisiones elásticas en dos dimensiones. Equipo Plano inclinado con canal de aluminio,
Objetivo COLISIONES EN DOS DIMENSIONES Estudiar las leyes de conservación del momento lineal y la energía mecánica en colisiones elásticas en dos dimensiones. Equipo Plano inclinado con canal de aluminio,
DINÁMICA. Son toda acción capaz de modificar el estado de movimiento del cuerpo (efecto dinámico) o producir deformaciones (efecto elástico).
 DINÁMICA La Dinámica es la parte de la Física que estudia las fuerzas. 1. FUERZAS Qué son? Son toda acción capaz de modificar el estado de movimiento del cuerpo (efecto dinámico) o producir deformaciones
DINÁMICA La Dinámica es la parte de la Física que estudia las fuerzas. 1. FUERZAS Qué son? Son toda acción capaz de modificar el estado de movimiento del cuerpo (efecto dinámico) o producir deformaciones
TERCERA EVALUACIÓN. Física del Nivel Cero A Abril 20 del 2012
 TERCERA EVALUACIÓN DE Física del Nivel Cero A Abril 20 del 2012 VERSION CERO (0) NOTA: NO ABRIR ESTA PRUEBA HASTA QUE SE LO AUTORICEN! Este examen, sobre 100 puntos, consta de 25 preguntas de opción múltiple
TERCERA EVALUACIÓN DE Física del Nivel Cero A Abril 20 del 2012 VERSION CERO (0) NOTA: NO ABRIR ESTA PRUEBA HASTA QUE SE LO AUTORICEN! Este examen, sobre 100 puntos, consta de 25 preguntas de opción múltiple
Olimpíada Argentina de Física
 Pruebas Preparatorias Primera Prueba: Cinemática - Dinámica Nombre:... D.N.I.:... Escuela:... - Antes de comenzar a resolver la prueba lea cuidadosamente TODO el enunciado de la misma. - Escriba su nombre
Pruebas Preparatorias Primera Prueba: Cinemática - Dinámica Nombre:... D.N.I.:... Escuela:... - Antes de comenzar a resolver la prueba lea cuidadosamente TODO el enunciado de la misma. - Escriba su nombre
EJERCICIOS DE SELECTIVIDAD ONDAS
 EJERCICIOS DE SELECTIVIDAD ONDAS 1. La ecuación de una onda armónica que se propaga por una cuerda es: y (x, t) = 0,08 cos (16 t - 10 x) (S.I.) a) Determine el sentido de propagación de la onda, su amplitud,
EJERCICIOS DE SELECTIVIDAD ONDAS 1. La ecuación de una onda armónica que se propaga por una cuerda es: y (x, t) = 0,08 cos (16 t - 10 x) (S.I.) a) Determine el sentido de propagación de la onda, su amplitud,
Movimiento armónico simple. Movimiento armónico simple Cuestiones
 Movimiento armónico simple Cuestiones (99-R) Una partícula describa un movimiento armónico simple de amplitud A y frecuencia f. a) Represente gráficamente la posición y la velocidad de la partícula en
Movimiento armónico simple Cuestiones (99-R) Una partícula describa un movimiento armónico simple de amplitud A y frecuencia f. a) Represente gráficamente la posición y la velocidad de la partícula en
SEGUNDA EVALUACIÓN DE FÍSICA NIVEL 0B Curso de Nivel Cero - Invierno del 2010
 ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL INSTITUTO DE CIENCIAS FÍSICAS SEGUNDA EVALUACIÓN DE FÍSICA NIVEL 0B Curso de Nivel Cero - Invierno del 2010 VERSIÓN 0 NOMBRE: Este examen consta de 25 preguntas,
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL INSTITUTO DE CIENCIAS FÍSICAS SEGUNDA EVALUACIÓN DE FÍSICA NIVEL 0B Curso de Nivel Cero - Invierno del 2010 VERSIÓN 0 NOMBRE: Este examen consta de 25 preguntas,
Actividades del final de la unidad
 Actividades del final de la unidad. Un cuerpo baja por un plano inclinado y sube, a continuación, por otro con igual inclinación, alcanzando en ambos la misma altura al deslizar sin rozamiento. Este movimiento,
Actividades del final de la unidad. Un cuerpo baja por un plano inclinado y sube, a continuación, por otro con igual inclinación, alcanzando en ambos la misma altura al deslizar sin rozamiento. Este movimiento,
Guía de Ejercicios Electroestática, ley de Coulomb y Campo Eléctrico
 NOMBRE: LEY DE COULOMB k= 9 x 10 9 N/mc² m e = 9,31 x 10-31 Kg q e = 1,6 x 10-19 C g= 10 m/s² F = 1 q 1 q 2 r 4 π ε o r 2 E= F q o 1. Dos cargas puntuales Q 1 = 4 x 10-6 [C] y Q 2 = -8 x10-6 [C], están
NOMBRE: LEY DE COULOMB k= 9 x 10 9 N/mc² m e = 9,31 x 10-31 Kg q e = 1,6 x 10-19 C g= 10 m/s² F = 1 q 1 q 2 r 4 π ε o r 2 E= F q o 1. Dos cargas puntuales Q 1 = 4 x 10-6 [C] y Q 2 = -8 x10-6 [C], están
Energía. Tiene distintas formas:
 Trabajo y energia Contenido Energía: definición, unidades Trabajo: Potencia Teorema del trabajo y la energía cinética Tipos de energía: cinética y potencial Formas de energía: térmica, nuclear, magnética,
Trabajo y energia Contenido Energía: definición, unidades Trabajo: Potencia Teorema del trabajo y la energía cinética Tipos de energía: cinética y potencial Formas de energía: térmica, nuclear, magnética,
PROBLEMAS: DINÁMICA_ENERGÍA_1 (Select)
 FÍSICA IES Los Álamos PROBLEMAS: DINÁMICA_ENERGÍA_1 (Select) 1. Explique y razone la veracidad o falsedad de las siguientes afirmaciones: a. El trabajo realizado por todas las fuerzas que actúan sobre
FÍSICA IES Los Álamos PROBLEMAS: DINÁMICA_ENERGÍA_1 (Select) 1. Explique y razone la veracidad o falsedad de las siguientes afirmaciones: a. El trabajo realizado por todas las fuerzas que actúan sobre
TEMA 12: UN MUNDO EN MOVIMIENTO
 TEMA 12: UN MUNDO EN MOVIMIENTO 1- MOVIMIENTO El movimiento de un cuerpo es el cambio de posición respecto a otros objetos que sirven como sistema de referencia. Llamamos trayectoria del movimiento de
TEMA 12: UN MUNDO EN MOVIMIENTO 1- MOVIMIENTO El movimiento de un cuerpo es el cambio de posición respecto a otros objetos que sirven como sistema de referencia. Llamamos trayectoria del movimiento de
y d dos vectores de igual módulo, dirección y sentido contrario.
 MINI ENSAYO DE FÍSICA Nº 1 1. Sean c r r y d dos vectores de igual módulo, dirección y sentido contrario. r El vector resultante c - d r tiene A) dirección y sentido igual a c r y el cuádruplo del módulo
MINI ENSAYO DE FÍSICA Nº 1 1. Sean c r r y d dos vectores de igual módulo, dirección y sentido contrario. r El vector resultante c - d r tiene A) dirección y sentido igual a c r y el cuádruplo del módulo
(99-R) Un movimiento armónico simple viene descrito por la expresión:
 Movimiento armónico simple Cuestiones (99-R) Una partícula describa un movimiento armónico simple de amplitud A y frecuencia f. a) Represente gráficamente la posición y la velocidad de la partícula en
Movimiento armónico simple Cuestiones (99-R) Una partícula describa un movimiento armónico simple de amplitud A y frecuencia f. a) Represente gráficamente la posición y la velocidad de la partícula en
GUIA Nº5: Cuerpo Rígido
 GUIA Nº5: Cuerpo Rígido Problema 1. La figura muestra una placa que para el instante representado se mueve de manera que la aceleración del punto C es de 5 cm/seg2 respecto de un sistema de referencia
GUIA Nº5: Cuerpo Rígido Problema 1. La figura muestra una placa que para el instante representado se mueve de manera que la aceleración del punto C es de 5 cm/seg2 respecto de un sistema de referencia
CINEMÁTICA: CONCEPTOS BÁSICOS
 CINEMÁTICA: CONCEPTOS BÁSICOS 1. MOVIMIENTO Y SISTEMA DE REFERENCIA. Sistema de referencia. Para decidir si algo o no está en movimiento necesitamos definir con respecto a qué, es decir, se necesita especificar
CINEMÁTICA: CONCEPTOS BÁSICOS 1. MOVIMIENTO Y SISTEMA DE REFERENCIA. Sistema de referencia. Para decidir si algo o no está en movimiento necesitamos definir con respecto a qué, es decir, se necesita especificar
XXVII Olimpiada Española de Física
 XXVII Olimpiada Española de Física FASE LOCAL-UNIVERSIDADES DE GALICIA- 26 de febrero de 2016 APELLIDOS...NOMBRE... CENTRO... Nota: En el caso de que la respuesta a alguna de las cuestiones planteadas
XXVII Olimpiada Española de Física FASE LOCAL-UNIVERSIDADES DE GALICIA- 26 de febrero de 2016 APELLIDOS...NOMBRE... CENTRO... Nota: En el caso de que la respuesta a alguna de las cuestiones planteadas
BOLETÍN EJERCICIOS TEMA 4 TRABAJO Y ENERGÍA
 Curso 2011-2012 BOLETÍN EJERCICIOS TEMA 4 TRABAJO Y ENERGÍA 1. Halla la energía potencial gravitatoria de un libro de 500 gramos que se sitúa a 80 cm de altura sobre una mesa. Calcula la energía cinética
Curso 2011-2012 BOLETÍN EJERCICIOS TEMA 4 TRABAJO Y ENERGÍA 1. Halla la energía potencial gravitatoria de un libro de 500 gramos que se sitúa a 80 cm de altura sobre una mesa. Calcula la energía cinética
MANUAL DE LABORATORIO DE FÍSICA GENERAL 9ª Edición EXPERIENCIA N 03
 MOVIMIENTO DE UN PROYECTIL EXPERIENCIA N 03 Galileo Galilei Nació en Pisa el 15 de febrero de 1564. Consiguió completar la última más importante de sus obras: los Discorsi e dimostrazioni matematiche intorno
MOVIMIENTO DE UN PROYECTIL EXPERIENCIA N 03 Galileo Galilei Nació en Pisa el 15 de febrero de 1564. Consiguió completar la última más importante de sus obras: los Discorsi e dimostrazioni matematiche intorno
Universidad Nacional del Litoral Facultad de Ingeniería y Ciencias Hídricas GUÍA DE PROBLEMAS
 UNIDAD V: CUERPO RÍGIDO GUÍA DE PROBLEMAS 1) a) Calcular los valores de los momentos de cada una de las fuerzas mostradas en la figura respecto del punto O, donde F1 = F = F3 = 110N y r1 = 110 mm, r =
UNIDAD V: CUERPO RÍGIDO GUÍA DE PROBLEMAS 1) a) Calcular los valores de los momentos de cada una de las fuerzas mostradas en la figura respecto del punto O, donde F1 = F = F3 = 110N y r1 = 110 mm, r =
PROBLEMAS INTERACCIÓN ELECTROMAGNÉTICA
 PROBLEMAS INTERACCIÓN ELECTROMAGNÉTICA 1) Dadas dos cargas eléctricas positivas, iguales, situadas a una distancia r, calcula el valor que ha de tener una carga negativa situada en el punto medio del segmento
PROBLEMAS INTERACCIÓN ELECTROMAGNÉTICA 1) Dadas dos cargas eléctricas positivas, iguales, situadas a una distancia r, calcula el valor que ha de tener una carga negativa situada en el punto medio del segmento
FÍSICA 2º Bachillerato Ejercicios: Interacción gravitatoria
 1(9) Ejercicio 1 Un bloque de 50 Kg de masa asciende una distancia de 6 m por un plano inclinado 37 º y que presenta un coeficiente de rozamiento de 0 2, aplicándole una fuerza constante de 490 N paralela
1(9) Ejercicio 1 Un bloque de 50 Kg de masa asciende una distancia de 6 m por un plano inclinado 37 º y que presenta un coeficiente de rozamiento de 0 2, aplicándole una fuerza constante de 490 N paralela
Examen de Física-1, 1 Ingeniería Química Examen final. Enero de 2015 Problemas (Dos puntos por problema).
 Examen de Física-, Ingeniería Química Examen final. Enero de 205 Problemas (Dos puntos por problema). Problema : La posición de una partícula móvil en el plano Oxy viene dada por : x(t) = 2 t 2 y(t) =
Examen de Física-, Ingeniería Química Examen final. Enero de 205 Problemas (Dos puntos por problema). Problema : La posición de una partícula móvil en el plano Oxy viene dada por : x(t) = 2 t 2 y(t) =
W F e m g h 500 9,8 t t t 50 Potencia practica 2450 Rendimiento= 100 = 100 = 82% Potencia teorica 3000
 TEMA TRABAJO, POTENIA Y ENERGÍA. Un cuerpo de 5 kg se deja caer desde una altura de 0 metros. alcula el trabajo realizado por el peso del cuerpo. W=F e = P h=m g h=5 9,8 0=470 J. Sobre un cuerpo de 0 kg
TEMA TRABAJO, POTENIA Y ENERGÍA. Un cuerpo de 5 kg se deja caer desde una altura de 0 metros. alcula el trabajo realizado por el peso del cuerpo. W=F e = P h=m g h=5 9,8 0=470 J. Sobre un cuerpo de 0 kg
Districte universitari de Catalunya
 SERIE 3 PAU. Curso 2003-2004 FÍSICA Districte universitari de Catalunya Resuelva el problema P1 y responda a las cuestiones C1 y C2. Escoja una de las opciones (A o B) y resuelva el problema P2 y responda
SERIE 3 PAU. Curso 2003-2004 FÍSICA Districte universitari de Catalunya Resuelva el problema P1 y responda a las cuestiones C1 y C2. Escoja una de las opciones (A o B) y resuelva el problema P2 y responda
Movimiento en línea recta (mov. En una dimensión)
 Movimiento en línea recta (mov. En una dimensión) CINEMÁTICA CINEMÁTICA Es el estudio del movimiento de los objetos Clasificación del movimiento: Movimiento traslacional Movimiento rotacional Movimiento
Movimiento en línea recta (mov. En una dimensión) CINEMÁTICA CINEMÁTICA Es el estudio del movimiento de los objetos Clasificación del movimiento: Movimiento traslacional Movimiento rotacional Movimiento
Tema 5. Análisis dinámico con dos grados de libertad.
 Tema 5. Análisis dinámico con dos grados de libertad. Objetivo Obtener las dos componentes de la posición, velocidad y aceleración de un punto. Representar gráficamente esas magnitudes de diferentes maneras.
Tema 5. Análisis dinámico con dos grados de libertad. Objetivo Obtener las dos componentes de la posición, velocidad y aceleración de un punto. Representar gráficamente esas magnitudes de diferentes maneras.
