Apuntes de Inteligencia Artificial
|
|
|
- Esteban Santos Maldonado
- hace 8 años
- Vistas:
Transcripción
1 PONTIFICIA UNIVERSIDAD CATÓLICA DEL ECUADOR FACULTAD DE INGENIERÍA Apuntes de Inteligencia Artificial Laboratorio: Redes con Conexiones hacia adelante JORGE AGUILAR JARAMILLO 83 Jorge Aguilar J.
2 LABORATORIO: REDES CON CONEXIONES HACIA ADELANTE OBJETIVOS Poner en práctica los conocimientos adquiridos sobre el perceptrón multicapa Aprender cómo usar los algoritmos de retro propagación para entrenar redes con conexiones hacia adelante. Conocer que funciones implementa Matlab, para este objetivo y usarlas Conocer los fundamentos para crear conjuntos de entrenamiento que permitan entrenar bien las redes. Entrenar la red para que simule una respuesta hacia nuevas entradas. MARCO TEÓRICO REDES CON RETRO PROPAGACIÓN El algoritmo de retro propagación es una generalización de la regla de aprendizaje Widrow Hoff. Esta adaptación es para redes multicapa y funciones de transferencia diferenciables no lineales. La retro propagación estándar es un algoritmo de gradiente descendiente, que como en la regla de aprendizaje de Widrow Hoff los pesos de la red son modificados a lo largo del negativo de la función gradiente de desempeño. El término de retro propagación se refiere a la forma en la que el gradiente se calcula para redes multicapa no lineales. Existe un número de variaciones en el algoritmo básico que se basan en otras técnicas estándar de optimización, tales como la gradiente conjugada y los métodos de Newton. El Neural Network de Matlab implementa algunas de estas variaciones. Las redes con retro propagación bien entrenadas tienden a brindar soluciones razonables al recibir entradas totalmente desconocidas Este tipo de redes, con bias, una capa sigmuidal y una capa de salida lineal son susceptibles de aproximar cualquier función en un número finito de discontinuidades. Jorge Aguilar J. Laboratorio: Redes con Conexiones hacia adelante 84
3 ARQUITECTURA DE LA RED CON RETROPROPAGACIÓN La arquitectura de red neuronal más utilizada para el algoritmo de retro propagación es la red multicapa con conexiones hacia delante El modelo de una neurona es como se muestra en el siguiente grafico. Ilustración 1 Neurona elemental con R entradas. (Fuente, Matlab) Cada entrada está representada por un valor apropiado, que Matlab lo simboliza con p. La suma ponderada,, de los pesos y el bias (umbral) con los datos de entrada forma la entrada a la función de transferencia f. Las neuronas deben usar cualquier función diferenciable para generar sus salidas. Función Sigmuidal genera salidas entre 0 y 1 Función Tangencial: Salidas entre 1 y 1 Función Lineal, la salida puede ser cualquier valor Ilustración 2. Funciones de tranferencia (Matlab) Las funciones más usadas por este tipo de redes son: la función sigmuidal logsig, tangencial (tansig) y lineal (purelin). Jorge Aguilar J. Laboratorio: Redes con Conexiones hacia adelante 85
4 Si la última capa de una red multicapa tiene neuronas sigmuidales, entonces la red se limita a un rango pequeño entre 0 y 1. Si se utilizan neuronas lineales en la capa de salida, teóricamente los resultados pueden tomar cualquier valor. En retro propagación es importante calcular las derivadas de las funciones de transferencia utilizadas. Cada una de las funciones de transferencia mencionadas contiene una derivada correspondiente: Matlab las implementa como: dtansig, dlogsig, y dpurelin. Para obtener el nombre de la derivada de una función de transferencia se debe invocar a la función de transferencia con la cadena: Código 1.- Comando para obtener la derivada de una función de transferencia REDES CON CONEXIÓN HACIA ADELANTE Las redes Conexión hacia adelante tienen frecuentemente una o más capas ocultas de neuronas sigmuidales seguidas de una capa de salida de neuronas lineales. Muchas capas de neuronas con funciones de transferencia no lineales permiten a la red aprender relaciones lineales y no lineales entre vectores de entrada y salidas. La capa lineal de salida permite a la red producir valores fuera del rango de 1 a +1. Por otra parte, si se necesita limitar las salidas de la red a un valor específico, entonces la capa de salida debe usar una función sigmuidal de transferencia (como logsig.) Este tipo de redes nos permitirá tener un rango especial de respuestas. Ilustración 3 Red con funciones: tansig y purelin Esta red puede ser utilizada como un aproximador general de funciones. Ya que puede aproximar cualquier función que tenga un número finito de discontinuidades, teniendo el suficiente número de neuronas en la capa oculta. Para entrenar una red, generalmente se tienen 4 pasos en el proceso de entrenamiento 1. Configurar los datos de entrenamiento Jorge Aguilar J. Laboratorio: Redes con Conexiones hacia adelante 86
5 2. Crear el objeto red: función newff 3. Entrenar la red : función train 4. Simular la respuesta de la red para nuevas entradas: función sim CONFIGURAR LOS DATOS DE ENTRENAMIENTO En un proyecto de redes neuronales, el llegar al conjunto final de datos, puede consumir el 60% de todo el proyecto. Pero una vez obtenidos los datos, en Matlab, estos deben definirse como en dos variables: una para los datos de entrada y la segunda variable en la que consten los respectivos valores de salida. CREANDO UNA RED CON CONEXIÓN HACIA ADELANTE (NEWFF) Una vez que se tiene los datos de entrada y salida deseada, para entrenar una red con conexión hacia adelante necesitamos crear el objeto red. La función newff crea una red con conexión hacia adelante y requiere de cuatro argumentos de entradas y devuelve el objeto de red. 1. El primer argumento es una matriz de los mínimos y máximos b 1 de las Ni entradas (Nix2 valores, para cada uno de los N elementos del vector de entrada). 2. El segundo argumento es un arreglo que contiene los tamaños de cada capa. 3. El tercer argumento es un arreglo que contiene los nombres de las funciones de transferencia que se usarán en cada capa. 4. El último argumento contiene el nombre del algoritmo de entrenamiento a ser usado. Veamos un ejemplo: Código 2.- creación de una red neuronal en Matlab Asignamos al objeto net, la estructura de la red: Una red de dos capas 2, dos vectores. Los valores para el primer elemento del vector de entrada están en el rango de 1 hasta 2, los valores del segundo elemento del vector están entre 0 y 5. Existen tres neuronas en la primera capa (capa oculta) y una neurona en la segunda capa (de salida). 1 Matlab implementa la función mm=minmax(x) que obtiene estos valores, X representa los datos de entrada 2 Ya que las neuronas de entrada solamente reciben los datos, Matlab, no la trata como una capa de neuronas Jorge Aguilar J. Laboratorio: Redes con Conexiones hacia adelante 87
6 La función de transferencia en la primera capa es tansig y la función de transferencia en la capa de salida es lineal y el algoritmo de de entrenamiento es traingd. Este comando crea el objeto red y además inicializa los pesos y los bias de la red, entonces la red se encuentra lista para entrenar. Reinicializando los pesos Aunque la función anterior ya inicializa los pesos y bias, si se requiere una re inicialización de los mismos puede hacérselo con el comando init. Esta función toma un objeto red como entrada y devuelve un objeto red con todos los pesos y los bias re inicializados. Aquí vemos como una red puede ser inicializada (o re inicializada): ENTRENAMIENTO Una vez que los pesos y los bias han sido inicializados, la red está lista para ser entrenada. La red puede ser entrenada para aproximación de funciones (regresión no lineal), asociación de patrones o clasificación de patrones. El proceso de entrenamiento requiere un conjunto de ejemplos que tenga un comportamiento apropiado para la red entradas p (ó X) y salidas t (ó Yd). Durante el entrenamiento los pesos y los bias de la red son ajustados iterativamente para minimizar la función de costo o error de la red net.performfcn. La función de desempeño predeterminada para redes con conexiónes hacia adelante es el error medio cuadrático mse, el promedio del error al cuadrado entre las salidas de la red a y los objetivos t. Todos los algoritmos de entrenamiento usan la función del gradiente de desempeño para determinar cómo ajustar los pesos, la gradiente es determina usando una técnica llamada retro propagación, que involucra la realización de hacer cálculos hacia atrás de la red. Los cálculos de retro propagación se derivan usando la regla de la cadena. ALGORITMO DE RETROPROPAGACIÓN Hay muchas variaciones del algoritmo de retro propagación, la implementación más simple de aprendizaje por retro propagación actualiza los pesos y los bias de la red en la dirección en la que la función de desempeño decrezca más rápido el negativo de la gradiente. Una iteración del algoritmo puede escribirse de la siguiente manera: Jorge Aguilar J. Laboratorio: Redes con Conexiones hacia adelante 88
7 Ecuación 1..- Una Iteración del Algoritmo de Retropropagación Donde W W ij es un vector de pesos y bias concurrentes. es la tasaa de aprendizaje. es el gradiente actual y u Existen dos formas diferentes de implementar el algoritmo de gradiente descendente; el modo incremental y por lotes. En el modo incremental, el gradiente es calculado y los pesos son actualizados después de que cadaa ejemplo se aplica a la red. En el modo por lotes todos los ejemplos (una época) son aplicadas a la red antes de que se actualicen los pesos. ENTRENAMIENTO POR LOTES Aquí los pesos y los bias de la red se actualizarán únicamente después de que todo el conjunto de entrenamiento ha sido aplicado a la red. Los gradientes calculados en cada ejemplo de entrenamiento son sumados para determinar el cambio en los pesos y los bias. Gradiente descendente: En el entrenamiento por lotes la función de gradiente descendente más empinada es traingd. Los pesos y los bias son actualizados en dirección del negativo del gradiente de la función de desempeño. Si se requiere entrenar una red usando esta función se debee cambiar la red de trainfcn a traingd, entonces llamar a la función train. Existe solo una función de entrenamiento asociada a una red en particular. Existen siete parámetros de entrenamiento asociados a traingd : epochs, show, goal, time, min grad, max_fail, y lr. La tasa de aprendizaje lr se multiplica cada vez con el negativo de la gradiente para determinar los cambios a realizarse a los pesos y a los bias. Mientras más grande sea la tasa de aprendizaje más grande es el salto. Si la tasa de aprendizaje es muy grande el algoritmo se vuelve inestablee y si la tasa de aprendizaje es muy pequeña, el algoritmo se demorará en converger. El estado de aprendizaje se mostrará en cada iteración del algoritmo. Los demás parámetros determinarán cuando se detendrá el entrenamiento. El entrenamiento finalizará si el número de iteraciones excede al parámetro epochs, si la función de desempeño encuentra su meta, si la magnitud de la gradiente es menor a min_grad, o si el tiempo de entrenamiento es mayor que time segundos. El siguiente código crea un conjunto de entradas p y objetivos t. Para entrenamiento por lotes todos los vectores de entradaa serán colocados en una matriz. Jorge Aguilar J. Laboratorio: Redes con Conexiones hacia adelante 89
8 Código 3.- Valores iniciales de entrenamiento por lotes para una red de retropropagación Luego crearemos la red con conexión hacia adelante. Aquí usaremos la función minmax para determinar el rango de las entradas a usarse en la creación de la red. Código 4.- Creación de la red con conexión hacia adelante En este punto, podremos modificar algunos de los valores predeterminados de entrenamientos Código 5.- Modificación de los valores iniciales predeterminados Si no se requiere cambiar los valores predeterminados de entrenamiento los comandos anteriores no serán necesarios. Estamos listos para entrenar la red. Código Entrenamiento de la red Jorge Aguilar J. Laboratorio: Redes con Conexiones hacia adelante 90
9 El registro de entrenamiento tr contiene la información acerca del progreso del entrenamiento. Ahora la red entrenada puede ser simulada para obtener su respuesta a las entradas del conjunto de entrenamiento. Código 7.- Despliegue de las salidas de la red luego del entrenamiento GRADIENTE DESCENDIENTE CON MOMENTO: Adicional a traingd, existe otro algoritmo por lotes para redes con conexión hacia adelante que frecuentemente provee mayor convergencia: traingdm. El momento permite a la red responder no solo al gradiente local sino también a las tendencias más recientes en la superficie de error. Actuando como un filtro pasa bajos el momento permite a la red ignorar las pequeñas imperfecciones de la superficie de error. Sin un momento la red puede atascarse en un mínimo local impidiendo su labor. El momento puede añadirse al aprendizaje con retro propagación realizando cambios en los pesos iguales a la suma de la fracción del último cambio de pesos y el nuevo cambio sugerido por la regla de retro propagación. La magnitud del efecto que último cambio de pesos permite tener es mediada por una constante de momento, mc, que puede ser cualquier número entre 0 y 1. Cuando la constante de momento es 0, el cambio de pesos es basado únicamente en la gradiente. Cuando la constante de momento es 0, el nuevo cambio de pesos se iguala al último cambio de pesos y el gradiente se ignora simplemente. La gradiente es calculada sumando los gradientes calculados en cada ejemplo de entrenamiento y los pesos y los bias son actualizados únicamente cuando todos los ejemplos de entrenamiento han sido presentados. Si la nueva función de entrenamiento en alguna iteración excede la función de desempeño en una previa iteración con un valor mayor a un valor predefinido max_perf_inc (comúnmente 1.04), los nuevos pesos y bias son descartados y el coeficiente de momento se vuelve cero. Esta función se llama con el comando traingdm, y contiene los mismos argumentos usados para traingd excepto que los parámetros de aprendizaje mc (coeficiente de momento), lr (tasa de aprendizaje) y max_perf_inc (máximo incremento del desempeño) pueden ser personalizados. En el siguiente código se recrea la red anterior y se la entrena con la función de gradiente descendente con momento. (Los parámetros de entrenamiento son reiniciados a los valores predeterminados cada vez que net.trainfcn se cambia a traingdm.) Jorge Aguilar J. Laboratorio: Redes con Conexiones hacia adelante 91
10 Código Inicialización de la red Con conexión hacia adelante Código 9.- Entrenamiento de la red Notemos que desde que se reinicializaron los pesos y los bias antes del entrenamiento (llamando a newff nuevamente), obtenemos diferente error medio cuadrático de lo que obtuvimos usando traingd. Si reiniciaríamos nuevamente la red con traingdm podríamos obtener incluso un error medio cuadrático distinto. La opción al azar de pesos y bias iniciales afectara el desempeño del algoritmo. Si se desea comparar el desempeño de diferentes algoritmos se debe probar cada vez usando diferentes conjuntos de pesos y bias iniciales y establecer una media de las diferentes corridas hechas 3. En resumen, la arquitectura de una red multicapa no está completamente limitada al problema a ser resuelto. El número de capas entre las entradas a la red y la capa de salida así como el tamaño 3 Una muestra estadísticamente significativa es de mínimo 30 corridas Jorge Aguilar J. Laboratorio: Redes con Conexiones hacia adelante 92
11 de las capas son cuestión del diseñador. La red de dos capas sigmuidal / lineal puede representar cualquier relación funcional entre las entradas y las salidas si la capa sigmuidal tiene la cantidad suficiente de neuronas. ALGORITMOS IMPLEMENTADOS POR MATLAB: De los algoritmos revisados en teoría, solamente los cuatro primeros tienen que ver con ella. El resto de algoritmos que implementa Matlab se los implementa en forma diferente. Función traingd traingdm traingdx trainrp traincgf traincgp traincgb Descripción Gradiente descendente básico, puede usarse en entrenamiento de modo incremental Gradiente descendente con momentun. Generalmente más rápido que traingd. Puede usarse en entrenamiento de modo incremental. Tasa de aprendizaje adaptativa. Entrenamiento más rápido que traingd, pero solo puede ser usado en modo de entrenamiento batch (por lotes). Backpropagation flexible. Simple algoritmo de entrenamiento en modo batch, con rápida convergencia y mínimos requerimientos de almacenamiento. Algoritmo de gradiente conjugado Fletcher Reeves. Tiene los Requerimientos de almacenamiento menores de los algoritmos de gradiente conjugado. Algoritmo de gradiente conjugado Polak Ribiére. Requerimientois de almacenamiento ligeramente mayores que traincgf. CXonvergencia más rápida sobre algunos problemas. Algoritmo de gradiente conjugado, Powell Beale. Requerimientois de almacenamiento ligeramente mayores que traincgp. Generalmente convergencia más rápida. trainscg Algoritmo de gradiente conjugado escalado (Scaled conjugate gradient). Solo el algoritmo de gradiente conjugado que no requiere búsqueda lineal. Un algoritmo de entrenamiento de propósito general, muy bueno. trainbfg trainoss trainlm BFGS método quasi Newton. Requiere almacenamiento de la Hessian matrix aproximada y tiene más cálculo en cada iteración, pero usualmente converge en pocas iteraciones Método One step secant. Compromiso entre los métodos gradiente conjugado métodos quasi Newton. Algoritmo Levenberg Marquardt. El algoritmo de entrenamiento más rápido para redes de tamaño moderado. Tiene características de reducción de memoria para conjuntos de entrenamiento grandes. Jorge Aguilar J. Laboratorio: Redes con Conexiones hacia adelante 93
12 trainbr trainlm Regularización Bayesiana. Modificación del algoritmo de entrenamiento Levenberg Levenberg Marquardt para producir redes que generalizan bien. Reduce la dificultad de determinar la arquitectura óptima de la red. Tabla 1.- Algoritmos que implementa Matlab para un PMC La tabla 1, presenta una lista que resume las funciones para entrenamiento de redes con retro propagación que contiene el Neural Network Toolbox de Matlab: SOBRE ENTRENAMIENTO Un problema que puede ocurrir al entrenar redes neuronales es que la red puede sobredimensionar el conjunto de entrenamiento y no realizar bien la generalización para datos diferentes al conjunto de entrenamiento. Esto puede prevenirse realizando un entrenamiento con trainbr, además puede prevenirse usando una detención temprana con cualquier otra rutina de entrenamiento, esto requiere que el usuario pase un conjunto de validaciones al algoritmo de entrenamiento adicional al conjunto de entrenamiento. Para producir un mejor entrenamiento es muy útil analizar si la respuesta de la red después del entrenamiento está completa. Matriz de confusión. En el campo de Inteligencia Artificial se usa la matriz de confusión en el aprendizaje supervisado. En la que las columnas representan las instancias predichas (la salida del sistema, Y) y las filas las instancias reales (los yd). De esta forma es muy fácil saber que clase está confundiendo el sistema. Para aclarar este concepto, revise el ejercicio 1 y los resultados de la tabla 2 y 3 REVISIÓN DE ALGUNOS DEMOS DE MATLAB: Realizar los siguientes demos y contestar las preguntas planteadas. GENERALIZACIÓN EN REDES CON RETROPROPAGACIÓN Existe el problema que al tener muchas neuronas ocultas, la red pierde la capacidad de generalizar y se presta a errores, la demostración nnd11gn, ilustra este hecho. Para probar esta demostración basta con modificar el número de neuronas ocultas y el grado de dificultad de manera que se visualice que la red tiende a aprender en forma exacta los datos de entrenamiento, pero pierde la capacidad de generalizar, como se ilustra en la figura a continuación Jorge Aguilar J. Laboratorio: Redes con Conexiones hacia adelante 94
13 Resultado para una red con 3 neuronas ocultas Resultado para una red con 9 neuronas ocultas Ilustración 4. Al aumentar en número de neuronas la red aprende muy bien los datos con los que aprendió, pero pierde la capacidad de generalización, es decir comete errores con datos nuevos Pregunta: Qué ocurre cuando se aumenta la complejidad del problema, como lo explica? FUNCIÓN DE GRADIENTE DESCENDIENTE (MÁS EMPINADA) RETRO PROPAGACIÓN Ilustración 5. Gradiente Descendiente W1(1,1) W2(1,1) Esquina Inferior Derecha Jorge Aguilar J. Laboratorio: Redes con Conexiones hacia adelante 95
14 Esta aplicación muestra tres superficies de error, aquí se puede observar como el algoritmo alcanza el primer mínimo que encuentra. Probar cada región. Preguntas: Identifique la arquitectura de la red de la ilustración 7? Pruebe en las regiones sin líneas, si la respuesta no se desplaza: que significa esto y cómo se explica? Qué significa la superficie, qué representa? FUNCIÓN DE GRADIENTE DESCENDIENTE CON MOMENTO RETROPROPAGACIÓN Este algoritmo, es el mismo anterior, solamente que se añade el término de momento. Ilustración 6. Gradiente Descendiente con Momento Preguntas: 1. En qué lugares se acelera la convergencia con el término momento y en cuáles no ocurre lo mismo? Cómo lo explica? 2. Por lo general, se aconseja utilizar un valor de la tasa de aprendizaje (u) menor a 1, como explica el uso de valores más altos? Jorge Aguilar J. Laboratorio: Redes con Conexiones hacia adelante 96
15 3. Cómo influye la tasa de aprendizaje en el desempeño de una red con Función de Gradiente Descendiente con Momento? TAREA DE LABORATORIO: PERCEPTRON MULTICAPA Y CLASIFICACIÓN DE PATRONES UN PEQUEÑO PROBLEMA. 1. Genere un conjunto que representen dos clases con aproximadamente el mismo número de datos para cada clase. La primera clase que sean los datos que se posicionen dentro de un círculo y las fuera del circulo la clase 2. a) Veamos el código en Matlab para generar los datos. cont1=0; % definimos dos contadores para la primera y segunda clase cont2=0; xc=2.5/2; % definimos un radio de 2.5 para que el número de datos sea aproximadamente el mismo para cada clase. hold on; X= rand(2,500)*2.5; % generación aleatoria de números (x1 y x2) entre 0 y 2.5 for i = 1:500 % Verificamos si caen dentro del circulo y le asignamos la clase 0 (o -1) if (sqrt((x(1,i)-xc)^2 + (X(2,i)-xc)^2 )) > 1; cont1=cont1+1; Yd(i) = 0; plot(x(1,i),x(2,i),'bo'); elseif (sqrt((x(1,i)-xc)^2 + (X(2,i)-xc)^2 )) <1; % Si no es así le asignamos como clase 1 cont2=cont2+1; Yd(i) = 1; plot(x(1,i),x(2,i),'r*'); end end Veamos los resultados Para esta corrida, el número de datos de la clase 1 es 248 y el de la segunda es 252 Jorge Aguilar J. Laboratorio: Redes con Conexiones hacia adelante 97
16 Ilustración 7 Datos generados que representan la clase 1 (rojo) y la clase 1 (azul). a) Una vez que tenemos los datos tanto de entrada (variable X) y de salida (variable Yd), separemos el 50% para datos de entrenamiento, 25% para validación y 25% para prueba y entrenemos la red. Q=500; % En primer lugar definimos los índices para las 3 tipos de datos iprueba = 2:4:Q; ivalida = 4:4:Q; ientren = [1:4:Q 3:4:Q]; % Con estos índices separamos los datos respectivos val.p = X(:,ivalida); val.t = Yd(:,ivalida); pru.p = X(:,iprueba); pru.t = Yd(:,iprueba); entx = X(:,ientren); entyd = Yd(:,ientren); red = newff(minmax(entx),[5 1],{'tansig' 'logsig'},'traingd'); % En este punto podemos redefinir los parámetros de la red % Dejemos los parámetros sin modificar y Entrenamos la red. [red,tr]=train(red,entx,entyd,[],[],val,pru); Los parámetros definidos por defecto no son los mejores para este algoritmo, por lo que la respuesta de la red es muy mala. Luego de entrenar la red, se obtiene el grafico de la figura Jorge Aguilar J. Laboratorio: Redes con Conexiones hacia adelante 98
17 10 0 Performance is , Goal is 0 Training-Blue Validation-Green Test-Red Epochs Ilustración 8. Como puede observarse los datos de entrenamiento normalmente generan un error menor, pero en este caso hemos modificado el número de épocas. b) Finalmente simulemos la red para observar que tan bien está generalizando para los datos de entrenamiento y validación y prueba. Yt=sim(red,entX); Yv=sim(red,val.X); c) Grafique los datos para cada conjunto y verifique si clasifica bien Como se observa en el grafico, la clasificación es muy pobre d) Cuál es el número de datos clasificados correctamente y fallidos para cada conjunto. Clase 1 Clase 2 Clase Clase Tabla 2.- La matriz muestra que la red clasifica bien como clase 1 solo 42 datos y falla en 78, mientas que 106 como clase 2 y falla en 24 Jorge Aguilar J. Laboratorio: Redes con Conexiones hacia adelante 99
18 Aumente el número de épocas a y pruebe nuevamente los resultados y entrene nuevamente la red y verifique las respuestas de la misma. Los resultados son mejores pero aún se pueden mejorar. En este punto hay que trabajar con diferentes hacer pruebas con los diferentes parámetros de la red Otra opción es cambiar de algoritmo. Uno de los mejores algoritmos para estas redes es el Levenberg Marquardt. Si entrenamos con este algoritmo, la red prácticamente clasifica el 100% de los datos de manera correcta tanto de los datos de entrenamiento como los de validación. No es necesario realizar cambios a los parámetros definidos por defecto. red = newff(minmax(entx),[5 1],{'tansig' 'logsig'},'trainlm'); Entrenado y simulando la red se tienen los siguientes resultados Entrenamiento Clase 1 Clase 2 Clase Clase Validación Clase 1 Clase 2 Clase Clase Tabla 3.- matriz de confusión tanto para los datos de entrenamiento y los datos de validación. Como se observa la red clasifica muy bien todos los datos a excepción de uno de la clase 2 que lo clasifica como clase 1. TRABAJO A REALIZAR 2. Qué cambia si en vez de dos clases se tiene 3 clases. Genere un problema de 3 clases e intente resolverlo. a. NOTA. Tenga en cuenta la codificación b. Reporte resultados, para entrenamiento y validación. 3. Descarge el archivo de datos lab2train1, y el archivo de prueba lab2test1 del servidor. Cada ejemplo contiene un vector de 4 datos (una fila en el archivo). Los dos primeros elementos de cada vector da las coordenadas del dato y el tercer elemento es el valor objetivo (0 or 1). Use los datos de entrenamiento para entrenar una red PMC. Entonces pruebe la red entrenada con los datos de prueba. Usted debe usar el algoritmo desarrollado en clase. Para cada experimento descrito luego debe repetir el mismo experimento 10 veces y reportar la media y desviacion estándar del resultado. Los sigueintes parámetros serán usados, a menos que se diga lo contrario. Jorge Aguilar J. Laboratorio: Redes con Conexiones hacia adelante 100
19 Maximo número de épocas usadas para el entrenamiento = 1000, net.trainparam.epochs=1000 Datos de entrada serán escalados a [ 5, 5], y las muestras de salida a [ ]. La tasa de aprendizaje por defecto μ = 0.1 (net.trainparam.lr) y momento = 0.8. net.trainparam.mc Las neuronas ocultas usan funciones de activación tangente hyperbolica y las de salida función de activación sigmuidal. La configuración del PMC será (dos neuronas de entrada, 2 ocultas y 2 de salida). Consideremos el primer caso: Tabule el valor medio y la desviación estándar del conjunto de prueba para una tasa de aprendizaje de μ = 0.01, 0.1, 0.2, 0.4, 0.8. Para cada valor de μ use dos valores diferentes de momento: β = 0 y 0.8. Recuerde que para cada combinación de u y β se debe realizar 10 ensayos. Discuta los resultados brevemente. El siguiente programa en Matlab nos permite realizar esta tarea: En este código no está considerado el hecho de escalar los datos de entrada ni de salida. date=load('lab2train1.txt'); datp=load('lab2test1.txt'); xe=date(:,1:2); yde=date(:,3:4); xp=datp(:,1:2); ydp=datp(:,3:4); for k=1:2 if k==1 beta=0; else beta=0.8; end for j=1:5 for i=1:10 if j==1 net = newff(minmax(xe'),[2 2],{'tansig' 'logsig'},'traingdm'); net.trainparam.epochs=1000; net.trainparam.lr=0.01; net.trainparam.mc=beta; net=train(net,xe',ydp'); y=sim(net,xp'); [C, R] = CONFMAT(y', ydp); rate(i,j+5*(k-1))=r(1); else net = newff(minmax(xe'),[2 2],{'tansig' 'logsig'},'traingdm'); net.trainparam.epochs=1000; net.trainparam.lr=0.1*(j-1); net.trainparam.mc=beta; net=train(net,xe',ydp'); y=sim(net,xp'); Jorge Aguilar J. Laboratorio: Redes con Conexiones hacia adelante 101
20 end end end end [C, R] = CONFMAT(y', ydp); rate(i,j+5*(k-1))=r(1); m=mean(rate); ds=std(rate); x=[0.01, 0.1, 0.2, 0.4, 0.8]; subplot(2,1,1) plot(x,m(1:5),x(1:5),m(1:5)+ds(1:5),'m',x(1:5),m(1:5)- ds(1:5),'m'); title('perceptrón Multicapa'); xlabel('u'); ylabel('tasa de aciertos'); subplot(2,1,2) plot(x,m(6:10),x,m(6:10)+ds(6:10),'m',x,m(6:10)-ds(6:10),'m'); xlabel('u'); ylabel('tasa de aciertos'); 100 Perceptrón Multicapa: caso a) beta= Perceptrón Multicapa: caso b) beta= taza de aprendizaje: u Ilustración 9. resultados de promediar 10 corridas para los cinco valores de u con los dos valores de beta. Jorge Aguilar J. Laboratorio: Redes con Conexiones hacia adelante 102
21 a) Tabule el valor medio y la desviación estándar de la tasa de clasificación del conjunto de prueba cuando se tiene un PMC 2-h-2 donde el número de neuronas ocultas h = 2, 5, 20. Discuta los resultados brevemente. b) Tabule el valor medio y la desviación estándar de la tasa de clasificación para el conjunto de prueba cuando la configuración del PMC contiene más de una capa oculta. Realice experimentos específicamente para las siguientes: 2-3-2, , Discuta los resultados brevemente. c) Basado en los resultados experimentales llevados en (a) - (c), determine cuál será la mejor selección de μ y β y la configuración del PMC que de resultados satisfactorios. Brevemente justifique su selección d) Para la red seleccionada en la parte (d), ilustre la región de decisión de cada clase en el espacio de entrada 2D x 1 -x 2. Un camino es evaluar la salida del PMC sobre una malla de puntos dentro de una región cuadrada con fronteras ( 10, 10) y (10, 10). En Matlab, la función meshgrid será útil para generar el grafico NOTA. Para la tasa de clasificación puede usar la matriz de confusión codificada en el archivo confmat.m (Ian T Nabney, 2001), descargue el archivo del directorio de laboratorio : [C, Tasa] = confmat(y, Yd) Donde Y es la salida calculada por la red y Yd la salida conocida. C es la matriz de confusión y Tasa es un vector con dos números: El porcentaje de datos correctamente clasificados y el número de datos. 4. Entrene al PMC usando validación en tres formas Descarge los archivos vino1.txt, vino2.txt, y vino3.txt del servidor. Estas son 3 particiones de los datos para el propósito de reconocimiento de vino. El espacio de entrada o de características es de dimensión 13, y hay 3 clases. El objetivo de este problema es encontrar la configuración óptima de un PMC con una capa oculta, usando la validación de tres formas. La función de activación para la capa de salida será sigmoidal y para la capa oculta será tangente hyperbolica (tangencial). Para cada valor de h, lleve los siguientes pasos de entrenamientos y prueba: Entrene con vino1, vino2, y pruebe la red entrenada usando vino3. Entrene con vino2, vino3, y pruebe la red entrenada usando vino1. Entrene con vino3, vino1, y pruebe la red entrenada usando vino2. Revise el ejemplo que viene en Matlab en la sección Sample Training Session del capítulo de Backpropagation. Aquí se hace un pre-análisis de los datos. Jorge Aguilar J. Laboratorio: Redes con Conexiones hacia adelante 103
22 Los resultados de prueba serán promediados anadiendo la correspondiente matriz de confusión y calcule la tasa de clasificación de la matriz de confusión combinada. Nuestro objetivo es seleccionar el valor de h, 1 h 10 que rinda la clasificación más alta y calcule de acuerdo al siguiente método. (a) (1.0 puntos) Discuta los pasos que realizó para llevar el análisis de los datos y preprocesamiento antes de aplicarlos al algoritmo de entrenamiento del PMC. (b) (1.0 puntos, CC) Suministre una tabla que liste el valor de h, versus la correspondiente clasificación. Discuta brevemente la ventaja potencial y desventaja de esta aproximación Jorge Aguilar J. Laboratorio: Redes con Conexiones hacia adelante 104
ANEXO A DESCRIPCIÓN DE LAS FUNCIONES UTILIZADAS EN MATLAB
 333 ANEXO A DESCRIPCIÓN DE LAS FUNCIONES UTILIZADAS EN MATLAB 1. Red tipo Perceptrón: Las siguientes son las herramientas de redes neuronales del Matlab 5.3: utilizadas en el entrenamiento de las redes
333 ANEXO A DESCRIPCIÓN DE LAS FUNCIONES UTILIZADAS EN MATLAB 1. Red tipo Perceptrón: Las siguientes son las herramientas de redes neuronales del Matlab 5.3: utilizadas en el entrenamiento de las redes
El Perceptrón Multicapa
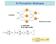 El Perceptrón Multicapa N entradas M neuronas de salida L: neuronas en la capa oculta E = 1 p M ( zi ( k) yi ( k) ) k = 1 i= 1 Implementación de la función XOR Regiones de clasificación en función del
El Perceptrón Multicapa N entradas M neuronas de salida L: neuronas en la capa oculta E = 1 p M ( zi ( k) yi ( k) ) k = 1 i= 1 Implementación de la función XOR Regiones de clasificación en función del
Neural Network Toolbox
 Neural Network Toolbox Sistemas Conexionistas - Curso 07/08 La Neural Network Toolbox es un paquete de Matlab que contiene una serie de funciones para crear y trabajar con redes de neuronas artificiales.
Neural Network Toolbox Sistemas Conexionistas - Curso 07/08 La Neural Network Toolbox es un paquete de Matlab que contiene una serie de funciones para crear y trabajar con redes de neuronas artificiales.
3. MATLAB TOOLBOX. 1. Configurar los datos de entrenamiento 2. Crear la red 3. Entrenar la red 4. Simular la respuesta de la red con nuevas entradas
 3. MATLAB TOOLBOX 3.1. INTRODUCCIÓN El objetivo de este capítulo es explicar el uso del toolbox de matlab para entrenar redes neuronales con el algoritmo backpropagation de tipo feedforward, para resolver
3. MATLAB TOOLBOX 3.1. INTRODUCCIÓN El objetivo de este capítulo es explicar el uso del toolbox de matlab para entrenar redes neuronales con el algoritmo backpropagation de tipo feedforward, para resolver
Apuntes de Inteligencia Artificial
 PONTIFICIA UNIVERSIDAD CATÓLICA DEL ECUADOR FACULTAD DE INGENIERÍA Apuntes de Inteligencia Artificial Laboratorio: Perceptrón Simple JORGE AGUILAR JARAMILLO LABORATORIO : NEURONA Y PERCEPTRON SIMPPLE Objetivos.
PONTIFICIA UNIVERSIDAD CATÓLICA DEL ECUADOR FACULTAD DE INGENIERÍA Apuntes de Inteligencia Artificial Laboratorio: Perceptrón Simple JORGE AGUILAR JARAMILLO LABORATORIO : NEURONA Y PERCEPTRON SIMPPLE Objetivos.
TLU(s) MULTICAPAS. Se pueden implementar funciones en TLU con más de una capa.
 TLU(s) MULTICAPAS Se pueden implementar funciones en TLU con más de una capa 1 05 2 15 2 3 z 3 15 2 4 05 No eisten, en la actualidad, mecanismos de entrenamiento que permita conocer los pesos sinápticos
TLU(s) MULTICAPAS Se pueden implementar funciones en TLU con más de una capa 1 05 2 15 2 3 z 3 15 2 4 05 No eisten, en la actualidad, mecanismos de entrenamiento que permita conocer los pesos sinápticos
Tema: Aprendizaje Supervisado.
 Sistemas Expertos e Inteligencia Artificial. Guía No. 9 1 Tema: Aprendizaje Supervisado. Facultad: Ingeniería Escuela: Computación Asignatura: Sistemas Expertos e Inteligencia Artificial Objetivos Específicos
Sistemas Expertos e Inteligencia Artificial. Guía No. 9 1 Tema: Aprendizaje Supervisado. Facultad: Ingeniería Escuela: Computación Asignatura: Sistemas Expertos e Inteligencia Artificial Objetivos Específicos
CAPITULO 5 DISEÑO DE UN CLASIFICADOR DE
 Capitulo 5. Diseño de un Clasificador de Patrones. 60 CAPITULO 5 DISEÑO DE UN CLASIFICADOR DE PATRONES. En este capítulo se presenta un problema simple de clasificación de patrones, en el cual se pondrán
Capitulo 5. Diseño de un Clasificador de Patrones. 60 CAPITULO 5 DISEÑO DE UN CLASIFICADOR DE PATRONES. En este capítulo se presenta un problema simple de clasificación de patrones, en el cual se pondrán
Aprendizaje Automatizado. Redes Neuronales Artificiales
 Aprendizaje Automatizado Redes Neuronales Artificiales Introducción Otra forma de emular características propias de los humanos: memorizar y asociar hechos. Se aprende de la experiencia. El cerebro humano
Aprendizaje Automatizado Redes Neuronales Artificiales Introducción Otra forma de emular características propias de los humanos: memorizar y asociar hechos. Se aprende de la experiencia. El cerebro humano
UNIVERSIDAD CARLOS III MADRID
 UNIVERSIDAD CARLOS III MADRID PROYECTO FIN DE CARRERA INGENIERÍA INDUSTRIAL Desarrollo de una interfaz gráfica de redes neuronales usando Matlab AUTOR: ALFONSO MORENO RODRÍGUEZ TUTOR: ISABEL GONZÁLEZ FARIAS
UNIVERSIDAD CARLOS III MADRID PROYECTO FIN DE CARRERA INGENIERÍA INDUSTRIAL Desarrollo de una interfaz gráfica de redes neuronales usando Matlab AUTOR: ALFONSO MORENO RODRÍGUEZ TUTOR: ISABEL GONZÁLEZ FARIAS
Inteligencia Artificial (Curso ) Grado en Ingeniería Informática - Ingeniería del Software
 Inteligencia Artificial (Curso 0-0) Grado en Ingeniería Informática - Ingeniería del Software Redes neuronales Cuestión : Decir si las siguientes afirmaciones son verdaderas o falsas: Si tomamos la función
Inteligencia Artificial (Curso 0-0) Grado en Ingeniería Informática - Ingeniería del Software Redes neuronales Cuestión : Decir si las siguientes afirmaciones son verdaderas o falsas: Si tomamos la función
Inteligencia Artificial II (Curso ) Ejercicios propuestos del tema 5
 Inteligencia Artificial II (Curso 0-0) Ejercicios propuestos del tema Ejercicio : Diseñar un perceptrón simple con n valores de entrada y función umbral de activación que sirva para calcular la función
Inteligencia Artificial II (Curso 0-0) Ejercicios propuestos del tema Ejercicio : Diseñar un perceptrón simple con n valores de entrada y función umbral de activación que sirva para calcular la función
REDES NEURONALES ADAPTABLES
 REDES NEURONALES ADAPTABLES Unidad 3: Redes neuronales artificiales y modelos de entrenamiento SubTemas 3.2 Perceptron simple Arquitectura Regla delta Multi Layer Perceptrón 3.3 Redes Neuronales Adaptables
REDES NEURONALES ADAPTABLES Unidad 3: Redes neuronales artificiales y modelos de entrenamiento SubTemas 3.2 Perceptron simple Arquitectura Regla delta Multi Layer Perceptrón 3.3 Redes Neuronales Adaptables
ANEXO II.- TEORÍA SOBRE REDES NEURONALES ARTIFICIALES
 ANEXO II.- TEORÍA SOBRE REDES NEURONALES ARTIFICIALES 1. Concepto de red neuronal artificial Una red neuronal artificial (RNA) es un modelo matemático que intenta reproducir el modo de funcionamiento y
ANEXO II.- TEORÍA SOBRE REDES NEURONALES ARTIFICIALES 1. Concepto de red neuronal artificial Una red neuronal artificial (RNA) es un modelo matemático que intenta reproducir el modo de funcionamiento y
Perceptrón simple y perceptrón multicapa
 UNL - FICH - Departamento de Informática - Ingeniería Informática Inteligencia Computacional Guía de trabajos prácticos Perceptrón simple y perceptrón multicapa. Objetivos Aplicar diferentes arquitecturas
UNL - FICH - Departamento de Informática - Ingeniería Informática Inteligencia Computacional Guía de trabajos prácticos Perceptrón simple y perceptrón multicapa. Objetivos Aplicar diferentes arquitecturas
Redes Neuronales. Las redes neuronales son modelos computacionales que buscan imitar el funcionamiento
 Redes Neuronales Las redes neuronales son modelos computacionales que buscan imitar el funcionamiento de las neuronas biológicas. Se usan principalmente para el reconocimiento de patrones complejos. Para
Redes Neuronales Las redes neuronales son modelos computacionales que buscan imitar el funcionamiento de las neuronas biológicas. Se usan principalmente para el reconocimiento de patrones complejos. Para
Aprendizaje Automatizado. Redes Neuronales Artificiales
 Aprendizaje Automatizado Redes Neuronales Artificiales Introducción Una forma de emular características propias de los humanos: memorizar y asociar hechos. Se aprende de la experiencia. El cerebro humano
Aprendizaje Automatizado Redes Neuronales Artificiales Introducción Una forma de emular características propias de los humanos: memorizar y asociar hechos. Se aprende de la experiencia. El cerebro humano
Análisis de Datos. Red de función de base radial. Profesor: Dr. Wilfrido Gómez Flores
 Análisis de Datos Red de función de base radial Profesor: Dr. Wilfrido Gómez Flores 1 Introducción Las funciones de base radial han sido utilizadas en diversas técnicas de reconocimiento de patrones como
Análisis de Datos Red de función de base radial Profesor: Dr. Wilfrido Gómez Flores 1 Introducción Las funciones de base radial han sido utilizadas en diversas técnicas de reconocimiento de patrones como
CAPÍTULO 4 IMPLEMENTACIÓN DE LA TRANSFORMADA DE DISTANCIA CON UN
 CAPÍTULO 4 IMPLEMENTACIÓN DE LA TRANSFORMADA DE DISTANCIA CON UN PERCEPTRÓN MULTICAPA EN MATLAB 4.1 Matlab Matlab ha demostrado ser un programa de desarrollo muy completo en distintas áreas, más que nada
CAPÍTULO 4 IMPLEMENTACIÓN DE LA TRANSFORMADA DE DISTANCIA CON UN PERCEPTRÓN MULTICAPA EN MATLAB 4.1 Matlab Matlab ha demostrado ser un programa de desarrollo muy completo en distintas áreas, más que nada
Relación 7 - Redes neuronales
 Sistemas Inteligentes 0-0 Relación - Redes neuronales Problemas Ejercicio. Explicar cómo se usaría una red neuronal para obtener un reconocedor de letras escritas a mano. Describir con precisión qué estructura
Sistemas Inteligentes 0-0 Relación - Redes neuronales Problemas Ejercicio. Explicar cómo se usaría una red neuronal para obtener un reconocedor de letras escritas a mano. Describir con precisión qué estructura
3.7 IDENTIFICACION DE UN SISTEMA DINÁMICO NO LINEAL Descripción del Problema: La identificación de un sistema consiste en
 301 3.7 IDENTIFICACION DE UN SISTEMA DINÁMICO NO LINEAL 3.7.1 Descripción del Problema: La identificación de un sistema consiste en determinar una función que relacione las variables de entrada con las
301 3.7 IDENTIFICACION DE UN SISTEMA DINÁMICO NO LINEAL 3.7.1 Descripción del Problema: La identificación de un sistema consiste en determinar una función que relacione las variables de entrada con las
Neural Network Toolbox
 Neural Network Toolbox Sistemas Conexionistas - Curso 08/09 La Neural Network Toolbox es un paquete de Matlab que contiene una serie de funciones para crear y trabajar con redes de neuronas artificiales.
Neural Network Toolbox Sistemas Conexionistas - Curso 08/09 La Neural Network Toolbox es un paquete de Matlab que contiene una serie de funciones para crear y trabajar con redes de neuronas artificiales.
Perceptrón Simple. Aspectos Prácticos y Algoritmos Redes Neuronales, DC-FCEyN-UBA. Rosana Matuk Primer Cuatrimestre 2018
 Perceptrón Simple Aspectos Prácticos y Algoritmos Redes Neuronales, DC-FCEyN-UBA Rosana Matuk Primer Cuatrimestre 2018 Rosana Matuk (DC-FCEyN-UBA) Perceptrón simple Primer Cuatrimestre 2018 1 / 29 Objetivo
Perceptrón Simple Aspectos Prácticos y Algoritmos Redes Neuronales, DC-FCEyN-UBA Rosana Matuk Primer Cuatrimestre 2018 Rosana Matuk (DC-FCEyN-UBA) Perceptrón simple Primer Cuatrimestre 2018 1 / 29 Objetivo
Tema 2 Primeros Modelos Computacionales
 Universidad Carlos III de Madrid OpenCourseWare Redes de Neuronas Artificiales Inés M. Galván - José Mª Valls Tema 2 Primeros Modelos Computacionales 1 Primeros Modelos Computacionales Perceptron simple
Universidad Carlos III de Madrid OpenCourseWare Redes de Neuronas Artificiales Inés M. Galván - José Mª Valls Tema 2 Primeros Modelos Computacionales 1 Primeros Modelos Computacionales Perceptron simple
Análisis de Datos. Validación de clasificadores. Profesor: Dr. Wilfrido Gómez Flores
 Análisis de Datos Validación de clasificadores Profesor: Dr. Wilfrido Gómez Flores 1 Introducción La mayoría de los clasificadores que se han visto requieren de uno o más parámetros definidos libremente,
Análisis de Datos Validación de clasificadores Profesor: Dr. Wilfrido Gómez Flores 1 Introducción La mayoría de los clasificadores que se han visto requieren de uno o más parámetros definidos libremente,
UNIVERSIDAD AUTONOMA DEL ESTADO DE MEXICO CENTRO UNIVERSITARIO UAEM ATLACOMULCO REPORTE DE INVESTIGACION
 UNIVERSIDAD AUTONOMA DEL ESTADO DE MEXICO CENTRO UNIVERSITARIO UAEM ATLACOMULCO REPORTE DE INVESTIGACION Qué es el momento en una red backpropagation? U.A. REDES NEURONALES INTEGRANTES: JESUS BARRIOS CRESCENCIO
UNIVERSIDAD AUTONOMA DEL ESTADO DE MEXICO CENTRO UNIVERSITARIO UAEM ATLACOMULCO REPORTE DE INVESTIGACION Qué es el momento en una red backpropagation? U.A. REDES NEURONALES INTEGRANTES: JESUS BARRIOS CRESCENCIO
Optimización en Ingeniería
 Optimización en Ingeniería Departamento de Computación CINVESTAV-IPN Av. IPN No. 2508 Col. San Pedro Zacatenco México, D.F. 07300 email: [email protected] El Método de Marquardt Algoritmo Paso 1:
Optimización en Ingeniería Departamento de Computación CINVESTAV-IPN Av. IPN No. 2508 Col. San Pedro Zacatenco México, D.F. 07300 email: [email protected] El Método de Marquardt Algoritmo Paso 1:
Uso de una red neuronal multicapa para el reconocimiento de caracteres griegos. Skynet Reloaded
 Uso de una red neuronal multicapa para el reconocimiento de caracteres griegos: Skynet Reloaded...decided our fate in a microsecond... P. García H. Rajchert I. Scena Sistemas de Inteligencia Artificial
Uso de una red neuronal multicapa para el reconocimiento de caracteres griegos: Skynet Reloaded...decided our fate in a microsecond... P. García H. Rajchert I. Scena Sistemas de Inteligencia Artificial
Detección Multiusuario para DS-CDMA basado en SVM
 9 Otra técnica basada en el aprendizaje y más conocida que la anterior es la basada en. Vamos a realizar una pequeña comparativa teórica de sobre ambas técnicas de clasificación. Estudiaremos los conceptos
9 Otra técnica basada en el aprendizaje y más conocida que la anterior es la basada en. Vamos a realizar una pequeña comparativa teórica de sobre ambas técnicas de clasificación. Estudiaremos los conceptos
TUTORIAL SOBRE REDES NEURONALES APLICADAS EN INGENIERIA ELECTRICA Y SU IMPLEMENTACIÓN EN UN SITIO WEB
 TUTORIAL SOBRE REDES NEURONALES APLICADAS EN INGENIERIA ELECTRICA Y SU IMPLEMENTACIÓN EN UN SITIO WEB MARIA ISABEL ACOSTA BUITRAGO CAMILO ALFONSO ZULUAGA MUÑOZ UNIVERSIDAD TECNOLOGICA DE PEREIRA FACULTAD
TUTORIAL SOBRE REDES NEURONALES APLICADAS EN INGENIERIA ELECTRICA Y SU IMPLEMENTACIÓN EN UN SITIO WEB MARIA ISABEL ACOSTA BUITRAGO CAMILO ALFONSO ZULUAGA MUÑOZ UNIVERSIDAD TECNOLOGICA DE PEREIRA FACULTAD
Redes Neuronales Artificiales El Perceptrón
 1 Sistemas Expertos e Inteligencia Artificial / Guía IX / Ciclo 01-2018 Facultad: Ingeniería Escuela: Computación Asignatura: Sistemas Expertos e Inteligencia Artificial Redes Neuronales Artificiales El
1 Sistemas Expertos e Inteligencia Artificial / Guía IX / Ciclo 01-2018 Facultad: Ingeniería Escuela: Computación Asignatura: Sistemas Expertos e Inteligencia Artificial Redes Neuronales Artificiales El
BACK-PROPAGATION: UN ALGORITMO DE ENTRENAMIENTO PARA REDES NEURONALES
 BACK-PROPAGATION: UN ALGORITMO DE ENTRENAMIENTO PARA REDES NEURONALES Paul Acquatella B. Universidad Simón Bolívar, Valle de Sartenejas, Caracas, Venezuela. [email protected] Resumen Este trabajo presenta
BACK-PROPAGATION: UN ALGORITMO DE ENTRENAMIENTO PARA REDES NEURONALES Paul Acquatella B. Universidad Simón Bolívar, Valle de Sartenejas, Caracas, Venezuela. [email protected] Resumen Este trabajo presenta
Técnicas de inteligencia artificial. Aprendizaje: Perceptrón multi-capa
 Técnicas de inteligencia artificial Aprendizaje: Perceptrón multi-capa Índice Regla delta Modelo computacional Neuronas e hiperplanos Entrenamiento como ajuste supervisado No-separabilidad lineal Backpropagation
Técnicas de inteligencia artificial Aprendizaje: Perceptrón multi-capa Índice Regla delta Modelo computacional Neuronas e hiperplanos Entrenamiento como ajuste supervisado No-separabilidad lineal Backpropagation
Las Redes Neuronales Artificiales y su importancia como herramienta en la toma de decisiones. Villanueva Espinoza, María del Rosario CAPÍTULO V
 CAPÍTULO V V. ALGORITMOS NEURONALES Los modelos neuronales utilizan varios algoritmos de estimación, aprendizaje o entrenamiento para encontrar los valores de los parámetros del modelo, que en la jerga
CAPÍTULO V V. ALGORITMOS NEURONALES Los modelos neuronales utilizan varios algoritmos de estimación, aprendizaje o entrenamiento para encontrar los valores de los parámetros del modelo, que en la jerga
OPENCOURSEWARE REDES DE NEURONAS ARTIFICIALES Inés M. Galván José M. Valls. Tema 6: Redes de Neuronas Recurrentes
 OPENCOURSEWARE REDES DE NEURONAS ARTIFICIALES Inés M. Galván José M. Valls Tema 6: Redes de Neuronas Recurrentes En este tema se estudian las redes de neuronas recurrentes. Se presentan en primer lugar
OPENCOURSEWARE REDES DE NEURONAS ARTIFICIALES Inés M. Galván José M. Valls Tema 6: Redes de Neuronas Recurrentes En este tema se estudian las redes de neuronas recurrentes. Se presentan en primer lugar
Redes Neuronales Artificiales
 Algoritmo de retropropagación Back propagation Es utilizado para entrenar redes neuronales multicapa. Exige que la función de activación de las neuronas sea derivable y creciente. Las funciones comúnmente
Algoritmo de retropropagación Back propagation Es utilizado para entrenar redes neuronales multicapa. Exige que la función de activación de las neuronas sea derivable y creciente. Las funciones comúnmente
Entrenamiento de redes neuronales Fernando Berzal,
 Entrenamiento de redes neuronales Fernando Berzal, [email protected] Entrenamiento de redes neuronales Modos de entrenamiento Preprocesamiento de los datos Funciones de activación Inicialización de los pesos
Entrenamiento de redes neuronales Fernando Berzal, [email protected] Entrenamiento de redes neuronales Modos de entrenamiento Preprocesamiento de los datos Funciones de activación Inicialización de los pesos
Perceptrón multicapa. Diego Milone y Leonardo Rufiner Inteligencia Computacional Departamento de Informática FICH-UNL
 Perceptrón multicapa Diego Milone y Leonardo Rufiner Inteligencia Computacional Departamento de Informática FICH-UNL Organización Un poco de historia... Cómo resolver el problema XOR? Métodos de gradiente
Perceptrón multicapa Diego Milone y Leonardo Rufiner Inteligencia Computacional Departamento de Informática FICH-UNL Organización Un poco de historia... Cómo resolver el problema XOR? Métodos de gradiente
Práctica 10. Redes Neuronales
 Práctica 10 Redes Neuronales En esta práctica trabajaremos con un sistema de aprendizaje basado en ejemplos que ya hemos visto con anterioridad (k-vecinos) y una implementación de las redes neuronales.
Práctica 10 Redes Neuronales En esta práctica trabajaremos con un sistema de aprendizaje basado en ejemplos que ya hemos visto con anterioridad (k-vecinos) y una implementación de las redes neuronales.
CAPÍTULO 3. Las redes neuronales artificiales, ANNs por sus siglas en inglés, son el resultado de varias
 CAPÍTULO 3 REDES NEURONALES ARTIFICIALES 3.1 Introducción Las redes neuronales artificiales, ANNs por sus siglas en inglés, son el resultado de varias décadas de investigaciones desarrolladas en torno
CAPÍTULO 3 REDES NEURONALES ARTIFICIALES 3.1 Introducción Las redes neuronales artificiales, ANNs por sus siglas en inglés, son el resultado de varias décadas de investigaciones desarrolladas en torno
Redes Neuronales Artificiales
 Redes Neuronales Artificiales Introducción a la Robótica Inteligente Álvaro Gutiérrez de abril de 208 [email protected] www.robolabo.etsit.upm.es Mapas Predicción Robótica M l M r W ij S S 2 S 3 S 4
Redes Neuronales Artificiales Introducción a la Robótica Inteligente Álvaro Gutiérrez de abril de 208 [email protected] www.robolabo.etsit.upm.es Mapas Predicción Robótica M l M r W ij S S 2 S 3 S 4
Redes de Neuronas de Base Radial
 Redes de Neuronas de Base Radial 1 Introducción Redes multicapa con conexiones hacia delante Única capa oculta Las neuronas ocultas poseen carácter local Cada neurona oculta se activa en una región distinta
Redes de Neuronas de Base Radial 1 Introducción Redes multicapa con conexiones hacia delante Única capa oculta Las neuronas ocultas poseen carácter local Cada neurona oculta se activa en una región distinta
Redes Neuronales Multicapa
 Undécima sesión 16 de abril de 2010 Relación entre capas y conjuntos bajo estudio Estructura Regla de decisión XOR Clases no linealmente separables Regiones generalizadas Una capa Regiones separables con
Undécima sesión 16 de abril de 2010 Relación entre capas y conjuntos bajo estudio Estructura Regla de decisión XOR Clases no linealmente separables Regiones generalizadas Una capa Regiones separables con
Aprendizaje: Perceptrón multi-capa
 Técnicas de inteligencia artificial Asignatura troncal: 4.5cr, 4ºCurso Ing Inf Aprendizaje: Perceptrón multi-capa 2003-2004 F.Escolano, O.Colomina, M.A. Cazorla Perceptrón 1 Indice Regla delta Modelo computacional
Técnicas de inteligencia artificial Asignatura troncal: 4.5cr, 4ºCurso Ing Inf Aprendizaje: Perceptrón multi-capa 2003-2004 F.Escolano, O.Colomina, M.A. Cazorla Perceptrón 1 Indice Regla delta Modelo computacional
CONCLUSIONES. La teoría de Redes Neuronales Artificiales, presenta grandes ventajas con
 319 CONCLUSIONES La teoría de Redes Neuronales Artificiales, presenta grandes ventajas con respecto a otros modelos típicos de solución de problemas de Ingeniería, una de ellas es su inspiración en modelos
319 CONCLUSIONES La teoría de Redes Neuronales Artificiales, presenta grandes ventajas con respecto a otros modelos típicos de solución de problemas de Ingeniería, una de ellas es su inspiración en modelos
Definir un Equipo de Fútbol óptimo mediante Redes Neuronales Artificiales
 Definir un Equipo de Fútbol óptimo mediante Redes Neuronales Artificiales Abstract Este trabajo tiene como objetivo analizar, experimentar y comprender el funcionamiento y las características de los Sistemas
Definir un Equipo de Fútbol óptimo mediante Redes Neuronales Artificiales Abstract Este trabajo tiene como objetivo analizar, experimentar y comprender el funcionamiento y las características de los Sistemas
Neural Network Toolbox de MATLAB
 Neural Network Toolbox de MATLAB Instructor: Ciencias Computacionales - INAOE Septiembre 2006 Agenda. Introducción a las Redes Neuronales Artificiales 2. Introducción al Neural Network Toolbox 3. Redes
Neural Network Toolbox de MATLAB Instructor: Ciencias Computacionales - INAOE Septiembre 2006 Agenda. Introducción a las Redes Neuronales Artificiales 2. Introducción al Neural Network Toolbox 3. Redes
DISEÑO EXPERIMENTAL Y OPTIMIZACIÓN DE SISTEMAS CON MÚLTIPLES RESPUESTAS
 DISEÑO EXPERIMENTAL Y OPTIMIZACIÓN DE SISTEMAS CON MÚLTIPLES RESPUESTAS Parte 5: Redes neuronales Héctor Goicoechea E-mail: [email protected] http://www.fbcb.unl.edu.ar/laboratorios/ladaq/ Redes Neuronales
DISEÑO EXPERIMENTAL Y OPTIMIZACIÓN DE SISTEMAS CON MÚLTIPLES RESPUESTAS Parte 5: Redes neuronales Héctor Goicoechea E-mail: [email protected] http://www.fbcb.unl.edu.ar/laboratorios/ladaq/ Redes Neuronales
Inteligencia Computacional
 Inteligencia Computacional Práctica de redes neuronales Reconocimiento óptico de caracteres MNIST Curso 2017-2018 Máster en Ingeniería Informática Departamento de Ciencias de la Computación e Inteligencia
Inteligencia Computacional Práctica de redes neuronales Reconocimiento óptico de caracteres MNIST Curso 2017-2018 Máster en Ingeniería Informática Departamento de Ciencias de la Computación e Inteligencia
Redes Neuronales Artificiales
 Red de Hopfield Almacenar un conjunto de p patrones de forma tal que cuando se presente un nuevo patrón, la red responda produciendo alguno de los patrones previamente almacenados que más se parezca al
Red de Hopfield Almacenar un conjunto de p patrones de forma tal que cuando se presente un nuevo patrón, la red responda produciendo alguno de los patrones previamente almacenados que más se parezca al
Neural Network Toolbox de MATLAB
 Neural Network Toolbox de MATLAB Instructor: Ciencias Computacionales - INAOE Septiembre 26 Agenda. Introducción a las Redes Neuronales Artificiales 2. Introducción al 3. Redes Perceptrón 4. Redes Backpropagation
Neural Network Toolbox de MATLAB Instructor: Ciencias Computacionales - INAOE Septiembre 26 Agenda. Introducción a las Redes Neuronales Artificiales 2. Introducción al 3. Redes Perceptrón 4. Redes Backpropagation
Aplicación de diferentes arquitecturas de RNA sobre datos de paquetes de red en Matlab con y sin reducción de características.
 Aplicación de diferentes arquitecturas de RNA sobre datos de paquetes de red en Matlab con y sin reducción de características. Judith M Carbonell Alfonso 1, Donnie DeFreitas Ortega 2 1 Instituto Finaly.
Aplicación de diferentes arquitecturas de RNA sobre datos de paquetes de red en Matlab con y sin reducción de características. Judith M Carbonell Alfonso 1, Donnie DeFreitas Ortega 2 1 Instituto Finaly.
Reconocimiento automático de palabras en documentos históricos usando redes neuronales convolucionales
 Reconocimiento automático de palabras en documentos históricos usando redes neuronales convolucionales Dra. Ma. de Guadalupe García Hernández Departamento de Ingeniería Electrónica Objetivo general Aplicar
Reconocimiento automático de palabras en documentos históricos usando redes neuronales convolucionales Dra. Ma. de Guadalupe García Hernández Departamento de Ingeniería Electrónica Objetivo general Aplicar
Aprendizaje Automatizado. Redes Neuronales Artificiales
 Aprendizaje Automatizado Redes Neuronales Artificiales Introducción Una forma de emular características propias de los humanos: memorizar y asociar hechos. Se aprende de la experiencia. El cerebro humano
Aprendizaje Automatizado Redes Neuronales Artificiales Introducción Una forma de emular características propias de los humanos: memorizar y asociar hechos. Se aprende de la experiencia. El cerebro humano
LIM. Modelización del conjunto motor-transmisión de un automóvil a partir de datos experimentales. Trabajo final de grado
 Trabajo final de grado Modelización del conjunto motor-transmisión de un automóvil a partir de datos experimentales Autor Alfonso Ramón Varela Olmedo Tutores Miguel Ángel Naya Villaverde Emilio Sanjurjo
Trabajo final de grado Modelización del conjunto motor-transmisión de un automóvil a partir de datos experimentales Autor Alfonso Ramón Varela Olmedo Tutores Miguel Ángel Naya Villaverde Emilio Sanjurjo
Inteligencia Artificial. Aprendizaje neuronal. Ing. Sup. en Informática, 4º. Curso académico: 2011/2012 Profesores: Ramón Hermoso y Matteo Vasirani
 Inteligencia Artificial Aprendizaje neuronal Ing. Sup. en Informática, 4º Curso académico: 20/202 Profesores: Ramón Hermoso y Matteo Vasirani Aprendizaje Resumen: 3. Aprendizaje automático 3. Introducción
Inteligencia Artificial Aprendizaje neuronal Ing. Sup. en Informática, 4º Curso académico: 20/202 Profesores: Ramón Hermoso y Matteo Vasirani Aprendizaje Resumen: 3. Aprendizaje automático 3. Introducción
Redes Neuronales Artificiales
 Redes Neuronales Artificiales Alejandro Osses Vecchi 11 de julio de 2009 1. Introducción Comenzaremos con una definición simple y general de Red Neuronal para, en las próximas secciones, explicar y profundizar
Redes Neuronales Artificiales Alejandro Osses Vecchi 11 de julio de 2009 1. Introducción Comenzaremos con una definición simple y general de Red Neuronal para, en las próximas secciones, explicar y profundizar
Red Neuronal Artificial
 índice RN Supervisadas - Introducción - El Perceptrón y la estructura multicapa MLP - El aprendizaje retropropagado: BP - Aplicaciones y ejemplos - Características y limitaciones P Campoy 1 Red Neuronal
índice RN Supervisadas - Introducción - El Perceptrón y la estructura multicapa MLP - El aprendizaje retropropagado: BP - Aplicaciones y ejemplos - Características y limitaciones P Campoy 1 Red Neuronal
Área Académica: Instituto de Ciencias Básicas e Ingeniería, Sistemas Computacionales
 Área Académica: Instituto de Ciencias Básicas e Ingeniería, Sistemas Computacionales Tema: Perceptron Parte I Profesor: Víctor Tomás T. Mariano. Alumnos: Leticia Hernández Hernández Agustín Hernández Espinoza
Área Académica: Instituto de Ciencias Básicas e Ingeniería, Sistemas Computacionales Tema: Perceptron Parte I Profesor: Víctor Tomás T. Mariano. Alumnos: Leticia Hernández Hernández Agustín Hernández Espinoza
Redes neuronales con funciones de base radial
 Redes neuronales con funciones de base radial Diego Milone y Leonardo Rufiner Inteligencia Computacional Departamento de Informática FICH-UNL Organización: RBF-NN Motivación y orígenes RBF Arquitectura
Redes neuronales con funciones de base radial Diego Milone y Leonardo Rufiner Inteligencia Computacional Departamento de Informática FICH-UNL Organización: RBF-NN Motivación y orígenes RBF Arquitectura
Redes Neuronales. Parte II. Facultad de Ciencias Exactas y Tecnología Universidad Nacional de Tucumán Mg. Ing. Gustavo E. Juárez
 Redes Neuronales Parte II Facultad de Ciencias Exactas y Tecnología Universidad Nacional de Tucumán Mg. Ing. Gustavo E. Juárez UNIDAD TEMÁTICA : REDES NEURONALES Introducción. De/iniciones. Topologías
Redes Neuronales Parte II Facultad de Ciencias Exactas y Tecnología Universidad Nacional de Tucumán Mg. Ing. Gustavo E. Juárez UNIDAD TEMÁTICA : REDES NEURONALES Introducción. De/iniciones. Topologías
Reconocimiento de Patrones
 Reconocimiento de Patrones Técnicas de validación (Clasificación Supervisada) Jesús Ariel Carrasco Ochoa Instituto Nacional de Astrofísica, Óptica y Electrónica Clasificación Supervisada Para qué evaluar
Reconocimiento de Patrones Técnicas de validación (Clasificación Supervisada) Jesús Ariel Carrasco Ochoa Instituto Nacional de Astrofísica, Óptica y Electrónica Clasificación Supervisada Para qué evaluar
4. El perceptrón. 4.1 Introducción. 4.2 Consideraciones básicas
 4. El perceptrón 4.1 Introducción El perceptrón es la forma más simple de una red neuronal usada para la clasificación de un tipo especial de patrones, los linealmente separables (es decir, patrones que
4. El perceptrón 4.1 Introducción El perceptrón es la forma más simple de una red neuronal usada para la clasificación de un tipo especial de patrones, los linealmente separables (es decir, patrones que
Capítulo 5: CONTROL INVERSO ADAPTATIVO
 Capítulo 5: CONTROL INVERSO INTRODUCCIÓN 5.. INTRODUCCIÓN Un sistema de control inverso adaptativo se muestra en la Figura 5. Si el controlador fuese ideal, su función de transferencia sería: C( z) M (
Capítulo 5: CONTROL INVERSO INTRODUCCIÓN 5.. INTRODUCCIÓN Un sistema de control inverso adaptativo se muestra en la Figura 5. Si el controlador fuese ideal, su función de transferencia sería: C( z) M (
Resolución de Ecuaciones no lineales. Juan Manuel Rodríguez Prieto
 Resolución de Ecuaciones no lineales Juan Manuel Rodríguez Prieto Resolución de Ecuaciones no lineales Objetivos Aprender a resolver ecuaciones de la forma: f () = 0 Donde f es una función no-lineal de
Resolución de Ecuaciones no lineales Juan Manuel Rodríguez Prieto Resolución de Ecuaciones no lineales Objetivos Aprender a resolver ecuaciones de la forma: f () = 0 Donde f es una función no-lineal de
Redes neuronales en control de sistemas
 Redes neuronales en control de sistemas Marco Teórico Las redes neuronales tratan de emular ciertas características propias de los humanos, una muy importante es la experiencia. El ser humano es capaz
Redes neuronales en control de sistemas Marco Teórico Las redes neuronales tratan de emular ciertas características propias de los humanos, una muy importante es la experiencia. El ser humano es capaz
CAPÍTULO Inteligencia Artificial y Redes Neuronales Artificiales
 CAPÍTULO 1 INTRODUCCIÓN 1.1 Inteligencia Artificial y Redes Neuronales Artificiales Durante las últimas décadas se han ido desarrollando investigaciones importantes en el área de la inteligencia artificial.
CAPÍTULO 1 INTRODUCCIÓN 1.1 Inteligencia Artificial y Redes Neuronales Artificiales Durante las últimas décadas se han ido desarrollando investigaciones importantes en el área de la inteligencia artificial.
CONCEPTOS BÁSICOS (Freeman capt.1; Neural Nets capt. 4,5 y 7)
 Tema 1: Conceptos Básicos Sistemas Conexionistas 1 CONCEPTOS BÁSICOS (Freeman capt.1; Neural Nets capt. 4,5 y 7) 1.- Introducción. 1.1.- Redes Neuronales de Tipo Biológico. 1.2.- Redes Neuronales dirigidas
Tema 1: Conceptos Básicos Sistemas Conexionistas 1 CONCEPTOS BÁSICOS (Freeman capt.1; Neural Nets capt. 4,5 y 7) 1.- Introducción. 1.1.- Redes Neuronales de Tipo Biológico. 1.2.- Redes Neuronales dirigidas
CONTROL PREDICTIVO CON REDES NEURONALES COMO MODELO, UTILIZANDO EL METODO DE NEWTON-RAPHSON PARA LOGRAR LA MINIMIZACION DE LA FUNCION DE COSTO
 Scientia et Technica Año XV, No 41, Mayo de 2009. Universidad Tecnológica de Pereira. ISSN 0122-1701 203 CONTROL PREDICTIVO CON REDES NEURONALES COMO MODELO, UTILIZANDO EL METODO DE NEWTON-RAPHSON PARA
Scientia et Technica Año XV, No 41, Mayo de 2009. Universidad Tecnológica de Pereira. ISSN 0122-1701 203 CONTROL PREDICTIVO CON REDES NEURONALES COMO MODELO, UTILIZANDO EL METODO DE NEWTON-RAPHSON PARA
Redes Neuronales. Introducción. José Manuel Quero Reboul Dpto. Ingeniería Electrónica Universidad de Sevilla
 Redes Neuronales Introducción José Manuel Quero Reboul Dpto. Ingeniería Electrónica Universidad de Sevilla Indice Motivación Arquitectura Leyes de Aprendizae Aplicaciones DILEMA MEMORIA CALCULO Aritmética
Redes Neuronales Introducción José Manuel Quero Reboul Dpto. Ingeniería Electrónica Universidad de Sevilla Indice Motivación Arquitectura Leyes de Aprendizae Aplicaciones DILEMA MEMORIA CALCULO Aritmética
Tema 15: Combinación de clasificadores
 Tema 15: Combinación de clasificadores p. 1/21 Tema 15: Combinación de clasificadores Abdelmalik Moujahid, Iñaki Inza, Pedro Larrañaga Departamento de Ciencias de la Computación e Inteligencia Artificial
Tema 15: Combinación de clasificadores p. 1/21 Tema 15: Combinación de clasificadores Abdelmalik Moujahid, Iñaki Inza, Pedro Larrañaga Departamento de Ciencias de la Computación e Inteligencia Artificial
Resolución de Ecuaciones no lineales. Juan Manuel Rodríguez Prieto
 Resolución de Ecuaciones no lineales Juan Manuel Rodríguez Prieto Resolución de Ecuaciones no lineales Objetivos Aprender a resolver ecuaciones de la forma: f () = 0 Donde f es una función no-lineal de
Resolución de Ecuaciones no lineales Juan Manuel Rodríguez Prieto Resolución de Ecuaciones no lineales Objetivos Aprender a resolver ecuaciones de la forma: f () = 0 Donde f es una función no-lineal de
OCW-V.Muto Métodos de interpolación Cap. XI CAPITULO XI. METODOS DE INTERPOLACION 1. EL METODO DE INTERPOLACION DE LA POSICION FALSA
 CAPITULO XI. METODOS DE INTERPOLACION 1. EL METODO DE INTERPOLACION DE LA POSICION FALSA Los métodos de interpolación que vamos a discutir en el resto de este capítulo son muy útiles para determinar los
CAPITULO XI. METODOS DE INTERPOLACION 1. EL METODO DE INTERPOLACION DE LA POSICION FALSA Los métodos de interpolación que vamos a discutir en el resto de este capítulo son muy útiles para determinar los
INTRODUCTION TO MACHINE LEARNING ISABELLE GUYON
 INTRODUCTION TO MACHINE LEARNING ISABELLE GUYON 2008-02-31 Notas tomadas por: María Eugenia Rojas Qué es Machine Learning? El proceso de aprendizaje de maquina consiste en tener una gran base de datos
INTRODUCTION TO MACHINE LEARNING ISABELLE GUYON 2008-02-31 Notas tomadas por: María Eugenia Rojas Qué es Machine Learning? El proceso de aprendizaje de maquina consiste en tener una gran base de datos
Tema 8: Redes Neuronales
 Tema 8: Redes Neuronales Pedro Larrañaga, Iñaki Inza, Abdelmalik Moujahid Intelligent Systems Group Departamento de Ciencias de la Computación e Inteligencia Artificial Universidad del País Vasco http://www.sc.ehu.es/isg/
Tema 8: Redes Neuronales Pedro Larrañaga, Iñaki Inza, Abdelmalik Moujahid Intelligent Systems Group Departamento de Ciencias de la Computación e Inteligencia Artificial Universidad del País Vasco http://www.sc.ehu.es/isg/
PONTIFICIA UNIVERSIDAD CATOLICA DEL ECUADOR FACULTAD DE INGENIERIA ESCUELA DE SISTEMAS
 PONTIFICIA UNIVERSIDAD CATOLICA DEL ECUADOR FACULTAD DE INGENIERIA 1. DATOS INFORMATIVOS MATERIA O MODULO: CODIGO: CARRERA: NIVEL: No. CREDITOS 4 CREDITOS TEORIA: 3 CREDITOS PRACTICA: 1 ESCUELA DE SISTEMAS
PONTIFICIA UNIVERSIDAD CATOLICA DEL ECUADOR FACULTAD DE INGENIERIA 1. DATOS INFORMATIVOS MATERIA O MODULO: CODIGO: CARRERA: NIVEL: No. CREDITOS 4 CREDITOS TEORIA: 3 CREDITOS PRACTICA: 1 ESCUELA DE SISTEMAS
Introducción a Las redes Neuronales (Neurales) CO-6612
 a Las redes Neuronales (Neurales) CO-6612 Coordenadas iniciales: Prof. Minaya Villasana Oficina: CBI-112 Extension: 906 3386 forma más fácil (preferida) de contacto: [email protected] Bibliografia: Simon
a Las redes Neuronales (Neurales) CO-6612 Coordenadas iniciales: Prof. Minaya Villasana Oficina: CBI-112 Extension: 906 3386 forma más fácil (preferida) de contacto: [email protected] Bibliografia: Simon
OPTIMIZACIÓN VECTORIAL
 OPTIMIZACIÓN VECTORIAL Métodos de Búsqueda Directa Utilizan sólo valores de la función Métodos del Gradiente Métodos de Segundo Orden Requieren valores aproimados de la primera derivada de f) Además de
OPTIMIZACIÓN VECTORIAL Métodos de Búsqueda Directa Utilizan sólo valores de la función Métodos del Gradiente Métodos de Segundo Orden Requieren valores aproimados de la primera derivada de f) Además de
FUNCIONES DE GENERACIÓN DE NÚMEROS ALEATORIOS NÚMEROS ALEATORIOS UNIFORMES
 FUNCIONES DE GENERACIÓN DE NÚMEROS ALEATORIOS Hay muchos problemas de ingeniería que requieren números aleatorios para obtener una solución. En algunos casos, esos números sirven para crear una simulación
FUNCIONES DE GENERACIÓN DE NÚMEROS ALEATORIOS Hay muchos problemas de ingeniería que requieren números aleatorios para obtener una solución. En algunos casos, esos números sirven para crear una simulación
Análisis de Datos. Introducción al aprendizaje supervisado. Profesor: Dr. Wilfrido Gómez Flores
 Análisis de Datos Introducción al aprendizaje supervisado Profesor: Dr. Wilfrido Gómez Flores 1 Conceptos básicos Desde la antigüedad, el problema de buscar patrones en datos es fundamental en diversas
Análisis de Datos Introducción al aprendizaje supervisado Profesor: Dr. Wilfrido Gómez Flores 1 Conceptos básicos Desde la antigüedad, el problema de buscar patrones en datos es fundamental en diversas
Optimización Fernando Berzal,
 Optimización Fernando Berzal, [email protected] Backpropagation Convergencia del gradiente descendente Momentos Tasas de aprendizaje adaptativas rprop& rmsprop 1 En la práctica Algoritmo de aprendizaje de
Optimización Fernando Berzal, [email protected] Backpropagation Convergencia del gradiente descendente Momentos Tasas de aprendizaje adaptativas rprop& rmsprop 1 En la práctica Algoritmo de aprendizaje de
