3.Dependencias funcionales.
|
|
|
- Eduardo Soler Farías
- hace 7 años
- Vistas:
Transcripción
1 3.Dependencias funcionales. 3.1 Definiciones básicas. Una dependencia funcional es una restricción inherente a la semántica de los atributos que se expresa en la forma : X Y ( X e Y son descriptores, esto es, conjuntos de atributos ) y se lee X implica Y. El significado, ya aclarado en la introducción, es que, a cada valor de X, le corresponde uno solo de Y. Si X X : X Y, se dice que la dependencia es total. En caso contrario, se dice que es parcial. Si Z : Z X = Ф, Z Y = Ф, X Z, ( Z X ), Z Y ; de la dependencia se dice que es transitiva. Un esquema de relación R viene definido por el par ( T, L ), siendo T el conjunto de atributos y L el conjunto de dependencias. Una clave del esquema es un descriptor K ( subconjunto de T ), tal que : K T, siendo ésta una dependencia total. 3.2 Axiomas de Armstrong. Los Axiomas de Armstrong son más bien reglas de inferencia. Estas reglas permiten deducir todas las dependencias funcionales que tienen lugar entre un conjunto dado de atributos, como consecuencia de las dependencias dato, esto es, de las que se asumen como ciertas a partir del conocimiento del problema. Las dependencias dato equivalen a los axiomas de una teoría ( en sentido lógico ) y los Axiomas de Armstrong son el conjunto completo de reglas deductivas que nos permite deducir cualquier otra dependencia cierta ( teorema de la teoría ). Los Axiomas de Armstrong son : 1
2 Reflexividad : X, X X Proyectividad : { X Y, Z Y } X Z Aumentatividad : { X Y, Z X} Z Y Aditividad :{ X Y, Z V } X Z Y V Transitividad : { X Z, Z Y } X Y El carácter correcto de estas reglas, es obvio y, en todo caso, fácilmente demostrable. Lo que ya es más complicado es demostrar el carácter completo del conjunto, demostración que pertenece al campo de la Lógica y no es en todo caso objeto de este curso básico de Bases de Datos. Lo importante para nosotros es que este resultado ( la completitud del conjunto ), nos permite abordar y resolver una serie de problemas fundamentales que luego nos conducirán al establecimiento de algoritmos de diseño sencillos y fiables. Estos problemas fundamentales, son : Cierre de un conjunto de dependencias. Equivalencia lógica de esquemas. Deducción de dependencias. Cierre de un descriptor respecto de un conjunto de dependencias..cálculo de las claves de un esquema. 3.3 Cierre de un conjunto de dependencias. Equivalencia de esquemas. Sea el esquema R ( T, L ). El cierre del conjunto L de dependencias funcionales es el conjunto de todas las dependencias ciertas ( deducibles a partir de L mediante los Axiomas de Armstrong ). El cierre se representa por L +. Dos conjuntos de dependencias, L y M, relativas al mismo universo T de atributos, son equivalentes si L + = M +, en cuyo caso R ( T, L ) y S ( T, M ) son esquemas equivalentes ( representaciones alternativas y equivalentes del mismo problema ). 2
3 3.4 Deducción de dependencias. Cierre de un descriptor respecto de un conjunto de dependencias. El problema de deducción puede plantearse en estos términos : Dado un esquema R ( T, L ), y dada la dependencia X Y ( no perteneciente a L ), establecer el carácter cierto o falso de la misma. La solución ( teórica ) es, obviamente, calcular L +, y ver si X Y pertenece o no al cierre calculado. El problema radica en la extraordinaria complejidad computacional del cálculo de un cierre ( el libro de Ullmann citado en la bibliografía básica comenta casi siempre algo acerca de la complejidad computacional de los algoritmos que propone ), así que no calcularemos L + en ningún caso. El cierre de un descriptor X respecto de un conjunto de dependencias L, se representa por X + L ( se omite el subíndice si no hay ambigüedad ). El cierre se define así: X X + Z X + : X Z Es decir : X implica a su cierre y no existe ningún superconjunto del mismo que sea implicado por X ( el cierre, en ese sentido, es un conjunto máximo ). A diferencia del cálculo del cierre de un conjunto de dependencias, el cálculo del cierre de un descriptor es computacionalmente simple y permite resolver el problema antes planteado mediante una simple estrategia. Para saber si X Y es cierta en relación a R( T, L ), calculamos X +. Si Y X la dependencia es cierta y no lo es en caso contrario. Si se trata de analizar la equivalencia de dos representaciones del mismo problema, esto es, si R( T, L ) S( T, M ), hay que establecer la equivalencia de los conjuntos M y L de dependencias funcionales. M y L serán equivalentes si sus cierres coinciden. (X Y ) {M-L} se calcula el cierre X + L. Si Y es un subconjunto de dicho cierre en todos los casos, pasamos a calcular V + M, ( V Z ) { L M }. Si Z es un subconjunto del cierre en todos los casos, L y M son conjuntos equivalentes. 3.5 Cálculo del cierre de un descriptor respecto de un conjunto de dependencias funcionales. 3
4 Es un proceso iterativo. Sea X el descriptor y L = { f 1,,f n } el conjunto de dependencias. Se calcula la secuencia X 0,, X i,, X n =X + en la forma siguiente : X 0= X X i+1 =X i { atributos de la derecha de las dependencias en L implicadas por subconjuntos de X i }. Si X i =X i+1, X i es el cierre. Si X i =T, X i es el cierre. Ejemplo: X=BD, f 1 = AB C, f 2 =C A, f 3 =BC D, f 4 = ACD B, f 5 =D EG, f 6 =CG BD, f 7 =BE C, f 8 = CE AG X 0 =BD X 1 =BDEG (usando f 5 ) X 2 =BDEGC ( usando f 7 ) X 3 =BDEGCA ( usando f 2 ) Como no hay más atributos, éste es el cierre. 3.6 Recubrimiento no redundante. Si dos conjuntos de dependencias funcionales, L y M, son equivalentes, o sea, tienen sus cierres iguales ; se dice que L es un recubrimiento de M ( y recíprocamente ). Dado el conjunto L de dependencias funcionales, M es un recubrimiento no redundante si : L M Toda dependencia en M es de la forma X A (segundos miembros simples ) Ningún implicante contiene atributos superfluos ( un atributo es superfluo si su supresión no altera el cierre del conjunto ). 4
5 No hay dependencias redundantes ( una dependencia es redundante si su supresión no altera el cierre del conjunto ). Ejemplo : Calcular un recubrimiento no redundante de : L={ AB C, C A, BC D, ACD B, D EG, BE C, CG BD, CE AG } Aplicando el axioma de proyectividad : L 1 ={ AB C, C A, BC D, ACD B, D E, D G, BE C, CG B, CG D, CE A, CE G } Cuando hay redundancies obvias, pueden ( y deben ) ser eliminadas cuanto antes, pues esto contribuirá a simplificar el problema en su conjunto. Un rápido examen, permite observar que, ya que C A, CE A es redundante y puede eliminarse. Asimismo, ACD B puede sustituirse por CD B. Nos queda el conjunto L 2 en el que, por comodidad de notación, vamos a identificar cada elemento mediante un número de orden : L 2 = { AB C (1 ), C A ( 2 ), BC D ( 3 ), CD B ( 4 ), D E ( 5 ), D G ( 6 ), BE C ( 7 ), CG B ( 8 ), CG D ( 9 ), CE G ( 10 ) } Eliminación de atributos superfluos: Si una dependencia viene implicada por un atributo simple, es obvio que éste no es superfluo. Analicemos los implicantes compuestos : AB C. Si A fuese superfluo, B no podrá serlo, y recíprocamente. Supongamos que se elimina A. Nos queda B C. Si es cierta, A es superfluo Calculamos B + L2 y se obtiene B A no es superfluo. Si eliminamos B,nos queda A C. El cierre A + L2 es A. B no es superfluo. Repitiendo este proceso para todos los implicantes compuestos, puede verse que no hay atributos superfluos (y es un ejercicio muy recomendable para fijar los conceptos ). 5
6 Eliminación de dependencias redundantes : Podemos seguir el orden que queramos, llegando eventualmente a recubrimientos no redundantes distintos, pero equivalentes. Para ver si (1) es redundante, la elimino y calculo AB + L2-{1} : AB + L2-{1}=AB. Como C no pertenece al cierre, (1) no es redundante. Repetimos el proceso: C + L2-{2}= C, así que (2) no es redundante. BC + L2-{3}=ABC, así que (3) no es redundante. CD + L2-{4}=CDAEGB, así que (4) es redundante y se suprime, siendo L 3 =L 2 -{4} D + L3-{5}=DG, así que (5) no es redundante. D + L3-{6}=DE, así que (6) no es redundante. BE + L3-{7}=BE, así que (7) no es redundante. CG + L3-{8}=CGAD, así que (8) no es redundante. CG + L3-{9}=CGABD, así que (9 ) es redundante y se suprime, siendo L 4 =L 3 -{9} CE + L4-{10}=CEA, así que (10) no es redundante. Un recubrimiento no redundante de L es, por tanto : AB C ; C A ; BC D ; D E ; D G ; BE C ; CG B ; CE G En problemas de diseño y cálculo de claves, trabajaremos siempre con recubrimientos no redundantes. 3.7 Determinación de las claves de un esquema. Ahora ya podemos formular la base del procedimiento. Sea el esquema R ( T, L ) con T un conjunto de n atributos. Para calcular las claves, vamos generando los posibles descriptores a partir de los elementos de T, y vamos calculando los cierres respecto de L. Si X + L=T, X es clave ( y ya ignoramos sus superconjuntos ). 6
7 Lo malo es que el número de descriptores a explorar ( en el caso peor ) es 2 n, y es que el problema de calcular todas las claves de un esquema es del tipo NPcompleto, por lo que todos los algoritmos existentes para su computación requieren de mucho tiempo para su ejecución. Afortunadamente, los problemas de diseño sólo requieren del conocimiento de al menos una clave, y, determinar una clave, no suele ser complicado. En este curso, y por limitación del tiempo disponible para impartir este tema, nos limitaremos a calcular una clave de R ( T, L ) para luego rediseñar el esquema en forma de proyecciones normalizadas. 3.8 Cálculo de una clave del esquema R ( T, L ). Lo primero que debe hacerse, es calcular un recubrimiento no redundante de L.Esto despeja un poco los datos de partida y facilita el cálculo de la(s) clave(s), sea cual sea el procedimiento empleado. Ya hemos dicho que el cálculo de todas las claves no es una necesidad en la práctica del diseño. Sólo tendría un sentido si lo que se pretende es establecer el nivel de normalización de un esquema ( enfoque analítico ), para validar un diseño. Pero, ya que partimos de algoritmos que aseguran la normalización del resultado, no tiene más interés en este curso. Ahora bien, para diseñar correctamente, necesitamos conocer al menos una clave. Afortunadamente, esto no es muy complicado. Sea L un conjunto no redundante de dependencias funcionales. Distinguiremos cuatro conjuntos de atributos : I={ atributos que aparecen sólo como implicantes } D={ atributos que aparecen sólo como implicados } ID={ atributos que aparecen como implicantes e implicados } N={ atributos que no aparecen en ninguna dependencia } Es fácil razonar lo siguiente : Los atributos de I forman parte de todas las claves. Los atributos de N forman parte de todas las claves. Los atributos de D no forman parte de ninguna clave. Los atributos de ID pueden formar parte o no de alguna clave. 7
8 Un procedimiento sencillo para determinar una clave, es por tanto el siguiente : 1. Calcular Z=I N. Z es el núcleo del proceso ( intersección de todas las claves, pudiendo ser en algún caso el conjunto vacío ) 2. Calcular Z +. Si este cierre es T, Z es la clave (única) del esquema. Si no es así, sigue la búsqueda de una clave. 3. Z 0 =Z, Z i =Z i-1 { A j }, A j ID 4. Calcular ( Z i ) +. Si este cierre es T, Z i es, en general una superclave del esquema ( es clave o contiene alguna clave ) 5. La(s) clave(s) contenida(s) en Z i se extrae(n) por eliminación de posibles atributos superfluos (distintos de los del núcleo y del último añadido ). En el ejemplo del apartado anterior para cálculo de un recubrimiento no redundante, es fácil ver : ID ={ A B C D E G } I=φ, N=φ, D= φ Z 0 =φ. Z 1 =A, A + =A Z 2 =AB, AB + =T AB es una clave. (Nota: Con relación al punto 3,en el que el núcleo se va incrementando con atributos del conjunto ID, si se diese el caso de que el cierre de Z i incluyese elementos de ID, es obvio que será innecesario añadirlos. Esto es una heurística que puede agilizar el proceso). 8
Diseño de Base de Datos
 Diseño de Base de Datos DISEÑO DE BASE DE DATOS 1 Lectura No. 10 Nombre: Forma normal de Boyce y Codd Contextualización La normalización es un proceso mediante el cual se hace la transformación de datos
Diseño de Base de Datos DISEÑO DE BASE DE DATOS 1 Lectura No. 10 Nombre: Forma normal de Boyce y Codd Contextualización La normalización es un proceso mediante el cual se hace la transformación de datos
Normalización. Conceptos adicionales
 Normalización. Conceptos adicionales Definición formal de normalización Descomposición sin pérdida de información ni de semántica de la relación universal (o de una colección de relaciones equivalentes
Normalización. Conceptos adicionales Definición formal de normalización Descomposición sin pérdida de información ni de semántica de la relación universal (o de una colección de relaciones equivalentes
TEMA I: LOS CONCEPTOS FUNDAMENTALES DE LA TEORÍA DE LA COMPUTABILIDAD
 1 Asignatura: Lógica 3 Curso 2004-2005 Profesor: Juan José Acero 20 25 de Octubre del 2004 TEMA I: LOS CONCEPTOS FUNDAMENTALES DE LA TEORÍA DE LA COMPUTABILIDAD 1. El concepto de algoritmo. Los matemáticos
1 Asignatura: Lógica 3 Curso 2004-2005 Profesor: Juan José Acero 20 25 de Octubre del 2004 TEMA I: LOS CONCEPTOS FUNDAMENTALES DE LA TEORÍA DE LA COMPUTABILIDAD 1. El concepto de algoritmo. Los matemáticos
Dependencias funcionales
 Dependencias funcionales Bases de datos Emi Höss Ejercicio 2, Práctica normalización Considerar los siguientes conjuntos de dependencias funcionales FD1: {BC D, ACD B, CG B, CG D, AB C, C B, D E, BE C,
Dependencias funcionales Bases de datos Emi Höss Ejercicio 2, Práctica normalización Considerar los siguientes conjuntos de dependencias funcionales FD1: {BC D, ACD B, CG B, CG D, AB C, C B, D E, BE C,
Bases de Datos. Tema 7 (parte 1) Teoría de la Normalización. Francisco Ruiz abr UCLM-ESI (F.Ruiz)
 Bases de Datos Tema 7 (parte 1) Teoría de la Normalización Francisco Ruiz abr-2001 documentación preparada con ayuda de Esperanza Marcos (Universidad Rey Juan Carlos) y Mario Piattini (Universidad de Castilla-La
Bases de Datos Tema 7 (parte 1) Teoría de la Normalización Francisco Ruiz abr-2001 documentación preparada con ayuda de Esperanza Marcos (Universidad Rey Juan Carlos) y Mario Piattini (Universidad de Castilla-La
Teoría de Conjuntos. Conjunto es: colección de cosas, o una colección determinada de objetos.
 Teoría de Conjuntos Apuntes Fernando Toscano tomados por A.Diz-Lois La teoría de conjuntos es una herramienta formal semántica que trata de dotar de significado, o lo que es lo mismo dotar de interpretación.
Teoría de Conjuntos Apuntes Fernando Toscano tomados por A.Diz-Lois La teoría de conjuntos es una herramienta formal semántica que trata de dotar de significado, o lo que es lo mismo dotar de interpretación.
5. Dependencias multivaluadas.
 5. Dependencias multivaluadas. 5.1 Definiciones básicas. Una dependencia multivaluada es una sentencia que se escribe : X Y y cuyo significado intuitivo es el siguiente : A cada valor de X se le asocia
5. Dependencias multivaluadas. 5.1 Definiciones básicas. Una dependencia multivaluada es una sentencia que se escribe : X Y y cuyo significado intuitivo es el siguiente : A cada valor de X se le asocia
Teoría de conjuntos. Tema 1: Teoría de Conjuntos.
 Tema 1: Teoría de Conjuntos. La teoría de Conjuntos es actualmente una de las más importantes dentro de la matemática. Muchos de los problemas que se le han presentado a esta disciplina en los últimos
Tema 1: Teoría de Conjuntos. La teoría de Conjuntos es actualmente una de las más importantes dentro de la matemática. Muchos de los problemas que se le han presentado a esta disciplina en los últimos
Espacio de Funciones Medibles
 Capítulo 22 Espacio de Funciones Medibles Igual que la σ-álgebra de los conjuntos medibles, la familia de funciones medibles, además de contener a todas las funciones razonables (por supuesto son medibles
Capítulo 22 Espacio de Funciones Medibles Igual que la σ-álgebra de los conjuntos medibles, la familia de funciones medibles, además de contener a todas las funciones razonables (por supuesto son medibles
Restricción de valor único. Indispensable para diseñar esquemas de bases de datos que eliminen al redundancia.
 CC42A Auxiliar #3 Dependencias funcionales, reglas, axiomas de Armstrong, cerradura de dependencias Martes, 03 de Septiembre de 2002 Profesor: Claudio Gutiérrez Auxiliar: Tania Gallardo Consultas a tgallard@dcc.uchile.cl
CC42A Auxiliar #3 Dependencias funcionales, reglas, axiomas de Armstrong, cerradura de dependencias Martes, 03 de Septiembre de 2002 Profesor: Claudio Gutiérrez Auxiliar: Tania Gallardo Consultas a tgallard@dcc.uchile.cl
Profesor: Rafa González Jiménez. Instituto Santa Eulalia ÍNDICE
 TEMA 5: DERIVADAS. APLICACIONES. ÍNDICE 5..- Derivada de una función en un punto. 5...- Tasa de variación media. Interpretación geométrica. 5..2.- Tasa de variación instantánea. Derivada de una función
TEMA 5: DERIVADAS. APLICACIONES. ÍNDICE 5..- Derivada de una función en un punto. 5...- Tasa de variación media. Interpretación geométrica. 5..2.- Tasa de variación instantánea. Derivada de una función
2. SISTEMAS DE ECUACIONES LINEALES. Introducción
 2. SISTEMAS DE ECUACIONES LINEALES Introducción El presente curso trata sobre álgebra lineal. Al buscarla palabra lineal en un diccionario se encuentra, entre otras definiciones la siguiente: lineal, perteneciente
2. SISTEMAS DE ECUACIONES LINEALES Introducción El presente curso trata sobre álgebra lineal. Al buscarla palabra lineal en un diccionario se encuentra, entre otras definiciones la siguiente: lineal, perteneciente
Proyecciones. Producto escalar de vectores. Aplicaciones
 Proyecciones La proyección de un punto A sobre una recta r es el punto B donde la recta perpendicular a r que pasa por A corta a la recta r. Con un dibujo se entiende muy bien. La proyección de un segmento
Proyecciones La proyección de un punto A sobre una recta r es el punto B donde la recta perpendicular a r que pasa por A corta a la recta r. Con un dibujo se entiende muy bien. La proyección de un segmento
Conjuntos finitos y conjuntos numerables
 Tema 3 Conjuntos finitos y conjuntos numerables En este tema vamos a usar los números naturales para contar los elementos de un conjunto, o dicho con mayor precisión, para definir los conjuntos finitos
Tema 3 Conjuntos finitos y conjuntos numerables En este tema vamos a usar los números naturales para contar los elementos de un conjunto, o dicho con mayor precisión, para definir los conjuntos finitos
Tema 2. Grupos. 3. El conjunto de matrices de orden 2 con coeficientes enteros (o reales) con la suma es un grupo conmutativo.
 Tema 2. Grupos. 1 Grupos Definición 1 Un grupo es una estructura algebraica (G, ) tal que la operación binaria verifica: 1. * es asociativa 2. * tiene elemento neutro 3. todo elemento de G tiene simétrico.
Tema 2. Grupos. 1 Grupos Definición 1 Un grupo es una estructura algebraica (G, ) tal que la operación binaria verifica: 1. * es asociativa 2. * tiene elemento neutro 3. todo elemento de G tiene simétrico.
ANX-PR/CL/001-02 GUÍA DE APRENDIZAJE. ASIGNATURA Control estadistico de procesos. CURSO ACADÉMICO - SEMESTRE 2015-16 - Primer semestre
 ANX-PR/CL/001-02 GUÍA DE APRENDIZAJE ASIGNATURA Control estadistico de procesos CURSO ACADÉMICO - SEMESTRE 2015-16 - Primer semestre GA_05IO_55000602_1S_2015-16 Datos Descriptivos Nombre de la Asignatura
ANX-PR/CL/001-02 GUÍA DE APRENDIZAJE ASIGNATURA Control estadistico de procesos CURSO ACADÉMICO - SEMESTRE 2015-16 - Primer semestre GA_05IO_55000602_1S_2015-16 Datos Descriptivos Nombre de la Asignatura
Números enteros. Dado cualquier número natural, éste siempre será menor que su sucesor, luego los naturales son ordenados.
 Números naturales y cardinales Números enteros Los elementos del conjunto N = {1,2,3, } se denominan números naturales. Si a este conjunto le unimos el conjunto formado por el cero, obtenemos N 0 = {0,1,2,
Números naturales y cardinales Números enteros Los elementos del conjunto N = {1,2,3, } se denominan números naturales. Si a este conjunto le unimos el conjunto formado por el cero, obtenemos N 0 = {0,1,2,
Divisibilidad y congruencias
 Divisibilidad y congruencias Ana Rechtman Bulajich y Carlos Jacob Rubio Barrios Revista Tzaloa, año 1, número 2 Empecemos por explicar el significado de la palabra divisibilidad. En este texto vamos a
Divisibilidad y congruencias Ana Rechtman Bulajich y Carlos Jacob Rubio Barrios Revista Tzaloa, año 1, número 2 Empecemos por explicar el significado de la palabra divisibilidad. En este texto vamos a
Campos gravitatorios en el espacio muestral
 Campos gravitatorios en el espacio muestral Dept. Lenguajes y Ciencias de la Computación Septiembre, 2004 1/28 Enfocando el problema Aprendizaje supervisado Clasificación dicotómica (2 clases) Atributos
Campos gravitatorios en el espacio muestral Dept. Lenguajes y Ciencias de la Computación Septiembre, 2004 1/28 Enfocando el problema Aprendizaje supervisado Clasificación dicotómica (2 clases) Atributos
Ámbito Científico-Tecnológico Módulo III Bloque 3 Unidad 2 Cuanto más, mejor y viceversa
 Ámbito Científico-Tecnológico Módulo III Bloque 3 Unidad 2 Cuanto más, mejor y viceversa Seguro que alguna vez has tenido en tus manos algún cuadernillo de pasatiempos o has realizado algún test psicotécnico
Ámbito Científico-Tecnológico Módulo III Bloque 3 Unidad 2 Cuanto más, mejor y viceversa Seguro que alguna vez has tenido en tus manos algún cuadernillo de pasatiempos o has realizado algún test psicotécnico
1.Introducción al Modelo Relacional.
 1.Introducción al Modelo Relacional. 1.1 Qué es un Modelo?. Cuando en teoría de diseño de bases de datos se emplea el término "modelo", esto no tiene el mismo significado que en Lógica. En Lógica por "modelo"
1.Introducción al Modelo Relacional. 1.1 Qué es un Modelo?. Cuando en teoría de diseño de bases de datos se emplea el término "modelo", esto no tiene el mismo significado que en Lógica. En Lógica por "modelo"
Práctica 3. CÁLCULO DE LA FUNCIÓN SENO UTILIZANDO UN DESARROLLO EN SERIE
 PROGRAMACIÓN (EUI). Curso 2001-2002 Práctica 3. CÁLCULO DE LA FUNCIÓN SENO UTILIZANDO UN DESARROLLO EN SERIE F. Marqués y N. Prieto Índice General 1 Introducción 1 2 El problema 1 2.1 Desarrollo en serie
PROGRAMACIÓN (EUI). Curso 2001-2002 Práctica 3. CÁLCULO DE LA FUNCIÓN SENO UTILIZANDO UN DESARROLLO EN SERIE F. Marqués y N. Prieto Índice General 1 Introducción 1 2 El problema 1 2.1 Desarrollo en serie
Optimización en Ingeniería
 Optimización en Ingeniería Departamento de Computación CINVESTAV-IPN Av. IPN No. 2508 Col. San Pedro Zacatenco México, D.F. 07300 email: ccoello@cs.cinvestav.mx Método de Búsqueda de Fibonacci Algoritmo
Optimización en Ingeniería Departamento de Computación CINVESTAV-IPN Av. IPN No. 2508 Col. San Pedro Zacatenco México, D.F. 07300 email: ccoello@cs.cinvestav.mx Método de Búsqueda de Fibonacci Algoritmo
Matemáticas I: Hoja 1
 Matemáticas I: Hoja 1 1. Números complejos Hasta ahora, hemos visto que los números reales son aquellos que poseen una expresión decimal y que podemos representar en una recta infinita. No obstante, para
Matemáticas I: Hoja 1 1. Números complejos Hasta ahora, hemos visto que los números reales son aquellos que poseen una expresión decimal y que podemos representar en una recta infinita. No obstante, para
Estructuras de control. Secuencial, condicional y repetitivas.
 Estructuras de control. Secuencial, condicional y repetitivas. 1 Estructuras de control. Hemos visto en los diagramas de flujo y pseudo-código que: 1) Se piden datos de entrada (al usuario) Asiganción
Estructuras de control. Secuencial, condicional y repetitivas. 1 Estructuras de control. Hemos visto en los diagramas de flujo y pseudo-código que: 1) Se piden datos de entrada (al usuario) Asiganción
Conjuntos disjuntos (Relaciones de equivalencia)
 Conjuntos disjuntos (Relaciones de equivalencia) Una relación R se define en un conjunto C si para todo par de elementos (a,b),a,b C,a R b es verdadera o falsa. Una relación de equivalencia es una relación
Conjuntos disjuntos (Relaciones de equivalencia) Una relación R se define en un conjunto C si para todo par de elementos (a,b),a,b C,a R b es verdadera o falsa. Una relación de equivalencia es una relación
VALORES EXACTOS DE FUNCIONES TRIGONOMÉTRICAS (SENO Y COSENO)
 VALORES EXACTOS DE FUNCIONES TRIGONOMÉTRICAS (SENO Y COSENO) En trigonometría plana, es fácil de encontrar el valor exacto de la función seno y coseno de los ángulos de 30, 5 y 60, gracias a la ayuda de
VALORES EXACTOS DE FUNCIONES TRIGONOMÉTRICAS (SENO Y COSENO) En trigonometría plana, es fácil de encontrar el valor exacto de la función seno y coseno de los ángulos de 30, 5 y 60, gracias a la ayuda de
El cuerpo de los números reales
 Capítulo 1 El cuerpo de los números reales 1.1. Introducción Existen diversos enfoques para introducir los números reales: uno de ellos parte de los números naturales 1, 2, 3,... utilizándolos para construir
Capítulo 1 El cuerpo de los números reales 1.1. Introducción Existen diversos enfoques para introducir los números reales: uno de ellos parte de los números naturales 1, 2, 3,... utilizándolos para construir
VALOR ABSOLUTO. Definición.- El valor absoluto de un número real, x, se define como:
 VALOR ABSOLUTO Cualquier número a tiene su representación en la recta real. El valor absoluto de un número representa la distancia del punto a al origen. Observe en el dibujo que la distancia del al origen
VALOR ABSOLUTO Cualquier número a tiene su representación en la recta real. El valor absoluto de un número representa la distancia del punto a al origen. Observe en el dibujo que la distancia del al origen
Representación de números enteros: el convenio complemento a dos
 Representación de números enteros: el convenio complemento a dos Apellidos, nombre Martí Campoy, Antonio (amarti@disca.upv.es) Departamento Centro Informàtica de Sistemes i Computadors Escola Tècnica Superior
Representación de números enteros: el convenio complemento a dos Apellidos, nombre Martí Campoy, Antonio (amarti@disca.upv.es) Departamento Centro Informàtica de Sistemes i Computadors Escola Tècnica Superior
Universidad Nacional del Sur Departamento de Ciencias e Ingeniería de la Computación Elementos de Bases de Datos 2do. Cuatrimestre de 2004
 2do. Cuatrimestre de 2004 Elementos de Bases de Datos Dpto.Ciencias e Ingeniería de la Computación Universidad Nacional del Sur Lic. María Mercedes Vitturini [mvitturi@cs.uns.edu.ar] Clase 9 1er. Cuatrimestre
2do. Cuatrimestre de 2004 Elementos de Bases de Datos Dpto.Ciencias e Ingeniería de la Computación Universidad Nacional del Sur Lic. María Mercedes Vitturini [mvitturi@cs.uns.edu.ar] Clase 9 1er. Cuatrimestre
PUNTOS Y VECTORES EN EL PLANO
 PUNTOS Y VECTORES EN EL PLANO PUNTOS EN EL PLANO Tomando como referencia los ejes cartesianos del plano, un punto se representa mediante un par ordenado (a, b) de números reales, es decir, mediante un
PUNTOS Y VECTORES EN EL PLANO PUNTOS EN EL PLANO Tomando como referencia los ejes cartesianos del plano, un punto se representa mediante un par ordenado (a, b) de números reales, es decir, mediante un
Introducción a la Geometría Computacional
 Dr. Eduardo A. RODRÍGUEZ TELLO CINVESTAV-Tamaulipas 8 de enero del 2013 Dr. Eduardo RODRÍGUEZ T. (CINVESTAV) Introducción a la GC 8 de enero del 2013 1 / 17 1 Introducción a la Geometría Computacional
Dr. Eduardo A. RODRÍGUEZ TELLO CINVESTAV-Tamaulipas 8 de enero del 2013 Dr. Eduardo RODRÍGUEZ T. (CINVESTAV) Introducción a la GC 8 de enero del 2013 1 / 17 1 Introducción a la Geometría Computacional
Práctica 2 Métodos de búsqueda para funciones de una variable
 Práctica 2 Métodos de búsqueda para funciones de una variable Introducción Definición 1. Una función real f se dice que es fuertemente cuasiconvexa en el intervalo (a, b) si para cada par de puntos x 1,
Práctica 2 Métodos de búsqueda para funciones de una variable Introducción Definición 1. Una función real f se dice que es fuertemente cuasiconvexa en el intervalo (a, b) si para cada par de puntos x 1,
4. Método Simplex de Programación Lineal
 Temario Modelos y Optimización I 4. Método Simplex de Programación Lineal A- Resolución de problemas, no particulares, con representación gráfica. - Planteo ordenado de las inecuaciones. - Introducción
Temario Modelos y Optimización I 4. Método Simplex de Programación Lineal A- Resolución de problemas, no particulares, con representación gráfica. - Planteo ordenado de las inecuaciones. - Introducción
Dependencia e independencia lineal
 CAPíTULO 3 Dependencia e independencia lineal En este capítulo estudiaremos tres conceptos de gran importancia para el desarrollo del álgebra lineal: el concepto de conjunto generador, el concepto de conjunto
CAPíTULO 3 Dependencia e independencia lineal En este capítulo estudiaremos tres conceptos de gran importancia para el desarrollo del álgebra lineal: el concepto de conjunto generador, el concepto de conjunto
Relaciones IIC1253. IIC1253 Relaciones 1 / 32
 Relaciones IIC1253 IIC1253 Relaciones 1 / 32 Relaciones binarias Dado: conjunto A R es una relación binaria sobre A si R A A. Para indicar que a,b A están relacionados a través de R usamos las notaciones:
Relaciones IIC1253 IIC1253 Relaciones 1 / 32 Relaciones binarias Dado: conjunto A R es una relación binaria sobre A si R A A. Para indicar que a,b A están relacionados a través de R usamos las notaciones:
TEORÍA DE LA NORMALIZACIÓN GESTIÓN Y MODELACIÓN DE DATOS
 TEORÍA DE LA NORMALIZACIÓN GESTIÓN Y MODELACIÓN DE DATOS Problemas que se pueden presentar en un esquema relacional CcEmpleado Nombre Departamento CiudadDpto Jefe 39288271 Sonia Maria Osorio Ventas Cali
TEORÍA DE LA NORMALIZACIÓN GESTIÓN Y MODELACIÓN DE DATOS Problemas que se pueden presentar en un esquema relacional CcEmpleado Nombre Departamento CiudadDpto Jefe 39288271 Sonia Maria Osorio Ventas Cali
Tema 4 Probabilidad condicionada: teoremas básicos. Independencia de sucesos
 Tema 4 Probabilidad condicionada: teoremas básicos. Independencia de sucesos 1. Probabilidad condicionada. Espacio de probabilidad condicionado La probabilidad condicionada es uno de los conceptos clave
Tema 4 Probabilidad condicionada: teoremas básicos. Independencia de sucesos 1. Probabilidad condicionada. Espacio de probabilidad condicionado La probabilidad condicionada es uno de los conceptos clave
PROGRAMACIÓN LINEAL. 1. Introducción
 PROGRAMACIÓN LINEAL 1. Introducción La programación lineal es una técnica matemática relativamente reciente (siglo XX), que consiste en una serie de métodos y procedimientos que permiten resolver problemas
PROGRAMACIÓN LINEAL 1. Introducción La programación lineal es una técnica matemática relativamente reciente (siglo XX), que consiste en una serie de métodos y procedimientos que permiten resolver problemas
3.1 Reglas de equivalencia
 3.1 Reglas de equivalencia En esta sección estudiarás y aplicarás algunas reglas de equivalencia de proposiciones lógicas. Es decir, vamos a empezar a aplicar algunas reglas que nos permitirán transformar
3.1 Reglas de equivalencia En esta sección estudiarás y aplicarás algunas reglas de equivalencia de proposiciones lógicas. Es decir, vamos a empezar a aplicar algunas reglas que nos permitirán transformar
Oliverio J. Santana Jaria. Sistemas Digitales Ingeniería Técnica en Informática de Sistemas Curso 2006 2007
 Oliverio J. Santana Jaria Sistemas Digitales Ingeniería Técnica en Informática de Sistemas Curso 2006 2007 7. Álgebra de Boole Este El que éxito resulta de la diseñar tecnología y fabricar digital circuitos
Oliverio J. Santana Jaria Sistemas Digitales Ingeniería Técnica en Informática de Sistemas Curso 2006 2007 7. Álgebra de Boole Este El que éxito resulta de la diseñar tecnología y fabricar digital circuitos
A partir de la definición obtenemos las siguientes propiedades para estas funciones:
 Capítulo 1 Conjuntos Supondremos conocidas las nociones básicas sobre teoría de conjuntos, tales como subconjuntos, elementos, unión, intersección, complemento, diferencia, diferencia simétrica, propiedades
Capítulo 1 Conjuntos Supondremos conocidas las nociones básicas sobre teoría de conjuntos, tales como subconjuntos, elementos, unión, intersección, complemento, diferencia, diferencia simétrica, propiedades
Reglas de derivación. 4.1. Sumas, productos y cocientes. Tema 4
 Tema 4 Reglas de derivación Aclarado el concepto de derivada, pasamos a desarrollar las reglas básicas para el cálculo de derivadas o, lo que viene a ser lo mismo, a analizar la estabilidad de las funciones
Tema 4 Reglas de derivación Aclarado el concepto de derivada, pasamos a desarrollar las reglas básicas para el cálculo de derivadas o, lo que viene a ser lo mismo, a analizar la estabilidad de las funciones
TEMA 2: EL INTERÉS SIMPLE
 TEMA 2: EL INTERÉS SIMPLE 1.- CAPITALIZACIÓN SIMPLE 1.1.- CÁLCULO DEL INTERÉS: Recibe el nombre de capitalización simple la ley financiera según la cual los intereses de cada periodo de capitalización
TEMA 2: EL INTERÉS SIMPLE 1.- CAPITALIZACIÓN SIMPLE 1.1.- CÁLCULO DEL INTERÉS: Recibe el nombre de capitalización simple la ley financiera según la cual los intereses de cada periodo de capitalización
Autómatas finitos no deterministas (AFnD)
 Autómatas finitos no deterministas (AFnD) Elvira Mayordomo Universidad de Zaragoza 1 de octubre de 2012 Contenido de este tema Introducción y ejemplos de autómatas finitos no deterministas Definición de
Autómatas finitos no deterministas (AFnD) Elvira Mayordomo Universidad de Zaragoza 1 de octubre de 2012 Contenido de este tema Introducción y ejemplos de autómatas finitos no deterministas Definición de
Modelo Relacional. Bibliografía: Fundamentos de bases de datos Korth, Silberschatz
 Modelo Relacional Bibliografía: Fundamentos de bases de datos Korth, Silberschatz Modelos de datos Colección de herramientas conceptuales para describir datos, relaciones entre ellos, semántica asociada
Modelo Relacional Bibliografía: Fundamentos de bases de datos Korth, Silberschatz Modelos de datos Colección de herramientas conceptuales para describir datos, relaciones entre ellos, semántica asociada
Conjuntos y relaciones
 Conjuntos y relaciones Introducción Propiedades de las relaciones Sobre un conjunto Reflexivas Simétricas y transitivas Cerradura Relaciones de equivalencia Órdenes parciales Diagramas de Hasse Introducción
Conjuntos y relaciones Introducción Propiedades de las relaciones Sobre un conjunto Reflexivas Simétricas y transitivas Cerradura Relaciones de equivalencia Órdenes parciales Diagramas de Hasse Introducción
descripción del argumento identificador tipo longitud condición restricción
 Recuerde que estos son apuntes muy simplificados que deberá completar con la bibliografía PROGRAMACIÓN 0 Prof. Dolores Cuiñas H. recomendada APUNTES Nº. METODOLOGÍA PARA LA CONSTRUCCIÓN DE PROGRAMAS. Presentaremos
Recuerde que estos son apuntes muy simplificados que deberá completar con la bibliografía PROGRAMACIÓN 0 Prof. Dolores Cuiñas H. recomendada APUNTES Nº. METODOLOGÍA PARA LA CONSTRUCCIÓN DE PROGRAMAS. Presentaremos
Universidad Nacional del Sur Departamento de Ciencias e Ingeniería de la Computación Elementos de Bases de Datos 2do. Cuatrimestre de 2004
 2do. Cuatrimestre de 2004 Elementos de Bases de Datos Dpto.Ciencias e Ingeniería de la Computación Universidad Nacional del Sur Lic. María Mercedes Vitturini [mvitturi@cs.uns.edu.ar] Qué constituye un
2do. Cuatrimestre de 2004 Elementos de Bases de Datos Dpto.Ciencias e Ingeniería de la Computación Universidad Nacional del Sur Lic. María Mercedes Vitturini [mvitturi@cs.uns.edu.ar] Qué constituye un
CURSOSO. Aritmética: Númerosnaturalesyenteros. Númerosracionalesyfraciones. MATEMÁTICAS. AntonioF.CostaGonzález
 CURSOSO CURSOSO MATEMÁTICAS Aritmética: Númerosnaturalesyenteros. Númerosracionalesyfraciones. AntonioF.CostaGonzález DepartamentodeMatemáticasFundamentales FacultaddeCiencias Índice 1 Introducción y objetivos
CURSOSO CURSOSO MATEMÁTICAS Aritmética: Númerosnaturalesyenteros. Númerosracionalesyfraciones. AntonioF.CostaGonzález DepartamentodeMatemáticasFundamentales FacultaddeCiencias Índice 1 Introducción y objetivos
Parte 1: Introducción a la lógica funcional Parte 2: Introducción a la teoría intuitiva de conjuntos
 Parte 1: Introducción a la lógica funcional Parte 2: Introducción a la teoría intuitiva de conjuntos Material preparado por: Prof. Ana María Tosetti Revisado y complementado por: Ing. Freddy Rabín Catedrático
Parte 1: Introducción a la lógica funcional Parte 2: Introducción a la teoría intuitiva de conjuntos Material preparado por: Prof. Ana María Tosetti Revisado y complementado por: Ing. Freddy Rabín Catedrático
4. " $#%&' (#) para todo $#* (desigualdad triangular).
 10 Capítulo 2 Espacios Métricos 21 Distancias y espacios métricos Definición 211 (Distancia) Dado un conjunto, una distancia es una aplicación que a cada par le asocia un número real y que cumple los siguientes
10 Capítulo 2 Espacios Métricos 21 Distancias y espacios métricos Definición 211 (Distancia) Dado un conjunto, una distancia es una aplicación que a cada par le asocia un número real y que cumple los siguientes
si este límite es finito, y en este caso decimos que f es integrable (impropia)
 Capítulo 6 Integrales impropias menudo resulta útil poder integrar funciones que no son acotadas, e incluso integrarlas sobre recintos no acotados. En este capítulo desarrollaremos brevemente una teoría
Capítulo 6 Integrales impropias menudo resulta útil poder integrar funciones que no son acotadas, e incluso integrarlas sobre recintos no acotados. En este capítulo desarrollaremos brevemente una teoría
Vemos que t3 y t4 serían las mismas tuplas que las dadas. En este caso no se agregan tuplas.
 EJERCICIOS DE DEPENDENCIAS MULTIVALUADAS (DMV): EJERCICIO 1: La relación R(X,Y,Z) satisface las DMV X->->Y. Si r contiene las tuplas (0,1,2) y (0,3,4), Qué otras tuplas deben aparecer necesariamente en
EJERCICIOS DE DEPENDENCIAS MULTIVALUADAS (DMV): EJERCICIO 1: La relación R(X,Y,Z) satisface las DMV X->->Y. Si r contiene las tuplas (0,1,2) y (0,3,4), Qué otras tuplas deben aparecer necesariamente en
SUBCONJUNTOS y CONJUNTO POTENCIA. COMP 2501: Estructuras Computacionales Discretas I Dra. Madeline Ortiz Rodríguez 3 de septiembre de 2013
 1 SUBCONJUNTOS y CONJUNTO POTENCIA COMP 2501: Estructuras Computacionales Discretas I Dra. Madeline Ortiz Rodríguez 3 de septiembre de 2013 2 Material de Estudio Libro de Koshy: páginas 71-72, 78-84. Vídeos
1 SUBCONJUNTOS y CONJUNTO POTENCIA COMP 2501: Estructuras Computacionales Discretas I Dra. Madeline Ortiz Rodríguez 3 de septiembre de 2013 2 Material de Estudio Libro de Koshy: páginas 71-72, 78-84. Vídeos
f (x) (1+[f (x)] 2 ) 3 2 κ(x) =
![f (x) (1+[f (x)] 2 ) 3 2 κ(x) = f (x) (1+[f (x)] 2 ) 3 2 κ(x) =](/thumbs/40/20918876.jpg) MATEMÁTICAS II - EXAMEN PRIMER PARCIAL - 4/11/11 Grado: Ing. Electrónica Rob. y Mec. Ing. Energía Ing. Organización Ind. Nombre y Apellidos: Ejercicio 1. La curvatura de una función f en un punto x viene
MATEMÁTICAS II - EXAMEN PRIMER PARCIAL - 4/11/11 Grado: Ing. Electrónica Rob. y Mec. Ing. Energía Ing. Organización Ind. Nombre y Apellidos: Ejercicio 1. La curvatura de una función f en un punto x viene
Tema 4: Múltiplos y Divisores
 Tema 4: Múltiplos y Divisores Índice 1. Introducción. 2. Múltiplos de un número. 3. Divisores de un número. 4. Criterios de divisibilidad. 5. Números primos y números compuestos. 6. Descomposición de un
Tema 4: Múltiplos y Divisores Índice 1. Introducción. 2. Múltiplos de un número. 3. Divisores de un número. 4. Criterios de divisibilidad. 5. Números primos y números compuestos. 6. Descomposición de un
Recopilación de preguntas de exámenes anteriores de dependencias funcionales y normalización
 Recopilación de preguntas de exámenes anteriores de dependencias funcionales y normalización 1.- Dado el siguiente esquema y conjunto de dependencias funcionales: R={A, B, C, D, E, F, G}, DF={BD->A, C->D,
Recopilación de preguntas de exámenes anteriores de dependencias funcionales y normalización 1.- Dado el siguiente esquema y conjunto de dependencias funcionales: R={A, B, C, D, E, F, G}, DF={BD->A, C->D,
Lógica Proposicional, Teoremas y Demostraciones
 Lógica Proposicional, Teoremas y Demostraciones Manuel Maia 19 de marzo de 2012 1 Proposiciones Una proposición es una oración declarativa o una expresión matemática que es verdadera o es falsa, pero no
Lógica Proposicional, Teoremas y Demostraciones Manuel Maia 19 de marzo de 2012 1 Proposiciones Una proposición es una oración declarativa o una expresión matemática que es verdadera o es falsa, pero no
DISEÑO LÓGICO DE UNA BASE DE DATOS EN EL MODELO RELACIONAL (Teoría de la Normalización)
 Tema IV: Teoría de la Normalización 41 Noción intuitiva de las primeras formas normales 42 Dependencias funcionales 43 Definición formal de las tres primeras formas normales 44 Forma Normal de Boyce y
Tema IV: Teoría de la Normalización 41 Noción intuitiva de las primeras formas normales 42 Dependencias funcionales 43 Definición formal de las tres primeras formas normales 44 Forma Normal de Boyce y
Expresiones algebraicas
 Expresiones algebraicas Expresiones algebraicas Las expresiones algebraicas Elementos de una expresión algebraica Números de cualquier tipo Letras Signos de operación: sumas, restas, multiplicaciones y
Expresiones algebraicas Expresiones algebraicas Las expresiones algebraicas Elementos de una expresión algebraica Números de cualquier tipo Letras Signos de operación: sumas, restas, multiplicaciones y
Normalización de Modelos Relacionales
 Normalización de Modelos Relacionales Grupo de Ingeniería del Software y Bases de Datos Universidad de Sevilla octubre 2012 Objetivos de este tema Conocer las problemas que presentan los no normalizados.
Normalización de Modelos Relacionales Grupo de Ingeniería del Software y Bases de Datos Universidad de Sevilla octubre 2012 Objetivos de este tema Conocer las problemas que presentan los no normalizados.
Teoría de Autómatas y Lenguajes Formales. Capítulo 1: Introducción. Teoría de Autómatas y Lenguajes formales es un repaso a la informática teórica.
 Teoría de Autómatas y Lenguajes Formales Capítulo 1: Introducción Holger Billhardt holger.billhardt@urjc.es Introducción Teoría de Autómatas y Lenguajes formales es un repaso a la informática teórica.
Teoría de Autómatas y Lenguajes Formales Capítulo 1: Introducción Holger Billhardt holger.billhardt@urjc.es Introducción Teoría de Autómatas y Lenguajes formales es un repaso a la informática teórica.
La herramienta ArtEM: Aritmética Entera y Modular
 La herramienta ArtEM: Aritmética Entera y Modular 1. Introducción La herramienta ArtEM (Aritmética Entera y Modular) es una aplicación informática programada en Visual Basic y desarrollada con el fin de
La herramienta ArtEM: Aritmética Entera y Modular 1. Introducción La herramienta ArtEM (Aritmética Entera y Modular) es una aplicación informática programada en Visual Basic y desarrollada con el fin de
Cardinalidad. Teorema 0.3 Todo conjunto infinito contiene un subconjunto infinito numerable.
 Cardinalidad Dados dos conjuntos A y B, decimos que A es equivalente a B, o que A y B tienen la misma potencia, y lo notamos A B, si existe una biyección de A en B Es fácil probar que es una relación de
Cardinalidad Dados dos conjuntos A y B, decimos que A es equivalente a B, o que A y B tienen la misma potencia, y lo notamos A B, si existe una biyección de A en B Es fácil probar que es una relación de
Matrices. p ij = a ik b kj = a i1 b 1j + a i2 b 2j + + a in b nj.
 Matrices Introducción Una matriz de m filas y n columnas con elementos en el cuerpo K es un rectángulo de elementos de K (es decir, números) del tipo a a 2 a n a 2 a 22 a 2n A = (a ij ) = a m a m2 a mn
Matrices Introducción Una matriz de m filas y n columnas con elementos en el cuerpo K es un rectángulo de elementos de K (es decir, números) del tipo a a 2 a n a 2 a 22 a 2n A = (a ij ) = a m a m2 a mn
TEMA 1. NÚMEROS REALES Y COMPLEJOS
 TEMA 1. NÚMEROS REALES Y COMPLEJOS 1.1 DEFINICIÓN AXIOMATICA DE LOS NÚMEROS REALES 1.1.1 Axiomas de cuerpo En admitimos la existencia de dos operaciones internas la suma y el producto, con estas operaciones
TEMA 1. NÚMEROS REALES Y COMPLEJOS 1.1 DEFINICIÓN AXIOMATICA DE LOS NÚMEROS REALES 1.1.1 Axiomas de cuerpo En admitimos la existencia de dos operaciones internas la suma y el producto, con estas operaciones
Complejidad algorítmica. Algoritmos y Estructuras de Datos II (Programación I) Mgter. Vallejos, Oscar A.
 Complejidad algorítmica Complejidad Algorítmica En particular, usualmente se estudia la eficiencia de un algoritmo en tiempo (de ejecución), espacio (de memoria) o número de procesadores (en algoritmos
Complejidad algorítmica Complejidad Algorítmica En particular, usualmente se estudia la eficiencia de un algoritmo en tiempo (de ejecución), espacio (de memoria) o número de procesadores (en algoritmos
Teoremas de Circuitos
 1 Teoremas de Circuitos Existen varios métodos para simplificar la resolución de circuitos eléctricos y que son básicos para la aplicación de la Electrotecnia a otras disciplinas relacionadas como los
1 Teoremas de Circuitos Existen varios métodos para simplificar la resolución de circuitos eléctricos y que son básicos para la aplicación de la Electrotecnia a otras disciplinas relacionadas como los
Existen distintas formas de representar una función lógica, entre las que podemos destacar las siguientes:
 Función booleana Se denomina función lógica o booleana a aquella función matemática cuyas variables son binarias y están unidas mediante los operadores del álgebra de Boole suma lógica (+), producto lógico
Función booleana Se denomina función lógica o booleana a aquella función matemática cuyas variables son binarias y están unidas mediante los operadores del álgebra de Boole suma lógica (+), producto lógico
Dependencias Funcionales. Bibliografía: Fundamentos de bases de datos Korth, Silberschatz
 Dependencias Funcionales Bibliografía: Fundamentos de bases de datos Korth, Silberschatz Conceptos básicos Las DF son un tipo particular de restricción. Permiten expresar hechos acerca de la realidad que
Dependencias Funcionales Bibliografía: Fundamentos de bases de datos Korth, Silberschatz Conceptos básicos Las DF son un tipo particular de restricción. Permiten expresar hechos acerca de la realidad que
Normalización. Carlos A. Olarte Bases de Datos I
 Carlos A. Olarte Bases de Datos I Outline 1 Introducción 2 Dependencias Funcionales 3 Diseño de Bases de Datos 4 Forma Normal Boyce-Codd (FNBC) 5 3FN 6 Dependneicas Funcionales Multivaluadas 7 4FN Introducción
Carlos A. Olarte Bases de Datos I Outline 1 Introducción 2 Dependencias Funcionales 3 Diseño de Bases de Datos 4 Forma Normal Boyce-Codd (FNBC) 5 3FN 6 Dependneicas Funcionales Multivaluadas 7 4FN Introducción
Es la cantidad de electricidad (electrones) que recorre un circuito eléctrico en una unidad. Q t I =
 3º E.S.O. UNIDAD DIDÁCTICA: EL CIRCUITO ELÉCTRICO Intensidad de corriente eléctrica (medida de una corriente eléctrica) Es la cantidad de electricidad (electrones) que recorre un circuito eléctrico en
3º E.S.O. UNIDAD DIDÁCTICA: EL CIRCUITO ELÉCTRICO Intensidad de corriente eléctrica (medida de una corriente eléctrica) Es la cantidad de electricidad (electrones) que recorre un circuito eléctrico en
Matemáticas Propedéutico para Bachillerato. Introducción
 ctividad 1. Notación de Conjuntos. Introducción La Teoría de Conjuntos fue introducida por el matemático alemán George Cantor. Desde pequeños hemos estado en contacto con ella, por ejemplo, quién de ustedes
ctividad 1. Notación de Conjuntos. Introducción La Teoría de Conjuntos fue introducida por el matemático alemán George Cantor. Desde pequeños hemos estado en contacto con ella, por ejemplo, quién de ustedes
ÁLGEBRA LINEAL Y GEOMETRÍA ANALÍTICA (0250)
 Universidad Central de Venezuela Facultad de Ingeniería Ciclo Básico Departamento de Matemática Aplicada ÁLGEBRA LINEAL Y GEOMETRÍA ANALÍTICA (0250) Semestre 1-2011 Mayo 2011 Álgebra Lineal y Geometría
Universidad Central de Venezuela Facultad de Ingeniería Ciclo Básico Departamento de Matemática Aplicada ÁLGEBRA LINEAL Y GEOMETRÍA ANALÍTICA (0250) Semestre 1-2011 Mayo 2011 Álgebra Lineal y Geometría
1. INTRODUCCIÓN A LA MODELIZACIÓN CONCEPTUAL DE DATOS
 TEMA 5: MODELIZACIÓN CONCEPTUAL DE DATOS 1. INTRODUCCIÓN A LA MODELIZACIÓN CONCEPTUAL DE DATOS 2. MODELO CONCEPTUAL DE DATOS 2.1. Características Generales. 2.2. Pasos para su Desarrollo. 2.3. Añadir Detalles
TEMA 5: MODELIZACIÓN CONCEPTUAL DE DATOS 1. INTRODUCCIÓN A LA MODELIZACIÓN CONCEPTUAL DE DATOS 2. MODELO CONCEPTUAL DE DATOS 2.1. Características Generales. 2.2. Pasos para su Desarrollo. 2.3. Añadir Detalles
Números naturales, principio de inducción
 , principio de inducción. Conjuntos inductivos. Denotaremos por IN al conjunto de números naturales, IN {,,, 4, 5, 6,...}, cuyos elementos son suma de un número finito de unos. Recordemos que IN es cerrado
, principio de inducción. Conjuntos inductivos. Denotaremos por IN al conjunto de números naturales, IN {,,, 4, 5, 6,...}, cuyos elementos son suma de un número finito de unos. Recordemos que IN es cerrado
Es la cantidad de electricidad (electrones) que recorre un circuito eléctrico en una unidad. Q t I =
 3º E.S.O. UNIDAD DIDÁCTICA: EL CIRCUITO ELÉCTRICO Intensidad de corriente eléctrica (medida de una corriente eléctrica) Es la cantidad de electricidad (electrones) que recorre un circuito eléctrico en
3º E.S.O. UNIDAD DIDÁCTICA: EL CIRCUITO ELÉCTRICO Intensidad de corriente eléctrica (medida de una corriente eléctrica) Es la cantidad de electricidad (electrones) que recorre un circuito eléctrico en
RSA: Implementación. Ya resolvimos (3), ahora vamos a resolver (2). IIC3242 Complejidad Probabiĺıstica 28 / 77
 RSA: Implementación Para poder implementar RSA necesitamos algoritmos eficientes para los siguientes problemas: (1) Generar primos P y Q (2) Generar números e y d tales que e d modφ(n) = 1 (3) Calcular
RSA: Implementación Para poder implementar RSA necesitamos algoritmos eficientes para los siguientes problemas: (1) Generar primos P y Q (2) Generar números e y d tales que e d modφ(n) = 1 (3) Calcular
Ejemplo 1. Ejemplo introductorio
 . -Jordan. Ejemplo 1. Ejemplo introductorio. -Jordan Dos especies de insectos se crían juntas en un recipiente de laboratorio. Todos los días se les proporcionan dos tipos de alimento A y B. 1 individuo
. -Jordan. Ejemplo 1. Ejemplo introductorio. -Jordan Dos especies de insectos se crían juntas en un recipiente de laboratorio. Todos los días se les proporcionan dos tipos de alimento A y B. 1 individuo
Inteligencia Artificial
 Programa de la Asignatura: Inteligencia Artificial Código: 773 Carrera: Ingeniería en Computación Plan: 2008 Carácter: Obligatoria Unidad Académica: Secretaría Académica Curso: Tercer Año Segundo cuatrimestre
Programa de la Asignatura: Inteligencia Artificial Código: 773 Carrera: Ingeniería en Computación Plan: 2008 Carácter: Obligatoria Unidad Académica: Secretaría Académica Curso: Tercer Año Segundo cuatrimestre
Curso Completo de Electrónica Digital. 3.7. Simplificación de funciones booleanas
 CURSO Curso Completo de Electrónica Digital Departamento de Electronica y Comunicaciones Universidad Pontifica de Salamanca en Madrid Prof. Juan González Gómez Capítulo 3 ALGEBRA DE BOOLE Continuación...
CURSO Curso Completo de Electrónica Digital Departamento de Electronica y Comunicaciones Universidad Pontifica de Salamanca en Madrid Prof. Juan González Gómez Capítulo 3 ALGEBRA DE BOOLE Continuación...
Lógica de Predicados
 Lógica de Predicados En las últimas décadas, ha aumentado considerablemente el interés de la informática por la aplicación de la lógica a la programación. De hecho, ha aparecido un nuevo paradigma de programación,
Lógica de Predicados En las últimas décadas, ha aumentado considerablemente el interés de la informática por la aplicación de la lógica a la programación. De hecho, ha aparecido un nuevo paradigma de programación,
Facultad de Informática UCM - Examen Parcial Convocatoria de Febrero Curso 2009/2010 Grupo A Bases de Datos y Sistemas de la Información SOLUCIÓN
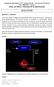 Facultad de Informática UCM - Examen Parcial Convocatoria de Febrero Curso 2009/2010 Grupo A Bases de Datos y Sistemas de la Información Ejercicio 1: 2 puntos SOLUCIÓN a) Se desea diseñar un diagrama Entidad
Facultad de Informática UCM - Examen Parcial Convocatoria de Febrero Curso 2009/2010 Grupo A Bases de Datos y Sistemas de la Información Ejercicio 1: 2 puntos SOLUCIÓN a) Se desea diseñar un diagrama Entidad
Operaciones lógicas principales: Negación, Conjunción y Disyunción
 Operaciones lógicas principales: Negación, Conjunción y Disyunción Definiciones informales. A es verdadera A es falsa A B es verdadera A es verdadera y B es verdadera A B es verdadera A es verdadera o
Operaciones lógicas principales: Negación, Conjunción y Disyunción Definiciones informales. A es verdadera A es falsa A B es verdadera A es verdadera y B es verdadera A B es verdadera A es verdadera o
f n = 0 si n = 0 (ER)
 1. El significado de la recursión La recursión (en particular la iteración) es una componente fundamental de los lenguajes de programación. Vamos aquí a mostrar cuales son las dificultades que surgen al
1. El significado de la recursión La recursión (en particular la iteración) es una componente fundamental de los lenguajes de programación. Vamos aquí a mostrar cuales son las dificultades que surgen al
Práctica 2 - Hay diferentes infinitos?- A. Propiedades básicas de los Conjuntos
 Cálculo Avanzado Primer Cuatrimestre de 2011 Práctica 2 - Hay diferentes infinitos?- Llamaremos número cardinal de M al concepto general que, por medio de nuestra activa capacidad de pensar, surge del
Cálculo Avanzado Primer Cuatrimestre de 2011 Práctica 2 - Hay diferentes infinitos?- Llamaremos número cardinal de M al concepto general que, por medio de nuestra activa capacidad de pensar, surge del
Conceptos básicos de la matemática
 , 1 2 Contents 1 Conceptos básicos de la matemática 5 1.1 Introducción................................... 5 1.2 Conjuntos.................................... 5 1.2.1 Clases de conjuntos...........................
, 1 2 Contents 1 Conceptos básicos de la matemática 5 1.1 Introducción................................... 5 1.2 Conjuntos.................................... 5 1.2.1 Clases de conjuntos...........................
Universidad Politécnica de Puerto Rico Departamento de Ciencias y Matemáticas. Preparado por: Prof. Manuel Capella-Casellas, M.A.Ed.
 Universidad Politécnica de Puerto Rico Departamento de Ciencias y Matemáticas Preparado por: Prof. Manuel Capella-Casellas, M.A.Ed. Agosto, 00 Notación exponencial La notación exponencial se usa para repetir
Universidad Politécnica de Puerto Rico Departamento de Ciencias y Matemáticas Preparado por: Prof. Manuel Capella-Casellas, M.A.Ed. Agosto, 00 Notación exponencial La notación exponencial se usa para repetir
, y efectuar la multiplicación 10000
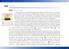 1.5 Figura 1.10: Las ecuaciones representan un cierto equilibrio entre los dos miembros separados por el signo igual. 1.5.1 La idea de ecuación Muchos problemas que se plantean en la vida real consisten
1.5 Figura 1.10: Las ecuaciones representan un cierto equilibrio entre los dos miembros separados por el signo igual. 1.5.1 La idea de ecuación Muchos problemas que se plantean en la vida real consisten
MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN CLASE # 5
 MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN CLASE # 5 OPERACIONES CON LOS NÚMEROS REALES En R se de nen dos operaciones: Suma o adición y producto o multiplicación: Si a 2 R y
MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN CLASE # 5 OPERACIONES CON LOS NÚMEROS REALES En R se de nen dos operaciones: Suma o adición y producto o multiplicación: Si a 2 R y
Topología de R n. Beatriz Porras
 Producto escalar, métrica y norma asociada. Topología de R n Beatriz Porras 1 Producto escalar, métrica y norma asociada Consideramos el espacio vectorial R n sobre el cuerpo R; escribimos los vectores
Producto escalar, métrica y norma asociada. Topología de R n Beatriz Porras 1 Producto escalar, métrica y norma asociada Consideramos el espacio vectorial R n sobre el cuerpo R; escribimos los vectores
Representación de números enteros: el convenio complemento a uno
 Representación de números enteros: el convenio complemento a uno Apellidos, nombre Martí Campoy, Antonio (amarti@disca.upv.es) Departamento Centro Informàtica de Sistemes i Computadors Escola Tècnica Superior
Representación de números enteros: el convenio complemento a uno Apellidos, nombre Martí Campoy, Antonio (amarti@disca.upv.es) Departamento Centro Informàtica de Sistemes i Computadors Escola Tècnica Superior
FRAGMENTACIÓN DE TABLAS
 2 FRAGMENTACIÓN DE TABLAS Contenido: 2.1. Introducción Fragmentación de tablas 2.1.1. Definición. 2.2. Tipos de Fragmentación 2.2.1. Fragmentación Horizontal 2.2.2. Fragmentación Vertical 2.2.3. Fragmentación
2 FRAGMENTACIÓN DE TABLAS Contenido: 2.1. Introducción Fragmentación de tablas 2.1.1. Definición. 2.2. Tipos de Fragmentación 2.2.1. Fragmentación Horizontal 2.2.2. Fragmentación Vertical 2.2.3. Fragmentación
Atributos Los atributos son las columnas de un relación y describen características particulares de ella.
 Unidad III: Modelo relacional 3.1 Estructura básica Tablas El modelo relacional proporciona una manera simple de representar los datos: una tabla bidimensional llamada relación. título año duración tipo
Unidad III: Modelo relacional 3.1 Estructura básica Tablas El modelo relacional proporciona una manera simple de representar los datos: una tabla bidimensional llamada relación. título año duración tipo
Conjuntos Un conjunto es una colección de objetos. A cada uno de esos objetos se llama elemento del conjunto.
 1 TEORÍA DE CONJUNTOS: IDEAS BÁSICAS Conjuntos Un conjunto es una colección de objetos. A cada uno de esos objetos se llama elemento del conjunto. Un conjunto puede darse enumerando todos y cada uno de
1 TEORÍA DE CONJUNTOS: IDEAS BÁSICAS Conjuntos Un conjunto es una colección de objetos. A cada uno de esos objetos se llama elemento del conjunto. Un conjunto puede darse enumerando todos y cada uno de
Teoría elemental de números
 Teoría elemental de números Matemática discreta 1 Resultados previos Axioma: todo subconjunto no vacío de N tiene mínimo, con el orden usual en N. Toda sucesión decreciente en N converge. 2 Divisibilidad
Teoría elemental de números Matemática discreta 1 Resultados previos Axioma: todo subconjunto no vacío de N tiene mínimo, con el orden usual en N. Toda sucesión decreciente en N converge. 2 Divisibilidad
Terminología Equivalente
 Normalización La normalización de bases de datos es un proceso que consiste en designar y aplicar una serie de reglas a las relaciones obtenidas tras el paso del modelo entidadrelación almodelo relacional.
Normalización La normalización de bases de datos es un proceso que consiste en designar y aplicar una serie de reglas a las relaciones obtenidas tras el paso del modelo entidadrelación almodelo relacional.
Ibero Rubik. Cubo de 5x5x5 Método para principiantes
 Ibero Rubik Cubo de 5x5x5 Método para principiantes 1 Copyright 2013 Ibero Rubik. Esta obra está sujeta a la licencia Reconocimiento-NoComercial-CompartirIgual 3.0 Unported de Creative Commons. Para ver
Ibero Rubik Cubo de 5x5x5 Método para principiantes 1 Copyright 2013 Ibero Rubik. Esta obra está sujeta a la licencia Reconocimiento-NoComercial-CompartirIgual 3.0 Unported de Creative Commons. Para ver
