INTRODUCCIÓN A LA ESTADÍSTICA
|
|
|
- Emilia Maestre Páez
- hace 9 años
- Vistas:
Transcripción
1 INTRODUCCIÓN A LA ESTADÍSTICA Autor: Clara Laguna 1.1 INTRODUCCIÓN. QUÉ ES LA ESTADÍSTICA? Cuando coloquialmente se habla de estadística, se suele pensar en una relación de datos numéricos presentada de forma ordenada y sistemática. Esta idea es la consecuencia del concepto popular que existe sobre el término y que cada vez está más extendido debido a la influencia de nuestro entorno, ya que hoy día es casi imposible que cualquier medio de difusión, periódico, radio, televisión, etc., no nos aborde diariamente con cualquier tipo de información estadística. Sólo cuando nos adentramos en un mundo más específico como es el campo de la investigación de las Ciencias Sociales: Medicina, Biología, Psicología,...percibimos que la Estadística se convierte en la única herramienta que permite dar luz y obtener resultados, y por tanto beneficios, en cualquier tipo de estudio, cuyos movimientos y relaciones, por su variabilidad intrínseca, no puedan ser abordadas desde la perspectiva de las leyes deterministas. Desde un punto de vista más amplio, podemos decir que la Estadística se utiliza como tecnología al servicio de las ciencias donde la variabilidad y la incertidumbre forman parte de su naturaleza. La Estadística es la rama de las matemáticas aplicadas que permite estudiar fenómenos cuyos resultados son en parte inciertos. Al estudiar sistemas biológicos, esta incertidumbre se debe al desconocimiento de muchos de los mecanismos fisiológicos, a la incapacidad de medir todos los determinantes de la enfermedad y a los errores de medida que inevitablemente se producen. Así, al realizar observaciones en clínica o en salud pública, los resultados obtenidos contienen una parte sistemática o estructural, que aporta información sobre las relaciones entre las variables estudiadas, y una parte de ruido aleatorio. El objeto de la estadística consiste en extraer la máxima información sobre estas relaciones estructurales a partir de los datos recogidos. Definición: Historia de la Estadística: Su raíz: STATUS=cosas del estado. Durante el siglo pasado, era considerada como la Ciencia del Estado. Sus orígenes: El recuento. Las civilizaciones antiguas recogían datos sobre población, producción agrícola y renta. Tal cantidad de información debía ser resumida en valores numéricos para su interpretación y uso en la toma de decisiones políticas. La Estadística se ocupa de los métodos y procedimientos para recoger, clasificar, resumir, hallar regularidades y analizar los datos, siempre y cuando la variabilidad e 01. Introducción a la Estadística 1-12
2 incertidumbre sea una causa intrínseca de los mismos; así como de realizar inferencias a partir de ellos, con la finalidad de ayudar a la toma de decisiones y en su caso formular predicciones. La estadística es la ciencia que permite tomar decisiones en situaciones de incertidumbre A qué nos referimos cuándo hablamos de variabilidad? Cuando nos referimos a una determinada característica (p.ej. nivel de ácido úrico) en los individuos de una población nos estamos refiriendo a una distribución de valores. La observación de un determinado grupo de pacientes nos proporciona información acerca de esta distribución. Los resultados que observamos se relacionan con la distribución poblacional. Sin embargo, observaciones distintas proporcionan resultados distintos (aunque compatibles), por ejemplo un mismo tratamiento aplicado a grupos distintos de pacientes proporcionará resultados distintos. La Bioestadística es la rama de la estadística que estudia la utilización de métodos estadísticos en problemas médicos y biológicos. Enseña y ayuda a investigar en todas las áreas de las Ciencias de la Vida donde la variabilidad no es la excepción sino la regla. Podemos clasificar la Estadística en descriptiva, cuando los resultados del análisis no pretenden ir más allá del conjunto de datos, e inferencial cuando el objetivo del estudio es derivar las conclusiones obtenidas a un conjunto de datos más amplio. Estadística descriptiva: Describe, analiza y representa un grupo de datos utilizando métodos numéricos y gráficos que resumen y presentan la información contenida en ellos. Estadística inferencial: Apoyándose en el cálculo de probabilidades y a partir de datos muestrales, efectúa estimaciones, decisiones, predicciones u otras generalizaciones sobre un conjunto mayor de datos. Su tarea fundamental es la de hacer inferencias acerca de la población a partir de una muestra extraída de la misma. El análisis de una base de datos siempre partirá de técnicas simples de resumen de los datos y presentación de los resultados. A partir de estos resultados iniciales, y en función del diseño del estudio y de las hipótesis preestablecidas, se aplicarán las técnicas de inferencia estadística que permitirán obtener conclusiones acerca de las relaciones entre las variables estudiadas. Las técnicas de estadística descriptiva no precisan de asunciones para su interpretación, pero la información que proporcionan no es fácilmente generalizable. La estadística inferencial permite esta generalización, pero requiere ciertas asunciones que deben verificarse para tener un grado razonable de seguridad en las inferencias. 1.2 CONCEPTOS BÁSICOS Vamos a definir algunos conceptos básicos y fundamentales a los cuales haremos referencia continuamente: 01. Introducción a la Estadística 2-12
3 Unidad estadística, Individuo o Elemento: personas u objetos que contienen cierta información que se desea estudiar y que pertenecen a la población en estudio. Población: conjunto de individuos o elementos que cumplen ciertas propiedades y entre los cuales se desea estudiar un determinado fenómeno. Muestra: subconjunto representativo de una población. Estadístico: función definida sobre los valores numéricos de una muestra. Parámetro: función definida sobre los valores numéricos de características medibles de una población. Estimador: función de los valores de una muestra que se elabora para indagar el valor de un parámetro de la población de la que procede la muestra. Los parámetros poblacionales se denotan con letras del alfabeto griego, mientras que los estimadores muestrales se denotan con letras de nuestro alfabeto. Así, por ejemplo, la media del colesterol en una población, que se denotaría por μ, es un parámetro que se estima a partir de la media de los valores de colesterol en una muestra obtenida en esa población, que se representaría por x. Variables o caracteres: característica observable que varía entre los diferentes individuos de una población. Las variables pueden dividirse en cualitativas y cuantitativas. Modalidades o categorías: posibles valores de una variable. Las modalidades deben ser a la vez exhaustivas y mutuamente excluyentes (cada elemento posee una y sólo una de las modalidades posibles). Las modalidades pueden agruparse en clases (intervalos) Tipos de variables Variables cualitativas: Se usan con datos que representan categorías que son mutuamente excluyentes, aunque se utilicen números para cada categoría no representan cantidades. Para su medición usamos escalas: Nominales: no hay relación entre las categorías. Una escala nominal sólo permite clasificar (no jerarquizar ni ordenar). Ej.: Género, nacionalidad, situación geográfica Distinguimos dos tipos de variables cualitativas o categóricas nominales: Dicotómicas o binarias: sano/enfermo, hombre/mujer Policotómicas (con varias categorías): grupo sanguíneo (A/B/AB) Ordinales: sus posibles categorías se encuentran jerarquizadas y ordenadas. Ej.: Mejoría a un tratamiento, satisfacción de un usuario, grado de dolor 01. Introducción a la Estadística 3-12
4 Es buena idea codificar las variables cualitativas asignando un código numérico a cada categoría ( etiqueta ) para poder procesarlas con facilidad. Ojo! Aunque se codifiquen como números, debemos recordar siempre el verdadero tipo de las variables con las que estamos trabajando y su significado cuando vayamos a usar programas estadísticos. No todo está permitido con cualquier tipo de variable! Variables cuantitativas: Se usan con datos que se expresan mediante cantidades numéricas que permiten hacer operaciones matemáticas. Existen los siguientes tipos: Discretas: sólo puede tomar valores enteros. Ej.: Nº de hijos, nº de intervenciones Continuas: Si sus posibles valores están en un conjunto infinito. Las podemos categorizar en intervalos (trataremos este tema en la clase práctica con SPSS). Ej.: Edad, peso, tensión arterial En la tabla se resumen los distintos tipos de variables y su utilidad: TIPO DE VARIABLE SIRVE PARA Cualitativa nominal Cualitativa ordinal Cuantitativa discreta Cuantitativa continua CLASIFICAR JERARQUIZAR CONTAR MEDIR Figura Introducción a la Estadística 4-12
5 Aquí tenéis un ejemplo de base de datos en SPSS: Figura Introducción a la Estadística 5-12
6 1.3 MUESTREO Cuando se decide cuantificar sólo una parte de las unidades de una población y a partir de esta información estimar sus parámetros, entonces estamos planteando un problema de muestreo. La estadística habitualmente estudia sólo una muestra de individuos. Se entiende por muestra al subconjunto de una población de mayor tamaño. Se entiende por población o universo al conjunto de todos los individuos o elementos (unidades de análisis) que cumplen ciertas características. Al proceso de extracción de una muestra a partir de una población se le denomina muestreo. A la interpretación del tratamiento estadístico de unos datos que acaba generalizándolos a toda la población se le llama inferencia. POBLACIÓN Muestreo Inferencia MUESTRA Figura 1.3 El muestreo es una herramienta de la investigación científica, su función básica es determinar qué parte de la realidad en estudio (población o universo) debe de examinarse con la finalidad de hacer inferencias sobre el todo de la que procede. Un proceso inductivo (que va de lo particular a lo general) se asocia inevitablemente a la posibilidad de cometer errores. El error es mayor en la medida que la muestra sea más pequeña, y sobre todo, cuando la muestra no refleja o representa la realidad sobre la que recaen las conclusiones de la inferencia. El error que se comete debido al hecho de que se sacan conclusiones sobre cierta población, a partir de la observación de sólo una parte de ella, se denomina error de muestreo. Dentro del proceso de selección de una muestra, la población suele dividirse en unidades de muestreo las cuales deben de cubrir por entero a la población, en otras palabras, todo miembro de la población o unidad de análisis pertenece a una y sólo una unidad de muestreo. Una unidad de muestreo puede contener un conjunto de unidades de análisis, incluso, un conjunto de unidades de muestreo correspondientes a una etapa posterior. La lista de las unidades de muestreo, recibe el nombre de marco muestral. 01. Introducción a la Estadística 6-12
7 Ejemplo 1.1. Supongamos que se estudia una población de escolares a fin de conocer la prevalencia de cierta dolencia. Cada escolar es una unidad de análisis pero, en lugar de contar con un listado de escolares, se tiene un listado de colegios (alguno de los cuales se elegirán para el estudio).una vez hecha esta selección, se toman algunas aulas de los colegios elegidos. Finalmente, dentro de estas últimas se eligen alumnos que integran la muestra definitiva. El listado de colegios primero, el de las aulas que tiene cada colegio seleccionado y el de niños, correspondiente a cada aula elegida dentro de los colegios de la muestra, constituyen el marco muestral del estudio. Puesto que hay tres procesos escalonados de selección, existen en este caso las llamadas unidades de muestreo de primera, segunda y tercera etapa. Figura 1.4 Podemos resumir en estos cuatro puntos las ventajas que la utilización de muestras presenta con respecto a la enumeración completa de la población: Coste reducido. Si los datos se obtienen de una pequeña fracción del total, los gastos de recogida y tratamiento de los datos se reducen. Incluso si la obtención de información en toda la población es factible, suele ser mucho más eficiente la utilización de técnicas de muestreo. Mayor rapidez. Los datos pueden ser más fácilmente recolectados y estudiados si se utiliza una muestra que si se emplean todos los elementos de la población. Por tanto, el uso de técnicas de muestreo es especialmente importante cuando se necesita la información con carácter urgente. Mayor flexibilidad y mayores posibilidades de estudio. La disponibilidad de registros completos es limitada. Muy a menudo, la única alternativa posible para la realización de un estudio es la obtención de datos por muestreo. Mayor control de calidad del proceso de recogida de datos. Al recoger datos en un número menor de efectivos, resulta más fácil recoger un número mayor de variables por individuo, así como tener un mejor control de la calidad del proceso de recogida de datos. La teoría de muestreo persigue un doble objetivo. Por un lado, estudia las técnicas que permiten obtener muestras representativas de la población de forma eficiente. Por otro lado, indica cómo utilizar los resultados del muestreo para estimar los parámetros poblacionales, conociendo a la vez el grado de incertidumbre de las estimaciones. 01. Introducción a la Estadística 7-12
8 Así, la teoría de muestreo pretende dar respuesta a varias preguntas de interés: Cómo se eligen a los individuos que componen la muestra? Cuántos individuos formarán parte de la muestra? Cómo se cuantifican las diferencias existentes entre los resultados obtenidos en la muestra y los que hubiéramos obtenido si el estudio se hubiera llevado a cabo en toda la población? Técnicas de muestreo La característica más importante de una muestra es que debe ser representativa de la población objeto de estudio para poder extrapolar los resultados a la población total. Las nociones de muestra representativa y de muestra probabilística suelen identificarse erróneamente como una y la misma. Como consecuencia puede ocurrir que, al admitir que la muestra no fue seleccionada por vía del azar, el investigador sienta que su estudio carece del rigor científico necesario. La noción que mejor sintetiza la idea de representatividad es la siguiente: Lo que debe procurarse es que la muestra tenga internamente el mismo grado de diversidad que la población Los métodos para seleccionar una muestra representativa son numerosos, podemos clasificarlos en: Probabilístico: Todos los individuos tienen la misma probabilidad de ser elegidos para formar parte de la muestra (principio de equiprobabilidad). No Probabilístico: La elección de los individuos no depende de la probabilidad, sino del proceso de toma de decisiones del investigador (las muestras seleccionadas por decisiones subjetivas tienden a estar sesgadas). MUESTREO PROBABILISTICO Los procedimientos probabilísticos reducen la carga subjetiva que podría influir en la elección de las unidades que se van a estudiar, y sobre todo, permiten medir el grado de precisión con que se realizan las estimación de los parámetros poblacionales. El azar no necesariamente inyecta representatividad a cada muestra que se obtenga, sino lo que realmente asegura es la imparcialidad en la conducta del investigador. Se considera que el método de selección de la muestra tiene un carácter estadísticamente riguroso cuando su diseño cumple las siguientes condiciones: A cada elemento de la población, se le otorgue una probabilidad conocida de pertenecer a la muestra. Y por supuesto, esta probabilidad no sea nula. 01. Introducción a la Estadística 8-12
9 Vamos a describir brevemente los principales procedimientos probabilísticos de selección de muestras: Muestreo aleatorio simple Muestreo sistemático Muestreo aleatorio estratificado Muestreo por conglomerados Muestreo polietápico Muestreo aleatorio simple (m.a.s.) Es el más sencillo y conocido de los distintos tipos de muestreo probabilístico. Supongamos que se pretende seleccionar una muestra de tamaño n a partir de una población de N unidades. Un muestreo aleatorio simple es aquel en el que cada unidad de muestreo de la población tiene la misma probabilidad de ser seleccionado. Puede probarse que el m.a.s. es un procedimiento equiprobabilístico; es decir, todas las unidades de la población tienen la misma probabilidad n/n de ser elegidas en la muestra. A la probabilidad que tiene cada individuo de pertenecer a la muestra se le denomina fracción de muestreo: f= n/n Para la selección de una m.a.s., se enumeran previamente las unidades de la población de 1 a N y a continuación se seleccionan n números distintos entre 1 y N utilizando algún procedimiento aleatorio (mediante una tabla de números aleatorios o un generador de números aleatorios por ordenador). Ejemplo 1.2 Elegir una muestra aleatoria de 5 estudiantes en un grupo de estadística de 20 alumnos. Extraer una muestra a partir de historias clínicas del Servicio de Planificación Familiar de un Hospital. Muestreo sistemático Cuando los elementos de la población están ordenados en una lista, podemos muestrear de la siguiente forma: Ejemplo 1.3 En primer lugar, se calcula la constante de muestreo k=n/n. Se elige aleatoriamente un número de arranque r entre 1 y k, donde k es la parte entera de N/n Se le suma a r (primera unidad elegida) la constante k sucesivamente hasta completar el tamaño de la muestra. De un conjunto de unidades queremos seleccionar Introducción a la Estadística 9-12
10 La constante de muestreo será K = 1000/200 = 5, por tanto se escogerá a una de cada cinco. La primera será sorteada entre los números del 1 al 5; si el elegido es el 2, el siguiente sería el 7 (2+k), y así hasta completar la muestra. Muestreo estratificado Cuando se desea asegurar la representatividad de determinados subgrupos o estratos de la población, la alternativa más sencilla es seleccionar por separado distintas submuestras dentro de cada estrato. Los estratos han de definir subgrupos de población que sean internamente homogéneos con respecto a la característica o parámetro de interés y, por tanto, heterogéneos entre sí. En la práctica, los estratos se definen en función de variables fáciles de medir previamente y relevantes para el tema objeto de estudio (edad, sexo, área geográfica de residencia). En general, el número de estratos L ha de ser reducido (rara vez resulta eficiente utilizar más de 5 estratos) y el tamaño por estrato no debe ser muy pequeño. Para la selección de una muestra estratificada de tamaño n, la población de N unidades se divide en L estratos de tamaños N 1, N 2,..., N L, cuya suma es igual a N. 1. Decidir el número de variables elegidas para la estratificación. 2. Elegir las variables de la estratificación e indicar el orden de estas variables, escogiendo como primera la que más discrimina. 3. Distribuir la muestra en cada estrato, AFIJACIÓN. Que la muestra sea representativa de cada estrato y que cada estrato esté suficientemente representado para poder tomar como válidos los resultados obtenidos. En el muestreo estratificado, es necesario determinar cómo se distribuye el tamaño muestral total n entre los distintos estratos; es decir, la asignación de los tamaños muestrales n 1,..., n L. El procedimiento utilizado con mayor frecuencia es la afijación proporcional: el tamaño de la muestra de cada estrato es proporcional al tamaño del estrato correspondiente con respecto a la población total. Ejemplo 1.4 Tenemos una población con N= y queremos distribuir una muestra de tamaño n= 600 personas en L= 3 estratos. La distribución de la población por edades es la siguiente: Grupo A: habitantes <18 años Grupo B: habitantes años Grupo C: habitantes >60 años Asignamos por Afijación Proporcional a cada estrato su tamaño muestral: n L= (n/n)xn L Estrato 1. Grupo A: 600x (1.500 / ) = 90 hab. Estrato 2. Grupo B: 600x (6.500 / ) = 390 hab. Estrato 3. Grupo C: 600x (2.000 / ) = 120 hab. 01. Introducción a la Estadística 10-12
11 Muestreo por conglomerados La aplicación de los diseños muestrales anteriores requiere de la enumeración u ordenación de todos los elementos de la población. Sin embargo, a menudo no se dispone de una lista completa o, aun disponiendo de tal lista, resulta muy costoso obtener información de las unidades muestreadas. Por ejemplo, si se seleccionara una muestra aleatoria simple de 1000 individuos de una gran ciudad, los individuos seleccionados estarían muy dispersos y la recogida de información sería extraordinariamente laboriosa. En tales circunstancias, una alternativa consiste en clasificar a la población en grupos o conglomerados, para así seleccionar una muestra de estos conglomerados y después tomar a todas o a una parte de las unidades incluidas dentro de los conglomerados seleccionados. Los conglomerados acostumbran a ser agrupaciones naturales de individuos como hogares, hospitales, colegios, provincias, etc. A diferencia de la estratificación, las diferencias dentro de cada conglomerado deben ser máximas: en cada conglomerado debe haber unidades representativas de toda la población, de lo contrario se perdería información al seleccionar únicamente algunos de ellos. Los resultados no varían si se selecciona uno u otro conglomerado. El número de conglomerados es típicamente elevado, de los cuales suele seleccionarse un número relativamente pequeño para resolver el problema de la dispersión muestral. Ejemplo 1.5 Si queremos extraer una muestra para un estudio epidemiológico en niños escolarizados en Zaragoza, con edades comprendidas entre 5 y 14 años, a partir de una lista completa de las aulas de todos los centros escolares, podemos elegir aleatoriamente un cierto número de aulas (conglomerados) de manera que la muestra estaría formada por todos los niños de las aulas seleccionadas. Muestreo polietápico Los diseños muestrales empleados en la práctica se realizan combinando las técnicas descritas anteriormente. En muchas situaciones, resulta más apropiado obtener la muestra final en diferentes etapas o pasos. En un muestreo polietápico, la población se divide en grupos exhaustivos y mutuamente excluyentes, que constituyen las llamadas unidades de primera etapa; cada una de ellas se desagrega a su vez en subgrupos o unidades de segunda etapa, y así sucesivamente, hasta llegar en una última etapa a los elementos o unidades de análisis. La selección de unidades en cada una de las etapas se realiza mediante una técnica de muestreo diferente y la muestra final será la resultante de aplicar sucesivamente cada una de estas técnicas. Ejemplo 1.6 Para obtener una muestra de pacientes diabéticos ingresados en nuestro país, en una primera etapa se escoge una muestra de hospitales, y en la segunda etapa, una muestra de pacientes diabéticos ingresados en los hospitales elegidos. 01. Introducción a la Estadística 11-12
12 MUESTREO NO PROBABILISTICO Los métodos de muestreo no probabilístico son aquellos en los que las unidades de análisis se recogen según criterios del investigador y no utilizando métodos en los que interviene el azar, de modo que no es posible estimar la probabilidad que tiene cada elemento de ser incluido en la muestra y no todos los elementos tienen posibilidad de ser incluidos. No garantizan la representatividad de la muestra y por lo tanto no permiten realizar estimaciones inferenciales sobre la población. Al igual que en los anteriores existen diferentes tipos de muestro no probabilístico: por cuotas, por conveniencia, método bola de nieve, Tamaño muestral Una vez abordados los diferentes diseños de muestreo es decir, como se obtiene la muestra, uno de los puntos que preocupa a la mayoría de los investigadores es cuantos individuos debe tener la muestra es decir que tamaño. Buscamos una fórmula que nos de un "número mágico" de sujetos que formen nuestra muestra. No vamos a entrar en fórmulas de cálculo de tamaño muestral (ver material de apoyo) puesto que para comprender su desarrollo necesitamos tener algunos conceptos estadísticos que todavía no hemos desarrollado. Sin embargo, vamos a tener en cuenta algunas consideraciones: El tamaño de la muestra estará en función de cuan frecuente sea lo que deseamos medir. Si lo que quiero estudiar es muy frecuente, necesitaré una muestra más pequeña, que si se da con menor frecuencia. Sin embargo, nosotros calculamos el tamaño muestral para conocer algo que desconocemos y, sin embargo, debemos de partir de un conocimiento de su valor (en la mayoría de los casos por otros estudios) para saber que tamaño de muestra elegimos. El tamaño de la muestra estará en función del máximo error de muestreo que se esté dispuesto a admitir al estimar un parámetro (a menor error necesitamos mayor muestra). Se supone, por tanto, que hay un error máximo, lo cual no siempre es fácil de determinar a priori y, en cualquier caso, se trata de una decisión esencialmente subjetiva. Cuanto más complejo es el diseño que utilizamos, mayor será la muestra que necesitaremos, puesto que el efecto del diseño nos hace aumentar el tamaño de la muestra para conseguir el mismo grado de precisión. 01. Introducción a la Estadística 12-12
Fase 2. Estudio de mercado: ESTADÍSTICA
 1. CONCEPTO DE ESTADÍSTICA. ESTADÍSTICA DESCRIPTIVA 2. 3. TABLA DE FRECUENCIAS 4. REPRESENTACIONES GRÁFICAS 5. TIPOS DE MEDIDAS: A. MEDIDAS DE POSICIÓN B. MEDIDAS DE DISPERSIÓN C. MEDIDAS DE FORMA 1 1.
1. CONCEPTO DE ESTADÍSTICA. ESTADÍSTICA DESCRIPTIVA 2. 3. TABLA DE FRECUENCIAS 4. REPRESENTACIONES GRÁFICAS 5. TIPOS DE MEDIDAS: A. MEDIDAS DE POSICIÓN B. MEDIDAS DE DISPERSIÓN C. MEDIDAS DE FORMA 1 1.
Conceptos básicos estadísticos
 Conceptos básicos estadísticos Población Población, en estadística, también llamada universo o colectivo, es el conjunto de elementos de referencia sobre el que se realizan las observaciones. El concepto
Conceptos básicos estadísticos Población Población, en estadística, también llamada universo o colectivo, es el conjunto de elementos de referencia sobre el que se realizan las observaciones. El concepto
Matemáticas 2.º Bachillerato. Intervalos de confianza. Contraste de hipótesis
 Matemáticas 2.º Bachillerato Intervalos de confianza. Contraste de hipótesis Depto. Matemáticas IES Elaios Tema: Estadística Inferencial 1. MUESTREO ALEATORIO Presentación elaborada por el profesor José
Matemáticas 2.º Bachillerato Intervalos de confianza. Contraste de hipótesis Depto. Matemáticas IES Elaios Tema: Estadística Inferencial 1. MUESTREO ALEATORIO Presentación elaborada por el profesor José
Tema 1: Introducción
 Estadística Universidad de Salamanca Curso 2010/2011 Outline 1 Estadística 2 Outline 1 Estadística 2 La estadística es una ciencia que comprende la recopilación, tabulación, análisis e interpretación de
Estadística Universidad de Salamanca Curso 2010/2011 Outline 1 Estadística 2 Outline 1 Estadística 2 La estadística es una ciencia que comprende la recopilación, tabulación, análisis e interpretación de
CAPÍTULO I. INTRODUCCIÓN. Cuando se requiere obtener información de una población, y se desean obtener los mejores
 CAPÍTULO I. INTRODUCCIÓN I.1 Breve Descripción Cuando se requiere obtener información de una población, y se desean obtener los mejores y más completos resultados, el censo es una opción para dar una respuesta
CAPÍTULO I. INTRODUCCIÓN I.1 Breve Descripción Cuando se requiere obtener información de una población, y se desean obtener los mejores y más completos resultados, el censo es una opción para dar una respuesta
UNIDAD 12.- Estadística. Tablas y gráficos (tema12 del libro)
 UNIDAD 12.- Estadística. Tablas y gráficos (tema12 del libro) 1. ESTADÍSTICA: CLASES Y CONCEPTOS BÁSICOS En sus orígenes históricos, la Estadística estuvo ligada a cuestiones de Estado (recuentos, censos,
UNIDAD 12.- Estadística. Tablas y gráficos (tema12 del libro) 1. ESTADÍSTICA: CLASES Y CONCEPTOS BÁSICOS En sus orígenes históricos, la Estadística estuvo ligada a cuestiones de Estado (recuentos, censos,
2.- Tablas de frecuencias
 º BACHILLERATO MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II TEMA 3.- ESTADÍSTICA DESCRIPTIVA PROFESOR: RAFAEL NÚÑEZ -----------------------------------------------------------------------------------------------------------------------------------------------------------------
º BACHILLERATO MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II TEMA 3.- ESTADÍSTICA DESCRIPTIVA PROFESOR: RAFAEL NÚÑEZ -----------------------------------------------------------------------------------------------------------------------------------------------------------------
Teorema Central del Límite (1)
 Teorema Central del Límite (1) Definición. Cualquier cantidad calculada a partir de las observaciones de una muestra se llama estadístico. La distribución de los valores que puede tomar un estadístico
Teorema Central del Límite (1) Definición. Cualquier cantidad calculada a partir de las observaciones de una muestra se llama estadístico. La distribución de los valores que puede tomar un estadístico
Diseños de muestreo (II)
 Diseños de muestreo (II) Muestreo estratificado El muestreo estratificado es un diseño de muestreo probabilístico en el que dividimos a la población en subgrupos o estratos. La estratificación puede basarse
Diseños de muestreo (II) Muestreo estratificado El muestreo estratificado es un diseño de muestreo probabilístico en el que dividimos a la población en subgrupos o estratos. La estratificación puede basarse
ESTADÍSTICA. Población Individuo Muestra Muestreo Valor Dato Variable Cualitativa ordinal nominal. continua
 ESTADÍSTICA Población Individuo Muestra Muestreo Valor Dato Variable Cualitativa ordinal nominal Cuantitativa discreta continua DISTRIBUCIÓN DE FRECUENCIAS Frecuencia absoluta: fi Frecuencia relativa:
ESTADÍSTICA Población Individuo Muestra Muestreo Valor Dato Variable Cualitativa ordinal nominal Cuantitativa discreta continua DISTRIBUCIÓN DE FRECUENCIAS Frecuencia absoluta: fi Frecuencia relativa:
Ing. Eduardo Cruz Romero w w w. tics-tlapa. c o m
 Ing. Eduardo Cruz Romero [email protected] w w w. tics-tlapa. c o m La estadística es tan vieja como la historia registrada. En la antigüedad los egipcios hacían censos de las personas y de los bienes
Ing. Eduardo Cruz Romero [email protected] w w w. tics-tlapa. c o m La estadística es tan vieja como la historia registrada. En la antigüedad los egipcios hacían censos de las personas y de los bienes
Estadística. Introducción a la Estadística Descriptiva. Área de Matemática Cerp Florida Reforma de Ed. Inicial y Primaria,
 Estadística Introducción a la Estadística Descriptiva Área de Matemática Cerp Florida Reforma de Ed. Inicial y Primaria, 2009 1 Contenido de Estadística según la Propuesta Programática para el año 2009
Estadística Introducción a la Estadística Descriptiva Área de Matemática Cerp Florida Reforma de Ed. Inicial y Primaria, 2009 1 Contenido de Estadística según la Propuesta Programática para el año 2009
1 Introducción. 2 Modelo. Hipótesis del modelo MODELO DE REGRESIÓN LOGÍSTICA
 MODELO DE REGRESIÓN LOGÍSTICA Introducción A grandes rasgos, el objetivo de la regresión logística se puede describir de la siguiente forma: Supongamos que los individuos de una población pueden clasificarse
MODELO DE REGRESIÓN LOGÍSTICA Introducción A grandes rasgos, el objetivo de la regresión logística se puede describir de la siguiente forma: Supongamos que los individuos de una población pueden clasificarse
Estadística Inferencial. Estadística Descriptiva
 INTRODUCCIÓN Estadística: Ciencia que trata sobre la teoría y aplicación de métodos para coleccionar, representar, resumir y analizar datos, así como realizar inferencias a partir de ellos. Recogida y
INTRODUCCIÓN Estadística: Ciencia que trata sobre la teoría y aplicación de métodos para coleccionar, representar, resumir y analizar datos, así como realizar inferencias a partir de ellos. Recogida y
1. LAS PRÁCTICAS DE OBSERVACIÓN 2. LA ENTREVISTA 3. EL GRUPO DE DISCUSIÓN 4. EL PROCESO DE INVESTIGACIÓN MEDIANTE ENCUESTA
 4. TÉCNICAS BÁSICAS DE INVESTIGACIÓN SOCIAL 1. LAS PRÁCTICAS DE OBSERVACIÓN 2. LA ENTREVISTA 3. EL GRUPO DE DISCUSIÓN 4. EL PROCESO DE INVESTIGACIÓN MEDIANTE ENCUESTA 1. LAS PRÁCTICAS DE OBSERVACIÓN Consiste
4. TÉCNICAS BÁSICAS DE INVESTIGACIÓN SOCIAL 1. LAS PRÁCTICAS DE OBSERVACIÓN 2. LA ENTREVISTA 3. EL GRUPO DE DISCUSIÓN 4. EL PROCESO DE INVESTIGACIÓN MEDIANTE ENCUESTA 1. LAS PRÁCTICAS DE OBSERVACIÓN Consiste
Metodología de la Investigación [DII-711] Capítulo 7: Selección de la Muestra
![Metodología de la Investigación [DII-711] Capítulo 7: Selección de la Muestra Metodología de la Investigación [DII-711] Capítulo 7: Selección de la Muestra](/thumbs/48/24875184.jpg) Metodología de la Investigación [DII-711] Capítulo 7: Selección de la Muestra Dr. Ricardo Soto [[email protected]] [http://www.inf.ucv.cl/ rsoto] Escuela de Ingeniería Informática Pontificia Universidad
Metodología de la Investigación [DII-711] Capítulo 7: Selección de la Muestra Dr. Ricardo Soto [[email protected]] [http://www.inf.ucv.cl/ rsoto] Escuela de Ingeniería Informática Pontificia Universidad
Área Académica: Gestión Tecnológica. Asignatura (Estadística para el Desarrollo Tecnológico, 3er Semestre) Tema: Muestra y Muestreo
 Área Académica: Gestión Tecnológica. Asignatura (Estadística para el Desarrollo Tecnológico, 3er Semestre) Tema: Muestra y Muestreo Profesor: Dr. Ernesto Bolaños Rodríguez Periodo: Enero-Junio de 01 Tema:Sample
Área Académica: Gestión Tecnológica. Asignatura (Estadística para el Desarrollo Tecnológico, 3er Semestre) Tema: Muestra y Muestreo Profesor: Dr. Ernesto Bolaños Rodríguez Periodo: Enero-Junio de 01 Tema:Sample
ESTADÍSTICA DESCRIPTIVA
 ESTADÍSTICA DESCRIPTIVA Medidas de tendencia central y de dispersión Giorgina Piani Zuleika Ferre 1. Tendencia Central Son un conjunto de medidas estadísticas que determinan un único valor que define el
ESTADÍSTICA DESCRIPTIVA Medidas de tendencia central y de dispersión Giorgina Piani Zuleika Ferre 1. Tendencia Central Son un conjunto de medidas estadísticas que determinan un único valor que define el
Pregunta 1. Pregunta 2. Pregunta 3. Pregunta 4. Pregunta 5. Pregunta 6. Pregunta 7. Comenzado el lunes, 25 de marzo de 2013, 17:24
 Comenzado el lunes, 25 de marzo de 2013, 17:24 Estado Finalizado Finalizado en sábado, 30 de marzo de 2013, 17:10 Tiempo empleado 4 días 23 horas Puntos 50,00/50,00 Calificación 10,00 de un máximo de 10,00
Comenzado el lunes, 25 de marzo de 2013, 17:24 Estado Finalizado Finalizado en sábado, 30 de marzo de 2013, 17:10 Tiempo empleado 4 días 23 horas Puntos 50,00/50,00 Calificación 10,00 de un máximo de 10,00
MEDIDAS DE TENDENCIA CENTRAL
 MEDIDAS DE TENDENCIA CENTRAL Al describir grupos de observaciones, con frecuencia es conveniente resumir la información con un solo número. Este número que, para tal fin, suele situarse hacia el centro
MEDIDAS DE TENDENCIA CENTRAL Al describir grupos de observaciones, con frecuencia es conveniente resumir la información con un solo número. Este número que, para tal fin, suele situarse hacia el centro
UNIVERSIDAD AUTONOMA DE SANTO DOMINGO
 UNIVERSIDAD AUTONOMA DE SANTO DOMINGO FACULTAD DE CIENCIAS ECONOMICAS Y SOCIALES DEPARTAMENTO DE ESTADISITICA CATEDRA Estadística Especializada ASIGNATURA Estadística Industrial (EST-121) NUMERO DE CREDITOS
UNIVERSIDAD AUTONOMA DE SANTO DOMINGO FACULTAD DE CIENCIAS ECONOMICAS Y SOCIALES DEPARTAMENTO DE ESTADISITICA CATEDRA Estadística Especializada ASIGNATURA Estadística Industrial (EST-121) NUMERO DE CREDITOS
INTRODUCCION AL MARKETING
 INTRODUCCION AL MARKETING Tema 5 LA INVESTIGACIÓN COMERCIAL Y EL MARKETING CONTENIDOS BASICOS OBJETIVOS a) Comprender la importancia del Sistema de Información de Marketing b) Componentes del S.I.M c)
INTRODUCCION AL MARKETING Tema 5 LA INVESTIGACIÓN COMERCIAL Y EL MARKETING CONTENIDOS BASICOS OBJETIVOS a) Comprender la importancia del Sistema de Información de Marketing b) Componentes del S.I.M c)
SOCIOLOGÍA: MÉTODOS DE INVESTIGACIÓN
 SOCIOLOGÍA: MÉTODOS DE INVESTIGACIÓN Existen varios métodos posibles de investigación social, varias formas de aplicar el análisis científico al plano de la realidad social. Los más utilizados hoy en día
SOCIOLOGÍA: MÉTODOS DE INVESTIGACIÓN Existen varios métodos posibles de investigación social, varias formas de aplicar el análisis científico al plano de la realidad social. Los más utilizados hoy en día
INFERENCIA ESTADISTICA
 1 INFERENCIA ESTADISTICA Es una rama de la Estadística que se ocupa de los procedimientos que nos permiten analizar y extraer conclusiones de una población a partir de los datos de una muestra aleatoria,
1 INFERENCIA ESTADISTICA Es una rama de la Estadística que se ocupa de los procedimientos que nos permiten analizar y extraer conclusiones de una población a partir de los datos de una muestra aleatoria,
CAPITULO III MARCO METODOLOGICO. Tipo de Investigación
 CAPITULO III MARCO METODOLOGICO Tipo de Investigación En este aspecto usted debe describir el tipo de investigación, en el cual se ubica el estudio. Cada investigador podrá construir su método, de acuerdo
CAPITULO III MARCO METODOLOGICO Tipo de Investigación En este aspecto usted debe describir el tipo de investigación, en el cual se ubica el estudio. Cada investigador podrá construir su método, de acuerdo
INTERVALOS DE CONFIANZA. La estadística en cómic (L. Gonick y W. Smith)
 INTERVALOS DE CONFIANZA La estadística en cómic (L. Gonick y W. Smith) EJEMPLO: Será elegido el senador Astuto? 2 tamaño muestral Estimador de p variable aleatoria poblacional? proporción de personas que
INTERVALOS DE CONFIANZA La estadística en cómic (L. Gonick y W. Smith) EJEMPLO: Será elegido el senador Astuto? 2 tamaño muestral Estimador de p variable aleatoria poblacional? proporción de personas que
El conjunto de datos obtenidos en un estudio se pueden describir en base a tres elementos esenciales:
 Análisis de datos en los estudios epidemiológicos Análisis de datos en los estudios epidemiológicos ntroducción En este capitulo, de continuación de nuestra serie temática de formación en metodología de
Análisis de datos en los estudios epidemiológicos Análisis de datos en los estudios epidemiológicos ntroducción En este capitulo, de continuación de nuestra serie temática de formación en metodología de
Tema 5 Algunas distribuciones importantes
 Algunas distribuciones importantes 1 Modelo Bernoulli Distribución Bernoulli Se llama experimento de Bernoulli a un experimento con las siguientes características: 1. Se realiza un experimento con dos
Algunas distribuciones importantes 1 Modelo Bernoulli Distribución Bernoulli Se llama experimento de Bernoulli a un experimento con las siguientes características: 1. Se realiza un experimento con dos
Conceptos de Estadística
 117 118 CAPÍTULO 12 CONCEPTOS DE ESTADÍSTICA La estadística es el conjunto de métodos o técnicas que se aplican a la recolección, organización, presentación, análisis e interpretación de datos numéricos.
117 118 CAPÍTULO 12 CONCEPTOS DE ESTADÍSTICA La estadística es el conjunto de métodos o técnicas que se aplican a la recolección, organización, presentación, análisis e interpretación de datos numéricos.
Nivel de Satisfacción en los afiliados. Régimen Estatal de Protección Social en Salud Zacatecas
 Nivel de Satisfacción en los afiliados 2012 Régimen Estatal de Protección Social en Salud Zacatecas Nivel de Satisfacción de los Afiliados Justificación A fin de cumplir con los objetivos del Régimen Estatal
Nivel de Satisfacción en los afiliados 2012 Régimen Estatal de Protección Social en Salud Zacatecas Nivel de Satisfacción de los Afiliados Justificación A fin de cumplir con los objetivos del Régimen Estatal
Capítulo 3. Desarrollo Metodológico de la Investigación.
 Capítulo 3. Desarrollo Metodológico de la Investigación. El presente capitulo tiene el objetivo de desarrollar la ruta metodológica utilizada para abordar nuestro objeto de estudio. (cuadro No.2), en el
Capítulo 3. Desarrollo Metodológico de la Investigación. El presente capitulo tiene el objetivo de desarrollar la ruta metodológica utilizada para abordar nuestro objeto de estudio. (cuadro No.2), en el
POBLACIÓN o UNIVERSO - Totalidad de unidades de análisis del conjunto a estudiar. - Conjunto de individuos, objetos, elementos o
 Población y Muestra Lic. Silvia Beatriz D Angelo (U.N.N.E.; U.C.P.) Población y Unidad elemental POBLACIÓN o UNIVERSO - Totalidad de unidades de análisis del conjunto a estudiar. - Conjunto de individuos,
Población y Muestra Lic. Silvia Beatriz D Angelo (U.N.N.E.; U.C.P.) Población y Unidad elemental POBLACIÓN o UNIVERSO - Totalidad de unidades de análisis del conjunto a estudiar. - Conjunto de individuos,
ANALISIS E INTERPRETACION DE DATOS SOBRE PERMANENCIA Y GASTOS DE LOS ALUMNOS EN LA UNIVERSIDAD NACIONAL DE INGENIERIA
 ANALISIS E INTERPRETACION DE DATOS SOBRE PERMANENCIA Y GASTOS DE LOS ALUMNOS EN LA UNIVERSIDAD NACIONAL DE INGENIERIA Jack Marlon Martínez Abregu e-mail: [email protected] IvánJosé Pazos Alvarado
ANALISIS E INTERPRETACION DE DATOS SOBRE PERMANENCIA Y GASTOS DE LOS ALUMNOS EN LA UNIVERSIDAD NACIONAL DE INGENIERIA Jack Marlon Martínez Abregu e-mail: [email protected] IvánJosé Pazos Alvarado
Muestreo. Tipos de muestreo. Álvaro José Flórez. Febrero - Junio Facultad de Ingenierías. 1 Escuela de Ingeniería Industrial y Estadística
 Muestreo Tipos de muestreo Álvaro José Flórez 1 Escuela de Ingeniería Industrial y Estadística Facultad de Ingenierías Febrero - Junio 2012 Introducción Todos los métodos probabilísticos de muestreo están
Muestreo Tipos de muestreo Álvaro José Flórez 1 Escuela de Ingeniería Industrial y Estadística Facultad de Ingenierías Febrero - Junio 2012 Introducción Todos los métodos probabilísticos de muestreo están
Tema 5. Contraste de hipótesis (I)
 Tema 5. Contraste de hipótesis (I) CA UNED de Huelva, "Profesor Dr. José Carlos Vílchez Martín" Introducción Bienvenida Objetivos pedagógicos: Conocer el concepto de hipótesis estadística Conocer y estimar
Tema 5. Contraste de hipótesis (I) CA UNED de Huelva, "Profesor Dr. José Carlos Vílchez Martín" Introducción Bienvenida Objetivos pedagógicos: Conocer el concepto de hipótesis estadística Conocer y estimar
Conceptos Básicos de Inferencia
 Conceptos Básicos de Inferencia Álvaro José Flórez 1 Escuela de Ingeniería Industrial y Estadística Facultad de Ingenierías Febrero - Junio 2012 Inferencia Estadística Cuando obtenemos una muestra, conocemos
Conceptos Básicos de Inferencia Álvaro José Flórez 1 Escuela de Ingeniería Industrial y Estadística Facultad de Ingenierías Febrero - Junio 2012 Inferencia Estadística Cuando obtenemos una muestra, conocemos
DISTRIBUCIÓN N BINOMIAL
 DISTRIBUCIÓN N BINOMIAL COMBINACIONES En muchos problemas de probabilidad es necesario conocer el número de maneras en que r objetos pueden seleccionarse de un conjunto de n objetos. A esto se le denomina
DISTRIBUCIÓN N BINOMIAL COMBINACIONES En muchos problemas de probabilidad es necesario conocer el número de maneras en que r objetos pueden seleccionarse de un conjunto de n objetos. A esto se le denomina
Micro y Macroeconomía
 Micro y Macroeconomía 1 Sesión No. 6 Nombre: Teoría del consumidor Contextualización: La microeconomía como herramienta de análisis nos permite el poder comprender el comportamiento de las personas en
Micro y Macroeconomía 1 Sesión No. 6 Nombre: Teoría del consumidor Contextualización: La microeconomía como herramienta de análisis nos permite el poder comprender el comportamiento de las personas en
ESTADÍSTICA CON EXCEL
 ESTADÍSTICA CON EXCEL 1. INTRODUCCIÓN La estadística es la rama de las matemáticas que se dedica al análisis e interpretación de series de datos, generando unos resultados que se utilizan básicamente en
ESTADÍSTICA CON EXCEL 1. INTRODUCCIÓN La estadística es la rama de las matemáticas que se dedica al análisis e interpretación de series de datos, generando unos resultados que se utilizan básicamente en
Agro 6998 Conferencia 2. Introducción a los modelos estadísticos mixtos
 Agro 6998 Conferencia Introducción a los modelos estadísticos mixtos Los modelos estadísticos permiten modelar la respuesta de un estudio experimental u observacional en función de factores (tratamientos,
Agro 6998 Conferencia Introducción a los modelos estadísticos mixtos Los modelos estadísticos permiten modelar la respuesta de un estudio experimental u observacional en función de factores (tratamientos,
INSTITUTO NACIONAL DE ESTADÍSTICAS (INE) 29 de Abril de 2016
 ANEXO ESTADÍSTICO 1 : COEFICIENTES DE VARIACIÓN Y ERROR ASOCIADO AL ESTIMADOR ENCUESTA NACIONAL DE EMPLEO (ENE) INSTITUTO NACIONAL DE ESTADÍSTICAS (INE) 9 de Abril de 016 1 Este anexo estadístico es una
ANEXO ESTADÍSTICO 1 : COEFICIENTES DE VARIACIÓN Y ERROR ASOCIADO AL ESTIMADOR ENCUESTA NACIONAL DE EMPLEO (ENE) INSTITUTO NACIONAL DE ESTADÍSTICAS (INE) 9 de Abril de 016 1 Este anexo estadístico es una
Probabilidad y Estadística
 Probabilidad y Estadística Probabilidad Conceptos como probabilidad, azar, aleatorio son tan viejos como la misma civilización. Y es que a diario utilizamos el concepto de probabilidad: Quizá llueva mañana
Probabilidad y Estadística Probabilidad Conceptos como probabilidad, azar, aleatorio son tan viejos como la misma civilización. Y es que a diario utilizamos el concepto de probabilidad: Quizá llueva mañana
Encuesta sobre Equipamiento y Uso de Tecnologías de la Información y Comunicación (TIC) en los Hogares
 1 / 10 Encuesta sobre Equipamiento y Uso de Tecnologías de la Información y Comunicación (TIC) en los Hogares A continuación se muestra un ejemplo del proceso de realización de encuestas en el INE, desde
1 / 10 Encuesta sobre Equipamiento y Uso de Tecnologías de la Información y Comunicación (TIC) en los Hogares A continuación se muestra un ejemplo del proceso de realización de encuestas en el INE, desde
Otra característica poblacional de interés es la varianza de la población, 2, y su raíz cuadrada, la desviación estándar de la población,. La varianza
 CARACTERÍSTICAS DE LA POBLACIÓN. Una pregunta práctica en gran parte de la investigación de mercado tiene que ver con el tamaño de la muestra. La encuesta, en principio, no puede ser aplicada sin conocer
CARACTERÍSTICAS DE LA POBLACIÓN. Una pregunta práctica en gran parte de la investigación de mercado tiene que ver con el tamaño de la muestra. La encuesta, en principio, no puede ser aplicada sin conocer
BLOQUE I: GEOMETRÍA PLANA Y FIGURAS GEOMÉTRICAS. Ecuaciones y sistemas. 2 (20 horas) Funciones y gráficas. 2 (20 horas) Estadística y probabilidad
 PROGRAMACIÓN DIDÁCTICA Materia IV Período FBPI Tramo II Ámbito Científico-Tecnológico Bloque I Geometría plana y figuras geométricas Créditos 3 (30 horas) Bloque II Créditos Ecuaciones y sistemas 2 (20
PROGRAMACIÓN DIDÁCTICA Materia IV Período FBPI Tramo II Ámbito Científico-Tecnológico Bloque I Geometría plana y figuras geométricas Créditos 3 (30 horas) Bloque II Créditos Ecuaciones y sistemas 2 (20
DIPLOMADO EN ESTADÍSTICA APLICADA
 DIPLOMADO EN ESTADÍSTICA APLICADA DIPLOMADO EN ESTADÍSTICA APLICADA FUNDAMENTACIÓN El Diplomado en Estadística Aplicada posibilitará la actualización profesional y el desarrollo de competencias específicas
DIPLOMADO EN ESTADÍSTICA APLICADA DIPLOMADO EN ESTADÍSTICA APLICADA FUNDAMENTACIÓN El Diplomado en Estadística Aplicada posibilitará la actualización profesional y el desarrollo de competencias específicas
CONTENIDOS MÍNIMOS BLOQUE 2. NÚMEROS
 CONTENIDOS Y CRITERIOS DE EVALUACIÓN DE MATEMÁTICAS 1º DE ESO. Bloque 1: Contenidos Comunes Este bloque de contenidos será desarrollado junto con los otros bloques a lo largo de todas y cada una de las
CONTENIDOS Y CRITERIOS DE EVALUACIÓN DE MATEMÁTICAS 1º DE ESO. Bloque 1: Contenidos Comunes Este bloque de contenidos será desarrollado junto con los otros bloques a lo largo de todas y cada una de las
Tema 5. Muestreo y distribuciones muestrales
 Tema 5. Muestreo y distribuciones muestrales Contenidos Muestreo y muestras aleatorias simples La distribución de la media en el muestreo La distribución de la varianza muestral Lecturas recomendadas:
Tema 5. Muestreo y distribuciones muestrales Contenidos Muestreo y muestras aleatorias simples La distribución de la media en el muestreo La distribución de la varianza muestral Lecturas recomendadas:
Distribuciones de probabilidad
 Distribuciones de probabilidad Prof, Dr. Jose Jacobo Zubcoff Departamento de Ciencias del Mar y Biología Aplicada Inferencia estadística: Parte de la estadística que estudia grandes colectivos a partir
Distribuciones de probabilidad Prof, Dr. Jose Jacobo Zubcoff Departamento de Ciencias del Mar y Biología Aplicada Inferencia estadística: Parte de la estadística que estudia grandes colectivos a partir
4. NÚMEROS PSEUDOALEATORIOS.
 4. NÚMEROS PSEUDOALEATORIOS. En los experimentos de simulación es necesario generar valores para las variables aleatorias representadas estas por medio de distribuciones de probabilidad. Para poder generar
4. NÚMEROS PSEUDOALEATORIOS. En los experimentos de simulación es necesario generar valores para las variables aleatorias representadas estas por medio de distribuciones de probabilidad. Para poder generar
GUION TÉCNICO AUDIO. El Conjunto De Los Números Reales. realidad, es una ciencia resultado de más de 4 mil años de
 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. El Conjunto De Los Números Reales. Hablar de matemáticas, no es solo referirse a números. En realidad, es
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. El Conjunto De Los Números Reales. Hablar de matemáticas, no es solo referirse a números. En realidad, es
2. METODOLOGÍA. Los tipos fundamentales de Estudios de Investigación, como nos recuerda Bavaresco, son cuatro:
 2. METODOLOGÍA Para llevar a cabo este estudio es necesario utilizar una metodología de investigación, debido a que el no contar con los métodos y técnicas necesarias que nos guíen a través de una investigación
2. METODOLOGÍA Para llevar a cabo este estudio es necesario utilizar una metodología de investigación, debido a que el no contar con los métodos y técnicas necesarias que nos guíen a través de una investigación
Simulación I. Investigación Operativa, Grado en Estadística y Empresa, 2011/12
 Simulación I Prof. José Niño Mora Investigación Operativa, Grado en Estadística y Empresa, 2011/12 Esquema Modelos de simulación y el método de Montecarlo Ejemplo: estimación de un área Ejemplo: estimación
Simulación I Prof. José Niño Mora Investigación Operativa, Grado en Estadística y Empresa, 2011/12 Esquema Modelos de simulación y el método de Montecarlo Ejemplo: estimación de un área Ejemplo: estimación
A. Menéndez Taller CES 15_ Confiabilidad. 15. Confiabilidad
 15. Confiabilidad La confiabilidad se refiere a la consistencia de los resultados. En el análisis de la confiabilidad se busca que los resultados de un cuestionario concuerden con los resultados del mismo
15. Confiabilidad La confiabilidad se refiere a la consistencia de los resultados. En el análisis de la confiabilidad se busca que los resultados de un cuestionario concuerden con los resultados del mismo
Tipos de gráficas y selección según los datos CIENCIA, TECNOLOGIA Y AMBIENTE
 Tipos de gráficas y selección según los datos CIENCIA, TECNOLOGIA Y AMBIENTE Objetivos 2 Identificar los tipos de gráficas. Definir los conceptos tablas y cuadros Reconocer las partes de una gráfica. Construir
Tipos de gráficas y selección según los datos CIENCIA, TECNOLOGIA Y AMBIENTE Objetivos 2 Identificar los tipos de gráficas. Definir los conceptos tablas y cuadros Reconocer las partes de una gráfica. Construir
3.1. Administración de la medición y de la información estratégica:
 Unidad III Aspectos Generales Sobre la Gestión de la Calidad 3.1. Administración de la medición y de la información estratégica: Los siguientes criterios corresponden a la administración de la medición
Unidad III Aspectos Generales Sobre la Gestión de la Calidad 3.1. Administración de la medición y de la información estratégica: Los siguientes criterios corresponden a la administración de la medición
2. Recolección de información - Medidas de posición: moda, media aritmética, mínimo, máximo - Frecuencia absoluta, relativa y porcentual
 Prueba Escrita de matemática / Nivel: Sétimo año 1. Estadística - Unidad estadística - Características - Datos u observaciones - Población - Muestra - Variabilidad de los datos - Variables cuantitativas
Prueba Escrita de matemática / Nivel: Sétimo año 1. Estadística - Unidad estadística - Características - Datos u observaciones - Población - Muestra - Variabilidad de los datos - Variables cuantitativas
Estadística descriptiva y métodos diagnósticos
 2.2.1. Estadística descriptiva y métodos diagnósticos Dra. Ana Dorado Díaz Consejería de Sanidad Diplomado en Salud Pública Diplomado en Salud Pública - 2 Objetivos específicos 1. El alumno aprenderá a
2.2.1. Estadística descriptiva y métodos diagnósticos Dra. Ana Dorado Díaz Consejería de Sanidad Diplomado en Salud Pública Diplomado en Salud Pública - 2 Objetivos específicos 1. El alumno aprenderá a
TEMA 3. Población y muestra
 TEMA 3. Población y muestra Alicia Nieto Reyes BIOESTADÍSTICA Alicia Nieto Reyes (BIOESTADÍSTICA) TEMA 3. Población y muestra 1 / 7 Conceptos de población y muestra Objetivo principal de la estadística:
TEMA 3. Población y muestra Alicia Nieto Reyes BIOESTADÍSTICA Alicia Nieto Reyes (BIOESTADÍSTICA) TEMA 3. Población y muestra 1 / 7 Conceptos de población y muestra Objetivo principal de la estadística:
Objetivos. Epígrafes 3-1. Francisco José García Álvarez
 Objetivos Entender el concepto de variabilidad natural de un procesos Comprender la necesidad de los gráficos de control Aprender a diferenciar los tipos de gráficos de control y conocer sus limitaciones.
Objetivos Entender el concepto de variabilidad natural de un procesos Comprender la necesidad de los gráficos de control Aprender a diferenciar los tipos de gráficos de control y conocer sus limitaciones.
CAPITULO XII PUENTES DE CORRIENTE ALTERNA
 CAPITULO XII PUENTES DE CORRIENTE ALTERNA 2. INTRODUCCION. En el Capítulo IX estudiamos el puente de Wheatstone como instrumento de medición de resistencias por el método de detección de cero. En este
CAPITULO XII PUENTES DE CORRIENTE ALTERNA 2. INTRODUCCION. En el Capítulo IX estudiamos el puente de Wheatstone como instrumento de medición de resistencias por el método de detección de cero. En este
POBLACIÓN Y MUESTREO. Metodología de la Investigación 7/11/08 Danny Freira
 POBLACIÓN Y MUESTREO Metodología de la Investigación 7/11/08 Danny Freira Planificación Operativa En que consiste? En prever las operaciones que deberán realizarse para poner en práctica la estrategia
POBLACIÓN Y MUESTREO Metodología de la Investigación 7/11/08 Danny Freira Planificación Operativa En que consiste? En prever las operaciones que deberán realizarse para poner en práctica la estrategia
Protocolo de la investigación.
 Protocolo de la investigación. Francisco Javier Jiménez Méndez Mecatrónica El protocolo de una investigación puede ser basado en dos tipos de conocimientos, el popular y el científico, el conocimiento
Protocolo de la investigación. Francisco Javier Jiménez Méndez Mecatrónica El protocolo de una investigación puede ser basado en dos tipos de conocimientos, el popular y el científico, el conocimiento
Objetivos del tema. Qué es una hipótesis? Test de Hipótesis Introducción a la Probabilidad y Estadística. Contrastando una hipótesis
 Objetivos del tema Conocer el proceso para contrastar hipótesis y su relación con el método científico. Diferenciar entre hipótesis nula y alternativa Nivel de significación Test de Hipótesis Introducción
Objetivos del tema Conocer el proceso para contrastar hipótesis y su relación con el método científico. Diferenciar entre hipótesis nula y alternativa Nivel de significación Test de Hipótesis Introducción
Socioestadística I Análisis estadístico en Sociología
 Análisis estadístico en Sociología Capítulo 4 TEORÍA DE LA PROBABILIDAD Y SUS PRINCIPIOS. ESTADÍSTICA INFERENCIAL 1. INTRODUCCIÓN A LA ESTADÍSTICA INFERENCIAL En los capítulos anteriores, hemos utilizado
Análisis estadístico en Sociología Capítulo 4 TEORÍA DE LA PROBABILIDAD Y SUS PRINCIPIOS. ESTADÍSTICA INFERENCIAL 1. INTRODUCCIÓN A LA ESTADÍSTICA INFERENCIAL En los capítulos anteriores, hemos utilizado
13. Utilizar la fórmula del término general y de la suma de n términos consecutivos
 Contenidos mínimos 3º ESO. 1. Contenidos. Bloque I: Aritmética y álgebra. 1. Utilizar las reglas de jerarquía de paréntesis y operaciones, para efectuar cálculos con números racionales, expresados en forma
Contenidos mínimos 3º ESO. 1. Contenidos. Bloque I: Aritmética y álgebra. 1. Utilizar las reglas de jerarquía de paréntesis y operaciones, para efectuar cálculos con números racionales, expresados en forma
La síntesis estadística como cuarta etapa del método estadístico. Medidas de resumen para variables cualitativas. Razones, proporciones y tasas.
 La síntesis estadística como cuarta etapa del método estadístico. Medidas de resumen para variables cualitativas. Razones, proporciones y tasas. Introducción La cuarta etapa del método estadístico se denomina
La síntesis estadística como cuarta etapa del método estadístico. Medidas de resumen para variables cualitativas. Razones, proporciones y tasas. Introducción La cuarta etapa del método estadístico se denomina
4.12 Ciertos teoremas fundamentales del cálculo de probabilidades
 1 de 9 15/10/2006 05:57 a.m. Nodo Raíz: 4. Cálculo de probabilidades y variables Siguiente: 4.14 Tests diagnósticos Previo: 4.10 Probabilidad condicionada e independencia de 4.12 Ciertos teoremas fundamentales
1 de 9 15/10/2006 05:57 a.m. Nodo Raíz: 4. Cálculo de probabilidades y variables Siguiente: 4.14 Tests diagnósticos Previo: 4.10 Probabilidad condicionada e independencia de 4.12 Ciertos teoremas fundamentales
Técnicas Cuantitativas para el Management y los Negocios I
 Técnicas Cuantitativas para el Management y los Negocios I Licenciado en Administración Módulo II: ESTADÍSTICA INFERENCIAL Contenidos Módulo II Unidad 4. Probabilidad Conceptos básicos de probabilidad:
Técnicas Cuantitativas para el Management y los Negocios I Licenciado en Administración Módulo II: ESTADÍSTICA INFERENCIAL Contenidos Módulo II Unidad 4. Probabilidad Conceptos básicos de probabilidad:
1º CURSO BIOESTADÍSTICA
 E.U.E. MADRID CRUZ ROJA ESPAÑOLA UNIVERSIDAD AUTÓNOMA DE MADRID CURSO ACADÉMICO 2012/2013 1º CURSO BIOESTADÍSTICA Coordinación: Eva García-Carpintero Blas Profesores: María de la Torre Barba Fernando Vallejo
E.U.E. MADRID CRUZ ROJA ESPAÑOLA UNIVERSIDAD AUTÓNOMA DE MADRID CURSO ACADÉMICO 2012/2013 1º CURSO BIOESTADÍSTICA Coordinación: Eva García-Carpintero Blas Profesores: María de la Torre Barba Fernando Vallejo
Estadística. Análisis de datos.
 Estadística Definición de Estadística La Estadística trata del recuento, ordenación y clasificación de los datos obtenidos por las observaciones, para poder hacer comparaciones y sacar conclusiones. Un
Estadística Definición de Estadística La Estadística trata del recuento, ordenación y clasificación de los datos obtenidos por las observaciones, para poder hacer comparaciones y sacar conclusiones. Un
ANEXO 1. CONCEPTOS BÁSICOS. Este anexo contiene información que complementa el entendimiento de la tesis presentada.
 ANEXO 1. CONCEPTOS BÁSICOS Este anexo contiene información que complementa el entendimiento de la tesis presentada. Aquí se exponen técnicas de cálculo que son utilizados en los procedimientos de los modelos
ANEXO 1. CONCEPTOS BÁSICOS Este anexo contiene información que complementa el entendimiento de la tesis presentada. Aquí se exponen técnicas de cálculo que son utilizados en los procedimientos de los modelos
LA ENCUESTA. Manuel Montañés Serrano
 LA ENCUESTA INTRODUCCIÓN Para dar a conocer cómo se distribuye la población respecto a un significante socialmente cristalizados es adecuado recurrir a la explotación primaria de fuentes secundarias o
LA ENCUESTA INTRODUCCIÓN Para dar a conocer cómo se distribuye la población respecto a un significante socialmente cristalizados es adecuado recurrir a la explotación primaria de fuentes secundarias o
Histogramas. Para crear un histograma. Para crear un histograma podemos utilizar el procedimiento Generador de gráficos en el Menú: o Gráficos:
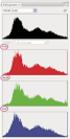 SPSS: GRÁFICOS HISTOGRAMAS Histogramas Los histogramas son útiles para mostrar la distribución de una única variable de escala. Los datos se agrupan y se resumen utilizando el estadístico de porcentaje
SPSS: GRÁFICOS HISTOGRAMAS Histogramas Los histogramas son útiles para mostrar la distribución de una única variable de escala. Los datos se agrupan y se resumen utilizando el estadístico de porcentaje
U.D.1: Análisis estadístico de una variable Consideraciones iniciales: Propuesta: 1.1 Distribución de frecuencias. Variables Cualitativas: Ejemplo
 U.D.1: Análisis estadístico de una variable Consideraciones iniciales: - Población: Es el conjunto de todos los elementos que cumplen una determinada característica. Ej.: Alumnos del colegio. - Individuo:
U.D.1: Análisis estadístico de una variable Consideraciones iniciales: - Población: Es el conjunto de todos los elementos que cumplen una determinada característica. Ej.: Alumnos del colegio. - Individuo:
Tema1: Introducción a La Estadística 1.1-1
 1 Tema1: Introducción a La Estadística 1.1-1 Determine a cuáles de los términos se hacen referencia en el siguiente estudio : población, muestra, parámetro, estadístico, variable, data. Se quiere saber
1 Tema1: Introducción a La Estadística 1.1-1 Determine a cuáles de los términos se hacen referencia en el siguiente estudio : población, muestra, parámetro, estadístico, variable, data. Se quiere saber
M ÉTODO DE MUESTREO DE GEOSINTÉTICOS PARA ENSAYOS I.N.V. E
 M ÉTODO DE MUESTREO DE GEOSINTÉTICOS PARA ENSAYOS I.N.V. E 908 07 1. OBJETO 1.1 Esta práctica cubre dos procedimientos para el muestreo de geosintéticos para ser ensayados. Se requiere que las instrucciones
M ÉTODO DE MUESTREO DE GEOSINTÉTICOS PARA ENSAYOS I.N.V. E 908 07 1. OBJETO 1.1 Esta práctica cubre dos procedimientos para el muestreo de geosintéticos para ser ensayados. Se requiere que las instrucciones
Mapas de Puntos. Cartografía a Temática Cuantitativa. Cartografía de superficie
 Cartografía a Temática Cuantitativa Cartografía de superficie En la cartografía a temática tica cuantitativa existe el concepto de superficie estadística. stica. La superficie estadística stica es una
Cartografía a Temática Cuantitativa Cartografía de superficie En la cartografía a temática tica cuantitativa existe el concepto de superficie estadística. stica. La superficie estadística stica es una
Centro Asociado Palma de Mallorca. Tutor: Antonio Rivero Cuesta
 Centro Asociado Palma de Mallorca Arquitectura de Ordenadores Tutor: Antonio Rivero Cuesta Unidad Didáctica 1 Representación de la Información y Funciones Lógicas Tema 1 Representación de la Información
Centro Asociado Palma de Mallorca Arquitectura de Ordenadores Tutor: Antonio Rivero Cuesta Unidad Didáctica 1 Representación de la Información y Funciones Lógicas Tema 1 Representación de la Información
Tema 4. Probabilidad Condicionada
 Tema 4. Probabilidad Condicionada Presentación y Objetivos. En este tema se dan reglas para actualizar una probabilidad determinada en situaciones en las que se dispone de información adicional. Para ello
Tema 4. Probabilidad Condicionada Presentación y Objetivos. En este tema se dan reglas para actualizar una probabilidad determinada en situaciones en las que se dispone de información adicional. Para ello
La investigación para la conservación y gestión del patrimonio cultural. Dra en Arq. Karim Chew
 La investigación para la conservación y gestión del patrimonio cultural Dra en Arq. Karim Chew Trabajo Final de Maestría. Tesis Una proposición original y creativa que debe ser demostrada mediante pruebas
La investigación para la conservación y gestión del patrimonio cultural Dra en Arq. Karim Chew Trabajo Final de Maestría. Tesis Una proposición original y creativa que debe ser demostrada mediante pruebas
Problema, Objetivos y Justificación. Corina Flores Villarroel Programa MEMI
 Problema, Objetivos y Justificación Corina Flores Villarroel Contenidos Qué es un problema? Cómo definir un problema? Formulación del problema Cómo redactar un problema De dónde salen los objetivos? Qué
Problema, Objetivos y Justificación Corina Flores Villarroel Contenidos Qué es un problema? Cómo definir un problema? Formulación del problema Cómo redactar un problema De dónde salen los objetivos? Qué
Medidas de centralización
 1 1. Medidas de centralización Medidas de centralización Hemos visto cómo el estudio del conjunto de los datos mediante la estadística permite realizar representaciones gráficas, que informan sobre ese
1 1. Medidas de centralización Medidas de centralización Hemos visto cómo el estudio del conjunto de los datos mediante la estadística permite realizar representaciones gráficas, que informan sobre ese
Introducción a la Estadística y al Análisis de Datos. UCR ECCI CI-1352 Probabilidad y Estadística Prof. M.Sc. Kryscia Daviana Ramírez Benavides
 Introducción a la Estadística y al Análisis de Datos UCR ECCI CI-135 Probabilidad y Estadística Prof. M.Sc. Kryscia Daviana Ramírez Benavides Fundamentos de la Estadística La estadística recoge, ordena
Introducción a la Estadística y al Análisis de Datos UCR ECCI CI-135 Probabilidad y Estadística Prof. M.Sc. Kryscia Daviana Ramírez Benavides Fundamentos de la Estadística La estadística recoge, ordena
UNIVERSIDAD AUTONOMA DE SANTO DOMINGO
 UNIVERSIDAD AUTONOMA DE SANTO DOMINGO FACULTAD DE CIENCIAS ECONOMICAS Y SOCIALES DEPARTAMENTO DE ESTADISITICA CATEDRA Estadística Especializada ASIGNATURA Estadística Descriptiva Para Psicólogos (EST-225)
UNIVERSIDAD AUTONOMA DE SANTO DOMINGO FACULTAD DE CIENCIAS ECONOMICAS Y SOCIALES DEPARTAMENTO DE ESTADISITICA CATEDRA Estadística Especializada ASIGNATURA Estadística Descriptiva Para Psicólogos (EST-225)
CAPITULO V METODOLOGÍA DE LA INVESTIGACIÓN
 CAPITULO V METODOLOGÍA DE LA INVESTIGACIÓN Población y Muestra: El tipo de investigación es un estudio correlacional que consiste en ver la relación entre la variable independiente y dependiente. La población
CAPITULO V METODOLOGÍA DE LA INVESTIGACIÓN Población y Muestra: El tipo de investigación es un estudio correlacional que consiste en ver la relación entre la variable independiente y dependiente. La población
Ciencia que tiene por objeto el estudio de las poblaciones humanas y que trata de:
 DEMOGRAFÍA 1 1- DEFINICIÓN: Ciencia que tiene por objeto el estudio de las poblaciones humanas y que trata de: n Tamaño, composición y distribución geográfica en un momento dado y de sus cambios en el
DEMOGRAFÍA 1 1- DEFINICIÓN: Ciencia que tiene por objeto el estudio de las poblaciones humanas y que trata de: n Tamaño, composición y distribución geográfica en un momento dado y de sus cambios en el
Las operaciones con números irracionales
 Las operaciones con números irracionales Antes de empezar a sumar, restar, multiplicar, y realizar cualquier tipo de las operaciones con números irracionales, debemos comprender como extraer, e introducir
Las operaciones con números irracionales Antes de empezar a sumar, restar, multiplicar, y realizar cualquier tipo de las operaciones con números irracionales, debemos comprender como extraer, e introducir
ESTUDIO CIS nº BARÓMETRO SANITARIO, 2013 (Tercera oleada) FICHA TÉCNICA DISEÑO MUESTRAL GENERAL DEL BARÓMETRO SOBRE EL SISTEMA SANITARIO.
 ESTUDIO CIS nº 3002 BARÓMETRO SANITARIO, 2013 (Tercera oleada) FICHA TÉCNICA DISEÑO MUESTRAL GENERAL DEL BARÓMETRO SOBRE EL SISTEMA SANITARIO. 2013 Convenio: Ministerio de Sanidad, Servicios Sociales e
ESTUDIO CIS nº 3002 BARÓMETRO SANITARIO, 2013 (Tercera oleada) FICHA TÉCNICA DISEÑO MUESTRAL GENERAL DEL BARÓMETRO SOBRE EL SISTEMA SANITARIO. 2013 Convenio: Ministerio de Sanidad, Servicios Sociales e
INSTITUTO TECNOLÓGICO DE APIZACO TEORÍA DE CONJUNTOS CONJUNTOS Y TÉCNICAS DE CONTEO
 TEORÍA DE CONJUNTOS CONJUNTOS Y TÉCNICAS DE CONTEO DEFINICIÓN Y NOTACIÓN DE CONJUNTOS El término conjunto juega un papel fundamental en el desarrollo de las matemáticas modernas; Además de proporcionar
TEORÍA DE CONJUNTOS CONJUNTOS Y TÉCNICAS DE CONTEO DEFINICIÓN Y NOTACIÓN DE CONJUNTOS El término conjunto juega un papel fundamental en el desarrollo de las matemáticas modernas; Además de proporcionar
El método deductivo: es aquel que parte de datos generales aceptados como validos para llegar a una conclusión de tipo particular.
 Que es el conocimiento? La metodología Dicho determino esta compuesto del vocablo método y el sustantivo griego logos que significa juicio, estudio, esta palabra se puede definir como La descripción, el
Que es el conocimiento? La metodología Dicho determino esta compuesto del vocablo método y el sustantivo griego logos que significa juicio, estudio, esta palabra se puede definir como La descripción, el
Este documento enumera los diferentes tipos de Diagramas Matriciales y su proceso de construcción.
 DIAGRAMA MATRICIAL 1.- INTRODUCCIÓN Este documento enumera los diferentes tipos de Diagramas Matriciales y su proceso de construcción. Muestra su potencial, como herramienta indispensable para la planificación
DIAGRAMA MATRICIAL 1.- INTRODUCCIÓN Este documento enumera los diferentes tipos de Diagramas Matriciales y su proceso de construcción. Muestra su potencial, como herramienta indispensable para la planificación
PRIMER ENCUENTRO. Licenciatura en Enseñanza de la Matemática Mg. Lucía C. Sacco
 PRIMER ENCUENTRO Unidad Nº1 Unidad Nº1: Estadística descriptiva Tipos de estadística: descriptiva e inferencial. Tipos de variables. Niveles de medición: datos de nivel nominal, de nivel ordinal, de nivel
PRIMER ENCUENTRO Unidad Nº1 Unidad Nº1: Estadística descriptiva Tipos de estadística: descriptiva e inferencial. Tipos de variables. Niveles de medición: datos de nivel nominal, de nivel ordinal, de nivel
DEPARTAMENTO DE MATEMÁTICAS. IES GALLICUM
 UNIDAD I: NÚMEROS (6 Horas) 1.- Repasar el cálculo con números racionales y potencias de exponente entero. 2.- Resolver problemas de la vida cotidiana en los que intervengan los números racionales. 1.-
UNIDAD I: NÚMEROS (6 Horas) 1.- Repasar el cálculo con números racionales y potencias de exponente entero. 2.- Resolver problemas de la vida cotidiana en los que intervengan los números racionales. 1.-
INFERENCIA ESTADÍSTICA. Metodología de Investigación. Tesifón Parrón
 Metodología de Investigación Tesifón Parrón Contraste de hipótesis Inferencia Estadística Medidas de asociación Error de Tipo I y Error de Tipo II α β CONTRASTE DE HIPÓTESIS Tipos de Test Chi Cuadrado
Metodología de Investigación Tesifón Parrón Contraste de hipótesis Inferencia Estadística Medidas de asociación Error de Tipo I y Error de Tipo II α β CONTRASTE DE HIPÓTESIS Tipos de Test Chi Cuadrado
Probabilidad Condicional
 Probabilidad Condicional Algunas veces la ocurrencia de un evento A puede afectar la ocurrencia posterior de otro evento B; por lo tanto, la probabilidad del evento B se verá afectada por el hecho de que
Probabilidad Condicional Algunas veces la ocurrencia de un evento A puede afectar la ocurrencia posterior de otro evento B; por lo tanto, la probabilidad del evento B se verá afectada por el hecho de que
CONTRASTES DE HIPÓTESIS NO PARAMÉTRICOS
 CONTRASTES DE HIPÓTESIS NO PARAMÉTRICOS 1 POR QUÉ SE LLAMAN CONTRASTES NO PARAMÉTRICOS? A diferencia de lo que ocurría en la inferencia paramétrica, ahora, el desconocimiento de la población que vamos
CONTRASTES DE HIPÓTESIS NO PARAMÉTRICOS 1 POR QUÉ SE LLAMAN CONTRASTES NO PARAMÉTRICOS? A diferencia de lo que ocurría en la inferencia paramétrica, ahora, el desconocimiento de la población que vamos
