Transcripción

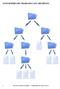
1 ÁRBOLES GENERALES Y Y ESTRUCTURAS DE ÍNDICES DEFINICIONES Y REPRESENTACIONES DEFINICIONES Y REPRESENTACIONES. NOMENCLATURA SOBRE ÁRBOLES. DECLARACIÓN Y REPRESENTACIÓN.. CONSTRUCCIÓN.. ÁRBOLES ÁRBOLES ROJO NEGRO. ÁRBOLES AVL. ÁRBOLES MULTIWAY. ÁRBOLES B. ÁRBOLES B+. ÁRBOLES HILVANADOS. ÁRBOLES GENERALES Y 1 ÁRBOLES GENERALES Y 2 DEFINICIONES Y REPRESENTACIONES UN BOSQUE ES UN GRAFO NO DIRIGIDO ACÍCLICO. UN ÁRBOL ES UNA ESTRUCTURA DE DATOS, QUE PUEDE DEFINIRSE DE FORMA RECURSIVA COMO: UNA ESTRUCTURA VACÍA O. UN ELEMENTO O CLAVE DE INFORMACIÓN (NODO) MÁS UN NÚMERO FINITO DE ESTRUCTURAS TIPO ÁRBOL, DISJUNTOS, LLAMADOS SUBÁRBOLES: SI DICHO NÚMERO DE ESTRUCTURAS ES INFERIOR O IGUAL A 2, SE TIENE UN ÁRBOL BINARIO. UN ÁRBOL ES UNA ESTRUCTURA NO SECUENCIAL. UN ÁRBOL ES UN TIPO DE GRAFO ACÍCLICO, CONEXO Y NO DIRIGIDO: ES UN GRAFO NO DIRIGIDO EN EL QUE EXISTE EXACTAMENTE UN CAMINO ENTRE TODO PAR DE NODOS. ESTA DEFINICIÓN PERMITE IMPLEMENTAR UN ÁRBOL Y SUS OPERACIONES EMPLEANDO LAS REPRESENTACIONES QUE SE UTILIZAN PARA LOS GRAFOS. ÁRBOLES GENERALES Y 3 DEFINICIONES Y REPRESENTACIONES LAS PRINCIPALES FORMAS DE REPRESENTACIÓN SON: MEDIANTE UN GRAFO. MEDIANTE UN DIAGRAMA ENCOLUMNADO: a b d c e f UNA ESTRUCTURA DE DATOS MUY UTILIZADA SON LOS ÁRBOLES : ESTOS ÁRBOLES TIENEN 0, 1 O 2 DESCENDIENTES COMO MÁXIMO. EL ÁRBOL DE LA FIGURA ES UN EJEMPLO VÁLIDO DE ÁRBOL BINARIO. ÁRBOLES GENERALES Y 4 DEFINICIONES Y REPRESENTACIONES NOMENCLATURA SOBRE ÁRBOLES ÁRBOLES GENERALES Y 5 ÁRBOLES GENERALES Y 6

2 NOMENCLATURA SOBRE ÁRBOLES NOMENCLATURA SOBRE ÁRBOLES RAÍZ: ES AQUEL ELEMENTO QUE NO TIENE ANTECESOR; EJEMPLO: a. RAMA: ES LA ARISTA ENTRE DOS NODOS. ANTECESOR: UN NODO X ES ANTECESOR DE UN NODO Y SI POR ALGUNA DE LAS RAMAS DE X SE PUEDE LLEGAR A Y. SUCESOR: UN NODO X ES SUCESOR DE UN NODO Y SI POR ALGUNA DE LAS RAMAS DE Y SE PUEDE LLEGAR A X. GRADO DE UN NODO: ES EL NÚMERO DE DESCENDIENTES DIRECTOS QUE TIENE. EJEMPLO: c TIENE GRADO 2, d TIENE GRADO 0, a TIENE GRADO 2. HOJA: ES UN NODO QUE NO TIENE DESCENDIENTES (GRADO 0). EJEMPLO: d. NODO INTERNO: ES AQUEL QUE TIENE AL MENOS UN DESCENDIENTE. NIVEL: ES EL NÚMERO DE RAMAS QUE HAY QUE RECORRER PARA LLEGAR DE LA RAÍZ A UN NODO. EJEMPLO: EL NIVEL DEL NODO a ES 1 (ES UN CONVENIO), EL NIVEL DEL NODO e ES 3. ALTURA: ES EL NIVEL MÁS ALTO DEL ÁRBOL. EN EL EJEMPLO LA ALTURA ES 3. ANCHURA: ES EL MAYOR VALOR DEL NÚMERO DE NODOS QUE HAY EN UN NIVEL. EN LA FIGURA LA ANCHURA ES 3. ÁRBOL BALANCEADO POR ALTURA: ES AQUEL EN DONDE TODOS LOS HIJOS O NODOS HOJA SE INTENTAN MANTENER A LA MISMA DISTANCIA DE LA RAÍZ. ÁRBOL BALANCEADO POR PESO: ES AQUEL EN DONDE LOS NODOS MÁS VISITADOS O UTILIZADOS SE MANTIENEN A POCA DISTANCIA DE LA RAÍZ. ÁRBOL RELLENO: SE DA CUANDO TODO NODO TIENE 2 HIJOS O BIEN ES HOJA. ÁRBOL BINARIO COMPLETO: ES UN ÁRBOL BINARIO RELLENO EN DÓNDE TODAS LAS HOJAS TIENEN LA MISMA PROFUNDIDAD. ÁRBOLES GENERALES Y 7 ÁRBOLES GENERALES Y 8 NOMENCLATURA SOBRE ÁRBOLES ACLARACIONES: SE HA DENOMINADO a A LA RAÍZ, PERO SE PUEDE OBSERVAR SEGÚN LA FIGURA QUE CUALQUIER NODO PODRÍA SER CONSIDERADO RAÍZ, BASTA CON GIRAR EL ÁRBOL. PODRÍA DETERMINARSE POR EJEMPLO QUE b FUERA LA RAÍZ Y a Y d LOS SUCESORES INMEDIATOS DE LA RAÍZ b. GENERALMENTE EN LAS IMPLEMENTACIONES SOBRE UN COMPUTADOR ES NECESARIA UNA JERARQUÍA, ES DECIR, QUE HAYA UNA ÚNICA RAÍZ. DECLARACIÓN Y REPRESENTACIÓN ÁRBOLES GENERALES Y 9 ÁRBOLES GENERALES Y 10 DECLARACIÓN Y REPRESENTACIÓN DECLARACIÓN Y REPRESENTACIÓN SE DEFINIRÁ EL ÁRBOL CON UNA CLAVE DE TIPO ENTERO (PUEDE SER CUALQUIER OTRO TIPO DE DATOS), Y DOS HIJOS: IZQUIERDO (izq) Y DERECHO (der). PARA REPRESENTAR LOS ENLACES CON LOS HIJOS SE UTILIZAN PUNTEROS. EL ÁRBOL VACÍO SE REPRESENTARÁ CON UN PUNTERO NULO. EN C UN ÁRBOL BINARIO PUEDE DECLARARSE DE LA SIGUIENTE MANERA: typedef struct tarbol int clave; struct tarbol *izq, *der; tarbol; ÁRBOLES GENERALES Y 11 ÁRBOLES GENERALES Y 12

3 DECLARACIÓN Y REPRESENTACIÓN DECLARACIÓN Y REPRESENTACIÓN UNA FORMA MÁS DETALLADA SERÍA: ESTRUCTURA TreeNode: template<class T> class TreeNode public: TreeNode(T e) : data(e), leftptr(null), rightptr(null) ; TreeNode(T e, TreeNode<T>* left, TreeNode<T>* right) : data(e), leftptr(left), rightptr(right) ; T data; TreeNode<T> *leftptr, *rightptr; ; ÁRBOLES GENERALES Y 13 ESTRUCTURA BinaryTree: template<class T> class BinaryTree public: BinaryTree(): root(null) ; BinaryTree(T rootvalue); BinaryTree(T rootvalue, const BinaryTree<T>& left, const BinaryTree<T>& right); BinaryTree<T>& operator= (const BinaryTree<T>& b); ~BinaryTree() Clear();; ÁRBOLES GENERALES Y 14 DECLARACIÓN Y REPRESENTACIÓN BinaryTree<T> Left() const; BinaryTree<T> Right() const; int IsEmpty() const return (root == NULL);; T& operator() () const; void Clear(); void Preorder(); void Inorder(); void Postorder(); protected: TreeNode<T>* root; ; DECLARACIÓN Y REPRESENTACIÓN LA REPRESENTACIÓN GRÁFICA ES LA SIGUIENTE: *leftptr data *rightptr ÁRBOLES GENERALES Y 15 ÁRBOLES GENERALES Y 16 DECLARACIÓN Y REPRESENTACIÓN ÁRBOLES GENERALES Y 17 ÁRBOLES GENERALES Y 18

4 SE CONSIDERAN DOS TIPOS DE RECORRIDO: RECORRIDO EN PROFUNDIDAD. RECORRIDO EN ANCHURA O A NIVEL. PUESTO QUE LOS ÁRBOLES NO SON SECUENCIALES COMO LAS LISTAS, HAY QUE BUSCAR ESTRATEGIAS ALTERNATIVAS PARA VISITAR TODOS LOS NODOS. RECORRIDOS EN PROFUNDIDAD RECORRIDO EN PREORDEN (PREORDER): CONSISTE EN VISITAR EL NODO ACTUAL (VISITAR PUEDE SER SIMPLEMENTE MOSTRAR LA CLAVE DEL NODO POR PANTALLA), Y DESPUÉS VISITAR EL SUBÁRBOL IZQUIERDO Y UNA VEZ VISITADO, VISITAR EL SUBÁRBOL DERECHO. ES UN PROCESO RECURSIVO POR NATURALEZA. PARA LA FIGURA EJEMPLO LAS VISITAS SERÍAN EN EL ORDEN SIGUIENTE: a,b,d,c,e,f. ÁRBOLES GENERALES Y 19 ÁRBOLES GENERALES Y 20 LA CODIFICACIÓN EN C ES LA SIGUIENTE: void preorden(tarbol *a) if (a!= NULL) visitar(a); preorden(a->izq); preorden(a->der); RECORRIDO EN INORDEN U ORDEN CENTRAL (INORDER): SE VISITA EL SUBÁRBOL IZQUIERDO, EL NODO ACTUAL, Y DESPUÉS SE VISITA EL SUBÁRBOL DERECHO. EN EL EJEMPLO DE LA FIGURA LAS VISITAS SERÍAN EN ESTE ORDEN: b,d,a,e,c,f. LA CODIFICACIÓN EN C ES LA SIGUIENTE: void inorden(tarbol *a) if (a!= NULL) inorden(a->izq); visitar(a); inorden(a->der); ÁRBOLES GENERALES Y 21 ÁRBOLES GENERALES Y 22 RECORRIDO EN POSTORDEN (POSTORDER): SE VISITAN PRIMERO EL SUBÁRBOL IZQUIERDO, DESPUÉS EL SUBÁRBOL DERECHO, Y POR ÚLTIMO EL NODO ACTUAL. EN EL EJEMPLO DE LA FIGURA EL RECORRIDO QUEDARÍA ASÍ: d,b,e,f,c,a. LA CODIFICACIÓN EN C ES LA SIGUIENTE: void postorden(arbol *a) if (a!= NULL) postorden(a->izq); postorden(a->der); visitar(a); LA VENTAJA DEL RECORRIDO EN POSTORDEN ES QUE PERMITE BORRAR EL ÁRBOL DE FORMA CONSISTENTE: SI VISITAR SE TRADUCE POR BORRAR EL NODO ACTUAL, AL EJECUTAR ESTE RECORRIDO SE BORRARÁ EL ÁRBOL O SUBÁRBOL QUE SE PASA COMO PARÁMETRO. LA RAZÓN PARA HACER ESTO ES QUE NO SE DEBE BORRAR UN NODO Y DESPUÉS SUS SUBÁRBOLES, PORQUE AL BORRARLO SE PUEDEN PERDER LOS ENLACES, Y AUNQUE NO SE PERDIERAN SE ROMPE CON LA REGLA DE MANIPULAR UNA ESTRUCTURA DE DATOS INEXISTENTE. ÁRBOLES GENERALES Y 23 ÁRBOLES GENERALES Y 24

5 EJEMPLOS DE RECORRIDOS DE ÁRBOLES : ÁRBOL PARA EJEMPLO DE RECORRIDOS EN AMPLITUD: ÁRBOLES GENERALES Y 25 ÁRBOLES GENERALES Y 26 RECORRIDOS EN AMPLITUD CONSISTE EN IR VISITANDO EL ÁRBOL POR NIVELES. PRIMERO SE VISITAN LOS NODOS DE NIVEL 1 (LA RAÍZ), DESPUÉS LOS NODOS DE NIVEL 2, ASÍ HASTA QUE YA NO QUEDEN MÁS. SI SE HACE EL RECORRIDO EN AMPLITUD DEL ÁRBOL DE LA FIGURA EJEMPLO SE VISITARÍAN LOS NODOS EN ESTE ORDEN: a,b,c,d,e,f. EN ESTE CASO EL RECORRIDO NO SE REALIZARÁ DE FORMA RECURSIVA SINO ITERATIVA, UTILIZANDO UNA COLA COMO ESTRUCTURA DE DATOS AUXILIAR: EL PROCEDIMIENTO CONSISTE EN ENCOLAR (SI NO ESTÁN VACÍOS) LOS SUBÁRBOLES IZQUIERDO Y DERECHO DEL NODO EXTRAIDO DE LA COLA, Y SEGUIR DESENCOLANDO Y ENCOLANDO HASTA QUE LA COLA ESTÉ VACÍA. EN LA CODIFICACIÓN QUE VIENE A CONTINUACIÓN NO SE IMPLEMENTAN LAS OPERACIONES SOBRE COLAS. ÁRBOLES GENERALES Y 27 LA CODIFICACIÓN EN C ES LA SIGUIENTE: void amplitud(tarbol *a) tcola cola; /* LAS CLAVES DE LA COLA SERÁN DE TIPO ÁRBOL BINARIO */ arbol *aux; if (a!= NULL) CrearCola(cola); encolar(cola, a); while (!colavacia(cola)) desencolar(cola, aux); visitar(aux); if (aux->izq!= NULL) encolar(cola, aux->izq); if (aux->der!= NULL) encolar(cola, aux->der); ÁRBOLES GENERALES Y 28 CONSTRUCCIÓN DE UN ÁRBOL BINARIO CONSTRUCCIÓN DE UN ÁRBOL BINARIO A CONTINUACIÓN SE ESTUDIA UN MÉTODO PARA CREAR UN ÁRBOL BINARIO QUE NO TENGA CLAVES REPETIDAS. SE PARTE DE SU RECORRIDO EN PREORDEN E INORDEN, ALMACENADOS EN SENDOS ARRAYS. ÁRBOLES GENERALES Y 29 ÁRBOLES GENERALES Y 30

6 CONSTRUCCIÓN DE UN ÁRBOL BINARIO PARTIENDO DE LOS RECORRIDOS PREORDEN E INORDEN DEL ÁRBOL DE LA FIGURA EJEMPLO PUEDE DETERMINARSE: QUE LA RAÍZ ES EL PRIMER ELEMENTO DEL RECORRIDO EN PREORDEN. ESE ELEMENTO SE BUSCA EN EL ARRAY INORDEN. LOS ELEMENTOS EN EL ARRAY INORDEN ENTRE IZQ Y LA RAÍZ FORMAN EL SUBÁRBOL IZQUIERDO. LOS ELEMENTOS ENTRE DER Y LA RAÍZ FORMAN EL SUBÁRBOL DERECHO. POR TANTO SE TIENE EL ÁRBOL SIGUIENTE: CONSTRUCCIÓN DE UN ÁRBOL BINARIO A CONTINUACIÓN COMIENZA UN PROCESO RECURSIVO. SE PROCEDE A CREAR EL SUBÁRBOL IZQUIERDO, CUYO TAMAÑO ESTÁ LIMITADO POR LOS ÍNDICES IZQ Y DER. LA SIGUIENTE POSICIÓN EN EL RECORRIDO EN PREORDEN ES LA RAÍZ DE ESTE SUBÁRBOL. QUEDA LO SIGUIENTE: ÁRBOLES GENERALES Y 31 ÁRBOLES GENERALES Y 32 CONSTRUCCIÓN DE UN ÁRBOL BINARIO EL SUBÁRBOL b TIENE UN SUBÁRBOL DERECHO, QUE NO TIENE NINGÚN DESCENDIENTE, SEGÚN INDICAN LOS ÍNDICES IZQ Y DER. SE HA OBTENIDO EL SUBÁRBOL IZQUIERDO COMPLETO DE LA RAÍZ a, PUESTO QUE b NO TIENE SUBÁRBOL IZQUIERDO: DESPUÉS SEGUIRÁ CONSTRUYÉNDOSE EL SUBÁRBOL DERECHO A PARTIR DE LA RAÍZ a. ÁRBOLES GENERALES Y 33 ÁRBOLES GENERALES Y 34 UN ES AQUEL QUE ES: UNA ESTRUCTURA VACÍA, O. UN ELEMENTO O CLAVE DE INFORMACIÓN (NODO) MÁS UN NÚMERO FINITO -A LO SUMO DOS- DE ESTRUCTURAS TIPO ÁRBOL, DISJUNTOS, LLAMADOS SUBÁRBOLES QUE CUMPLEN LO SIGUIENTE: TODAS LAS CLAVES DEL SUBÁRBOL IZQUIERDO AL NODO SON MENORES QUE LA CLAVE DEL NODO. TODAS LAS CLAVES DEL SUBÁRBOL DERECHO AL NODO SON MAYORES QUE LA CLAVE DEL NODO. AMBOS SUBÁRBOLES SON ÁRBOLES DE BÚSQUEDA. UN EJEMPLO DE ES EL SIGUIENTE: ÁRBOLES GENERALES Y 35 ÁRBOLES GENERALES Y 36

7 AL DEFINIR EL TIPO DE DATOS QUE REPRESENTA LA CLAVE DE UN NODO DENTRO DE UN ES NECESARIO QUE EN DICHO TIPO SE PUEDA ESTABLECER UNA RELACIÓN DE ORDEN. POR EJEMPLO, SUPONER QUE EL TIPO DE DATOS DE LA CLAVE ES UN PUNTERO (DA IGUAL A LO QUE APUNTE). EN EL EJEMPLO DE LA FIGURA LAS CLAVES SON NÚMEROS ENTEROS: DADA LA RAÍZ 4, LAS CLAVES DEL SUBÁRBOL IZQUIERDO SON MENORES QUE 4, Y LAS CLAVES DEL SUBÁRBOL DERECHO SON MAYORES QUE 4. ESTO SE CUMPLE TAMBIÉN PARA TODOS LOS SUBÁRBOLES. SI SE HACE EL RECORRIDO DE ESTE ÁRBOL EN ORDEN CENTRAL SE OBTIENE UNA LISTA DE LOS NÚMEROS ORDENADA DE MENOR A MAYOR. UNA VENTAJA FUNDAMENTAL ES QUE SON EN GENERAL MUCHO MÁS RÁPIDOS PARA LOCALIZAR UN ELEMENTO QUE UNA LISTA ENLAZADA. SON MÁS RÁPIDOS PARA INSERTAR Y BORRAR ELEMENTOS. SI EL ÁRBOL ESTÁ PERFECTAMENTE EQUILIBRADO (LA DIFERENCIA ENTRE EL N DE NODOS DEL SUBÁRBOL IZQUIERDO Y EL N DE NODOS DEL SUBÁRBOL DERECHO ES A LO SUMO 1, PARA TODOS LOS NODOS): EL NÚMERO DE COMPARACIONES NECESARIAS PARA LOCALIZAR UNA CLAVE ES APROXIMADAMENTE LOG N EN EL PEOR CASO. EL ALGORITMO DE INSERCIÓN EN UN ÁRBOL BINARIO DE BÚSQUEDA TIENE LA VENTAJA (SOBRE LOS ARRAYS ORDENADOS, DONDE SE EMPLEARÍA BÚSQUEDA DICOTÓMICA PARA LOCALIZAR UN ELEMENTO) DE QUE NO NECESITA HACER UNA REUBICACIÓN DE LOS ELEMENTOS DE LA ESTRUCTURA PARA QUE ESTA SIGA ORDENADA DESPUÉS DE LA INSERCIÓN. ÁRBOLES GENERALES Y 37 ÁRBOLES GENERALES Y 38 DICHO ALGORITMO FUNCIONA AVANZANDO POR EL ÁRBOL ESCOGIENDO LA RAMA IZQUIERDA O DERECHA EN FUNCIÓN DE LA CLAVE QUE SE INSERTA Y LA CLAVE DEL NODO ACTUAL, HASTA ENCONTRAR SU UBICACIÓN: INSERTAR LA CLAVE 7 EN EL ÁRBOL DE LA FIGURA REQUIERE AVANZAR POR EL ÁRBOL HASTA LLEGAR A LA CLAVE 8, E INTRODUCIR LA NUEVA CLAVE EN EL SUBÁRBOL IZQUIERDO A 8. EL ALGORITMO DE BORRADO EN ÁRBOLES ES ALGO MÁS COMPLEJO, PERO MÁS EFICIENTE QUE EL DE BORRADO EN UN ARRAY ORDENADO. ÁRBOLES GENERALES Y 39 OPERACIONES BÁSICAS SOBRE ÁRBOLES DE BÚSQUEDA BÚSQUEDA SI EL ÁRBOL NO ES DE BÚSQUEDA, ES NECESARIO EMPLEAR UNO DE LOS RECORRIDOS ANTERIORES SOBRE EL ÁRBOL PARA LOCALIZARLO. EL RESULTADO ES IDÉNTICO AL DE UNA BÚSQUEDA SECUENCIAL. APROVECHANDO LAS PROPIEDADES DEL ÁRBOL DE BÚSQUEDA SE PUEDE ACELERAR LA LOCALIZACIÓN: HAY QUE DESCENDER A LO LARGO DEL ÁRBOL A IZQUIERDA O DERECHA DEPENDIENDO DEL ELEMENTO QUE SE BUSCA. LA CODIFICACIÓN EN C ES LA SIGUIENTE: boolean buscar(tarbol *a, int elem) if (a == NULL) return FALSE; else if (a->clave < elem) return buscar(a->der, elem); else if (a->clave > elem) return buscar(a->izq, elem); else return TRUE; ÁRBOLES GENERALES Y 40 INSERCIÓN LA INSERCIÓN RESULTA PRÁCTICAMENTE IDÉNTICA A LA BÚSQUEDA. CUANDO SE LLEGA A UN ÁRBOL VACÍO SE CREA EL NODO EN EL PUNTERO QUE SE PASA COMO PARÁMETRO POR REFERENCIA, DE ESTA MANERA LOS NUEVOS ENLACES MANTIENEN LA COHERENCIA. SI EL ELEMENTO A INSERTAR YA EXISTE ENTONCES NO SE HACE NADA. LA CODIFICACIÓN EN C ES LA SIGUIENTE: void insertar(tarbol **a, int elem) if (*a == NULL) *a = (arbol *) malloc(sizeof(arbol)); (*a)->clave = elem; (*a)->izq = (*a)->der = NULL; else if ((*a)->clave < elem) insertar(&(*a)->der, elem); else if ((*a)->clave > elem) insertar(&(*a)->izq, elem); ÁRBOLES GENERALES Y 41 ÁRBOLES GENERALES Y 42

8 BORRADO LA OPERACIÓN DE BORRADO RESULTA SER ALGO MÁS COMPLICADA. EL ÁRBOL DEBE SEGUIR SIENDO DE BÚSQUEDA TRAS EL BORRADO. UNA VEZ ENCONTRADO EL NODO A BORRAR PUEDEN DARSE TRES CASOS: EL NODO NO TIENE DESCENDIENTES: SIMPLEMENTE SE BORRA. EL NODO TIENE AL MENOS UN DESCENDIENTE POR UNA SOLA RAMA: SE BORRA DICHO NODO Y SU PRIMER DESCENDIENTE SE ASIGNA COMO HIJO DEL PADRE DEL NODO BORRADO: EN EL ÁRBOL DE LA FIGURA SE BORRA EL NODO CUYA CLAVE ES 1, RESULTANDO EL SIGUIENTE ÁRBOL: ÁRBOLES GENERALES Y 43 EL NODO TIENE AL MENOS UN DESCENDIENTE POR CADA RAMA: AL BORRAR DICHO NODO ES NECESARIO MANTENER LA COHERENCIA DE LOS ENLACES Y LA ESTRUCTURA DE UN : LA SOLUCIÓN CONSISTE EN SUSTITUIR LA INFORMACIÓN DEL NODO QUE SE BORRA POR LA DE UNA DE LAS HOJAS Y BORRAR A CONTINUACIÓN DICHA HOJA: DEBE SER LA HOJA QUE CONTENGA UNA DE ESTAS DOS CLAVES: LA MAYOR DE LAS CLAVES MENORES AL NODO QUE SE BORRA: SI SE QUIERE BORRAR EL NODO 4 DEL ÁRBOL DE LA FIGURA EJEMPLO SE SUSTITUIRÁ LA CLAVE 4 POR LA CLAVE 2. LA MENOR DE LAS CLAVES MAYORES AL NODO QUE SE BORRA: SI SE QUIERE BORRAR EL NODO 4 DEL ÁRBOL DE LA FIGURA EJEMPLO SE SUSTITUIRÁ LA CLAVE 4 POR LA CLAVE 5. ÁRBOLES GENERALES Y 44 EL ALGORITMO DE BORRADO QUE SE MUESTRA A CONTINUACIÓN REALIZA LA SUSTITUCIÓN POR LA MAYOR DE LAS CLAVES MENORES, PARA LO CUAL ES NECESARIO: DESCENDER PRIMERO A LA IZQUIERDA DEL NODO QUE SE VA A BORRAR. AVANZAR SIEMPRE A LA DERECHA HASTA ENCONTRAR UN NODO HOJA. A CONTINUACIÓN SE MUESTRA GRÁFICAMENTE EL PROCESO DE BORRAR EL NODO DE CLAVE 4: ÁRBOLES GENERALES Y 45 LA CODIFICACIÓN EN C ES LA SIGUIENTE, DONDE EL PROCEDIMIENTO SUSTITUIR ES EL QUE DESCIENDE POR EL ÁRBOL CUANDO SE DA EL CASO DEL NODO CON DESCENCIENTES POR AMBAS RAMAS: void borrar(tarbol **a, int elem) void sustituir(tarbol **a, tarbol **aux); tarbol *aux; if (*a == NULL) /* no existe la clave */ return; if ((*a)->clave < elem) borrar(&(*a)->der, elem); else if ((*a)->clave > elem) borrar(&(*a)->izq, elem); else if ((*a)->clave == elem) aux = *a; if ((*a)->izq == NULL) *a = (*a)->der; else if ((*a)->der == NULL) *a = (*a)->izq; else sustituir(&(*a)->izq, &aux); /* se sustituye por la mayor de las menores */ free(aux); ÁRBOLES GENERALES Y 46 void sustituir(tarbol **a, tarbol **aux) if ((*a)->der!= NULL) sustituir(&(*a)->der, aux); else (*aux)->clave = (*a)->clave; *aux = *a; *a = (*a)->izq; ÁRBOLES ÁRBOLES GENERALES Y 47 ÁRBOLES GENERALES Y 48

9 ÁRBOLES COMO UNA FORMA DE ELIMINAR LAS BÚSQUEDAS EXHAUSTIVAS DE LOS ÁRBOLES EXISTEN LOS ÁRBOLES ESTOS SON ÁRBOLES EN CUYOS NODOS SE PERMITE TENER MÁS DE UNA CLAVE AL MISMO TIEMPO. LOS ÁRBOLES TIENEN MÁXIMO 2 HIJOS (DERECHO E IZQUIERDO). SI SE LE PERMITE AL NODO TENER 2 VALORES, ESTE PODRÁ TENER 3 LIGAS A SUBÁRBOLES Y UNO CON 3 VALORES PODRÁ TENER 4 LIGAS. UN ÁRBOL CON ESTAS CARACTERÍSTICAS PUEDE CONTENER ENTONCES NODOS CON 2, 3 O 4 LIGAS, DE AHÍ QUE SE LES LLAMA ÁRBOLES EN LOS ÁRBOLES TODOS LOS SUBÁRBOLES TIENEN LA MISMA ALTURA Y ESTÁN SIEMPRE BALANCEADOS. ESTOS ÁRBOLES SON MUY ATRACTIVOS PARA EL ALMACENAMIENTO Y RECUPERACIÓN DE CLAVES, SIN EMBARGO SON UN TANTO COMPLICADOS DE IMPLEMENTAR. ÁRBOLES LOS ÁRBOLES 2-3 SON UN TIPO DE ÁRBOL BALANCEADO POR ALTURA (HEIGHT BALANCED) EN DONDE TODOS LOS NODOS NO- TERMINALES TIENEN 2 Ó 3 DECENDIENTES Y TODOS LOS NODOS HOJA TIENEN LA MISMA LONGITUD (PATH LENGTH) O DISTANCIA DESDE LA RAÍZ. EN ESTOS ÁRBOLES SÓLO LAS HOJAS CONTIENEN LA INFORMACIÓN (VALORES). LOS NODOS NO-TERMINAMES CONTIENEN INDICADORES QUE CONSTAN DE 2 VALORES DE LOS CUALES EL IZQUIERDO ES EL MÁXIMO DEL SUBÁRBOL IZQUIERDO Y EL SEGUNDO VALOR ES EL VALOR MÁXIMO DEL SUBÁRBOL CENTRAL. ÁRBOLES GENERALES Y 49 ÁRBOLES GENERALES Y 50 ÁRBOLES ÁRBOLES ROJO - NEGRO ÁRBOL ÁRBOLES GENERALES Y 51 ÁRBOLES GENERALES Y 52 ÁRBOLES ROJO - NEGRO LOS ÁRBOLES ROJO-NEGRO SON ÁRBOLES EN DONDE CADA NODO TIENE UN COLOR YA SEA ROJO O NEGRO. ESTOS ÁRBOLES REPRESENTAN UNA MANERA DE TRANSFORMAR UN ÁRBOL EN UNO BINARIO, LO QUE SE PUEDE LOGRAR UTILIZANDO LOS SIGUIENTES LINEAMIENTOS: TODO NODO 2 ES TRANSFORMADO A UN NODO NEGRO CON DECENDIENTES NEGROS. TODO NODO 3 ES TRANSFORMADO EN UN NODO NEGRO CON UN HIJO ROJO Y UNO NEGRO. UN NODO 4 ES TRANSFORMADO A UN NODO NEGRO CON DOS HIJOS ROJOS. ÁRBOLES ROJO - NEGRO ESTO SATISFACE LAS SIGUIENTES PROPIEDADES: TODOS LOS NODOS TIENEN UN COLOR, YA SEA ROJO O NEGRO. TODA HOJA ES NEGRA. AMBOS DESCENDIENTES DE UN NODO ROJO SON SIEMPRE NODOS NEGROS. CADA CAMINO DESDE CUALQUIER NODO HASTA UNA HOJA DESCENDIENTE CONTIENE EL MISMO NÚMERO DE NODOS NEGROS. NO HAY DOS NODOS ROJOS ADYACENTES EN UN CAMINO. ÁRBOLES GENERALES Y 53 ÁRBOLES GENERALES Y 54

10 ÁRBOLES ROJO - NEGRO UN EJEMPLO DE TRANSFORMACIÓN DE LOS NODOS '3' Y '4' EN ROJO NEGRO ES EL SIGUIENTE: ÁRBOLES ROJO - NEGRO AL NÚMERO DE NODOS NEGROS EN EL CAMINO DE UN NODO A UNA HOJA DESCENDIENTE SE LE CONOCE COMO LA ALTURA - NEGRA DEL NODO. LA ALTURA - NEGRA DE UN ÁRBOL ROJO - NEGRO ES LA ALTURA NEGRA DE SU RAÍZ. EJEMPLO DE TRANSFORMACIÓN DE UN ÁRBOL EN UN ÁRBOL ROJO NEGRO: ÁRBOLES GENERALES Y 55 ÁRBOLES GENERALES Y 56 ÁRBOLES AVL ÁRBOLES GENERALES Y 57 ÁRBOLES AVL LA ESTRUCTURA DE DATOS MÁS VIEJA Y MEJOR CONOCIDA PARA ÁRBOLES BALANCEADOS ES EL ÁRBOL AVL. SU PROPIEDAD ES QUE LA ALTURA DE LOS SUBÁRBOLES DE CADA NODO DIFIERE EN NO MÁS DE 1. PARA MANTENERLO BALANCEADO ES NECESARIO SABER LA ALTURA O LA DIFERENCIA EN ALTURAS DE TODOS LOS SUBÁRBOLES: SE DEBE TENER QUE GUARDAR INFORMACIÓN ADICIONAL EN CADA NODO: UN CONTADOR DE LA DIFERENCIA ENTRE LAS ALTURAS DE SUS DOS SUBÁRBOLES. LOS ÁRBOLES AVL FUERON NOMBRADOS POR SUS DESARROLLADORES ADELSON - VELSKII Y LANDIS. PROBABLEMENTE LA PRINCIPAL CARACTERÍSTICA DE LOS ÁRBOLES AVL ES SU EXELENTE TIEMPO DE EJECUCIÓN PARA LAS DIFERENTES OPERACIONES (BÚSQUEDAS, ALTAS Y BAJAS). EN LAS SIGUIENTES DOS FIGURAS LA PRIMERA ES UN ÁRBOL AVL Y LA SEGUNDA NO LO ES YA QUE LOS SUBÁRBOLES DEL NODO L DIFIEREN EN ALTURA POR MÁS DE 1. ÁRBOLES GENERALES Y 58 ÁRBOLES AVL UN EJEMPLO DE ARBOL AVL ES EL ÁRBOL (a), MIENTRAS QUE EL ÁRBOL (b) NO LO ES. ÁRBOLES MULTIWAY ÁRBOLES GENERALES Y 59 ÁRBOLES GENERALES Y 60

11 ÁRBOLES MULTIWAY ÁRBOLES MULTIWAY LOS ÁRBOLES SON UTILIZADOS PARA ALMACENAR INFORMACIÓN Y PARA PODER ACCEDERLA. CUANDO SE TRATA DE VOLÚMENES MUY GRANDES DE DATOS ALMACENADOS EN DISCO DURO, LAS ESTRUCTURAS Y ESTRATEGIAS DE BÚSQUEDA VISTAS ANTERIORMENTE RESULTAN INEFICIENTES, ESPECIALMENTE POR EL ALTO NÚMERO DE ACCESOS AL DISCO. PARA EVITAR TENER QUE HACER MUCHOS ACCESOS A DISCO ES RAZONABLE TENER VARIAS CLAVES EN CADA NODO DEL ÁRBOL. CUANDO LA INFORMACIÓN DE VARIOS NODOS SE JUNTA FORMANDO PEQUEÑOS GRUPOS A ESTOS SE LES LLAMA PÁGINAS. SI EN CADA ACCESO A DISCO UN PROCEDIMIENTO PUEDE LEER TODA UNA PÁGINA DE DATOS EN LUGAR DE LEERLOS DE UNO EN UNO: SE PUEDE DISMINUIR SIGNIFICATIVAMENTE EL NÚMERO DE ACCESOS NECESARIOS PARA ENCONTRAR UN DETERMINADO DATO. ÁRBOLES GENERALES Y 61 A LOS ÁRBOLES QUE MANEJAN EN CADA NODO UNA PÁGINA SE LES LLAMA ÁRBOLES MULTIWAY : CADA NODO PODRÁ TENER UN MÁXIMO DE M VALORES O CLAVES Y POR CONSIGIENTE M + 1 LIGAS A SUS DECENDIENTES. LA BÚSQUEDA DE UNA CLAVE SERÍA ANÁLOGA A LA DE LOS ÁRBOLES INSERTAR UN DATO EN UN NODO M (ES DECIR, QUE YA ESTÉ LLENO, CON M - 1 ELEMENTOS) IMPLICA DIVIDIR DICHO NODO EN 2 NODOS DE TIPO M/2 (PARA ELLO SE ASUME QUE ES NÚMERO PAR): EJEMPLO, UN NODO 4 (QUE TIENE 3 ELEMENTOS) SE DIVIDE EN 2 NODOS DE TIPO 2, AL IGUAL QUE EN EL CASO DE LOS ÁRBOLES ÁRBOLES GENERALES Y 62 ÁRBOLES MULTIWAY EL TAMAÑO DE UNA PÁGINA NO ES TOTALMENTE ARBITRARIO: A MAYOR TAMAÑO EL TIEMPO PARA PROCESARLA ES MAYOR. DEPENDE TAMBIÉN DE LA CANTIDAD DE MEMORIA PRINCIPAL DISPONIBLE. ÁRBOLES B ÁRBOLES GENERALES Y 63 ÁRBOLES GENERALES Y 64 ÁRBOLES B ÁRBOLES B ESTE TIPO DE ÁRBOLES FUE LLAMADO ÁRBOLES B POR R. BAYER Y E. McCREIGHT, LOS PRIMEROS EN CONSIDERAR EL USO DE ESTOS ÁRBOLES DE TIPO MULTIWAY. UN ÁRBOL B DE ORDEN w CUMPLE CON LAS SIGUIENTES PROPIEDADES: TODA PÁGINA, EXCEPTO LA RAÍZ CONTIENE AL MENOS w CLAVES. LA RAÍZ CONTIENE AL MENOS UNA CLAVE. LA RAÍZ TIENE AL MENOS 2 DESCENDIENTES. TODA PÁGINA CONTIENE A LO SUMO 2 w CLAVES. TODA PÁGINA EXCEPTO LAS HOJAS TIENE m + 1 DECENDIENTES, DÓNDE m ES EL NÚMERO DE CLAVES EN LA PÁGINA. LAS HOJAS NO TIENEN DECENDIENTES. TODAS LAS HOJAS ESTÁN EN EL MISMO NIVEL. CADA NODO PÁGINA ES REPRESENTADO POR UNA ESTRUCTURA QUE TIENE: UN ESPACIO PARA 2 w CLAVES Y 2 w + 1 APUNTADORES HACIA SUS DECENDIENTES. UN CAMPO CON UN VALOR QUE INDICA EL NÚMERO ACTUAL DE CLAVES EN LA PÁGINA. ESTE TIPO DE ÁRBOLES SÓLO SON ÚTILES CUANDO SON DE ORDEN MAYOR O IGUAL A 3. LAS OPERACIONES DE ALTAS Y BAJAS EN UN ÁRBOL B NO ALTERAN SU BALANCE. ÁRBOLES GENERALES Y 65 ÁRBOLES GENERALES Y 66

12 ÁRBOLES B ALTAS Y BAJAS EN UN ÁRBOL B EJEMPLO DE UNA ALTA EN UN ÁRBOL B: SE DA DE ALTA EL DATO 50 : ÁRBOLES B EJEMPLO DE UNA BAJA EN UN ÁRBOL B: ÁRBOLES GENERALES Y 67 ÁRBOLES GENERALES Y 68 ÁRBOLES B ÁRBOLES B EJEMPLO PASO A PASO DE LA BAJA DEL N 76 EN UN ÁRBOL B: ÁRBOLES GENERALES Y 69 ÁRBOLES GENERALES Y 70 ÁRBOLES B+ ÁRBOLES B+ UNA VARIACIÓN A LOS ÁRBOLES B CONSISTE EN QUE TODAS LAS CLAVES ESTÁN EN LAS HOJAS MIENTRAS QUE LOS NODOS NO TERMINALES CONTIENEN LOS ÍNDICES PARA LAS CLAVES. ADICIONALMENTE LAS HOJAS ESTÁN CONECTADAS SECUENCIALMENTE. EN ESTOS ÁRBOLES SE REQUIEREN 2 TIPOS DE ESTRUCTURAS: UNA PARA REPRESENTAR LOS NODOS NO TERMINALES: IGUAL A LA DE LOS ÁRBOLES B. OTRAPARA LAS HOJAS: TIENE UN APUNTADOR ADICIONAL PARA APUNTAR A LA SIGUIENTE HOJA. ESTOS ÁRBOLES SON ESPECIALMENTE ÚTILES PARA APLICACIONES QUE REQUIEREN AMBOS TIPOS DE ACCESO, SECUENCIAL YALEATORIO. ÁRBOLES GENERALES Y 71 ÁRBOLES GENERALES Y 72

13 ÁRBOLES B+ ÁRBOLES B+ PARA BUSCAR UN DATO EN ESTOS ÁRBOLES ES NECESARIO RECORRER UN CAMINO COMPLETO HASTA LA HOJA CORRESPONDIENTE SIGUIENDO LOS ÍNDICES: EL TIEMPO DE BÚSQUEDA ES SIEMPRE CONSTANTE. LAS BAJAS SON DIFERENTES: CUANDO SE ELIMINA UN DATO SE TIENEN QUE MOVER Y REAJUSTAR ELEMENTOS PARA EVITAR HUECOS Y PARA QUE LA INFORMACIÓN EN LOS NODOS NO - TERMINALES ASOCIADOS NO CAMBIE. SI UNA PÁGINA TIENE MENOS DE LA MITAD DE ELEMENTOS (UNDERFLOW) ES NECESARIO BALANCEAR EL ÁRBOL. PARA BALANCEAR SE REDISTRIBUYEN LOS DATOS O SE CONCATENAN PÁGINAS. ÁRBOLES GENERALES Y 73 ÁRBOLES GENERALES Y 74 ÁRBOLES HILVANADOS ÁRBOLES HILVANADOS AL ESTUDIAR LA REPRESENTACIÓN ENLAZADA DE UN ÁRBOL BINARIO ES FÁCIL OBSERVAR QUE EXISTEN MUCHOS ENLACES NULOS. DE HECHO, PUEDEN EXISTIR MÁS ENLACES NULOS QUE PUNTEROS CON VALORES REALES. PARA UN ÁRBOL CON N NODOS, EXISTEN N+1 ENLACES NULOS DE LOS 2N ENLACES EXISTENTES EN LA REPRESENTACIÓN (MÁS DE LA MITAD). COMO EL ESPACIO DE MEMORIA OCUPADO POR LOS ENLACES NULOS ES EL MISMO QUE EL OCUPADO POR LOS NO NULOS, PODRÍA RESULTAR CONVENIENTE UTILIZAR ESTOS ENLACES NULOS PARA ALMACENAR ALGUNA INFORMACIÓN DE INTERÉS PARA LA MANIPULACIÓN DEL ÁRBOL BINARIO. UNA FORMA DE UTILIZAR ESTOS ENLACES ES SUSTITUIRLOS POR PUNTEROS A OTROS NODOS DEL ÁRBOL. ÁRBOLES GENERALES Y 75 ÁRBOLES GENERALES Y 76 ÁRBOLES HILVANADOS ÁRBOLES HILVANADOS LOS ENLACES NULOS SITUADOS EN EL SUBÁRBOL DERECHO DE UN NODO SE SUELEN REUTILIZAR PARA APUNTAR AL SUCESOR DE ESE NODO EN UN DETERMINADO RECORRIDO DEL ÁRBOL, POR EJEMPLO INFIJO. LOS ENLACES NULOS EN SUBÁRBOLES IZQUIERDOS SE UTILIZAN PARA APUNTAR AL PREDECESOR DEL NODO EN EL MISMO TIPO DE RECORRIDO. SI PARA ALGÚN NODO NO EXISTE PREDECESOR (PORQUE ES EL PRIMERO DEL RECORRIDO) O SUCESOR (PORQUE ES EL ÚLTIMO), SE MANTIENE CON VALOR NULO EL ENLACE CORRESPONDIENTE. OTRA VENTAJA ES LA POSIBILIDAD DE UN ACCESO RÁPIDO AL SUCESOR (O AL PREDECESOR) DE UN NODO, QUE ES UNA OPERACIÓN FRECUENTEMENTE NECESARIA. ÁRBOLES GENERALES Y 77 ÁRBOLES GENERALES Y 78

14 ÁRBOLES HILVANADOS ÁRBOLES HILVANADOS PARA PODER MANEJAR CORRECTAMENTE TODA LA INFORMACIÓN DE LA QUE SE DISPONE EN LA REPRESENTACIÓN HILVANADA (CON HILOS) DEL ÁRBOL BINARIO, ES NECESARIO PODER DISTINGUIR ENTRE LO QUE SON PUNTEROS NORMALES, QUE REPRESENTAN LAS RELACIONES REALES ENTRE LOS NODOS, Y LO QUE SON HILOS. ESTO SE PUEDE HACER AÑADIENDO DOS CAMPOS BOOLEANOS A LA REPRESENTACIÓN DE LOS NODOS DEL ÁRBOL. ESTOS NUEVOS CAMPOS INDICARÁN SI LOS ENLACES IZQUIERDO Y DERECHO SON HILOS O NO. CON EL OBJETO DE NO MANTENER ABSOLUTAMENTE NINGÚN ENLACE NULO Y PARA FACILITAR EL RECORRIDO DEL ÁRBOL, SE SUELE AÑADIR A LA ESTRUCTURA UN NODO RAÍZ QUE NO CONTIENE INFORMACIÓN REAL. EL NODO RAÍZ QUE REPRESENTA EL ÁRBOL VACÍO TENDRÁ LA ESTRUCTURA QUE SE MUESTRA EN LA FIGURA: ÁRBOLES GENERALES Y 79 ÁRBOLES GENERALES Y 80 ÁRBOLES HILVANADOS EN GENERAL, LA UTILIZACIÓN DE ENLACES HILOS SIMPLIFICA LOS ALGORITMOS DE RECORRIDO DEL ÁRBOL, POR LO QUE SON RECOMENDABLES CUANDO EL RECORRIDO DEL ÁRBOL ES UNA OPERACIÓN FRECUENTE. DESDE EL PUNTO DE VISTA DE LA MANIPULACIÓN GENERAL DEL ÁRBOL HAY QUE TENER EN CUENTA QUE: LA INSERCIÓN DE NUEVOS NODOS DEBE MANTENER EN TODO MOMENTO ESTA ESTRUCTURA DE ENLACES CON LOS NODOS SUCESOR Y PREDECESOR. CADA VEZ QUE SE INSERTE UN NODO SE DEBERÁ COMPROBAR SI EXISTEN ENLACES DE ESTE TIPO QUE DEBAN SER MODIFICADOS O CREADOS, ADEMÁS DE LOS PUNTEROS NORMALES QUE RELACIONAN LOS NODOS DEL ÁRBOL. ÁRBOLES GENERALES Y 81