Métodos en diferencias para problemas de contorno
|
|
|
- Juan José Figueroa Navarro
- hace 6 años
- Vistas:
Transcripción
1 Métodos numéricos de resolución de ecs. en derivadas parciales Curso Prácticas 1 y 2 Métodos en diferencias para problemas de contorno 1 Resultados sobre existencia de solución de un problema de contorno En esta primera parte, se van a resolver aproximadamente problemas de contorno lineales en ecuaciones diferenciales del tipo u (x) + p(x)u (x) + q(x)u(x) = r(x), x (a, b), (PC) a 0 u(a) a 1 u (a) = α, b 0 u(b) + b 1 u (b) = β, con a 0 + a 1 0, b 0 + b 1 0. Proposición 1 Si el problema de contorno lineal (PC) cumple que: 1. p(x), q(x) y r(x) son funciones continuas en [a, b], 2. q(x) 0 en [a, b], 3. a 0 + b 0 0; a 0 a 1 0 y b 0 b 1 0, entonces el (PC) tiene solución única. Proposición 2 (Principio del máximo) Se considera el siguiente problema de contorno lineal con condiciones de contorno de tipo Dirichlet { u (P CD) (x) + p(x)u (x) + q(x)u(x) = r(x), x (a, b), u(a) = α, u(b) = β, donde las funciones p(x), q(x) y r(x) son continuas en [a, b] y q(x) 0 en el intervalo [a, b]. Por la proposición anterior este problema tiene solución única, u(x). Si u(x) es una función no constante posee las siguientes propiedades: 1. Si r(x) 0 entonces u(x) no tiene ni máximos positivos ni mínimos negativos en (a, b). 2. Si r(x) q(x) 0 entonces u(x) no tiene ni máximos ni mínimos en (a, b). En adelante tomaremos una constante positiva M > 0 tal que p(x) M, en [a, b].
2 2 Algunos resultados sobre existencia y unicidad de sistemas de ecuaciones Definición Una matriz A n n es estrictamente diagonal dominante si a ii > n a ij, i = 1,..., n. j=1 j i Una matriz A n n es diagonal dominante si a ii n a ij, i = 1,..., n. (1) j=1 j i Proposición 3 Si A es estrictamente diagonal dominante, entonces es inversible. Por tanto, el sistema Au = b tiene solución única. Proposición 4 Sea A una matriz tridiagonal tal que a ii > 0, i = 1, 2,..., n, a i,i+1 < 0, i = 1, 2,..., n 1, a i+1,i < 0, i = 1, 2,..., n 1. Si la matriz A es diagonal dominante con la desigualdad (1) estricta al menos para una fila de la matriz, entonces A es inversible, luego el sistema Au = b tiene solución única.. 3 Diferencias finitas Se realiza una partición uniforme del intervalo [a, b] a = x 1 < x 2 < x 3 <... < x n < x n+1 = b, donde x i = a+(i 1) h, i = 1,..., n+1 son los nodos de la malla y h es el paso de discretización. Aplicando la ecuación diferencial del (PC) en los nodos interiores se obtienen las ecuaciones u (x i ) + p(x i )u (x i ) + q(x i )u(x i ) = r(x i ), i = 2,..., n. (2) Existen distintas formas de aproximar las derivadas de una función en un punto. Ejemplos de fórmulas para la primera y segunda derivada son las siguientes: u (x) u (x) u (x) u (x) u(x + h) 2u(x) + u(x h) h 2, (3) u(x + h) u(x h), 2h (4) u(x + h) u(x), h (5) u(x) u(x h). h (6)
3 Se denota por u i a la aproximación de la solución en el nodo x i. Entonces, al sustituir en cada punto interior de la malla x i la ecuación diferencial (2) por la ecuación discreta resultante de aproximar las derivadas por alguna de las fórmulas anteriores se obtiene (junto con las condiciones de contorno) un sistema de ecuaciones lineales tridiagonal. Definición Un esquema en diferencias finitas se dice que es convergente si [ ] max u(x i ) u i = 0, i lim h Método de diferencias centrales Consiste en utilizar las siguientes aproximaciones de las derivadas: u (x) u (x) u(x + h) 2u(x) + u(x h) h 2, u(x + h) u(x h). 2h Proposición 5 Supongamos que en el problema (PCD) las funciones p, q y r son continuas y que q(x) 0, en [a, b] Sea M como antes y supongamos que M h < 2. Entonces se cumplen las siguientes propiedades. 1. Si r(x) 0, la solución numérica obtenida por diferencias centrales o es constante o no puede alcanzar ni un máximo positivo ni un mínimo negativo en ningún nodo interior de la malla. 2. Si r(x) q(x) 0 entonces la solución numérica o es constante o no puede alcanzar ni máximos ni mínimos en el interior del dominio. 3. Supóngamos que u C 4 ([a, b]) es la solución del problema (PCD) y que existe w > 0 tal que q(x) w en [a, b]. Sea u i, i = 1,..., n+1 la solución numérica obtenida por el método de diferencias centrales. Entonces donde max i M 3 = max a x b u (x), u(x i ) u i C h2 12 (M 4 + 2MM 3 ), M 4 = max a x b uiv (x) C = max(1, 1/w). Las conclusiones 1. y 2. reciben el nombre de Principio del máximo discreto.
4 3.2 El método upwind La segunda derivada se aproxima como antes y la primera se aproxima en función del signo de p(x i ) u (x) u (x) u (x) u(x + h) 2u(x) + u(x h) h 2, u(x + h) u(x), h si p(x) < 0 u(x) u(x h), h si p(x) > 0. Proposición 6 Supongamos que en el problema (PCD) las funciones p, q y r son continuas y que q(x) 0, en [a, b] y sea M como antes. Entonces se cumplen las siguientes propiedades. 1. Si r(x) 0, la solución numérica obtenida por el método upwind o es constante o no puede alcanzar ni un máximo positivo ni un mínimo negativo en ningún nodo interior de la malla. 2. Si r(x) q(x) 0 entonces la solución numérica o es constante o no puede alcanzar ni máximos ni mínimos en el interior del dominio. 3. Supóngamos que u C 4 ([a, b]) es la solución del problema (PCD) y que existe w > 0 tal que q(x) w en [a, b]. Sea u i, i = 1,..., n + 1 la solución numérica obtenida por el método upwind. Entonces max i u(x i ) u i C h 12 (hm 4 + 6MM 2 ), donde M 2 = max a x b u (x), M 4 = max a x b uiv (x) C = max(1, 1/w). Las conclusiones 1. y 2. reciben de nuevo el nombre de Principio del máximo discreto.
5 4 Preliminares La notación que se va a usar es la siguiente: Extremos inferior y superior del intervalo de trabajo: a y b. Número de subintervalos de la malla: n. Paso de discretización h. u i es la aproximación numérica en el nodo i. Cuando discretices cualquier problema de la primera parte de la práctica vas a obtener un sistema tridiagonal de ecuaciones lineales. Tanto en el guión como en los ficheros escritos en MATLAB nos referiremos como: matriz(i, i) al elemento diagonal de la matriz correspondiente a la fila i o lo que es lo mismo el coeficiente de u i cuando se discretiza la ecuación diferencial en el nodo i. matriz(i, i + 1) es el elemento superdiagonal de la matriz correspondiente a la fila i o lo que es lo mismo el coeficiente de u i+1 cuando se discretiza la ecuación diferencial en el nodo i. matriz(i, i 1) es el elemento subdiagonal de la matriz correspondiente a a la fila i o lo que es lo mismo el coeficiente de u i 1 cuando se discretiza la ecuación diferencial en el nodo i. tind(i) es la componente i del vector de términos independientes del sistema. El esquema básico utilizado para resolver numéricamente los problemas de esta primera práctica contiene tres partes: Inicialización, donde se definen los parámetros del problema. Resolución, donde se define y se resuelve el sistema de ecuaciones. Resultados, donde se muestran las soluciones numéricas obtenidas. Importante. Los programas con los que se acompaña esta práctica están estructurados de forma que con muy pocos cambios vas a poder resolver cualquier problema de contorno lineal utilizando distintos esquemas. No te dediques exclusivamente a hacer los ejercicios que aquí se proponen. Llévate los ficheros MATLAB y haz los ejercicios y ejemplos que se vayan proponiendo en clase.
6 5 Ejercicios propuestos 5.1 Problema de difusión Se considera el problema: u (x) = e x, x (0, 2), (P1) u(0) = 1, u(2) = e Justifica que la única solución del problema (P1) es la función u(x) = e x. 2. Utiliza el método de diferencias finitas para discretizar el problema (P1) e indica cuáles de términos independientes. matriz(i, i 1) = matriz(i, i) = matriz(i, i + 1) = tind(i) = i = 2,..., n. matriz(1, 1) = tind(1) = matriz(n + 1, n + 1) = tind(n + 1) = 3. Estudia si el sistema anterior tiene solución única. 4. Edita el fichero edp1.m y observa lo siguiente: (a) Se definen: Extremos inferior y superior del intervalo de trabajo : a y b. Número de subintervalos de la malla: n. Paso de discretización: h. Coordenadas de cada uno de los nodos de la malla: x(i), i = 1,..., n + 1. Los coeficientes no nulos de la matriz del sistema: matriz(i, i 1), matriz(i, i), matriz(i, i + 1), i = 2,... n, matriz(1, 1) y matriz(n + 1, n + 1). (Compáralos con los obtenidos en el apartado (2)). El vector de términos independientes del sistema: tind(i), i = 1,..., n + 1. (Compáralo con el obtenido en el apartado (2)). (b) Se resuelve el sistema de ecuaciones. (c) Se calcula el error máximo y se dibuja tanto la solución numérica como la exacta.
7 5. Completa la siguiente tabla: n Error máximo 10 e 10 = e 20 = 40 e 40 = 80 e 80 = 160 e 160 = 6. Utilizando los resultados de la tabla anterior comprueba el orden del método. 5.2 Problema de reacción difusión Se considera el problema: u (x) + x 2 u(x) = x 6 + x 4 12x 2 2, x ( 1, 1), (P2) u( 1) = 2, u(1) = Justifica que la única solución del problema (P2) es la función u(x) = x 4 + x Utiliza el método de diferencias finitas para discretizar el problema (P2) e indica cuáles de términos independientes. matriz(i, i 1) = matriz(i, i) = matriz(i, i + 1) = tind(i) = i = 2,..., n. 3. Modifica el fichero edp1.m adecuadamente de forma que resuelva el problema (P2).
8 4. Completa la siguiente tabla: n Error máximo 10 e 10 = e 20 = 40 e 40 = 80 e 80 = 160 e 160 = 5.3 Problema de convección difusión. Se considera el problema: 1 (P3) 100 u (x) + u (x) = 0, x (0, 1), u(0) = 0, u(1) = Justifica que la única solución del problema (P3) es la función u(x) = e100(x 1) e e 100. Cumple la solución del problema (P3) el principio del máximo? 2. Utiliza el método de diferencias centrales para discretizar el problema (P3) e indica cuáles de términos independientes. matriz(i, i 1) = matriz(i, i) = matriz(i, i + 1) = tind(i) = i = 2,..., n. 3. Modifica el fichero edp1.m adecuadamente de forma que resuelva el problema (P3) por el método de diferencias centrales. Ejecuta el programa para n = 10. Cumple la solución numérica el principio del máximo discreto? Construye una malla de forma que se asegure que la solución numérica cumpla el principio del máximo.
9 4. Completa la siguiente tabla: n Error máximo 10 e 10 = e 20 = 40 e 40 = 80 e 80 = 160 e 160 = 5. Utiliza el método upwind para discretizar el problema (P3) e indica cuáles son los elementos no nulos de la matriz del sistema lineal que resulta, así como su vector de términos independientes. matriz(i, i 1) = matriz(i, i) = matriz(i, i + 1) = tind(i) = i = 2,..., n. 6. Modifica el fichero edp1.m adecuadamente de forma que resuelva el problema (P3) por el método upwind. Ejecuta el programa para n = 10. Cumple la solución numérica el principio del máximo discreto? 7. Completa la siguiente tabla e indica el orden de convergencia n Error máximo 40 e 40 = e 80 = 160 e 160 = 320 e 320 = 640 e 640 = 5.4 Condición de tipo Neumann En este ejercicio vamos a modificar el programa de forma que resuelva el siguiente problema de contorno con condiciones de contorno mixtas: u (x) + x 2 u(x) = x 6 + x 4 12x 2 2, x ( 1, 1), (P4) u ( 1) = 6, u(1) = 2.
10 4.1a Se considera la siguiente aproximación para u ( 1): u ( 1) u( 1 + h) u( 1) h Utiliza el método de diferencias finitas para discretizar el problema (P4) e indica cuáles de términos independientes. matriz(i, i 1) = matriz(i, i) = matriz(i, i + 1) = tind(i) = i = 2,..., n. matriz(1, 1) = tind(1) = matriz(1, 2) = 4.1b Modifica convenientemente el programa edp1.m y completa la siguiente tabla: n Error máximo 10 e 10 = e 20 = 40 e 40 = 80 e 80 = 160 e 160 = 4.1c Utiliza la tabla anterior para deducir el orden de convergencia. 4.2a Ahora se considera la aproximación : u ( 1) u( 1 + h) u( 1 h) 2h Utiliza el método de diferencias finitas para discretizar el problema (P4) e indica cuáles de términos independientes.
11 matriz(i, i 1) = matriz(i, i) = matriz(i, i + 1) = tind(i) = i = 2,..., n. matriz(1, 1) = tind(1) = matriz(1, 2) = 4.2b Modifica convenientemente el programa edp1.m y completa la siguiente tabla: n Error máximo 10 e 10 = e 20 = 40 e 40 = 80 e 80 = 160 e 160 = 4.2c Utiliza la tabla anterior para deducir el orden de convergencia. 4.3 Compara los órdenes de convergencia y razona a qué puede deberse esta diferencia. 5.5 La ecuación de Poisson Se considera el problema: { u = 12(x (P5) 2 + y 2 ), (x, y) Ω = (0, 1) (0, 1), u(x, y) = x 4 + y 4, (x, y) Ω = Γ. 1. Clasifica el problema de ecuaciones en derivadas parciales. 2. Utiliza el método de diferencias finitas para discretizar el problema (P5) e indica cuáles
12 de términos independientes. matriz(nodo, nodo 1) = matriz(nodo, nodo + 1) = matriz(nodo, nodo (n + 1)) = matriz(nodo, nodo + (n + 1)) = matriz(nodo, nodo) = tind(nodo) = matriz(nodo, nodo) = tind(nodo) = si el nodo es interior si el nodo está en la frontera 3. Edita el fichero edp2.m y observa lo siguiente: (a) Se definen: Los vértices del rectángulo: a, b, c y d. Número de subintervalos de la malla en la dirección x e y: n y m. Paso de discretización en la dirección x e y: h y k. Coordenadas de cada uno de los nodos de la malla: (x, y) Los coeficientes no nulos de la matriz del sistema. Compáralos con los obtenidos en el apartado (2)). El vector de términos independientes del sistema. Compáralo con el obtenido en el apartado (2)). (b) Se resuelve el sistema de ecuaciones. (c) Se calcula el error máximo y se dibuja tanto la solución numérica como la exacta. 4. Completa la siguiente tabla: n m Error máximo e 10,10 = e 20,20 = e 40,40 = e 80,80 = e 160,160 = 5. Utilizando los resultados de la tabla anterior comprueba el orden del método.
13 5.6 Una ecuación elíptica general con condiciones de contorno Dirichlet Se considera el problema: { u + ux + u (P6) y = 120xy + 60(x 2 y 2 ), (x, y) Ω = (0, 1) (0, 1), u(x, y) = 60 x 2 y 20 y 3, (x, y) Ω = Γ. 1. Utiliza el método de diferencias centrales para discretizar el problema (P6) e indica cuáles de términos independientes. matriz(nodo, nodo 1) = matriz(nodo, nodo + 1) = matriz(nodo, nodo (n + 1)) = matriz(nodo, nodo + (n + 1)) = matriz(nodo, nodo) = tind(nodo) = matriz(nodo, nodo) = tind(nodo) = si el nodo es interior si el nodo está en la frontera 2. Modifica el fichero edp2.m adecuadamente de forma que resuelva el problema (P6) por el método de diferencias centrales. Ejecuta el programa para n = m = 10. Cumple la solución numérica el principio del máximo discreto? Construye una malla de forma que se asegure que la solución numérica cumpla el principio del máximo. 3. Completa la siguiente tabla: n m Error máximo e 10,10 = e 20,20 = e 40,40 = e 80,80 = e 160,160 = 4. Utilizando los resultados de la tabla anterior comprueba el orden del método.
Método de diferencias finitas para ecuaciones diferenciales parciales elípticas. (Parte II)
 Método de diferencias finitas para ecuaciones diferenciales parciales elípticas (Parte II) Métodos numéricos para sistemas lineales Solución numérica de EDPs requiere resolver sistemas de ecuaciones lineales
Método de diferencias finitas para ecuaciones diferenciales parciales elípticas (Parte II) Métodos numéricos para sistemas lineales Solución numérica de EDPs requiere resolver sistemas de ecuaciones lineales
Interp r o p la l c a ió i n seccio i nal a l (S ( pl p i l n i e) Val a o l re r s pr p e r scri r t i os N (x)
 Introducción al método de los elementos finitos Métodos Numéricos 2 Laboratori de Càlcul Numèric (LaCàN) Dep. de Matemàtica Aplicada III Universitat Politècnica de Catalunya www-lacan.upc.es Ventajas del
Introducción al método de los elementos finitos Métodos Numéricos 2 Laboratori de Càlcul Numèric (LaCàN) Dep. de Matemàtica Aplicada III Universitat Politècnica de Catalunya www-lacan.upc.es Ventajas del
Resolución de sistemas de ecuaciones lineales
 Tema 2 Resolución de sistemas de ecuaciones lineales 21 Métodos directos de resolución de sistemas de ecuaciones lineales 211 Resolución de sistemas triangulares Definición 211 Una matriz A se dice triangular
Tema 2 Resolución de sistemas de ecuaciones lineales 21 Métodos directos de resolución de sistemas de ecuaciones lineales 211 Resolución de sistemas triangulares Definición 211 Una matriz A se dice triangular
Formulación de Galerkin El método de los elementos finitos
 Clase No. 28: MAT 251 Formulación de Galerkin El método de los elementos finitos Dr. Alonso Ramírez Manzanares Depto. de Matemáticas Univ. de Guanajuato e-mail: alram@ cimat.mx web: http://www.cimat.mx/
Clase No. 28: MAT 251 Formulación de Galerkin El método de los elementos finitos Dr. Alonso Ramírez Manzanares Depto. de Matemáticas Univ. de Guanajuato e-mail: alram@ cimat.mx web: http://www.cimat.mx/
MÉTODO DE DIFERENCIAS FINITAS (FDM)
 MÉTODO DE DIFERENCIAS FINITAS (FDM) MÉTODO DE DIFERENCIAS FINITAS (FDM) Cambia ecuaciones diferenciales ecuaciones en diferencias finitas a Relaciona el valor de la variable dependiente en un punto a valores
MÉTODO DE DIFERENCIAS FINITAS (FDM) MÉTODO DE DIFERENCIAS FINITAS (FDM) Cambia ecuaciones diferenciales ecuaciones en diferencias finitas a Relaciona el valor de la variable dependiente en un punto a valores
Sistemas de ecuaciones no lineales
 Práctica 6 Sistemas de ecuaciones no lineales En esta práctica revisaremos algunos métodos básicos para la resolución numérica de sistemas de ecuaciones no lineales 61 Método iterativo del punto fijo Partimos
Práctica 6 Sistemas de ecuaciones no lineales En esta práctica revisaremos algunos métodos básicos para la resolución numérica de sistemas de ecuaciones no lineales 61 Método iterativo del punto fijo Partimos
Métodos de elemento finito Formulación n de elemento finito en 2 dimensiones
 Métodos de elemento finito 7.4.. Método de Galerkin 7.4.. Formulación n de elemento finito en dimensiones Los métodos m de elemento finito (MEF) son una estrategia numérica alternativa muy popular para
Métodos de elemento finito 7.4.. Método de Galerkin 7.4.. Formulación n de elemento finito en dimensiones Los métodos m de elemento finito (MEF) son una estrategia numérica alternativa muy popular para
Simulación Numérica de Yacimientos
 Simulación Numérica de Yacimientos Dr. Fernando Rodríguez de la Garza email: frodriguezd@pep.pemex.com Tel: 5550871, 56 3017 al 19 Capítulo 3. Diferencias Finitas 1 3.1 Diferencias Finitas Considerar que
Simulación Numérica de Yacimientos Dr. Fernando Rodríguez de la Garza email: frodriguezd@pep.pemex.com Tel: 5550871, 56 3017 al 19 Capítulo 3. Diferencias Finitas 1 3.1 Diferencias Finitas Considerar que
Capítulo 3. Polinomios
 Capítulo 3 Polinomios 29 30 Polinomios de variable real 31 Polinomios de variable real 311 Evaluación de polinomios Para el cálculo eficiente de los valores de un polinomio se utiliza el algoritmo de Horner,
Capítulo 3 Polinomios 29 30 Polinomios de variable real 31 Polinomios de variable real 311 Evaluación de polinomios Para el cálculo eficiente de los valores de un polinomio se utiliza el algoritmo de Horner,
Diferencias finitas aplicadas a ecuaciones en derivadas parciales
 Diferencias finitas aplicadas a ecuaciones en derivadas parciales Segundo curso Grado en Física Índice Introducción Aproximación de FD de la ecuación de Laplace. Métodos iterativos. Aproximación de FD
Diferencias finitas aplicadas a ecuaciones en derivadas parciales Segundo curso Grado en Física Índice Introducción Aproximación de FD de la ecuación de Laplace. Métodos iterativos. Aproximación de FD
Tema 6: Resolución aproximada de sistemas de ecuaciones lineales
 Métodos Numéricos: Resumen y ejemplos Tema 6: Resolución aproximada de sistemas de ecuaciones lineales Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de
Métodos Numéricos: Resumen y ejemplos Tema 6: Resolución aproximada de sistemas de ecuaciones lineales Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de
Preliminares Problemas de Valor Inicial Problemas de Contorno ECUACIONES DIFERENCIALES ORDINARIAS
 ECUACIONES DIFERENCIALES ORDINARIAS Contenido Preliminares 1 Preliminares 2 3 El Método de Disparo Lineal Contenido Preliminares 1 Preliminares 2 3 El Método de Disparo Lineal Preliminares Las ecuaciones
ECUACIONES DIFERENCIALES ORDINARIAS Contenido Preliminares 1 Preliminares 2 3 El Método de Disparo Lineal Contenido Preliminares 1 Preliminares 2 3 El Método de Disparo Lineal Preliminares Las ecuaciones
Sistemas de Ecuaciones. Lineales III
 Sistemas de Ecuaciones Lineales III Pivoteo: Estrategia de pivoteo parcial Adaptación a matrices con estructuras particulares: Matrices banda y tridiagonales Método de holesky 52123-1 - DIM Universidad
Sistemas de Ecuaciones Lineales III Pivoteo: Estrategia de pivoteo parcial Adaptación a matrices con estructuras particulares: Matrices banda y tridiagonales Método de holesky 52123-1 - DIM Universidad
Métodos Numéricos: Ejercicios resueltos
 Métodos Numéricos: Ejercicios resueltos Tema 6: Resolución aproximada de sistemas de ecuaciones lineales Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica
Métodos Numéricos: Ejercicios resueltos Tema 6: Resolución aproximada de sistemas de ecuaciones lineales Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica
1.2 Valores y vectores propios. Método de las potencias y Rayleigh.
 20 Prelininares. 1.2 Valores y vectores propios. Método de las potencias y Rayleigh. 1.2.1 Cálculo del Polinomio Caracterstico: ALGORITMO DE SOURIAU. ENTRADA: la matriz A 1 = A, p 1 = traza(a 1 ), n =
20 Prelininares. 1.2 Valores y vectores propios. Método de las potencias y Rayleigh. 1.2.1 Cálculo del Polinomio Caracterstico: ALGORITMO DE SOURIAU. ENTRADA: la matriz A 1 = A, p 1 = traza(a 1 ), n =
Cálculo Numérico - CO3211. Ejercicios. d ) Sabiendo que la inversa de la matriz A = es A c d
 Cálculo Numérico - CO32 Ejercicios Decida cuáles de las siguientes proposiciones son verdaderas y cuáles son falsas Si una proposición es verdadera, demuéstrela, y si es falsa dé un contraejemplo: a Sea
Cálculo Numérico - CO32 Ejercicios Decida cuáles de las siguientes proposiciones son verdaderas y cuáles son falsas Si una proposición es verdadera, demuéstrela, y si es falsa dé un contraejemplo: a Sea
MÉTODOS NUMÉRICOS DE LA
 SEMINARIOS DE MODELACIÓN COMPUTACIONAL MÉTODOS NUMÉRICOS DE LA MODELACIÓN COMPUTACIONAL MARTÍN N DÍAZD, IGEOF-UNAM, MEXICO 1 Contenido Etapas de la Modelación Computacional Métodos Numéricos Método de
SEMINARIOS DE MODELACIÓN COMPUTACIONAL MÉTODOS NUMÉRICOS DE LA MODELACIÓN COMPUTACIONAL MARTÍN N DÍAZD, IGEOF-UNAM, MEXICO 1 Contenido Etapas de la Modelación Computacional Métodos Numéricos Método de
2. Sistemas de ecuaciones lineales
 2 Sistemas de ecuaciones lineales 2 Ejercicios resueltos Ejercicio 2 Estudiar el número de condición de Frobenius de la matriz a b A a + ε b Solución: El determinante de A es A ab + ba + ε b ε Si b 0 y
2 Sistemas de ecuaciones lineales 2 Ejercicios resueltos Ejercicio 2 Estudiar el número de condición de Frobenius de la matriz a b A a + ε b Solución: El determinante de A es A ab + ba + ε b ε Si b 0 y
1. El Teorema de Rolle Generalizado.
 Proyecto III: Los Teoremas de Rolle y del valor Medio Objetivos: Profundizar el estudio de algunos teoremas del cálculo diferencial 1 El Teorema de Rolle Generalizado La formulación más común del Teorema
Proyecto III: Los Teoremas de Rolle y del valor Medio Objetivos: Profundizar el estudio de algunos teoremas del cálculo diferencial 1 El Teorema de Rolle Generalizado La formulación más común del Teorema
INTRODUCCIÓN AL MÉTODO DEL ELEMENTO FINITO
 INTRODUCCIÓN AL MÉTODO DEL ELEMENTO FINITO El método del elemento finito es una técnica numérica para resolver problemas que se pueden describir por ecuaciones diferenciales parciales o que pueden ser
INTRODUCCIÓN AL MÉTODO DEL ELEMENTO FINITO El método del elemento finito es una técnica numérica para resolver problemas que se pueden describir por ecuaciones diferenciales parciales o que pueden ser
Solución de ecuaciones diferenciales por el método de elementos finitos
 Solución de ecuaciones diferenciales por el método de elementos finitos Departamento de Matemáticas Método de elemento finito Un problema del método de diferencias finitas es que al aplicarlo obtenemos
Solución de ecuaciones diferenciales por el método de elementos finitos Departamento de Matemáticas Método de elemento finito Un problema del método de diferencias finitas es que al aplicarlo obtenemos
MÉTODOS MATEMÁTICOS (Curso 2012-2013) Cuarto Curso de Ingeniero Industrial Departamento de Matemática Aplicada II. Universidad de Sevilla
 MÉTODOS MATEMÁTICOS (Curso 2012-2013) Cuarto Curso de Ingeniero Industrial Departamento de Matemática Aplicada II. Universidad de Sevilla Lección 7: Métodos Numéricos para Ecuaciones en Derivadas Parciales.
MÉTODOS MATEMÁTICOS (Curso 2012-2013) Cuarto Curso de Ingeniero Industrial Departamento de Matemática Aplicada II. Universidad de Sevilla Lección 7: Métodos Numéricos para Ecuaciones en Derivadas Parciales.
TEMA 5: INTERPOLACION NUMERICA
 Lino Alvarez - Aurea Martinez METODOS NUMERICOS TEMA 5: INTERPOLACION NUMERICA 1 EL PROBLEMA GENERAL DE INTER- POLACION En ocasiones se plantea el problema de que se conoce una tabla de valores de una
Lino Alvarez - Aurea Martinez METODOS NUMERICOS TEMA 5: INTERPOLACION NUMERICA 1 EL PROBLEMA GENERAL DE INTER- POLACION En ocasiones se plantea el problema de que se conoce una tabla de valores de una
IMPLEMENTACIÓN DE LOS MÉTODOS DE DIFERENCIAS FINITAS Y ELEMENTOS FINITOS Curso 2000 2001. Hoja 1. La ecuaciónde Poissonendimensión1
 Curso 000 00 Hoja. La ecuaciónde Poissonendimensión Consideremos el siguiente problema con condiciones de contorno de tipo Dirichlet { u (x+c(xu(x =f(x, a < x < b u(a =α, u(b =β ( donde c(x 0, x (a, b.
Curso 000 00 Hoja. La ecuaciónde Poissonendimensión Consideremos el siguiente problema con condiciones de contorno de tipo Dirichlet { u (x+c(xu(x =f(x, a < x < b u(a =α, u(b =β ( donde c(x 0, x (a, b.
May 4, 2012 CAPÍTULO 5: OPTIMIZACIÓN
 May 4, 2012 1. Optimización Sin Restricciones En toda esta sección D denota un subconjunto abierto de R n. 1.1. Condiciones Necesarias de Primer Orden. Proposición 1.1. Sea f : D R diferenciable. Si p
May 4, 2012 1. Optimización Sin Restricciones En toda esta sección D denota un subconjunto abierto de R n. 1.1. Condiciones Necesarias de Primer Orden. Proposición 1.1. Sea f : D R diferenciable. Si p
2. Cálculo diferencial de funciones de varias variables. Mayo, 2009
 Cálculo 2. Cálculo diferencial de funciones de varias variables Mayo, 2009 Definición IR 2 = {(x 1,x 2 )/x 1 IR,x 2 IR} Sean dos puntos a y b, de coordenadas respectivas (a 1,a 2 ) y (b 1,b 2 ). Definición
Cálculo 2. Cálculo diferencial de funciones de varias variables Mayo, 2009 Definición IR 2 = {(x 1,x 2 )/x 1 IR,x 2 IR} Sean dos puntos a y b, de coordenadas respectivas (a 1,a 2 ) y (b 1,b 2 ). Definición
Ecuaciones en Derivadas Parciales y Análisis Numérico
 Ecuaciones en Derivadas Parciales y Análisis Numérico Prácticas Capítulo 4. Series de Fourier. 4.1 Serie de Fourier Vamos a intentar representar algunas funciones por su serie de Fourier de senos. Tomamos
Ecuaciones en Derivadas Parciales y Análisis Numérico Prácticas Capítulo 4. Series de Fourier. 4.1 Serie de Fourier Vamos a intentar representar algunas funciones por su serie de Fourier de senos. Tomamos
Diferenciación numérica: Método de Euler explícito
 Clase No. 21: MAT 251 Diferenciación numérica: Método de Euler explícito Dr. Alonso Ramírez Manzanares Depto. de Matemáticas Univ. de Guanajuato e-mail: alram@ cimat.mx web: http://www.cimat.mx/ alram/met_num/
Clase No. 21: MAT 251 Diferenciación numérica: Método de Euler explícito Dr. Alonso Ramírez Manzanares Depto. de Matemáticas Univ. de Guanajuato e-mail: alram@ cimat.mx web: http://www.cimat.mx/ alram/met_num/
CÁLCULO NUMÉRICO (0258)
 CÁLCULO NUMÉRICO (58) Tema 5. Diferenciación e Integración Numérica Enero 5. Utilice la fórmula para calcular la derivada de f(x) = cos(x) en utilizar la fórmula. f(x + ) f(x) f'(x) x = y con =.. Estime
CÁLCULO NUMÉRICO (58) Tema 5. Diferenciación e Integración Numérica Enero 5. Utilice la fórmula para calcular la derivada de f(x) = cos(x) en utilizar la fórmula. f(x + ) f(x) f'(x) x = y con =.. Estime
SOLUCIÓN A LA ECUACIÓN EN DIFERENCIAS FINITAS. Hernández Cruz G. Berenice.
 SOLUCIÓN A LA ECUACIÓN EN DIFERENCIAS FINITAS Hernández Cruz G. Berenice. SOLUCIÓN A LA ECUACIÓN EN DIFERENCIAS FINITAS La solución de diferencias finitas es ocupada en los análisis numéricos, por ejemplo:
SOLUCIÓN A LA ECUACIÓN EN DIFERENCIAS FINITAS Hernández Cruz G. Berenice. SOLUCIÓN A LA ECUACIÓN EN DIFERENCIAS FINITAS La solución de diferencias finitas es ocupada en los análisis numéricos, por ejemplo:
Al considerar varios polígonos regulares inscritos resulta: perímetro del cuadrado < π. perímetro del 96 gono < π
 AMPLIACIÓN DE MATEMÁTICAS INTRODUCCIÓN Método Constructivo: Conjunto de instrucciones que permiten calcular la solución de un problema, bien en un número finito de pasos, bien en un proceso de paso al
AMPLIACIÓN DE MATEMÁTICAS INTRODUCCIÓN Método Constructivo: Conjunto de instrucciones que permiten calcular la solución de un problema, bien en un número finito de pasos, bien en un proceso de paso al
Métodos de factorización para resolver sistemas de ecuaciones lineales. 22 de agosto, 2012
 Cálculo numérico Métodos de factorización para resolver sistemas de ecuaciones lineales 22 de agosto, 2012 1 Factorización LU Considera el siguiente ejemplo de factorización LU de una matriz en un sistema
Cálculo numérico Métodos de factorización para resolver sistemas de ecuaciones lineales 22 de agosto, 2012 1 Factorización LU Considera el siguiente ejemplo de factorización LU de una matriz en un sistema
Introducción al Cálculo Numérico
 Tema 1 Introducción al Cálculo Numérico 1.1 Introducción El Cálculo Numérico, o como también se le denomina, el Análisis numérico, es la rama de las Matemáticas que estudia los métodos numéricos de resolución
Tema 1 Introducción al Cálculo Numérico 1.1 Introducción El Cálculo Numérico, o como también se le denomina, el Análisis numérico, es la rama de las Matemáticas que estudia los métodos numéricos de resolución
El método de los elementos finitos
 El método de los elementos finitos Segundo curso Grado en Física Índice Funciones continuas a trozos: elementos finitos Métodos variacionales Elementos finitos aplicados a la ecuación de Poisson Consideremos
El método de los elementos finitos Segundo curso Grado en Física Índice Funciones continuas a trozos: elementos finitos Métodos variacionales Elementos finitos aplicados a la ecuación de Poisson Consideremos
Dos matrices son iguales cuando tienen la misma dimensión y los elementos que ocupan el mismo lugar en ambas son iguales
 Introducción Las matrices aparecen por primera vez hacia el año 1850, introducidas por J.J. Sylvester. El desarrollo inicial de la teoría se debe al matemático W.R. Hamilton en 1853. En 1858, A. Cayley
Introducción Las matrices aparecen por primera vez hacia el año 1850, introducidas por J.J. Sylvester. El desarrollo inicial de la teoría se debe al matemático W.R. Hamilton en 1853. En 1858, A. Cayley
Sistemas de Ecuaciones. Lineales II
 Sistemas de Ecuaciones Lineales II Factorización LU: Eliminación Gaussiana Relación con la factorización LU 521230-1 - DIM Universidad de Concepción Solución de sistemas con matriz triangular Dadas L =
Sistemas de Ecuaciones Lineales II Factorización LU: Eliminación Gaussiana Relación con la factorización LU 521230-1 - DIM Universidad de Concepción Solución de sistemas con matriz triangular Dadas L =
Profesor Francisco R. Villatoro 29 de Mayo de 2000 NO SE PERMITEN APUNTES, FORMULARIOS O CALCULADORA NO OLVIDE RACIONALIZAR TODOS LOS RESULTADOS
 Examen Segundo Parcial Técnicas Numéricas (Técn. Comp.) Profesor Francisco R. Villatoro 9 de Mayo de 000 NO SE PERMITEN APUNTES FORMULARIOS O CALCULADORA NO OLVIDE RACIONALIZAR TODOS LOS RESULTADOS 1.
Examen Segundo Parcial Técnicas Numéricas (Técn. Comp.) Profesor Francisco R. Villatoro 9 de Mayo de 000 NO SE PERMITEN APUNTES FORMULARIOS O CALCULADORA NO OLVIDE RACIONALIZAR TODOS LOS RESULTADOS 1.
Métodos iterativos para sistemas de ecuaciones lineales
 Métodos iterativos para sistemas de ecuaciones lineales Natalia Boal - Manuel Palacios - Sergio Serrano Departamento de Matemática Aplicada Obetivos Trabaar con los métodos iterativos habituales (Jacobi,
Métodos iterativos para sistemas de ecuaciones lineales Natalia Boal - Manuel Palacios - Sergio Serrano Departamento de Matemática Aplicada Obetivos Trabaar con los métodos iterativos habituales (Jacobi,
LICENCIATURA EN FÍSICA
 PRÁCTICAS DE CÁLCULO NUMÉRICO AVANZADO LICENCIATURA EN FÍSICA CURSO ACADÉMICO 2005-06 PRÁCTICA 5: Método de disparo para problemas de contorno. En esta práctica nos ocuparemos de la resolución de problemas
PRÁCTICAS DE CÁLCULO NUMÉRICO AVANZADO LICENCIATURA EN FÍSICA CURSO ACADÉMICO 2005-06 PRÁCTICA 5: Método de disparo para problemas de contorno. En esta práctica nos ocuparemos de la resolución de problemas
FEM para Mecánica 3D. Miguel Ángel Otaduy. Animación Avanzada 7 de Marzo de 2014
 FEM para Mecánica 3D Miguel Ángel Otaduy Animación Avanzada 7 de Marzo de 2014 Índice Repaso Hoy Funciones de forma Formulación fuerte formulación débil Matriz de rigidez Ec. de elasticidad en 3D Deformación
FEM para Mecánica 3D Miguel Ángel Otaduy Animación Avanzada 7 de Marzo de 2014 Índice Repaso Hoy Funciones de forma Formulación fuerte formulación débil Matriz de rigidez Ec. de elasticidad en 3D Deformación
Flujo en acuífero confinado
 SESIÓN PRÁCTICA EDO CON CONDICIONES DE CONTORNO Flujo en acuífero confinado En esta sesión práctica se plantea el estudio del movimiento del agua a través de un medio poroso bajo una geometría de acuífero
SESIÓN PRÁCTICA EDO CON CONDICIONES DE CONTORNO Flujo en acuífero confinado En esta sesión práctica se plantea el estudio del movimiento del agua a través de un medio poroso bajo una geometría de acuífero
Splines (funciones polinomiales por trozos)
 Splines (funciones polinomiales por trozos) Problemas para examen Interpolación lineal y cúbica 1. Fórmulas para la interpolación lineal. Dados t 1,..., t n, x 1,..., x n R tales que t 1
Splines (funciones polinomiales por trozos) Problemas para examen Interpolación lineal y cúbica 1. Fórmulas para la interpolación lineal. Dados t 1,..., t n, x 1,..., x n R tales que t 1
MÉTODO DE DIFERENCIAS FINITAS Y EL USO DE MATLAB PARA ECUACIONES ELÍPTICAS SOBRE CONDUCTIVIDAD TÉRMICA
 UNIVERSIDAD NACIONAL DEL SANTA FACULTAD DE CIENCIAS DEPARTAMENTO DE MATEMÁTICA XIV CONVENCIÓN DE INVESTIGACIÓN MÉTODO DE DIFERENCIAS FINITAS Y EL USO DE MATLAB PARA ECUACIONES ELÍPTICAS SOBRE CONDUCTIVIDAD
UNIVERSIDAD NACIONAL DEL SANTA FACULTAD DE CIENCIAS DEPARTAMENTO DE MATEMÁTICA XIV CONVENCIÓN DE INVESTIGACIÓN MÉTODO DE DIFERENCIAS FINITAS Y EL USO DE MATLAB PARA ECUACIONES ELÍPTICAS SOBRE CONDUCTIVIDAD
Capítulo 3 El Método de los Elementos de Contorno y la Formulación Hipersingular.
 Capítulo 3 El Método de los Elementos de Contorno y la Formulación Hipersingular. 3.1. Introducción El Método de los Elementos de Contorno (MEC) se ha implantado firmemente en numerosos campos de la ingeniería
Capítulo 3 El Método de los Elementos de Contorno y la Formulación Hipersingular. 3.1. Introducción El Método de los Elementos de Contorno (MEC) se ha implantado firmemente en numerosos campos de la ingeniería
2. ANÁLISIS DEL TECHO DE UN AUDITORIO MEDIANTE FEM
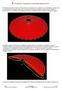 . ANÁLISIS DEL TECHO DE UN AUDITORIO MEDIANTE FEM El Objetivo es analizar el techo en forma de cono con abertura de un auditorio circular de diámetro igual a m, la altura total del cono sería.m, pero a
. ANÁLISIS DEL TECHO DE UN AUDITORIO MEDIANTE FEM El Objetivo es analizar el techo en forma de cono con abertura de un auditorio circular de diámetro igual a m, la altura total del cono sería.m, pero a
Unidad 2: Ecuaciones, inecuaciones y sistemas.
 Unidad 2: Ecuaciones, inecuaciones y sistemas 1 Unidad 2: Ecuaciones, inecuaciones y sistemas. 1.- Factorización de polinomios. M. C. D y m.c.m de polinomios. Un número a es raíz de un polinomio es 0.
Unidad 2: Ecuaciones, inecuaciones y sistemas 1 Unidad 2: Ecuaciones, inecuaciones y sistemas. 1.- Factorización de polinomios. M. C. D y m.c.m de polinomios. Un número a es raíz de un polinomio es 0.
Introducción: Visualización, Discretización,
 Introducción: Visualización, Discretización, Hardware y Métodos Numéricos Prof. M.C. Rivara 2011 M.C.Rivara 2011 1 Contenido Visualización Científica versus Visualización Realista Modelación de objetos
Introducción: Visualización, Discretización, Hardware y Métodos Numéricos Prof. M.C. Rivara 2011 M.C.Rivara 2011 1 Contenido Visualización Científica versus Visualización Realista Modelación de objetos
Matrices. Operaciones con matrices.
 Matrices. Operaciones con matrices. Ejercicio. Dadas las matrices ( ) ( ) 4 A = B = ( ) C = D = 4 5 ( ) 4 E = F = seleccione las que se pueden sumar y súmelas. Ejercicio. Dadas las matrices ( ) ( ) A =
Matrices. Operaciones con matrices. Ejercicio. Dadas las matrices ( ) ( ) 4 A = B = ( ) C = D = 4 5 ( ) 4 E = F = seleccione las que se pueden sumar y súmelas. Ejercicio. Dadas las matrices ( ) ( ) A =
Clasificación de Ecuaciones Diferenciales Parciales
 Clasificación de Ecuaciones Diferenciales Parciales Yarko Niño C. y Paulo Herrera R. Departamento de Ingeniería Civil, Universidad de Chile Semestre Primavera 2011 Calendario Cátedras sólo los miércoles.
Clasificación de Ecuaciones Diferenciales Parciales Yarko Niño C. y Paulo Herrera R. Departamento de Ingeniería Civil, Universidad de Chile Semestre Primavera 2011 Calendario Cátedras sólo los miércoles.
1. El Método de Diferencias Finitas
 1. El Método de Diferencias Finitas Por Guillermo Hernández García El Método consiste en una aproximación de derivadas parciales por expresiones algebraicas envolviendo los valores de la variable dependiente
1. El Método de Diferencias Finitas Por Guillermo Hernández García El Método consiste en una aproximación de derivadas parciales por expresiones algebraicas envolviendo los valores de la variable dependiente
Diagonalización de matrices
 7 Diagonalización de matrices 7.1. Matrices diagonalizables Existen diversos procesos en los que el estado en cada uno de sus pasos se puede representar por un determinado vector y en los que, además,
7 Diagonalización de matrices 7.1. Matrices diagonalizables Existen diversos procesos en los que el estado en cada uno de sus pasos se puede representar por un determinado vector y en los que, además,
Partial Differential Equation PDE Toolbox
 Partial Differential Equation PDE Toolbox Por: Henry Copete QUE ES PDE TOOLBOX? Es una herramienta de MATLAB que facilita la resolución de problemas de ecuaciones diferenciales parciales (EDP) La solución
Partial Differential Equation PDE Toolbox Por: Henry Copete QUE ES PDE TOOLBOX? Es una herramienta de MATLAB que facilita la resolución de problemas de ecuaciones diferenciales parciales (EDP) La solución
Métodos Numéricos con Diferencias Finitas para EDPs de evolución
 Práctica 6 Métodos Numéricos con Diferencias Finitas para EDPs de evolución En esta práctica resolveremos algunas ecuaciones en derivadas parciales mediante métodos numéricos que discretizan tanto el espacio
Práctica 6 Métodos Numéricos con Diferencias Finitas para EDPs de evolución En esta práctica resolveremos algunas ecuaciones en derivadas parciales mediante métodos numéricos que discretizan tanto el espacio
Ecuaciones e inecuaciones. Sistemas de ecuaciones e inecuaciones
 Ecuaciones e inecuaciones. Sistemas de ecuaciones e inecuaciones Álvarez S., Caballero M.V. y Sánchez M. a M. salvarez@um.es, m.victori@um.es, marvega@um.es Índice 1. Herramientas 6 1.1. Factorización
Ecuaciones e inecuaciones. Sistemas de ecuaciones e inecuaciones Álvarez S., Caballero M.V. y Sánchez M. a M. salvarez@um.es, m.victori@um.es, marvega@um.es Índice 1. Herramientas 6 1.1. Factorización
2. El Teorema del Valor Medio
 2.24 45 2. El Teorema del Valor Medio Comenzaremos esta sección recordando dos versiones del teorema del valor medido para funciones de 1-variable y por tanto ya conocidas: 2.22 Sea f : [a, b] R R una
2.24 45 2. El Teorema del Valor Medio Comenzaremos esta sección recordando dos versiones del teorema del valor medido para funciones de 1-variable y por tanto ya conocidas: 2.22 Sea f : [a, b] R R una
ECUACIONES DIFERENCIALES EN DERIVADAS PARCIALES
 Análisis Numérico II Ecuaciones Diferenciales en Derivadas Parciales ECUACIONES DIFERENCIALES EN DERIVADAS PARCIALES 1/4 Análisis Numérico II Ecuaciones Diferenciales en Derivadas Parciales ECUACIONES
Análisis Numérico II Ecuaciones Diferenciales en Derivadas Parciales ECUACIONES DIFERENCIALES EN DERIVADAS PARCIALES 1/4 Análisis Numérico II Ecuaciones Diferenciales en Derivadas Parciales ECUACIONES
Esta expresión polinómica puede expresarse como una expresión matricial de la forma; a 11 a 12 a 1n x 1 x 2 q(x 1, x 2,, x n ) = (x 1, x 2,, x n )
 Tema 3 Formas cuadráticas. 3.1. Definición y expresión matricial Definición 3.1.1. Una forma cuadrática sobre R es una aplicación q : R n R que a cada vector x = (x 1, x 2,, x n ) R n le hace corresponder
Tema 3 Formas cuadráticas. 3.1. Definición y expresión matricial Definición 3.1.1. Una forma cuadrática sobre R es una aplicación q : R n R que a cada vector x = (x 1, x 2,, x n ) R n le hace corresponder
Parte 3. Vectores y valores propios
 Parte 3. Vectores y valores propios Gustavo Montero Escuela Universitaria Politécnica Universidad de Las Palmas de Gran Canaria Curso 2004-2005 1 Introducción a los valores y vectores propios 2 3 4 5 Valores
Parte 3. Vectores y valores propios Gustavo Montero Escuela Universitaria Politécnica Universidad de Las Palmas de Gran Canaria Curso 2004-2005 1 Introducción a los valores y vectores propios 2 3 4 5 Valores
6.1 Transformada de Fourier
 6 Función de Green II. Dominios no acotados 23 a t e a PROBLEMAS DE AMPLIACIÓN DE MATEMÁTICAS t i c a s 2 o Ing. Telecomunicaciones CURSO 2009 2010 6 Función de Green II. Dominios no acotados 6.1 Transformada
6 Función de Green II. Dominios no acotados 23 a t e a PROBLEMAS DE AMPLIACIÓN DE MATEMÁTICAS t i c a s 2 o Ing. Telecomunicaciones CURSO 2009 2010 6 Función de Green II. Dominios no acotados 6.1 Transformada
Ficha de trabajo en clase 1 Introducción a MATLAB 04 de octubre de 2007
 A) Escalares, vectores, matrices Ficha de trabajo en clase Introducción a MATLAB 04 de octubre de 2007 En MATLAB, el símbolo = se llama operador de asignación. Asigna a una variable cuyo nombre está especificado
A) Escalares, vectores, matrices Ficha de trabajo en clase Introducción a MATLAB 04 de octubre de 2007 En MATLAB, el símbolo = se llama operador de asignación. Asigna a una variable cuyo nombre está especificado
1.IV Aproximación numérica de valores y vectores propios.
 .IV Aproximación numérica de valores y vectores propios. Manuel Palacios Departamento de Matemática Aplicada Centro Politécnico Superior. Universidad de Zaragoza Primavera 2007 Contents Introducción 2
.IV Aproximación numérica de valores y vectores propios. Manuel Palacios Departamento de Matemática Aplicada Centro Politécnico Superior. Universidad de Zaragoza Primavera 2007 Contents Introducción 2
r r a) Clasificar el sistema x = Ax en función del parámetro r R.
 Examen Final de Ecuaciones Diferenciales Fecha: 15 de junio de 2012 3 Problemas (7.5 puntos) Tiempo total: 3 horas Problema 1 [2.5 puntos]. Queremos dibujar el croquis de un sistema lineal 2D y realizar
Examen Final de Ecuaciones Diferenciales Fecha: 15 de junio de 2012 3 Problemas (7.5 puntos) Tiempo total: 3 horas Problema 1 [2.5 puntos]. Queremos dibujar el croquis de un sistema lineal 2D y realizar
2. Formas cuadráticas. Expresiones diagonales. Clasificación respecto a su signo.
 2. Formas cuadráticas. Expresiones diagonales. Clasificación respecto a su signo. 2.1 Formas cuadráticas. Expresión matricial y analítica. Expresiones diagonales. Definición 2.1 (Expresión matricial) Una
2. Formas cuadráticas. Expresiones diagonales. Clasificación respecto a su signo. 2.1 Formas cuadráticas. Expresión matricial y analítica. Expresiones diagonales. Definición 2.1 (Expresión matricial) Una
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A xcos(x)+b sen(x) Ejercicio 1.- [2 5 puntos] Sabiendo que lím x 0 x 3 es finito, calcula b y el valor del límite. Ejercicio 2.- Sean f : R R y g : R R las funciones definidas mediante f(x) = x(x
Opción A xcos(x)+b sen(x) Ejercicio 1.- [2 5 puntos] Sabiendo que lím x 0 x 3 es finito, calcula b y el valor del límite. Ejercicio 2.- Sean f : R R y g : R R las funciones definidas mediante f(x) = x(x
Clase. 1. Resolución de sistemas de ecuaciones lineales: preliminares
 Clase 1. Resolución de sistemas de ecuaciones lineales: preliminares 2. Método directo y exacto: Gauss 3. Método directo y exacto (II): descomposición LU 4. Métodos indirectos: Jacobi, Gauss-Seidel 2 Sistemas
Clase 1. Resolución de sistemas de ecuaciones lineales: preliminares 2. Método directo y exacto: Gauss 3. Método directo y exacto (II): descomposición LU 4. Métodos indirectos: Jacobi, Gauss-Seidel 2 Sistemas
CLASIFICACIÓN AFÍN DE CÓNICAS
 Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS CLASIFICACIÓN AFÍN DE CÓNICAS Sea E un R-espacio vectorial de dimensión. Sean E = e 1, e un plano vectorial de E y e 0 un
Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS CLASIFICACIÓN AFÍN DE CÓNICAS Sea E un R-espacio vectorial de dimensión. Sean E = e 1, e un plano vectorial de E y e 0 un
Métodos Matemáticos I
 E. de Ingenierías Industriales 2012-13 Métodos Matemáticos I Jesús Rojo Parte 3. Métodos en diferencias para las E.D.P. Las ecuaciones en derivadas parciales; ecuaciones de segundo orden Generalidades
E. de Ingenierías Industriales 2012-13 Métodos Matemáticos I Jesús Rojo Parte 3. Métodos en diferencias para las E.D.P. Las ecuaciones en derivadas parciales; ecuaciones de segundo orden Generalidades
Es una ecuación polinómica de grado uno con una o varias incógnitas. Por ejemplo, son ecuaciones lineales: 2x 3y 4z
 1. Ecuación lineal Es una ecuación polinómica de grado uno con una o varias incógnitas. Por ejemplo, son ecuaciones lineales: x y 4z 8 x 6y z 5 7y z 1. Sin embargo, no son, ecuaciones lineales: x y z 1,
1. Ecuación lineal Es una ecuación polinómica de grado uno con una o varias incógnitas. Por ejemplo, son ecuaciones lineales: x y 4z 8 x 6y z 5 7y z 1. Sin embargo, no son, ecuaciones lineales: x y z 1,
TEMA 8.- NORMAS DE MATRICES Y
 Álgebra II: Tema 8. TEMA 8.- NORMAS DE MATRICES Y NúMERO DE CONDICIóN Índice. Introducción 2. Norma vectorial y norma matricial. 2 2.. Norma matricial inducida por normas vectoriales......... 4 2.2. Algunos
Álgebra II: Tema 8. TEMA 8.- NORMAS DE MATRICES Y NúMERO DE CONDICIóN Índice. Introducción 2. Norma vectorial y norma matricial. 2 2.. Norma matricial inducida por normas vectoriales......... 4 2.2. Algunos
1. Matrices. Operaciones con matrices
 REPASO MUY BÁSICO DE MATRICES. Matrices. Operaciones con matrices.. Introducción Las matrices aparecieron por primera vez hacia el año 850, introducidas por el inglés J. J. Sylvester. Su desarrollo se
REPASO MUY BÁSICO DE MATRICES. Matrices. Operaciones con matrices.. Introducción Las matrices aparecieron por primera vez hacia el año 850, introducidas por el inglés J. J. Sylvester. Su desarrollo se
Preliminares Interpolación INTERPOLACIÓN Y APROXIMACIÓN POLINOMIAL
 INTERPOLACIÓN Y APROXIMACIÓN POLINOMIAL Contenido Preliminares 1 Preliminares Teorema 2 Contenido Preliminares Teorema 1 Preliminares Teorema 2 Teorema Preliminares Teorema Teorema: Serie de Taylor Supongamos
INTERPOLACIÓN Y APROXIMACIÓN POLINOMIAL Contenido Preliminares 1 Preliminares Teorema 2 Contenido Preliminares Teorema 1 Preliminares Teorema 2 Teorema Preliminares Teorema Teorema: Serie de Taylor Supongamos
SISTEMAS DE ECUACIONES. Un sistema de m ecuaciones lineales con n incógnitas, x 1, x 2,, x n es un conjunto de m igualdades de la forma:
 TEMA Sistemas de ecuaciones SISTEMAS DE ECUACIONES. DEFINICIÓN SISTEMAS DE ECUACIONES Un sistema de m ecuaciones lineales con n incógnitas,,,, n es un conjunto de m igualdades de la forma: a a an n b a
TEMA Sistemas de ecuaciones SISTEMAS DE ECUACIONES. DEFINICIÓN SISTEMAS DE ECUACIONES Un sistema de m ecuaciones lineales con n incógnitas,,,, n es un conjunto de m igualdades de la forma: a a an n b a
Expresiones algebraicas
 Polinomios Expresiones algebraicas Una expresión algebraica es cualquier combinación de números y letras relacionados por operaciones aritméticas: suma, resta, producto, división y potenciación. Ejemplos
Polinomios Expresiones algebraicas Una expresión algebraica es cualquier combinación de números y letras relacionados por operaciones aritméticas: suma, resta, producto, división y potenciación. Ejemplos
Tema 3 Álgebra Matemáticas I 1º Bachillerato. 1
 Tema 3 Álgebra Matemáticas I 1º Bachillerato. 1 TEMA 3 ÁLGEBRA 3.1 FACTORIZACIÓN DE POLINOMIOS LA DIVISIBILIDAD EN LOS POLINOMIOS Un polinomio P(x) es divisible por otro polinomio Q(x) cuando el cociente
Tema 3 Álgebra Matemáticas I 1º Bachillerato. 1 TEMA 3 ÁLGEBRA 3.1 FACTORIZACIÓN DE POLINOMIOS LA DIVISIBILIDAD EN LOS POLINOMIOS Un polinomio P(x) es divisible por otro polinomio Q(x) cuando el cociente
Problemas de Espacios Vectoriales
 Problemas de Espacios Vectoriales 1. Qué condiciones tiene que cumplir un súbconjunto no vacío de un espacio vectorial para que sea un subespacio vectorial de este? Pon un ejemplo. Sean E un espacio vectorial
Problemas de Espacios Vectoriales 1. Qué condiciones tiene que cumplir un súbconjunto no vacío de un espacio vectorial para que sea un subespacio vectorial de este? Pon un ejemplo. Sean E un espacio vectorial
CRITERIOS DE EVALUACIÓN 1º BACH. C. N. S. MATEMÁTICAS I
 CRITERIOS DE EVALUACIÓN 1º BACH. C. N. S. MATEMÁTICAS I UNIDAD 1 NÚMEROS REALES 1.1. Dados varios números, los clasifica en los distintos campos numéricos y los representa en la recta real. 1.2. Domina
CRITERIOS DE EVALUACIÓN 1º BACH. C. N. S. MATEMÁTICAS I UNIDAD 1 NÚMEROS REALES 1.1. Dados varios números, los clasifica en los distintos campos numéricos y los representa en la recta real. 1.2. Domina
Práctica II: Problemas de valor inicial en EDO s.
 AMPLIACIÓN DE MATEMÁTICAS o Ing. de Telecomunicación y Aeronáutica) Departamento de Matemática Aplicada II. Universidad de Sevilla CURSO ACADÉMICO 008-009 Práctica II: Problemas de valor inicial en EDO
AMPLIACIÓN DE MATEMÁTICAS o Ing. de Telecomunicación y Aeronáutica) Departamento de Matemática Aplicada II. Universidad de Sevilla CURSO ACADÉMICO 008-009 Práctica II: Problemas de valor inicial en EDO
ERRORES. , siempre que p 0.
 ERRORES Indice 1. Errores 2. Clases de errores 3. Números en coma flotante 4. Aritmética del punto flotante 4.1. Errores 4.2. Operaciones en punto flotante 4.3. Problemas con operaciones en punto flotante
ERRORES Indice 1. Errores 2. Clases de errores 3. Números en coma flotante 4. Aritmética del punto flotante 4.1. Errores 4.2. Operaciones en punto flotante 4.3. Problemas con operaciones en punto flotante
Cónicas. Clasificación.
 Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
VECTORES EN EL ESPACIO
 UNIDAD VECTORES EN EL ESPACIO Página 13 Problema 1 Halla el área de este paralelogramo en función del ángulo α: cm Área = 8 sen α = 40 sen α cm α 8 cm Halla el área de este triángulo en función del ángulo
UNIDAD VECTORES EN EL ESPACIO Página 13 Problema 1 Halla el área de este paralelogramo en función del ángulo α: cm Área = 8 sen α = 40 sen α cm α 8 cm Halla el área de este triángulo en función del ángulo
Tema 6: Modelos de probabilidad.
 Estadística 60 Tema 6: Modelos de probabilidad. 6.1 Modelos discretos. (a) Distribución uniforme discreta: La variable aleatoria X tiene una distribución uniforme discreta de parámetro n,que denoteramos
Estadística 60 Tema 6: Modelos de probabilidad. 6.1 Modelos discretos. (a) Distribución uniforme discreta: La variable aleatoria X tiene una distribución uniforme discreta de parámetro n,que denoteramos
TRABAJO DE MATEMÁTICAS. PENDIENTES DE 3º ESO. (2ª parte)
 TRABAJO DE MATEMÁTICAS PENDIENTES DE 3º ESO. (2ª parte) 1 OPERACIONES CON POLINOMIOS 1.-) Dados los polinomios: P(x) = 3x 2 + 3x - 1, Q(x) = 3x 2 + 2x + 1 y R(x) = -x 3 + 2x 2 +1. Calcular: a) P - Q R
TRABAJO DE MATEMÁTICAS PENDIENTES DE 3º ESO. (2ª parte) 1 OPERACIONES CON POLINOMIOS 1.-) Dados los polinomios: P(x) = 3x 2 + 3x - 1, Q(x) = 3x 2 + 2x + 1 y R(x) = -x 3 + 2x 2 +1. Calcular: a) P - Q R
Cálculo numérico. Sistemas de ecuaciones lineales.
 José Luis Morales http://allman.rhon.itam.mx/ jmorales Departamento de Matemáticas. ITAM. 2010. Las raíces de x 2 bx + c = 0. r = b ± b 2 4c 2 b = 3.6778, c = 0.0020798 r 1 = 3.67723441190... r 2 = 0.00056558809...
José Luis Morales http://allman.rhon.itam.mx/ jmorales Departamento de Matemáticas. ITAM. 2010. Las raíces de x 2 bx + c = 0. r = b ± b 2 4c 2 b = 3.6778, c = 0.0020798 r 1 = 3.67723441190... r 2 = 0.00056558809...
Matrices 3. Matrices. Verónica Briceño V. agosto 2012
 3 agosto 2012 En esta Presentación... En esta Presentación veremos: Matriz Inversa En esta Presentación... En esta Presentación veremos: Matriz Inversa Determinante En esta Presentación... En esta Presentación
3 agosto 2012 En esta Presentación... En esta Presentación veremos: Matriz Inversa En esta Presentación... En esta Presentación veremos: Matriz Inversa Determinante En esta Presentación... En esta Presentación
Matemáticas II, 2º BACH Fecha: 14 de noviembre de 2011 Sistemas de Ecuaciones Global 1ª evaluación Método de Gauss Álgebra de matrices Determinantes
 Fecha: 14 de noviembre de 2011 Global 1ª evaluación Matemáticas II, 2º BACH Sistemas de Ecuaciones Método de Gauss Álgebra de matrices Determinantes El alumno contestará a los ejercicios 1, 2, 3 y 4, o
Fecha: 14 de noviembre de 2011 Global 1ª evaluación Matemáticas II, 2º BACH Sistemas de Ecuaciones Método de Gauss Álgebra de matrices Determinantes El alumno contestará a los ejercicios 1, 2, 3 y 4, o
Tema 1: Matrices. Sistemas de ecuaciones. Determinantes
 Tema 1: Matrices. Sistemas de ecuaciones. Determinantes José M. Salazar Octubre de 2016 Tema 1: Matrices. Sistemas de ecuaciones. Determinantes Lección 1. Matrices. Sistemas de ecuaciones. Determinantes
Tema 1: Matrices. Sistemas de ecuaciones. Determinantes José M. Salazar Octubre de 2016 Tema 1: Matrices. Sistemas de ecuaciones. Determinantes Lección 1. Matrices. Sistemas de ecuaciones. Determinantes
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A Ejercicio 1.- Sea f : R R definida por f(x) = x 3 +ax 2 +bx+c. a) [1 75 puntos] Halla a,b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1 2 y que la recta tangente en
Opción A Ejercicio 1.- Sea f : R R definida por f(x) = x 3 +ax 2 +bx+c. a) [1 75 puntos] Halla a,b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1 2 y que la recta tangente en
si existe un entorno V de a contenido en A, tal que la diferencia f(x) f(a) no cambia de signo cuando x V :
 Capítulo 7 Extremos Relativos Una aplicación clásica del Teorema Local de Taylor es el estudio de los extremos relativos de una función escalar. Aunque la analogía con el caso de una variable es total,
Capítulo 7 Extremos Relativos Una aplicación clásica del Teorema Local de Taylor es el estudio de los extremos relativos de una función escalar. Aunque la analogía con el caso de una variable es total,
Ecuaciones Diferenciales
 1 Parte IV Ecuaciones Diferenciales Esta sección tiene como propósito dar algunos de los conceptos básicos relacionados con las ecuaciones diferenciales e ilustrar su importancia en la resolución de problemas
1 Parte IV Ecuaciones Diferenciales Esta sección tiene como propósito dar algunos de los conceptos básicos relacionados con las ecuaciones diferenciales e ilustrar su importancia en la resolución de problemas
Ecuación de Bessel Definición. Puntos singulares
 Capítulo 9 Ecuación de Bessel 9.1. Definición. Puntos singulares La ecuación de Bessel, una de las más importantes en física matemática, es una ecuación diferencial lineal de orden 2, x 2 y + xy +(x 2
Capítulo 9 Ecuación de Bessel 9.1. Definición. Puntos singulares La ecuación de Bessel, una de las más importantes en física matemática, es una ecuación diferencial lineal de orden 2, x 2 y + xy +(x 2
Análisis de Sensibilidad de los Resultados
 Pontificia Universidad Católica Escuela de Ingeniería Departamento de Ingeniería Industrial y de Sistemas Clase 22 Análisis de Sensibilidad de los Resultados ICS 02 Optimización Profesor : Claudio Seebach
Pontificia Universidad Católica Escuela de Ingeniería Departamento de Ingeniería Industrial y de Sistemas Clase 22 Análisis de Sensibilidad de los Resultados ICS 02 Optimización Profesor : Claudio Seebach
3. Determinantes. Propiedades. Depto. de Álgebra, curso
 Depto de Álgebra curso 06-07 3 Determinantes Propiedades Ejercicio 3 Use la definición para calcular el valor del determinante de cada una de las siguientes matrices: 3 0 0 α A = 5 4 0 A = 6 A 3 = 0 β
Depto de Álgebra curso 06-07 3 Determinantes Propiedades Ejercicio 3 Use la definición para calcular el valor del determinante de cada una de las siguientes matrices: 3 0 0 α A = 5 4 0 A = 6 A 3 = 0 β
Ejercicios Temas 3 y 4: Interpolación polinomial. Ajuste de curvas.
 Ejercicios Temas 3 y 4: Interpolación polinomial. Ajuste de curvas.. El número de personas afectadas por el virus contagioso que produce la gripe en una determinada población viene dado por la siguiente
Ejercicios Temas 3 y 4: Interpolación polinomial. Ajuste de curvas.. El número de personas afectadas por el virus contagioso que produce la gripe en una determinada población viene dado por la siguiente
IES Fco Ayala de Granada Junio de 2012 (Común Modelo 4) Soluciones Germán-Jesús Rubio Luna
 IES Fco Ayala de Granada Junio de 01 (Común Modelo 4) Soluciones Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo Junio 01 común Sea f : R R la función definida como f(x) = e x.(x ). [1 punto]
IES Fco Ayala de Granada Junio de 01 (Común Modelo 4) Soluciones Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo Junio 01 común Sea f : R R la función definida como f(x) = e x.(x ). [1 punto]
Bajo estas hipótesis la ley de Newton permite escribir las ecuaciones del cohete (ver Figura 1.1) como. = m(t) g + T (t), = g + dx dt (0) = v 0.
 CAPÍTULO 1 INTRODUCCIÓN Ejercicios resueltos Problema 1. Desarrolle un modelo simplificado de un coete como un cuerpo sujeto a la gravedad que se mueve en vertical por el empuje de una fuerza de propulsión
CAPÍTULO 1 INTRODUCCIÓN Ejercicios resueltos Problema 1. Desarrolle un modelo simplificado de un coete como un cuerpo sujeto a la gravedad que se mueve en vertical por el empuje de una fuerza de propulsión
Trabajo Práctico N 5: ESPACIOS VECTORIALES
 Trabajo Práctico N 5: ESPACIOS VECTORIALES Ejercicio 1: Determine si los siguientes conjuntos con las operaciones definidas en cada caso son o no espacios vectoriales. Para aquellos que no lo sean, indique
Trabajo Práctico N 5: ESPACIOS VECTORIALES Ejercicio 1: Determine si los siguientes conjuntos con las operaciones definidas en cada caso son o no espacios vectoriales. Para aquellos que no lo sean, indique
Cálculo. Licenciatura en CC. Químicas Tema n o 5 Resultados teóricos. Ecuaciones diferenciales ordinarias
 Cálculo. Licenciatura en CC. Químicas Tema n o 5 Resultados teóricos Ecuaciones diferenciales ordinarias 1. Ecuaciones diferenciales lineales de orden n Considera un número n de funcines de una variable
Cálculo. Licenciatura en CC. Químicas Tema n o 5 Resultados teóricos Ecuaciones diferenciales ordinarias 1. Ecuaciones diferenciales lineales de orden n Considera un número n de funcines de una variable
Tema 3: Espacios vectoriales
 Tema 3: Espacios vectoriales K denotará un cuerpo. Definición. Se dice que un conjunto no vacio V es un espacio vectorial sobre K o que es un K-espacio vectorial si: 1. En V está definida una operación
Tema 3: Espacios vectoriales K denotará un cuerpo. Definición. Se dice que un conjunto no vacio V es un espacio vectorial sobre K o que es un K-espacio vectorial si: 1. En V está definida una operación
Complementos de Análisis. Año 2016
 Complementos de Análisis. Año 2016 Práctica 8. Ecuaciones diferenciales ordinarias. 1 Modelando con ecuaciones diferenciales Modelar con ecuaciones diferenciales las siguientes situaciones. Intentar resolver
Complementos de Análisis. Año 2016 Práctica 8. Ecuaciones diferenciales ordinarias. 1 Modelando con ecuaciones diferenciales Modelar con ecuaciones diferenciales las siguientes situaciones. Intentar resolver
Matrices. José Vicente Romero Bauset. ETSIT-curso 2009/2010. José Vicente Romero Bauset Tema 1.- Matrices. 1
 Matrices José Vicente Romero Bauset ETSIT-curso 2009/2010 José Vicente Romero Bauset Tema 1- Matrices 1 Introducción Por qué estudiar las matrices? Son muchas las situaciones de la vida real en las que
Matrices José Vicente Romero Bauset ETSIT-curso 2009/2010 José Vicente Romero Bauset Tema 1- Matrices 1 Introducción Por qué estudiar las matrices? Son muchas las situaciones de la vida real en las que
