Análisis de Algoritmos
|
|
|
- Rosa María Franco Rivero
- hace 5 años
- Vistas:
Transcripción
1 Análisis de Algoritmos IIC1253 IIC1253 Análisis de Algoritmos 1 / 36
2 Complejidad de un algoritmo Un algoritmo A puede ser pensado como una función A : {0,1} {0,1} Qué tan general es esta representación? Qué restricciones hay que imponer sobre A? IIC1253 Análisis de Algoritmos 2 / 36
3 Complejidad de un algoritmo Un algoritmo A puede ser pensado como una función A : {0,1} {0,1} Qué tan general es esta representación? Qué restricciones hay que imponer sobre A? Ejercicio Represente un algoritmo para decidir si un número natural es primo con la notación anterior. IIC1253 Análisis de Algoritmos 2 / 36
4 Complejidad de un algoritmo A cada algoritmo A asociamos una función tiempo A : {0,1} N tal que: tiempo A (w): número de pasos realizados por A con entrada w Qué es un paso de un algoritmo? Qué operaciones debemos considerar? IIC1253 Análisis de Algoritmos 3 / 36
5 Complejidad de un algoritmo A cada algoritmo A asociamos una función tiempo A : {0,1} N tal que: tiempo A (w): número de pasos realizados por A con entrada w Qué es un paso de un algoritmo? Qué operaciones debemos considerar? Ejercicio En general, un algoritmo puede ser pensado como una función A : Γ Γ, donde Γ es un alfabeto finito. De un algoritmo Ord para ordenar una lista de números naturales. Calcule la función tiempo Ord. Suponga que el alfabeto utilizado es {0,1,#} Indique cuáles son las operaciones que deben ser consideradas IIC1253 Análisis de Algoritmos 3 / 36
6 Análisis de un algoritmo en el peor caso Para analizar un algoritmo vamos a considerar el peor caso. Para cada algoritmo A asociamos una función t A : N N tal que t A (n) = máx{tiempo A (w) w {0,1} y w = n}, donde w es el largo de w. IIC1253 Análisis de Algoritmos 4 / 36
7 Análisis de un algoritmo en el peor caso Para analizar un algoritmo vamos a considerar el peor caso. Para cada algoritmo A asociamos una función t A : N N tal que t A (n) = máx{tiempo A (w) w {0,1} y w = n}, donde w es el largo de w. Ejercicio Calcule la función t Ord para el algoritmo Ord construido en la transparencia anterior. IIC1253 Análisis de Algoritmos 4 / 36
8 Notación asintótica En muchos casos, nos interesa conocer el orden de un algoritmo en lugar de su complejidad exacta. Queremos decir que un algoritmo es lineal o cuadrático, en lugar de decir que su complejidad es 3n 2 +17n+22 Vamos a desarrollar notación para hablar del orden de un algoritmo. Vamos a considerar funciones de la forma f : N R + 0, donde R + = {r R r > 0} y R + 0 = R+ {0} Incluyen a las funciones definidas en las transparencias anteriores, y también sirven para modelar el tiempo de ejecución de un algoritmo IIC1253 Análisis de Algoritmos 5 / 36
9 La notación O(f) Sea f : N R + 0 Definición O(f) = {g : N R + 0 ( c R+ )( n 0 N) ( n n 0 )(g(n) c f(n))} IIC1253 Análisis de Algoritmos 6 / 36
10 La notación O(f) Sea f : N R + 0 Definición O(f) = {g : N R + 0 ( c R+ )( n 0 N) ( n n 0 )(g(n) c f(n))} Ejercicio Demuestre que 3n 2 +17n+22 O(n 2 ) IIC1253 Análisis de Algoritmos 6 / 36
11 Las notaciones Ω(f) y Θ(f) Definición Ω(f) = {g : N R + 0 ( c R+ )( n 0 N) Θ(f) = O(f) Ω(f) ( n n 0 )(c f(n) g(n))} IIC1253 Análisis de Algoritmos 7 / 36
12 Las notaciones Ω(f) y Θ(f) Definición Ω(f) = {g : N R + 0 ( c R+ )( n 0 N) Θ(f) = O(f) Ω(f) ( n n 0 )(c f(n) g(n))} Ejercicios 1. Demuestre que 3n 2 +17n +22 Θ(n 2 ) 2. Demuestre que g Θ(f) si y sólo si existen c,d R + y n 0 N tal que para todo n n 0 : c f(n) g(n) d f(n) IIC1253 Análisis de Algoritmos 7 / 36
13 Ejercicios 1. Sea p(n) un polinomio de grado k 0 con coeficientes en los números enteros. Demuestre que p(n) O(n k ). 2. Cuáles de las siguientes afirmaciones son ciertas? n 2 O(n) Si f(n) O(n), entonces f(n) 2 O(n 2 ) Si f(n) O(n), entonces 2 f(n) O(2 n ) 3. Decimos que f g si f O(g). Es un orden parcial? Es un orden total? 4. Decimos que f g si f Θ(g). Demuestre que es una relación de equivalencia. Indique qué es [f] IIC1253 Análisis de Algoritmos 8 / 36
14 Ecuaciones de recurrencia Suponga que tiene una lista ordenada (de menor a mayor) L de números naturales L tiene n elementos, para referirnos al elemento i-ésimo (1 i n) usamos la notación L[i] Cómo podemos verificar si un número a está en L? IIC1253 Análisis de Algoritmos 9 / 36
15 Ecuaciones de recurrencia: Búsqueda binaria Para verificar si un número a está en L usamos el siguiente algoritmo: encontrar(a, L, i, j) if i > j then return no else if i = j then if L[i] = a then return i else return no else p = i+j 2 if L[p] < a then return encontrar(a, L, p +1, j) else if L[p] > a then return encontrar(a, L, i, p 1) else return p Llamada inicial al algoritmo: encontrar(a, L, 1, n) IIC1253 Análisis de Algoritmos 10 / 36
16 Ecuaciones de recurrencia: Búsqueda binaria Cuál es la complejidad del algoritmo? Qué operaciones vamos a considerar? Cuál es el peor caso? IIC1253 Análisis de Algoritmos 11 / 36
17 Ecuaciones de recurrencia: Búsqueda binaria Cuál es la complejidad del algoritmo? Qué operaciones vamos a considerar? Cuál es el peor caso? Si contamos sólo las comparaciones, entonces la siguiente expresión define la complejidad del algoritmo: { c n = 1 T(n) = T( n 2 )+d n > 1 donde c N y d N son constantes tales que c 1 y d 1. IIC1253 Análisis de Algoritmos 11 / 36
18 Ecuaciones de recurrencia: Búsqueda binaria Cuál es la complejidad del algoritmo? Qué operaciones vamos a considerar? Cuál es el peor caso? Si contamos sólo las comparaciones, entonces la siguiente expresión define la complejidad del algoritmo: { c n = 1 T(n) = T( n 2 )+d n > 1 donde c N y d N son constantes tales que c 1 y d 1. Esta es una ecuación de recurrencia. IIC1253 Análisis de Algoritmos 11 / 36
19 Ecuaciones de recurrencia: Búsqueda binaria Cómo podemos solucionar una ecuación de recurrencia? Técnica básica: sustitución de variables IIC1253 Análisis de Algoritmos 12 / 36
20 Ecuaciones de recurrencia: Búsqueda binaria Cómo podemos solucionar una ecuación de recurrencia? Técnica básica: sustitución de variables Para la ecuación anterior usamos la sustitución n = 2 k. Vamos a resolver la ecuación suponiendo que n es una potencia de 2 Vamos a estudiar condiciones bajo las cuales el resultado para una potencia de 2 puede ser extendido a todo n Estas condiciones van a servir para cualquier potencia IIC1253 Análisis de Algoritmos 12 / 36
21 Ecuaciones de recurrencia: sustitución de variables Si realizamos la sustitución n = 2 k en la ecuación: { c n = 1 T(n) = T( n 2 )+d n > 1 obtenemos: T(2 k ) = { c k = 0 T(2 k 1 )+d k > 0 IIC1253 Análisis de Algoritmos 13 / 36
22 Ecuaciones de recurrencia: sustitución de variables Extendiendo la expresión anterior obtenemos: T(2 k ) = T(2 k 1 )+d = (T(2 k 2 )+d)+d = T(2 k 2 )+2d = (T(2 k 3 )+d)+2d = T(2 k 3 )+3d = IIC1253 Análisis de Algoritmos 14 / 36
23 Ecuaciones de recurrencia: sustitución de variables Extendiendo la expresión anterior obtenemos: T(2 k ) = T(2 k 1 )+d = (T(2 k 2 )+d)+d = T(2 k 2 )+2d = (T(2 k 3 )+d)+2d = T(2 k 3 )+3d = Deducimos la expresión general para k i 0: T(2 k ) = T(2 k i )+i d IIC1253 Análisis de Algoritmos 14 / 36
24 Ecuaciones de recurrencia: sustitución de variables Considerando i = k obtenemos: T(2 k ) = T(1)+k d = c +k d IIC1253 Análisis de Algoritmos 15 / 36
25 Ecuaciones de recurrencia: sustitución de variables Considerando i = k obtenemos: T(2 k ) = T(1)+k d = c +k d Dado que k = log 2 n, obtenemos que T(n) = c +d log 2 n para n potencia de 2. Vamos a definir notación para decir esto de manera formal IIC1253 Análisis de Algoritmos 15 / 36
26 Notaciones asintóticas condicionales Sea P un predicado sobre los números naturales. Definición O(f P) = {g : N R + 0 ( c R+ )( n 0 N) ( n n 0 )(n P g(n) c f(n))} IIC1253 Análisis de Algoritmos 16 / 36
27 Notaciones asintóticas condicionales Sea P un predicado sobre los números naturales. Definición O(f P) = {g : N R + 0 ( c R+ )( n 0 N) ( n n 0 )(n P g(n) c f(n))} Las notaciones Ω(f P) y Θ(f P) son definidas de manera análoga. IIC1253 Análisis de Algoritmos 16 / 36
28 Búsqueda en una lista ordenada: complejidad del algoritmo Sea POTENCIA 2 = {2 i i N} Para la función T que define la complejidad del procedimiento encontrar, tenemos que: T Θ(log 2 n POTENCIA 2 ) Podemos concluir que T Θ(log 2 n)? Vamos a estudiar este problema, pero antes vamos a ver un segundo ejemplo. IIC1253 Análisis de Algoritmos 17 / 36
29 Ordenamiento de una lista Ahora queremos ordenar una lista L de números naturales Utilizamos el algoritmo mergesort Si contamos sólo las comparaciones entre elementos de L, entonces la siguiente expresión define la complejidad de mergesort: { 0 n = 1 T(n) = T( n 2 )+T( n 2 )+(n 1) n > 1 IIC1253 Análisis de Algoritmos 18 / 36
30 Orden de mergesort Nuevamente utilizamos la sustitución n = 2 k, obteniendo: { T(2 k 0 k = 0 ) = 2 T(2 k 1 )+(2 k 1) k > 0 Desarrollando esta expresión obtenemos: T(2 k ) = 2 T(2 k 1 )+(2 k 1) = 2 (2 T(2 k 2 )+(2 k 1 1))+(2 k 1) = 2 2 T(2 k 2 )+2 k 2+2 k 1 = 2 2 T(2 k 2 )+2 2 k (1+2) = 2 2 (2 T(2 k 3 )+(2 k 2 1))+2 2 k (1+2) = 2 3 T(2 k 3 )+2 k k (1+2) = 2 3 T(2 k 3 )+3 2 k ( ) = IIC1253 Análisis de Algoritmos 19 / 36
31 Orden de mergesort Deducimos la expresión general para k i 0: i 1 T(2 k ) = 2 i T(2 k i )+i 2 k j=0 2 j = 2 i T(2 k i )+i 2 k 2 i +1 Considerando i = k obtenemos: T(2 k ) = 2 k T(1)+k 2 k 2 k +1 = k 2 k 2 k +1 Dado que k = log 2 n, concluimos que: T Θ(n log 2 n POTENCIA 2 ) IIC1253 Análisis de Algoritmos 20 / 36
32 Técnicas para solucionar ecuaciones de recurrencia Vamos a estudiar dos técnicas que nos permitan extender la solución a una ecuación de recurrencia encontrada usando sustitución de variables. Nos vamos a concentrar en la notación O Primera técnica: Utilizamos una sustitución de variable para encontrar una solución en un caso particular. Por ejemplo: T O(n log2 n POTENCIA 2 ) Usamos inducción para demostrar que la solución es válida en el caso general IIC1253 Análisis de Algoritmos 21 / 36
33 Construcción de soluciones usando inducción Consideremos la ecuación de recurrencia para el algoritmo de búsqueda en listas ordenadas: { c n = 1 T(n) = T( n 2 )+d n > 1 Sabemos que T O(log 2 n POTENCIA 2 ) Queremos demostrar entonces que: ( e R + )( n 0 N)( n n 0 )(T(n) e log 2 n) IIC1253 Análisis de Algoritmos 22 / 36
34 Construcción de soluciones usando inducción Veamos algunos valores de la función T para estimar e y n 0 : T(1) = c T(2) = c +d T(3) = c +d T(4) = c +2d En este caso necesitamos que n 0 2 y e (c +d) Por qué? Intentamos entonces con n 0 = 2 y e = (c +d) Por demostrar: ( n 2)(T(n) (c +d) log 2 n) IIC1253 Análisis de Algoritmos 23 / 36
35 Inducción fuerte Cuál es el principio de inducción adecuado para el problema anterior? Tenemos n 0 como punto de partida n 0 es un caso base, pero podemos tener otros Dado n > n 0 tal que n no es un caso base, suponemos que la propiedad se cumple para todo k {n 0,...,n 1} IIC1253 Análisis de Algoritmos 24 / 36
36 Inducción fuerte: Ejemplo Queremos demostrar que ( n 2)(T(n) (c +d) log 2 n) IIC1253 Análisis de Algoritmos 25 / 36
37 Inducción fuerte: Ejemplo Queremos demostrar que ( n 2)(T(n) (c +d) log 2 n) 2 es el punto de partida y el primer caso base IIC1253 Análisis de Algoritmos 25 / 36
38 Inducción fuerte: Ejemplo Queremos demostrar que ( n 2)(T(n) (c +d) log 2 n) 2 es el punto de partida y el primer caso base También 3 es un caso base ya que T(3) = T(1)+d y para T(1) no se cumple la propiedad IIC1253 Análisis de Algoritmos 25 / 36
39 Inducción fuerte: Ejemplo Queremos demostrar que ( n 2)(T(n) (c +d) log 2 n) 2 es el punto de partida y el primer caso base También 3 es un caso base ya que T(3) = T(1)+d y para T(1) no se cumple la propiedad Para n 4 tenemos que T(n) = T( n 2 )+d y n 2 2, por lo que resolvemos este caso de manera inductiva Suponemos que la propiedad se cumple para todo k {2,...,n 1} IIC1253 Análisis de Algoritmos 25 / 36
40 Inducción fuerte: Ejemplo Vamos a demostrar entonces que para { c n = 1 T(n) = T( n 2 )+d n > 1 se tiene que ( n 2)(T(n) (c +d) log 2 n) IIC1253 Análisis de Algoritmos 26 / 36
41 Inducción fuerte: Ejemplo Vamos a demostrar entonces que para { c n = 1 T(n) = T( n 2 )+d n > 1 se tiene que ( n 2)(T(n) (c +d) log 2 n) Casos base: T(2) = c +d = (c +d) log 2 2 T(3) = c +d < (c +d) log 2 3 IIC1253 Análisis de Algoritmos 26 / 36
42 Inducción fuerte: Ejemplo Vamos a demostrar entonces que para { c n = 1 T(n) = T( n 2 )+d n > 1 se tiene que ( n 2)(T(n) (c +d) log 2 n) Casos base: T(2) = c +d = (c +d) log 2 2 T(3) = c +d < (c +d) log 2 3 Caso inductivo: Suponemos que n 4 y para todo k {2,...,n 1}: T(k) (c +d) log 2 k IIC1253 Análisis de Algoritmos 26 / 36
43 Inducción fuerte: Ejemplo Tenemos que: T(n) = T( n 2 )+d (c +d) log 2 n 2 +d (c +d) log 2 n 2 +d = (c +d) log 2 n (c +d)+d = (c +d) log 2 n c < (c +d) log 2 n IIC1253 Análisis de Algoritmos 27 / 36
44 Una segunda técnica para solucionar ecuaciones de recurrencia Para definir esta segunda técnica necesitamos definir algunos términos. Una función f : N R + 0 es asintóticamente no decreciente si: ( n 0 N)( n n 0 )(f(n) f(n+1)) IIC1253 Análisis de Algoritmos 28 / 36
45 Una segunda técnica para solucionar ecuaciones de recurrencia Para definir esta segunda técnica necesitamos definir algunos términos. Una función f : N R + 0 es asintóticamente no decreciente si: ( n 0 N)( n n 0 )(f(n) f(n+1)) Ejemplo Las funciones log 2 n, n, n 5 y 2 n son asintóticamente no decrecientes IIC1253 Análisis de Algoritmos 28 / 36
46 Funciones b-armónicas Sea f : N R + 0 y b N tal que b > 0 f es una función b-armónica si f(b n) O(f(n)) IIC1253 Análisis de Algoritmos 29 / 36
47 Funciones b-armónicas Sea f : N R + 0 y b N tal que b > 0 f es una función b-armónica si f(b n) O(f(n)) Ejemplo Las funciones log 2 n, n y n 5 son b-armónicas para cualquier b (b > 0). La función 2 n no es 2-armónica. IIC1253 Análisis de Algoritmos 29 / 36
48 Una segunda técnica: extensión de soluciones Sean f,g : N R + 0, b N tal que b > 0, y POTENCIA b = {b i i N} IIC1253 Análisis de Algoritmos 30 / 36
49 Una segunda técnica: extensión de soluciones Sean f,g : N R + 0, b N tal que b > 0, y POTENCIA b = {b i i N} Teorema Si f,g son asintóticamente no decrecientes, g es b-armónica y f O(g POTENCIA b ), entonces f O(g). IIC1253 Análisis de Algoritmos 30 / 36
50 Una segunda técnica: demostración del teorema Como f es asintóticamente no decreciente: ( n 0 N)( n n 0 )(f(n) f(n+1)) Como g es asintóticamente no decreciente: ( n 1 N)( n n 1 )(g(n) g(n+1)) Como f O(g POTENCIA b ): ( c R + )( n 2 N)( n n 2 ) (n PONTENCIA b f(n) c g(n)) IIC1253 Análisis de Algoritmos 31 / 36
51 Una segunda técnica: demostración del teorema Como g es b-armónica: ( d R + )( n 3 N)( n n 3 )(g(b n) d g(n)) Sea n 4 = máx{1,n 0,n 1,n 2,n 3 } y n n 4 Como n 1, existe k 0 tal que: b k n < b k+1 Como n n 0 y f es asintóticamente no decreciente: f(n) f(b k+1 ) IIC1253 Análisis de Algoritmos 32 / 36
52 Una segunda técnica: demostración del teorema Como n n 2 y f O(g POTENCIA b ): f(b k+1 ) c g(b k+1 ) Dado que b k n, se tiene que b k+1 b n. Así, dado que n n 1 y g es asintóticamente no decreciente: g(b k+1 ) g(b n) Finalmente, dado que n n 3 y g es b-armónica: g(b n) d g(n) IIC1253 Análisis de Algoritmos 33 / 36
53 Una segunda técnica: demostración del teorema Combinando los resultados anteriores obtenemos: f(n) f(b k+1 ) c g(b k+1 ) c g(b n) c d g(n) Por lo tanto: ( n n 4 )(f(n) (c d) g(n)) Concluimos que f O(g). IIC1253 Análisis de Algoritmos 34 / 36
54 Una segunda técnica: el caso de mergesort La siguiente expresión define la complejidad de mergesort: { 0 n = 1 T(n) = T( n 2 )+T( n 2 )+(n 1) n > 1 Ya demostramos que T O(n log 2 n POTENCIA 2 ) Usando el último teorema, vamos a demostrar que T O(n log 2 n) IIC1253 Análisis de Algoritmos 35 / 36
55 Una segunda técnica: el caso de mergesort Ejercicio 1. Demuestre que T(n) y n log 2 n son asintóticamente no decrecientes Puede usar inducción fuerte para demostrar que T(n) es asintóticamente no decreciente 2. Demuestre que n log 2 n es 2-armónica 3. Use los ejercicios anteriores para concluir que T O(n log 2 n) IIC1253 Análisis de Algoritmos 36 / 36
Análisis de Algoritmos
 Análisis de Algoritmos IIC1253 IIC1253 Análisis de Algoritmos 1 / 36 Complejidad de un algoritmo Un algoritmo A puede ser pensado como una función A : {0,1} {0,1} Qué tan general es esta representación?
Análisis de Algoritmos IIC1253 IIC1253 Análisis de Algoritmos 1 / 36 Complejidad de un algoritmo Un algoritmo A puede ser pensado como una función A : {0,1} {0,1} Qué tan general es esta representación?
Demostrando cotas inferiores: Arboles de decisión
 Demostrando cotas inferiores: Arboles de decisión De la misma forma que la técnica basada en la mejor estrategia del adversario, vamos a utilizar los árboles de decisión para establecer una cota inferior
Demostrando cotas inferiores: Arboles de decisión De la misma forma que la técnica basada en la mejor estrategia del adversario, vamos a utilizar los árboles de decisión para establecer una cota inferior
Muchas de las ecuaciones de recurrencia que vamos a usar en este curso tienen la siguiente forma: ( c n =0 T (n) = a T (b n b.
 El Teorema Maestro Muchas de las ecuaciones de recurrencia que vamos a usar en este curso tienen la siguiente forma: ( c n =0 T (n) = a T (b n b c)+f (n) n 1 donde a, b y c son constantes, y f (n) es una
El Teorema Maestro Muchas de las ecuaciones de recurrencia que vamos a usar en este curso tienen la siguiente forma: ( c n =0 T (n) = a T (b n b c)+f (n) n 1 donde a, b y c son constantes, y f (n) es una
Algoritmos en teoría de números
 Algoritmos en teoría de números IIC2283 IIC2283 Algoritmos en teoría de números 1 / 92 Para recordar: aritmética modular Dados dos números a, b Z, si b > 0 entonces existen α, β Z tales que 0 β < b y a
Algoritmos en teoría de números IIC2283 IIC2283 Algoritmos en teoría de números 1 / 92 Para recordar: aritmética modular Dados dos números a, b Z, si b > 0 entonces existen α, β Z tales que 0 β < b y a
Análisis y Diseño de Algoritmos
 Análisis y Diseño de Algoritmos Notación Asintótica DR. JESÚS A. GONZÁLEZ BERNAL CIENCIAS COMPUTACIONALES INAOE Introducción Por qué el análisis de algoritmos? Determinar tiempos de respuesta (runtime)
Análisis y Diseño de Algoritmos Notación Asintótica DR. JESÚS A. GONZÁLEZ BERNAL CIENCIAS COMPUTACIONALES INAOE Introducción Por qué el análisis de algoritmos? Determinar tiempos de respuesta (runtime)
Un tercer ejemplo: verificación de primalidad
 Un tercer ejemplo: verificación de primalidad Vamos a ver un algoritmo aleatorizado para verificar si un número es primo. I Este algoritmo es más eficiente que los algoritmos sin componentes aleatorias
Un tercer ejemplo: verificación de primalidad Vamos a ver un algoritmo aleatorizado para verificar si un número es primo. I Este algoritmo es más eficiente que los algoritmos sin componentes aleatorias
Análisis de algoritmos.
 Análisis de algoritmos. - Introducción. - Notaciones asintóticas. - Ecuaciones de recurrencia. - Ejemplos. 1 Introducción Algoritmo: Conjunto de reglas para resolver un problema. Su ejecución requiere
Análisis de algoritmos. - Introducción. - Notaciones asintóticas. - Ecuaciones de recurrencia. - Ejemplos. 1 Introducción Algoritmo: Conjunto de reglas para resolver un problema. Su ejecución requiere
Tema 3.2: Eficiencia de algoritmos recursivos. Diseño y Análisis de Algoritmos
 Diseño y Análisis de Algoritmos Contenidos Contenidos 1 Introducción 2 3 Método general para resolución de relaciones de recurrencia URJC DAA 2 / 37 Introducción Análisis de algoritmos recursivos La matemática
Diseño y Análisis de Algoritmos Contenidos Contenidos 1 Introducción 2 3 Método general para resolución de relaciones de recurrencia URJC DAA 2 / 37 Introducción Análisis de algoritmos recursivos La matemática
Notación Asintótica. Temas. Introducción Notación O Notación Omega Notación Theta. Análisis de Algoritmos
 Notación Asintótica Análisis de Algoritmos Temas Introducción Notación O Notación Omega Notación Theta 1 Introducción Por qué el análisis de algoritmos? Determinar tiempos de respuesta (runtime) Determinar
Notación Asintótica Análisis de Algoritmos Temas Introducción Notación O Notación Omega Notación Theta 1 Introducción Por qué el análisis de algoritmos? Determinar tiempos de respuesta (runtime) Determinar
Complejidad computacional. Algoritmos y Estructuras de Datos I. Complejidad computacional. Notación O grande
 Complejidad computacional Algoritmos y Estructuras de Datos I Segundo cuatrimestre de 2014 Departamento de Computación - FCEyN - UBA Algoritmos - clase 10 Introducción a la complejidad computacional y
Complejidad computacional Algoritmos y Estructuras de Datos I Segundo cuatrimestre de 2014 Departamento de Computación - FCEyN - UBA Algoritmos - clase 10 Introducción a la complejidad computacional y
Multiplicación de matrices simétricas
 Multiplicación de matrices simétricas La traspuesta de una matriz A n n es definida como una matriz A T n n tal que A T [i, j] =A[j, i] paracadai, j 2{1,...,n} Además, una matriz A es simétrica si A =
Multiplicación de matrices simétricas La traspuesta de una matriz A n n es definida como una matriz A T n n tal que A T [i, j] =A[j, i] paracadai, j 2{1,...,n} Además, una matriz A es simétrica si A =
Cardinalidad IIC1253. IIC1253 Cardinalidad 1 / 23
 Cardinalidad IIC1253 IIC1253 Cardinalidad 1 / 23 Conjuntos con la misma cardinalidad Definición Decimos que dos conjuntos A y B son equinumerosos, denotado como A B, si existe una biyección f : A B. Ejemplo
Cardinalidad IIC1253 IIC1253 Cardinalidad 1 / 23 Conjuntos con la misma cardinalidad Definición Decimos que dos conjuntos A y B son equinumerosos, denotado como A B, si existe una biyección f : A B. Ejemplo
Cardinalidad IIC1253. IIC1253 Cardinalidad 1 / 23
 Cardinalidad IIC1253 IIC1253 Cardinalidad 1 / 23 Conjuntos con la misma cardinalidad Definición Decimos que dos conjuntos A y B son equinumerosos, denotado como A B, si existe una biyección f : A B. IIC1253
Cardinalidad IIC1253 IIC1253 Cardinalidad 1 / 23 Conjuntos con la misma cardinalidad Definición Decimos que dos conjuntos A y B son equinumerosos, denotado como A B, si existe una biyección f : A B. IIC1253
Resolviendo Recurrencias
 Resolviendo Recurrencias Mauro Jaskelioff 16/03/2015 Análisis de Algoritmos Queremos poder evaluar la performance de algoritmos. Para esto utilizamos Notación Asintótica Modelo de Costo basado en Lenguaje
Resolviendo Recurrencias Mauro Jaskelioff 16/03/2015 Análisis de Algoritmos Queremos poder evaluar la performance de algoritmos. Para esto utilizamos Notación Asintótica Modelo de Costo basado en Lenguaje
1/16. Coste de Algoritmos. 8 de abril de 2018
 1/16 Coste de Algoritmos Josefina Sierra Santibáñez 8 de abril de 2018 2/16 Coste de un Algoritmo Analizar un algoritmo significa, en el contexto de este curso, estimar los recursos que requiere. Aunque
1/16 Coste de Algoritmos Josefina Sierra Santibáñez 8 de abril de 2018 2/16 Coste de un Algoritmo Analizar un algoritmo significa, en el contexto de este curso, estimar los recursos que requiere. Aunque
Análisis y Diseño de Algoritmos. Complejidad Computacional
 Análisis y Diseño de Algoritmos Complejidad Computacional Multiplicación Método Tradicional Método Russé Método Particiones Complejidad Computacional Tan pronto como una máquina análitica exista, será
Análisis y Diseño de Algoritmos Complejidad Computacional Multiplicación Método Tradicional Método Russé Método Particiones Complejidad Computacional Tan pronto como una máquina análitica exista, será
Tiempo de Ejecución. Midiendo el Tiempo de Ejecución
 Tiempo de Ejecución Arturo Díaz Pérez Sección de Computación Departamento de Ingeniería Eléctrica CINVESTAV-IPN Av. Instituto Politécnico Nacional No. 2508 Col. San Pedro Zacatenco México, D. F. CP 07300
Tiempo de Ejecución Arturo Díaz Pérez Sección de Computación Departamento de Ingeniería Eléctrica CINVESTAV-IPN Av. Instituto Politécnico Nacional No. 2508 Col. San Pedro Zacatenco México, D. F. CP 07300
R no es enumerable. Por contradicción, supongamos que existe una biyección f : N! R. diagonalización de Cantor. Para cada i 2 N:
 R no es enumerable Por contradicción, supongamos que existe una biyección f : N! R. I Vamos a obtener una contradicción usando el método de diagonalización de Cantor. Para cada i 2 N: f (i) = n i.d i,0
R no es enumerable Por contradicción, supongamos que existe una biyección f : N! R. I Vamos a obtener una contradicción usando el método de diagonalización de Cantor. Para cada i 2 N: f (i) = n i.d i,0
Notación Asintótica 2
 Notación Asintótica 2 mat-151 1 Éxamen Rápido (6 minutos) Cada operación fundamental usa c milisegundos, cuánto tiempo toma contar hasta 1,000,000? Cuál es el valor de N? Cuál es el órden de complejidad
Notación Asintótica 2 mat-151 1 Éxamen Rápido (6 minutos) Cada operación fundamental usa c milisegundos, cuánto tiempo toma contar hasta 1,000,000? Cuál es el valor de N? Cuál es el órden de complejidad
Recurrencias y cómo resolverlas
 Recurrencias y cómo resolverlas Algoritmos y Estructuras de Datos II Departamento de Computación, Facultad de Ciencias Exactas y Naturales, Universidad de Buenos Aires 8 de septiembre de 2017 Algo2 (DC-FCEyN-UBA)
Recurrencias y cómo resolverlas Algoritmos y Estructuras de Datos II Departamento de Computación, Facultad de Ciencias Exactas y Naturales, Universidad de Buenos Aires 8 de septiembre de 2017 Algo2 (DC-FCEyN-UBA)
Algoritmos y Complejidad
 Algoritmos y Complejidad Técnicas y Herramientas Pablo R. Fillottrani Depto. Ciencias e Ingeniería de la Computación Universidad Nacional del Sur Primer Cuatrimestre 2014 Técnicas y Herramientas Técnicas
Algoritmos y Complejidad Técnicas y Herramientas Pablo R. Fillottrani Depto. Ciencias e Ingeniería de la Computación Universidad Nacional del Sur Primer Cuatrimestre 2014 Técnicas y Herramientas Técnicas
Técnicas y Herramientas. Algoritmos y Complejidad. Técnicas de Demostración. Técnicas y Herramientas. Herramientas Matemáticas Básicas
 Técnicas y Herramientas Técnicas y Herramientas Pablo R. Fillottrani Depto. Ciencias e Ingeniería de la Computación Universidad Nacional del Sur Primer Cuatrimestre 2014 Técnicas de Demostración Herramientas
Técnicas y Herramientas Técnicas y Herramientas Pablo R. Fillottrani Depto. Ciencias e Ingeniería de la Computación Universidad Nacional del Sur Primer Cuatrimestre 2014 Técnicas de Demostración Herramientas
Ejercicio. Usando la formulación del principio de inducción mostrada en la transparencia anterior, demuestre que: 2 2 n 1esdivisiblepor3. =2 n.
 Ejercicio Usando la formulación del principio de inducción mostrada en la transparencia anterior, demuestre que: n 1esdivisiblepor3 n i=0 ( ) n i = n IIC153 Inducción 18 / 30 Inducción estructural La forma
Ejercicio Usando la formulación del principio de inducción mostrada en la transparencia anterior, demuestre que: n 1esdivisiblepor3 n i=0 ( ) n i = n IIC153 Inducción 18 / 30 Inducción estructural La forma
Relaciones IIC1253. IIC1253 Relaciones 1 / 32
 Relaciones IIC1253 IIC1253 Relaciones 1 / 32 Relaciones binarias Dado: conjunto A R es una relación binaria sobre A si R A A. Para indicar que a,b A están relacionados a través de R usamos las notaciones:
Relaciones IIC1253 IIC1253 Relaciones 1 / 32 Relaciones binarias Dado: conjunto A R es una relación binaria sobre A si R A A. Para indicar que a,b A están relacionados a través de R usamos las notaciones:
Introducción y Comportamiento Asintótico
 Introducción y Comportamiento Asintótico M. Andrea Rodríguez-Tastets Ayudante: Erick Elejalde Universidad de Concepción,Chile www.inf.udec.cl\ andrea andrea@udec.cl I Semestre - 2014 1/64 Problemas and
Introducción y Comportamiento Asintótico M. Andrea Rodríguez-Tastets Ayudante: Erick Elejalde Universidad de Concepción,Chile www.inf.udec.cl\ andrea andrea@udec.cl I Semestre - 2014 1/64 Problemas and
Análisis y Diseño de Algoritmos
 Análisis y Diseño de Algoritmos Recurrencias DR. JESÚS A. GONZÁLEZ BERNAL CIENCIAS COMPUTACIONALES INAOE Introducción 2 Cuando un algoritmo se llama a sí mismo Su tiempo de ejecución se puede describir
Análisis y Diseño de Algoritmos Recurrencias DR. JESÚS A. GONZÁLEZ BERNAL CIENCIAS COMPUTACIONALES INAOE Introducción 2 Cuando un algoritmo se llama a sí mismo Su tiempo de ejecución se puede describir
1. Algoritmo, programa y pseudocódigo. Introducción al estudio de algoritmos. Ejemplos
 Introducción al estudio de algoritmos 1. Algoritmo, programa y pseudocódigo 2. Eficiencia y el principio de invarianza 3. Operaciones elementales 4. Casos mejor, peor y medio 5. Notación asintótica 6.
Introducción al estudio de algoritmos 1. Algoritmo, programa y pseudocódigo 2. Eficiencia y el principio de invarianza 3. Operaciones elementales 4. Casos mejor, peor y medio 5. Notación asintótica 6.
Teoría de Modelos Finitos: Motivación
 Teoría de Modelos Finitos: Motivación IIC3260 IIC3260 Teoría de Modelos Finitos: Motivación 1 / 29 Poder expresivo de una lógica: Caso finito Desde ahora en adelante nos vamos a concentrar en las estructuras
Teoría de Modelos Finitos: Motivación IIC3260 IIC3260 Teoría de Modelos Finitos: Motivación 1 / 29 Poder expresivo de una lógica: Caso finito Desde ahora en adelante nos vamos a concentrar en las estructuras
NOTACIÓN O GRANDE. El análisis de algoritmos estima el consumo de recursos de un algoritmo.
 NOTACIÓN O GRANDE El análisis de algoritmos estima el consumo de recursos de un algoritmo. Esto nos permite comparar los costos relativos de dos o más algoritmos para resolver el mismo problema. El análisis
NOTACIÓN O GRANDE El análisis de algoritmos estima el consumo de recursos de un algoritmo. Esto nos permite comparar los costos relativos de dos o más algoritmos para resolver el mismo problema. El análisis
Problemas recursivamente enumerables
 Problemas recursivamente enumerables Definición Un problema L es recursivamente enumerable si existe una máquina de Turing M tal que L = L(M). Nótese que M en la definición no necesariamente se detiene
Problemas recursivamente enumerables Definición Un problema L es recursivamente enumerable si existe una máquina de Turing M tal que L = L(M). Nótese que M en la definición no necesariamente se detiene
Introducción al análisis de algoritmos
 Estructura de Datos y Algoritmos Introducción al análisis de algoritmos 1. Eficiencia en tiempo de Ejecución Cuando resolvemos un problema nos vemos frecuentemente enfrentando una elección de programas,
Estructura de Datos y Algoritmos Introducción al análisis de algoritmos 1. Eficiencia en tiempo de Ejecución Cuando resolvemos un problema nos vemos frecuentemente enfrentando una elección de programas,
Estructuras de Datos. Clase 3 Análisis de algoritmos recursivos
 Clase 3 Análisis de algoritmos recursivos http://cs.uns.edu.ar/~sag Bahía Blanca, Argentina Notación asintótica (Big-Oh) Sean f(n) y g(n) : N R f(n) es O(g(n)) ssiexisten c real con c>0 y n 0 natural con
Clase 3 Análisis de algoritmos recursivos http://cs.uns.edu.ar/~sag Bahía Blanca, Argentina Notación asintótica (Big-Oh) Sean f(n) y g(n) : N R f(n) es O(g(n)) ssiexisten c real con c>0 y n 0 natural con
Complejidad computacional. Algoritmos y Estructuras de Datos I. Complejidad computacional. Notación O grande
 Complejidad computacional Algoritmos y Estructuras de Datos I Segundo cuatrimestre de 2015 Departamento de Computación - FCEyN - UBA Algoritmos - clase 10 Introducción a la complejidad computacional y
Complejidad computacional Algoritmos y Estructuras de Datos I Segundo cuatrimestre de 2015 Departamento de Computación - FCEyN - UBA Algoritmos - clase 10 Introducción a la complejidad computacional y
Conceptos Fundamentales del Análisis de Algoritmos II
 Conceptos Fundamentales del Análisis de Algoritmos II Dr. Eduardo A. RODRÍGUEZ TELLO CINVESTAV-Tamaulipas 17 de enero de 2018 Dr. Eduardo RODRÍGUEZ T. (CINVESTAV) Conceptos Fundamentales del Análisis II
Conceptos Fundamentales del Análisis de Algoritmos II Dr. Eduardo A. RODRÍGUEZ TELLO CINVESTAV-Tamaulipas 17 de enero de 2018 Dr. Eduardo RODRÍGUEZ T. (CINVESTAV) Conceptos Fundamentales del Análisis II
Estructuras de Datos y Algoritmos
 Ejercicio 1: Estructuras de Datos y Algoritmos Año 2018 Práctico 2: Evaluación de Algoritmos (Finalización: 27/08) Ingeniería en Computación - Ingeniería en Informática - Profesorado en Computación Dados
Ejercicio 1: Estructuras de Datos y Algoritmos Año 2018 Práctico 2: Evaluación de Algoritmos (Finalización: 27/08) Ingeniería en Computación - Ingeniería en Informática - Profesorado en Computación Dados
Problemas recursivamente enumerables
 Problemas recursivamente enumerables Definición Un problema L es recursivamente enumerable si existe una máquina de Turing M tal que L = L(M). Nótese que M en la definición no necesariamente se detiene
Problemas recursivamente enumerables Definición Un problema L es recursivamente enumerable si existe una máquina de Turing M tal que L = L(M). Nótese que M en la definición no necesariamente se detiene
Análisis de Algoritmos
 Parte de Algoritmos de la asignatura de Programación Master de Bioinformática Análisis de Algoritmos Web asignatura: http://dis.um.es/~domingo/algbio.html E-mail profesor: domingo@um.es Transparencias
Parte de Algoritmos de la asignatura de Programación Master de Bioinformática Análisis de Algoritmos Web asignatura: http://dis.um.es/~domingo/algbio.html E-mail profesor: domingo@um.es Transparencias
Análisis de algoritmos
 Tema 05: no recursivos M. en C. Edgardo Adrián Franco Martínez http://www.eafranco.com edfrancom@ipn.mx @edfrancom edgardoadrianfrancom 1 Contenido no recursivos La notación de Landau O La notación O Principio
Tema 05: no recursivos M. en C. Edgardo Adrián Franco Martínez http://www.eafranco.com edfrancom@ipn.mx @edfrancom edgardoadrianfrancom 1 Contenido no recursivos La notación de Landau O La notación O Principio
Ecuaciones de recurrencia. Abraham Sánchez López FCC/BUAP Grupo MOVIS
 Ecuaciones de recurrencia Abraham Sánchez López FCC/BUAP Grupo MOVIS Introducción, I Cuando se analiza la complejidad de un algoritmo recursivo, es frecuente que aparezcan funciones de costo también recursivas,
Ecuaciones de recurrencia Abraham Sánchez López FCC/BUAP Grupo MOVIS Introducción, I Cuando se analiza la complejidad de un algoritmo recursivo, es frecuente que aparezcan funciones de costo también recursivas,
Análisis de Algoritmos Primer Problemario Prof. Miguel A. Pizaña 22 de Mayo de 2007
 Análisis de Algoritmos Primer Problemario Prof. Miguel A. Pizaña 22 de Mayo de 2007 I Tareas 1. Dudar de todo, al menos una vez en la vida. 2. Que dice la paradoja de Zenón de Elea? Qué significa paradoja?
Análisis de Algoritmos Primer Problemario Prof. Miguel A. Pizaña 22 de Mayo de 2007 I Tareas 1. Dudar de todo, al menos una vez en la vida. 2. Que dice la paradoja de Zenón de Elea? Qué significa paradoja?
Resolución Proposicional
 Resolución Proposicional IIC2213 IIC2213 Resolución Proposicional 1 / 19 Resolución proposicional Sabemos que Σ = ϕ si y sólo si Σ { ϕ} es inconsistente. Cómo verificamos si Σ { ϕ} es inconsistente? El
Resolución Proposicional IIC2213 IIC2213 Resolución Proposicional 1 / 19 Resolución proposicional Sabemos que Σ = ϕ si y sólo si Σ { ϕ} es inconsistente. Cómo verificamos si Σ { ϕ} es inconsistente? El
Capítulo 1: Fundamentos: Lógica y Demostraciones Clase 3: Relaciones, Funciones, y Notación Asintótica
 Capítulo 1: Fundamentos: Lógica y Demostraciones Clase 3: Relaciones, Funciones, y Notación Asintótica Matemática Discreta - CC3101 Profesor: Pablo Barceló P. Barceló Matemática Discreta - Cap. 1: Fundamentos:
Capítulo 1: Fundamentos: Lógica y Demostraciones Clase 3: Relaciones, Funciones, y Notación Asintótica Matemática Discreta - CC3101 Profesor: Pablo Barceló P. Barceló Matemática Discreta - Cap. 1: Fundamentos:
IIC1253. IIC1253 Una introducción a la teoría de números (y a la criptografía) 1/45
 Una introducción a la teoría de números (y a la criptografía) IIC1253 IIC1253 Una introducción a la teoría de números (y a la criptografía) 1/45 Motivación: Criptografía de clave pública Se tiene dos funciones
Una introducción a la teoría de números (y a la criptografía) IIC1253 IIC1253 Una introducción a la teoría de números (y a la criptografía) 1/45 Motivación: Criptografía de clave pública Se tiene dos funciones
Complejidad computacional y asintótica
 Complejidad computacional y asintótica Complejidad computacional Indica el esfuerzo que hay que realizar para aplicar un algoritmo y lo costoso que éste resulta. La eficiencia suele medirse en términos
Complejidad computacional y asintótica Complejidad computacional Indica el esfuerzo que hay que realizar para aplicar un algoritmo y lo costoso que éste resulta. La eficiencia suele medirse en términos
Lógica Proposicional IIC2213. IIC2213 Lógica Proposicional 1/42
 Lógica Proposicional IIC2213 IIC2213 Lógica Proposicional 1/42 Por qué necesitamos la lógica? Necesitamos un lenguaje con una sintaxis precisa y una semántica bien definida. Queremos usar este lenguaje
Lógica Proposicional IIC2213 IIC2213 Lógica Proposicional 1/42 Por qué necesitamos la lógica? Necesitamos un lenguaje con una sintaxis precisa y una semántica bien definida. Queremos usar este lenguaje
Lógica Proposicional IIC2213. IIC2213 Lógica Proposicional 1/42
 Lógica Proposicional IIC2213 IIC2213 Lógica Proposicional 1/42 Por qué necesitamos la lógica? Necesitamos un lenguaje con una sintaxis precisa y una semántica bien definida. Queremos usar este lenguaje
Lógica Proposicional IIC2213 IIC2213 Lógica Proposicional 1/42 Por qué necesitamos la lógica? Necesitamos un lenguaje con una sintaxis precisa y una semántica bien definida. Queremos usar este lenguaje
Diseño y Análisis de Algoritmos
 1. Recursividad 2. "Dividir para Reinar" 3. Recursividad y Tabulación (Programación Dinámica) 4. Métodos Matemáticos Funciones discretas Notación O Ecuaciones de recurrencia 5. Casos de Estudio Breve descripción
1. Recursividad 2. "Dividir para Reinar" 3. Recursividad y Tabulación (Programación Dinámica) 4. Métodos Matemáticos Funciones discretas Notación O Ecuaciones de recurrencia 5. Casos de Estudio Breve descripción
Números naturales y recursividad
 Números naturales y recursividad Rafael F. Isaacs G. * Fecha: 12 de abril de 2004 Números naturales Cuál es el primer conjunto de números que estudiamos desde la escuela primaria? Se sabe que los números
Números naturales y recursividad Rafael F. Isaacs G. * Fecha: 12 de abril de 2004 Números naturales Cuál es el primer conjunto de números que estudiamos desde la escuela primaria? Se sabe que los números
Algoritmos Secuenciales y Recursivos
 Algoritmos Secuenciales y Recursivos M. Andrea Rodríguez-Tastets Ayudante: Erick Elejalde Universidad de Concepción,Chile www.inf.udec.cl\ andrea andrea@udec.cl I Semestre - 2014 1/45 Análisis secuencial
Algoritmos Secuenciales y Recursivos M. Andrea Rodríguez-Tastets Ayudante: Erick Elejalde Universidad de Concepción,Chile www.inf.udec.cl\ andrea andrea@udec.cl I Semestre - 2014 1/45 Análisis secuencial
IIC1253. IIC1253 Inducción 1/30
 Inducción IIC1253 IIC1253 Inducción 1/30 Inducción en los números naturales: Formulación intuitiva Si P es una propiedad tal que: Caso base : P se cumple para 0, Caso inductivo : si P se cumple para n,
Inducción IIC1253 IIC1253 Inducción 1/30 Inducción en los números naturales: Formulación intuitiva Si P es una propiedad tal que: Caso base : P se cumple para 0, Caso inductivo : si P se cumple para n,
Algoritmos de Búsqueda
 Introducción a la Computación Algoritmos de Búsqueda Esteban E. Mocskos (emocskos@dc.uba.ar) Facultad de Ciencias Exactas y Naturales, UBA CONICET 11/10/2017 E. Mocskos (UBA CONICET) Algoritmos de Búsqueda
Introducción a la Computación Algoritmos de Búsqueda Esteban E. Mocskos (emocskos@dc.uba.ar) Facultad de Ciencias Exactas y Naturales, UBA CONICET 11/10/2017 E. Mocskos (UBA CONICET) Algoritmos de Búsqueda
RSA: Implementación. Ya resolvimos (3), ahora vamos a resolver (2). IIC3242 Complejidad Probabiĺıstica 28 / 77
 RSA: Implementación Para poder implementar RSA necesitamos algoritmos eficientes para los siguientes problemas: (1) Generar primos P y Q (2) Generar números e y d tales que e d modφ(n) = 1 (3) Calcular
RSA: Implementación Para poder implementar RSA necesitamos algoritmos eficientes para los siguientes problemas: (1) Generar primos P y Q (2) Generar números e y d tales que e d modφ(n) = 1 (3) Calcular
Algoritmos y Estructuras de Datos Curso 06/07. Ejercicios
 6.1.(Clase) Un programa que utiliza la técnica divide y vencerás, divide un problema de tamaño n en a subproblemas de tamaño n/b. El tiempo g(n) de la resolución directa (caso base) se considerará constante.
6.1.(Clase) Un programa que utiliza la técnica divide y vencerás, divide un problema de tamaño n en a subproblemas de tamaño n/b. El tiempo g(n) de la resolución directa (caso base) se considerará constante.
Una pregunta pendiente
 Una pregunta pendiente Cómo podemos construir un generador (casi) uniforme para una relación? Recuerde el problema KS definido en la sección anterior y la relación: R KS = {((~a, b), ~x) ~a 2 N n y ~x
Una pregunta pendiente Cómo podemos construir un generador (casi) uniforme para una relación? Recuerde el problema KS definido en la sección anterior y la relación: R KS = {((~a, b), ~x) ~a 2 N n y ~x
1. Definiciones previas
 Universidad de Chile Facultad de Ciencias Físicas y Matemáticas Departamento de Ingeniería Matemática MA47A: Optimización Combinatorial Profesor: Roberto Cominetti Auxiliares: Raul Aliaga Diaz, Cristóbal
Universidad de Chile Facultad de Ciencias Físicas y Matemáticas Departamento de Ingeniería Matemática MA47A: Optimización Combinatorial Profesor: Roberto Cominetti Auxiliares: Raul Aliaga Diaz, Cristóbal
Análisis de la Complejidad de Algoritmos
 Análisis de la Complejidad de Algoritmos Gráficas estadística y minería de datos con python Miguel Cárdenas Montes Centro de Investigaciones Energéticas Medioambientales y Tecnológicas, Madrid, Spain miguel.cardenas@ciemat.es
Análisis de la Complejidad de Algoritmos Gráficas estadística y minería de datos con python Miguel Cárdenas Montes Centro de Investigaciones Energéticas Medioambientales y Tecnológicas, Madrid, Spain miguel.cardenas@ciemat.es
Clases de Complejidad
 Clases de Complejidad IIC3242 IIC3242 Clases de Complejidad 1 / 71 Clases de complejidad: Supuestos Vamos a definir y estudiar las propiedades fundamentales de algunas de las clases de complejidad más
Clases de Complejidad IIC3242 IIC3242 Clases de Complejidad 1 / 71 Clases de complejidad: Supuestos Vamos a definir y estudiar las propiedades fundamentales de algunas de las clases de complejidad más
Análisis y Diseño de Algoritmos
 Análisis y Diseño de Algoritmos Introducción: El Rol de los Algoritmos en Computación DR. JESÚS A. GONZÁLEZ BERNAL CIENCIAS COMPUTACIONALES INAOE Temario 2 1. Introducción 2. Notación Asintótica 3. Recurrencias
Análisis y Diseño de Algoritmos Introducción: El Rol de los Algoritmos en Computación DR. JESÚS A. GONZÁLEZ BERNAL CIENCIAS COMPUTACIONALES INAOE Temario 2 1. Introducción 2. Notación Asintótica 3. Recurrencias
Análisis de Algoritmos
 Análisis de Algoritmos Amalia Duch Barcelona, marzo de 2007 Índice 1. Costes en tiempo y en espacio 1 2. Coste en los casos mejor, promedio y peor 3 3. Notación asintótica 4 4. Coste de los algoritmos
Análisis de Algoritmos Amalia Duch Barcelona, marzo de 2007 Índice 1. Costes en tiempo y en espacio 1 2. Coste en los casos mejor, promedio y peor 3 3. Notación asintótica 4 4. Coste de los algoritmos
Lógica proposicional: Lectura única
 Lógica proposicional: Lectura única Una fórmula ϕ es atómica si ϕ = p, donde p P. Una fórmula ϕ es compuesta si no es atómica. - Si ϕ = ( α), entonces es un conectivo primario de ϕ y α es una subfórmula
Lógica proposicional: Lectura única Una fórmula ϕ es atómica si ϕ = p, donde p P. Una fórmula ϕ es compuesta si no es atómica. - Si ϕ = ( α), entonces es un conectivo primario de ϕ y α es una subfórmula
Arreglos. Algoritmos y Estructuras de Datos I. Arreglos en C++ Arreglos y listas
 Arreglos Algoritmos y Estructuras de Datos I Primer cuatrimestre 2007 Teórica de imperativo 3 Algoritmos de búsqueda secuencias de una cantidad fija de variables del mismo tipo se declaran con un nombre,,
Arreglos Algoritmos y Estructuras de Datos I Primer cuatrimestre 2007 Teórica de imperativo 3 Algoritmos de búsqueda secuencias de una cantidad fija de variables del mismo tipo se declaran con un nombre,,
La lógica de segundo orden: Sintaxis
 La lógica de segundo orden: Sintaxis Dado: Vocabulario L Definición La lógica de segundo orden (LSO) sobre L es definida como la extensión de LPO que incluye las siguientes reglas: Si t 1,..., t k son
La lógica de segundo orden: Sintaxis Dado: Vocabulario L Definición La lógica de segundo orden (LSO) sobre L es definida como la extensión de LPO que incluye las siguientes reglas: Si t 1,..., t k son
Algoritmos aleatorizados
 Algoritmos aleatorizados IIC2283 IIC2283 Algoritmos aleatorizados 1/109 Algoritmos aleatorizados Vamos a permitir a los algoritmos tener una componente aleatoria I En general esto significa que un algoritmo
Algoritmos aleatorizados IIC2283 IIC2283 Algoritmos aleatorizados 1/109 Algoritmos aleatorizados Vamos a permitir a los algoritmos tener una componente aleatoria I En general esto significa que un algoritmo
1. Ecuaciones de recurrencia
 PRÁCTICA NO 3. ALGORITMOS RECURRENTES 1. Ecuaciones de recurrencia Una ecuación de recurrencia es una expresión finita que define explícitamente una sucesión, en el cual un elemento de la sucesión se determina
PRÁCTICA NO 3. ALGORITMOS RECURRENTES 1. Ecuaciones de recurrencia Una ecuación de recurrencia es una expresión finita que define explícitamente una sucesión, en el cual un elemento de la sucesión se determina
Algoritmos aleatorizados
 Algoritmos aleatorizados IIC2283 IIC2283 Algoritmos aleatorizados 1/109 Algoritmos aleatorizados Vamos a permitir a los algoritmos tener una componente aleatoria I En general esto significa que un algoritmo
Algoritmos aleatorizados IIC2283 IIC2283 Algoritmos aleatorizados 1/109 Algoritmos aleatorizados Vamos a permitir a los algoritmos tener una componente aleatoria I En general esto significa que un algoritmo
Temario. Tipos de recursión. Eficiencia y recursión
 RECURSION Temario Tipos de recursión Eficiencia y recursión Tipos de RECURSION Según desde donde se realice el llamado recursivo: Directa: la función se llama a sí misma. Indirecta: la función A llama
RECURSION Temario Tipos de recursión Eficiencia y recursión Tipos de RECURSION Según desde donde se realice el llamado recursivo: Directa: la función se llama a sí misma. Indirecta: la función A llama
Recurrencias. Si a 0, a 1, a 2, es una progresión geométrica, entonces a 1 /a 0 = a 2 /a 1 = = a n+1 /a n = r, la razón común.
 Recurrencias Def. Progresión geométrica. Es una sucesión infinita de números, como: 5, 45, 135, donde el cociente de cualquier término entre su predecesor es una constante, llamada razón común. (Para nuestro
Recurrencias Def. Progresión geométrica. Es una sucesión infinita de números, como: 5, 45, 135, donde el cociente de cualquier término entre su predecesor es una constante, llamada razón común. (Para nuestro
Algorítmica y Lenguajes de Programación. Eficiencia y notación asintótica (i)
 Algorítmica y Lenguajes de Programación Eficiencia y notación asintótica (i) Eficiencia y notación asintótica. Introducción Para resolver un problema pueden existir varios algoritmos. Por tanto, es lógico
Algorítmica y Lenguajes de Programación Eficiencia y notación asintótica (i) Eficiencia y notación asintótica. Introducción Para resolver un problema pueden existir varios algoritmos. Por tanto, es lógico
Algoritmos de Ordenamiento
 Algoritmos de Ordenamiento Límite inferior y Alg. Lineales Andrés Becerra Sandoval Ponticia Universidad Javeriana 14 de julio de 2007 Lenguajes III Introducción Algoritmo Complejidad Bubble(burbuja) Θ(n
Algoritmos de Ordenamiento Límite inferior y Alg. Lineales Andrés Becerra Sandoval Ponticia Universidad Javeriana 14 de julio de 2007 Lenguajes III Introducción Algoritmo Complejidad Bubble(burbuja) Θ(n
Complejidad de algoritmos recursivos
 Tema 3. Complejidad de algoritmos recursivos 1. INTRODUCCIÓN... 1 CLASIFICACIÓN DE FUNCIONES RECURSIVAS... 1 DISEÑO DE FUNCIONES RECURSIVAS... 2 2. VENTAJAS E INCONVENIENTES DE LA RECURSIVIDAD... 4 3.
Tema 3. Complejidad de algoritmos recursivos 1. INTRODUCCIÓN... 1 CLASIFICACIÓN DE FUNCIONES RECURSIVAS... 1 DISEÑO DE FUNCIONES RECURSIVAS... 2 2. VENTAJAS E INCONVENIENTES DE LA RECURSIVIDAD... 4 3.
Tema 01: Fundamentos del Análisis Asintótico de Algoritmos
 Tema 01: Fundamentos del Análisis Asintótico de Algoritmos Noviembre, 2003 CS0218: Algoritmos y Programación II Introducción En Ciencias de la Computación se presenta con frecuencia la situación de analizar
Tema 01: Fundamentos del Análisis Asintótico de Algoritmos Noviembre, 2003 CS0218: Algoritmos y Programación II Introducción En Ciencias de la Computación se presenta con frecuencia la situación de analizar
Máquinas de Turing IIC3242. IIC3242 Máquinas de Turing 1 / 42
 Máquinas de Turing IIC3242 IIC3242 Máquinas de Turing 1 / 42 Complejidad Computacional Objetivo: Medir la complejidad computacional de un problema. Vale decir: Medir la cantidad de recursos computacionales
Máquinas de Turing IIC3242 IIC3242 Máquinas de Turing 1 / 42 Complejidad Computacional Objetivo: Medir la complejidad computacional de un problema. Vale decir: Medir la cantidad de recursos computacionales
Algoritmos Iterativos de Búsqueda y Ordenación y sus tiempos
 Estructura de Datos y Algoritmos Algoritmos Iterativos de Búsqueda y Ordenación y sus tiempos 1. Algorimos de ordenación Discutiremos el problema de ordenar un array de elementos. A los efectos de simplificar
Estructura de Datos y Algoritmos Algoritmos Iterativos de Búsqueda y Ordenación y sus tiempos 1. Algorimos de ordenación Discutiremos el problema de ordenar un array de elementos. A los efectos de simplificar
Tema 2: Series numéricas
 Tema 2: Series numéricas Una serie infinita (o simplemente serie) es una suma formal de infinitos términos a + a 2 + a 3 + + + Al número se le denomin-ésimo término de la serie Se llama sucesión de sumas
Tema 2: Series numéricas Una serie infinita (o simplemente serie) es una suma formal de infinitos términos a + a 2 + a 3 + + + Al número se le denomin-ésimo término de la serie Se llama sucesión de sumas
Programación dinámica: un último ejemplo
 Programación dinámica: un último ejemplo Dado: matrices A m n, B n r, C r s de números enteros Para calcular A m n B n r el algoritmo usual realiza m n r multiplicaciones de números enteros Cuántas multiplicaciones
Programación dinámica: un último ejemplo Dado: matrices A m n, B n r, C r s de números enteros Para calcular A m n B n r el algoritmo usual realiza m n r multiplicaciones de números enteros Cuántas multiplicaciones
Demostración Contraejemplo. Métodos Indirectos
 DEMOSTRACION Una demostración de un teorema es una verificación escrita que muestra que el teorema es verdadero. Informalmente, desde el punto de vista de la lógica, una demostración de un teorema es un
DEMOSTRACION Una demostración de un teorema es una verificación escrita que muestra que el teorema es verdadero. Informalmente, desde el punto de vista de la lógica, una demostración de un teorema es un
Capítulo 1 LA COMPLEJIDAD DE LOS ALGORITMOS
 Capítulo 1 LA COMPLEJIDAD DE LOS ALGORITMOS 1.1 INTRODUCCIÓN En un sentido amplio, dado un problema y un dispositivo donde resolverlo, es necesario proporcionar un método preciso que lo resuelva, adecuado
Capítulo 1 LA COMPLEJIDAD DE LOS ALGORITMOS 1.1 INTRODUCCIÓN En un sentido amplio, dado un problema y un dispositivo donde resolverlo, es necesario proporcionar un método preciso que lo resuelva, adecuado
Máquinas de Turing IIC3242. IIC3242 Máquinas de Turing 1 / 45
 Máquinas de Turing IIC3242 IIC3242 Máquinas de Turing 1 / 45 Complejidad Computacional Objetivo: Medir la complejidad computacional de un problema. Vale decir: Medir la cantidad de recursos computacionales
Máquinas de Turing IIC3242 IIC3242 Máquinas de Turing 1 / 45 Complejidad Computacional Objetivo: Medir la complejidad computacional de un problema. Vale decir: Medir la cantidad de recursos computacionales
Reglas de derivación Sumas, productos y cocientes. Tema 4
 Tema 4 Reglas de derivación Aclarado el concepto de derivada, su significado analítico y sus interpretaciones geométrica y física, pasamos a desarrollar las reglas básicas para el cálculo de derivadas
Tema 4 Reglas de derivación Aclarado el concepto de derivada, su significado analítico y sus interpretaciones geométrica y física, pasamos a desarrollar las reglas básicas para el cálculo de derivadas
Propiedades de números enteros (lista de problemas para examen)
 Propiedades de números enteros (lista de problemas para examen) Denotamos por Z al conjunto de los números enteros y por N al conjunto de los números enteros positivos: N = 1, 2, 3,...}. Valor absoluto
Propiedades de números enteros (lista de problemas para examen) Denotamos por Z al conjunto de los números enteros y por N al conjunto de los números enteros positivos: N = 1, 2, 3,...}. Valor absoluto
Técnicas de diseño de algoritmos Divide y Vencerás
 Técnicas de diseño de algoritmos Divide y Vencerás Luis Javier Rodríguez Fuentes Amparo Varona Fernández Departamento de Electricidad y Electrónica Facultad de Ciencia y Tecnología, UPV/EHU luisjavier.rodriguez@ehu.es
Técnicas de diseño de algoritmos Divide y Vencerás Luis Javier Rodríguez Fuentes Amparo Varona Fernández Departamento de Electricidad y Electrónica Facultad de Ciencia y Tecnología, UPV/EHU luisjavier.rodriguez@ehu.es
Matemáticas Discretas
 Coordinación de Ciencias Computacionales - INAOE Matemáticas Discretas Cursos Propedéuticos 2011 Ciencias Computacionales INAOE Dr. Enrique Muñoz de Cote jemc@inaoep.mx http://ccc.inaoep.mx/~jemc Oficina
Coordinación de Ciencias Computacionales - INAOE Matemáticas Discretas Cursos Propedéuticos 2011 Ciencias Computacionales INAOE Dr. Enrique Muñoz de Cote jemc@inaoep.mx http://ccc.inaoep.mx/~jemc Oficina
CI2612: Algoritmos y Estructuras de Datos II. Recurrencias y el principio de dividir y conquistar. Recurrencias. Objetivos.
 CI2612: Algoritmos y Estructuras de Datos II Blai Bonet Universidad Simón Boĺıvar, Caracas, Venezuela Recurrencias y el principio de dividir y conquistar Objetivos Recurrencias Repasar los conceptos de
CI2612: Algoritmos y Estructuras de Datos II Blai Bonet Universidad Simón Boĺıvar, Caracas, Venezuela Recurrencias y el principio de dividir y conquistar Objetivos Recurrencias Repasar los conceptos de
Programación 2. Lección 8. Caracterización asintótica de la eficiencia de un algoritmo
 Programación 2 Lección 8. Caracterización asintótica de la eficiencia de un algoritmo 1 1. Funciones de coste de un algoritmo 2. Caracterización asintótica del coste Notación O Consecuencias prácticas
Programación 2 Lección 8. Caracterización asintótica de la eficiencia de un algoritmo 1 1. Funciones de coste de un algoritmo 2. Caracterización asintótica del coste Notación O Consecuencias prácticas
(TALF- ITIS- C) Clase 3 5 de Octubre de 2010
 (TALF- ITIS- C) Clase 3 5 de Octubre de 2010 Ac=vidades de par=cipación de alumnos 2 Alumnos : Blog de la Asignatura: hip://talf.blogspot.es/ 1 Alumno: BiograMa relacionada con la asignatura ACTIVIDADES
(TALF- ITIS- C) Clase 3 5 de Octubre de 2010 Ac=vidades de par=cipación de alumnos 2 Alumnos : Blog de la Asignatura: hip://talf.blogspot.es/ 1 Alumno: BiograMa relacionada con la asignatura ACTIVIDADES
Estructuras de Datos y Algoritmos
 Estructuras de Datos y Algoritmos Práctico 2: Evaluación de Algoritmos (Finalización: 03/09) Ingeniería en Computación - Ingeniería en Informática Año 2015 Ejercicio 1: Dados los siguientes vectores, correspondientes
Estructuras de Datos y Algoritmos Práctico 2: Evaluación de Algoritmos (Finalización: 03/09) Ingeniería en Computación - Ingeniería en Informática Año 2015 Ejercicio 1: Dados los siguientes vectores, correspondientes
Tema 2 Fundamentos de Complejidad Algorítmica
 Tema 2 Fundamentos de Complejidad Algorítmica Pablo Sánchez Dpto. Matemáticas, Estadística y Computación Universidad de Cantabria Santander (Cantabria, España) p.sanchez@unican.es Pablo Sánchez (MATESCO)
Tema 2 Fundamentos de Complejidad Algorítmica Pablo Sánchez Dpto. Matemáticas, Estadística y Computación Universidad de Cantabria Santander (Cantabria, España) p.sanchez@unican.es Pablo Sánchez (MATESCO)
Análisis de algoritmos
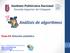 Tema 04: Notación asintótica M. en C. Edgardo Adrián Franco Martínez http://www.eafranco.com edfrancom@ipn.mx @edfrancom edgardoadrianfrancom 1 Contenido Introducción Asíntota Dominio asintótico Ejemplo
Tema 04: Notación asintótica M. en C. Edgardo Adrián Franco Martínez http://www.eafranco.com edfrancom@ipn.mx @edfrancom edgardoadrianfrancom 1 Contenido Introducción Asíntota Dominio asintótico Ejemplo
Especialidad La enseñanza de las matemáticas en secundaria Grupo B: Celaya. Inducción. 1. Principio de Inducción
 Especialidad La enseñanza de las matemáticas en secundaria Grupo B: Celaya Inducción 1. Principio de Inducción La inducción matemática es un método muy útil en algunas demostraciones. Se emplea generalmente
Especialidad La enseñanza de las matemáticas en secundaria Grupo B: Celaya Inducción 1. Principio de Inducción La inducción matemática es un método muy útil en algunas demostraciones. Se emplea generalmente
Límite superior y límite inferior de una sucesión
 Límite superior y límite inferior de una sucesión Objetivos. Definir las nociones de los límites superior e inferior de una sucesión y estudiar sus propiedades básicas. Requisitos. Supremo e ínfimo de
Límite superior y límite inferior de una sucesión Objetivos. Definir las nociones de los límites superior e inferior de una sucesión y estudiar sus propiedades básicas. Requisitos. Supremo e ínfimo de
RSA funciona correctamente
 RSA funciona correctamente Sean E y D construidas como fue mencionado en las transparencias anteriores. N = P Q, E(M) = M e modn y D(M) = M d modn Teorema (Rivest-Shamir-Adleman) Para cada M {0,...,N 1},
RSA funciona correctamente Sean E y D construidas como fue mencionado en las transparencias anteriores. N = P Q, E(M) = M e modn y D(M) = M d modn Teorema (Rivest-Shamir-Adleman) Para cada M {0,...,N 1},
Este documento es de distribución gratuita y llega gracias a El mayor portal de recursos educativos a tu servicio!
 Este documento es de distribución gratuita y llega gracias a Ciencia Matemática www.cienciamatematica.com El mayor portal de recursos educativos a tu servicio! EL MÉTODO DE INDUCCIÓN Lección de preparación
Este documento es de distribución gratuita y llega gracias a Ciencia Matemática www.cienciamatematica.com El mayor portal de recursos educativos a tu servicio! EL MÉTODO DE INDUCCIÓN Lección de preparación
ALGORITMOS INTRODUCCIÓN ALGORITMOS INTRODUCCIÓN AL ANÁLISIS Y AL DISEÑO DE AL ANÁLISIS Y AL DISEÑO DE UNIVERSIDAD AUTÓNOMA METROPOLITANA
 INTRODUCCIÓN AL ANÁLISIS Y AL DISEÑO DE ALGORITMOS El análisis de la complejidad de algoritmos, así como la discusión de las ventajas/desventajas, que tienen diferentes soluciones a los problemas clásicos,
INTRODUCCIÓN AL ANÁLISIS Y AL DISEÑO DE ALGORITMOS El análisis de la complejidad de algoritmos, así como la discusión de las ventajas/desventajas, que tienen diferentes soluciones a los problemas clásicos,
Matriz asociada a una transformación lineal respecto a un par de bases
 Matriz asociada a una transformación lineal respecto a un par de bases Ejercicios Objetivos Comprender cómo se describe una transformación lineal (que actúa en espacios vectoriales de dimensiones finitas)
Matriz asociada a una transformación lineal respecto a un par de bases Ejercicios Objetivos Comprender cómo se describe una transformación lineal (que actúa en espacios vectoriales de dimensiones finitas)
Análisis de Algoritmos
 January 15, 010 1 Pseudocódigo 3 Modelos de referencia Antes de analizar un algoritmo debemos tener un modelo de la implementación de la tecnología que se va a usar, incluyendo un modelo para los recursos
January 15, 010 1 Pseudocódigo 3 Modelos de referencia Antes de analizar un algoritmo debemos tener un modelo de la implementación de la tecnología que se va a usar, incluyendo un modelo para los recursos
Capitulo 1 Tema 3: Resolución de Recurrencias Asintóticas
 Capitulo 1 Tema 3: Resolución de Recurrencias Asintóticas Introducción En general, todos los problemas en los que alguna de sus variables solo puede tomar valores discretos dan lugar a modelos que involucran
Capitulo 1 Tema 3: Resolución de Recurrencias Asintóticas Introducción En general, todos los problemas en los que alguna de sus variables solo puede tomar valores discretos dan lugar a modelos que involucran
Un tercer problema NP-completo: Programación entera
 Un tercer problema NP-completo: Programación entera Un problema muy estudiado por su utilidad práctica: PROG-ENT = {(A, b) A x b es un sistema de ecuaciones lineales enteras que tiene solución}. Teorema
Un tercer problema NP-completo: Programación entera Un problema muy estudiado por su utilidad práctica: PROG-ENT = {(A, b) A x b es un sistema de ecuaciones lineales enteras que tiene solución}. Teorema
