Cardinalidad IIC1253. IIC1253 Cardinalidad 1 / 23
|
|
|
- Soledad Montes Santos
- hace 6 años
- Vistas:
Transcripción
1 Cardinalidad IIC1253 IIC1253 Cardinalidad 1 / 23
2 Conjuntos con la misma cardinalidad Definición Decimos que dos conjuntos A y B son equinumerosos, denotado como A B, si existe una biyección f : A B. Ejemplo N es equinumeroso con {2 i i N}. IIC1253 Cardinalidad 2 / 23
3 Un teorema útil Teorema (Schröder-Bernstein) A B si y sólo si existen funciones inyectivas f : A B y g : B A. Ejercicio Demuestre que N es equinumeroso con {2 i 3 j i,j N}. IIC1253 Cardinalidad 3 / 23
4 Otras definiciones útiles Definición Sean A y B dos conjuntos. Decimos que B es al menos tan numeroso como A, denotado como A B, si existe una función inyectiva f : A B Decimos que B es más numeroso que A, denotado como A B, si existe una función inyectiva f : A B y no existe una función inyectiva g : B A Observación Del teorema de Schröder-Bernstein: A B si y sólo si A B y B A IIC1253 Cardinalidad 4 / 23
5 Conjuntos enumerables Definición Un conjunto infinito A se dice enumerable si A N. Ejemplo Los conjuntos {2 i i N} y {2 i 3 j i,j N} son enumerables. IIC1253 Cardinalidad 5 / 23
6 Z es enumerable Para demostrar que Z es enumerable, basta demostrar que N N es enumerable. Por qué? Para demostrar que N N es enumerable: primero ordenamos los pares según la suma de sus valores, de menor a mayor; luego ordenamos los pares con la misma suma por el primer componente, de menor a mayor; y finalmente asignamos un número natural a cada par según el orden obtenido IIC1253 Cardinalidad 6 / 23
7 Z es enumerable (0, 0) 0 (0, 1) 1 (1, 0) 2 (0, 2) 3 (1, 1) 4 (2, 0) 5 (0, 3) 6 (1, 2) 7 (2, 1) 8 (3, 0) 9... IIC1253 Cardinalidad 7 / 23
8 Z es enumerable Fórmula obtenida: 0 i +j = 0 ( i+j 1 f(i,j) = ) k +1 +i i +j > 0 k=0 Vale decir: f(i,j) = { 0 i +j = 0 (i+j)(i+j+1) 2 +i i +j > 0 Por ejemplo: f(1,1) = 4 y f(3,0) = 9 IIC1253 Cardinalidad 8 / 23
9 Q es enumerable Para demostrar que Q es enumerable, basta demostrar que Z Z es enumerable. Por qué? Esto es consecuencia de un resultado más general: Teorema Para cada k 3, se tiene que N k es enumerable. Ejercicio Demuestre el teorema para k = 3, y luego generalice su construcción para k > 3. IIC1253 Cardinalidad 9 / 23
10 Ejercicios 1. Demuestre que el conjunto de todos los strings construidos con los símbolos 0 y 1 es enumerable 2. Sea Γ un conjunto finito de símbolos. Demuestre que el conjunto de todos los strings construidos con los símbolos de Γ es enumerable 3. Utilize el resultado anterior para concluir que el conjunto de los polinomios p(x) con coeficientes en los naturales es enumerable. IIC1253 Cardinalidad 10 / 23
11 R no es enumerable Por contradicción, supongamos que existe una biyección f : N R. Vamos a obtener una contradicción usando el método de diagonalización de Cantor Para cada i N: f(i) = n i.d i,0 d i,1...d i,i... donde n i Z y d i,j {0,...,9}, para cada j N IIC1253 Cardinalidad 11 / 23
12 R no es enumerable: Diagonalización Definimos un número r R usando la siguiente diagonal: f(0) = n 0.d 0,0 d 0,1 d 0,2 d 0,3... f(1) = n 1.d 1,0 d 1,1 d 1,2 d 1,3... f(2) = n 2.d 2,0 d 2,1 d 2,2 d 2,3... f(3) = n 3.d 3,0 d 3,1 d 3,2 d 3,3... f(i) = n i.d i,0 d i,1 d i,2 d i,3...d i,i... Propiedad fundamental de r: f(i) r para cada i N Usando esta propiedad obtenemos una contradicción: f no es sobre IIC1253 Cardinalidad 12 / 23
13 R no es enumerable: Diagonalización Definimos r como: r = 0.r 0 r 1 r 2... donde r i (i N) es definido como: { 5 si d i,i 5 r i = 4 si d i,i = 5 Por qué la demostración anterior no funciona si reemplazamos R por Q? IIC1253 Cardinalidad 13 / 23
14 R no es enumerable: Existencia de números trascendentes Un número a R es algebraico si existe un polinomio p(x) tal que: p(x) no es nulo, y los coeficientes de p(x) son números enteros p(a) = 0 Ejemplo Cada número en Q es algebraico, además 2 es algebraico. Un número a R es trascendente si no es algebraico. Existen números trascendentes? IIC1253 Cardinalidad 14 / 23
15 R no es enumerable: Existencia de números trascendentes Existencia de números trascendentes: Liouville (1850): 10 i! i=1 Hermite (1873): e Lindemann (1882): π Un argumento más simple: El conjunto de los polinomios p(x) con coeficientes enteros es enumerable Como R no es enumerable, concluimos que existen números trascendentes IIC1253 Cardinalidad 15 / 23
16 R no es enumerable: Nombres para los números Podemos asociar nombres a los números reales: 1264, mil doscientos sesenta y cuatro, 3.25, tres punto veinte y cinco, 2, raíz cuadrada positiva de 2, π, e, menor raíz del polinomio 3x 3 17x +1,... Podemos asociar un nombre a cada número real? Qué alfabeto usamos? IIC1253 Cardinalidad 16 / 23
17 R no es enumerable: Nombres para los números Consideramos el alfabeto ASCII que tiene 95 caracteres (que pueden ser impresos) Otros alfabetos puedes ser codificados usando este alfabeto: "3*x^3-17*x + 1", "pi" Podemos considerar un alfabeto más pequeño? 0 y 1? El conjunto de los strings que pueden construidos usando el alfabeto ASCII es enumerable Tenemos más números en R que nombres para ellos! IIC1253 Cardinalidad 17 / 23
18 Un teorema más general Teorema (Cantor) A 2 A Demostración: Si A =, tenemos que 2 A = { } y el teorema se cumple Suponemos que A Primero debemos mostrar una función inyectiva f : A 2 A Para cada a A: f(a) = {a} IIC1253 Cardinalidad 18 / 23
19 Teorema de Cantor: Demostración Ahora debemos demostrar que no existe una biyección g : A 2 A. Por contradicción, suponemos que g existe Definimos B A como sigue: B = {a A a g(a)} Como g es sobre, existe b A tal que g(b) = B. Se debe tener que b g(b) o b g(b) IIC1253 Cardinalidad 19 / 23
20 Teorema de Cantor: Demostración Consideramos los dos casos: b g(b) b B b g(b) b g(b) b B b g(b) En ambos casos obtenemos una contradicción. IIC1253 Cardinalidad 20 / 23
21 Teorema de Cantor: Problemas no decidibles Una propiedad P sobre N es un subconjunto de N. Por ejemplo, las siguientes son propiedades sobre N: PARES = {a N a es un número par} PRIMOS = {a N a es un número primo} Definición (informal) Una propiedad sobre N es decidible si existe un programa en Java (o Python) tal que: recibe como entrada n N; si n P retorna sí, en caso contrario retorna no IIC1253 Cardinalidad 21 / 23
22 Teorema de Cantor: Problemas no decidibles Ejemplo PARES y PRIMOS son decidibles. Existe una propiedad P no decidible? No existe un procedimiento mecánico que pueda verificar si un elemento está en P IIC1253 Cardinalidad 22 / 23
23 Teorema de Cantor: Problemas no decidibles Tenemos que: El conjunto de los programas en Java (o Python) es enumerable {P P es una propiedad sobre N} es equinumeroso con 2 N Por teorema de Cantor: N 2 N Concluimos que existen propiedades sobre N que no son decidibles IIC1253 Cardinalidad 23 / 23
Cardinalidad IIC1253. IIC1253 Cardinalidad 1 / 23
 Cardinalidad IIC1253 IIC1253 Cardinalidad 1 / 23 Conjuntos con la misma cardinalidad Definición Decimos que dos conjuntos A y B son equinumerosos, denotado como A B, si existe una biyección f : A B. IIC1253
Cardinalidad IIC1253 IIC1253 Cardinalidad 1 / 23 Conjuntos con la misma cardinalidad Definición Decimos que dos conjuntos A y B son equinumerosos, denotado como A B, si existe una biyección f : A B. IIC1253
R no es enumerable. Por contradicción, supongamos que existe una biyección f : N! R. diagonalización de Cantor. Para cada i 2 N:
 R no es enumerable Por contradicción, supongamos que existe una biyección f : N! R. I Vamos a obtener una contradicción usando el método de diagonalización de Cantor. Para cada i 2 N: f (i) = n i.d i,0
R no es enumerable Por contradicción, supongamos que existe una biyección f : N! R. I Vamos a obtener una contradicción usando el método de diagonalización de Cantor. Para cada i 2 N: f (i) = n i.d i,0
(TALF- ITIS- C) Clase 3 5 de Octubre de 2010
 (TALF- ITIS- C) Clase 3 5 de Octubre de 2010 Ac=vidades de par=cipación de alumnos 2 Alumnos : Blog de la Asignatura: hip://talf.blogspot.es/ 1 Alumno: BiograMa relacionada con la asignatura ACTIVIDADES
(TALF- ITIS- C) Clase 3 5 de Octubre de 2010 Ac=vidades de par=cipación de alumnos 2 Alumnos : Blog de la Asignatura: hip://talf.blogspot.es/ 1 Alumno: BiograMa relacionada con la asignatura ACTIVIDADES
1. Conjuntos y funciones
 PRACTICO 1: CONJUNTOS. 1. Conjuntos y funciones Es útil saber de memoria las siguientes propiedades de conjuntos y funciones. Tanto como saber las tablas. Ejercicio 1. Si I es un conjunto y A α es un conjunto
PRACTICO 1: CONJUNTOS. 1. Conjuntos y funciones Es útil saber de memoria las siguientes propiedades de conjuntos y funciones. Tanto como saber las tablas. Ejercicio 1. Si I es un conjunto y A α es un conjunto
1. Conjuntos y funciones
 Centro de Matemática Facultad de Ciencias Universidad de la República Introducción a la Topología Curso 2016 PRACTICO 1: CONJUNTOS. 1 1. Conjuntos y funciones Ejercicio 1. Si I es un conjunto y A α es
Centro de Matemática Facultad de Ciencias Universidad de la República Introducción a la Topología Curso 2016 PRACTICO 1: CONJUNTOS. 1 1. Conjuntos y funciones Ejercicio 1. Si I es un conjunto y A α es
Cardinalidad. Teorema 0.3 Todo conjunto infinito contiene un subconjunto infinito numerable.
 Cardinalidad Dados dos conjuntos A y B, decimos que A es equivalente a B, o que A y B tienen la misma potencia, y lo notamos A B, si existe una biyección de A en B Es fácil probar que es una relación de
Cardinalidad Dados dos conjuntos A y B, decimos que A es equivalente a B, o que A y B tienen la misma potencia, y lo notamos A B, si existe una biyección de A en B Es fácil probar que es una relación de
Práctica 2 -Cardinalidad- A. Propiedades básicas de los Conjuntos
 Cálculo Avanzado Segundo Cuatrimestre de 2012 Práctica 2 -Cardinalidad- A. Propiedades básicas de los Conjuntos Ejercicio 1. Demostrar las siguientes igualdades de conjuntos: i) B i I A i = i I(B A i ).
Cálculo Avanzado Segundo Cuatrimestre de 2012 Práctica 2 -Cardinalidad- A. Propiedades básicas de los Conjuntos Ejercicio 1. Demostrar las siguientes igualdades de conjuntos: i) B i I A i = i I(B A i ).
Práctica 2: Cardinalidad. Propiedades básicas de los conjuntos
 Cálculo Avanzado Segundo Cuatrimestre de 2014 Práctica 2: Cardinalidad Propiedades básicas de los conjuntos Ejercicio 1. Demostrar las siguientes igualdades de conjuntos: i) B i I A i = i I(B A i ). ii)
Cálculo Avanzado Segundo Cuatrimestre de 2014 Práctica 2: Cardinalidad Propiedades básicas de los conjuntos Ejercicio 1. Demostrar las siguientes igualdades de conjuntos: i) B i I A i = i I(B A i ). ii)
Espacios Vectoriales
 Espacios Vectoriales Espacios Vectoriales Verónica Briceño V. noviembre 2013 Verónica Briceño V. () Espacios Vectoriales noviembre 2013 1 / 47 En esta Presentación... En esta Presentación veremos: Espacios
Espacios Vectoriales Espacios Vectoriales Verónica Briceño V. noviembre 2013 Verónica Briceño V. () Espacios Vectoriales noviembre 2013 1 / 47 En esta Presentación... En esta Presentación veremos: Espacios
Un tercer ejemplo: verificación de primalidad
 Un tercer ejemplo: verificación de primalidad Vamos a ver un algoritmo aleatorizado para verificar si un número es primo. I Este algoritmo es más eficiente que los algoritmos sin componentes aleatorias
Un tercer ejemplo: verificación de primalidad Vamos a ver un algoritmo aleatorizado para verificar si un número es primo. I Este algoritmo es más eficiente que los algoritmos sin componentes aleatorias
Es claro que es una relación de equivalencia. Para ver que tener la misma cardinalidad y la cardinalidad están bien definidas queremos ver que
 Capítulo II Cardinalidad Finita II.1. Cardinalidad Definimos I n para n N como I n = {k N : 1 k n}. En particular I 0 =, puesto que 0 < 1. Esto es equivalente a la definición recursiva { si n = 0 I n =
Capítulo II Cardinalidad Finita II.1. Cardinalidad Definimos I n para n N como I n = {k N : 1 k n}. En particular I 0 =, puesto que 0 < 1. Esto es equivalente a la definición recursiva { si n = 0 I n =
Anillos. a + (b + c) = (a + b) + c. 3) Existe un elemento 0 en R, el cual llamaremos cero, tal que. a + 0 = 0 + a = a para todo a en R.
 Capítulo 7 Anillos 7.1 Definiciones Básicas El concepto de Anillo se obtiene como una generalización de los números enteros, en donde están definidas un par de operaciones, la suma y el producto, relacionadas
Capítulo 7 Anillos 7.1 Definiciones Básicas El concepto de Anillo se obtiene como una generalización de los números enteros, en donde están definidas un par de operaciones, la suma y el producto, relacionadas
Terminaremos el capítulo con una breve referencia a la teoría de cardinales.
 TEMA 5. CARDINALES 241 Tema 5. Cardinales Terminaremos el capítulo con una breve referencia a la teoría de cardinales. Definición A.5.1. Diremos que el conjunto X tiene el mismo cardinal que el conjunto
TEMA 5. CARDINALES 241 Tema 5. Cardinales Terminaremos el capítulo con una breve referencia a la teoría de cardinales. Definición A.5.1. Diremos que el conjunto X tiene el mismo cardinal que el conjunto
Conjuntos, relaciones y funciones Susana Puddu
 Susana Puddu 1. Repaso sobre la teoría de conjuntos. Denotaremos por IN al conjunto de los números naturales y por ZZ al de los enteros. Dados dos conjuntos A y B decimos que A está contenido en B o también
Susana Puddu 1. Repaso sobre la teoría de conjuntos. Denotaremos por IN al conjunto de los números naturales y por ZZ al de los enteros. Dados dos conjuntos A y B decimos que A está contenido en B o también
Ejercicio. Usando la formulación del principio de inducción mostrada en la transparencia anterior, demuestre que: 2 2 n 1esdivisiblepor3. =2 n.
 Ejercicio Usando la formulación del principio de inducción mostrada en la transparencia anterior, demuestre que: n 1esdivisiblepor3 n i=0 ( ) n i = n IIC153 Inducción 18 / 30 Inducción estructural La forma
Ejercicio Usando la formulación del principio de inducción mostrada en la transparencia anterior, demuestre que: n 1esdivisiblepor3 n i=0 ( ) n i = n IIC153 Inducción 18 / 30 Inducción estructural La forma
Introducción a la Lógica y la Computación
 Clase del 9 de septiembre de 2014 Cuestión a resolver Todas las Álgebras de Boole vistas (aunque estén camufladas como D 6 o D 30 ) son en definitiva (vía isomorfismo) de la forma P(X). O sea, son álgebras
Clase del 9 de septiembre de 2014 Cuestión a resolver Todas las Álgebras de Boole vistas (aunque estén camufladas como D 6 o D 30 ) son en definitiva (vía isomorfismo) de la forma P(X). O sea, son álgebras
Construcción axiomática del conjunto de los números naturales a partir de una condición sobre su cardinalidad
 Recibido: 8 de febrero 2016 Aceptado: 27 de febrero 2016 Construcción axiomática del conjunto de los números naturales a partir de una condición sobre su cardinalidad Axiomatic construction of the set
Recibido: 8 de febrero 2016 Aceptado: 27 de febrero 2016 Construcción axiomática del conjunto de los números naturales a partir de una condición sobre su cardinalidad Axiomatic construction of the set
Espacios vectoriales
 Espacios vectoriales [Versión preliminar] Prof. Isabel Arratia Z. Algebra Lineal 1 En el estudio de las matrices y, en particular, de los sistemas de ecuaciones lineales realizamos sumas y multiplicación
Espacios vectoriales [Versión preliminar] Prof. Isabel Arratia Z. Algebra Lineal 1 En el estudio de las matrices y, en particular, de los sistemas de ecuaciones lineales realizamos sumas y multiplicación
Multiplicación de matrices simétricas
 Multiplicación de matrices simétricas La traspuesta de una matriz A n n es definida como una matriz A T n n tal que A T [i, j] =A[j, i] paracadai, j 2{1,...,n} Además, una matriz A es simétrica si A =
Multiplicación de matrices simétricas La traspuesta de una matriz A n n es definida como una matriz A T n n tal que A T [i, j] =A[j, i] paracadai, j 2{1,...,n} Además, una matriz A es simétrica si A =
Subespacios de espacios vectoriales
 Subespacios de espacios vectoriales Objetivos. Estudiar la definición, el criterio y algunos ejemplos de subespacios vectoriales. Muchos espacios vectoriales importantes (por ejemplo, espacio de soluciones
Subespacios de espacios vectoriales Objetivos. Estudiar la definición, el criterio y algunos ejemplos de subespacios vectoriales. Muchos espacios vectoriales importantes (por ejemplo, espacio de soluciones
Conjuntos. Relaciones. Aplicaciones
 Conjuntos. Relaciones. Aplicaciones Conjuntos 1. Considera el subconjunto A de números naturales formado por los múltiplos de 4 y el conjunto B N de los números que terminan en 4. Comprueba que A B y B
Conjuntos. Relaciones. Aplicaciones Conjuntos 1. Considera el subconjunto A de números naturales formado por los múltiplos de 4 y el conjunto B N de los números que terminan en 4. Comprueba que A B y B
Inducción Matemática Conjuntos Funciones. Matemática Discreta. Agustín G. Bonifacio UNSL. Repaso de Inducción, Conjuntos y Funciones
 UNSL Repaso de Inducción, y Inducción Matemática (Sección 1.7 del libro) Supongamos que queremos demostrar enunciados del siguiente tipo: P(n) : La suma de los primeros n números naturales es n(n+1)
UNSL Repaso de Inducción, y Inducción Matemática (Sección 1.7 del libro) Supongamos que queremos demostrar enunciados del siguiente tipo: P(n) : La suma de los primeros n números naturales es n(n+1)
Semana04[1/17] Funciones. 21 de marzo de Funciones
![Semana04[1/17] Funciones. 21 de marzo de Funciones Semana04[1/17] Funciones. 21 de marzo de Funciones](/thumbs/73/69418199.jpg) Semana04[1/17] 21 de marzo de 2007 Composición de funciones Semana04[2/17] Pensemos que tenemos tres conjuntos no vacíos A, B, C, y dos funciones, f : A B y g : B C, como en el siguiente diagrama: Figura:
Semana04[1/17] 21 de marzo de 2007 Composición de funciones Semana04[2/17] Pensemos que tenemos tres conjuntos no vacíos A, B, C, y dos funciones, f : A B y g : B C, como en el siguiente diagrama: Figura:
Introducción a la indecidibilidad
 Introducción a la indecidibilidad José M. empere Departamento de istemas Informáticos y Computación Universidad Politécnica de Valencia Lenguajes y problemas Un problema será considerado cualquier cuestión
Introducción a la indecidibilidad José M. empere Departamento de istemas Informáticos y Computación Universidad Politécnica de Valencia Lenguajes y problemas Un problema será considerado cualquier cuestión
Dualidad. 1. Dual de una transformación lineal
 CAPíTULO 8 Dualidad 1. Dual de una transformación lineal En este capítulo volveremos a considerar el tema de la dualidad de espacios vectoriales. Se recuerda que si V es un espacio vectorial, definimos
CAPíTULO 8 Dualidad 1. Dual de una transformación lineal En este capítulo volveremos a considerar el tema de la dualidad de espacios vectoriales. Se recuerda que si V es un espacio vectorial, definimos
Teoría de Modelos Finitos: Motivación
 Teoría de Modelos Finitos: Motivación IIC3260 IIC3260 Teoría de Modelos Finitos: Motivación 1 / 29 Poder expresivo de una lógica: Caso finito Desde ahora en adelante nos vamos a concentrar en las estructuras
Teoría de Modelos Finitos: Motivación IIC3260 IIC3260 Teoría de Modelos Finitos: Motivación 1 / 29 Poder expresivo de una lógica: Caso finito Desde ahora en adelante nos vamos a concentrar en las estructuras
Capítulo 2. Conjuntos Finitos Funciones
 Capítulo 2 Conjuntos Finitos 2.1. Funciones Definición 2.1. Considere dos conjuntos A y B y suponga que a cada elemento x A es asociado un elemento de B, denotado por f(x). En este caso decimos que f es
Capítulo 2 Conjuntos Finitos 2.1. Funciones Definición 2.1. Considere dos conjuntos A y B y suponga que a cada elemento x A es asociado un elemento de B, denotado por f(x). En este caso decimos que f es
Máquinas de Turing IIC3242. IIC3242 Máquinas de Turing 1 / 42
 Máquinas de Turing IIC3242 IIC3242 Máquinas de Turing 1 / 42 Complejidad Computacional Objetivo: Medir la complejidad computacional de un problema. Vale decir: Medir la cantidad de recursos computacionales
Máquinas de Turing IIC3242 IIC3242 Máquinas de Turing 1 / 42 Complejidad Computacional Objetivo: Medir la complejidad computacional de un problema. Vale decir: Medir la cantidad de recursos computacionales
Ejercicios Resueltos 1 / Algebra / 2008
 Ejercicios Resueltos 1 / Algebra / 008 Profesora: María Leonor Varas (Sección 4) Auxiliares: Sebastián Astroza & Diego Morán A continuación veremos un ejemplo de un tipo de problemas de inducción, los
Ejercicios Resueltos 1 / Algebra / 008 Profesora: María Leonor Varas (Sección 4) Auxiliares: Sebastián Astroza & Diego Morán A continuación veremos un ejemplo de un tipo de problemas de inducción, los
Cálculo Infinitesimal 1. Cuestiones de examen (2010/2011 a 2015/2016)
 Cálculo Infinitesimal 1. Cuestiones de examen (2010/2011 a 2015/2016) 1. Justifíquese la verdad o falsedad de la siguiente afirmación: La suma de dos números irracionales iguales es irracional (enero 2011).
Cálculo Infinitesimal 1. Cuestiones de examen (2010/2011 a 2015/2016) 1. Justifíquese la verdad o falsedad de la siguiente afirmación: La suma de dos números irracionales iguales es irracional (enero 2011).
Departamento de Matemáticas
 MA5 Clase : Series de números reales Definición de Serie Elaborado por los profesores Edgar Cabello y Marcos González Definicion Dada una sucesión de escalares (a n ), definimos su sucesión de sumas parciales
MA5 Clase : Series de números reales Definición de Serie Elaborado por los profesores Edgar Cabello y Marcos González Definicion Dada una sucesión de escalares (a n ), definimos su sucesión de sumas parciales
Guia - Cardinalidad Conjuntos Infinitos
 MA1101-1 Introducción al Álgebra Profesor: Leonardo Sánchez C. Auxiliar: Marcelo Navarro Resumen Guia - Cardinalidad Conjuntos Infinitos A = B si existe una función f : A B biyectiva. A B si existe una
MA1101-1 Introducción al Álgebra Profesor: Leonardo Sánchez C. Auxiliar: Marcelo Navarro Resumen Guia - Cardinalidad Conjuntos Infinitos A = B si existe una función f : A B biyectiva. A B si existe una
Una pregunta pendiente
 Una pregunta pendiente Cómo podemos construir un generador (casi) uniforme para una relación? Recuerde el problema KS definido en la sección anterior y la relación: R KS = {((~a, b), ~x) ~a 2 N n y ~x
Una pregunta pendiente Cómo podemos construir un generador (casi) uniforme para una relación? Recuerde el problema KS definido en la sección anterior y la relación: R KS = {((~a, b), ~x) ~a 2 N n y ~x
Semana 14 [1/19] Polinomios. 8 de junio de Polinomios
![Semana 14 [1/19] Polinomios. 8 de junio de Polinomios Semana 14 [1/19] Polinomios. 8 de junio de Polinomios](/thumbs/57/40923686.jpg) Semana 14 [1/19] 8 de junio de 2007 División Semana 14 [2/19] Teorema de la División Al ser (K[x], +, ) un anillo, ocurre un fenómeno similar al de : Las divisiones deben considerar un posible resto. Teorema
Semana 14 [1/19] 8 de junio de 2007 División Semana 14 [2/19] Teorema de la División Al ser (K[x], +, ) un anillo, ocurre un fenómeno similar al de : Las divisiones deben considerar un posible resto. Teorema
Espacios vectoriales con producto interno
 Espacios vectoriales con producto interno Mariano Suárez-Alvarez 24 de junio, 2011 1. Espacios con producto interno... 1 2. Normas y distancias... 3 3. Ortogonalidad... 5 4. Proyectores ortogonales...
Espacios vectoriales con producto interno Mariano Suárez-Alvarez 24 de junio, 2011 1. Espacios con producto interno... 1 2. Normas y distancias... 3 3. Ortogonalidad... 5 4. Proyectores ortogonales...
Operaciones extendidas de conjuntos
 234 A. GENERALIDADES DE TEORÍA DE CONJUNTOS Tema 3. Operaciones extendidas de conjuntos En este tema extenderemos las operaciones de conjuntos anteriormente definidas a familias arbitrarias de conjuntos.
234 A. GENERALIDADES DE TEORÍA DE CONJUNTOS Tema 3. Operaciones extendidas de conjuntos En este tema extenderemos las operaciones de conjuntos anteriormente definidas a familias arbitrarias de conjuntos.
NÚMEROS COMPLEJOS 1.1. INTRODUCCIÓN 1.2. OPERACIONES CON COMPLEJOS
 NÚMEROS COMPLEJOS 1.1. INTRODUCCIÓN La ecuación x + 1 0 no tiene solución en el cuerpo de los números reales R ya que no existe un número real x tal que x 1. Necesitamos un conjunto que contenga a R, que
NÚMEROS COMPLEJOS 1.1. INTRODUCCIÓN La ecuación x + 1 0 no tiene solución en el cuerpo de los números reales R ya que no existe un número real x tal que x 1. Necesitamos un conjunto que contenga a R, que
Práctica 2 - Hay diferentes infinitos?- A. Propiedades básicas de los Conjuntos
 Cálculo Avanzado Primer Cuatrimestre de 2011 Práctica 2 - Hay diferentes infinitos?- Llamaremos número cardinal de M al concepto general que, por medio de nuestra activa capacidad de pensar, surge del
Cálculo Avanzado Primer Cuatrimestre de 2011 Práctica 2 - Hay diferentes infinitos?- Llamaremos número cardinal de M al concepto general que, por medio de nuestra activa capacidad de pensar, surge del
Conjuntos Infinitos. Ramón Espinoza Armenta AVC APOYO VIRTUAL PARA EL CONOCIMIENTO
 Ramón Espinoza Armenta AVC APOYO VIRTUAL PARA EL CONOCIMIENTO El estudio de los conjuntos infinitos se inicia con Las Paradojas del Infinito, la última obra del matemático checo Bernard Bolzano, publicada
Ramón Espinoza Armenta AVC APOYO VIRTUAL PARA EL CONOCIMIENTO El estudio de los conjuntos infinitos se inicia con Las Paradojas del Infinito, la última obra del matemático checo Bernard Bolzano, publicada
Los Números Reales. Capítulo Introducción.
 Capítulo 1 Los Números Reales 11 Introducción En este primer capítulo del libro introducimos el sistema de los Números Reales, que es la base sobre la cual se desarrolla el Análisis Matemático Los matemáticos
Capítulo 1 Los Números Reales 11 Introducción En este primer capítulo del libro introducimos el sistema de los Números Reales, que es la base sobre la cual se desarrolla el Análisis Matemático Los matemáticos
x (0) si f (x) = 2s 1, s > 1 d) f 3. Analizar la existencia de derivadas laterales y de derivada en a = 0, para las siguientes funciones:
 FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
Relaciones IIC1253. IIC1253 Relaciones 1 / 32
 Relaciones IIC1253 IIC1253 Relaciones 1 / 32 Relaciones binarias Dado: conjunto A R es una relación binaria sobre A si R A A. Para indicar que a,b A están relacionados a través de R usamos las notaciones:
Relaciones IIC1253 IIC1253 Relaciones 1 / 32 Relaciones binarias Dado: conjunto A R es una relación binaria sobre A si R A A. Para indicar que a,b A están relacionados a través de R usamos las notaciones:
Relaciones, Funciones y Enumerabilidad
 Relaciones, Funciones y Enumerabilidad Rafael F. Isaacs G. * Fecha: 10 de diciembre de 2004 El lector debe tener familiaridad tanto con las relaciones como con las funciones. Estos conceptos son básicos
Relaciones, Funciones y Enumerabilidad Rafael F. Isaacs G. * Fecha: 10 de diciembre de 2004 El lector debe tener familiaridad tanto con las relaciones como con las funciones. Estos conceptos son básicos
FUNCIONES MEROMORFAS. EL TEOREMA DE LOS RESIDUOS Y ALGUNAS DE SUS CONSECUENCIAS
 FUNCIONES MEROMORFAS. EL TEOREMA DE LOS RESIDUOS Y ALGUNAS DE SUS CONSECUENCIAS. FUNCIONES MEROMORFAS Definición.. Se dice que una función es meromorfa en un abierto Ω de C si f es holomorfa en Ω excepto
FUNCIONES MEROMORFAS. EL TEOREMA DE LOS RESIDUOS Y ALGUNAS DE SUS CONSECUENCIAS. FUNCIONES MEROMORFAS Definición.. Se dice que una función es meromorfa en un abierto Ω de C si f es holomorfa en Ω excepto
11.SISTEMAS DE ECUACIONES LINEALES DEFINICIÓN DE ECUACIÓN LINEAL DEFINICIÓN DE SISTEMA LINEAL Y CONJUNTO SOLUCIÓN
 ÍNDICE 11SISTEMAS DE ECUACIONES LINEALES 219 111 DEFINICIÓN DE ECUACIÓN LINEAL 219 112 DEFINICIÓN DE SISTEMA LINEAL Y CONJUNTO SOLUCIÓN 220 113 EQUIVALENCIA Y COMPATIBILIDAD 220 11 REPRESENTACIÓN MATRICIAL
ÍNDICE 11SISTEMAS DE ECUACIONES LINEALES 219 111 DEFINICIÓN DE ECUACIÓN LINEAL 219 112 DEFINICIÓN DE SISTEMA LINEAL Y CONJUNTO SOLUCIÓN 220 113 EQUIVALENCIA Y COMPATIBILIDAD 220 11 REPRESENTACIÓN MATRICIAL
Combinatoria Básica: Conteo
 Capítulo III Combinatoria Básica: Conteo En este capítulo continuamos determinando la cardinalidad de varios conjuntos interesantes, en particular, permutaciones y combinaciones. Como parte de esto encontramos
Capítulo III Combinatoria Básica: Conteo En este capítulo continuamos determinando la cardinalidad de varios conjuntos interesantes, en particular, permutaciones y combinaciones. Como parte de esto encontramos
CAPÍTULO 2 NOCIONES BÁSICAS DE TEORÍA DE CONJUNTOS
 CAPÍTULO 2 NOCIONES BÁSICAS DE TEORÍA DE CONJUNTOS 2.1. NOCIONES PRIMITIVAS Consideraremos tres nociones primitivas: Conjunto, Elemento y Pertenencia. Conjunto Podemos entender al conjunto como, colección,
CAPÍTULO 2 NOCIONES BÁSICAS DE TEORÍA DE CONJUNTOS 2.1. NOCIONES PRIMITIVAS Consideraremos tres nociones primitivas: Conjunto, Elemento y Pertenencia. Conjunto Podemos entender al conjunto como, colección,
Números complejos y Polinomios
 Semana 13 [1/14] 23 de mayo de 2007 Forma polar de los complejos Semana 13 [2/14] Raíces de la unidad Raíz n-ésima de la unidad Sean z C y n 2. Diremos que z es una raíz n-ésima de la unidad si z n = 1
Semana 13 [1/14] 23 de mayo de 2007 Forma polar de los complejos Semana 13 [2/14] Raíces de la unidad Raíz n-ésima de la unidad Sean z C y n 2. Diremos que z es una raíz n-ésima de la unidad si z n = 1
Departamento de Ingeniería Matemática - Universidad de Chile
 Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 08-2 SEMANA 7: ESPACIOS VECTORIALES 3.5. Generadores de un espacio vectorial Sea V un espacio vectorial
Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 08-2 SEMANA 7: ESPACIOS VECTORIALES 3.5. Generadores de un espacio vectorial Sea V un espacio vectorial
Geometría afín y proyectiva, 2016 SEMANA 4
 Geometría afín y proyectiva, 2016 SEMANA 4 Sonia L. Rueda ETS Arquitectura. UPM September 30, 2016 Geometría afín y proyectiva 1. Álgebra Lineal 2. Geometría afín y eucĺıdea 3. Cónicas y cuádricas Álgebra
Geometría afín y proyectiva, 2016 SEMANA 4 Sonia L. Rueda ETS Arquitectura. UPM September 30, 2016 Geometría afín y proyectiva 1. Álgebra Lineal 2. Geometría afín y eucĺıdea 3. Cónicas y cuádricas Álgebra
TEMA 6: DIVISIÓN DE POLINOMIOS RAÍCES MATEMÁTICAS 3º ESO
 TEMA 6: DIVISIÓN DE POLINOMIOS RAÍCES MATEMÁTICAS 3º ESO 1. División de polinomios Dados dos polinomios P (el dividendo) y D (el divisor), dividir P entre D es encontrar dos polinomios Q (el cociente)
TEMA 6: DIVISIÓN DE POLINOMIOS RAÍCES MATEMÁTICAS 3º ESO 1. División de polinomios Dados dos polinomios P (el dividendo) y D (el divisor), dividir P entre D es encontrar dos polinomios Q (el cociente)
TEMA 7. DIAGONALIZACION Y Y FORMAS CANONICAS 1. ENDOMORFISMOS NILPOTENTES
 TEMA 7. DIAGONALIZACION Y Y FORMAS CANONICAS 1. ENDOMORFISMOS NILPOTENTES Definición 1.1. Endomorfismo Nilpotente. Un endomorfismo T End(V ) es nilpotente si existe n N tal que f n 0. Definición 1.. Matriz
TEMA 7. DIAGONALIZACION Y Y FORMAS CANONICAS 1. ENDOMORFISMOS NILPOTENTES Definición 1.1. Endomorfismo Nilpotente. Un endomorfismo T End(V ) es nilpotente si existe n N tal que f n 0. Definición 1.. Matriz
Estructuras Discretas. Conjuntos. Conjuntos & Funciones. Especificación de Conjuntos.
 Estructuras Discretas Conjuntos Conjuntos & Funciones Claudio Lobos clobos@inf.utfsm.cl niversidad Técnica Federico Santa María Estructuras Discretas INF 152 Definición: conjunto n conjunto es una colección
Estructuras Discretas Conjuntos Conjuntos & Funciones Claudio Lobos clobos@inf.utfsm.cl niversidad Técnica Federico Santa María Estructuras Discretas INF 152 Definición: conjunto n conjunto es una colección
Definición 1. Dado un conjunto C una aplicación definida por : C C C
 ESTRUCTURAS ALGEBRAICAS. En matemáticas aparecen distintos conjuntos cuyos elementos podemos operar de alguna manera. Los conjuntos de números usuales: N, Z, Q, y R son unos ejemplos claros. Otros ejemplos
ESTRUCTURAS ALGEBRAICAS. En matemáticas aparecen distintos conjuntos cuyos elementos podemos operar de alguna manera. Los conjuntos de números usuales: N, Z, Q, y R son unos ejemplos claros. Otros ejemplos
Máquinas de Turing IIC3242. IIC3242 Máquinas de Turing 1 / 45
 Máquinas de Turing IIC3242 IIC3242 Máquinas de Turing 1 / 45 Complejidad Computacional Objetivo: Medir la complejidad computacional de un problema. Vale decir: Medir la cantidad de recursos computacionales
Máquinas de Turing IIC3242 IIC3242 Máquinas de Turing 1 / 45 Complejidad Computacional Objetivo: Medir la complejidad computacional de un problema. Vale decir: Medir la cantidad de recursos computacionales
Conjuntos. 17 {perro, gato, 17, x 2 }
 Conjuntos Qué es un conjunto? Informalmente, es una agrupación de cosas, o una descripción que dice qué elementos están y qué elementos no están. Para describir un conjunto usamos llavecitas y enumeramos
Conjuntos Qué es un conjunto? Informalmente, es una agrupación de cosas, o una descripción que dice qué elementos están y qué elementos no están. Para describir un conjunto usamos llavecitas y enumeramos
Formulaciones equivalentes del Axioma de Elección
 Formulaciones equivalentes del Axioma de Elección MARU SARAZOLA Resumen En este documento presentamos algunas formulaciones equivalentes del axioma de elección. En la primera sección, se presenta el enunciado
Formulaciones equivalentes del Axioma de Elección MARU SARAZOLA Resumen En este documento presentamos algunas formulaciones equivalentes del axioma de elección. En la primera sección, se presenta el enunciado
Uno de los más importantes conceptos en Matemática se refiere a un tipo particular de relación entre elementos de dos conjuntos; las funciones.
 MATEMÁTICA GENERAL 005, HERALDO GONZALEZ S 37 FUNCIONES Uno de los más importantes conceptos en Matemática se reiere a un tipo particular de relación entre elementos de dos conjuntos; las unciones Una
MATEMÁTICA GENERAL 005, HERALDO GONZALEZ S 37 FUNCIONES Uno de los más importantes conceptos en Matemática se reiere a un tipo particular de relación entre elementos de dos conjuntos; las unciones Una
Definición 1.2. Sea (K, +, ) un dominio de integridad. Un polinomio de grado n sobre K es una expresión de la forma
 Polinomios Definición 1.1. Un conjunto K junto con dos operaciones definidas en él que denotaremos por + : K K K : K K K para las cuales se cumplen las siguientes propiedades: Asociatividad Conmutatividad
Polinomios Definición 1.1. Un conjunto K junto con dos operaciones definidas en él que denotaremos por + : K K K : K K K para las cuales se cumplen las siguientes propiedades: Asociatividad Conmutatividad
2. Los números naturales, enteros y racionales 1
 - Fernando Sánchez - - Cálculo I 2Los números naturales, enteros y racionales Números naturales 24 09 2015 Se llaman números naturales a los elementos del conjunto N = {1, 2, 3,...}. En este conjunto hay
- Fernando Sánchez - - Cálculo I 2Los números naturales, enteros y racionales Números naturales 24 09 2015 Se llaman números naturales a los elementos del conjunto N = {1, 2, 3,...}. En este conjunto hay
Álgebra y Trigonometría
 Álgebra y Trigonometría Conceptos fundamentales del Álgebra Universidad de Antioquia Departamento de Matemáticas 1. Números Reales El conjunto de los números reales está constituido por diferentes clases
Álgebra y Trigonometría Conceptos fundamentales del Álgebra Universidad de Antioquia Departamento de Matemáticas 1. Números Reales El conjunto de los números reales está constituido por diferentes clases
Teorema de incompletitud de Gödel
 Teorema de incompletitud de Gödel Theorem (Gödel) Th(N) es una teoría indecidible. IIC2213 Teorías 79 / 109 Teorema de incompletitud de Gödel Theorem (Gödel) Th(N) es una teoría indecidible. Corolario
Teorema de incompletitud de Gödel Theorem (Gödel) Th(N) es una teoría indecidible. IIC2213 Teorías 79 / 109 Teorema de incompletitud de Gödel Theorem (Gödel) Th(N) es una teoría indecidible. Corolario
Cuadrados mágicos y matrices de permutación
 Cuadrados mágicos y matrices de permutación Alexey Beshenov (cadadr@gmail.com) 13 de agosto de 016 Estos son mis apuntes para una pequeña presentación para los alumnos del Programa Jóvenes Talento de la
Cuadrados mágicos y matrices de permutación Alexey Beshenov (cadadr@gmail.com) 13 de agosto de 016 Estos son mis apuntes para una pequeña presentación para los alumnos del Programa Jóvenes Talento de la
AMPLIACIÓN DE MATEMÁTICAS
 AMPLIACIÓN DE MATEMÁTICAS EJEMPLOS DE EXTENSIONES DE CUERPOS. Comenzamos con el primer ejemplo. Aquí ya vamos a ver las ideas que después desarrollaremos. Ejemplo 1. Consideramos el polinomio x 2 2 Q[x]
AMPLIACIÓN DE MATEMÁTICAS EJEMPLOS DE EXTENSIONES DE CUERPOS. Comenzamos con el primer ejemplo. Aquí ya vamos a ver las ideas que después desarrollaremos. Ejemplo 1. Consideramos el polinomio x 2 2 Q[x]
1. Sucesiones. Sucesiones. Compacidad. {( 1) n, n N} = { 1, 1, 1, 1, 1, 1,... } es una sucesión de elementos del conjunto { 1, 1}, y la familia
 1.. De una manera informal, una sucesión es una familia de elementos de un conjunto, ordenada según el índice de los números naturales. Los elementos pueden estar repetidos o no. Por ejemplo la familia
1.. De una manera informal, una sucesión es una familia de elementos de un conjunto, ordenada según el índice de los números naturales. Los elementos pueden estar repetidos o no. Por ejemplo la familia
Resolución Proposicional
 Resolución Proposicional IIC2213 IIC2213 Resolución Proposicional 1 / 19 Resolución proposicional Sabemos que Σ = ϕ si y sólo si Σ { ϕ} es inconsistente. Cómo verificamos si Σ { ϕ} es inconsistente? El
Resolución Proposicional IIC2213 IIC2213 Resolución Proposicional 1 / 19 Resolución proposicional Sabemos que Σ = ϕ si y sólo si Σ { ϕ} es inconsistente. Cómo verificamos si Σ { ϕ} es inconsistente? El
Problemas de VC para EDVC elaborados por C. Mora, Tema 4
 Problemas de VC para EDVC elaborados por C. Mora, Tema 4 Ejercicio Determinar las funciones enteras f para las que Solución f( + w) = f()f(w), w C. En primer lugar, f(0) = f(0 + 0) = f(0)f(0) = f(0) 2,
Problemas de VC para EDVC elaborados por C. Mora, Tema 4 Ejercicio Determinar las funciones enteras f para las que Solución f( + w) = f()f(w), w C. En primer lugar, f(0) = f(0 + 0) = f(0)f(0) = f(0) 2,
Espacios vectoriales con producto interno
 Espacios vectoriales con producto interno Problemas teóricos En todos los problemas relacionados con el caso complejo se supone que el producto interno es lineal con respecto al segundo argumento. Definición
Espacios vectoriales con producto interno Problemas teóricos En todos los problemas relacionados con el caso complejo se supone que el producto interno es lineal con respecto al segundo argumento. Definición
Extensiones finitas.
 2. EXTENSIONES ALGEBRAICAS. Hemos dividido este tema en dos secciones: Extensiones finitas, y Clausura algebraica. En la primera relacionamos extensión finita y extensión algebraica: probamos que toda
2. EXTENSIONES ALGEBRAICAS. Hemos dividido este tema en dos secciones: Extensiones finitas, y Clausura algebraica. En la primera relacionamos extensión finita y extensión algebraica: probamos que toda
Semana03[1/17] Funciones. 16 de marzo de Funciones
![Semana03[1/17] Funciones. 16 de marzo de Funciones Semana03[1/17] Funciones. 16 de marzo de Funciones](/thumbs/48/24900626.jpg) Semana03[1/17] 16 de marzo de 2007 Introducción Semana03[2/17] Ya que conocemos el producto cartesiano A B entre dos conjuntos A y B, podemos definir entre ellos algún tipo de correspondencia. Es decir,
Semana03[1/17] 16 de marzo de 2007 Introducción Semana03[2/17] Ya que conocemos el producto cartesiano A B entre dos conjuntos A y B, podemos definir entre ellos algún tipo de correspondencia. Es decir,
Ceros en extensiones.
 1. EXTENSIONES DE CUERPOS. Varios son los objetivos de este tema. El primero de ellos, resultado debido a Kronecker, es probar que todo polinomio con coeficientes en un cuerpo tiene una raíz en un cuerpo
1. EXTENSIONES DE CUERPOS. Varios son los objetivos de este tema. El primero de ellos, resultado debido a Kronecker, es probar que todo polinomio con coeficientes en un cuerpo tiene una raíz en un cuerpo
Reconocer y utilizar las propiedades sencillas de la topología métrica.
 3 Funciones continuas De entre todas las aplicaciones que pueden definirse entre dos espacios métrico, las aplicaciones continuas ocupan un papel preponderante. Su estudio es fundamental no sólo en topología,
3 Funciones continuas De entre todas las aplicaciones que pueden definirse entre dos espacios métrico, las aplicaciones continuas ocupan un papel preponderante. Su estudio es fundamental no sólo en topología,
Estructuras Algebraicas
 Tema 1 Estructuras Algebraicas Definición 1 Sea A un conjunto no vacío Una operación binaria (u operación interna) en A es una aplicación : A A A Es decir, tenemos una regla que a cada par de elementos
Tema 1 Estructuras Algebraicas Definición 1 Sea A un conjunto no vacío Una operación binaria (u operación interna) en A es una aplicación : A A A Es decir, tenemos una regla que a cada par de elementos
Curso Propedéutico de Cálculo Sesión 1: Funciones
 Curso Propedéutico de Cálculo Sesión 1: Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico Esquema 1 2 Esquema 1 2 El cálculo se basa en las propiedades de los
Curso Propedéutico de Cálculo Sesión 1: Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico Esquema 1 2 Esquema 1 2 El cálculo se basa en las propiedades de los
Entscheidungsproblem I TEORÍA DE LA COMPUTACIÓN MÁQUINAS DE TURING Y DECIDIBILIDAD. Máquinas de Turing (TM) Procedimiento efectivo
 Entscheidungsproblem I TEORÍA DE LA COMPUTACIÓN MÁQUINAS DE TURING Y DECIDIBILIDAD Francisco Hernández Quiroz Departamento de Matemáticas Facultad de Ciencias, UNAM E-mail: fhq@ciencias.unam.mx Página
Entscheidungsproblem I TEORÍA DE LA COMPUTACIÓN MÁQUINAS DE TURING Y DECIDIBILIDAD Francisco Hernández Quiroz Departamento de Matemáticas Facultad de Ciencias, UNAM E-mail: fhq@ciencias.unam.mx Página
Demostración Contraejemplo. Métodos Indirectos
 DEMOSTRACION Una demostración de un teorema es una verificación escrita que muestra que el teorema es verdadero. Informalmente, desde el punto de vista de la lógica, una demostración de un teorema es un
DEMOSTRACION Una demostración de un teorema es una verificación escrita que muestra que el teorema es verdadero. Informalmente, desde el punto de vista de la lógica, una demostración de un teorema es un
EL CUERPO ORDENADO REALES
 CAPÍTULO I. EL CUERPO ORDENADO DE LOS NÚMEROS REALES SECCIONES A. Elementos notables en R. B. Congruencias. Conjuntos numerables. C. Método de inducción completa. D. Desigualdades y valor absoluto. E.
CAPÍTULO I. EL CUERPO ORDENADO DE LOS NÚMEROS REALES SECCIONES A. Elementos notables en R. B. Congruencias. Conjuntos numerables. C. Método de inducción completa. D. Desigualdades y valor absoluto. E.
1. Problemas de inducción.
 Proyecto I: Más sobre números reales Objetivos: Profundizar el estudio de los números reales. 1. Problemas de inducción. Ejercicio 1.1 Sea n. Definiremos los coeficientes binomiales ( n ) mediante la expresión
Proyecto I: Más sobre números reales Objetivos: Profundizar el estudio de los números reales. 1. Problemas de inducción. Ejercicio 1.1 Sea n. Definiremos los coeficientes binomiales ( n ) mediante la expresión
1.3. El teorema de los valores intermedios
 Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 07-2 Importante: Visita regularmente http://www.dim.uchile.cl/calculo. Ahí encontrarás
Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 07-2 Importante: Visita regularmente http://www.dim.uchile.cl/calculo. Ahí encontrarás
Algoritmos aleatorizados
 Algoritmos aleatorizados IIC2283 IIC2283 Algoritmos aleatorizados 1/109 Algoritmos aleatorizados Vamos a permitir a los algoritmos tener una componente aleatoria I En general esto significa que un algoritmo
Algoritmos aleatorizados IIC2283 IIC2283 Algoritmos aleatorizados 1/109 Algoritmos aleatorizados Vamos a permitir a los algoritmos tener una componente aleatoria I En general esto significa que un algoritmo
Estructuras algebraicas
 Semana 10[1/14] 26 de abril de 2007 Semana 10[2/14] Grupos Un grupo es un caso particular de una estructura algebraica. Veremos que esta noción rescata ampliamente las propiedades de estructuras tales
Semana 10[1/14] 26 de abril de 2007 Semana 10[2/14] Grupos Un grupo es un caso particular de una estructura algebraica. Veremos que esta noción rescata ampliamente las propiedades de estructuras tales
La trascendencia de e y π
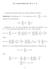 La trascendencia de e y π Comenzamos introduciendo unos convenios útiles de notación: Definición 1 Escribiremos h r = r!, de modo que si fz) = m c r z r C[z], entonces fh) representará fh) = m c r h r
La trascendencia de e y π Comenzamos introduciendo unos convenios útiles de notación: Definición 1 Escribiremos h r = r!, de modo que si fz) = m c r z r C[z], entonces fh) representará fh) = m c r h r
Topología y Transitividad del Shift Unilateral.
 Topología y Transitividad del Shift Unilateral. Eleonora Catsigeras Asesoramiento a Odalis Sofía Ortega 2. Directora de Posgrado: Cristina Lizana 3 3 de Agosto de 205 Consideremos el conjunto {0,, al que
Topología y Transitividad del Shift Unilateral. Eleonora Catsigeras Asesoramiento a Odalis Sofía Ortega 2. Directora de Posgrado: Cristina Lizana 3 3 de Agosto de 205 Consideremos el conjunto {0,, al que
Matemática Discreta TEORÍA DE CONJUNTOS
 Matemática Discreta Instructor: Marcos Villagra Clase # Escriba: Arturo Ramón González Osorio 30/10/17 TEORÍA DE CONJUNTOS Definición 1 Conjuntos: Es una colección de elementos que pueden ser finitos o
Matemática Discreta Instructor: Marcos Villagra Clase # Escriba: Arturo Ramón González Osorio 30/10/17 TEORÍA DE CONJUNTOS Definición 1 Conjuntos: Es una colección de elementos que pueden ser finitos o
TEORÍA DE NÚMEROS Curso 2004/2005 Lista 1
 TEORÍA DE NÚMEROS Curso 2004/2005 Lista 1 Repaso de congruencias y divisibilidad 1. Sea H = {5, 9, 13, 17, 21,... }. Decimos que n H es H-primo si no tiene divisores propios en H. Demostrar que la factorización
TEORÍA DE NÚMEROS Curso 2004/2005 Lista 1 Repaso de congruencias y divisibilidad 1. Sea H = {5, 9, 13, 17, 21,... }. Decimos que n H es H-primo si no tiene divisores propios en H. Demostrar que la factorización
Algoritmos aleatorizados
 Algoritmos aleatorizados IIC2283 IIC2283 Algoritmos aleatorizados 1/109 Algoritmos aleatorizados Vamos a permitir a los algoritmos tener una componente aleatoria I En general esto significa que un algoritmo
Algoritmos aleatorizados IIC2283 IIC2283 Algoritmos aleatorizados 1/109 Algoritmos aleatorizados Vamos a permitir a los algoritmos tener una componente aleatoria I En general esto significa que un algoritmo
AMPLIACIÓN DE MATEMÁTICAS
 AMPLIACIÓN DE MATEMÁTICAS GRUPOS PRODUCTO Y COCIENTE. El producto cartesiano de dos grupos y el conjunto cociente de un grupo respecto de ciertas relaciones, son dos formas de construir nuevos grupos.
AMPLIACIÓN DE MATEMÁTICAS GRUPOS PRODUCTO Y COCIENTE. El producto cartesiano de dos grupos y el conjunto cociente de un grupo respecto de ciertas relaciones, son dos formas de construir nuevos grupos.
CLAVE DE EXAMEN Matemática para computación 1 código de curso: 960
 universidad de san carlos Facultad de Ingeniería Escuela de Ciencias Departamento de Matemática clave-960-1-m-2-00-2012 CLAVE DE EXAMEN Matemática para computación 1 código de curso: 960 Datos de la clave
universidad de san carlos Facultad de Ingeniería Escuela de Ciencias Departamento de Matemática clave-960-1-m-2-00-2012 CLAVE DE EXAMEN Matemática para computación 1 código de curso: 960 Datos de la clave
Eliminación de cuantificadores
 Eliminación de cuantificadores Teorema Si una teoría admite eliminación de cuantificadores, y existe un algoritmo que construye ϕ sc a partir de ϕ, entonces es decidible. Cómo se demuestra este teorema?
Eliminación de cuantificadores Teorema Si una teoría admite eliminación de cuantificadores, y existe un algoritmo que construye ϕ sc a partir de ϕ, entonces es decidible. Cómo se demuestra este teorema?
4.2. Funciones inyectivas, sobreyectivas y biyectivas
 4.. Funciones inyectivas, sobreyectivas y biyectivas En esta sección estudiaremos tres conceptos básicos sobre funciones. 4... Funciones inyectivas Definición 4.. Sea f una función de en. Diremos que f
4.. Funciones inyectivas, sobreyectivas y biyectivas En esta sección estudiaremos tres conceptos básicos sobre funciones. 4... Funciones inyectivas Definición 4.. Sea f una función de en. Diremos que f
Tema 1: Fundamentos.
 Tema 1: Fundamentos. 1. Nociones básicas de la Teoría de Conjuntos. Definición. Un conjunto es una colección de objetos. A los objetos de un conjunto se les llama elementos del conjunto. Se denominará
Tema 1: Fundamentos. 1. Nociones básicas de la Teoría de Conjuntos. Definición. Un conjunto es una colección de objetos. A los objetos de un conjunto se les llama elementos del conjunto. Se denominará
Valores y Vectores Propios
 Valores y Vectores Propios Iván Huerta Facultad de Matemáticas Pontificia Universidad Católica de Chile ihuerta@mat.puc.cl Segundo Semestre, 1999 Definición Valores y Vectores Propios Valores y Vectores
Valores y Vectores Propios Iván Huerta Facultad de Matemáticas Pontificia Universidad Católica de Chile ihuerta@mat.puc.cl Segundo Semestre, 1999 Definición Valores y Vectores Propios Valores y Vectores
Conjuntos. Un conjunto es una colección de objetos. Si a es un objeto y R es un conjunto entonces por. a R. se entiende que a pertenece a R.
 Conjuntos Un conjunto es una colección de objetos. Si a es un objeto y R es un conjunto entonces por se entiende que a pertenece a R. a R Normalmente, podremos definir a un conjunto de dos maneras: Por
Conjuntos Un conjunto es una colección de objetos. Si a es un objeto y R es un conjunto entonces por se entiende que a pertenece a R. a R Normalmente, podremos definir a un conjunto de dos maneras: Por
José Humberto Serrano Devia Página 1
 Similitudes entre el espacio y las series de Fourier Funciones Ortogonales En esta sección se muestra la forma en que los conceptos vectoriales de producto interno, o producto escalar, y el de ortogonalidad
Similitudes entre el espacio y las series de Fourier Funciones Ortogonales En esta sección se muestra la forma en que los conceptos vectoriales de producto interno, o producto escalar, y el de ortogonalidad
Demostrando cotas inferiores: Arboles de decisión
 Demostrando cotas inferiores: Arboles de decisión De la misma forma que la técnica basada en la mejor estrategia del adversario, vamos a utilizar los árboles de decisión para establecer una cota inferior
Demostrando cotas inferiores: Arboles de decisión De la misma forma que la técnica basada en la mejor estrategia del adversario, vamos a utilizar los árboles de decisión para establecer una cota inferior
2 Ecuaciones Algebraicas y Trascendentes
 2 Ecuaciones Algebraicas y Trascendentes 2.1 Introducción Las sucesiones asintóticas son una herramienta usada en el análisis de las soluciones de problemas que surgen en la Teoría de Perturbaciones. En
2 Ecuaciones Algebraicas y Trascendentes 2.1 Introducción Las sucesiones asintóticas son una herramienta usada en el análisis de las soluciones de problemas que surgen en la Teoría de Perturbaciones. En
MÉTODOS DE DEMOSTRACIÓN
 2016-1 1 Presentación 2 Métodos de Demostración Sobre métodos de demostración algunas preguntas de interés 1 Qué es una demostración? Sobre métodos de demostración algunas preguntas de interés 1 Qué es
2016-1 1 Presentación 2 Métodos de Demostración Sobre métodos de demostración algunas preguntas de interés 1 Qué es una demostración? Sobre métodos de demostración algunas preguntas de interés 1 Qué es
Tema 2: Diagonalización
 TEORÍA DE ÁLGEBRA II: Tema 2. DIPLOMATURA DE ESTADÍSTICA 1 Tema 2: Diagonalización 1 Introducción Sea f : R n R n lineal. Dada una base B de R n podemos asociar a f la matriz A 1 = [f, B] M n. Si C es
TEORÍA DE ÁLGEBRA II: Tema 2. DIPLOMATURA DE ESTADÍSTICA 1 Tema 2: Diagonalización 1 Introducción Sea f : R n R n lineal. Dada una base B de R n podemos asociar a f la matriz A 1 = [f, B] M n. Si C es
Álgebra. Curso de junio de Grupo B
 Álgebra. Curso 2008-2009 9 de junio de 2009. Grupo B Primera parte Ejercicio. 1. Sea D un dominio noetheriano que no es un cuerpo. Demuestra que son equivalentes: (a) D es un dominio de Dedekind. (b) Todo
Álgebra. Curso 2008-2009 9 de junio de 2009. Grupo B Primera parte Ejercicio. 1. Sea D un dominio noetheriano que no es un cuerpo. Demuestra que son equivalentes: (a) D es un dominio de Dedekind. (b) Todo
Formas canónicas de Jordan
 Capítulo 6 Formas canónicas de Jordan 61 Subespacios propios generalizados Introducción En el capítulo anterior se han estudiado los endomorfismos diagonalizables y se han dado condiciones necesarias y
Capítulo 6 Formas canónicas de Jordan 61 Subespacios propios generalizados Introducción En el capítulo anterior se han estudiado los endomorfismos diagonalizables y se han dado condiciones necesarias y
