SISTEMAS CRISTALINOS NOCIONES PRELIMINARES
|
|
|
- María del Carmen Soto Martínez
- hace 7 años
- Vistas:
Transcripción
1 SISTEMAS CRISTALINOS NOCIONES PRELIMINARES Los Sistemas Cristalinos y sus Clases. Ya sabemos que la materia cristalina viene caracterizada por un determinado tipo de red cristalina la cual en último, término se define por las características de su malla, es decir, del paralelepípedo elemental en cuyos vértices estén situados los nudos de la red más próximos (véase la fig. 1). Fig. 1.- Conjunto reticular, con partículas periódicamente ordenadas en las tres direcciones del espacio OX, OY, OZ Es el caso, que pueden existir siete tipos de redes cristalinas distintas, definidas por su malla que caracterizan a su vez a otros tantos sistemas; cristalinos. Cada tipo de red tiene sus características simétricas propias que aparecen reflejadas de alguna manera en la simetría propia, de los cristales correspondientes al sistema. La observación de los cristales dio a conocer muy pronto que muchos de ellos tienen los mismos elementos de simetría, aunque velados con formas geométricas muy distintas. No fue difícil clasificarlos en grupos, procurando incluir en cada uno aquellas formas que tuvieran sus ejes y planos de simetría en igual número y de la misma naturaleza. Así, por ejemplo, si examinamos el cubo veremos que tiene tres ejes cuaternarios, cuatro ternarios y seis binarios; además de tres planos principales y seis secundarios. Los mismos elementos simétricos tiene él rombododecaedro, el triaquisoctaedro, el octaedro regular, etc. El tetraedro, por ejemplo, tiene tres ejes binarios, cuatro ternarios seis planos de simetría; aunque no tiene exactamente el mismo número de elementos de simetría que el cubo, con todo tiene determinados elementos que les son comunes, como son, por ejemplo, los cuatro ejes ternarios.
2 Esto da pie a que los cristales que tienen los mismos elementos comunes de simetría se puedan agrupar en clases, y a que las clases que tengan ciertos elementos de simetría comunes se agrupen en sistemas. Así, por ejemplo, el cubo, el octaedro, el rombododecaedro, etc.., se agrupan en la clase holoédrica del sistema regular; el tetraedro corresponde a la clase tetraédrica del mismo sistema regular, etc. Y todas estas clases que tienen los mismos elementos de simetría. comunes (los cuatro ejes ternarios) se agrupan formando el sistema regular. SISTEMAS CRISTALINOS SON, POR TANTO, EL CONJUNTO DE: FORMAS QUE POSEEN DETERMINADO NÚMERO DE ELEMENTOS DE SIMETRÍA. COMUNES Y DE LA MISMA NATURALEZA. CLASES DE SIMETRÍA SON EL CONJUNTO DE FORMAS QUE POSEEN LA TOTALIDAD DE LOS ELEMENTOS DE SIMETRÍA COMUNES. Atendiendo a los elementos de simetría sólo puede haber 32 tipos o clases de cristales diferentes; y en efecto, no.solo no se han encontrado más, sino que para alguna de estas 32 clases no se han encontrado todavía representantes. Cristales Holoédricos y Meroédricos: Hemiedria y Tetartoedría. Cristales Holoédricos u Holoedros son aquellos que, no han sufrido ninguna modificación en sus elementos geométricos, o lo han sufrido en todos. Los derivados de estos que solo han sufrido modificaciones en parte de sus elementos se llaman meroedros Ejemplo de los primeros, le tenemos en el cubo y en el octaedro (que resulta de la truncados de todos los vértices del cubo); entre los segundos podemos contar el tetraedro, que se origina por la truncados de la mitad de los vértices del cubo. a) Si la modificación sólo afecta a la mitad de sus elementos, se llama HEMIEDRÍA. (Ejemplo, el tetraedro, que puede considerarse como procedente del cubo, por truncamiento de sus vértices alternos.) b) Si la modificación afecta a la cuarta parte de sus elementos, se llama TETARTOEDRÍA. (Ejemplo, el dodecaedro pentagonal plagiédrico.) c) Y si afecta a la octava parte, se denomina OGDOEDRÍA. Las formas meroédricas son una aparente excepción de la ley de simetría, puesto que sólo modifican parte de sus elementos y no todos como exige esta ley. Pero en los casos de meroedría, un examen más detenido nos hace ver que si la modificación afecta solamente a un cierto orden en relación con la simetría primitiva, ésta queda así restringida, pero no derogada.
3 Por ejemplo: la HEMEDRÍA en un cubo conduce a un tetraedro, y a que los ejes cuaternarios del cubo se degraden (bajen de categoría simétrica) a binarios; pero no se han hallado cubos que tengan truncados los cuatro vértices que corresponden a un polo de un eje cuaternario, o sólo truncados dos vértices contiguos de los ocho existentes o cualesquiera de las disposiciones imaginables que realmente anularían la simetría. * Clases de Hemiedria: CRISTALES PARAMORFOS, ANTIMORFOS Y ENANTIOMORFOS. HEMIMORFIA.- Atendiendo a la naturaleza de su simetría, los hemiedros comprenden tres clases: A) Unos tienen centro de simetría (luego también caras paralelas); se llaman parahemiedros, paramorfos o hemiedros paralelos, y son superponibles por giro en torno de un eje. (Diploedro.) B) Otros no tienen centro de simetría (luego tampoco caras paralelas): a) De éstos, unos conservan los planos de simetría compatibles con la ausencia del centro, y son superponibles (los dos derivados de un mismo holoedro) por giro en torno de un eje; son los antihemiedros, antimorfos o hemiedros inclinados (Déltoedros). (Adviértase que si son superponibles son iguales.) b) Otros no son superponibles, pero son simétricos con relación a un plano (como las dos manos unidas por las palmas); se llaman enantiomorfos, giroedros o plagiedros (Giroedros), y suprimen todos los elementos de simetría de la forma holoédrica, menos los ejes. c) En los sistemas en que existen ejes de naturaleza única, pueden presentarse cristales desigualmente conformados en las extremidades de dichos ejes. Este fenómeno se llama hemimorfía, y los cristales que la presentan hemimorfos (Fig 2) Fig. 2.-cristales hemimórficos. A, de Greenockita (Cds), piramidal diexagonal: P, prima hexagonal de primera especie; a, b, g, hemipirámides exagonales superiores de primera especie; n, ídem inferior; ni y o, pedión básicos superior e inferior (según Roso de Luna). B. de Turmalina, piramidal ditrigonal : P,.prisma trigonal de
4 segunda especie, negativo; p, prisma hexagonai de primera especie; v, )hemipírámide hexagonal de primera especie; x y o, hemipirámides trigonales de segunda especie, positiva y negativa (según Rolo de Luna). Las formas meroédricas tienen una simetría de grado inferior a la de las holoédricas de que derivan, pero sin llegarse a confundir con la que presentan las de otro sistema. Así, por ejemplo, los tres ejes cuaternarios del sistema regular pasan a ser binarios en el tetraedro; pero no por eso se confunde la simetría de éste con la del sistema rómbico (que también tiene tres ejes binarios), porque los ejes ternarios conservan su naturaleza y desaparecen planos y el centro de simetría. Formas Abiertas y Cerradas. El concepto de forma cristalina es exclusivamente cristalográfico y nada tiene que ver con el geométrico. Supongamos dos planos que se cortan o que se disponen en posición paralela; es claro que no cierran enteramente un espacio, sino que a lo más lo cerrarán en aquella parte en que se cortan formando un ángulo diedro, pero el espacio quedará abierto en todas las demás direcciones. Con tres planos, tampoco podremos cerrar un espacio. Todas estas formas reciben el nombre de abiertas, en contraposición a las que presentan un espacio limitado por todas partes y que se denominan cerradas. Las formas poliédricas que se estudian en geometría son todas cerradas. Las formas abiertas son puramente teóricas e inexistentes en la naturaleza, la cual jamás podrá presentarlas; pero responden a un concepto objetivo y se admiten en Cristalografía, puesto que sirven de base para la explicación científica de las formas geométricas; son una abstracción de la forma real poliédrica que hace el cristalógrafo. La combinación de formas abiertas da formas cerradas, constituyendo los poliedros geométricos. Formas Abiertas Primarias. Todas las formas abiertas pueden combinarse, y de hecho se combinan entre sí para dar las formas geométricas que presenta la Naturaleza. Estas formas primarias, llamadas también generadoras fundamentales, son las siguientes: 1.º EL PEDION.- Está constituido por una sola cara indefinida, que es, por lo tanto, asimétrica. Suele combinarse con la hemipirámide abierta, cerrando este poliedro y constituyendo la pirámide geométrica. Carece de todo elemento de simetría (figura 3-p).
5 2.º EL PINACOIDE.- Está formado por dos caras paralelas e indefinidas, que exigen centro de simetría. Suelen combinarse con los prismas, cerrándolos por sus bases (Fig. 3-pi). 3.º EL DOMO.-Tiene como único elemento de simetría el plano. Consiste en la unión de dos caras indefinidas, formando un diedro en forma de tejado. Suelen combinarse entre sí para originar prismas (Fig. 3-d). 4.º EL ESFENOIDE.-Consiste también en dos caras indefinidas y cruzadas, pero que son el resultado de la repetición de un plano por razón del eje binario, su único elemento de simetría (Fig. 3-s). 5.º EL PRISMA.-Es la combinación de cuatro planos, manteniendo paralelas sus aristas de intersección y formando, por lo tanto, zona sus cuatro caras. Sus bordes libres quedan indefinidos. Estas formas tienen centro, eje y plano de simetría (Fig. 3-m). Fig. 3.-Las cinco formas abiertas primarias: p, pedion; pi, pinacoide (centro de simetría 0); d, domo (plano de simetría); s, esfenoide (eje binarlo E); m, prisma (eje binario E, plano de simetría P perpendicular a él, y, como consecuencia, centro de simetría 0). Formas Simples y Compuestas: DOMINANTES Y SUBORDINADAS.-Las formas cerradas pueden presentarse de dos maneras: a) Unos cristales no presentan más que caras correspondientes a una sola forma holoédrica o meroédrica, y se denominan Sformas simples. b) Otros, por el contrario, están constituidos por la asociación de caras de dos o más formas simples, y se llaman formas compuestas. En las formas simples las caras del cristal tienen la misma notación. Tal es el octaedro de la figura 4-A. En las compuestas, las caras del cristal tienen distinta notación, aunque cada forma simple que la constituye conserva la suya característica. Tal es la figura 4-B, que es la combinación de un cubo (caras cuadradas) y un octaedro (caras triangulares). En toda forma compuesta, las caras de una forma simple limitan y a su vez quedan limitadas por las caras de la otra, subsistiendo en conjunto fragmento: de una y otra forma; este
6 modo de coexistencia de formas explica por qué las formas compuestas no ofrecen ángulos entrantes, presentándose como poliedros convexos. Fig. 4.-Formas simples y compuestas: A, forma simple (octaedro); B, forma compuesta de cubo y octaedro (las caras del cubo aparecen rayadas). En toda combinación de formas simples las caras de una de ellas suelen presentarse más desarrolladas y visibles que las de la otra; la primera forma se llama dominante y la segunda, subordinada. Las formas compuestas tienen los mismos elementos de simetría que las simples que las constituyen; esto las distingue de las maclas. Forma Geométrica Fundamental o Forma Tipo. En la holoedría de cada sistema se puede considerar a una de sus formas como tipo o generadora, de la cual se pueden hacer derivar todas las demás, por modificación de algunos de sus elementos geométricos. Aunque en principio se podría tomar como tipo cualquiera de los holoédros, es preferible tomar como punto de partida aquél cuyas caras coincidan con las del paralelepípedo fundamental. (fig. 9) Modificando los elementos geométricos de este paralelepípedo, por truncadura, biselamiento y apuntamiento, se obtienen las otras seis formas cristalinas, de las siete que son propias de cada clase de simetría. Las formas hemiédricas, se obtienen por la "supresión" de determinadas caras en cada uno de los siete holoedros, prolongando las contiguas para que cierren el poliedro restante. Dominio Fundamental. de un cristal es el Triedro que tiene su vértice en el centro del cristal, estando limitados por todos los elementos de simetría del mismo y sin tener ninguno en su interior. Limitado en una cara del cristal; origina un tetraedro elemental que esta repetido un numero exacto de veces en su interior, dependiendo de su forma y dimensiones las características cristalográficas y geométricas del cristal.
7 Si tomamos un cubo (Fig. 5-A) y trazamos sus tres planos principales y los seis secundarios, el poliedro nos quedará dividido en 48 fragmentos. cada uno de los cuales tendrá por vértice común el centro geométrico del poliedro, y por base un triángulo que coincide con una cara del cristal. Este fragmento recibe el nombre de DOMINIO FUNDAMENTAL Extrayendo uno de estos fragmentos, como se extrae una tajada de melón, y examinándolo cuidadosamente, se advierte (Fg. 5-B): 1. º Que estos fragmentos son pirámides de base triangular, por lo que al dominio se le llama también TETRAEDRO ELEMENTAL O FUNDAMENTAL 2. º Que las tres caras (interiores en el poliedro) COT, COB y BOT coinciden con tres planos de simetría (Fig. 5-A). Fig. 5-El dominio fundamental en el cubo. A, Cubo dividido en 48 dominios fundaménteles, mediante planos de simetría. Partiendo de un punto A, en el interior de un dominio fundamental, se obtienen otros 47, mediante las operaciones de simetría indicadas por los ejes y planos propios del cristal. B, Da dominio fundamental aislado, que está limitado por todos los elementos de simetría del cristal, sin que en su interior exista ninguno. 3. El dominio queda por tanto encerrado entre planos que lo limitan y separan de los demás dominios. 4. º Que la cara basas CTB, se confunde con la cara del cubo de la que forma parte. 5. º Que las tres aristas (interiores en el poliedros CO, TO, BO, son las intersecciones de los tres planos de simetría indicados; y coinciden con tres ejes de simetría del cubo, aunque de diversa categoría: el primero, CO, con el eje cuaternario; y el segundo, TO, con el ternario; y el tercero, BO, con el binario (Fig. A y B). 6. º Que los elementos de simetría (centro, ejes y planos) no se encuentran en el interior del dominio como atravesándolo, sino que se hallan en las superficies limitantes que lo separan de los demás. 7. º Que en el interior del dominio todas las direcciones son desiguales; pero estas direcciones las tienen idénticas todos los demás dominios. 8. º Que el vértice de la pirámide O es a la vez centro geométrico del poliedro y centro de simetría.
8 9.º Que la cara básica CTB es un triángulo exactamente igual a los 47 restantes externos del cristal y con los mismos elementos de simetría; y en consecuencia cada pirámide es también exactamente igual a las 47 restantes. 10. º Que las tres aristas de esta cara básica representan las tres únicas modalidades distintas de los planos de simetría respecto al cubo; puesto que la arista CB pertenece al plano principal la TB y la CT a planos secundarios, pero la primera coincide con la arista del cubo, al paso que la otra es diagonal a una de sus caras. 11. º Respecto a su posición en el poliedro, cada una de estas caras es idéntica a sus alternas y simétrica a sus adyacentes; y lo mismo puede decirse de sus respectivas pirámides. Las CONSECUENCIAS que se derivan de estas observaciones son: 1.ª Que el cubo no es más que un conjunto de dominios tan perfectamente unidos que no queda entre ellos intersticio alguno. 2.ª Que el centro del cubo es el punto de exacta coincidencia de todos los vértices de los dominios. 3.ª Que todo dominio está limitado por planos, que serán de simetría cuando el sistema a que pertenece el cristal lo permita. 4.ª Que el dominio es asimétrico, pues incluye a todos y a sólo los elementos de simetría de la clase y está limitado por ellos, comprendiendo todas sus distintas categorías. En su interior no caben, por tanto, dos o más posiciones equivalentes. 5.ª Que en el dominio están representados todos los elementos de simetría de la clase; o sea, de sus direcciones posibles y equivalentes (4). 6.ª Que los ejes de simetría, como contenidos en los planos de simetría, pueden coincidir con la intersección de éstos o situarse entre dos de ellos; pero nunca penetrar en el dominio. 7.ª Que para verificar operaciones de simetría en un poliedro regular, puede tomarse indistintamente cualquiera de estos dominios, puesto que todos son idénticos. 8.ª Que con un solo dominio puede reconstruirse toda la forma cristalina, conocidos los elementos de simetría de la clase, puesto que un cristal es la repetición de un determinado número de dominios. 9.ª Que todo punto de un dominio tiene su homólogo en los demás dominios del poliedro, con el que coincidirá por operaciones de simetría. 10.ª Que dentro de un dominio no puede haber dos puntos homólogos. 11.ª Que para estudiar un cristal basta estudiar uno de sus dominios cualquiera.
9 12.ª Que en toda forma cristalina hay tantos dominios como operaciones de simetría; este dominio define con su forma y dimensiones las constantes geométricas del cristal. 13.ª Averiguar el número de dominios equivale a investigar, por consiguiente, el número máximo de caras que tendrá el poliedro. NOTA.-Todo lo dicho del cubo como poliedro, puede aplicarse a la proyección estereográfica del mismo cubo (Fig. 6-A), en la que el dominio fundamental es CBT: y de su dominio fundamental aislado (Fig. 6-B) en la esfera. * Construcción del Dominio Fundamental: Según todo lo que antecede, la construcción del dominio fundamental se reduce a trazar en el poliedro regular (o en la esfera, si se trata de una proyección estereográfica), a cuyo centro geométrico se hayan transportado los elementos de simetría. planos diametrales conteniendo a lo:: ejes de tal suerte que cada uno de ellos esté rodeado de tantos dominios fundamentales equivalentes como unidades tiene su orden (Pardillo). El estudio de la posición del polo en el dominio, determinará la estructura de la forma geométrica; y el de sus elementos de simetría precisará el sistema cristalino, y dentro de él la clase a que pertenece dicha forma. SIMBOLOS VARIABLES E INVARIABLES EN EL DOMINIO FUNDAMENTAL.- Tratándose de -proyecciones, el polo o bien puede caer en el cruce de dos planos de simetría, o bien puede caer en la Intersección de un plano con la superficie esférica, o, finalmente, en el interior del dominio (Fig-. 6-B). Fig. 6-.A, El dominio fundamental del cubo, en proyección estereográfica, que esta limitado por planos de simetría, y tiene en cada vértice Un eje binario. Uno temario v otro cuaternario. B, Diferentes posiciones del polo P, P', P", en el dominio fundamental. En el primer caso está claro que el pollo P tiene su posición fija inmutable, por lo que su símbolo será invariable. En el segundo (P'), el polo, sin apartarse de dicha
10 intersección, puede aproximarse mas a uno u otro de sus extremos, lo mismo que el polo que cae en el interior del dominio (P") puede ocupar variadísimas posiciones dentro de él; en estos dos últimos casos el polo tiene una posición mutable, por lo que su símbolo será variable. Y como el símbolo de la cara depende de la inclinación que ésta tiene respecto a los ejes cristalográficos o ejes de coordenadas, se deduce que las formas cristalográficas de símbolo invariable o constante son idénticas, al paso que las de símbolo variable no son idénticas puesto que sus respectivas formas poliédricas tendrán sus caras formando entre sí ángulos muy variados. Según esto, en el sistema regular las formas INVARIABLES son: el cubo, el octaedro y el rombododecaedro, cuyos polos caen en los ejes (cuaternario, ternario y binario), por lo que todos los cubos, octaedros y rombo dodecaedros son iguales. Todas las demás formas son variables, por lo que habrá muchas variedades de tetraquisexaedros, de trapezoedros, etc. * Numero de dominios fundamentales de una clase de simetría: Como en el interior de cada dominio fundamental no existe ningún elemento de simetría, todas las direcciones contenidas en él serán distintas, y, por lo tanto, hallar el número de dominios equivale a determinar el de direcciones equivalentes de la clase. Siendo n el grado de un eje de simetría, a partir de una dirección inicial A (Fig. 5-A) se obtendrán en total n direcciones equivalentes, es decir (n-1) nuevas (sin contar la inicial). Y si en vez de un eje de simetría fuesen p los de grado n, tendríamos que el número de direcciones equivalentes originadas por esos ejes sería: N,=1 + (n-1) p. Suponiendo que además de ejes de grado n haya también otros de. grado n' en número p'; otros de grado n", en número p", etc., el número total de direcciones equivalentes sería ahora, por un razonamiento análogo. N,=1 + (n-1)p + (n -1)p' + (n"-1)p" + '... Y si, finalmente, suponemos que además existen planos de simetría o centro de simetría, habrá que duplicar el número total de direcciones equivalentes, aunque si
11 existen ambas cosas a la vez no, habrá que multiplicar por 4, sino solamente por 2, ya que el efecto de unos y otro es el mismo y único. La fórmula general del número total posible de dominios será, por tanto: N = [1+(n-1)p+(n'-1)p +...]2 Pongamos un ejemplo, sobre el cubo del sistema regular (Fig. 5-A) que representa la clase holoédrica de este sistema: De la posición inicial A, el eje binario B' origina la b; el ternario, T', las t1 y t2; el cuaternario C, las a1 a2 y a3, lo cual está de acuerda con la fórmula hallada. Teniendo en cuenta que hay seis ejes binarios, cuatro ternarios, y tres cuaternarios; y que también hay centro de simetría, la fórmula nos da, para el número de direcciones equivalentes a la A, o para ei número de dominios: N = [1 + (2-1) 6 + (3-1) 4 + (4-1) 3] 2= [ ] 2=48. y efectivamente, según puede verse en la citada figura el cubo tiene ocho dominios sobre cada cara, y como son seis caras, en total, N = 8 x 6 = 48. Deducción de Formas por la Posición del Polo. Como todos los dominios del cristal son absolutamente idénticos, y en cada uno están: incluidos todos los elementos de simetría de la clase a que pertenece el cristal, el polo de una cara ha de caer necesariamente dentro de este dominio. Pero, los dominios son pirámides de base esférica triangular cuyo vértice coincide con el centro de la esfera. El polo cae en este triángulo, pudiendo ocupar, como es natural, una de: estas posiciones: a) en uno de los tres vértices; b) en una de las tres aristas; c) en el interior del dominio. Cada una de estas posiciones originará una forma o poliedro distinto; y como en total son siete, habrá para cada clase SIETE FORMAS CRISTALOCRÁFICAS DISTINTAS. Si la forma es holoédrica el cristal tendrá todos los dominios, y el polo se repetirá en cada uno de ellos, guardando en todos idéntica posición. Si la forma es hemiédrica, el cristal tendrá la mitad de dominios que tiene la clase holoédrica, y el polo se, repetirá en cada uno de ellos, por lo que el poliedro tendrá la mitad de polos, es decir, la mitad de caras que tiene la forma holoédrica fundamental.
12 En las formas tetratoédricas, el cristal tiene la cuarta parte de dominios que la forma fundamental, por lo que tendrá la cuarta parte de polos, y en consecuencia, la cuarta parte de caras. * Deduccion de Formas Meroedricas: POR SUPRESIÓN DE DOMINIOS FUNDAMENTALES. Para, hacer más patente y comprensible la manera cómo de una forma holoédrica pueden derivarse las formas meroédricas del sistema, por supresión de dominios fundamentales (que corresponden en este caso a caras poiiédricas), representaremos gráficamente en cada sistema la forma fundamental extendida, y se repetirá en cada una de las clases meroédricas, rayando las caras que se suprimen en dicha forma fundamental, con lo cual las no suprimidas constituyen el conjunto de dominios propios de la clase, objeto de estudio. Esta derivación de formas se presenta también en forma de quebrado, dando a cada cara del poliedro un número ordenado, y colocando en el numerador las que corresponden a la hemipirámide superior, y en el denominador las de la hemipirámide inferior. Y se tachan en cada forma los números que corresponden a las caras suprimidas, para que quede más patente la correspondencia de las no suprimidas con las de la forma poliédrica representada. * Deduccion de las Formas de una Clase Cristalina de Simetría: Basta para ello conocer -el -dominio fundamental y los elementos de simetría propios de la clase, y el problema queda reducido al estudio de las siete posiciones del polo de una cara en dicho dominio, tal como se ha indicado anteriormente. Las características geométricas de cada forma son el resultado de su condición simétrica y de la posición del polo, pudiendo ocurrir que una misma forma, geométrica pertenezca a diferentes clases de simetría, en cada una de las cuales tendrá simetría distinta. Número de caras de una Forma Cristalina.. No es lo mismo cara que dominio fundamental. El número de ambos sólo coincide en la forma general (hkl). Si queremos hallar el número de caras de una determinada forma cristalina, podemos partir del número de dominios fundamentales característicos del sistema a que corresponde, teniendo además en cuenta la posición, del polo en el dominio fundamental, y si se trata de una holoedría o meroedría.
13 1.º Si el polo de la cara está en el interior del dominio (P" de la Fig. 6-B), el número de caras es el mismo que el de dominios. 2.º Si está situado el polo sobre un plano de simetría (P' de la Fig. 6-P), el número de caras será la mitad del de dominios. 3.º Si el polo coincide con un eje de simetría de orden n (P de la Fig. 6-B), el número de caras se obtendrá dividiendo el número de dominios por n. 4º Si en el caso anterior el polo, además de estar sobre un eje de orden n, está sobre un plano de simetría (éste es el caso más general), el número de caras se obtiene dividiendo por 2 la fórmula obtenida en el caso tercero. 5º Si se trata de una forma meroédrica, el número de caras será la mitad, cuarta y octava parte (según sea hemiédrica, tetraédrica u ogdoédrica, respectivamente) del obtenido en cualquiera de los casos anteriores. Simetría Real y Simetría Aparente. Es frecuente que en las clases meroédricas, la simetría aparente de una forma sea muy distinta de la que realmente tiene. Cuando el polo de una cara esta en posición tal con relación al dominio fundamental, que pertenece a la vez a dos o mas dominios contiguos (siempre que no esté localizado en su interior), por ejemplo los polos P y P' de la fig. 6-B, ocurre que al suprimir un determinado número de dominios según determinada ley, para obtener una forma meroédrica, sólo se suprimen en realidad parte de dichos polos, o lo que es lo mismo, parte de las caras de la forma holoédrica originaria (pero no caras completas), y al extenderse de nuevo las que han quedado, para cerrar espacio, reconstruyen la forma primitiva. Si, por ejemplo, en el cubo (Fig. 5-A) suprimimos los dominios I-II-III-IV, y los correspondientes de las demás caras, claro es que las partes de cara de cubo respetadas (dominios V-VI-VII-VIII, etc.) al prolongarse reconstruyen el cubo. Así se comprende que ciertas formas holoédricas, sean comunes a muchas hedierais y tetartoedrías, como veremos al estudiar los sistemas. Sin embargo, casi siempre es posible decidir, por pequeños, detalles externos, como son las figuras de corrosión, estrías, caras subordinadas, etc., la verdadera simetría de una determinada forma cristalina.
14 Fig. 7.- Simetría real y simetría aparente: el cubo de la figura A no tiene, a causa de las estrías y figuras de sus caras, planos diagonales de simetría, y los ejes cuaternarios solamente son binarios. II cubo de la figu ra 3, que sólo presenta cuatro vértices alternos truncados, carece de planos diametrales de símetría, de ejes binarios y de centro; además sus ejes cuartanarios sólo son binarios. Por ejemplo, el cubo como forma geométrica existe en las cinco clases de simetría del sistema regular, pero estos cubos se diferencian por tener diferentes elementos de simetría, lo cual se manifiesta de muy diversas formas; unas veces, por la presencia de estrías o figuras geométricas sobre sus caras, que reducen su simetría (figura 7-A), haciendo, por ejemplo, que los ejes cuaternarios sean sólo binarios y que, sin embargo, persistan los cuatro ternarios y los tres planos; y otras veces será por la presencia de caras suplementarias que, en vez de aparecer en todos los vértices (Fig. 7-B), sólo aparecen en algunos respetando los ejes ternarios, pero haciendo desaparecer los binarios y transformando los cuaternarios en binarios. En el primer supuesto, el cubo sería de la hemiedría dodecaédrica, y en el segundo de la tetraédrica. * Poliedros de Primera, Segunda y Tercera Especie: Se da el caso de que ciertas formas, geométricamente iguales, son distintas desde el punto de vista cristalográfico, por tener distinta posición respecto a los ejes cristalográficos, con lo cual también la notación de sus caras es distinta. Esto puede ocurrir en todos los sistemas, excepto en el Regular. A tales cristales, para distinguirlos, se les denomina de "primera", de "segunda", de "tercera" y hasta de "cuarta" especie.
15 Fig. 8.-Formas de La, 2a y 3a especies: en la figura A, se representa una proforma o de.1a especie (prisma tetragonal); en h figura B, una deutoforma o de 2.a especie, cuyas caras son pínacoidales, y en la figura C, una tritoforma o de 3a especie, cuyas caras lo son del prisma ditetragonal., Pongamos un ejemplo: En la figura 81 se representan los ejes cristalográficos horizontales, y relacionados con ellos un prisma tetragonal, que ocupa tres posiciones distintas. En Ia figura A, las caras del prisma son realmente prismáticas, porque cortan a los dos ejes; y corresponden a un prisma tetragonai (110) porque lo hacen a la misma distancia om=on. A una forma corno ésta se )a llama de primera especie o protoforma (protoprisma, protopirámide, etc.). En la figura B, las caras del prisma son en realidad pinacoidales. porque cortan a un solo eje y son paralelas al otro horizontal, siendo su notación(100). Por esta razón, a esta forma se la denomina de segunda especie o dento -( =falsa) forma; (deuto-prisma, etc.). En la figura C, las caras del prisma tetragonal son también prismáticas, porque cortan a los dos ejes horizontales, pero lo hacen a distinta distancia (om, on), por lo cual dichas caras corresponden en realidad a un prisma ditetragonal, cuya notación es (hko): es decir, que este prisma tetragonal se ha originado por el desarrollo de la mitad de las caras de un prisma ditetragonal. A una forma en estas condiciones se la denomina de tercera especie o trito-forma.
16 * Característica Simétrica: En cada sistema hay uno o varios elementos de simetría que no solo se encuentran en cada una de sus formas, sino en solo ellas, constituyendo así su característica peculiar. Este o estos elementos señalan la característica simétrica del sistema; y ellos bastan para poder reconocer y clasificar rápidamente cualquier forma bajo su aspecto simétrico. Adviértase que las formas holoédricas no tienen los mismos elementos de simetría que las hemiédricas del mismo sistema; sin embargo, en cada sistema siempre existe una característica simétrica común a todas sus clases; por ejemplo, en el sistema regular, cuatro ejes ternarios. Esto no es sino una consecuencia de la manera como se pueden combinar los diferentes elementos de simetría a partir de las cinco formas primarias(fig. 3); añadiendo a cada una de ellas un eje binario, ternario, cuaternario y senario, obtendremos otras tantas características simétricas que nos definen los sistemas rómbico, trigonal, tetragonal y hexagonal. Cualquiera otra combinación, teóricamente posible, de elementos de simetría para que puedan originar una clase, ha de corresponder a la simetría posible en Un paralelepípedo, y fácilmente se ve que la única posibilidad reside en la coexistencia de cuatro ejes terrarios cuando el paralelepípedo es un cubo, resultando entonces el sistema regular. Orientación de un Cristal. Orientar un cristal es colocarlo en tal posición ante nosotros que al observarlo, descubramos fácilmente en él la situación y relación de sus elementos de simetría Fig. 9.- Modo de orientar un cristal (cubo) en el espacie, cogiéndole con los dedos índice I pulgar de la mano izquierda, por los extremos del eje cristalográfico vertical. Esto lo obtendremos localizando en el cristal sus respectivos EJES CRISTALOGRÁFICOS; y como éstos se toman, a ser posible, de sus ejes de simetría, los cuales guardan íntima relación entre sí y con todos los demás elementos de
17 simetría, una vez orientado el cristal se aprecia de un golpe de vista todo el conjunto simétrico del poliedro. Aún más: como las caras del cristal están también relacionadas con los ejes cristalográficos (puesto que son coordenadas) y con sus y de conjunto de todo el complejo cristalográfico del poliedro. *ORIENTACIÓN DEL CRISTAL EQUIVALE, POR LO TANTO, A ORIENTAR SUS EJES CRISTALOGRÁFICOS (fig. 9) Fig. 9: Los ejes cristalográficos se orientan siempre: El ZZ' (c) en posición vertical; el XX' (a) en posición antero-posterior; y el YY' (b), en posición transversal, o sea, de derecha a izquierda. Por lo tanto, lo primero que se ha de hacer es buscar el tercer efe cristalográfico ZZ' y colocarlo en posición vertical. Se toma el cristal entre el pulgar y el índice de la mano izquierda (como indica la figura 82) y se hacen apoyar las yemas de estos dedos en
18 los extremos de dicho eje ideal, cuidando de mantener el cristal, durante el giro, siempre con dicho eje en posición vertical. Con esto; en la mayor parte de los casos quedarán ya automáticamente localizados los otros ejes en posición horizontal. Valiéndonos del índice de la mano derecha, haremos girar al poliedro en torno del supuesto eje vertical, con lo cual obligaremos a uno de los restantes ejes cristalográficos horizontales a situarse en posición antero-posterior, es decir, de frente al observador. Este eje será el XX' (a). El tercer eje quedará en posición más o menos transversal; éste será el eje YY' (b). Con esto tenemos colocados adecuadamente, con respecto al espacio, los tres ejes cristalográficos; es decir, TENEMOS ORIENTADO EL CRISTAL (Fig. 83). Los sistemas hexagonal y trigonal tienen excepcionalmente CUATRO EJES CRISTALOGRÁFICOS.
Módulo 3. Introducción a la cristalografía
 Módulo 3. Introducción a la cristalografía Poliedros cristalográficos recortables Un método muy recomendable para estudiar la forma y simetría de los cristales consiste en construir poliedros recortables.
Módulo 3. Introducción a la cristalografía Poliedros cristalográficos recortables Un método muy recomendable para estudiar la forma y simetría de los cristales consiste en construir poliedros recortables.
Cuerpos Geométricos. Volúmenes de Cuerpos Geométricos
 Cuerpos Geométricos. Volúmenes de Cuerpos Geométricos Un cuerpo geométrico es un elemento que existe en la realidad o que somos capaces de concebir, llamado sólido, el cual ocupa un volumen en el espacio,
Cuerpos Geométricos. Volúmenes de Cuerpos Geométricos Un cuerpo geométrico es un elemento que existe en la realidad o que somos capaces de concebir, llamado sólido, el cual ocupa un volumen en el espacio,
Geometría. Cuerpos Geométricos. Trabajo
 Geometría Cuerpos Geométricos Trabajo CUERPOS GEOMÉTRICOS 1. Clasifique los cuerpos geométricos. Dos grupos de sólidos geométricos del espacio presentan especial interés: 1.1. Poliedros: Aquellos cuerpos
Geometría Cuerpos Geométricos Trabajo CUERPOS GEOMÉTRICOS 1. Clasifique los cuerpos geométricos. Dos grupos de sólidos geométricos del espacio presentan especial interés: 1.1. Poliedros: Aquellos cuerpos
SUPERFICIES POLIÉDRICAS CONVEXAS
 SUPERFICIES POLIÉDRICAS CONVEXAS OBJETIVOS Conocer las características y relaciones métricas del te tra - edro, hexaedro o cubo y octaedro, para su represen tación en el sistema diédrico en sus múltiples
SUPERFICIES POLIÉDRICAS CONVEXAS OBJETIVOS Conocer las características y relaciones métricas del te tra - edro, hexaedro o cubo y octaedro, para su represen tación en el sistema diédrico en sus múltiples
MSC J. Fco. Jafet Pérez L. Conceptos Geométricos Objetos Básicos
 Gráficos por Computadora MSC J. Fco. Jafet Pérez L. Conceptos Geométricos Objetos Básicos Objetos básicos Punto, Línea, Plano y Espacio Punto: Ubicación, sin longitud, anchura ni altura. (El punto representa
Gráficos por Computadora MSC J. Fco. Jafet Pérez L. Conceptos Geométricos Objetos Básicos Objetos básicos Punto, Línea, Plano y Espacio Punto: Ubicación, sin longitud, anchura ni altura. (El punto representa
CLASIFICAR POLIEDROS. Nombre: Curso: Fecha:
 CLASIICAR POLIEDROS OBJETIVO 1 Nombre: Curso: eca: POLIEDROS Un poliedro es un cuerpo geométrico que está limitado por cuatro o más polígonos. Los polígonos que limitan al poliedro se llaman caras. Los
CLASIICAR POLIEDROS OBJETIVO 1 Nombre: Curso: eca: POLIEDROS Un poliedro es un cuerpo geométrico que está limitado por cuatro o más polígonos. Los polígonos que limitan al poliedro se llaman caras. Los
Punto. Recta. Semirrecta. Segmento. Rectas Secantes. Rectas Paralelas. Rectas Perpendiculares
 Punto El punto es un objeto geométrico que no tiene dimensión y que sirve para indicar una posición. A Recta Es una sucesión continua e indefinida de puntos en una sola dimensión. Semirrecta Es una línea
Punto El punto es un objeto geométrico que no tiene dimensión y que sirve para indicar una posición. A Recta Es una sucesión continua e indefinida de puntos en una sola dimensión. Semirrecta Es una línea
Un punto divide a una recta en dos semirrectas. Ese punto es el origen de ambas semirrectas.
 Una línea recta es una línea que no tiene principio ni fin. Una semirrecta es una línea que tiene principio pero no tiene final. o Un punto divide a una recta en dos semirrectas. Ese punto es el origen
Una línea recta es una línea que no tiene principio ni fin. Una semirrecta es una línea que tiene principio pero no tiene final. o Un punto divide a una recta en dos semirrectas. Ese punto es el origen
Autor: 2º ciclo de E.P.
 1 Autor: 2º ciclo de E.P. Una línea recta es una línea que no tiene principio ni fin. Una semirrecta es una línea que tiene principio pero no tiene final. o Un punto divide a una recta en dos semirrectas.
1 Autor: 2º ciclo de E.P. Una línea recta es una línea que no tiene principio ni fin. Una semirrecta es una línea que tiene principio pero no tiene final. o Un punto divide a una recta en dos semirrectas.
SIMETRÍA INFINITA. nt = kt
 SIMETRÍA INFINITA Al considerar el cristal como un medio periódico en el cual un grupo de átomos (el motivo) se repite en las tres dimensiones del espacio, de manera que entre dos puntos homólogos de dos
SIMETRÍA INFINITA Al considerar el cristal como un medio periódico en el cual un grupo de átomos (el motivo) se repite en las tres dimensiones del espacio, de manera que entre dos puntos homólogos de dos
unidad 10 Cuerpos geométricos
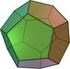 unidad 10 Cuerpos geométricos Poliedros. Características Página 1 Poliedro es un cuerpo cerrado limitado por caras planas que son polígonos. Aristas son los lados de las caras. Cada dos caras contiguas
unidad 10 Cuerpos geométricos Poliedros. Características Página 1 Poliedro es un cuerpo cerrado limitado por caras planas que son polígonos. Aristas son los lados de las caras. Cada dos caras contiguas
Tema 8: Cuerpos geométricos. Matemáticas Específicas para Maestros 1º Grado en Educación Primaria
 Tema 8: Cuerpos geométricos Matemáticas Específicas para Maestros 1º Grado en Educación Primaria Definiciones Cuerpos geométricos Poliedros. Elementos. Clasificaciones: o Poliedros cóncavos y convexos.
Tema 8: Cuerpos geométricos Matemáticas Específicas para Maestros 1º Grado en Educación Primaria Definiciones Cuerpos geométricos Poliedros. Elementos. Clasificaciones: o Poliedros cóncavos y convexos.
CRISTALOGRAFÍA GEOMÉTRICA TEMA 4 SIMETRÍA PUNTUAL
 CRISTALOGRAFÍA GEOMÉTRICA TEMA 4 SIMETRÍA PUNTUAL ÍNDICE 4.1 Introducción 4.2 Grupos puntuales y clases cristalinas 4.3 Reglas que condicionan la presencia de varios elementos de simetría en un mismo grupo
CRISTALOGRAFÍA GEOMÉTRICA TEMA 4 SIMETRÍA PUNTUAL ÍNDICE 4.1 Introducción 4.2 Grupos puntuales y clases cristalinas 4.3 Reglas que condicionan la presencia de varios elementos de simetría en un mismo grupo
TEMA 9 CUERPOS GEOMÉTRICOS
 Tel: 98 9 6 91 Fax: 98 1 89 96 TEMA 9 CUERPOS GEOMÉTRICOS Objetivos / Criterios de evaluación O.1.1 Conocer las fórmulas de áreas y volúmenes de figuras geométricas sencillas de D. O.1. Resolver problemas
Tel: 98 9 6 91 Fax: 98 1 89 96 TEMA 9 CUERPOS GEOMÉTRICOS Objetivos / Criterios de evaluación O.1.1 Conocer las fórmulas de áreas y volúmenes de figuras geométricas sencillas de D. O.1. Resolver problemas
Maquetería 02: Poliedros, cuerpos redondos y su construcción
 Maquetería 02: Poliedros, cuerpos redondos y su construcción Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
Maquetería 02: Poliedros, cuerpos redondos y su construcción Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
CUERPOS. Poliedros: Aquellos cuerpos geométricos totalmente limitados por polígonos, como por ejemplo, el prisma, la pirámide; etc.
 CUERPOS Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede calcular el volumen del mismo
CUERPOS Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede calcular el volumen del mismo
Maquetería 02: Poliedros, cuerpos redondos y su construcción
 Maquetería 02: Poliedros, cuerpos redondos y su construcción Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
Maquetería 02: Poliedros, cuerpos redondos y su construcción Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta.
 POLIEDROS Ejercicio nº 1.- a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
POLIEDROS Ejercicio nº 1.- a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
Cuerpos geométricos son porciones de espacio limitadas por superficies planas o curvas. CUERPOS GEOMÉTRICOS PRISMAS PIRÁMIDES CILINDROS CONOS ESFERAS
 UNIDAD DIDÁCTICA CUERPOS GEOMÉTRICOS 1. CUERPOS GEOMÉTRICOS En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos
UNIDAD DIDÁCTICA CUERPOS GEOMÉTRICOS 1. CUERPOS GEOMÉTRICOS En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos
ESTRU R C U T C UR U A R S A D E D LOS O MAT A ERI R AL A ES
 ESTRUCTURAS DE LOS MATERIALES Cristalina CRISTALINOS METALES COMPUESTOS IÓNICOS COMPUESTOS COMPLEJOS COV.-ION. SÓLIDOS COVALENTES COVALENTE PURO SÓLIDOS MOLECULARES NO CRISTALINOS (AMORFOS) VIDRIOS INORGÁNICOS
ESTRUCTURAS DE LOS MATERIALES Cristalina CRISTALINOS METALES COMPUESTOS IÓNICOS COMPUESTOS COMPLEJOS COV.-ION. SÓLIDOS COVALENTES COVALENTE PURO SÓLIDOS MOLECULARES NO CRISTALINOS (AMORFOS) VIDRIOS INORGÁNICOS
10- Los poliedros. Aprende a reconocer los poliedros en nuestro entorno; identifica sus elementos y aprende a clasificarlos.
 Aprende a reconocer los poliedros en nuestro entorno; identifica sus elementos y aprende a clasificarlos. Impreso por Juan Carlos Vila Vilariño Centro PASTORIZA (Nº 3) Sumario 1 Los poliedros... 3 1.1
Aprende a reconocer los poliedros en nuestro entorno; identifica sus elementos y aprende a clasificarlos. Impreso por Juan Carlos Vila Vilariño Centro PASTORIZA (Nº 3) Sumario 1 Los poliedros... 3 1.1
MATEMÁTICAS 2º DE ESO LOE
 MATEMÁTICAS º DE ESO LOE TEMA XII: POLIEDROS Y CUERPOS REDONDOS Poliedros: o Elementos. o Tipos. Poliedros regulares. Cubos. Prismas: elementos, clases. Pirámides: elementos, clases. Áreas laterales y
MATEMÁTICAS º DE ESO LOE TEMA XII: POLIEDROS Y CUERPOS REDONDOS Poliedros: o Elementos. o Tipos. Poliedros regulares. Cubos. Prismas: elementos, clases. Pirámides: elementos, clases. Áreas laterales y
CUERPOS GEOMÉTRICOS (CONCEPTOS BÁSICOS)
 CUERPOS GEOMÉTRICOS (CONCEPTOS BÁSICOS) Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede
CUERPOS GEOMÉTRICOS (CONCEPTOS BÁSICOS) Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede
TEMA 5: Cuerpos geométricos CONTENIDOS:
 CONTENIDOS: - Prismas y pirámides: descripción, elementos y clasificación. - Cilindro, cono y esfera: descripción y elementos. - Realización de clasificaciones de cuerpos geométricos atendiendo a diferentes
CONTENIDOS: - Prismas y pirámides: descripción, elementos y clasificación. - Cilindro, cono y esfera: descripción y elementos. - Realización de clasificaciones de cuerpos geométricos atendiendo a diferentes
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA
 RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
Trabajo de Investigación Cuerpos Geométricos
 Saint George s College Área de Matemáticas y sus Aplicaciones Tercera Unidad Trabajo de Investigación Cuerpos Geométricos Integrantes: -Stefan Jercic -Ignacio Larrain -Cristian Majluf Curso: 10 E Profesora:
Saint George s College Área de Matemáticas y sus Aplicaciones Tercera Unidad Trabajo de Investigación Cuerpos Geométricos Integrantes: -Stefan Jercic -Ignacio Larrain -Cristian Majluf Curso: 10 E Profesora:
MAQUETERÍA 02: POLIEDROS, CUERPOS REDONDOS Y SU CONSTRUCCIÓN
 MAQUETERÍA 02: POLIEDROS, CUERPOS REDONDOS Y SU CONSTRUCCIÓN Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
MAQUETERÍA 02: POLIEDROS, CUERPOS REDONDOS Y SU CONSTRUCCIÓN Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
SÓLIDOS EN EL ESPACIO TRIDIMENSIONAL
 G3D1: Sólidos convexos y cóncavos SÓLIDOS EN EL ESPACIO TRIDIMENSIONAL Pon tres ejemplos de objetos cotidianos que sean convexos: Pon tres ejemplos de objetos cotidianos que sean cóncavos: G3D2: Caracterización
G3D1: Sólidos convexos y cóncavos SÓLIDOS EN EL ESPACIO TRIDIMENSIONAL Pon tres ejemplos de objetos cotidianos que sean convexos: Pon tres ejemplos de objetos cotidianos que sean cóncavos: G3D2: Caracterización
POLIEDROS. Ejercicio nº 1.- a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta.
 POLIEDROS Ejercicio nº 1.- De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
POLIEDROS Ejercicio nº 1.- De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
TEMA 4. Geometría. Teoría. Matemáticas
 1 1.- Rectas y ángulos La geometría se basa en tres conceptos fundamentales que forman parte del espacio geométrico, es decir, el conjunto formado por todos los puntos: El punto La recta El plano Partiendo
1 1.- Rectas y ángulos La geometría se basa en tres conceptos fundamentales que forman parte del espacio geométrico, es decir, el conjunto formado por todos los puntos: El punto La recta El plano Partiendo
MYP (MIDDLE YEARS PROGRAMME)
 MYP (MIDDLE YEARS PROGRAMME) 2014-2015 Fecha 19/05/2015 APUNTES DE GEOMETRÍA 2º ESO 1. EL TEOREMA DE PITÁGORAS El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa
MYP (MIDDLE YEARS PROGRAMME) 2014-2015 Fecha 19/05/2015 APUNTES DE GEOMETRÍA 2º ESO 1. EL TEOREMA DE PITÁGORAS El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa
31. SISTEMA AXONOMÉTRICO. LA RECTA Y EL PLANO
 31. SISTEMA AXONOMÉTRICO. LA RECTA Y EL PLANO 31.1. Representación de la recta. Si un punto se representaba por cuatro proyecciones, la recta se representa igual por cuatro proyecciones. Proyecciones de
31. SISTEMA AXONOMÉTRICO. LA RECTA Y EL PLANO 31.1. Representación de la recta. Si un punto se representaba por cuatro proyecciones, la recta se representa igual por cuatro proyecciones. Proyecciones de
DIBUJO TÉCNICO. UNIDAD DIDÁCTICA VI: Geometría 3D (III)
 UNIDAD DIDÁCTICA VI: Geometría 3D (III) 1 ÍNDICE Página: 2 SUPERFICIES PRISMÁTICAS.. 2 2.1 PRISMAS 2 3 SUPERFICIES PIRAMIDALES.. 3 3.1 PIRÁMIDES 4 4 SECCIONES PLANAS. 5 5 DESARROLLOS Y TRANSFORMADAS...
UNIDAD DIDÁCTICA VI: Geometría 3D (III) 1 ÍNDICE Página: 2 SUPERFICIES PRISMÁTICAS.. 2 2.1 PRISMAS 2 3 SUPERFICIES PIRAMIDALES.. 3 3.1 PIRÁMIDES 4 4 SECCIONES PLANAS. 5 5 DESARROLLOS Y TRANSFORMADAS...
CUERPOS EN EL ESPACIO
 CUERPOS EN EL ESPACIO 1. Poliedros. 2. Fórmula de Euler. 3. Prismas. 4. Paralelepípedos. Ortoedros. 5. Pirámides. 6. Cuerpos de revolución. 6.1. Cilindros. 6.2. Conos. 6.3. Esferas. 6.4. Coordenadas geográficas.
CUERPOS EN EL ESPACIO 1. Poliedros. 2. Fórmula de Euler. 3. Prismas. 4. Paralelepípedos. Ortoedros. 5. Pirámides. 6. Cuerpos de revolución. 6.1. Cilindros. 6.2. Conos. 6.3. Esferas. 6.4. Coordenadas geográficas.
TEMA 7 Las formas y las medidas que nos rodean. 2. Repaso a las figuras planas elementales
 TEMA 7 Las formas y las medidas que nos rodean 1. Introducción 1.1. Qué es la geometría? Es una rama de la matemática que se ocupa del estudio de las propiedades de las figuras geométricas en el plano
TEMA 7 Las formas y las medidas que nos rodean 1. Introducción 1.1. Qué es la geometría? Es una rama de la matemática que se ocupa del estudio de las propiedades de las figuras geométricas en el plano
PROBFlfiFlfi GEOMETRIA POR. CñTEDRñTICO DE MfiTEMñTICñS. En EL. Instituto BcnEral y Técnica de Lagrana LOGROÑO IMPRENTA Y LIBRERÍA MODERNA
 PROBFlfiFlfi DE GEOMETRIA POR Miguel Hayos y Julia CñTEDRñTICO DE MfiTEMñTICñS En EL Instituto BcnEral y Técnica de Lagrana LOGROÑO IMPRENTA Y LIBRERÍA MODERNA 1913 GEOMETRIA POR Miguel Hayos y Julia
PROBFlfiFlfi DE GEOMETRIA POR Miguel Hayos y Julia CñTEDRñTICO DE MfiTEMñTICñS En EL Instituto BcnEral y Técnica de Lagrana LOGROÑO IMPRENTA Y LIBRERÍA MODERNA 1913 GEOMETRIA POR Miguel Hayos y Julia
Bases Matemáticas para la Educación Primaria. Guía de Estudio. Tema 4: Figuras geométricas
 Bases Matemáticas para la Educación Primaria Guía de Estudio Tema 4: Figuras geométricas 1 Conceptos geométricos En la clase de matemáticas, y en los textos escolares, encontramos expresiones tales como:
Bases Matemáticas para la Educación Primaria Guía de Estudio Tema 4: Figuras geométricas 1 Conceptos geométricos En la clase de matemáticas, y en los textos escolares, encontramos expresiones tales como:
ELEMENTOS DE UN POLIEDRO. PRINCIPALES POLIEDROS REGULARES
 OBJETIVO 1 ELEMENTOS DE UN POLIEDRO. PRINCIPALES POLIEDROS REGULARES NOMBRE: CURSO: ECHA: CONCEPTO DE POLIEDRO Vértice Arista Cara Un poliedro es un cuerpo geométrico cuyas caras son polígonos. Los elementos
OBJETIVO 1 ELEMENTOS DE UN POLIEDRO. PRINCIPALES POLIEDROS REGULARES NOMBRE: CURSO: ECHA: CONCEPTO DE POLIEDRO Vértice Arista Cara Un poliedro es un cuerpo geométrico cuyas caras son polígonos. Los elementos
Área: Ciencia y Tecnología Asignatura: MATEMÁTICA. Título. Trabajo Práctico Cuerpos. Año: Pag.1/7
 Área: Ciencia y Tecnología Asignatura: MATEMÁTICA Título Trabajo Práctico Cuerpos Curso 1 Año Año: 2007 Pag.1/7 CUERPOS GEOMÉTRICOS Escribe en tu carpeta cómo se llama el cuerpo geométrico al que se parece
Área: Ciencia y Tecnología Asignatura: MATEMÁTICA Título Trabajo Práctico Cuerpos Curso 1 Año Año: 2007 Pag.1/7 CUERPOS GEOMÉTRICOS Escribe en tu carpeta cómo se llama el cuerpo geométrico al que se parece
Preparado por el Arqto. Jing Chang Lou
 POLIIEDROS A P U N T E D O C E N T E Preparado por el Arqto. Jing Chang Lou U N I V ER S I D A D D E C H I L E F AC U L T A D D E A R Q U I T EC T U R A Y U R B A N I S MO D EPARTAMENTO C I ENCIAS DE L
POLIIEDROS A P U N T E D O C E N T E Preparado por el Arqto. Jing Chang Lou U N I V ER S I D A D D E C H I L E F AC U L T A D D E A R Q U I T EC T U R A Y U R B A N I S MO D EPARTAMENTO C I ENCIAS DE L
Se dice que un poliedro es regular cuando sus caras son polígonos regulares iguales y sus ángulos poliedros tienen el mismo número de caras.
 LOS POLIEDROS: El cubo, la pirámide, la esfera, el cilindro... son figuras sólidas. Observando tales figuras, vemos que algunos sólidos, como el cubo y la pirámide, tienen su superficie exterior formada
LOS POLIEDROS: El cubo, la pirámide, la esfera, el cilindro... son figuras sólidas. Observando tales figuras, vemos que algunos sólidos, como el cubo y la pirámide, tienen su superficie exterior formada
Figura en el espacio o cuerpo geométrico es el conjunto de puntos que no están contenidos en un mismo plano, es la porción de espacio limitado.
 Cuenca, 11 de noviembre de 2013 Clase 13 Geometría del espacio Figuras geométricas en el espacio Definiciones: Geometría del espacio: Rama de las matemáticas encargada de las propiedades y medida de las
Cuenca, 11 de noviembre de 2013 Clase 13 Geometría del espacio Figuras geométricas en el espacio Definiciones: Geometría del espacio: Rama de las matemáticas encargada de las propiedades y medida de las
Preguntas tipo OLIMPIADA DE DIBUJO TÉCNICO MARZO 2014
 E S C U E L A T É C N I C A S U P E R I O R D E A R Q U I T E C T U R A U N I V E R S I D A D D E N A V A R R A Preguntas tipo OLIMPIADA DE DIBUJO TÉCNICO MARZO 2014 G E O M E T R Í A M É T R I C A. T
E S C U E L A T É C N I C A S U P E R I O R D E A R Q U I T E C T U R A U N I V E R S I D A D D E N A V A R R A Preguntas tipo OLIMPIADA DE DIBUJO TÉCNICO MARZO 2014 G E O M E T R Í A M É T R I C A. T
11 CONOCER LOS POLIEDROS Y DIFERENCIAR
 REPASO Y APOYO OBJETIVO 1 11 CONOCER LOS POLIEDROS Y DIERENCIAR LOS POLIEDROS REGULARES Nombre: Curso: echa: CONCEPTO DE POLIEDRO Vértice Un poliedro es un cuerpo geométrico cuyas caras son polígonos.
REPASO Y APOYO OBJETIVO 1 11 CONOCER LOS POLIEDROS Y DIERENCIAR LOS POLIEDROS REGULARES Nombre: Curso: echa: CONCEPTO DE POLIEDRO Vértice Un poliedro es un cuerpo geométrico cuyas caras son polígonos.
31. SISTEMA AXONOMÉTRICO. LA RECTA Y EL PLANO
 31. SISTEMA AXONOMÉTRICO. LA RECTA Y EL PLANO 31.1. Representación de la recta. Si un punto se representaba por cuatro proyecciones, la recta se representa igual por cuatro proyecciones. Tenemos la recta
31. SISTEMA AXONOMÉTRICO. LA RECTA Y EL PLANO 31.1. Representación de la recta. Si un punto se representaba por cuatro proyecciones, la recta se representa igual por cuatro proyecciones. Tenemos la recta
Elementos del cilindro
 Definición de cilindro Un cilindro es un cuerpo geométrico engendrado por un rectángulo que gira alrededor de uno de sus lados. Desarrollo del cilindro Elementos del cilindro Eje Es el lado fijo alrededor
Definición de cilindro Un cilindro es un cuerpo geométrico engendrado por un rectángulo que gira alrededor de uno de sus lados. Desarrollo del cilindro Elementos del cilindro Eje Es el lado fijo alrededor
MODULO I. LABORATORIO GEMOLÓGICO MLLOPIS
 3.1 I 3.1 INTRODUCCIÓN A LA CRIST RISTAL ALOGRAFÍA La Cristalografía es la Ciencia que estudia la materia cristalina, y siendo el mineral un cristal natural, estudiará sus caracteres cristalográficos.
3.1 I 3.1 INTRODUCCIÓN A LA CRIST RISTAL ALOGRAFÍA La Cristalografía es la Ciencia que estudia la materia cristalina, y siendo el mineral un cristal natural, estudiará sus caracteres cristalográficos.
UNIDAD 11 Figuras en el espacio
 Pág. 1 de 5 I. Conoces de cursos anteriores los poliedros regulares y algunas de sus características. Has reforzado ese conocimiento y lo has ampliado a los poliedros semirregulares? 1 Dibuja, a partir
Pág. 1 de 5 I. Conoces de cursos anteriores los poliedros regulares y algunas de sus características. Has reforzado ese conocimiento y lo has ampliado a los poliedros semirregulares? 1 Dibuja, a partir
ÁLGEBRA LINEAL II Práctica
 ÁLGEBRA LINEAL II Práctica 3.1-3.2 Geometría afín. (Curso 2013 2014) 1. En un espacio afín real de dimensión 3, se consideran dos sistemas de referencia R = O, ē 1, ē 2, ē 3 } y R = P, ū 1, ū 2, ū 3 },
ÁLGEBRA LINEAL II Práctica 3.1-3.2 Geometría afín. (Curso 2013 2014) 1. En un espacio afín real de dimensión 3, se consideran dos sistemas de referencia R = O, ē 1, ē 2, ē 3 } y R = P, ū 1, ū 2, ū 3 },
38. CUERPOS SÓLIDOS: DESARROLLOS Y TRANSFORMADAS Desarrollo de los Poliedros Regulares.
 1 38. CUERPOS SÓLIDOS: DESARROLLOS Y TRANSFORMADAS. 38.1. Desarrollo de los Poliedros Regulares. 38.1.1. Tetraedro. Dado que los poliedros regulares tienen sus caras iguales, el desarrollo de los mismos
1 38. CUERPOS SÓLIDOS: DESARROLLOS Y TRANSFORMADAS. 38.1. Desarrollo de los Poliedros Regulares. 38.1.1. Tetraedro. Dado que los poliedros regulares tienen sus caras iguales, el desarrollo de los mismos
* * * GEOMETRÍA DESCRIPTIVA * * * ÍNDICE
 ÍNDICE 1.- CONCEPTO DE PROYECCIÓN.... 1 Proyección de un punto.... 1 Clasificación de las proyecciones.... 1 Sistema Diédrico...3 Sistema de Planos Acotados...3 Sistema Axonométrico...3 Sistema Cónico...4
ÍNDICE 1.- CONCEPTO DE PROYECCIÓN.... 1 Proyección de un punto.... 1 Clasificación de las proyecciones.... 1 Sistema Diédrico...3 Sistema de Planos Acotados...3 Sistema Axonométrico...3 Sistema Cónico...4
A mi muy querida profesora que con ansias debe estar esperando mi trabajo. I. Introducción pag. 4
 MONOGRAFÍA NOMBRE : COLEGIO : GRADO : IVº B TEMA : Geometría del Espacio PROFESORA : FECHA : 30 de Noviembre DEDICATORIA A mi muy querida profesora que con ansias debe estar esperando mi trabajo índice
MONOGRAFÍA NOMBRE : COLEGIO : GRADO : IVº B TEMA : Geometría del Espacio PROFESORA : FECHA : 30 de Noviembre DEDICATORIA A mi muy querida profesora que con ansias debe estar esperando mi trabajo índice
POLIEDROS. ÁREAS Y VOLÚMENES.
 7. POLIEDROS. ÁREAS Y VOLÚMENES. EN ESTA UNIDAD VAS A APRENDER CUERPOS GEOMÉTRICOS POLIEDROS POLIEDROS REGULARES PRISMAS PIRÁMIDES CARACTERÍSTICAS DEFINICIÓN ELEMENTOS DEFINICIÓN ELEMENTOS - Tetaedro.
7. POLIEDROS. ÁREAS Y VOLÚMENES. EN ESTA UNIDAD VAS A APRENDER CUERPOS GEOMÉTRICOS POLIEDROS POLIEDROS REGULARES PRISMAS PIRÁMIDES CARACTERÍSTICAS DEFINICIÓN ELEMENTOS DEFINICIÓN ELEMENTOS - Tetaedro.
FIGURAS DEL ESPACIO. ÁREAS Y VOLÚMENES
 POLIEDROS : Cuerpo sólido limitado por polígonos, llamados caras; en la que algunas de las caras confluyen en líneas rectas, llamadas aristas; y algunas de las aristas confluyen en puntos,llamados vértices.
POLIEDROS : Cuerpo sólido limitado por polígonos, llamados caras; en la que algunas de las caras confluyen en líneas rectas, llamadas aristas; y algunas de las aristas confluyen en puntos,llamados vértices.
CUERPOS GEOMÉTRICOS. Los cuerpos geométricos son porciones de espacio limitadas por superficies planas o curvas.
 CUERPOS GEOMÉTRICOS CUERPOS GEOMÉTRICOS.- Los cuerpos geométricos son porciones de espacio limitadas por superficies planas o curvas. Clasificamos, en el siguiente esquema, los cuerpos geométricos: POLIEDROS.-
CUERPOS GEOMÉTRICOS CUERPOS GEOMÉTRICOS.- Los cuerpos geométricos son porciones de espacio limitadas por superficies planas o curvas. Clasificamos, en el siguiente esquema, los cuerpos geométricos: POLIEDROS.-
Módulo diseñado por: Docente María Cristina Marín Valdés
 Módulo diseñado por: Docente María Cristina Marín Valdés I.E. Eduardo Fernández Botero Amalfi (Ant) 2018 CONTENIDOS CONTENIDO PÁGINA Concepto de poliedros. 3 Clases de poliedros 3 Teorema de Euler. 4 Áreas
Módulo diseñado por: Docente María Cristina Marín Valdés I.E. Eduardo Fernández Botero Amalfi (Ant) 2018 CONTENIDOS CONTENIDO PÁGINA Concepto de poliedros. 3 Clases de poliedros 3 Teorema de Euler. 4 Áreas
INTRODUCCIÓN A LOS POLIEDROS
 INTRODUCCIÓN A LOS POLIEDROS AUTORIA MIGUEL ÁNGEL GUERRERO MOLINA TEMÁTICA POLIEDROS ETAPA BACHILLERATO Resumen Este artículo pretende dar una visión general de los poliedros. Trataremos su clasificación,
INTRODUCCIÓN A LOS POLIEDROS AUTORIA MIGUEL ÁNGEL GUERRERO MOLINA TEMÁTICA POLIEDROS ETAPA BACHILLERATO Resumen Este artículo pretende dar una visión general de los poliedros. Trataremos su clasificación,
El cubo o hexaedro regular
 El cubo o hexaedro regular Como los ángulos de un cuadrado miden 90, solo podemos formar un poliedro de caras cuadradas, tres por cada vértice. La suma de las caras que están unidas en cada vértice será:
El cubo o hexaedro regular Como los ángulos de un cuadrado miden 90, solo podemos formar un poliedro de caras cuadradas, tres por cada vértice. La suma de las caras que están unidas en cada vértice será:
a 2 = = 1600 ; a = 40 A = = 80. Iguales A = 361 1:150
 uno es agudo y el otro es obtuso. Á = (48. 5 ) / 2 = 120 D 2 = 20 2 + 10 2 + 6 2 = 536 ; D = 23 15 V = V S + V c = 2 / 3. π 125 + 1 / 3. π 25. 3 = 325/3. π Área = lado x lado = l 2 Los paralelepípedos
uno es agudo y el otro es obtuso. Á = (48. 5 ) / 2 = 120 D 2 = 20 2 + 10 2 + 6 2 = 536 ; D = 23 15 V = V S + V c = 2 / 3. π 125 + 1 / 3. π 25. 3 = 325/3. π Área = lado x lado = l 2 Los paralelepípedos
Diagonal: es un segmento que une dos vértices no consecutivos del poliedro. Puede trazarse en una misma cara o entre distintas caras.
 CLASIFICASION DE CUERPOS GEOMETRICOS 1 2 Cuerpos Geométrico s Ángulo diedro: es el ángulo formado por dos caras del poliedro. El ángulo formado por tres o más caras que concurren en un vértice, se denomina
CLASIFICASION DE CUERPOS GEOMETRICOS 1 2 Cuerpos Geométrico s Ángulo diedro: es el ángulo formado por dos caras del poliedro. El ángulo formado por tres o más caras que concurren en un vértice, se denomina
Dibujo y geometría descriptiva II 2014
 ` CONTENIDO 1. Conceptos básicos Cuerpos geométricos Intersección 2. Intersección entre planos y sólidos. 3. Intersección de plano con prisma 4. Intersección de plano con cilindro. 5. Intersección de sólido
` CONTENIDO 1. Conceptos básicos Cuerpos geométricos Intersección 2. Intersección entre planos y sólidos. 3. Intersección de plano con prisma 4. Intersección de plano con cilindro. 5. Intersección de sólido
ÍNDICE DE SISTEMAS Y MODELOS CRISTALOGRÁFICOS
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA CUNOR - CARRERA DE GEOLOGÍA CURSO DE MINERALOGÍA GENERAL PRÁCTICA No. 1 Realización de modelos Cristalográficos en 3D. ÍNDICE DE SISTEMAS Y MODELOS CRISTALOGRÁFICOS
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA CUNOR - CARRERA DE GEOLOGÍA CURSO DE MINERALOGÍA GENERAL PRÁCTICA No. 1 Realización de modelos Cristalográficos en 3D. ÍNDICE DE SISTEMAS Y MODELOS CRISTALOGRÁFICOS
UNIDAD 1: LA MATERIA CRISTALINA
 UNIDAD 1: LA MATERIA CRISTALINA CONCEPTOS MATERIA CRISTALINA: Aquella cuyas partículas están perfectamente ordenadas en el espacio, ocupando posiciones fijas y a distancias regulares unas de otras, formando
UNIDAD 1: LA MATERIA CRISTALINA CONCEPTOS MATERIA CRISTALINA: Aquella cuyas partículas están perfectamente ordenadas en el espacio, ocupando posiciones fijas y a distancias regulares unas de otras, formando
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: DIBUJO TÉCNICO II
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2014-2015 MATERIA: DIBUJO TÉCNICO II INSTRUCCIONES GENERALES Y CALIFICACIÓN Después
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2014-2015 MATERIA: DIBUJO TÉCNICO II INSTRUCCIONES GENERALES Y CALIFICACIÓN Después
POLIEDROS. POLIEDROS Prof. Annabella Zapattini. Definición: Llamamos poliedro a la región del espacio limitada por polígonos planos.
 POLIEDROS Definición: Llamamos poliedro a la región del espacio limitada por polígonos planos. Definiciones: Llamamos caras de un poliedro a los polígonos que lo definen. Llamamos aristas a los segmentos
POLIEDROS Definición: Llamamos poliedro a la región del espacio limitada por polígonos planos. Definiciones: Llamamos caras de un poliedro a los polígonos que lo definen. Llamamos aristas a los segmentos
APLICACIÓN DE DESARROLLOS
 TEMA: DESARROLLOS DESARROLLOS Es el proceso de trazar una superficie geométrica sobre un plano de tal manera que se pueda extender para mostrar la superficie desarrollada. De tal manera que al cortarla
TEMA: DESARROLLOS DESARROLLOS Es el proceso de trazar una superficie geométrica sobre un plano de tal manera que se pueda extender para mostrar la superficie desarrollada. De tal manera que al cortarla
Contenido. Tema 11. Geometría en el espacio. 1. Poliedros Regulares o sólidos Platónicos Teorema de Euler Prismas...
 Tema 11. Geometría en el espacio Contenido 1. Poliedros Regulares o sólidos Platónicos... 2 2. Teorema de Euler... 3 3. Prismas... 3 4. Pirámides... 5 5. Cilindro... 7 6. Cono... 8 7. Esfera... 9 8. Coordenadas
Tema 11. Geometría en el espacio Contenido 1. Poliedros Regulares o sólidos Platónicos... 2 2. Teorema de Euler... 3 3. Prismas... 3 4. Pirámides... 5 5. Cilindro... 7 6. Cono... 8 7. Esfera... 9 8. Coordenadas
2.2 Simetría en los sólidos cristalinos
 2.2 Simetría en los sólidos cristalinos Observación: Distribución de las caras en los cristales Sentido de proporción y equilibrio geométrico Simetría externa de los cristales permite: - Placer estético
2.2 Simetría en los sólidos cristalinos Observación: Distribución de las caras en los cristales Sentido de proporción y equilibrio geométrico Simetría externa de los cristales permite: - Placer estético
ÁLGEBRA LINEAL II Práctica
 ÁLGEBRA LINEAL II Práctica 3.1-3.2 Geometría afín. (Curso 2015 2016) 1. En el espacio afín IR 3 se considera la referencia canónica R y la referencia R = (1, 0, 1); (1, 1, 0), (1, 1, 1), (1, 0, 0)}. Denotamos
ÁLGEBRA LINEAL II Práctica 3.1-3.2 Geometría afín. (Curso 2015 2016) 1. En el espacio afín IR 3 se considera la referencia canónica R y la referencia R = (1, 0, 1); (1, 1, 0), (1, 1, 1), (1, 0, 0)}. Denotamos
Poliedro cóncavo: es aquel que no cumple la propiedad anterior. Una recta puede cortarlo por más de dos puntos.
 El sistema diédrico D13 El prisma Poliedros Poliedro es un cuerpo geométrico limitado por polígonos. Caras del poliedro son los polígonos que lo limitan. Vértices son los vértices de las caras. Aristas
El sistema diédrico D13 El prisma Poliedros Poliedro es un cuerpo geométrico limitado por polígonos. Caras del poliedro son los polígonos que lo limitan. Vértices son los vértices de las caras. Aristas
ÁLGEBRA LINEAL II Práctica
 ÁLGEBRA LINEAL II Práctica 3.1-3.2 Geometría afín. (Curso 2012 2013) 1. En un espacio afín real de dimensión 3, se consideran dos sistemas de referencia R = O, ē 1, ē 2, ē 3 } y R = P, ū 1, ū 2, ū 3 },
ÁLGEBRA LINEAL II Práctica 3.1-3.2 Geometría afín. (Curso 2012 2013) 1. En un espacio afín real de dimensión 3, se consideran dos sistemas de referencia R = O, ē 1, ē 2, ē 3 } y R = P, ū 1, ū 2, ū 3 },
1. Dualidad de poliedros. 2. Prismas y antiprismas. 3. Estructuras espaciales. 4. Secciones y simetrías de poliedros. 5. Macizamiento del espacio
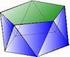 5. Poliedros Matemáticas 2º ESO 1. Dualidad de poliedros 2. Prismas y antiprismas 3. Estructuras espaciales 4. Secciones y simetrías de poliedros 5. Macizamiento del espacio 6. Coordenadas en el espacio
5. Poliedros Matemáticas 2º ESO 1. Dualidad de poliedros 2. Prismas y antiprismas 3. Estructuras espaciales 4. Secciones y simetrías de poliedros 5. Macizamiento del espacio 6. Coordenadas en el espacio
Problema 1. Cuántos triángulos rectángulos se pueden formar que tengan sus vértices en vértices de una caja?
 Nota4: Soluciones problemas propuestos Problema 1. Cuántos triángulos rectángulos se pueden formar que tengan sus vértices en vértices de una caja? Solución: Consideremos primero todos aquellos triángulos
Nota4: Soluciones problemas propuestos Problema 1. Cuántos triángulos rectángulos se pueden formar que tengan sus vértices en vértices de una caja? Solución: Consideremos primero todos aquellos triángulos
32. SISTEMA PERSPECTIVA CABALLERA
 32. SISTEMA PERSPECTIVA CABALLERA 32.1. Elementos del sistema. En el sistema de perspectiva caballera continuamos utilizando un triedro trirectangulo y las proyecciones cilindrica del mismo modo que en
32. SISTEMA PERSPECTIVA CABALLERA 32.1. Elementos del sistema. En el sistema de perspectiva caballera continuamos utilizando un triedro trirectangulo y las proyecciones cilindrica del mismo modo que en
Los cuerpos geométricos.
 Los cuerpos geométricos. Se denominan cuerpos geométricos a aquellos elementos que, ya sean reales o ideales que existen en la realidad o pueden concebirse mentalmente ocupan un volumen en el espacio desarrollándose
Los cuerpos geométricos. Se denominan cuerpos geométricos a aquellos elementos que, ya sean reales o ideales que existen en la realidad o pueden concebirse mentalmente ocupan un volumen en el espacio desarrollándose
Bases Matemáticas para la Educación Primaria. Guía de Estudio. Tema: Figuras geométricas
 Bases Matemáticas para la Educación Primaria Guía de Estudio Tema: Figuras geométricas 1 Conceptos geométricos En la clase de matemáticas, y en los textos escolares, encontramos expresiones tales como:
Bases Matemáticas para la Educación Primaria Guía de Estudio Tema: Figuras geométricas 1 Conceptos geométricos En la clase de matemáticas, y en los textos escolares, encontramos expresiones tales como:
ÁLGEBRA LINEAL II Práctica
 ÁLGEBRA LINEAL II Práctica 3.1-3.2 Geometría afín. (Curso 2016 2017) 1. En el espacio afín IR 3 se considera la referencia canónica R y la referencia R = {(1, 0, 1); (1, 1, 0), (1, 1, 1), (1, 0, 0)}. Denotamos
ÁLGEBRA LINEAL II Práctica 3.1-3.2 Geometría afín. (Curso 2016 2017) 1. En el espacio afín IR 3 se considera la referencia canónica R y la referencia R = {(1, 0, 1); (1, 1, 0), (1, 1, 1), (1, 0, 0)}. Denotamos
5. Cristales y agregados minerales en Naturaleza
 5. Cristales y agregados minerales en Naturaleza En la naturaleza los minerales se encuentran en la forma de los cristales mas o menos bien formados, granos irregulares, agregados mono- y poliminerales,
5. Cristales y agregados minerales en Naturaleza En la naturaleza los minerales se encuentran en la forma de los cristales mas o menos bien formados, granos irregulares, agregados mono- y poliminerales,
CUERPOS GEOMÉTRICOS EN EL PLANO Y EN EL ESPACIO: APLICACIONES DIDÁCTICAS.
 CUERPOS GEOMÉTRICOS EN EL PLANO Y EN EL ESPACIO: APLICACIONES DIDÁCTICAS. Resumen AUTORIA FERNANDO VALLEJO LÓPEZ TEMÁTICA DIDÁCTICA DE LA MATEMÁTICA ETAPA ESO EN ÉSTE ARTÍCULO, SE ESTUDIAN LOS CUERPOS
CUERPOS GEOMÉTRICOS EN EL PLANO Y EN EL ESPACIO: APLICACIONES DIDÁCTICAS. Resumen AUTORIA FERNANDO VALLEJO LÓPEZ TEMÁTICA DIDÁCTICA DE LA MATEMÁTICA ETAPA ESO EN ÉSTE ARTÍCULO, SE ESTUDIAN LOS CUERPOS
Grupos espaciales de simetría
 Grupos espaciales de simetría La simetría de los átomos que constituyen el cristal se describe con un grupo de simetría espacial constituido por un subgrupo de traslación (el retículo) y determinados elementos
Grupos espaciales de simetría La simetría de los átomos que constituyen el cristal se describe con un grupo de simetría espacial constituido por un subgrupo de traslación (el retículo) y determinados elementos
CUERPOS GEOMÉTRICOS. 2º E.S.O. PUNTOS, RECTAS Y PLANOS EN EL ESPACIO DETERMINACIÓN DE PUNTOS, RECTAS Y PLANOS DETERMINACIÓN DE PUNTOS, RECTAS Y PLANOS
 CUERPOS GEOMÉTRICOS. PUNTOS, RECTAS Y PLANOS EN EL ESPACIO 2º E.S.O. DETERMINACIÓN DE PUNTOS, RECTAS Y PLANOS Determinación de puntos: DETERMINACIÓN DE PUNTOS, RECTAS Y PLANOS Determinación de una recta:
CUERPOS GEOMÉTRICOS. PUNTOS, RECTAS Y PLANOS EN EL ESPACIO 2º E.S.O. DETERMINACIÓN DE PUNTOS, RECTAS Y PLANOS Determinación de puntos: DETERMINACIÓN DE PUNTOS, RECTAS Y PLANOS Determinación de una recta:
GEOMETRÍA DEL ESPACIO
 GEOMETRÍA DEL ESPACIO Lic. Saúl Villamizar Valencia 33 1 GEOMETRÍA DEL ESPACIO Definición: Es la parte de la geometría que estudia las propiedades de las figuras y sólidos geométricos cuyos elementos
GEOMETRÍA DEL ESPACIO Lic. Saúl Villamizar Valencia 33 1 GEOMETRÍA DEL ESPACIO Definición: Es la parte de la geometría que estudia las propiedades de las figuras y sólidos geométricos cuyos elementos
Figuras de tres dimensiones
 Figuras de tres dimensiones Poliedros: cuerpos geométricos limitados por 4 o más superficies planas que son polígonos. Poliedros regulares: todas las caras de igual forma y tamaño. Solo existen 5. Prismas
Figuras de tres dimensiones Poliedros: cuerpos geométricos limitados por 4 o más superficies planas que son polígonos. Poliedros regulares: todas las caras de igual forma y tamaño. Solo existen 5. Prismas
Geometría. Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid
 Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
Geometría. Ángulos. Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid
 Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
GEOMETRÍA. Convexos Llano (Plano) Cóncavo Giro. Consecutivos Adyacentes Diedro Complementario Suplementario
 GEOMETRÍA Angulo.- Es la abertura comprendida entre dos rectas que se encuentran en un punto. Estas rectas se llaman lados del ángulo, y el punto de encuentro se denomina vértice. Un ángulo suele designarse
GEOMETRÍA Angulo.- Es la abertura comprendida entre dos rectas que se encuentran en un punto. Estas rectas se llaman lados del ángulo, y el punto de encuentro se denomina vértice. Un ángulo suele designarse
MINISTERIO DE EDUCACIÓN PÚBLICA DIRECCIÓN DE DESARROLLO CURRICULAR DEPARTAMENTO DE PRIMERO Y SEGUNDO CICLOS ASESORÍA NACIONAL DE MATEMÁTICA
 MINISTERIO DE EDUCACIÓN PÚBLICA DIRECCIÓN DE DESARROLLO CURRICULAR DEPARTAMENTO DE PRIMERO Y SEGUNDO CICLOS ASESORÍA NACIONAL DE MATEMÁTICA Área matemática: Geometría Primer periodo 20XX Habilidad(es)
MINISTERIO DE EDUCACIÓN PÚBLICA DIRECCIÓN DE DESARROLLO CURRICULAR DEPARTAMENTO DE PRIMERO Y SEGUNDO CICLOS ASESORÍA NACIONAL DE MATEMÁTICA Área matemática: Geometría Primer periodo 20XX Habilidad(es)
REGULARES.
 Diédrico Poliedros REGULARES http://www.edu.xunta.es/contidos/premios/p2004/b/poliedros/poliedros.html POLIEDROS Los poliedros son los cuerpos geométricos limitados por polígonos. Poliedros regulares son
Diédrico Poliedros REGULARES http://www.edu.xunta.es/contidos/premios/p2004/b/poliedros/poliedros.html POLIEDROS Los poliedros son los cuerpos geométricos limitados por polígonos. Poliedros regulares son
Poliedros y cuerpos redondos para imprimir
 Poliedros y cuerpos redondos para imprimir Nombre Curso: Fecha: Escribe en la parte derecha lo que falta. 1. Los cuerpos redondos. La geometría del espacio estudia los cuerpos que tienen tres dimensiones:
Poliedros y cuerpos redondos para imprimir Nombre Curso: Fecha: Escribe en la parte derecha lo que falta. 1. Los cuerpos redondos. La geometría del espacio estudia los cuerpos que tienen tres dimensiones:
GUÍA CUERPOS GEOMÉTRICOS Nº1 POLIEDROS. NOMBRE. FECHA: 03/10/2018. Tercero básico
 GUÍA CUERPOS GEOMÉTRICOS Nº1 POLIEDROS NOMBRE. FECHA: 03/10/2018. Tercero básico 1- Qué son los cuerpos geométricos? Un sólido o cuerpo geométrico es una figura geométrica de tres dimensiones (largo, ancho
GUÍA CUERPOS GEOMÉTRICOS Nº1 POLIEDROS NOMBRE. FECHA: 03/10/2018. Tercero básico 1- Qué son los cuerpos geométricos? Un sólido o cuerpo geométrico es una figura geométrica de tres dimensiones (largo, ancho
Sistema diédrico: poliedros regulares y pirámides. Icosaedro (modificación de la fotografía: Eneágono del Banco de imágenes del ISFTIC)
 UNIDAD 6 Sistema diédrico: poliedros regulares y pirámides Icosaedro (modificación de la fotografía: Eneágono del Banco de imágenes del ISFTIC) L a representación de los poliedros debe abordarse desde
UNIDAD 6 Sistema diédrico: poliedros regulares y pirámides Icosaedro (modificación de la fotografía: Eneágono del Banco de imágenes del ISFTIC) L a representación de los poliedros debe abordarse desde
Introducción. Este trabajo será realizado con los siguientes fines :
 Introducción Este trabajo será realizado con los siguientes fines : Aprender mas sobre la geometría analítica. Tener mejores conceptos sobre ella ; los cuales me pueden ayudar con las pruebas ICFES. Otro
Introducción Este trabajo será realizado con los siguientes fines : Aprender mas sobre la geometría analítica. Tener mejores conceptos sobre ella ; los cuales me pueden ayudar con las pruebas ICFES. Otro
ACTIVIDADES PARA LA SESIÓN PRIMERA
 ACTIVIDADES PARA LA SESIÓN PRIMERA AUTOR: Begoña Soler de Dios 1 Máster en Profesor de Educación Secundaria Esp. Matemáticas 1 besode@alumni.uv.es Sesión 1 1. Los poliedros regulares convexos: Cuántos
ACTIVIDADES PARA LA SESIÓN PRIMERA AUTOR: Begoña Soler de Dios 1 Máster en Profesor de Educación Secundaria Esp. Matemáticas 1 besode@alumni.uv.es Sesión 1 1. Los poliedros regulares convexos: Cuántos
Homología y Afinidad IES BELLAVISTA
 Homología y Afinidad IES BELLAVISTA La proyectividad es una transformación geométrica que transforma unos elementos geométricos en otros (puntos, rectas, haces de rectas, formas planas, etc.) mediante
Homología y Afinidad IES BELLAVISTA La proyectividad es una transformación geométrica que transforma unos elementos geométricos en otros (puntos, rectas, haces de rectas, formas planas, etc.) mediante
Perspectiva y Geometría Descriptiva I
 Cuadernillo de ejercicios y preguntas El filósofo Eric Hoffer dice: "Los que están aprendiendo heredarán la Tierra, mientras que los que ya saben estarán perfectamente equipados para vivir en un mundo
Cuadernillo de ejercicios y preguntas El filósofo Eric Hoffer dice: "Los que están aprendiendo heredarán la Tierra, mientras que los que ya saben estarán perfectamente equipados para vivir en un mundo
12 ÁNGULOS EN DIÉDRICO
 12-1 Apuntes de dibujo técnico Patxi Aguirrezabal M artin 12 ÁNGULOS EN DIÉDRICO Ángulos de la recta con los planos de proyección. Ángulo de dos rectas y bisectriz del ángulo. Ángulo de recta y plano.
12-1 Apuntes de dibujo técnico Patxi Aguirrezabal M artin 12 ÁNGULOS EN DIÉDRICO Ángulos de la recta con los planos de proyección. Ángulo de dos rectas y bisectriz del ángulo. Ángulo de recta y plano.
Figura plana Área Ejemplo Cuadrado. Área =
 ersión: Septiembre 01 Áreas y volúmenes Por Sandra Elvia Pérez Márquez Áreas de figuras planas Las aplicaciones de las figuras planas requieren, por lo general, conocer (o calcular) dos características
ersión: Septiembre 01 Áreas y volúmenes Por Sandra Elvia Pérez Márquez Áreas de figuras planas Las aplicaciones de las figuras planas requieren, por lo general, conocer (o calcular) dos características
APLICACIÓN DE LAS FUNCIONES AL ESTUDIO DE MOSAICOS Y POLIEDROS
 APLICACIÓN DE LAS FUNCIONES AL ESTUDIO DE MOSAICOS Y POLIEDROS 1. Introducción La investigación que se presenta a continuación tiene su origen en mi función de director de trabajos de investigación realizados
APLICACIÓN DE LAS FUNCIONES AL ESTUDIO DE MOSAICOS Y POLIEDROS 1. Introducción La investigación que se presenta a continuación tiene su origen en mi función de director de trabajos de investigación realizados
Definición: Un prisma es un cuerpo geométrico (un poliedro) que tiene dos bases iguales y paralelas entre sí,
 CONOCE LAS MATEMÁTICAS. CEIP Manuel Siurot (La Palma del Cdo.) Definición: Un prisma es un cuerpo geométrico (un poliedro) que tiene dos bases iguales y paralelas entre sí, llamadas BASES (que pueden ser
CONOCE LAS MATEMÁTICAS. CEIP Manuel Siurot (La Palma del Cdo.) Definición: Un prisma es un cuerpo geométrico (un poliedro) que tiene dos bases iguales y paralelas entre sí, llamadas BASES (que pueden ser
IES CUADERNO Nº 8 NOMBRE: FECHA: / / Cuerpos geométricos
 Cuerpos geométricos Contenidos 1. Poliedros Definición Elementos de un poliedro 2. Tipos de poliedros Prismas Prismas regulares Desarrollo de un prisma recto Paralelepípedos Pirámides Pirámides regulares
Cuerpos geométricos Contenidos 1. Poliedros Definición Elementos de un poliedro 2. Tipos de poliedros Prismas Prismas regulares Desarrollo de un prisma recto Paralelepípedos Pirámides Pirámides regulares
