3. ARITMÉTICA MODULAR Congruencias de números enteros. Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM.
|
|
|
- Ángela Soler Ortíz
- hace 8 años
- Vistas:
Transcripción
1 3.1. Congruencias de números enteros Definición de congruencia Dado un número entero fijo p>1 y dos números enteros cualesquiera a, b Z, sedicequea es congruente con b módulo p, yseindicaa b (mod p), si p (a b). Es fácil ver que a b (mod p) si y sólo si coinciden los restos de dividir los números a y b por p, que se llaman residuos módulo p. En módulo p los posibles residuos son: 0, 1, 2,...,p 1. Propiedades La relación de congruencia módulo p>1 verifica las siguientes propiedades: 1. Reflexiva: a b (mod p), para todo a Z. 2. Simétrica: a b (mod p) = b a (mod p). 3. Transitiva: a b (mod p) yb c (mod p) = a c (mod p). Por verificar estas tres propiedades, se dice que la relación de congruencia es una relación de equivalencia. Relación de equivalencia Se llama relación de equivalencia sobre un conjunto A a cualquier relación R entre sus elementos que verifica las siguientes tres propiedades: 1. Reflexiva: ara, para cualquier a A. 2. Antisimétrica: si arb entonces bra. 3. Transitiva: si arb y brc, entonces arc. Una relación de equivalencia R sobre un conjunto A produce una partición del conjunto en subconjuntos disjuntos, llamados clases de equivalencia, cada uno de ellos formados por elementos que están relacionados entre sí. Esta partición se representa por A/R y se llama conjunto cociente. El conjunto Z p Cada clase del conjunto cociente de Z por la relación de congruencia módulo p está formada por todos los números enteros con el mismo residuo módulo p. Puesto que hay p posibles residuos habrá p clases distintas, cada una de ellas asociada a un residuo r, 0 r p 1, y que se representa por [r] p, r p ó r si no hay lugar a error. El conjunto de todas las clases se representa por Z p,esdecir: Z p = 0, 1, 2,...,p 1 donde r = {a Z : a r (mod p)} = {np + r : n Z} 1. Estudia si son ciertas las siguientes congruencias: (a) 2 4 (mod 2) ; (b) 13 2 (mod 5) ; (c) 15 3 (mod 3) ; (d) 20 4 (mod 7). 2. Describe los conjuntos Z 2 y Z Demuestra que si n 5 es primo, entonces n 1 (mod 6) ó n 5 (mod 6), es decir, n 1 6 ó n (a) Cierta; (b) Cierta; (c) Cierta; (d) No es cierta. 2. Z 2 = 0, 1, Z 5 = 0, 1, 2, 3, Prueba que los número congruentes con 0, 2, 3 y 4 no son primos.
2 3.2. Residuos de operaciones aritméticas Residuos de operaciones aritméticas Dado un número entero p>1, si a α (mod p) yb β (mod p), entonces: (a + b) (α + β) (modp) ab αβ (mod p) a b α b (mod p) Ojo!: No es cierto, en general, que a b α β (mod p). Simplificación de congruencias de productos Si mcd(c, p) = 1 entonces: ac bc (mod p) = a b (mod p) En general: ac bc (mod p) = a b (mod p mcd(c,p) ) Criterios de divisibilidad Si n = a k a k 1...a 2 a 1 a 0 = k i=0 a i10 i, con 0 a i 9, entonces: n es divisible por 2 si y sólo si a 0 es divisible por 2. n es divisible por 3 si y sólo si k i=0 a i es divisible por 3. n es divisible por 4 si y sólo si a 1 a 0 = 10a 1 + a 0 es divisible por 4 ( 2a 1 + a 0 es divisible por 4). n es divisible por 5 si y sólo si a 0 es divisible por 5 ( a 0 =0óa 0 = 5). n es divisible por 9 si y sólo si k i=0 a i es divisible por 9. n es divisible por 11 si y sólo si k i=0 ( 1)i a i es divisible por 11. Regla del nueve El producto de números naturales debe verificar la siguiente regla, conocida como regla del nueve: n = a k a k 1...a 2 a 1 a 0 = k i=0 a i10 i, con 0 a i 9 k l m = b l b l 1...b 2 b 1 b 0 = l i=0 b i10 i = n m a i b i (mod 9), con 0 b i 9 1. Halla el residuo módulo 7 del resultado de las siguientes operaciones sin realizarlas: (a) ; (b) Comprueba si N = y M = son divisibles por Qué cifra falta en la igualdad 14! = ? 4. Usa la regla del nueve para qué dos de las siguientes operaciones son falsas. Qué se puede decir de la otra? (a) = ; (b) = ; (c) = Qué dígito falta en la operación: = ? i=0 i=0 1. (a) 4; (b) N no y M si (a) Falsa; (b) Falsa; (c) La regla del nueve no implica falsedad, luego puede estar bien
3 3.3. Aritmética en Z p Operaciones en Z p La compatibilidad de la congruencia con la suma y el producto de números enteros permite definir en Z p las operaciones suma y producto, para cada 0 a, b < p, como: Suma: a + b = a + b Producto: a b = a b Divisores de cero Se llaman divisores de cero a cualesquiera a, b Z p, con a = 0 = b, tales que a b = 0. Es fácil ver que: Existen divisores de cero en Z p p no es primo (es compuesto) Elementos inversibles Se dice que a Z p es un elemento inversible ó unidad si existe b Z p tal que a b = 1, y se indica a 1 = b y a 1 para referirse a cualquier elemento de la clase. Es fácil ver que para cualquier p>1 existen elementos inversibles. Se representa por U p al conjunto de todos los elementos inversibles de Z p. Estructura de U p a U p mcd(a, p) =1 En consecuencia, si p es primo: U p = Z p 0. Si a, b U p entonces: a b U p, a 1 U p,ya U p = U p. 1. Construye las tablas de sumar y multiplicar en Z 2, Z 5 y Z Halla los divisores de cero y los elementos inversibles en Z 6, Z 7, Z 8 y Z Halla los siguientes inversos: (a) de 6enZ 17 ; (b) de 3enZ 10 ; (c) de 5enZ 12 ; (d) de 7enZ 16 ; (e) de 5enZ 13 ; (f) de 777 en Z (a) Demuestra que todos los elementos de Z 11 0,excepto1y10, se pueden agrupar de dos en dos de manera que cada uno de ellos es el inverso del otro. (b) Demuestra que 10! 1 (mod 11). (c) Demuestra que si p es primo los únicos elementos de Z p que coinciden con su inverso son 1yp 1. (d) Demuestra que si p es primo entonces (p 1)! 1(modp) (Teorema de Wilson, 1770). (e) Halla, sin calculadora, el resto de dividir 15! por Las tablas que se obtienen al sumar y multiplicar todos sus elementos entre sí. Divisores de cero: 2y3, 3y4. Divisores de cero: 2y4, 4y4, 4y6. 2. Z 6 : Inversibles: 1 1 = 1, 5 1 ; Z 8 : = 5. Inversibles: 1 1 = 1, 3 1 = 3, 5 1 = 5, 7 1 ; = 7. Divisores de cero: no hay. Z 7 : Inversibles: 1 1 = 1, 2 1 = 4, 3 1 = 5, 4 1 = 2, 5 1 = 3, 6 1 ; = 6. Divisores de cero: 3y5, 3y10, 5y6, 5y9, 5y12, 6y10, 9y10, 10 y 12. Z 15 : Inversibles: 1 1 = 1, 2 1 = 8, 4 1 = 4, 7 1 = 13, 8 1 = 2, 11 1 = 11, 13 1 = 7, = (a) 3; (b) 7; (c) 5; (d) 7; (e) 8; (f) (a) Se hallan los inversos de todos y se agrupan. (b) Usa las agrupaciones obtenidas en el apartado anterior. (c) Se impone la condición de que un elemento coincide con su inverso. (d) Utiliza en mismo argumento que en (b). (e) Utiliza el teorema de Wilson.
4 3.4. Residuos de potencias Cálculo residuos de potencias Para calcular el residuo de x = módulo 22 se puede proceder como sigue: 1. En primer lugar, puesto que (mod 22): x = (mod 22). 2. Se expresa el exponente en base 2: 46 = = = Se calcula el residuo de la potencia a partir de los residuos que tienen por exponente las potencias de 2: 13 2 = (mod 22) 13 4 = = (mod 22) 13 8 = = 25 3 (mod 22) = =9 9 (mod 22) = = (mod 22) = = = (mod 22) 4. El residuo de la potencia pedida es: x = (mod 22). Función de Euler Para cada número natural n, se define la función de Euler Φ(n) como el número de naturales menores que n relativamente primos con n, es decir: Φ(n) = {x N :1 x n ymcd(x, n) =1} donde A es el cardinal o número de elementos del conjunto A. Para los primeros números naturales, la función de Euler es: n Φ(n) Propiedades 1. Para cualquier número entero p>1: Φ(p) = U p. 2. Si p es primo, entonces: Φ(p α )=p α p α Si mcd(a, b) = 1, entonces: Φ(ab) = Φ(a)Φ(b). 4. Si n = p α 1 1 pα pα k k, con cada p i primo, entonces: Φ(n) =n p1 p2 p k. Teorema de Euler Si mcd(a, p) = 1, entonces: a Φ(p) 1(modp). Teorema de Fermat Si p es primo y no es divisor a, entonces: a p 1 1(modp). 1. Calcula el último dígito de las siguientes potencias: 6 20,7 93 y Calcula el resto de de las siguientes divisiones: (a) : 11; (b) 3 47 : 23; (c) 3 15 : 17; (d) : 13; (e) : 20; (f) : Calcula el residuo de en los módulos 2, 5 y 7.
5 4. Comprueba que (mod 11) y (mod 31), y concluye que (mod 341). 5. Realiza en Z 203 la siguiente operación: Demuestra que para cualquier n Z las últimas cifras de n y n 5 son iguales. 1. 6, 7 y (a) 5; (b) 4; (c) 6; (d) 8; (e) 1; (f) , 1 y Comprueba que son ciertas las dos primeras afirmaciones, y úsalas para obtener la última Consecuencia de que, por el teorema de Fermat, si 0 a 9 entonces a 4 1 (mod 10).
6 3.5. Ecuaciones lineales de congruencias Ecuaciones lineales de congruencias Se llama ecuación lineal de congruencias a cualquier ecuación de la forma ax b (mod p), donde a, b Z y p>1, y se llama solución a cualquier x Z que verifica la ecuación. Resolución La condición necesaria y suficiente para que la ecuación en congruencias ax b (mod p) tenga solución en x es que la ecuación ax + py = b tenga solución en x e y, y esta ecuación tiene solución si y sólo si mcd(a, p) b. Por tanto: ax b (mod p) tiene solución en x mcd(a, p) b Para resolver la ecuación se procede según el caso: Si mcd(a, p) = 1, es solución cualquier x a 1 b (mod p), donde a 1 es el inverso de a módulo p. La solución es única en Z p. Si mcd(a, p) =d>1, con d b, es solución cualquier: x x 0 + tp d (mod p), t =0, 1, 2,...,d 1 donde x 0 es una solución particular de x en la ecuación diofántica ax + py = b. La ecuación tiene exactamente d soluciones en Z p. 1. Hallar todas las soluciones enteras de las ecuaciones: (a) 5x +2 5 (mod 7); (b) 3x +4 5 (mod 6); (c) 12x 9 (mod 27); (d) 8x 12 (mod 28); (e) 5x 1 (mod 11); (f) 4x 3 (mod 7); (g) 5x 7 (mod 15). 2. Resuelve las siguientes ecuaciones: (a) 66x = 42 en Z 168 ; (b) 21x = 18 en Z 30 ; (c) 35x = 42 en Z (a) x =7k + 2, k Z; (b) No tiene solución; (c) x 3, 12, 21 (mod 27); (d) x 5, 12, 19, 26 (mod 28); (e) x 9 (mod 11); (f) x 6 (mod 7); (g) No tiene solución. 2. (a) x 21, 49, 77, 105, 133, 161 (mod 168); (b) x 3, 13, 23 (mod 30); (c) x 3, 10, 17, 24, 31, 38, 45 (mod 49).
7 3.6. Sistemas lineales de congruencias Sistemas lineales de congruencias x a 1 (mod p 1 ) x a 2 (mod p 2 ) Se llama sistema lineal de congruencias a un conjunto de ecuaciones del tipo: (). x a n (mod p n ) Teorema chino del resto Si a i,p i Z con p i > 1ymcd(p i,p j ) = 1 (primos entre sí) para i = j, entonces el sistema de congruencias () tiene solución única en Z p con p = p 1 p 2...p n. Además, la solución es: p p p x a 1 q 1 + a 2 q a n q n (mod p) p 1 p 2 p n donde q i es tal que q i p p i 1(modp i ), 1 i n. 1. (a) Qué enteros dan resto 1 al dividirlos por 2 y por 3? (b) Qué enteros divisibles por 5 dan resto 1 al dividirlos por 3? 2. Halla un número natural cuyos restos al dividirlo por 3, 4, 5 y 6 sean, respectivamente, 2, 3, 4 y 5. (Brahmegupta, siglo VII) 3. Resuelve los siguientes sistemas de congruencias: x 2 (mod 3) x 2 (mod 5) (a) x 3 (mod 5) (b) 2x 1 (mod 7) x 2 (mod 7) 3x 4 (mod 11) (c) x 2 (mod 4) x 1 (mod 6) 4. Encuentra los números enteros n tales que n + 1 es múltiplo de 3, n +3 es múltiplo de 4 y n +5 es múltiplo de Sabiendo que mcd(b, 561) = 1, justifica las siguientes afirmaciones: (a) El número b verifica que: b 2 1 (mod 3), b 10 1 (mod 11) y b 16 1 (mod 17). (b) El número b verifica que: b (mod 3), b (mod 11) y b (mod 17). (c) El número b verifica que: b (mod 561). 6. Resuelve los siguientes sistemas de congruencias: 120x 180 (mod 450) 4x 11 (mod 15) (a) (b) 24x 76 (mod 100) 10x 8 (mod 12) (c) 168x 24 (mod 220) 56x 40 (mod 68) 7. Unos piratas encuentran en una isla desierta un cofre repleto de monedas de oro, en el que no caben más de Si los 5 cabecillas del grupo se reparten equitativamente el tesoro les sobra 1 moneda, si incluyen a los oficiales en el reparto son 13 y les sobran 6 monedas, y si incluyen a los 18 miembros de la tripulación les sobran 9 monedas. Cuántas monedas contiene el cofre? 8. Una banda de 17 piratas se reúne para repartirse un cofre con más de 100 monedas de oro, sobrando 1 moneda después del reparto. En la consiguiente pelea, muere un pirata y vuelve a hacerse el reparto sobrando de nuevo 1 moneda. Cuál es menor número de monedas que puede contener el cofre? Supongamos que la solución anterior es el número real de monedas en el cofre y que la historia continúa: siempre que sobran monedas en el reparto hay pelea y muere un pirata. Cuántos piratas quedarán vivos cuando en el reparto no sobre ninguna moneda?
8 9. Se reparten cuatro bolsas iguales de caramelos entre tres grupos de niños. En el primer grupo, que tiene cinco niños, se reparten dos bolsas y sobra un caramelo. En el segundo grupo, de seis niños, se reparte una bolsa y sobran dos caramelos. En el tercer grupo, de siete niños, se reparte una bolsa y sobran tres caramelos. Sabiendo que el número total de caramelos no llega a 500, cuántos caramelos contiene cada bolsa? 10. Un distribuidor de equipos informáticos efectuó un pedido de entre 1000 y 1500 equipos a un fabricante que se los envió en contenedores completos con capacidad para 68 equipos cada uno. El distribuidor los repartió a los diferentes puntos de venta usado furgonetas con capacidad para 20 equipos, dejando 32 equipos sin repartir en el almacén. Cuántos equipos pidió el distribuidor a la fábrica? 11. Se dispone de una cantidad par de monedas, menor que 600, que se quieren disponer en filas. Si se ordenan en filas de 17 monedas, sobran 8. Si se consideran únicamente la mitad de las monedas iniciales y se ordenan en filas de 7 monedas, sobran 3. Cuántas monedas hay? Es única la solución? 1. (a) x =6k + 1, k Z; (b) x = 15k + 10, k Z k 1, k (a) x 23 (mod 105); (b) x 137 (mod 385); (c) No tiene solución. 4. x 65 (mod 84). 5. (a) Aplica el teorema de Fermat; (b) Consecuencia inmediata de (a); (c) Consecuencia inmediata de (b). 6. (a) No tiene solución; (b) x 14 (mod 30); (c) x 8 (mod 935) monedas monedas. 13 piratas caramelos equipos , 314 o 552 monedas.
9 3.7. Dígitos de control Los dígitos de control, que se utilizan para detectar errores en la transmisión de datos. Número de identificación fiscal: NIF El número de identificación fiscal (NIF) está formado por el número del documento nacional de identidad (DNI), formado por 8 dígitos, seguido de una letra del alfabeto. Para encontrar la letra del alfabeto asociada al DNI con número N = n 1 n 2 n 3 n 4 n 5 n 6 n 7 n 8 se procede así: 1. Se halla el resíduo de N módulo 23: N x (mod 23). 2. Se determina la letra correspondiente a x en la siguiente identificación: 0 T 3 A 6 Y 9 D 12 N 15 S 18 H 21 K 1 R 4 G 7 F 10 X 13 J 16 Q 19 L 22 E 2 W 5 M 8 P 11 B 14 Z 17 V 20 C 3. Si x X, el número de NIF es: n 1 n 2 n 3 n 4 n 5 n 6 n 7 n 8 X. El NIF detecta si ha habido errores, y permite recuperar un dígito perdido en la transmisión, siempre que se sepa el lugar que ocupa. El número ISBN El ISBN (International Standard Book Number) es un número de 10 cifras que identifica de forma única cualquier libro editado en el mundo. Un organismo internacional ( marca las directrices sobre este número. Sus 10 cifras están estructuradas en cuatro bloques, XX-XXX-XXXX-X, donde: El primero es el indicador geográfico. A España le corresponde el 84. El segundo bloque corresponde a la editorial. El tercer número corresponde al libro (dentro de su editorial). El último bloque lo constituye un dígito de control. En el ISBN x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 el último dígito es: x 10 (x 1 +2x 2 +3x 3 +4x 4 +5x 5 +6x 6 +7x 7 +8x 8 +9x 9 ) (mod 11) teniendo en cuenta que cuando x 10 = 10 se sustituye por la letra X. Así, por ejemplo, el ISBN corresponde al libro de Matemática Discreta de N.L. Biggs (3311) publicado en España (84) por la editorial Vicens-Vives (316) con dígito de control: = (mod 11) El dígito de control permite detectar errores y recuperar un dígito perdido en la transmisión, siempre que se sepa el lugar que ocupa. Número de cuenta corriente En número de cuenta corriente consta de 20 dígitos distribuidos en la siguiente estructura: E 1 E 2 E 3 E 4 O 1 O 2 O 3 O 4 XY C 1 C 2 C 3 C 4 C 5 C 6 C 7 C 8 C 9 C 10 donde los cuatro primeros dígitos identifican la entidad, los cuatro siguientes la oficina, los dos siguientes son dígitos de control y los diez últimos identifican la cuenta. Los dígitos de control controlan el primero a la oficina y la entidad y el segundo al número de cuenta, y se calculan como sigue: X (7E 1 + 3E 2 + 6E 3 +E 4 + 2O 1 + 4O 2 + 8O 3 + 5O 4 ) (mod 11) Y (10C 1 + 9C 2 + 7C 3 + 3C 4 + 6C 5 +C 6 + 2C 7 + 4C 8 + 8C 9 + 5C 10 ) (mod 11) poniendo, en ambos casos, un 1 cuando el resultado es 10.
10 1. Verifica que el NIF correspondiente a tu DNI es el correcto. Si cambias alguno de sus dígitos, cuál sería la letra correspondiente? 2. Por un error de transmisión se ha recibido la siguiente información sobre el NIF de una persona: Z. Cuál es el número que falta? 1. Calcula la letra que corresponde a tu DNI y verifica que es la que aparece en tu NIF. 2. El número 6.
11 3.8. Criptografía La criptografía se ocupa del problema de cifrar (encriptar) y descifrar (desencriptar) mensajes para su transmisión secreta, pudiendo ser: Criptografía simétrica: cuando se utiliza la misma clave para cifrar y descifrar. El principal problema de la criptografía simétrica es que para descifrar es necesario conocer la clave con la que se ha cifrado y, por tanto, hay que enviar la clave junto con el mensaje, pudiendo ser interceptado y descifrado fácilmente. Criptografía asimétrica: cuando se utilizan claves distintas para cifrar y descifrar. En la criptografía asimétrica la clave que se utiliza para cifrar puede ser pública siempre que la clave para descifrar sea privada, es decir, conocida simplemente por el destinatario, ni siquiera por el remitente. Dos ejemplos de criptografía simétrica son los cifrados de Cesar y los cifrados lineales. criptografía asimétrica son los cifrados de clave pública (RSA). Un ejemplo de de Codificación del alfabeto En criptografía, cada letra del alfabeto (y el espacio) se puede codificar con dos dígitos según la siguiente tabla: = 00 D = 04 H = 08 L = 12 O = 16 S = 20 W = 24 A = 01 E = 05 I = 09 M = 13 P = 17 T = 21 X = 25 B = 02 F = 06 J = 10 N = 14 Q = 18 U = 22 Y = 26 C = 03 G = 07 K = 11 Ñ = 15 R = 19 V = 23 Z = 27 Cifrados de Cesar El cifrado de Cesar con clave k 1 cifra los mensajes sumando k en módulo 28 al código numérico de cada letra. Para descifrar el mensaje se realiza la operación inversa, es decir, se resta k en módulo 28 al código numérico de cada una de las letras recibidas. Hay tantos cifrados de Cesar como valores posibles de k, es decir, 28. Por tanto, son códigos fáciles de romper, ya que habría que hacer un máximo de 28 pruebas hasta obtener un mensaje comprensible. Ejemplo Para cifrar el texto JULIO CESAR con clave k = 3: JULIO CESAR (se suma 3 en módulo 28) MXÑLRCFHVDU El mensaje a enviar sería MXÑLRCFHVDU, que se descifraría así: MXÑLRCFHVDU (se resta 3 en módulo 28) JULIO CESAR Cifrados lineales Es una variante sobre los cifrados de Cesar. El cifrado lineal con clave (a, b) cifra los mensajes aplicando al código numérico de cada letra la transformación lineal: n m an + b (mod 28) Para descifrar el mensaje se realiza la operación inversa: m n a 1 (m b) (mod 28)
12 por lo que hay que tener en cuenta que a debe tener inverso en Z 28, es decir, ha de ser primo con 28. En consecuencia, el número cifrados lineales distintos es Φ(28) 28 = = 336. Estos cifrados son algo más difíciles de romper que los de Cesar, pero relativamente fáciles de romper con ordenador, ya que habría que hacer un máximo de 336 pruebas hasta obtener un mensaje comprensible. Ejemplo Para cifrar el texto JULIO CESAR con el cifrado lineal de clave (3, 1): JULIO CESAR (se aplica la operación 3n + 1 en módulo 28) CKI TAJOEDB El mensaje a enviar sería CKI TAJOEDB, que se descifraría, teniendo en cuenta que 3 1 = 19 en Z 28, así: CKI TAJOEDB (se aplica la operación 19(m 1) en módulo 28) JULIO CESAR 1. Utiliza el cifrado de Cesar con clave k = 7 para cifrar y descifrar el mensaje: VAMOS A CENAR EN CASA. 2. Utiliza el cifrado lineal con clave (5, 3) para cifrar y descifrar el mensaje: VAMOS A CENAR EN CASA. 3. Utiliza el cifrado lineal con clave (3, 0) para cifrar el mensaje: HOLA A TODOS. 1. CHSVZGHGJLTHYGLTGJHZH 2. JHNBUCHCQARHPCARCQHUH 3. WSHC C GSLSD
13 3.9. Cifrado de clave pública: RSA El cifrado de clave pública RSA fue desarrollado en 1978 por R.L. Rivest, A. Shamir y L. Adleman, debiendo su nombre a las iniciales de sus autores. El método completo RSA El proceso completo de cifrado y descifrado de un mensaje consta de los pasos que se enumeran a continuación y que se realizan, como ejemplo con el mensaje El código. 1. El mensaje se reagrupa en bloques de letras de igual longitud r, llamadas palabras. Si r = 2: EL CODIGO = EL C OD IG O 2. Usando la codificación del alfabeto dada en 2.8, cada palabra se codifica como un número de 2 r dígitos, llamado también palabra. EL C OD IG O = La clave pública, llamada así porque puede ser conocida por cualquier persona, está formada por una pareja de enteros positivos (n, e) elegidos de tal forma que: n sea primo con cualquier palabra del texto, lo que se garantiza si cualquier divisor primo de n es mayor que la mayor palabra posible del texto. En la práctica, se elige n = pq como el producto de dos números primos mayores que la mayor palabra del texto. e sea primo con Φ(n) =(p 1)(q 1). En el ejemplo que estamos considerando, la mayor palabra del texto es 2727, dos números primos mayores que esta palabra son p = 2729 y q = 2741, y entonces n = pq = = En este caso, Φ(n) =(p 1)(q 1) = = y, puesto que Φ(n) no es divisible por 3, se puede elegir e = 3. En consecuencia, se elige y publica la clave pública ( , 3). 4. La clave privada, llamada así porque sólo es conocida por el receptor del mensaje, está formada por la pareja de enteros positivos (n, d), donde n es el mismo de la clave pública y d = e 1 (mod Φ(n)), cuya existencia queda garantizada al ser e primo con Φ(n). En el ejemplo, d =3 1 (mod ) = , y la clave privada es ( , ). 5. El cifrado: cada palabra N se cifra como C = N e (mod n). En el ejemplo: N = 0512 = C = (mod ) = N = 0003 = C = (mod ) = 27 N = 1604 = C = (mod ) = N = 0907 = C = (mod ) = N = 1600 = C = (mod ) = El mensaje cifrado a enviar sería: El descifrado: cada palabra recibida C se descifra como N = C d (mod n), ya que, al ser ed+αφ(n) =1 para algún α Z y N Φ(n) 1(modn) (por ser n primo con cualquier palabra N del texto), se tiene que: C d (mod n) =N ed (mod n) =N ed N Φ(n) α (mod n) =N ed+αφ(n) (mod n) =N (mod n)
14 En el ejemplo: C = = N = (mod ) = 512 C = 27 = N = (mod ) = 3 C = = N = (mod ) = 1604 C = = N = (mod ) = 907 C = = N = (mod ) = 1600 Puesto que r = 2, cada palabra debe tener 2 2 = 4 dígitos, por lo que para obtener el mensaje hay que completar las palabra con los ceros necesarios hasta obtener los cuatro dígitos, y decodificarla: = EL C OD IG O = EL CODIGO Seguridad del método Puesto que la clave pública (n, e) es conocida por todos, la seguridad del método de cifrado RSA consiste en la privacidad de la clave privada (n, d), es decir, del número d y, puesto que d = e 1 (mod Φ(n)), la seguridad radica en la dificultad de obtener Φ(n) =(p 1)(q 1), que en última instancia radica en la dificultad de obtener la descomposición n = pq. Si los números primos p y q se eligen suficientemente grandes, el problema de descomposición de n es prácticamente imposible en la actualidad. El método de trabajo Para enviarse mensajes cifrados un grupo indeterminado de personas, cada una de ellas publica sus claves (n i,e i ), i 1, manteniendo en secreto su clave privada (n i,d i ). Cuando i quiere enviar un mensaje a j lo cifra con la clave privada de j, y el mensaje sólo lo podrá descifrar j (que es el único que conoce la clave privada correspondiente). 1. Tomando r = 1, encuentra la clave privada correspondiente a la clave pública (899, 11). 2. Cifra y descifra el mensaje Es un secreto con r = 1 y clave pública (899, 11). 1. (n, d) = (899, 611). 2. Mensaje cifrado:
Divisibilidad y números primos
 Divisibilidad y números primos Divisibilidad En muchos problemas es necesario saber si el reparto de varios elementos en diferentes grupos se puede hacer equitativamente, es decir, si el número de elementos
Divisibilidad y números primos Divisibilidad En muchos problemas es necesario saber si el reparto de varios elementos en diferentes grupos se puede hacer equitativamente, es decir, si el número de elementos
Módulo 9 Sistema matemático y operaciones binarias
 Módulo 9 Sistema matemático y operaciones binarias OBJETIVO: Identificar los conjuntos de números naturales, enteros, racionales e irracionales; resolver una operación binaria, representar un número racional
Módulo 9 Sistema matemático y operaciones binarias OBJETIVO: Identificar los conjuntos de números naturales, enteros, racionales e irracionales; resolver una operación binaria, representar un número racional
CRIPTOGRAFÍA SIMÉTRICA Y ASIMÉTRICA
 CRIPTOGRAFÍA SIMÉTRICA Y ASIMÉTRICA Para generar una transmisión segura de datos, debemos contar con un canal que sea seguro, esto es debemos emplear técnicas de forma que los datos que se envían de una
CRIPTOGRAFÍA SIMÉTRICA Y ASIMÉTRICA Para generar una transmisión segura de datos, debemos contar con un canal que sea seguro, esto es debemos emplear técnicas de forma que los datos que se envían de una
POLINOMIOS Y FRACCIONES ALGEBRAICAS
 POLINOMIOS Y FRACCIONES ALGEBRAICAS Página 66 PARA EMPEZAR, REFLEXIONA Y RESUELVE Múltiplos y divisores. Haz la división: 4 + 5 0 + 5 A la vista del resultado, di dos divisores del polinomio 4 + 5 0. (
POLINOMIOS Y FRACCIONES ALGEBRAICAS Página 66 PARA EMPEZAR, REFLEXIONA Y RESUELVE Múltiplos y divisores. Haz la división: 4 + 5 0 + 5 A la vista del resultado, di dos divisores del polinomio 4 + 5 0. (
EJERCICIOS SOBRE : DIVISIBILIDAD
 1.- Múltiplo de un número. Un número es múltiplo de otro cuando lo contiene un número exacto de veces. De otra forma sería: un número es múltiplo de otro cuando la división del primero entre el segundo
1.- Múltiplo de un número. Un número es múltiplo de otro cuando lo contiene un número exacto de veces. De otra forma sería: un número es múltiplo de otro cuando la división del primero entre el segundo
Ecuaciones de primer grado con dos incógnitas
 Ecuaciones de primer grado con dos incógnitas Si decimos: "las edades de mis padres suman 120 años", podemos expresar esta frase algebraicamente de la siguiente forma: Entonces, Denominamos x a la edad
Ecuaciones de primer grado con dos incógnitas Si decimos: "las edades de mis padres suman 120 años", podemos expresar esta frase algebraicamente de la siguiente forma: Entonces, Denominamos x a la edad
Polinomios: Definición: Se llama polinomio en "x" de grado "n" a una expresión del tipo
 Polinomios: Definición: Se llama polinomio en "x" de grado "n" a una expresión del tipo P (x) = a 0 x n + a 1 x n 1 +... + a n Donde n N (número natural) ; a 0, a 1, a 2,..., a n son coeficientes reales
Polinomios: Definición: Se llama polinomio en "x" de grado "n" a una expresión del tipo P (x) = a 0 x n + a 1 x n 1 +... + a n Donde n N (número natural) ; a 0, a 1, a 2,..., a n son coeficientes reales
2. Aritmética modular Ejercicios resueltos
 2. Aritmética modular Ejercicios resueltos Ejercicio 2.1 Probar, mediante congruencias, que 3 2n+5 + 2 4n+1 es divisible por 7 cualquiera que sea el entero n 1. Trabajando módulo 7 se tiene que 3 2n+5
2. Aritmética modular Ejercicios resueltos Ejercicio 2.1 Probar, mediante congruencias, que 3 2n+5 + 2 4n+1 es divisible por 7 cualquiera que sea el entero n 1. Trabajando módulo 7 se tiene que 3 2n+5
ECUACIONES DIOFÁNTICAS LINEALES
 ARITMÉTICA MODULAR II En primer lugar vamos a introducir las ecuaciones diofánticas lineales y posteriormente veremos las ecuaciones lineales en congruencias. ECUACIONES DIOFÁNTICAS LINEALES Ejercicio
ARITMÉTICA MODULAR II En primer lugar vamos a introducir las ecuaciones diofánticas lineales y posteriormente veremos las ecuaciones lineales en congruencias. ECUACIONES DIOFÁNTICAS LINEALES Ejercicio
EXPRESIONES ALGEBRAICAS. POLINOMIOS
 EXPRESIONES ALGEBRAICAS. POLINOMIOS 1. EXPRESIONES ALGEBRAICAS. Estas expresiones del área son expresiones algebraicas, ya que además de números aparecen letras. Son también expresiones algebraicas: bac,
EXPRESIONES ALGEBRAICAS. POLINOMIOS 1. EXPRESIONES ALGEBRAICAS. Estas expresiones del área son expresiones algebraicas, ya que además de números aparecen letras. Son también expresiones algebraicas: bac,
Biblioteca Virtual Ejercicios Resueltos
 EJERCICIO 13 13 V a l o r n u m é r i c o Valor numérico de expresiones compuestas P r o c e d i m i e n t o 1. Se reemplaza cada letra por su valor numérico 2. Se efectúan las operaciones indicadas Hallar
EJERCICIO 13 13 V a l o r n u m é r i c o Valor numérico de expresiones compuestas P r o c e d i m i e n t o 1. Se reemplaza cada letra por su valor numérico 2. Se efectúan las operaciones indicadas Hallar
1º) Siempre que se pueda, hay que sacar factor común: :a b ± a c ± a d ± = a (b ± c ± d ± ):
 Pág. 1 de 7 FAC T O R I Z AC I Ó N D E P O L I N O M I O S Factorizar (o descomponer en factores) un polinomio consiste en sustituirlo por un producto indicado de otros de menor grado tales que si se multiplicasen
Pág. 1 de 7 FAC T O R I Z AC I Ó N D E P O L I N O M I O S Factorizar (o descomponer en factores) un polinomio consiste en sustituirlo por un producto indicado de otros de menor grado tales que si se multiplicasen
Apuntes de Matemática Discreta 9. Funciones
 Apuntes de Matemática Discreta 9. Funciones Francisco José González Gutiérrez Cádiz, Octubre de 004 Universidad de Cádiz Departamento de Matemáticas ii Lección 9 Funciones Contenido 9.1 Definiciones y
Apuntes de Matemática Discreta 9. Funciones Francisco José González Gutiérrez Cádiz, Octubre de 004 Universidad de Cádiz Departamento de Matemáticas ii Lección 9 Funciones Contenido 9.1 Definiciones y
ESTRUCTURAS ALGEBRAICAS 1
 ESTRUCTURAS ALGEBRAICAS Se da la relación entre dos conjuntos mediante el siguiente diagrama: (, ) (2, 3) (, 4) (, 2) (7, 8) (, ) (3, 3) (5, ) (6, ) (, 6)........ 5 6......... 2 5 i) Observa la correspondencia
ESTRUCTURAS ALGEBRAICAS Se da la relación entre dos conjuntos mediante el siguiente diagrama: (, ) (2, 3) (, 4) (, 2) (7, 8) (, ) (3, 3) (5, ) (6, ) (, 6)........ 5 6......... 2 5 i) Observa la correspondencia
Polinomios y fracciones algebraicas
 UNIDAD Polinomios y fracciones algebraicas U n polinomio es una expresión algebraica en la que las letras y los números están sometidos a las operaciones de sumar, restar y multiplicar. Los polinomios,
UNIDAD Polinomios y fracciones algebraicas U n polinomio es una expresión algebraica en la que las letras y los números están sometidos a las operaciones de sumar, restar y multiplicar. Los polinomios,
1.4.- D E S I G U A L D A D E S
 1.4.- D E S I G U A L D A D E S OBJETIVO: Que el alumno conozca y maneje las reglas empleadas en la resolución de desigualdades y las use para determinar el conjunto solución de una desigualdad dada y
1.4.- D E S I G U A L D A D E S OBJETIVO: Que el alumno conozca y maneje las reglas empleadas en la resolución de desigualdades y las use para determinar el conjunto solución de una desigualdad dada y
Qué son los monomios?
 Qué son los monomios? Recordemos qué es una expresión algebraica. Definición Una expresión algebraica es aquella en la que se utilizan letras, números y signos de operaciones. Si se observan las siguientes
Qué son los monomios? Recordemos qué es una expresión algebraica. Definición Una expresión algebraica es aquella en la que se utilizan letras, números y signos de operaciones. Si se observan las siguientes
Ecuaciones de segundo grado
 3 Ecuaciones de segundo grado Objetivos En esta quincena aprenderás a: Identificar las soluciones de una ecuación. Reconocer y obtener ecuaciones equivalentes. Resolver ecuaciones de primer grado Resolver
3 Ecuaciones de segundo grado Objetivos En esta quincena aprenderás a: Identificar las soluciones de una ecuación. Reconocer y obtener ecuaciones equivalentes. Resolver ecuaciones de primer grado Resolver
342 SOBRE FORMAS TERNARIAS DE SEGUNDO GRADO.
 342 SOBRE FORMAS TERNARIAS DE SEGUNDO GRADO. ALGUNAS APLICACIONES A LA TEORIA DE LAS FORMAS BINARIAS. Encontrar una forma cuya duplicación produce una forma dada del género principal. Puesto que los elementos
342 SOBRE FORMAS TERNARIAS DE SEGUNDO GRADO. ALGUNAS APLICACIONES A LA TEORIA DE LAS FORMAS BINARIAS. Encontrar una forma cuya duplicación produce una forma dada del género principal. Puesto que los elementos
Los polinomios. Un polinomio es una expresión algebraica con una única letra, llamada variable. Ejemplo: 9x 6 3x 4 + x 6 polinomio de variable x
 Los polinomios Los polinomios Un polinomio es una expresión algebraica con una única letra, llamada variable. Ejemplo: 9x 6 3x 4 + x 6 polinomio de variable x Elementos de un polinomio Los términos: cada
Los polinomios Los polinomios Un polinomio es una expresión algebraica con una única letra, llamada variable. Ejemplo: 9x 6 3x 4 + x 6 polinomio de variable x Elementos de un polinomio Los términos: cada
Colegio Las Tablas Tarea de verano Matemáticas 3º ESO
 Colegio Las Tablas Tarea de verano Matemáticas º ESO Nombre: C o l e g i o L a s T a b l a s Tarea de verano Matemáticas º ESO Resolver la siguiente ecuación: 5 5 6 Multiplicando por el mcm(,,6) = 6 y
Colegio Las Tablas Tarea de verano Matemáticas º ESO Nombre: C o l e g i o L a s T a b l a s Tarea de verano Matemáticas º ESO Resolver la siguiente ecuación: 5 5 6 Multiplicando por el mcm(,,6) = 6 y
DIVISIBILIDAD SOLUCIÓN:
 DIVISIBILIDAD 1. Si a, b y c son números naturales tales que c = a. b, se dice: a) c es divisor de a y de b. b) c es múltiplo de a y de b. c) a y b son múltiplos de c. Todo número descompuesto en un producto
DIVISIBILIDAD 1. Si a, b y c son números naturales tales que c = a. b, se dice: a) c es divisor de a y de b. b) c es múltiplo de a y de b. c) a y b son múltiplos de c. Todo número descompuesto en un producto
Programa para el Mejoramiento de la Enseñanza de la Matemática en ANEP Proyecto: Análisis, Reflexión y Producción. Fracciones
 Fracciones. Las fracciones y los números Racionales Las fracciones se utilizan cotidianamente en contextos relacionados con la medida, el reparto o como forma de relacionar dos cantidades. Tenemos entonces
Fracciones. Las fracciones y los números Racionales Las fracciones se utilizan cotidianamente en contextos relacionados con la medida, el reparto o como forma de relacionar dos cantidades. Tenemos entonces
Lección 1-Introducción a los Polinomios y Suma y Resta de Polinomios. Dra. Noemí L. Ruiz Limardo 2009
 Lección 1-Introducción a los Polinomios y Suma y Resta de Polinomios Dra. Noemí L. Ruiz Limardo 2009 Objetivos de la Lección Al finalizar esta lección los estudiantes: Identificarán, de una lista de expresiones
Lección 1-Introducción a los Polinomios y Suma y Resta de Polinomios Dra. Noemí L. Ruiz Limardo 2009 Objetivos de la Lección Al finalizar esta lección los estudiantes: Identificarán, de una lista de expresiones
by Tim Tran: https://picasaweb.google.com/lh/photo/sdo00o8wa-czfov3nd0eoa?full-exif=true
 by Tim Tran: https://picasaweb.google.com/lh/photo/sdo00o8wa-czfov3nd0eoa?full-exif=true I. FUNDAMENTOS 3. Representación de la información Introducción a la Informática Curso de Acceso a la Universidad
by Tim Tran: https://picasaweb.google.com/lh/photo/sdo00o8wa-czfov3nd0eoa?full-exif=true I. FUNDAMENTOS 3. Representación de la información Introducción a la Informática Curso de Acceso a la Universidad
TEMA: ECUACIONES CON NÚMEROS NATURALES ECUACIONES DE PRIMER GRADO CON UNA INCÓGNITA.
 TEMA: ECUACIONES CON NÚMEROS NATURALES INTRODUCCIÓN: Las ecuaciones sirven, básicamente, para resolver problemas ya sean matemáticos, de la vida diaria o de cualquier ámbito- y, en ese caso, se dice que
TEMA: ECUACIONES CON NÚMEROS NATURALES INTRODUCCIÓN: Las ecuaciones sirven, básicamente, para resolver problemas ya sean matemáticos, de la vida diaria o de cualquier ámbito- y, en ese caso, se dice que
Lección 9: Polinomios
 LECCIÓN 9 c) (8 + ) j) [ 9.56 ( 9.56)] 8 q) (a x b) d) ( 5) 4 k) (6z) r) [k 0 (k 5 k )] e) (. 0.) l) (y z) s) (v u ) 4 f) ( 5) + ( 4) m) (c d) 7 t) (p + q) g) (0 x 0.) n) (g 7 g ) Lección 9: Polinomios
LECCIÓN 9 c) (8 + ) j) [ 9.56 ( 9.56)] 8 q) (a x b) d) ( 5) 4 k) (6z) r) [k 0 (k 5 k )] e) (. 0.) l) (y z) s) (v u ) 4 f) ( 5) + ( 4) m) (c d) 7 t) (p + q) g) (0 x 0.) n) (g 7 g ) Lección 9: Polinomios
Definición 1.1.1. Dados dos números naturales m y n, una matriz de orden o dimensión m n es una tabla numérica rectangular con m filas y n columnas.
 Tema 1 Matrices Estructura del tema. Conceptos básicos y ejemplos Operaciones básicas con matrices Método de Gauss Rango de una matriz Concepto de matriz regular y propiedades Determinante asociado a una
Tema 1 Matrices Estructura del tema. Conceptos básicos y ejemplos Operaciones básicas con matrices Método de Gauss Rango de una matriz Concepto de matriz regular y propiedades Determinante asociado a una
Cifras significativas e incertidumbre en las mediciones
 Unidades de medición Cifras significativas e incertidumbre en las mediciones Todas las mediciones constan de una unidad que nos indica lo que fue medido y un número que indica cuántas de esas unidades
Unidades de medición Cifras significativas e incertidumbre en las mediciones Todas las mediciones constan de una unidad que nos indica lo que fue medido y un número que indica cuántas de esas unidades
1.3 Números racionales
 1.3 1.3.1 El concepto de número racional Figura 1.2: Un reparto no equitativo: 12 5 =?. Figura 1.3: Un quinto de la unidad. Con los números naturales y enteros es imposible resolver cuestiones tan simples
1.3 1.3.1 El concepto de número racional Figura 1.2: Un reparto no equitativo: 12 5 =?. Figura 1.3: Un quinto de la unidad. Con los números naturales y enteros es imposible resolver cuestiones tan simples
NÚMEROS NATURALES Y NÚMEROS ENTEROS
 NÚMEROS NATURALES Y NÚMEROS ENTEROS Los números naturales surgen como respuesta a la necesidad de nuestros antepasados de contar los elementos de un conjunto (por ejemplo los animales de un rebaño) y de
NÚMEROS NATURALES Y NÚMEROS ENTEROS Los números naturales surgen como respuesta a la necesidad de nuestros antepasados de contar los elementos de un conjunto (por ejemplo los animales de un rebaño) y de
OBJETIVOS CONTENIDOS PROCEDIMIENTOS. Cálculo de los múltiplos y divisores de un número. Criterios de divisibilidad por 2, 3, 5 y 10.
 _ 9-.qxd //7 9:7 Página 9 Divisibilidad INTRODUCCIÓN El concepto de divisibilidad requiere dominar la multiplicación, división y potenciación de números naturales. Es fundamental dedicar el tiempo necesario
_ 9-.qxd //7 9:7 Página 9 Divisibilidad INTRODUCCIÓN El concepto de divisibilidad requiere dominar la multiplicación, división y potenciación de números naturales. Es fundamental dedicar el tiempo necesario
Matrices Invertibles y Elementos de Álgebra Matricial
 Matrices Invertibles y Elementos de Álgebra Matricial Departamento de Matemáticas, CCIR/ITESM 12 de enero de 2011 Índice 91 Introducción 1 92 Transpuesta 1 93 Propiedades de la transpuesta 2 94 Matrices
Matrices Invertibles y Elementos de Álgebra Matricial Departamento de Matemáticas, CCIR/ITESM 12 de enero de 2011 Índice 91 Introducción 1 92 Transpuesta 1 93 Propiedades de la transpuesta 2 94 Matrices
DÍGITOS DE CONTROL: APLICACIONES DE LA ARITMÉTICA DE NÚMEROS ENTEROS A LA VIDA REAL
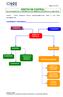 DÍGITOS DE CONTROL: APLICACIONES DE LA ARITMÉTICA DE NÚMEROS ENTEROS A LA VIDA REAL Autores: Cristina Steegmann Pascual (csteegmann@uoc.edu), Ángel A. Juan Pérez (ajuanp@uoc.edu). ESQUEMA DE CONTENIDOS
DÍGITOS DE CONTROL: APLICACIONES DE LA ARITMÉTICA DE NÚMEROS ENTEROS A LA VIDA REAL Autores: Cristina Steegmann Pascual (csteegmann@uoc.edu), Ángel A. Juan Pérez (ajuanp@uoc.edu). ESQUEMA DE CONTENIDOS
Grupos. Subgrupos. Teorema de Lagrange. Operaciones.
 1 Tema 1.-. Grupos. Subgrupos. Teorema de Lagrange. Operaciones. 1.1. Primeras definiciones Definición 1.1.1. Una operación binaria en un conjunto A es una aplicación α : A A A. En un lenguaje más coloquial
1 Tema 1.-. Grupos. Subgrupos. Teorema de Lagrange. Operaciones. 1.1. Primeras definiciones Definición 1.1.1. Una operación binaria en un conjunto A es una aplicación α : A A A. En un lenguaje más coloquial
La nueva criba de Eratóstenes Efraín Soto Apolinar 1 F.I.M.E. U.A.N.L. San Nicolás, N.L. México. efrain@yalma.fime.uanl.mx
 La nueva criba de Eratóstenes Efraín Soto Apolinar 1 F.I.M.E. U.A.N.L. San Nicolás, N.L. México. efrain@yalma.fime.uanl.mx Resumen Se dan algunas definiciones básicas relacionadas con la divisibilidad
La nueva criba de Eratóstenes Efraín Soto Apolinar 1 F.I.M.E. U.A.N.L. San Nicolás, N.L. México. efrain@yalma.fime.uanl.mx Resumen Se dan algunas definiciones básicas relacionadas con la divisibilidad
AMPLIACIÓN DE MATEMÁTICAS. REPASO DE MATEMÁTICAS DISCRETA. CONGRUENCIAS. En el conjunto de los números enteros
 AMPLIACIÓN DE MATEMÁTICAS REPASO DE MATEMÁTICAS DISCRETA. CONGRUENCIAS. En el conjunto de los números enteros Z = {..., n,..., 2, 1, 0, 1, 2, 3,..., n, n + 1,...} tenemos definidos una suma y un producto
AMPLIACIÓN DE MATEMÁTICAS REPASO DE MATEMÁTICAS DISCRETA. CONGRUENCIAS. En el conjunto de los números enteros Z = {..., n,..., 2, 1, 0, 1, 2, 3,..., n, n + 1,...} tenemos definidos una suma y un producto
CURSO BÁSICO DE MATEMÁTICAS PARA ESTUDIANTES DE ECONÓMICAS Y EMPRESARIALES
 INECUACIONES NOTA IMPORTANTE: El signo de desigualdad de una inecuación puede ser,, < o >. Para las cuestiones teóricas que se desarrollan en esta unidad únicamente se utilizará la desigualdad >, siendo
INECUACIONES NOTA IMPORTANTE: El signo de desigualdad de una inecuación puede ser,, < o >. Para las cuestiones teóricas que se desarrollan en esta unidad únicamente se utilizará la desigualdad >, siendo
4º ESO 1. ECUAC. 2º GRADO Y UNA INCÓGNITA
 4º ESO 1. ECUAC. 2º GRADO Y UNA INCÓGNITA Una ecuación con una incógnita es de segundo grado si el exponente de la incógnita es dos. Ecuaciones de segundo grado con una incógnita son: Esta última ecuación
4º ESO 1. ECUAC. 2º GRADO Y UNA INCÓGNITA Una ecuación con una incógnita es de segundo grado si el exponente de la incógnita es dos. Ecuaciones de segundo grado con una incógnita son: Esta última ecuación
De dos incógnitas. Por ejemplo, x + y 3 = 4. De tres incógnitas. Por ejemplo, x + y + 2z = 4. Y así sucesivamente.
 3 Ecuaciones 17 3 Ecuaciones Una ecuación es una igualdad en la que aparecen ligados, mediante operaciones algebraicas, números y letras Las letras que aparecen en una ecuación se llaman incógnitas Existen
3 Ecuaciones 17 3 Ecuaciones Una ecuación es una igualdad en la que aparecen ligados, mediante operaciones algebraicas, números y letras Las letras que aparecen en una ecuación se llaman incógnitas Existen
9.1 Primeras definiciones
 Tema 9- Grupos Subgrupos Teorema de Lagrange Operaciones 91 Primeras definiciones Definición 911 Una operación binaria en un conjunto A es una aplicación α : A A A En un lenguaje más coloquial una operación
Tema 9- Grupos Subgrupos Teorema de Lagrange Operaciones 91 Primeras definiciones Definición 911 Una operación binaria en un conjunto A es una aplicación α : A A A En un lenguaje más coloquial una operación
3 POLINOMIOS Y FRACCIONES ALGEBRAICAS
 POLINOMIOS Y FRACCIONES ALGEBRAICAS PARA EMPEZAR Un cuadrado tiene 5 centímetros de lado. Escribe la epresión algebraica que da el área cuando el lado aumenta centímetros. A ( 5) Señala cuáles de las siguientes
POLINOMIOS Y FRACCIONES ALGEBRAICAS PARA EMPEZAR Un cuadrado tiene 5 centímetros de lado. Escribe la epresión algebraica que da el área cuando el lado aumenta centímetros. A ( 5) Señala cuáles de las siguientes
TEMA 2 POLINOMIOS Y FRACCIONES ALGEBRAICAS
 Matemáticas B 4º E.S.O. Tema : Polinomios y fracciones algebraicas. 1 TEMA POLINOMIOS Y FRACCIONES ALGEBRAICAS.1 COCIENTE DE POLINOMIOS 4º.1.1 COCIENTE DE MONOMIOS 4º El cociente de un monomio entre otro
Matemáticas B 4º E.S.O. Tema : Polinomios y fracciones algebraicas. 1 TEMA POLINOMIOS Y FRACCIONES ALGEBRAICAS.1 COCIENTE DE POLINOMIOS 4º.1.1 COCIENTE DE MONOMIOS 4º El cociente de un monomio entre otro
Tema 3. Medidas de tendencia central. 3.1. Introducción. Contenido
 Tema 3 Medidas de tendencia central Contenido 31 Introducción 1 32 Media aritmética 2 33 Media ponderada 3 34 Media geométrica 4 35 Mediana 5 351 Cálculo de la mediana para datos agrupados 5 36 Moda 6
Tema 3 Medidas de tendencia central Contenido 31 Introducción 1 32 Media aritmética 2 33 Media ponderada 3 34 Media geométrica 4 35 Mediana 5 351 Cálculo de la mediana para datos agrupados 5 36 Moda 6
Los números racionales
 Los números racionales Los números racionales Los números fraccionarios o fracciones permiten representar aquellas situaciones en las que se obtiene o se debe una parte de un objeto. Todas las fracciones
Los números racionales Los números racionales Los números fraccionarios o fracciones permiten representar aquellas situaciones en las que se obtiene o se debe una parte de un objeto. Todas las fracciones
BASES Y DIMENSIÓN. Propiedades de las bases. Ejemplos de bases.
 BASES Y DIMENSIÓN Definición: Base. Se llama base de un espacio (o subespacio) vectorial a un sistema generador de dicho espacio o subespacio, que sea a la vez linealmente independiente. β Propiedades
BASES Y DIMENSIÓN Definición: Base. Se llama base de un espacio (o subespacio) vectorial a un sistema generador de dicho espacio o subespacio, que sea a la vez linealmente independiente. β Propiedades
EJERCICIOS DE MATEMÁTICAS I HOJA 4. Ejercicio 1. Se consideran los vectores
 EJERCICIOS DE MATEMÁTICAS I HOJA 4 Ejercicio 1. Se consideran los vectores u 1 = (1, 1, 0, 1), u 2 = (0, 2, 1, 0), u 3 = ( 1, 1, 1, 1), u 4 = (2, 2, 1, 0) de R 4. Expresa, si es posible, los vectores u
EJERCICIOS DE MATEMÁTICAS I HOJA 4 Ejercicio 1. Se consideran los vectores u 1 = (1, 1, 0, 1), u 2 = (0, 2, 1, 0), u 3 = ( 1, 1, 1, 1), u 4 = (2, 2, 1, 0) de R 4. Expresa, si es posible, los vectores u
Apuntes de Matemática Discreta 7. Relaciones de Orden
 Apuntes de Matemática Discreta 7. Relaciones de Orden Francisco José González Gutiérrez Cádiz, Octubre de 2004 Universidad de Cádiz Departamento de Matemáticas ii Lección 7 Relaciones de Orden Contenido
Apuntes de Matemática Discreta 7. Relaciones de Orden Francisco José González Gutiérrez Cádiz, Octubre de 2004 Universidad de Cádiz Departamento de Matemáticas ii Lección 7 Relaciones de Orden Contenido
Datos del autor. Nombres y apellido: Germán Andrés Paz. Lugar de nacimiento: Rosario (Código Postal 2000), Santa Fe, Argentina
 Datos del autor Nombres y apellido: Germán Andrés Paz Lugar de nacimiento: Rosario (Código Postal 2000), Santa Fe, Argentina Correo electrónico: germanpaz_ar@hotmail.com =========0========= Introducción
Datos del autor Nombres y apellido: Germán Andrés Paz Lugar de nacimiento: Rosario (Código Postal 2000), Santa Fe, Argentina Correo electrónico: germanpaz_ar@hotmail.com =========0========= Introducción
Ejercicios de divisibilidad con soluciones. 1 De entre los siguientes números: 405, 316, 814, 1085 y 340: a) Hay alguno que sea divisible por 3?
 Ejercicios de divisibilidad con soluciones 1 De entre los siguientes números: 405, 316, 814, 1085 y 340: a) Hay alguno que sea divisible por 3? b) Cuáles son divisibles por 4? c) Cuáles tienen por divisor
Ejercicios de divisibilidad con soluciones 1 De entre los siguientes números: 405, 316, 814, 1085 y 340: a) Hay alguno que sea divisible por 3? b) Cuáles son divisibles por 4? c) Cuáles tienen por divisor
Capítulo 7 Teoría de los Números
 Capítulo 7 Teoría de los Números Seguridad Informática y Criptografía Ultima actualización del archivo: 01/03/06 Este archivo tiene: 75 diapositivas v 4.1 Material Docente de Libre Distribución Dr. Jorge
Capítulo 7 Teoría de los Números Seguridad Informática y Criptografía Ultima actualización del archivo: 01/03/06 Este archivo tiene: 75 diapositivas v 4.1 Material Docente de Libre Distribución Dr. Jorge
1. SISTEMAS DIGITALES
 1. SISTEMAS DIGITALES DOCENTE: ING. LUIS FELIPE CASTELLANOS CASTELLANOS CORREO ELECTRÓNICO: FELIPECASTELLANOS2@HOTMAIL.COM FELIPECASTELLANOS2@GMAIL.COM PAGINA WEB MAESTROFELIPE.JIMDO.COM 1.1. INTRODUCCIÓN
1. SISTEMAS DIGITALES DOCENTE: ING. LUIS FELIPE CASTELLANOS CASTELLANOS CORREO ELECTRÓNICO: FELIPECASTELLANOS2@HOTMAIL.COM FELIPECASTELLANOS2@GMAIL.COM PAGINA WEB MAESTROFELIPE.JIMDO.COM 1.1. INTRODUCCIÓN
EJERCICIOS RESUELTOS SOBRE ERRORES DE REDONDEO
 EJERCICIOS RESUELTOS SOBRE ERRORES DE REDONDEO 1º) Considérese un número estrictamente positivo del sistema de números máquina F(s+1, m, M, 10). Supongamos que tal número es: z = 0.d 1 d...d s 10 e Responde
EJERCICIOS RESUELTOS SOBRE ERRORES DE REDONDEO 1º) Considérese un número estrictamente positivo del sistema de números máquina F(s+1, m, M, 10). Supongamos que tal número es: z = 0.d 1 d...d s 10 e Responde
Números Reales. MathCon c 2007-2009
 Números Reales z x y MathCon c 2007-2009 Contenido 1. Introducción 2 1.1. Propiedades básicas de los números naturales....................... 2 1.2. Propiedades básicas de los números enteros........................
Números Reales z x y MathCon c 2007-2009 Contenido 1. Introducción 2 1.1. Propiedades básicas de los números naturales....................... 2 1.2. Propiedades básicas de los números enteros........................
Polinomios y Fracciones Algebraicas
 Tema 4 Polinomios y Fracciones Algebraicas En general, a lo largo de este tema trabajaremos con el conjunto de los números reales y, en casos concretos nos referiremos al conjunto de los números complejos.
Tema 4 Polinomios y Fracciones Algebraicas En general, a lo largo de este tema trabajaremos con el conjunto de los números reales y, en casos concretos nos referiremos al conjunto de los números complejos.
Función exponencial y Logaritmos
 Eje temático: Álgebra y funciones Contenidos: Función exponencial y Logaritmos Nivel: 4 Medio Función exponencial y Logaritmos 1. Funciones exponenciales Existen numerosos fenómenos que se rigen por leyes
Eje temático: Álgebra y funciones Contenidos: Función exponencial y Logaritmos Nivel: 4 Medio Función exponencial y Logaritmos 1. Funciones exponenciales Existen numerosos fenómenos que se rigen por leyes
Ejercicios Resueltos del Tema 4
 70 Ejercicios Resueltos del Tema 4 1. Traduce al lenguaje algebraico utilizando, para ello, una o más incógnitas: La suma de tres números consecutivos Un número más la mitad de otro c) El cuadrado de la
70 Ejercicios Resueltos del Tema 4 1. Traduce al lenguaje algebraico utilizando, para ello, una o más incógnitas: La suma de tres números consecutivos Un número más la mitad de otro c) El cuadrado de la
1. Números Reales 1.1 Clasificación y propiedades
 1. Números Reales 1.1 Clasificación y propiedades 1.1.1 Definición Número real, cualquier número racional o irracional. Los números reales pueden expresarse en forma decimal mediante un número entero,
1. Números Reales 1.1 Clasificación y propiedades 1.1.1 Definición Número real, cualquier número racional o irracional. Los números reales pueden expresarse en forma decimal mediante un número entero,
INTERPOLACIÓN POLINÓMICA Y LA DIVISIÓN DE SECRETOS
 INTERPOLACIÓN POLINÓMICA Y LA DIVISIÓN DE SECRETOS Ángela Rojas Matas, Universidad de Córdoba Alberto Cano Rojas, Universidad de Córdoba RESUMEN. La división o reparto de secretos es un tema de completa
INTERPOLACIÓN POLINÓMICA Y LA DIVISIÓN DE SECRETOS Ángela Rojas Matas, Universidad de Córdoba Alberto Cano Rojas, Universidad de Córdoba RESUMEN. La división o reparto de secretos es un tema de completa
TALLER DE DETECTIVES: DESCIFRANDO MENSAJES SECRETOS. 1. Introducción
 TALLER DE DETECTIVES: DESCIFRANDO MENSAJES SECRETOS charamaria@gmail.com Resumen. Notas del taller para estudiantes Taller de Detectives: descifrando mensajes secretos dictado durante el tercer festival
TALLER DE DETECTIVES: DESCIFRANDO MENSAJES SECRETOS charamaria@gmail.com Resumen. Notas del taller para estudiantes Taller de Detectives: descifrando mensajes secretos dictado durante el tercer festival
Matemáticas I: Hoja 3 Espacios vectoriales y subespacios vectoriales
 Matemáticas I: Hoa 3 Espacios vectoriales y subespacios vectoriales Eercicio 1. Demostrar que los vectores v 1, v 2, v 3, v 4 expresados en la base canónica forman una base. Dar las coordenadas del vector
Matemáticas I: Hoa 3 Espacios vectoriales y subespacios vectoriales Eercicio 1. Demostrar que los vectores v 1, v 2, v 3, v 4 expresados en la base canónica forman una base. Dar las coordenadas del vector
, o más abreviadamente: f ( x)
 TEMA 5: 1. CONCEPTO DE FUNCIÓN Observa los siguientes ejemplos: El precio de una llamada telefónica depende de su duración. El consumo de gasolina de un coche depende de la velocidad del mismo. La factura
TEMA 5: 1. CONCEPTO DE FUNCIÓN Observa los siguientes ejemplos: El precio de una llamada telefónica depende de su duración. El consumo de gasolina de un coche depende de la velocidad del mismo. La factura
QUIERES COMPROBAR CÓMO LAS REDES DETECTAN Y CORRIGEN ERRORES?
 QUIERES COMPROBAR CÓMO LAS REDES DETECTAN Y CORRIGEN ERRORES? AUTORÍA MARÍA CATALÁ CARBONERO TEMÁTICA DETECCIÓN Y CORRECCIÓN DE ERRORES ETAPA CICLO MEDIO Y SUPERIOR DE INFORMÁTICA Resumen Hoy en día las
QUIERES COMPROBAR CÓMO LAS REDES DETECTAN Y CORRIGEN ERRORES? AUTORÍA MARÍA CATALÁ CARBONERO TEMÁTICA DETECCIÓN Y CORRECCIÓN DE ERRORES ETAPA CICLO MEDIO Y SUPERIOR DE INFORMÁTICA Resumen Hoy en día las
Tema 1: Fundamentos de lógica, teoría de conjuntos y estructuras algebraicas: Apéndice
 Tema 1: Fundamentos de lógica, teoría de conjuntos y estructuras algebraicas: Apéndice 1 Polinomios Dedicaremos este apartado al repaso de los polinomios. Se define R[x] ={a 0 + a 1 x + a 2 x 2 +... +
Tema 1: Fundamentos de lógica, teoría de conjuntos y estructuras algebraicas: Apéndice 1 Polinomios Dedicaremos este apartado al repaso de los polinomios. Se define R[x] ={a 0 + a 1 x + a 2 x 2 +... +
Materia: Informática. Nota de Clases Sistemas de Numeración
 Nota de Clases Sistemas de Numeración Conversión Entre Sistemas de Numeración 1. EL SISTEMA DE NUMERACIÓN 1.1. DEFINICIÓN DE UN SISTEMA DE NUMERACIÓN Un sistema de numeración es un conjunto finito de símbolos
Nota de Clases Sistemas de Numeración Conversión Entre Sistemas de Numeración 1. EL SISTEMA DE NUMERACIÓN 1.1. DEFINICIÓN DE UN SISTEMA DE NUMERACIÓN Un sistema de numeración es un conjunto finito de símbolos
XLIV Olimpiada Matemática Española Fase nacional 2008 (Valencia) PRIMERA SESIÓN (28 de marzo)
 Fase nacional 008 (Valencia) PRIMERA SESIÓN (8 de marzo).- Halla dos enteros positivos a y b conociendo su suma y su mínimo común múltiplo. Aplícalo en el caso de ue la suma sea 97 y el mínimo común múltiplo
Fase nacional 008 (Valencia) PRIMERA SESIÓN (8 de marzo).- Halla dos enteros positivos a y b conociendo su suma y su mínimo común múltiplo. Aplícalo en el caso de ue la suma sea 97 y el mínimo común múltiplo
Tema 07. LÍMITES Y CONTINUIDAD DE FUNCIONES
 Tema 07 LÍMITES Y CONTINUIDAD DE FUNCIONES Límite de una función en un punto Vamos a estudiar el comportamiento de las funciones f ( ) g ( ) ENT[ ] h ( ) i ( ) en el punto Para ello, damos a valores próimos
Tema 07 LÍMITES Y CONTINUIDAD DE FUNCIONES Límite de una función en un punto Vamos a estudiar el comportamiento de las funciones f ( ) g ( ) ENT[ ] h ( ) i ( ) en el punto Para ello, damos a valores próimos
Apuntes de Matemática Discreta 11. Teorema Fundamental de la Aritmética
 Apuntes de Matemática Discreta 11. Teorema Fundamental de la Aritmética Francisco José González Gutiérrez Cádiz, Octubre de 2004 Universidad de Cádiz Departamento de Matemáticas ii Lección 11 Teorema Fundamental
Apuntes de Matemática Discreta 11. Teorema Fundamental de la Aritmética Francisco José González Gutiérrez Cádiz, Octubre de 2004 Universidad de Cádiz Departamento de Matemáticas ii Lección 11 Teorema Fundamental
a < b y se lee "a es menor que b" (desigualdad estricta) a > b y se lee "a es mayor que b" (desigualdad estricta)
 Desigualdades Dadas dos rectas que se cortan, llamadas ejes (rectangulares si son perpendiculares, y oblicuos en caso contrario), un punto puede situarse conociendo las distancias del mismo a los ejes,
Desigualdades Dadas dos rectas que se cortan, llamadas ejes (rectangulares si son perpendiculares, y oblicuos en caso contrario), un punto puede situarse conociendo las distancias del mismo a los ejes,
3. Operaciones con funciones.
 GRADO DE INGENIERÍA AEROESPACIAL. CURSO 00. Lección. Funciones derivada. 3. Operaciones con funciones. En esta sección veremos cómo podemos combinar funciones para construir otras nuevas. Especialmente
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 00. Lección. Funciones derivada. 3. Operaciones con funciones. En esta sección veremos cómo podemos combinar funciones para construir otras nuevas. Especialmente
Naturaleza binaria. Conversión decimal a binario
 Naturaleza binaria En los circuitos digitales sólo hay 2 voltajes. Esto significa que al utilizar 2 estados lógicos se puede asociar cada uno con un nivel de tensión, así se puede codificar cualquier número,
Naturaleza binaria En los circuitos digitales sólo hay 2 voltajes. Esto significa que al utilizar 2 estados lógicos se puede asociar cada uno con un nivel de tensión, así se puede codificar cualquier número,
Unidad I. 1.1 Sistemas numéricos (Binario, Octal, Decimal, Hexadecimal)
 Unidad I Sistemas numéricos 1.1 Sistemas numéricos (Binario, Octal, Decimal, Hexadecimal) Los computadores manipulan y almacenan los datos usando interruptores electrónicos que están ENCENDIDOS o APAGADOS.
Unidad I Sistemas numéricos 1.1 Sistemas numéricos (Binario, Octal, Decimal, Hexadecimal) Los computadores manipulan y almacenan los datos usando interruptores electrónicos que están ENCENDIDOS o APAGADOS.
Tema 3. Polinomios y fracciones algebraicas
 Tema. Polinomios y fracciones algebraicas. Monomios.. Definiciones.. Operaciones con monomios. Polinomios.. Definiciones.. Operaciones con polinomios. Factorización de un polinomio.. Teorema del resto.
Tema. Polinomios y fracciones algebraicas. Monomios.. Definiciones.. Operaciones con monomios. Polinomios.. Definiciones.. Operaciones con polinomios. Factorización de un polinomio.. Teorema del resto.
Sistemas de dos ecuaciones lineales con dos incógnitas
 Sistemas de dos ecuaciones lineales con dos incógnitas Una ecuación lineal con dos incógnitas es una epresión de la forma a b c donde a, b c son los coeficientes (números) e son las incógnitas. Gráficamente
Sistemas de dos ecuaciones lineales con dos incógnitas Una ecuación lineal con dos incógnitas es una epresión de la forma a b c donde a, b c son los coeficientes (números) e son las incógnitas. Gráficamente
EJERCICIOS SOBRE : NÚMEROS ENTEROS
 1.- Magnitudes Absolutas y Relativas: Se denomina magnitud a todo lo que se puede medir cuantitativamente. Ejemplo: peso de un cuerpo, longitud de una cuerda, capacidad de un recipiente, el tiempo que
1.- Magnitudes Absolutas y Relativas: Se denomina magnitud a todo lo que se puede medir cuantitativamente. Ejemplo: peso de un cuerpo, longitud de una cuerda, capacidad de un recipiente, el tiempo que
Como ya se sabe, existen algunas ecuaciones de segundo grado que no tienen ninguna solución real. Tal es el caso de la ecuación x2 + 1 = 0.
 NÚMEROS COMPLEJOS. INTRO. ( I ) Como ya se sabe, existen algunas ecuaciones de segundo grado que no tienen ninguna solución real. Tal es el caso de la ecuación x2 + 1 = 0. Si bien esto no era un problema
NÚMEROS COMPLEJOS. INTRO. ( I ) Como ya se sabe, existen algunas ecuaciones de segundo grado que no tienen ninguna solución real. Tal es el caso de la ecuación x2 + 1 = 0. Si bien esto no era un problema
Plan de mejora de las competencias lectoras en la ESO. PERFECTOS, AMIGOS Y GEMELOS
 Plan de mejora de las competencias lectoras en la ESO. PERFECTOS, AMIGOS Y GEMELOS Las categorías en las que se clasifican los números enteros son numerosas y atienden a diversos criterios, siendo los
Plan de mejora de las competencias lectoras en la ESO. PERFECTOS, AMIGOS Y GEMELOS Las categorías en las que se clasifican los números enteros son numerosas y atienden a diversos criterios, siendo los
Julio César Mendoza T. Ingeniería de Sistemas Quito
 46 Julio César Mendoza T. Ingeniería de Sistemas Quito 47 RESUMEN En el presente artículo se presenta una breve introducción a la criptografía sin profundizar en las matemáticas que soportan los algoritmos
46 Julio César Mendoza T. Ingeniería de Sistemas Quito 47 RESUMEN En el presente artículo se presenta una breve introducción a la criptografía sin profundizar en las matemáticas que soportan los algoritmos
Unidad 1 números enteros 2º ESO
 Unidad 1 números enteros 2º ESO 1 2 Conceptos 1. Concepto de número entero: diferenciación entre número entero, natural y fraccionario. 2. Representación gráfica y ordenación. 3. Valor absoluto de un número
Unidad 1 números enteros 2º ESO 1 2 Conceptos 1. Concepto de número entero: diferenciación entre número entero, natural y fraccionario. 2. Representación gráfica y ordenación. 3. Valor absoluto de un número
 UNIDAD 2 Configuración y operación de un sistema de cómputo Representación de datos Conceptos El concepto de bit (abreviatura de binary digit) es fundamental para el almacenamiento de datos Puede representarse
UNIDAD 2 Configuración y operación de un sistema de cómputo Representación de datos Conceptos El concepto de bit (abreviatura de binary digit) es fundamental para el almacenamiento de datos Puede representarse
6 Ecuaciones de 1. er y 2. o grado
 8985 _ 009-08.qd /9/07 5:7 Página 09 Ecuaciones de. er y. o grado INTRODUCCIÓN La unidad comienza diferenciando entre ecuaciones e identidades, para pasar luego a la eposición de los conceptos asociados
8985 _ 009-08.qd /9/07 5:7 Página 09 Ecuaciones de. er y. o grado INTRODUCCIÓN La unidad comienza diferenciando entre ecuaciones e identidades, para pasar luego a la eposición de los conceptos asociados
REPASO NÚMEROS NATURALES Y NÚMEROS ENTEROS
 SUMA REPASO NÚMEROS NATURALES Y NÚMEROS ENTEROS NÚMEROS NATURALES (N) 1. Características: Axiomas de Giuseppe Peano (*): El 1 es un número natural. Si n es un número natural, entonces el sucesor (el siguiente
SUMA REPASO NÚMEROS NATURALES Y NÚMEROS ENTEROS NÚMEROS NATURALES (N) 1. Características: Axiomas de Giuseppe Peano (*): El 1 es un número natural. Si n es un número natural, entonces el sucesor (el siguiente
Múltiplos y divisores
 2 Múltiplos y divisores Objetivos En esta quincena aprenderás a: Saber si un número es múltiplo de otro. Reconocer las divisiones exactas. Hallar todos los divisores de un número. Reconocer los números
2 Múltiplos y divisores Objetivos En esta quincena aprenderás a: Saber si un número es múltiplo de otro. Reconocer las divisiones exactas. Hallar todos los divisores de un número. Reconocer los números
Sistemas de numeración
 Sistemas de numeración Un sistema de numeración es un conjunto de símbolos y reglas que permiten representar datos numéricos. Los sistemas de numeración actuales son sistemas posicionales, que se caracterizan
Sistemas de numeración Un sistema de numeración es un conjunto de símbolos y reglas que permiten representar datos numéricos. Los sistemas de numeración actuales son sistemas posicionales, que se caracterizan
UNIDAD 1. LOS NÚMEROS ENTEROS.
 UNIDAD 1. LOS NÚMEROS ENTEROS. Al final deberás haber aprendido... Interpretar y expresar números enteros. Representar números enteros en la recta numérica. Comparar y ordenar números enteros. Realizar
UNIDAD 1. LOS NÚMEROS ENTEROS. Al final deberás haber aprendido... Interpretar y expresar números enteros. Representar números enteros en la recta numérica. Comparar y ordenar números enteros. Realizar
Conjuntos, Relaciones y Grupos. Problemas de examen.
 Conjuntos, Relaciones y Grupos. Problemas de examen. Mayo 2006 1. La función f es definida por (a) Halle el recorrido exacto, A, de f. f : R R donde f(x) = e senx 1. (b) (i) Explique por qué f no es inyectiva.
Conjuntos, Relaciones y Grupos. Problemas de examen. Mayo 2006 1. La función f es definida por (a) Halle el recorrido exacto, A, de f. f : R R donde f(x) = e senx 1. (b) (i) Explique por qué f no es inyectiva.
Una relación R de un conjunto A en un conjunto B es un subconjunto R de A x B.
 Una relación R de un conjunto A en un conjunto B es un subconjunto R de A x B. Sea R una relación de un conjunto A en un conjunto B. Se dice que un elemento a de A está relacionado con un elemento b de
Una relación R de un conjunto A en un conjunto B es un subconjunto R de A x B. Sea R una relación de un conjunto A en un conjunto B. Se dice que un elemento a de A está relacionado con un elemento b de
Unidad Didáctica. Códigos Binarios
 Unidad Didáctica Códigos Binarios Programa de Formación Abierta y Flexible Obra colectiva de FONDO FORMACION Coordinación Diseño y maquetación Servicio de Producción Didáctica de FONDO FORMACION (Dirección
Unidad Didáctica Códigos Binarios Programa de Formación Abierta y Flexible Obra colectiva de FONDO FORMACION Coordinación Diseño y maquetación Servicio de Producción Didáctica de FONDO FORMACION (Dirección
1. MEDIDAS DE TENDENCIA CENTRAL
 1. MEDIDAS DE TENDENCIA CENTRAL Lo importante en una tendencia central es calcular un valor central que actúe como resumen numérico para representar al conjunto de datos. Estos valores son las medidas
1. MEDIDAS DE TENDENCIA CENTRAL Lo importante en una tendencia central es calcular un valor central que actúe como resumen numérico para representar al conjunto de datos. Estos valores son las medidas
VII. Estructuras Algebraicas
 VII. Estructuras Algebraicas Objetivo Se analizarán las operaciones binarias y sus propiedades dentro de una estructura algebraica. Definición de operación binaria Operaciones como la suma, resta, multiplicación
VII. Estructuras Algebraicas Objetivo Se analizarán las operaciones binarias y sus propiedades dentro de una estructura algebraica. Definición de operación binaria Operaciones como la suma, resta, multiplicación
SISTEMAS DE NUMERACIÓN. Sistema decimal
 SISTEMAS DE NUMERACIÓN Sistema decimal Desde antiguo el Hombre ha ideado sistemas para numerar objetos, algunos sistemas primitivos han llegado hasta nuestros días, tal es el caso de los "números romanos",
SISTEMAS DE NUMERACIÓN Sistema decimal Desde antiguo el Hombre ha ideado sistemas para numerar objetos, algunos sistemas primitivos han llegado hasta nuestros días, tal es el caso de los "números romanos",
VI Olimpiada de Informática del estado de Guanajuato Solución Examen Teórico
 I.- En todos los problemas siguientes de esta sección, encuentra qué número (o números) debe seguir según la sucesión, y explica el por qué. 1) 1, 4, 27, 256,? (5 puntos) R = 3125 Observa que 1=1 1, 4=2
I.- En todos los problemas siguientes de esta sección, encuentra qué número (o números) debe seguir según la sucesión, y explica el por qué. 1) 1, 4, 27, 256,? (5 puntos) R = 3125 Observa que 1=1 1, 4=2
UNIDAD 6. POLINOMIOS CON COEFICIENTES ENTEROS
 UNIDAD 6. POLINOMIOS CON COEFICIENTES ENTEROS Unidad 6: Polinomios con coeficientes enteros. Al final deberás haber aprendido... Expresar algebraicamente enunciados sencillos. Extraer enunciados razonables
UNIDAD 6. POLINOMIOS CON COEFICIENTES ENTEROS Unidad 6: Polinomios con coeficientes enteros. Al final deberás haber aprendido... Expresar algebraicamente enunciados sencillos. Extraer enunciados razonables
Relaciones binarias. ( a, b) = ( c, d) si y solamente si a = c y b = d
 Relaciones binarias En esta sección estudiaremos formalmente las parejas de objetos que comparten algunas características o propiedades en común. La estructura matemática para agrupar estas parejas en
Relaciones binarias En esta sección estudiaremos formalmente las parejas de objetos que comparten algunas características o propiedades en común. La estructura matemática para agrupar estas parejas en
Apuntes de Matemática Discreta 1. Conjuntos y Subconjuntos
 Apuntes de Matemática Discreta 1. Conjuntos y Subconjuntos Francisco José González Gutiérrez Cádiz, Octubre de 2004 Universidad de Cádiz Departamento de Matemáticas ii Lección 1 Conjuntos y Subconjuntos
Apuntes de Matemática Discreta 1. Conjuntos y Subconjuntos Francisco José González Gutiérrez Cádiz, Octubre de 2004 Universidad de Cádiz Departamento de Matemáticas ii Lección 1 Conjuntos y Subconjuntos
Transformación de binario a decimal. Transformación de decimal a binario. ELECTRÓNICA DIGITAL
 ELECTRÓNICA DIGITAL La electrónica es la rama de la ciencia que se ocupa del estudio de los circuitos y de sus componentes, que permiten modificar la corriente eléctrica amplificándola, atenuándola, rectificándola
ELECTRÓNICA DIGITAL La electrónica es la rama de la ciencia que se ocupa del estudio de los circuitos y de sus componentes, que permiten modificar la corriente eléctrica amplificándola, atenuándola, rectificándola
Estructuras de Datos y Algoritmos Práctica I - Curso 2012/13
 Estructuras de Datos y Algoritmos Práctica I - Curso 2012/13 Rompiendo el Código Enigma Introducción y objetivos Como un pequeño homenaje a Alan Turing en su año conmemorativo, las prácticas de este curso
Estructuras de Datos y Algoritmos Práctica I - Curso 2012/13 Rompiendo el Código Enigma Introducción y objetivos Como un pequeño homenaje a Alan Turing en su año conmemorativo, las prácticas de este curso
Matrices: Conceptos y Operaciones Básicas
 Matrices: Conceptos y Operaciones Básicas Departamento de Matemáticas, CCIR/ITESM 8 de septiembre de 010 Índice 111 Introducción 1 11 Matriz 1 113 Igualdad entre matrices 11 Matrices especiales 3 115 Suma
Matrices: Conceptos y Operaciones Básicas Departamento de Matemáticas, CCIR/ITESM 8 de septiembre de 010 Índice 111 Introducción 1 11 Matriz 1 113 Igualdad entre matrices 11 Matrices especiales 3 115 Suma
