ANÁLISIS DEL CÓDIGO MATLAB DE PARTIDA EN CPU

Transcripción

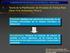
1 II. ANÁLISIS DEL CÓDIGO MATLAB DE PARTIDA EN CPU Como punto de partida se escogió un código MATLAB que debía ser adaptado a CUDA con el objetivo de explorar la nueva tecnología y realizar comparaciones. Este código había sido probado y su corrección había sido comprobada. Sería por tanto el patrón elegido para comparar y medir la eficiencia de CUDA. El código tiene por objeto resolver la ecuación del calor mediante el Método de los Elementos Finitos. 1. MALLADO La solución se busca en un dominio cuadrado de superficie unidad que se somete a mallado con un patrón sencillo de triángulos. Se generan archivos que identifican este mallado que serán usados por los códigos de resolución. En el mallado se definen también las condiciones de contorno según Neumann y Dirichlet. El Mallado se realiza mediante la herramienta de Ecuaciones Diferenciales Parciales (PDE Toolbox) de MATLAB que se ilustra en la figura 1. Esta herramienta permite modificar el grado de mallado en sucesivos pasos para ir aumentando su detalle y por tanto la precisión de las operaciones. Este aumento se traduce en un aumento del número de triángulos y de nodos. Fig. 1: Punto de partida: Mallado del problema. 83

2 CÓDIGO TRATAMALLA: Gracias a éste código auxiliar, facilitado por el tutor, se genera a partir de los parámetros del mallado 4 archivos con extensión.dat. Estos archivos son los que se usan para la ejecución del programa y describen en su totalidad el mallado y las condiciones de contorno. Triangulos.dat: Este archivo contiene los nodos de cada triángulo. Cada línea corresponde al triángulo que lleva el mismo número y contiene tres vértices que son los nodos del triángulo. Coordenadas.dat: Es un archivo ordenado donde cada línea corresponde al nodo que lleva el mismo número y contiene las coordenadas x e y de dicho nodo. Neumann.dat: Es un archivo que describe las condiciones de contorno Neumann. En cada línea encontramos descrito el lado de Neumann correspondiente mediante el primer nodo que lo forma, el segundo nodo y el subdominio al que pertenece dicho lado. Dirichlet.dat: De igual modo este archivo describe las condiciones de contorno de Dirichlet. Cada línea corresponde a un lado Dirichlet descrito mediante su primer nodo, su segundo nodo y el subdominio al que pertenece. 2. CÓDIGO SECUENCIAL Esta parte está constituida por el archivo femp4 y por archivos auxiliares. Realiza las siguientes tareas: 1. Inicialización y definición de variables. 2. Lectura de archivos 3. Generación de matrices locales y su ensamblado en la matriz de Rigidez. 4. Generación del vector de elementos independientes definido según las condiciones de contorno Dirichlet y Neumann. 5. Resolución de problema y obtención del vector X. 6. Comprobación de la precisión del resultado con respecto a la solución correcta. 7. Representación. En Matlab la matriz de rigidez se define y almacena como matriz dispersa (Sparse). 84

3 Todas estas operaciones se realizan en la CPU. En las versiones multiprocesador, algunas de las tareas se comparten entre los distintos microprocesadores del equipo de manera transparente para el usuario, realizándose una ejecución en paralelo. Sin embargo, el control de dicha ejecución, en todo momento, lo realizan la aplicación y el sistema operativo. 3. BUCLES E IDENTIFICACIÓN DE CUELLOS DE BOTELLA (BLOQUES) Para proceder a la adaptación del código se tuvieron presentes los siguientes objetivos: - El sistema debe ser acelerado mediante la tecnología CUDA; es decir usando paralelización basado en el modelo Una Instrucción-Datos Múltiples. - El sistema debe gestionar la memoria de manera eficiente permitiendo manejar matrices grandes y por tanto mallados muy finos. Por tanto se pretendían aprovechar dos características fundamentales del problema conocidas de antemano: - Que la Matriz de rigidez, es una matriz Real, Cuadrada, Dispersa, Simétrica y con diagonal principal no-nula. - Que a la hora de resolver el sistema se debe tener presente que se debe desarrollar un SOLVER rápido apropiado para matrices dispersas. Mediante inspección del código se identificaron los bloques iterativos como cuellos de botellas y se decidió analizarlos para someterlos a aceleración con la tecnología CUDA. En un análisis teórico previo para decidir su prioridad se ordenaron del siguiente modo: - Bloque I: Resolución de problema y obtención del vector Solución (X). Es el bloque identificado en el código MATLAB con el comentario % RESOLVER y que realiza la resolución mediante la orden MATLAB:x[Lib]=A[Lib]\B[Lib]. - Bloque II: Generación de matrices de rigidez: En MATLAB se señala este bloque como potencialmente lento por la propia aplicación. Está identificado por el comentario % ENSAMBLADO MATRIZ + FUERZAS VOLUMETRICAS (f) e invoca un programa auxiliar para la generación de matrices locales y su ensamblado. - Bloque III: Generación del vector de elementos independientes definido según las condiciones de contorno Dirichlet y Neumann. MODIFICACIONES INTRODUCIDAS EN EL CÓDIGO ORIGINAL: El código Matlab original fue modificado insertando líneas de comando que no modificaban sus tareas sino que aportaban mayor información. 85

4 En concreto se insertó un comando para generar un archivo en formato martix market con extensión.mtx que almacenaba la matriz de rigidez para poder ser usada en la comprobación de los solvers CUDA. Esto se hizo mediante la orden mmwrite('a_matlab.mtx',a). Esta orden se apoya en la función mmwrite codificada en el archivo mmio.c y disponible en el sitio Web Matrix Market. Esta función permite el almacenamiento de una matriz en un archivo en formato MM. También está disponible la función inversa que carga una matriz desde un archivo MM a la memoria del sistema. Ambas son funciones C convencionales. También se insertó una instrucción para generar un archivo que contenía el vector de elementos independientes con extensión.dat con el mismo fin. Esto se hizo con la orden save file.dat array -ascii disponible en MATLAB. Esto permitiría comparar los valores de la Matriz de Rigidez y del Vector de términos independientes con aquellos obtenidos por la aplicación CUDA, mediante la inspección de los archivo. Se insertaron también instrucciones tic y toc antes y después de A\B para medir el tiempo que tardaba la CPU en ejecutar esa instrucción y compararlo con el tiempo de ejecución del equivalente paralelo en los solvers CUDA. Pero también se usaron para medir el tiempo de ejecución global, colocándolos al principio y al final de código. Como criterio de comparación de la exactitud de las soluciones se decidió usar la Norma de tal forma que también se insertó una orden para ofrecer en pantalla el resultado de: Norma (B-A X)/Norma (B). 86

5 4. ANEXOS ANEXO I: Código MATLAB de Partida con las modificaciones usadas. function u=femp4 tic %medida de tiempo de ejecuciã³n load coordenadas.dat; load triangulos.dat; load neumann.dat; load dirichlet.dat; numnodos=size(coordenadas,1); numtriang=size(triangulos,1); numladosdir=size(dirichlet,1); numladosneu=size(neumann,1); % no se usa % CREACION DE LA LISTA DE NODOS DIRICHLET dirichlet=[dirichlet(:,[1 3]);dirichlet(:,[2 3])]; [Dir,distintos]=unique(dirichlet(:,1)); save DIR.dat Dir -ascii save dirich.dat dirichlet -ascii subdir=dirichlet(distintos,2); Lib=setdiff(1:numNodos,Dir); A=sparse(numNodos,numNodos); b=zeros(numnodos,1); % nodos incognita % ENSAMBLADO MATRIZ + FUERZAS VOLUMETRICAS (f) for j=1:numtriang tri=triangulos(j,:); % vertices del triangulo # j vertices=coordenadas(tri,:); % coordenadas de sus vertices [R,M,jacob]=local(vertices); % rigidez y masa local A(tri,tri)=A(tri,tri)+0*M+R; % ensamblado baricentro=sum(vertices)/3; % baricentro del triangulo aux=(jacob/6)*f(baricentro); %contribucion b(tri)=b(tri)+aux*[1;1;1]; end mmwrite('a_matlab.mtx',a); % CONDICIONES NEUMANN (g) for j=1:numladosneu lado=neumann(j,1:2); % extremos del lado # j subd=neumann(j,3); % subdominio del lado #j coord=coordenadas(lado,:); % coordenadas de los extremos ptomedio=sum(coord)/2; % punto medio del lado longitud=norm(coord(1,:)-coord(2,:)); % longitud del lado aux=longitud*g(ptomedio,subd)/2; % contribucion; b(lado)=b(lado)+aux*[1;1]; end 87

6 save BN.dat b -ascii % CONDICIONES DIRICHLET (u_d) coordir=coordenadas(dir,:); % coordenadas de los nodos Dirichlet u=zeros(numnodos,1); % para la solucion u(dir)=u_d(coordir,subdir); % evalï ½o u_d en los nodos Dirichlet save UD.dat u -ascii b=b-a*u; % A*u=A(:,Dir)*u(Dir) porque u(lib)=0 save temp.dat b -ascii % RESOLVER u(lib)=a(lib,lib)\b(lib); save x.dat u -ascii toc K=b-A*u; save dif.dat K -ascii norm(b-a*u)/norm(b) trisurf(triangulos,coordenadas(:,1),coordenadas(:,2),u),... view(0,90),... colorbar,... shading interp; exacta=u_ex(coordenadas); save exacta.dat u_ex -ascii err=abs(exacta-u); pause trisurf(triangulos,coordenadas(:,1),coordenadas(:,2),err),... view(0,90),... colorbar,... shading interp; 88