Problema 1. Se considera un triángulo equilátero de lado 1 y centro O, comoeldelafigura.
|
|
|
- Martín Ortiz de Zárate Navarrete
- hace 5 años
- Vistas:
Transcripción
1 Problema 1. Se considera un triángulo equilátero de lado 1 y centro O, comoeldelafigura. O C Un rayo parte de O y se refleja en los tres lados,, C y C, (en el orden dado), hasta alcanzar el vértice. Determinalalongitudmínima del recorrido del rayo. Nota: Cuando el rayo se refleja en un lado, los ángulos de entrada (incidencia) y salida (reflexión) coinciden. Solución. Como el rayo se refleja en los lados indicados, basta con desarrollar el camino recorrido por el rayo, para ello desdoblamos el triángulo según la siguiente figura. O C P O C Esta figura nos indica que existe un único camino para ir del punto O al punto reflejándose en los lados del triángulo en el orden indicado. Para calcular la distancia recorrida por el rayo, basta considerar el triángulo P O ; es un triángulo rectángulo del que tenemos que calcular la hipotenusa O. Sabemos que O P es igual a 1. La distancia P es = 7 de la altura h = del triángulo. En este caso tenemos: (O ) =(O P ) +(P) = Por lo tanto la distancia O es: ( ) ( = 9. Problema. Calcula las soluciones reales de la ecuación: 4 97 X + 4 X =5. ) = = = 1. 1
2 Solución. Si llamamos a = 4 97 x y b = 4 x, se verifica: a + b =5 a 4 + b 4 =97 Para resolver este sistema procedemos como sigue: 5 = (a + b) = a +ab + b ydeaquísetienea + b =5 ab. Por otro lado 65 = (a + b) 4 = a 4 + b 4 +4ab(a + b )+6a b = ab a b, ydeaquísetienea b 50ab + 64 = 0. Entonces ab es una raíz de z 50z + 64 = 0; como las raíces son 44 y 6, estudiamos cada uno de estos casos. Si ab = 44, entonces a y b son las soluciones del sistema a + b =5, luego de la ecuación ab =44 z 5z +44=0; ésta no tiene raíces reales. Si ab = 6, entonces a y b son raíces de la ecuación z 5z + 6 = 0, que tiene las raíces y. Si b =, entonces x = 81, y si x =, entonces x = 16. Éstas son las únicas raíces reales de la ecuación dada. Solución.[lternativa] Si llamamos a = 4 97 x y b = 4 x, se verifica: a + b =5 a 4 + b 4 =97 Utilizamos una variable temporal t yescribimosa = 5 + t, b = 5 t. entonces se verifica: ( ) 4 ( ) 4 ( ) ( ) = a 4 + b 4 = + t + t =t 4 +1 t +. Simplificando resulta: 16t t 151 = 0 El valor de t es ± 1. Se tiene entonces: b = =; Entonces al igualar b = 4 x,resulta: b = 5 1 =. b = x =81, b = x =16, que son las únicas dos soluciones reales de la ecuación dada. Problema. Dado el polinomio P (X) =X 4 + X + X + X +, en el que cada cuadrado representa un hueco donde se colocará un coeficiente, se plantea el siguiente juego entre dos jugadores: lternativamente, el primer y el segundo jugador eligen un hueco vacío y colocan en él un entero no nulo hasta rellenar todos los cuatro huecos. Si el polinomio resultante tiene al menos dos raíces enteras gana el segundo jugador, en otro caso el ganador es el primero. Prueba que, eligiendo la estrategia adecuada, el primer jugador siempre puede ganar.
3 Solución. Nota: El enunciado presenta cierta ambigüedad: hay que distinguir si dos raíces enteras significa que éstas son distintas, o por el contrario pueden ser raíces dobles. El caso de dos raíces distintas es sencillo; basta con la primera jugada para el primer jugador. En el caso de raíces dobles tiene que hacer uso también de la segunda jugada. Una posible estrategia es: (i) El primer jugador coloca un -1 en el lugar a 4, quedando el polinomio en la forma: X 4 + X + X + X 1 De esta forma el primer jugador fuerza a que las posibles raíces enteras del polinomio sean 1 y 1. (ii) El segundo jugador coloca a i 0 en uno de los huecos. (iii) El primer jugador coloca a j 0 en uno de los huecos. (iv) El segundo jugador coloca a k 0 en el único hueco restante. Observa que el polinomio tiene ahora la forma X 4 + a 1 X + a X + a X 1yquelasposibles raíces enteras (distintas) de este polinomio son 1 y -1, ya que el término independiente es 1. Cuando 1 es una raíz se tiene 1 + a 1 + a + a 1 = 0, esto es, a 1 + a + a = 0, y cuando 1 es una raíz se tiene 1 a 1 + a a 1 = 0, esto es a 1 + a a =0. Sean cuales sean los valores de a 1,a,a se tendrá siemprea = 0, lo que implica que a =0, y esto no está permitido por las reglas del juego. Por lo tanto el caso de dos raíces distintas está resuelto. En el caso en el que las dos raíces sean iguales. Si 1 es una raíz doble, entonces se verifica a 1 + a + a =0y4+a 1 +a + a =0,porlo tanto se tiene: a 1 + a + a =0 4+a 1 +a =0 siendo a =4+a 1 y a = 4 a 1. Si 1 es una raíz doble, entonces se verifica a 1 + a a =0y4 a 1 +a a =0,porlo tanto se tiene: a 1 + a a =0 4 a 1 +a =0 siendo a = 4+a 1 y a = 4+a 1. Está claro que si el segundo jugador hace a i = a, entonces el primer jugador puede colocar a j = a 1 de forma que 4 a 1 a y 4+a 1 a, de esta forma no habrá dosraíces enteras. Por el contrario, si el primer jugador hace a i = a 1, basta tomar a de forma que a 4 a 1 y a 4+a 1.Elcasodea i = a se hace de la misma forma. Problema 4. Supongamos que tenemos un tablero con dieciséiscasillasdispuestasencuatro filas y cuatro columnas. (a) Prueba que se pueden colocar siete fichas, nunca dos en la misma casilla, de forma que al eliminar dos filas y dos columnas cualesquiera, siempre quede alguna ficha sin eliminar. (b) Prueba que si se colocan seis fichas, nunca dos en la misma casilla, siempre se puede eliminar dos filas y dos columnas de forma que todas las fichas sean eliminadas.
4 Solución. (a).unasolución es: (b). Si se tienen 6 fichas en el tablero, alguna columna tendrá al menos dos fichas; eliminamos esa columna. Quedan, como máximo 4 fichas, y exactamente tres columnas. Por el mismo procedimiento podemos ahora eliminar una columna de forma que nos queden. como máximo, dos fichas en el tablero. El tercer y cuarto paso consiste en eliminar dos filas de forma que no queden fichas en el tablero. Problema 5. Se considera un tetraedro regular como el de la figura. Si el punto E recorre la arista. Cuándo el ángulo ĈED es máximo? E D C Solución. Supongamos que el tetraedro tiene arista de longitud 1, sea α el ángulo CED y x la longitud del segmento E. Si aplicamos el Teorema del coseno al triángulo EC tenemos: EC = x +1 x cos 60 o = x +1 x. Por simetría se tiene que la longitud EC es igual a la longitud ED. DenuevoporelTeorema del coseno, ahora para el triángulo ECD, se tiene 1=(x x +1)+(x x +1) ( x x +1) cos α 4
5 1=(x x + 1)(1 cos α). Despejando se tiene: 1 cos α =1 (x x +1). (1) Por ser la función cos decreciente en el primer cuadrante, par encontrar el valor máximo de α tenemos que buscar el valor de x [0, 1] que haga mínima la función dada en (1), o equivalentemente que haga mínimo el denominador x x + 1. Es evidente que este mínimo se alcanza para x = 1. La respuesta es: cuando el punto E es el punto medio del lado. Podemos calcular en este caso el valor de α; setiene:α = arccos 1. Problema 6. Decimos que un conjunto E de números naturales es especial cuando al tomar dos elementos cualesquiera distintos a, b E se tiene que (a b) divide al producto ab. (a) Encuentra un conjunto especial formado por tres elementos. (b) Existe un conjunto especial formado por cuatro números naturales que están en progresión aritmética? Solución. (a). Un conjunto especial de tres elementos es {,, 4. (b). Supongamos que {x, x + y, x +y, x +y forman un conjunto especial. Podemos suponer que x e y son primos relativos, pues si llamamos d = mcd{x, y y d 1, tomando x = x/d e y = y/d tenemos un conjunto especial {x,x + y,x +y,x +y con x e y primos relativos. Sean pues x e y primos relativos. Por ser el conjunto especial y divide a x(x + y), y existe un entero k tal que x(x + y) =y k,porlotantox = y k xy = y(yk x), lo que implica que y = 1 al ser un divisor común de x e y. sí pues el conjunto especial es de la forma {x, x +1,x+,x+. l ser especial 4 es un divisor de x(x +)yde (x +1)(x + ), pero uno de ellos es un número impar, lo que es una contradicción. Por lo tanto la suposición de que existe un conjunto especial formado por cuatro términos en progresión aritmética es falsa. 5
Curso Curso
 Problema 77. Se considera un triángulo equilátero de lado 1 y centro O, y vértices A, B y C. Un rayo luminoso parte de O, se refleja una vez en cada uno de los tres lados, AB, AC y BC (en el orden dado)
Problema 77. Se considera un triángulo equilátero de lado 1 y centro O, y vértices A, B y C. Un rayo luminoso parte de O, se refleja una vez en cada uno de los tres lados, AB, AC y BC (en el orden dado)
Seminario de problemas-eso. Curso Hoja 14
 Seminario de problemas-eso. Curso 011-1. Hoja 14 6. Determina el valor de m tal que la ecuación en x x 4 (3m + )x + m = 0 tenga cuatro raíces en progresión aritmética. Como la suma de las cuatro raíces
Seminario de problemas-eso. Curso 011-1. Hoja 14 6. Determina el valor de m tal que la ecuación en x x 4 (3m + )x + m = 0 tenga cuatro raíces en progresión aritmética. Como la suma de las cuatro raíces
SOLUCIONES ENERO 2018
 Página 1 de 9 SOLUCIONES ENERO 018 Soluciones extraídas del libro: XVIII CONCURSO DE PRIMAVERA 014 Obtenibles en http://www.concursoprimavera.es#libros NIVEL: Segundo ciclo de la E. S. O. AUTORES: Colectivo
Página 1 de 9 SOLUCIONES ENERO 018 Soluciones extraídas del libro: XVIII CONCURSO DE PRIMAVERA 014 Obtenibles en http://www.concursoprimavera.es#libros NIVEL: Segundo ciclo de la E. S. O. AUTORES: Colectivo
2. Hallar las soluciones enteras de la ecuación. x 4 + y 4 = 3x 3 y.
 Sesión 1. Se considera un polígono regular de 90 vértices, numerados del 1 al 90 de manera aleatoria. Probar que siempre podemos encontrar dos vértices consecutivos cuyo producto es mayor o igual que 014.
Sesión 1. Se considera un polígono regular de 90 vértices, numerados del 1 al 90 de manera aleatoria. Probar que siempre podemos encontrar dos vértices consecutivos cuyo producto es mayor o igual que 014.
TALLER DE MATEMÁTICAS NOTAS. Toda expresión algebraica del tipo. a n x n + a n 1 x n a 1 x + a 0. es un polinomio de grado n, si a n 0.
 NOTAS Toda expresión algebraica del tipo es un polinomio de grado n, si a n 0. a n x n + a n 1 x n 1 +... + a 1 x + a 0 RELACIONES DE DIVISIBILIDAD 1) x n a n = (x a)(x n 1 + ax n 2 + a 2 x n 3 +... +
NOTAS Toda expresión algebraica del tipo es un polinomio de grado n, si a n 0. a n x n + a n 1 x n 1 +... + a 1 x + a 0 RELACIONES DE DIVISIBILIDAD 1) x n a n = (x a)(x n 1 + ax n 2 + a 2 x n 3 +... +
no descompone no descompone no descompone
 Problema 1. Sea I n el conjunto de los n primeros números naturales impares. Por ejemplo: I 3 = {1, 3, 5, I 6 = {1, 3, 5, 7, 9, 11, etc. Para qué números n el conjunto I n se puede descomponer en dos partes
Problema 1. Sea I n el conjunto de los n primeros números naturales impares. Por ejemplo: I 3 = {1, 3, 5, I 6 = {1, 3, 5, 7, 9, 11, etc. Para qué números n el conjunto I n se puede descomponer en dos partes
PREEVALUACIÓN CURSO 0 SOLUCIONES
 PREEVALUACIÓN CURSO SOLUCIONES Problema. Dado el número decimal 68, encuentra su representación binaria. Solución. Para encontrar la representación binaria del número, lo pondremos en una columna, en la
PREEVALUACIÓN CURSO SOLUCIONES Problema. Dado el número decimal 68, encuentra su representación binaria. Solución. Para encontrar la representación binaria del número, lo pondremos en una columna, en la
SEGUNDO NIVEL. Problema 1 Hallar todos los números naturales a tales que para todo natural n el número n( a + n) no es un cuadrado perfecto.
 PRIMER NIVEL PRIMER DÍA Problema 1 Se tiene un tablero rectangular de 2 13. En cada casilla de la fila inferior hay una ficha y las 13 fichas están numeradas de 1 a 13, de menor a mayor; la fila superior
PRIMER NIVEL PRIMER DÍA Problema 1 Se tiene un tablero rectangular de 2 13. En cada casilla de la fila inferior hay una ficha y las 13 fichas están numeradas de 1 a 13, de menor a mayor; la fila superior
XIII. SegundaFecha. Primer Nivel. 30 de Mayo de 2015 Soluciones. Individual
 XIII SegundaFecha 30 de Mayo de 2015 Soluciones Individual Primer Nivel 1 Un cuadrado mágico es un tablero cuadriculado cuadrado, en el cual, en cada casilla se escribe un numero natural de manera tal
XIII SegundaFecha 30 de Mayo de 2015 Soluciones Individual Primer Nivel 1 Un cuadrado mágico es un tablero cuadriculado cuadrado, en el cual, en cada casilla se escribe un numero natural de manera tal
Trabajo 2. Jonathan A. Trejos O. El primer problema es uno típico de teoría de números, en el cual se puede apreciar la simetría.
 Trabajo Jonathan A. Trejos O. 1 Primer problema El primer problema es uno típico de teoría de números, en el cual se puede apreciar la simetría. Enunciado 1 Halle y pruebe una bonita fórmula para el producto
Trabajo Jonathan A. Trejos O. 1 Primer problema El primer problema es uno típico de teoría de números, en el cual se puede apreciar la simetría. Enunciado 1 Halle y pruebe una bonita fórmula para el producto
PRUEBA REGIONAL OJM 2012
 PRUE REGIONL OJM 2012 Problemas y Soluciones Problema 1 de Primer y Segundo ño. El área de la siguiente figura, construida con cuadrados idénticos, es 72 cm 2. uál es su perímetro? Solución: La figura
PRUE REGIONL OJM 2012 Problemas y Soluciones Problema 1 de Primer y Segundo ño. El área de la siguiente figura, construida con cuadrados idénticos, es 72 cm 2. uál es su perímetro? Solución: La figura
PREEVALUACIÓN CURSO 0 SOLUCIONES
 PREEVALUACIÓN CURSO 0 SOLUCIONES Problema. Dado el número decimal 9, encuentra su representación binaria. Solución. Para encontrar la representación binaria del número, lo pondremos en una columna, en
PREEVALUACIÓN CURSO 0 SOLUCIONES Problema. Dado el número decimal 9, encuentra su representación binaria. Solución. Para encontrar la representación binaria del número, lo pondremos en una columna, en
SOLUCIONES SEPTIEMBRE 2016
 Página de 9 SOLUCIONES SEPTIEMBRE 206 Soluciones extraídas de los libros: XII CONCURSO DE PRIMAVERA 2008 XV CONCURSO DE PRIMAVERA 20 XVI CONCURSO DE PRIMAVERA 202 Obtenibles en http://www.concursoprimavera.es#libros
Página de 9 SOLUCIONES SEPTIEMBRE 206 Soluciones extraídas de los libros: XII CONCURSO DE PRIMAVERA 2008 XV CONCURSO DE PRIMAVERA 20 XVI CONCURSO DE PRIMAVERA 202 Obtenibles en http://www.concursoprimavera.es#libros
Unidad 2 Polinomios PÁGINA 28 SOLUCIONES. Sacar factor común. a) b) Evaluar un polinomio en un punto.
 Unidad Polinomios PÁGINA 8 SOLUCIONES Sacar factor común. a) b) 3x 6 3 ( x ) 3 5x 10x 5x 5 x( x x1) Evaluar un polinomio en un punto. Dado el polinomio P(x) = x 4 x 3 x + 1, podemos asegurar que: a) P(1)
Unidad Polinomios PÁGINA 8 SOLUCIONES Sacar factor común. a) b) 3x 6 3 ( x ) 3 5x 10x 5x 5 x( x x1) Evaluar un polinomio en un punto. Dado el polinomio P(x) = x 4 x 3 x + 1, podemos asegurar que: a) P(1)
Seminario de problemas. Curso Hoja 17
 Seminario de problemas. Curso 015-15. Hoja 17 11. [Olimpiada Matemática de Española, 00, Islas Canarias] Las alturas de un triángulo ABC se cortan en un punto H. Sabemos que AB = CH. Determinad el valor
Seminario de problemas. Curso 015-15. Hoja 17 11. [Olimpiada Matemática de Española, 00, Islas Canarias] Las alturas de un triángulo ABC se cortan en un punto H. Sabemos que AB = CH. Determinad el valor
Nivel: A partir de 4ESO. Solución: La relación entre la apotema y el lado del hexágono es la misma que entre la altura y
 Página 1 de 9 SOLUCIONES MAYO 2017 Soluciones extraídas de los libros: XVI CONCURSO DE PRIMAVERA 2012 XVII CONCURSO DE PRIMAVERA 2013 Obtenibles en http://www.concursoprimavera.es#libros AUTORES: Colectivo
Página 1 de 9 SOLUCIONES MAYO 2017 Soluciones extraídas de los libros: XVI CONCURSO DE PRIMAVERA 2012 XVII CONCURSO DE PRIMAVERA 2013 Obtenibles en http://www.concursoprimavera.es#libros AUTORES: Colectivo
EJERCICIOS DE GEOMETRÍA PLANA. 1. Hallar las ecuaciones paramétricas de la recta r que pasa por el punto ( 2, 2) tiene como vector director el vector
 EJERCICIOS DE GEOMETRÍA PLANA Hallar las ecuaciones paramétricas de la recta r que pasa por el punto (, ) tiene como vector director el vector v i j A y x a + vt La ecuación paramétrica de una recta es
EJERCICIOS DE GEOMETRÍA PLANA Hallar las ecuaciones paramétricas de la recta r que pasa por el punto (, ) tiene como vector director el vector v i j A y x a + vt La ecuación paramétrica de una recta es
PRIMERA PRUEBA. 28 DE AGOSTO DE 1999 PROBLEMAS
 PRIMERA PRUEBA. 8 DE AGOSTO DE 1999 PROBLEMAS 1. Fíjate en la primera estrella, la cual está formada por 1 triángulos equiláteros. Cada número indica cuántos triángulos negros tienen vértice allí. a. Copia
PRIMERA PRUEBA. 8 DE AGOSTO DE 1999 PROBLEMAS 1. Fíjate en la primera estrella, la cual está formada por 1 triángulos equiláteros. Cada número indica cuántos triángulos negros tienen vértice allí. a. Copia
TEMA 3. POLINOMIOS Y FRACCIONES ALGEBRAICAS. Ficha 1. P x
 Ficha. Dados los siguientes polinomios, ordenarlos en orden decreciente, indicar cuál es su grado, decir cuántos términos tiene, señalar cuál es el término independiente, calcular su valor numérico para
Ficha. Dados los siguientes polinomios, ordenarlos en orden decreciente, indicar cuál es su grado, decir cuántos términos tiene, señalar cuál es el término independiente, calcular su valor numérico para
Seminario de problemas Curso Soluciones HOJA 4
 Seminario de problemas Curso 04-5 Soluciones HOJA 4. Sea ABCD un trapecio cuya base mayor es AB. Las diagonales AC y BD se cortan en el punto P. Si llamamos respectivamente A, A, A y A a las áreas de los
Seminario de problemas Curso 04-5 Soluciones HOJA 4. Sea ABCD un trapecio cuya base mayor es AB. Las diagonales AC y BD se cortan en el punto P. Si llamamos respectivamente A, A, A y A a las áreas de los
b) Si la ficha con el número x y la ficha con el número y son de distinto color, entonces la ficha con el número x y se pinta de color rojo.
 Sesión 1 1. Tenemos 50 fichas numeradas del 1 al 50, y hay que colorearlas de rojo o azul. Sabemos que la ficha 5 es de color azul. Para la coloración del resto de fichas se siguen las siguientes reglas:
Sesión 1 1. Tenemos 50 fichas numeradas del 1 al 50, y hay que colorearlas de rojo o azul. Sabemos que la ficha 5 es de color azul. Para la coloración del resto de fichas se siguen las siguientes reglas:
IES FONTEXERÍA MUROS. 18-X-2013 Nombre y apellidos:...
 IES FONTEXERÍA MUROS MATEMÁTICAS 2º E.S.O-A (Desdoble 1) 1º Examen (1ª Evaluación) 18-X-201 Nombre y apellidos:... 1. Contesta estas cuestiones: a) Qué es un monomio?. Un monomio es una expresión algebraica
IES FONTEXERÍA MUROS MATEMÁTICAS 2º E.S.O-A (Desdoble 1) 1º Examen (1ª Evaluación) 18-X-201 Nombre y apellidos:... 1. Contesta estas cuestiones: a) Qué es un monomio?. Un monomio es una expresión algebraica
I.P.A.O.(Granada) EXAMEN DE ANDALUCIA 2002 J.A. Romero
 1. - Se dan las rectas r 1 : x + y - 2 = 0. r 2 : x + 2y-3 = 0 r 3 : 3 x + y - 4 = 0 Hallar los vértices A, B y C de un triángulo sabiendo que el radio de la circunferencia circunscrita es 2 y que r 1
1. - Se dan las rectas r 1 : x + y - 2 = 0. r 2 : x + 2y-3 = 0 r 3 : 3 x + y - 4 = 0 Hallar los vértices A, B y C de un triángulo sabiendo que el radio de la circunferencia circunscrita es 2 y que r 1
GEOMETRÍA. Septiembre 94. Determinar la ecuación del plano que pasa por el punto M (1, 0, [1,5 puntos]
![GEOMETRÍA. Septiembre 94. Determinar la ecuación del plano que pasa por el punto M (1, 0, [1,5 puntos] GEOMETRÍA. Septiembre 94. Determinar la ecuación del plano que pasa por el punto M (1, 0, [1,5 puntos]](/thumbs/86/94405582.jpg) Matemáticas II Pruebas de Acceso a la Universidad GEOMETRÍA Junio 94 1 Sin resolver el sistema, determina si la recta x y + 1 = 0 es exterior, secante ó tangente a la circunferencia (x 1) (y ) 1 Razónalo
Matemáticas II Pruebas de Acceso a la Universidad GEOMETRÍA Junio 94 1 Sin resolver el sistema, determina si la recta x y + 1 = 0 es exterior, secante ó tangente a la circunferencia (x 1) (y ) 1 Razónalo
Seminario de problemas. Curso Hoja 7
 Seminario de problemas. Curso 015-16. Hoja 7 37. Determinar un número de cinco cifras tal que su cuadrado termine en las mismas cinco cifras colocadas en el mismo orden. La forma más simple de resolver
Seminario de problemas. Curso 015-16. Hoja 7 37. Determinar un número de cinco cifras tal que su cuadrado termine en las mismas cinco cifras colocadas en el mismo orden. La forma más simple de resolver
Trigonometría. 1. Ángulos
 Trigonometría Ángulos Hasta ahora se han considerado los ángulos como la porción del plano comprendida entre dos semirrectas con el origen común De esta manera, la medida de un ángulo está comprendida
Trigonometría Ángulos Hasta ahora se han considerado los ángulos como la porción del plano comprendida entre dos semirrectas con el origen común De esta manera, la medida de un ángulo está comprendida
Tema 3: Expresiones algebraicas
 .1 Polinomios Tema : Expresiones algebraicas Determina cuáles de las siguientes expresiones son polinomios. Cuando lo sean, dí cuáles son sus monomios(términos), su grado, término principal, término independiente,
.1 Polinomios Tema : Expresiones algebraicas Determina cuáles de las siguientes expresiones son polinomios. Cuando lo sean, dí cuáles son sus monomios(términos), su grado, término principal, término independiente,
EJERCICIOS Y PROBLEMAS RESUELTOS
 Ecuaciones de Segundo Grado -- página 1 EJERCICIOS Y PROBLEMAS RESUELTOS Ejercicio 1: Indica si son ecuaciones de segundo grado las siguientes ecuaciones: a) 5 + 8 + b) + + ( )( + ) c) + 1 a) El primer
Ecuaciones de Segundo Grado -- página 1 EJERCICIOS Y PROBLEMAS RESUELTOS Ejercicio 1: Indica si son ecuaciones de segundo grado las siguientes ecuaciones: a) 5 + 8 + b) + + ( )( + ) c) + 1 a) El primer
Soluciones Fase Local Viernes 15 y sábado 16 de enero de 2016
 LII Olimpiada Matemática Española Soluciones Fase Local Viernes 15 y sábado 16 de enero de 2016 Olimpiada Matemática Española RSME 1. En la primera fila de un tablero 5 5 se colocan 5 fichas que tienen
LII Olimpiada Matemática Española Soluciones Fase Local Viernes 15 y sábado 16 de enero de 2016 Olimpiada Matemática Española RSME 1. En la primera fila de un tablero 5 5 se colocan 5 fichas que tienen
MODELO DE RESPUESTA SEGUNDA PRUEBA INTEGRAL MATEMÁTICA I ( ) Lapso
 Primera Prueba Integral Lapso 004-7-76-77 UNIVERSIDAD NACIONAL ABIERTA CENTRO LOCAL METROPOLITANO ÁREA DE MATEMÁTICA MODELO DE RESPUESTA SEGUNDA PRUEBA INTEGRAL MATEMÁTICA I (7 76 77) Lapso.004- OBJ PTA
Primera Prueba Integral Lapso 004-7-76-77 UNIVERSIDAD NACIONAL ABIERTA CENTRO LOCAL METROPOLITANO ÁREA DE MATEMÁTICA MODELO DE RESPUESTA SEGUNDA PRUEBA INTEGRAL MATEMÁTICA I (7 76 77) Lapso.004- OBJ PTA
= a + b + c a + 1 b + 1 ) La desigualdad anterior se cumple cuando uno de los factores del número
 1.- Sean a, b i c tres números reales positivos cuyo producto es 1. Demuestra que, si la suma de estos números es mayor que la suma de sus inveros, entonces exactamente uno de ellos es mayor que 1. Solución.
1.- Sean a, b i c tres números reales positivos cuyo producto es 1. Demuestra que, si la suma de estos números es mayor que la suma de sus inveros, entonces exactamente uno de ellos es mayor que 1. Solución.
XVIII Olimpíada Matemática Rioplatense San Isidro, 7 de Diciembre de Nivel A Primer Día
 Nivel A Primer Día 1. En una caja hay 2009 bolitas numeradas del 1 al 2009, y fuera de la caja hay bolitas sin numerar. Andrés repite el siguiente procedimiento hasta que quedee sólo una bolita en la caja.
Nivel A Primer Día 1. En una caja hay 2009 bolitas numeradas del 1 al 2009, y fuera de la caja hay bolitas sin numerar. Andrés repite el siguiente procedimiento hasta que quedee sólo una bolita en la caja.
LA RECTA Y SUS ECUACIONES
 UNIDAD LA RECTA Y SUS ECUACIONES EJERCICIOS RESUELTOS Objetivo general. Al terminar esta Unidad resolverás ejercicios y problemas correspondientes a las rectas en el plano y sus ecuaciones. Objetivo. Recordarás
UNIDAD LA RECTA Y SUS ECUACIONES EJERCICIOS RESUELTOS Objetivo general. Al terminar esta Unidad resolverás ejercicios y problemas correspondientes a las rectas en el plano y sus ecuaciones. Objetivo. Recordarás
Olimpiada Paceña de Matemática
 Olimpiada Paceña de Matemática Carrera de Matemática Instituto de Investigación Matemática, Facultad de Ciencias Puras y Naturales, Universidad Mayor de San Andrés, La Paz, Bolivia. Cuaderno N 3 Banco
Olimpiada Paceña de Matemática Carrera de Matemática Instituto de Investigación Matemática, Facultad de Ciencias Puras y Naturales, Universidad Mayor de San Andrés, La Paz, Bolivia. Cuaderno N 3 Banco
Enunciados de problemas de números.
 Nº. Enunciados de problemas de números. Hallar un número de 4 cifras que sea igual al cubo de la suma de las cifras. 2 Demostrar que si a, b y c son números racionales arbitrarios, los polinomios: n -2
Nº. Enunciados de problemas de números. Hallar un número de 4 cifras que sea igual al cubo de la suma de las cifras. 2 Demostrar que si a, b y c son números racionales arbitrarios, los polinomios: n -2
EJERCICIOS PROPUESTOS. Escribe las expresiones algebraicas correspondientes. a) Tres números consecutivos. b) Tres números pares consecutivos.
 EJERCICIOS PROPUESTOS 4.1 Relaciona cada enunciado con su expresión algebraica. Múltiplo de 3. Número par. El cuadrado de un número más 3. Un número más 5. El triple de un número más 7. 2x x 5 3x x 2 3
EJERCICIOS PROPUESTOS 4.1 Relaciona cada enunciado con su expresión algebraica. Múltiplo de 3. Número par. El cuadrado de un número más 3. Un número más 5. El triple de un número más 7. 2x x 5 3x x 2 3
EJERCICIOS PROPUESTOS. Escribe las expresiones algebraicas correspondientes. a) Tres números consecutivos. b) Tres números pares consecutivos.
 EJERCICIOS PROPUESTOS 4.1 Relaciona cada enunciado con su expresión algebraica. Múltiplo de 3. Número par. El cuadrado de un número más 3. Un número más 5. El triple de un número más 7. 2x x 5 3x x 2 3
EJERCICIOS PROPUESTOS 4.1 Relaciona cada enunciado con su expresión algebraica. Múltiplo de 3. Número par. El cuadrado de un número más 3. Un número más 5. El triple de un número más 7. 2x x 5 3x x 2 3
Cuarta Fase Nivel Se tiene los siguientes tableros de 4 4: Tablero 1. Tablero 2
 Capítulo 8 Cuarta Fase 8.. Nivel. Se tiene los siguientes tableros de 4 4: Tablero Tablero Mateo debe eliminar algunos números de cada tablero de tal modo que la suma de los números que queden en cada
Capítulo 8 Cuarta Fase 8.. Nivel. Se tiene los siguientes tableros de 4 4: Tablero Tablero Mateo debe eliminar algunos números de cada tablero de tal modo que la suma de los números que queden en cada
PRUEBAS DE ACCESO A LA UNIVERSIDAD PARA ALUMNOS DE BACHILLERATO LOE Septiembre 2013 MATEMÁTICAS II. CÓDIGO 158
 PRUEBAS DE ACCESO A LA UNIVERSIDAD PARA ALUMNOS DE BACHILLERATO LOE Septiembre 2013 MATEMÁTICAS II. CÓDIGO 158 OBSERVACIONES IMPORTANTES: El alumno deberá responder a todas las cuestiones de una de las
PRUEBAS DE ACCESO A LA UNIVERSIDAD PARA ALUMNOS DE BACHILLERATO LOE Septiembre 2013 MATEMÁTICAS II. CÓDIGO 158 OBSERVACIONES IMPORTANTES: El alumno deberá responder a todas las cuestiones de una de las
1 Primera Sesión Ejercicio Ejercicio Ejercicio
 Problemas de la XXXVIII Olimpiada Matemática Española Primera Fase (Murcia) Archena, 18 de enero de 2002 IES Vicente Medina" http://www.fmath.um.es/rsme/38olimpiada.html 1 Primera Sesión 2 1.1 Ejercicio
Problemas de la XXXVIII Olimpiada Matemática Española Primera Fase (Murcia) Archena, 18 de enero de 2002 IES Vicente Medina" http://www.fmath.um.es/rsme/38olimpiada.html 1 Primera Sesión 2 1.1 Ejercicio
C2. El problema en el plano.
 C. Sea CD un cuadrilátero convexo y P un punto interior. Determina cuáles son las condiciones que deben cumplir el cuadrilátero y el punto P para que los cuatro triángulos P, PC, PCD i PD tengan la misma
C. Sea CD un cuadrilátero convexo y P un punto interior. Determina cuáles son las condiciones que deben cumplir el cuadrilátero y el punto P para que los cuatro triángulos P, PC, PCD i PD tengan la misma
Prueba clasificatoria - PAUTAS Olimpiada Nacional de Matemáticas Chile Primera prueba Nivel menor
 Prueba clasificatoria - PAUTAS Olimpiada Nacional de Matemáticas Chile 008 Primera prueba Nivel menor Problema 1 Se tienen 80 naranjas apiladas en una pirámide triangular Cuántas naranjas hay en la base
Prueba clasificatoria - PAUTAS Olimpiada Nacional de Matemáticas Chile 008 Primera prueba Nivel menor Problema 1 Se tienen 80 naranjas apiladas en una pirámide triangular Cuántas naranjas hay en la base
Primera Fase Primera sesión Viernes mañana, 17 de enero de 2014
 Primera sesión Viernes mañana, 17 de enero de 2014 1. Tenemos 50 fichas numeradas del 1 al 50, y hay que colorearlas de rojo o azul. Sabemos que la ficha 5 es de color azul. Para la coloración del resto
Primera sesión Viernes mañana, 17 de enero de 2014 1. Tenemos 50 fichas numeradas del 1 al 50, y hay que colorearlas de rojo o azul. Sabemos que la ficha 5 es de color azul. Para la coloración del resto
NÚMEROS ENTEROS. (1) Laura anotó en fichas las temperaturas a partir de las 8 de la mañana, pero las fichas de le
 NÚMEROS ENTEROS Matemática Año (1) Laura anotó en fichas las temperaturas a partir de las 8 de la mañana, pero las fichas de le desordenaron. Ayudá a Laura a escribir la temperatura correspondiente a cada
NÚMEROS ENTEROS Matemática Año (1) Laura anotó en fichas las temperaturas a partir de las 8 de la mañana, pero las fichas de le desordenaron. Ayudá a Laura a escribir la temperatura correspondiente a cada
Viernes mañana Problema 1. Sean a 1, b 1 números naturales cuyo máximo común divisor y mínimo común múltiplo designamos por D y M, respectivamente.
 Soluciones Viernes mañana Problema 1. Sean a 1, b 1 números naturales cuo máximo común divisor mínimo común múltiplo designamos por D M, respectivamente. Si a b son los respectivos cocientes obtenidos
Soluciones Viernes mañana Problema 1. Sean a 1, b 1 números naturales cuo máximo común divisor mínimo común múltiplo designamos por D M, respectivamente. Si a b son los respectivos cocientes obtenidos
Olimpiada Recreativa de Matemática Prueba Nacional Séptimo Grado
 Olimpiada Recreativa de Matemática Séptimo Grado Problema 1. Se tienen siete monedas: todas iguales en forma y tamaño, pero dos de ellas son un poco más pesadas que las otras cinco. Si tienes una balanza
Olimpiada Recreativa de Matemática Séptimo Grado Problema 1. Se tienen siete monedas: todas iguales en forma y tamaño, pero dos de ellas son un poco más pesadas que las otras cinco. Si tienes una balanza
EXAMEN SEGUNDO NIVEL SOLUCIONARIO
 XXVI OLIMPIADA COSTARRICENSE DE MATEMÁTICA UCR-UN A-IT CR-UN ED-MEP-MICIT SEGUNDA ELIMINATORIA NACIONAL EXAMEN SEGUNDO NIVEL SOLUCIONARIO 2014 SOLUCIONARIO EXAMEN SEGUNDO NIVEL SEGUNDA ELIMINATORIA 2014
XXVI OLIMPIADA COSTARRICENSE DE MATEMÁTICA UCR-UN A-IT CR-UN ED-MEP-MICIT SEGUNDA ELIMINATORIA NACIONAL EXAMEN SEGUNDO NIVEL SOLUCIONARIO 2014 SOLUCIONARIO EXAMEN SEGUNDO NIVEL SEGUNDA ELIMINATORIA 2014
Segunda Fase Nivel 1
 apítulo 6 Segunda Fase 6.1. Nivel 1 1. Ocho amigos fueron al cine. Ellos pagaron en total 78 soles por sus entradas, incluyendo 2 gaseosas. Si una entrada al cine cuesta lo mismo que 3 gaseosas, cuántos
apítulo 6 Segunda Fase 6.1. Nivel 1 1. Ocho amigos fueron al cine. Ellos pagaron en total 78 soles por sus entradas, incluyendo 2 gaseosas. Si una entrada al cine cuesta lo mismo que 3 gaseosas, cuántos
Seminario de problemas. Curso Hoja 9
 Seminario de problemas. Curso 204-5. Hoja 9 57. Se pincha aleatoriamente un punto P en el interior de un triángulo equilátero ABC. Cuál es la probabilidad de que los segmentos P A, P B y P C sean los lados
Seminario de problemas. Curso 204-5. Hoja 9 57. Se pincha aleatoriamente un punto P en el interior de un triángulo equilátero ABC. Cuál es la probabilidad de que los segmentos P A, P B y P C sean los lados
A) 7 B) 111 C) 567 D) 722 E) 728. El número que desconoce Sara se representa por la variable x, estableciendo la siguiente ecuación:
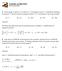 CANGURO MATEMÁTICO Portal Fuenterrebollo 1. Sara escoge un número, lo divide por 7, al resultado le suma 7 y finalmente multiplica la suma por 7. De esta manera consigue el número 777. Cuál número fue
CANGURO MATEMÁTICO Portal Fuenterrebollo 1. Sara escoge un número, lo divide por 7, al resultado le suma 7 y finalmente multiplica la suma por 7. De esta manera consigue el número 777. Cuál número fue
Problemas de fases nacionales e internacionales
 Problemas de fases nacionales e internacionales 1.- (China 1993). Dado el paralelogramo ABCD, se consideran dos puntos E, F sobre la diagonal AC e interiores al paralelogramo. Demostrar que si existe una
Problemas de fases nacionales e internacionales 1.- (China 1993). Dado el paralelogramo ABCD, se consideran dos puntos E, F sobre la diagonal AC e interiores al paralelogramo. Demostrar que si existe una
Definiciones I. Una solución de una ecuación son aquellos valores que al sustituirlos en la ecuación hacen que la igualdad sea cierta.
 Ecuaciones Definiciones I Una ecuación es una igualdad algebraica que se verifica únicamente para un conjunto determinado de valores de las variables o indeterminadas que forman la ecuación. a + b 2 =
Ecuaciones Definiciones I Una ecuación es una igualdad algebraica que se verifica únicamente para un conjunto determinado de valores de las variables o indeterminadas que forman la ecuación. a + b 2 =
RECUPERACIÓN DE MATEMÁTICAS PENDIENTES DE 2º ESO
 RECUPERACIÓN DE MATEMÁTICAS PENDIENTES DE º ESO BLOQUE I. NÚMEROS. * Divisibilidad y números enteros Ejercicio nº 1.- Calcula todos los divisores de 5. Ejercicio nº.- Calcula: a mín.c.m. 0, 60, 90 b máx.c.d.
RECUPERACIÓN DE MATEMÁTICAS PENDIENTES DE º ESO BLOQUE I. NÚMEROS. * Divisibilidad y números enteros Ejercicio nº 1.- Calcula todos los divisores de 5. Ejercicio nº.- Calcula: a mín.c.m. 0, 60, 90 b máx.c.d.
Ecuaciones e inecuaciones. Sistemas de ecuaciones e inecuaciones
 de ecuaciones e inecuaciones Álvarez S., Caballero M.V. y Sánchez M. a M. salvarez@um.es, m.victori@um.es, marvega@um.es 1 Índice 1. Definiciones 3 2. Herramientas 5 2.1. Factorización de polinomios: Regla
de ecuaciones e inecuaciones Álvarez S., Caballero M.V. y Sánchez M. a M. salvarez@um.es, m.victori@um.es, marvega@um.es 1 Índice 1. Definiciones 3 2. Herramientas 5 2.1. Factorización de polinomios: Regla
GEOMETRÍ A ANALÍ TÍCA
 GEOMETRÍ A ANALÍ TÍCA En este tema estudiaremos vectores (definición, características, operaciones) de forma geométrica y analítica. Además veremos los conceptos de vector director, pendiente de una recta
GEOMETRÍ A ANALÍ TÍCA En este tema estudiaremos vectores (definición, características, operaciones) de forma geométrica y analítica. Además veremos los conceptos de vector director, pendiente de una recta
Control Global de la 1ª Evaluación Matemáticas Aplicadas a las Ciencias Sociales 1º de Bachillerato
 Control Global de la ª Evaluación Matemáticas Aplicadas a las Ciencias Sociales º de Bachillerato. 5,5 puntos). Resolver las siguientes ecuaciones: a) b) log log ) c) d) ) ).,5 puntos). Dado el polinomio
Control Global de la ª Evaluación Matemáticas Aplicadas a las Ciencias Sociales º de Bachillerato. 5,5 puntos). Resolver las siguientes ecuaciones: a) b) log log ) c) d) ) ).,5 puntos). Dado el polinomio
Seminario de problemas. Curso Hoja 5
 Seminario de problemas. Curso 015-16. Hoja 5 5. En un triángulo acutángulo ABC, con AB AC, sea V la intersección de la bisectriz de A con BC y sea D el pie de la altura desde A a BC. Si E y F son las intersecciones
Seminario de problemas. Curso 015-16. Hoja 5 5. En un triángulo acutángulo ABC, con AB AC, sea V la intersección de la bisectriz de A con BC y sea D el pie de la altura desde A a BC. Si E y F son las intersecciones
Problemas resueltos correspondientes a la selectividad de Matemáticas II de septiembre de 2011, Andalucía
 Problemas resueltos correspondientes a la selectividad de Matemáticas II de septiembre de 011, Andalucía Pedro González Ruiz septiembre de 011 1. Opción A Problema 1.1 Calcular la base y la altura del
Problemas resueltos correspondientes a la selectividad de Matemáticas II de septiembre de 011, Andalucía Pedro González Ruiz septiembre de 011 1. Opción A Problema 1.1 Calcular la base y la altura del
PRUEBA DE CUARTO GRADO.
 PRUEBA DE CUARTO GRADO. Francisco tiene 10 cajas y 44 monedas. Quiere poner las monedas en las cajas repartiéndolas de modo que cada caja contenga un número distinto de monedas. Puede hacerlo? Si puede,
PRUEBA DE CUARTO GRADO. Francisco tiene 10 cajas y 44 monedas. Quiere poner las monedas en las cajas repartiéndolas de modo que cada caja contenga un número distinto de monedas. Puede hacerlo? Si puede,
BANCO DE PROBLEMAS DÍA 2
 XXVIII OLIMPID COSTRRICENSE DE MTEMÁTIC UN - UCR - TEC - UNED - MEP - MICITT NCO DE PROLEMS DÍ 2 I Nivel 7 Martes 15 de noviembre del 2016 Geometría 1. Sean el C recto en, F un punto tal que F C, F el
XXVIII OLIMPID COSTRRICENSE DE MTEMÁTIC UN - UCR - TEC - UNED - MEP - MICITT NCO DE PROLEMS DÍ 2 I Nivel 7 Martes 15 de noviembre del 2016 Geometría 1. Sean el C recto en, F un punto tal que F C, F el
Soluciones de la Etapa Final Estatal de la 27 a Olimpiada Mexicana de Matemáticas, 2013
 Soluciones de la tapa Final statal de la 27 a Olimpiada Mexicana de Matemáticas, 2013 1 Cinco equipos sto ocurrirá si, por ejemplo, 4 de los equipos ganan todos sus juegos contra los otros 5 (obteniendo
Soluciones de la tapa Final statal de la 27 a Olimpiada Mexicana de Matemáticas, 2013 1 Cinco equipos sto ocurrirá si, por ejemplo, 4 de los equipos ganan todos sus juegos contra los otros 5 (obteniendo
TALLER DE MATEMÁTICAS 1 ECUACIONES POLINÓMICAS
 TALLER DE MATEMÁTICAS 1 ECUACIONES POLINÓMICAS NOTAS Toda expresión algebraica del tipo a n x n + a n 1 x n 1 + + a 1 x + a 0 es un polinomio de grado n, si a n 0. Es bien conocida la fórmula que da las
TALLER DE MATEMÁTICAS 1 ECUACIONES POLINÓMICAS NOTAS Toda expresión algebraica del tipo a n x n + a n 1 x n 1 + + a 1 x + a 0 es un polinomio de grado n, si a n 0. Es bien conocida la fórmula que da las
Ecuaciones segundo F H G I K J H G I K J. Cómo se llama al nº que está dentro de la raíz? Despeja x en las siguientes ecuaciones:
 Ecuaciones segundo 1 Cuadrado Raíz 1 Qué es el cuadrado de un número? Calcula: a)( ) b) 7 c) 16 d) 0 e) 4 f ) 0 g) 4 Cómo se llama al nº que está dentro de la raíz? Despeja en las siguientes ecuaciones:
Ecuaciones segundo 1 Cuadrado Raíz 1 Qué es el cuadrado de un número? Calcula: a)( ) b) 7 c) 16 d) 0 e) 4 f ) 0 g) 4 Cómo se llama al nº que está dentro de la raíz? Despeja en las siguientes ecuaciones:
Entrenamiento de Principio de Casillas. Olimpiada de Matemáticas en Chiapas
 UNIVERSIDAD AUTÓNOMA DE CHIAPAS FACULTAD DE CIENCIAS EN FÍSICA Y MATEMÁTICAS Entrenamiento de Olimpiada de Matemáticas en Chiapas Mayo del 2017 Introducción La versión más simple del principio de las casillas
UNIVERSIDAD AUTÓNOMA DE CHIAPAS FACULTAD DE CIENCIAS EN FÍSICA Y MATEMÁTICAS Entrenamiento de Olimpiada de Matemáticas en Chiapas Mayo del 2017 Introducción La versión más simple del principio de las casillas
Fase Local OLIMPIADA MATEMÁTICA ESPAÑOLA
 OLIMPIADA MATEMÁTICA ESPAÑOLA Fase Local Mañana del Sábado 1 Dado un número entero n escrito en el sistema de numeración decimal, formamos el número entero k restando del número formado por las tres últimas
OLIMPIADA MATEMÁTICA ESPAÑOLA Fase Local Mañana del Sábado 1 Dado un número entero n escrito en el sistema de numeración decimal, formamos el número entero k restando del número formado por las tres últimas
Soluciones del examen final estatal de la 24 a OLIMPIADA MEXICANA DE MATEMÁTICAS
 Soluciones del examen final estatal de la 24 a OLIMPID MEXICN DE MTEMÁTICS 1 Como 01 9 = 45, que es múltiplo de 9, bastará ver si es posible lograr que un número con todos los dígitos sea múltiplo de 11
Soluciones del examen final estatal de la 24 a OLIMPID MEXICN DE MTEMÁTICS 1 Como 01 9 = 45, que es múltiplo de 9, bastará ver si es posible lograr que un número con todos los dígitos sea múltiplo de 11
RAZONES TRIGONOMÉTRICAS
 RAZONES TRIGONOMÉTRICAS Las Razones trigonométricas se definen comúnmente como el cociente entre dos lados de un triangulo rectángulo asociado a sus ángulos. SENO, COSENO Y TANGENTE Recordarás que eisten
RAZONES TRIGONOMÉTRICAS Las Razones trigonométricas se definen comúnmente como el cociente entre dos lados de un triangulo rectángulo asociado a sus ángulos. SENO, COSENO Y TANGENTE Recordarás que eisten
1. He escrito el No he escrito el He escrito el No he escrito el 4.
 º Nivel. El número que está justamente entre 8 y 0 es 80 B) 0 C) 8 E) 80. Halla la suma de todos los primos comprendidos entre y 00 que verifiquen ser múltiplos de más y múltiplos de 5 menos. 8 B) 7 C)
º Nivel. El número que está justamente entre 8 y 0 es 80 B) 0 C) 8 E) 80. Halla la suma de todos los primos comprendidos entre y 00 que verifiquen ser múltiplos de más y múltiplos de 5 menos. 8 B) 7 C)
LIV OME - FASE CERO, COMUNIDAD DE MADRID
 LIV OME - FSE ERO, OMUNIDD DE MDRID 24 de noviembre de 2017 1. olocamos cifras en los huecos del número 2, una en cada hueco, para formar un número de tres cifras. De cuántas formas podemos hacerlo para
LIV OME - FSE ERO, OMUNIDD DE MDRID 24 de noviembre de 2017 1. olocamos cifras en los huecos del número 2, una en cada hueco, para formar un número de tres cifras. De cuántas formas podemos hacerlo para
ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- Enteros
 Resumen teoría Prof. Alcón ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- Z = N {0} N Enteros Las operaciones + y. son cerradas en Z, es decir la suma de dos números enteros es un número entero y el producto
Resumen teoría Prof. Alcón ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- Z = N {0} N Enteros Las operaciones + y. son cerradas en Z, es decir la suma de dos números enteros es un número entero y el producto
Enunciados y Soluciones
 LIV Olimpiada matemática Española (Concurso Final) Enunciados Soluciones 1. Determina todos los enteros positivos x, tales que 2x + 1 sea un cuadrado perfecto, pero entre los números 2x + 2, 2x + 3,, 3x
LIV Olimpiada matemática Española (Concurso Final) Enunciados Soluciones 1. Determina todos los enteros positivos x, tales que 2x + 1 sea un cuadrado perfecto, pero entre los números 2x + 2, 2x + 3,, 3x
Unidad 7 Producto vectorial y mixto. Aplicaciones. Superficie esférica
 Unidad 7 Producto vectorial y mixto. Aplicaciones. Superficie esférica PÁGINA 157 SOLUCIONES 1. La recta es x y + z = 0 x y z = 0. Puede ser el vector: 3. La altura es la distancia entre los planos, es
Unidad 7 Producto vectorial y mixto. Aplicaciones. Superficie esférica PÁGINA 157 SOLUCIONES 1. La recta es x y + z = 0 x y z = 0. Puede ser el vector: 3. La altura es la distancia entre los planos, es
GEOMETRÍA. (x 1) 2 +(y 2) 2 =1. Razónalo. x y + z = 2. :3x 3z +1= 0 es doble de la distancia al plano π 2. : x + y 1= 0. Razónalo.
 GEOMETRÍA 1. (Junio, 1994) Sin resolver el sistema, determina si la recta x +3y +1= 0 es exterior, secante o tangente a la circunferencia (x 1) +(y ) =1. Razónalo.. (Junio, 1994) Dadas las ecuaciones de
GEOMETRÍA 1. (Junio, 1994) Sin resolver el sistema, determina si la recta x +3y +1= 0 es exterior, secante o tangente a la circunferencia (x 1) +(y ) =1. Razónalo.. (Junio, 1994) Dadas las ecuaciones de
SOLUCIÓN PRIMERA ELIMINATORIA NACIONAL NIVEL C
 XXIV OLIMPIADA COSTARRICENSE DE MATEMÁTICA MEP ITCR UCR UNA UNED - MICIT SOLUCIÓN PRIMERA ELIMINATORIA NACIONAL NIVEL C 01 1. Un factor de la factorización completa de corresponde a mx y + 9y m x y x 4
XXIV OLIMPIADA COSTARRICENSE DE MATEMÁTICA MEP ITCR UCR UNA UNED - MICIT SOLUCIÓN PRIMERA ELIMINATORIA NACIONAL NIVEL C 01 1. Un factor de la factorización completa de corresponde a mx y + 9y m x y x 4
Capítulo 2. Determinantes Introducción. Definiciones
 Capítulo 2 Determinantes 2.1. Introducción. Definiciones Si nos centramos en la resolución de un sistema A x = b con A una matriz n n, podemos calcular A 1 y la resolución es inmendiata. El problema es
Capítulo 2 Determinantes 2.1. Introducción. Definiciones Si nos centramos en la resolución de un sistema A x = b con A una matriz n n, podemos calcular A 1 y la resolución es inmendiata. El problema es
TEMA 3. POLINOMIOS Y FRACCIONES ALGEBRAICAS. Ficha 0
 Ficha 0 Un monomio es una expresión algebraica formada por el producto de un número, llamado coeficiente, por una o más variables con exponente natural o cero, llamadas parte literal. El grado es la suma
Ficha 0 Un monomio es una expresión algebraica formada por el producto de un número, llamado coeficiente, por una o más variables con exponente natural o cero, llamadas parte literal. El grado es la suma
TORNEO DE PRIMAVERA CUENCA DEL PLATA PRIMER NIVEL Primera Prueba
 TORNEO DE PRIMAVERA 2012 CUENCA DEL PLATA PRIMER NIVEL Primera Prueba Lee con atención: 1- Es posible consultar libros o apuntes y usar calculadora. 2- Solamente se pueden usar los elementos propios. 3-
TORNEO DE PRIMAVERA 2012 CUENCA DEL PLATA PRIMER NIVEL Primera Prueba Lee con atención: 1- Es posible consultar libros o apuntes y usar calculadora. 2- Solamente se pueden usar los elementos propios. 3-
TEMA 9. TRIGONOMETRÍA
 TEMA 9. TRIGONOMETRÍA 1. LOS ÁNGULOS Y SU MEDIDA. La trigonometría es la parte de las matemáticas que se encarga de la medida de los lados y los ángulos de un triángulo. ÁNGULO Un ángulo en el plano es
TEMA 9. TRIGONOMETRÍA 1. LOS ÁNGULOS Y SU MEDIDA. La trigonometría es la parte de las matemáticas que se encarga de la medida de los lados y los ángulos de un triángulo. ÁNGULO Un ángulo en el plano es
TRIGONOMETRÍA. 1. Ángulos. 2. Razones trigonométricas de ángulos agudos
 TRIGONOMETRÍA 1 Ángulos Hasta ahora se han considerado los ángulos como la porción del plano comprendida entre dos semirrectas con el origen común De esta manera, el ángulo está comprendido entre 0 y 360
TRIGONOMETRÍA 1 Ángulos Hasta ahora se han considerado los ángulos como la porción del plano comprendida entre dos semirrectas con el origen común De esta manera, el ángulo está comprendido entre 0 y 360
Tema 9 Funciones elementales
 Tema 9 Funciones elementales 9.1Gráfica de una función. Signo simetría. PÁGINA 175 EJERCICIOS 1. Encuentra los puntos de corte con los ejes de las siguientes funciones estudia su signo. 3 c) f 1 c.1) Cortes
Tema 9 Funciones elementales 9.1Gráfica de una función. Signo simetría. PÁGINA 175 EJERCICIOS 1. Encuentra los puntos de corte con los ejes de las siguientes funciones estudia su signo. 3 c) f 1 c.1) Cortes
Facultad de Ciencias Naturales y Museo Trabajo Práctico Nº
 TRABAJO PRÁCTICO Nº 1 CONTENIDOS: Geometría. Progresiones aritméticas y geométricas. Coordenadas cartesianas y polares Parte I: Geometría 1) Las siguientes afirmaciones son verdaderas o falsas: a. los
TRABAJO PRÁCTICO Nº 1 CONTENIDOS: Geometría. Progresiones aritméticas y geométricas. Coordenadas cartesianas y polares Parte I: Geometría 1) Las siguientes afirmaciones son verdaderas o falsas: a. los
a + b 2 ab + a2 + b 2 Si aplicamos la desigualdad entre las medias aritmética y geométrica al miembro de la izquierda obtenemos 2 2ab + a2 + b =
 Sesión 3 1. Sean a, b números positivos. Probar que a + b a + b ab +. Solución 1. La desigualdad equivale a ab + a +b a + b. Si aplicamos la desigualdad entre las medias aritmética y geométrica al miembro
Sesión 3 1. Sean a, b números positivos. Probar que a + b a + b ab +. Solución 1. La desigualdad equivale a ab + a +b a + b. Si aplicamos la desigualdad entre las medias aritmética y geométrica al miembro
Geometría del Plano. Física Geográfica. Licenciatura de Humanidades. Febrero-Mayo,
 Geometría del Plano. Física Geográfica. Licenciatura de Humanidades. Febrero-Mayo, 2007. 17 Indice. 1. Líneas y Curvas. 2. Ángulos en el plano. 3. Medida de un ángulo. 4. Tipos de Ángulos. 5. Teorema de
Geometría del Plano. Física Geográfica. Licenciatura de Humanidades. Febrero-Mayo, 2007. 17 Indice. 1. Líneas y Curvas. 2. Ángulos en el plano. 3. Medida de un ángulo. 4. Tipos de Ángulos. 5. Teorema de
Matemáticas Nivel Medio Matemáticas Ap.CC.SS.I
 Matemáticas Nivel Medio Matemáticas Ap.CC.SS.I Martes, 1 de abril de 01 1 hora y 15 minutos. NOMBRE Y APELLIDOS CALIFICACIÓN 1. La superficie de un triángulo isósceles mide cm y uno de sus lados iguales
Matemáticas Nivel Medio Matemáticas Ap.CC.SS.I Martes, 1 de abril de 01 1 hora y 15 minutos. NOMBRE Y APELLIDOS CALIFICACIÓN 1. La superficie de un triángulo isósceles mide cm y uno de sus lados iguales
Teoría de Números. 1. Introducción. Factorización Algebraica. Olimpiada de Matemáticas en Tamaulipas
 Teoría de Números Factorización Algebraica Olimpiada de Matemáticas en Tamaulipas 1. Introducción El matemático, físico y astrónomo Carl Friedrich Gauss (1777-1855) fue uno de los más importantes personajes
Teoría de Números Factorización Algebraica Olimpiada de Matemáticas en Tamaulipas 1. Introducción El matemático, físico y astrónomo Carl Friedrich Gauss (1777-1855) fue uno de los más importantes personajes
Seminario de problemas. Curso Hoja 20
 Seminario de problemas. Curso 014-15. Hoja 0 13. Dada una semicircunferencia de diámetro AB = R, se considera la cuerda CD de longitud fija c. Sea E la intersección de AC con BD y F la intersección de
Seminario de problemas. Curso 014-15. Hoja 0 13. Dada una semicircunferencia de diámetro AB = R, se considera la cuerda CD de longitud fija c. Sea E la intersección de AC con BD y F la intersección de
Soluciones oficiales de los problemas de la Final de la XXI Olimpiada Nacional de Matemática 2009
 Soluciones oficiales de los problemas de la Final de la XXI Olimpiada Nacional de Matemática 009 Comisión Académica 1 Nivel Menor Problema 1. Considere un triángulo cuyos lados miden 1, r y r. Determine
Soluciones oficiales de los problemas de la Final de la XXI Olimpiada Nacional de Matemática 009 Comisión Académica 1 Nivel Menor Problema 1. Considere un triángulo cuyos lados miden 1, r y r. Determine
Ecuaciones e inecuaciones. Sistemas de ecuaciones e inecuaciones
 Ecuaciones e inecuaciones. Sistemas de ecuaciones e inecuaciones Álvarez S., Caballero M.V. y Sánchez M. a M. salvarez@um.es, m.victori@um.es, marvega@um.es Índice 1. Herramientas 6 1.1. Factorización
Ecuaciones e inecuaciones. Sistemas de ecuaciones e inecuaciones Álvarez S., Caballero M.V. y Sánchez M. a M. salvarez@um.es, m.victori@um.es, marvega@um.es Índice 1. Herramientas 6 1.1. Factorización
Problemas Tema 1 Solución a problemas de Repaso de 1ºBachillerato - Hoja 05 - Problemas 1, 2, 3, 5
 Asignatura: Matemáticas II ºBachillerato Problemas Tema 1: Solución a problemas de Repaso de 1ºBachillerato - Hoja 05 - Problemas 1,, 3, 5 página 1/7 Problemas Tema 1 Solución a problemas de Repaso de
Asignatura: Matemáticas II ºBachillerato Problemas Tema 1: Solución a problemas de Repaso de 1ºBachillerato - Hoja 05 - Problemas 1,, 3, 5 página 1/7 Problemas Tema 1 Solución a problemas de Repaso de
a) Cuántos cm. mide la hipotenusa? (2 puntos) A
 OOMM º ESO Cantabria 05.ág. 0.-GEOMETRIA EN EL TABLERO En un tablero de ajedrez, el lado de cada casilla mide 0 cm. Formamos un triángulo rectángulo. Cada cateto del triángulo rectángulo tiene dos casillas
OOMM º ESO Cantabria 05.ág. 0.-GEOMETRIA EN EL TABLERO En un tablero de ajedrez, el lado de cada casilla mide 0 cm. Formamos un triángulo rectángulo. Cada cateto del triángulo rectángulo tiene dos casillas
14 CUERPOS GEOMÉTRICOS. VOLÚMENES
 EJERCICIOS PARA ENTRENARSE Poliedros 14.33 Calcula la suma de los ángulos de las caras que concurren en un vértice de los poliedros regulares. Qué observas? TETRAEDO: En un vértice concurren tres triángulos
EJERCICIOS PARA ENTRENARSE Poliedros 14.33 Calcula la suma de los ángulos de las caras que concurren en un vértice de los poliedros regulares. Qué observas? TETRAEDO: En un vértice concurren tres triángulos
EJERCICIOS DE VERANO MATEMÁTICAS 3º ESO
 EJERCICIOS DE VERANO MATEMÁTICAS 3º ESO Página 1 de 14 Entregar el día del examen de recuperación de matemáticas. Será condición indispensable para aprobar la asignatura. 1. Calcula: NUMEROS ENTEROS. FRACCIONES.
EJERCICIOS DE VERANO MATEMÁTICAS 3º ESO Página 1 de 14 Entregar el día del examen de recuperación de matemáticas. Será condición indispensable para aprobar la asignatura. 1. Calcula: NUMEROS ENTEROS. FRACCIONES.
IES ATENEA. GLOBAL/RECUPERACIÓN. MATEMÁTICAS B. 4º ESO. Nombre: , simplificando el resultado. Q(x) = 2x 3x 9x + 10.
 IES ATENEA GLOBAL/RECUPERACIÓN MATEMÁTICAS B 4º ESO Nombre: Evaluación: Primera Fecha: 4 de enero de 011 NOTA Ejercicio nº 1- a) Epresar como un solo radical 4 0 b) Racionaliza la epresión 6, simplificando
IES ATENEA GLOBAL/RECUPERACIÓN MATEMÁTICAS B 4º ESO Nombre: Evaluación: Primera Fecha: 4 de enero de 011 NOTA Ejercicio nº 1- a) Epresar como un solo radical 4 0 b) Racionaliza la epresión 6, simplificando
UNIDAD 2 ELEMENTOS BASICOS DE TRIGONOMETRÍA.
 UNIDAD 2 ELEMENTOS BASICOS DE TRIGONOMETRÍA http://www.uaeh.edu.mx/virtual ELEMENTOS BASICOS DE TRIGONOMETRÍA. Introducción. La trigonometría es el área de las matemáticas que se encarga de calcular los
UNIDAD 2 ELEMENTOS BASICOS DE TRIGONOMETRÍA http://www.uaeh.edu.mx/virtual ELEMENTOS BASICOS DE TRIGONOMETRÍA. Introducción. La trigonometría es el área de las matemáticas que se encarga de calcular los
Unidad 8 Áreas y Volúmenes
 Unidad 8 Áreas y Volúmenes PÁGINA 132 SOLUCIONES Unidades de medida. Pasa a centímetros cuadrados las siguientes cantidades. a) b) c) Pasa a metros cúbicos las siguientes unidades. a) b) c) Cuántos litros
Unidad 8 Áreas y Volúmenes PÁGINA 132 SOLUCIONES Unidades de medida. Pasa a centímetros cuadrados las siguientes cantidades. a) b) c) Pasa a metros cúbicos las siguientes unidades. a) b) c) Cuántos litros
Facultad de Ciencias Naturales y Museo Trabajo Práctico Nº
 CONTENIDOS: Geometría. Progresiones aritméticas y geométricas. Coordenadas cartesianas y polares Parte I: Geometría 1) Las siguientes afirmaciones son verdaderas o falsas: a. los pares de ángulos alternos
CONTENIDOS: Geometría. Progresiones aritméticas y geométricas. Coordenadas cartesianas y polares Parte I: Geometría 1) Las siguientes afirmaciones son verdaderas o falsas: a. los pares de ángulos alternos
