Operaciones aritméticas en Maple
|
|
|
- Aurora Revuelta Sevilla
- hace 9 años
- Vistas:
Transcripción
1 Operaciones aritméticas en Maple José Luis Torres Rodríguez * Febrero 2011 Gracias a los diversos tipos de datos disponibles, a las constantes simbólicas (por ejemplo Pi), a las funciones aritméticas y de manipulación numérica con las que cuenta, es posible utilizar Maple para realizar calculos numéricos y evaluar expresiones aritméticas. Esto, aunado a su capacidad para manejar números de precisión infinita y al manejo de aritmética racional, real y compleja, nos permiten considerar a este sistema como un poderoso ambiente para el manejo de operaciones artitméticas en general. Tales características de Maple son tratadas a lo largo de esta sección. 1. Funciones aritméticas Anteriormente habian sido presentados los operadores artiméticos soportados por Maple, así como los operadores relacionales y algunas de las funciones elementales predefinidas en este sistema (vease el capítulo Elementos Básicos de Maple y el capítulo Uso de Funciones). Además de las ya mencionadas, existen algunas otras funciones, útiles en la manipulación de expresiones aritméticas. Entre ellas tenemos las que se muestran en la tabla 1. Nombre Cociente entero Residuo entero Función iquo(x) irem(x) Máximo común divisor entre a y b: mcd(a, b) Mínimo común multiplo entre a y b lcm(a, b) Signo Signo complejo Factorización en productos de primos signum(x) csignum(x) ifactor(x) Cuadro 1: Funciones aritméticas Otras funciones útiles para realizar cálculos numéricos son las trigonométricas, con sus respectivas formas inversas, hiperbólicas e hiperbólicas inversas, además de los operadores lógicos (todos ellos mencionados anteriormente). Ejemplos sobre el uso de éstos son presentados en las siguientes secciones. * Coordinación de Cómputo, Facultad de Ciencias, UNAM 1
2 2. Uso de Maple como calculadora Maple tiene la capacidad de realizar cualquier tipo de operación aritmética, por ejemplo: > 4 + 5; > * ; > 892/ ; ,35 2, > 7/36 + 5/8 + 3/5; Además, puede manipular números muy grandes, tanto enteros como de punto flotante (en ocasiones es utilizada la notación decimal). > 100!; > exp(245.0); \ \ , Nota: ademas del uso tradicional que se le da al operador / para expresar cocientes en la forma: a/b, Maple 8 también permite usarlo de la siguiente manera: / (a, b) más aun, puede ser usado como: / (c) lo cual es equivalente a la expresión: 1/c Nótese que para hacer uso del operador como se describe aqui, éste debe estar delimitado por acentos agudos. Por ejemplo: > / (7,36) = 7/36; > / (Pi*3!) = 1/(Pi*3!); 7 36 = π = 1 6 π 2
3 Este sistema nos proporciona diversas funciones por medio de las cuales podemos hacer manipulaciones sobre expresiones aritméticas o números, por ejemplo: Obtención de la parte fraccionaria. > frac(evalf(sqrt(2))); 0, Factorización de un entero, en productos de potencias de números primos. > ifactor(-29!); (2) 25 (3) 13 (5) 6 (7) 4 (11) 2 (13) 2 (17) (19) (23) (29) Este tipo de expresiones aritméticas pueden ser expandidas usando la función expand: > expand( %); Obtención del máximo común divisor y el mínimo común multiplo para dos enteros. > gcd(26764, 4686); > lcm(49234, 18932); Podemos verificar si una expresión arirmética corresponde a un número primo. > isprime(11); > isprime(23!); > isprime(1323); false false También podemos evaluar expresiones como la conjetura de Fermat (según la cual 2 (2n) + 1 es un número primo para n natural), para diferentes valores. Probaremos para n = 1, 2, 3, 4, 5. > isprime(2^(2^1) + 1); > isprime(2^(2^2) + 1); > isprime(2^(2^3) + 1); > isprime(2^(2^4) + 1); > isprime(2^(2^5) + 1); false 3
4 Podemos calcular el primer primo mayor que un número cualquiera. Por ejemplo, calcularemos el primer número primo mayor que > nextprime(4568); Verifiquemos el resultado: > isprime( %); 4583 También podemos calcular el primer primo menor que un número. Calculemos el primero menor que 4568 y verifiquemos el resultado: > prevprime(4568); 4567 > isprime( %); Recuérdese que generalmente Maple realiza las operaciones utilizando artimética racional, lo cual quiere decir que las operaciones con enteros o fracciones siempre generan resultados enteros o fracciones. Por ejemplo: > 21! + 56^2 + 8/5-16/9; No obstante, Maple realiza automáticamente algunas simplificaciones sencillas sobre racionales de tal manera que sean expresados en su forma más simple. Por ejemplo: > 4/8; > /876432; Cuando trabajamos con expresiones racionales, es necesario aplicar evalf para obtener un número de punto flotante, o bien, se debe incluir en la expresión por lo menos un número de punto flotante. > evalf(21! + 56^2 + 8/5-16/9); > 21! + 56^2 + 8/5-16/9.0; 0, , Este forma de operar de Maple permite obtener resultados más exactos, pues se evitan todos los errores que puedan surgir al hacer redondeos o aproximaciones de números. Por otro lado, podemos también calcular el residuo y el cociente de una expresión artitmética racional: > irem(89234, 45); > iquo(89234, 45);
5 Otras operaciones útiles son las exponenciaciones: > 8^8; > 25^(2^3); En estas operaciones es necesario utilizar paréntesis para asociar. Por ejemplo: > 2^2^2^2; Error, ^ unexpected Nos genera un mensaje de error, la forma correcta es: > 2^(2^(2^2)); Las operaciones de exponenciación pueden ser utilizadas en general para calcular x p, donde p es un exponente entero, racional o decimal. Por ejemplo: > 4^(1/2); 4 > evalf(8^(2.8)); > evalf(34^pi); 2, , ,43258 También podemos calcular modulos: > mod 8; > 8! mod 3; 2 0 > mod 7; 4 La expresión a mod b"nos devuelve el residuo al calcular la división entera a b. Recuérdese que esta operación únicamente está definida para a y b enteros. Veamos otro ejemplo. Comprobaremos a continuación que es una raíz del polinomio x 8 40 x x x > subs(x = sqrt(2) + sqrt(3) + sqrt(5), x^8-40*x^ *x^4 - > 960*x^ ); % % % % %1 := ,
6 Existen varias funciones más que nos permiten llevar a cabo operaciones sobre números, a continuación listaremos algunas de ellas: add. Nos permite calcular la suma de una suceción de valores. mul. Nos permite calcular el producto de una sucesión de valores. Si, Ci. Estas funciones están definidas de la siguiente forma: Para toda x compleja: Si(x) = int(sin(t)/t, t=0..x) Ci(x) = gamma + ln(x) + int((cos(t)-1)/t, t=0..x) factorset(n). Calcula los factores primos de un entero n. ithprime(i). Calcula el i-esimo primo. Randpoly, Randprime. Permiten calcular polinomios aleatorios sobre un campo finito. rand. Genera números aleatorios. numer, denom. Devuelven el numerador y denominador de una expresión, respectivamente. frem. Esta función devuelve r = x - y*n, donde n es el entero mas cercano a x/y. irem, iquo. Devuelven el residuo entero y cociente entero de dos expresiones, respectivamente. rem, quo. Calculan el residuo y cociente de dos polinomios. También puede consultarse la ayuda del paquete numtheory, para obtener información de diversas funciones propias de Teoría de Números. 3. Precisión de una operación y aproximaciones de punto flotante Maple es capaz de manejar números de punto flotante de precisión arbitraria, para ello es necesario utilizar la función evalf; ésta nos permite indicar a Maple con cuantos dígitos debe realizarse un cálculo numérico, con lo cual podemos obtener aproximaciones de diferente orden, para expresiones aritméticas. Para ejemplificar lo anterior, calcularemos a continuación el cuadrado del número Pi con quinientos digitos de precisión: > evalf(pi^2, 500); 9, \ \ \ \ \ \ \ \ A continuación obtendremos los primeros 200 dígitos de la parte fraccionaria del resultado de la instrucción anterior: 6
7 > frac(evalf( %, 200)); 0, \ \ \ De forma predeterminada, Maple solo muestra los primeros 10 dígitos en cualquier operación de punto flotante (tomando en cuenta parte entera y fraccionaria). Por ejemplo: > evalf(exp(4.8)); 121, Este número de dígitos está determinado por una variable global definida por Maple, conocida como Digits. (Consultese la página de ayuda de Digits y otras variables de ambiente usando?envvar). Veamos el valor que contiene esta variable: > Digits; 10 Al modificar el valor de esta variable, también modificamos el número de dígitos utilizados al hacer este tipo de evaluaciones. Por ejemplo, asignemosle el valor de 25: > Digits := 25; Calculemos nuevamente evalf(e 4.8 ): Digits := 25 > evalf(exp(4.8)); 121, Nótese como ahora obtenemos 25 dígitos en lugar de 10. La cantidad de dígitos a desplegar tambien puede ser ajustado por medio de la opción Preferences del menú File, seleccionando la ficha Numerics. 4. Números complejos Los números complejos son operados de la misma forma que los reales. Estos números son considerados por Maple como polinómios en términos del símbolo I, el cual representa la raiz cuadrada de menos uno. Maple utiliza siempre la relación i = 0 para evaluar expresiones que contienen este tipo de números. Veamos un ejemplo: > (4 + 2*I)/(2-5*I); I 0, , I Podemos observar que al aplicar evalf a un complejo, esta función evalúa tanto la parte real como la parte imaginaria de este número. > ( sin(234)*i)*( exp(4)*pi*i); (32768 sin(234) I) ( e 4 π I) Nótese que este último resultado no está evaluado. Existe una función que nos permite hacer este tipo de evaluaciones para complejos, su nombre es evalc (vease su página de ayuda). 7
8 > evalc( %); sin(234) e 4 π + ( 9879 sin(234) e 4 π) I Otras funciones útiles en el manejo de complejos son: Re. Parte real de un complejo. Im. Parte imaginaria. conjugate. Conjugado complejo. abs. Módulo. argument. Argumento de un complejo. csgn. Para un número complejo determina en que parte del plano se encuentra éste. signum. Devuelve el sígno de una expresión real o compleja. polar. Calcula la forma polar de un número complejo. Veamos a continuación algunos ejemplos. Considerese el siguiente número: > com1 := (12/ *I)*(234/92 - sin(9)*i); ( ) 2 com1 := I) ( sin(9) I Calcularemos sus partes real e imaginaria: > Re(com1); > Im(com1); sin(9) sin(9) Calcularemos su conjugado, su módulo, su argumento y su signo como número complejo: > conjugate(com1); ( 2 ) ( 117 ) I 46 + sin(9) I > abs(com1); > argument(com1); > csgn(com1); sin(9) arctan 791 sin(9) sin(9) Este último resultado es calculado de la siguiente forma: 8
9 1: si la parte real es positiva o si la parte real es cero y la imaginaria positiva. 0: si el complejo es 0, y -1: en otro caso. Podemos incluir variables dentro de expresiones dadas en términos de complejos. En este caso, Maple asume que dichas variables representan números reales, por lo cual son manejadas como tales. Por ejemplo: > (a + b*i)*c; > Re( %); > Im( % %); (a + b I) c R((a + b I) c) I((a + b I) c) Las expresiones obtenidas representan las partes real e imaginaria del numero complejo, se muestran de forma simbólica ya que contienen valores indeterminados. 5. Sumatorias Maple puede efectuar sumas tanto de números reales como de complejos. Una forma de hacer esta operación es a través de la función sum. La sintaxis es la siguiente: sum(expr(x), x=a..b); Donde expr(x) es una expresión (real o compleja), dada en términos de x; mientras que a y b son enteros, tales que a<b. Esta función calcula la suma expr(a) + expr(a + 1) + expr(a + 2) expr(b). Veamos algunos ejemplos: > sum(x + x^2*sin(x), x=1..10); 55 + sin(1) + 4 sin(2) + 9 sin(3) + 16 sin(4) + 25 sin(5) + 36 sin(6) + 49 sin(7) + 64 sin(8) + 81 sin(9) sin(10) 89, > sum((4*r + Pi*r*I), r=2..20); I π , I Recuérdese que esta función tiene una forma inerte. Veamos otros ejemplos: > Sum((1 - i)/(1 + i), i=1..15); > value( %); 15 i=1 1 i 1 + i ,
10 Esta función también nos permite manipular sumas indefinidas: > Sum((1 - i)/(1 + i), i=1..n); > subs(n = 17, %); n i=1 17 i=1 1 i 1 + i 1 i 1 + i 12, Veamos algunos ejemplos más con números complejos: > Sum((2 + k*i)/(2 - k*i), k=0..10); k I 2 k I > evalc( %); ( 10 k=0 k=0 ( ) ) ( 10 ( ) ) k 2 k2 4 k 4 + k k 2 I k=0 4, , I > sum((234 + sin(t)^2*i), t=1..10); sin(2) 2 I + sin(9) 2 I + sin(4) 2 I + sin(6) 2 I + sin(8) 2 I + sin(10) 2 I + sin(1) 2 I + sin(3) 2 I + sin(5) 2 I + sin(7) 2 I , I Otra forma de calcular sumas es por medio de la instrucción add, la cual nos permite obtener la suma de una sucesión de valores; su sintaxis es similar a la de sum. Por ejemplo: > add(sin(i)^2, i=1..20); sin(1) 2 + sin(2) 2 + sin(3) 2 + sin(4) 2 + sin(5) 2 + sin(6) 2 + sin(7) 2 + sin(8) 2 + sin(9) 2 + sin(10) 2 + sin(11) 2 + sin(12) 2 + sin(13) 2 + sin(14) 2 + sin(15) 2 + sin(16) 2 + sin(17) 2 + sin(18) 2 + sin(19) 2 + sin(20) 2 10, A diferencia de sum, la función add no tiene una forma inerte y no puede realizar sumas simbólicas, solo puede sumar datos numéricos explícitos. 10
11 6. Productos Otro tipo de operaciones válidas son los productos, tanto de números reales como de complejos. Una forma de calcularlos es por medio de la función product, su sintaxis es la siguiente: product(expr(x), x=a..b); En donde expr(x) es una expresión (real o compleja) en términos de x, y a, b son números enteros tales que a<b. Esta función también tiene una forma inerte. Consultese su página de ayuda.veamos algunos ejemplos: > Product((j + 2)/(j + 3), j=1..10) = product((j + 2)/(j + 3), j=1..10); > product(d!*sin(d), d=1..20); 10 j=1 j + 2 j + 3 = \ \ sin(1) sin(2) sin(3) sin(4) sin(5) sin(6) sin(7) sin(8) sin(9) sin(10) sin(11) sin(12) sin(13) sin(14) sin(15) sin(16) sin(17) sin(18) sin(19) sin(20) 0, Esta función también nos permite manipular productos indefinidos: > product((k + 3)/k^2, k=1..n); > subs(n = 10, %); 1 6 Γ(n + 4) Γ(n + 1) Γ(14) Γ(11) 2 0, Además, también se pueden calcular productos de complejos: > product(i/(j + 3*I), j=1..10); n= I 0, , I > Product(n*I/(4 + 2*I), n=6..15) = evalf(product(n*i/(4 + 2*I), > n=6..15)); 15 ( ) 5 I n = 258, , I 11
12 Otra función que nos permite calcular productos es mul, la cual calcula el producto de una secuencia explícita de valores. A diferencia de pruduct, esta función no tiene una forma inerte. Su tintaxis es similar a la de product. Por ejemplo: > datos:=[2, Pi, 4, 5*Pi, 8, 10]; > mul(x - i, i=datos); datos := [2, π, 4, 5 π, 8, 10] (x 2) (x π) (x 4) (x 5 π) (x 8) (x 10) Podemos usar la función expand para obtener el resultado del producto > expand( %); x 6 24 x x 4 6 x 5 π x 4 π 1176 x 3 π 624 x x 2 π + 5 x 4 π x 3 π x 2 π x π x x π π 2 12
FUNCIONES, VARIABLES Y CARPETAS EN LA CALCULADORA CLASSPAD 300
 2. FUNCIONES, VARIABLES Y CARPETAS EN LA CALCULADORA CLASSPAD 300 FUNCIONES DISPONIBLES EN LA CLASSPAD La calculadora Classpad 300 ofrece una amplia relación de funciones a las que, en su mayoría se accede
2. FUNCIONES, VARIABLES Y CARPETAS EN LA CALCULADORA CLASSPAD 300 FUNCIONES DISPONIBLES EN LA CLASSPAD La calculadora Classpad 300 ofrece una amplia relación de funciones a las que, en su mayoría se accede
CURSOSO. Aritmética: Númerosnaturalesyenteros. Númerosracionalesyfraciones. MATEMÁTICAS. AntonioF.CostaGonzález
 CURSOSO CURSOSO MATEMÁTICAS Aritmética: Númerosnaturalesyenteros. Númerosracionalesyfraciones. AntonioF.CostaGonzález DepartamentodeMatemáticasFundamentales FacultaddeCiencias Índice 1 Introducción y objetivos
CURSOSO CURSOSO MATEMÁTICAS Aritmética: Númerosnaturalesyenteros. Númerosracionalesyfraciones. AntonioF.CostaGonzález DepartamentodeMatemáticasFundamentales FacultaddeCiencias Índice 1 Introducción y objetivos
La suma de dos números.
 1 Números Mathematica es una herramienta matemática que, esencialmente, funciona como una calculadora. La secuencia básica consiste, entonces, en introducir una expresión y ordenarle a Mathematica que
1 Números Mathematica es una herramienta matemática que, esencialmente, funciona como una calculadora. La secuencia básica consiste, entonces, en introducir una expresión y ordenarle a Mathematica que
Capítulo 1. El Conjunto de los números Reales
 Capítulo El Conjunto de los números Reales Contenido. El conjunto de los números Naturales................................. 4. El conjunto de los números Enteros................................... 4. El
Capítulo El Conjunto de los números Reales Contenido. El conjunto de los números Naturales................................. 4. El conjunto de los números Enteros................................... 4. El
operaciones inversas Para unificar ambas operaciones, se define la potencia de exponente fraccionario:
 Potencias y raíces Potencias y raíces Potencia operaciones inversas Raíz exponente índice 7 = 7 7 7 = 4 4 = 7 base base Para unificar ambas operaciones, se define la potencia de exponente fraccionario:
Potencias y raíces Potencias y raíces Potencia operaciones inversas Raíz exponente índice 7 = 7 7 7 = 4 4 = 7 base base Para unificar ambas operaciones, se define la potencia de exponente fraccionario:
POTENCIAS. MÚLTIPLOS Y DIVISORES. MÁXIMO COMÚN DIVISOR Y MÍNIMO COMÚN MÚLTIPLO.
 1. LOS NÚMEROS NATURALES POTENCIAS. MÚLTIPLOS Y DIVISORES. MÁXIMO COMÚN DIVISOR Y MÍNIMO COMÚN MÚLTIPLO. 2. LOS NÚMEROS ENTEROS. VALOR ABSOLUTO DE UN NÚMERO ENTERO. REPRESENTACIÓN GRÁFICA. OPERACIONES.
1. LOS NÚMEROS NATURALES POTENCIAS. MÚLTIPLOS Y DIVISORES. MÁXIMO COMÚN DIVISOR Y MÍNIMO COMÚN MÚLTIPLO. 2. LOS NÚMEROS ENTEROS. VALOR ABSOLUTO DE UN NÚMERO ENTERO. REPRESENTACIÓN GRÁFICA. OPERACIONES.
Tema 2. FUNCIONES, VARIABLES Y CARPETAS EN LA CALCULADORA CLASSPAD
 Tema 2. FUNCIONES, VARIABLES Y CARPETAS EN LA CALCULADORA CLASSPAD Introducción. Funciones disponibles en la Classpad. Variables y carpetas. Actividades propuestas. INTRODUCCIÓN En los siguientes apartados
Tema 2. FUNCIONES, VARIABLES Y CARPETAS EN LA CALCULADORA CLASSPAD Introducción. Funciones disponibles en la Classpad. Variables y carpetas. Actividades propuestas. INTRODUCCIÓN En los siguientes apartados
UNIVERSIDAD SAN MARCOS
 Prof. Edwin Gerardo Acuña Acuña UNIVERSIDAD SAN MARCOS ALGEBRA Este capítulo estudia los conceptos básicos del álgebra, una de las disciplinas de la matemática que tiene más aplicaciones en diversos campos.
Prof. Edwin Gerardo Acuña Acuña UNIVERSIDAD SAN MARCOS ALGEBRA Este capítulo estudia los conceptos básicos del álgebra, una de las disciplinas de la matemática que tiene más aplicaciones en diversos campos.
Lección 8: Potencias con exponentes enteros
 GUÍA DE MATEMÁTICAS III Lección 8: Potencias con exponentes enteros Cuando queremos indicar productos de factores iguales, generalmente usamos la notación exponencial. Por ejemplo podemos expresar x, como
GUÍA DE MATEMÁTICAS III Lección 8: Potencias con exponentes enteros Cuando queremos indicar productos de factores iguales, generalmente usamos la notación exponencial. Por ejemplo podemos expresar x, como
Unidad 1 Números. Los números naturales son aquellos que se utilizan para contar los elementos de un conjunto.
 Unidad 1 Números 1.- Números Naturales Los números naturales son aquellos que se utilizan para contar los elementos de un conjunto. El conjunto de números naturales se representa por la letra N Operaciones
Unidad 1 Números 1.- Números Naturales Los números naturales son aquellos que se utilizan para contar los elementos de un conjunto. El conjunto de números naturales se representa por la letra N Operaciones
TEMA 2: TEORÍA DE CONJUNTOS Y CONJUNTOS NUMÉRICOS.
 TEMA 2: TEORÍA DE CONJUNTOS Y CONJUNTOS NUMÉRICOS. TEORÍA DE CONJUNTOS. Definiciones. Se define un conjunto como una colección de objetos o cosas, se nombran con letras mayúsculas (A, B...). Cada uno de
TEMA 2: TEORÍA DE CONJUNTOS Y CONJUNTOS NUMÉRICOS. TEORÍA DE CONJUNTOS. Definiciones. Se define un conjunto como una colección de objetos o cosas, se nombran con letras mayúsculas (A, B...). Cada uno de
MATEMÁTICAS 2º ESO. TEMA 1
 MATEMÁTICAS 2º ESO. TEMA 1 1. DIVISIBILIDAD Y NÚMEROS ENTEROS 1. Los divisores son siempre menores o iguales que el número. 2. Los múltiplos siempre son mayores o iguales que el número. 3. Para saber si
MATEMÁTICAS 2º ESO. TEMA 1 1. DIVISIBILIDAD Y NÚMEROS ENTEROS 1. Los divisores son siempre menores o iguales que el número. 2. Los múltiplos siempre son mayores o iguales que el número. 3. Para saber si
Recordar las principales operaciones con expresiones algebraicas.
 Capítulo 1 Álgebra Objetivos Recordar las principales operaciones con expresiones algebraicas. 1.1. Números Los números naturales se denotarán por N y están constituidos por 0, 1, 2, 3... Con estos números
Capítulo 1 Álgebra Objetivos Recordar las principales operaciones con expresiones algebraicas. 1.1. Números Los números naturales se denotarán por N y están constituidos por 0, 1, 2, 3... Con estos números
Los números naturales
 Los números naturales Los números naturales Los números naturales son aquellos que sirven para contar. Se suelen representar utilizando las cifras del 0 al 9. signo suma o resultado Suma: 9 + 12 = 21 sumandos
Los números naturales Los números naturales Los números naturales son aquellos que sirven para contar. Se suelen representar utilizando las cifras del 0 al 9. signo suma o resultado Suma: 9 + 12 = 21 sumandos
UNIDAD I. ALGORITMOS
 UNIDAD I. ALGORITMOS 1.1 Definición Un algoritmo es una serie de pasos organizados que describe el proceso que se debe seguir, para dar solución a un problema específico. 1.2 Tipos Cualitativos: Son aquellos
UNIDAD I. ALGORITMOS 1.1 Definición Un algoritmo es una serie de pasos organizados que describe el proceso que se debe seguir, para dar solución a un problema específico. 1.2 Tipos Cualitativos: Son aquellos
CURSO BÁSICO DE MATEMÁTICAS PARA ESTUDIANTES DE ECONÓMICAS Y EMPRESARIALES. Unidad didáctica 4. Números reales y números complejos
 NÚMEROS REALES Como se ha señalado anteriormente la necesidad de resolver diversos problemas de origen aritmético y geométrico lleva a ir ampliando sucesivamente los conjuntos numéricos, N Z Q, y a definir
NÚMEROS REALES Como se ha señalado anteriormente la necesidad de resolver diversos problemas de origen aritmético y geométrico lleva a ir ampliando sucesivamente los conjuntos numéricos, N Z Q, y a definir
CURSO BÁSICO DE MATEMÁTICAS PARA ESTUDIANTES DE ECONÓMICAS Y EMPRESARIALES. Unidad didáctica 4. Números reales y números complejos
 NÚMEROS REALES NÚMEROS NATURALES Y NÚMEROS ENTEROS Los números naturales surgen como respuesta a la necesidad de nuestros antepasados de contar los elementos de un conjunto (por ejemplo los animales de
NÚMEROS REALES NÚMEROS NATURALES Y NÚMEROS ENTEROS Los números naturales surgen como respuesta a la necesidad de nuestros antepasados de contar los elementos de un conjunto (por ejemplo los animales de
CLASIFICACION DE LAS EXPRESIONES ALGEBRAICAS. Las expresiones algebraicas se clasifican en: a) racionales; b) irracionales.
 Capítulo 3.-EXPRESIONES ALGEBRAICAS OBJETIVOS INSTRUCTIVOS Que el alumno: Distinga la clasificación de las expresiones algebraicas. Aprenda las operaciones con monomios y polinomios y sus aplicaciones
Capítulo 3.-EXPRESIONES ALGEBRAICAS OBJETIVOS INSTRUCTIVOS Que el alumno: Distinga la clasificación de las expresiones algebraicas. Aprenda las operaciones con monomios y polinomios y sus aplicaciones
MODULO DE LOGARITMO. 1 log 2 4 16. log N x b N N se llama antilogaritmo, b > 0 y b 1. Definición de Logaritmo. Liceo n 1 Javiera Carrera 2011
 MODULO DE LOGARITMO Nombre:.. Curso : Medio Los aritmos están creados para facilitar los cálculos numéricos. Por aritmo podemos convertir los productos en sumas, los cocientes en restas, las potencias
MODULO DE LOGARITMO Nombre:.. Curso : Medio Los aritmos están creados para facilitar los cálculos numéricos. Por aritmo podemos convertir los productos en sumas, los cocientes en restas, las potencias
Polinomios Primero que todo vamos a definirlos como aquella expresión algebraica de la forma: P(x) = a n x n + a n - 1 x n - 1 + a n - 2 x n - 2 +...
 Polinomios Primero que todo vamos a definirlos como aquella expresión algebraica de la forma: P(x) = a n x n + a n - 1 x n - 1 + a n - 2 x n - 2 +... + a 1 x 1 + a 0 Siendo a n, a n -1... a 1, a o números,
Polinomios Primero que todo vamos a definirlos como aquella expresión algebraica de la forma: P(x) = a n x n + a n - 1 x n - 1 + a n - 2 x n - 2 +... + a 1 x 1 + a 0 Siendo a n, a n -1... a 1, a o números,
1. El sistema de los números reales
 1. El sistema de los números reales Se iniciará definiendo el conjunto de números que conforman a los números reales, en la siguiente figura se muestra la forma en la que están contenidos estos conjuntos
1. El sistema de los números reales Se iniciará definiendo el conjunto de números que conforman a los números reales, en la siguiente figura se muestra la forma en la que están contenidos estos conjuntos
2. ENTIDADES PRIMITIVAS PARA EL DESARROLLO DE ALGORITMOS
 2. ENTIDADES PRIMITIVAS PARA EL DESARROLLO DE ALGORITMOS 2.1 Tipos De Datos Todos los datos tienen un tipo asociado con ellos. Un dato puede ser un simple carácter, tal como b, un valor entero tal como
2. ENTIDADES PRIMITIVAS PARA EL DESARROLLO DE ALGORITMOS 2.1 Tipos De Datos Todos los datos tienen un tipo asociado con ellos. Un dato puede ser un simple carácter, tal como b, un valor entero tal como
Unidad 1: Números reales.
 Unidad 1: Números reales. 1 Unidad 1: Números reales. 1.- Números racionales e irracionales Números racionales: Son aquellos que se pueden escribir como una fracción. 1. Números enteros 2. Números decimales
Unidad 1: Números reales. 1 Unidad 1: Números reales. 1.- Números racionales e irracionales Números racionales: Son aquellos que se pueden escribir como una fracción. 1. Números enteros 2. Números decimales
LOGARITMOS. El logaritmo de un número es, entonces, el exponente a que debe elevarse otro número que llamado base, para que dé el primer número.
 LOGARITMOS A. DEFINICIONES La función y=2 x se puede representar gráficamente. Para ello se debe tabular de la siguiente forma. X - -4-3 -2-1 0 1 2 3 Y=2 x 0.0625.125.25.5 1 2 4 8 La gráfica sería esta:
LOGARITMOS A. DEFINICIONES La función y=2 x se puede representar gráficamente. Para ello se debe tabular de la siguiente forma. X - -4-3 -2-1 0 1 2 3 Y=2 x 0.0625.125.25.5 1 2 4 8 La gráfica sería esta:
GUIA PRACTICA PARA LA APLICACIÓN DE MS EXCEL TECNOLOGIA/ INFORMATICA
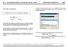 Fórmulas y funciones De la barra de menú seleccionmos la opción insertar y haciendo clic en la opción f x se desplegará el siguiente cuadro de diálogo a partir del cual escogeremos la función adecuada
Fórmulas y funciones De la barra de menú seleccionmos la opción insertar y haciendo clic en la opción f x se desplegará el siguiente cuadro de diálogo a partir del cual escogeremos la función adecuada
Utiliza los números ordinales al resolver problemas planteados de manera oral.
 T G CONTENIDOS APRENDIZAJES ESPERADOS ESTÁNDARES 1.2.1 Identificación y uso de los números ordinales para colocar objetos o para indicar el lugar que ocupan dentro de una colección de hasta 10 elementos.
T G CONTENIDOS APRENDIZAJES ESPERADOS ESTÁNDARES 1.2.1 Identificación y uso de los números ordinales para colocar objetos o para indicar el lugar que ocupan dentro de una colección de hasta 10 elementos.
Area Académica: Licenciatura en Administración. Profesor: I.E.C. Roxana Sifuentes Carrillo
 Area Académica: Licenciatura en Administración Asignatura: Matemáticas Básicas Profesor: I.E.C. Roxana Sifuentes Carrillo Periodo: Julio-Diciembre 2011 Tema: Basic Concepts of Algebra Abstract Algebra
Area Académica: Licenciatura en Administración Asignatura: Matemáticas Básicas Profesor: I.E.C. Roxana Sifuentes Carrillo Periodo: Julio-Diciembre 2011 Tema: Basic Concepts of Algebra Abstract Algebra
Término algebraico. (Informal) Es la multiplicación o división de factores literales y coeficiente numéricos
 Término algebraico. (Informal) Es la multiplicación o división de factores literales y coeficiente numéricos 7ax³ y² 3x²y ; - ; 4a²b³c 5 Todo término algebraico se compone de un factor literal (letras)
Término algebraico. (Informal) Es la multiplicación o división de factores literales y coeficiente numéricos 7ax³ y² 3x²y ; - ; 4a²b³c 5 Todo término algebraico se compone de un factor literal (letras)
Tema 1: Números Reales.
 Tema 1: Números Reales. En este tema, estudiaremos lo que son los números reales, el conjunto de los números reales y los distintos subconjuntos (Naturales, Enteros, Racionales e Irracionales), así como
Tema 1: Números Reales. En este tema, estudiaremos lo que son los números reales, el conjunto de los números reales y los distintos subconjuntos (Naturales, Enteros, Racionales e Irracionales), así como
Fracciones numéricas enteras
 Números racionales Fracciones numéricas enteras En matemáticas, una fracción numérica entera expresa la división de un número entero en partes iguales. Una fracción numérica consta de dos términos: El
Números racionales Fracciones numéricas enteras En matemáticas, una fracción numérica entera expresa la división de un número entero en partes iguales. Una fracción numérica consta de dos términos: El
Tema 2 Cálculos básicos con wxmaxima
 Tema 2 Cálculos básicos con wxmaxima Objetivos 1. Llevar a cabo cálculos básicos con variables. 2. Llevar a cabo cálculos básicos con expresiones algebraicas. 3. Llevar a cabo cálculos básicos con polinomios
Tema 2 Cálculos básicos con wxmaxima Objetivos 1. Llevar a cabo cálculos básicos con variables. 2. Llevar a cabo cálculos básicos con expresiones algebraicas. 3. Llevar a cabo cálculos básicos con polinomios
k k N b Sistemas Númericos Sistemas con Notación Posicional (1) Sistemas con Notación Posicional (2) Sistemas Decimal
 Sistemas con Notación Posicional (1) Sistemas Númericos N b = a n-1 *b n-1 + a n-2 *b n-2 +... + a 0 *b 0 +a -1 *b - 1 + a -2 *b -2 +... + a -m *b -m Sistemas con Notación Posicional (2) N b : Número en
Sistemas con Notación Posicional (1) Sistemas Númericos N b = a n-1 *b n-1 + a n-2 *b n-2 +... + a 0 *b 0 +a -1 *b - 1 + a -2 *b -2 +... + a -m *b -m Sistemas con Notación Posicional (2) N b : Número en
Contenidos mínimos 4B ESO. 1. Contenidos. Bloque I: Aritmética y álgebra.
 Contenidos mínimos 4B ESO. 1. Contenidos. Bloque I: Aritmética y álgebra. 1. Clasificar distintos tipos de números: naturales, enteros, racionales y reales. 2. Operar con números reales y aplicar las propiedades
Contenidos mínimos 4B ESO. 1. Contenidos. Bloque I: Aritmética y álgebra. 1. Clasificar distintos tipos de números: naturales, enteros, racionales y reales. 2. Operar con números reales y aplicar las propiedades
lasmatemáticas.eu Pedro Castro Ortega materiales de matemáticas
 º ESO 1. Expresiones algebraicas En matemáticas es muy común utilizar letras para expresar un resultado general. Por ejemplo, el área de un b h triángulo es base por altura dividido por dos y se expresa
º ESO 1. Expresiones algebraicas En matemáticas es muy común utilizar letras para expresar un resultado general. Por ejemplo, el área de un b h triángulo es base por altura dividido por dos y se expresa
N = {1, 2, 3, 4, 5,...}
 Números y Funciones.. Números Los principales tipos de números son:. Los números naturales son aquellos que sirven para contar. N = {,,, 4, 5,...}. Los números enteros incluyen a los naturales y a sus
Números y Funciones.. Números Los principales tipos de números son:. Los números naturales son aquellos que sirven para contar. N = {,,, 4, 5,...}. Los números enteros incluyen a los naturales y a sus
MATEMÁTICA MÓDULO 1 Eje temático: Números y proporcionalidad
 MATEMÁTICA MÓDULO 1 Eje temático: Números y proporcionalidad 1. CONJUNTOS NUMÉRICOS Empezaremos este curso de preparación PSU revisando los diferentes conjuntos numéricos con los que has trabajado tanto
MATEMÁTICA MÓDULO 1 Eje temático: Números y proporcionalidad 1. CONJUNTOS NUMÉRICOS Empezaremos este curso de preparación PSU revisando los diferentes conjuntos numéricos con los que has trabajado tanto
Polinomios. 1.- Funciones cuadráticas
 Polinomios 1.- Funciones cuadráticas Definición 1 (Función polinomial) Sea n un entero no negativo y sean a n, a n 1,..., a, a 1, a 0 número s reales con a n 0. La función se denomina función polinomial
Polinomios 1.- Funciones cuadráticas Definición 1 (Función polinomial) Sea n un entero no negativo y sean a n, a n 1,..., a, a 1, a 0 número s reales con a n 0. La función se denomina función polinomial
IV NÚMEROS FRACCIONARIOS.
 IV NÚMEROS FRACCIONARIOS.. Qué es una fracción?. Fracciones equivalentes. Definición. Reconocimiento. Obtención.. Simplificación de fracciones.. Comparación de fracciones.. Operaciones con fracciones.
IV NÚMEROS FRACCIONARIOS.. Qué es una fracción?. Fracciones equivalentes. Definición. Reconocimiento. Obtención.. Simplificación de fracciones.. Comparación de fracciones.. Operaciones con fracciones.
SESIÓN 1 PRE-ALGEBRA, CONCEPTOS Y OPERACIONES ARITMÉTICAS BÁSICAS
 SESIÓN 1 PRE-ALGEBRA, CONCEPTOS Y OPERACIONES ARITMÉTICAS BÁSICAS I. CONTENIDOS: 1. Introducción: de la aritmética al álgebra. 2. Números reales y recta numérica. 3. Operaciones aritméticas básicas con
SESIÓN 1 PRE-ALGEBRA, CONCEPTOS Y OPERACIONES ARITMÉTICAS BÁSICAS I. CONTENIDOS: 1. Introducción: de la aritmética al álgebra. 2. Números reales y recta numérica. 3. Operaciones aritméticas básicas con
Preparación para Álgebra 1 de Escuela Superior
 Preparación para Álgebra 1 de Escuela Superior Este curso cubre los conceptos mostrados a continuación. El estudiante navega por trayectos de aprendizaje basados en su nivel de preparación. Usuarios institucionales
Preparación para Álgebra 1 de Escuela Superior Este curso cubre los conceptos mostrados a continuación. El estudiante navega por trayectos de aprendizaje basados en su nivel de preparación. Usuarios institucionales
Universidad Politécnica de Puerto Rico Departamento de Ciencias y Matemáticas. Preparado por: Prof. Manuel Capella-Casellas, M.A.Ed.
 Universidad Politécnica de Puerto Rico Departamento de Ciencias y Matemáticas Preparado por: Prof. Manuel Capella-Casellas, M.A.Ed. Agosto, 00 Notación exponencial La notación exponencial se usa para repetir
Universidad Politécnica de Puerto Rico Departamento de Ciencias y Matemáticas Preparado por: Prof. Manuel Capella-Casellas, M.A.Ed. Agosto, 00 Notación exponencial La notación exponencial se usa para repetir
Teoría de errores. Departamento de Análisis Matemático Universidad de La Laguna
 Teoría de errores BENITO J. GONZÁLEZ RODRÍGUEZ ([email protected]) DOMINGO HERNÁNDEZ ABREU ([email protected]) MATEO M. JIMÉNEZ PAIZ ([email protected]) M. ISABEL MARRERO RODRÍGUEZ ([email protected]) ALEJANDRO SANABRIA
Teoría de errores BENITO J. GONZÁLEZ RODRÍGUEZ ([email protected]) DOMINGO HERNÁNDEZ ABREU ([email protected]) MATEO M. JIMÉNEZ PAIZ ([email protected]) M. ISABEL MARRERO RODRÍGUEZ ([email protected]) ALEJANDRO SANABRIA
ENTIDADES PRIMITIVAS PARA EL DESARROLLO DE ALGORITMOS Tipos de datos Expresiones Operadores y operandos Identificadores como localidades de memoria
 ENIDADES PRIMIIVAS PARA EL DESARROLLO DE ALGORIMOS ipos de datos Expresiones Operadores y operandos Identificadores como localidades de memoria ipos De Datos odos los datos tienen un tipo asociado con
ENIDADES PRIMIIVAS PARA EL DESARROLLO DE ALGORIMOS ipos de datos Expresiones Operadores y operandos Identificadores como localidades de memoria ipos De Datos odos los datos tienen un tipo asociado con
SISTEMAS DE NUMERACIÓN
 SISTEMAS DE NUMERACIÓN INDICE. 1. DEFINICIÓN DE SISTEMAS DE NUMERACIÓN.... 1 2. TEOREMA FUNDAMENTAL DE LA NUMERACIÓN... 3 3. SISTEMAS DECIMAL, BINARIO, OCTAL Y HEXADECIMAL.... 5 3.1. SISTEMA DECIMAL...
SISTEMAS DE NUMERACIÓN INDICE. 1. DEFINICIÓN DE SISTEMAS DE NUMERACIÓN.... 1 2. TEOREMA FUNDAMENTAL DE LA NUMERACIÓN... 3 3. SISTEMAS DECIMAL, BINARIO, OCTAL Y HEXADECIMAL.... 5 3.1. SISTEMA DECIMAL...
POLINOMIOS. Un polinomio es una expresión algebraica (conjunto de. números y letras que representan números, conectados por las
 POLINOMIOS Teoría 1.- Qué es un polinomio? Un polinomio es una expresión algebraica (conjunto de números y letras que representan números, conectados por las operaciones de suma, resta, multiplicación,
POLINOMIOS Teoría 1.- Qué es un polinomio? Un polinomio es una expresión algebraica (conjunto de números y letras que representan números, conectados por las operaciones de suma, resta, multiplicación,
MATEMÁTICAS - 6º curso
 MATEMÁTICAS 6º curso TEMA 1. OPERACIONES CON NÚMEROS NATURALES 1. Realizar sumas y restas dadas. 2. Efectuar multiplicaciones dadas. 3. Realizar divisiones dadas. 4. Clasificar las divisiones en exactas
MATEMÁTICAS 6º curso TEMA 1. OPERACIONES CON NÚMEROS NATURALES 1. Realizar sumas y restas dadas. 2. Efectuar multiplicaciones dadas. 3. Realizar divisiones dadas. 4. Clasificar las divisiones en exactas
www.matesxronda.net José A. Jiménez Nieto
 NÚMEROS REALES 1. NÚMEROS IRRACIONALES: CARACTERIZACIÓN. En el tema correspondiente a números racionales hemos visto que estos números tienen una característica esencial: su expresión decimal es exacta
NÚMEROS REALES 1. NÚMEROS IRRACIONALES: CARACTERIZACIÓN. En el tema correspondiente a números racionales hemos visto que estos números tienen una característica esencial: su expresión decimal es exacta
Tema 2. Divisibilidad. Múltiplos y submúltiplos.
 Tema 2. Divisibilidad. Múltiplos y submúltiplos. En el tema 1, se ha mostrado como realizar cuentas con números naturales y enteros. Antes de conocer otras clases de números, los racionales, irracionales
Tema 2. Divisibilidad. Múltiplos y submúltiplos. En el tema 1, se ha mostrado como realizar cuentas con números naturales y enteros. Antes de conocer otras clases de números, los racionales, irracionales
EL CONJUNTO DE LOS NÚMEROS REALES
 MÓDULO 1 Curso: Matemática EL CONJUNTO DE LOS NÚMEROS REALES UNIVERSIDAD DE PANAMÁ CENTRO REGIONAL UNIVERSITARIO DE BOCAS DEL TORO Introducción Los estudiantes que inician el curso de Matemática a nivel
MÓDULO 1 Curso: Matemática EL CONJUNTO DE LOS NÚMEROS REALES UNIVERSIDAD DE PANAMÁ CENTRO REGIONAL UNIVERSITARIO DE BOCAS DEL TORO Introducción Los estudiantes que inician el curso de Matemática a nivel
Tema 1 Conjuntos numéricos
 Tema 1 Conjuntos numéricos En este tema: 1.1 Números naturales. Divisibilidad 1.2 Números enteros 1.3 Números racionales 1.4 Números reales 1.5 Potencias y radicales 1.7 Logaritmos decimales 1.1 NÚMEROS
Tema 1 Conjuntos numéricos En este tema: 1.1 Números naturales. Divisibilidad 1.2 Números enteros 1.3 Números racionales 1.4 Números reales 1.5 Potencias y radicales 1.7 Logaritmos decimales 1.1 NÚMEROS
Complejos, C. Reales, R. Fraccionarios
 NÚMEROS COMPLEJOS Como ya sabemos, conocemos distintos cuerpos numéricos en matemáticas como por ejemplo el cuerpo de los números racionales, irracionales, enteros, negativos,... Sin embargo, para completar
NÚMEROS COMPLEJOS Como ya sabemos, conocemos distintos cuerpos numéricos en matemáticas como por ejemplo el cuerpo de los números racionales, irracionales, enteros, negativos,... Sin embargo, para completar
Ejercicio 1: Realiza las siguientes divisiones por el método tradicional y por Ruffini: a)
 Tema 2: Ecuaciones, Sistemas e Inecuaciones. 2.1 División de polinomios. Regla de Ruffini. Polinomio: Expresión algebraica formada por la suma y/o resta de varios monomios. Terminología: o Grado del polinomio:
Tema 2: Ecuaciones, Sistemas e Inecuaciones. 2.1 División de polinomios. Regla de Ruffini. Polinomio: Expresión algebraica formada por la suma y/o resta de varios monomios. Terminología: o Grado del polinomio:
6to GRADO. Operaciones con decimales HOJAS DE TRABAJO
 6to GRADO Operaciones con decimales HOJAS DE TRABAJO Multiplicar y dividir por potencias de diez Mueve el punto decimal dependiendo de la cantidad de ceros el punto decimal se mueve a la derecha el punto
6to GRADO Operaciones con decimales HOJAS DE TRABAJO Multiplicar y dividir por potencias de diez Mueve el punto decimal dependiendo de la cantidad de ceros el punto decimal se mueve a la derecha el punto
1 of 18 10/25/2011 6:42 AM
 Prof. Anneliesse SánchezDepartamento de MatemáticasUniversidad de Puerto Rico en AreciboEn esta sección discutiremos Expresiones algebraicas y polinomios. Discutiremos los siguientes tópicos: Introducción
Prof. Anneliesse SánchezDepartamento de MatemáticasUniversidad de Puerto Rico en AreciboEn esta sección discutiremos Expresiones algebraicas y polinomios. Discutiremos los siguientes tópicos: Introducción
Repaso de Álgebra. Los subconjuntos de los reales de relevancia para nuestra discusión serán denotados según indicamos a continuación:
 Repaso de Álgebra Preliminares: En esta sección trabajaremos con los siguientes temas: I Los números reales: racionales e irracionales II Valor absoluto: nociones básicas III Expresiones algebraicas: evaluación,
Repaso de Álgebra Preliminares: En esta sección trabajaremos con los siguientes temas: I Los números reales: racionales e irracionales II Valor absoluto: nociones básicas III Expresiones algebraicas: evaluación,
Ámbito Científico y Tecnológico. Repaso de números enteros y racionales
 Ámbito Científico y Tecnológico. Repaso de números enteros y racionales 1 Prioridad de las operaciones Si en una operación aparecen sumas, o restas y multiplicaciones o divisiones, el resultado varía según
Ámbito Científico y Tecnológico. Repaso de números enteros y racionales 1 Prioridad de las operaciones Si en una operación aparecen sumas, o restas y multiplicaciones o divisiones, el resultado varía según
Expresión, Operador, Operando, Asignación, Prioridad
 4. EXPRESIONES Y OPERADORES Conceptos: Resumen: Expresión, Operador, Operando, Asignación, Prioridad En este tema se presentan los siguientes elementos de la programación: las expresiones y los operadores.
4. EXPRESIONES Y OPERADORES Conceptos: Resumen: Expresión, Operador, Operando, Asignación, Prioridad En este tema se presentan los siguientes elementos de la programación: las expresiones y los operadores.
CAPITULO II. ENTIDADES PRIMITIVAS PARA EL DESARROLLO DE ALGORITMOS
 CAPIULO II. ENIDADES PRIMIIVAS PARA EL DESARROLLO DE ALGORIMOS 2.1 ipos de datos 2.2 Expresiones 2.3 Operadores y operandos 2.4 Identificadores como localidades de memoria OBJEIVO EDUCACIONAL: El alumno:
CAPIULO II. ENIDADES PRIMIIVAS PARA EL DESARROLLO DE ALGORIMOS 2.1 ipos de datos 2.2 Expresiones 2.3 Operadores y operandos 2.4 Identificadores como localidades de memoria OBJEIVO EDUCACIONAL: El alumno:
MATERIALES DIDÁCTICOS
 MATERIALES DIDÁCTICOS LUIS QUINTANAR MEDINA* Ejercitaremos el despeje en ecuaciones de primer grado y lo haremos a tres niveles: El primero en que solo se consideran expresiones directas, la habilidad
MATERIALES DIDÁCTICOS LUIS QUINTANAR MEDINA* Ejercitaremos el despeje en ecuaciones de primer grado y lo haremos a tres niveles: El primero en que solo se consideran expresiones directas, la habilidad
Luis Zegarra A. Sucesiones, inducción y sumatorias 97
 Luis Zegarra A. Sucesiones, inducción y sumatorias 97 Note que a i representa a una suma desde el primer término de la sucesión i a para i hasta el último término que en este caso es a n para i n. Es decir,
Luis Zegarra A. Sucesiones, inducción y sumatorias 97 Note que a i representa a una suma desde el primer término de la sucesión i a para i hasta el último término que en este caso es a n para i n. Es decir,
3. Resolver triángulos rectángulos utilizando las definiciones de las razones trigonométricas.
 Contenidos mínimos MI. 1. Contenidos. Bloque I: Aritmética y Álgebra. 1. Conocer las clases de números, los conjuntos numéricos: naturales, enteros, racionales, reales y complejos y las propiedades que
Contenidos mínimos MI. 1. Contenidos. Bloque I: Aritmética y Álgebra. 1. Conocer las clases de números, los conjuntos numéricos: naturales, enteros, racionales, reales y complejos y las propiedades que
Expresiones algebraicas
 Expresiones algebraicas Una expresión algebraica es una combinación de letras y números relacionadas por los signos de las operaciones: adición, sustracción, multiplicación, división y potenciación. Las
Expresiones algebraicas Una expresión algebraica es una combinación de letras y números relacionadas por los signos de las operaciones: adición, sustracción, multiplicación, división y potenciación. Las
TUTORIAL INTRODUCTORIO DE MATLAB
 TUTORIAL INTRODUCTORIO DE MATLAB (PVB Parte I) Consejos y tips para tener en cuenta. Si la forma de la interface o la disposición de las ventanas cambia de configuración, ya sea que se desordenen o se
TUTORIAL INTRODUCTORIO DE MATLAB (PVB Parte I) Consejos y tips para tener en cuenta. Si la forma de la interface o la disposición de las ventanas cambia de configuración, ya sea que se desordenen o se
Una sucesión infinita es una función cuyo dominio es el conjunto de los enteros positivos. Podemos denotar una sucesión como una lista
 Cap 9 Sec 9.1 9.3 Una sucesión infinita es una función cuyo dominio es el conjunto de los enteros positivos. Podemos denotar una sucesión como una lista a 1, a 2, a 3, a n, Donde cada a k es un término
Cap 9 Sec 9.1 9.3 Una sucesión infinita es una función cuyo dominio es el conjunto de los enteros positivos. Podemos denotar una sucesión como una lista a 1, a 2, a 3, a n, Donde cada a k es un término
POLINOMIOS Y FRACCIONES ALGEBRAICAS
 POLINOMIOS Y FRACCIONES ALGEBRAICAS Definición de monomio. Expresión algebraica formada por el producto de un número finito de constantes y variables con exponente natural. Al producto de las constantes
POLINOMIOS Y FRACCIONES ALGEBRAICAS Definición de monomio. Expresión algebraica formada por el producto de un número finito de constantes y variables con exponente natural. Al producto de las constantes
TEMA 1: NÚMEROS REALES
 TEMA 1: NÚMEROS REALES 3º ESO Matemáticas Apuntes para trabajo del alumnos en el aula. 1. Fracciones. Números racionales Si se multiplican o dividen el numerador y el denominador de una fracción por un
TEMA 1: NÚMEROS REALES 3º ESO Matemáticas Apuntes para trabajo del alumnos en el aula. 1. Fracciones. Números racionales Si se multiplican o dividen el numerador y el denominador de una fracción por un
Los números enteros. > significa "mayor que". Ejemplo: 58 > 12 < significa "menor que". Ejemplo: 3 < 12 Cualquier número positivo siempre es mayor
 Los números enteros Los números enteros Los números enteros son aquellos que permiten contar tanto los objetos que se tienen, como los objetos que se deben. Enteros positivos: precedidos por el signo +
Los números enteros Los números enteros Los números enteros son aquellos que permiten contar tanto los objetos que se tienen, como los objetos que se deben. Enteros positivos: precedidos por el signo +
Fracciones. 1. Concepto de fracción 1.a. Las fracciones en nuestra vida Lee el texto de pantalla. 1.b. Definición y elementos de una fracción
 1. Concepto de fracción 1.a. Las fracciones en nuestra vida Lee el texto de pantalla. Fracciones Pon, al menos tres ejemplos de 1ª Forma: utilización de fracciones en el lenguaje habitual. Uno original
1. Concepto de fracción 1.a. Las fracciones en nuestra vida Lee el texto de pantalla. Fracciones Pon, al menos tres ejemplos de 1ª Forma: utilización de fracciones en el lenguaje habitual. Uno original
Introducción al análisis numérico
 Introducción al análisis numérico Javier Segura Universidad de Cantabria Cálculo Numérico I. Tema 1 Javier Segura (Universidad de Cantabria) Introducción al análisis numérico CNI 1 / 26 Contenidos: 1 Sistemas
Introducción al análisis numérico Javier Segura Universidad de Cantabria Cálculo Numérico I. Tema 1 Javier Segura (Universidad de Cantabria) Introducción al análisis numérico CNI 1 / 26 Contenidos: 1 Sistemas
MATEMÁTICAS Versión impresa NÚMEROS REALES
 MATEMÁTICAS Versión impresa NÚMEROS REALES 1. EL CONJUNTO DE LOS NÚMEROS REALES 1.1. Números naturales El conjunto de los números naturales se representa con el símbolo. Los números naturales son los más
MATEMÁTICAS Versión impresa NÚMEROS REALES 1. EL CONJUNTO DE LOS NÚMEROS REALES 1.1. Números naturales El conjunto de los números naturales se representa con el símbolo. Los números naturales son los más
Qué Tipos de Datos se Almacenan en OpenOffice.org Calc?
 Qué Tipos de Datos se Almacenan en OpenOffice.org Calc? Se puede ingresar cualquier dato en una celda de la hoja de cálculo. OpenOffice.org Calc está en condiciones de comprobar automáticamente el tipo
Qué Tipos de Datos se Almacenan en OpenOffice.org Calc? Se puede ingresar cualquier dato en una celda de la hoja de cálculo. OpenOffice.org Calc está en condiciones de comprobar automáticamente el tipo
UNIDAD III Artificios de Integración
 UNIDAD III Artificios de Integración 8 UNIDAD III ARTIFICIOS DE INTEGRACIÓN La integración depende, en última instancia, del empleo adecuado de las formas básicas de integración. Cuando en un caso no sucede
UNIDAD III Artificios de Integración 8 UNIDAD III ARTIFICIOS DE INTEGRACIÓN La integración depende, en última instancia, del empleo adecuado de las formas básicas de integración. Cuando en un caso no sucede
INSTITUCION EDUCATIVA LA PRESENTACION
 INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMATICAS ASIGNATURA: MATEMATICAS DOCENTE: HUGO HERNAN BEDOYA Y LUIS LOPEZ TIPO DE GUIA: NIVELACION PERIODO GRADO FECHA DURACION 8 A/B Abril
INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMATICAS ASIGNATURA: MATEMATICAS DOCENTE: HUGO HERNAN BEDOYA Y LUIS LOPEZ TIPO DE GUIA: NIVELACION PERIODO GRADO FECHA DURACION 8 A/B Abril
Convertir unidades de longitud Determinar el perímetro de triángulo y cuadrilátero Determinar el volumen de prismas rectos.
 Colegio Preuniversitario Dr. Luis Alfredo Duvergé Mejía Listado de contenidos en matemática a estudiar para ingresar al 6to Grado Nivel Básico. Números y operaciones. Leer y escribe los números de mayores
Colegio Preuniversitario Dr. Luis Alfredo Duvergé Mejía Listado de contenidos en matemática a estudiar para ingresar al 6to Grado Nivel Básico. Números y operaciones. Leer y escribe los números de mayores
UNIDAD III 3.2 USO DE FUNCIONES MATEMÁTICAS LÓGICAS Y DE BUSQUEDA
 EXCEL BASICO UNIDAD III 3.2 USO DE FUNCIONES MATEMÁTICAS LÓGICAS Y DE BUSQUEDA Autor: M.T.E Silvia M. Hernández Hermosillo Actualización: Lic. Angélica Sánchez Ángeles 3.1 FORMATOS DE NUMEROS Se pueden
EXCEL BASICO UNIDAD III 3.2 USO DE FUNCIONES MATEMÁTICAS LÓGICAS Y DE BUSQUEDA Autor: M.T.E Silvia M. Hernández Hermosillo Actualización: Lic. Angélica Sánchez Ángeles 3.1 FORMATOS DE NUMEROS Se pueden
Matemática Empresarial
 Corporación Universitaria Minuto de Dios - UNITOLIMA GUIA DE TRABAJO 1. Matemática Empresarial Guía N.001 F. Elaboración: 19 febrero /11 F. 1 Revisión: 19 febrero /11 Pagina 1 de 6 TEMA: Números reales
Corporación Universitaria Minuto de Dios - UNITOLIMA GUIA DE TRABAJO 1. Matemática Empresarial Guía N.001 F. Elaboración: 19 febrero /11 F. 1 Revisión: 19 febrero /11 Pagina 1 de 6 TEMA: Números reales
IES Juan García Valdemora NÚMEROS REALES Departamento de Matemáticas NÚMEROS REALES
 NÚMEROS REALES. NÚMEROS RACIONALES Desde la aparición de las sociedades humanas los números desempeñan un papel fundamental para ordenar y contar los elementos de un conjunto. Así surgen, en primer lugar,
NÚMEROS REALES. NÚMEROS RACIONALES Desde la aparición de las sociedades humanas los números desempeñan un papel fundamental para ordenar y contar los elementos de un conjunto. Así surgen, en primer lugar,
UNIDAD DE APRENDIZAJE II UNIDAD DE APRENDIZAJE 2 ( 12 HORAS)
 UNIDAD DE APRENDIZAJE II UNIDAD DE APRENDIZAJE HORAS) Saberes procedimentales Saberes declarativos Identifica y realiza operaciones básicas con expresiones aritméticas. Jerarquía de las operaciones aritméticas.
UNIDAD DE APRENDIZAJE II UNIDAD DE APRENDIZAJE HORAS) Saberes procedimentales Saberes declarativos Identifica y realiza operaciones básicas con expresiones aritméticas. Jerarquía de las operaciones aritméticas.
Representación de los números naturales
 Números naturales El conjunto de los números naturales se representa por la letra, y está formado por: N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9,...} Los números naturales sirven para contar los elementos de un
Números naturales El conjunto de los números naturales se representa por la letra, y está formado por: N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9,...} Los números naturales sirven para contar los elementos de un
Competencias que se favorecen. Validar procedimientos y resultados. Manejar técnicas eficientemente.
 Introducción En este bloque resolverás cálculos numéricos que implican el uso de un orden jerárquico e involucran el uso de números enteros, decimales y fraccionarios. En el caso de la geometría justificarás
Introducción En este bloque resolverás cálculos numéricos que implican el uso de un orden jerárquico e involucran el uso de números enteros, decimales y fraccionarios. En el caso de la geometría justificarás
UNIDAD 2: LÍMITES DE FUNCIONES.CONTINUIDAD = 3 2
 UNIDAD 2: LÍMITES DE FUNCIONES.CONTINUIDAD 1.- Límites en el Infinito: lim x + f(x) = L Se dice que el límite de f (x) cuando x tiende a + es L ϵ Ɽ, si podemos hacer que f(x) se aproxime a L tanto como
UNIDAD 2: LÍMITES DE FUNCIONES.CONTINUIDAD 1.- Límites en el Infinito: lim x + f(x) = L Se dice que el límite de f (x) cuando x tiende a + es L ϵ Ɽ, si podemos hacer que f(x) se aproxime a L tanto como
UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN
 UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN FACULTAD DE INGENIERÍA MECÁNICA Y ELÉCTRICA LABORATORIO DE INGENIERÍA DE CONTROL PRACTICA N 1 INTRODUCCIÓN Y COMANDOS DEL MATLAB OBJETIVO Familiarizarse con el modo de
UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN FACULTAD DE INGENIERÍA MECÁNICA Y ELÉCTRICA LABORATORIO DE INGENIERÍA DE CONTROL PRACTICA N 1 INTRODUCCIÓN Y COMANDOS DEL MATLAB OBJETIVO Familiarizarse con el modo de
[email protected]
 Titulo: RADICACION Año escolar: 3er. año de bachillerato Autor: José Luis Albornoz Salazar Ocupación: Ing Civil. Docente Universitario País de residencia: Venezuela Correo electrónico: [email protected]
Titulo: RADICACION Año escolar: 3er. año de bachillerato Autor: José Luis Albornoz Salazar Ocupación: Ing Civil. Docente Universitario País de residencia: Venezuela Correo electrónico: [email protected]
UNIDAD 1: NÚMEROS NATURALES
 UNIDAD 1: NÚMEROS NATURALES 1. Calcula: Ya conoces las cuatro operaciones básicas, la suma, la resta, multiplicación y división. Cuando te aparezcan varias operaciones para realizar debes saber la siguiente
UNIDAD 1: NÚMEROS NATURALES 1. Calcula: Ya conoces las cuatro operaciones básicas, la suma, la resta, multiplicación y división. Cuando te aparezcan varias operaciones para realizar debes saber la siguiente
CAPITULO 2. ELEMENTOS Y OPERACIONES DE LAS EXPRESIONES ALGEBRAICAS. Cuando nos encontramos con dos o más términos algebraicos en un
 CAPITULO 2. ELEMENTOS Y OPERACIONES DE LAS EXPRESIONES ALGEBRAICAS. Cuando nos encontramos con dos o más términos algebraicos en un conjunto relacionado, los matemáticos dicen que tratamos con una expresión
CAPITULO 2. ELEMENTOS Y OPERACIONES DE LAS EXPRESIONES ALGEBRAICAS. Cuando nos encontramos con dos o más términos algebraicos en un conjunto relacionado, los matemáticos dicen que tratamos con una expresión
CURSO BÁSICO DE MATEMÁTICAS PARA ESTUDIANTES DE ECONÓMICAS Y EMPRESARIALES
 Unidad didáctica. Ecuaciones, inecuaciones y sistemas de ecuaciones e inecuaciones CONCEPTOS ECUACIONES Una ecuación es una igualdad entre dos epresiones en las que aparece una o varias incógnitas. En
Unidad didáctica. Ecuaciones, inecuaciones y sistemas de ecuaciones e inecuaciones CONCEPTOS ECUACIONES Una ecuación es una igualdad entre dos epresiones en las que aparece una o varias incógnitas. En
1 Números racionales
 8 _ 0-0.qxd //0 : Página Números racionales INTRODUCCIÓN Esta unidad desarrolla conceptos y técnicas ya conocidos de otros cursos. Sin embargo, es conveniente repasar las distintas interpretaciones que
8 _ 0-0.qxd //0 : Página Números racionales INTRODUCCIÓN Esta unidad desarrolla conceptos y técnicas ya conocidos de otros cursos. Sin embargo, es conveniente repasar las distintas interpretaciones que
MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN CLASE # 5
 MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN CLASE # 5 OPERACIONES CON LOS NÚMEROS REALES En R se de nen dos operaciones: Suma o adición y producto o multiplicación: Si a 2 R y
MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN CLASE # 5 OPERACIONES CON LOS NÚMEROS REALES En R se de nen dos operaciones: Suma o adición y producto o multiplicación: Si a 2 R y
APUNTES DE MATEMÁTICAS
 APUNTES DE MATEMÁTICAS NÚMEROS NATURALES: Son los que utilizamos para contar Ejemplo: Contar el número de alumnos de la clase, escribir el número de la matrícula de un coche Se representan N{0,1,2, } Ejercicio:
APUNTES DE MATEMÁTICAS NÚMEROS NATURALES: Son los que utilizamos para contar Ejemplo: Contar el número de alumnos de la clase, escribir el número de la matrícula de un coche Se representan N{0,1,2, } Ejercicio:
T. P. Números Racionales: Q. a es igual a 1?, cuándo es menor?, cuándo es mayor?
 T. P. Números Racionales Q Si a b pertenecen a los enteros, a b SIEMPRE pertenece a los enteros? Exploren las distintas posibilidades (positivos negativos. Den ejemplos de acuerdo con cada caso posible.
T. P. Números Racionales Q Si a b pertenecen a los enteros, a b SIEMPRE pertenece a los enteros? Exploren las distintas posibilidades (positivos negativos. Den ejemplos de acuerdo con cada caso posible.
Representación de la información
 Prof. Rodrigo Araya E. [email protected] Universidad Técnica Federico Santa María Departamento de Informática Valparaíso, 1 er Semestre 2006 1 2 3 4 5 Contenido En el mundo que vivimos estamos rodeados
Prof. Rodrigo Araya E. [email protected] Universidad Técnica Federico Santa María Departamento de Informática Valparaíso, 1 er Semestre 2006 1 2 3 4 5 Contenido En el mundo que vivimos estamos rodeados
CURSO BÁSICO DE MATEMÁTICAS PARA ESTUDIANTES DE ECONÓMICAS Y EMPRESARIALES. Unidad didáctica 4. Números reales y números complejos
 CONCEPTOS NÚMEROS COMPLEJOS En el conjunto de los números reales, una ecuación tan sencilla como x + = 0 no se puede resolver ya que es equivalente a x = - y no existe ningún número real cuyo cuadrado
CONCEPTOS NÚMEROS COMPLEJOS En el conjunto de los números reales, una ecuación tan sencilla como x + = 0 no se puede resolver ya que es equivalente a x = - y no existe ningún número real cuyo cuadrado
en coma flotante Oliverio J. Santana Jaria Sistemas Digitales Ingeniería Técnica en Informática de Sistemas Curso 2006 2006
 Oliverio J. Santana Jaria Sistemas Digitales Ingeniería Técnica en Informática de Sistemas Curso 2006 2006 4. Representación n de números n en coma flotante Para La números representar fraccionarios números
Oliverio J. Santana Jaria Sistemas Digitales Ingeniería Técnica en Informática de Sistemas Curso 2006 2006 4. Representación n de números n en coma flotante Para La números representar fraccionarios números
UNIDAD IV CONTENIDO TEMÁTICO
 UNIDAD IV CONTENIDO TEMÁTICO OPERACIONES CON FRACCIONES ALGEBRAICAS I.S.C. Alejandro de Fuentes Martínez 1 ESQUEMA-RESUMEN RESUMEN DE LA UNIDAD IV Conceptos Mínimo común múltiplo OPERACIONES CON FRACCIONES
UNIDAD IV CONTENIDO TEMÁTICO OPERACIONES CON FRACCIONES ALGEBRAICAS I.S.C. Alejandro de Fuentes Martínez 1 ESQUEMA-RESUMEN RESUMEN DE LA UNIDAD IV Conceptos Mínimo común múltiplo OPERACIONES CON FRACCIONES
Se dice que dos monomios son semejantes cuando tienen la misma parte literal
 Expresiones algebraicas 1 MONOMIOS Conceptos Un monomio es una expresión algebraica en la que las únicas operaciones que aparecen entre las variables son el producto y la potencia de exponente natural.
Expresiones algebraicas 1 MONOMIOS Conceptos Un monomio es una expresión algebraica en la que las únicas operaciones que aparecen entre las variables son el producto y la potencia de exponente natural.
REGLAS DE LOS SIGNOS
 1. 1 UNIDAD 1 REGLAS DE LOS SIGNOS Objetivo general. Al terminar esta Unidad resolverás ejercicios y problemas en los que apliques las reglas de los signos. Objetivos específicos: 1. Recordarás las reglas
1. 1 UNIDAD 1 REGLAS DE LOS SIGNOS Objetivo general. Al terminar esta Unidad resolverás ejercicios y problemas en los que apliques las reglas de los signos. Objetivos específicos: 1. Recordarás las reglas
Números Reales. 87 ejercicios para practicar con soluciones. 1 Ordena de menor a mayor las siguientes fracciones: y
 Números Reales. 8 ejercicios para practicar con soluciones Ordena de menor a mayor las siguientes fracciones: y 8 Reducimos a común denominador: 0 80 0 00 0 y 0 0 0 0 0 0 8 0 El orden de las fracciones,
Números Reales. 8 ejercicios para practicar con soluciones Ordena de menor a mayor las siguientes fracciones: y 8 Reducimos a común denominador: 0 80 0 00 0 y 0 0 0 0 0 0 8 0 El orden de las fracciones,
Apuntes de matemáticas 2º ESO Curso 2013-2014. Lenguaje algebraico.
 Lenguaje algebraico. Expresiones algebraicas Trabajar en álgebra consiste en manejar relaciones numéricas en las que una o más cantidades son desconocidas. Estas cantidades se llaman variables, incógnitas
Lenguaje algebraico. Expresiones algebraicas Trabajar en álgebra consiste en manejar relaciones numéricas en las que una o más cantidades son desconocidas. Estas cantidades se llaman variables, incógnitas
2. OPERACIONES ALGEBRAICAS BÁSICAS.
 Prácticas de Matemáticas I y Matemáticas II con DERIVE 30 2. OPERACIONES ALGEBRAICAS BÁSICAS. En este apartado vamos a realizar las operaciones algebraicas básicas que nos permiten utilizar DERIVE como
Prácticas de Matemáticas I y Matemáticas II con DERIVE 30 2. OPERACIONES ALGEBRAICAS BÁSICAS. En este apartado vamos a realizar las operaciones algebraicas básicas que nos permiten utilizar DERIVE como
3.2 DIVIDIR UN POLINOMIO POR x a. REGLA DE RUFFINI
 TEMA 3 ÁLGEBRA MATEMÁTICAS CCSSI 1º BACH 1 TEMA 3 ÁLGEBRA 3.1 DIVISIÓN DE POLINOMIOS COCIENTE DE MONOMIOS El cociente de un monomio por otro monomio de grado inferior es un nuevo monomio cuyo grado es
TEMA 3 ÁLGEBRA MATEMÁTICAS CCSSI 1º BACH 1 TEMA 3 ÁLGEBRA 3.1 DIVISIÓN DE POLINOMIOS COCIENTE DE MONOMIOS El cociente de un monomio por otro monomio de grado inferior es un nuevo monomio cuyo grado es
