ÓPTICA ÓPTICA GEOMÉTRICA
|
|
|
- Ernesto Aguilera Aguirre
- hace 9 años
- Vistas:
Transcripción
1 ÓPTICA ÓPTICA GEOMÉTRICA IES La Magdalena. Avilés. Asturias En la óptica geométrica se estudian los cambios de dirección experimentados por los rayos de luz cuando son reflejados o refractados mediante representaciones geométricas. Para trazar el camino de los rayos se tiene en cuenta lo siguiente: La luz cuando se propaga en un medio homogéneo lo hace en línea recta. Se supone que el tamaño de los obstáculos que la luz encuentra en su camino son muy grandes en comparación con su longitud de onda. Por tanto, no tienen lugar procesos de difracción. El trazado de los rayos se realiza siguiendo las leyes estudiadas para la reflexión y la refracción. Los rayos luminosos son reversibles. La imagen de un punto se forma en la intersección de los rayos. Si divergen después de la reflexión o la refracción, la imagen se forma en la intersección de su prolongación (en sentido opuesto al de propagación) Reflexión en espejos planos Los rayos que llegan a un espejo se reflejan siguiendo las leyes de la reflexión. Un rayo que incida perpendicularmente al espejo se refleja sobre si mismo. La imagen se forma en la intersección de los rayos. Aparentemente está "en el interior del espejo", al otro lado de la superficie reflectante es derecha (no está invertida),del mismo tamaño, y a una distancia (s') igual a la que se sitúa el objeto del espejo (s). Las imágenes que se forman al prolongar los rayos se denominan virtuales, ya que no pueden ser recogidas por una pantalla Imagen: Virtual Derecha Del mismo tamaño Distancia imagen=distancia objeto Las imágenes formadas por reflexión en un espejo plano presentan lo que se conoce con el nombre de inversión lateral ya que la derecha y la izquierda en el objeto y la imagen están invertidas. 1
2 S situamos dos espejos planos uno junto al otro, la imagen de uno se puede reflejar en el otro produciendo una repetición del objeto inicial. El número de imágenes formadas dependerá del ángulo entre los espejos. I E2 I I E1 Se muestra ahora (derecha) un esquema de la reflexión de un objeto en dos espejos que forman un ángulo de 60 0 (E 1 y E 2 ). Los espejos se reflejan dando imágenes situadas en idéntica posición que los originales (ángulo de 60 0 ). De manera similar al caso anterior las imágenes formadas sirven como objeto para el siguiente espejo. Se obtienen cinco imágenes. De forma general el número de imágenes formadas (N) depende del ángulo formado por los espejos : En la imagen (izquierda) puede verse como dos espejos que forman un ángulo de 90 0 (E 1 y E 2 ) se reflejan mutuamente dando las correspondiente imágenes (E' 1 y E' 2 ). El objeto inicial situado entre ambos se refleja en E 1 obteniéndose la correspondiente imagen I E1, y en E 2 obteniéndose I E2. Tanto I E1 cono I E2 sirven a su vez de objetos para la reflexión en los espejos E' 2 y E' 1 dando la imagen común I. Como resultado de las reflexiones se obtienen tres imágenes. N = 360 α 1 Ejemplo 1 Dos espejos planos están colocados perpendicularmente entre sí. Un rayo que se desplaza en un plano perpenduicular a ambos es reflejado primero en uno y luego en el otro. CUál es la dirección final del rayo respecto a su dirección original? Solución: i 1 r 1 i 2 r 2 Como se puede observar en la figura el rayo se refleja en dirección paralela al incidente, aunque en sentido contrario. El ángulo de refracción final (segunda refracción) puede calcularse fácilmente considerando el triángulo rectángulo formado por la intersección de las normales a ambas caras (líneas discontinuas): r 1 + i 2 = 90 0 Como: i 1 = r 1 e i 2 = r 2 r 1 + r 2 = 90 0 ; i 1 + r 2 = 90 0 ; r 2 = i 1 Por ejemplo para un ángulo de incidencia de 30 0 : r 2 = =
3 Reflexión en espejos esféricos Los espejos curvos, como su nombre indica, presentan cierta curvatura en la superficie reflectante. Dependiendo del tipo de curvatura tendremos espejos hiperbólicos, parabólicos, elípticos o esféricos. Aquí se considerarán únicamente estos últimos Los espejos esféricos pueden ser cóncavos o convexos (ver figura). Espejo esférico cóncavo Espejo esférico convexo Los elementos básicos de un espejo esférico son (ver figura): Eje del espejo (línea central). Centro óptico (O). Radio de curvatura (r). Centro de curvatura (C). Foco del espejo (f) o punto en el que se reflejan los rayos que inciden paralelamente al eje del espejo. El foco del espejo se sitúa sobre el eje óptico y a una distancia del centro óptico igual a la mitad del radio. La obtención de las imágenes por reflexión en espejos esféricos se realiza teniendo en cuenta la trayectoria de algunos rayos característicos: La imagen se formará en el punto en que se corten los rayos (imagen real) o sus prolongaciones (imagen virtual) Cualquier rayo paralelo al eje del espejo se refleja pasando por el foco (el foco es la imagen de un punto situado en el infinito). Aplicando el principio de reversibilidad de los rayos podremos afirmar que todo rayo que incida pasando por el foco se reflejará paralelamente al eje del espejo (la imagen del foco está en el infinito). Cualquier rayo que incida pasando por el centro de curvatura se refleja sobre si mismo (ya que incide perpendicularmente al espejo). Lo anterior se aplica rigurosamente a rayos que incidan en el espejo en la zona próxima al eje óptico (rayos paraxiales). Si la zona de incidencia está alejada de la zona central del espejo los rayos que inciden paralelamente al eje óptico no se reflejan pasando exactamente por el foco. La imagen entonces no es nítida, sino algo borrosa, efecto conocido con el nombre de aberración esférica. La aberración de los espejos esféricos se puede evitar diafragmando los rayos para eliminar los que inciden lejos de la zona paraxial. El problema es que haciendo esto se disminuye la luminosidad de la imagen. Si en lugar de un espejo esférico se utiliza un espejo parabólico se evita este tipo de aberración. Zona paraxial Aberración esférica 3
4 Obtención de imágenes en espejos trazando los rayos característicos. Espejo cóncavo: imagen real, más pequeña e invertida. Espejo convexo: imagen virtual, más pequeña y derecha. En los espejos cóncavos la imagen es real e invertida si el objeto se sitúa más allá del foco y virtual y derecha si el objeto se sitúa entre el foco y el espejo. Si el objeto se sitúa más allá del centro de curvatura, la imagen es más pequeña que el objeto. A medida que acercamos el objeto la imagen (invertida) aumenta su tamaño hasta que se hace igual al del objeto cuando éste está situado justo en el centro de curvatura. A partir de ahí la imagen (aún invertida) se hace cada vez mayor. Cuando situamos el objeto en el foco la imagen se forma en el infinito (no se observa la imagen) y cuando el objeto se sitúa entre el foco y el espejo la imagen es virtual, derecha y mayor. Imágenes en un espejo cóncavo Esquema 1. Objeto más lejos del centro de curvatura. Imagen real, invertida y más pequeña. Esquema 2. Objeto en el centro de curvatura. Imagen real, invertida y de igual tamaño. Esquema 3. Objeto entre el centro de curvatura y el foco. Imagen real, invertida y mayor. Esquema 4. Objeto entre el foco y el espejo. Imagen virtual, derecha y mayor. En los espejos convexos la imagen es siempre virtual, derecha y más pequeña que el objeto. Su tamaño disminuye a medida que el objeto se aleja del espejo y aumenta si nos acercamos. 4
5 A partir de la figura que se muestra a la derecha se puede deducir una ecuación que nos permite realizar cálculos en espejos esféricos: P: objeto (un punto) P': imagen s : distancia objeto s': distancia imagen r: radio de curvatura Para los triángulos rectángulos con vértices en P, C y P' se cumple: d d d tg α = ;tg β = ;tg γ = s s' r Si suponemos ángulos pequeños (zona paraxial) podemos suponer que la tangente es aproximadamente igual al ángulo (en radianes). Luego: En el triángulo PAP' se cumple: d d d α ; β ; γ s s' r β = α + 2 ϕ Por tanto: En el triángulo PAC se cumple: α + β = 2γ γ = ϕ + α Cuando el objeto se sitúa en el foco (s = f) la imagen estará situada en el infinito (s' = ). Por tanto: 1 r + 0 = 2 ; f = = 1 f r 2 s s' f Para aplicar la fórmula es necesario utilizar un conjunto de normas: d d 2d + = s s' r = s s' r A O En los esquemas la luz se propaga de izquierda a derecha. Los distancias tienen signo positivo si se miden hacia la derecha del centro óptico y negativo cuando se miden hacia la izquierda. Las distancia medidas en vertical (altura del objeto y de la imagen) se consideran positivas si se miden hacia arriba del eje óptico y negativas cuando se miden hacia abajo. El aumento lateral (m) de la imagen puede obtenerse a partir del esquema que se muestra a la derecha: y' tg ϕ = s' y' s' m = = y y s tg( ϕ ) = tg ϕ = s Un aumento negativo (s y s' negativas) indica que la imagen está invertida. Un aumento positivo (s positiva y s'negativa) indica que la imagen está derecha. Si el aumento es mayor que 1, la imagen es mayor que el objeto (y ' >y). Si el aumento es menor que 1, la imagen es menor que el objeto (y ' <y). Tanto la posición de la imagen como el aumento puede obtenerse realizando el correspondiente dibujo a escala. 5
6 Ejemplo 2 Un espejo esférico, plateado por ambos lados, tiene un radio de curvatura de 8 cm. Determinar de forma gráfica y analítica la posición y el tamaño de la imagen de un objeto de 1,0 cm de altura situado a 10,0, 8,0 y 2,0 cm del espejo: a) Cuando la reflexión se produce por la parte cóncava. b) Cuando la reflexión se produce por la parte convexa. Solución: a) Espejo cóncavo (el dibujo no está hecho a escala) La resolución gráfica del problema (teniendo en cuenta que el foco está a una distancia igual a la mitad del radio de curvatura) nos indica que en los dos primeros casos (s = 10,0 y 8,0 cm) la imagen es real e invertida, más pequeña cuando el objeto se sitúa más allá del centro de curvatura y del mismo tamaño que éste cuando se sitúa justo en el centro de curvatura. Si el objeto se sitúa entre el foco y el espejo (s = 3,0 cm) la imagen será virtual, derecha y más grande que el objeto Para la resolución analítica hacemos uso de la ecuación general para los espejos esféricos y la fórmula del aumento. Los criterios de signo son los que se recogen en la página anterior. Cálculo de la distancia imagen y el aumento: s = 10,0 cm 1 ; s', cm s + 1 s' = 1 1 f s' = 1 f 1 s = 1 1 ( ) = 6 = 3 = 20 = y' s' 6, 7cm m = = = y s 10, 0cm Imagen situada a la izquierda (s' negativa), real, invertida (y' negativa) y más pequeña. s = 8,0 cm 1 ; s', cm s + 1 s' = 1 1 f s' = 1 f 1 s = 1 1 ( ) = 4 = 8 = Imagen situada en el centro de curvatura (s' negativa), real, invertida (y' negativa) e igual. s = 2,0 cm y' s' 8, 0cm m = = = y s 8, 0cm = 0, 67;y' = my = 0, 67. 1, 0cm = 0, 67cm = 1, 0;y' = my = 1, 0. 1, 0cm = 1, 0cm 1 ; s', cm s + 1 s' = 1 1 f s' = 1 f 1 s = 1 ( ) 1 ( ) = 1 = = y' s', cm m = = = 4 0 y s 2, 0cm = 2, 0;y' = my = 2, 0. 1, 0cm = 2, 0cm Imagen situada a la derecha (s' positiva), virtual, derecha (y' positiva) y mayor. 6
7 b) Espejo cónvexo (el dibujo no está a escala) La resolución gráfica nos indica ahora que la imagen es siempre virtual, derecha y más pequeña y su tamaño crece a medida que nos aproximamos al espejo. Cálculo de la distancia imagen y el aumento: s = 10,0 cm = ; = = s' = 2, 9cm s s' f s' f s 4 ( 10) y' s' ( 2, 9cm ) m = = = y s Imagen situada a la derecha (s' positiva), virtual, derecha (y' positiva) y más pequeña. s = 8,0 cm = ; = = s' = 2, 7cm s s' f s' f s 4 ( 8) Imagen situada a la derecha (s' positiva), virtual, derecha (y' positiva) y más pequeña. s = 2,0 cm Imagen situada a la derecha (s' positiva), virtual, derecha (y' positiva) y más pequeña. Ejemplo 3 (Oviedo ) Se utiliza un pequeño espejo cóncavo de 50 cm de distancia focal para ampliar las imágenes de nuestra cara. Determine la posición (respecto del centro del espejo) y tamaño de la imagen de nuestra boca de 5,0 cm cuando la situamos a una distancia de 25 cm del centro del espejo (suponga que la boca está centrada respecto del espejo) Solución: ( 10, 0cm ) y' s', cm m = = = 2 7 y s 8, 0cm = ; = = s' = 0, 75cm s s' f s' f s 4 ( 2) y' s', cm m = = = 0 75 y s 2, 0cm = 0, 29;y' = my = 0, 29. 1, 0cm = 0, 29cm = 0, 34;y' = my = 0, 34. 1, 0cm = 0, 34cm = 0, 38;y' = my = 0, 38. 1, 0cm = 0, 38cm = ; = = = s' = 50, 0cm s s' f s' f s ( 50) ( 25) 50 y' s' 50 m = = = = 2 ;y' = my = 2. 5, 0cm = 10, 0cm y s ( 25) La imagen será virtual (s' positiva), derecha (y' positiva) y de tamaño doble que el objeto. 7
8 Refracción en lentes delgadas En óptica recibe el nombre de dioptrio cualquier superficie que separe dos medios con distinto índice de refracción. La superficie del agua o del vidrio es un dioptrio plano. Además del plano, el dioptrio más común (debido a su facilidad de fabricación) es el dioptrio esférico, la mayor parte de las lentes están limitadas por superficies esféricas. Los dioptrios esféricos tienen dos focos: El foco imagen es el punto en el que, tras refractarse, coinciden los rayos que llegan el dioptrio en dirección paralela al eje óptico. Es la imagen correspondiente a un punto situado en el infinito. El foco objeto es el punto que tras pasar los rayos por él se refractan paralelos al eje óptico. La imagen del foco objeto está situada en el infinito. En un diopotrio convexo el foco imagen está situado a la derecha y el foco objeto a la izquierda. En un dioptrio cóncavo los focos objeto e imagen están situados al revés que en uno convexo: el foco imagen se sitúa a la izquierda y el foco objeto a la derecha. Una lente es un sistema óptico limitado por dos dioptrios de los cuales uno, al menos, es esférico. La desviación del rayo es consecuencia de la refracción en ambos dioptrios, aunque en las lentes delgadas se considera que la desviación del rayo tiene lugar en el centro de la lente. En las lentes convergentes los rayos se refractan y emergen aproximándose al eje de la lente. En las divergentes el rayo emerge alejándose del eje de la lente. El que una lente sea convergente o divergente depende de su geometría. Lentes divergentes Izquierda: lente divergente (bicóncava) Derecha: lente convergente (biconvexa) Lentes convergentes 8
9 Los focos de una lente son puntos característicos de las mismas, que están situados simétricamente respecto del centro de la lente. Una lente tiene dos focos: el foco objeto y el foco imagen (ver figura). El foco objeto (f) es un punto del eje óptico tal que todo rayo que incide en la lente pasando por él se refracta paralelamente al eje de la lente (imagen en el infinito) El foco imagen (f') es el punto del eje óptico por el que pasa todo rayo refractado resultado de una incidencia paralela al eje de la lente. En una lente convergente el foco objeto se sitúa a la izquierda y el foco imagen a la derecha. En una lente divergente el foco objeto se sitúa a la derecha y el foco imagen a la izquierda. Lente convergente Foco imagen Lente divergente Foco objeto Foco objeto Foco imagen Si suponemos que el espesor de la lente es pequeño (lentes delgadas) se pueden considerar los siguientes rayos característicos: Cualquier rayo paralelo al eje de la lente se refracta pasando por el foco imagen. Todo rayo que incida pasando por el foco objeto se refracta paralelamente al eje de la lente. Cualquier rayo que incida pasando por el centro de la lente no sufre refracción alguna.. La distancia focal de una lente delgada situada en el aire depende del índice de refracción de la lente y de los radios de curvatura de sus superficies: = ( n 1) f' R1 R 2 9
10 La ecuación que relaciona distancia objeto (s), distancia imagen (s') y distancia focal imagen (f'), para las lentes delgadas es: = s' s f' Los criterios de signos son análogos a los fijados para los espejos: positivo hacia la derecha y hacia arriba, negativo a la izquierda y hacia abajo Se define la potencia de una lente como la inversa de su distancia focal imagen. La potencia de una lente está relacionada con su capacidad para hacer converger o divergir los rayos de luz. A mayor potencia mayor capacidad de convergencia o divergencia de los rayos. Las lentes con mayor potencia tienen una distancia focal corta. La unidad en el Sistema Internacional es la dioptría (D) que se define como la potencia de una lente que tenga un metro de distancia focal P = 1 Para sistemas formados por varias lentes la potencia se obtiene sumando la potencia de las lentes que integran el sistema. f' Para calcular el aumento lateral de la imagen formada por una lente: y' s' m = = y s Las imágenes en las lentes delgadas se obtienen a partir del trazado de los rayos característicos. La imagen se formará en el punto en el que se corten los rayos (imagen real) o sus prolongaciones (imagen virtual) Rayos característicos en lentes Rayo paralelo al eje se refracta pasando por el foco imagen (f'). Rayo que pasa por el centro óptico de la lente, no se refracta. Rayo que pasa por el foco objeto (f) se refracta paralelo al eje. Ejemplo 4 (Oviedo ) Usando una lente convergente con distancias focales f = f ' = 4,0 cm, mediante un diagrama de rayos, determine la posición y el aumento lateral de la imagen que produce dicha lente de un objeto de 1,5 cm de altura situado perpendicularmente al eje óptico a 6,0 cm de la lente y expónganse las características de dicha imagen. Solución: 10
11 Imagen real, invertida y mayor que el objeto Los datos cuantitativos solicitados pueden obtenerse a partir de un dibujo a escala. A continuación se obtienen de forma analítica: = ; = + = + = ; s' = 12, 0cm s' s f' s' f' s 4 ( 6) 12 y' s' 12 m = = = = 2 ; y' = my = 2., 1 5cm = 3, 0cm y s ( 6) Los datos obtenidos coinciden con los obtenidos a partir del diagrama de rayos: Imagen situada a la derecha, real (s ' positiva), invertida (y' negativa), mayor que el objeto. Ejemplo 5 (Oviedo ) Usando una lente divergente con distancias focales f = f ' = 5,0 cm, mediante un diagrama de rayos, determine la posición y el aumento lateral de la imagen que produce dicha lente de un objeto de 1,5 cm de altura situado perpendicularmente al eje óptico a 8,0 cm de la lente y expónganse las características de dicha imagen. Solución: Imagen virtual, derecha y más pequeña que el objeto = ; = + = + = ; s' = 3, 1cm s' s f' s' f' s ( 5) ( 8) 40 y' s' ( 3,) 1 m = = = = 0, 39 ; y' = my = 0, 39., 1 5cm = 0, 59cm y s ( 8) Imagen situada a la izquierda, virtual (s ' negativa), derecha (y' positiva), más pequeña que el objeto. Ejemplo 6 (Oviedo ) Qué es la dioptría? Calcule el número de dioptrías de una lente de distancia focal 25 cm Solución: La dioptría (D) es la unidad (S.I.) de medida de la potencia de una lente, que se define como el inverso de la distancia focal. Una dioptría es la potencia de una lente que tenga una distancia focal de 1,0 m. Dimensionalmente: 1 1 P = ; P = L f 1 1D = 1m Para una lente de distancia focal 25 cm: P = ;P = = 4m = 4D f 0, 25m 11
12 Ejemplo 7 (Oviedo ) Encontrar mediante un diagrama de rayos la imagen creada por: a) Una lente convergente de 2,0 cm de distancia focal de un objeto situado a 4,0 cm. b) Un espejo plano de un objeto situado a 2,0 cm. Describir en ambos casos las características más importantes de la imagen Solución: a) Imagen real, invertida e igual que el objeto Analíticamente (como no se conoce el tamaño del objeto, el aumento se calcula para comprobar - únicamente que la imagen es invertida y del mismo tamaño que el objeto): = ; = + = + = ; s' = 4, 0cm s' s f' s' f' s 2 ( 4) 4 y' s' 4 m = = = = 1 ; y' = my = 1.xcm = xcm y s ( 4) Imagen situada a la derecha, real (s ' positiva), invertida (y' negativa), e igual que el objeto. b) Un espejo plano forma siempre una imagen virtual, derecha y del mismo tamaño que el objeto que se encuentra situada a la misma distancia del espejo. La imagen presentará inversión lateral: la izquierda y la derecha está invertidas respecto del objeto. 12
13 Combinando dos o más elementos ópticos (lentes, espejos... etc) podemos construir sistemas ópticos. En esto sistemas, o instrumentos ópticos, en muchas ocasiones, la imagen formada por uno de los elementos sirve de objeto para el otro. 1. Cámara oscura. Cámara fotográfica. El instrumento óptico más simple es la cámara oscura, donde no existe ningún elemento óptico, sólo un pequeño orificio que, debido a la propagación rectilínea de la luz, forma una imagen invertida de la imagen. La primera cámara oscura de la que se tiene noticia fue construida por Aristóteles (384 a.c a.c.). Esta es su propia descripción del invento: "Se hace pasar la luz a través de un pequeño agujero hecho en un cuarto cerrado por todos sus lados. En la pared opuesta al agujero, se formará la imagen de lo que se encuentre enfrente". 2. Lupa Un simple lente convergente nos permite ver los objetos aumentados si los situamos entre el foco y la lente. Se obtiene una imagen virtual, derecha y de mayor tamaño, situada detrás del objeto. La potencia de la lupa depende de su distancia focal. Las lupas más potentes tienen una distancia focal corta, lo que se consigue dando un radio de curvatura pequeño a la lente (lente muy curvada). 3. Microscopio Sistemas (instrumentos) ópticos Leonardo da Vinci (en la segunda mitad del s XV) redescubre la cámara oscura que fue muy utilizada posteriormente para dibujar objetos. En el s. XVI Giovanni Battista della Porta dotó a la cámara oscura de una lente biconvexa que mejoraba notablemente la nitidez de la imagen. La cámara oscura evolucionó con el tiempo hacia la cámara fotográfica, en la que la imagen se forma sobre una película fotosensible. Imagen Objeto El microscopio ya es un verdadero sistema óptico. Se utiliza para ver objetos muy próximos y de pequeño tamaño. Consta de dos lentes convergentes. La que se sitúa más próxima al ojo se denomina ocular y la que está próxima al objeto, objetivo. El objeto se coloca a una distancia mayor que la distancia focal del objetivo y su imagen (real) ampliada, sirve de objeto para la segunda lente. Si la imagen de la primera lente se coloca entre el foco y la segunda lente, ésta proporcionará una imagen nuevamente ampliada. 13
14 4. Anteojo de Galileo El objetivo es una lente convergente con una gran distancia focal y el ocular una lente divergente. Los rayos, al proceder de un objeto lejano inciden prácticamente paralelos formando la imagen en el plano focal imagen del objetivo. Antes de formarse esta imagen se encuentran con el ocular (lente divergente), cuyo foco objeto coincide con el imagen del objetivo, de forma que los rayos se refractan paralelos, y la imagen final (virtual) se forma en el infinito (el ojo forma en la retina las imágenes situadas en el infinito sin acomodación alguna). La imagen formada en la retina es mayor y derecha. Distancia entre lentes: f ob '- f oc 5. Telescopio astronómico (o de Kepler) Se utiliza para ver objetos grandes situados a mucha distancia. Consta de dos lentes convergentes, objetivo y ocular. Como el objeto está a una distancia muy grande los rayos procedentes de él llegan paralelos, con lo que se refractan en el objetivo formando una imagen en el plano focal imagen (plano que contiene al foco imagen). El foco imagen del objetivo y el foco objeto del ocular coinciden, por tanto la imagen formada por el ocular (virtual) se encuentra en el infinito. Es invertida y mayor. Distancia entre lentes: f ob '+ f oc En los sistemas telescópicos (que forman la imagen en el infinito) se define el aumento angular (M) como el cociente entre el ángulo subtendido por la imagen final y el objeto: y tg( ϕ') ϕ ' = y f oc' ϕ' f oc' f ob' f ob' M = = = ; M = y ϕ y f oc' f oc' tg( ϕ) tg( ϕ) ϕ = f f ob' ob' ϕ' M = ϕ 14
ÓPTICA GEOMÉTRICA. Es el fenómeno que se observa cuando un rayo de luz incide sobre una superficie y se refleja. Su estudio se basa en dos leyes:
 ONDAS LUMINOSAS La luz que nos llega del sol (luz blanca), está compuesta por rayos de luz de diferentes colores. Este conjunto de rayos constituye lo que se llama espectro visible, el cual, es una zona
ONDAS LUMINOSAS La luz que nos llega del sol (luz blanca), está compuesta por rayos de luz de diferentes colores. Este conjunto de rayos constituye lo que se llama espectro visible, el cual, es una zona
Bolilla 12: Óptica Geométrica
 Bolilla 12: Óptica Geométrica 1 Bolilla 12: Óptica Geométrica Los contenidos de esta bolilla están relacionados con los principios primarios que rigen el comportamiento de los instrumentos ópticos. La
Bolilla 12: Óptica Geométrica 1 Bolilla 12: Óptica Geométrica Los contenidos de esta bolilla están relacionados con los principios primarios que rigen el comportamiento de los instrumentos ópticos. La
Porqué es útil estudiar los espejos y las lentes como elementos ópticos? A qué se le conoce como distancia focal de una lente o espejo?
 Porqué es útil estudiar los espejos y las lentes como elementos ópticos? A qué se le conoce como distancia focal de una lente o espejo? Cómo depende la distancia focal del material que forma un espejo?
Porqué es útil estudiar los espejos y las lentes como elementos ópticos? A qué se le conoce como distancia focal de una lente o espejo? Cómo depende la distancia focal del material que forma un espejo?
Lentes delgadas Clasificación de las lentes Según su forma Lentes convergentes Lentes divergentes Según su grosor
 Lentes delgadas Una lente delgada es un sistema óptico centrado formado por dos dioptrios, uno de los cuales, al menos, es esférico, y en el que los dos medios refringentes extremos poseen el mismo índice
Lentes delgadas Una lente delgada es un sistema óptico centrado formado por dos dioptrios, uno de los cuales, al menos, es esférico, y en el que los dos medios refringentes extremos poseen el mismo índice
ÓPTICA GEOMÉTRICA 1. Conceptos básicos. 2. Espejos planos. 3. Espejos esféricos. 4. Dioptrios. 5. Lentes delgadas. 6. La visión.
 ÓPTICA GEOMÉTRICA 1. Conceptos básicos. 2. Espejos planos. 3. Espejos esféricos. 4. Dioptrios. 5. Lentes delgadas. 6. La visión. Física 2º bachillerato Óptica geométrica 1 ÓPTICA GEOMÉTRICA La óptica geométrica
ÓPTICA GEOMÉTRICA 1. Conceptos básicos. 2. Espejos planos. 3. Espejos esféricos. 4. Dioptrios. 5. Lentes delgadas. 6. La visión. Física 2º bachillerato Óptica geométrica 1 ÓPTICA GEOMÉTRICA La óptica geométrica
13. Por qué no se observa dispersión cuando la luz blanca atraviesa una lámina de vidrio de caras planas y paralelas? 14. Sobre una lámina de vidrio,
 PROBLEMAS ÓPTICA 1. Una de las frecuencias utilizadas en telefonía móvil (sistema GSM) es de 900 MHz. Cuántos fotones GSM necesitamos para obtener la misma energía que con un solo fotón de luz violeta,
PROBLEMAS ÓPTICA 1. Una de las frecuencias utilizadas en telefonía móvil (sistema GSM) es de 900 MHz. Cuántos fotones GSM necesitamos para obtener la misma energía que con un solo fotón de luz violeta,
TEMA 4: OPTICA. s, y s, y Espejos y lentes FINALIDAD: dado un objeto imagen
 4.2.- Espejos y lentes FINALIDAD: dado un objeto imagen s, y s, y Objeto o imagen real: aquél para el cual los rayos de luz se cruzan de forma real. El punto de corte se puede recoger en una pantalla Figura
4.2.- Espejos y lentes FINALIDAD: dado un objeto imagen s, y s, y Objeto o imagen real: aquél para el cual los rayos de luz se cruzan de forma real. El punto de corte se puede recoger en una pantalla Figura
LAS LENTES Y SUS CARACTERÍSTICAS
 LAS LENTES Y SUS CARACTERÍSTICAS Las lentes son cuerpos transparentes limitados por dos superficies esféricas o por una esférica y una plana, las lentes se emplean a fin de desviar las rayos luminosos
LAS LENTES Y SUS CARACTERÍSTICAS Las lentes son cuerpos transparentes limitados por dos superficies esféricas o por una esférica y una plana, las lentes se emplean a fin de desviar las rayos luminosos
Física 2 Biólogos y Geólogos - Curso de Verano 2006 Turno: Tarde
 Física 2 Biólogos y Geólogos - Curso de Verano 2006 Turno: Tarde Serie 2: Objetos. Formación de imágenes. Imágenes. Dioptras esféricas y planas. Espejos esféricos y planos. Lentes delgadas, sistemas de
Física 2 Biólogos y Geólogos - Curso de Verano 2006 Turno: Tarde Serie 2: Objetos. Formación de imágenes. Imágenes. Dioptras esféricas y planas. Espejos esféricos y planos. Lentes delgadas, sistemas de
Física P.A.U. ÓPTICA 1 ÓPTICA
 Física P.A.U. ÓPTICA 1 ÓPTICA PROBLEMAS DIOPTRIO PLANO 1. Un rayo de luz de frecuencia 5 10¹⁴ Hz incide con un ángulo de incidencia de 30 sobre una lámina de vidrio de caras plano-paralelas de espesor
Física P.A.U. ÓPTICA 1 ÓPTICA PROBLEMAS DIOPTRIO PLANO 1. Un rayo de luz de frecuencia 5 10¹⁴ Hz incide con un ángulo de incidencia de 30 sobre una lámina de vidrio de caras plano-paralelas de espesor
1. El (los) espejo(s) que puede(n) formar una imagen virtual, derecha y de igual tamaño que el objeto observado, es (son)
 Programa Estándar Anual Nº Guía práctica Ondas V: imágenes en espejos y lentes Ejercicios PSU 1. El (los) espejo(s) que puede(n) formar una imagen virtual, derecha y de igual tamaño que el objeto observado,
Programa Estándar Anual Nº Guía práctica Ondas V: imágenes en espejos y lentes Ejercicios PSU 1. El (los) espejo(s) que puede(n) formar una imagen virtual, derecha y de igual tamaño que el objeto observado,
LUZ Y ÓPTICA. Propagación de la luz
 LUZ Y ÓPTICA Propagación de la luz La luz se propaga en línea recta en un medio homogéneo. La hipótesis de la propagación de la luz explica varios fenómenos entre los que se puede resaltar: Cuando un rayo
LUZ Y ÓPTICA Propagación de la luz La luz se propaga en línea recta en un medio homogéneo. La hipótesis de la propagación de la luz explica varios fenómenos entre los que se puede resaltar: Cuando un rayo
REFRACCIÓN DE LA LUZ
 1 Nombre OBJETIVOS: Ud. Deberá ser capaz de : 1. definir la refracción de la luz 2. comprender el comportamiento que tiene la luz frente a distintos medios 3. describir la ley de refracción 4. describir
1 Nombre OBJETIVOS: Ud. Deberá ser capaz de : 1. definir la refracción de la luz 2. comprender el comportamiento que tiene la luz frente a distintos medios 3. describir la ley de refracción 4. describir
ÁREA DE FÍSICA GUÍA DE APLICACIÓN TEMA: ACÚSTICA Y ÓPTICA GUÍA: 1203 ESTUDIANTE: FECHA:
 ÁREA DE FÍSICA GUÍA DE APLICACIÓN TEMA: ACÚSTICA Y ÓPTICA GUÍA: 1203 ESTUDIANTE: E-MAIL: FECHA: ACÚSTICA Resuelva cada uno de los siguientes problemas haciendo el proceso completo. 1. Un estudiante golpea
ÁREA DE FÍSICA GUÍA DE APLICACIÓN TEMA: ACÚSTICA Y ÓPTICA GUÍA: 1203 ESTUDIANTE: E-MAIL: FECHA: ACÚSTICA Resuelva cada uno de los siguientes problemas haciendo el proceso completo. 1. Un estudiante golpea
UNIVERSIDAD NACIONAL DE MISIONES
 OPTICA GEOMÉTRICA PROBLEMAS PROPUESTOS 1: Un rayo que se propaga por el aire incide en la superficie de un bloque de hielo transparente (n h =1,309) formando un ángulo de 40º con la normal a dicha superficie.
OPTICA GEOMÉTRICA PROBLEMAS PROPUESTOS 1: Un rayo que se propaga por el aire incide en la superficie de un bloque de hielo transparente (n h =1,309) formando un ángulo de 40º con la normal a dicha superficie.
ÓPTICA GEOMÉTRICA: REFLEXIÓN Y REFRACCIÓN DE LA LUZ
 1 ÓPTICA GEOMÉTRICA: REFLEXIÓN Y REFRACCIÓN DE LA LUZ INTRODUCCIÓN TEÓRICA: La característica fundamental de una onda propagándose por un medio es su velocidad (v), y naturalmente, cuando la onda cambia
1 ÓPTICA GEOMÉTRICA: REFLEXIÓN Y REFRACCIÓN DE LA LUZ INTRODUCCIÓN TEÓRICA: La característica fundamental de una onda propagándose por un medio es su velocidad (v), y naturalmente, cuando la onda cambia
Ejercicios Repaso Tema 5: Óptica geométrica
 Cuestiones y Problemas Ejercicios Repaso Tema 5: Óptica geométrica Dpto. de Física 1. Una esfera de vidrio de paredes delgadas y radio R está llena de agua. A una distancia 3R de su superficie se coloca
Cuestiones y Problemas Ejercicios Repaso Tema 5: Óptica geométrica Dpto. de Física 1. Una esfera de vidrio de paredes delgadas y radio R está llena de agua. A una distancia 3R de su superficie se coloca
FÍSICA de 2º de BACHILLERATO ÓPTICA -GEOMÉTRICA-
 FÍSICA de 2º de BACHILLERATO ÓPTICA -GEOMÉTRICA- EJERCICIOS RESUELTOS QUE HAN SIDO PROPUESTOS EN LOS EXÁMENES DE LAS PRUEBAS DE ACCESO A ESTUDIOS UNIVERSITARIOS EN LA COMUNIDAD DE MADRID (1996 2013) DOMINGO
FÍSICA de 2º de BACHILLERATO ÓPTICA -GEOMÉTRICA- EJERCICIOS RESUELTOS QUE HAN SIDO PROPUESTOS EN LOS EXÁMENES DE LAS PRUEBAS DE ACCESO A ESTUDIOS UNIVERSITARIOS EN LA COMUNIDAD DE MADRID (1996 2013) DOMINGO
4. Dioptrios. Vamos a estudiar dioptrios esféricos con rayos paraxiales. La ecuación de un dioptrio esférico para rayos paraxiales
 4. Dioptrios. Un dioptrio es la superficie de separación entre dos medios con distinto índice de refracción, pero isótropos, homogéneos y transparente. Un rayo paraxial es aquel que forma un ángulo muy
4. Dioptrios. Un dioptrio es la superficie de separación entre dos medios con distinto índice de refracción, pero isótropos, homogéneos y transparente. Un rayo paraxial es aquel que forma un ángulo muy
Magnetismo y Óptica Departamento de Física Universidad de Sonora. Óptica Geométrica
 Magnetismo y Óptica 2006 Departamento de Física Universidad de Sonora 1 Óptica Geométrica 2 1 Temas 1. Formación de imágenes por reflexión: En espejos planos En espejos esféricos 2. Formación de imágenes
Magnetismo y Óptica 2006 Departamento de Física Universidad de Sonora 1 Óptica Geométrica 2 1 Temas 1. Formación de imágenes por reflexión: En espejos planos En espejos esféricos 2. Formación de imágenes
ESPEJOS ESFERICOS. Figura 29. Definición de términos para los espejos esféricos.
 ESPEJOS ESFERICOS Los mismos métodos geométricos aplicados a la reflexión de la luz desde un espejo plano se pueden utilizar para un espejo curvo. El ángulo de incidencia sigue siendo igual que el ángulo
ESPEJOS ESFERICOS Los mismos métodos geométricos aplicados a la reflexión de la luz desde un espejo plano se pueden utilizar para un espejo curvo. El ángulo de incidencia sigue siendo igual que el ángulo
Webpage:
 Magnetismo y Óptica Dr. Roberto Pedro Duarte Zamorano E-mail: [email protected] Webpage: http://rpduarte.fisica.uson.mx 2016 Departamento de Física Universidad de Sonora A. Magnetismo
Magnetismo y Óptica Dr. Roberto Pedro Duarte Zamorano E-mail: [email protected] Webpage: http://rpduarte.fisica.uson.mx 2016 Departamento de Física Universidad de Sonora A. Magnetismo
Formación de imágenes
 ormación de imágenes Espejos esféricos: Cóncavos Convexos Lentes Convergentes Divergentes Salir Espejos esféricos cóncavos ormación de imágenes en el espejo esférico. a mayor distancia que el centro de
ormación de imágenes Espejos esféricos: Cóncavos Convexos Lentes Convergentes Divergentes Salir Espejos esféricos cóncavos ormación de imágenes en el espejo esférico. a mayor distancia que el centro de
Problemas de Óptica II. Óptica geométrica 2º de bachillerato. Física
 1 Problemas de Óptica II. Óptica geométrica 2º de bachillerato. Física 1. Los índices de refracción de un dioptrio esférico cóncavo, de 20,0 cm de radio, son 1,33 y 1,54 para el primero y el segundo medios.
1 Problemas de Óptica II. Óptica geométrica 2º de bachillerato. Física 1. Los índices de refracción de un dioptrio esférico cóncavo, de 20,0 cm de radio, son 1,33 y 1,54 para el primero y el segundo medios.
Lentes Clasificación Se clasifican en dos grupos convergentes (positivas) y divergentes (negativas), las cuales a su vez pueden adoptar formas
 Lentes Clasificación Se clasifican en dos grupos convergentes (positivas) y divergentes (negativas), las cuales a su vez pueden adoptar formas distintas. Estas geometrías de lentes tienen las siguientes
Lentes Clasificación Se clasifican en dos grupos convergentes (positivas) y divergentes (negativas), las cuales a su vez pueden adoptar formas distintas. Estas geometrías de lentes tienen las siguientes
LENTES Y ÓPTICA DEL OJO
 LENTES Y ÓPTICA DEL OJO OBJETIVOS En las investigaciones 2 y 3 vimos que si la luz atraviesa superficies de separación entre dos medios diferentes se desvía. Este hecho ha sido empleado para la construcción
LENTES Y ÓPTICA DEL OJO OBJETIVOS En las investigaciones 2 y 3 vimos que si la luz atraviesa superficies de separación entre dos medios diferentes se desvía. Este hecho ha sido empleado para la construcción
Práctica de Óptica Geométrica
 Práctica de Determinación de la distancia focal de lentes delgadas convergentes y divergentes 2 Pre - requisitos para realizar la práctica.. 2 Bibliografía recomendada en referencia al modelo teórico 2
Práctica de Determinación de la distancia focal de lentes delgadas convergentes y divergentes 2 Pre - requisitos para realizar la práctica.. 2 Bibliografía recomendada en referencia al modelo teórico 2
PRÁCTICA Nº3 REFLEXIÓN Y REFRACCIÓN
 PRÁCTICA Nº3 REFLEXIÓN Y REFRACCIÓN 1.- Equipamiento y montaje Componentes del equipo Los accesorios necesarios para la realización de la presente práctica se enumeran a continuación: 1. Caja de Almacenamiento
PRÁCTICA Nº3 REFLEXIÓN Y REFRACCIÓN 1.- Equipamiento y montaje Componentes del equipo Los accesorios necesarios para la realización de la presente práctica se enumeran a continuación: 1. Caja de Almacenamiento
Distancia focal de una lente convergente (método del desplazamiento) Fundamento
 Distancia focal de una lente convergente (método del desplazamiento) Fundamento En una lente convergente delgada se considera el eje principal como la recta perpendicular a la lente y que pasa por su centro.
Distancia focal de una lente convergente (método del desplazamiento) Fundamento En una lente convergente delgada se considera el eje principal como la recta perpendicular a la lente y que pasa por su centro.
UN SISTEMA PARA RESOLVER PROBLEMAS DE ÓPTICA. Guillermo Becerra Córdova. Universidad Autónoma Chapingo. Dpto. de Preparatoria Agrícola.
 UN SISTEMA PARA RESOLVER PROBLEMAS DE ÓPTICA Guillermo Becerra Córdova Universidad Autónoma Chapingo Dpto. de Preparatoria Agrícola Área de Física E-mail: [email protected] Resumen Dentro de los cursos
UN SISTEMA PARA RESOLVER PROBLEMAS DE ÓPTICA Guillermo Becerra Córdova Universidad Autónoma Chapingo Dpto. de Preparatoria Agrícola Área de Física E-mail: [email protected] Resumen Dentro de los cursos
PROBLEMAS LUZ Y ÓPTICA SELECTIVIDAD
 PROBLEMAS LUZ Y ÓPTICA SELECTIVIDAD 1.- Un objeto luminoso de 2mm de altura está situado a 4m de distancia de una pantalla. Entre el objeto y la pantalla se coloca una lente esférica delgada L, de distancia
PROBLEMAS LUZ Y ÓPTICA SELECTIVIDAD 1.- Un objeto luminoso de 2mm de altura está situado a 4m de distancia de una pantalla. Entre el objeto y la pantalla se coloca una lente esférica delgada L, de distancia
Departamento de Física y Química
 1 PAU Física, septiembre 2011 OPCIÓN A Cuestión 1.- Un espejo esférico convexo, proporciona una imagen virtual de un objeto que se encuentra a 3 m del espejo con un tamaño 1/5 del de la imagen real. Realice
1 PAU Física, septiembre 2011 OPCIÓN A Cuestión 1.- Un espejo esférico convexo, proporciona una imagen virtual de un objeto que se encuentra a 3 m del espejo con un tamaño 1/5 del de la imagen real. Realice
BLOQUE 4.2 ÓPTICA GEOMÉTRICA
 BLOQUE 4.2 ÓPTICA GEOMÉTRICA 1- DE QUÉ TRATA LA ÓPTICA GEOMÉTRICA? El desarrollo de la Óptica y de sus usos o aplicaciones discurrió prácticamente al margen de la discusión relativa a la naturaleza de
BLOQUE 4.2 ÓPTICA GEOMÉTRICA 1- DE QUÉ TRATA LA ÓPTICA GEOMÉTRICA? El desarrollo de la Óptica y de sus usos o aplicaciones discurrió prácticamente al margen de la discusión relativa a la naturaleza de
7. Cónicas. Propiedades métricas y ópticas
 Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 49 7. Cónicas. Propiedades métricas y ópticas Cónicas Círcunferencias, elipses, parábolas, e hipérbolas son llamadas secciones cónicas
Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 49 7. Cónicas. Propiedades métricas y ópticas Cónicas Círcunferencias, elipses, parábolas, e hipérbolas son llamadas secciones cónicas
EXAMEN FÍSICA 2º BACHILLERATO TEMA 4: ÓPTICA
 INSTRUCCIONES GENERALES Y VALORACIÓN La prueba consiste de dos opciones, A y B, y el alumno deberá optar por una de las opciones y resolver las tres cuestiones y los dos problemas planteados en ella, sin
INSTRUCCIONES GENERALES Y VALORACIÓN La prueba consiste de dos opciones, A y B, y el alumno deberá optar por una de las opciones y resolver las tres cuestiones y los dos problemas planteados en ella, sin
Óptica. Radio Microondas Infrarrojo Visible Ultravioleta Rayos X Rayos. plano. 2ª ley: el ángulo de incidencia es igual que el ángulo de reflexión.
 Óptica Espectro electromagnético (m) 10-1 10-3 7 10-7 4,5 10-7 10-9 10-11 Radio Microondas Inrarrojo Visible Ultravioleta Rayos X Rayos (Hz) 10 9 10 11 4 10 14 8 10 14 10 17 10 19 Hipótesis de Planck Energía
Óptica Espectro electromagnético (m) 10-1 10-3 7 10-7 4,5 10-7 10-9 10-11 Radio Microondas Inrarrojo Visible Ultravioleta Rayos X Rayos (Hz) 10 9 10 11 4 10 14 8 10 14 10 17 10 19 Hipótesis de Planck Energía
Espejos CAPÍTULO 4. Editorial Contexto - - Canelones Espejos planos, imágenes
 APÍTULO 4 interacciones campos y ondas / física 1º b.d. ESPEJOS apítulo 4 43 Espejos Espejos planos, imágenes En la figura 1 representamos un fuente puntual de luz ubicada en A y un espejo plano. En ella
APÍTULO 4 interacciones campos y ondas / física 1º b.d. ESPEJOS apítulo 4 43 Espejos Espejos planos, imágenes En la figura 1 representamos un fuente puntual de luz ubicada en A y un espejo plano. En ella
Capítulo 21 Óptica 1
 Capítulo 21 Óptica 1 Reflexión y refracción Las leyes de la reflexión y de la refracción nos dicen lo siguiente: Los rayos incidente, reflejado y transmitido están todos en un mismo plano, perpendicular
Capítulo 21 Óptica 1 Reflexión y refracción Las leyes de la reflexión y de la refracción nos dicen lo siguiente: Los rayos incidente, reflejado y transmitido están todos en un mismo plano, perpendicular
FÍSICA 2º BACHILLERATO
 PROBLEMAS DE ÓPTICA 1.- Un faro sumergido en un lago dirige un haz de luz hacia la superficie del lago con î = 40º. Encontrar el ángulo refractado. ( n agua = 1,33 ) SOLUCIÓN 58,7º 2.- Encontrar el ángulo
PROBLEMAS DE ÓPTICA 1.- Un faro sumergido en un lago dirige un haz de luz hacia la superficie del lago con î = 40º. Encontrar el ángulo refractado. ( n agua = 1,33 ) SOLUCIÓN 58,7º 2.- Encontrar el ángulo
UNIDAD 7 Trazo de curvas
 UNIDAD 7 Trazo de curvas El trazo de curvas se emplea en la construcción de vías para conectar dos líneas de diferente dirección o pendiente. Estas curvas son circulares y verticales. CURVAS CIRCULARES:
UNIDAD 7 Trazo de curvas El trazo de curvas se emplea en la construcción de vías para conectar dos líneas de diferente dirección o pendiente. Estas curvas son circulares y verticales. CURVAS CIRCULARES:
FICHAS COMPLEMENTARIAS. REFLEXIÓN
 FICHAS COMPLEMENTARIAS. REFLEXIÓN I.- DESCRIPCIÓN DE LOS COMPONENTES Para realizar las prácticas de óptica vas a usar: 1.- Banco óptico: es una base metálica sobre la que colocar los diferentes montajes.
FICHAS COMPLEMENTARIAS. REFLEXIÓN I.- DESCRIPCIÓN DE LOS COMPONENTES Para realizar las prácticas de óptica vas a usar: 1.- Banco óptico: es una base metálica sobre la que colocar los diferentes montajes.
PRÁCTICA Nº.- LENTES.
 PRÁCTICA Nº.- LENTES. Objetivo: Estudiar la ormación de imágenes de lentes delgadas y determinar la distancia ocal y la potencia de una lente convergente y de una lente divergente. undamento teórico: La
PRÁCTICA Nº.- LENTES. Objetivo: Estudiar la ormación de imágenes de lentes delgadas y determinar la distancia ocal y la potencia de una lente convergente y de una lente divergente. undamento teórico: La
Óptica Física y Geométrica
 Óptica Física y Geométrica INDICE Diversas teorías acerca de la luz 1 Propagación de las ondas electromagnéticas 3 Ondas electromagnéticas. La luz. 3 Índice de refracción de la luz 4 Reflexión de la luz
Óptica Física y Geométrica INDICE Diversas teorías acerca de la luz 1 Propagación de las ondas electromagnéticas 3 Ondas electromagnéticas. La luz. 3 Índice de refracción de la luz 4 Reflexión de la luz
ÓPTICA GEOMÉTRICA IDEAS PRINCIPALES
 3 ÓPTICA GEOMÉTRICA IDEAS PRINCIPALES Modelo de rayos Sombras y penumbras Velocidad de la luz Imágenes reales y virtuales Mecanismo de visión Reflexión especular y difusa Espejos planos y esféricos Lentes
3 ÓPTICA GEOMÉTRICA IDEAS PRINCIPALES Modelo de rayos Sombras y penumbras Velocidad de la luz Imágenes reales y virtuales Mecanismo de visión Reflexión especular y difusa Espejos planos y esféricos Lentes
Física 2º Bach. Óptica 01/04/09
 Física 2º Bach. Óptica 0/04/09 DEPARTAMENTO DE FÍSICA E QUÍMICA Problemas Nombre: [3 PUNTO /UNO]. Un objeto O está situado a 30 cm del vértice de un espejo cóncavo, tal y como indica la figura. Se observa
Física 2º Bach. Óptica 0/04/09 DEPARTAMENTO DE FÍSICA E QUÍMICA Problemas Nombre: [3 PUNTO /UNO]. Un objeto O está situado a 30 cm del vértice de un espejo cóncavo, tal y como indica la figura. Se observa
a) la imagen de un plano perpendicular al eje óptico es otro plano perpendicular
 .- CONCEPTOS BÁSICOS: RAYO, DIOPTRIO, OBJETO, IMAGEN... La Óptica geométrica se ocupa de la propagación de la luz y de la formación de las imágenes que ésta produce sin tener para nada en cuenta su naturaleza.
.- CONCEPTOS BÁSICOS: RAYO, DIOPTRIO, OBJETO, IMAGEN... La Óptica geométrica se ocupa de la propagación de la luz y de la formación de las imágenes que ésta produce sin tener para nada en cuenta su naturaleza.
Capítulo 23. Microscopios
 Capítulo 23 Microscopios 1 Aumento angular El aumento angular m (a) de una lente convergente viene dado por: m (a) = tan θ rmim tan θ ob = q 0.25 (d + q )p en donde d es la separación entre la lente y
Capítulo 23 Microscopios 1 Aumento angular El aumento angular m (a) de una lente convergente viene dado por: m (a) = tan θ rmim tan θ ob = q 0.25 (d + q )p en donde d es la separación entre la lente y
TEMA 10: INSTRUMENTOS ÓPTICOS.
 TEMA 10: INSTRUMENTOS ÓPTICOS. 10.1. El ojo humano. De forma muy simplificada, podemos considerar que el ojo humano está constituido por una lente (formada por la córnea y el cristalino) y una superficie
TEMA 10: INSTRUMENTOS ÓPTICOS. 10.1. El ojo humano. De forma muy simplificada, podemos considerar que el ojo humano está constituido por una lente (formada por la córnea y el cristalino) y una superficie
ÓPTICA. Agradecimientos al profesor Camilo Reyes
 ÓPTICA Agradecimientos al profesor Camilo Reyes ÓPTICA Aplicación de lentes, espejos y prismas a instrumentos que controlan y manipulan la luz. CONVERGENTES (positivas) DIVERGENTES (negativas) TIPOS BÁSICOS
ÓPTICA Agradecimientos al profesor Camilo Reyes ÓPTICA Aplicación de lentes, espejos y prismas a instrumentos que controlan y manipulan la luz. CONVERGENTES (positivas) DIVERGENTES (negativas) TIPOS BÁSICOS
OPTICA GEOMÉTRICA. Física de 2º de Bachillerato
 OPTICA GEOMÉTRICA Física de 2º de Bachillerato La luz se propaga en el vacío a la velocidad de la luz, que es constante, nunca se detiene. Da igual a qué velocidad persigamos un rayo de luz; siempre se
OPTICA GEOMÉTRICA Física de 2º de Bachillerato La luz se propaga en el vacío a la velocidad de la luz, que es constante, nunca se detiene. Da igual a qué velocidad persigamos un rayo de luz; siempre se
Reflexión de la luz MATERIALES MONTAJE
 Reflexión de la luz Espejos planos Estamos acostumbrados a usar los espejos sin plantearnos que ocurre con los rayos de luz que inciden sobre ellos. Vamos a estudiar el comportamiento de la luz primero
Reflexión de la luz Espejos planos Estamos acostumbrados a usar los espejos sin plantearnos que ocurre con los rayos de luz que inciden sobre ellos. Vamos a estudiar el comportamiento de la luz primero
PROBLEMAS DE OPTIMIZACIÓN
 1 PROBLEMAS DE OPTIMIZACIÓN Planteamiento y resolución de los problemas de optimización Se quiere construir una caja, sin tapa, partiendo de una lámina rectangular de cm de larga por de ancha. Para ello
1 PROBLEMAS DE OPTIMIZACIÓN Planteamiento y resolución de los problemas de optimización Se quiere construir una caja, sin tapa, partiendo de una lámina rectangular de cm de larga por de ancha. Para ello
Guía de Estudio Algebra y Trigonometría Para Ciencias Agropecuarias
 Guía de Estudio Para Ciencias Agropecuarias Unidad: Geometría Analítica Los siguientes ejercicios están relacionados con los principales temas de Geometría Analítica e involucra todos los conocimientos
Guía de Estudio Para Ciencias Agropecuarias Unidad: Geometría Analítica Los siguientes ejercicios están relacionados con los principales temas de Geometría Analítica e involucra todos los conocimientos
Practica nº n 5: Fenómenos de Difracción.
 Facultad de Farmacia Universidad de Granada Departamento de Química Física Practica nº n 5: Fenómenos de Difracción. OBJETIVOS 1.Observar los fenómenos de difracción Rendija simple Rendija doble 2.Calcular
Facultad de Farmacia Universidad de Granada Departamento de Química Física Practica nº n 5: Fenómenos de Difracción. OBJETIVOS 1.Observar los fenómenos de difracción Rendija simple Rendija doble 2.Calcular
CURSO 2006/2007 TEMA 1:
 HOJA DE PROBLEMAS ÓPTICA I CURSO 2006/2007 TEMA 1: 1.1.- La anchura de banda del espectro de emisión de una fuente láser es: ν = 30 MHz. Cuál es la duración del pulso luminoso emitido por la fuente? Cuál
HOJA DE PROBLEMAS ÓPTICA I CURSO 2006/2007 TEMA 1: 1.1.- La anchura de banda del espectro de emisión de una fuente láser es: ν = 30 MHz. Cuál es la duración del pulso luminoso emitido por la fuente? Cuál
Tema: La luz Eje temático: Física, El sonido La luz La electricidad Contenido: La luz. Propagación de la Luz. Cuándo decimos que algo está iluminado?
 Tema: La luz Eje temático: Física, El sonido La luz La electricidad Contenido: La luz Propagación de la Luz Cuándo decimos que algo está iluminado? Podemos calificar a los objetos de brillantes, opacos
Tema: La luz Eje temático: Física, El sonido La luz La electricidad Contenido: La luz Propagación de la Luz Cuándo decimos que algo está iluminado? Podemos calificar a los objetos de brillantes, opacos
La Luz y las ondas electromagnéticas. La luz y las ondas electromagnéticas Cuestiones
 La luz y las ondas electromagnéticas Cuestiones (96-E) a) Qué se entiende por interferencia de la luz? b) Por qué no observamos la interferencia de la luz producida por los dos faros de un automóvil? (96-E)
La luz y las ondas electromagnéticas Cuestiones (96-E) a) Qué se entiende por interferencia de la luz? b) Por qué no observamos la interferencia de la luz producida por los dos faros de un automóvil? (96-E)
I.E.S. Sierra de Mijas Curso 2014-15 PROBLEMAS DE SELECTIVIDAD DEL TEMA 4: ÓPTICA
 PROBLEMAS DE SELECTIVIDAD DEL TEMA 4: ÓPTICA Selectividad Andalucía 2001: 1. a) Indique qué se entiende por foco y por distancia focal de un espejo. Qué es una imagen virtual? b) Con ayuda de un diagrama
PROBLEMAS DE SELECTIVIDAD DEL TEMA 4: ÓPTICA Selectividad Andalucía 2001: 1. a) Indique qué se entiende por foco y por distancia focal de un espejo. Qué es una imagen virtual? b) Con ayuda de un diagrama
Sol: d = 2'12. sen (30-19'47) = 0'39 cm
 www.preparadores.eu Física y Química 1 FÍSICA Y QUÍMICA CURSO: 2015-2016 SEMANA: 9ª PROFESOR: Ána Gómez Gómez TEMAS: 26 y 27 1.Una persona padece presbicia. Tiene el punto próximo situado a 0'75 m del
www.preparadores.eu Física y Química 1 FÍSICA Y QUÍMICA CURSO: 2015-2016 SEMANA: 9ª PROFESOR: Ána Gómez Gómez TEMAS: 26 y 27 1.Una persona padece presbicia. Tiene el punto próximo situado a 0'75 m del
3.3.6 Introducción a los Instrumentos Ópticos
 GUÍA DE ESTUDIO Complemento a la Unidad 3.3 LUZ 3.3.6 Introducción a los Instrumentos Ópticos. Instrumentos de Lente.. Imágenes Reales... El Proyector Opera con el objeto (diapositiva) muy cerca de la
GUÍA DE ESTUDIO Complemento a la Unidad 3.3 LUZ 3.3.6 Introducción a los Instrumentos Ópticos. Instrumentos de Lente.. Imágenes Reales... El Proyector Opera con el objeto (diapositiva) muy cerca de la
MYP (MIDDLE YEARS PROGRAMME)
 MYP (MIDDLE YEARS PROGRAMME) 2014-2015 Fecha 19/05/2015 APUNTES DE GEOMETRÍA 2º ESO 1. EL TEOREMA DE PITÁGORAS El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa
MYP (MIDDLE YEARS PROGRAMME) 2014-2015 Fecha 19/05/2015 APUNTES DE GEOMETRÍA 2º ESO 1. EL TEOREMA DE PITÁGORAS El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa
SELECTIVIDAD LOGSE: ÓPTICA GEOMÉTRICA PROBLEMAS RESUELTOS
 SELECTIVIDAD LOGSE: ÓPTICA GEOMÉTRICA PROBLEMAS RESUELTOS JUNIO 96 C3. Explica por qué cuando se observa desde el aire un remo sumergido parcialmente en el agua parece estar doblado. Ayúdate de construcciones
SELECTIVIDAD LOGSE: ÓPTICA GEOMÉTRICA PROBLEMAS RESUELTOS JUNIO 96 C3. Explica por qué cuando se observa desde el aire un remo sumergido parcialmente en el agua parece estar doblado. Ayúdate de construcciones
Refracción en lámina de caras planas y paralelas
 Refracción en lámina de caras planas y paralelas Fundamento Un medio material que esté formado por dos caras planas y paralelas, siendo su espesor e, forma lo que se llama una lámina de caras planas y
Refracción en lámina de caras planas y paralelas Fundamento Un medio material que esté formado por dos caras planas y paralelas, siendo su espesor e, forma lo que se llama una lámina de caras planas y
Volumen de Sólidos de Revolución
 60 CAPÍTULO 4 Volumen de Sólidos de Revolución 6 Volumen de sólidos de revolución Cuando una región del plano de coordenadas gira alrededor de una recta l, se genera un cuerpo geométrico denominado sólido
60 CAPÍTULO 4 Volumen de Sólidos de Revolución 6 Volumen de sólidos de revolución Cuando una región del plano de coordenadas gira alrededor de una recta l, se genera un cuerpo geométrico denominado sólido
Preuniversitario Esperanza Joven Curso Física Intensivo, Módulo Común. Ondas III; La luz
 Preuniversitario Esperanza Joven Curso Física Intensivo, Módulo Común Guía 11 Ondas III; La luz Nombre: Fecha: Naturaleza de la luz 1. Teoría corpuscular: Newton formula que la luz estaba formada por pequenos
Preuniversitario Esperanza Joven Curso Física Intensivo, Módulo Común Guía 11 Ondas III; La luz Nombre: Fecha: Naturaleza de la luz 1. Teoría corpuscular: Newton formula que la luz estaba formada por pequenos
TEMA: LA LUZ. - Concepto - Tipos - Leyes. - Concepto. - Espejos. - Concepto. - Índice de refracción. - Lentes. - Prisma óptico
 TEMA: LA LUZ LA LUZ - Concepto - Características - Propagación - La materia y la luz - Instrumentos ópticos -Reflexión - Refracción - Concepto - Tipos - Leyes - Espejos - Concepto - Índice de refracción
TEMA: LA LUZ LA LUZ - Concepto - Características - Propagación - La materia y la luz - Instrumentos ópticos -Reflexión - Refracción - Concepto - Tipos - Leyes - Espejos - Concepto - Índice de refracción
Problemas de Óptica. PAU (PAEG)
 1. (Junio 09 ) Observamos una pequeña piedra que esta incrustada bajo una plancha de hielo, razona si su profundidad aparente es mayor o menor que su profundidad real. Traza un diagrama de rayos para justificar
1. (Junio 09 ) Observamos una pequeña piedra que esta incrustada bajo una plancha de hielo, razona si su profundidad aparente es mayor o menor que su profundidad real. Traza un diagrama de rayos para justificar
Aplicación: cálculo de áreas XII APLICACIÓN: CÁLCULO DE ÁREAS
 XII APLICACIÓN: CÁLCULO DE ÁREAS El estudiante, hasta este momento de sus estudios, está familiarizado con el cálculo de áreas de figuras geométricas regulares a través del uso de fórmulas, como el cuadrado,
XII APLICACIÓN: CÁLCULO DE ÁREAS El estudiante, hasta este momento de sus estudios, está familiarizado con el cálculo de áreas de figuras geométricas regulares a través del uso de fórmulas, como el cuadrado,
Proyecto. Tema 6 sesión 2: Generación de Rectas, Circunferencias y Curvas. Geometría Analítica. Isidro Huesca Zavaleta
 Geometría Analítica Tema 6 sesión 2: Generación de Rectas, Circunferencias y Curvas Isidro Huesca Zavaleta La Integración de dos Ciencias La Geometría Analítica nació de la integración de dos ciencias
Geometría Analítica Tema 6 sesión 2: Generación de Rectas, Circunferencias y Curvas Isidro Huesca Zavaleta La Integración de dos Ciencias La Geometría Analítica nació de la integración de dos ciencias
R=mv/qBvmax=AAAωF=kxB=µoI/2πd; ;ertyuied3rgfghjklzxc;e=mc 2
 E=hf;p=mv;F=dp/dt;I=Q/t;Ec=mv 2 /2; TEMA 6: ÓPTICA F=KQq/r 2 ;L=rxp;x=Asen(ωt+φo);v=λf c 2 =1/εoµo;A=πr 2 ;T 2 =4π 2 /GMr 3 ;F=ma; L=dM/dtiopasdfghjklzxcvbvv=dr/dt; M=rxF;sspmoqqqqqqqqqqqp=h/λ; Ejercicios
E=hf;p=mv;F=dp/dt;I=Q/t;Ec=mv 2 /2; TEMA 6: ÓPTICA F=KQq/r 2 ;L=rxp;x=Asen(ωt+φo);v=λf c 2 =1/εoµo;A=πr 2 ;T 2 =4π 2 /GMr 3 ;F=ma; L=dM/dtiopasdfghjklzxcvbvv=dr/dt; M=rxF;sspmoqqqqqqqqqqqp=h/λ; Ejercicios
III Unidad Modulación
 1 Modulación Análoga (AM, FM). Digital (MIC). 2 Modulación Longitud de onda Es uno de los parámetros de la onda sinusoidal. Es la distancia que recorre la onda sinusoidal en un ciclo (Hertz). Su unidad
1 Modulación Análoga (AM, FM). Digital (MIC). 2 Modulación Longitud de onda Es uno de los parámetros de la onda sinusoidal. Es la distancia que recorre la onda sinusoidal en un ciclo (Hertz). Su unidad
PRÁCTICA 14. Reflexión y refracción
 PRÁCTICA 14 Reflexión y refracción Laboratorio de Física General Objetivos Generales 1. Determinar la ley que rige la reflexión de la luz. 2. Estudiar la ley de la refracción de la luz. Equipo y materiales
PRÁCTICA 14 Reflexión y refracción Laboratorio de Física General Objetivos Generales 1. Determinar la ley que rige la reflexión de la luz. 2. Estudiar la ley de la refracción de la luz. Equipo y materiales
Unidad V. 5.1 Recta tangente y recta normal a una curva en un punto. Curvas ortogonales.
 Unidad V Aplicaciones de la derivada 5.1 Recta tangente y recta normal a una curva en un punto. Curvas ortogonales. Una tangente a una curva es una recta que toca la curva en un solo punto y tiene la misma
Unidad V Aplicaciones de la derivada 5.1 Recta tangente y recta normal a una curva en un punto. Curvas ortogonales. Una tangente a una curva es una recta que toca la curva en un solo punto y tiene la misma
VIBRACIÓN Y ONDAS. Se denomina rayo a la línea perpendicular a los frentes de onda, como se muestra en la figura.
 VIBRACIÓN Y ONDAS DEFINICIÓN DE ONDA Una partícula realiza un movimiento vibratorio cuando realiza una oscilación alrededor del punto de equilibrio. Un ejemplo de movimiento vibratorio lo constituye la
VIBRACIÓN Y ONDAS DEFINICIÓN DE ONDA Una partícula realiza un movimiento vibratorio cuando realiza una oscilación alrededor del punto de equilibrio. Un ejemplo de movimiento vibratorio lo constituye la
2.2 Rectas en el plano
 2.2 Al igual que ocurre con el punto, en geometría intrínseca, el concepto de recta no tiene definición, sino que constituye otro de sus conceptos iniciales, indefinibles. Desde luego se trata de un conjunto
2.2 Al igual que ocurre con el punto, en geometría intrínseca, el concepto de recta no tiene definición, sino que constituye otro de sus conceptos iniciales, indefinibles. Desde luego se trata de un conjunto
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA
 RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
Introducción. Flujo Eléctrico.
 Introducción La descripción cualitativa del campo eléctrico mediante las líneas de fuerza, está relacionada con una ecuación matemática llamada Ley de Gauss, que relaciona el campo eléctrico sobre una
Introducción La descripción cualitativa del campo eléctrico mediante las líneas de fuerza, está relacionada con una ecuación matemática llamada Ley de Gauss, que relaciona el campo eléctrico sobre una
Unidad 3: Razones trigonométricas.
 Unidad 3: Razones trigonométricas 1 Unidad 3: Razones trigonométricas. 1.- Medida de ángulos: grados y radianes. Las unidades de medida de ángulos más usuales son el grado sexagesimal y el radián. Se define
Unidad 3: Razones trigonométricas 1 Unidad 3: Razones trigonométricas. 1.- Medida de ángulos: grados y radianes. Las unidades de medida de ángulos más usuales son el grado sexagesimal y el radián. Se define
FORMACIÓN DE IMÁGENES CON LENTES
 Laboratorio de Física de Procesos Biológicos FORMACIÓN DE IMÁGENES CON LENTES Fecha: 19/12/2005 1. Objetivo de la práctica Estudio de la posición y el tamaño de la imagen de un objeto formada por una lente
Laboratorio de Física de Procesos Biológicos FORMACIÓN DE IMÁGENES CON LENTES Fecha: 19/12/2005 1. Objetivo de la práctica Estudio de la posición y el tamaño de la imagen de un objeto formada por una lente
7. Difracción n de la luz
 7. Difracción n de la luz 7.1. La difracción 1 7. Difracción de la luz. 2 Experiencia de Grimaldi (1665) Al iluminar una pantalla opaca con una abertura pequeña, se esperaba que en la pantalla de observación
7. Difracción n de la luz 7.1. La difracción 1 7. Difracción de la luz. 2 Experiencia de Grimaldi (1665) Al iluminar una pantalla opaca con una abertura pequeña, se esperaba que en la pantalla de observación
Práctica 5: El telemicroscopio
 LABORATORIO DE ÓPTICA (ÓPTICA INSTRUMENTAL) CURSO 009/10 Práctica 5: El telemicroscopio 5.1 Objetivo de la práctica El objetivo de esta práctica es el estudio y comprensión de los fundamentos ópticos del
LABORATORIO DE ÓPTICA (ÓPTICA INSTRUMENTAL) CURSO 009/10 Práctica 5: El telemicroscopio 5.1 Objetivo de la práctica El objetivo de esta práctica es el estudio y comprensión de los fundamentos ópticos del
No es otra cosa, que la representación de los resultados de una función sobre el plano carteciano.
 FUNCIONES GRAFICAS No es otra cosa, que la representación de los resultados de una función sobre el plano carteciano. INTÉRVALOS Un intervalo es el conjunto de todos los números reales entre dos números
FUNCIONES GRAFICAS No es otra cosa, que la representación de los resultados de una función sobre el plano carteciano. INTÉRVALOS Un intervalo es el conjunto de todos los números reales entre dos números
TEMA 4: OPTICA. Ojo normal! 4.4 El ojo como sistema óptico Características del ojo normal (emétrope): Córnea: parte protuberante del ojo
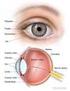 Ojo normal! Características del ojo normal (emétrope): Córnea: parte protuberante del ojo Figura 32.45 Tipler 5ª Ed. Características del ojo normal (emétrope): Córnea: parte protuberante del ojo Iris:
Ojo normal! Características del ojo normal (emétrope): Córnea: parte protuberante del ojo Figura 32.45 Tipler 5ª Ed. Características del ojo normal (emétrope): Córnea: parte protuberante del ojo Iris:
SESIÓN 10 DERIVACIÓN DE FUNCIONES TRIGONOMÉTRICAS DIRECTAS
 SESIÓN 0 DERIVACIÓN DE FUNCIONES TRIGONOMÉTRICAS DIRECTAS I. CONTENIDOS:. Derivadas de funciones trigonométricas directas. Ejercicios resueltos. Estrategias Centradas en el Aprendizaje: Ejercicios propuestos
SESIÓN 0 DERIVACIÓN DE FUNCIONES TRIGONOMÉTRICAS DIRECTAS I. CONTENIDOS:. Derivadas de funciones trigonométricas directas. Ejercicios resueltos. Estrategias Centradas en el Aprendizaje: Ejercicios propuestos
TEMA IV EL OJO EMÉTROPE. VI - Tamaño de la imagen sobre la retina de un objeto extenso
 TEMA IV EL OJO EMÉTRO I - Concepto de ojo emétropre II - Punto remoto III - La ecuación de Gauss en el ojo emétrope IV - Imagen de un punto enfocado V - El círculo de desenfoque VI - Tamaño de la imagen
TEMA IV EL OJO EMÉTRO I - Concepto de ojo emétropre II - Punto remoto III - La ecuación de Gauss en el ojo emétrope IV - Imagen de un punto enfocado V - El círculo de desenfoque VI - Tamaño de la imagen
MEDIDA DE FOCALES Y RADIOS DE CURVATURA DE ESPEJOS
 SESIÓN 1 MEDIDA DE FOCALES Y RADIOS DE CURVATURA DE ESPEJOS TRABAJO PREVIO: MEDIDA DE FOCALES CONCEPTOS FUNDAMENTALES Aproximación paraxial Los ángulos con el eje óptico se aproximan por ángulos pequeños
SESIÓN 1 MEDIDA DE FOCALES Y RADIOS DE CURVATURA DE ESPEJOS TRABAJO PREVIO: MEDIDA DE FOCALES CONCEPTOS FUNDAMENTALES Aproximación paraxial Los ángulos con el eje óptico se aproximan por ángulos pequeños
22. DETERMINACIÓN DE ÍNDICES DE REFRACCIÓN
 22. DETERMINACIÓN DE ÍNDICES DE REFRACCIÓN OBJETIVOS Determinación del índice de refracción de un cuerpo semicircular, así como del ángulo límite. Observación de la dispersión cromática. Determinación
22. DETERMINACIÓN DE ÍNDICES DE REFRACCIÓN OBJETIVOS Determinación del índice de refracción de un cuerpo semicircular, así como del ángulo límite. Observación de la dispersión cromática. Determinación
1) Enuncie el principio de Fermat. Demuestre a través de este principio la ley de reflexión de la luz en un espejo plano.
 Unidad 3: ÓPTICA Principio de Fermat. Reflexión. Espejos. Refracción. Ley de Snell. Lentes. Prisma. Fibras ópticas. Luz como fenómeno electromagnético. Luz como fenómeno corpuscular. Interferencia. Polarización.
Unidad 3: ÓPTICA Principio de Fermat. Reflexión. Espejos. Refracción. Ley de Snell. Lentes. Prisma. Fibras ópticas. Luz como fenómeno electromagnético. Luz como fenómeno corpuscular. Interferencia. Polarización.
TEMA - IV ESPEJOS. 1. ESPEJOS ESFÉRICOS.
 IV - 0 TEMA - IV ESPEJOS.. ESPEJOS ESFÉRICOS... Poición de la imagen..2. Foco y ditancia focal..3. Potencia..4. Formación de imágene..4.. Marcha de lo rayo..4.2. Imágene en epejo cóncavo..4.3. Imágene
IV - 0 TEMA - IV ESPEJOS.. ESPEJOS ESFÉRICOS... Poición de la imagen..2. Foco y ditancia focal..3. Potencia..4. Formación de imágene..4.. Marcha de lo rayo..4.2. Imágene en epejo cóncavo..4.3. Imágene
Relación Problemas Tema 9: La luz y las ondas electromagnéticas
 Relación Problemas Tema 9: La luz y las ondas electromagnéticas Problemas 1. Una onda electromagnética (o.e.m.) cuya frecuencia es de 10 14 Hz y cuyo campo eléctrico, de 2 V/m de amplitud, está polarizado
Relación Problemas Tema 9: La luz y las ondas electromagnéticas Problemas 1. Una onda electromagnética (o.e.m.) cuya frecuencia es de 10 14 Hz y cuyo campo eléctrico, de 2 V/m de amplitud, está polarizado
INSTITUCION EDUCATIVA NACIONAL LOPERENA DEPARTAMENTO DE CIENCIAS NATURALES. FISICA I. CUESTIONARIO GENERAL IV PERIODO.
 INSTITUCION EDUCATIVA NACIONAL LOPERENA DEPARTAMENTO DE CIENCIAS NATURALES. FISICA I. CUESTIONARIO GENERAL IV PERIODO. NOTA: Es importante que cada una de las cuestiones así sean tipo Icfes, deben ser
INSTITUCION EDUCATIVA NACIONAL LOPERENA DEPARTAMENTO DE CIENCIAS NATURALES. FISICA I. CUESTIONARIO GENERAL IV PERIODO. NOTA: Es importante que cada una de las cuestiones así sean tipo Icfes, deben ser
23. MICROSCOPIO COMPUESTO: DETERMINACIÓN DE SU AUMENTO y MEDIDA DE ÁREAS MICROSCÓPICAS
 23. MICROSCOPIO COMPUESTO: DETERMINACIÓN DE SU AUMENTO y MEDIDA DE ÁREAS MICROSCÓPICAS OBJETIVO El objetivo de la práctica es familiarizarse con el uso del microscopio, determinar el aumento lineal de
23. MICROSCOPIO COMPUESTO: DETERMINACIÓN DE SU AUMENTO y MEDIDA DE ÁREAS MICROSCÓPICAS OBJETIVO El objetivo de la práctica es familiarizarse con el uso del microscopio, determinar el aumento lineal de
10. ÓPTICA GEOMÉTRICA.
 Optica 19 10. ÓPTICA GEOMÉTRICA. Desarrollamos la unidad de acuerdo con el siguiente hilo conductor: 1. De qué trata la Óptica geométrica? Conceptos básicos en Óptica geométrica. 2. Cómo se forman las
Optica 19 10. ÓPTICA GEOMÉTRICA. Desarrollamos la unidad de acuerdo con el siguiente hilo conductor: 1. De qué trata la Óptica geométrica? Conceptos básicos en Óptica geométrica. 2. Cómo se forman las
COMPROBACIÓN DE RELACIONES PARAXIALES
 SESIÓN 4: COMPROBACIÓN DE RELACIONES PARAXIALES TRABAJO PREVIO CONCEPTOS FUNDAMENTALES Aproximación paraxial Aproximación de ángulos con el eje óptico pequeños (sen σ σ, tg σ σ). En aproximación paraxial
SESIÓN 4: COMPROBACIÓN DE RELACIONES PARAXIALES TRABAJO PREVIO CONCEPTOS FUNDAMENTALES Aproximación paraxial Aproximación de ángulos con el eje óptico pequeños (sen σ σ, tg σ σ). En aproximación paraxial
MINI ENSAYO DE FÍSICA Nº 4
 MINI ENSAYO DE FÍSICA Nº 4 TEMA: ONDAS Y ÓPTICA 1. Con respecto a las ondas mecánicas, cuál de las siguientes afirmaciones es correcta? A) Las tres afirmaciones siguientes son verdaderas. B) Si se refractan
MINI ENSAYO DE FÍSICA Nº 4 TEMA: ONDAS Y ÓPTICA 1. Con respecto a las ondas mecánicas, cuál de las siguientes afirmaciones es correcta? A) Las tres afirmaciones siguientes son verdaderas. B) Si se refractan
UNIDAD EDUCATIVA SALESIANA CARDENAL SPELLMAN
 UNIDAD EDUCATIVA SALESIANA CARDENAL SPELLMAN CUESTIONARIO DE OPTATIVA II: FISICA-CÁLCULO DIFERENCIAL TERCERO DE BACHILLERATO (Examen Escrito de Grado) Dr. Eduardo Cadena Cazares 1.- ANALIZAR LA INFORMACIÓN
UNIDAD EDUCATIVA SALESIANA CARDENAL SPELLMAN CUESTIONARIO DE OPTATIVA II: FISICA-CÁLCULO DIFERENCIAL TERCERO DE BACHILLERATO (Examen Escrito de Grado) Dr. Eduardo Cadena Cazares 1.- ANALIZAR LA INFORMACIÓN
Cuadriláteros y circunferencia
 CLAVES PARA EMPEZAR Un triángulo isósceles tiene dos lados iguales: b c. Como es rectángulo, se cumple el teorema de Pitágoras: 10 2 b 2 b 2 100 2b 2 b 7,07. Los dos lados miden 7,07 cm cada uno. r A C
CLAVES PARA EMPEZAR Un triángulo isósceles tiene dos lados iguales: b c. Como es rectángulo, se cumple el teorema de Pitágoras: 10 2 b 2 b 2 100 2b 2 b 7,07. Los dos lados miden 7,07 cm cada uno. r A C
TALLER DE EXPERIMENTOS SENCILLOS DE ÓPTICA
 GRINCEF TALLER DE EXPERIMENTOS SENCILLOS DE ÓPTICA Hebert Elías Lobo Manuel Villarreal Iris Materán Jesús Rosario Autores Jesús Briceño Juan Carlos Díaz Yasmelis Rivas Juan Lobo Co-autores Experiencias
GRINCEF TALLER DE EXPERIMENTOS SENCILLOS DE ÓPTICA Hebert Elías Lobo Manuel Villarreal Iris Materán Jesús Rosario Autores Jesús Briceño Juan Carlos Díaz Yasmelis Rivas Juan Lobo Co-autores Experiencias
PROBLEMAS DE ÓPTICA RESUELTOS
 PROBLEMAS DE ÓPTICA RESUELTOS PROBLEMAS DEL CURSO En el fondo de un recipiente con agua de 1 m de profundidad hay un foco que emite luz en todas las direcciones. Si en la vertical del foco y en la superficie
PROBLEMAS DE ÓPTICA RESUELTOS PROBLEMAS DEL CURSO En el fondo de un recipiente con agua de 1 m de profundidad hay un foco que emite luz en todas las direcciones. Si en la vertical del foco y en la superficie
