MÓDULO SOBRE PROGRAMACIÓN MATLAB
|
|
|
- Teresa Miguélez Agüero
- hace 9 años
- Vistas:
Transcripción
1 8 MÓDULO SOBRE PROGRAMACIÓN MATLAB Francisco Muñoz Paba M.Sc correo: 8 SIMULACIÓN DE SISTEMAS DINÁMICOS OBJETIVOS Al terminar éste módulo el lector estará en condiciones de: Utilizar y aplicar los diferentes bloques de las bibliotecas Sources, Continuos, Commonly used blocks, Sinks, Discrete y Math operations a problemas específicos de la ingeniería. Crear un nuevo modelo, arrastrando y colocando los bloques necesarios para su simulación dinámica. Crear iconos personalizados para los bloques. Examinar la señal que pasa a través de cualquier línea seleccionada. Modificar y seleccionar la visualización y el rango de la señal visualizada. Simular sistemas dinámicos, utilizando ecuaciones diferenciales ordinarias. Modelar sistemas de ecuaciones algebraicas lineales y no lineales. Modelar y simular virtualmente cualquier tipo de sistema dinámico del mundo real Evaluar diseños y corregir las fallas del diseño antes de construir el prototipo. Desarrollar estrategias de control en sistemas dinámicos. INTRODUCCIÓN En el módulo 7, se analizan las variables con subíndices y arreglos, se definen los arreglos unidimensionales, bidimensionales, se generan arreglos y se acceden a sus elementos. Este módulo hace una introducción del software de SIMULINK para modelar, simular y analizar sistemas dinámicos. Una definición aproximada para el término Simulación es el desarrollo y uso de modelos para el estudio de la dinámica de sistemas existentes o hipotéticos. Los modelos matemáticos de sistemas de tiempos continuos consisten de una combinación de ecuaciones algebraicas y ecuaciones diferenciales y los modelos de tiempo discreto son una mezcla de ecuaciones algebraicas y de diferencia. Qué es Simulink? Simulink, es un software para utilizar con MATLAB para modelar, simular y analizar sistemas dinámicos. Para modelar, Simulink proporciona una interfaz gráfica de usuario (GUI) para construir los modelos con diagramas de bloques, utilizando el ratón para realizar operaciones cómo pulsar, arrastrar y colocar de forma que los sistemas Universidad del Atlántico-Facultad de Ingeniería.
2 dinámicos, se simulan en forma interactiva. Soporta sistemas lineales y no lineales, modelados en tiempo continuo, discreto, muestreado o un híbrido de los dos. La Interfaz Gráfica de Usuario. Una interfaz gráfica se usa para convertir un diagrama de bloque de esta clase directamente en Simulink y simula gráficamente el funcionamiento del sistema. Se puede crear una GUI, pulsando y arrastrando bloques desde la Biblioteca de Bloques, tales cómo Clock, Digital Clock, Signal Generator al área de diseño. La ventana Simulink Block Library Cuando iniciemos Simulink, se visualiza una ventana Simulink Library Browser, como se muestra en la figura 8., que contiene la biblioteca de los bloques de Simulink, presentando una lista con su respectivo icono en forma de un explorador de Windows. Añada bloques a su modelo copiándolos desde una biblioteca de bloques, que se encuentra en la parte izquierda de la pantalla o desde otro modelo. Después de haber añadido los bloques a la ventana modelo, se convierten en objetos o elementos programables de la ventana modelo. La ventana Simulink Block Library contiene una biblioteca de bloques Sources, Continuous, Discontinuities, Commonly used blocks, Sinks, Discrete, Math operations, User defined functions, Signal routing y otros más. Figura 8. El Navegador de biblioteca de Simulink. La biblioteca de Simulink contiene los bloques para representar los modelos matemáticos de componentes que comúnmente ocurren en sistemas dinámicos. Los bloques son agrupados en carpetas de acuerdo a la función. Una vez seleccionado el nombre de la lista (o icono) se abre la sección en el Navegador de Biblioteca de Simulink con los símbolos o iconos de la carpeta seleccionada. Por ejemplo, pulsando la carpeta Sources (fuentes), se abre la ventana mostrada en la figura 8.2. Para construir un modelo en Simulink de un sistema, seleccione los bloques apropiados y conéctelos de tal forma que represente el modelo matemático. Universidad del Atlántico-Facultad de Ingeniería. 2
3 Figura 8.2 El Navegador de Biblioteca y la Biblioteca Sources con sus bloques. Establecer los parámetros de los bloques. La ventana parámetros permite modificar las características o valores de propiedad de los objetos de la ventana modelo. La asignación de valores es una cualidad de uno de los objetos de la ventana modelo. Por ejemplo, se puede variar su tamaño, su alineación o color. Puede visualizar la ventana parámetros de un bloque haciendo doble clic sobre el bloque o seleccione Parameters en el menú Simulation, examinando el cuadro de diálogo que aparece. Biblioteca Sources. Contiene los bloques que originan señales. La tabla 8. que se muestra a continuación describe los bloques de la biblioteca Sources. Tabla 8. Nombre del bloque Clock Describe los bloques de la biblioteca Sources Descripción Visualiza y proporciona el tiempo de simulación. Band -Limited White Noise Introduce ruido blanco en un sistema continuo. Chirp Signal Genera una onda senoidal de frecuencia creciente. Universidad del Atlántico-Facultad de Ingeniería. 3
4 Constant Counter Free-Running lim Counter Limited 2:34 Digital Clock untitled.mat From File Salida de la constante especificada por el parámetro constant value. La salida es normalmente un entero no asignado con el número de bits especificado. Se usa el número más pequeño de bits para representar el límite superior. Genera tiempo de simulación en el intervalo de muestreo especificado Lee los valores del tiempo y la salida de la primera matriz en el archivo M especificado. simin From Workspace Lee datos de una matriz definida en el espacio de trabajo. Ground In Usado para señales de entradas ground Suministra un puerto de entrada para un subsistema. Pulse Generator Genera pulsos a intervalos regulares. Genera una función rampa. Ramp Genera números al azar normalmente distribuidos. Random Number Repeating Sequence Repeating Sequence Interpolated Genera señales periódicas formadas arbitrariamente. Salida de secuencia de tiempo discreto y repite puntos interpolados entre datos. Repeating Sequence Stair Signal Signal Builder Salida y secuencia repetida de tiempo discreto. Crea y genera grupos de señales intercambiables cuyas formas de ondas son trazos lineales. Universidad del Atlántico-Facultad de Ingeniería. 4
5 Signal Generator Generador de varias ondas: seno, coseno, cuadrada y aleatoria. Salida de una onda senoidal. Sine Wave Step Salida de un paso. de un paso Salida. Uniform Random Number Salida de una señal al azar uniformemente distribuida. Biblioteca Sinks. Contiene los bloques que visualizan o escriben su salida. La tabla 8.2 que se muestra a continuación describe los bloques de la biblioteca Sinks. Tabla 8.2 Describe los bloques de la biblioteca Sinks Nombre del bloque Descripción Display Floating Scope Out Suministra Visualización un puerto numérica a la de salida valores para a un la entrada. subsistema o modelo. Scope Scope flotante. flotante. Suministra un puerto a la salida para un subsistema o modelo. Usado para visualizar señales a la salida. Scope STOP Stop Simulation Para la simulación cuando la entrada es distinta de cero. Terminator Usado para terminar señales a la salida. untitled.mat To File Escribe datos a un archivo. simout To Workspace Escribe datos en una matriz en el espacio de trabajo. Universidad del Atlántico-Facultad de Ingeniería. 5
6 Visualiza gráfica X-Y de señales en la ventana de figuras de MATLAB. XY Graph Su primer modelo con Simulink. Crear un modelo con Simulink es muy sencillo. Para comprobar esta afirmación pruebe el modelo Generador de ondas de señales. Hay tres pasos principales para crear un modelo:. Abrir la ventana de Modelo. 2. Seleccionar, poner e interconectar los bloques. 3. Establecer los parámetros de los bloques. Para crear un modelo sencillo, siga los pasos del siguiente ejemplo 8., que consiste en un generador de ondas de señales y un osciloscopio. Cuando ejecute el modelo, observará la respuesta, una onda sinusoidal en el osciloscopio. Crear la interfaz gráfica de usuario. Utilice los siguientes procedimientos para iniciar Simulink.. Pulse el botón inicio de Window XP, señale a programas y señale después a la carpeta MATLAB 7.0. Los iconos de la carpeta Matlab 7.0 aparecerán en una lista. 2. En la línea de comando de Matlab, escriba simulink: >> Simulink o pulse el icono de Simulink Aparecerá la ventana Simulink Library Browser, visualizando los iconos de sus bibliotecas de bloques, tal cómo muestra la figura 8.3. Figura 8.3 Ventana Navegador de Biblioteca de Simulink. 3. Genere una ventana de Modelo, seleccionando New Model en el menú File de la ventana Navegador de Biblioteca de Simulink. Universidad del Atlántico-Facultad de Ingeniería. 6
7 Haga clic en el icono Stay on top, para que la Ventana de Modelo se mantenga en la parte superior de la ventana. Aparecerá la Ventana de Modelo vacía, tal cómo se muestra en la figura 8.4 Figura 8.4 Ventana de Modelo de Simulink. 4. Seleccione File Save 5. Guarde su Modelo con el nombre simple _ modelo. Ejemplo 8. Generador de ondas de señales. Para éste primer Modelo, utilizamos un bloque Signal Generator y un bloque Scope de las bibliotecas Sources y Sinks respectivamente. Iconos Biblioteca Bloques. Sources Signal Generator Signal Generator Scope Sinks Scope. Para dibujar un bloque mediante la biblioteca de bloques. a) Abra la biblioteca Sources haciendo doble clic sobre el icono Sources. Simulink visualiza una ventana que contiene todos los bloques de la biblioteca Sources; estos bloques son fuentes de señales. La ventana de la biblioteca Sources tiene el aspecto que se ilustra en la figura 8.2 b) Para copiar el bloque Signal Generator desde la biblioteca de bloques Sources, haga clic sobre el bloque Signal Generator y arrástrelo a la ventana de su modelo. Cuando libere el botón del ratón, Simulink visualiza el icono del bloque, tal como se ilustra en la figura 8.7 Universidad del Atlántico-Facultad de Ingeniería. 7
8 c) Puede visualizar los parámetros del bloque Signal Generator, haciendo doble clic sobre el bloque y examinar el cuadro de diálogo que aparece. En la figura 8.6, se muestra cómo se visualiza éste cuadro de diálogo. Figura 8.5 Ventana Biblioteca Sinks. Figura 8.6 Ventana Parámetros del bloque Sources. d) Abra la biblioteca Sinks haciendo doble clic sobre el icono Sinks. Simulink visualiza una ventana que contiene todos los bloques de la biblioteca Sinks; estos bloques visualizan o escriben su salida. La ventana de la biblioteca Sinks tiene el aspecto que se ilustra en la figura 8.5. e) Para copiar el bloque Scope desde la biblioteca de bloques Sinks, haga clic sobre el bloque Scope y arrástrelo a la ventana de su modelo. Cuando libere el botón del ratón, Simulink visualiza el icono del bloque Scope, tal como se muestra en la figura 8.7. Puede visualizar los parámetros del bloque Scope, haciendo doble clic sobre el bloque, luego pulse el icono parameters en la ventana Scope y examine el cuadro de diálogo que aparece. En la figura 8.8, se muestra cómo se visualiza éste cuadro de diálogo. f) Con los bloques ya copiados en la ventana del Modelo, ahora conecte los bloques. Si examina los iconos de los bloques, verá un signo en forma de ángulo a la derecha del bloque Signal Generator y uno a la izquierda del bloque Scope. El símbolo > apuntando hacia fuera de un bloque es un puerto de salida; si el símbolo apunta hacia el bloque es un puerto de entrada. Cuando los bloque se conectan los símbolos del puerto desaparecen. g) Conecte el bloque Signal Generator al bloque Scope. Posicione el puntero del ratón sobre el puerto de salida en el lado derecho del bloque Signal Generator. Presione y mantenga pulsado el botón del ratón. Observe que el botón cambia a una forma de una cruz. Manteniendo pulsado el botón del ratón, mueva el cursor al puerto de entrada del bloque Scope. Observe que el cursor mantiene su forma de cruz y que una línea conecta el bloque Signal Generator con el puerto de entrada del bloque Scope. Ahora libere el botón del ratón. Los bloques se conectan, tal cómo se ilustra en la figura 8.7 Universidad del Atlántico-Facultad de Ingeniería. 8
9 Signal Generator Scope Figura 8.7 Ventana de Modelo Figura 8.8 Ventana Parámetros de Scope. El bloque Signal Generator, se utiliza para generar ondas de señales. Las características se modifican mediante el establecimiento de los parámetros del bloque Signal Generator. El bloque Scope se utiliza para representar las ondas de señales. Observará que el bloque Scope es una representación gráfica de un osciloscopio. 2. Establecer los parámetros de los bloques. El siguiente paso es establecer los parámetros de los bloques que ha creado. Las ventanas Source Block Parameters: Signal Generator y Scope Parameters, ilustradas en las figuras 8.6 y 8.8 respectivamente, proporcionan una manera fácil de establecer los parámetros de los bloques utilizados en éste Modelo. En el ejemplo 8. Generador de ondas, necesitará cambiar los valores de dos parámetros. Use el valor predeterminado para las demás propiedades. Objeto Parámetro Valor Signal Generator Amplitude :2 Wave form sine Frequency rad/sec Time(t) Use simulation time. Scope Time range Establecer el tiempo de simulación. En la Ventana de Modelo de Simulink, seleccione Simulation Configuration Parameters. Se abre la ventana de diálogo Configuración Parameters, cómo se ilustra en la figura 8.9 En el campo Stop time, ingrese 20. En la casilla Type, seleccione Variable-step y en la lista desplegable de Solver, seleccione Discrete (no continuous states). Pulse OK. El software actualiza los valores de los parámetros con sus cambios. Cierre el cuadro de diálogo Configuration Parameters. Después de introducir sus cambios de Configuration Parameters, está listo para simular el simple _ modelo y visualizar los resultados de la simulación. Universidad del Atlántico-Facultad de Ingeniería. 9
10 Figura 8.9 Ventana de Configuration Parameters. 4. Ejecutar el Modelo. Para ejecutar el Modelo, hay dos maneras de ejecutarlo: a) En la ventana de Modelo de Simulink, seleccione Simulation Star. b) Pulse el icono ejecutar en la barra de herramientas. La simulación se ejecuta, deteniéndose cuando alcanza el tiempo de simulación especificado en la ventana de diálogo Configuration Parameters. Pulse dos veces el icono Scope en la Ventana de Modelo para ver la respuesta de la simulación, tal cómo aparece ilustrada en la figura 8.0. Figura 8.0 Respuesta de la simulación del simple _ modelo. Puede pulsar el botón Autoscale en la ventana de visualización de Scope para obtener una mejor visualización de los gráficos. El siguiente código en MATLAB, realiza la misma simulación del generador de ondas de señales de la función seno. >> t=0:0.0:20; >> y=sin(t); >> y2=2*sin(t); >> plot(t,y,t,y2),grid on Universidad del Atlántico-Facultad de Ingeniería. 0
11 Resumen de los bloques utilizados en los ejemplos. El Bloque Scope de la biblioteca Sinks. El bloque Scope visualiza simulaciones de formas de ondas con respecto al tiempo. Puede tener múltiples ejes y un rango de tiempo común. Puede ajustar el tiempo, el rango de los valores de entradas visualizados, redimensionar la ventana Scope y modificar los valores de los parámetros durante la simulación. El Bloque Mux de la biblioteca Commonly used block. El bloque Mux combina sus entradas con una sola salida. Una entrada puede ser un escalar, un vector, o una señal de matriz. La salida de un bloque Mux es un vector. El Bloque Signal Generator de la Biblioteca Sources. El bloque Signal Generator produce una de las cuatro formas diferentes de ondas: Onda Seno, Onda cuadrada, Onda sawtooth y Onda aleatoria. Los parámetros de la señal se pueden expresar en Hertz (por defecto) o radianes por segundo. Se puede invertir la forma de onda especificando un signo negativo en la amplitud en la ventana de parámetros del bloque. El bloque Fcn de la Biblioteca User Defined Functions. Para el bloque Fcn a su entrada se aplica una expresión específica y se escribe como u. Si u es un vector, u(i) representa el elemento i del vector; u() o u sólo representa el primer elemento. La expresión especificada puede consistir de una constante numérica, operadores aritméticos, operadores relacionales, operadores lógicos, y las funciones matemáticas abs, acos, asin, atan, atan2, ceil,, cos, cosh, exp, fabs, floor, hypot, ln, log, log0, pow, power, rem, sgn, sin, sinh, sqrt, tan y tanh. El bloque Gain de la biblioteca Commonly Used Block. El Gain bloque multiplica la entrada por un parámetro constant value. La entrada y el constant value puede ser un escalar, vector o una matriz. Especifique el valor del bloque Gain en el parámetro Gain. La multiplicación del parámetro es especificado en Elementwise o matrix multiplication. Para la multiplicación de matriz éste parámetro nos indica el orden de la multiplicación. Universidad del Atlántico-Facultad de Ingeniería.
12 Grafica de una función trigonométrica. EJEMPLO 8.2 Simule el movimiento armónico simple representado por la ecuación x(t)=acos(wt + ) Dónde: x(t) = Elongación A = La amplitud = 5 cm w = 2 f = Frecuencia angular= 5 rad/seg. f = /T = Frecuencia. T= período= 2 / w = Angulo de fase = / 2 fase = (wt + ). Abrimos la Ventana de Modelo, pulsando el icono Stay on top De la biblioteca de Simulink, insertamos los siguientes bloques a la Ventana de Modelo, guardado con el nombre: Ejemplo8_2_simulink. Icono Biblioteca Cantidad Bloque Clock Constant Sources Clock Commonly used blocks Constant Gain Math Operations Gain Sum sin Trigonometric Function Trigonometric Function Scope Scope Universidad del Atlántico-Facultad de Ingeniería. 2
13 2. El próximo paso es conectar estos bloques como muestra la siguiente ilustración: 0 5 cos 5 Clock Gain Trigonometric Function Gain Scope pi/2 Constant Cómo opera la simulación en el diagrama de bloques? El bloque Clock visualiza y proporciona el tiempo de simulación. El bloque Gain multiplica el 5 por el tiempo del bloque Clock y el bloque Sum calcula el argumento (wt + pi/2) para que el bloque Trigonometric Function con la función Cos determine su valor. El bloque Gain multiplica su entrada por 5 y el bloque Scope visualiza la respuesta de la simulación. 3. Establecer los parámetros de los bloques. El siguiente paso es establecer los parámetros de los bloques que ha creado. Pulse dos veces el botón izquierdo del ratón en cada bloque e ingrese los siguientes valores. Objeto Parámetro Valor Clock Decimation 0 Gain gain 5 Gain 2 Gain 5 Multiplication Element-wise (k.*u) Constant Constan Value pi/2 Sum icon shape round List of signs ++ Trigonometric Function Function cos Output signal type auto Scope Time range 0 4. Establecer el tiempo de simulación. En la barra de herramientas seleccione Simulation Configuration Parameter. En la etiqueta Selec seleccione Solver. En la etiqueta Simulation time: en la casilla Star time, ingrese cero, en la casilla Stop time, ingrese 0, en la casilla Type, seleccione Variable-step y en la lista desplegable de Solver, seleccione Discrete (no continuous states). Pulse OK. 5. Ejecutar el Modelo. Para ejecutar el Modelo, hay dos maneras de ejecutarlo: ) En la ventana de Modelo de Simulink, seleccione Simulation Star. 2) Pulse el icono ejecutar en la barra de herramientas. Universidad del Atlántico-Facultad de Ingeniería. 3
14 Pulse dos veces el icono Scope de la ventana de Modelo para ver la respuesta de la simulación, tal como aparece ilustrada en la figura 8.. Figura 8. Grafica de la simulación del movimiento armónico simple. El siguiente código en MATLAB, realiza la misma simulación del movimiento armónico: >> t=0:0.0:0; >> x=5*cos(5*t+pi/2); >> plot(t,x,'-d') Descripción de los bloques utilizados en los ejemplos. El bloque Clock de la biblioteca Sources. Clock El bloque Clock visualiza y determina el tiempo de simulación. En la ventana de parámetros se puede ingresar en la casilla Decimation el tiempo estimado. El bloque Constant de la biblioteca Commonly used blocks. Constant El bloque Constant genera un valor constante real o complejo. Constant value, especifica el valor constante a la salida. El bloque genera a la salida un escalar, un vector o una matriz, dependiendo de: La dimensión del parámetro Constant value. La setting del parámetro Interpret vector Parameters as -D. El bloque Sum de la biblioteca Math operations. El bloque Sum, Add y Substrac opera la suma o la resta en sus entradas. Este bloque puede sumar o sustraer a las entradas un escalar, un vector o una matriz. Se pueden especificar las operaciones de los bloques con el parámetro List of signs. Los Universidad del Atlántico-Facultad de Ingeniería. 4
15 caracteres más (+), menos (-) y el espaciador ( ), indican las operaciones que se deben efectuar a la entrada. Sistemas de primer orden. Los sistemas dinámicos de tiempo continuo son de primer orden si la derivada más alta de la variable dependiente que aparece en el modelo matemático es de primer orden. Los sistemas en que una cantidad de materia o energía cambian a una velocidad dependiente de la cantidad de materia o energía son típicamente de primer orden. La figura 8.2 ilustra el sistema de primer orden con las variables de entrada y salida. La representación escalar de un sistema de primer orden es: dy/dt =g(t,y,f) (8.) Dónde: t f(t) y(t) es la variable de tiempo continuo. es la entrada del sistema. es la salida del sistema. g(t,y,f) es la derivada de la función, que relaciona la velocidad de y con los tres argumentos. f(t) dy/dt y(t) Figura 8.2 Sistema de primer orden. De la ley de conservación de masa: Acumulación = Entrada Salida Balance de masa en el sistema: dy/dt = f(t) y(t) (8.2) Considere un caso especial de un sistema de primer orden, donde la función derivada es una función lineal explícita y la entrada / salida están dadas por: g(t,y,f) = a 0 f(t) b 0 y(t) (8.3) Donde a 0 y b 0 son constantes. Combinando las ecuaciones (8.) y (8.2) obtenemos: dy/dt + b 0 y = a 0 f(t) (8.4) En el caso que varíe el tiempo, uno o ambos de los parámetros del sistema lineal a 0 y b 0 son funciones de la variable independiente t. La ecuación (8.3) es expresada comúnmente cómo: τdy/dt + y = κf(t) (8.5) Donde τ y κ están relacionados por las siguientes ecuaciones: τ = /a 0 κ=b 0 /a 0 (8.6) Universidad del Atlántico-Facultad de Ingeniería. 5
16 Respuesta a una entrada escalón de un sistema de primer orden. Cuando la entrada u(t) es una constante, esto es, f(t)=a, la solución de la ecuación (8.5) para y(t) se obtiene usando la transformada de Laplace o por los métodos clásicos. La solución exacta por transformada de Laplace es: ( ) ( ( )) (8.7) Observe que la respuesta escalón cambia de 0 hasta A y la condición inicial es cero en todas las respuestas. La constante A mide la amplitud de la entrada y no es un parámetro inherente del sistema. Los parámetros del sistema son κ y t. El primer parámetro κ es llamado la ganancia del estado estacionario. Recibe este nombre porque el valor de la salida, y() es fácilmente calculada de: ( ) ( ) κ A (8.8) Respuesta a una entrada en rampa de un sistema de primer orden. Cuando la entrada u(t) es una variable independiente, esto es, f(t)=t, t >0. La solución de la ecuación (8.5) para y(t) se obtiene usando la transformada de Laplace o por los métodos clásicos. La solución exacta por transformada de Laplace es: y(t) = κτ (t + exp(- t/τ)) + y(0)exp( - t/τ)/ τ (8.9) Muchos sistemas dinámicos del mundo real son modelados por la ecuación diferencial de primer orden (ecuación 8.4), bajo ciertas condiciones. Para sistemas más complejos a menudo tienen comportamientos similares con los sistemas de primer orden bajo ciertas condiciones. Para modelos de sistemas de orden superior se pueden reducir a modelos de sistemas de ecuaciones diferenciales de primer orden. El siguiente modelo ejemplo 8.3 ilustra el uso de Simulink para simular ecuaciones diferenciales ordinarias con valor inicial. Ejemplo 8.3 Modele el siguiente sistema de primer orden: Solución de una ecuación diferencial dy/dt = - 3y + f(t) y(0) = y 0 Dónde: f(t) es una función. a) Encontrar la respuesta del sistema para una entrada de escalón f(t) =, t > 0 b) Encontrar la respuesta para una entrada de rampa f(t) = t, t >0 c) Encontrar las respuestas para la entrada de escalón y de rampa, cuando la constante b 0 es cero. Parte a). Abrimos la Ventana de Modelo, pulsando el icono Stay on top. De las bibliotecas de Simulink, insertamos los siguientes bloques a la Ventana de Modelo, guardado con el nombre: Ejemplo8_3_simulink. Universidad del Atlántico-Facultad de Ingeniería. 6
17 Icono Biblioteca Cantidad Bloque Step Sources Escalón Commonly Used Block Suma s Integrator Gain Integrador Ganancia Scope Osciloscopio 2. El próximo paso es conectar estos bloques como muestra la siguiente ilustración: Step s Integrator Scope -3 Gain Cómo opera la simulación en el diagrama de bloques? El bloque Sum recibe la señal del bloque Step y del producto (-3y) del bloque Gain. El bloque Gain multiplica la salida y del bloque Integrator por (-3) y el bloque Scope grafica la respuesta de la simulación. 3. Establecer los parámetros de los bloques. El siguiente paso es establecer los parámetros de los bloques que ha creado. Objeto Parámetro Valor Step Step time Initial value 0 Sum Icon shape rectangular List of signs ++ Integrator External reset none Initial condition source none Universidad del Atlántico-Facultad de Ingeniería. 7
18 Initial condition 0 Gain Gain - 3 Multiplication Element-wise (k.*u) Scope Number of axes Time range 0 Tick labels Bottons axis only 4. Establecer el tiempo de simulación. En la barra de herramientas seleccione Simulation Configuration Parameter. En la etiqueta Selec seleccione Solver. En la etiqueta Simulation time: en la casilla Star time, ingrese cero, en la casilla Stop time, ingrese 0, en la casilla Type, seleccione Variable-step y en la lista desplegable de Solver, seleccione ode45 (Dorman-Prince). Pulse OK. 5. Ejecutar el Modelo. Para ejecutar el Modelo, hay dos maneras de ejecutarlo: ) En la ventana de Modelo de Simulink, seleccione Simulation Star. 2) Pulse el icono ejecutar en la barra de herramientas. Pulse dos veces el icono Scope de la Ventana de Modelo para ver la respuesta de la simulación, tal como aparece ilustrada en la figura 8.2. Figura 8.2 Respuesta de la simulación de la ecuación diferencial de primer orden. Puede pulsar el botón Autoscale en la ventana de visualización del bloque Scope para obtener una mejor visualización de los gráficos. El siguiente código en MATLAB, realiza la misma simulación de la ecuación diferencial. >> Eq=@(t,y) (-3*y + ); >> [t,y]=ode45(eq,[0:0.0:0],0); >> plot(t,y,'--') Universidad del Atlántico-Facultad de Ingeniería. 8
19 Sistemas de segundo orden. Los modelos de entrada-salida de Sistemas Dinámicos de Tiempo Continuo, donde la derivada más alta de la variable dependiente es de segundo orden son clasificados de segundo orden. Los sistemas de segundo orden resultan cuando hay dos tanques de energía presentes. Se analizarán sistemas lineales de segundo orden, que puedan ser manipulados de acuerdo a la ecuación (8.2), relacionando una salida y(t) y una entrada f(t) con los parámetros genéricos del sistema A, K, B y M. La siguiente ecuación es un modelo de un sistema mecánico masa resorte amortiguador: Dónde: M es la masa del objeto, en kg K es la constante del resorte N/m. B es el coeficiente de amortiguamiento en N s/m y es el desplazamiento vertical en m. A es una constante. f(t) es la fuerza externa que actúa sobre el objeto. ( ) (8.2) El siguiente Modelo Ejemplo 8.4 ilustra el uso de Simulink para simular ecuaciones diferenciales ordinarias de segundo orden con valor inicial. Ejemplo 8.4 Grafica de una E.D.O de segundo orden. Simule el siguiente sistema mecánico masa resorte amortiguador de segundo orden: x(0)=0 x Ꞌ (0)=0.5 ( ) Dónde: M=Kg B=4 Ns/m K=3 N/m A= 3m. f(t)= es una onda seno. Solución. Expresando la ecuación diferencial de segundo orden en un sistema de ecuaciones diferenciales de primer orden para resolverlo por un método numérico multi paso de quinto orden. El sistema de ecuaciones diferenciales de primer orden obtenido es: ( ) Dónde: f(t) es la fuerza externa. KK K M f(t) B Universidad del Atlántico-Facultad de Ingeniería. 9
20 Abrimos la Ventana de Modelo, pulsando el icono Stay on top. De las bibliotecas de Simulink, insertamos los siguientes bloques a la Ventana de Modelo, guardado con el nombre: Ejemplo8_4_simulink. Icono Biblioteca Cantidad Bloque Sine Wave Sources Onda sinusoidal. Commonly Used Block 3 Ganancia Gain Suma. s Integrator Integrador Scope Osciloscopio Mux. 2. El próximo paso es conectar estos bloques como muestra la siguiente ilustración. Universidad del Atlántico-Facultad de Ingeniería. 20
21 Cómo opera la simulación en el diagrama de bloques? El bloque Add, recibe la señal del bloque Sine Wave que es multiplicada por 3 en el bloque Gain, el producto (-4x 2 ) del bloque Gain2 y el producto (-3x ) del bloque Gain3. El primer bloque Integrator genera la segunda variable x 2 que es multiplicada por (-4) en el bloque Gain2 y el segundo bloque Integrator2 genera la primera variable x que es multiplicada por (-3) en el bloque Gain3. El bloque Mux combina los valores de x / x 2 en una salida para que el bloque Scope grafique la respuesta de la simulación. 3. Establecer los parámetros de los bloques. El siguiente paso es establecer los parámetros de los bloques que ha creado. Objeto Parámetro Valor Sine Wave Sine Type Time based Time(t) Simulation use time. Amplitude Frequency rad/seg. Gain Gain 3 Gain2 Gain - 4 Gain3 Gain - 3 Add Icon shape Rectangular. List of signs Integrator External reset none Initial condition source interna. Initial condition 0 Integrator2 External reset none Initial condition source interna. Initial condition 0.5 Mux Number of inputs 2 Scope Number of axes Time range auto Tick labels Bottom axis only. Decimation 4. Establecer el tiempo de simulación. En la barra de herramientas seleccione Simulation Configuration Parameter. En la etiqueta Selec seleccione Solver. En la etiqueta Simulation time: en la casilla Star time, ingrese cero, en la casilla Stop time, ingrese 0, en la casilla Type, seleccione Variable-step y en la lista desplegable de Solver, seleccione ode45 (Dorman-Prince). Pulse OK. 5. Ejecutar el Modelo. Para ejecutar el Modelo, hay dos maneras de ejecutarlo: 3) En la ventana de Modelo de Simulink, seleccione Simulation Star. 4) Pulse el icono ejecutar en la barra de herramientas. Pulse dos veces el icono Scope de la Ventana de Modelo para ver la respuesta de la simulación, tal como aparece ilustrada en la figura 8.3. Universidad del Atlántico-Facultad de Ingeniería. 2
22 Figura 8.3 Respuesta de la simulación de la ecuación diferencial de segundo orden. Puede pulsar el botón Autoscale en la ventana de visualización del bloque Scope para obtener una mejor visualización de los gráficos. El siguiente código en MATLAB, realiza la misma simulación de la ecuación diferencial de segundo orden. >> Eq=inline('[y(2);-4*y(2)-3*y()+ 3*sin(t)]','t','y'); >> [t,y]=ode45(eq,[0:0.:0],[0 0.5]); >> plot(t,y(:,),'-d',t,y(:,2),'*r') Descripción de los bloques utilizados en los ejemplos. La Biblioteca User Defined Funtions a) Bloque Fcn f(u) Fcn El boque de expresión general. Use u cómo el nombre de la variable de entrada. Ejemplo: sin(u()*exp(2.3*( - u(2)))) b) Bloque Interpreted Matlab Fcn Interpreted MATLAB Fcn Interpreted MATLAB Function El bloque Interpreted Matlab Function, pasa los valores de entrada a una función de Matlab para evaluación. Ejemplo: sin, sin(u), foo(u(),u(2)). c) Bloque Interpreted Matlab Fcn u fcn MATLAB Function y El bloque MATLAB Function, se pueden escribir funciones de Matlab para usarlas en los modelos de Simulink. Se crea la función de MATLAB para ejecutar la simulación y genera el código para los objetivos de Simulink. Universidad del Atlántico-Facultad de Ingeniería. 22
23 El bloque Inport de la Biblioteca Sources. In El bloque Inport crea un puerto de entrada para subsistemas. El bloque Product de la Biblioteca Math Operations. Product El bloque Product, multiplica y divide escalares y no escalares o multiplica e invierte matrices. Por defecto, las salidas del bloque Product es el resultado de dos entradas: Dos escalares, un escalar y un no escalar o dos no escalares que tengan las mismas dimensiones. Los valores de los parámetros que especifica éste comportamiento son: Multiplication: Element-wise(.*) Number of inputs: 2 Ejemplo 8.5 Simulación de la ecuación de Van der Pol. Modele y simule la siguiente ecuación diferencial de segundo orden por el método de Runge Kutta de quinto orden: ( ) ( ) ( ) Donde es un parámetro escalar. Reduciendo el sistema de segundo orden. Expresando esta ecuación en un sistema de ecuaciones diferenciales de primer orden: ( ) y = y 2 = Suponga un valor de para. Solución:. Abrimos la Ventana de Modelo, pulsando el icono Stay on top De la biblioteca de Simulink, insertamos los siguientes bloques a la Ventana de Modelo, guardado con el nombre: Ejemplo8_5_simulink. Icono Biblioteca Cantidad Nombre f(u) User Defined Funtions Función definida por el usuario Fcn Product Math Operations Operaciones matemáticas Ganancia. Universidad del Atlántico-Facultad de Ingeniería Sustracción.
24 Gain Subtract s Integrator Scope Out 2. El próximo paso es conectar estos bloques como muestra la siguiente ilustración. y ECUACIÓN DE VAN DER POL (-u*u) Fcn Product Gain s Integrator y2 s y Integrator Out y2 Scope Y'' + (Y^2 - )Y' + Y =0 Y(0)=Y'(0)= 2 Out2 Cómo opera la simulación en el diagrama de bloques? El bloque Product, multiplica la expresión ( u*u) del bloque Fcn por la variable y 2 del bloque Integrator, esta nueva expresión es multiplicada por en el bloque Gain. El bloque Sum, realiza la operación de la expresión [ ( u*u)*y 2 y ]. El bloque Mux combina las variables y /y 2 en una sola salida para que el bloque Scope, grafique la respuesta de la simulación. Universidad del Atlántico-Facultad de Ingeniería. 24
25 3. Establecer los parámetros de los bloques. El siguiente paso es establecer los parámetros de los bloques que ha creado. Objeto Parámetro Valor Fcn Expression ( u*u) Sample time - Product Number of input 2 Gain Gain Sum List of signs - + Integrator Initial condition Integrator Initial condition Scope Number axes Mux List of input 2 4. Establecer el tiempo de simulación. En la barra de herramientas seleccione Simulation Configuration Parameter. En la etiqueta Selec seleccione Solver. En la etiqueta Simulation time: en la casilla Star time, ingrese cero, en la casilla Stop time, ingrese 0, en Max step size, ingrese 0, en Min step size, ingrese e 5, en la casilla Type, seleccione Variable-step y en la lista desplegable de Solver, seleccione ode45 (Dorman-Prince). Pulse OK. 5. Ejecutar el Modelo. Para ejecutar el Modelo, hay dos maneras de ejecutarlo: 5) En la ventana de Modelo de Simulink, seleccione Simulation Star. 6) Pulse el icono ejecutar en la barra de herramientas. Pulse dos veces el icono Scope de la Ventana de Modelo para ver la respuesta de la simulación, tal como aparece ilustrada en la figura 8.4. Figura 8.4 Respuesta de la simulación de la ecuación de Van der Pol. Puede pulsar el botón Autoscale en la ventana de visualización del bloque Scope para obtener una mejor visualización de los gráficos. El siguiente código en MATLAB, realiza la misma simulación de la ecuación de Van der Pol. >> Eq=inline('[y(2);(-y()^2)*y(2)-y()]','t','y'); >> [t,y]=ode45(eq,[0:0.0:0],[ ]); >> plot(t,y(:,),'--b',t,y(:,2),'-r') Universidad del Atlántico-Facultad de Ingeniería. 25
26 Ejemplo 8.6 Ingresando una expresión en el bloque Fcn Modele y simule la siguiente expresión matemática: ( ) ( ( ( )) ) 0 Solución:. Abrimos la Ventana de Modelo, pulsando el icono Stay on top De la biblioteca de Simulink, insertamos los siguientes bloques a la Ventana de Modelo, guardado con el nombre: Ejemplo8_6_simulink. Icono Biblioteca Cantidad Nombre Clock Sources Reloj f(u) Fcn User Defined Funtions Función Constant Commony Used Block 2 Valor Constante Product Gain Ganancia Suma o Resta Scope Osciloscopio 2. El próximo paso es conectar estos bloques como muestra la siguiente ilustración. Universidad del Atlántico-Facultad de Ingeniería. 26
27 Cómo opera la simulación en el diagrama de bloques? El bloque Clock determina el tiempo de simulación y se suministra a la expresión matemática definida por el usuario (bloque Fcn) y el bloque Product, la multiplica por el valor constante del bloque Constant, luego se multiplica por un Gain de 0. del bloque Gain. El bloque Sum, realiza la operación para que el bloque Scope visualice la respuesta de la simulación. 3. Establecer los parámetros de los bloques. El siguiente paso es establecer los parámetros de los bloques que ha creado. Objeto Parámetro Valor Clock Decimation 0 Fcn Expression exp(0.2*sin(3*u)) Constant Constant value 0. Constant Constant value 0. Product Number of inputs 2 Gain Gain Sum List of signs +- Scope Number of axes 4. Establecer el tiempo de simulación. En la barra de herramientas seleccione Simulation Configuration Parameter. En la etiqueta Selec seleccione Solver. En la etiqueta Simulation time: en la casilla Star time, ingrese cero, en la casilla Stop time, ingrese 0, en la casilla Type, seleccione Variable-step y en la lista desplegable de Solver, seleccione Discrete (no continuous states). Pulse OK. 5. Ejecutar el Modelo. Para ejecutar el Modelo, hay dos maneras de ejecutarlo: 7) En la ventana de Modelo de Simulink, seleccione Simulation Star. 8) Pulse el icono ejecutar en la barra de herramientas. Pulse dos veces el icono Scope de la Ventana de Modelo para ver la respuesta de la simulación, tal como aparece ilustrada en la figura 8.5. Figura 8.5 Respuesta de la simulación de la expresión matemática. Universidad del Atlántico-Facultad de Ingeniería. 27
28 Puede pulsar el botón Autoscale en la ventana de visualización del bloque Scope para obtener una mejor visualización de los gráficos. El siguiente código en MATLAB, realiza la misma simulación de la expresión matemática. >> t=0:0.:0; >> I= 0.*(exp(0.2*sin(3*t))-); >> plot(t,i,'--b') Universidad del Atlántico-Facultad de Ingeniería. 28
MÓDULO SOBRE PROGRAMACIÓN MATLAB
 8 MÓDULO SOBRE PROGRAMACIÓN MATLAB Francisco Muñoz Paba M.Sc 8 SIMULACIÓN DE SISTEMAS DINÁMICOS OBJETIVOS Al terminar éste módulo el estudiante estará en condiciones de: Utilizar y aplicar los diferentes
8 MÓDULO SOBRE PROGRAMACIÓN MATLAB Francisco Muñoz Paba M.Sc 8 SIMULACIÓN DE SISTEMAS DINÁMICOS OBJETIVOS Al terminar éste módulo el estudiante estará en condiciones de: Utilizar y aplicar los diferentes
MATLAB. (PARTE III) APLICACIONES EN CONTROL CON SIMULINK SIMULINK
 UNIVERSIDAD NACIONAL EXPERIMENTAL DEL TACHIRA DEPARTAMENTO DE INGENIERIA ELECTRONICA NUCLEO DE INSTRUMENTACION CONTROL Y SEÑALES LABORATORIO DE INSTRUMENTACION Y CONTROL MATLAB. (PARTE III) APLICACIONES
UNIVERSIDAD NACIONAL EXPERIMENTAL DEL TACHIRA DEPARTAMENTO DE INGENIERIA ELECTRONICA NUCLEO DE INSTRUMENTACION CONTROL Y SEÑALES LABORATORIO DE INSTRUMENTACION Y CONTROL MATLAB. (PARTE III) APLICACIONES
INTRODUCCION A SIMULINK
 INTRODUCCION A SIMULINK Simulink es un software que funciona bajo la plataforma de Matlab y es una herramienta muy útil para modelar, simular y analizar sistemas, tanto lineales como no lineales. Permite
INTRODUCCION A SIMULINK Simulink es un software que funciona bajo la plataforma de Matlab y es una herramienta muy útil para modelar, simular y analizar sistemas, tanto lineales como no lineales. Permite
Docente: Gabriel Rafael Lacayo Saballos Martes 15 de mayo de
 Tema: Aplicaciones de la simulación Industrial. Objetivo General: UNIVERSIDAD NACIONAL DE INGENIERÍA Conocer e implementar ejemplos usando el software Simulink. Objetivos Específicos del Laboratorio: Integrantes:
Tema: Aplicaciones de la simulación Industrial. Objetivo General: UNIVERSIDAD NACIONAL DE INGENIERÍA Conocer e implementar ejemplos usando el software Simulink. Objetivos Específicos del Laboratorio: Integrantes:
INFORMÁTICA MATLAB GUÍA 5 Simulink
 1. INTRODUCCIÓN Es un entorno de diagramas de bloques orientados a la simulación y generación de código en varios campos de la ciencia. Se pueden simular sistemas de tipo mecánico, eléctrico, electrónico
1. INTRODUCCIÓN Es un entorno de diagramas de bloques orientados a la simulación y generación de código en varios campos de la ciencia. Se pueden simular sistemas de tipo mecánico, eléctrico, electrónico
Creación de nuevo modelo en Simulink
 Creación de nuevo modelo en Para editar un modelo Abrir la ventana de un nuevo modelo Conectar los bloques Añadir bloques Cambiar el tamaño de los bloques Modificar etiquetas y añadir anotaciones Parametrizar
Creación de nuevo modelo en Para editar un modelo Abrir la ventana de un nuevo modelo Conectar los bloques Añadir bloques Cambiar el tamaño de los bloques Modificar etiquetas y añadir anotaciones Parametrizar
INTRODUCCION A SIMULINK
 INTRODUCCION A SIMULINK Matlab (Matrix Laboratory) es un sistema basado en matrices para realizar cálculos matemáticos y de ingeniería. Entre las múltiples herramientas que presenta este programa se encuentra
INTRODUCCION A SIMULINK Matlab (Matrix Laboratory) es un sistema basado en matrices para realizar cálculos matemáticos y de ingeniería. Entre las múltiples herramientas que presenta este programa se encuentra
Guía Para Utilizar Utilizar Simulink Nota: Para la siguiente guía se utilizó como base el programa Matlab 7.0
 Guía Para Utilizar Utilizar Simulink Nota: Para la siguiente guía se utilizó como base el programa Matlab 7.0 Una vez instalado el programa en el ordenador se tienen varias opciones de acceso a él: a)
Guía Para Utilizar Utilizar Simulink Nota: Para la siguiente guía se utilizó como base el programa Matlab 7.0 Una vez instalado el programa en el ordenador se tienen varias opciones de acceso a él: a)
Lab 1: Representación de señales en System Generator
 Introducción Objetivos Lab 1: Representación de señales en System Generator Este laboratorio guia al asistente a través de las herramientas System Generator y Simulink para analizar la representación de
Introducción Objetivos Lab 1: Representación de señales en System Generator Este laboratorio guia al asistente a través de las herramientas System Generator y Simulink para analizar la representación de
CURSO Introducción al modelado y análisis de Sistemas con SIMULINK
 CURSO 2013-2014 Introducción al modelado y análisis de Sistemas con SIMULINK k b x f(t) m Automatización y Control Ingeniería de Sistemas y Automática Universidad de Oviedo 0 Contenido 0 Contenido... 1
CURSO 2013-2014 Introducción al modelado y análisis de Sistemas con SIMULINK k b x f(t) m Automatización y Control Ingeniería de Sistemas y Automática Universidad de Oviedo 0 Contenido 0 Contenido... 1
Simulink. Capítulo Inicio de Simulink
 Capítulo 1 Simulink 1.1. Inicio de Simulink Para usar Simulink debemos estar trabajando con MATLAB. Simulink se puede iniciar con una pulsación en el icono de Simulink mostrado en la figura 17.1 y que
Capítulo 1 Simulink 1.1. Inicio de Simulink Para usar Simulink debemos estar trabajando con MATLAB. Simulink se puede iniciar con una pulsación en el icono de Simulink mostrado en la figura 17.1 y que
Práctica 2: Modelizado y Simulación de Sistemas No Lineales
 Práctica 2: Modelizado y Simulación de Sistemas No Lineales 1. Simulación con Simulink Simulink permite la simulación de sistemas, lineales y no lineales, haciendo uso de una interfaz gráfica basada en
Práctica 2: Modelizado y Simulación de Sistemas No Lineales 1. Simulación con Simulink Simulink permite la simulación de sistemas, lineales y no lineales, haciendo uso de una interfaz gráfica basada en
Lab 2: Sumador/Restador en System Generator
 Lab 2: Sumador/Restador en System Generator Introducción Objetivos Este laboratorio guia al asistente a través de las herramientas System Generator y Simulink para analizar la representación de números
Lab 2: Sumador/Restador en System Generator Introducción Objetivos Este laboratorio guia al asistente a través de las herramientas System Generator y Simulink para analizar la representación de números
Práctica 3.Simulación de sistemas
 Práctica 3.Simulación de sistemas OBJETIVOS DE LA PRÁCTICA 1. Conocer la herramienta Simulink y sus posibilidades para realizar simulaciones de sistemas. 2. Realizar la simulación de un sistema dinámico
Práctica 3.Simulación de sistemas OBJETIVOS DE LA PRÁCTICA 1. Conocer la herramienta Simulink y sus posibilidades para realizar simulaciones de sistemas. 2. Realizar la simulación de un sistema dinámico
TEORÍA DE SISTEMAS. Un ejemplo de representación de un sistema mediante Simulink sería el siguiente:
 TEORÍA DE SISTEMAS PRÁCTICA 2: INTRODUCCIÓN A SIMULINK 1. CARACTERÍSTICAS BÁSICAS DE SIMULINK Funcionalidad básica: simulación de sistemas dinámicos. Características principales: - Se trata de un entorno
TEORÍA DE SISTEMAS PRÁCTICA 2: INTRODUCCIÓN A SIMULINK 1. CARACTERÍSTICAS BÁSICAS DE SIMULINK Funcionalidad básica: simulación de sistemas dinámicos. Características principales: - Se trata de un entorno
Prácticas de Tecnología Electrónica. Tutorial de PSpice
 Prácticas de Tecnología Electrónica Iniciar PSpice y crear un proyecto Hacer clic en el menú Inicio Todos los programas PSpice Student Capture Student Figura 1: Vista inicial de PSpice Student. Una vez
Prácticas de Tecnología Electrónica Iniciar PSpice y crear un proyecto Hacer clic en el menú Inicio Todos los programas PSpice Student Capture Student Figura 1: Vista inicial de PSpice Student. Una vez
Guía para la realización de prácticas de Control
 Guía para la realización de prácticas de Control Ésta guía tiene la finalidad de asistir al alumno de Control en la resolución de prácticas de la materia. Las bases teóricas usadas en la misma están cubiertas
Guía para la realización de prácticas de Control Ésta guía tiene la finalidad de asistir al alumno de Control en la resolución de prácticas de la materia. Las bases teóricas usadas en la misma están cubiertas
CURSO Modelado y análisis de Sistemas con SIMULINK
 CURSO 2013-2014 Modelado y análisis de Sistemas con SIMULINK k b x f(t) m Automatización y Control Ingeniería de Sistemas y Automática Universidad de Oviedo 0 Contenido 0 Contenido... 1 1 MATLAB y SIMULINK...
CURSO 2013-2014 Modelado y análisis de Sistemas con SIMULINK k b x f(t) m Automatización y Control Ingeniería de Sistemas y Automática Universidad de Oviedo 0 Contenido 0 Contenido... 1 1 MATLAB y SIMULINK...
Simulación de sistemas con Simulink
 Curso: 2006/2007 Asignatura: Automatización de Procesos Industriales. Grupo: IOI Simulación de sistemas con Simulink 1.1 INTRODUCCIÓN A SIMULINK...2 1.1.1 CREACIÓN DE UN MODELO...3 1.2 SIMULACIÓN DE UN
Curso: 2006/2007 Asignatura: Automatización de Procesos Industriales. Grupo: IOI Simulación de sistemas con Simulink 1.1 INTRODUCCIÓN A SIMULINK...2 1.1.1 CREACIÓN DE UN MODELO...3 1.2 SIMULACIÓN DE UN
Análisis espectral de señales periódicas son Simulink
 1 Análisis espectral de señales periódicas son Simulink 2 3 8.1. Captura de un modelo Simulink es un entorno profesional de simulación, lo que quiere decir dos cosas: poco amigable y sus librerías son
1 Análisis espectral de señales periódicas son Simulink 2 3 8.1. Captura de un modelo Simulink es un entorno profesional de simulación, lo que quiere decir dos cosas: poco amigable y sus librerías son
Manual de Introducción a SIMULINK
 Manual de Introducción a SIMULINK Autor: José Ángel Acosta Rodríguez 2004 Capítulo Ejemplo.. Modelado de un sistema dinámico En este ejemplo se realizará el modelado de un sistema dinámico muy sencillo.
Manual de Introducción a SIMULINK Autor: José Ángel Acosta Rodríguez 2004 Capítulo Ejemplo.. Modelado de un sistema dinámico En este ejemplo se realizará el modelado de un sistema dinámico muy sencillo.
PRÁCTICA Nº 2 INTRODUCCIÓN A SIMULINK DE MATLAB
 UNIVERSIDAD NACIONAL EXPERIMENTAL FRANCISCO DE MIRANDA COMPLEJO ACADÉMICO EL SABINO PROGRAMA DE INGENIERÍA QUÍMICA DPTO DE MECÁNICA Y TECNOLOGÍA DE LA PRODUCCIÓN DINÁMICA Y CONTROL DE PROCESOS PRÁCTICA
UNIVERSIDAD NACIONAL EXPERIMENTAL FRANCISCO DE MIRANDA COMPLEJO ACADÉMICO EL SABINO PROGRAMA DE INGENIERÍA QUÍMICA DPTO DE MECÁNICA Y TECNOLOGÍA DE LA PRODUCCIÓN DINÁMICA Y CONTROL DE PROCESOS PRÁCTICA
Teoría de Sistemas y Señales
 Teoría de Sistemas y Señales Problemas Propuestos Serie 5 Descripción: Análisis de Sistemas Lineales Estacionarios en TC en el dominio Transformado de Laplace. Álgebra de bloques. 1. Obtenga la Transformada
Teoría de Sistemas y Señales Problemas Propuestos Serie 5 Descripción: Análisis de Sistemas Lineales Estacionarios en TC en el dominio Transformado de Laplace. Álgebra de bloques. 1. Obtenga la Transformada
PRÁCTICA Nº 1 INTRODUCCIÓN A MATLAB TOOLBOX DE CONTROL Y SIMULINK
 UNIVERSIDAD NACIONAL EXPERIMENTAL FRANCISCO DE MIRANDA COMPLEJO ACADÉMICO EL SABINO PROGRAMA DE INGENIERÍA QUÍMICA DPTO DE MECÁNICA Y TECNOLOGÍA DE LA PRODUCCIÓN DINÁMICA Y CONTROL DE PROCESOS PRÁCTICA
UNIVERSIDAD NACIONAL EXPERIMENTAL FRANCISCO DE MIRANDA COMPLEJO ACADÉMICO EL SABINO PROGRAMA DE INGENIERÍA QUÍMICA DPTO DE MECÁNICA Y TECNOLOGÍA DE LA PRODUCCIÓN DINÁMICA Y CONTROL DE PROCESOS PRÁCTICA
Seminario de Simulink/WinCon
 Seminario de Simulink/WinCon INEL5508 - Control Digital Jesús David González-Llorente Universidad De Puerto Rico Recinto Universitario De Mayagüez Departamento de Ingeniería Eléctrica y de Computadoras
Seminario de Simulink/WinCon INEL5508 - Control Digital Jesús David González-Llorente Universidad De Puerto Rico Recinto Universitario De Mayagüez Departamento de Ingeniería Eléctrica y de Computadoras
Introducción a MATLAB y LabVIEW
 Facultad: Ingeniería Escuela: Ingeniería Biomédica Asignatura: Procesamiento de Señales Biomédicas Introducción a MATLAB y LabVIEW Objetivo. Realizar operaciones básicas en el lenguaje de programación
Facultad: Ingeniería Escuela: Ingeniería Biomédica Asignatura: Procesamiento de Señales Biomédicas Introducción a MATLAB y LabVIEW Objetivo. Realizar operaciones básicas en el lenguaje de programación
3 y un vector Y 2 que contenga el cálculo de Y2 = 4X
 Laboratorio 1. Introducción a MATLAB y Simulink. 1. Uso de MATLAB. Manejo de Vectores y Matrices: Usando el editor de MATLAB, escriba el código necesario para generar: a. Vectores (1x1) (3x1) y (1x7),
Laboratorio 1. Introducción a MATLAB y Simulink. 1. Uso de MATLAB. Manejo de Vectores y Matrices: Usando el editor de MATLAB, escriba el código necesario para generar: a. Vectores (1x1) (3x1) y (1x7),
PRÁCTICA N 1 INTRODUCCIÒN A MATLAB Y UTILIZACIÓN DE LAS MATEMÁTICAS COMO HERRAMIENTAS PRIMORDIAL EN EL ANÁLISIS DE SISTEMAS DE CONTROL
 UNIVERSIDAD NACIONAL EXPERIMENTAL FRANCISCO DE MIRANDA COMPLEJO ACADÉMICO EL SABINO PROGRAMA DE INGENIERÍA QUÍMICA DPTO DE MECÁNICA Y TECNOLOGÍA DE LA PRODUCCIÓN LABORATORIO DE DINÁMICA Y CONTROL DE PROCESOS
UNIVERSIDAD NACIONAL EXPERIMENTAL FRANCISCO DE MIRANDA COMPLEJO ACADÉMICO EL SABINO PROGRAMA DE INGENIERÍA QUÍMICA DPTO DE MECÁNICA Y TECNOLOGÍA DE LA PRODUCCIÓN LABORATORIO DE DINÁMICA Y CONTROL DE PROCESOS
UNIVERSIDAD NACIONAL DE INGENIERÍA Departamento de Lenguajes y Simulación Guía de laboratorio I
 Tema: Uso del software MATLAB para graficar Funciones. Objetivo General: Conocer e implementar Funciones Lineales en MATLAB. Objetivos Específicos del Laboratorio: Integrantes: 1. Conocer el software MATLAB.
Tema: Uso del software MATLAB para graficar Funciones. Objetivo General: Conocer e implementar Funciones Lineales en MATLAB. Objetivos Específicos del Laboratorio: Integrantes: 1. Conocer el software MATLAB.
Operaciones básicas con hojas de cálculo
 Operaciones básicas con hojas de cálculo Insertar hojas de cálculo. Para insertar rápidamente una hoja de cálculo nueva al final de las hojas de cálculo existentes, haga clic en la ficha Insertar hoja
Operaciones básicas con hojas de cálculo Insertar hojas de cálculo. Para insertar rápidamente una hoja de cálculo nueva al final de las hojas de cálculo existentes, haga clic en la ficha Insertar hoja
MODULO 1 - EXCEL BÁSICO
 SELECCIÓN Selección de una celda Para seleccionar una única celda sólo tienes que hacer clic sobre la celda. Selección de un rango de celdas Continuas: Seleccione la primera celda y con clic sostenido
SELECCIÓN Selección de una celda Para seleccionar una única celda sólo tienes que hacer clic sobre la celda. Selección de un rango de celdas Continuas: Seleccione la primera celda y con clic sostenido
INDICE PARTE I AMBIENTE DE TRABAJO Instalación de Winplot 1.2. Conociendo Winplot Ambiente de trabajo. 1.4.
 INDICE PARTE I AMBIENTE DE TRABAJO 1.1. Instalación de Winplot 1.2. Conociendo Winplot. 1.3. Ambiente de trabajo. 1.4. Barra de menú PARTE II CONSTRUCCIÓN DE GRÁFICAS 2.1. Ubicación de una coordenada x,y
INDICE PARTE I AMBIENTE DE TRABAJO 1.1. Instalación de Winplot 1.2. Conociendo Winplot. 1.3. Ambiente de trabajo. 1.4. Barra de menú PARTE II CONSTRUCCIÓN DE GRÁFICAS 2.1. Ubicación de una coordenada x,y
Manual de usuario MetaTrader 4 TraderNovo:
 Manual de usuario MetaTrader 4 TraderNovo: Aquí está una foto que muestra la pantalla principal MT4: Menú principal (acceder al menú y los ajustes del programa); Barras de herramientas (acceso rápido a
Manual de usuario MetaTrader 4 TraderNovo: Aquí está una foto que muestra la pantalla principal MT4: Menú principal (acceder al menú y los ajustes del programa); Barras de herramientas (acceso rápido a
Profesor(a): Ing. Miriam Cerón Brito
 Área Académica: Informática Tema: Hoja electrónica Profesor(a): Ing. Miriam Cerón Brito Periodo: Enero Junio 2014 Abstract: This presentation show the spreadsheet's characteristics and show the principals
Área Académica: Informática Tema: Hoja electrónica Profesor(a): Ing. Miriam Cerón Brito Periodo: Enero Junio 2014 Abstract: This presentation show the spreadsheet's characteristics and show the principals
SIMULACIÓN DE CIRCUITOS EN RÉGIMEN TRANSITORIO Y CORRIENTE ALTERNA
 SIMULACIÓN DE CIRCUITOS EN RÉGIMEN TRANSITORIO Y CORRIENTE ALTERNA 4.1. Medidas con el osciloscopio El osciloscopio es un instrumento que sirve para visualizar señales periódicas. Nos permite, entre otras
SIMULACIÓN DE CIRCUITOS EN RÉGIMEN TRANSITORIO Y CORRIENTE ALTERNA 4.1. Medidas con el osciloscopio El osciloscopio es un instrumento que sirve para visualizar señales periódicas. Nos permite, entre otras
Computación Aplicada. Universidad de Las Américas. Aula virtual de Computación Aplicada. Módulo de Excel 2013 LIBRO 6
 Computación Aplicada Universidad de Las Américas Aula virtual de Computación Aplicada Módulo de Excel 2013 LIBRO 6 Contenido FORMA DE HACER CÁLCULOS... 3 QUÉ SON LAS FÓRMULAS Y QUÉ LAS FUNCIONES?... 4
Computación Aplicada Universidad de Las Américas Aula virtual de Computación Aplicada Módulo de Excel 2013 LIBRO 6 Contenido FORMA DE HACER CÁLCULOS... 3 QUÉ SON LAS FÓRMULAS Y QUÉ LAS FUNCIONES?... 4
1.1 Experimentación y simulación con un servomecanismo
 1.1 Experimentación y simulación con un servomecanismo El objetivo de esta práctica es tener un primer contacto con un sistema real, observando y midiendo su comportamiento dinámico, y comparando los resultados
1.1 Experimentación y simulación con un servomecanismo El objetivo de esta práctica es tener un primer contacto con un sistema real, observando y midiendo su comportamiento dinámico, y comparando los resultados
SimPowerSystems. Los componentes utilizados son agrupados en la librería denominado powerlib. Pasos para implementar el modelo
 SimPowerSystems Introducción Es una herramienta de MATLAB que trabaja en entorno Simulink, el cual nos permite construir modelos que simulan un Sistema de Potencia Eléctrico. Un Sistema de Potencia Eléctrico,
SimPowerSystems Introducción Es una herramienta de MATLAB que trabaja en entorno Simulink, el cual nos permite construir modelos que simulan un Sistema de Potencia Eléctrico. Un Sistema de Potencia Eléctrico,
CONTROL DE PROCESOS QUÍMICOS
 UNIVERSIDAD NACIONAL EXPERIMENTAL POLITECNICA ANTONIO JOSÉ DE SUCRE VICERRECTORADO BARQUISIMETO DEPARTAMENTO DE INGENIERÍA QUÍMICA CONTROL DE PROCESOS QUÍMICOS Prof: Ing. (MSc). Juan Enrique Rodríguez
UNIVERSIDAD NACIONAL EXPERIMENTAL POLITECNICA ANTONIO JOSÉ DE SUCRE VICERRECTORADO BARQUISIMETO DEPARTAMENTO DE INGENIERÍA QUÍMICA CONTROL DE PROCESOS QUÍMICOS Prof: Ing. (MSc). Juan Enrique Rodríguez
INTRODUCCIÓN A XCOS (SCILAB)
 CACHEME.ORG INTRODUCCIÓN A XCOS (SCILAB) CREACIÓN Y RESOLUCIÓN DE MODELOS CON XCOS (SCILAB) Noviembre 2012 www.cacheme.org Índice de Contenido 1. NOTA... 2 2. INTRODUCCIÓN.... 2 3. Superbloques y Enmascaramiento
CACHEME.ORG INTRODUCCIÓN A XCOS (SCILAB) CREACIÓN Y RESOLUCIÓN DE MODELOS CON XCOS (SCILAB) Noviembre 2012 www.cacheme.org Índice de Contenido 1. NOTA... 2 2. INTRODUCCIÓN.... 2 3. Superbloques y Enmascaramiento
Practica No. 2 MODELADO DE UN MOTOR DC. Pontificia Universidad Javeriana Facultad de Ingeniería Departamento de Electrónica Laboratorio de Control
 Practica No. 2 MODELADO DE UN MOTOR DC Pontificia Universidad Javeriana Facultad de Ingeniería Departamento de Electrónica Laboratorio de Control 1. Introducción En esta práctica se realiza la formulación
Practica No. 2 MODELADO DE UN MOTOR DC Pontificia Universidad Javeriana Facultad de Ingeniería Departamento de Electrónica Laboratorio de Control 1. Introducción En esta práctica se realiza la formulación
Práctica N 2 Simulink como herramienta para resolver ecuaciones diferenciales
 Universidad Simón Bolívar Ingeniería Electrónica SEÑALES Y SISTEMAS I Práctica N Simulink como herramienta para resolver ecuaciones diferenciales Preparación Revisar el help que sobre Simulink tiene Matlab
Universidad Simón Bolívar Ingeniería Electrónica SEÑALES Y SISTEMAS I Práctica N Simulink como herramienta para resolver ecuaciones diferenciales Preparación Revisar el help que sobre Simulink tiene Matlab
CONTROLADORES DE CANCELACIÓN I Controladores de tiempo mínimo
 SISTEMAS DE CONTROL PRÁCTICAS DE SISTEMAS DE CONTROL CONTROLADORES DE CANCELACIÓN I Controladores de tiempo mínimo 1. OBJETIVOS Los objetivos de esta práctica son: Diseñar y estudiar el funcionamiento
SISTEMAS DE CONTROL PRÁCTICAS DE SISTEMAS DE CONTROL CONTROLADORES DE CANCELACIÓN I Controladores de tiempo mínimo 1. OBJETIVOS Los objetivos de esta práctica son: Diseñar y estudiar el funcionamiento
Integrador, realimentación y control
 Prctica 1 Integrador, realimentación y control El programa Simulink es un programa incluido dentro de Matlab que sirve para realizar la integración numérica de ecuaciones diferenciales a efectos de simular
Prctica 1 Integrador, realimentación y control El programa Simulink es un programa incluido dentro de Matlab que sirve para realizar la integración numérica de ecuaciones diferenciales a efectos de simular
DINAMICA POBLACIONAL. DINAMICA DE SISTEMAS EJERCICIOS - Juan Martín García 87
 DINAMICA POBLACIONAL Una población se halla formada inicialmente por 1000 individuos, su tasa de natalidad es del 5% semanal, y su esperanza media de vida es de 100 semanas. No hay migraciones y la distribución
DINAMICA POBLACIONAL Una población se halla formada inicialmente por 1000 individuos, su tasa de natalidad es del 5% semanal, y su esperanza media de vida es de 100 semanas. No hay migraciones y la distribución
2 MATLAB para mecatrónica. Alfaomega. Material Web. Simulink 2 GUIDE 15
 2 MATLAB para mecatrónica Capítulo Material Web Simulink 2 GUIDE 15 2 MATLAB para mecatrónica 2.1. 2.1 Simulink Simulink es un ambiente interactivo de programación de bloques para modelar y simular una
2 MATLAB para mecatrónica Capítulo Material Web Simulink 2 GUIDE 15 2 MATLAB para mecatrónica 2.1. 2.1 Simulink Simulink es un ambiente interactivo de programación de bloques para modelar y simular una
PRACTICA 1 LABORATORIO DE INGENIERÍA DE SISTEMAS INTRODUCCIÓN A MATLAB
 PRACTICA 1 LABORATORIO DE INGENIERÍA DE SISTEMAS INTRODUCCIÓN A MATLAB Introducción a Matlab 1 1. Introducción El objetivo de esta práctica es adquirir los conocimientos básicos para familiarizarse con
PRACTICA 1 LABORATORIO DE INGENIERÍA DE SISTEMAS INTRODUCCIÓN A MATLAB Introducción a Matlab 1 1. Introducción El objetivo de esta práctica es adquirir los conocimientos básicos para familiarizarse con
AUTOMATIZACIÓN INDUSTRIAL INTRODUCCIÓN AL PROGRAMA SIMULINK
 3º INGENIERÍA TÉCNICA INDUSTRIAL, ESPECIALIDAD MECÁNICA AUTOMATIZACIÓN INDUSTRIAL PRÁCTICA 7 INTRODUCCIÓN AL PROGRAMA SIMULINK 1 1. CARACTERÍSTICAS BÁSICAS DE SIMULINK Funcionalidad básica: simulación
3º INGENIERÍA TÉCNICA INDUSTRIAL, ESPECIALIDAD MECÁNICA AUTOMATIZACIÓN INDUSTRIAL PRÁCTICA 7 INTRODUCCIÓN AL PROGRAMA SIMULINK 1 1. CARACTERÍSTICAS BÁSICAS DE SIMULINK Funcionalidad básica: simulación
GUÍA USO DE REGLA Y COMPÁS
 GUÍA USO DE REGLA Y COMPÁS Esta es una guía que presenta los procedimientos esenciales que le permitirán aprender a utilizar el procesador geométrico Regla y Compás: ingreso al software, descripción de
GUÍA USO DE REGLA Y COMPÁS Esta es una guía que presenta los procedimientos esenciales que le permitirán aprender a utilizar el procesador geométrico Regla y Compás: ingreso al software, descripción de
Insertando Texto Dinámico y Estático en la Ventana Gráfica de GeoGebra
 Insertando Texto Dinámico y Estático en la Ventana Gráfica de GeoGebra GeoGebra Manual Taller 5 Judith and Markus Hohenwarter www.geogebra.org Traducción y adaptación María Asunción Montes Tabla de Contenido
Insertando Texto Dinámico y Estático en la Ventana Gráfica de GeoGebra GeoGebra Manual Taller 5 Judith and Markus Hohenwarter www.geogebra.org Traducción y adaptación María Asunción Montes Tabla de Contenido
Figura 61: Barras de Herramientas para la edición de Formularios
 1. FORMULARIOS Un documento estándar muestra información: una carta o reporte, por ejemplo. Típicamente el lector tiende a modificar algo o nada. Un formulario tiene secciones que no pueden modificarse
1. FORMULARIOS Un documento estándar muestra información: una carta o reporte, por ejemplo. Típicamente el lector tiende a modificar algo o nada. Un formulario tiene secciones que no pueden modificarse
Mathematics 4.0 Microsoft Mathematics 4.0
 Mathematics 4.0 Microsoft Mathematics 4.0 Es una aplicación para profesores de matemáticas y ciencias que brinda una forma útil y potente para introducir los conceptos a sus alumnos. Esta aplicación de
Mathematics 4.0 Microsoft Mathematics 4.0 Es una aplicación para profesores de matemáticas y ciencias que brinda una forma útil y potente para introducir los conceptos a sus alumnos. Esta aplicación de
ACTIVIDADES PEDAGÓGICAS: lee el material que se te presenta a continuación y responde estas preguntas en tu cuaderno:
 ACTIVIDADES PEDAGÓGICAS: lee el material que se te presenta a continuación y responde estas preguntas en tu cuaderno: 1. Qué son los accesorios de Windows? 2. Dónde encuentro los accesorios de Windows?
ACTIVIDADES PEDAGÓGICAS: lee el material que se te presenta a continuación y responde estas preguntas en tu cuaderno: 1. Qué son los accesorios de Windows? 2. Dónde encuentro los accesorios de Windows?
CLASE 1 INTRODUCCIÓN A MATLAB
 Prof. Alexander Hoyo Clase 1 Introducción a MATLAB pág. 1 de 12 CLASE 1 INTRODUCCIÓN A MATLAB MATLAB es un software de computación técnica de alto nivel que integra cómputo, visualización y programación
Prof. Alexander Hoyo Clase 1 Introducción a MATLAB pág. 1 de 12 CLASE 1 INTRODUCCIÓN A MATLAB MATLAB es un software de computación técnica de alto nivel que integra cómputo, visualización y programación
. Manual General para el Uso del Software Graphmatica.
 1. Manual General para el Uso del Software Graphmatica. http://www.graphmatica.com/espanol/grmat0n.html Graphmatica es un software de uso libre muy fácil de utilizar y que puede ser descargado de Internet
1. Manual General para el Uso del Software Graphmatica. http://www.graphmatica.com/espanol/grmat0n.html Graphmatica es un software de uso libre muy fácil de utilizar y que puede ser descargado de Internet
DINAMICA POBLACIONAL. Podemos observar que hay un bucle positivo (nacimientos población) y otro bucle este negativo (población defunciones)..
 DINAMICA POBLACIONAL Una población se halla formada inicialmente por 1000 individuos, su tasa de natalidad es del 5% semanal, y su esperanza media de vida es de 100 semanas. No hay migraciones y la distribución
DINAMICA POBLACIONAL Una población se halla formada inicialmente por 1000 individuos, su tasa de natalidad es del 5% semanal, y su esperanza media de vida es de 100 semanas. No hay migraciones y la distribución
4.1 Conceptos Básicos de Matlab. Matlab es creado por The MathWorks, el cual es un idioma de alto rendimiento
 MATLAB CAPÍTULO 4 Realización Activa en 4.1 Conceptos Básicos de es creado por The MathWorks, el cual es un idioma de alto rendimiento para la informática técnica. Integra cómputo, visualización, y programación
MATLAB CAPÍTULO 4 Realización Activa en 4.1 Conceptos Básicos de es creado por The MathWorks, el cual es un idioma de alto rendimiento para la informática técnica. Integra cómputo, visualización, y programación
GUIA DE USO GRAPHMATICA
 GUIA DE USO GRAPHMATICA Ingreso de funciones a. El ingreso de funciones se hace en el renglón blanco de entrada. Autor: Gustavo Rodriguez Para ingresar una ecuación se puede realizar en la forma explícita
GUIA DE USO GRAPHMATICA Ingreso de funciones a. El ingreso de funciones se hace en el renglón blanco de entrada. Autor: Gustavo Rodriguez Para ingresar una ecuación se puede realizar en la forma explícita
Dirección de Tecnologías de Información DTI PUCP. Creación de pregunta calculada de opción múltiple - sincronizada
 Dirección de Tecnologías de Información DTI PUCP Creación de pregunta calculada de opción múltiple - sincronizada Las preguntas calculadas de opción múltiple son similares a las preguntas de opción múltiple,
Dirección de Tecnologías de Información DTI PUCP Creación de pregunta calculada de opción múltiple - sincronizada Las preguntas calculadas de opción múltiple son similares a las preguntas de opción múltiple,
Figura 17 Barra de iconos
 2. MANEJO DE HERRAMIENTAS AVANZADAS 2.1.Ordenamiento Especifica los criterios de clasificación para visualizar los datos. Para acceder a este comando de un clic en el Símbolo Ordenar en las barras de base
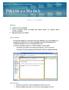
2. MANEJO DE HERRAMIENTAS AVANZADAS 2.1.Ordenamiento Especifica los criterios de clasificación para visualizar los datos. Para acceder a este comando de un clic en el Símbolo Ordenar en las barras de base
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO ESCUELA NACIONAL COLEGIO DE CIENCIAS Y HUMANIDADES MATERIA: TALLER DE CÓMPUTO MATERIAL DE APOYO
 UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO ESCUELA NACIONAL COLEGIO DE CIENCIAS Y HUMANIDADES MATERIA: TALLER DE CÓMPUTO MATERIAL DE APOYO NOMENCLATURA : NOMBRE: M U VI-18 Práctica Construcciones geométricas
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO ESCUELA NACIONAL COLEGIO DE CIENCIAS Y HUMANIDADES MATERIA: TALLER DE CÓMPUTO MATERIAL DE APOYO NOMENCLATURA : NOMBRE: M U VI-18 Práctica Construcciones geométricas
2.2 CREAR TABLAS Y GRÁFICOS.
 2.2 CREAR TABLAS Y GRÁFICOS. INSERTAR UNA TABLA Y DARLE FORMATO La forma más habitual de comenzar a trabajar con tablas es a través de la ficha Insertar, tabla. A continuación Word le ofrece las siguientes
2.2 CREAR TABLAS Y GRÁFICOS. INSERTAR UNA TABLA Y DARLE FORMATO La forma más habitual de comenzar a trabajar con tablas es a través de la ficha Insertar, tabla. A continuación Word le ofrece las siguientes
TRABAJO DE EXCEL 1. QUÉ ES UNA FÓRMULA EN EXCEL?
 TRABAJO DE EXCEL 1. QUÉ ES UNA FÓRMULA EN EXCEL? Las fórmulas en Excel son expresiones que se utilizan para realizar cálculos o procesamiento de valores, produciendo un nuevo valor que será asignado a
TRABAJO DE EXCEL 1. QUÉ ES UNA FÓRMULA EN EXCEL? Las fórmulas en Excel son expresiones que se utilizan para realizar cálculos o procesamiento de valores, produciendo un nuevo valor que será asignado a
LABORATORIO DE CIRCUITOS ELÉCTRICOS PRÁCTICA N 8 SIMULACIÓN: RESPUESTA EN CIRCUITOS DE PRIMER Y SEGUNDO ORDEN
 FACULTAD DE INGENIERÍA ELÉCTRICA Y ELECTRÓNICA Carrera de Ingeniería Electrónica y Control Carrera de Ingeniería Electrónica y Telecomunicaciones Carrera de Ingeniería Electrónica y Redes de Información
FACULTAD DE INGENIERÍA ELÉCTRICA Y ELECTRÓNICA Carrera de Ingeniería Electrónica y Control Carrera de Ingeniería Electrónica y Telecomunicaciones Carrera de Ingeniería Electrónica y Redes de Información
Introducción al MATLAB
 Introducción al MATLAB Dr. Luis Javier Morales Mendoza FIEC Universidad Veracruzana Poza Rica - Tuxpan Índice 1. Introducción al Matlab 2. Operaciones Aritméticas 3. Vectores y Matrices 4. Funciones Matemáticas
Introducción al MATLAB Dr. Luis Javier Morales Mendoza FIEC Universidad Veracruzana Poza Rica - Tuxpan Índice 1. Introducción al Matlab 2. Operaciones Aritméticas 3. Vectores y Matrices 4. Funciones Matemáticas
Arreglos y Clusters MATRICES: CLUSTERS: Creación de matrices y clusters con controles e indicadores.
 Arreglos y Clusters Vamos a examinar la variedad y tipos de arreglos de datos y le da una introducción a la creación y manipulación de matrices y clusters. MATRICES: Una matriz, que se compone de elementos
Arreglos y Clusters Vamos a examinar la variedad y tipos de arreglos de datos y le da una introducción a la creación y manipulación de matrices y clusters. MATRICES: Una matriz, que se compone de elementos
Centro de Bachillerato Tecnológico. Manual de prácticas. Visual Basic 6.0. Nivel Básico. Industrial y de servicios No. 231.
 Centro de Bachillerato Tecnológico Industrial y de servicios No. 231 Manual de prácticas de Visual Basic 6.0 Nivel Básico Profesor: Lic. Leonel Orozco Celaya [email protected] Guía de prácticas I Prof.
Centro de Bachillerato Tecnológico Industrial y de servicios No. 231 Manual de prácticas de Visual Basic 6.0 Nivel Básico Profesor: Lic. Leonel Orozco Celaya [email protected] Guía de prácticas I Prof.
Diagramación digital
 Diagramación digital CONTENIDO GUÍAS GUÍA 1 GUÍA 2 GUÍA 3 GUÍA 4 GUÍA 5 GUÍA 6 GUÍA 7 GUÍA 8 GUÍA 9 y 10 GUÍA 1 INTRODUCCIÓN Contenidos Presentación de la planificación. Presentación de la plataforma
Diagramación digital CONTENIDO GUÍAS GUÍA 1 GUÍA 2 GUÍA 3 GUÍA 4 GUÍA 5 GUÍA 6 GUÍA 7 GUÍA 8 GUÍA 9 y 10 GUÍA 1 INTRODUCCIÓN Contenidos Presentación de la planificación. Presentación de la plataforma
MANUAL AVANZADO DE SIMULINK PARA LA ASIGNATURA FUNDAMENTOS DE AUTOMÁTICA. ESCUELA DE INGENIERÍAS INDUSTRIALES. UNIVERSIDAD DE VALLADOLID.
 MANUAL AVANZADO DE SIMULINK PARA LA ASIGNATURA FUNDAMENTOS DE AUTOMÁTICA. ESCUELA DE INGENIERÍAS INDUSTRIALES. UNIVERSIDAD DE VALLADOLID. Documento original: Manual de simulink para la asignatura de teoría
MANUAL AVANZADO DE SIMULINK PARA LA ASIGNATURA FUNDAMENTOS DE AUTOMÁTICA. ESCUELA DE INGENIERÍAS INDUSTRIALES. UNIVERSIDAD DE VALLADOLID. Documento original: Manual de simulink para la asignatura de teoría
LA HOJA DE CÁLCULO HOJA DE CÁLCULO:
 LA HOJA DE CÁLCULO HOJA DE CÁLCULO: es una herramienta que permite realizar cálculos u operaciones matemáticas, estadísticas financieras y de tabla de base de datos. También se pueden crear y extraer gráficos
LA HOJA DE CÁLCULO HOJA DE CÁLCULO: es una herramienta que permite realizar cálculos u operaciones matemáticas, estadísticas financieras y de tabla de base de datos. También se pueden crear y extraer gráficos
analizar y estudiar las herramientas que MatLab ofrece para realizar la simulación del
 CAPÍTULO 4 Herramientas de MatLab Una vez que se ha estudiado y se conocen tanto las características del robot, como la teoría de los sistemas de control así como la teoría de la lógica difusa, es momento
CAPÍTULO 4 Herramientas de MatLab Una vez que se ha estudiado y se conocen tanto las características del robot, como la teoría de los sistemas de control así como la teoría de la lógica difusa, es momento
MÁSTER OFICIAL EN SISTEMAS ELECTRÓNICOS AVANZADOS, SISTEMAS INTELIGENTES. Asignatura: Convertidores Avanzados de Potencia.
 MÁSTER OFICIAL EN SISTEMAS ELECTRÓNICOS AVANZADOS, SISTEMAS INTELIGENTES Asignatura: Convertidores Avanzados de Potencia Práctica 0 Introducción al Matlab/SIMULINK y análisis de potencia 1.- OBJETIVOS.
MÁSTER OFICIAL EN SISTEMAS ELECTRÓNICOS AVANZADOS, SISTEMAS INTELIGENTES Asignatura: Convertidores Avanzados de Potencia Práctica 0 Introducción al Matlab/SIMULINK y análisis de potencia 1.- OBJETIVOS.
Introducción al manejo de Simuladores
 Facultad de Ciencias Exactas y Tecnología - UNT Introducción al manejo de Simuladores Microcap 10 Autor: Ing. Miguel Valdez Edición: Ing. Marcelo Abdala 28/03/2012 Simulación de Circuitos Eléctricos INTRODUCCIÓN
Facultad de Ciencias Exactas y Tecnología - UNT Introducción al manejo de Simuladores Microcap 10 Autor: Ing. Miguel Valdez Edición: Ing. Marcelo Abdala 28/03/2012 Simulación de Circuitos Eléctricos INTRODUCCIÓN
Profesor: Marcelo Rebellato. Teórico 3. Teclado
 Profesor: Marcelo Rebellato Teórico 3 Teclado Repaso Cerrar: Permite cerrar la ventana, cuadro de diálogo u aplicación abierta. Si la misma es un programa donde el usuario realizo actividades que no guardo,
Profesor: Marcelo Rebellato Teórico 3 Teclado Repaso Cerrar: Permite cerrar la ventana, cuadro de diálogo u aplicación abierta. Si la misma es un programa donde el usuario realizo actividades que no guardo,
3 HERRAMIENTAS PARA CIRCUITOS DE CA. Objetivo
 3 Muchos circuitos electrónicos operan con corriente alterna (CA). El diseño de circuitos requiere usar herramientas para medir componentes e impedancias, así como para el despliegue del comportamiento
3 Muchos circuitos electrónicos operan con corriente alterna (CA). El diseño de circuitos requiere usar herramientas para medir componentes e impedancias, así como para el despliegue del comportamiento
Cátedra: Fundamentos de Informática para Ingeniería Química. Introducción al manejo de Matlab 6.5
 Cátedra: Fundamentos de Informática para Ingeniería Química Introducción al manejo de Matlab 6.5 Introducción al manejo de Matlab 6.5 Matlab se puede inicializar como cualquier otra aplicación de Windows,
Cátedra: Fundamentos de Informática para Ingeniería Química Introducción al manejo de Matlab 6.5 Introducción al manejo de Matlab 6.5 Matlab se puede inicializar como cualquier otra aplicación de Windows,
Microsoft Office XP Excel XP (III)
 PRÁCTICA 3 HOJA DE CÁLCULO Microsoft Office XP Excel XP (III) 1. Escenarios. Con esta herramienta de análisis es posible evaluar distintas estrategias para comparar y ajustar distintos datos o resultados.
PRÁCTICA 3 HOJA DE CÁLCULO Microsoft Office XP Excel XP (III) 1. Escenarios. Con esta herramienta de análisis es posible evaluar distintas estrategias para comparar y ajustar distintos datos o resultados.
Generalidades sobre Excel
 Generalidades sobre Excel Temas Introducción Funciones Suma, Promedio, Max, Min, etc Gráficos Introducción Al ingresar a Excel aparece una hoja de cálculo, que permite tratar datos que pueden organizarse
Generalidades sobre Excel Temas Introducción Funciones Suma, Promedio, Max, Min, etc Gráficos Introducción Al ingresar a Excel aparece una hoja de cálculo, que permite tratar datos que pueden organizarse
CALCULO GRADO EN INGEN. INFORM. DEL SOFTWARE PRACTICA 1. INTRODUCCIÓN A MATLAB
 CALCULO GRADO EN INGEN. INFORM. DEL SOFTWARE. 12-13 PRACTICA 1. INTRODUCCIÓN A MATLAB Qué es MATLAB? MATLAB es la abreviatura de MATrix LABoratory (laboratorio de matrices). Se trata de un software matemático
CALCULO GRADO EN INGEN. INFORM. DEL SOFTWARE. 12-13 PRACTICA 1. INTRODUCCIÓN A MATLAB Qué es MATLAB? MATLAB es la abreviatura de MATrix LABoratory (laboratorio de matrices). Se trata de un software matemático
Nos muestra el contenido de la celda activa, es decir, la casilla donde estamos situados.
 La barra de fórmulas Nos muestra el contenido de la celda activa, es decir, la casilla donde estamos situados. La barra de etiquetas Permite movernos por las distintas hojas del libro de trabajo. Las barras
La barra de fórmulas Nos muestra el contenido de la celda activa, es decir, la casilla donde estamos situados. La barra de etiquetas Permite movernos por las distintas hojas del libro de trabajo. Las barras
AUTOMATIZACIÓN INDUSTRIAL
 Universidad Carlos III de Madrid Departamento de Ingeniería de Sistemas y Automática AUTOMATIZACIÓN INDUSTRIAL Práctica 1 Introducción a los autómatas programables Marzo 2008 Ramiro Diez Automatización
Universidad Carlos III de Madrid Departamento de Ingeniería de Sistemas y Automática AUTOMATIZACIÓN INDUSTRIAL Práctica 1 Introducción a los autómatas programables Marzo 2008 Ramiro Diez Automatización
GUIA BÁSICA DE KALGEBRA
 GUIA BÁSICA DE KALGEBRA KAlgebra es una calculadora gráfica basada en MathML. Aunque en un principio estuvo orientado a MathML, actualmente puede ser usado por cualquier persona, aunque posea pocos conocimientos
GUIA BÁSICA DE KALGEBRA KAlgebra es una calculadora gráfica basada en MathML. Aunque en un principio estuvo orientado a MathML, actualmente puede ser usado por cualquier persona, aunque posea pocos conocimientos
PRÁCTICA NÚMEROS REALES Y COMPLEJOS CURSO Práctica 1 (21- IX-2016)
 PRÁCTICA NÚMEROS REALES Y COMPLEJOS CURSO 016-017 Prácticas Matlab Práctica 1 (1- IX-016) Objetivos Iniciarse en el uso de Matlab. Conocer comandos básicos de Matlab para realizar cálculos con números
PRÁCTICA NÚMEROS REALES Y COMPLEJOS CURSO 016-017 Prácticas Matlab Práctica 1 (1- IX-016) Objetivos Iniciarse en el uso de Matlab. Conocer comandos básicos de Matlab para realizar cálculos con números
Procesamiento Analógico de Señales
 Procesamiento Analógico de Señales Departamento de Electrónica y Automática Facultad de Ingeniería Generación de señales con SIMetrix Andrés Lage Angel Veca Mario Ruiz Edición 2013 Generación de Señales
Procesamiento Analógico de Señales Departamento de Electrónica y Automática Facultad de Ingeniería Generación de señales con SIMetrix Andrés Lage Angel Veca Mario Ruiz Edición 2013 Generación de Señales
CIRCUITOS ELECTRÓNICOS. Práctica nº 1. Software de simulación de circuitos
 CIRCUITOS ELECTRÓNICOS Práctica nº 1 Software de simulación de circuitos Trabajo a realizar en la práctica La práctica consiste en introducir al alumno en la utilización de la herramienta software LTspice
CIRCUITOS ELECTRÓNICOS Práctica nº 1 Software de simulación de circuitos Trabajo a realizar en la práctica La práctica consiste en introducir al alumno en la utilización de la herramienta software LTspice
Oscar Ignacio Botero H. Diana Marcela Domínguez P. SIMULADOR PROTEUS MÓDULO GRÁFICOS (GRAPHS)
 Oscar Ignacio Botero H. SIMULADOR PROTEUS MÓDULO GRÁFICOS (GRAPHS) Para insertar las graficas en los circuitos a simular, se activa el icono En este modo se encuentran las siguientes opciones: GRAFICA
Oscar Ignacio Botero H. SIMULADOR PROTEUS MÓDULO GRÁFICOS (GRAPHS) Para insertar las graficas en los circuitos a simular, se activa el icono En este modo se encuentran las siguientes opciones: GRAFICA
MODULO I. Avanzando en Windows Informática II Actividades Permanentes
 MODULO I Avanzando en Windows 2000 Informática II Actividades Permanentes Año 2003/2004 TABLA DE CONTENIDOS 1.1 EL PANEL DE CONTROL Descripción...3 Elementos y funcionalidad...4 1.2 EL EXPLORADOR DE WINDOWS
MODULO I Avanzando en Windows 2000 Informática II Actividades Permanentes Año 2003/2004 TABLA DE CONTENIDOS 1.1 EL PANEL DE CONTROL Descripción...3 Elementos y funcionalidad...4 1.2 EL EXPLORADOR DE WINDOWS
Hoja electrónica Microsoft Excel
 Hoja electrónica Microsoft Excel Son programas que facilitan el manejo de datos y procesamiento de operaciones de cálculo en diversas áreas. Se utilizan para realizar operaciones: Aritméticas Estructuras
Hoja electrónica Microsoft Excel Son programas que facilitan el manejo de datos y procesamiento de operaciones de cálculo en diversas áreas. Se utilizan para realizar operaciones: Aritméticas Estructuras
