DIAGRAMAS DE MINKOWSKI
|
|
|
- María Isabel Campos Jiménez
- hace 8 años
- Vistas:
Transcripción
1 DIAGRAMAS DE MINKOWSKI
2 Hermann Minkowski (22 de junio de de enero de 1909) fue un matemáticoalemán de origen judío que desarrolló la teoría geométrica de los números. Sus trabajos más destacados fueron realizados en las áreas de la teoría de números, la física matemática y la teoría de la relatividad
3 Los diagramas espacio-tiempo de Minkowski Considerando para fines ilustrativos una velocidad de la luz de c = 1 metro por segundo, eldiagrama espacio-tiempo para un rayo de luz es el siguiente: La especificación de una coordenada x de una partícula material, nos indica la posición en la cual se encuentra la partícula y del tiempo t al que corresponde esta coordenada, se dice que determina un evento o un suceso
4 El lugar en un plano x-t de los eventos que representan las coordenadas apareadas de una partícula en varios instantes se conoce en los estudios de la relatividad como línea del mundo (world line) y también como línea del universo Los eventos para un mismo y único observador están separados en el espacio por una distancia x = x2 - x1 y en el tiempo por una distancia t = t2 - t1
5 Para que en un diagrama espacio-tiempo tanto el eje horizontal como el eje vertical usen el mismo tipo de unidades, se acostumbra multiplicar el tiempo en el eje vertical que corresponde al tiempo por la constante universal absoluta que es la velocidad de la luz c, ya que con ello ct se convierte en una distancia que está medida en metros, no en segundos.
6 En la gráfica anterior, se representan dos eventos distintos, uno en la posición x1 en un tiempo representado en la posición ct1, y el otro evento ocurriendo en la posición x2 en un tiempo representado en la posición ct2. Poniendo números y usando una velocidad de la luz igual a c = 1 metro/segundo, las coordenadas respectivas de cada evento y la distancia entre ambos eventos es: x1 = 1 metro x2 = 2 metros ct1 = 1 metro ct2 = 3 metros x = x2 - x1 = 2 metros - 1 metro = 1 metro c t = ct2 - ct1 = 3 metros - 1 metro = 2 metros
7 PROBLEMA: Una varilla de medir de tres metros de largo se encuentra en reposo en el marco de referencia del observador O, y sus extremos coinciden con las coordenadas x1 = 2 metros y x2 = 5 metros. Trazar las líneas del mundo de los extremos de la vara de medir en un diagrama espaciotiempo del observador O. No es un requisito indispensable que en la construcción de un diagrama del espacio-tiempo se utilicen ejes ortogonales (perpendiculares, puestos en ángulos rectos el uno con respecto al otro).
8 Es posible trazar ejes principales que no son perpendiculares entre si. Obsérvese la manera de leer las coordenadas de un punto cualesquiera en este tipo de diagrama, trazando desde el punto líneas paralelas a uno de los ejes principales hasta topar con el eje principal de la otra coordenada.
9 Y a continuación tenemos otro diagrama espacio-tiempo en el cual los ejes principales tampoco son perpendiculares: El diagrama espaciotiempo nos dá la distancia x que separa dos eventos E1 y E2, y nos dá también la distancia c t que separa a dichos eventos. Pero este diagrama espacio-tiempo describe la situación de un solo observador
10 Para trazar un diagrama espaciotiempo combinado juntando a dos observadores diferentes que están en movimiento relativo el uno con respecto al otro a una velocidad V, trazamos primero el eje-t del marco de referencia S sobre el diagrama espacio-tiempo del observador en reposo usando para ello la velocidad relativa entre ambos observadores. No es necesario que los orígenes de los diagramas espacio-tiempo del observador O y del observador O coincidan. Construiremos un diagrama en el que ambos orígenes coinciden.
11 Suponiendo que la velocidad relativa entre ambos marcos de referencia es de V = 0.4c (o.4 metros/segundo) entonces para moverse una distancia x = 1 metro el observador O debe de haberse movido en un tiempo t = x/v = 2.5 segundos con respecto al origen, y para moverse una distancia x = 2 metros el observador O debe de haberse movido en un tiempo t = x/v = 5 segundos. Todos estos puntos están conectados con una línea recta, la cual trazamos sobre el diagrama como se muestra arriba. Esta recta corresponde al tiempo t del marco de referencia S
12 Este es el diagrama espaciotiempo desde la perspectiva del observador O en reposo. Si queremos, podemos dibujar también el diagrama espacio-tiempo desde la perspectiva del observador O cuando este se considera en reposo y cuando ve al observador O en movimiento hacia la izquierda
13 Lo que se a hecho fue tomar el diagrama básico para un observador O en reposo en un marco de referencia S, trazando sobre el mismo la línea que marca la trayectoria de un rayo de luz con una pendiente de 45 grados que corresponde a una velocidad c de 1 metro por segundo:
14 y sobre este diagrama, usando como referencia común la bisectriz que ambos diagramas deben tener identificando en el mismo la línea del mundo de un rayo de luz común a ambos observadores O y O en los marcos de referencia S y S, hemos agregado al diagrama del observador estacionario O el siguiente diagrama espacio-tiempo de O
15 Luego el diagrama espaciotiempo resultante combinando a ambos observadores desde la perspectiva del observador estacionario O:
16 PROBLEMA: Representar en un diagrama espaciotiempo cuatro eventos distintos cuyas coordenadas son las siguientes: E1(x1, c t1) = (1, 2) E2(x2, c t2) = (2, 5) E3(x 1, c t 1) = (4, 1) E4(x 2, c t 2) = (2, 2)
17 Los eventos E1 y E2 están especificados sobre las coordenadas del observador en reposo O en su marco de referencia S, y en el diagrama espaciotiempo combinado estarán ubicados en las siguientes posiciones (se han representado los dos eventos en el diagrama con unos cuadritos de color púrpura):
18 Los eventos E3 y E4 están especificados sobre las coordenadas del observador en movimiento O en su marco de referencia S, y en el diagrama espaciotiempo combinado estarán ubicados en las siguientes posiciones (se han representado los dos eventos en el diagrama con unos cuadritos de color verde):
19 Cuanto más alta sea la velocidad relativa V entre dos marcos de referencia acercándose o alejándose a una velocidad cada vez más cercana a la velocidad de la luz, tanto más se irán cerrando los ejes que corresponden al marco de referencia en movimiento S como podemos apreciarlo en el siguiente diagrama espacio-tiempo:
20 En el diagrama espacio-tiempo anterior, tenemos sobrepuestos a tres observadores, el observador que consideramos estacionario, el observador O que se está moviendo a una velocidad relativa V con respecto al observador O, y un tercer observador O que se está moviendo a una velocidad todavía mayor con respecto al observador O. Nótese cómo se van cerrando cada vez más y más los ejes coordenados x-t de un observador móvil conforme va aumentando su velocidad V con respecto al observador estacionario.
21 Cuando se prescinde de un diagrama espacio-tiempo como el caso en el que se vaya a efectuar un cálculo numérico, para la especificación completa de un mismo evento E cualquiera se deben especificar cuatro coordenadas, las coordenadas (x,t) del evento en el marco de referencia S, y las coordenadas (x,t ) del evento en el marco de referencia S, de modo tal que un evento quedará registrado como E(x,t,x,t ) en forma completa. Esto es válido para cualquier evento. El único evento que tendrá las mismas coordenadas tanto para S como para S será el que ocurra en el punto común de origen, o sea E(x,t,x,t ) = (0,0,0,0).
22 En el siguiente diagrama espacio-tiempo tenemos un evento A. Trazando una línea horizontal hacia la izquierda hasta llegar al eje vertical ct podemos obtener el valor de ct con lo cual podemos obtener el tiempo, y trazando una línea vertical hacia abajo podemos obtener la coordenada de la distancia x. Del mismo evento A podemos hacia la línea ct una línea paralela a la coordenada x con lo cual obtenemos el valor de ct, y podemos trazar hacia abajo otra línea paralela a ct con lo cual obtenemos el valor de x.
Los diagramas espacio-tiempo de Minkowski
 24/05/2013 DIAGRAMAS DE MINKOWSKI 1 Hermann Minkowski (22 de junio de 1864-12 de enero de 1909) fue un matemáticoalemán de origen judío que desarrolló la teoría geométrica de los números. Sus trabajos
24/05/2013 DIAGRAMAS DE MINKOWSKI 1 Hermann Minkowski (22 de junio de 1864-12 de enero de 1909) fue un matemáticoalemán de origen judío que desarrolló la teoría geométrica de los números. Sus trabajos
Proyecto Guao PLANO REAL
 PLANO REAL María vive 2 cuadras al norte y una cuadra al este de la escuela, Carlos vive tres cuadras al sur y dos cuadras al oeste de la escuela. Cuál es la línea más corta de conexión a sus casas? EL
PLANO REAL María vive 2 cuadras al norte y una cuadra al este de la escuela, Carlos vive tres cuadras al sur y dos cuadras al oeste de la escuela. Cuál es la línea más corta de conexión a sus casas? EL
Tema 3. Magnitudes escalares y vectoriales
 1 de 13 09/07/2012 12:51 Tema 3. Magnitudes escalares y vectoriales Algunos derechos reservados por manelzaera Como sabes, una magnitud es todo aquello que se puede medir. Por ejemplo, la fuerza, el tiempo,
1 de 13 09/07/2012 12:51 Tema 3. Magnitudes escalares y vectoriales Algunos derechos reservados por manelzaera Como sabes, una magnitud es todo aquello que se puede medir. Por ejemplo, la fuerza, el tiempo,
Ref: Cinemática Vectorial
 Nombre: Curso: Introducción En la ciencia uno de las avances más notables es cuando la logra sistematizar la información en relación a la descripción del movimiento, utilizando los conceptos básicos de
Nombre: Curso: Introducción En la ciencia uno de las avances más notables es cuando la logra sistematizar la información en relación a la descripción del movimiento, utilizando los conceptos básicos de
T2. ESPACIO, TIEMPO Y ESPACIOTIEMPO: DIAGRAMAS DE MINKOWSKI
 T2. ESPACIO, TIEMPO Y ESPACIOTIEMPO: DIAGRAMAS DE MINKOWSKI 1. Introducción: postulados de la relatividad especial 2. Definición de tiempo 2.1 Qué es medir el tiempo? 2.2 Sistema común de tiempos 2.3 Dilatación
T2. ESPACIO, TIEMPO Y ESPACIOTIEMPO: DIAGRAMAS DE MINKOWSKI 1. Introducción: postulados de la relatividad especial 2. Definición de tiempo 2.1 Qué es medir el tiempo? 2.2 Sistema común de tiempos 2.3 Dilatación
La longitud de la barra 2 vista desde el sistema de referencia de la barra 1 será: 1 v 2 c v2
 RELATIVIDAD ESPECIAL Dos barras de igual longitud propia l 0 se acercan moviéndose en dirección longitudinal paralelamente a un eje común con una misma velocidad v respecto al sistema de referencia del
RELATIVIDAD ESPECIAL Dos barras de igual longitud propia l 0 se acercan moviéndose en dirección longitudinal paralelamente a un eje común con una misma velocidad v respecto al sistema de referencia del
CINEMÁTICA: ESTUDIO DEL MOVIMIENTO. Cinemática es la parte de la Física que estudia la descripción del movimiento de los cuerpos.
 CINEMÁTICA: ESTUDIO DEL MOVIMIENTO Cinemática es la parte de la Física que estudia la descripción del movimiento de los cuerpos. 1. Cuándo un cuerpo está en movimiento? Para hablar de reposo o movimiento
CINEMÁTICA: ESTUDIO DEL MOVIMIENTO Cinemática es la parte de la Física que estudia la descripción del movimiento de los cuerpos. 1. Cuándo un cuerpo está en movimiento? Para hablar de reposo o movimiento
Materia: Matemática de 5to Tema: Ecuación vectorial. Marco Teórico
 Materia: Matemática de 5to Tema: Ecuación vectorial Marco Teórico Como ya sabemos y = mx + b es la forma pendiente-intersección de una recta. Mientras que esta ecuación funciona bien en el espacio de dos
Materia: Matemática de 5to Tema: Ecuación vectorial Marco Teórico Como ya sabemos y = mx + b es la forma pendiente-intersección de una recta. Mientras que esta ecuación funciona bien en el espacio de dos
Dinámica relativista: E = mc 2 y movimiento acelerado
 Tema 7 Dinámica relativista: E = mc 2 y movimiento acelerado 7.1 Introducción Hemos visto que conviene considerar el espaciotiempo como un espacio cuadridimensional en el que podemos localizar sucesos
Tema 7 Dinámica relativista: E = mc 2 y movimiento acelerado 7.1 Introducción Hemos visto que conviene considerar el espaciotiempo como un espacio cuadridimensional en el que podemos localizar sucesos
3. Cinemática de la partícula: Sistemas de referencia
 3. Cinemática de la partícula: Sistemas de referencia 3.1.- Cinemática de la partícula 3.2.- Coordenadas intrínsecas y polares 3.3.- Algunos casos particulares de especial interés 3.1.- Cinemática de la
3. Cinemática de la partícula: Sistemas de referencia 3.1.- Cinemática de la partícula 3.2.- Coordenadas intrínsecas y polares 3.3.- Algunos casos particulares de especial interés 3.1.- Cinemática de la
I. INTRODUCCIÓN MECANICA MECANICA DE CUERPO RIGIDOS MECÁNICA DE CUERPO DEFORMABLE MECÁNICA DE FLUIDOS
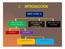 I. INTRODUCCIÓN MECANICA MECANICA DE CUERPO RIGIDOS MECÁNICA DE CUERPO DEFORMABLE MECÁNICA DE FLUIDOS ESTATICA DINAMICA CINEMATICA CINETICA II. NOCION DE CINEMATICA La cinemática (del griegoκινεω, kineo,
I. INTRODUCCIÓN MECANICA MECANICA DE CUERPO RIGIDOS MECÁNICA DE CUERPO DEFORMABLE MECÁNICA DE FLUIDOS ESTATICA DINAMICA CINEMATICA CINETICA II. NOCION DE CINEMATICA La cinemática (del griegoκινεω, kineo,
Física I. TEMA I. Vectores. Ing. Alejandra Escobar UNIVERSIDAD FERMÍN TORO VICE RECTORADO ACADÉMICO FACULTAD DE INGENIERÍA
 Física I TEMA I. Vectores UNIVERSIDAD FERMÍN TORO VICE RECTORADO ACADÉMICO FACULTAD DE INGENIERÍA Ing. Alejandra Escobar TEMA I. VECTORES Magnitudes Una magnitud se define como toda aquella propiedad que
Física I TEMA I. Vectores UNIVERSIDAD FERMÍN TORO VICE RECTORADO ACADÉMICO FACULTAD DE INGENIERÍA Ing. Alejandra Escobar TEMA I. VECTORES Magnitudes Una magnitud se define como toda aquella propiedad que
Cinemática: Conceptos Básicos del Movimiento, Movimiento Rectilíneo Uniforme y Movimiento Rectilíneo Uniforme Acelerado.
 Temática Estudiante Cinemática: Conceptos Básicos del Movimiento, Movimiento Rectilíneo Uniforme y Movimiento Rectilíneo Uniforme Acelerado. Fecha Conceptos Básicos de Movimiento Mecánica: Rama de la Física
Temática Estudiante Cinemática: Conceptos Básicos del Movimiento, Movimiento Rectilíneo Uniforme y Movimiento Rectilíneo Uniforme Acelerado. Fecha Conceptos Básicos de Movimiento Mecánica: Rama de la Física
DIBUJO ILUSTRATIVO: CABALLERA ESCORZADA
 SEMANA N 11: DIBUJO ILUSTRATIVO: CABALLERA ESCORZADA 1 10.1 DEFINICIÓN DE PROYECCION OBLICUA. En la proyección oblicua los rayos visuales son paralelos entre sí pero oblicuos (diferente de 90º) al plano
SEMANA N 11: DIBUJO ILUSTRATIVO: CABALLERA ESCORZADA 1 10.1 DEFINICIÓN DE PROYECCION OBLICUA. En la proyección oblicua los rayos visuales son paralelos entre sí pero oblicuos (diferente de 90º) al plano
FUNCIONES 1. FUNCIONES Y SUS GRAFICAS.
 FUNCIONES 1. FUNCIONES Y SUS GRAFICAS. Una de las grandes inquietudes de los seres humanos a través de la historia ha sido la de describir los fenómenos naturales, sus cambios las relaciones entre unos
FUNCIONES 1. FUNCIONES Y SUS GRAFICAS. Una de las grandes inquietudes de los seres humanos a través de la historia ha sido la de describir los fenómenos naturales, sus cambios las relaciones entre unos
INTRODUCCIÓN A LAS MATEMÁTICAS SUPERIORES. Tema 3 EL PLANO Y LAS GRÁFICAS EL PLANO CARTESIANO. COORDENADAS Y DISTANCIA ENTRE PUNTOS.
 INTRODUCCIÓN A LAS MATEMÁTICAS SUPERIORES Tema EL PLANO Y LAS GRÁFICAS EL PLANO CARTESIANO. COORDENADAS Y DISTANCIA ENTRE PUNTOS. C.- Qué es cómo se representa un sistema de coordenadas cartesianas rectangulares
INTRODUCCIÓN A LAS MATEMÁTICAS SUPERIORES Tema EL PLANO Y LAS GRÁFICAS EL PLANO CARTESIANO. COORDENADAS Y DISTANCIA ENTRE PUNTOS. C.- Qué es cómo se representa un sistema de coordenadas cartesianas rectangulares
para aterrizar finalmente en otro aeropuerto en el noroeste de los controladores aéreos. Los caminos de estos dos aviones se cruzan?
 Materia: Matemáticas de 4to año Tema: Combinación lineal de dos o más vectores Control del tráfico aéreo es el seguimiento de dos aviones en las proximidades de su aeropuerto. En un momento dado, un avión
Materia: Matemáticas de 4to año Tema: Combinación lineal de dos o más vectores Control del tráfico aéreo es el seguimiento de dos aviones en las proximidades de su aeropuerto. En un momento dado, un avión
UNIDAD XVII LA LINEA RECTA. Modulo 4 Ecuación de la recta
 UNIDAD XVII LA LINEA RECTA Modulo 4 Ecuación de la recta OBJETIVO Encontrar y determinar la ecuación de una recta, conocidos los puntos de intersección con los ejes coordenados. 4. 1. LINEA RECTA. Lugar
UNIDAD XVII LA LINEA RECTA Modulo 4 Ecuación de la recta OBJETIVO Encontrar y determinar la ecuación de una recta, conocidos los puntos de intersección con los ejes coordenados. 4. 1. LINEA RECTA. Lugar
Relatividad: la misma historia según distintos protagonistas
 Tema 3 Relatividad: la misma historia según distintos protagonistas 3. La historia Un tren que mide 00 m circula a la increíble velocidad de 3/2 veces la velocidad de la luz. El tren pasa por una estación
Tema 3 Relatividad: la misma historia según distintos protagonistas 3. La historia Un tren que mide 00 m circula a la increíble velocidad de 3/2 veces la velocidad de la luz. El tren pasa por una estación
Cómo identificar los puntos de tangencia de rectas tangentes a una circunferencia dada, y que pasan por un punto dado
 Cómo identificar los puntos de tangencia de rectas tangentes a una circunferencia dada y que pasan por un punto dado El procedimiento aquí presentado combina conceptos tanto de la geometría clásica como
Cómo identificar los puntos de tangencia de rectas tangentes a una circunferencia dada y que pasan por un punto dado El procedimiento aquí presentado combina conceptos tanto de la geometría clásica como
ECUACIONES DE RECTAS Y PLANOS
 ECUACIONES DE RECTAS Y PLANOS Una recta en el plano está determinada cuando se dan dos puntos cualesquiera de la recta, o un punto de la recta y su dirección (su pendiente o ángulo de inclinación). La
ECUACIONES DE RECTAS Y PLANOS Una recta en el plano está determinada cuando se dan dos puntos cualesquiera de la recta, o un punto de la recta y su dirección (su pendiente o ángulo de inclinación). La
TEMA 4 REPRESENTACION DE OBJETOS.VISTAS
 TEMA 4 REPRESENTACION DE OBJETOS.VISTAS INDICE 1. INTRODUCCION... 2 2. SISTEMAS DE REPRESENTACION... 2 2.1 PROYECCIONES... 3 2.2 TIPO DE PROYECCIONES... 3 2.3 ELEMENTOS DE LOS SISTEMAS DE REPRESENTACION...
TEMA 4 REPRESENTACION DE OBJETOS.VISTAS INDICE 1. INTRODUCCION... 2 2. SISTEMAS DE REPRESENTACION... 2 2.1 PROYECCIONES... 3 2.2 TIPO DE PROYECCIONES... 3 2.3 ELEMENTOS DE LOS SISTEMAS DE REPRESENTACION...
DE LA GRÁFICA A LA EXPRESIÓN ALGEBRAICA
 De la gráfica a la expresión algebraica DE LA GRÁFICA A LA EXPRESIÓN ALGEBRAICA Rectas, Parábolas, Hipérbolas, Exponenciales Logarítmicas LA RECTA Comencemos localizando el punto donde la recta corta al
De la gráfica a la expresión algebraica DE LA GRÁFICA A LA EXPRESIÓN ALGEBRAICA Rectas, Parábolas, Hipérbolas, Exponenciales Logarítmicas LA RECTA Comencemos localizando el punto donde la recta corta al
m=0 La ecuación de una recta se puede obtener a partir de dos puntos por los que pase la recta: y y1 = m(x x1)
 Recta Una propiedad importante de la recta es su pendiente. Para determinar este coeficiente m en una recta que no sea vertical, basta tener dos puntos (, y) & (, y) que estén sobre la recta, la pendiente
Recta Una propiedad importante de la recta es su pendiente. Para determinar este coeficiente m en una recta que no sea vertical, basta tener dos puntos (, y) & (, y) que estén sobre la recta, la pendiente
PREGUNTAS DE OPCION MULTIPLE (Deben presentar su respectiva justificación, caso contrario no tendrán validez) (Del 1 al 11, 3 puntos c/u)
 ESCUELA SUPERIOR POLITECNICA DEL LITORAL INSTITUTO DE CIENCIAS FISICAS PRIMERA EVALUACION DE FISICA GENERAL I II TERMINO 2011-2012 Nombre: Paralelo: 01 Ing. Francisca Flores N. PREGUNTAS DE OPCION MULTIPLE
ESCUELA SUPERIOR POLITECNICA DEL LITORAL INSTITUTO DE CIENCIAS FISICAS PRIMERA EVALUACION DE FISICA GENERAL I II TERMINO 2011-2012 Nombre: Paralelo: 01 Ing. Francisca Flores N. PREGUNTAS DE OPCION MULTIPLE
Planos y Rectas. 19 de Marzo de 2012
 el Geometría en el Planos y Rectas Universidad Autónoma Metropolitana Unidad Iztapalapa 19 de Marzo de 2012 el Anteriormente vimos que es posible encontrar un número infinito de vectores, no paralelos
el Geometría en el Planos y Rectas Universidad Autónoma Metropolitana Unidad Iztapalapa 19 de Marzo de 2012 el Anteriormente vimos que es posible encontrar un número infinito de vectores, no paralelos
Problemas Fundamentales sobre Cinemática Errática
 Problemas Fundamentales sobre Cinemática Errática F12-9 La partícula viaja a lo largo de una pista recta de manera que su posición se describe por la gráfica. Construya la gráfica para el mismo intervalo
Problemas Fundamentales sobre Cinemática Errática F12-9 La partícula viaja a lo largo de una pista recta de manera que su posición se describe por la gráfica. Construya la gráfica para el mismo intervalo
VECTORES Y SUS ELEMENTOS
 VECTORES Y SUS ELEMENTOS Los conjuntos de números naturales, enteros y racionales estudiados, te han permitido expresar distintas situaciones y resolver muchos problemas. En este sentido, algunas cantidades
VECTORES Y SUS ELEMENTOS Los conjuntos de números naturales, enteros y racionales estudiados, te han permitido expresar distintas situaciones y resolver muchos problemas. En este sentido, algunas cantidades
UNIDAD Nº 4:CINEMATICA DEL CUERPO RIGIDO.
 UNIDAD Nº 4:CINEMATICA DEL CUERPO RIGIDO. 1 Concepto de trayectoria y corrimiento de un punto perteneciente a un cuerpo. Traslación y rotación de un cuerpo. Hipótesis de pequeñas rotaciones. Cupla de rotaciones.
UNIDAD Nº 4:CINEMATICA DEL CUERPO RIGIDO. 1 Concepto de trayectoria y corrimiento de un punto perteneciente a un cuerpo. Traslación y rotación de un cuerpo. Hipótesis de pequeñas rotaciones. Cupla de rotaciones.
MATEMÁTICAS 2º DE ESO
 MATEMÁTICAS 2º DE ESO LOE TEMA VII: FUNCIONES Y GRÁFICAS Coordenadas cartesianas. Concepto de función. Tabla y ecuación. Representación gráfica de una función. Estudio gráfico de una función. o Continuidad
MATEMÁTICAS 2º DE ESO LOE TEMA VII: FUNCIONES Y GRÁFICAS Coordenadas cartesianas. Concepto de función. Tabla y ecuación. Representación gráfica de una función. Estudio gráfico de una función. o Continuidad
MATEMÁTICAS 2º DE ESO
 MATEMÁTICAS 2º DE ESO LOMCE TEMA VII: FUNCIONES Y GRÁFICAS Coordenadas cartesianas. Concepto de función. Tabla y ecuación. Representación gráfica de una función. Estudio gráfico de una función. o Continuidad
MATEMÁTICAS 2º DE ESO LOMCE TEMA VII: FUNCIONES Y GRÁFICAS Coordenadas cartesianas. Concepto de función. Tabla y ecuación. Representación gráfica de una función. Estudio gráfico de una función. o Continuidad
Bases para el estudio del movimiento mecánico
 Vectores 1 ases para el estudio del movimiento mecánico SR: Cuerpos que se toman como referencia para describir el movimiento del sistema bajo estudio. Se le asocia z(t) (t) (t) Observador Sistema de Coordenadas
Vectores 1 ases para el estudio del movimiento mecánico SR: Cuerpos que se toman como referencia para describir el movimiento del sistema bajo estudio. Se le asocia z(t) (t) (t) Observador Sistema de Coordenadas
I. INTRODUCCIÓN MECANICA MECANICA DE CUERPO RIGIDOS MECÁNICA DE CUERPO DEFORMABLE MECÁNICA DE FLUIDOS
 I. INTRODUCCIÓN MECANICA MECANICA DE CUERPO RIGIDOS MECÁNICA DE CUERPO DEFORMABLE MECÁNICA DE FLUIDOS ESTATICA DINAMICA CINEMATICA CINETICA II. NOCION DE CINEMATICA La cinemática (del griegoκινεω, kineo,
I. INTRODUCCIÓN MECANICA MECANICA DE CUERPO RIGIDOS MECÁNICA DE CUERPO DEFORMABLE MECÁNICA DE FLUIDOS ESTATICA DINAMICA CINEMATICA CINETICA II. NOCION DE CINEMATICA La cinemática (del griegoκινεω, kineo,
PRIMERA EVALUACIÓN. FÍSICA Junio 19 del 2014 (11h30-13h30)
 PRIMERA EVALUACIÓN DE FÍSICA Junio 19 del 2014 (11h30-13h30) Como aspirante a la ESPOL me comprometo a combatir la mediocridad y actuar con honestidad, por eso no copio ni dejo copiar" NOMBRE: FIRMA: VERSIÓN
PRIMERA EVALUACIÓN DE FÍSICA Junio 19 del 2014 (11h30-13h30) Como aspirante a la ESPOL me comprometo a combatir la mediocridad y actuar con honestidad, por eso no copio ni dejo copiar" NOMBRE: FIRMA: VERSIÓN
PRIMERA EVALUACIÓN. FÍSICA Junio 19 del 2014 (08h30-10h30)
 PRIMERA EVALUACIÓN DE FÍSICA Junio 19 del 2014 (08h30-10h30) Como aspirante a la ESPOL me comprometo a combatir la mediocridad y actuar con honestidad, por eso no copio ni dejo copiar" NOMBRE: FIRMA: VERSIÓN
PRIMERA EVALUACIÓN DE FÍSICA Junio 19 del 2014 (08h30-10h30) Como aspirante a la ESPOL me comprometo a combatir la mediocridad y actuar con honestidad, por eso no copio ni dejo copiar" NOMBRE: FIRMA: VERSIÓN
Instituto de Matemática y Física 1 Universidad de Talca
 Instituto de Matemática y Física 1 Universidad de Talca 1. El plano cartesiano Para representar puntos en un plano, definidos por un par ordenado de números reales, se utiliza generalmente el sistema de
Instituto de Matemática y Física 1 Universidad de Talca 1. El plano cartesiano Para representar puntos en un plano, definidos por un par ordenado de números reales, se utiliza generalmente el sistema de
Destino Matemáticas. Dominino de Destrezas y Conceptos: Curso III (Windows / Macintosh Versión 5.0) Guía del Usuario (Network)
 Destino Matemáticas Dominino de Destrezas y Conceptos: Curso III (Windows / Macintosh Versión 5.0) Guía del Usuario (Network) TM 16 17 2002 Riverdeep Interactive Learning Limited y sus licenciadores Riverdeep,
Destino Matemáticas Dominino de Destrezas y Conceptos: Curso III (Windows / Macintosh Versión 5.0) Guía del Usuario (Network) TM 16 17 2002 Riverdeep Interactive Learning Limited y sus licenciadores Riverdeep,
Antecedentes: Distancia entre dos puntos.
 Antecedentes: Distancia entre dos puntos. Tinoco, G. (2013). Antecedentes: Distancia entre dos puntos. [Manuscrito no publicado]. México: UAEM. Espacio de Formación Multimodal Antecedentes Coordenadas
Antecedentes: Distancia entre dos puntos. Tinoco, G. (2013). Antecedentes: Distancia entre dos puntos. [Manuscrito no publicado]. México: UAEM. Espacio de Formación Multimodal Antecedentes Coordenadas
UNIDAD 3 LA RECTA Y SU ECUACIÓN CARTESIANA. Dada la ecuación de dos rectas. Determinará si se cortan, si son paralelas o perpendiculares. Y l.
 UNIDAD 3 LA RECTA SU ECUACIÓN CARTESIANA OBJETIVOS ESPECÍFICOS. Al término de la unidad, el alumno: Conocerá las distintas formas de representación de la recta e identificará cuál de ellas conviene usar.
UNIDAD 3 LA RECTA SU ECUACIÓN CARTESIANA OBJETIVOS ESPECÍFICOS. Al término de la unidad, el alumno: Conocerá las distintas formas de representación de la recta e identificará cuál de ellas conviene usar.
1. Magnitudes características del movimiento: trayectoria, posición, desplazamiento, espacio recorrido, velocidad y aceleración.
 BLOQUE 2. Fuerzas y movimientos. Tema 2: Características generales del movimiento 1. Magnitudes características del movimiento: trayectoria, posición, desplazamiento, espacio recorrido, velocidad y aceleración.
BLOQUE 2. Fuerzas y movimientos. Tema 2: Características generales del movimiento 1. Magnitudes características del movimiento: trayectoria, posición, desplazamiento, espacio recorrido, velocidad y aceleración.
ASIGNATURA: FISICA PERIODO: 3 DOCENTE: LIC. DIEGO JAIMES FECHA: ESTUDIANTE: GRADO: 7- Cinemática
 Cinemática Cinemática, es el estudio del movimiento sin atender a sus causas. Se entiende por movimiento, el cambio de posición de una partícula con relación al tiempo y a un punto de referencia. El término
Cinemática Cinemática, es el estudio del movimiento sin atender a sus causas. Se entiende por movimiento, el cambio de posición de una partícula con relación al tiempo y a un punto de referencia. El término
PUCMM FIS 101 Prof. Remigia cabrera Genao 2014
 Posición (m) Unidad II. Cinemática Rectilínea PROBLEMAS PARA RESOLVER EN LA CLASE 1. Para el móvil del gráfico determine lo que se le pide abajo, si se mueve en una recta nortesur: 7.00 6.00 5.00 4.00
Posición (m) Unidad II. Cinemática Rectilínea PROBLEMAS PARA RESOLVER EN LA CLASE 1. Para el móvil del gráfico determine lo que se le pide abajo, si se mueve en una recta nortesur: 7.00 6.00 5.00 4.00
INTERPRETACIÓN DE GRÁFICOS
 Facultad de Ingeniería Mecánica y Eléctrica FIME Universidad Autónoma de Nuevo León UANL Nuevo León, México M.C. Gabriel F. Martínez Alonso FIME UANL INTERPRETACIÓN DE GRÁFICOS GRÁFICOS: La elaboración
Facultad de Ingeniería Mecánica y Eléctrica FIME Universidad Autónoma de Nuevo León UANL Nuevo León, México M.C. Gabriel F. Martínez Alonso FIME UANL INTERPRETACIÓN DE GRÁFICOS GRÁFICOS: La elaboración
también lo hace la masa, pero el cociente permanece constante. m K, en donde K se conoce con el nombre de V V [m 3 ] m [kg]
![también lo hace la masa, pero el cociente permanece constante. m K, en donde K se conoce con el nombre de V V [m 3 ] m [kg] también lo hace la masa, pero el cociente permanece constante. m K, en donde K se conoce con el nombre de V V [m 3 ] m [kg]](/thumbs/63/48713393.jpg) Proporciones Proporción directa Dadas dos magnitudes físicas, si están relacionadas, de manera que se duplica una, entonces se duplicará la otra. Si se triplica una, la otra quedará multiplicada por tres.
Proporciones Proporción directa Dadas dos magnitudes físicas, si están relacionadas, de manera que se duplica una, entonces se duplicará la otra. Si se triplica una, la otra quedará multiplicada por tres.
GUÍA 6: CIRCUITOS MAGNÉTICOS Electricidad y Magnetismo
 GUÍA 6: CIRCUITOS MAGNÉTICOS Primer Cuatrimestre 2013 Docentes: Dr. Alejandro Gronoskis Lic. María Inés Auliel Andrés Sabater Universidad Nacional de Tres de febrero Depto de Ingeniería Universidad de
GUÍA 6: CIRCUITOS MAGNÉTICOS Primer Cuatrimestre 2013 Docentes: Dr. Alejandro Gronoskis Lic. María Inés Auliel Andrés Sabater Universidad Nacional de Tres de febrero Depto de Ingeniería Universidad de
TEORÍA TEMA 6 CENTRO DE FUERZAS PARALELAS. A- Centro de fuerzas paralelas caso dos fuerzas- caso n fuerzas. Definición centro de fuerzas paralelas.
 TEORÍA TEMA 6 CENTRO DE FUERZAS PARALELAS A- Centro de fuerzas paralelas caso dos fuerzas- caso n fuerzas. Definición centro de fuerzas paralelas. B- Caso de fuerzas paralelas de igual sentido (gráfico)
TEORÍA TEMA 6 CENTRO DE FUERZAS PARALELAS A- Centro de fuerzas paralelas caso dos fuerzas- caso n fuerzas. Definición centro de fuerzas paralelas. B- Caso de fuerzas paralelas de igual sentido (gráfico)
Respecto a los conceptos de velocidad y rapidez media, es correcto afirmar que
 Nº Guía práctica Movimiento II: movimientos con velocidad constante Física Estándar Anual Ejercicios PSU 1. 2. Respecto a los conceptos de velocidad y rapidez media, es correcto afirmar que I) II) III)
Nº Guía práctica Movimiento II: movimientos con velocidad constante Física Estándar Anual Ejercicios PSU 1. 2. Respecto a los conceptos de velocidad y rapidez media, es correcto afirmar que I) II) III)
Ecuaciones Lineales en Dos Variables
 Ecuaciones Lineales en Dos Variables Una ecuación lineal en dos variables tiene la forma general a + b + c = 0; donde a, b, c representan números reales las tres no pueden ser iguales a cero a la misma
Ecuaciones Lineales en Dos Variables Una ecuación lineal en dos variables tiene la forma general a + b + c = 0; donde a, b, c representan números reales las tres no pueden ser iguales a cero a la misma
32. SISTEMA PERSPECTIVA CABALLERA
 32. SISTEMA PERSPECTIVA CABALLERA 32.1. Elementos del sistema. En el sistema de perspectiva caballera continuamos utilizando un triedro trirectangulo y las proyecciones cilindrica del mismo modo que en
32. SISTEMA PERSPECTIVA CABALLERA 32.1. Elementos del sistema. En el sistema de perspectiva caballera continuamos utilizando un triedro trirectangulo y las proyecciones cilindrica del mismo modo que en
Isométricos. Ing. Carlos Camacho Soto Escuela de Ingeniería Civil Universidad de Costa Rica IC-302. Setiembre 2005
 Isométricos Ing. Carlos Camacho Soto Escuela de Ingeniería Civil Universidad de Costa Rica IC-302 Setiembre 2005 Resumen Los dibujos isométricos son un tipo de dibujo en perspectiva, en la cual se trata
Isométricos Ing. Carlos Camacho Soto Escuela de Ingeniería Civil Universidad de Costa Rica IC-302 Setiembre 2005 Resumen Los dibujos isométricos son un tipo de dibujo en perspectiva, en la cual se trata
ESTUDIO Y ANÁLISIS DEL MOVIMIENTO DE DOS CUERPOS DESDE DISTINTOS SISTEMAS DE REFERENCIA INERCIALES
 FAENA Fis - 126 ESTUDIO Y ANÁLISIS DEL MOVIMIENTO DE DOS CUERPOS DESDE DISTINTOS SISTEMAS DE REFERENCIA INERCIALES Omayra Pérez ([email protected]) Bernardo Fernández ([email protected])
FAENA Fis - 126 ESTUDIO Y ANÁLISIS DEL MOVIMIENTO DE DOS CUERPOS DESDE DISTINTOS SISTEMAS DE REFERENCIA INERCIALES Omayra Pérez ([email protected]) Bernardo Fernández ([email protected])
7. Cónicas. Propiedades métricas y ópticas
 Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 49 7. Cónicas. Propiedades métricas y ópticas Cónicas Círcunferencias, elipses, parábolas, e hipérbolas son llamadas secciones cónicas
Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 49 7. Cónicas. Propiedades métricas y ópticas Cónicas Círcunferencias, elipses, parábolas, e hipérbolas son llamadas secciones cónicas
Magnitudes vectoriales y escalares.
 Magnitudes vectoriales y escalares https://sites.google.com/site/fisicadeterceroedwar/temas/magnitudes-escalares-y-vectoriales Magnitudes escalares Son aquellas que quedan completamente especificadas con
Magnitudes vectoriales y escalares https://sites.google.com/site/fisicadeterceroedwar/temas/magnitudes-escalares-y-vectoriales Magnitudes escalares Son aquellas que quedan completamente especificadas con
t'' B' t' La recta "t" es la trayectoria de la gota de agua
 EJERCICIO 1 ABD y BDC son dos planos que forman parte de un tejado. Trazar una horizontal del plano ABD de cota 3 Dibujar la trayectoria de una gota de agua que parte de un punto medio de la recta BC B"
EJERCICIO 1 ABD y BDC son dos planos que forman parte de un tejado. Trazar una horizontal del plano ABD de cota 3 Dibujar la trayectoria de una gota de agua que parte de un punto medio de la recta BC B"
PARÁBOLA { } Según esta definición y haciendo referencia al gráfico, se tiene:
 PARÁBOLA Definición.- Una parábola es el conjunto de todos los puntos en el plano que equidista de una recta fija, llamada directriz, y un punto fijo, denominado foco, que no pertenece a la recta, es decir:
PARÁBOLA Definición.- Una parábola es el conjunto de todos los puntos en el plano que equidista de una recta fija, llamada directriz, y un punto fijo, denominado foco, que no pertenece a la recta, es decir:
Movimiento curvilíneo. Magnitudes cinemáticas
 Movimiento curvilíneo. Magnitudes cinemáticas Movimiento curvilíneo Supongamos que el movimiento tiene lugar en el plano XY, Situamos un origen, y unos ejes, y representamos la trayectoria del móvil, es
Movimiento curvilíneo. Magnitudes cinemáticas Movimiento curvilíneo Supongamos que el movimiento tiene lugar en el plano XY, Situamos un origen, y unos ejes, y representamos la trayectoria del móvil, es
Sistema de coordenadas cartesianas. Ecuación de la recta y de la circunferencia.
 Clase 4 Sistema de coordenadas cartesianas. Ecuación de la recta y de la circunferencia. Clase 4... 1 1. Sistema de Coordenadas Cartesianas... 2 1.a. Punto medio... 3 1.b. Distancia entre dos puntos...
Clase 4 Sistema de coordenadas cartesianas. Ecuación de la recta y de la circunferencia. Clase 4... 1 1. Sistema de Coordenadas Cartesianas... 2 1.a. Punto medio... 3 1.b. Distancia entre dos puntos...
MATHEMATICA. Geometría - Recta. Ricardo Villafaña Figueroa. Material realizado con Mathematica. Ricardo Villafaña Figueroa
 MATHEMATICA Geometría - Recta Material realizado con Mathematica 2 Contenido Sistema de Coordenadas... 3 Distancia entre dos puntos... 3 Punto Medio... 5 La Recta... 8 Definición de recta... 8 Pendiente
MATHEMATICA Geometría - Recta Material realizado con Mathematica 2 Contenido Sistema de Coordenadas... 3 Distancia entre dos puntos... 3 Punto Medio... 5 La Recta... 8 Definición de recta... 8 Pendiente
LECCIÓN Nº 04 LA PARABOLA
 LECCIÓN Nº 04 LA PARABOLA Parábola El conjunto de puntos del plano tales que están a la misma distancia de una recta dada y de un punto dado F que no este sobre recibe el nombre de parábola. El punto F
LECCIÓN Nº 04 LA PARABOLA Parábola El conjunto de puntos del plano tales que están a la misma distancia de una recta dada y de un punto dado F que no este sobre recibe el nombre de parábola. El punto F
En general un cuerpo puede tener dos tipos distintos de movimiento simultáneamente.
 TORQUE Y EQUILIBRIO DE CUERPO RÍGIDO. En general un cuerpo puede tener dos tipos distintos de movimiento simultáneamente. De traslación a lo largo de una trayectoria, de rotación mientras se está trasladando,
TORQUE Y EQUILIBRIO DE CUERPO RÍGIDO. En general un cuerpo puede tener dos tipos distintos de movimiento simultáneamente. De traslación a lo largo de una trayectoria, de rotación mientras se está trasladando,
CINEMATICA ESCALAR I Conceptos Básicos y Gráficos
 Dpto Física PSN/2012 CINEMATICA ESCALAR I Conceptos Básicos y Gráficos La Física sistematiza la información y realiza la descripción del movimiento de un cuerpo y para ello utiliza algunos conceptos básicos
Dpto Física PSN/2012 CINEMATICA ESCALAR I Conceptos Básicos y Gráficos La Física sistematiza la información y realiza la descripción del movimiento de un cuerpo y para ello utiliza algunos conceptos básicos
V E C T O R E S L I B R E S E N E L P L A N O
 V E C T O R E S L I B R E S E N E L P L A N O 1. V E C T O R E S F I J O S Y V E C T O R E S L I B R E S E N E L P L A N O Existen magnitudes como la fuerza, la velocidad, la aceleración, que no quedan
V E C T O R E S L I B R E S E N E L P L A N O 1. V E C T O R E S F I J O S Y V E C T O R E S L I B R E S E N E L P L A N O Existen magnitudes como la fuerza, la velocidad, la aceleración, que no quedan
CAPÍTULO 3: PORCIONES Y NÚMEROS ENTEROS
 CAPÍTULO 3: PORCIONES Y NÚMEROS ENTEROS Fecha: Caja de herramientas 2014 CPM Educational Program. All rights reserved. 22 Capítulo 3: Porciones y números enteros Fecha: 23 2014 CPM Educational Program.
CAPÍTULO 3: PORCIONES Y NÚMEROS ENTEROS Fecha: Caja de herramientas 2014 CPM Educational Program. All rights reserved. 22 Capítulo 3: Porciones y números enteros Fecha: 23 2014 CPM Educational Program.
Grupo A B C D E Docente: Fís. Dudbil Olvasada Pabon Riaño Materia: Oscilaciones y Ondas
 Ondas mecánicas Definición: Una onda mecánica es la propagación de una perturbación a través de un medio. Donde. Así, la función de onda se puede escribir de la siguiente manera, Ondas transversales: Son
Ondas mecánicas Definición: Una onda mecánica es la propagación de una perturbación a través de un medio. Donde. Así, la función de onda se puede escribir de la siguiente manera, Ondas transversales: Son
Tutorial MT-b16. Matemática Tutorial Nivel Básico. Geometría analítica en línea recta
 12345678901234567890 M ate m ática Tutorial MT-b16 Matemática 2006 Tutorial Nivel Básico Geometría analítica en línea recta Matemática 2006 Tutorial Geometría analítica en línea recta Marco teórico: 1.
12345678901234567890 M ate m ática Tutorial MT-b16 Matemática 2006 Tutorial Nivel Básico Geometría analítica en línea recta Matemática 2006 Tutorial Geometría analítica en línea recta Marco teórico: 1.
Materia: Matemática de Octavo Tema: Plano Cartesiano
 Materia: Matemática de Octavo Tema: Plano Cartesiano Kaitlyn entró en la clase de matemáticas y vio la siguiente imagen mostrada en el proyector. Su maestra les pidió a todos en la clase que duplicaran
Materia: Matemática de Octavo Tema: Plano Cartesiano Kaitlyn entró en la clase de matemáticas y vio la siguiente imagen mostrada en el proyector. Su maestra les pidió a todos en la clase que duplicaran
Profesor: Carlos Arroyave Valencia GUÍA 2 TEMA: VECTORES - OPERACIONES MAGNITUDES FÍSICAS
 INSTITUTO TECNICO INDUSTRIAL PASCUAL BRAVO ÁREA: CIENCIAS NATURALES Y EDUCACIÓN AMBIENTAL (FÍSICA) GRADO: 10 JORNADA: Tarde PERÍODO: II Profesor: Carlos Arroyave Valencia GUÍA 2 TEMA: VECTORES - OPERACIONES
INSTITUTO TECNICO INDUSTRIAL PASCUAL BRAVO ÁREA: CIENCIAS NATURALES Y EDUCACIÓN AMBIENTAL (FÍSICA) GRADO: 10 JORNADA: Tarde PERÍODO: II Profesor: Carlos Arroyave Valencia GUÍA 2 TEMA: VECTORES - OPERACIONES
Bloque 3. Funciones. 1. Análisis de funciones
 Bloque 3. Funciones 1. Análisis de funciones 1. Concepto de función Una función es una relación entre dos magnitudes, de tal manera que a cada valor de la primera le corresponde un único valor de la segunda,
Bloque 3. Funciones 1. Análisis de funciones 1. Concepto de función Una función es una relación entre dos magnitudes, de tal manera que a cada valor de la primera le corresponde un único valor de la segunda,
TEMA VI: ÁNGULOS ENTRE ELEMENTOS
 TEMA VI: ÁNGULOS ENTRE ELEMENTOS 6.1.D Ángulo entre dos rectas El cálculo del ángulo de dos rectas que se cortan es sencillo. Si las rectas se cruzan, el ángulo es el formado entre una de las rectas y
TEMA VI: ÁNGULOS ENTRE ELEMENTOS 6.1.D Ángulo entre dos rectas El cálculo del ángulo de dos rectas que se cortan es sencillo. Si las rectas se cruzan, el ángulo es el formado entre una de las rectas y
PROCEDIMIENTO TEÓRICO
 1 CONSTANTE DE GRAVITACIÓN UNIVERSAL, SU VALOR EXACTO. EN EL SISTEMA INTERNACIONAL DE UNIDADES, VALE: G = 6,6718190396304099151153489 x 10 11 N m kg G = 6,6718190396304099151153489 x 10 11 m 3 kg 1 s CONSTANTE
1 CONSTANTE DE GRAVITACIÓN UNIVERSAL, SU VALOR EXACTO. EN EL SISTEMA INTERNACIONAL DE UNIDADES, VALE: G = 6,6718190396304099151153489 x 10 11 N m kg G = 6,6718190396304099151153489 x 10 11 m 3 kg 1 s CONSTANTE
TEMA 12: UN MUNDO EN MOVIMIENTO
 TEMA 12: UN MUNDO EN MOVIMIENTO 1- MOVIMIENTO El movimiento de un cuerpo es el cambio de posición respecto a otros objetos que sirven como sistema de referencia. Llamamos trayectoria del movimiento de
TEMA 12: UN MUNDO EN MOVIMIENTO 1- MOVIMIENTO El movimiento de un cuerpo es el cambio de posición respecto a otros objetos que sirven como sistema de referencia. Llamamos trayectoria del movimiento de
Lección 50. Funciones II. Plano cartesiano
 Lección 50 Funciones II Plano cartesiano Un sistema de coordenadas rectangulares o cartesianas, llamado también plano cartesiano o plano xy, está formado por dos rectas coordenadas perpendiculares (rectas
Lección 50 Funciones II Plano cartesiano Un sistema de coordenadas rectangulares o cartesianas, llamado también plano cartesiano o plano xy, está formado por dos rectas coordenadas perpendiculares (rectas
Unidades de medida Una conversión muy útil x 3,6 3,6
 Recordemos Unidades de medida Una conversión muy útil Si necesitamos pasar desde a o viceversa, podemos seguir este sencillo procedimiento. m s km h m s x 3,6 km h m s 3,6 km h Gráficos Para graficar,
Recordemos Unidades de medida Una conversión muy útil Si necesitamos pasar desde a o viceversa, podemos seguir este sencillo procedimiento. m s km h m s x 3,6 km h m s 3,6 km h Gráficos Para graficar,
Apéndice A. Vectores: propiedades y operaciones básicas.
 Vectores 145 Apéndice A. Vectores: propiedades y operaciones básicas. Una clasificación básica de las distintas propiedades físicas medibles, establece que estas pueden dividirse en dos tipos: a) Aquellas
Vectores 145 Apéndice A. Vectores: propiedades y operaciones básicas. Una clasificación básica de las distintas propiedades físicas medibles, establece que estas pueden dividirse en dos tipos: a) Aquellas
Guía de Matemática Segundo Medio
 Guía de Matemática Segundo Medio Aprendizaje Esperado:. Analizan la ecuación de la recta; establecen la dependencia entre las variables y la expresan gráfica y algebraicamente.. Identifican e interpretan
Guía de Matemática Segundo Medio Aprendizaje Esperado:. Analizan la ecuación de la recta; establecen la dependencia entre las variables y la expresan gráfica y algebraicamente.. Identifican e interpretan
DEPARTAMENTO DE FISICA DOCENTE: ING. JOEL PACO S.
 .1.- INTRODUCION Las propiedades físicas en la mecánica deben expresarse por una magnitud y una cierta unidad que las permita medir y comparar entre si, sin embargo debido a que en algunos casos esa información
.1.- INTRODUCION Las propiedades físicas en la mecánica deben expresarse por una magnitud y una cierta unidad que las permita medir y comparar entre si, sin embargo debido a que en algunos casos esa información
UTalca - Versión Preliminar
 1. Definición La parábola es el lugar geométrico de todos los puntos del plano que equidistan de un punto y una recta dada. Más claramente: Dados (elementos bases de la parábola) Una recta L, llamada directriz
1. Definición La parábola es el lugar geométrico de todos los puntos del plano que equidistan de un punto y una recta dada. Más claramente: Dados (elementos bases de la parábola) Una recta L, llamada directriz
MATEMÁTICAS III CUADERNILLO DE ACTIVIDADES Y TAREAS. Bachillerato General, Modalidad Mixta
 Bachillerato General, Modalidad Mixta MATEMÁTICAS III CUADERNILLO DE ACTIVIDADES Y TAREAS. Nombre del Alumn@ Día de la clase de matemáticas Hora de la clase de matemáticas Maestra: María Luisa Rubalcava
Bachillerato General, Modalidad Mixta MATEMÁTICAS III CUADERNILLO DE ACTIVIDADES Y TAREAS. Nombre del Alumn@ Día de la clase de matemáticas Hora de la clase de matemáticas Maestra: María Luisa Rubalcava
Secciones Cónicas. 0.1 Parábolas
 Secciones Cónicas 0.1 Parábolas Las secciones cónicas, también llamadas cónicas, se obtienen cortando un cono circular recto doble con un plano. Al cambiar la posición del plano se tiene un círculo, una
Secciones Cónicas 0.1 Parábolas Las secciones cónicas, también llamadas cónicas, se obtienen cortando un cono circular recto doble con un plano. Al cambiar la posición del plano se tiene un círculo, una
Física I. Estática y Dinámica. Leyes de Newton. Ejercicios. Ing. Alejandra Escobar
 Física I Estática y Dinámica. Leyes de Newton. Ejercicios UNIVERSIDAD FERMÍN TORO VICE RECTORADO ACADÉMICO FACULTAD DE INGENIERÍA Ing. Alejandra Escobar 15 cm 10 cm 6 cm GUÍA DE EJERCICIOS 1. Encontrar
Física I Estática y Dinámica. Leyes de Newton. Ejercicios UNIVERSIDAD FERMÍN TORO VICE RECTORADO ACADÉMICO FACULTAD DE INGENIERÍA Ing. Alejandra Escobar 15 cm 10 cm 6 cm GUÍA DE EJERCICIOS 1. Encontrar
FUNDAMENTOS DE LA REPRESENTACIÓN GRÁFICA EN INGENIERÍA. Ing. Guillermo Verger Cátedra: Representación Gráfica
 FUNDAMENTOS DE LA REPRESENTACIÓN GRÁFICA EN INGENIERÍA Ing. Guillermo Verger Cátedra: Representación Gráfica http://www.ingverger.com.ar El Dibujo de Ingeniería como lenguaje gráfico Representación de
FUNDAMENTOS DE LA REPRESENTACIÓN GRÁFICA EN INGENIERÍA Ing. Guillermo Verger Cátedra: Representación Gráfica http://www.ingverger.com.ar El Dibujo de Ingeniería como lenguaje gráfico Representación de
2018-I. Profesor: NELSON ENRIQUE TORRES BERMONT Web:
 2018-I Profesor: NELSON ENRIQUE TORRES BERMONT Email: [email protected] Web: https://unipamplona.wordpress.com/ SISTEMAS DE REFERENCIA Es aquel lugar del espacio en donde en forma real o
2018-I Profesor: NELSON ENRIQUE TORRES BERMONT Email: [email protected] Web: https://unipamplona.wordpress.com/ SISTEMAS DE REFERENCIA Es aquel lugar del espacio en donde en forma real o
Interpretación geométrica de la derivada
 Interpretación geométrica de la derivada El matemático francés ierre de Fermat (60 665) al estudiar máimos mínimos de ciertas funciones observó que en aquellos puntos en los que la curva presenta un máimo
Interpretación geométrica de la derivada El matemático francés ierre de Fermat (60 665) al estudiar máimos mínimos de ciertas funciones observó que en aquellos puntos en los que la curva presenta un máimo
Elementos de geometría analítica
 UNIDAD 7: APLIQUEMOS ELEMENTOS DE GEOMETRIA ANALITICA. Introducción Elementos de geometría analítica En esta unidad última nos ocuparemos del estudio de los conceptos más fundamentales de la geometría
UNIDAD 7: APLIQUEMOS ELEMENTOS DE GEOMETRIA ANALITICA. Introducción Elementos de geometría analítica En esta unidad última nos ocuparemos del estudio de los conceptos más fundamentales de la geometría
Física 2º Bto. (A y B) Movimiento ondulatorio. Campos gravitatorio y eléctrico 19 marzo 2008
 Alumno o alumna: Puntuación: 1. El oscilador armónico Una partícula de 1,4 kg de masa se conecta a un muelle de masa despreciable y constante recuperadora k = 15 N/m, de manera que el sistema se mueve
Alumno o alumna: Puntuación: 1. El oscilador armónico Una partícula de 1,4 kg de masa se conecta a un muelle de masa despreciable y constante recuperadora k = 15 N/m, de manera que el sistema se mueve
Introducción. Cuerpo Rígido. Mecánica Racional 20 TEMA 4: Cinemática de los Cuerpos Rígidos.
 Introducción. La cinemática de cuerpos rígidos estudia las relaciones existentes entre el tiempo, las posiciones, las velocidades y las aceleraciones de las diferentes partículas que forman un cuerpo rígido.
Introducción. La cinemática de cuerpos rígidos estudia las relaciones existentes entre el tiempo, las posiciones, las velocidades y las aceleraciones de las diferentes partículas que forman un cuerpo rígido.
METODOLOGÍA DEL ANÁLISIS DE VELOCIDADES Y ACELERACIONES POR EL MÉTODO DEL POLÍGONO.
 METODOLOGÍA DEL ANÁLISIS DE VELOCIDADES Y ACELERACIONES POR EL MÉTODO DEL POLÍGONO. INTRODUCCIÓN Para una mejor apreciación del estudio de la dinámica se clasifica en dos ramas: cinemática y cinética.
METODOLOGÍA DEL ANÁLISIS DE VELOCIDADES Y ACELERACIONES POR EL MÉTODO DEL POLÍGONO. INTRODUCCIÓN Para una mejor apreciación del estudio de la dinámica se clasifica en dos ramas: cinemática y cinética.
Revisión de Relatividad Especial 1
 Revisión de Relatividad Especial 1 Esta entrada está orientada para aquellos que necesitan una presentación breve de los conceptos básicos de la relatividad especial. Por lo tanto, esto es útil para los
Revisión de Relatividad Especial 1 Esta entrada está orientada para aquellos que necesitan una presentación breve de los conceptos básicos de la relatividad especial. Por lo tanto, esto es útil para los
ITM, Institución universitaria. Guía de Laboratorio de Física Mecánica. Práctica 5: MUA. vt (4) Implementos
 ITM, Institución universitaria Guía de Laboratorio de Física Mecánica Práctica 5: MUA Implementos Soporte universal (3), nueces (3), varilla corta (), flexómetro, carro, sensor digital de tiempo y fotocompuertas,
ITM, Institución universitaria Guía de Laboratorio de Física Mecánica Práctica 5: MUA Implementos Soporte universal (3), nueces (3), varilla corta (), flexómetro, carro, sensor digital de tiempo y fotocompuertas,
CONOCER LA FUNCIÓN DE PROPORCIONALIDAD DIRECTA
 0 REPASO APOO CONOCER LA FUNCIÓN DE PROPORCIONALIDAD DIRECTA OBJETIVO Una función de proporcionalidad directa, se epresa de la forma: y = m, siendo m un número cualquiera. La representación gráfica de
0 REPASO APOO CONOCER LA FUNCIÓN DE PROPORCIONALIDAD DIRECTA OBJETIVO Una función de proporcionalidad directa, se epresa de la forma: y = m, siendo m un número cualquiera. La representación gráfica de
18. PERSPECTIVA CABALLERA.
 18. PERSPECTIVA CABALLERA. La perspectiva caballera es un sistema de representación que utiliza la proyección paralela oblicua, en el que las dimensiones del plano proyectante frontal, como las de los
18. PERSPECTIVA CABALLERA. La perspectiva caballera es un sistema de representación que utiliza la proyección paralela oblicua, en el que las dimensiones del plano proyectante frontal, como las de los
El análisis cartesiano (René Descartes ) descubrió que las ecuaciones pueden tener una representación gráfica.
 Capítulo 4. Estudio de la línea recta El análisis cartesiano (René Descartes 1596-1650) descubrió que las ecuaciones pueden tener una representación gráfica. Para lograr esa representación gráfica es necesario
Capítulo 4. Estudio de la línea recta El análisis cartesiano (René Descartes 1596-1650) descubrió que las ecuaciones pueden tener una representación gráfica. Para lograr esa representación gráfica es necesario
SISTEMA DIÉDRICO: PUNTO, RECTA, PLANO: Sistemas de representación. El Sistema diédrico ELEMENTOS DEL SISTEMA DIÉDRICO
 SISTEMA DIÉDRICO (I) TEMA 8: 2º DE BAC/Página 1 de 21 SISTEMA DIÉDRICO: PUNTO, RECTA, PLANO: CLASES DE PROYECCIÓN: Proyección de un punto sobre un plano es la intersección del rayo proyectante que pasa
SISTEMA DIÉDRICO (I) TEMA 8: 2º DE BAC/Página 1 de 21 SISTEMA DIÉDRICO: PUNTO, RECTA, PLANO: CLASES DE PROYECCIÓN: Proyección de un punto sobre un plano es la intersección del rayo proyectante que pasa
