Diseño de algoritmos
|
|
|
- Vicente Saavedra Moreno
- hace 5 años
- Vistas:
Transcripción
1 Diseño de algoritmos Algoritmos de Vuelta Atrás Jesús Bermúdez de Andrés Universidad del País Vasco/Euskal Herriko Unibertsitatea (UPV/EHU) Curso
2 1 Algoritmos de vuelta atrás El coloreado de mapas Número mínimo de monedas Suma de subconjunto El problema de la mochila
3 Algoritmos de vuelta atrás (1/2) Hay problemas para los que no se conoce mejor solución que la que consiste, básicamente, en una búsqueda sistemática en un espacio de propuestas posibles de solución. La técnica de vuelta atrás consiste en construir la solución de un problema mediante extensiones de ensayos parciales de solución. En general, se parte del ensayo neutro [ ] y en un estado intermedio del proceso, tras haber construido el ensayo parcial [x 1,..., x i ], se tantea sistemáticamente con cada posibilidad x i+1 de extender el ensayo: si [x 1,..., x i, x i+1 ] es un ensayo aceptable, se extiende [x 1,..., x i ] a [x 1,..., x i, x i+1 ] y se continúa con este último ensayo parcial. si ninguna de las posibilidades para x i+1 hacen que [x 1,..., x i, x i+1 ] sea aceptable entonces significa que el ensayo [x 1,..., x i ] no es extensible a solución, por consiguiente retiramos la última opción x i añadida a ese ensayo y continuamos con el ensayo parcial [x 1,..., x i 1 ] tanteando otra posible opción.
4 Árbol de ensayos
5 Algoritmos de vuelta atrás (2/2) Esta estrategia equivale al recorrido en profundidad de un árbol impĺıcito (ya que ese árbol no está representado por ninguna estructura de datos) comenzando desde la raíz, tal que cada nodo se corresponde con un ensayo parcial y cada arista que parte de un nodo se corresponde con una opción de tanteo. Cuando un ensayo no es aceptable equivale a podar la posible rama del árbol que pudiera crecer desde ese nodo. Cuanto más inteligente sea la poda más eficiente será el algoritmo. Las hojas de ese árbol impĺıcito se corresponden con ensayos no extensibles a solución o bien con ensayos que son solución.
6 Esquema de vuelta atrás que calcula todas las soluciones proc Ensayar (E) if Solución(E) then gestionar el E solución {else } for cada posibilidad p de extender E loop if Es aceptable(e + p) then Ensayar (E + p) Debe retirarse la cláusula {else } en caso de que haya soluciones que sean prefijos de otras soluciones.
7 Esquema de vuelta atrás que calcula la primera solución proc Ensayar (E, éxito) if Solución(E) then gestionar el E solución éxito true else for cada posibilidad p de extender E loop if Es aceptable(e + p) then Ensayar (E + p, éxito) if éxito then return
8 Análisis de un algoritmo de vuelta atrás Un modo de aproximarse al análisis de la eficiencia de los algoritmos de vuelta atrás es analizar el árbol impĺıcito de ensayos explorado por el algoritmo: 1 contar el número de ensayos explorados. 2 analizar el coste de calcular las posibilidades de extender cada ensayo y el coste de generar cada nuevo ensayo. 3 analizar el coste de comprobación de la aceptación de un ensayo. Hay que observar que el resultado es una cota superior. El rendimiento real del algoritmo puede ser mucho mejor, ya que la función de aceptación de ensayos puede podar una cantidad considerable de ramas del árbol impĺıcito. De hecho, la utilidad de los algoritmos de vuelta atrás depende principalmente de la capacidad de aplicación de funciones de aceptación que poden convenientemente ramas del árbol de ensayos. Evaluación usando un Método de Montecarlo.
9 El coloreado de mapas Calcular todas las formas posibles de colorear los países de un mapa poĺıtico, usando sólo cuatro colores, de manera que ningún par de países fronterizos esté pintado del mismo color. Representamos el mapa mediante un grafo no dirigido en el que los nodos representan a los países y cada arista representa que sus extremos son países fronterizos. En particular, representaremos un mapa con n países mediante una matriz de adyacencia F (1..n, 1..n) con valores booleanos.
10 Árbol de ensayos para Cuatro colores Un ensayo de longitud k consiste en la lista de colores (tomados de los cuatro posibles) que se han asignado a los países numerados con [1,..., k]. Representamos los ensayos con un vector color(1..n) con valores en el conjunto {1, 2, 3, 4} que representa a los cuatro colores. En cada momento del proceso sólo son representativos los k primeros componentes del vector color. Cuando k llegue a ser n y se satisfaga la condición de aceptación tendremos una solución del problema. Una extensión de un ensayo de longitud k consiste en dar color al país número k + 1. Supongamos que tenemos un ensayo de longitud k que satisface las restricciones del problema, entonces una extensión de ese ensayo es aceptable si el color asignado al país número k + 1 es distinto del color asignado a sus adyacentes que estén numerados del 1 al k.
11 Algoritmo Cuatro colores (1/2) La llamada inicial debe ser Cuatro colores(0, F, color) proc Cuatro colores(k, F (1..n, 1..n), color(1..n)) {k: número de países coloreados} if k = n then Imprimir(color(1..n)) else for C in 1..,4 loop color(k + 1) C if Es aceptable(f, color, k + 1) then Cuatro colores(k + 1, F, color)
12 Algoritmo Cuatro colores (2/2) func Es aceptable(f, color, último) return boolean {último: índice del último país coloreado} acept true país 1 while país < último acept loop if F (país, último) color(país)=color(último) then acept false end if país país + 1 end loop return acept
13 Número mínimo de monedas (1/2) Dadas n de monedas, de valores v 1,..., v n respectivamente, determinar cual es el número mínimo de monedas que necesitamos para sumar una determinada cantidad C. Un ensayo será una secuencia de los valores de esas monedas, que denominaremos SEC. Para completar la representación de un ensayo tendremos: una variable suma que representa la suma de los valores de SEC, una variable long que representa la longitud de SEC y una variable k que representa el subíndice de la moneda que hay que considerar a continuación. La parte del esquema de vuelta atrás dedicada a gestionar el ensayo solución sirve para memorizar la mejor solución encontrada hasta el momento. La solución óptima será la que quede registrada en la secuencia OPT, de longitud longopt.
14 Árbol de ensayos para Número mínimo de monedas
15 Número mínimo de monedas (2/2) Suponemos ordenados los valores de monedas, de manera que v 1 v 2... v n Ensayo: Un secuencia de valores de monedas Las posibilidades de extender un ensayo [v i,..., v k 1 ] son v k... v n El ensayo [v i,..., v k 1, v k ] es aceptable si su longitud es menor que longopt y su suma menor o igual que C Un ensayo es solución si su suma es igual a C
16 Algoritmo MinMonedas Para podar algunas ramas del árbol de ensayos, asumimos que tenemos ordenadas las monedas de manera que v 1... v n. proc MinMonedas(SEC, k, long, suma, OPT, longopt ) if suma = C then if long < longopt then OPT SEC longopt long else while (k n) (1 + long < longopt ) (suma + v k C) loop SEC[1 + long] v k MinMonedas(SEC, k + 1, 1 + long, suma + v k, OPT, longopt ) k k + 1 La llamada inicial debe ser MinMonedas(SEC, 1, 0, 0, OPT, n + 1)
17 Variación de Número mínimo de monedas Qué modificaciones debemos hacer en el algoritmo MinMonedas si disponemos de tantas monedas como se desee de cada valor v 1,..., v n? Una vez analizada la modificación del árbol de ensayos, observamos que basta con sustituir el valor de k + 1 por k en la llamada recursiva, es decir: MinMonedas(SEC, k, 1 + long, suma + v k, OPT, longopt )
18 Suma de subconjunto Disponemos de valores V = {V 1,..., V n } enteros positivos y queremos saber todas las formas posibles de sumar D con subconjuntos de V. Un ensayo constará de un vector conjunto de ceros y unos, de manera que conjunto[i] = 1 representa que V i pertenece al subconjunto seleccionado y conjunto[i] = 0 representa que no. Tendremos dos variables: suma que representa la suma de los valores del subconjunto seleccionado y resto que representa la suma de los valores que quedan todavía por considerar. La variable j representa el subíndice del valor de V que hay que considerar a continuación. Para podar más ramas es importante considerar los valores de V en orden creciente: Suponemos que V 1... V n. Un ensayo es aceptable si suma + resto D (para que sea posible llegar a sumar D) y suma D (para que la suma del ensayo no exceda de la cantidad a sumar).
19 Algoritmo SumaSubconjunto proc SumaSubconjunto(suma, resto, j, conjunto) if suma = D then Imprimir(conjunto[1..j 1]) else if suma + V j D then conjunto[j] 1 SumaSubconjunto(suma + V j, resto V j, j + 1, conjunto) if suma + resto V j D then conjunto[j] 0 SumaSubconjunto(suma, resto V j, j + 1, conjunto) La llamada inicial debe ser SumaSubconjunto(0, n i=1 V i, 1, conjunto)
20 El problema de la mochila (1/2) Dado M 0 y dados n objetos con valores unitarios (v 1,..., v n ) y pesos (p 1,..., p n ) respectivamente, queremos calcular un vector (x 1,..., x n ) de valores x i = 0, 1 tal que se maximice restringido a que n x i v i i=1 n x i p i M i=1
21 El problema de la mochila (2/2) Hay varias opciones para la definición de los ensayos. Una posibilidad simple es la siguiente: los ensayos son vectores de longitud i n con valores 0, 1 que representan las opciones tomadas con respecto a los objetos numerados con {1,..., i}; x i = 0 representa la opción de no poner el objeto i en la mochila y x i = 1 representa la opción de ponerlo. Los ensayos se representan mediante un vector X(1..n) y una variable j; el valor de la variable j representa el identificador del objeto que debe estudiarse a continuación para extender el ensayo. Cuando j = n + 1 significa que tenemos un ensayo de longitud n
22 Algoritmo Mochila 0 1 {XOPT(1..n) y VOPT : mejor solución encontrada hasta el momento y su valor, repectivamente} {SV y SP: valor y peso, respectivamente, del ensayo en curso X } {M: capacidad de la mochila y V(1..n) y P(1..n) los valores y pesos respectivos de los objetos} {j: índice del objeto que puede extender el ensayo} proc Mochila 0 1(SP, SV, X, j, VOPT, XOPT) if j = n+1 then if SV > VOPT then XOPT(1..n) X(1..n) VOPT SV end if else for k in 0..1 loop if SP + k P(j) M then X(j) k Mochila 0 1(SP + X(j) P(j), SV + X(j) V(j), X, j+1, VOPT, XOPT) La llamada inicial deberá ser Mochila 0 1(0, 0, X, 1, 0, XOPT)
23 Algoritmo alternativo a Mochila 0 1 (1/5) 1 En primer lugar, en vez de buscar soluciones de longitud n, consideramos solución cualquier ensayo cuyo peso no exceda la capacidad de la mochila. 2 En este caso, tenemos soluciones que son prefijos de otras soluciones. 3 Para podar ramas que ya no son prometedoras, utilizaremos un criterio que aprovecha lo que conocemos de este problema para el caso de las fracciones de objetos (véase algoritmos voraces). 4 Diremos que la extensión de un ensayo es aceptable si cabe alguna esperanza de que mejore el beneficio de la mejor carga de mochila encontrada hasta el momento.
24 Algoritmo alternativo a Mochila 0 1 (2/5) Asumimos que v 1 p 1 v 2 p 2... vn p n Consideremos que tenemos el ensayo (x 1,..., x i ) con peso = i j=1 x jp j y valor = i j=1 x jv j. Imaginemos que podemos añadir al ensayo (x 1,..., x i ) los objetos completos siguientes numerados hasta el k 1, y que excedemos la capacidad M de la mochila si añadimos el objeto número k completo. Entonces, el peso cota que podemos llevar en la mochila, partiendo del ensayo (x 1,..., x i ) es peso cota = peso + y una cota superior del beneficio sería valor cota = (valor + k 1 j=i+1 k 1 j=i+1 p j v j ) + (M peso cota) v k p k
25 Algoritmo alternativo a Mochila 0 1 (3/5) Si valor OPT es el máximo valor conseguido hasta el momento, diremos que (x 1,..., x i ) es aceptable si: 1 peso M (su peso no excede la capacidad de la mochila) y 2 valor cota > valor OPT (y promete más que lo conocido)
26 Algoritmo alternativo a Mochila 0 1 (4/5) {Precondición: v 1 p 1 v 2 p 2... vn p n } proc Mochila 0 1 V(X, SP, SV, i, VOPT, XOPT) if SV > VOPT then XOPT(1..i) X(1..i) VOPT SV end if if i < n then for s in 0..1 loop if SP + s P(i+1) M Es aceptable(x, i+1, s, SP, SV, VOPT) then X(i+1) s Mochila 0 1 V(X, SP + s P(i+1), SV + s V(i+1), i+1, VOPT, XOPT) La llamada inicial debe ser: Mochila 0 1 V(X, 0, 0, 0, 0, XOPT)
27 Algoritmo alternativo a Mochila 0 1 (5/5) func Es aceptable(x, e, X e, SP, SV, VOPT) return boolean k e peso cota SP + X e P(e) SV SV + X e V(e) while k < n peso cota M loop k k + 1 peso cota peso cota + P(k) SV SV + V(k) end loop if peso cota > M then {k es el primer objeto que no cabe} peso cota peso cota - P(k) SV SV - V(k) valor cota SV + (M - peso cota) V(k)/P(k) else {peso cota M y k=n} valor cota SV end if return valor cota > VOPT
Diseño de algoritmos
 Diseño de algoritmos Jesús Bermúdez de Andrés. UPV-EHU Guías para la solución de ejercicios: Vuelta atrás Curso 2008-09 1. Escriba un algoritmo de vuelta atrás para determinar el mínimo número de monedas
Diseño de algoritmos Jesús Bermúdez de Andrés. UPV-EHU Guías para la solución de ejercicios: Vuelta atrás Curso 2008-09 1. Escriba un algoritmo de vuelta atrás para determinar el mínimo número de monedas
Diseño de algoritmos
 Diseño de algoritmos Programación Dinámica Jesús Bermúdez de Andrés Universidad del País Vasco/Euskal Herriko Unibertsitatea (UPV/EHU) Curso 2008-09 1 Programación Dinámica Definición de la técnica Funciones
Diseño de algoritmos Programación Dinámica Jesús Bermúdez de Andrés Universidad del País Vasco/Euskal Herriko Unibertsitatea (UPV/EHU) Curso 2008-09 1 Programación Dinámica Definición de la técnica Funciones
Diseño de algoritmos. Universidad del País Vasco/Euskal Herriko Unibertsitatea (UPV/EHU) Curso
 Diseño de algoritmos Montículos Jesús Bermúdez de Andrés Universidad del País Vasco/Euskal Herriko Unibertsitatea (UPV/EHU) Curso 2008-09 1 Montículos Ordenación por Montículo Montículos Un montículo (binario)
Diseño de algoritmos Montículos Jesús Bermúdez de Andrés Universidad del País Vasco/Euskal Herriko Unibertsitatea (UPV/EHU) Curso 2008-09 1 Montículos Ordenación por Montículo Montículos Un montículo (binario)
Diseño de algoritmos
 Diseño de algoritmos Análisis de algoritmos Jesús Bermúdez de Andrés Universidad del País Vasco/Euskal Herriko Unibertsitatea (UPV/EHU) Curso 2008-09 1 Análisis de algoritmos Qué analizamos? Función de
Diseño de algoritmos Análisis de algoritmos Jesús Bermúdez de Andrés Universidad del País Vasco/Euskal Herriko Unibertsitatea (UPV/EHU) Curso 2008-09 1 Análisis de algoritmos Qué analizamos? Función de
Algoritmos y Estructuras de Datos Tema 2: Diseño de Algoritmos
 Algoritmos y Estructuras de Datos Tema 2: Diseño de Algoritmos 1! 1. Algoritmos recursivos " 1.1 Algoritmos recursivos. Recursión simple " 1.2 Algoritmos con vuelta atrás y ejemplos! 2. Complejidad de
Algoritmos y Estructuras de Datos Tema 2: Diseño de Algoritmos 1! 1. Algoritmos recursivos " 1.1 Algoritmos recursivos. Recursión simple " 1.2 Algoritmos con vuelta atrás y ejemplos! 2. Complejidad de
1. Método general. 2. Análisis de tiempos de ejecución. 3. Ejemplos de aplicación Problema de las 8 reinas Problema de la mochila 0/1.
 Backtracking. Método general. 2. Análisis de tiempos de ejecución. 3. Ejemplos de aplicación. 3.. Problema de las 8 reinas. 3.2. Problema de la mochila 0/. Método general El backtracking (método de retroceso
Backtracking. Método general. 2. Análisis de tiempos de ejecución. 3. Ejemplos de aplicación. 3.. Problema de las 8 reinas. 3.2. Problema de la mochila 0/. Método general El backtracking (método de retroceso
PARTE II: ALGORÍTMICA
 PARTE II: ALGORÍTMICA 5.. Método general 5.2. Análisis de tiempos de ejecución 5.3. Ejemplos de aplicación 5.3.. Problema de la mochila 0/ 5.3.2. Problema de la asignación 5.3.3. Resolución de juegos A.E.D.
PARTE II: ALGORÍTMICA 5.. Método general 5.2. Análisis de tiempos de ejecución 5.3. Ejemplos de aplicación 5.3.. Problema de la mochila 0/ 5.3.2. Problema de la asignación 5.3.3. Resolución de juegos A.E.D.
Multiplicación de matrices simétricas
 Multiplicación de matrices simétricas La traspuesta de una matriz A n n es definida como una matriz A T n n tal que A T [i, j] =A[j, i] paracadai, j 2{1,...,n} Además, una matriz A es simétrica si A =
Multiplicación de matrices simétricas La traspuesta de una matriz A n n es definida como una matriz A T n n tal que A T [i, j] =A[j, i] paracadai, j 2{1,...,n} Además, una matriz A es simétrica si A =
x x 2 s s= (x 1, x 2 ) ... ? (sin explorar) M= (x 1, x 2, x 3, x 4,..., x n ) valor(m) =?
 Exploración de grafos Grafos Recorridos sobre grafos Búsqueda primero en profundidad Búsqueda primero en anchura Backtracking ( vuelta atrás ) Descripción general Espacio de soluciones Implementación Ejemplos
Exploración de grafos Grafos Recorridos sobre grafos Búsqueda primero en profundidad Búsqueda primero en anchura Backtracking ( vuelta atrás ) Descripción general Espacio de soluciones Implementación Ejemplos
Diseño de algoritmos
 Diseño de algoritmos Jesús Bermúdez de Andrés. UPV-EHU Guías para la solución de ejercicios: Análisis de algoritmos Curso 2008-09 1. Con un algoritmo de función de coste temporal f(n) = n 3 resolvemos
Diseño de algoritmos Jesús Bermúdez de Andrés. UPV-EHU Guías para la solución de ejercicios: Análisis de algoritmos Curso 2008-09 1. Con un algoritmo de función de coste temporal f(n) = n 3 resolvemos
ANÁLISIS Y DISEÑO DE ALGORITMOS
 ANÁLISIS Y DISEÑO DE ALGORITMOS CURSO 26/27 BOLETÍN DE PROBLEMAS: ALGORITMOS VORACES Ejercicio 1 Sean n personas, representadas por los Enteros : 1..n, puestas en círculo, y m, un Entero no negativo cualquiera,
ANÁLISIS Y DISEÑO DE ALGORITMOS CURSO 26/27 BOLETÍN DE PROBLEMAS: ALGORITMOS VORACES Ejercicio 1 Sean n personas, representadas por los Enteros : 1..n, puestas en círculo, y m, un Entero no negativo cualquiera,
Planteamiento General
 Algoritmos de Ramificación y Poda Ejemplos de Aplicación Problema de la Mochila entera Problema del Rompecabezas Problema de la Asignación Problema del Viajante Se aplica a problemas que cumplen: Se puedan
Algoritmos de Ramificación y Poda Ejemplos de Aplicación Problema de la Mochila entera Problema del Rompecabezas Problema de la Asignación Problema del Viajante Se aplica a problemas que cumplen: Se puedan
El Juego como Problema de Búsqueda
 El Juego como Problema de Búsqueda En este algoritmo identificamos dos jugadores: max y min. El objetivo es encontrar la mejor movida para max. Supondremos que max mueve inicialmente y que luego se turnan
El Juego como Problema de Búsqueda En este algoritmo identificamos dos jugadores: max y min. El objetivo es encontrar la mejor movida para max. Supondremos que max mueve inicialmente y que luego se turnan
Problema ejemplo. El Arte de la Programación Rápida. Backtracking
 El Arte de la Programación Rápida Backtracking Problema ejemplo Vamos a analizar la técnica de backtracking a través de un ejemplo. El problema de las 8 reinas Cómo ubicar 8 reinas en un tablero sin que
El Arte de la Programación Rápida Backtracking Problema ejemplo Vamos a analizar la técnica de backtracking a través de un ejemplo. El problema de las 8 reinas Cómo ubicar 8 reinas en un tablero sin que
Apuntes de Teórico PROGRAMACIÓN 3. Backtracking. Versión 1.4
 Apuntes de Teórico PROGRAMACIÓN 3 Backtracking Versión 1.4 2 Índice Introducción... 4 Problema de las n reinas... 4 Espacio de soluciones... 5 Colorear un mapa... 9 Hallar una solución... 10 Hallar todas
Apuntes de Teórico PROGRAMACIÓN 3 Backtracking Versión 1.4 2 Índice Introducción... 4 Problema de las n reinas... 4 Espacio de soluciones... 5 Colorear un mapa... 9 Hallar una solución... 10 Hallar todas
Algoritmos mas complejos. Algoritmos y Estructuras de Datos II (Programación I) Mgter. Vallejos, Oscar A.
 Algoritmos mas complejos Divide y Vencerás Técnica empleada en cosas dispares. También en el diseño de algoritmos. (ordenación: Quicksort; Mergesort). Consiste básicamente en dividir un problema original
Algoritmos mas complejos Divide y Vencerás Técnica empleada en cosas dispares. También en el diseño de algoritmos. (ordenación: Quicksort; Mergesort). Consiste básicamente en dividir un problema original
ÁRBOLES CRISTIAN ALFREDO MUÑOZ ÁLVAREZ JUAN DAVID LONDOÑO CASTRO JUAN PABLO CHACÓN PEÑA EDUARDO GONZALES
 ÁRBOLES CRISTIAN ALFREDO MUÑOZ ÁLVAREZ JUAN DAVID LONDOÑO CASTRO JUAN PABLO CHACÓN PEÑA EDUARDO GONZALES ÁRBOL Un árbol es un grafo no dirigido, conexo, sin ciclos (acíclico), y que no contiene aristas
ÁRBOLES CRISTIAN ALFREDO MUÑOZ ÁLVAREZ JUAN DAVID LONDOÑO CASTRO JUAN PABLO CHACÓN PEÑA EDUARDO GONZALES ÁRBOL Un árbol es un grafo no dirigido, conexo, sin ciclos (acíclico), y que no contiene aristas
Complejidad computacional. Algoritmos y Estructuras de Datos I. Complejidad computacional. Notación O grande
 Complejidad computacional Algoritmos y Estructuras de Datos I Segundo cuatrimestre de 2014 Departamento de Computación - FCEyN - UBA Algoritmos - clase 10 Introducción a la complejidad computacional y
Complejidad computacional Algoritmos y Estructuras de Datos I Segundo cuatrimestre de 2014 Departamento de Computación - FCEyN - UBA Algoritmos - clase 10 Introducción a la complejidad computacional y
GRAFOS. Tomado de: Joyanes Aguilar Luis, Estructuras de datos en Java. CASOS
 GRAFOS Tomado de: Joyanes Aguilar Luis, Estructuras de datos en Java. CASOS 1.4 El recorrido del cartero Imaginemos un grafo que representa el mapa de las calles de un barrio. Una calle va de una esquina
GRAFOS Tomado de: Joyanes Aguilar Luis, Estructuras de datos en Java. CASOS 1.4 El recorrido del cartero Imaginemos un grafo que representa el mapa de las calles de un barrio. Una calle va de una esquina
Los grafos son estructuras de datos Representan relaciones entre objetos. Son aplicables en. Relaciones arbitrarias, es decir No jerárquicas.
 ESTRUCTURA DE DATOS Los grafos son estructuras de datos Representan relaciones entre objetos Relaciones arbitrarias, es decir No jerárquicas Son aplicables en Química Modem Geografía Ing. Eléctrica e Industrial,
ESTRUCTURA DE DATOS Los grafos son estructuras de datos Representan relaciones entre objetos Relaciones arbitrarias, es decir No jerárquicas Son aplicables en Química Modem Geografía Ing. Eléctrica e Industrial,
1. GRAFOS : CONCEPTOS BASICOS
 1. GRAFOS : CONCEPTOS BASICOS Sea V un conjunto finito no vacio y sea E V x V. El par (V, E) es un grafo no dirigido, donde V es un conjunto de vértices o nodos y E es un conjunto de aristas. Denotaremos
1. GRAFOS : CONCEPTOS BASICOS Sea V un conjunto finito no vacio y sea E V x V. El par (V, E) es un grafo no dirigido, donde V es un conjunto de vértices o nodos y E es un conjunto de aristas. Denotaremos
Algoritmos y Complejidad
 Algoritmos y Complejidad Algoritmos greedy Pablo R. Fillottrani Depto. Ciencias e Ingeniería de la Computación Universidad Nacional del Sur Primer Cuatrimestre 2017 Algoritmos greedy Generalidades Problema
Algoritmos y Complejidad Algoritmos greedy Pablo R. Fillottrani Depto. Ciencias e Ingeniería de la Computación Universidad Nacional del Sur Primer Cuatrimestre 2017 Algoritmos greedy Generalidades Problema
Parte de Algoritmos de la asignatura de Programación Master de Bioinformática. Búsqueda exhaustiva
 Parte de Algoritmos de la asignatura de Programación Master de Bioinformática Búsqueda exhaustiva Web asignatura: http://dis.um.es/~domingo/algbio.html E-mail profesor: domingo@um.es Transparencias preparadas
Parte de Algoritmos de la asignatura de Programación Master de Bioinformática Búsqueda exhaustiva Web asignatura: http://dis.um.es/~domingo/algbio.html E-mail profesor: domingo@um.es Transparencias preparadas
TEMA 5 El tipo grafo. Tipo grafo
 TEMA 5 El tipo grafo PROGRAMACIÓN Y ESTRUCTURAS DE DATOS Tipo grafo 1. Concepto de grafo y terminología 2. Especificación algebraica. Representación de grafos.1. Recorrido en profundidad o DFS.2. Recorrido
TEMA 5 El tipo grafo PROGRAMACIÓN Y ESTRUCTURAS DE DATOS Tipo grafo 1. Concepto de grafo y terminología 2. Especificación algebraica. Representación de grafos.1. Recorrido en profundidad o DFS.2. Recorrido
Análisis de algoritmos
 Tema 10: Algoritmos ávidos M. en C. Edgardo Adrián Franco Martínez http://www.eafranco.com edfrancom@ipn.mx @edfrancom edgardoadrianfrancom 1 Contenido Introducción Algoritmos ávidos Forma general de un
Tema 10: Algoritmos ávidos M. en C. Edgardo Adrián Franco Martínez http://www.eafranco.com edfrancom@ipn.mx @edfrancom edgardoadrianfrancom 1 Contenido Introducción Algoritmos ávidos Forma general de un
Apuntes de Teórico de Programación 3. Apuntes de Teórico PROGRAMACIÓN 3. Greedy. Versión 1.1
 Apuntes de Teórico PROGRAMACIÓN 3 Greedy Versión 1.1 1 Índice Índice... Introducción... 3 Ejemplo 1 (problema de las monedas)... 3 Ejemplo (problema de la mochila)... 4 Aplicaciones del método Greedy a
Apuntes de Teórico PROGRAMACIÓN 3 Greedy Versión 1.1 1 Índice Índice... Introducción... 3 Ejemplo 1 (problema de las monedas)... 3 Ejemplo (problema de la mochila)... 4 Aplicaciones del método Greedy a
B s ú que u da p rim i ero o e n n p rof o u f n u d n id i ad: E tr t ate t gia i L I L FO B s ú que u da p rim i ero o e n n a nc n h c u h r u a:
 Búsqueda sin información Fernando Berzal, berzal@acm.org Búsqueda sin información Recorridos sobre grafos Búsqueda en anchura (BFS) Búsqueda en profundidad (DFS) Descenso iterativo (IDS) [ vuelta atrás
Búsqueda sin información Fernando Berzal, berzal@acm.org Búsqueda sin información Recorridos sobre grafos Búsqueda en anchura (BFS) Búsqueda en profundidad (DFS) Descenso iterativo (IDS) [ vuelta atrás
Programación Dinámica
 Programación Dinámica La técnica de programación dinámica se aplica en general a problemas de optimización. l igual que "dividir y conquistar", el problema es dividido en subproblemas de tamaños menores
Programación Dinámica La técnica de programación dinámica se aplica en general a problemas de optimización. l igual que "dividir y conquistar", el problema es dividido en subproblemas de tamaños menores
Introducción a los árboles. Lección 11
 Introducción a los árboles Lección 11 Árbol: Conjunto de elementos de un mismo tipo, denominados nodos, que pueden representarse en un grafo no orientado, conexo y acíclico, en el que existe un vértice
Introducción a los árboles Lección 11 Árbol: Conjunto de elementos de un mismo tipo, denominados nodos, que pueden representarse en un grafo no orientado, conexo y acíclico, en el que existe un vértice
Tema: Algoritmos Backtracking.
 Programación IV. Guía 12 1 Facultad: Ingeniería Escuela: Computación Asignatura: Programación IV Tema: Algoritmos Backtracking. Objetivos Específicos Comprender el funcionamiento de un Algoritmo Backtracking.
Programación IV. Guía 12 1 Facultad: Ingeniería Escuela: Computación Asignatura: Programación IV Tema: Algoritmos Backtracking. Objetivos Específicos Comprender el funcionamiento de un Algoritmo Backtracking.
Algoritmos Voraces. Diseño y Análisis de Algoritmos
 Algoritmos Voraces Diseño y Análisis de Algoritmos Contenidos Contenidos 1 Introducción 2 Ejemplos básicos 3 Cambio de monedas 4 Problema de la mochila 5 Problemas de planificación de tareas 6 Patrones
Algoritmos Voraces Diseño y Análisis de Algoritmos Contenidos Contenidos 1 Introducción 2 Ejemplos básicos 3 Cambio de monedas 4 Problema de la mochila 5 Problemas de planificación de tareas 6 Patrones
Algoritmos y Estructuras de Datos Curso 06/07. Ejercicios
 9..En un problema de backtracking estamos interesados en almacenar de forma explícita el árbol recorrido por el algoritmo. De cada nodo del árbol sólo necesitamos saber un número, que indica el orden en
9..En un problema de backtracking estamos interesados en almacenar de forma explícita el árbol recorrido por el algoritmo. De cada nodo del árbol sólo necesitamos saber un número, que indica el orden en
Tema 4y 5. Algoritmos voraces. Algoritmos sobre grafos
 Tema 4y 5. Algoritmos voraces. Algoritmos sobre grafos Objetivos: Estudio de la técnica de diseño de algoritmos voraces Estudio de algunos problemas clásicos: Indice: Mochila con fraccionamiento Algoritmos
Tema 4y 5. Algoritmos voraces. Algoritmos sobre grafos Objetivos: Estudio de la técnica de diseño de algoritmos voraces Estudio de algunos problemas clásicos: Indice: Mochila con fraccionamiento Algoritmos
(x 1,x 2,x 3,,x n ),...,x n
 Exploración de grafos Grafos Recorridos sobre grafos Búsqueda primero en profundidad Búsqueda primero en anchura ( vuelta atrás ) Descripción general Espacio de soluciones Implementación Ejemplos Branch
Exploración de grafos Grafos Recorridos sobre grafos Búsqueda primero en profundidad Búsqueda primero en anchura ( vuelta atrás ) Descripción general Espacio de soluciones Implementación Ejemplos Branch
Parte de Algoritmos de la asignatura de Programación Master de Bioinformática. Grafos
 Parte de Algoritmos de la asignatura de Programación Master de Bioinformática Grafos Web asignatura: http://dis.um.es/~domingo/algbio.html E-mail profesor: domingo@um.es Transparencias preparadas a partir
Parte de Algoritmos de la asignatura de Programación Master de Bioinformática Grafos Web asignatura: http://dis.um.es/~domingo/algbio.html E-mail profesor: domingo@um.es Transparencias preparadas a partir
Teoría de redes y optimización en redes
 Teoría de redes y optimización en redes Pedro Sánchez Martín Contenidos Definiciones básicas Árbol generador mínimo de expansión Camino mínimo Algoritmo Dkstra Algoritmo Bellman-Ford Fluo máximo Fluo de
Teoría de redes y optimización en redes Pedro Sánchez Martín Contenidos Definiciones básicas Árbol generador mínimo de expansión Camino mínimo Algoritmo Dkstra Algoritmo Bellman-Ford Fluo máximo Fluo de
Algoritmo de ramificación y acotación
 Algoritmo de ramificación y acotación Investigación Operativa Ingeniería Técnica en Informática de Gestión UC3M Curso 08/09 Descripción de los objetivos En esta práctica desarrollaremos el algoritmo de
Algoritmo de ramificación y acotación Investigación Operativa Ingeniería Técnica en Informática de Gestión UC3M Curso 08/09 Descripción de los objetivos En esta práctica desarrollaremos el algoritmo de
El TAD Grafo. El TAD Grafo
 ! Esta representación resulta útil cuando el número de vértices se conoce previamente y permanecerá fijo durante la resolución del problema, pero resulta ineficiente si necesitamos añadir o eliminar vértices
! Esta representación resulta útil cuando el número de vértices se conoce previamente y permanecerá fijo durante la resolución del problema, pero resulta ineficiente si necesitamos añadir o eliminar vértices
Parte de Algoritmos de la asignatura de Programación Master de Bioinformática. Avance rápido
 Parte de Algoritmos de la asignatura de Programación Master de Bioinformática Avance rápido Web asignatura: http://dis.um.es/~domingo/algbio.html E-mail profesor: domingo@um.es Transparencias preparadas
Parte de Algoritmos de la asignatura de Programación Master de Bioinformática Avance rápido Web asignatura: http://dis.um.es/~domingo/algbio.html E-mail profesor: domingo@um.es Transparencias preparadas
Introducción al análisis de algoritmos
 Estructura de Datos y Algoritmos Introducción al análisis de algoritmos 1. Eficiencia en tiempo de Ejecución Cuando resolvemos un problema nos vemos frecuentemente enfrentando una elección de programas,
Estructura de Datos y Algoritmos Introducción al análisis de algoritmos 1. Eficiencia en tiempo de Ejecución Cuando resolvemos un problema nos vemos frecuentemente enfrentando una elección de programas,
Curso: Métodos de Monte Carlo Unidad 3, Sesión 7: Problemas de conteo
 Curso: Métodos de Monte Carlo Unidad 3, Sesión 7: Problemas de conteo Departamento de Investigación Operativa Instituto de Computación, Facultad de Ingeniería Universidad de la República, Montevideo, Uruguay
Curso: Métodos de Monte Carlo Unidad 3, Sesión 7: Problemas de conteo Departamento de Investigación Operativa Instituto de Computación, Facultad de Ingeniería Universidad de la República, Montevideo, Uruguay
Árboles de Expansión Mínima. Matemática Discreta. Agustín G. Bonifacio UNSL
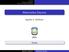 UNSL Árboles Definiciones y Ejemplos Caracterización Un árbol T es un grafo simple que satisface lo siguiente: si v y w son vértices en T, entonces existe una trayectoria simple única de v a w. Un árbol
UNSL Árboles Definiciones y Ejemplos Caracterización Un árbol T es un grafo simple que satisface lo siguiente: si v y w son vértices en T, entonces existe una trayectoria simple única de v a w. Un árbol
Algoritmos y Estructuras de Datos Tema 2: Diseño de Algoritmos
 Algoritmos y Estructuras de Datos Tema 2: Diseño de Algoritmos 1! 1. Algoritmos recursivos " 1.1 Algoritmos recursivos. Recursión simple " 1.2 Algoritmos con vuelta atrás y ejemplos! 2. Complejidad de
Algoritmos y Estructuras de Datos Tema 2: Diseño de Algoritmos 1! 1. Algoritmos recursivos " 1.1 Algoritmos recursivos. Recursión simple " 1.2 Algoritmos con vuelta atrás y ejemplos! 2. Complejidad de
Algoritmos voraces (greedy)
 Dr. Eduardo A. RODRÍGUEZ TELLO CINVESTAV-Tamaulipas 21 de marzo de 2018 Dr. Eduardo RODRÍGUEZ T. (CINVESTAV) Algoritmos voraces 21 de marzo de 2018 1 / 45 1 Algoritmos voraces (greedy) Aplicaciones de
Dr. Eduardo A. RODRÍGUEZ TELLO CINVESTAV-Tamaulipas 21 de marzo de 2018 Dr. Eduardo RODRÍGUEZ T. (CINVESTAV) Algoritmos voraces 21 de marzo de 2018 1 / 45 1 Algoritmos voraces (greedy) Aplicaciones de
Centro Asociado Palma de Mallorca. Tutor: Antonio Rivero Cuesta
 Centro Asociado Palma de Mallorca Lógica y Estructuras Discretas Tutor: Antonio Rivero Cuesta Tema 5 Teoría de Grafos Conceptos Básicos Un grafo consta de: Grafo Un conjunto de nodos, Un conjunto de aristas
Centro Asociado Palma de Mallorca Lógica y Estructuras Discretas Tutor: Antonio Rivero Cuesta Tema 5 Teoría de Grafos Conceptos Básicos Un grafo consta de: Grafo Un conjunto de nodos, Un conjunto de aristas
NIVEL 17: ESTRUCTURAS NO LINEALES
 1 NIVEL 17: ESTRUCTURAS NO LINEALES Recorridos y Algorítmica de Grafos 2 Agenda Recorridos de grafos Recorridos Planos Recorridos en profundidad Recorridos por niveles Recorridos Heurísticos Algorítmica
1 NIVEL 17: ESTRUCTURAS NO LINEALES Recorridos y Algorítmica de Grafos 2 Agenda Recorridos de grafos Recorridos Planos Recorridos en profundidad Recorridos por niveles Recorridos Heurísticos Algorítmica
ARBOLES BINARIOS ORDENADOS. REPRESENTACIÓN Y OPERACIONES
 ARBOLES BINARIOS ORDENADOS. REPRESENTACIÓN Y OPERACIONES TEMAS Recorrido de un árbol Máximo y mínimo Búsqueda de un elemento Borrado de un nodo 3 Características ARBOLES - CONCEPTOS Cada elemento del árbol
ARBOLES BINARIOS ORDENADOS. REPRESENTACIÓN Y OPERACIONES TEMAS Recorrido de un árbol Máximo y mínimo Búsqueda de un elemento Borrado de un nodo 3 Características ARBOLES - CONCEPTOS Cada elemento del árbol
Teoría de grafos y optimización en redes
 Teoría de grafos y optimización en redes José María Ferrer Caja Universidad Pontificia Comillas Definiciones básicas Grafo: Conjunto de nodos (o vértices) unidos por aristas G = (V,E) Ejemplo V = {,,,,
Teoría de grafos y optimización en redes José María Ferrer Caja Universidad Pontificia Comillas Definiciones básicas Grafo: Conjunto de nodos (o vértices) unidos por aristas G = (V,E) Ejemplo V = {,,,,
Análisis y Complejidad de Algoritmos. Arboles Binarios. Arturo Díaz Pérez
 Análisis y Complejidad de Algoritmos Arboles Binarios Arturo Díaz Pérez Arboles Definiciones Recorridos Arboles Binarios Profundidad y Número de Nodos Arboles-1 Arbol Un árbol es una colección de elementos,
Análisis y Complejidad de Algoritmos Arboles Binarios Arturo Díaz Pérez Arboles Definiciones Recorridos Arboles Binarios Profundidad y Número de Nodos Arboles-1 Arbol Un árbol es una colección de elementos,
ARBOLES B. Lo que si es cierto es que la letra B no significa "binario", ya que:
 ARBOLES B El problema original comienza con la necesidad de mantener índices en almacenamiento externo para acceso a bases de datos, es decir, con el grave problema de la lentitud de estos dispositivos
ARBOLES B El problema original comienza con la necesidad de mantener índices en almacenamiento externo para acceso a bases de datos, es decir, con el grave problema de la lentitud de estos dispositivos
Heurísticas en el recorrido de árboles de soluciones
 Heurísticas en el recorrido de árboles de soluciones. Árboles de soluciones. Repaso de backtracking y branch and bound. Uso de heurísicas en backtracking 4. Uso de heurísticas en branch and bound . Árboles
Heurísticas en el recorrido de árboles de soluciones. Árboles de soluciones. Repaso de backtracking y branch and bound. Uso de heurísicas en backtracking 4. Uso de heurísticas en branch and bound . Árboles
Coloreo de Grafos. Algoritmos y Estructuras de Datos III
 Coloreo de Grafos Algoritmos y Estructuras de Datos III Coloreo de nodos Definiciones: Un coloreo (válido) de los nodos de un grafo G = (V, X ) es una asignación f : V C, tal que f (v) f (u) (u, v) E.
Coloreo de Grafos Algoritmos y Estructuras de Datos III Coloreo de nodos Definiciones: Un coloreo (válido) de los nodos de un grafo G = (V, X ) es una asignación f : V C, tal que f (v) f (u) (u, v) E.
Apellidos:... Nombre:...
 Apellidos:....................................... Nombre:........................................ Introducción a la Inteligencia Artificial 1 er Parcial de Teoría 12 Noviembre 2004 Ejercicio 1: Responder
Apellidos:....................................... Nombre:........................................ Introducción a la Inteligencia Artificial 1 er Parcial de Teoría 12 Noviembre 2004 Ejercicio 1: Responder
Todos los Pares de Rutas más Cortas (All-Pairs Shortest Paths) DR. JESÚS A. GONZÁLEZ BERNAL CIENCIAS COMPUTACIONALES INAOE
 Todos los Pares de Rutas más Cortas (All-Pairs Shortest Paths) DR. JESÚS A. GONZÁLEZ BERNAL CIENCIAS COMPUTACIONALES INAOE Problema de Encontrar todos los Pares de Rutas más Cortas 2 Encontrar las rutas
Todos los Pares de Rutas más Cortas (All-Pairs Shortest Paths) DR. JESÚS A. GONZÁLEZ BERNAL CIENCIAS COMPUTACIONALES INAOE Problema de Encontrar todos los Pares de Rutas más Cortas 2 Encontrar las rutas
Este material es de uso exclusivo para clase de algoritmos y estructura de datos, la información de este documento fue tomada textualmente de varios
 CLASE GRAFOS Este material es de uso exclusivo para clase de algoritmos y estructura de datos, la información de este documento fue tomada textualmente de varios libros por lo que está prohibida su impresión
CLASE GRAFOS Este material es de uso exclusivo para clase de algoritmos y estructura de datos, la información de este documento fue tomada textualmente de varios libros por lo que está prohibida su impresión
Apuntes elaborados por: Aaron Asencio, Eduardo Quevedo, Raquel López Revisado por: Javier Miranda el???
 Apuntes elaborados por: Aaron Asencio, duardo Quevedo, Raquel López Revisado por: Javier Miranda el??? Tema 9: rafos Los grafos no son más que la versión general de un árbol, es decir, cualquier nodo de
Apuntes elaborados por: Aaron Asencio, duardo Quevedo, Raquel López Revisado por: Javier Miranda el??? Tema 9: rafos Los grafos no son más que la versión general de un árbol, es decir, cualquier nodo de
Tema 7: Árboles ESTRUCTURAS DE DATOS 1
 Tema 7: Árboles ESTRUCTURAS DE DATOS 1 Contenidos Definiciones Conceptos de Árboles Binarios Especificación algebraica Implementaciones Programación con Árboles Binarios Árboles Binarios de Búsqueda Introducción
Tema 7: Árboles ESTRUCTURAS DE DATOS 1 Contenidos Definiciones Conceptos de Árboles Binarios Especificación algebraica Implementaciones Programación con Árboles Binarios Árboles Binarios de Búsqueda Introducción
Algoritmos de búsqueda en grafos I
 I Dr. Eduardo A. RODRÍGUEZ TELLO CINVESTAV-Tamaulipas 7 de febrero de 2018 Dr. Eduardo RODRÍGUEZ T. (CINVESTAV) Búsqueda en grafos I 7 de febrero de 2018 1 / 36 1 Representación computacional de grafos
I Dr. Eduardo A. RODRÍGUEZ TELLO CINVESTAV-Tamaulipas 7 de febrero de 2018 Dr. Eduardo RODRÍGUEZ T. (CINVESTAV) Búsqueda en grafos I 7 de febrero de 2018 1 / 36 1 Representación computacional de grafos
Coloreo de vértices Definiciones: Coloreo de Grafos. Cotas para χ Proposición: Si H es un subgrafo de G entonces χ(h) χ(g).
 Coloreo de vértices Definiciones: Coloreo de Grafos Algoritmos y Estructuras de Datos III Un coloreo (válido) de los vértices de un grafo G = (V, X ) es una asignación f : V C, tal que f (v) f (u) (u,
Coloreo de vértices Definiciones: Coloreo de Grafos Algoritmos y Estructuras de Datos III Un coloreo (válido) de los vértices de un grafo G = (V, X ) es una asignación f : V C, tal que f (v) f (u) (u,
Análisis y Diseño de Algoritmos
 Análisis y Diseño de Algoritmos Algoritmos Voraces DR. JESÚS A. GONZÁLEZ BERNAL CIENCIAS COMPUTACIONALES INAOE Introducción Siempre toman la mejor opción en cada momento (punto de decisión del algoritmo)
Análisis y Diseño de Algoritmos Algoritmos Voraces DR. JESÚS A. GONZÁLEZ BERNAL CIENCIAS COMPUTACIONALES INAOE Introducción Siempre toman la mejor opción en cada momento (punto de decisión del algoritmo)
Tema 10: Árbol binario de búsqueda
 Tema 10: Árbol binario de búsqueda M. en C. Edgardo Adrián Franco Martínez http://www.eafranco.com edfrancom@ipn.mx @edfrancom edgardoadrianfrancom (Prof. Edgardo A. Franco) 1 Contenido Árbol binario de
Tema 10: Árbol binario de búsqueda M. en C. Edgardo Adrián Franco Martínez http://www.eafranco.com edfrancom@ipn.mx @edfrancom edgardoadrianfrancom (Prof. Edgardo A. Franco) 1 Contenido Árbol binario de
Grafos: algunas definiciones
 Grafos: algunas definiciones Un grafo dirigido G es un par (V, E), donde V es un conjunto finito de nodos (o vértices) y E es una relación binaria sobre V. Un grafo no dirigido G es un par (V, E), donde
Grafos: algunas definiciones Un grafo dirigido G es un par (V, E), donde V es un conjunto finito de nodos (o vértices) y E es una relación binaria sobre V. Un grafo no dirigido G es un par (V, E), donde
Cálculo del valor acumulado de los elementos de una secuencia
 Ejercicios Resueltos del tema 10 Contenido Cálculo del valor acumulado de los elementos de una secuencia... 1 Secuencias. Esquemas recursivos finales... 9 Esquemas sobre tipos recursivos... 14 Algoritmos
Ejercicios Resueltos del tema 10 Contenido Cálculo del valor acumulado de los elementos de una secuencia... 1 Secuencias. Esquemas recursivos finales... 9 Esquemas sobre tipos recursivos... 14 Algoritmos
Relación de Ejercicios. Programación Paralela 4º de Grado en Ingeniería Informática.
 1. Por qué el modelo de programación que se sigue al programar con MPI es independiente de la asignación? 2. Describir gráficamente una solución eficiente para realizar una operación de reducción global
1. Por qué el modelo de programación que se sigue al programar con MPI es independiente de la asignación? 2. Describir gráficamente una solución eficiente para realizar una operación de reducción global
Algoritmos y Estructuras de Datos II
 27 de mayo de 2013 Clase de hoy 1 Repaso Divide y vencerás Algoritmos voraces 2 3 Divide y vencerás Algoritmos voraces Repaso cómo vs. qué 3 partes 1 análisis de algoritmos 2 tipos de datos 3 técnicas
27 de mayo de 2013 Clase de hoy 1 Repaso Divide y vencerás Algoritmos voraces 2 3 Divide y vencerás Algoritmos voraces Repaso cómo vs. qué 3 partes 1 análisis de algoritmos 2 tipos de datos 3 técnicas
ANÁLISIS Y DISEÑO DE ALGORITMOS
 ANÁLISIS Y DISEÑO DE ALGORITMOS CURSO 2005/2006 BOLETÍN DE PROBLEMAS: ALGORITMOS VORACES Ejercicio 1 Sean n personas, representadas por los Enteros : 1..n, puestas en círculo, y m, un Entero no negativo
ANÁLISIS Y DISEÑO DE ALGORITMOS CURSO 2005/2006 BOLETÍN DE PROBLEMAS: ALGORITMOS VORACES Ejercicio 1 Sean n personas, representadas por los Enteros : 1..n, puestas en círculo, y m, un Entero no negativo
Apuntes de Teórico PROGRAMACIÓN 3
 Apuntes de Teórico PROGRAACIÓN Programación Dinámica Versión. Índice Índice... Introducción... Principio de optimalidad...5 Ejemplo: Camino de menor costo...6 Ejemplo: problema de la mochila...6 Aplicación
Apuntes de Teórico PROGRAACIÓN Programación Dinámica Versión. Índice Índice... Introducción... Principio de optimalidad...5 Ejemplo: Camino de menor costo...6 Ejemplo: problema de la mochila...6 Aplicación
259. El número de combinaciones de m objetos entre un conjunto de n, denotado por n, para n 1 y 0 m n, se puede definir recursivamente por: m
 258. Aplicar el algoritmo de programación dinámica para el problema del cambio de monedas sobre el siguiente ejemplo: n = 3, P = 9, c = (1, 3, 4). Qué ocurre si multiplicamos P y c por un valor constante,
258. Aplicar el algoritmo de programación dinámica para el problema del cambio de monedas sobre el siguiente ejemplo: n = 3, P = 9, c = (1, 3, 4). Qué ocurre si multiplicamos P y c por un valor constante,
Tema 2, 3 y 4 GRUPO 82 - INGENIERÍA INFORMÁTICA. Bernardo D Auria. 3 Diciembre Departamento de Estadística. Universidad Carlos III de Madrid
 Bernardo D Auria Departamento de Estadística Universidad Carlos III de Madrid GRUPO 82 - INGENIERÍA INFORMÁTICA Diciembre 2008 Ejercicio T2-JN12 Comprueba que el problema lineal min x x 1 + x 2 2x x +
Bernardo D Auria Departamento de Estadística Universidad Carlos III de Madrid GRUPO 82 - INGENIERÍA INFORMÁTICA Diciembre 2008 Ejercicio T2-JN12 Comprueba que el problema lineal min x x 1 + x 2 2x x +
Algoritmos: Exploración de grafos
 Algoritmos: Exploración de grafos Alberto Valderruten LFCIA - Departamento de Computación Facultad de Informática Universidad de A Coruña, España www.lfcia.org/alg www.fi.udc.es Contenido Juegos de estrategia
Algoritmos: Exploración de grafos Alberto Valderruten LFCIA - Departamento de Computación Facultad de Informática Universidad de A Coruña, España www.lfcia.org/alg www.fi.udc.es Contenido Juegos de estrategia
Estructuras de Datos Orientadas a Objetos. Pseudocódigo y aplicaciones en C#.NET. Capítulo 9.- Grafos
 Capítulo 9.- Grafos Cuestionario 9.1 Se pueden representar los nodos de un grafo como un conjunto de elementos 9.2 Se pueden representar los arcos de un grafo como un conjunto de tuplas 9.3 Los grafos
Capítulo 9.- Grafos Cuestionario 9.1 Se pueden representar los nodos de un grafo como un conjunto de elementos 9.2 Se pueden representar los arcos de un grafo como un conjunto de tuplas 9.3 Los grafos
Tema: Recorrido de Grafos. Ruta más corta
 PED104. Guía N 12 Página 1 Facultad: Ingeniería Escuela: Computación Asignatura: Programación con Estructuras de Datos Tema: Recorrido de Grafos. Ruta más corta Competencia Desarrolla sistemas de información
PED104. Guía N 12 Página 1 Facultad: Ingeniería Escuela: Computación Asignatura: Programación con Estructuras de Datos Tema: Recorrido de Grafos. Ruta más corta Competencia Desarrolla sistemas de información
Problemas de programación entera: El método Ramifica y Acota. Investigación Operativa, Grado en Estadística y Empresa, 2011/12
 Problemas de programación entera: El método Ramifica y Acota Prof. José Niño Mora Investigación Operativa, Grado en Estadística y Empresa, 2011/12 Esquema La estrategia Divide y vencerás Árboles de enumeración
Problemas de programación entera: El método Ramifica y Acota Prof. José Niño Mora Investigación Operativa, Grado en Estadística y Empresa, 2011/12 Esquema La estrategia Divide y vencerás Árboles de enumeración
Complejidad computacional. Algoritmos y Estructuras de Datos I. Complejidad computacional. Notación O grande
 Complejidad computacional Algoritmos y Estructuras de Datos I Segundo cuatrimestre de 2015 Departamento de Computación - FCEyN - UBA Algoritmos - clase 10 Introducción a la complejidad computacional y
Complejidad computacional Algoritmos y Estructuras de Datos I Segundo cuatrimestre de 2015 Departamento de Computación - FCEyN - UBA Algoritmos - clase 10 Introducción a la complejidad computacional y
A) PREORDEN B) INORDEN C) POSTORDEN D) NIVELES
 Capitulo 5. Arboles 1. Al recorrer el siguiente árbol en se visitan más nodos para llegar al número 38. Justifique su respuesta mostrando cada uno de los recorridos. Tipo de Recorrido Recorrido A) PREORDEN
Capitulo 5. Arboles 1. Al recorrer el siguiente árbol en se visitan más nodos para llegar al número 38. Justifique su respuesta mostrando cada uno de los recorridos. Tipo de Recorrido Recorrido A) PREORDEN
Propiedades (1/2) Soluciones Ejercicios Tema 14. Representación de Grafo (I) Propiedades (2/2) Grado del grafo: 6 V = 7 E = 12
 Soluciones Ejercicios Tema Ejercicios Adaptados de Apuntes y Exámenes de EDA Germán Moltó gmolto@dsic.upv.es Estructuras de Datos y Algoritmos Escuela Técnica Superior de Ingeniería Informática Universidad
Soluciones Ejercicios Tema Ejercicios Adaptados de Apuntes y Exámenes de EDA Germán Moltó gmolto@dsic.upv.es Estructuras de Datos y Algoritmos Escuela Técnica Superior de Ingeniería Informática Universidad
Búsqueda en línea y Búsqueda multiagente
 Búsqueda en línea y Búsqueda multiagente Ingeniería Informática, 4º Curso académico: 2011/2012 Profesores: Ramón Hermoso y Matteo Vasirani 1 Tema 2: Agentes basados en Búsqueda Resumen: 2. Agentes basados
Búsqueda en línea y Búsqueda multiagente Ingeniería Informática, 4º Curso académico: 2011/2012 Profesores: Ramón Hermoso y Matteo Vasirani 1 Tema 2: Agentes basados en Búsqueda Resumen: 2. Agentes basados
Inteligencia Artificial
 I.T. en Informática de Sistemas, 3º Curso académico: 2009/2010 Profesores: Sascha Ossowski y Ramón Hermoso 1 Tema 2: Búsqueda Resumen: 2. Búsqueda 2.1. Agentes de resolución de problemas 2.2. Búsqueda
I.T. en Informática de Sistemas, 3º Curso académico: 2009/2010 Profesores: Sascha Ossowski y Ramón Hermoso 1 Tema 2: Búsqueda Resumen: 2. Búsqueda 2.1. Agentes de resolución de problemas 2.2. Búsqueda
ESTRUCTURA DE DATOS Y ALGORITMOS Titulación: Ingeniero Técnico en Informática de Gestión Curso: 2º Nombre y apellidos: Nota:
 Nombre y apellidos: Nota: NOTA FINAL: Nota Practica (1 punto) + Nota Examen (9 punto) Es indispensable aprobar el examen (4,5 puntos) para aprobar la asignatura (5 puntos) La práctica es opcional Duración:
Nombre y apellidos: Nota: NOTA FINAL: Nota Practica (1 punto) + Nota Examen (9 punto) Es indispensable aprobar el examen (4,5 puntos) para aprobar la asignatura (5 puntos) La práctica es opcional Duración:
ARBOLES GENERADORES. Orlando Arboleda Molina. 16 de septiembre de Escuela de Ingeniería de Sistemas y Computación de La Universidad del Valle
 ARBOLES GENERADORES Orlando Arboleda Molina Escuela de Ingeniería de Sistemas y Computación de La Universidad del Valle 16 de septiembre de 2008 Contenido Árboles generadores Algoritmo búsqueda por profundidad
ARBOLES GENERADORES Orlando Arboleda Molina Escuela de Ingeniería de Sistemas y Computación de La Universidad del Valle 16 de septiembre de 2008 Contenido Árboles generadores Algoritmo búsqueda por profundidad
Matemáticas Discretas
 Coordinación de Ciencias Computacionales - INAOE Matemáticas Discretas Cursos Propedéuticos 2011 Ciencias Computacionales INAOE Dr. Enrique Muñoz de Cote jemc@inaoep.mx http://ccc.inaoep.mx/~jemc Oficina
Coordinación de Ciencias Computacionales - INAOE Matemáticas Discretas Cursos Propedéuticos 2011 Ciencias Computacionales INAOE Dr. Enrique Muñoz de Cote jemc@inaoep.mx http://ccc.inaoep.mx/~jemc Oficina
CAPÍTULO 4 PROGRAMACIÓN LINEAL ENTERA
 CAPÍTULO 4 PROGRAMACIÓN LINEAL ENTERA Programación Lineal Entera Es una técnica que permite modelar y resolver problemas cuya característica principal es que el conjunto de soluciones factibles es discreto.
CAPÍTULO 4 PROGRAMACIÓN LINEAL ENTERA Programación Lineal Entera Es una técnica que permite modelar y resolver problemas cuya característica principal es que el conjunto de soluciones factibles es discreto.
Sugerencia: transformar el problema en un problema sobre grafos, teniendo en cuenta las casillas y las posiciones accesibles desde cada una.
 3. Modificar el algoritmo voraz del problema de la mochila visto en clase, para tratar el caso en que no se permita partir los objetos (es decir, un objeto se coge entero o no se coge nada). Comprobar
3. Modificar el algoritmo voraz del problema de la mochila visto en clase, para tratar el caso en que no se permita partir los objetos (es decir, un objeto se coge entero o no se coge nada). Comprobar
Búsqueda en espacio de estados
 Búsqueda en espacio de estados Departamento de Ciencias de la Computación e Inteligencia Artificial Universidad de Sevilla Inteligencia Artificial CCIA, US Búsqueda en espacio de estados IA 1 / 35 Metodología
Búsqueda en espacio de estados Departamento de Ciencias de la Computación e Inteligencia Artificial Universidad de Sevilla Inteligencia Artificial CCIA, US Búsqueda en espacio de estados IA 1 / 35 Metodología
Algoritmos pseudo-polinomiales
 Análisis de Algoritmos Algoritmos pseudo-polinomiales Dra. Elisa Schaeffer elisa.schaeffer@gmail.com PISIS / FIME / UANL Algoritmos pseudo-polinomiales p. 1 HAMILTON PATH es NP-completo La reducción es
Análisis de Algoritmos Algoritmos pseudo-polinomiales Dra. Elisa Schaeffer elisa.schaeffer@gmail.com PISIS / FIME / UANL Algoritmos pseudo-polinomiales p. 1 HAMILTON PATH es NP-completo La reducción es
Tema: Algoritmos para la ruta más corta en un Grafo.
 Programación IV. Guía No. 10 1 Facultad: Ingeniería Escuela: Computación Asignatura: Programación IV Tema: Algoritmos para la ruta más corta en un Grafo. Objetivos Específicos Definir el concepto de camino
Programación IV. Guía No. 10 1 Facultad: Ingeniería Escuela: Computación Asignatura: Programación IV Tema: Algoritmos para la ruta más corta en un Grafo. Objetivos Específicos Definir el concepto de camino
Algoritmos glotones. mat-151
 Algoritmos glotones (greedy) mat-151 Alonso Ramirez Manzanares Computación y Algoritmos 04.06.2009 Algoritmos glotones Algoritmos utilizados en problemas de optimización. Estos algoritmos siguen típicamente
Algoritmos glotones (greedy) mat-151 Alonso Ramirez Manzanares Computación y Algoritmos 04.06.2009 Algoritmos glotones Algoritmos utilizados en problemas de optimización. Estos algoritmos siguen típicamente
Demostrando cotas inferiores: Arboles de decisión
 Demostrando cotas inferiores: Arboles de decisión De la misma forma que la técnica basada en la mejor estrategia del adversario, vamos a utilizar los árboles de decisión para establecer una cota inferior
Demostrando cotas inferiores: Arboles de decisión De la misma forma que la técnica basada en la mejor estrategia del adversario, vamos a utilizar los árboles de decisión para establecer una cota inferior
Algoritmos para caminos más cortos (2) comp-420
 lgoritmos para caminos más cortos (2) comp-420 lgoritmo * escrito totalmente en 1968 por Peter art, Nils Nilsson y ertram Raphael. n 1964 Nils Nilsson inventó un método que utiliza una heurística para
lgoritmos para caminos más cortos (2) comp-420 lgoritmo * escrito totalmente en 1968 por Peter art, Nils Nilsson y ertram Raphael. n 1964 Nils Nilsson inventó un método que utiliza una heurística para
MATRIZ DE ARBOLES DE DECISION
 MATRIZ DE ARBOLES DE DECISION Los árboles son un subconjunto importante de los grafos, y son una herramienta útil para describir estructuras que presentan algún tipo de jerarquía. Las dificultades de las
MATRIZ DE ARBOLES DE DECISION Los árboles son un subconjunto importante de los grafos, y son una herramienta útil para describir estructuras que presentan algún tipo de jerarquía. Las dificultades de las
Algoritmos de búsqueda con espacio de memoria limitado
 Algoritmos de búsqueda con espacio de memoria limitado Los métodos de búsqueda por primero el mejor, tales como A, no escalan bien a grandes problemas de búsqueda debido a su consumo de memoria, mientras
Algoritmos de búsqueda con espacio de memoria limitado Los métodos de búsqueda por primero el mejor, tales como A, no escalan bien a grandes problemas de búsqueda debido a su consumo de memoria, mientras
OBJETIVOS ÍNDICE BIBLIOGRAFÍA
 OBJETIVOS Tema 9: GRAFOS Primera Parte Estructuras de Datos y Algoritmos Curso 2002/03 Definiciones formales de grafo y conceptos relacionados Estructuras de datos para representar grafos Algoritmos para
OBJETIVOS Tema 9: GRAFOS Primera Parte Estructuras de Datos y Algoritmos Curso 2002/03 Definiciones formales de grafo y conceptos relacionados Estructuras de datos para representar grafos Algoritmos para
Grafos. Suponiendo que e = [u, v]. Entonces los nodos u y v se llaman extremos de e y u y v se dice que son nodos adyacentes o vecinos.
![Grafos. Suponiendo que e = [u, v]. Entonces los nodos u y v se llaman extremos de e y u y v se dice que son nodos adyacentes o vecinos. Grafos. Suponiendo que e = [u, v]. Entonces los nodos u y v se llaman extremos de e y u y v se dice que son nodos adyacentes o vecinos.](/thumbs/54/33802392.jpg) Grafos Los grafos son estructuras que constan de vértices o nodos y de aristas o arcos que conectan los vértices entre sí. Un grafo G consiste en dos cosas: 1. Un conjunto V de elementos llamados nodos
Grafos Los grafos son estructuras que constan de vértices o nodos y de aristas o arcos que conectan los vértices entre sí. Un grafo G consiste en dos cosas: 1. Un conjunto V de elementos llamados nodos
Modelos de Redes: Problemas de la Ruta más m s corta. M. En C. Eduardo Bustos Farías
 Modelos de Redes: Problemas de la Ruta más m s corta M. En C. Eduardo Bustos Farías as Problemas de la Ruta más m s corta 2 Problemas de la Ruta más m s corta Se trata de encontrar la ruta de menor distancia,
Modelos de Redes: Problemas de la Ruta más m s corta M. En C. Eduardo Bustos Farías as Problemas de la Ruta más m s corta 2 Problemas de la Ruta más m s corta Se trata de encontrar la ruta de menor distancia,
INDICE INTRODUCCION1 DESARROLLO2 GRAFOS (CONCEPTO).2 ARISTAS...2 VERTICES2 CAMINOS.3 CLASIFICACION DE GRAFOS...3 GRAFOS EULERIANOS.
 INDICE INTRODUCCION1 DESARROLLO2 GRAFOS (CONCEPTO).2 ARISTAS...2 VERTICES2 CAMINOS.3 CLASIFICACION DE GRAFOS...3 GRAFOS EULERIANOS.7 GRAFOS CONEXOS7 ÁRBOLES..7 BOSQUES DE ÁRBOLES...8 RECORRIDO DE UN GRAFO..8
INDICE INTRODUCCION1 DESARROLLO2 GRAFOS (CONCEPTO).2 ARISTAS...2 VERTICES2 CAMINOS.3 CLASIFICACION DE GRAFOS...3 GRAFOS EULERIANOS.7 GRAFOS CONEXOS7 ÁRBOLES..7 BOSQUES DE ÁRBOLES...8 RECORRIDO DE UN GRAFO..8
2. Desarrolla una especificación informal genérica para el TAD árbol binario. Incluir operaciones para crear y modificar el árbol.
 1. Escribe una especificación informal para los distintos métodos de ordenación que conozcas. La especificación debe ser genérica, es decir trabajar con elementos de cualquier tipo. En qué se diferencia
1. Escribe una especificación informal para los distintos métodos de ordenación que conozcas. La especificación debe ser genérica, es decir trabajar con elementos de cualquier tipo. En qué se diferencia
ESTRUCTURA DE DATOS Y ALGORITMOS Titulación: Ingeniero Técnico en Informática de Gestión Curso: 2º Nombre y apellidos: Nota:
 Nombre y apellidos: Nota: Escribe tu nombre y apellidos en esta hoja e inmediatamente en todas las suplementarias, incluso las de sucio. El no hacerlo puede suponer tu expulsión Puedes utilizar el lápiz
Nombre y apellidos: Nota: Escribe tu nombre y apellidos en esta hoja e inmediatamente en todas las suplementarias, incluso las de sucio. El no hacerlo puede suponer tu expulsión Puedes utilizar el lápiz
Descubrir los árboles como paradigma de los tipos Recursivos de Datos
 TEMA 5 ÁRBOLES(*) Una de las estructuras las datos más importantes y prominentes que existen es el árbol. No es un árbol en el sentido botánico de la palabra, sino uno de naturaleza más abstracta. Todos
TEMA 5 ÁRBOLES(*) Una de las estructuras las datos más importantes y prominentes que existen es el árbol. No es un árbol en el sentido botánico de la palabra, sino uno de naturaleza más abstracta. Todos
