PERCEPTRONES SIMPLE, MULTICAPA Y BACKPROPAGATION
|
|
|
- Sebastián Salinas Vidal
- hace 5 años
- Vistas:
Transcripción
1 UNIVERSIDAD DE BUENOS AIRES FACULTAD DE INGENIERÍA MAESTRÍA EN SIMULACIÓN NUMÉRICA Y CONTROL TRABAJO PRACTICO 2: PERCEPTRONES SIMPLE, MULTICAPA Y BACKPROPAGATION Presentada como requisito parcial para la aprobación del curso Sistemas Adaptativos y Redes Neuronales. Estudiante: Fredy Andrés Mercado Navarro DNI: Profesor titular: Sergio Lew Clases Prácticas: Ana Laura Vadnjal 8 de diciembre de 2013 Buenos Aires, Argentina
2 Resumen Un perceptrón es una red de capas de neuronas alimentadas hacia adelante, que puede tener varias entradas y varias salidas, donde las salidas son función de las entradas. En el perceptrón se busca actualizar los pesos sinápticos de forma iterativa a través del algoritmo de propagación del error hacia atrás (Backpropagation). Existen perceptrones simples, sin capas ocultas y perceptrones de varias capas. El perceptrón simple puede resolver solamente aquellos problemas que sean linealmente separables, esto es, problemas cuyas salidas estén clasificadas en dos categorías diferentes y que permitan que su espacio de entrada sea dividido en estas dos regiones por medio de un hiperplano de características similares. Un ejemplo de este tipo de problemas son las funciones lógicas OR y AND. Para aquellos problemas que no son linealmente separables se emplean perceptrones multicapa, como es el caso del aprendizaje de la función XOR.
3 Índice general 1. Teoría Perceptron Simple Algoritmo de aprendizaje Perceptrón Multicapa Propagación hacia atrás Procedimiento Back-propagation Error cuadrático medio Ejercicios teóricos Punto Desarrollo Punto Desarrollo Punto Desarrollo Ejercicios prácticos Punto Desarrollo Conclusión Punto Desarrollo Conclusión Punto Desarrollo Resultados Comentarios y Conclusiones 21 1
4 Índice de figuras 1.1. Perceptrón simple Red hacia adelante de dos capas. Notación para unidades y pesos Tipos de bordes de decisión que pueden ser formados por perceptrones simples y perceptrones de varias capas con una y dos capas de unidades escondidas. Lo anterior para dos entradas y una sola salida. Las partes sombreadas corresponden a regiones de decisión para la clase A. Tomada de [5] Clasificacion de la función OR de 2 entradas Curva de error cuadrático medio con eje x logarítmico para perceptron simple de 2 entradas Curva de error cuadrático medio con eje x logarítmico para perceptron simple de 4 entradas Curva de error cuadrático medio con eje x logarítmico para perceptron multicapa de 4 entradas aprendiendo una función f(x,y,z) Curvas de f(x,y,z) deseada y de la salida actual del perceptron para z e y constantes. 0 x 2π Curvas de f(x,y,z) deseada y de la salida actual del perceptron para x y z constantes. 0 y 2π Curvas de f(x,y,z) deseada y de la salida actual del perceptron para x e y constantes. 1 z
5 Índice de cuadros 3.1. Tabla de verdad - Puerta OR de 2 entradas Tabla de verdad - Puerta OR de 4 entradas Tabla de verdad - Puerta XOR de 2 entradas Tabla de verdad - Puerta XOR de 4 entradas Parámetros utilizados para el aprendizaje de la función
6 Capítulo 1 Teoría 1.1. Perceptron Simple Es un método de aprendizaje supervisado. Consiste de un proceso iterativo, donde vamos hallando términos w ij mejores partiendo de un punto de partida arbitrario. El perceptrón simple solo posee una capa por definición y es una red con aprendizaje hacia adelante (feed forward). La matriz de pesos w ij es, por definición, asimétrica, es decir, todas las conexiones son unidireccionales, lo que significa que no existe una función de energía. Figura 1.1: Perceptrón simple. ( N ) O i = g w ik ξ k θ i O = k=1 O 1 O 2... O NN N: cantidad de entradas. i: neurona i. ξ µ k : patrón de entrada. Como vector es ξµ. ζ µ i : patrón de salida particular (patrón objetivo). O µ i : patrón de salida actual. µ: número de patrón. 4
7 La salida deseada es: O µ i = ζ µ i Los pesos w ij se convierten en un vector de pesos w = (w 1, w 2,..., w N ), una componente para cada entrada. Para cada patrón µ. sgn(w ξ µ ) = ζ µ w 1 sgn w 2 P = ζ µ w 3 Utilizamos la función signo para obtener ±1 en lugar de 0 o Algoritmo de aprendizaje Este algoritmo es útil para problemas linealmente separables. Los pasos para actualizar los pesos sinápticos son: 1. Recorrer los patrones uno por uno. 2. Para cada patrón recorrer las unidades de salida una por una. 3. Para cada unidad de salida comparar si la salida actual es la deseada. 4. Si lo es no realizar ningún cambio. 5. Si no, aplicar la regla de Hebb, es decir, agregar a cada conexión algo proporcional al producto de la entrada y la salida deseada. Dicho de otra forma: w new ik = w old ik + w ik η: tasa de aprendizaje. w ik = η (ζ µ i O µ i ) ξµ k 1.2. Perceptrón Multicapa El perceptrón simple no aplica para redes hacia adelante (feed-forward) con capas intermedias (ocultas) entre las capas de entrada y salida. Una red con una sola capa oculta puede representar cualquier función Booleana, incluyendo funciones que no son linealmente separables como la función XOR, que trataremos en el punto práctico 2. Se usará el método de propagación del error hacia atrás para hacer que el perceptrón multicapa aprenda una función particular. 5
8 Propagación hacia atrás Este algoritmo da una receta para ir cambiando los pesos w pq en cualquier red hacia adelante. Las unidades escondidas se denotan por V j, las entradas por ξ k y las salidas por O i. w jk son conexiones entre las entradas y las unidades escondidas y W ij son las conexiones entre las unidades escondidas y las de salida. i se refiere a unidades de salida, j a unidades escondidas y k a una terminal de entrada, µ indica el patrón, N la cantidad de unidades de entrada y p la cantidad de patrones de entrada (µ=1,2,...,p). Figura 1.2: Red hacia adelante de dos capas. Notación para unidades y pesos. Para un patrón µ, la unidad escondida j recibe una entrada neta h µ j = k w jk ξ µ k y produce la salida La unidad de salida i recibe entonces V µ j = g(h µ j ) = sgn(hµ j ) h µ i = j W ij V µ j y produce para la salida final O µ i = g(h µ i ) = sgn(hµ i ) Los umbrales pueden implementarse como una unidad de entrada extra fijada en 1 y conectada a todas las unidades de la red. La medida del error es E[w] = 1 (ζ µ i O µ i 2 )2 µi que es una función contínua y diferenciable de cada peso. 6
9 Para las conexiones que van de la última capa oculta hacia la capa de salida la regla del gradiente descendente resulta en: W ij = η µ δ µ i V µ j δ µ i = g (h µ i )[ζµ i O µ i ] Para las conexiones entre la capa de entrada y la primera capa oculta tenemos: w jk = η µ δ µ j ξµ k δ µ j = g (h µ j ) i W ij δ µ i La regla general es: w pq = η δ salida V entrada patrones Importante La regla de actualización es local. El cambio de los pesos para una conexión sólo depende de las cantidades de los dos extremos de esa conexión. Es normal usar una función sigmoidea para la función de activación g(h). Debe ser diferenciable y saturarse en ambos extremos. β a menudo es 1. g(h) = tanh βh g (h) = β(1 g(h) 2 ) Procedimiento Back-propagation Tomando un patrón µ a la vez. Consideremos una red con M capas m = 1, 2,..., M y usemos Vi m para la salida de la i-ésima unidad en la m-ésima capa. Vi o será sinónimo para ξ i, la i-ésima entrada. m etiqueta capas, no patrones. wij m es la conexión desde V m 1 j hasta Vi m. El procedimiento de propagación hacia atrás sigue los siguientes puntos: 1. Inicializar los pesos a valores aleatorios pequeños. 2. Seleccionar un patrón ξ µ k y aplicarlo a la capa de entrada (m = 0) de modo que V 0 k = ξ µ k k 3. Propagar la señal hacia adelante a través de la red usando ( ) Vi m = g(h m i ) = g wij m V m 1 j j para cada i y m hasta que las salidas finales V M i hayan sido calculadas. 7
10 4. Calcular los deltas para las capas de salida δ M i = g (h M i )[ζ µ i V µ i ] comparando las salidas actuales V M i con las salidas deseadas ζ µ i para el patrón µ que está siendo considerado. 5. Calcular los deltas para las capas anteriores propagando el error hacia atrás δ m 1 i = g (h m 1 i ) j w m ji δ m j para m = M, M 1,..., 2 hasta que se calcule una delta para cada unidad (neurona). 6. Usar para actualizar todas las conexiones de acuerdo a w m ij = ηδ m i V m 1 j (1.1) w new ij = w old ij + w ij (1.2) 7. Volver al paso 2 y repetir para el próximo patrón [4] Error cuadrático medio El cálculo del error cuadrático medio que se empleará para la estimación del error entre los datos de salida deseados y las salidas actuales es: ECM = 1 n n (O i ζ i ) 2 i=1 Donde n es la cantidad de datos de los vectores de salida (4 para dos entradas y 16 para 4 entradas binarias), O i es una componente del vector de la salida actual (estimada) y ζ i es una componente del vector de la salida deseada. 8
11 Capítulo 2 Ejercicios teóricos 2.1. Punto 1 Explicar la siguiente ecuación: C(p + 1, N) = C(p, N) + D (2.1) donde C(p, N) es la cantidad de combinaciones posibles de p puntos en posición general, pertenecientes a dos clases distintas, que pueden ser separados por un hiperplano en un espacio de dimensión N (Ver Capacity of the simple perceptron, Hertz, Krogh y Palmer, pág. 113) Desarrollo La ecuación 2.1 surge en el contexto de la determinación del poder computacional de un perceptrón a raíz de la siguiente pregunta: Cuántas dicotomías es posible encontrar si lanzo una distribución aleatoria de p puntos en un espacio de N dimensiones, si cada punto puede tomar una de dos características (clases)? Entiéndase por dicotomía a un estado de los p puntos que pueda ser dividido por un hiperplano, entendiendo que un hiperplano es un sub-espacio de dimensión (N 1). Si los puntos están en un espacio bidimensional (N = 2), el hiperplano correspondiente es una línea recta que separa dos grupos de puntos. Cada grupo con una característica distintiva. La respuesta a la pregunta anterior se dotó con el símbolo C(p, N), donde p es la cantidad de patrones de entrada (a almacenar) y N la cantidad de unidades o neuronas de entrada, que corresponde a la dimensión del problema. Para poder responder a la pregunta correctamente se utiliza el método de inducción matemática, donde se demostrará el cálculo para el aumento de las dicotomías para un paso de (p) a (p + 1) patrones, con N constante, así: 1. Suponer que tenemos un grupo de p patrones (puntos) en un espacio de dimensión N. La cantidad de dicotomías que tendría este grupo de puntos estaría dada entonces por C(p, N). 9
12 2. Supongamos ahora que al grupo de puntos anterior agregamos otro punto (patrón) P que se encuentre en posición general, al igual que los demás. Estar en posición general indica que el punto posee independencia lineal y un hiperplano que pase por el origen no cortará más de un punto en cierta posición. 3. Ahora, algunas de las dicotomías del grupo original de p puntos pueden conseguirse con hiperplanos que pasen por el origen O y por el punto P. A ésta cantidad de dicotomías se le llamará D. 4. Para cada una de las D dicotomías hay dos nuevas dicotomías, la primera si corremos el punto infinitesimalmente hacia una clase y la segunda si lo corremos hacia la otra clase. Esto ocurre porque cuando los puntos están en posición general, cualquier hiperplano que pase a través de P permite clasificarlo sin afectar la dicotomía de los p puntos que estaba dada por ese mismo hiperplano. 5. Para las C(p, N) D dicotomías restantes, los dos nuevos posibles conjuntos que incluyen P deben ser separables, y como consecuencia, habrá una dicotomía nueva para cada dicotomía de los p puntos. Los puntos anteriores nos llevan a que el número C(p + 1, N) de dicotomías lineales del grupo que incluye el punto P está dado por: C(p + 1, N) = C(p, N) D + 2D = C(p, N) + D Recordemos que D es la cantidad de dicotomías lineales del grupo de puntos p que pudieron haber sido separadas por un hiperplano que pase a través del punto P, pero este número es simplemente C(p, N 1), porque al imponer la condición de que el hiperplano pase por el punto P estamos convirtiendo el problema en uno de dimensión (N-1), ya que los puntos podrían separarse (clasificarse) sin necesidad de que se encuentren en el espacio de dimensión N, simplemente proyectándolos en un espacio de dimensión (N-1). Una muestra de esto es tener un espacio de dimensión 3 y proyectar los puntos sobre un espacio de dimensión 2 (un plano perpendicular a la línea que une el origen y el punto P ), que es justo lo que se observa en la Figura 5.12 del texto de Hertz, Krogh y Palmer [4]. La observación anterior permite obtener la expresión: C(p + 1, N) = C(p, N) + C(p, N 1) La explicación de la ecuación anterior es un paso intermedio para finalmente demostrar, iterando para p, p 1, p 2,..., 1 que la cantidad de dicotomías posibles para una cantidad de puntos aleatorios (patrones) p en un espacio de N dimensiones es: C(p, N) = 2 N 1 i=0 ( ) p 1 i Este punto teórico fue desarrollado con ayuda de las referencias [2], [3] y [6] Punto 2 Demostrar que cualquier función binaria puede ser implementada con algún perceptrón multicapa. 10
13 Desarrollo Los perceptrones multicapa integran las capacidades de los perceptrones simples, que solo tienen una capa de entrada y una de salida. Estos perceptrones simples pueden modelar funciones con entradas linealmente separables, mientras que los perceptrones multicapa pueden modelar funciones que no son linealmente separables, como la función OR exclusiva. Dentro del grupo de las 16 funciones binarias que existen tenemos un grupo de funciones con salidas que son linealmente separables y otro grupo con funciones con salidas que no lo son. Sabemos que el perceptron simple puede modelar las que son linealmente separables, y esta ventaja se aprovecha para modelar las demás funciones binarias que no son linealmente separables. Una clave para modelar las funciones no separables son las funciones NOR y NAND, las cuales son ambas linealmente separables y pueden ser representadas por un perceptrón simple. Al combinar estas funciones en dos capas es posible generar las demás funciones booleanas que no pudieron ser modeladas con el perceptrón simple. Esto nos demuestra que cualquier función binaria puede ser representada por un perceptrón multicapa, mejor aún, es posible hacerlo con un perceptrón de una sola capa oculta [1] Punto 3 El borde de decisión (decision boundary) de un perceptrón simple es un hiperplano. Explique cómo es el límite de decisión de un perceptrón de dos o tres capas (siempre con una sola neurona de salida) Desarrollo El perceptrón simple (con una capa de entrada y una de salida) forma bordes de decisión de medio plano, separando los patrones de entrada por clases o grupos. A continuación se explica como son los bordes de decisión para un perceptron de dos y tres capas con una sola neurona de salida, ya que el comportamiento de los perceptrones con varias salidas es más complejo debido a que las regiones de decisión están bordeadas por curvas suaves en lugar de segmentos de líneas rectas. Bordes de decisión para un perceptrón de dos capas Un perceptrón de dos capas puede formar regiones de decisión convexas en el espacio ocupado por los patrones de entrada. Estas regiones incluyen polígonos convexos y regiones no limitadas como las que se aprecian en la fila del medio de la Figura 2.1. El término convexo significa que cualquier línea que una puntos sobre el borde de una región sólo pasa a través de puntos por dentro de esa misma región. Las regiones convexas están formadas por la intersección de regiones de medio plano formadas por cada nodo en la primera capa del perceptrón multicapa. Cada nodo de la primera capa se comporta como un perceptrón simple. Las regiones convexas tienen a lo sumo tantos lados como nodos tenga la primera capa (ver fila del medio y columna 5 de la Figura 2.1). 11
14 Figura 2.1: Tipos de bordes de decisión que pueden ser formados por perceptrones simples y perceptrones de varias capas con una y dos capas de unidades escondidas. Lo anterior para dos entradas y una sola salida. Las partes sombreadas corresponden a regiones de decisión para la clase A. Tomada de [5]. Bordes de decisión para un perceptrón de tres capas Un perceptrón de tres capas puede formar regiones de decisión arbitrariamente complejas. Esto puede demostrarse construyendo la red pensando en particionar la región de decisión en hipercubos pequeños (cuadrados, cuando se tienen dos entradas). Cada hipercubo requiere 2N nodos en la primera capa, uno para cada lado del hipercubo, y un nodo en la segunda capa que tome la salida lógica AND de los nodos de la primera capa. Los hipercubos se asignan a las regiones de decisión apropiadas conectando la salida de los nodos de la segunda capa solo al nodo de salida que corresponde a la región de decisión en la que se encuentra el hipercubo de ese nodo y realizando una operación logica OR en cada nodo de salida. Este procedimiento de construcción es capaz de generar las regiones desconectadas y no convexas que se muestran en la fila más baja de la Figura 2.1. Finalmente, los perceptrones de tres capas pueden generar, a diferencia de los de dos capas, una región de decisión totalmente cerrada, también puede tener varias regiones del mismo tipo cerradas y aisladas entre si, y regiones cerradas dentro de regiones de clase diferente, como también se puede apreciar en la columna 5, fila 4 de la Figura 2.1 [5]. 12
15 Capítulo 3 Ejercicios prácticos 3.1. Punto 1 Implemente un perceptrón simple que aprenda la función lógica OR de 2 y de 4 entradas Desarrollo En el Cuadro 3.1 se observa la tabla de verdad para la función OR de 2 entradas, donde SALIDA=1 si A=1 o B=1, y en el Cuadro 3.2 la tabla de verdad para 4 entradas, donde SALIDA=1 si A, B, C o D son iguales a 1. Se elaboró un programa en Matlab para aprender estas dos funciones. El usuario elige entre correr para 2 o 4 entradas y elige el número máximo de iteraciones que permitirá que corra el programa, al igual que el valor de la constante de aprendizaje. Los pesos iniciales a partir de los cuales comenzará el proceso de aprendizaje y actualización de pesos se toman aleatorios con la función rand(). Por cada iteración se corre un ciclo que barre los patrones enseñados unos por uno. Si la salida de cada patrón es diferente a la salida deseada entonces se actualiza el vector de pesos como indican las ecuaciones 1.1 y 1.2. El proceso descrito anteriomente se repite hasta que no existe ninguna diferencia entre la salida deseada y la salida actual. Se empleó la función signo, lo que garantiza que el error podrá descender hasta cero para este caso donde tenemos una función binaria. Para el caso práctico de este ejercicio representamos el 0 por el -1 y el 1 por el +1. A todas las entradas de este punto práctico y de los siguientes se les adicionó una entrada fija en 1 para tener en cuenta el umbral. Los pesos obtenidos para el caso de 2 entradas son w 1 = 0,7502, w 2 = 0,2344 y w 3 = 0,6387. Para el caso de 4 entradas se obtuvieron Patrón Entrada A Entrada B Salida A o B Cuadro 3.1: Tabla de verdad - Puerta OR de 2 entradas. 13
16 w 1 = 0,1816, w 2 = 0,1655, w 3 = 0,5952, w 4 = 0,3869 y w 5 = 1,0898. Con estos pesos se podría comprobar el aprendizaje de la función OR de 2 y 4 entradas. En la Figura 3.1 se observa la clasificación del perceptron simple para la función OR de 2 entradas, donde se tienen 4 puntos en el espacio de clases de dos dimensiones, +1 y -1. Aquí se observa que el perceptrón logra clasificar los patrones (puntos) de entrada, separando aquellos que satisfacen la función de los que sí lo hacen. En este caso, graficamos la línea normal al vector de pesos, que separa una clase (-1) de la otra (+1). Figura 3.1: Clasificacion de la función OR de 2 entradas Conclusión Se logró implementar el perceptrón simple para la función OR de 2 y 4 entradas. Para ambos casos el vector de pesos w converge en pocas iteraciones. Para 2 entradas en 3 iteraciones o menos, y para 4 entradas en 7 iteraciones o menos. Esto depende de las componentes aleatorias iniciales de w Punto 2 Implemente un perceptrón multicapa que aprenda la función lógica XOR de 4 entradas (utilizando el algoritmo Backpropagation) Desarrollo Se implementará también el aprendizaje de la función XOR para 2 entradas, aunque el ejercicio no lo pida. En el Cuadro 3.3 se encuentra la tabla de verdad para la función lógica XOR de 2 entradas y en el Cuadro 3.4 la tabla de verdad para la función de 4 entradas. Para dos entradas la salida es igual a 1 si A y B son diferentes y 0 si A y B son iguales. La función XOR es asociativa, así que para 4 entradas la salida es igual a 1 si la suma de entradas iguales a 1 es impar. Para el aprendizaje de la función XOR de 2 y 4 entradas se elaboró un programa de MATLAB que lee los números de entrada reemplazando ceros por -1. Se adiciona también una entrada fija siempre en 1 para reemplazar el uso de un umbral. Las constantes η y 14
17 Patrón A B C D Salida A o B Cuadro 3.2: Tabla de verdad - Puerta OR de 4 entradas. Patrón A B Salida A o B Cuadro 3.3: Tabla de verdad - Puerta XOR de 2 entradas. Patrón A B C D Salida A o B Cuadro 3.4: Tabla de verdad - Puerta XOR de 4 entradas. 15
18 β se mantienen constantes, al igual que el número de neuronas de la única capa oculta que se utilizó para la red del perceptrón. El usuario define también un error cuadrático medio mínimo que debe mejorarse para detener la corrida del ciclo de iteraciones de actualización de los pesos de las conexiones entre neuronas del perceptrón. En términos generales, el algoritmo calcula la salida de las neuronas de la capa oculta y luego la salida de la neurona de la capa de salida. Luego calcula un delta por neurona para cada capa. Si el error cuadrático medio entre las salidas deseadas y las actuales es mayor que el permitido el ciclo se repite hasta que el ECM actual sea menor que el ECM permitido. Para el caso de la función XOR de 2 entradas, las entradas al perceptrón son 3. Como se empleó solo una capa oculta la cantidad de pesos entre la capa de entrada y la de salida es, para el ejemplo de la Figura 3.2, de 3 6 = 18 pesos, mientras que los pesos de la capa oculta hacia la capa de salida son sólo 6, uno por neurona. Para el caso de la función XOR de 4 entradas, las entradas al perceptrón serían 5, los pesos entre la capa de entrada y la oculta 5 10 = 50 y de la capa oculta hacia la capa de salida 10 (ver variables W 1 y W 2 en el programa de Matlab). En la Figura 3.2 se observa como progresa el ECM para el aprendizaje de la función XOR de 2 entradas y en la Figura 3.3 para la función XOR de 4 entradas. Figura 3.2: Curva de error cuadrático medio con eje x logarítmico para perceptron simple de 2 entradas Conclusión Se implementó un algoritmo para el aprendizaje de la función XOR de 2 y 4 entradas para un perceptron con una sola capa oculta. El algoritmo de propagación del error hacia atrás calcula un delta de peso para cada neurona de cada capa. El algoritmo diseñado permite variar el número de neuronas de la capa oculta, pero no el número de capas. Mientras menor es el ECM permitido mejores son las aproximaciones de las salidas ac- 16
19 Figura 3.3: Curva de error cuadrático medio con eje x logarítmico para perceptron simple de 4 entradas. tuales comparadas con las deseadas y mejores las estimaciones de los pesos de cada capa de conexiones que llevan al aprendizaje de la función Punto 3 Implemente una red con aprendizaje Backpropagation que aprenda la siguiente función: f(x, y, z) = sen (x) + cos (y) + z donde x e y están en el intervalo [0, 2π] y z está en el intervalo [ 1, 1] Desarrollo La función tiene 3 entradas (4 con el umbral), x, y, z y una salida f(x, y, z). El propósito del ejercicio es enseñar a la red uno por uno todos los patrones, que serían combinaciones de x, y, z e ir corrigiendo los pesos con base en la diferencia entre f(x, y, z) y la salida actual. A continuación se resume lo que se realizó. En primer lugar, el algoritmo que se utilizó para el ejercicio es en escencia el mismo algoritmo de un perceptrón multicapa feedforward con backpropagation del punto 2. Los parámetros que determina el usuario para correr el programa son: las constantes η y β, un número máximo de iteraciones (MAXITER), el número de neuronas de la única capa oculta (NNEURONAS), el error cuadrático medio permisible (MIN ECM), la cantidad de datos a evaluar por cada eje coordenado (NDATOS) y un número (PROD) que tiene la función de escalar los valores de f(x, y, z) enseñados a un intervalo [ 1, 1], ya que estamos utilizando la función sigmoidea tanh para el umbral. El número usado para escalar f(x, y, z) enseñado es P ROD = 1/3 y el usado para escalar de vuelta la salida es su inverso, es decir 3, dado que el valor máximo de f(x, y, z) es +3 y el valor mínimo es -3. La expresión utilizada para escalar f(x, y, z) es entonces: 17
20 Parámetro Valor Constante de aprendizaje η 0.1 Constante (steepness parameter) β 1 Limite de iteraciones MAXITER Neuronas de capa oculta NNEURONAS 20 Error permisible MIN ECM Datos por eje coordenado NDATOS 10 Total de patrones enseñados a la red 1000 Número de entradas (coordenadas+umbral) 3+1=4 Cuadro 3.5: Parámetros utilizados para el aprendizaje de la función. f(x, y, z) escalada = (sin x + cos y + z) P ROD A diferencia del ejercicio 2, en éste ejercicio le enseñamos a la red 1000 patrones (10x10x10 datos), donde tendremos una entrada por cada coordenada y otra fija en 1 para el umbral. La ejecución del programa sigue el mismo algoritmo del ejercicio 2, donde se realiza una actualización de pesos cada vez que se enseña un nuevo patrón. Al final, el programa sale del ciclo iterativo cuando el Error Cuadrático Medio desciende por debajo de MIN ECM Resultados Para demostrar la funcionalidad del programa para aprender una función se corrió un ejercicio con los parámetros consignados en el Cuadro 3.5. En la Figura 3.4 se aprecia el gráfico logaritmico de la convergencia del error cuadrático medio en función del número de iteraciones. Para comprobar lo anterior se compararon gráficamente los valores del campo escalar f(x, y, z) manteniendo constantes dos de las tres variables, lo que da como resultado un gráfico 2D que corresponde al valor de la función sobre una línea recta producto de la intersección de los dos planos que define cada una de las coordenadas que se deja constante. En la Figura 3.5 se aprecia el gráfico de f(x, y, z) manteniendo constantes z e y en el intervalo 0 x 2π. Los valores de la salida deseada y la salida actual coinciden bastante bien. La forma de la función que predomina es claramente la de la función seno, que es la que transforma los valores de x. La Figura 3.6 muestra resultados similares a los de la Figura 3.5. Aquí la forma de la función que predomina es la de la función coseno, que es aquella que transforma los valores de Y, mientras que la Figura 3.7 muestra también buena coincidencia entre los valores deseados y la salida del perceptrón. Todo indica que los pesos fueron modificados exitosamente y el aprendizaje del perceptrón se realizó correctamente. 18
21 Figura 3.4: Curva de error cuadrático medio con eje x logarítmico para perceptron multicapa de 4 entradas aprendiendo una función f(x,y,z). Figura 3.5: Curvas de f(x,y,z) deseada y de la salida actual del perceptron para z e y constantes. 0 x 2π. 19
22 Figura 3.6: Curvas de f(x,y,z) deseada y de la salida actual del perceptron para x y z constantes. 0 y 2π. Figura 3.7: Curvas de f(x,y,z) deseada y de la salida actual del perceptron para x e y constantes. 1 z 1. 20
23 Capítulo 4 Comentarios y Conclusiones La cantidad de dicotomías que se pueden obtener a partir de una distribución aleatoria de patrones, para un perceptrón simple, está dada por una expresión que relaciona la cantidad de patrones de entrada y la cantidad de unidades de la primera capa. La ecuación fue deducida por inducción matemática teniendo en cuenta las dicotomías que resultan al adicionar un nuevo patrón e imponer que el hiperplano pase por el punto que define el estado de dicho patrón y el origen. Se aprovecha la proyección de los puntos sobre un plano de dimensión (N-1) para concluir que las dicotomías que se suman a las ya conocidas son las que resultan de hallar las dicotomías para el mismo número de puntos (patrones) pero con una dimensión menor (N-1). Los bordes de decisión del perceptron de dos capas pueden formar regiones de decisión convexas abiertas o cerradas, mientras que los bordes de decisión del perceptron de tres capas pueden formar regiones arbitrariamente complejas que pueden tener zonas de decisión aisladas y también zonas excluidas dentro de una región de decisión cerrada. El aprendizaje del perceptrón multicapa depende de parámetros de aprendizaje como η y β. Mientras menor sea la constante de aprendizaje más tiempo le tomará aprender a la red, sin embargo, esto garantiza una mejor aproximación de la solución deseada al emplear pasos de iteración más cortos que facilitan hallar mínimos locales. La facilidad de aprendizaje del perceptrón depende también del número de neuronas de las capas ocultas y del número de capas. En este trabajo práctico se demostrón que las funciones lógicas OR de 2 y 4 entradas pueden se aprendidas por un perceptrón simple, y que la función XOR de 2 y 4 entradas puede ser aprendida por un perceptrón multicapa con una sola capa oculta. El perceptrón con una sola capa oculta y función de activación sigmoidea tanh puede aprender una función contínua de varias variables. Dado que la salida del perceptrón estudiado va entre -1 y 1 se escaló la función de entrada para enseñar a la red valores que estuvieran dentro de ese intervalo. Luego se escaló de vuelta la salida para obtener los valores originales de f(x, y, z). 21
24 Bibliografía [1] Coppin, B. Artificial Intelligence Illuminated. Jones and Bartlet Publishers, [2] Engel, A., and den Broeck, C. V. Statistical Mechanics of Learning. Cambridge University Press, [3] Hassoun, M. H. Fundamentals of Artificial Neural Networks. The MIT Press, [4] Hertz, J., Krogh, A., and Palmer, R. G. Introduction to the theory of neural computation. Addison-Wesley, [5] Lippmann, R. P. An introduction to computing with neural nets. IEEE ASSP Magazine 3, 4 (1987), [6] Sampolinsky, H. Introduction: The Perceptron. MIT,
Redes Neuronales. Las redes neuronales son modelos computacionales que buscan imitar el funcionamiento
 Redes Neuronales Las redes neuronales son modelos computacionales que buscan imitar el funcionamiento de las neuronas biológicas. Se usan principalmente para el reconocimiento de patrones complejos. Para
Redes Neuronales Las redes neuronales son modelos computacionales que buscan imitar el funcionamiento de las neuronas biológicas. Se usan principalmente para el reconocimiento de patrones complejos. Para
Técnicas de inteligencia artificial. Aprendizaje: Perceptrón multi-capa
 Técnicas de inteligencia artificial Aprendizaje: Perceptrón multi-capa Índice Regla delta Modelo computacional Neuronas e hiperplanos Entrenamiento como ajuste supervisado No-separabilidad lineal Backpropagation
Técnicas de inteligencia artificial Aprendizaje: Perceptrón multi-capa Índice Regla delta Modelo computacional Neuronas e hiperplanos Entrenamiento como ajuste supervisado No-separabilidad lineal Backpropagation
REDES NEURONALES ADAPTABLES
 REDES NEURONALES ADAPTABLES Unidad 3: Redes neuronales artificiales y modelos de entrenamiento SubTemas 3.2 Perceptron simple Arquitectura Regla delta Multi Layer Perceptrón 3.3 Redes Neuronales Adaptables
REDES NEURONALES ADAPTABLES Unidad 3: Redes neuronales artificiales y modelos de entrenamiento SubTemas 3.2 Perceptron simple Arquitectura Regla delta Multi Layer Perceptrón 3.3 Redes Neuronales Adaptables
Redes Neuronales Artificiales
 Algoritmo de retropropagación Back propagation Es utilizado para entrenar redes neuronales multicapa. Exige que la función de activación de las neuronas sea derivable y creciente. Las funciones comúnmente
Algoritmo de retropropagación Back propagation Es utilizado para entrenar redes neuronales multicapa. Exige que la función de activación de las neuronas sea derivable y creciente. Las funciones comúnmente
Tema 2 Primeros Modelos Computacionales
 Universidad Carlos III de Madrid OpenCourseWare Redes de Neuronas Artificiales Inés M. Galván - José Mª Valls Tema 2 Primeros Modelos Computacionales 1 Primeros Modelos Computacionales Perceptron simple
Universidad Carlos III de Madrid OpenCourseWare Redes de Neuronas Artificiales Inés M. Galván - José Mª Valls Tema 2 Primeros Modelos Computacionales 1 Primeros Modelos Computacionales Perceptron simple
Aprendizaje: Perceptrón multi-capa
 Técnicas de inteligencia artificial Asignatura troncal: 4.5cr, 4ºCurso Ing Inf Aprendizaje: Perceptrón multi-capa 2003-2004 F.Escolano, O.Colomina, M.A. Cazorla Perceptrón 1 Indice Regla delta Modelo computacional
Técnicas de inteligencia artificial Asignatura troncal: 4.5cr, 4ºCurso Ing Inf Aprendizaje: Perceptrón multi-capa 2003-2004 F.Escolano, O.Colomina, M.A. Cazorla Perceptrón 1 Indice Regla delta Modelo computacional
Redes Neuronales Multicapa
 Undécima sesión 16 de abril de 2010 Relación entre capas y conjuntos bajo estudio Estructura Regla de decisión XOR Clases no linealmente separables Regiones generalizadas Una capa Regiones separables con
Undécima sesión 16 de abril de 2010 Relación entre capas y conjuntos bajo estudio Estructura Regla de decisión XOR Clases no linealmente separables Regiones generalizadas Una capa Regiones separables con
Relación 7 - Redes neuronales
 Sistemas Inteligentes 0-0 Relación - Redes neuronales Problemas Ejercicio. Explicar cómo se usaría una red neuronal para obtener un reconocedor de letras escritas a mano. Describir con precisión qué estructura
Sistemas Inteligentes 0-0 Relación - Redes neuronales Problemas Ejercicio. Explicar cómo se usaría una red neuronal para obtener un reconocedor de letras escritas a mano. Describir con precisión qué estructura
Inteligencia Artificial (Curso ) Grado en Ingeniería Informática - Ingeniería del Software
 Inteligencia Artificial (Curso 0-0) Grado en Ingeniería Informática - Ingeniería del Software Redes neuronales Cuestión : Decir si las siguientes afirmaciones son verdaderas o falsas: Si tomamos la función
Inteligencia Artificial (Curso 0-0) Grado en Ingeniería Informática - Ingeniería del Software Redes neuronales Cuestión : Decir si las siguientes afirmaciones son verdaderas o falsas: Si tomamos la función
Inteligencia Artificial. Aprendizaje neuronal. Ing. Sup. en Informática, 4º. Curso académico: 2011/2012 Profesores: Ramón Hermoso y Matteo Vasirani
 Inteligencia Artificial Aprendizaje neuronal Ing. Sup. en Informática, 4º Curso académico: 20/202 Profesores: Ramón Hermoso y Matteo Vasirani Aprendizaje Resumen: 3. Aprendizaje automático 3. Introducción
Inteligencia Artificial Aprendizaje neuronal Ing. Sup. en Informática, 4º Curso académico: 20/202 Profesores: Ramón Hermoso y Matteo Vasirani Aprendizaje Resumen: 3. Aprendizaje automático 3. Introducción
RED NEURONAL DE KOHONEN
 UNIVERSIDAD DE BUENOS AIRES FACULTAD DE INGENIERÍA MAESTRÍA EN SIMULACIÓN NUMÉRICA Y CONTROL TRABAJO PRACTICO 3: RED NEURONAL DE KOHONEN Presentada como requisito parcial para la aprobación del curso Sistemas
UNIVERSIDAD DE BUENOS AIRES FACULTAD DE INGENIERÍA MAESTRÍA EN SIMULACIÓN NUMÉRICA Y CONTROL TRABAJO PRACTICO 3: RED NEURONAL DE KOHONEN Presentada como requisito parcial para la aprobación del curso Sistemas
Inteligencia Artificial II (Curso ) Ejercicios propuestos del tema 5
 Inteligencia Artificial II (Curso 0-0) Ejercicios propuestos del tema Ejercicio : Diseñar un perceptrón simple con n valores de entrada y función umbral de activación que sirva para calcular la función
Inteligencia Artificial II (Curso 0-0) Ejercicios propuestos del tema Ejercicio : Diseñar un perceptrón simple con n valores de entrada y función umbral de activación que sirva para calcular la función
Tema: Aprendizaje Supervisado.
 Sistemas Expertos e Inteligencia Artificial. Guía No. 9 1 Tema: Aprendizaje Supervisado. Facultad: Ingeniería Escuela: Computación Asignatura: Sistemas Expertos e Inteligencia Artificial Objetivos Específicos
Sistemas Expertos e Inteligencia Artificial. Guía No. 9 1 Tema: Aprendizaje Supervisado. Facultad: Ingeniería Escuela: Computación Asignatura: Sistemas Expertos e Inteligencia Artificial Objetivos Específicos
TLU(s) MULTICAPAS. Se pueden implementar funciones en TLU con más de una capa.
 TLU(s) MULTICAPAS Se pueden implementar funciones en TLU con más de una capa 1 05 2 15 2 3 z 3 15 2 4 05 No eisten, en la actualidad, mecanismos de entrenamiento que permita conocer los pesos sinápticos
TLU(s) MULTICAPAS Se pueden implementar funciones en TLU con más de una capa 1 05 2 15 2 3 z 3 15 2 4 05 No eisten, en la actualidad, mecanismos de entrenamiento que permita conocer los pesos sinápticos
Métodos de Aprendizaje en Redes Neuronales
 11 de abril de 2011 Entrenamiento de redes feedforward (Backpropagation) Siendo {z m, t m } m=1...n un conjunto de n patrones de entrenamiento, con z m las entradas conocidas para el m ésimo patrón y
11 de abril de 2011 Entrenamiento de redes feedforward (Backpropagation) Siendo {z m, t m } m=1...n un conjunto de n patrones de entrenamiento, con z m las entradas conocidas para el m ésimo patrón y
SISTEMAS INTELIGENTES
 SISTEMAS INTELIGENTES T10: Redes Neuronales.aic.uniovi.es/ssii Índice Redes Neuronales Artificiales Fundamentos biológicos Perceptrón Funciones de activación Redes de neuronas Entrenamiento: Perceptrón
SISTEMAS INTELIGENTES T10: Redes Neuronales.aic.uniovi.es/ssii Índice Redes Neuronales Artificiales Fundamentos biológicos Perceptrón Funciones de activación Redes de neuronas Entrenamiento: Perceptrón
Redes Neuronales. Introducción. José Manuel Quero Reboul Dpto. Ingeniería Electrónica Universidad de Sevilla
 Redes Neuronales Introducción José Manuel Quero Reboul Dpto. Ingeniería Electrónica Universidad de Sevilla Indice Motivación Arquitectura Leyes de Aprendizae Aplicaciones DILEMA MEMORIA CALCULO Aritmética
Redes Neuronales Introducción José Manuel Quero Reboul Dpto. Ingeniería Electrónica Universidad de Sevilla Indice Motivación Arquitectura Leyes de Aprendizae Aplicaciones DILEMA MEMORIA CALCULO Aritmética
Aprendizaje no supervisado
 OPENCOURSEWARE REDES DE NEURONAS ARTIFICIALES Inés M. Galván José M. Valls Tema 4 1 Introducción Aprendizaje competitvo Otros algoritmos de agrupación 2 1 Introducción Características principales de las
OPENCOURSEWARE REDES DE NEURONAS ARTIFICIALES Inés M. Galván José M. Valls Tema 4 1 Introducción Aprendizaje competitvo Otros algoritmos de agrupación 2 1 Introducción Características principales de las
Introducción a las Redes Neuronales
 Introducción a las Redes Neuronales Perceptrón Simple William Campillay-LLanos williamcampillay@gmail.com https://sites.google.com/site/williamcampillay/home Departamento de Matemática, Física y Estadística.
Introducción a las Redes Neuronales Perceptrón Simple William Campillay-LLanos williamcampillay@gmail.com https://sites.google.com/site/williamcampillay/home Departamento de Matemática, Física y Estadística.
4. El perceptrón. 4.1 Introducción. 4.2 Consideraciones básicas
 4. El perceptrón 4.1 Introducción El perceptrón es la forma más simple de una red neuronal usada para la clasificación de un tipo especial de patrones, los linealmente separables (es decir, patrones que
4. El perceptrón 4.1 Introducción El perceptrón es la forma más simple de una red neuronal usada para la clasificación de un tipo especial de patrones, los linealmente separables (es decir, patrones que
Tema 8: Redes Neuronales
 Tema 8: Redes Neuronales Pedro Larrañaga, Iñaki Inza, Abdelmalik Moujahid Intelligent Systems Group Departamento de Ciencias de la Computación e Inteligencia Artificial Universidad del País Vasco http://www.sc.ehu.es/isg/
Tema 8: Redes Neuronales Pedro Larrañaga, Iñaki Inza, Abdelmalik Moujahid Intelligent Systems Group Departamento de Ciencias de la Computación e Inteligencia Artificial Universidad del País Vasco http://www.sc.ehu.es/isg/
Aprendizaje Automatizado. Redes Neuronales Artificiales
 Aprendizaje Automatizado Redes Neuronales Artificiales Introducción Otra forma de emular características propias de los humanos: memorizar y asociar hechos. Se aprende de la experiencia. El cerebro humano
Aprendizaje Automatizado Redes Neuronales Artificiales Introducción Otra forma de emular características propias de los humanos: memorizar y asociar hechos. Se aprende de la experiencia. El cerebro humano
Redes Neuronales Multicapa
 4 de abril de 2011 Relación entre capas y conjuntos bajo estudio Estructura Regla de decisión XOR Clases no linealmente separables Regiones generalizadas Una capa Regiones separables con hiperplanos Dos
4 de abril de 2011 Relación entre capas y conjuntos bajo estudio Estructura Regla de decisión XOR Clases no linealmente separables Regiones generalizadas Una capa Regiones separables con hiperplanos Dos
CONCLUSIONES. La teoría de Redes Neuronales Artificiales, presenta grandes ventajas con
 319 CONCLUSIONES La teoría de Redes Neuronales Artificiales, presenta grandes ventajas con respecto a otros modelos típicos de solución de problemas de Ingeniería, una de ellas es su inspiración en modelos
319 CONCLUSIONES La teoría de Redes Neuronales Artificiales, presenta grandes ventajas con respecto a otros modelos típicos de solución de problemas de Ingeniería, una de ellas es su inspiración en modelos
OPENCOURSEWARE REDES DE NEURONAS ARTIFICIALES Inés M. Galván José M. Valls. Tema 6: Redes de Neuronas Recurrentes
 OPENCOURSEWARE REDES DE NEURONAS ARTIFICIALES Inés M. Galván José M. Valls Tema 6: Redes de Neuronas Recurrentes En este tema se estudian las redes de neuronas recurrentes. Se presentan en primer lugar
OPENCOURSEWARE REDES DE NEURONAS ARTIFICIALES Inés M. Galván José M. Valls Tema 6: Redes de Neuronas Recurrentes En este tema se estudian las redes de neuronas recurrentes. Se presentan en primer lugar
Perceptrón multicapa. Diego Milone y Leonardo Rufiner Inteligencia Computacional Departamento de Informática FICH-UNL
 Perceptrón multicapa Diego Milone y Leonardo Rufiner Inteligencia Computacional Departamento de Informática FICH-UNL Organización Un poco de historia... Cómo resolver el problema XOR? Métodos de gradiente
Perceptrón multicapa Diego Milone y Leonardo Rufiner Inteligencia Computacional Departamento de Informática FICH-UNL Organización Un poco de historia... Cómo resolver el problema XOR? Métodos de gradiente
Redes neuronales con funciones de base radial
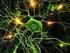 Redes neuronales con funciones de base radial Diego Milone y Leonardo Rufiner Inteligencia Computacional Departamento de Informática FICH-UNL Organización: RBF-NN Motivación y orígenes RBF Arquitectura
Redes neuronales con funciones de base radial Diego Milone y Leonardo Rufiner Inteligencia Computacional Departamento de Informática FICH-UNL Organización: RBF-NN Motivación y orígenes RBF Arquitectura
Perceptrones Fernando Berzal,
 Fernando Berzal, berzal@acm.org Introducción Redes neuronales artificiales Modelos de redes Modelo de neurona artificial Funciones de activación La neurona de McCulloch y Pitts El algoritmo de aprendizaje
Fernando Berzal, berzal@acm.org Introducción Redes neuronales artificiales Modelos de redes Modelo de neurona artificial Funciones de activación La neurona de McCulloch y Pitts El algoritmo de aprendizaje
Detección Multiusuario para DS-CDMA basado en SVM
 9 Otra técnica basada en el aprendizaje y más conocida que la anterior es la basada en. Vamos a realizar una pequeña comparativa teórica de sobre ambas técnicas de clasificación. Estudiaremos los conceptos
9 Otra técnica basada en el aprendizaje y más conocida que la anterior es la basada en. Vamos a realizar una pequeña comparativa teórica de sobre ambas técnicas de clasificación. Estudiaremos los conceptos
Perceptrón Simple. Aspectos Prácticos y Algoritmos Redes Neuronales, DC-FCEyN-UBA. Rosana Matuk Primer Cuatrimestre 2018
 Perceptrón Simple Aspectos Prácticos y Algoritmos Redes Neuronales, DC-FCEyN-UBA Rosana Matuk Primer Cuatrimestre 2018 Rosana Matuk (DC-FCEyN-UBA) Perceptrón simple Primer Cuatrimestre 2018 1 / 29 Objetivo
Perceptrón Simple Aspectos Prácticos y Algoritmos Redes Neuronales, DC-FCEyN-UBA Rosana Matuk Primer Cuatrimestre 2018 Rosana Matuk (DC-FCEyN-UBA) Perceptrón simple Primer Cuatrimestre 2018 1 / 29 Objetivo
Conceptos básicos V:
 C261-69 69 Tópicos Avanzados: Redes Neuronales Artificiales Conceptos básicos Dra. Ma. del Pilar Gómez Gil Primavera 2009 pgomez@acm.org V:13-01-09 Modelo Básico y Abstracto de un Neurón Artificial x 0
C261-69 69 Tópicos Avanzados: Redes Neuronales Artificiales Conceptos básicos Dra. Ma. del Pilar Gómez Gil Primavera 2009 pgomez@acm.org V:13-01-09 Modelo Básico y Abstracto de un Neurón Artificial x 0
Resolución de Ecuaciones No Lineales
 Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Métodos Computacionales Contenido 1 Introducción Introducción 2 Localización de Raíces Localización de Raíces 3 Métodos Iterativos
Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Métodos Computacionales Contenido 1 Introducción Introducción 2 Localización de Raíces Localización de Raíces 3 Métodos Iterativos
Métodos de modelado y clasificación de patrones. clasificación de patrones
 FUNDAMENTOS DEL RECONOCIMIENTO AUTOMÁTICO DE LA VOZ Métodos de modelado y clasificación de patrones Agustín Álvarez Marquina Introducción. Modelado y clasificación de patrones Objetivos: Agrupar el conjunto
FUNDAMENTOS DEL RECONOCIMIENTO AUTOMÁTICO DE LA VOZ Métodos de modelado y clasificación de patrones Agustín Álvarez Marquina Introducción. Modelado y clasificación de patrones Objetivos: Agrupar el conjunto
Introducción. Existen dos aproximaciones para resolver el problema de clasificación: Aproximación Generativa (vista en el Tema 3) Basada en:
 Introducción Eisten dos aproimaciones para resolver el problema de clasificación: Aproimación Generativa (vista en el Tema 3) Basada en: Modelar p(,w)=p( w)p(w) p( w) es la distribución condicional de
Introducción Eisten dos aproimaciones para resolver el problema de clasificación: Aproimación Generativa (vista en el Tema 3) Basada en: Modelar p(,w)=p( w)p(w) p( w) es la distribución condicional de
Redes de Neuronas de Base Radial
 Redes de Neuronas de Base Radial 1 Introducción Redes multicapa con conexiones hacia delante Única capa oculta Las neuronas ocultas poseen carácter local Cada neurona oculta se activa en una región distinta
Redes de Neuronas de Base Radial 1 Introducción Redes multicapa con conexiones hacia delante Única capa oculta Las neuronas ocultas poseen carácter local Cada neurona oculta se activa en una región distinta
Formulación del problema de la ruta más corta en programación lineal
 Formulación del problema de la ruta más corta en programación lineal En esta sección se describen dos formulaciones de programación lineal para el problema de la ruta más corta. Las formulaciones son generales,
Formulación del problema de la ruta más corta en programación lineal En esta sección se describen dos formulaciones de programación lineal para el problema de la ruta más corta. Las formulaciones son generales,
Tema 6. Reconocimiento de voz
 Tema 6. Reconocimiento de voz 6.1.- Introducción 6.2.- Problemática 6.3.- Clasificación 6.4.- Esquema de trabajo 6.5.- Técnicas de reconocimiento 6.6.- Conclusiones 6.1.- Introducción Reconocimiento de
Tema 6. Reconocimiento de voz 6.1.- Introducción 6.2.- Problemática 6.3.- Clasificación 6.4.- Esquema de trabajo 6.5.- Técnicas de reconocimiento 6.6.- Conclusiones 6.1.- Introducción Reconocimiento de
Redes Neuronales Artificiales
 Redes Neuronales Artificiales Claudio Javier Tablada Germán Ariel Torres Resumen. Una Red Neuronal Artificial es un modelo matemático inspirado en el comportamiento biológico de las neuronas y en la estructura
Redes Neuronales Artificiales Claudio Javier Tablada Germán Ariel Torres Resumen. Una Red Neuronal Artificial es un modelo matemático inspirado en el comportamiento biológico de las neuronas y en la estructura
ANEXO II.- TEORÍA SOBRE REDES NEURONALES ARTIFICIALES
 ANEXO II.- TEORÍA SOBRE REDES NEURONALES ARTIFICIALES 1. Concepto de red neuronal artificial Una red neuronal artificial (RNA) es un modelo matemático que intenta reproducir el modo de funcionamiento y
ANEXO II.- TEORÍA SOBRE REDES NEURONALES ARTIFICIALES 1. Concepto de red neuronal artificial Una red neuronal artificial (RNA) es un modelo matemático que intenta reproducir el modo de funcionamiento y
Algebra lineal y conjuntos convexos
 Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
CI5438. Inteligencia Artificial II Clase 6: Redes Multicapas - Back. Cap 20.5 Russel & Norvig Cap 4 Mitchell
 CI5438. Inteligencia Artificial II Clase 6: Redes Multicapas - Backpropagation Cap 20.5 Russel & Norvig Cap 4 Mitchell Universidad Simón Boĺıvar 8 de Octubre de 2008 Redes Multicapas de Unidades Sigmoidales
CI5438. Inteligencia Artificial II Clase 6: Redes Multicapas - Backpropagation Cap 20.5 Russel & Norvig Cap 4 Mitchell Universidad Simón Boĺıvar 8 de Octubre de 2008 Redes Multicapas de Unidades Sigmoidales
ALGUNOS COMENTARIOS SOBRE GENERALIZACION EN BACKPROPAGATION
 ALGUNOS COMENTARIOS SOBRE GENERALIZACION EN BACKPROPAGATION En una RN entrenada, si las salidas calculadas por la red con nuevos ejemplos están próimas a los valores deseados, hay generalización (Haykin,
ALGUNOS COMENTARIOS SOBRE GENERALIZACION EN BACKPROPAGATION En una RN entrenada, si las salidas calculadas por la red con nuevos ejemplos están próimas a los valores deseados, hay generalización (Haykin,
CURSO DE METODOS NUMERICOS Año Académico Curso Tercero de Matemáticas EXAMEN FINAL FEBRERO
 Año Académico 2000-2001 Curso Tercero de Matemáticas EXAMEN FINAL FEBRERO 1. Dá el enunciado y demuestra el teorema de convergencia del método del punto fijo. (2 puntos) 2. Resuelve el siguiente sistema
Año Académico 2000-2001 Curso Tercero de Matemáticas EXAMEN FINAL FEBRERO 1. Dá el enunciado y demuestra el teorema de convergencia del método del punto fijo. (2 puntos) 2. Resuelve el siguiente sistema
Clase 9 Programación No Lineal
 Pontificia Universidad Católica Escuela de Ingeniería Departamento de Ingeniería Industrial y de Sistemas Clase 9 Programación No Lineal ICS 110 Optimización Profesor : Claudio Seebach Apuntes de Clases
Pontificia Universidad Católica Escuela de Ingeniería Departamento de Ingeniería Industrial y de Sistemas Clase 9 Programación No Lineal ICS 110 Optimización Profesor : Claudio Seebach Apuntes de Clases
Tema 5: Introducción a las redes neuronales
 Tema 5: Introducción a las redes neuronales F. J. Martín Mateos, J. L. Ruiz Reina et al. Dpto. Ciencias de la Computación e Inteligencia Artificial Universidad de Sevilla nteligencia Artificial IA 2017
Tema 5: Introducción a las redes neuronales F. J. Martín Mateos, J. L. Ruiz Reina et al. Dpto. Ciencias de la Computación e Inteligencia Artificial Universidad de Sevilla nteligencia Artificial IA 2017
Examen Parcial. Attr1: A, B Attr2: A, B, C Attr3 1, 2, 3 Attr4; a, b Attr5: 1, 2, 3, 4
 Aprenentatge 0-03 Q Examen Parcial Nombre: (Examen ) Instrucciones. (0 puntos) Este examen dura horas. Responded todas las preguntas en estas hojas. Para las preguntas test poned un circulo alrededor de
Aprenentatge 0-03 Q Examen Parcial Nombre: (Examen ) Instrucciones. (0 puntos) Este examen dura horas. Responded todas las preguntas en estas hojas. Para las preguntas test poned un circulo alrededor de
CAPÍTULO 3. Las redes neuronales artificiales, ANNs por sus siglas en inglés, son el resultado de varias
 CAPÍTULO 3 REDES NEURONALES ARTIFICIALES 3.1 Introducción Las redes neuronales artificiales, ANNs por sus siglas en inglés, son el resultado de varias décadas de investigaciones desarrolladas en torno
CAPÍTULO 3 REDES NEURONALES ARTIFICIALES 3.1 Introducción Las redes neuronales artificiales, ANNs por sus siglas en inglés, son el resultado de varias décadas de investigaciones desarrolladas en torno
TUTORIAL SOBRE REDES NEURONALES APLICADAS EN INGENIERIA ELECTRICA Y SU IMPLEMENTACIÓN EN UN SITIO WEB
 TUTORIAL SOBRE REDES NEURONALES APLICADAS EN INGENIERIA ELECTRICA Y SU IMPLEMENTACIÓN EN UN SITIO WEB MARIA ISABEL ACOSTA BUITRAGO CAMILO ALFONSO ZULUAGA MUÑOZ UNIVERSIDAD TECNOLOGICA DE PEREIRA FACULTAD
TUTORIAL SOBRE REDES NEURONALES APLICADAS EN INGENIERIA ELECTRICA Y SU IMPLEMENTACIÓN EN UN SITIO WEB MARIA ISABEL ACOSTA BUITRAGO CAMILO ALFONSO ZULUAGA MUÑOZ UNIVERSIDAD TECNOLOGICA DE PEREIRA FACULTAD
Al considerar varios polígonos regulares inscritos resulta: perímetro del cuadrado < π. perímetro del 96 gono < π
 AMPLIACIÓN DE MATEMÁTICAS INTRODUCCIÓN Método Constructivo: Conjunto de instrucciones que permiten calcular la solución de un problema, bien en un número finito de pasos, bien en un proceso de paso al
AMPLIACIÓN DE MATEMÁTICAS INTRODUCCIÓN Método Constructivo: Conjunto de instrucciones que permiten calcular la solución de un problema, bien en un número finito de pasos, bien en un proceso de paso al
Tema 9: Introducción a las redes neuronales
 D. Balbontín Noval F. J. Martín Mateos J. L. Ruiz Reina Dpto. Ciencias de la Computación e Inteligencia Artificial Universidad de Sevilla Neuronas artificiales: inspiración biológica El aprendizaje en
D. Balbontín Noval F. J. Martín Mateos J. L. Ruiz Reina Dpto. Ciencias de la Computación e Inteligencia Artificial Universidad de Sevilla Neuronas artificiales: inspiración biológica El aprendizaje en
Tema 1: Vectores y Matrices
 Tema 1: Vectores y Matrices Curso 2016/2017 Ruzica Jevtic Universidad San Pablo CEU Madrid Índice de contenidos Vectores y operaciones básicas Combinaciones lineales Producto escalar interior interno punto
Tema 1: Vectores y Matrices Curso 2016/2017 Ruzica Jevtic Universidad San Pablo CEU Madrid Índice de contenidos Vectores y operaciones básicas Combinaciones lineales Producto escalar interior interno punto
1. Método de bisección
 Cálculo Infinitesimal y Numérico. E.T.S. de Ingeniería Informática. Universidad de Sevilla 1 Tema 1: resolución de ecuaciones. Ejercicios y Problemas Nota: Abreviación usual en estos ejercicios: C.D.E.
Cálculo Infinitesimal y Numérico. E.T.S. de Ingeniería Informática. Universidad de Sevilla 1 Tema 1: resolución de ecuaciones. Ejercicios y Problemas Nota: Abreviación usual en estos ejercicios: C.D.E.
Redes Neuronales Artificiales
 Red de Hopfield Almacenar un conjunto de p patrones de forma tal que cuando se presente un nuevo patrón, la red responda produciendo alguno de los patrones previamente almacenados que más se parezca al
Red de Hopfield Almacenar un conjunto de p patrones de forma tal que cuando se presente un nuevo patrón, la red responda produciendo alguno de los patrones previamente almacenados que más se parezca al
Análisis Matemático II Curso 2018 Práctica introductoria
 Análisis Matemático II Curso 018 Práctica introductoria Cónicas - Sus ecuaciones y gráficas 1. Encontrar la forma estándar de cada cónica y graficar. a) x + y 6y = 0 b) x + y 1 = 0 c) x(x + 1) y = 4 d)
Análisis Matemático II Curso 018 Práctica introductoria Cónicas - Sus ecuaciones y gráficas 1. Encontrar la forma estándar de cada cónica y graficar. a) x + y 6y = 0 b) x + y 1 = 0 c) x(x + 1) y = 4 d)
Producto Escalar. AMD Grado en Ingeniería Informática. AMD Grado en Ingeniería Informática (UM) Producto Escalar 1 / 31
 Producto Escalar AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Producto Escalar 1 / 31 Objetivos Al finalizar este tema tendrás que: Saber usar el producto escalar. Calcular
Producto Escalar AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Producto Escalar 1 / 31 Objetivos Al finalizar este tema tendrás que: Saber usar el producto escalar. Calcular
Perceptrón simple y perceptrón multicapa
 UNL - FICH - Departamento de Informática - Ingeniería Informática Inteligencia Computacional Guía de trabajos prácticos Perceptrón simple y perceptrón multicapa. Objetivos Aplicar diferentes arquitecturas
UNL - FICH - Departamento de Informática - Ingeniería Informática Inteligencia Computacional Guía de trabajos prácticos Perceptrón simple y perceptrón multicapa. Objetivos Aplicar diferentes arquitecturas
Inteligencia Artificial II
 Inteligencia Artificial II Introducción a Redes Neuronales D. Balbontín Noval Dpto. Ciencias de la Computación e Inteligencia Artificial Universidad de Sevilla Inteligencia Artificial II - Tema 4 p. 1/43
Inteligencia Artificial II Introducción a Redes Neuronales D. Balbontín Noval Dpto. Ciencias de la Computación e Inteligencia Artificial Universidad de Sevilla Inteligencia Artificial II - Tema 4 p. 1/43
Análisis Numérico para Ingeniería. Clase Nro. 7
 Análisis Numérico para Ingeniería Clase Nro. 7 Sistemas de Ecuaciones No Lineales Temas a tratar: Método de Bisección. Método de Punto Fijo. Método de Punto Fijo Sistemático. Método de Newton-Raphson.
Análisis Numérico para Ingeniería Clase Nro. 7 Sistemas de Ecuaciones No Lineales Temas a tratar: Método de Bisección. Método de Punto Fijo. Método de Punto Fijo Sistemático. Método de Newton-Raphson.
Capítulo 5: CONTROL INVERSO ADAPTATIVO
 Capítulo 5: CONTROL INVERSO INTRODUCCIÓN 5.. INTRODUCCIÓN Un sistema de control inverso adaptativo se muestra en la Figura 5. Si el controlador fuese ideal, su función de transferencia sería: C( z) M (
Capítulo 5: CONTROL INVERSO INTRODUCCIÓN 5.. INTRODUCCIÓN Un sistema de control inverso adaptativo se muestra en la Figura 5. Si el controlador fuese ideal, su función de transferencia sería: C( z) M (
Matrices, determinantes y sistemas de ecuaciones lineales
 Matrices, determinantes y sistemas de ecuaciones lineales David Ariza-Ruiz 10 de octubre de 2012 1 Matrices Una matriz es una tabla numérica rectangular de m filas y n columnas dispuesta de la siguiente
Matrices, determinantes y sistemas de ecuaciones lineales David Ariza-Ruiz 10 de octubre de 2012 1 Matrices Una matriz es una tabla numérica rectangular de m filas y n columnas dispuesta de la siguiente
Análisis de Datos. Perceptrón multicapa. Profesor: Dr. Wilfrido Gómez Flores
 Análisis de Datos Perceptrón multicapa Profesor: Dr. Wilfrido Gómez Flores 1 Introducción De acuerdo con el consejo de la IEEE Neural Networks de 1996, inteligencia artificial (IA) es el estudio de cómo
Análisis de Datos Perceptrón multicapa Profesor: Dr. Wilfrido Gómez Flores 1 Introducción De acuerdo con el consejo de la IEEE Neural Networks de 1996, inteligencia artificial (IA) es el estudio de cómo
El Perceptrón Multicapa
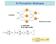 El Perceptrón Multicapa N entradas M neuronas de salida L: neuronas en la capa oculta E = 1 p M ( zi ( k) yi ( k) ) k = 1 i= 1 Implementación de la función XOR Regiones de clasificación en función del
El Perceptrón Multicapa N entradas M neuronas de salida L: neuronas en la capa oculta E = 1 p M ( zi ( k) yi ( k) ) k = 1 i= 1 Implementación de la función XOR Regiones de clasificación en función del
Convergencia Lineal y el algoritmo de
 Convergencia Lineal y el algoritmo de bisección 1 Introducción Claudio Fernández - Olga Funes El algoritmo de bisección es usualmente el primer algoritmo presentado en un curso de análisis numérico para
Convergencia Lineal y el algoritmo de bisección 1 Introducción Claudio Fernández - Olga Funes El algoritmo de bisección es usualmente el primer algoritmo presentado en un curso de análisis numérico para
Un vector está representado por cuatro elementos: origen, dirección, sentido y módulo.
 CÁLCULO VECTORIAL Escalares y vectores. Al estudiar la Física nos encontramos con dos tipos diferentes de magnitudes físicas: magnitudes escalares y magnitudes vectoriales.son magnitudes escalares aquellas
CÁLCULO VECTORIAL Escalares y vectores. Al estudiar la Física nos encontramos con dos tipos diferentes de magnitudes físicas: magnitudes escalares y magnitudes vectoriales.son magnitudes escalares aquellas
Fundamentos de Programación Entera. A. Revisión. Carlos Testuri Germán Ferrari
 Fundamentos de Programación Entera A. Revisión Carlos Testuri Germán Ferrari Departamento de Investigación Operativa Instituto de Computación Facultad de Ingeniería Universidad de la República 2012-2018
Fundamentos de Programación Entera A. Revisión Carlos Testuri Germán Ferrari Departamento de Investigación Operativa Instituto de Computación Facultad de Ingeniería Universidad de la República 2012-2018
Las Redes Neuronales Artificiales y su importancia como herramienta en la toma de decisiones. Villanueva Espinoza, María del Rosario CAPÍTULO V
 CAPÍTULO V V. ALGORITMOS NEURONALES Los modelos neuronales utilizan varios algoritmos de estimación, aprendizaje o entrenamiento para encontrar los valores de los parámetros del modelo, que en la jerga
CAPÍTULO V V. ALGORITMOS NEURONALES Los modelos neuronales utilizan varios algoritmos de estimación, aprendizaje o entrenamiento para encontrar los valores de los parámetros del modelo, que en la jerga
Redes Neuronales. Elementos básicos de las redes neuronales Carlos Andrés Delgado S.
 Redes Neuronales Elementos básicos de las redes neuronales carlos.andres.delgado@correounivalle.edu.co Carlos Andrés Delgado S. Facultad de Ingeniería. Universidad del Valle Agosto de 2017 Contenido 1
Redes Neuronales Elementos básicos de las redes neuronales carlos.andres.delgado@correounivalle.edu.co Carlos Andrés Delgado S. Facultad de Ingeniería. Universidad del Valle Agosto de 2017 Contenido 1
BACK-PROPAGATION: UN ALGORITMO DE ENTRENAMIENTO PARA REDES NEURONALES
 BACK-PROPAGATION: UN ALGORITMO DE ENTRENAMIENTO PARA REDES NEURONALES Paul Acquatella B. Universidad Simón Bolívar, Valle de Sartenejas, Caracas, Venezuela. acquatella@usb.ve Resumen Este trabajo presenta
BACK-PROPAGATION: UN ALGORITMO DE ENTRENAMIENTO PARA REDES NEURONALES Paul Acquatella B. Universidad Simón Bolívar, Valle de Sartenejas, Caracas, Venezuela. acquatella@usb.ve Resumen Este trabajo presenta
Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados
 Capítulo 5 Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados En este tema iniciamos el estudio de los conceptos geométricos de distancia y perpendicularidad en K n. Empezaremos con las definiciones
Capítulo 5 Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados En este tema iniciamos el estudio de los conceptos geométricos de distancia y perpendicularidad en K n. Empezaremos con las definiciones
Redes Neuronales Artificiales
 Redes Neuronales Artificiales Introducción a la Robótica Inteligente Álvaro Gutiérrez de abril de 208 aguti@etsit.upm.es www.robolabo.etsit.upm.es Mapas Predicción Robótica M l M r W ij S S 2 S 3 S 4
Redes Neuronales Artificiales Introducción a la Robótica Inteligente Álvaro Gutiérrez de abril de 208 aguti@etsit.upm.es www.robolabo.etsit.upm.es Mapas Predicción Robótica M l M r W ij S S 2 S 3 S 4
M a t e m á t i c a s I I 1
 Matemáticas II Matemáticas II CASTILLA Y LEÓN CONVOCATORIA SEPTIEMBRE 9 SOLUCIÓN DE LA PRUEBA DE ACCESO AUTOR: José Luis Pérez Sanz Prueba A Problemas a) f(x) x El denominador de f(x) nunca se anula; por
Matemáticas II Matemáticas II CASTILLA Y LEÓN CONVOCATORIA SEPTIEMBRE 9 SOLUCIÓN DE LA PRUEBA DE ACCESO AUTOR: José Luis Pérez Sanz Prueba A Problemas a) f(x) x El denominador de f(x) nunca se anula; por
Introducción a las Redes Neuronales mediante el paquete neuralnet
 Introducción a las Redes Neuronales mediante el paquete neuralnet El paquete neuralnet es un paquete de muy sencilla utilización que permite la aplicación, visulaización e implementación de redes neuronales.
Introducción a las Redes Neuronales mediante el paquete neuralnet El paquete neuralnet es un paquete de muy sencilla utilización que permite la aplicación, visulaización e implementación de redes neuronales.
Inteligencia Artificial II
 Inteligencia Artificial II Introducción a Redes Neuronales Delia Balbontín Noval Francisco Jesús Martín Mateos José Luis Ruiz Reina Dpto. Ciencias de la Computación e Inteligencia Artificial Universidad
Inteligencia Artificial II Introducción a Redes Neuronales Delia Balbontín Noval Francisco Jesús Martín Mateos José Luis Ruiz Reina Dpto. Ciencias de la Computación e Inteligencia Artificial Universidad
CÁLCULO NUMÉRICO I (Tema 2 - Relación 1)
 CÁLCULO NUMÉRICO I (Tema - Relación 1) 1 Cuáles de los siguientes algoritmos son finitos? a) Cálculo del producto de dos números enteros. b) Cálculo de la división de dos números enteros. c) Cálculo de
CÁLCULO NUMÉRICO I (Tema - Relación 1) 1 Cuáles de los siguientes algoritmos son finitos? a) Cálculo del producto de dos números enteros. b) Cálculo de la división de dos números enteros. c) Cálculo de
Una ecuación lineal de n-incógnitas es una igualdad de la forma:
 página 1/39 Teoría Tema 6 Ecuación lineal Una ecuación lineal de n-incógnitas es una igualdad de la forma: a 1 x 1 +a 2 x 2 +a 3 x 3 +...+a n x n =c Donde a 1,a 2, a 3,..., a n,c son números reales. En
página 1/39 Teoría Tema 6 Ecuación lineal Una ecuación lineal de n-incógnitas es una igualdad de la forma: a 1 x 1 +a 2 x 2 +a 3 x 3 +...+a n x n =c Donde a 1,a 2, a 3,..., a n,c son números reales. En
02. Resolver sistemas de ecuaciones lineales por el método de Gauss.
 3.6 Criterios específicos de evaluación. 01. Conocer lo que significa que un sistema sea incompatible o compatible, determinado o indeterminado, y aplicar este conocimiento para formar un sistema de un
3.6 Criterios específicos de evaluación. 01. Conocer lo que significa que un sistema sea incompatible o compatible, determinado o indeterminado, y aplicar este conocimiento para formar un sistema de un
1 Método de la bisección. 1.1 Teorema de Bolzano Teorema 1.1 (Bolzano) Contenido
 E.T.S. Minas: Métodos Matemáticos Resumen y ejemplos Tema 3: Solución aproximada de ecuaciones Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña
E.T.S. Minas: Métodos Matemáticos Resumen y ejemplos Tema 3: Solución aproximada de ecuaciones Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña
2 Obtener el término general de las siguientes sucesiones definidas por recurrencia: y0 = a > 0
 CÁLCULO NUMÉRICO I (Ejercicios Temas 1 y ) 1 Cuáles de los siguientes algoritmos son finitos? (a) Cálculo del producto de dos números enteros. (b) Cálculo de la división de dos números enteros. (c) Cálculo
CÁLCULO NUMÉRICO I (Ejercicios Temas 1 y ) 1 Cuáles de los siguientes algoritmos son finitos? (a) Cálculo del producto de dos números enteros. (b) Cálculo de la división de dos números enteros. (c) Cálculo
Regresión polinomial y factores
 Capítulo Regresión polinomial y factores.. Regresión polinomial Si una función media tiene un predictor X pueden usarse sus potencias enteras para aproximar E (Y X). El caso más simple es la regresión
Capítulo Regresión polinomial y factores.. Regresión polinomial Si una función media tiene un predictor X pueden usarse sus potencias enteras para aproximar E (Y X). El caso más simple es la regresión
PROPUESTA A. f(x) = x 3 + ax 2 + bx + c,
 PROPUESTA A 1A. Dada la función f(x) = x 3 + ax 2 + bx + c, calcula los parámetros a, b, c R sabiendo que: La recta tangente a la gráfica de f(x) en el punto de abcisa x = 1 tiene pendiente 3. f(x) tiene
PROPUESTA A 1A. Dada la función f(x) = x 3 + ax 2 + bx + c, calcula los parámetros a, b, c R sabiendo que: La recta tangente a la gráfica de f(x) en el punto de abcisa x = 1 tiene pendiente 3. f(x) tiene
Resolución de Ecuaciones no lineales. Juan Manuel Rodríguez Prieto
 Resolución de Ecuaciones no lineales Juan Manuel Rodríguez Prieto Resolución de Ecuaciones no lineales Objetivos Aprender a resolver ecuaciones de la forma: f () = 0 Donde f es una función no-lineal de
Resolución de Ecuaciones no lineales Juan Manuel Rodríguez Prieto Resolución de Ecuaciones no lineales Objetivos Aprender a resolver ecuaciones de la forma: f () = 0 Donde f es una función no-lineal de
3.7 IDENTIFICACION DE UN SISTEMA DINÁMICO NO LINEAL Descripción del Problema: La identificación de un sistema consiste en
 301 3.7 IDENTIFICACION DE UN SISTEMA DINÁMICO NO LINEAL 3.7.1 Descripción del Problema: La identificación de un sistema consiste en determinar una función que relacione las variables de entrada con las
301 3.7 IDENTIFICACION DE UN SISTEMA DINÁMICO NO LINEAL 3.7.1 Descripción del Problema: La identificación de un sistema consiste en determinar una función que relacione las variables de entrada con las
Valores y vectores propios
 Valores y vectores propios Tareas adicionales Algunos de estos problemas compuso Gustavo Antonio Sandoval Angeles (como parte de su servicio social). Estos problemas son más difíciles o más laboriosos
Valores y vectores propios Tareas adicionales Algunos de estos problemas compuso Gustavo Antonio Sandoval Angeles (como parte de su servicio social). Estos problemas son más difíciles o más laboriosos
Optimización en Ingeniería
 Optimización en Ingeniería Departamento de Computación CINVESTAV-IPN Av. IPN No. 2508 Col. San Pedro Zacatenco México, D.F. 07300 email: ccoello@cs.cinvestav.mx El Método de Marquardt Algoritmo Paso 1:
Optimización en Ingeniería Departamento de Computación CINVESTAV-IPN Av. IPN No. 2508 Col. San Pedro Zacatenco México, D.F. 07300 email: ccoello@cs.cinvestav.mx El Método de Marquardt Algoritmo Paso 1:
INDICE. Procedimiento 4. Mutación Paramétrica. 8
 INDICE Introducción. 3 Objetivo 4 Procedimiento 4 Algoritmo Principal. 6 Inicialización de la Población 6 Función de Aptitud.. 7 Selección de la Nueva Población. 7 Mutación Estructural 8 Mutación Paramétrica.
INDICE Introducción. 3 Objetivo 4 Procedimiento 4 Algoritmo Principal. 6 Inicialización de la Población 6 Función de Aptitud.. 7 Selección de la Nueva Población. 7 Mutación Estructural 8 Mutación Paramétrica.
Método de mínimos cuadrados (Continuación)
 Clase No. 11: MAT 251 Método de mínimos cuadrados (Continuación) Dr. Alonso Ramírez Manzanares CIMAT A.C. e-mail: alram@ cimat.mx web: http://www.cimat.mx/ alram/met_num/ Dr. Joaquín Peña Acevedo CIMAT
Clase No. 11: MAT 251 Método de mínimos cuadrados (Continuación) Dr. Alonso Ramírez Manzanares CIMAT A.C. e-mail: alram@ cimat.mx web: http://www.cimat.mx/ alram/met_num/ Dr. Joaquín Peña Acevedo CIMAT
Redes neuronales Back Propagation. Enrique Calot 4 de octubre de 2009
 Redes neuronales Back Propagation Enrique Calot 4 de octubre de 2009 1 1. Introducción Una red neuronal de tipo back propagation permite aprender mediante un conjunto de ejemplo (entrada-salida) comunmente
Redes neuronales Back Propagation Enrique Calot 4 de octubre de 2009 1 1. Introducción Una red neuronal de tipo back propagation permite aprender mediante un conjunto de ejemplo (entrada-salida) comunmente
GUIA DE EJERCICIOS TIPO PSU ECUACIONES Y FUNCIONES DE SEGUNDO GRADO MATEMÁTICA COMÚN
 GUIA DE EJERCICIOS TIPO PSU ECUACIONES Y FUNCIONES DE SEGUNDO GRADO MATEMÁTICA COMÚN 1) El vértice de la parábola f ( x) x² 8x 5 corresponde al par ordenado: a) (4,11) b) (4, 11) c) ( 8,5) d) ( 4,11) e)
GUIA DE EJERCICIOS TIPO PSU ECUACIONES Y FUNCIONES DE SEGUNDO GRADO MATEMÁTICA COMÚN 1) El vértice de la parábola f ( x) x² 8x 5 corresponde al par ordenado: a) (4,11) b) (4, 11) c) ( 8,5) d) ( 4,11) e)
Análisis de Datos. Red de función de base radial. Profesor: Dr. Wilfrido Gómez Flores
 Análisis de Datos Red de función de base radial Profesor: Dr. Wilfrido Gómez Flores 1 Introducción Las funciones de base radial han sido utilizadas en diversas técnicas de reconocimiento de patrones como
Análisis de Datos Red de función de base radial Profesor: Dr. Wilfrido Gómez Flores 1 Introducción Las funciones de base radial han sido utilizadas en diversas técnicas de reconocimiento de patrones como
Puntos y Vectores. 16 de Marzo de 2012
 Geometría en Puntos y Vectores Universidad Autónoma Metropolitana Unidad Iztapalapa 16 de Marzo de 2012 Introducción En Geometría analítica plana las relaciones y las propiedades geométricas se expresan
Geometría en Puntos y Vectores Universidad Autónoma Metropolitana Unidad Iztapalapa 16 de Marzo de 2012 Introducción En Geometría analítica plana las relaciones y las propiedades geométricas se expresan
Coordinación de Matemática II (MAT022)
 Coordinación de Matemática II (MAT022) Guía de ejercicios N 6 parte Complementos Espacios Vectoriales En los ejercicios que siguen utilizamos la siguientes notaciones: R n [x es el espacio vectorial sobre
Coordinación de Matemática II (MAT022) Guía de ejercicios N 6 parte Complementos Espacios Vectoriales En los ejercicios que siguen utilizamos la siguientes notaciones: R n [x es el espacio vectorial sobre
Determinantes. = a 11a 22 a 12 a 21 = ( 3) ( 5) ( 4) 7 = 15 ( 28) = = 43
 Determinante de una matriz cuadrada Toda matriz cuadrada A lleva asociado un número, llamado determinante de A, y que denotaremos mediante el símbolo. Este número, entre otras cosas, permite saber cuándo
Determinante de una matriz cuadrada Toda matriz cuadrada A lleva asociado un número, llamado determinante de A, y que denotaremos mediante el símbolo. Este número, entre otras cosas, permite saber cuándo
Redes Neuronales Artificiales
 Redes Neuronales Artificiales Alejandro Osses Vecchi 11 de julio de 2009 1. Introducción Comenzaremos con una definición simple y general de Red Neuronal para, en las próximas secciones, explicar y profundizar
Redes Neuronales Artificiales Alejandro Osses Vecchi 11 de julio de 2009 1. Introducción Comenzaremos con una definición simple y general de Red Neuronal para, en las próximas secciones, explicar y profundizar
Una variable es una cantidad que se simboliza por una literal y que puede tomar diferentes valores.
 MATEMÁTICAS BÁSICAS TEORÍA DE ECUACIONES DEFINICIÓN DE OLINOMIO Y DE ECUACIÓN Una variable es una cantidad que se simboliza por una literal y que puede tomar diferentes valores. Una constante es una magnitud
MATEMÁTICAS BÁSICAS TEORÍA DE ECUACIONES DEFINICIÓN DE OLINOMIO Y DE ECUACIÓN Una variable es una cantidad que se simboliza por una literal y que puede tomar diferentes valores. Una constante es una magnitud
