EXPERIMENTOS COMPUTACIONALES EN UN
|
|
|
- Natividad María Pilar Núñez Mora
- hace 5 años
- Vistas:
Transcripción
1 EXPERIMENTOS COMPUTACIONALES EN UN ESTUDIO DE SIMULACIÓN DE MODELOS DE REGRESIÓN PARA UNA MEJOR COMPRENSIÓN DE LAS HERRAMIENTAS RANDOM FORESTS Y CONDITIONAL TREES SEPTIEMBRE 2016 TRABAJO FIN DE GRADO PARA LA OBTENCIÓN DEL TÍTULO DE GRADUADO EN INGENIERÍA EN TECNOLOGÍAS INDUSTRIALES Álvaro Rollón de Pinedo DIRECTORES DEL TRABAJO FIN DE GRADO: José Mira McWilliams Francisco Javier Cara Cañas
2
3 Dedicatoria y agradecimientos Es fácil mentir a través de la Estadística. Es imposible decir la verdad sin ella. Andrejs Dunkels. A mis padres, Eduardo y Myriam, sin cuyo apoyo constante jamás habría llegado hasta aquí. A mi hermana Ángela, una de las principales razones por las cuales merece la pena levantarse por la mañana. A mis tutores, José Mira y Javier Cara, y a la profesora Camino González, que en todo momento estuvieron disponibles para cualquier consulta. A todos mis amigos, pero especialmente a Iván, Patricia Manchado, Alberto, Belén, Héctor, Nacho, Dani, Andrés, Víctor y Magda, que hacen que no haya día por el que no merezca la pena ir a la Escuela. También quiero mencionar a Patricia Martín, uno de los ejemplos en los que más me miro, y a Hua Chen, cuya ayuda en la redacción de este texto ha sido inestimable. Finalmente, a todos los profesores de esta Escuela que consiguen despertar las ganas de aprender y superarme a mí mismo, sean cuales sean las dicultades a las que haya que enfrentarse. 1
4 2 Escuela Técnica Superior de Ingenieros Industriales (UPM)
5 Resumen El presente Trabajo de Fin de Grado tiene como objetivo fundamental la realización de experimentos y simulaciones que permitan mejorar la comprensión que se posee de una de las herramientas estadísticas más potentes de las últimas décadas, especialmente en problemas de regresión y clasicación, los Random Forests. Descripción de Random Forest Los algoritmos de Bosques Aleatorios surgen como la evolución natural de los modelos estadísticos de árboles individuales de decisión, entre los cuales se pueden destacar dos principalmente: CART y los Conditional Inference Trees. En base a estos dos modelos más simples es posible construir dichos Bosques a través de una técnica conocida como Bagging (Bootstrap Aggregating), que permite mejorar la capacidad de los diversos algoritmos de Aprendizaje Automático, aumentando su estabilidad, reduciendo su varianza y previniendo el problema que supone el fenómeno del overtting (sobreajuste) en casos en los que se manejan grandes cantidades de datos. Básicamente, el proceso consiste en tomar de manera aleatoria una cantidad determinada de variables (un subconjunto de todas las variables posibles) con las cuales construir cada uno de los árboles individuales, realizándose con ellos una predicción concreta, que posteriormente será ponderada a través del cálculo de la media de cada uno de dichos árboles, para generar la predicción nal del Random Forest. Si bien es cierto que este proceder se ha demostrado válido en numerosas aplicaciones y tiene gran cantidad de ventajas, el hecho de que en muchos aspectos se comporte como una caja negra a la que sencillamente se le introduce información y directamente aporte una solución al problema, hace que conocer en detalle sus capacidades y características constituya un problema considerablemente complejo. Para solventarlo, se realizarán una serie de simulaciones programadas que permitan facilitar la comprensión de la herramienta. Las pruebas que se irán realizando tendrán en cuenta diversos parámetros a modicar para posteriormente poder analizar la respuesta. En general, se generarán variables aleatorias de diferentes características y número de observaciones. Asimismo, dicho conjunto de variables en ocasiones se generará de tal manera que las mismas estén correlacionadas (variaciones en el valor numérico de las mismas tienen relación con variaciones de las demás) o sean totalmente independientes dependiendo del caso. Asimismo, también se observará el efecto que tiene la introducción de ruido en el sistema, pudiéndose observar la adaptación de Random Forests a modelos deterministas y no deterministas. 3
6 Los modelos Como es natural en cualquier problema de regresión, las variables dependientes son el resultado de una serie de relaciones matemáticas entre las variables independientes o regresores que, en general, no son conocidas a priori. Sin embargo, para facilitar la comprensión de los resultados obtenidos en los diversos experimentos, se emplearán dos modelos relativamente sencillos, que son además muy empleados en el caso de la regresión: El modelo lineal múltiple y el modelo lineal múltiple con interacciones de segundo orden entre las variales. El hecho de que en el segundo caso no se hayan incluido interacciones de orden tres o superior obedece al hecho de que rara vez en un proceso real se da dicha situación. El primer modelo se puede representar (incluyendo el ruido) como: y = n β i x i + ε i i=1 mientras que el segundo, para un ejemplo de tres variables con ruido tiene la siguiente forma: Los Experimentos y = β 0 + β 1 x 1 + β 2 x 2 + α 1 x α 2 x 1 x 2 + α 3 x ε A lo largo de todo el documento se llevan a cabo gran cantidad de simulaciones. Sin embargo, los principales experimentos realizados para analizar la repuesta de los modelos de Random Forest son los siguientes: Variación del número de variables: Una de las grandes ventajas de los árboles de decisión es su gran capacidad para el manejo de enormes cantidades de datos y variables y aun así proporcionar buenos resultados, característica que se quería comprobar en este apartado. En este tipo de experimentos se modicará la cantidad de variables (llegándose a los centenares), y con el número de observaciones que se tiene de la misma. En general, se proporcionará poca información al sistema, de tal manera que la tarea de encontrar las relaciones entre las mismas resulte aún más complicado. El haber procedido de esta manera permite comprobar cómo incluso el ajuste de modelos lineales (que teóricamente deberían arrojar resultados mucho mejores que los árboles de decisión en estos casos concretos), falla a partir de cierto punto en el que le falta demasiada información para ajustar un modelo correcto (problema de dimensionalidad). Sin embargo, se comprueba que Random Forest se mantiene robusto pese a que está claramente desfavorecido en este caso. 4 Escuela Técnica Superior de Ingenieros Industriales (UPM)
7 EXPERIMENTOS PARA MODELOS DE ÁRBOLES Un ejemplo en el cual se aprecia dicho fenómeno es el siguiente, realizado con un modelo lineal sin interacción, con variables correlacionadas y con ruido: Figura 1: Tasa de acierto en un modelo lineal sin interacción, con regresores correlacionados y con ruido Dimensionalidad: Si bien está claro que los algoritmos realizados con árboles de decisión poseen una gran robustez a la hora de tratar con problemas en los que se posee poca información, es decir, en los cuales o bien la información está muy dispersa o sencillamente no hay sucientes datos para tantas variables explicativas, al nal todo modelo matemático está sujeto a este tipo de problema. La intención de dicho experimento era forzar hasta tal punto al sistema que incluso los modelos de árboles tuvieran complicaciones serias a la hora de abordarlos. Tras diversas simulaciones, en las cuales se analizó la variación del MAPE 1 se llegó a encontrar una relación exponencial entre la necesidad de observaciones de las variables y la cantidad de las mismas, estando en todo momento dicha relación acotada por la bisectriz del primer cuadrante, es decir, se necesitan más observaciones, como es lógico. Para llegar a dichas conclusiones fue necesario analizar modelos de Random Forest que llegaron a estar construidos hasta con 3000 variables y observaciones (nueve millones de datos). Número de árboles: El número de árboles que se incluyen en el Bosque Aleatorio es uno de los parámetros más discutidos en cuanto a la inuencia que pueden tener en la precisión de las predicciones o la aparición de fenómenos como el sobreajuste. En principio la metodología del Bagging 2 resulta muy ecaz en estos modelos a la hora de evitar el overtting, de modo que en principio un aumento del tamaño del bosque únicamente debería redundar en un aumento del coste computacional del análisis y quizá en un aumento de la precisión. 1 Mean Absolute Percentage Error, medida del error típica en estadística. 2 Bootstrap Aggregating Álvaro Rollón de Pinedo 5
8 En general se ha podido comprobar que Random Forest posee una fuerte resistencia al sobreajuste y se produce una rápida convergencia hacia la solución con el aumento de dicho número. Figura 2: Dependencia del MAPE con el número de árboles. Modelo con interacción de 3 variables correlacionadas con ruido. mtry: El parámetro conocido como mtry hace referencia a la cantidad de variables que se emplearán a la hora de analizar cómo conseguir la mayor mejora posible de un determinado parámetro, como puede ser la ganancia de información según se va ramicando el árbol. En general, es considerado uno de los parámetros que más inuyen en la calidad del Random Forest que se ajuste a un modelo concreto, de forma que lo esperable es que haya un gran sensibilidad de la precisión de las predicciones ante variaciones de dicho parámetro. En los experimentos llevados a cabo en los cuales se varía el mtry, se analiza la respuesta que aportan los modelos a lo largo de todo el espacio de valores que puede tomar, tomando un mayor o menor paso de análisis en función de la cantidad de variables y de observaciones consideradas. Conviene señalar que los valores de mtry recomendados para los casos de regresión han de oscilar en torno a n 3 para los casos de regresión y n para clasicación, siempre a nivel teórico y siendo n el número de variables implicadas, de modo que resulta interesante analizar si la experiencia corrobora la teoría. Importancia de variables: Se trata de un concepto complicado de denir pero que pretende expresar la relevancia que tienen los diversos regresores en la respuesta. Existen diversos métodos de medición indirecta de la misma, de modo que en función del caso se intentará comprobar hasta qué punto los métodos implementados en los diversos algoritmos a analizar se acercan a la relevancia ponderada que se puede asignar a cada regresor dado que el modelo con el que se generan las repuestas es conocido a priori. 6 Escuela Técnica Superior de Ingenieros Industriales (UPM)
9 EXPERIMENTOS PARA MODELOS DE ÁRBOLES Intervalos de conanza: Resulta una característica típica de la mayoría de documentos relativos al comportamiento de Random Forest el análisis de la calidad de las predicciones en función del error relativo (independientemente de cómo se mida), dejando de lado un aspecto fundamental del análisis estadístico en cualquier proceso de regresión o que implique problemas de predicción: la incertidumbre sobre la misma. Se denomina intervalo de conanza al número o dupla de número a partir del cual o entre los cuales es posible encontrar el parámetro estimado con una cierta probabilidad, de modo que se puede emplear como una medida de la incertidumbre. En el caso de Random Forest, dichos intervalos serán construidos mostrando dónde se sitúa la predicción del conjunto respecto de la totalidad de predicciones de cada árbol individual. Un gráco de ejemplo de cómo se pueden observar dichas predicciones e intervalos es el siguiente: Figura 3: Intervalos de conanza para predicciones con modelo lineal con 5 variables con interacción. Palabras Clave: Random Forest, Árboles de decisión, MAPE, Intervalo de conanza, Conditional Inference Trees, Bagging, Aprendizaje Automático. Códigos UNESCO:120304, , , , , Álvaro Rollón de Pinedo 7
10 8 Escuela Técnica Superior de Ingenieros Industriales (UPM)
11 Índice general Resumen 3 1. Introducción Antecedentes Estado del Arte Machine Learning Usos del Aprendizaje automático Redes Neuronales Máquina de Vectores Soporte Árboles de decisión Maldición de la dimensionalidad Objetivos Metodología Herramientas empleadas Introducción Classication and Regression Trees, CART Principios básicos de CART La función impureza Random Forest Out Of Bag Error Overtting Validación Cruzada Importancia de variables
12 ÍNDICE GENERAL Incremento del Error Cuadrático Medio Conditional Inference Trees Paquete Estadístico R Funciones más empleadas MAPE Experimentos con Modelo de Regresión Lineal Múltiple Introducción El modelo Aspectos a analizar Parámetros que variar Procedimiento Experimentos Independientes Cambio de variables Correlacionadas Modelo determinista Modelo no Determinista Cambio de variables no Correlacionadas Modelo Determinista Modelo no Determinista Búsqueda de la Maldición de la Dimensionalidad para los modelos de árboles Dependencia del número de árboles Experimentos con mtry Variación de mtry con 100 observaciones Variación de mtry con 200 observaciones Variación de mtry con 300 observaciones Importancia de variables Experimento 1 de Importancia de Variables, 10 regresores y 50 observaciones Experimento 2 de Importancia de Variables, 10 regresores y 150 observaciones Escuela Técnica Superior de Ingenieros Industriales (UPM)
13 EXPERIMENTOS PARA MODELOS DE ÁRBOLES Experimento 3 de Importancia de Variables, 10 regresores y 300 observaciones Experimentos con Sistema Lineal con Interacción Introducción El modelo Experimentos Independientes Cambio de variables Correlacionadas Modelo determinista Modelo no determinista Cambio de variables no Correlacionadas Modelo determinista Modelo no determinista Dependencia respecto del número de árboles Experimentos con mtry Variación de mtry con 100 observaciones Variación de mtry con 200 observaciones Variación de mtry con 300 observaciones Intervalos de Conanza Introducción Descripción de los Intervalos Experimento 1: 20 variables Esperimento 2: 40 variables Experimento 3: 60 variables Bibliografía Conclusión y Líneas Futuras Conclusión Líneas futuras Planicación temporal y presupuesto 87 Álvaro Rollón de Pinedo 11
14 ÍNDICE GENERAL 8.1. Estructura de Descomposición del Proyecto (EDP) Diagrama de Gantt Presupuesto del TFG Bibliografía 93 Apéndices 93 Índice de Figuras 99 Índice de Tablas 101 Índice de Códigos Escuela Técnica Superior de Ingenieros Industriales (UPM)
15 Capítulo 1 Introducción 1.1. Antecedentes En un mundo en constante evolución, la revolución digital supuso un aumento extraordinario de la cantidad de información que la humanidad era capaz de generar. El año 2002, en el cual la cantidad de datos digitales generados igualó a la de analógicos, es habitualmente considerado el punto de inicio de la conocida como Era digital, y supuso un hito a partir del cual la generación y almacenamiento de información sufrieron un crecimiento exponencial hasta el día de hoy. Según Martin Hilbert, profesor de la Universidad de California, en el año 2007 la humanidad tenía una capacidad de almacenamiento de aproximadamente 300 exabytes 1, lo cual equivale al número de estrellas en nuestra galaxia como bits por persona. Ese mismo año la humanidad transrió unos 65 exabytes a través de medios de comunicación bidireccionales. Naturalmente, estas cifras no han hecho otra cosa que incrementarse masivamente los años posteriores, de tal manera que para poder hacer uso de tan tremenda cantidad de información se hace imprescindible apartar los modelos de tratamiento de datos tradicionales y recurrir a técnicas más modernas que permitan analizar tan colosal cantidad de información, conocida como Big Data Estado del Arte A continuación se realizará un bosquejo del estado actual de la ciencia estadística y computacional, que en muchos casos se solapan en tanto en cuanto ambos campos están especialmente interesados en las técnicas de análisis de datos Machine Learning El Aprendizaje automático, más conocido por su nomenclatura en inglés, Machine Learning es una disciplina computacional pertenciente al campo de la inteligencia articial bytes 13
16 1.2. ESTADO DEL ARTE cuyo objetivo primordial es la búsqueda de patrones en el análisis de un fenómeno a partir de una muestra aleatorizada de variables y respuestas. Asimismo, su característica más importante es el diseño de programas capaces de aprender por ellos mismos a través de la experiencia de los datos previos analizados. Por supuesto, esta idea general es en la práctica extremadamente complicada, pues en el momento en el que el input del sistema son centenares o incluso miles de variables, todas ellas distintas entre sí, la variabilidad de posibles outputs del sistema es aparentemente impredecible, razón por la cual los diversos algoritmos de Machine Learning se diseñan de tal manera que todo el conocimiento que vayan adquiriendo se vaya convirtiendo en experiencia que nutra al sistema y le ayude a aprender. Cabe distinguir dos tipos generales de aprendizaje llevados a cabo por este tipo de algoritmos: el conocido como Aprendizaje supervisado, en el cual el algoritmo se encarga de establecer algún tipo de correspondencia (función) entre las variables de entrada y las salidas asignadas. El otro caso típico es el de Aprendizaje no supervisado, en el cual el sistema es únicamente alimentado con variables de entrada, de tal manera que se vuelve crítico reconocer los patrones establecidos entre los inputs. Naturalmente, existen otros tipos intermedios, como el Aprendizaje semisupervisado, en el cual solo se alimenta al sistema con un porcentaje de las respuestas totales conocidas, o el Aprendizaje mediante ensayo y error. Conviene señalar que el aprendizaje supervisado es el que está más orientado a las típicas labores de regresión y predicción estadística, pues es capaz de diferenciar qué conjunto de conclusiones es satisfactorio, mientras que el no supervisado es más frecuentemente empleado en labores de clasicación de las variables suministradas al sistema, en base a patrones que el algoritmo pudiera ser capaz de reconocer Usos del Aprendizaje automático Existen innidad de usos para las diversas técnicas de Machine Learning, como pueden ser el modelado de funciones de densidad, empleo en optimización de problemas o, más en relación con el presente trabajo, clasicación y regresión, las cuales se relacionan también con modelado de funciones de densidad de probabilidad condicionadas. En el caso de Clasicación, dado un conjunto de variables de entrada y de salida (Aprendizaje supervisado), el objetivo es la asignación de una determinada categoría (los outputs del sistema)a los nuevos datos que se pretenden clasicar. Ahondando en la nomenclatura, en el caso del Aprendizaje Automático, las categorías que se asignan a las variables se suelen denominar Clases, mientras que las observaciones son más comúnmente conocidas como Instancias. En cuanto a la Regresión, se trata de un campo cuyo objetivo es encontrar la relación entre una variable dependiente escalar, en función de una serie de variables explicativas. Los modelos de regresión son ampliamente utilizados para multitud de aplicaciones, pero conviene destacar las más importantes. Primeramente, estos modelos pueden ser empleados en labores de predicción, de tal manera que en base a las respuestas previamente obtenidas por parte de las variables explicativas del conjunto de entrenamiento ( training set), el sistema es capaz de predecir con mayor o menor precisión la posible respuesta a nuevas observaciones. Otro uso típico de los modelos de regresión es el estudio de la relación entre la respuesta y los regresores, en denitiva, el objetivo es el análisis de cómo 14 Escuela Técnica Superior de Ingenieros Industriales (UPM)
17 EXPERIMENTOS PARA MODELOS DE ÁRBOLES de importante es cada regresor a la hora de conocer la respuesta. Entre los muchos modelos que existen, conviene destacar los siguientes, que asimismo son los más utilizados hoy en día Redes Neuronales Las Redes Neuronales Articiales (en inglés, Articial Neural Networks) son un modelo estadístico de Aprendizaje automático que se inspira en los modelos de procesamiento y tratamiento de información de sistemas biológicos reales, si bien a una escala mucho menor. La base de las mismas es la cooperación de conjuntos de nodos (neuronas) que permanentemente colaboran entre sí para dar respuesta al estímulo de entrada, de tal manera que durante su etapa de aprendizaje (se le proporcionan al sistema las respuestas apropiadas a los estímulos), la red va generando de forma autónoma su modelo neuronal. Este proceder tiene la ventaja del almacenamiento de información redundante y contraste de la misma, de tal manera que en caso de que parte de la red maneje información errónea, el conjunto de la red es robusto ante errores, además de poseer una gran tolerancia ante variables de entrada no relevantes, o ruido. A modo de resumen, la salida que cada neurona aportará a la siguiente será combinación de tres funciones. La primera de ellas es conocida como Función de Propagación, en la cual la salida será una combinación de las entradas multiplicada cada una de ellas por un peso. En base a ella, la Función de Activación de la neurona puede o no actuar sobre la respuesta, para nalmente aplicarse a la respuesta la conocida como Función de Transferencia, que acota los tipos de salida que se pueden obtener de cada neurona y facilita la comunicación e interconexión entre ellas. Figura 1.1: Esquema de una Red Neuronal Álvaro Rollón de Pinedo 15
18 1.2. ESTADO DEL ARTE Máquina de Vectores Soporte Las Máquinas de Vectores Soporte (Support Vector Machines) son otro conjunto de algoritmos de Machine Learning de tipo supervisado especialmente empleados en labores de clasicación y regresión. Intuitivamente, dado un conjunto de puntos que quiere ser sometido a una clasicación, las Máquinas de Vectores Soporte (MVS) se encargan de encontrar una separación óptima entre dichos puntos, siendo cada conjunto de puntos pertenciente a una categoría. Generalmente, ello se consigue mediante la proyección de dichos puntos en subespacios de dimensión superior a la inicialmente considerada, de tal manera que se facilita la tarea de encontrar un hiperplano capaz de realizar la separación óptima entre las variables. Esta última es una de las características fundamentales de las MVS, ya que la cantidad de posibilidades de separación es innita. Al vector que está conformado por el conjunto de puntos más cercano al mencionado hiperplano es al que se conoce en la literatura como Vector Soporte. Típicamente las variables predictoras se denominan atributos, mientras que al factor principal de clasicación se lo conoce como característica. Conviene destacar la importancia de la proyección en subespacios de superior superior de los atributos. La utilidad de esta metodología es que permite una separación mucho más eciente de las variables de otra manera no serían tan sencillas de separar como con un hiperplano (en dos dimensiones sería una recta, siendo muy complicado separar el conjunto de puntos de forma eciente con dicho elemento geométrico). Esta mencionada proyección se logra a través de funciones conocidas como Kernel, entre las cuales se puede destacar la Polinomial/homogénea, o la Radial Gaussiana. Figura 1.2: Esquema del funcionamiento de la función Kernel 16 Escuela Técnica Superior de Ingenieros Industriales (UPM)
19 Árboles de decisión EXPERIMENTOS PARA MODELOS DE ÁRBOLES Los árboles de decisión son herramientas o algoritmos cuya nalidad fundamental radica en la toma de decisiones en base a criterios determinados en cada uno de sus nodos u "hojas", de tal manera que en función de las características que toma la entrada del sistema, se produzca una salida determinada en base a un criterio establecido. Este tipo de algoritmos se analizarán en profundidad en capítulos posteriores Maldición de la dimensionalidad La Maldición de la dimensionalidad es un concepto en realidad simple pero completamente antintuitivo, razón por la cual tardó un tiempo considerable en ser contemplada por parte de la comunidad cientíca. Se trata de un problema que se hace evidente en el momento en el que se procede al manejo de gran cantidad de datos (Razón por la cual es importante tenerlo en consideración en todo tipo de temas relacionados con Big Data). Resulta que en el caso de fenómenos que se pretenden explicar estudiando la variación de muchas variables, la cantidad de datos necesarios para que exista la posibilidad de ajustar un modelo va creciendo exponencialmente con el número de variables. Ello supone un gran contratiempo en el momento en el que se sabe a ciencia cierta que un fenómeno depende de demasiadas variables en comparación con el tamaño de muestra y la cantidad de datos de la que se dispone. Debido a ello, la capacidad de medir de alguna manera la importancia de las variables en función de las cuales quiere dar respuesta a un cierto caso resulta fundamental, para poder seleccionar las menos relevantes y despreciar su efecto en el caso de que no se disponga de un tamaño de muestra lo sucientemente grande. En general, la mayoría de algoritmos de aprendizaje son susceptibles de padecer en mayor o menor medida este efecto, y teniendo en cuenta que la mayoría trabajan con Big data, la robustez de los mismos ante el manejo de grandes cantidades de datos (necesaria para hacer viable el manejo de muchas variables), resulta una faceta importante a tener en cuenta a la hora de seleccionar qué algoritmo sería el óptimo. Este problema de dimensionalidad, debido a su carácter antintuitivo, es frecuentemente explicado a través de ejemplos sencillos. Uno típico es el siguiente: Si se quisiera localizar una moneda en una linea de 100 metros en la carretera, no resultaría muy complicado, ya que solo sería necesario recorrerla hasta encontrarla y en poco tiempo se podría. La posición de la moneda solo depende de la variable distancia, resulta un problema unidimensional. Si en cambio se extiende el conjunto posible de puntos en los que puede estar la moneda a un cuadrado de metros, el mismo problema de encontrar la moneda, con un número mayor de variables, no solo no resulta más sencillo sino que se complica, y lo mismo sucede en el caso de un cubo de dimensiones análogas, de modo que la dicultad del problema además es exponencial. Por supuesto, dicho ejemplo no quiere decir que para explicar un fenómeno complejo que dependa de muchas variables lo idóneo sea seleccionar solo una de ellas, ya que las Álvaro Rollón de Pinedo 17
20 1.3. OBJETIVOS demás también aportarán información, sino que en el momento en el que la dimensionalidad del problema crece, el número de datos que se deben aportar también debe hacerlo, y de manera exponencial, para evita la contingencia de que la cantidad de datos de que se dispone sea insuciente Objetivos El presente Trabajo de Fin de Grado tiene como objetivo primordial expandir el conocimiento que se tiene de una de las herramientas de análisis estadístico más utilizadas hoy en día: los conocidos como Random Forest. Si bien está claro que su potencial en el análisis y tratamiento de datos está más que demostrado, aun no se ha llevado a cabo un análisis riguroso de algunas de sus capacidades fundamentales y de cómo estos algoritmos manejan la información para obtener los buenos resultados que obviamente proporcionan. Más especícamente, este documento busca ayudar a mejorar la comprensión de los Random Forest en algunas de sus aplicaciones más típicas, en particular la Regresión y el análisis de importancia de variables. Si bien está claro que un gran avance en la compresión de esta herramienta no es sencillo de abordar en un proyecto de la dimensión de un Trabajo de Fin de Grado, sí es posible mostrar un acercamiento a cómo analizar de forma exhaustiva el comportamiento de los Random Forest, así como aportar ciertas conclusiones o características interesantes que son únicamente abordables a través de la simulación o la experiencia. Otro gran objetivo es el análisis de la incertidumbre que este tipo de modelos arrojan en sus resultados. Actualmente, la inmensa mayoría de los usos de este tipo de herramientas estadísticas modernas se focalizan en la obtención de resultados muy concretos sin entrar tanto a analizar la incertidumbre de los mismos. Parte del presente trabajo se centrará en la creación de intervalos de conanza en cuanto a la calidad de las predicciones o clasicaciones realizados con los diversos modelos que se analizarán. Asimismo, es bien sabido que Random Forest, si bien es una técnica en general no demasiado susceptible al tipo de variables que tenga que analizar, o al tipo de modelo (ya sea simulado o real) que se aplica, sí es cierto que se han encontrado deciencias en su funcionamiento en cuanto al sesgo que pueda llegar a tener por ciertos tipos de variables o con ciertos valores de sus parámetros. Es interesante comprobar hasta qué punto sucede este fenómeno o si es algo que sucede siempre o solo en algunos casos concretos Metodología La metodología seguida es consistente a lo largo del trabajo, y se puede resumir en cuatro puntos fundamentales: Denir el experimento de simulación a realizar. Escritura del código en R. 18 Escuela Técnica Superior de Ingenieros Industriales (UPM)
21 EXPERIMENTOS PARA MODELOS DE ÁRBOLES Análisis de los resultados arrojados por parte del código y comprobación de su consistencia para asegurar que no se han cometido errores. Conclusiones sobre los resultados arrojados por el modelo y contraste con lo esperado. Como es lógico, la complejidad de los modelos a analizar no debe ser excesiva, de tal manera que se facilite su análisis. Por ejemplo, no sería útil denir un modelo matemático tan complejo que no fuera posible saber si los resultados que arroja el modelo son realistas o están sesgados de alguna manera. De igual forma, conviene que los experimentos a realizar tengan una solución de sobra conocida que permita contrastar los resultados. Álvaro Rollón de Pinedo 19
22 1.4. METODOLOGÍA 20 Escuela Técnica Superior de Ingenieros Industriales (UPM)
23 Capítulo 2 Herramientas empleadas 2.1. Introducción En el presente capítulo se dará una visión general del conjunto de herramientas, tanto estadísticas como computacionales, de las cuales se hará uso a lo largo del proyecto. La comprensión del funcionamiento de dichas herramientas es fundamental para poder realizar un análisis exhaustivo y más o menos profundo de los resultados que se obtengan Classication and Regression Trees, CART Los Árboles de Clasicación y Regresión (CART por sus siglas en inglés, Breiman, Friedman, Olshen, y Stone 1984 ), son una técnica estadística no paramétrica que permite resolver con acierto problemas de clasicación en los que las variables implicadas pueden ser tanto continuas como discretas. El nombre que se asigna al árbol depende fundamentalmente de la naturaleza de la variable respuesta, de tal manera que en caso de ser continua el árbol se denominará de Regresión, y en caso contrario de Clasicación. En las propias palabras de Breiman: "Tanto en los casos de Clasicación como de Regresión, el principal objetivo de CART es producir un conjunto preciso de variables clasicadoras que permitan descubrir la estructura predictiva del modelo en consideración". En denitiva, CART es una herramienta cuya nalidad fundamental es encontrar una relación entre variables explicativas para dar respuesta a un cierto fenómeno. El empleo de la metodología CART tiene ciertas ventajas frente a otros algoritmos de clasicación. Más concretamente, Breiman destaca los siguientes puntos frente a otros tipos de técnicas similares: CART no realiza asunciones acerca de las posibles distribuciones de probabilidad de las variables independientes y dependientes, lo cual es extremadamente útil en el análisis de sistemas reales. Las variables explicativas pueden ser tanto continuas como discretas (categóricas). 21
24 2.2. CLASSIFICATION AND REGRESSION TREES, CART CART no es afectado por los típicos problemas de los modelos paramétricos, como pueden ser la correlación entre las variables o la heterocedasticidad. Es capaz de descubrir interacciones entre las variables explicativas. Los árboles producidos con CART no varían ante transformaciones monótonas de las variables explicativas. La principal ventaja de CART es que es capaz de lidiar con grandes cantidades de variables y datos, pudiendo distinguir qué variables son las más relevantes a la hora de realizar el análisis. La estructura de los árboles resultantes es intuitiva y de fácil comprensión para cualquier persona independientemente del campo de aplicación Principios básicos de CART Según la doctora Jia Li, profesora de la Penn State University, la construcción de un Árbol de Clasicación y Regresión depende de tres elementos fundamentales: La selección de cómo partir un nodo. En qué momento declarar a un nodo terminal o continuar partiéndolo. La asignación de una clase a cada nodo terminal Cumpliendo con lo anterior, un CART ya terminado debería tener un aspecto similar al siguiente: Figura 2.1: Ejemplo sencillo de un CART Así, para conseguir crear el árbol, será necesaria la generación de un conjunto de preguntas binarias que permitan moverse por una rama u otra, así como un criterio de bondad de partición aplicable a todo nodo analizado. También es necesario establecer un criterio de parada para decidir cuándo parar de partir los nodos, además de otro criterio que permita asignar una clase a cada nodo terminal. Lo que se conoce como bondad de partición es medible a partir de la conocida como Función de Impureza (Impurity Function). Resulta bastante intuitiva la idea de que lo 22 Escuela Técnica Superior de Ingenieros Industriales (UPM)
25 EXPERIMENTOS PARA MODELOS DE ÁRBOLES más deseable es que cada nodo que se separe debe ser todo lo puro posible, es decir, que a la hora de asignar una clase determinada a un nodo terminal todos los datos ahí asignados resulten ser muy homogéneos y de la misma naturaleza La función impureza La función impureza (φ) resulta ser una medida indirecta de la llamada "pureza"de cada nodo. Dicha función está compuesta por unas n-uplas de números: (p 1,..., p n ) que satisfacen: p j 0 y n p j = 1. Asimismo, debe cumplir las propiedades: j=0 φ tiene un máximo único en ( 1 n,..., 1 n ) φ solo tiene mínimos únicos en (1, 0,..., 0), (0, 1, 0,..., 0)...(0, 0,..., 1) φ es una función simétrica en p j, es decir, la permutación de cualquier par de p j deja la función invariante Así, dada una fución impureza φ es posible denir la impureza i(t) de un nodo t de la siguiente manera: i(t) = φ(p(1 t), p(2 t),..., p(n t)) donde p(j t) es la probabilidad estimada de que a un nodo t le sea asignada la clase j. A partir de estas consideraciones, es posible calcular la pureza de los nodos asociados a un CART, con lo cual es asimismo posible establecer una tasa de error de clasicación en el árbol. Existen tres funciones habitualmente empleadas como funciones de impureza en la mayoría de Árboles de Regresión: n Entropía: p j log 1, y en caso de que p j = 0, emplear el límite: lím p j log p j p j j j=0 Tasa de error de Clasicación:1 max j p j Índice de Gini: n p j (1 p j ) = 1 n j=1 p 2 j j=1 Existe bastante aceptación en torno al hecho de que el Índice de Gini es el que suele funcionar mejor en la mayoría de los casos. Como es lógico, la construcción del CART se va realizando empleando siempre el criterio de que la función impureza elegida alcance un mínimo, y se va realizando la clasicación de variables con dicho objetivo, hasta llegar al árbol resultante con la máxima pureza posible en los nodos. Por supuesto, como ya se ha mencionado es imprescindible establecer un criterio de parada, pues si no sería posible por ejemplo seguir haciendo particiones hasta que en cada nodo hoja o terminal hubiera un único dato, de tal manera que evidentemente la pureza Álvaro Rollón de Pinedo 23
26 2.2. CLASSIFICATION AND REGRESSION TREES, CART de todos esos nodos sería del 100 %, pero resultaría en un árbol gigantesco de proporciones inmanejables, que además no proporcionaría ninguna información, además de aumentarse ostensiblemente el coste computacional. 24 Escuela Técnica Superior de Ingenieros Industriales (UPM)
27 2.3. Random Forest EXPERIMENTOS PARA MODELOS DE ÁRBOLES Una vez entendidas las bases de cómo funciona CART y los árboles de decisión en general, es posible proceder a una explicación somera de las bases en las que se apoya el algoritmo de Random Forest (Bosques o Selvas Aleatorios, aunque rara vez se los llama así) para realizar sus predicciones. Primeramente, se genera un conjunto de árboles, de tal manera que la nueva observación es aplicada a cada uno de dichos árboles y, mediante un proceso de "votación", a la observación le es asignada la clase más votada. Conviene recalcar que no todos los árboles se construyen de la misma manera, de forma que, en general, pueden arrojar resultados distintos. Profundizando en la manera en la que el bosque es construido, cada árbol de decisión se diseña así: Dado un tamaño de muestra N, se escogen de esa misma muestra N datos de forma aleatoria, pero con reemplazamiento. Dicha metodología seguida de selección de muestras con reemplazamiento es lo que se conoce como Bootstrapping, y es un método muy generalizado empleado tanto en Random Forest como en otras técnicas de Machine Learning. Dadas M variables de entrada, se escoge un número considerablemente inferior m M de variables para que en cada nodo se vayan seleccionando nuevas de forma aleatoria para buscar la mejor partición posible de cada nodo. El número de variables m escogido es constante en todo el Random Forest. Se genera cada árbol sin podar hasta la máxima extensión posible. Teniendo estos factores en cuenta, según el paper original de Random Forest la tasa de error de un Random Forest es dependiente de dos parámetros fundamentales: La correlación existente entre árboles. A mayor correlación entre distintos árboles del bosque mayor será en general la tasa de error del algoritmo. Este problema es paliado en parte gracias a la aleatorización con la que se se toman las variables explicativas. La fuerza de cada árbol individual. La existencia de árboles que aporten mucha información mejora en general la capacidad predictiva del Random Forest. Conviene tener en cuenta que ambos factores son muy sensibles a parámetro m, de forma que la disminuir su valor, se reduce sensiblemente la correlación entre árboles, pero es menos probable que aporten una mayor cantidad de información de manera global. Existen diversas razones por las cuales los Random Forest son tan ampliamente empleados actualmente, entre las cuales cabe destacar: Es uno de los algoritmos existentes más precisos. Es capaz de manejar cantidades enormes de datos y variables. Puede arrojar resultados de importancia de variables en la clasicación. Álvaro Rollón de Pinedo 25
28 2.4. OVERFITTING Sigue siendo capaz de realizar aproximaciones relativamente precisas aun desconociendo parte de la información. Es capaz de captar la interacción entre las distintas variables explicativas Out Of Bag Error El Out Of Bag Error (OOB) es un concepto de error aplicado generalmente a los diversos algoritmos que emplean el modelo de toma de muestras con reemplazamiento conocido como bootstrapping. Para cada conjunto de variables, el OOB representa el error cometido por el conjunto de árboles que no contienen esas determinadas variables, y por lo tanto no las tienen en cuenta a la hora de realizar sus particiones nodales. En el caso de Random Forest, es típico observar un decremento continuado del OOB con el aumento del número de árboles generados, llegándose en general a un valor asintótico al llegar al orden de centenares de árboles, por lo que la mayoría de los programas que manejan los Random Forests tienen un número determinado de árboles que generan por defecto, para reducir el coste computacional de los cálculos y simulaciones, además de evitar incurrir en otros peligros como el overtting. Una representación de la reducción del OOB error en un modelo ejemplo de Random Forest es la siguiente: Figura 2.2: Ejemplo sencillo de la disminución del OOB con el número de árboles 2.4. Overtting El concepto de overtting (sobreajuste), es un término comúnmente empleado en algoritmos de Machine Learning y estadística en general. En ambos ámbitos es típica la necesidad de tener que ajustar un modelo estadístico a un conjunto de variables explicativas, de tal manera que siempre se busque un ajuste todo lo preciso que se pueda. 26 Escuela Técnica Superior de Ingenieros Industriales (UPM)
29 EXPERIMENTOS PARA MODELOS DE ÁRBOLES Sin embargo, dependiendo de los procedimientos que se empleen o el tipo de modelo que se ajuste a un determinado conjunto de datos, así como el ruido que los mismos puedan tener, es posible terminar con un modelo que se ajuste con mucha precisión a los datos de partida, pero que resulte incapaz de predecir cualquier conjunto de valores que se hallen fuera de dicho intervalo de actuación. Ello resulta en el concepto de Overtting o Sobreajuste. Se trata de un concepto muy similar al conocido problema de interpolación polinomial por el cual en numerosas ocasiones ajustar un polinomio de grado muy grande resulta en valores ridículos fuera del intervalo de actuación de las variables que se emplearon en la generación del modelo. Existen diversas técnicas generales que permiten subsanar este problema común, como la poda de los árboles, obligándoles a aportar una ganancia mínima de información para permitir la partición de un nodo, técnicas de variación cruzada etc. En el caso de Random Forest, por la forma en la que está diseñado el algoritmo, es considerablemente improbable que se produzca el fenómeno de overtting, sin embargo, dependiendo del número de variables que se empleen en la creación de los árboles (antes denotado por la letra m), o incluso en función del número de árboles que se generen, existe la posibilidad de que se produzca dicho fenómeno, si bien es un tema sobre el que precisamente se quiere investigar en este trabajo. También es conocido el aumento de la tendencia al sobreajuste por parte de los modelos estadísticos ante la falta de datos, de forma que si existe una ausencia severa de los mismos, aumenta la tendencia. Un buen ejemplo es el típico caso ofrecido por Mathworks,Inc. en el cual se muestra cómo el ajuste de un polinomio de primer grado ofrece unos resultados razonables en cuanto a la variación poblacional de EEUU, mientras que un modelo parabólico se aproxima aún mejor, pero al intentar ajustar un polinomio de grado 6 la curva presenta valores absurdos fuera del intervalo de los datos aportados: Figura 2.3: Caso de overtting en el modelo poblacional de EEUU Álvaro Rollón de Pinedo 27
30 2.5. VALIDACIÓN CRUZADA 2.5. Validación Cruzada La Validación Cruzada (Cross Validation) es una técnica empleada en el manejo de grandes cantidades de datos cuya nalidad es garantizar la independencia de los resultados obtenidos a la hora de realizar una partición de los datos empleados como set de entrenamiento y prueba, típicamente conocidos como training set y test set. Resulta muy útil en la generación de algoritmos de inteligencia articial o Aprendizaje Automático, ya que permite comprobar que los resultados que se obtengan sean en general independientes de la muestra elegida. Este método consiste en una variación del llamado Holdout method, por el cual dada una muestra de datos, éstos son separados en dos conjuntos de datos bien diferenciados, los ya mencionados training set y test set. El modelo que se desea generar se hará empleando únicamente los datos contenidos en el set de entrenamiento, para posteriormente vericar los resultados de las predicciones con el set de prueba, ya que en este conjunto de información son conocidas las variables de entrada y las respuestas que éstas generan. Como es lógico, este proceder es válido únicamente en el caso del Aprendizaje supervisado. Sin embargo, si bien es cierto que el Holdout method es una técnica práctica a la hora de analizar datos, resulta inconsistente por sí mismo, ya que no hay manera de garantizar que no haya sesgo o independencia a la hora de elegir las variables con las que se generará el modelo. Dicho problema se puede paliar parcialmente aleatorizando la muestra antes de elegir qué conjuntos de variable explicativas y respuesta formarán parte del test de entrenamiento (procedimiento que por otra parte se seguirá a lo largo de todo este Trabajo de Fin de Grado). En cualquier caso, para asegurar la independencia de los resultados obtenidos de la muestra, la manera más sencilla y práctica de conseguirlo es mediante la validación cruzada. Existen dos tipos fundamentales de Cross validation, siendo el primero de ellos el que, por su mayor sencillez y claridad el que se empleará en este documento. Ambos modelos se engloban en lo que se conoce como validación cruzada no exhaustiva, que es con mucho el tipo más empleado. El otro tipo, la validación exhaustiva, tiene un coste computacional en general más alto, ya que contemplan todas las posibles combinaciones de datos a la hora de realizar el muestreo. K-fold cross validation : Este tipo de validación cruzada consiste en dividir la muestra completa en K subconjuntos, de manera que en cada ocasión se elegirá uno de dichos subconjuntos, que constituirá el conjunto de prueba, mientras que el modelo a considerar se generará con el resto de subconjuntos. Será necesario repetir este proceder con cada uno de los K subconjuntos seleccionados, de manera que el trabajo a realizar es mucho mayor, ya que será necesario generar K veces más modelos que lo inicialmente previsto. Una vez se tienen en cuenta todos los modelo creados con este proceder, lo más común es utilizar la media aritmética de los resultados para obtener los valores que se querían predecir. 28 Escuela Técnica Superior de Ingenieros Industriales (UPM)
31 EXPERIMENTOS PARA MODELOS DE ÁRBOLES Figura 2.4: Esquema del proceder empleando K-fold validation Validación cruzada aleatoria: Es una manera de proceder menos empleada pero que también arroja buenos resultados en general. En este caso, en vez de aletorizar los datos y dividirlos en secciones, primero se aleatoriza y posteriormente, se selcciona qué datos pasarán a formar parte del set e entrenamiento también de manera aleatoria. Por supuesto, será necesario denir qué cantidad de datos (en número) van a formar parte de cada conjunto de entrenamiento, así como el número de iteraciones que se pretende realizar. Surgen cierto problemas derivados de este proceder, como por ejemplo que existe una probabilidad alta de solapes entre training set y test set, además de que habrá muestras evaluadas repetidas veces y otras que sencillamente no se tendrán en cuenta. Dicho problema se puede abordar aumentando el número de iteraciones, pero ello conlleva como contrapartida el aumento del riesgo de overtting. Figura 2.5: Ejemplo de lo anterior con 3 iteraciones Álvaro Rollón de Pinedo 29
32 2.6. IMPORTANCIA DE VARIABLES 2.6. Importancia de variables El concepto Importancia de variables es quizá uno de los más habitualmente empleados en campos estadísticos como problemas de regresión o clasicación, y sin embargo sigue siendo uno de los más complejos de denir y sobre todo de medir. A grandes rasgos el análisis de la Importancia de variables pretende expresar cómo varía la variable dependiente (normalmente denotada por Y ) ante cambios en las variables de entrada (las X), buscando en cierta forma expresar la sensibilidad de la respuesta ante cambios en los inputs. Sin embargo, aunque conceptualmente resulte una idea sencilla de asimilar, resulta tremendamente complejo medir dicha dependencia debido a la multitud de factores que inuyen. Probablemente la manera más ilustrativa de explicar dicha dicultad sea con un ejemplo práctico sencillo, pero que permite dar una idea de la magnitud del problema. Supóngase un modelo de regresión lineal básico como el siguiente: y = β 0 + β 1 x 1 + β 2 x 2 + ε j En este caso, sin tener en cuenta los residuos, se puede armar que la variable respuesta y depende de cinco factores: β 0, β 1, x 1, β 2, x 2. Un análisis de importancia de variables típico pretendería establecer cuál de las dos variables explicativas, x 1 o x 2, tiene más peso en la respuesta del modelo. La primera consideración que se tiene es bastante intuitiva, la importancia de cada una de las variables será función de los valores que tomen sus coecientes, ya que si, por ejemplo, β 1 fuera diez veces mayor que β 2, los valores que pudiera tomar la primera variable sería mucho más importantes que los de la segunda, que en ciertos casos podría incluso considerarse como irrelevante. En el siguiente ejemplo simulado, ambas variables explicativas toman valores aleatorios comprendidos entre cero y diez mediante una distribución uniforme, mientras que los coecientes β 1 y β 2 toman respectivamente los valores 10 y 1, de tal manera que la mayor inuencia en la respuesta se asigna a la variable x 1. En este ejemplo, se ha representado en azul el valor real de la respuesta, mientras que en negro se representa el mismo modelo pero sin considerar el valor de la variable x 2, como si β 2 = 0, mientras que en rojo aparece el caso inverso, en el cual no se considera la primera variable explicativa. En este caso resulta sencillo armar que x 1 es la variable más signicativa, pero no es tan sencillo cuanticar dicha relación. 30 Escuela Técnica Superior de Ingenieros Industriales (UPM)
33 EXPERIMENTOS PARA MODELOS DE ÁRBOLES Figura 2.6: Variación de la respuesta ante alteraciones del modelo Asimismo, existe otra posibilidad, que es que el rango de variación de los valores que toman las variables sea muy dispar, por ejemplo, variando una entre 0 y 10, y otra entre 10 3 y 10 5, con lo cual la variable de menor rango resultaría prácticamente despreciable. Este es en realidad otro problema típico en diversos campos de análisis de datos que se puede corregir hasta cierto punto mediante escalado de las variables implicadas, usualmente haciéndolas variar entre cero y uno. Otro problema que se tiene que tener en consideración es la distribución de las variables, ya que incluso hablando de una misma variable puede que haya un porcentaje alto de valores con un rango muy estrecho de variación, como sucedería por ejemplo en una distribución gaussiana de poca amplitud, o en otras ocasiones tener un rango mucho mayor. En denitiva, diferencias en las distribuciones de probabilidad de las variables explicativas dicultan el análisis de importancia, y más aún cuando dichas funciones son desconocidas a priori. Finalmente, un último factor a considerar es la posibilidad de que las variables que conforman el modelo puedan ser continuas o discretas, de manera que sus diferencias dicultan aún más la labor de comparar su relevancia. Si bien no se ha profundizado en la cuestión, ha quedado clara la dicultad de realizar un análisis de Importancia de Variables incluso en los ejemplos más sencillos, máxime si dichos modelos son desconocidos, con centenares o miles de variables, y todas distintas entre sí en todos los aspectos. Álvaro Rollón de Pinedo 31
34 2.6. IMPORTANCIA DE VARIABLES Incremento del Error Cuadrático Medio A pesar de las dicultades ya mencionadas, sí que existen métodos que, al menos de forma indirecta, permiten medir hasta cierto punto la importancia de las variables a partir de las cuales se ha conformado un modelo. Uno de los ejemplos más típicos es el del Incremento del Error Cuadrático Medio (ECM). Dicha forma de cálculo se basa en el conocido concepto de Error Cuadrático Medio, muy empleado en estadística, así como en ajustes por mínimos cuadrados. En el caso de estudio, denotando por ŷ al valor predicho de la respuesta, y, consecuentemente, como y al valor real de la misma, para todo el conjunto de respuestas obtenidas, se calcula el ECM a partir de la expresión: ECM = 1 n n (ŷ y) 2 j=1 Este error es asimismo el segundo momento sobre el origen del error cometido, de modo que también aporta información sobre la varianza y el sesgo del estimador, en este caso ŷ, de hecho, para un estimador insesgado, el Error Cuadrático Medio se corresponde con la varianza. Para el caso concreto de Random Forest, los grácos más típicos empleados en el análisis de importancia de variables tienen un forma similar a la siguiente: Figura 2.7: Importancia de Variables 32 Escuela Técnica Superior de Ingenieros Industriales (UPM)
35 EXPERIMENTOS PARA MODELOS DE ÁRBOLES Generalmente estos grácos pueden representar dos cosas. La primera de ellas puede ser el Incremento de ECM, el cual es un parámetro que mide indirectamente la importancia de cada variable observando cúanto varía el Out Of Bag error en caso de permutar una de las variables con las que se había realizado el modelo, de tal manera que se computa de media dicha variación de error al dejar fuera unas variables u otras. En base a cómo varía dicho parámetro de error se estima la importancia de cada variable considerada. La otra posibilidad es que dichos grácos hagan referencia al incremento de pureza que se produce en cada nodo si se eligen unas variables u otras a la hora de ralizar los splits (particiones) de los mismos. Conviene recordar que la pureza viene dada por una función de impureza, la cual normalmente es el índice de Gini en los problemas de clasicación. En términos generales el criterio más empleado es el de incremento de ECM, y solo se usaría el criterio de la pureza de nodos en los casos en los que el coste temporal de emplear el modelo anterior fuera excesivo. Dado que en términos de trabajo de cálculo, el incremento de ECM requiere en la mayoría de los casos entre el 5 y el 25 % más, en este trabajo se ofrecerán generalmente ambos grácos, que además en ocasiones otorgarán importancias distintas a cada variable. Álvaro Rollón de Pinedo 33
36 2.7. CONDITIONAL INFERENCE TREES 2.7. Conditional Inference Trees Los Conditional Inference Trees (ctrees), son una evolución de los típicos árboles de clasicación, así como otras técnicas dedicadas al mismo campo, como pueden ser los CART o los algoritmos C4.5, pretenden así mismo solucionar los problemas más comunes que este tipo de modelos presentan. El primero de dichos problemas es el ya comentado overtting al que tienden la mayoría de los árboles si no se lleva una tarea apropiada de poda, pruning, en la cual se pretende reducción del tamaño del árbol mediante la eliminación de ramas en las cuales se compruebe que aportan poca información global. Asimismo, el empleo del pruning conjuntamente con el establecimiento de un criterio de parada en los nodos del árbol reduce considerablemente el riesgo de sobreajuste. El segundo problema de este tipo de algoritmos es el sesgo que se produce hacia ciertas variables correlacionadas y que actúan como entrada del sistema. Ambos problemas son exhaustivamente analizados en el paper: Hothorn, Hornik y Zeileis (2006), en el cual aportan su solución, a la par que introducen el nuevo concepto de Conditional Tree. A nivel básico, una diferencia importante entre este tipo de árboles y los mas clásicos es la sistematización del algoritmo en el aspecto del pruning, de modo que los árboles construidos no se dejan crecer indenidamente, sino que se van sosticando según se van construyendo. Sin embargo, el aspecto diferencial que es más importante destacar es la manera en la que se realizan los splits nodales de los árboles. En vez utilizar la metodología clásica (que por ejemplo utiliza CART), los Conditional trees realizan un test de signicación en cada nodo para determinar qué variable emplear en la partición en lugar de simplemente elegir la variable que maximice la ganancia de información. Si bien estos mecanismos de análisis no son el centro de este Trabajo, dado que su programación es similar a la de los demás algoritmos,se realizarán comparaciones entre los resultados que aportan los ctrees, y los correspondientes bosques generados con ellos Paquete Estadístico R Todos los análisis estadísticos llevados a cabo en este Trabajo de Fin de Grado han sido realizados empleando R. R es tanto un lenguaje de programación como un entorno de desarrollo que permite la realización de los más complejos (y también básicos) procedimientos de estadística y está especícamente diseñado para el tratamiento de datos e información, razón por la cual es ampliamente utilizado en campos tan diversos como la Minería de datos, matemáticas nancieras y campos biológicos, especialmente en el ámbito sanitario. Forma parte del GNU project, de modo que se trata de un software gratuito, escrito principalmente en C y Fortran, y es compatible con la mayoría de sistemas operativos comerciales convencionales. Asimismo, posee una amplia variedad de packages, que permi- 34 Escuela Técnica Superior de Ingenieros Industriales (UPM)
37 EXPERIMENTOS PARA MODELOS DE ÁRBOLES ten ampliar considerablemente sus opciones expandiendo las funciones a ámbitos como el análisis mediante árboles de decisión, series temporales, modelos avanzados de regresión, modelado lineal y no lineal, o problemas de clasicación. Otro gran fuerte del paquete R es la posibilidad de realizar grácos muy variados, con posibilidad de ser interactivos e incluir simbología matemática. Figura 2.8: Muestra de las posibilidades grácas de R La mayoría de posibilidades de expansión vienen recogidas en la página web del proyecto CRAN, en la cual aparece asimismo una lista con todos los packages más importantes. Sin embargo, a la hora de trabajar es mucho más práctico emplear el programa Rstudio, el cual es un IDE (Integrated Development Environment ), diseñado para facilitar el manejo del entorno de R, de modo que todo el código fuente y los grácos empleados en el presente trabajo han sido realizados con dicha IDE Funciones más empleadas A la hora de la escritura del código fuente de los programas que conforman las simulaciones que se han realizado, han sido empleadas, como es natural, gran cantidad de funciones implementadas en los distintos packages de R. Si bien no es de interés comentar la totalidad de las que se han usado, sí puede resultar útil mencionar la utilidad de las más importantes, especialmente en el caso de que se desee consultar el código adjunto en los anexos del Trabajo. randomforest(). Ajusta un modelo de Random Forest dado un conjunto de variables y observaciones de las mismas, así como la respuesta ante dichos valores tomados. Es necesario especicar cuál es la variable dependiente, y conviene que los datos se le pasen aleatorizados. lm(). Similar a la función anterior, pero en lugar de devolver un modelo de bosque aleatorio proporciona un modelo lineal compatible con los datos que se le pasan como argumentos. Calcula los coecientes del modelo que proporciona. glm(). Igual que las anteriores, pero el modelo ajustado es uno Lineal Generalizado, el cual aúna varios, como el de Regresión Lineal, Regresión Logística y la Regresión de Poisson. Álvaro Rollón de Pinedo 35
38 2.9. MAPE rpart(). Ajusta un CART y realiza una clasicación en categorías en función de las variables explicativas. ctree(). Exactamente lo mismo que la función anterior, pero en lugar emplear un modelo CART, ajusta un Conditional Inference Tree. genpositivedefmat(). Pasándole como argumento un número entero, devuelve una matriz cuadrada de dicho orden denida positiva y simétrica, de modo que puede ser empleada para generar de manera rápida matrices de covarianzas aleatorias que se pueden usar para correlacionar rápidamente tantas variables como se desee. diag(). Retorna una matriz identidad (diagonal de unos) del orden que se le pasa como argumento. Útil para emplear como matriz de covarianzas si se quiere que las variables sean independientes. sample(). Realiza permutaciones de los valores deseados de manera aleatoria. Los datos pueden estar contenidos en un vector, una matriz, un dataframe etc. ggplot(). Genera grácos más variados y estéticos que los predenidos originalmente por el paquete R. mvrnorm(). Devuelve un vector con tantas variables y observaciones de las mismas generadas cada una según una distribución normal diferente. Es necesario pasar como argumento un vector de medias de cada una de las variables que se desea generar, así como una matriz de covarianzas de las mismas, de modo que si se desea se pueden correlacionar las variables que convenga. Es una manera fácil y rápida de generar gran cantidad de variables independientes o no MAPE El conocido como MAPE (del inglés: Mean Absolute Percentage Error ), también conocido como MAPD (Mean Absolute Percentage Deviation ) es un parámetro que permite pretende medir la precisión de una determinada predicción realizada con un algoritmo. La fórmula que permite calcularlo es la siguiente: MAP E = n j=1 Ŷ Y Y Es uno de los datos más empleados para mostrar y comparar resultados estadísticos, ya que aporta información de una manera clara y sencilla, y su cálculo no es complejo. Además, analizar su variación con la modicación de una variable del modelo permite estimar cómo varía la calidad del mismo en función del parámetro analizado. Una gráca de ejemplo de la evolución del MAPE de dos modelos estadísticos en función de las variables que analiza cada modelo es la siguiente: Sin embargo, a pesar de su utilidad innegable, y de ser uno de los parámetros más mostrados en la literatura, el MAPE tiene diversos problemas severos que es necesario 36 Escuela Técnica Superior de Ingenieros Industriales (UPM)
39 EXPERIMENTOS PARA MODELOS DE ÁRBOLES Figura 2.9: Ejemplo de la evolución del MAPE de un Modelo de Random Forest y uno de Conditional Inference Trees tener en cuenta a la hora de emplearlo, ya que puede dar lugar a interpretaciones erróneas o fallos de programas en caso contrario: Imposibilidad de manejar valores reales de cero: Ya que hay un cociente entre el valor real de la predicción, el MAPE no contempla la posibilidad de que dicho valor sea cero, ya que tendría que dividir por el mismo, de modo que el conjunto de números a manejar está limitado. Rango de las predicciones: Aunque en ningún momento se divida por cero, si el rango de las predicciones es en algunos tramos muy cercano a dicho punto, el valor numérico del MAPE se incrementaría drásticamente y resulta complicado de comparar con otros, ya que incluso aun siendo una predicción considerablemente buena, su MAPE sería elevado. Es importante tener en cuenta estos dos problemas cuando se trabaja con variables escaladas entre cero y uno. Inexistencia de límite superior: Los errores estimados mediante MAPE pueden superar, para valores predichos relativamente grandes, el 100 % de error incluso por órdenes de magnitud, dicultando la tarea de medir dichos errores. Realiza una estimación parcial en tanto en cuanto a la hora de seleccionar un modelo estadístico óptimo es probable que se decante por aquel cuyas predicciones son más pequeñas, incluso para un mismo nivel teórico de calidad de la predicción. Diferencias de porcentajes de error: La metodología de cálculo del error de MAPE otorga mayor peso a los errores de predicción cuando el valor predicho es negativo que en los positivos, lo cual constituye un caso más de parcialidad, ya que para un error de la misma magnitud según MAPE el de los valores negativos será mucho mayor. Álvaro Rollón de Pinedo 37
40 2.9. MAPE 38 Escuela Técnica Superior de Ingenieros Industriales (UPM)
41 Capítulo 3 Experimentos con Modelo de Regresión Lineal Múltiple 3.1. Introducción En el presente capítulo se mostrarán los experimentos, resultados y conclusiones que se han realizado sobre un modelo de regresión lineal simple. A lo largo del mismo se irán realizando las variaciones de parámetros (número de variables consideradas, observaciones de cada una de las variables, árboles empleados...) de tal manera que los resultados puedan compararse y vericarse de la manera más sistemática y concienzuda posible con la nalidad de extraer toda la información y conclusiones posibles del modelo de Random Forest. Para facilitar la interpretación de los resultados obtenidos, en general se procurará generar los experimentos en condiciones de ceteris paribus, cambiando únicamente la variable cuya inuencia se desea estudiar en cada momento. Se procederá así con todas las variables que sean escogidas como de interés, y una vez hecho esto, se evaluará la variación conjunta de varias y su impacto en las predicciones El modelo El modelo objeto de estudio es uno de los más importantes y estudiados históricamente en la ciencia Estadística. Se enseña en cualquier curso de regresión y sus propiedades, utilidades y limitaciones son de sobra conocidas. Estos hechos, añadidos a la simplicidad matemática de la relación entre la variable respuesta y las variables explicativas son las principales razones de su elección. 39
42 3.3. ASPECTOS A ANALIZAR Inicialmente se considerará un modelo determinista (carente de ruido) en el cual para ciertos valores de las variables explicativas la respuesta está perfectamente denida. Dicho modelo, para n variables es el que sigue: y = n β i x i i=1 Como se puede observar, cada una de las variables estará multiplicada por un coeciente β i, que como ya se mencionó en capítulos anteriores inuye signicativamente en la importancia de la variable, por lo que resulta fundamental controlar su rango y valor concreto en todo momento. Todos los modelos lineales que se generarán a lo largo del documento se realizan de la misma manera. Primeramente, es creado un vector, que se denominará de importancias, cuya dimensión coincide con el número de variables que se considerarán en dicho modelo lineal, de tal manera que los valores almacenados en el mismo puedan servir como coecientes de las variables. Posteriormente, se genera un vector para cada variable de la dimensión del número de observaciones que se van a emplear. La manera de crear dichos conjuntos de variables diferirá en función de la distribución de probabilidad con la que se generen, así como el rango que se les quiera dar, o incluso si son categóricas o continuas. Según se vayan realizando experimentos, irán cambiando aspectos aspectos del modelo. Efectivamente, el primer aspecto que se tendrá en cuenta es la correlación de las variables, y se analizarán tanto el caso en el que las variables son independientes como el caso en el que no, pero hay otro factor muy importante a tener en cuenta, que es el determinismo. Se comprobarán tanto la respuesta de los modelos en el caso determinista como en el que no, en el cual se introducirá un ruido blanco que haga variar la respuesta ante entradas de variables idénticas, de modo que el modelo de regresión quedará con el aspecto siguiente: y = n β i x i + ε i i=1 El último término añadido resulta fundamental en el análisis de la respuesta, y diculta considerablemente la interpretación de los resultados y la elaboración de un modelo que los ajuste. Resulta de interés conocer la distribución de probabilidad con la cual se generan dichos sumandos Aspectos a analizar Parámetros que variar Hay innidad de parámetros que se pueden ir cambiando para analizar la respuesta del sistema ante dichos cambios. Sin embargo, no todos serán de utilidad, por lo que será necesario seleccionar cuáles serán más representativos de los cambios del sistema, vericándose dicha relación con la respuesta. Los parámetros que se variarán son: 40 Escuela Técnica Superior de Ingenieros Industriales (UPM)
43 EXPERIMENTOS PARA MODELOS DE ÁRBOLES Número de variables: Uno de los mantras más repetidos por los defensores de Random Forest es su capacidad de aportar buenos resultados aun con cantidades enormes de variables predictivas. Se intentará contrastar hasta qué punto ello es cierto. Número de observaciones: Es esperable que haya una gran sensibilidad a la cantidad de observaciones que se hagan de las variables explicativas. Parámetro mtry: Se trata de uno de los parámetros fundamentales de la función randomforest. Expresa el número de variables que tomará en cuenta cada árbol a la hora de realizar los splits nodales. Parámetro ntree: expresa el número de árboles que generará el Bosque Aleatorio. Presumiblemente, si es demasiado pequeño la precisión del modelo debería resentirse, mientra que si es demasiado elevado podría producirse el fenómeno del overtting. Modicar este parámetro podría ayudar a comprobar hasta qué punto es cierta la supesta resistencia de los modelos de Random Forest a dicho fenómeno Procedimiento En los apartados siguientes se realizarán experimentos en los cuales se generará un número concreto de variables, cada una con sus coecientes, y posteriormente se calculará la respuesta que otorgan según el modelo. Una vez hecho, se dividirá la muestra en un training set y un test set, de forma que con el primero se ajusten los modelos de regresión requeridos, y con el segundo se elaboran las predicciones que se contrastarán con los resultados almacenados en el set de prueba. Finalmente, según los resultados que se deseen analizar, se construirán grácos que faciliten la interpretación de las tasas de acierto de cada modelo. En general, se considerará acierto todo resultado en el que el error relativo entre la predicción y el valor real sea menor que el 1 %: Error = y ŷ y si 0,01 acierto > 0,01 fallo Álvaro Rollón de Pinedo 41
44 3.4. EXPERIMENTOS INDEPENDIENTES 3.4. Experimentos Independientes Cambio de variables Correlacionadas Modelo determinista En este experimento se comprobará cómo, a igualdad de los demás parámetros, la variación del número de variables que componen el modelo de regresión considerado cambia considerablemente la capacidad predictiva de los modelos objeto de estudio. No se modicarán los parámetros por defecto que asignan las funciones de R para cada caso. En el caso de randomforest, el número de árboles predeterminados son 500 (ntree=500 ) y dado que se trata de un caso de regresión y no de clasicación, las variables empleadas en la construcción de los árboles serán p, siendo p el número total de variables. 3 Asimismo, la cantidad de observaciones que se proporcionan sobre cada variable es de 600. Se irá comprobando cómo varía la capacidad predictiva de cada modelo desde una variable hasta tener que manejar resultados producidos con un sistema dependiente de 500 variables. Asimismo, en este primer caso todas las variables están correlacionadas. Los resultados arrojados se muestran en la siguiente gráca, donde en azul se representa la tasa de acierto de Random Forest, en verde la de Conditional Forest y en rojo la de un ajuste puramente lineal. Figura 3.1: Tasa de acierto de los modelos en función del número de variables que manejan El primer efecto que salta a la vista son las oscilaciones que experimenta el modelo lineal generado en el momento en el que tiene que ajustar pocos cientos de variables. Si bien a priori parece un suceso digno de análisis exhaustivo, en realidad se trata de la conocida necesidad de un número mínimo de observaciones para ajustar un modelo lineal dependiendo de cuántas variables independientes existan. Para evidenciar este efecto, se aporta un nuevo gráco con un número mucho menor de variables (hasta 40), y solo 50 observaciones por variable. Rápidamente se aprecia el mismo efecto: 42 Escuela Técnica Superior de Ingenieros Industriales (UPM)
45 EXPERIMENTOS PARA MODELOS DE ÁRBOLES Figura 3.2: Ejemplo de la limitación del modelo lineal Este problema podría ser un buen caso de ejemplo para comprobar el efecto de la maldición de la dimensionalidad, en el que la cantidad de datos de los que se dispone para explicar un fenómeno es sensiblemente inferior a los necesarios ya que dicho fenómeno depende de una cantidad de variables de orden muy superior, de modo que no es viable pretender exlicarlos con ellos. Esta tendencia es bien conocida y denota cómo tanto Random Forest como los Conditional Forests son capaces de adaptarse mejor al sistema que un modelo de regresión lineal que a priori debería ser capaz de predecir con muchísima mejor precisión el modelo analizado, y de hecho lo hace, ya que su tasa de acierto es del 100 % cuando dispone del tamaño de muestra requerido. Sin embargo, en el momento en el que la cantidad de variables se hace excesivo, empeora rápidamente sus resultados, sensibilidad que no muestran ninguno de los modelos de árboles, que por el contrario se muestran capaces de ajustar con una precisión de casi el 100 % cuando se los obliga a manejar gran cantidad de variables siempre que el modelo sea determinista. Al menos sin la introducción de ruido blanco, queda clara la robustez de los modelos de Bosques Aleatorios frente a gran cantidad de variables y observaciones, ya que en este caso, teniendo en cuenta que se analizaban 500 variables con 600 observaciones cada una, el número de datos a manejar era de Modelo no Determinista En este caso se generarán datos con un modelo igual, pero introduciendo una componente aleatoria del orden de magnitud de las variables de entrada. De esta manera se consigue la construcción de un modelo no determinista en el cual para unas variables de entrada concretas, el output sea diferente cada vez. El problema del aumento del número de variables en el lineal sigue apreciándose de manera similar al caso anterior, de modo que a partir de cierto momento se resiente su capacidad si el número de observaciones se mantiene constante. Álvaro Rollón de Pinedo 43
46 3.4. EXPERIMENTOS INDEPENDIENTES Figura 3.3: Tasa de acierto al aumentar el número de variables de los distintos modelos si se introduce ruido Existe una reducción considerable en la capacidad predictiva tanto de Random Forest como de Conditional Forest claramente debida a la inclusión de ruido. Sin embargo, ambos consiguen estabilizarse de manera similar a la del caso anterior, llegando a tasas de acierto cercanas al 100 %,si bien es cierto que de forma más lenta. En términos generales, se puede armar que los modelos de regresión generados con árboles son capaces de aproximar con gran acierto casos de regresión lineal en los cuales hay correlación entre las variables, siendo un aspecto muy signicativo la mejora de la capacidad predictiva cuando se les exige el manejo de gran cantidad de regresores Cambio de variables no Correlacionadas En la presente sección se llevarán a cabo exactamente los mismos experimentos, pero siendo las variables indpendientes (no hay correlación entre ellas), tanto con ruido (modelo no determinista) como sin el mismo (modelo determinista). Modelo Determinista Bajo las mismas consideraciones que en el caso de variables correlacionadas, los resultados obtenidos son los siguientes: En este caso, dado que el problema que se debe analizar es considerablemente más sencillo, todos los modelos poseen mayor capacidad predictiva y sus tasas de acierto son próximas al 100 % en la inmensa mayoría de los casos, independientemente del número de variables. 44 Escuela Técnica Superior de Ingenieros Industriales (UPM)
47 EXPERIMENTOS PARA MODELOS DE ÁRBOLES Figura 3.4: Tasa de acierto al aumentar el número de variables, sin estar éstas correlacionadas, de los distintos modelos si no se introduce ruido Modelo no Determinista Tomando ahora un caso en el que la variables sean independientes pero con la inclusión de ruido en la respuesta, los resultados aportados por los distintos modelos son los siguientes: Figura 3.5: Tasa de acierto al aumentar el número de variables, sin estar éstas correlacionadas, con ruido. La respuesta observada resulta muy similar a la anterior, apreciándose sin embargo un retardo a la hora de alcanzar el valor de régimen permanente. Álvaro Rollón de Pinedo 45
48 3.4. EXPERIMENTOS INDEPENDIENTES Búsqueda de la Maldición de la Dimensionalidad para los modelos de árboles En los experimentos realizados en las secciones anteriores los resultados han sido en gran parte los esperados, comprobándose la capacidad de Random Forest de trabajar con datasets de gran tamaño, incluyendo muchas variables. Sin embargo, resulta interesante comprobar en qué momento estos algoritmos de gran robustez sucumben a la Curse of dimensionality, no siendo capaces de manejar tantas variables en función de tan pocos datos. Se han realizado experimentos de gran coste computacional, y se observa que a partir de cierto punto el MAPE se comporta de la siguiente manera: Figura 3.6: Aparición de la Curse of dimensionality en el caso de los modelos de árboles analizando como parámetro explicativo el MAPE Para estos experimentos se ha procedido de la manera siguiente: Se ha jado el número total de variables máximo con el que se va a generar el modelo, de tal manera que para un número de observaciones por variable de igual tamaño, se va incrementando progresivamente la cantidad de variables para generar el modelo hasta observar cómo el error se dispara. Para dar una idea del coste de procesamiento de datos del último experimento, algunos datos de los parámetros implicados en los cálculos son los siguientes: La matriz de observaciones (las variables por columnas y las observaciones por las) alcanzó un tamaño de , con nueve millones de elementos. El modelo que ajustó la última cantidad de datos con Conditional Inference Trees tenía un peso de 2.9Gb. La matriz de varianzas y covarianzas con la que se correlacionaron las variables tenía un peso de 19.2Mb (siendo solo una matriz de números). 46 Escuela Técnica Superior de Ingenieros Industriales (UPM)
49 EXPERIMENTOS PARA MODELOS DE ÁRBOLES El modelo lineal con el que se ajustó dicha cantidad de datos y variables ocupaba más de 100 Mb. Se ha elaborado una tabla que describe el momento en el que los modelos de árboles empiezan a fallar, representándose la cantidad de variables en el que lo hacen dada una cantidad de observaciones concreta. Número de datos Número de variables hasta el fallo Tabla 3.1: Para cada cantidad de datos, número de variables hasta que se produce el error en el sistema Si se representan grácamente dichos puntos, se pueden observar ciertas características interesantes: Figura 3.7: Representación de los puntos en los que los modelos empiezan a fallar Los puntos que aparecen en la gura anterior hacen referencia al momento en el que los modelos empiezan a arrojar resultados erróneos y se ven incapaces de predecir con la precisión anterior a causa de la falta de observaciones. Como se puede apreciar, si bien al principio parece que la relación entre la necesidad de observaciones y variables es lineal, se comprueba que ello solo es una impresión óptica, y que en realidad dicha tendencia es exponencial, necesitándose cada vez más observaciones de las variables explicativas según aumenta su número. La otra observación clara que se puede realizar es el hecho de que en todo momento los puntos se encuentran por encima de la bisectriz, de modo que, como parece intuitivo, siempre debe haber más observaciones que variables explicativas. Resulta un caso análogo a tener más variables que ecuaciones en un sistema de ecuaciones. Álvaro Rollón de Pinedo 47
50 3.4. EXPERIMENTOS INDEPENDIENTES Dependencia del número de árboles Si bien existe relativo consenso en torno al hecho de que un aumento del número de árboles a la hora de ajustar modelos de árboles de regresión no supone una gran diferencia en cuanto a los resultados a partir de un número mínimo de árboles, conviene comprobar la resistencia al overtting de Random Forest, al menos en cuanto al número de árboles seleccionados. En esta simulación se ha repetido un experimento con variables correlacionadas y con ruido, llegando a 100 variables con 300 observaciones por cada una. En ella, el número de variables se va incrementando progresivamente hasta llegar al centenar, generándose cada vez los modelos con árboles. Los resultados obtenidos son los siguientes: Figura 3.8: Evolución del MAPE en los modelos generados con árboles. Dos aspectos se pueden resaltar de la gura: Efectivamente, la posibilidad de que se produzca overtting en un modelo de Random Forest es extremadamente pequeña, como demuestra el hecho de que las predicciones realizadas con este modelo no dieren signicativamente en los resultados si se comparan con los MAPEs de los experimentos anteriores. Uno de los aspectos más aceptados en cuanto al funcionamiento de los Random Forests es el hecho de que, si bien el coste computacional de incrementar la cantidad de árboles que conforman el Bosque Aleatorio, la precisión en las predicciones también aumenta. Sin embargo, no está claro hasta qué punto dicha armación es cierta. Desde luego, realizando el mismo experimento con 500 árboles en lugar de con la diferencia en los resultados aportados por el MAPE es inapreciable. 48 Escuela Técnica Superior de Ingenieros Industriales (UPM)
51 EXPERIMENTOS PARA MODELOS DE ÁRBOLES Figura 3.9: Evolución del MAPE en los modelos generados con 500 árboles. Como se puede apreciar, los valores entre los que se mueve son muy similares. En realidad, la conclusión evidente es que la inuencia del número de árboles se estabiliza rápidamente con los pocos centenares, de modo que aumentar el número a partir de cierto momento apenas supone mejora de precisión y sin embargo sí un mayor consumo de recursos. Álvaro Rollón de Pinedo 49
52 3.5. EXPERIMENTOS CON MTRY 3.5. Experimentos con mtry A la hora de construir cada árbol que se incluirá en el Random Forest, hay un parámetro clave que inuye en cómo acabará siendo la forma nal de cada uno de esos árboles. Dicho parámetro es el conocido como mtry, y expresa la cantidad de variables de las totales que se usarán a la hora de decidir cómo realizar los splits nodales. Básicamente, si se tiene un número total n de variables explicativas, a la hora de realizar las particiones de cada nodo se tomará un número muy inferior de variables para realizarlas, de forma que se agiliza considerablemente el tiempo de ejecución de los algoritmos, y favorece la aleatorización. Sin embargo, pese a ser uno de los parámetros que más inuyen en la evolución de los Bosques aleatorios, no está realmente clara cuál es la tendencia que se sufre según varía mtry, razón por la cual se han realizado los siguientes experimentos. En general, Breiman recomienda tomar los valores n 3 para realizar regresión, y n para clasicación. Sin embargo, al evaluar la evolución del MAPE según va cambiando mtry, para un caso de 200 variables y 400 observaciones, y para un caso de 300 variables y 600 observaciones, los resultados obtenidos son los siguientes: Figura 3.10: Evolución del MAPE variando el mtry de 20 en 20 hasta llegar a 200 variables. 50 Escuela Técnica Superior de Ingenieros Industriales (UPM)
53 EXPERIMENTOS PARA MODELOS DE ÁRBOLES Figura 3.11: Evolución del MAPE variando el mtry de 30 en 30 hasta llegar a 300 variables. En ambos casos se ha estudiado la evolución del MAPE con el incremento de mtry de tal manera que el paso de aumento sea la décima parte del número total de variables, en un caso 300, y en el otro 200. En teoría, dado que se está abordando un problema de regresión, los valores óptimos de mtry deberían rondar las 100 variables y las 70 en cada caso, de tal manera que el MAPE fuera mínimo en ambos casos. Sin embargo, analizando las grácas anteriores se observa que no es posible distinguir una tendencia clara, además de que decir que el mínimo MAPE se situará en los valores predichos resulta como mínimo aventurado. Asimismo, al manejar modelos lineales tan grandes, es complicado observar ninguna tendencia por parte de un parámetro tan importante variado con un paso de esos órdenes de magnitud. Es por esta razón que los siguientes experimentos se han diseñado con 10 variables y distintas cantidades de observaciones: 100, 200 y 300. Finalmente, para contrastar la validez de los resultados, en cada uno de los experimentos anteriores se han realizado 10 replicaciones, y los resultados que se muestran son las medias de los individuales Variación de mtry con 100 observaciones En este caso (y en los dos siguientes) en cada una de las 10 replicaciones se irá incrementado progresivamente, de uno en uno, el número de variables que se tomarán en el mtry, hasta llegar a diez, y se observará qué valor ronda el óptimo, es decir, un número entero cercano a 10. Con 100 observaciones los resultados son: 3 Álvaro Rollón de Pinedo 51
54 3.5. EXPERIMENTOS CON MTRY Figura 3.12: Evolución del MAPE variando el mtry de 1 en 1 hasta llegar a 10 variables. Esos mismos datos, recogiendo los MAPEs de Random Forest y Conditional Forest en una tabla, son los siguientes: Tabla abscisa MRF MCF 1 1 0, , , , , , , , , , , , , , , , , ,01177 Tabla 3.2: Tabla de MAPEs con mtry de 1 en 1 y 100 observaciones Se han marcado en negrita los valores para los cuales el MAPE es mínimo entre todos los valores estudiados. Está claro que existe una depresión cerca de los valores para los cuales teóricamente se obtienen mejores resultados en el caso de regresión. A priori, observando la media de los valores de las 10 replicaciones, no se encuentra razón para pensar que dicha armación no se cumpla. 52 Escuela Técnica Superior de Ingenieros Industriales (UPM)
55 EXPERIMENTOS PARA MODELOS DE ÁRBOLES Variación de mtry con 200 observaciones En este apartado se llevará a cabo el mismo experimento, con 10 replicaciones también, pero variando el número de observaciones que se le proporciona a los modelos. En la gura se aprecia cómo varía el MAPE con el mismo paso y número de variables. Figura 3.13: Evolución del MAPE variando el mtry de 1 en 1 hasta llegar a 10 variables con 200 observaciones. La tabla correspondiente a dichos datos es: Tabla abscisa MRF MCF 1 1 0, , , , , , , , , , , , , , , , , ,09692 Tabla 3.3: Tabla de MAPEs con mtry de 1 en 1 y 200 observaciones En este experimento, si bien es cierto que el valor mínimo no sucede exactamente en las inmediaciones de 10, existe un valle en el MAPE en el entorno de dicho valor, con 3 lo que las predicciones llevadas a cabo con valores de mtry tomados en esa zona tendrán más posibilidades de arrojar resultados más precisos que en otras zonas. Álvaro Rollón de Pinedo 53
56 3.5. EXPERIMENTOS CON MTRY Variación de mtry con 300 observaciones Esta será la última iteración del proceso, aumentando el número de observaciones a 300 pero manteniendo el resto de variables del problema, aumentándose mtry de la misma manera que las veces anteriores. Figura 3.14: Evolución del MAPE variando el mtry de 1 en 1 hasta llegar a 10 variables con 300 observaciones. Y la tabla de datos correspondientes es: Tabla3 abscisa MRF MCF 1 1 0, , , , , , , , , , , , , , , , , ,08929 Tabla 3.4: Tabla de MAPEs con mtry de 1 en 1 y 300 observaciones Este caso resulta análogo al anterior, sucediendo que el mínimo MAPE no se alcanza exactamente en el punto de trabajo recomendado, pero en dicho sitio se observa un valle del parámetro, de modo que resulta una zona cómoda de trabajo a la hora de minimizar el error. Trabajar en otras zonas, si bien puede resultar recomendable en casos determinados, supone un riesgo, ya que tal y como se ha visto, en el caso de estarse trabajando con algoritmos de regresión resulta bastante frecuente el tener una región en el entorno recomendado en la cual el valor de las tasas de error disminuye considerablemente, mientras que dicha seguridad desaparece trabajando en otras zonas. 54 Escuela Técnica Superior de Ingenieros Industriales (UPM)
57 EXPERIMENTOS PARA MODELOS DE ÁRBOLES En cualquier caso, para maximizar la tasa de acierto de los árboles, la única manera relativamente segura de localizar los puntos óptimos es realizar un muestreo a lo largo de toda la región de trabajo. También existen funciones de R diseñadas para localizar los mejores valores para cada caso particular. Es este el caso de la función tunerf(). La necesidad de este tipo de funciones se hace evidente en ejemplos como el siguiente, en el cual el valle del valor óptimo de mtry se encuentra desplazado a zonas superiores a las del 50 % de regresores: Figura 3.15: Ejemplo de caso en el cual el error se reduce en una zona distinta de n 3 para realizar regresión. Álvaro Rollón de Pinedo 55
58 3.6. IMPORTANCIA DE VARIABLES 3.6. Importancia de variables El objetivo primordial de esta sección es evaluar la capacidad de los algoritmos de árboles de captar cómo de inuyentes son las distintas variables explicativas en la variable dependiente(y ). Este hecho resulta fundamental para cualquier algoritmo de Machine Learning, y en general para cualquier algoritmo que maneje grandes cantidades de datos, ya que, como se ha tenido ocasión de comprobar, son susceptibles de tener problemas de dimensionalidad. Es por esto que resulta de vital importancia seleccionar qué variables son las más y las menos inuyentes en la respuesta, pues de esa manera es fácil seleccionar cuáles son innegociables de eliminar para reducir la dimensionalidad del problema, y cuáles las ideales en caso de necesitarse simplicar el problema. Este proceder se conoce a menudo como Selección de atributos, Reducción de rango o Selección de variables. Las razones principales por las cuales se realizan este tipo de simplicaciones son las siguientes: Facilitar la interpretación de datos y resultados: Elegir un número reducido de variables, si bien puede empeorar los resultados de un modelo (aunque como se ha visto, a veces también mejorarlos), facilita en gran medida la interpretabilidad del problema, pudiéndose también apreciar tendencias o errores con mayor facilidad. Además de ello, a la hora de exponer las conclusiones a un público no técnico o no especialista en la materia la tarea es considerablemente más simple. Tiempos de computación: Resulta obvio que ajustar un mismo modelo o algoritmo a un caso más sencillo acorta la tarea, característica que resulta crítica en caso de manejarse gran cantidad de datos, en las cuales reducciones de tiempos de computación incluso de pequeños porcentajes pueden suponer acortamientos del orden de horas o días. Menor tendencia de los modelos al sobreajuste, resultando en soluciones más sencillas de generalizar. Esta característica, al igual que la primera, hace referencia a la relevancia que tiene encontrar el número óptimo de regresores, debiéndose elegir un número ni demasiado grande ni demasiado pequeño. En el caso de los experimentos que se van a realizar, por razones de interpretabilidad de los resultados se generarán modelos con diez regresores relevantes. De esta manera, se facilitará la tarea de interpretación de los grácos de importancia de variables, que como ya se ha mencionado, pueden estar basados en el Incremento porcentual de Error Cuadrático Medio al realizar permutaciones de las variables en el momento de realizar los splits, o en el incremento de pureza que se aprecia al incluir o no cierta variable como criterio de partición de cada nodo. Finalmente, el número de experimentos a realizar será 3, de igual manera que con los de mtry, incrementando la cantidad de datos aportados al modelo progresivamente. En todos ellos, las variables que se generarán son independientes de distribución uniforme. La anchura de los intervalos en los que se pueden generar las variables son aleatorios entre ciertos valores, y el lugar en el que están centrados también lo es. Conviene señalar que, dado que la naturaleza de cómo se generan las variables es 56 Escuela Técnica Superior de Ingenieros Industriales (UPM)
59 EXPERIMENTOS PARA MODELOS DE ÁRBOLES diferente entre sí, es necesario realizar un escalado de las mismas. Para ello, se le resta a cada valor de cada variable el mínimo que toma la misma, y se divide entre el máximo menos el mínimo valor que toma cada variable. De forma más gráca, el código con el que se realiza el escalado es: 1 for ( i in 1 : k ) 2 { 3 X1 [ i ] = ( X1s [ i ] min ( X1s ) ) / ( max( X1s) min ( X1s ) ) 4 X2 [ i ] = ( X2s [ i ] min ( X2s ) ) / ( max( X2s) min ( X2s ) ) 5 X3 [ i ] = ( X3s [ i ] min ( X3s ) ) / ( max( X3s) min ( X3s ) ) 6 X4 [ i ] = ( X4s [ i ] min ( X4s ) ) / ( max( X4s) min ( X4s ) ) 7 X5 [ i ] = ( X5s [ i ] min ( X5s ) ) / ( max( X5s) min ( X5s ) ) 8 X6 [ i ] = ( X6s [ i ] min ( X6s ) ) / ( max( X6s) min ( X6s ) ) 9 X7 [ i ] = ( X7s [ i ] min ( X7s ) ) / ( max( X7s) min ( X7s ) ) 10 X8 [ i ] = ( X8s [ i ] min ( X8s ) ) / ( max( X8s) min ( X8s ) ) 11 X9 [ i ] = ( X9s [ i ] min ( X9s ) ) / ( max( X9s) min ( X9s ) ) 12 X10 [ i ] = ( X10s [ i ] min ( X10s ) ) / ( max( X10s) min ( X10s ) ) 13 } Código 3.1: Código empleado en el escalado de las 10 variables Experimento 1 de Importancia de Variables, 10 regresores y 50 observaciones En este experimento, se generan 10 variables con distribución uniforme en anchuras de intervalo aleatorias, asignándose asimismo coecientes aleatorios para generar así el modelo lineal que se desea evaluar. Dicho modelo será determinista en este caso, para comprobar cómo de bien es capaz Random Forest de captar las importancias. En el presente caso, solo se proporcionarán 50 observaciones de cada variable a los modelos. Se ha obtenido la siguiente tabla de datos: TablaI Medias Coecientes Valor 1 305,9256 0, , ,4850 3, , ,0247 0, , ,3952 0, , ,9251 0, , ,6232 2, , ,5571 3, , ,8977 2, , ,7452 4, , ,4354 1, ,1535 Tabla 3.5: Tabla de importancia de variables con 10 regresores y 50 observaciones Álvaro Rollón de Pinedo 57
60 3.6. IMPORTANCIA DE VARIABLES En dicha tabla se pretende expresar una ponderación intuitiva del peso que cada regresor tiene en la respuesta. La manera en la que se ha procedido es la siguiente: Se calcula la media de todos los valores que toma una variable, y realizándolo para todas ellas se obtiene la columna de Medias. La siguiente no es más que la columna de coecientes asociados a cada regresor, mientras que por último la columna nal es el producto de las dos anteriores, de forma que el valor aportado debe resultar una suerte de ponderación entre el peso que posee cada variable y su coeciente asociado. Resulta de interés comparar dichos valores con los que aporta el modelo de Random Forest a través de la función varimpplot(): Figura 3.16: Grácos de importancia de variables con 10 regresores y 50 observaciones Como ya se explicó en una de las secciones del capítulo anterior, el primer gráco hace referencia al incremento de Error Cuadrático Medio producido por la permutación de cada variable, y el segundo mide la importancia a través del incremento de pureza. Como se puede comprobar, a grandes rasgos Random Forest es capaz de ponderar correctamente la importancia que cada variable tiene en la respuesta, de forma que a las variables a las que en la tabla le corresponden números mayores tienen asignadas mayores importancias. Por supuesto, hay que tener en cuenta el hecho de el concepto importancia es relativo, y el hecho de que los números aportados por la tabla no asignen la importancia igual que los dos parámetros de los grácos no quiere decir que estos últimos sean incorrectos. En cualquier caso, es cierto que los dos grácos tampoco aportan exactamente los mismos resultados, de modo que en general, las conclusiones aportadas por los mismos deben ser tomadas como orientativas, y nunca como axiomas inamovibles. 58 Escuela Técnica Superior de Ingenieros Industriales (UPM)
61 EXPERIMENTOS PARA MODELOS DE ÁRBOLES Experimento 2 de Importancia de Variables, 10 regresores y 150 observaciones Este experimento incrementa el número de observaciones por variable a 150, de modo que, ante la mayor cantidad de información proporcionada, es esperable una mejora en la asignación de importancias respecto al caso anterior. Las variables se generan exactamente de la misma manera, de modo que se debe tener en cuenta la aleatoridad con la que se generan las mismas. La tabla análoga al experimento anterior es: TablaII Medias Coecientes Valor 1 223,4726 1, , ,3173 2, , ,4274 4, , ,7753 3, , ,4907 0, , ,2766 2, , ,9937 0, , ,9023 4, , ,4242 0, , ,2357 4, ,9477 Tabla 3.6: Tabla de importancia de variables con 10 regresores y 150 observaciones Mientras que los grácos arrojados por el programa son: Figura 3.17: Grácos de importancia de variables con 10 regresores y 150 observaciones Álvaro Rollón de Pinedo 59
62 3.6. IMPORTANCIA DE VARIABLES Como se puede apreciar, en este caso los resultados que se observan tanto en la tabla como en el análisis de Random Forest son análogos, y se da la máxima importancia a las mismas variables y concuerdan en el hecho de que las menos importantes son la número cinco y la novena. Sin embargo, se puede observar un valor anómalo en el análisis efectuado mediante la técnica del Error Cuadrático Medio, ya que arma que la variable número 10 es irrelevante, mientras que resulta evidente que tiene más peso que otras en el valor nal de la variable dependiente. Finalmente, se puede resaltar el hecho de que en este caso el análisis llevado a cabo con criterios de pureza de nodo, si bien no selecciona como más importante la variable correcta, en su conjunto no comete errores del calibre de la anterior Experimento 3 de Importancia de Variables, 10 regresores y 300 observaciones En este último experimento se realizará el mismo análisis pero duplicando el número de observaciones que se tiene de los regresores, llegando a un valor de 300. En este caso, los resultados obtenidos son sensiblemente diferentes entre los que se muestran en la tabla y los que se observan en los grácos de importancia. Este suceso resulta cuanto menos curioso teniendo en cuenta que se trata del experimento en el que más información se proporciona a los modelos de Random Forest. La tabla con las ponderaciones asignadas a cada variable es la siguiente: TablaIII Medias Coecientes Valor 1 171,5066 3, , ,1046 2, , ,4611 3, , ,8989 1, , ,5975 2, , ,3894 4, , ,0118 4, , ,0010 2, , ,4717 4, , ,6343 3, ,8569 Tabla 3.7: Tabla de importancia de variables con 10 regresores y 300 observaciones Los grácos de importancias para dicho experimento son: 60 Escuela Técnica Superior de Ingenieros Industriales (UPM)
63 EXPERIMENTOS PARA MODELOS DE ÁRBOLES Figura 3.18: Grácos de importancia de variables con 10 regresores y 300 observaciones Como se puede apreciar, hay una variación enorme entre la información que aporta la tabla y la que parecen aportar los grácos de importancia. Si bien ambas medidas de importancia captan cuál es la variable más relevante, de las cuatro variables más importantes solo consideran relevantes a dos. Dejando de lado el hecho de que por denición la medición de la importancia es compleja, en este caso particular es probable que este tipo de errores provengan de que en la generación aleatoria de variables y coecientes las variables resultantes son muy similares (los valores que se asigan en la ponderación no dieren sensiblemente), de modo que discernir cuál es la más importante resulta mucho más complicado. Álvaro Rollón de Pinedo 61
64 3.6. IMPORTANCIA DE VARIABLES 62 Escuela Técnica Superior de Ingenieros Industriales (UPM)
65 Capítulo 4 Experimentos con Sistema Lineal con Interacción 4.1. Introducción En esta sección se realizará el análisis del otro modelo objeto de estudio del presente Trabajo de Fin de Grado: el modelo lineal múltiple con interacción entre las variables. El interés de este modelo radica en el hecho de que, aunque ya no sea el típico modelo lineal tradicional, aún así es uno de los ejemplos más utilizados en diversos análisis estadísticos, ya que generaliza el concepto de regresión lineal a un orden superior. Como es lógico, la generalización máxima sería llevando a cabo interacción de todos los órdenes entre todas las variables, sin embargo, son raros los casos en los que las interacciones entre variables de orden superior a tres son relevantes. Este último hecho, junto a la dicultad computacional de experimentos de órdenes superiores, hacen que truncar en este punto la regresión lineal sea deseable, y en base a eso se diseñarán los distintos experimentos El modelo En este capítulo se apostará por la búsqueda de brevedad en las explicaciones para evitar redundancias innecesarias con los capítulos anteriores, en los cuales ya se introdujeron varios de los conceptos que en este se emplean. Dicho esto, conviene describir a nivel general el modelo de Regresión Lineal Múltiple con interacción. Para el caso de una respuesta dependiente de dos variables, tiene la forma siguiente en el caso de ser determinista: y = β 0 + β 1 x 1 + β 2 x 2 + α 1 x α 2 x 1 x 2 + α 3 x 2 2 Como es evidente, ya que hay que tener en cuenta las interacciones, la complejidad 63
66 4.2. EL MODELO del modelo respecto al anterior es muchísimo mayor para el mismo número de variables, de modo que a priori debería resultar más complicado ajustar un modelo estadístico de regresión. Introduciendo ruido, para cada observación se cumple la relación: y = β 0 + β 1 x 1 + β 2 x 2 + α 1 x α 2 x 1 x 2 + α 3 x ε En general, los coecientes α i tienen un valor sensiblemente menor a los β i, que son los asociados a los regresores de primer orden. Para realizar la generación de dichos modelos el procedimiento empleado es el siguiente: Dada una matriz con todas las variables y observaciones, primero se creará una matriz de ceros con tantas las como observaciones por variable y tantas columnas como la que se denominará dimensión característica de las interacciones. Esta dimensión hace referencia a la cantidad de nuevas variables que se crearían si cada interacción binaria entre las originales se considerara una nueva variable. Dicha dimensión característica se puede calcular con la siguiente expresión, donde n es el número de variables: dim = n j j=1 Así, para tres variables, existen seis interacciones binarias posibles, que serían las siguientes: x 2 1, x 2 2, x 2 3, x 1 x 2, x 1 x 3, x 2 x 3, Resulta evidente que el crecimiento del número de dichos factores es muy rápido, de modo que a la hora de realizar las simulaciones es un parámetro a tener en cuenta para no incluir demasiadas variables, o para aumentar el paso a la hora de analizar, lo cual reduciría la precisión pero también los tiempos de simulación. Una vez creada dicha matriz, se procede a generar una matriz auxiliar maux cuadrada de dimensión n n, y un vector de dimensión la característica. Así, maux se irá rellenando por las con todas las posibles interacciones que cada variable puede experimentar, de modo que la primera la posee todos los productos de la primera variable, la segunda todos los de la segunda etc. Posteriormente, se procede a incluir por las todos los elementos de la matriz triangular superior en el otro vector auxiliar, el cual nalmente pasará a convertirse en la nueva la de la matriz de variables que se quería crear originalmente. Este procedimiento se llevará a cabo con todas las observaciones. Un ejemplo de matriz y vectores auxiliares para el caso de tres variables son los siguientes: 64 Escuela Técnica Superior de Ingenieros Industriales (UPM)
67 EXPERIMENTOS PARA MODELOS DE ÁRBOLES x 2 1 x 1 x 2 x 1 x 3 x 2 x 1 x 2 2 x 2 x 3 x 3 x 1 x 3 x 2 x 2 3 (x 2 1, x 1 x 2, x 1 x 3, x 2 2, x 2 x 3, x 2 3) Y este último vector es el que se incluiría en la la correspondiente de la matriz de ceros original. El código (en R) que implementa este procedimiento es el siguiente: 1 l i b r a r y ( reshape2 ) 2 l i b r a r y ( t a b l e s ) 3 4 num_datos=2 5 num_var=2 6 7 covar = genpositivedefmat (num_var) 8 mu = rep (0, num_var) 9 10 for ( q in 1 : num_var) 11 {mu[ q ] = r u n i f (1, 0,100)} Datos = mvrnorm( num_datos, mu, covar$sigma ) 14 dim = for ( i in 1 : num_var) 17 {dim = dim +i } varaux = matrix (0, nrow=num_datos, ncol=dim ) maux = matrix (0, num_var, num_var) 22 vaux = rep (0, dim ) for ( f in 1 : num_datos ) 25 { 26 maux = matrix (0, num_var, num_var) 27 vaux = rep (0, dim ) for ( i in 1 : num_var) 30 { for ( j in 1 : num_var) 31 {maux [ i, j ] = Datos [ f, i ] Datos [ f, j ] } 32 } for ( i in 1 : num_var) 35 { for ( j in i : num_var) 36 {vaux [ min ( which(0==vaux ) ) ] = maux [ i, j ] } 37 } Álvaro Rollón de Pinedo 65
68 4.3. EXPERIMENTOS INDEPENDIENTES 38 varaux [ f, ] = vaux 39 } v a r i a b l e s = Datos for ( i in 1 : dim ) 44 { v a r i a b l e s = cbind ( v a r i a b l e s, varaux [, i ] ) } Código 4.1: Código empleado para generar las interacciones necesarias. En los experimentos realizados con este modelo, se procurará replicar los realizados en el capítulo anterior en la medida de lo posible, aunque a una escala menor en lo que a número de variables se reere, para que los experimentos sean viables. En el momento en el que se introdujeran 50 variables, el problema computacional ya es equivalente a tener 1275 en el caso anterior. Esos órdenes de magnitud solo se alcanzaron en el experimento de búsqueda de la Maldición de la Dimensionalidad, de modo que está justicada la reducción. Es importante subrayar que en experimentos reales es improbable que se produzcan interacciones de segundo orden entre todas las variables, de modo que considerar todas ellas responde únicamente a la búsqueda de la máxima generalidad matemática. Otro procedimiento podría haber sido la selección de un número concreto de variables al azar y realizar sus productos de forma aleatoria. Por último, los criterios de acierto a emplear son los mismos que los del capítulo anterior, considerando un 1 % de error relativo como máximo admisible, así como el criterio del MAPE. Asimismo, los parámetros a cambiar en los experimentos son también los empleados en el capítulo anterior, Número de variables, Número de observaciones, Parámetro mtry y ntree Experimentos Independientes Cambio de variables Correlacionadas Modelo determinista En este primer caso se omitirá el ruido en la generación de la variable respuesta y se procederá a estudiar la reacción de los diversos modelos cuando hay 20 variables implicadas y 600 observaciones por cada una de ellas. La elección de estos números obedece a criterios de coste en las simulaciones pero al mismo tiempo buscan conseguir que el ajuste de modelo lineal se pueda realizar, ya que si tomando menor número de observaciones el rango de las mismas resulta insuciente, es decir, se necesita más información para ajustar el modelo (Rank deciency), quedando tasas de acierto como las siguientes: 66 Escuela Técnica Superior de Ingenieros Industriales (UPM)
69 EXPERIMENTOS PARA MODELOS DE ÁRBOLES Figura 4.1: Ejemplo de Rank deciency en un modelo lineal Este caso es similar al problema de dimensionalidad que se mostró en el capítulo anterior, pero en estos experimentos es particularmente problemático debido al aumento exponencial del número de variables. Los resultados obtenidos de este experimento con modelo determinista son: Figura 4.2: Modelo con interacción y variables correlacionadas sin ruido. Dicha gráca permite observar las tasas de acierto de cada modelo. El primer aspecto que salta a la vista es el hecho de que, al igual que en los ejemplos del capítulo anterior, el modelo lineal ajustado posee una tasa de acierto del 100 %, de modo que sigue siendo el que mejor realiza la regresión de los datos. El hecho de que experimente una bajada por debajo de la tasa de acierto de Random Forest se debe a que está en el límite de su capacidad de ajuste con la información suministrada. Álvaro Rollón de Pinedo 67
70 4.3. EXPERIMENTOS INDEPENDIENTES Finalmente, es destacable el hecho de que, ya que el lineal sabe qué tipo de modelo tiene que ajustar, su resistencia a los problemas de dimensionalidad es muy grande, incluso aunque en teoría la falta de información debería impedir conseguir buenos resultados, en este caso es capaz de acertar debido a que está especícamente diseñado para ajustar dicho modelo. Modelo no determinista La introducción de ruido en la respuesta provoca unos resultados considerablemente diferentes a los observados en el anterior apartado, reduciéndose con mucho la precisión de los mismos. Es importante señalar que, al igual que los coecientes de los regresores de segundo orden son de un orden de magnitud menor que los originales, el ruido asociado a los mismos también lo es. Las tasas de acierto del modelo con variables correlacionadas no determinista son las siguientes: Figura 4.3: Modelo con interacción y variables correlacionadas con ruido. La respuesta que ha dado el sistema con 20 variables (y sus interacciones) y 600 observaciones incluyendo ruido es muy diferente. Se observa primeramente una gran bajada en la tasa de acierto que proporcionan todos los modelos, si bien es cierto que los modelos de árboles son bastante estables y poseen una progresiva mejora según va aumentando el número de variables. Sin embargo, la característica más reseñable es que, incluso con un gran número de observaciones, el modelo lineal posee un acierto muy pobre en el momento en el que le es introducida una componente aleatoria. Finalmente, el MAPE arrojado por los modelos de árboles varía de la siguiente manera: Cuyos resultados son congruentes con las tasas de acierto consideradas. 68 Escuela Técnica Superior de Ingenieros Industriales (UPM)
71 EXPERIMENTOS PARA MODELOS DE ÁRBOLES Figura 4.4: MAPE del modelo con interacción y variables correlacionadas con ruido Cambio de variables no Correlacionadas Modelo determinista En este caso, como se ha indicado, no hay correlación entre las variables, de modo que la matriz de covarianzas es diagonal. En este caso, el predecir la respuesta es más sencillo debido a que las relaciones entre los regresores son más evidentes. Los resultados son los siguientes para el modelo determinista: Figura 4.5: Respuesta de los modelos ante un modelo lineal con interacción y sin correlación de variables ni ruido. Resulta evidente que el modelo que tiene mas problemas de adaptación a la relación entre las variables es el de Random Forest creado con Conditional Inference Trees. Sin embargo, queda patente la capacidad de todos los modelos de estimar este tipo de relaciones. Álvaro Rollón de Pinedo 69
72 4.4. DEPENDENCIA RESPECTO DEL NÚMERO DE ÁRBOLES Modelo no determinista Se trata del último caso de análisis del comportamiento de los modelos en función del incremento de variables que conforman la respuesta. Las variables no tienen correlación entre sí pero existe inclusión de ruido en la respuesta. La respuesta de los modelos es la siguiente: Figura 4.6: Respuesta de los modelos ante un modelo lineal con interacción y sin correlación de variables pero con ruido. Lo que más llama la atención es la similaridad con el caso en el que sí había correlación. A tenor de estos resultados, parece que la correlación de variables solo tiene una inuencia sensible en el caso de modelos deterministas, en el momento en el que aparece ruido en el sistema no es posible apreciarla Dependencia respecto del número de árboles Al igual que en el caso abordado en el capítulo anterior, es esperable que el número de árboles no resulte ser una variable decisiva en cuanto a lo que la calidad de las predicciones se reere. Sin embargo, resulta interestante comprobar la velocidad a la que la tasa de error converge. Las variables empleadas a lo largo de estos experimentos estarán correlacionadas. Primeramente, se hará una comprobación grosera, con un paso de 5, desde 5 árboles a 400 y con 20 variables buscándose algún tipo de tendencia en la variación del MAPE de los modelos de árboles. Los resultados son los siguientes: 70 Escuela Técnica Superior de Ingenieros Industriales (UPM)
73 EXPERIMENTOS PARA MODELOS DE ÁRBOLES Figura 4.7: Dependencia del error MAPE con el número de árboles hasta 400 en un modelo lineal con interacción. Como se puede observar, no se aprecia una dependencia clara del número de árboles. Dado que el número era realmente grande (y aun así menor del predenido en las librerías de R), se ha decidido probar con números menores de árboles, con lo cual sería esperable más varianza en los primeros valores del MAPE, y una posterior estabilización. En la siguiente prueba, el número máximo de árboles se ha reducido de 400 a 50, pero manteniendo el de variables en 20. Recuérdese que aunque el número de regresores sea 20, las variables introducidas al modelo son muchas más, en este caso 230, debido a las interacciones. Figura 4.8: Dependencia del error MAPE con el número de árboles hasta 50 en un modelo lineal con interacción. Álvaro Rollón de Pinedo 71
74 4.4. DEPENDENCIA RESPECTO DEL NÚMERO DE ÁRBOLES Nuevamente, aunque se ha pasado a analizar un número mínimo de árboles y la precisión de las observaciones es mucho mayor, ya que el paso se ha reducido a uno, de forma que sea apreciable la variación del MAPE con la inclusión de cada árbol nuevo, los resultados siguen oscilando de la misma manera. Otra posible explicación de este fenómeno es la gran cantidad de variables e interacciones introducidas. Puede ser que al ser un número tan grande, además de que las variables están correlacionadas, o bien el sistema capta rápidamente la relación entre ellas o se declara completamente incapaz de hacerlo. La única otra manera de apreciar dicha posibilidad es reduciendo el número de variables. En este caso, se pasará a 3 regresores más sus interacciones. Los resultados obtenidos son: Figura 4.9: Dependencia del error MAPE con el número de árboles hasta 50 en un modelo lineal con interacción y 3 regresores. Finalmente, ahora sí es posible apreciar un cambio de patrón en el MAPE a partir de cierto número, pudiéndose ver las oscilaciones del sistema hasta alcanzar un valor que aparenta ser un régimen permanente. Sin embargo, a pesar de los últimos resultados, resulta evidente que la dependencia de la calidad de las predicciones con el número de árboles es, como mucho, leve, especialmente a partir de las pocas decenas. 72 Escuela Técnica Superior de Ingenieros Industriales (UPM)
75 4.5. Experimentos con mtry EXPERIMENTOS PARA MODELOS DE ÁRBOLES En esta sección se realizarán experimentos idénticos a los realizados en el capítulo anterior variando el parámetro mtry, es decir, la cantidad de variables empleadas en la realización de los splits nodales. Dicho valor irá aumentando progresivamente de uno en uno hasta llegar al número máximo de variables contando las interacciones entre las mismas. Como ya se apreció en el anterior experimento, la dependencia con este parámetro es sensible, de modo que no es despreciable en absoluto, y las tasas de error varían considerablemente entre tomar unos valores u otros. Los tres experimentos realizados harán cambios en el número de observaciones por variable, al igual que en el caso del capítulo anterior. El número de variables a evaluar será 5 en todo caso, sin contar con las interacciones. Las variables se escalarán, mientras que el número de replicaciones de cada experimento se mantendrá en 10, de modo que los resultados que se muestran son la media ponderada de dichas replicaciones. Dado que este caso también es de regresión y no de clasicación, el valor teórico óptimo para la mayoría de los casos debería rondar p, siendo p el número de variables 3 que se introducen a los modelos de Bosques Aleatorios Variación de mtry con 100 observaciones Aportando solo 100 observaciones por variable, la variación del MAPE según aumenta mtry viene dada por: Figura 4.10: Dependencia del error MAPE en el modelo con interacción variando mtry con 100 observaciones Álvaro Rollón de Pinedo 73
76 4.5. EXPERIMENTOS CON MTRY La tabla de datos medios con la que se ha construido el gráco es: TABLAI abscisa MRF MCF 2 2 0,0378 0, ,0209 0, ,0221 0, ,0237 0, ,0205 0, ,0427 0, ,0257 0, ,0423 0, ,0192 0,0217 Tabla 4.1: Datos de la variación del MAPE con mtry con 100 observaciones. Nuevamente, y de forma congruente con la teoría, existe en intervalo en el entorno de la tercera parte del número de variables introducidas a los modelos en el cual el error desciende y, en general, se obtienen buenos resultados predictivos con dichos valores. Tal y como sucedía en algunos casos de los experimentos con el modelo Lineal puro, el valor mínimo del MAPE no se encuentra en la región de trabajo recomendada, pero sin embargo sí que existe un valle de bajo error que garantiza más abilidad a la hora de trabajar Variación de mtry con 200 observaciones En este experimento se ha duplicado la información aportada al sistema, de modo que existen 200 observaciones por cada variable independiente. La tabla con los datos es: TABLAI abscisa MRF MCF 2 2 0,0212 0, ,0220 0, ,0255 0, ,0209 0, ,0289 0, ,0266 0, ,0300 0, ,0263 0, ,0224 0,0223 Tabla 4.2: Datos de la variación del MAPE con mtry con 200 observaciones. 74 Escuela Técnica Superior de Ingenieros Industriales (UPM)
77 EXPERIMENTOS PARA MODELOS DE ÁRBOLES Y su representación gráca es la siguiente: Figura 4.11: Dependencia del error MAPE en el modelo con interacción variando mtry con 200 observaciones Como se puede comprobar, los resultados medios obtenidos ponderando las 10 replicaciones no son en este caso tan congruentes con la teoría como los anteriores. Primeramente, hay una gran oscilación de resultados en el entorno de mtry = p 3 de modo que dicha zona de trabajo resulta no ser tan segura como en otras simulaciones, ya que, como es apreciable, el valle de error del MAPE aparece desplazado a valores menores de los que se suponen óptimos. Sí que es cierto que dicho valle no está muy alejado de la que se puede considerar como zona de trabajo, el problema de este caso es que existe un pico de error entre ambos Variación de mtry con 300 observaciones En este último experimento, el número de variables ha aumentado a 300, con lo que es esperable que los modelos tengan informacion de sobra para ajustarse sin problemas a la respuesta. De nuevo se han llevado a cabo 10 replicaciones del experimento de simulación, y los valores medios obtenidos resultan interesantes, ya que muestran un comportamiento disimilar respecto de todas las simulaciones llevadas a cabo. La tabla con los datos obtenidos se muestra en la página siguiente: Álvaro Rollón de Pinedo 75
78 4.5. EXPERIMENTOS CON MTRY TABLAI abscisa MRF MCF 2 2 0,0228 0, ,0274 0, ,0235 0, ,0232 0, ,0222 0, ,0237 0, ,0221 0, ,0217 0, ,0259 0, Tabla 4.3: Datos de la variación del MAPE con mtry con 300 observaciones. Mientras que la representación gráca de dichos resultados resulta ser: Figura 4.12: Dependencia del error MAPE en el modelo con interacción variando mtry con 300 observaciones Este caso, de nuevo resulta ser más típico que el anterior, ya que se puede apreciar cómo, si bien el mínimo error no es alcanzado en el punto de trabajo especicado, sí es cierto que en este caso el entorno general de trabajo coincide con una región de MAPE aceptable, si bien es cierto que no parece tan conveniente como era en el caso de 100 observaciones. En cualquier caso, está claro que de forma general (ni mucho menos siempre), a falta de un buen criterio de decisión como puede ser un muestreo de los porcentajes de error asociados a cada valor de mtry, puede ser conveniente asignar un valor jo de la tercera parte de las variables. Además de esto, la otra razón de tomar dichos valores es que al tener en cuenta menos variables para cada árbol, se agilizaría el proceso de construcción de los modelos. 76 Escuela Técnica Superior de Ingenieros Industriales (UPM)
79 Capítulo 5 Intervalos de Conanza 5.1. Introducción Una característica muy frecuente en las publicaciones que analizan actualmente la capacidad predictiva de los modelos de Random Forest, tanto en los elaborados con CART y con Conditional Inference Trees es el hecho de que, generalmente, o bien se centran en el análisis del modelo matemático en sí de una manera que se podría denir como analítica, o producen un resultado y buscan analizar la precisión del mismo a través de un parámetro auxiliar como puede ser el MAPE para inferir a través del mismo las capacidades de los modelos. Sin embargo, esta manera de atacar a los diferentes casos deja de lado un problema fundamental de especial interés en el análisis estadístico. A menudo el valor de una predicción en sí, ya sea en un problema de regresión, predicción de series temporales etc. no es tan importante como la incertidumbre que a él se asocia. De dicha necesidad surgen los intervalos de conanza Descripción de los Intervalos Un intervalo de conanza es un parámetro estadístico constituido por un número o una dupla de números a partir del cual o entre los cuales existe una probabilidad determinada de encontrar el valor que se estima en un determinado problema. A la probabilidad de fallar la estimación realizada a través de dicho intervalo se la conoce como nivel de signicación, y es generalmente representada por la letra griega α. Típicamente, los valores que α suele tomar son el 1, 5 y 10 por ciento, si bien por supuesto dicha precisión depende del problema determinado. Lógicamente, la probabilidad de acierto es 1 - α. En general, la construcción de los intervalos requiere conocer la distribución de probabilidad del parámetro que se desea estimar. Por ejemplo, en el caso de que dicho parámetro siga una normal, resulta sencillo crear el intervalo de la precisión deseada a través de la siguiente expresión: 77
80 5.3. EXPERIMENTO 1: 20 VARIABLES µ ˆµ ± z α/2 σ n Donde µ sería el valor real del parámetro que se desea estimar, ˆµ la estimación que se hace del mismo, n el tamaño de la muestra, σ la desviación típica de la misma, y z α/2 el valor leído en las tablas de la normal estándar en función de la precisión que se exija al intervalo. Otra manera de realizar dicho cálculo es a través de la Igualdad de Chebychev. Dado que en el caso de los modelos de árboles no se posee tanta información sobre las variables, ya que generalmente solo se dispone de un conjunto de datos de diferentes naturalezas, este tipo de procedimientos resultan poco prácticos e inecientes. Por estas razones, a la hora de evaluar la incertidumbre de las predicciones realizadas con los modelos generados se procederá de manera diferente. Como en los modelos de Random Forest las predicciones se generan a través de las medias ponderadas de las predicciones de los árboles individuales, tiene sentido generar el intervalo empleando las predicciones individuales de cada árbol, de modo que si, por ejemplo, se dispone de 1000 árboles, es posible generar dicho intervalo con α = 5 % cogiendo (una vez ordenadas las predicciones de menor a mayor) desde el número 25 al 975. Mediante este método se irán generando diversos intervalos de conanza con diferentes niveles de signicación, tomando la cantidad de árboles correspondiente. En los experimentos de este capítulo, se realizarán los intervalos de conanza asociados a un modelo lineal con correlación entre variables. En los tres experimentos, se probarán diferentes órdenes de magnitud de variables y observaciones para comprobar la diversidad de resultados Experimento 1: 20 variables En este apartado se realizarán las predicciones sobre un modelo lineal con 20 variables y se irán incrementando el numero de observaciones para comprobar la variación en las anchuras de los intervalos. Las cantidades de las observaciones son el doble, cinco y diez veces el número de variables. En la siguiente tabla se resume cómo varían las anchuras de los intervalos de conanza según se van incrementando las observaciones, para los intervalos de nivel de signicación 1, 5 y Escuela Técnica Superior de Ingenieros Industriales (UPM)
81 EXPERIMENTOS PARA MODELOS DE ÁRBOLES Observaciones 1 % 5 % 10 % 40 0,0113 0,0113 0, ,0152 0,0152 0, ,0122 0,0122 0,0088 Tabla 5.1: Variación de las anchuras de los intervalos de conanza con 40, 100 y 200 observaciones Como se ve, las anchuras decrecen al aumentar el índice de signicación(como es lógico). Resulta interesante sin embargo subrayar el hecho de que aumentar el número de observaciones no hace mejorar las anchuras máximas de los intervalos de forma inmediata. La representación gráca de las predicciones con sus respectivos intervalos en el caso de 200 observaciones es: Figura 5.1: Predicción e intervalos de conanza con 20 variables y 200 observaciones 5.4. Esperimento 2: 40 variables En este apartado se llevará a cabo el mismo experimento pero con 40 variables, incrementando las observaciones de manera análoga al caso anterior. La tabla con los resultados es: Observaciones 1 % 5 % 10 % 80 0,0229 0,0229 0, ,0221 0,0216 0, ,0166 0,0163 0,0142 Tabla 5.2: Variación de las anchuras de los intervalos de conanza con 80, 200 y 400 observaciones Álvaro Rollón de Pinedo 79
82 5.5. EXPERIMENTO 3: 60 VARIABLES En este caso los resultados referentes a las anchuras de los intervalos son mucho más típicos, ya que la tendencia es en todos los casos a reducirse con el incremento de la signicación y las observaciones. Para el caso de 200 observaciones, la representación gráca de los intervalos es: Figura 5.2: Predicción e intervalos de conanza con 40 variables y 200 observaciones 5.5. Experimento 3: 60 variables Este será el último caso objeto de estudio y la metodología seguida es la misma que en los casos anteriores. La tabla de datos es la siguiente: Observaciones 1 % 5 % 10 % 120 0,0302 0,0301 0, ,0298 0,0293 0, ,0369 0,0341 0,0256 Tabla 5.3: Variación de las anchuras de los intervalos de conanza con 120, 300 y 600 observaciones En este caso, si bien sigue siendo cierto que la anchura disminuye de forma inversa al aumento del índice de signicación, en todos los casos aumenta con el número de observaciones, lo cual supone un fenómeno curioso y digno de estudio. Ha de ser tenido en cuenta el hecho de que en ciertas situaciones, como ya se ha tenido la ocasión de comprobar en apartados anteriores del presente trabajo, un aumento de las observaciones por variable no es concluyente a la hora de mejorar la precisión de los modelos. 80 Escuela Técnica Superior de Ingenieros Industriales (UPM)
83 EXPERIMENTOS PARA MODELOS DE ÁRBOLES Finalmente se adjunta la gráca obtenida para el caso en el que se han tomado las 600 observaciones por variable y sus intervalos de conanza asociados: Figura 5.3: Predicción e intervalos de conanza con 60 variables y 600 observaciones Finalmente, es muy destacable el hecho de que la incertidumbre asociada a los intervalos es como mucho un uno por ciento, de modo que se puede armar que en general las predicciones de dichos intervalos son considerablemente precisas. Álvaro Rollón de Pinedo 81
84 5.5. EXPERIMENTO 3: 60 VARIABLES 82 Escuela Técnica Superior de Ingenieros Industriales (UPM)
85 Capítulo 6 Conclusión y Líneas Futuras 6.1. Conclusión En este Trabajo de Fin de Grado se ha realizado un análisis exhaustivo de las capacidades de los modelos de Random Forest como herramienta para resolver problemas de regresión estadística en modelos típicos lineales. Al margen del resto de conclusiones, cabe destacar el hecho de que, en términos generales los Bosques Aleatorios, tanto los realizados con CART como con Conditional Inference Trees son una herramienta útil y de gran adaptabilidad ante prácticamente cualquier tipo de cambio. Al margen de este hecho, cabe destacar los siguientes aspectos sobre los modelos de Random Forest: Es apreciable un aumento de la precisión en la mayoría de los casos según aumenta el número de variables que conforman el problema. Existe sensibilidad a la correlación de las variables y al ruido, pero ambos son leves frente a otros modelos. Tienen gran robustez frente a la dimensionalidad de los problemas, siendo capaces de manejar poca información en proporción al número de variables. La cantidad de árboles que conforman el Random Forest no es una variable muy signicativa en su calidad, convergiendo en general hacia la solución con pocas decenas de árboles. Presentan muy pocos problemas de sobreajuste (overtting). El parámetro mtry tiene una inuencia decisiva en la tasa de error cometida, y en general es conveniente adaptarlo a cada problema especíco. Random Forest es una herramienta potente a la hora de captar la importancia de las variables que conforman un determinado proceso, pero de todos los resultados que pueden aportar, este es el que más reservas debe generar ya que depende mucho 83
86 6.2. LÍNEAS FUTURAS del método de cálculo y es fácil que aunque la generalidad esté correcta, haya algún error grave puntual enmascarado. Los intervalos de conanza generados a partir de las predicciones de los árboles individuales son relativamente estrechos, con una anchura generalmente inferior al 1 % del valor predicho, de modo que la incertidumbre asociada a dichos valores es pequeña Líneas futuras Este proyecto de investigación tiene gran cantidad de posibilidades de ampliación en vistas a una mayor profundización de los experimentos expuesto, o extensión a otro tipo de modelos de regresión. En ese aspecto, cabe destacar: Análisis de nuevos modelos típicamente utilizados en Ciencia y Tecnología, como modelos tipo Arrhenius por ejemplo. Realización de los mismos experimentos aumentando el número de replicaciones. Hallar una relación analítica aproximada que explique las necesidades de información de Random Forest para no incurrir en problemas de dimensionalidad. Análisis de la anchura de los intervalos de conanza en función de los tamaños de los conjuntos de entrenamiento y prueba. 84 Escuela Técnica Superior de Ingenieros Industriales (UPM)
87 Capítulo 7 Planicación temporal y presupuesto 7.1. Estructura de Descomposición del Proyecto (EDP) La Estructura de Descomposición del Proyecto, EDP, es una representación esquemática de la jerarquía que han de tener las diferentes partes que conforman un proyecto, llegando a la unidad mínima, que está constituida por los entregables de dicho proyecto. La EDP constituye una herramienta ecaz con la cual poder observar de un vistazo los niveles fundamentales en los que se divide un proyecto. Asimismo, transmite información sobre el alcance del mismo (en este caso, el Trabajo de Fin de Grado), si bien es cierto que no aporta información en cuanto a la cronología que lo rige. Finalmente, dado que debe ser un elemento de fácil manejo e interpretación, no ha de tener un tamaño demasiado grande para que su utilidad no quede coartada por su complejidad. En las páginas siguientes viene adjuntada la EDP del presente trabajo Diagrama de Gantt El conocido como diagrama de Gantt es un diagrama de barras que permite representar la cronología de las diversas tareas asociadas a un proyecto. Resulta ser una herramienta gráca de sencilla interpretación en la cual la planicación del mismo queda patente. Sin embargo, los diagramas de Gantt tienen como contrapartida su incapacidad para mostrar las relaciones entre las distintas partes representadas, por ello a menudo se conjuntan con información complementaria como la proporcionada por la EDP. En las siguientes páginas se muestra detalladamente el diagrama de Gantt del trabajo. 85
88 7.2. DIAGRAMA DE GANTT EDP Estudios Previos Prácticas con R Experimentos con el modelo Lineal Experimentos con modelo Lineal e interacciones Lectura de los "papers" Lectura del manual básico Cantidad de variables Cantidad de variables Lectura de ejemplos Aplicación a ejemplos simples Dimensionalidad Número de árboles Aprendizaje de aplicaciones reales Pruebas con CART Número de Árboles Variación de mtry Pruebas con Random Forest Variación de mtry Intervalos de Confianza Importancia de variables Figura 7.1: Estructura de Descomposición del Proyecto 86 Escuela Técnica Superior de Ingenieros Industriales (UPM)
Métodos de Remuestreo en Aprendizaje Automático
 Métodos de Remuestreo en Aprendizaje Automático en datos, en hipótesis, y algunos otros trucos: Cross-validation, Bootstrap, Bagging, Boosting, Random Subspaces Lo que sabemos hasta ahora: Hemos visto
Métodos de Remuestreo en Aprendizaje Automático en datos, en hipótesis, y algunos otros trucos: Cross-validation, Bootstrap, Bagging, Boosting, Random Subspaces Lo que sabemos hasta ahora: Hemos visto
Aprendizaje Automatizado
 Aprendizaje Automatizado Aprendizaje Automatizado Programas que mejoran su comportamiento con la experiencia. Dos formas de adquirir experiencia: A partir de ejemplos suministrados por un usuario (un conjunto
Aprendizaje Automatizado Aprendizaje Automatizado Programas que mejoran su comportamiento con la experiencia. Dos formas de adquirir experiencia: A partir de ejemplos suministrados por un usuario (un conjunto
MASTER DE INGENIERÍA BIOMÉDICA. Métodos de ayuda al diagnóstico clínico. Tema 6: Árboles de decisión.
 MASTER DE INGENIERÍA BIOMÉDICA. Métodos de ayuda al diagnóstico clínico. Tema 6: Árboles de decisión. 1 Objetivos del tema Conocer en qué consiste un árbol de decisión. Aprender los problemas que pueden
MASTER DE INGENIERÍA BIOMÉDICA. Métodos de ayuda al diagnóstico clínico. Tema 6: Árboles de decisión. 1 Objetivos del tema Conocer en qué consiste un árbol de decisión. Aprender los problemas que pueden
Técnicas Multivariadas Avanzadas
 Métodos basados en árboles Universidad Nacional Agraria La Molina 2014-2 Introducción Introducción Se describen métodos basados en árboles para regresión y clasicación. Estos métodos requieren estraticar
Métodos basados en árboles Universidad Nacional Agraria La Molina 2014-2 Introducción Introducción Se describen métodos basados en árboles para regresión y clasicación. Estos métodos requieren estraticar
Análisis de Datos. Introducción al aprendizaje supervisado. Profesor: Dr. Wilfrido Gómez Flores
 Análisis de Datos Introducción al aprendizaje supervisado Profesor: Dr. Wilfrido Gómez Flores 1 Conceptos básicos Desde la antigüedad, el problema de buscar patrones en datos es fundamental en diversas
Análisis de Datos Introducción al aprendizaje supervisado Profesor: Dr. Wilfrido Gómez Flores 1 Conceptos básicos Desde la antigüedad, el problema de buscar patrones en datos es fundamental en diversas
Identificación mediante el método de los mínimos cuadrados
 Ingeniería de Control Identificación mediante el método de los mínimos cuadrados Daniel Rodríguez Ramírez Teodoro Alamo Cantarero Contextualización del tema Conocimientos relevantes aprendidos previamente:
Ingeniería de Control Identificación mediante el método de los mínimos cuadrados Daniel Rodríguez Ramírez Teodoro Alamo Cantarero Contextualización del tema Conocimientos relevantes aprendidos previamente:
Conjuntos de Clasificadores (Ensemble Learning)
 Aprendizaje Automático Segundo Cuatrimestre de 2016 Conjuntos de Clasificadores (Ensemble Learning) Gracias a Ramiro Gálvez por la ayuda y los materiales para esta clase. Bibliografía: S. Fortmann-Roe,
Aprendizaje Automático Segundo Cuatrimestre de 2016 Conjuntos de Clasificadores (Ensemble Learning) Gracias a Ramiro Gálvez por la ayuda y los materiales para esta clase. Bibliografía: S. Fortmann-Roe,
Introducción a los sistemas Multiclasificadores. Carlos J. Alonso González Departamento de Informática Universidad de Valladolid
 Introducción a los sistemas Multiclasificadores Carlos J. Alonso González Departamento de Informática Universidad de Valladolid Contenido 1. Combinación de modelos 2. Descomposición bias-varianza 3. Bagging
Introducción a los sistemas Multiclasificadores Carlos J. Alonso González Departamento de Informática Universidad de Valladolid Contenido 1. Combinación de modelos 2. Descomposición bias-varianza 3. Bagging
Unidad V: Estadística aplicada
 Unidad V: Estadística aplicada 5.1 Inferencia estadística: Concepto, Estimación, Prueba de hipótesis La Inferencia Estadística es la parte de la estadística matemática que se encarga del estudio de los
Unidad V: Estadística aplicada 5.1 Inferencia estadística: Concepto, Estimación, Prueba de hipótesis La Inferencia Estadística es la parte de la estadística matemática que se encarga del estudio de los
Repaso de conceptos de álgebra lineal
 MÉTODOS AVANZADOS EN APRENDIZAJE ARTIFICIAL: TEORÍA Y APLICACIONES A PROBLEMAS DE PREDICCIÓN Manuel Sánchez-Montañés Luis Lago Ana González Escuela Politécnica Superior Universidad Autónoma de Madrid Repaso
MÉTODOS AVANZADOS EN APRENDIZAJE ARTIFICIAL: TEORÍA Y APLICACIONES A PROBLEMAS DE PREDICCIÓN Manuel Sánchez-Montañés Luis Lago Ana González Escuela Politécnica Superior Universidad Autónoma de Madrid Repaso
Correlación. El coeficiente de correlación mide la fuerza o el grado de asociación entre dos variables (r)
 Correlación El coeficiente de correlación mide la fuerza o el grado de asociación entre dos variables (r) El coeficiente de correlación lineal de Pearson (r) permite medir el grado de asociación entre
Correlación El coeficiente de correlación mide la fuerza o el grado de asociación entre dos variables (r) El coeficiente de correlación lineal de Pearson (r) permite medir el grado de asociación entre
Estadística con R. Clasificadores
 Estadística con R Clasificadores Análisis discriminante lineal (estadístico) Árbol de decisión (aprendizaje automático) Máquina soporte vector (aprendizaje automático) Análisis discriminante lineal (AD)
Estadística con R Clasificadores Análisis discriminante lineal (estadístico) Árbol de decisión (aprendizaje automático) Máquina soporte vector (aprendizaje automático) Análisis discriminante lineal (AD)
CART s. Walter Sosa-Escudero. Universisad de San Andres y CONICET
 Universisad de San Andres y CONICET Motivacion Modelo flexible e interpretable para la relacion entre Y y X. Arboles: partir el espacio de atributos en rectangulos, y ajustar un modelo simple para Y dentro
Universisad de San Andres y CONICET Motivacion Modelo flexible e interpretable para la relacion entre Y y X. Arboles: partir el espacio de atributos en rectangulos, y ajustar un modelo simple para Y dentro
Aprendizaje Automático
 id3 id3 como búsqueda Cuestiones Adicionales Regresión Lineal. Árboles y Reglas de Regresión Ingeniería Informática Fernando Fernández Rebollo y Daniel Borrajo Millán Grupo de Planificación y Aprendizaje
id3 id3 como búsqueda Cuestiones Adicionales Regresión Lineal. Árboles y Reglas de Regresión Ingeniería Informática Fernando Fernández Rebollo y Daniel Borrajo Millán Grupo de Planificación y Aprendizaje
INTRODUCCION A LA SIMULACION DE MODELOS. Simulación es la descripción de un sistema a través de modelos que se pueden aplicar a varias disciplinas.
 Tema N 1 Definiciones INTRODUCCION A LA SIMULACION DE MODELOS Simulación es la descripción de un sistema a través de modelos que se pueden aplicar a varias disciplinas. La simulación esencialmente es una
Tema N 1 Definiciones INTRODUCCION A LA SIMULACION DE MODELOS Simulación es la descripción de un sistema a través de modelos que se pueden aplicar a varias disciplinas. La simulación esencialmente es una
Tareas de la minería de datos: clasificación. CI-2352 Intr. a la minería de datos Prof. Braulio José Solano Rojas ECCI, UCR
 Tareas de la minería de datos: clasificación CI-2352 Intr. a la minería de datos Prof. Braulio José Solano Rojas ECCI, UCR Tareas de la minería de datos: clasificación Clasificación (discriminación) Empareja
Tareas de la minería de datos: clasificación CI-2352 Intr. a la minería de datos Prof. Braulio José Solano Rojas ECCI, UCR Tareas de la minería de datos: clasificación Clasificación (discriminación) Empareja
CRITERIOS DE SELECCIÓN DE MODELOS
 Inteligencia artificial y reconocimiento de patrones CRITERIOS DE SELECCIÓN DE MODELOS 1 Criterios para elegir un modelo Dos decisiones fundamentales: El tipo de modelo (árboles de decisión, redes neuronales,
Inteligencia artificial y reconocimiento de patrones CRITERIOS DE SELECCIÓN DE MODELOS 1 Criterios para elegir un modelo Dos decisiones fundamentales: El tipo de modelo (árboles de decisión, redes neuronales,
CONCLUSIONES Y RECOMENDACIONES
 CONCLUSIONES Y RECOMENDACIONES 1. Esta página web brinda al usuario la posibilidad de desplazar uno o más puntos de la muestra para observar la forma de la curva discriminante antes y después de dichos
CONCLUSIONES Y RECOMENDACIONES 1. Esta página web brinda al usuario la posibilidad de desplazar uno o más puntos de la muestra para observar la forma de la curva discriminante antes y después de dichos
Nota de los autores... vi
 ÍNDICE Nota de los autores... vi 1 Qué es la estadística?... 1 1.1 Introducción... 2 1.2 Por qué se debe estudiar estadística?... 2 1.3 Qué se entiende por estadística?... 4 1.4 Tipos de estadística...
ÍNDICE Nota de los autores... vi 1 Qué es la estadística?... 1 1.1 Introducción... 2 1.2 Por qué se debe estudiar estadística?... 2 1.3 Qué se entiende por estadística?... 4 1.4 Tipos de estadística...
Aprendizaje Automático para el Análisis de Datos GRADO EN ESTADÍSTICA Y EMPRESA. Ricardo Aler Mur
 Aprendizaje Automático para el Análisis de Datos GRADO EN ESTADÍSTICA Y EMPRESA Ricardo Aler Mur EVALUACIÓN Evaluación: entrenamiento y test Una vez obtenido el conocimiento es necesario validarlo para
Aprendizaje Automático para el Análisis de Datos GRADO EN ESTADÍSTICA Y EMPRESA Ricardo Aler Mur EVALUACIÓN Evaluación: entrenamiento y test Una vez obtenido el conocimiento es necesario validarlo para
Clustering: Auto-associative Multivariate Regression Tree (AAMRT)
 Introducción Tipos Validación AAMRT Clustering: Auto-associative Multivariate Regression Tree (AAMRT) Miguel Bernal C Quantil 12 de diciembre de 2013 Miguel Bernal C Quantil Matemáticas Aplicadas Contenido
Introducción Tipos Validación AAMRT Clustering: Auto-associative Multivariate Regression Tree (AAMRT) Miguel Bernal C Quantil 12 de diciembre de 2013 Miguel Bernal C Quantil Matemáticas Aplicadas Contenido
4. NÚMEROS PSEUDOALEATORIOS.
 4. NÚMEROS PSEUDOALEATORIOS. En los experimentos de simulación es necesario generar valores para las variables aleatorias representadas estas por medio de distribuciones de probabilidad. Para poder generar
4. NÚMEROS PSEUDOALEATORIOS. En los experimentos de simulación es necesario generar valores para las variables aleatorias representadas estas por medio de distribuciones de probabilidad. Para poder generar
D conjunto de N patrones etiquetados, cada uno de los cuales está caracterizado por n variables predictoras X 1,..., X n y la variable clase C.
 Tema 10. Árboles de Clasificación Pedro Larrañaga, Iñaki Inza, Abdelmalik Moujahid Departamento de Ciencias de la Computación e Inteligencia Artificial Universidad del País Vasco Euskal Herriko Unibertsitatea
Tema 10. Árboles de Clasificación Pedro Larrañaga, Iñaki Inza, Abdelmalik Moujahid Departamento de Ciencias de la Computación e Inteligencia Artificial Universidad del País Vasco Euskal Herriko Unibertsitatea
El modelo de regresión múltiple
 El de regresión múltiple Simple El de regresión múltiple es la extensión a k variables explicativas del de regresión simple. La estructura del de regresión múltiple es la siguiente: y = f (x 1,..., x k
El de regresión múltiple Simple El de regresión múltiple es la extensión a k variables explicativas del de regresión simple. La estructura del de regresión múltiple es la siguiente: y = f (x 1,..., x k
Support Vector Machines
 Support Vector Machines Métodos Avanzados en Aprendizaje Artificial Luis F. Lago Fernández Manuel Sánchez-Montañés Ana González Universidad Autónoma de Madrid 6 de abril de 2010 L. Lago - M. Sánchez -
Support Vector Machines Métodos Avanzados en Aprendizaje Artificial Luis F. Lago Fernández Manuel Sánchez-Montañés Ana González Universidad Autónoma de Madrid 6 de abril de 2010 L. Lago - M. Sánchez -
7. ANÁLISIS DE VARIABLES CUANTITATIVAS: REGRESIÓN LINEAL SIMPLE
 ESCUELA UNIVERSITARIA DE ENFERMERIA DE TERUEL 1 er CURSO DE GRADO DE ENFERMERIA Estadística en Ciencias de la Salud 7. ANÁLISIS DE VARIABLES CUANTITATIVAS: REGRESIÓN LINEAL SIMPLE PROFESOR Dr. Santiago
ESCUELA UNIVERSITARIA DE ENFERMERIA DE TERUEL 1 er CURSO DE GRADO DE ENFERMERIA Estadística en Ciencias de la Salud 7. ANÁLISIS DE VARIABLES CUANTITATIVAS: REGRESIÓN LINEAL SIMPLE PROFESOR Dr. Santiago
7. PARAMETRIZACIÓN SOBRE LA RED DE PRUEBA
 7. PARAMETRIZACIÓN SOBRE LA RED DE PRUEBA 7.1. Red de prueba Para realizar el análisis de los parámetros del problema e intentar encontrar los valores óptimos de estos se ha hecho uso de un modelo de ciudad
7. PARAMETRIZACIÓN SOBRE LA RED DE PRUEBA 7.1. Red de prueba Para realizar el análisis de los parámetros del problema e intentar encontrar los valores óptimos de estos se ha hecho uso de un modelo de ciudad
VIII Jornadas de Usuarios de R
 VIII Jornadas de Usuarios de R Análisis del Abandono en el Sector Bancario Predicción del abandono de clientes Albacete, 17 de Noviembre de 2016 I. INDICE : Modelo Abandonos I. COMPRENSIÓN DEL NEGOCIO
VIII Jornadas de Usuarios de R Análisis del Abandono en el Sector Bancario Predicción del abandono de clientes Albacete, 17 de Noviembre de 2016 I. INDICE : Modelo Abandonos I. COMPRENSIÓN DEL NEGOCIO
Generalmente, el objetivo de cualquier estudio de econometría es la. búsqueda de relaciones matemáticas que permitan explicar el comportamiento
 5. METODOLOGÍA ECONOMÉTRICA. Generalmente, el objetivo de cualquier estudio de econometría es la búsqueda de relaciones matemáticas que permitan explicar el comportamiento de una variable económica a partir
5. METODOLOGÍA ECONOMÉTRICA. Generalmente, el objetivo de cualquier estudio de econometría es la búsqueda de relaciones matemáticas que permitan explicar el comportamiento de una variable económica a partir
Aprendizaje Automatizado. Árboles de Clasificación
 Aprendizaje Automatizado Árboles de Clasificación Árboles de Clasificación Estudiaremos un algoritmo para la creación del árbol. Selección de atributos comenzando en el nodo raíz. Proceso recursivo. Árboles
Aprendizaje Automatizado Árboles de Clasificación Árboles de Clasificación Estudiaremos un algoritmo para la creación del árbol. Selección de atributos comenzando en el nodo raíz. Proceso recursivo. Árboles
Estadística Descriptiva: Elementos Básicos. José Enrique Martín García Universidad Politécnica de Gimialcón (Copyright 2016)
 Estadística Descriptiva: Elementos Básicos José Enrique Martín García Universidad Politécnica de Gimialcón (Copyright 2016) Población Población estadística, también llamada universo o colectivo, es el
Estadística Descriptiva: Elementos Básicos José Enrique Martín García Universidad Politécnica de Gimialcón (Copyright 2016) Población Población estadística, también llamada universo o colectivo, es el
Aprendizaje: Boosting y Adaboost
 Técnicas de Inteligencia Artificial Aprendizaje: Boosting y Adaboost Boosting 1 Indice Combinando clasificadores débiles Clasificadores débiles La necesidad de combinar clasificadores Bagging El algoritmo
Técnicas de Inteligencia Artificial Aprendizaje: Boosting y Adaboost Boosting 1 Indice Combinando clasificadores débiles Clasificadores débiles La necesidad de combinar clasificadores Bagging El algoritmo
El Perceptrón Multicapa
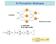 El Perceptrón Multicapa N entradas M neuronas de salida L: neuronas en la capa oculta E = 1 p M ( zi ( k) yi ( k) ) k = 1 i= 1 Implementación de la función XOR Regiones de clasificación en función del
El Perceptrón Multicapa N entradas M neuronas de salida L: neuronas en la capa oculta E = 1 p M ( zi ( k) yi ( k) ) k = 1 i= 1 Implementación de la función XOR Regiones de clasificación en función del
CRITERIOS DE EVALUACIÓN DE MATEMÁTICAS DE 4º ESO (Currículo oficial)
 CRITERIOS DE EVALUACIÓN DE MATEMÁTICAS DE 4º ESO (Currículo oficial) Los criterios de evaluación que se exponen son los correspondientes al Real Decreto 1631/2006 al que remite el Decreto 231/2007 de 31
CRITERIOS DE EVALUACIÓN DE MATEMÁTICAS DE 4º ESO (Currículo oficial) Los criterios de evaluación que se exponen son los correspondientes al Real Decreto 1631/2006 al que remite el Decreto 231/2007 de 31
Tema 10: Introducción a los problemas de Asociación y Correlación
 Tema 10: Introducción a los problemas de Asociación y Correlación Estadística 4 o Curso Licenciatura en Ciencias Ambientales Licenciatura en Ciencias Ambientales (4 o Curso) Tema 10: Asociación y Correlación
Tema 10: Introducción a los problemas de Asociación y Correlación Estadística 4 o Curso Licenciatura en Ciencias Ambientales Licenciatura en Ciencias Ambientales (4 o Curso) Tema 10: Asociación y Correlación
ÍNDICE. Prefacio... xi
 ÍNDICE Prefacio... xi Capítulo 1 Introducción... 1 1.1 Por qué hay que tomar este curso y quién utiliza la estadística?... 2 1.2 Historia... 3 1.3 Subdivisiones de la estadística... 4 1.4 Un enfoque simple
ÍNDICE Prefacio... xi Capítulo 1 Introducción... 1 1.1 Por qué hay que tomar este curso y quién utiliza la estadística?... 2 1.2 Historia... 3 1.3 Subdivisiones de la estadística... 4 1.4 Un enfoque simple
Tareas de la minería de datos: clasificación. PF-5028 Minería de datos Prof. Braulio José Solano Rojas UCR
 Tareas de la minería de datos: clasificación PF-5028 Minería de datos Prof. Braulio José Solano Rojas UCR Tareas de la minería de datos: clasificación Clasificación (discriminación) Empareja o asocia datos
Tareas de la minería de datos: clasificación PF-5028 Minería de datos Prof. Braulio José Solano Rojas UCR Tareas de la minería de datos: clasificación Clasificación (discriminación) Empareja o asocia datos
Clasificadores Débiles - AdaBoost
 Capítulo 3 Clasificadores Débiles - AdaBoost El término boosting hace referencia a un tipo de algoritmos cuya finalidad es encontrar una hipótesis fuerte a partir de utilizar hipótesis simples y débiles.
Capítulo 3 Clasificadores Débiles - AdaBoost El término boosting hace referencia a un tipo de algoritmos cuya finalidad es encontrar una hipótesis fuerte a partir de utilizar hipótesis simples y débiles.
Índice general. Prefacio...5
 Índice general Prefacio...5 Capítulo 1 Introducción...13 1.1 Introducción...13 1.2 Los datos...19 1.3 Etapas en los procesos de big data...20 1.4 Minería de datos...21 1.5 Estructura de un proyecto de
Índice general Prefacio...5 Capítulo 1 Introducción...13 1.1 Introducción...13 1.2 Los datos...19 1.3 Etapas en los procesos de big data...20 1.4 Minería de datos...21 1.5 Estructura de un proyecto de
Caso 105. Tamaño de muestra y potencia de una prueba. Diseño de experimentos. Jesús López Fidalgo
 Caso 105. Tamaño de muestra y potencia de una prueba. Diseño de experimentos. Jesús López Fidalgo Caso Práctico El objetivo de este ejercicio es analizar diferentes tipos de pruebas estadísticas en las
Caso 105. Tamaño de muestra y potencia de una prueba. Diseño de experimentos. Jesús López Fidalgo Caso Práctico El objetivo de este ejercicio es analizar diferentes tipos de pruebas estadísticas en las
Contenidos Programáticos
 Página 1 de 6 FACULTAD: CIENCIAS ECONÓMICAS Y EMPRESARIALES PROGRAMA: ADMINISTRACIÓN DE EMPRESAS DEPARTAMENTO DE: ADMINISTRACIÓN CURSO: ESTADISTICA I CÓDIGO: 157011 ÁREA: BÁSICA REQUISITOS: CORREQUISITO:
Página 1 de 6 FACULTAD: CIENCIAS ECONÓMICAS Y EMPRESARIALES PROGRAMA: ADMINISTRACIÓN DE EMPRESAS DEPARTAMENTO DE: ADMINISTRACIÓN CURSO: ESTADISTICA I CÓDIGO: 157011 ÁREA: BÁSICA REQUISITOS: CORREQUISITO:
PROGRAMACIÓN ABREVIADA DE MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES I
 PROGRAMACIÓN ABREVIADA DE MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES I 1- CONTENIDOS Bloque 1. Procesos, métodos y actitudes en matemáticas Planificación del proceso de resolución de problemas. 1- Estrategias
PROGRAMACIÓN ABREVIADA DE MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES I 1- CONTENIDOS Bloque 1. Procesos, métodos y actitudes en matemáticas Planificación del proceso de resolución de problemas. 1- Estrategias
Análisis de regresión y correlación lineal
 Análisis de regresión y correlación lineal En las unidades anteriores hemos aplicado metodologías estadísticas para analizar la información de una variable desde una o más muestras utilizando las herramientas
Análisis de regresión y correlación lineal En las unidades anteriores hemos aplicado metodologías estadísticas para analizar la información de una variable desde una o más muestras utilizando las herramientas
proporcionan respuestas muy diferentes a este problema, obteniendo que la solución asociada a la norma l
 6 Conclusiones Con la teoría de muestreo de Nyquist, a medida que el ancho de banda de la señal aumenta, también lo hace la frecuencia de muestreo, de forma que para ciertos tipos de señales la tarea de
6 Conclusiones Con la teoría de muestreo de Nyquist, a medida que el ancho de banda de la señal aumenta, también lo hace la frecuencia de muestreo, de forma que para ciertos tipos de señales la tarea de
ORIENTACIONES PARA LA MATERIA DE MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II. EBAU 2018
 ORIENTACIONES PARA LA MATERIA DE MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II. EBAU 2018 Criterios de evaluación Criterios específicos NÚMEROS Y ÁLGEBRA Matrices 1. Conocer el concepto de matriz y
ORIENTACIONES PARA LA MATERIA DE MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II. EBAU 2018 Criterios de evaluación Criterios específicos NÚMEROS Y ÁLGEBRA Matrices 1. Conocer el concepto de matriz y
Análisis de Datos. Validación de clasificadores. Profesor: Dr. Wilfrido Gómez Flores
 Análisis de Datos Validación de clasificadores Profesor: Dr. Wilfrido Gómez Flores 1 Introducción La mayoría de los clasificadores que se han visto requieren de uno o más parámetros definidos libremente,
Análisis de Datos Validación de clasificadores Profesor: Dr. Wilfrido Gómez Flores 1 Introducción La mayoría de los clasificadores que se han visto requieren de uno o más parámetros definidos libremente,
Modelos de Scoring para Riesgo de Crédito
 Modelos de Scoring para Riesgo de Crédito Los modelos de scoring de riesgo, dentro del proceso de otorgamiento de crédito, están orientados a anticipar comportamiento futuro. Podemos dividirlos en tres
Modelos de Scoring para Riesgo de Crédito Los modelos de scoring de riesgo, dentro del proceso de otorgamiento de crédito, están orientados a anticipar comportamiento futuro. Podemos dividirlos en tres
INTRODUCCIÓN. Capítulo OBJETIVO
 Capítulo 1 INTRODUCCIÓN La cuantización es un proceso que ha tomado gran importancia en las comunicaciones en general desde el momento en que las comunicaciones analógicas comenzaron a ser desplazadas
Capítulo 1 INTRODUCCIÓN La cuantización es un proceso que ha tomado gran importancia en las comunicaciones en general desde el momento en que las comunicaciones analógicas comenzaron a ser desplazadas
ARBOLES DE DECISION. Miguel Cárdenas-Montes. 1 Introducción. Objetivos: Entender como funcionan los algoritmos basados en árboles de decisión.
 ARBOLES DE DECISION Miguel Cárdenas-Montes Los árboles de decisión son estructuras lógicas con amplia utilización en la toma de decisión, la predicción y la minería de datos. Objetivos: Entender como funcionan
ARBOLES DE DECISION Miguel Cárdenas-Montes Los árboles de decisión son estructuras lógicas con amplia utilización en la toma de decisión, la predicción y la minería de datos. Objetivos: Entender como funcionan
Modelado de Objetos 3D II
 Decimotercera sesión 12 de abril de 2011 Operaciones sobre mallas Generación de Mallas Discretización (Muestreo) Las operaciones de generación y de modicación de mallas se hacen sobre espacios discretos
Decimotercera sesión 12 de abril de 2011 Operaciones sobre mallas Generación de Mallas Discretización (Muestreo) Las operaciones de generación y de modicación de mallas se hacen sobre espacios discretos
MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES I Y II CONTENIDOS BACHILLERATO
 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES I Y II CONTENIDOS BACHILLERATO BLOQUE 1. PROCESOS, MÉTODOS Y ACTITUDES EN MATEMÁTICAS Los contenidos de este bloque se desarrollan de forma simultánea al resto
MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES I Y II CONTENIDOS BACHILLERATO BLOQUE 1. PROCESOS, MÉTODOS Y ACTITUDES EN MATEMÁTICAS Los contenidos de este bloque se desarrollan de forma simultánea al resto
Universidad Técnica de Babahoyo CORRELACIÓN DE VARIABLES Y REGRESIÓN LINEAL
 Universidad Técnica de Babahoyo CORRELACIÓN DE VARIABLES Y REGRESIÓN LINEAL OBJETIVO Analizar las Diferentes formas de Describir la Relación entre dos variables numéricas Trazar un diagrama de dispersión
Universidad Técnica de Babahoyo CORRELACIÓN DE VARIABLES Y REGRESIÓN LINEAL OBJETIVO Analizar las Diferentes formas de Describir la Relación entre dos variables numéricas Trazar un diagrama de dispersión
EXPERIMENTOS COMPUTACIONALES EN UN ESTUDIO DE SIM
 EXPERIMENTOS COMPUTACIONALES EN UN ESTUDIO DE SIMULACIÓN DE MODELOS DE SERIES TEMPORALES PARA UNA MEJOR COMPRENSIÓN DE LAS HERRAMIENTAS RANDOM FOREST Y CONDITIONAL TREES SEPTIEMBRE 2016 TRABAJO FIN DE
EXPERIMENTOS COMPUTACIONALES EN UN ESTUDIO DE SIMULACIÓN DE MODELOS DE SERIES TEMPORALES PARA UNA MEJOR COMPRENSIÓN DE LAS HERRAMIENTAS RANDOM FOREST Y CONDITIONAL TREES SEPTIEMBRE 2016 TRABAJO FIN DE
Máster en comunicaciones. Clase 2. Modelos predictores.
 Máster en comunicaciones. Clase 2. Modelos predictores. 1. Introducción Uno de los cometidos más importantes de la estadística es la explotación de los datos observados de una o más características de
Máster en comunicaciones. Clase 2. Modelos predictores. 1. Introducción Uno de los cometidos más importantes de la estadística es la explotación de los datos observados de una o más características de
Unidad IV: Distribuciones muestrales
 Unidad IV: Distribuciones muestrales 4.1 Función de probabilidad En teoría de la probabilidad, una función de probabilidad (también denominada función de masa de probabilidad) es una función que asocia
Unidad IV: Distribuciones muestrales 4.1 Función de probabilidad En teoría de la probabilidad, una función de probabilidad (también denominada función de masa de probabilidad) es una función que asocia
Sobreajuste - Overfitting
 Sobreajuste - Overfitting Miguel Cárdenas-Montes Cuando se evalúa la calidad de un modelo o un ajuste, es importante medir el error en el conjunto de entrenamiento y en la predicción. La utilización exclusiva
Sobreajuste - Overfitting Miguel Cárdenas-Montes Cuando se evalúa la calidad de un modelo o un ajuste, es importante medir el error en el conjunto de entrenamiento y en la predicción. La utilización exclusiva
Técnicas Multivariadas Avanzadas
 Métodos de remuestreo Universidad Nacional Agraria La Molina 2014-2 Error de entrenamiento y prueba Estimación del error de predicción Los métodos de remuestreo constituyen una herramienta importante e
Métodos de remuestreo Universidad Nacional Agraria La Molina 2014-2 Error de entrenamiento y prueba Estimación del error de predicción Los métodos de remuestreo constituyen una herramienta importante e
RESUMEN PROGRAMACIÓN ESTADÍSTICA I. 3. Diseñar tablas estadísticas para coleccionar y ordenar datos.
 RESUMEN PROGRAMACIÓN ESTADÍSTICA I OBJETIVOS 1. Conocer los principales conceptos usados en Estadística: población, muestra e individuo. 2. Diferenciar los tres tipos de variables estadísticas: cualitativas,
RESUMEN PROGRAMACIÓN ESTADÍSTICA I OBJETIVOS 1. Conocer los principales conceptos usados en Estadística: población, muestra e individuo. 2. Diferenciar los tres tipos de variables estadísticas: cualitativas,
TEMA 3.- EL ANALISIS ESTADISTICO DE LA INFORMACION (MODELIZACION) DIFERENTES TIPOS DE PROCEDIMIENTOS ESTADISTICOS
 TEMA 3.- EL ANALISIS ESTADISTICO DE LA INFORMACION (MODELIZACION) PROCEDIMIENTOS ESTADISTICOS CONSTRUCCION DE MODELOS DIFERENTES TIPOS DE PROCEDIMIENTOS ESTADISTICOS Cada procedimiento es aplicable a un
TEMA 3.- EL ANALISIS ESTADISTICO DE LA INFORMACION (MODELIZACION) PROCEDIMIENTOS ESTADISTICOS CONSTRUCCION DE MODELOS DIFERENTES TIPOS DE PROCEDIMIENTOS ESTADISTICOS Cada procedimiento es aplicable a un
Figura 1: Propiedades de textura: (a) Suavidad, (b) Rugosidad y (c) Regularidad
 3 TEXTURA 3.1 CONCEPTO DE LA TEXTURA La textura es una característica importante utilizada en segmentación, identificación de objetos o regiones de interés en una imagen y obtención de forma. El uso de
3 TEXTURA 3.1 CONCEPTO DE LA TEXTURA La textura es una característica importante utilizada en segmentación, identificación de objetos o regiones de interés en una imagen y obtención de forma. El uso de
Capítulo 4. Reconocimiento de patrones. A lo largo del siglo pasado, se llevó a cabo investigación en el área de
 Capítulo 4 Reconocimiento de patrones 4.1 Reconocimiento de patrones como un campo de estudios A lo largo del siglo pasado, se llevó a cabo investigación en el área de reconocimiento de patrones en todas
Capítulo 4 Reconocimiento de patrones 4.1 Reconocimiento de patrones como un campo de estudios A lo largo del siglo pasado, se llevó a cabo investigación en el área de reconocimiento de patrones en todas
TEMA 1: SISTEMAS MODELADOS POR ECUACIONES DIFERENCIALES EN INGENIERÍA QUÍMICA. CLASIFICACIÓN. GENERALIDADES.
 TEMA 1: SISTEMAS MODELADOS POR ECUACIONES DIFERENCIALES EN INGENIERÍA QUÍMICA. CLASIFICACIÓN. GENERALIDADES. 1. INTRODUCCIÓN. PLANTEAMIENTO DE PROBLEMAS EN INGENIERÍA QUÍMICA 2. PROBLEMAS EXPRESADOS MEDIANTE
TEMA 1: SISTEMAS MODELADOS POR ECUACIONES DIFERENCIALES EN INGENIERÍA QUÍMICA. CLASIFICACIÓN. GENERALIDADES. 1. INTRODUCCIÓN. PLANTEAMIENTO DE PROBLEMAS EN INGENIERÍA QUÍMICA 2. PROBLEMAS EXPRESADOS MEDIANTE
Posibles trabajos HIA
 Posibles trabajos HIA Posibles trabajos Comparar otras herramientas de Minería de Datos con Weka Estudiar la influencia del ruido en bagging y boosting Estudiar la influencia del parámetro de poda en J48
Posibles trabajos HIA Posibles trabajos Comparar otras herramientas de Minería de Datos con Weka Estudiar la influencia del ruido en bagging y boosting Estudiar la influencia del parámetro de poda en J48
Anexo. Guía de uso de la herramienta Java de identificación.
 Anexo. Guía de uso de la herramienta Java de identificación. En este apartado se va a explicar una aplicación ("ejsidentescalon") que se ha desarrollado en JAVA, mediante el paquete Easy Java Simulations
Anexo. Guía de uso de la herramienta Java de identificación. En este apartado se va a explicar una aplicación ("ejsidentescalon") que se ha desarrollado en JAVA, mediante el paquete Easy Java Simulations
Conclusiones. Somos la suma de nuestras decisiones. WOODY ALLEN Delitos y Faltas (1989)
 Capítulo 7 Conclusiones Somos la suma de nuestras decisiones WOODY ALLEN Delitos y Faltas (1989) En este trabajo se ha presentado una nueva estrategia para construir árboles de decisión que ha conseguido
Capítulo 7 Conclusiones Somos la suma de nuestras decisiones WOODY ALLEN Delitos y Faltas (1989) En este trabajo se ha presentado una nueva estrategia para construir árboles de decisión que ha conseguido
Aux 6. Introducción a la Minería de Datos
 Aux 6. Introducción a la Minería de Datos Gastón L Huillier 1,2, Richard Weber 2 glhuilli@dcc.uchile.cl 1 Departamento de Ciencias de la Computación Universidad de Chile 2 Departamento de Ingeniería Industrial
Aux 6. Introducción a la Minería de Datos Gastón L Huillier 1,2, Richard Weber 2 glhuilli@dcc.uchile.cl 1 Departamento de Ciencias de la Computación Universidad de Chile 2 Departamento de Ingeniería Industrial
Programa Oficial de Asignatura. Ficha Técnica. Presentación. Competencias y/o resultados del aprendizaje. Estadística
 Ficha Técnica Titulación: Grado en Administración y Dirección de Empresas Plan BOE: BOE número 67 de 19 de marzo de 2014 Asignatura: Módulo: Métodos cuantitativos de la empresa Curso: 1º Créditos ECTS:
Ficha Técnica Titulación: Grado en Administración y Dirección de Empresas Plan BOE: BOE número 67 de 19 de marzo de 2014 Asignatura: Módulo: Métodos cuantitativos de la empresa Curso: 1º Créditos ECTS:
ANÁLISIS DE DATOS. Jesús García Herrero
 ANÁLISIS DE DATOS Jesús García Herrero ANALISIS DE DATOS EJERCICIOS Una empresa de seguros de automóviles quiere utilizar los datos sobre sus clientes para obtener reglas útiles que permita clasificar
ANÁLISIS DE DATOS Jesús García Herrero ANALISIS DE DATOS EJERCICIOS Una empresa de seguros de automóviles quiere utilizar los datos sobre sus clientes para obtener reglas útiles que permita clasificar
BOLETÍN OFICIAL DEL ESTADO
 Núm. 108 Sábado 6 de mayo de 2017 Sec. I. Pág. 36879 Bloque 1. Procesos, métodos y actitudes en matemáticas. Competencia matemática Matemáticas orientadas a las enseñanzas académicas Identifica patrones,
Núm. 108 Sábado 6 de mayo de 2017 Sec. I. Pág. 36879 Bloque 1. Procesos, métodos y actitudes en matemáticas. Competencia matemática Matemáticas orientadas a las enseñanzas académicas Identifica patrones,
Aprendizaje Automático
 Aprendizaje Automático Andrea Mesa 21 de mayo de 2010 Aprendizaje automático Otras denominaciones: machine learning, statistical learning, data mining, inteligencia artificial. Las técnicas de Aprendizaje
Aprendizaje Automático Andrea Mesa 21 de mayo de 2010 Aprendizaje automático Otras denominaciones: machine learning, statistical learning, data mining, inteligencia artificial. Las técnicas de Aprendizaje
MATEMÁTICAS CRITERIOS DE EVALUACIÓN Y CALIFICACIÓN BACHILLERATO CURSO
 MATEMÁTICAS CRITERIOS DE EVALUACIÓN Y CALIFICACIÓN BACHILLERATO CURSO 2006-07 1 MATEMÁTICAS I 1º BACHILLERATO CRITERIOS DE EVALUACIÓN Utilizar las estrategias del cálculo con números reales para resolver
MATEMÁTICAS CRITERIOS DE EVALUACIÓN Y CALIFICACIÓN BACHILLERATO CURSO 2006-07 1 MATEMÁTICAS I 1º BACHILLERATO CRITERIOS DE EVALUACIÓN Utilizar las estrategias del cálculo con números reales para resolver
CRITERIOS DE EVALUACIÓN EN LA E. S. O
 CRITERIOS DE EVALUACIÓN EN LA E. S. O CRITERIOS DE EVALUACIÓN 1º E. S. O... 2 CRITERIOS DE EVALUACIÓN 2º E. S. O... 3 CRITERIOS DE EVALUACIÓN 3º E. S. O... 4 CRITERIOS DE EVALUACIÓN 4º E. S. O opción A...
CRITERIOS DE EVALUACIÓN EN LA E. S. O CRITERIOS DE EVALUACIÓN 1º E. S. O... 2 CRITERIOS DE EVALUACIÓN 2º E. S. O... 3 CRITERIOS DE EVALUACIÓN 3º E. S. O... 4 CRITERIOS DE EVALUACIÓN 4º E. S. O opción A...
Qué es? Primer paso Representación en un sistema de coordenadas. numéricos Cada punto muestra el valor de cada pareja de datos (X e Y)
 Gráfico de dispersión Qué es? Primer paso Representación en un sistema de coordenadas cartesianas de los datos numéricos Cada punto muestra el valor de cada pareja de datos (X e Y) Gráfico de dispersión
Gráfico de dispersión Qué es? Primer paso Representación en un sistema de coordenadas cartesianas de los datos numéricos Cada punto muestra el valor de cada pareja de datos (X e Y) Gráfico de dispersión
Combinación de Clasificadores
 Combinación de Clasificadores Parte 1: Métodos de comité, Bagging, Boosting Reconocimiento de Patrones Departamento de Procesamiento de Señales Instituto de Ingeniería Eléctrica Facultad de Ingeniería,
Combinación de Clasificadores Parte 1: Métodos de comité, Bagging, Boosting Reconocimiento de Patrones Departamento de Procesamiento de Señales Instituto de Ingeniería Eléctrica Facultad de Ingeniería,
CAPÍTULO 4 METODOLOGÍA PROPUESTA
 CAPÍTULO 4 METODOLOGÍA PROPUESTA En este capítulo, se describen los métodos utilizados en el procedimiento propuesto para obtener soluciones del PLIDMC. En la actualidad, muchos de los problemas de optimización
CAPÍTULO 4 METODOLOGÍA PROPUESTA En este capítulo, se describen los métodos utilizados en el procedimiento propuesto para obtener soluciones del PLIDMC. En la actualidad, muchos de los problemas de optimización
LABORATORIO No. 0. Cálculo de errores en las mediciones. 0.1 Introducción
 LABORATORIO No. 0 Cálculo de errores en las mediciones 0.1 Introducción Es bien sabido que la especificación de una magnitud físicamente medible requiere cuando menos de dos elementos: Un número y una
LABORATORIO No. 0 Cálculo de errores en las mediciones 0.1 Introducción Es bien sabido que la especificación de una magnitud físicamente medible requiere cuando menos de dos elementos: Un número y una
Carteras minoristas. árbol de decisión. Ejemplo: Construcción de un scoring de concesión basado en un DIRECCIÓN GENERAL DE SUPERVISIÓN
 Carteras minoristas Ejemplo: Construcción de un scoring de concesión basado en un árbol de decisión Grupo de Tesorería y Modelos de Gestión de Riesgos Sergio Gavilá II Seminario sobre Basilea II Validación
Carteras minoristas Ejemplo: Construcción de un scoring de concesión basado en un árbol de decisión Grupo de Tesorería y Modelos de Gestión de Riesgos Sergio Gavilá II Seminario sobre Basilea II Validación
Aprendizaje no supervisado
 OPENCOURSEWARE REDES DE NEURONAS ARTIFICIALES Inés M. Galván José M. Valls Tema 4 1 Introducción Aprendizaje competitvo Otros algoritmos de agrupación 2 1 Introducción Características principales de las
OPENCOURSEWARE REDES DE NEURONAS ARTIFICIALES Inés M. Galván José M. Valls Tema 4 1 Introducción Aprendizaje competitvo Otros algoritmos de agrupación 2 1 Introducción Características principales de las
Tema 12: Introducción a la Estadística.
 MOLEDO GUGLIOTTA VICTOR Tratamiento de los datos Tema 12: Introducción a la Estadística. Al intentar interpretar la realidad a través de las herramientas que nos aporta la Estadística, lo primero que se
MOLEDO GUGLIOTTA VICTOR Tratamiento de los datos Tema 12: Introducción a la Estadística. Al intentar interpretar la realidad a través de las herramientas que nos aporta la Estadística, lo primero que se
GUÍA DOCENTE DE LA ASIGNATURA ESTADÍSTICA APLICADA
 GUÍA DOCENTE DE LA ASIGNATURA ESTADÍSTICA APLICADA DATOS BÁSICOS DE LA ASIGNATURA Nombre: Titulación: Centro: Tipo: Créditos: Curso: Prerrequisitos: Profesor: Dpto.: Estadística Aplicada. Licenciatura
GUÍA DOCENTE DE LA ASIGNATURA ESTADÍSTICA APLICADA DATOS BÁSICOS DE LA ASIGNATURA Nombre: Titulación: Centro: Tipo: Créditos: Curso: Prerrequisitos: Profesor: Dpto.: Estadística Aplicada. Licenciatura
GUIÓN ASIGNATURA DE MATEMÁTICAS ORIENTADAS A LAS ENSEÑANZAS APLICADAS 4ºESO 17/18
 GUIÓN ASIGNATURA DE MATEMÁTICAS ORIENTADAS A LAS ENSEÑANZAS APLICADAS 4ºESO 17/18 1. MATERIAL A TENER: Libro de texto. Bolígrafo azul o negro. Bolígrafo rojo, para corregir ejercicios y Pruebas Cortas.
GUIÓN ASIGNATURA DE MATEMÁTICAS ORIENTADAS A LAS ENSEÑANZAS APLICADAS 4ºESO 17/18 1. MATERIAL A TENER: Libro de texto. Bolígrafo azul o negro. Bolígrafo rojo, para corregir ejercicios y Pruebas Cortas.
Tema 2 Primeros Modelos Computacionales
 Universidad Carlos III de Madrid OpenCourseWare Redes de Neuronas Artificiales Inés M. Galván - José Mª Valls Tema 2 Primeros Modelos Computacionales 1 Primeros Modelos Computacionales Perceptron simple
Universidad Carlos III de Madrid OpenCourseWare Redes de Neuronas Artificiales Inés M. Galván - José Mª Valls Tema 2 Primeros Modelos Computacionales 1 Primeros Modelos Computacionales Perceptron simple
Objetivos. Epígrafes 3-1. Francisco José García Álvarez
 Objetivos Entender el concepto de variabilidad natural de un procesos Comprender la necesidad de los gráficos de control Aprender a diferenciar los tipos de gráficos de control y conocer sus limitaciones.
Objetivos Entender el concepto de variabilidad natural de un procesos Comprender la necesidad de los gráficos de control Aprender a diferenciar los tipos de gráficos de control y conocer sus limitaciones.
UNIDAD 7: SISTEMAS DE ECUACIONES. CONTENIDOS
 UNIDAD 7: SISTEMAS DE ECUACIONES. * Ecuaciones lineales con dos incógnitas. * Sistemas de 2 ecuaciones con 2 incógnitas. Resolución gráfica y analítica. * Sistemas equivalentes. * Tipos de sistemas de
UNIDAD 7: SISTEMAS DE ECUACIONES. * Ecuaciones lineales con dos incógnitas. * Sistemas de 2 ecuaciones con 2 incógnitas. Resolución gráfica y analítica. * Sistemas equivalentes. * Tipos de sistemas de
Representaciones gráficas de las distribuciones bidimensionales de frecuencias... 74
 Índice 1. Introducción al R 15 1.1. Introducción............................. 15 1.2. El editor de objetos R....................... 18 1.3. Datos en R............................. 19 1.3.1. Vectores...........................
Índice 1. Introducción al R 15 1.1. Introducción............................. 15 1.2. El editor de objetos R....................... 18 1.3. Datos en R............................. 19 1.3.1. Vectores...........................
Conocimiento de Matemáticas de 4º ESO. a) Contenidos, temporalización y secuenciación. Bloque 1. Planificación del proceso de resolución de
 Conocimiento de Matemáticas de 4º ESO. a) Contenidos, temporalización y secuenciación. Bloque 1. Planificación del proceso de resolución de problemas: análisis de la situación, selección y relación entre
Conocimiento de Matemáticas de 4º ESO. a) Contenidos, temporalización y secuenciación. Bloque 1. Planificación del proceso de resolución de problemas: análisis de la situación, selección y relación entre
CENTRO UNIVERSITARIO UAEM ZUMPANGO INGENIERO EN COMPUTACIÓN MUESTRAS ALEATORIAS Y DISTRIBUCIONES DE MUESTREO
 CENTRO UNIVERSITARIO UAEM ZUMPANGO INGENIERO EN COMPUTACIÓN MUESTRAS ALEATORIAS Y DISTRIBUCIONES DE MUESTREO ELABORÓ: M. EN C. LUIS ENRIQUE KU MOO FECHA: AGOSTO DE 2017 UNIDAD DE APRENDIZAJE PROBABILIDAD
CENTRO UNIVERSITARIO UAEM ZUMPANGO INGENIERO EN COMPUTACIÓN MUESTRAS ALEATORIAS Y DISTRIBUCIONES DE MUESTREO ELABORÓ: M. EN C. LUIS ENRIQUE KU MOO FECHA: AGOSTO DE 2017 UNIDAD DE APRENDIZAJE PROBABILIDAD
5. Descripción teórica de los modelos econométricos. La naturaleza del estudio que esta tesis pretende realizar nos lleva a enfrentarnos
 5. Descripción teórica de los modelos econométricos El problema de la auto-selección La naturaleza del estudio que esta tesis pretende realizar nos lleva a enfrentarnos inevitablemente a un problema de
5. Descripción teórica de los modelos econométricos El problema de la auto-selección La naturaleza del estudio que esta tesis pretende realizar nos lleva a enfrentarnos inevitablemente a un problema de
MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II DISTRITO ÚNICO DE ANDALUCÍA
 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II DISTRITO ÚNICO DE ANDALUCÍA CONTENIDOS Y OBJETIVOS MÍNIMOS PARA EL CURSO 2007/08. 1. INTRODUCCIÓN A LOS CONTENIDOS. ( Decreto 208/2002. B.O.J.A. de 20.08.02
MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II DISTRITO ÚNICO DE ANDALUCÍA CONTENIDOS Y OBJETIVOS MÍNIMOS PARA EL CURSO 2007/08. 1. INTRODUCCIÓN A LOS CONTENIDOS. ( Decreto 208/2002. B.O.J.A. de 20.08.02
La econometría : una mirada de pájaro
 La econometría : una mirada de pájaro Contenido Objetivo Definición de Econometría Modelos determinista y estocástico Metodología de la econometría Propiedades de un modelo econométrico Supuestos de un
La econometría : una mirada de pájaro Contenido Objetivo Definición de Econometría Modelos determinista y estocástico Metodología de la econometría Propiedades de un modelo econométrico Supuestos de un
1 - TEORIA DE ERRORES : distribución de frecuencias
 - TEORIA DE ERRORES : distribución de frecuencias CONTENIDOS Distribución de Frecuencias. Histograma. Errores de Apreciación. Propagación de errores. OBJETIVOS Representar una serie de datos mediante un
- TEORIA DE ERRORES : distribución de frecuencias CONTENIDOS Distribución de Frecuencias. Histograma. Errores de Apreciación. Propagación de errores. OBJETIVOS Representar una serie de datos mediante un
INTELIGENCIA EN REDES DE COMUNICACIÓN TRABAJO FIN DE CURSO. Las cuatro en raya
 INTELIGENCIA EN REDES DE COMUNICACIÓN TRABAJO FIN DE CURSO Las cuatro en raya Por Javier Martín Manzano Alejandro Bárcena Berzosa INFORME TÉCNICO El trabajo que se ha realizado, es un programa que consta
INTELIGENCIA EN REDES DE COMUNICACIÓN TRABAJO FIN DE CURSO Las cuatro en raya Por Javier Martín Manzano Alejandro Bárcena Berzosa INFORME TÉCNICO El trabajo que se ha realizado, es un programa que consta
Part I. Descripción estadística de dos variables. Estadística I. Mario Francisco. Variable. bidimensional. Distribuciones de frecuencias
 Part I Descripción de dos variables Introducción Si para un mismo individuo observamos simultáneamente k obtendremos como resultado una variable k-dimensional. Nos ocuparemos del estudio de las variables
Part I Descripción de dos variables Introducción Si para un mismo individuo observamos simultáneamente k obtendremos como resultado una variable k-dimensional. Nos ocuparemos del estudio de las variables
Dada f : [a, b] R R, continua, se plantea el problema de encontrar ceros de f, es decir raíces de la ecuación
![Dada f : [a, b] R R, continua, se plantea el problema de encontrar ceros de f, es decir raíces de la ecuación Dada f : [a, b] R R, continua, se plantea el problema de encontrar ceros de f, es decir raíces de la ecuación](/thumbs/59/43345437.jpg) Tema 8 Ceros de funciones Versión: 23 de abril de 2009 8.1 Introducción Dada f : [a, b] R R, continua, se plantea el problema de encontrar ceros de f, es decir raíces de la ecuación f(x) = 0. (8.1) La
Tema 8 Ceros de funciones Versión: 23 de abril de 2009 8.1 Introducción Dada f : [a, b] R R, continua, se plantea el problema de encontrar ceros de f, es decir raíces de la ecuación f(x) = 0. (8.1) La
Simulación INC SATCA 1 : Carrera:
 Datos Generales de la asignatura. Nombre de la asignatura: Clave de la asignatura: SATCA 1 : Carrera: Simulación INC-1027 2-2-4 Ingeniería Industrial Presentación. Esta asignatura aporta al perfil profesional
Datos Generales de la asignatura. Nombre de la asignatura: Clave de la asignatura: SATCA 1 : Carrera: Simulación INC-1027 2-2-4 Ingeniería Industrial Presentación. Esta asignatura aporta al perfil profesional
Carrera: Ingeniería Civil CIM 0531
 1.- DATOS DE LA ASIGNATURA Nombre de la asignatura: Carrera: Clave de la asignatura: Horas teoría-horas práctica-créditos: Probabilidad y Estadística Ingeniería Civil CIM 0531 3 2 8 2.- HISTORIA DEL PROGRAMA
1.- DATOS DE LA ASIGNATURA Nombre de la asignatura: Carrera: Clave de la asignatura: Horas teoría-horas práctica-créditos: Probabilidad y Estadística Ingeniería Civil CIM 0531 3 2 8 2.- HISTORIA DEL PROGRAMA
Estabilización Inteligente de Sistemas Eléctricos de Potencia (Parte II)
 ANEXO AL INFORME DEL PROYECTO INDIVIDUAL ESTABILIZACIÓN INTELIGENTE DE SISTEMAS ELÉCTRICOS DE POTENCIA (Parte II). CLAVE CGPI: 20071307 DIRECTOR: M. en C. FRANCISCO JAVIER VILLANUEVA MAGAÑA. I. RESUMEN.
ANEXO AL INFORME DEL PROYECTO INDIVIDUAL ESTABILIZACIÓN INTELIGENTE DE SISTEMAS ELÉCTRICOS DE POTENCIA (Parte II). CLAVE CGPI: 20071307 DIRECTOR: M. en C. FRANCISCO JAVIER VILLANUEVA MAGAÑA. I. RESUMEN.
Part VII. Estadística I. Mario Francisco. Introducción a la inferencia. Estimación puntual. Propiedades deseables de los estimadores
 Part VII La inferencia puede definirse como el conjunto de métodos mediante cuales podemos extraer información sobre distintas características de interés de cierta distribución de probabilidad de la cual
Part VII La inferencia puede definirse como el conjunto de métodos mediante cuales podemos extraer información sobre distintas características de interés de cierta distribución de probabilidad de la cual
TEMA 1: INTRODUCCIÓN N AL PROCESADO Y ANÁLISIS DE DATOS
 Procesado y Análisis de Datos Ambientales. Curso 2009-2010. José D. Martín, Emilio Soria, Antonio J. Serrano TEMA 1: INTRODUCCIÓN N AL PROCESADO Y ANÁLISIS DE DATOS ÍNDICE Introducción. Selección de variables.
Procesado y Análisis de Datos Ambientales. Curso 2009-2010. José D. Martín, Emilio Soria, Antonio J. Serrano TEMA 1: INTRODUCCIÓN N AL PROCESADO Y ANÁLISIS DE DATOS ÍNDICE Introducción. Selección de variables.
