Introducción a Mathematica
|
|
|
- Eugenia Duarte Reyes
- hace 8 años
- Vistas:
Transcripción
1 Introduccion a mathematica.nb Introducción a Mathematica Mathematica es un paquete de software matemático, de uso fácil y gran capacidad, que nos permitirá realizar las operaciones necesarias para resolver problemas que ya se abordaron en su momento en las diferentes asignaturas de matemáticas en cuatrimestres anteriores. En este primer apartado nos iniciaremos en el conocimiento básico de las funciones más importantes de Mathematica que nos serán imprescindibles para el posterior desarrollo de las prácticas de las diversas asignaturas. En cada práctica se hará un estudio de los comandos específicos que son necesarios para el desarrollo de las mismas.- Estructura interna de Mathematica Este paquete tiene una estructura que permite su utilización en diferentes entornos, Pc, Mac, Unix, etc. Para ello está dispuesto en dos partes fundamentales. El Kernel (motor de cálculo ) y el Front End (Interfaz de comunicación con el usuario). Cuando se comienza a utilizar el programa se activa el Front End con lo que se puede comenzar a introducir datos y expresiones. En el momento en que se desea realizar la primera operación se activa el Kernel que es el módulo que realiza el cálculo. En el Kernel se encuentran introducidos los procedimientos de cálculo relacionados con una gran cantidad de operaciones ( las más habituales ). Sin embargo, dada la potencia de cálculo del paquete, operaciones y procedimientos más complejos se encuentran almacenados en diferentes Packages que deben ser activados antes de realizar los cálculos con ese tipo de sentencias. En el entorno Windows en que nos movemos, el Front End está dispuesto de manera que todo el desarrollo realizado puede ser almacenado prácticamente como en un editor de texto y tiene además todas las características de conectividad con otros paquetes que funcionen en el mismo entorno windows (OLE). También, muchos de los comandos que ejecuta Mathematica han sido introducidos en ventanas gráficas Palettes que permiten una más rápida implementación de las sentencias y evitan memorizar parte de los comandos utilizados. Todas estas características permiten un manejo sencillo y rápido de modo que, con una pequeña introducción a las funciones básicas, al modo de introducir datos y la utilización de la ayuda, se puede manejar con soltura en un corto espacio de tiempo.
2 Introduccion a mathematica.nb Introducción de datos y operaciones Comenzar a trabajar con Mathematica es muy sencillo, basta con introducir la operación que se desea realizar y pulsar las teclas Shift + Intro. Así Mathematica realiza la operación In[]:= 2 3 Out[]= 6 De este modo las operaciones quedan numeradas en el orden en que se van realizando, con lo que se pueden ir utilizando los resultados previos con solo indicar en que momento se obtuvieron. El resultado de la última operación se puede recuperar utilizando el símbolo %, el penúltimo mediante %% y en general el resultado de la k-ésima operación con el símbolo %k.por tanto, la siguiente operación hace referencia al resultado obtenido en la primera operación In[2]:= H3 + 9Lê% Out[2]= 2 En Mathematica el producto de dos factores se puede representar tanto por el asterisco como por un espacio en blanco. Es importante recordar que cuando se opera con variables no es lo mismo escribir x y que xy ya que Mathematica en el primer caso entiende x*y mientras que en el segundo considera una nueva variable llamada (xy). Las operaciones algebraicas comunes y el orden de evaluación de los diferentes factores sigue el mismo criterio que cualquier lenguaje de programación. En cualquier caso siempre se puede controlar la operación que se realiza colocando paréntesis. 3.- Precisión en el cálculo Mathemática intenta siempre llegar al resultado más aproximado en cada operacion que realiza y siempre que puede llega al resultado exacto. De este modo cuando se realiza el cociente de dos números enteros matemática da como resultado dicho cociente puesto que si sacara un número decimal perdería precisión. In[3]:= 3 ê 5 Out[3]= 3 5
3 Introduccion a mathematica.nb 3 Lo mismo sucede cuando se realizan operaciones con variables. Siempre que no se pueda simplificar Mathematica presenta el valor que se ha introducido. In[4]:= Out[4]= Hx^3+ 5Lêx^2 5 + x 3 x 2 En ocasiones puede interesar llegar a un resultado aproximado en vez de al resultado exacto, para hacerse una idea del orden de magnitud del resultado obtenido. Para ello se pueden aplicar tres métodos a) Introducir alguno de los factores de la operación que se desea realizar de forma aproximada. Para ello basta con poner en forma decimal algún factor. Ej: 0 = 0.0 ( con poner tan solo el punto decimal es suficiente) In[5]:= 3. ê 5 Out[5]= 0.6 b) Utilizar el comando N[ ]. Con este comando se puede obtener el resultado de forma aproximada e incluso indicar el número de decimales que se desea que aparezcan. Primero se introduce la operación a realizar y separado con una coma el número de dígitos significativos. In[6]:= N@20 ê 7, 5D Out[6]=.765 c) Utilizar el comando N pero al final de la expresión que se desea evaluar de la siguiente manera expr //N ( Por defecto Mathematica presenta 6 dígitos significativos ). In[7]:= 20 ê 7 êê N Out[7]= Comandos y variables predefinidas Mathematica incorpora tanto sus propios comandos como algunas variables de uso muy frecuente de modo que la primera letra es siempre mayúscula. Para evitar confusiones o errores entre las variables definidas por el usuario y las ya definidas por el programa se recomienda definir variables propias que comiencen por letras minúsculas. Entre las variables definidas en el programa se encuentran Pi, E, I.
4 Introduccion a mathematica.nb 4 In[8]:= N@PiD Out[8]= In[9]:= N@ED Out[9]= In[0]:= Out[0]=, H L En cuanto a los comandos, todos ellos comienzan también con mayúscula y además el argumento que introducimos así como el resto de datos para el control de la operación van entre corchetes. Comando[arg, control_, control_2,... ] In[]:= Out[]= Cos@Pi ê 3D 2 In[2]:= Plot3D@Sin@x yd, 8x, 2, 2<, 8 y, 2, 2<D Out[2]= SurfaceGraphics 4..- Funciones Matemáticas Comunes Las funciones matemáticas más comunmente utilizadas pueden introducirse directamente atendiendo al comando o también mediante las paletas que proporciona Mathematica. Para uitlizar estas Paletas basta con situarse en la barra superior en el comando File y en Palettes seleccionar la paleta Basic Calculations. En esta paleta aparecen tanto funciones como comandos muy utilizados. Por ejemplo, para indicar que se desea realizar una raiz cuadrada se puede utilizar el comando Sqrt[ ] o también se puede utilizar el icono correspondiente que aparece en la paleta è!!!! Ñ en este caso basta
5 Introduccion a mathematica.nb 5 con rellenar el recuadro con la expresión que se desea evaluar. En esta paleta también aparecen funciones trigonometricas tanto directas como inversas Sin[ ], ArcCos[ ], y las correspondientes expresiones Hiperbólicas Cosh[ ], ArcTanh[ ]. Repasando esta paleta se pueden encontrar funciones como el factorial!, el entero mas cercano a x Round[x], etc. Ejercicios de las secciónes 2,3,4 - Utilice N para calcular p con 50 decimales. - Utilice N para ver a que entero se aproxima E p. A continuación utilizar los comandos Floor[E p ] y Ceiling[E p ]. - Calcule dos números aleatorios con Random[ ] y a continuación multiplíquelos 5.- Listas En muchas ocasiones es necesario utilizar datos que se encuentran relacionados entre si y que pueden ser todos ellos el argumento de una función. En esas ocasiones utilizamos listas para definir todos estos elementos. Una lista contiene elementos que se encuentran separados por comas de la siguiente manera: In[3]:= 8, 3, 6, 9, 2< Out[3]= 8, 3, 6, 9, 2< De este modo todos estos elementos se pueden utilizar como una única variable. In[4]:= 2^% Out[4]= 82, 8, 64, 52, 4096< En una lista se pueden introducir elementos que no sean del mismo tipo, como valores numéricos, variables, texto, etc. En estos casos deberemos referirnos a uno específicamente para poder realizar la operación correspondiente. Para ello se considera la posición que ocupa dicho elemento en la lista y se hace referencia a él de la siguiente manera: In[5]:= a = 82.4, x, 8 2, 6<, Pi< Out[5]= 82.4, x, 82, 6<, π< Una vez definida la lista pasamos a operar con los elementos de la misma. La expresión a[[i]] hace referencia al elemento i-esimo de la lista.
6 Introduccion a mathematica.nb 6 In[6]:= 3 a@@dd Out[6]= 7.2 In[7]:= a@@2dd ^3 Out[7]= x 3 In[8]:= Out[8]= Cos@a@@4DDD In[9]:= 2 a@@3dd Out[9]= 84, 2< El tercer elemento de la lista es a su vez una lista por lo que se puede hacer referencia al elemento en si, a[[3]], o a cada uno de los elementos que lo componen a[[3,]] y a[[3,2]] pudiendo operar con ellos por separado In[20]:= a@@2dd^a@@3, DD Out[20]= x 2 In[2]:= a@@2dd ^a@@3, 2DD Out[2]= x 6 Este tipo de listas tienen gran aplicación, para dar límites de integración, zonas donde se desea dibujar una función y fundamentalmente para el trabajo con matrices. Toda matriz se expresa como una lista, de modo que se puede definir un vector como una lista unidimensional {,2,3}mientras que una matriz es una lista bidimensional {{,3,5},{2,4,6}} (matriz 2x3). Mathematica cuando devuelve resultados también los devuelve en forma de lista, por ejemplo cuando proporciona las raices de un polinomio. Ejemplos: In[22]:= Plot@x^2, 8x, 3, 3<D
7 Introduccion a mathematica.nb Out[22]= Graphics In[23]:= Integrate@x^2, 8x, 0, 2<D Out[23]= 8 3 In[24]:= a = 88, 3, 5<, 8 2, 4, 6<< Out[24]= 88, 3, 5<, 82, 4, 6<< In[25]:= MatrixForm@aD Out[25]//MatrixForm= J N In[26]:= Out[26]= 2 x^2 5 x 4 == 0, xd êênd 88x.85577<, 8x 3.774<, 8x << Las operaciones 24 y 25 hacen referencia a operaciones con matrices. La 24 define una matriz de dos filas y tres columnas mientras que MatrixForm[ ] representa la Lista anterior en forma matricial. La última operación calcula las raices de la ecuación y devuelve una lista de tres listas cada una de ellas con un elemento ( una solución de la ecuación). Como veremos posteriormente, no será necesario memorizar todo este tipo de comandos puesto que una de las herramientas más útiles de Mathematica 3.0 (las paletas de comandos) nos permitirá introducir estas sentencias de otra forma Utilizando el comando Table se pueden generar listas sin dar explícitamente cada uno de los elementos que la componen. Basta con indicar la expresión a través de la que se genera y el número de elementos que la componen de la siguiente manera: Table[expresión,{i, min,max,paso}] donde la expresión es una expresión en la que i variará entre los valores mínimo y máximo especificados y considerando el paso indicado en la lista. In[27]:= Table@x^i, 8i, 2, 9, 2<D Out[27]= 8x 2,x 4,x 6,x 8 <
8 Introduccion a mathematica.nb 8 Se pueden generar de esta manera listas de varias dimensiones, introduciendo en vez de una única expresión una lista de expresiones In[28]:= Table@8E^Hj 2L, j 2 ê 3<, 8 j, 3, 5<D Out[28]= 98, 2<, 9 2, 8 3 =, 9 3, 0 3 == Si no se indica el paso se considera que vale uno. De igual manera, si no se indica el valor mínimo se comienza desde uno In[29]:= Table@i, 8 i, 4<D Out[29]= 8, 2, 3, 4< Asi como conseguimos listas dimensiones introduciendo varias expresiones,también se pueden conseguir listas de este tipo introduciendo varios índices. In[30]:= Table@i + j, 8 i,, 3<, 8 j, 2, 5<D Out[30]= 883, 4, 5, 6<, 84, 5, 6, 7<, 85, 6, 7, 8<< In[3]:= MatrixForm@%D Out[3]//MatrixForm= i y j z k { Se ha obtenido una matriz bidimensional en las columnas hacen referencia a todos distintos valores de j (2,3,4,5) mientras que las filas hacen referencia a los valores de i (,2,3) Ejercicios de la sección 5 - Utilice Table para hacer una lista de cinco nueves - Utilice Table para hacer una lista conjunta de los cuadrados y los cubos de los numeros pares del uno al nueve - Utilice Table para crear una lista con las potencias de x de 2 a 9 con paso 3 - Seleccione de la lista anterior x 5 y evalúelo para x = 2 - Crear con el comando Table una matriz 3 x Funciones definidas por el usuario
9 Introduccion a mathematica.nb 9 En general los ejercicios que realizaremos con Mathematica no serán únicamente operaciones aritméticas sino que se necesitará utilizar funciones definidas por el usuario para realizar el análisis de las mismas asi como para operar con elllas. Por ello se debe aprender a definir funciones de una o varias variables, así como evaluar las mismas para cualquier punto. 6..-Definición de funciones Para definir funciones, igual que cualquier otra variable definida por el usuario, se recomienda utilizar palabras que empiecen por minúscula o letras minúsculas, para evitar que las variables definidas por el usuario se confundan con variables o comandos propios de Mathematica. La definición de funciones es muy sencilla basta con indicar la expresión correspondiente de la siguiente manera: In[32]:= f@x_d := x^3+ 2 x^2+ 3x+ 5 Esta sentencia no da ningún resultado puesto que tan solo se trata de una definición. Para ver que efectivamente la expresión que se ha introducido se corresponde con la deseada basta con preguntar cual es la función f que se ha definido, de la siguiente manera: In[33]:=?f Global`f f@x_d := x 3 + 2x 2 + 3x+ 5 Es fundamental definir de esta manera las funciones, colocando como variable independiente la variable x_, este símbolo permite considerar la variable x como una variable global que puede ser tanto un valor numérico como una expresión en la que haya definidas otras variables In[34]:= f@y zd Out[34]= Hy zl + 2 Hy zl 2 + Hy zl 3 In[35]:= f@3d Out[35]= 59 Del mismo modo se pueden asignar valores a las variables de las funciones a través de la expresión /. de la forma siguiente: In[36]:= f@xd ê. x > 3
10 Introduccion a mathematica.nb 0 Out[36]= 59 In[37]:= f@xd ê. x > u + v Out[37]= Hu + vl + 2 Hu + vl 2 + Hu + vl 3 El símbolo /. se puede considerar como "Tal que" de forma que la última operación se puede traducir como: calcular cuanto vale f[x] tal que x=a+b. Lo mismo que se ha realizado para una función de una variable se podría reañizar para funciones de varias variables. In[38]:= m@x_, y_d := x^2+ 2 y x+ 5 x + 2 In[39]:= m@x, yd ê. 8x > 2, y > 5< Out[39]= 36 In[40]:= m@x, yd ê. 8x > r s, y > t< Out[40]= Hr sl + Hr sl Hr sl t Las funciones que se han definido hasta el momento tienen un dominio que para las funciones polinómicas, por ejemplo, es todo el conjunto de los números reales. Sin embargo se pueden definir también funciones a trozos, definiendo en cada caso en que dominio esta definida la función. Se pueden representar este tipo de funciones de tres formas distintas..- Asignando sucesivamente los valores de la función en cada intervalo. In[4]:= g@x_ ê; x < 2D := 3x; g@x_ ê; 2 <= x <= 2D := 6; g@x_ ê; x > 2D := 3 x In[44]:= Plot@g@xD, 8x, 4, 4<, PlotRange > 80, 2<D Out[44]= Graphics Se ha definido la función g[x] dividida en tres trozos,x<-2, -2<=x<=2, x>2. Se puede definir la misma función con el comando Which:
11 Introduccion a mathematica.nb In[45]:= h@x_d := Which@ x < 2, 3 x, 2 <= x <= 2, 6, x > 2, 3 xd In[46]:= Plot@h@xD, 8x, 4, 4<D Out[46]= Graphics En este caso se definen los intervalos y seguidos con comas los valores de la función en estos intervalos de la forma: Which[intervalo, valor, intervalo2,valor,...] Por último, otra forma de definir funciones a trozos es introduciendo el comando if In[47]:= j@x_d := If@x < 3, 2, x 2D In[48]:= Plot@j@xD, 8x, 0, 6<D Out[48]= Graphics En este caso debido a la nomenclatura del comando If tan solo se pueden dividir en dos intervalos ya que se pueden asignar valores distintos en función de que se cumpla la condición o no se cumpla. El comando If se define de la siguiente manera: If [condición,expresión,expresión2]. De esta manera si se cumple la condición se ejecuta la expresión y si no se cumple la expresión se ejecuta la expresión Operando con expresiones algebraicas Cuando se opera con expresiones algebraicas Mathematica proporciona el resultado exacto ( si puede conseguirlo ). Sin embargo las expresiones que se obtienen pueden parecer muy complejas puesto que en ese proceso el paquete no se preocupa de reducir al máximo la expresión. Por ello
12 Introduccion a mathematica.nb 2 siempre que las expresiones resulten complejas es muy ùtil considerar el comando Simplify[ ] que simplifica al máximo la expresión con que se trabaja. Por ejemplo: In[49]:= x^3+ 3 x^2+ 3 x + Out[49]= + 3x+ 3x 2 + x 3 In[50]:= Simplify@%D Out[50]= H + xl 3 In[5]:= x 4 x Out[5]= H 2 ArcTan@xD + Log@ + xd Log@ + xdl 4 In[52]:= Out[52]= D@%, xd 4 J + x + x 2 + x 2 N In[53]:= Out[53]= Simplify@%D + x 4 En las tres ùltimas operaciones se ha realizado una integral indefinida, a continuación se ha realizado la derivada del resultado y por ùltimo se ha simplificado la expresión En este último ejemplo vemos como obtenemos el resultado inicial al derivar el resultado obtenido de la integral anterior, aunque si no hubieramos utilizado el comando Simplify[ ] resultaría difícil darse cuenta de ello. Otra operación que se puede realizar es la de obtener los factores de una expresión algebraica, muy ùtil para obtener las raices de un polinomio, por ejemplo. Para ello se utiliza el comando Factor[ ] In[54]:= + 4x+ 6x 2 + 4x 3 + x y + 36 x y + 36 x 2 y + 2 x 3 y + 54 y x y x 2 y y x y y 4 Out[54]= + 4x+ 6x 2 + 4x 3 + x y + 36 x y + 36 x 2 y + 2 x 3 y + 54 y x y x 2 y y x y y 4 In[55]:= Factor@%D Out[55]= H + x + 3yL 4
13 Introduccion a mathematica.nb 3 In[56]:= Plot3D@%%, 8x, 5, 5<, 8y, 2, 2<D Out[56]= SurfaceGraphics In[57]:= << Graphics`ImplicitPlot` In[58]:= ImplicitPlot@ + x + 3 y == 0, 8x, 5, 5<D Out[58]= Graphics De este modo la representación en dos dimensiones indica los puntos de corte de la superficie definida con el plano z=0. Del mismo modo puede interesar en ocasiones obtener el desarrollo completo de una expresión algebraica que está simplificada. Para ello se utiliza le comando Expand[ ] como veremos en el siguiente ejemplo In[59]:= Hx^2+ L^2 Hx + 2L^3 Out[59]= H2 + xl 3 H + x 2 L 2 In[60]:= Expand@%D Out[60]= x + 22 x x x x 5 + 6x 6 + x 7 Ejercicios de la sección 6 - Representar como f(x) la función ( x+2 )Hx - L 2 Hx - 2L 3 - Dibujar dicha función con el comando Plot entre x = -3, x = 3
14 Introduccion a mathematica.nb 4 - Expandir la expresión de f(x) hasta obtener un polinomio de grado 6 en x - Aplicar la expresión Factor [ ] para llegar a la expresión de partida. 7.- Paletas Una de las mejoras sustanciales de Mathematica 3.0 en cuanto a la comunicación con el usuario es la presentación de paletas que permiten introducir sentencias y realizar operaciones de forma más sencilla. Para algunas sentencias de Mathematica como Sqrt[ ] ( Raiz Cuadrada ), Sum[ ] ( Sumatorio ), Product[ ] ( Producto ),etc. resulta complicado escribir en el notebook cual es la operación que se desea realizar, mientras que con las paletas estas operaciones vienen representadas por sus símbolos matemáticos por lo que basta con introducir los datos de la operación para que ésta se pueda llevar a cabo. Los símbolos que utilizan estas paletas para realizar las operaciones anteriores son: è!!!! Ñ Ñ Ñ, Ñ=Ñ Ñ, Ñ=Ñ Ñ. Introduciendo en los recuadros los valores deseados se completa la sentencia con lo que se puede realizar la operación. Basta con pulsar el tabulador para pasar de un recuadro a otro e ir llenando la sentencia completa. En este sentido Mathematica 3.0 introduce ya como predefinidas una serie de paletas en las que se representan tanto comandos, como operaciones, caracteres, matrices,etc. Para ver todas ellas basta con activar en el menu File la palabra Palettes con lo que se puede ver todas las paletas predefinidas. Una de las aplicaciones mas comodas de las paletas es la definición de matrices puesto que partiendo de matrices 2 x 2 que aparecen en la paleta se puede llegar a conseguir matrices de cualquier dimensión. Se aumenta el número de filas con el comando " Control + Intro" mientras que el número de columnas aumenta al pulsar "Control +," 8.- Gráficos con Mathematica Una herramienta de apoyo muy importante a la hora de resolver una gran cantidad de problemas matemáticos ( sobre todo de una y dos variables ) es la representación de funciones. De esta manera se pueden ver cuales son los extremos de una función, sus asíntotas, etc. Mathematica dispone de una gran cantidad de comandos que permiten representar curvas y superfi-
15 Introduccion a mathematica.nb 5 cies. En este apartado se hará una exposición general de los comandos que se utilizarán posteriormente en las prácticas de las diferentes asignaturas. Debido a que la nomenclatura es exactamente igual se introducirán de forma conjunta las expresiones de dibujo en dos y tres variables Plot, Plot3D Estos comandos generan la función f en un recinto definido por el usuario. La forma de expresarlo es la siguiente: Plot[ f, {x,x_min,x_max}] Plot3D[f, {x,x_min,x_max},{y,y_min,y_max}] Ejemplos: Definimos previamente dos funciones, una de una variable y otra de dos variables y posteriormente las representamos. In[6]:= f@x_d := Sin@xD + x^2ê 2 In[62]:= g@x_, y_d := x^2+ y x 2y A continuación pasamos a representar ambas funciones In[63]:= Plot@f@xD, 8x, Pi, Pi<D Out[63]= Graphics In[64]:= Plot3D@g@x, yd, 8x, 2, 2<, 8y, 2, 2<D
16 Introduccion a mathematica.nb 6 Out[64]= SurfaceGraphics Estos dos comandos permiten dibujar funciones de la forma y = f(x) o z = g(x,y). Por otro lado una grán cantidad de funciones no vienen representadas de forma explícita e incluso es imposible despejar una de las variables en función del resto. Por ello se necesita otra serie de comandos que nos permitan representar esas funciones. Las otras dos formas en que mas habitualmente se presentan las funciones son la forma paramétrica y la forma implícita. A continuación veremos como se representan las funciones cuando viene definidas de esta manera ParametricPlot, ParametricPlot3D Estos comandos permiten representar funciones que vienen definidas a través de parámetros. Una función de dos variables se representaría de la siguiente manera: x = x(t) y = y(t)a medida que varía el parametro se obtienen puntos de la curva. Para el caso de tres dimensiones a través de expresiones paramétricas se pueden representar tanto curvas como superficies. Una curva se representa de la siguiente manera: x = x(t) y = y(t)variando t se obtiene una familia simplemente infinita de puntos ( una curva ) z = z(t) Para representar una superficie se necesitan dos parámetros, de forma que se obtiene una familia doblemente infinita de puntos que generan la superficie. La superficie se reptresenta de la siguiente manera: x=x( u,v) y=y( u,v) z=z( u,v) Vista esta introducción podemos presentar la forma de utilizar los comandos ParametricPlot y ParametricPlot3D. ParametricPlot [{x,y},{t,t_min,t_max}] ParametricPlot3D[{x,y,z},{u,u_min,u_max},{v,v_min,v_max}] In[65]:= ParametricPlot@8Cos@5 td, Sin@3 td<, 8t, 0, 2 π<d
17 Introduccion a mathematica.nb Out[65]= Graphics La función representada es x=cos[5*t],y=sin[3*t]. Para el caso de ParametricPlot3D veremos un ejemplo de una curva y otro de una superficie. In[66]:= ParametricPlot3D@8Cos@5 td, Sin@3 td, Sin@tD<, 8t, 0, 2 π<d Out[66]= Graphics3D Se trata de una curva puesto que tan solo se tiene un parámetro. La función es de la forma: x=cos[5t] y=sin[3t] z=sin[t] Para el caso de una superficie: In[67]:= ParametricPlot3D@8Cos@uD Cos@vD, Sin@uD Cos@vD, Sin@vD<, 8u, 0, 2 Pi<, 8v, Pi, Pi<D
18 Introduccion a mathematica.nb Out[67]= Graphics3D La superficie representada es : x=cos[u]*cos[v] y=sin[u]*cos[v] z=sin[v] ImplicitPlot Este comando se emplea para representar funciones definidas de forma implicita de dos variables. Para poder utilizar estos comandos se debe hacer referencia a paquetes especificos que tienen los programas con los que se ejecutan estos comandos. Para cargar estos paquetes se debe ejecutar la siguiente orden: <<Graphics`ImplicitPlot` Estas instrucciones permiten cargar la librerís de tipo grafico que permite representar funciones implicitas de dos variables. In[68]:= << Graphics`ImplicitPlot` Una vez cargadas las librerías, pasamos a explicar la nomenclatura de cada uno de los dos comandos. ImplicitPlot[eq,{x,x_min,x_max}]. Donde eq es la ecuación que define la función implicita y se introduce además el intervalo donde se dibuja la función. In[69]:= ImplicitPlot@x^2+ y^2 4 == 0, 8x, 3, 3<D
19 Introduccion a mathematica.nb Out[69]= Graphics In[70]:= h@x_, y_d := 3 x + 5 y In[7]:= ImplicitPlot@h@x, yd == 3, 8x, 3, 3<D Out[7]= Graphics In[72]:= Show@%, %%%D Out[72]= Graphics In[73]:= ImplicitPlot@8x^2+ y^2 4 == 0, h@x, yd == 3<, 8x, 3, 3<D
20 Introduccion a mathematica.nb Out[73]= Graphics En los dos últimos ejemplos se han presentado dos formas distintas de representar varias finciones en un mismo gráfico. El comando Show[ ] permite representar diferentes gráficos combinados. Mientras que el comando ImplicitPlot permite representar varios gráficos a la vez agrupados entre llaves El comando ImplicitPLot3D representa funciones de tres variables en forma implícita. La nomenclatura es de la siguiente forma: ImplicitPlot3D[eq,{x,x_min,x_max},{y,y_min,y_max},{z,z_min,z_max}] Ejemplos: Ejercicios de la sección 8 - Dibujar la función sen(x)/x así como la función sen(x) en el intervalo (-0,0) - Dibujar la función x*y - Dibujar la función paramétrica x = 4 Cos(-t / 4)+7 Cos(t) y = 4 Sin(-t / 4)+7 Sin(t) Desde 0 a 8Pi - Dibujar la funcion x= Cos(u)Sin(v) y= Cos(u)Cos(v) z=v - Dibujar la función : 4x^2+y^2= 9.- Packages Una de las caracteríaticas más importantes de Mathematica es que se trata de un sistema extensible. Es decir, hay una gran cantidad de funciones matemáticas, constantes, etc. que están introducidas en el programa. Pero utilizando el lenguaje de Mathematica se pueden añadir más funciones a las ya existentes. En general, cuando se realizan las operaciones mas comunes es suficiente con el programa para que se puedan ejecutar. Sin embargo cuando se trabaja en un campo específico, hay una serie de funci-
21 Introduccion a mathematica.nb 2 ones que no están especificadas en Mathematica y se introducen de otro modo. En estos casos se pueden utilizar los Mathematica Packages que son librerías en las que se encuentran definidos procedimientos de cálculo relacionados con operaciones matemáticas mas específicas. Estos Packages consisten en funciones definidas en el lenguaje de Mathematica que le permiten al programa realizar estas operaciones mas complejas. Para poder utilizar las funciones que se encuentran en estos Packages en primer lugar se debe indicar a Mathematica que se van a utilizar en la sesión funciones específicas de ese paquete. Para ello se carga el paquete en cuestión de la siguiente manera: In[74]:= << Calculus`VectorAnalysis` Una vez cargado este Package ya se pueden realizar operaciones relacionadas con los comando que introduce este fichero como pueden ser el cálculo de la divergencia, del gradiente, etc In[75]:= Grad@5 x^2 y^3 z^4, Cartesian@x, y, zdd Out[75]= 80 x y 3 z 4,5x 2 y 2 z 4,20x 2 y 3 z 3 < Existen una gran cantidad de Packages que ya vienen cargados en la instalación de Mathematicas referentes a diversos campos como son : Algebra, Cálculo, Matemática Discreta, Geometría, Gráficos, Algebra Lineal, Estadística,etc. Dentro de cada uno de estos campos se encuentran diversos Packages que se van cargando. Para ver con detenimiento los distintos Packages que proporciona Mathematica utilice la ayuda de Mathematica y en el apartado de Add-ons seleccione el campo Standard Packages. A partir de aqui seleccionando cada uno de los campos se pueden ver los diferentes Packages que existen para cada rama matemática. Como se puede apreciar al cargar el paquete en la sesion de Mathematica se hace referencia al campo general del paquete (en nuestro caso Calculus) y a continuación encerrado entre tildes " ` " el paquete particular que se desea cargar (`VectorAnalysis`). Recordando operaciones que se hicieron en su momento, al explicar ImplicitPlot e ImplicitPlot3D vimos como se tenían que cargar dos paquetes que se encontraban en el directorio Graphics que eran: <<Graphics`ImplicitPlot` <<Graphics`ImplicitPlot3D` 0.- Resolución de Ecuaciones Mathematica dispone de un amplio grupo de sentencias que permiten resolver ecuaciones. Dependiendo del tipo de ecuación que se desee resolver y las variables y parámetros que tenga será conveniente utilizar uno u otro de los comandos que a continuación se exponen. Roots[ ecuación, variable ] permite obtener las raices de una ecuación polinómica en la variable que
22 Introduccion a mathematica.nb 22 se indica en la expresión. Este comando funcionará correctamente siempre que se pueda obtener de forma exacta la raiz del polinomio. In[76]:= Out[76]= Roots@Hx + 2L^3 Hx 3L == 0, xd x 3»» x 2»» x 2»» x 2 In[77]:= Out[77]= Roots@Hx + y L Hx 2L == 0, xd x 2»» x y In[78]:= Out[78]= Roots@Hx + y L Hx 2L == 0, yd y x La expresión Roots[ ] devuelve todas las raices de la ecuación.en caso de haber mas de una solución relaciona todas ellas mediante operadores lógicos ( significa OR, && significa AND ). En caso que no se pueda obtener el valor exacto de la raiz se utilizarà el comando NRoots[ ] que proporciona una solución aproximada. In[79]:= Out[79]= Roots@x^7+ x + 4 == 0, xd x Root@4 + # + # 7 &, D»» x Root@4 + # + # 7 &, 2D»»x Root@4 + # + # 7 &, 3D»» x Root@4 + # + # 7 &, 4D»»x Root@4 + # + # 7 &, 5D»» x Root@4 + # + # 7 &, 6D»»x Root@4 + # + # 7 &, 7D In[80]:= NRoots@x^7+ x + 4 == 0, xd Out[80]= x.6076»» x »» x »» x »» x »» x »» x En este último ejemplo se puede ver como intentando obtener las raices con el comando Roots no se llega a una solución por lo que hay que buscar la solución aproximada. Para un caso mas general en que se desea resolver una ecuación cualquiera se utiliza el comando Solve[ ] que funciona de la misma manera que el comando Roots[ ] In[8]:= Solve@Hx + 2L^3 Hx 3L == 0, xd Out[8]= 88x 2<, 8x 2<, 8x 2<, 8x 3<< Los resultados se presentan en una lista en que se asignan a x un valor con el signo x->. Cuando no se pueden obtener los valores exactos la solución queda en función del comando Root y se puede obtener la solución aproximada aplicando el comando N[ ]
23 Introduccion a mathematica.nb 23 In[82]:= Out[82]= Solve@x^7+ x + 4 == 0, xd 88x Root@4 + # + # 7 &, D<, 8x Root@4 + # + # 7 &, 2D<, 8x Root@4 + # + # 7 &, 3D<, 8x Root@4 + # + # 7 &, 4D<, 8x Root@4 + # + # 7 &, 5D<, 8x Root@4 + # + # 7 &, 6D<, 8x Root@4 + # + # 7 &, 7D<< In[83]:= Out[83]= N@%D 88x.6076<, 8x <, 8x <, 8x <, 8x <, 8x <, 8x << Este Comando permite resolver ecuaciones que no sean polinómicas como por ejemplo: In[84]:= Solve@Sin@xD Cos@xD == 0, xd Solve::ifun : Inverse functions are being used by Solve, so some solutions may not be found; use Reduce for complete solution information. More Out[84]= 98x 0<, 9x π π =, 9x 2 2 == En este caso se obtienen algunas soluciones triviales y devuelve un mensaje que indica la posible existencia de mas soluciones Este comando Solve permite también resolver sistemas de ecuaciones que se representan en una lista o bien unidas a través del símbolo && (And). Ejemplos de este tipo se verán en las prácticas correspondientes al Algebra. En muchas ocasiones se emplean parámetros que pueden ir variando según se desee y que mejoran o empeoran el comportamiento de un sistema. Por ello es muy interesante, poder resolver ecuaciones en las que se encuentren parámetros. Para ello el comando mas indicado en el paquete Mathematica es Reduce[ ]. La forma de presentarlo es idéntica a los anteriores. Veamos algún ejemplo: In[85]:= Clear@a, xd In[86]:= Reduce@3 a x^3 2 x + 3 == 0, xd Out[86]= a 0&&x 3 2»» a 0&&Hx Root@3 2#+ 3a# 3 &, D»»x Root@3 2#+ 3a# 3 &, 2D»» x Root@3 2#+ 3a# 3 &, 3DL En este ejemplo se ve claramente el funcionamiento del comando. Si a vale cero logicamente se trata de una ecuación en que solo hay una raiz. Si a es distinto de cero se obtienen tres raices distintas dado que estamos estudiando un polinomio de grado tres.
24 Introduccion a mathematica.nb 24 Este comando también se puede emplear cuando se trabaja con un sistema de ecuaciones como en el caso anterior, definiendo todos ellos entre llaves o con el símbolo &&. Ej: In[87]:= Clear@a, r, sd In[88]:= 882, a<, 83, <<.8r, s< == 80, < Out[88]= 82 r+ as,3r+ s< 80, < In[89]:= Out[89]= Reduce@%, 8r, s<d 2 + 3a 0&&r a && s 3r 2 + 3a Resuelve el sistema matricial considerando el valor del parámetro a. Lógicamente el valor del determinante de la matriz tiene que ser no nulo ya que el rango debe ser dos para que exista solución. Cuando no se pueden obtener soluciones mediante los comandos que se han explicado se debe pasar a los métodos iterativos para la obtención de soluciones de la ecuación. Para ello se utiliza el comando FindRoot[ecuación,{x,sol_aprox}] en el que se indica la ecuación que se desea resolver y un valor cercano a la solución de la ecuación. Debido a esto se recomienda anteriormente dibujar la función para tener una idea aproximada de la posición de la solución. Ejemplo: Calcular las soluciones de la ecuación x Sin[x]-/2= 0 In[90]:= Plot@x Sin@xD ê 2, 8x, 0, 4<D Out[90]= Graphics In[9]:= FindRoot@x Sin@xD ê 2 == 0, 8x, <D Out[9]= 8x < In[92]:= FindRoot@x Sin@xD ê 2 == 0, 8x, 3<D Out[92]= 8x < Ejercicios de la sección 0
25 Introduccion a mathematica.nb 25 - Resolver x^2+2x+2=0 - Resolver x^2+a x+2=0 - Calcular raices de la ecuación Tan[x] == Cos[x] en el intervalo [0, Pi]
Introducción a Mathematica
 Introducción a Mathematica Mathematica es un paquete de software matemático, de uso fácil y gran capacidad, que nos permitirá realizar las operaciones necesarias para resolver problemas que ya se abordaron
Introducción a Mathematica Mathematica es un paquete de software matemático, de uso fácil y gran capacidad, que nos permitirá realizar las operaciones necesarias para resolver problemas que ya se abordaron
N = {1, 2, 3, 4, 5,...}
 Números y Funciones.. Números Los principales tipos de números son:. Los números naturales son aquellos que sirven para contar. N = {,,, 4, 5,...}. Los números enteros incluyen a los naturales y a sus
Números y Funciones.. Números Los principales tipos de números son:. Los números naturales son aquellos que sirven para contar. N = {,,, 4, 5,...}. Los números enteros incluyen a los naturales y a sus
GUIA PRACTICA PARA LA APLICACIÓN DE MS EXCEL TECNOLOGIA/ INFORMATICA
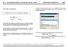 Fórmulas y funciones De la barra de menú seleccionmos la opción insertar y haciendo clic en la opción f x se desplegará el siguiente cuadro de diálogo a partir del cual escogeremos la función adecuada
Fórmulas y funciones De la barra de menú seleccionmos la opción insertar y haciendo clic en la opción f x se desplegará el siguiente cuadro de diálogo a partir del cual escogeremos la función adecuada
CURSOSO. Aritmética: Númerosnaturalesyenteros. Númerosracionalesyfraciones. MATEMÁTICAS. AntonioF.CostaGonzález
 CURSOSO CURSOSO MATEMÁTICAS Aritmética: Númerosnaturalesyenteros. Númerosracionalesyfraciones. AntonioF.CostaGonzález DepartamentodeMatemáticasFundamentales FacultaddeCiencias Índice 1 Introducción y objetivos
CURSOSO CURSOSO MATEMÁTICAS Aritmética: Númerosnaturalesyenteros. Númerosracionalesyfraciones. AntonioF.CostaGonzález DepartamentodeMatemáticasFundamentales FacultaddeCiencias Índice 1 Introducción y objetivos
OPERADORES LÓGICOS Y RELACIONALES. CICLOS Y ESTRUCTURAS DE CONTROL. MÉTODOS DE RESOLUCIÓN DE UNA ECUACIÓN NO LINEAL.
 2.1.-Resol.ec. no lineales.nb 126 OPERADORES LÓGICOS Y RELACIONALES. CICLOS Y ESTRUCTURAS DE CONTROL. MÉTODOS DE RESOLUCIÓN DE UNA ECUACIÓN NO LINEAL. Operadores lógicos y relacionales Los operadores lógicos
2.1.-Resol.ec. no lineales.nb 126 OPERADORES LÓGICOS Y RELACIONALES. CICLOS Y ESTRUCTURAS DE CONTROL. MÉTODOS DE RESOLUCIÓN DE UNA ECUACIÓN NO LINEAL. Operadores lógicos y relacionales Los operadores lógicos
INSTRUCCIONES PARA EL USO DEL SOFTWARE (IS)
 INSTRUCCIONES PARA EL USO DEL SOFTWARE (IS) Pantalla Inicial de DERIVE for Windows Teniendo instalado el programa DERIVE sobre Windows, podemos ingresar al sistema de las siguientes formas: Haciendo clic
INSTRUCCIONES PARA EL USO DEL SOFTWARE (IS) Pantalla Inicial de DERIVE for Windows Teniendo instalado el programa DERIVE sobre Windows, podemos ingresar al sistema de las siguientes formas: Haciendo clic
La suma de dos números.
 1 Números Mathematica es una herramienta matemática que, esencialmente, funciona como una calculadora. La secuencia básica consiste, entonces, en introducir una expresión y ordenarle a Mathematica que
1 Números Mathematica es una herramienta matemática que, esencialmente, funciona como una calculadora. La secuencia básica consiste, entonces, en introducir una expresión y ordenarle a Mathematica que
UNIDAD I. ALGORITMOS
 UNIDAD I. ALGORITMOS 1.1 Definición Un algoritmo es una serie de pasos organizados que describe el proceso que se debe seguir, para dar solución a un problema específico. 1.2 Tipos Cualitativos: Son aquellos
UNIDAD I. ALGORITMOS 1.1 Definición Un algoritmo es una serie de pasos organizados que describe el proceso que se debe seguir, para dar solución a un problema específico. 1.2 Tipos Cualitativos: Son aquellos
CURSO BÁSICO DE MATEMÁTICAS PARA ESTUDIANTES DE ECONÓMICAS Y EMPRESARIALES. Unidad didáctica 4. Números reales y números complejos
 NÚMEROS REALES NÚMEROS NATURALES Y NÚMEROS ENTEROS Los números naturales surgen como respuesta a la necesidad de nuestros antepasados de contar los elementos de un conjunto (por ejemplo los animales de
NÚMEROS REALES NÚMEROS NATURALES Y NÚMEROS ENTEROS Los números naturales surgen como respuesta a la necesidad de nuestros antepasados de contar los elementos de un conjunto (por ejemplo los animales de
Lección 8: Potencias con exponentes enteros
 GUÍA DE MATEMÁTICAS III Lección 8: Potencias con exponentes enteros Cuando queremos indicar productos de factores iguales, generalmente usamos la notación exponencial. Por ejemplo podemos expresar x, como
GUÍA DE MATEMÁTICAS III Lección 8: Potencias con exponentes enteros Cuando queremos indicar productos de factores iguales, generalmente usamos la notación exponencial. Por ejemplo podemos expresar x, como
1. Conocimientos previos. 1 Funciones exponenciales y logarítmicas.
 . Conocimientos previos. Funciones exponenciales y logarítmicas.. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Intervalos y sus definiciones básicas.
. Conocimientos previos. Funciones exponenciales y logarítmicas.. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Intervalos y sus definiciones básicas.
Polinomios. 1.- Funciones cuadráticas
 Polinomios 1.- Funciones cuadráticas Definición 1 (Función polinomial) Sea n un entero no negativo y sean a n, a n 1,..., a, a 1, a 0 número s reales con a n 0. La función se denomina función polinomial
Polinomios 1.- Funciones cuadráticas Definición 1 (Función polinomial) Sea n un entero no negativo y sean a n, a n 1,..., a, a 1, a 0 número s reales con a n 0. La función se denomina función polinomial
VALOR ABSOLUTO. Definición.- El valor absoluto de un número real, x, se define como:
 VALOR ABSOLUTO Cualquier número a tiene su representación en la recta real. El valor absoluto de un número representa la distancia del punto a al origen. Observe en el dibujo que la distancia del al origen
VALOR ABSOLUTO Cualquier número a tiene su representación en la recta real. El valor absoluto de un número representa la distancia del punto a al origen. Observe en el dibujo que la distancia del al origen
UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN
 UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN FACULTAD DE INGENIERÍA MECÁNICA Y ELÉCTRICA LABORATORIO DE INGENIERÍA DE CONTROL PRACTICA N 1 INTRODUCCIÓN Y COMANDOS DEL MATLAB OBJETIVO Familiarizarse con el modo de
UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN FACULTAD DE INGENIERÍA MECÁNICA Y ELÉCTRICA LABORATORIO DE INGENIERÍA DE CONTROL PRACTICA N 1 INTRODUCCIÓN Y COMANDOS DEL MATLAB OBJETIVO Familiarizarse con el modo de
INTRODUCCIÓN a DERIVE 6. PANTALLA DE EXPRESIONES ALGEBRAICAS
 INTRODUCCIÓN a DERIVE 6. Existen tres clases de pantallas: La pantalla de Álgebra (para expresiones algebraicas) y las pantallas gráficas que permiten representar gráficas en dos dimensiones (ventana 2D)
INTRODUCCIÓN a DERIVE 6. Existen tres clases de pantallas: La pantalla de Álgebra (para expresiones algebraicas) y las pantallas gráficas que permiten representar gráficas en dos dimensiones (ventana 2D)
3. Resolver triángulos rectángulos utilizando las definiciones de las razones trigonométricas.
 Contenidos mínimos MI. 1. Contenidos. Bloque I: Aritmética y Álgebra. 1. Conocer las clases de números, los conjuntos numéricos: naturales, enteros, racionales, reales y complejos y las propiedades que
Contenidos mínimos MI. 1. Contenidos. Bloque I: Aritmética y Álgebra. 1. Conocer las clases de números, los conjuntos numéricos: naturales, enteros, racionales, reales y complejos y las propiedades que
Unidad 1. Las fracciones.
 Unidad 1. Las fracciones. Ubicación Curricular en España: 4º, 5º y 6º Primaria, 1º, 2º y 3º ESO. Objetos de aprendizaje. 1.1. Concepto de fracción. Identificar los términos de una fracción. Escribir y
Unidad 1. Las fracciones. Ubicación Curricular en España: 4º, 5º y 6º Primaria, 1º, 2º y 3º ESO. Objetos de aprendizaje. 1.1. Concepto de fracción. Identificar los términos de una fracción. Escribir y
8. ESPACIOS VECTORIALES Y APLICACIONES LINEALES.
 Prácticas de Matemáticas I y Matemáticas II con DERIVE-5 6 8. ESPACIOS VECTORIALES Y APLICACIONES LINEALES. 8.. DEPENDENCIA E INDEPENDENCIA LINEAL DE VECTORES. COMBINACIÓN LINEAL. EJEMPLO 8.. Estudiar
Prácticas de Matemáticas I y Matemáticas II con DERIVE-5 6 8. ESPACIOS VECTORIALES Y APLICACIONES LINEALES. 8.. DEPENDENCIA E INDEPENDENCIA LINEAL DE VECTORES. COMBINACIÓN LINEAL. EJEMPLO 8.. Estudiar
Práctica 7. Integración de funciones de dos variables. Teorema de Fubini. Cambio de variable a coordenadas polares.
 Práctica 7. Integración de funciones de dos variables. Teorema de Fubini. Cambio de variable a coordenadas polares. Análisis Matemático II. Departamento de Matemáticas. Diplomatura en Estadística / Ingeniería
Práctica 7. Integración de funciones de dos variables. Teorema de Fubini. Cambio de variable a coordenadas polares. Análisis Matemático II. Departamento de Matemáticas. Diplomatura en Estadística / Ingeniería
IES Fco Ayala de Granada Septiembre de 2013 (Modelo 3 Especifico) Solucíon Germán-Jesús Rubio Luna. Opción A
 Opción A Ejercicio opción A, modelo 3 Septiembre 03 específico x Sea f la función definida por f(x) = para x > 0, x (donde ln denota el logaritmo neperiano) ln(x) [ 5 puntos] Estudia y determina las asíntotas
Opción A Ejercicio opción A, modelo 3 Septiembre 03 específico x Sea f la función definida por f(x) = para x > 0, x (donde ln denota el logaritmo neperiano) ln(x) [ 5 puntos] Estudia y determina las asíntotas
CURSO BÁSICO DE MATEMÁTICAS PARA ESTUDIANTES DE ECONÓMICAS Y EMPRESARIALES. Unidad didáctica 4. Números reales y números complejos
 NÚMEROS REALES Como se ha señalado anteriormente la necesidad de resolver diversos problemas de origen aritmético y geométrico lleva a ir ampliando sucesivamente los conjuntos numéricos, N Z Q, y a definir
NÚMEROS REALES Como se ha señalado anteriormente la necesidad de resolver diversos problemas de origen aritmético y geométrico lleva a ir ampliando sucesivamente los conjuntos numéricos, N Z Q, y a definir
Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos:
 1 CONOCIMIENTOS PREVIOS. 1 Logaritmos. 1. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Operaciones básicas con números reales. Propiedades de
1 CONOCIMIENTOS PREVIOS. 1 Logaritmos. 1. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Operaciones básicas con números reales. Propiedades de
CURSO BÁSICO DE MATEMÁTICAS PARA ESTUDIANTES DE ECONÓMICAS Y EMPRESARIALES
 Unidad didáctica. Ecuaciones, inecuaciones y sistemas de ecuaciones e inecuaciones CONCEPTOS ECUACIONES Una ecuación es una igualdad entre dos epresiones en las que aparece una o varias incógnitas. En
Unidad didáctica. Ecuaciones, inecuaciones y sistemas de ecuaciones e inecuaciones CONCEPTOS ECUACIONES Una ecuación es una igualdad entre dos epresiones en las que aparece una o varias incógnitas. En
Sistemas de Ecuaciones y Matrices
 Sistemas de Ecuaciones y Matrices 0.1 Sistemas de ecuaciones Consideremos las gráficas de dos funciones f y g como en la figura siguiente: P Q y = fx y = gx En la práctica, en ocasiones hay que encontrar
Sistemas de Ecuaciones y Matrices 0.1 Sistemas de ecuaciones Consideremos las gráficas de dos funciones f y g como en la figura siguiente: P Q y = fx y = gx En la práctica, en ocasiones hay que encontrar
Curvas en paramétricas y polares
 Capítulo 10 Curvas en paramétricas y polares Introducción Después del estudio detallado de funciones reales de variable real expresadas en forma explícita y con coordenadas cartesianas, que se ha hecho
Capítulo 10 Curvas en paramétricas y polares Introducción Después del estudio detallado de funciones reales de variable real expresadas en forma explícita y con coordenadas cartesianas, que se ha hecho
Tema 2. Sistemas de ecuaciones lineales
 Tema 2. Sistemas de ecuaciones lineales Estructura del tema. Definiciones básicas Forma matricial de un sistema de ecuaciones lineales Clasificación de los sistemas según el número de soluciones. Teorema
Tema 2. Sistemas de ecuaciones lineales Estructura del tema. Definiciones básicas Forma matricial de un sistema de ecuaciones lineales Clasificación de los sistemas según el número de soluciones. Teorema
www.matesxronda.net José A. Jiménez Nieto
 NÚMEROS REALES 1. NÚMEROS IRRACIONALES: CARACTERIZACIÓN. En el tema correspondiente a números racionales hemos visto que estos números tienen una característica esencial: su expresión decimal es exacta
NÚMEROS REALES 1. NÚMEROS IRRACIONALES: CARACTERIZACIÓN. En el tema correspondiente a números racionales hemos visto que estos números tienen una característica esencial: su expresión decimal es exacta
SESIÓN 1 PRE-ALGEBRA, CONCEPTOS Y OPERACIONES ARITMÉTICAS BÁSICAS
 SESIÓN 1 PRE-ALGEBRA, CONCEPTOS Y OPERACIONES ARITMÉTICAS BÁSICAS I. CONTENIDOS: 1. Introducción: de la aritmética al álgebra. 2. Números reales y recta numérica. 3. Operaciones aritméticas básicas con
SESIÓN 1 PRE-ALGEBRA, CONCEPTOS Y OPERACIONES ARITMÉTICAS BÁSICAS I. CONTENIDOS: 1. Introducción: de la aritmética al álgebra. 2. Números reales y recta numérica. 3. Operaciones aritméticas básicas con
Contenidos mínimos 4B ESO. 1. Contenidos. Bloque I: Aritmética y álgebra.
 Contenidos mínimos 4B ESO. 1. Contenidos. Bloque I: Aritmética y álgebra. 1. Clasificar distintos tipos de números: naturales, enteros, racionales y reales. 2. Operar con números reales y aplicar las propiedades
Contenidos mínimos 4B ESO. 1. Contenidos. Bloque I: Aritmética y álgebra. 1. Clasificar distintos tipos de números: naturales, enteros, racionales y reales. 2. Operar con números reales y aplicar las propiedades
Práctica 2ª : OPERADORES LÓGICOS Y RELACIONALES. CICLOS Y ESTRUCTURAS DE CONTROL. MÉTODOS DE RESOLUCIÓN DE UNA ECUACIÓN NO LINEAL.
 practica2sr.nb 1 Apellidos y Nombre: Práctica 2ª : OPERADORES LÓGICOS Y RELACIONALES. CICLOS Y ESTRUCTURAS DE CONTROL. MÉTODOS DE RESOLUCIÓN DE UNA ECUACIÓN NO LINEAL. Operadores lógicos y relacionales
practica2sr.nb 1 Apellidos y Nombre: Práctica 2ª : OPERADORES LÓGICOS Y RELACIONALES. CICLOS Y ESTRUCTURAS DE CONTROL. MÉTODOS DE RESOLUCIÓN DE UNA ECUACIÓN NO LINEAL. Operadores lógicos y relacionales
Definición(2) La base (r) de un sistema de numeración especifica el número de dígitos o cardinal* de dicho conjunto ordenado. Las bases más utilizadas
 Sistemas numéricos MIA José Rafael Rojano Cáceres Arquitectura de Computadoras I Definición(1) Un sistema de representación numérica es un sistema de lenguaje que consiste en: un conjunto ordenado de símbolos
Sistemas numéricos MIA José Rafael Rojano Cáceres Arquitectura de Computadoras I Definición(1) Un sistema de representación numérica es un sistema de lenguaje que consiste en: un conjunto ordenado de símbolos
UNIDAD 2: LÍMITES DE FUNCIONES.CONTINUIDAD = 3 2
 UNIDAD 2: LÍMITES DE FUNCIONES.CONTINUIDAD 1.- Límites en el Infinito: lim x + f(x) = L Se dice que el límite de f (x) cuando x tiende a + es L ϵ Ɽ, si podemos hacer que f(x) se aproxime a L tanto como
UNIDAD 2: LÍMITES DE FUNCIONES.CONTINUIDAD 1.- Límites en el Infinito: lim x + f(x) = L Se dice que el límite de f (x) cuando x tiende a + es L ϵ Ɽ, si podemos hacer que f(x) se aproxime a L tanto como
Funciones de varias variables.
 Funciones de varias variables. Definición. Hasta ahora se han estudiado funciones de la forma y = f (x), f :D Estas funciones recibían el nombre de funciones reales de variable real ya que su valor y dependía
Funciones de varias variables. Definición. Hasta ahora se han estudiado funciones de la forma y = f (x), f :D Estas funciones recibían el nombre de funciones reales de variable real ya que su valor y dependía
P. A. U. LAS PALMAS 2005
 P. A. U. LAS PALMAS 2005 OPCIÓN A: J U N I O 2005 1. Hallar el área encerrada por la gráfica de la función f(x) = x 3 4x 2 + 5x 2 y la rectas y = 0, x = 1 y x = 3. x 3 4x 2 + 5x 2 es una función polinómica
P. A. U. LAS PALMAS 2005 OPCIÓN A: J U N I O 2005 1. Hallar el área encerrada por la gráfica de la función f(x) = x 3 4x 2 + 5x 2 y la rectas y = 0, x = 1 y x = 3. x 3 4x 2 + 5x 2 es una función polinómica
Curso Propedéutico de Cálculo Sesión 2: Límites y Continuidad
 y Laterales Curso Propedéutico de Cálculo Sesión 2: y Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico y Esquema Laterales 1 Laterales 2 y Esquema Laterales
y Laterales Curso Propedéutico de Cálculo Sesión 2: y Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico y Esquema Laterales 1 Laterales 2 y Esquema Laterales
La herramienta ArtEM: Aritmética Entera y Modular
 La herramienta ArtEM: Aritmética Entera y Modular 1. Introducción La herramienta ArtEM (Aritmética Entera y Modular) es una aplicación informática programada en Visual Basic y desarrollada con el fin de
La herramienta ArtEM: Aritmética Entera y Modular 1. Introducción La herramienta ArtEM (Aritmética Entera y Modular) es una aplicación informática programada en Visual Basic y desarrollada con el fin de
Aplicaciones de las Derivadas
 Tema 4 Aplicaciones de las Derivadas 4.1 Introducción Repasaremos en este Tema algunas de las aplicaciones fundamentales de las derivadas. Muchas de ellas son ya conocidas por tratarse de conceptos explicados
Tema 4 Aplicaciones de las Derivadas 4.1 Introducción Repasaremos en este Tema algunas de las aplicaciones fundamentales de las derivadas. Muchas de ellas son ya conocidas por tratarse de conceptos explicados
Tabla de Derivadas. Función Derivada Función Derivada. f (x) n+1. f (x) y = f (x) y = ln x. y = cotg f (x) y = ( 1 cotg 2 f (x)) f (x) = f (x)
 Matemáticas aplicadas a las CCSS - Derivadas Tabla de Derivadas Función Derivada Función Derivada y k y 0 y y y y y f ) y f ) f ) y n y n n y f ) n y n f ) n f ) y y n y y f ) y n n+ y f ) n y f ) f )
Matemáticas aplicadas a las CCSS - Derivadas Tabla de Derivadas Función Derivada Función Derivada y k y 0 y y y y y f ) y f ) f ) y n y n n y f ) n y n f ) n f ) y y n y y f ) y n n+ y f ) n y f ) f )
SISTEMAS DE NUMERACIÓN
 SISTEMAS DE NUMERACIÓN INDICE. 1. DEFINICIÓN DE SISTEMAS DE NUMERACIÓN.... 1 2. TEOREMA FUNDAMENTAL DE LA NUMERACIÓN... 3 3. SISTEMAS DECIMAL, BINARIO, OCTAL Y HEXADECIMAL.... 5 3.1. SISTEMA DECIMAL...
SISTEMAS DE NUMERACIÓN INDICE. 1. DEFINICIÓN DE SISTEMAS DE NUMERACIÓN.... 1 2. TEOREMA FUNDAMENTAL DE LA NUMERACIÓN... 3 3. SISTEMAS DECIMAL, BINARIO, OCTAL Y HEXADECIMAL.... 5 3.1. SISTEMA DECIMAL...
Introducción a MATLAB
 Introducción a MATLAB Sistemas Conexionistas - Curso 07/08 MATLAB es un sistema interactivo basado en matrices para cálculos científicos y de ingeniería. Se pueden resolver problemas numéricos relativamente
Introducción a MATLAB Sistemas Conexionistas - Curso 07/08 MATLAB es un sistema interactivo basado en matrices para cálculos científicos y de ingeniería. Se pueden resolver problemas numéricos relativamente
Introducción a MATLAB
 Introducción a MATLAB Sistemas Conexionistas - Curso 08/09 MATLAB es un sistema interactivo basado en matrices que se utiliza para cálculos científicos y de ingeniería. Puede resolver problemas numéricos
Introducción a MATLAB Sistemas Conexionistas - Curso 08/09 MATLAB es un sistema interactivo basado en matrices que se utiliza para cálculos científicos y de ingeniería. Puede resolver problemas numéricos
Cálculo científico y técnico con HP49g/49g+/48gII/50g Módulo 3: Aplicaciones Tema 3.2 Determinación aproximada de extremos: Método de Newton-Raphson
 Cálculo científico y técnico con HP49g/49g+/48gII/50g Módulo 3: Aplicaciones Tema 3.2 Determinación aproximada de extremos: Método de Newton-Raphson Francisco Palacios Escuela Politécnica Superior de Ingeniería
Cálculo científico y técnico con HP49g/49g+/48gII/50g Módulo 3: Aplicaciones Tema 3.2 Determinación aproximada de extremos: Método de Newton-Raphson Francisco Palacios Escuela Politécnica Superior de Ingeniería
IES Fco Ayala de Granada Junio de 2011 (Específico 2 Modelo 1) Soluciones Germán-Jesús Rubio Luna
 PRUEBA DE ACCESO A LA UNIVERSIDAD MATEMÁTICAS II DE ANDALUCÍA CURSO 010-011 Opción A Ejercicio 1, Opción A, Modelo especifico de Junio de 011 [ 5 puntos] Una ventana normanda consiste en un rectángulo
PRUEBA DE ACCESO A LA UNIVERSIDAD MATEMÁTICAS II DE ANDALUCÍA CURSO 010-011 Opción A Ejercicio 1, Opción A, Modelo especifico de Junio de 011 [ 5 puntos] Una ventana normanda consiste en un rectángulo
MATEMATICA APLICADA A LA ARQUITECTURA: REPRESENTACIÓN GRÁFICA DE CURVAS PLANAS CON MATHEMATICA
 MATEMATICA APLICADA A LA ARQUITECTURA: REPRESENTACIÓN GRÁFICA DE CURVAS PLANAS CON MATHEMATICA AUTORÍA CARMEN MARIA REINOSO MAROTO TEMÁTICA ARQUITECTURA, MATEMATICAS ETAPA FORMACIÓN PROFESIONAL GRADO SUPERIOR
MATEMATICA APLICADA A LA ARQUITECTURA: REPRESENTACIÓN GRÁFICA DE CURVAS PLANAS CON MATHEMATICA AUTORÍA CARMEN MARIA REINOSO MAROTO TEMÁTICA ARQUITECTURA, MATEMATICAS ETAPA FORMACIÓN PROFESIONAL GRADO SUPERIOR
Anexo C. Introducción a las series de potencias. Series de potencias
 Anexo C Introducción a las series de potencias Este apéndice tiene como objetivo repasar los conceptos relativos a las series de potencias y al desarrollo de una función ne serie de potencias en torno
Anexo C Introducción a las series de potencias Este apéndice tiene como objetivo repasar los conceptos relativos a las series de potencias y al desarrollo de una función ne serie de potencias en torno
Tema 2 Cálculos básicos con wxmaxima
 Tema 2 Cálculos básicos con wxmaxima Objetivos 1. Llevar a cabo cálculos básicos con variables. 2. Llevar a cabo cálculos básicos con expresiones algebraicas. 3. Llevar a cabo cálculos básicos con polinomios
Tema 2 Cálculos básicos con wxmaxima Objetivos 1. Llevar a cabo cálculos básicos con variables. 2. Llevar a cabo cálculos básicos con expresiones algebraicas. 3. Llevar a cabo cálculos básicos con polinomios
Los números naturales
 Los números naturales Los números naturales Los números naturales son aquellos que sirven para contar. Se suelen representar utilizando las cifras del 0 al 9. signo suma o resultado Suma: 9 + 12 = 21 sumandos
Los números naturales Los números naturales Los números naturales son aquellos que sirven para contar. Se suelen representar utilizando las cifras del 0 al 9. signo suma o resultado Suma: 9 + 12 = 21 sumandos
Pruebas de Acceso a enseñanzas universitarias oficiales de grado Castilla y León
 Selectividad Junio 05 Pruebas de Acceso a enseñanzas universitarias oficiales de grado Castilla y León MATEMÁTICAS II EJERCICIO Nº páginas: INDICACIONES:.- OPTATIVIDAD: El alumno deberá escoger una de
Selectividad Junio 05 Pruebas de Acceso a enseñanzas universitarias oficiales de grado Castilla y León MATEMÁTICAS II EJERCICIO Nº páginas: INDICACIONES:.- OPTATIVIDAD: El alumno deberá escoger una de
UNIDAD DE APRENDIZAJE II UNIDAD DE APRENDIZAJE 2 ( 12 HORAS)
 UNIDAD DE APRENDIZAJE II UNIDAD DE APRENDIZAJE HORAS) Saberes procedimentales Saberes declarativos Identifica y realiza operaciones básicas con expresiones aritméticas. Jerarquía de las operaciones aritméticas.
UNIDAD DE APRENDIZAJE II UNIDAD DE APRENDIZAJE HORAS) Saberes procedimentales Saberes declarativos Identifica y realiza operaciones básicas con expresiones aritméticas. Jerarquía de las operaciones aritméticas.
Los números enteros. > significa "mayor que". Ejemplo: 58 > 12 < significa "menor que". Ejemplo: 3 < 12 Cualquier número positivo siempre es mayor
 Los números enteros Los números enteros Los números enteros son aquellos que permiten contar tanto los objetos que se tienen, como los objetos que se deben. Enteros positivos: precedidos por el signo +
Los números enteros Los números enteros Los números enteros son aquellos que permiten contar tanto los objetos que se tienen, como los objetos que se deben. Enteros positivos: precedidos por el signo +
3.1 Representación gráfica de curvas bidimensionales.
 Tema 3 Curvas y superficies Versión: 6 de febrero de 29 3. Representación gráfica de curvas bidimensionales. La representación gráfica de una curva en un ordenador es una linea poligonal construida uniendo
Tema 3 Curvas y superficies Versión: 6 de febrero de 29 3. Representación gráfica de curvas bidimensionales. La representación gráfica de una curva en un ordenador es una linea poligonal construida uniendo
Funciones reales de variable real: Gráficas, límites y continuidad.
 Cálculo Matemático. Práctica 3. Curso 2009-2010. AMRP. 1 Funciones reales de variable real: Gráficas, límites y continuidad. Práctica 3 (Específica de la asignatura de Cálculo Matemático en E.U.A.T.) Introducción
Cálculo Matemático. Práctica 3. Curso 2009-2010. AMRP. 1 Funciones reales de variable real: Gráficas, límites y continuidad. Práctica 3 (Específica de la asignatura de Cálculo Matemático en E.U.A.T.) Introducción
CURSO CERO DE MATEMATICAS. Apuntes elaborados por Domingo Pestana Galván. y José Manuel Rodríguez García
 INGENIEROS INDUSTRIALES Y DE TELECOMUNICACIONES CURSO CERO DE MATEMATICAS Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica
INGENIEROS INDUSTRIALES Y DE TELECOMUNICACIONES CURSO CERO DE MATEMATICAS Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica
CAPÍTULO 3: DETERMINANTES Y SISTEMAS DE ECUACIONES
 CAPÍTULO 3: DETERMINANTES Y SISTEMAS DE ECUACIONES Parte A: determinantes. A.1- Definición. Por simplificar, consideraremos que a cada matriz cuadrada se le asocia un número llamado determinante que se
CAPÍTULO 3: DETERMINANTES Y SISTEMAS DE ECUACIONES Parte A: determinantes. A.1- Definición. Por simplificar, consideraremos que a cada matriz cuadrada se le asocia un número llamado determinante que se
Introducción al análisis numérico
 Introducción al análisis numérico Javier Segura Universidad de Cantabria Cálculo Numérico I. Tema 1 Javier Segura (Universidad de Cantabria) Introducción al análisis numérico CNI 1 / 26 Contenidos: 1 Sistemas
Introducción al análisis numérico Javier Segura Universidad de Cantabria Cálculo Numérico I. Tema 1 Javier Segura (Universidad de Cantabria) Introducción al análisis numérico CNI 1 / 26 Contenidos: 1 Sistemas
Sistemas de ecuaciones lineales
 Sistemas de ecuaciones lineales Este tema resulta fundamental en la mayoría de las disciplinas, ya que son muchos los problemas científicos y de la vida cotidiana que requieren resolver simultáneamente
Sistemas de ecuaciones lineales Este tema resulta fundamental en la mayoría de las disciplinas, ya que son muchos los problemas científicos y de la vida cotidiana que requieren resolver simultáneamente
Tema 2. FUNCIONES, VARIABLES Y CARPETAS EN LA CALCULADORA CLASSPAD
 Tema 2. FUNCIONES, VARIABLES Y CARPETAS EN LA CALCULADORA CLASSPAD Introducción. Funciones disponibles en la Classpad. Variables y carpetas. Actividades propuestas. INTRODUCCIÓN En los siguientes apartados
Tema 2. FUNCIONES, VARIABLES Y CARPETAS EN LA CALCULADORA CLASSPAD Introducción. Funciones disponibles en la Classpad. Variables y carpetas. Actividades propuestas. INTRODUCCIÓN En los siguientes apartados
ESCEMMat ESCENARIOS MULTIMEDIA EN FORMACIÓN DE FUTUROS PROFESORES DE MATEMÁTICAS DE SECUNDARIA
 ASIGNATURA: METODOLOGÍA MATEMÁTICA CURSO: Op. 2ci.; 2007-2008 PROFESORA: Inés M. Gómez-Chacón CARÁCTER/CRÉDITOS: 7,5 DEPARTAMENTO: ÁLGEBRA FACULTAD DE CC. MATEMÁTICAS, UNIVERSIDAD COMPLUTENSE DE MADRID
ASIGNATURA: METODOLOGÍA MATEMÁTICA CURSO: Op. 2ci.; 2007-2008 PROFESORA: Inés M. Gómez-Chacón CARÁCTER/CRÉDITOS: 7,5 DEPARTAMENTO: ÁLGEBRA FACULTAD DE CC. MATEMÁTICAS, UNIVERSIDAD COMPLUTENSE DE MADRID
3.2 DIVIDIR UN POLINOMIO POR x a. REGLA DE RUFFINI
 TEMA 3 ÁLGEBRA MATEMÁTICAS CCSSI 1º BACH 1 TEMA 3 ÁLGEBRA 3.1 DIVISIÓN DE POLINOMIOS COCIENTE DE MONOMIOS El cociente de un monomio por otro monomio de grado inferior es un nuevo monomio cuyo grado es
TEMA 3 ÁLGEBRA MATEMÁTICAS CCSSI 1º BACH 1 TEMA 3 ÁLGEBRA 3.1 DIVISIÓN DE POLINOMIOS COCIENTE DE MONOMIOS El cociente de un monomio por otro monomio de grado inferior es un nuevo monomio cuyo grado es
UNIVERSIDAD SAN MARCOS
 Prof. Edwin Gerardo Acuña Acuña UNIVERSIDAD SAN MARCOS ALGEBRA Este capítulo estudia los conceptos básicos del álgebra, una de las disciplinas de la matemática que tiene más aplicaciones en diversos campos.
Prof. Edwin Gerardo Acuña Acuña UNIVERSIDAD SAN MARCOS ALGEBRA Este capítulo estudia los conceptos básicos del álgebra, una de las disciplinas de la matemática que tiene más aplicaciones en diversos campos.
Ejercicio 1: Realiza las siguientes divisiones por el método tradicional y por Ruffini: a)
 Tema 2: Ecuaciones, Sistemas e Inecuaciones. 2.1 División de polinomios. Regla de Ruffini. Polinomio: Expresión algebraica formada por la suma y/o resta de varios monomios. Terminología: o Grado del polinomio:
Tema 2: Ecuaciones, Sistemas e Inecuaciones. 2.1 División de polinomios. Regla de Ruffini. Polinomio: Expresión algebraica formada por la suma y/o resta de varios monomios. Terminología: o Grado del polinomio:
k k N b Sistemas Númericos Sistemas con Notación Posicional (1) Sistemas con Notación Posicional (2) Sistemas Decimal
 Sistemas con Notación Posicional (1) Sistemas Númericos N b = a n-1 *b n-1 + a n-2 *b n-2 +... + a 0 *b 0 +a -1 *b - 1 + a -2 *b -2 +... + a -m *b -m Sistemas con Notación Posicional (2) N b : Número en
Sistemas con Notación Posicional (1) Sistemas Númericos N b = a n-1 *b n-1 + a n-2 *b n-2 +... + a 0 *b 0 +a -1 *b - 1 + a -2 *b -2 +... + a -m *b -m Sistemas con Notación Posicional (2) N b : Número en
5.1. Recta tangente, normal e intersección de curvas. Recta tangente
 5. Aplicaciones de la Derivada 5.1. Recta tangente, normal e intersección de curvas Recta tangente Desde la escuela primaria se sabe que la recta tangente en un punto de una circunferencia es aquella recta
5. Aplicaciones de la Derivada 5.1. Recta tangente, normal e intersección de curvas Recta tangente Desde la escuela primaria se sabe que la recta tangente en un punto de una circunferencia es aquella recta
Resolver ecuaciones de segundo grado con WIRIS
 RESOLVER ECUACIONES DE SEGUNDO GRADO CON WIRIS Programación Resolver ecuaciones de segundo grado con WIRIS Objetivos específicos Requisitos mínimos Contenidos Criterios de evaluación Conocer el motor matemático
RESOLVER ECUACIONES DE SEGUNDO GRADO CON WIRIS Programación Resolver ecuaciones de segundo grado con WIRIS Objetivos específicos Requisitos mínimos Contenidos Criterios de evaluación Conocer el motor matemático
1. El sistema de los números reales
 1. El sistema de los números reales Se iniciará definiendo el conjunto de números que conforman a los números reales, en la siguiente figura se muestra la forma en la que están contenidos estos conjuntos
1. El sistema de los números reales Se iniciará definiendo el conjunto de números que conforman a los números reales, en la siguiente figura se muestra la forma en la que están contenidos estos conjuntos
Cálculo diferencial y aplicaciones
 PRÁCTICA 3 Cálculo diferencial y aplicaciones En esta práctica utilizaremos, entre otras, las órdenes específicas Limit, Series y Normal, del programa Mathematica para estudiar límites, continuidad y derivabilidad
PRÁCTICA 3 Cálculo diferencial y aplicaciones En esta práctica utilizaremos, entre otras, las órdenes específicas Limit, Series y Normal, del programa Mathematica para estudiar límites, continuidad y derivabilidad
CLASE 11 USO DE CONDICIONALES Y VECTORES
 CLASE 11 USO DE CONDICIONALES Y VECTORES Condicional de Descartes. Para sacar un mayor provecho a este comando es importante entender cómo funciona su estructura lógica. Para ello se recomienda escribir
CLASE 11 USO DE CONDICIONALES Y VECTORES Condicional de Descartes. Para sacar un mayor provecho a este comando es importante entender cómo funciona su estructura lógica. Para ello se recomienda escribir
Departamento de Matemáticas. Matemáticas. 2º Bachillerato
 Matemáticas 2º Bachillerato 1.- CONTENIDOS DE MATEMÁTICAS II QUE SERVIRÁN DE BASE PARA LA ELABORACIÓN DE LAS PROPUESTAS DE EXAMEN EN LAS PRUEBAS DE ACCESO A LA UNIVERSIDAD DE EXTREMADURA CURSO 2006-2007
Matemáticas 2º Bachillerato 1.- CONTENIDOS DE MATEMÁTICAS II QUE SERVIRÁN DE BASE PARA LA ELABORACIÓN DE LAS PROPUESTAS DE EXAMEN EN LAS PRUEBAS DE ACCESO A LA UNIVERSIDAD DE EXTREMADURA CURSO 2006-2007
POTENCIAS. MÚLTIPLOS Y DIVISORES. MÁXIMO COMÚN DIVISOR Y MÍNIMO COMÚN MÚLTIPLO.
 1. LOS NÚMEROS NATURALES POTENCIAS. MÚLTIPLOS Y DIVISORES. MÁXIMO COMÚN DIVISOR Y MÍNIMO COMÚN MÚLTIPLO. 2. LOS NÚMEROS ENTEROS. VALOR ABSOLUTO DE UN NÚMERO ENTERO. REPRESENTACIÓN GRÁFICA. OPERACIONES.
1. LOS NÚMEROS NATURALES POTENCIAS. MÚLTIPLOS Y DIVISORES. MÁXIMO COMÚN DIVISOR Y MÍNIMO COMÚN MÚLTIPLO. 2. LOS NÚMEROS ENTEROS. VALOR ABSOLUTO DE UN NÚMERO ENTERO. REPRESENTACIÓN GRÁFICA. OPERACIONES.
Práctica 2 Métodos de búsqueda para funciones de una variable
 Práctica 2 Métodos de búsqueda para funciones de una variable Introducción Definición 1. Una función real f se dice que es fuertemente cuasiconvexa en el intervalo (a, b) si para cada par de puntos x 1,
Práctica 2 Métodos de búsqueda para funciones de una variable Introducción Definición 1. Una función real f se dice que es fuertemente cuasiconvexa en el intervalo (a, b) si para cada par de puntos x 1,
2.4. Números complejos
 2.4 Números complejos 95 83 Relaciones temperatura-latitud a tabla siguiente contiene promedios de temperaturas anuales para los hemisferios norte y sur a varias latitudes. atitud Hemisf. N. Hemisf. S.
2.4 Números complejos 95 83 Relaciones temperatura-latitud a tabla siguiente contiene promedios de temperaturas anuales para los hemisferios norte y sur a varias latitudes. atitud Hemisf. N. Hemisf. S.
Problemas de 4 o ESO. Isaac Musat Hervás
 Problemas de 4 o ESO Isaac Musat Hervás 5 de febrero de 01 Índice general 1. Problemas de Álgebra 7 1.1. Números Reales.......................... 7 1.1.1. Los números....................... 7 1.1.. Intervalos.........................
Problemas de 4 o ESO Isaac Musat Hervás 5 de febrero de 01 Índice general 1. Problemas de Álgebra 7 1.1. Números Reales.......................... 7 1.1.1. Los números....................... 7 1.1.. Intervalos.........................
SISTEMAS DE ECUACIONES LINEALES
 1 SISTEMAS DE ECUACIONES LINEALES Una ecuación es un enunciado o proposición que plantea la igualdad de dos expresiones, donde al menos una de ellas contiene cantidades desconocidas llamadas variables
1 SISTEMAS DE ECUACIONES LINEALES Una ecuación es un enunciado o proposición que plantea la igualdad de dos expresiones, donde al menos una de ellas contiene cantidades desconocidas llamadas variables
TEMA 2: EL INTERÉS SIMPLE
 TEMA 2: EL INTERÉS SIMPLE 1.- CAPITALIZACIÓN SIMPLE 1.1.- CÁLCULO DEL INTERÉS: Recibe el nombre de capitalización simple la ley financiera según la cual los intereses de cada periodo de capitalización
TEMA 2: EL INTERÉS SIMPLE 1.- CAPITALIZACIÓN SIMPLE 1.1.- CÁLCULO DEL INTERÉS: Recibe el nombre de capitalización simple la ley financiera según la cual los intereses de cada periodo de capitalización
2. OPERACIONES ALGEBRAICAS BÁSICAS.
 Prácticas de Matemáticas I y Matemáticas II con DERIVE 30 2. OPERACIONES ALGEBRAICAS BÁSICAS. En este apartado vamos a realizar las operaciones algebraicas básicas que nos permiten utilizar DERIVE como
Prácticas de Matemáticas I y Matemáticas II con DERIVE 30 2. OPERACIONES ALGEBRAICAS BÁSICAS. En este apartado vamos a realizar las operaciones algebraicas básicas que nos permiten utilizar DERIVE como
TEMA 2: TEORÍA DE CONJUNTOS Y CONJUNTOS NUMÉRICOS.
 TEMA 2: TEORÍA DE CONJUNTOS Y CONJUNTOS NUMÉRICOS. TEORÍA DE CONJUNTOS. Definiciones. Se define un conjunto como una colección de objetos o cosas, se nombran con letras mayúsculas (A, B...). Cada uno de
TEMA 2: TEORÍA DE CONJUNTOS Y CONJUNTOS NUMÉRICOS. TEORÍA DE CONJUNTOS. Definiciones. Se define un conjunto como una colección de objetos o cosas, se nombran con letras mayúsculas (A, B...). Cada uno de
Universidad de Oriente Núcleo de Bolívar Departamento de Ciencias Área de Matemática Asignatura: Matemática (0081714)
 Universidad de Oriente Núcleo de Bolívar Departamento de Ciencias Área de Matemática Asignatura: Matemática (0081714) UNIDAD N 1 (FUNCIONES) Profesora: Yulimar Matute Octubre 2011 Función Constante: Se
Universidad de Oriente Núcleo de Bolívar Departamento de Ciencias Área de Matemática Asignatura: Matemática (0081714) UNIDAD N 1 (FUNCIONES) Profesora: Yulimar Matute Octubre 2011 Función Constante: Se
Expresión, Operador, Operando, Asignación, Prioridad
 4. EXPRESIONES Y OPERADORES Conceptos: Resumen: Expresión, Operador, Operando, Asignación, Prioridad En este tema se presentan los siguientes elementos de la programación: las expresiones y los operadores.
4. EXPRESIONES Y OPERADORES Conceptos: Resumen: Expresión, Operador, Operando, Asignación, Prioridad En este tema se presentan los siguientes elementos de la programación: las expresiones y los operadores.
Lógica de Predicados
 Lógica de Predicados En las últimas décadas, ha aumentado considerablemente el interés de la informática por la aplicación de la lógica a la programación. De hecho, ha aparecido un nuevo paradigma de programación,
Lógica de Predicados En las últimas décadas, ha aumentado considerablemente el interés de la informática por la aplicación de la lógica a la programación. De hecho, ha aparecido un nuevo paradigma de programación,
5. Producto de dos binomios de la forma: ( ax + c)( bx d )
 PRODUCTOS NOTABLES Y FACTORIZACIÓN. Productos Notables: Son polinomios que se obtienen de la multiplicación entre dos o más polinomios que poseen características especiales o expresiones particulares,
PRODUCTOS NOTABLES Y FACTORIZACIÓN. Productos Notables: Son polinomios que se obtienen de la multiplicación entre dos o más polinomios que poseen características especiales o expresiones particulares,
CURSO BÁSICO DE MATEMÁTICAS PARA ESTUDIANTES DE ECONÓMICAS Y EMPRESARIALES. Unidad didáctica 4. Números reales y números complejos
 CONCEPTOS NÚMEROS COMPLEJOS En el conjunto de los números reales, una ecuación tan sencilla como x + = 0 no se puede resolver ya que es equivalente a x = - y no existe ningún número real cuyo cuadrado
CONCEPTOS NÚMEROS COMPLEJOS En el conjunto de los números reales, una ecuación tan sencilla como x + = 0 no se puede resolver ya que es equivalente a x = - y no existe ningún número real cuyo cuadrado
Expresiones algebraicas
 Expresiones algebraicas Expresiones algebraicas Las expresiones algebraicas Elementos de una expresión algebraica Números de cualquier tipo Letras Signos de operación: sumas, restas, multiplicaciones y
Expresiones algebraicas Expresiones algebraicas Las expresiones algebraicas Elementos de una expresión algebraica Números de cualquier tipo Letras Signos de operación: sumas, restas, multiplicaciones y
Unidad 1 Números. Los números naturales son aquellos que se utilizan para contar los elementos de un conjunto.
 Unidad 1 Números 1.- Números Naturales Los números naturales son aquellos que se utilizan para contar los elementos de un conjunto. El conjunto de números naturales se representa por la letra N Operaciones
Unidad 1 Números 1.- Números Naturales Los números naturales son aquellos que se utilizan para contar los elementos de un conjunto. El conjunto de números naturales se representa por la letra N Operaciones
2. OPERACIONES ALGEBRAICAS BÁSICAS.
 Operaciones algebraicas básicas 27 2. OPERACIONES ALGEBRAICAS BÁSICAS. En este apartado vamos a realizar las operaciones algebraicas básicas que nos permiten utilizar DERIVE como herramienta de cálculo.
Operaciones algebraicas básicas 27 2. OPERACIONES ALGEBRAICAS BÁSICAS. En este apartado vamos a realizar las operaciones algebraicas básicas que nos permiten utilizar DERIVE como herramienta de cálculo.
MATEMÁTICAS Versión impresa NÚMEROS REALES
 MATEMÁTICAS Versión impresa NÚMEROS REALES 1. EL CONJUNTO DE LOS NÚMEROS REALES 1.1. Números naturales El conjunto de los números naturales se representa con el símbolo. Los números naturales son los más
MATEMÁTICAS Versión impresa NÚMEROS REALES 1. EL CONJUNTO DE LOS NÚMEROS REALES 1.1. Números naturales El conjunto de los números naturales se representa con el símbolo. Los números naturales son los más
SEMINARIO VIRTUAL WOLFRAM MATHEMATICA ALGEBRA DE MATRICES
 SEMINARIO VIRTUAL WOLFRAM MATHEMATICA ALGEBRA DE MATRICES TEMA Y PROPÓSITO: Demostrar mediante ejemplos sencillos el uso de Wolfram Mathematica para resolver problemas de Álgebra de Matrices. OBJETIVOS:
SEMINARIO VIRTUAL WOLFRAM MATHEMATICA ALGEBRA DE MATRICES TEMA Y PROPÓSITO: Demostrar mediante ejemplos sencillos el uso de Wolfram Mathematica para resolver problemas de Álgebra de Matrices. OBJETIVOS:
1.4 SISTEMAS HOMOGÉNEOS DE ECUACIONES. 36 CAPÍTULO 1 Sistemas de ecuaciones lineales y matrices
 36 CAPÍTULO Sistemas de ecuaciones lineales y matrices Escriba, en un comentario, la ecuación del polinomio cúbico que se ajusta a los cuatro puntos. Sea x el vector columna que contiene las coordenadas
36 CAPÍTULO Sistemas de ecuaciones lineales y matrices Escriba, en un comentario, la ecuación del polinomio cúbico que se ajusta a los cuatro puntos. Sea x el vector columna que contiene las coordenadas
POLINOMIOS Y FRACCIONES ALGEBRAICAS
 POLINOMIOS Y FRACCIONES ALGEBRAICAS Definición de monomio. Expresión algebraica formada por el producto de un número finito de constantes y variables con exponente natural. Al producto de las constantes
POLINOMIOS Y FRACCIONES ALGEBRAICAS Definición de monomio. Expresión algebraica formada por el producto de un número finito de constantes y variables con exponente natural. Al producto de las constantes
Cálculo científico y técnico con HP49g/49g+/48gII/50g Módulo 2: Recursos avanzados Tema 2.1 Resolución numérica de ecuaciones
 Cálculo científico y técnico con HP49g/49g+/48gII/50g Módulo 2: Recursos avanzados Tema 2.1 Resolución numérica de ecuaciones Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad
Cálculo científico y técnico con HP49g/49g+/48gII/50g Módulo 2: Recursos avanzados Tema 2.1 Resolución numérica de ecuaciones Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad
UNIDAD 2: INTRODUCCIÓN AL LENGUAJE DE PROGRAMACiÓN R
 UNIDAD 2: INTRODUCCIÓN AL LENGUAJE DE PROGRAMACiÓN R Técnicas Inteligentes en Bioinformática Máster en Lógica, Computación e Inteligencia Artificial Dpto. Ciencias de la Computación e Inteligencia Artificial
UNIDAD 2: INTRODUCCIÓN AL LENGUAJE DE PROGRAMACiÓN R Técnicas Inteligentes en Bioinformática Máster en Lógica, Computación e Inteligencia Artificial Dpto. Ciencias de la Computación e Inteligencia Artificial
1. DIFERENCIABILIDAD EN VARIAS VARIABLES
 1 1. DIFERENCIABILIDAD EN VARIAS VARIABLES 1.1. DERIVADAS DIRECCIONALES Y PARCIALES Definición 1.1. Sea f : R n R, ā R n y v R n. Se define la derivada direccional de f en ā y en la dirección de v como:
1 1. DIFERENCIABILIDAD EN VARIAS VARIABLES 1.1. DERIVADAS DIRECCIONALES Y PARCIALES Definición 1.1. Sea f : R n R, ā R n y v R n. Se define la derivada direccional de f en ā y en la dirección de v como:
PUNTOS, RECTAS Y PLANOS EN EL ESPACIO
 6 PUNTOS, RECTAS Y PLANOS EN EL ESPACIO El objetivo de esta unidad es conocer distintos elementos de la geometría en el espacio, y las distintas relaciones que tienen entre ellos. Se estudia lo que es
6 PUNTOS, RECTAS Y PLANOS EN EL ESPACIO El objetivo de esta unidad es conocer distintos elementos de la geometría en el espacio, y las distintas relaciones que tienen entre ellos. Se estudia lo que es
Tema 1. Cálculo diferencial
 Tema 1. Cálculo diferencial 1 / 57 Una función es una herramienta mediante la que expresamos la relación entre una causa (variable independiente) y un efecto (variable dependiente). Las funciones nos permiten
Tema 1. Cálculo diferencial 1 / 57 Una función es una herramienta mediante la que expresamos la relación entre una causa (variable independiente) y un efecto (variable dependiente). Las funciones nos permiten
Ing. Ramón Morales Higuera
 MATRICES. Una matriz es un conjunto ordenado de números. Un determinante es un número. CONCEPTO DE MATRIZ. Se llama matriz a un conjunto ordenado de números, dispuestos en filas y Las líneas horizontales
MATRICES. Una matriz es un conjunto ordenado de números. Un determinante es un número. CONCEPTO DE MATRIZ. Se llama matriz a un conjunto ordenado de números, dispuestos en filas y Las líneas horizontales
Cálculo Diferencial - Parcial No. 2
 Cálculo Diferencial - Parcial No. 2 Departamento de Matemáticas - Universidad de los Andes Marzo 18 de 2010 Juro solemnemente abstenerme de copiar o de incurrir en actos que puedan conducir a la trampa
Cálculo Diferencial - Parcial No. 2 Departamento de Matemáticas - Universidad de los Andes Marzo 18 de 2010 Juro solemnemente abstenerme de copiar o de incurrir en actos que puedan conducir a la trampa
ESCEMMat ESCENARIOS MULTIMEDIA EN FORMACIÓN DE FUTUROS PROFESORES DE MATEMÁTICAS DE SECUNDARIA
 ASIGNATURA: METODOLOGÍA MATEMÁTICA CURSO: Op. 2ci.; 2007-2008 PROFESORA: Inés M. Gómez-Chacón CARÁCTER/CRÉDITOS: 7,5 DEPARTAMENTO: ÁLGEBRA FACULTAD DE CC. MATEMÁTICAS, UNIVERSIDAD COMPLUTENSE DE MADRID
ASIGNATURA: METODOLOGÍA MATEMÁTICA CURSO: Op. 2ci.; 2007-2008 PROFESORA: Inés M. Gómez-Chacón CARÁCTER/CRÉDITOS: 7,5 DEPARTAMENTO: ÁLGEBRA FACULTAD DE CC. MATEMÁTICAS, UNIVERSIDAD COMPLUTENSE DE MADRID
I.E.S. Emperatriz María de Austria Página 1
 .-INTRODUCCIÓN: Derive para Windows tiene todas las ventajas que ofrece este sistema operativo de Microsoft, utiliza todos los periféricos que aporta Windows para manejar sus aplicaciones y se puede comunicar
.-INTRODUCCIÓN: Derive para Windows tiene todas las ventajas que ofrece este sistema operativo de Microsoft, utiliza todos los periféricos que aporta Windows para manejar sus aplicaciones y se puede comunicar
Sistemas de ecuaciones lineales
 Sistemas.nb 1 Sistemas de ecuaciones lineales Práctica de Álgebra Lineal, E.U.A.T., Curso 2005 2006 En esta práctica aprenderemos a discutir y resolver sistemas de ecuaciones lineales con el ordenador.
Sistemas.nb 1 Sistemas de ecuaciones lineales Práctica de Álgebra Lineal, E.U.A.T., Curso 2005 2006 En esta práctica aprenderemos a discutir y resolver sistemas de ecuaciones lineales con el ordenador.
Matemáticas Febrero 2013 Modelo A
 Matemáticas Febrero 0 Modelo A. Calcular el rango de 0 0 0. 0 a) b) c). Cuál es el cociente de dividir P(x) = x x + 9 entre Q(x) = x +? a) x x + x 6. b) x + x + x + 6. c) x x + 5x 0.. Diga cuál de las
Matemáticas Febrero 0 Modelo A. Calcular el rango de 0 0 0. 0 a) b) c). Cuál es el cociente de dividir P(x) = x x + 9 entre Q(x) = x +? a) x x + x 6. b) x + x + x + 6. c) x x + 5x 0.. Diga cuál de las
Ecuaciones diferenciales lineales con coeficientes constantes
 Tema 4 Ecuaciones diferenciales lineales con coeficientes constantes Una ecuación diferencial lineal de orden n tiene la forma a 0 (x)y (n) + a 1 (x)y (n 1) + + a n 1 (x)y + a n (x)y = b(x) (41) Vamos
Tema 4 Ecuaciones diferenciales lineales con coeficientes constantes Una ecuación diferencial lineal de orden n tiene la forma a 0 (x)y (n) + a 1 (x)y (n 1) + + a n 1 (x)y + a n (x)y = b(x) (41) Vamos
