4.1.- EXPRESIONES LOGICAS
|
|
|
- Lorena Redondo Nieto
- hace 9 años
- Vistas:
Transcripción
1 4.1.- EXPRESIONES LOGICAS Una expresión lógica únicamente puede tomar dos valores que son : o Este tipo de expresiones permiten crear estructuras de control dentro del programa FORTRAN que dependiendo de los valores obtenidos por la expresión se bifurcan y recorren caminos alternativos. A la hora de construir una expresión lógica FORTRAN cuenta con una serie de operadores lógicos que se aplican siempre entre dos elementos del mismo tipo, bien numéricos o bien tipo carácter. Una vez construida la expresión esta únicamente puede tomar dos valores cierto o falso. Los operadores en FORTRAN son los siguientes: OPERADOR SIGNIFICADO.EQ. Igual que ( = ).NE. No igual que ( ).LT. Menor que (< ).LE. Menor o igual que ( ).GT. Mayor que (> ).GE. Mayor o igual que ( ) Supongamos que una variable real A posee un valor de 5.6 y otra variable real B posee un valor de 7.8, la siguiente tabla muestra los valores de lógicos para una serie de expresiones lógicas: EXPRESION VALOR (A.gt. 50.0) (A.ge. B) (A.ne.B) Por otro lado, hay otro tipo de operadores lógicos que son utilizados únicamente entre expresiones lógicas, en concreto.not. opera sobre una sola expresión lógica y el resto sobre dos. La siguiente tabla muestra este tipo de operadores y sus significado. OPERADOR.NOT..AND..OR..XOR..EQV..NEQV. SIGNIFICADO Cambia el valor de la expresión lógica a su opuesto Cierto únicamente si ambas expresiones lógicas son ciertas Cierto si una de las expresiones es cierta Cierto únicamente si una de las expresiones lógicas es cierto Cierto si ambas expresiones tiene el mismo valor Cierto si ambas expresiones no tienen el mismo valor Supongamos dos variables con valores A=2.0 y B=10.0, entonces:.not. (a.lt. b) (a.ne. b).and. (a.lt. b) (ambas expresiones lógicas son ciertas) (a.lt. b).or. (a.gt. b) (una de las expresiones lógicas es cierta) (a.ne. b).xor. (a.lt. b) (ambas expresiones son ciertas) (a.lt. b).eqv. (a.gt. b) (los resultados de las expresiones no son iguales) (a.lt. b).neqv. (a.gt. b) (los resultados de las expresiones no son iguales) Grupo de Electromagnetismo 1
2 Cuando en una misma expresión lógica compuesta existen varios operadores la prioridad de mayor a menor es: 1. Paréntesis 2. Operadores aritméticos (**, *, /, +, -) 3. Operadores lógicos (.lt.,.gt.,.eq.,.ne.,.le.,.ge.) 4..not. 5..and. 6..or. 7..eqv. and.neqv. Cuando en una misma expresión existen operadores de la misma prioridad las operaciones se realizaran recorriendo la expresión de izquierda a derecha ESTRUCTURAS DE CONTROL Una vez vistas las posibilidades que ofrecen la conjunción de expresiones lógicas, así como su funcionamiento podemos introducir las estructuras de control. Este tipo de estructuras son fundamentales en el desarrollo de un programa FORTRAN y permiten implementar bifurcaciones operacionales que son indispensables en la mayoría de los programas. La sentencia FORTRAN que permite este tipo de estructuras es la sentencia IF (lógico) la cual tiene una estructura como la que se muestra a continuación: Sentencias nº 1 ejecutadas cuando expresión logica= Sentencias nº 2 ejecutadas cuando expresión logica= En caso de no existir o no ser necesarias las sentencias nº 2, la sentencia no es de uso obligado. En ese caso el Bloque IF queda del siguiente modo: Sentencias nº 1 ejecutadas cuando expresión logica= : Programa que lee dos números y nos dice por pantalla cual de ellos es el mayor. P R O G R A M M A Y O R R E A L A, B P R I N T *, D A M E A P R I N T *, D A M E B R E A D *, B I F ( A. G E. B ) T H E N P R I N T *, A E S M A Y O R P R I N T *, B E S M A Y O R Grupo de Electromagnetismo 2
3 I F Obsérvese que el programa responderá que A es mayor, cuando A=B, lo que no es muy correcto. Analizando el problema observamos que deberíamos haber tenido en cuenta el caso. Para ello podemos incluir otra sentencia IF del siguiente modo: P R O G R A M M A Y O R R E A L A, B P R I N T *, D A M E A P R I N T *, D A M E B R E A D *, B I F ( A. E Q. B ) T H E N P R I N T *, A = B I F ( A. G E. B ) T H E N P R I N T *, A E S M A Y O R P R I N T *, B E S M A Y O R I F I F De la modificación anterior es preciso observar detenidamente dos cuestiones: a) Al existir dos sentencia IF, su anidamiento debe respetarse. Esto significa que las sentencias y del segundo IF nunca deberán se escritas con posterioridad a las sentencia y de del primer IF. ANIDAMIENTO CORRECTO ANIDAMIENTO INCORRECTO b) Al aumentar el numero de sentencia anidadas es muy conveniente para una correcta comprensión y lectura del programa aplicar tabulaciones hacia la derecha para cada bloque IF, con el fin de que cada bloque quede alineado verticalmente y separado de los demás bloques. Grupo de Electromagnetismo 3
4 Dentro de la estructura IF existe una variante permitida en la que no es necesario poner las sentencia y, su estructura es: IF (expresión lógica) Sentencia ejecutable que se aplicará cuando expresión logica= Programa que lea un carácter y si es la letra S escribe la palabra YES, sino que no escriba nada P R O G R A M C U A D R A D O C H A R A C T E R * 1 A P R I N T *, D A M E U N A L E T R A I F ( A. E Q. S ) P R I N T *, Y E S Al introducir por teclado un carácter que será leído por la sentencia READ*,A este deberá ser introducido entrecomillado, es decir : 'S'. Por ultimo, dentro de la construcción de varios bloques IF entrelazados se establece una nueva forma que responde a la siguiente estructura: IF (expresión lógica 1) THEN Sentencias nº 1 ejecutadas cuando expresión lógica 1 = IF (expresión lógica 2) THEN Sentencias nº 2 ejecutadas cuando expresión lógica 2 = IF (expresión lógica 3) THEN Sentencias nº 3 ejecutadas cuando expresión lógica 2 = IF (expresión lógica N) THEN Sentencias nº N ejecutadas cuando expresión lógica N = Sentencias nº N+1 ejecutadas cuando expresión lógica 1 = De manera gráfica puede explicarse fácilmente la estructura anterior como se puede ver a continuación: Grupo de Electromagnetismo 4
5 condicion logica 1 sentencias nº 1 condicion logica 2 sentencias nº 2 condicion logica 3 sentencias nº 3 condicion logica N sentencias nº N sentencias nº N+1 EJERCICIO 4.1 Realizar un programa que lea un numero por pantalla y comunique al usuario si es par o impar. EJERCICIO 4.2 Realizar un programa que lea un valor entero comprendido entre 1 y 5 y presente por pantalla la vocal a,e,i,o,u en función del numero leído. El programa deberá advertir al usuario en caso de que el valor introducido no este en el intervalo [1,5]. EJERCICIO 4.3 Realizar un programa que lea una letra del abecedario y diga al usuario si se trata de una vocal o no. EJERCICIO 4.4 Programar la ecuación de 2º grado Ax 2 + B x + C = 0, con la capacidad de dar como resultado las raíces complejas. EJERCICIO 4.5 Realizar un programa que calcule el modulo y el argumento de un numero complejo (a+bi), poniendo especial cuidado en la ubicación del argumento resultante en el cuadrante correcto. Grupo de Electromagnetismo 5
Operando1 operador de relación Operando2
 PROGRAMACIÓN 10 Prof. Dolores Cuiñas H. Recuerde que estos son apuntes muy simplificados que deberá completar con la bibliografía recomendada APUNTES Nº 5 ESTRUCTURAS DE CONTROL SELECTIAS O ESTRUCTURAS
PROGRAMACIÓN 10 Prof. Dolores Cuiñas H. Recuerde que estos son apuntes muy simplificados que deberá completar con la bibliografía recomendada APUNTES Nº 5 ESTRUCTURAS DE CONTROL SELECTIAS O ESTRUCTURAS
Capítulo 3. Prueba de escritorio 1: l a P S 3 2 10. Salida por pantalla 1. Prueba de escritorio 2: l a P S 5 7 24 35. Salida por pantalla 2 35
 Capítulo 3 Procesos con estructuras de selección Procesos con estructuras de selección Los procesos lineales vistos en el capítulo anterior permiten solucionar un muy reducido número de problemas, ya que
Capítulo 3 Procesos con estructuras de selección Procesos con estructuras de selección Los procesos lineales vistos en el capítulo anterior permiten solucionar un muy reducido número de problemas, ya que
Programcaión Básica. Secuencias de Control y Repetición. Arturo Vega González.
 Programación Básica Arturo Vega González [email protected] Division de Ciencias e Ingenierías Universidad de Guanajuato Campus León Sesión 5 Universidad de Guanajuato, DCI, Campus León 1 / 31 Universidad
Programación Básica Arturo Vega González [email protected] Division de Ciencias e Ingenierías Universidad de Guanajuato Campus León Sesión 5 Universidad de Guanajuato, DCI, Campus León 1 / 31 Universidad
Estructuras de control
 Estructuras de control El flujo secuencial de acciones en un algoritmo puede ser alterado por medio de las denominadas estructuras de control, las cuales se resumen a continuación: Estructuras de selección
Estructuras de control El flujo secuencial de acciones en un algoritmo puede ser alterado por medio de las denominadas estructuras de control, las cuales se resumen a continuación: Estructuras de selección
UNIDAD I. ALGORITMOS
 UNIDAD I. ALGORITMOS 1.1 Definición Un algoritmo es una serie de pasos organizados que describe el proceso que se debe seguir, para dar solución a un problema específico. 1.2 Tipos Cualitativos: Son aquellos
UNIDAD I. ALGORITMOS 1.1 Definición Un algoritmo es una serie de pasos organizados que describe el proceso que se debe seguir, para dar solución a un problema específico. 1.2 Tipos Cualitativos: Son aquellos
ENTIDADES PRIMITIVAS PARA EL DESARROLLO DE ALGORITMOS Tipos de datos Expresiones Operadores y operandos Identificadores como localidades de memoria
 ENIDADES PRIMIIVAS PARA EL DESARROLLO DE ALGORIMOS ipos de datos Expresiones Operadores y operandos Identificadores como localidades de memoria ipos De Datos odos los datos tienen un tipo asociado con
ENIDADES PRIMIIVAS PARA EL DESARROLLO DE ALGORIMOS ipos de datos Expresiones Operadores y operandos Identificadores como localidades de memoria ipos De Datos odos los datos tienen un tipo asociado con
2. ENTIDADES PRIMITIVAS PARA EL DESARROLLO DE ALGORITMOS
 2. ENTIDADES PRIMITIVAS PARA EL DESARROLLO DE ALGORITMOS 2.1 Tipos De Datos Todos los datos tienen un tipo asociado con ellos. Un dato puede ser un simple carácter, tal como b, un valor entero tal como
2. ENTIDADES PRIMITIVAS PARA EL DESARROLLO DE ALGORITMOS 2.1 Tipos De Datos Todos los datos tienen un tipo asociado con ellos. Un dato puede ser un simple carácter, tal como b, un valor entero tal como
Expresión, Operador, Operando, Asignación, Prioridad
 4. EXPRESIONES Y OPERADORES Conceptos: Resumen: Expresión, Operador, Operando, Asignación, Prioridad En este tema se presentan los siguientes elementos de la programación: las expresiones y los operadores.
4. EXPRESIONES Y OPERADORES Conceptos: Resumen: Expresión, Operador, Operando, Asignación, Prioridad En este tema se presentan los siguientes elementos de la programación: las expresiones y los operadores.
CAPITULO II. ENTIDADES PRIMITIVAS PARA EL DESARROLLO DE ALGORITMOS
 CAPIULO II. ENIDADES PRIMIIVAS PARA EL DESARROLLO DE ALGORIMOS 2.1 ipos de datos 2.2 Expresiones 2.3 Operadores y operandos 2.4 Identificadores como localidades de memoria OBJEIVO EDUCACIONAL: El alumno:
CAPIULO II. ENIDADES PRIMIIVAS PARA EL DESARROLLO DE ALGORIMOS 2.1 ipos de datos 2.2 Expresiones 2.3 Operadores y operandos 2.4 Identificadores como localidades de memoria OBJEIVO EDUCACIONAL: El alumno:
.LE. <= MENOR O IGUAL QUE .GE. >= MAYOR O IGUAL QUE. Tabla 2.1: Operadores lógicos relacionales Fortran
 2 ESTRUCTURAS DE CONTROL CONDICIONALES Hasta ahora, todas las sentencias que forman los programas se ejecutan. Sin embargo, hay ocasiones en que un determinado conjunto de sentencias se deben ejecutar
2 ESTRUCTURAS DE CONTROL CONDICIONALES Hasta ahora, todas las sentencias que forman los programas se ejecutan. Sin embargo, hay ocasiones en que un determinado conjunto de sentencias se deben ejecutar
$0 Representa al parámetro cero o nombre del programa $1 Representa al parámetro uno $2 Representa al parámetro dos
 PROGRAMACIÓN DE SHELL SCRIPTS EN LINUX El shell es un intérprete de órdenes, pero el shell no es solamente eso; los intérpretes de órdenes de Linux son auténticos lenguajes de programación. Como tales,
PROGRAMACIÓN DE SHELL SCRIPTS EN LINUX El shell es un intérprete de órdenes, pero el shell no es solamente eso; los intérpretes de órdenes de Linux son auténticos lenguajes de programación. Como tales,
LÓGICA - DECISIONES. Hay dos tipos de expresiones lógicas: las expresiones lógicas relacionales y las expresiones lógicas combinacionales.
 LÓGICA - DECIONES Los valores lógicos: constantes, variables y expresiones lógicas, permiten controlar la ejecución de las sentencias de un programa. Hay dos tipos de expresiones lógicas: las expresiones
LÓGICA - DECIONES Los valores lógicos: constantes, variables y expresiones lógicas, permiten controlar la ejecución de las sentencias de un programa. Hay dos tipos de expresiones lógicas: las expresiones
SESIÓN DE EJERCICIOS E1
 SESIÓN DE EJERCICIOS E1 Primera parte: ejercicios test (soluciones al final) A resolver antes de comenzar la sesión en el aula Ejercicio 1 Qué definición de constantes es la correcta en lenguaje C? a)
SESIÓN DE EJERCICIOS E1 Primera parte: ejercicios test (soluciones al final) A resolver antes de comenzar la sesión en el aula Ejercicio 1 Qué definición de constantes es la correcta en lenguaje C? a)
Variables lógicas y sentencia IF. Seminario de Computación Verano de 2009
 Variables lógicas y sentencia IF Seminario de Computación Verano de 2009 Variables lógicas: Solo pueden tomar 2 valores:.true. y.false. (verdadero o falso). Existen operadores que aplicados a variables
Variables lógicas y sentencia IF Seminario de Computación Verano de 2009 Variables lógicas: Solo pueden tomar 2 valores:.true. y.false. (verdadero o falso). Existen operadores que aplicados a variables
Programación de los problemas de Física en.
 Programación de los problemas de Física en. TEMA 1: INTRODUCCIÓN A LA PROGRAMACIÓN 1.2. ORDENADOR COMO CALCULADORA 1.3.ORDENADOR COMO CALCULADORA PROGRAMABLE 1.4. DIAGRAMAS DE FLUJO 1.5. CODIFICAR O PROGRAMAR
Programación de los problemas de Física en. TEMA 1: INTRODUCCIÓN A LA PROGRAMACIÓN 1.2. ORDENADOR COMO CALCULADORA 1.3.ORDENADOR COMO CALCULADORA PROGRAMABLE 1.4. DIAGRAMAS DE FLUJO 1.5. CODIFICAR O PROGRAMAR
Proposiciones Condicionales
 SENTENCIAS CONDICIONALES SIMPLES: if- Anteriormente se discutió que una de las estructuras utilizadas en la programación estructurada es la Estructura Selectiva o Condicional. Se explican aquí las sentencias
SENTENCIAS CONDICIONALES SIMPLES: if- Anteriormente se discutió que una de las estructuras utilizadas en la programación estructurada es la Estructura Selectiva o Condicional. Se explican aquí las sentencias
LOS NÚMEROS ENTEROS NÚMEROS POSITIVOS Y NÚMEROS NEGATIVOS
 LOS NÚMEROS ENTEROS NÚMEROS POSITIVOS Y NÚMEROS NEGATIVOS Para indicar las temperaturas por encima de cero ponemos delante del número el signo más y a las que son por debajo de cero, el signo menos. Para
LOS NÚMEROS ENTEROS NÚMEROS POSITIVOS Y NÚMEROS NEGATIVOS Para indicar las temperaturas por encima de cero ponemos delante del número el signo más y a las que son por debajo de cero, el signo menos. Para
UNIVERSIDAD SAN MARCOS
 Prof. Edwin Gerardo Acuña Acuña UNIVERSIDAD SAN MARCOS ALGEBRA Este capítulo estudia los conceptos básicos del álgebra, una de las disciplinas de la matemática que tiene más aplicaciones en diversos campos.
Prof. Edwin Gerardo Acuña Acuña UNIVERSIDAD SAN MARCOS ALGEBRA Este capítulo estudia los conceptos básicos del álgebra, una de las disciplinas de la matemática que tiene más aplicaciones en diversos campos.
Estructuras de control. Secuencial, condicional y repetitivas.
 Estructuras de control. Secuencial, condicional y repetitivas. 1 Estructuras de control. Hemos visto en los diagramas de flujo y pseudo-código que: 1) Se piden datos de entrada (al usuario) Asiganción
Estructuras de control. Secuencial, condicional y repetitivas. 1 Estructuras de control. Hemos visto en los diagramas de flujo y pseudo-código que: 1) Se piden datos de entrada (al usuario) Asiganción
MICROSOFT EXCEL QUÉ ES MICROSOFT EXCEL?
 MICROSOFT EXCEL QUÉ ES MICROSOFT EXCEL? Excel es un paquete especializado en cálculos de todo tipo y gráficas, especialmente creado para Nominas, Inventarios, Base de datos, etc. Podría seguir con la lista
MICROSOFT EXCEL QUÉ ES MICROSOFT EXCEL? Excel es un paquete especializado en cálculos de todo tipo y gráficas, especialmente creado para Nominas, Inventarios, Base de datos, etc. Podría seguir con la lista
Operaciones aritméticas
 Operaciones aritméticas Operador aritmético Operación Ejemplo Resultado Potencia 4 3 64 Multiplicación 8.25 7 57.75 / División 15 / 4 3.75 Suma 125.78 62.50 188.28 Resta 65.30 32.33 32.97 mod Módulo (residuo)
Operaciones aritméticas Operador aritmético Operación Ejemplo Resultado Potencia 4 3 64 Multiplicación 8.25 7 57.75 / División 15 / 4 3.75 Suma 125.78 62.50 188.28 Resta 65.30 32.33 32.97 mod Módulo (residuo)
REGLAS DE LOS SIGNOS
 1. 1 UNIDAD 1 REGLAS DE LOS SIGNOS Objetivo general. Al terminar esta Unidad resolverás ejercicios y problemas en los que apliques las reglas de los signos. Objetivos específicos: 1. Recordarás las reglas
1. 1 UNIDAD 1 REGLAS DE LOS SIGNOS Objetivo general. Al terminar esta Unidad resolverás ejercicios y problemas en los que apliques las reglas de los signos. Objetivos específicos: 1. Recordarás las reglas
TEMA 4. ESTRUCTURAS DE CONTROL
 M.P. Sesmero, P. de Toledo, F.J. Ordoñez, J. Gómez-Romero, J.A. Iglesias, J.L. Mira Programación TEMA 4. ESTRUCTURAS DE CONTROL Grado en Ingeniería en Tecnologías Industriales Programación CONTENIDOS 4.1.
M.P. Sesmero, P. de Toledo, F.J. Ordoñez, J. Gómez-Romero, J.A. Iglesias, J.L. Mira Programación TEMA 4. ESTRUCTURAS DE CONTROL Grado en Ingeniería en Tecnologías Industriales Programación CONTENIDOS 4.1.
Competencias que se favorecen. Validar procedimientos y resultados. Manejar técnicas eficientemente.
 Introducción En este bloque resolverás cálculos numéricos que implican el uso de un orden jerárquico e involucran el uso de números enteros, decimales y fraccionarios. En el caso de la geometría justificarás
Introducción En este bloque resolverás cálculos numéricos que implican el uso de un orden jerárquico e involucran el uso de números enteros, decimales y fraccionarios. En el caso de la geometría justificarás
CURSO BÁSICO DE MATEMÁTICAS PARA ESTUDIANTES DE ECONÓMICAS Y EMPRESARIALES. Unidad didáctica 4. Números reales y números complejos
 NÚMEROS REALES Como se ha señalado anteriormente la necesidad de resolver diversos problemas de origen aritmético y geométrico lleva a ir ampliando sucesivamente los conjuntos numéricos, N Z Q, y a definir
NÚMEROS REALES Como se ha señalado anteriormente la necesidad de resolver diversos problemas de origen aritmético y geométrico lleva a ir ampliando sucesivamente los conjuntos numéricos, N Z Q, y a definir
CAPITULO 2. ELEMENTOS Y OPERACIONES DE LAS EXPRESIONES ALGEBRAICAS. Cuando nos encontramos con dos o más términos algebraicos en un
 CAPITULO 2. ELEMENTOS Y OPERACIONES DE LAS EXPRESIONES ALGEBRAICAS. Cuando nos encontramos con dos o más términos algebraicos en un conjunto relacionado, los matemáticos dicen que tratamos con una expresión
CAPITULO 2. ELEMENTOS Y OPERACIONES DE LAS EXPRESIONES ALGEBRAICAS. Cuando nos encontramos con dos o más términos algebraicos en un conjunto relacionado, los matemáticos dicen que tratamos con una expresión
SESIÓN DE EJERCICIOS E1
 SESIÓN DE EJERCICIOS E1 Primera parte: ejercicios test Ejercicio 1 Qué definición de constantes es la correcta en lenguaje C? a) #define N=25; b) #define N 25 c) int N=25; d) int N 25 Ejercicio 2 La expresión
SESIÓN DE EJERCICIOS E1 Primera parte: ejercicios test Ejercicio 1 Qué definición de constantes es la correcta en lenguaje C? a) #define N=25; b) #define N 25 c) int N=25; d) int N 25 Ejercicio 2 La expresión
Análisis de problemas
 Análisis de problemas La resolución de problemas implica el desarrollo de habilidades del pensamiento. Nuestra capacidad d de enfrentar problemas aumenta con la práctica. Existen algunos textos con problemas
Análisis de problemas La resolución de problemas implica el desarrollo de habilidades del pensamiento. Nuestra capacidad d de enfrentar problemas aumenta con la práctica. Existen algunos textos con problemas
8.1.- ENTRADA Y SALIDA CON FORMATO
 8.1.- ENTRADA Y SALIDA CON FORMATO El presente capitulo va a estar dedicado exclusivamente a presentar las diferentes maneras que FORTRAN ofrece para leer y escribir datos de cualquier tipo mediante un
8.1.- ENTRADA Y SALIDA CON FORMATO El presente capitulo va a estar dedicado exclusivamente a presentar las diferentes maneras que FORTRAN ofrece para leer y escribir datos de cualquier tipo mediante un
SISTEMA DE NUMERACIÓN BINARIO
 SISTEMA DE NUMERACIÓN BINARIO Cuando se trabaja en una computadora, los datos son convertidos en números dígitos que, a su vez, son representados como pulsaciones o pulsos electrónicos. En la actualidad
SISTEMA DE NUMERACIÓN BINARIO Cuando se trabaja en una computadora, los datos son convertidos en números dígitos que, a su vez, son representados como pulsaciones o pulsos electrónicos. En la actualidad
1. Conocimientos previos. 1 Funciones exponenciales y logarítmicas.
 . Conocimientos previos. Funciones exponenciales y logarítmicas.. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Intervalos y sus definiciones básicas.
. Conocimientos previos. Funciones exponenciales y logarítmicas.. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Intervalos y sus definiciones básicas.
TEMA 1: NÚMEROS REALES
 TEMA 1: NÚMEROS REALES 3º ESO Matemáticas Apuntes para trabajo del alumnos en el aula. 1. Fracciones. Números racionales Si se multiplican o dividen el numerador y el denominador de una fracción por un
TEMA 1: NÚMEROS REALES 3º ESO Matemáticas Apuntes para trabajo del alumnos en el aula. 1. Fracciones. Números racionales Si se multiplican o dividen el numerador y el denominador de una fracción por un
Inecuaciones y Ecuación cuadrática
 Inecuaciones Desigualdades Inecuaciones y Ecuación cuadrática Llamaremos desigualdades a expresiones de la forma a > b, a < b, a b ó a b. Las desigualdades cumplen con las siguientes propiedades: Propiedad
Inecuaciones Desigualdades Inecuaciones y Ecuación cuadrática Llamaremos desigualdades a expresiones de la forma a > b, a < b, a b ó a b. Las desigualdades cumplen con las siguientes propiedades: Propiedad
UNIDAD II FUNCIONES. Ing. Ronny Altuve Esp.
 República Bolivariana de Venezuela Universidad Alonso de Ojeda Administración Mención Gerencia y Mercadeo UNIDAD II FUNCIONES Ing. Ronny Altuve Esp. Ciudad Ojeda, Septiembre de 2015 Función Universidad
República Bolivariana de Venezuela Universidad Alonso de Ojeda Administración Mención Gerencia y Mercadeo UNIDAD II FUNCIONES Ing. Ronny Altuve Esp. Ciudad Ojeda, Septiembre de 2015 Función Universidad
LUGAR GEOMÉTRICO DE LAS RAICES (LGR)
 LUGAR GEOMÉTRICO DE LAS RAICES (LGR) DEFINICIÓN: El lugar geométrico de las raíces es la trayectoria formada por las raíces de una ecuación polinómica cuando un parámetro de ésta varía. En el caso de Sistemas
LUGAR GEOMÉTRICO DE LAS RAICES (LGR) DEFINICIÓN: El lugar geométrico de las raíces es la trayectoria formada por las raíces de una ecuación polinómica cuando un parámetro de ésta varía. En el caso de Sistemas
Universidad Politécnica de Puerto Rico Departamento de Ciencias y Matemáticas. Preparado por: Prof. Manuel Capella-Casellas, M.A.Ed.
 Universidad Politécnica de Puerto Rico Departamento de Ciencias y Matemáticas Preparado por: Prof. Manuel Capella-Casellas, M.A.Ed. Agosto, 00 Notación exponencial La notación exponencial se usa para repetir
Universidad Politécnica de Puerto Rico Departamento de Ciencias y Matemáticas Preparado por: Prof. Manuel Capella-Casellas, M.A.Ed. Agosto, 00 Notación exponencial La notación exponencial se usa para repetir
Introducción a las sentencias de control
 INSTRUCCIONES DE CONTROL CONTENIDOS 1. Introducción a las sentencias de control. 2. Instrucciones o sentencias condicionales: IF, IF-ELSE, SWITCH. 3. Instrucciones o sentencias repetitivas o iterativas:
INSTRUCCIONES DE CONTROL CONTENIDOS 1. Introducción a las sentencias de control. 2. Instrucciones o sentencias condicionales: IF, IF-ELSE, SWITCH. 3. Instrucciones o sentencias repetitivas o iterativas:
Ejercicio 1: Realiza las siguientes divisiones por el método tradicional y por Ruffini: a)
 Tema 2: Ecuaciones, Sistemas e Inecuaciones. 2.1 División de polinomios. Regla de Ruffini. Polinomio: Expresión algebraica formada por la suma y/o resta de varios monomios. Terminología: o Grado del polinomio:
Tema 2: Ecuaciones, Sistemas e Inecuaciones. 2.1 División de polinomios. Regla de Ruffini. Polinomio: Expresión algebraica formada por la suma y/o resta de varios monomios. Terminología: o Grado del polinomio:
Resolución de Problemas y Algoritmos
 RESOLUCIÓN DE PROBLEMAS Y ALGORITMOS CLASE Estructura de control condicional. Luciano H. Tamargo http://cs.uns.edu.ar/~lt Depto. de Ciencias e Ingeniería de la Computación Universidad Nacional del Sur,
RESOLUCIÓN DE PROBLEMAS Y ALGORITMOS CLASE Estructura de control condicional. Luciano H. Tamargo http://cs.uns.edu.ar/~lt Depto. de Ciencias e Ingeniería de la Computación Universidad Nacional del Sur,
Utiliza los números ordinales al resolver problemas planteados de manera oral.
 T G CONTENIDOS APRENDIZAJES ESPERADOS ESTÁNDARES 1.2.1 Identificación y uso de los números ordinales para colocar objetos o para indicar el lugar que ocupan dentro de una colección de hasta 10 elementos.
T G CONTENIDOS APRENDIZAJES ESPERADOS ESTÁNDARES 1.2.1 Identificación y uso de los números ordinales para colocar objetos o para indicar el lugar que ocupan dentro de una colección de hasta 10 elementos.
Teoría de conjuntos. Tema 1: Teoría de Conjuntos.
 Tema 1: Teoría de Conjuntos. La teoría de Conjuntos es actualmente una de las más importantes dentro de la matemática. Muchos de los problemas que se le han presentado a esta disciplina en los últimos
Tema 1: Teoría de Conjuntos. La teoría de Conjuntos es actualmente una de las más importantes dentro de la matemática. Muchos de los problemas que se le han presentado a esta disciplina en los últimos
Lógica y compuertas (Parte 2): Circuitos Combinacionales y Secuenciales
 Práctica 4 Lógica y compuertas (Parte 2): Circuitos Combinacionales y Secuenciales Objetivos de la práctica: que el alumno domine Circuitos lógicos y diagramas de compuertas Introducción a equivalencias
Práctica 4 Lógica y compuertas (Parte 2): Circuitos Combinacionales y Secuenciales Objetivos de la práctica: que el alumno domine Circuitos lógicos y diagramas de compuertas Introducción a equivalencias
Algoritmos. Luis Castellanos & Angela Galea marzo de 2012
 Luis Castellanos & Angela Galea marzo de 2012 Contenido 1. Introducción. 2. Qué es un Algoritmo 3. Tipos de 4. Para qué sirven los algoritmos? 5. Lenguaje de Programación 6. Tipos de Datos 7. Tipos de
Luis Castellanos & Angela Galea marzo de 2012 Contenido 1. Introducción. 2. Qué es un Algoritmo 3. Tipos de 4. Para qué sirven los algoritmos? 5. Lenguaje de Programación 6. Tipos de Datos 7. Tipos de
Pertenencia y no pertenencia
 Colegio San Benito Abad Institución Educativa Distrital NIT 830.068.785-7* DANE 11100186634 Inscripción en Secretaria Educación N. 6534. acuerdo creación N 17 de 29-10-1992 Aprobación según Resolución
Colegio San Benito Abad Institución Educativa Distrital NIT 830.068.785-7* DANE 11100186634 Inscripción en Secretaria Educación N. 6534. acuerdo creación N 17 de 29-10-1992 Aprobación según Resolución
RELACIÓN ENTRE LA GRÁFICA DE UNA FUNCIÓN f y LA DE SU INVERSA f -1
 RELACIÓN ENTRE LA GRÁFICA DE UNA FUNCIÓN f y LA DE SU INVERSA f -1 Sabemos que la función inversa 1 Si f a b, entonces f b a 1 f (o recíproca) de f cumple la siguiente condición: Por lo tanto: 1 f f 1
RELACIÓN ENTRE LA GRÁFICA DE UNA FUNCIÓN f y LA DE SU INVERSA f -1 Sabemos que la función inversa 1 Si f a b, entonces f b a 1 f (o recíproca) de f cumple la siguiente condición: Por lo tanto: 1 f f 1
operaciones inversas Para unificar ambas operaciones, se define la potencia de exponente fraccionario:
 Potencias y raíces Potencias y raíces Potencia operaciones inversas Raíz exponente índice 7 = 7 7 7 = 4 4 = 7 base base Para unificar ambas operaciones, se define la potencia de exponente fraccionario:
Potencias y raíces Potencias y raíces Potencia operaciones inversas Raíz exponente índice 7 = 7 7 7 = 4 4 = 7 base base Para unificar ambas operaciones, se define la potencia de exponente fraccionario:
VALOR ABSOLUTO EN LA RECTA NUMÉRICA
 VALOR ABSOLUTO EN LA RECTA NUMÉRICA 1 CONTENIDO 1. Distancia entre dos puntos. 2. Punto medio. 3. Valor Absoluto. 4. Ecuaciones e Inecuaciones con valor Absoluto 2 Concepto de distancia entre dos puntos
VALOR ABSOLUTO EN LA RECTA NUMÉRICA 1 CONTENIDO 1. Distancia entre dos puntos. 2. Punto medio. 3. Valor Absoluto. 4. Ecuaciones e Inecuaciones con valor Absoluto 2 Concepto de distancia entre dos puntos
GUIA PRACTICA PARA LA APLICACIÓN DE MS EXCEL TECNOLOGIA/ INFORMATICA
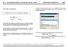 Fórmulas y funciones De la barra de menú seleccionmos la opción insertar y haciendo clic en la opción f x se desplegará el siguiente cuadro de diálogo a partir del cual escogeremos la función adecuada
Fórmulas y funciones De la barra de menú seleccionmos la opción insertar y haciendo clic en la opción f x se desplegará el siguiente cuadro de diálogo a partir del cual escogeremos la función adecuada
N = {1, 2, 3, 4, 5,...}
 Números y Funciones.. Números Los principales tipos de números son:. Los números naturales son aquellos que sirven para contar. N = {,,, 4, 5,...}. Los números enteros incluyen a los naturales y a sus
Números y Funciones.. Números Los principales tipos de números son:. Los números naturales son aquellos que sirven para contar. N = {,,, 4, 5,...}. Los números enteros incluyen a los naturales y a sus
5. Al simplificar. expresión se obtiene:
 ARITMÉTICA. [ ( 7 ) 9 ( 7 )] es igual a : 5. El resultado de simplificar la expresión. 5 5 5 7 7, 6 + es igual a: 5 9 7 6 5 5. El valor de 75 6 5 5 ( 5 )( 65 ) log es igual a: 5 5 5. Al simplificar Mayo
ARITMÉTICA. [ ( 7 ) 9 ( 7 )] es igual a : 5. El resultado de simplificar la expresión. 5 5 5 7 7, 6 + es igual a: 5 9 7 6 5 5. El valor de 75 6 5 5 ( 5 )( 65 ) log es igual a: 5 5 5. Al simplificar Mayo
1. El sistema de los números reales
 1. El sistema de los números reales Se iniciará definiendo el conjunto de números que conforman a los números reales, en la siguiente figura se muestra la forma en la que están contenidos estos conjuntos
1. El sistema de los números reales Se iniciará definiendo el conjunto de números que conforman a los números reales, en la siguiente figura se muestra la forma en la que están contenidos estos conjuntos
CENTRO DE EDUCACIÓN MEDIA CURSO CERO. Departamento: Matemáticas y Física. Área Académica: Matemáticas. Nombre de la materia: Curso Cero
 CENTRO DE EDUCACIÓN MEDIA CURSO CERO DATOS DE IDENTIFICACIÓN CENTRO DE EDUCACIÓN MEDIA Departamento: Matemáticas y Física. Área Académica: Matemáticas BACHILLERATO Nombre de la materia: Curso Cero Tipo
CENTRO DE EDUCACIÓN MEDIA CURSO CERO DATOS DE IDENTIFICACIÓN CENTRO DE EDUCACIÓN MEDIA Departamento: Matemáticas y Física. Área Académica: Matemáticas BACHILLERATO Nombre de la materia: Curso Cero Tipo
INSTITUCION EDUCATIVA LA PRESENTACION
 INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMATICAS ASIGNATURA: MATEMATICAS DOCENTE: HUGO HERNAN BEDOYA Y LUIS LOPEZ TIPO DE GUIA: NIVELACION PERIODO GRADO FECHA DURACION 8 A/B Abril
INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMATICAS ASIGNATURA: MATEMATICAS DOCENTE: HUGO HERNAN BEDOYA Y LUIS LOPEZ TIPO DE GUIA: NIVELACION PERIODO GRADO FECHA DURACION 8 A/B Abril
Guía Práctica N 14: Función Logarítmica
 Fuente: Pre Universitario Pedro de Valdivia Guía Práctica N 4: Función Logarítmica LOGARITMOS FUNCIÓN LOGARÍTMICA DEFINICIÓN El logaritmo de un número real positivo b en base a, positiva y distinta de,
Fuente: Pre Universitario Pedro de Valdivia Guía Práctica N 4: Función Logarítmica LOGARITMOS FUNCIÓN LOGARÍTMICA DEFINICIÓN El logaritmo de un número real positivo b en base a, positiva y distinta de,
Los datos de una cuenta bancaria. (Dato compuesto por: nombre, apellidos, etc.) La capital de Canadá. ("Ottawa" > Dato de tipo cadena)
 Solución del Ejercicio 1 - Clasificar datos (Tipos de datos - Pseudocódigo CEE) Datos simples: El número de botones de una camisa. (Por ejemplo: 8 > Dato numérico entero) La altura de una torre. (Por ejemplo:
Solución del Ejercicio 1 - Clasificar datos (Tipos de datos - Pseudocódigo CEE) Datos simples: El número de botones de una camisa. (Por ejemplo: 8 > Dato numérico entero) La altura de una torre. (Por ejemplo:
Bloque 15. Valor absoluto: funciones lineales y cuadráticas
 Bloque 15 Valor absoluto: funciones lineales y cuadráticas Bloque 15 Valor absoluto: Funciones lineales y cuadráticas Presentación El bloque tiene como propósitos centrales (i) (ii) Determinar el dominio
Bloque 15 Valor absoluto: funciones lineales y cuadráticas Bloque 15 Valor absoluto: Funciones lineales y cuadráticas Presentación El bloque tiene como propósitos centrales (i) (ii) Determinar el dominio
Los números enteros. > significa "mayor que". Ejemplo: 58 > 12 < significa "menor que". Ejemplo: 3 < 12 Cualquier número positivo siempre es mayor
 Los números enteros Los números enteros Los números enteros son aquellos que permiten contar tanto los objetos que se tienen, como los objetos que se deben. Enteros positivos: precedidos por el signo +
Los números enteros Los números enteros Los números enteros son aquellos que permiten contar tanto los objetos que se tienen, como los objetos que se deben. Enteros positivos: precedidos por el signo +
Centro Universitario UAEM Zumpango Ingeniería en Computación
 Centro Universitario UAEM Zumpango Agosto 2016 Universidad Autónoma del Estado de México Centro Universitario UAEM Zumpango UA: Programación Estructurada Tema: Estructuras de control de flujo selectivas
Centro Universitario UAEM Zumpango Agosto 2016 Universidad Autónoma del Estado de México Centro Universitario UAEM Zumpango UA: Programación Estructurada Tema: Estructuras de control de flujo selectivas
GUIÓN DE PRÁCTICAS 3: ESTRUCTURAS CONDICIONALES
 GUIÓN DE PRÁCTICAS 3: ESTRUCTURAS CONDICIONALES Introducción. En este guión vamos a introducir aquellas estructuras en C que nos permiten seleccionar qué parte del código queremos que se ejecute. A este
GUIÓN DE PRÁCTICAS 3: ESTRUCTURAS CONDICIONALES Introducción. En este guión vamos a introducir aquellas estructuras en C que nos permiten seleccionar qué parte del código queremos que se ejecute. A este
Capítulo 1. Algoritmos, diagramas de flujo y programas.
 Capítulo 1. Algoritmos, diagramas de flujo y programas. 1.1 Problemas y algoritmos 1.2 Diagramas de flujo 1.2.1 Reglas para la construcción de diagramas de flujo 1.3 Conceptos fundamentales 1.3.1 Tipos
Capítulo 1. Algoritmos, diagramas de flujo y programas. 1.1 Problemas y algoritmos 1.2 Diagramas de flujo 1.2.1 Reglas para la construcción de diagramas de flujo 1.3 Conceptos fundamentales 1.3.1 Tipos
Operadores aritméticos
 Bloque 3.2 Operadores aritméticos Suma : x + y Resta : x y Multiplicación : x * y División : x / y Módulo : x % y (resto de la división Si los operandos son enteros tipo del resultado
Bloque 3.2 Operadores aritméticos Suma : x + y Resta : x y Multiplicación : x * y División : x / y Módulo : x % y (resto de la división Si los operandos son enteros tipo del resultado
Tema: Estructuras de Selección en C#.
 2 Programación I Tema: Estructuras de Selección en C#. Programación I. Guía 4 3 Facultad: Ingeniería Escuela: Ingeniería en Computación Asignatura: Programación I Objetivos Utilizar las instrucciones de
2 Programación I Tema: Estructuras de Selección en C#. Programación I. Guía 4 3 Facultad: Ingeniería Escuela: Ingeniería en Computación Asignatura: Programación I Objetivos Utilizar las instrucciones de
Se llama factores o divisores, a las expresiones algebraicas que multiplicadas entre sí, dan como producto la primera expresión.
 FACTORIZACION Se llama factores o divisores, a las expresiones algebraicas que multiplicadas entre sí, dan como producto la primera expresión. Al proceso de encontrar los factores o divisores a partir
FACTORIZACION Se llama factores o divisores, a las expresiones algebraicas que multiplicadas entre sí, dan como producto la primera expresión. Al proceso de encontrar los factores o divisores a partir
El pseudocódigo es una herramienta de programación en la que las instrucciones se escriben en palabras similares al inglés o español, que facilitan
 El pseudocódigo es una herramienta de programación en la que las instrucciones se escriben en palabras similares al inglés o español, que facilitan tanto la escritura como la lectura de programas En esencia,
El pseudocódigo es una herramienta de programación en la que las instrucciones se escriben en palabras similares al inglés o español, que facilitan tanto la escritura como la lectura de programas En esencia,
Combinación Lineal. Departamento de Matemáticas, CCIR/ITESM. 10 de enero de 2011
 Combinación Lineal Departamento de Matemáticas, CCIR/ITESM 10 de enero de 011 Índice.1. Introducción............................................... 1.. Combinación lineal entre vectores...................................
Combinación Lineal Departamento de Matemáticas, CCIR/ITESM 10 de enero de 011 Índice.1. Introducción............................................... 1.. Combinación lineal entre vectores...................................
Tipos de Funciones. 40 Ejercicios para practicar con soluciones. 1 Representa en los mismos ejes las siguientes funciones: 1 x
 Tipos de Funciones. 40 Ejercicios para practicar con soluciones Representa en los mismos ejes las siguientes funciones: a) y = ; b) y = ; c) y = y= y= y= Representa las siguientes funciones: a) y = b)
Tipos de Funciones. 40 Ejercicios para practicar con soluciones Representa en los mismos ejes las siguientes funciones: a) y = ; b) y = ; c) y = y= y= y= Representa las siguientes funciones: a) y = b)
POTENCIAS. MÚLTIPLOS Y DIVISORES. MÁXIMO COMÚN DIVISOR Y MÍNIMO COMÚN MÚLTIPLO.
 1. LOS NÚMEROS NATURALES POTENCIAS. MÚLTIPLOS Y DIVISORES. MÁXIMO COMÚN DIVISOR Y MÍNIMO COMÚN MÚLTIPLO. 2. LOS NÚMEROS ENTEROS. VALOR ABSOLUTO DE UN NÚMERO ENTERO. REPRESENTACIÓN GRÁFICA. OPERACIONES.
1. LOS NÚMEROS NATURALES POTENCIAS. MÚLTIPLOS Y DIVISORES. MÁXIMO COMÚN DIVISOR Y MÍNIMO COMÚN MÚLTIPLO. 2. LOS NÚMEROS ENTEROS. VALOR ABSOLUTO DE UN NÚMERO ENTERO. REPRESENTACIÓN GRÁFICA. OPERACIONES.
Tema 6 Lenguaje Algebraico. Ecuaciones
 Tema 6 Lenguaje Algebraico. Ecuaciones 1. El álgebra El álgebra es una rama de las matemáticas que emplea números y letras con las operaciones aritméticas de sumar, restar, multiplicar, dividir, potencias
Tema 6 Lenguaje Algebraico. Ecuaciones 1. El álgebra El álgebra es una rama de las matemáticas que emplea números y letras con las operaciones aritméticas de sumar, restar, multiplicar, dividir, potencias
El lenguaje C. 3. Una instrucción que se ejecutará si la condición es verdadera.
 Principios de Programación El lenguaje C 1. Instrucciones de control 1.1. Secuencia, selección, iteración Por lo regular en un programa los enunciados son ejecutados uno después del otro, en el orden en
Principios de Programación El lenguaje C 1. Instrucciones de control 1.1. Secuencia, selección, iteración Por lo regular en un programa los enunciados son ejecutados uno después del otro, en el orden en
DESCOMPOSICIÓN FACTORIAL
 6. 1 UNIDAD 6 DESCOMPOSICIÓN FACTORIAL Objetivo general. Al terminar esta Unidad resolverás ejercicios y problemas en los que apliques la factorización de polinomios cuyos términos tienen coeficientes
6. 1 UNIDAD 6 DESCOMPOSICIÓN FACTORIAL Objetivo general. Al terminar esta Unidad resolverás ejercicios y problemas en los que apliques la factorización de polinomios cuyos términos tienen coeficientes
DISEÑO ESTRUCTURADO USANDO HERRAMIENTAS DE
 DISEÑO ESTRUCTURADO USANDO HERRAMIENTAS DE REPRESENTACIÓN DE ALGORITMOS PSEUDOCÓDIGO El pseudocódigo es una herramienta de programación en la que las instrucciones se escriben en palabras similares al
DISEÑO ESTRUCTURADO USANDO HERRAMIENTAS DE REPRESENTACIÓN DE ALGORITMOS PSEUDOCÓDIGO El pseudocódigo es una herramienta de programación en la que las instrucciones se escriben en palabras similares al
Convertir unidades de longitud Determinar el perímetro de triángulo y cuadrilátero Determinar el volumen de prismas rectos.
 Colegio Preuniversitario Dr. Luis Alfredo Duvergé Mejía Listado de contenidos en matemática a estudiar para ingresar al 6to Grado Nivel Básico. Números y operaciones. Leer y escribe los números de mayores
Colegio Preuniversitario Dr. Luis Alfredo Duvergé Mejía Listado de contenidos en matemática a estudiar para ingresar al 6to Grado Nivel Básico. Números y operaciones. Leer y escribe los números de mayores
Prof. Dr. Paul Bustamante
 Nombre: Carné: Examen C++ - Junio Informática II Fundamentos de Programación Prof. Dr. Paul Bustamante Examen Grupo B Programación en C++ Pág. 1 ÍNDICE ÍNDICE... 1 1. Introducción.... 1 1.1 Ejercicio 1:
Nombre: Carné: Examen C++ - Junio Informática II Fundamentos de Programación Prof. Dr. Paul Bustamante Examen Grupo B Programación en C++ Pág. 1 ÍNDICE ÍNDICE... 1 1. Introducción.... 1 1.1 Ejercicio 1:
I.E.S. CUADERNO Nº 3 NOMBRE: FECHA: / / Los números enteros
 Los números enteros Contenidos 1. Los números enteros Introducción La recta numérica Valor absoluto Ordenar enteros Opuesto de un número entero 2. Suma y diferencia de enteros Suma de dos enteros Suma
Los números enteros Contenidos 1. Los números enteros Introducción La recta numérica Valor absoluto Ordenar enteros Opuesto de un número entero 2. Suma y diferencia de enteros Suma de dos enteros Suma
CURSO BÁSICO DE MATEMÁTICAS PARA ESTUDIANTES DE ECONÓMICAS Y EMPRESARIALES. Unidad didáctica 4. Números reales y números complejos
 NÚMEROS REALES NÚMEROS NATURALES Y NÚMEROS ENTEROS Los números naturales surgen como respuesta a la necesidad de nuestros antepasados de contar los elementos de un conjunto (por ejemplo los animales de
NÚMEROS REALES NÚMEROS NATURALES Y NÚMEROS ENTEROS Los números naturales surgen como respuesta a la necesidad de nuestros antepasados de contar los elementos de un conjunto (por ejemplo los animales de
Conocimientos previos
 Ficha de Aprendizaje Tema: Estructura condicional Logro @ # n 11 Conoce las estructuras de control condicional. Usa las estructuras de control condicional: if else, if else if, switch case. Conocimientos
Ficha de Aprendizaje Tema: Estructura condicional Logro @ # n 11 Conoce las estructuras de control condicional. Usa las estructuras de control condicional: if else, if else if, switch case. Conocimientos
Clase adicional 2. Estructuras básicas de control. Temas
 Clase adicional 2 Temas Estructuras de control Sentencia condicional Iteración Clases Definir una clase Crear una instancia de una clase Campos estáticos Problemas de la clase adicional Problema de diseño
Clase adicional 2 Temas Estructuras de control Sentencia condicional Iteración Clases Definir una clase Crear una instancia de una clase Campos estáticos Problemas de la clase adicional Problema de diseño
Teoría de Conjuntos. Conjunto es: colección de cosas, o una colección determinada de objetos.
 Teoría de Conjuntos Apuntes Fernando Toscano tomados por A.Diz-Lois La teoría de conjuntos es una herramienta formal semántica que trata de dotar de significado, o lo que es lo mismo dotar de interpretación.
Teoría de Conjuntos Apuntes Fernando Toscano tomados por A.Diz-Lois La teoría de conjuntos es una herramienta formal semántica que trata de dotar de significado, o lo que es lo mismo dotar de interpretación.
Matemáticas Propedéutico para Bachillerato. Introducción
 ctividad 1. Notación de Conjuntos. Introducción La Teoría de Conjuntos fue introducida por el matemático alemán George Cantor. Desde pequeños hemos estado en contacto con ella, por ejemplo, quién de ustedes
ctividad 1. Notación de Conjuntos. Introducción La Teoría de Conjuntos fue introducida por el matemático alemán George Cantor. Desde pequeños hemos estado en contacto con ella, por ejemplo, quién de ustedes
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág. Página 7 PRACTICA Números reales a) Clasifica los siguientes números como racionales o irracionales: ; 9 ;, 7; ),; ; b) Alguno de ellos es entero? c) Ordénalos de menor a mayor. a) Racionales: ; 9
Pág. Página 7 PRACTICA Números reales a) Clasifica los siguientes números como racionales o irracionales: ; 9 ;, 7; ),; ; b) Alguno de ellos es entero? c) Ordénalos de menor a mayor. a) Racionales: ; 9
INTRODUCCIÓN AL TURBO PASCAL.
 PROGRAMACIÓN 10 Prof. Dolores Cuiñas H. APUNTES Nº 2. Recuerde que estos son apuntes muy simplificados que deberá completar con la bibliografía recomendada INTRODUCCIÓN AL TURBO PASCAL. El lenguaje Turbo
PROGRAMACIÓN 10 Prof. Dolores Cuiñas H. APUNTES Nº 2. Recuerde que estos son apuntes muy simplificados que deberá completar con la bibliografía recomendada INTRODUCCIÓN AL TURBO PASCAL. El lenguaje Turbo
FUNCIONES CUADRÁTICAS. PARÁBOLAS
 FUNCIONES CUADRÁTICAS. PARÁBOLAS 1. FUNCIONES CUADRÁTICAS Representemos, en función de la longitud de la base (x), el área (y) de todos los rectángulos de perímetro 1 metros. De ellos, cuáles son las medidas
FUNCIONES CUADRÁTICAS. PARÁBOLAS 1. FUNCIONES CUADRÁTICAS Representemos, en función de la longitud de la base (x), el área (y) de todos los rectángulos de perímetro 1 metros. De ellos, cuáles son las medidas
La Jerarquía de Chomsky
 La Apuntes sobre la Complejidad Universidad de Cantabria Esquema Motivación 1 Motivación 2 Ideas y Nociones Motivación Como se ha mencionado anteriormente, los lenguajes son conjuntos de palabras definidos
La Apuntes sobre la Complejidad Universidad de Cantabria Esquema Motivación 1 Motivación 2 Ideas y Nociones Motivación Como se ha mencionado anteriormente, los lenguajes son conjuntos de palabras definidos
Capítulo 5 IDENTIFICADORES, VARIABLES Y CONSTANTES. Presentación resumen del libro: "EMPEZAR DE CERO A PROGRAMAR EN lenguaje C"
 Presentación resumen del libro: "EMPEZAR DE CERO A PROGRAMAR EN lenguaje C" Autor: Carlos Javier Pes Rivas ([email protected]) Capítulo 5 IDENTIFICADORES, VARIABLES Y CONSTANTES 1 OBJETIVOS Saber qué
Presentación resumen del libro: "EMPEZAR DE CERO A PROGRAMAR EN lenguaje C" Autor: Carlos Javier Pes Rivas ([email protected]) Capítulo 5 IDENTIFICADORES, VARIABLES Y CONSTANTES 1 OBJETIVOS Saber qué
UNIDAD 2: INTRODUCCIÓN AL LENGUAJE DE PROGRAMACiÓN R
 UNIDAD 2: INTRODUCCIÓN AL LENGUAJE DE PROGRAMACiÓN R Técnicas Inteligentes en Bioinformática Máster en Lógica, Computación e Inteligencia Artificial Dpto. Ciencias de la Computación e Inteligencia Artificial
UNIDAD 2: INTRODUCCIÓN AL LENGUAJE DE PROGRAMACiÓN R Técnicas Inteligentes en Bioinformática Máster en Lógica, Computación e Inteligencia Artificial Dpto. Ciencias de la Computación e Inteligencia Artificial
RAZONES TRIGONOMÉTRICAS
 RAZONES TRIGONOMÉTRICAS.- PRIMERAS DEFINICIONES Se denomina ángulo en el plano a la porción de plano comprendida entre dos semirrectas con un origen común denominado vértice. Ángulo central es el ángulo
RAZONES TRIGONOMÉTRICAS.- PRIMERAS DEFINICIONES Se denomina ángulo en el plano a la porción de plano comprendida entre dos semirrectas con un origen común denominado vértice. Ángulo central es el ángulo
6. EJERCICIOS RESUELTOS
 CLASE : CICLOS. CICLOS CLASE. EJERCICIOS RESUELTOS 0. Desarrollar un algoritmo que imprima desde el numero hasta el 0 C= Mientras C
CLASE : CICLOS. CICLOS CLASE. EJERCICIOS RESUELTOS 0. Desarrollar un algoritmo que imprima desde el numero hasta el 0 C= Mientras C
OPERADORES LÓGICOS JAVASCRIPT. EJEMPLOS. RELACIONALES MAYOR, MENOR, IGUAL, DISTINTO. AND, OR, NOT. CORTO- CIRCUITO (CU01117E)
 APRENDERAPROGRAMAR.COM OPERADORES LÓGICOS JAVASCRIPT. EJEMPLOS. RELACIONALES MAYOR, MENOR, IGUAL, DISTINTO. AND, OR, NOT. CORTO- CIRCUITO (CU01117E) Sección: Cursos Categoría: Tutorial básico del programador
APRENDERAPROGRAMAR.COM OPERADORES LÓGICOS JAVASCRIPT. EJEMPLOS. RELACIONALES MAYOR, MENOR, IGUAL, DISTINTO. AND, OR, NOT. CORTO- CIRCUITO (CU01117E) Sección: Cursos Categoría: Tutorial básico del programador
UNIDAD III: Elementos del Lenguaje QuickBASIC OBJETIVO GENERAL:
 UNIDAD III: Elementos del Lenguaje QuickBASIC OBJETIVO GENERAL: Aprender los tipos de datos que soporta este lenguaje de programación. 3.1 Números en QuickBASIC QuickBASIC soporta cuatro tipos de números:
UNIDAD III: Elementos del Lenguaje QuickBASIC OBJETIVO GENERAL: Aprender los tipos de datos que soporta este lenguaje de programación. 3.1 Números en QuickBASIC QuickBASIC soporta cuatro tipos de números:
Evaluación 1ª Examen 1º Grupo: 4º ESO Fecha: 9 de octubre 2008. Nota ) 1'9 0'6 : 0'125 7-5/4
 Departamento de Matemáticas Evaluación 1ª Examen 1º Grupo: 4º ESO Fecha: 9 de octubre 008 Nota 1. Obtén la fracción generatriz de los siguientes números decimales: a) 0'57 b) 1'9 ) c) 0'15. Obtén el número
Departamento de Matemáticas Evaluación 1ª Examen 1º Grupo: 4º ESO Fecha: 9 de octubre 008 Nota 1. Obtén la fracción generatriz de los siguientes números decimales: a) 0'57 b) 1'9 ) c) 0'15. Obtén el número
2. Estructuras condicionales
 2. Estructuras condicionales Fundamentos de Informática Dpto. Lenguajes y Sistemas Informáticos Curso 2012 / 2013 Índice Estructuras condicionales 1. Ej07: Cond. simple 2. Ej08: Cond. doble 3. Ej09: Cond.
2. Estructuras condicionales Fundamentos de Informática Dpto. Lenguajes y Sistemas Informáticos Curso 2012 / 2013 Índice Estructuras condicionales 1. Ej07: Cond. simple 2. Ej08: Cond. doble 3. Ej09: Cond.
Area Académica: Licenciatura en Administración. Profesor: I.E.C. Roxana Sifuentes Carrillo
 Area Académica: Licenciatura en Administración Asignatura: Matemáticas Básicas Profesor: I.E.C. Roxana Sifuentes Carrillo Periodo: Julio-Diciembre 2011 Tema: Basic Concepts of Algebra Abstract Algebra
Area Académica: Licenciatura en Administración Asignatura: Matemáticas Básicas Profesor: I.E.C. Roxana Sifuentes Carrillo Periodo: Julio-Diciembre 2011 Tema: Basic Concepts of Algebra Abstract Algebra
UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE SEGUNDO GRADO Y FUNCIÓN CUADRÁTICA
 C u r s o : Matemática Material N 6 GUÍA TEÓRICO PRÁCTICA Nº UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE SEGUNDO GRADO Y FUNCIÓN CUADRÁTICA Una ecuación de segundo grado es una ecuación de la forma, o que
C u r s o : Matemática Material N 6 GUÍA TEÓRICO PRÁCTICA Nº UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE SEGUNDO GRADO Y FUNCIÓN CUADRÁTICA Una ecuación de segundo grado es una ecuación de la forma, o que
INSTITUTO NACIONAL SUPERIOR DEL PROFESORADO TÉCNICO - TÉCNICO SUPERIOR EN INFORMÁTICA APLICADA - PROGRAMACIÓN I
 RESOLUCIÓN DE PROBLEMAS Y ALGORITMOS La principal razón para que las personas aprendan lenguajes de programación es utilizar una computadora como una herramienta para la resolución de problemas. Cinco
RESOLUCIÓN DE PROBLEMAS Y ALGORITMOS La principal razón para que las personas aprendan lenguajes de programación es utilizar una computadora como una herramienta para la resolución de problemas. Cinco
f (x) (1+[f (x)] 2 ) 3 2 κ(x) =
![f (x) (1+[f (x)] 2 ) 3 2 κ(x) = f (x) (1+[f (x)] 2 ) 3 2 κ(x) =](/thumbs/40/20918876.jpg) MATEMÁTICAS II - EXAMEN PRIMER PARCIAL - 4/11/11 Grado: Ing. Electrónica Rob. y Mec. Ing. Energía Ing. Organización Ind. Nombre y Apellidos: Ejercicio 1. La curvatura de una función f en un punto x viene
MATEMÁTICAS II - EXAMEN PRIMER PARCIAL - 4/11/11 Grado: Ing. Electrónica Rob. y Mec. Ing. Energía Ing. Organización Ind. Nombre y Apellidos: Ejercicio 1. La curvatura de una función f en un punto x viene
Prácticas de JavaScript
 Control de flujo If (condición) [else ] Prácticas de JavaScript if (a==b) document.write( iguales ); else if(a>b) document.write( a mayor que b ); else document.write( b mayor que a ); Bucles for (inicial;condición;incremento)
Control de flujo If (condición) [else ] Prácticas de JavaScript if (a==b) document.write( iguales ); else if(a>b) document.write( a mayor que b ); else document.write( b mayor que a ); Bucles for (inicial;condición;incremento)
