UNIVERSIDAD COMPLUTENSE DE MADRID
|
|
|
- Encarnación Segura Cabrera
- hace 9 años
- Vistas:
Transcripción
1 INSTRUCCIONES GENERALES Y VALORACIÓN TIEMPO: Una hora y treinta minutos. INSTRUCCIONES: El examen presenta dos opciones A y B; el alumno deberá elegir una de ellas y contestar razonadamente a los cuatro ejercicios de que consta dicha opción. Para la realización de esta prueba puede utilizarse calculadora científica, siempre que no disponga de capacidad de representación gráfica o de cálculo simbólico. PUNTUACIÓN: La puntuación máxima de cada ejercicio se indica en el encabezamiento del mismo. Ejercicio 1. (Puntuación máxima: 3 puntos) Sean las matrices OPCIÓN A (a) Determínese si A y B son invertibles y, en su caso, calcúlese la matriz inversa. (b) Resuélvase la ecuación matricial X A - B = 2I, siendo I la matriz identidad de orden tres. (c) Calcúlese A 86. Ejercicio 2. (Puntuación máxima 3 puntos) Sean las funciones f(x) = x 2 + ax + b, g(x) = -x 2 + c (a) Determínense a, b y c, sabiendo que las gráficas de ambas funciones se cortan en los puntos (- 2, -3) y (1, 0). (b) Hállese la ecuación de la recta tangente a la gráfica de g(x) en el punto (-2, -3). (c) Calcúlese el área de la región limitada por las gráficas de f(x) y g(x). Ejercicio 3. (Puntuación máxima 2 puntos) El peso de los perros adultos de una cierta raza es una variable aleatoria que se distribuye normalmente con desviación típica 0,6 kg. Una muestra aleatoria de 30 animales ha dado un peso medio de 7,4 kg.
2 (a) Calcúlese un intervalo de confianza al 99% para el peso medio de los perros adultos de esta raza. (b) Qué tamaño mínimo debe tener la muestra para tener una confianza del 95% de que la media muestral no se diferencie en más de 0,3 kg de la media de la población? Ejercicio 4. (Puntuación máxima: 2 puntos) En un videoclub quedan 8 copias de la película A, 9 de la B y 5 de la C. Entran tres clientes consecutivamente y cada uno elige una copia al azar. Calcúlese la probabilidad de que: (a) Los tres escojan la misma película. (b) Dos escojan la película A y el otro la C. Ejercicio 1. (Puntuación máxima 3 puntos) OPCIÓN B Un hipermercado inicia una campaña de ofertas. En la primera de ellas descuenta un 4% en un cierto producto A, un 6% en el producto B y un 5% en el producto C. A las dos semanas pone en marcha la segunda oferta descontando un 8% sobre el precio inicial de A, un 10% sobre el precio inicial de B y un 6% sobre el precio inicial de C. Se sabe que si un cliente compra durante la primera oferta un producto A, dos B y tres C, se ahorra 16 euros respecto del precio inicial. Si compra tres productos A, uno B y cinco C en la segunda oferta, el ahorro es de 29 euros. Si compra un producto A, uno B y uno C, sin ningún tipo de descuento, debe abonar 135 euros. Calcúlese el precio de cada producto antes de las ofertas. Ejercicio 2. (Puntuación máxima: 3 puntos) Sea la función Calcúlense: (a) Los intervalos donde es creciente y decreciente. (b) Las coordenadas de sus máximos y mínimos relativos. (c) El valor de x para el que es máxima la pendiente de la recta tangente a la gráfica de f (x). Ejercicio 3. (Puntuación máxima 2 puntos)
3 En un laboratorio se obtuvieron seis determinaciones del ph de una solución, con los resultados siguientes: 7,91 7,94 7,90 7,93 7,89 7,91 Se supone que la población de todas las determinaciones del ph de la solución tiene una distribución normal de media desconocida con desviación típica igual a 0,02. (a) Determínese un intervalo de confianza al 98% para la media de todas las determinaciones del ph de la misma solución obtenidas con el mismo método. (b) Con el mismo nivel de confianza anterior, cuál debe ser el tamaño mínimo de la muestra para que la amplitud del intervalo de confianza sea a lo sumo 0,02? Ejercicio 4. (Puntuación máxima: 2 puntos) Con el objetivo de recaudar fondos para un viaje, los alumnos de un instituto realizan una rifa con 500 números. Un alumno compra dos números. (a) Si sólo hay un premio, qué probabilidad tiene el alumno de que le toque a él? (b) Si hay dos premios, qué probabilidad tiene el alumno de que le toque al menos uno de ellos?
4
5 - Ejercicio 1. (Puntuación máxima: 3 puntos) CRITERIOS ESPECÍFICOS DE CORRECCIÓN OPCIÓN A Cálculo correcto de A -1 comprobación de que no existe B -1 : 1 punto. Resolución correcta de la ecuación: 1 punto. Cálculo correcto de A 86 : 1 punto. - Ejercicio 2. (Puntuación máxima: 3 puntos) Cálculo correcto de a, b y c: 1 punto. Determinación correcta de la pendiente: O,5 puntos. Cálculo correcto de la ecuación de la tangente: O,5 puntos. Planteamiento correcto de la integral definida: O,5 puntos. Determinación correcta del área pedida: O,5 puntos. - Ejercicio 3. (Puntuación máxima: 2 puntos) Planteamiento correcto del intervalo de confianza: 1 punto. Cálculo correcto del tamaño muestral pedido: 1 punto. - Ejercicio 4. (Puntuación máxima: 2 puntos) OPCIÓN B - Ejercicio 1. (Puntuación máxima: 3 puntos) Planteamiento correcto del sistema de ecuaciones a resolver: 1,5 puntos. Resolución correcta del mismo: 1,5 puntos. - Ejercicio 2. (Puntuación máxima: 3 puntos) - Ejercicio 3. (Puntuación máxima: 2 puntos) Planteamiento correcto del intervalo de confianza: 1 punto. Cálculo correcto del tamaño muestral pedido: 1 punto. - Ejercicio 4. (Puntuación máxima: 2 puntos)
Propuesta A. =, despeja y calcula la matriz X. (0.75 ptos)
 Pruebas de Acceso a Enseñanzas Universitarias Oficiales de Grado (015) Materia: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II El alumno deberá contestar a una de las dos opciones propuestas A o B. Se
Pruebas de Acceso a Enseñanzas Universitarias Oficiales de Grado (015) Materia: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II El alumno deberá contestar a una de las dos opciones propuestas A o B. Se
Propuesta A. 2 0 b) Dada la ecuación matricial: X = , despeja y calcula la matriz X. (0.75 ptos) 2 1
 Pruebas de Acceso a Enseñanzas Universitarias Oficiales de Grado (015) Materia: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II El alumno deberá contestar a una de las dos opciones propuestas A o B. Se
Pruebas de Acceso a Enseñanzas Universitarias Oficiales de Grado (015) Materia: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II El alumno deberá contestar a una de las dos opciones propuestas A o B. Se
INFORMACIÓN SOBRE LA PRUEBA DE ACCESO (PAU) A LA UNIVERSIDAD DE OVIEDO. CURSO 2015/2016
 INFORMACIÓN SOBRE LA PRUEBA DE ACCESO (PAU) A LA UNIVERSIDAD DE OVIEDO. CURSO 2015/2016 Materia: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II 1. COMENTARIOS Y/O ACOTACIONES RESPECTO AL TEMARIO EN RELACIÓN
INFORMACIÓN SOBRE LA PRUEBA DE ACCESO (PAU) A LA UNIVERSIDAD DE OVIEDO. CURSO 2015/2016 Materia: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II 1. COMENTARIOS Y/O ACOTACIONES RESPECTO AL TEMARIO EN RELACIÓN
x + 3y 3 2x y 4 2x + y 24
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2012-2013 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2012-2013 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
INSTRUCCIONES GENERALES Y VALORACIÓN
 UNIVERSIDADES P ÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO 215-216 MATERIA: MATEMÁTICAS II MODELO INSTRUCCIONES GENERALES Y VALORACIÓN Después
UNIVERSIDADES P ÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO 215-216 MATERIA: MATEMÁTICAS II MODELO INSTRUCCIONES GENERALES Y VALORACIÓN Después
PARTE COMÚN MATERIA: FUNDAMENTOS DE MATEMÁTICAS
 CALIFICACIÓN: Consejería de Educación, Ciencia y Cultura PRUEBAS DE ACCESO A CICLOS FORMATIVOS DE GRADO SUPERIOR DE FORMACIÓN PROFESIONAL Junio 2011 Resolución de 9 de marzo de 2011 (DOCM de 5 de abril)
CALIFICACIÓN: Consejería de Educación, Ciencia y Cultura PRUEBAS DE ACCESO A CICLOS FORMATIVOS DE GRADO SUPERIOR DE FORMACIÓN PROFESIONAL Junio 2011 Resolución de 9 de marzo de 2011 (DOCM de 5 de abril)
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2012-2013 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2012-2013 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD OPCIÓN A
 OPCIÓN A 1 a 1/ 0 Se consideran las matrices A = y B =, 0 1 3/ 4 0 siendo a un número real cualquiera 014 a) (1 punto) Obtenga la matriz A 3 b) (15 puntos) Para a =, resuelva la ecuación matricial A X
OPCIÓN A 1 a 1/ 0 Se consideran las matrices A = y B =, 0 1 3/ 4 0 siendo a un número real cualquiera 014 a) (1 punto) Obtenga la matriz A 3 b) (15 puntos) Para a =, resuelva la ecuación matricial A X
Selectividad Junio 2007 JUNIO 2007
 Bloque A JUNIO 2007 1.- Julia, Clara y Miguel reparten hojas de propaganda. Clara reparte siempre el 20 % del total, Miguel reparte 100 hojas más que Julia. Entre Clara y Julia reparten 850 hojas. Plantea
Bloque A JUNIO 2007 1.- Julia, Clara y Miguel reparten hojas de propaganda. Clara reparte siempre el 20 % del total, Miguel reparte 100 hojas más que Julia. Entre Clara y Julia reparten 850 hojas. Plantea
JUNIO 2010. Opción A. 1 2 3
 JUNIO 2010 Opción A 2 3 1 1.- Sean las matrices: A 0 1 2 y B 5 3 1 Halla una matriz X tal que 2X BA AB. 2 0 1 3 3 2. 1 2 3 2.- La cantidad C de tomates (en kg) que se obtienen de una planta de tomate depende
JUNIO 2010 Opción A 2 3 1 1.- Sean las matrices: A 0 1 2 y B 5 3 1 Halla una matriz X tal que 2X BA AB. 2 0 1 3 3 2. 1 2 3 2.- La cantidad C de tomates (en kg) que se obtienen de una planta de tomate depende
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2004 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 6: TEORÍA DE MUESTRAS
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 004 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 6: TEORÍA DE MUESTRAS Junio, Ejercicio 3, Parte II, Opción A Junio, Ejercicio 3, Parte II, Opción B Reserva
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 004 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 6: TEORÍA DE MUESTRAS Junio, Ejercicio 3, Parte II, Opción A Junio, Ejercicio 3, Parte II, Opción B Reserva
SELECTIVIDAD. Exámenes de PAU de Matemáticas II de la Comunidad de Madrid.
 SELECTIVIDAD Exámenes de PAU de Matemáticas II de la Comunidad de Madrid. Contenido del fichero: Modelos de examen y pruebas de las convocatorias de junio y septiembre desde el curso 2001-2002 hasta 2012-2013.
SELECTIVIDAD Exámenes de PAU de Matemáticas II de la Comunidad de Madrid. Contenido del fichero: Modelos de examen y pruebas de las convocatorias de junio y septiembre desde el curso 2001-2002 hasta 2012-2013.
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Curso 2014-2015 Modelo 1 CIENCIAS SOCIALES II Instrucciones: a) Duración: 1 hora y 30 minutos b) Elija una de las dos opciones propuestas y conteste los ejercicios de la opción elegida c) En cada ejercicio,
Curso 2014-2015 Modelo 1 CIENCIAS SOCIALES II Instrucciones: a) Duración: 1 hora y 30 minutos b) Elija una de las dos opciones propuestas y conteste los ejercicios de la opción elegida c) En cada ejercicio,
Examen de Matemáticas Aplicadas a las CC. Sociales II (Junio 2015-coincidente) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Junio 015-coincidente) Selectividad-Opción A Tiempo: 90 minutos Problema 1 ( puntos) Se considera el sistema de ecuaciones dependiente del parámetro
Examen de Matemáticas Aplicadas a las CC. Sociales II (Junio 015-coincidente) Selectividad-Opción A Tiempo: 90 minutos Problema 1 ( puntos) Se considera el sistema de ecuaciones dependiente del parámetro
Apellidos Nombre DNI / NIE Centro de examen PARTE COMÚN MATERIA: FUNDAMENTOS DE MATEMÁTICAS
 CALIFICACIÓN: PRUEBAS DE ACCESO A CICLOS FORMATIVOS DE GRADO SUPERIOR DE FORMACIÓN PROFESIONAL SEPTIEMBRE DE 2012 Resolución de 27 de abril de 2012 (DOCM de 30 de abril) Instrucciones Generales PARTE COMÚN
CALIFICACIÓN: PRUEBAS DE ACCESO A CICLOS FORMATIVOS DE GRADO SUPERIOR DE FORMACIÓN PROFESIONAL SEPTIEMBRE DE 2012 Resolución de 27 de abril de 2012 (DOCM de 30 de abril) Instrucciones Generales PARTE COMÚN
MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES Y CRITERIOS GENERALES DE CALIFICACIÓN
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MODELO DE EXAMEN CURSO 2014-2015 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MODELO DE EXAMEN CURSO 2014-2015 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES
x = 0, la recta tangente a la gráfica de f (x)
 CÁLCULO DIFERENCIAL JUNIO 004 1. Sea la función e y = estúdiese su monotonía, etremos relativos y asíntotas. (Solución: Es derivable en todos los puntos ecepto en =0. Creciente si < 0. No tiene asíntotas
CÁLCULO DIFERENCIAL JUNIO 004 1. Sea la función e y = estúdiese su monotonía, etremos relativos y asíntotas. (Solución: Es derivable en todos los puntos ecepto en =0. Creciente si < 0. No tiene asíntotas
Pruebas de acceso a enseñanzas universitarias oficiales de grado Castilla y León
 Pruebas de acceso a enseñanzas universitarias oficiales de grado Castilla y León MATEMÁTICAS APLICAAS A LAS CIENCIAS SOCIALES EJERCICIO Nº Páginas 2 OPTATIVIA: EL ALUMNO EBERÁ ESCOGER UNA E LAS OS OPCIONES
Pruebas de acceso a enseñanzas universitarias oficiales de grado Castilla y León MATEMÁTICAS APLICAAS A LAS CIENCIAS SOCIALES EJERCICIO Nº Páginas 2 OPTATIVIA: EL ALUMNO EBERÁ ESCOGER UNA E LAS OS OPCIONES
DISTRIBUCIONES DE PROBABILIDAD
 DISTRIBUCIONES DE PROBABILIDAD Se llama variable aleatoria a toda función que asocia a cada elemento del espacio muestral E un número real. Una variable aleatoria discreta es aquella que sólo puede tomar
DISTRIBUCIONES DE PROBABILIDAD Se llama variable aleatoria a toda función que asocia a cada elemento del espacio muestral E un número real. Una variable aleatoria discreta es aquella que sólo puede tomar
PRUEBAS DE ACCESO A LA UNIVERSIDAD L.O.E.
 PRUEBAS DE ACCESO A LA UNIVERSIDAD L.O.E. CURSO 014-015 CONVOCATORIA: MATERIA: MATEMATICAS APLICADAS A LAS CC. SS. 1 - Cada alumno debe elegir sólo una de las pruebas (A o B). - Cada una de las preguntas
PRUEBAS DE ACCESO A LA UNIVERSIDAD L.O.E. CURSO 014-015 CONVOCATORIA: MATERIA: MATEMATICAS APLICADAS A LAS CC. SS. 1 - Cada alumno debe elegir sólo una de las pruebas (A o B). - Cada una de las preguntas
PRUEBAS DE ACCESO A LA UNIVERSIDAD L.O.E.
 PRUEBAS DE ACCESO A LA UNIVERSIDAD L.O.E. CURSO 01-013 CONVOCATORIA: MATERIA: MATEMATICAS APLICADAS A LAS CC. SS. - Cada alumno debe elegir sólo una de las pruebas (A o B). - Cada una de las preguntas
PRUEBAS DE ACCESO A LA UNIVERSIDAD L.O.E. CURSO 01-013 CONVOCATORIA: MATERIA: MATEMATICAS APLICADAS A LAS CC. SS. - Cada alumno debe elegir sólo una de las pruebas (A o B). - Cada una de las preguntas
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID MATERIA: MATEMÁTICAS APLICADAS A LAS CC. SOCIALES
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) (Curso 2004-2005) MATERIA: MATEMÁTICAS APLICADAS A LAS CC. SOCIALES MODELO DE PRUEBA INSTRUCCIONES GENERALES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) (Curso 2004-2005) MATERIA: MATEMÁTICAS APLICADAS A LAS CC. SOCIALES MODELO DE PRUEBA INSTRUCCIONES GENERALES
Matemáticas II PRUEBA DE ACCESO A LA UNIVERSIDAD 2013 BACHILLERATO FORMACIÓN PROFESIONAL CICLOS FORMATIVOS DE GRADO SUPERIOR.
 PRUEBA DE ACCESO A LA UNIVERSIDAD 0 Matemáticas II BACHILLERATO FORMACIÓN PROFESIONAL CICLOS FORMATIVOS DE GRADO SUPERIOR Examen Criterios de Corrección y Calificación UNIBERTSITATERA SARTZEKO PROBAK 0ko
PRUEBA DE ACCESO A LA UNIVERSIDAD 0 Matemáticas II BACHILLERATO FORMACIÓN PROFESIONAL CICLOS FORMATIVOS DE GRADO SUPERIOR Examen Criterios de Corrección y Calificación UNIBERTSITATERA SARTZEKO PROBAK 0ko
Pruebas de Acceso a Enseñanzas Universitarias Oficiales de Grado (PAEG) Matemáticas aplicadas a las Ciencias Sociales II - Junio 2011 - Propuesta B
 Pruebas de Acceso a Enseñanzas Universitarias Oficiales de Grado (PAEG) Matemáticas aplicadas a las Ciencias Sociales II - Junio 2011 - Propuesta B 1. Queremos invertir una cantidad de dinero en dos tipos
Pruebas de Acceso a Enseñanzas Universitarias Oficiales de Grado (PAEG) Matemáticas aplicadas a las Ciencias Sociales II - Junio 2011 - Propuesta B 1. Queremos invertir una cantidad de dinero en dos tipos
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2014-2015 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2014-2015 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
EJERCICIOS RESUELTOS TEMA 7
 EJERCICIOS RESUELTOS TEMA 7 7.1. Seleccione la opción correcta: A) Hay toda una familia de distribuciones normales, cada una con su media y su desviación típica ; B) La media y la desviaciones típica de
EJERCICIOS RESUELTOS TEMA 7 7.1. Seleccione la opción correcta: A) Hay toda una familia de distribuciones normales, cada una con su media y su desviación típica ; B) La media y la desviaciones típica de
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO 015-016 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II Instrucciones: a) Duración: 1 hora y 30 minutos. b) Elija una de las dos opciones
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO 015-016 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II Instrucciones: a) Duración: 1 hora y 30 minutos. b) Elija una de las dos opciones
[email protected]!!91.501.36.88!!28007!madrid!
 CONTINUIDAD Y DERIVABILIDAD. TEOREMAS Y APLICACIONES DE LAS DERIVADAS 1.- junio 1994 Se sabe que y = f (x) e y = g (x) son dos curvas crecientes en x = a. Analícese si la curva y = f(x) g(x) ha de ser,
CONTINUIDAD Y DERIVABILIDAD. TEOREMAS Y APLICACIONES DE LAS DERIVADAS 1.- junio 1994 Se sabe que y = f (x) e y = g (x) son dos curvas crecientes en x = a. Analícese si la curva y = f(x) g(x) ha de ser,
MATERIA: MATEMÁTICAS APLICACADAS A LAS CIENCIAS SOCIALES
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBAS DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) MODELO DE EXAMEN (Curso 2002-2003) MATERIA: MATEMÁTICAS APLICACADAS A LAS CIENCIAS SOCIALES INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBAS DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) MODELO DE EXAMEN (Curso 2002-2003) MATERIA: MATEMÁTICAS APLICACADAS A LAS CIENCIAS SOCIALES INSTRUCCIONES
LA DISTRIBUCIÓN NORMAL
 LA DISTRIBUCIÓN NORMAL En estadística y probabilidad se llama distribución normal, distribución de Gauss o distribución gaussiana, a una de las distribuciones de probabilidad que con más frecuencia aparece
LA DISTRIBUCIÓN NORMAL En estadística y probabilidad se llama distribución normal, distribución de Gauss o distribución gaussiana, a una de las distribuciones de probabilidad que con más frecuencia aparece
OPCIÓN A m. y B =
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID EVALUACIÓN PARA EL ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2017-2018 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID EVALUACIÓN PARA EL ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2017-2018 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
DOCUMENTO 3: DISTRIBUCIÓN DE PROBABILIDAD DE V. A. CONTINUA: LA DISTRIBUCIÓN NORMAL
 DOCUMENTO 3: DISTRIBUCIÓN DE PROBABILIDAD DE V. A. CONTINUA: LA DISTRIBUCIÓN NORMAL 3.1 INTRODUCCIÓN Como ya sabes, una distribución de probabilidad es un modelo matemático que nos ayuda a explicar los
DOCUMENTO 3: DISTRIBUCIÓN DE PROBABILIDAD DE V. A. CONTINUA: LA DISTRIBUCIÓN NORMAL 3.1 INTRODUCCIÓN Como ya sabes, una distribución de probabilidad es un modelo matemático que nos ayuda a explicar los
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2016) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2016) Selectividad-Opción A Tiempo: 90 minutos k 1 0 Problema 1 (2 puntos) Se considera la matriz A = 7 k k 1 1 k a) Estudíese para qué
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2016) Selectividad-Opción A Tiempo: 90 minutos k 1 0 Problema 1 (2 puntos) Se considera la matriz A = 7 k k 1 1 k a) Estudíese para qué
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2012-2013 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2012-2013 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
Tema Contenido Contenidos Mínimos
 1 Números racionales - Fracciones equivalentes. - Simplificación de fracciones. - Representación y comparación de los números fraccionarios. - Operaciones con números fraccionarios. - Ordenación de los
1 Números racionales - Fracciones equivalentes. - Simplificación de fracciones. - Representación y comparación de los números fraccionarios. - Operaciones con números fraccionarios. - Ordenación de los
MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II DISTRITO ÚNICO DE ANDALUCÍA
 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II DISTRITO ÚNICO DE ANDALUCÍA CONTENIDOS, OBJETIVOS MÍNIMOS, DIRECTRICES Y CRITERIOS GENERALES CURSO 2008/09. 1. INTRODUCCIÓN A LOS CONTENIDOS. ( Decreto
MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II DISTRITO ÚNICO DE ANDALUCÍA CONTENIDOS, OBJETIVOS MÍNIMOS, DIRECTRICES Y CRITERIOS GENERALES CURSO 2008/09. 1. INTRODUCCIÓN A LOS CONTENIDOS. ( Decreto
UNIVERSIDAD COMPLUTENSE DE MADRID
 INSTRUCCIONES GENERALES Y VALORACIÓN INSTRUCCIONES: El examen presenta dos opciones A y B; el alumno deberá elegir una de ellas y contestar razonadamente a los cuatro ejercicios de que consta dicha opción.
INSTRUCCIONES GENERALES Y VALORACIÓN INSTRUCCIONES: El examen presenta dos opciones A y B; el alumno deberá elegir una de ellas y contestar razonadamente a los cuatro ejercicios de que consta dicha opción.
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2013) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II Septiembre 2013 Selectividad-Opción A Tiempo: 90 minutos Problema 1 2 puntos Se consideran las matrices A = 3 8. 3 5 0 2 3 0 y B = a Calcúlese la matriz
Examen de Matemáticas Aplicadas a las CC. Sociales II Septiembre 2013 Selectividad-Opción A Tiempo: 90 minutos Problema 1 2 puntos Se consideran las matrices A = 3 8. 3 5 0 2 3 0 y B = a Calcúlese la matriz
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2013) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2013) Selectividad-Opción A Tiempo: 90 minutos 0 2 Problema 1 (2 puntos) Se consideran las matrices A y B 3 0 3 8. 3 5 a) Calcúlese la
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2013) Selectividad-Opción A Tiempo: 90 minutos 0 2 Problema 1 (2 puntos) Se consideran las matrices A y B 3 0 3 8. 3 5 a) Calcúlese la
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2014-2015 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2014-2015 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MODELO CURSO 2012-2013 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MODELO CURSO 2012-2013 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
RELACIÓN DE EJERCICIOS DE REPASO DE MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES I
 Dto. de MATEMÁTICAS RELACIÓN DE EJERCICIOS DE REPASO DE MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES I 1. Calcular, de forma exacta las siguientes operaciones. a) 1, 0, b) 0,7:0,916. Representa el conjunto
Dto. de MATEMÁTICAS RELACIÓN DE EJERCICIOS DE REPASO DE MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES I 1. Calcular, de forma exacta las siguientes operaciones. a) 1, 0, b) 0,7:0,916. Representa el conjunto
5. Al simplificar. expresión se obtiene:
 ARITMÉTICA. [ ( 7 ) 9 ( 7 )] es igual a : 5. El resultado de simplificar la expresión. 5 5 5 7 7, 6 + es igual a: 5 9 7 6 5 5. El valor de 75 6 5 5 ( 5 )( 65 ) log es igual a: 5 5 5. Al simplificar Mayo
ARITMÉTICA. [ ( 7 ) 9 ( 7 )] es igual a : 5. El resultado de simplificar la expresión. 5 5 5 7 7, 6 + es igual a: 5 9 7 6 5 5. El valor de 75 6 5 5 ( 5 )( 65 ) log es igual a: 5 5 5. Al simplificar Mayo
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID EVALUACIÓN PARA EL ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2017-2018 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID EVALUACIÓN PARA EL ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2017-2018 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
Nombre: Solución: a) N(
 1998 JUNIO OPCIÓN A Un fabricante de electrodomésticos sabe que la vida media de éstos sigue una distribución normal con media µ = 100 meses y desviación típica σ = 12 meses. Determínese el mínimo tamaño
1998 JUNIO OPCIÓN A Un fabricante de electrodomésticos sabe que la vida media de éstos sigue una distribución normal con media µ = 100 meses y desviación típica σ = 12 meses. Determínese el mínimo tamaño
Contenidos mínimos 4B ESO. 1. Contenidos. Bloque I: Aritmética y álgebra.
 Contenidos mínimos 4B ESO. 1. Contenidos. Bloque I: Aritmética y álgebra. 1. Clasificar distintos tipos de números: naturales, enteros, racionales y reales. 2. Operar con números reales y aplicar las propiedades
Contenidos mínimos 4B ESO. 1. Contenidos. Bloque I: Aritmética y álgebra. 1. Clasificar distintos tipos de números: naturales, enteros, racionales y reales. 2. Operar con números reales y aplicar las propiedades
EJERCICIOS PAU MAT II CC SOC. ARAGÓN Autor: Fernando J. Nora Costa-Ribeiro Más ejercicios y soluciones en fisicaymat.wordpress.com.
 FUNCIONES 1- a) Dada la función:, Definida para 0, 0, encontrar el punto (x,y) que maximiza f sujeto a la restricción x+y=36. b) Calcular: Aragón 2014 Opción A Junio 2- Dada la función: Calcular: a) Dominio
FUNCIONES 1- a) Dada la función:, Definida para 0, 0, encontrar el punto (x,y) que maximiza f sujeto a la restricción x+y=36. b) Calcular: Aragón 2014 Opción A Junio 2- Dada la función: Calcular: a) Dominio
El conjunto de los complejos. Escritura cartesiana y binómica. Representación gráfica.
 Tramo A Números complejos Disciplina, esfuerzo y perseverancia en la búsqueda de resultados. Valoración del lenguaje preciso, claro y conciso de la Matemática como organizador del pensamiento. Valoración
Tramo A Números complejos Disciplina, esfuerzo y perseverancia en la búsqueda de resultados. Valoración del lenguaje preciso, claro y conciso de la Matemática como organizador del pensamiento. Valoración
OPCIÓN A. dependiente del parámetro real a.
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID EVALUACIÓN PARA EL ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2017-2018 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II MODELO
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID EVALUACIÓN PARA EL ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2017-2018 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II MODELO
Prueba de hipótesis. 1. Considerando lo anterior específica: a. La variable de estudio: b. La población: c. El parámetro. d. Estimador puntual:
 Prueba de hipótesis Problema Un grupo de profesores, de cierto estado de la república, plantea una investigación acerca del aprendizaje de las ciencias naturales en la escuela primaria. Uno de los objetivos
Prueba de hipótesis Problema Un grupo de profesores, de cierto estado de la república, plantea una investigación acerca del aprendizaje de las ciencias naturales en la escuela primaria. Uno de los objetivos
OPCIÓN A. x 2 2x si x < 1,
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID EVALUACIÓN PARA EL ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2016-2017 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID EVALUACIÓN PARA EL ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2016-2017 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
Microcurrículo del ÁREA DE: MATEMÁTICAS. Unidad y temas. Logro e Indicadores Indicadores De Logro
 Microcurrículo del ÁREA DE: MATEMÁTICAS fecha Grado noveno Sesión 1-10 (semanas) Unidad Unidad y temas Temas Unidad #1.Conjunto de los números imaginarios. Números Imaginarios: Concepto, operaciones básicas
Microcurrículo del ÁREA DE: MATEMÁTICAS fecha Grado noveno Sesión 1-10 (semanas) Unidad Unidad y temas Temas Unidad #1.Conjunto de los números imaginarios. Números Imaginarios: Concepto, operaciones básicas
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2015-2016 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2015-2016 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
Examen de Matemáticas Aplicadas a las CC. Sociales II (Modelo 2008) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Modelo 28) Selectividad-Opción A Tiempo: 9 minutos Problema 1 (3 puntos) Dadas las matrices A = y B = 1 1 2 1 1 n 1 1 1, X = a) Hallar los valores
Examen de Matemáticas Aplicadas a las CC. Sociales II (Modelo 28) Selectividad-Opción A Tiempo: 9 minutos Problema 1 (3 puntos) Dadas las matrices A = y B = 1 1 2 1 1 n 1 1 1, X = a) Hallar los valores
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2015-coincidente) Selectividad-Opción A Tiempo: 90 minutos 5 7 C = 1 5
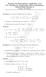 Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2015-coincidente) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (2 puntos) Considérense las matrices ( ) ( ) ( ) 1 2 3 2 5 7 A =,
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2015-coincidente) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (2 puntos) Considérense las matrices ( ) ( ) ( ) 1 2 3 2 5 7 A =,
RELACIÓN DE EJERCICIOS SOBRANTES DE MATEMÁTICAS APLICADAS A LAS CIENCIAS (Segundo Bachillerato L.O.G.S.E.) Ponencia Andaluza, Abril 2001.
 RELACIÓN DE EJERCICIOS SOBRANTES DE MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II (Segundo Bachillerato L.O.G.S.E.) Ponencia Andaluza, Abril 001. Nota: Esta relación de ejercicios la ha elaborado la
RELACIÓN DE EJERCICIOS SOBRANTES DE MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II (Segundo Bachillerato L.O.G.S.E.) Ponencia Andaluza, Abril 001. Nota: Esta relación de ejercicios la ha elaborado la
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2010 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 010 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva 1, Ejercicio, Opción A Reserva
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 010 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva 1, Ejercicio, Opción A Reserva
Inferencia estadística Estimación - 1. MasMates.com Colecciones de ejercicios
 1. Una ciudad de 2000 habitantes está poblada por personas de pelo negro, rubio o castaño. Se ha seleccionado, mediante muestreo aleatorio estratificado con afijación proporcional, una muestra constituida
1. Una ciudad de 2000 habitantes está poblada por personas de pelo negro, rubio o castaño. Se ha seleccionado, mediante muestreo aleatorio estratificado con afijación proporcional, una muestra constituida
ÍNDICE CAPITULO UNO CAPITULO DOS. Pág.
 ÍNDICE CAPITULO UNO Pág. Concepto de Estadística 1 Objetivo 1 Diferencia entre estadísticas y estadística 1 Uso de la estadística 1 Divisiones de la estadística 1 1. Estadística Descriptiva 1 2. Estadística
ÍNDICE CAPITULO UNO Pág. Concepto de Estadística 1 Objetivo 1 Diferencia entre estadísticas y estadística 1 Uso de la estadística 1 Divisiones de la estadística 1 1. Estadística Descriptiva 1 2. Estadística
P. A. U. LAS PALMAS 2005
 P. A. U. LAS PALMAS 2005 OPCIÓN A: J U N I O 2005 1. Hallar el área encerrada por la gráfica de la función f(x) = x 3 4x 2 + 5x 2 y la rectas y = 0, x = 1 y x = 3. x 3 4x 2 + 5x 2 es una función polinómica
P. A. U. LAS PALMAS 2005 OPCIÓN A: J U N I O 2005 1. Hallar el área encerrada por la gráfica de la función f(x) = x 3 4x 2 + 5x 2 y la rectas y = 0, x = 1 y x = 3. x 3 4x 2 + 5x 2 es una función polinómica
IES Fco Ayala de Granada Junio de 2011 (Específico 2 Modelo 1) Soluciones Germán-Jesús Rubio Luna
 PRUEBA DE ACCESO A LA UNIVERSIDAD MATEMÁTICAS II DE ANDALUCÍA CURSO 010-011 Opción A Ejercicio 1, Opción A, Modelo especifico de Junio de 011 [ 5 puntos] Una ventana normanda consiste en un rectángulo
PRUEBA DE ACCESO A LA UNIVERSIDAD MATEMÁTICAS II DE ANDALUCÍA CURSO 010-011 Opción A Ejercicio 1, Opción A, Modelo especifico de Junio de 011 [ 5 puntos] Una ventana normanda consiste en un rectángulo
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2012) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2012) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (3 puntos) Un pintor dispone de dos tipos de pintura para realizar su trabajo.
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2012) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (3 puntos) Un pintor dispone de dos tipos de pintura para realizar su trabajo.
Distribución muestral de proporciones. Algunas secciones han sido tomadas de: Apuntes de Estadística Inferencial Instituto Tecnológico de Chiuhuahua
 Distribución muestral de proporciones Algunas secciones han sido tomadas de: Apuntes de Estadística Inferencial Instituto Tecnológico de Chiuhuahua Distribución muestral de Proporciones Existen ocasiones
Distribución muestral de proporciones Algunas secciones han sido tomadas de: Apuntes de Estadística Inferencial Instituto Tecnológico de Chiuhuahua Distribución muestral de Proporciones Existen ocasiones
DISTRIBUCIONES DE PROBABILIDAD (RESUMEN)
 DISTRIBUCIONES DE PROBABILIDAD (RESUMEN) VARIABLE ALEATORIA: un experimento produce observaciones numéricas que varían de muestra a muestra. Una VARIABLE ALEATORIA se define como una función con valores
DISTRIBUCIONES DE PROBABILIDAD (RESUMEN) VARIABLE ALEATORIA: un experimento produce observaciones numéricas que varían de muestra a muestra. Una VARIABLE ALEATORIA se define como una función con valores
Examen de Matemáticas Aplicadas a las CC. Sociales II-Coincidente (Junio 2017) Selectividad-Opción A Tiempo: 90 minutos 2 3 A = , y B = 3 5 1
 Examen de Matemáticas Aplicadas a las CC. Sociales II-Coincidente (Junio 217) Selectividad-Opción A Tiempo: 9 minutos Problema 1 (2 puntos) Considérense las matrices ( ) ( ) 1 2 2 A =, y B = 5 1 1 4 a)
Examen de Matemáticas Aplicadas a las CC. Sociales II-Coincidente (Junio 217) Selectividad-Opción A Tiempo: 9 minutos Problema 1 (2 puntos) Considérense las matrices ( ) ( ) 1 2 2 A =, y B = 5 1 1 4 a)
IES Fco Ayala de Granada Septiembre de 2013 (Modelo 3 Especifico) Solucíon Germán-Jesús Rubio Luna. Opción A
 Opción A Ejercicio opción A, modelo 3 Septiembre 03 específico x Sea f la función definida por f(x) = para x > 0, x (donde ln denota el logaritmo neperiano) ln(x) [ 5 puntos] Estudia y determina las asíntotas
Opción A Ejercicio opción A, modelo 3 Septiembre 03 específico x Sea f la función definida por f(x) = para x > 0, x (donde ln denota el logaritmo neperiano) ln(x) [ 5 puntos] Estudia y determina las asíntotas
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2015 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 05 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 05 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva,
Estudio de funciones mediante límites y derivadas
 Estudio de funciones mediante límites y derivadas Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios españoles El precio
Estudio de funciones mediante límites y derivadas Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios españoles El precio
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES Y CRITERIOS
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES Y CRITERIOS
1.- CONCEPTO DE FUNCIÓN
 .- CONCEPTO DE FUNCIÓN Actividades del alumno/a Explica porqué la siguiente gráfica no corresponde a una función: Porque a un valor de x, por ejemplo x =, le corresponde más de un valor de y. .- CONCEPTO
.- CONCEPTO DE FUNCIÓN Actividades del alumno/a Explica porqué la siguiente gráfica no corresponde a una función: Porque a un valor de x, por ejemplo x =, le corresponde más de un valor de y. .- CONCEPTO
Pruebas de Acceso a las Universidades de Castilla y León
 Pruebas de Acceso a las Universidades de Castilla y León MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES EJERCICIO Nº páginas 2 Tablas OPTATIVIDAD: EL ALUMNO DEBERÁ ESCOGER UNA DE LAS DOS OPCIONES Y DESARROLLAR
Pruebas de Acceso a las Universidades de Castilla y León MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES EJERCICIO Nº páginas 2 Tablas OPTATIVIDAD: EL ALUMNO DEBERÁ ESCOGER UNA DE LAS DOS OPCIONES Y DESARROLLAR
CÁLCULO DE PRIMITIVAS Y ÁREAS POR INTEGRALES
 CÁLCULO DE PRIMITIVAS Y ÁREAS POR INTEGRALES RELACIÓN DE PROBLEMAS DE SELECTIVIDAD º DE BACHILLERATO CIENCIAS DEPARTAMENTO DE MATEMÁTICAS COLEGIO MARAVILLAS TERESA GONZÁLEZ GÓMEZ .-Hallar una primitiva
CÁLCULO DE PRIMITIVAS Y ÁREAS POR INTEGRALES RELACIÓN DE PROBLEMAS DE SELECTIVIDAD º DE BACHILLERATO CIENCIAS DEPARTAMENTO DE MATEMÁTICAS COLEGIO MARAVILLAS TERESA GONZÁLEZ GÓMEZ .-Hallar una primitiva
Examen de Matemáticas II (Modelo 2018) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas II (Modelo 208) Selectividad-Opción A Tiempo: 90 minutos 0 Problema (2,5 puntos) Dadas las matrices A = 0 0, y I = 0 0 0 0 0 se pide: 0 0 a) (,5 puntos) Obtener los valores de m para
Examen de Matemáticas II (Modelo 208) Selectividad-Opción A Tiempo: 90 minutos 0 Problema (2,5 puntos) Dadas las matrices A = 0 0, y I = 0 0 0 0 0 se pide: 0 0 a) (,5 puntos) Obtener los valores de m para
Grado en Química Bloque 1 Funciones de una variable
 Grado en Química Bloque Funciones de una variable Sección.5: Aplicaciones de la derivada. Máximos y mínimos (absolutos) de una función. Sea f una función definida en un conjunto I que contiene un punto
Grado en Química Bloque Funciones de una variable Sección.5: Aplicaciones de la derivada. Máximos y mínimos (absolutos) de una función. Sea f una función definida en un conjunto I que contiene un punto
IES Francisco Ayala Modelo 1 (Septiembre) de 2007 Solución Germán Jesús Rubio Luna. Opción A
 IES Francisco Ayala Modelo (Septiembre) de 7 Germán Jesús Rubio Luna Opción A Ejercicio n de la opción A de septiembre, modelo de 7 3x+ Sea f: (,+ ) R la función definida por f(x)= x. [ 5 puntos] Determina
IES Francisco Ayala Modelo (Septiembre) de 7 Germán Jesús Rubio Luna Opción A Ejercicio n de la opción A de septiembre, modelo de 7 3x+ Sea f: (,+ ) R la función definida por f(x)= x. [ 5 puntos] Determina
ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES
 ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES 1. Sea f : (0, + ) definida como f () = Ln a) Probar que la función derivada f es decreciente en todo su dominio. b) Determinar los intervalos de crecimiento
ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES 1. Sea f : (0, + ) definida como f () = Ln a) Probar que la función derivada f es decreciente en todo su dominio. b) Determinar los intervalos de crecimiento
6. ESTIMACIÓN DE PARÁMETROS
 PROBABILIDAD Y ESTADÍSTICA Sesión 7 6. ESTIMACIÓN DE PARÁMETROS 6.1 Características el estimador 6. Estimación puntual 6..1 Métodos 6..1.1 Máxima verosimilitud 6..1. Momentos 6.3 Intervalo de confianza
PROBABILIDAD Y ESTADÍSTICA Sesión 7 6. ESTIMACIÓN DE PARÁMETROS 6.1 Características el estimador 6. Estimación puntual 6..1 Métodos 6..1.1 Máxima verosimilitud 6..1. Momentos 6.3 Intervalo de confianza
Módulo Programación lineal. 3 Medio Diferenciado
 Módulo Programación lineal 3 Medio Diferenciado Profesor: Galo Páez Nombre: Curso :. Sabemos que una ecuación lineal de dos variables tiene la forma con ó y representa siempre una recta en el plano. Ahora
Módulo Programación lineal 3 Medio Diferenciado Profesor: Galo Páez Nombre: Curso :. Sabemos que una ecuación lineal de dos variables tiene la forma con ó y representa siempre una recta en el plano. Ahora
TEMARIO EXAMEN MATEMÁTICA SÉPTIMO AÑO BÁSICO 2012 3 DE DICIEMBRE
 SÉPTIMO AÑO BÁSICO 2012 NÚMEROS Ejercicios combinados con enteros, con y sin paréntesis. Solución de problemas con enteros Solución de problemas, aplicando proporción directa e inversa. Propiedades de
SÉPTIMO AÑO BÁSICO 2012 NÚMEROS Ejercicios combinados con enteros, con y sin paréntesis. Solución de problemas con enteros Solución de problemas, aplicando proporción directa e inversa. Propiedades de
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID EVALUACIÓN PARA EL ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2018-2019 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II Modelo
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID EVALUACIÓN PARA EL ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2018-2019 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II Modelo
OPCIÓN A B = A 1 B C 1 B A X = C
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2014-2015 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2014-2015 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES
REACTIVOS MATEMÁTICAS 3
 REACTIVOS MATEMÁTICAS 3 1.- Una es una igualdad en la cual hay términos conocidos y términos desconocidos. El término desconocido se llama incógnita y se representa por letras. a) Literal. b) Ecuación.
REACTIVOS MATEMÁTICAS 3 1.- Una es una igualdad en la cual hay términos conocidos y términos desconocidos. El término desconocido se llama incógnita y se representa por letras. a) Literal. b) Ecuación.
Examen de Matemáticas Aplicadas a las CC. Sociales II (Modelo 2018) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Modelo 208) Selectividad-Opción A Tiempo: 90 minutos 0 a a Problema (2 puntos) Se considera la matriz A = a 0 a a a 0 a) Determínese para qué valores
Examen de Matemáticas Aplicadas a las CC. Sociales II (Modelo 208) Selectividad-Opción A Tiempo: 90 minutos 0 a a Problema (2 puntos) Se considera la matriz A = a 0 a a a 0 a) Determínese para qué valores
P (X 5) = P (x = 5) + P (X = 6) + P (X = 7) + P (X = 8) = 0.005416467 + 0.051456432 + 0.79334918 + 0.663420431 = 0.999628249
 Hoja 3: robabilidad y variables aleatorias 1. La probabilidad de que un enfermo se recupere tomando un nuevo fármaco es 0.95. Si se les administra a 8 enfermos, hallar: a La probabilidad de que se recuperen
Hoja 3: robabilidad y variables aleatorias 1. La probabilidad de que un enfermo se recupere tomando un nuevo fármaco es 0.95. Si se les administra a 8 enfermos, hallar: a La probabilidad de que se recuperen
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD OPCIÓN A
 DE 00 OPCIÓN A a) (.5 puntos) Resuelva el siguiente sistema y clasifíquelo atendiendo al número de soluciones: x + y + z = 0 x + 3y z = 17 4x + 5y + z = 17 b) (0.75 puntos) A la vista del resultado anterior,
DE 00 OPCIÓN A a) (.5 puntos) Resuelva el siguiente sistema y clasifíquelo atendiendo al número de soluciones: x + y + z = 0 x + 3y z = 17 4x + 5y + z = 17 b) (0.75 puntos) A la vista del resultado anterior,
Ejemplo Traza la gráfica de los puntos: ( 5, 4), (3, 2), ( 2, 0), ( 1, 3), (0, 4) y (5, 1) en el plano cartesiano.
 Plano cartesiano El plano cartesiano se forma con dos rectas perpendiculares, cuyo punto de intersección se denomina origen. La recta horizontal recibe el nombre de eje X o eje de las abscisas y la recta
Plano cartesiano El plano cartesiano se forma con dos rectas perpendiculares, cuyo punto de intersección se denomina origen. La recta horizontal recibe el nombre de eje X o eje de las abscisas y la recta
Examen de Matemáticas Aplicadas a las CC. Sociales II (Modelo 2019) Selectividad-Opción A Tiempo: 90 minutos
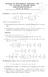 Examen de Matemáticas Aplicadas a las CC. Sociales II (Modelo 9) Selectividad-Opción A Tiempo: 9 minutos Problema ( puntos) Se consideran lan matrices 3 5 A = 3 6 y B = 3 3 m donde m es un parámetro real.
Examen de Matemáticas Aplicadas a las CC. Sociales II (Modelo 9) Selectividad-Opción A Tiempo: 9 minutos Problema ( puntos) Se consideran lan matrices 3 5 A = 3 6 y B = 3 3 m donde m es un parámetro real.
