Capítulo 5. Medición
|
|
|
- Francisco José Gallego Santos
- hace 9 años
- Vistas:
Transcripción
1 Actividad Club Cabri cabri.com 1 Capítulo 5 1. Aumento (archivo enlargement.cg3) Cree un triángulo ABC in el plano base. Cree un punto S en el espacio. Cree la pirámide de base ABC y vértice S. Hágala demarcada (estilo Vacío). Cree un punto A sobre el borde AS. Construya un plano paralelo al plano base que pase por A. Cree la sección A B C de la pirámide a través de este plano. Muestre de nueva la parte escondida usy o Mostrar Objetos Escondidos en el menú Mostrar. a) Calcule de dos formas la proporción del aumento cuy o se transforma la SABC en SA B C. b) Calcule de dos formas la proporción de las áreas de los triángulos ABC y A B C. Verifique que ambos resultados sean los mismo cuando se cambia A. c) Calcule de dos formas la proporción de los volúmenes de las pirámides SABC y SA B C. Verifique que ambos resultados sean los mismo cuando se cambia A. 2. Volúmenes : un cilindro y un prisma (archivo 2vases.cg3) Se colocan dos recipientes sobre un plano. Uno de ellos es un cilindro y el otro un prisma rectángulo de base triangular y de la misma altura. El prisma está lleno de agua. El agua se vierte en el cilindro. Puede calcular a qué nivel llega el agua? Marque un punto en el eje del cilindro a la altura donde calcula llega el nivel. Usando las herramientas Area, Volumen y Calculadora, construya el punto en el eje del cilindro que indica el nivel del agua. Verifique con la herramienta Volúmen. Comentario: Las figuras se pueden haber diseñado con anterioridad y dejar que los estudiantes simplemente respondan las preguntas. A continuación damos algunas explicaciones para la construcción de los dos recipientes. Pasos en la construcción de los recipientes Abra un nuevo archivo. Borre el origen y los vectores. Cree un circulo en el plano horizontal y una línea perpendicular al plano que pasa por el centro del circulo. Cree un punto esta línea. Cree el vector de origen en el centro del circulo y el punto como extremo de la línea. Cree el cilindro con el círculo como base Capítulo 5 1 Cabrilog
2 2 Actividad Club Cabri cabri.com y la altura determinada por el vector (herramienta Cilindro). Cree un triangulo cualquiera sobre el plano y una línea perpendicular a él, que pase por el vértice del triangulo. Construya un plano paralelo al plano horizontal, que pase por la parte superior del cilindro en su intersección con el punto extremo del eje y que corte también la perpendicular al triangulo. Esconda ese plano. Cree el vector con origen en el vértice y extremo en el punto de intersección recién creado. Construya el prisma definido por el triángulo y este vector. Elija los colores que desee para los sólidos y esconda la construcción de la línea s. Construcción del punto que indica el nivel de agua en el cilindro. Muestre el volumen del prisma y el área de la base del cilindro. Use la calculadora para calcular la proporción del volumen dividido por el área. El resultado es la altura esperada del nivel del agua. Use la herramienta Transferencia de Medida para crear un punto sobre el vector del cilindro para esa altura. El mismo problema se puede proponer para una pirámide, o un cono en vez del prisma y el cilindro. Dependiendo del sólido, se debe introducir un factor a la división. Capítulo 5 2 Cabrilog
3 Actividad Club Cabri cabri.com 3 Aporte de Cabri 3D Con Cabri3D es posible modificar el problema cambiando el tamaño de la base del prisma o la altura del cilindro. Esto demuestra el poder de la fórmula del volumen. Cabri 3D también permite que los estudiantes confirmen la exactitud de su construcción, mostrando el volumen de la parte del cilindro llena de agua. Debe ser igual al volumen del prisma. 2. Volumen de un cubo y de la esfera inscrita en él (archivo inscribedesferaincubo.cg3) Cree a cubo. Construya la esfera con un radio la mitad del lado del cubo. Calcule la proporción del volumen de la esfera y el cubo. Cambie el tamaño del cubo. Por qué no cambia la proporción? Solución: La proporción siempre será igual a 0.53 (redondeando). No varía porque la proporción de sus volúmenes siempre es igual (4/3) π 1/8. 4. Construya un sólido con un volumen dado sin recurrir a la calculadora de Cabri (archivo pyramidandcube1.cg3) Cree un cubo. Cree un cuadrado en el plano base con su lado igual al doble del lado del cubo. Construya una pirámide a partir de este cuadrado cuyo volumen sea el mismo del cubo. Un archivo ya preparado puede contener tanto el cubo como el cuadrado. La construcción puede verificarse mostrando el volumen del cubo y el de la pirámide. Caso general usando la calculadora de Cabri3D (archivo pyrámidandcubo2.cg3 Cree un cubo. Cree un cuadrado en el plano base. Construya una pirámide sobre este cuadrado, con el mismo volumen del cubo. 5. Areas (archivo areaspherecylinder.cg3) Cree una esfera con centre en el origen de los vectores. Construya el círculo resultante de la intersección de la esfera con el plano base (herramienta Curva de Intersección). Cree un cilindro a partir de este círculo y con la misma área lateral de la esfera. Varíe el radio de la esfera. Para qué valores es el radio de la esfera menor que la altura del cilindro? Para cuales mayor? Capítulo 5 3 Cabrilog
4 4 Actividad Club Cabri cabri.com 6. Volúmenes: una esfera y un cilindro (archivo ballinavase.cg3) Un recipiente cilíndrico contiene agua con una bola adentro. Construya la simulación, mostrando el nivel del agua que cambia en función del radio de la bola en el agua. Construya el recipiente como un cilindro. Con la base un circulo de centro O en el plano base y otro cilindro representando el agua, en color azul. Cree un punto C sobre el eje del cilindro y construya la esfera de centro C y radio CO. Calcule el aumento en el nivel del agua cuando se pone la bola en el recipiente. Construya el nuevo cilindro de agua. Al arrastrar el punto C (e.g. cambiar el tamaño de la bola) podrá ver como el nivel del agua cambia. Hay un punto en el cual el radio de la bola se hace mayor que el del cilindro! La herramienta Redefinición le permite redefinir el punto C como perteneciente al segmento y restringir la variación de C de forma que el radio de la bola siempre sea menor que el radio del cilindro. Capítulo 5 4 Cabrilog
5 Actividad Club Cabri cabri.com 5 Aporte de la herramienta Redefinición en modelos La herramienta Redefinición es muy útil en simulaciones. Permite que el usuario tenga en cuenta limitantes que se descubren solo después de un primer intento, sin necesidad de destruir del todo la simulación; simplemente añade la nueva limitante. Grafica del nivel del agua en el recipiente como función del radio de la bola. Cree el punto de coordenadas (0, OC, h) donde h es el nivel del agua de los vectores dados al iniciar Cabri 3D. Obtenga su trazado (Herramienta Trayectoria) arrastrando C. La curva así obtenida es una función cubica. (muy plana en su mínimo. 7. Radio del corte de una esfera como función de la altura de la sección (archivo crosssectionsphere.cg3) Construya una esfera de centro O y radio OA. Cree un punto H en la línea perpendicular al plano horizontal que pasa por O. Construya la sección de la esfera con el plano paralelo al plano horizontal que pasa por H. Sea h = OH y r = HP. En un plano paralelo al horizontal, construya el punto M cuyas coordenadas son h y r. Arrastre H y observe la trayectoria de M. Aventure una explicación, verifíquela con Cabri y pruébela. 8. Geodésica sobre un cubo (archivo shortestpathoncube.cg3) Capítulo 5 5 Cabrilog
6 6 Actividad Club Cabri cabri.com Cree un cubo. Cree dos puntos A y B en dos caras adyacentes. Construya el sendero más corto entre A y B. El principio consiste en reemplazar ese sendero con uno planar y aplicar la propiedad de que en un plano la distancia más corta es la línea recta. La grafica de la variación de la suma AM+MB en función de RM se muestra en un plano vertical. En un cilindro (archivo geodesiccylinder.cg3) El principio es el mismo, pero el plano se obtiene desenrollando el cilindro o el cono en un plano. Presupone que uno sabe cuál es el resultado del desenvolvimiento del cilindro o del cono.. En un cilindro Dos puntos A y B se crean en una misma mitad del cilindro. (ángulo acb < 180 ). Un punto A en el cilindro se determina con una proyección a sobre la base círculo y su altura aa. La proyección de la superficie lateral es un rectángulo escogido sobre el plano vertical OO C. El punto correspondiente de la proyección se construye por medio de estos dos números: la longitud del arco Oa se transfiere por el rayo oc y produce el punto a. El punto A es el punto de la proyección llevado a a y con la misma altura de A. El punto B corresponde a B y es construido desde B de la misma forma. La distancia más corta entre A y B es el segmento A B. La distancia más corta entre A y B es la trayectoria del punto M cuyo punto correspondiente en la proyección es M que describe el segmento A B. Cree un punto variable M sobre A B. Construya el punto correspondiente M sobre el cilindro y obtenga la trayectoria de M cuando se arrastra M. A partir de la construcción se puede determinar que z M es proporcional a la longitud del arco Om. La geodésica entre A y B pertenece a una hélice. La propiedad de la tangente de la hélice en ángulo constante con el eje del cilindro Capítulo 5 6 Cabrilog
7 Actividad Club Cabri cabri.com 7 también puede derivarse de esta construcción. Se obtienen ciertos casos particulares cuando A y B tienen la misma altura o cuando A y B se encuentran en la misma línea vertical. La construcción puede verificarse en cada caso. Capítulo 5 7 Cabrilog
Desarrollo de Poliedros Regulares: Generalidades. Ejercicios Resueltos. Ejercicio 1 Ejercicio 2 Ejercicio 3 Ejercicio 4 Ejercicio 5
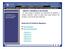 DESARROLLO DE POLIEDROS REGULARES UNIDAD IV: DESARROLLO DE SÓLIDOS En esta unidad se dibujarán las superficies de poliedros y cuerpos redondos modelos. Los temas de esta unidad son: sobre un plano para
DESARROLLO DE POLIEDROS REGULARES UNIDAD IV: DESARROLLO DE SÓLIDOS En esta unidad se dibujarán las superficies de poliedros y cuerpos redondos modelos. Los temas de esta unidad son: sobre un plano para
ÁREAS DE CUERPOS GEOMÉTRICOS Poliedros. Para calcular el área de un poliedro calculamos el área de cada una de sus caras y las sumamos.
 TEMA 9: ÁREAS Y VOLÚMENES DE CUERPOS GEOMÉTRICOS POLIEDROS REGULARES Un poliedro se llama regular cunado cumple las dos condiciones siguientes: Sus caras son polígonos regulares idénticos. En cada vértice
TEMA 9: ÁREAS Y VOLÚMENES DE CUERPOS GEOMÉTRICOS POLIEDROS REGULARES Un poliedro se llama regular cunado cumple las dos condiciones siguientes: Sus caras son polígonos regulares idénticos. En cada vértice
VOLUMENES. Los cuerpos en el espacio (sólidos) poseen tres dimensiones: largo, ancho y profundidad
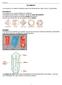 VOLUMENES Los cuerpos en el espacio (sólidos) poseen tres dimensiones: largo, ancho y profundidad POLIEDROS Un poliedro es un cuerpo limitado por polígonos Los polígonos que limiten el poliedro, se llaman
VOLUMENES Los cuerpos en el espacio (sólidos) poseen tres dimensiones: largo, ancho y profundidad POLIEDROS Un poliedro es un cuerpo limitado por polígonos Los polígonos que limiten el poliedro, se llaman
16. exacto 17. 18. coordenadas geográficas
 15. Historia muda: 16. En la siguiente figura aparece la mitad y un cuarto de esfera de radio 4 cm. Calcule el valor exacto en términos de π,de las áreas totales y los dos volúmenes. 17. Se coloca una
15. Historia muda: 16. En la siguiente figura aparece la mitad y un cuarto de esfera de radio 4 cm. Calcule el valor exacto en términos de π,de las áreas totales y los dos volúmenes. 17. Se coloca una
Unidad didáctica 3. Cálculo de superficies y volúmenes
 Unidad didáctica. Cálculo de superficies y volúmenes.1 Cálculo de superficies. En el presente apartado se estudiarán las superficies, perímetros y relaciones geométricas más importantes de las principales
Unidad didáctica. Cálculo de superficies y volúmenes.1 Cálculo de superficies. En el presente apartado se estudiarán las superficies, perímetros y relaciones geométricas más importantes de las principales
Área de paralelogramos, triángulos y trapecios (páginas 314 318)
 NOMRE FECHA PERÍODO Área de paralelogramos, triángulos y trapecios (páginas 34 38) Cualquier lado de un paralelogramo o triángulo puede usarse como base. La altitud de un paralelogramo es un segmento de
NOMRE FECHA PERÍODO Área de paralelogramos, triángulos y trapecios (páginas 34 38) Cualquier lado de un paralelogramo o triángulo puede usarse como base. La altitud de un paralelogramo es un segmento de
XIX OLIMPIADA NACIONAL DE MATEMÁTICA TERCERA RONDA REGIONAL - 1 DE SETIEMBRE DE 2007 - NIVEL 1. Nombre y Apellido:... C.I.:...
 TERCERA RONDA REGIONAL - 1 DE SETIEMBRE DE 2007 - NIVEL 1 Nombre y Apellido:..................................... C.I.:.................. Grado:......... Sección:........ Puntaje:........... Los dibujos
TERCERA RONDA REGIONAL - 1 DE SETIEMBRE DE 2007 - NIVEL 1 Nombre y Apellido:..................................... C.I.:.................. Grado:......... Sección:........ Puntaje:........... Los dibujos
13 POLIEDROS REPRESENTACIÓN DE POLIEDROS
 13-1 Curso de Dibujo Técnico. 2º de Bachillerato Patxi Aguirrezabal Martin 13 POLIEDROS TETRAEDRO. CUBO. OCTAEDRO. PRISMA. PIRÁMIDE. CONO. CILINDRO. ICOSAEDRO. DODECAEDRO. ESFERA. Contornos aparente y
13-1 Curso de Dibujo Técnico. 2º de Bachillerato Patxi Aguirrezabal Martin 13 POLIEDROS TETRAEDRO. CUBO. OCTAEDRO. PRISMA. PIRÁMIDE. CONO. CILINDRO. ICOSAEDRO. DODECAEDRO. ESFERA. Contornos aparente y
EJERCICIOS Nº 10: GEOMETRIA ANALITICA. se extiende hacia cada extremo en una longitud igual a su longitud original. Halle las coordenadas de
 EJERCICIOS Nº 1: GEOMETRIA ANALITICA 1) Determine x si el punto A (x,3) equidista de B ( 3, ) y de C (7,4) Respuesta ) Determine los puntos de trisección del segmento de recta AB donde A( 6, 9), B(6,9)
EJERCICIOS Nº 1: GEOMETRIA ANALITICA 1) Determine x si el punto A (x,3) equidista de B ( 3, ) y de C (7,4) Respuesta ) Determine los puntos de trisección del segmento de recta AB donde A( 6, 9), B(6,9)
Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm.
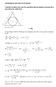 OPTIMIZACION DE FUNCIONES Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm. S = пrg Si los triángulos DCO y DAB que son semejantes, pues OC AB y poseen un
OPTIMIZACION DE FUNCIONES Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm. S = пrg Si los triángulos DCO y DAB que son semejantes, pues OC AB y poseen un
SUBRAYE LA RESPUESTA CORRECTA EN CADA PREGUNTA.
 CUADERNILLO DE GEOMETRIA I.- SUBRAYE LA RESPUESTA CORRECTA EN CADA PREGUNTA. 1.- SON LOS TRIÁNGULOS QUE TIENEN TODOS LOS ÁNGULOS IGUALES. A) EQUILÁTERO B) ACUTÁNGULO C) ISÓSCELES D) ESCALENO E) RECTÁNGULO
CUADERNILLO DE GEOMETRIA I.- SUBRAYE LA RESPUESTA CORRECTA EN CADA PREGUNTA. 1.- SON LOS TRIÁNGULOS QUE TIENEN TODOS LOS ÁNGULOS IGUALES. A) EQUILÁTERO B) ACUTÁNGULO C) ISÓSCELES D) ESCALENO E) RECTÁNGULO
MATEMÁTICAS 1º DE ESO
 MATEMÁTICAS 1º DE ESO LOE TEMA XII: POLIEDROS Y CUERPOS DE REDONDOS Poliedros. o Elementos de un poliedro y desarrollo plano. Prismas. o Elementos y tipos de prismas. Pirámides. o Elementos y tipos de
MATEMÁTICAS 1º DE ESO LOE TEMA XII: POLIEDROS Y CUERPOS DE REDONDOS Poliedros. o Elementos de un poliedro y desarrollo plano. Prismas. o Elementos y tipos de prismas. Pirámides. o Elementos y tipos de
CORRECCIÓN DE ACTIVIDADES GEOMETRÍA LINEAL
 CORRECCIÓN DE ACTIVIDADES GEOMETRÍA LINEAL *. Responde a las siguientes preguntas en tu cuaderno. a) Qué es una recta? Dibújala. Recta: sucesión infinita de puntos (no tiene principio ni fin). Las rectas
CORRECCIÓN DE ACTIVIDADES GEOMETRÍA LINEAL *. Responde a las siguientes preguntas en tu cuaderno. a) Qué es una recta? Dibújala. Recta: sucesión infinita de puntos (no tiene principio ni fin). Las rectas
RAZONES TRIGONOMÉTRICAS
 RAZONES TRIGONOMÉTRICAS Razones trigonométricas de los ángulos de un triángulo rectángulo eran esas relaciones entre los lados de dicho triángulo rectángulo. Seno: Se define el seno del ángulo como el
RAZONES TRIGONOMÉTRICAS Razones trigonométricas de los ángulos de un triángulo rectángulo eran esas relaciones entre los lados de dicho triángulo rectángulo. Seno: Se define el seno del ángulo como el
11 Cuerpos geométricos
 89485 _ 0369-0418.qxd 1/9/07 15:06 Página 369 Cuerpos geométricos INTRODUCCIÓN Los poliedros, sus elementos y tipos ya son conocidos por los alumnos del curso anterior. Descubrimos y reconocemos de nuevo
89485 _ 0369-0418.qxd 1/9/07 15:06 Página 369 Cuerpos geométricos INTRODUCCIÓN Los poliedros, sus elementos y tipos ya son conocidos por los alumnos del curso anterior. Descubrimos y reconocemos de nuevo
1 Calcula en la siguiente figura el elemento que falta: 2 Calcula en la siguiente figura el elemento que falta:
 1 Calcula en la siguiente figura el elemento que falta: Calcula en la siguiente figura el elemento que falta: Calcula el valor de la diagonal de un ortoedro de aristas cm, 4 cm y 5 cm. 4 Comprueba la fórmula
1 Calcula en la siguiente figura el elemento que falta: Calcula en la siguiente figura el elemento que falta: Calcula el valor de la diagonal de un ortoedro de aristas cm, 4 cm y 5 cm. 4 Comprueba la fórmula
Colegio LOPE DE VEGA Luis de Medina, 12 28805 Alcalá de Henares DIBUJO TÉCNICO II EJERCICIOS DE APOYO
 Colegio LOPE DE VEGA Luis de Medina, 12 28805 Alcalá de Henares DIBUJO TÉCNICO II EJERCICIOS DE APOYO 1º.- Deducir razonadamente el valor del ángulo α marcado en la figura sabiendo que esta representa
Colegio LOPE DE VEGA Luis de Medina, 12 28805 Alcalá de Henares DIBUJO TÉCNICO II EJERCICIOS DE APOYO 1º.- Deducir razonadamente el valor del ángulo α marcado en la figura sabiendo que esta representa
TETRAEDRO CUBO OCTAEDRO DODECAEDRO ICOSAEDRO
 6.- SÓLIDOS Al finalizar el sexto curso de Educación Primaria, los estudiantes deben describir cuerpos geométricos usando el vocabulario apropiado con términos como vértices, caras, aristas, planos, diedros,
6.- SÓLIDOS Al finalizar el sexto curso de Educación Primaria, los estudiantes deben describir cuerpos geométricos usando el vocabulario apropiado con términos como vértices, caras, aristas, planos, diedros,
Práctica 06. Instituto Tecnológico de Costa Rica Escuela de Matemática Matemática General. I. Plantee y resuelva los siguientes problemas:
 Instituto Tecnológico de Costa Rica Escuela de Matemática Matemática General I. Plantee y resuelva los siguientes problemas: Práctica 06 Geometría 1) Un árbol proyecta una sombra de 5 m en el mismo instante
Instituto Tecnológico de Costa Rica Escuela de Matemática Matemática General I. Plantee y resuelva los siguientes problemas: Práctica 06 Geometría 1) Un árbol proyecta una sombra de 5 m en el mismo instante
Guía del docente. 1. Descripción curricular:
 Guía del docente. 1. Descripción curricular: - Nivel: NB6º, 8º Básico. - Subsector: Matemática. - Unidad temática: Geometría. - Palabras claves: Geometría; Volumen; Figuras geométricas; - Contenidos curriculares:
Guía del docente. 1. Descripción curricular: - Nivel: NB6º, 8º Básico. - Subsector: Matemática. - Unidad temática: Geometría. - Palabras claves: Geometría; Volumen; Figuras geométricas; - Contenidos curriculares:
Trigonometría, figuras planas
 El polígono Un polígono es una figura plana limitada por tres o más segmentos. El perímetro de un polígono es igual a la suma de las longitudes de sus lados. El perímetro de una circunferencia se llama
El polígono Un polígono es una figura plana limitada por tres o más segmentos. El perímetro de un polígono es igual a la suma de las longitudes de sus lados. El perímetro de una circunferencia se llama
a) A la mitad del número le sumo 3 y el resultado es 8 ( ) 9 b) En la ecuación 3x = 54 Qué valor puede tomar x? ( ) Rombo
 Guía Matemáticas 3 ELIGE LA RESPUESTA CORRECTA.. Anota en el paréntesis de la derecha la letra que corresponda. a) A la mitad del número le sumo 3 y el resultado es 8 9 b) En la ecuación 3 = 54 Qué valor
Guía Matemáticas 3 ELIGE LA RESPUESTA CORRECTA.. Anota en el paréntesis de la derecha la letra que corresponda. a) A la mitad del número le sumo 3 y el resultado es 8 9 b) En la ecuación 3 = 54 Qué valor
UNIDAD X - GEOMETRIA. Ejercitación
 UNIDAD X - GEOMETRIA Programa Analítico Segmentos. Operaciones con segmentos. Ángulos. Clasificación de los ángulos: Complementarios, suplementarios, adyacentes, alternos-internos, opuestos por el vértice.
UNIDAD X - GEOMETRIA Programa Analítico Segmentos. Operaciones con segmentos. Ángulos. Clasificación de los ángulos: Complementarios, suplementarios, adyacentes, alternos-internos, opuestos por el vértice.
RELACION DE PROBLEMAS DE GEOMETRIA. Problemas propuestos para la prueba de acceso del curso 1996/97.
 RELACION DE PROBLEMAS DE GEOMETRIA Problemas propuestos para la prueba de acceso del curso 996/97. º. - Explica cómo se puede hallar el área de un triángulo, a partir de sus coordenadas, en el espacio
RELACION DE PROBLEMAS DE GEOMETRIA Problemas propuestos para la prueba de acceso del curso 996/97. º. - Explica cómo se puede hallar el área de un triángulo, a partir de sus coordenadas, en el espacio
UNIDAD IV ÁREAS DE FIGURAS PLANAS
 UNIDAD IV ÁREAS DE FIGURAS PLANAS COMPETENCIAS E INDICADORES DE DESEMPEÑO Identifica las áreas de figuras planas, volumen y superficie. CONCEPTOS DE PERÍMETRO Y AREA DE UNA FIGURA PLANA Se llama perímetro
UNIDAD IV ÁREAS DE FIGURAS PLANAS COMPETENCIAS E INDICADORES DE DESEMPEÑO Identifica las áreas de figuras planas, volumen y superficie. CONCEPTOS DE PERÍMETRO Y AREA DE UNA FIGURA PLANA Se llama perímetro
ACTIVIDAD INTRODUCTORIA: El regalo para mi hermano.
 Grado 7 Matemáticas Conozcamos otros sistemas de medidas, el sistema internacional y el sistema inglés. TEMA: DESCRIPCIÓN DEL ÁREA EN CUERPOS GEOMÉTRICOS Nombre: Grado: ACTIVIDAD INTRODUCTORIA: El regalo
Grado 7 Matemáticas Conozcamos otros sistemas de medidas, el sistema internacional y el sistema inglés. TEMA: DESCRIPCIÓN DEL ÁREA EN CUERPOS GEOMÉTRICOS Nombre: Grado: ACTIVIDAD INTRODUCTORIA: El regalo
Conceptos básicos de Geometría
 Conceptos básicos de geometría La geometría trata de la medición y de las propiedades de puntos, líneas, ángulos, planos y sólidos, así como de las relaciones que guardan entre sí. A continuación veremos
Conceptos básicos de geometría La geometría trata de la medición y de las propiedades de puntos, líneas, ángulos, planos y sólidos, así como de las relaciones que guardan entre sí. A continuación veremos
1. Aplique el método de inducción matemática para probar las siguientes proposiciones. e) f) es divisible por 6. a) b) c) d) e) f)
 1. Aplique el método de inducción matemática para probar las siguientes proposiciones. a) b) c) d) e) f) es divisible por 6. g) 2. Halle la solución de las siguientes desigualdades de primer orden. g)
1. Aplique el método de inducción matemática para probar las siguientes proposiciones. a) b) c) d) e) f) es divisible por 6. g) 2. Halle la solución de las siguientes desigualdades de primer orden. g)
EJERCICIOS BLOQUE III: GEOMETRÍA
 EJERCICIOS BLOQUE III: GEOMETRÍA (00-M-A-4) (5 puntos) Determina el centro y el radio de la circunferencia que pasa por el origen de coordenadas, tiene su centro en el semieje positivo de abscisas y es
EJERCICIOS BLOQUE III: GEOMETRÍA (00-M-A-4) (5 puntos) Determina el centro y el radio de la circunferencia que pasa por el origen de coordenadas, tiene su centro en el semieje positivo de abscisas y es
4. GEOMETRÍA // 4.4. ÁREAS Y VOLÚMENES.
 4. GEOMETRÍA // 4.4. ÁREAS Y VOLÚMENES. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS. 4.4.1. Áreas de polígonos. El área de un triángulo es Área(ABC) = 1 2 ch = 1 cb sin α 2 Si el triángulo
4. GEOMETRÍA // 4.4. ÁREAS Y VOLÚMENES. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS. 4.4.1. Áreas de polígonos. El área de un triángulo es Área(ABC) = 1 2 ch = 1 cb sin α 2 Si el triángulo
La geometría de los sólidos
 LECCIÓN CONDENSADA 10.1 La geometría de los sólidos En esta lección Conocerás los poliedros, que incluyen a los prismas y las pirámides Conocerás los sólidos con superficies curvas, que incluyen a las
LECCIÓN CONDENSADA 10.1 La geometría de los sólidos En esta lección Conocerás los poliedros, que incluyen a los prismas y las pirámides Conocerás los sólidos con superficies curvas, que incluyen a las
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág. PÁGINA EJERCICIOS Unidades de volumen Transforma en metros cúbicos: a) 50 dam b) 0,08 hm c) 0, km d) 5 80 dm e) 500 hl f) 0 000 l a) 50 dam = 50 000 m b) 0,08 hm = 8 000 m c) 0, km = 0 000 000 m d)
Pág. PÁGINA EJERCICIOS Unidades de volumen Transforma en metros cúbicos: a) 50 dam b) 0,08 hm c) 0, km d) 5 80 dm e) 500 hl f) 0 000 l a) 50 dam = 50 000 m b) 0,08 hm = 8 000 m c) 0, km = 0 000 000 m d)
Ángulos. Semejanza. ABE ˆ, ACE ˆ o ADE ˆ son ángulos inscritos en la. n 2 180º. En la circunferencia:
 GEOMETRÍA Ángulos En la circunferencia: ABE ˆ, ACE ˆ o ADE ˆ son ángulos inscritos en la circunferencia y son todos iguales. AOE ˆ es el ángulo central correspondiente y su medida es dos veces la medida
GEOMETRÍA Ángulos En la circunferencia: ABE ˆ, ACE ˆ o ADE ˆ son ángulos inscritos en la circunferencia y son todos iguales. AOE ˆ es el ángulo central correspondiente y su medida es dos veces la medida
Nº caras. Nº vértices
 Tipo De Caras (Ángulo Interior) Triángulo Equilátero (60º) Cuadrado (90º) Pentágono (108º) Hexágono (10º) Nº caras por vértice Suma de los ángulos de cada vértice Nº caras Nº vértices Nº aristas C + V
Tipo De Caras (Ángulo Interior) Triángulo Equilátero (60º) Cuadrado (90º) Pentágono (108º) Hexágono (10º) Nº caras por vértice Suma de los ángulos de cada vértice Nº caras Nº vértices Nº aristas C + V
Los poliedros y sus elementos
 Los poliedros y sus elementos De las siguientes figuras, rodea las que sean poliedros o tengan forma de poliedro. Dibuja y escribe el nombre de tres objetos que tengan forma de poliedro. espuesta libre
Los poliedros y sus elementos De las siguientes figuras, rodea las que sean poliedros o tengan forma de poliedro. Dibuja y escribe el nombre de tres objetos que tengan forma de poliedro. espuesta libre
Guía de Trabajo Volumen. Nombre: Curso: Fecha: Cuerpos geométricos
 Departamento de Matemática Profesora: Diosa Loyola Angel Âdâx àâ xáyâxüéé àx ÄÄxäx ÑÉÜ Ät áxçwt wxä vtâw ÄÄÉÊ Guía de Trabajo Volumen 1 Nombre: Curso: Fecha: Cuerpos geométricos Los cuerpos geométricos
Departamento de Matemática Profesora: Diosa Loyola Angel Âdâx àâ xáyâxüéé àx ÄÄxäx ÑÉÜ Ät áxçwt wxä vtâw ÄÄÉÊ Guía de Trabajo Volumen 1 Nombre: Curso: Fecha: Cuerpos geométricos Los cuerpos geométricos
GEOMETRÍA. 1. Líneas y ángulos. Partimos de la existencia de infinitos puntos cuyo conjunto llamamos ESPACIO.
 1. Líneas y ángulos Partimos de la existencia de infinitos puntos cuyo conjunto llamamos ESPACIO. Los puntos del espacio se consideran agrupados en conjuntos parciales de infinitos puntos llamados PLANOS.
1. Líneas y ángulos Partimos de la existencia de infinitos puntos cuyo conjunto llamamos ESPACIO. Los puntos del espacio se consideran agrupados en conjuntos parciales de infinitos puntos llamados PLANOS.
EJERCICIOS BLOQUE III: GEOMETRÍA
 EJERCICIOS BLOQUE III: GEOMETRÍA (00-M-A-4) (5 puntos) Determina el centro y el radio de la circunferencia que pasa por el origen de coordenadas, tiene su centro en el semieje positivo de abscisas y es
EJERCICIOS BLOQUE III: GEOMETRÍA (00-M-A-4) (5 puntos) Determina el centro y el radio de la circunferencia que pasa por el origen de coordenadas, tiene su centro en el semieje positivo de abscisas y es
Seminario de problemas-bachillerato. Curso 2012-13. Hoja 4
 Seminario de problemas-bachillerato. Curso 2012-13. Hoja 4 25. El número 2 x es la mayor potencia entera de 2 entre las que tienen nueve dígitos en base 10, y sus nueve dígitos son distintos. Usando que
Seminario de problemas-bachillerato. Curso 2012-13. Hoja 4 25. El número 2 x es la mayor potencia entera de 2 entre las que tienen nueve dígitos en base 10, y sus nueve dígitos son distintos. Usando que
CUERPOS GEOMÉTRICOS. Clases de cuerpos geométricos. Los poliedros. Los poliedros regulares.
 CUERPOS GEOMÉTRICOS. Se denominan cuerpos geométricos a aquellos elementos que, ya sean reales o ideales - que existen en la realidad o pueden concebirse mentalmente - ocupan un volumen en el espacio desarrollándose
CUERPOS GEOMÉTRICOS. Se denominan cuerpos geométricos a aquellos elementos que, ya sean reales o ideales - que existen en la realidad o pueden concebirse mentalmente - ocupan un volumen en el espacio desarrollándose
Sistemas de Representación y Dibujo Técnico Año 2015. Geometría Básica
 EL PUNTO Geometría Básica El punto es la entidad geométrica más pequeña y finita. Se puede definir por intersección de 2 rectas. En un plano, se puede definir por medio de 2 coordenadas. En el espacio,
EL PUNTO Geometría Básica El punto es la entidad geométrica más pequeña y finita. Se puede definir por intersección de 2 rectas. En un plano, se puede definir por medio de 2 coordenadas. En el espacio,
Área de paralelogramos (páginas 546 549)
 A NOMRE FECHA PERÍODO Área de paralelogramos (páginas 546 549) Un paralelogramo es un cuadrilátero con dos pares de lados paralelos. La base es cualquiera de los lados y la altura es la distancia más corta
A NOMRE FECHA PERÍODO Área de paralelogramos (páginas 546 549) Un paralelogramo es un cuadrilátero con dos pares de lados paralelos. La base es cualquiera de los lados y la altura es la distancia más corta
TRANSFORMACIONES DEL PLANO
 PROBLEMAS DE GEOMETRÍA. TRANSFORMACIONES DEL PLANO 1. Un producto de dos simetrías axiales de ejes perpendiculares A qué transformación corresponde? En qué se transforma un segmento vertical? ( ) 2. Cuál
PROBLEMAS DE GEOMETRÍA. TRANSFORMACIONES DEL PLANO 1. Un producto de dos simetrías axiales de ejes perpendiculares A qué transformación corresponde? En qué se transforma un segmento vertical? ( ) 2. Cuál
LA RECTA. Ax By C 0. y y m x x. y mx b. Geometría Analítica 2 ECUACIÓN GENERAL. Teorema: ECUACIÓN PUNTO - PENDIENTE .
 LA RECTA En geometría definimos a la recta como la sucesión infinita de puntos uno a continuación de otro en la misma dirección. En el plano cartesiano, la recta es el lugar geométrico de todos los puntos
LA RECTA En geometría definimos a la recta como la sucesión infinita de puntos uno a continuación de otro en la misma dirección. En el plano cartesiano, la recta es el lugar geométrico de todos los puntos
Guia PSU Matemática IV Medio PERÍMETROS, ÁREAS Y VOLÚMENES
 PERÍMETROS, ÁREAS Y VOLÚMENES Antes de entrar al análisis de fórmulas referente al perímetro, área y volumen de figuras geométricas, repasemos estos temas y efectuemos ejercicios pertinentes Llamamos área
PERÍMETROS, ÁREAS Y VOLÚMENES Antes de entrar al análisis de fórmulas referente al perímetro, área y volumen de figuras geométricas, repasemos estos temas y efectuemos ejercicios pertinentes Llamamos área
LA ECUACIÓN DE UN CÍRCULO 10.1.1 10.1.2
 Capítulo 10 L ECUCIÓN DE UN CÍRCUL 10.1.1 10.1.2 Los alumnos han calculado las circunferencias áreas de círculos, de partes de los círculos, han usado las propiedades de los círculos en problemas de aplicación
Capítulo 10 L ECUCIÓN DE UN CÍRCUL 10.1.1 10.1.2 Los alumnos han calculado las circunferencias áreas de círculos, de partes de los círculos, han usado las propiedades de los círculos en problemas de aplicación
1. Ángulos en la circunferencia
 1. Ángulos en la circunferencia Ángulo central. Es el que tiene el vértice en el centro de la circunferencia. Se identifica con el arco, de modo que escribiremos α = Figura 1: Ángulo central, inscrito
1. Ángulos en la circunferencia Ángulo central. Es el que tiene el vértice en el centro de la circunferencia. Se identifica con el arco, de modo que escribiremos α = Figura 1: Ángulo central, inscrito
UNIDAD 10 CUERPOS GEOMÉTRICOS. Objetivo General.
 UNIDAD 10 CUERPOS GEOMÉTRICOS Objetivo General. Al terminar ésta unidad identificarás los diferentes tipos de Cuerpos Geométricos, resolverás ejercicios y problemas en los que apliques definiciones y fórmulas.
UNIDAD 10 CUERPOS GEOMÉTRICOS Objetivo General. Al terminar ésta unidad identificarás los diferentes tipos de Cuerpos Geométricos, resolverás ejercicios y problemas en los que apliques definiciones y fórmulas.
Hoja de problemas nº 7. Introducción a la Geometría
 Hoja de problemas nº 7 Introducción a la Geometría 1. Un rectángulo tiene de área 135 u 2 a. Si sus lados miden números enteros, averigua cuáles pueden ser sus dimensiones. b. Cortamos los vértices como
Hoja de problemas nº 7 Introducción a la Geometría 1. Un rectángulo tiene de área 135 u 2 a. Si sus lados miden números enteros, averigua cuáles pueden ser sus dimensiones. b. Cortamos los vértices como
SÓLIDOS Y RAZONES DE SEMEJANZA 11.1.1 11.1.3
 Capítulo 11 SÓLIDOS Y RAZONES DE SEMEJANZA 11.1.1 11.1. En este capítulo, los alumnos analizarán las figuras tridimensionales, que se conocen como sólidos. Revisarán cómo calcular el área de superficie
Capítulo 11 SÓLIDOS Y RAZONES DE SEMEJANZA 11.1.1 11.1. En este capítulo, los alumnos analizarán las figuras tridimensionales, que se conocen como sólidos. Revisarán cómo calcular el área de superficie
Los cuerpos geométricos
 Los cuerpos geométricos Se denominan cuerpos geométricos a aquellos elementos que, ya sean reales o ideales que existen en la realidad o pueden concebirse mentalmente ocupan un volumen en el espacio desarrollándose
Los cuerpos geométricos Se denominan cuerpos geométricos a aquellos elementos que, ya sean reales o ideales que existen en la realidad o pueden concebirse mentalmente ocupan un volumen en el espacio desarrollándose
PERÍMETROS Y ÁREAS DE FIGURAS PLANAS UNIDADE 13 1º ESO Halla la superficie y el perímetro del recinto marrón:
 PERÍMETROS Y ÁREAS DE FIGURAS PLANAS UNIDADE 13 1º ESO Halla la superficie y el perímetro del recinto marrón: Calcula el perímetro y el área de esta figura: Calcula el perímetro y el área de esta figura:
PERÍMETROS Y ÁREAS DE FIGURAS PLANAS UNIDADE 13 1º ESO Halla la superficie y el perímetro del recinto marrón: Calcula el perímetro y el área de esta figura: Calcula el perímetro y el área de esta figura:
Trigonometría y problemas métricos
 Trigonometría y problemas métricos 1) En un triángulo rectángulo, los catetos miden 6 y 8 centímetros. Calcula la medida de la altura sobre la hipotenusa y la distancia desde su pie hasta los extremos.
Trigonometría y problemas métricos 1) En un triángulo rectángulo, los catetos miden 6 y 8 centímetros. Calcula la medida de la altura sobre la hipotenusa y la distancia desde su pie hasta los extremos.
Geometría en 3D. Problemas del capítulo. 1. Cuáles son las diferencias entre prismas y pirámides, y entre cilindros y conos?
 Geometría en 3D. Problemas del capítulo 1. Cuáles son las diferencias entre prismas y pirámides, y entre cilindros y conos? 2. Qué es volumen y cómo lo encontramos? 3. Cómo se relacionan los volúmenes
Geometría en 3D. Problemas del capítulo 1. Cuáles son las diferencias entre prismas y pirámides, y entre cilindros y conos? 2. Qué es volumen y cómo lo encontramos? 3. Cómo se relacionan los volúmenes
Created with novapdf Printer (www.novapdf.com)
 GEOMETRÍA LONGITUDES Longitud de la circunferencia Es una línea curva cerrada que equidistan todos sus puntos del centro. Radio Centro: punto situado a igual distancia de todos los puntos de la circunferencia.
GEOMETRÍA LONGITUDES Longitud de la circunferencia Es una línea curva cerrada que equidistan todos sus puntos del centro. Radio Centro: punto situado a igual distancia de todos los puntos de la circunferencia.
PROBLEMAS METRICOS. r 3
 PROBLEMAS METRICOS 1. Hallar el área del triángulo de vértices A(1,1), B(2,3) y C(5,2). 2. Halla las ecuaciones de las bisectrices determinadas por las rectas y=3x e y=1/3 x. Comprueba que ambas bisectrices
PROBLEMAS METRICOS 1. Hallar el área del triángulo de vértices A(1,1), B(2,3) y C(5,2). 2. Halla las ecuaciones de las bisectrices determinadas por las rectas y=3x e y=1/3 x. Comprueba que ambas bisectrices
Sistema Diédrico. Punto y recta
 Sistema Diédrico. Punto y recta Dibujo Técnico Ejercicios del alumno. Uso en el Centro Pág. 1 Si un punto del espacio se encuentra por encima del plano horizontal, su cota es positiva y en el sistema diédrico
Sistema Diédrico. Punto y recta Dibujo Técnico Ejercicios del alumno. Uso en el Centro Pág. 1 Si un punto del espacio se encuentra por encima del plano horizontal, su cota es positiva y en el sistema diédrico
[email protected]
 Titulo: CENTRO DE GRAVEDAD, CENTRO DE MASA Y CENTROIDE. Año escolar: Estática - Ingeniería Autor: José Luis Albornoz Salazar Ocupación: Ing Civil. Docente Universitario País de residencia: Venezuela Correo
Titulo: CENTRO DE GRAVEDAD, CENTRO DE MASA Y CENTROIDE. Año escolar: Estática - Ingeniería Autor: José Luis Albornoz Salazar Ocupación: Ing Civil. Docente Universitario País de residencia: Venezuela Correo
1. Determinar las ecuaciones paramétricas y la ecuación continua de las rectas que pasan por el punto A y con el vector de dirección dado:
 CAPÍTULO. GEOMETRÍA AFÍN.. Problemas. Determinar las ecuaciones paramétricas y la ecuación continua de las rectas que pasan por el punto A y con el vector de dirección dado: a) A(,, ), v = (,, ) ; b) A(0,
CAPÍTULO. GEOMETRÍA AFÍN.. Problemas. Determinar las ecuaciones paramétricas y la ecuación continua de las rectas que pasan por el punto A y con el vector de dirección dado: a) A(,, ), v = (,, ) ; b) A(0,
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág. 1 PÁGINA 255 EJERCICIOS Construcciones y ejes de simetría 1 a) Halla el ángulo central de un octógono regular. b) Dibuja un octógono regular inscrito en una circunferencia de 5 cm de radio, construyendo
Pág. 1 PÁGINA 255 EJERCICIOS Construcciones y ejes de simetría 1 a) Halla el ángulo central de un octógono regular. b) Dibuja un octógono regular inscrito en una circunferencia de 5 cm de radio, construyendo
3. Si la capacidad de un cubo es 8 litros, entonces la suma de las medidas de todas las aristas del cubo es
 Programa Estándar Anual Nº Guía práctica Poliedros Ejercicios PSU 1. Si la arista de un cubo mide 4 cm, entonces el área del cubo mide Matemática A) 12 cm 2 D) 96 cm 2 B) 48 cm 2 E) 576 cm 2 C) 64 cm 2
Programa Estándar Anual Nº Guía práctica Poliedros Ejercicios PSU 1. Si la arista de un cubo mide 4 cm, entonces el área del cubo mide Matemática A) 12 cm 2 D) 96 cm 2 B) 48 cm 2 E) 576 cm 2 C) 64 cm 2
EJERCICIOS PROPUESTOS
 EJERCICIOS PROPUESTOS 1) En cada ejercicio hallar la ecuación de la circunferencia que cumple: 1) El radio es igual a 6 y las coordenadas de su centro son ( 1, 2). 2) Su centro es el origen de coordenadas
EJERCICIOS PROPUESTOS 1) En cada ejercicio hallar la ecuación de la circunferencia que cumple: 1) El radio es igual a 6 y las coordenadas de su centro son ( 1, 2). 2) Su centro es el origen de coordenadas
A = A < θ R = A + B + C = C+ B + A. b) RESTA O DIFERENCIA DE VECTORES ANÁLISIS VECTORIAL. Es una operación que tiene por finalidad hallar un
 ANÁLISIS VECTORIAL MAGNITUD FÍSICA Es todo aquello que se puede medir. CLASIFICACIÓN DE MAGNITUDES POR NATURALEZA MAGNITUD ESCALAR: Magnitud definida por completo mediante un número y la unidad de medida
ANÁLISIS VECTORIAL MAGNITUD FÍSICA Es todo aquello que se puede medir. CLASIFICACIÓN DE MAGNITUDES POR NATURALEZA MAGNITUD ESCALAR: Magnitud definida por completo mediante un número y la unidad de medida
Lección 14: Volúmenes de algunos cuer pos
 LECCIÓN 14 Lección 14: Volúmenes de algunos cuer pos Concepto de volumen En un cuerpo sólido podemos medir su volumen, lo que, como en el caso de las longitudes y las áreas significa ver cuántas veces
LECCIÓN 14 Lección 14: Volúmenes de algunos cuer pos Concepto de volumen En un cuerpo sólido podemos medir su volumen, lo que, como en el caso de las longitudes y las áreas significa ver cuántas veces
EXAMEN GEOMETRÍA. 5. Halla el perímetro y el área de un triángulo isósceles cuyos lados miden 5, 5 y 8 cms., respectivamente.
 1. Supongamos una circunferencia de radio 90/ð cms. y un ángulo cuyo vértice coincida con el centro de la circunferencia. Halla: a) La longitud de arco de circunferencia que abarca un ángulo de 501. b)
1. Supongamos una circunferencia de radio 90/ð cms. y un ángulo cuyo vértice coincida con el centro de la circunferencia. Halla: a) La longitud de arco de circunferencia que abarca un ángulo de 501. b)
Manual de teoría: Geometría Matemática Bachillerato
 Manual de teoría: Geometría Matemática Bachillerato Realizado por José Pablo Flores Zúñiga Geometría: José Pablo Flores Zúñiga Página 1 Contenido: 3) Geometría 3.1 Círculo y Circunferencia 3. Polígonos
Manual de teoría: Geometría Matemática Bachillerato Realizado por José Pablo Flores Zúñiga Geometría: José Pablo Flores Zúñiga Página 1 Contenido: 3) Geometría 3.1 Círculo y Circunferencia 3. Polígonos
17. POLÍGONOS REGULARES
 17. POLÍGONOS REGULARES 17.1. Características generales Los polígonos regulares son los que tienen los lados y los ángulos iguales, es decir, son equiláteros y equiángulos. Son inscriptibles y circunscriptibles.
17. POLÍGONOS REGULARES 17.1. Características generales Los polígonos regulares son los que tienen los lados y los ángulos iguales, es decir, son equiláteros y equiángulos. Son inscriptibles y circunscriptibles.
ÁLGEBRA LINEAL II Práctica 3.1-3.2
 ÁLGEBRA LINEAL II Práctica 3.1-3.2 Geometría afín. (Curso 2014 2015) 1. En el espacio afín IR 3 se considera la referencia canónica R y la referencia R = (1, 0, 1); (1, 1, 0), (1, 1, 1), (1, 0, 0)}. Denotamos
ÁLGEBRA LINEAL II Práctica 3.1-3.2 Geometría afín. (Curso 2014 2015) 1. En el espacio afín IR 3 se considera la referencia canónica R y la referencia R = (1, 0, 1); (1, 1, 0), (1, 1, 1), (1, 0, 0)}. Denotamos
ÁREAS Y VOLÚMENES DE CUERPOS GEOMÉTRICOS.
 PRISMAS 1.) Las dimensiones de un ortoedro son a = 7 cm, b = 5 cm y c = 10 cm. Dibuja esquemáticamente su desarrollo y calcula su área, su volumen y la longitud de la diagonal. Sol: 310 cm 2 ; 350 cm 3
PRISMAS 1.) Las dimensiones de un ortoedro son a = 7 cm, b = 5 cm y c = 10 cm. Dibuja esquemáticamente su desarrollo y calcula su área, su volumen y la longitud de la diagonal. Sol: 310 cm 2 ; 350 cm 3
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2015 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 015 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva 1, Ejercicio 4, Opción A Reserva 1, Ejercicio
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 015 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva 1, Ejercicio 4, Opción A Reserva 1, Ejercicio
OLIMPÍADA JUVENIL DE MATEMÁTICA 2011 CANGURO MATEMÁTICO PRUEBA PRELIMINAR CUARTO AÑO
 OLIMPÍADA JUVENIL DE MATEMÁTICA 2011 CANGURO MATEMÁTICO PRUEBA PRELIMINAR CUARTO AÑO RESPONDE LA PRUEBA EN LA HOJA DE RESPUESTA ANEXA 1. En un cruce peatonal se alternan franjas blancas y negras, cada
OLIMPÍADA JUVENIL DE MATEMÁTICA 2011 CANGURO MATEMÁTICO PRUEBA PRELIMINAR CUARTO AÑO RESPONDE LA PRUEBA EN LA HOJA DE RESPUESTA ANEXA 1. En un cruce peatonal se alternan franjas blancas y negras, cada
ESTALMAT-Andalucía. Geometría dinámica con Cabri Géomètre
 Geometría dinámica con Cabri Géomètre SAEM THALES Material recopilado y elaborado por: Encarnación Amaro Parrado Agustín Carrillo de Albornoz Torres Granada, 28 de marzo de 2008-2 - Actividades para practicar
Geometría dinámica con Cabri Géomètre SAEM THALES Material recopilado y elaborado por: Encarnación Amaro Parrado Agustín Carrillo de Albornoz Torres Granada, 28 de marzo de 2008-2 - Actividades para practicar
Identificación de figuras planas
 Unidad 03: Comparando y caracterizando figuras. Grado 02 Matemáticas Clase: Identificación de figuras planas Nombre: Introducción Escribe el nombre y dibuja la figura de acuerdo a las características mencionadas.
Unidad 03: Comparando y caracterizando figuras. Grado 02 Matemáticas Clase: Identificación de figuras planas Nombre: Introducción Escribe el nombre y dibuja la figura de acuerdo a las características mencionadas.
Ejercicios Resueltos de Derivadas y sus aplicaciones:
 Ejercicios Resueltos de Derivadas y sus aplicaciones: 1.- Sea la curva paramétrica definida por, con. a) Halle. b) Para qué valor(es) de, la curva tiene recta tangente vertical? 2.- Halle para : a) b)
Ejercicios Resueltos de Derivadas y sus aplicaciones: 1.- Sea la curva paramétrica definida por, con. a) Halle. b) Para qué valor(es) de, la curva tiene recta tangente vertical? 2.- Halle para : a) b)
VOLUMENES DE SÓLIDOS DE REVOLUCION
 OLUMENES DE SÓLIDOS DE REOLUCION Los sólidos de revolución son sólidos que se generan al girar una región plana alrededor de un eje. Por ejemplo: el cono es un sólido que resulta al girar un triángulo
OLUMENES DE SÓLIDOS DE REOLUCION Los sólidos de revolución son sólidos que se generan al girar una región plana alrededor de un eje. Por ejemplo: el cono es un sólido que resulta al girar un triángulo
1 Indica cuál es el valor de los ángulo Â, Bˆ. en las siguientes figuras: a) b) 2 Calcula los ángulos dados por letras:
 1 Indica cuál es el valor de los ángulo Â, Bˆ y Ĉ en las siguientes figuras: a) b) Calcula los ángulos dados por letras: 3 Calcula el valor del ángulo A. 4 Dados los ángulos los mismos. a 45 0 30.y b 6
1 Indica cuál es el valor de los ángulo Â, Bˆ y Ĉ en las siguientes figuras: a) b) Calcula los ángulos dados por letras: 3 Calcula el valor del ángulo A. 4 Dados los ángulos los mismos. a 45 0 30.y b 6
10 FIGURAS Y CUERPOS GEOMÉTRICOS
 10 FIGURAS Y CUERPOS GEOMÉTRICOS EJERCICIOS PROPUESTOS 10.1 Indica cuál de estos poliedros es cóncavo y cuál es convexo. a) Cóncavo b) Convexo 10. Completa la siguiente tabla. Caras (C ) Vértices (V )
10 FIGURAS Y CUERPOS GEOMÉTRICOS EJERCICIOS PROPUESTOS 10.1 Indica cuál de estos poliedros es cóncavo y cuál es convexo. a) Cóncavo b) Convexo 10. Completa la siguiente tabla. Caras (C ) Vértices (V )
UNIDAD I. ÁNGULOS, TRIÁNGILOS, POLÍGONOS Y CIRCUNFERENCIA. Tema. Triángulos
 UNIDAD I. ÁNGULOS, TRIÁNGILOS, POLÍGONOS Y CIRCUNFERENCIA Tema. Triángulos TRIÁNGULOS Así como nuestro alrededor está lleno de objetos que nos ejemplifican claramente el concepto de ángulo, también existen
UNIDAD I. ÁNGULOS, TRIÁNGILOS, POLÍGONOS Y CIRCUNFERENCIA Tema. Triángulos TRIÁNGULOS Así como nuestro alrededor está lleno de objetos que nos ejemplifican claramente el concepto de ángulo, también existen
MUNICIPIO DE MEDELLÍN ÁREA DE MATEMÁTICAS: GEOMETRÍA ANALÍTICA. 3. Determinar analíticamente cuando dos rectas son paralelas o perpendiculares.
 ESTUDIO ANALÍTICO DE LA LÍNEA RECTA Y APLICACIONES SEMESTRE II VERSIÓN 03 FECHA: Septiembre 29 de 2011 MUNICIPIO DE MEDELLÍN ÁREA DE MATEMÁTICAS: GEOMETRÍA ANALÍTICA LOGROS: 1. Hallar la dirección, la
ESTUDIO ANALÍTICO DE LA LÍNEA RECTA Y APLICACIONES SEMESTRE II VERSIÓN 03 FECHA: Septiembre 29 de 2011 MUNICIPIO DE MEDELLÍN ÁREA DE MATEMÁTICAS: GEOMETRÍA ANALÍTICA LOGROS: 1. Hallar la dirección, la
21. Círculo y recta Matemáticas II, 2012-II. Por qué el círculo y la recta son tan importantes?
 . Círculo recta Matemáticas II, -II. Círculo recta Por qué el círculo la recta son tan importantes? Los dos objetos geométricos más importantes aparte del punto son sin duda la recta el círculo. La recta
. Círculo recta Matemáticas II, -II. Círculo recta Por qué el círculo la recta son tan importantes? Los dos objetos geométricos más importantes aparte del punto son sin duda la recta el círculo. La recta
Si ningún alumno hace algún comentario, el profesor pregunta si están mirando los lados del octágono.
 65 7) Prisma octagonal. Al iniciar la clase, el profesor coloca las ligas del geospacio, ante todos los alumnos, o solicita que algunos de ellos lo hagan, mientras él los dirige. Ya formado el prisma octagonal,
65 7) Prisma octagonal. Al iniciar la clase, el profesor coloca las ligas del geospacio, ante todos los alumnos, o solicita que algunos de ellos lo hagan, mientras él los dirige. Ya formado el prisma octagonal,
EJERCICIOS. ÁREAS Y VOLÚMENES.
 EJERCICIOS. ÁREAS Y VOLÚMENES. Teorema de Tales 1. Sean los triángulos ABC, AB'C'.Calcula el valor desconocido x. 2. Dos triángulos semejantes tienen una superficie de 20cm 2 y 30cm 2 respectivamente.
EJERCICIOS. ÁREAS Y VOLÚMENES. Teorema de Tales 1. Sean los triángulos ABC, AB'C'.Calcula el valor desconocido x. 2. Dos triángulos semejantes tienen una superficie de 20cm 2 y 30cm 2 respectivamente.
Conceptos Básicos. Las líneas rectas podemos encontrarlas en el doblez de una hoja de papel, en un hilo estirado, en la arista de una puerta, etc.
 3. Geometría Desde el jardinero que traza un jardín, el navegante que fija y traza la ruta del próximo viaje, el arquitecto que hace los planos para la construcción de un grandioso edificio, el ingeniero
3. Geometría Desde el jardinero que traza un jardín, el navegante que fija y traza la ruta del próximo viaje, el arquitecto que hace los planos para la construcción de un grandioso edificio, el ingeniero
La geometría de los sólidos
 LECCIÓN CONDENSADA 10.1 La geometría de los sólidos En esta lección Conocerás los poliedros, que incluyen a los prismas y las pirámides Conocerás los sólidos con superficies curvas, que incluyen a los
LECCIÓN CONDENSADA 10.1 La geometría de los sólidos En esta lección Conocerás los poliedros, que incluyen a los prismas y las pirámides Conocerás los sólidos con superficies curvas, que incluyen a los
CÁLCULO DIFERENCIAL (SEMESTRE 01-2010) EJERCICIOS COMPLEMENTARIOS SECCIÓN 1.1 DEL TEXTO GUÍA
 CÁLCULO DIFERENCIAL (SEMESTRE 01-2010) EJERCICIOS COMPLEMENTARIOS SECCIÓN 1.1 DEL TEXTO GUÍA 1. Expresar el área de un triángulo equilátero como función de la altura h del triángulo. 2. Se va a construir
CÁLCULO DIFERENCIAL (SEMESTRE 01-2010) EJERCICIOS COMPLEMENTARIOS SECCIÓN 1.1 DEL TEXTO GUÍA 1. Expresar el área de un triángulo equilátero como función de la altura h del triángulo. 2. Se va a construir
Departamento de Tecnología I.E.S. San José (Villanueva de la Serena) Bloque de contenidos: EXPRESIÓN GRÁFICA
 SISTEMAS DE REPRESENTACIÓN. No es habitual, que la persona que diseña un objeto sea luego la misma que se encarga de su construcción. Por ello, la información gráfica tiene que ser accesible a todas las
SISTEMAS DE REPRESENTACIÓN. No es habitual, que la persona que diseña un objeto sea luego la misma que se encarga de su construcción. Por ello, la información gráfica tiene que ser accesible a todas las
Unidad 3 Lección 1. Unidad 3 Lección 1 Nombre
 Unidad 3 Lección 1 Prueba A 1. Un segmento dibujado desde el centro de un círculo hasta el borde del mismo, se llama un. 2. Todos los radios de un círculo tienen el mismo. 3. Escriba una ecuación que represente
Unidad 3 Lección 1 Prueba A 1. Un segmento dibujado desde el centro de un círculo hasta el borde del mismo, se llama un. 2. Todos los radios de un círculo tienen el mismo. 3. Escriba una ecuación que represente
INTEGRALES TRIPLES. 46. Dada la integral la integral de todas las formas posibles. f(x, y, z) dzdydx, dibujar la región de integración y escribir
 INTEGALES TIPLES. 46. Dada la integral la integral de todas las formas posibles. f(,, ) ddd, dibujar la región de integración escribir Teniendo en cuenta la gráfica adjunta, si D 1, D 2 D 3 son las proecciones
INTEGALES TIPLES. 46. Dada la integral la integral de todas las formas posibles. f(,, ) ddd, dibujar la región de integración escribir Teniendo en cuenta la gráfica adjunta, si D 1, D 2 D 3 son las proecciones
Volúmenes de cuerpos geométricos
 Volúmenes de cuerpos geométricos TEORÍA Cuerpos geométricos En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos
Volúmenes de cuerpos geométricos TEORÍA Cuerpos geométricos En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos
UNIDAD 12. GEOMETRÍA DEL ESPACIO (II). CUERPOS DE REVOLUCIÓN.
 UNIDAD 12. GEOMETRÍA DEL ESPACIO (II). CUERPOS DE REVOLUCIÓN. Unidad 12: Geometría del espacio (II). Cuerpos de revolución. Al final deberás haber aprendido... Describir cuerpos de revolución e identificar
UNIDAD 12. GEOMETRÍA DEL ESPACIO (II). CUERPOS DE REVOLUCIÓN. Unidad 12: Geometría del espacio (II). Cuerpos de revolución. Al final deberás haber aprendido... Describir cuerpos de revolución e identificar
8. POLÍGONOS REGULARES 8.1. CARACTERÍSTICAS GENERALES
 8. POLÍGONOS REGULARES 8.1. CARACTERÍSTICAS GENERALES Los polígonos regulares son los que tienen los lados y los ángulos iguales, es decir, son equiláteros y equiángulos. Son inscriptibles y circunscriptibles.
8. POLÍGONOS REGULARES 8.1. CARACTERÍSTICAS GENERALES Los polígonos regulares son los que tienen los lados y los ángulos iguales, es decir, son equiláteros y equiángulos. Son inscriptibles y circunscriptibles.
[email protected]!!91.501.36.88!!28007!madrid!
 CONTINUIDAD Y DERIVABILIDAD. TEOREMAS Y APLICACIONES DE LAS DERIVADAS 1.- junio 1994 Se sabe que y = f (x) e y = g (x) son dos curvas crecientes en x = a. Analícese si la curva y = f(x) g(x) ha de ser,
CONTINUIDAD Y DERIVABILIDAD. TEOREMAS Y APLICACIONES DE LAS DERIVADAS 1.- junio 1994 Se sabe que y = f (x) e y = g (x) son dos curvas crecientes en x = a. Analícese si la curva y = f(x) g(x) ha de ser,
Colegio Universitario Boston. Geometría
 34 Conceptos ásicos Triángulo: Se define como la figura geométrica plana, cerrada de tres lados. Triángulo equilátero: Es el triángulo que tiene sus tres lados iguales y sus tres ángulos internos iguales,
34 Conceptos ásicos Triángulo: Se define como la figura geométrica plana, cerrada de tres lados. Triángulo equilátero: Es el triángulo que tiene sus tres lados iguales y sus tres ángulos internos iguales,
PROBLEMAS DE SEMEJANZA
 PROBLEMAS DE SEMEJANZA 1. En una fotografía, María y Fernando miden 2,5 cm y 2,7 cm, respectivamente; en la realidad, María tiene una altura de 167,5 cm. A qué escala está hecha la foto? Qué altura tiene
PROBLEMAS DE SEMEJANZA 1. En una fotografía, María y Fernando miden 2,5 cm y 2,7 cm, respectivamente; en la realidad, María tiene una altura de 167,5 cm. A qué escala está hecha la foto? Qué altura tiene
EJERCICIOS PROPUESTOS
 EJERCICIOS PROPUESTOS ) Dadas las coordenadas del punto A(, ). Hallar la ecuación de la recta (r) paralela al eje por dicho punto. Hallar la ecuación de la recta (p) paralela al eje por dicho punto. )
EJERCICIOS PROPUESTOS ) Dadas las coordenadas del punto A(, ). Hallar la ecuación de la recta (r) paralela al eje por dicho punto. Hallar la ecuación de la recta (p) paralela al eje por dicho punto. )
Proyecciones. Producto escalar de vectores. Aplicaciones
 Proyecciones La proyección de un punto A sobre una recta r es el punto B donde la recta perpendicular a r que pasa por A corta a la recta r. Con un dibujo se entiende muy bien. La proyección de un segmento
Proyecciones La proyección de un punto A sobre una recta r es el punto B donde la recta perpendicular a r que pasa por A corta a la recta r. Con un dibujo se entiende muy bien. La proyección de un segmento
La circunferencia y el círculo
 La circunferencia y el círculo Contenidos 1. La circunferencia. La circunferencia Elementos de la circunferencia. 2. Posiciones relativas. Punto y circunferencia. Recta y circunferencia. Dos circunferencias.
La circunferencia y el círculo Contenidos 1. La circunferencia. La circunferencia Elementos de la circunferencia. 2. Posiciones relativas. Punto y circunferencia. Recta y circunferencia. Dos circunferencias.
MATEMÁTICAS II PROBLEMAS DE GEOMETRÍA PAU ANDALUCÍA
 1 MATEMÁTICAS II PROBLEMAS DE GEOMETRÍA PAU ANDALUCÍA Ejercicio 1. (Junio 2006-A) Considera el plano π de ecuación 2x + y z + 2 = 0 y la recta r de ecuación x 5 z 6 = y =. 2 m (a) [1 punto] Halla la posición
1 MATEMÁTICAS II PROBLEMAS DE GEOMETRÍA PAU ANDALUCÍA Ejercicio 1. (Junio 2006-A) Considera el plano π de ecuación 2x + y z + 2 = 0 y la recta r de ecuación x 5 z 6 = y =. 2 m (a) [1 punto] Halla la posición
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: DIBUJO TÉCNICO 11
 y UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2014-2015 MATERIA: DIBUJO TÉCNICO 11 INSTRUCCIONES GENERALES Y CALIFICACIÓN
y UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2014-2015 MATERIA: DIBUJO TÉCNICO 11 INSTRUCCIONES GENERALES Y CALIFICACIÓN
COLEGIO TIRSO DE MOLINA DEPARTAMENTO DE DIBUJO TÉCNICO CURSO 2010-11 DIBUJO TÉCNICO II
 DIBUJO TÉCNICO II TEMA 2: PROPORCIONALIDAD Y SEMEJANZA Media proporcional Teoremas del Cateto y la Altura Figuras equivalentes Figuras semejantes y sus diferencias con las homotéticas Razón de semejanza
DIBUJO TÉCNICO II TEMA 2: PROPORCIONALIDAD Y SEMEJANZA Media proporcional Teoremas del Cateto y la Altura Figuras equivalentes Figuras semejantes y sus diferencias con las homotéticas Razón de semejanza
