CONOCIMIENTOS TEÓRICOS
|
|
|
- Natalia Herrera Márquez
- hace 7 años
- Vistas:
Transcripción
1 7 Sistema diédrico. Poliedros regulares UNIDAD CONOCIMIENTOS TEÓRICOS 1 Superficies y cuerpos. Introducción 1.1 Concepto de superficie 1.2 Generación y clasificación 1.3 Poliedros regulares 1.4 Fórmula de Euler 1.5 Poliedros conjugados 2 Características de los diferentes poliedros regulares 2.1 Tetraedro: elementos y relaciones 2.2 Hexaedro: elementos y relaciones 2.3 Octaedro: elementos y relaciones 2.4 Dodecaedro e icosaedro APLICACIONES PRÁCTICAS 1 Representaciones de los poliedros regulares 1.1 El tetraedro 1.2 El hexaedro o cubo 1.3 El octaedro 1.4 El dodecaedro 1.5 El icosaedro 2 Secciones planas, desarrollos y transformadas 2.1 Secciones planas de los poliedros 2.2 Intersecciones recta-poliedro 2.3 Desarrollos 3 Presencia de los poliedros regulares 3.1 Antecedentes históricos 3.2 Poliedros y arte CUESTIONES Y EJERCICIOS
2 UNIDAD 7 CONOCIMIENTOS TEÓRICOS Sistema diédrico. Poliedros regulares En los próximos apartados nos introduciremos en el estudio de superficies y cuerpos, un terreno mucho más concreto que el explorado en las dos últimas unidades, a las que recurriremos en busca de recursos (movimientos, posiciones favorables...) con los que resolver las representaciones de los poliedros regulares en proyecciones diédricas. 1 SUPERFICIES Y CUERPOS. INTRODUCCIÓN No debemos confundir los conceptos de cuerpo y superficie. El cuerpo, o sólido en la terminología de la mayoría del sorfware 3D, siempre hace referencia a un volumen determinado al que poder asociar propiedades como el peso, la densidad, centro de gravedad, etc.; la superficie, que puede ser ilimitada, coincide con la envoltura imaginaria que rodea a un cuerpo. En el caso de un cubo, todas sus superficies son planas y en el caso de una esfera son curvas; otros cuerpos, como el cono, tienen superficies planas y curvas. Fig. 1 Fig Concepto de superficie Una superficie es el lugar geométrico de las posiciones sucesivas de una línea, denominada generatriz, que cambia de posición, o de posición y forma, según una ley determinada. A las líneas que determinan el movimiento de la generatriz, se las denomina directriz de la superficie. En una superficie de revolución, cónica en el ejemplo de la figura 1, la generatriz gira alrededor de una recta fija a la que denominamos eje, y a la cual está invariablemente ligada. El plano es la superficie más elemental. En su generación, tanto la generatriz como la directriz son líneas rectas. La unión de dos o más planos define los siguientes ángulos: Fig. 3 Fig. 4 Ángulo diedro, formado por dos planos con una intersección o arista común i (Fig. 2). Cuando son tres los planos que, concurrentes dos a dos, tienen un punto común llamado vértice, la forma geométrica que configuran se denomina ángulo triedro. Un triedro característico es el denominado triedro trirrectángulo, formado por tres planos ortogonales entre sí (Fig. 3); sus tres ángulos diedros serán rectos y cada arista es perpendicular al plano de las otras dos. Ángulo poliedro, formado por más de tres planos, con un vértice V común entre ellos y limitado por sus intersecciones respectivas llamadas aristas (Fig. 4). Cada plano del ángulo poliedro se denomina cara, y el ángulo formado por dos caras consecutivas, diedro. Si prolongando una de las caras del poliedro todo él queda situado a un mismo lado respecto a esta cara, el poliedro es convexo; en caso contrario sería cóncavo. 136
3 Sistema diédrico. Poliedros regulares CONOCIMIENTOS TEÓRICOS UNIDAD Generación y clasificación Una primera clasificación agrupa las superficies en limitadas o ilimitadas; entre las primeras se incluyen las cerradas, que encierran un volumen determinado y dan lugar a los cuerpos que estudiaremos en esta unidad y en la próxima. Una superficie puede generarse de dos maneras distintas: 1.Como lugar geométrico de las posiciones de una línea cualquiera, que se mueve en el espacio de acuerdo con una ley determinada. 2.Como envolvente de otra superficie, que a su vez se mueve en el espacio de acuerdo con una ley determinada. Clasificaremos las superficies atendiendo a la forma de su generatriz y a las leyes a que responda su movimiento, las cuales condicionan la forma de la directriz. Un primer gran grupo de superficies son las regladas, cuya generatriz es una recta; a su vez se subdividen en desarrollables y alabeadas. Las primeras pueden extenderse sobre un plano sin experimentar deformación ni rotura, e incluyen a las poliédricas (regulares e irregulares) y a las radiales o radiadas (cónicas y cilíndricas). Las superficies alabeadas no pueden desarrollarse sobre un plano como las desarrollables. Kisho Kurokawa. Torre Nakagin, Las superficies curvas tienen por generatriz una curva, pero no son desarrollables ni alabeadas; entre éstas se encuentran la esfera y el toro. 1.3 Poliedros regulares Un poliedro es una figura tridimensional cerrada, formada por varios planos que se interseccionan en el espacio. Cada polígono formado en la intersección de una cara con las otras del poliedro, define una de las caras del poliedro. Los segmentos comunes a dos caras son las aristas, y la intersección de éstas forma cada uno de los vértices del poliedro. Un poliedro es regular cuando sus caras están formadas por el mismo polígono regular y los ángulos poliedros son también iguales entre sí. Todos los poliedros regulares son convexos y en cada uno de ellos existe un centro geométrico único que, a su vez, es el centro de las esferas inscrita, circunscrita y tangente a las aristas del poliedro. La primera es tangente a todas sus caras en los puntos centrales de éstas, y su diámetro coincide con la distancia entre caras opuestas; la segunda pasa por todos sus vértices, mientras que la tercera es tangente a todas las aristas en sus respectivos puntos medios, y su diámetro es igual a la distancia entre aristas opuestas. 137
4 UNIDAD 7 CONOCIMIENTOS TEÓRICOS Sistema diédrico. Poliedros regulares Sabiendo que para formar un ángulo poliedro la suma de los ángulos de las caras concurrentes en un vértice no puede llegar a ser 360, en cuyo caso formarían un ángulo plano, y que el mínimo de caras concurrentes en un vértice ha de ser tres, los poliedros regulares convexos no pueden ser más que los cinco siguientes: Si el polígono de la cara es un triángulo equilátero, las caras concurrentes en cada vértice pueden ser tres, cuatro o cinco (Fig. 5), dando lugar, respectivamente, a los siguientes poliedros: tetraedro, octaedro e icosaedro. Piet Blom. Kubuswowing. Roterdam. Fig. 5 Fig. 6 Si el polígono de la cara es un cuadrado, sólo pueden ser tres las caras concurrentes en cada vértice, ya que con cuatro llegarían al ángulo de 360º (Fig. 6). El poliedro formado es un hexaedro o cubo. Cuando el polígono de la cara es un pentágono regular, cuyos ángulos interiores miden 72º, únicamente pueden ser tres las caras concurrentes en cada vértice, ya que con cuatro superarían los 360º (Fig. 7). El poliedro formado es un dodecaedro. Con caras formadas por hexágonos (ángulos interiores de 120º) ya no es posible formar ningún poliedro regular, pues con el mínimo de tres caras por vértice alcanzaríamos los 360º. Fig
5 Sistema diédrico. Poliedros regulares CONOCIMIENTOS TEÓRICOS UNIDAD Fórmula de Euler En la siguiente tabla recogemos las características geométricas de los poliedros regulares convexos: Poliedro Polígono caras Nº caras Vértices Aristas Ángulo poliedro (caras por vértice) Tetraedro Triángulo Triedro Hexaedro Cuadrado Triedro trirrectángulo Octaedro Triángulo Tetraedro Icosaedro Triángulo Pentaedro Dodecaedro Pentágono Triedro El número de aristas de cada poliedro será igual al total de aristas de todas sus caras (obtenido multiplicando su número por los lados de cada una) dividido por dos, que son las caras que concurren en cada arista. El número de vértices se obtiene dividiendo el número total de vértices del conjunto de caras del poliedro (obtenido multiplicando el número de caras por los vértices de cada una) entre el número de caras que concurren en cada vértice. En cada uno de los poliedros, los números de caras, vértices y aristas están relacionados por la fórmula de Euler: nº de caras + nº de vértices = nº de aristas Poliedros conjugados Fig. 8 Llamamos conjugados a dos poliedros en los que el número de caras de uno de ellos coincide con el número de vértices del otro y viceversa. El punto central de las caras de un hexaedro o cubo define la posición de cada uno de los vértices de su poliedro conjugado, el octaedro, inscrito en el mismo (Fig. 8). De forma similar, uniendo los puntos centrales de las caras de un octaedro, formaremos el cubo conjugado e inscrito en él, tal como podemos apreciar en la representación perspectiva de la figura 9. Otro par de poliedros conjugados, con las mismas propiedades descritas, son el dodecaedro y el icosaedro. El tetraedro es el poliedro conjugado de sí mismo. Fig
6 UNIDAD 7 CONOCIMIENTOS TEÓRICOS Sistema diédrico. Poliedros regulares 2 CARACTERÍSTICAS DE LOS DIFERENTES POLIEDROS REGULARES En este apartado realizaremos la descripción de los diferentes poliedros regulares, así como las relaciones entre algunos elementos lineales característicos de cada uno de ellos, cuyo conocimiento nos facilitará su representación en proyecciones diédricas. En todos los poliedros regulares es posible establecer una sección plana, que denominamos sección principal y que, pasando por su centro geométrico, contiene y relaciona sus principales magnitudes. Fig Tetraedro: elementos y relaciones El tetraedro es un poliedro regular convexo, cuyas cuatro caras son triángulos equiláteros; cada uno de sus cuatro vértices es el elemento común a las tres caras y aristas que concurren en ellos (Fig. 10). La arista y la altura h del tetraedro se relacionan mediante un triángulo rectángulo que hemos representado en la figura anterior; un triángulo en el que la hipotenusa es la arista, siendo sus catetos la altura y la proyección a de la arista sobre una de las caras del poliedro. Fig. 11 La sección principal es la intersección del tetraedro con un plano que pase por una de sus aristas y por su centro geométrico (Fig. 11); esta intersección es un triángulo isósceles de base la arista a del tetraedro, cuyos lados iguales coinciden con la altura h c de cada una de las caras. En la sección principal, la altura referida a la arista coincide con la mínima distancia entre aristas opuestas, d a, del tetraedro. Analizadas las características de la sección principal, podemos construirla de forma independiente del poliedro al cual pertenece; así lo hemos realizado en la figura 12, conocida la arista a del tetraedro: Fig. 12 Con la arista a como lado, construimos el triángulo equilátero ABC. Determinamos la altura h c correspondiente a la cara representada. El triángulo isósceles de base a y lados iguales a la altura h c, es la sección principal; su altura d a es la distancia entre aristas opuestas. Siendo r y R los radios, respectivamente, de las esferas inscrita y circunscrita en el poliedro, ambos aparecen contenidos y relacionados en la sección principal (Fig. 13): Fig. 13 R es la hipotenusa de un triángulo rectángulo que tiene por catetos el radio r de la esfera inscrita y el radio del polígono de la cara, 2/3 de la altura de la cara h c por ser ésta un triángulo equilátero. 140
7 Sistema diédrico. Poliedros regulares CONOCIMIENTOS TEÓRICOS UNIDAD Hexaedro: elementos y relaciones El hexaedro es un poliedro regular convexo, cuyas seis caras son cuadrados y sus ángulos poliedros son triedros trirrectángulos; cada uno de sus ocho vértices es el elemento común a las tres caras y aristas que concurren en ellos (Fig. 14). Mediante el triángulo rectángulo de la figura 15, a partir de la arista a del cubo podemos determinar la diagonal d de cada una de sus caras; un segundo triángulo rectángulo nos permite determinar la diagonal D del poliedro. Fig. 14 La relación entre las tres magnitudes anteriores la veíamos también en la representación del primer cubo en perspectiva. A partir de cualquiera de ellas podemos determinar, gráficamente, el segmento representativo de la longitud de las otras dos; así, conociendo la diagonal D del cubo, resolvemos las longitudes de la arista a y de la diagonal d de la cara (Fig. 16): Con centro en el punto medio del segmento D trazamos una semicircunferencia, arco capaz de 90º cuyo diámetro sea su longitud. Dividimos D en tres partes iguales y por la primera de ellas levantamos una perpendicular al segmento D hasta cortar al arco. Los catetos del triángulo rectángulo formado responden a las longitudes buscadas de a y d. La sección principal del hexaedro es la representada en la figura 17: un rectángulo de lados a y d que, como vemos también en la figura 18, relaciona, en la forma indicada anteriormente, estas magnitudes con la diagonal D del cubo. En la figura 19 indicamos las secciones producidas por otros planos que, pasando también por el centro geométrico del poliedro, tienen una inclinación diferente a la del plano que nos produce la sección principal. Fig. 15 Fig. 16 Al igual que vimos en el tetraedro, los radios r y R de las esferas inscrita y circunscrita están relacionados mediante un triángulo rectángulo (Fig. 20): R es la hipotenusa de un triángulo rectángulo que tiene por catetos el radio r de la esfera inscrita y el radio del polígono de la cara (1/2 de la diagonal d de la cara, por ser ésta un cuadrado). Fig. 17 Fig. 18 Fig. 19 Fig
8 UNIDAD 7 CONOCIMIENTOS TEÓRICOS Sistema diédrico. Poliedros regulares 2.3 Octaedro: elementos y relaciones El octaedro es un poliedro regular convexo formado por ocho caras, todas ellas triángulos equiláteros (Fig. 21). Tiene seis vértices y doce aristas. Las caras opuestas son paralelas dos a dos y la distancia entre ellas es una magnitud que se determina a partir de la sección principal, y que utilizaremos en alguna de sus representaciones diédricas. Fig. 21 Fig. 22 Las tres diagonales son iguales y perpendiculares y se cortan en sus puntos medios, puntos que coinciden con el centro geométrico del poliedro. Conocida la arista, podemos determinar la longitud de la diagonal D mediante la construcción del triángulo rectángulo de la figura 22. La sección principal es la intersección del octaedro con un plano que pasa por su centro geométrico y por las alturas de dos pares de caras opuestas (Fig. 23). Esta intersección es un rombo, cuyo lado coincide con la altura h c del triángulo de las caras y cuyas diagonales son la arista a y la diagonal D del octaedro; la distancia d c entre lados opuestos de la sección principal coincide con la mínima distancia entre aristas opuestas del octaedro. En la figura 24 disponemos perpendicularmente los valores conocidos de arista y diagonal, cortándose en sus respectivos puntos medios, para fijar la posición de las diagonales del rombo que nos permiten trazar la sección principal; en ella determinamos el segmento d c de la distancia entre caras. La figura 25, con la representación de media sección principal, es una simplificación de la anterior: Fig. 23 Un triángulo isósceles de base a y altura la mitad de la diagonal, D/2. La altura, trazada en relación a uno de los lados iguales, coincide con la distancia entre caras d c y con el diámetro de la esfera inscrita en el octaedro. 2.4 Dodecaedro e icosaedro Fig. 24 Fig. 25 Fig. 26 El dodecaedro es un poliedro regular convexo formado por doce caras, las cuales son pentágonos regulares (Fig. 26). Tiene veinte vértices y treinta aristas, y sus ángulos poliedros son triedros. En su geometría destaca la simetría; su centro geométrico o de gravedad lo es también de simetría; así, cada vértice, arista o cara tiene su simétrica u opuesta en relación a este centro de la figura. Las aristas opuestas son paralelas y las caras opuestas, además de paralelas, aparecen giradas 180º una respecto a la otra. 142
9 Sistema diédrico. Poliedros regulares CONOCIMIENTOS TEÓRICOS UNIDAD 7 Si en el pentágono existe una relación áurea entre la diagonal d y la arista a, en el dodecaedro existe esta relación entre la distancia entre aristas opuestas da y la diagonal d de cada una de las caras. Podemos establecer: da d d = = a La sección principal es la producida en el dodecaedro por un plano que contiene dos aristas opuestas, paralelas entre sí como acabamos de señalar. Dicha sección es un hexágono irregular, representado en la figura anterior, en el que los dos lados paralelos menores coinciden con la arista del poliedro y el resto de lados, también paralelos dos a dos, tienen por longitud la altura de los polígonos de las caras. La sección principal puede inscribirse en un cuadrado cuyo lado es igual a la distancia entre aristas opuestas d a. Otra sección característica en el dodecaedro es la producida por un plano paralelo a una de sus caras; la sección es un pentágono regular, cuyo lado coincide con la diagonal de las caras y cuya diagonal es la distancia entre aristas opuestas. Este pentágono sección justifica la relación áurea entre la distancia entre aristas opuestas y la diagonal de las caras. El icosaedro es un poliedro regular convexo formado por veinte caras, todas ellas triángulos equiláteros (Fig. 27). Tiene doce vértices y treinta aristas, y sus ángulos poliedros son pentaedros. El poliedro puede descomponerse en dos pirámides pentagonales, regulares e iguales, de bases paralelas y en un sólido prismático intermedio, de base pentagonal, limitado lateralmente por diez triángulos equiláteros. Como en el dodecaedro, la figura tiene un centro geométrico que también lo es de simetría; las aristas y caras opuestas son paralelas, y cada par de estas últimas están giradas 180º una en relación a la otra. Fig. 27 La sección principal es la producida por un plano que, conteniendo su centro geométrico, pasa por dos aristas opuestas. Esta sección es un hexágono irregular en el que los dos lados paralelos menores coinciden con la arista del poliedro, y el resto de lados, también paralelos dos a dos, coinciden con la altura de los triángulos de las caras. Como en el dodecaedro, podemos trazar quince secciones del tipo de la descrita. Las secciones producidas por dos planos perpendiculares a una de las diagonales del poliedro, y que pasen por alguno de sus vértices, son dos pentágonos regulares de lado igual a la arista del icosaedro y desfasados 180º uno en relación al otro. Si el plano perpendicular a una de las diagonales pasa por su punto medio, el polígono sección es un decágono de lado igual a la mitad de la arista del poliedro. 143
10 UNIDAD 7 APLICACIONES PRÁCTICAS Sistema diédrico. Poliedros regulares Conocidas las principales características de los poliedros regulares, en los próximos apartados efectuaremos su representación gráfica en las posiciones más características respecto a los planos de proyección. 1 REPRESENTACIONES DE LOS POLIEDROS REGULARES 1.1 El tetraedro El dato más habitual, al abordar sus proyecciones diédricas, es su arista; veamos, a partir de la misma, las representaciones más habituales: Con una cara paralela a uno de los planos de proyección En la representación de la figura 28, suponemos al tetraedro con una de sus caras contenida en el plano horizontal de proyección, por lo que la proyección de la misma sobre este plano estará en verdadera magnitud, triángulo equilátero A B C de lado igual a la arista del poliedro; la proyección vertical A B C estará situada en la LT. Fig. 28 La proyección horizontal del cuarto vértice, E, coincide con el centro geométrico de la cara proyectada en verdadera magnitud. Para situar la proyección vertical, E, debemos encontrar la altura h del tetraedro; altura que determinamos mediante una construcción auxiliar sobre su representación en planta, abatiendo el triángulo rectángulo formado por la arista, su proyección ortogonal sobre la base y la propia altura. En este triángulo, A E es el primero de los catetos; la magnitud del segundo, h, se determina sobre la perpendicular al anterior al situar como hipotenusa una longitud igual a la arista a. Conocidas las proyecciones horizontales y verticales de los cuatro vértices, realizamos su unión prestando especial atención a la visibilidad de las aristas. Los contornos aparentes son siempre visibles en su totalidad, mientras que la visibilidad del resto de aristas depende de la dirección en que se ha obtenido la proyección a la que pertenecen. Con una de sus caras contenida en un plano α cualquiera Ejemplo de pirámide en el patio del museo de Louvre, Paris. Conocidas las trazas h α - v α del plano y la arista a del tetraedro, abatimos el plano para poder representar en verdadera magnitud la cara contenida en él. En la figura 29 hemos abatido el plano α sobre el horizontal de proyección, representando sobre el mismo la verdadera magnitud de la cara ABC; conocida esta cara, determinamos la altura h del tetraedro con la construcción auxiliar utilizada en la primera representación del poliedro. 144
11 7 Sistema diédrico. Poliedros regulares APLICACIONES PRÁCTICAS UNIDAD Fig. 29 Utilizando horizontales auxiliares del plano α que hacemos pasar por cada uno de sus vértices, desabatimos la cara ABC en sus proyecciones A B C - A B C ; por el centro de cada una de éstas, trazamos la perpendicular r r a las trazas del plano. Sobre esta perpendicular, y a la distancia h del centro, O O, de la base, se encontrarán las proyecciones del cuarto vértice del tetraedro. Para poder medir la verdadera magnitud de la altura h sobre la recta oblicua r, giramos ésta hasta la posición de recta horizontal mediante un eje de punta no representado, que hacemos pasar por O O ; sobre la proyección O M 1, situamos la verdadera magnitud de la altura h y deshacemos el giro para determinar las proyecciones E E del cuarto vértice. La representación de las aristas en ambas proyecciones, de acuerdo a la visibilidad correspondiente, nos completa el trazado. Con una arista sobre el PH y la opuesta paralela al mismo Tanto la arista contenida en el PH como la paralela a él, tendrán la proyección horizontal en verdadera magnitud; sus proyecciones A B y C E reflejarán la perpendicularidad existente entre las mismas en el tetraedro. El trazado del contorno aparente nos completa la proyección horizontal (Fig. 30). Fig
12 UNIDAD 7 APLICACIONES PRÁCTICAS Sistema diédrico. Poliedros regulares La proyección vertical de la arista inferior, A B, se halla sobre LT y la de la arista opuesta, C E, será paralela a la línea de tierra a una distancia de ésta igual a la mínima distancia entre aristas opuestas d a. Encontramos esta distancia en la sección principal del tetraedro, o abatiendo en la representación en planta el triángulo rectángulo formado por la altura de la cara h c, su proyección ortogonal sobre la base y la distancia entre aristas opuestas. Conocidas las proyecciones verticales de los cuatro vértices, completamos la proyección homónima del tetraedro con el trazado de las aristas correspondientes, visibles o no según la dirección de la proyección efectuada. 1.2 El hexaedro o cubo Conocida su arista a, obtendremos las proyecciones correspondientes a las posiciones más habituales: Con una cara apoyada o paralela a uno de los planos de proyección Con una de las caras en la posición solicitada, la opuesta se proyectará coincidente con ella, y las cuatro restantes son proyectantes respecto al plano horizontal. La proyección horizontal es un cuadrado de lado igual a la arista del cubo, (Fig. 31); las cuatro aristas perpendiculares a los planos paralelos al PH son verticales, y tienen su proyección vertical en verdadera magnitud. Fig. 31 Al estudiar la visibilidad de la proyección vertical, recordamos que las aristas que forman el contorno aparente del cuerpo son siempre visibles; para conocer la visibilidad de las aristas interiores, examinamos la proyección horizontal observando que, al mirar la figura perpendicularmente a LT, la arista BF es la primera que se ve, por tanto, es visible en proyección vertical; por idéntica razón, la arista DH es oculta y la representamos con línea discontinua. Con una cara situada en un plano cualquiera Al conocer el plano que contiene una de las caras del hexaedro, podemos encontrar las proyecciones diédricas del poliedro de forma similar a la utilizada en la representación del tetraedro, con una de sus caras contenidas en un plano α cualquiera, de la figura 29. En este caso, buscaremos una resolución diferente a partir de una posición favorable del plano la cual nos facilite los trazados (Fig. 32). Un cambio de plano vertical transforma el plano oblicuo inicial en uno de canto, con la nueva traza vertical en la posición v α1 ; lo abatimos sobre el PH, dibujando en verdadera magnitud la cara ABCD contenida en él. 146
13 7 Sistema diédrico. Poliedros regulares APLICACIONES PRÁCTICAS UNIDAD Fig. 32 Desabatida en sus proyecciones A B C D A 1 B 1 C 1 D 1, esta última situada en la traza proyectante del plano de canto, trazamos por ellas las perpendiculares al plano auxiliar que, dada la posición del plano, serán rectas frontales. Sobre las perpendiculares a v α1 trazadas por A 1, B 1 etc., medimos la longitud real de la arista del cubo, completando de esta forma la proyección vertical auxiliar. Referimos los vértices de la base superior a las perpendiculares a h α1 trazadas por A, B etc., obteniendo las proyecciones E, F, G y H correspondientes a la proyección horizontal de la cara superior del cubo. Con estas proyecciones completamos la proyección horizontal del hexaedro. Para representar la proyección vertical en la posición del plano α, determinamos las proyecciones verticales de los vértices ABCD correspondientes a la base inferior. Para ello utilizamos rectas auxiliares, horizontales del plano α, que hacemos pasar por las proyecciones A, B... Por las nuevas proyecciones A, B, levantamos perpendiculares a la traza vertical v α del plano y referimos a ellas los vértices E, F, G y H de la base superior. El paralelismo entre las proyecciones de aristas paralelas en el espacio nos ayuda en el trazado de las diferentes aristas. El estudio de la visibilidad, según el punto de vista de cada una de las proyecciones, completa las proyecciones solicitadas del hexaedro. 147
14 UNIDAD 7 APLICACIONES PRÁCTICAS Sistema diédrico. Poliedros regulares Con una diagonal perpendicular al horizontal de proyección Esta representación la podemos efectuar de dos maneras; mediante la primera de ellas (Fig. 33), disponemos el hexaedro con una de sus caras paralela o contenida en el PH y dispuesto, en relación al PV, de tal forma que una de sus diagonales, la AG en el ejemplo, sea una recta frontal. Fig. 33 A partir de esta posición auxiliar inicial, efectuamos un cambio de plano horizontal para que la diagonal anterior quede en posición de recta vertical; para ello disponemos la LT 1 perpendicular a la proyección vertical A G. Referimos los alejamientos de la proyección horizontal anterior y representamos la visibilidad de las diferentes aristas, según la nueva dirección de proyección. Del análisis de la representación anterior, extraemos las conclusiones que nos permiten representar el hexaedro en la posición solicitada de manera directa (Fig. 34), sin utilizar proyecciones auxiliares. El cubo queda inscrito en una esfera cuyo diámetro es la diagonal principal A - G. Dividiendo esta diagonal en tres partes iguales, obtenemos los vértices C y E que, unidos con A y G, nos dan el contorno aparente del poliedro en proyección vertical; proyección que completamos con las aristas D H y B F, coincidentes por pertenecer al mismo plano proyectante. Fig. 34 En proyección horizontal, el contorno de la figura es un hexágono regular inscrito en una circunferencia cuyo radio coincide con la proyección horizontal del segmento A E. Referimos vértices según la correspondencia entre proyecciones y trazamos las aristas de acuerdo a la visibilidad del conjunto; observamos, por ejemplo, que la arista GC, por ser la de mayor cota, será visible en proyección horizontal; al contrario, la arista AE es la de menor cota y se representa oculta en la misma proyección. 148
15 7 Sistema diédrico. Poliedros regulares APLICACIONES PRÁCTICAS UNIDAD Con una arista en uno de los planos de proyección Conocemos las proyecciones de la arista AE; por estar contenida en el PH, su proyección sobre este plano estará en verdadera magnitud. Buscamos una proyección auxiliar vertical en la que la arista AE se vea como recta de punta (Fig. 35); para ello efectuamos un cambio de plano vertical en la dirección de la proyección A E. En la nueva proyección vertical las caras perpendiculares a AE se verán en verdadera magnitud, por lo que dibujamos un cuadrado con uno de sus vértices en A 1 E 1, lado igual a la proyección A E, y con cualquier inclinación al no tener condiciones al respecto. Fig. 35 Las caras que pasan por los vértices A y E, por ser perpendiculares a la arista definida por ambos, serán planos verticales y sus proyecciones horizontales serán segmentos perpendiculares a A E. De la proyección auxiliar obtendremos la correspondencia de los vértices que forman el cubo y, también, las cotas que, conocida la proyección horizontal, nos permitirán completar la proyección vertical. En el estudio de la visibilidad horizontal, la arista A E es oculta al ser la de menor cota de todas las que forman el poliedro. En la visibilidad vertical, al comparar los alejamientos de los vértices D y F, es mayor el del segundo de ellos, por lo que las tres aristas que concurren en él son visibles, a la inversa de lo que ocurre con las aristas concurrentes en el vértice D. 149
16 UNIDAD 7 APLICACIONES PRÁCTICAS Sistema diédrico. Poliedros regulares 1.3 El octaedro Como en los poliedros anteriores, suponemos conocida su arista para obtener las siguientes representaciones: Con una de sus diagonales perpendicular al PH Con una diagonal EF representada como una recta vertical (Fig. 36), el contorno aparente, A B C D, de la proyección horizontal es un cuadrado de lado igual a la arista del octaedro. Las diagonales A C y B D tienen la misma longitud que la diagonal E F, todas ellas en verdadera magnitud. Sobre las dos primeras diagonales se proyectan, horizontalmente, las ocho aristas restantes. En proyección vertical, los vértices E y F están en los extremos de la diagonal correspondiente, mientras que los otros cuatro se hallan sobre el plano medio del octaedro, horizontal y de cota igual a la mitad de la longitud de la diagonal. Completamos el trazado con la representación de las aristas y el estudio de su visibilidad. Fig. 36 Con una cara apoyada en el plano horizontal Empezamos por representar la proyección horizontal (Fig. 37); en ella el triángulo A B F está en verdadera magnitud, correspondiendo a la proyección horizontal de la cara contenida en PH. La cara opuesta, C D E, paralela a la anterior y al PH, también está en verdadera magnitud y se proyecta según un triángulo equilátero desfasado 180º en relación al anterior. La unión de las proyecciones de los seis vértices define el contorno aparente y nos completa la proyección horizontal. Fig
17 7 Sistema diédrico. Poliedros regulares APLICACIONES PRÁCTICAS UNIDAD En proyección vertical, las caras ABF y CDE se proyectan como dos planos horizontales, el primero de ellos coincidente con LT y el segundo con una cota igual a la distancia entre caras opuestas. Determinamos ésta con una construcción auxiliar, realizada sobre la representación en planta: abatimos sobre el horizontal el triángulo rectángulo que tiene por catetos la distancia entre caras y la proyección horizontal de la altura de una cara, y por hipotenusa, la verdadera magnitud de esta última. Con el plano medio situado en un plano α dado En el plano α dado, conocemos también las proyecciones de la arista AB del octaedro (Fig. 38). Abatimos el plano sobre el horizontal de proyección (al ser un plano de canto, el abatimiento de v α coincide con LT) y representamos en verdadera magnitud la sección ABCD. Al desabatir, tendremos las proyecciones, C D y C D, de los otros dos vértices de la sección. Por su centro O O trazamos la perpendicular r al plano de canto; ésta será una frontal sobre cuya proyección vertical mediremos la verdadera magnitud de la diagonal del poliedro, para completar la posición de los vértices E y F que referimos a la proyección horizontal de la recta r. El estudio en la forma acostumbrada de la visibilidad de las aristas completa la representación solicitada. Fig
18 UNIDAD 7 APLICACIONES PRÁCTICAS Sistema diédrico. Poliedros regulares 1.4 El dodecaedro De los dos últimos poliedros regulares efectuaremos una única representación para cada uno de ellos. Al dodecaedro lo suponemos situado con una de sus caras paralela o contenida en el plano horizontal de proyección; la cara opuesta también será, lógicamente, paralela. Conocemos un único dato del poliedro que queremos representar: su arista (Fig. 39). Fig. 39 Dibujamos la proyección horizontal del pentágono regular ABCDE y de dos de las caras contiguas, las que comparten entre sí la arista BF; la representación efectuada de éstas últimas equivale a su abatimiento sobre el PH, utilizando para ello como charnelas las aristas A B y B C. Al desabatir las dos posiciones del vértice (F), la intersección de las perpendiculares a las respectivas charnelas definirá su proyección F sobre el plano horizontal. Por simetría respecto al centro del pentágono ABCDE, definiremos la posición de las proyecciones horizontales de los vértices G, H, I y J; todas ellas se encuentran sobre una circunferencia, concéntrica con la circunscrita a la cara A B C D E, en la que también se hallan las proyecciones de los vértices K, L, M, N y O, formando un decágono regular. La cara superior del dodecaedro tiene por proyección horizontal un pentágono P Q R S T, centrado con la proyección de la base inferior y desfasado 36º en relación a la misma. Completamos la proyección horizontal del 152
19 7 Sistema diédrico. Poliedros regulares APLICACIONES PRÁCTICAS UNIDAD poliedro representando el resto de aristas; las que parten de los vértices de la base inferior son ocultas, mientras que las que parten de los vértices de la base superior son vistas. Para poder representar la proyección vertical, necesitamos determinar las cotas de sus diferentes vértices. Los vértices de la base inferior, A, B, C, D y E, tienen la proyección vertical sobre LT. La cota z 1, común a los vértices F, G, H, I y J, la determinamos mediante el abatimiento sobre el PH de un triángulo rectángulo que tiene por hipotenusa la arista en verdadera magnitud y por catetos, la proyección de esta arista y la cota buscada z 1 ; la figura 40 ilustra en perspectiva los trazados descritos. De forma similar buscamos la cota z 2 de los vértices K, L, M, N y O; la figura 41 justifica el triángulo rectángulo abatido en la representación en planta, triángulo que tiene por hipotenusa la altura de una de las caras y por catetos, la proyección de ésta y la cota buscada z 2. Fig. 40 A partir del plano horizontal, que definen las proyecciones verticales de los vértices anteriores, trasladamos nuevamente la cota z 1 para situar el plano horizontal en el que se hallan las proyecciones verticales de los vértices de la base superior P, Q, R, S y T. Uniendo las proyecciones verticales de los veinte vértices y estudiando la visibilidad de las aristas según los alejamientos respectivos, completaremos la proyección vertical del poliedro. 1.5 El icosaedro Fig. 41 Lo representamos con la diagonal MN, que une dos de sus vértices opuestos, perpendicular al plano horizontal de proyección (Fig. 42). En esta posición, los pentágonos ABCDE y FGHIJ, bases de las dos pirámides en que podemos descomponer la figura, tendrán la proyección horizontal en verdadera magnitud por estar contenidos en planos paralelos al PH. Determinar la proyección horizontal del poliedro supone trazar dos pentágonos regulares centrados, de lados iguales a la arista del icosaedro, y desfasados 36º uno en relación al otro. Su punto central es la proyección horizontal de la diagonal MN; punto que unimos con los correspondientes vértices de los dos pentágonos y con la visibilidad que se desprende de la diferencia de cota entre M y N. En proyección vertical situamos N sobre LT. El plano horizontal que definen las proyecciones de los vértices Fig
20 UNIDAD 7 APLICACIONES PRÁCTICAS Sistema diédrico. Poliedros regulares A, B se halla a una cota z 1 respecto a LT, cota que determinamos con el abatimiento sobre el plano horizontal del triángulo rectángulo que tiene por hipotenusa la arista del icosaedro y por catetos, la proyección de esta arista y la cota z 1 que pretendemos determinar. La figura 43 describe, en perspectiva, la construcción efectuada sobre la proyección horizontal. A partir del plano horizontal anterior, buscamos la cota z 2 de un segundo plano horizontal, el que definen los vértices F, G, H, mediante un triángulo rectángulo similar al descrito que, en representación perspectiva, vemos en la figura 44. Por simetría del icosaedro, la cota de M respecto al anterior plano horizontal vuelve a ser z 1. Fig. 43 Fig. 44 Dada la posición de la planta respecto al plano vertical de proyección, las aristas vistas y ocultas quedan confundidas en una única proyección vertical, lo que facilita los trazados. De esta posición también se desprende que la arista ND es frontal, por lo que también podríamos determinar la proyección vertical D, sobre la perpendicular a LT trazada por D, mediante un arco de centro N y cuyo radio es la longitud de la arista. 2 SECCIONES PLANAS, DESARROLLOS Y TRANSFORMADAS Determinar la sección que un plano produce en un cuerpo, poliedro regular en nuestro caso, o la intersección de éste con una recta, no son más que dos aplicaciones de las intersecciones entre elementos fundamentales, las cuales estudiamos en la unidad 11 de Dibujo técnico 1. Lo veremos en los próximos apartados. 154
21 7 Sistema diédrico. Poliedros regulares APLICACIONES PRÁCTICAS UNIDAD 2.1 Secciones planas de los poliedros Denominamos sección plana a la intersección de un plano con un cuerpo. En la descripción efectuada de los diferentes poliedros, además de la denominada sección principal, hemos hablado de otras secciones características; por ejemplo, la sección hexagonal producida en un cubo por un plano que, pasando por el centro del poliedro, sea perpendicular a una de sus diagonales. En general, para determinar una sección plana cualquiera, deberemos buscar los puntos de intersección de cada una de las aristas del cuerpo con el plano; dichos puntos de intersección serán los vértices del polígono sección. Veamos dos ejemplos, con dos posiciones de planos diferentes: Sección plana de un tetraedro por un plano proyectante Partimos de las dos proyecciones del tetraedro y de las trazas del plano sector, en este caso un plano α de canto (Fig. 45). Fig. 45 Por ser el plano proyectante vertical, los puntos de intersección con el poliedro serán los de intersección de su traza vertical con las proyecciones verticales de las aristas del tetraedro. Así, directamente, encontramos las proyecciones verticales 1, 2, 3 de los vértices del polígono sección. Referimos las anteriores proyecciones a las correspondientes aristas de la proyección horizontal del tetraedro, y tendremos la proyección horizontal de la sección. Si queremos conocer la sección producida por el plano α en verdadera magnitud, abatiremos dicho plano; en la figura hemos realizado el abatimiento sobre el plano horizontal, obteniendo la sección plana (1) - (2) - (3) en verdadera magnitud. 155
22 UNIDAD 7 APLICACIONES PRÁCTICAS Sistema diédrico. Poliedros regulares Sección plana de un hexaedro por un plano cualquiera Para determinar la sección que un plano produce en una figura cuando el plano es oblicuo a los de proyección, podemos proceder de dos maneras: determinando la intersección de cada una de las aristas con el plano, en una aplicación de la intersección recta-cuerpo que veremos en el próximo apartado, o, más fácilmente, colocando el plano en posición de plano proyectante; de esta segunda manera, la sección que produce el plano se verá como una recta y su determinación es inmediata, como ya hemos visto en el ejemplo anterior. Suponemos el hexaedro representado en la figura 46 y cuya sección por un plano α, oblicuo a los de proyección, queremos determinar. Representamos una nueva LT, perpendicular a la traza horizontal h α del plano, para definir un cambio de plano vertical de proyección, en relación al cual el plano α pasará a ser proyectante vertical o de canto. Fig. 46 Buscamos la nueva traza vertical v α1 y la nueva proyección vertical del cubo; los puntos en que v α1 intersecciona con las aristas de la nueva proyección vertical son los vértices del polígono sección que, mediante perpendiculares a las respectivas líneas de tierra, pasamos a las proyecciones iniciales del cubo. Al referir 1 y 2, utilizamos la cota de la proyección vertical auxiliar. 156
23 7 Sistema diédrico. Poliedros regulares APLICACIONES PRÁCTICAS UNIDAD Como en la sección plana anterior, el abatimiento del plano proyectante sobre uno de los de proyección nos sirve para determinar la verdadera magnitud de la sección plana buscada. Observemos en la sección abatida que las aristas (1) - (4) y (2) (3), producidas como intersección del plano α sobre dos caras paralelas de un mismo cuerpo, son también paralelas. Cualquier sección plana la resolveremos tal como hemos efectuado en los ejemplos anteriores: si el plano es proyectante, encontraremos directamente el polígono sección en la intersección de la traza proyectante del plano con las aristas del cuerpo (si el plano fuera horizontal o frontal, tendríamos, además, la proyección no proyectante de la sección en verdadera magnitud), y, si el plano es oblicuo, efectuaremos un cambio de plano para conseguir la posición de plano proyectante con las ventajas derivadas de la misma. 2.2 Intersecciones recta-poliedro Hallar la intersección de una recta con un sólido consiste en determinar los puntos de entrada y salida de la recta en el sólido. Para ello utilizaremos un plano auxiliar que contenga a la recta (Fig. 47), y determinaremos la sección que dicho plano produce en el sólido; los puntos de intersección entre la sección y la recta son los puntos buscados. Fig. 47 En proyecciones diédricas, hemos buscado las intersecciones entre una recta r y un octaedro, conocidas las proyecciones de ambos (Fig. 48). Coincidente con la proyección horizontal de la recta, definimos la traza proyectante de un plano vertical auxiliar; su intersección con la proyección horizontal de las aristas del poliedro define la posición de los vértices 1, 2, 3, 4, 5 y 6 de la sección auxiliar. Referimos los vértices anteriores a la proyección vertical de las aristas del octaedro; su unión representa la proyección vertical de la sección auxiliar, y la intersección de ésta con la proyección vertical r determina las proyecciones verticales, P y Q, de los puntos buscados. A continuación, referiremos éstos a la proyección horizontal r de la recta. En ambas proyecciones representamos con trazo discontinuo el segmento comprendido entre los puntos P y Q, para diferenciar la parte de la recta que atraviesa el interior del poliedro. No añadimos más ejemplos ya que, independientemente del poliedro de que se trate, siempre utilizaremos un procedimiento idéntico al que acabamos de ver. Fig
24 UNIDAD 7 APLICACIONES PRÁCTICAS Sistema diédrico. Poliedros regulares 2.3 Desarrollos Al clasificar las superficies al inicio del tema, las poliédricas (entre las que se incluyen los poliedros regulares) figuraban dentro de las denominadas desarrollables. Esto significa que la superficie exterior asociada a cada uno de ellos puede extenderse sobre un plano. Al estar formados por polígonos regulares, representar su desarrollo no presenta mayor dificultad que la de dibujar cada una de sus caras en contacto con las contiguas; así lo hemos realizado para cada uno de ellos en la figura 49. Poliedros aplicados en la arquitectura. Fig. 49 El desarrollo del hexaedro corresponde al representado en la figura 46. Sobre el mismo hemos indicado la sección que en el poliedro producía un plano α; a esta representación se la denomina transformada de la sección. Tanto las aristas que definen el desarrollo de la superficie del sólido, como los segmentos correspondientes a la transformada de la sección plana, han de ser siempre las verdaderas magnitudes de los mismos. 158
25 7 Sistema diédrico. Poliedros regulares APLICACIONES PRÁCTICAS UNIDAD 3 PRESENCIA DE LOS POLIEDROS REGULARES En la naturaleza encontramos estructuras poliédricas como, por ejemplo, los cristales de diversas sustancias. Así, el tetraedro aparece en la estructura cristalina del sodio; el cubo, en la de la sal común; el octaedro, en la de los diamantes naturales, y el dodecaedro, en la de las piritas. La estructura del modelo de la cadena de ADN está formada, también, por una serie de dodecaedros superpuestos en espiral. 3.1 Antecedentes históricos Algunos pueblos neolíticos conocían la existencia de formas geométricas que recuerdan a algunos poliedros (Fig. 47). Así lo demuestran algunos vestigios encontrados en zonas de Escocia. Estos restos se hallan localizados en la actualidad en el Ashmolean Museum de Oxford, se trata de piedras esculpidas, cuya forma recuerda a la de algunos poliedros (cubo, dodecaedro, icosaedro ), de las que se sospecha que pudieron ser usadas como elementos de juego o decoración. Fig. 47 En excavaciones realizadas cerca de Pádova (Italia), se halló un dodecaedro etrusco, que probablemente era usado como juguete (Fig. 48). En el antiguo Egipto, encontramos referencias más concretas a algunos poliedros (cubo, tetraedro, octaedro, pirámide...). La utilización de la forma piramidal como sepultura de los faraones egipcios pone de manifiesto cierta conexión entre los poliedros y aspectos religiosos y místicos. Sin embargo, y aunque estos sólidos ya se conocían en tiempos prepitagóricos, fueron Pitágoras y su escuela quienes iniciaron su estudio; se les supone conocedores del tetraedro, el cubo y el dodecaedro. Los otros dos restantes poliedros regulares, el icosaedro y el octaedro, se atribuyen a Teeteto ( a. C.), amigo y alumno de Platón, a quien se debe el estudio sistemático de los cinco poliedros regulares. Se les llama también sólidos platónicos por el papel que tienen en el diálogo de Platón El Timeo, donde pone de manifiesto su relación con los elementos primarios: hexaedro-tierra, tetraedro-fuego, octaedro-aire e icosaedro-agua; al dodecaedro, tan distinto por sus caras de los otros poliedros, lo asoció con el universo, la representación del Todo, la Quintaesencia (Fig. 49). Kepler, siglos más tarde, asocia sus doce caras con los doce signos del Zodíaco. Fig. 48 Fig
26 UNIDAD 7 APLICACIONES PRÁCTICAS Sistema diédrico. Poliedros regulares Euclides, en el libro XIII de los Elementos, mejoró los trabajos de Teeteto en relación con los sólidos platónicos, probando que los únicos poliedros convexos regulares, con caras y ángulos en los vértices iguales, eran los sólidos platónicos. Ya en el Renacimiento volvemos a encontrar numerosas referencias y representaciones de los poliedros regulares. Alberto Durero ( ) centró su atención en estos poliedros, ya que le servían de modelos en sus estudios de perspectiva; los representó mediante su desarrollo sobre un plano. Leonardo Da Vinci utilizó los poliedros para la decoración del libro De Divina Proportione del franciscano Luca Pacioli ( ), donde éste estudia las relaciones entre dodecaedro e icosaedro y la denominada divina proporción. En la representación de Leonardo, con los poliedros huecos o vacíos, se observan simultáneamente sus partes frontal y posterior (Fig. 50). Fig. 50 Aproximadamente un siglo después, el astrónomo alemán Johannes Kepler encuentra en los poliedros regulares una explicación a las órbitas de los planetas alrededor del Sol: creía que los radios de sus órbitas circulares estaban en proporción con los radios de las esferas inscritas en los sólidos platónicos, al estar éstos dispuestos uno dentro de otro. Además, sistematiza y desarrolla todo los que se conocía en su época sobre estos poliedros. 3.2 Poliedros y arte El período histórico en el que la conexión entre arte y poliedros fue más fructífera es, sin duda, el Renacimiento. Además de los dibujos de Leonardo ya reseñados, encontramos otros ejemplos en los que éstos aparecen representados: En el primer retrato conocido de un matemático, el de Luca Pacioli, observamos sobre la mesa un dodecaedro y, en la parte superior izquierda, un poliedro semirregular transparente, figura 51. Es obra del pintor veneciano Jacopo de Barbari; en él, Pacioli aparece haciendo una demostración geométrica a un joven, identificado como el Duque de Urbino. Fig
27 Sistema diédrico. Poliedros regulares APLICACIONES PRÁCTICAS UNIDAD 7 Destacamos también los famosos mosaicos (Fig. 52), realizados con maderas de diversas tonalidades, elaborados por Fra Giovanni, donde se muestran poliedros y esquemas de poliedros. En la escuela alemana renacentista, además de la referencia ya realizada a Durero, encontramos al orfebre Jamnitzer ( ), uno de los más creativos artistas poliedrales tal y como vemos en sus esculturas de la figura 53. Fig. 52 Fig. 53 El pintor holandés Maurits Escher ( ), considerado uno de los artistas del siglo XX más vinculado a las matemáticas, también utilizó los poliedros en algunas de sus obras. En un grabado sobre madera, titulado Estrellas (Fig. 54), muestra un cielo poliedral en el que fácilmente identificamos poliedros regulares y otras composiciones derivadas de los mismos. En el campo de la arquitectura, encontramos poliedros regulares y truncamientos de los mismos en la Sagrada Familia de Gaudí; en la cripta del templo barcelonés, también utiliza Gaudí dodecaedros para construir originales lámparas. Tomando como referencia este poliedro regular o el icosaedro, pueden construirse cúpulas geodésicas como la del museo Dalí de Figueres (Fig. 55). Fig. 54 Fig
13 POLIEDROS REPRESENTACIÓN DE POLIEDROS
 13-1 Curso de Dibujo Técnico. 2º de Bachillerato Patxi Aguirrezabal Martin 13 POLIEDROS TETRAEDRO. CUBO. OCTAEDRO. PRISMA. PIRÁMIDE. CONO. CILINDRO. ICOSAEDRO. DODECAEDRO. ESFERA. Contornos aparente y
13-1 Curso de Dibujo Técnico. 2º de Bachillerato Patxi Aguirrezabal Martin 13 POLIEDROS TETRAEDRO. CUBO. OCTAEDRO. PRISMA. PIRÁMIDE. CONO. CILINDRO. ICOSAEDRO. DODECAEDRO. ESFERA. Contornos aparente y
Sistema Diédrico. Punto y recta
 Sistema Diédrico. Punto y recta Dibujo Técnico Ejercicios del alumno. Uso en el Centro Pág. 1 Si un punto del espacio se encuentra por encima del plano horizontal, su cota es positiva y en el sistema diédrico
Sistema Diédrico. Punto y recta Dibujo Técnico Ejercicios del alumno. Uso en el Centro Pág. 1 Si un punto del espacio se encuentra por encima del plano horizontal, su cota es positiva y en el sistema diédrico
APLICACIONES PRÁCTICAS
 6 UNIDAD Sistema diédrico. Verdaderas magnitudes CONOCIMIENTOS TEÓRICOS 1 Distancias entre elementos fundamentales. Posiciones favorables de resolución 1.1 Entre dos puntos 1.2 Entre punto y plano 1.3
6 UNIDAD Sistema diédrico. Verdaderas magnitudes CONOCIMIENTOS TEÓRICOS 1 Distancias entre elementos fundamentales. Posiciones favorables de resolución 1.1 Entre dos puntos 1.2 Entre punto y plano 1.3
Sistemas de Representación y Dibujo Técnico Año 2015. Geometría Básica
 EL PUNTO Geometría Básica El punto es la entidad geométrica más pequeña y finita. Se puede definir por intersección de 2 rectas. En un plano, se puede definir por medio de 2 coordenadas. En el espacio,
EL PUNTO Geometría Básica El punto es la entidad geométrica más pequeña y finita. Se puede definir por intersección de 2 rectas. En un plano, se puede definir por medio de 2 coordenadas. En el espacio,
Carlos Quesada Dominguez ANEXO AL LIBRO DE SISTEMA DIEDRICO
 ANEXO AL LIBRO DE SISTEMA DIEDRICO 1 RECTA Y PLANO Dadas dos rectas (r y s) que se cortan y sus trazas están fuera de los limites del papel. Hallar las trazas del plano que determinan. 1º.- Trazar una
ANEXO AL LIBRO DE SISTEMA DIEDRICO 1 RECTA Y PLANO Dadas dos rectas (r y s) que se cortan y sus trazas están fuera de los limites del papel. Hallar las trazas del plano que determinan. 1º.- Trazar una
D18 Poliedros regulares
 El sistema diédrico D18 Poliedros regulares Clases de poliedros regulares convexos No pueden existir más de cinco clases de poliedros regulares convexos. Teniendo en cuenta que la suma de las caras de
El sistema diédrico D18 Poliedros regulares Clases de poliedros regulares convexos No pueden existir más de cinco clases de poliedros regulares convexos. Teniendo en cuenta que la suma de las caras de
Desarrollo de Poliedros Regulares: Generalidades. Ejercicios Resueltos. Ejercicio 1 Ejercicio 2 Ejercicio 3 Ejercicio 4 Ejercicio 5
 DESARROLLO DE POLIEDROS REGULARES UNIDAD IV: DESARROLLO DE SÓLIDOS En esta unidad se dibujarán las superficies de poliedros y cuerpos redondos modelos. Los temas de esta unidad son: sobre un plano para
DESARROLLO DE POLIEDROS REGULARES UNIDAD IV: DESARROLLO DE SÓLIDOS En esta unidad se dibujarán las superficies de poliedros y cuerpos redondos modelos. Los temas de esta unidad son: sobre un plano para
Poliedro cóncavo: es aquel que no cumple la propiedad anterior. Una recta puede cortarlo por más de dos puntos.
 El sistema diédrico D13 El prisma Poliedros Poliedro es un cuerpo geométrico limitado por polígonos. Caras del poliedro son los polígonos que lo limitan. Vértices son los vértices de las caras. Aristas
El sistema diédrico D13 El prisma Poliedros Poliedro es un cuerpo geométrico limitado por polígonos. Caras del poliedro son los polígonos que lo limitan. Vértices son los vértices de las caras. Aristas
17. POLÍGONOS REGULARES
 17. POLÍGONOS REGULARES 17.1. Características generales Los polígonos regulares son los que tienen los lados y los ángulos iguales, es decir, son equiláteros y equiángulos. Son inscriptibles y circunscriptibles.
17. POLÍGONOS REGULARES 17.1. Características generales Los polígonos regulares son los que tienen los lados y los ángulos iguales, es decir, son equiláteros y equiángulos. Son inscriptibles y circunscriptibles.
Ángulos. Semejanza. ABE ˆ, ACE ˆ o ADE ˆ son ángulos inscritos en la. n 2 180º. En la circunferencia:
 GEOMETRÍA Ángulos En la circunferencia: ABE ˆ, ACE ˆ o ADE ˆ son ángulos inscritos en la circunferencia y son todos iguales. AOE ˆ es el ángulo central correspondiente y su medida es dos veces la medida
GEOMETRÍA Ángulos En la circunferencia: ABE ˆ, ACE ˆ o ADE ˆ son ángulos inscritos en la circunferencia y son todos iguales. AOE ˆ es el ángulo central correspondiente y su medida es dos veces la medida
Dibujo Técnico Polígonos regulares
 19. POLÍGONOS REGULARES 19.1. Características generales Los polígonos regulares son los que tienen los lados y los ángulos iguales, es decir, son equiláteros y equiángulos. Son inscriptibles y circunscriptibles.
19. POLÍGONOS REGULARES 19.1. Características generales Los polígonos regulares son los que tienen los lados y los ángulos iguales, es decir, son equiláteros y equiángulos. Son inscriptibles y circunscriptibles.
LOS POLÍGONOS, PROPIEDADES Y CONSTRUCCIONES. 1. DEFINICIÓN Y TIPOS DE POLÍGONOS. DEFINICIÓN. ELEMENTOS GENERALES DE UN POLÍGONO.
 LOS POLÍGONOS, PROPIEDADES Y CONSTRUCCIONES. 1. DEFINICIÓN Y TIPOS DE POLÍGONOS. DEFINICIÓN. Polígono es la superficie plana limitada por una línea poligonal cerrada. Línea poligonal es la figura formada
LOS POLÍGONOS, PROPIEDADES Y CONSTRUCCIONES. 1. DEFINICIÓN Y TIPOS DE POLÍGONOS. DEFINICIÓN. Polígono es la superficie plana limitada por una línea poligonal cerrada. Línea poligonal es la figura formada
MATEMÁTICAS 1º DE ESO
 MATEMÁTICAS 1º DE ESO LOE TEMA XII: POLIEDROS Y CUERPOS DE REDONDOS Poliedros. o Elementos de un poliedro y desarrollo plano. Prismas. o Elementos y tipos de prismas. Pirámides. o Elementos y tipos de
MATEMÁTICAS 1º DE ESO LOE TEMA XII: POLIEDROS Y CUERPOS DE REDONDOS Poliedros. o Elementos de un poliedro y desarrollo plano. Prismas. o Elementos y tipos de prismas. Pirámides. o Elementos y tipos de
Colegio LOPE DE VEGA Luis de Medina, 12 28805 Alcalá de Henares DIBUJO TÉCNICO II EJERCICIOS DE APOYO
 Colegio LOPE DE VEGA Luis de Medina, 12 28805 Alcalá de Henares DIBUJO TÉCNICO II EJERCICIOS DE APOYO 1º.- Deducir razonadamente el valor del ángulo α marcado en la figura sabiendo que esta representa
Colegio LOPE DE VEGA Luis de Medina, 12 28805 Alcalá de Henares DIBUJO TÉCNICO II EJERCICIOS DE APOYO 1º.- Deducir razonadamente el valor del ángulo α marcado en la figura sabiendo que esta representa
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: DIBUJO TÉCNICO 11
 y UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2014-2015 MATERIA: DIBUJO TÉCNICO 11 INSTRUCCIONES GENERALES Y CALIFICACIÓN
y UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2014-2015 MATERIA: DIBUJO TÉCNICO 11 INSTRUCCIONES GENERALES Y CALIFICACIÓN
8. POLÍGONOS REGULARES 8.1. CARACTERÍSTICAS GENERALES
 8. POLÍGONOS REGULARES 8.1. CARACTERÍSTICAS GENERALES Los polígonos regulares son los que tienen los lados y los ángulos iguales, es decir, son equiláteros y equiángulos. Son inscriptibles y circunscriptibles.
8. POLÍGONOS REGULARES 8.1. CARACTERÍSTICAS GENERALES Los polígonos regulares son los que tienen los lados y los ángulos iguales, es decir, son equiláteros y equiángulos. Son inscriptibles y circunscriptibles.
11 Cuerpos geométricos
 89485 _ 0369-0418.qxd 1/9/07 15:06 Página 369 Cuerpos geométricos INTRODUCCIÓN Los poliedros, sus elementos y tipos ya son conocidos por los alumnos del curso anterior. Descubrimos y reconocemos de nuevo
89485 _ 0369-0418.qxd 1/9/07 15:06 Página 369 Cuerpos geométricos INTRODUCCIÓN Los poliedros, sus elementos y tipos ya son conocidos por los alumnos del curso anterior. Descubrimos y reconocemos de nuevo
Created with novapdf Printer (www.novapdf.com)
 GEOMETRÍA LONGITUDES Longitud de la circunferencia Es una línea curva cerrada que equidistan todos sus puntos del centro. Radio Centro: punto situado a igual distancia de todos los puntos de la circunferencia.
GEOMETRÍA LONGITUDES Longitud de la circunferencia Es una línea curva cerrada que equidistan todos sus puntos del centro. Radio Centro: punto situado a igual distancia de todos los puntos de la circunferencia.
GEOMETRÍA. 1. Líneas y ángulos. Partimos de la existencia de infinitos puntos cuyo conjunto llamamos ESPACIO.
 1. Líneas y ángulos Partimos de la existencia de infinitos puntos cuyo conjunto llamamos ESPACIO. Los puntos del espacio se consideran agrupados en conjuntos parciales de infinitos puntos llamados PLANOS.
1. Líneas y ángulos Partimos de la existencia de infinitos puntos cuyo conjunto llamamos ESPACIO. Los puntos del espacio se consideran agrupados en conjuntos parciales de infinitos puntos llamados PLANOS.
Liceo N 1 Javiera Carrera 8 años 2011
 GUIA DE ESTUDIO : Cuerpos geométricos Prof. Juan Schuchhardt E. DEFINICIÓN: Los poliedros son aquellos cuerpos geométricos que están limitados por superficies planas y de contorno poligonal. Un poliedro
GUIA DE ESTUDIO : Cuerpos geométricos Prof. Juan Schuchhardt E. DEFINICIÓN: Los poliedros son aquellos cuerpos geométricos que están limitados por superficies planas y de contorno poligonal. Un poliedro
TEMA 2. DIBUJO TÉCNICO
 TEMA 2. DIBUJO TÉCNICO 1.PARALELISMO Y PERPENDICULARIDAD Dos rectas son paralelas cuando mantienen siempre la misma distancia entre ellas y nunca llegan a unirse. Dos rectas son perpendiculares cuando
TEMA 2. DIBUJO TÉCNICO 1.PARALELISMO Y PERPENDICULARIDAD Dos rectas son paralelas cuando mantienen siempre la misma distancia entre ellas y nunca llegan a unirse. Dos rectas son perpendiculares cuando
Polígonos y circunferencia
 826464 _ 055-070.qxd 12/2/07 09:22 Página 55 Polígonos y circunferencia INTRODUCCIÓN RESUMEN DE LA UNIDAD Nos introducimos en el estudio de los polígonos, recordando contenidos trabajados por los alumnos
826464 _ 055-070.qxd 12/2/07 09:22 Página 55 Polígonos y circunferencia INTRODUCCIÓN RESUMEN DE LA UNIDAD Nos introducimos en el estudio de los polígonos, recordando contenidos trabajados por los alumnos
AREA Y PERIMETRO DE LAS FIGURAS GEOMETRICAS
 AREA Y PERIMETRO DE LAS FIGURAS GEOMETRICAS Figura geométrica Consiste de una línea o de un conjunto de líneas que representarán un objeto dado. Polígono Es una poligonal cerrada (el origen del primer
AREA Y PERIMETRO DE LAS FIGURAS GEOMETRICAS Figura geométrica Consiste de una línea o de un conjunto de líneas que representarán un objeto dado. Polígono Es una poligonal cerrada (el origen del primer
Los cuerpos geométricos
 Los cuerpos geométricos Se denominan cuerpos geométricos a aquellos elementos que, ya sean reales o ideales que existen en la realidad o pueden concebirse mentalmente ocupan un volumen en el espacio desarrollándose
Los cuerpos geométricos Se denominan cuerpos geométricos a aquellos elementos que, ya sean reales o ideales que existen en la realidad o pueden concebirse mentalmente ocupan un volumen en el espacio desarrollándose
Segmento : porción de recta comprendida entre dos de sus puntos, llamados extremos.
 ÍNDICE Elementos fundamentales Ángulos Triángulos y cuadriláteros Áreas y volúmenes Poliedros ELEMENTOS FUNDAMENTALES DE GEOMETRÍA Conceptos fundamentales Punto Recta Plano Semirecta : porción de recta
ÍNDICE Elementos fundamentales Ángulos Triángulos y cuadriláteros Áreas y volúmenes Poliedros ELEMENTOS FUNDAMENTALES DE GEOMETRÍA Conceptos fundamentales Punto Recta Plano Semirecta : porción de recta
38. CUERPOS SÓLIDOS: DESARROLLOS Y TRANSFORMADAS Desarrollo de los Poliedros Regulares.
 1 38. CUERPOS SÓLIDOS: DESARROLLOS Y TRANSFORMADAS. 38.1. Desarrollo de los Poliedros Regulares. 38.1.1. Tetraedro. Dado que los poliedros regulares tienen sus caras iguales, el desarrollo de los mismos
1 38. CUERPOS SÓLIDOS: DESARROLLOS Y TRANSFORMADAS. 38.1. Desarrollo de los Poliedros Regulares. 38.1.1. Tetraedro. Dado que los poliedros regulares tienen sus caras iguales, el desarrollo de los mismos
Conceptos básicos de Geometría
 Conceptos básicos de geometría La geometría trata de la medición y de las propiedades de puntos, líneas, ángulos, planos y sólidos, así como de las relaciones que guardan entre sí. A continuación veremos
Conceptos básicos de geometría La geometría trata de la medición y de las propiedades de puntos, líneas, ángulos, planos y sólidos, así como de las relaciones que guardan entre sí. A continuación veremos
Preparado por el Arqto. Jing Chang Lou
 POLIIEDROS A P U N T E D O C E N T E Preparado por el Arqto. Jing Chang Lou U N I V ER S I D A D D E C H I L E F AC U L T A D D E A R Q U I T EC T U R A Y U R B A N I S MO D EPARTAMENTO C I ENCIAS DE L
POLIIEDROS A P U N T E D O C E N T E Preparado por el Arqto. Jing Chang Lou U N I V ER S I D A D D E C H I L E F AC U L T A D D E A R Q U I T EC T U R A Y U R B A N I S MO D EPARTAMENTO C I ENCIAS DE L
PERSPECTIVA ISOMÉTRICA. INTERSECCIONES CON RECTAS Y PLANOS. SECCIONES PLANAS.
 PERSPECTIVA ISOMÉTRICA. INTERSECCIONES CON RECTAS Y PLANOS. SECCIONES PLANAS. 1. INTERSECCIÓN ENTRE PLANOS DADOS POR SUS TRAZAS. 1.1. INTERSECCIÓN DE DOS PLANOS CUALESQUIERA. Es la recta común a los dos
PERSPECTIVA ISOMÉTRICA. INTERSECCIONES CON RECTAS Y PLANOS. SECCIONES PLANAS. 1. INTERSECCIÓN ENTRE PLANOS DADOS POR SUS TRAZAS. 1.1. INTERSECCIÓN DE DOS PLANOS CUALESQUIERA. Es la recta común a los dos
2. Construcción de polígonos regulares conociendo el radio
 Polígonos regulares 1. Características Polígono regular es el que tiene sus lados iguales y sus ángulos iguales. Un polígono regular puede ser inscrito y circunscrito a una circunferencia cuyo centro es
Polígonos regulares 1. Características Polígono regular es el que tiene sus lados iguales y sus ángulos iguales. Un polígono regular puede ser inscrito y circunscrito a una circunferencia cuyo centro es
Tema 5: Polígonos. Mediatriz de un segmento : Es la recta perpendicular trazada en su punto medio.
 Tema 5: Polígonos 5.1 Elementos Fundamentales de Geometría Mediatriz de un segmento : Es la recta perpendicular trazada en su punto medio. A P * B Cualquier punto P de la mediatriz equidista de los extremos
Tema 5: Polígonos 5.1 Elementos Fundamentales de Geometría Mediatriz de un segmento : Es la recta perpendicular trazada en su punto medio. A P * B Cualquier punto P de la mediatriz equidista de los extremos
COLEGIO TIRSO DE MOLINA DEPARTAMENTO DE DIBUJO TÉCNICO CURSO 2010-11 DIBUJO TÉCNICO II
 DIBUJO TÉCNICO II TEMA 2: PROPORCIONALIDAD Y SEMEJANZA Media proporcional Teoremas del Cateto y la Altura Figuras equivalentes Figuras semejantes y sus diferencias con las homotéticas Razón de semejanza
DIBUJO TÉCNICO II TEMA 2: PROPORCIONALIDAD Y SEMEJANZA Media proporcional Teoremas del Cateto y la Altura Figuras equivalentes Figuras semejantes y sus diferencias con las homotéticas Razón de semejanza
Sistema Diédrico Índice de contenido
 Sistema Diédrico Índice de contenido Sistema Diédrico Fundamentos La geometría descriptiva es la ciencia que estudia la representación de los elementos del espacio sobre el plano.... 2 El punto... 3 Conceptos
Sistema Diédrico Índice de contenido Sistema Diédrico Fundamentos La geometría descriptiva es la ciencia que estudia la representación de los elementos del espacio sobre el plano.... 2 El punto... 3 Conceptos
CUERPOS GEOMÉTRICOS. Clases de cuerpos geométricos. Los poliedros. Los poliedros regulares.
 CUERPOS GEOMÉTRICOS. Se denominan cuerpos geométricos a aquellos elementos que, ya sean reales o ideales - que existen en la realidad o pueden concebirse mentalmente - ocupan un volumen en el espacio desarrollándose
CUERPOS GEOMÉTRICOS. Se denominan cuerpos geométricos a aquellos elementos que, ya sean reales o ideales - que existen en la realidad o pueden concebirse mentalmente - ocupan un volumen en el espacio desarrollándose
SUPERFICIES POLIÉDRICAS CONVEXAS
 SUPERFICIES POLIÉDRICAS CONVEXAS OBJETIVOS Conocer las características y relaciones métricas del te tra - edro, hexaedro o cubo y octaedro, para su represen tación en el sistema diédrico en sus múltiples
SUPERFICIES POLIÉDRICAS CONVEXAS OBJETIVOS Conocer las características y relaciones métricas del te tra - edro, hexaedro o cubo y octaedro, para su represen tación en el sistema diédrico en sus múltiples
1. Polígonos. 1.1 Definición
 1.1 Definición 1. Polígonos Es toda figura plana, cerrada, limitada por un número finito de lados rectos. De acuerdo al número de lados, los más utilizados se clasifican en: Triángulos 3 lados Cuadriláteros
1.1 Definición 1. Polígonos Es toda figura plana, cerrada, limitada por un número finito de lados rectos. De acuerdo al número de lados, los más utilizados se clasifican en: Triángulos 3 lados Cuadriláteros
CORRECCIÓN DE ACTIVIDADES GEOMETRÍA LINEAL
 CORRECCIÓN DE ACTIVIDADES GEOMETRÍA LINEAL *. Responde a las siguientes preguntas en tu cuaderno. a) Qué es una recta? Dibújala. Recta: sucesión infinita de puntos (no tiene principio ni fin). Las rectas
CORRECCIÓN DE ACTIVIDADES GEOMETRÍA LINEAL *. Responde a las siguientes preguntas en tu cuaderno. a) Qué es una recta? Dibújala. Recta: sucesión infinita de puntos (no tiene principio ni fin). Las rectas
FIGURAS PLANAS. Esto es un segmento: Esto es una línea poligonal abierta, formada por la unión de varios segmentos:
 FIGURAS PLANAS Esto es un segmento: Esto es una línea poligonal abierta, formada por la unión de varios segmentos: Y esto, una línea poligonal cerrada en la que se unen el extremo inicial del primer segmento
FIGURAS PLANAS Esto es un segmento: Esto es una línea poligonal abierta, formada por la unión de varios segmentos: Y esto, una línea poligonal cerrada en la que se unen el extremo inicial del primer segmento
Unidad didáctica 3. Cálculo de superficies y volúmenes
 Unidad didáctica. Cálculo de superficies y volúmenes.1 Cálculo de superficies. En el presente apartado se estudiarán las superficies, perímetros y relaciones geométricas más importantes de las principales
Unidad didáctica. Cálculo de superficies y volúmenes.1 Cálculo de superficies. En el presente apartado se estudiarán las superficies, perímetros y relaciones geométricas más importantes de las principales
DIBUJO TÉCNICO II. Construcción de polígonos regulares a partir de su lado o del radio de la circunferencia circunscrita.
 TEMA 4: POLÍGONOS DIBUJO TÉCNICO II Líneas y puntos notables de un triángulo: o o o o o Ortocentro y triángulo órtico. Baricentro. Incentro y circunferencia inscrita. Circuncentro y circunferencia circunscrita.
TEMA 4: POLÍGONOS DIBUJO TÉCNICO II Líneas y puntos notables de un triángulo: o o o o o Ortocentro y triángulo órtico. Baricentro. Incentro y circunferencia inscrita. Circuncentro y circunferencia circunscrita.
1.- Punto: Intersección de dos rectas. No tiene dimensiones (ni largo, ni ancho, ni alto).
 1.- Punto: Intersección de dos rectas. No tiene dimensiones (ni largo, ni ancho, ni alto). 6.- Espacio: Conjunto de puntos con tres dimensiones: largo, ancho y alto. Es infinito, sin límites. 2.- Recta:
1.- Punto: Intersección de dos rectas. No tiene dimensiones (ni largo, ni ancho, ni alto). 6.- Espacio: Conjunto de puntos con tres dimensiones: largo, ancho y alto. Es infinito, sin límites. 2.- Recta:
13 CUERPOS GEOMÉTRICOS
 13 CUERPOS GEOMÉTRICOS EJERCICIOS PROPUESTOS 13.1 Observa la figura y di qué elemento geométrico determinan la recta y el plano. r α La recta r y el plano determinan un punto. 13.2 Con los cuatro puntos
13 CUERPOS GEOMÉTRICOS EJERCICIOS PROPUESTOS 13.1 Observa la figura y di qué elemento geométrico determinan la recta y el plano. r α La recta r y el plano determinan un punto. 13.2 Con los cuatro puntos
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO.
 UNIVERSIDDES PÚLICS DE L COMUNIDD DE MDRID PRUE DE CCESO LS ENSEÑNZS UNIVERSITRIS OFICILES DE GRDO MTERI: DIUJO TÉCNICO II Curso 2010-2011 INSTRUCCIONES Y CRITERIOS GENERLES DE CLIFICCIÓN La prueba consiste
UNIVERSIDDES PÚLICS DE L COMUNIDD DE MDRID PRUE DE CCESO LS ENSEÑNZS UNIVERSITRIS OFICILES DE GRDO MTERI: DIUJO TÉCNICO II Curso 2010-2011 INSTRUCCIONES Y CRITERIOS GENERLES DE CLIFICCIÓN La prueba consiste
Trigonometría y problemas métricos
 Trigonometría y problemas métricos 1) En un triángulo rectángulo, los catetos miden 6 y 8 centímetros. Calcula la medida de la altura sobre la hipotenusa y la distancia desde su pie hasta los extremos.
Trigonometría y problemas métricos 1) En un triángulo rectángulo, los catetos miden 6 y 8 centímetros. Calcula la medida de la altura sobre la hipotenusa y la distancia desde su pie hasta los extremos.
Dibujo Técnico Cuerpos Sólidos Redondos: Desarrollos y Transformadas.
 38. CUERPOS SÓLIDOS REDONDOS: DESARROLLOS Y TRANSFORMADAS. 38.6. Desarrollo del cilindro. 38.6.1. Cilindro recto. En realidad el trabajar con un cilindro es lo mismo que trabajar con un prisma pero este
38. CUERPOS SÓLIDOS REDONDOS: DESARROLLOS Y TRANSFORMADAS. 38.6. Desarrollo del cilindro. 38.6.1. Cilindro recto. En realidad el trabajar con un cilindro es lo mismo que trabajar con un prisma pero este
GENERALIDADES SISTEMAS DE PROYECCIÓN
 GENERALIDADES Todos los sistemas de representación, tienen como objetivo representar sobre una superficie bidimensional, los objetos que son tridimensionales en el espacio y cumplen una condición fundamental,
GENERALIDADES Todos los sistemas de representación, tienen como objetivo representar sobre una superficie bidimensional, los objetos que son tridimensionales en el espacio y cumplen una condición fundamental,
Dibujo Técnico Sistema diédrico.- Cambios de plano, giros y ángulos. ÁNGULOS.
 30. SISTEMA DIÉDRICO.- CAMBIOS DE PLANO, GIROS Y ÁNGULOS. 30.1. Cambios de plano. Los cambios de planos de proyección consisten en tomar o elegir otros planos de proyección de forma que los elementos que
30. SISTEMA DIÉDRICO.- CAMBIOS DE PLANO, GIROS Y ÁNGULOS. 30.1. Cambios de plano. Los cambios de planos de proyección consisten en tomar o elegir otros planos de proyección de forma que los elementos que
5. POLÍGONOS. 5.1 Definición y notación de polígonos
 5. POLÍGONOS 5.1 Definición y notación de polígonos Un polígono es una figura geométrica limitada por segmentos de recta denominados lados, donde el extremo de un segmento es el origen del otro. E D Etimológicamente,
5. POLÍGONOS 5.1 Definición y notación de polígonos Un polígono es una figura geométrica limitada por segmentos de recta denominados lados, donde el extremo de un segmento es el origen del otro. E D Etimológicamente,
ÁREAS DE CUERPOS GEOMÉTRICOS Poliedros. Para calcular el área de un poliedro calculamos el área de cada una de sus caras y las sumamos.
 TEMA 9: ÁREAS Y VOLÚMENES DE CUERPOS GEOMÉTRICOS POLIEDROS REGULARES Un poliedro se llama regular cunado cumple las dos condiciones siguientes: Sus caras son polígonos regulares idénticos. En cada vértice
TEMA 9: ÁREAS Y VOLÚMENES DE CUERPOS GEOMÉTRICOS POLIEDROS REGULARES Un poliedro se llama regular cunado cumple las dos condiciones siguientes: Sus caras son polígonos regulares idénticos. En cada vértice
Volúmenes de cuerpos geométricos
 Volúmenes de cuerpos geométricos TEORÍA Cuerpos geométricos En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos
Volúmenes de cuerpos geométricos TEORÍA Cuerpos geométricos En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos
RESUMEN GEOMETRÍA SAINT MARY SCHOOL. PROF. JUAN K. BOLAÑOS M. Geometría Elemental
 Geometría Elemental Punto Sólo tiene posición. No posee longitud, anchura ni espesor. Se representa por un. Se designa por medio de una letra mayúscula colocada cerca del punto gráfico. Línea recta Es
Geometría Elemental Punto Sólo tiene posición. No posee longitud, anchura ni espesor. Se representa por un. Se designa por medio de una letra mayúscula colocada cerca del punto gráfico. Línea recta Es
Hoja de problemas nº 7. Introducción a la Geometría
 Hoja de problemas nº 7 Introducción a la Geometría 1. Un rectángulo tiene de área 135 u 2 a. Si sus lados miden números enteros, averigua cuáles pueden ser sus dimensiones. b. Cortamos los vértices como
Hoja de problemas nº 7 Introducción a la Geometría 1. Un rectángulo tiene de área 135 u 2 a. Si sus lados miden números enteros, averigua cuáles pueden ser sus dimensiones. b. Cortamos los vértices como
Lección 17: Polígonos básicos
 Lección 17: Polígonos básicos Un polígono es una figura cerrada formada por segmentos de recta que no se cruzan entre sí. Los segmentos se llaman lados del polígono. Los polígonos pueden ser convexos,
Lección 17: Polígonos básicos Un polígono es una figura cerrada formada por segmentos de recta que no se cruzan entre sí. Los segmentos se llaman lados del polígono. Los polígonos pueden ser convexos,
UNIDAD 10. FIGURAS PLANAS: POLÍGONOS CIRCUNFERENCIA Y CÍRCULO
 UNIDAD 10. FIGURAS PLANAS: POLÍGONOS CIRCUNFERENCIA Y CÍRCULO 1. POLÍGONOS: DEFINÍCIÓN, ELEMENTOS Y CLASIFICACIÓN. 2. POLÍGONOS REGULARES E IRREGULARES. 3. TRIÁNGULOS Y CUADRILÁTEROS: CLASIFICACIÓN. 4.
UNIDAD 10. FIGURAS PLANAS: POLÍGONOS CIRCUNFERENCIA Y CÍRCULO 1. POLÍGONOS: DEFINÍCIÓN, ELEMENTOS Y CLASIFICACIÓN. 2. POLÍGONOS REGULARES E IRREGULARES. 3. TRIÁNGULOS Y CUADRILÁTEROS: CLASIFICACIÓN. 4.
DIBUJO TÉCNICO II BLOQUE 1_TRAZADOS GEOMÉTRICOS
 En este tema se establecen algunas de las relaciones geométricas que pueden presentar dos figuras planas entre si. 1. Proporcionalidad 1.1. Teorema de Tales. División de un segmento en partes iguales.
En este tema se establecen algunas de las relaciones geométricas que pueden presentar dos figuras planas entre si. 1. Proporcionalidad 1.1. Teorema de Tales. División de un segmento en partes iguales.
Propiedades y clasificación de triángulos
 MT-22 Clase Propiedades y clasificación de triángulos Síntesis de la clase Ángulos Polígonos convexos Clasificación de ángulos Relaciones angulares Regulares Irregulares 0º < Agudo < 90 Recto = 90 90º
MT-22 Clase Propiedades y clasificación de triángulos Síntesis de la clase Ángulos Polígonos convexos Clasificación de ángulos Relaciones angulares Regulares Irregulares 0º < Agudo < 90 Recto = 90 90º
8. LA CIRCUNFERENCIA Y EL CÍRCULO. 8.1. La Circunferencia. 8.2. El circulo. Dibujo Técnico La Circunferencia y el círculo
 8. LA CIRCUNFERENCIA Y EL CÍRCULO 8.1. La Circunferencia. Una circunferencia es una línea curva, cerrada y plana, cuyos puntos están a la misma distancia de otro interior al que llamamos centro, es decir:
8. LA CIRCUNFERENCIA Y EL CÍRCULO 8.1. La Circunferencia. Una circunferencia es una línea curva, cerrada y plana, cuyos puntos están a la misma distancia de otro interior al que llamamos centro, es decir:
10 FIGURAS Y CUERPOS GEOMÉTRICOS
 10 FIGURAS Y CUERPOS GEOMÉTRICOS EJERCICIOS PROPUESTOS 10.1 Indica cuál de estos poliedros es cóncavo y cuál es convexo. a) Cóncavo b) Convexo 10. Completa la siguiente tabla. Caras (C ) Vértices (V )
10 FIGURAS Y CUERPOS GEOMÉTRICOS EJERCICIOS PROPUESTOS 10.1 Indica cuál de estos poliedros es cóncavo y cuál es convexo. a) Cóncavo b) Convexo 10. Completa la siguiente tabla. Caras (C ) Vértices (V )
* * * GEOMETRÍA DESCRIPTIVA * * *
 Superficies. Llamamos superficie a una lámina, infinitamente delgada, que recubre un cuerpo o que separa dos regiones del espacio. Una superficie puede engendrarse de dos maneras distintas: a). Como lugar
Superficies. Llamamos superficie a una lámina, infinitamente delgada, que recubre un cuerpo o que separa dos regiones del espacio. Una superficie puede engendrarse de dos maneras distintas: a). Como lugar
UNIVERSIDAD NACIONAL DE ASUNCIÓN FACULTAD DE INGENIERÍA CURSO PREPARATORIO DE INGENIERÍA (CPI) EJERCITARIO PRÁCTICO DE GEOMETRÍA ANALÍTICA
 UNIVERSIDAD NACIONAL DE ASUNCIÓN FACULTAD DE INGENIERÍA CURSO PREPARATORIO DE INGENIERÍA (CPI) EJERCITARIO PRÁCTICO DE GEOMETRÍA ANALÍTICA AÑO 014 CURSO PREPARATORIO DE INGENIERÍA CPI-014 TRASLACIÓN Y/O
UNIVERSIDAD NACIONAL DE ASUNCIÓN FACULTAD DE INGENIERÍA CURSO PREPARATORIO DE INGENIERÍA (CPI) EJERCITARIO PRÁCTICO DE GEOMETRÍA ANALÍTICA AÑO 014 CURSO PREPARATORIO DE INGENIERÍA CPI-014 TRASLACIÓN Y/O
Clasificación de triángulos: Un triángulo es un polígono de tres lados. Un triángulo está determinado por:
 Un triángulo es un polígono de tres lados. Un triángulo está determinado por: 1. Tres segmentos de recta que se denominan lados. 2. Tres puntos no alineados que se llaman vértices. Los vértices se escriben
Un triángulo es un polígono de tres lados. Un triángulo está determinado por: 1. Tres segmentos de recta que se denominan lados. 2. Tres puntos no alineados que se llaman vértices. Los vértices se escriben
CONOCIMIENTOS TEÓRICOS. 1 Cambios de plano 1.1 Nuevas proyecciones del punto 1.2 Nuevas proyecciones de la recta 1.3 Nuevas proyecciones del plano
 5 Sistema diédrico. Movimientos UNIDAD CONOCIMIENTOS TEÓRICOS 1 Cambios de plano 1.1 Nuevas proyecciones del punto 1.2 Nuevas proyecciones de la recta 1.3 Nuevas proyecciones del plano 2 Giros 2.1 Giro
5 Sistema diédrico. Movimientos UNIDAD CONOCIMIENTOS TEÓRICOS 1 Cambios de plano 1.1 Nuevas proyecciones del punto 1.2 Nuevas proyecciones de la recta 1.3 Nuevas proyecciones del plano 2 Giros 2.1 Giro
RELACION DE PROBLEMAS DE GEOMETRIA. Problemas propuestos para la prueba de acceso del curso 1996/97.
 RELACION DE PROBLEMAS DE GEOMETRIA Problemas propuestos para la prueba de acceso del curso 996/97. º. - Explica cómo se puede hallar el área de un triángulo, a partir de sus coordenadas, en el espacio
RELACION DE PROBLEMAS DE GEOMETRIA Problemas propuestos para la prueba de acceso del curso 996/97. º. - Explica cómo se puede hallar el área de un triángulo, a partir de sus coordenadas, en el espacio
Conceptos Básicos. Las líneas rectas podemos encontrarlas en el doblez de una hoja de papel, en un hilo estirado, en la arista de una puerta, etc.
 3. Geometría Desde el jardinero que traza un jardín, el navegante que fija y traza la ruta del próximo viaje, el arquitecto que hace los planos para la construcción de un grandioso edificio, el ingeniero
3. Geometría Desde el jardinero que traza un jardín, el navegante que fija y traza la ruta del próximo viaje, el arquitecto que hace los planos para la construcción de un grandioso edificio, el ingeniero
SOLUCIONES A LAS ACTIVIDADES DE CADA EPÍGRAFE
 Pág. 1 PÁGINA 19 REFLEXIONA Las cajas, los contenedores y la caseta son poliedros. También es un poliedro la figura que forma la caja que pende de la grúa con las cuatro cuerdas que la sostienen. Cuántas
Pág. 1 PÁGINA 19 REFLEXIONA Las cajas, los contenedores y la caseta son poliedros. También es un poliedro la figura que forma la caja que pende de la grúa con las cuatro cuerdas que la sostienen. Cuántas
Los poliedros y sus elementos
 Los poliedros y sus elementos De las siguientes figuras, rodea las que sean poliedros o tengan forma de poliedro. Dibuja y escribe el nombre de tres objetos que tengan forma de poliedro. espuesta libre
Los poliedros y sus elementos De las siguientes figuras, rodea las que sean poliedros o tengan forma de poliedro. Dibuja y escribe el nombre de tres objetos que tengan forma de poliedro. espuesta libre
SUBRAYE LA RESPUESTA CORRECTA EN CADA PREGUNTA.
 CUADERNILLO DE GEOMETRIA I.- SUBRAYE LA RESPUESTA CORRECTA EN CADA PREGUNTA. 1.- SON LOS TRIÁNGULOS QUE TIENEN TODOS LOS ÁNGULOS IGUALES. A) EQUILÁTERO B) ACUTÁNGULO C) ISÓSCELES D) ESCALENO E) RECTÁNGULO
CUADERNILLO DE GEOMETRIA I.- SUBRAYE LA RESPUESTA CORRECTA EN CADA PREGUNTA. 1.- SON LOS TRIÁNGULOS QUE TIENEN TODOS LOS ÁNGULOS IGUALES. A) EQUILÁTERO B) ACUTÁNGULO C) ISÓSCELES D) ESCALENO E) RECTÁNGULO
TRIÁNGULOS. TEOREMA DE PITÁGORAS.
 TRIÁNGULOS. TEOREMA DE PITÁGORAS. Un triángulo ABC es la figura geométrica del plano formada por 3 segmentos llamados lados cuyos extremos se cortan a en 3 puntos llamados vértices. Los vértices se escriben
TRIÁNGULOS. TEOREMA DE PITÁGORAS. Un triángulo ABC es la figura geométrica del plano formada por 3 segmentos llamados lados cuyos extremos se cortan a en 3 puntos llamados vértices. Los vértices se escriben
Colegio Universitario Boston. Geometría
 34 Conceptos ásicos Triángulo: Se define como la figura geométrica plana, cerrada de tres lados. Triángulo equilátero: Es el triángulo que tiene sus tres lados iguales y sus tres ángulos internos iguales,
34 Conceptos ásicos Triángulo: Se define como la figura geométrica plana, cerrada de tres lados. Triángulo equilátero: Es el triángulo que tiene sus tres lados iguales y sus tres ángulos internos iguales,
* * * GEOMETRÍA DESCRIPTIVA * * * ÍNDICE
 ÍNDICE 1.- CONCEPTO DE PROYECCIÓN.... 1 Proyección de un punto.... 1 Clasificación de las proyecciones.... 1 Sistema Diédrico...3 Sistema de Planos Acotados...3 Sistema Axonométrico...3 Sistema Cónico...4
ÍNDICE 1.- CONCEPTO DE PROYECCIÓN.... 1 Proyección de un punto.... 1 Clasificación de las proyecciones.... 1 Sistema Diédrico...3 Sistema de Planos Acotados...3 Sistema Axonométrico...3 Sistema Cónico...4
Dibujo Técnico Triángulos 9. TRIÁNGULOS. Según los lados.
 9. TRIÁNGULOS 9.1. Características generales. Un triángulo es una figura plana limitada por tres rectas que se cortan dos a dos, determinando los segmentos que son los lados del triángulo. Para que tres
9. TRIÁNGULOS 9.1. Características generales. Un triángulo es una figura plana limitada por tres rectas que se cortan dos a dos, determinando los segmentos que son los lados del triángulo. Para que tres
Proporcionalidad geométrica
 TEMA 9: Proporcionalidad geométrica INTRODUCCIÓN: THALES DE MILETO Thales, filósofo, astrónomo y matemático griego nació en Mileto en el año 624 a. de C. y murió a la edad de 78 años durante la quincuagésima
TEMA 9: Proporcionalidad geométrica INTRODUCCIÓN: THALES DE MILETO Thales, filósofo, astrónomo y matemático griego nació en Mileto en el año 624 a. de C. y murió a la edad de 78 años durante la quincuagésima
EJERCICIOS BLOQUE III: GEOMETRÍA
 EJERCICIOS BLOQUE III: GEOMETRÍA (00-M-A-4) (5 puntos) Determina el centro y el radio de la circunferencia que pasa por el origen de coordenadas, tiene su centro en el semieje positivo de abscisas y es
EJERCICIOS BLOQUE III: GEOMETRÍA (00-M-A-4) (5 puntos) Determina el centro y el radio de la circunferencia que pasa por el origen de coordenadas, tiene su centro en el semieje positivo de abscisas y es
1. ESQUEMA - RESUMEN Página. 2. EJERCICIOS DE INICIACIÓN Página. 3. EJERCICIOS DE DESARROLLO Página. 4. EJERCICIOS DE AMPLIACIÓN Página
 1. ESQUEMA - RESUMEN Página 2 2. EJERCICIOS DE INICIACIÓN Página 7 3. EJERCICIOS DE DESARROLLO Página 7 4. EJERCICIOS DE AMPLIACIÓN Página 9 5. EJERCICIOS DE REFUERZO Página 12 6. EJERCICIOS RESUELTOS
1. ESQUEMA - RESUMEN Página 2 2. EJERCICIOS DE INICIACIÓN Página 7 3. EJERCICIOS DE DESARROLLO Página 7 4. EJERCICIOS DE AMPLIACIÓN Página 9 5. EJERCICIOS DE REFUERZO Página 12 6. EJERCICIOS RESUELTOS
Dibujo Técnico División de la circunferencia en partes iguales. 1º.-Bach. IGUALES. 18.1. División de la circunferencia en tres y seis partes iguales.
 18. DIVISIÓN DE LA CIRCUNFERENCIA EN PARTES IGUALES 18.1. División de la circunferencia en tres y seis partes iguales. Trazamos dos diámetros perpendiculares AB y CD. Con centro en C y radio R trazamos
18. DIVISIÓN DE LA CIRCUNFERENCIA EN PARTES IGUALES 18.1. División de la circunferencia en tres y seis partes iguales. Trazamos dos diámetros perpendiculares AB y CD. Con centro en C y radio R trazamos
1º BACH SISTEMA DIÉDRICO III
 SISTEMA DIÉDRICO III ABATIMIENTOS, GIROS, CAMBIOS DE PLANO. SISTEMA DIÉDRICO III: ABATIMIENTOS, CAMBIOS DE PLANO Y GIROS 1- ABATIMIENTOS Los abatimientos se utilizan para hallar la verdadera magnitud (
SISTEMA DIÉDRICO III ABATIMIENTOS, GIROS, CAMBIOS DE PLANO. SISTEMA DIÉDRICO III: ABATIMIENTOS, CAMBIOS DE PLANO Y GIROS 1- ABATIMIENTOS Los abatimientos se utilizan para hallar la verdadera magnitud (
PÁGINA 196. 1 Di qué tipo de prisma es cada uno de los siguientes. Indica cuáles son regulares. Dibuja el desarrollo del primero de ellos.
 Soluciones a las actividades de cada epígrafe PÁGINA 196 1 Di qué tipo de prisma es cada uno de los siguientes. Indica cuáles son regulares. Dibuja el desarrollo del primero de ellos. a) b) c) d) a) Triangular,
Soluciones a las actividades de cada epígrafe PÁGINA 196 1 Di qué tipo de prisma es cada uno de los siguientes. Indica cuáles son regulares. Dibuja el desarrollo del primero de ellos. a) b) c) d) a) Triangular,
VOLUMENES. Los cuerpos en el espacio (sólidos) poseen tres dimensiones: largo, ancho y profundidad
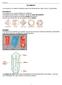 VOLUMENES Los cuerpos en el espacio (sólidos) poseen tres dimensiones: largo, ancho y profundidad POLIEDROS Un poliedro es un cuerpo limitado por polígonos Los polígonos que limiten el poliedro, se llaman
VOLUMENES Los cuerpos en el espacio (sólidos) poseen tres dimensiones: largo, ancho y profundidad POLIEDROS Un poliedro es un cuerpo limitado por polígonos Los polígonos que limiten el poliedro, se llaman
Sistema Diédrico (II). Superficies poliédricas y radiadas: Representación
 Sistema Diédrico (II). Superficies poliédricas y radiadas: Representación Comenzamos una nueva unidad didáctica en la que desarrollaremos los conceptos y procedimientos sobre superficies poliédricas y
Sistema Diédrico (II). Superficies poliédricas y radiadas: Representación Comenzamos una nueva unidad didáctica en la que desarrollaremos los conceptos y procedimientos sobre superficies poliédricas y
PERÍMETROS Y ÁREAS DE FIGURAS PLANAS UNIDADE 13 1º ESO Halla la superficie y el perímetro del recinto marrón:
 PERÍMETROS Y ÁREAS DE FIGURAS PLANAS UNIDADE 13 1º ESO Halla la superficie y el perímetro del recinto marrón: Calcula el perímetro y el área de esta figura: Calcula el perímetro y el área de esta figura:
PERÍMETROS Y ÁREAS DE FIGURAS PLANAS UNIDADE 13 1º ESO Halla la superficie y el perímetro del recinto marrón: Calcula el perímetro y el área de esta figura: Calcula el perímetro y el área de esta figura:
Preguntas tipo OLIMPIADA DE DIBUJO TÉCNICO MARZO 2014
 E S C U E L A T É C N I C A S U P E R I O R D E A R Q U I T E C T U R A U N I V E R S I D A D D E N A V A R R A Preguntas tipo OLIMPIADA DE DIBUJO TÉCNICO MARZO 2014 G E O M E T R Í A M É T R I C A. T
E S C U E L A T É C N I C A S U P E R I O R D E A R Q U I T E C T U R A U N I V E R S I D A D D E N A V A R R A Preguntas tipo OLIMPIADA DE DIBUJO TÉCNICO MARZO 2014 G E O M E T R Í A M É T R I C A. T
UNIDAD 10 CUERPOS GEOMÉTRICOS. Objetivo General.
 UNIDAD 10 CUERPOS GEOMÉTRICOS Objetivo General. Al terminar ésta unidad identificarás los diferentes tipos de Cuerpos Geométricos, resolverás ejercicios y problemas en los que apliques definiciones y fórmulas.
UNIDAD 10 CUERPOS GEOMÉTRICOS Objetivo General. Al terminar ésta unidad identificarás los diferentes tipos de Cuerpos Geométricos, resolverás ejercicios y problemas en los que apliques definiciones y fórmulas.
TRANSFORMACIONES DEL PLANO
 PROBLEMAS DE GEOMETRÍA. TRANSFORMACIONES DEL PLANO 1. Un producto de dos simetrías axiales de ejes perpendiculares A qué transformación corresponde? En qué se transforma un segmento vertical? ( ) 2. Cuál
PROBLEMAS DE GEOMETRÍA. TRANSFORMACIONES DEL PLANO 1. Un producto de dos simetrías axiales de ejes perpendiculares A qué transformación corresponde? En qué se transforma un segmento vertical? ( ) 2. Cuál
SISTEMA DIÉDRICO PERTENENCIA VISIBILIDAD VISIBILIDAD 3º PROYECCIÓN PLANOS NO DADOS POR SUS TRAZAS
 SISTEMA DIÉDRICO PERTENENCIA 1. Dado un plano cualquiera cuya traza horizontal forma 40º con la LT y 60º la traza vertical, situar pasando por un punto A que le pertenece y de altura 30 mm, todas sus rectas
SISTEMA DIÉDRICO PERTENENCIA 1. Dado un plano cualquiera cuya traza horizontal forma 40º con la LT y 60º la traza vertical, situar pasando por un punto A que le pertenece y de altura 30 mm, todas sus rectas
ÁLGEBRA LINEAL II Práctica 3.1-3.2
 ÁLGEBRA LINEAL II Práctica 3.1-3.2 Geometría afín. (Curso 2014 2015) 1. En el espacio afín IR 3 se considera la referencia canónica R y la referencia R = (1, 0, 1); (1, 1, 0), (1, 1, 1), (1, 0, 0)}. Denotamos
ÁLGEBRA LINEAL II Práctica 3.1-3.2 Geometría afín. (Curso 2014 2015) 1. En el espacio afín IR 3 se considera la referencia canónica R y la referencia R = (1, 0, 1); (1, 1, 0), (1, 1, 1), (1, 0, 0)}. Denotamos
1.- 3.- Las áreas de dos polígonos semejantes son 121 cm 2 y 324 cm 2. Si el perímetro del primero es 44 cm, cuál es el perímetro del segundo?
 olegio-laret 1.- 10m 7m 30m SMINRIO MTMÁTIS l dibujo presenta un método aproximado para medir la anchura de un río sin necesidad más que de tomar medidas en una orilla. Situándonos en el punto hemos realizado
olegio-laret 1.- 10m 7m 30m SMINRIO MTMÁTIS l dibujo presenta un método aproximado para medir la anchura de un río sin necesidad más que de tomar medidas en una orilla. Situándonos en el punto hemos realizado
POLIGONOS. Nº DE LADOS NOMBRE 3 Triángulos 4 Cuadriláteros 5 Pentágonos 6 Hexágonos 7 Heptágonos 8 Octógonos 9 Eneágonos 10 Decágonos
 1 POLIGONO POLIGONOS Polígono es la superficie plana limitada por una línea poligonal cerrada. Lados Vértices Polígono regular es el que tiene todos sus lados y ángulos iguales, mientras que polígono irregular
1 POLIGONO POLIGONOS Polígono es la superficie plana limitada por una línea poligonal cerrada. Lados Vértices Polígono regular es el que tiene todos sus lados y ángulos iguales, mientras que polígono irregular
21.3. Rectas tangentes exteriores a dos circunferencias.
 21. TANGENCIAS 21.1. Características generales. Tangencia entre recta y circunferencia: una recta t es tangente a una circunferencia de centro O en un punto T cuando es perpendicular en T al radio OT.
21. TANGENCIAS 21.1. Características generales. Tangencia entre recta y circunferencia: una recta t es tangente a una circunferencia de centro O en un punto T cuando es perpendicular en T al radio OT.
CONOCIMIENTOS TEÓRICOS. 1 Características del sistema axonométrico
 9 Axonometría ortogonal y oblicua UNIDAD CONOCIMIENTOS TEÓRICOS 1 Características del sistema axonométrico 2 Proyección de los elementos fundamentales 2.1 Representación del punto 2.2 Representación de
9 Axonometría ortogonal y oblicua UNIDAD CONOCIMIENTOS TEÓRICOS 1 Características del sistema axonométrico 2 Proyección de los elementos fundamentales 2.1 Representación del punto 2.2 Representación de
EJERCICIOS BLOQUE III: GEOMETRÍA
 EJERCICIOS BLOQUE III: GEOMETRÍA (00-M-A-4) (5 puntos) Determina el centro y el radio de la circunferencia que pasa por el origen de coordenadas, tiene su centro en el semieje positivo de abscisas y es
EJERCICIOS BLOQUE III: GEOMETRÍA (00-M-A-4) (5 puntos) Determina el centro y el radio de la circunferencia que pasa por el origen de coordenadas, tiene su centro en el semieje positivo de abscisas y es
A G R. Diédrico 17. Cuerpos 4. Tetraedro
 Dibujar los tetraedros, de igual arista, en las cuatro posiciones siguientes: 1. Apoyado por la cara AB en el PH (la posición de la izquierda). 2. on una arista, la AB en el PH y la opuesta horizontal.
Dibujar los tetraedros, de igual arista, en las cuatro posiciones siguientes: 1. Apoyado por la cara AB en el PH (la posición de la izquierda). 2. on una arista, la AB en el PH y la opuesta horizontal.
Dibujo Técnico Secciones Planas
 37. SECCIONES PLANAS 37.1. INTRODUCCIÓN. Para hallar la sección plano de un cuerpo geométrico se pueden emplear tres métodos: a.- Por intersección de aristas o generatrices del cuerpo con el plano. b.-
37. SECCIONES PLANAS 37.1. INTRODUCCIÓN. Para hallar la sección plano de un cuerpo geométrico se pueden emplear tres métodos: a.- Por intersección de aristas o generatrices del cuerpo con el plano. b.-
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág. 1 PÁGINA 255 EJERCICIOS Construcciones y ejes de simetría 1 a) Halla el ángulo central de un octógono regular. b) Dibuja un octógono regular inscrito en una circunferencia de 5 cm de radio, construyendo
Pág. 1 PÁGINA 255 EJERCICIOS Construcciones y ejes de simetría 1 a) Halla el ángulo central de un octógono regular. b) Dibuja un octógono regular inscrito en una circunferencia de 5 cm de radio, construyendo
A = 180-90 - 62 = 28. 8 GEOMETRíA DEL PLA 8 = 720-145 - 125-105 - 130-160 = 55. b) 720 = 90: ~ B- 110 + 8+ 150 + 90 = 440 + 28 ==> B = 140 C
 8 GEOMETRíA DEL PLA EJERCCOS PROPUESTOS Calcula la medida del ángulo que falta en cada figura. a) b) a) En un triángulo, la suma de las medidas de sus ángulos es 180, A = 180-90 - 6 = 8 El ángulo mide
8 GEOMETRíA DEL PLA EJERCCOS PROPUESTOS Calcula la medida del ángulo que falta en cada figura. a) b) a) En un triángulo, la suma de las medidas de sus ángulos es 180, A = 180-90 - 6 = 8 El ángulo mide
CONOCIMIENTOS TEÓRICOS APLICACIONES PRÁCTICAS. 2 Secciones planas e intersecciones 2.1 Secciones planas de sólidos 2.2 Intersección recta-cuerpo
 8 UNIDAD Superficies radiales CONOCIMIENTOS TEÓRICOS 1 Superficies radiales de vértice propio 1.1 Concepto y clasificación 1.2 La pirámide: clasificación y elementos 1.3 El cono: clasificación y elementos
8 UNIDAD Superficies radiales CONOCIMIENTOS TEÓRICOS 1 Superficies radiales de vértice propio 1.1 Concepto y clasificación 1.2 La pirámide: clasificación y elementos 1.3 El cono: clasificación y elementos
Tema 9 Cuerpos geométricos
 9.1 Prismas Tema 9 Cuerpos geométricos PÁGINA 196 ACTIVIDADES 1. Dí de que tipo es cada uno de los siguientes prismas: a) Prisma recto triangular. Es regular pues la base es un triángulo equilátero. b)
9.1 Prismas Tema 9 Cuerpos geométricos PÁGINA 196 ACTIVIDADES 1. Dí de que tipo es cada uno de los siguientes prismas: a) Prisma recto triangular. Es regular pues la base es un triángulo equilátero. b)
12.1. Clasificación de los cuadriláteros según su paralelismo.
 12. CUADRILÁTEROS 12.1. Clasificación de los cuadriláteros según su paralelismo. Según la cantidad de pares de lados que sean paralelos, los cuadriláteros se clasifican en tres tipos : Paralelogramos:
12. CUADRILÁTEROS 12.1. Clasificación de los cuadriláteros según su paralelismo. Según la cantidad de pares de lados que sean paralelos, los cuadriláteros se clasifican en tres tipos : Paralelogramos:
Vistas de un objeto VISTAS DE UN OBJETO
 Vistas de un objeto VISTAS DE UN OBJETO CONCEPTO DE VISTA Una de las formas en que podemos representar los objetos en Tecnología es mediante sus vistas. Pero, qué se entiende por vista de un objeto? cómo
Vistas de un objeto VISTAS DE UN OBJETO CONCEPTO DE VISTA Una de las formas en que podemos representar los objetos en Tecnología es mediante sus vistas. Pero, qué se entiende por vista de un objeto? cómo
1º ESO GEOMETRÍA PLANA: ÁNGULOS Y TRIÁNGULOS
 1º ESO GEOMETRÍA PLANA: ÁNGULOS Y TRIÁNGULOS 1.- ÁNGULOS Un ángulo es la porción de plano limitada por dos semirrectas o rayos que tienen el mismo origen. Los lados del ángulo son las semirrectas que lo
1º ESO GEOMETRÍA PLANA: ÁNGULOS Y TRIÁNGULOS 1.- ÁNGULOS Un ángulo es la porción de plano limitada por dos semirrectas o rayos que tienen el mismo origen. Los lados del ángulo son las semirrectas que lo
Tema 8 Cuerpos en el espacio
 Tema 8 Cuerpos en el espacio Poliedros La primera distinción que debemos hacer es entre los poliedros, que son cuerpos geométricos limitados por polígonos, y los cuerpos de revolución, donde una forma
Tema 8 Cuerpos en el espacio Poliedros La primera distinción que debemos hacer es entre los poliedros, que son cuerpos geométricos limitados por polígonos, y los cuerpos de revolución, donde una forma
