TEMA: EJES DE COORDENADAS
|
|
|
- María Rosario Ojeda Giménez
- hace 9 años
- Vistas:
Transcripción
1 TEMA: EJES DE COORDENADAS Se llaman ejes de coordenadas cartesianas a dos rectas del plano numeradas y perpendiculares. El eje horizontal recibe el nombre de eje de abscisas o eje de las X. El eje vertical se llama eje de ordenadas o eje de las Y. El punto donde se cortan los ejes se llama origen de coordenadas. Un punto P del plano se representa mediante una pareja de números ( x, y ) llamados coordenadas del punto. Para localizar el punto de coordenadas ( x, y ) se traza una vertical por el número x del eje de abcisas a continuación se traza una horizontal por el número y del eje de ordenadas. El punto de corte de las líneas trazadas es el punto en cuestión. Observa cómo se representa el punto de coordenadas ( - 3, - 6 ) Ordenada Abscis
2 Observa cómo se reprensentan los puntos de coordenadas ( 2, 3 ) ; ( - 2, 1 ) ; ( - 3, - 5 ) ; ( 7, - 2 ) Los ejes de coordenadas dividen el plano en cuatro cuadrantes El punto (-3, -6) está situado en el 3er cuadrante y el punto (-1, 2) está situado en el 2º cuadrante.
3 Nombre y Apellido:... Tema: ejes cartesianos Trabajo Práctico N 1 1) Representar los siguientes puntos en el plano cartesiano: a) P = 3;2 P = 2;3 P = 5;0 b) P = 3;3 P = 4;3 P = 3; 0 c) P = 2;5 P = 0;2 P = 0;0 d) P = 0;3 P = 2; 0 P = 4;4 e) P = 5;5 P = 2;2 P = 0;0 2) Ubicar los siguientes puntos A, B, C en un plano cartesiano y averiguar las coordenadas del punto D para que ABCD se un rectángulo: ( 1;3 ) ( 1;5 ) ( 5;5 ) A = B = C = 3) Representar los siguientes puntos en un plano cartesiano y agregar dos punto mas de modo tal que queden alineados con los otros tres: a) P = 2;3 Q = 2;5 T = 2;0 b) R = 5;5 S = 2;2 G = 0; 0 c) M = 1;3 N = 3;3 H = 0;3 d) A = 1;2 B = 5;6 C = 4;5 4) Representar las coordenadas en los siguientes planos e indiquen que tipo de figura representan:,,,, ( ) a) a = 1;1 b = 3;2 c = 4;4 d = 2;3 b) a = 1;1 b = 1;7 c = 4;6 ( ) c) a = 1;1 b = 4;6 c = 8;6 d = 11;1 ( ) d) a = 2; 4 b = 4;6 c = 6;4 d = 4;1 e) a = 1;5 b = 4;5 c = 1;1 ( ) ( ) ) f a = 2;2 b = 5;1 c = 8;2 d = 9;5 e = 8;8 f = 5;9 g = 2;8 h = 1;5
4 Nombre y Apellido:... Tema: ejes cartesianos Trabajo Práctico N 2 Ejercicio nº 1: Muchos niños de Retamar van al colegio a Cabo de Gata. Suelen ir en bicicleta. La primera clase empieza a las ocho y cuarto, lo que significa que la mayor parte de los alumnos ya salen de casa a las siete y media, porque llegar tarde... La distancia de Retamar al colegio es de (casi) 10 kilómetros. Las cuatro gráficas que vienen a continuación muestran cómo las cosas son distintas para Carmen, Fernando, Maruja y Yolanda cuando van al colegio. YOLANDA: Yo siempre salgo con calma. Porque yo me digo, a esas horas de la mañana no te puedes precipitar... Ya en el camino empiezo a pedalear más deprisa, porque no me gusta llegar tarde. FERNANDO: Esta mañana con la moto al cole guay del Paraguay. Bien rápido. Pero cuando casi había llegado, ploff, ploff, sin gasolina! Yo, hasta la coronilla! Moto de la mano y andando el resto. Llegué por los pelos. CARMEN: Acababa de salir de casa, cuando me di cuenta que hoy tenemos gimnasia. Y me había olvidado el chandal y las zapatillas. Que tonta verdad? Otra vez a casa para buscarlos. Después tuve que pedalear muy deprisa para llegar a tiempo. MARUJA: 1.- A quién corresponde cada gráfica? 2.- Imagínate lo que puede haber dicho Maruja.
5 Aquí tienes otra vez la gráfica de Yolanda, pero esta vez, con mayor precisión. DISTANCIA :30 7:35 7:40 7:45 7:50 7:55 8:00 8:05 8:10 8:15 8:20 TIEM PO Úsala para contestar a las siguientes preguntas: 3.- Cuántos Km había recorrido Yolanda a las 7:45? Cuántos minutos tardó Yolanda en los 5 primeros Km? Cuántos Km pedaleó entre las ocho menos cuarto y las ocho? 4.- Cómo se puede saber que Yolanda ha ido a la misma velocidad en los primeros 25 minutos (de 7:30 a 7:55)? 5.- Si Yolanda hubiera seguido con la misma velocidad, habría llegado a tiempo al colegio? Cuántos minutos de adelanto o atraso? Cómo has encontrado la respuesta? 6.- Entre qué horas, aproximadamente, fue mayor la velocidad de Yolanda? Cómo lo puedes saber? Intenta calcular a qué velocidad pedaleaba en esos momentos.
6 Nombre y Apellido:... Tema: ejes cartesianos Trabajo Práctico N La siguiente gráfica describe la variación del ruido de una moto: a) Cuánto tiempo ha durado el ruido de la moto? Cuál ha sido la intensidad máxima? b) Había ruido antes de llegar la moto? Qué intensidad de ruido se oye al acabar de pasar la moto? c) Cuál es la intensidad del ruido a los 5 segundos? d) En qué momento o momentos, la intensidad del ruido es de 90 decibelios? e) Cuánto tiempo dura el ruido máximo? 2.- La siguiente gráfica representa la variación de la velocidad de un coche: a) Cuánto tiempo ha durado su viaje? b) Qué velocidad llevaba el coche a las dos horas de viaje? c) Cuándo ha llevado el coche una velocidad de 60 km/h d) En qué tramos aumentó la velocidad? Cuándo la disminuyó? e) Qué significado das a los tramos horizontales? f) Cuál es la velocidad máxima alcanzada? Cuándo ha descansado? Cuánto tiempo? 3.- En una casa había una temperatura de 10º a la una de la tarde. Hemos ido observando el termómetro desde esa hora hasta las siete de la tarde y la temperatura ha ido cambiando de la
7 forma siguiente: durante las dos horas siguientes va subiendo hasta que alcanza la temperatura máxima ( 20º ). Después baja y entre las cuatro y las cinco se mantiene constante ( 18º ). Sigue bajando a partir de las cinco y a las seis llega a ser de 15º. De nuevo empieza a subir y llega a los 18º cuanto son las siete. Dibuja la gráfica correspondiente a la situación anterior 4.- La siguiente gráfica representa una excursión en autobús de un grupo de estudiantes, reflejando el tiempo ( en horas ) y la distancia al instituto ( en km ): a) A cuántos km estaba el lugar que visitaron? b) Cuánto tiempo duró la visita al lugar? c) Hubo alguna parada a la ida? Y a la vuelta? d) Cuánto duró la excursión completa? 5.- Se va a organizar una excursión y el precio por persona va a depender del número de excursionistas. El número máximo de plazas es de 60 y el mínimo, de 10. Se admiten solamente grupos con un número de personas que resulte múltiplo de 10. La siguiente gráfica muestra la situación:
8 a) Qué significa tiene el punto ( 20, 8 ) Y el ( 40, 4 ) b) Por qué hemos dibujado la gráfica sólo entre 10 y 60? 6.- Construye una gráfica que represente lo mejor posible las siguientes situaciones: 5) Altura de una pelota que bota, según pasa el tiempo 6) Coste de una llamada telefónica en función de su duración 7) Distancia a casa durante un paseo de ida y vuelta de 30 de duración 8) Nivel del agua en una piscina vacía al llenarla
INTERPRETACIÓN DE FUNCIONES
 INTERPRETACIÓN DE FUNCIONES 1º) Se va a organizar una excursión y el precio por persona va a depender del número de personas que vayan a dicha excursión. El número máximo de plazas es de 60, y el mínimo,
INTERPRETACIÓN DE FUNCIONES 1º) Se va a organizar una excursión y el precio por persona va a depender del número de personas que vayan a dicha excursión. El número máximo de plazas es de 60, y el mínimo,
EJERCICIOS RESUELTOS DE MÍNIMOS TEMA 6 FUNCIONES Y GRÁFICAS 3º ESO
 EJERCICIOS RESUELTOS DE MÍNIMOS TEMA 6 FUNCIONES Y GRÁFICAS 3º ESO Ejercicio nº 1.- La siguiente gráfica representa una excursión en autobús de un grupo de estudiantes, reflejando el tiempo (en horas)
EJERCICIOS RESUELTOS DE MÍNIMOS TEMA 6 FUNCIONES Y GRÁFICAS 3º ESO Ejercicio nº 1.- La siguiente gráfica representa una excursión en autobús de un grupo de estudiantes, reflejando el tiempo (en horas)
3º ESO TEMA 7.- FUNCIONES Y GRÁFICAS. Página web del profesor: Profesor: Rafael Núñez Nogales
 3º ESO TEMA 7.- FUNCIONES Y GRÁFICAS Página web del profesor: http://www.iesmontesorientales.es/mates/ 1.-LAS FUNCIONES Y SUS GRÁFICAS. (Págs: 13 y 133) 1.1.- Qué es una función? Esta gráfica representa
3º ESO TEMA 7.- FUNCIONES Y GRÁFICAS Página web del profesor: http://www.iesmontesorientales.es/mates/ 1.-LAS FUNCIONES Y SUS GRÁFICAS. (Págs: 13 y 133) 1.1.- Qué es una función? Esta gráfica representa
TEMA 7. FUNCIONES. - Variables dependiente e independiente.
 TEMA 7. FUNCIONES 7.1. Definiciones. - Función. - Variables dependiente e independiente. - Imagen y antiimagen. - Interpretación de gráficas. - Dominio y recorrido. 7.2. Propiedades de las funciones. -
TEMA 7. FUNCIONES 7.1. Definiciones. - Función. - Variables dependiente e independiente. - Imagen y antiimagen. - Interpretación de gráficas. - Dominio y recorrido. 7.2. Propiedades de las funciones. -
Resolución de exámenes. NOTA: La opción resaltada en naranja es la opción correcta.
 Resolución de exámenes NOTA: La opción resaltada en naranja es la opción correcta. Geometría Ejercicio 1: La suma de los ángulos internos de un cuadrilátero vale: A. Depende el cuadrilátero B. 90 C. 360
Resolución de exámenes NOTA: La opción resaltada en naranja es la opción correcta. Geometría Ejercicio 1: La suma de los ángulos internos de un cuadrilátero vale: A. Depende el cuadrilátero B. 90 C. 360
I.E.S. HAYGÓN CURSO 2011/20121 NOMBRE Y APELLIDOS FECHA TEMA 7: FUNCIONES
 NOMBRE Y APELLIDOS FECHA TEMA 7: FUNCIONES 1. La siguiente gráfica representa una excursión en autobús de un grupo de estudiantes, reflejando el tiempo (en horas) y la distancia al instituto (en kilómetros):
NOMBRE Y APELLIDOS FECHA TEMA 7: FUNCIONES 1. La siguiente gráfica representa una excursión en autobús de un grupo de estudiantes, reflejando el tiempo (en horas) y la distancia al instituto (en kilómetros):
Ejes cartesianos. Coordenadas de un punto
 Ejes cartesianos. Coordenadas de un punto Los elementos de una función son: la variable independiente la variable dependiente, que se representa sobre el eje horizontal o eje de abscisas,, que se representa
Ejes cartesianos. Coordenadas de un punto Los elementos de una función son: la variable independiente la variable dependiente, que se representa sobre el eje horizontal o eje de abscisas,, que se representa
Indica si las funciones son lineales y, en ese caso, determina su pendiente y su crecimiento o decrecimiento.
 . RECTAS y FUNCIONES AFINES Indica si las funciones son lineales y, en ese caso, determina su pendiente y su crecimiento o decrecimiento. a) y = c) y = e) y = b) y = d) y = + f) y = a) No es lineal. c)
. RECTAS y FUNCIONES AFINES Indica si las funciones son lineales y, en ese caso, determina su pendiente y su crecimiento o decrecimiento. a) y = c) y = e) y = b) y = d) y = + f) y = a) No es lineal. c)
TEMA 7: FUNCIONES. 7.1 Características e interpretación de una función
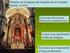 TEMA 7: FUNCIONES 7.1 Características e interpretación de una función 1. Un ciclista decide salir de ruta y durante un tiempo pedalea por un camino hasta que llega a una zona de descanso en donde se detiene
TEMA 7: FUNCIONES 7.1 Características e interpretación de una función 1. Un ciclista decide salir de ruta y durante un tiempo pedalea por un camino hasta que llega a una zona de descanso en donde se detiene
Materia: Matemática de Octavo Tema: Plano Cartesiano
 Materia: Matemática de Octavo Tema: Plano Cartesiano Kaitlyn entró en la clase de matemáticas y vio la siguiente imagen mostrada en el proyector. Su maestra les pidió a todos en la clase que duplicaran
Materia: Matemática de Octavo Tema: Plano Cartesiano Kaitlyn entró en la clase de matemáticas y vio la siguiente imagen mostrada en el proyector. Su maestra les pidió a todos en la clase que duplicaran
Trabajo Práctico 2 - ECUACIÓN DE LA RECTA
 Trabajo Práctico - ECUACIÓN DE LA RECTA ) Un barril tiene una capacidad de 00 litros. El barril se encuentra sobre una balanza y al echarle distintas cantidades de un aceite, se puede tomar el peso que
Trabajo Práctico - ECUACIÓN DE LA RECTA ) Un barril tiene una capacidad de 00 litros. El barril se encuentra sobre una balanza y al echarle distintas cantidades de un aceite, se puede tomar el peso que
I.E.S. CUADERNO Nº 11 NOMBRE: FECHA: / / Tablas y gráficas
 Tablas y gráficas Contenidos 1. Sistema de ejes coordenados Ejes cartesianos Coordenadas de un punto 2. Gráficas cartesianas Interpretar gráficas de puntos Interpretar gráficas continuas 3. Tablas y gráficas
Tablas y gráficas Contenidos 1. Sistema de ejes coordenados Ejes cartesianos Coordenadas de un punto 2. Gráficas cartesianas Interpretar gráficas de puntos Interpretar gráficas continuas 3. Tablas y gráficas
1. [2014] [EXT-A] En una localidad la concentración de polen de olivo, medida en granos de polen/m 3 de aire, se puede ajustar a la
![1. [2014] [EXT-A] En una localidad la concentración de polen de olivo, medida en granos de polen/m 3 de aire, se puede ajustar a la 1. [2014] [EXT-A] En una localidad la concentración de polen de olivo, medida en granos de polen/m 3 de aire, se puede ajustar a la](/thumbs/54/33992632.jpg) 1. [2014] [EXT-A] En una localidad la concentración de polen de olivo, medida en granos de polen/m 3 de aire, se puede ajustar a la función f(t) = t3 3-22t2 +448t-2600, siendo t el tiempo medido en semanas,
1. [2014] [EXT-A] En una localidad la concentración de polen de olivo, medida en granos de polen/m 3 de aire, se puede ajustar a la función f(t) = t3 3-22t2 +448t-2600, siendo t el tiempo medido en semanas,
tema 6: ecuaciones curso 2010/2011
 nombre: ecuaciones apellidos: Una ecuación es un igualdad entre expresiones algebraicas expresión algebraica 1 = expresión algebraica 2 En una ecuación hay dos miembros separados por un signo igual =.
nombre: ecuaciones apellidos: Una ecuación es un igualdad entre expresiones algebraicas expresión algebraica 1 = expresión algebraica 2 En una ecuación hay dos miembros separados por un signo igual =.
Interpretación de gráficas 1
 Interpretación de gráficas 1 Dos ejemplos sencillos. 1. El precio de un bolígrafo en la papelería cercana es de 0,30. Calcula y escribe en la tabla siguiente el precio de los bolígrafos que se indican.
Interpretación de gráficas 1 Dos ejemplos sencillos. 1. El precio de un bolígrafo en la papelería cercana es de 0,30. Calcula y escribe en la tabla siguiente el precio de los bolígrafos que se indican.
Características globales de las funciones
 Características globales de las funciones. Funciones Considera los rectángulos con un lado de doble longitud que el otro. Expresa el perímetro y el área en función del lado menor. P = (x + x) = x A = x
Características globales de las funciones. Funciones Considera los rectángulos con un lado de doble longitud que el otro. Expresa el perímetro y el área en función del lado menor. P = (x + x) = x A = x
FUNCIONES y = f(x) ESO3
 Las correspondencias entre conjunto de valores o magnitudes se pueden expresar de varias formas: con un enunciado, con una tabla, con una gráfica, o con una fórmula o expresión algebraica o analítica.
Las correspondencias entre conjunto de valores o magnitudes se pueden expresar de varias formas: con un enunciado, con una tabla, con una gráfica, o con una fórmula o expresión algebraica o analítica.
UNIDADES 1 y 2: FRACCIONES Y DECIMALES. POTENCIAS Y RAÍCES. NÚMEROS APROXIMADOS. 1º.- Ordena de menor a mayor las siguientes fracciones:
 UNIDADES y : FRACCIONES Y DECIMALES. POTENCIAS Y RAÍCES. NÚMEROS APROXIMADOS. º.- Ordena de menor a mayor las siguientes fracciones: ; 6 5 7 4 ; 5 4 ; ; ; 8 6 9 º.- Efectúa las siguientes operaciones y
UNIDADES y : FRACCIONES Y DECIMALES. POTENCIAS Y RAÍCES. NÚMEROS APROXIMADOS. º.- Ordena de menor a mayor las siguientes fracciones: ; 6 5 7 4 ; 5 4 ; ; ; 8 6 9 º.- Efectúa las siguientes operaciones y
La recta en el plano.
 1 CONOCIMIENTOS PREVIOS. 1 La recta en el plano. 1. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Intervalos y sus definiciones básicas. Representación
1 CONOCIMIENTOS PREVIOS. 1 La recta en el plano. 1. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Intervalos y sus definiciones básicas. Representación
TEMA 3: El movimiento rectilíneo
 Física y Química Curso 2011/12 4º E.S.O. TEMA 3: El movimiento rectilíneo 1.- Las ecuaciones de los movimientos de dos móviles que se mueven por la misma trayectoria, en las unidades del S.I. son respectivamente:
Física y Química Curso 2011/12 4º E.S.O. TEMA 3: El movimiento rectilíneo 1.- Las ecuaciones de los movimientos de dos móviles que se mueven por la misma trayectoria, en las unidades del S.I. son respectivamente:
Solución: Las rectas paralelas a estas tienen la misma pendiente, es decir 2; por tanto la ecuación es:
 Representa las rectas y = x + e y = x y calcula el punto que tienen en común El punto que tienen en común estas dos rectas se obtiene resolviendo el siguiente sistema de ecuaciones: y = x + y = x 3 x =,
Representa las rectas y = x + e y = x y calcula el punto que tienen en común El punto que tienen en común estas dos rectas se obtiene resolviendo el siguiente sistema de ecuaciones: y = x + y = x 3 x =,
Funciones. Generalidades
 Funciones. Generalidades 1.- Se suelta un globo que se eleva y, al alcanzar cierta altura, estalla. La siguiente gráfica representa la altura, con el paso del tiempo, a la que se encuentra el globo hasta
Funciones. Generalidades 1.- Se suelta un globo que se eleva y, al alcanzar cierta altura, estalla. La siguiente gráfica representa la altura, con el paso del tiempo, a la que se encuentra el globo hasta
Ecuaciones de la forma. y se sabe que pasa por el punto ( 4 ;16 ), cuál es la ecuación de la recta? con m > 0. contenga los puntos ( 2;? por qué?
 Ecuaciones de la forma y = m. Haga las gráficas de y = y = y = y = y y y y y y a. Como son las rectas b. Cuales son simétricas respecto al origen c. La recta y que tipo de simetría presenta respecto a
Ecuaciones de la forma y = m. Haga las gráficas de y = y = y = y = y y y y y y a. Como son las rectas b. Cuales son simétricas respecto al origen c. La recta y que tipo de simetría presenta respecto a
INTERPRETACIÓN DE GRÁFICAS
 INTERPRETACIÓN DE GRÁFICAS Ejercicio nº 1.- La siguiente gráfica representa una excursión en autobús de un grupo de estudiantes, reflejando el tiempo (en horas) y la distancia al instituto (en kilómetros):
INTERPRETACIÓN DE GRÁFICAS Ejercicio nº 1.- La siguiente gráfica representa una excursión en autobús de un grupo de estudiantes, reflejando el tiempo (en horas) y la distancia al instituto (en kilómetros):
EJERCICIOS DE REPASO DE MATEMÁTICAS I PENDIENTES
 EJERCICIOS DE REPASO DE MATEMÁTICAS I PENDIENTES 1 er PARCIAL 1. Obtén los valores reales que cumplen las siguientes condiciones: x+ x 3 5 x 1/ =1. Opera y expresa el resultado en notación científic (5,
EJERCICIOS DE REPASO DE MATEMÁTICAS I PENDIENTES 1 er PARCIAL 1. Obtén los valores reales que cumplen las siguientes condiciones: x+ x 3 5 x 1/ =1. Opera y expresa el resultado en notación científic (5,
MATEMÁTICA: TRABAJO PRÁCTICO 2. Funciones. 1) Carlos está enfermo. Veamos la gráfica de la evolución de su temperatura.
 ILSE-2º Año- MATEMÁTICA: TRABAJO PRÁCTICO 2 Funciones 1) Carlos está enfermo. Veamos la gráfica de la evolución de su temperatura. a) Cuántos días ha estado enfermo el paciente? (Se considera normal una
ILSE-2º Año- MATEMÁTICA: TRABAJO PRÁCTICO 2 Funciones 1) Carlos está enfermo. Veamos la gráfica de la evolución de su temperatura. a) Cuántos días ha estado enfermo el paciente? (Se considera normal una
Observando la gráfica anterior, responder:
 1. Un ciclista decide salir de ruta y durante un tiempo pedalea por un camino hasta que llega a una zona de descanso en donde se detiene para comer. A continuación, sigue avanzando durante otro rato más,
1. Un ciclista decide salir de ruta y durante un tiempo pedalea por un camino hasta que llega a una zona de descanso en donde se detiene para comer. A continuación, sigue avanzando durante otro rato más,
FISICA I HOJA 3 ESCUELA POLITÉCNICA DE INGENIERÍA DE MINAS Y ENERGIA 3. CINEMÁTICA FORMULARIO
 3. CINEMÁTICA FORMULARIO 3.1) El golpe de una piedra al caer a un pozo se oye al cabo de 4,33 s. Calcular la profundidad del pozo sabiendo que la velocidad del sonido es 330 m.s -1. 3.2) Un ascensor sube
3. CINEMÁTICA FORMULARIO 3.1) El golpe de una piedra al caer a un pozo se oye al cabo de 4,33 s. Calcular la profundidad del pozo sabiendo que la velocidad del sonido es 330 m.s -1. 3.2) Un ascensor sube
GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA
 ESCUELA PREPARATORIA OFICIAL No. 268 GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA Profra: Citlalli Artemisa García García 1) Qué es la pendiente? 2) Cómo es la pendiente de rectas
ESCUELA PREPARATORIA OFICIAL No. 268 GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA Profra: Citlalli Artemisa García García 1) Qué es la pendiente? 2) Cómo es la pendiente de rectas
Ejemplo Traza la gráfica de los puntos: ( 5, 4), (3, 2), ( 2, 0), ( 1, 3), (0, 4) y (5, 1) en el plano cartesiano.
 Plano cartesiano El plano cartesiano se forma con dos rectas perpendiculares, cuyo punto de intersección se denomina origen. La recta horizontal recibe el nombre de eje X o eje de las abscisas y la recta
Plano cartesiano El plano cartesiano se forma con dos rectas perpendiculares, cuyo punto de intersección se denomina origen. La recta horizontal recibe el nombre de eje X o eje de las abscisas y la recta
MATEMÁTICAS 2º DE ESO
 MATEMÁTICAS 2º DE ESO LOE TEMA VII: FUNCIONES Y GRÁFICAS Coordenadas cartesianas. Concepto de función. Tabla y ecuación. Representación gráfica de una función. Estudio gráfico de una función. o Continuidad
MATEMÁTICAS 2º DE ESO LOE TEMA VII: FUNCIONES Y GRÁFICAS Coordenadas cartesianas. Concepto de función. Tabla y ecuación. Representación gráfica de una función. Estudio gráfico de una función. o Continuidad
C.P.F.P.A. San Francisco de Asís. Dolores. EJERCICIOS 2ª EVALUACIÓN. FÍSICA
 EJERCICIOS 2ª EVALUACIÓN. FÍSICA 1. Un tren de alta velocidad (AVE) viaja durante media hora con una velocidad constante de 252 Km/h. A continuación reduce su velocidad hasta pararse en 14 s. a) Describe
EJERCICIOS 2ª EVALUACIÓN. FÍSICA 1. Un tren de alta velocidad (AVE) viaja durante media hora con una velocidad constante de 252 Km/h. A continuación reduce su velocidad hasta pararse en 14 s. a) Describe
INSTITUTO SANTA CECILIA - MATEMÁTICA
 INSTITUTO SANTA CECILIA - MATEMÁTICA MÓDULO DE ORIENTACIÓN Cursos: 1º A y B 1) Se colocaron 15 filas con 35 árboles en un bosque. Para el siguiente año se quiere cuadruplicar la cantidad de árboles. Señalar
INSTITUTO SANTA CECILIA - MATEMÁTICA MÓDULO DE ORIENTACIÓN Cursos: 1º A y B 1) Se colocaron 15 filas con 35 árboles en un bosque. Para el siguiente año se quiere cuadruplicar la cantidad de árboles. Señalar
EJERCICIOS RESUELTOS TEMA 11 Y 12. FUNCIONES. FUNCIÓN LINEAL Y CUADRÁTICA. Apellidos y Nombre:.Curso: 3º E.S.O. Grupo:.
 EJERCICIS RESUELTS TEMA 11 1. FUNCINES. FUNCIÓN LINEAL CUADRÁTICA Apellidos y Nombre:.Curso: º E.S.. Grupo:. 1 El coste del recibo del teléfono depende de los minutos hablados y una cuota fija de 1 euros.
EJERCICIS RESUELTS TEMA 11 1. FUNCINES. FUNCIÓN LINEAL CUADRÁTICA Apellidos y Nombre:.Curso: º E.S.. Grupo:. 1 El coste del recibo del teléfono depende de los minutos hablados y una cuota fija de 1 euros.
s(m) t(s) TEMA 1: EL MOVIMIENTO CARACTERÍSTICAS DEL MOVIMIENTO
 TEMA 1: EL MOVIMIENTO CARACTERÍSTICAS DEL MOVIMIENTO 1. Por qué se dice que todos los movimientos son relativos?. Responde de forma razonada las siguientes cuestiones: a. Cómo se clasifican los movimientos
TEMA 1: EL MOVIMIENTO CARACTERÍSTICAS DEL MOVIMIENTO 1. Por qué se dice que todos los movimientos son relativos?. Responde de forma razonada las siguientes cuestiones: a. Cómo se clasifican los movimientos
Física 4º E.S.O. 2015/16
 Física 4º E.S.O. 2015/16 TEMA 3: El movimiento rectilíneo Ficha número 6 1.- Las ecuaciones de los movimientos de dos móviles que se mueven por la misma trayectoria, en las unidades del S.I. son respectivamente:
Física 4º E.S.O. 2015/16 TEMA 3: El movimiento rectilíneo Ficha número 6 1.- Las ecuaciones de los movimientos de dos móviles que se mueven por la misma trayectoria, en las unidades del S.I. son respectivamente:
Sistema de coordenadas. Plano cartesiano
 Geometría analítica La geometría analítica estudia las figuras geométricas mediante técnicas básicas del análisis matemático y del álgebra en un determinado sistema de coordenadas.. Actualmente la geometría
Geometría analítica La geometría analítica estudia las figuras geométricas mediante técnicas básicas del análisis matemático y del álgebra en un determinado sistema de coordenadas.. Actualmente la geometría
UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE LA RECTA
 C u r s o : Matemática Material N 8 GUÍA TEÓRICO PRÁCTICA Nº 5 UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE LA RECTA SISTEMA CARTESIANO ORTOGONAL Para determinar la posición de los puntos de un plano usando
C u r s o : Matemática Material N 8 GUÍA TEÓRICO PRÁCTICA Nº 5 UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE LA RECTA SISTEMA CARTESIANO ORTOGONAL Para determinar la posición de los puntos de un plano usando
UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE LA RECTA
 C u r s o : Matemática Material N 18 UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE LA RECTA GUÍA TEÓRICO PRÁCTICA Nº 15 SISTEMA CARTESIANO ORTOGONAL Para determinar la posición de los puntos de un plano usando
C u r s o : Matemática Material N 18 UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE LA RECTA GUÍA TEÓRICO PRÁCTICA Nº 15 SISTEMA CARTESIANO ORTOGONAL Para determinar la posición de los puntos de un plano usando
Representación gráfica de funciones. De la fórmula a la tabla. Resolución de problemas
 REPRESENTACIÓN DE PUNTOS EN EL PLANO RELACIÓN ENTRE DOS MAGNITUDES Ejes de coordenadas y coordenadas de puntos FUNCIÓN Tipos: - Lineal. - Afín. - Constante. - De proporcionalidad inversa. - Cuadrática.
REPRESENTACIÓN DE PUNTOS EN EL PLANO RELACIÓN ENTRE DOS MAGNITUDES Ejes de coordenadas y coordenadas de puntos FUNCIÓN Tipos: - Lineal. - Afín. - Constante. - De proporcionalidad inversa. - Cuadrática.
Tablas y gráficas. Objetivos. Antes de empezar. 1.Sistema de ejes coordenados pág. 178 Ejes cartesianos Coordenadas de un punto
 11 Tablas y gráficas Objetivos En esta quincena aprenderás a: Representar puntos en el plano Calcular las coordenadas de un punto Construir e interpretar gráficas cartesianas Construir e interpretar tablas
11 Tablas y gráficas Objetivos En esta quincena aprenderás a: Representar puntos en el plano Calcular las coordenadas de un punto Construir e interpretar gráficas cartesianas Construir e interpretar tablas
Función de proporcionalidad directa
 Gráficos de proporcionalidad Resultados de Aprendizaje: Generar gráficos a partir de tablas de datos Calcular constantes de proporcionalidad Diseñar gráficos que representan relaciones proporcionales Síntesis
Gráficos de proporcionalidad Resultados de Aprendizaje: Generar gráficos a partir de tablas de datos Calcular constantes de proporcionalidad Diseñar gráficos que representan relaciones proporcionales Síntesis
El análisis cartesiano (René Descartes ) descubrió que las ecuaciones pueden tener una representación gráfica.
 Capítulo 4. Estudio de la línea recta El análisis cartesiano (René Descartes 1596-1650) descubrió que las ecuaciones pueden tener una representación gráfica. Para lograr esa representación gráfica es necesario
Capítulo 4. Estudio de la línea recta El análisis cartesiano (René Descartes 1596-1650) descubrió que las ecuaciones pueden tener una representación gráfica. Para lograr esa representación gráfica es necesario
1 Indica cuáles de las siguientes parábolas están abiertas hacia arriba y cuáles hacia abajo:
 Indica cuáles de las siguientes parábolas están abiertas hacia arriba y cuáles hacia abajo: 3 + x y = 3 x x + x 3 + x y = 3 x x + x Abierta hacia arriba Abierta hacia abajo Abierta hacia abajo Calcula
Indica cuáles de las siguientes parábolas están abiertas hacia arriba y cuáles hacia abajo: 3 + x y = 3 x x + x 3 + x y = 3 x x + x Abierta hacia arriba Abierta hacia abajo Abierta hacia abajo Calcula
Por ejemplo, la necesidad de representar el dinero adeudado, temperatura bajo cero, profundidades con respecto al nivel del mar, etc.
 NÚMEROS ENTEROS 1. LOS NÚMEROS ENTEROS. Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el sustraendo, pero en la vida nos encontramos con operaciones de este
NÚMEROS ENTEROS 1. LOS NÚMEROS ENTEROS. Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el sustraendo, pero en la vida nos encontramos con operaciones de este
GUIA Nº3. FUNCIONES 2º MEDIO A) 30 B) 20 C) 10 D) 0 E) -10. A) sólo I B) sólo III C) I y II D) II y III E) I, II y III
 Colegio Raimapu Departamento de Matemática GUIA Nº. FUNCIONES º MEDIO 1. Si f(x)= x + 10 y f(b)= 0, entonces b es igual a: A) 0 B) 0 C) 10 D) 0 E) -10. Si f(x) = x ; Cuál(es) de las siguientes afirmaciones
Colegio Raimapu Departamento de Matemática GUIA Nº. FUNCIONES º MEDIO 1. Si f(x)= x + 10 y f(b)= 0, entonces b es igual a: A) 0 B) 0 C) 10 D) 0 E) -10. Si f(x) = x ; Cuál(es) de las siguientes afirmaciones
COLEGIO NIÑO JESÚS CURSO 2013/2014. Nombre: Curso:
 COLEGIO NIÑO JESÚS CURSO 2013/2014 Nombre: Curso: RAP MATEMÁTICAS 3º ESO. PRIMER TRIMESTRE. 1. Calcula: 5 2 28 14 7 3 5 2. Efectúa y simplifica: 1 1 1 1 2 : 3 2 3 3 2 3. Un campesino tiene alimento para
COLEGIO NIÑO JESÚS CURSO 2013/2014 Nombre: Curso: RAP MATEMÁTICAS 3º ESO. PRIMER TRIMESTRE. 1. Calcula: 5 2 28 14 7 3 5 2. Efectúa y simplifica: 1 1 1 1 2 : 3 2 3 3 2 3. Un campesino tiene alimento para
1. Conceptos básicos para estudiar el movimiento.
 Contenidos Tema 4: EL MOVIMIENTO 1. CONCEPTOS BÁSICOS PARA ESTUDIAR EL MOVIMIENTO. 2. LA VELOCIDAD 3. ECUACIÓN DEL MOVIMIENTO 4. MOVIMIENTO RECTILÍNEO Y UNIFORME (M.R.U.) 5. LA ACELERACIÓN 6. MOVIMIENTO
Contenidos Tema 4: EL MOVIMIENTO 1. CONCEPTOS BÁSICOS PARA ESTUDIAR EL MOVIMIENTO. 2. LA VELOCIDAD 3. ECUACIÓN DEL MOVIMIENTO 4. MOVIMIENTO RECTILÍNEO Y UNIFORME (M.R.U.) 5. LA ACELERACIÓN 6. MOVIMIENTO
GEOMETRÍA ANALÍTICA DEL PLANO
 GEOMETRÍA ANALÍTICA DEL PLANO 1 UNIDAD DIDÁCTICA 5: Geometría analítica del plano 1. ÍNDICE 1. Sistemas de referencia y coordenadas puntuales 2. Distancia entre dos puntos del plano 3. Coordenadas del
GEOMETRÍA ANALÍTICA DEL PLANO 1 UNIDAD DIDÁCTICA 5: Geometría analítica del plano 1. ÍNDICE 1. Sistemas de referencia y coordenadas puntuales 2. Distancia entre dos puntos del plano 3. Coordenadas del
Funciones y gráficas. La bruja de Agnesi
 3 Funciones y gráficas La bruja de Agnesi Los ágiles dedos acariciaban las cuerdas y arrancaban dulces sonidos al arpa. María Agnesi se relajó por un momento. Oír a su hermana Teresa tocar el arpa hacía
3 Funciones y gráficas La bruja de Agnesi Los ágiles dedos acariciaban las cuerdas y arrancaban dulces sonidos al arpa. María Agnesi se relajó por un momento. Oír a su hermana Teresa tocar el arpa hacía
D1 Generalidades: El punto
 El sistema diédrico D1 Generalidades: El punto Generalidades Proyección ortogonal de un punto sobre un plano Proyección ortogonal o, simplemente proyección de un punto sobre un plano, es el pie de la perpendicular
El sistema diédrico D1 Generalidades: El punto Generalidades Proyección ortogonal de un punto sobre un plano Proyección ortogonal o, simplemente proyección de un punto sobre un plano, es el pie de la perpendicular
1 Las gráficas siguientes representan a un móvil que se mueve con movimiento uniformemente acelerado. Explica su significado.
 1 Las gráficas siguientes representan a un móvil que se mueve con movimiento uniformemente acelerado. Explica su significado. Gráfica A. Representa la variación de la posición con el tiempo, como en tiempos
1 Las gráficas siguientes representan a un móvil que se mueve con movimiento uniformemente acelerado. Explica su significado. Gráfica A. Representa la variación de la posición con el tiempo, como en tiempos
Funciones: Tablas, gráficos y fórmulas
 Funciones: Tablas, gráficos y fórmulas TEMA: FUNCIONES Una función es una relación entre dos magnitudes de forma que a cada valor de la primera magnitud, llamada variable independiente, le corresponde
Funciones: Tablas, gráficos y fórmulas TEMA: FUNCIONES Una función es una relación entre dos magnitudes de forma que a cada valor de la primera magnitud, llamada variable independiente, le corresponde
UNIDAD DE APRENDIZAJE III
 UNIDAD DE APRENDIZAJE III Saberes procedimentales 1. Utiliza correctamente el lenguaje algebraico, geométrico y trigonométrico.. Identifica la simbología propia de la geometría y la trigonometría. Saberes
UNIDAD DE APRENDIZAJE III Saberes procedimentales 1. Utiliza correctamente el lenguaje algebraico, geométrico y trigonométrico.. Identifica la simbología propia de la geometría y la trigonometría. Saberes
8.- GEOMETRÍA ANÁLITICA
 8.- GEOMETRÍA ANÁLITICA 1.- PROBLEMAS EN EL PLANO 1. Dados los puntos A = (1, 2), B = (-1, 3), C = (3, 4) y D = (1, 0) halla las coordenadas de los vectores AB, BC, CD, DA y AC. Solución: AB = (-2, 1),
8.- GEOMETRÍA ANÁLITICA 1.- PROBLEMAS EN EL PLANO 1. Dados los puntos A = (1, 2), B = (-1, 3), C = (3, 4) y D = (1, 0) halla las coordenadas de los vectores AB, BC, CD, DA y AC. Solución: AB = (-2, 1),
UNIDAD 10. LAS FUNCIONES LINEALES ESQUEMA DE LA UNIDAD FICHA DE TRABAJO A FICHA DE TRABAJO B SOLUCIONES
 UNIDAD. LAS FUNCIONES LINEALES ESQUEMA DE LA UNIDAD FICHA DE TRABAJO A FICHA DE TRABAJO B SOLUCIONES ESQUEMA DE LA UNIDAD LAS FUNCIONES LINEALES Nombre y apellidos:... Curso:... Fecha:... LAS FUNCIONES
UNIDAD. LAS FUNCIONES LINEALES ESQUEMA DE LA UNIDAD FICHA DE TRABAJO A FICHA DE TRABAJO B SOLUCIONES ESQUEMA DE LA UNIDAD LAS FUNCIONES LINEALES Nombre y apellidos:... Curso:... Fecha:... LAS FUNCIONES
INSTITUCIÓN EDUCATIVA INSTITUTO AGRICOLA JORNADA DIURNA GUÍA DE TRABAJO # 11 AREA: MATEMÁTICAS AGISNATURA: ARITMÉTICA GRADO: SEXTO
 AREA: MATEMÁTICAS AGISNATURA: ARITMÉTICA GRADO: SEXTO Instrucciones. Lee cuidadosamente los conceptos, los ejemplos y desarrolla los ejercicios propuestos. No olvides guardar esta guía de trabajo en tu
AREA: MATEMÁTICAS AGISNATURA: ARITMÉTICA GRADO: SEXTO Instrucciones. Lee cuidadosamente los conceptos, los ejemplos y desarrolla los ejercicios propuestos. No olvides guardar esta guía de trabajo en tu
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág. PÁGIN 5 EJERCICIOS Interpretación de puntos Dibuja sobre un papel cuadriculado unos ejes coordenados y representa los siguientes puntos: (, ); (, 7); C (4, ); D ( 4, ); E ( 6, ); F (0, 5); G (, 0);
Pág. PÁGIN 5 EJERCICIOS Interpretación de puntos Dibuja sobre un papel cuadriculado unos ejes coordenados y representa los siguientes puntos: (, ); (, 7); C (4, ); D ( 4, ); E ( 6, ); F (0, 5); G (, 0);
INTERPRETACIÓN DE GRÁFICAS
 INTERPRETACIÓN DE GRÁFICAS 1. En la siguiente gráfica tienes dibujada una vasija y, a su derecha, la gráfica correspondiente que relaciona la altura del agua con el tiempo de llenado: Completa las otras
INTERPRETACIÓN DE GRÁFICAS 1. En la siguiente gráfica tienes dibujada una vasija y, a su derecha, la gráfica correspondiente que relaciona la altura del agua con el tiempo de llenado: Completa las otras
Curso º ESO. UNIDAD 8: FUNCIONES Departamento de Matemáticas IES Fray Bartolomé de las Casas (Morón)
 Curso 2º ESO UNIDAD 8: FUNCIONES Departamento de Matemáticas IES Fray Bartolomé de las Casas (Morón) OBJETIVOS CONTENIDOS PROCEDIMIENTOS 1. Conocer qué es una función y cómo expresarla. 2. Reconocer las
Curso 2º ESO UNIDAD 8: FUNCIONES Departamento de Matemáticas IES Fray Bartolomé de las Casas (Morón) OBJETIVOS CONTENIDOS PROCEDIMIENTOS 1. Conocer qué es una función y cómo expresarla. 2. Reconocer las
LA RECTA Y SUS ECUACIONES
 UNIDAD LA RECTA Y SUS ECUACIONES EJERCICIOS RESUELTOS Objetivo general. Al terminar esta Unidad resolverás ejercicios y problemas correspondientes a las rectas en el plano y sus ecuaciones. Objetivo. Recordarás
UNIDAD LA RECTA Y SUS ECUACIONES EJERCICIOS RESUELTOS Objetivo general. Al terminar esta Unidad resolverás ejercicios y problemas correspondientes a las rectas en el plano y sus ecuaciones. Objetivo. Recordarás
ECUACIÓN GENERAL DE LA RECTA
 ECUACIÓN GENERAL DE LA RECTA Sugerencias para quien imparte el curso En los ejemplos que se proponen, se debe tratar en la medida de lo posible que el propio alumno encuentre las respuestas y llegue a
ECUACIÓN GENERAL DE LA RECTA Sugerencias para quien imparte el curso En los ejemplos que se proponen, se debe tratar en la medida de lo posible que el propio alumno encuentre las respuestas y llegue a
que asocia a cada número entero su triple menos dos:
 Dada la función f que asocia a cada número entero su triple menos dos: a) Escribe la epresión que nos proporciona f 0,, b) Calcula la imagen para ) Dada la siguiente función : ), ) y 0) a) Calcula b) Determina
Dada la función f que asocia a cada número entero su triple menos dos: a) Escribe la epresión que nos proporciona f 0,, b) Calcula la imagen para ) Dada la siguiente función : ), ) y 0) a) Calcula b) Determina
1 Función de proporcionalidad y = mx
 Unidad. Funciones lineales y cuadráticas Función de proporcionalidad y = mx Página. Dibuja sobre unos ejes cartesianos, en papel cuadriculado, dos rectas que pasen por el origen y que tengan pendientes
Unidad. Funciones lineales y cuadráticas Función de proporcionalidad y = mx Página. Dibuja sobre unos ejes cartesianos, en papel cuadriculado, dos rectas que pasen por el origen y que tengan pendientes
unicoos Funciones lineales Objetivos 1.Función de proporcionalidad directa pág. 170 Definición Representación gráfica
 10 Funciones lineales Objetivos En esta lección aprenderás a: Identificar problemas en los que intervienen magnitudes directamente proporcionales. Calcular la función que relaciona a esas magnitudes a
10 Funciones lineales Objetivos En esta lección aprenderás a: Identificar problemas en los que intervienen magnitudes directamente proporcionales. Calcular la función que relaciona a esas magnitudes a
INSTITUCIÓN EDUCATIVA SAN PEDRO CLAVER DEPARTAMENTO DE INGLÉS FECHA: 31 DE AGOSTO AL 11 DE SEPTIEMBRE 2015
 DOCENTE: Juan de Dios Varelas GRADO: 5º A-B-C-D- E - F TEMA: EL CUBO Y ORTOEDRO FECHA: 31 DE AGOSTO AL 11 DE SEPTIEMBRE 2015 ESTANDAR: construyo y descompongo figuras y sólidos a partir de condiciones
DOCENTE: Juan de Dios Varelas GRADO: 5º A-B-C-D- E - F TEMA: EL CUBO Y ORTOEDRO FECHA: 31 DE AGOSTO AL 11 DE SEPTIEMBRE 2015 ESTANDAR: construyo y descompongo figuras y sólidos a partir de condiciones
CALCULO DIFERENCIAL Escuela Colombiana de Ingeniería. Geometría Analítica = Unión de Álgebra con la Geometría.
 PRELIMINARES. COORDENADAS EN UN PLANO Cuando se trabaja un sistema de coordenadas Geometría Analítica = Unión de Álgebra con la Geometría. La geometría Analítica se origina al asignar coordenadas numéricas
PRELIMINARES. COORDENADAS EN UN PLANO Cuando se trabaja un sistema de coordenadas Geometría Analítica = Unión de Álgebra con la Geometría. La geometría Analítica se origina al asignar coordenadas numéricas
FICHA 2: Ejercicios ecuación MU y gráficas
 FICHA 2: Ejercicios ecuación MU y gráficas 1. Escribe la ecuación del movimiento en los casos: a) S 0 = 0 m con v = 2 m/s b) S 0 = 2 m con v = 5 m/s c) S 0 = -5 m con v = -3 5 m/s d) S 0 = 0 5 m con v
FICHA 2: Ejercicios ecuación MU y gráficas 1. Escribe la ecuación del movimiento en los casos: a) S 0 = 0 m con v = 2 m/s b) S 0 = 2 m con v = 5 m/s c) S 0 = -5 m con v = -3 5 m/s d) S 0 = 0 5 m con v
En mi pueblo han hecho un carril-bici que une los edificios más importantes con la fuente de la plaza.
 EL CARRIL-BICI En mi pueblo han hecho un carril-bici que une los edificios más importantes con la fuente de la plaza. PREGUNTA 1. Fíjate en el dibujo y responde: A. Cuál es la forma geométrica que tiene
EL CARRIL-BICI En mi pueblo han hecho un carril-bici que une los edificios más importantes con la fuente de la plaza. PREGUNTA 1. Fíjate en el dibujo y responde: A. Cuál es la forma geométrica que tiene
TEMA 1: MOVIMIENTO RECTILÍNEO UNIFORME.
 Física y Química 4 ESO M.R.U. Pág. 1 TEMA 1: MOVIMIENTO RECTILÍNEO UNIFORME. La cinemática es la parte de la física que estudia el movimiento de los cuerpos. Cuando un cuerpo cambia de posición a lo largo
Física y Química 4 ESO M.R.U. Pág. 1 TEMA 1: MOVIMIENTO RECTILÍNEO UNIFORME. La cinemática es la parte de la física que estudia el movimiento de los cuerpos. Cuando un cuerpo cambia de posición a lo largo
COLEGIO INTERNACIONAL SEK-CATALUNYA
 COLEGIO INTERNACIONAL SEK-CATALUNYA Curso 01/13 4º ESO Ejercicios: Cinemática AUTOEVALUACIÓN Ejercicio 1: Dos móviles se encuentran a 500 m de distancia y se acercan con velocidades de 0 m/s y 15 m/s dirigidas
COLEGIO INTERNACIONAL SEK-CATALUNYA Curso 01/13 4º ESO Ejercicios: Cinemática AUTOEVALUACIÓN Ejercicio 1: Dos móviles se encuentran a 500 m de distancia y se acercan con velocidades de 0 m/s y 15 m/s dirigidas
EL MOVIMIENTO EJERCICIOS
 EL MOVIMIENTO EJERCICIOS MOVIMIENTO RECTILÍNEO UNIFORME 1) Un móvil con Movimiento Rectilíneo Uniforme (MRU) tiene una velocidad de 3 m/s. Calcula la distancia que recorre en 12 segundos. 2) La velocidad
EL MOVIMIENTO EJERCICIOS MOVIMIENTO RECTILÍNEO UNIFORME 1) Un móvil con Movimiento Rectilíneo Uniforme (MRU) tiene una velocidad de 3 m/s. Calcula la distancia que recorre en 12 segundos. 2) La velocidad
TEMA 2: EL MOVIMIENTO
 TEMA 2: EL MOVIMIENTO 1.- Introducción. 2.- Características del movimiento. 2.1.- Posición. 2.2.- Trayectoria. 2.3.- Desplazamiento. 2.4.- Velocidad. 2.5.- Aceleración. 1.- INTRODUCCIÓN La Cinemática es
TEMA 2: EL MOVIMIENTO 1.- Introducción. 2.- Características del movimiento. 2.1.- Posición. 2.2.- Trayectoria. 2.3.- Desplazamiento. 2.4.- Velocidad. 2.5.- Aceleración. 1.- INTRODUCCIÓN La Cinemática es
En la notación C(3) se indica el valor de la cuenta para 3 kilowatts-hora: C(3) = 60 (3) = 1.253
 Eje temático: Álgebra y funciones Contenidos: Operatoria con expresiones algebraicas Nivel: 2 Medio Funciones 1. Funciones En la vida diaria encontramos situaciones en las que aparecen valores que varían
Eje temático: Álgebra y funciones Contenidos: Operatoria con expresiones algebraicas Nivel: 2 Medio Funciones 1. Funciones En la vida diaria encontramos situaciones en las que aparecen valores que varían
TRABAJO PRÁCTICO N 1: CONCEPTOS BÁSICOS
 PROFESORADO EN EDUCACIÓN SECUNDARIA DE LA MODALIDAD TÉCNICO PROFESIONAL EN CONCURRENCIA CON EL TÍTULO DE BASE. ESPACIO CURRICULAR: FÍSICA AÑO: 010 PROFESORES: BERTONI, JUAN; ; CATALDO JORGE; ; GARCÍA,
PROFESORADO EN EDUCACIÓN SECUNDARIA DE LA MODALIDAD TÉCNICO PROFESIONAL EN CONCURRENCIA CON EL TÍTULO DE BASE. ESPACIO CURRICULAR: FÍSICA AÑO: 010 PROFESORES: BERTONI, JUAN; ; CATALDO JORGE; ; GARCÍA,
CINEMÁTICA 1. Sistema de referencia. 2. Trayectoria. 3. Velocidad. 4. Aceleración. 5. Movimientos simples. 6. Composición de movimientos.
 CINEMÁTICA 1. Sistema de referencia. 2. Trayectoria. 3. Velocidad. 4. Aceleración. 5. Movimientos simples. 6. Composición de movimientos. Física 1º bachillerato Cinemática 1 CINEMÁTICA La cinemática es
CINEMÁTICA 1. Sistema de referencia. 2. Trayectoria. 3. Velocidad. 4. Aceleración. 5. Movimientos simples. 6. Composición de movimientos. Física 1º bachillerato Cinemática 1 CINEMÁTICA La cinemática es
OBJETIVOS CONTENIDOS PROCEDIMIENTOS
 898 _ 09-08.qd /9/0 :0 Página 9 Funciones INTRODUCCIÓN Partiendo de la representación de los números enteros en la recta numérica, introducimos la representación de puntos en el plano mediante la asignación
898 _ 09-08.qd /9/0 :0 Página 9 Funciones INTRODUCCIÓN Partiendo de la representación de los números enteros en la recta numérica, introducimos la representación de puntos en el plano mediante la asignación
CENTRO ESCOLAR REPUBLICA DE NICARAGUA EXAMEN PRIMER PERIODO DE MATEMÁTICA NOVENO GRADO
 CENTRO ESCOLAR REPUBLICA DE NICARAGUA EXAMEN PRIMER PERIODO DE MATEMÁTICA NOVENO GRADO Alumno: sección: lista: Profesor: Santos Jonathan Tzun Meléndez. Periodo: I INDICACIONES: La prueba consta de veinticinco
CENTRO ESCOLAR REPUBLICA DE NICARAGUA EXAMEN PRIMER PERIODO DE MATEMÁTICA NOVENO GRADO Alumno: sección: lista: Profesor: Santos Jonathan Tzun Meléndez. Periodo: I INDICACIONES: La prueba consta de veinticinco
I.E.S. HAYGÓN CURSO 2011/20121 NOMBRE Y APELLIDOS FECHA REPASO EXAMEN DE RECUPERACIÓN
 NOMBRE Y APELLIDOS FECHA REPASO EXAMEN DE RECUPERACIÓN 1. Calcula y simplifica el resultado. 3 4 1 9 1 2 a) 6 45 9 10 5 15 2 2 1 3 1 b) : 4 2 2 3 2 2. Calcula 3. a) El 28% de 375. b) Halla el tanto por
NOMBRE Y APELLIDOS FECHA REPASO EXAMEN DE RECUPERACIÓN 1. Calcula y simplifica el resultado. 3 4 1 9 1 2 a) 6 45 9 10 5 15 2 2 1 3 1 b) : 4 2 2 3 2 2. Calcula 3. a) El 28% de 375. b) Halla el tanto por
5 2,7; ; ; 3; 3,2
 Actividades de recuperación para septiembre 3º ESO, MATEMÁTICAS La recuperación de la asignatura consta de dos partes: Entregar los siguientes ejercicios resueltos correctamente. Aprobar el examen de recuperación.
Actividades de recuperación para septiembre 3º ESO, MATEMÁTICAS La recuperación de la asignatura consta de dos partes: Entregar los siguientes ejercicios resueltos correctamente. Aprobar el examen de recuperación.
MATEMÁTICA - TERCERO - REVISIÓN INTEGRADORA. 1) Determinar k y h para que las rectas kx+2y-h=0, 4x+ky-2=0, se corten en un punto.
 MATEMÁTICA - TERCERO - REVISIÓN INTEGRADORA ) Determinar k y h para que las rectas kxy-h=0, 4xky-=0, se corten en un punto ) La recta r: 5 x y 9 = 0, corta a la recta y = x en el punto A Obtener la ecuación
MATEMÁTICA - TERCERO - REVISIÓN INTEGRADORA ) Determinar k y h para que las rectas kxy-h=0, 4xky-=0, se corten en un punto ) La recta r: 5 x y 9 = 0, corta a la recta y = x en el punto A Obtener la ecuación
Localizando pares ordenados
 DMINI DE ÁLGEBRA: Curso I MÓDUL 2: Ecuaciones funciones lineales Localizando pares ordenados Realiza las siguientes actividades, mientras trabajas con el tutorial.. La recta numérica horizontal se conoce
DMINI DE ÁLGEBRA: Curso I MÓDUL 2: Ecuaciones funciones lineales Localizando pares ordenados Realiza las siguientes actividades, mientras trabajas con el tutorial.. La recta numérica horizontal se conoce
MANZANAS. Un granjero plantó árboles de manzana siguiendo un patrón cuadrado. Para protegerlos del viento, plantó pinos alrededor del huerto.
 AZAA Un granjero plantó árboles de manzana siguiendo un patrón cuadrado. ara protegerlos del viento, plantó pinos alrededor del huerto. A continuación se presentan diagramas de esta situación, donde podrás
AZAA Un granjero plantó árboles de manzana siguiendo un patrón cuadrado. ara protegerlos del viento, plantó pinos alrededor del huerto. A continuación se presentan diagramas de esta situación, donde podrás
PRUEBA DE LA EVALUACIÓN DE DIAGNÓSTICO
 Alumno/a Nº: Grupo: Centro: Localidad: Provincia: Eres chica o chico? Chica Chico Marca con una cruz (X) PRUEBA DE LA EVALUACIÓN DE DIAGNÓSTICO COMPETENCIA BÁSICA EN MATEMÁTICAS 4º Educación Primaria INSTRUCCIONES
Alumno/a Nº: Grupo: Centro: Localidad: Provincia: Eres chica o chico? Chica Chico Marca con una cruz (X) PRUEBA DE LA EVALUACIÓN DE DIAGNÓSTICO COMPETENCIA BÁSICA EN MATEMÁTICAS 4º Educación Primaria INSTRUCCIONES
UNIDAD DIDÁCTICA 5: Geometría analítica del plano
 UNIDAD DIDÁCTICA 5: Geometría analítica del plano 1. ÍNDICE 1. Sistemas de referencia y coordenadas puntuales 2. Distancia entre dos puntos del plano 3. Coordenadas del punto medio de un segmento 4. La
UNIDAD DIDÁCTICA 5: Geometría analítica del plano 1. ÍNDICE 1. Sistemas de referencia y coordenadas puntuales 2. Distancia entre dos puntos del plano 3. Coordenadas del punto medio de un segmento 4. La
NOMBRE Y APELLIDOS REPASO DE MATEMÁTICAS 1ºESO
 NOMBRE Y APELLIDOS REPASO DE MATEMÁTICAS 1ºESO 1. Responde a las preguntas y justifica tu respuesta: a) El número 14 es divisor de 56? Explica por qué. b) El número 310 es múltiplo de 31? Explica por qué.
NOMBRE Y APELLIDOS REPASO DE MATEMÁTICAS 1ºESO 1. Responde a las preguntas y justifica tu respuesta: a) El número 14 es divisor de 56? Explica por qué. b) El número 310 es múltiplo de 31? Explica por qué.
Dirección Regional de Educación de Lima Metropolitana EVALUACIÓN DIAGNÓSTICA. MATEMÁTICA Sexto Grado PRIMARIA
 Dirección Regional de Educación de Lima Metropolitana EVALUACIÓN DIAGNÓSTICA 1 9 3 1/2 8 6 5 X < 7 % MATEMÁTICA Sexto Grado PRIMARIA Institución Educativa: Nombres y apellidos: Grado y sección : Fecha:
Dirección Regional de Educación de Lima Metropolitana EVALUACIÓN DIAGNÓSTICA 1 9 3 1/2 8 6 5 X < 7 % MATEMÁTICA Sexto Grado PRIMARIA Institución Educativa: Nombres y apellidos: Grado y sección : Fecha:
6 si x -4 (x+2) 2 si -4 < x -1 4 si x > x+1 si 0 x 1 x si 1 < x < 3 6-x si 3 x 4
 . Calcula la derivada de las siguientes funciones:. y = 2-2 +2 2. y = 2-2 2 +2. y = 2 -ln +e 4. y = 2 e 2 5. y = e 6. y = 2 ln 2 7. y = 2-8. y = e. y = 2 + 4. y = ln 2-5. y = 2 2 2 6. y = 2-9. y = e 2
. Calcula la derivada de las siguientes funciones:. y = 2-2 +2 2. y = 2-2 2 +2. y = 2 -ln +e 4. y = 2 e 2 5. y = e 6. y = 2 ln 2 7. y = 2-8. y = e. y = 2 + 4. y = ln 2-5. y = 2 2 2 6. y = 2-9. y = e 2
Departamento de Matemáticas. Nombre:.Grupo:..
 I.E.S. Mar Mediterráneo Matemáticas º E.S.O e) 2 [5 (7 2)] f) 22 - [5 - (8 - )] - 6 g) (-5) 2 - (-2) + (-) 6 h) 8 0 : 5 + 6 : 2 i) 5 : [2 + (2-7) + 5] j) 5 (8 - ) (2-7) 5 ( - 6) k) + 6 : 9 50 : [2 + (7
I.E.S. Mar Mediterráneo Matemáticas º E.S.O e) 2 [5 (7 2)] f) 22 - [5 - (8 - )] - 6 g) (-5) 2 - (-2) + (-) 6 h) 8 0 : 5 + 6 : 2 i) 5 : [2 + (2-7) + 5] j) 5 (8 - ) (2-7) 5 ( - 6) k) + 6 : 9 50 : [2 + (7
Ejercicios 1ª EVALUACIÓN. FÍSICA Movimiento Rectilíneo Uniforme (MRU)
 Ejercicios 1ª EVALUACIÓN. FÍSICA Movimiento Rectilíneo Uniforme (MRU) 1. Cuál de los siguientes movimientos es más rápido, el del sonido que viaja a 340 m/s o el de un avión comercial que viaja a 1.080
Ejercicios 1ª EVALUACIÓN. FÍSICA Movimiento Rectilíneo Uniforme (MRU) 1. Cuál de los siguientes movimientos es más rápido, el del sonido que viaja a 340 m/s o el de un avión comercial que viaja a 1.080
EJERCICIOS MÓDULO 6. 1) Graficar aproximadamente cada ángulo dado en un sistema de ejes cartesianos:
 Seminario Universitario Matemática EJERCICIOS MÓDULO 1) Graficar aproximadamente cada ángulo dado en un sistema de ejes cartesianos: a) 5 b ) 170 c ) 0 d ) 75 e) 10 f ) 50 g ) 0 h ) 87 i ) 08 j ) 700 k
Seminario Universitario Matemática EJERCICIOS MÓDULO 1) Graficar aproximadamente cada ángulo dado en un sistema de ejes cartesianos: a) 5 b ) 170 c ) 0 d ) 75 e) 10 f ) 50 g ) 0 h ) 87 i ) 08 j ) 700 k
Bloque 2. Geometría. 3. La recta. 1. Definición de recta
 Bloque 2. Geometría 3. La recta 1. Definición de recta Para representar puntos en un plano (superficie de dos dimensiones) utilizamos dos rectas graduadas y perpendiculares, cuyo corte es el punto 0 de
Bloque 2. Geometría 3. La recta 1. Definición de recta Para representar puntos en un plano (superficie de dos dimensiones) utilizamos dos rectas graduadas y perpendiculares, cuyo corte es el punto 0 de
CUADERNO Nº 11 NOMBRE: FECHA: / / Funciones. Interpretar y relacionar tabla, gráfica y fórmula de una relación funcional.
 Funciones Contenidos 1. Relaciones funcionales Tablas, gráficas y fórmulas. Variables Dominio y recorrido 2. Representación gráfica A partir de tabla o fórmula Unos símbolos muy útiles 3. Propiedades generales
Funciones Contenidos 1. Relaciones funcionales Tablas, gráficas y fórmulas. Variables Dominio y recorrido 2. Representación gráfica A partir de tabla o fórmula Unos símbolos muy útiles 3. Propiedades generales
MATEMÁTICAS III CUADERNILLO DE ACTIVIDADES Y TAREAS. Bachillerato General, Modalidad Mixta
 Bachillerato General, Modalidad Mixta MATEMÁTICAS III CUADERNILLO DE ACTIVIDADES Y TAREAS. Nombre del Alumn@ Día de la clase de matemáticas Hora de la clase de matemáticas Maestra: María Luisa Rubalcava
Bachillerato General, Modalidad Mixta MATEMÁTICAS III CUADERNILLO DE ACTIVIDADES Y TAREAS. Nombre del Alumn@ Día de la clase de matemáticas Hora de la clase de matemáticas Maestra: María Luisa Rubalcava
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág. 1 PÁGIN 88 JRIIOS Representación de puntos 1 Representa los siguientes puntos: (, 3), (, 1), (0, ), (1, 5), (3, 3). Representa los siguientes puntos: (, ), (0, 5), (, ), (, 0), (3, 1). Pág. 3 Representa
Pág. 1 PÁGIN 88 JRIIOS Representación de puntos 1 Representa los siguientes puntos: (, 3), (, 1), (0, ), (1, 5), (3, 3). Representa los siguientes puntos: (, ), (0, 5), (, ), (, 0), (3, 1). Pág. 3 Representa
4. Medida de ángulos y de tiempo
 30 4. Medida de ángulos y de tiempo 1. Medida de ángulos Cuánto mide un ángulo recto? Y un ángulo llano? Un ángulo recto mide 90 y un ángulo llano 180 659 : 8,6 C = 76,62; R = 0,068 1. Estima la medida
30 4. Medida de ángulos y de tiempo 1. Medida de ángulos Cuánto mide un ángulo recto? Y un ángulo llano? Un ángulo recto mide 90 y un ángulo llano 180 659 : 8,6 C = 76,62; R = 0,068 1. Estima la medida
1) A cuántos m/s equivale la velocidad de un móvil que se desplaza a 72 km/h? Solución: 20 m/s
 Problemas MRU 1) A cuántos m/s equivale la velocidad de un móvil que se desplaza a 72 km/h? Solución: 20 m/s 2) Un móvil viaja en línea recta con una velocidad media de 1.200 cm/s durante 9 s, y luego
Problemas MRU 1) A cuántos m/s equivale la velocidad de un móvil que se desplaza a 72 km/h? Solución: 20 m/s 2) Un móvil viaja en línea recta con una velocidad media de 1.200 cm/s durante 9 s, y luego
