En l actualitat, una part important dels objectes que es fabriquen estan fets sota algun tipus de forma corba geomètrica.
|
|
|
- Luis David Aguirre Rojo
- hace 6 años
- Vistas:
Transcripción
1 06 orbes geomètriques En l actualitat, una part important dels objectes que es fabriquen estan fets sota algun tipus de forma corba geomètrica. Si prestem atenció al nostre entorn, ens adonarem que en molts dels objectes que ens envolten hi són presents les corbes tècniques i les corbes còniques; per exemple, des de la forma de paràbola que alguns ulls de pont tenen fins a la forma d oval o ovoide amb què s han dissenyat certes culleres. La natura també contribueix a crear aquest tipus de formes; els meandres d alguns rius, o el vent en modelar les sorres dels deserts, donen testimoni d aquest tipus de figures geomètriques.
2 6. orbes geomètriques 6.. orbes tècniques 6.. orbes geomètriques Es defineix una línia com a corba geomètrica quan s aparta constantment de la direcció recta sense formar angles, i la trajectòria dels punts que la formen és contínua i, a més, compleix una determinada norma. Hi ha dos grups de corbes geomètriques: les denominades planes i les torcejades. Una corba rep el nom de plana quan tots els seus punts estan situats en un mateix pla; i corba torcejada quan quatre dels seus punts no es troben al mateix pla. Segons la forma que tinguin de generar-se, les corbes planes es divideixen en corbes tècniques i corbes còniques, que tenen propietats específiques i diferents entre si. 6.. orbes tècniques Les corbes tècniques tenen moltes aplicacions en la resolució de problemes de dibuix tècnic, tant si provenen de l àmbit del disseny industrial, arquitectònic o gràfic. Les corbes d aquest tipus es configuren mitjançant la unió d arcs de circumferència que són tangents entre si, i donen lloc a la formació de figures planes que poden ser tancades: oval, ovoide; o obertes: espirals, evolvent del cercle, etc. cc. val ccc efinició És una corba plana i tancada, simètrica en relació amb els seus dos eixos perpendiculars i formada per quatre arcs de circumferència iguals dos a dos. ccc onstrucció d ovals continuació es desenvolupen alguns dels traçats d ovals més utilitzats en dibuix tècnic. val coneixent l eix menor '. Es traça la mediatriu de l eix menor, i s obté el punt. la mediatriu es troba l eix major de l oval.. mb centre a i radi es dibuixa una circumferència que talla l eix major en els punts i ; s uneixen aquests punts amb i allargant aquestes rectes.. mb radi i centre a i, respectivament, es tracen dos arcs que determinen els punts i, Q i Q, punts de tangència entre els arcs que forman l oval. Q Q'. er últim, amb centre a i, i radi, es tracen els altres dos arcs per unir amb Q, i amb Q ; així queda determinat l oval. (ig. 6.) ig. 6.. val coneixent l eix menor. 08
3 6. orbes geomètriques 6.. orbes tècniques val coneixent l eix major (primer procediment). Es divideix l eix major en tres parts iguals, i es determinen els punts i. mb centre en aquests punts i radi igual a / d, per exemple, es tracen dues circumferències que es tallen en els punts i. '. S uneixen mitjançant rectes els punts i amb i, s obtenen els quatre punts de tangència: i, i Q i Q.. mb centre a i respectivament, i radi, es fan dos arcs fins a unir els punts amb i Q amb Q. ixí, queda resolt l oval que es demanava (ig. 6.). ' ' ' Q Q' ig. 6.. val coneixent l eix major, primer procediment. val coneixent l eix major (segon procediment). Es divideix l eix major en quatre parts iguals, i s obtenen els punts i que corresponen als punts i a l eix dividit. Es tracen dues circumferències amb centre a i, respectivament, i radi igual a / d, és a dir,. '. Es tracen dos arcs amb centre també a i, respectivament, i radi igual a.. n els arcs es tallen, es troben els punts i, centres dels arcs majors de l oval. er trobar els punts de tangència s uneixen els centres i amb els altres centres i, i, a partir d aquí, se segueix el mateix procediment que a l exercici anterior (ig. 6.). Q ' = ' ' ' = Q' ig. 6.. val coneixent l eix major, segon procediment. val òptim coneixent tots dos eixos. Es traça un arc de centre a amb radi que talla la prolongació de, eix menor, en el punt. S uneix amb, i es descriu un arc de radi amb centre a fins a tallar el segment a V.. Es dibuixa la mediatriu d V, que talla la prolongació d en el punt o dins el propi segment, i el semieix major en el punt. Es determinen els punts simètrics de i en relació amb els eixos de l oval, i. Q ' V Q'. S uneixen els punts i amb i, respectivament, i es tracen els arcs de centre i amb radi i, s obtenen els punts Q i Q i i. '. er últim, es dibuixen els arcs de centre i amb radi i fins als punts de tangència anteriorment traçats: Q i Q, i i ; així s aconsegueix construir l oval (ig. 6.). ' ig. 6.. val òptim coneixent tots dos eixos. 09
4 6. orbes geomètriques 6.. orbes tècniques val inscrit en un rombe Q Q'. Es parteix d un rombe qualsevol. es dels vèrtexs dels angles de major valor del rombe, es tracen rectes perpendiculars als costats oposats a ells, que tallen l eix major i determinen els punts i, i als costats del rombe a i, i Q i Q. '. Els punts,, i són els centres dels quatre arcs que formen l oval que es demanava.. mb centre a i respectivament, i radi, es tracen dos arcs fins a unir amb, i Q amb Q. e la mateixa manera, amb centre a i, es tracen dos arcs fins a unir amb Q i amb Q, així es determina la construcció de l oval (ig. 6.). ig. 6.. val inscrit en un rombe. val isomètric Q 0 Q' En el cas que els angles majors de l oval on s hagi d inscriure l oval valguin 0º, i per tant els menors valguin 60º, l oval inscrit s anomena isomètric. La seva construcció es realitza de la mateixa manera que en el cas descrit anteriorment. 60 La raó d adoptar aquest nom ve donada perquè aquesta figura es fa servir en dibuix isomètric per substituir, de manera aproximada, l el lipse que tingui el mateix valor d eixos que l oval. (ig. 6.6). ' cc. voide ccc efinició ig val isomètric. L ovoide és una corba plana i tancada, simètrica només en relació amb el seu eix major, i formada per quatre arcs de circumferència, dels quals dos són iguals i els altres dos són desiguals. ccc onstrucció d ovoides continuació es desenvolupen alguns dels traçats d ovoides més utilitzats en dibuix tècnic. ' ig val coneixent l eix menor. voide coneixent l eix menor. Es dibuixa la mediatriu de l eix conegut, i s obté el punt. mb centre a i radi, es traça una circumferència que talla la mediatriu en el punt.. S uneixen els punts i amb, amb la qual cosa s arriba a les rectes r i s. Es tracen dos arcs amb radi i centre als punts i, de manera que s obtenen els punts i.. mb centre a i radi o, es descriu l últim arc que configura l ovoide que es demanava. (ig. 6.7). 0
5 6. orbes geomètriques 6.. orbes tècniques voide coneixent l eix major. Es divideix l eix major en sis parts iguals, i per la segona divisió es traça una perpendicular a l eix. Es fa centre en aquesta mateixa divisió, és a dir, a la i, amb radi -6, es descriu un arc que determina els punts i Q.. S uneixen i Q amb el punt, cinquena divisió d. Es fa centre al punt i, amb radi o Q es dibuixa una semicircumferència i s obtenen sobre el segment Q els punts H i I. mb centre a i Q, respectivament, i radi I, es tracen els arcs que determinen els punts i.. er últim, amb centre al punt, i amb radi, es traça un arc per acabar de construir l ovoide que es demana (ig. 6.8). voide coneixent tots dos eixos. Es pren l eix menor i se n traça la mediatriu, i s obté el punt. mb centre a i radi, es dibuixa una circumferència que talla la mediatriu en els punts i J. es d i sobre aquesta mediatriu, es porta el valor de l eix major, i d aquesta manera queden situats els eixos de l ovoide.. mb centre a J i radi J, es dibuixa una circumferència. partir de i sobre, es porta la magnitud J i s obté el punt. Es determina la mediatriu de J; i s obté el punt sobre el segment.. Es troba el simètric de sobre, i s obté el punt. S uneixen els punts i amb J, determinen els punts de tangència Q i Q.. er últim, amb centre a i respectivament, i radi, es tracen els arcs fins a unir amb Q i amb Q, amb la qual cosa s obté l ovoide que es buscava (ig. 6.9). H I Q ' = 6 ig voide coneixent l eix major. J cc. Espiral ccc efinició Q Q' ig voide coneixent tots dos eixos. L espiral és una corba plana, oberta i contínua que es configura en expansió per un punt que es desplaça de manera uniforme al llarg d una recta, que està fixa en un punt pel qual gira amb un valor angular constant. Una espiral es defineix pels elements següents: as: és la distància longitudinal amb què es desplaça un punt de la corba en una volta completa. És a dir, és la distància entre dues espires consecutives. Espira: és la part de la corba descrita a cada volta. ucli: és a partir d on es genera, en expansió, l espiral. Els nuclis poden ser lineals si els centres estan situats en una línia, o poligonals si són els vèrtexs dels polígons els centres que generen la corba. Radis vectors: són la prolongació, o bé de la línia on estan situats els centres del nucli o bé dels costats del polígon que fa de nucli.
6 6. orbes geomètriques 6.. orbes tècniques ccc onstrucció d espirals continuació es desenvolupen alguns dels traçats d espirals més utilitzats en dibuix tècnic. Espiral logarítmica. En aquesta corba es comprova que el moviment de translació no és uniforme, sinó que segueix una progressió geomètrica, de manera que el pas és variable. E. er construir-la, es tracen dos eixos perpendiculars entre si, i s obté el punt on es tallen. Es traça un triangle rectangle, els catets del qual formen amb la hipotenusa els angles que es volen deixar constants durant el recorregut del punt generador. artim del triangle escollit.. el punt es traça una perpendicular a la hipotenusa, i això determina sobre l altre eix el punt pel qual, al seu torn, es traça una altra perpendicular al segment i s obté el punt sobre l altre eix, i així successivament. ig Espiral logarítmica.. Es tracen les mediatrius dels segments que contenen els punts,,,, etc., i on aquestes tallin les bisectrius dels angles rectes que formen la línia poligonal definida per aquests s obtenen els centres,,, etc. dels diferents arcs de circumferència que configuren l espiral. escrits aquests amb els seus radis particulars,,, etc. i units convenientment, donen com a resultat la construcció de l espiral com pot apreciar-se a la igura 6.0. aso Espiral d rquímedes coneixent el pas. Es divideix el segment en un nombre qualsevol de parts iguals, per exemple dotze. mb centre a i amb radis, fins a, es tracen circumferències.. Es divideix la circumferència en dotze parts iguals i es tracen els radis respectius. La intersecció d aquests radis amb els arcs corresponents determinen els diversos punts que configuren l espiral, punts que, units amb traç continu, determinen la corba que es demana (ig. 6.) as ig. 6.. Espiral d rquímedes.
7 6. orbes geomètriques 6.. orbes tècniques cc. Voluta ccc efinició Es denomina voluta la corba plana, oberta i contínua composta per arcs de circumferència, tangents entre ells, els centres dels quals són els vèrtexs d un polígon bàsicament regular. ccc onstrucció de volutes continuació es desenvolupen alguns dels traçats de volutes més utilitzats en dibuix tècnic. Volutes de nucli triangular, quadrangular i hexagonal. La construcció d aquest tipus de volutes és molt senzill: només cal fixar-ne la posició dels centres i la longitud del radi inicial. bserva, a les igures 6., 6. i 6., com en el dibuix de cada una d elles, els traçats per construir-les es repeteixen a partir de la primera volta, els seus arcs es desenvolupen de manera paral lela. 6 6 ig. 6.. Voluta de nucli triangular. ig. 6.. Voluta de nucli quadrangular. ig. 6.. Voluta de nucli hexagonal. Voluta jònica. Es parteix d una circumferència la longitud de la qual és igual al pas en què es vol construir la voluta. S hi inscriu un quadrat i s hi tracen paral leles als costats pels dos punts mitjos d aquests, i s obtenen els punts 9, 0, i.. Es divideixen els segments 9- i 0- en sis parts iguals, i es numeren de la manera indicada a la igura 6.. Es dibuixen les diagonals del quadrat prolongant-les; en aquestes diagonals es troben els punts de tangència de la voluta.. mb centre a i radi, es traça un arc fins a la diagonal i es determina el punt E, amb centre a i radi E, es traça un altre arc fins a tallar la següent diagonal en el punt, i així successivament (ig. 6.) ig. 6.. Voluta jònica.
8 6. orbes geomètriques ctivitats Qüestions efineix de manera raonada les preguntes següents:. Què és una corba geomètrica? lassifica-les.. Què és un oval?. ibuixa un oval òptim coneixent-ne tots dos eixos i explica per escrit els passos seguits per construir-lo.. ibuixa un oval isomètric inscrit en un rombe i explica per escrit els passos seguits per construir-lo.. Què és un ovoide? 6. ibuixa un ovoide coneixent-ne tots dos eixos i explica per escrit els passos seguits per construir-lo. 7. En què es diferencia un oval d un ovoide? 8. Què és una espiral? escriu com es generen les espirals, i quins elements les configuren. 9. ibuixa una espiral logarítmica i explica per escrit els passos seguits per construir-la. 0. Què és una voluta?. Quina característica tenen en comú l oval, l ovoide i l espiral? Exercicis. ibuixa un oval sabent que el seu eix menor mesura 7 mm.. ibuixa un oval sabent que el seu eix major mesura 6 mm.. ibuixa un oval òptim sabent que els seus eixos mesuren 67 mm i mm, respectivament. 9. ibuixa a escala : la clau de dues boques de la igura ixa t com estan fetes les espirals de les igures 6.7 i 6.8. Intenta reproduir-les esbrinant quins han estat els seus processos de construcció. 7. ibuixa un ovoide sabent que el seu eix major mesura 67 mm.. ibuixa un ovoide sabent que els seus eixos mesuren 67 mm i mm, respectivament. 0 R9 R0 6. ibuixa una espiral d rquímedes sabent que el seu pas mesura 0 mm. 7 ig Exercici 0, primera figura de model. 7. ibuixa una voluta de nucli hexagonal, sabent que el costat de l hexàgon mesura mm ibuixa una voluta jònica sabent que la circumferència la longitud de la qual és igual al pas té un radi de 8 mm. R R 0 = = 6 = 8 0 = 60 = 6 ig Exercici 9, figura de model. ig Exercici 0, segona figura de model.
9 6. orbes geomètriques 6.. orbes còniques 6.. orbes còniques eje Les corbes còniques s obtenen en seccionar un con de revolució amb un pla secant. Un con de revolució és un cos geomètric que pot considerar-se engendrat per una línia recta denominada generatriu, que es mou fixa en un punt (centre de generació o vèrtex del con), al voltant d un eix i amb una direcció circular anomenada directriu. (ig. 6.9). cc. lassificació de les corbes còniques La posició del pla secant en relació amb l eix del con possibilita diferents tipus de corbes. més de la circumferència, que es genera quan el pla secant (o pla secció) és perpendicular a l eix del con, són figures còniques l el lipse, la paràbola i la hipèrbola. Si el pla secció és paral lel a l eix i talla el con, la secció és una hipèrbola. És a dir, a < b (ig. 6.). Generatriu Vèrtex V irectriu Si el pla secció és oblic i talla totes les generatrius del con, la secció és una el lipse. És a dir, a > b (ig. 6.0). Si el pla secció és oblic a l eix i paral lel a una de les generatrius del con, la secció és una paràbola. És a dir, a = b (ig. 6.). ig Elements d un con de revolució. ig El lipse. És convenient apuntar que les corbes còniques, excepte la circumferència, ja estudiada, es construeixen per mitjà de l obtenció de punts que configuren la corba, i que posteriorment cal unir-los, o bé a mà alçada o mitjançant l ús de plantilles de corbes. ig. 6.. Hipérbola. ig. 6.. arábola.
10 6. orbes geomètriques 6.. orbes còniques cc. Elements de les corves còniques Vegem els elements més importants que formen les corbes còniques i que són necessaris per construirles: ocus: són els punts i de contacte de les esferes inscrites al con amb el pla secant que genera les seccions còniques, i estan situats a l eix de simetria. L el lipse i la hipèrbola tenen dos focus, i la paràbola en té només un. Vèrtexs: són els punts extrems dels eixos de la corba. Eixos: amb aquest terme es denominen els eixos de simetria de la corba. Tant l el lipse com la hipèrbola tenen dos eixos de simetria que són perpendiculars entre ells. La paràbola en té només un. entre: és el punt on es tallen els eixos de simetria i, per tant, el centre de la corba. irectrius: són les rectes d intersecció que fa el pla secant (que genera la corba cònica) amb els plans que contenen les circumferències tangents de les esferes amb el con. ircumferència principal: és el lloc geomètric de les projeccions dels focus sobre les rectes tangents a la cònica. El centre d aquesta circumferència és el centre de l el lipse o de la hipèrbola i el radi és igual a la meitat del seu eix major. En el cas de la paràbola, el radi és infinit. ircumferència focal: és el lloc geomètric dels punts simètrics de l altre focus en relació amb les rectes tangents a la cònica. El centre d aquestes circumferències són els focus i els radis són la longitud de l eix major en el cas de l el lipse i la hipèrbola. la paràbola, el radi és infinit. Radis vectors ercle focal ircumferència principal cc. El lipse És una corba plana i tancada, lloc geomètric de tots els punts del pla, la suma de distàncies dels quals a dos punts fixos, anomenats focus i, és constant i igual a l eix major. ccc Elements de l el lipse + = Eix menor o virtual = a = a ' Els elements més significatius que configuren l el lipse són els següents: (ig. 6.): Eixos: té dos eixos i perpendiculars entre ells, que es tallen en el punt, centre de l el lipse. L eix major s anomena eix real o principal, i l eix menor, secundari o virtual. questa corba és simètrica en relació amb aquests eixos. ocus: anomenats i, estan situats en l eix real, i es troben fent centre en un dels extrems de l eix virtual o, i radi igual al semieix real. istància focal: és la distància que existeix entre tots dos focus. istancia focal Radis vectors: són les rectes que uneixen un punt qualsevol de l el lipse amb els focus. Eix major o real. ircumferència principal: és la que es determina fent centre a, centre de l el lipse, i radi igual al semieix major. ig. 6.. Elements de l el lipse. + ' = ircumferència focal: l el lipse té dues circumferències focals. er dibuixar-les es pren com a radi l eix real i centre i, respectivament. 6
11 6. orbes geomètriques 6.. orbes còniques La nomenclatura més utilitzada en geometria per denominar els eixos i la distància focal és la següent: Eix major o real = = a; semieix major o real a. Eix menor o virtual = = b; semieix menor o virtual = b. istància focal = = c. ccc onstrucció de l el lipse continuació es desenvolupen alguns dels traçats de l el lipse més utilitzats en dibuix tècnic. El lipse coneixent tots dos eixos. er punts. Es tracen dues rectes perpendiculars i s obté en el tall el punt. Sobre aquestes se situen els eixos de l el lipse = a i = b. mb centre a o i radi, es traça un arc que talla l eix real en els punts i, focus de la corba.. Es divideix en un nombre de parts la distància focal,,, etc. mb centre a i radi es tracen dos arcs; amb radi i centre a es tracen uns altres dos arcs que tallen els dos anteriors a E i, punts de l el lipse.. mb centre a i radi, es tornen a traçar dos arcs; amb radi i centre a es tracen uns altres dos arcs que tallen els anteriors en els punts G i H, uns altres dos punts de la corba. Repetim aquesta operació prenent altres punts,, etc. de l eix real per seguir trobant punts de l el lipse i, finalment, s uneixen els punts determinats manualment o amb plantilles, amb la qual cosa s obté l el lipse que es demanava. (ig. 6.). G E 6 ' H ig. 6.. onstrucció de l el lipse per punts. 7
12 6. orbes geomètriques 6.. orbes còniques H G E = = ' ' ' ' ' El lipse coneixent tots dos eixos. er feixos projectius. Es dibuixa un rectangle de costats iguals al valor dels eixos de l el lipse. Es tracen els eixos dins aquest rectangle. Es divideixen els segments i E en el mateix nombre de parts i iguals a cada segment. En aquest cas, cinc.. Les interseccions dels raigs,, i amb els raigs,, i, respectivament, determinen diferents punts de l el lipse E,, G i H.. bserva que els punts de la corba en els altres tres quadrants de l el lipse s han obtingut aplicant el mateix mètode. er últim, només queda unir aquests punts per completar l el lipse (ig. 6.). ig. 6.. onstrucció de l el lipse per feixos projectius. El lipse coneixent tots dos eixos. er circumferències concèntriques o afinitat. Es dibuixen dues circumferències concèntriques de radis iguals als valors dels semieixos major i menor. Es tracen diferents radis de les dues circumferències. E. els extrems dels radis de la circumferència major, es tracen rectes paral leles a l eix menor. els extrems dels radis de la circumferència menor, es tracen paral leles a l eix major.. Els punts d intersecció de les respectives paral leles determinen punts de l el lipse buscada (ig. 6.6). ig onstrucció de l el lipse per afinitat. 8
13 6. orbes geomètriques 6.. orbes còniques El lipse coneixent tots dos eixos. ètode de la tira de paper. quest és un mètode senzill i ràpid per traçar el lipses. El procediment està basat en la definició d el lipse. onsisteix, per tant, a marcar sobre una tira de paper, amb traços petits, la longitud del semieix major i la del semieix menor.. Es fa coincidir el punt sobre el semieix major de l el lipse que es dibuixarà, i el punt sobre el semieix menor, i és un punt de l el lipse. Repetint aquest procediment s aconsegueixen nous punts, tants com es desitgin.. al no oblidar que els punts i de la tira de paper han de coincidir sempre sobre els eixos de l el lipse que es vol dibuixar. er últim, només cal unir els punts trobats de manera manual o amb plantilles per determinar la corba (ig. 6.7) ig onstrucció de l el lipse pel mètode de la tira de paper. 9
14 6. orbes geomètriques 6.. orbes còniques El lipse coneixent tots dos diàmetres conjugats onat un diàmetre qualsevol JK d una el lipse, el seu conjugat és el lloc geomètric dels punts mitjos de totes les cordes paral leles a JK. Es pot observar a la igura 6.8 que la corda E, paral lela al diàmetre JK, és tallada a, que és un punt mig, pel diàmetre.. Es parteix dels diàmetres conjugats i. Es dibuixa una circumferència de diàmetre igual al major dels diàmetres conjugats. Sobre aquesta es traça un altre diàmetre, perpendicular a.. Es divideix en n parts, per exemple sis, i s hi tracen paral leles a i. Es tracen els segments que uneixen els punts amb, i amb.. n les cordes tallen la circumferència, es tracen paral leles a i que tallen les paral leles al diàmetre conjugat en els punts E i E, i, etc., i així successivament; d aquesta manera es van determinant els punts de l el lipse buscada (ig. 6.9). E J E ' K E' = 6 ig iàmetres conjugats d una el lipse. ' ' ig El lipse coneixent-ne tots dos diàmetres conjugats. eterminació dels eixos d una el lipse coneixent tots dos diàmetres conjugats J. Es parteix dels diàmetres conjugats i. er es traça una perpendicular al diàmetre, i es porta a partir de el semidiàmetre a cada costat, és a dir, = = Q. Q E. S uneix el punt amb i Q, i es troba la bisectriu de l angle Q; aquesta recta conté l eix major de l el lipse. er es traça una perpendicular a l eix major; aquesta recta conté l eix menor. I per es traça una paral lela; on aquesta talli el segment s obtindrà el punt J.. J és el valor del semieix menor i J, el del semieix major. Es traslladen aquestes magnituds a partir d a tots dos costats dels eixos, i queden determinats i E, eixos de l el lipse buscada. (ig. 6.0) ig eterminació dels eixos d una el lipse coneixent tots dos diàmetres conjugats. 0
15 6. orbes geomètriques 6.. orbes còniques cc. Hipèrbola La hipèrbola és una corba plana i oberta, lloc geomètric de tots els punts del pla la diferència de distància dels quals a dos punts fixos, anomenats focus i, és constant i igual a l eix real, és a dir, a la distància entre els vèrtexs V i V. ccc Elements de la hipèrbola = ' Eix real Els elements més significatius que configuren la hipèrbola són els següents: (ig. 6.): Eix imaginari Eixos: té dos eixos:, eix real, i, eix imaginari; són perpendiculars entre ells i es tallen al punt. L eix real conté els vèrtexs i de cada branca de la corba. La hipèrbola consta de dues branques simètriques en relació amb els dos eixos. En aquesta corba, la distància des del centre de simetria a cada focus és igual a la distància, quan és un extrem de l eix real i, un extrem de l eix imaginari. questa propietat permet, si es coneix un dels eixos i els focus, determinar l altre eix (ig. 6.); i, lògicament, si es coneixen tots dos eixos, es poden obtenir els focus (ig. 6.). ocus: denominats i, estan situats a l eix real i es troben fent centre a i radi igual a la distància. istància focal: és la distància que hi ha entre tots dos focus. ig. 6.. eterminació dels focus de la hipérbola. Radis vectors: són les rectes que uneixen un punt qualsevol de la hipèrbola amb els focus. Eix imaginari ' Eix real ig. 6.. eterminació de l eix real de la hipérbola. b eix imaginari erc. focal erc. principal a Eix real c istància focal ig. 6.. Elements de la hipérbola. erc. focal ' Radis vectors ircumferència principal: és la que es determina fent centre a, centre de la hipèrbola, i radi igual a la distància del semieix real. ircumferència focal: la hipèrbola té dues circumferències focals. er dibuixar-les es pren com a radi l eix real, i com a centre, i, respectivament. símptotes: són rectes que passen pel centre de la hipèrbola, i són tangents a aquesta a l infinit; a més, són simètriques en relació amb els eixos i. Es determinen traçant la circumferència principal amb centre a. Es dibuixen rectes tangents des del focus a la circumferència, i així es determinen els punts de tangència i. S uneixen aquests punts amb i s obtenen totes dues asímptotes (ig. 6.). H ' ig. 6.. eterminació de les asímptotes de la hipérbola.
16 6. orbes geomètriques 6.. orbes còniques La nomenclatura més utilitzada en geometria per denominar els eixos i la distància focal és la següent: Eix real = = a; semieix menor o virtual a. Eix imaginari = = b; semieix major o real = b. istància focal = = c. ccc onstrucció de la hipèrbola continuació es desenvolupen alguns dels traçats de la hipèrbola més utilitzats en dibuix tècnic. Hipèrbola coneixent tots dos eixos. er punts ' ' ' '. Un cop situats els eixos i, es procedeix a determinar els focus; amb centre a i radi, es traça un arc, i on aquest talla l eix real es troben els focus i.. Se situen punts arbitraris: i, i, etc., sobre l eix real a un i l altre costat dels focus, i, respectivament. mb radi i centre a i es fan dos arcs; amb radi i centre a i es descriuen uns altres dos arcs, que tallen els anteriors i determinen els punts i, i i, de la corba de totes dues branques.. Repetint aquesta operació tantes vegades com punts hi hagi marcats sobre l eix, s obté la resta dels punts de la hipèrbola. er últim, s uneixen amb plantilles de corbes o a mà alçada fins acabar les dues branques de la corba (ig. 6.). ig. 6.. onstrucció de la hipèrbola coneixent tots dos eixos. Hipèrbola coneixent les asímptotes i els vèrtexs '' '' J I ''' ' ' ' ''' ig Hipèrbola coneixent les asímptotes i els vèrtexs.. Es tracen paral leles a les asímptotes pels vèrtexs i, i s obtenen sobre aquestes els punts i. Es porta sobre les asímptotes la distància =, i es determinen els punts,, etc., pels quals es tracen paral leles a l asímptota.. Es divideix el segment en parts, que estan a / de la distància (punt ), a / (punt I), a / (punt J), etc., de manera que les paral leles traçades pels punts, I, J, etc. tallen les traçades per a, per a, i així successivament.. Els punts de l altra meitat de la branca en què s ha treballat poden obtenir-se trobant els simètrics, en relació amb els eixos de la corba, dels ja determinats, com també els punts de l altra branca (ig. 6.6).
17 6. orbes geomètriques 6.. orbes còniques cc E. aràbola Semiparàmetre La paràbola és una corba plana i oberta, lloc geomètric de tots els punts del pla equidistants d un de fix anomenat focus i d una recta d denominada directriu. irectriu = ccc Elements de la paràbola Els elements més significatius que configuren la hipèrbola són els següents (ig. 6.7): Eix: té només un eix de simetria, perpendicular a la directriu, i que conté el vèrtex i el focus. Radis vectors: són les rectes que uneixen un punt qualsevol de la paràbola amb el focus. ircumferència principal: té un radi infinit i és tangent a la paràbola en el seu vèrtex. Radis vectors aràmetre Eix ircumferència focal: també té un radi infinit i es converteix en una recta que coincideix amb la directriu. aràmetre: és la longitud de la corda de la paràbola, perpendicular a l eix, que passa pel focus. Semiparàmetre: és la distància des del focus fins a la directriu. ig Elements de la parábola. ccc onstrucció de la paràbola continuació es desenvolupen alguns dels traçats de la paràbola més utilitzats en dibuix tècnic. aràbola coneixent la directriu i el focus. er punts. Es dibuixen la directriu d i el focus, i es troba el punt mig del segment, que és el vèrtex de la corba. partir del focus se situen punts arbitraris:,,, etc., i s hi tracen paral leles a la directriu d. ' '. renent com a radis les distàncies,, etc., i fent sempre centre al punt, es tracen arcs que tallen, respectivament, les rectes que passen per,,, etc., i s obtenen els punts i, i, i així successivament. ig onstrucció de la parábola coneixent la directriu i el focus.. En unir aquests punts amb traç continu, resulta la paràbola buscada (ig. 6.8). aràbola coneixent el vèrtex, l eix i un punt de la corba. Se situen les dades que tenim i es determina el punt, simètric de en relació amb l eix. el vèrtex de la corba es traça una perpendicular a l eix, i per i es tracen les paral leles a l eix; on aquestes es tallen a la perpendicular s obtenen els punts i. = 6. Es divideixen i en un nombre de parts iguals, per exemple, sis. er les divisions obtingudes sobre es tracen paral leles a l eix. S uneixen amb el vèrtex els punts de la divisó, i on aquestes rectes tallen les paral leles s obtenen els punts,,, etc. Els punts,,, etc. es troben per simetria.. Unint els punts així determinats amb una línia contínua, s obté la paràbola que es demana (ig. 6.9). ig aràbola coneixent el vèrtex, l eix i un punt d aquesta. ' ' ' ' ' ' = 6'
18 6. orbes geomètriques ctivitats Qüestions Respon de manera raonada les preguntes següents:. om s obtenen les corbes còniques? lassifica-les.. omenta els elements més importants que formen les corbes còniques.. Què és una el lipse? Quina nomenclatura es fa servir per denominar els eixos i la distància focal?. omenta els elements que configuren l el lipse.. ibuixa una el lipse coneixent-ne tots dos eixos, per punts, i explica per escrit els passos seguits per construir-la. 6. Què és una hipèrbola? Quina nomenclatura es fa servir per denominar els eixos i la distància focal? 7. omenta els elements que formen la hipèrbola. 8. ibuixa una hipèrbola coneixent-ne les asímptotes i explica per escrit els passos seguits per construir-la. 9. Què és una paràbola? 0. omenta els elements que configuren la paràbola. Exercicis. ibuixa una el lipse per punts, sabent que els seus eixos tenen una longitud de 6 mm i mm, respectivament.. ibuixa una el lipse per feixos projectius, sabent que els seus eixos tenen una longitud de 69 mm i 7 mm, respectivament.. ibuixa una el lipse, sabent que el seu eix major mesura 68 mm i la seva distància focal, 6 mm.. ibuixa una el lipse per circumferències concèntriques o afinitat, sabent que els seus eixos mesuren 7 mm i 7 mm, respectivament.. ibuixa una el lipse pel mètode de la tira de paper, sabent que dos dels seus diàmetres conjugats mesuren 78 mm i 6 mm, respectivament, i l angle menor que formen entre ells és de º. 6. ibuixa una hipèrbola per punts, sabent que = 6 mm, i = 7 mm. 7. ibuixa una hipèrbola sabent que = 6 mm, i = 7 mm, fent servir per construir-la les asímptotes de la corba. 8. ibuixa una paràbola per punts, sabent que la distància entre el vértex de la corba i el seu focus és de mm. ig Exercici 9, figures d exemple. 9. mb ajuda d el lipses, que pots fer mitjançant el traçats geomètrics estudiats, dissenya dues figures ornamentals de manera similar a les que et proposem en la igura 6.0.
DIBUIX TÈCNIC PER A CICLE SUPERIOR DE PRIMÀRIA
 DIBUIX TÈCNIC PER A CICLE SUPERIOR DE PRIMÀRIA Abans de començar cal tenir uns coneixements bàsics que estudiareu a partir d ara. PUNT: No es pot definir, però podem dir que és la marca més petita que
DIBUIX TÈCNIC PER A CICLE SUPERIOR DE PRIMÀRIA Abans de començar cal tenir uns coneixements bàsics que estudiareu a partir d ara. PUNT: No es pot definir, però podem dir que és la marca més petita que
GEOMETRIA PLANA 1. ELS ANGLES 1.1. DEFINICIÓ 1.2. CLASSIFICACIÓ
 GEOMETRIA PLANA 1. ELS ANGLES 1.1. DEFINICIÓ Representem un punt A en un pla i tracem dues semirectes amb origen en aquest punt. El punt A serà el vèrtex de l angle i cada semirecta serà el costat. 1..
GEOMETRIA PLANA 1. ELS ANGLES 1.1. DEFINICIÓ Representem un punt A en un pla i tracem dues semirectes amb origen en aquest punt. El punt A serà el vèrtex de l angle i cada semirecta serà el costat. 1..
TRIANGLES. TEOREMA DE PITÀGORES.
 TRIANGLES. TEOREMA DE PITÀGORES. Un triangle ABC és la figura geomètrica del plànol formada per 3 segments anomenats costats els extrems dels quals es tallen a en 3 punts anomenats vèrtexs. Els vèrtexs
TRIANGLES. TEOREMA DE PITÀGORES. Un triangle ABC és la figura geomètrica del plànol formada per 3 segments anomenats costats els extrems dels quals es tallen a en 3 punts anomenats vèrtexs. Els vèrtexs
La porció limitada per una línia poligonal tancada és un
 PLA Si n és el nombre de costats del polígon: El nombre de diagonals és La suma dels seus angles és 180º ( n 2 ). La porció limitada per una línia poligonal tancada és un Entre les seves propietats destaquem
PLA Si n és el nombre de costats del polígon: El nombre de diagonals és La suma dels seus angles és 180º ( n 2 ). La porció limitada per una línia poligonal tancada és un Entre les seves propietats destaquem
UN POLÍGON és una superficie plana
 UNITAT 10 - FIGURES PLANES RECORDA 4t. Primària UN POLÍGON és una superficie plana limitada per segments rectes. Cadascún d aquests segments és un COSTAT i cada punt on s uneixen dos costats forman un
UNITAT 10 - FIGURES PLANES RECORDA 4t. Primària UN POLÍGON és una superficie plana limitada per segments rectes. Cadascún d aquests segments és un COSTAT i cada punt on s uneixen dos costats forman un
UNITAT 8. FIGURES PLANES
 1. Fes servir aquests punts per traçar dues línies poligonals més de cada tipus, apart de les dels exemples: Línia poligonal oberta Línia poligonal oberta creuada Línia poligonal tancada Línia poligonal
1. Fes servir aquests punts per traçar dues línies poligonals més de cada tipus, apart de les dels exemples: Línia poligonal oberta Línia poligonal oberta creuada Línia poligonal tancada Línia poligonal
Matemàtiques, Ciència i Tecnologia 8. TRIGONOMETRIA UNITAT 3 ÀREES I VOLUMS. Unitat 3 ÀREES I VOLUMS
 70 Unitat 3 ÀREES I VOLUMS què treballaràs? En acabar la unitat has de ser capaç de: Reconèixer unitats de mesura d una àrea. Interpretar fórmules d àrees de figures planes. Aplicar fórmules d àrees de
70 Unitat 3 ÀREES I VOLUMS què treballaràs? En acabar la unitat has de ser capaç de: Reconèixer unitats de mesura d una àrea. Interpretar fórmules d àrees de figures planes. Aplicar fórmules d àrees de
Tema 2: GEOMETRIA ANALÍTICA AL PLA
 Tema : GEOMETRIA ANALÍTICA AL PLA Vector El vector AB és el segment orientat amb origen al punt A i extrem al punt B b a A B Les projeccions del vector sobre els eixos són les components del vector: a
Tema : GEOMETRIA ANALÍTICA AL PLA Vector El vector AB és el segment orientat amb origen al punt A i extrem al punt B b a A B Les projeccions del vector sobre els eixos són les components del vector: a
Sector circular i Segment circular.
 Tema: poligons, circumferència i cercle Activitats de consolidació Pàgina 1 de 8 1. Explica quines són les semblances i diferències entre: Línia poligonal i polígon. Circumferència i cercle. Sector circular
Tema: poligons, circumferència i cercle Activitats de consolidació Pàgina 1 de 8 1. Explica quines són les semblances i diferències entre: Línia poligonal i polígon. Circumferència i cercle. Sector circular
POLÍGONS, CIRCUMFERÈNCIA I CERCLE
 POLÍGONS, CIRCUMFERÈNCIA I CERCLE POLÍGONS Polígon és la figura plana tancada formada per n segments P 1P,PP3,P3P4,...,Pn P1 ( n 3 ) anomenats costats, essent els punts P,P,... els vèrtexs. 1 Pn L angle
POLÍGONS, CIRCUMFERÈNCIA I CERCLE POLÍGONS Polígon és la figura plana tancada formada per n segments P 1P,PP3,P3P4,...,Pn P1 ( n 3 ) anomenats costats, essent els punts P,P,... els vèrtexs. 1 Pn L angle
FITXA 1: Polígons. Conceptes
 FITXA 1: Polígons. Conceptes A.1. REPASSA ELS TEUS CONEIXEMENTS. 1. Escriu la lletra de les figures equilàteres. A, D 2. Escriu el nom de les figures equiangulars. A, D 3. Anomena les figures que tenen
FITXA 1: Polígons. Conceptes A.1. REPASSA ELS TEUS CONEIXEMENTS. 1. Escriu la lletra de les figures equilàteres. A, D 2. Escriu el nom de les figures equiangulars. A, D 3. Anomena les figures que tenen
Unitat 2 TEOREMA DE TALES. TEOREMA DE PITÀGORES. RAONS TRIGONOMÈTRIQUES UNITAT 2 TEOREMA DE TALES.
 Unitat 2 TEOREMA DE TALES. TEOREMA DE PITÀGORES. RAONS TRIGONOMÈTRIQUES 41 42 Matemàtiques, Ciència i Tecnologia 8. TRIGONOMETRIA UNITAT 2 QUÈ TREBALLARÀS? què treballaràs? En acabar la unitat has de ser
Unitat 2 TEOREMA DE TALES. TEOREMA DE PITÀGORES. RAONS TRIGONOMÈTRIQUES 41 42 Matemàtiques, Ciència i Tecnologia 8. TRIGONOMETRIA UNITAT 2 QUÈ TREBALLARÀS? què treballaràs? En acabar la unitat has de ser
FITXA 1: Angles consecutius i adjacents
 FITXA 1: Angles consecutius i adjacents A.1. OBSERVA AQUESTES FIGURES I FES EL QUE S INDICA: Consecutius Adjacents Oposats 1. Col loca aquests noms en la figura corresponent: angles adjacents, angles oposats
FITXA 1: Angles consecutius i adjacents A.1. OBSERVA AQUESTES FIGURES I FES EL QUE S INDICA: Consecutius Adjacents Oposats 1. Col loca aquests noms en la figura corresponent: angles adjacents, angles oposats
Proves d accés a la Universitat per a més grans de 25 anys Convocatòria 2013
 Pàgina 1 de 5 Sèrie 3 Opció A A1.- Digueu de quin tipus és la progressió numèrica següent i calculeu la suma dels seus termes La progressió és geomètrica de raó 2 ja que cada terme s obté multiplicant
Pàgina 1 de 5 Sèrie 3 Opció A A1.- Digueu de quin tipus és la progressió numèrica següent i calculeu la suma dels seus termes La progressió és geomètrica de raó 2 ja que cada terme s obté multiplicant
j Unitat 6. Rectes en el pla
 MATEMÀTIQUES 9 4. Calcula a a sabent que a b, b b 4 i que l angle que formen els vectors a i b mesura 0º. b b 4 b 4 b a b a b cos a a cos 0º a cos 0º a a a 9. Els punts A(, ), B(, ) i C(, ) són tres vèrtexs
MATEMÀTIQUES 9 4. Calcula a a sabent que a b, b b 4 i que l angle que formen els vectors a i b mesura 0º. b b 4 b 4 b a b a b cos a a cos 0º a cos 0º a a a 9. Els punts A(, ), B(, ) i C(, ) són tres vèrtexs
SOLUCIONARI Unitat 5
 SOLUCIONARI Unitat 5 Comencem Escriu tres equacions que no tinguin solució en el conjunt. Resposta oberta. Per exemple: a) x b) 5x 0 c) x Estableix tres equacions que no tinguin solució en el conjunt.
SOLUCIONARI Unitat 5 Comencem Escriu tres equacions que no tinguin solució en el conjunt. Resposta oberta. Per exemple: a) x b) 5x 0 c) x Estableix tres equacions que no tinguin solució en el conjunt.
PROVES D ACCÉS A CICLES FORMATIUS DE GRAU SUPERIOR Convocatòria maig de 2005 DIBUIX TÈCNIC
 PROVES D ACCÉS A CICLES FORMATIUS DE GRAU SUPERIOR Convocatòria maig de 2005 DIBUIX TÈCNIC 1º A Donada la perspectiva de la figura dibuixa, a mà alçada, les tres vistes de la mateixa Dada la perspectiva
PROVES D ACCÉS A CICLES FORMATIUS DE GRAU SUPERIOR Convocatòria maig de 2005 DIBUIX TÈCNIC 1º A Donada la perspectiva de la figura dibuixa, a mà alçada, les tres vistes de la mateixa Dada la perspectiva
UNITAT 3: TRIGONOMETRIA
 UNITAT 3: TRIGONOMETRIA 1. Angles Anomenem angle a l'espai del pla tancat per dues semirectes que tenen un mateix origen. Podem classificar els angles segons la seva obertura en tres tipus: agut, recte
UNITAT 3: TRIGONOMETRIA 1. Angles Anomenem angle a l'espai del pla tancat per dues semirectes que tenen un mateix origen. Podem classificar els angles segons la seva obertura en tres tipus: agut, recte
TEMA 10: Cossos geomètrics
 TEMA 10: Cossos geomètrics 4tESO CB Cossos geomètrics: podem diferenciar poliedres i cossos de revolució I. Poliedre És una figura tridimensional limitat per cares que tenen forma de polígon: triangles,
TEMA 10: Cossos geomètrics 4tESO CB Cossos geomètrics: podem diferenciar poliedres i cossos de revolució I. Poliedre És una figura tridimensional limitat per cares que tenen forma de polígon: triangles,
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 30 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE Activitat 1 Completa la taula següent: Graus Minuts Segons 30º 30 x 60 = 1.800 1.800 x 60 = 108.000 45º 2.700 162.000 120º 7.200 432.000 270º 16.200 972.000
30 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE Activitat 1 Completa la taula següent: Graus Minuts Segons 30º 30 x 60 = 1.800 1.800 x 60 = 108.000 45º 2.700 162.000 120º 7.200 432.000 270º 16.200 972.000
Políedres regulars Cossos de revolució
 Políedres regulars Cossos de revolució Políedre. Un políedre és un cos limitat per cares poligonals. Angle díedre. Angle políedre anomena angle díedre d un políedre el que està format per dues cares que
Políedres regulars Cossos de revolució Políedre. Un políedre és un cos limitat per cares poligonals. Angle díedre. Angle políedre anomena angle díedre d un políedre el que està format per dues cares que
EXERCICIS PROPOSATS. 3 cm
 EXERCICIS PROPOSATS 1.1 Calcula el perímetre de les figures següents. a), b) cm cm cm a) p,5 8 5 1 b) p 9 cm 1. Calcula el perímetre d aquestes figures. a) Un quadrat de 6 centímetres de costat. b) Un
EXERCICIS PROPOSATS 1.1 Calcula el perímetre de les figures següents. a), b) cm cm cm a) p,5 8 5 1 b) p 9 cm 1. Calcula el perímetre d aquestes figures. a) Un quadrat de 6 centímetres de costat. b) Un
Geometria. Àrees i volums de cossos geomètrics
 Geometria. Àrees i volums de cossos geomètrics Àrea de figures planes... Àrea dels paral lelograms... Àrea del quadrat... Àrea del rectangle... 3 Àrea del rombe... 4 Àrea del paral lelogram... 4 Àrea dels
Geometria. Àrees i volums de cossos geomètrics Àrea de figures planes... Àrea dels paral lelograms... Àrea del quadrat... Àrea del rectangle... 3 Àrea del rombe... 4 Àrea del paral lelogram... 4 Àrea dels
RECONÈIXER ELS PRISMES I PIRÀMIDES PRINCIPALS. CALCULAR-NE LES ÀREES
 OBJECTIU RECONÈIXER ELS PRISMES I PIRÀMIDES PRINCIPALS. CALCULAR-NE LES ÀREES 10 NOM: CURS: DATA: CONCEPTE DE PRISMA Un prisma és un poliedre format per dues bases iguals i paral leles, les cares laterals
OBJECTIU RECONÈIXER ELS PRISMES I PIRÀMIDES PRINCIPALS. CALCULAR-NE LES ÀREES 10 NOM: CURS: DATA: CONCEPTE DE PRISMA Un prisma és un poliedre format per dues bases iguals i paral leles, les cares laterals
= 1+ β, essent α i β paràmetres reals. a la recta r 2. i el pla Π d equació
 Problema A Setembre 0 + y z = En l espai es té la recta r i el pla Π d equacions r x + mz = 0, on x y z = 0 m és un paràmetre real a) Un vector director de la recta r b) El valor de m per al qual la recta
Problema A Setembre 0 + y z = En l espai es té la recta r i el pla Π d equacions r x + mz = 0, on x y z = 0 m és un paràmetre real a) Un vector director de la recta r b) El valor de m per al qual la recta
Problemes de Geometria per a l ESO 171
 roblemes de Geometria per a l ESO 171 1701- Siga un triangle acutangle i i E les altures Si E = 5, E = 3, = etermineu E 3 x 5 Siga = x plicant el teorema de itàgores al triangle rectangle = 15 plicant
roblemes de Geometria per a l ESO 171 1701- Siga un triangle acutangle i i E les altures Si E = 5, E = 3, = etermineu E 3 x 5 Siga = x plicant el teorema de itàgores al triangle rectangle = 15 plicant
D55. El mirall o superfície reflectant. Còncau. part interna. Convex. El mirall o superfície reflectant. correspon a la. part externa.
 D55 Aplicacions de la llei de la reflexió als miralls. Miralls plans Miralls esfèrics o corbs Còncau El mirall o superfície reflectant correspon a la part interna. Convex El mirall o superfície reflectant
D55 Aplicacions de la llei de la reflexió als miralls. Miralls plans Miralls esfèrics o corbs Còncau El mirall o superfície reflectant correspon a la part interna. Convex El mirall o superfície reflectant
LLOCS GEOMÈTRICS. CÒNIQUES
 LLOCS GEOMÈTRICS. CÒNIQUES Pàgina REFLEXIONA I RESOL Còniques obertes: paràboles i hipèrboles Completa la taula següent, en què a és l angle que formen les generatrius amb l eix, e, de la cònica i b l
LLOCS GEOMÈTRICS. CÒNIQUES Pàgina REFLEXIONA I RESOL Còniques obertes: paràboles i hipèrboles Completa la taula següent, en què a és l angle que formen les generatrius amb l eix, e, de la cònica i b l
quaderns de matemàtiques
 1 quaderns de matemàtiques trigonometria 2 AUTOR / RECOPILADOR: Xavier Vilardell Bascompte xevi.vb@gmail.com CURS: 2007-2008 ÚLTIMA REVISIÓ: 22 de gener de 2008 Aquests quaderns de matemàtiques han estat
1 quaderns de matemàtiques trigonometria 2 AUTOR / RECOPILADOR: Xavier Vilardell Bascompte xevi.vb@gmail.com CURS: 2007-2008 ÚLTIMA REVISIÓ: 22 de gener de 2008 Aquests quaderns de matemàtiques han estat
Tema 1: TRIGONOMETRIA
 Tema : TRIGONOMETRIA Raons trigonomètriques d un angle - sinus ( projecció sobre l eix y ) sin α sin α [, ] - cosinus ( projecció sobre l eix x ) cos α cos α [ -, ] - tangent tan α sin α / cos α tan α
Tema : TRIGONOMETRIA Raons trigonomètriques d un angle - sinus ( projecció sobre l eix y ) sin α sin α [, ] - cosinus ( projecció sobre l eix x ) cos α cos α [ -, ] - tangent tan α sin α / cos α tan α
TEMA 6 : Geometria en l espai. Activitats
 TEMA 6 : Geometria en l espai Activitats 1. Siguin els punts A(1,2,3), B(0,1,3) i C(2,3,1) a) Trobeu el vector b) Calculeu el mòdul del vector c) Trobeu el vector unitari d igual direcció que el vector
TEMA 6 : Geometria en l espai Activitats 1. Siguin els punts A(1,2,3), B(0,1,3) i C(2,3,1) a) Trobeu el vector b) Calculeu el mòdul del vector c) Trobeu el vector unitari d igual direcció que el vector
Resolucions de l autoavaluació del llibre de text
 Pàg. 1 de 1 Tenim els vectors u(3,, 1), v ( 4, 0, 3) i w (3,, 0): a) Formen una base de Á 3? b) Troba m per tal que el vector (, 6, m) sigui perpendicular a u. c) Calcula u, ì v i ( u, v). a) Per tal que
Pàg. 1 de 1 Tenim els vectors u(3,, 1), v ( 4, 0, 3) i w (3,, 0): a) Formen una base de Á 3? b) Troba m per tal que el vector (, 6, m) sigui perpendicular a u. c) Calcula u, ì v i ( u, v). a) Per tal que
Geometria Analítica del pla
 Geometria Analítica del pla Continguts 1. Vectors Vectors fixos i vectors lliures Operacions amb vectors Combinació lineal de vectors Punt mitjà d un segment Producte escalar Aplicacions del producte escalar
Geometria Analítica del pla Continguts 1. Vectors Vectors fixos i vectors lliures Operacions amb vectors Combinació lineal de vectors Punt mitjà d un segment Producte escalar Aplicacions del producte escalar
DOSSIER DE RECUPERACIÓ CURS VISUAL I PLÀSTICA 3ESO PROF: CATERINA PUPPO
 INSTITUT ELS TRES TURONS ÀMBIT ARTÍSTIC DOSSIER DE RECUPERACIÓ CURS 2017-2018 VISUAL I PLÀSTICA 3ESO PROF: CATERINA PUPPO Per superar l assignatura s ha de presentar a l exàmen de setembre junt amb el
INSTITUT ELS TRES TURONS ÀMBIT ARTÍSTIC DOSSIER DE RECUPERACIÓ CURS 2017-2018 VISUAL I PLÀSTICA 3ESO PROF: CATERINA PUPPO Per superar l assignatura s ha de presentar a l exàmen de setembre junt amb el
En aquest tema estudiarem bàsicament els triangles, relacions entre ells i punts distingits.
 1 Triangles En aquest tema estudiarem bàsicament els triangles, relacions entre ells i punts distingits. 1.1 Propietats bàsiques riteris d igualtat. Els següents criteris ens asseguren que dos triangles
1 Triangles En aquest tema estudiarem bàsicament els triangles, relacions entre ells i punts distingits. 1.1 Propietats bàsiques riteris d igualtat. Els següents criteris ens asseguren que dos triangles
DIBUIX TÈCNIC, 2n BATXILLERAT. 1r CRÈDIT: GEOMETRIA PLANA
 DIUIX TÈCNIC, 2n ATXILLERAT 1r CRÈDIT: GEOMETRIA LANA IES uig de la Creu 1 INDEX 1.- TEMA 1: ROORCIONALITAT 1.1.- directa e invsa 1.2.- quarta i tca proporcional 1.3.- mitjana proporcional: teorema del
DIUIX TÈCNIC, 2n ATXILLERAT 1r CRÈDIT: GEOMETRIA LANA IES uig de la Creu 1 INDEX 1.- TEMA 1: ROORCIONALITAT 1.1.- directa e invsa 1.2.- quarta i tca proporcional 1.3.- mitjana proporcional: teorema del
TEMA 4 : Matrius i Determinants
 TEMA 4 : Matrius i Determinants MATRIUS 4.1. NOMENCLATURA. DEFINICIÓ Una matriu és un conjunt de mxn elements distribuïts en m files i n columnes, A= Aquesta és una matriu de m files per n columnes. És
TEMA 4 : Matrius i Determinants MATRIUS 4.1. NOMENCLATURA. DEFINICIÓ Una matriu és un conjunt de mxn elements distribuïts en m files i n columnes, A= Aquesta és una matriu de m files per n columnes. És
10 Àlgebra vectorial. on 3, -2 i 4 són les projeccions en els eixos x, y, y z respectivament.
 10 Àlgebra vectorial ÀLGEBR VECTORIL Índe P.1. P.. P.3. P.4. P.5. P.6. Vectors Suma i resta vectorial Producte d un escalar per un vector Vector unitari Producte escalar Producte vectorial P.1. Vectors
10 Àlgebra vectorial ÀLGEBR VECTORIL Índe P.1. P.. P.3. P.4. P.5. P.6. Vectors Suma i resta vectorial Producte d un escalar per un vector Vector unitari Producte escalar Producte vectorial P.1. Vectors
Semblança. Teorema de Tales
 Semblança. Teorema de Tales Dos polígons són semblants si el angles corresponents són iguals i els costats corresponents són proporcionals. ABCDE A'B'C'D'E' si: Â = Â',Bˆ = Bˆ', Ĉ = Ĉ', Dˆ = Dˆ', Ê = Ê'
Semblança. Teorema de Tales Dos polígons són semblants si el angles corresponents són iguals i els costats corresponents són proporcionals. ABCDE A'B'C'D'E' si: Â = Â',Bˆ = Bˆ', Ĉ = Ĉ', Dˆ = Dˆ', Ê = Ê'
Geometria / GE 2. Perpendicularitat S. Xambó
 Geometria / GE 2. Perpendicularitat S. Xambó Vectors perpendiculars Ortogonal d un subespai Varietats lineals ortogonals Projecció ortogonal Càlcul efectiu de la projecció ortogonal Aplicació: ortonormalització
Geometria / GE 2. Perpendicularitat S. Xambó Vectors perpendiculars Ortogonal d un subespai Varietats lineals ortogonals Projecció ortogonal Càlcul efectiu de la projecció ortogonal Aplicació: ortonormalització
Exercicis de rectes en el pla
 Equacions de la recta 1. Escriu les diferents equacions de la recta que passa pel punt P(3, 4) i que té com a vector director el vector v = ( 5, 2). 2. Per a la recta d equació director. 6 + y = 1, escriu
Equacions de la recta 1. Escriu les diferents equacions de la recta que passa pel punt P(3, 4) i que té com a vector director el vector v = ( 5, 2). 2. Per a la recta d equació director. 6 + y = 1, escriu
TEMA 4 : Geometria analítica al pla. Vectors i la Recta. Activitats
 TEMA 4 : Geometria analítica al pla. Vectors i la Recta Activitats 1. Donats els punts A(2,1), B(6,5),i C(-1,4): a) Representa els vectors AB i CA i estudia totes les seves característiques b) Calcula
TEMA 4 : Geometria analítica al pla. Vectors i la Recta Activitats 1. Donats els punts A(2,1), B(6,5),i C(-1,4): a) Representa els vectors AB i CA i estudia totes les seves característiques b) Calcula
VECTORS I RECTES AL PLA. Exercici 1 Tenint en compte quin és l'origen i quin és l'extrem, anomena els següents vectors: D
 VECTORS I RECTES AL PLA Un vector és un segment orientat que és determinat per dos punts, A i B, i l'ordre d'aquests. El primer dels punts s'anomena origen i el segons es denomina extrem, i s'escriu AB.
VECTORS I RECTES AL PLA Un vector és un segment orientat que és determinat per dos punts, A i B, i l'ordre d'aquests. El primer dels punts s'anomena origen i el segons es denomina extrem, i s'escriu AB.
I. SISTEMA DIÈDRIC 3. DISTÀNCIES I ANGLES DIBUIX TÈCNIC
 DIBUIX TÈCNIC I. SISTEMA DIÈDRIC 3. DISTÀNCIES I ANGLES 1. Dist. d un punt a una recta - Abatiment del pla format per la recta i el punt 2. Dist. d un punt a un pla - Canvi de pla posant el pla de perfil
DIBUIX TÈCNIC I. SISTEMA DIÈDRIC 3. DISTÀNCIES I ANGLES 1. Dist. d un punt a una recta - Abatiment del pla format per la recta i el punt 2. Dist. d un punt a un pla - Canvi de pla posant el pla de perfil
Figures planes, propietats mètriques
 Figures planes, propietats mètriques Continguts 1. Angles en la circumferència Angle central i angle inscrit 2. Semblança Figures semblants Semblança de triangles, criteris 3. Triangles rectangles Teorema
Figures planes, propietats mètriques Continguts 1. Angles en la circumferència Angle central i angle inscrit 2. Semblança Figures semblants Semblança de triangles, criteris 3. Triangles rectangles Teorema
6. Calcula l obertura de l angle que falta. Digues de quin tipus d angles es tracta. 6
 Geometria dossier estiu 2012 2C 1. Dibuixa dues rectes, m i n, que siguin: a) Paral leles horitzontalment. c) Paral leles verticalment. b) Secants. d) Perpendiculars. 6 2. Dibuixa una recta qualsevol m
Geometria dossier estiu 2012 2C 1. Dibuixa dues rectes, m i n, que siguin: a) Paral leles horitzontalment. c) Paral leles verticalment. b) Secants. d) Perpendiculars. 6 2. Dibuixa una recta qualsevol m
QUADERN d ESTUDI de RECTES TANGENTS
 QUADERN d ESTUDI de RECTES TANGENTS per a les PAU i 2n de Batxillerat Autor: Pepe Ródenas Borja pepe.rodenas.borja@gmail.com http://manifoldo.weebly.com Descripció del material: Aquest quadern consisteix
QUADERN d ESTUDI de RECTES TANGENTS per a les PAU i 2n de Batxillerat Autor: Pepe Ródenas Borja pepe.rodenas.borja@gmail.com http://manifoldo.weebly.com Descripció del material: Aquest quadern consisteix
Problemes de Geometria per a l ESO 178
 Problemes de Geometria per a l EO 17 1771- alculeu el perímetre de la figura KöMaL, K04 01 19 19 olució: onsiderem el pentàgon DE Les rectes i DE s intersecten en el punt P PD = 90º PD = DE = 01 19 = 0
Problemes de Geometria per a l EO 17 1771- alculeu el perímetre de la figura KöMaL, K04 01 19 19 olució: onsiderem el pentàgon DE Les rectes i DE s intersecten en el punt P PD = 90º PD = DE = 01 19 = 0
16 febrer 2016 Integrals exercicis. 3 Integrals
 I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 16 febrer 2016 Integrals exercicis 3 Integrals 28. Troba una funció primitiva de les següents funcions: () = 1/ () = 3 h() = 2 () = 4 () = cos () = sin () =
I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 16 febrer 2016 Integrals exercicis 3 Integrals 28. Troba una funció primitiva de les següents funcions: () = 1/ () = 3 h() = 2 () = 4 () = cos () = sin () =
Visual i Plàstica Dossier de recuperació curs r d'eso
 Visual i Plàstica Dossier de recuperació curs 2011-2012 3r d'eso 1 EL COLOR Colors primaris, secundaris i terciaris 1. El cercle cromàtic Situa en aquest cercle cromàtic els 3 colors primaris, els 3 colors
Visual i Plàstica Dossier de recuperació curs 2011-2012 3r d'eso 1 EL COLOR Colors primaris, secundaris i terciaris 1. El cercle cromàtic Situa en aquest cercle cromàtic els 3 colors primaris, els 3 colors
SÈRIE 3 PAU. Curs DIBUIX TÈCNIC
 SÈRIE 3 PAU. Curs 2003-2004 DIBUIX TÈCNIC L examen consta de la realització de tres dibuixos: el dibuix 1, una de les dues opcions del dibuix 2 i una de les dues opcions del dibuix 3. Escolliu entre l
SÈRIE 3 PAU. Curs 2003-2004 DIBUIX TÈCNIC L examen consta de la realització de tres dibuixos: el dibuix 1, una de les dues opcions del dibuix 2 i una de les dues opcions del dibuix 3. Escolliu entre l
Problemes de Geometria per a l ESO 206
 Problemes de Geometria per a l ESO 06 05- onada una circumferència de centre O i radi R, dibuixem les cordes i iguals al costat del quadrat inscrit i la corda igual a costat de l hexàgon regular a) alculeu
Problemes de Geometria per a l ESO 06 05- onada una circumferència de centre O i radi R, dibuixem les cordes i iguals al costat del quadrat inscrit i la corda igual a costat de l hexàgon regular a) alculeu
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 59 Activitat 1 Llegeix atentament el teorema de Tales. Creus que també és certa la proporció següent? Per què? AB CD A B C D El teorema de Tales diu: AB (A B
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 59 Activitat 1 Llegeix atentament el teorema de Tales. Creus que també és certa la proporció següent? Per què? AB CD A B C D El teorema de Tales diu: AB (A B
Deduce razonadamente en que casos los planos π 1 y π 2 son o no paralelos:
 GEOMETRÍA Junio 98 Deduce razonadamente en que casos los planos y son o no paralelos: a) : x + y + z = y : x + y z = 4 b) : x y + z = 4 y : x y + z = Obtén la distancia entre los planos y cuando sean paralelos.
GEOMETRÍA Junio 98 Deduce razonadamente en que casos los planos y son o no paralelos: a) : x + y + z = y : x + y z = 4 b) : x y + z = 4 y : x y + z = Obtén la distancia entre los planos y cuando sean paralelos.
x x 1 x 11= 7) y = 6 3x-2 12) y = e 5x (3x 2-6)
 Derivació1/ 1.- Calculeu la primera derivada de les funcions següents, simplificant el resultat el màim possible. 1) y = - 4 4 + - ) y 6 4 4 = + 3 3) y = 3 + 4) y = ) 3 y = 6) y = ( + ) 1 + 7) ( 3) y =
Derivació1/ 1.- Calculeu la primera derivada de les funcions següents, simplificant el resultat el màim possible. 1) y = - 4 4 + - ) y 6 4 4 = + 3 3) y = 3 + 4) y = ) 3 y = 6) y = ( + ) 1 + 7) ( 3) y =
CONCEPTES BÀSICS SOBRE SUPERFÍCIES GEOMÈTRIQUES
 CONCEPTES BÀSICS SOBRE SUPERFÍCIES GEOMÈTRIQUES Entenem per superfície el lloc geomètric de les successives posicions d una línia que es mou a l espai, seguint una llei determinada i contínua. Aquesta
CONCEPTES BÀSICS SOBRE SUPERFÍCIES GEOMÈTRIQUES Entenem per superfície el lloc geomètric de les successives posicions d una línia que es mou a l espai, seguint una llei determinada i contínua. Aquesta
MMF 10 / 1. Mecànica 5. Dinàmica del sòlid rígid: tensor d inèrcia S. Xambó
 MMF 10 / 1. Mecànica 5. Dinàmica del sòlid rígid: tensor d inèrcia S. Xambó Preliminars matemàtics Tensor d inèrcia Teorema d Steiner Moment angular Energia cinètica Moments d inèrcia Moments i eixos principals
MMF 10 / 1. Mecànica 5. Dinàmica del sòlid rígid: tensor d inèrcia S. Xambó Preliminars matemàtics Tensor d inèrcia Teorema d Steiner Moment angular Energia cinètica Moments d inèrcia Moments i eixos principals
CONVOCATÒRIA D INCIDÈNCIES. Proves d'accés a Cicles Formatius de Grau Superior Dibuix Tècnic
 CONVOCATÒRIA D INCIDÈNCIES Proves d'accés a Cicles Formatius de Grau Superior 2001 Part específica Dibuix Tècnic Per accedir a cicles formatius de grau superior: Navegació, pesca i transport marítim. Disseny
CONVOCATÒRIA D INCIDÈNCIES Proves d'accés a Cicles Formatius de Grau Superior 2001 Part específica Dibuix Tècnic Per accedir a cicles formatius de grau superior: Navegació, pesca i transport marítim. Disseny
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 PAU 2012
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 1 1 k 1.- Determineu el rang de la matriu A = 1 k 1 en funció del valor del paràmetre k. k 1 1 [2 punts] En ser la matriu
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 1 1 k 1.- Determineu el rang de la matriu A = 1 k 1 en funció del valor del paràmetre k. k 1 1 [2 punts] En ser la matriu
Els catets d un triangle rectangle mesuren 5 i 13 centímetres. Calcula n el valor de la hipotenusa.
 1 LONGITUDS I ÀREES EXERCICIS PER A ENTRENAR-SE Teorema de Pitàgores 1.8 Els catets d un triangle rectangle mesuren i 1 centímetres. Calcula n el valor de la hipotenusa. Si fem servir el teorema de Pitàgores:
1 LONGITUDS I ÀREES EXERCICIS PER A ENTRENAR-SE Teorema de Pitàgores 1.8 Els catets d un triangle rectangle mesuren i 1 centímetres. Calcula n el valor de la hipotenusa. Si fem servir el teorema de Pitàgores:
Dibuix Tècnic. Sistemes de representació
 Dibuix Tècnic Sistemes de representació El dibuix és una ferramenta que ens ajuda a representar la realitat. plànol esbós realitat Representar la realitat mitjançant dibuixos Dibuixos en 2D Dibuixos en
Dibuix Tècnic Sistemes de representació El dibuix és una ferramenta que ens ajuda a representar la realitat. plànol esbós realitat Representar la realitat mitjançant dibuixos Dibuixos en 2D Dibuixos en
FUNCIONS REALS. MATEMÀTIQUES-1
 FUNCIONS REALS. 1. El concepte de funció. 2. Domini i recorregut d una funció. 3. Característiques generals d una funció. 4. Funcions definides a intervals. 5. Operacions amb funcions. 6. Les successions
FUNCIONS REALS. 1. El concepte de funció. 2. Domini i recorregut d una funció. 3. Característiques generals d una funció. 4. Funcions definides a intervals. 5. Operacions amb funcions. 6. Les successions
INTERACCIÓ GRAVITATÒRIA
 INTERACCIÓ GRAVITATÒRIA REPÀS FÓRMULES DE MOVIMENT MRU MRUA CAIGUDA LLIURE MRUA on MCU LLEIS DE KEPLER 1ª. Tots els planetes es mouen al voltant del sol seguint òrbites el líptiques. El Sol està a un dels
INTERACCIÓ GRAVITATÒRIA REPÀS FÓRMULES DE MOVIMENT MRU MRUA CAIGUDA LLIURE MRUA on MCU LLEIS DE KEPLER 1ª. Tots els planetes es mouen al voltant del sol seguint òrbites el líptiques. El Sol està a un dels
CONVOCATÒRIA ORDINÀRIA. Proves d'accés a Cicles Formatius Error! Marcador no definido.de Grau Superior Dibuix Tècnic
 CONVOCATÒRIA ORDINÀRIA Proves d'accés a Cicles Formatius Error! Marcador no definido.de Grau Superior 2000 Part específica Dibuix Tècnic Per accedir a cicles formatius de grau superior: Navegació, pesca
CONVOCATÒRIA ORDINÀRIA Proves d'accés a Cicles Formatius Error! Marcador no definido.de Grau Superior 2000 Part específica Dibuix Tècnic Per accedir a cicles formatius de grau superior: Navegació, pesca
Proporcionalitat i percentatges
 Proporcionalitat i percentatges Proporcions... 2 Propietats de les proporcions... 2 Càlul del quart proporcional... 3 Proporcionalitat directa... 3 Proporcionalitat inversa... 5 El tant per cent... 6 Coneixement
Proporcionalitat i percentatges Proporcions... 2 Propietats de les proporcions... 2 Càlul del quart proporcional... 3 Proporcionalitat directa... 3 Proporcionalitat inversa... 5 El tant per cent... 6 Coneixement
Districte Universitari de Catalunya
 Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val
Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val
Unitat didàctica 7. Desenvolupament i superfície del cossos geomètrics
 Unitat didàctica 7. Desenvolupament i superfície del cossos geomètrics Reflexiona Quantes cares té aquest poliedre? Quantes cares són triangles? I quadrilàters? Compta el nombre d arestes i vèrtexs que
Unitat didàctica 7. Desenvolupament i superfície del cossos geomètrics Reflexiona Quantes cares té aquest poliedre? Quantes cares són triangles? I quadrilàters? Compta el nombre d arestes i vèrtexs que
Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera:
 Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera: ax + by = k a x + b y = k Coeficients de les incògnites: a, a, b, b. Termes independents:
Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera: ax + by = k a x + b y = k Coeficients de les incògnites: a, a, b, b. Termes independents:
EXERCICIS PROPOSATS. Observa la figura i digues quin element geomètric determinen la recta i el pla.
 13 COSSOS GEOMÈTRICS EXERCICIS PROPOSTS 13.1 Observa la figura i digues quin element geomètric determinen la recta i el pla. r α La recta r i el pla determinen un punt. 13.2 mb els quatre punts que delimiten
13 COSSOS GEOMÈTRICS EXERCICIS PROPOSTS 13.1 Observa la figura i digues quin element geomètric determinen la recta i el pla. r α La recta r i el pla determinen un punt. 13.2 mb els quatre punts que delimiten
Càlcul d'àrees i volums.
 Càlcul d'àrees i volums. Exemple 1. Donada la figura següent: Calcula'n: superfície volum Resolució: Fixem-nos que la superfície està formada per tres objectes.: 1. la base del cilindre 2. la paret del
Càlcul d'àrees i volums. Exemple 1. Donada la figura següent: Calcula'n: superfície volum Resolució: Fixem-nos que la superfície està formada per tres objectes.: 1. la base del cilindre 2. la paret del
Vector unitari Els vectors unitaris tenen de mòdul la unitat. Calculem el vector unitari del vector següent manera: ( ) ( )
 GEOMETRIA EN L ESPAI VECTORS EN L ESPAI OPERACIONS AMB VECTORS Un vector és un segment orientat en l espai que té un mòdul, una direcció i un sentit coneguts: té un extrem i un origen (Exemple: vector
GEOMETRIA EN L ESPAI VECTORS EN L ESPAI OPERACIONS AMB VECTORS Un vector és un segment orientat en l espai que té un mòdul, una direcció i un sentit coneguts: té un extrem i un origen (Exemple: vector
UNITAT 3: SISTEMES D EQUACIONS
 UNITAT 3: SISTEMES D EQUACIONS 1. EQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITES L equació x + y = 3 és una equació de primer grau amb dues incògnites : x i y. Per calcular les solucions escollim un valor
UNITAT 3: SISTEMES D EQUACIONS 1. EQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITES L equació x + y = 3 és una equació de primer grau amb dues incògnites : x i y. Per calcular les solucions escollim un valor
Problemes de Geometria per a l ESO Calculeu l àrea d un cercle tal que té un hexàgon inscrit de costats consecutius 1, 1, 1, 2, 2, 2.
 Problemes de Geometria per a l SO 7 6- alculeu l àrea d un cercle tal que té un hexàgon inscrit de costats consecutius,,,,, Siga l hexàgon inscrit en la circumferència de centre O i radi r Siga α O, β
Problemes de Geometria per a l SO 7 6- alculeu l àrea d un cercle tal que té un hexàgon inscrit de costats consecutius,,,,, Siga l hexàgon inscrit en la circumferència de centre O i radi r Siga α O, β
PROVES D ACCÉS A CFGS
 PROVES D ACCÉS A CFGS DIBUIX TÈCNIC TEMARI BLOC 1: TRAÇATS FONAMENTALS EN EL PLA 1.1 Instruments de dibuix 1.1.1 Coneixement de diferents tipus de paper (opac, transparent, milimetrat, etc.). 1.1.2 Llapis
PROVES D ACCÉS A CFGS DIBUIX TÈCNIC TEMARI BLOC 1: TRAÇATS FONAMENTALS EN EL PLA 1.1 Instruments de dibuix 1.1.1 Coneixement de diferents tipus de paper (opac, transparent, milimetrat, etc.). 1.1.2 Llapis
Els fulls de càlcul. Tabla 1 : Calculadora
 Els fulls de càlcul Els Fulls de càlcul tenen etiquetes de columna (A, B, C,...) i etiquetes de files (1, 2, 3,...). Aquestes etiquetes constitueixen les coordenades per les quals s identifica una cel
Els fulls de càlcul Els Fulls de càlcul tenen etiquetes de columna (A, B, C,...) i etiquetes de files (1, 2, 3,...). Aquestes etiquetes constitueixen les coordenades per les quals s identifica una cel
Cognoms i Nom: Examen parcial de Física - CORRENT CONTINU 3 d Octubre del 2013
 Examen parcial de Física - COENT CONTINU Model Qüestions: 50% de l examen cada qüestió només hi ha una resposta correcta. Encercleu-la de manera clara. Puntuació: correcta = 1 punt, incorrecta = -0.25
Examen parcial de Física - COENT CONTINU Model Qüestions: 50% de l examen cada qüestió només hi ha una resposta correcta. Encercleu-la de manera clara. Puntuació: correcta = 1 punt, incorrecta = -0.25
Geometria / GQ 2. Invariants euclidians de les còniques S. Xambó
 Geometria / GQ 2. Invariants euclidians de les còniques S. Xambó,, Classificació de còniques mitjançant invariants Obtenció de les equacions reduïdes i canòniques a partir dels invariants Exemple: àrea
Geometria / GQ 2. Invariants euclidians de les còniques S. Xambó,, Classificació de còniques mitjançant invariants Obtenció de les equacions reduïdes i canòniques a partir dels invariants Exemple: àrea
Districte Universitari de Catalunya
 Proves d accés a la universitat Convocatòria 2014 Dibuix tècnic Sèrie 3 Indiqueu les opcions triades: Exercici 1: Opció A Opció B Exercici 2: Opció A Opció B Exercici 3: Opció A Opció B Qualificació 1
Proves d accés a la universitat Convocatòria 2014 Dibuix tècnic Sèrie 3 Indiqueu les opcions triades: Exercici 1: Opció A Opció B Exercici 2: Opció A Opció B Exercici 3: Opció A Opció B Qualificació 1
TEMA 1: Trigonometria
 TEMA 1: Trigonometria La trigonometria, és la part de la geometria dedicada a la resolució de triangles, es a dir, a determinar els valors dels angles i dels costats d un triangle. 1.1 MESURA D ANGLES
TEMA 1: Trigonometria La trigonometria, és la part de la geometria dedicada a la resolució de triangles, es a dir, a determinar els valors dels angles i dels costats d un triangle. 1.1 MESURA D ANGLES
ACTIVITATS FINALS. Segments proporcionals. Teorema de Tales. a) AB = 2 cm i CD = 5 cm. b) AB = 7,5 cm i CD = 15 cm. c) AB = 1 m i CD = 30 dm.
 TIVITTS INLS Segments proporcionals 33 34 a) cm i b) 7, i c) m i 30 dm d) 7 mm i 0,4 dm 35 4 5 36 3 7 37 a) cm E GH 0 cm b) E 9 cm GH Teorema de Tales 43 a) b) 3 cm, cm,, 3, 44 a) e) 4,,8 cm cm b) f )
TIVITTS INLS Segments proporcionals 33 34 a) cm i b) 7, i c) m i 30 dm d) 7 mm i 0,4 dm 35 4 5 36 3 7 37 a) cm E GH 0 cm b) E 9 cm GH Teorema de Tales 43 a) b) 3 cm, cm,, 3, 44 a) e) 4,,8 cm cm b) f )
DERIVADES. TÈCNIQUES DE DERIVACIÓ
 UNITAT 7 DERIVADES. TÈCNIQUES DE DERIVACIÓ Pàgina 56 Tangents a una corba y f (x) 5 5 9 4 Troba, mirant la gràfica i les rectes traçades, f'(), f'(9) i f'(4). f'() 0; f'(9) ; f'(4) 4 Digues uns altres
UNITAT 7 DERIVADES. TÈCNIQUES DE DERIVACIÓ Pàgina 56 Tangents a una corba y f (x) 5 5 9 4 Troba, mirant la gràfica i les rectes traçades, f'(), f'(9) i f'(4). f'() 0; f'(9) ; f'(4) 4 Digues uns altres
QUADERN Núm. 9 NOM: DATA: / /
 Cossos geomètrics Continguts 1. Poliedres Definició Elements d un poliedre 2. Tipus de poliedres Prismes Prismes regulars Desenvolupament d un prisma recte Paral lelepípedes Piràmides Piràmides regulars
Cossos geomètrics Continguts 1. Poliedres Definició Elements d un poliedre 2. Tipus de poliedres Prismes Prismes regulars Desenvolupament d un prisma recte Paral lelepípedes Piràmides Piràmides regulars
1.- Sabem que el vector (2, 1, 1) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c. . cx by +2z = b
 Oficina d Organització de Proves d Accés a la Universitat Pàgina de 5 PAU 0 - Sabem que el vector (,, ) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c cx by +z = b Calculeu el valor
Oficina d Organització de Proves d Accés a la Universitat Pàgina de 5 PAU 0 - Sabem que el vector (,, ) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c cx by +z = b Calculeu el valor
En la actualidad, una parte importante de los objetos que se fabrican están realizados bajo algún tipo de forma curva geométrica.
 06 urvas geométricas En la actualidad, una parte importante de los objetos que se fabrican están realizados bajo algún tipo de forma curva geométrica. Si prestamos atención a nuestro entorno, nos damos
06 urvas geométricas En la actualidad, una parte importante de los objetos que se fabrican están realizados bajo algún tipo de forma curva geométrica. Si prestamos atención a nuestro entorno, nos damos
Districte Universitari de Catalunya
 Proves d Accés a la Universitat. Curs 2012-2013 Matemàtiques Sèrie 4 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts.
Proves d Accés a la Universitat. Curs 2012-2013 Matemàtiques Sèrie 4 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts.
Proves d accés a la universitat Convocatòria 2016 Dibuix tècnic Sèrie 3 Indiqueu les opcions triades:
 Proves d accés a la universitat Convocatòria 2016 Dibuix tècnic Sèrie 3 Indiqueu les opcions triades: Exercici 1: Opció A Exercici 2: Opció A Exercici 3: Opció A Opció B Opció B Opció B Qualificació 1
Proves d accés a la universitat Convocatòria 2016 Dibuix tècnic Sèrie 3 Indiqueu les opcions triades: Exercici 1: Opció A Exercici 2: Opció A Exercici 3: Opció A Opció B Opció B Opció B Qualificació 1
Gràficament: una funció és contínua en un punt si en aquest punt el seu gràfica no es trenca
 Funcions contínues Funcions contínues Continuïtat d una funció Si x 0 és un nombre, la funció f(x) és contínua en aquest punt si el límit de la funció en aquest punt coincideix amb el valor de la funció
Funcions contínues Funcions contínues Continuïtat d una funció Si x 0 és un nombre, la funció f(x) és contínua en aquest punt si el límit de la funció en aquest punt coincideix amb el valor de la funció
Generalitat de Catalunya Departament d Educació Institut El Palau. Nivell: 1r ESO. Matèria: Matemàtiques. Nom:
 Nivell: 1r ESO Matèria: Matemàtiques Nom: Unitat 1: Divisibilitat Múltiples i divisors 1. Digues si són certes o falses les frases següents i el perquè: a) 4 és divisor de 32 b) 12 és un divisor de 4.
Nivell: 1r ESO Matèria: Matemàtiques Nom: Unitat 1: Divisibilitat Múltiples i divisors 1. Digues si són certes o falses les frases següents i el perquè: a) 4 és divisor de 32 b) 12 és un divisor de 4.
2.Igualtat. 3.Gir. 4.Simetria. 6.Semblança. 7.Escales
 DIBUIX TÈCNIC 3. TRANSFORMACIONS GEOMÈTRIQUES. ESCALES 1.Transformacions isomètriques 2.Igualtat 3.Gir 4.Simetria 5.Transformacions isomòrfiques 6.Semblança 7.Escales COL LEGI ST. JOSEP SANT SADURNÍ D
DIBUIX TÈCNIC 3. TRANSFORMACIONS GEOMÈTRIQUES. ESCALES 1.Transformacions isomètriques 2.Igualtat 3.Gir 4.Simetria 5.Transformacions isomòrfiques 6.Semblança 7.Escales COL LEGI ST. JOSEP SANT SADURNÍ D
Proves d accés a la universitat Dibuix tècnic Sèrie 1 Indiqueu les opcions triades: Convocatòria 2017
 Proves d accés a la universitat Dibuix tècnic Sèrie 1 Indiqueu les opcions triades: Exercici 1: Opció A Exercici 2: Opció A Exercici 3: Opció A Opció B Opció B Opció B Qualificació 1 Exercicis 2 3 Suma
Proves d accés a la universitat Dibuix tècnic Sèrie 1 Indiqueu les opcions triades: Exercici 1: Opció A Exercici 2: Opció A Exercici 3: Opció A Opció B Opció B Opció B Qualificació 1 Exercicis 2 3 Suma
MECANISMES DE TRANSMISSIÓ DE MOVIMENT.
 MECANISMES DE TRANSMISSIÓ DE MOVIMENT. 1. El títol d aquest capítol fa referència a elements que s encarreguen de transmetre moviments entre dos o més punts. En els següents dibuixos es representen diversos
MECANISMES DE TRANSMISSIÓ DE MOVIMENT. 1. El títol d aquest capítol fa referència a elements que s encarreguen de transmetre moviments entre dos o més punts. En els següents dibuixos es representen diversos
XXXV OLIMPÍADA MATEMÀTICA
 XXXV OLIMPÍADA MATEMÀTICA Primera fase (Catalunya) 10 de desembre de 1999, de 16 a 0h. 1. Amb quadrats i triangles equilàters de costat unitat es poden construir polígons convexos. Per exemple, es poden
XXXV OLIMPÍADA MATEMÀTICA Primera fase (Catalunya) 10 de desembre de 1999, de 16 a 0h. 1. Amb quadrats i triangles equilàters de costat unitat es poden construir polígons convexos. Per exemple, es poden
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 55 Activitat 1 Dels nombres següents, indica quins són enters. a) 4 b) 0,25 c) 2 d) 3/5 e) 0 f) 1/2 g) 9 Els nombres enters són: 4, 2, 0 i 9. Activitat 2 Si la
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 55 Activitat 1 Dels nombres següents, indica quins són enters. a) 4 b) 0,25 c) 2 d) 3/5 e) 0 f) 1/2 g) 9 Els nombres enters són: 4, 2, 0 i 9. Activitat 2 Si la
( b) ( a) Matemàtiques - Activitats d estiu 4t ESO + = NOMBRES REALS. 1. Calcula, extraient factors fora dels radicals:
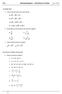 NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
TEMA 4 : Programació lineal
 TEMA 4 : Programació lineal 4.1. SISTEMES D INEQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITA La solució d aquest sistema és l intersecció de les regions que correspon a la solució de cadascuna de les inequacions
TEMA 4 : Programació lineal 4.1. SISTEMES D INEQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITA La solució d aquest sistema és l intersecció de les regions que correspon a la solució de cadascuna de les inequacions
LA RECTA. Exercicis d autoaprenentatge 1. Siga la gràfica següent:
 LA RECTA Recordeu: Una recta és una funció de la forma y = mx + n, on m i n són nombres reals. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall
LA RECTA Recordeu: Una recta és una funció de la forma y = mx + n, on m i n són nombres reals. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall
TASCA D ESTIU. 1er ESO
 ED. PLÀSTICA I VISUAL TASCA D ESTIU. 1er ESO IMPORTANT: LA PRESENTACIÓ DE TOTS ELS TREBALLS DE LA RECUPERACIÓ SON OBLIGATORIS. TAMBÉ, LA BONA PRESENTACIÓ I LA ELABORACIÓ CORRECTE DE L ACTIVITAT. S han
ED. PLÀSTICA I VISUAL TASCA D ESTIU. 1er ESO IMPORTANT: LA PRESENTACIÓ DE TOTS ELS TREBALLS DE LA RECUPERACIÓ SON OBLIGATORIS. TAMBÉ, LA BONA PRESENTACIÓ I LA ELABORACIÓ CORRECTE DE L ACTIVITAT. S han
