Sólidos Arquimedianos
|
|
|
- Santiago Maidana Segura
- hace 7 años
- Vistas:
Transcripción
1 Sólidos Arquimedianos El hacedor del universo creó el orden a partir del caos primigenio de los elementos por medio de las formas y los números esenciales de los poliedros, en una acción que culmina ese ordenamiento en la disposición armónica de los cinco elementos en el universo físico Platón
2 Tras los cinco poliedros platónicos surge otro grupo de cuerpos de gran poder, belleza y regularidad: los llamados sólidos arquimedianos, por ser Arquímedes el primero que los nombra, aunque algunos eran conocidos desde mucho tiempo atrás. Sólidos Arquimedianos
3 Se define como poliedros Arquimedianos, poliedros con caras regulares y vértices iguales, por ello son también conocidos como poliedros semirregulares. Los poliedros arquimedianos pueden ser obtenidos mediante manipulaciones de los platónicos. Sólidos Arquimedianos
4 Sólidos Arquimedianos
5 Sólidos Arquimedianos
6 Tanto los sólidos platónicos como los arquimedianos pueden estar circunscritos por una esfera, pero sólo los platónicos pueden estar tanto inscritos como circunscritos en una esfera. Los sólidos arquimedianos pueden estar inscritos en 2 ó 3 esferas. Sólidos Arquimedianos
7 Siete sólidos arquimedianos se pueden obtener truncando sólidos platónicos: Sólidos Arquimedianos 1. el tetraedro truncado 2. el cuboctaedro 3. el cubo truncado 4. el octaedro truncado 5. el icosidodecaedro 6. el icosaedro truncado. 7. el dodecaedro truncado
8 Sólidos Arquimedianos El resto de los sólidos arquimedianos, puede obtenerse mediante sucesivas operaciones de truncamiento y desplazamiento radial de las caras.
9 Sólidos Arquimedianos
10 Los 13 sólidos arquimedianos corresponden a los 13 toroides horizontales que corren a lo largo del cuerpo humano desde la base en el perineo hasta la coronilla. Se acomodan proporcionalmente a cada persona si se toma la medida unitaria de la barbilla a la nariz y se reproduce esta media sobre el cuerpo. Sólidos Arquimedianos
11 A diferencia de los 5 toroides verticales correspondientes a los 5 sólidos platónicos que se encuentran localizados en los puntos específicos ya mencionados; estos 13 toroides se disponen transversalmente a la médula espinal, por ello los conocemos como toroides horizontales. En el sistema egipcio de chakras eran bien conocidos por su relación con el manejo de la fuerza centrante en el cuerpo. Sólidos Arquimedianos
12 Sólidos Arquimedianos
13 La diferencia entre los sólidos platónicos y arquimedianos en el cuerpo y su relación con el Toroide central es que la energía que se distribuye, producto de la interacción de cada sólido platónico, fluye vertical, es decir, paralelo a la columna vertebral mientras que la energía que se distribuye del toroide que surge de cada uno de los 13 sólidos arquimedianos, ocurre transversalmente a la columna vertebral. En suma, hay 5 toroides verticales y 13 toroides horizontales básicos en el cuerpo humano. Sólidos Arquimedianos
14 Sólidos Arquimedianos
15 Sólidos Arquimedianos
16 Fullerenos
17 El fullereno es la tercera forma molecular más estable del carbono, tras el grafito y el diamante. La primera vez que se encontró un fullereno fue en 1985: Su naturaleza y forma se han hecho ampliamente conocidas en la ciencia y en la cultura en general, por sus características físicas, químicas, matemáticas y estéticas. Se destaca tanto por su versatilidad para la síntesis de nuevos compuestos como por la armonía de la configuración paradigmática de las moléculas con hexágonos y pentágonos: el icosaedro truncado y los cuerpos geométricos semejantes, con mayor número de caras. Reciben su nombre de Buckminster Fuller, que empleó la configuración de hexágonos y pentágonos en domos geodésicos Fullerenos
ACTIVIDADES PARA LA SESIÓN SEXTA
 ACTIVIDADES PARA LA SESIÓN SEXTA AUTOR: Begoña Soler de Dios 1 Máster en Profesor de Educación Secundaria Esp. Matemáticas 1 [email protected] Sesión 6 POLIEDROS ARQUIMEDIANOS 1. Qué se ve en la imagen?
ACTIVIDADES PARA LA SESIÓN SEXTA AUTOR: Begoña Soler de Dios 1 Máster en Profesor de Educación Secundaria Esp. Matemáticas 1 [email protected] Sesión 6 POLIEDROS ARQUIMEDIANOS 1. Qué se ve en la imagen?
ESTALMAT-Andalucía Actividades 05/06 Sesión: nº 22 Fecha: 10 de junio de 2006 Título: Construcción de Poliedros deltaedros-
 Hoja número 0. CONSTRUYENDO POLIEDROS. El material que tienes sobre la mesa se llama CREATOR o POLYDRON. Consta de piezas polígonos regulares- que pueden engarzarse para formar cuerpos como los sólidos
Hoja número 0. CONSTRUYENDO POLIEDROS. El material que tienes sobre la mesa se llama CREATOR o POLYDRON. Consta de piezas polígonos regulares- que pueden engarzarse para formar cuerpos como los sólidos
REGULARES.
 Diédrico Poliedros REGULARES http://www.edu.xunta.es/contidos/premios/p2004/b/poliedros/poliedros.html POLIEDROS Los poliedros son los cuerpos geométricos limitados por polígonos. Poliedros regulares son
Diédrico Poliedros REGULARES http://www.edu.xunta.es/contidos/premios/p2004/b/poliedros/poliedros.html POLIEDROS Los poliedros son los cuerpos geométricos limitados por polígonos. Poliedros regulares son
SUPERFICIES POLIÉDRICAS CONVEXAS
 SUPERFICIES POLIÉDRICAS CONVEXAS OBJETIVOS Conocer las características y relaciones métricas del te tra - edro, hexaedro o cubo y octaedro, para su represen tación en el sistema diédrico en sus múltiples
SUPERFICIES POLIÉDRICAS CONVEXAS OBJETIVOS Conocer las características y relaciones métricas del te tra - edro, hexaedro o cubo y octaedro, para su represen tación en el sistema diédrico en sus múltiples
De los sólidos platónicos a los balones de fútbol y de allí a los ovoides
 De los sólidos platónicos a los balones de fútbol y de allí a los ovoides MarthaCeciliaMosqueraUrrutia DocentedeMatemáticasAplicadasalaquímica UniversidadSurcolombiana Sitio:http://marthamosqueramatematicas.blogspot.com/
De los sólidos platónicos a los balones de fútbol y de allí a los ovoides MarthaCeciliaMosqueraUrrutia DocentedeMatemáticasAplicadasalaquímica UniversidadSurcolombiana Sitio:http://marthamosqueramatematicas.blogspot.com/
UP I Universidad de Palermo
 Poliedros Cuerpos tridimensionales formados por caras planas. Sus caras son siempre figuras geométricas de aristas rectas. En forma de polígonos Sus aristas, segmento que une a las caras, deben tener igual
Poliedros Cuerpos tridimensionales formados por caras planas. Sus caras son siempre figuras geométricas de aristas rectas. En forma de polígonos Sus aristas, segmento que une a las caras, deben tener igual
a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta.
 POLIEDROS Ejercicio nº 1.- a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
POLIEDROS Ejercicio nº 1.- a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
Polígonos y poliedros
 Polígonos y poliedros Rojo central (1980). El científico se ocupa de demostrar hechos, para comprobarlos, las mentes más estrictas utilizan ecuaciones matemáticas, luego vienen otros hombres, que aplican
Polígonos y poliedros Rojo central (1980). El científico se ocupa de demostrar hechos, para comprobarlos, las mentes más estrictas utilizan ecuaciones matemáticas, luego vienen otros hombres, que aplican
10- Los poliedros. Aprende a reconocer los poliedros en nuestro entorno; identifica sus elementos y aprende a clasificarlos.
 Aprende a reconocer los poliedros en nuestro entorno; identifica sus elementos y aprende a clasificarlos. Impreso por Juan Carlos Vila Vilariño Centro PASTORIZA (Nº 3) Sumario 1 Los poliedros... 3 1.1
Aprende a reconocer los poliedros en nuestro entorno; identifica sus elementos y aprende a clasificarlos. Impreso por Juan Carlos Vila Vilariño Centro PASTORIZA (Nº 3) Sumario 1 Los poliedros... 3 1.1
unidad 10 Cuerpos geométricos
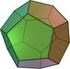 unidad 10 Cuerpos geométricos Poliedros. Características Página 1 Poliedro es un cuerpo cerrado limitado por caras planas que son polígonos. Aristas son los lados de las caras. Cada dos caras contiguas
unidad 10 Cuerpos geométricos Poliedros. Características Página 1 Poliedro es un cuerpo cerrado limitado por caras planas que son polígonos. Aristas son los lados de las caras. Cada dos caras contiguas
CUERPOS GEOMÉTRICOS (CONCEPTOS BÁSICOS)
 CUERPOS GEOMÉTRICOS (CONCEPTOS BÁSICOS) Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede
CUERPOS GEOMÉTRICOS (CONCEPTOS BÁSICOS) Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede
SISTEMA DIÉDRICO POLIEDROS REGULARES DIBUJO TÉCNICO 2º BACH.
 SISTEMA DIÉDRICO POLIEDROS REGULARES DIBUJO TÉCNICO. ANA BALLESTER JIMÉNEZ 0 SISTEMA DIÉDRICO: REPRESENTACIÓN DE POLIEDROS REGULARES DEFINICIÓN DE POLIEDRO: Sólido geométrico limitado por caras planas.
SISTEMA DIÉDRICO POLIEDROS REGULARES DIBUJO TÉCNICO. ANA BALLESTER JIMÉNEZ 0 SISTEMA DIÉDRICO: REPRESENTACIÓN DE POLIEDROS REGULARES DEFINICIÓN DE POLIEDRO: Sólido geométrico limitado por caras planas.
La lección de hoy es sobre Platónicos Sólidos. El cuál es la expectativa para el aprendizaje del estudiante R.4.G.4
 R.4.G.4-Becky Blankenship-Platonic Solids. La lección de hoy es sobre Platónicos Sólidos. El cuál es la expectativa para el aprendizaje del estudiante R.4.G.4 Primero, Qué son Platónicos Sólidos? Son Poliedros
R.4.G.4-Becky Blankenship-Platonic Solids. La lección de hoy es sobre Platónicos Sólidos. El cuál es la expectativa para el aprendizaje del estudiante R.4.G.4 Primero, Qué son Platónicos Sólidos? Son Poliedros
CUERPOS GEOMÉTRICOS. Un polígono es una figura compuesta por tres o más segmentos rectos (lados) que cierran una región en el espacio.
 CUERPOS GEOMÉTRICOS 07 Comprende que son los cuerpos geométricos e identifica las partes que los componen. En Presentación de Contenidos recuerdan qué son los polígonos para comprender cómo se forman los
CUERPOS GEOMÉTRICOS 07 Comprende que son los cuerpos geométricos e identifica las partes que los componen. En Presentación de Contenidos recuerdan qué son los polígonos para comprender cómo se forman los
PÁGINA 98. a) Tetraedro = 2 Cubo = 2 Octaedro = 2 Dodecaedro = 2 Icosaedro = 2
 PÁGINA 98 Pág. 1 1 Haz una tabla con el número de caras, vértices y aristas de los cinco poliedros regulares. a) Comprueba que los cinco cumplen la fórmula de Euler. [Recuerda: c + v = a + ]. b) Comprueba
PÁGINA 98 Pág. 1 1 Haz una tabla con el número de caras, vértices y aristas de los cinco poliedros regulares. a) Comprueba que los cinco cumplen la fórmula de Euler. [Recuerda: c + v = a + ]. b) Comprueba
Un poliedro es un cuerpo geométrico que tiene todas sus caras planas y formadas por polígonos.
 CUERPOS GEOMÉTRICOS Los cuerpos geométricos son figuras geométricas tridimensionales (tienen alto, ancho y largo) que ocupan un lugar en el espacio. 1. POLIEDROS. 1.1. DEFINICIÓN. Un poliedro es un cuerpo
CUERPOS GEOMÉTRICOS Los cuerpos geométricos son figuras geométricas tridimensionales (tienen alto, ancho y largo) que ocupan un lugar en el espacio. 1. POLIEDROS. 1.1. DEFINICIÓN. Un poliedro es un cuerpo
CUERPOS. Poliedros: Aquellos cuerpos geométricos totalmente limitados por polígonos, como por ejemplo, el prisma, la pirámide; etc.
 CUERPOS Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede calcular el volumen del mismo
CUERPOS Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede calcular el volumen del mismo
Preparado por el Arqto. Jing Chang Lou
 POLIIEDROS A P U N T E D O C E N T E Preparado por el Arqto. Jing Chang Lou U N I V ER S I D A D D E C H I L E F AC U L T A D D E A R Q U I T EC T U R A Y U R B A N I S MO D EPARTAMENTO C I ENCIAS DE L
POLIIEDROS A P U N T E D O C E N T E Preparado por el Arqto. Jing Chang Lou U N I V ER S I D A D D E C H I L E F AC U L T A D D E A R Q U I T EC T U R A Y U R B A N I S MO D EPARTAMENTO C I ENCIAS DE L
PÁGINA Describe y calcula la longitud del trayecto más corto que debe recorrer la lagartija para ir de A a B en cada caso.
 PÁGIN 213 Pág. 1 0 Describe y calcula la longitud del trayecto más corto que debe recorrer la lagartija para ir de a en cada caso. 1 m 1 m 3 m En el tercer caso, y son centros de dos caras en una pirámide
PÁGIN 213 Pág. 1 0 Describe y calcula la longitud del trayecto más corto que debe recorrer la lagartija para ir de a en cada caso. 1 m 1 m 3 m En el tercer caso, y son centros de dos caras en una pirámide
Cuerpos geométricos son porciones de espacio limitadas por superficies planas o curvas. CUERPOS GEOMÉTRICOS PRISMAS PIRÁMIDES CILINDROS CONOS ESFERAS
 UNIDAD DIDÁCTICA CUERPOS GEOMÉTRICOS 1. CUERPOS GEOMÉTRICOS En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos
UNIDAD DIDÁCTICA CUERPOS GEOMÉTRICOS 1. CUERPOS GEOMÉTRICOS En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos
Punto. Recta. Semirrecta. Segmento. Rectas Secantes. Rectas Paralelas. Rectas Perpendiculares
 Punto El punto es un objeto geométrico que no tiene dimensión y que sirve para indicar una posición. A Recta Es una sucesión continua e indefinida de puntos en una sola dimensión. Semirrecta Es una línea
Punto El punto es un objeto geométrico que no tiene dimensión y que sirve para indicar una posición. A Recta Es una sucesión continua e indefinida de puntos en una sola dimensión. Semirrecta Es una línea
ESQUEMA GENERAL DE LA CLASIFICACIÓN DE LOS CUERPOS GEOMÉTRICOS REGULARES ESFERA
 ESQUEMA GENERAL DE LA CLASIFICACIÓN DE LOS CUERPOS GEOMÉTRICOS POLIEDROS REGULARES Tetraedro ( 4 triángulos equiláteros) Hexaedro o cubo( 6 cuadrados) Octaedro( 8 triángulos equiláteros) Dodecaedro ( 12
ESQUEMA GENERAL DE LA CLASIFICACIÓN DE LOS CUERPOS GEOMÉTRICOS POLIEDROS REGULARES Tetraedro ( 4 triángulos equiláteros) Hexaedro o cubo( 6 cuadrados) Octaedro( 8 triángulos equiláteros) Dodecaedro ( 12
ELEMENTOS DE UN POLIEDRO. PRINCIPALES POLIEDROS REGULARES
 OBJETIVO 1 ELEMENTOS DE UN POLIEDRO. PRINCIPALES POLIEDROS REGULARES NOMBRE: CURSO: ECHA: CONCEPTO DE POLIEDRO Vértice Arista Cara Un poliedro es un cuerpo geométrico cuyas caras son polígonos. Los elementos
OBJETIVO 1 ELEMENTOS DE UN POLIEDRO. PRINCIPALES POLIEDROS REGULARES NOMBRE: CURSO: ECHA: CONCEPTO DE POLIEDRO Vértice Arista Cara Un poliedro es un cuerpo geométrico cuyas caras son polígonos. Los elementos
Curso: GeoGebra como herramienta para aprender y enseñar matemática en forma dinámica Profesor Tutor: Laura del Río y Fabiana Pauletich.
 Módulo 5 GEOMETRÍA 3D CONTENIDOS Durante el desarrollo de este módulo podrás utilizar las herramientas disponibles en GeoGebra para: Construir sólidos y explorar sus propiedades. Profundizar acerca del
Módulo 5 GEOMETRÍA 3D CONTENIDOS Durante el desarrollo de este módulo podrás utilizar las herramientas disponibles en GeoGebra para: Construir sólidos y explorar sus propiedades. Profundizar acerca del
Dibujo y geometría descriptiva II 2014
 ` CONTENIDO 1. Conceptos básicos Cuerpos geométricos Intersección 2. Intersección entre planos y sólidos. 3. Intersección de plano con prisma 4. Intersección de plano con cilindro. 5. Intersección de sólido
` CONTENIDO 1. Conceptos básicos Cuerpos geométricos Intersección 2. Intersección entre planos y sólidos. 3. Intersección de plano con prisma 4. Intersección de plano con cilindro. 5. Intersección de sólido
Heurística de los poliedros platónicos para la investigación de la realidad de altas restricciones
 Vol. IV, No. 1, enero - abril, 2013, pp. 59-77 PROBLEMAS SOCIALES DE LA CIENCIA Y LA TECNOLOGÍA Heurística de los poliedros platónicos para la investigación de la realidad de altas restricciones Carlos
Vol. IV, No. 1, enero - abril, 2013, pp. 59-77 PROBLEMAS SOCIALES DE LA CIENCIA Y LA TECNOLOGÍA Heurística de los poliedros platónicos para la investigación de la realidad de altas restricciones Carlos
Figuras de tres dimensiones
 Figuras de tres dimensiones Poliedros: cuerpos geométricos limitados por 4 o más superficies planas que son polígonos. Poliedros regulares: todas las caras de igual forma y tamaño. Solo existen 5. Prismas
Figuras de tres dimensiones Poliedros: cuerpos geométricos limitados por 4 o más superficies planas que son polígonos. Poliedros regulares: todas las caras de igual forma y tamaño. Solo existen 5. Prismas
Conceptos geométricos II
 Conceptos geométricos II Ángulo Ángulos Consecutivos Ángulos Alternos y Ángulos Correspondientes Polígono Polígono Regular Polígono Irregular Triángulo Cuadrilátero Superficie Círculo Superficie reglada
Conceptos geométricos II Ángulo Ángulos Consecutivos Ángulos Alternos y Ángulos Correspondientes Polígono Polígono Regular Polígono Irregular Triángulo Cuadrilátero Superficie Círculo Superficie reglada
Taller 6 La fórmula de Euler y los Sólidos Platónicos Profesor: Maximiliano Leyton
 Taller 6 La fórmula de Euler y los Sólidos Platónicos Profesor: Maximiliano Leyton I. Fórmula de Euler Ejercicio 1. Considere un cuadrado y escoja arbitrariamente 10 puntos en su interior. Utilizando estos
Taller 6 La fórmula de Euler y los Sólidos Platónicos Profesor: Maximiliano Leyton I. Fórmula de Euler Ejercicio 1. Considere un cuadrado y escoja arbitrariamente 10 puntos en su interior. Utilizando estos
11 CONOCER LOS POLIEDROS Y DIFERENCIAR
 REPASO Y APOYO OBJETIVO 1 11 CONOCER LOS POLIEDROS Y DIERENCIAR LOS POLIEDROS REGULARES Nombre: Curso: echa: CONCEPTO DE POLIEDRO Vértice Un poliedro es un cuerpo geométrico cuyas caras son polígonos.
REPASO Y APOYO OBJETIVO 1 11 CONOCER LOS POLIEDROS Y DIERENCIAR LOS POLIEDROS REGULARES Nombre: Curso: echa: CONCEPTO DE POLIEDRO Vértice Un poliedro es un cuerpo geométrico cuyas caras son polígonos.
Matemática. Desafío. GUÍA DE EJERCITACIÓN AVANZADA Cuerpos geométricos GUICEN032MT22-A16V1
 GUÍ DE EJERCITCIÓN VNZD Cuerpos geométricos Programa Entrenamiento Desafío GUICEN02MT22-16V1 Matemática Una semiesfera tiene un área total de 4π cm 2. Si se corta por la mitad, de manera de formar dos
GUÍ DE EJERCITCIÓN VNZD Cuerpos geométricos Programa Entrenamiento Desafío GUICEN02MT22-16V1 Matemática Una semiesfera tiene un área total de 4π cm 2. Si se corta por la mitad, de manera de formar dos
Tema 8: Cuerpos geométricos. Matemáticas Específicas para Maestros 1º Grado en Educación Primaria
 Tema 8: Cuerpos geométricos Matemáticas Específicas para Maestros 1º Grado en Educación Primaria Definiciones Cuerpos geométricos Poliedros. Elementos. Clasificaciones: o Poliedros cóncavos y convexos.
Tema 8: Cuerpos geométricos Matemáticas Específicas para Maestros 1º Grado en Educación Primaria Definiciones Cuerpos geométricos Poliedros. Elementos. Clasificaciones: o Poliedros cóncavos y convexos.
POLIEDROS. Ejercicio nº 1.- a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta.
 POLIEDROS Ejercicio nº 1.- De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
POLIEDROS Ejercicio nº 1.- De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
TEMA 45 POLIEDROS TEOREMA DE EULER SÓLIDOS PLATÓNICOS Y ARQUIMEDIANOS
 ACADEMIA ADOS TEMA 45 POLIEDROS TEOREMA DE EULER SÓLIDOS PLATÓNICOS Y ARQUIMEDIANOS 1. INTRODUCCIÓN. 2. POLIEDROS. 2.1. DEFINICIÓN Y ELEMENTOS. 2.2. GÉNERO Y ESPECIE. 2.3. DESCOMPOSICIÓN DE UN POLIEDRO.
ACADEMIA ADOS TEMA 45 POLIEDROS TEOREMA DE EULER SÓLIDOS PLATÓNICOS Y ARQUIMEDIANOS 1. INTRODUCCIÓN. 2. POLIEDROS. 2.1. DEFINICIÓN Y ELEMENTOS. 2.2. GÉNERO Y ESPECIE. 2.3. DESCOMPOSICIÓN DE UN POLIEDRO.
Tema 11 Cuerpos geométricos
 Tema 11 Cuerpos geométricos 11.1 Poliedros regulares y semirregulares Tareas 11/11/: todos los ejercicios de la página 08. Además, completa la tabla análoga de los poliedros duales para el icosaedro y
Tema 11 Cuerpos geométricos 11.1 Poliedros regulares y semirregulares Tareas 11/11/: todos los ejercicios de la página 08. Además, completa la tabla análoga de los poliedros duales para el icosaedro y
 http://www.matesymas.es/ MATERIAL PLOT El material PLOT está formado por láminas de cartulina troquelada y gomas elásticas de colores para realizar las uniones. De las láminas de cartulina se obtienen
http://www.matesymas.es/ MATERIAL PLOT El material PLOT está formado por láminas de cartulina troquelada y gomas elásticas de colores para realizar las uniones. De las láminas de cartulina se obtienen
Figura en el espacio o cuerpo geométrico es el conjunto de puntos que no están contenidos en un mismo plano, es la porción de espacio limitado.
 Cuenca, 11 de noviembre de 2013 Clase 13 Geometría del espacio Figuras geométricas en el espacio Definiciones: Geometría del espacio: Rama de las matemáticas encargada de las propiedades y medida de las
Cuenca, 11 de noviembre de 2013 Clase 13 Geometría del espacio Figuras geométricas en el espacio Definiciones: Geometría del espacio: Rama de las matemáticas encargada de las propiedades y medida de las
SOLUCIONES MINIMOS 2º ESO TEMA 8 CUERPOS GEOMÉTRICOS
 SOLUCIONES MINIMOS º ESO TEMA 8 CUERPOS GEOMÉTRICOS Ejercicio nº 1.- Escribe el nombre de cada uno de los elementos de este poliedro: Ejercicio nº.- Cuáles de las siguientes figuras son poliedros? Por
SOLUCIONES MINIMOS º ESO TEMA 8 CUERPOS GEOMÉTRICOS Ejercicio nº 1.- Escribe el nombre de cada uno de los elementos de este poliedro: Ejercicio nº.- Cuáles de las siguientes figuras son poliedros? Por
Se dice que un poliedro es regular cuando sus caras son polígonos regulares iguales y sus ángulos poliedros tienen el mismo número de caras.
 LOS POLIEDROS: El cubo, la pirámide, la esfera, el cilindro... son figuras sólidas. Observando tales figuras, vemos que algunos sólidos, como el cubo y la pirámide, tienen su superficie exterior formada
LOS POLIEDROS: El cubo, la pirámide, la esfera, el cilindro... son figuras sólidas. Observando tales figuras, vemos que algunos sólidos, como el cubo y la pirámide, tienen su superficie exterior formada
Euler y un balón de fútbol
 sigma 36 Euler y un balón de fútbol José Ignacio Royo Prieto (*) y Martín Saralegi Aranguren (**) Se podría pensar que el logotipo de la Liga de Campeones de la UEFA representa el balón con el que juegan
sigma 36 Euler y un balón de fútbol José Ignacio Royo Prieto (*) y Martín Saralegi Aranguren (**) Se podría pensar que el logotipo de la Liga de Campeones de la UEFA representa el balón con el que juegan
APLICACIÓN DE LAS FUNCIONES AL ESTUDIO DE MOSAICOS Y POLIEDROS
 APLICACIÓN DE LAS FUNCIONES AL ESTUDIO DE MOSAICOS Y POLIEDROS 1. Introducción La investigación que se presenta a continuación tiene su origen en mi función de director de trabajos de investigación realizados
APLICACIÓN DE LAS FUNCIONES AL ESTUDIO DE MOSAICOS Y POLIEDROS 1. Introducción La investigación que se presenta a continuación tiene su origen en mi función de director de trabajos de investigación realizados
Preguntas tipo OLIMPIADA DE DIBUJO TÉCNICO MARZO 2014
 E S C U E L A T É C N I C A S U P E R I O R D E A R Q U I T E C T U R A U N I V E R S I D A D D E N A V A R R A Preguntas tipo OLIMPIADA DE DIBUJO TÉCNICO MARZO 2014 G E O M E T R Í A M É T R I C A. T
E S C U E L A T É C N I C A S U P E R I O R D E A R Q U I T E C T U R A U N I V E R S I D A D D E N A V A R R A Preguntas tipo OLIMPIADA DE DIBUJO TÉCNICO MARZO 2014 G E O M E T R Í A M É T R I C A. T
INTRODUCCIÓN A LOS POLIEDROS
 INTRODUCCIÓN A LOS POLIEDROS AUTORIA MIGUEL ÁNGEL GUERRERO MOLINA TEMÁTICA POLIEDROS ETAPA BACHILLERATO Resumen Este artículo pretende dar una visión general de los poliedros. Trataremos su clasificación,
INTRODUCCIÓN A LOS POLIEDROS AUTORIA MIGUEL ÁNGEL GUERRERO MOLINA TEMÁTICA POLIEDROS ETAPA BACHILLERATO Resumen Este artículo pretende dar una visión general de los poliedros. Trataremos su clasificación,
Geometría en el espacio
 Geometría en el espacio 3º E.S.O. PARTE TEÓRICA 1.- Define los siguientes conceptos: Poliedro: Vértice de un poliedro: Cara de un poliedro: Arista de un poliedro: Poliedro regular: 2.- Di cuáles son los
Geometría en el espacio 3º E.S.O. PARTE TEÓRICA 1.- Define los siguientes conceptos: Poliedro: Vértice de un poliedro: Cara de un poliedro: Arista de un poliedro: Poliedro regular: 2.- Di cuáles son los
Grupos Puntuales de Simetría
 Grupos Puntuales de Simetría Operación de Simetría: Transformación de la posición de un cuerpo tal que la posición final es físicamente indistinguible de la inicial y las distancias entre todas las parejas
Grupos Puntuales de Simetría Operación de Simetría: Transformación de la posición de un cuerpo tal que la posición final es físicamente indistinguible de la inicial y las distancias entre todas las parejas
MATEMÁTICAS (GEOMETRÍA)
 COLEGIO COLOMBO BRITÁNICO Formación en la Libertad y para la Libertad MATEMÁTICAS (GEOMETRÍA) GRADO:7 O DOCENTE: Nubia E. Niño C. FECHA: 8 / 07 / 15 Guía Didáctica 3-2 Desempeños: * Reconoce y clasifica
COLEGIO COLOMBO BRITÁNICO Formación en la Libertad y para la Libertad MATEMÁTICAS (GEOMETRÍA) GRADO:7 O DOCENTE: Nubia E. Niño C. FECHA: 8 / 07 / 15 Guía Didáctica 3-2 Desempeños: * Reconoce y clasifica
Área: Ciencia y Tecnología Asignatura: MATEMÁTICA. Título. Trabajo Práctico Cuerpos. Año: Pag.1/7
 Área: Ciencia y Tecnología Asignatura: MATEMÁTICA Título Trabajo Práctico Cuerpos Curso 1 Año Año: 2007 Pag.1/7 CUERPOS GEOMÉTRICOS Escribe en tu carpeta cómo se llama el cuerpo geométrico al que se parece
Área: Ciencia y Tecnología Asignatura: MATEMÁTICA Título Trabajo Práctico Cuerpos Curso 1 Año Año: 2007 Pag.1/7 CUERPOS GEOMÉTRICOS Escribe en tu carpeta cómo se llama el cuerpo geométrico al que se parece
Sólidos Platónicos. herramienta para el proceso de consciencia
 herramienta para el proceso de consciencia Platón definió las siete formas principales en la Geometría Sagrada: Los cinco sólidos, el círculo y la espiral.! La característica de los sólidos platónicos
herramienta para el proceso de consciencia Platón definió las siete formas principales en la Geometría Sagrada: Los cinco sólidos, el círculo y la espiral.! La característica de los sólidos platónicos
GEOMETRÍA POLIEDROS. Los ángulos diedros y los ángulos poliedros determinados por las caras son los ángulos diedros y ángulos poliedros del poliedro.
 GEOMETRÍA POLIEDROS Poliedro. Un poliedro es la unión de cuatro o más regiones poligonales tales que cada uno de sus lados pertenecen precisamente a dos regiones adyacentes no coplanares. Las regiones
GEOMETRÍA POLIEDROS Poliedro. Un poliedro es la unión de cuatro o más regiones poligonales tales que cada uno de sus lados pertenecen precisamente a dos regiones adyacentes no coplanares. Las regiones
FIGURAS DEL ESPACIO. ÁREAS Y VOLÚMENES
 POLIEDROS : Cuerpo sólido limitado por polígonos, llamados caras; en la que algunas de las caras confluyen en líneas rectas, llamadas aristas; y algunas de las aristas confluyen en puntos,llamados vértices.
POLIEDROS : Cuerpo sólido limitado por polígonos, llamados caras; en la que algunas de las caras confluyen en líneas rectas, llamadas aristas; y algunas de las aristas confluyen en puntos,llamados vértices.
Poliedros Regulares Convexos
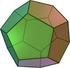 Poliedros Regulares Convexos Características y relaciones entre ellos AUTOR: Begoña Soler de Dios 1 Máster en Profesor de Educación Secundaria Esp. Matemáticas 1 [email protected] Poliedros Regulares
Poliedros Regulares Convexos Características y relaciones entre ellos AUTOR: Begoña Soler de Dios 1 Máster en Profesor de Educación Secundaria Esp. Matemáticas 1 [email protected] Poliedros Regulares
Diferencias entre Figuras y
 10 Lección Refuerzo Matemáticas Diferencias entre Figuras y Cuerpos Geométricos APRENDO JUGANDO Competencia Aplica conocimientos acerca de las principales características de polígonos y cuerpos geométricos.
10 Lección Refuerzo Matemáticas Diferencias entre Figuras y Cuerpos Geométricos APRENDO JUGANDO Competencia Aplica conocimientos acerca de las principales características de polígonos y cuerpos geométricos.
Sistema Diédrico (II). Superficies poliédricas y radiadas: Representación
 Sistema Diédrico (II). Superficies poliédricas y radiadas: Representación Comenzamos una nueva unidad didáctica en la que desarrollaremos los conceptos y procedimientos sobre superficies poliédricas y
Sistema Diédrico (II). Superficies poliédricas y radiadas: Representación Comenzamos una nueva unidad didáctica en la que desarrollaremos los conceptos y procedimientos sobre superficies poliédricas y
UNIDAD 11 Figuras en el espacio
 Pág. 1 de 5 I. Conoces de cursos anteriores los poliedros regulares y algunas de sus características. Has reforzado ese conocimiento y lo has ampliado a los poliedros semirregulares? 1 Dibuja, a partir
Pág. 1 de 5 I. Conoces de cursos anteriores los poliedros regulares y algunas de sus características. Has reforzado ese conocimiento y lo has ampliado a los poliedros semirregulares? 1 Dibuja, a partir
Maquetería 02: Poliedros, cuerpos redondos y su construcción
 Maquetería 02: Poliedros, cuerpos redondos y su construcción Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
Maquetería 02: Poliedros, cuerpos redondos y su construcción Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
APÉNDICE I. Solución a los Ejercicios Propuestos
 APÉNDICE I Solución a los Ejercicios Propuestos 1 Adyacentes. Problema Este ejercicio consiste en lograr acomodar números naturales del 1 al 8. Lo importante es que dos números consecutivos no queden juntos
APÉNDICE I Solución a los Ejercicios Propuestos 1 Adyacentes. Problema Este ejercicio consiste en lograr acomodar números naturales del 1 al 8. Lo importante es que dos números consecutivos no queden juntos
ACTIVIDADES PARA LA SESIÓN PRIMERA
 ACTIVIDADES PARA LA SESIÓN PRIMERA AUTOR: Begoña Soler de Dios 1 Máster en Profesor de Educación Secundaria Esp. Matemáticas 1 [email protected] Sesión 1 1. Los poliedros regulares convexos: Cuántos
ACTIVIDADES PARA LA SESIÓN PRIMERA AUTOR: Begoña Soler de Dios 1 Máster en Profesor de Educación Secundaria Esp. Matemáticas 1 [email protected] Sesión 1 1. Los poliedros regulares convexos: Cuántos
Maquetería 02: Poliedros, cuerpos redondos y su construcción
 Maquetería 02: Poliedros, cuerpos redondos y su construcción Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
Maquetería 02: Poliedros, cuerpos redondos y su construcción Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
Poliedros y cuerpos redondos para imprimir
 Poliedros y cuerpos redondos para imprimir Nombre Curso: Fecha: Escribe en la parte derecha lo que falta. 1. Los cuerpos redondos. La geometría del espacio estudia los cuerpos que tienen tres dimensiones:
Poliedros y cuerpos redondos para imprimir Nombre Curso: Fecha: Escribe en la parte derecha lo que falta. 1. Los cuerpos redondos. La geometría del espacio estudia los cuerpos que tienen tres dimensiones:
Área del rectángulo y del cuadrado
 59 Área del rectángulo y del cuadrado El área del rectángulo es el producto de su base por su altura. El área del cuadrado es su lado elevado al cuadrado. 1. Mide con una regla y completa. Área del rectángulo:
59 Área del rectángulo y del cuadrado El área del rectángulo es el producto de su base por su altura. El área del cuadrado es su lado elevado al cuadrado. 1. Mide con una regla y completa. Área del rectángulo:
Un punto divide a una recta en dos semirrectas. Ese punto es el origen de ambas semirrectas.
 Una línea recta es una línea que no tiene principio ni fin. Una semirrecta es una línea que tiene principio pero no tiene final. o Un punto divide a una recta en dos semirrectas. Ese punto es el origen
Una línea recta es una línea que no tiene principio ni fin. Una semirrecta es una línea que tiene principio pero no tiene final. o Un punto divide a una recta en dos semirrectas. Ese punto es el origen
El número de caras de cada uno coincide con el número de vértices del otro. Además, los dos cuerpos geométricos tienen el mismo número de aristas.
 1 Dibuja, a partir del cubo, un octaedro regular, de modo que se aprecie la dualidad entre ellos. elaciona el número de caras, aristas y vértices de uno con el de otro. Pág. 1 Los vértices del octaedro
1 Dibuja, a partir del cubo, un octaedro regular, de modo que se aprecie la dualidad entre ellos. elaciona el número de caras, aristas y vértices de uno con el de otro. Pág. 1 Los vértices del octaedro
Geometría. Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid
 Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
Geometría. Ángulos. Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid
 Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
Autor: 2º ciclo de E.P.
 1 Autor: 2º ciclo de E.P. Una línea recta es una línea que no tiene principio ni fin. Una semirrecta es una línea que tiene principio pero no tiene final. o Un punto divide a una recta en dos semirrectas.
1 Autor: 2º ciclo de E.P. Una línea recta es una línea que no tiene principio ni fin. Una semirrecta es una línea que tiene principio pero no tiene final. o Un punto divide a una recta en dos semirrectas.
MAQUETERÍA 02: POLIEDROS, CUERPOS REDONDOS Y SU CONSTRUCCIÓN
 MAQUETERÍA 02: POLIEDROS, CUERPOS REDONDOS Y SU CONSTRUCCIÓN Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
MAQUETERÍA 02: POLIEDROS, CUERPOS REDONDOS Y SU CONSTRUCCIÓN Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
Guía para maestros - Matemáticas 6 0 grado
 Guía para maestros - Matemáticas 6 0 grado 1 Unidad Sólidos geométricos (15 horas) Expectativas de logro Establecen las diferencias y analogías (semejanzas) entre prismas, pirámides, conos, cilindros y
Guía para maestros - Matemáticas 6 0 grado 1 Unidad Sólidos geométricos (15 horas) Expectativas de logro Establecen las diferencias y analogías (semejanzas) entre prismas, pirámides, conos, cilindros y
IES FONTEXERÍA MUROS. 14-II-2014 Nombre y apellidos:.
 IES FONTEXERÍA MUROS MATEMÁTICAS º E.S.O-A (Desdoble 1) 1º Examen (ª Evaluación) 14-II-014 Nombre y apellidos:. 1. Completa las siguientes definiciones: a) Un poliedro es un cuerpo geométrico tridimensional
IES FONTEXERÍA MUROS MATEMÁTICAS º E.S.O-A (Desdoble 1) 1º Examen (ª Evaluación) 14-II-014 Nombre y apellidos:. 1. Completa las siguientes definiciones: a) Un poliedro es un cuerpo geométrico tridimensional
Cuerpos geométricos. Volúmenes
 4 uerpos geométricos. Volúmenes. Poliedros Un poliedro es un cuerpo geométrico limitado por cuatro o más polígonos planos. Los elementos de un poliedro son: aras: son los polígonos que lo delimitan. ristas:
4 uerpos geométricos. Volúmenes. Poliedros Un poliedro es un cuerpo geométrico limitado por cuatro o más polígonos planos. Los elementos de un poliedro son: aras: son los polígonos que lo delimitan. ristas:
Contenido. Tema 11. Geometría en el espacio. 1. Poliedros Regulares o sólidos Platónicos Teorema de Euler Prismas...
 Tema 11. Geometría en el espacio Contenido 1. Poliedros Regulares o sólidos Platónicos... 2 2. Teorema de Euler... 3 3. Prismas... 3 4. Pirámides... 5 5. Cilindro... 7 6. Cono... 8 7. Esfera... 9 8. Coordenadas
Tema 11. Geometría en el espacio Contenido 1. Poliedros Regulares o sólidos Platónicos... 2 2. Teorema de Euler... 3 3. Prismas... 3 4. Pirámides... 5 5. Cilindro... 7 6. Cono... 8 7. Esfera... 9 8. Coordenadas
UNIDAD 7. SUPERFICIES POLIÉDRICAS.
 UNIDAD 7. SUPERFICIES POLIÉDRICAS. OBJETIVOS Conocer las características y determinar la sección principal de cada uno de los poliedros regulares. Obtener la representación en el sistema diédrico de los
UNIDAD 7. SUPERFICIES POLIÉDRICAS. OBJETIVOS Conocer las características y determinar la sección principal de cada uno de los poliedros regulares. Obtener la representación en el sistema diédrico de los
congruentes es porque tienen la misma longitud AB = CD y, cuando dos ángulos DEF son congruentes es porque tienen la misma medida
 COLEGIO COLMBO BRITÁNICO DEPARTAMENTO DE MATEMÁTICAS GEOMETRÍA NOVENO GRADO PROFESORES: RAÚL MARTÍNEZ, JAVIER MURILLO Y JESÚS VARGAS CONGRUENCIA Y SEMEJANZA Cuando tenemos dos segmentos escribimos AB CD
COLEGIO COLMBO BRITÁNICO DEPARTAMENTO DE MATEMÁTICAS GEOMETRÍA NOVENO GRADO PROFESORES: RAÚL MARTÍNEZ, JAVIER MURILLO Y JESÚS VARGAS CONGRUENCIA Y SEMEJANZA Cuando tenemos dos segmentos escribimos AB CD
a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta.
 POLIEDROS Ejercicio nº 1.- a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
POLIEDROS Ejercicio nº 1.- a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA
 RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
4. GEOMETRÍA // 4.4. POLIEDROS.
 4. GEOMETRÍA // 4.4. POLIEDROS. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS. Bibliografía. 1. Alsina, C., Pérez, R., Ruiz, C., Simetría dinámica, Serie Matemáticas: Cultura y aprendizaje,
4. GEOMETRÍA // 4.4. POLIEDROS. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS. Bibliografía. 1. Alsina, C., Pérez, R., Ruiz, C., Simetría dinámica, Serie Matemáticas: Cultura y aprendizaje,
Poliedros Regulares- Patricia Muñoz. Poliedros Regulares. D.I. Patricia Muñoz. Laboratorio de Morfología SICyT - FADU - UBA
 Poliedros Regulares- Patricia Muñoz 1 Poliedros Regulares D.I. Patricia Muñoz Laboratorio de Morfología SICyT - FADU - UBA Cátedra de Morfología Especial 1 Carrera de Diseño Industrial FADU - UBA Poliedros
Poliedros Regulares- Patricia Muñoz 1 Poliedros Regulares D.I. Patricia Muñoz Laboratorio de Morfología SICyT - FADU - UBA Cátedra de Morfología Especial 1 Carrera de Diseño Industrial FADU - UBA Poliedros
DE PRISMAS Y POLIEDROS. A LA BÚSQUEDA DEL CUBOIDE PERFECTO
 DE PRISMAS Y POLIEDROS. A LA BÚSQUEDA DEL CUBOIDE PERFECTO De poliedros En el espacio euclídeo tridimensional podemos resumir algunas nociones básicas de geometría clásica Un poliedro es la zona espacial
DE PRISMAS Y POLIEDROS. A LA BÚSQUEDA DEL CUBOIDE PERFECTO De poliedros En el espacio euclídeo tridimensional podemos resumir algunas nociones básicas de geometría clásica Un poliedro es la zona espacial
TRABAJO GEO 5: TALLERES 9 COLEGIO LUIS CARLOS GALÁN SARMIENTO
 TRABAJO GEO 5: Logikubo: Es un material didáctico utilizado para construir figuras geométricas planas. Consta de 9 piezas y 2 dados. 1) Construir un cubo. (Saca la ficha verde y la blanca) 2) Determinar
TRABAJO GEO 5: Logikubo: Es un material didáctico utilizado para construir figuras geométricas planas. Consta de 9 piezas y 2 dados. 1) Construir un cubo. (Saca la ficha verde y la blanca) 2) Determinar
5to Parcial de Geometría Euclidiana. 2) Sea p un polígono tal que se puede descomponer en n polígonos simples
 5to Parcial de Geometría Euclidiana AREAS y VOLUMENES Definición 55 (Área) Se define el área como una función A definida del conjunto de todos los polígonos P en R + (A : P R + ), con las siguientes propiedades:
5to Parcial de Geometría Euclidiana AREAS y VOLUMENES Definición 55 (Área) Se define el área como una función A definida del conjunto de todos los polígonos P en R + (A : P R + ), con las siguientes propiedades:
Poliedros Semiregulares - Patricia Muñoz y col.
 1 Poliedros Semiregulares D.I. Patricia Muñoz Con la colaboración de D.C.V. Nora Pereyra Laboratorio de Morfología SICyT - FADU - UBA Cátedra de Morfología Especial 1 Carrera de Diseño Industrial FADU
1 Poliedros Semiregulares D.I. Patricia Muñoz Con la colaboración de D.C.V. Nora Pereyra Laboratorio de Morfología SICyT - FADU - UBA Cátedra de Morfología Especial 1 Carrera de Diseño Industrial FADU
Cuerpos Geométricos Son aquellos elementos que ocupan un volumen en el espacio se componen de tres partes: alto, ancho y largo.
 CUERPOS GEOMÉTRICOS 06 Describe qué son e identifica las características de los cuerpos geométricos. El maestro comenta qué es, cómo se forman y cuáles son las partes de un cuerpo geométrico. Los alumnos
CUERPOS GEOMÉTRICOS 06 Describe qué son e identifica las características de los cuerpos geométricos. El maestro comenta qué es, cómo se forman y cuáles son las partes de un cuerpo geométrico. Los alumnos
Tema 2. Geometría en el espacio
 Tema 2. Geometría en el espacio Matemáticas I La geometría espacial o geometría en el espacio es la rama de la geometría que se ocupa de las propiedades y medidas de las figuras geométricas en el espacio
Tema 2. Geometría en el espacio Matemáticas I La geometría espacial o geometría en el espacio es la rama de la geometría que se ocupa de las propiedades y medidas de las figuras geométricas en el espacio
DIBUJO TÉCNICO BACHILLERATO LÁMINAS. TEMA 7 SISTEMA DIÉDRICO II. Superficies y figuras. Departamento de Artes Plásticas y Dibujo
 DIBUJO TÉCNICO BACHILLERATO LÁMINAS TEMA 7 SISTEMA DIÉDRICO II. Superficies y figuras. Departamento de Artes Plásticas y Dibujo 1.- Construir un TETRAEDRO. Los puntos A y B son dos vértices del mismo y
DIBUJO TÉCNICO BACHILLERATO LÁMINAS TEMA 7 SISTEMA DIÉDRICO II. Superficies y figuras. Departamento de Artes Plásticas y Dibujo 1.- Construir un TETRAEDRO. Los puntos A y B son dos vértices del mismo y
Figura plana Área Ejemplo Cuadrado. Área =
 ersión: Septiembre 01 Áreas y volúmenes Por Sandra Elvia Pérez Márquez Áreas de figuras planas Las aplicaciones de las figuras planas requieren, por lo general, conocer (o calcular) dos características
ersión: Septiembre 01 Áreas y volúmenes Por Sandra Elvia Pérez Márquez Áreas de figuras planas Las aplicaciones de las figuras planas requieren, por lo general, conocer (o calcular) dos características
Cursillo. Descubriendo Cabri 3D a través de situaciones de aprendizaje para los alumnos
 XVII Congreso Colombiano de Matemáticas, Agosto 2009 Cali Cursillo Colette Laborde Universidad Joseph Fourier, [email protected] Descubriendo Cabri 3D a través de situaciones de aprendizaje para
XVII Congreso Colombiano de Matemáticas, Agosto 2009 Cali Cursillo Colette Laborde Universidad Joseph Fourier, [email protected] Descubriendo Cabri 3D a través de situaciones de aprendizaje para
MATEMÁTICAS 2º DE ESO LOE
 MATEMÁTICAS º DE ESO LOE TEMA XII: POLIEDROS Y CUERPOS REDONDOS Poliedros: o Elementos. o Tipos. Poliedros regulares. Cubos. Prismas: elementos, clases. Pirámides: elementos, clases. Áreas laterales y
MATEMÁTICAS º DE ESO LOE TEMA XII: POLIEDROS Y CUERPOS REDONDOS Poliedros: o Elementos. o Tipos. Poliedros regulares. Cubos. Prismas: elementos, clases. Pirámides: elementos, clases. Áreas laterales y
Modulo IV Los Sólidos Platónicos
 Modulo IV Los Sólidos Platónicos Qué vamos aprender en este Módulo? Estrella Madre, el Secreto de la Vida. Características metafísicas de los sólidos Platónicos Visión Psicogeométrica Nuestra estructura
Modulo IV Los Sólidos Platónicos Qué vamos aprender en este Módulo? Estrella Madre, el Secreto de la Vida. Características metafísicas de los sólidos Platónicos Visión Psicogeométrica Nuestra estructura
P O L I E D R O S y C U E R P O S R E D O N D O S
 Universidad Nacional de Córdoba Facultad de Arquitectura, Urbanismo y Diseño MATEMÁTICA [DISEÑO INDUSTRIAL] P O L I E D R O S y C U E R P O S R E D O N D O S UBICACIÓN DEL TEMA EN CRONOGRAMA DE MATEMÁTICA
Universidad Nacional de Córdoba Facultad de Arquitectura, Urbanismo y Diseño MATEMÁTICA [DISEÑO INDUSTRIAL] P O L I E D R O S y C U E R P O S R E D O N D O S UBICACIÓN DEL TEMA EN CRONOGRAMA DE MATEMÁTICA
Raúl Panqueva Escuela Colombiana de Ingeniería Julio Garavito
 ENVOLVIENDO ESFERAS CON TIRAS DE PAPEL Raúl Panqueva Escuela Colombiana de Ingeniería Julio Garavito [email protected] Una esfera se puede rodear con varias tiras de papel que se entrelazan y unen
ENVOLVIENDO ESFERAS CON TIRAS DE PAPEL Raúl Panqueva Escuela Colombiana de Ingeniería Julio Garavito [email protected] Una esfera se puede rodear con varias tiras de papel que se entrelazan y unen
SÓLIDOS EN EL ESPACIO TRIDIMENSIONAL
 G3D1: Sólidos convexos y cóncavos SÓLIDOS EN EL ESPACIO TRIDIMENSIONAL Pon tres ejemplos de objetos cotidianos que sean convexos: Pon tres ejemplos de objetos cotidianos que sean cóncavos: G3D2: Caracterización
G3D1: Sólidos convexos y cóncavos SÓLIDOS EN EL ESPACIO TRIDIMENSIONAL Pon tres ejemplos de objetos cotidianos que sean convexos: Pon tres ejemplos de objetos cotidianos que sean cóncavos: G3D2: Caracterización
CUERPOS GEOMÉTRICOS. Los cuerpos geométricos son porciones de espacio limitadas por superficies planas o curvas.
 CUERPOS GEOMÉTRICOS CUERPOS GEOMÉTRICOS.- Los cuerpos geométricos son porciones de espacio limitadas por superficies planas o curvas. Clasificamos, en el siguiente esquema, los cuerpos geométricos: POLIEDROS.-
CUERPOS GEOMÉTRICOS CUERPOS GEOMÉTRICOS.- Los cuerpos geométricos son porciones de espacio limitadas por superficies planas o curvas. Clasificamos, en el siguiente esquema, los cuerpos geométricos: POLIEDROS.-
Diagonal: es un segmento que une dos vértices no consecutivos del poliedro. Puede trazarse en una misma cara o entre distintas caras.
 CLASIFICASION DE CUERPOS GEOMETRICOS 1 2 Cuerpos Geométrico s Ángulo diedro: es el ángulo formado por dos caras del poliedro. El ángulo formado por tres o más caras que concurren en un vértice, se denomina
CLASIFICASION DE CUERPOS GEOMETRICOS 1 2 Cuerpos Geométrico s Ángulo diedro: es el ángulo formado por dos caras del poliedro. El ángulo formado por tres o más caras que concurren en un vértice, se denomina
SISTEMASS DE REPRESENTACIÓNN Geometría Básica
 SISTEMASS DE REPRESENTACIÓNN Geometría Básica Coordinadora de Cátedra: Ing. Canziani, Mónica Profesores: Arq. Aubin, Mónica Arq. Magenta, Gabriela Ing. Medina, Noemí Ing. Nassipián, Rosana V. Ing. Borgnia,
SISTEMASS DE REPRESENTACIÓNN Geometría Básica Coordinadora de Cátedra: Ing. Canziani, Mónica Profesores: Arq. Aubin, Mónica Arq. Magenta, Gabriela Ing. Medina, Noemí Ing. Nassipián, Rosana V. Ing. Borgnia,
POLIEDROS. POLIEDROS Prof. Annabella Zapattini. Definición: Llamamos poliedro a la región del espacio limitada por polígonos planos.
 POLIEDROS Definición: Llamamos poliedro a la región del espacio limitada por polígonos planos. Definiciones: Llamamos caras de un poliedro a los polígonos que lo definen. Llamamos aristas a los segmentos
POLIEDROS Definición: Llamamos poliedro a la región del espacio limitada por polígonos planos. Definiciones: Llamamos caras de un poliedro a los polígonos que lo definen. Llamamos aristas a los segmentos
4. GEOMETRÍA // 4.4. POLIEDROS.
 4. GEOMETRÍA // 4.4. POLIEDROS. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS Curso 2011-2012 Bibliografía. Bibliografía. 1. Alsina, C., Pérez, R., Ruiz, C., Simetría dinámica, Serie Matemáticas:
4. GEOMETRÍA // 4.4. POLIEDROS. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS Curso 2011-2012 Bibliografía. Bibliografía. 1. Alsina, C., Pérez, R., Ruiz, C., Simetría dinámica, Serie Matemáticas:
Dossier Volumen II. Índice
 Índice Introducción 1 Sólidos platónicos 4 Bocetos y estudios preliminares 6 El módulo 8 Antecedentes 10 Estudio 11 Planta, alzado y perfil 13 Perspectivas Axonométrica 14 Caballera 15 Cónica Central 16
Índice Introducción 1 Sólidos platónicos 4 Bocetos y estudios preliminares 6 El módulo 8 Antecedentes 10 Estudio 11 Planta, alzado y perfil 13 Perspectivas Axonométrica 14 Caballera 15 Cónica Central 16
4. GEOMETRÍA // 4.5. POLIEDROS.
 4. GEOMETRÍA // 4.5. POLIEDROS. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS. Bibliografía. 1. Alsina, C., Pérez, R., Ruiz, C., Simetría dinámica, Serie Matemáticas: Cultura y aprendizaje,
4. GEOMETRÍA // 4.5. POLIEDROS. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS. Bibliografía. 1. Alsina, C., Pérez, R., Ruiz, C., Simetría dinámica, Serie Matemáticas: Cultura y aprendizaje,
POLIEDROS E CORPOS REDONDOS
 Escribe na parte dereita o que falta. POLIEDROS E CORPOS REDONDOS 1. Os corpos redondos. A xeometría do espazo estuda os corpos que teñen tres dimensións: lonxitude, anchura e altura. Os corpos que teñen
Escribe na parte dereita o que falta. POLIEDROS E CORPOS REDONDOS 1. Os corpos redondos. A xeometría do espazo estuda os corpos que teñen tres dimensións: lonxitude, anchura e altura. Os corpos que teñen
D18 Poliedros regulares
 El sistema diédrico D18 Poliedros regulares Clases de poliedros regulares convexos No pueden existir más de cinco clases de poliedros regulares convexos. Teniendo en cuenta que la suma de las caras de
El sistema diédrico D18 Poliedros regulares Clases de poliedros regulares convexos No pueden existir más de cinco clases de poliedros regulares convexos. Teniendo en cuenta que la suma de las caras de
