Polígonos y poliedros
|
|
|
- Patricia Castillo Cruz
- hace 9 años
- Vistas:
Transcripción
1 Polígonos y poliedros Rojo central (1980). El científico se ocupa de demostrar hechos, para comprobarlos, las mentes más estrictas utilizan ecuaciones matemáticas, luego vienen otros hombres, que aplican estos conocimientos y los traducen en objetos concretos con aplicabilidad práctica. El artista por su parte demuestra la otra realidad del universo, aquella que no es tangible, aquella que no se puede demostrar a través de esas fórmulas matemáticas: es la realidad sensible, son dos formas de explorar, descubrir y explicar el universo, los cuales normalmente marchan paralelas" Jesús Rafael Soto (Venezuela, ).
2 El mundo de los poliedros Pasamos del mundo de los polígonos (figuras planas o bidimensionales) al mundo de los poliedros (cuerpos en el espacio tridimensional). En el proceso de fabricación de piezas y en la construcción de edificios tiene especial importancia la interpretación del plano de la pieza o del edificio, para luego construir el modelo, réplica de la pieza que se producirá posteriormente. Así también construimos cuerpos a partir de sus respectivas redes o planos, lo que nos permite proyectar edificios y estructuras de uso en la construcción y el diseño. Las figuras representadas son cuerpos geométricos en el espacio, limitados por un número finito de superficies planas. Estos cuerpos reciben el nombre de poliedros. Las superficies planas en cuestión son polígonos y se denominan caras del poliedro. Observa cualquiera de los poliedros que están dibujados y algunos de sus elementos característicos: a) Cómo definirías cada uno de sus elementos? b) Cuántas caras, vértices y aristas tiene? c) Cuántas caras, como mínimo, habrá que juntar en un vértice? d) Cuánto pueden sumar, como máximo, los ángulos de las caras que concurren en un mismo vértice? Se denomina orden del vértice al número de caras que concurren a un mismo vértice. Este poliedro tiene orden del vértice 3. Vértice Cara Este es un poliedro que tiene 14 vértices, 21 aristas y nueve caras. Este cuerpo geométrico no es un poliedro. 18 Por qué el cuerpo de la derecha no es un poliedro?
3 Clasificación de poliedros Una clasificación de los poliedros es la siguiente: Poliedros Convexos No convexos (cóncavos) Se caracterizan porque cada uno de ellos se puede apoyar en una superficie plana sobre cada una de sus caras. Se caracterizan porque cada uno de ellos no se puede apoyar en una superficie plana sobre alguna de sus caras. Regulares (sólo hay 5) No regulares Regulares estrellados (hay 4) No regulares Se caracterizan porque todas sus caras son polígonos regulares congruentes y en cada vértice concurre el mismo número de caras. Se caracterizan porque son poliedros con caras no congruentes y en el caso de la segunda figura, aunque sus caras son congruentes no tienen el mismo número de caras en cada vértice. Decide: cuáles de los siguientes cuerpos son poliedros? Cuáles son convexos? Cuáles son cóncavos? Cuáles son regulares? y cuáles son irregulares? Explica en cada caso el porqué de tu decisión. A B C E F G H D 19
4 El mundo de los poliedros regulares Los poliedros regulares convexos son conocidos con el nombre de sólidos platónicos en honor al filosofo griego Platón ( a.c.) que los cita en el Timeo, pero lo cierto es que no se sabe en que época llegaron a conocerse. Algunos investigadores asignan el cubo, el tetraedro y el dodecaedro a Pitágoras (siglo IV a.c.) y el octaedro e icosaedro a Teeteto ( a.c.). Para Platón los elementos últimos de la materia son los poliedros regulares, asignando el fuego al tetraedro (el fuego tiene la forma del tetraedro, pues es el elemento mas pequeño, ligero, móvil y agudo), la tierra al cubo (el poliedro mas sólido de los cinco), el aire al octaedro (para los griegos el aire, de tamaño, peso y fluidez, en cierto modo intermedios, se compone de octaedros) y el agua al icosaedro (el agua, el más móvil y fluido de los elementos, debe tener como forma propia o "semilla, el icosaedro, el sólido más cercano a la esfera y, por tanto, el que con mayor facilidad puede rodar), mientras que al dodecaedro le asignó el Universo. Como los griegos ya tenían asignados los cuatro elementos dejaban sin pareja al dodecaedro, por lo que lo relacionaron con el Universo como conjunción de los otros cuatro. La forma del dodecaedro es la que los dioses emplean para disponer las constelaciones en los cielos. Dios lo utilizó para todo cuando dibujó el orden final. En cada uno de los poliedros abajo representados cuenta el número de vértices V, el número de aristas A y el número de caras C. Calcula V-A+C. Qué número se obtiene? La relación resultante fue demostrada por Euler. Icosaedro (agua) (universo) Tetraedro (fuego) Observa los cinco poliedros regulares, las caras idénticas que se encuentran en cada vértice y el elemento que representan. Platón (Grecia a.c.) Octaedro (aire) Cubo (tierra) Poliedro regular Hexaedro regular o cubo Tetraedro regular regular Icosaedro regular Octaedro regular Modelo Caras 6 cuadrados 4 triángulos equiláteros 12 pentágonos regulares 20 triángulos equiláteros 8 triángulos equiláteros Vértices Aristas Aristas por vértice
5 Euclides (Grecia, s. III a.c.) demostró, de forma algebraica, porqué sólo existen cinco tipos de poliedros regulares convexos. Supongamos que se pueda construir un poliedro regular convexo cuyas caras sean polígonos regulares de n lados. Luego, el ángulo de cada vértice del polígono mide (n-2) n x 180. Si el orden del vértice de un poliedro regular es p, entonces la suma de los ángulos de un vértice del poliedro es: p [ (n-2) x 180 ]. Pero esta suma tiene que ser menor que 360, n porque si fuera igual a 360 las caras estarían en un plano y no se tendría una figura sólida. Luego: p[ (n-2) n x 180 ] < 360 p[ (n-2) n ] < 2 p(n-2) < 2n pn -2p -2n < 0 pn - 2p - 2n +4 < 4 p (n-2) - 2 (n-2) < 4 (p-2)(n-2) < 4 Como cada cara de un poliedro regular debe tener más de dos lados y más de dos caras deben concurrir en cada vértice, vemos que p y n deben ser mayores que 2. Las únicas soluciones (n,p) a esta desigualdad son (3,3), (3,4), (3,5) (4,3) y (5,3). La tabla a la derecha justifica lo anterior. α α 360 /n 2α = =(n-2) 180 n n n p n-2 p-2 (n-2)(p-2) Figura Tetraedro Octaedro Icosaedro Cubo O Proyección de Schlegel Los sólidos platónicos pueden además ser proyectados sobre un plano. Esta proyección se obtiene eligiendo una cara y proyectando los lados del poliedro platónico desde un punto O por encima del centro de esta cara. La figura que se obtiene se llama diagrama de Schlegel. También se pueden obtener si rompemos una cara y estiramos las restantes caras sobre la pared, sin romper las aristas. Observa el diagrama de Schlegel del cubo. Parte de las características del poliedro (como la conexión entre vértices y lados) se preserva en su correspondiente diagrama de Schlegel. Esto facilita el estudio de determinados problemas, tales como recorrido y coloración. En el caso de los sólidos platónicos estos diagramas son únicos (no depende de la cara desde la que se proyecte). También se pueden hacer los desarrollos planos tal como se enseñan en Educación Básica (1ª y 2ª etapas) además de los diagramas de Schlegel de los poliedros platónicos. Estos desarrollos los presentamos en la página siguiente. E A B E F A D C H G F A B D C H G B 21 E F
6 Vista Desarrollo plano Diagrama de Schlegel Hexaedro regular o cubo Tetraedro Icosaedro Octaedro Como hemos visto sólo existen cinco poliedros regulares convexos. Si eliminamos la condición de ser convexo tenemos cuatro más. Éstos son conocidos como los poliedros de Kepler- Poinsot o poliedros regulares estrellados. Johannes Kepler (Holanda, ), en 1619, se dio cuenta que existían dos maneras diferentes de pegar 12 pentagramas (pentágonos estrellados) a lo largo de sus aristas para obtener un sólido regular. Si 5 de ellos se unen en un sólo vértice, obtendremos el pequeño dodecaedro estrellado que tiene doce vértices. Si son 3 pentagramas los que se encuentran en cada vértice, obtenemos el gran dodecaedro estrellado que tiene 20 vértices. 22
7 Pequeño dodecaedro estrellado Gran dodecaedro estrellado Posteriormente, en 1809, Louis Poinsot (Francia, ) descubrió los otros dos poliedros no convexos regulares, el gran icosaedro y el pequeño dodecaedro. Pequeño dodecaedro Gran icosaedro Universo Icosaedro 2, Material: acero inoxidable. 23 Icosaedro stellato, Materiales: acero inoxidable y cemento. El escultor Attilio Pierelli (Italia, ) utilizó, en la década de los 80, figuras como el dodecaedro, el icosaedro, el hipercubo y otras para realizar sus obras. Fuente:
8 Pero, existen otros tipos de poliedros? Sí, entre estos se encuentran los poliedros semirregulares que son 17. Un poliedro convexo es semirregular si sus caras son polígonos regulares de dos o tres tipos. Entre estos sólidos están los arquimedianos, ya que se creen fueron descubiertos por Arquímedes, aunque no se tiene ninguna prueba documental que lo acredite. Existen 13 sólidos arquimedianos. Siete de ellos se obtienen por truncamiento de los sólidos platónicos, es decir, por cortes de esquinas, acción que se puede ejecutar de varias maneras. Así, los denominados con el nombre del sólido platónico de origen más el término, se obtienen al dividir cada arista en tres partes y cortar por estas divisiones. Si dividimos la arista a la mitad y truncamos, sólo obtenemos dos nuevos poliedros: el cuboctaedro y el icosidodecaedro. Sus nombres se deben al hecho de que al realizar el proceso de truncamiento que acabamos de describir, en el caso de un cubo y un octaedro (respectivamente, icosaedro y dodecaedro) obtenemos el mismo poliedro. El cubo chato y el dodecaedro chato se obtienen con otro procedimiento. Tetraedro Cubo Cuboctaedro Octaedro Rombocuboctaedro Cuboctaedro Cubo chato chato Icosidodecaedro Icosaedro Romboicosidodecaedro 24 Icosidodecaedro
10- Los poliedros. Aprende a reconocer los poliedros en nuestro entorno; identifica sus elementos y aprende a clasificarlos.
 Aprende a reconocer los poliedros en nuestro entorno; identifica sus elementos y aprende a clasificarlos. Impreso por Juan Carlos Vila Vilariño Centro PASTORIZA (Nº 3) Sumario 1 Los poliedros... 3 1.1
Aprende a reconocer los poliedros en nuestro entorno; identifica sus elementos y aprende a clasificarlos. Impreso por Juan Carlos Vila Vilariño Centro PASTORIZA (Nº 3) Sumario 1 Los poliedros... 3 1.1
Punto. Recta. Semirrecta. Segmento. Rectas Secantes. Rectas Paralelas. Rectas Perpendiculares
 Punto El punto es un objeto geométrico que no tiene dimensión y que sirve para indicar una posición. A Recta Es una sucesión continua e indefinida de puntos en una sola dimensión. Semirrecta Es una línea
Punto El punto es un objeto geométrico que no tiene dimensión y que sirve para indicar una posición. A Recta Es una sucesión continua e indefinida de puntos en una sola dimensión. Semirrecta Es una línea
Figura en el espacio o cuerpo geométrico es el conjunto de puntos que no están contenidos en un mismo plano, es la porción de espacio limitado.
 Cuenca, 11 de noviembre de 2013 Clase 13 Geometría del espacio Figuras geométricas en el espacio Definiciones: Geometría del espacio: Rama de las matemáticas encargada de las propiedades y medida de las
Cuenca, 11 de noviembre de 2013 Clase 13 Geometría del espacio Figuras geométricas en el espacio Definiciones: Geometría del espacio: Rama de las matemáticas encargada de las propiedades y medida de las
Cuerpos geométricos son porciones de espacio limitadas por superficies planas o curvas. CUERPOS GEOMÉTRICOS PRISMAS PIRÁMIDES CILINDROS CONOS ESFERAS
 UNIDAD DIDÁCTICA CUERPOS GEOMÉTRICOS 1. CUERPOS GEOMÉTRICOS En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos
UNIDAD DIDÁCTICA CUERPOS GEOMÉTRICOS 1. CUERPOS GEOMÉTRICOS En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos
MATEMÁTICAS (GEOMETRÍA)
 COLEGIO COLOMBO BRITÁNICO Formación en la Libertad y para la Libertad MATEMÁTICAS (GEOMETRÍA) GRADO:7 O DOCENTE: Nubia E. Niño C. FECHA: 8 / 07 / 15 Guía Didáctica 3-2 Desempeños: * Reconoce y clasifica
COLEGIO COLOMBO BRITÁNICO Formación en la Libertad y para la Libertad MATEMÁTICAS (GEOMETRÍA) GRADO:7 O DOCENTE: Nubia E. Niño C. FECHA: 8 / 07 / 15 Guía Didáctica 3-2 Desempeños: * Reconoce y clasifica
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA
 RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
Un poliedro es un cuerpo geométrico que tiene todas sus caras planas y formadas por polígonos.
 CUERPOS GEOMÉTRICOS Los cuerpos geométricos son figuras geométricas tridimensionales (tienen alto, ancho y largo) que ocupan un lugar en el espacio. 1. POLIEDROS. 1.1. DEFINICIÓN. Un poliedro es un cuerpo
CUERPOS GEOMÉTRICOS Los cuerpos geométricos son figuras geométricas tridimensionales (tienen alto, ancho y largo) que ocupan un lugar en el espacio. 1. POLIEDROS. 1.1. DEFINICIÓN. Un poliedro es un cuerpo
CUERPOS GEOMÉTRICOS. Un polígono es una figura compuesta por tres o más segmentos rectos (lados) que cierran una región en el espacio.
 CUERPOS GEOMÉTRICOS 07 Comprende que son los cuerpos geométricos e identifica las partes que los componen. En Presentación de Contenidos recuerdan qué son los polígonos para comprender cómo se forman los
CUERPOS GEOMÉTRICOS 07 Comprende que son los cuerpos geométricos e identifica las partes que los componen. En Presentación de Contenidos recuerdan qué son los polígonos para comprender cómo se forman los
Diagonal: es un segmento que une dos vértices no consecutivos del poliedro. Puede trazarse en una misma cara o entre distintas caras.
 CLASIFICASION DE CUERPOS GEOMETRICOS 1 2 Cuerpos Geométrico s Ángulo diedro: es el ángulo formado por dos caras del poliedro. El ángulo formado por tres o más caras que concurren en un vértice, se denomina
CLASIFICASION DE CUERPOS GEOMETRICOS 1 2 Cuerpos Geométrico s Ángulo diedro: es el ángulo formado por dos caras del poliedro. El ángulo formado por tres o más caras que concurren en un vértice, se denomina
DE PRISMAS Y POLIEDROS. A LA BÚSQUEDA DEL CUBOIDE PERFECTO
 DE PRISMAS Y POLIEDROS. A LA BÚSQUEDA DEL CUBOIDE PERFECTO De poliedros En el espacio euclídeo tridimensional podemos resumir algunas nociones básicas de geometría clásica Un poliedro es la zona espacial
DE PRISMAS Y POLIEDROS. A LA BÚSQUEDA DEL CUBOIDE PERFECTO De poliedros En el espacio euclídeo tridimensional podemos resumir algunas nociones básicas de geometría clásica Un poliedro es la zona espacial
SOLUCIONES MINIMOS 2º ESO TEMA 8 CUERPOS GEOMÉTRICOS
 SOLUCIONES MINIMOS º ESO TEMA 8 CUERPOS GEOMÉTRICOS Ejercicio nº 1.- Escribe el nombre de cada uno de los elementos de este poliedro: Ejercicio nº.- Cuáles de las siguientes figuras son poliedros? Por
SOLUCIONES MINIMOS º ESO TEMA 8 CUERPOS GEOMÉTRICOS Ejercicio nº 1.- Escribe el nombre de cada uno de los elementos de este poliedro: Ejercicio nº.- Cuáles de las siguientes figuras son poliedros? Por
Geometría en el espacio. Poliedros
 Geometría en el espacio. Gemma Hermida Granado Trinidad Gómez Ramírez 28 de junio de 2006 Geometría en el espacio. 1 Programación de la unidad Objetivos didácticos Conceptos Procedimientos Actitudes Criterios
Geometría en el espacio. Gemma Hermida Granado Trinidad Gómez Ramírez 28 de junio de 2006 Geometría en el espacio. 1 Programación de la unidad Objetivos didácticos Conceptos Procedimientos Actitudes Criterios
IES CUADERNO Nº 8 NOMBRE: FECHA: / / Cuerpos geométricos
 Cuerpos geométricos Contenidos 1. Poliedros Definición Elementos de un poliedro 2. Tipos de poliedros Prismas Prismas regulares Desarrollo de un prisma recto Paralelepípedos Pirámides Pirámides regulares
Cuerpos geométricos Contenidos 1. Poliedros Definición Elementos de un poliedro 2. Tipos de poliedros Prismas Prismas regulares Desarrollo de un prisma recto Paralelepípedos Pirámides Pirámides regulares
Geometría. Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid
 Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
Poliedros Regulares Convexos
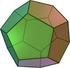 Poliedros Regulares Convexos Características y relaciones entre ellos AUTOR: Begoña Soler de Dios 1 Máster en Profesor de Educación Secundaria Esp. Matemáticas 1 [email protected] Poliedros Regulares
Poliedros Regulares Convexos Características y relaciones entre ellos AUTOR: Begoña Soler de Dios 1 Máster en Profesor de Educación Secundaria Esp. Matemáticas 1 [email protected] Poliedros Regulares
Diferencias entre Figuras y
 10 Lección Refuerzo Matemáticas Diferencias entre Figuras y Cuerpos Geométricos APRENDO JUGANDO Competencia Aplica conocimientos acerca de las principales características de polígonos y cuerpos geométricos.
10 Lección Refuerzo Matemáticas Diferencias entre Figuras y Cuerpos Geométricos APRENDO JUGANDO Competencia Aplica conocimientos acerca de las principales características de polígonos y cuerpos geométricos.
Matemática. Desafío. GUÍA DE EJERCITACIÓN AVANZADA Cuerpos geométricos GUICEN032MT22-A16V1
 GUÍ DE EJERCITCIÓN VNZD Cuerpos geométricos Programa Entrenamiento Desafío GUICEN02MT22-16V1 Matemática Una semiesfera tiene un área total de 4π cm 2. Si se corta por la mitad, de manera de formar dos
GUÍ DE EJERCITCIÓN VNZD Cuerpos geométricos Programa Entrenamiento Desafío GUICEN02MT22-16V1 Matemática Una semiesfera tiene un área total de 4π cm 2. Si se corta por la mitad, de manera de formar dos
Geometría. Cuerpos Geométricos. Trabajo
 Geometría Cuerpos Geométricos Trabajo CUERPOS GEOMÉTRICOS 1. Clasifique los cuerpos geométricos. Dos grupos de sólidos geométricos del espacio presentan especial interés: 1.1. Poliedros: Aquellos cuerpos
Geometría Cuerpos Geométricos Trabajo CUERPOS GEOMÉTRICOS 1. Clasifique los cuerpos geométricos. Dos grupos de sólidos geométricos del espacio presentan especial interés: 1.1. Poliedros: Aquellos cuerpos
SÓLIDOS EN EL ESPACIO TRIDIMENSIONAL
 G3D1: Sólidos convexos y cóncavos SÓLIDOS EN EL ESPACIO TRIDIMENSIONAL Pon tres ejemplos de objetos cotidianos que sean convexos: Pon tres ejemplos de objetos cotidianos que sean cóncavos: G3D2: Caracterización
G3D1: Sólidos convexos y cóncavos SÓLIDOS EN EL ESPACIO TRIDIMENSIONAL Pon tres ejemplos de objetos cotidianos que sean convexos: Pon tres ejemplos de objetos cotidianos que sean cóncavos: G3D2: Caracterización
Trabajo de Investigación Cuerpos Geométricos
 Saint George s College Área de Matemáticas y sus Aplicaciones Tercera Unidad Trabajo de Investigación Cuerpos Geométricos Integrantes: -Stefan Jercic -Ignacio Larrain -Cristian Majluf Curso: 10 E Profesora:
Saint George s College Área de Matemáticas y sus Aplicaciones Tercera Unidad Trabajo de Investigación Cuerpos Geométricos Integrantes: -Stefan Jercic -Ignacio Larrain -Cristian Majluf Curso: 10 E Profesora:
MÓDULO Nº 3. Nivelación. Matemática Módulo Nº3. Contenidos. Polígonos Circunferencia y Círculo Volúmenes
 MÓDULO Nº 3 Nivelación Matemática 2005 Módulo Nº3 Contenidos Polígonos Circunferencia y Círculo Volúmenes Nivelación Polígonos Polígono Regular: Son aquellos polígonos que tienen todos sus lados y ángulos
MÓDULO Nº 3 Nivelación Matemática 2005 Módulo Nº3 Contenidos Polígonos Circunferencia y Círculo Volúmenes Nivelación Polígonos Polígono Regular: Son aquellos polígonos que tienen todos sus lados y ángulos
Cuerpos geométricos. Volúmenes
 4 uerpos geométricos. Volúmenes. Poliedros Un poliedro es un cuerpo geométrico limitado por cuatro o más polígonos planos. Los elementos de un poliedro son: aras: son los polígonos que lo delimitan. ristas:
4 uerpos geométricos. Volúmenes. Poliedros Un poliedro es un cuerpo geométrico limitado por cuatro o más polígonos planos. Los elementos de un poliedro son: aras: son los polígonos que lo delimitan. ristas:
Recuerda lo fundamental
 12 Figuras planas y espaciales Recuerda lo fundamental Curso:... Fecha:... TRIÁNGULOS Mediana de un triángulo es un segmento que...... Las tres medianas de un triángulo se cortan en el...... Las mediatrices
12 Figuras planas y espaciales Recuerda lo fundamental Curso:... Fecha:... TRIÁNGULOS Mediana de un triángulo es un segmento que...... Las tres medianas de un triángulo se cortan en el...... Las mediatrices
11 POLIEDROS EJERCICIOS. 6 Cuántas caras, vértices y aristas hay en los siguientes poliedros? a) b) c)
 11 POLIEROS EJERIIOS 1 ibuja una línea recta en tu cuaderno. escribe algún segmento real en el techo de la clase que se cruce con la línea que has dibujado. 6 uántas caras, vértices y aristas hay en los
11 POLIEROS EJERIIOS 1 ibuja una línea recta en tu cuaderno. escribe algún segmento real en el techo de la clase que se cruce con la línea que has dibujado. 6 uántas caras, vértices y aristas hay en los
MYP (MIDDLE YEARS PROGRAMME)
 MYP (MIDDLE YEARS PROGRAMME) 2014-2015 Fecha 19/05/2015 APUNTES DE GEOMETRÍA 2º ESO 1. EL TEOREMA DE PITÁGORAS El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa
MYP (MIDDLE YEARS PROGRAMME) 2014-2015 Fecha 19/05/2015 APUNTES DE GEOMETRÍA 2º ESO 1. EL TEOREMA DE PITÁGORAS El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa
Ámbito científico tecnológico
 Dirección Xeral de Educación, Formación Profesional e Innovación Educativa Educación secundaria para personas adultas Ámbito científico tecnológico Educación a distancia semipresencial Módulo Unidad didáctica
Dirección Xeral de Educación, Formación Profesional e Innovación Educativa Educación secundaria para personas adultas Ámbito científico tecnológico Educación a distancia semipresencial Módulo Unidad didáctica
congruentes es porque tienen la misma longitud AB = CD y, cuando dos ángulos DEF son congruentes es porque tienen la misma medida
 COLEGIO COLMBO BRITÁNICO DEPARTAMENTO DE MATEMÁTICAS GEOMETRÍA NOVENO GRADO PROFESORES: RAÚL MARTÍNEZ, JAVIER MURILLO Y JESÚS VARGAS CONGRUENCIA Y SEMEJANZA Cuando tenemos dos segmentos escribimos AB CD
COLEGIO COLMBO BRITÁNICO DEPARTAMENTO DE MATEMÁTICAS GEOMETRÍA NOVENO GRADO PROFESORES: RAÚL MARTÍNEZ, JAVIER MURILLO Y JESÚS VARGAS CONGRUENCIA Y SEMEJANZA Cuando tenemos dos segmentos escribimos AB CD
Conceptos geométricos II
 Conceptos geométricos II Ángulo Ángulos Consecutivos Ángulos Alternos y Ángulos Correspondientes Polígono Polígono Regular Polígono Irregular Triángulo Cuadrilátero Superficie Círculo Superficie reglada
Conceptos geométricos II Ángulo Ángulos Consecutivos Ángulos Alternos y Ángulos Correspondientes Polígono Polígono Regular Polígono Irregular Triángulo Cuadrilátero Superficie Círculo Superficie reglada
III: Geometría para maestros. Capitulo 1: Figuras geométricas
 III: Geometría para maestros. Capitulo : Figuras geométricas SELECCIÓN DE EJERCICIOS RESUELTOS SITUACIONES INTRODUCTORIAS En un libro de primaria encontramos este enunciado: Dibuja un polígono convexo
III: Geometría para maestros. Capitulo : Figuras geométricas SELECCIÓN DE EJERCICIOS RESUELTOS SITUACIONES INTRODUCTORIAS En un libro de primaria encontramos este enunciado: Dibuja un polígono convexo
TEMA 9 CUERPOS GEOMÉTRICOS
 Tel: 98 9 6 91 Fax: 98 1 89 96 TEMA 9 CUERPOS GEOMÉTRICOS Objetivos / Criterios de evaluación O.1.1 Conocer las fórmulas de áreas y volúmenes de figuras geométricas sencillas de D. O.1. Resolver problemas
Tel: 98 9 6 91 Fax: 98 1 89 96 TEMA 9 CUERPOS GEOMÉTRICOS Objetivos / Criterios de evaluación O.1.1 Conocer las fórmulas de áreas y volúmenes de figuras geométricas sencillas de D. O.1. Resolver problemas
Qué son los cuerpos geométricos?
 Qué son los cuerpos geométricos? Definición Los cuerpos geométricos son regiones cerradas del espacio. Una caja de tetrabrick es un ejemplo claro de la figura que en matemáticas se conoce con el nombre
Qué son los cuerpos geométricos? Definición Los cuerpos geométricos son regiones cerradas del espacio. Una caja de tetrabrick es un ejemplo claro de la figura que en matemáticas se conoce con el nombre
a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta.
 POLIEDROS Ejercicio nº 1.- a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
POLIEDROS Ejercicio nº 1.- a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
Hay 5 sólidos platónicos
 1 Un sólido es un poliedro, o sea una figura tridimensional conformada por planos de diversas formas (polígonos) que se intersectan. Hay 5 sólidos platónicos Fueron estudiados y descriptos por los geómetras
1 Un sólido es un poliedro, o sea una figura tridimensional conformada por planos de diversas formas (polígonos) que se intersectan. Hay 5 sólidos platónicos Fueron estudiados y descriptos por los geómetras
POLÍGONOS POLÍGONOS. APM Página 1
 POLÍGONOS 1. Polígonos. 1.1. Elementos de un polígono. 1.2. Suma de los ángulos interiores de un polígono. 1.3. Diagonales de un polígono. 1.4. Clasificación de los polígonos. 2. Polígonos regulares. Elementos.
POLÍGONOS 1. Polígonos. 1.1. Elementos de un polígono. 1.2. Suma de los ángulos interiores de un polígono. 1.3. Diagonales de un polígono. 1.4. Clasificación de los polígonos. 2. Polígonos regulares. Elementos.
Liceo N 1 Javiera Carrera 8 años 2011
 GUIA DE ESTUDIO : Cuerpos geométricos Prof. Juan Schuchhardt E. DEFINICIÓN: Los poliedros son aquellos cuerpos geométricos que están limitados por superficies planas y de contorno poligonal. Un poliedro
GUIA DE ESTUDIO : Cuerpos geométricos Prof. Juan Schuchhardt E. DEFINICIÓN: Los poliedros son aquellos cuerpos geométricos que están limitados por superficies planas y de contorno poligonal. Un poliedro
Los cuerpos geométricos
 Los cuerpos geométricos Se denominan cuerpos geométricos a aquellos elementos que, ya sean reales o ideales que existen en la realidad o pueden concebirse mentalmente ocupan un volumen en el espacio desarrollándose
Los cuerpos geométricos Se denominan cuerpos geométricos a aquellos elementos que, ya sean reales o ideales que existen en la realidad o pueden concebirse mentalmente ocupan un volumen en el espacio desarrollándose
Minicurso de Teoría de Gráficas Escuela de Verano 2014 por María Luisa Pérez Seguí Facultad de Ciencias Físico-Matemáticas, Universidad Michoacana
 Minicurso de Teoría de Gráficas Escuela de Verano 014 por María Luisa Pérez Seguí Facultad de Ciencias Físico-Matemáticas, Universidad Michoacana Índice 1. Conceptos básicos 1 1.1. Nomenclatura...................................
Minicurso de Teoría de Gráficas Escuela de Verano 014 por María Luisa Pérez Seguí Facultad de Ciencias Físico-Matemáticas, Universidad Michoacana Índice 1. Conceptos básicos 1 1.1. Nomenclatura...................................
CONOCER Y DIFERENCIAR LOS POLIEDROS REGULARES
 OJETIVO 1 CONOCER Y DIERENCIR LOS POLIEDROS REGULRES NOMRE: CURSO: ECH: CONCEPTO DE POLIEDRO Vértice Un poliedro es un cuerpo geométrico cuyas caras son polígonos. Los elementos del poliedro son: Caras:
OJETIVO 1 CONOCER Y DIERENCIR LOS POLIEDROS REGULRES NOMRE: CURSO: ECH: CONCEPTO DE POLIEDRO Vértice Un poliedro es un cuerpo geométrico cuyas caras son polígonos. Los elementos del poliedro son: Caras:
ELEMENTOS Y CLASES DE ÁNGULOS
 Apellidos: Curso: Grupo: Nombre: Fecha: ELEMENTOS Y CLASES DE ÁNGULOS Dos rectas que se cortan forman 4 regiones llamadas ángulos. Las partes de un ángulo son: los lados: son las semirrectas que lo forman.
Apellidos: Curso: Grupo: Nombre: Fecha: ELEMENTOS Y CLASES DE ÁNGULOS Dos rectas que se cortan forman 4 regiones llamadas ángulos. Las partes de un ángulo son: los lados: son las semirrectas que lo forman.
Soluciones oficiales Clasificación Olimpiada Nacional Nivel Mayor
 Soluciones oficiales Clasificación Olimpiada Nacional 009 Comisión Académica Nivel Maor Problema 1. Calcule todas las soluciones m, n de números enteros que satisfacen la ecuación m n = 009 (n + 1) Solución.
Soluciones oficiales Clasificación Olimpiada Nacional 009 Comisión Académica Nivel Maor Problema 1. Calcule todas las soluciones m, n de números enteros que satisfacen la ecuación m n = 009 (n + 1) Solución.
11. MOSAICOS. El ángulo interior de un polígono regular de n lados es
 11. MOSAICOS Cuando una o varias piezas recubren un plano sin solaparse tenemos un recubrimiento o mosaico. Los mosaicos más sencillos son los que solo utilizan una pieza de una única forma y tamaño. Aun
11. MOSAICOS Cuando una o varias piezas recubren un plano sin solaparse tenemos un recubrimiento o mosaico. Los mosaicos más sencillos son los que solo utilizan una pieza de una única forma y tamaño. Aun
Cuerpos geométricos OBJETIVOS CONTENIDOS PROCEDIMIENTOS. Elementos de un poliedro y su desarrollo. Los poliedros regulares y sus características.
 826464 _ 0385-0396.qxd /2/07 09:27 Página 385 Cuerpos geométricos INTRODUCCIÓN Esta unidad completa la serie dedicada a la Geometría y afianza su comprensión mediante la descripción y desarrollo de las
826464 _ 0385-0396.qxd /2/07 09:27 Página 385 Cuerpos geométricos INTRODUCCIÓN Esta unidad completa la serie dedicada a la Geometría y afianza su comprensión mediante la descripción y desarrollo de las
DIBUJO TÉCNICO II EJERCICIOS DE APOYO. Prof. Jesús Macho Martínez
 DIBUJO TÉCNICO II EJERCICIOS DE APOYO Esta obra de Jesús Macho Martínez está bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported 1º.- Deducir razonadamente el valor del ángulo α marcado
DIBUJO TÉCNICO II EJERCICIOS DE APOYO Esta obra de Jesús Macho Martínez está bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported 1º.- Deducir razonadamente el valor del ángulo α marcado
RESUMEN DE FORMULAS EJERCICIOS de APLICACIÓN POLIEDROS
 RESUMEN DE FORMULAS EJERCICIOS de APLICACIÓN POLIEDROS. 1.-Calcule la superficie total de un tetraedro cuya arista mide 2 (12 3 ) 2.- Se tiene un tetraedro cuya arista mide 6 3 cm. Calcular.- 2.1.-La superficie
RESUMEN DE FORMULAS EJERCICIOS de APLICACIÓN POLIEDROS. 1.-Calcule la superficie total de un tetraedro cuya arista mide 2 (12 3 ) 2.- Se tiene un tetraedro cuya arista mide 6 3 cm. Calcular.- 2.1.-La superficie
Geometría Básica 43 UNIVERSIDAD DE LOS ANDES - TÁCHIRA DEPARTAMENTO DE CIENCIAS CARRERA EDUCACIÓN BÁSICA INTEGRAL
 Geometría Básica 43 POLIGONOS UNIVERSIDAD DE LOS ANDES - TÁCHIRA DEPARTAMENTO DE CIENCIAS CARRERA EDUCACIÓN BÁSICA INTEGRAL SEGMENTOS CONCATENADOS Y CONSECUTIVOS Consideremos los segmentos ab y bc, donde
Geometría Básica 43 POLIGONOS UNIVERSIDAD DE LOS ANDES - TÁCHIRA DEPARTAMENTO DE CIENCIAS CARRERA EDUCACIÓN BÁSICA INTEGRAL SEGMENTOS CONCATENADOS Y CONSECUTIVOS Consideremos los segmentos ab y bc, donde
4. GEOMETRÍA // 4.4. POLIEDROS.
 4. GEOMETRÍA // 4.4. POLIEDROS. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS Curso 2011-2012 Bibliografía. Bibliografía. 1. Alsina, C., Pérez, R., Ruiz, C., Simetría dinámica, Serie Matemáticas:
4. GEOMETRÍA // 4.4. POLIEDROS. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS Curso 2011-2012 Bibliografía. Bibliografía. 1. Alsina, C., Pérez, R., Ruiz, C., Simetría dinámica, Serie Matemáticas:
DESCRIPCIÓN Y CLASIFICACIÓN DE POLÍGONOS
 DESCRIPCIÓN Y CLASIFICACIÓN DE POLÍGONOS 1.1.1 1.1.2 Las figuras geométricas, como los polígonos, aparecen en muchos lugares. En estas lecciones, los alumnos estudiarán más atentamente los polígonos y
DESCRIPCIÓN Y CLASIFICACIÓN DE POLÍGONOS 1.1.1 1.1.2 Las figuras geométricas, como los polígonos, aparecen en muchos lugares. En estas lecciones, los alumnos estudiarán más atentamente los polígonos y
Departamento de Educación Plástica y Visual. Unidad 3: Polígonos. 3º ESO EDUCACIÓN PLÁSTICA Y VISUAL UNIDAD 3: POLÍGONOS.
 EDUCACIÓN PLÁSTICA Y VISUAL UNIDAD 3: POLÍGONOS Página 1 de 15 1. POLÍGONOS 1.1. Conocimiento de los polígonos regulares Polígono: Proviene de la palabra compuesta de Poli (muchos) Gonos (ángulos). Se
EDUCACIÓN PLÁSTICA Y VISUAL UNIDAD 3: POLÍGONOS Página 1 de 15 1. POLÍGONOS 1.1. Conocimiento de los polígonos regulares Polígono: Proviene de la palabra compuesta de Poli (muchos) Gonos (ángulos). Se
Polígono. Superficie plana limitada por una línea poligonal cerrada.
 POLÍGONO B C r A d O a l E D Polígono. Superficie plana limitada por una línea poligonal cerrada. r O r =a Elementos, puntos y líneas en los polígonos. (Regulares) LADO Cada uno de los segmentos de la
POLÍGONO B C r A d O a l E D Polígono. Superficie plana limitada por una línea poligonal cerrada. r O r =a Elementos, puntos y líneas en los polígonos. (Regulares) LADO Cada uno de los segmentos de la
MATEMÁTICAS (GEOMÉTRÍA)
 COLEGIO COLOMBO BRITÁNICO Formación en la Libertad y para la Libertad MATEMÁTICAS (GEOMÉTRÍA) GRADO:6 O DOCENTE: Nubia E. Niño C. FECHA: 9 / 06 / 15 Guía Didáctica 3 1 Desempeños: * Identifica, clasifica
COLEGIO COLOMBO BRITÁNICO Formación en la Libertad y para la Libertad MATEMÁTICAS (GEOMÉTRÍA) GRADO:6 O DOCENTE: Nubia E. Niño C. FECHA: 9 / 06 / 15 Guía Didáctica 3 1 Desempeños: * Identifica, clasifica
DEF Diremos que dos diedros son Adyacentes si tienen una cara común y las otras opuestas.
 1. PRIMERAS DEFINICIONES. DEF Dados dos semiplanos en el espacio α y β con un borde común r y situados en planos distintos, llamaremos Diedro Convexo al conjunto de puntos comunes a los semiespacios limitados
1. PRIMERAS DEFINICIONES. DEF Dados dos semiplanos en el espacio α y β con un borde común r y situados en planos distintos, llamaremos Diedro Convexo al conjunto de puntos comunes a los semiespacios limitados
Triángulos. Definición y clasificación
 Profr. Efraín Soto polinar. Triángulos En esta sección empezamos el estudio de las figuras geométricas planas creadas de segmentos de rectas. uando la figura está formada por tres segmentos de recta y
Profr. Efraín Soto polinar. Triángulos En esta sección empezamos el estudio de las figuras geométricas planas creadas de segmentos de rectas. uando la figura está formada por tres segmentos de recta y
5º de E. Primaria LOS CUERPOS GEOMÉTRICOS -TEMA 15
 LOS POLIEDROS Los poliedros son cuerpos geométricos que tienen todas sus caras formadas por polígonos. Muchos objetos de nuestro alrededor tienen forma de poliedro: Los elementos de un poliedro son caras,
LOS POLIEDROS Los poliedros son cuerpos geométricos que tienen todas sus caras formadas por polígonos. Muchos objetos de nuestro alrededor tienen forma de poliedro: Los elementos de un poliedro son caras,
Polígono Polígono es la porción del plano limitada por rectas que se cortan dos a dos.
 Geometría plana B6 Triángulos Polígono Polígono es la porción del plano limitada por rectas que se cortan dos a dos. Clasificación de los polígonos Según el número de lados los polígonos se llaman: Triángulo
Geometría plana B6 Triángulos Polígono Polígono es la porción del plano limitada por rectas que se cortan dos a dos. Clasificación de los polígonos Según el número de lados los polígonos se llaman: Triángulo
IE FINCA LA MESA TALLERR DE COMPETENCIAS BÁSICAS. Nombre: Grado: Costrucciones
 IE FINCA LA MESA TALLERR DE COMPETENCIAS BÁSICAS Nombre: Grado: 9 5 1. Costrucciones 2. las rectas y puntos notables de un triángulo Sabemos que los polígonos son figuras cerradas planas, de lados rectos,
IE FINCA LA MESA TALLERR DE COMPETENCIAS BÁSICAS Nombre: Grado: 9 5 1. Costrucciones 2. las rectas y puntos notables de un triángulo Sabemos que los polígonos son figuras cerradas planas, de lados rectos,
PLAN DE RECUPERACIÓN DE MATEMÁTICAS 3º ESO (Tercer Trimestre) (Para alumnos de 4º de ESO)
 PLAN DE RECUPERACIÓN DE MATEMÁTICAS 3º ESO (Tercer Trimestre) (Para aumnos de 4º de ESO) NOMBRE: Para aprobar as matemáticas pendientes de cursos anteriores es obigatorio reaizar e pan de recuperación
PLAN DE RECUPERACIÓN DE MATEMÁTICAS 3º ESO (Tercer Trimestre) (Para aumnos de 4º de ESO) NOMBRE: Para aprobar as matemáticas pendientes de cursos anteriores es obigatorio reaizar e pan de recuperación
Se denomina mosaico a un recubrimiento del plano mediante piezas llamadas teselas sin dejar huecos y sin solapamiento.
 Qué entendemos por Mosaico? Se denomina mosaico a un recubrimiento del plano mediante piezas llamadas teselas sin dejar huecos y sin solapamiento. En otro lenguaje, formar un mosaico es embaldosar una
Qué entendemos por Mosaico? Se denomina mosaico a un recubrimiento del plano mediante piezas llamadas teselas sin dejar huecos y sin solapamiento. En otro lenguaje, formar un mosaico es embaldosar una
Cuerpos geométricos. Objetivos. Antes de empezar. 1. Poliedros...pág. 138 Definición Elementos de un poliedro
 8 Cuerpos geométricos. Objetivos En esta quincena aprenderás a: Identificar que es un poliedro. Determinar los elementos de un poliedro: Caras, aristas y vértices. Clasificar los poliedros. Especificar
8 Cuerpos geométricos. Objetivos En esta quincena aprenderás a: Identificar que es un poliedro. Determinar los elementos de un poliedro: Caras, aristas y vértices. Clasificar los poliedros. Especificar
D18 Poliedros regulares
 El sistema diédrico D18 Poliedros regulares Clases de poliedros regulares convexos No pueden existir más de cinco clases de poliedros regulares convexos. Teniendo en cuenta que la suma de las caras de
El sistema diédrico D18 Poliedros regulares Clases de poliedros regulares convexos No pueden existir más de cinco clases de poliedros regulares convexos. Teniendo en cuenta que la suma de las caras de
MATEMÁTICAS 2º ESO SEMEJANZA Y TEOREMA DE THALES
 MATEMÁTICAS º ESO SEMEJANZA Y TEOREMA DE THALES S1 SEMEJANZA DE FIGURAS. RAZÓN DE SEMEJANZA O ESCALA. Dos figuras son semejantes si tienen la misma forma, aunque quizá distinto tamaño. La razón de semejanza
MATEMÁTICAS º ESO SEMEJANZA Y TEOREMA DE THALES S1 SEMEJANZA DE FIGURAS. RAZÓN DE SEMEJANZA O ESCALA. Dos figuras son semejantes si tienen la misma forma, aunque quizá distinto tamaño. La razón de semejanza
Programa Entrenamiento MT-22
 Programa Entrenamiento MT- SOLUCIONARIO Guía de ejercitación avanzada SGUICEN0MT-A6V TABLA DE CORRECCIÓN Guía de ejercitación ÍTEM ALTERNATIVA HABILIDAD D E B 4 C 5 C Comprensión 6 B 7 E Comprensión 8
Programa Entrenamiento MT- SOLUCIONARIO Guía de ejercitación avanzada SGUICEN0MT-A6V TABLA DE CORRECCIÓN Guía de ejercitación ÍTEM ALTERNATIVA HABILIDAD D E B 4 C 5 C Comprensión 6 B 7 E Comprensión 8
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
 ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO 1. Área y volumen del ortoedro y del cubo. 1.1. Área y volumen del ortoedro. 1.2. Cálculo de la diagonal del ortoedro. 1.3. Área y volumen del cubo. 2. Área y
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO 1. Área y volumen del ortoedro y del cubo. 1.1. Área y volumen del ortoedro. 1.2. Cálculo de la diagonal del ortoedro. 1.3. Área y volumen del cubo. 2. Área y
Geometría del espacio
 Áreas y volumenes de cuerpos geométricos Un poliedro es un cuerpo geométrico que está limitado por cuatro o más polígonos. Los elementos de un poliedro son: Caras del poliedro: son los polígonos que lo
Áreas y volumenes de cuerpos geométricos Un poliedro es un cuerpo geométrico que está limitado por cuatro o más polígonos. Los elementos de un poliedro son: Caras del poliedro: son los polígonos que lo
Polígonos y Poliedros
 09 Lección Apertura Matemáticas Polígonos y s Competencia Socializa sus ideas y llega a acuerdos con los que asimila conceptos relacionados con polígonos y poliedros. Diseño instruccional El maestro aclarará
09 Lección Apertura Matemáticas Polígonos y s Competencia Socializa sus ideas y llega a acuerdos con los que asimila conceptos relacionados con polígonos y poliedros. Diseño instruccional El maestro aclarará
open green road Guía Matemática CUERPOS GEOMÉTRICOS tutora: Jacky Moreno .co
 Guía Matemática CUERPOS GEOMÉTRICOS tutora: Jacky Moreno.co 1. Geometría en el espacio Al observar nuestro alrededor podemos notar una infinidad de objetos que ocupan un lugar en el espacio físico en el
Guía Matemática CUERPOS GEOMÉTRICOS tutora: Jacky Moreno.co 1. Geometría en el espacio Al observar nuestro alrededor podemos notar una infinidad de objetos que ocupan un lugar en el espacio físico en el
Seminario de problemas-eso. Curso Hoja 10
 Seminario de problemas-eso. Curso 011-1. Hoja 10 5. Dado un triángulo cualquiera, demuestra que es posible recubrir el plano con infinitos triángulos iguales al dado, de forma que estos triángulos no se
Seminario de problemas-eso. Curso 011-1. Hoja 10 5. Dado un triángulo cualquiera, demuestra que es posible recubrir el plano con infinitos triángulos iguales al dado, de forma que estos triángulos no se
Los cuerpos geométricos
 Los cuerpos geométricos Los poliedros y sus elementos Clasifica estos cuerpos en poliedros y no poliedros. A B C D E F G poliedros> B, D, E, F A, C, G no poliedros > Cuenta las caras, los vértices y las
Los cuerpos geométricos Los poliedros y sus elementos Clasifica estos cuerpos en poliedros y no poliedros. A B C D E F G poliedros> B, D, E, F A, C, G no poliedros > Cuenta las caras, los vértices y las
TEMA 9: FIGURAS GEOMÉTRICAS ESPACIALES
 TEMA 9: FIGURAS GEOMÉTRICAS ESPACIALES Matías Arce, Sonsoles Blázquez, Tomás Ortega, Cristina Pecharromán 1. INTRODUCCIÓN...1 2. SUPERFICIES POLIÉDRICAS. POLIEDROS...1 3. FIGURAS DE REVOLUCIÓN...3 4. POLIEDROS
TEMA 9: FIGURAS GEOMÉTRICAS ESPACIALES Matías Arce, Sonsoles Blázquez, Tomás Ortega, Cristina Pecharromán 1. INTRODUCCIÓN...1 2. SUPERFICIES POLIÉDRICAS. POLIEDROS...1 3. FIGURAS DE REVOLUCIÓN...3 4. POLIEDROS
Cuadriláteros y circunferencia
 CLAVES PARA EMPEZAR Un triángulo isósceles tiene dos lados iguales: b c. Como es rectángulo, se cumple el teorema de Pitágoras: 10 2 b 2 b 2 100 2b 2 b 7,07. Los dos lados miden 7,07 cm cada uno. r A C
CLAVES PARA EMPEZAR Un triángulo isósceles tiene dos lados iguales: b c. Como es rectángulo, se cumple el teorema de Pitágoras: 10 2 b 2 b 2 100 2b 2 b 7,07. Los dos lados miden 7,07 cm cada uno. r A C
GEOMETRÍA SAGRADA. Ejemplos y dibujos vectoriales JUNIO de 2009 - Roberto García
 GEOMETRÍA SAGRADA Ejemplos y dibujos vectoriales JUNIO de 2009 - Roberto García Génesis 1:1 En el principio creó Dios los cielos y la tierra. Espacio tridimensional definido Espacio tridimensional creado
GEOMETRÍA SAGRADA Ejemplos y dibujos vectoriales JUNIO de 2009 - Roberto García Génesis 1:1 En el principio creó Dios los cielos y la tierra. Espacio tridimensional definido Espacio tridimensional creado
POLÍGONO ÁNGULOS DE UN POLÍGONO CLASIFICACIÓN: La denominación de polígono palabra compuesta de poli, del griego: muchos; y gonos del griego: ángulos
 POLÍGONO La denominación de polígono palabra compuesta de poli, del griego: muchos; y gonos del griego: ángulos Un polígono es una porción del plano limitada por una línea poligonal cerrada. Los segmentos
POLÍGONO La denominación de polígono palabra compuesta de poli, del griego: muchos; y gonos del griego: ángulos Un polígono es una porción del plano limitada por una línea poligonal cerrada. Los segmentos
Geometría 2D: Preguntas Capítulo Relaciones Geométricas, Perímetro y Circunferencia
 Geometría 2D: Preguntas Capítulo Relaciones Geométricas, Perímetro y Circunferencia 1. Cuáles son algunas de las relaciones especiales entre los ángulos? 2. Explique qué es un polígono y cómo determinar
Geometría 2D: Preguntas Capítulo Relaciones Geométricas, Perímetro y Circunferencia 1. Cuáles son algunas de las relaciones especiales entre los ángulos? 2. Explique qué es un polígono y cómo determinar
MATEMÁTICAS Y SU DIDÁCTICA
 MATEMÁTICAS Y SU DIDÁCTICA ESCUELA UNIVERSITARIA DE MAGISTERIO SAGRADO CORAZÓN UNIVERSIDAD DE CÓRDOBA Curso académico: 2011 2012 ACTIVIDADES DE GEOMETRÍA TRABAJO EN GRUPO Las siguientes actividades se
MATEMÁTICAS Y SU DIDÁCTICA ESCUELA UNIVERSITARIA DE MAGISTERIO SAGRADO CORAZÓN UNIVERSIDAD DE CÓRDOBA Curso académico: 2011 2012 ACTIVIDADES DE GEOMETRÍA TRABAJO EN GRUPO Las siguientes actividades se
Circunradio y Volumen de Poliedros
 Circunradio y Volumen de Poliedros Julio Castiñeira Merino. Introducción A mis queridos nietos Santiago, Gonzalo y Nicolás Una parte importante de los poliedros convexos con caras regulares son inscribibles
Circunradio y Volumen de Poliedros Julio Castiñeira Merino. Introducción A mis queridos nietos Santiago, Gonzalo y Nicolás Una parte importante de los poliedros convexos con caras regulares son inscribibles
1. Descompón cada uno de estos números. 2. Escribe cómo se leen estos números. 3. Compara y escribe el signo < o > según corresponda. 4. Calcula.
 Trabajo de recuperación del área de matemáticas de 6º de primaria. 1. Descompón cada uno de estos números. 8.603.058 39.090.001 410.901.100 639.000.072 2. Escribe cómo se leen estos números. 10.196.364
Trabajo de recuperación del área de matemáticas de 6º de primaria. 1. Descompón cada uno de estos números. 8.603.058 39.090.001 410.901.100 639.000.072 2. Escribe cómo se leen estos números. 10.196.364
Tema 2: Figuras geométricas
 Tema 2: Figuras geométricas En este tema empezaremos a estudiar: 1. la circunferencia. 2. los triángulos. 3. los cuadriláteros. 4. los poĺıgonos. 1 2 La circunferencia (p. 31) El cerebro humano es muy
Tema 2: Figuras geométricas En este tema empezaremos a estudiar: 1. la circunferencia. 2. los triángulos. 3. los cuadriláteros. 4. los poĺıgonos. 1 2 La circunferencia (p. 31) El cerebro humano es muy
CUBO. Truncado FICHA TÉCNICA
 CUBO Truncado Este material está aconsejado para ayudar a construir el siguiente conocimiento: C Continuar haciendo clasificaciones, en este caso, de poliedros. C Concepto de ángulo en el espacio como
CUBO Truncado Este material está aconsejado para ayudar a construir el siguiente conocimiento: C Continuar haciendo clasificaciones, en este caso, de poliedros. C Concepto de ángulo en el espacio como
Soluciones Primer Nivel - 5º Año de Escolaridad
 Primer Nivel - 5º Año de Escolaridad Problema 1. La diagonal del cuadrado mide cm. El cuadrado se descompone en cuatro triángulos rectángulos cuyos catetos miden 1cm. Las áreas de estos triángulos miden
Primer Nivel - 5º Año de Escolaridad Problema 1. La diagonal del cuadrado mide cm. El cuadrado se descompone en cuatro triángulos rectángulos cuyos catetos miden 1cm. Las áreas de estos triángulos miden
EJERCICIOS DE LOS TEMAS 9 y 10.GEOMETRÍA
 1.- Dos triángulos ABC y A C son semejantes y la razón de semejanza entre el primero y el segundo es,4. Calcula las longitudes de los lados que faltan sabiendo que AB = 0 cm, BC = 15 cm y A C = 10 cm.
1.- Dos triángulos ABC y A C son semejantes y la razón de semejanza entre el primero y el segundo es,4. Calcula las longitudes de los lados que faltan sabiendo que AB = 0 cm, BC = 15 cm y A C = 10 cm.
CONCEPTO DE POLÍGONO. RECONOCER Y CLASIFICAR POLÍGONOS
 OBJETIVO 1 CONCEPTO DE POLÍGONO. RECONOCER Y CLASIICAR POLÍGONOS NOMBRE: CURSO: ECHA: POLÍGONOS Varios segmentos unidos entre sí forman una línea poligonal. Una línea poligonal cerrada es un polígono.
OBJETIVO 1 CONCEPTO DE POLÍGONO. RECONOCER Y CLASIICAR POLÍGONOS NOMBRE: CURSO: ECHA: POLÍGONOS Varios segmentos unidos entre sí forman una línea poligonal. Una línea poligonal cerrada es un polígono.
TEORÍA DE POLIEDROS Y CONSTRUCCIÓN DE
 TEORÍA DE POLIEDROS Y CONSTRUCCIÓN DE Vicente Viana Martínez Vicente Viana Martínez Pág 1 CONSTRUCCIÓN DE UN OMNIPOLIEDRO Introducción. Definiciones Un poliedro es un cuerpo geométrico totalmente limitado
TEORÍA DE POLIEDROS Y CONSTRUCCIÓN DE Vicente Viana Martínez Vicente Viana Martínez Pág 1 CONSTRUCCIÓN DE UN OMNIPOLIEDRO Introducción. Definiciones Un poliedro es un cuerpo geométrico totalmente limitado
CUERPOS GEOMÉTRICOS. POLIEDROS
 INTRODUCCIÓN CUERPOS GEOMÉTRICOS - POLIEDROS Este texto te servirá para que estudies los contenidos sobre poliedros que fueron desarrollados por los distintos grupos en clases y tiene como objetivos que
INTRODUCCIÓN CUERPOS GEOMÉTRICOS - POLIEDROS Este texto te servirá para que estudies los contenidos sobre poliedros que fueron desarrollados por los distintos grupos en clases y tiene como objetivos que
SOLUCIONES A LAS ACTIVIDADES DE CADA EPÍGRAFE
 Pág. 1 PÁGINA 246 REFLEXIONA En la inauguración de la Casa de la Cultura observamos, entre otras, las siguientes figuras: Todas ellas son polígonos. Cuáles crees que son regulares? Explica por qué crees
Pág. 1 PÁGINA 246 REFLEXIONA En la inauguración de la Casa de la Cultura observamos, entre otras, las siguientes figuras: Todas ellas son polígonos. Cuáles crees que son regulares? Explica por qué crees
Talento Matemático 2002/2003. Real Academia de Ciencias
 Volvemos al hermoso tema de la simetría. Además de la imágenes de multitud de objetos y de seres vivos que poseen simetrías recuerdas en qué consistía una simetría desde el punto de vista matemático?,
Volvemos al hermoso tema de la simetría. Además de la imágenes de multitud de objetos y de seres vivos que poseen simetrías recuerdas en qué consistía una simetría desde el punto de vista matemático?,
TEMA 10: FORMAS Y FIGURAS PLANAS. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco.
 2009 TEMA 10: FORMAS Y FIGURAS PLANAS. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco. Manuel González de León. mgdl 01/01/2009 TEMA 10: FORMAS Y FIGURAS PLANAS. 1. Polígonos. 2.
2009 TEMA 10: FORMAS Y FIGURAS PLANAS. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco. Manuel González de León. mgdl 01/01/2009 TEMA 10: FORMAS Y FIGURAS PLANAS. 1. Polígonos. 2.
COLEGIO COLOMBO BRITÁNICO Formación en la Libertad y para la Libertad MATEMÁTICAS (GEOMETRÍA)
 COLEGIO COLOMBO BRITÁNICO Formación en la Libertad y para la Libertad MATEMÁTICAS (GEOMETRÍA) GRADO:7 O DOCENTE: Nubia E. Niño C. FECHA: 9 / 06 / 15 Guía Didáctica 3-1 Desempeño: Determina la clasificación
COLEGIO COLOMBO BRITÁNICO Formación en la Libertad y para la Libertad MATEMÁTICAS (GEOMETRÍA) GRADO:7 O DOCENTE: Nubia E. Niño C. FECHA: 9 / 06 / 15 Guía Didáctica 3-1 Desempeño: Determina la clasificación
CUERPOS GEOMÉTRICOS EN EL PLANO Y EN EL ESPACIO: APLICACIONES DIDÁCTICAS.
 CUERPOS GEOMÉTRICOS EN EL PLANO Y EN EL ESPACIO: APLICACIONES DIDÁCTICAS. Resumen AUTORIA FERNANDO VALLEJO LÓPEZ TEMÁTICA DIDÁCTICA DE LA MATEMÁTICA ETAPA ESO EN ÉSTE ARTÍCULO, SE ESTUDIAN LOS CUERPOS
CUERPOS GEOMÉTRICOS EN EL PLANO Y EN EL ESPACIO: APLICACIONES DIDÁCTICAS. Resumen AUTORIA FERNANDO VALLEJO LÓPEZ TEMÁTICA DIDÁCTICA DE LA MATEMÁTICA ETAPA ESO EN ÉSTE ARTÍCULO, SE ESTUDIAN LOS CUERPOS
Definición y Clasificación de Polígonos. Definición
 Definición y Clasificación de Polígonos Además del triángulo hay una gran cantidad de otras figuras geométricas delimitadas por segmentos de recta que son importantes en geometría. Definición Polígono
Definición y Clasificación de Polígonos Además del triángulo hay una gran cantidad de otras figuras geométricas delimitadas por segmentos de recta que son importantes en geometría. Definición Polígono
MATEMÁTICAS (TIC) REPASO BIMESTRAL (3P) TALLER DE REPASO PARA EL BIMESTRAL 3P
 COLEGIO COLOMBO BRITANICO Formación en la Libertad y para la Libertad MATEMÁTICAS (TIC) REPASO BIMESTRAL (3P) GRADO:7 O DOCENTES: Natalia A. Gil V. Nubia E. Niño C. FECHA: 18 / 08 /15 Taller Adicional
COLEGIO COLOMBO BRITANICO Formación en la Libertad y para la Libertad MATEMÁTICAS (TIC) REPASO BIMESTRAL (3P) GRADO:7 O DOCENTES: Natalia A. Gil V. Nubia E. Niño C. FECHA: 18 / 08 /15 Taller Adicional
MATEMÁTICAS 1º DE ESO
 MATEMÁTICAS 1º DE ESO LOE TEMA XII: POLIEDROS Y CUERPOS DE REDONDOS Poliedros. o Elementos de un poliedro y desarrollo plano. Prismas. o Elementos y tipos de prismas. Pirámides. o Elementos y tipos de
MATEMÁTICAS 1º DE ESO LOE TEMA XII: POLIEDROS Y CUERPOS DE REDONDOS Poliedros. o Elementos de un poliedro y desarrollo plano. Prismas. o Elementos y tipos de prismas. Pirámides. o Elementos y tipos de
geometría 2008 cbc taller de dibujo cátedra arq. víctor murgia
 geometría 2008 cbc taller de dibujo cátedra arq. víctor murgia CBC TALLER DE DIBUJO Cátedra Arq. VÍCTOR MURGIA 2008 3 INTRODUCCIÓN AL LENGUAJE GEOMÉTRICO línea recta Este texto trata sobre conceptos básicos
geometría 2008 cbc taller de dibujo cátedra arq. víctor murgia CBC TALLER DE DIBUJO Cátedra Arq. VÍCTOR MURGIA 2008 3 INTRODUCCIÓN AL LENGUAJE GEOMÉTRICO línea recta Este texto trata sobre conceptos básicos
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: DIBUJO TÉCNICO II
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2014-2015 MATERIA: DIBUJO TÉCNICO II INSTRUCCIONES GENERALES Y CALIFICACIÓN Después
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2014-2015 MATERIA: DIBUJO TÉCNICO II INSTRUCCIONES GENERALES Y CALIFICACIÓN Después
MATEMÁTICAS 1º DE ESO
 MATEMÁTICAS 1º DE ESO LOMCE TEMA X: POLÍGONOS Y CIRCUNFERENCIAS Triángulos. Elementos y relaciones. Tipos de triángulos. Rectas y puntos notables: o Mediatrices y circuncentro. o Bisectrices e incentro.
MATEMÁTICAS 1º DE ESO LOMCE TEMA X: POLÍGONOS Y CIRCUNFERENCIAS Triángulos. Elementos y relaciones. Tipos de triángulos. Rectas y puntos notables: o Mediatrices y circuncentro. o Bisectrices e incentro.
1 NOCIONES BÁSICAS SOBRE CONJUNTOS. SÍMBOLOS.
 UNIDAD 1.- CONCEPTOS REQUERIDOS CONJUNTOS. AXIOMAS DE PERTENENCIA, PARALELISMO, ORDEN Y PARTICIÓN. 1 NOCIONES BÁSICAS SOBRE CONJUNTOS. SÍMBOLOS. 1.1 Determinaciones de un conjunto. Un conjunto queda determinado
UNIDAD 1.- CONCEPTOS REQUERIDOS CONJUNTOS. AXIOMAS DE PERTENENCIA, PARALELISMO, ORDEN Y PARTICIÓN. 1 NOCIONES BÁSICAS SOBRE CONJUNTOS. SÍMBOLOS. 1.1 Determinaciones de un conjunto. Un conjunto queda determinado
Estrellas en la Sagrada Familia de Gaudí: Un contexto nuevo para estudiar poliedros.
 Comunicación Estrellas en la Sagrada Familia de Gaudí. Un contexto nuevo para estudiar poliedros. Estrellas en la Sagrada Familia de Gaudí: Un contexto nuevo para estudiar poliedros. María de los Desamparados
Comunicación Estrellas en la Sagrada Familia de Gaudí. Un contexto nuevo para estudiar poliedros. Estrellas en la Sagrada Familia de Gaudí: Un contexto nuevo para estudiar poliedros. María de los Desamparados
EJERCICIOS MÓDULO 4. Geometría plana. 1) Cuántos vértices tiene un polígono cuyo número total de diagonales es 9?
 Seminario Universitario Matemática EJERCICIOS MÓDULO 4 Geometría plana 1) Cuántos vértices tiene un polígono cuyo número total de diagonales es 9? ) Cuántos lados tiene un polígono en el cual la suma de
Seminario Universitario Matemática EJERCICIOS MÓDULO 4 Geometría plana 1) Cuántos vértices tiene un polígono cuyo número total de diagonales es 9? ) Cuántos lados tiene un polígono en el cual la suma de
Vistas de un objeto VISTAS DE UN OBJETO
 Vistas de un objeto VISTAS DE UN OBJETO CONCEPTO DE VISTA Una de las formas en que podemos representar los objetos en Tecnología es mediante sus vistas. Pero, qué se entiende por vista de un objeto? cómo
Vistas de un objeto VISTAS DE UN OBJETO CONCEPTO DE VISTA Una de las formas en que podemos representar los objetos en Tecnología es mediante sus vistas. Pero, qué se entiende por vista de un objeto? cómo
CLASIFICACIÓN DE POLÍGONOS: SU DIDÁCTICA.
 CLASIFICACIÓN DE POLÍGONOS: SU DIDÁCTICA. AUTORIA FERNANDO VALLEJO LÓPEZ TEMÁTICA DIDÁCTICA DE LA MATEMÁTICA ETAPA ESO Resumen EN ÉSTE ARTÍCULO, ESTUDIAMOS LA CLASIFICACIÓN DE POLÍGONOS. HACEMOS UNA CLASIFICACIÓN
CLASIFICACIÓN DE POLÍGONOS: SU DIDÁCTICA. AUTORIA FERNANDO VALLEJO LÓPEZ TEMÁTICA DIDÁCTICA DE LA MATEMÁTICA ETAPA ESO Resumen EN ÉSTE ARTÍCULO, ESTUDIAMOS LA CLASIFICACIÓN DE POLÍGONOS. HACEMOS UNA CLASIFICACIÓN
DE LA GEOMETRÍA EUCLIDIANA A LA GEOMETRÍA NO EUCLIDIANA, UNA TRANSFORMACIÓN DE LAS FORMAS GEOMÉTRICAS. PRIMERA PARTE.
 DE LA GEOMETRÍA EUCLIDIANA A LA GEOMETRÍA NO EUCLIDIANA, UNA TRANSFORMACIÓN DE LAS FORMAS GEOMÉTRICAS PRIMERA PARTE Dra Dina Rochman Beer Profesor-investigador titular C del Departamento de Teoría y Procesos
DE LA GEOMETRÍA EUCLIDIANA A LA GEOMETRÍA NO EUCLIDIANA, UNA TRANSFORMACIÓN DE LAS FORMAS GEOMÉTRICAS PRIMERA PARTE Dra Dina Rochman Beer Profesor-investigador titular C del Departamento de Teoría y Procesos
FICHAS DE PRÁCTICAS 6º PRIMARIA MATEMÁTICAS
 FICHAS DE PRÁCTICAS 6º PRIMARIA MATEMÁTICAS UNIDAD DIDÁCTICA : ÁLGEBRA Y ARITMÉTICA Crucigrama numérico de operaciones combinadas Duración Estimada: 50 min Mejorar el cálculo de sumas, restas y operaciones
FICHAS DE PRÁCTICAS 6º PRIMARIA MATEMÁTICAS UNIDAD DIDÁCTICA : ÁLGEBRA Y ARITMÉTICA Crucigrama numérico de operaciones combinadas Duración Estimada: 50 min Mejorar el cálculo de sumas, restas y operaciones
