Espectroscopia vibracional
|
|
|
- Marina Cordero Ferreyra
- hace 5 años
- Vistas:
Transcripción
1 Espectroscopia vibracional Prof. Jesús Hernández Trujillo Facultad de Química, UNAM Espectroscopía vibr./jesús Hernández T p. 1
2 Contenido Series de Taylor a segundo orden. Formas cuadráticas. Modos normales. Espectroscopia vibracional de moléculas poliatómicas. Espectroscopía vibr./jesús Hernández T p. 2
3 Series de Taylor a segundo orden Expansión de z = f(x,y) a segundo orden alrededor de r 0 = (x 0,y 0 ): (1) f(x,y) = f(x 0,y 0 )+ 1 2! [ 2 f x 2 [ f x (x x 0 )+ f y r0 (x x 0 ) f x y r0 (y y 0 ) ] r0 + 2 f y 2 ] (y y 0 ) r0 + r0 (x x 0 )(y y 0 ) Espectroscopía vibr./jesús Hernández T p. 3
4 Si (x 0,y 0 ) = (0,0): [ f(x,y) = f(0,0)+ 1 2! [ 2 f x 2 f x (x)+ f ] (0,0) y (y) + (0,0) x y (xy)+ 2 f (0,0) y 2 r0 (x) f ] (y) 2 (0,0) +... (2) = f(0,0)+ ( f 2! (x,y) x 2 ( f x, f (x,y) y) (0,0) ) 2 f 2 f y x x y 2 f y 2 ( x (0,0) y ) + = f(0,0)+ f (0,0) (x,y)+(x,y) H (0,0) ( x y ) Espectroscopía vibr./jesús Hernández T p. 4
5 La matriz (3) H = ( 2 f x 2 2 f y x se llama el Hessiano de f(x,y). 2 f x y 2 f y 2 ) Si f(0,0) es un mínimo: (4) f(x,y) = 1 2! (x,y) ( h11 h 12 h 21 h 22 )( x y ) f(x,y) se comporta localmente como una función cuadrática. Espectroscopía vibr./jesús Hernández T p. 5
6 Ejemplo: Expresa f(x,y) = sen(2x 2 +xy +3y 2 ) como serie de Taylor a segundo orden alrededor de (0,0). f(0,0) = 0 f(0,0) = (0,0) ( 4 1 H = 1 2 ) Por lo tanto: f(x,y) = 1 2 (x,y) ( )( x y ) = 2x 2 +xy +3y Espectroscopía vibr./jesús Hernández T p. 6
7 Gráficamente: sen(2x 2 +xy +3y 2 ) 2x 2 +xy +3y 2 Espectroscopía vibr./jesús Hernández T p. 7
8 Formas cuadráticas Ecuación cuadrática en dos variables: ax 2 +2bxy +cy 2 = d Espectroscopía vibr./jesús Hernández T p. 8
9 Formas cuadráticas Ecuación cuadrática en dos variables: ax 2 +2bxy +cy 2 = d Forma cuadrática en dos variables: q(x,y) = ax 2 +2bxy +cy 2 Espectroscopía vibr./jesús Hernández T p. 8
10 Ejemplos: f(x,y) = x 2 +y Espectroscopía vibr./jesús Hernández T p. 9
11 Ejemplos: f(x,y) = x 2 +y 2 Contornos: f(x,y) = k En este caso: circunferencias Espectroscopía vibr./jesús Hernández T p. 9
12 f(x,y) = 2x 2 +xy +3y 2 Espectroscopía vibr./jesús Hernández T p. 10
13 f(x,y) = 2x 2 +xy +3y 2 Contornos? Espectroscopía vibr./jesús Hernández T p. 10
14 f(x,y) = 2x 2 +xy +3y 2 Contornos? Elipses Espectroscopía vibr./jesús Hernández T p. 10
15 f(x,y) = 2x 2 +xy +3y 2 Contornos? Elipses Gráficas de las ecuaciones cuadráticas: cónicas Espectroscopía vibr./jesús Hernández T p. 10
16 Cualquier forma cuadrática q(x,y) = ax 2 +2bxy +cy 2 puede expresarse como un producto matricial: ( ) ( )( ) a b x x y = X t MX b c y donde X = ( x y ) y M = ( a b b c ) Espectroscopía vibr./jesús Hernández T p. 11
17 Forma cuadrática en n variables {x 1,x 2,...,x n }: q(x 1,x 2,...,x n ) = n n λ ij x i x j i j En forma matricial: q(x 1,x 2,...,x n ) = X t ΛX donde la matriz Λ tiene elementos (Λ) ij = λ ij Espectroscopía vibr./jesús Hernández T p. 12
18 A partir de la matriz Λ es posible obtener una matriz simétrica tal que M = 1 2 ( Λ+Λ t ) q(x 1,x 2,...,x n ) = X t MX M es simétrica pues M t = M Además, toda matriz simétrica es diagonalizable Espectroscopía vibr./jesús Hernández T p. 13
19 Mediante una transformación lineal, es posible reducir cualquier forma cuadrática a la forma canónica: q(x 1,x 2,...,x n) = n i d i (x i )2 = X t DX en las variables {x 1,x 2,...,x n}, donde D = d d d n.. Espectroscopía vibr./jesús Hernández T p. 14
20 A partir de M se obtiene la matriz diagonal D mediante la ecuación de valores propios: o de manera equivalente: Mv = dv Mv = div; (M di)v = 0 Espectroscopía vibr./jesús Hernández T p. 15
21 A partir de M se obtiene la matriz diagonal D mediante la ecuación de valores propios: o de manera equivalente: Mv = dv Mv = div; (M di)v = 0 Los valores propios se obtienen a partir de det(m di) = 0 Espectroscopía vibr./jesús Hernández T p. 15
22 Sustituir d = d 1,d = d 2,... en la ecuación de valores propios: (M d 1 I)v 1 = 0, (M di)v 2 = 0... Para obtener los vectores propios: v 1 = v 1 1 v 1 2., v2 = v 2 1 v 2 2.,... Espectroscopía vibr./jesús Hernández T p. 16
23 La transformación lineal (rotación de coordenadas) se lleva a cabo con la matriz v 1 1 v2 1. V = v1 2 v Espectroscopía vibr./jesús Hernández T p. 17
24 La transformación lineal (rotación de coordenadas) se lleva a cabo con la matriz v 1 1 v2 1. V = v1 2 v La matriz diagonal es D = V t MV Espectroscopía vibr./jesús Hernández T p. 17
25 La transformación lineal (rotación de coordenadas) se lleva a cabo con la matriz v 1 1 v2 1. V = v1 2 v La matriz diagonal es D = V t MV Las nuevas coordenadas son X = V t X Espectroscopía vibr./jesús Hernández T p. 17
26 Ejemplo: Describe la cónica 2x 2 +xy +3y 2 = 2 La ecuación puede escribirse en forma matricial como X t MX = 2 donde X = ( x y ) y M = ( ) Espectroscopía vibr./jesús Hernández T p. 18
27 D = ( ) = ( ) y la matriz ( ) V = realiza la transformación a las nuevas coordenadas: ) ) X = ( x y = V t X = ( 0.383x+0.924y 0.924x y Espectroscopía vibr./jesús Hernández T p. 19
28 Es decir, la matriz V realiza la rotación al nuevo sistema de coordenadas x = 0.383x+0.924y y = 0.924x+0.383y de donde x = 0.383x 0.924y y = 0.924x y Mediante combinaciones lineales de los vectores base {î,ĵ} se obtiene {î,ĵ } Espectroscopía vibr./jesús Hernández T p. 20
29 Es decir, la matriz V realiza la rotación al nuevo sistema de coordenadas x = 0.383x+0.924y y = 0.924x+0.383y de donde x = 0.383x 0.924y y = 0.924x y Mediante combinaciones lineales de los vectores base {î,ĵ} se obtiene {î,ĵ } Calcula los vectores î y ĵ Espectroscopía vibr./jesús Hernández T p. 20
30 Al sustituir x y y en 2x 2 +xy +3y 2 = 2 se obtiene la ecuación de la cónica en los ejes x y y : o bien 3.208(x ) (y ) 2 = 2 ( x ) 2 + ( y ) 2 = Espectroscopía vibr./jesús Hernández T p. 21
31 Al sustituir x y y en 2x 2 +xy +3y 2 = 2 se obtiene la ecuación de la cónica en los ejes x y y : o bien 3.208(x ) (y ) 2 = 2 ( x ) 2 + ( y ) 2 = A qué tipo de lugar geométrico corresponde? Espectroscopía vibr./jesús Hernández T p. 21
32 Se trata de una elipse: y x y x x y y son los ejes principales Espectroscopía vibr./jesús Hernández T p. 22
Química Cuántica I Formas cuadráticas
 Formas cuadráticas/jesús Hernández Trujillo p. 1/16 Química Cuántica I Formas cuadráticas Prof. Jesús Hernández Trujillo Facultad de Química, UNAM Formas cuadráticas/jesús Hernández Trujillo p. 2/16 Ecuación
Formas cuadráticas/jesús Hernández Trujillo p. 1/16 Química Cuántica I Formas cuadráticas Prof. Jesús Hernández Trujillo Facultad de Química, UNAM Formas cuadráticas/jesús Hernández Trujillo p. 2/16 Ecuación
Fundamentos de espectroscopia: Vibraciones poliatómicas. Jesús Hernández Trujillo. Noviembre de Vibraciones poli/jht 1 / 36
 Fundamentos de espectroscopia: Vibraciones poliatómicas Jesús Hernández Trujillo Noviembre de 2017 Vibraciones poli/jht 1 / 36 Formas cuadráticas En un punto crítico, en ocasiones, una funciónf(x,y) puede
Fundamentos de espectroscopia: Vibraciones poliatómicas Jesús Hernández Trujillo Noviembre de 2017 Vibraciones poli/jht 1 / 36 Formas cuadráticas En un punto crítico, en ocasiones, una funciónf(x,y) puede
Teoría de catástrofes
 Teoría de catástrofes Jesús Hernández Trujillo Facultad de Química, UNAM Marzo de 2012 Teoría de catástrofes/jht p. 1 Contenido Espacio de configuración. Formas cuadráticas y cúbicas. Lemas de Morse y
Teoría de catástrofes Jesús Hernández Trujillo Facultad de Química, UNAM Marzo de 2012 Teoría de catástrofes/jht p. 1 Contenido Espacio de configuración. Formas cuadráticas y cúbicas. Lemas de Morse y
Vibraciones de moléculas poliatómicas
 Vibraciones moleculares/jesús Hernández T p. 1/15 Vibraciones de moléculas poliatómicas Prof. Jesús Hernández Trujillo Facultad de Química, UNAM Vibraciones moleculares/jesús Hernández T p. 2/15 Modos
Vibraciones moleculares/jesús Hernández T p. 1/15 Vibraciones de moléculas poliatómicas Prof. Jesús Hernández Trujillo Facultad de Química, UNAM Vibraciones moleculares/jesús Hernández T p. 2/15 Modos
Operadores Lineales en Espacios con Producto Interno
 Operadores Lineales en Espacios con Producto Interno Definición y propiedades elementales del adjunto de un operador Al combinar las transformaciones lineales y el producto interno en un espacio vectorial
Operadores Lineales en Espacios con Producto Interno Definición y propiedades elementales del adjunto de un operador Al combinar las transformaciones lineales y el producto interno en un espacio vectorial
PRIMER CONTROL. 13 de Noviembre de 2012.
 GRAO EN QUÍMICA. MATEMÁTICAS. (Evaluación continua) PRIMER CONTROL. 13 de Noviembre de 2012. 1.- Sea f : R 3 R 3 la aplicación lineal f(x, y, z) = (x + z, 2x + ay az, 4x + z), (a R) a) Matriz de la aplicación
GRAO EN QUÍMICA. MATEMÁTICAS. (Evaluación continua) PRIMER CONTROL. 13 de Noviembre de 2012. 1.- Sea f : R 3 R 3 la aplicación lineal f(x, y, z) = (x + z, 2x + ay az, 4x + z), (a R) a) Matriz de la aplicación
Esta expresión polinómica puede expresarse como una expresión matricial de la forma; a 11 a 12 a 1n x 1 x 2 q(x 1, x 2,, x n ) = (x 1, x 2,, x n )
 Tema 3 Formas cuadráticas. 3.1. Definición y expresión matricial Definición 3.1.1. Una forma cuadrática sobre R es una aplicación q : R n R que a cada vector x = (x 1, x 2,, x n ) R n le hace corresponder
Tema 3 Formas cuadráticas. 3.1. Definición y expresión matricial Definición 3.1.1. Una forma cuadrática sobre R es una aplicación q : R n R que a cada vector x = (x 1, x 2,, x n ) R n le hace corresponder
Departamento de Ingeniería Matemática - Universidad de Chile
 Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 8-7 Formas cuadráticas SEMANA 4: FORMAS CUADRÁTICAS 7 Formas cuadráticas y matrices definidas positivas
Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 8-7 Formas cuadráticas SEMANA 4: FORMAS CUADRÁTICAS 7 Formas cuadráticas y matrices definidas positivas
Matemáticas Empresariales II. Formas cuadráticas
 Matemáticas Empresariales II Lección 7 Formas cuadráticas Manuel León Navarro Colegio Universitario Cardenal Cisneros M. León Matemáticas Empresariales II 1 / 17 Definición de Formas cuadráticas Sea V
Matemáticas Empresariales II Lección 7 Formas cuadráticas Manuel León Navarro Colegio Universitario Cardenal Cisneros M. León Matemáticas Empresariales II 1 / 17 Definición de Formas cuadráticas Sea V
APUNTES DE MATEMÁTICAS UNIVERSIDAD DE SEVILLA GRADOS EN ECONOMÍA Y ADMINISTRACIÓN DE EMPRESAS PRIMER CURSO
 APUNTES E MATEMÁTICAS EXÁMENES RESUELTOS E MATEMÁTICAS I EPARTAMENTO E ECONOMÍA APLICAA I UNIVERSIA E SEVILLA GRAOS EN ECONOMÍA Y AMINISTRACIÓN E EMPRESAS PRIMER CURSO Jesús Muñoz San Miguel http://www.personal.us.es/jmiguel
APUNTES E MATEMÁTICAS EXÁMENES RESUELTOS E MATEMÁTICAS I EPARTAMENTO E ECONOMÍA APLICAA I UNIVERSIA E SEVILLA GRAOS EN ECONOMÍA Y AMINISTRACIÓN E EMPRESAS PRIMER CURSO Jesús Muñoz San Miguel http://www.personal.us.es/jmiguel
Álgebra Lineal UCR. Sétimo tema, 2013
 Álgebra Lineal UCR Sétimo tema, 2013 Presentaciones basadas principalmente en Arce,C, Castillo,W y González, J. (2004) Álgebra lineal. Tercera edición. UCR. San Pedro. Otras fuentes serán mencionadas cuando
Álgebra Lineal UCR Sétimo tema, 2013 Presentaciones basadas principalmente en Arce,C, Castillo,W y González, J. (2004) Álgebra lineal. Tercera edición. UCR. San Pedro. Otras fuentes serán mencionadas cuando
Hoja de diagonalización MATEMÁTICAS I
 Hoja de diagonalización MATEMÁTICAS I 007-008 1.- En los siguientes casos estudiar si f es una aplicación lineal y en caso afirmativo hallar una matriz A tal que f(x) = Ax, así como los subespacios vectoriales
Hoja de diagonalización MATEMÁTICAS I 007-008 1.- En los siguientes casos estudiar si f es una aplicación lineal y en caso afirmativo hallar una matriz A tal que f(x) = Ax, así como los subespacios vectoriales
UNIVERSIDAD DE SEVILLA. DEPARTAMENTO DE ECONOMÍA APLICADA I. BOLETÍN DE PROBLEMAS DE MATEMÁTICAS I. GRADO EN ECONOMÍA.
 UNIVERSIA E SEVILLA. EPARTAMENTO E ECONOMÍA APLICAA I. BOLETÍN E PROBLEMAS E MATEMÁTICAS I. GRAO EN ECONOMÍA. BLOQUE I: CÁLCULO IFERENCIAL. Tema 1: Funciones de una variable Problema 1 Estudiar la continuidad
UNIVERSIA E SEVILLA. EPARTAMENTO E ECONOMÍA APLICAA I. BOLETÍN E PROBLEMAS E MATEMÁTICAS I. GRAO EN ECONOMÍA. BLOQUE I: CÁLCULO IFERENCIAL. Tema 1: Funciones de una variable Problema 1 Estudiar la continuidad
Fundamentos matemáticos. Tema 3 Geometría del plano y del espacio
 Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es
Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es
Fundamentos matemáticos. Tema 3 Geometría del plano y del espacio
 Grado en Ingeniería agrícola y del medio rural Tema 3 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2017 Licencia Creative Commons 4.0 Internacional J.
Grado en Ingeniería agrícola y del medio rural Tema 3 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2017 Licencia Creative Commons 4.0 Internacional J.
Parte II - Prácticas 8 a 9. Álgebra A 62 ÁLGEBRA A 62 (INGENIERÍA)
 Parte II - Prácticas 8 a 9 Álgebra A 62 Ingeniería 2015 CICLO BÁSICO COMÚN UBA ÁLGEBRA A 62 (INGENIERÍA) Práctica 8 Introducción a las transformaciones lineales Definiciones y propiedades Transformaciones
Parte II - Prácticas 8 a 9 Álgebra A 62 Ingeniería 2015 CICLO BÁSICO COMÚN UBA ÁLGEBRA A 62 (INGENIERÍA) Práctica 8 Introducción a las transformaciones lineales Definiciones y propiedades Transformaciones
1 CÓNICAS Cónicas. Estudio particular. 1 x y. 1 x y. a 00 a 01 a 02 a 10 a 11 a 12 a 20 a 21 a 22
 CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
Soluciones de la hoja de diagonalización MATEMÁTICAS I
 Soluciones de la hoja de diagonalización MATEMÁTICAS I 9- - En los siguientes casos estudiar si f es una aplicación lineal y, en caso afirmativo, hallar una matriz A tal que f(x) Ax, así como los subespacios
Soluciones de la hoja de diagonalización MATEMÁTICAS I 9- - En los siguientes casos estudiar si f es una aplicación lineal y, en caso afirmativo, hallar una matriz A tal que f(x) Ax, así como los subespacios
INSTITUCIÓN EDUCATIVA HÉCTOR ABAD GÓMEZ
 INSTITUCIÓN EDUCATIVA HÉCTOR ABAD GÓMEZ CONTENIDOS DEL AREA PERIODO: 01 MATEMATICAS Y ESTADISTICA DOCENTE: ADRIANA ZULAY VILLA URIBE GRADO 10 MATEMATICAS Propósito Conocer y Comprender las razones y funciones
INSTITUCIÓN EDUCATIVA HÉCTOR ABAD GÓMEZ CONTENIDOS DEL AREA PERIODO: 01 MATEMATICAS Y ESTADISTICA DOCENTE: ADRIANA ZULAY VILLA URIBE GRADO 10 MATEMATICAS Propósito Conocer y Comprender las razones y funciones
TÉCNICA SUPERIOR DE INGENIERÍA INFORMÁTICA
 ESCUELA ESTUDIOS DE TÉCNICA SUPERIOR DE INGENIERÍA INFORMÁTICA DEPARTAMENTO DE INGENIERÍA INFORMÁTICA MATEMÁTICA APLICADA I ÁLGERA LINEAL OLETINES DE PROLEMAS Curso 8-9 Sistemas de ecuaciones lineales.
ESCUELA ESTUDIOS DE TÉCNICA SUPERIOR DE INGENIERÍA INFORMÁTICA DEPARTAMENTO DE INGENIERÍA INFORMÁTICA MATEMÁTICA APLICADA I ÁLGERA LINEAL OLETINES DE PROLEMAS Curso 8-9 Sistemas de ecuaciones lineales.
Cónicas y cuádricas. Circunferencia Elipse Parábola Hipérbola
 Grado en Óptica y Optometría Curso 2009-2010 Cónicas y cuádricas. Curvas cónicas Entre las curvas, quizás más importante y con más renombre, figuran las conocidas como curvas cónicas, cuyo nombre proviene
Grado en Óptica y Optometría Curso 2009-2010 Cónicas y cuádricas. Curvas cónicas Entre las curvas, quizás más importante y con más renombre, figuran las conocidas como curvas cónicas, cuyo nombre proviene
Función lineal y cuadrática. Curvas de primer y segundo grado.
 Tema 5 Función lineal y cuadrática. Curvas de primer y segundo grado. 5.0.1 Ecuaciones en dos variables. Una linea del plano es el conjunto de puntos (x, y), cuyas coordenadas satisfacen la ecuación F
Tema 5 Función lineal y cuadrática. Curvas de primer y segundo grado. 5.0.1 Ecuaciones en dos variables. Una linea del plano es el conjunto de puntos (x, y), cuyas coordenadas satisfacen la ecuación F
Vibraciones de moléculas poliatómicas
 Vibraciones oleculares/jesús Hernández T p. 1/14 Vibraciones de oléculas poliatóicas Prof. Jesús Hernández Trujillo Facultad de Quíica, UNAM Vibraciones oleculares/jesús Hernández T p. 2/14 odos (coordenadas)
Vibraciones oleculares/jesús Hernández T p. 1/14 Vibraciones de oléculas poliatóicas Prof. Jesús Hernández Trujillo Facultad de Quíica, UNAM Vibraciones oleculares/jesús Hernández T p. 2/14 odos (coordenadas)
CONJUNTO R n. = (5, 2, 10) de 3, son linealmente. = (2,1,3) y v 3. = (0,1, 1) y u 3. = (2,0,3, 1), u 3. = (1,1, 0,m), v 2
 CONJUNTO R n.- Considerar los vectores u = (, -3, ) y v = (, -, ) de 3 : a) Escribir, si es posible, los vectores (, 7, -4) y (, -5, 4) como combinación lineal de u y v. b) Para qué valores de x es el
CONJUNTO R n.- Considerar los vectores u = (, -3, ) y v = (, -, ) de 3 : a) Escribir, si es posible, los vectores (, 7, -4) y (, -5, 4) como combinación lineal de u y v. b) Para qué valores de x es el
CLASIFICACIÓN AFÍN DE CÓNICAS
 Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS CLASIFICACIÓN AFÍN DE CÓNICAS Sea E un R-espacio vectorial de dimensión. Sean E = e 1, e un plano vectorial de E y e 0 un
Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS CLASIFICACIÓN AFÍN DE CÓNICAS Sea E un R-espacio vectorial de dimensión. Sean E = e 1, e un plano vectorial de E y e 0 un
Hoja de diagonalización MATEMÁTICAS I
 Hoja de diagonalización MATEMÁTICAS I 8-9.- En los siguientes casos estudiar si f es una aplicación lineal y en caso afirmativo hallar una matriz A tal que f(x) Ax así como los subespacios vectoriales
Hoja de diagonalización MATEMÁTICAS I 8-9.- En los siguientes casos estudiar si f es una aplicación lineal y en caso afirmativo hallar una matriz A tal que f(x) Ax así como los subespacios vectoriales
Trabajo Práctico N 5: ESPACIOS VECTORIALES. Ejercicio 1:
 6 Trabajo Práctico N 5: ESPACIOS VECTORIALES Ejercicio : Determine si los siguientes conjuntos con las operaciones definidas en cada caso son o no espacios vectoriales. Para aquellos que no lo sean, indique
6 Trabajo Práctico N 5: ESPACIOS VECTORIALES Ejercicio : Determine si los siguientes conjuntos con las operaciones definidas en cada caso son o no espacios vectoriales. Para aquellos que no lo sean, indique
Una ecuación de segundo grado en dos variables se puede expresar. (x y) y + (D E) x y = x
 Unidad. Transformaciones.4 Eliminación de términos mitos Eliminación de los términos mitos de la ecuación general de do grado en dos variables Una ecuación de segundo grado en dos variables se puede epresar
Unidad. Transformaciones.4 Eliminación de términos mitos Eliminación de los términos mitos de la ecuación general de do grado en dos variables Una ecuación de segundo grado en dos variables se puede epresar
Prácticas de Matemáticas II: Álgebra lineal
 Prácticas de Matemáticas II: Álgebra lineal Jesús Getán y Eva Boj Facultat d Economia i Empresa Universitat de Barcelona Marzo de 2014 Jesús Getán y Eva Boj Prácticas de Matemáticas II: Álgebra lineal
Prácticas de Matemáticas II: Álgebra lineal Jesús Getán y Eva Boj Facultat d Economia i Empresa Universitat de Barcelona Marzo de 2014 Jesús Getán y Eva Boj Prácticas de Matemáticas II: Álgebra lineal
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A xcos(x)+b sen(x) Ejercicio 1.- [2 5 puntos] Sabiendo que lím x 0 x 3 es finito, calcula b y el valor del límite. Ejercicio 2.- Sean f : R R y g : R R las funciones definidas mediante f(x) = x(x
Opción A xcos(x)+b sen(x) Ejercicio 1.- [2 5 puntos] Sabiendo que lím x 0 x 3 es finito, calcula b y el valor del límite. Ejercicio 2.- Sean f : R R y g : R R las funciones definidas mediante f(x) = x(x
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A Ejercicio 1.- [2 5 puntos] Halla las dimensiones del rectángulo de área máxima inscrito en un triángulo isósceles de 6 metros de base (el lado desigual) y 4 metros de alto. Ejercicio 2.- Sean
Opción A Ejercicio 1.- [2 5 puntos] Halla las dimensiones del rectángulo de área máxima inscrito en un triángulo isósceles de 6 metros de base (el lado desigual) y 4 metros de alto. Ejercicio 2.- Sean
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A Ejercicio 1.- Sea f : R R definida por f(x) = x 3 +ax 2 +bx+c. a) [1 75 puntos] Halla a,b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1 2 y que la recta tangente en
Opción A Ejercicio 1.- Sea f : R R definida por f(x) = x 3 +ax 2 +bx+c. a) [1 75 puntos] Halla a,b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1 2 y que la recta tangente en
MATRICES. 1.- Calcular: g) 0 a b a 0 c b c 0. x x x. x + a b c a x + b c a b x + c. a b b b a b b b a
 MATRICES 1.- Calcular: a) 3 2 5 2 1 4 3 1 6 b) 2 1 3 4 2 5 6 0 2 c) 3 1 5 0 5 4 6 3 1 3 2 1 6 7 5 4 d) 7 6 8 5 6 7 10 6 7 8 8 9 8 7 9 6 e) 1 3 2 1 3 5 3 2 3 6 2 2 6 4 5 3 f) 1 1 1 1 1 1 1 g) 1 1 1 1 1
MATRICES 1.- Calcular: a) 3 2 5 2 1 4 3 1 6 b) 2 1 3 4 2 5 6 0 2 c) 3 1 5 0 5 4 6 3 1 3 2 1 6 7 5 4 d) 7 6 8 5 6 7 10 6 7 8 8 9 8 7 9 6 e) 1 3 2 1 3 5 3 2 3 6 2 2 6 4 5 3 f) 1 1 1 1 1 1 1 g) 1 1 1 1 1
Valores y Vectores Propios
 Valores y Vectores Propios Iván Huerta Facultad de Matemáticas Pontificia Universidad Católica de Chile ihuerta@mat.puc.cl Segundo Semestre, 1999 Definición Valores y Vectores Propios Valores y Vectores
Valores y Vectores Propios Iván Huerta Facultad de Matemáticas Pontificia Universidad Católica de Chile ihuerta@mat.puc.cl Segundo Semestre, 1999 Definición Valores y Vectores Propios Valores y Vectores
Tema 2.- Formas Cuadráticas.
 Álgebra. 004 005. Ingenieros Industriales. Departamento de Matemática Aplicada II. Universidad de Sevilla. Tema.- Formas Cuadráticas. Definición y representación matricial. Clasificación de las formas
Álgebra. 004 005. Ingenieros Industriales. Departamento de Matemática Aplicada II. Universidad de Sevilla. Tema.- Formas Cuadráticas. Definición y representación matricial. Clasificación de las formas
Superficie cónica. Cuando una recta g que corta a otra recta e, gira alrededor de ella, genera una superficie cónica
 CÓNICAS Superficie cónica Cuando una recta g que corta a otra recta e, gira alrededor de ella, genera una superficie cónica V Las cónicas como secciones de un cono. Circunferencia Al cortar la superficie
CÓNICAS Superficie cónica Cuando una recta g que corta a otra recta e, gira alrededor de ella, genera una superficie cónica V Las cónicas como secciones de un cono. Circunferencia Al cortar la superficie
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A Ejercicio 1.- Sea f : R R definida por f(x) = x 3 +ax 2 +bx+c. a) [1 75 puntos] Halla a,b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1 2 y que la recta tangente en
Opción A Ejercicio 1.- Sea f : R R definida por f(x) = x 3 +ax 2 +bx+c. a) [1 75 puntos] Halla a,b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1 2 y que la recta tangente en
ÁLGEBRA LINEAL II Práctica
 ÁLGEBRA LINEAL II Práctica 2.1-2.2 Espacios Euclídeos. Ortogonalidad (Curso 2011 2012) 1. Se considera un espacio euclídeo de dimensión 3, y en él una base {ē 1, ē 2, ē 3 } tal que el módulo de ē 1 y el
ÁLGEBRA LINEAL II Práctica 2.1-2.2 Espacios Euclídeos. Ortogonalidad (Curso 2011 2012) 1. Se considera un espacio euclídeo de dimensión 3, y en él una base {ē 1, ē 2, ē 3 } tal que el módulo de ē 1 y el
Álgebra II (61.08, 81.02) Primer cuatrimestre 2017 Práctica 5. Diagonalización de matrices hermíticas. Formas Cuadráticas.
 Álgebra II (61.08, 81.02) Primer cuatrimestre 2017 Práctica 5. Diagonalización de matrices hermíticas. Formas Cuadráticas. Nota: en todos los ejercicios, salvo que se indique lo contrario, (, ) representa
Álgebra II (61.08, 81.02) Primer cuatrimestre 2017 Práctica 5. Diagonalización de matrices hermíticas. Formas Cuadráticas. Nota: en todos los ejercicios, salvo que se indique lo contrario, (, ) representa
Tema 3.1. Espacio eucĺıdeo. Diagonalización ortogonal
 Tema 3.1. Espacio eucĺıdeo. Diagonalización ortogonal Definición 1. Sea V un espacio vectorial sobre un cuerpo K. Llamamos forma bilineal a toda aplicación f : V V K ( x, y) f( x, y) que verifica: 1. f(
Tema 3.1. Espacio eucĺıdeo. Diagonalización ortogonal Definición 1. Sea V un espacio vectorial sobre un cuerpo K. Llamamos forma bilineal a toda aplicación f : V V K ( x, y) f( x, y) que verifica: 1. f(
DIAGONALIZACIÓN DE MATRICES CUADRADAS
 DIAGONALIZACIÓN DE MATRICES CUADRADAS.- Considerar los vectores u = (, -, ) y v = (, -, ) de : a) Escribir, si es posible, los vectores (, 7, -4) y (, -5, 4) como combinación lineal de u y v. b) Para qué
DIAGONALIZACIÓN DE MATRICES CUADRADAS.- Considerar los vectores u = (, -, ) y v = (, -, ) de : a) Escribir, si es posible, los vectores (, 7, -4) y (, -5, 4) como combinación lineal de u y v. b) Para qué
Termodinámica estadística: Repaso de diferenciales
 Termodinámica estadística: Repaso de diferenciales Prof. Jesús Hernández Trujillo 1 Diferenciales 1.1 Diferencial total La diferencial total de z = φ(x, y) se define por dφ = ( ) φ dx + Facultad de Química,
Termodinámica estadística: Repaso de diferenciales Prof. Jesús Hernández Trujillo 1 Diferenciales 1.1 Diferencial total La diferencial total de z = φ(x, y) se define por dφ = ( ) φ dx + Facultad de Química,
ÁLGEBRA LINEAL. EXAMEN EXTRAORDINARIO 2 de julio de 2012 Duración del examen: 3 horas Fecha publicación notas: 11 de julio
 ÁLGEBRA LINEAL EXAMEN EXTRAORDINARIO 2 de julio de 22 Duración del examen: 3 horas Fecha publicación notas: de julio Fecha revisión examen: 3 de julio Apellidos: Nombre: Grupo: Titulación: ESCRIBA EL APELLIDO
ÁLGEBRA LINEAL EXAMEN EXTRAORDINARIO 2 de julio de 22 Duración del examen: 3 horas Fecha publicación notas: de julio Fecha revisión examen: 3 de julio Apellidos: Nombre: Grupo: Titulación: ESCRIBA EL APELLIDO
Matrices. Operaciones con matrices.
 Matrices. Operaciones con matrices. Ejercicio. Dadas las matrices ( ) ( ) 4 A = B = ( ) C = D = 4 5 ( ) 4 E = F = seleccione las que se pueden sumar y súmelas. Ejercicio. Dadas las matrices ( ) ( ) A =
Matrices. Operaciones con matrices. Ejercicio. Dadas las matrices ( ) ( ) 4 A = B = ( ) C = D = 4 5 ( ) 4 E = F = seleccione las que se pueden sumar y súmelas. Ejercicio. Dadas las matrices ( ) ( ) A =
a n1 a n2 a nn x n a ij x i x j = [x] t B A+At ) t = At +(A t ) t = At +A x j x i = s ij x i x j + s ji x j x i 2 x i x j + a ij + a ji
![a n1 a n2 a nn x n a ij x i x j = [x] t B A+At ) t = At +(A t ) t = At +A x j x i = s ij x i x j + s ji x j x i 2 x i x j + a ij + a ji a n1 a n2 a nn x n a ij x i x j = [x] t B A+At ) t = At +(A t ) t = At +A x j x i = s ij x i x j + s ji x j x i 2 x i x j + a ij + a ji](/thumbs/84/89039875.jpg) 16 Fundamentos de Matemáticas : Álgebra Lineal Capítulo 1 Formas cuadráticas Aunque, pueda parecernos que vamos a estudiar un nuevo concepto, un caso particular de las formas cudráticas ya ha sido estudiado,
16 Fundamentos de Matemáticas : Álgebra Lineal Capítulo 1 Formas cuadráticas Aunque, pueda parecernos que vamos a estudiar un nuevo concepto, un caso particular de las formas cudráticas ya ha sido estudiado,
Diagonalización. Índice General. Nelson Möller. 1 Matrices Semejantes 2. 2 Matrices diagonalizables 2
 Diagonalización Nelson Möller Índice General 1 Matrices Semejantes 2 2 Matrices diagonalizables 2 3 Polinomio característico de una matriz 4 3.2 Valores propios.... 5 4 Vectores propios. 6 4.1 Ejemplo...
Diagonalización Nelson Möller Índice General 1 Matrices Semejantes 2 2 Matrices diagonalizables 2 3 Polinomio característico de una matriz 4 3.2 Valores propios.... 5 4 Vectores propios. 6 4.1 Ejemplo...
3.8 Ejercicios propuestos
 3.8 Ejercicios propuestos Ejercicio 3.7 Consideremos la aplicación lineal f : R 3 R 3 definida por f(x, y, z) =(2x + y, z,0) a) Determinar Ker f y hallar una base de dicho subespacio. b) Hallar el rango
3.8 Ejercicios propuestos Ejercicio 3.7 Consideremos la aplicación lineal f : R 3 R 3 definida por f(x, y, z) =(2x + y, z,0) a) Determinar Ker f y hallar una base de dicho subespacio. b) Hallar el rango
Direcciones invariantes
 Direcciones invariantes as transformaciones lineales mandan lineas paralelas en lineas paralelas, así que podemos decir sin ambigüedad que envían cada dirección en el espacio a otra dirección. Si una dirección
Direcciones invariantes as transformaciones lineales mandan lineas paralelas en lineas paralelas, así que podemos decir sin ambigüedad que envían cada dirección en el espacio a otra dirección. Si una dirección
OPERADORES LINEALES EN ESPACIOS CON PRODUCTO INTERNO Adjunto de un operador
 OPERADORES LINEALES EN ESPACIOS CON PRODUCTO INTERNO Adjunto de un operador Sea V un espacio con producto interno y sea T : V V un operador lineal. Un operador T * : V V se dice que es un adjunto de T
OPERADORES LINEALES EN ESPACIOS CON PRODUCTO INTERNO Adjunto de un operador Sea V un espacio con producto interno y sea T : V V un operador lineal. Un operador T * : V V se dice que es un adjunto de T
Respuestas ejercicios edición 2007 Sección 3.3: Transformación de coordenadas Ejercicio 3-1
 Editorial Mc Graw Hill. Edición 007 Respuestas ejercicios edición 007 Sección 3.3: Transformación de coordenadas Ejercicio 3-1 a) Simetría respecto de ambos ejes y respecto del origen. b) Simetría respecto
Editorial Mc Graw Hill. Edición 007 Respuestas ejercicios edición 007 Sección 3.3: Transformación de coordenadas Ejercicio 3-1 a) Simetría respecto de ambos ejes y respecto del origen. b) Simetría respecto
Tema 8 Ecuaciones diferenciales
 Tema 8 Ecuaciones diferenciales 1. ECUACIONES DIFERENCIALES ORDINARIAS Definición 1.1: Ecuación diferencial Se llama ecuación diferencial de orden n a una ecuación que relaciona la variable independiente
Tema 8 Ecuaciones diferenciales 1. ECUACIONES DIFERENCIALES ORDINARIAS Definición 1.1: Ecuación diferencial Se llama ecuación diferencial de orden n a una ecuación que relaciona la variable independiente
Cónicas. Al añadirle a cualquier cónica sus puntos al infinito se obtiene una curva cerrada en el plano proyectivo.
 ónicas Todas las cónicas del plano afn pueden completarse anadiendoles sus puntos al infnito para obtener cónicas en el plano proyectivo. Las elipses ya están completas, pero a cada parábola hay que añadirle
ónicas Todas las cónicas del plano afn pueden completarse anadiendoles sus puntos al infnito para obtener cónicas en el plano proyectivo. Las elipses ya están completas, pero a cada parábola hay que añadirle
Relación 1. Espacios vectoriales
 MATEMÁTICAS PARA LA EMPRESA Curso 2007/08 Relación 1. Espacios vectoriales 1. (a) En IR 2 se consideran las operaciones habituales: (x, y) + (x, y ) = (x + x, y + y ) λ(x, y) = (λx, λy) Demuestra que IR
MATEMÁTICAS PARA LA EMPRESA Curso 2007/08 Relación 1. Espacios vectoriales 1. (a) En IR 2 se consideran las operaciones habituales: (x, y) + (x, y ) = (x + x, y + y ) λ(x, y) = (λx, λy) Demuestra que IR
ALGEBRA LINEAL - Práctica N 8 - Segundo cuatrimestre de 2017 Espacios vectoriales con producto interno
 Departamento de Matemática - Facultad de Ciencias Exactas y Naturales - UBA ALGEBRA LINEAL - Práctica N 8 - Segundo cuatrimestre de 07 Espacios vectoriales con producto interno En esta práctica, todos
Departamento de Matemática - Facultad de Ciencias Exactas y Naturales - UBA ALGEBRA LINEAL - Práctica N 8 - Segundo cuatrimestre de 07 Espacios vectoriales con producto interno En esta práctica, todos
RESUMEN DEL TEMA 7 VALORES Y VECTORES PROPIOS
 RESUMEN DEL TEMA 7 VALORES Y VECTORES PROPIOS 1. Determinantes El determinante de una matriz cuadrada n n A = a 21 a 22 a 2n a n1 a n2 a nn es un número real, y se representa por: A = a 21 a 22 a 2n a
RESUMEN DEL TEMA 7 VALORES Y VECTORES PROPIOS 1. Determinantes El determinante de una matriz cuadrada n n A = a 21 a 22 a 2n a n1 a n2 a nn es un número real, y se representa por: A = a 21 a 22 a 2n a
x +3y 2t = 1 2x +y +z +t = 2 3x y +z t = 7 2x +6y +z +t = a (a) Realizamos transformaciones elementales sobre la matriz ampliada del sistema
 UCM Matemáticas II Examen Final, 8/05/014 Soluciones 1 Dado el parámetro a R, se considera el sistema lineal x +y t = 1 x +y +z +t = x y +z t = 7 x +6y +z +t = a (a (6 puntos Discutir el sistema según
UCM Matemáticas II Examen Final, 8/05/014 Soluciones 1 Dado el parámetro a R, se considera el sistema lineal x +y t = 1 x +y +z +t = x y +z t = 7 x +6y +z +t = a (a (6 puntos Discutir el sistema según
a n1 a n2 a nn Es decir, una forma cuadrática es un polinomio homogéneo de grado 2 y n variables.
 Capítulo 7 Formas cuadráticas. Aunque, pueda parecernos que vamos a estudiar un nuevo concepto, un caso particular de las formas cudráticas ya ha sido estudiado, pues el cuadrado de la norma de un vector
Capítulo 7 Formas cuadráticas. Aunque, pueda parecernos que vamos a estudiar un nuevo concepto, un caso particular de las formas cudráticas ya ha sido estudiado, pues el cuadrado de la norma de un vector
Clase 8 Nociones Básicas de Convexidad
 Pontificia Universidad Católica Escuela de Ingeniería Departamento de Ingeniería Industrial y de Sistemas Clase 8 Nociones Básicas de Convexidad ICS 1102 Optimización Profesor : Claudio Seebach Apuntes
Pontificia Universidad Católica Escuela de Ingeniería Departamento de Ingeniería Industrial y de Sistemas Clase 8 Nociones Básicas de Convexidad ICS 1102 Optimización Profesor : Claudio Seebach Apuntes
a ij x i x j = [x] t B A+At ) t = At +(A t ) t = At +A x i x j + a ij + a ji x j x i = s ij x i x j + s ji x j x i 2
![a ij x i x j = [x] t B A+At ) t = At +(A t ) t = At +A x i x j + a ij + a ji x j x i = s ij x i x j + s ji x j x i 2 a ij x i x j = [x] t B A+At ) t = At +(A t ) t = At +A x i x j + a ij + a ji x j x i = s ij x i x j + s ji x j x i 2](/thumbs/65/53464617.jpg) 68 Matemáticas I : Álgebra Lineal Tema 7 Formas cuadráticas Aunque, pueda parecernos que vamos a estudiar un nuevo concepto, un caso particular de las formas cudráticas ya ha sido estudiado, pues el cuadrado
68 Matemáticas I : Álgebra Lineal Tema 7 Formas cuadráticas Aunque, pueda parecernos que vamos a estudiar un nuevo concepto, un caso particular de las formas cudráticas ya ha sido estudiado, pues el cuadrado
Trabajo Práctico N 5: ESPACIOS VECTORIALES
 Trabajo Práctico N 5: ESPACIOS VECTORIALES Ejercicio 1: Determine si los siguientes conjuntos con las operaciones definidas en cada caso son o no espacios vectoriales. Para aquellos que no lo sean, indique
Trabajo Práctico N 5: ESPACIOS VECTORIALES Ejercicio 1: Determine si los siguientes conjuntos con las operaciones definidas en cada caso son o no espacios vectoriales. Para aquellos que no lo sean, indique
Cálculo II: Integrales de línea: Independencia de la trayectoria, diferenciales
 Cálculo II: Integrales de línea: Independencia de la trayectoria, diferenciales Prof Jesús Hernández Trujillo Facultad de Química, UNAM 1. Independencia de la trayectoria Considérese la integral de línea
Cálculo II: Integrales de línea: Independencia de la trayectoria, diferenciales Prof Jesús Hernández Trujillo Facultad de Química, UNAM 1. Independencia de la trayectoria Considérese la integral de línea
Diferenciación de funciones f : R n R m. f(x, y) = ( e xy, x 2 + y, 2x 3 y 2) r(h) (h 1, h 2 ) e. 2(1 + h 1 ) 3 (3 + h 2 ) h 1 12h 2
 Funciones de R n en R m Diferenciación de funciones f : R n R m Definición. Considere la función f : A R n R m definida en un conjunto abierto A de R n y sea x 0 A. Se dice que esta función es diferenciable
Funciones de R n en R m Diferenciación de funciones f : R n R m Definición. Considere la función f : A R n R m definida en un conjunto abierto A de R n y sea x 0 A. Se dice que esta función es diferenciable
Extremos Locales. Un punto x 0 es un punto crítico de f si Df(x 0 ) = 0. Un punto crítico que no es un extremo local se llama punto silla.
 Extremos Locales Entre las caracteristicas geometricas básicas de la gráficas de una función estan sus puntos extremos, en los cuales la función alcanza sus valores mayor y menor. Definicón.- Si f : u
Extremos Locales Entre las caracteristicas geometricas básicas de la gráficas de una función estan sus puntos extremos, en los cuales la función alcanza sus valores mayor y menor. Definicón.- Si f : u
Cónicas. Clasificación.
 Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
La ecuación general de segundo grado
 La ecuación general de segundo grado Las cónicas cuyos ejes son paralelos a los ejes coordenados tienen ecuaciones de la forma Ax 2 +By 2 +Cx+Dy=E, y de esta ecuación es fácil deducir su forma. Pero cuando
La ecuación general de segundo grado Las cónicas cuyos ejes son paralelos a los ejes coordenados tienen ecuaciones de la forma Ax 2 +By 2 +Cx+Dy=E, y de esta ecuación es fácil deducir su forma. Pero cuando
MATEMÁTICAS I Examen Extraordinario Diciembre 17-I-2011 CUESTIONES TIPO TEST
 MATEMÁTICAS I Examen Extraordinario Diciembre 17-I-011 NOTA: CUESTIONES TIPO TEST SOLO HAY UNA RESPUESTA CORRECTA EN CADA CUESTION RESPUESTA CORRECTA: + 0. PUNTOS RESPUESTA INCORRECTA: - 0.1 PUNTOS RESPUESTA
MATEMÁTICAS I Examen Extraordinario Diciembre 17-I-011 NOTA: CUESTIONES TIPO TEST SOLO HAY UNA RESPUESTA CORRECTA EN CADA CUESTION RESPUESTA CORRECTA: + 0. PUNTOS RESPUESTA INCORRECTA: - 0.1 PUNTOS RESPUESTA
CONVEXIDAD DE CONJUNTOS.-
 CONVEXIDAD DE CONJUNTOS.- Conjunto convexo Conjunto no convexo No lo es ya que se trata de la circunferencia de centro (0,0) y radio 1. Dos puntos de ella, por ejemplo, son los de coordenadas (1, 0) y
CONVEXIDAD DE CONJUNTOS.- Conjunto convexo Conjunto no convexo No lo es ya que se trata de la circunferencia de centro (0,0) y radio 1. Dos puntos de ella, por ejemplo, son los de coordenadas (1, 0) y
TEOREMA DE TAYLOR y EXTREMOS SIN RESTRICCIONES
 TEOREMA DE TAYLOR y EXTREMOS SIN RESTRICCIONES Para una función de una variable puede construirse una mejor aproximación mediante una función cuadrática que mediante una función lineal, para las funciones
TEOREMA DE TAYLOR y EXTREMOS SIN RESTRICCIONES Para una función de una variable puede construirse una mejor aproximación mediante una función cuadrática que mediante una función lineal, para las funciones
Empezaremos por el Álgebra lineal porque:
 Empezaremos por el Álgebra lineal porque: Las soluciones de una ecuación diferencial, como la ecuación de Schroedinger, son base de algún espacio vectorial. Las operaciones de simetría son transformaciones
Empezaremos por el Álgebra lineal porque: Las soluciones de una ecuación diferencial, como la ecuación de Schroedinger, son base de algún espacio vectorial. Las operaciones de simetría son transformaciones
CÓNICAS. 1. Dada la cónica x 2 + 2xy y 2 2x 2y + 4 = 0, se pide su clasicación y los elementos característicos de la misma. = 1
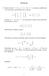 CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
Figura 1: Pendiente de una recta no vertical a partir de dos puntos cualesquiera sobre la recta.
 Rectas en el Plano Pendiente de una recta La pendiente de una recta no vertical es la razón de cambio vertical con respecto a la cantidad de cambio horizontal entre dos puntos. Para los puntos (x 1, y
Rectas en el Plano Pendiente de una recta La pendiente de una recta no vertical es la razón de cambio vertical con respecto a la cantidad de cambio horizontal entre dos puntos. Para los puntos (x 1, y
PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A Ejercicio 1.- Sea f : (0,+ ) R la función definida por f(x) = 3x + 1 x. (a) [1 5 puntos] Determina los intervalos de crecimiento y de decrecimiento y los extremos relativos de f (puntos donde
Opción A Ejercicio 1.- Sea f : (0,+ ) R la función definida por f(x) = 3x + 1 x. (a) [1 5 puntos] Determina los intervalos de crecimiento y de decrecimiento y los extremos relativos de f (puntos donde
Métodos Estadísticos Multivariados
 Métodos Estadísticos Multivariados Victor Muñiz ITESM Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre 2011 1 / 34 Álgebra matricial y vectores aleatorios Una matriz es un arreglo
Métodos Estadísticos Multivariados Victor Muñiz ITESM Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre 2011 1 / 34 Álgebra matricial y vectores aleatorios Una matriz es un arreglo
MATEMÁTICAS I 13 de junio de 2007
 MATEMÁTICAS I 13 de junio de 2007 2º EXAMEN PARCIAL Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0.2 puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- Si
MATEMÁTICAS I 13 de junio de 2007 2º EXAMEN PARCIAL Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0.2 puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- Si
CAPÍTULO 4 OPERADORES LINEALES EN ESPACIOS CON PRODUCTO INTERNO
 CAPÍULO 4 OPERADORES LINEALES EN ESPACIOS CON PRODUCO INERNO Adjunto de un operador En un espacio vectorial V con producto interno, cada operador lineal tiene un operador llamado su adjunto que también
CAPÍULO 4 OPERADORES LINEALES EN ESPACIOS CON PRODUCO INERNO Adjunto de un operador En un espacio vectorial V con producto interno, cada operador lineal tiene un operador llamado su adjunto que también
Simetría en química. Laura Gasque
 Simetría en química Laura Gasque 2016-1 2 Laura Gasque 2016-1 3 Bibliografía básica Primeras tres o cuatro clases: Unidad I y II del curso de Cálculo II Cotton F.A. Chemical Applications of Group Theory
Simetría en química Laura Gasque 2016-1 2 Laura Gasque 2016-1 3 Bibliografía básica Primeras tres o cuatro clases: Unidad I y II del curso de Cálculo II Cotton F.A. Chemical Applications of Group Theory
10. Aplicaciones del cálculo diferencial.
 10 Aplicaciones del cálculo diferencial 101 Teorema de la función implícita Habitualmente, estamos acostumbrados a trabajar con funciones denidas de forma explícita, es decir, tales que la variable dependiente
10 Aplicaciones del cálculo diferencial 101 Teorema de la función implícita Habitualmente, estamos acostumbrados a trabajar con funciones denidas de forma explícita, es decir, tales que la variable dependiente
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A Ejercicio 1.- Sea la función f: (0,+ ) R definida por f(x) = ln(x), donde ln denota logaritmo x neperiano. a) [1 punto] Estudia y determina las asíntotas de la gráfica de f. b) [1 5 puntos] Halla
Opción A Ejercicio 1.- Sea la función f: (0,+ ) R definida por f(x) = ln(x), donde ln denota logaritmo x neperiano. a) [1 punto] Estudia y determina las asíntotas de la gráfica de f. b) [1 5 puntos] Halla
Escuela Universitaria Politécnica Examen de Cálculo - Febrero - Curso 01/02
 Escuela Universitaria Politécnica Examen de Cálculo - Febrero - Curso 0/02 x 2 + y 4. (a) Comprueba que el siguiente límite no existe lim (x,y) (0,0) x 2 + y. 2 (b) Busca una trayectoria a través de la
Escuela Universitaria Politécnica Examen de Cálculo - Febrero - Curso 0/02 x 2 + y 4. (a) Comprueba que el siguiente límite no existe lim (x,y) (0,0) x 2 + y. 2 (b) Busca una trayectoria a través de la
ALGEBRA. Escuela Politécnica Superior de Málaga
 ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) x u + f
 1 228 Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) z u = f x x u + f y y u z v = f x x v + f y y v z w = f x
1 228 Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) z u = f x x u + f y y u z v = f x x v + f y y v z w = f x
3º B.D. opción Social-Económico Matemática III. Parábola.
 Parábola. Definición: Lugar geométrico de los puntos del plano que equidistan de un punto fijo F, llamado foco y de una recta fija z llamada directriz. Siendo F no perteneciente a z. Entonces siendo P
Parábola. Definición: Lugar geométrico de los puntos del plano que equidistan de un punto fijo F, llamado foco y de una recta fija z llamada directriz. Siendo F no perteneciente a z. Entonces siendo P
Tema 3.3. Aplicaciones afines. Cónicas y cuádricas
 Tema 3.3. Aplicaciones afines. Cónicas y cuádricas Definición 1. Sean A = (P, V, f) y A = (P, V, f ) dos espacios afines tales que V y V son espacios vectoriales sobre un mismo cuerpo. Una función θ :
Tema 3.3. Aplicaciones afines. Cónicas y cuádricas Definición 1. Sean A = (P, V, f) y A = (P, V, f ) dos espacios afines tales que V y V son espacios vectoriales sobre un mismo cuerpo. Una función θ :
ALGEBRA. Escuela Politécnica Superior de Málaga
 ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
FINAL DE ÁLGEBRA Y GEOMETRÍA ANALÍTICA 30 mayo 2006 Tema 1
 FINAL DE ÁLGEBRA Y GEOMETRÍA ANALÍTICA 0 mayo 006 Tema Apellido y nombres:... 4 5 Calificación final ) Dadas las rectas : x y + z = r : r : ( x, y, z) = (,,) + λ(, ) x z + k = 0 k para que las rectas sean
FINAL DE ÁLGEBRA Y GEOMETRÍA ANALÍTICA 0 mayo 006 Tema Apellido y nombres:... 4 5 Calificación final ) Dadas las rectas : x y + z = r : r : ( x, y, z) = (,,) + λ(, ) x z + k = 0 k para que las rectas sean
Trabajo Práctico N 5: ESPACIOS VECTORIALES
 Trabajo Práctico N 5: ESPACIOS VECTORIALES Ejercicio 1: Determine si los siguientes conjuntos con las operaciones definidas en cada caso son o no espacios vectoriales. Para aquellos que no lo sean, indique
Trabajo Práctico N 5: ESPACIOS VECTORIALES Ejercicio 1: Determine si los siguientes conjuntos con las operaciones definidas en cada caso son o no espacios vectoriales. Para aquellos que no lo sean, indique
MATEMÁTICAS I 2º EXAMEN PARCIAL 12 junio de 2009
 Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0.2 puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- Un sistema generador G de R 3 : a) Está constituido por
Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0.2 puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- Un sistema generador G de R 3 : a) Está constituido por
Docente Matemáticas. Marzo 11 de 2013
 Geometría Analítica Ana María Beltrán Docente Matemáticas Marzo 11 de 2013 1 Geometría Analítica Definición 1. Un lugar geométrico es el conjunto de todos los puntos del plano que tienen una característica
Geometría Analítica Ana María Beltrán Docente Matemáticas Marzo 11 de 2013 1 Geometría Analítica Definición 1. Un lugar geométrico es el conjunto de todos los puntos del plano que tienen una característica
1. Clasifica las siguientes cónicas dando su ecuación reducida, centro o vértice y ejes (si es posible): (1.d) x 2 + y 2 + 2x + 1 = 0
 Clasificación de cónicas.. Clasifica las siguientes cónicas dando su ecuación reducida, centro o vértice y ejes si es posible:.a x xy + y + x y + 0.b x + xy y 6x + y 0.c x + xy + y x y 0.d x + y + x +
Clasificación de cónicas.. Clasifica las siguientes cónicas dando su ecuación reducida, centro o vértice y ejes si es posible:.a x xy + y + x y + 0.b x + xy y 6x + y 0.c x + xy + y x y 0.d x + y + x +
Curso MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2011-2012 MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN El alumno
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2011-2012 MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN El alumno
p x
 UNIVERSIDD NCIONL UÓNOM DE MÉXICO FCULD DE INGENIERÍ DIVISIÓN DE CIENCIS BÁSICS ÁLGEBR LINEL SERIE RNSFORMCIONES LINELES 1. Sean el espacio vectorial real P ax bx c a, b, c correspondencia es a) Si D es
UNIVERSIDD NCIONL UÓNOM DE MÉXICO FCULD DE INGENIERÍ DIVISIÓN DE CIENCIS BÁSICS ÁLGEBR LINEL SERIE RNSFORMCIONES LINELES 1. Sean el espacio vectorial real P ax bx c a, b, c correspondencia es a) Si D es
si existe un entorno V de a contenido en A, tal que la diferencia f(x) f(a) no cambia de signo cuando x V :
 Capítulo 12 Extremos Relativos Una aplicación clásica del Teorema Local de Taylor, que vimos en el capítulo anterior, es el estudio de los extremos relativos de una función escalar. Aunque la analogía
Capítulo 12 Extremos Relativos Una aplicación clásica del Teorema Local de Taylor, que vimos en el capítulo anterior, es el estudio de los extremos relativos de una función escalar. Aunque la analogía
Primer Examen, Invierno 2017.
 Primer Examen, Invierno 2017. Problema 1. Encuentre la ecuación del plano que pasa por 3 puntos cuyas coordenadas son A = (3, 1,2), B = (2,4,3), C = (4,7,1). (1 punto) Problema 2. Encuentre el valor de
Primer Examen, Invierno 2017. Problema 1. Encuentre la ecuación del plano que pasa por 3 puntos cuyas coordenadas son A = (3, 1,2), B = (2,4,3), C = (4,7,1). (1 punto) Problema 2. Encuentre el valor de
Algebra Matricial.
 Algebra Matricial Dr. Alfonso Alba Cadena fac@galia.fc.uaslp.mx Facultad de Ciencias UASLP Unidad I Fundamentos de matrices 1 Introducción Una matriz es un arreglo rectangular de números. Algunos ejemplos
Algebra Matricial Dr. Alfonso Alba Cadena fac@galia.fc.uaslp.mx Facultad de Ciencias UASLP Unidad I Fundamentos de matrices 1 Introducción Una matriz es un arreglo rectangular de números. Algunos ejemplos
Matemáticas para la Empresa
 Matemáticas para la Empresa 1 o D.C.E. 1 o L.A.D.E. Curso 2008/09 Relación 2. Aplicaciones Lineales. Diagonalización. Formas Cuadráticas 1. Estudia si son lineales las aplicaciones siguientes: a) La aplicación
Matemáticas para la Empresa 1 o D.C.E. 1 o L.A.D.E. Curso 2008/09 Relación 2. Aplicaciones Lineales. Diagonalización. Formas Cuadráticas 1. Estudia si son lineales las aplicaciones siguientes: a) La aplicación
Introducción a la geometría analítica
 Introducción a la geometría analítica Prof. Yoel Gutiérrez 1 Sistema de coordenadas rectangulares 1.1 sistema coordenado rectangular El sistema coordenado rectangular, indicado en la figura 1, consta de
Introducción a la geometría analítica Prof. Yoel Gutiérrez 1 Sistema de coordenadas rectangulares 1.1 sistema coordenado rectangular El sistema coordenado rectangular, indicado en la figura 1, consta de
