Métodos Estadísticos Multivariados
|
|
|
- Ramón Tebar Campos
- hace 5 años
- Vistas:
Transcripción
1 Métodos Estadísticos Multivariados Victor Muñiz ITESM Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
2 Álgebra matricial y vectores aleatorios Una matriz es un arreglo de números en n renglones y d columnas: x 11 x 12 x 1d x 21 x 22 x 2d X = (x ij ) = x n1 x n2 x nd (n d) Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
3 Álgebra matricial y vectores aleatorios Una matriz es un arreglo de números en n renglones y d columnas: x 11 x 12 x 1d x 21 x 22 x 2d X = (x ij ) = x n1 x n2 x nd Un vector es una matriz con 1 columna: x 1 x 2 x =. x n (n d) Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
4 Álgebra matricial Operaciones y propiedades básicas Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
5 Operaciones y propiedades básicas Operaciones básicas: Transpuesta A T = (a ji ) Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
6 Operaciones y propiedades básicas Operaciones básicas: Transpuesta A T = (a ji ) Suma A (n d) + B (n d) = (a ij ) + (b ij ) = C (n d) Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
7 Operaciones y propiedades básicas Operaciones básicas: Transpuesta A T = (a ji ) Suma A (n d) + B (n d) = (a ij ) + (b ij ) = C (n d) Multiplicación por un escalar ca = (c a ij ) Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
8 Operaciones y propiedades básicas Operaciones básicas: Multiplicación ( d ) A (n d) B (d m) = C (n m) = a ik b kj, k=1 es decir, multiplicar cada renglón de A por cada columna de B. Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
9 Operaciones y propiedades básicas Operaciones básicas: Multiplicación ( d ) A (n d) B (d m) = C (n m) = a ik b kj, es decir, multiplicar cada renglón de A por cada columna de B. Observa que, si las columnas de A no son iguales a los renglones de B, la operación no estará definida. Observa también que, en general, la multiplicación es no conmutativa: AB BA k=1 Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
10 Operaciones y propiedades básicas Algunas propiedades (suponiendo que están definidas las operaciones): Conmutatividad de la suma A + B = B + A Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
11 Operaciones y propiedades básicas Algunas propiedades (suponiendo que están definidas las operaciones): Conmutatividad de la suma A + B = B + A Distributividad respecto a la suma A(B + C) = AB + AC, sin embargo, en general A(B + C) BA + CA Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
12 Operaciones y propiedades básicas Algunas propiedades (suponiendo que están definidas las operaciones): Conmutatividad de la suma A + B = B + A Distributividad respecto a la suma A(B + C) = AB + AC, sin embargo, en general A(B + C) BA + CA Asociatividad A(BC) = (AB)C Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
13 Operaciones y propiedades básicas Algunas propiedades (suponiendo que están definidas las operaciones): Conmutatividad de la suma A + B = B + A Distributividad respecto a la suma A(B + C) = AB + AC, sin embargo, en general A(B + C) BA + CA Asociatividad A(BC) = (AB)C Transpuestas (A T ) T = A, (AB) T = B T A T, (A + B) T = A T + B T Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
14 Álgebra matricial Algunos tipos básicos de matrices Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
15 Tipos básicos de matrices Matriz cuadrada: A (d d) Nota que, el producto A 2 = AA (en general A k ) está definido solo para este tipo de matrices. Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
16 Tipos básicos de matrices Matriz cuadrada: A (d d) Nota que, el producto A 2 = AA (en general A k ) está definido solo para este tipo de matrices. Matriz simétrica: A = A T Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
17 Tipos básicos de matrices Matriz cuadrada: A (d d) Nota que, el producto A 2 = AA (en general A k ) está definido solo para este tipo de matrices. Matriz simétrica: A = A T Matriz diagonal: diag(d 1,..., d n ) = d d d n (n n) Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
18 Tipos básicos de matrices Algunos tipos especiales de matrices: Vector y matriz de unos: n =., 1 m1 T n = (m n) Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
19 Tipos básicos de matrices Algunos tipos especiales de matrices: Vector y matriz de unos: n =., 1 m1 T n = (m n) Matriz identidad: I = diag(1 n ) = (n n) Observa que para cualquier matriz A de tamaño adecuado, IA = AI = A. Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
20 Álgebra matricial Características básicas Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
21 Características básicas Independencia lineal: Un conjunto de k renglones (o columnas) de A son linealmente independientes si k j=1 c ja j = 0 implica que existen constantes c j = 0 j, c j R, es decir, ningun renglón (o columna) de este conjunto puede expresarse como una combinación lineal de los (k 1) renglones restantes. Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
22 Características básicas Independencia lineal: Un conjunto de k renglones (o columnas) de A son linealmente independientes si k j=1 c ja j = 0 implica que existen constantes c j = 0 j, c j R, es decir, ningun renglón (o columna) de este conjunto puede expresarse como una combinación lineal de los (k 1) renglones restantes. Ejemplo Considera la matriz X = Los vectores columna x 1 y x 4 son linealmente dependientes, así como x 1, x 2 y x 3, pero x 1 y x 2 son linealmente independientes.. Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
23 Características básicas Rango: el rango de una matriz A n d es el máximo número de columnas (renglones) linealmente independientes. Si rango(a n d ) = mín(n, d), se dice que A es de rango completo. Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
24 Características básicas Rango: el rango de una matriz A n d es el máximo número de columnas (renglones) linealmente independientes. Si rango(a n d ) = mín(n, d), se dice que A es de rango completo. Determinante: Consideremos una matriz cuadrada A n n. Su determinante está dado por { A = a 11 si k = 1 d j=1 a ij A ij ( 1) i+j si k > 1, donde A ij es la matriz A (d 1) (d 1) obtenida al eliminar el renglón i y la columna j. Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
25 Características básicas Rango: el rango de una matriz A n d es el máximo número de columnas (renglones) linealmente independientes. Si rango(a n d ) = mín(n, d), se dice que A es de rango completo. Determinante: Consideremos una matriz cuadrada A n n. Su determinante está dado por { A = a 11 si k = 1 d j=1 a ij A ij ( 1) i+j si k > 1, donde A ij es la matriz A (d 1) (d 1) obtenida al eliminar el renglón i y la columna j. Ejemplo (Determinante) Considera las matrices A (2 2) y B (3 3) para obtener A y B. Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
26 Características básicas Matriz singular y no singular: Considera una matriz cuadrada A de tamaño n. A es no singular si Rango(A) = n, lo que implica que Ax = 0 solo si x = 0, es decir, sus columnas (renglones) son linealmente independientes. En caso contrario, se dice que A es singular. Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
27 Características básicas Matriz singular y no singular: Considera una matriz cuadrada A de tamaño n. A es no singular si Rango(A) = n, lo que implica que Ax = 0 solo si x = 0, es decir, sus columnas (renglones) son linealmente independientes. En caso contrario, se dice que A es singular. Inversa: Si A es cuadrada y no singular, su inversa A 1 es una matriz tal que AA 1 = A 1 A = I Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
28 Características básicas También, la inversa está relacionada con el determinante mediante donde C es la adjunta de A. A 1 = C A, Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
29 Características básicas También, la inversa está relacionada con el determinante mediante donde C es la adjunta de A. A 1 = C A, Si A es una matriz cuadrada, de tamaño n, lo siguiente es equivalente: 1 A es singular, es decir Ax = 0 implica que x = 0 2 A 0 3 Existe su inversa, tal que AA 1 = A 1 A = I Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
30 Características básicas Algunos resultados útiles. Sean A y B matrices cuadradas de tamaño n y no singulares. 1 (A 1 ) T = (A T ) 1 2 (AB) 1 = B 1 A 1 3 Si una columna o renglón de A es cero, A = 0. 4 Si A tiene renglones o columnas ideénticos, A = 0. 5 Si A = diag(a 1,..., a n ), con los elementos de la diagonal diferentes de cero, entonces A 1 = diag(a1 1,..., a 1 n ). Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
31 Características básicas Algunos resultados útiles. Sean A y B matrices cuadradas de tamaño n y no singulares. 1 (A 1 ) T = (A T ) 1 2 (AB) 1 = B 1 A 1 3 Si una columna o renglón de A es cero, A = 0. 4 Si A tiene renglones o columnas ideénticos, A = 0. 5 Si A = diag(a 1,..., a n ), con los elementos de la diagonal diferentes de cero, entonces A 1 = diag(a1 1,..., a 1 n ). Traza: Para una matriz A cuadrada de tamaño n, su traza es la suma de la diagonal n tr(a) = i=1 a ii Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
32 Características básicas Un método para invertir una matriz: Eliminación de Gauss-Jordan. Consideremos las matrices elementales cuadradas E 1, E 2,... E k, obtenidas al aplicar solo una operación elemental de renglón a I, por ejemplo: E 1 = E 2 = ( ( c ), intercambia renglón 1 y 2 ), multiplica renglón 1 por c Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
33 Características básicas Eliminación de Gauss-Jordan. Teorema Sea A una matriz cuadrada e invertible. Supongamos que una secuencia de operaciones elementales de renglón reduce A a la matriz identidad. Entonces, A 1 se obtiene aplicando la misma secuencia de operaciones a la matriz identidad. Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
34 Características básicas Eliminación de Gauss-Jordan. Teorema Sea A una matriz cuadrada e invertible. Supongamos que una secuencia de operaciones elementales de renglón reduce A a la matriz identidad. Entonces, A 1 se obtiene aplicando la misma secuencia de operaciones a la matriz identidad. Ejemplo Obtener la inversa de A = ( ) Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
35 Características básicas Valores y vectores propios Definición (Eigenvalores) Sea A una matriz cuadrada de tamaño n. Los escalares λ 1, λ 2,..., λ n que satisfacen A λi = 0 (1) son llamados eigenvalores o valores propios de A Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
36 Características básicas Valores y vectores propios Definición (Eigenvalores) Sea A una matriz cuadrada de tamaño n. Los escalares λ 1, λ 2,..., λ n que satisfacen A λi = 0 (1) son llamados eigenvalores o valores propios de A La ecuación (1) es llamada ecuación característica. Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
37 Características básicas Valores y vectores propios Definición (Eigenvalores) Sea A una matriz cuadrada de tamaño n. Los escalares λ 1, λ 2,..., λ n que satisfacen A λi = 0 (1) son llamados eigenvalores o valores propios de A La ecuación (1) es llamada ecuación característica. El lado izquierdo de (1) es un polinomio de grado n en λ, y puede mostrarse que tiene exáctamente n raíces, no necesariamente diferentes y pueden ser reales o complejas. Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
38 Características básicas Valores y vectores propios Definición (Eigenvectores) Sea A una matriz cuadrada de tamaño n con eigenvalores λ 1, λ 2,..., λ n. Si x i 0 tal que Ax i = λ i x i = 0, (2) entonces x i es un eigenvector (o vector propio) de A asociado al eigenvalor λ i. Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
39 Características básicas Valores y vectores propios Definición (Eigenvectores) Sea A una matriz cuadrada de tamaño n con eigenvalores λ 1, λ 2,..., λ n. Si x i 0 tal que Ax i = λ i x i = 0, (2) entonces x i es un eigenvector (o vector propio) de A asociado al eigenvalor λ i. Si x i es un eigenvector de A, también lo es kx i, es decir, los eigenvectores son invariantes bajo la multiplicación por un escalar. Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
40 Características básicas Valores y vectores propios Definición (Eigenvectores) Sea A una matriz cuadrada de tamaño n con eigenvalores λ 1, λ 2,..., λ n. Si x i 0 tal que Ax i = λ i x i = 0, (2) entonces x i es un eigenvector (o vector propio) de A asociado al eigenvalor λ i. Si x i es un eigenvector de A, también lo es kx i, es decir, los eigenvectores son invariantes bajo la multiplicación por un escalar. Ejemplo (En clase...) Obtener los valores y vectores propios de ( 1 0 A = 1 3 ). Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
41 Características básicas Ortogonalidad de vectores y matrices Dos vectores a y b de tamaño n son ortogonales si a T b = a, b = a 1 b 1 + a 2 b a n b n = 0. Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
42 Características básicas Ortogonalidad de vectores y matrices Dos vectores a y b de tamaño n son ortogonales si a T b = a, b = a 1 b 1 + a 2 b a n b n = 0. Un vector a está normalizado si a T a = 1, lo cual se logra haciendo a (a T a) 1/2 Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
43 Características básicas Ortogonalidad de vectores y matrices Dos vectores a y b de tamaño n son ortogonales si a T b = a, b = a 1 b 1 + a 2 b a n b n = 0. Un vector a está normalizado si a T a = 1, lo cual se logra haciendo a (a T a) 1/2 Dos vectores a y b de tamaño n son ortonormales si son ortogonales y están normalizados, es decir a T a = b T b = 1 y a T b = 0 Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
44 Características básicas Definición (Matriz ortogonal) Una matriz cuadrada A de tamaño n es ortogonal si sus columnas son normalizadas y mutuamente ortogonales, de forma tal que AA T = A T A = I Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
45 Características básicas Definición (Matriz ortogonal) Una matriz cuadrada A de tamaño n es ortogonal si sus columnas son normalizadas y mutuamente ortogonales, de forma tal que AA T = A T A = I Observa que, lo anterior es cierto para matrices cuadradas, es decir, si sus columnas son ortogonales, también sus renglones, pero en general B T B = I c pero BB T I r Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
46 Características básicas Algunos aspectos geométricos. Norma o longitud: a = ( ) 1/2 a T a Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
47 Características básicas Algunos aspectos geométricos. Norma o longitud: a = ( ) 1/2 a T a Distancia entre 2 vectores: a b = ( ) 1/2 (a b) T (a b) Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
48 Características básicas Algunos aspectos geométricos. Norma o longitud: a = ( ) 1/2 a T a Distancia entre 2 vectores: a b = ( ) 1/2 (a b) T (a b) Ángulo entre 2 vectores: cos θ = at b a b Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
49 Características básicas Ejemplo en R 2 Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
50 Características básicas Ejemplo en R 2. 2 vectores ortogonales Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
51 Características básicas Ejemplo en R 2. 2 vectores ortogonales Una matriz real, cuadrada, de tamaño n define una base para el espacio vectorial R n. Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
52 Álgebra matricial Descomposición espectral y formas cuadráticas Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
53 Descomposiciones espectrales y formas cuadráticas Teorema (Descomposición de Jordan) Cualquier matriz simétrica A de tamaño n puede escribirse como A = VΛV T = n λ i v i vi T, i=1 donde Λ es una matriz diagonal que contiene los eigenvalores de A y V es una matriz ortogonal cuyas columnas son los eigenvectores correspondientes. Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
54 Descomposiciones espectrales y formas cuadráticas Definición (Forma cuadrática) Una forma cuadrática en el vector x de tamaño d es una función de la forma x T Ax = a ij x i x j = a ii xi 2 + a ij x i x j, i j i=1 i j para i, j = 1,..., d, y donde A es una matriz simétrica. Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
55 Descomposiciones espectrales y formas cuadráticas Un resultado importante Resultado Para cualquier matriz simétrica A, existe una transformación ortogonal y = V T x tal que x T Ax = i λ i y 2 i Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
56 Descomposiciones espectrales y formas cuadráticas Definición (Positividad) Una matriz simétrica A de tamaño n es positiva definida si y es positiva semidefinida si x T Ax > 0 para x 0 x T Ax 0 para x 0 Usualmente también se escribe A > 0 y A 0 para una matriz positiva definida y positiva semidefinida, respectívamente. Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
57 Descomposiciones espectrales y formas cuadráticas Resultado Si A es positiva definida, λ i > 0 para i = 1,..., n. Si A es positiva semidefinida, λ i 0 para i = 1,..., n. Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
58 Descomposiciones espectrales y formas cuadráticas Resultado Si A es positiva definida, λ i > 0 para i = 1,..., n. Si A es positiva semidefinida, λ i 0 para i = 1,..., n. Lo anterior nos da una forma de caracterizar las matrices simétricas mediante su descomposición espectral. Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
59 Álgebra matricial Vectores y matrices aleatorias Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
60 Vectores y matrices aleatorias Una matriz aleatoria X (vector aleatorio) es una matriz cuyas entradas son variables aleatorias. El valor esperado es la matriz formada por los valores esperados de cada entrada: E(X) = E(x 11 ) E(x 12 ) E(x 1d ) E(x 21 ) E(x 22 ) E(x 2d ) E(x n1 ) E(x n2 ) E(x nd ) Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
61 Vectores y matrices aleatorias Vector de promedios y matrices de covarianzas. E(x 1 ) E(x 2 ) E(x) = µ =. E(x d ) Σ = E(x µ)(x µ) T = E(x 1 µ 1 ) 2 E(x 1 µ 1 )(x 2 µ 2 ) E(x 1 µ 1 )(x d µ d ) E(x 2 µ 2 )(x 1 µ 1 ) E(x 2 µ 2 ) 2 E(x 2 µ 2 )(x d µ d ) E(x d µ d )(x 1 µ 1 ) E(x d µ d )(x 2 µ 2 ) E(x d µ d ) 2 Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
62 Vectores y matrices aleatorias Σ = σ 11 σ 12 σ 1d σ 21 σ 22 σ 2d σ d1 σ d2 σ dd Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre / 34
Definición (matriz): Definición (dimensión de una matriz): Si una matriz tiene m renglones y n columnas se dice que es de dimensión m n.
Índice general 1. Álgebra de Matrices 1 1.1. Conceptos Fundamentales............................ 1 1.1.1. Vectores y Matrices........................... 1 1.1.2. Transpuesta................................
Tema 1. 1 Álgebra lineal. Aurea Grané Departamento de Estadística Universidad Carlos III de Madrid. 1.1 Vectores de R n. 1. Vectores. 2.
Aurea Grané. Máster en Estadística. Universidade Pedagógica. 1 Aurea Grané. Máster en Estadística. Universidade Pedagógica. 2 Tema 1 Álgebra lineal 1. Vectores 2. Matrices 1 Álgebra lineal Aurea Grané
APÉNDICE A. Algebra matricial
APÉNDICE A Algebra matricial El estudio de la econometría requiere cierta familiaridad con el álgebra matricial. La teoría de matrices simplifica la descripción, desarrollo y aplicación de los métodos
CONTENIDOS MATEMÁTICAS II SEGUNDA EVALUACIÓN CURSO 2017/2018 MATRICES
CONTENIDOS MATEMÁTICAS II SEGUNDA EVALUACIÓN CURSO 2017/2018 Unidades: - Matrices (Bloque Álgebra) - Determinantes (Bloque Álgebra) - Sistemas de ecuaciones lineales (Bloque Álgebra) - Vectores (Bloque
MATRIZ Una matriz de orden (tamaño) mxn sobre el campo de los complejos es un arreglo rectangular de la forma a 11 a 12 a 1n a ] a m1 a m2 a mn
![MATRIZ Una matriz de orden (tamaño) mxn sobre el campo de los complejos es un arreglo rectangular de la forma a 11 a 12 a 1n a ] a m1 a m2 a mn](/thumbs/79/78966751.jpg "MATRIZ Una matriz de orden (tamaño) mxn sobre el campo de los complejos es un arreglo rectangular de la forma a 11 a 12 a 1n a ] a m1 a m2 a mn")
MATRIZ Una matriz de orden (tamaño) mxn sobre el campo de los complejos es un arreglo rectangular de la forma a 11 a 12 a 1n a [ 21 a 22 a 2n ] a m1 a m2 a mn con m renglones y n columnas, donde los a
Algebra Lineal * Working draft: México, D.F., a 17 de noviembre de 2010.
Algebra Lineal * José de Jesús Ángel Ángel jjaa@mathcommx Working draft: México, DF, a 17 de noviembre de 2010 Un resumen de los principales temas tratados en un curso de Álgebra Lineal Contenido 1 Sistemas
ALGEBRA y ALGEBRA LINEAL
520142 ALGEBRA y ALGEBRA LINEAL Primer Semestre, Universidad de Concepción CAPITULO 7. MATRICES DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas 1 Definición: Matriz Sean
Repaso de álgebra de matrices y probabilidad. Javier Santibáñez (IIMAS, UNAM) Regresión Semestre / 58
Repaso de álgebra de matrices y probabilidad Javier Santibáñez (IIMAS, UNAM) Regresión Semestre 2017-2 1 / 58 Preliminares Definición (matriz) Una matriz de dimensión m n es un arreglo rectangular de números
Gustavo Rodríguez Gómez. Agosto Dicembre 2011
Computación Científica Gustavo Rodríguez Gómez INAOE Agosto Dicembre 2011 1 / 44 Capítulo III Descomposición de Matrices 2 / 44 1 Descomposición de Matrices Notación Matrices Operaciones con Matrices 2
1 Vectores de R n. Tema 1. Álgebra matricial. 1.2 Dependencia lineal
Diplomatura en Estadística 1 Tema 1. Álgebra matricial 1. Vectores 1.1 Definiciones básicas 1.2 Dependencia lineal 2. Matrices 2.1 Rango de una matriz 2.2 Matrices cuadradas 3. Vectores y valores propios
MATRICES. Se denomina matriz de dimensión m n a todo conjunto cuyos elementos están dispuestos en m filas y n columnas. o simplemente A = (a.
MATRICES Se denomina matriz de dimensión m n a todo conjunto cuyos elementos están dispuestos en m filas y n columnas A= 2 1 5 0 3 8 A es de dimensión 2 3. a a a En general una matriz de dimensión 2 3
Estadística III Repaso de Algebra Lineal
Repaso de Algebra Lineal Vectores Un vector columna de dimensión n 1 es una serie de números dispuestos como sigue: x 1 x 2 x =. x n Un vector fila de dimensión 1 p es una serie de números dispuestos como
Tema 1. Espacios Vectoriales. Sistemas de ecuaciones.
Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Álgebra Lineal Escuela Politécnica Superior Universidad de Málaga Emilio Muñoz-Velasco (Basado en los apuntes de Jesús Medina e Inmaculada Fortes)
Matrices. Definiciones básicas de matrices. José de Jesús Angel Angel.
Matrices Definiciones básicas de matrices wwwmathcommx José de Jesús Angel Angel jjaa@mathcommx MathCon c 2007-2009 Contenido 1 Matrices 3 11 Matrices cuadradas 5 12 Matriz transpuesta 5 13 Elementos de
Eigenvalores y eigenvectores
Eigenvalores y eigenvectores Los dos problemas principales del álgebra lineal son: resolver sistemas lineales de la forma Ax = b y resolver el problema de eigenvalores. En general, una matriz actúa sobre
Clase 7 Herramientas de Álgebra Lineal
Clase 7 Herramientas de Álgebra Lineal 1 Formas cuadráticas La descomposición en valores singulares 3 Normas de matrices 4 Ejercicios Dada una matriz M R n n, la función escalar x T Mx, donde x R n, es
1.5.3 Sistemas, Matrices y Determinantes
1.5.3 Sistemas, Matrices y Determinantes 24. Sean las matrices 3 0 4 1 A= 1 2 B = 0 2 1 1 C = 1 4 2 3 1 5 1 5 2 D = 1 0 1 E = 3 2 4 6 1 3 1 1 2 4 1 3 a Calcular cuando se pueda: 3C D, ABC, ABC, ED, DE,
ELEMENTOS DE ALGEBRA LINEAL
ELEMENTOS DE ALGEBRA LINEAL Matriz Una matriz de orden o dimensión n x p es una ordenación rectangular de elementos dispuestos en n filas y p columnas de la siguiente forma: a11 a1 a1p a1 a a p A an1 an
Matrices: repaso. Denotaremos con M m n el conjunto de matrices de tamaño m n, o sea, de m filas y n columnas. Una matriz A M m n es de la forma A =
Matrices: repaso Denotaremos con M m n el conjunto de matrices de tamaño m n, o sea, de m filas y n columnas Una matriz A M m n es de la forma a 11 a 1n A = a m1 a mn Denotaremos A ij = a ij el coeficiente
Tema 1. Espacios Vectoriales. Sistemas de ecuaciones.
Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Álgebra Lineal Escuela Politécnica Superior Universidad de Málaga Emilio Muñoz-Velasco (Basado en los apuntes de Jesús Medina e Inmaculada Fortes)
Matrices y Sistemas de Ecuaciones lineales
Matrices y Sistemas de Ecuaciones lineales Llamaremos M m n (K) al conjunto de las matrices A = (a ij ) (i = 1, 2,..., m; j = 1, 2,..., n) donde los elementos a ij pertenecen a un cuerpo K. Las matrices,
Contenido. 2 Operatoria con matrices. 3 Determinantes. 4 Matrices elementales. 1 Definición y tipos de matrices
elementales Diciembre 2010 Contenido Definición y tipos de matrices elementales 1 Definición y tipos de matrices 2 3 4 elementales 5 elementales Definición 1.1 (Matriz) Una matriz de m filas y n columnas
Algebra Lineal Aplicada para Modelos Lineales
Algebra Lineal Aplicada para Modelos Lineales Yuri Miranda Gonzáles Universidad Mayor de San Andrés Carrera de Estadística Abril 203 En el área de modelos lineales y econometría, la necesidad de contar
Tema 1: Matrices. Sistemas de ecuaciones. Determinantes
Tema 1: Matrices. Sistemas de ecuaciones. Determinantes José M. Salazar Octubre de 2016 Tema 1: Matrices. Sistemas de ecuaciones. Determinantes Lección 1. Matrices. Sistemas de ecuaciones. Determinantes
Matrices. Álgebra de matrices.
Matrices. Álgebra de matrices. 1. Definiciones generales Definición 1.1 Si m y n son dos números naturales, se llama matriz de números reales de orden m n a una aplicación A : {1, 2, 3,..., m} {1, 2, 3,...,
23/10/14. Algebra Matricial $ $ ' ' ' $ & & & # # I 3 I 2 = 1 0 $ DEFINICION DE MATRIZ 2.1 CONCEPTOS DE MATRICES CONCEPTOS DE MATRICES. $ n. ! a.
/0/ Algebra Matricial. OPERACIONES DE DEFINICION DE MATRIZ Si A es una matriz de m x n (esto es una matriz con m filas y n columnas) la entrada escalar en la i-ésima fila y la j-ésima columna de A se denota
Matrices y determinantes
Matrices y determinantes Las matrices y los determinantes son herramientas del álgebra de gran utilidad en muchas disciplinas. Los campos de aplicación de la teoría de las matrices y de los determinantes
Vectores y Matrices. Tema 3: Repaso de Álgebra Lineal Parte I. Contenidos
Tema 3: Repaso de Álgebra Lineal Parte I Virginia Mazzone Contenidos Vectores y Matrices Bases y Ortonormailizaciòn Norma de Vectores Ecuaciones Lineales Algenraicas Ejercicios Vectores y Matrices Los
Repaso de conceptos de álgebra lineal
MÉTODOS AVANZADOS EN APRENDIZAJE ARTIFICIAL: TEORÍA Y APLICACIONES A PROBLEMAS DE PREDICCIÓN Manuel Sánchez-Montañés Luis Lago Ana González Escuela Politécnica Superior Universidad Autónoma de Madrid Repaso
Álgebra lineal Prof: Leonid Fridman
Álgebra lineal Prof: Leonid Fridman Vectores y subespacios lineales Vector: Un vector en Rn es una n-tupla de números reales Espacio lineal: Un conjunto no vacío L de elementos x, y, z, que satisface las
Definición: Dos matrices A y B son iguales si tienen el mismo orden y coinciden los elementos que ocupan el mismo lugar.
UNIDAD 03: MATRICES Y DETERMINANTES. 3.1 Conceptos de Matrices. 3.1.1 Definición de matriz. Definición: Se lama matriz de orden m x n a un arreglo rectangular de números dispuestos en m renglones y n columnas.
CAPÍTULO 1. Preliminares
CAPÍTULO 1 Preliminares En este capítulo se recopilan algunas definiciones y algunos resultados básicos que servirán de referencia en el desarrollo de los capítulos posteriores Se consideran aquí varios
Clase 8 Matrices Álgebra Lineal
Clase 8 Matrices Álgebra Lineal Código Escuela de Matemáticas - Facultad de Ciencias Universidad Nacional de Colombia Matrices Definición Una matriz es un arreglo rectangular de números denominados entradas
Espacios Vectoriales, Valores y Vectores Propios
, Valores y Vectores Propios José Juan Rincón Pasaye, División de Estudios de Postgrado FIE-UMSNH Curso Propedéutico de Matemáticas para la Maestría en Ciencias opciones: Sistemas de Control y Sistemas
BOLETÍN DE MATRICES 2 IES A Sangriña Curso 2016/ Calcula la matriz inversa, si existe, usando el método de Gauss:
*** OBLIGATORIOS *** 1. Efectúa todos los posibles productos: 2. Calcula la matriz inversa, si existe, usando el método de Gauss: 3. Sean y. Encuentra X para que cumpla: 3 X 2 A = 5 B 4. Encuentra dos
6.5.7 Orientación de un espacio vectorial eucĺıdeo Producto vectorial Diagonalización de formas bilineales simétricas...
Contents 6 Formas Bilineales y Producto Escalar 3 6.1 Formas bilineales............................... 3 6.1.1 Matriz de una forma bilineal....................... 4 6.1. Formas bilineales simétricas.......................
Definición Dados dos números naturales m y n, una matriz de orden o dimensión m n es una tabla numérica rectangular con m filas y n columnas.
Tema 1 Matrices 1.1. Conceptos básicos y ejemplos Definición 1.1.1. Dados dos números naturales m y n, una matriz de orden o dimensión m n es una tabla numérica rectangular con m filas y n columnas. NOTA:
Matrices y sistemas de ecuaciones
Matrices y sistemas de ecuaciones María Muñoz Guillermo maria.mg@upct.es U.P.C.T. Matemáticas I M. Muñoz (U.P.C.T.) Matrices y sistemas de ecuaciones Matemáticas I 1 / 59 Definición de Matriz Matrices
de la forma ), i =1,..., m, j =1,..., n, o simplemente por (a i j ).
INTRODUCCIÓN. MATRICES Y DETERMINANTES Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de ecuaciones lineales, de las ecuaciones diferenciales y de las derivadas parciales.
1. Las matrices se denotan con letras mayúsculas. Por ejemplo, A, B, C, X,...
CAPÍTULO 1 ALGEBRA MATRICIAL 11 Introducción Definición 111 (Matriz) Definimos una matriz como un arreglo rectangular de elementos, llamados escalares, sobre un álgebra F Más que hacer referencia especifica
Matemáticas Discretas TC1003
Matemáticas Discretas TC13 Matrices: Conceptos y Operaciones Básicas Departamento de Matemáticas ITESM Matrices: Conceptos y Operaciones Básicas Matemáticas Discretas - p. 1/25 Una matriz A m n es un arreglo
Operaciones con matrices
Operaciones con matrices Objetivos: Distinguir y realizar los cálculos con las operaciones matriciales básicas. Introducción: Las operaciones matriciales permiten el abordaje de los métodos del álgebra
Matrices y Sistemas Lineales
Matrices y Sistemas Lineales Natalia Boal María Luisa Sein-Echaluce Universidad de Zaragoza Matrices sobre IR ó C. Definición Dado un conjunto K (IR ó C) y dos conjuntos finitos de índices I = {,, m} J
MENORES, COFACTORES Y DETERMINANTES
MENORES, COFACTORES Y DETERMINANTES 1. Introducción. 2. Determinante de una matriz de 3 x 3. 3. Menores y cofactores. 4. Determinante de una matriz de n x n. 5. Matriz triangular. 6. Determinante de una
Tema 1 CÁLCULO MATRICIAL y ECUACIONES LINEALES
Tema 1 CÁLCULO MATRICIAL y ECUACIONES LINEALES Prof. Rafael López Camino Universidad de Granada 1 Matrices Definición 1.1 Una matriz (real) de n filas y m columnas es una expresión de la forma a 11...
ÁLGEBRA Ejercicios no resueltos de la Práctica 3
ÁLGEBRA Ejercicios no resueltos de la Práctica 3 Matrices y determinantes (Curso 2007 2008) 15. Encontrar la (única) respuesta correcta, de entre las indicadas, a las siguientes cuestiones: (b) En una
Conceptos Preliminares
Conceptos Preliminares Igualdad de matrices Definición: Dos matrices son iguales cuando tienen la misma dimensión y los elementos que ocupan la misma posición en ambas son iguales. Estas matrices cumplen
2. Problemas. Espacios Vectoriales. Álgebra Lineal- Propedéutico Mayo de 2012
2. Problemas. Espacios Vectoriales. Álgebra Lineal- Propedéutico Mayo de 2012 1. En R 2 se define la suma: (a 1, b 1 ) + (a 2, b 2 ) = (a 1 + a 2, b 1 + b 2 ) y el producto por un escalar: λ(a, b) = (0,
Valores y vectores propios
Valores y vectores propios Departamento de Matemáticas, CCIR/ITESM 4 de enero de 20 Índice 8.. Definición de valor y vector propio.................................. 8.2. Determinación de los valores propios.................................
1 Clase sobre determinantes
1 Clase sobre determinantes Una herramienta muy útil cuando trabajamos con matrices y con el producto de matrices, es su interpretación como: una colección de números, A = [a ij ] ; como una colección
Tema 1: Matrices y Determinantes
Tema 1: Matrices y Determinantes September 14, 2009 1 Matrices Definición 11 Una matriz es un arreglo rectangular de números reales a 11 a 12 a 1m a 21 a 22 a 2m A = a n1 a n2 a nm Se dice que una matriz
ALN. Repaso matrices. In. Co. Facultad de Ingeniería Universidad de la República
ALN Repaso matrices In. Co. Facultad de Ingeniería Universidad de la República Definiciones básicas - Vectores Definiciones básicas - Vectores Construcciones Producto interno: ( x, y n i x y i i ' α Producto
GRADO: Ingeniería en Tecnologías Industriales CURSO: 1º CUATRIMESTRE: 1º
SESIÓN SEMANA DENOMINACIÓN ASIGNATURA: Álgebra Lineal GRADO: Ingeniería en Tecnologías Industriales CURSO: 1º CUATRIMESTRE: 1º La asignatura tiene 28 sesiones que se distribuyen a lo largo de 14 semanas
102 EJERCICIOS DE ALGEBRA LINEAL por Francisco Rivero Mendoza Ph.D.
102 EJERCICIOS DE ALGEBRA LINEAL por Francisco Rivero Mendoza Ph.D. Tema 1. Espacios Vectoriales. 1. Dar la definición de cuerpo. Dar tres ejemplos de cuerpos. Dar un ejemplo de un cuerpo finito 2. Defina
Algebra lineal Matrices
Algebra lineal Matrices Una matriz A un arreglo rectangular de números dispuestos en m renglones (filas) y n columnas. Fila 1 La componente o elemento ij de A, denotado por es el número que aparece en
Tema 4: Matrices y Determinantes. Algunas Notas sobre Matrices y Determinantes. Álgebra Lineal. Curso
Tema 4: Matrices y Determinantes Algunas Notas sobre Matrices y Determinantes Álgebra Lineal Curso 2004-2005 Prof. Manu Vega Índice 1. Determinantes 3 2. Regla de Sarrus 3 3. Propiedades de los determinantes
Universidad de Buenos Aires - Facultad de Ciencias Exactas y Naturales - Departamento de Matemática Segundo Cuatrimestre de 2002 ÁLGEBRA LINEAL
Universidad de Buenos Aires - Facultad de Ciencias Exactas y Naturales - Departamento de Matemática Segundo Cuatrimestre de 2002 ÁLGEBRA LINEAL Práctica N 2: Matrices Ejercicio 1 Probar que los siguientes
ÁLGEBRA MATRICIAL. 1. La traspuesta de A es A; (A ) = A. 2. La inversa de A 1 es A; (A 1 ) 1 = A. 3. (AB) = B A.
ÁLGEBRA MATRICIAL. 1. La traspuesta de A es A; A = A. 2. La inversa de A 1 es A; A 1 1 = A. 3. AB = B A. 4. Las matrices A A y AA son simétricas. 5. AB 1 = B 1 A 1, si A y B son no singulares. 6. Los escalares
MATRICES, DETERMINANTES Y SISTEMAS DE ECUACIONES LINEALES
6 de Abril de MATRICES, DETERMINANTES Y SISTEMAS DE ECUACIONES LINEALES (Clase ) Departamento de Matemática Aplicada Facultad de Ingeniería Universidad Central de Venezuela . Producto de matrices. Aplicaciones
Sistemas Lineales y Matrices
Profesores Hernán Giraldo y Omar Saldarriaga Instituto de Matemáticas Facultad de Ciencias Exactas y Naturales Universidad de Antioquia 2014 Ejemplo Solución de sistemas de ecuaciones lineales, usaremos
Multivariante Curso Cálculo matricial
Multivariante Curso 06-07 1 Cálculo matricial Introducción La información de partida en el análisis multivariante es una tabla de datos correspondiente a la medición de distintas variables sobre varios
Vectores en el plano UNIDAD I: MATRICES. Dirección de un vector. Sentido de un vector
UNIDAD I: MATRICES Vectores en el plano Un vector,, es un segmento con una dirección que va del punto A (origen) al punto B (etremo).un vector es un segmento orientado que va del punto A (origen) al punto
Matemáticas. Álgebra lineal (parte final ampliada)
Master en Estadística e Investigación Operativa Matemáticas Álgebra lineal (parte final ampliada) Vera Sacristán Departament de Matemàtica Aplicada II Facultat de Matemàtiques i Estadística Universitat
Matrices, Determinantes y Sistemas Lineales.
12 de octubre de 2014 Matrices Una matriz A m n es una colección de números ordenados en filas y columnas a 11 a 12 a 1n f 1 a 21 a 22 a 2n f 2....... a m1 a m2 a mn f m c 1 c 2 c n Decimos que la dimensión
Es decir, det A = producto de diagonal principal producto de diagonal secundaria. Determinante de una matriz cuadrada de orden 3
1.- DETERMINANTE DE UNA MATRIZ CUADRADA Determinante de una matriz cuadrada de orden 1 Dada una matriz cuadrada de orden 1, A = (a), se define det A = det (a) = a Determinante de una matriz cuadrada de
Análisis Multivariado. Leticia Gracia Medrano V
Análisis Multivariado Leticia Gracia Medrano V Septiembre 207 ii Capítulo Introducción Álgebra lineal Empezaremos tomando la siguiente matriz: X X 2 X j X p X 2 X 2 X 2j X 2p X = X i X i2 X ij X ip X n
Capitulo 6. Matrices y determinantes
Capitulo 6. Matrices y determinantes Objetivo. El alumno aplicará los conceptos fundamentales de las matrices, determinantes y sus propiedades a problemas que requieran de ellos para su resolución. Contenido.
3.1. Operaciones con matrices. (Suma, resta, producto y traspuesta)
Operaciones con matrices Suma, resta, producto y traspuesta Suma, resta y multiplicación por escalares Las matrices de un tamaño fijo m n se pueden sumar entre sí y esta operación de sumar se puede definir
ÁLGEBRA LINEAL I NOTAS DE CLASE UNIDAD 2
ÁLGEBRA LINEAL I NOTAS DE CLASE UNIDAD 2 Abstract Estas notas conciernen al álgebra de matrices y serán actualizadas conforme el material se cubre Las notas no son substituto de la clase pues solo contienen
Elementos de una matriz.
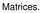Matrices. Elementos de una matriz. Renglón. Columnas. A=[a ij ] A-Nombre de la matriz. a-número. i-renglón. j-columna. i j-orden de la matriz. Ejercicio. Indica el orden de la matriz. Indica el valor de
Matrices y sistemas lineales
Capítulo 2 Matrices y sistemas lineales 2.1 Definiciones básicas Una matriz es una tabla rectangular de números, es decir, una distribución ordenada de números. Los números de la tabla se conocen con el
PROBLEMAS DE ÁLGEBRA LINEAL INGENIERÍA DE TELECOMUNICACIONES - E.T.S.I.T. CURSO 2005/06
PROBLEMAS DE ÁLGEBRA LINEAL INGENIERÍA DE TELECOMUNICACIONES - E.T.S.I.T. CURSO 200/06 1. Utilizar el método de eliminación de Gauss para resolver el sistema de ecuaciones lineales siguiente: 2 x 1 2 x
Vectores y matrices. Problemas para examen
Vectores y matrices Problemas para examen Operaciones lineales con vectores 1. Programación: la suma de dos vectores. Escriba una función que calcule x + y, donde x, y R n. Calcule el número de flops.
TEMA V. Pues bien, a estas caracterizaciones de los sistemas de ecuaciones lineales se las llamó matrices. En el caso del sistema considerado tenemos:
TEMA V 1. MATRICES Y SISTEMAS DE ECUACIONES LINEALES. Sea el siguiente sistema de ecuaciones lineales: Realmente quien determina la naturaleza y las soluciones del sistema, no son las incógnitas: x, y,
Ejercicios de Álgebra Lineal Parcial 1
Ejercicios de Álgebra Lineal Parcial 1 1. Ejercicios de respuesta corta ( ) 3 1 a) Si A = encuentre la entrada c 6 2 12 de la matriz A 2 { x 3y = 1 b) Si para k R el sistema tiene solución única, verique
PROGRAMA DE EXAMEN. Unidad Nº1: Matrices y Función Determinante
Ministerio de Cultura y Educación Universidad Nacional de San Juan Fac. de Ciencias Exactas Físicas y Naturales Ciclo Lectivo 2018 PROGRAMA DE EXAMEN Cátedra: ALGEBRA LINEAL Carrera: Licenciatura en Geofísica
MATRICES. Se simboliza tal matriz por y se le llamará una matriz x o matriz de orden x (que se lee por ).
1 MATRICES 1 Una matriz es una disposición rectangular de números (Reales); la forma general de una matriz con filas y columnas es Se simboliza tal matriz por y se le llamará una matriz x o matriz de orden
Material para el examen parcial 1
Algebra Lineal 2, FAMAT-UG, aug-dic, 2009 Material para el examen parcial 1 (17 oct, 2009) Definiciones: Hay que saber las definiciones precisas de todos los siguientes términos, y conocer ejemplos concretos
INSTITUTO POLITÉCNICO NACIONAL
INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA, ESIME ZACATENCO SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN POSGRADO EN INGENIERÍA ELÉCTRICA CURSO DE PROPÓSITO ESPECIFICO
Matrices ortogonales y descomposición QR
Matrices ortogonales y descomposición QR Problemas para examen Agradezco a Aldo Iván Leal García por varias correcciones importantes. Invertibilidad por la izquierda y por la derecha (repaso) 1. Conceptos
Propiedades de los Determinantes
Propiedades de los Determinantes Departamento de Matemáticas, CCIR/ITESM 26 de mayo de 2010 Índice 19.1. Propiedades............................................... 1 19.2. La adjunta de una matriz cuadrada..................................
Matrices: Una ordenación de números dispuestos en filas y columnas, encerrados entre corchetes
Matrices: Una ordenación de números dispuestos en filas y columnas, encerrados entre corchetes Ejemplos: Verifican ciertas reglas o algebra, denominada algebra de matrices.la matriz representa en general
Capítulo 1: Diagonalización de matrices
Capítulo : Diagonalización de matrices Matrices y determinantes Definición Una matriz es un arreglo rectangular de números reales a a a m a A a a m a n a n a nm La matriz es de orden n m si consta de n
6.8. Descomposición mediante valores singulares. v 2 =
68 Descomposición mediante valores singulares Los valores singulares de una matriz m n Supongamos que A es una matriz real cualquiera Los autovalores de A T A tienen la siguiente propiedad A T Ax = λx
dia G o n a l i z a c i ó n
Unidad elementos característicos dia G o n a l i z a c i ó n Objetivos: Al inalizar la unidad, el alumno: Encontrará los valores y los vectores característicos de una matriz. Utilizará los elementos característicos
3. ÁLGEBRA LINEAL // 3.1. SISTEMAS DE
3. ÁLGEBRA LINEAL // 3.1. SISTEMAS DE ECUACIONES LINEALES Y MATRICES COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS Curso 2011-2012 3.1.1. Resolución de sistemas de ecuaciones lineales. Método
UNIVERSIDAD AUTÓNOMA DE CHIAPAS Facultad de Contaduría y Administración, Campus I
Facultad de Negocios, Campus IV Programa descriptivo por unidad de competencia Programa educativo Licenciatura en Ingeniería en Desarrollo y Tecnologías de Software Modalidad Presencial Clave MA04 H S
Producto tensorial entre tensores
Tensores cartesianos Producto tensorial entre tensores Producto tensorial entre tensores Se define el producto tensorial entre los tensores S CT(m) y T CT(n) como el tensor S T CT(n + m): S T = S i1...i
Definición de matriz Una matriz A es un conjunto de números dispuestos en filas y en columnas.
1.- CONCEPTO DE MATRIZ. TIPOS DE MATRICES Definición de matriz Una matriz A es un conjunto de números dispuestos en filas y en columnas. 1 3 4 Por ejemplo, A = es una matriz de 2 filas y 3 columnas 0 5
Algebra Matricial.
Algebra Matricial Dr. Alfonso Alba Cadena fac@galia.fc.uaslp.mx Facultad de Ciencias UASLP Unidad I Fundamentos de matrices 1 Introducción Una matriz es un arreglo rectangular de números. Algunos ejemplos
Sistemas de ecuaciones lineales. Matrices
Dpto de MATEMÁTICA APLICADA A LOS RECURSOS NATURALES Sección departamental en la ETSI de Montes Algebra Sistemas de ecuaciones lineales Matrices Sistemas lineales Solución de un sistema lineal Sistemas
1 0 4/ 5 13/
1 1 1 7 1 0 4/ 5 13/ 5 R1 R 1+1/5R3 0 0 0 2 R2 R3 0 5 9 22 0 5 9 22 0 0 0 2 Como la matriz tiene un renglón (0, 0, 0, 2) indica que el sistema no tiene solución ya que no existe un número que sea 2 y al
Álgebra Lineal. Ejercicios de evaluación. Grado en Ingeniería Informática Doble Grado en Ingeniería Informática y Administración de Empresas
Álgebra Lineal Ejercicios de evaluación Grado en Ingeniería Informática Doble Grado en Ingeniería Informática y Administración de Empresas AUTORES: J. S ALAS, A. T ORRENTE Y E.J.S. V ILLASEÑOR Problema
3. ÁLGEBRA LINEAL // 3.1. SISTEMAS DE
3. ÁLGEBRA LINEAL // 3.1. SISTEMAS DE ECUACIONES LINEALES Y MATRICES COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS // Curso 2017-18 3.1.1. Resolución de sistemas de ecuaciones lineales. Método
Apuntes de modelos lineales
Apuntes de modelos lineales Clases Nos. 1 al 3 Ernesto Ponsot Balaguer Dr. en Estadística, MSc. en Estadística Aplicada, Ing. de Sistemas http://webdelprofesor.ula.ve/economia/ernesto E-mail: ernesto@ula.ve
Valores singulares. Producto escalar y ortogonalidad. Proposición. Curso < x, y >= si F = C. Si x C n x i=1
Valores singulares Curso 2017-18 1 Producto escalar y ortogonalidad < x, y >= n y i x i = y T x si F = R, n y i x i = y x Si x C n x x = n x i 2 = x 2 2. si F = C Si x, y C n x y = y x, pero si x, y R
Matrices y determinantes
Matrices y determinantes 1 Ejemplo Cuál es el tamaño de las siguientes matrices? Cuál es el elemento a 21, b 23, c 42? 2 Tipos de matrices Matriz renglón o vector renglón Matriz columna o vector columna