CUENCA DEL ALTO PARANÁ Soluciones - Primer Nivel
|
|
|
- Lorenzo Ruiz Navarrete
- hace 7 años
- Vistas:
Transcripción
1 CUENCA DEL ALTO PARANÁ Soluciones - Primer Nivel Problema 1: Si se traza una recta m paralela a r que pase por el centro del rectángulo, éste quedará seccionado en dos trapecios iguales. En efecto, trazando paralelas a los lados del rectángulo por los puntos de intersección de m con el borde del rectángulo, como muestra la gura, se forman dos triángulos iguales, uno en cada trapecio. La igualdad de estos triángulos se debe a que tienen un par de ángulos iguales, alternos internos entre paralelas, y el lado adyacente a estos ángulos, es común. Figura 1 Por otra parte, hay dos rectángulos, uno en cada trapecio. Estos rectángulos tienen uno de sus lados igual a un lado del rectángulo dado como se observa en la Figura 1. En la Figura 2, al trazar la diagonal del rectángulo, quedan formados 2 triángulos que resultan iguales por tenerlos 3 ángulos iguales y un par de lados correspondientes de igual longitud, precisamente los lados que se encuentran sobre la diagonal del rectángulo. Figura 2 1
2 Los lados opuestos al vértice común en estos triángulos son lados de los rectángulos anteriormente considerados en cada trapecio, y por lo tanto dichos rectángulos son iguales Comentario: Otra solución más simple se apoya en el hecho que el rectángulo (o un paralelogramo) es simétrico respecto de su centro, es decir, si el rectángulo se hiciera rotar 180 o alrededor de su centro, se obtiene el mismo rectángulo mientras que los trapecios en ambos lados de la recta m, se superponen uno en el otro. Problema 2: En el triángulo BCD, su base CD es un tercio de la base AC de ABC, mientras que la altura correpondiente en BCD y ABC es común. El área de BCD es entonces 1 3 del área de ABC, es decir 4cm2. Luego el área de ABD es 8cm 2. Como AED y EBD comparten la altura sobre AE y EB respectivamente, y AE = EB, resulta que AED y EBD tienen la misma área, o sea, ambas áreas miden 4m 2. Problema 3: El cubo quedará formado por 3 pisos de 9 dados cada uno. Cada piso puede tomar uno de los tipos que se muestra en la gura: Dos pisos vecinos deberán ser de tipo distinto por las condiciones de ensamble, es decir, necesariamente el cubo tendrá dos pisos de un tipo y uno de otro tipo. En cada piso hay 5 dados de un color, negro o blanco, y 4 del otro color, respectivamente blanco o negro. Por ejemplo, la situación siguiente: En conclusión, se necesitan 14 dados de un color y 13 dados del otro color. 2
3 CUENCA DEL ALTO PARANÁ Soluciones - Segundo Nivel Problema 1: El triángulo puede ser descompuesto en 3 triángulos, todos ellos con una altura de 2cm y los distintos lados del triángulo como las bases correspondientes, tal como lo ilustra la gura. La suma de las áreas de estos 3 triángulos coincide con el área del triángulo dado y de alli se obtiene que el perímetro buscado es 21cm. Problema 2: El tirante puede cortarse en forma longitudinal en cuatro partes para pegar las piezas de a 2 como se indica en la gura. Problema 3: Juntando los caminos recorridos por los amigos que salen desde las esquinas opuestas A y C, se obtiene un camino desde A hasta C, sin vueltas ni retrocesos, lo que equivale en cuadras, a un camino desde A a B y desde B hasta C como se ve en la gura: 3
4 Análogamente ocurre con los amigos que salen desde las esquinas opuestas B y D. Se conluye que el perímetro de la ciudad es de 60 cuadras. El número de cuadras desde A hasta B por el número de cuadras desde B hasta C es 200, por coincidir con el número de manzanas de la ciudad. Por otra parte, el número de cuadras desde A hasta B más el número de cuadras desde B hasta C es 30. Descomponiendo 200 en factores primos, resulta 200 = y los números de cuadras buscados surgen de una descomposición de 200 en dos factores cuya suma sea igual a 30. Estos dos factores se obtienen distribuyendo los primos 2; 2; 2; 5; 5 en dos grupos. Si los dos 5 quedan en un mismo grupo, el factor correspondiente será 25 pues este grupo no admite otro primo por que superaría a 30 y el otro factor debe ser 8. En este caso la suma supera a 30. Los 5 deben estar, uno en cada factor; los 2 no pueden estar todos en un mismo factor, por los tanto ambos factores deben ser múltiplos de 10, y no hay otra solución que 10 y 20. Comentario: Para quienes conozcan la ecuación cuadrática, si a y b son los lados del rectángulo, a + b = 30 y ab = 200 lleva a la ecuación : x 2 30x = 0 cuyas raíces son: es decir 20 y p
5 CUENCA DEL ALTO PARANÁ Soluciones - Tercer Nivel Problema 1: Con las notaciones de la gura, el farol no será mojado si la distancia entre E y F es mayor que 8. Para calcular dicha distancia, aplicamos dos veces Pitágoras: AC 2 = = 61 y EF 2 = = 65 Se concluye que EF = p 65 > 8. Problema 2: Solución 1: Usaremos el siguiente principio: Si un cuadrilátero tiene sus diagonales perpendiculares, entonces su área es un medio del producto de las diagonales. El hexágono regular se puede descomponer en 6 cuadriláteros en la situación mencionada, donde en cada uno de ellos una diagonal es un lado del hexágono inscripto y la otra es igual al lado r del hexágono regular. El área del hexágono 5
6 regular es, por una parte, la suma de las áreas de los 6 cuadriláteros que lo componen, esto es 1 2p r, donde p es el perímetro del hexágono inscripto. Por otra parte, es igual a perímetro por apotema sobre 2, es decir 1 26r 2 = 6r. Igualando ambos resultados y simpli cando se obtiene p = 12cm. Solución 2: Usaremos el siguiente principio: En un triángulo isósceles ABC, si desde un punto P en la base AB se trazan los segmentos P Q y P R perpendiculares a los lados iguales, como lo muestra la gura, la suma P Q + P R = h, donde h es la altura correspondiente a los lados iguales. Esta situación se aplica a cada uno de los triángulos equiláteros que componen el hexágono regular, donde el punto P es, en cada caso, un vértice del hexágono inscripto. Luego el perímetro del hexágono inscripto es 6 veces la altura del triángulo equilátrero, es decir 6 veces la apotema del hexágono regular, igual a 12cm. Problema 3: La diagonal BD del cuadrilátero, descompone a la altura h del triángulo ACE en los segementos h 0 y h" según muestra la gura. El área del cuadrilátero es igual a la del triángulo ABD más la del triángulo BCD, es decir: 1 2 BD h" BD h0 = 1 2 BD (h" + h0 ) = 1 2 BD h Dado que AE = BD, el área de ACE resulta igual a la del cuadrilátero ABCD, es decir a 9cm 2. 6
Soluciones Nota nº 1
 Soluciones Nota nº 1 Problemas Propuestos 1- En el paralelogramo ABCD el ángulo en el vértice A es 30º Cuánto miden los ángulos en los vértices restantes? Solución: En un paralelogramo, los ángulos contiguos
Soluciones Nota nº 1 Problemas Propuestos 1- En el paralelogramo ABCD el ángulo en el vértice A es 30º Cuánto miden los ángulos en los vértices restantes? Solución: En un paralelogramo, los ángulos contiguos
TORNEOS GEOMÉTRICOS 2016 Primera Ronda. Primer Nivel - 5º Año de Escolaridad
 TORNEOS GEOMÉTRICOS 2016 Primera Ronda Primer Nivel - 5º Año de Escolaridad 1- En el triángulo rectángulo ABC cuyo ángulo en C mide 48º se trazan la bisectrices de los ángulos B y C, que se cortan en O.
TORNEOS GEOMÉTRICOS 2016 Primera Ronda Primer Nivel - 5º Año de Escolaridad 1- En el triángulo rectángulo ABC cuyo ángulo en C mide 48º se trazan la bisectrices de los ángulos B y C, que se cortan en O.
TORNEOS GEOMÉTRICOS Primera Ronda Primer Nivel - 5º Año de Escolaridad
 TORNEOS GEOMÉTRICOS 2017. Primera Ronda Primer Nivel - 5º Año de Escolaridad Problema 1. El hexágono regular de la figura tiene área 6cm 2. Halla el área de la región sombreada. Solución: El triángulo
TORNEOS GEOMÉTRICOS 2017. Primera Ronda Primer Nivel - 5º Año de Escolaridad Problema 1. El hexágono regular de la figura tiene área 6cm 2. Halla el área de la región sombreada. Solución: El triángulo
TORNEO DE LAS CUENCAS 2013 Segunda Ronda Primera Prueba Primer Nivel
 TORNEO DE LAS CUENCAS 2013 Segunda Ronda Primera Prueba Primer Nivel Problema 1- Los cuadraditos de la cuadrícula son de 1 cm por 1 cm. Halla el área del triángulo inscripto. Solución: El área puede ser
TORNEO DE LAS CUENCAS 2013 Segunda Ronda Primera Prueba Primer Nivel Problema 1- Los cuadraditos de la cuadrícula son de 1 cm por 1 cm. Halla el área del triángulo inscripto. Solución: El área puede ser
TORNEOS GEOMÉTRICOS 2015 Segunda Ronda 5º Grado SOLUCIONES
 TORNEOS GEOMÉTRICOS 015 Segunda Ronda 5º Grado SOLUCIONES Problema 1- Un paralelogramo de 5 cm de área, tiene por vértices al centro de un hexágono regular y a otros tres vértices del hexágono, como muestra
TORNEOS GEOMÉTRICOS 015 Segunda Ronda 5º Grado SOLUCIONES Problema 1- Un paralelogramo de 5 cm de área, tiene por vértices al centro de un hexágono regular y a otros tres vértices del hexágono, como muestra
TORNEOS GEOMÉTRICOS 2016 Segunda Ronda. Soluciones 1º Nivel
 TORNEOS GEOMÉTRICOS 2016 Segunda Ronda Soluciones 1º Nivel 1. Halla la suma de los ángulos marcados en el cuadrilátero inscripto en la circunferencia, como indica la figura. Solución: Por la propiedad
TORNEOS GEOMÉTRICOS 2016 Segunda Ronda Soluciones 1º Nivel 1. Halla la suma de los ángulos marcados en el cuadrilátero inscripto en la circunferencia, como indica la figura. Solución: Por la propiedad
Primer Nivel. Solución: Por los valores de los lados del triángulo, éste debe ser un triángulo rectángulo, y en consecuencia su área es (3 4 ) 6
 Primer Nivel Problema 1- Los lados de un cuadrado de área 4cm se han dividido en cuatro partes iguales. Halla el área del cuadrado sombreado. Solución: Trazando los segmentos adicionales indicados en la
Primer Nivel Problema 1- Los lados de un cuadrado de área 4cm se han dividido en cuatro partes iguales. Halla el área del cuadrado sombreado. Solución: Trazando los segmentos adicionales indicados en la
Soluciones Primer Nivel
 Soluciones Primer Nivel Torneos Geométricos 2017 2º Ronda 1. En un papel cuadriculado con cuadrados de un centímetro de lado, se ha dibujado un cuadrilátero con vértices en los nodos del mismo (vértices
Soluciones Primer Nivel Torneos Geométricos 2017 2º Ronda 1. En un papel cuadriculado con cuadrados de un centímetro de lado, se ha dibujado un cuadrilátero con vértices en los nodos del mismo (vértices
TORNEOS GEOMÉTRICOS Segunda Ronda. Primer Nivel - 5º Año de Escolaridad. Apellido Nombres. DNI Tu Escuela. Localidad Provincia
 TORNEOS GEOMÉTRICOS 2017. Segunda Ronda Primer Nivel - 5º Año de Escolaridad Apellido Nombres DNI Tu Escuela. Tu domicilio: Calle. Nº Piso Dpto C.P... Localidad Provincia Lee con atención: 1- Es posible
TORNEOS GEOMÉTRICOS 2017. Segunda Ronda Primer Nivel - 5º Año de Escolaridad Apellido Nombres DNI Tu Escuela. Tu domicilio: Calle. Nº Piso Dpto C.P... Localidad Provincia Lee con atención: 1- Es posible
SOLUCIONES PRIMER NIVEL
 SOLUCIONES PRIMER NIVEL 1. Los cuatro polígonos de la figura son regulares. Halla los valores de los tres ángulos, de vértice A limitados por dos lados de los polígonos dados, indicados en la figura. Solución:
SOLUCIONES PRIMER NIVEL 1. Los cuatro polígonos de la figura son regulares. Halla los valores de los tres ángulos, de vértice A limitados por dos lados de los polígonos dados, indicados en la figura. Solución:
Problema 1. Cuántos triángulos rectángulos se pueden formar que tengan sus vértices en vértices de una caja?
 Nota4: Soluciones problemas propuestos Problema 1. Cuántos triángulos rectángulos se pueden formar que tengan sus vértices en vértices de una caja? Solución: Consideremos primero todos aquellos triángulos
Nota4: Soluciones problemas propuestos Problema 1. Cuántos triángulos rectángulos se pueden formar que tengan sus vértices en vértices de una caja? Solución: Consideremos primero todos aquellos triángulos
TORNEOS GEOMÉTRICOS Primera Ronda Primer Nivel - 5º Año de Escolaridad Apellido Nombres DNI Tu Escuela.. Localidad Provincia
 Primer Nivel - 5º Año de Escolaridad Problema 1. El hexágono regular de la figura tiene área 6cm 2. Halla el área de la región sombreada. Problema 2. Usando sólo una regla sin marcas, dibujar en la cuadrícula
Primer Nivel - 5º Año de Escolaridad Problema 1. El hexágono regular de la figura tiene área 6cm 2. Halla el área de la región sombreada. Problema 2. Usando sólo una regla sin marcas, dibujar en la cuadrícula
Soluciones Primer Nivel - 5º Año de Escolaridad
 Primer Nivel - 5º Año de Escolaridad Problema 1. La diagonal del cuadrado mide cm. El cuadrado se descompone en cuatro triángulos rectángulos cuyos catetos miden 1cm. Las áreas de estos triángulos miden
Primer Nivel - 5º Año de Escolaridad Problema 1. La diagonal del cuadrado mide cm. El cuadrado se descompone en cuatro triángulos rectángulos cuyos catetos miden 1cm. Las áreas de estos triángulos miden
Triángulo equilátero conocida su altura con el cartabón. Sobre una recta, r, se sitúa el punto, B.
 Elementos geométricos / Triángulo 31 Triángulo equilátero conocida su altura con el cartabón Sobre una recta, r, se sitúa el punto, B. Se traza por el punto, B, la recta perpendicular a la recta, r, y
Elementos geométricos / Triángulo 31 Triángulo equilátero conocida su altura con el cartabón Sobre una recta, r, se sitúa el punto, B. Se traza por el punto, B, la recta perpendicular a la recta, r, y
EJERCICIOS ÁREAS DE REGIONES PLANAS
 EJERCICIOS ÁREAS DE REGIONES PLANAS 1. En un triángulo equilátero se inscribe una circunferencia de radio R y otra de radio r tangente a dos de los lados y a la primera circunferencia, hallar el área que
EJERCICIOS ÁREAS DE REGIONES PLANAS 1. En un triángulo equilátero se inscribe una circunferencia de radio R y otra de radio r tangente a dos de los lados y a la primera circunferencia, hallar el área que
8. POLÍGONOS Y FIGURAS CIRCULARES
 8. POLÍGONOS Y FIGURAS CIRCULARES 1. Los ángulos del triángulo ABC de la siguiente gura miden: m A = 60 o, m B = 100 o. Prolongando AB tal que BD = BC, los ángulos del triángulo CBD miden: a) B 80 o, C
8. POLÍGONOS Y FIGURAS CIRCULARES 1. Los ángulos del triángulo ABC de la siguiente gura miden: m A = 60 o, m B = 100 o. Prolongando AB tal que BD = BC, los ángulos del triángulo CBD miden: a) B 80 o, C
TALLER # 4 DE GEOMETRÍA EUCLIDIANA SEMEJANZAS Y RELACIONES MÉTRICAS. Universidad de Antioquia
 TALLER # 4 DE GEOMETRÍA EUCLIDIANA SEMEJANZAS Y RELACIONES MÉTRICAS Universidad de Antioquia Profesor: Manuel J. Salazar J. 1. El producto de las medidas de las diagonales de un cuadrilátero inscrito es
TALLER # 4 DE GEOMETRÍA EUCLIDIANA SEMEJANZAS Y RELACIONES MÉTRICAS Universidad de Antioquia Profesor: Manuel J. Salazar J. 1. El producto de las medidas de las diagonales de un cuadrilátero inscrito es
Soluciones Nota nº 2. Problemas propuestos 1. El segmento AC es una diagonal del cuadrado ABCD. Reconstruir el cuadrado.
 Soluciones Nota nº 2 Problemas propuestos 1. El segmento AC es una diagonal del cuadrado ABCD. Reconstruir el cuadrado. Si el segmento AC fuera una diagonal del rectángulo ABCD, que no es cuadrado, es
Soluciones Nota nº 2 Problemas propuestos 1. El segmento AC es una diagonal del cuadrado ABCD. Reconstruir el cuadrado. Si el segmento AC fuera una diagonal del rectángulo ABCD, que no es cuadrado, es
TORNEOS GEOMÉTRICOS 2016 Primera Ronda. Primer Nivel - 5º Año de Escolaridad. Apellido Nombres.. DNI Tu Escuela. Localidad Provincia
 Primer Nivel - 5º Año de Escolaridad 1- En el triángulo rectángulo ABC cuyo ángulo en C mide 48º se trazan la bisectrices de los ángulos B y C, que se cortan en O. Calcula la medida de los ángulos del
Primer Nivel - 5º Año de Escolaridad 1- En el triángulo rectángulo ABC cuyo ángulo en C mide 48º se trazan la bisectrices de los ángulos B y C, que se cortan en O. Calcula la medida de los ángulos del
Cuadriláteros y circunferencia
 CLAVES PARA EMPEZAR Un triángulo isósceles tiene dos lados iguales: b c. Como es rectángulo, se cumple el teorema de Pitágoras: 10 2 b 2 b 2 100 2b 2 b 7,07. Los dos lados miden 7,07 cm cada uno. r A C
CLAVES PARA EMPEZAR Un triángulo isósceles tiene dos lados iguales: b c. Como es rectángulo, se cumple el teorema de Pitágoras: 10 2 b 2 b 2 100 2b 2 b 7,07. Los dos lados miden 7,07 cm cada uno. r A C
TORNEOS GEOMÉTRICOS 2016 Segunda Ronda. Primer Nivel - 5º Año de Escolaridad. Apellido Nombres.. DNI Tu Escuela. Localidad Provincia
 TORNEOS GEOMÉTRICOS 2016 Segunda Ronda Primer Nivel - 5º Año de Escolaridad justificar tus respuestas. hacerla cada participante. 1. Halla la suma de los ángulos marcados en el cuadrilátero inscripto en
TORNEOS GEOMÉTRICOS 2016 Segunda Ronda Primer Nivel - 5º Año de Escolaridad justificar tus respuestas. hacerla cada participante. 1. Halla la suma de los ángulos marcados en el cuadrilátero inscripto en
A 2 TEMA 10. POLÍGONOS ÁREAS Y PERÍMETROS TRIÁNGULOS CUADRILÁTEROS POLÍGONOS REGULARES CIRCUNFERENCIA CÍRCULO TEOREMA DE PITÁGORAS:
 TEMA 10. POLÍGONOS ÁREAS Y PERÍMETROS ELEMENTOS CLASIFICACIÓN TRIÁNGULOS CUADRILÁTEROS POLÍGONOS REGULARES CIRCUNFERENCIA CÍRCULO A b h A b a A perímetro apotema A r TEOREMA DE PITÁGORAS: a b c 1 POLÍGONOS
TEMA 10. POLÍGONOS ÁREAS Y PERÍMETROS ELEMENTOS CLASIFICACIÓN TRIÁNGULOS CUADRILÁTEROS POLÍGONOS REGULARES CIRCUNFERENCIA CÍRCULO A b h A b a A perímetro apotema A r TEOREMA DE PITÁGORAS: a b c 1 POLÍGONOS
ARITMÉTICA. 1. Resolver las siguientes ecuaciones en Q. 2 x + 5. d) ( ) 2. g) 0,86 x 0,73 = 1. x = 1 4 3x. = x + + l) ( ) ( )( ) m) ( )( ) ( ) 2
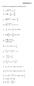 1. Resolver las siguientes ecuaciones en Q. ARITMÉTICA a) b) 3. x + 1 = 3 83 3,90x x = 3 31 c) 0,x + x 4,16 = 6 x + 3 1 + 4 = x + 1 d) ( ) e) f) x x + = 0,3 0, 6x 3 0, 6 1x + 6x = 0,3 8 g) 0,86 x 0,73
1. Resolver las siguientes ecuaciones en Q. ARITMÉTICA a) b) 3. x + 1 = 3 83 3,90x x = 3 31 c) 0,x + x 4,16 = 6 x + 3 1 + 4 = x + 1 d) ( ) e) f) x x + = 0,3 0, 6x 3 0, 6 1x + 6x = 0,3 8 g) 0,86 x 0,73
FORMULARIO (ÁREAS DE FIGURAS PLANAS)
 FORMULARIO (ÁREAS DE FIGURAS PLANAS) Rectángulo Triángulo Paralelogramo Cuadrado Cuadrilátero cuyos lados forman ángulos de 90º. Es la porción de plano limitada por tres segmentos de recta. Cuadrilátero
FORMULARIO (ÁREAS DE FIGURAS PLANAS) Rectángulo Triángulo Paralelogramo Cuadrado Cuadrilátero cuyos lados forman ángulos de 90º. Es la porción de plano limitada por tres segmentos de recta. Cuadrilátero
MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN ÁREA Y PERÍMETRO DE FIGURAS PLANAS Y TEOREMA DE PITÁGORAS
 MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN ÁREA Y PERÍMETRO DE FIGURAS PLANAS Y TEOREMA DE PITÁGORAS ÁREA Y PERÍMETRO DE FIGURAS PLANAS LINEA POLIGONAL: Se llama línea poligonal
MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN ÁREA Y PERÍMETRO DE FIGURAS PLANAS Y TEOREMA DE PITÁGORAS ÁREA Y PERÍMETRO DE FIGURAS PLANAS LINEA POLIGONAL: Se llama línea poligonal
EJERCICIOS MÓDULO 4. Geometría plana. 1) Cuántos vértices tiene un polígono cuyo número total de diagonales es 9?
 Seminario Universitario Matemática EJERCICIOS MÓDULO 4 Geometría plana 1) Cuántos vértices tiene un polígono cuyo número total de diagonales es 9? ) Cuántos lados tiene un polígono en el cual la suma de
Seminario Universitario Matemática EJERCICIOS MÓDULO 4 Geometría plana 1) Cuántos vértices tiene un polígono cuyo número total de diagonales es 9? ) Cuántos lados tiene un polígono en el cual la suma de
Lección 1.1: Perímetro y área. Parte A - Figuras regulares e irregulares
 Unidad 7.5: Geometría Tema 1: Figuras bidimensionales Lección 1.1: Perímetro y área Parte A - Figuras regulares e irregulares Los polígonos Los ángulos son las regiones que forman los lados al cortarse.
Unidad 7.5: Geometría Tema 1: Figuras bidimensionales Lección 1.1: Perímetro y área Parte A - Figuras regulares e irregulares Los polígonos Los ángulos son las regiones que forman los lados al cortarse.
ARITMÉTICA. 1. Resolver las siguientes ecuaciones en Q. 2 x + 5. d) ( x ) ( x ) x = x + = x. l) ( ) ( )( ) + = + + o) ( x ) 2.
 1. Resolver las siguientes ecuaciones en Q. ARITMÉTICA a) b) 3. x + 1 = 3 83 3,90x x = 3 31 c) 0,x + x 4,16 = 6 d) ( x ) ( x ) + 3 1 = + 1 4 e) f) g) x x + = 0,3 0, 6x 3 0, 6 1x + 6x = 0,3 8 0,86x 0,73
1. Resolver las siguientes ecuaciones en Q. ARITMÉTICA a) b) 3. x + 1 = 3 83 3,90x x = 3 31 c) 0,x + x 4,16 = 6 d) ( x ) ( x ) + 3 1 = + 1 4 e) f) g) x x + = 0,3 0, 6x 3 0, 6 1x + 6x = 0,3 8 0,86x 0,73
Cuadrilátero conocido su lado, AB, con la escuadra. Se apoya la escuadra por su hipotenusa sobre la regla y se traza el lado, AB, del cuadrado.
 Elementos geométricos / Cuadrilátero 47 Cuadrilátero conocido su lado, AB, con la escuadra Se apoya la escuadra por su hipotenusa sobre la regla y se traza el lado, AB, del cuadrado. Se desliza hacia arriba
Elementos geométricos / Cuadrilátero 47 Cuadrilátero conocido su lado, AB, con la escuadra Se apoya la escuadra por su hipotenusa sobre la regla y se traza el lado, AB, del cuadrado. Se desliza hacia arriba
TORNEOS GEOMÉTRICOS 2018 Segunda Ronda. Primer Nivel - 5º Año de Escolaridad. Apellido Nombres. Calle..N Piso.Dpto..CP.. Localidad.Provincia.
 TORNEOS GEOMÉTRICOS 2018 Segunda Ronda Primer Nivel - 5º Año de Escolaridad Apellido Nombres. DNI.. Tu Escuela. Tu Domicilio Calle..N Piso.Dpto..CP.. Localidad.Provincia. Lee con atención: 1- Es posible
TORNEOS GEOMÉTRICOS 2018 Segunda Ronda Primer Nivel - 5º Año de Escolaridad Apellido Nombres. DNI.. Tu Escuela. Tu Domicilio Calle..N Piso.Dpto..CP.. Localidad.Provincia. Lee con atención: 1- Es posible
2. De acuerdo a lo determinado en el numeral anterior, alguno de los polígonos es simple?. Justifique su respuesta.
 8.16 EJERCICIOS PROPUESTOS Temas: Poligonal. Polígonos. Cuadriláteros convexos. 1. En las figuras siguientes B está entre A y C; K, está entre S y M; D, H, V, T son colineales. O está entre P y Q y O está
8.16 EJERCICIOS PROPUESTOS Temas: Poligonal. Polígonos. Cuadriláteros convexos. 1. En las figuras siguientes B está entre A y C; K, está entre S y M; D, H, V, T son colineales. O está entre P y Q y O está
FIGURAS GEOMETRICAS PLANAS
 UNIDAD 9 FIGURAS GEOMETRICAS PLANAS Objetivo General Al terminar esta Unidad entenderás y aplicaras los conceptos generales de las figuras geométricas planas, y resolverás ejercicios y problemas con figuras
UNIDAD 9 FIGURAS GEOMETRICAS PLANAS Objetivo General Al terminar esta Unidad entenderás y aplicaras los conceptos generales de las figuras geométricas planas, y resolverás ejercicios y problemas con figuras
Plan de Animación para la enseñanza de las Matemáticas
 FIGURAS PLANAS CÓMO DETERMINAR AREAS DE FIGURAS PLANAS Las FIGURAS PLANAS son aquellas que están limitadas por líneas rectas o curvas, además de que todos sus puntos están contenidos en un solo plano.
FIGURAS PLANAS CÓMO DETERMINAR AREAS DE FIGURAS PLANAS Las FIGURAS PLANAS son aquellas que están limitadas por líneas rectas o curvas, además de que todos sus puntos están contenidos en un solo plano.
Semejanza. Razones. Teorema de Thales. Proporciones. a = b. c d
 Semejanza Razones Razones y proporciones Teorema de Thales Triángulos semejantes Teoremas de semejanza Teoremas de Euclides Perímetro y Área a) Razón. Es el cuociente entre dos números (positivos). b)
Semejanza Razones Razones y proporciones Teorema de Thales Triángulos semejantes Teoremas de semejanza Teoremas de Euclides Perímetro y Área a) Razón. Es el cuociente entre dos números (positivos). b)
Bloque 33 Guía: Ubicación de puntos, distancia y longitudes en el plano cartesiano SGUICEG047EM33-A17V1
 SGUICEG047EM33-A17V1 Bloque 33 Guía: Ubicación de puntos, distancia longitudes en el plano cartesiano TABLA DE CORRECCIÓN UBICACIÓN DE PUNTOS, DISTANCIAS Y LONGITUDES EN EL PLANO CARTESIANO N Clave Dificultad
SGUICEG047EM33-A17V1 Bloque 33 Guía: Ubicación de puntos, distancia longitudes en el plano cartesiano TABLA DE CORRECCIÓN UBICACIÓN DE PUNTOS, DISTANCIAS Y LONGITUDES EN EL PLANO CARTESIANO N Clave Dificultad
4. Resolver un triángulo rectángulo e isósceles en el que la hipotenusa tiene 9 pies de longitud.
 7 CAPÍTULO SIETE Ejercicios propuestos 7.5 Triángulos 1. Construya de ser posible los siguientes triángulos ABC. En caso de que existan, determine sus cuatro puntos característicos empleando regla y compás.
7 CAPÍTULO SIETE Ejercicios propuestos 7.5 Triángulos 1. Construya de ser posible los siguientes triángulos ABC. En caso de que existan, determine sus cuatro puntos característicos empleando regla y compás.
1. Encuentra cuánto vale el ángulo exterior θ en la siguiente figura si son conocidos los ángulos α y β. El ángulo θ se llama ángulo exterior en C.
 1. Encuentra cuánto vale el ángulo exterior θ en la siguiente figura si son conocidos los ángulos α y β. El ángulo θ se llama ángulo exterior en C. 2. En un triángulo rectángulo, los ángulos agudos están
1. Encuentra cuánto vale el ángulo exterior θ en la siguiente figura si son conocidos los ángulos α y β. El ángulo θ se llama ángulo exterior en C. 2. En un triángulo rectángulo, los ángulos agudos están
ACTIVIDADES PROPUESTAS
 GEOMETRÍA DINÁMICA ACTIVIDADES PROPUESTAS 1. Dibujar un pentágono y trazar sus diagonales. 2. A partir de una circunferencia c y de un punto exterior A, trazar la circunferencia que tiene centro en el
GEOMETRÍA DINÁMICA ACTIVIDADES PROPUESTAS 1. Dibujar un pentágono y trazar sus diagonales. 2. A partir de una circunferencia c y de un punto exterior A, trazar la circunferencia que tiene centro en el
TALLER # 5 de GEOMETRÍA EUCLIDIANA ÁREAS Y VOLÚMENES. Universidad de Antioquia. Departamento de Matemáticas. Septiembre 2008
 TALLER # 5 de GEOMETRÍA EUCLIDIANA ÁREAS Y VOLÚMENES Universidad de Antioquia Departamento de Matemáticas Septiembre 2008 1. Sea ABCD un rectángulo, E punto medio de, a) Calcular el área del rectángulo
TALLER # 5 de GEOMETRÍA EUCLIDIANA ÁREAS Y VOLÚMENES Universidad de Antioquia Departamento de Matemáticas Septiembre 2008 1. Sea ABCD un rectángulo, E punto medio de, a) Calcular el área del rectángulo
donde n es el numero de lados. n APOTEMA: Es la altura de un triangulo formado por el centro del polígono regular y dos vértices consecutivos.
 Polígonos regulares 1 POLIGONOS REGULARES DEFINICION: Un polígono regular es el que tiene todos sus lados y sus ángulos congruentes. DEFINICION: Un polígono esta inscrito en una circunferencia si sus vértices
Polígonos regulares 1 POLIGONOS REGULARES DEFINICION: Un polígono regular es el que tiene todos sus lados y sus ángulos congruentes. DEFINICION: Un polígono esta inscrito en una circunferencia si sus vértices
TORNEO DE PRIMAVERA CUENCA DEL PLATA PRIMER NIVEL Primera Prueba
 TORNEO DE PRIMAVERA 2012 CUENCA DEL PLATA PRIMER NIVEL Primera Prueba Lee con atención: 1- Es posible consultar libros o apuntes y usar calculadora. 2- Solamente se pueden usar los elementos propios. 3-
TORNEO DE PRIMAVERA 2012 CUENCA DEL PLATA PRIMER NIVEL Primera Prueba Lee con atención: 1- Es posible consultar libros o apuntes y usar calculadora. 2- Solamente se pueden usar los elementos propios. 3-
Geometría básica Autor: Noelia Torres Costa
 Geometría básica Autor: Noelia Torres Costa 1 Presentación del curso La Geometría es una de las ramas de las Matemáticas más atractivas para estudiar. Aunque no lo parezca, todo nuestro entorno está lleno
Geometría básica Autor: Noelia Torres Costa 1 Presentación del curso La Geometría es una de las ramas de las Matemáticas más atractivas para estudiar. Aunque no lo parezca, todo nuestro entorno está lleno
Olimpiadas de Matemáticas
 Taller Áreas 1. En la figura, el cuadrado P QRS es 3 3. Los puntos T y U, estan sobre el lado QR de tal forma que QT = T U = UR = 1. Los puntos V y W, estan sobre el lado RS de tal forma que RV = V W =
Taller Áreas 1. En la figura, el cuadrado P QRS es 3 3. Los puntos T y U, estan sobre el lado QR de tal forma que QT = T U = UR = 1. Los puntos V y W, estan sobre el lado RS de tal forma que RV = V W =
Guía Nº 3. CONTENIDOS: Perímetro y Área Nombre: Marque la alternativa correcta. Realice sus cálculos al costado de cada ejercicio.
 SUBSECTOR : Electivo de Álgebra y Geometría NIVELES : IIIº/VIº Medio PROFESORES : Martín Andrés Martínez Santana AÑO : 017 CONTENIDOS: Perímetro y Área Nombre: Guía Nº IIIº/IV Marque la alternativa correcta.
SUBSECTOR : Electivo de Álgebra y Geometría NIVELES : IIIº/VIº Medio PROFESORES : Martín Andrés Martínez Santana AÑO : 017 CONTENIDOS: Perímetro y Área Nombre: Guía Nº IIIº/IV Marque la alternativa correcta.
FIGURAS PLANAS. Es una figura plana delimitada por una línea poligonal cerrada.
 1.- Qué es un polígono? FIGURAS PLANAS Es una figura plana delimitada por una línea poligonal cerrada. Los elementos de un polígono son: - Lado: Se llama lado a cada segmento que limita un polígono - Vértice:
1.- Qué es un polígono? FIGURAS PLANAS Es una figura plana delimitada por una línea poligonal cerrada. Los elementos de un polígono son: - Lado: Se llama lado a cada segmento que limita un polígono - Vértice:
SOLUCIONES A LAS ACTIVIDADES DE CADA EPÍGRAFE
 Pág. 1 PÁGINA 232 REFLEXIONA Para decidir el tipo de suelo que se pondrá en la Casa de la Cultura, hay varios mosaicos. Estos mosaicos tienen cinco tipos de losetas: Todas estas losetas son cuadriláteros.
Pág. 1 PÁGINA 232 REFLEXIONA Para decidir el tipo de suelo que se pondrá en la Casa de la Cultura, hay varios mosaicos. Estos mosaicos tienen cinco tipos de losetas: Todas estas losetas son cuadriláteros.
Mª Rosa Villegas Pérez
 Mª Rosa Villegas Pérez FIGURAS PLANAS G.T. Elaboración de Materiales y Recursos Didácticos en un Centro TIC. Polígonos.- / 14 POLÍGONOS Un polígono es una figura plana y cerrada formada al unir tres o
Mª Rosa Villegas Pérez FIGURAS PLANAS G.T. Elaboración de Materiales y Recursos Didácticos en un Centro TIC. Polígonos.- / 14 POLÍGONOS Un polígono es una figura plana y cerrada formada al unir tres o
RAZONAMIENTO GEOMÉTRICO
 RAZONAMIENTO GEOMÉTRICO Fundamentos de Matemáticas I Razonamiento geométrico Video Previo a la actividad: Áreas y perímetros de cuerpos y figuras planas Video Previo a la actividad: Áreas y perímetros
RAZONAMIENTO GEOMÉTRICO Fundamentos de Matemáticas I Razonamiento geométrico Video Previo a la actividad: Áreas y perímetros de cuerpos y figuras planas Video Previo a la actividad: Áreas y perímetros
Tema 2 2 Geometría métrica en el pla no
 Tema Geometría métrica en el pla no CONCEPTOS BÁSICOS Figuras básicas en el plano: puntos, rectas, semirrectas, segmentos y ángulos Los polígonos y su clasificación según los ángulos internos y según el
Tema Geometría métrica en el pla no CONCEPTOS BÁSICOS Figuras básicas en el plano: puntos, rectas, semirrectas, segmentos y ángulos Los polígonos y su clasificación según los ángulos internos y según el
DIBUJO TÉCNICO BACHILLERATO TRABAJOS - LÁMINAS TEMA 3. POLÍGONOS. Departamento de Artes Plásticas y Dibujo
 DIBUJO TÉCNICO BACHILLERATO TRABAJOS - LÁMINAS TEMA 3. POLÍGONOS. Departamento de Artes Plásticas y Dibujo 1. Construir un triángulo equilátero conocida la altura. 2. Construir un triángulo isósceles conocida
DIBUJO TÉCNICO BACHILLERATO TRABAJOS - LÁMINAS TEMA 3. POLÍGONOS. Departamento de Artes Plásticas y Dibujo 1. Construir un triángulo equilátero conocida la altura. 2. Construir un triángulo isósceles conocida
Problemas y ejercicios de áreas de polígonos
 Problemas y ejercicios de áreas de polígonos 1Un campo rectangular tiene 170 m de base y 28 m de altura. Calcular: 1Las hectáreas que tiene. 2El precio del campo si el metro cuadrado cuesta 15. 2 Calcula
Problemas y ejercicios de áreas de polígonos 1Un campo rectangular tiene 170 m de base y 28 m de altura. Calcular: 1Las hectáreas que tiene. 2El precio del campo si el metro cuadrado cuesta 15. 2 Calcula
Unidad nº 6 Figuras planas 13
 Unidad nº 6 Figuras planas 13 Cuestiones 3 1 Puede ser que la suma de los ángulos de un polígono sea 40º Justifica tu respuesta. Debería cumplirse 180º (n ) = 40º, que no se cumple para ningún valor entero
Unidad nº 6 Figuras planas 13 Cuestiones 3 1 Puede ser que la suma de los ángulos de un polígono sea 40º Justifica tu respuesta. Debería cumplirse 180º (n ) = 40º, que no se cumple para ningún valor entero
TRIÁNGULOS Y CUADRILÁTEROS
 TEMA 8.- POLÍGONOS TRIÁNGULOS Y CUADRILÁTEROS 1.- POLÍGONOS.- La definición de polígono viene dada por POLI= varios y GONO= ángulo. Clasificación de los polígonos según el número de lados: así son los
TEMA 8.- POLÍGONOS TRIÁNGULOS Y CUADRILÁTEROS 1.- POLÍGONOS.- La definición de polígono viene dada por POLI= varios y GONO= ángulo. Clasificación de los polígonos según el número de lados: así son los
Cuaderno: LIMPIEZA Y ORGANIZACIÓN Realización de TAREAS TEMA 12 FIGURAS PLANAS Y ESPACIALES ALUMNO/A: Nº
 Cuaderno: LIMPIEZA Y ORGANIZACIÓN Realización de TAREAS SATISFACTORIO ACEPTABLE MEJORABLE TEMA 12 FIGURAS PLANAS Y ESPACIALES ALUMNO/A: Nº Ejercicios TEMA 12 FIGURAS PLANAS Y ESPACIALES (1º ESO) Página
Cuaderno: LIMPIEZA Y ORGANIZACIÓN Realización de TAREAS SATISFACTORIO ACEPTABLE MEJORABLE TEMA 12 FIGURAS PLANAS Y ESPACIALES ALUMNO/A: Nº Ejercicios TEMA 12 FIGURAS PLANAS Y ESPACIALES (1º ESO) Página
Á REAS Y PERÍMETROS DE FIGURAS SENCILLAS
 Pág. 1 Á REAS Y PERÍMETROS DE FIGURAS SENCILLAS Halla el área y el perímetro de las figuras coloreadas de los siguientes ejercicios: 1 a) b) 5 dm 4 cm 2 cm 5 cm 8 cm 2 a) b) 5 m 8 m 17 m 15 m 3 a) b) 5
Pág. 1 Á REAS Y PERÍMETROS DE FIGURAS SENCILLAS Halla el área y el perímetro de las figuras coloreadas de los siguientes ejercicios: 1 a) b) 5 dm 4 cm 2 cm 5 cm 8 cm 2 a) b) 5 m 8 m 17 m 15 m 3 a) b) 5
TORNEOS DE LAS CUENCAS - TORNEO DE PRIMAVERA SOLUCIONES
 TORNEOS DE LAS CUENCAS - TORNEO DE PRIMAVERA 2012 SOLUCIONES PRIMER NIVEL (Primera Prueba) Problema 1-Dado que la suma de los ángulos interiores de un triángulo es 180º, en el triángulo de la figura el
TORNEOS DE LAS CUENCAS - TORNEO DE PRIMAVERA 2012 SOLUCIONES PRIMER NIVEL (Primera Prueba) Problema 1-Dado que la suma de los ángulos interiores de un triángulo es 180º, en el triángulo de la figura el
Problemas Propuestos
 Problemas Propuestos 1. Dos planos paralelos, a 4cm de distancia uno del otro y con la inclinación indicada en la figura, seccionan un cilindro de cm de radio en su base. Hallar el volumen del cuerpo limitado
Problemas Propuestos 1. Dos planos paralelos, a 4cm de distancia uno del otro y con la inclinación indicada en la figura, seccionan un cilindro de cm de radio en su base. Hallar el volumen del cuerpo limitado
Elementos del cilindro
 Definición de cilindro Un cilindro es un cuerpo geométrico engendrado por un rectángulo que gira alrededor de uno de sus lados. Desarrollo del cilindro Elementos del cilindro Eje Es el lado fijo alrededor
Definición de cilindro Un cilindro es un cuerpo geométrico engendrado por un rectángulo que gira alrededor de uno de sus lados. Desarrollo del cilindro Elementos del cilindro Eje Es el lado fijo alrededor
LA RECTA Y SUS ECUACIONES
 UNIDAD 1 LA RECTA Y SUS ECUACIONES PROBLEMAS PROPUESTOS Objetivo general. Al terminar esta Unidad resolverás ejercicios y problemas correspondientes a las rectas en el plano y sus ecuaciones. Objetivos
UNIDAD 1 LA RECTA Y SUS ECUACIONES PROBLEMAS PROPUESTOS Objetivo general. Al terminar esta Unidad resolverás ejercicios y problemas correspondientes a las rectas en el plano y sus ecuaciones. Objetivos
13Soluciones a los ejercicios y problemas PÁGINA 250
 PÁGINA 50 Pág. 1 Á REAS Y PERÍMETROS DE FIGURAS SENCILLAS Halla el área y el perímetro de las figuras coloreadas de los siguientes ejercicios: 1 a) b) 5 dm 4 cm cm 5 cm 8 cm a) 5 5 dm b) 8 8 cm P 5 4 0
PÁGINA 50 Pág. 1 Á REAS Y PERÍMETROS DE FIGURAS SENCILLAS Halla el área y el perímetro de las figuras coloreadas de los siguientes ejercicios: 1 a) b) 5 dm 4 cm cm 5 cm 8 cm a) 5 5 dm b) 8 8 cm P 5 4 0
Tema 8. Teorema de Pitágoras. Semejanza
 Material necesario: Escuadra Cartabón Regla Transportador de ángulos Compás Calculadora Libro de texto nuevo!!!!!!!!!!!!!! Tema 8. Teorema de Pitágoras. Semejanza 8.1 Teorema de Pitágoras Página 17 Actividades
Material necesario: Escuadra Cartabón Regla Transportador de ángulos Compás Calculadora Libro de texto nuevo!!!!!!!!!!!!!! Tema 8. Teorema de Pitágoras. Semejanza 8.1 Teorema de Pitágoras Página 17 Actividades
OLIMPÍADA POPULAR ESTUDIANTIL DE MATEMÁTICA TEMARIO DE ENSEÑANZA PREUNIVERSITARIA CURSO
 OLIMPÍADA POPULAR ESTUDIANTIL DE MATEMÁTICA TEMARIO DE ENSEÑANZA PREUNIVERSITARIA CURSO 00 00 Los estudiantes de 0mo grado deben resolver los problemas al 4 Los estudiantes de no grado deben resolver los
OLIMPÍADA POPULAR ESTUDIANTIL DE MATEMÁTICA TEMARIO DE ENSEÑANZA PREUNIVERSITARIA CURSO 00 00 Los estudiantes de 0mo grado deben resolver los problemas al 4 Los estudiantes de no grado deben resolver los
. M odulo 7 Geometr ıa Gu ıa de Ejercicios
 . Módulo 7 Geometría Guía de Ejercicios Índice Unidad I. Conceptos y elementos de geometría. Ejercicios Resueltos... pág. 02 Ejercicios Propuestos... pág. 09 Unidad II. Áreas y perímetros de figuras planas.
. Módulo 7 Geometría Guía de Ejercicios Índice Unidad I. Conceptos y elementos de geometría. Ejercicios Resueltos... pág. 02 Ejercicios Propuestos... pág. 09 Unidad II. Áreas y perímetros de figuras planas.
Geometría. Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid
 Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
Geometría. Ángulos. Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid
 Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
TALLER 3 GEOMETRÍA VECTORIAL Y ANALÍTICA FACULTAD DE INGENIERÍA UNIVERSIDAD DE ANTIOQUIA
 TALLER GEOMETRÍA VECTORIAL Y ANALÍTICA FACULTAD DE INGENIERÍA UNIVERSIDAD DE ANTIOQUIA. 20-2 Profesor: Jaime Andres Jaramillo González Parte del material ha sido tomado de documentos de los profesores
TALLER GEOMETRÍA VECTORIAL Y ANALÍTICA FACULTAD DE INGENIERÍA UNIVERSIDAD DE ANTIOQUIA. 20-2 Profesor: Jaime Andres Jaramillo González Parte del material ha sido tomado de documentos de los profesores
12Soluciones a los ejercicios y problemas
 Soluciones a los ejercicios y problemas PÁGINA 9 Pág. P RACTICA Puntos Si los puntos 6 6 y son vértices de un cuadrado cuál es el cuarto vértice? 6 6 P P Los puntos y son vértices de un paralelogramo.
Soluciones a los ejercicios y problemas PÁGINA 9 Pág. P RACTICA Puntos Si los puntos 6 6 y son vértices de un cuadrado cuál es el cuarto vértice? 6 6 P P Los puntos y son vértices de un paralelogramo.
Geometría. Problemas de Semejanza. Olimpiada de Matemáticas en Tamaulipas
 Geometría Problemas de Semejanza Olimpiada de Matemáticas en Tamaulipas 1. Problemas Antes de comenzar con los problemas, es conveniente recordar o asegurarse que los olímpicos tienen presentes el tema
Geometría Problemas de Semejanza Olimpiada de Matemáticas en Tamaulipas 1. Problemas Antes de comenzar con los problemas, es conveniente recordar o asegurarse que los olímpicos tienen presentes el tema
PROBLEMAS DE POLÍGONOS.
 PROBLEMAS DE POLÍGONOS. 1. Construir un rombo sabiendo que: El punto M divide al segmento, en cuyos extremos se encuentran los focos de la elipse que pasa por A, en la razón 4/5. El punto M está más cerca
PROBLEMAS DE POLÍGONOS. 1. Construir un rombo sabiendo que: El punto M divide al segmento, en cuyos extremos se encuentran los focos de la elipse que pasa por A, en la razón 4/5. El punto M está más cerca
SOLUCIÓN PRIMERA ELIMINATORIA NACIONAL NIVEL C
 XXIV OLIMPIADA COSTARRICENSE DE MATEMÁTICA MEP ITCR UCR UNA UNED - MICIT SOLUCIÓN PRIMERA ELIMINATORIA NACIONAL NIVEL C 01 1. Un factor de la factorización completa de corresponde a mx y + 9y m x y x 4
XXIV OLIMPIADA COSTARRICENSE DE MATEMÁTICA MEP ITCR UCR UNA UNED - MICIT SOLUCIÓN PRIMERA ELIMINATORIA NACIONAL NIVEL C 01 1. Un factor de la factorización completa de corresponde a mx y + 9y m x y x 4
CICLO ESCOLAR: SEMESTRE: ENERO JUNIO 2018 ACTIVIDAD DE INTEGRADORA ETAPA 2 DE MATEMÁTICAS II FECHA: MARZO 2018
 UANL UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN CICLO ESCOLAR: 2017 2018 SEMESTRE: ENERO JUNIO 2018 ACTIVIDAD DE INTEGRADORA ETAPA 2 DE MATEMÁTICAS II FECHA: MARZO 2018 ELABORÓ: ACADEMIA DE MATEMÁTICAS SEGUNDO
UANL UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN CICLO ESCOLAR: 2017 2018 SEMESTRE: ENERO JUNIO 2018 ACTIVIDAD DE INTEGRADORA ETAPA 2 DE MATEMÁTICAS II FECHA: MARZO 2018 ELABORÓ: ACADEMIA DE MATEMÁTICAS SEGUNDO
Tema 10: Problemas métricos en el plano
 Tema 10: Problemas métricos en el plano 10.1 Relaciones angulares Construye un polígono de cinco lados, divídelo en triángulos para averiguar la suma de los ángulos interiores del pentágono. Nuestro pentágono
Tema 10: Problemas métricos en el plano 10.1 Relaciones angulares Construye un polígono de cinco lados, divídelo en triángulos para averiguar la suma de los ángulos interiores del pentágono. Nuestro pentágono
2.-GEOMETRÍA PLANA O EUCLIDIANA
 2.-GEOMETRÍA PLANA O EUCLIDIANA 2.2.-Cuadriláteros. Definición, clasificación y notación. Clasificación de los cuadriláteros: Paralelogramos y no paralelogramos. Los cuadriláteros son los polígonos de
2.-GEOMETRÍA PLANA O EUCLIDIANA 2.2.-Cuadriláteros. Definición, clasificación y notación. Clasificación de los cuadriláteros: Paralelogramos y no paralelogramos. Los cuadriláteros son los polígonos de
open green road Guía Matemática CUADRILÁTEROS tutora: Jacky Moreno .co
 Guía Matemática CUADRILÁTEROS tutora: Jacky Moreno.co 1. Polígonos Epistemológicamente, la palabra polígono significa muchos ángulos. Los polígonos son figuras cerradas planas que están formadas por la
Guía Matemática CUADRILÁTEROS tutora: Jacky Moreno.co 1. Polígonos Epistemológicamente, la palabra polígono significa muchos ángulos. Los polígonos son figuras cerradas planas que están formadas por la
Tutorial MT-b10. Matemática Tutorial Nivel Básico. Cuadriláteros
 134567890134567890 M ate m ática Tutorial MT-b10 Matemática 006 Tutorial Nivel Básico Cuadriláteros Matemática 006 Tutorial Cuadriláteros Marco teórico: 1. Definición: Polígono de cuatro lados, cuya suma
134567890134567890 M ate m ática Tutorial MT-b10 Matemática 006 Tutorial Nivel Básico Cuadriláteros Matemática 006 Tutorial Cuadriláteros Marco teórico: 1. Definición: Polígono de cuatro lados, cuya suma
EF AB. Hallar la longitud del segmento BE si AC+BD+CE+DF=30. 3 a) 10 b) 14 c) 20 d) 8 e) Ning.
 UNIVERSIDAD MAYOR DE SAN SIMÓN FACULTAD DE CIENCIAS Y TECNOLOGÍA CURSO PREFACULTATIVO GESTIÓN II-2012 PRÁCTICA Nº 1 GEOMETRÍA 1. Sobre una línea recta se consideran los puntos consecutivos A, B y C; luego
UNIVERSIDAD MAYOR DE SAN SIMÓN FACULTAD DE CIENCIAS Y TECNOLOGÍA CURSO PREFACULTATIVO GESTIÓN II-2012 PRÁCTICA Nº 1 GEOMETRÍA 1. Sobre una línea recta se consideran los puntos consecutivos A, B y C; luego
( 2) 1. Simplificar las siguientes expresiones usando propiedades de la potenciación: a) f) 5 0 b) 2 6 : 2 3 g) 2 4.
 DO AÑO. 014 TRABAJO PRÁCTICO 0 1. Simplificar las siguientes expresiones usando propiedades de la potenciación: a) 5.. f) 5 0 b) 6 : g) 4. - + c) 5-5. 5 h) 5 d) ( 5 ) 5 i) e) Esta Guía 0 contiene los prerrequisitos
DO AÑO. 014 TRABAJO PRÁCTICO 0 1. Simplificar las siguientes expresiones usando propiedades de la potenciación: a) 5.. f) 5 0 b) 6 : g) 4. - + c) 5-5. 5 h) 5 d) ( 5 ) 5 i) e) Esta Guía 0 contiene los prerrequisitos
TALLER 3 GEOMETRÍA VECTORIAL Y ANALÍTICA FACULTAD DE INGENIERÍA UNIVERSIDAD DE ANTIOQUIA
 TALLER GEOMETRÍA VECTORIAL Y ANALÍTICA FACULTAD DE INGENIERÍA UNIVERSIDAD DE ANTIOQUIA. 20-2 Profesor: Jaime Andrés Jaramillo González (jaimeaj@conceptocomputadores.com) Parte del material ha sido tomado
TALLER GEOMETRÍA VECTORIAL Y ANALÍTICA FACULTAD DE INGENIERÍA UNIVERSIDAD DE ANTIOQUIA. 20-2 Profesor: Jaime Andrés Jaramillo González (jaimeaj@conceptocomputadores.com) Parte del material ha sido tomado
MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN CLASE #3
 MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN CLASE #3 ÁREA Y PERÍMETRO DE FIGURAS PLANAS LINEA POLIGONAL: Se llama línea poligonal a la gura formada por la unión de segmentos de
MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN CLASE #3 ÁREA Y PERÍMETRO DE FIGURAS PLANAS LINEA POLIGONAL: Se llama línea poligonal a la gura formada por la unión de segmentos de
UNIDAD 8 Geometría analítica
 Pág. 1 de 5 I. Sabes hallar puntos medios de segmentos, puntos simétricos de otros y ver si varios puntos están alineados? 1 Los puntos A( 1, 3), B(2, 6), C (7, 2) y D( 5, 3) son vértices de un cuadrilátero.
Pág. 1 de 5 I. Sabes hallar puntos medios de segmentos, puntos simétricos de otros y ver si varios puntos están alineados? 1 Los puntos A( 1, 3), B(2, 6), C (7, 2) y D( 5, 3) son vértices de un cuadrilátero.
POLIGONOS. Nº DE LADOS NOMBRE 3 Triángulos 4 Cuadriláteros 5 Pentágonos 6 Hexágonos 7 Heptágonos 8 Octógonos 9 Eneágonos 10 Decágonos
 1 POLIGONO POLIGONOS Polígono es la superficie plana limitada por una línea poligonal cerrada. Lados Vértices Polígono regular es el que tiene todos sus lados y ángulos iguales, mientras que polígono irregular
1 POLIGONO POLIGONOS Polígono es la superficie plana limitada por una línea poligonal cerrada. Lados Vértices Polígono regular es el que tiene todos sus lados y ángulos iguales, mientras que polígono irregular
III: Geometría para maestros. Capitulo 1: Figuras geométricas
 III: Geometría para maestros. Capitulo : Figuras geométricas SELECCIÓN DE EJERCICIOS RESUELTOS SITUACIONES INTRODUCTORIAS En un libro de primaria encontramos este enunciado: Dibuja un polígono convexo
III: Geometría para maestros. Capitulo : Figuras geométricas SELECCIÓN DE EJERCICIOS RESUELTOS SITUACIONES INTRODUCTORIAS En un libro de primaria encontramos este enunciado: Dibuja un polígono convexo
TEMA 10: FORMAS Y FIGURAS PLANAS. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco.
 2009 TEMA 10: FORMAS Y FIGURAS PLANAS. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco. Manuel González de León. mgdl 01/01/2009 TEMA 10: FORMAS Y FIGURAS PLANAS. 1. Polígonos. 2.
2009 TEMA 10: FORMAS Y FIGURAS PLANAS. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco. Manuel González de León. mgdl 01/01/2009 TEMA 10: FORMAS Y FIGURAS PLANAS. 1. Polígonos. 2.
Figuras planas. Definiciones
 Figuras planas Definiciones Polígono: definición Un polígono es una figura plana (yace en un plano) cerrada por tres o más segmentos. Los lados de un polígono son cada uno de los segmentos que delimitan
Figuras planas Definiciones Polígono: definición Un polígono es una figura plana (yace en un plano) cerrada por tres o más segmentos. Los lados de un polígono son cada uno de los segmentos que delimitan
Nivel: A partir de 4ESO. Solución: La relación entre la apotema y el lado del hexágono es la misma que entre la altura y
 Página 1 de 9 SOLUCIONES MAYO 2017 Soluciones extraídas de los libros: XVI CONCURSO DE PRIMAVERA 2012 XVII CONCURSO DE PRIMAVERA 2013 Obtenibles en http://www.concursoprimavera.es#libros AUTORES: Colectivo
Página 1 de 9 SOLUCIONES MAYO 2017 Soluciones extraídas de los libros: XVI CONCURSO DE PRIMAVERA 2012 XVII CONCURSO DE PRIMAVERA 2013 Obtenibles en http://www.concursoprimavera.es#libros AUTORES: Colectivo
XX OLIMPIADA NACIONAL DE MATEMÁTICA SEGUNDA RONDA COLEGIAL - 1 DE AGOSTO DE NIVEL 1. Nombre y Apellido:... Grado:... Sección:...
 SEGUNDA RONDA COLEGIAL - 1 DE AGOSTO DE 2008 - NIVEL 1 Nombre y Apellido:................................. Grado:....... Sección:...... Puntaje:.......... Los dibujos correspondientes a los problemas de
SEGUNDA RONDA COLEGIAL - 1 DE AGOSTO DE 2008 - NIVEL 1 Nombre y Apellido:................................. Grado:....... Sección:...... Puntaje:.......... Los dibujos correspondientes a los problemas de
Seminario de problemas-eso. Curso Hoja 14
 Seminario de problemas-eso. Curso 011-1. Hoja 14 6. Determina el valor de m tal que la ecuación en x x 4 (3m + )x + m = 0 tenga cuatro raíces en progresión aritmética. Como la suma de las cuatro raíces
Seminario de problemas-eso. Curso 011-1. Hoja 14 6. Determina el valor de m tal que la ecuación en x x 4 (3m + )x + m = 0 tenga cuatro raíces en progresión aritmética. Como la suma de las cuatro raíces
ÁNGULOS. 2. En el triángulo ABC, el ángulo B se obtiene aumentando en 50% el ángulo A o también reduciendo en 25% el ángulo C. Cuál es la medida de B?
 ENTRENAMIENTO COMPETENCIA COTORRA 2015 GEOMETRÍA (PROBLEMAS INTRODUCTORIOS) IIS AMIR MADRID GARZÓN Enero / 2015 ÁNGULOS 1. Cuántos ángulos hay en la siguiente figura? a) 13 b) 14 c) 21 d) 18 2. En el triángulo
ENTRENAMIENTO COMPETENCIA COTORRA 2015 GEOMETRÍA (PROBLEMAS INTRODUCTORIOS) IIS AMIR MADRID GARZÓN Enero / 2015 ÁNGULOS 1. Cuántos ángulos hay en la siguiente figura? a) 13 b) 14 c) 21 d) 18 2. En el triángulo
8 GEOMETRÍA DEL PLANO
 8 GEOMETRÍ DEL PLNO EJERIIOS PR ENTRENRSE Ángulos y triángulos 8.6 Halla la medida del ángulo p en el siguiente triángulo. 6 4 180 6 p 4 p 180 6 4 11 8.7 alcula la suma de los ángulos interiores de un
8 GEOMETRÍ DEL PLNO EJERIIOS PR ENTRENRSE Ángulos y triángulos 8.6 Halla la medida del ángulo p en el siguiente triángulo. 6 4 180 6 p 4 p 180 6 4 11 8.7 alcula la suma de los ángulos interiores de un
a) Las mediatrices de un triángulo se cortan en un punto llamado... b) Las bisectrices de un triángulo se cortan en un punto llamado...
 Geometría Plana 3º E.S.O. PARTE TEÓRICA 1.- Define para un triángulo los siguientes conceptos: Mediatriz: Bisectriz: Mediana: Altura: 2.- Completa las siguientes frases: a) Las mediatrices de un triángulo
Geometría Plana 3º E.S.O. PARTE TEÓRICA 1.- Define para un triángulo los siguientes conceptos: Mediatriz: Bisectriz: Mediana: Altura: 2.- Completa las siguientes frases: a) Las mediatrices de un triángulo
POLÍGONOS POLÍGONOS. APM Página 1
 POLÍGONOS 1. Polígonos. 1.1. Elementos de un polígono. 1.2. Suma de los ángulos interiores de un polígono. 1.3. Diagonales de un polígono. 1.4. Clasificación de los polígonos. 2. Polígonos regulares. Elementos.
POLÍGONOS 1. Polígonos. 1.1. Elementos de un polígono. 1.2. Suma de los ángulos interiores de un polígono. 1.3. Diagonales de un polígono. 1.4. Clasificación de los polígonos. 2. Polígonos regulares. Elementos.
NIVEL 6 CÓDIGO SECCIÓN 1: ALTERNATIVA MÚLTIPLE. Cuántos números de 4 dígitos hay de la forma a99b que sean divisibles entre 54?
 Problema 1. Cuántos números de 4 dígitos hay de la forma a99b que sean divisibles entre 54? A. 3 B. 4 C. 5 6 Como 54 = 2 27 = 2 3 3, 9 tiene que dividir a a99b, luego 9 divide a a + b. Además 2 divide
Problema 1. Cuántos números de 4 dígitos hay de la forma a99b que sean divisibles entre 54? A. 3 B. 4 C. 5 6 Como 54 = 2 27 = 2 3 3, 9 tiene que dividir a a99b, luego 9 divide a a + b. Además 2 divide
MATEMÁTICA-PRIMER AÑO REVISIÓN INTEGRADORA. A) Reproduce la siguiente figura, luego trace las bisectrices de los ángulos ACD y BCD.
 Universidad de Buenos Aires Instituto Libre de Segunda Enseñanza MATEMÁTICA-PRIMER AÑO REVISIÓN INTEGRADORA Construcciones con regla no graduada y compás A) Reproduce la siguiente figura, luego trace las
Universidad de Buenos Aires Instituto Libre de Segunda Enseñanza MATEMÁTICA-PRIMER AÑO REVISIÓN INTEGRADORA Construcciones con regla no graduada y compás A) Reproduce la siguiente figura, luego trace las
SOLUCIONES SEPTIEMBRE 2016
 Página de 9 SOLUCIONES SEPTIEMBRE 206 Soluciones extraídas de los libros: XII CONCURSO DE PRIMAVERA 2008 XV CONCURSO DE PRIMAVERA 20 XVI CONCURSO DE PRIMAVERA 202 Obtenibles en http://www.concursoprimavera.es#libros
Página de 9 SOLUCIONES SEPTIEMBRE 206 Soluciones extraídas de los libros: XII CONCURSO DE PRIMAVERA 2008 XV CONCURSO DE PRIMAVERA 20 XVI CONCURSO DE PRIMAVERA 202 Obtenibles en http://www.concursoprimavera.es#libros
Fundación Uno. 2. En la figura, BD es una altura del triángulo ABC. Cuál es el valor de b a?
 ENCUENTRO # 51 TEMA: Semejanza de triángulo. CONTENIDOS: 1. Razones y proporciones(teorema de Tales). 2. Criterios de Semejanza. 3. Ejercicios de aplicación. Ejercicio Reto 1. Examen de la UNI 2014 En
ENCUENTRO # 51 TEMA: Semejanza de triángulo. CONTENIDOS: 1. Razones y proporciones(teorema de Tales). 2. Criterios de Semejanza. 3. Ejercicios de aplicación. Ejercicio Reto 1. Examen de la UNI 2014 En
Problemas de geometría analítica
 Universidad de Costa Rica Instituto Tecnológico de Costa Rica Problemas de geometría analítica Tomados del libro Geometría Moderna de Moise y Downs 1. Conteste para cada figura las preguntas siguientes:
Universidad de Costa Rica Instituto Tecnológico de Costa Rica Problemas de geometría analítica Tomados del libro Geometría Moderna de Moise y Downs 1. Conteste para cada figura las preguntas siguientes:
