El álgebra de los valores propios
|
|
|
- Magdalena Rodríguez Poblete
- hace 7 años
- Vistas:
Transcripción
1 Capítulo 9 El álgebra de los valores propios 9.1. Introducción El objetivo de este tema es proporcionar las ideas matemáticas que se usan en el cálculo numérico de los valores propios de matrices. En parte es un repaso de conceptos ya estudiado en cursos básicos de Álgebra Lineal pero el énfasis se pone en aquellos aspectos que son importantes en el análisis numérico. Así, mientras que el objetivo teórico último, en relación con los valores y vectores propios, es la obtención de la forma canónica de Jordan que proporciona un sistema completo de invariantes para la semejanza (o conjugación) de matrices, ésta es de muy poca relevancia desde el punto de vista numérico. La razón es que la forma canónica de Jordan es altamente inestable y, salvo que se usen algoritmos simbólicos, rara vez se puede obtener con fiabilidad. A lo largo de este tema veremos que uno de los problemas es que las transformaciones de semejanza no son recomendables para la obtención de los valores y vectores propios de matrices. En su lugar, mucho más fiables son las transformaciones de semejanza unitaria. Este planteamiento nos conduce a estudiar 179
2 180 El álgebra de los valores propios con detalle la forma de Schur (compleja y real) que sería el objetivo final de los algoritmos de cálculo de valores propios. En este primer tema sobre valores propios nos centraremos en los aspectos teóricos que nos permitirán comprender mejor los algoritmos que veremos en el siguiente tema. Empezaremos repasando los conceptos de Algebra Lineal relacionados con los valores y vectores propios. Entre otras cosas veremos que el conjunto de las matrices con valores propios distintos forman un conjunto denso en el espacio de las matrices cuadradas; lo cual, desde un punto de vista numérico, hace prácticamente indistinguibles las matrices con valores propios distintos de las que no tienen esta propiedad. Por ello, las matrices que tienen valores propios repetidos se llaman matrices defectuosas. Veremos que no ser defectuosa equivale a ser diagonalizable por semejanza (o conjungación). La mayor parte de los problemas en los que hay que calcular valores propios suelen involucrar matrices de números reales. Pero como éstas pueden tener valores propios complejos y la teoría básica es la misma para matrices reales o complejas, en todo este tema, y salvo que se especifique lo contrario, F representará indistintamente el cuerpo de los números reales o el de los complejos Valores y vectores propios Si A P F n n, λ 0 P C es un valor propio (o autovalor) de A si existe un vector no nulo x P C n tal que Ax λ 0 x Al conjunto de valores propios (distintos) de A lo denotaremos por ΛpAq; y a éste conjunto se le conoce con el nombre de espectro de A. En algunos libros y artículos se le suele denotar por σpaq, pero cada vez se utiliza más la notación que se empleará aquí: ΛpAq. Si λ 0 P ΛpAq, los vectores x 0 para los que Ax λ 0 x se llaman vectores propios o autovectores de A asociados al valor propio λ 0. Para λ 0 P ΛpAq sea S λ0 tx P C n Ax λ 0 xu Este conjunto es un subespacio vectorial de C n que se llama subespacio propio de A asociado a λ 0. Como x P S λ0 ô pλ 0 I n Aqx 0
3 9.2 Valores y vectores propios 181 resulta que el subespacio propio de A asociado a λ 0 es Kerpλ 0 I n Aq. Además si x P S λ0 entonces pλ 0 I n AqAx Apλ 0 I n Aqx 0, de modo que Ax P S λ0. Los subespacios que cumplen esta propiedad (x P S Ñ Ax P S) se llaman subespacios invariantes por A. Así pues, los subespacios propios de A son invariantes por A (o A-invariantes). La siguiente propiedad pone de manifiesto que vectores propios asociados a valores propios distintos son linealmente independientes Proposición 9.1 Sea A P F n n y tλ 1,..., λ s u ΛpAq. (a) Si para i 1,..., s, x i es un vector propio de A asociado al valor propio λ i, entonces los vectores x 1,..., x s son linealmente independientes. (b) La suma Kerpλ 1 I n Aq Kerpλ s I n Aq es directa. Demostración.- (a) Lo demostraremos por contradicción. Recordemos que ΛpAq es el conjunto de los valores propios de A y, por lo tanto λ i λ j para i j. Con los vectores x 1,..., x s construímos la matriz X x 1 x s. Si x1,..., x s no son linealmente dependientes, entonces rang X r s y hay r columnas de X, digamos x i1,..., x ir que son linealmente independientes y vectores propios asociados a los valores propios λ i1,..., λ ir. Sea x j una columna de X tal que j R ti 1,..., i r u, entonces x j α 1 x i1 α r x ir. Como x j P Kerpλ j I n Aq y Ax ik λ ik x ik, k 1,..., s, resulta que 0 pλ j I n Aqx j pλ j I n Aqpα 1 x i1 α r x ir q α 1 pλ j λ i1 qx i1 α r pλ j λ ir qx ir Y como x i1,..., x ir son linealmente independientes α k pλ j λ ik q 0, k 1,..., r. Pero x j 0, de modo que al menos un α k 0. Para ese índice k concluímos que necesariamente λ j λ ik contradiciendo que todos los valores propios son distintos.
4 182 El álgebra de los valores propios (b) Hay que demostrar que si R i Kerpλ i I n Aq, entonces para j 1,..., s M j R 1 X X R j 1 X R j 1 X X R s t0u. Si 0 x P M j para algún j, entonces Ax λ j x λ j pv 1 v j 1 v j 1 v s q, v i P Kerpλ i I n Aq. Así pλ i λ j qv i λ i v i λ j v i Av i λ j x A ij ij ij ij ij v i λ j x Ax λ j x 0 Pero, por el apartado (a), los vectores v 1,..., v j 1, v j 1,..., v s son linealmente independientes. Por consiguiente λ i λ j para i 1,..., j 1, j 1,..., s, lo que es imposible porque son todos distintos. Introducimos ahora los conceptos de multiplicidad algebraica y geométrica. Definición 9.2 Para λ 0 P ΛpAq se define la multiplicidad geométrica de λ 0 como la dimensión del subespacio propio de A asociado a λ 0, y se denota por mg A pλ 0 q: mg A pλ 0 q dim Kerpλ 0 I n Aq Por otra parte, λ 0 P ΛpAq ô Dx 0 t. q. pλ 0 I n Aqx 0 ô detpλ 0 I n Aq 0 Si λ denota una indeterminada, la matriz λi n A está definida en Frλs, el anillo de los polinomios en la indeterminada λ con coeficientes en F; i.e. λi n A P Frλs n n Como Frλs es una anillo conmutativo, podemos calcular el determinante de λi n A. Es fácil ver que éste es un polinomio de grado n con coeficiente principal 1: detpλi n Aq λ n p 1 λ n 1 p n 1 λ p n. Los polinomios cuyo coeficiente principal es 1 se llaman polinomios mónicos. Y al polinomio mónico detpλi n Aq se le llama polinomio característico de A. Lo denotaremos por p A pλq detpλi n Aq.
5 9.2 Valores y vectores propios 183 Si factorizamos este polinomio en C, se descompone como producto de potencias de factores lineales: ppλq pλ λ 1 q m 1 pλ λ 1 q m 2... pλ λ 1 q ms, λ i λ j, entonces ΛpAq tλ 1, λ 2,..., λ s u porque λ 0 P ΛpAq si y sólo si detpλ 0 I n Aq 0, tal y como hemos visto más arriba. Definición 9.3 Al número m i se le llama multiplicidad algebraica de λ i como valor propio de A, y se representa por ma A pλ i q. En otras palabras, la multiplicidad algebraica de un valor propio es su multiplicidad como raíz del polinomio característico. Cuando no haya posibilidad de confusión, en la notación de las multiplicidades algebraica y geométrica (ma A pλ 0 q y mg A pλ 0 q) suprimiremos los subíndices que hacen referencia a la matriz. Por otra parte, si A, B P F n n son semejantes; i.e., A T 1 BT para alguna matriz T P Gl n pfq, entonces tienen el mismo polinomio característico, p A pλq p B pλq. En efecto, p A pλq detpλi n Aq detpλi n T 1 BT q detpt 1 pλi n BqT q detpt 1 q detpt q detpλi n Bq detpλi n Bq p B pλq. Una consecuendia de esta propiedad es que ΛpAq ΛpBq y para cada λ 0 P ΛpAq ΛpBq, ma A pλ 0 q ma B pλ 0 q. También es cierto que mg A pλ 0 q mg B pλ 0 q porque Kerpλ 0 I n Aq T 1 Kerpλ 0 I n Bq, lo cual se demuestra por doble inclusión como sigue: x P Kerpλ 0 I n Aq ô pλ 0 I n Aqx 0 ô T 1 pλ 0 I n BqT x 0 ô ô pλ 0 I n BqT x 0 ô T x P Kerpλ 0 I n Bq ô x P T 1 Kerpλ 0 I n Bq. Además, como T es invertible, dim Kerpλ 0 I n Aq dim Kerpλ 0 I n Bq. Las multiplicidades algebraica y geométrica de cada valor propio están relacionadas tay y como muestra la siguiente proposición.
6 184 El álgebra de los valores propios Proposición 9.4 Para A P F n n y λ 0 P ΛpAq,mapλ 0 q mgpλ 0 q. Demostración.- Sea mgpλ 0 q r y tt 1,..., t r u una base del subespacio propio Kerpλ 0 I n Aq. Ampliamos esta base tt 1,..., t r, t r 1,..., t n u para obtener S λ0 una base de C n. Pongamos T t 1 t 2 t n la matriz cuyas columnas son los vectores de la base escogida. Y sea B T 1 AT. Veamos la forma que tiene esta matriz: AT At 1 At r At r 1 At n λ0 t 1 λ 0 t r y r 1 y n λ t 1 t r t r 1 t 0 I r C n T B. 0 D Así Por lo tanto λi n B pλ λ0 qi r C. 0 λi n r D detpλi n Bq pλ λ 0 q r detpλi n r Dq. Como A y B tienen para cada valor propio las mismas multiplicidades algebraicas y geométricas y λ 0 podría ser valor propio de D, concluimos que r mgpλ 0 q mapλ 0 q. Definición 9.5 Sea A P F n n y λ 0 P ΛpAq. (a) Si mgpλ 0 q mapλ 0 q entonces se dice que λ 0 es un valor propio defectuoso de A. En caso contrario se dice que es no defectuoso. La matriz A se dice que es defectuosa si tiene algún valor propio defectuoso y en caso contrario se dice que es no defectuosa. (b) Si mapλ 0 q 1 entonces se dice que λ 0 es un valor propio simple de A. La matriz A se dice que es simple si todos sus valores propios son simples. (c) Los valores propios no defectuosos que no son simple se llaman semisimples. La matriz A se dice que es semisimple si sus valores propios son simples o semisimples.
7 9.2 Valores y vectores propios 185 Debe notarse que para una matriz es lo mismo ser semisimple o ser no defectuosa y que las matrices simples tiene todos sus valores propios distintos. En el extremo opuesto, las matrices cuyos valores propios tienen todos multiplicidad geométrica 1, se llaman no derogatorias. Las matrices simples son a la vez no defectuosas y no derogatorias. Posiblemente la denominación de matriz defectuosa se debe al hecho de que casi todas las matrices son no defectuosas. Veremos que, en efecto, el conjunto de matrices no defectuosas es un conjunto abierto y denso en el conjunto de todas las matrices cuadradas. En otras palabras, tan cerca como se quiera de una matriz defectuosa hay matrices que no lo son. También se dice que la propiedad ser no defectuosa es genérica para las matrices. Definición 9.6 A P F n n se dice que es diagonalizable si es semejante a una matriz diagonal. Si A es diagonalizable, las matrices diagonales a las que es semejante son matrices cuyos elementos diagonales son los valores propios (en algún orden) de A. En efecto, si T 1 AT D Diagpd 1,..., d n q entonces A y D tienen el mismo polinomio característico. Pero detpλi n Dq pλ d 1 qpλ d 2 q... pλ d n q; así que d 1,..., d n son los valores propios (quizá repetidos) de D y, por lo tanto, de A. Proposición 9.7 A P F n n es no defectuosa si y sólo si es diagonalizable. Demostración.- Claramente si A es diagonalizable es no defectuosa porque la mutiplicidad algebraica de sus valores propios es 1. Recíprocamente, si A es no defectuosa entonces para cada λ 0 P ΛpAq se tiene que mapλ 0 q mgpλ 0 q. Supongamos ΛpAq tλ 1,..., λ s u y mapλ i q mgpλ i q m i, i 1,..., s.
8 186 El álgebra de los valores propios Esto significa que dim Kerpλ i I n Aq m i y m 1 m s n. Pero por la Proposición 9.1 la suma Kerpλ 1 Aq Kerpλ s I n Aq es directa, de modo que dimpkerpλ 1 Aq Kerpλ s I n Aqq m 1 m s n. Es decir, C n Kerpλ 1 Aq ` ` Kerpλ s I n Aq. Así, si tt ii,..., t imi u es una base de Kerpλ i I n Aq y T t 11 t 1m1 t s1 t sms, las columnas de T forman una base de C n y consecuentemente T es invertible. Ahora AT At 11 At 1m1 At s1 At sms λ 1 t 11 λ 1 t 1m1 λ s t s1 λ s t sms λ 1... t 11 t 1m1 t s1 t sms λ 1... λ s... T D λ s Como T es invertible, T 1 AT D con D diagonal. La demostración nos proporciona la siguiente información: Si A es diagonalizable y formamos una matriz T cuyas columnas sean vectores propios asociados a los valores propios de A (un vector propio por cada valor propio) entonces T es invertible y T 1 AT es una matriz diagonal cuyos elementos diagonales son los valores propios de A. Pero el recíproco también es cierto: si T 1 AT D es diagonal, entonces los valores propios de A son los elementos diagonales de D y la i-ésima columna de T es un vector propio de A asociado al valor propio que ocupa la i-ésima posición de la diagonal de D. Si A no es diagonalizable, todavía podemos encontrar una matriz T, no singular, tal que T 1 AT es casi diagonal: Teorema 9.8 (Forma canónica de Jordan) Dada A P F n n existe una matriz no singular T P C n n tal que T 1 AT J es la forma canónica de Jordan de A. Es decir, J es una matriz diagonal por bloques J DiagpJ n1 pλ 1 q, J n2 pλ 2 q,..., J ns pλ s qq
9 9.2 Valores y vectores propios 187 y J ni pλ i q DiagpJ ni1 pλ i q, J ni2 pλ i q,..., J niri pλ i qq con J nij pλ i q λ i λ i λ i λ i J es única salvo permutación de sus bloques diagonales. P C n ij n ij. Demostraciones de este teorema pueden encontrarse en muchos libros de Álgebra Lineal. La forma canónica de Jordan ofrece toda la información sobre la estructura propia de la matriz A. En efecto, sus valores propios son λ 1,..., λ s ; la multiplicidad geométrica de λ i es n i y su multiplicidad geométrica es r i, el número de bloques diagonales en J ni pλ i q. Pero calcular numéricamente la forma canónica de Jordan es una tarea difícil, si no imposible, por dos razones especialmente: No depende continuamente de A de modo que los errores de redondeo, por pequeños que sean pueden cambiarla completamente. Ejemplo 9.9 Sea J n p0q una matriz en forma de Jordan. Para ε todo lo perqueño que se quiera, si se añade el número i ε al elemento en la posición pi, iq de J n p0q la matriz resultante tiene n valores propios distintos y es, por lo tanto, diagonalizable. Su forma de Jordan será Diagpε, 2ε,..., nεq. La distancia entre J n p0q y esta matriz diagonal es, en la norma de Frobenius, mayor que n 1. Por lo tanto, pequeñas modificaciones en los elementos de J n p0q producen una matriz cuya forma de Jordan está lejos de la forma de Jordan de J n p0q (que es ella misma). Por lo tanto la aplicación que a cada matriz le asocia su forma de Jordan no es continua.
10 188 El álgebra de los valores propios No se puede calcular de forma estable en general. En realidad, éste es un problema incluso cuando la forma de Jordan es diagonal: si T 1 AT J y T está muy mal condicionada (κpt q }T } }T 1 } es muy grande) los valores propios obtenidos pueden estar muy lejos de los exactos. El siguiente resultado nos da muestra de ello. Teorema 9.10 (Teorema de Bauer-Fike) Sea A P F n n una matriz diagonalizable y sea T P Gl n pcq tal que T 1 AT D Diagpλ 1,..., λ n q. Entonces, para cada λ P ΛpA Eq, E P F n n, se tiene que mín 1 i n λ i λ }T } }T 1 } }E} donde } } es cualquier norma de matriz inducida por una norma de vector l p. Recordemos que el número de condición de T es κpt q }T } }T 1 }, de modo que este resultado nos dice que si T está mal condicionada entonces los valores propios de A E pueden estar muy lejos de los de A aunque E sea muy pequeña. El siguiente ejemplo nos lo muestra. Ejemplo 9.11 Sean A ,9990 1, ,9623 T 0 0,0005 0, ,1925 Entonces T 1 AT Diagp1, 0,9990, 2q. Y si entonces E ΛpA Eq t0,9995 0,0044i, 0,9995 0,0044i, 2, 0001u El error en el cálculo de los valores propios sería 2 órdenes de magnitud mayor que el de la perturbación. Nótese que κpt q 6, Lo que sería deseable es poder utilizar matrices cuyo número de condición fuera lo más pequeño posible. Estas matrices son las matrices unitarias. Sin embargo, sólo algunas matrices pueden reducirse a forma diagonal usando matrices unitarias tal y como veremos más adelante.
11 9.2 Valores y vectores propios 189 Demostración Si λ P ΛpAq entonces mín 1 i n λ i λ 0 y no hay nada que demostrar. Supondremos entonces que λ R ΛpAq de modo que λ λ i para todo i 1,..., n y λi n D es invertible. Como λ P ΛpA Eq, existe un vector no nulo x P C n tal que pa Eqx λx. Así Pongamos Entonces o Ex pλi n Aqx pλi n T DT 1 qx T pλi n DqT 1 x. T 1 x y. T 1 Ex pλi n Dqy y pλi n Dq 1 T 1 Ex pλi n Dq 1 T 1 ET y. Tomando normas de vector y las correspondientes normas de matriz inducidas }y} }pλi n Dq 1 } }T 1 } }E} }T } }y}. Como y 0 1 }pλi n Dq 1 } }T 1 } }E} }T } (9.1) 1 Ahora bien pλi n Dq 1 1 Diag,...,, y para cualquier matriz λ λ 1 λ λ n diagonal B Diagpb 1,..., b n q y para cualquier norma de matriz inducida por una norma de vector l p se tiene que En efecto pero }B} máx 1 i n b i }B} máx }Bx} p }x} p1 Bx b 1 x 1 b 2 x 2. b n x n Así, para cualquier x P F n unitario tenemos que }Bx} p máx 1 i n b i }x} p máx 1 i n b i
12 190 El álgebra de los valores propios Por otra parte, si máx b i b k y tomamos x e k, el k-ésimo vector canónico, 1 i n resulta que }Bx} p b k. En conclusión, para cualquier x P F n unitario, }Bx} p máx b i y hay un x de norma 1 tal que }Bx} p máx b i. Por consiguiente 1 i n 1 i n }B} máx }Bx} p máx b i. }x} p1 1 i n Continuando con la demostración del teorema, tomando cualquier norma de matriz inducida por una norma de vector l p }pλi n Dq 1 1 } máx 1 i n λ λ i 1 mín 1 i n λ λ i. Sustituyendo en (9.1) concluímos que que es lo que se quería demostrar. mín 1 i n λ λ i }T } }T 1 } }E} 9.3. Semejanza Unitaria En general no se puede diagonalizar una matriz cualquiera usando matrices unitarias, pero sí se puede triangularizar. Para calcular los valores propios esto es suficiente porque los valores propios de una matriz triangular son también sus elementos diagonales. El siguiente resultado nos muestra cómo reducir una matriz cualquiera a forma triangular mediante semejanza unitaria. Pero primero la definción de lo que significa este concepto. Definición 9.12 Dos matrices A, B P C n n se dice que son unitariamente semejantes si existe una matriz unitaria U P C n n tal que B U AU. Si A, B P R n n y existe una matriz ortogonal P P R n n tal que B P T AP entonces se dice que A y B son ortogonalmente semejantes. Teorema 9.13 (Teorema de Schur) Si A P F n n entonces A es unitariamente semejante a una matriz triangular superior. Los valores propios de A son los elementos diagonales de dicha matriz triangular.
13 9.3 Semejanza Unitaria 191 Recordemos que F R o C. El teorema dice que tanto si A es real como compleja existe una matriz unitaria U P C n n tal que U AU T con T triangular superior. De la propia demostración del teorema se desprenderá que si A es real y sus valores propios son todos reales entonces U también puede tomarse real y, por lo tnato, ortogonal. Sin embargo, si A tiene valores propios complejos no reales entonces U es necesariamente compleja. Demostración.- La demostración es por inducción sobre n. Si n 1 no hay nada que probar porque A ras ya es triangular. Suponemos entonces que el teorema está demostrado para matrices de orden hasta n 1. Sea A P C n n y λ 1 P ΛpAq. Sea u un vector propio unitario de A asociado a λ 1 y U u U 1 una matriz unitaria. Así, el espacio generado por las columnas de U 1 es U u AU U 1 u K. Entonces u A u U Au u AU 1 1 U 1 Au U 1 AU 1 Como Au λ 1 u y u es un vector de norma euclídea 1, u Au λ 1. Y como U 1 u K, U 1 Au λ 1 U 1 u 0. Por lo tanto, si ponemos B U 1 AU y c u AU 1, se tiene que U λ1 c AU. 0 B Ahora, B es de tamaño pn 1q pn 1q por lo que aplicando la hipótesis de inducción se tiene que existe una matrix unitaria V P C pn 1q pn 1q tal que V BV T 1 es una matriz triangular superior. Entonces V U AU 1 0 λ1 a T, 0 V 0 T donde a c V, es una matriz triangular superior. Teniendo en cuenta que 0 V es una matriz unitaria y que, por consiguiente, A y T son semejantes, se concluye ± que detpλi n Aq detpλi n T q n pλ t ii q; i.e., los valores propios de A son i1 los elementos diagonales de T. Esto termina la demostración del teorema. Una consecuencia importante del Teorema de Schur es el siguiente resultado Corolario 9.14 El conjunto de las matrices complejas de tamaño n n con valores propios distintos es denso en C n n.
14 192 El álgebra de los valores propios Im t 77 +e 7 t 66 =t 77 e 6 + t 66 t 55 +e 5 e 4 + t 44 t 33 = = e 2 + t 22 t 11 =t 22 t 44 e 3 + t 33 e 1 + t 11 t 55 Re Figura 9.1: Distintos elementos para la diagonal de E T. El radio de cada disco es ε menor que n 1{2 Demostración.- Hay que probar que dada A P C n n y dado ε 0 existe una matriz A 1 P C n n con todos sus valores propios distintos tal que }A A 1 } ε en alguna norma. Usaremos la norma de Frobenius. Por el Teorema de Schur existe una matriz unitaria U P C n n tal que U AU T rt ij s. Tal y como se muestra en la Figura 9.1 se pueden escoger n números complejos e 1,..., e n tales que: (a) e i ε n 1{2, y (b) t 11 e 1, t 22 e 2,..., t nn e n sean todos números distintos De esta forma, si E Diagpe 1,..., e n q entonces T E es triangular superior con los números t 11 e 1, t 22 e 2,..., t nn e n en la diagonal; siendo estos números sus valores propios. Ahora, si A 1 U pa EqU y teniendo en cuenta que la norma de Frobenius es unitariamente invariante, resulta que }A A 1 } F }U T U U pe T qu} F }U EU} F }E} F ε 2 p e 1 2 e n 2 q 1{2 ε 2 1{2 ε n n
15 9.3 Semejanza Unitaria 193 que es lo que se quería demostrar. Este resultado nos muestra una vez más que sólo es razonable intentar calcular numéricamente los valores propios de matrices diagonalizables y que con altísima probabilidad los valores propios que puedan devolver los algoritmos van a ser todos distintos. Por otra parte, si A P R n n es real se desearía poder reducir A a forma triangular usando matrices ortogonales reales; i.e., usando aritmética real que es más barata desde el punto de vista del cálculo. Ahora bien, una matriz real puede tener valores propios complejos aunque éstos deben aparecer en pares conjugados. Esto es debido a que detpλi n Aq se factoriza en R en factores lineales o cuadráticos; los primeros corresponden a raíces reales y los segundos tienen raíces complejas pero ambas conjugadas, debido a que los coeficientes de los factores son reales. Así pues, no es posible obtener una matriz triangular realizando transformaciones ortogonales sobre una matriz real si ésta tiene valores propios complejos. A lo más que podemos aspirar es a obtener una matriz triangular por bloques con bloques diagonales de tamaño 2 2 a lo más. Teorema 9.15 (Teorema de Schur real) Si A P R n n, existe una matriz ortogonal P P R n n tal que P T AP T, con T una matriz cuasi triangular superior. Es decir, T es una matriz triangular superior por bloques con bloques diagonales de tamaño 1 1 o 2 2. Los valores propios de A son los valores propios de los bloques diagonales de T. Los bloques de tamaño 1 1 corresponden a valores propios de A reales y los de tamaño 2 2 a sus valores propios complejos conjugados. Demostración.- Se hace por inducción sobre n como en el caso complejo. Si n 1 no hay nada que demostrar así que supondremos demostrado el teorema para matrices de tamaño menor o igual que n 1. Sea A P R n n y λ un valor propio de A. Si λ P R entonces admite un vector propio, u, real y unitario. Que sea real es consecuencia de que es solución del sistema pλi n Aqx 0, siendo λi n A una matriz de números reales y las soluciones de los sistemas se obtienen mediante operaciones sin salir del cuerpo. Así Au λu y se procede como en el caso del teorema de Schur complejo. Si λ es un número complejo entonces λ es también valor propio. Y si u es un vector propio de A asociado a λ, ū es un vector propio de A asociado a s λ. En efecto, Asu s Asu Au λu s λsu
16 194 El álgebra de los valores propios Pongamos u R u su 2 u I u su 2i siendo i la unidad imaginaria. Así u R, u I P R n 1 y u R, u I u, su. Sea ru u R u I y U r QR su factorización QR real (i.e., Q es real con columnas ortonormales y R es real) Así Im Q u R, u I y podemos escoger una matriz Q r Q Q r tal que U es real y ortogonal. Ahora U T AU Q T rq T A Q Q r Q T AQ rq T AQ Q T A r Q r Q T A r Q Pongamos B Q T AQ y observemos que B P R 2 2 porque Q P R n 2. Así AQ QB y Q r T AQ Q r T QB 0 porque las columnas de Q y Q r son ortonormales. Por lo tanto U T B Q AU T A Q r 0 Q r T A Q r Como r Q T A r Q P R pn 2q pn 2q, aplicamos la hipótesis de inducción a esta matriz como en el caso complejo. Falta demostrar que los valores propios de B son λ y λ. s En efecto, como u y su son vectores propios asociados a valores propios distintos, son linealmente independientes. Y es fácil ver que también u R y u I lo son. Y como U r ur u I QR resulta que R es invertible. Así Ahora bien Au R u su A 2 AQR A u R u I AuR Au I. λ 2 u λ 2 su 1 2 pλpu R iu I q s λpur iu I qq 1 2 ppλ s λqur ipλ λqu I q Repλqu R Impλqu I. De la misma forma Au I Impλqu R Repλqu I. Entonces Repλq Impλq A u R u I AuR Au I ur u I Impλq Repλq.
17 9.4 Vectores propios a la izquierda 195 Como B Q T AQ resulta que AQR QBR QRR 1 BR y QR u R consiguiente Repλq Impλq R 1 BR Impλq Repλq y esta matriz tiene λ y λ s como valores propios. u I. Por 9.4. Vectores propios a la izquierda A los vectores propios, tal y como han sido definidos, se les suele llamar vectores propios a la derecha. La razón es que, en ocasiones, se usan también vectores propios a la izquierda y es necesario distinguirlos. Definición 9.16 Si A P F n n y λ 0 es un valor propio de A, se dice que un vector no nulo y P C n 1 es un vector propio a la izquierda de A asociado al valor propio λ 0 si y A y λ 0. El subespacio propio a la izquierda de A asociado a λ 0 es el conjunto de vectores propios por la izquierda junto con el vector 0. Debe observarse que los valores propios de A y A están relacionados mediante conjugación. Es decir, λ 0 P ΛpAq si y sólo si s λ0 P ΛpA q. Como, además, conjugando y trasponiendo se tiene que y A y λ 0 ô A y s λ0 y, el siguiente resultado se sigue de forma inmediata. Proposición 9.17 y P C n 1 es un vector propio a la izquierda de A asociado al valor propio λ 0 si y sólo si es un vector propio a la derecha de A asociado al valor propio s λ0. Si la matriz A es diagonalizable; o incluso, si λ 0 es un valor propio simple de A aunque A no sea diagonalizable, entonces en su forma canónica de Jordan el bloque
18 196 El álgebra de los valores propios correspondiente a λ 0 es de tamaño 1 1. Por lo tanto, si T 1 AT J y λ 0 está en la posición pi, iq de J entonces siendo y i λ y i A λ 0 y i y Ax i λ 0 x i, la i-ésima fila de T 1 y x i la i-ésima columna de T. Como T 1 T es la matriz identidad se sigue que y x 1. Sin embargo, si λ 0 es un valor propio con un bloque de Jordan de tamaño mayor que 1 este producto escalar es cero. Para verlo basta considerar el caso en el que A es de la forma J n pλ 0 q. En este caso, un vector propio por la derecha de A es e T y un vector propio por la izquierda es e n Qué pasa, finalmente, si λ 0 es semisimple pero no simple?. En este caso hay más de un bloque de Jordan de A asociado a λ 0, pero todos ellos son de tamaño 1 1; i.e., las mutiplicidades algebraicas y geométricas de λ 0 son iguales y mayores que 1. Hay vectores propios a la izquierda y a la derecha cuyo producto escalar es 1, pero los hay también que son ortogonales. El producto escalar entre los vectores propios por la izquierda y la derecha de un valor propio juega un papel fundamental en el análisis del condicionamiento del problema de calcular los valores propios de una matriz. Los vectores propios a la izquierda se pueden usar para proporcionar otra forma de construir una forma de Schur de una matriz. El proceso sería el siguiente (se detalla sólo el caso complejo, el real sería similar): Si A P C n n y λ P ΛpAq sea u P C n 1 un vector propio a la izquierda de A de norma euclídea 1 asociado a λ. Con este vector se construye una matriz unitaria U que tiene el vector u como última columna:... Entonces U AU U 1 u A U 1 U U 1 u. U u 1 AU 1 u AU 1 U 1 Au u Au.
19 9.5 Matrices unitariamente diagonalizables 197 Pero u Au λu u λ y u AU 1 λu U 1 0 porque las columnas de U 1 son ortonormales a u. Así U U AU 1 AU 1 U 1 Au 0 λ y aplicamos el proceso de inducción a U 1 AU 1 para obtener una matriz triangular Matrices unitariamente diagonalizables Hemos visto que toda matriz compleja es unitariamente semejante a una matriz triangular (teorema de Schur). Algunas tienen la propiedad más fuerte de ser semejantes a una matriz diagonal. Son las matrices normales. Las introducimos, sin embargo, de otra forma. Definición 9.18 Una matriz A P C n n se dice que es normal si conmuta con su traspuesta conjugada. Es decir, si AA A A. Con esta definición vemos que las matrices unitarias y las matrices hermíticas son ejemplos de matrices normales. En efecto, si U P C n n es unitaria entonces U U UU I n. Y is H P C n n es hermítica entonces H H y toda matriz conmuta consigo misma. Veamos ahora que las matrices normales así definidas son precisamente las que son unitariamente diagonalizables. Teorema 9.19 Una matriz es normal si y sólo si es unitariamente diagonalizable. Demostración.- Si A P C n n es unitariamente diagonalizable entonces U AU D con U P C n n unitaria y D Diagpλ 1,..., λ n q. Entonces A UDU y A UD U U DU s
20 198 El álgebra de los valores propios En consecuencia A A U s DU UDU U s DDU Y como D y s D son diagonales, conmutan. Es decir, y A es normal. A A U s DDU UD s DU UDU U s DU AA, Recíprocamente, por el teorema de Schur para cada A P C n n existe una matriz unitaria U P C n n tal que U AU T, una matriz triangular superior. Si A es normal entonces A A AA y esto equivale a que T T T T. Veamos, por inducción sobre el tamaño de T, n, que esto sólo es posible si T es diagonal. Si n 1 no hay nada que demostrar. Supongamos la propiedad demostrada para matrices de tamaño a lo más n 1 y sea T una matriz triangular superior tal que T T T T. Pongamos Entonces Por una parte Y por otra T t11 t 12 0 T 22 T st11 0 t 12 T 22 T T t11 2 t 12t 12 t 12T 22 T 22 t 12 T 22 T 22 T T t11 2 s t11 t 12 t 11 t 12 T 22T 22 Para que estas dos matrices sean iguales debe suceder que t 12t Pero t 12t 12 }t 12 } 2 2 y }t 12 } 2 0 si y sólo si t En consecuencia T t T 22 y T T T T si y sólo si T 22 T 22 T 22T 22. Aplicando la hipótesis de inducción a T 22 concluímos que T 22, y por lo tanto T, son diagonales. Este resultado (que las matrices normales sean unitariamente diagonalizables) se conoce con el nombre de Teorema espectral para las matrices normales. Y éste, a
21 9.6 Teoría de Perturbación 199 su vez, se expresa diciendo que una matriz A P F n n es normal si y sólo si se puede escribir en la forma con v 1,..., v n vectores ortonormales. A ņ i1 λ i v i v i Se trata, en efecto, de otra forma de escribir U AU Diagpλ 1,..., λ n q porque si V U entonces V es unitaria y A V Diagpλ 1,..., λ n qv λ 1 v 1 v 1 λ nv n v n. v 1. v n λ 1... λ n v 1 v n Hay dos tipos de matrices normales especialmente importantes: las matrices unitarias y las matrices hermíticas (ortogonales y simétricas en el caso real). Las matrices unitarias (ortogonales) son las matrices normales cuyos valores propios están en la circunferencia unidad (i.e., tienen módulo 1). Y las matrices hermíticas (simétricas) son las matrices unitarias cuyos valores propios son números reales. SE deja como ejercicio probar ambas caracterizaciones Teoría de Perturbación El Teorema de Bauer-Fike (Teorema 9.10) es un ejemplo típico de un resultado de perturbación cuantitativa de valores propios. Es decir, es un resultado sobre cómo varían los valores propios de una matriz al someterla a una perturbación aditiva (pequeña, habitualmente). Hay muchos otros resultados de este tipo (véase por ejemplo [24]), pero en esta sección nos centraremos en lo que se conoce como perturbación cualitativa. En particular estudiaremos la continuidad y diferenciabilidad de los valores propios como funciones de la matriz. El objetivo final es encontrar una expresión simple para el número de condición del problema de calcular un valor propio de una matriz.
22 200 El álgebra de los valores propios Continuidad de los valores propios En el Ejemplo 9.9 hemos visto que, en general, la Forma de Jordan de una matriz no depende continuamente de ésta. Este hecho implica que pequeños cambios en la matriz dada pueden resultar en grandes modificaciones en su Forma de Jordan. Esto no significa que no sea posible calcular numéricamente la forma de Jordan de ciertas matrices (de hecho lo es) pero el diseño de cualquier algoritmo con este propósito deberá tener en cuenta este problema de falta de continuidad y en particular el hecho de que el conjunto de matrices simples es denso en F n n (Corolario 9.14). Tanto este Corolario como el Ejemplo 9.9 reflejan que el problema estriba en la preservación de los tamaños de los bloques de Jordan por pequeñas perturbaciones. Ahora nos proponemos mostrar que es ahí y sólo ahí donde están las dificultades teóricas. Es decir, el objetivo es demostrar que los valores propios de una matriz dependen continuamente de la matriz, y que en el caso de ser simples lo hacen diferenciablemente. Este resultado nos permitirá definir el número de condición del problema de calcular valores propios simples. El problema que queremos abordar es el de calcular los valores propios de cada matriz A P F n n. La primera dificultad que nos encontramos para plantear la función que define este problema es cuál es su conjunto de llegada. El conjunto de partida está claro: F n n (F R o C) pero hay una pequeña dificultad para definir correctamente el conjunto de llegada. Por ejemplo, los valores propios de la matriz 1 3 A 0 2 son tanto p1, 2q como p2, 1q. En otras palabras, mirando ΛpAq como una n-tupla de números complejos (posiblemente repetidos), ésta está determinada salvo una permutación de sus componentes. Esto nos conduce a considerar en el conjunto C n la siguiente relación de equivalencia: pλ 1,..., λ n q pµ 1,..., µ n q ô λ i µ σpiq, i 1,..., n para alguna permutación σ P Σ n, el grupo de permutaciones de orden n. Al correspondiente conjunto cociente lo representamos como C n {. Así el problema de calcular los valores propios de una matriz queda definido por la aplicación: f : F n n Ñ C n { A r λ rpλ1,..., λ n qs
23 9.6 Teoría de Perturbación 201 donde ΛpAq pλ 1,..., λ n q son los valores propios de A en algún orden. A los elementos de C n { los llamaremos n-tuplas desordenadas de números complejos. Nuestro objetvo es demostrar que f es una función continua. Para ello debemos dotar a C n { de una topología. Lo más natural es considerar en C n la topología habitual (la derivada de cualquier norma) y en C n { la correspondiente topología cociente; es decir, la topología más fina que hace que la proyección canónica π : C n Ñ C n { λ pλ 1,..., λ n q r λ rpλ1,..., λ n qs sea una función continua. En otras palabras U C n { abierto si y sólo si π 1 puq C n abierto. Otra forma de dotar a C n { de una topología es a través de una métrica. Para rλ, rµ P C n { se define la distancia de emparejamiento óptimo entre estas dos n-tuplas desordenadas de la siguiente forma: dpr λ, rµq mín máx λ j µ σpjq 1 j n σpσ n donde pλ 1,..., λ n q y pµ 1,..., µ n q son dos representantes cualesquiera de r λ y rµ, respectivamente, y Σ n es el grupo simétrico de orden n (i.e., el grupo de permutaciones de orden n). Es fácil demostrar que dpr λ, rµq no depende de los representates elegidos para r λ y rµ. También se puede demostrar que d es, en efecto, una métrica para C n { y que la topología cociente y la derivada de esta métrica son las misma; es decir, que un subconjunto de C n { es abierto en la topolodía cociente si y sólo si es abierto en la topología derivada de la distancia de emparejamiento óptimo. No lo haremos aquí y se deja como ejercicio (véase [1, Ex. VI.I.1]). Necesitamos ahora analizar de cerca el polinomio característico de una matriz A. Recordemos que p A pλq detpλi n Aq. Un análisis minucioso de este determinante revela (véase por ejemplo el Teorema de [14]) que si p A pλq λ n a 1 λ n 1 a n 1 λ a n entonces a k 1 i 1... i k n p 1q k det Api 1 : i k, i 1 : i k q donde Api 1 : i k, i 1 : i k q es la submatriz principal de A formada por las filas y columnas i 1,..., i k. En particular, a 1 trpaq y a n p 1q n det A. Esta representación
24 202 El álgebra de los valores propios Im Im nº ceros de f= nº ceros de f+g Γ Re Γ 2 Γ 1 µ 32 λ(triple) 3 µ 31 µ 12 λ(doble) 1 µ 11 µ 33 Re z f(z) > g(z) µ 23 µ 21 (cuadruple) µ 22 Γ 3 µ 24 λ 2 Figura 9.2: Interpretación del Teorema de Rouché Figura 9.3: Valores propios de A E en las bolas disjuntas centradas en los valores propios de A con igual multiplicidad explíta de p A pλq es importante porque muestra que los coeficientes del polinomio característico de una matriz son funciones continuas de ésta. Veremos enseguida que esta propiedad es crucial para demostrar que los valores propios, que son las raíces del polinomio característico, son funciones continuas de la matriz. Para lograr este objetivo haremos uso de un importante resultado sobre funciones analíticas de una variable compleja (ver Figura 9.2): Lema 9.20 (Teorema de Rouché) Sean f y g dos funciones analíticas en el interior y sobre un contorno cerrado simple Γ C. Si fpzq gpzq en todo punto de Γ entonces las funciones f y f g tienen el mismo número de ceros, contando sus multiplicidades, dentro de Γ. Ahora podemos demostrar que los valores propios son funciones continuas de la matriz. Teorema 9.21 La aplicación f : F n n Ñ C n { A r λ rpλ1,..., λ n qs que a cada matriz le asocia la n-tupla desordenada de sus valores propios (contando multiplicidades) es una función continua cuando en F n n se considera la topología habitual y en C n { la derivada de la distancia de emparejamiento óptimo.
25 9.6 Teoría de Perturbación 203 Demostración.- Sea } } una norma en F n n. Debemos demostrar 0 existe δ tal que si }A A} r δ y rµ es la n-tupla desordenada de valores propios de ra entonces dpr λ, rµq ε. Supongamos fijado un ε 0 y denotemos por λ i1,...,λ is los valores propios distintos de A. Sea m j la multiplicidad algebraica de λ ij, j 1,..., s. Sea B ξ pλ ij q la bola con centro en λ ij y radio ξ. Tomamos ξ de modo que ξ ε y que las bolas B ξ pλ ij q sean disjuntas dos a dos (véase la Figura 9.3). Nuestro objetivo es demostrar que existe un número real positivo δ tal que si }A A} r δ entonces en el interior de cada bola B ξ pλ ij q hay exactamente m j valores propios (quizá repetidos) de A r (véase de nuevo la Figura 9.3). Así pues, la distancia de λ ij a los m j valores propios de A r en B ξ pλ ij q es menor que ξ. Esto implica que hay una forma de emparejar los valores propios de A y A r (existe una permutación σ) tal que máx λ j µ σpjq ξ. Es decir, 1 j n dpr λ, rµq ε, que es lo que se quiere demostrar. Sea p A pλq λ n a 1 λ n 1 a n 1 λ a n el polinomio característico de A y sea Γ j la circunferencias que forma la frontera de la bola B ξ pλ ij q. Consideremos la función polinomial g : C Ñ C z z n a 1 z n 1 a n 1 z a n Esta es una función analítica que no se anula en ningún punto de Γ j y que tiene en el interior de cada Γ j un único cero de multiplicidad m j. Como Γ j es compacto y g es una función continua g alcanza en Γ j su mínimo que es distinto de cero porque, como acabamos de decir, g no se anula en Γ j. Sea η j mín gpzq 0. zpγ j Para este número η j 0 existe ρ j 0 tal que si a k b k ρ j para k 1,..., n y hpzq z n b 1 z n 1 b n 1 z b n entonces gpzq hpzq η j para todo z P Γ j. En efecto, gpzq hpzq z n a 1 b 1 z n 1 a n 1 b n 1 z a n b n ρ j ņ Como Γ j es compacto, la función n z k alcanza su máximo en Γ j, digamos M j. k0 Escogiendo 0 ρ j η{m j concluímos que gpzq hpzq η j. Por consiguiente, si ponemos qpzq hpzq gpzq resulta que qpzq η j mín gpzq gpzq para todo zpγ j z P Γ j. Por el Teorema de Rouché, gpzq y gpzq qpzq hpzq tienen el mismo número de ceros en el interior de Γ j. Es decir, hpzq tiene m j ceros en el interior de B ξ pλ ij q. k0 z k
26 204 El álgebra de los valores propios Sea, finalmente, ρ mín ρ j. Por la continuidad de los coeficientes del polinomio 1 j s característico respecto de la matriz, existe δ 0 tal que si }A A} r δ y pa rpλq λ n b 1 λ n 1 b 1 λ b 0 es el polinomio característico de A, r entonces ak b k ρ para k 1,..., n. En conclusión, para j 1,..., s, m j valores propios de A r están en el interior de B ξ pλ ij q, que es lo que se quería demostrar. Corolario 9.22 El conjunto de matrices simples de F n n es abierto Demostración.- Es una consecuencia inmediata del Teorema En efecto, sea A una matriz con valores propios simples λ 1,..., λ n y sea ξ 0 tal que B ξ pλ i qxb ξ pλ i q H para i j. De acuerdo con la demostración del Teorema 9.21 existe un δ ta que si }A A} r δ entonces A r tiene un único valor propio en cada Bξ pλ i q. En consecuencia, ra es simple. Esto demuestra que el conjunto de matrices simple es abierto Localización de los valores propios Tal y como hemos comentado en la introducción de esta sección, nuestro objetivo final es calcular el número de condición de los valores propios de una matriz. Veremos que los valores propios simples son funciones diferenciables y para ello utilizaremos un resultado auxiliar que es importante en sí mismo porque sirve para localizar aproximadamente los valores propios de una matriz, es el llamado Teorema de Gerschgorin: Teorema 9.23 (Teorema de Gerschgorin) Sea A P C n n y ρ i n j1 ji a ij, i 1,..., n. Entonces todos los valores propios de A están localizados en la unión de los n discos: n i1 tz P C : z a ii ρ i u : GpAq. Además, si la unión de k de estos n discos forma una región conexa que es disjunta de los restantes n k discos, entonces en dicha región hay precisamente k valores propios de A.
27 9.6 Teoría de Perturbación 205 Demostración.- Sea λ un valor propio de A y x un vector propio asociado a λ. Pongamos x rx i s y sea x p la componente no nula de x da mayor módulo: x p x i, i 1,..., n. Como Ax λx tenemos que: que es equivalente a λx p raxs p x p pλ a pp q ņ j1 ņ j1 jp a pj x j La desigualdad triangular nos permite concluir que x p λ a pp n j1 jp a pj x j n j1 jp a pj x j. a pj x j n j1 jp a pj x j x p n j1 jp a pj x p ρ p Así pues, λ a pp ρ p para algún p; es decir, λ está en el disco cerrado con centro en a pp y radio ρ p. Puesto que no sabemos qué p corresponde a cada valor propio λ (salvo que conozcamos un vector propio asociado, que es tanto como conocer el propio valor propio, y entonces no estaríamos interesados en localizarlo porque lo conoceríamos exactamente), sólo podemos concluir que cada valor propio λ está en la unión de todos los posibles discos. Esto es GpAq. Para demostrar la segunda parte escribimos A D C con D Diagpa 11,..., a nn q y por lo tanto C es la misma matriz que A salvo que los elementos diagonales son todos cero. Para t P r0, 1s definimos Bptq D tc, de forma que Bp0q D y Bp1q A. Observamos que por lo que GpBptqq n i1 ρ i ptq ņ j1 ji b ij ptq ņ j1 ji tz P C : z b ii ptq ρ i ptqu ta ij tρ i n i1 tz P C : z a ii tρ i u
28 206 El álgebra de los valores propios Por simplicidad vamos a suponer que la región conexa que es unión de k discos y disjunta de los restantes es la formada por los primeros k discos. Denotemos a esta región por G k, i. e. G k : k i1 tz P C : z a ii ρ i u y por G c k GpAq G k su complementario respecto de GpAq. Así G k X G c k H. Está claro que en G k hay k valores propios de Ap0q D y los restantes n k están en G c k. Vamos a demostrar que esto mismo sucede para todo Aptq con t P r0, 1s. Tomando un ε 0 para que la unión de los discos Dpa ii, εq esté en G k para i 1,..., k y en G c k para i k 1,..., n, por la continuidad de los valores propios, resulta que existe un δ 0 tal que si }E} δ entonces Ap0q E tiene k valores propios en G k y n k en G c k. En particular existe un t 0 0 tal que para t P r0, t 0 q, k valores propios de Aptq están en G k y n k en G c k. Si t 0 1 ya hemos terminado. Si no, para probar que Aptq tiene k valores propios en G k y n k en G c k para todo t P r0, 1s procedemos por contradicción. Podemos suponer que existe t 1 P rt 0, 1s tal que Aptq tiene k valores propios en G k y n k en G c k para t P r0, t 1q y Apt 1 q tiene menos de k valores propios en G k y más de n k en G c k. Si fuera al revés; es decir, si Apt 1 q tuviera menos de n k valores propios en G c k y más de k en G k se procedería de forma similar. Veamos que esto conduce a una contradicción. En efecto, sean λ 1,..., λ s los valores propios no repetidos de Apt 1 q en G k y λ s 1,..., λ r los que están en G c k. Sea ε 0 un número real tal que la unión de los discos Dpλ i, εq está en G k para i 1,..., s y en G c k para i s 1,..., r. Tal y como hemos razonado más arriba, por la continuidad de los valores propios, existe un δt 0 tal que Apt 1 δtq tiene en s Dpλ i, εq tantos valores propios como Apt 1 q y lo mismo en r is 1 i1 Dpλ i, εq. Es decir, Apt 1 δtq tiene menos de k valores propios en G k y más de n k en G c k ; lo que es una contradicción porque t 1 δt t 1 y para t t 1 la suposición es que Aptq tiene exactamente k valores propios en G k y n k en G c k. Lo siguiente es un ejemplo de aplicación del Teorema de Gerschgorin
29 9.6 Teoría de Perturbación 207 Ejemplo 9.24 La siguiente matriz A puede verse como una perturbación de la matriz Diagp1, 2q. Sus valores propios pueden calcularse a mano: y Qué resultado nos proporciona el Teorema de Gerschgorin? Según este teorema, los valores propios de A deben estar en el intervalo r1 10 4, s y r2 10 4, s. Por qué en la recta real? El Teorema de Gerschgorin garantiza que hay un valor propio en la bola de centro 1 y radio 10 4 y otro en la de centro 2 y el mismo radio. Pero A es real de modo que si sus valores propios fueran complejos deberían ser conjugado uno del otro y no podría uno estar en una bola y otro en la otra. Por lo tanto deben ser reales. El teorema de Gerschgorin en el ejemplo anterior nos da una idea de que los valores propios de A están próximos a 1 y 2 pero la precisión es escasa. Hay resultados que mejoran el resultado de este teorema pero no proseguiremos en esa dirección. El lector interesado puede consultar los libros [12, 26], por ejemplo Diferenciabilidad de los valores propios simples Podemos ahora afrontar el problema de la diferenciabilidad de los valores propios. Veremos que los valores propios simples son funciones diferenciales de la matriz. Cuando los valores propios no son simples esta propiedad de diferenciabilidad puede fallar. Consideremos, por ejemplo, la siguiente matriz n n A ε 0 El polinomio característico de esta matriz es λ n ε de modo que A tiene como valores propios las n raíces complejas de ε: λ n? ε. λ es diferenciable como función de ε pero dλ dε ε 1 n 1 n
30 208 El álgebra de los valores propios que es 8 en ε 0 y para n 2. En otras palabras λ no es diferenciable en ε 0 cuando n 2. Esto no significa que no puedan calcularse los número de condición de valores propios múltiples, sino que no se puede hacer usando la diferencial. Centraremos nuestra atención en los valores propios simples. El primer problema a la hora de hablar de la diferenciabilidad de los valores propios simples es el de definir de forma adecuada una función que asocie a una matriz un valor propio simple. Esto lo podemos hacer localmente con ayuda del teorema de continuidad de los valores propios. En efecto, este teorema nos asegura que si λ 0 es un valor propio simple de A P F n n y δ 0 es cualquier número real para el que las bolas con centro en los valores propios de A y radio δ son disjuntas dos a dos, entonces existe un número real ε 0 tal que si r A P Bε paq resulta que en la bola B δ pλ 0 q hay un único valor propio de r A. Esto nos permite definir localmente, en el entorno de una matriz A con un valor propio simple λ 0, una función que asocia a cada matriz de dicho entorno el único valor propio simple que tiene en el entorno fijado de λ 0 : f : B δ paq Ñ B ɛ pλ 0 q ra r λ0 (9.2) Con esta notación tenemos el siguiente resultado Teorema 9.25 Sea A P F n n, λ 0 un valor simple de A. Existen bolas abiertas B ε paq y B δ pλ 0 q tales que la función definida en (9.2) es diferenciable en todo B ε paq. Además, si x, y son vectores propios de A, por la derecha e izquierda respectivamente, asociados a λ 0 y E r A A con r A P Bε paq entonces rλ 0 λ 0 y Ex y x Op}E} 2 q. (9.3) Demostración: Para probar que f es diferenciable, supongamos que hemos demostrado la propiedad (9.3) para el valor propio simple λ 0 de A. Esto significa que para A te P B ε paq se tiene que fpa teq fpaq t y Ex y x Op t }E} 2 q. Por lo tanto fpa lím tñ0 teq fpaq t y Ex y x
31 9.6 Teoría de Perturbación 209 y esto significa que f es diferenciable y es la diferencial de f en A. f 1 paqpeq y Ex y x Así pues sólo debemos demostrar (9.3). Supongamos para ello que J T 1 AT es la forma de Jordan de A del Teorema 9.8. En realidad, nos interesa considerar una leve variación de esta forma clásica de Jordan. Se trata de lo siguiente. Supongamos que z 0 es un número complejo y que J n pλq es un bloque de Jordan. Definamos D z Diagpz, z 2,..., z n q. Esta matriz es invertible y D z 1 J n D z difiere de J n en que los elementos en la subdiagonal superior son todos iguales a z en vez de ser todos iguales a 1. Este procedimiento para un bloque de Jordan se puede generalizar a cualquier matriz en forma de Jordan de modo que podemos suponer que la matriz J T 1 AT de más arriba es la forma de Jordan de A con δ{3 en vez de 1 en la superdiagonal. Dado que δ es un número tal que las bolas centradas en los valores propios de A y radio δ son disjuntas dos a dos, la distancia de λ 0 a cualquier otro valor propio de A es mayor que δ. Además, como x, y son vectores propios de A por la derecha e izquierda, podemos suponer que el elemento en la posición p1, 1q de J es λ 0, que x es la primera columna de T y que y es la primera fila de T 1. Si no fuera así podrímos sustituir x por x 1 x y que también sería un valor propio de A x por la derecha asociado a λ 0 y tendrímos que y x 1 1, que es lo que se necesita. Sea E una matriz tal que r A A E P Bε paq y rj T 1 pa EqT Si denotamos por y i a la i-ésima fila de T 1 y por x j a la j-ésima columna de T resulta que el elemento en la posición pi, jq de J r es rj ij y i Ex j y i Ax j y i Ex j J ij. Así pues, si ponemos ɛ ij y i Ex j, tenemos que rj 11 y 1 Ax 1 y 1 Ex 1 λ 0 ɛ 11, rj ii y i Ax i y i Ex i λ i ɛ ii si i 1,
Valores propios de matrices
 Valores propios de matrices Curso 2017-18 1 Definiciones y resultados previos Si A P F nˆn, λ 0 P C valor propio de A si Dv 0 P C n, v 0 0, tal que Av 0 λ 0 v 0 ô pλ 0 I n Aqv 0 0. v 0 es un vector propio
Valores propios de matrices Curso 2017-18 1 Definiciones y resultados previos Si A P F nˆn, λ 0 P C valor propio de A si Dv 0 P C n, v 0 0, tal que Av 0 λ 0 v 0 ô pλ 0 I n Aqv 0 0. v 0 es un vector propio
6.6. Diagonalización de matrices simétricas o hermitianas. Ejemplo de una diagonalización de una matriz simétrica
 6.6 Diagonalización de matrices simétricas o hermitianas Ejemplo de una diagonalización de una matriz simétrica Matrices hermitianas Los autovalores de las matrices reales simétricas o complejas hermitianas
6.6 Diagonalización de matrices simétricas o hermitianas Ejemplo de una diagonalización de una matriz simétrica Matrices hermitianas Los autovalores de las matrices reales simétricas o complejas hermitianas
Clase 7 Herramientas de Álgebra Lineal
 Clase 7 Herramientas de Álgebra Lineal 1 Formas cuadráticas La descomposición en valores singulares 3 Normas de matrices 4 Ejercicios Dada una matriz M R n n, la función escalar x T Mx, donde x R n, es
Clase 7 Herramientas de Álgebra Lineal 1 Formas cuadráticas La descomposición en valores singulares 3 Normas de matrices 4 Ejercicios Dada una matriz M R n n, la función escalar x T Mx, donde x R n, es
Espacios vectoriales
 CAPíTULO 2 Espacios vectoriales 1. Definición de espacio vectorial Es frecuente representar ciertas magnitudes físicas (velocidad, fuerza,...) mediante segmentos orientados o vectores. Dados dos de tales
CAPíTULO 2 Espacios vectoriales 1. Definición de espacio vectorial Es frecuente representar ciertas magnitudes físicas (velocidad, fuerza,...) mediante segmentos orientados o vectores. Dados dos de tales
Diagonalización de Endomorfismos
 Tema 5 Diagonalización de Endomorfismos 5.1 Introducción En este tema estudiaremos la diagonalización de endomorfismos. La idea central de este proceso es determinar, para una aplicación lineal f : E E,
Tema 5 Diagonalización de Endomorfismos 5.1 Introducción En este tema estudiaremos la diagonalización de endomorfismos. La idea central de este proceso es determinar, para una aplicación lineal f : E E,
TEMA III: DIAGONALIZACIÓN.
 TEMA III: DIAGONALIZACIÓN. OBJETIVOS: Generales: 1. Captar el motivo que justifica el problema de la diagonalización de endomorfismos. 2. Resolver y aplicar dicho problema cuando sea posible. Específicos:
TEMA III: DIAGONALIZACIÓN. OBJETIVOS: Generales: 1. Captar el motivo que justifica el problema de la diagonalización de endomorfismos. 2. Resolver y aplicar dicho problema cuando sea posible. Específicos:
Tema 11.- Autovalores y Autovectores.
 Álgebra 004-005 Ingenieros Industriales Departamento de Matemática Aplicada II Universidad de Sevilla Tema - Autovalores y Autovectores Definición, propiedades e interpretación geométrica La ecuación característica
Álgebra 004-005 Ingenieros Industriales Departamento de Matemática Aplicada II Universidad de Sevilla Tema - Autovalores y Autovectores Definición, propiedades e interpretación geométrica La ecuación característica
Autovalores y autovectores Diagonalización y formas canónicas
 Autovalores y autovectores Diagonalización y formas canónicas Autovalores y autovectores.propiedades Sea V un espacio vectorial sobre K y f End(V ). Fijada una base de V, existirá una matriz cuadrada A,
Autovalores y autovectores Diagonalización y formas canónicas Autovalores y autovectores.propiedades Sea V un espacio vectorial sobre K y f End(V ). Fijada una base de V, existirá una matriz cuadrada A,
Diagonalización. Tema Valores y vectores propios Planteamiento del problema Valores y vectores propios
 61 Matemáticas I : Álgebra Lineal Tema 6 Diagonalización 61 Valores y vectores propios 611 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial
61 Matemáticas I : Álgebra Lineal Tema 6 Diagonalización 61 Valores y vectores propios 611 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial
ÁLGEBRA Ejercicios no resueltos de la Práctica 3
 ÁLGEBRA Ejercicios no resueltos de la Práctica 3 Matrices y determinantes (Curso 2007 2008) 15. Encontrar la (única) respuesta correcta, de entre las indicadas, a las siguientes cuestiones: (b) En una
ÁLGEBRA Ejercicios no resueltos de la Práctica 3 Matrices y determinantes (Curso 2007 2008) 15. Encontrar la (única) respuesta correcta, de entre las indicadas, a las siguientes cuestiones: (b) En una
ALGEBRA LINEAL Segundo Semestre. Parte II
 1 Universidad Nacional de La Plata Facultad de Ciencias Astronómicas y Geofísicas ALGEBRA LINEAL 2015 Segundo Semestre Parte II 2 1. Valores y Vectores propios. Diagonalización.Forma de Jordan. 1.1. Polinomios
1 Universidad Nacional de La Plata Facultad de Ciencias Astronómicas y Geofísicas ALGEBRA LINEAL 2015 Segundo Semestre Parte II 2 1. Valores y Vectores propios. Diagonalización.Forma de Jordan. 1.1. Polinomios
Formas canónicas de Jordan
 Capítulo 6 Formas canónicas de Jordan 61 Subespacios propios generalizados Introducción En el capítulo anterior se han estudiado los endomorfismos diagonalizables y se han dado condiciones necesarias y
Capítulo 6 Formas canónicas de Jordan 61 Subespacios propios generalizados Introducción En el capítulo anterior se han estudiado los endomorfismos diagonalizables y se han dado condiciones necesarias y
Tema 2: Teorema de estructura de los grupos abelianos finitamente generados.
 ESTRUCTURAS ALGEBRAICAS GRADO EN MATEMÁTICAS. CURSO 215/216 Tema 2: Teorema de estructura de los grupos abelianos finitamente generados. 1.1. Grupo abeliano libre. Bases. Definición 1.1. El grupo Z n con
ESTRUCTURAS ALGEBRAICAS GRADO EN MATEMÁTICAS. CURSO 215/216 Tema 2: Teorema de estructura de los grupos abelianos finitamente generados. 1.1. Grupo abeliano libre. Bases. Definición 1.1. El grupo Z n con
Tema 9: REDUCCIÓN POR SEMEJANZA DE UNA MATRIZ. DIAGONALIZACIÓN
 Álgebra I - Curso 2005/06 - Grupos M1 y M2 Tema 9: REDUCCIÓN POR SEMEJANZA DE UNA MATRIZ DIAGONALIZACIÓN por Mario López Gómez 1 Valores y vectores propios Definición- Dada una matriz cuadrada A K n n,
Álgebra I - Curso 2005/06 - Grupos M1 y M2 Tema 9: REDUCCIÓN POR SEMEJANZA DE UNA MATRIZ DIAGONALIZACIÓN por Mario López Gómez 1 Valores y vectores propios Definición- Dada una matriz cuadrada A K n n,
Podemos pues formular los dos problemas anteriores en términos de matrices.
 Tema 5 Diagonalización 51 Introducción Valores y vectores propios 511 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial V de dimensión
Tema 5 Diagonalización 51 Introducción Valores y vectores propios 511 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial V de dimensión
Parte 3. Vectores y valores propios
 Parte 3. Vectores y valores propios Gustavo Montero Escuela Universitaria Politécnica Universidad de Las Palmas de Gran Canaria Curso 2004-2005 1 Introducción a los valores y vectores propios 2 3 4 5 Valores
Parte 3. Vectores y valores propios Gustavo Montero Escuela Universitaria Politécnica Universidad de Las Palmas de Gran Canaria Curso 2004-2005 1 Introducción a los valores y vectores propios 2 3 4 5 Valores
Determinantes. Reducción de matrices. Caso diagonalizable
 Tema 4 Determinantes Reducción de matrices Caso diagonalizable En este tema consideraremos matrices cuadradas y, para ellas, introduciremos el concepto de autovalor de una matriz Veremos también cómo algunas
Tema 4 Determinantes Reducción de matrices Caso diagonalizable En este tema consideraremos matrices cuadradas y, para ellas, introduciremos el concepto de autovalor de una matriz Veremos también cómo algunas
AUTOVALORES Y AUTOVECTORES
 12 de Julio de 2011 AUTOVALORES Y AUTOVECTORES (Clase 01) Departamento de Matemática Aplicada Facultad de Ingeniería Universidad Central de Venezuela 1 Puntos a tratar 1. Valores y vectores propios 2.
12 de Julio de 2011 AUTOVALORES Y AUTOVECTORES (Clase 01) Departamento de Matemática Aplicada Facultad de Ingeniería Universidad Central de Venezuela 1 Puntos a tratar 1. Valores y vectores propios 2.
Profesor Francisco R. Villatoro 13 de Diciembre de 1999 SOLUCIONES. 1. Una matriz A de n n es diagonalmente dominante (estrictamente) por filas si
 Cuarta relación de problemas Técnicas Numéricas Profesor Francisco R. Villatoro 13 de Diciembre de 1999 SOLUCIONES 1. Una matriz A de n n es diagonalmente dominante estrictamente por filas si a ii > a
Cuarta relación de problemas Técnicas Numéricas Profesor Francisco R. Villatoro 13 de Diciembre de 1999 SOLUCIONES 1. Una matriz A de n n es diagonalmente dominante estrictamente por filas si a ii > a
Solución de problemas I 1
 Universidad Autónoma de Madrid Álgebra II. Físicas. Curso 5 6 Solución de problemas I Álgebra II Curso 5-6. Proyecciones en el producto escalar estándar Ejercicio 7.7. (a) Dada la ecuación x + y z, dar
Universidad Autónoma de Madrid Álgebra II. Físicas. Curso 5 6 Solución de problemas I Álgebra II Curso 5-6. Proyecciones en el producto escalar estándar Ejercicio 7.7. (a) Dada la ecuación x + y z, dar
Tema 3: Espacios vectoriales
 Tema 3: Espacios vectoriales K denotará un cuerpo. Definición. Se dice que un conjunto no vacio V es un espacio vectorial sobre K o que es un K-espacio vectorial si: 1. En V está definida una operación
Tema 3: Espacios vectoriales K denotará un cuerpo. Definición. Se dice que un conjunto no vacio V es un espacio vectorial sobre K o que es un K-espacio vectorial si: 1. En V está definida una operación
Capítulo 1: Diagonalización de matrices
 Capítulo : Diagonalización de matrices Matrices y determinantes Definición Una matriz es un arreglo rectangular de números reales a a a m a A a a m a n a n a nm La matriz es de orden n m si consta de n
Capítulo : Diagonalización de matrices Matrices y determinantes Definición Una matriz es un arreglo rectangular de números reales a a a m a A a a m a n a n a nm La matriz es de orden n m si consta de n
Matrices y sistemas de ecuaciones
 Matrices y sistemas de ecuaciones María Muñoz Guillermo maria.mg@upct.es U.P.C.T. Matemáticas I M. Muñoz (U.P.C.T.) Matrices y sistemas de ecuaciones Matemáticas I 1 / 59 Definición de Matriz Matrices
Matrices y sistemas de ecuaciones María Muñoz Guillermo maria.mg@upct.es U.P.C.T. Matemáticas I M. Muñoz (U.P.C.T.) Matrices y sistemas de ecuaciones Matemáticas I 1 / 59 Definición de Matriz Matrices
Transformaciones Lineales
 Transformaciones Lineales En lo que sigue denotaremos por K al conjunto R ó C Definición Sean V y W dos K-ev (espacios vectoriales sobre K Se llama transformación lineal de V en W a toda función T : V
Transformaciones Lineales En lo que sigue denotaremos por K al conjunto R ó C Definición Sean V y W dos K-ev (espacios vectoriales sobre K Se llama transformación lineal de V en W a toda función T : V
Definición Dados dos números naturales m y n, una matriz de orden o dimensión m n es una tabla numérica rectangular con m filas y n columnas.
 Tema 1 Matrices 1.1. Conceptos básicos y ejemplos Definición 1.1.1. Dados dos números naturales m y n, una matriz de orden o dimensión m n es una tabla numérica rectangular con m filas y n columnas. NOTA:
Tema 1 Matrices 1.1. Conceptos básicos y ejemplos Definición 1.1.1. Dados dos números naturales m y n, una matriz de orden o dimensión m n es una tabla numérica rectangular con m filas y n columnas. NOTA:
Transformaciones Lineales y Espacio Dual
 Transformaciones Lineales y Espacio Dual Juan Pablo De Rasis 22 de abril de 2018 El presente artículo tiene como objetivo la exposición de soluciones a problemas de Álgebra Lineal concernientes a transformaciones
Transformaciones Lineales y Espacio Dual Juan Pablo De Rasis 22 de abril de 2018 El presente artículo tiene como objetivo la exposición de soluciones a problemas de Álgebra Lineal concernientes a transformaciones
AP = A p 1 p 2 p n = Ap 1 Ap 2. λ 1 p 21 λ 2 p 22 λ n p 2n. .. = λ 1 p 1 λ 2 p 2
 Capítulo 6 Diagonalización 6 Valores y vectores propios 6 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial V, nos planteamos el problema
Capítulo 6 Diagonalización 6 Valores y vectores propios 6 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial V, nos planteamos el problema
Sea V un conjunto no vacío (cuyos elementos se llamarán vectores) y sea K un cuerpo (cuyos elementos se llamarán escalares).
 Capítulo 6 Espacios Vectoriales 6.1 Definiciones Sea V un conjunto no vacío (cuyos elementos se llamarán vectores) y sea K un cuerpo (cuyos elementos se llamarán escalares). Definición 6.1.1 Se dice que
Capítulo 6 Espacios Vectoriales 6.1 Definiciones Sea V un conjunto no vacío (cuyos elementos se llamarán vectores) y sea K un cuerpo (cuyos elementos se llamarán escalares). Definición 6.1.1 Se dice que
Sesión 18: Diagonalización (I) Método práctico para diagonalizar una matriz cuadrada A M nxn K
 Sesión 8: Diagonalización (I) Método práctico para diagonalizar una matriz cuadrada A M nxn K ) Calculamos los valores propios de A y sus multiplicidades algebraicas con: d A λ = det A λi nxn = Si d A
Sesión 8: Diagonalización (I) Método práctico para diagonalizar una matriz cuadrada A M nxn K ) Calculamos los valores propios de A y sus multiplicidades algebraicas con: d A λ = det A λi nxn = Si d A
Diagonalización de matrices. Kepler C k
 Kepler C k 24 Índice. Problema de diagonalización 3.. Semejanza de matrices................................. 3.2. Valores propios y vectores propios........................... 3.3. Matrices y valores propios...............................
Kepler C k 24 Índice. Problema de diagonalización 3.. Semejanza de matrices................................. 3.2. Valores propios y vectores propios........................... 3.3. Matrices y valores propios...............................
Parte 3. Vectores y valores propios
 Parte 3. Vectores y valores propios Gustavo Montero Escuela Universitaria Politécnica Universidad de Las Palmas de Gran Canaria Curso 2006-2007 Valores y vectores propios Valor propio Se dice que el número
Parte 3. Vectores y valores propios Gustavo Montero Escuela Universitaria Politécnica Universidad de Las Palmas de Gran Canaria Curso 2006-2007 Valores y vectores propios Valor propio Se dice que el número
TEMA 8.- NORMAS DE MATRICES Y
 Álgebra II: Tema 8. TEMA 8.- NORMAS DE MATRICES Y NúMERO DE CONDICIóN Índice. Introducción 2. Norma vectorial y norma matricial. 2 2.. Norma matricial inducida por normas vectoriales......... 4 2.2. Algunos
Álgebra II: Tema 8. TEMA 8.- NORMAS DE MATRICES Y NúMERO DE CONDICIóN Índice. Introducción 2. Norma vectorial y norma matricial. 2 2.. Norma matricial inducida por normas vectoriales......... 4 2.2. Algunos
4. Endomorfismos. 2 Autovalores y autovectores. 1 Introducción. 2.1 Definición y propiedades. 2.2 Subespacios característicos.
 Tema III Capítulo 4 Endomorfismos Álgebra Lineal I Departamento de Métodos Matemáticos y de Representación UDC 4 Endomorfismos 1 Introducción Vimos en el capítulo anterior que un endomorfismo es una aplicación
Tema III Capítulo 4 Endomorfismos Álgebra Lineal I Departamento de Métodos Matemáticos y de Representación UDC 4 Endomorfismos 1 Introducción Vimos en el capítulo anterior que un endomorfismo es una aplicación
f(x, y, z, t) = (x + y t, x + 2y z 3t, 3x + 5y 2z 7t).
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Álgebra Convocatoria de enero de 20 de enero de 20 (2.5 p.) ) Se considera la aplicación lineal f : R 4 R definida por: f(x y
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Álgebra Convocatoria de enero de 20 de enero de 20 (2.5 p.) ) Se considera la aplicación lineal f : R 4 R definida por: f(x y
Álgebra Lineal. Maestría en Ciencias Matemáticas. x y + z = 1 x y z = 3 2x y z = 1. x + y + 2z = 1 4x 2ty + 5z = 2 x y + tz = 1
 Álgebra Lineal Maestría en Ciencias Matemáticas Resuelva el siguiente sistema usando la factorización LU o P T LU (según sea el caso) x y + z = x y z = 3 2x y z = 2 Calcule A usando el algoritmo de Gauss-Jordan:
Álgebra Lineal Maestría en Ciencias Matemáticas Resuelva el siguiente sistema usando la factorización LU o P T LU (según sea el caso) x y + z = x y z = 3 2x y z = 2 Calcule A usando el algoritmo de Gauss-Jordan:
ÁLGEBRA LINEAL Problemas, 2006/2007
 ÁLGEBRA LINEAL Problemas, 2006/2007 Nota: si no se especifíca lo contrario suponemos que las matrices y espacios vectoriales están definidos sobre un cuerpo K arbitrario 1 Una matriz A de orden n n se
ÁLGEBRA LINEAL Problemas, 2006/2007 Nota: si no se especifíca lo contrario suponemos que las matrices y espacios vectoriales están definidos sobre un cuerpo K arbitrario 1 Una matriz A de orden n n se
Valores y Vectores Propios
 Valores y Vectores Propios Iván Huerta Facultad de Matemáticas Pontificia Universidad Católica de Chile ihuerta@mat.puc.cl Segundo Semestre, 1999 Definición Valores y Vectores Propios Valores y Vectores
Valores y Vectores Propios Iván Huerta Facultad de Matemáticas Pontificia Universidad Católica de Chile ihuerta@mat.puc.cl Segundo Semestre, 1999 Definición Valores y Vectores Propios Valores y Vectores
1.2 Valores y vectores propios. Método de las potencias y Rayleigh.
 20 Prelininares. 1.2 Valores y vectores propios. Método de las potencias y Rayleigh. 1.2.1 Cálculo del Polinomio Caracterstico: ALGORITMO DE SOURIAU. ENTRADA: la matriz A 1 = A, p 1 = traza(a 1 ), n =
20 Prelininares. 1.2 Valores y vectores propios. Método de las potencias y Rayleigh. 1.2.1 Cálculo del Polinomio Caracterstico: ALGORITMO DE SOURIAU. ENTRADA: la matriz A 1 = A, p 1 = traza(a 1 ), n =
Vectores y Valores Propios
 Capítulo 11 Vectores y Valores Propios Las ideas de vector y valor propio constituyen conceptos centrales del álgebra lineal y resultan una valiosa herramienta en la solución de numerosos problemas de
Capítulo 11 Vectores y Valores Propios Las ideas de vector y valor propio constituyen conceptos centrales del álgebra lineal y resultan una valiosa herramienta en la solución de numerosos problemas de
6.5.7 Orientación de un espacio vectorial eucĺıdeo Producto vectorial Diagonalización de formas bilineales simétricas...
 Contents 6 Formas Bilineales y Producto Escalar 3 6.1 Formas bilineales............................... 3 6.1.1 Matriz de una forma bilineal....................... 4 6.1. Formas bilineales simétricas.......................
Contents 6 Formas Bilineales y Producto Escalar 3 6.1 Formas bilineales............................... 3 6.1.1 Matriz de una forma bilineal....................... 4 6.1. Formas bilineales simétricas.......................
Tema 3: Forma canónica de Jordan de una matriz.
 Forma canónica de Jordan de una matriz 1 Tema 3: Forma canónica de Jordan de una matriz. 1. Planteamiento del problema. Matrices semejantes. Matrices triangularizables. El problema que nos planteamos en
Forma canónica de Jordan de una matriz 1 Tema 3: Forma canónica de Jordan de una matriz. 1. Planteamiento del problema. Matrices semejantes. Matrices triangularizables. El problema que nos planteamos en
Cálculo de autovalores
 Cálculo de autovalores Damián Ginestar Peiró Departamento de Matemática Aplicada Universidad Politécnica de Valencia Curso 2011-2012 (UPV) Cálculo de autovalores Curso 2011-2012 1 / 28 Índice 1 Preliminares
Cálculo de autovalores Damián Ginestar Peiró Departamento de Matemática Aplicada Universidad Politécnica de Valencia Curso 2011-2012 (UPV) Cálculo de autovalores Curso 2011-2012 1 / 28 Índice 1 Preliminares
Formas canónicas reales
 Capítulo 7 Formas canónicas reales Introducción Sea V un espacio vectorial sobre C, f End(V y M B (f = A M(n n Sea λ = a + bi es una autovalor complejo de f de multiplicidad m Para tal autovalor complejo
Capítulo 7 Formas canónicas reales Introducción Sea V un espacio vectorial sobre C, f End(V y M B (f = A M(n n Sea λ = a + bi es una autovalor complejo de f de multiplicidad m Para tal autovalor complejo
Ejercicio 1 Explica por qué el coste de invertir una matriz utilizando el algoritmo LU es de orden
 CUESTIONES Ejercicio 1 Explica por qué el coste de invertir una matriz utilizando el algoritmo LU es de orden cúbico Ejercicio 2 Explica por qué si λ 1 ě λ 2 ě ě λ n son los valores propios de la matrix
CUESTIONES Ejercicio 1 Explica por qué el coste de invertir una matriz utilizando el algoritmo LU es de orden cúbico Ejercicio 2 Explica por qué si λ 1 ě λ 2 ě ě λ n son los valores propios de la matrix
Examen Final - soluciones
 Algebra Lineal 2, FAMAT-UG, agsto-dic, 2009 PARTE A (60 puntos). Cierto o Falso. Examen Final - soluciones 9 dic, 2009 1. Para todo operador ortogonal T en R n, det(t ) = 1. Falso. T : (x 1,..., x n )
Algebra Lineal 2, FAMAT-UG, agsto-dic, 2009 PARTE A (60 puntos). Cierto o Falso. Examen Final - soluciones 9 dic, 2009 1. Para todo operador ortogonal T en R n, det(t ) = 1. Falso. T : (x 1,..., x n )
L(a, b, c, d) = (a + c, 2a 2b + 2c + d, a c, 4a 4b + 4c + 2d).
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Álgebra Convocatoria de enero de 1 18 de enero de 1 (5 p. 1 Para cada α R se considera el siguiente subespacio de R 4 : U α =
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Álgebra Convocatoria de enero de 1 18 de enero de 1 (5 p. 1 Para cada α R se considera el siguiente subespacio de R 4 : U α =
a ij x i x j = [x] t B A+At ) t = At +(A t ) t = At +A x i x j + a ij + a ji x j x i = s ij x i x j + s ji x j x i 2
![a ij x i x j = [x] t B A+At ) t = At +(A t ) t = At +A x i x j + a ij + a ji x j x i = s ij x i x j + s ji x j x i 2 a ij x i x j = [x] t B A+At ) t = At +(A t ) t = At +A x i x j + a ij + a ji x j x i = s ij x i x j + s ji x j x i 2](/thumbs/65/53464617.jpg) 68 Matemáticas I : Álgebra Lineal Tema 7 Formas cuadráticas Aunque, pueda parecernos que vamos a estudiar un nuevo concepto, un caso particular de las formas cudráticas ya ha sido estudiado, pues el cuadrado
68 Matemáticas I : Álgebra Lineal Tema 7 Formas cuadráticas Aunque, pueda parecernos que vamos a estudiar un nuevo concepto, un caso particular de las formas cudráticas ya ha sido estudiado, pues el cuadrado
Valores y vectores propios
 Valores y vectores propios Problemas teóricos El los siguientes problemas se denota por L(V ) conjunto de los operadores lineales en un espacio vectorial V (en otras palabras, de las transformaciones lineales
Valores y vectores propios Problemas teóricos El los siguientes problemas se denota por L(V ) conjunto de los operadores lineales en un espacio vectorial V (en otras palabras, de las transformaciones lineales
Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1. Se llama producto escalar sobre un espacio vectorial real V a cualquier aplicación
 Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 6 Espacios euclídeos 6.1 Producto escalar. Espacio euclídeo Se llama producto escalar sobre un espacio vectorial real V a cualquier aplicación
Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 6 Espacios euclídeos 6.1 Producto escalar. Espacio euclídeo Se llama producto escalar sobre un espacio vectorial real V a cualquier aplicación
Álgebra II(61.08, 81.02) Segundo cuatrimestre 2017 Práctica 4. Autovalores y autovectores de matrices. Diagonalización.
 Álgebra II(6108, 8102) Segundo cuatrimestre 2017 Práctica 4 Autovalores y autovectores de matrices Diagonalización Nota: salvo indicación particular, se considera que todas las matrices pertenecen a C
Álgebra II(6108, 8102) Segundo cuatrimestre 2017 Práctica 4 Autovalores y autovectores de matrices Diagonalización Nota: salvo indicación particular, se considera que todas las matrices pertenecen a C
Espacios vectoriales con producto escalar
 147 Fundamentos de Matemáticas : Álgebra Lineal Capítulo 10 Espacios vectoriales con producto escalar 10.1 Producto escalar. Norma. Distancia Definición 71.- Un producto escalar o producto interior en
147 Fundamentos de Matemáticas : Álgebra Lineal Capítulo 10 Espacios vectoriales con producto escalar 10.1 Producto escalar. Norma. Distancia Definición 71.- Un producto escalar o producto interior en
Departamento de Ingeniería Matemática - Universidad de Chile
 Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 08-2 SEMANA 7: ESPACIOS VECTORIALES 3.5. Generadores de un espacio vectorial Sea V un espacio vectorial
Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 08-2 SEMANA 7: ESPACIOS VECTORIALES 3.5. Generadores de un espacio vectorial Sea V un espacio vectorial
RESUMEN DEL TEMA 7 VALORES Y VECTORES PROPIOS
 RESUMEN DEL TEMA 7 VALORES Y VECTORES PROPIOS 1. Determinantes El determinante de una matriz cuadrada n n A = a 21 a 22 a 2n a n1 a n2 a nn es un número real, y se representa por: A = a 21 a 22 a 2n a
RESUMEN DEL TEMA 7 VALORES Y VECTORES PROPIOS 1. Determinantes El determinante de una matriz cuadrada n n A = a 21 a 22 a 2n a n1 a n2 a nn es un número real, y se representa por: A = a 21 a 22 a 2n a
Álgebra Lineal UCR. Sétimo tema, 2013
 Álgebra Lineal UCR Sétimo tema, 2013 Presentaciones basadas principalmente en Arce,C, Castillo,W y González, J. (2004) Álgebra lineal. Tercera edición. UCR. San Pedro. Otras fuentes serán mencionadas cuando
Álgebra Lineal UCR Sétimo tema, 2013 Presentaciones basadas principalmente en Arce,C, Castillo,W y González, J. (2004) Álgebra lineal. Tercera edición. UCR. San Pedro. Otras fuentes serán mencionadas cuando
Álgebra Lineal - Grado de Estadística. Examen final 27 de junio de 2014 APELLIDOS, NOMBRE:
 Álgebra Lineal - Grado de Estadística Examen final 7 de junio de 4 APELLIDOS, NOMBRE: DNI: irma Primer parcial Ejercicio Consideremos matrices A m m, B, C n n, Pruebe que bajo la hipótesis de que las inversas
Álgebra Lineal - Grado de Estadística Examen final 7 de junio de 4 APELLIDOS, NOMBRE: DNI: irma Primer parcial Ejercicio Consideremos matrices A m m, B, C n n, Pruebe que bajo la hipótesis de que las inversas
a n1 a n2 a nn x n a ij x i x j = [x] t B A+At ) t = At +(A t ) t = At +A x j x i = s ij x i x j + s ji x j x i 2 x i x j + a ij + a ji
![a n1 a n2 a nn x n a ij x i x j = [x] t B A+At ) t = At +(A t ) t = At +A x j x i = s ij x i x j + s ji x j x i 2 x i x j + a ij + a ji a n1 a n2 a nn x n a ij x i x j = [x] t B A+At ) t = At +(A t ) t = At +A x j x i = s ij x i x j + s ji x j x i 2 x i x j + a ij + a ji](/thumbs/84/89039875.jpg) 16 Fundamentos de Matemáticas : Álgebra Lineal Capítulo 1 Formas cuadráticas Aunque, pueda parecernos que vamos a estudiar un nuevo concepto, un caso particular de las formas cudráticas ya ha sido estudiado,
16 Fundamentos de Matemáticas : Álgebra Lineal Capítulo 1 Formas cuadráticas Aunque, pueda parecernos que vamos a estudiar un nuevo concepto, un caso particular de las formas cudráticas ya ha sido estudiado,
dia G o n a l i z a c i ó n
 Unidad elementos característicos dia G o n a l i z a c i ó n Objetivos: Al inalizar la unidad, el alumno: Encontrará los valores y los vectores característicos de una matriz. Utilizará los elementos característicos
Unidad elementos característicos dia G o n a l i z a c i ó n Objetivos: Al inalizar la unidad, el alumno: Encontrará los valores y los vectores característicos de una matriz. Utilizará los elementos característicos
Espacios vectoriales con producto interno
 Espacios vectoriales con producto interno Mariano Suárez-Alvarez 24 de junio, 2011 1. Espacios con producto interno... 1 2. Normas y distancias... 3 3. Ortogonalidad... 5 4. Proyectores ortogonales...
Espacios vectoriales con producto interno Mariano Suárez-Alvarez 24 de junio, 2011 1. Espacios con producto interno... 1 2. Normas y distancias... 3 3. Ortogonalidad... 5 4. Proyectores ortogonales...
Acerca del Teorema de Gershgorin
 Acerca del Teorema de Gershgorin La siguiente nota se refiere al Teorema de Gershgorin y está motivada parcialmente por la parte c) de dicho teorema que puede verse en las notas de Geometría y Algebra
Acerca del Teorema de Gershgorin La siguiente nota se refiere al Teorema de Gershgorin y está motivada parcialmente por la parte c) de dicho teorema que puede verse en las notas de Geometría y Algebra
Tema 4: Sistemas de ecuaciones lineales.
 Tema 4: Sistemas de ecuaciones lineales 1 Rango de una matriz Definición Sea A Mat n m (K) Se llama rango de filas de A, y se denota por rg f (A) la dimensión del subespacio vectorial generado por las
Tema 4: Sistemas de ecuaciones lineales 1 Rango de una matriz Definición Sea A Mat n m (K) Se llama rango de filas de A, y se denota por rg f (A) la dimensión del subespacio vectorial generado por las
Descomposición en forma canónica de Jordan (Segunda versión)
 Descomposición en forma canónica de Jordan (Segunda versión) Francisco J. Bravo S. 1 de septiembre de 211 En esta guía se presentan los resultados necesarios para poder construir la forma de Jordan sin
Descomposición en forma canónica de Jordan (Segunda versión) Francisco J. Bravo S. 1 de septiembre de 211 En esta guía se presentan los resultados necesarios para poder construir la forma de Jordan sin
Apéndice sobre ecuaciones diferenciales lineales
 Apéndice sobre ecuaciones diferenciales lineales Juan-Miguel Gracia 10 de febrero de 2008 Índice 2 Determinante wronskiano. Wronskiano de f 1 (t), f 2 (t),..., f n (t). Derivada de un determinante de funciones.
Apéndice sobre ecuaciones diferenciales lineales Juan-Miguel Gracia 10 de febrero de 2008 Índice 2 Determinante wronskiano. Wronskiano de f 1 (t), f 2 (t),..., f n (t). Derivada de un determinante de funciones.
Transformaciones lineales autoadjuntas (hermíticas)
 Transformaciones lineales autoadjuntas (hermíticas) Objetivos. Estudiar propiedades elementales de transformaciones lineales autoadjuntas. Demostrar que para toda transformación lineal autoadjunta en un
Transformaciones lineales autoadjuntas (hermíticas) Objetivos. Estudiar propiedades elementales de transformaciones lineales autoadjuntas. Demostrar que para toda transformación lineal autoadjunta en un
UNIVERSIDAD SIMON BOLIVAR MA1116 abril-julio de 2009 Departamento de Matemáticas Puras y Aplicadas. Ejercicios sugeridos para :
 IX / 9 UNIVERSIDAD SIMON BOLIVAR MA6 abril-julio de 9 Ejercicios sugeridos para : los temas de las clases del 3 de junio y de julio de 9. Temas : Autovalores y autovectores. Matrices similares; diagonalización.
IX / 9 UNIVERSIDAD SIMON BOLIVAR MA6 abril-julio de 9 Ejercicios sugeridos para : los temas de las clases del 3 de junio y de julio de 9. Temas : Autovalores y autovectores. Matrices similares; diagonalización.
Descomposición en valores singulares de una matriz
 Descomposición en valores singulares de una matriz Estas notas están dedicadas a demostrar una extensión del teorema espectral conocida como descomposición en valores singulares (SVD en inglés) de gran
Descomposición en valores singulares de una matriz Estas notas están dedicadas a demostrar una extensión del teorema espectral conocida como descomposición en valores singulares (SVD en inglés) de gran
Álgebra Lineal. Ejercicios de evaluación. Grado en Ingeniería Informática Doble Grado en Ingeniería Informática y Administración de Empresas
 Álgebra Lineal Ejercicios de evaluación Grado en Ingeniería Informática Doble Grado en Ingeniería Informática y Administración de Empresas AUTORES: J. S ALAS, A. T ORRENTE Y E.J.S. V ILLASEÑOR Problema
Álgebra Lineal Ejercicios de evaluación Grado en Ingeniería Informática Doble Grado en Ingeniería Informática y Administración de Empresas AUTORES: J. S ALAS, A. T ORRENTE Y E.J.S. V ILLASEÑOR Problema
Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados
 Capítulo 5 Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados En este tema iniciamos el estudio de los conceptos geométricos de distancia y perpendicularidad en K n. Empezaremos con las definiciones
Capítulo 5 Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados En este tema iniciamos el estudio de los conceptos geométricos de distancia y perpendicularidad en K n. Empezaremos con las definiciones
Cálculo Numérico III Curso 2010/11
 Cálculo Numérico III Curso 2010/11 Problemas del Tema 1 1. Sean {x 0, x 1,..., x n } IR con x i x j si i j. Hoja de problemas - Parte I a) Hallar el polinomio de grado n que interpola a la función en los
Cálculo Numérico III Curso 2010/11 Problemas del Tema 1 1. Sean {x 0, x 1,..., x n } IR con x i x j si i j. Hoja de problemas - Parte I a) Hallar el polinomio de grado n que interpola a la función en los
2 Polinomio característico de una matriz
 Lección 4: Teoría de Operadores 1 Semejanza Sean A, B M n,n. Se dice A es semejante con B cuando existe una matriz regular P GL n de suerte que B = P 1 AP. Si A es semejante con B, entonces B es semejante
Lección 4: Teoría de Operadores 1 Semejanza Sean A, B M n,n. Se dice A es semejante con B cuando existe una matriz regular P GL n de suerte que B = P 1 AP. Si A es semejante con B, entonces B es semejante
Práctica 5. Autovalores y autovectores. Diagonalización de matrices y de transformaciones lineales.
 Práctica 5 Autovalores y autovectores Diagonalización de matrices y de transformaciones lineales Nota: salvo indicación particular, se considera que todas las matrices pertenecen a C n n 1 Encuentre los
Práctica 5 Autovalores y autovectores Diagonalización de matrices y de transformaciones lineales Nota: salvo indicación particular, se considera que todas las matrices pertenecen a C n n 1 Encuentre los
MAT1202: Algebra Lineal GUIA N 6 Otoño 2002 Valores y Vectores Propios
 Pontificia Universidad Católica de Chile Facultad de Matemáticas MAT1202: Algebra Lineal GUIA N 6 Otoño 2002 Valores y Vectores Propios 1. Determine los valores y vectores propios de 0 3 A + I = 1 3 A
Pontificia Universidad Católica de Chile Facultad de Matemáticas MAT1202: Algebra Lineal GUIA N 6 Otoño 2002 Valores y Vectores Propios 1. Determine los valores y vectores propios de 0 3 A + I = 1 3 A
Soluciones a los ejercicios del examen final C =. 1 0
 Universidade de Vigo Departamento de Matemática Aplicada II E T S E de Minas Álgebra Lineal Curso 205/6 de enero de 206 Soluciones a los ejercicios del examen final Se considera el subespacio U {X M 2
Universidade de Vigo Departamento de Matemática Aplicada II E T S E de Minas Álgebra Lineal Curso 205/6 de enero de 206 Soluciones a los ejercicios del examen final Se considera el subespacio U {X M 2
a n1 a n2 a nn Es decir, una forma cuadrática es un polinomio homogéneo de grado 2 y n variables.
 Capítulo 7 Formas cuadráticas. Aunque, pueda parecernos que vamos a estudiar un nuevo concepto, un caso particular de las formas cudráticas ya ha sido estudiado, pues el cuadrado de la norma de un vector
Capítulo 7 Formas cuadráticas. Aunque, pueda parecernos que vamos a estudiar un nuevo concepto, un caso particular de las formas cudráticas ya ha sido estudiado, pues el cuadrado de la norma de un vector
Departamento de Ingeniería Matemática - Universidad de Chile
 Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 8-7 Formas cuadráticas SEMANA 4: FORMAS CUADRÁTICAS 7 Formas cuadráticas y matrices definidas positivas
Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 8-7 Formas cuadráticas SEMANA 4: FORMAS CUADRÁTICAS 7 Formas cuadráticas y matrices definidas positivas
Matrices. Álgebra de matrices.
 Matrices. Álgebra de matrices. 1. Definiciones generales Definición 1.1 Si m y n son dos números naturales, se llama matriz de números reales de orden m n a una aplicación A : {1, 2, 3,..., m} {1, 2, 3,...,
Matrices. Álgebra de matrices. 1. Definiciones generales Definición 1.1 Si m y n son dos números naturales, se llama matriz de números reales de orden m n a una aplicación A : {1, 2, 3,..., m} {1, 2, 3,...,
VALORES Y VECTORES PROPIOS
 45 Capítulo 6 VALORES Y VECTORES PROPIOS Martínez Héctor Jairo Sanabria Ana María Semestre, 7 6 Introducción Aunque, en general, la imagen de un vector bajo una transformación de un espacio vectorial en
45 Capítulo 6 VALORES Y VECTORES PROPIOS Martínez Héctor Jairo Sanabria Ana María Semestre, 7 6 Introducción Aunque, en general, la imagen de un vector bajo una transformación de un espacio vectorial en
ÁLGEBRA LINEAL I Algunas soluciones a la Práctica 3
 ÁLGEBRA LINEAL I Algunas soluciones a la Práctica 3 Matrices y determinantes (Curso 2011 2012) 2. Sea A una matriz diagonal n n y supongamos que todos los elementos de su diagonal son distintos entre sí.
ÁLGEBRA LINEAL I Algunas soluciones a la Práctica 3 Matrices y determinantes (Curso 2011 2012) 2. Sea A una matriz diagonal n n y supongamos que todos los elementos de su diagonal son distintos entre sí.
APÉNDICE A. Algebra matricial
 APÉNDICE A Algebra matricial El estudio de la econometría requiere cierta familiaridad con el álgebra matricial. La teoría de matrices simplifica la descripción, desarrollo y aplicación de los métodos
APÉNDICE A Algebra matricial El estudio de la econometría requiere cierta familiaridad con el álgebra matricial. La teoría de matrices simplifica la descripción, desarrollo y aplicación de los métodos
5. Autovalores y autovectores
 172 Autovalores y autovectores Al ser x 0 = y = P 1 x 0yportanto,λ es un autovalor de A. Recíprocamente, si λ es un autovalor de A existe un vector x 0talque A x = λx y por tanto, 5. Autovalores y autovectores
172 Autovalores y autovectores Al ser x 0 = y = P 1 x 0yportanto,λ es un autovalor de A. Recíprocamente, si λ es un autovalor de A existe un vector x 0talque A x = λx y por tanto, 5. Autovalores y autovectores
6.8. Descomposición mediante valores singulares. v 2 =
 68 Descomposición mediante valores singulares Los valores singulares de una matriz m n Supongamos que A es una matriz real cualquiera Los autovalores de A T A tienen la siguiente propiedad A T Ax = λx
68 Descomposición mediante valores singulares Los valores singulares de una matriz m n Supongamos que A es una matriz real cualquiera Los autovalores de A T A tienen la siguiente propiedad A T Ax = λx
sup si A no es acotado.
 Capítulo 5 Teoría de Baire 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y la
Capítulo 5 Teoría de Baire 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y la
1. ESPACIO EUCLÍDEO. ISOMETRÍAS
 1 1. ESPACIO EUCLÍDEO. ISOMETRÍAS Muchos de los fenómenos que se investigan en la geometría utilizan nociones como las de longitud de un vector y ángulo entre vectores. Para introducir estos dos conceptos
1 1. ESPACIO EUCLÍDEO. ISOMETRÍAS Muchos de los fenómenos que se investigan en la geometría utilizan nociones como las de longitud de un vector y ángulo entre vectores. Para introducir estos dos conceptos
Universidad Nacional de Colombia Departamento de Matemáticas Álgebra Lineal - Grupo 1 Resumen Unidad n 3
 Universidad Nacional de Colombia Departamento de Matemáticas 1000003-5 Álgebra Lineal - Grupo 1 Resumen Unidad n 3 Vectores en R n Definición. El conjunto de las n-tuplas ordenadas de números reales se
Universidad Nacional de Colombia Departamento de Matemáticas 1000003-5 Álgebra Lineal - Grupo 1 Resumen Unidad n 3 Vectores en R n Definición. El conjunto de las n-tuplas ordenadas de números reales se
Matrices ortogonales y descomposición QR
 Matrices ortogonales y descomposición QR Problemas para examen Agradezco a Aldo Iván Leal García por varias correcciones importantes. Invertibilidad por la izquierda y por la derecha (repaso) 1. Conceptos
Matrices ortogonales y descomposición QR Problemas para examen Agradezco a Aldo Iván Leal García por varias correcciones importantes. Invertibilidad por la izquierda y por la derecha (repaso) 1. Conceptos
Transformaciones lineales
 CAPíTULO 4 Transformaciones lineales En este capítulo estudiamos las primeras propiedades de las transformaciones lineales entre espacios vectoriales. 1. Construcciones de transformaciones lineales Lema
CAPíTULO 4 Transformaciones lineales En este capítulo estudiamos las primeras propiedades de las transformaciones lineales entre espacios vectoriales. 1. Construcciones de transformaciones lineales Lema
1. DIAGONALIZACIÓN Y FORMAS CANÓNICAS
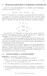 1 1. DIAGONALIZACIÓN Y FORMAS CANÓNICAS Sea f : V V un endomorfismo de V, f End(V, con V un K-espacio vectorial de dimensión n, y sean B = {e 1,..., e n } B = {e 1,..., e n} bases de V. La matriz de f
1 1. DIAGONALIZACIÓN Y FORMAS CANÓNICAS Sea f : V V un endomorfismo de V, f End(V, con V un K-espacio vectorial de dimensión n, y sean B = {e 1,..., e n } B = {e 1,..., e n} bases de V. La matriz de f
Espacios vectoriales reales.
 Tema 3 Espacios vectoriales reales. 3.1 Espacios vectoriales. Definición 3.1 Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe el nombre
Tema 3 Espacios vectoriales reales. 3.1 Espacios vectoriales. Definición 3.1 Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe el nombre
Introducción a la Teoría de Códigos
 Introducción a la Teoría de Códigos M.A.García, L. Martínez, T.Ramírez Facultad de Ciencia y Tecnología. UPV/EHU Resumen Teórico Tema 1: PRELIMINARES SOBRE ÁLGEBRA LINEAL Mayo de 2017 Tema 1 Preliminares
Introducción a la Teoría de Códigos M.A.García, L. Martínez, T.Ramírez Facultad de Ciencia y Tecnología. UPV/EHU Resumen Teórico Tema 1: PRELIMINARES SOBRE ÁLGEBRA LINEAL Mayo de 2017 Tema 1 Preliminares
Métodos Matemáticos: Análisis Funcional
 Licenciatura en Ciencias y Técnicas Estadísticas Universidad de Sevilla http://euler.us.es/ renato/clases.html Espacios eucĺıdeos Definición Se dice que un espacio vectorial E es un espacio eucĺıdeo si
Licenciatura en Ciencias y Técnicas Estadísticas Universidad de Sevilla http://euler.us.es/ renato/clases.html Espacios eucĺıdeos Definición Se dice que un espacio vectorial E es un espacio eucĺıdeo si
Tema 5: Diagonalización de matrices: Apéndice
 Tema : Diagonalización de matrices: Apéndice Más aplicaciones de la diagonalización. Diagonalización de matrices simétricas reales Tiene especial interés la diagonalización de matrices simétricas. Supongamos
Tema : Diagonalización de matrices: Apéndice Más aplicaciones de la diagonalización. Diagonalización de matrices simétricas reales Tiene especial interés la diagonalización de matrices simétricas. Supongamos
Tema 1. Espacios Vectoriales. Sistemas de ecuaciones.
 Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Álgebra Lineal Escuela Politécnica Superior Universidad de Málaga Emilio Muñoz-Velasco (Basado en los apuntes de Jesús Medina e Inmaculada Fortes)
Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Álgebra Lineal Escuela Politécnica Superior Universidad de Málaga Emilio Muñoz-Velasco (Basado en los apuntes de Jesús Medina e Inmaculada Fortes)
Ba s e, d i M e n s i ó n y Mat r i z
 Unidad 4 Ba s e, d i M e n s i ó n y Mat r i z de transición Objetivos: Al inalizar la unidad, el alumno: Conocerá la deinición de base de un espacio vectorial Identiicará bases canónicas para algunos
Unidad 4 Ba s e, d i M e n s i ó n y Mat r i z de transición Objetivos: Al inalizar la unidad, el alumno: Conocerá la deinición de base de un espacio vectorial Identiicará bases canónicas para algunos
