1. ESTUDIO DE ROBUSTEZ EN REDES DEPENDIENDO DE SU TOPOLOGÍA
|
|
|
- Julián Castro Ponce
- hace 7 años
- Vistas:
Transcripción
1 . ESTUDIO DE ROBUSTEZ EN REDES DEPENDIENDO DE SU TOPOLOGÍA A continuación, se intentarán aplicar algunas de las definiciones vistas anteriormente a redes con distinta topología con objeto de analizar el grado de robustez de cada una de ellas. Se le llama topología de red a la disposición de los elementos físicos que la componen. Las topologías más comunes son: Anillo: Los nodos se disponen en línea, formando figuras planas cerradas. Cada nodo está unido mediante aristas, una o varias, tanto al nodo anterior como al siguiente. El incremento del número de aristas entre pares aumenta la fiabilidad. Figura 4 Son necesarias técnicas para acceder al medio compartido y evitar colisiones. Puede entenderse como un mallado parcial (explicado en este mismo punto más adelante. Ver figura 7) con dos caminos disjuntos entre cada par de nodos. Bus: Conexión de cada nodo mediante una arista propia a una arista común. Pueden producirse colisiones en el bus. Es necesario la existencia de un mecanismo que permita a los distintos nodos ponerse de acuerdo sobre quién va a acceder al bus en cada instante. Un nodo no depende del resto para que exista su tráfico por el bus por lo que la fiabilidad aumenta notablemente. Topología de bajo coste, muy utilizada en las redes de área local, donde el número de nodos no es muy elevado. 79
2 Figura 5 Modelaremos, en posteriores análisis, la topología en bus mediante un grafo camino. Estrella: Todos los nodos están conectados únicamente a un nodo central que actúa como distribuidor del tráfico. Es la estructura más simple de todas las estudiadas. Permite una rápida comunicación. Resulta óptimo para áreas geográficas no muy extensas con un número de nodos no muy elevado. Alto costo del medio físico. Su fiabilidad depende mucho del nodo central, que ha de tener una gran capacidad. En general, es pequeña ya que al fallar un nodo se queda incomunicada la parte de la red que pende de él. Figura 6 Existe una topología, el árbol, muy similar a la estrella. La diferencia radica en que los nodos que en la estrella no son centrales, funcionan como tal para otra serie de nodos a los cuales denominaremos secundarios. Con ella, se establecen jerarquías fácilmente. Esta topología es usada, por ejemplo, en el bucle de abonado en la red telefónica conmutada. 80
3 Malla: Cada nodo está conectado a uno o varios nodos. Diremos que el mallado es total si todas las conexiones posibles entre nodos en el grafo existen. En este caso, todos los nodos presentan las mismas características en cuanto a concentración de tráfico. Si no existen todas las conexiones posibles entre nodos, el mallado será parcial. El número de medios físicos usados es muy elevado. La eficiencia de los enlaces dependerá, por supuesto, del tráfico que vaya por ellos, pero si consideramos que este tráfico entre nodos es el mismo que en otras configuraciones (suponiendo que ambas configuraciones poseen el mismo número de nodos), la eficiencia anteriormente nombrada será muy baja. Al tener tantos enlaces entre nodos, si por todos ellos viaja la misma cantidad de flujo, esta será muy pequeña. Si no viajase la misma cantidad de flujo, algunos enlaces quizás tendrían un rendimiento elevado, pero la mayoría tendrían un rendimiento nulo. Por otra parte, es una estructura muy fiable, pues existen muchos caminos alternativos para llegar de un nodo a otro. Suele usarse en el núcleo de las redes. Figura 7 Sería necesario comentar que existen también topologías hibridas, en las que se mezclan características y propiedades de diferentes topologías básicas. Son estas topologías mixtas las que, en general, se dan en redes reales. Algunas estructuras que se repiten con frecuencia son por ejemplo el anillo-estrella o el bus-estrella. Hasta ahora hemos realizado un análisis cualitativo de las distintas topologías. Si analizamos ahora matemáticamente con las magnitudes y propiedades expuestas en los apartados y 3, la fiabilidad de las distintas configuraciones llegamos a las 8
4 siguientes conclusiones en las diferentes topologías. Consideraremos en todos los casos que el peso de las aristas es unitario. 4. Anillo simple Figura 8 Hemos numerado los nodos de a n, con objeto de facilitar la explicación de todos los cálculos realizados al tener una referencia. No obstante, esta numeración podría ser rehecha con cualquier numeración secuencial al ser todos los nodos iguales (configuración simétrica en cualquier dirección del plano). Si tomamos como referencia el nodo número, Si n es par, el nodo más alejado de es el. Si n es impar, existen dos nodos cuya distancia hasta este origen es mayor que la distancia de cualquier otro nodo del grafo a él. Además, estos dos nodos están a la misma distancia del vértice considerado como origen. Los dos vértices son el y el. Por tanto: Si n es par, la menor distancia entre los dos nodos más alejados, es decir, el diámetro, es. Si n es impar, el diámetro es. Es un grafo regular en el cual todos los vértices tienen valencia, por lo que el valor medio de grado es. La longitud característica del grafo es: Si n es par, Si n es impar, 8
5 El coeficiente de agrupación, obtenido mediante las ec. (3) y (4) es nulo. El razonamiento seguido para obtener este resultado ha sido: Cualquier subgrafo de G está compuesto por 3 nodos conectados en camino. Sin embargo el subgrafo G i no incluye el nodo i solo los vecinos. Con lo cual, si quitamos del subgrafo que ya teníamos el nodo i, el subgrafo con el cual trabajamos estará formado por dos nodos aislados, no conectados entre sí. El número de aristas será 0, y por tanto, los coeficientes c i serán nulos. La eficiencia media de la red es: Si n es par, Si n es impar, Como vemos, en ambos casos, el sumatorio es una suma parcial de la serie armónica. La eficiencia global es igual que la media, ya que el estudio es topológico y la eficiencia ideal sería. La eficiencia local, al igual que el coeficiente de agrupamiento y, por la misma razón, es nulo. El coste de la red es: El grafo es conexo, con una vértice-conectividad = y una arista-conectividad =. Otras propiedades son: La cohesividad, ch(v), de todos los vértices es la misma, ch(v)=. El i-degree, ξ(i), tiene valor para i n-. Tanto la dureza de vértices, t V (G), como la de aristas toman valor uno. La persistencia del grafo, tanto la de vértices, ρ V (G), como la de arista, ρ E (G), es. Máximo incremento de distancia entre dos nodos causada por la eliminación de un vértice en la red: 4, para i =. 83
6 Máximo incremento de distancia entre dos nodos causada por la eliminación de una arista en la red:, para i =. Máximo diámetro del grafo causada por la eliminación de un vértice en el mismo:, para i =. Máximo diámetro del grafo causada por la eliminación de una arista en el mismo:, para i =. Conectividad principal,, es igual a, ya que es (n-) en los n! casos. 4. Estrella Figura 9 Al igual que antes la numeración de los nodos puede ser rehecha, siendo válidos todos los cálculos realizados para cualquier numeración. Independientemente de si n es par o impar, los nodos más alejados de la red están a una distancia =. El diámetro de la red es. No es un grafo regular, ya que todos los nodos tendrán valencia, excepto el central, que tendrá valencia n-. El grado medio es, por tanto: La longitud de camino característica es. El coeficiente de agrupación es nulo. El razonamiento seguido para obtenerlo ha sido: Si recordamos la definición proporcionada del coeficiente de agrupación veremos como todos los vértices de grado nulo o unitario, poseían un coeficiente nulo. Eso ocurre con cada subgrafo centrado en un vértice i exterior. Cuando el vértice i es el central, lo que ocurre es que todos los 84
7 nodos exteriores quedan desconectados. Al no haber ninguna arista el coeficiente de agrupamiento es nulo. La eficiencia media de la red es La eficiencia global es igual que la eficiencia media, por ser la eficiencia del grafo ideal unitaria. Por otra parte, la eficiencia local es: Recordemos que la expresión de la eficiencia local es :,, Donde. Si falta el nodo central, al no ser conexo, la eficiencia local es nula. Si falta cualquiera de los nodos exteriores el subgrafo correspondiente estaría formado por un solo nodo, por lo que la eficiencia también sería nula. En conclusión, la eficiencia local es nula. El coste de la red es: El grafo es conexo, con una vértice-conectividad = y una arista-conectividad =. Otras propiedades son: La cohesividad, ch(v), de todos los vértices exteriores es la misma, ch(v)=0. La del vértice central es. El i-degree, ξ(i), tiene valor para i=. Para el resto de valores de i, i n-, es 0. No puedo borrar ninguna arista sin que el grafo sea inconexo. 85
8 La dureza de vértices, t v (G), es (Si suprimimos el nodo central tendríamos los n- nodos exteriores aislados. Al suprimir cualquiera de los nodos exteriores tendríamos solo una componente conexa). La dureza de aristas, t E (G), es 0,5. Si eliminamos una arista tenemos dos componentes, si suprimimos dos aristas tenemos 3 componentes, si eliminamos tres aristas nos quedan 4 componentes, y así, siempre tendremos componente más que arista suprimida. El menor cociente de todos los nombrados (este valor es mayor a mas aristas suprimidas) es. La persistencia de vértices, ρ v (G), es, ya que en cuanto retiro el nodo central el grafo se hace totalmente inconexo. El diámetro, D, adquiere valor infinito. La persistencia de aristas, ρ E (G), es n-, ya que necesitaría quitar todas las aristas para incrementar el diámetro. Además, cuando esto se produce el grafo queda no conexo. Conectividad media, = 0. He de colocar siempre todas las aristas para lograr que sea conexo. El resto de las propiedades calculadas en el apartado anterior, en el caso del anillo, no tiene sentido calcularlas en este ya que el grafo deja de ser conexo. 4.3 Mallado completo Figura 0 Los dos nodos más alejados de la red están a distancia. Este es el diámetro, independientemente del número de nodos. Es un grafo regular en el cual todos los vértices tienen valencia n-, por lo que el valor medio de grado es n-. Tanto la longitud característica del grafo como el coeficiente de agrupación toman valor. 86
9 La eficiencia media de la red, la eficiencia global y la eficiencia local también son unitarias desde el punto de vista topológico. El tener a nuestra disposición un enlace dedicado entre cada par de nodos eleva el coste hasta su valor máximo, la unidad. El grafo es conexo, con una vértice-conectividad = n- (necesito quitar todos los nodos, excepto para dejar este aislado) y una arista-conectividad = n-. Otras propiedades son: La cohesividad de todos los vértices es la misma, ch(v) =. El i-degree tiene valor: i(n-i) para i n-. La dureza de vértices, t v (G), es infinita, por definición. La dureza de aristas, t E (G), es Ya que si no quito todas las aristas, el número de componentes es uno. Cuando las quitamos todas quedan n componentes aislados. La persistencia de vértices, ρ v (G), es n-, mientras que la de aristas, ρ E (G), es. Máximo incremento de distancia entre dos nodos causada por la eliminación de i vértices en la red: 0,. Máximo incremento de distancia entre dos nodos causada por la eliminación de i aristas en la red:, Máximo diámetro del grafo causado por la eliminación de i vértices en el mismo: 0,. Máximo diámetro del grafo causada por la eliminación de i aristas en el mismo:, Conectividad media: En este caso, es muy complejo el cálculo de la conectividad media. Por eso, únicamente lo acotaremos usando una de las propiedades vistas anteriormente cuando se definió la magnitud 3 A medida que crece el número de nodos esta acotación nos aporta menos información del valor de la variable. 87
10 4.4 Bus Figura Los dos nodos más alejados de la red están a una distancia n-, por lo que el diámetro de la red es n-. El grafo no es regular. Los nodos intermedios tienen un grado de valor, mientras que los de los extremos (son dos nodos) solo tienen grado. El valor medio de grado es, por tanto: La longitud característica del grafo es:
11 El coeficiente de agrupación es nulo. En los nodos intermedios el subgrafo estará formado por dos nodos aislados, sin ninguna arista, por lo que el coeficiente correspondiente a estos nodos es cero. En los nodos extremos tenemos un único nodo aislado. Este es el caso hoja, ya explicado en el tercer apartado. La eficiencia media de la red es: Esta expresión es más difícil de desarrollar que L, matemáticamente hablando. Sin embargo, podemos acotarla log log La eficiencia local es nula. Si quito un nodo cualquiera el grafo es no conexo. El coste de la red es: El grafo es conexo, con una Vértice-conectividad = y una arista-conectividad =. Otras propiedades son: La cohesividad de todos los vértices extremos es ch(v)=0. Si suprimo ese vértice extremo el vértice-conectividad seguirá siendo, igual que cuando el vértice estaba presente. La cohesividad de los vértices intermedios es ch(v)=. Cuando el vértice a analizar esta presente el vértice-conectividad es. Cuando no lo está, esta magnitud es 0. No debo quitar ningún nodo para hacerlo disconexo porque ya lo es. Estos resultados son lógicos. Como ya vimos los valores son mayores () cuando el nodo es central, mientras que son pequeños (valores negativos incluso) cuanto más exterior es el nodo al grafo. 89
12 El i-degree tiene valor para i n-. La dureza de vértices, t V (G), es 0,5. Analicemos el por qué. La supresión de cualquier vértice extremo, no nos permite la aplicación de la expresión de dureza conocida, ya que únicamente tenemos un elemento conexo. La opción con la cual conseguiríamos un mayor número de componentes es suprimiendo nodos alternos del camino. El mínimo valor de t(g) se alcanzaría si suprimimos un nodo, quedándonos aislados dos componentes. La dureza de aristas, t E (G), es 0,5. Cada vez que eliminamos una aristas, tendremos el número de aristas eliminadas más uno elementos disconexos. El menos valor de este cociente se produce cuando sólo hay una arista eliminada y, por tanto, dos subgrafos. La persistencia de vértices del grafo, ρ V (G), es. Si quito algún vértice el diámetro se hace infinito; el grafo es inconexo. Igual ocurre con las aristas, por lo que, ρ E (G) =. Conectividad media, = 0, ya que siempre las he de colocar todas para que el grafo sea conexo. El resto de propiedades calculadas en los apartados 4. y 4.3 no tiene sentido calcularlas en este, ya que el grafo deja de ser conexo. 4.5 Árbol Esta topología requiere un análisis algo diferente del realizado hasta ahora, ya que no sigue un esquema concreto, una estructura predecible en función del número de nodos. Como ya se comentó en el punto de la memoria, un árbol es un grafo conexo y sin ciclos. Consideraremos un árbol con n vértices, enraizado en el vértice 0 ( en la figura ), con b niveles: num j es el número de vértices que cuelgan del nodo j pad j es el número del nodo padre del nodo j. 90
13 Dist ij será la distancia entre el nodo i y el j. Niv j es el nivel en el cual se encuentra el nodo j. Figura No es un grafo regular. Sus nodos tendrán valencia (del enlace a su nodo padre, su nodo de nivel superior) mas el número de nodos que cuelguen de él, es decir: +num j. El valor de grado medio será, por tanto: Dado que el grafo no tiene una estructura predecible en función del número de nodos, algunas de las magnitudes calculadas en otros casos serán expresadas simplemente en función de la distancia entre nodos. Para calcular la distancia entre dos nodos cualquiera u y v del grafo, podríamos aplicar el algoritmo de Dijsktra, ya explicado en el punto.. Sin embargo, hemos implementado un algoritmo que resuelve este mismo problema, de forma más eficaz para este caso concreto. Hace uso de las variables mostradas sobre la figura. Algoritmo Antes de comenzar, definimos las variables locales: hijo, hijo. Inicializamos: hijo = u, hijo =v, dist = 0.. Paso : los dos nodos introducidos son el mismo? Si u = v, dist uv = 0. Finaliza aquí el algoritmo. Si no es así, vamos al paso.. Paso : Niveles 9
14 Si el niv hijo = niv hijo, seguimos con el paso 4. Si no es así, vamos al paso Paso 3: Niveles desiguales. Si niv hijo > niv hijo, dist uv = dist uv +, hijo=pad hijo Si niv hijo < niv hijo, dist uv = dist uv +, hijo=pad hijo Volvemos a. 4. Paso 4: hijo = hijo? Si es así, aquí finaliza el algoritmo. Si no, hijo = pad u, hijo = pad v, dist uv = dist uv + Vamos al paso 4. Si realizase el algoritmo entre cada par de nodos obtendría una matriz {dist ij } formada por las distancias entre cada par de nodos del grafo. Con estos valores de distancias, podríamos calcular el valor de la longitud de camino característica, el diámetro y la eficiencia media siguiendo la definición del punto 3. El coste de la red es: El grafo es conexo, con una Vértice-conectividad = y una arista-conectividad =. Otras propiedades son: La cohesividad de todos los vértices finales por cada rama es la misma, ch(v)=0. La magnitud vértice -conectividad tiene el mismo valor tanto si están presentes como si no: su valor es la unidad. La correspondiente a los vértices intermedios es, ya que si el vértice no está presente, el grafo es disconexo sin necesidad de quitar ningún nodo. El i-degree, en este caso, no tiene valor modelable. El grafo que estamos suponiendo en todos los casos es genérico, sin embargo, no podemos 9
15 suponer ningún árbol genérico. El valor del i-degree dependerá del número de nodos de cada nivel, y del número de nodos hijos de cada nodo padre. Si podemos decir que el -degree es, ya que solo sería necesario borrar una arista para aislar un extremo. Calcularemos, al final de esta lista de propiedades esta magnitud en un grafo ejemplo. Para calcular la dureza de vértices, t v (G), evaluaremos si + num j > num 0 para algún valor de j. Si no es así, t v (G) =. Si encontramos ese valor, t v (G) =. La dureza mínima se consigue al eliminar un solo vértice. La dureza de aristas, t E (G), es más simple de calcular. Por cada arista suprimida tendremos (+número de aristas suprimidas) componentes, con lo que el menor valor de dureza se consigue al eliminar una solo arista. t E (G) = 0,5. Tanto la persistencia de vértices, ρ v (G), como la de aristas, ρ E (G), es, ya que en cuanto retiro el nodo central o una arista cualquiera, el grafo se hace no conexo, por lo que ya se ha producido el incremento de diámetro. El nuevo valor de diámetro es infinito. Conectividad media, = 0. He de colocar siempre todas las aristas para lograr que sea conexo. El resto de propiedades calculadas en los apartados 4. y 4.3 no tiene sentido calcularlas en este, ya que el grafo deja de ser conexo. Ejemplo Usaremos como ejemplo el árbol de la figura, en el que el nodo n sea el nodo número 9 y este unido con línea continua al nodo , j 9 ú , j 9 93
16 , j ,7 La matriz de distancias calculada con ese algoritmo es: El diámetro sería 5. La longitud de camino característica es,55. La eficiencia media es 0,5088. El coste es 0,0833. La dureza de vértices sería 0,5. Se obtiene al quitar el nodo 3. El i-degree es: Para i = :. Solo sería necesario borrar la arista 7-9, o la -4 o cualquier otra que vaya a un vértice extremo para tener dos subgrafos, uno de ellos con una sóla componente. Para i = :. Si suprimimos la arista 3-7, obtenemos el grafo de dos componentes formado por los nodos 7 y 9. Sería la única posibilidad de poder obtener este subgrafo. Con esto, nos damos cuenta, de que en el árbol solo sería calculable el -degree en caso de que existiese una rama-camino con dos saltos. Sino no podría tener un subgrafo de dos componentes al borrar ninguna arista. Para i = 3:. Eliminaríamos la arista - para obtenerla. Para i = 4:. Suprimiríamos la arista -3. Me quedaría el subgrafo formado por los nodos,,4,5. 94
17 Tan solo sería necesario calcular hasta ese valor por las propiedades de simetría. 4.6 Comparativa de propiedades PROPIEDAD\TOPOLOGÍA ANILLO ESTRELLA MALLADO COMPLETO n par n impar n par n impar n par n impar Diámetro, D Grado medio, k med Longitud de camino característica, L 4 4 Coeficiente de 0 0 agrupamiento, C Vértice conectividad n Arista conectividad n Eficiencia media, E Eficiencia local, E local 0 0 Coste, Co(G) Cohesividad, ch(v) ch(vért.exterior) = 0 ch(vért.central) = i degree, ξ(i), i n i=, i(n i) e.o.c 0 Dureza, t(g) t v (G) t E (G) 0,5 Persistencia, ρ(g) Máx. incremento de la distancia entre nodos causada por la eliminación de i vértices, c i Máx. incremento de la distancia entre nodos causada por la eliminación de i aristas, e i Máx. incremento del diámetro causado por la eliminación de i vértices, f i ρ v (G) n ρ E (G) n n 4, para i = n, para i = 95 n 0,, n, para i = 0,
18 Máx. incremento del diámetro causado por la eliminación de i aristas, t i Conectividad Media, n, para i =, 0 TABLA VIII PROPIEDAD\TOPOLOGÍA BUS ARBOL n par n impar n par n impar Diámetro, D n á,, Grado medio, k med Longitud de camino característica, L 3 L = 96 n( n ) Coeficiente de 0 0 agrupamiento, C Vértice conectividad Arista conectividad Eficiencia media, E E = n ( n ) u, v G, u v dist u, v dist u u, v G, u v, v Eficiencia local, E local 0 0 Coste, Co(G) Cohesividad, ch(v) ch(vértice extremo) = 0 ch(vértice intermedio) = Ch(vértice extremo) = 0 Ch(vértice intermedio) = i degree, ξ(i), i n Dureza, t(g) t v (G) 0,5 Evalúa: Persistencia, ρ(g) Máx. incremento de la distancia entre nodos causada por la eliminación de i vértices, c i Máx. incremento de la distancia entre nodos causada por la eliminación de i aristas, e i Máx. incremento del diámetro causado por la eliminación de i vértices, + num j > num 0 t E (G) 0,5 0,5 ρ v (G) ρ E (G) Si, para algún valor de j: No se verifica para ningún valor de j: Se ha implementado un algoritmo para calcular las distancias entre nodos. En esta tabla, todas las magnitudes están en función de las distancias así calculadas.
19 f i Máx. incremento del diámetro causado por la eliminación de i aristas, t i Conectividad Media, 0 0 TABLA IX Es difícil afirmar una respuesta para la pregunta: Qué topología es más robusta? En cualquier caso, analizaremos estos resultados y los compararemos todos, excepto la topología árbol, de la cual, por las razones que ya se comentaron anteriormente, no se poseen expresiones en función del número de nodos. La topología que posee un menor diámetro es el mallado completo. La que posee sus dos nodos más alejados más distantes, es el bus. En medio esta el anillo y la estrella. En general, el diámetro de la estrella será menor que el del anillo. El grado medio es mayor en el mallado completo. El bus y la estrella poseen el mismo valor. Este para un número de nodos pequeño será menor que el del anillo. Sin embargo, cuando el número de nodos se eleva el grado medio del anillo es el menor de todos. La separación típica de nodos es mínima en el mallado completo. Después, le sigue la estrella, a continuación el anillo y, por último, el bus. El coeficiente de agrupamiento, al igual que la eficiencia local, es nulo para todas las topologías excepto para el mallado. La vértice-conectividad y la arista conectividad son mayores en el mallado completo. Después, la topología en anillo y, por último, las dos restantes. La secuencia de mejor a peor valor de dureza de vértices es la siguiente: mallado total, anillo, bus y estrella. La secuencia en el mismo orden según la dureza de aristas es la misma. La persistencia de vértices es notablemente mejor en el mallado completo. El resto de topologías presentan el mismo valor. En el caso de la persistencia de aristas, el mejor caso es la estrella. Sin embargo, este último resultado es indiferente a la hora de comprobar la robustez, ya que si, es cierto que el diámetro no se incrementa, pero el grafo resulta ser disconexo. 97
20 Con respecto a las magnitudes de distancias incrementales y secuencias, diremos que no han sido calculadas ni en el caso de la estrella ni en el bus. Entre los otros dos, son mejores los valores del mallado completo. Tras este pequeño análisis, vemos como la topología más robusta es, sin duda, el mallado completo. En segundo lugar, atendiendo únicamente a la robustez, situaríamos el anillo, que presenta mejores condiciones de dureza, mejor valor de vértice conectividad y arista conectividad y mejores características de distancias incrementales y secuencias (en los otros dos casos el grafo se queda disconexo en algunos casos), manteniendo un tercer puesto en separación típica de nodos y si el número de nodos es pequeño un segundo en valores de grado medio. En tercer lugar, situaríamos la estrella, ya que presenta prácticamente las mismas características que el bus, pero en general los nodos están más próximos. En cuanto al coste que supone alcanzar la eficiencia en esa topología, el que el mallado completo sea más robusto implica que su coste es el mayor. Las siguientes topologías en coste son la estrella y el bus. Por último, el anillo. Para valores de n>>, el coste de estas tres topologías es el mismo. 98
Grafos y Redes. 3. Resolución: Dibujar el camino sin levantar el lápiz y pasando sólo una vez por cada arco o arista.
 Grafos y Redes. Nodos: vértices, 2, 3 2. Arcos: aristas, conexión entre nodos. 2, 54, etc. 3. Resolución: Dibujar el camino sin levantar el lápiz y pasando sólo una vez por cada arco o arista. 4. Grado
Grafos y Redes. Nodos: vértices, 2, 3 2. Arcos: aristas, conexión entre nodos. 2, 54, etc. 3. Resolución: Dibujar el camino sin levantar el lápiz y pasando sólo una vez por cada arco o arista. 4. Grado
Centro Asociado Palma de Mallorca. Tutor: Antonio Rivero Cuesta
 Centro Asociado Palma de Mallorca Lógica y Estructuras Discretas Tutor: Antonio Rivero Cuesta Tema 5 Teoría de Grafos Conceptos Básicos Un grafo consta de: Grafo Un conjunto de nodos, Un conjunto de aristas
Centro Asociado Palma de Mallorca Lógica y Estructuras Discretas Tutor: Antonio Rivero Cuesta Tema 5 Teoría de Grafos Conceptos Básicos Un grafo consta de: Grafo Un conjunto de nodos, Un conjunto de aristas
Grafos. Suponiendo que e = [u, v]. Entonces los nodos u y v se llaman extremos de e y u y v se dice que son nodos adyacentes o vecinos.
![Grafos. Suponiendo que e = [u, v]. Entonces los nodos u y v se llaman extremos de e y u y v se dice que son nodos adyacentes o vecinos. Grafos. Suponiendo que e = [u, v]. Entonces los nodos u y v se llaman extremos de e y u y v se dice que son nodos adyacentes o vecinos.](/thumbs/54/33802392.jpg) Grafos Los grafos son estructuras que constan de vértices o nodos y de aristas o arcos que conectan los vértices entre sí. Un grafo G consiste en dos cosas: 1. Un conjunto V de elementos llamados nodos
Grafos Los grafos son estructuras que constan de vértices o nodos y de aristas o arcos que conectan los vértices entre sí. Un grafo G consiste en dos cosas: 1. Un conjunto V de elementos llamados nodos
En la fig. 1 se representa el grafo, G=(V,A) donde: V = {1, 2, 3, 4, 5, 6} A = { {1,2}, {1,3}, {1,5}, {3}, {3,4}, {4,5}, {5,6} }
 Unidad 1 Parte 1 - Teoría de Grafos Introducción En este capítulo veremos la noción matemática de grafo y propiedades de los mismos. En capítulos subsiguientes veremos las estructuras de datos utilizadas
Unidad 1 Parte 1 - Teoría de Grafos Introducción En este capítulo veremos la noción matemática de grafo y propiedades de los mismos. En capítulos subsiguientes veremos las estructuras de datos utilizadas
Teoría de grafos y optimización en redes
 Teoría de grafos y optimización en redes José María Ferrer Caja Universidad Pontificia Comillas Definiciones básicas Grafo: Conjunto de nodos (o vértices) unidos por aristas G = (V,E) Ejemplo V = {,,,,
Teoría de grafos y optimización en redes José María Ferrer Caja Universidad Pontificia Comillas Definiciones básicas Grafo: Conjunto de nodos (o vértices) unidos por aristas G = (V,E) Ejemplo V = {,,,,
Es un conjunto de objetos llamados vértices o nodos unidos por enlaces llamados aristas o arcos, que permiten representar relaciones binarias entre
 Es un conjunto de objetos llamados vértices o nodos unidos por enlaces llamados aristas o arcos, que permiten representar relaciones binarias entre elementos de un conjunto. Típicamente, un grafo se representa
Es un conjunto de objetos llamados vértices o nodos unidos por enlaces llamados aristas o arcos, que permiten representar relaciones binarias entre elementos de un conjunto. Típicamente, un grafo se representa
Un grafo G = (V, E) se dice finito si V es un conjunto finito.
 1 Grafos: Primeras definiciones Definición 1.1 Un grafo G se define como un par (V, E), donde V es un conjunto cuyos elementos son denominados vértices o nodos y E es un subconjunto de pares no ordenados
1 Grafos: Primeras definiciones Definición 1.1 Un grafo G se define como un par (V, E), donde V es un conjunto cuyos elementos son denominados vértices o nodos y E es un subconjunto de pares no ordenados
Grafos. AMD Grado en Ingeniería Informática. AMD Grado en Ingeniería Informática (UM) Grafos 1 / 30
 Grafos AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Grafos / 0 Objetivos Al finalizar este tema tendréis que: Conocer la terminología básica de la teoría de grafos. Pasar
Grafos AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Grafos / 0 Objetivos Al finalizar este tema tendréis que: Conocer la terminología básica de la teoría de grafos. Pasar
Grafos. Amalia Duch Brown Octubre de 2007
 Grafos Amalia Duch Brown Octubre de 2007 Índice 1. Definiciones Básicas Intuitivamente un grafo es un conjunto de vértices unidos por un conjunto de líneas o flechas dependiendo de si el grafo es dirigido
Grafos Amalia Duch Brown Octubre de 2007 Índice 1. Definiciones Básicas Intuitivamente un grafo es un conjunto de vértices unidos por un conjunto de líneas o flechas dependiendo de si el grafo es dirigido
III Unidad Planificación y diseño de una red (LAN)
 Recordemos: Una red de área local, Es un conjunto de Equipos y dispositivos de hardware unidos entre sí con el fin de compartir recursos en una zona geográfica limitada. Planificación y diseño de la red.
Recordemos: Una red de área local, Es un conjunto de Equipos y dispositivos de hardware unidos entre sí con el fin de compartir recursos en una zona geográfica limitada. Planificación y diseño de la red.
Introducción a la Teoría de Grafos
 Introducción a la Teoría de Grafos Flavia Bonomo fbonomo@dc.uba.ar do. Cuatrimestre 009 Programa Introducción a la teoría de grafos Problemas de camino mínimo Problemas de flujo máximo Programación lineal
Introducción a la Teoría de Grafos Flavia Bonomo fbonomo@dc.uba.ar do. Cuatrimestre 009 Programa Introducción a la teoría de grafos Problemas de camino mínimo Problemas de flujo máximo Programación lineal
Introducción. Flujo Eléctrico.
 Introducción La descripción cualitativa del campo eléctrico mediante las líneas de fuerza, está relacionada con una ecuación matemática llamada Ley de Gauss, que relaciona el campo eléctrico sobre una
Introducción La descripción cualitativa del campo eléctrico mediante las líneas de fuerza, está relacionada con una ecuación matemática llamada Ley de Gauss, que relaciona el campo eléctrico sobre una
Formulación del problema de la ruta más corta en programación lineal
 Formulación del problema de la ruta más corta en programación lineal En esta sección se describen dos formulaciones de programación lineal para el problema de la ruta más corta. Las formulaciones son generales,
Formulación del problema de la ruta más corta en programación lineal En esta sección se describen dos formulaciones de programación lineal para el problema de la ruta más corta. Las formulaciones son generales,
Tema 3: El Método Simplex. Algoritmo de las Dos Fases.
 Tema 3: El Método Simplex Algoritmo de las Dos Fases 31 Motivación Gráfica del método Simplex 32 El método Simplex 33 El método Simplex en Formato Tabla 34 Casos especiales en la aplicación del algoritmo
Tema 3: El Método Simplex Algoritmo de las Dos Fases 31 Motivación Gráfica del método Simplex 32 El método Simplex 33 El método Simplex en Formato Tabla 34 Casos especiales en la aplicación del algoritmo
Árboles. Un grafo no dirigido es un árbol si y sólo si existe una ruta unica simple entre cualquiera dos de sus vértices.
 ÁRBOLES Árboles Un grafo conectado que no contiene circuitos simples. Utilizados desde 1857, por el matemático Ingles Arthur Cayley para contar ciertos tipos de componentes químicos. Un árbol es un grafo
ÁRBOLES Árboles Un grafo conectado que no contiene circuitos simples. Utilizados desde 1857, por el matemático Ingles Arthur Cayley para contar ciertos tipos de componentes químicos. Un árbol es un grafo
3. ASOCIACIÓN ENTRE DOS VARIABLES CUALITATIVAS
 1. INTRODUCCIÓN Este tema se centra en el estudio conjunto de dos variables. Dos variables cualitativas - Tabla de datos - Tabla de contingencia - Diagrama de barras - Tabla de diferencias entre frecuencias
1. INTRODUCCIÓN Este tema se centra en el estudio conjunto de dos variables. Dos variables cualitativas - Tabla de datos - Tabla de contingencia - Diagrama de barras - Tabla de diferencias entre frecuencias
TEMA I. Teoría de Circuitos
 TEMA I Teoría de Circuitos Electrónica II 2009-2010 1 1 Teoría de Circuitos 1.1 Introducción. 1.2 Elementos básicos 1.3 Leyes de Kirchhoff. 1.4 Métodos de análisis: mallas y nodos. 1.5 Teoremas de circuitos:
TEMA I Teoría de Circuitos Electrónica II 2009-2010 1 1 Teoría de Circuitos 1.1 Introducción. 1.2 Elementos básicos 1.3 Leyes de Kirchhoff. 1.4 Métodos de análisis: mallas y nodos. 1.5 Teoremas de circuitos:
un conjunto cuyos elementos denominaremos vectores y denotaremos por es un espacio vectorial si verifica las siguientes propiedades:
 CAPÍTULO 2: ESPACIOS VECTORIALES 2.1- Definición y propiedades. 2.1.1-Definición: espacio vectorial. Sea un cuerpo conmutativo a cuyos elementos denominaremos escalares o números. No es necesario preocuparse
CAPÍTULO 2: ESPACIOS VECTORIALES 2.1- Definición y propiedades. 2.1.1-Definición: espacio vectorial. Sea un cuerpo conmutativo a cuyos elementos denominaremos escalares o números. No es necesario preocuparse
Tema 5: Semejanza. 1.- Introducción: Concepto de Escala y Teorema de Pitágoras.
 Tema 5: Semejanza. En este tema nos dedicaremos al estudio de los triángulos y polígonos, y dedicaremos un apartado a un famoso teorema, que nos será de utilidad para entender la semejanza entre ellos:
Tema 5: Semejanza. En este tema nos dedicaremos al estudio de los triángulos y polígonos, y dedicaremos un apartado a un famoso teorema, que nos será de utilidad para entender la semejanza entre ellos:
Amplificadores Operacionales
 Amplificadores Operacionales Configuraciones básicas del amplificador operacional Los amplificadores operacionales se pueden conectar según dos circuitos amplificadores básicos: las configuraciones (1)
Amplificadores Operacionales Configuraciones básicas del amplificador operacional Los amplificadores operacionales se pueden conectar según dos circuitos amplificadores básicos: las configuraciones (1)
DIVISIBILIDAD NÚMEROS NATURALES
 DIVISIBILIDAD NÚMEROS NATURALES MÚLTIPLOS Un número a es múltiplo de otro b cuando es el resultado de multiplicarlo por otro número c. a = b c Ejemplo: 12 es múltiplo de 2, ya que resulta de multiplicar
DIVISIBILIDAD NÚMEROS NATURALES MÚLTIPLOS Un número a es múltiplo de otro b cuando es el resultado de multiplicarlo por otro número c. a = b c Ejemplo: 12 es múltiplo de 2, ya que resulta de multiplicar
Semana 09 [1/28] Sucesiones. 29 de abril de Sucesiones
![Semana 09 [1/28] Sucesiones. 29 de abril de Sucesiones Semana 09 [1/28] Sucesiones. 29 de abril de Sucesiones](/thumbs/49/25360651.jpg) Semana 09 [1/28] 29 de abril de 2007 Semana 09 [2/28] Definición Sucesión Una sucesión real es una función: f : N R n f (n) Observaciones Para distinguir a una sucesión de las demás funciones, se ocupará
Semana 09 [1/28] 29 de abril de 2007 Semana 09 [2/28] Definición Sucesión Una sucesión real es una función: f : N R n f (n) Observaciones Para distinguir a una sucesión de las demás funciones, se ocupará
Tipos de redes de distribución. Obras de abastecimiento y de saneamiento 3º ITOP
 Tipos de redes de distribución Redes ramificadas El agua circula por la red en un único sentido, es decir, el agua solo puede seguir un camino para llegar a cada uno de los nudos del sistema Arteria maestra
Tipos de redes de distribución Redes ramificadas El agua circula por la red en un único sentido, es decir, el agua solo puede seguir un camino para llegar a cada uno de los nudos del sistema Arteria maestra
Análisis y síntesis de sistemas digitales combinacionales
 Análisis Algoritmo de análisis, para un circuito lógico combinacional Síntesis. Conceptos Circuitos combinacionales bien construidos Circuitos combinacionales mal construidos Criterios de optimización
Análisis Algoritmo de análisis, para un circuito lógico combinacional Síntesis. Conceptos Circuitos combinacionales bien construidos Circuitos combinacionales mal construidos Criterios de optimización
UNIDAD 10: ECUACIONES DE SEGUNDO GRADO.
 UNIDAD 10: ECUACIONES DE SEGUNDO GRADO. 10.1 Estudio elemental de la ecuación de segundo grado. Expresión general. 10.2 Resolución de ecuaciones de segundo grado completas e incompletas. 10.3 Planteamiento
UNIDAD 10: ECUACIONES DE SEGUNDO GRADO. 10.1 Estudio elemental de la ecuación de segundo grado. Expresión general. 10.2 Resolución de ecuaciones de segundo grado completas e incompletas. 10.3 Planteamiento
Derivada de una función en un punto. Función derivada. Diferencial de una función en un punto. dy = f (x) dx. Derivada de la función inversa
 Derivada de una función en un punto Las tres expresiones son equivalentes. En definitiva, la derivada de una función en un punto se obtiene como el límite del cociente incremental: el incremento del valor
Derivada de una función en un punto Las tres expresiones son equivalentes. En definitiva, la derivada de una función en un punto se obtiene como el límite del cociente incremental: el incremento del valor
CONTENIDOS. 1. Procesos Estocásticos y de Markov. 2. Cadenas de Markov en Tiempo Discreto (CMTD) 3. Comportamiento de Transición de las CMTD
 CONTENIDOS 1. Procesos Estocásticos y de Markov 2. Cadenas de Markov en Tiempo Discreto (CMTD) 3. Comportamiento de Transición de las CMTD 4. Comportamiento Estacionario de las CMTD 1. Procesos Estocásticos
CONTENIDOS 1. Procesos Estocásticos y de Markov 2. Cadenas de Markov en Tiempo Discreto (CMTD) 3. Comportamiento de Transición de las CMTD 4. Comportamiento Estacionario de las CMTD 1. Procesos Estocásticos
TEMA 1. MATRICES, DETERMINANTES Y APLICACIÓN DE LOS DETERMINANTES. CONCEPTO DE MATRIZ. LA MATRIZ COMO EXPRESIÓN DE TABLAS Y GRAFOS.
 TEMA 1. MATRICES, DETERMINANTES Y APLICACIÓN DE LOS DETERMINANTES. 1. MATRICES. CONCEPTO DE MATRIZ. LA MATRIZ COMO EXPRESIÓN DE TABLAS Y GRAFOS. DEFINICIÓN: Las matrices son tablas numéricas rectangulares
TEMA 1. MATRICES, DETERMINANTES Y APLICACIÓN DE LOS DETERMINANTES. 1. MATRICES. CONCEPTO DE MATRIZ. LA MATRIZ COMO EXPRESIÓN DE TABLAS Y GRAFOS. DEFINICIÓN: Las matrices son tablas numéricas rectangulares
TEST DE RAZONAMIENTO NUMÉRICO. Consejos generales
 TEST DE RAZONAMIENTO NUMÉRICO Consejos generales 1 I. INTRODUCCIÓN En lo relativo a los cálculos de porcentajes, es fundamental tener en cuenta que los porcentajes, en realidad, son referencias abstractas,
TEST DE RAZONAMIENTO NUMÉRICO Consejos generales 1 I. INTRODUCCIÓN En lo relativo a los cálculos de porcentajes, es fundamental tener en cuenta que los porcentajes, en realidad, son referencias abstractas,
Un paquete de problemas de potenciación
 Un paquete de problemas de potenciación Betina Zolkower- Adriana Rabino- Ana Bressan A continuación se presenta una serie de problemas de potenciación y distintas estrategias de resolución. Betina Zolkower
Un paquete de problemas de potenciación Betina Zolkower- Adriana Rabino- Ana Bressan A continuación se presenta una serie de problemas de potenciación y distintas estrategias de resolución. Betina Zolkower
TEMA 11 CONMUTACIÓN DE PAQUETES
 TEMA 11 CONMUTACIÓN DE PAQUETES La conmutación de circuitos fue diseñada para transmisión de voz o Recursos dedicados a una llamada en particular o Parte considerable del tiempo la conexión de datos no
TEMA 11 CONMUTACIÓN DE PAQUETES La conmutación de circuitos fue diseñada para transmisión de voz o Recursos dedicados a una llamada en particular o Parte considerable del tiempo la conexión de datos no
Sistemas de ecuaciones lineales
 Sistemas de ecuaciones lineales Sistemas de ecuaciones lineales Generalidades Definición [Sistema de ecuaciones lineales] Un sistema de m ecuaciones lineales con n incógnitas, es un conjunto de m igualdades
Sistemas de ecuaciones lineales Sistemas de ecuaciones lineales Generalidades Definición [Sistema de ecuaciones lineales] Un sistema de m ecuaciones lineales con n incógnitas, es un conjunto de m igualdades
MAXIMOS Y MINIMOS RELATIVOS
 MAXIMOS Y MINIMOS RELATIVOS Con cierta frecuencia nos encontramos con la necesidad de buscar la mejor forma de hacer algo. En muchas ocasiones a través de los poderosos mecanismos de cálculo diferencial
MAXIMOS Y MINIMOS RELATIVOS Con cierta frecuencia nos encontramos con la necesidad de buscar la mejor forma de hacer algo. En muchas ocasiones a través de los poderosos mecanismos de cálculo diferencial
Figura 3.1. Grafo orientado.
 Leyes de Kirchhoff 46. ECUACIONES DE INTERCONEXION. Leyes de Kirchhoff..1. Definiciones. Una red está formada por la interconexión de componentes en sus terminales; y deben cumplirse simultáneamente las
Leyes de Kirchhoff 46. ECUACIONES DE INTERCONEXION. Leyes de Kirchhoff..1. Definiciones. Una red está formada por la interconexión de componentes en sus terminales; y deben cumplirse simultáneamente las
Tema 3: Criterios serie paralelo y mixto. Resolución de problemas.
 Tema 3. Circuitos serie paralelo y mixto. Resolución de problemas En el tema anterior viste como se comportaban las resistencias, bobinas y condensadores cuando se conectaban a un circuito de corriente
Tema 3. Circuitos serie paralelo y mixto. Resolución de problemas En el tema anterior viste como se comportaban las resistencias, bobinas y condensadores cuando se conectaban a un circuito de corriente
Tema 7: Geometría Analítica. Rectas.
 Tema 7: Geometría Analítica. Rectas. En este tema nos centraremos en estudiar la geometría en el plano, así como los elementos que en este aparecen como son los puntos, segmentos, vectores y rectas. Estudiaremos
Tema 7: Geometría Analítica. Rectas. En este tema nos centraremos en estudiar la geometría en el plano, así como los elementos que en este aparecen como son los puntos, segmentos, vectores y rectas. Estudiaremos
6. Mosaicos y movimientos. en el plano
 6. Mosaicos y movimientos en el plano Ámbito científico 1. Mosaicos 2. Módulos planos 3. Diseña mosaicos 4. Ejemplos de mosaicos 5. Ejemplos de tramas 6. Mosaicos semiregulares I 7. Libro de espejos 8.
6. Mosaicos y movimientos en el plano Ámbito científico 1. Mosaicos 2. Módulos planos 3. Diseña mosaicos 4. Ejemplos de mosaicos 5. Ejemplos de tramas 6. Mosaicos semiregulares I 7. Libro de espejos 8.
TIPOS DE REDES. Conrado Perea
 TIPOS DE REDES Conrado Perea TIPOS DE REDES Primero vamos a clasificarlas por su extensión geográfica. LAN, redes de are local, local área network, es un sistema de interconexión de equipos informáticos
TIPOS DE REDES Conrado Perea TIPOS DE REDES Primero vamos a clasificarlas por su extensión geográfica. LAN, redes de are local, local área network, es un sistema de interconexión de equipos informáticos
PREGUNTAS TIPO EXAMEN- ESTADÍSTICA DESCRIPTIVA 2
 PREGUNTAS TIPO EXAMEN- ESTADÍSTICA DESCRIPTIVA 2 Preg. 1. Para comparar la variabilidad relativa de la tensión arterial diastólica y el nivel de colesterol en sangre de una serie de individuos, utilizamos
PREGUNTAS TIPO EXAMEN- ESTADÍSTICA DESCRIPTIVA 2 Preg. 1. Para comparar la variabilidad relativa de la tensión arterial diastólica y el nivel de colesterol en sangre de una serie de individuos, utilizamos
Una ecuación puede tener ninguna, una o varias soluciones. Por ejemplo: 5x 9 = 1 es una ecuación con una incógnita con una solución, x = 2
 Podemos definir a las ecuaciones como una igualdad entre expresiones algebraicas (encadenamiento de números y letras ligados por operaciones matemáticas diversas),en la que intervienen una o más letras,
Podemos definir a las ecuaciones como una igualdad entre expresiones algebraicas (encadenamiento de números y letras ligados por operaciones matemáticas diversas),en la que intervienen una o más letras,
Tema 14: Sistemas Secuenciales
 Tema 14: Sistemas Secuenciales Objetivos: (CONTADORES) Introducción. Características de los contadores. Contadores Asíncronos. Contadores Síncronos. 1 INTRODUCCIÓN Los contadores son sistemas secuenciales
Tema 14: Sistemas Secuenciales Objetivos: (CONTADORES) Introducción. Características de los contadores. Contadores Asíncronos. Contadores Síncronos. 1 INTRODUCCIÓN Los contadores son sistemas secuenciales
Fracciones Algebraicas
 Fracciones Algebraicas 1 Conceptos básicos Definición 1 Una fracción algebraica en la indeterminada x (o cualquier otra letra) es una expresión de la forma, donde tanto P como Q son polinomios con coeficientes
Fracciones Algebraicas 1 Conceptos básicos Definición 1 Una fracción algebraica en la indeterminada x (o cualquier otra letra) es una expresión de la forma, donde tanto P como Q son polinomios con coeficientes
Definición 1.1 Sea G = (V, A) un grafo no dirigido. G se denomina árbol si es conexo y no contiene ciclos.
 Matemática Discreta y Lógica 2 1. Árboles Árboles Definición 1.1 Sea G = (V, A) un grafo no dirigido. G se denomina árbol si es conexo y no contiene ciclos. Como un lazo es un ciclo de longitud 1, un árbol
Matemática Discreta y Lógica 2 1. Árboles Árboles Definición 1.1 Sea G = (V, A) un grafo no dirigido. G se denomina árbol si es conexo y no contiene ciclos. Como un lazo es un ciclo de longitud 1, un árbol
Tema 2.- Formas Cuadráticas.
 Álgebra. 004 005. Ingenieros Industriales. Departamento de Matemática Aplicada II. Universidad de Sevilla. Tema.- Formas Cuadráticas. Definición y representación matricial. Clasificación de las formas
Álgebra. 004 005. Ingenieros Industriales. Departamento de Matemática Aplicada II. Universidad de Sevilla. Tema.- Formas Cuadráticas. Definición y representación matricial. Clasificación de las formas
Retículos y Álgebras de Boole
 Retículos y Álgebras de Boole Laboratorio de Matemática Discreta Jesús Martínez Mateo jmartinez@fi.upm.es Práctica 1. Ordenación topológica A. Herramientas necesarias Para la práctica que vamos a realizar
Retículos y Álgebras de Boole Laboratorio de Matemática Discreta Jesús Martínez Mateo jmartinez@fi.upm.es Práctica 1. Ordenación topológica A. Herramientas necesarias Para la práctica que vamos a realizar
UNIVERSIDAD TECNOLOGICA DE PEREIRA PROGRAMA DE TECNOLOGIA ELECTRICA
 UNERSDAD TECNOLOGCA DE PERERA PROGRAMA DE TECNOLOGA ELECTRCA Curso Básico de Análisis de Sistemas Eléctricos de Potencia Antonio Escobar Zuluaga Pereira - Risaralda - Colombia 0 Matriz admitancia Y BUS
UNERSDAD TECNOLOGCA DE PERERA PROGRAMA DE TECNOLOGA ELECTRCA Curso Básico de Análisis de Sistemas Eléctricos de Potencia Antonio Escobar Zuluaga Pereira - Risaralda - Colombia 0 Matriz admitancia Y BUS
Tema: Los Grafos y su importancia para la optimización de redes.
 Tema: Los Grafos y su importancia para la optimización de redes. Qué son los Grafos? Un grafo es una dupla G= {X,U}, donde X es un conjunto finito y no vacio de elementos llamados vértices y U es el conjunto
Tema: Los Grafos y su importancia para la optimización de redes. Qué son los Grafos? Un grafo es una dupla G= {X,U}, donde X es un conjunto finito y no vacio de elementos llamados vértices y U es el conjunto
RESOLUCIÓN DE SISTEMAS MEDIANTE DETERMINANTES
 UNIDD 4 RESOLUCIÓN DE SISTEMS MEDINTE DETERMINNTES Página 00 Resolución de sistemas mediante determinantes x y Resuelve, aplicando x = e y =, los siguientes sistemas de ecuaciones: x 5y = 7 5x + 4y = 6x
UNIDD 4 RESOLUCIÓN DE SISTEMS MEDINTE DETERMINNTES Página 00 Resolución de sistemas mediante determinantes x y Resuelve, aplicando x = e y =, los siguientes sistemas de ecuaciones: x 5y = 7 5x + 4y = 6x
SISTEMAS DE ECUACIONES
 SISTEMAS DE ECUACIONES Ecuación es una igualdad que contiene por lo menos una incógnita, que se representa por medio de una letra, cuyo valor se debe averiguar. Por ejemplo: 3x + 2 = 4 donde debemos calcular
SISTEMAS DE ECUACIONES Ecuación es una igualdad que contiene por lo menos una incógnita, que se representa por medio de una letra, cuyo valor se debe averiguar. Por ejemplo: 3x + 2 = 4 donde debemos calcular
TEMA 8. GEOMETRÍA ANALÍTICA.
 TEMA 8. GEOMETRÍA ANALÍTICA. 8..- El plano. Definimos el plano euclideo como el conjunto de puntos ( x, y) R. Así, cada punto del plano posee dos coordenadas. Para representar puntos del plano utilizaremos
TEMA 8. GEOMETRÍA ANALÍTICA. 8..- El plano. Definimos el plano euclideo como el conjunto de puntos ( x, y) R. Así, cada punto del plano posee dos coordenadas. Para representar puntos del plano utilizaremos
Electrotecnia General Tema 26 TEMA 26 CÁLCULO DE REDES DE DISTRIBUCIÓN II
 TEMA 26 CÁLCULO DE REDES DE DISTRIBUCIÓN II 26.1. DISTRIBUCIONES PERFECTAMENTE CERRADAS CON TENSIÓN CONSTANTE Y SECCIÓN UNIFORME. Las distribuciones perfectamente cerradas son aquellas en las que el distribuidor
TEMA 26 CÁLCULO DE REDES DE DISTRIBUCIÓN II 26.1. DISTRIBUCIONES PERFECTAMENTE CERRADAS CON TENSIÓN CONSTANTE Y SECCIÓN UNIFORME. Las distribuciones perfectamente cerradas son aquellas en las que el distribuidor
Para construir un diagrama PERT se han de tener en cuenta las siguientes reglas
 Construcción de diagramas de PERT. Apunte para la confección del TP. Modalidad de entrega y/o presentación a convenir. Realizar la diagramación de algún proceso real o simulado a elección utilizando la
Construcción de diagramas de PERT. Apunte para la confección del TP. Modalidad de entrega y/o presentación a convenir. Realizar la diagramación de algún proceso real o simulado a elección utilizando la
Espacios Vectoriales Asturias: Red de Universidades Virtuales Iberoamericanas 1
 Espacios Vectoriales 201 6Asturias: Red de Universidades Virtuales Iberoamericanas 1 Índice 1 Espacios Vectoriales... 4 1.1 Definición de espacio vectorial... 4 1.2 Definición de subespacio vectorial...
Espacios Vectoriales 201 6Asturias: Red de Universidades Virtuales Iberoamericanas 1 Índice 1 Espacios Vectoriales... 4 1.1 Definición de espacio vectorial... 4 1.2 Definición de subespacio vectorial...
1 SISTEMAS DE ECUACIONES LINEALES. MÉTODO DE GAUSS
 1 SISTEMAS DE ECUACIONES LINEALES. MÉTODO DE GAUSS 1.1 SISTEMAS DE ECUACIONES LINEALES Una ecuación lineal es una ecuación polinómica de grado 1, con una o varias incógnitas. Dos ecuaciones son equivalentes
1 SISTEMAS DE ECUACIONES LINEALES. MÉTODO DE GAUSS 1.1 SISTEMAS DE ECUACIONES LINEALES Una ecuación lineal es una ecuación polinómica de grado 1, con una o varias incógnitas. Dos ecuaciones son equivalentes
Unidad 8 Áreas y Volúmenes
 Unidad 8 Áreas y Volúmenes PÁGINA 132 SOLUCIONES Unidades de medida. Pasa a centímetros cuadrados las siguientes cantidades. a) b) c) Pasa a metros cúbicos las siguientes unidades. a) b) c) Cuántos litros
Unidad 8 Áreas y Volúmenes PÁGINA 132 SOLUCIONES Unidades de medida. Pasa a centímetros cuadrados las siguientes cantidades. a) b) c) Pasa a metros cúbicos las siguientes unidades. a) b) c) Cuántos litros
lím lím Veamos como ejemplo el límite de la función polinómica f(x)=3x 2-8 en 1: x 1 (3x2 )-lím 8 x 1 =2 x 1 x)2 -lím x 1 8 =
 LÍMITES LECCIÓN 7 Índice: Cálculo de ites en un punto. Epresión indeterminada L/0. Epresión indeterminada 0/0. Algunos ites de funciones irracionales. Otras técnicas básicas para el cálculo de ites. Problemas..-
LÍMITES LECCIÓN 7 Índice: Cálculo de ites en un punto. Epresión indeterminada L/0. Epresión indeterminada 0/0. Algunos ites de funciones irracionales. Otras técnicas básicas para el cálculo de ites. Problemas..-
Determinantes. Determinante de orden uno. a 11 = a 11 5 = 5
 DETERMINANTES Determinantes Concepto de determinante A cada matriz cuadrada A se le asigna un escalar particular denominado determinante de A, denotado por A o por det (A). A = Determinante de orden uno
DETERMINANTES Determinantes Concepto de determinante A cada matriz cuadrada A se le asigna un escalar particular denominado determinante de A, denotado por A o por det (A). A = Determinante de orden uno
Algoritmos para determinar Caminos Mínimos en Grafos
 Problemas de camino mínimo Algoritmos para determinar Caminos Mínimos en Grafos Algoritmos y Estructuras de Datos III DC, FCEN, UBA, C 202 Problemas de camino mínimo Dado un grafo orientado G = (V, E)
Problemas de camino mínimo Algoritmos para determinar Caminos Mínimos en Grafos Algoritmos y Estructuras de Datos III DC, FCEN, UBA, C 202 Problemas de camino mínimo Dado un grafo orientado G = (V, E)
UNIVERSIDAD MAYOR DE SAN SIMÓN FACULTAD DE CIENCIAS Y TECNOLOGÍA INGENIERÍA DE SISTEMAS BÚSQUEDA PRIMERO EL MEJOR
 UNIVERSIDAD MAYOR DE SAN SIMÓN FACULTAD DE CIENCIAS Y TECNOLOGÍA INGENIERÍA DE SISTEMAS BÚSQUEDA PRIMERO EL MEJOR INTEGRANTES: Caricari Cala Aquilardo Villarroel Fernandez Fructuoso DOCENTE: Lic. Garcia
UNIVERSIDAD MAYOR DE SAN SIMÓN FACULTAD DE CIENCIAS Y TECNOLOGÍA INGENIERÍA DE SISTEMAS BÚSQUEDA PRIMERO EL MEJOR INTEGRANTES: Caricari Cala Aquilardo Villarroel Fernandez Fructuoso DOCENTE: Lic. Garcia
EJERCICIO 26 DE EXCEL
 EJERCICIO 26 DE EXCEL TABLAS EN EXCEL Tablas En las versiones anteriores de Excel esta característica se conocía como Listas, ahora en esta nueva versión se denomina Tablas. Las tablas facilitan la administración
EJERCICIO 26 DE EXCEL TABLAS EN EXCEL Tablas En las versiones anteriores de Excel esta característica se conocía como Listas, ahora en esta nueva versión se denomina Tablas. Las tablas facilitan la administración
1 ÁLGEBRA DE MATRICES
 1 ÁLGEBRA DE MATRICES 1.1 DEFINICIONES Las matrices son tablas numéricas rectangulares. Se dice que una matriz es de dimensión m n si tiene m filas y n columnas. Cada elemento de una matriz se designa
1 ÁLGEBRA DE MATRICES 1.1 DEFINICIONES Las matrices son tablas numéricas rectangulares. Se dice que una matriz es de dimensión m n si tiene m filas y n columnas. Cada elemento de una matriz se designa
RELACIÓN DE PROBLEMAS DE CLASE DE PROGRAMACIÓN LINEAL ENTERA
 RELACIÓN DE PROBLEMAS DE CLASE DE PROGRAMACIÓN LINEAL ENTERA SIMPLEX Y LINEAL ENTERA a Resuelve el siguiente problema con variables continuas positivas utilizando el método simple a partir del vértice
RELACIÓN DE PROBLEMAS DE CLASE DE PROGRAMACIÓN LINEAL ENTERA SIMPLEX Y LINEAL ENTERA a Resuelve el siguiente problema con variables continuas positivas utilizando el método simple a partir del vértice
DETERMINANTES Profesor: Fernando Ureña Portero
 : CONCEPTO, CÁLCULO DE. Definición: A cada matriz cuadrada A=a ij, de orden n, se le asigna un número real, denominado determinante de A, denotado por A o por det (A). A =det (A)= 1.-Determinante de orden
: CONCEPTO, CÁLCULO DE. Definición: A cada matriz cuadrada A=a ij, de orden n, se le asigna un número real, denominado determinante de A, denotado por A o por det (A). A =det (A)= 1.-Determinante de orden
Sistemas de ecuaciones lineales dependientes de un parámetro
 Vamos a hacer uso del Teorema de Rouché-Frobenius para resolver sistemas de ecuaciones lineales de primer grado. En particular, dedicaremos este artículo a resolver sistemas de ecuaciones lineales que
Vamos a hacer uso del Teorema de Rouché-Frobenius para resolver sistemas de ecuaciones lineales de primer grado. En particular, dedicaremos este artículo a resolver sistemas de ecuaciones lineales que
APUNTADORES. Un apuntador es un objeto que apunta a otro objeto. Es decir, una variable cuyo valor es la dirección de memoria de otra variable.
 APUNTADORES Un apuntador es un objeto que apunta a otro objeto. Es decir, una variable cuyo valor es la dirección de memoria de otra variable. No hay que confundir una dirección de memoria con el contenido
APUNTADORES Un apuntador es un objeto que apunta a otro objeto. Es decir, una variable cuyo valor es la dirección de memoria de otra variable. No hay que confundir una dirección de memoria con el contenido
Sistemas de Ecuaciones Lineales y Matrices
 Capítulo 4 Sistemas de Ecuaciones Lineales y Matrices El problema central del Álgebra Lineal es la resolución de ecuaciones lineales simultáneas Una ecuación lineal con n-incógnitas x 1, x 2,, x n es una
Capítulo 4 Sistemas de Ecuaciones Lineales y Matrices El problema central del Álgebra Lineal es la resolución de ecuaciones lineales simultáneas Una ecuación lineal con n-incógnitas x 1, x 2,, x n es una
SISTEMAS INFORMÁTICOS PROGRAMACION I - Contenidos Analíticos Ing. Alejandro Guzmán M. TEMA 2. Diseño de Algoritmos
 TEMA 2 Diseño de Algoritmos 7 2. DISEÑO DE ALGORITMOS 2.1. Concepto de Algoritmo En matemáticas, ciencias de la computación y disciplinas relacionadas, un algoritmo (del griego y latín, dixit algorithmus
TEMA 2 Diseño de Algoritmos 7 2. DISEÑO DE ALGORITMOS 2.1. Concepto de Algoritmo En matemáticas, ciencias de la computación y disciplinas relacionadas, un algoritmo (del griego y latín, dixit algorithmus
Estática de Vigas. 20 de mayo de 2006
 Estática de Vigas 0 de mayo de 006 Los elementos estructurales que vamos a estudiar en este capítulo estarán sometidos a fuerzas o distribuciones aplicadas lateral o transversalmente a sus ejes y el objetivo
Estática de Vigas 0 de mayo de 006 Los elementos estructurales que vamos a estudiar en este capítulo estarán sometidos a fuerzas o distribuciones aplicadas lateral o transversalmente a sus ejes y el objetivo
CORRIENTE CONTINUA I : RESISTENCIA INTERNA DE UNA FUENTE
 eman ta zabal zazu Departamento de Física de la Materia Condensada universidad del país vasco euskal herriko unibertsitatea FACULTAD DE CIENCIA Y TECNOLOGÍA UNIVERSIDAD DEL PAÍS VASCO DEPARTAMENTO de FÍSICA
eman ta zabal zazu Departamento de Física de la Materia Condensada universidad del país vasco euskal herriko unibertsitatea FACULTAD DE CIENCIA Y TECNOLOGÍA UNIVERSIDAD DEL PAÍS VASCO DEPARTAMENTO de FÍSICA
Tema 3: Sistemas de ecuaciones lineales
 Tema 3: Sistemas de ecuaciones lineales 1. Introducción Los sistemas de ecuaciones resuelven problemas relacionados con situaciones de la vida cotidiana que tiene que ver con las Ciencias Sociales. Nos
Tema 3: Sistemas de ecuaciones lineales 1. Introducción Los sistemas de ecuaciones resuelven problemas relacionados con situaciones de la vida cotidiana que tiene que ver con las Ciencias Sociales. Nos
Sistemas de ecuaciones lineales
 Sistemas de ecuaciones lineales TIPOS DE SISTEMAS. DISCUSIÓN DE SISTEMAS. Podemos clasificar los sistemas según el número de soluciones: Incompatible. No tiene solución Compatible. Tiene solución. Compatible
Sistemas de ecuaciones lineales TIPOS DE SISTEMAS. DISCUSIÓN DE SISTEMAS. Podemos clasificar los sistemas según el número de soluciones: Incompatible. No tiene solución Compatible. Tiene solución. Compatible
Se inicia con las especificaciones del módulo fotovoltaico.
 Con base en las especificaciones técnicas del inversor SB 3000U y de un módulo fotovoltaico de 175 watts, indicar los valores los parámetros característicos requeridos para el dimensionamiento del sistema.
Con base en las especificaciones técnicas del inversor SB 3000U y de un módulo fotovoltaico de 175 watts, indicar los valores los parámetros característicos requeridos para el dimensionamiento del sistema.
2.1 Reglas básicas de derivación y ritmos o velocidades de cambio
 PRIMER BIMESTRE Guía didáctica: Cálculo La ecuación de la velocidad instantánea es la derivada de la función posición: La velocidad instantánea para t = 2s, es 8 m/s Esperamos, que con los ejemplos resueltos
PRIMER BIMESTRE Guía didáctica: Cálculo La ecuación de la velocidad instantánea es la derivada de la función posición: La velocidad instantánea para t = 2s, es 8 m/s Esperamos, que con los ejemplos resueltos
Valoración del Impacto de Contingencias de Subestaciones en los Sistemas Eléctricos de Potencia. Noviembre 2012
 Valoración del Impacto de Contingencias de Subestaciones en los Sistemas Eléctricos de Potencia Noviembre 2012 CONTENIDO 1. Metodología General. 2. Índice de Severidad Operativa. 3. Índice de Riesgo de
Valoración del Impacto de Contingencias de Subestaciones en los Sistemas Eléctricos de Potencia Noviembre 2012 CONTENIDO 1. Metodología General. 2. Índice de Severidad Operativa. 3. Índice de Riesgo de
MEDIDA DE POTENCIA EN TRIFÁSICA MÉTODO DE LOS DOS VATÍMETROS
 Práctica Nº 6 MEDID DE POTENI EN TRIFÁSI MÉTODO DE OS DOS VTÍMETROS 1. Objetivos a) Medida de la potencia activa, reactiva y el factor de potencia, en una red trifásica a tres hilos (sin neutro), utilizando
Práctica Nº 6 MEDID DE POTENI EN TRIFÁSI MÉTODO DE OS DOS VTÍMETROS 1. Objetivos a) Medida de la potencia activa, reactiva y el factor de potencia, en una red trifásica a tres hilos (sin neutro), utilizando
6. Diagramas de flujo.
 Ingeniería de Control I Tema 6 Diagramas de flujo 1 6. Diagramas de flujo. Representación en DF Simplificaciones Fórmula de Mason Formas de Kalman Sistemas MIMO Diagramas de Flujo 2 1 Bibliografía Señales
Ingeniería de Control I Tema 6 Diagramas de flujo 1 6. Diagramas de flujo. Representación en DF Simplificaciones Fórmula de Mason Formas de Kalman Sistemas MIMO Diagramas de Flujo 2 1 Bibliografía Señales
SESIÓN 10 DERIVACIÓN DE FUNCIONES TRIGONOMÉTRICAS DIRECTAS
 SESIÓN 0 DERIVACIÓN DE FUNCIONES TRIGONOMÉTRICAS DIRECTAS I. CONTENIDOS:. Derivadas de funciones trigonométricas directas. Ejercicios resueltos. Estrategias Centradas en el Aprendizaje: Ejercicios propuestos
SESIÓN 0 DERIVACIÓN DE FUNCIONES TRIGONOMÉTRICAS DIRECTAS I. CONTENIDOS:. Derivadas de funciones trigonométricas directas. Ejercicios resueltos. Estrategias Centradas en el Aprendizaje: Ejercicios propuestos
V B. g (1) V B ) g, (2) +ρ B. =( m H. m H (3) ρ 1. ρ B. Aplicando al aire la ecuación de estado de los gases perfectos, en la forma.
 Un globo de aire caliente de volumen =, m 3 está abierto por su parte inferior. La masa de la envoltura es =,87 kg y el volumen de la misma se considera despreciable. La temperatura inicial del aire es
Un globo de aire caliente de volumen =, m 3 está abierto por su parte inferior. La masa de la envoltura es =,87 kg y el volumen de la misma se considera despreciable. La temperatura inicial del aire es
2007 Carmen Moreno Valencia
 Tema VIII. Grafos Grafos 1 2007 Carmen Moreno Valencia 1. Grafos, digrafos y multigrafos 2. Grafos eulerianos 3. Matrices de adyacencia e incidencia 4. Exploración de grafos pesados 1. Grafos, digrafos
Tema VIII. Grafos Grafos 1 2007 Carmen Moreno Valencia 1. Grafos, digrafos y multigrafos 2. Grafos eulerianos 3. Matrices de adyacencia e incidencia 4. Exploración de grafos pesados 1. Grafos, digrafos
Los valores obtenidos de speedup tienden a incrementarse hasta los ocho procesadores. al usar diez procesadores éste se mantiene igual o decrece. Esto
 En la Figura 6.9 se muestra el speedup obtenido en el tiempo de ejecución al ejecutar la aplicación con las distintas pol ticas de mapping, que pueden ser comparadas con el caso ideal. En el Apéndice D
En la Figura 6.9 se muestra el speedup obtenido en el tiempo de ejecución al ejecutar la aplicación con las distintas pol ticas de mapping, que pueden ser comparadas con el caso ideal. En el Apéndice D
5.- Construcción de la Matriz Admitancia de Barra del Sistema
 MATRIZ ADMITANCIA DE BARRA 5.- Construcción de la Matri Admitancia de Barra del Sistema Encontradas las matrices de admitancia de barra elementales, estas se pueden combinar para formar la matri Admitancia
MATRIZ ADMITANCIA DE BARRA 5.- Construcción de la Matri Admitancia de Barra del Sistema Encontradas las matrices de admitancia de barra elementales, estas se pueden combinar para formar la matri Admitancia
Tema 3: Espacios vectoriales
 Tema 3: Espacios vectoriales K denotará un cuerpo. Definición. Se dice que un conjunto no vacio V es un espacio vectorial sobre K o que es un K-espacio vectorial si: 1. En V está definida una operación
Tema 3: Espacios vectoriales K denotará un cuerpo. Definición. Se dice que un conjunto no vacio V es un espacio vectorial sobre K o que es un K-espacio vectorial si: 1. En V está definida una operación
Experiencia 2. Laboratorio de Redes 2010, UTFSM. Valparaíso, 25 de marzo de 2011
 Experiencia 2 Laboratorio de Redes 2010, UTFSM Valparaíso, 25 de marzo de 2011 Índice 1. Simulación de Redes 3 1.1. Introducción.......................................... 3 1.2. Tipos de Simulación.....................................
Experiencia 2 Laboratorio de Redes 2010, UTFSM Valparaíso, 25 de marzo de 2011 Índice 1. Simulación de Redes 3 1.1. Introducción.......................................... 3 1.2. Tipos de Simulación.....................................
Grafos. Algoritmos y Estructuras de Datos III
 Grafos Algoritmos y Estructuras de Datos III Grafos Un grafo G = (V, X ) es un par de conjuntos, donde V es un conjunto de puntos o nodos o vértices y X es un subconjunto del conjunto de pares no ordenados
Grafos Algoritmos y Estructuras de Datos III Grafos Un grafo G = (V, X ) es un par de conjuntos, donde V es un conjunto de puntos o nodos o vértices y X es un subconjunto del conjunto de pares no ordenados
Matriz de Insumo - Producto
 Matriz de Insumo - Producto Introducción En esta sección vamos a suponer que en la economía de un país hay sólo tres sectores: industria (todas las fábricas juntas), agricultura (todo lo relacionado a
Matriz de Insumo - Producto Introducción En esta sección vamos a suponer que en la economía de un país hay sólo tres sectores: industria (todas las fábricas juntas), agricultura (todo lo relacionado a
1. Lección 9 - Continuidad y Derivabilidad
 1. Lección 9 - Continuidad y Derivabilidad 1.1. Continuidad El concepto de continuación es el mismo que el visto en el primer cuatrimestre pero generalizado al caso de los campos escalares. Así, sea la
1. Lección 9 - Continuidad y Derivabilidad 1.1. Continuidad El concepto de continuación es el mismo que el visto en el primer cuatrimestre pero generalizado al caso de los campos escalares. Así, sea la
LAS CIENCIAS DE LA PLANIFICACIÓN
 LAS CIENCIAS DE LA PLANIFICACIÓN 5. EL PROBLEMA DEL VIAJANTE (PV) (The Traveling Salesman Problem TSP) Un problema como el de las vacaciones, pero vital para las empresas, es el problema del viajante (PV):
LAS CIENCIAS DE LA PLANIFICACIÓN 5. EL PROBLEMA DEL VIAJANTE (PV) (The Traveling Salesman Problem TSP) Un problema como el de las vacaciones, pero vital para las empresas, es el problema del viajante (PV):
V. ESTUDIO DE LA ENTONACIÓN.
 V. ESTUDIO DE LA ENTONACIÓN. V.. Modelo de entonación. La entonación es la variación de la frecuencia de vibración de las cuerdas vocales a lo largo de una frase. Existe una relación estrecha entre el
V. ESTUDIO DE LA ENTONACIÓN. V.. Modelo de entonación. La entonación es la variación de la frecuencia de vibración de las cuerdas vocales a lo largo de una frase. Existe una relación estrecha entre el
Visión artificial y Robótica Modelos de movimiento y mapas. Depto. de Ciencia de la Computación e Inteligencia Artificial
 Visión artificial y Robótica Modelos de movimiento y mapas Depto. de Ciencia de la Computación e Inteligencia Artificial Contenidos Sistemas de coordenadas Localización de objetos en el espacio Modelos
Visión artificial y Robótica Modelos de movimiento y mapas Depto. de Ciencia de la Computación e Inteligencia Artificial Contenidos Sistemas de coordenadas Localización de objetos en el espacio Modelos
CINEMÁTICA: CONCEPTOS BÁSICOS
 CINEMÁTICA: CONCEPTOS BÁSICOS 1. MOVIMIENTO Y SISTEMA DE REFERENCIA. Sistema de referencia. Para decidir si algo o no está en movimiento necesitamos definir con respecto a qué, es decir, se necesita especificar
CINEMÁTICA: CONCEPTOS BÁSICOS 1. MOVIMIENTO Y SISTEMA DE REFERENCIA. Sistema de referencia. Para decidir si algo o no está en movimiento necesitamos definir con respecto a qué, es decir, se necesita especificar
LAS CIENCIAS DE LA PLANIFICACIÓN
 LAS CIENCIAS DE LA PLANIFICACIÓN 1. MODELIZACIÓN CON GRAFOS El objetivo de las ciencias de la planificación es encontrar el mejor método para resolver un problema, y si es posible encontrar la solución
LAS CIENCIAS DE LA PLANIFICACIÓN 1. MODELIZACIÓN CON GRAFOS El objetivo de las ciencias de la planificación es encontrar el mejor método para resolver un problema, y si es posible encontrar la solución
Tema 2: Determinantes
 Tema 2: Determinantes 1. Introducción En este tema vamos a asignar a cada matriz cuadrada de orden, un número real que llamaremos su determinante y escribiremos. Vamos a ver cómo se calcula. Consideremos
Tema 2: Determinantes 1. Introducción En este tema vamos a asignar a cada matriz cuadrada de orden, un número real que llamaremos su determinante y escribiremos. Vamos a ver cómo se calcula. Consideremos
POST-OPTIMIZACIÓN Y SENSIBILIDAD EN PROBLEMAS LINEALES.
 POST-OPTIMIZACIÓN Y SENSIBILIDAD EN PROBLEMAS LINEALES. Una de las hipótesis básicas de los problemas lineales es la constancia de los coeficientes que aparecen en el problema. Esta hipótesis solamente
POST-OPTIMIZACIÓN Y SENSIBILIDAD EN PROBLEMAS LINEALES. Una de las hipótesis básicas de los problemas lineales es la constancia de los coeficientes que aparecen en el problema. Esta hipótesis solamente
Estudio de fallas asimétricas
 Departamento de Ingeniería Eléctrica Universidad Nacional de Mar del Plata Área Electrotecnia Estudio de fallas asimétricas Autor: Ingeniero Gustavo L. Ferro Prof. Adjunto Electrotecnia EDICION 2012 1.
Departamento de Ingeniería Eléctrica Universidad Nacional de Mar del Plata Área Electrotecnia Estudio de fallas asimétricas Autor: Ingeniero Gustavo L. Ferro Prof. Adjunto Electrotecnia EDICION 2012 1.
Tema 1. Conceptos básicos
 Tema 1. Conceptos básicos 1. Introducción... 1 2. Conceptos básicos... 2 2.1. Circuito eléctrico... 2 2.2. Teoría de Circuitos... 2 3. Magnitudes de un circuito: Tensión e intensidad... 3 3.1. Carga y
Tema 1. Conceptos básicos 1. Introducción... 1 2. Conceptos básicos... 2 2.1. Circuito eléctrico... 2 2.2. Teoría de Circuitos... 2 3. Magnitudes de un circuito: Tensión e intensidad... 3 3.1. Carga y
Enunciados de los problemas (1)
 Enunciados de los problemas (1) Problema 1. El peso de tres manzanas y dos naranjas es de 255 gramos. El peso de dos manzanas y tres naranjas es de 285 gramos. Si todas las manzanas son del mismo peso
Enunciados de los problemas (1) Problema 1. El peso de tres manzanas y dos naranjas es de 255 gramos. El peso de dos manzanas y tres naranjas es de 285 gramos. Si todas las manzanas son del mismo peso
Determinantes. Concepto de determinante A cada matriz cuadrada A se le asigna un número denominado determinante de A, denotado por A o por det (A).
 Determinantes Concepto de determinante A cada matriz cuadrada A se le asigna un número denominado determinante de A, denotado por A o por det (A). A = Determinante de orden uno a 11 = a 11 5 = 5 Determinante
Determinantes Concepto de determinante A cada matriz cuadrada A se le asigna un número denominado determinante de A, denotado por A o por det (A). A = Determinante de orden uno a 11 = a 11 5 = 5 Determinante
Rentas Ciertas MATEMÁTICA FINANCIERA. Rentas Ciertas: Ejemplo. Rentas Ciertas. Ejemplo (1) C C C C C
 Rentas Ciertas MATEMÁTICA FINANCIERA RENTAS CIERTAS I Luis Alcalá UNSL Segundo Cuatrimeste 06 A partir de ahora, utilizaremos capitalización compuesta como ley financiera por defecto, salvo que expĺıcitamente
Rentas Ciertas MATEMÁTICA FINANCIERA RENTAS CIERTAS I Luis Alcalá UNSL Segundo Cuatrimeste 06 A partir de ahora, utilizaremos capitalización compuesta como ley financiera por defecto, salvo que expĺıcitamente
Ruta más Corta con una sóla Fuente de Inicio (Single-Source Shortest Paths) DR. JESÚS A. GONZÁLEZ BERNAL CIENCIAS COMPUTACIONALES INAOE
 Ruta más Corta con una sóla Fuente de Inicio (Single-Source Shortest Paths) 1 DR. JESÚS A. GONZÁLEZ BERNAL CIENCIAS COMPUTACIONALES INAOE Problema de Encontrar la Ruta más Corta 2 Se requiere llegar de
Ruta más Corta con una sóla Fuente de Inicio (Single-Source Shortest Paths) 1 DR. JESÚS A. GONZÁLEZ BERNAL CIENCIAS COMPUTACIONALES INAOE Problema de Encontrar la Ruta más Corta 2 Se requiere llegar de
Capítulo 10. Efectos de superficie. Sistema respiratorio
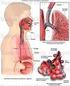 Capítulo 10 Efectos de superficie. Sistema respiratorio 1 Tensión superficial El coeficiente de tensión superficial γ es la fuerza por unidad de longitud que hay que realizar para aumentar una superficie:
Capítulo 10 Efectos de superficie. Sistema respiratorio 1 Tensión superficial El coeficiente de tensión superficial γ es la fuerza por unidad de longitud que hay que realizar para aumentar una superficie:
