Reactores Multifásicos
|
|
|
- Gonzalo Mendoza Contreras
- hace 9 años
- Vistas:
Transcripción
1 Capítulo 11 Reactores Multifásicos Dr. Fernando Tiscareño Lechuga Departamento de Ingeniería Química Instituto Tecnológico de Celaya
2 Multifásicos { Sólido-Líquido Fases involucradas Sólido-Líquido-Gas { Reactores en Suspensión A tratar Reactores de Lecho Percolador Suspensión: Líquido y sólido Tanque agitado ( y el gas?) Lecho percolador: Empacado pero el líquido no llena todos los espacios vacíos Existen muchas subclasificaciones que se pueden modelar con los principios que veremos: transporte, columnas de burbujeo en suspensión, de película descendente,... Laguna: No cubriremos reactores con reactivos sólidos: altos hornos, fabricación de cemento, cerámicas, combustión de carbón,... No incluiremos correlaciones para los parámetros c Dr. Fernando Tiscareño L./p2
3 Reactores en Suspensión Producción de agentes quelatantes Hidrogenaciones de glucosa y ácidos grasos Aplicaciones Oxidación parcial de etileno ( ambos reactivos gaseosos??) Tratamiento de aguas residuales Emulsiones (dos fases líquidas) Fase continua: Líquido Mezclado perfecto Fase dispersa: Burbujas de gas Flujo tapón Muy importante: Cuidar las unidades!!! Volumen-de-qué? Qué es la retención, R b? Variable de diseño: V L cuál volumen? Resistencias significativas: Masa interna y externa? Calor interna y externa? c Dr. Fernando Tiscareño L./p3
4 ) ) ( Velocidad de reacción #%$ & Líquido! "! Concentración C ) + + ( (C ) (C ),-/.,-. C' C ) ( C ' * C ) * Qué pasaría si alguna resistencia fuera despreciable? Qué pasa en la interfase g-l? c Dr. Fernando Tiscareño L./p4
5 A (G) + B (L) Productos Ley de Henry? Unidades? Solubilidad de NH 3 o CO 2? Si C AL C BL, orden de reacción respecto a B? Variable de Diseño, V L Ecuación de diseño: B.M. de j en el líquido V L = V L C j L0 C jl1 ( r Lj ) 1 (11.1) Velocidad de reacción = Resistencia externa ( r Lj ) = (k s a s ) j (C j L C js ) (11.2) Unidades? De qué depende C j s? Puede (C jl C js ) 0? c Dr. Fernando Tiscareño L./p5
6 Velocidad para el reactivo gaseoso i B.M. de i en el líquido ( r Li ) = 1 V L = 1 VL 0 VL (k G a b ) i [C ig (C ig ) igl ] dv L V L C il V L (11.3) (k L a b ) i [(C il ) igl C il ] dv L V L C il V L 0 V L (11.4) = (k s a s ) i (C il C is ) (11.5) Qué es V L C il V L? Cómo se evalúan las integrales? B.M. en las burbujas (Unidades) df ig dv G = 1 R b (k G a b ) i [C ig (C ig ) igl ] d( V G C ig ) dv L = (k G a b ) i [C ig (C ig ) igl ] d(c ig) dv L 1 V G (k G a b ) i [C ig (C ig ) igl ] c Dr. Fernando Tiscareño L./p6
7 Velocidad para el reactivo gaseoso i Suposiciones en la interfase g l: (C il ) igl = H i (C ig ) igl (k G a b ) i [C ig (C ig ) igl ] = (k L a b ) i [(C il ) igl C il ] (C ig ) igl = (k Ga b ) i C ig + (k L a b ) i C il (k G a b ) i + H i (k L a b ) i (11.7) Del B.M. en las burbujas (Unidades) d(c ig) 1 (k G a b ) i [C ig (C ig ) dv L V igl ] ( G ) ( ) (kg a b ) i Hi k Li = C ig V G k Gi + H i k Li ( ) ( ) (kg a b ) i kli C il V G k Gi + H i k Li Integrando qué se supone constante? ( C ig = C ig0 C ) [ ( ) ] 1 il e 1 1 VL (k G a b ) + i H i (k L a b ) i V G + C il (11.8) H i H i c Dr. Fernando Tiscareño L./p7
8 Velocidad para el reactivo gaseoso i B.M. Global en las burbujas: VL 0 (k G a b ) i [C ig (C ig ) igl ] dv L = V G [C ig0 C ig1 ] Retomando la Ec y Ec con [V L ] total y C ig1 : ( r Li ) = 1 V L = V G V L VL (k G a b ) i [C ig (C ig ) igl ] dv L V L C il (11.3) 0 V L ( C ig0 C ) ( [ ( ) 1 ]) il 1 e VL (k G a b ) i H i (k L a b ) i V G V L C il (11.9) H i V L Ventaja: Ec. Diferencial Ec. Algebraica! Suposiciones involucradas? c Dr. Fernando Tiscareño L./p8
9 Dificultad Matemática El gas i se alimenta puro o C ig Cte. (C ig ) igl y (C il ) igl? El reactivo líquido j no interviene en la cinética; si primer orden, solución analítica sí interviene en la expre- C ig no es constante y C j L sión cinética; y C ig no es constante y C j L sí interviene en la cinética, pero además: V G, k G, k L y a b dependen de V L c Dr. Fernando Tiscareño L./p9
10 Ecuaciones de Diseño: 1 o varias reacciones Para reactivos gaseosos ( r Li ) 1 = V G V L ( C ig0 C ) ( [ ( ) 1 ]) il 1 e VL (k G a b ) i H i (k L a b ) i V G V L C il (11.9) H i V L = (k s a s ) i (C il C is ) (11.5) = η r i (C is, C j s ) (11.10) Para reactivos líquidos ( r Lj ) 1 = V C j L0 C jl L V L (11.11) = (k s a s ) j (C j L C js ) (11.2) = ν j η r i (C is, C j s ν ) (11.12) i Número de ecuaciones y variables? Ecuaciones simultáneas? Si significativos la resistencia interna: r L = ρ P ( Volumen de catalizador Volumen de líquido ) r P = ( ) Peso de catalizador Volumen de líquido r P c Dr. Fernando Tiscareño L./p10
11 Algoritmo secuencial: 1 rxn y V L conocido PASO Procedimiento 1 Suponer C il : 0 < C il < H i C ig0 2 Calcular ( r Li ) de la Ecuación Calcular C is de la Ecuación Calcular ( r Lj ) de la Ecuación Calcular C j s con la Ecuación Obtener ( r Li ) de la Ecuación o, si los efectos internos son significativos, de un procedimiento algorítmico adicional a partir de las concentraciones en la superficie 7 Calcular V L de la Ecuación Comparar, Es [V L ] Paso 7 = [V L ] conocida? NO: regresar al Paso 1; y SÍ: terminar. c Dr. Fernando Tiscareño L./p11
12 Algoritmo secuencial: 1 rxn y C j L1 conocido PASO Procedimiento 1 Suponer V L 2 Calcular ( r Lj ) de la Ecuación Calcular ( r Li ) de la Ecuación Calcular C il de la Ecuación Calcular C is de la Ecuación Calcular C j s de la Ecuación Obtener ( r Li ) de la Ecuación o, si los efectos internos son significativos, de un procedimiento algorítmico adicional a partir de las concentraciones en la superficie 8 Comparar, Es [( r Li )] Paso 3 = [( r Li )] Paso 7? NO: regresar al Paso 1; y SÍ: terminar. c Dr. Fernando Tiscareño L./p12
13 Ejemplo 11.1: Suspensión A (l) + 2 B (g) Productos ( r B ) = k C B 2 = 1, 200 lt2 s mol g C B 2 atm y 30 C [ρgh 0]; La expresión es intrínseca y C B implica a B absorbido Partículas esféricas d P = cm y [ρ P ] seco = 1 g cm 3 Para Φ = d P ρp k C Bs 2 D e < 5, η = Φ 0.1 Φ Φ Φ 4 B donde D eb = cm2 s V L = 1 lt s y C A0 = 0.55 M; El líquido entra saturado con B V G = 200 lt s y y B0 = condiciones de operación; H A = 0.06 k s = 0.03 cm s ; k L = 0.02 cm s ; k G = 0.5 cm s ; y a cm b = 2 2 cm 3 de líquido R b = 0.1 y R s = 0.08 (Carga de catalizador, razón de volúmenes referido a V L ) a) Si f A = 0.65, V L y t residencia del líquido? b) C B L1?, C BL0?; y c) V recipiente? si 30 % ocupado por accesorios y espacio sobre el nivel de líquido c Dr. Fernando Tiscareño L./p13
14 Ejemplo 11.1 (Continuación 1) G.I., T, P y y B 0 C BG0 = M Ley de Henry considerando líquido entra saturado: Geometría: πd 2 / 1 6 πd3 Por qué R s? Para evaluar η: 1000? Φ = d P 2 C BL0 = C BG0 H B = M a s = R s 6 d P = 120 cm 1 ρ P 1000 k C Bs D eb = C Bs c Dr. Fernando Tiscareño L./p14
15 Ejemplo 11.1 (Continuación 2) Ec (Ojo: líq. entra sat.!), Ec. 11.5, Ec y Ec. 11.1: ( r LB ) 1 = V G V L Sustituyendo: ( C BG0 C ) ( [ ( ) 1 ]) BL1 1 e VL (k G a b ) B H B (k L a b ) B V G V L (C BL1 C BL0 ) H B V L = (k s a s ) B (C BL1 C Bs ) 2 = 1000 η(c Bs ) R s ρ P k C ( ) Bs = V C AL0 C AL1 L ν A ν V L B ( r LB ) 1 = 200 ( C ) ( ) BL1 1 e V L 83,533 1 (C BL ) V L 0.06 V L (A) = 3.6 (C BL1 C Bs ) (B) = 96, 000 C 2 Bs ( C Bs 2, 400C Bs C 2s B C Bs ) (C) ( ) = 1 (D) 0.5 V L 4 Ec. y 4 Incógnitas, opciones de solución? c Dr. Fernando Tiscareño L./p15
16 Ejemplo 11.1 (Continuación 3) Solución numérica: 5 mol V L = 13, 772 lt, ( r LB ) 1 = s lt, C BL1 = M y C Bs = M C BL1 C Bs, significado? Φ = η = 0.919, significado? Tiempo de residencia porque V L : t L = V L V = h L Ec sustituyendo [V L ] interno = [V L ] total : C ig1 = ( Volumen del recipiente: ) e 13,772 83, Volumen debajo del nivel 0.7 V recipiente = V L (1 + R b + R s ) = 0.7 Con reactores multifásicos volumen-de-qué! = M = 23, 220 lt c Dr. Fernando Tiscareño L./p16
17 Ejemplo 11.2: Suspensión 2 A (g) + B 2 C r L1 = k 1 C 2 A C B = 150 lt2 C 2 s mol 2 A C B A (g) + B Subproductos r L2 = k 2 C A C B = 0.16 lt C s mol A C B A (g) + C Subproductos r L3 = k 3 C A C C = 0.12 lt C s mol A C C Las constantes incluyen los efectos internos de masa V L = 20 m 3 ; V L = 80 lt s y C B0 = 0.05 M V G = 2 m3 s y y A 0 = 10 atm y 120 C; H A = 0.3 R b = 0.3 y R s = 0.05 (Carga de catalizador, razón de volúmenes referido a V L ) d P = cm y k s = cm s ; d b = 0.1 cm y k L = cm s Concentraciones en los efluentes? Efectos de las resistencias a la transferencia de masa? c Dr. Fernando Tiscareño L./p17
18 Ejemplo 11.2 (Continuación 1) G.I., T, P y y A 0 C AG0 = M Geometría: πd 2 / 1 6 πd3 a b = R b 6 d b = 18 cm 1 a s = R s 6 d P = 12 cm 1 Qué significan a b y a s? Cuál es la base? 3 rxnes independientes 3 ec. diseño y 3 de transferencia de masa Estequiometría: ( r LA ) = 2 k 1 C As 2 C Bs + k 2 C As C Bs + k 3 C As C Cs ( r LB ) = k 1 C As 2 C Bs + k 2 C As C Bs (+r LC ) = 2 k 1 C As 2 C Bs k 3 C As C Cs Resistencias en la burbuja: implicaciones de 1 (k G a b ) i 1 H i (k L a b ) i? c Dr. Fernando Tiscareño L./p18
19 Ejemplo 11.2 (Continuación 2) Ecuaciones de diseño (Ec y 11.1) 2k 1 C As 2 C Bs + k 2 C As C Bs + k 3 C As C Cs = V G V L k 1 C As 2 C Bs + k 2 C As C Bs = V L V L (C BL0 C BL ) ( C AG0 C ) ( ) AL 1 e H A(k L a b ) V L V G V L C AL H A V L (A) (B) 2 k 1 C As 2 C Bs k 3 C As C Cs = V L V L (C CL ) E.E. de la transferencia de masa: (k s a s )(C AL C As ) = 2 k 1 C As 2 C Bs + k 2 C As C Bs + k 3 C As C Cs (D) (k s a s )(C BL C Bs ) = k 1 C As 2 C Bs + k 2 C As C Bs (E) (k s a s )(C Cs C CL ) = 2 k 1 C As 2 C Bs k 3 C As C Cs (F) Dónde quedó el B.M. en la burbuja? qué son estas ec. de diseño? Suposiciones implicadas en la Ecuación A? y si no se cumplen? Y se más de un reactivo gaseoso? Y si los efectos internos no estuvieran incluidos? (C) c Dr. Fernando Tiscareño L./p19
20 Ejemplo 11.2 (Continuación 3) Sustituyendo valores, condiciones iniciales? Resultados: 300 C As 2 C Bs C As C Bs C As C Cs = C AL (A) 150 C As 2 C Bs C As C Bs = C BL (B) 300 C As 2 C Bs 0.12 C As C Cs = C CL (C) 300 C As 2 C Bs C As C Bs C As C Cs = (C AL C As ) (D) 150 C As 2 C Bs C As C Bs = (C BL C Bs ) (E) 300 C As 2 C Bs 0.12 C As C Cs = (C Cs C CL ) (F) C AL = M C BL = M C CL = M C As = M C Bs = M C Cs = M Resistencias externa de masa significativas? f B = y R B C = Ec C AG1 = M; Significado de C AG1 +C AG0 2 H A = M? Resistencia en la burbuja? c Dr. Fernando Tiscareño L./p20
21 Reactores de Lecho Percolador Oxidación de compuestos orgánicos Hidrogenación de compuestos orgánicos Algunas aplicaciones ( Hidrodesulfurización!!) Tratamiento de Aguas Residuales Tres fases: sólido-líquido-gas El líquido se embebe dentro del catalizador poroso como un absorbedor Operación industrial: flujos concurrentes Condiciones isotérmicas ( por qué) Aumentar la solubilidad: P ( y T?) c Dr. Fernando Tiscareño L./p21
22 Hidráulica $ %'&% () (# +*, -,& -.!#" "# / 0"- '&% () (# +*, -,& !#" " Operación concurrente c Dr. Fernando Tiscareño L./p22
23 ! Velocidad de reacción Corriente de Gas Concentración C " $ C (C" $ ) & (C % ) ' () ' ( ) C # C "! " C # Líquido Similar a suspensión? Fase dispersa; líquido fluye en una dirección ; y órdenes de magnitud c Dr. Fernando Tiscareño L./p23
24 Reacción y transferencia Aumentar la solubilidad: P ( y T?, ks y absorción) Para reactivos líquidos j Para reactivos gaseosos i ( r W j ) = (k c a c ) j (C j L C js ) (11.13) ( r W i ) = (k c a c ) i (C il C is ) (11.14) Expresiones cinéticas y efectos internos r W s Velocidades locales! Resistencias en la interfase g-l ( Unidades de a L?) (k G a L ) i [C ig (C ig ) igl ] = (k L a L ) i [(C il ) igl C il ] (k L a L ) i [H i C ig C il ] ( r W i ) Suposición: Fases uniformemente distribuidas Modelo unidimensional c Dr. Fernando Tiscareño L./p24
25 Transferencia = reacción? Primer orden para i, en otros textos: ( r W i ) =? ( H i H i (k G a L ) i + 1 (k L a L ) i + 1 (k c a c ) i + 1 η k ) C ig = k 0 C ig V C V C w Gas C Líquido V V C Catalizador w + w Y para suspensión, OK? por qué? Entonces, su utilidad? c Dr. Fernando Tiscareño L./p25
26 Ecuaciones de Diseño (generales en E.E.) d(c j L ) dw = 1 V L ( r W j ) (11.15) d(c i G) dw d(c i L) dw = 1 = ( 1)θ V G (k L a L ) i (H i C i G C i L) (11.16) θ = V L [( r W i ) (k La L ) i (H i C i G C i L)] (11.17) { 0 para operación concurrente; y 1 para operación a contracorriente. Despreciando resistencia g-l de lado del gas Expresiones cinéticas y efectos internos r W s Base: W (V L es utilizado en otros textos) c Dr. Fernando Tiscareño L./p26
27 Primer Orden: Solución anaĺıtica Efectos internos y externos al sólido [ 1 ( r Wi ) = η k C is = + 1 ] 1 C il = k ap C il (k c a c ) i η k Despejando del B.M. de i en el gas C il = H i C ig + ( 1) θ VG d(c ig ) (k L a L ) i dw Derivando suponiendo constantes los parámetros, y si no? d(c il ) dw = H i d(c ig ) dw + VG d 2 (C ig ) ( 1)θ (k L a L ) i dw 2 Rearreglamos del B.M. de i en el líquido V L d(c il ) V L [ d(c ig ) H i dw + VG d 2 (C ig ) ( 1)θ (k L a L ) i dw 2 dw = k ap C il + (k L a L ) i (H i C ig C il ) ] [ ] = k ap H i C ig + ( 1) θ VG d(c ig ) (k L a L ) i dw ( 1) θ VG d(c ig ) dw (11.18) c Dr. Fernando Tiscareño L./p27
28 Solución anaĺıtica (Continuación) Reagrupando d 2 [ (C ig ) (kl a L ) i + + k ap + ( 1) dw 2 V L V θ(k ] La L ) i H i d(cig ) L V G dw Solución General m 1 = 1 [ (kl a L ) i 2 V L [ 1 (kl a L ) i + 4 V L m 2 = 1 [ (kl a L ) i 2 V L [ 1 (kl a L ) i 4 V L C.F. [C ig ] w=0 = C 1 + C 2 C ig = C 1 e m 1 w + C 2 e m 2 w + k ap + ( 1) V θ(k ] La L ) i H i L V G + k ap V L + ( 1) θ(k La L ) i H i V G + k ap + ( 1) V θ(k ] La L ) i H i L V G + k ap V L + ( 1) θ(k La L ) i H i V G + ( 1)θ (k La L ) i k ap H i V G VL C ig = 0 ] 2 ( 1) θ (k La L ) i k ap H i V G VL (11.19) ] 2 ( 1) θ (k La L ) i k ap H i V G VL (11.20) c Dr. Fernando Tiscareño L./p28
29 Solución anaĺıtica (Continuación 2) Segunda C.F.? o Primera derivada en w = 0? Derivando la solución general dc ig dw = m 1 C 1 e m 1 w + m 2 C 2 e m 2 w Evaluando en w = 0 e e igualando a B.M. de i en el gas [ ] d(cig ) = ( 1)θ (k L a L ) i (H i [C ig ] w=0 C il0 ) = m 1 C 1 + m 2 C 2 dw w=0 V G Evaluando C 1 y C 2 Perfil ( y si concurrente? si líquido entra saturado?) C ig = [C ig] w=0 (m 2 e m 1 w m 1 e m 2 w ) + ( 1)θ (k L a L ) i (H i [C ig ] w=0 C il0 ) (e m 2 m 1 V m 1 w e m 2 w ) G (m 2 m 1 ) (11.21) Derivandola y sustituyendo en B.M. en el gas C il = H i [C ig ] w=0 (m 2 e m 1 w m 1 e m 2 w ) + ( 1)θ H i (k L a L ) i (H i [C ig ] w=0 C il0 ) (e m 2 m 1 V m 1 w e m 2 w ) G (m 2 m 1 ) + m 1 m 2 VG [C ig ] w=0 (k L a L ) i (m 2 m 1 ) (em 1 w e m 2 w ) + (H i [C ig ] w=0 C il0 ) (m 1 e m 1 w m 2 e m 2 w ) (11.22) m 2 m 1 c Dr. Fernando Tiscareño L./p29
30 Solución anaĺıtica (Continuación 3) Y la [f j ] 1 o C j L1? Opción 1: B.M. para j en líquido en ν j ν i (r Wi ) con perfil conocido Opción 2: B.M. Líquido de j B.M. Líquido+Gas de i C j L1 = C jl0 ( νj ν i ) [ C il0 C il1 + ( 1) θ ( VG V L ) ([C ig ] w=0 [C ig ] w=w ) ] (11.23) c Dr. Fernando Tiscareño L./p30
31 Ejemplo 11.3: Percolador Catalizador: W =5,000 Kg, d P =0.08 cm y ρ P = 1 25 atm y 300 C g cm A (g) + B (l) C (l) r = k C A = 0.02 lt g s C A D il = cm2 s Líquido: 1 lt s, 0.2 moles de B lt y H A = 0.05 y libre de A Gas: 20 lt s y y A0 = 0.02; k La L = lt g s mol de A absorbido mol de A gaseoso lt / lt y k c a c = lt g s a) Perfiles para C A G, C AL, C As y C BL b) [f A ] absorbida y f B? c) Si W =10,000 Kg, C A G, C AL, y C BL de salida? c Dr. Fernando Tiscareño L./p31
32 Ejemplo 11.3 (Continuación 1) G.I., T, P y y A 0 C AG0 = M Solución analítica Problema propuesto Usaremos solución numérica η = independiente de w por qué?; 0.5? ρp k Φ S = R = ( ) 1000 = D e Constante aparente referente a mol de A k ap = [ (k c a c ) i η 0.5 k ] 1 = [ Concentración en la superficie: efecto constante ] 1 = lt g s C As = k ap η 0.5 k C AL = C AL c Dr. Fernando Tiscareño L./p32
33 Ejemplo 11.3 (Continuación 2) Ecuaciones de diseño d(c BL ) dw = 1 2 k ap C AL = V 3 C AL L d(c AG ) dw = (k La L ) A (H A C AG C AL ) = V 5 (0.05 C AG C AL ) G d(c AL ) dw = 1 [k ap C AL (k L a L ) A (H A C AG C AL )] V L = C AG C AL C.I.: C BL0 = 0.2 M y C AL0 = 0, G.I. C AG0 = mol lt Qué implica comparar curvas para C AL vs. C As y C AL vs. H A C AG? c Dr. Fernando Tiscareño L./p33
34 Ejemplo 11.3 (Continuación 3) Concentración de A, M C C Peso de Catalizador, Kg Concentración de B, M c Dr. Fernando Tiscareño L./p34
35 Ejemplo 11.3 (Continuación 4) Concentración de A, M H C C Peso de Catalizador, Kg c Dr. Fernando Tiscareño L./p35
36 Ejemplo 11.3 (Continuación 5) b) En 5,000 Kg: C AG1 = M, C AL1 = M y C BL1 = M [f A ] Absorbida = F [ ] AG0 F AG1 CAG0 C AG1 = = F AG0 Diferencia? C AG0 f B = C BL0 C BL1 C BL0 = Para V G constante = [F A ] absorbidos = V G (C AG0 C AG1 ) = 20 ( ) = moles s [F A ] reaccionaron = V L (C BL0 C BL1 ) ν A = 1 ( ) 0.5 = moles ν s B V L (C AL1 C AL0 ) = 1 ( moles 0) = s Reactivo limitante? Limita la velocidad? Alimentado en menor proporción? c) En 10,000 Kg: C AG1 = M, C AL1 = M y C BL1 = M c Dr. Fernando Tiscareño L./p36
37 Líquido saturado con i (k L a L ) i C il H i C ig Ecuaciones de diseño dadas Indeterminaciones d(c ig ) dw = ( 1)θ ( ) (0) V G d(c il ) dw = 1 [( r Wi ) ( ) (0)] V L Derivando la Ley de Henry: d(c il) d(c dw = H ig ) i dw Combinando éste con B.M.s para i en gas y líquido d(c ig ) dw = ( 1)θ ( r Wi ) (si i muy poco soluble) ( 1)θ ( r Wi ) (11.24) V G + H i VL V G Si primer orden: d(c ig ) dw = ( 1)θ k ap C il ( 1)θ k ap H i C ig V G + H i VL V G + H i VL C ig = C ig0 e ( 1)θ V G +H i VL k ap H i w Varias Reacciones o Reactivos? Solución numérica c Dr. Fernando Tiscareño L./p37
38 Recapitulación Tratamos modelos idealizados Flujo tapón y mezclado perfecto No se presentaron correlaciones ni métodos para los parámetros Reactor en suspensión Sistema mixto algebraico-global y diferencial Se desarrollo un procedimiento con sólo ecuaciones algebraicas Reactor de lecho percolador Sistema de ecuaciones diferenciales Solución analítica para primer orden respecto al gas i Se supusieron distr. homogéneas Mode. unidimensionales Existen otras clasificaciones para reactores multifásicos... c Dr. Fernando Tiscareño L./p38
Capítulo 14: Equilibrio químico
 Capítulo 14: Equilibrio químico Dr. Alberto Santana Universidad de Puerto Rico Recinto Universitario de Mayagüez Departamento de Química QUIM 3002 Química general II, Cap. 14: Eq. químico p.1 Concepto
Capítulo 14: Equilibrio químico Dr. Alberto Santana Universidad de Puerto Rico Recinto Universitario de Mayagüez Departamento de Química QUIM 3002 Química general II, Cap. 14: Eq. químico p.1 Concepto
Reactores Isotérmicos en Fase Gaseosa
 Capítulo 5 Reactores Isotérmicos en Fase Gaseosa Dr. Fernando Tiscareño Lechuga Departamento de Ingeniería Química Instituto Tecnológico de Celaya Por qué dividir en dos capítulos? Mismas ecuaciones de
Capítulo 5 Reactores Isotérmicos en Fase Gaseosa Dr. Fernando Tiscareño Lechuga Departamento de Ingeniería Química Instituto Tecnológico de Celaya Por qué dividir en dos capítulos? Mismas ecuaciones de
Operaciones Básicas de Transferencia de Materia Problemas Tema 6
 1º.- En una torre de relleno, se va a absorber acetona de una corriente de aire. La sección de la torre es de 0.186 m 2, la temperatura de trabajo es 293 K y la presión total es de 101.32 kpa. La corriente
1º.- En una torre de relleno, se va a absorber acetona de una corriente de aire. La sección de la torre es de 0.186 m 2, la temperatura de trabajo es 293 K y la presión total es de 101.32 kpa. La corriente
C: GASES Y PRESIÓN DE VAPOR DEL AGUA
 hecho el vacío. Calcula a) Cantidad de gas que se tiene ; b) la presión en los dos recipientes después de abrir la llave de paso y fluir el gas de A a B, si no varía la temperatura. C) Qué cantidad de
hecho el vacío. Calcula a) Cantidad de gas que se tiene ; b) la presión en los dos recipientes después de abrir la llave de paso y fluir el gas de A a B, si no varía la temperatura. C) Qué cantidad de
TEMA 3: CINÉTICA HOMOGÉNEA. REACCIONES SIMPLES CQA-3/1
 TEMA 3: CINÉTICA HOMOGÉNEA. REACCIONES SIMPLES CQA-3/1 CARACTERÍSTICAS DE LAS REACCIONES HOMOGÉNEAS Todas las sustancias reaccionantes se encuentran en una sola fase Velocidad de reacción: Objetivo principal
TEMA 3: CINÉTICA HOMOGÉNEA. REACCIONES SIMPLES CQA-3/1 CARACTERÍSTICAS DE LAS REACCIONES HOMOGÉNEAS Todas las sustancias reaccionantes se encuentran en una sola fase Velocidad de reacción: Objetivo principal
Tema 12 Termoquímica. Desprende o absorbe calor? Cuánto calor? Criterio de espontaneidad En qué dirección se produce? Reacciones Químicas
 Tema 1 Estequiometría Cuánto se produce? Cuánto reacciona? Tema 15 Equilibrio Cuándo se alcanza? Cómo modificarlo? Tema 12 Termoquímica Desprende o absorbe calor? Cuánto calor? Criterio de espontaneidad
Tema 1 Estequiometría Cuánto se produce? Cuánto reacciona? Tema 15 Equilibrio Cuándo se alcanza? Cómo modificarlo? Tema 12 Termoquímica Desprende o absorbe calor? Cuánto calor? Criterio de espontaneidad
INGENIERO. JOSMERY SÁNCHEZ
 UNIVERSIDAD NACIONAL EXPERIMENTAL FRANCISCO DE MIRANDA COMPLEJO ACADÉMICO "EL SABINO" PROGRAMA DE INGENIERÍA MECÁNICA AREA DE TECNOLOGÍA UNIDAD CURRICULAR: TERMODINÁMICA APLICADA REALIZADO POR: INGENIERO.
UNIVERSIDAD NACIONAL EXPERIMENTAL FRANCISCO DE MIRANDA COMPLEJO ACADÉMICO "EL SABINO" PROGRAMA DE INGENIERÍA MECÁNICA AREA DE TECNOLOGÍA UNIDAD CURRICULAR: TERMODINÁMICA APLICADA REALIZADO POR: INGENIERO.
Respuesta: a) La fracción molar de NaCl es 0,072 b) La concentración másica volumétrica de NaCl es 0,231 g/cc
 Ejercicio 1: La densidad a 4 ºC de una solución acuosa de NaCl al 20% en peso es 1,155 g/cc a) Calcule la fracción molar de NaCl b) Calcule la concentración másica volumétrica de NaCl La masa molecular
Ejercicio 1: La densidad a 4 ºC de una solución acuosa de NaCl al 20% en peso es 1,155 g/cc a) Calcule la fracción molar de NaCl b) Calcule la concentración másica volumétrica de NaCl La masa molecular
líquido sólido Interfase sólido-líquido
 INTERFASES La mayoría de los procesos fisicoquímicos naturales y artificiales ocurren en sistemas heterogéneos en donde las diferentes fases que las componen están separadas por una interfase, definida
INTERFASES La mayoría de los procesos fisicoquímicos naturales y artificiales ocurren en sistemas heterogéneos en donde las diferentes fases que las componen están separadas por una interfase, definida
DEPARTAMENTO DE INGENIERÍA QUÍMICA. Laboratorio de Ingeniería Química BALANCE DE ENERGÍA EN ESTADO NO ESTACIONARIO
 DEPARAMENO DE INGENIERÍA QUÍMICA Laboratorio de Ingeniería Química BALANCE DE ENERGÍA EN ESADO NO ESACIONARIO 1. INRODUCCIÓN El sistema al que se va a plantear el balance de energía calorífica consiste
DEPARAMENO DE INGENIERÍA QUÍMICA Laboratorio de Ingeniería Química BALANCE DE ENERGÍA EN ESADO NO ESACIONARIO 1. INRODUCCIÓN El sistema al que se va a plantear el balance de energía calorífica consiste
Masas atómicas (g/mol): O = 16; S = 32; Zn = 65,4. Sol: a) 847 L; b) 710,9 g; c) 1,01 atm.
 1) Dada la siguiente reacción química: 2 AgNO3 + Cl2 N2O5 + 2 AgCl + ½ O2. a) Calcule los moles de N2O5 que se obtienen a partir de 20 g de AgNO3. b) Calcule el volumen de O2 obtenido, medido a 20 ºC y
1) Dada la siguiente reacción química: 2 AgNO3 + Cl2 N2O5 + 2 AgCl + ½ O2. a) Calcule los moles de N2O5 que se obtienen a partir de 20 g de AgNO3. b) Calcule el volumen de O2 obtenido, medido a 20 ºC y
TEMA 1: SISTEMAS MODELADOS POR ECUACIONES DIFERENCIALES EN INGENIERÍA QUÍMICA. CLASIFICACIÓN. GENERALIDADES.
 TEMA 1: SISTEMAS MODELADOS POR ECUACIONES DIFERENCIALES EN INGENIERÍA QUÍMICA. CLASIFICACIÓN. GENERALIDADES. 1. INTRODUCCIÓN. PLANTEAMIENTO DE PROBLEMAS EN INGENIERÍA QUÍMICA 2. PROBLEMAS EXPRESADOS MEDIANTE
TEMA 1: SISTEMAS MODELADOS POR ECUACIONES DIFERENCIALES EN INGENIERÍA QUÍMICA. CLASIFICACIÓN. GENERALIDADES. 1. INTRODUCCIÓN. PLANTEAMIENTO DE PROBLEMAS EN INGENIERÍA QUÍMICA 2. PROBLEMAS EXPRESADOS MEDIANTE
Ecuaciones diferenciales de primer orden: Aplicaciones a la Ingeniería Química
 Lección 7 Ecuaciones diferenciales de primer orden: Aplicaciones a la Ingeniería Química 1 Ecuaciones Diferenciales en Cinética Química Ecuación estequiométrica: o a A b B = p P q Q 0 = a A b B... p P
Lección 7 Ecuaciones diferenciales de primer orden: Aplicaciones a la Ingeniería Química 1 Ecuaciones Diferenciales en Cinética Química Ecuación estequiométrica: o a A b B = p P q Q 0 = a A b B... p P
Examen de problemas. PROBLEMA 1 Considere la siguiente reacción: C(s) + CO 2 (g) 2CO(g)
 PROBLEMA 1 Considere la siguiente reacción: C(s) + CO 2 (g) 2CO(g) a) A partir de qué temperatura es espontánea o dejará de serlo? Suponga que r Hº y r Sº no dependen de la temperatura. b) Calcule el valor
PROBLEMA 1 Considere la siguiente reacción: C(s) + CO 2 (g) 2CO(g) a) A partir de qué temperatura es espontánea o dejará de serlo? Suponga que r Hº y r Sº no dependen de la temperatura. b) Calcule el valor
TEMA 6 EQUILIBRIO QUÍMICO
 TEMA 6 EQUILIBRIO QUÍMICO ÍNDICE 1. Equilibrio químico homogéneo y heterogéneo 2. Concentraciones en equilibrio 3. Constante de equilibrio K c 4. Constantes de equilibrio K p y K c 5. Cociente de reacción
TEMA 6 EQUILIBRIO QUÍMICO ÍNDICE 1. Equilibrio químico homogéneo y heterogéneo 2. Concentraciones en equilibrio 3. Constante de equilibrio K c 4. Constantes de equilibrio K p y K c 5. Cociente de reacción
GUÍA N 3: Equilibrio Químico y Cinética Química
 1 PRIMERA PARTE: Ejercicios de desarrollo. 1.- Defina los siguientes términos: a) Reacción irreversible b) Reacción reversible c) Equilibrio químico d) Constante de equilibrio e) Principio de Le Chatelier
1 PRIMERA PARTE: Ejercicios de desarrollo. 1.- Defina los siguientes términos: a) Reacción irreversible b) Reacción reversible c) Equilibrio químico d) Constante de equilibrio e) Principio de Le Chatelier
Clasificación de la materia hasta el nivel atómico
 1. Estequiometría Clasificación de la materia hasta el nivel atómico Materia puede separarse por un proceso físico? SÍ NO Mezcla es homogénea? Sustancia puede descomponerse por un proceso químico? SÍ NO
1. Estequiometría Clasificación de la materia hasta el nivel atómico Materia puede separarse por un proceso físico? SÍ NO Mezcla es homogénea? Sustancia puede descomponerse por un proceso químico? SÍ NO
Química 2º Bach. Recuperación 1ª Evaluación 13/01/05
 Química º Bach. Recuperación 1ª Evaluación 13/1/5 DEPARTAMENT DE FÍSIA E QUÍMIA Nombre: 1. alcula a partir de qué temperatura será espontánea la reacción de descomposición del tetraóxido de dinitrógeno
Química º Bach. Recuperación 1ª Evaluación 13/1/5 DEPARTAMENT DE FÍSIA E QUÍMIA Nombre: 1. alcula a partir de qué temperatura será espontánea la reacción de descomposición del tetraóxido de dinitrógeno
Capítulo 10. Efectos de superficie. Sistema respiratorio
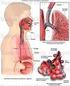 Capítulo 10 Efectos de superficie. Sistema respiratorio 1 Tensión superficial El coeficiente de tensión superficial γ es la fuerza por unidad de longitud que hay que realizar para aumentar una superficie:
Capítulo 10 Efectos de superficie. Sistema respiratorio 1 Tensión superficial El coeficiente de tensión superficial γ es la fuerza por unidad de longitud que hay que realizar para aumentar una superficie:
EJERCICIOS DE TERMOQUÍMICA
 EJERCICIOS DE TERMOQUÍMICA En los exámenes de Acceso a la Universidad se proponen una serie de cuestiones (más teóricas) y problemas (prácticos) para resolver. En estos apuntes vamos a resolver ambos tipos
EJERCICIOS DE TERMOQUÍMICA En los exámenes de Acceso a la Universidad se proponen una serie de cuestiones (más teóricas) y problemas (prácticos) para resolver. En estos apuntes vamos a resolver ambos tipos
GUIA DE PROBLEMAS. Velocidad de aproximación al equilibrio = kr(c-ceq)
 GUIA DE PROBLEMAS 1. La conversión de hidrógeno molecular de la forma orto a la forma para es catalizada por NiO. Se dipone de un catalizador soportado con un área específica de 305 m 2 /g y un volumen
GUIA DE PROBLEMAS 1. La conversión de hidrógeno molecular de la forma orto a la forma para es catalizada por NiO. Se dipone de un catalizador soportado con un área específica de 305 m 2 /g y un volumen
UNIDAD 2. CINÉTICA QUÍMICA
 UNIDAD 2. CINÉTICA QUÍMICA Introducción. Velocidad de reacción Cómo se producen las reacciones químicas Ecuación de la velocidad de reacción Factores que afectan a la velocidad de reacción Mecanismo de
UNIDAD 2. CINÉTICA QUÍMICA Introducción. Velocidad de reacción Cómo se producen las reacciones químicas Ecuación de la velocidad de reacción Factores que afectan a la velocidad de reacción Mecanismo de
Tema 3: Diagramas de fases. Problemas resueltos
 Tema 3: Diagramas de fases Problemas resueltos Problema 1. Dos metales y tienen puntos de fusión a 1400 y 1300 respectivamente. El metal presenta dos cambios alotrópicos a los 900,, y a los 700,, de forma
Tema 3: Diagramas de fases Problemas resueltos Problema 1. Dos metales y tienen puntos de fusión a 1400 y 1300 respectivamente. El metal presenta dos cambios alotrópicos a los 900,, y a los 700,, de forma
de aire. Determinar la composicion de la mezcla resultante. Cuál es el porcentaje en exceso de aire, suponiendo conversion completa?
 C A P Í T U L O 2 Dada la importancia que tienen los procesos de combustión en la generación de contaminantes, en este capítulo se han incluido algunos ejercicios relacionados con la combustión estequiométrica.
C A P Í T U L O 2 Dada la importancia que tienen los procesos de combustión en la generación de contaminantes, en este capítulo se han incluido algunos ejercicios relacionados con la combustión estequiométrica.
Índice Matemáticas 11
 5 Índice Índice Matemáticas 11 I. Símbolos, operaciones aritméticas, leyes 12 1. Símbolos generales 12 2. Símbolos de la teoría de conjuntos 12 3. Símbolos de lógica 12 4. Operaciones artiméticas 13 5.
5 Índice Índice Matemáticas 11 I. Símbolos, operaciones aritméticas, leyes 12 1. Símbolos generales 12 2. Símbolos de la teoría de conjuntos 12 3. Símbolos de lógica 12 4. Operaciones artiméticas 13 5.
Sustancia que tiene una composición química fija. Una sustancia pura no tiene que ser de un solo elemento, puede ser mezcla homogénea.
 Sustancia que tiene una composición química fija. Una sustancia pura no tiene que ser de un solo elemento, puede ser mezcla homogénea. Mezcla de aceite y agua Mezcla de hielo y agua Las sustancias existen
Sustancia que tiene una composición química fija. Una sustancia pura no tiene que ser de un solo elemento, puede ser mezcla homogénea. Mezcla de aceite y agua Mezcla de hielo y agua Las sustancias existen
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2005 QUÍMICA TEMA 4: ENERGÍA DE LAS REACCIONES QUÍMICAS
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 5 QUÍMICA TEMA 4: ENERGÍA DE LAS REACCIONES QUÍMICAS Junio, Ejercicio 6, Opción A Reserva 1, Ejercicio 4, Opción A Reserva 1, Ejercicio 6, Opción B Reserva, Ejercicio
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 5 QUÍMICA TEMA 4: ENERGÍA DE LAS REACCIONES QUÍMICAS Junio, Ejercicio 6, Opción A Reserva 1, Ejercicio 4, Opción A Reserva 1, Ejercicio 6, Opción B Reserva, Ejercicio
CAPITULO VII BOMBEO HIDRÁULICO TIPO JET (A CHORRO)
 GENERALIDADES. CAPITULO VII BOMBEO HIDRÁULICO TIPO JET (A CHORRO) El bombeo hidráulico tipo jet es un sistema artificial de producción especial, a diferencia del tipo pistón, no ocupa partes móviles y
GENERALIDADES. CAPITULO VII BOMBEO HIDRÁULICO TIPO JET (A CHORRO) El bombeo hidráulico tipo jet es un sistema artificial de producción especial, a diferencia del tipo pistón, no ocupa partes móviles y
Universidad Nacional de Córdoba. Facultad de Ciencias Exactas Físicas y Naturales. Cátedra de Mecánica de los Fluidos. Carrea de Ingeniería Civil
 Universidad Nacional de Córdoba Facultad de Ciencias Exactas Físicas y Naturales Cátedra de Mecánica de los Fluidos Carrea de Ingeniería Civil FLUJO COMPRESIBLE DR. ING. CARLOS MARCELO GARCÍA 2011 A modo
Universidad Nacional de Córdoba Facultad de Ciencias Exactas Físicas y Naturales Cátedra de Mecánica de los Fluidos Carrea de Ingeniería Civil FLUJO COMPRESIBLE DR. ING. CARLOS MARCELO GARCÍA 2011 A modo
ANEXO 1. DEPARTAMENTO DE: Química. ASIGNATURA: Química Tecnológica. CARRERAS - PLAN: Licenciatura en Química - Plan 1997.
 1 Corresponde al Anexo I de la Resolución N 93/02 ANEXO 1 DEPARTAMENTO DE: Química ASIGNATURA: Química Tecnológica. CARRERAS - PLAN: Licenciatura en Química - Plan 1997 CURSO: Cuarto REGIMEN: Cuatrimestral
1 Corresponde al Anexo I de la Resolución N 93/02 ANEXO 1 DEPARTAMENTO DE: Química ASIGNATURA: Química Tecnológica. CARRERAS - PLAN: Licenciatura en Química - Plan 1997 CURSO: Cuarto REGIMEN: Cuatrimestral
Análisis esquemático simplificado de una torre de enfriamiento.
 Análisis esquemático simplificado de una torre de enfriamiento. En el diagrama el aire con una humedad Y 2 y temperatura t 2 entra por el fondo de la torre y la abandona por la parte superior con una humedad
Análisis esquemático simplificado de una torre de enfriamiento. En el diagrama el aire con una humedad Y 2 y temperatura t 2 entra por el fondo de la torre y la abandona por la parte superior con una humedad
LA MATERIA: ESTADOS DE AGREGACIÓN
 LA MATERIA: ESTADOS DE AGREGACIÓN 1. PROPIEDADES DE LA MATERIA Materia: es todo aquello que existe, tiene masa y ocupa un volumen, los distintos tipos de materia se llaman sustancias. El sistema material
LA MATERIA: ESTADOS DE AGREGACIÓN 1. PROPIEDADES DE LA MATERIA Materia: es todo aquello que existe, tiene masa y ocupa un volumen, los distintos tipos de materia se llaman sustancias. El sistema material
El ejemplo que a continuación se detalla no pertenece a ninguna empresa en particular, pretende ser una aclaración a lo detallado en esta guía.
 CAPÍTULO 1 Introducción 1.1 INTRODUCCIÓN Se recomienda la lectura de este capítulo una vez leído el correspondiente a su instalación afectada en el anexo I de la Directiva 2003/87 y que a su vez ha sido
CAPÍTULO 1 Introducción 1.1 INTRODUCCIÓN Se recomienda la lectura de este capítulo una vez leído el correspondiente a su instalación afectada en el anexo I de la Directiva 2003/87 y que a su vez ha sido
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2014
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 014 QUÍMICA TEMA 5: EQUILIBRIO QUÍMICO Junio, Ejercicio 3, Opción A Reserva 1, Ejercicio 3, Opción A Reserva 1, Ejercicio 6, Opción B Reserva, Ejercicio 5, Opción
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 014 QUÍMICA TEMA 5: EQUILIBRIO QUÍMICO Junio, Ejercicio 3, Opción A Reserva 1, Ejercicio 3, Opción A Reserva 1, Ejercicio 6, Opción B Reserva, Ejercicio 5, Opción
CINÉTICA QUÍMICA. Dr. Hugo Cerecetto. Prof. Titular de Química
 CINÉTICA QUÍMICA Dr. Hugo Cerecetto Prof. Titular de Química Temario 2) La reacción química: - Nociones de Termoquímica y Termodinámica. Conceptos de entalpía y entropía de reacción. Energía libre. Espontaneidad
CINÉTICA QUÍMICA Dr. Hugo Cerecetto Prof. Titular de Química Temario 2) La reacción química: - Nociones de Termoquímica y Termodinámica. Conceptos de entalpía y entropía de reacción. Energía libre. Espontaneidad
Lección 4. Ecuaciones diferenciales. 1. Ecuaciones diferenciales de primer orden. Trayectorias ortogonales.
 GRADO DE INGENIERÍA AEROESPACIAL. CURSO 0.. Ecuaciones diferenciales de primer orden. Traectorias ortogonales. Muchas aplicaciones problemas de la ciencia, la ingeniería la economía se formulan en términos
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 0.. Ecuaciones diferenciales de primer orden. Traectorias ortogonales. Muchas aplicaciones problemas de la ciencia, la ingeniería la economía se formulan en términos
TEMA 4: CINÉTICA HOMOGÉNEA: REACCIONES MÚLTIPLES Y CATALIZADAS CQA-4/1
 TEMA 4: CINÉTICA HOMOGÉNEA: REACCIONES MÚLTIPLES Y CATALIZADAS CQA-4/1 CINÉTICA DE REACCIONES MÚLTIPLES Reacciones múltiples : Reacciones con más de una ecuación cinética que describe su comportamiento.
TEMA 4: CINÉTICA HOMOGÉNEA: REACCIONES MÚLTIPLES Y CATALIZADAS CQA-4/1 CINÉTICA DE REACCIONES MÚLTIPLES Reacciones múltiples : Reacciones con más de una ecuación cinética que describe su comportamiento.
1º) Dado el sistema de equilibrio representado por la siguiente ecuación:
 EJERCICIOS DE EQUILIBRIO QUÍMICO 1º) Dado el sistema de equilibrio representado por la siguiente ecuación: NH4HS (s) NH3 (g) + H2S (g) Indique, razonadamente, cómo varían las concentraciones de las especies
EJERCICIOS DE EQUILIBRIO QUÍMICO 1º) Dado el sistema de equilibrio representado por la siguiente ecuación: NH4HS (s) NH3 (g) + H2S (g) Indique, razonadamente, cómo varían las concentraciones de las especies
Los enlaces C F son polares pero la geometría tetraédrica
 1 PAU Química. Modelo 2010 PRIMERA PARTE Cuestión 1. Dadas las siguientes sustancias: CO 2, CF 4, H 2 CO y HF: a) Escriba las estructuras de Lewis de sus moléculas. b) Explique sus geometrías por la teoría
1 PAU Química. Modelo 2010 PRIMERA PARTE Cuestión 1. Dadas las siguientes sustancias: CO 2, CF 4, H 2 CO y HF: a) Escriba las estructuras de Lewis de sus moléculas. b) Explique sus geometrías por la teoría
Propiedades físicas y mecánicas de los materiales Parte I
 Propiedades físicas y mecánicas de los materiales Parte I Propiedades físicas y mecánicas de los materiales Capítulo 1. Conceptos generales Tipos de materiales Metodología para el estudio de materiales
Propiedades físicas y mecánicas de los materiales Parte I Propiedades físicas y mecánicas de los materiales Capítulo 1. Conceptos generales Tipos de materiales Metodología para el estudio de materiales
Diseño de Reactores Heterogéneos Catalíticos Reactores de Lecho Fijo
 Diseño de Reactores Heterogéneos Catalíticos Reactores de Lecho Fio En un reactor catalítico de lecho fio para llevar a cabo una reacción fluido-sólido, el catalizador se presenta coo un lecho de partículas
Diseño de Reactores Heterogéneos Catalíticos Reactores de Lecho Fio En un reactor catalítico de lecho fio para llevar a cabo una reacción fluido-sólido, el catalizador se presenta coo un lecho de partículas
Las sustancias reaccionan entre sí. REACCIÓN QUÍMICA: proceso en el cual una o varias sustancias cambian para formar sustancias nuevas
 Las sustancias reaccionan entre sí. REACCIÓN QUÍMICA: proceso en el cual una o varias sustancias cambian para formar sustancias nuevas LEY DE LAVOISIER: Los átomos no se crean ni se destruyen durante cualquier
Las sustancias reaccionan entre sí. REACCIÓN QUÍMICA: proceso en el cual una o varias sustancias cambian para formar sustancias nuevas LEY DE LAVOISIER: Los átomos no se crean ni se destruyen durante cualquier
Termodinámica y Máquinas Térmicas
 Termodinámica y Máquinas Térmicas Tema 04. Funciones de Estado Inmaculada Fernández Diego Severiano F. Pérez Remesal Carlos J. Renedo Estébanez DPTO. DE INGENIERÍA ELÉCTRICA Y ENERGÉTICA Este tema se publica
Termodinámica y Máquinas Térmicas Tema 04. Funciones de Estado Inmaculada Fernández Diego Severiano F. Pérez Remesal Carlos J. Renedo Estébanez DPTO. DE INGENIERÍA ELÉCTRICA Y ENERGÉTICA Este tema se publica
TEMA 13: Termodinámica
 QUÍMICA I TEMA 13: Termodinámica Tecnólogo Minero Temario ü Procesos espontáneos ü Entropía ü Segunda Ley de la Termodinámica ü Energía libre de Gibbs ü Energía libre y equilibrio químico Procesos espontáneos
QUÍMICA I TEMA 13: Termodinámica Tecnólogo Minero Temario ü Procesos espontáneos ü Entropía ü Segunda Ley de la Termodinámica ü Energía libre de Gibbs ü Energía libre y equilibrio químico Procesos espontáneos
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2007 QUÍMICA TEMA 1: LA TRANSFORMACIÓN QUÍMICA
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 007 QUÍMICA TEMA 1: LA TRANSFORMACIÓN QUÍMICA Junio, Ejercicio 4, Opción A Junio, Ejercicio 5, Opción B Reserva 1, Ejercicio, Opción B Reserva, Ejercicio 5, Opción
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 007 QUÍMICA TEMA 1: LA TRANSFORMACIÓN QUÍMICA Junio, Ejercicio 4, Opción A Junio, Ejercicio 5, Opción B Reserva 1, Ejercicio, Opción B Reserva, Ejercicio 5, Opción
Programa de Acceso Inclusivo, Equidad y Permanencia PAIEP U. de Santiago. Química
 Equilibrio Químico Programa de Acceso Inclusivo, Equidad y Permanencia RECUERDA QUE: el Equilibrio Químico, se presenta cuando reacciones opuestas ocurren a velocidades iguales. La velocidad a la que se
Equilibrio Químico Programa de Acceso Inclusivo, Equidad y Permanencia RECUERDA QUE: el Equilibrio Químico, se presenta cuando reacciones opuestas ocurren a velocidades iguales. La velocidad a la que se
Un sistema se encuentra en un estado de equilibrio químico cuando su composición no varía con el tiempo.
 Un sistema se encuentra en un estado de equilibrio químico cuando su composición no varía con el tiempo. N 2 g 3 H 2 g 2 NH 3 g 2 NH 3 g N 2 g 3 H 2 g concentración H 2 N 2 NH 3 concentración NH 3 H 2
Un sistema se encuentra en un estado de equilibrio químico cuando su composición no varía con el tiempo. N 2 g 3 H 2 g 2 NH 3 g 2 NH 3 g N 2 g 3 H 2 g concentración H 2 N 2 NH 3 concentración NH 3 H 2
Unidad 3. 1. En qué casos serán iguales los calores de reacción a presión constante (Q p ) y a volumen constante (Q v )? Razone la respuesta ( 2 p)
 Unidad 3 OPCIÓN A 1. En qué casos serán iguales los calores de reacción a presión constante (Q p ) y a volumen constante (Q v )? Razone la respuesta ( 2 p) La ecuación que relaciona Q p y Q v es: Q p =
Unidad 3 OPCIÓN A 1. En qué casos serán iguales los calores de reacción a presión constante (Q p ) y a volumen constante (Q v )? Razone la respuesta ( 2 p) La ecuación que relaciona Q p y Q v es: Q p =
Ing. Sol de María Jiménez González
 Ing. Sol de María Jiménez González 1 02 de junio I Tutoría Presencial 16 de junio II Tutoría Presencial Entrega de Tarea 30 de junio: I Examen Ordinario 14 de julio III Tutoría Presencial Entrega de proyecto
Ing. Sol de María Jiménez González 1 02 de junio I Tutoría Presencial 16 de junio II Tutoría Presencial Entrega de Tarea 30 de junio: I Examen Ordinario 14 de julio III Tutoría Presencial Entrega de proyecto
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2012 QUÍMICA TEMA 4: ENERGÍA DE LAS REACCIONES QUÍMICAS
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 1 QUÍMICA TEMA 4: ENERGÍA DE LAS REACCIONES QUÍMICAS Junio, Ejercicio 4, Opción A Junio, Ejercicio 6, Opción B Reserva 1, Ejercicio 3, Opción B Reserva, Ejercicio
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 1 QUÍMICA TEMA 4: ENERGÍA DE LAS REACCIONES QUÍMICAS Junio, Ejercicio 4, Opción A Junio, Ejercicio 6, Opción B Reserva 1, Ejercicio 3, Opción B Reserva, Ejercicio
- Leyes ponderales: Las leyes ponderales relacionan las masas de las sustancias que intervienen en una reacción química.
 FÍSICA Y QUÍMICA 4ºESO COLEGIO GIBRALJAIRE CÁLCULOS QUÍMICOS 1.- LA REACCIÓN QUÍMICA. LEYES PONDERALES Una reacción química es el proceso en el que, mediante una reorganización de enlaces y átomos, una
FÍSICA Y QUÍMICA 4ºESO COLEGIO GIBRALJAIRE CÁLCULOS QUÍMICOS 1.- LA REACCIÓN QUÍMICA. LEYES PONDERALES Una reacción química es el proceso en el que, mediante una reorganización de enlaces y átomos, una
[ A ], [ B ]...: concentraciones molares de los reactivos en un momento dado.
![[ A ], [ B ]...: concentraciones molares de los reactivos en un momento dado. [ A ], [ B ]...: concentraciones molares de los reactivos en un momento dado.](/thumbs/49/25484895.jpg) VELOCIDAD MEDIA DE UNA REACCIÓN aa + b B c C + d D [ A] [ B] [ C] [ D] Vmedia = = = = a b c d A Velocidad de disminución de los reactivos: a Velocidad de aumento de los productos: ECUACIÓN DE VELOCIDAD
VELOCIDAD MEDIA DE UNA REACCIÓN aa + b B c C + d D [ A] [ B] [ C] [ D] Vmedia = = = = a b c d A Velocidad de disminución de los reactivos: a Velocidad de aumento de los productos: ECUACIÓN DE VELOCIDAD
MATEMÁTICA TICA SUPERIOR APLICADA. Ejemplos de Ecuaciones No Lineales en
 MATEMÁTICA TICA SUPERIOR APLICADA Ejemplos de Ecuaciones No Lineales en Ingeniería a Química Universidad Tecnológica Nacional Facultad Regional Rosario Ejemplos de Aplicación A continuación n se presentan
MATEMÁTICA TICA SUPERIOR APLICADA Ejemplos de Ecuaciones No Lineales en Ingeniería a Química Universidad Tecnológica Nacional Facultad Regional Rosario Ejemplos de Aplicación A continuación n se presentan
TEMA 5. MAGNITUDES FISICAS Y UNIDADES DE MEDIDA. 4ª. PARTE
 1 TEMA 5. MAGNITUDES FISICAS Y UNIDADES DE MEDIDA. 4ª. PARTE Mario Melo Araya Ex Profesor Universidad de Chile [email protected] 11. EQUIVALENCIAS Y CONVERSION DE UNIDADES DE MEDIDA. Para toda magnitud
1 TEMA 5. MAGNITUDES FISICAS Y UNIDADES DE MEDIDA. 4ª. PARTE Mario Melo Araya Ex Profesor Universidad de Chile [email protected] 11. EQUIVALENCIAS Y CONVERSION DE UNIDADES DE MEDIDA. Para toda magnitud
Volumen de Sólidos de Revolución
 60 CAPÍTULO 4 Volumen de Sólidos de Revolución 6 Volumen de sólidos de revolución Cuando una región del plano de coordenadas gira alrededor de una recta l, se genera un cuerpo geométrico denominado sólido
60 CAPÍTULO 4 Volumen de Sólidos de Revolución 6 Volumen de sólidos de revolución Cuando una región del plano de coordenadas gira alrededor de una recta l, se genera un cuerpo geométrico denominado sólido
Modelado y simulación de un proceso de nivel
 Modelado y simulación de un proceso de nivel Carlos Gaviria Febrero 14, 2007 Introduction El propósito de este sencillo ejercicio es el de familiarizar al estudiante con alguna terminología del control
Modelado y simulación de un proceso de nivel Carlos Gaviria Febrero 14, 2007 Introduction El propósito de este sencillo ejercicio es el de familiarizar al estudiante con alguna terminología del control
Electricidad y calor. Dr. Roberto Pedro Duarte Zamorano. Departamento de Física
 Electricidad y calor Dr. Roberto Pedro Duarte Zamorano Departamento de Física 2011 A. Termodinámica Temario 1. Temperatura y Ley Cero. (3horas) 2. Calor y transferencia de calor. (5horas) 3. Gases ideales
Electricidad y calor Dr. Roberto Pedro Duarte Zamorano Departamento de Física 2011 A. Termodinámica Temario 1. Temperatura y Ley Cero. (3horas) 2. Calor y transferencia de calor. (5horas) 3. Gases ideales
MEDIOS DE CONTROL DE EMISIÓN DE CONTAMINANTES
 CAPÍTULO 11 MEDIOS DE CONTROL DE EMISIÓN DE CONTAMINANTES Fuente: National Geographic - Noviembre 2000 INTRODUCCIÓN Por lo general los contaminantes del aire aún en su fuente de emisión, por ejemplo en
CAPÍTULO 11 MEDIOS DE CONTROL DE EMISIÓN DE CONTAMINANTES Fuente: National Geographic - Noviembre 2000 INTRODUCCIÓN Por lo general los contaminantes del aire aún en su fuente de emisión, por ejemplo en
SEGUNDO DE BACHILLERATO QUÍMICA. a A + b B c C + d D
 TEMA 5. CINÉTICA QUÍMICA a A + b B c C + d D 1 d[a] 1 d[b] 1 d[c] 1 d[d] mol v = = = + = + a dt b dt c dt d dt L s El signo negativo en la expresión de velocidad es debido a que los reactivos desaparecen,
TEMA 5. CINÉTICA QUÍMICA a A + b B c C + d D 1 d[a] 1 d[b] 1 d[c] 1 d[d] mol v = = = + = + a dt b dt c dt d dt L s El signo negativo en la expresión de velocidad es debido a que los reactivos desaparecen,
LAS REACCIONES QUÍMICAS.
 1 Ajustes de reacciones químicas. LAS REACCIONES QUÍMICAS. Ejercicios de la unidad 8 1.- Ajusta por tanteo las siguientes reacciones químicas: a) C 3 H 8 + O CO + H O; b) Na + H O NaOH + H ; c) KOH + H
1 Ajustes de reacciones químicas. LAS REACCIONES QUÍMICAS. Ejercicios de la unidad 8 1.- Ajusta por tanteo las siguientes reacciones químicas: a) C 3 H 8 + O CO + H O; b) Na + H O NaOH + H ; c) KOH + H
6.2.- Reacciones de oxidación reducción
 350 Reacciones de transferencia de electrones 6.2.- Reacciones de oxidación reducción Aspectos teóricos: Valoraciones redox 6.2.1. Valoraciones redox. Equivalentes de oxidación-reducción Las reacciones
350 Reacciones de transferencia de electrones 6.2.- Reacciones de oxidación reducción Aspectos teóricos: Valoraciones redox 6.2.1. Valoraciones redox. Equivalentes de oxidación-reducción Las reacciones
PRÁCTICA 10. TORRE DE REFRIGERACIÓN POR AGUA
 PRÁCTICA 10. TORRE DE REFRIGERACIÓN POR AGUA OBJETIVO GENERAL: Familiarizar al alumno con los sistemas de torres de refrigeración para evacuar el calor excedente del agua. OBJETIVOS ESPECÍFICOS: Investigar
PRÁCTICA 10. TORRE DE REFRIGERACIÓN POR AGUA OBJETIVO GENERAL: Familiarizar al alumno con los sistemas de torres de refrigeración para evacuar el calor excedente del agua. OBJETIVOS ESPECÍFICOS: Investigar
Problemas Química Propuestos en las P.A.U. Termoquímica
 A) Relaciones Termoquimicas ( H, U) 1.- Calcula la variación de energía interna ( Uº) para la reacción de combustión del benceno líquido, C 6 H 6 (l), si el proceso se realiza a presión de 1 atm y 25ºC.
A) Relaciones Termoquimicas ( H, U) 1.- Calcula la variación de energía interna ( Uº) para la reacción de combustión del benceno líquido, C 6 H 6 (l), si el proceso se realiza a presión de 1 atm y 25ºC.
Sustancias puras, procesos de cambios de fase, diagramas de fase. Estado 3 Estado 4 Estado 5. P =1 atm T= 100 o C. Estado 3 Estado 4.
 TERMODINÁMICA Departamento de Física Carreras: Ing. Industrial y Mecánica Trabajo Práctico N 2: PROPIEDADES DE LAS SUSTANCIAS PURAS La preocupación por el hombre y su destino debe ser el interés primordial
TERMODINÁMICA Departamento de Física Carreras: Ing. Industrial y Mecánica Trabajo Práctico N 2: PROPIEDADES DE LAS SUSTANCIAS PURAS La preocupación por el hombre y su destino debe ser el interés primordial
Contenidos mínimos Física y Química 3º ESO
 Contenidos mínimos Física y Química 3º ESO EL TRABAJO CIENTÍFICO Etapas del método científico. Magnitudes y unidades. Cambio de unidades. Sistema Internacional de Unidades (SI). Representación de gráficas
Contenidos mínimos Física y Química 3º ESO EL TRABAJO CIENTÍFICO Etapas del método científico. Magnitudes y unidades. Cambio de unidades. Sistema Internacional de Unidades (SI). Representación de gráficas
CAPITULO V TERMODINAMICA - 115 -
 CAPIULO V ERMODINAMICA - 5 - 5. EL GAS IDEAL Es el conjunto de un gran número de partículas diminutas o puntuales, de simetría esférica, del mismo tamaño y de igual volumen, todas del mismo material. Por
CAPIULO V ERMODINAMICA - 5 - 5. EL GAS IDEAL Es el conjunto de un gran número de partículas diminutas o puntuales, de simetría esférica, del mismo tamaño y de igual volumen, todas del mismo material. Por
4.3 Problemas de aplicación 349
 4. Problemas de aplicación 49 4. Problemas de aplicación Ejemplo 4.. Circuito Eléctrico. En la figura 4.., se muestra un circuito Eléctrico de mallas en el cual se manejan corrientes, una en cada malla.
4. Problemas de aplicación 49 4. Problemas de aplicación Ejemplo 4.. Circuito Eléctrico. En la figura 4.., se muestra un circuito Eléctrico de mallas en el cual se manejan corrientes, una en cada malla.
TUTORIAL BÁSICO DE MECÁNICA FLUIDOS
 TUTORIAL BÁSICO DE MECÁNICA FLUIDOS El tutorial es básico pues como habréis visto en muchos de ellos es haceros entender no sólo la aplicación práctica de cada teoría sino su propia existencia y justificación.
TUTORIAL BÁSICO DE MECÁNICA FLUIDOS El tutorial es básico pues como habréis visto en muchos de ellos es haceros entender no sólo la aplicación práctica de cada teoría sino su propia existencia y justificación.
Física y Química 1ºBachillerato Ejemplo Examen. Formulación. (1 puntos) Formula correctamente los siguientes compuestos: Ioduro de Calcio:
 Física y Química 1ºBachillerato Ejemplo Examen Formulación. (1 puntos) Formula correctamente los siguientes compuestos: Óxido Fosfórico: Silano: Carburo Potásico: Ácido perclórico: Fosfato de Sodio: Hidruro
Física y Química 1ºBachillerato Ejemplo Examen Formulación. (1 puntos) Formula correctamente los siguientes compuestos: Óxido Fosfórico: Silano: Carburo Potásico: Ácido perclórico: Fosfato de Sodio: Hidruro
Soluciones. DESCRIPCION MACROSCOPICA DE UN GAS IDEAL (Serway, Cap 19, vol I)
 Soluciones DESCRIPCION MACROSCOPICA DE UN GAS IDEAL (Serway, Cap 19, vol I) 1. Demuestre que 1 mol de cualquier gas a presión atmosférica de 101 kpa y temperatura de 0ºC ocupa un volumen de 22,4 L. n =
Soluciones DESCRIPCION MACROSCOPICA DE UN GAS IDEAL (Serway, Cap 19, vol I) 1. Demuestre que 1 mol de cualquier gas a presión atmosférica de 101 kpa y temperatura de 0ºC ocupa un volumen de 22,4 L. n =
Tema VII: Introducción a las Reacciones Heterogéneas
 Clasificación de las reacciones químicas en función del número de fases: Homogéneas o monofásicas: homogeneidad, isotropía Líquidos miscibles, gases, sólidos disueltos en un mismo disolvente Ej. Formación
Clasificación de las reacciones químicas en función del número de fases: Homogéneas o monofásicas: homogeneidad, isotropía Líquidos miscibles, gases, sólidos disueltos en un mismo disolvente Ej. Formación
Capítulo 8. Termodinámica
 Capítulo 8 Termodinámica 1 Temperatura La temperatura es la propiedad que poseen los cuerpos, tal que su valor para ellos es el mismo siempre que estén en equilibrio térmico. Principio cero de la termodinámica:
Capítulo 8 Termodinámica 1 Temperatura La temperatura es la propiedad que poseen los cuerpos, tal que su valor para ellos es el mismo siempre que estén en equilibrio térmico. Principio cero de la termodinámica:
En cinética, se asume que las reacciones se completan desde los reactivos hacia los productos, es decir, se asume que son irreversibles.
 Resumen 4 FUNDAMENTOS DEL EQUILIBRIO QUÍMICO Adaptado de http://apchemistrynmsi.wikispaces.com/ap+chemistry+class+lecture+notes+and+instructional+videos por el profesor Julio Clavijo para los grupos de
Resumen 4 FUNDAMENTOS DEL EQUILIBRIO QUÍMICO Adaptado de http://apchemistrynmsi.wikispaces.com/ap+chemistry+class+lecture+notes+and+instructional+videos por el profesor Julio Clavijo para los grupos de
Unidad 0 CÁLCULOS QUÍMICOS. Unidad 0. Cálculos químicos
 Unidad 0 CÁLCULOS QUÍMICOS Unidad 0. Cálculos químicos 1 0. Leyes ponderales Leyes que rigen las combinaciones químicas. Se basan en la experimentación y miden cuantitativamente la cantidad de materia
Unidad 0 CÁLCULOS QUÍMICOS Unidad 0. Cálculos químicos 1 0. Leyes ponderales Leyes que rigen las combinaciones químicas. Se basan en la experimentación y miden cuantitativamente la cantidad de materia
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2002 QUÍMICA TEMA 4: ENERGÍA DE LAS REACCIONES QUÍMICAS
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA QUÍMICA TEMA 4: ENERGÍA DE LAS REACCIONES QUÍMICAS Junio, Ejercicio 5, Opción B Reserva, Ejercicio 4, Opción A Reserva, Ejercicio 6, Opción B Reserva 3, Ejercicio
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA QUÍMICA TEMA 4: ENERGÍA DE LAS REACCIONES QUÍMICAS Junio, Ejercicio 5, Opción B Reserva, Ejercicio 4, Opción A Reserva, Ejercicio 6, Opción B Reserva 3, Ejercicio
FISICOQUÍMICA APLICADA
 UNIVERSIDAD NACIONAL DE TUCUMAN FACULTAD DE BIOQUIMICA QUIMICA Y FARMACIA INSTITUTO DE QUIMICA FISICA San Miguel de Tucumán República Argentina FISICOQUÍMICA APLICADA Cambio de fase. Superficies. Coloides
UNIVERSIDAD NACIONAL DE TUCUMAN FACULTAD DE BIOQUIMICA QUIMICA Y FARMACIA INSTITUTO DE QUIMICA FISICA San Miguel de Tucumán República Argentina FISICOQUÍMICA APLICADA Cambio de fase. Superficies. Coloides
UNIDAD 1 La materia y sus cambios
 UNIDAD 1 La materia y sus cambios Tema 1.3 Propiedades características de las sustancias: físicas, organolépticas, químicas; intensivas y extensivas. NMLV 1 Propiedades de las sustancias Organolépticas
UNIDAD 1 La materia y sus cambios Tema 1.3 Propiedades características de las sustancias: físicas, organolépticas, químicas; intensivas y extensivas. NMLV 1 Propiedades de las sustancias Organolépticas
TEMA 2 CONCEPTOS BÁSICOS Cálculos estequiométricos
 TEMA 2 CONCEPTOS BÁSICOS Cálculos estequiométricos ÍNDICE 1. Ecuaciones (reacciones) químicas 2. Cálculos estequiométricos. Reactivo limitante y reacciones consecutivas 3. Pureza de un reactivo 4. Rendimiento
TEMA 2 CONCEPTOS BÁSICOS Cálculos estequiométricos ÍNDICE 1. Ecuaciones (reacciones) químicas 2. Cálculos estequiométricos. Reactivo limitante y reacciones consecutivas 3. Pureza de un reactivo 4. Rendimiento
Universidad de Oriente Núcleo de Bolívar Unidad de cursos básicos Matemáticas IV. María Palma Roselvis Flores
 Universidad de Oriente Núcleo de Bolívar Unidad de cursos básicos Matemáticas IV Profesor: Cristian Castillo Bachilleres: Yessica Flores María Palma Roselvis Flores Ciudad Bolívar; Marzo de 2010 Movimiento
Universidad de Oriente Núcleo de Bolívar Unidad de cursos básicos Matemáticas IV Profesor: Cristian Castillo Bachilleres: Yessica Flores María Palma Roselvis Flores Ciudad Bolívar; Marzo de 2010 Movimiento
TERMODINÁMICA 1. En la fermentación de la glucosa (C6H12O6) se obtiene etanol (C2H5OH) y CO2. Si la entalpía de combustión de la glucosa es de 15.
 TERMODINÁMICA 1. En la fermentación de la glucosa (C6H12O6) se obtiene etanol (C2H5OH) y CO2. Si la entalpía de combustión de la glucosa es de 15.63 kj/g y la del etanol es de 29.72 kj/g, a) Calcular la
TERMODINÁMICA 1. En la fermentación de la glucosa (C6H12O6) se obtiene etanol (C2H5OH) y CO2. Si la entalpía de combustión de la glucosa es de 15.63 kj/g y la del etanol es de 29.72 kj/g, a) Calcular la
Clase 2: Sustancias puras
 Teórico Física Térmica 2012 02 de Marzo de 2012 Agenda... 1 Referencias 2 Sustancias puras Intro Propiedades independientes 3 Fases Definiciones Cambios (o transiciones) de fase Mezcla Superficies P-v-T
Teórico Física Térmica 2012 02 de Marzo de 2012 Agenda... 1 Referencias 2 Sustancias puras Intro Propiedades independientes 3 Fases Definiciones Cambios (o transiciones) de fase Mezcla Superficies P-v-T
Procesos Industriales I BALANCES DE MATERIA
 BALANCES DE MATERIA Cuando se diseña un nuevo proceso o cuando se analiza uno ya existente, es necesario tener en cuenta las restricciones impuestas por la naturaleza. Por ejemplo, si en un reactor se
BALANCES DE MATERIA Cuando se diseña un nuevo proceso o cuando se analiza uno ya existente, es necesario tener en cuenta las restricciones impuestas por la naturaleza. Por ejemplo, si en un reactor se
Primer principio. Calor a presión y volumen constante.
 TERMOQUÍMICA. Primer principio. Calor a presión y volumen constante. 1.- a) Primer principio de la Termodinámica. b) Q v y Q p ; relación entre ambas. 2.- En un recipiente cerrado a volumen constante tiene
TERMOQUÍMICA. Primer principio. Calor a presión y volumen constante. 1.- a) Primer principio de la Termodinámica. b) Q v y Q p ; relación entre ambas. 2.- En un recipiente cerrado a volumen constante tiene
Tema 5 Tratamientos térmicos EUETI Escola Universitaria de Enxeñería Técnica Industrial
 Tratamiento de Residuos Tema 5 Tratamientos térmicos EUETI Escola Universitaria de Enxeñería Técnica Industrial INCINERACIÓN DE RESIDUOS Definición: Es el procesamiento térmico de los residuos sólidos
Tratamiento de Residuos Tema 5 Tratamientos térmicos EUETI Escola Universitaria de Enxeñería Técnica Industrial INCINERACIÓN DE RESIDUOS Definición: Es el procesamiento térmico de los residuos sólidos
LA TIOUREA (TU) EN LA ELECTROREFINACIÓN DE COBRE
 UNIVERSIDAD DE SANTIAGO DE CHILE FACULTAD DE INGENIERIA DEPARTAMENTO DE INGENIERIA METALURGICA LA TIOUREA (TU) EN LA ELECTROREFINACIÓN DE COBRE Profesor Dr. GERARDO CIFUENTES MOLINA 2013 www.ufrgs.br/cyted-recmet/wordpress/
UNIVERSIDAD DE SANTIAGO DE CHILE FACULTAD DE INGENIERIA DEPARTAMENTO DE INGENIERIA METALURGICA LA TIOUREA (TU) EN LA ELECTROREFINACIÓN DE COBRE Profesor Dr. GERARDO CIFUENTES MOLINA 2013 www.ufrgs.br/cyted-recmet/wordpress/
TEMA 7: POROSIDAD Y ÁREA SUPERFICIAL
 1 TEMA 7: POROSIDAD Y ÁREA SUPERFICIAL 1.- Clasificación de los poros de acuerdo a su tamaño Los materiales porosos se clasifican como microporosos con un tamaño de poro de 0.3-2 nm, mesoporosos de 2-50
1 TEMA 7: POROSIDAD Y ÁREA SUPERFICIAL 1.- Clasificación de los poros de acuerdo a su tamaño Los materiales porosos se clasifican como microporosos con un tamaño de poro de 0.3-2 nm, mesoporosos de 2-50
IV UNIDAD TRANSFERENCIA DE MASA
 IV UNIDAD TRANSFERENCIA DE MASA La transferencia de masa es la tendencia de uno o más componentes de una mezcla a transportarse desde una zona de alta concentración del o de los componentes a otra zona
IV UNIDAD TRANSFERENCIA DE MASA La transferencia de masa es la tendencia de uno o más componentes de una mezcla a transportarse desde una zona de alta concentración del o de los componentes a otra zona
OBTENCIÓN DE NaHCO 3 (P 4)
 OBTENCIÓN DE NaHCO 3 (P 4) Objetivos - Estudio descriptivo del NaHCO 3, y de sus usos industriales - Adquisición de conocimiento básicos sobre generación química de gases en el laboratorio - Realización
OBTENCIÓN DE NaHCO 3 (P 4) Objetivos - Estudio descriptivo del NaHCO 3, y de sus usos industriales - Adquisición de conocimiento básicos sobre generación química de gases en el laboratorio - Realización
Tema 6. Termodinámica y cinética
 Tema 6. Termodinámica y cinética A) Termodinámica Por qué algunas reacciones químicas son espontáneas a ciertas temperaturas? Existe alguna forma de predecir si una reacción va a producirse en unas condiciones
Tema 6. Termodinámica y cinética A) Termodinámica Por qué algunas reacciones químicas son espontáneas a ciertas temperaturas? Existe alguna forma de predecir si una reacción va a producirse en unas condiciones
Instituto Carlos Tejedor Educación Secundaria Fisicaquímica Segundo año A Profesor Carlos Castañón. Trabajo Práctico: Leyes de los gases
 Instituto Carlos Tejedor Educación Secundaria Fisicaquímica Segundo año A Profesor Carlos Castañón Trabajo Práctico: Leyes de los gases 1) La ley de Boyle establece que, a temperatura constante, la presión
Instituto Carlos Tejedor Educación Secundaria Fisicaquímica Segundo año A Profesor Carlos Castañón Trabajo Práctico: Leyes de los gases 1) La ley de Boyle establece que, a temperatura constante, la presión
Química. Equilibrio ácido-base Nombre:
 Química DEPARTAMENTO DE FÍSICA E QUÍMICA Equilibrio ácido-base 25-02-08 Nombre: Cuestiones y problemas 1. a) Qué concentración tiene una disolución de amoníaco de ph =10,35? [1½ PUNTO] b) Qué es una disolución
Química DEPARTAMENTO DE FÍSICA E QUÍMICA Equilibrio ácido-base 25-02-08 Nombre: Cuestiones y problemas 1. a) Qué concentración tiene una disolución de amoníaco de ph =10,35? [1½ PUNTO] b) Qué es una disolución
A continuación se presenta la información de la altura promedio para el año de 1998 en Holanda de hombres y mujeres jóvenes.
 M150: Creciendo A) Presentación del problema LOS JOVENES CRECEN MAS ALTO A continuación se presenta la altura promedio para el año de 1998 en Holanda de hombres y mujeres jóvenes. B) Preguntas del problema
M150: Creciendo A) Presentación del problema LOS JOVENES CRECEN MAS ALTO A continuación se presenta la altura promedio para el año de 1998 en Holanda de hombres y mujeres jóvenes. B) Preguntas del problema
La física de la chimenea solar
 La física de la chimenea solar Víctor Romero Rochín Instituto de Física, Uniersidad Nacional Autónoma de México. Apartado Postal 20-364, 01000 México, D.F, Mexico. Electronic address: [email protected]
La física de la chimenea solar Víctor Romero Rochín Instituto de Física, Uniersidad Nacional Autónoma de México. Apartado Postal 20-364, 01000 México, D.F, Mexico. Electronic address: [email protected]
FLUJO DE AGUA EN EL SUELO Y ZONA NO SATURADA
 Lección 7. Flujo de agua en el suelo. Ley de Darcy. Conductividad hidráulica. Relación entre conductividad hidráulica y tensión. Ecuaciones que rigen la infiltración vertical. Ecuación de Richards. Capacidad
Lección 7. Flujo de agua en el suelo. Ley de Darcy. Conductividad hidráulica. Relación entre conductividad hidráulica y tensión. Ecuaciones que rigen la infiltración vertical. Ecuación de Richards. Capacidad
3.- Con el diagrama de equilibrio Cu-Ni, haga el análisis de fases para una aleación del 50% de Cu a: 1400ºC, 1300ºC, 1200ºC 1100ºC.
 1.- Con el diagrama de equilibrio Cu-Ni que se adjunta, describir el enfriamiento lento de una aleación del 3% de Ni y determinar su composición a 12ºC. 2.- Una aleación compuesta de 2 Kg de Cu y 2 Kg
1.- Con el diagrama de equilibrio Cu-Ni que se adjunta, describir el enfriamiento lento de una aleación del 3% de Ni y determinar su composición a 12ºC. 2.- Una aleación compuesta de 2 Kg de Cu y 2 Kg
IES Atenea (S.S. de los Reyes) Departamento de Física y Química. PAU Química. Junio 2009 PRIMERA PARTE
 1 PAU Química. Junio 2009 PRIMERA PARTE Cuestión 1. La primera y segunda energía de ionización para el átomo A, cuya configuración electrónica es 1s 2 2s 1, son 520 y 7300 kj mol 1, respectivamente: a)
1 PAU Química. Junio 2009 PRIMERA PARTE Cuestión 1. La primera y segunda energía de ionización para el átomo A, cuya configuración electrónica es 1s 2 2s 1, son 520 y 7300 kj mol 1, respectivamente: a)
CLASE Nº 2 ESTEQUIOMETRÍA
 UNIVERSIDAD NACIONAL EXPERIMENTAL POLITECNICA ANTONIO JOSÉ DE SUCRE VICERRECTORADO BARQUISIMETO DEPARTAMENTO DE INGENIERÍA QUÍMICA QUÍMICA GENERAL CLASE Nº 2 ESTEQUIOMETRÍA 1 Estequiometría Leyes que rigen
UNIVERSIDAD NACIONAL EXPERIMENTAL POLITECNICA ANTONIO JOSÉ DE SUCRE VICERRECTORADO BARQUISIMETO DEPARTAMENTO DE INGENIERÍA QUÍMICA QUÍMICA GENERAL CLASE Nº 2 ESTEQUIOMETRÍA 1 Estequiometría Leyes que rigen
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2010 QUÍMICA TEMA 1: LA TRANSFORMACIÓN QUÍMICA
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 010 QUÍMICA TEMA 1: LA TRANSFORMACIÓN QUÍMICA Junio, Ejercicio, Opción B Reserva 1, Ejercicio 5, Opción A Reserva 1, Ejercicio 5, Opción B Reserva, Ejercicio
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 010 QUÍMICA TEMA 1: LA TRANSFORMACIÓN QUÍMICA Junio, Ejercicio, Opción B Reserva 1, Ejercicio 5, Opción A Reserva 1, Ejercicio 5, Opción B Reserva, Ejercicio
