Dimensiones Perspectivas:
|
|
|
- Adrián San Martín Medina
- hace 9 años
- Vistas:
Transcripción
1 5.2. PERSPECTIVA OBLICUA O ANGULAR DE DOS PUN- TOS DE FUGA. Al igual que ocurre con la perspectiva frontal esta perspectiva queda definida por la disposición del objeto, que ha de estar situado de manera que las caras laterales sean oblicuas respecto del plano del cuadro, así pues se obtienen dos puntos de fuga (f-f=). Esta oblicuidad puede ser cualquiera, pero la más comúnmente elegida es aquella en la que las caras laterales forman ángulos de 301 y 601 con el P.C. (esto es así por ser de fácil construcción con la escuadra y el cartabón) Las visuales paralelas a las aristas horizontales del prisma cortan al P.C. (a la L.H.) En los puntos F-F=, puntos de fuga de las paralelas a estas dos direcciones. Dichas visuales forman ángulos de 901, es necesario considerar esto a la hora de colocar el dibujo en el papel, pues cuando un punto de fuga se acerca al principal (P) el otro se aleja de él. Las aristas laterales no tienen punto de fuga, siendo consideradas perpendiculares a la L.T. Dimensiones Perspectivas: En el apartado al describir los elementos de referencia se nombraron dos puntos M-M= llamados puntos métricos, que están asociados a los puntosa de fuga F-F=, respectivamente, y que sirven para transformar las medidas reales en dimensiones perspectivas sobre las rectas que fugan a éstos. Los puntos métricos se obtienen tomando sobre la L.H. y a partir de los de fuga, la distancia de cada uno de éstos al punto de vista V. El punto M dista de F la magnitud F-V,, y el M= está a la distancia de F=-V de F=. Estos puntos son los equivalentes a los de distancia (D-D=) de la perspectiva frontal. La mayor parte de lo explicado en el apartado homólogo a este de la perspectiva frontal, referente a las operaciones para efectuar mediciones perspectivas sobre los tipos de rectas más frecuentes es válido para la perspectiva oblicua, exceptuando alguna diferencia en las rectas que fugan a F-F=. Para estudiar el proceso a seguir para tomar dimensiones perspectivas sobre el tipo de rectas anteriormente citado utilizaremos el conjunto de rectas y segmentos empleado en las figuras. PÁG Nº 12 DEPARTAMENTO DE DIBUJO CURSO
2 I.E.S. TORRE DE LOS GUZMANES LA ALGABA (SEVILLA) A) MÉTODOS PERSPECTIVOS: Trazar la perspectiva oblicua de una figura cualquiera (plana o tridimensional) requiere conocer las particularidades de su forma real así como la ubicación respecto al plano del cuadro, sólo queda escoger el método más apropiado a las dimensiones y circunstancias espaciales de la figura. 1.- Método Directo o de las trazas de rayos proyectantes. En este método se desarrollan conceptos y procedimientos propios de bachillerato, no obstante la simplicidad de su planteamiento y de trazado le convierten en un método perspectivo rápido y apropiado para figuras simples. 1. Una vez situados el plano del cuadro, según el ángulo dado (301 ó 601 generalmente), y el punto de vista (v=-v) se une la proyección horizontal de éste (v en planta) con los vértices en proyección horizontal de la figura (a-b-c-d-e-f-g-h), estas rectas cortarán al plano del cuadro en los puntos 1, 2, 3 y Se repite el procedimiento anterior empleando la proyección vertical del punto de vista (v= en alzado) y los vértices de la figura en proyección vertical (a=-b=-c=-d=-e=-f=-g=-h=) 3. Se levantan perpendiculares (respecto de la línea de tierra de la figura) desde los puntos 1, 2, 3 y 4 hasta que corten a las rectas anteriores (a=v=, b=v=, c=v=,..), los puntos intersección de estas rectas determinan la perspectiva lineal de la figura, no obstante ésta no viene dada en verdadera magnitud, por lo tanto es necesario abatir el plano del cuadro para determinarla. 4. El abatimiento del plano del cuadro no se debe realizar de manera convencional, pues el resultado sería una perspectiva cónica simétrica. Para evitar esto el orden de colocación de los puntos 1, 2, 3 y 4 se hace de manera inversa sobre la prolongación de la línea de tierra. Las alturas de transportan trazando paralelas a la L.T. ( no se usan ni la línea del horizonte ni los puntos de fuga) DEPARTAMENTO DE DIBUJO CURSO PÁG. Nº13
3 2.- Método de las prolongaciones. Si en el método anteriormente desarrollado no se empleaban los puntos de fuga, en éste es imprescindible su uso. Para determinar estos puntos otros que permitan el trazado de la perspectiva lineal de la figura se sigue el siguiente método: 1º. Una vez situados el plano del cuadro, según el ángulo dado (301 ó 601 generalmente), y el punto de vista (v=-v) se trazan paralelas a las aristas en proyección horizontal de la figura (ad, eh, ab, ef,..), las intersecciones con el plano del cuadro determinan los puntos de fuga (F=-F). Considerando los ángulos predeterminados ( ) estas paralelas formarán un ángulo de 901 cuyo vértice será v. 2º. Se prolongan las aristas bases (planta) de la figura hasta que corten al plano del cuadro (puntos 1, 2, 3). 3º. Sobre la L.T. se transportan los puntos anteriores siguiendo el método anterior (evitando así la simetría) y los puntos de fuga sobre la L.H., esta línea viene determinada por la proyección vertical (v=) del punto de vista. 4º. Unir los puntos anteriores con los puntos de fuga determinado así la proyección lineal. La altura (o alturas) de la figura se toman a partir de la L.T. (perpendicularmente) en verdadera magnitud. 5º. Como la figura de la ilustración n1 134 está apoyada sobre el P.G. con una arista (b-f) situada en el P.C., ésta viene dada en verdadera magnitud, la proyección lineal de la arista a-e se determina a partir de la arista b-f, uniendo el vértice f con el punto de fuga F y trazando una perpendicular desde a hasta cortar a la recta f-f en el punto e. 6º. Se repite el paso anterior para determinar las restantes alturas de la figura. PÁG Nº 14 DEPARTAMENTO DE DIBUJO CURSO
4 I.E.S. TORRE DE LOS GUZMANES LA ALGABA (SEVILLA) 3.- Método de los puntos métricos (medidores). Este método es muy parecido al anterior, si bien no hay que determinar las intersecciones de la figura con el P.C. ya que se emplean las medidas reales de la figura, es imprescindible el concurso de los puntos métricos (M-M=) 1º. Una vez situados el plano del cuadro, según el ángulo dado (301 ó 601 generalmente), y el punto de vista (v=-v) se trazan paralelas a las aristas en proyección horizontal de la figura (ad, eh, ab, ef,..), las intersecciones con el plano del cuadro determinan los puntos de fuga (F=-F). Considerando los ángulos predeterminados ( ) estas paralelas formarán un ángulo de 901 cuyo vértice será v. 2º. Sobre la L.T. se transportan las medidas reales de la figura (a-b 1-2, b-c 2-3) y los puntos de fuga sobre la L.H., para determinar los puntos métricos (M-M=) se trazan arcos de centro F-F= y radio F-v, F=-v. 3º. Se unen los puntos transportados sobre la L.T. (1 y 3) con los métricos (1-M, 3-M=) y el punto b (ó 2) con los de fuga (F-F=) la intersección de estas rectas con las anteriores determinan las dimensiones en perspectiva de la figura. 4º. Para trazar las alturas (y sus correspondientes dimensiones) se sigue lo explicado en los pasos 41 y 51 del método anteriormente explicado). DEPARTAMENTO DE DIBUJO CURSO PÁG. Nº15
5 4.- Método de coordenadas. El fundamento de este método está en determinar la situación de un punto a partir de la representación perspectiva de sus coordenadas. Para ello es preciso determinar las coordenadas de los puntos en proyección horizontal (planta) según el sistema cartesiano (x = 1-2, 3-4,... y= 1-a, 2-d, 4-c,...), esto se consigue de la siguiente manera: 1º. Una vez situados el plano del cuadro, según el ángulo dado (301 ó 601 generalmente), y el punto de vista (v=-v) se trazan desde los vértices en proyección horizontal (planta) perpendiculares al plano del cuadro hasta cortarlo en los puntos 1, 2 y 4. 2º. Sobre la L.T. se transportan los puntos anteriormente determinados (1, 2 y 4), además de las distancias correspondientes al eje de coordenadas y (1-a, 2-d,..) Siempre a partir de su punto correspondiente, por ejemplo la distancia 1-a se transporta sobre la L.T. desde el punto 1, y así sucesivamente. 3º. En este método no empleamos los puntos de fuga F-F=, consideramos la perspectiva como una frontal (pues los puntos de coordenadas viene determinados por rectas paralelas y perpendiculares al P.C.) Así pues los puntos anteriores (1, 2, 3, A, D, C) fugarán hacia P o hacia D-D=, según sea su coordenada: las coordenadas x fugan hacia P y las Y hacia D-D=, por ejemplo el punto 1 fuga hacia P mientras que su coordenada y, distancia 1-A, fuga hacia D=. La intersección de ambas rectas determinan la perspectiva del punto A. En la ilustración se han dibujado los puntos de fuga F-F= para demostrar que en ambos casos la perspectiva es la misma. 4º. Para trazar las alturas (y sus correspondientes dimensiones) se sigue el método explicado en la perspectiva frontal, trazado de segmentos verticales. Como ejemplo en la figura se ha levantado una perpendicular a la L.T. desde el punto 4 de magnitud igual a la altura del prisma, uniendo el extremo libre (g) con el punto principal P mediante una recta, está cortará a la perpendicular trazada por el punto C determinado el punto G. PÁG Nº 16 DEPARTAMENTO DE DIBUJO CURSO
6 I.E.S. TORRE DE LOS GUZMANES LA ALGABA (SEVILLA) B) FIGURAS SECCIONADAS POR EL PLANO DEL CUADRO: En todos los casos anteriores las figuras estaban situadas por detrás del P.C., y aunque esto sea lo normal, podemos encontrar otras disposiciones: que la figura tenga una parte situada por delante del P.C. (luego estará seccionada por él) o bien que se encuentre situada totalmente por delante de dicho plano. En la figura se observa como el prisma está cortado por el Plano del Cuadro, estando sus vértices B y F situados por delante de él. La sección del P.C. sobre la base del prisma genera varios puntos (2 y 3) la distancia entre ellos vendrá dada en verdadera magnitud, para resolver la perspectiva de la figura se ha utilizado el método de las prolongaciones. La resolución de este tipo de ejercicios es sencilla, ya que al estar la figura seccionada por el Plano del Cuadro nos determina una serie de puntos sobre la L.T. que facilitan la obtención de la perspectiva, además tenemos la referencia para obtener verdaderas magnitudes. 1º. Se aplica lo desarrollado en el método de las prolongaciones, desarrollado en la figura anterior: pasos del 11 al 51. 2º. Al prolongar las rectas F-2 y F=-3 se cortarán el un punto (B) que será la proyección lineal del vértice situado por delante del P.C. 3º. La alturas se toman sobre la L.T. en verdadera magnitud y preferentemente a partir de los puntos 2 ó 3. 4º. Se observa en la figura como la distancia del segmento BF excede a la verdadera magnitud, esto es así por encontrarse por delante del P.C. DEPARTAMENTO DE DIBUJO CURSO PÁG. Nº17
7 C) FIGURAS SITUADAS POR DELANTE DEL PLANO DEL CUADRO: En este caso la figura tiene todos su vértices situados por delante del plano del cuadro. Para resolver este ejercicio situaremos la planta abatida sobre el Plano del Cuadro, que por estar por delante de éste la disposición de la planta respecto a la L.T. no variará. El punto de vista se sitúa abatido sobre el P.C. usando como charnela la L.T. 1º. Trazamos desde V rectas paralelas a las aristas bases del prisma hasta que corten a la L.T., por estos puntos de corte levantamos perpendiculares hasta cortar a la L.H. en los puntos F-F=. 2º. Unimos mediante rectas el punto de vista (V) con los vértices de la base del prisma (a, b, c y d) hasta cortar a la L.T. por estos puntos determinados trazamos perpendiculares. 3º. Se prolongan las aristas bases hasta cortar a la L.T. determinado una serie de puntos. Se unen éstos con los puntos de fuga F-F= mediante rectas hasta que corten a las perpendiculares anteriores; por ejemplo al unir el punto de vista V con el vértice b mediante una recta esta determina un punto en la L.T. B=, prolongando la arista que contiene a b determinamos otro punto sobre la L.T: 1, al unir el punto 1 con F mediante una recta cortará a la perpendicular trazada a la L.T. por B= determinado el punto B. 4º. Para trazar las alturas sólo hay que llevar las verdaderas magnitudes a partir de un punto situado en la L.T. En la figura 137 se ha hecho empelando el punto 1 (verdadera magnitud 1-F1) PÁG Nº 18 DEPARTAMENTO DE DIBUJO CURSO
11. UNIDAD DIDACTICA 11.- PERSPECTIVA CÓNICA.
 11. UNIDAD DIDACTICA 11.- PERSPECTIVA CÓNICA. Rafael Sanzio (1483-1520) Los desposorios de la Virgen. Alberto Durero (1741-1528) grabado en madera fundamentos de la perspectiva lineal. 11.1. INTRODUCCIÓN
11. UNIDAD DIDACTICA 11.- PERSPECTIVA CÓNICA. Rafael Sanzio (1483-1520) Los desposorios de la Virgen. Alberto Durero (1741-1528) grabado en madera fundamentos de la perspectiva lineal. 11.1. INTRODUCCIÓN
LA PERSPECTIVA CÓNICA FRONTAL: LAS BASES DEL DIBUJO ARTÍSTICO.
 . 1. INTRODUCCIÓN. La perspectiva cónica o lineal permite representar los objetos tal y como los vemos en la realidad. El resultado de la representación dependerá de la posición que ocupan éstos en el
. 1. INTRODUCCIÓN. La perspectiva cónica o lineal permite representar los objetos tal y como los vemos en la realidad. El resultado de la representación dependerá de la posición que ocupan éstos en el
19. SISTEMA CÓNICO GENERALIDADES Aplicaciones
 19. SISTEMA CÓNICO 19.1. GENERALIDADES. La perspectiva cónica es un sistema de representación gráfico basado en la proyección de un cuerpo tridimensional sobre un plano auxiliándose en rectas proyectantes
19. SISTEMA CÓNICO 19.1. GENERALIDADES. La perspectiva cónica es un sistema de representación gráfico basado en la proyección de un cuerpo tridimensional sobre un plano auxiliándose en rectas proyectantes
SISTEMA CÓNICO CENTRO JUAN XXIII-CARTUJA. GRANADA 2º BACHILLER. DIBUJO TÉCNICO PERSPECTIVA CÓNICA 1
 SISTEMA CÓNICO La perspectiva cónica es sin duda el sistema descriptivo que consigue una representación de las piezas más parecida a la realidad. Podríamos considerar dos tipos diferentes de perspectiva
SISTEMA CÓNICO La perspectiva cónica es sin duda el sistema descriptivo que consigue una representación de las piezas más parecida a la realidad. Podríamos considerar dos tipos diferentes de perspectiva
PERSPECTIVA CÓNICA. similitud con la imagen que aparecería a un espectador, al mirar al objeto con un sólo ojo desde un punto determinado.
 1 Perspectiva cónica 3º ESO PERSPECTIVA CÓNICA Fig.1 En la pers. cónica se supone al espectador situado en un punto próximo al objeto que se observa por lo que el haz de rayos visuales que dirige el espectador
1 Perspectiva cónica 3º ESO PERSPECTIVA CÓNICA Fig.1 En la pers. cónica se supone al espectador situado en un punto próximo al objeto que se observa por lo que el haz de rayos visuales que dirige el espectador
Dibujo Técnico Cuerpos Sólidos Redondos: Desarrollos y Transformadas.
 38. CUERPOS SÓLIDOS REDONDOS: DESARROLLOS Y TRANSFORMADAS. 38.6. Desarrollo del cilindro. 38.6.1. Cilindro recto. En realidad el trabajar con un cilindro es lo mismo que trabajar con un prisma pero este
38. CUERPOS SÓLIDOS REDONDOS: DESARROLLOS Y TRANSFORMADAS. 38.6. Desarrollo del cilindro. 38.6.1. Cilindro recto. En realidad el trabajar con un cilindro es lo mismo que trabajar con un prisma pero este
12 ÁNGULOS EN DIÉDRICO
 12-1 Apuntes de dibujo técnico Patxi Aguirrezabal M artin 12 ÁNGULOS EN DIÉDRICO Ángulos de la recta con los planos de proyección. Ángulo de dos rectas y bisectriz del ángulo. Ángulo de recta y plano.
12-1 Apuntes de dibujo técnico Patxi Aguirrezabal M artin 12 ÁNGULOS EN DIÉDRICO Ángulos de la recta con los planos de proyección. Ángulo de dos rectas y bisectriz del ángulo. Ángulo de recta y plano.
G1 Generalidades. Perspectiva cónica. Perspectiva cónica
 Perspectiva cónica G1 Generalidades Perspectiva cónica Elementos fundamentales: Los elementos fundamentales son tres: El objeto a representar, el punto de vista (V) desde el que se observa al objeto y
Perspectiva cónica G1 Generalidades Perspectiva cónica Elementos fundamentales: Los elementos fundamentales son tres: El objeto a representar, el punto de vista (V) desde el que se observa al objeto y
Unidad Didáctica 8. Dibujo Geométrico
 Unidad Didáctica 8 Dibujo Geométrico 1.- Tazados Geométricos Básicos Trazados Rectas Paralelas Rectas paralelas. Las que no llegan nunca a cortarse, o se cortan en el infinito. Con Escuadra y Cartabón:
Unidad Didáctica 8 Dibujo Geométrico 1.- Tazados Geométricos Básicos Trazados Rectas Paralelas Rectas paralelas. Las que no llegan nunca a cortarse, o se cortan en el infinito. Con Escuadra y Cartabón:
INTRODUCCIÓN A LA PERSPECTIVA CÓNICA FRONTAL
 INTRODUCCIÓN A LA PERSPECTIVA CÓNICA FRONTAL El sistema cónico se diferencia de los demás sistemas de representación estudiados (sistema diédrico y sistemas axonométricos) en el criterio de proyección
INTRODUCCIÓN A LA PERSPECTIVA CÓNICA FRONTAL El sistema cónico se diferencia de los demás sistemas de representación estudiados (sistema diédrico y sistemas axonométricos) en el criterio de proyección
ANA BALLESTER DIBUJO TÉCNICO 1º BACH 1
 ANA BALLESTER DIBUJO TÉCNICO 1º BACH 1 PERSPECTIVA CÓNICA. FUNDAMENTOS. La perspectiva cónica es la representación de una escena o de un objeto desde un determinado punto de vista; dicho punto es el centro
ANA BALLESTER DIBUJO TÉCNICO 1º BACH 1 PERSPECTIVA CÓNICA. FUNDAMENTOS. La perspectiva cónica es la representación de una escena o de un objeto desde un determinado punto de vista; dicho punto es el centro
INTRODUCCIÓN A LA PERSPECTIVA CÓNICA OBLICUA
 INTRODUCCIÓN A LA PERSPECTIVA CÓNICA OBLICUA El sistema cónico se diferencia de los demás sistemas de representación estudiados (sistema diédrico y sistemas axonométricos) en el criterio de proyección
INTRODUCCIÓN A LA PERSPECTIVA CÓNICA OBLICUA El sistema cónico se diferencia de los demás sistemas de representación estudiados (sistema diédrico y sistemas axonométricos) en el criterio de proyección
Perspectiva del Campidoglio, en Roma.
 La perspectiva es el arte de dibujar volúmenes (objetos tridimensionales) en un plano (superficie bidimensional) para recrear la profundidad y la posición relativa de los objetos. Perspectiva del Campidoglio,
La perspectiva es el arte de dibujar volúmenes (objetos tridimensionales) en un plano (superficie bidimensional) para recrear la profundidad y la posición relativa de los objetos. Perspectiva del Campidoglio,
HOMOLOGÍA Y AFINIDAD 1. HOMOLOGÍA
 HOMOLOGÍA Y AFINIDAD 1. HOMOLOGÍA La Homología es una transformación geométrica de una figura plana en otra. Se utiliza con mucha frecuencia en geometría descriptiva y por lo tanto en dibujo industrial.
HOMOLOGÍA Y AFINIDAD 1. HOMOLOGÍA La Homología es una transformación geométrica de una figura plana en otra. Se utiliza con mucha frecuencia en geometría descriptiva y por lo tanto en dibujo industrial.
GEOMETRÍA TANGENCIAS - 1
 GEOMETRÍA TANGENCIAS - 1 TANGENCIAS BÁSICAS Recordemos que dos líneas se dice que son tangentes cuando tienen un solo punto común sin cortarse. Para resolver cualquier problema de tangencias de rectas
GEOMETRÍA TANGENCIAS - 1 TANGENCIAS BÁSICAS Recordemos que dos líneas se dice que son tangentes cuando tienen un solo punto común sin cortarse. Para resolver cualquier problema de tangencias de rectas
A RG. Diédrico 21. Sección 2. Prisma Oblicuo por un proyectante Hoja 1/2. α 2 α' 2 F ' 4 2 4' 2' 1' 3' E 2 3'' 1'' 2'' 4'' 5''
 α 2 G R α 2 α' 2 F 2 5 2 5' 50 4 2 4' 2 2 1 2 2' 1' 3 2 3' E 2 D 2 B 2 2 C 2 V V' 3'' 1'' 2'' 4'' 5'' D 1 4 1 4 0 C 1 3 1 3 0 2 0 B 1 2 1 E 1 5 1 5 0 1 1 1 F F 1 1 0 1 2 3 4 5 1 C B D E Recortables a la
α 2 G R α 2 α' 2 F 2 5 2 5' 50 4 2 4' 2 2 1 2 2' 1' 3 2 3' E 2 D 2 B 2 2 C 2 V V' 3'' 1'' 2'' 4'' 5'' D 1 4 1 4 0 C 1 3 1 3 0 2 0 B 1 2 1 E 1 5 1 5 0 1 1 1 F F 1 1 0 1 2 3 4 5 1 C B D E Recortables a la
PERSPECTIVAS PARALELAS:
 Perspectivas - Principios operativos básicos 1 PERSPECTIVAS PARALELAS: Principios generales de construcción Las perspectivas paralelas son de gran utilidad para el trabajo rápido a mano alzada y para visualizar
Perspectivas - Principios operativos básicos 1 PERSPECTIVAS PARALELAS: Principios generales de construcción Las perspectivas paralelas son de gran utilidad para el trabajo rápido a mano alzada y para visualizar
31. SISTEMA AXONOMÉTRICO. LA RECTA Y EL PLANO
 31. SISTEMA AXONOMÉTRICO. LA RECTA Y EL PLANO 31.1. Representación de la recta. Si un punto se representaba por cuatro proyecciones, la recta se representa igual por cuatro proyecciones. Proyecciones de
31. SISTEMA AXONOMÉTRICO. LA RECTA Y EL PLANO 31.1. Representación de la recta. Si un punto se representaba por cuatro proyecciones, la recta se representa igual por cuatro proyecciones. Proyecciones de
Preparado por el Arqto. Jing Chang Lou
 POLIIEDROS A P U N T E D O C E N T E Preparado por el Arqto. Jing Chang Lou U N I V ER S I D A D D E C H I L E F AC U L T A D D E A R Q U I T EC T U R A Y U R B A N I S MO D EPARTAMENTO C I ENCIAS DE L
POLIIEDROS A P U N T E D O C E N T E Preparado por el Arqto. Jing Chang Lou U N I V ER S I D A D D E C H I L E F AC U L T A D D E A R Q U I T EC T U R A Y U R B A N I S MO D EPARTAMENTO C I ENCIAS DE L
Dibujo Técnico Secciones Planas
 37. SECCIONES PLANAS 37.1. INTRODUCCIÓN. Para hallar la sección plano de un cuerpo geométrico se pueden emplear tres métodos: a.- Por intersección de aristas o generatrices del cuerpo con el plano. b.-
37. SECCIONES PLANAS 37.1. INTRODUCCIÓN. Para hallar la sección plano de un cuerpo geométrico se pueden emplear tres métodos: a.- Por intersección de aristas o generatrices del cuerpo con el plano. b.-
TEMA 5. CURVAS CÓNICAS.
 5.1. GENERALIDADES. TEMA 5. CURVAS CÓNICAS. Se denominan secciones cónicas a aquellas superficies que son producidas por la intersección de un plano con una superficie cónica de revolución (una superficie
5.1. GENERALIDADES. TEMA 5. CURVAS CÓNICAS. Se denominan secciones cónicas a aquellas superficies que son producidas por la intersección de un plano con una superficie cónica de revolución (una superficie
PRUEBAS DE ACCESO A LA UNIVERSIDAD L.O.G.S.E.
 PRUEBAS DE ACCESO A LA UNIVERSIDAD L.O.G.S.E. CURSO 2.006-2.007 - CONVOCATORIA: DIBUJO TÉCNICO EL ALUMNO DEBE ELEGIR Y DESARROLLAR, OBLIGATORIAMENTE, LOS EJERCICIOS DEL BLOQUE I ó LOS DEL BLOQUE II. BLOQUE
PRUEBAS DE ACCESO A LA UNIVERSIDAD L.O.G.S.E. CURSO 2.006-2.007 - CONVOCATORIA: DIBUJO TÉCNICO EL ALUMNO DEBE ELEGIR Y DESARROLLAR, OBLIGATORIAMENTE, LOS EJERCICIOS DEL BLOQUE I ó LOS DEL BLOQUE II. BLOQUE
8. UNIDAD DIDACTICA 8: TANGENCIAS Y ENLACES
 8. UNIDAD DIDACTICA 8: TANGENCIAS Y ENLACES 8.1. TANGENCIAS Se dice que dos figuras planas son tangentes cuando tienen un solo punto en común, al que se conoce como punto de tangencia. Las tangencias pueden
8. UNIDAD DIDACTICA 8: TANGENCIAS Y ENLACES 8.1. TANGENCIAS Se dice que dos figuras planas son tangentes cuando tienen un solo punto en común, al que se conoce como punto de tangencia. Las tangencias pueden
Sistema axonométrico. Con el estudio de esta Unidad nos proponemos alcanzar los siguientes objetivos:
 UNIDAD 9 Sistema axonométrico E l sistema axonométrico se divide en ortogonal y oblicuo según sea la dirección de proyección. La axonometría ortogonal puede ser isométrica, dimétrica o trimétrica según
UNIDAD 9 Sistema axonométrico E l sistema axonométrico se divide en ortogonal y oblicuo según sea la dirección de proyección. La axonometría ortogonal puede ser isométrica, dimétrica o trimétrica según
1º BACH SISTEMA DIÉDRICO III
 SISTEMA DIÉDRICO III ABATIMIENTOS, GIROS, CAMBIOS DE PLANO. SISTEMA DIÉDRICO III: ABATIMIENTOS, CAMBIOS DE PLANO Y GIROS 1- ABATIMIENTOS Los abatimientos se utilizan para hallar la verdadera magnitud (
SISTEMA DIÉDRICO III ABATIMIENTOS, GIROS, CAMBIOS DE PLANO. SISTEMA DIÉDRICO III: ABATIMIENTOS, CAMBIOS DE PLANO Y GIROS 1- ABATIMIENTOS Los abatimientos se utilizan para hallar la verdadera magnitud (
Sistema cónico de 10perspectiva lineal
 UNIDAD Sistema cónico de 10perspectiva lineal Línea de horizonte y puntos de fuga (Ilustración de los autores utilizando la fotografía de la Tumba del Sulta n del cementerio de la mezquita Al Mashun, Medan,
UNIDAD Sistema cónico de 10perspectiva lineal Línea de horizonte y puntos de fuga (Ilustración de los autores utilizando la fotografía de la Tumba del Sulta n del cementerio de la mezquita Al Mashun, Medan,
PRUEBAS DE ACCESO A LA UNIVERSIDAD L.O.G.S.E.
 PRUEBAS DE ACCESO A LA UNIVERSIDAD L.O.G.S.E. CURSO 2.004-2.005 - CONVOCATORIA: DIBUJO TÉCNICO EL ALUMNO DEBE ELEGIR Y DESARROLLAR, OBLIGATORIAMENTE, LOS EJERCICIOS DEL BLOQUE I ó LOS DEL BLOQUE II. BLOQUE
PRUEBAS DE ACCESO A LA UNIVERSIDAD L.O.G.S.E. CURSO 2.004-2.005 - CONVOCATORIA: DIBUJO TÉCNICO EL ALUMNO DEBE ELEGIR Y DESARROLLAR, OBLIGATORIAMENTE, LOS EJERCICIOS DEL BLOQUE I ó LOS DEL BLOQUE II. BLOQUE
EJERCICIOS DE DISTANCIAS PROCEDIMIENTOS DE EJECUCIÓN
 EJERCICIOS DE DISTANCIAS PROCEDIMIENTOS DE EJECUCIÓN 1-2-3.- Procedimiento: - Explicados en teoría 1) 2) 3) 4.- Procedimiento: - Trazar el plano P perpendicular a la recta R, pasando por el punto A, ayudándome
EJERCICIOS DE DISTANCIAS PROCEDIMIENTOS DE EJECUCIÓN 1-2-3.- Procedimiento: - Explicados en teoría 1) 2) 3) 4.- Procedimiento: - Trazar el plano P perpendicular a la recta R, pasando por el punto A, ayudándome
PRUEBAS DE ACCESO A LA UNIVERSIDAD MATERIAS DE MODALIDAD: FASE GENERAL Y ESPECÍFICA OPCIÓN A
 PRUEBAS DE ACCESO A LA UNIVERSIDAD MATERIAS DE MODALIDAD: FASE GENERAL Y ESPECÍFICA CURSO 2013-2014 CONVOCATORIA: JULIO MATERIA: DIBUJO TÉCNICO EL ALUMNO DEBE ELEGIR Y DESARROLLAR, OBLIGATORIAMENTE, LOS
PRUEBAS DE ACCESO A LA UNIVERSIDAD MATERIAS DE MODALIDAD: FASE GENERAL Y ESPECÍFICA CURSO 2013-2014 CONVOCATORIA: JULIO MATERIA: DIBUJO TÉCNICO EL ALUMNO DEBE ELEGIR Y DESARROLLAR, OBLIGATORIAMENTE, LOS
38. CUERPOS SÓLIDOS: DESARROLLOS Y TRANSFORMADAS Desarrollo de los Poliedros Regulares.
 1 38. CUERPOS SÓLIDOS: DESARROLLOS Y TRANSFORMADAS. 38.1. Desarrollo de los Poliedros Regulares. 38.1.1. Tetraedro. Dado que los poliedros regulares tienen sus caras iguales, el desarrollo de los mismos
1 38. CUERPOS SÓLIDOS: DESARROLLOS Y TRANSFORMADAS. 38.1. Desarrollo de los Poliedros Regulares. 38.1.1. Tetraedro. Dado que los poliedros regulares tienen sus caras iguales, el desarrollo de los mismos
ÁNGULOS ÁNGULO FORMADO ENTRE DOS RECTAS
 ÁNGULOS ÁNGULO FORMADO ENTRE DOS RECTAS QUE SE CORTAN 1 - Se halla el plano que forman R y S. 2 Se abaten las dos rectas para hallar el ángulo. Se puede abatir con el método directo, o con el método tradicional
ÁNGULOS ÁNGULO FORMADO ENTRE DOS RECTAS QUE SE CORTAN 1 - Se halla el plano que forman R y S. 2 Se abaten las dos rectas para hallar el ángulo. Se puede abatir con el método directo, o con el método tradicional
2º BACH. SISTEMA DIÉDRICO [ABATIMIENTOS, CAMBIOS DE PLANOS, GIROS Y ÁNGULOS]
![2º BACH. SISTEMA DIÉDRICO [ABATIMIENTOS, CAMBIOS DE PLANOS, GIROS Y ÁNGULOS] 2º BACH. SISTEMA DIÉDRICO [ABATIMIENTOS, CAMBIOS DE PLANOS, GIROS Y ÁNGULOS]](/thumbs/53/33097240.jpg) 2º BACH. SISTEMA DIÉDRICO [ABATIMIENTOS, CAMBIOS DE PLANOS, GIROS Y ÁNGULOS] ABATIMIENTOS ABATIMIENTO DE UN PUNTO CONTENIDO EN UN PLANO. Sobre el P.H. Sobre el P.V. 1 ABATIMIENTO DE UNA RECTA CONTENIDA
2º BACH. SISTEMA DIÉDRICO [ABATIMIENTOS, CAMBIOS DE PLANOS, GIROS Y ÁNGULOS] ABATIMIENTOS ABATIMIENTO DE UN PUNTO CONTENIDO EN UN PLANO. Sobre el P.H. Sobre el P.V. 1 ABATIMIENTO DE UNA RECTA CONTENIDA
MINIMA DISTANCIA DE UN PUNTO A UN CONO. Y A UNA ESFERA
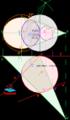
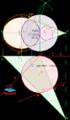 E J E R C I C I O S D E D I E D R I C O MINIMA DISTANCIA DE UN PUNTO A UN CONO. Y A UNA ESFERA Sea un cono recto apoyado en el plano horizontal y un punto exterior ( A ). 1º) Uniremos la proyección horizontal
E J E R C I C I O S D E D I E D R I C O MINIMA DISTANCIA DE UN PUNTO A UN CONO. Y A UNA ESFERA Sea un cono recto apoyado en el plano horizontal y un punto exterior ( A ). 1º) Uniremos la proyección horizontal
PERSPECTIVA CÓNICA. La perspectiva cónica, también llamada lineal, es el sistema de representación que más se asemeja a
 I.E.S. TORRE E LOS GUZMANES ERSECTIVA CÓNICA. Rafael Sanzio (1483-1520) Los desposorios de la Virgen. Alberto urero (1741-1528) grabado en madera fundamentos de la perspectiva lineal. 1. INTROUCCIÓN Y
I.E.S. TORRE E LOS GUZMANES ERSECTIVA CÓNICA. Rafael Sanzio (1483-1520) Los desposorios de la Virgen. Alberto urero (1741-1528) grabado en madera fundamentos de la perspectiva lineal. 1. INTROUCCIÓN Y
18. PERSPECTIVA CABALLERA.
 18. PERSPECTIVA CABALLERA. La perspectiva caballera es un sistema de representación que utiliza la proyección paralela oblicua, en el que las dimensiones del plano proyectante frontal, como las de los
18. PERSPECTIVA CABALLERA. La perspectiva caballera es un sistema de representación que utiliza la proyección paralela oblicua, en el que las dimensiones del plano proyectante frontal, como las de los
11. CURVAS TÉCNICAS ÓVALO Definición Construcción de óvalos
 11. CURVAS TÉCNICAS Las curvas técnicas tienen muchas aplicaciones en la resolución de problemas de dibujo técnico, ya sean éstos provenientes del ámbito del diseño industrial, arquitectónico o gráfico.
11. CURVAS TÉCNICAS Las curvas técnicas tienen muchas aplicaciones en la resolución de problemas de dibujo técnico, ya sean éstos provenientes del ámbito del diseño industrial, arquitectónico o gráfico.
D1 Generalidades: El punto
 El sistema diédrico D1 Generalidades: El punto Generalidades Proyección ortogonal de un punto sobre un plano Proyección ortogonal o, simplemente proyección de un punto sobre un plano, es el pie de la perpendicular
El sistema diédrico D1 Generalidades: El punto Generalidades Proyección ortogonal de un punto sobre un plano Proyección ortogonal o, simplemente proyección de un punto sobre un plano, es el pie de la perpendicular
ESCUELA DE INGENIERÍA AERONÁUTICA Y DEL ESPACIO EXPRESIÓN GRÁFICA 3 a POE Fecha: 15/04/2013 2º CONTROL DE EXPRESIÓN GRÁFICA. NORMAS E INFORMACIÓN
 º CONTROL DE EXPRESIÓN GRÁFICA. NORMAS E INFORMACIÓN 1º El carnet de la Escuela se debe situar en lugar visible. º El alumno debe cumplimentar los casilleros de identificación con apellidos, nombre, grupo
º CONTROL DE EXPRESIÓN GRÁFICA. NORMAS E INFORMACIÓN 1º El carnet de la Escuela se debe situar en lugar visible. º El alumno debe cumplimentar los casilleros de identificación con apellidos, nombre, grupo
31. SISTEMA AXONOMÉTRICO. LA RECTA Y EL PLANO
 31. SISTEMA AXONOMÉTRICO. LA RECTA Y EL PLANO 31.1. Representación de la recta. Si un punto se representaba por cuatro proyecciones, la recta se representa igual por cuatro proyecciones. Tenemos la recta
31. SISTEMA AXONOMÉTRICO. LA RECTA Y EL PLANO 31.1. Representación de la recta. Si un punto se representaba por cuatro proyecciones, la recta se representa igual por cuatro proyecciones. Tenemos la recta
Sistema Diédrico (II). Superficies poliédricas y radiadas. Secciones
 Sistema Diédrico (II). Superficies poliédricas y radiadas. Secciones En el tema anterior realizamos cambios en las superficies mediante intersecciones y tangencias con rectas o planos. Ahora vamos a ampliar
Sistema Diédrico (II). Superficies poliédricas y radiadas. Secciones En el tema anterior realizamos cambios en las superficies mediante intersecciones y tangencias con rectas o planos. Ahora vamos a ampliar
PERSPECTIVA REAL - Plano del cuadro inclinado Procedimiento de las proyectantes visuales, utilizando la 2da. proyección.
 ANEP Formación Docente Uruguay Educa Comunicación Visual - Dibujo Técnico Prof. Carlos Spalvier PERSPECTIVA REAL - Plano del cuadro inclinado Procedimiento de las proyectantes visuales, utilizando la 2da.
ANEP Formación Docente Uruguay Educa Comunicación Visual - Dibujo Técnico Prof. Carlos Spalvier PERSPECTIVA REAL - Plano del cuadro inclinado Procedimiento de las proyectantes visuales, utilizando la 2da.
18. TANGENCIAS Características generales Rectas tangentes a una circunferencia desde un punto exterior.
 18. TANGENCIAS 18.1. Características generales. Tangencia entre recta y circunferencia: una recta t es tangente a una circunferencia de centro O en un punto T cuando es perpendicular en T al radio OT.
18. TANGENCIAS 18.1. Características generales. Tangencia entre recta y circunferencia: una recta t es tangente a una circunferencia de centro O en un punto T cuando es perpendicular en T al radio OT.
DIÉDRICO: SECCIÓN PLANA EN UN HEXAEDRO (unidades en milímetros)
 1 / 14 DIÉDRICO: SECCIÓN PLANA EN UN HEXAEDRO (unidades en milímetros) Dibujar un hexaedro apoyado en el plano horizontal de proyección diédrica de forma que su base esté inscrita en una circunferencia
1 / 14 DIÉDRICO: SECCIÓN PLANA EN UN HEXAEDRO (unidades en milímetros) Dibujar un hexaedro apoyado en el plano horizontal de proyección diédrica de forma que su base esté inscrita en una circunferencia
PRUEBAS DE ACCESO A LA UNIVERSIDAD MATERIAS DE MODALIDAD: FASE GENERAL Y ESPECÍFICA
 PRUEBAS DE ACCESO A LA UNIVERSIDAD MATERIAS DE MODALIDAD: FASE GENERAL Y ESPECÍFICA CURSO 2.011-2.012 CONVOCATORIA: JUNIO MATERIA: DIBUJO TÉCNICO EL ALUMNO DEBE ELEGIR Y DESARROLLAR, OBLIGATORIAMENTE,
PRUEBAS DE ACCESO A LA UNIVERSIDAD MATERIAS DE MODALIDAD: FASE GENERAL Y ESPECÍFICA CURSO 2.011-2.012 CONVOCATORIA: JUNIO MATERIA: DIBUJO TÉCNICO EL ALUMNO DEBE ELEGIR Y DESARROLLAR, OBLIGATORIAMENTE,
Carlos Quesada Dominguez ANEXO AL LIBRO DE SISTEMA DIEDRICO
 ANEXO AL LIBRO DE SISTEMA DIEDRICO 1 RECTA Y PLANO Dadas dos rectas (r y s) que se cortan y sus trazas están fuera de los limites del papel. Hallar las trazas del plano que determinan. 1º.- Trazar una
ANEXO AL LIBRO DE SISTEMA DIEDRICO 1 RECTA Y PLANO Dadas dos rectas (r y s) que se cortan y sus trazas están fuera de los limites del papel. Hallar las trazas del plano que determinan. 1º.- Trazar una
Sistema diédrico: prisma, cono y cilindro
 UNIDAD 7 Sistema diédrico: prisma, cono y cilindro Capitel basado en el prisma y el cilindro (Modificación de la fotografía de la Mezquita de las Tornerías, Toledo, de Luana Fischer Ferreira, del Banco
UNIDAD 7 Sistema diédrico: prisma, cono y cilindro Capitel basado en el prisma y el cilindro (Modificación de la fotografía de la Mezquita de las Tornerías, Toledo, de Luana Fischer Ferreira, del Banco
A RG. Diédrico 32. Cubo apaoyado en plano oblicuo Hoja 1/2
 Dibujar las proyecciones, con partes vistas y ocultas, de un cubo de arista 50 mm, apoyado en el plano α, dicha arista, 45 mm del vértice del plano y tiene de cota cero. El cubo está en el primer cuadrante.
Dibujar las proyecciones, con partes vistas y ocultas, de un cubo de arista 50 mm, apoyado en el plano α, dicha arista, 45 mm del vértice del plano y tiene de cota cero. El cubo está en el primer cuadrante.
Sistema de planos acotados
 Sistema de planos acotados 1. Fundamentos y elementos del sistema El sistema de planos acotados o sistema acotado, es una variante del sistema diédrico en el que se ha sustituido el plano Vertical de proyección
Sistema de planos acotados 1. Fundamentos y elementos del sistema El sistema de planos acotados o sistema acotado, es una variante del sistema diédrico en el que se ha sustituido el plano Vertical de proyección
EDUCACIÓN PLÁSTICA Y VISUAL UNIDAD 2: TANGENCIAS EN LAS CIRCUNFERENCIAS
 EDUCACIÓN PLÁSTICA Y VISUAL UNIDAD 2: TANGENCIAS EN LAS CIRCUNFERENCIAS 1. TANGENCIAS EN LAS CIRCUNFERENCIAS Decimos que dos elementos geométricos son tangentes cuando tienen un punto en común. Las tangencias
EDUCACIÓN PLÁSTICA Y VISUAL UNIDAD 2: TANGENCIAS EN LAS CIRCUNFERENCIAS 1. TANGENCIAS EN LAS CIRCUNFERENCIAS Decimos que dos elementos geométricos son tangentes cuando tienen un punto en común. Las tangencias
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO OPCIÓN A
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: DIBUJO TÉCNICO II Curso 2009-2010 INSTRUCCIONES GENERALES Y VALORACIÓN La prueba
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: DIBUJO TÉCNICO II Curso 2009-2010 INSTRUCCIONES GENERALES Y VALORACIÓN La prueba
CURVAS TÉCNICAS: ÓVALOS, OVOIDES Y ESPIRALES
 GEOMETRÍA CURVAS TÉCNICAS 1 CURVAS TÉCNICAS: ÓVALOS, OVOIDES Y ESPIRALES Los óvalos y ovoides pertenecen al grupo de los enlaces denominados cerrados, dado que comienzan y terminan en un mismo punto. También
GEOMETRÍA CURVAS TÉCNICAS 1 CURVAS TÉCNICAS: ÓVALOS, OVOIDES Y ESPIRALES Los óvalos y ovoides pertenecen al grupo de los enlaces denominados cerrados, dado que comienzan y terminan en un mismo punto. También
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: DIBUJO TÉCNICO II
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2014-2015 MATERIA: DIBUJO TÉCNICO II INSTRUCCIONES GENERALES Y CALIFICACIÓN Después
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2014-2015 MATERIA: DIBUJO TÉCNICO II INSTRUCCIONES GENERALES Y CALIFICACIÓN Después
UNIDAD Nº 6 GEOMETRÍA DESCRIPTIVA PROYECCIÓN DIÉDRICA O DE MONGE
 UNIDAD Nº 6 GEOMETRÍA DESCRIPTIVA PROYECCIÓN DIÉDRICA O DE MONGE REPRESENTACION DE SEGMENTOS DE RECTAS: Un segmento de recta se proyecta sobre un plano bajo la forma de una recta, con la excepción que
UNIDAD Nº 6 GEOMETRÍA DESCRIPTIVA PROYECCIÓN DIÉDRICA O DE MONGE REPRESENTACION DE SEGMENTOS DE RECTAS: Un segmento de recta se proyecta sobre un plano bajo la forma de una recta, con la excepción que
DE LA RECTA PROYECCIONES DEL
 44 Punto, SISTEM NMÉTIC: recta, plano y cuerpos PECCINES DEL PUNT PECCINES DE L ECT PECCINES DEL PLN ECTS CNTENIDS EN PLNS Plano definido por dos rectas que se cortan INTESECCIÓN DE PLNS INTESECCIÓN DE
44 Punto, SISTEM NMÉTIC: recta, plano y cuerpos PECCINES DEL PUNT PECCINES DE L ECT PECCINES DEL PLN ECTS CNTENIDS EN PLNS Plano definido por dos rectas que se cortan INTESECCIÓN DE PLNS INTESECCIÓN DE
Autor: Arqto. Jing Chang Lou
 SIISTEMA DIIEDRIICO A P U N T E D O C E N T E Autor: Arqto. Jing Chang Lou BIBLIOGRAFÍA SISTEMA DIÉDRICO Ferrer Muñoz, José Luis Ediciones Paraninfo (1999) GEOMETRÍA DESCRIPTIVA Izquierdo Asensi, Fernando
SIISTEMA DIIEDRIICO A P U N T E D O C E N T E Autor: Arqto. Jing Chang Lou BIBLIOGRAFÍA SISTEMA DIÉDRICO Ferrer Muñoz, José Luis Ediciones Paraninfo (1999) GEOMETRÍA DESCRIPTIVA Izquierdo Asensi, Fernando
11. ALGUNOS PROBLEMAS CON TRIÁNGULOS
 11. ALGUNOS PROBLEMAS CON TRIÁNGULOS Estos problemas son ejemplos de aplicación de las propiedades estudiadas. 11.1. Determinar la posición de un topógrafo que tiene tres vértices geodésicos A,B,C, si
11. ALGUNOS PROBLEMAS CON TRIÁNGULOS Estos problemas son ejemplos de aplicación de las propiedades estudiadas. 11.1. Determinar la posición de un topógrafo que tiene tres vértices geodésicos A,B,C, si
A RG. Diédrico 13. Abatimientos Hoja 1/2
 menor cota, es horizontal; 2 - El otro vértice, él E, contiguo al A esta en el P; 3 - El pentágono está en el 1º A G R F 2 A 2 F 1 E B 1 2 A LA D 1 0 1 B 1LB 0 menor cota, es horizontal; 2 - El otro vértice,
menor cota, es horizontal; 2 - El otro vértice, él E, contiguo al A esta en el P; 3 - El pentágono está en el 1º A G R F 2 A 2 F 1 E B 1 2 A LA D 1 0 1 B 1LB 0 menor cota, es horizontal; 2 - El otro vértice,
1. Lugar geométrico de los centros de las circunferencias que pasen por un punto fijo
 Unidad 1. Dibujo Geométrico 1. Lugar geométrico de los centros de las circunferencias que pasen por un punto fijo 2. Circunferencia que pasa por dos o tres puntos 1.5. Circunferencia que pasa por dos puntos
Unidad 1. Dibujo Geométrico 1. Lugar geométrico de los centros de las circunferencias que pasen por un punto fijo 2. Circunferencia que pasa por dos o tres puntos 1.5. Circunferencia que pasa por dos puntos
TEMA 4 REPRESENTACION DE OBJETOS.VISTAS
 TEMA 4 REPRESENTACION DE OBJETOS.VISTAS INDICE 1. INTRODUCCION... 2 2. SISTEMAS DE REPRESENTACION... 2 2.1 PROYECCIONES... 3 2.2 TIPO DE PROYECCIONES... 3 2.3 ELEMENTOS DE LOS SISTEMAS DE REPRESENTACION...
TEMA 4 REPRESENTACION DE OBJETOS.VISTAS INDICE 1. INTRODUCCION... 2 2. SISTEMAS DE REPRESENTACION... 2 2.1 PROYECCIONES... 3 2.2 TIPO DE PROYECCIONES... 3 2.3 ELEMENTOS DE LOS SISTEMAS DE REPRESENTACION...
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: DIBUJO TÉCNICO II Curso 2011-2012 INSTRUCCIONES Y CRITERIOS GENERALES DE CALIFICACIÓN
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: DIBUJO TÉCNICO II Curso 2011-2012 INSTRUCCIONES Y CRITERIOS GENERALES DE CALIFICACIÓN
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2011-2012 MATERIA: DIBUJO TÉCNICO II INSTRUCCIONES Y CRITERIOS GENERALES DE CALIFICACIÓN
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2011-2012 MATERIA: DIBUJO TÉCNICO II INSTRUCCIONES Y CRITERIOS GENERALES DE CALIFICACIÓN
TORNEOS GEOMÉTRICOS Primera Ronda Primer Nivel - 5º Año de Escolaridad
 TORNEOS GEOMÉTRICOS 2017. Primera Ronda Primer Nivel - 5º Año de Escolaridad Problema 1. El hexágono regular de la figura tiene área 6cm 2. Halla el área de la región sombreada. Solución: El triángulo
TORNEOS GEOMÉTRICOS 2017. Primera Ronda Primer Nivel - 5º Año de Escolaridad Problema 1. El hexágono regular de la figura tiene área 6cm 2. Halla el área de la región sombreada. Solución: El triángulo
OPCIÓN A. A1.- Construir el triángulo del que se conoce la longitud de su lado AC y la longitud de las medianas m c = 40 mm y m a = 55 mm.
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: DIBUJO TÉCNICO II Curso 2010-2011 2 INSTRUCCIONES Y CRITERIOS GENERALES DE
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: DIBUJO TÉCNICO II Curso 2010-2011 2 INSTRUCCIONES Y CRITERIOS GENERALES DE
ESTUDIO GRÁFICO DE LA ELIPSE.
 Curvas Cónicas para Dibujo y Matemáticas. Aplicación web Dibujo Técnico para ESO y Bachillerato Matemáticas para Bachillerato Educación Plástica y Visual Autor: José Antonio Cuadrado Vicente. ESTUDIO GRÁFICO
Curvas Cónicas para Dibujo y Matemáticas. Aplicación web Dibujo Técnico para ESO y Bachillerato Matemáticas para Bachillerato Educación Plástica y Visual Autor: José Antonio Cuadrado Vicente. ESTUDIO GRÁFICO
EDUCACIÓN PLÁSTICA Y VISUAL BLOQUE: GEOMETRÍA CUADERNO ADAPTADO 1º E.S.O. Alumno/a: Curso escolar: Grupo: 1º
 EDUCACIÓN PLÁSTICA Y VISUAL BLOQUE: GEOMETRÍA CUADERNO ADAPTADO 1º E.S.O. Alumno/a: Curso escolar: Grupo: 1º TEMA 1. TRAZADOS GEOMÉTRICOS (tema 7 del libro) INTRODUCCIÓN: LOS MATERIALES DE DIBUJO Vamos
EDUCACIÓN PLÁSTICA Y VISUAL BLOQUE: GEOMETRÍA CUADERNO ADAPTADO 1º E.S.O. Alumno/a: Curso escolar: Grupo: 1º TEMA 1. TRAZADOS GEOMÉTRICOS (tema 7 del libro) INTRODUCCIÓN: LOS MATERIALES DE DIBUJO Vamos
2.-GEOMETRÍA PLANA O EUCLIDIANA
 2.-GEOMETRÍA PLANA O EUCLIDIANA 2.2.-Cuadriláteros. Definición, clasificación y notación. Clasificación de los cuadriláteros: Paralelogramos y no paralelogramos. Los cuadriláteros son los polígonos de
2.-GEOMETRÍA PLANA O EUCLIDIANA 2.2.-Cuadriláteros. Definición, clasificación y notación. Clasificación de los cuadriláteros: Paralelogramos y no paralelogramos. Los cuadriláteros son los polígonos de
MATERIAS DE MODALIDAD: FASES GENERAL Y ESPECÍFICA CURSO JUNIO
 PRUEBAS DE ACCESO A LA UNIVERSIDAD MATERIAS DE MODALIDAD: FASES GENERAL Y ESPECÍFICA CURSO 2015 2016 MATERIA: DIBUJO TÉCNICO II (2) Convocatoria: JUNIO EL ALUMNO DEBE ELEGIR Y DESARROLLAR, OBLIGATORIAMENTE,
PRUEBAS DE ACCESO A LA UNIVERSIDAD MATERIAS DE MODALIDAD: FASES GENERAL Y ESPECÍFICA CURSO 2015 2016 MATERIA: DIBUJO TÉCNICO II (2) Convocatoria: JUNIO EL ALUMNO DEBE ELEGIR Y DESARROLLAR, OBLIGATORIAMENTE,
Manejo de las herramientas de Dibujo
 Manejo de las herramientas de Dibujo Una vez aprendidos los instrumentos de dibujo más básicos, en la siguiente ficha, vas a descubrir para que sirven en la práctica, y vas a poder adquirir soltura en
Manejo de las herramientas de Dibujo Una vez aprendidos los instrumentos de dibujo más básicos, en la siguiente ficha, vas a descubrir para que sirven en la práctica, y vas a poder adquirir soltura en
22 CURVAS CÓNICAS- HIPÉRBOLAS
 22 CURVAS CÓNICAS- HIPÉRBOLAS 22.1 Características generales. La hipérbola se obtiene al cortar la superficie cónica por un plano paralelo al eje que corta las dos hojas de la cónica. 22.2 Focos y directrices.
22 CURVAS CÓNICAS- HIPÉRBOLAS 22.1 Características generales. La hipérbola se obtiene al cortar la superficie cónica por un plano paralelo al eje que corta las dos hojas de la cónica. 22.2 Focos y directrices.
28. SISTEMA DIÉDRICO.- DISTANCIAS, VERDADERAS MAGNITUDES.
 28. SISTEMA DIÉDRICO.- DISTANCIAS, VERDADERAS MAGNITUDES. 28.1. Verdaderas magnitudes. 28.1.1. Distancia entre dos puntos. Tenemos en el espacio dos puntos A y B, la distancia entre ellos es el segmento
28. SISTEMA DIÉDRICO.- DISTANCIAS, VERDADERAS MAGNITUDES. 28.1. Verdaderas magnitudes. 28.1.1. Distancia entre dos puntos. Tenemos en el espacio dos puntos A y B, la distancia entre ellos es el segmento
PRUEBAS DE ACCESO A LA UNIVERSIDAD MATERIAS DE MODALIDAD: FASE GENERAL Y ESPECÍFICA
 PRUEBAS DE ACCESO A LA UNIVERSIDAD MATERIAS DE MODALIDAD: FASE GENERAL Y ESPECÍFICA CURSO 2.013-2.014 CONVOCATORIA: JUNIO MATERIA: DIBUJO TÉCNICO 1 EL ALUMNO DEBE ELEGIR Y DESARROLLAR, OBLIGATORIAMENTE,
PRUEBAS DE ACCESO A LA UNIVERSIDAD MATERIAS DE MODALIDAD: FASE GENERAL Y ESPECÍFICA CURSO 2.013-2.014 CONVOCATORIA: JUNIO MATERIA: DIBUJO TÉCNICO 1 EL ALUMNO DEBE ELEGIR Y DESARROLLAR, OBLIGATORIAMENTE,
Unidad 4Transformaciones geométricas
 4.1. Dados los puntos A, B y C sobre una recta r, de manera que AB = 20 mm y BC = 20 mm, determina sobre r el punto D para que la razón doble (ABCD) = 19/14. 1. Por los puntos A y B de la recta r se trazan
4.1. Dados los puntos A, B y C sobre una recta r, de manera que AB = 20 mm y BC = 20 mm, determina sobre r el punto D para que la razón doble (ABCD) = 19/14. 1. Por los puntos A y B de la recta r se trazan
UNIDAD Nº 6 GEOMETRÍA DESCRIPTIVA PROYECCIÓN DIÉDRICA O DE MONGE
 UNIDAD Nº 6 GEOMETRÍA DESCRIPTIVA PROYECCIÓN DIÉDRICA O DE MONGE CUERPOS: POLIEDROS Se denomina superficie poliédrica aquella que está formada por varios poligonos consecutivos. Estos son las caras de
UNIDAD Nº 6 GEOMETRÍA DESCRIPTIVA PROYECCIÓN DIÉDRICA O DE MONGE CUERPOS: POLIEDROS Se denomina superficie poliédrica aquella que está formada por varios poligonos consecutivos. Estos son las caras de
OBJETIVOS: Relacionar espacialmente las proyecciones diédricas que describen a un objeto en sus tres dimensiones
 Pg. 1 OBJETIVOS: Relacionar espacialmente las proyecciones diédricas que describen a un objeto en sus tres dimensiones CONOCIMIENTOS: Elementos esenciales del Sistema Diédrico Nomenclatura Coordenadas
Pg. 1 OBJETIVOS: Relacionar espacialmente las proyecciones diédricas que describen a un objeto en sus tres dimensiones CONOCIMIENTOS: Elementos esenciales del Sistema Diédrico Nomenclatura Coordenadas
\ I OPCIÓN I PROBLEMA: SISTEMA DIÉDRICO.
 OPCIÓN I PROBLEMA: SISTEMA DIÉDRICO. Dadas las proyecciones horizontal y vertical de un sólido, asf como las trazas de un plano P, se pide: 1.- Determinar las proyecciones de la sección producida por el
OPCIÓN I PROBLEMA: SISTEMA DIÉDRICO. Dadas las proyecciones horizontal y vertical de un sólido, asf como las trazas de un plano P, se pide: 1.- Determinar las proyecciones de la sección producida por el
Dibujo Técnico Sistema diédrico.- Cambios de plano, giros y ángulos. ÁNGULOS.
 30. SISTEMA DIÉDRICO.- CAMBIOS DE PLANO, GIROS Y ÁNGULOS. 30.1. Cambios de plano. Los cambios de planos de proyección consisten en tomar o elegir otros planos de proyección de forma que los elementos que
30. SISTEMA DIÉDRICO.- CAMBIOS DE PLANO, GIROS Y ÁNGULOS. 30.1. Cambios de plano. Los cambios de planos de proyección consisten en tomar o elegir otros planos de proyección de forma que los elementos que
TEMA VI: ÁNGULOS ENTRE ELEMENTOS
 TEMA VI: ÁNGULOS ENTRE ELEMENTOS 6.1.D Ángulo entre dos rectas El cálculo del ángulo de dos rectas que se cortan es sencillo. Si las rectas se cruzan, el ángulo es el formado entre una de las rectas y
TEMA VI: ÁNGULOS ENTRE ELEMENTOS 6.1.D Ángulo entre dos rectas El cálculo del ángulo de dos rectas que se cortan es sencillo. Si las rectas se cruzan, el ángulo es el formado entre una de las rectas y
Polígonos IES BELLAVISTA
 Polígonos IES BELLAVISTA Polígonos: definiciones Un polígono es la porción de plano limitada por rectas que se cortan. Polígono regular: el que tiene todos los lados y ángulos iguales. Polígono irregular:
Polígonos IES BELLAVISTA Polígonos: definiciones Un polígono es la porción de plano limitada por rectas que se cortan. Polígono regular: el que tiene todos los lados y ángulos iguales. Polígono irregular:
1. Conocimientos básicos de dibujo geométrico
 1. Conocimientos básicos de dibujo geométrico Los trazados que veremos en este capítulo se harán fundamentalmente con el uso de un compás, por considerar que en el taller hay trazados muy grandes en los
1. Conocimientos básicos de dibujo geométrico Los trazados que veremos en este capítulo se harán fundamentalmente con el uso de un compás, por considerar que en el taller hay trazados muy grandes en los
INTERSECCIONES. POSICIONES RELATIVAS. DISTANCIAS
 INTERSECCIONES. POSICIONES RELATIVAS. DISTANCIAS OBJETIVOS Recordar los principios que rigen las intersecciones geo - métricas entre recta y plano y de estos entre sí, para apli - car, con dominio, el
INTERSECCIONES. POSICIONES RELATIVAS. DISTANCIAS OBJETIVOS Recordar los principios que rigen las intersecciones geo - métricas entre recta y plano y de estos entre sí, para apli - car, con dominio, el
27.1. Representación del Plano. Trazas del plano
 27. SISTEMA DIÉDRICO.- EL PLANO. 27.1. Representación del Plano. Trazas del plano Se llaman trazas de un plano a las rectas que resultan de la intersección de este plano con los planos de proyección. Por
27. SISTEMA DIÉDRICO.- EL PLANO. 27.1. Representación del Plano. Trazas del plano Se llaman trazas de un plano a las rectas que resultan de la intersección de este plano con los planos de proyección. Por
22. CURVAS CÓNICAS-ELIPSE
 22. CURVAS CÓNICAS-ELIPSE 22.1. Características generales. Las curvas cónicas son las secciones planas de un cono de revolución. El cono de revolución es la superficie que genera una recta r al girar alrededor
22. CURVAS CÓNICAS-ELIPSE 22.1. Características generales. Las curvas cónicas son las secciones planas de un cono de revolución. El cono de revolución es la superficie que genera una recta r al girar alrededor
SISTEMA DIÉDRICO. Introducción
 Introducción SISTEMA DIÉDRICO El Sistema Diédrico o de Monge es un Sistema de Representación sobre el plano de cuerpos y elementos geométricos del espacio. Emplea la proyección cilíndrica ortogonal según
Introducción SISTEMA DIÉDRICO El Sistema Diédrico o de Monge es un Sistema de Representación sobre el plano de cuerpos y elementos geométricos del espacio. Emplea la proyección cilíndrica ortogonal según
El Sistema Diédrico Ortogonal II
 DIBUJO TÉCNICO I El Sistema Diédrico Ortogonal II Como se expuso en la anterior unidad didáctica, este sistema está basado en el uso de dos planos de proyección, denominados horizontal y vertical, que
DIBUJO TÉCNICO I El Sistema Diédrico Ortogonal II Como se expuso en la anterior unidad didáctica, este sistema está basado en el uso de dos planos de proyección, denominados horizontal y vertical, que
PRUEBAS DE ACCESO A LA UNIVERSIDAD L.O.G.S.E. BLOQUE I
 PRUEBAS DE ACCESO A LA UNIVERSIDAD L.O.G.S.E. CURSO 2.008-2.009 CONVOCATORIA: JUNIO MATERIA: DIBUJO TÉCNICO EL ALUMNO DEBE ELEGIR Y DESARROLLAR, OBLIGATORIAMENTE, LOS EJERCICIOS DEL BLOQUE I ó LOS DEL
PRUEBAS DE ACCESO A LA UNIVERSIDAD L.O.G.S.E. CURSO 2.008-2.009 CONVOCATORIA: JUNIO MATERIA: DIBUJO TÉCNICO EL ALUMNO DEBE ELEGIR Y DESARROLLAR, OBLIGATORIAMENTE, LOS EJERCICIOS DEL BLOQUE I ó LOS DEL
Pruebas de Acceso a las Universidades de Castilla y León
 Pruebas de Acceso a las Universidades de Castilla y León DIBUJO TÉCNICO Texto para los Alumnos 9 páginas Antes de empezar a trabajar has de tener en cuenta lo siguiente: OPTATIVIDAD: Debes escoger una
Pruebas de Acceso a las Universidades de Castilla y León DIBUJO TÉCNICO Texto para los Alumnos 9 páginas Antes de empezar a trabajar has de tener en cuenta lo siguiente: OPTATIVIDAD: Debes escoger una
INDICE Prologo 1. Proyecciones y escalas Sistema diedrico 2. Punto y recta Recta.- 3. El plano 4. Intersecciones y paralelismo
 INDICE Prologo 7 1. Proyecciones y escalas 1.1. Proyección. Sus clases.- 1.2. Proyección cónica.- 1.3. Invariantes de 9 la proyección cónica.- 1.4. Proyección cilíndrica.- 15. Objeto de la geometría descriptiva.
INDICE Prologo 7 1. Proyecciones y escalas 1.1. Proyección. Sus clases.- 1.2. Proyección cónica.- 1.3. Invariantes de 9 la proyección cónica.- 1.4. Proyección cilíndrica.- 15. Objeto de la geometría descriptiva.
SISTEMA DIÉDRICO PERTENENCIA VISIBILIDAD VISIBILIDAD 3º PROYECCIÓN PLANOS NO DADOS POR SUS TRAZAS
 SISTEMA DIÉDRICO PERTENENCIA 1. Dado un plano cualquiera cuya traza horizontal forma 40º con la LT y 60º la traza vertical, situar pasando por un punto A que le pertenece y de altura 30 mm, todas sus rectas
SISTEMA DIÉDRICO PERTENENCIA 1. Dado un plano cualquiera cuya traza horizontal forma 40º con la LT y 60º la traza vertical, situar pasando por un punto A que le pertenece y de altura 30 mm, todas sus rectas
Dibujo Técnico Curvas técnicas
 22 CURVAS TÉCNICAS En la actualidad, una parte importante de los objetos que se fabrican están realizados bajo algún tipo de forma curva geométrica. Si prestamos atención a nuestro entorno, nos damos cuenta
22 CURVAS TÉCNICAS En la actualidad, una parte importante de los objetos que se fabrican están realizados bajo algún tipo de forma curva geométrica. Si prestamos atención a nuestro entorno, nos damos cuenta
ANA BALLESTER JIMÉNEZ SISTEMAS DE REPRESENTACIÓN TEMA 2 SISTEMAS DE REPRESENTACIÓN I: SISTEMA DIÉDRICO, VISTAS Y ACOTACIÓN
 1 TEMA 2 I: SISTEMA DIÉDRICO, VISTAS Y ACOTACIÓN 2 1. LA GEOMETRÍA DESCRIPTIVA La Geometría Descriptiva es la parte de la Geometría que tiene por objeto la representación de cuerpos tridimensionales sobre
1 TEMA 2 I: SISTEMA DIÉDRICO, VISTAS Y ACOTACIÓN 2 1. LA GEOMETRÍA DESCRIPTIVA La Geometría Descriptiva es la parte de la Geometría que tiene por objeto la representación de cuerpos tridimensionales sobre
Sistema Diédrico Índice de contenido
 Sistema Diédrico Índice de contenido Sistema Diédrico Fundamentos La geometría descriptiva es la ciencia que estudia la representación de los elementos del espacio sobre el plano.... 2 El punto... 3 Conceptos
Sistema Diédrico Índice de contenido Sistema Diédrico Fundamentos La geometría descriptiva es la ciencia que estudia la representación de los elementos del espacio sobre el plano.... 2 El punto... 3 Conceptos
S. Diédrico - 1 SISTEMAS DE PROYECCIÓN
 S. Diédrico - 1 SISTEMA DIÉDRICO El sistema diédrico es un sistema de proyecciones cilíndricas y ortogonales, es decir, que las rectas proyectantes son paralelas entre sí y perpendiculares a los planos
S. Diédrico - 1 SISTEMA DIÉDRICO El sistema diédrico es un sistema de proyecciones cilíndricas y ortogonales, es decir, que las rectas proyectantes son paralelas entre sí y perpendiculares a los planos
25. SISTEMA DIÉDRICO.- EL PLANO.
 25. SISTEMA DIÉDRICO.- EL PLANO. 25.1. Representación del Plano. Trazas del plano Se llaman trazas de un plano a las rectas que resultan de la intersección de este plano con los planos de proyección. Por
25. SISTEMA DIÉDRICO.- EL PLANO. 25.1. Representación del Plano. Trazas del plano Se llaman trazas de un plano a las rectas que resultan de la intersección de este plano con los planos de proyección. Por
DIBUJO TÉCNICO BACHILLERATO TEMA 6. SISTEMA DIÉDRICO. Departamento de Artes Plásticas y Dibujo
 DIBUJO TÉCNICO BCHILLERTO TEM 6. SISTEM DIÉDRICO Departamento de rtes Plásticas y Dibujo TEM 5. CURVS. TEM 6. EL SISTEM DIÉDRICO. 1º BCH. CONCEPTOS. 1.Proyectividad y sistemas de representación Del espacio
DIBUJO TÉCNICO BCHILLERTO TEM 6. SISTEM DIÉDRICO Departamento de rtes Plásticas y Dibujo TEM 5. CURVS. TEM 6. EL SISTEM DIÉDRICO. 1º BCH. CONCEPTOS. 1.Proyectividad y sistemas de representación Del espacio
DIBUJO TÉCNICO II EJERCICIOS DE APOYO. Prof. Jesús Macho Martínez
 DIBUJO TÉCNICO II EJERCICIOS DE APOYO Esta obra de Jesús Macho Martínez está bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported 1º.- Deducir razonadamente el valor del ángulo α marcado
DIBUJO TÉCNICO II EJERCICIOS DE APOYO Esta obra de Jesús Macho Martínez está bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported 1º.- Deducir razonadamente el valor del ángulo α marcado
También puede dibujarse la perspectiva caballera con los ejes formando otros ángulos, lo que ofrece una vista ligeramente distinta del objeto.
 Concepto de perspectiva. La perspectiva es el intento de dibujar en una sola representación y sobre una superficie plana (papel), que únicamente posee dos dimensiones, objetos que en la realidad tiene
Concepto de perspectiva. La perspectiva es el intento de dibujar en una sola representación y sobre una superficie plana (papel), que únicamente posee dos dimensiones, objetos que en la realidad tiene
La representación gráfica de las tres dimensiones TECNOLOGÍA
 La representación gráfica de las tres dimensiones TECNOLOGÍA Las vistas de un objeto Podemos representar todos los detalles de un objeto tridimensional dibujando lo que vemos de él desde diferentes posiciones.
La representación gráfica de las tres dimensiones TECNOLOGÍA Las vistas de un objeto Podemos representar todos los detalles de un objeto tridimensional dibujando lo que vemos de él desde diferentes posiciones.
POLÍGONOS REGULARES. Ejemplo: Hexágono 360º / 6 = 60º. TRIÁNGULO 3 120º 60º 180º (3-2)= 180º CUADRADO 4 90º 90º 180º (4-2)= 360º
 A B G C F LADO D E A B G C F D E APOTEMA DIAGONALES RADIO 360º / n (180º- ) ELEMENTOS Y PROPIEDADES DE LOS POLÍGONOS REGULARES. (Ilustración nº 1). Diagonal: Es el segmento que une dos vértices no consecutivos.
A B G C F LADO D E A B G C F D E APOTEMA DIAGONALES RADIO 360º / n (180º- ) ELEMENTOS Y PROPIEDADES DE LOS POLÍGONOS REGULARES. (Ilustración nº 1). Diagonal: Es el segmento que une dos vértices no consecutivos.
Tema 7: Superficies regladas desarrollables. Pirámide-cono, prisma-cilindro.
 Tema 7: Superficies regladas desarrollables. Pirámide-cono, prisma-cilindro. Definición y representación diédrica. Las superficies regladas están generadas por el movimiento de una recta. En las superficies
Tema 7: Superficies regladas desarrollables. Pirámide-cono, prisma-cilindro. Definición y representación diédrica. Las superficies regladas están generadas por el movimiento de una recta. En las superficies
