LAS LENTES PROGRESIVAS
|
|
|
- Mercedes Cruz Saavedra
- hace 8 años
- Vistas:
Transcripción
1 COMPENDIO DE OFTÁLMICA / LAS LENTES PROGRESIVAS LAS LENTES PROGRESIVAS CAPÍTULO DE 4 3. CONCEPCIÓN DE LAS LENTES PROGRESIVAS Principios de concepción de las lentes oftálmicas Fig. 9: Formación de la imagen en la esfera del remoto. 1) La lente oftálmica como un sistema óptico La lente oftálmica es un sistema óptico concebido para que forme la imagen de los obetos leanos en la esfera del remoto. Esta esfera abstracta representa la combinación óptica obeto de la fóvea del oo en rotación, sin acomodación. La imagen de un punto obeto formada en esta esfera suele ser una mancha borrosa en vez de un punto nítido, debido a la existencia de aberraciones. Para medir la calidad de la imagen de un punto obeto cualquiera, el diseñador de la lente envía un conunto de rayos luminosos, que parten del obeto y que se refractan a través de la lente, y calcula sus intersecciones con la esfera del remoto. La calidad de la imagen viene determinada por el diámetro de la mancha borrosa creada en esta esfera. Los diseñadores de lentes se esfuerzan por meorar la calidad de esta imagen controlando, en la medida de lo posible, las aberraciones ópticas de la lente. Asimismo, los diseñadores se preocupan Fig. 10: Modelo oo-lente. por la calidad de la imagen formada en la retina. Para conseguirlo, tienen que determinar las características del sistema óptico formado por la lente y el oo. Las características de la lente se conocen perfectamente, pero las del oo son más difíciles de determinar. Así pues, es necesario conocer las características de los diferentes dioptrios del oo (córnea, cristalino), sus posiciones relativas (profundidad de las cámaras, longitud del oo) y los índices de refracción de los diferentes medios transparentes del oo humano. Para ello se utilizan modelos de oo que representan a un individuo común. Otros datos necesarios para los cálculos son la posición y la orientación de la lente delante del oo: distancia oo-lente, ángulo pantoscópico, curvatura de la montura. Partiendo de todo esto, se puede analizar el sistema óptico oolente y definir todas sus características. ) La tecnología de los frentes de onda Esta tecnología consiste en calcular la lente considerando los frentes de onda luminosa que la atraviesan. El principio consiste en modelar la onda con una forma lo más regular posible para cada dirección de mirada antes de que penetre en el oo a través de la pupila. En la prác- 46 IMAGEN AÑO 9 VOL. 9 JUL-AGO MÉXICO 007
2 Fig. 11: Cálculo de la imagen. tica, la onda se descompone en una serie de ondas elementales: las primeras corresponden a la refracción del usuario y las siguientes a las aberraciones ópticas (véase la figura 1). Las superficies de la lente se calculan de manera que se minimicen y controlen las aberraciones en función de las necesidades fisiológicas de los usuarios. Esta tecnología se aplicó por primera vez a las lentes oftálmicas para el diseño de la lente Varilux Physio (véase más adelante). Fig. 1: Tecnología de los frentes de onda: a) Frente de onda. b) Descomposición del frente de onda. 3) Programa de optimización y función de mérito La concepción de los sistemas ópticos optimizados no puede realizarse en una única etapa. Generalmente, se recurre a un proceso repetitivo, durante el cual se utiliza un programa de optimización. En primer lugar, se definen un sistema óptico inicial y una función de mérito destinada a observar el rendimiento global del sistema óptico. Después de analizar el sistema óptico inicial, el programa de optimización calcula los nuevos parámetros de un sistema óptico meorado. Este proceso se repite hasta que se obtiene un sistema óptico de características óptimas. La función de mérito es un número, en cierto modo una nota, que se da a la lente para medir su rendimiento. Tiene en cuenta un gran número de puntos en la lente. En cada uno de esos puntos, al que se le asigna un coeficiente de ponderación, un valor obetivo es asignado a cada característica óptica: potencia, astigmatismo, efectos prismáticos y a sus gradientes. El valor de la función de mérito se calcula en cada punto de la lente mediante la suma ponderada de las diferencias cuadráticas entre las características ópticas deseadas T y las características de A del sistema. A continuación, se evalúa el rendimiento global de la lente mediante la suma ponderada de los valores de la función de mérito calculada en todos los puntos de la lente, según la fórmula siguiente: i= m = n Función de mérito Pi W T A i= 1 = 1 En la que: Pi representa el peso atribuido al punto i W representa el peso atribuido a la característica óptica T representa el valor deseado de la característica óptica A representa el valor en curso de la característica óptica La función de mérito es un método de cálculo utilizado habitualmente para la definición de sistemas con limitaciones múltiples y parcialmente contradictorias. Aplicada al cálculo de las lentes oftálmicas, permite relacionar en- IMAGEN AÑO 9 VOL. 9 JUL-AGO MÉXICO
3 tre sí las exigencias fisiológicas con el cálculo de las lentes. Fig. 13: Programa de optimización. Concepción de las lentes progresivas 1) Exigencias ópticas de una lente progresiva Las características ópticas de una lente progresiva se determinan mediante experimentación clínica con el obetivo de conseguir que se respete al máximo la fisiología del oo y de la visión. Estas características ópticas se dividen en dos categorías: características que deben contemplar valores bien determinados o limitaciones obligatorias. características que deben mantenerse por debao de unos umbrales determinados. a) Exigencias de progresión de potencia La función primera de una lente progresiva es proporcionar al usuario una buena visión de cerca y a distancia intermedia, al tiempo que conservar una visión nítida de leos. Esta eficacia se basa en el respeto imperativo de las potencias de visión de leos y de cerca, mientras que en lo que respecta a la progresión, es más flexible. Más concretamente: Posicionamiento en altura de la zona de visión de cerca: consideraciones fisiológicas, como la tensión de los músculos oculomotores o la zona restringida para la fusión binocular cuando miramos hacia abao, abogan por una posición alta de la visión de cerca en la lente. Esto implica una progresión relativamente corta que comporta una variación más rápida de las aberraciones periféricas. Un buen término medio consiste en situar la zona de visión próxima para una inclinación de la mirada del orden de 5º. Perfil de progresión de potencia: la progresión de la potencia a lo largo de la meridiana de la lente debe permitir al usuario explorar el campo obeto sin imponerle fatigosos movimientos verticales de la cabeza. Esto se obtiene definiendo el perfil de progresión de forma que se respete la coordinación natural de los movimientos verticales de los oos y de la cabeza, así como la orientación del horóptero vertical zona de puntos en el espacio que son vistos binocularmente simples con el cual está relacionada la inclinación natural de los documentos durante la lectura. Posicionamiento horizontal de la zona de visión próxima: debe adaptarse a la convergencia natural de los oos al valor de la adición y a la corrección del usuario en visión de leos. La convergencia natural de las líneas de mirada cuando se baa la vista y la distancia de lectura media, definen el descentramiento de la zona de visión de cerca que se debe realizar. Además, como la agudeza visual disminuye con la edad, los présbitas avanzados leen más cerca que los présbitas incipientes para procurarse un efecto de amplificación, implica que la zona de visión próxima debe descentrarse más con el aumento de la adición. Por último, los efectos prismáticos de la corrección en visión de leos desplazan sensiblemente el punto de impacto del oo en la lente: la zona de visión próxima debe descentrarse más para un hipermétrope que para un miope. b) Exigencias de percepción visual Para una visión foveal óptima, las aberraciones de imagen deben minimizarse en toda la superficie de la lente y en particular a lo largo de la meridiana de progresión. En la zona central de la lente, es importante equilibrar potencia, as- 48 IMAGEN AÑO 9 VOL. 9 JUL-AGO MÉXICO 007
4 después se integran en el programa de optimización de la lente. Fig. 15: Modelización del sistema lente + oo. Fig. 14: Progresión de potencia. tigmatismo y prisma vertical entre los oos derecho e izquierdo para respetar la fusión motriz y sensorial de las imágenes en visión binocular. Esto se realiza mediante una concepción asimétrica de la superficie de la lente progresiva combinada con un posicionamiento lateral adecuado de la meridiana. En la periferia de la lente, utilizada en visión extrafoveal, las aberraciones no se pueden eliminar completamente. En esta zona, las exigencias de calidad de la imagen son menos elevadas, pero el control de los efectos prismáticos sigue siendo importante. La percepción del movimiento es una función clave de la periferia de la lente donde el gradiente de variación de las aberraciones residuales es más importante que su valor absoluto. Para modelar los efectos de las lentes oftálmicas sobre la visión periférica, se utiliza un modelo de oo diferente del utilizado para la visión central. Se toma el oo en posición fia mirando una reilla y se toman los rayos emitidos desde cada punto del espacio obeto pasando por el centro de la pupila tras su refracción por los dos elementos dióptricos de la lente. Se estudia la posición de estos rayos y sus lugares de intercepción de la retina. De esta manera se obtiene información sobre el rendimiento de la lente en visión dinámica, fundamentalmente cuando el sueto mueve la cabeza o se desplaza. Las exigencias ópticas descritas anteriormente se introducen en la función de mérito y a) Modelo utilizado para la visión central: los rayos se emiten desde el punto observado y se enfocan en la retina. b) Modelo utilizado para la visión periférica: los rayos se emiten desde cada punto del espacio obeto. Se presta más atención a la posición de la imagen en la retina que a la calidad. c) Combinación de los modelos de visión central y visión periférica: el diseñador debe gestionar los dos efectos simultáneamente. IMAGEN AÑO 9 VOL. 9 JUL-AGO MÉXICO
5 Personalización de lentes progresivas Las tecnologías recientes de fabricación mediante retallado directo permiten calcular y realizar lentes progresivas personalizadas para cada usuario. Así se pueden integrar características propias del comportamiento de cada individuo. Por eemplo, la coordinación específica de los movimientos de los oos y de la cabeza para lo cual se varía la dimensión del campo central y la suavidad periférica del diseño en función de la medición del comportamiento de cada persona (véase más adelante la explicación detallada del Varilux Ipseo). Por otra parte, en el cálculo de la lente progresiva se pueden integrar parámetros relativos a la prescripción, al centrado y al montae de la lente. ) Estudios clínicos y bucle dióptrico Al finalizar el proceso de optimización y cálculo de la lente, se proponen diferentes diseños de superficies progresivas. Se fabrican prototipos de lentes de cada tipo y se prueban mediante ensayos clínicos muy rigurosos realizados a doble ciego (ni el paciente ni el experimentador conocen la naturaleza exacta de la lente probada). El protocolo seguido para estos ensayos tiene como obetivo garantizar que no se producirá ninguna influencia, ni por parte de los pacientes ni por parte de los responsables del test, en la evaluación clínica de los diseños. Así se controlan: la representatividad de la muestra de pacientes probada, la naturaleza del equipamiento utilizado anteriormente, el orden de desarrollo de los ensayos, el tiempo que se han llevado las lentes, el control y los austes de las monturas, de los materiales, los tratamientos y la precisión del centrado. Se efectúan evaluaciones comparativas de las lentes mediante el análisis en profundidad de los comentarios y observaciones expresadas por los pacientes. Se analiza su significado en materia estadística. Estos estudios conducen a la selección de la meor superficie progresiva. Cabe destacar aquí que es muy difícil, incluso imposible, establecer una relación formal entre el cálculo de las características de las lentes y la satisfacción de los usuarios. Por este motivo cualquier innovación se valida sistemáticamente a través del proceso de bucle dióptrico (figura 16). Éste consiste en traducir cualquier nueva idea fisiológica en un cálculo de diseño de superficie, realizar una serie de lentes prototipos, medir estas lentes para comprobar su conformidad y someterlas a la evaluación clínica de los pacientes. Si la innovación se confirma Fig. 16: El Bucle dióptrico. La única innovación real es la que perciben los usuarios. con un meor rendimiento visual y una mayor satisfacción de los pacientes, puede propiciar el nacimiento de una nueva lente progresiva. De no ser el caso, serían de todas maneras datos nuevos que enriquecen los conocimientos del equipo de diseño y el proceso iterativo del bucle dióptrico continúa sobre nuevas bases. 4. DESCRIPCIÓN Y CONTROL DE LAS LENTES PROGRESIVAS Representación gráfica de las lentes progresivas Los diseñadores de lentes utilizan diferentes métodos de representación gráfica para mostrar las características ópticas de las lentes progresivas. A menudo se refieren a las características ópticas de las lentes, es decir, a las relativas al sistema oo + lente, las cuales permiten diferenciar las características de las superficies progresivas y también describir su geometría. Las características que se describen más a menudo son las siguientes: 1) Perfil de potencia La curva representa la progresión de potencia de la lente a lo largo de su meridiana, desde 50 IMAGEN AÑO 9 VOL. 9 JUL-AGO MÉXICO 007
6 la visión de leos hasta la visión de cerca. Esta progresión de potencia es el resultado de la variación continua de la curvatura de la lente entre la parte superior y la inferior. Este perfil de potencia describe la función primera de la lente y permite evaluar la longitud de progresión. Fig. 18: Curvas isométricas de las características de una lente progresiva. a) Esfera. Fig. 17: Perfil de potencia de una lente progresiva. ) Curvas isométricas Se trata de un mapa bidimensional de la lente que representa la distribución de la potencia o el astigmatismo. El mapa muestra unas líneas de valor dióptrico constante (isoesfera o isocilindro). Entre dos líneas consecutivas, la esfera o el cilindro varían tomando un valor constante, 0,50 D en estos eemplos. Cabe observar que estos dos tipos de registros no debería presentarse nunca por separado ya que son interdependientes. 3) Gráfico de reilla Este tipo de gráfico permite poner de manifiesto la distribución de los efectos prismáticos de la lente mostrando cómo influyen en la forma de un reilla rectangular observada a través de la lente. 4) Gráficos tridimensionales Las representaciones tridimensionales proyec- b) Cilindro. tan verticalmente el valor de una característica óptica determinada en cada punto de la lente con respecto a un plano de referencia. Se puede utilizar para mostrar una distribución de potencia, de astigmatismo, de efectos prismáticos o los gradientes de estas características. Estos gráficos tridimensionales muestran más claramente las características de las lente que las curvas isométricas. IMAGEN AÑO 9 VOL. 9 JUL-AGO MÉXICO
7 Fig. 19: Gráfico de reilla de una lente progresiva. Interpretación de los gráficos: Aunque sean útiles en el proceso de diseño de las lentes estos gráficos sólo son simples representaciones de las características de las lentes progresivas y no reflean la satisfacción de los usuarios. Como tales, estos gráficos no se pueden utilizar para predecir la confort de los pacientes, ni para realizar comparaciones cualitativas entre lentes progresivas. Sólo los estudios clínicos, realizados en condiciones perfectamente controladas y en los que participe una muestra de pacientes representativa de la población présbita, pueden proporcionar las bases fiables de evaluación y de comparación cualitativa de las lentes progresivas. Fig. 0: Gráficos tridimensionales de las características de una lente progresiva. Medición y control de las superficies progresivas El control de la conformidad de las superficies progresivas es una actividad crucial para los diseñadores y fabricantes de lentes progresivas. Fig. 1: Medición y control de una superficie progresiva. Se puede realizar por medio de métodos de medición tridimensionales que analicen la topografía de la superficie o métodos deflectométricos que analicen la desviación de los rayos luminosos producida por la superficie. Estos datos de medición pueden compararse directamente con las ecuaciones teóricas de la superficie para comprobar su conformidad. También se pueden evaluar por medio de herramientas de simulación que recreen las condiciones de uso de la lente por el oo para facilitar una evaluación usuario de la superficie. Durante las fases de fabricación de las lentes, también se pueden utilizar frontofocómetros tradicionales para medir la potencia, el astigmatismo y el prisma en los puntos seleccionados de la lente. 5 IMAGEN AÑO 9 VOL. 9 JUL-AGO MÉXICO 007
8 COMPLEMENTO Descripción matemática de las superficies progresivas Descripción matemática de las superficies Cualquier superficie definida mediante una ecuación z=f (x,y) se puede expresar matemáticamente en un sistema de coordenadas 3D de referencia Oxyz, siendo xoy el plano tangencial a la superficie en el punto O, mediante una ecuación de segundo grado, más unos términos de grado más elevado. Esta superficie de segundo grado es osculadora con la superficie en el punto O (es decir, que sus curvaturas son idénticas a las de la superficie real) y se define con la ecuación: z = rx + sxy + ty en la que r, s, t son derivaciones locales de la superficie: r = d z / dx, s = d z / dxdy, t = d z / dy Esta superficie de segundo grado define el ee local y las curvaturas principales de la superficie en O. Por otro lado, toda superficie que pueda asimilarse localmente a una superficie tórica, caracterizada por sus curvaturas principales octogonales C1 y C y por su ee derivan de las siguientes ecuaciones: C. C 1 r. t s = ( 1 + p + q ) + ( + ) ( curvatura total) C C t p r q p q s = / 3 curvatura media. 1 + p + q en la que p = dx/dz et q = dz/dy Ee = Arctg(m) en la que m es la solución de la ecuación cuadrática = ( + ) t. p. q s 1+ q. m + t. 1 + p r. 1 q. m + s. 1 + p r. p. q 0 Fig. A: Descripción local de una superficie. Caracterización matemática de las superficies en un ámbito circular Cualquier parte de una superficie complea puede definirse utilizando un sistema de referencia conocido como los polinomios de Zernike. Este sistema se utiliza para expresar la superficie en forma matemática mediante la suma de una serie de polinomios específicos. Los diez primeros polinomios de Zernike permiten unas aplicaciones relevantes en matemáticas y física: el 5º da acceso a la curvatura media de la superficie, el 4º y el 6º a su cilindro y a su ee y el 7º y el 10º a su pendiente de variación de curvatura. La superficie de la lente se expresa en forma matemática con la fórmula: = i= i= 0 f y, z Z. P P1: polinomio de Zernike en la que Z1: coeficientes y,z: variables reducidas Pistón 1 Z0 Desviación en y y Z1 Desviación en z z Z Asti + 45º y.z Z3 Desenfoque -1+y +.z Z4 Asti 0,90º z -y Z5 Coma tr y 3y.z -y 3 Z6 Coma y -y+3y.z +3y 3 Z7 Coma z -z+3z.y +3.z 3 Z8 Coma tr z z 3-3zy Z9 Expansión de una superficie en los 10 primeros polinomios de Zernike. IMAGEN AÑO 9 VOL. 9 JUL-AGO MÉXICO
9 z=f(x,y), p, q, r, s, t en un punto de coordenadas x,y se deducen de los valores de las ordenadas próximas a este punto mediante su combinación en una matriz cuadrada. Estas características se calculan según las fórmulas siguientes: Fig. B: Descomposición de una superficie con ayuda de los polinomios de Zernike. Modelización matemática de superficies con funciones polinomiales mediante B-splines: Cualquier superficie bi-regular se puede representar mediante un conunto de abscisas y de ordenadas distribuidas uniformente por la superficie según una reilla de referencia regular. Las características locales de la superficie z = λ i,. a df x p = = w. a + 1 a dx ( i, ) (, ) df y q = = w. ai + 1 a dy d f r = = dx d f s = = dxdy d f t = dy con xx w,. a + a a i ( i, i, ) xy w. ai +, + ai +, + a a + ( ) yy = w. a + a a x y xx xy yy λ i, w i, w w w w,,,,,, son los coeficientes tabulados. Fig. C: Modelos de una superficie con funciones B-splines. 54 IMAGEN AÑO 9 VOL. 9 JUL-AGO MÉXICO 007
LAS LENTES PROGRESIVAS
 IMAGEN PERIODISMO CON VISIÓN COMPENDIO DE OFTÁLMICA / LAS LENTES PROGRESIVAS LAS LENTES PROGRESIVAS CAPÍTULO 1 DE 4 Fig. 1: Los présbitas una población en aumento. Introducción Desde su introducción por
IMAGEN PERIODISMO CON VISIÓN COMPENDIO DE OFTÁLMICA / LAS LENTES PROGRESIVAS LAS LENTES PROGRESIVAS CAPÍTULO 1 DE 4 Fig. 1: Los présbitas una población en aumento. Introducción Desde su introducción por
Las Lentes Progresivas
 COMPENDIO DE ÓPTICA OFTÁLMICA COMPENDIO DE ÓPTICA OFTÁLMICA LAS LENTES PROGRESIVAS Las Lentes Progresivas Copyright 2006 ESSILOR ACADEMY EUROPE, 13 rue Moreau, 75012 París, Francia - Todos los derechos
COMPENDIO DE ÓPTICA OFTÁLMICA COMPENDIO DE ÓPTICA OFTÁLMICA LAS LENTES PROGRESIVAS Las Lentes Progresivas Copyright 2006 ESSILOR ACADEMY EUROPE, 13 rue Moreau, 75012 París, Francia - Todos los derechos
TECNOLOGÍA AL SERVICIO DE TU VISIÓN
 TECNOLOGÍA AL SERVICIO DE TU VISIÓN 2 1 sedna HD En el desarrollo de lentes progresivas, es difícil decidir cuál es la mejor distribución de potencia que permita la mejor calidad de visión a todas las
TECNOLOGÍA AL SERVICIO DE TU VISIÓN 2 1 sedna HD En el desarrollo de lentes progresivas, es difícil decidir cuál es la mejor distribución de potencia que permita la mejor calidad de visión a todas las
EL TRAZADO DE RAYOS: DIFERENTES TECNICAS, SUS VENTAJAS E INCONVENIENTES.
 EL TRAZADO DE RAYOS: DIFERENTES TECNICAS, SUS VENTAJAS E INCONVENIENTES. EL TRAZADO DE RAYOS: ES EL METODO QUE SE UTILIZA PARA EL CALCULO DE MAGNITUDES OPTICAS DE UNA LENTE OFTALMICA EN POSICION DE USO.
EL TRAZADO DE RAYOS: DIFERENTES TECNICAS, SUS VENTAJAS E INCONVENIENTES. EL TRAZADO DE RAYOS: ES EL METODO QUE SE UTILIZA PARA EL CALCULO DE MAGNITUDES OPTICAS DE UNA LENTE OFTALMICA EN POSICION DE USO.
MANUAL DE LENTES PROGRESIVAS CAPÍTULO 1 L a s L e n t e s P r o g r e s i v a s
 CAPÍTULO 1 L a s L e n t e s P r o g r e s i v a s CAPÍTULO 1 Las Lentes Progresivas OBJETIVO Proporcionar al présbita una corrección adecuada a sus necesidades. Utilizar la misma gafa para todas las distancias.
CAPÍTULO 1 L a s L e n t e s P r o g r e s i v a s CAPÍTULO 1 Las Lentes Progresivas OBJETIVO Proporcionar al présbita una corrección adecuada a sus necesidades. Utilizar la misma gafa para todas las distancias.
SEDNAOFFICE OCUPACIONAL DE ALTA DEFINICIÓN
 SEDNAOFFICE OCUPACIONAL DE ALTA DEFINICIÓN 2 SEDNAOFICCE sedna HD office ha sido diseñada priorizando las zonas de visión intermedia y cerca para poder realizar cómodamente actividades con ordenador, lectura,
SEDNAOFFICE OCUPACIONAL DE ALTA DEFINICIÓN 2 SEDNAOFICCE sedna HD office ha sido diseñada priorizando las zonas de visión intermedia y cerca para poder realizar cómodamente actividades con ordenador, lectura,
Características oculares que reducen la calidad de la imagen. Aberraciones esférica y cromática.
 Tema IX. Características oculares que reducen la calidad de la imagen. Aberraciones esférica y cromática. La imagen formada por el sistema óptico del ojo no es perfecta porque el ojo sufre aberraciones
Tema IX. Características oculares que reducen la calidad de la imagen. Aberraciones esférica y cromática. La imagen formada por el sistema óptico del ojo no es perfecta porque el ojo sufre aberraciones
U N I V E R S I D A D N A C I O N A L D E L S U R 1/6
 U N I V E R S I D A D N A C I O N A L D E L S U R 1/6 DEPARTAMENTO DE: FÍSICA PROGRAMA DE: ÓPTICA OFTÁLMICA II Carreras: Tecnicatura Universitaria en Óptica HORAS DE CLASE TEÓRICAS PRÁCTICAS CÓDIGO: 3328
U N I V E R S I D A D N A C I O N A L D E L S U R 1/6 DEPARTAMENTO DE: FÍSICA PROGRAMA DE: ÓPTICA OFTÁLMICA II Carreras: Tecnicatura Universitaria en Óptica HORAS DE CLASE TEÓRICAS PRÁCTICAS CÓDIGO: 3328
TVD Digital ULTIM. Digital. Diseños de lentes progresivas
 Digital Laboratorio Óptico Premium Diseños de lentes progresivas La familia de diseños progresivos Digital Ultim representa una solución única que incorpora múltiples diseños de lentes personalizables.
Digital Laboratorio Óptico Premium Diseños de lentes progresivas La familia de diseños progresivos Digital Ultim representa una solución única que incorpora múltiples diseños de lentes personalizables.
NUEVA GAMA VARILUX CLASSIC
 NUEVA GAMA VARILUX CLASSIC Solo supera a NO TODAS LAS LENTES PROGRESIVAS SON IGUALES * INNOVACIÓN CONSUMIDOR Las lentes Varilux, inventadas en 1959, fueron las primeras lentes progresivas del mundo. Cada
NUEVA GAMA VARILUX CLASSIC Solo supera a NO TODAS LAS LENTES PROGRESIVAS SON IGUALES * INNOVACIÓN CONSUMIDOR Las lentes Varilux, inventadas en 1959, fueron las primeras lentes progresivas del mundo. Cada
POLINOMIOS DE ZERNIKE CON ABERRACIONES DE UNA ONDA. Pedro Soto López.
 POLINOMIOS DE ZERNIKE CON ABERRACIONES DE UNA ONDA Pedro Soto López. Universidad Politécnica de Tulancingo. Calle Ingenierías N.100, Huapalcalco, Hgo, México. [email protected]. Resumen Al detectar
POLINOMIOS DE ZERNIKE CON ABERRACIONES DE UNA ONDA Pedro Soto López. Universidad Politécnica de Tulancingo. Calle Ingenierías N.100, Huapalcalco, Hgo, México. [email protected]. Resumen Al detectar
PLIEGO DE PRESCRIPCIONES TÉCNICAS
 PLIEGO DE PRESCRIPCIONES TÉCNICAS EXPEDIENTE: 307 /11 OBJETO: SUMINISTRO DE LENTES GRADUADAS BIENES QUE IMPLICA EL SUMINISTRO: Lentes Correctoras graduadas, ajustadas a las características técnicas recogidas
PLIEGO DE PRESCRIPCIONES TÉCNICAS EXPEDIENTE: 307 /11 OBJETO: SUMINISTRO DE LENTES GRADUADAS BIENES QUE IMPLICA EL SUMINISTRO: Lentes Correctoras graduadas, ajustadas a las características técnicas recogidas
Física II- Curso de Verano. Clase 7
 Física II- Curso de Verano Clase 7 Formación de imágenes: ESPEJOS PLANOS Leyes de reflexión Imagen virtual, formada por la prolongación de los rayos Distancia imagen = distancia objeto d o =d i No invierte
Física II- Curso de Verano Clase 7 Formación de imágenes: ESPEJOS PLANOS Leyes de reflexión Imagen virtual, formada por la prolongación de los rayos Distancia imagen = distancia objeto d o =d i No invierte
VARILUX PHYSIO SHORT. Visión en alta resolución, ahora en monturas pequeñas
 VARILUX PHYSIO SHORT Visión en alta resolución, ahora en monturas pequeñas Diseñado específi camente para monturas pequeñas, Varilux Physio Short permite una altura mínima de 14mm, proporcionando la máxima
VARILUX PHYSIO SHORT Visión en alta resolución, ahora en monturas pequeñas Diseñado específi camente para monturas pequeñas, Varilux Physio Short permite una altura mínima de 14mm, proporcionando la máxima
DISEÑOS DE LENTES PROGRESIVOS
 DISEÑOS DE LENTES PROGRESIVOS La familia de diseños progresivos DYNAMIC ID Y HD, representa una solución única que incorpora múltiples diseños de lentes personalizables. Gracias a un amplio abanico de
DISEÑOS DE LENTES PROGRESIVOS La familia de diseños progresivos DYNAMIC ID Y HD, representa una solución única que incorpora múltiples diseños de lentes personalizables. Gracias a un amplio abanico de
PRESENTACIÓN. Evolución Tecnológica. Qué es Free-Form? Surface Power. Convencional. Limitaciones. Limitaciones. Proceso free-form.
 indice presentación monofocal free form first - perfect first perfect personalizados LOA lector personal expert personal complet personal novel LOA sport LOA drive elite FF revolution FF bifocal FF reader
indice presentación monofocal free form first - perfect first perfect personalizados LOA lector personal expert personal complet personal novel LOA sport LOA drive elite FF revolution FF bifocal FF reader
4.1Caracterización Del Ojo Normal Mexicano. Con un grupo de 71 ojos se realizó un análisis del promedio de las aberraciones de los
 Capítulo 4 Resultados y Discusión 4.1Caracterización Del Ojo Normal Mexicano Con un grupo de 71 ojos se realizó un análisis del promedio de las aberraciones de los ojos de estos pacientes. Estas personas
Capítulo 4 Resultados y Discusión 4.1Caracterización Del Ojo Normal Mexicano Con un grupo de 71 ojos se realizó un análisis del promedio de las aberraciones de los ojos de estos pacientes. Estas personas
4 Localización de terremotos
 513430 - Sismología Apl. y de Explor. 31 4 Localización de terremotos 4.1 Localización de sismos locales Fig 30: Gráfico de la ruptura en la superficie de una falla. La ruptura se propaga desde el punto
513430 - Sismología Apl. y de Explor. 31 4 Localización de terremotos 4.1 Localización de sismos locales Fig 30: Gráfico de la ruptura en la superficie de una falla. La ruptura se propaga desde el punto
La potencia concentrada en un sistema perfectamente equilibrado.
 Mr Orange Concebido para romper moldes. La generación Kappa ha supuesto una gran aportación. Mr Orange llega ahora para darle mucho más. Más funciones integradas, entre otras, lectura óptica y gestión
Mr Orange Concebido para romper moldes. La generación Kappa ha supuesto una gran aportación. Mr Orange llega ahora para darle mucho más. Más funciones integradas, entre otras, lectura óptica y gestión
Hipermetropía: concepto, clasificación, punto remoto, grado de ametropía.
 Tema VI. Hipermetropía: concepto, clasificación, punto remoto, grado de ametropía. La hipermetropía es una ametropía esférica en la que los rayos procedentes de un punto objeto distante (rayos paralelos
Tema VI. Hipermetropía: concepto, clasificación, punto remoto, grado de ametropía. La hipermetropía es una ametropía esférica en la que los rayos procedentes de un punto objeto distante (rayos paralelos
Sumario. Efectos ópticos de un prisma. Objeto binocular efectivo. Neutralización óptica con prismas en visión binocular
 Sumario Efectos ópticos de un prisma Objeto binocular efectivo Neutralización óptica con prismas en visión binocular 7-1 1. Efectos ópticos de un prisma 1 Prisma oftálmico o delgado Ángulo apical < 10
Sumario Efectos ópticos de un prisma Objeto binocular efectivo Neutralización óptica con prismas en visión binocular 7-1 1. Efectos ópticos de un prisma 1 Prisma oftálmico o delgado Ángulo apical < 10
LABORATORIO No. 0. Cálculo de errores en las mediciones. 0.1 Introducción
 LABORATORIO No. 0 Cálculo de errores en las mediciones 0.1 Introducción Es bien sabido que la especificación de una magnitud físicamente medible requiere cuando menos de dos elementos: Un número y una
LABORATORIO No. 0 Cálculo de errores en las mediciones 0.1 Introducción Es bien sabido que la especificación de una magnitud físicamente medible requiere cuando menos de dos elementos: Un número y una
BACHILLERATO FÍSICA 9. ÓPTICA GEOMÉTRICA. Dpto. de Física y Química. R. Artacho
 BACHILLERATO FÍSICA 9. ÓPTICA GEOMÉTRICA R. Artacho Dpto. de Física y Química Índice CONTENIDOS 1. Introducción a la óptica geométrica 2. Óptica de la reflexión. Espejos planos y esféricos 3. Óptica de
BACHILLERATO FÍSICA 9. ÓPTICA GEOMÉTRICA R. Artacho Dpto. de Física y Química Índice CONTENIDOS 1. Introducción a la óptica geométrica 2. Óptica de la reflexión. Espejos planos y esféricos 3. Óptica de
DEPARTAMENTO DE MATEMÁTICAS 1
 2.8. MATEMÁTICAS ACADÉMICAS 3º ESO: CONTENIDOS. Bloque 1. Contenidos comunes. Planificación del proceso de resolución de problemas: análisis de la situación, selección y relación entre los datos, selección
2.8. MATEMÁTICAS ACADÉMICAS 3º ESO: CONTENIDOS. Bloque 1. Contenidos comunes. Planificación del proceso de resolución de problemas: análisis de la situación, selección y relación entre los datos, selección
Espace Ideal Digital
 Espace Ideal Digital La tecnología digital y nuestros ojos Cada vez más, la tecnología digital cumple papeles muy importantes en nuestra vida diaria. Todos los días, nuestra mayor fuente de información,
Espace Ideal Digital La tecnología digital y nuestros ojos Cada vez más, la tecnología digital cumple papeles muy importantes en nuestra vida diaria. Todos los días, nuestra mayor fuente de información,
Tema 1. Consideraciones. CONTACTOLOGIA II María Isabel Soro Martínez Diego García Ayuso
 Tema 1. Consideraciones ópticas de las LC Introducción Objetivo adaptación LC Compensación óptica de ametropías y anisometropías. Debemos conocer: Potencia de la LC (plano de SCA). Cambios visuales respecto
Tema 1. Consideraciones ópticas de las LC Introducción Objetivo adaptación LC Compensación óptica de ametropías y anisometropías. Debemos conocer: Potencia de la LC (plano de SCA). Cambios visuales respecto
MaxView. Análisis de áreas de visión según método Sheedy* MÁS CAMPO VISUAL DE CERCA, E INVARIABLE A LOS CAMBIOS DE ADICIÓN
 www.indo.es MaxView MÁS CAMPO VISUAL DE CERCA, E INVARIABLE A LOS CAMBIOS DE ADICIÓN MaxView es una lente dentro de la familia de Progresivos FreeMax que incorpora nuevas tecnologías exclusivas de diseño
www.indo.es MaxView MÁS CAMPO VISUAL DE CERCA, E INVARIABLE A LOS CAMBIOS DE ADICIÓN MaxView es una lente dentro de la familia de Progresivos FreeMax que incorpora nuevas tecnologías exclusivas de diseño
ÓPTICA GEOMÉTRICA. ESPEJOS Y LENTES
 80 0 ÓPTICA GEOMÉTRICA. ESPEJOS Y LENTES j Actividades. Define los siguientes conceptos: dioptrio, eje óptico, radio de curvatura, imagen real y centro óptico. Dioptrio: conjunto formado por dos medios
80 0 ÓPTICA GEOMÉTRICA. ESPEJOS Y LENTES j Actividades. Define los siguientes conceptos: dioptrio, eje óptico, radio de curvatura, imagen real y centro óptico. Dioptrio: conjunto formado por dos medios
ÓPTICA GEOMÉTRICA. Teniendo en cuenta que se trata de ángulos paraxiales, la expresión se puede simplificar a: En el triángulo APC:
 ÓPTICA GEOMÉTRICA Conceptos generales: Imágenes reales. No se ven a simple vista, pero pueden recogerse sobre una pantalla. Se forman por la intersección de rayos convergentes. Imágenes virtuales. No existen
ÓPTICA GEOMÉTRICA Conceptos generales: Imágenes reales. No se ven a simple vista, pero pueden recogerse sobre una pantalla. Se forman por la intersección de rayos convergentes. Imágenes virtuales. No existen
DISTRIBUCIÓN PRIORIZADA DE ÍTEMS MATEMÁTICAS 2018
 MINISTERIO DE EDUCACIÓN PÚBLICA DIRECCIÓN DE GESTIÓN Y EVALUACIÓN DE LA CALIDAD Departamento de Evaluación Académica y Certificación Número de ítems por habilidades generales del Programa de estudio Pruebas
MINISTERIO DE EDUCACIÓN PÚBLICA DIRECCIÓN DE GESTIÓN Y EVALUACIÓN DE LA CALIDAD Departamento de Evaluación Académica y Certificación Número de ítems por habilidades generales del Programa de estudio Pruebas
7. Difracción n de la luz
 7. Difracción n de la luz 7.1. La difracción 1 7. Difracción de la luz. 2 Experiencia de Grimaldi (1665) Al iluminar una pantalla opaca con una abertura pequeña, se esperaba que en la pantalla de observación
7. Difracción n de la luz 7.1. La difracción 1 7. Difracción de la luz. 2 Experiencia de Grimaldi (1665) Al iluminar una pantalla opaca con una abertura pequeña, se esperaba que en la pantalla de observación
Procesamiento Digital de Imágenes
 Procesamiento Digital de Imágenes Unidad I (c): Percepción de imágenes Departamento de Informática - FICH Universidad Nacional del Litoral 18 de marzo de 2011 Unidad I (c): Percepción de imágenes p. 1
Procesamiento Digital de Imágenes Unidad I (c): Percepción de imágenes Departamento de Informática - FICH Universidad Nacional del Litoral 18 de marzo de 2011 Unidad I (c): Percepción de imágenes p. 1
Guía Óptica. Área de Físico-Química. 4to año 2016
 Guía Óptica Área de Físico-Química 4to año 2016 Pág. 1 de 10 Espejos Reflexión de la luz: Es el fenómeno que se observa cuando un rayo de luz incide sobre una superficie y se refleja. En este fenómeno
Guía Óptica Área de Físico-Química 4to año 2016 Pág. 1 de 10 Espejos Reflexión de la luz: Es el fenómeno que se observa cuando un rayo de luz incide sobre una superficie y se refleja. En este fenómeno
MINISTERIO DE EDUCACIÓN PÚBLICA DIRECCIÓN DE GESTIÓN Y EVALUACIÓN DE LA CALIDAD Departamento de Evaluación Académica y Certificación
 MINISTERIO DE EDUCACIÓN PÚBLICA DIRECCIÓN DE GESTIÓN Y EVALUACIÓN DE LA CALIDAD Departamento de Evaluación Académica y Certificación Número de ítems por habilidades generales del Programa de estudio Pruebas
MINISTERIO DE EDUCACIÓN PÚBLICA DIRECCIÓN DE GESTIÓN Y EVALUACIÓN DE LA CALIDAD Departamento de Evaluación Académica y Certificación Número de ítems por habilidades generales del Programa de estudio Pruebas
3.1 Ametropías Miopía
 3 A m e t r o p í a s y A l t e r a c i o n e s d e l a V isi ó n B i n o c u l a r En este capítulo se abordarán tanto los problemas de refracción, que necesitan una compensación óptica, como los más
3 A m e t r o p í a s y A l t e r a c i o n e s d e l a V isi ó n B i n o c u l a r En este capítulo se abordarán tanto los problemas de refracción, que necesitan una compensación óptica, como los más
VISIÓN y PERCEPCIÓN VISUAL
 VISIÓN y PERCEPCIÓN VISUAL PROCESO DE LA VISIÓN El ojo es la «ventana» avanzada del cerebro que comprende el bulbo del ojo y el nervio óptico. El ojo es una prolongación del sistema nervioso central que
VISIÓN y PERCEPCIÓN VISUAL PROCESO DE LA VISIÓN El ojo es la «ventana» avanzada del cerebro que comprende el bulbo del ojo y el nervio óptico. El ojo es una prolongación del sistema nervioso central que
P = potencia del componente esférico de la R = potencia del sistema lagrimal inducido por la ZOPT( en este caso PLP es cero porque r =r )
 Como el eje más plano de la lente es alineado con el meridiano más plano de la córnea, la potencia de la lente lagrimal es cero, y por lo tanto la potencia del meridiano más plano del sistema óptico compuesto
Como el eje más plano de la lente es alineado con el meridiano más plano de la córnea, la potencia de la lente lagrimal es cero, y por lo tanto la potencia del meridiano más plano del sistema óptico compuesto
ANEXO 1. CALIBRADO DE LOS SENSORES.
 ANEXO 1. CALIBRADO DE LOS SENSORES. Las resistencias dependientes de la luz (LDR) varían su resistencia en función de la luz que reciben. Un incremento de la luz que reciben produce una disminución de
ANEXO 1. CALIBRADO DE LOS SENSORES. Las resistencias dependientes de la luz (LDR) varían su resistencia en función de la luz que reciben. Un incremento de la luz que reciben produce una disminución de
ÓPTICA GEOMÉTRICA Tipos de imágenes Imagen real Imagen virtual Imágenes en los espejos planos
 ÓPTICA GEOMÉTRICA Tipos de imágenes Imagen real, es cuando está formada sobre los propios rayos. Estas imágenes se pueden recoger sobre una pantalla. Imagen virtual, es cuando está formada por la prolongación
ÓPTICA GEOMÉTRICA Tipos de imágenes Imagen real, es cuando está formada sobre los propios rayos. Estas imágenes se pueden recoger sobre una pantalla. Imagen virtual, es cuando está formada por la prolongación
NATURAL ÒPTICS MOLLERUSSA Ciutat de Lleida, Mollerussa (Lleida)
 Alteraciones visuales Lo ves todo correctamente? Aquí encontrarás una explicación de las alteraciones visuales más frecuentes. En Natural Optics, recomendamos que te hagas una revisión anual de la vista
Alteraciones visuales Lo ves todo correctamente? Aquí encontrarás una explicación de las alteraciones visuales más frecuentes. En Natural Optics, recomendamos que te hagas una revisión anual de la vista
EVOCO (Evaluador de la Visión en Ojos con Córnea Operada) *
 EVOCO (Evaluador de la Visión en Ojos con Córnea Operada) * Se propone el desarrollo de un programa informático para la evaluación del efecto de corrección de la ametropía y de la calidad de la visión
EVOCO (Evaluador de la Visión en Ojos con Córnea Operada) * Se propone el desarrollo de un programa informático para la evaluación del efecto de corrección de la ametropía y de la calidad de la visión
transparent ÓPTICA GEOMÉTRICA Prof. Jorge Rojo Carrascosa 27 de febrero de 2017
 transparent www.profesorjrc.es 27 de febrero de 2017 Conceptos Básicos 1 En medios isótropos y homogeneos, el rayo luminoso se propaga en ĺınea recta. 2 El cruce de dos o más rayos no afectan a la trayectoria.
transparent www.profesorjrc.es 27 de febrero de 2017 Conceptos Básicos 1 En medios isótropos y homogeneos, el rayo luminoso se propaga en ĺınea recta. 2 El cruce de dos o más rayos no afectan a la trayectoria.
Estadística de dos variables
 Versión: Estadística de dos variables 19 de septiembre de 013 1 Introducción En el Tema 1 se consideran las variables estadísticas unidimensionales, es decir, cada individuo de la muestra se describe de
Versión: Estadística de dos variables 19 de septiembre de 013 1 Introducción En el Tema 1 se consideran las variables estadísticas unidimensionales, es decir, cada individuo de la muestra se describe de
FACULTAD/DEPTO./CENTRO: 1. DATOS GENERALES. ÁREA/MÓDULO: Profesionales MODALIDAD: PRESENCIAL: X VIRTUAL BIMODAL 2. JUSTIFICACIÓN
 Página 1 de 5 PROGRAMA: OPTOMETRÍA PLAN DE ESTUDIOS: 4 ACTA DE CONSEJO DE 146 DE 2010 FACULTAD/DEPTO./CENTRO: ASIGNATURA/MÓDULO/SEMINARIO: ÓPTICA OFTÁLMICA I 1. DATOS GENERALES CÓDIGO: CRÉDITOS ACADÉMICO
Página 1 de 5 PROGRAMA: OPTOMETRÍA PLAN DE ESTUDIOS: 4 ACTA DE CONSEJO DE 146 DE 2010 FACULTAD/DEPTO./CENTRO: ASIGNATURA/MÓDULO/SEMINARIO: ÓPTICA OFTÁLMICA I 1. DATOS GENERALES CÓDIGO: CRÉDITOS ACADÉMICO
Mapa Curricular: Funciones y Modelos
 A.PR.11.2.1 Determina el dominio y el alcance de las funciones a partir de sus diferentes representaciones. A.PR.11.2.2 Identifica y aplica las relaciones entre los puntos importantes de una función (ceros,
A.PR.11.2.1 Determina el dominio y el alcance de las funciones a partir de sus diferentes representaciones. A.PR.11.2.2 Identifica y aplica las relaciones entre los puntos importantes de una función (ceros,
Conocimiento de Matemáticas 2º ESO. a) Contenidos.
 Conocimiento de Matemáticas 2º ESO. a) Contenidos. Bloque 1. Contenidos comunes. Planificación del proceso de resolución de problemas: análisis de la situación, selección y relación entre los datos, selección
Conocimiento de Matemáticas 2º ESO. a) Contenidos. Bloque 1. Contenidos comunes. Planificación del proceso de resolución de problemas: análisis de la situación, selección y relación entre los datos, selección
UNIDAD 1 DIBUJO TÉCNICO
 UNIDAD 1 DIBUJO TÉCNICO 1.1.- INTRODUCCIÓN 1.2.- SISTEMAS DE REPRESENTACIÓN 1.3.- SISTEMA AXONOMÉTRICO 1.4.- SISTEMA CÓNICO 1.1.- INTRODUCCIÓN GEOMETRÍA DESCRIPTIVA: Es un sistema científico que permite
UNIDAD 1 DIBUJO TÉCNICO 1.1.- INTRODUCCIÓN 1.2.- SISTEMAS DE REPRESENTACIÓN 1.3.- SISTEMA AXONOMÉTRICO 1.4.- SISTEMA CÓNICO 1.1.- INTRODUCCIÓN GEOMETRÍA DESCRIPTIVA: Es un sistema científico que permite
9. Diferenciación de funciones reales de varias variables reales Diferenciación DERIVADAS PARCIALES
 9.1. Diferenciación 9.1.1. DERIVADAS PARCIALES Derivadas parciales de una función de dos variables Se llaman primeras derivadas parciales de una función f(x, y) respecto de x e y a las funciones: f x (x,
9.1. Diferenciación 9.1.1. DERIVADAS PARCIALES Derivadas parciales de una función de dos variables Se llaman primeras derivadas parciales de una función f(x, y) respecto de x e y a las funciones: f x (x,
ÍNDICE RECUPERACIÓN DE MATEMÁTICAS 1º ESO..1 RECUPERACIÓN DE MATEMÁTICAS 2º ESO..4 RECUPERACIÓN DE MATEMÁTICAS 3º ESO..8
 ÍNDICE RECUPERACIÓN DE MATEMÁTICAS 1º ESO..1 RECUPERACIÓN DE MATEMÁTICAS 2º ESO..4 RECUPERACIÓN DE MATEMÁTICAS 3º ESO..8 RECUPERACIÓN DE MATEMÁTICAS 1º ESO CONTENIDOS Números, medidas y operaciones Números
ÍNDICE RECUPERACIÓN DE MATEMÁTICAS 1º ESO..1 RECUPERACIÓN DE MATEMÁTICAS 2º ESO..4 RECUPERACIÓN DE MATEMÁTICAS 3º ESO..8 RECUPERACIÓN DE MATEMÁTICAS 1º ESO CONTENIDOS Números, medidas y operaciones Números
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL INSTITUTO DE CIENCIAS FÍSICAS I TÉRMINO PRIMERA EVALUACIÓN DE FÍSICA D SOLUCIÓN
 ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL INSTITUTO DE CIENCIAS FÍSICAS I TÉRMINO 2011-2012 PRIMERA EVALUACIÓN DE FÍSICA D SOLUCIÓN PRIMERA PARTE: Ejercicios de opción múltiple (2 puntos c/u) 1) Un rayo
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL INSTITUTO DE CIENCIAS FÍSICAS I TÉRMINO 2011-2012 PRIMERA EVALUACIÓN DE FÍSICA D SOLUCIÓN PRIMERA PARTE: Ejercicios de opción múltiple (2 puntos c/u) 1) Un rayo
5. MODELO DE ANÁLISIS DEL CICLO TERMODINÁMICO. El método aplicado para modelar el ciclo de la Turbina se basa en el ciclo
 60 5. MODELO DE ANÁLISIS DEL CICLO TERMODINÁMICO El método aplicado para modelar el ciclo de la Turbina se basa en el ciclo Brayton para el cual se hicieron algunas simplificaciones que se especifican
60 5. MODELO DE ANÁLISIS DEL CICLO TERMODINÁMICO El método aplicado para modelar el ciclo de la Turbina se basa en el ciclo Brayton para el cual se hicieron algunas simplificaciones que se especifican
NOMBRE: 9 de FEBRERO de Evaluación de los Contenidos Teóricos impartidos durante el curso académico 2008/09
 Evaluación de los Contenidos Teóricos impartidos durante el curso académico 2008/09 Total de la Prueba 130 Puntos. /////// Total Ejercicio 40 Puntos. Pregunta Bien 4 Puntos. Pregunta Mal -2 Puntos. Pregunta
Evaluación de los Contenidos Teóricos impartidos durante el curso académico 2008/09 Total de la Prueba 130 Puntos. /////// Total Ejercicio 40 Puntos. Pregunta Bien 4 Puntos. Pregunta Mal -2 Puntos. Pregunta
Ministerio de Educación Pública Dirección de Gestión y Evaluación de la Calidad Departamento de Evaluación Académica y Certificación.
 Matemáticas Distribución de ítems para la prueba nacional Modalidad Académica (Diurnos Nocturnos) Convocatorias 016 ESTIMADO DOCENTE: En la modalidad de colegios académico, la Prueba de Bachillerato 016
Matemáticas Distribución de ítems para la prueba nacional Modalidad Académica (Diurnos Nocturnos) Convocatorias 016 ESTIMADO DOCENTE: En la modalidad de colegios académico, la Prueba de Bachillerato 016
CORRELACION Y REGRESIÓN LINEAL
 LECCION Nº 5 CORRELACION Y REGRESIÓN LINEAL OBJETIVOS ESPECIFICOS Diferenciar los conceptos de correlación lineal, y regresión lineal. Determinar el índice o coeficiente de correlación en una distribución
LECCION Nº 5 CORRELACION Y REGRESIÓN LINEAL OBJETIVOS ESPECIFICOS Diferenciar los conceptos de correlación lineal, y regresión lineal. Determinar el índice o coeficiente de correlación en una distribución
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE V
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-11--V---17 CURSO: Matemática Intermedia SEMESTRE: Segundo CÓDIGO DEL CURSO: 11 TIPO DE EXAMEN: Segundo Examen
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-11--V---17 CURSO: Matemática Intermedia SEMESTRE: Segundo CÓDIGO DEL CURSO: 11 TIPO DE EXAMEN: Segundo Examen
Funciones de Interpolación para Termómetros Digitales
 Funciones de Interpolación para Termómetros Digitales Andy Barrientos A. Laboratorio de Termometría 01. Introducción. La presentación propone considerar funciones interpoladoras del tipo polinomial; así
Funciones de Interpolación para Termómetros Digitales Andy Barrientos A. Laboratorio de Termometría 01. Introducción. La presentación propone considerar funciones interpoladoras del tipo polinomial; así
TABLA DE ESPECIFICACIONES DE HABILIDADES Y CONOCIMIENTOS QUE SE MEDIRÁN EN LAS PRUEBAS DE CERTIFICACIÓN DE BACHILLERATO.
 TABLA DE ESPECIFICACIONES DE HABILIDADES Y CONOCIMIENTOS QUE SE MEDIRÁN EN LAS PRUEBAS DE CERTIFICACIÓN DE BACHILLERATO. 1 DISTRIBUCIÓN SEGÚN HABILIDADES GENERALES ÁREA 1: GEOMETRÍA. Habilidad 1: Representar
TABLA DE ESPECIFICACIONES DE HABILIDADES Y CONOCIMIENTOS QUE SE MEDIRÁN EN LAS PRUEBAS DE CERTIFICACIÓN DE BACHILLERATO. 1 DISTRIBUCIÓN SEGÚN HABILIDADES GENERALES ÁREA 1: GEOMETRÍA. Habilidad 1: Representar
WEBS RECOMENDADAS. s1.htm
 WEBS RECOMENDADAS NÚMEROS RACIONALES E IRRACIONALES http://descartes.cnice.mec.es/3_eso/numeros_reales_aproximaciones/numero s1. Presenta los números racionales http://descartes.cnice.mec.es/3_eso/numeros_reales_aproximaciones/numero
WEBS RECOMENDADAS NÚMEROS RACIONALES E IRRACIONALES http://descartes.cnice.mec.es/3_eso/numeros_reales_aproximaciones/numero s1. Presenta los números racionales http://descartes.cnice.mec.es/3_eso/numeros_reales_aproximaciones/numero
Física 2 ByG / curso de verano 2017 Guía 2: Óptica geométrica. Dioptras, espejos, lentes delgadas e instrumentos.
 Guía 2: Óptica geométrica. Dioptras, espejos, lentes delgadas e instrumentos. A. Dioptras Espacio objeto : Espacio imagen : semi-espacio de donde viene la luz el otro semi-espacio, hacia donde avanza la
Guía 2: Óptica geométrica. Dioptras, espejos, lentes delgadas e instrumentos. A. Dioptras Espacio objeto : Espacio imagen : semi-espacio de donde viene la luz el otro semi-espacio, hacia donde avanza la
RADIACIÓN ELECTROMAGNÉTICA
 LUZ Y VISIÓN RADIACIÓN ELECTROMAGNÉTICA LUZ: ENERGIA ELECTROMAGNETICA EMITIDA DENTRO DE LA PORCION VISIBLE DEL ESPECTRO ESPECTRO ELECTROMAGNÉTICO RADIACION ULTRAVIOLETA RADIACION INFRARROJA 380-435 nm
LUZ Y VISIÓN RADIACIÓN ELECTROMAGNÉTICA LUZ: ENERGIA ELECTROMAGNETICA EMITIDA DENTRO DE LA PORCION VISIBLE DEL ESPECTRO ESPECTRO ELECTROMAGNÉTICO RADIACION ULTRAVIOLETA RADIACION INFRARROJA 380-435 nm
MÉTODOS DE PROYECCIÓN PARA LA REPRESENTACIÓN DE OBJETOS Unidad 1. El dibujo técnico en el plano
 MÉTODOS DE PROYECCIÓN PARA LA REPRESENTACIÓN DE OBJETOS Unidad 1. El dibujo técnico en el plano Las representaciones pictóricas, suelen ser las opciones más adecuadas para mostrar el producto final plasmado
MÉTODOS DE PROYECCIÓN PARA LA REPRESENTACIÓN DE OBJETOS Unidad 1. El dibujo técnico en el plano Las representaciones pictóricas, suelen ser las opciones más adecuadas para mostrar el producto final plasmado
Estéreo dinámico. Estéreo dinámico
 Estéreo dinámico 1 Vectores locales de desplazamiento Dada una secuencia de imagenes Tomadas a intervalos Movimiento absoluto: movimiento independiente de la cámara Movimiento relativo: movimiento debido
Estéreo dinámico 1 Vectores locales de desplazamiento Dada una secuencia de imagenes Tomadas a intervalos Movimiento absoluto: movimiento independiente de la cámara Movimiento relativo: movimiento debido
Lentes delgadas (aprox. paraxial + delgadas)
 Lentes delgadas (aprox. paraxial + delgadas) Formación de imágenes con lentes CONVERGENTES O POSITIVAS Objeto más allá del foco: Imagen REAL, INVERTIDA Objeto más cerca del foco: Imagen VIRTUAL, DERECHA,
Lentes delgadas (aprox. paraxial + delgadas) Formación de imágenes con lentes CONVERGENTES O POSITIVAS Objeto más allá del foco: Imagen REAL, INVERTIDA Objeto más cerca del foco: Imagen VIRTUAL, DERECHA,
Teoría de errores. 4 Otro de estos ejemplos pueden ser el de la medición de la densidad de un compuesto sólido o la velocidad de la luz.
 1. Preliminar Cuando se realizan mediciones siempre estamos sujetos a los errores, puesto que ninguna medida es perfecta. Es por ello, que nunca se podrá saber con certeza cual es la medida real de ningún
1. Preliminar Cuando se realizan mediciones siempre estamos sujetos a los errores, puesto que ninguna medida es perfecta. Es por ello, que nunca se podrá saber con certeza cual es la medida real de ningún
Laboratori de Mecànica de Fluids i Motors Tèrmics. E.U.P.M. Departament de Màquines i Motors Tèrmics. U.P.C. Prof: J.J. de Felipe
 1 TEMA 4. - ANÁLISIS DIMENSIONAL Y SEMEJANZA. 1. - Introducción. En los temas anteriores hemos analizado el comportamiento de fluidos en el ámbito de estática, en donde cualquier tipo de problema, se puede
1 TEMA 4. - ANÁLISIS DIMENSIONAL Y SEMEJANZA. 1. - Introducción. En los temas anteriores hemos analizado el comportamiento de fluidos en el ámbito de estática, en donde cualquier tipo de problema, se puede
TEMA 5.- LA LUPA (MICROSCOPIO SIMPLE)
 1/ 27 TEM 5.- L LUP (MICROSCOPIO SIMPLE) Introducción. umento visual. Distancia de visión equivalente. Potencia equivalente. Valores normalizados del aumento visual. Campo visual. Profundidad de enfoque.
1/ 27 TEM 5.- L LUP (MICROSCOPIO SIMPLE) Introducción. umento visual. Distancia de visión equivalente. Potencia equivalente. Valores normalizados del aumento visual. Campo visual. Profundidad de enfoque.
MAXIMA RVD HOJA DE PRODUCTO
 MAXIMA RVD HOJA DE PRODUCTO INDOHORIZONS is a division of: Descripción Lente progresiva Premium Plus, fabricada con FreeMax, la tecnología de talla desarrollada y patentada por Indo. Las dos características
MAXIMA RVD HOJA DE PRODUCTO INDOHORIZONS is a division of: Descripción Lente progresiva Premium Plus, fabricada con FreeMax, la tecnología de talla desarrollada y patentada por Indo. Las dos características
1. El (los) espejo(s) que puede(n) formar una imagen virtual, derecha y de igual tamaño que el objeto observado, es (son)
 Programa Estándar Anual Nº Guía práctica Ondas V: imágenes en espejos y lentes Ejercicios PSU 1. El (los) espejo(s) que puede(n) formar una imagen virtual, derecha y de igual tamaño que el objeto observado,
Programa Estándar Anual Nº Guía práctica Ondas V: imágenes en espejos y lentes Ejercicios PSU 1. El (los) espejo(s) que puede(n) formar una imagen virtual, derecha y de igual tamaño que el objeto observado,
3. Propagación n de la luz en los medios no conductores. Leyes de la reflexión y de la refracción
 3. Propagación n de la luz en los medios no conductores. Leyes de la reflexión y de la refracción 1 3. Propagación de la luz en los medios no conductores. Leyes de la reflexión y de la refracción. 2 Índice
3. Propagación n de la luz en los medios no conductores. Leyes de la reflexión y de la refracción 1 3. Propagación de la luz en los medios no conductores. Leyes de la reflexión y de la refracción. 2 Índice
SENTIDO DE LA VISTA. ADILENE ARREDONDO H. 5ª 1 Anatomía y Fisiología humana
 SENTIDO DE LA VISTA ADILENE ARREDONDO H. 5ª 1 Anatomía y Fisiología humana CUESTIONARIO 1. Qué órgano es el receptor del sentido de la vista? 2. Qué es el ojo? 3. Cuál es la función de los ojos? 4. Qué
SENTIDO DE LA VISTA ADILENE ARREDONDO H. 5ª 1 Anatomía y Fisiología humana CUESTIONARIO 1. Qué órgano es el receptor del sentido de la vista? 2. Qué es el ojo? 3. Cuál es la función de los ojos? 4. Qué
Escuela Pública Experimental Desconcentrada Nº3 Dr. Carlos Juan Rodríguez Matemática 3º Año Ciclo Básico de Secundaria Teoría Nº 2 Segundo Trimestre
 Potenciación de polinomios Para resolver la potencia de un monomio se deben aplicar las propiedades de la potenciación. n n n ab a b a) 6 x x 9x b) x x 8x c) Cuadrado de un binomio El cuadrado de un binomio
Potenciación de polinomios Para resolver la potencia de un monomio se deben aplicar las propiedades de la potenciación. n n n ab a b a) 6 x x 9x b) x x 8x c) Cuadrado de un binomio El cuadrado de un binomio
7 La teoría de rayos geométricos
 51434 - Sismología 69 7 La teoría de rayos geométricos La teoría de rayos sísmicos es análoga a la de óptica geométrica y (con la excepción de la conversión entre ondas P y SV) las reglas de ésta se aplican
51434 - Sismología 69 7 La teoría de rayos geométricos La teoría de rayos sísmicos es análoga a la de óptica geométrica y (con la excepción de la conversión entre ondas P y SV) las reglas de ésta se aplican
Pot = 6,65 D ZVN con Pot
 Hoja 2: onvergencia 1) uáles son los valores de convergencia de un sujeto miope de refracción R = -5.5 D cuando observa sin y con su neutralización óptica usual (P VP, V = 15 mm) un objeto sobre la línea
Hoja 2: onvergencia 1) uáles son los valores de convergencia de un sujeto miope de refracción R = -5.5 D cuando observa sin y con su neutralización óptica usual (P VP, V = 15 mm) un objeto sobre la línea
TEMA 4: OPTICA. Ojo normal! 4.4 El ojo como sistema óptico Características del ojo normal (emétrope): Córnea: parte protuberante del ojo
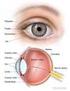 Ojo normal! Características del ojo normal (emétrope): Córnea: parte protuberante del ojo Figura 32.45 Tipler 5ª Ed. Características del ojo normal (emétrope): Córnea: parte protuberante del ojo Iris:
Ojo normal! Características del ojo normal (emétrope): Córnea: parte protuberante del ojo Figura 32.45 Tipler 5ª Ed. Características del ojo normal (emétrope): Córnea: parte protuberante del ojo Iris:
Práctica 5: El telemicroscopio
 LABORATORIO DE ÓPTICA (ÓPTICA INSTRUMENTAL) CURSO 009/10 Práctica 5: El telemicroscopio 5.1 Objetivo de la práctica El objetivo de esta práctica es el estudio y comprensión de los fundamentos ópticos del
LABORATORIO DE ÓPTICA (ÓPTICA INSTRUMENTAL) CURSO 009/10 Práctica 5: El telemicroscopio 5.1 Objetivo de la práctica El objetivo de esta práctica es el estudio y comprensión de los fundamentos ópticos del
Perspectiva óptica del material de policarbonato
 Perspectiva óptica del material de policarbonato JP Wei, Ph. D. Noviembre de 2011 Introducción Entre los materiales desarrollados para anteojos, el policarbonato tiene varias propiedades únicas y ofrece
Perspectiva óptica del material de policarbonato JP Wei, Ph. D. Noviembre de 2011 Introducción Entre los materiales desarrollados para anteojos, el policarbonato tiene varias propiedades únicas y ofrece
Metodología 3. METODOLOGÍA
 3. METODOLOGÍA En este capítulo se presenta la aplicación del método analítico para el cálculo de la irradiación por reflexión de la luz solar en la superficie de los helióstatos y la del receptor, en
3. METODOLOGÍA En este capítulo se presenta la aplicación del método analítico para el cálculo de la irradiación por reflexión de la luz solar en la superficie de los helióstatos y la del receptor, en
Regresión: implica la obtención de una ecuación mediante la que podamos estimar el valor medio de una variable.
 1 DEFINICIONES PREVIAS Regresión: implica la obtención de una ecuación mediante la que podamos estimar el valor medio de una variable. Correlación: es la cuantificación del grado de relación existente
1 DEFINICIONES PREVIAS Regresión: implica la obtención de una ecuación mediante la que podamos estimar el valor medio de una variable. Correlación: es la cuantificación del grado de relación existente
ECUACIONES EMPÍRICAS
 17 ECUACIONES EMPÍRICAS 1. OBJETIVOS 1.1 Determinar la ecuación empírica del periodo del péndulo simple 1. Desarrollar métodos gráficos analíticos para tener información del eperimento en estudio.. FUNDAMENTO
17 ECUACIONES EMPÍRICAS 1. OBJETIVOS 1.1 Determinar la ecuación empírica del periodo del péndulo simple 1. Desarrollar métodos gráficos analíticos para tener información del eperimento en estudio.. FUNDAMENTO
Bolilla 12: Óptica Geométrica
 Bolilla 12: Óptica Geométrica 1 Bolilla 12: Óptica Geométrica Los contenidos de esta bolilla están relacionados con los principios primarios que rigen el comportamiento de los instrumentos ópticos. La
Bolilla 12: Óptica Geométrica 1 Bolilla 12: Óptica Geométrica Los contenidos de esta bolilla están relacionados con los principios primarios que rigen el comportamiento de los instrumentos ópticos. La
LUZ Y VISION. agosto 2011
 LUZ Y VISION agosto 2011 RADIACIÓN ELECTROMAGNÉTICA LUZ: ENERGIA ELECTROMAGNETICA EMITIDA DENTRO DE LA PORCION VISIBLE DEL ESPECTRO ESPECTRO ELECTROMAGNÉTICO RADIACION ULTRAVIOLETA RADIACION INFRARROJA
LUZ Y VISION agosto 2011 RADIACIÓN ELECTROMAGNÉTICA LUZ: ENERGIA ELECTROMAGNETICA EMITIDA DENTRO DE LA PORCION VISIBLE DEL ESPECTRO ESPECTRO ELECTROMAGNÉTICO RADIACION ULTRAVIOLETA RADIACION INFRARROJA
LAS LENTES Y SUS CARACTERÍSTICAS
 LAS LENTES Y SUS CARACTERÍSTICAS Las lentes son cuerpos transparentes limitados por dos superficies esféricas o por una esférica y una plana, las lentes se emplean a fin de desviar las rayos luminosos
LAS LENTES Y SUS CARACTERÍSTICAS Las lentes son cuerpos transparentes limitados por dos superficies esféricas o por una esférica y una plana, las lentes se emplean a fin de desviar las rayos luminosos
2. Distancia entre dos puntos. Punto medio de un segmento
 Geometría 1 Geometría anaĺıtica Una ecuación de primer grado con dos incógnitas x e y tiene infinitas soluciones Por ejemplo x + y = 3 tiene como soluciones (0, 3), (1, ), ( 1, 4), etc Hasta ahora se han
Geometría 1 Geometría anaĺıtica Una ecuación de primer grado con dos incógnitas x e y tiene infinitas soluciones Por ejemplo x + y = 3 tiene como soluciones (0, 3), (1, ), ( 1, 4), etc Hasta ahora se han
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL INSTITUTO DE CIENCIAS FÍSICAS II TÉRMINO PRIMERA EVALUACIÓN DE FÍSICA GENERAL II SOLUCIÓN
 ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL INSTITUTO DE CIENCIAS FÍSICAS II TÉRMINO 2011-2012 PRIMERA EVALUACIÓN DE FÍSICA GENERAL II SOLUCIÓN PRIMERA PARTE: Ejercicios de opción múltiple (2 puntos c/u)
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL INSTITUTO DE CIENCIAS FÍSICAS II TÉRMINO 2011-2012 PRIMERA EVALUACIÓN DE FÍSICA GENERAL II SOLUCIÓN PRIMERA PARTE: Ejercicios de opción múltiple (2 puntos c/u)
PRODUCTO ESTUDIO SOBRE LA SATISFACCIÓN DE LOS USUARIOS DE LENTES PROGRESIVAS REALIZADO EN ESTABLECIMIENTOS ÓPTICOS
 PRODUCTO ESTUDIO SOBRE LA SATISFACCIÓN DE LOS USUARIOS DE LENTES PROGRESIVAS REALIZADO EN ESTABLECIMIENTOS ÓPTICOS Conseguir que una persona présbita se adapte a las lentes progresivas es un acto técnico
PRODUCTO ESTUDIO SOBRE LA SATISFACCIÓN DE LOS USUARIOS DE LENTES PROGRESIVAS REALIZADO EN ESTABLECIMIENTOS ÓPTICOS Conseguir que una persona présbita se adapte a las lentes progresivas es un acto técnico
Imagen retiniana: posición y tamaño.
 Tema IV. Imagen retiniana: posición y tamaño. La imagen retiniana es invertida y menor que el objeto (como son las imágenes formadas por una lente convexa) y es reinvertida psicológicamente en la corteza
Tema IV. Imagen retiniana: posición y tamaño. La imagen retiniana es invertida y menor que el objeto (como son las imágenes formadas por una lente convexa) y es reinvertida psicológicamente en la corteza
Pruebas de nivel Matemática. Primer Semestre 2016
 Pruebas de nivel Matemática Primer Semestre 2016 Nivel Contenidos Aprendizajes Esperados 5º Básico Unidad Números Naturales. Unidad Números Naturales. Lectura y escritura de números naturales. Composición
Pruebas de nivel Matemática Primer Semestre 2016 Nivel Contenidos Aprendizajes Esperados 5º Básico Unidad Números Naturales. Unidad Números Naturales. Lectura y escritura de números naturales. Composición
b) Procedimiento: 0.25 puntos. Cálculos: 0.25 puntos.
 MATEMÁTICAS II CRITERIOS ESPECÍFICOS DE CORRECCIÓN Todas las respuestas deberán estar debidamente justificadas. En todos los ejercicios, aunque el procedimiento seguido sea diferente al propuesto en el
MATEMÁTICAS II CRITERIOS ESPECÍFICOS DE CORRECCIÓN Todas las respuestas deberán estar debidamente justificadas. En todos los ejercicios, aunque el procedimiento seguido sea diferente al propuesto en el
Transformación bidimensional proyectiva (8 parámetros)
 www.topoedu.es Los mejores recursos especializados en topografía y geodesia, nunca vistos hasta ahora. Hojas técnicas de cálculo: Transformación bidimensional proyectiva (8 parámetros) Solución mediante
www.topoedu.es Los mejores recursos especializados en topografía y geodesia, nunca vistos hasta ahora. Hojas técnicas de cálculo: Transformación bidimensional proyectiva (8 parámetros) Solución mediante
MATEMÁTICAS ORIENTADAS A LAS ENSEÑANZAS APLICADAS CONTENIDOS
 MATEMÁTICAS ORIENTADAS A LAS ENSEÑANZAS APLICADAS CONTENIDOS BLOQUE 1. PROCESOS, MÉTODOS Y ACTITUDES EN MATEMÁTICAS Los contenidos de este bloque se desarrollan de forma simultánea al resto de bloques
MATEMÁTICAS ORIENTADAS A LAS ENSEÑANZAS APLICADAS CONTENIDOS BLOQUE 1. PROCESOS, MÉTODOS Y ACTITUDES EN MATEMÁTICAS Los contenidos de este bloque se desarrollan de forma simultánea al resto de bloques
PROBLEMAS DE ÓPTICA (Selectividad) FÍSICA 2º Bachillerato
 PROBLEMAS DE ÓPTICA (Selectividad) FÍSICA 2º Bachillerato 1. (Junio 1997 ) a) Describe el funcionamiento óptico de un microscopio y analiza las características de sus imágenes. Deduce la expresión de su
PROBLEMAS DE ÓPTICA (Selectividad) FÍSICA 2º Bachillerato 1. (Junio 1997 ) a) Describe el funcionamiento óptico de un microscopio y analiza las características de sus imágenes. Deduce la expresión de su
