Utilización de la fórmula de Black y Scholes. para valorar opciones
|
|
|
- Lidia Belmonte Tebar
- hace 6 años
- Vistas:
Transcripción
1 Utilización de la fórmula de Black y Scholes para valorar opciones Pablo Fernández* Profesor del IESE Titular de la Cátedra PricewaterhouseCoopers de Corporate Finance fernandezpa@iese.edu Web: RESUMEN Este documento muestra: a) cómo utilizar la fórmula de Black y Scholes para valorar opciones; b) cómo cambia el valor de la opción cuando cambian los parámetros de la opción; c) qué es la cartera réplica de la opción; d) cómo calcular la volatilidad; e) cómo afecta el ejercicio anticipado al valor de la opción; f) cómo afecta el reparto de dividendos al valor de la opción; y e) qué es la volatilidad implícita. Palabras clave: opción, put, call, volatilidad, volatilidad implícita,. JEL: G12, G31, M21 3 de abril de 28 xlhp IESE. Universidad de Navarra Camino del Cerro del Águila Madrid 1 Electronic copy available at:
2 1. Fórmula de Black y Scholes La fórmula de Black y Scholes para valorar opciones que no reparten dividendos es: C = S N(x) - K r -t -t LnS siendo [ /(Kr )] x = σ t N(x σ σ t + 2 t ) T = t Hoy Fecha de ejercicio C = Precio de la opción de compra hoy (T = ) en pesetas. t = Período de vigencia de la opción de compra. r = 1 + tasa de interés sin riesgo entre T = y t. En otras palabras, r es el número de pesetas que tendremos en t invirtiendo 1 peseta hoy en deuda sin riesgo. σ = Volatilidad anual de la acción en tanto por uno. Así, si la volatilidad de la acción es 2%, introduciremos σ =,2. K = Precio de ejercicio de la opción de compra en pesetas. S = Precio de la acción en t = en pesetas. N(x) = Valor de la función de probabilidad acumulada de una distribución normal estándar. 2. Uso de la fórmula de Black y Scholes Ya tenemos la fórmula de Black y Scholes, y ahora en esta sección vamos a ver cómo podemos utilizarla. En primer lugar, vamos a aplicar la fórmula suponiendo que tenemos todos los datos necesarios, y a continuación veremos cómo obtenemos los datos y de dónde los derivamos. Todas las operaciones incluidas en la fórmula de Black y Scholes son muy fáciles de realizar, con excepción de la función N (x). Sabemos que N (x) es una integral que no tiene una solución explícita. Sin embargo, la mayoría de los libros de estadística contienen tablas con la función de probabilidad acumulada de una distribución normal. También existen aproximaciones polinómicas a la fórmula. Describimos a continuación dos de ellas: Aproximación polinómica 1 para calcular N (x): Para x : N (x) = 1 N (x) [a1 k + a2 k2 + a3 k3], (1) donde: k = 1 / (1 + W x); W =,33267; a1 =, ; a2 =,121676; 1 e 2π a3 =,937298; x 2 / 2 N' (x) = Nótese que la fórmula es aproximada para x únicamente. Para x < debe hacerse uso de la propiedad N ( x) = 1 N (x). Esta aproximación es correcta hasta la cuarta cifra decimal. 2 Electronic copy available at:
3 Aproximación polinómica 2 para calcular N (x) Para x > : N (x) = 1 N (x) [b1 k + b2 k2 + b3 k3 + b4 k4 + b5 k5] (2) donde: k = 1 / (1 + W x); W =, ; b1 =, ; b2 =, ; 1 e 2π b3 = 1, ; b4 = 1, ; b5 = 1, ; x 2 / 2 N' (x) = Nótese que esta fórmula es también aproximada únicamente para x >. Para x < se hace uso de la propiedad N ( x) = 1 N (x). Esta aproximación es correcta hasta la sexta cifra decimal y es la que utilizamos en los cálculos que vienen a continuación. Ejemplo. Cálculo del valor de una opción de compra con 3 meses de vigor (la opción se podrá ejercer cualquier día hasta dentro de 3 meses) con precio de ejercicio de 4 pesetas. El precio de la acción hoy es 5 pesetas; la volatilidad anual esperada es del 3% (,3), y el tipo de interés sin riesgo a 3 meses anualizado es del 1%. La acción no pagará dividendos durante los próximos 3 meses. Tenemos todos los datos precisos para calcular el valor de la opción: S = 5; K = 4; σ =,3; r = 1,1 y t =,25; σ t =,15; S / K r t = 1, ; x = 1, ; x σ t = 1, ; N (x) =, ; N (x σ t) =, El valor de la opción de compra, por consiguiente, es: C = 5 x, x 1,1,25 x, = 11,8 pesetas. Estos cálculos pueden realizarse muy fácilmente con una calculadora programable o con una hoja electrónica. Ejemplo. Calcular el valor de una «call» sobre una acción de IBM que tiene un precio de ejercicio de $45 y fecha de ejercicio dentro de 156 días. La cotización actual de la acción de IBM es de $44, y la tasa de interés sin riesgo anual es 7%. La volatilidad esperada de la acción de IBM es,31. No se esperan dividendos de dicha acción durante los próximos seis meses. Aplicando la fórmula de Black y Scholes, resulta: «call» = $3, Influencia de los parámetros en el valor de la opción Al tratar de cuantificar la sensibilidad del valor de la opción respecto a la variación de alguno de los parámetros, utilizaremos las Tablas 1 a 5, y también daremos la cuantificación más matemática, que viene dada por la derivada parcial del valor de la opción con respecto a la variable que estamos examinando. Las Tablas 1, 2, 3, 4 y 5 muestran cómo cambia el valor de la opción cuando cambian los parámetros que la caracterizan. La Tabla 1 es la tabla base a la que irán referidas las demás. Nótese cómo en la Tabla 1, para el tipo de interés igual a 1% y el precio de ejercicio de 4 pesetas, el valor de la «call» es 11,8, como habíamos obtenido anteriormente. 3
4 Tabla 1. Valores de distintas opciones de compra (El valor de la opción se calcula utilizando la fórmula de Black y Scholes) r K 1,3 1,5 1,1 1,15 1,2 3 22,21 23,64 27,7 21,3 213, ,74 16,51 11,8 114,88 118, ,66 32,84 35,8 38,76 41,7 6 4,91 5,23 6,5 6,94 7,88 7,44,48,59,72,86 S = 5 pesetas; t =,25 años; σ =,3 Tabla 2. Valores de distintas opciones de compra (El valor de la opción se calcula utilizando la fórmula de Black y Scholes) r K 1,3 1,5 1,1 1,15 1,2 3 24,58 27,38 214,7 22,32 226, ,4 115,24 123,3 13,48 137, ,69 48,3 53,92 59,87 65, ,7 15,15 18,2 21,11 24,4 7 3,5 3,86 4,87 6,2 7,32 S = 5 pesetas; t =,5 años; σ =,3 1. t, tiempo hasta la fecha de ejercicio La única diferencia entre las Tablas 1 y 2 es el tiempo hasta la expiración. Las opciones de la Tabla 1 tienen un tiempo hasta la expiración de tres meses, mientras que las opciones de la Tabla 2 tienen un tiempo hasta la expiración de 6 meses. Nótese cómo el precio de las opciones de la Tabla 2 es superior al precio de las opciones de la Tabla 1 con iguales características (excepto el tiempo hasta la expiración). Este resultado es acorde con la intuición de que una opción tendrá más valor cuanto mayor sea su período de vigencia. Para una cuantificación más exacta de cómo cambia el precio de la opción con respecto al tiempo hasta la expiración, necesitamos calcular la derivada parcial de la fórmula de Black y Scholes con respecto al tiempo, la cual viene dada por la expresión 1 : C S σn' (x) Kr - t = + Ln(r) N(x σ t) > t 2 t Nótese como: cuando t >, entonces C > MAX [S K, ]; cuando t >, entonces C > S. Demostración: Si t = ; entonces r t = 1, y 1 Se suele denominar Theta = C / t. 4
5 x = lim [Ln (S) Ln (K) + t Ln (r) +,5 σ 2 t] / [σ t] t > = + si S > K = si S < K N (+ ) = 1 y N ( ) =. Por tanto: C = S K si S > K, y C = si S < K. Si t = ; entonces r =, y x = lim [Ln (S) Ln (K) + t Ln(r) +,5 σ 2 t] / [σ t] =. Como N ( ) = 1, C = S. t > 2. r, tasa de interés En todas las Tablas vemos cómo el precio de la opción aumenta cuando aumenta el tipo de interés. La intuición detrás de esto es muy sencilla: el valor actual neto del precio de ejercicio es menor cuanto mayor es el tipo de interés y, por consiguiente, mayor es el precio de la opción de compra. Para cuantificar más exactamente la variación del precio de la opción cuando varía la tasa de interés, hacemos la derivada parcial de la fórmula de Black y Scholes con respecto al tipo de interés 2 : C - t 1 = t Kr Ln(r) N(x σ t) > r Cuando r >, entonces C > S. Demostración: cuando r >, x > y N (x) = 1. Igualmente: Cuando r >, r t >. Por tanto: C > S. La intuición detrás de este resultado es que cuando el tipo de interés tiende a infinito, el valor actual neto del precio de ejercicio es cero, con lo cual el valor de la opción será igual al precio de la acción. 3. K, precio de ejercicio En las Tablas 1 a 4 podemos observar cómo el precio de la opción disminuye cuando aumenta el precio del ejercicio. Este resultado es intuitivamente evidente, puesto que cuanto más tengamos que pagar por la misma acción en la fecha de ejercicio, menor será el precio de la opción correspondiente. La cuantificación más exacta de la variación del precio de la opción cuando cambia el precio del ejercicio viene dada por: C = - r -t N(x σ t) < K Cuando K >, entonces C > S; y cuando K >, entonces C >. Demostración: cuando K =, entonces x =, porque Ln () = ; N ( ) = 1 y C = S. Cuando K =, entonces x =, N ( ) =. Por otro lado; lim K N ( ln K) =. Por consiguiente C >. K > 2 Se suele denominar Rho = C / r. 5
6 La intuición detrás de estos resultados es la siguiente: cuando K =, no hemos de pagar nada para hacernos con una acción en el futuro. Como el valor actual neto del precio de la acción en la fecha de ejercicio es el precio de la acción hoy, es claro que una opción de compra es equivalente a poseer una acción y, por tanto, C = S. Cuando K tiende a infinito, quiere decir que hemos de pagar una cantidad en la fecha de ejercicio, que con seguridad será superior al precio de la acción; por consiguiente, nunca ejerceremos esa opción, por lo cual su valor es cero. 4. σ, volatilidad La única diferencia entre la Tabla 3 y la 1 es la volatilidad de la acción. La Tabla 3 es 5%, mientras que la Tabla 1 es 3%. Podemos observar cómo el precio de la opción es mayor cuanto mayor es la volatilidad. Una volatilidad mayor implica una mayor probabilidad de valores altos y valores bajos de la acción en la fecha de ejercicio. Comoquiera que el poseedor de la opción no está obligado a ejercitarla, esto quiere decir que se beneficiará de la probabilidad mayor de valores altos o se verá perjudicado por la probabilidad mayor de valores más bajos en el precio de la acción; por consiguiente, una mayor volatilidad implica un mayor precio de la opción. Tabla 3. Valores de distintas opciones de compra (El valor de la opción se calcula utilizando la fórmula de Black y Scholes) r K 1,3 1,5 1,1 1,15 1,2 3 22,88 24,27 27,62 21,79 213, ,63 115,14 118,79 122,3 125, ,42 52,53 55,26 57,94 6, ,42 2,1 21,5 22,99 24,49 7 6,44 6,7 7,35 8,1 8,69 S = 5 pesetas; t =,25 años; σ =,5 Para cuantificar más exactamente la variación el precio de la opción cuando se produce un cambio en la volatilidad, derivamos la expresión de Black y Scholes con respecto a la volatilidad 3 : C =S t N'(x) > σ Cuando σ >, entonces C > Max [S K r t, ] Cuando σ >, entonces C > So. Demostración: Si σ =, entonces: x = + si S > K r t y = si S < K r t. Por tanto, N (x) = 1 si So > K r t = si So < K r t, y C = Max [So K r t, ] Si σ >, entonces x > + y x + σ t >. Como N ( ) = 1 y N ( ) =, entonces C = So. 3 Se suele denominar Vega = C / σ. 6
7 Cuando la volatilidad de la acción es cero, podemos considerar la acción como un instrumento de renta fija, ya que si σ =, la acción carece de riesgo. El valor actual neto del precio a pagar en la fecha de ejercicio es K r -t, y el valor actual neto del precio de la acción en la fecha de ejercicio es, por definición, el precio de la acción hoy; por consiguiente: C = Max [S K r -t, ]. Cuando la volatilidad tiende a infinito, el precio de la opción tiende hacia el precio de la acción, porque su valor actual neto del precio de ejercicio pasa a ser insignificante con respecto al valor actual neto del precio de la acción en la fecha de ejercicio. 5. S, precio de la acción En la Tabla 4 hemos incrementado el precio de la acción con respecto a la Tabla 1. Nótese cómo el precio de la opción es superior en la Tabla 4. La intuición detrás de este resultado es que siendo todas las demás características iguales, cuanto mayor es el precio de la acción hoy mayor es la probabilidad de que sea también mayor el precio de la acción en la fecha de ejercicio. Tabla 4. Valores de distintas opciones de compra (El valor de la opción se calcula utilizando la fórmula de Black y Scholes) r K 1,3 1,5 1,1 1,15 1,2 3 32,21 33,64 37,6 31,3 313, ,1 24,91 29,46 213,77 217, ,69 19,8 114,92 119,82 124, ,99 39,41 42,96 46,51 5,4 7 8,39 8,89 1,19 11,57 13,2 S = 6 pesetas; t =,25 años; σ =,3 La expresión de la derivada parcial de la fórmula de Black y Scholes con respecto al precio de la acción tiene mucha importancia en la construcción de una cartera réplica, como veremos más adelante, y se denomina delta. Delta = = C / S = N (x) > Cuando S >, entonces C > y > Cuando S >, entonces C > y > 1. Demostración: cuando S >, entonces x > porque Ln () =. Por tanto, C =. Cuando S >, entonces x > + y C >. Cuando el valor de la acción tiende a cero (la empresa está en quiebra), entonces el precio de la opción de compra también es, lógicamente, cero. Cuando el valor de la acción tiende a infinito, el valor actual neto del precio del ejercicio es una cantidad despreciable con respecto al precio de la acción y, por consiguiente, el precio de la opción tiende también a infinito. 7
8 Tabla 5. Valores de una «call» (pesetas) según la fórmula de Black y Scholes) r = 1,1; K = 5 pesetas; σ = 3% t S (pesetas) 1 mes 3 meses 6 meses 12 meses 24 meses,833 años,25 años,5 años 1, año 2, años 2,,,,8 2,14 25,,,2,87 7,78 3,,1,41 4,16 19,18 35,,29 2,79 12,58 37,26 4,8 2,83 1,57 28,19 61,9 45 2,67 12,97 27,21 51,68 92, ,25 35,8 53,92 82,46 127, ,53 71,2 89,43 119,18 166,6 6 14,19 114,92 131,27 16,36 28, ,97 162,69 177,3 24,68 252, ,96 212,1 224,96 251,1 298, ,96 261,83 274,1 298,88 345, ,96 311,79 323,58 347,52 392,94 La Tabla 5 nos muestra la variación del precio de una opción cuando cambia el precio de la acción y el tiempo hasta el ejercicio. Los resultados son los apuntados ya anteriormente. La Figura 1 muestra la representación gráfica de la Tabla 5. Figura 1. Valor de una opción de compra según la fórmula de Black y Scholes r = 1,1; K = 5 pesetas; Volatilidad = 3% t = 24 meses 25 C Valores intermedios: 1, 3, 6 y 12 meses t = S (pesetas) En la Figura 2 se observa la evolución creciente del valor de la opción de compra europea a medida que mayor es el tiempo que transcurre hasta el ejercicio de la misma. También se puede ver 8
9 que, para un número determinado de meses hasta el vencimiento, el valor de la opción de compra es mayor conforme menor es el precio de ejercicio. Figura 2. Valor de una «call» según la fórmula de Black y Scholes S = 5 pesetas; r = 1,1; Volatilidad= 3% La línea intermedia corresponde a una «call at the money» (K = 5) 2 K = 4 15 C 1 5 K = 5 K = Tiempo hasta el ejercicio (meses) Precisamente, la Figura 3 muestra también cómo afecta, en términos de menor valor de la opción de compra, el hecho de ir aumentando el precio de ejercicio de la misma. También se observa que, dado un determinado precio de ejercicio, la opción de compra a la que le falta más tiempo hasta el vencimiento es la que tiene un mayor valor. Figura 3. Valor de una «call» europea según la fórmula de Black y Scholes S = 5 pesetas; σ = 3%; r = 1, C t = 1 año 4 t = 1 mes t = 3 meses K (pesetas) La Figura 4 muestra la diferencia entre el precio de dos opciones que son iguales en todos sus parámetros, excepto en el precio de ejercicio. Una de ellas tiene el precio de ejercicio de 5 ptas., y otra, de 6 ptas. Nótese cómo siempre la opción con precio de ejercicio de 5 ptas. tiene un valor superior al de la opción con precio de ejercicio de 6 ptas. 9
10 Figura 4. Valor de una «call» según la fórmula de Black y Scholes r = 1,1; t = 6 meses; Volatilidad =,3 C K = K = S (pesetas) La Figura 5 nos muestra los valores correspondientes a tres opciones que difieren únicamente en la volatilidad de la acción a la que se refiere; las volatilidades son,2,,4 y,6. Nótese cómo cuanto mayor es la volatilidad, mayor es el precio de la opción si consideramos los demás parámetros constantes. Figura 5. Valor de una «call» según la fórmula de Black y Scholes r = 1,1; K = 5 pesetas; t = 6 meses C σ =,6 σ =, S (pesetas) La Figura 6 muestra la evolución en el valor de una opción de compra en relación a la volatilidad de la acción a la que se refiere: cuanto mayor es la volatilidad, mayor es el valor de la opción. Nótese que la influencia de la volatilidad es mayor conforme mayor es el precio de ejercicio de la opción. 1
11 Figura 6. Valor de una «call» europea según la fórmula de Black y Scholes S = 5 pesetas; r = 1,1; t = 6 meses C K = 4 K = 5 K = 6 % 1% 2% 3% 4% 5% 6% 7% 8% Volatilidad La Figura 7 muestra la influencia del tipo de interés en el valor de la opción de compra. Nótese de nuevo cómo cuanto mayor es el tipo de interés, mayor es el valor de la opción de compra Figura 7. Valor de una «call» según la fórmula de Black y Scholes t = 6 meses; K = 5 pesetas; Volatilidad =,3 C 2 r = 1, La línea intermedia corresponde a r =1,1 r = 1, S (pesetas) En la Figura 8 también se observa la forma en la que afecta el tipo de interés al valor de la opción de compra: éste crece conforme aumenta el tipo de interés, siendo el incremento más acusado conforme menor es el precio de ejercicio de la opción. 11
12 Figura 8. Valor de una «call» europea según la fórmula de Black y Scholes S = 5 pesetas; t = 6 meses; σ = 3% C K = 4 r K = 5 K = 6 1, 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 4. Cartera réplica equivalente a la opción de compra La derivación de la fórmula de Black y Scholes se basa en que es posible formar una cartera con acciones y bonos que constituye una perfecta réplica de una opción de compra. Esta cartera se ha de ir modificando según cambia el valor de la acción, y también con el transcurso del tiempo. La cartera réplica de una opción de compra está compuesta en todo momento por acciones y por dinero prestado, o, lo que es lo mismo, bonos vendidos a crédito 4. Es importante señalar de nuevo que con las hipótesis bajo las que se ha derivado la fórmula de Black y Scholes, la cartera réplica es factible de construirse. Cartera réplica de una opción de compra de valor C y parámetros K, t, r, σ y S Una opción de compra = cartera réplica compuesta por: acciones y B pesetas prestadas 5 a devolver en t, en todo momento, donde: = C / S = N (x), y B = K r t N (x σ t) Nótese cómo cuando S >, entonces > 1 y >, entonces >. La Figura 9 muestra el valor de en función del precio de la acción. La Figura nos permite ver cómo aunque no se modifique el precio de la acción la de una opción varía con el paso del tiempo. 4 Alternativamente, la cartera réplica puede construirse con bonos y «forwards». Un «forward» es equivalente a comprar una acción con dinero prestado. Por ello, la cartera réplica puede construirse comprando inicialmente algunos bonos y contratos «forward». Posteriormente, basta ir modificando el número de «forwards» para replicar la opción. 5 Tomar prestadas B pesetas es equivalente a vender a crédito bonos cupón cero (o pagarés) que caducan en t y que tienen un valor nominal de K N (x σ t). 12
13 Figura 9. Delta de una opción de compra según la fórmula de Black y Scholes r = 1,1; K = 5 pesetas; Volatilidad =,3 Delta 1,,9,8,7,6 t = 24 meses,5,4 t = 1 mes,3,2,1 Valores intermedios: 3, 6 y 12 meses, S (pesetas) En la Figura 1 se observa la evolución de la según el tiempo que falta hasta el ejercicio de la opción. También se observa que, dado un número determinado de meses hasta el ejercicio, el valor de la es mayor conforme menor es el precio de ejercicio. No obstante, los valores de la según diferentes precios de ejercicio empiezan siendo muy dispares cuando el tiempo hasta el ejercicio es escaso, mientras que acaban convergiendo dentro de un rango cuando el número de meses hasta el ejercicio es elevado. Figura 1. Delta de una «call» europea según la fórmula de Black y Scholes S = 5 pesetas; r = 1,1; σ = 3% Delta 1,,9,8,7,6,5,4,3,2,1, K = 4 K = 5 K = Tiempo hasta el ejercicio (meses) La Figura 11 muestra cómo afecta al valor de la el tipo de interés. Nótese que la influencia del incremento en el tipo de interés en el valor de la es mayor conforme mayor es el precio de ejercicio de la opción. 13
14 Figura 11. Delta de una «call» europea según la fórmula de Black y Scholes S = 5 pesetas; t = 6 meses; σ = 3% Delta 1,,9,8,7,6,5,4,3,2,1, K = 4 K = 5 K = 6 1, 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 r En la Figura 12 se observa la influencia de la volatilidad de las acciones que componen la cartera y del precio de ejercicio de la opción de compra en el valor de la. Mientras que para valores reducidos de volatilidad hay una gran dispersión entre la según sea el precio de ejercicio, a medida que aquellos empiezan a ser elevados se produce una convergencia en los valores de la. Delta Figura 12. Delta de una «call» europea según la fórmula de Black y Scholes S = 5 pesetas; t = 6 meses; r = 1,1 1,,9,8,7,6,5,4,3,2,1, K = 4 K = 5 K = 6 % 1% 2% 3% 4% 5% 6% 7% 8% Volatilidad 14
15 La Figura 13 muestra la evolución del valor de la de una opción de compra según sea el precio de ejercicio de la misma. Nótese que, según se reduce el tiempo que falta hasta el ejercicio, la tendencia se va acentuando. Delta Figura 13. Delta de una «call» europea según la fórmula de Black y Scholes S = 5 pesetas; σ = 3%; r = 1,1 1,,9,8,7,6,5,4,3,2,1, t = 1 mes t = 1 año t = 3 meses K (pesetas) La Figura 14 muestra el impacto de la volatilidad en la de una opción. 1, Figura 14. Delta de una «call» según la fórmula de Black y Scholes r = 1,1; K = 5 pesetas; t = 6 meses,8 Delta,6,4 Volatilidad = 1,2.5 Volatilidad =,2, Se define Gamma (Γ) de una opción como la derivada de delta con respecto al precio de la acción 6. Nótese que gamma indica el número de acciones en que hemos de variar la cartera réplica cuando el precio de la acción varía en una peseta. Γ = 2 C / S 2 = / S = N (x) / (S σ t) S (pesetas) 6 Es también la segunda derivada parcial del precio de la opción con respecto al precio de la acción. 15
16 La elasticidad de una opción (Ω) es el cambio porcentual en el valor de la opción cuando el precio de la acción cambia en 1%, y se calcula: Ω = [ C / S] / [C / S] = [ C / C] / [ S / S] = S / C = N (x) S / C. 5. Parámetros necesarios para calcular el precio de una opción Para utilizar la fórmula de Black y Scholes (o el método binomial) necesitamos conocer cinco parámetros: el precio de la acción, S; el precio de ejercicio, K; el tiempo hasta la fecha de ejercicio, t; el tipo de interés sin riesgo, r, y la volatilidad, σ. Los tres primeros parámetros son directamente observables, y uno más el tipo de interés (r) es también casi directamente observable, pero hemos de hacer la salvedad siguiente: r = 1 + R, siendo R interés anual. Por ejemplo, si el tipo de interés es del 1%, entonces R =,1 y r = 1,1. Un ejemplo. Supongamos que un pagaré del Estado que da derecho a su poseedor a cobrar 1 pesetas dentro de 6 meses (182 días) se puede comprar hoy por 95 pesetas. Si estamos interesados en calcular el precio de una opción que se puede ejercitar el mismo día que vence el pagaré, calcularemos r del siguiente modo: t = 182 / 365 =,49863; r t =,95; r =,95 1/t =,95 1/,49863 = 1,183 Nos queda únicamente estimar la volatilidad de la acción a la que se refiere la opción. Hay que notar que la volatilidad relevante que es la que hemos incluido en la fórmula de Black y Scholes es la volatilidad entre momento actual y el día en que expira la opción. Sin embargo, en muchas ocasiones se utiliza la volatilidad histórica como una estimación de la futura volatilidad. Esto será apropiado cuando no se prevea en el futuro ninguna alteración sustancial que haga pensar que el período que tenemos por delante sea distinto (en términos de volatilidad) que el período histórico sobre el que estamos midiendo la volatilidad. Para medir la volatilidad histórica hemos de precisar sobre qué período la hemos de medir. La regla más común es tomar un período histórico de duración igual al período de vigencia de la opción. Veamos cómo se calcula la volatilidad con un ejemplo. Supongamos que estamos interesados en calcular el precio de una opción con 2 semanas hasta la fecha de ejercicio. Por tanto, estimaremos la volatilidad de la acción en las 2 semanas anteriores. En la Tabla 6 hacemos el ejercicio con precios semanales, pero se podría hacer exactamente igual con precios diarios. La columna (1) de la Tabla 6 es el precio de la acción. Hay que tener en cuenta que si la acción pagó algún dividendo a lo largo de estas 2 semanas, éste se ha de sumar a la cotización. Del mismo modo, habría que ajustar la cotización si hubiese habido una ampliación de capital. La columna (2) es el precio de la acción de la semana dividido por el precio de la semana anterior. La columna (3) es el logaritmo neperiano de la columna (2), esto es, el rendimiento semanal de la acción. La volatilidad anual es precisamente la desviación estándar del rendimiento de la acción en un año. La varianza es el cuadrado de la desviación estándar. La estimación sin sesgo de la varianza semanal de R t viene dada por la expresión 7 : (R t µ) 2 / 19 =,1849 donde µ es la media de R t, esto es: (R t ) / 2 =,9563, con lo cual la estimación de la varianza anual es: 52 x,1849 =, La volatilidad anual es la raíz cuadrada de esta cantidad, esto es:, Aunque el estimador de máxima verosimilitud de la varianza es (R t µ) 2 / n, este estimador resulta sesgado. 16
17 Tabla 6. Cálculo de la volatilidad de una acción Semana S t D t = S t /S t-1 R t = Ln(D t ) R t µ (R t µ) 2 (1) (2) (3) (4) (5) ,961538,39221,48784, ,8,7968,1595, ,22222,21979,12416, ,74534,71887,62324, ,98414,1624,25586, ,96352,4455,518, ,39755,38985,29423, ,933824,68468,7831, ,86614,8367,7354, ,4229,4117,3167, ,1391,139,8173, ,,,9563, ,13889,13793,4231, ,53425,5246,42484, ,928479,7428,83771, ,39216,38466,2893, ,99566,9479,1942, ,21769,21535,11972, ,51931,5627,4164, ,99623,385,13367,1787 Suma 2,2984,191256, Media 72,7619 1,1492,9563 Desviación estándar semanal =,435 (Varianza semanal =,1849) Varianza anual =,96168 Desviación estandar anual =,3111 = Volatilidad anual = 31,11% 6. Razones por las que el modelo es muy exacto Llegado a este punto, es probable que el lector esté pensando que la derivación del modelo es un interesante ejercicio matemático, pero que las hipótesis en que se basa son muy poco realistas. Una de las hipótesis era que no existían comisiones ni impuestos diferenciales. Esta puede ser una hipótesis no muy plausible para un pequeño inversor particular, pero ciertamente lo es para los grandes inversores, que son los que al final fijan las cotizaciones, pues son los que pueden aprovechar el arbitraje en bandas más estrechas. La segunda hipótesis asumía que se puede tomar prestado e invertir dinero a la tasa de interés sin riesgo. Esta no es una hipótesis que se aleje de la realidad para los mayores inversores. La tercera hipótesis es que la tasa de interés r es conocida y constante durante la vida de la opción. Aunque sabemos que la tasa de interés varía, el permitir que la tasa de interés sea aleatoria introduce una pequeña y despreciable variación. Las hipótesis de mercado continuo y del movimiento supuesto para el precio de la acción vienen determinadas por la distribución logarítmico normal que hemos supuesto para el precio de la acción. Hay tres factores que hacen que el precio de la acción evolucione de modo ligeramente distinto que en la distribución logarítmico normal: 17
18 1. La volatilidad no es constante, sino que es inversamente proporcional al precio de la acción. 2. Se producen cambios aleatorios en la volatilidad. 3. De todos es sabido que el precio de las acciones se mueve en ocasiones a saltos. Afortunadamente, estos tres efectos tienden a amortiguarse mutuamente, con lo que el efecto conjunto de los tres es despreciable. El efecto 1 causa infravaloración para aquellas opciones en las que el precio de la acción es sensiblemente menor que el precio de ejercicio de la opción, y sobrevaloración para aquellas opciones en las que el precio de ejercicio es sensiblemente menor al precio de la acción. Los factores 2 y 3 producen sobrevaloración para opciones con precio de ejercicio superior al valor de la acción e infravaloración (normalmente) para aquellas opciones cuyo precio de ejercicio es menor que el precio de la acción. En general, el modelo de Black y Scholes es un modelo muy útil y muy exacto. Para el caso en que la acción a la que se refiere la opción pague dividendos durante la vida de la opción, hay dos procedimientos para ajustar el valor. El procedimiento menos exacto es seguir utilizando la fórmula de Black y Scholes y ajustar el parámetro S: en lugar de introducir el precio de la acción, introduciremos el precio de la acción menos el valor actual neto de los dividendos que esperamos que pague la acción durante el período de vigencia de la opción. Hay otro método que es exacto y que consiste en el empleo del método binomial. De cualquier modo, las divergencias entre estos dos métodos son cuando el tiempo hasta el ejercicio no es muy grande muy pequeñas. 7. Ejercicio anticipado de la opción La fórmula de Black y Scholes supone que la opción nunca se ejercerá antes de la fecha de ejercicio. En caso de ser una opción europea, esto viene obligado por las características del contrato. En caso de ser una opción americana sobre una acción que no reparte dividendos, ya hemos visto que la fecha óptima de ejercicio de la «call» es la fecha de ejercicio: en cualquier momento anterior al mismo, es preferible vender la opción en el mercado secundario a ejercitarla. El ejercicio anticipado de la «call» puede ser racional, únicamente, en el caso en que la acción reparta dividendos. En este caso, puede ser óptimo ejercitar la «call» el día inmediatamente anterior al reparto del dividendo. De nuevo podemos utilizar dos métodos para estudiar la posibilidad del ejercicio anticipado. El primero consiste en evaluar la opción según la fórmula de Black y Scholes con el tiempo comprendido entre hoy y la fecha en que la acción vaya a repartir el dividendo, sin hacer ningún ajuste en S, y valorar la opción entre hoy y la fecha de ejercicio haciendo el ajuste indicado de dividendos en S, esto es, restando a S el valor actual neto de los dividendos esperados durante el período de vigencia de la opción. Si el primer valor resulta superior al segundo, entonces puede ser óptimo el ejercicio anticipado. El segundo procedimiento más exacto es utilizar la fórmula binomial. De nuevo y salvo que la opción tenga una larga duración (superior a un año) o que los dividendos sean muy elevados las dos fórmulas producen resultados muy similares. 18
19 8. Comprobación empírica de la fórmula de Black y Scholes. Fórmulas alternativas Desde que Black y Scholes dieron a conocer su popular fórmula, numerosos estudiosos han publicado investigaciones tratando de comprobar si los precios de mercado se ajustan a la fórmula. El primer estudio fue publicado por Galai, en 1977; posteriormente, Trippi, Manaster y muchos otros publicaron estudios tratando de comprobar la posibilidad de conseguir beneficios extraordinarios utilizando estrategias de compra y venta de opciones utilizando la fórmula de Black y Scholes. Todos estos estudios originales tuvieron algunos errores técnicos que fueron resueltos por Rubistein en La conclusión general es que el modelo de Black y Scholes nos proporciona una herramienta extremadamente valiosa y precisa para calcular los precios de las opciones, y que ninguno de los otros modelos desarrollados con posterioridad para valorar las opciones lo mejora sustancialmente. Se han desarrollado muchas fórmulas alternativas a la de Black y Scholes para valorar opciones. La mayoría de ellas surgen de considerar que el precio del activo subyacente no evoluciona como supone la fórmula de Black y Scholes 8, sino de otro modo. Cox y Ross (1976) derivaron fórmulas alternativas según que el movimiento del subyacente siguiera un proceso de difusión, un proceso de saltos o un proceso con elasticidad de la varianza constante 9. Merton (1976) propuso un proceso de saltos con difusión. Merton (1973) fue el primero en desarrollar fórmulas suponiendo los tipos de interés aleatorios. Hull y White (1987), Johnson y Shanno (1987), Scott (1977) y Wiggins (1987) publicaron fórmulas de valoración con volatilidad del subyacente aleatoria. En las revistas especializadas siguen apareciendo fórmulas de valoración para distintas hipótesis sobre el movimiento del subyacente. Como es evidente que la volatilidad del subyacente no es constante, muchos investigadores dedicaron sus esfuerzos a desarrollar métodos de valoración (la mayoría numéricos) de opciones con volatilidad aleatoria. De aquí surgen los métodos denominados ARCH («autoregressive conditional heteroskedasticity») y GARCH («generalized autoregressive conditional heteroskedasticity») 1. Se han realizado muchos test para ver si estos modelos valoran mejor las opciones que la fórmula de Black y Scholes, casi siempre comparando los resultados con los precios de mercado, pero los resultados no son concluyentes y todavía la fórmula de Black y Scholes (o el método binomial o la simulación con volatilidad constante) sigue siendo la más utilizada. En lo que respecta a opciones sobre divisas, Melino y Turnbull (1995) ofrecen un trabajo muy interesante que compara la fórmula de Black y Scholes (utilizando la volatilidad histórica o la volatilidad implícita) con otra fórmula con volatilidad aleatoria. Lo interesante del artículo radica (más que en las conclusiones a que llegan) en que realizan la comparación de las dos fórmulas en base al ajuste de las carteras réplicas asociadas a ambas fórmulas Opción de venta («put») Podemos obtener el valor y las propiedades de una opción de venta europea a partir de los de la opción de compra análoga y haciendo uso de la «put-call parity»: C = S + P K r t La fórmula de Black y Scholes para valorar opciones de venta europeas viene dada por: 8 Volatilidad constante, tipo de interés constante, sin saltos. 9 Cox y Rubinstein (1985), en las páginas 36-37, exponen con claridad estas fórmulas. 1 Véase artículos de Engle y Mustafa (1992), y Kang y Brorsen (1995). 11 Una buena recopilación de la literatura financiera sobre este tema se encuentra en Bates, David S., «Testing Option Pricing Models», Wharton,
20 C = K r -t N(w + σ -t LnKr / S σ t t ) σ t 2 siendo [ ] w= = - x - S N(w) Es importante recordar que debido a la posibilidad de ejercicio óptimo anticipado, el valor de una «put» americana es siempre superior al de una «put» europea con idénticas características. Para S =, w =, y la «put» europea vale P = K r t. La «put» americana vale K. Las Tablas 7, 8, 9, 1 y 11 muestran cómo cambia el valor de una opción de venta europea cuando cambian los parámetros que la caracterizan. Estas Tablas, y las Figuras 15 a 22, permiten comprobar cómo los parámetros afectan el valor de una «put». Podemos escribir más precisamente la sensibilidad del valor de una «put» europea al cambio en el valor de sus parámetros. La Figura 15 muestra cómo el valor de una «put» puede aumentar o disminuir cuando aumenta el tiempo hasta la fecha de ejercicio: P / t = C / t K r t Ln (r) > = <. En las Figuras 16 y 17 se observa la evolución del valor de la opción de venta cuando varía el precio de ejercicio y el tiempo que falta hasta el mismo. Se puede apreciar cómo el valor de la «put» aumenta cuando lo hace el precio de ejercicio. La Figura 18 muestra cómo el valor de una «put» aumenta cuando aumenta el precio de ejercicio: P / K = C / K + r -t = r -t [1 N (x σ t)] >. La Figura 19 muestra cómo el valor de una «put» aumenta cuando aumenta la volatilidad de la acción a que se refiere: P / σ = C / σ = S t N (x) >. En la Figura 2 se observa la relación entre el valor de la «put» y la volatilidad: la «put» vale más conforme mayor es la volatilidad de la acción subyacente. La Figura 21 muestra cómo el valor de una «put» disminuye cuando aumenta el tipo de interés: P / r = [ C / r] t K r -t-1 = t K r -t-1 [N (x σ t) 1] <. En la Figura 22 se puede apreciar que el valor de la «put» disminuye a medida que aumenta el tipo de interés. Además, esa disminución es más acusada cuanto mayor es el precio de ejercicio de la opción. Las Figuras 15, 18, 19 y 21 permiten comprobar cómo el valor de una «put» disminuye cuando aumenta el precio de la acción a que se refiere: P / S = [ C / S] 1 = N (x) 1 < Γ = 2 P / S 2 = 2 C / S 2 = / S = N (x) / (S σ t) Ω = [ P / S] / [P / S] = [ P / P] / [ S / S] = S / P = [N (x) 1] S / C Podemos construir la cartera réplica de una opción de venta europea análogamente a como hicimos para una «call»: 2
21 Cartera réplica de una opción de venta («put») europea de valor P y parámetros K, t, r y S Una opción de venta = cartera réplica compuesta por: acciones vendidas a crédito («short») y B pesetas invertidas 12 en todo momento y a devolver en t, donde: = P / S = N (w) = 1 N (x) y B = K r -t N (w σ t). Tabla 7. Valores de distintas «puts» europeas (El valor de la opción se calcula utilizando la fórmula de Black y Scholes) r K 1,3 1,5 1,1 1,15 1,2 3,,,,, 4 1,8 1,66 1,38 1,14, ,98 26,78 24,3 21,59 19,42 6 1,49 97,95 91,93 86,34 81, ,28 191,99 184,11 176,68 169,67 S = 5 pesetas; t =,25 años; σ =,3 Tabla 8. Valores de distintas «puts» europeas (El valor de la opción se calcula utilizando la fórmula de Black y Scholes) r K 1,3 1,5 1,1 1,15 1,2 3,17,15,11,7,5 4 6,17 5,6 4,41 3,49 2, ,36 35,98 3,65 26,12 22, ,27 1,69 9,1 8,61 72, ,23 186,99 172,29 158,78 146,33 S = 5 pesetas; t =,5 años; σ =,3 Tabla 9. Valores de distintas «puts» europeas (El valor de la opción se calcula utilizando la fórmula de Black y Scholes) r K 1,3 1,5 1,1 1,15 1,2 3,67,63,55,48,43 4 1,69 1,29 9,37 8,56 7, ,74 46,46 43,49 4,77 38, , 112,73 17,37 12,39 97, ,29 198,21 19,86 183,97 177,5 S = 5 pesetas; t =,25 años; σ =,5 12 Invertir B pesetas es equivalente a comprar bonos cupón cero (o pagarés) que vencen en t y que tienen un valor nominal de K N (w σ t). 21
22 Tabla 1. Valores de distintas «puts» europeas (El valor de la opción se calcula utilizando la fórmula de Black y Scholes) r K 1,3 1,5 1,1 1,15 1,2 3,48,44,35,29, ,38 21,42 19,22 17,27 15, ,57 96,34 91,6 86,13 81, ,67 192,83 186, 179,56 173, ,85 291,52 283,52 275,97 268,82 S = 4 pesetas; t =,25 años; σ =,3 Tabla 11. Valores de distintas «puts» europeas (El valor de la opción se calcula utilizando la fórmula de Black y Scholes) r = 1,1; K = 5 pesetas; σ =,3 t S (pesetas) 1 mes 3 meses 6 meses 12 meses 24 meses,833 años,25 años,5 años 1, año 2, años 2 296,4 288,23 276,73 254,63 215, ,4 238,23 226,76 25,41 171, 3 196,4 188,24 177,14 158,71 132, ,4 138,51 129,52 117,12 1, ,13 91,6 87,31 82,73 75, ,72 51,19 53,94 56,23 55, ,3 24,3 3,65 37, 4, ,58 9,42 16,17 23,73 29,82 6,23 3,14 8, 14,91 21,74 65,1,91 3,76 9,22 15,84 7,,24 1,7 5,64 11,55 3 Figura 15. Valor de una «put» europea según la fórmula de Black y Scholes r = 1,1; K = 5 pesetas; Volatilidad =,3 25 P 2 15 Valores intermedios: 1, 3, 6 y 12 meses 1 t = 24 meses 5 t = S (pesetas) 22
23 Figura 16. Valor de una «put» europea según la fórmula de Black y Scholes S = 5 pesetas; r = 1,1; Volatilidad = 3% 1 8 K = 6 P K = 5 K = Tiempo hasta el ejercicio (meses) Figura 17. Valor de una «put» europea según la fórmula de Black y Scholes S = 5 pesetas; σ = 3%; r = 1, t = 1 mes P 1 La línea intermedia corresponde a t = 3 meses t = 1 año K (pesetas) 23
24 Figura 18. Valor de una «put» europea según la fórmula de Black y Scholes r = 1,1; t = 6 meses; Volatilidad =, P K = 5 K = S (pesetas) Figura 19. Valor de una «put» europea según la fórmula de Black y Scholes r = 1,1; K = 5 pesetas; t = 6 meses P σ =,2 σ =, S (pesetas) 24
25 P Figura 2. Valor de una «put» europea según la fórmula de Black y Scholes S = 5 pesetas; r = 1,1; t = 6 meses K = 6 K = 5 K = 4 % 1% 2% 3% 4% 5% 6% 7% 8% Volatilidad Figura 21. Valor de una opción de venta según la fórmula de Black y Scholes t = 6 meses; K = 5 pesetas; Volatilidad =, P r = 1,3 r = 1, La línea intermedia corresponde a r = 1, S (pesetas) 25
26 Figura 22. Valor de una «put» europea según la fórmula de Black y Scholes S = 5 pesetas; t = 6 meses; σ = 3% P 6 K = 6 4 K = 5 2 K = 4 1, 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 r 1. La distribución normal La Figura 23 es la representación de la distribución de probabilidad normal estándar (de media cero y varianza unidad), que viene dada por: N' (x) = 1 e 2π x 2 /2 Figura 23. N (x),45,4,35,3 N'(x),25,2,15,1,5 2,5 2 1,5 1,5,5 1 1,5 2 2,5 x 26
27 La Figura 24 es la representación de N(x). Recordemos que N (x) es el área comprendida debajo de la distribución de probabilidad normal estándar de la Figura 23 (de media cero y varianza unidad) entre y x. N(x) se denomina función de probabilidad acumulada de una distribución normal estándar. La Figura 24 permite apreciar que N ( x) = 1 N (x). La Figura 25 es la representación de la distribución logarítmico normal. Se obtiene directamente de la Figura 23. La rentabilidad de las acciones se asemeja a la distribución normal, mientras que el precio de las acciones se asemeja a la distribución logarítmico normal. N(x) Figura 24. N(x) 1,9,8,7,6,5,4,3,2,1 2,5 2 1,5 1,5,5 1 1,5 2 2,5 x,7 Figura 25. Distribución logarítmico normal,6,5 f [exp (x)],4,3,2,1, exp (x) 27
28 12. Valoración de opciones sobre acciones que reparten dividendos Para valorar opciones europeas sobre acciones que reparten dividendos es necesario realizar un ajuste en la fórmula de Black y Scholes: se introduce S D (el precio de la acción menos el valor actual de los dividendos), en lugar del precio de la acción. Ejemplo. Vimos en el ejemplo de la sección 2 que el valor de una «call» europea sobre una acción que no reparte dividendos con las siguientes características: S = 5; K = 4; σ =,3; r = 1,1 y t =,25, es 11,8 pesetas. Si la acción repartiese un dividendo de 1 pesetas dentro de dos meses, el valor de la «call» europea sería 11,44 pesetas. Este valor se obtiene introduciendo en la fórmula S D (49,158 = 5 1/ 1,1 2/12 ), en lugar de 5. Análogamente, el valor de la «put» europea sobre la acción, si no reparte dividendos, es 1,38 pesetas. Notar que se cumple la «put-call parity» (12.1): 11,8 = 5 + 1,38 4 x 1,1-3/12. El valor de la «put» europea sobre la acción, si existe un dividendo de 1 pesetas dentro de 2 meses, sería 1,86 pesetas 13. Notar que se cumple la «put-call parity» (1.4): 11,44 = 5 1/ 1,1 2/12 + 1,86 4 x 1,1-3/12. Merton desarrolló una fórmula para valorar opciones europeas en que los dividendos se suponen continuos y dependientes del precio de la acción. Si los dividendos anuales de la acción son el d% de su cotización y los paga de modo continuo, el valor de la «call» viene dado por: Fórmula para valorar opciones con dividendos continuos C = S (1 + d) -t N (x) K r -t N (x σ t) P = K r -t N ( x + σ t) S (1 + d) -t N ( x) (3) siendo x = Ln (S (1 + d) -t / K r -t ) / (σ t) + σ t / 2 Nótese que S (1+d) -t no es más que el precio actual de la acción menos el valor actual de los dividendos. Ejemplo. Si una acción que hoy tiene un precio de 5 pesetas reparte continuamente un dividendo anual del 8% (d =,8), el valor actual de tener una acción dentro de un año es 5/1,8 = 462,96296 pesetas. Expresando el dividendo como interés continuo, esto significa que estamos suponiendo que la acción reparte en cada instante un dividendo anual equivalente al 7,69614% de su cotización (, = ln[1,8]). Véase que esto es equivalente a suponer que la acción pagará a lo largo del año un único dividendo igual al 7,4747% (1 1/1,8) de su cotización. Si el dividendo no es continuo y constante a lo largo de la vida de la opción, (3) es correcta siempre que d sea el dividendo promedio. Cuando las opciones de compra son americanas, el valor correcto se obtiene únicamente utilizando el método binomial. Sin embargo, existen algunas aproximaciones: 1) Valorar la opción como si fuese europea siguiendo el procedimiento descrito. 13 Esta valoración es aproximada. Si el dividendo es pequeño en relación al precio de la acción, la aproximación es muy buena. El valor exacto de opciones sobre acciones que reparten dividendos se obtiene con el método binomial. 28
29 2) Calcular el valor de varias opciones europeas: una con fecha de ejercicio en el final de la vida de la opción, y otras con fecha de ejercicio en cada fecha en que la acción reparta dividendos 14. El valor de la opción será el mayor de todos estos valores. 3) Utilizar otras fórmulas más sofisticadas y exactas, como la de Whaley, Roll y Geske 15. El propio Whaley realizó una comprobación de los tres métodos y encontró que el tercero (error = 1,1%) es un poco más exacto que el segundo (error = 1,5%), y éste, a su vez, más exacto que el primero (error = 2,1%). En resumen, podemos decir que para la valoración de opciones existen dos métodos fundamentales. El denominado método binomial puede aplicarse en todos los casos, pero exige un elevado número de cálculos (si bien fáciles de programar en ordenador). El segundo método consiste en el empleo de la fórmula de Black y Scholes, relativamente sencilla, pero cuya validez está limitada a ciertos casos. En la práctica, la utilización de un método u otro depende del tipo de opción a valorar, según se indica en el siguiente Cuadro: Sin dividendos «Put» «Call» Opción europea Black-Scholes Black-Scholes Opción americana Binomial Black-Scholes Con dividendos «Put» «Call» Opción europea Binomial o Black-Scholes corregida Opción americana Binomial Binomial o Black- Scholes corregida 13. Volatilidad implícita En muchas ocasiones conocemos el precio de las opciones; por ejemplo, cuando vemos sus precios en el mercado. La cuestión que entonces nos preguntamos con frecuencia es cuál es la volatilidad implícita en ese precio, esto es, qué volatilidad hemos de utilizar en la fórmula de valoración para obtener el precio que observamos en el mercado. Ejemplo. Calcular la volatilidad implícita de las siguientes opciones europeas sobre una acción de la empresa X, que se podrán ejercer dentro de 5 meses; r = 1,1. El precio de la acción de X es 4 pesetas. K «Call» «Put» 3 118,5 6, ,5 37,92 5 2,28 1,82 14 Este método lo introdujo Fischer Black en su artículo «Fact and Fantasy in the Use of Options», Financial Analysts Journal, julio-agosto de 1975, págs Véanse: Whaley, Robert E., «Valuation of American Call Options on Dividend-Paying Stocks», Journal of Financial Economics, vol. 1, 1982, págs , y Geske, Robert y Richard Roll, «On Valuing American Call Options with the Black-Scholes European Formula», Journal of Finance, junio de 1984, págs
30 Solución Para todas las opciones se comprueba que la volatilidad anual de la acción (suponiendo que no repartirá dividendos durante los próximos 5 meses) es 45% anual. Apéndice 1 UTILIZACION DE LA FORMULA DE BLACK Y SCHOLES PARA VALORAR OPCIONES Hipótesis bajo las que se ha derivado la fórmula de Black y Scholes Las hipótesis necesarias para derivar la fórmula de Black y Scholes son las siguientes: H1: no hay costes de transacción, ni comisiones ni impuestos diferenciales. Esto no significa que no se admita la existencia de impuestos, sino que los impuestos afectan de igual modo al rendimiento de las acciones que al de la deuda. H2: se puede tomar dinero prestado e invertir en renta fija al mismo tipo de interés y sin restricciones. H3: la tasa de interés sin riesgo, r, es conocida y constante en el intervalo comprendido entre T = y T = t. H4: La venta a crédito de acciones, con total uso del dinero procedente de la venta, no tiene ninguna restricción. H5: Se pueden comprar y vender acciones continuamente. H6: El movimiento del precio de la acción se puede describir como un proceso de difusión. Una implicación directa de esta hipótesis es que el rendimiento diario de la acción seguirá una distribución normal. H7: La acción a la que se refiere la «call» no paga dividendos entre T = y T = t. Con estas hipótesis, Black y Scholes demostraron que se puede construir una cartera de valores (cartera réplica) con acciones y bonos (o tomando dinero prestado) de manera que el rendimiento de la cartera réplica sea exactamente igual que el rendimiento de una opción de compra en un intervalo de tiempo muy corto (dt). Haciendo cambios continuos en la composición de la cartera réplica (con el transcurso del tiempo y cuando cambia el precio de la acción), es posible lograr que la cartera réplica tenga un comportamiento idéntico al de la opción. Por tanto, el precio de la opción será en T = igual al precio de la cartera réplica. Las hipótesis pueden parecer poco razonables para un inversor pequeño. Sin embargo, son bastante aceptables para los inversores institucionales, los cuales cumplen las cinco primeras hipótesis adecuadamente. La hipótesis H7 simplemente hace referencia a que no habrá dividendos entre T= y T = t. Para el caso de que la acción reciba dividendos, la fórmula de Black y Scholes se adapta muy fácilmente. 3
Deducción de las fórmulas de Black-Scholes mediante valor esperado del pago futuro
 Deducción de las fórmulas de Black-Scholes mediante valor esperado del pago futuro Alexis Sánchez Tello de Meneses 4 Septiembre 04 Abstract Se desarrollará a partir del modelo de evolución log-normal para
Deducción de las fórmulas de Black-Scholes mediante valor esperado del pago futuro Alexis Sánchez Tello de Meneses 4 Septiembre 04 Abstract Se desarrollará a partir del modelo de evolución log-normal para
COMO SE ANALIZAN Y VALORAN LOS WARRANTS?
 2 COMO SE ANALIZAN Y VALORAN LOS WARRANTS? 2.1. El precio del warrant 2.2. Qué variables afectan el valor temporal? 2.3. Para que sirven las griegas? 2.4. Cuáles son las herramientas de análisis de los
2 COMO SE ANALIZAN Y VALORAN LOS WARRANTS? 2.1. El precio del warrant 2.2. Qué variables afectan el valor temporal? 2.3. Para que sirven las griegas? 2.4. Cuáles son las herramientas de análisis de los
Pablo Fernández. IESE. Valoración de opciones por simulación 1 VALORACIÓN DE OPCIONES POR SIMULACIÓN Pablo Fernández IESE
 Pablo Fernández. IESE. Valoración de opciones por simulación 1 VALORACIÓN DE OPCIONES POR SIMULACIÓN Pablo Fernández IESE 1. Fórmulas utilizadas en la simulación de la evolución del precio de una acción
Pablo Fernández. IESE. Valoración de opciones por simulación 1 VALORACIÓN DE OPCIONES POR SIMULACIÓN Pablo Fernández IESE 1. Fórmulas utilizadas en la simulación de la evolución del precio de una acción
RIESGO SISTEMÁTICO Y RIESGO NO SISTEMÁTICO. TEORÍA DEL EQUILIBRIO EN EL MERCADO DE CAPITALES
 RIESGO SISTEMÁTICO Y RIESGO NO SISTEMÁTICO. TEORÍA DEL EQUILIBRIO EN EL MERCADO DE CAPITALES 1 Riesgo Sistemático y Riesgo no Sistemático. Teoría del Equilibrio en el Mercado de Capitales http://ciberconta.unizar.es/leccion/fin004/120.htm
RIESGO SISTEMÁTICO Y RIESGO NO SISTEMÁTICO. TEORÍA DEL EQUILIBRIO EN EL MERCADO DE CAPITALES 1 Riesgo Sistemático y Riesgo no Sistemático. Teoría del Equilibrio en el Mercado de Capitales http://ciberconta.unizar.es/leccion/fin004/120.htm
1. La Distribución Normal
 1. La Distribución Normal Los espacios muestrales continuos y las variables aleatorias continuas se presentan siempre que se manejan cantidades que se miden en una escala continua; por ejemplo, cuando
1. La Distribución Normal Los espacios muestrales continuos y las variables aleatorias continuas se presentan siempre que se manejan cantidades que se miden en una escala continua; por ejemplo, cuando
MÓDULO 5: MERCADO DE PRODUCTOS DERIVADOS
 MÓDULO 5: MERCADO DE PRODUCTOS DERIVADOS TEST DE AUTOEVALUACIÓN 5.1_MODULO 5 1. El precio de una opción PUT es de 3,00, vencimiento 1 semana, precio de ejercicio 14 y la cotización del subyacente 12. Indica
MÓDULO 5: MERCADO DE PRODUCTOS DERIVADOS TEST DE AUTOEVALUACIÓN 5.1_MODULO 5 1. El precio de una opción PUT es de 3,00, vencimiento 1 semana, precio de ejercicio 14 y la cotización del subyacente 12. Indica
AVISO A LOS SOCIOS LIQUIDADORES, OPERADORES Y PÚBLICO EN GENERAL CÁLCULO DEL PRECIO O PRIMA DE LIQUIDACIÓN DIARIA PARA OPCIONES.
 México, D.F., a 10 de marzo de 2008. AVISO A LOS SOCIOS LIQUIDADORES, OPERADORES Y PÚBLICO EN GENERAL CÁLCULO DEL PRECIO O PRIMA DE LIQUIDACIÓN DIARIA PARA OPCIONES. A continuación se da a conocer el nuevo
México, D.F., a 10 de marzo de 2008. AVISO A LOS SOCIOS LIQUIDADORES, OPERADORES Y PÚBLICO EN GENERAL CÁLCULO DEL PRECIO O PRIMA DE LIQUIDACIÓN DIARIA PARA OPCIONES. A continuación se da a conocer el nuevo
1.1.-TIPOLOGIA DE ACCIONES ACCIONES PREFERENTES.
 1.1.-TIPOLOGIA DE ACCIONES. 1.1.1.- ACCIONES PREFERENTES. Podemos decir que las acciones preferentes o privilegiadas son como valores híbridos ya que tienen características comunes con las acciones ordinarias
1.1.-TIPOLOGIA DE ACCIONES. 1.1.1.- ACCIONES PREFERENTES. Podemos decir que las acciones preferentes o privilegiadas son como valores híbridos ya que tienen características comunes con las acciones ordinarias
INVERTIR EN VOLATILIDAD: STRADDLES Y STRANGLES
 INVERTIR EN VOLATILIDAD: STRADDLES Y STRANGLES Como ya hemos explicado en alguna otra ocasión, la volatilidad no sólo es uno de los estadísticos que se utiliza habitualmente para medir el riesgo de las
INVERTIR EN VOLATILIDAD: STRADDLES Y STRANGLES Como ya hemos explicado en alguna otra ocasión, la volatilidad no sólo es uno de los estadísticos que se utiliza habitualmente para medir el riesgo de las
OPTIMIZACIÓN Y SIMULACIÓN PARA LA EMPRESA. Tema 5 Simulación
 OPTIMIZACIÓN Y SIMULACIÓN PARA LA EMPRESA Tema 5 Simulación ORGANIZACIÓN DEL TEMA Sesiones: Introducción Ejemplos prácticos Procedimiento y evaluación de resultados INTRODUCCIÓN Simulación: Procedimiento
OPTIMIZACIÓN Y SIMULACIÓN PARA LA EMPRESA Tema 5 Simulación ORGANIZACIÓN DEL TEMA Sesiones: Introducción Ejemplos prácticos Procedimiento y evaluación de resultados INTRODUCCIÓN Simulación: Procedimiento
PASEO ALEATORIO. MOVIMIENTO BROWNIANO
 PASEO ALEATORIO. MOVIMIENTO BROWNIANO Jorge Estévez Grupo ER El movimiento browniano es el movimiento aleatorio que se observa en algunas partículas microscópicas que se hallan en un medio fluido (por
PASEO ALEATORIO. MOVIMIENTO BROWNIANO Jorge Estévez Grupo ER El movimiento browniano es el movimiento aleatorio que se observa en algunas partículas microscópicas que se hallan en un medio fluido (por
LOS PROYECTOS DE INVERSIÓN ANALIZADOS COMO OPCIONES REALES. Preparado por: Mg Carlos Mario Ramírez Gil
 LOS PROYECTOS DE INVERSIÓN ANALIZADOS COMO OPCIONES REALES Preparado por: Mg Carlos Mario Ramírez Gil PLAN DE TEMAS Evaluación financiera proyectos de inversión OPCIONES REALES Proyectos de inversión analizados
LOS PROYECTOS DE INVERSIÓN ANALIZADOS COMO OPCIONES REALES Preparado por: Mg Carlos Mario Ramírez Gil PLAN DE TEMAS Evaluación financiera proyectos de inversión OPCIONES REALES Proyectos de inversión analizados
Discretas. Continuas
 UNIDAD 0. DISTRIBUCIÓN TEÓRICA DE PROBABILIDAD Discretas Binomial Distribución Teórica de Probabilidad Poisson Normal Continuas Normal Estándar 0.1. Una distribución de probabilidad es un despliegue de
UNIDAD 0. DISTRIBUCIÓN TEÓRICA DE PROBABILIDAD Discretas Binomial Distribución Teórica de Probabilidad Poisson Normal Continuas Normal Estándar 0.1. Una distribución de probabilidad es un despliegue de
El Movimiento Browniano en la modelización del par EUR/USD
 MÁSTER UNIVERSITARIO EN DIRECCIÓN FINANCIERA Y FISCAL TESINA FIN DE MÁSTER El Movimiento Browniano en la modelización del par EUR/USD Autor: José Vicente González Cervera Directores: Dr. Juan Carlos Cortés
MÁSTER UNIVERSITARIO EN DIRECCIÓN FINANCIERA Y FISCAL TESINA FIN DE MÁSTER El Movimiento Browniano en la modelización del par EUR/USD Autor: José Vicente González Cervera Directores: Dr. Juan Carlos Cortés
VI. Criterios de Evaluación de Inversiones
 VI. Criterios de Evaluación de Inversiones Criterios de Evaluación de Inversiones Los criterios o indicadores de evaluación de inversiones son índices que nos ayudan a determinar si un proyecto es o no
VI. Criterios de Evaluación de Inversiones Criterios de Evaluación de Inversiones Los criterios o indicadores de evaluación de inversiones son índices que nos ayudan a determinar si un proyecto es o no
La importancia de la diversificación. Dirección de Inversiones BBVA Banca Privada
 La importancia de la diversificación Dirección de Inversiones BBVA Banca Privada Índice 1 Introducción 2 Rentabilidad y riesgo 3 Rentabilidad y riesgo de una cartera 4 La importancia de la diversificación
La importancia de la diversificación Dirección de Inversiones BBVA Banca Privada Índice 1 Introducción 2 Rentabilidad y riesgo 3 Rentabilidad y riesgo de una cartera 4 La importancia de la diversificación
Tratamiento de Riesgo Avanzado de Carteras
 t Tratamiento de Riesgo Avanzado de Carteras Dossier Comercial Departamento Comercial Febrero 2012 2 T Edificio RD Sistemas TRAC Dossier Comercial Versión 2.0 Valencia, 560 4º 08026 BARCELONA Calle Margarita
t Tratamiento de Riesgo Avanzado de Carteras Dossier Comercial Departamento Comercial Febrero 2012 2 T Edificio RD Sistemas TRAC Dossier Comercial Versión 2.0 Valencia, 560 4º 08026 BARCELONA Calle Margarita
MERCADOS FINANCIEROS
 MERCADOS FINANCIEROS 1. Mercados financieros: conceptos generales Mercados financieros: lugar donde se intercambian y negocian los activos financieros. Tres funciones de los mercados financieros: Determinar
MERCADOS FINANCIEROS 1. Mercados financieros: conceptos generales Mercados financieros: lugar donde se intercambian y negocian los activos financieros. Tres funciones de los mercados financieros: Determinar
IESE Universidad de Navarra Barcelona-Madrid
 Barcelona-Madrid 2- APLICACIONES DE LOS DERIVADOS PARA CUBRIR LA GESTION DE CARTERAS Y PARA CUBRIR RIESGOS (*) En esta nota se presentan algunas de las aplicaciones más frecuentes de los derivados para
Barcelona-Madrid 2- APLICACIONES DE LOS DERIVADOS PARA CUBRIR LA GESTION DE CARTERAS Y PARA CUBRIR RIESGOS (*) En esta nota se presentan algunas de las aplicaciones más frecuentes de los derivados para
TEMA 4. Series de potencias
 TEMA 4 Series de potencias. Introducción En el tema anterior hemos estudiado la aproximación polinómica local de funciones mediante el polinomio de Taylor correspondiente. En particular, vimos para la
TEMA 4 Series de potencias. Introducción En el tema anterior hemos estudiado la aproximación polinómica local de funciones mediante el polinomio de Taylor correspondiente. En particular, vimos para la
La volatilidad implícita
 La volatilidad implícita La volatilidad es uno de los parámetros con mayor peso dentro de la valoración de opciones. Afecta igualmente a call y a put, provocando aumentos de sus primas cuando aumenta y
La volatilidad implícita La volatilidad es uno de los parámetros con mayor peso dentro de la valoración de opciones. Afecta igualmente a call y a put, provocando aumentos de sus primas cuando aumenta y
DURACIÓN Y VOLATILIDAD DE LOS BONOS. PDF created with pdffactory trial version
 DURACIÓN Y VOLATILIDAD DE LOS BONOS Duración y Volatilidad de los Bonos Los precios de los títulos que ofrecen una renta fija al inversor, fluctúan en forma inversa a los cambios en la tasa de interés,
DURACIÓN Y VOLATILIDAD DE LOS BONOS Duración y Volatilidad de los Bonos Los precios de los títulos que ofrecen una renta fija al inversor, fluctúan en forma inversa a los cambios en la tasa de interés,
Otra característica poblacional de interés es la varianza de la población, 2, y su raíz cuadrada, la desviación estándar de la población,. La varianza
 CARACTERÍSTICAS DE LA POBLACIÓN. Una pregunta práctica en gran parte de la investigación de mercado tiene que ver con el tamaño de la muestra. La encuesta, en principio, no puede ser aplicada sin conocer
CARACTERÍSTICAS DE LA POBLACIÓN. Una pregunta práctica en gran parte de la investigación de mercado tiene que ver con el tamaño de la muestra. La encuesta, en principio, no puede ser aplicada sin conocer
VII ANÁLISIS DE RENTABILIDAD: APLICACIÓN DE CRITERIOS
 VII ANÁLISIS DE RENTABILIDAD: APLICACIÓN DE CRITERIOS 7.1. ENCUADRE Estudio de Viabilidad Definición Inicial Plan Planificación Temporal Planificación Económica Planificación Financiera Análisis de Rentabilidad
VII ANÁLISIS DE RENTABILIDAD: APLICACIÓN DE CRITERIOS 7.1. ENCUADRE Estudio de Viabilidad Definición Inicial Plan Planificación Temporal Planificación Económica Planificación Financiera Análisis de Rentabilidad
Glosario de términos. Introducción a las Matemáticas Financieras
 Introducción a las Matemáticas Financieras Carlos Mario Morales C 2012 1 Amortización y capitalización UNIDAD 4: AMORTIZACIÓN Y CAPITALIZACIÓN OBJETIVO Al finalizar la unidad los estudiantes estarán en
Introducción a las Matemáticas Financieras Carlos Mario Morales C 2012 1 Amortización y capitalización UNIDAD 4: AMORTIZACIÓN Y CAPITALIZACIÓN OBJETIVO Al finalizar la unidad los estudiantes estarán en
FUNCIONAMIENTO DE LOS WARRANTS
 FUNCIONAMIENTO DE LOS WARRANTS Índice 1 Cómo funcionan los Warrants y Ejemplo 2 Factores que determinan la Prima del Warrant 3 Advertencias y Factores de Riesgos 4 Como es el proceso de contratación Cómo
FUNCIONAMIENTO DE LOS WARRANTS Índice 1 Cómo funcionan los Warrants y Ejemplo 2 Factores que determinan la Prima del Warrant 3 Advertencias y Factores de Riesgos 4 Como es el proceso de contratación Cómo
Trabajo No 1. Derivados Financieros
 Trabajo No 1. Derivados Financieros Norman Giraldo Gómez Escuela de Estadística - Universidad Nacional de Colombia ndgirald@unal.edu.co Marzo, 2010 1. Introducción Este trabajo consiste de un punto asignado
Trabajo No 1. Derivados Financieros Norman Giraldo Gómez Escuela de Estadística - Universidad Nacional de Colombia ndgirald@unal.edu.co Marzo, 2010 1. Introducción Este trabajo consiste de un punto asignado
Movimiento Browniano o proceso de Wiener
 1 Movimiento Browniano o proceso de Wiener Se dice que Z [ ] es un proceso de Wiener o movimiento Browniano si Z es una función definida en algún intervalo I = [, T ] (eventualmente puede ser T = + ),
1 Movimiento Browniano o proceso de Wiener Se dice que Z [ ] es un proceso de Wiener o movimiento Browniano si Z es una función definida en algún intervalo I = [, T ] (eventualmente puede ser T = + ),
LABORATORIO No. 0. Cálculo de errores en las mediciones. 0.1 Introducción
 LABORATORIO No. 0 Cálculo de errores en las mediciones 0.1 Introducción Es bien sabido que la especificación de una magnitud físicamente medible requiere cuando menos de dos elementos: Un número y una
LABORATORIO No. 0 Cálculo de errores en las mediciones 0.1 Introducción Es bien sabido que la especificación de una magnitud físicamente medible requiere cuando menos de dos elementos: Un número y una
Estadística. Generalmente se considera que las variables son obtenidas independientemente de la misma población. De esta forma: con
 Hasta ahora hemos supuesto que conocemos o podemos calcular la función/densidad de probabilidad (distribución) de las variables aleatorias. En general, esto no es así. Más bien se tiene una muestra experimental
Hasta ahora hemos supuesto que conocemos o podemos calcular la función/densidad de probabilidad (distribución) de las variables aleatorias. En general, esto no es así. Más bien se tiene una muestra experimental
La estrategia Protective Put y sus diferentes alternativas
 La estrategia Protective Put y sus diferentes alternativas Si existe una estrategia clásica con opciones, es la de utilizar una Put para proteger la cartera ante caídas del activo subyacente, es lo que
La estrategia Protective Put y sus diferentes alternativas Si existe una estrategia clásica con opciones, es la de utilizar una Put para proteger la cartera ante caídas del activo subyacente, es lo que
Aplicación a Portafolios en Colombia
 Administración de Riesgos Financieros: Aplicación a Portafolios en Colombia Tema 3: Riesgo I - ensibilidades Diego Jara diego.jara@quantil.com.co Facultad de Economía Educación Continuada Riesgo I Recordemos:
Administración de Riesgos Financieros: Aplicación a Portafolios en Colombia Tema 3: Riesgo I - ensibilidades Diego Jara diego.jara@quantil.com.co Facultad de Economía Educación Continuada Riesgo I Recordemos:
ANÁLISIS DE FRECUENCIAS
 ANÁLISIS DE FRECUENCIAS EXPRESIONES PARA EL CÁLCULO DE LOS EVENTOS PARA EL PERÍODO DE RETORNO T Y DE LOS RESPECTIVOS ERRORES ESTÁNDAR DE ESTIMACIÓN REQUERIDOS PARA LA DETERMINACIÓN DE LOS INTERVALOS DE
ANÁLISIS DE FRECUENCIAS EXPRESIONES PARA EL CÁLCULO DE LOS EVENTOS PARA EL PERÍODO DE RETORNO T Y DE LOS RESPECTIVOS ERRORES ESTÁNDAR DE ESTIMACIÓN REQUERIDOS PARA LA DETERMINACIÓN DE LOS INTERVALOS DE
VALORACION DE OPCIONES CON ARBOLES BINOMIALES
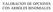 VALORACION DE OPCIONES CON ARBOLES BINOMIALES Modelo Binomial Simple Precio actual de la acción $20 Dentro de tres meses será $22 o $18 Precio Acción = $22 Precio Acción = $20 Precio Acción = $18 Una opción
VALORACION DE OPCIONES CON ARBOLES BINOMIALES Modelo Binomial Simple Precio actual de la acción $20 Dentro de tres meses será $22 o $18 Precio Acción = $22 Precio Acción = $20 Precio Acción = $18 Una opción
Estadística y sus aplicaciones en Ciencias Sociales 5. Estimación. Facultad de Ciencias Sociales, UdelaR
 Estadística y sus aplicaciones en Ciencias Sociales 5. Estimación Facultad de Ciencias Sociales, UdelaR Índice 1. Repaso: estimadores y estimaciones. Propiedades de los estimadores. 2. Estimación puntual.
Estadística y sus aplicaciones en Ciencias Sociales 5. Estimación Facultad de Ciencias Sociales, UdelaR Índice 1. Repaso: estimadores y estimaciones. Propiedades de los estimadores. 2. Estimación puntual.
El Banco M comercializa el depósito IBÉRDEP a un año. Este producto se caracteriza por:
 41.- Depósito Estructurado IBERDEP Autor: Constancio Zamora. Universidad de Sevilla El Banco M comercializa el depósito IBÉRDEP a un año. Este producto se caracteriza por: a. Se garantiza el capital invertido.
41.- Depósito Estructurado IBERDEP Autor: Constancio Zamora. Universidad de Sevilla El Banco M comercializa el depósito IBÉRDEP a un año. Este producto se caracteriza por: a. Se garantiza el capital invertido.
INSTITUTO DE FÍSICA FACULTAD DE INGENIERÍA FÍSICA ESTADÍSTICA
 INSTITUTO DE FÍSICA FACULTAD DE INGENIERÍA DIPLOMA DE ESPECIALIZACIÓN EN FÍSICA (ANEP UDELAR) FÍSICA ESTADÍSTICA Curso 013 Práctico II Fundamentos de Probabilidad y Estadística. Fecha de Entrega: 13 de
INSTITUTO DE FÍSICA FACULTAD DE INGENIERÍA DIPLOMA DE ESPECIALIZACIÓN EN FÍSICA (ANEP UDELAR) FÍSICA ESTADÍSTICA Curso 013 Práctico II Fundamentos de Probabilidad y Estadística. Fecha de Entrega: 13 de
Algunas Distribuciones Continuas de Probabilidad. UCR ECCI CI-1352 Probabilidad y Estadística Prof. M.Sc. Kryscia Daviana Ramírez Benavides
 Algunas Distribuciones Continuas de Probabilidad UCR ECCI CI-1352 Probabilidad y Estadística Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción El comportamiento de una variable aleatoria queda
Algunas Distribuciones Continuas de Probabilidad UCR ECCI CI-1352 Probabilidad y Estadística Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción El comportamiento de una variable aleatoria queda
Caso práctico: La gestión de carteras en INVESTING PARTNERS BANK.
 Caso práctico: La gestión de carteras en INVESTING PARTNERS BANK. Después de intensas entrevistas y pruebas un día recibe la excelente noticia de que ha sido seleccionado como Gestor de Carteras para un
Caso práctico: La gestión de carteras en INVESTING PARTNERS BANK. Después de intensas entrevistas y pruebas un día recibe la excelente noticia de que ha sido seleccionado como Gestor de Carteras para un
Práctica 4 TEOREMA CENTRAL DEL LÍMITE
 Práctica 4. Teorema Central del Límite 1 Práctica 4 TEOREMA CENTRAL DEL LÍMITE Objetivos: En esta práctica utilizaremos el paquete SPSS para ilustrar el Teorema Central del Límite. Además calcularemos
Práctica 4. Teorema Central del Límite 1 Práctica 4 TEOREMA CENTRAL DEL LÍMITE Objetivos: En esta práctica utilizaremos el paquete SPSS para ilustrar el Teorema Central del Límite. Además calcularemos
FONDO MUTUO SECURITY DOLAR MONEY MARKET SERIE A Folleto Informativo al cierre de marzo 2015
 FONDO MUTUO SECURITY DOLAR MONEY MARKET SERIE A Folleto Informativo al cierre de marzo 2015 Administradora RUN Patrimonio Serie Monto Mínimo ADMINISTRADORA GENERAL DE FONDOS SECURITY S.A. 8384 USD USD
FONDO MUTUO SECURITY DOLAR MONEY MARKET SERIE A Folleto Informativo al cierre de marzo 2015 Administradora RUN Patrimonio Serie Monto Mínimo ADMINISTRADORA GENERAL DE FONDOS SECURITY S.A. 8384 USD USD
ASIGNATURA: DECISIONES DE FINANCIAMIENTO
 ASIGNATURA: DECISIONES DE FINANCIAMIENTO FUENTES DE FINANCIAMIENTO A LARGO PLAZO DOS DECISIONES IMPORTANTES: En qué activos invertir y cómo financiar la inversión Decisión de Invertir Objetivo: Obtener
ASIGNATURA: DECISIONES DE FINANCIAMIENTO FUENTES DE FINANCIAMIENTO A LARGO PLAZO DOS DECISIONES IMPORTANTES: En qué activos invertir y cómo financiar la inversión Decisión de Invertir Objetivo: Obtener
( ) DISTRIBUCIÓN UNIFORME (o rectangular) 1 b a. para x > b DISTRIBUCIÓN DE CAUCHY. x ) DISTRIBUCIÓN EXPONENCIAL. α α 2 DISTRIBUCIÓN DE LAPLACE
 Estudiamos algunos ejemplos de distribuciones de variables aleatorias continuas. De ellas merecen especial mención las derivadas de la distribución normal (χ, t de Student y F de Snedecor), por su importancia
Estudiamos algunos ejemplos de distribuciones de variables aleatorias continuas. De ellas merecen especial mención las derivadas de la distribución normal (χ, t de Student y F de Snedecor), por su importancia
ACTIVIDAD 2: La distribución Normal
 Actividad 2: La distribución Normal ACTIVIDAD 2: La distribución Normal CASO 2-1: CLASE DE BIOLOGÍA El Dr. Saigí es profesor de Biología en una prestigiosa universidad. Está preparando una clase en la
Actividad 2: La distribución Normal ACTIVIDAD 2: La distribución Normal CASO 2-1: CLASE DE BIOLOGÍA El Dr. Saigí es profesor de Biología en una prestigiosa universidad. Está preparando una clase en la
III.1. Descomposición de la tasa de crecimiento
 Estos resultados nos indican que la explicación del menor nivel de producción per cápita de Andalucía frente al total nacional no hay que buscarla en las dotaciones de los factores productivos, resultado
Estos resultados nos indican que la explicación del menor nivel de producción per cápita de Andalucía frente al total nacional no hay que buscarla en las dotaciones de los factores productivos, resultado
1) Características del diseño en un estudio de cohortes.
 Departamento de Estadística Universidad Carlos III de Madrid BIOESTADISTICA (55-10536) Estudios de cohortes CONCEPTOS CLAVE 1) Características del diseño en un estudio de cohortes. ) Elección del tamaño
Departamento de Estadística Universidad Carlos III de Madrid BIOESTADISTICA (55-10536) Estudios de cohortes CONCEPTOS CLAVE 1) Características del diseño en un estudio de cohortes. ) Elección del tamaño
Estadistica II Tema 0. Repaso de conceptos básicos. Curso 2009/10
 Estadistica II Tema 0. Repaso de conceptos básicos Curso 2009/10 Tema 0. Repaso de conceptos básicos Contenidos Variables aleatorias y distribuciones de probabilidad La distribución normal Muestras aleatorias,
Estadistica II Tema 0. Repaso de conceptos básicos Curso 2009/10 Tema 0. Repaso de conceptos básicos Contenidos Variables aleatorias y distribuciones de probabilidad La distribución normal Muestras aleatorias,
A. CRITERIOS GENERALES DE LOS PRINCIPIOS DE INVERSIÓN DE LA ENTIDAD.
 DECLARACIÓN DE PRINCIPIOS DE INVERSIÓN DE E.P.S.V. ALEJANDRO ECHEVARRIA y DE LOS PLANES DE PREVISIÓN INTEGRADOS Aprobada por la Junta de Gobierno de la Entidad con fecha 16 de diciembre de 2015. Esta Declaración
DECLARACIÓN DE PRINCIPIOS DE INVERSIÓN DE E.P.S.V. ALEJANDRO ECHEVARRIA y DE LOS PLANES DE PREVISIÓN INTEGRADOS Aprobada por la Junta de Gobierno de la Entidad con fecha 16 de diciembre de 2015. Esta Declaración
Regresión múltiple. Demostraciones. Elisa Mª Molanes López
 Regresión múltiple Demostraciones Elisa Mª Molanes López El modelo de regresión múltiple El modelo que se plantea en regresión múltiple es el siguiente: y i = β 0 + β 1 x 1i + β 2 x 2i +...+ β k x ki +
Regresión múltiple Demostraciones Elisa Mª Molanes López El modelo de regresión múltiple El modelo que se plantea en regresión múltiple es el siguiente: y i = β 0 + β 1 x 1i + β 2 x 2i +...+ β k x ki +
Derivadas Parciales (parte 2)
 40 Derivadas Parciales (parte 2) Ejercicio: Si donde y. Determinar Solución: Consideraremos ahora la situación en la que, pero cada una de las variables e es función de dos variables y. En este caso tiene
40 Derivadas Parciales (parte 2) Ejercicio: Si donde y. Determinar Solución: Consideraremos ahora la situación en la que, pero cada una de las variables e es función de dos variables y. En este caso tiene
ESTIMACIÓN PUNTUAL Julián de la Horra Departamento de Matemáticas U.A.M.
 1 Introducción ESTIMACIÓN PUNTUAL Julián de la Horra Departamento de Matemáticas U.A.M. En este capítulo, vamos a abordar la Estimación Puntual, que es uno de los tres grandes conjuntos de técnicas que
1 Introducción ESTIMACIÓN PUNTUAL Julián de la Horra Departamento de Matemáticas U.A.M. En este capítulo, vamos a abordar la Estimación Puntual, que es uno de los tres grandes conjuntos de técnicas que
Análisis de duración y convexidad de una cartera de bonos soberanos de Venezuela con vencimiento en el periodo
 Análisis de duración y convexidad de una cartera de bonos soberanos de Venezuela con vencimiento en el periodo 2018-2038 Elaborado por: Cristina Vázquez Tutor: Javier Ríos Octubre 2016 Planteamiento del
Análisis de duración y convexidad de una cartera de bonos soberanos de Venezuela con vencimiento en el periodo 2018-2038 Elaborado por: Cristina Vázquez Tutor: Javier Ríos Octubre 2016 Planteamiento del
METODOS ESTADÍSTICOS
 METODOS ESTADÍSTICOS Introducción. Uno de los objetivos de la asignatura de Hidrología, es mostrar a los alumnos, las herramientas de cálculo utilizadas en Hidrología Aplicada para diseño de Obras Hidráulicas.
METODOS ESTADÍSTICOS Introducción. Uno de los objetivos de la asignatura de Hidrología, es mostrar a los alumnos, las herramientas de cálculo utilizadas en Hidrología Aplicada para diseño de Obras Hidráulicas.
PROBLEMA 1 Capítulo 6: MEDICIÓN Y GESTIÓN DEL RIESGO DE TIPO DE INTERÉS
 ROBLEMA Capítulo 6: MEDICIÓN Y GESTIÓN DEL RIESGO DE TIO DE INTERÉS Sabemos de una Obligación del Estado las siguientes características: Fecha de Emisión: 0-0-000 Fecha de vencimiento: 0-0-00 Cupón anual:
ROBLEMA Capítulo 6: MEDICIÓN Y GESTIÓN DEL RIESGO DE TIO DE INTERÉS Sabemos de una Obligación del Estado las siguientes características: Fecha de Emisión: 0-0-000 Fecha de vencimiento: 0-0-00 Cupón anual:
Matemática Financiera
 Matemática Financiera Patricia Kisbye Profesorado en Matemática Facultad de Matemática, Astronomía y Física 2011 Patricia Kisbye (FaMAF) 2011 1 / 70 Presentación de la materia Matemática financiera: ambiente
Matemática Financiera Patricia Kisbye Profesorado en Matemática Facultad de Matemática, Astronomía y Física 2011 Patricia Kisbye (FaMAF) 2011 1 / 70 Presentación de la materia Matemática financiera: ambiente
DEMANDA OFERTA MERCADO
 PARTE 1. Tomado de: Blanco Sánchez, Juan Manuel. Economía: teoría y práctica (5a. ed.)., España: McGraw-Hill España, 2008. p 17. http://site.ebrary.com/lib/unadsp/doc?id=10498596&ppg=30 ECONOMIA: La economía
PARTE 1. Tomado de: Blanco Sánchez, Juan Manuel. Economía: teoría y práctica (5a. ed.)., España: McGraw-Hill España, 2008. p 17. http://site.ebrary.com/lib/unadsp/doc?id=10498596&ppg=30 ECONOMIA: La economía
Medidas descriptivas I. Medidas de tendencia central A. La moda
 Medidas descriptivas I. Medidas de tendencia central A. La moda Preparado por: Roberto O. Rivera Rodríguez Coaching de matemática Escuela Eduardo Neuman Gandía 1 Introducción En muchas ocasiones el conjunto
Medidas descriptivas I. Medidas de tendencia central A. La moda Preparado por: Roberto O. Rivera Rodríguez Coaching de matemática Escuela Eduardo Neuman Gandía 1 Introducción En muchas ocasiones el conjunto
Estrategias Especulativas con Opciones Financieras: Diferenciales de Precios Bajistas (Bear Spreads)
 Estrategias Especulativas con Opciones Financieras: Diferenciales de Precios Bajistas (Bear Spreads) Apellidos, nombre Departamento Centro Burgos Simón, Clara; Cortés López, Juan Carlos; Navarro Quiles,
Estrategias Especulativas con Opciones Financieras: Diferenciales de Precios Bajistas (Bear Spreads) Apellidos, nombre Departamento Centro Burgos Simón, Clara; Cortés López, Juan Carlos; Navarro Quiles,
PARTE 4 ANUALIDADES T E M A S
 PATE 4 ANUALIDADES T E M A S Concepto de anualidad y aplicaciones principales Tipos principales de anualidades Valuación de anualidades ordinarias (vencidas) Valuación de anualidades adelantadas Construcción
PATE 4 ANUALIDADES T E M A S Concepto de anualidad y aplicaciones principales Tipos principales de anualidades Valuación de anualidades ordinarias (vencidas) Valuación de anualidades adelantadas Construcción
Derivada de la función compuesta. Regla de la cadena
 Derivada de la función compuesta. Regla de la cadena Cuando en las matemáticas de bachillerato se introduce el concepto de derivada, su significado y su interpretación geométrica, se pasa al cálculo de
Derivada de la función compuesta. Regla de la cadena Cuando en las matemáticas de bachillerato se introduce el concepto de derivada, su significado y su interpretación geométrica, se pasa al cálculo de
Lectura 1. Razones de Liquidez
 Lectura 1. Razones de Liquidez Un activo líquido está considerado como aquél que puede ser comercializado en un mercado activo, y que puede convertirse en efectivo con rapidez, al precio vigente en el
Lectura 1. Razones de Liquidez Un activo líquido está considerado como aquél que puede ser comercializado en un mercado activo, y que puede convertirse en efectivo con rapidez, al precio vigente en el
ANALISIS DE FRECUENCIA EN HIDROLOGIA JULIAN DAVID ROJO HERNANDEZ
 ANALISIS DE FRECUENCIA EN HIDROLOGIA JULIAN DAVID ROJO HERNANDEZ Probabilidad - Período de retorno y riesgo La probabilidad de ocurrencia de un fenómeno en hidrología puede citarse de varias Formas: El
ANALISIS DE FRECUENCIA EN HIDROLOGIA JULIAN DAVID ROJO HERNANDEZ Probabilidad - Período de retorno y riesgo La probabilidad de ocurrencia de un fenómeno en hidrología puede citarse de varias Formas: El
3. ASOCIACIÓN ENTRE DOS VARIABLES CUALITATIVAS
 1. INTRODUCCIÓN Este tema se centra en el estudio conjunto de dos variables. Dos variables cualitativas - Tabla de datos - Tabla de contingencia - Diagrama de barras - Tabla de diferencias entre frecuencias
1. INTRODUCCIÓN Este tema se centra en el estudio conjunto de dos variables. Dos variables cualitativas - Tabla de datos - Tabla de contingencia - Diagrama de barras - Tabla de diferencias entre frecuencias
MICROSOFT EXCEL PARA DIRECCIÓN FINANCIERA I. 1. Resolución de problemas de simulación de Montecarlo mediante el uso de la hoja de cálculo.
 MICROSOFT EXCEL PARA DIRECCIÓN FINANCIERA I. 1. Resolución de problemas de simulación de Montecarlo mediante el uso de la hoja de cálculo. Mediante el modelo de Hertz o Simulación de Montecarlo, trataremos
MICROSOFT EXCEL PARA DIRECCIÓN FINANCIERA I. 1. Resolución de problemas de simulación de Montecarlo mediante el uso de la hoja de cálculo. Mediante el modelo de Hertz o Simulación de Montecarlo, trataremos
MEDIDAS DE VARIABILIDAD
 MEDIDAS DE VARIABILIDAD 1 Medidas de variabilidad Qué son las medidas de variabilidad? Las medidas de variabilidad de una serie de datos, muestra o población, permiten identificar que tan dispersos o concentrados
MEDIDAS DE VARIABILIDAD 1 Medidas de variabilidad Qué son las medidas de variabilidad? Las medidas de variabilidad de una serie de datos, muestra o población, permiten identificar que tan dispersos o concentrados
INTRODUCCIÓN AL ANÁLISIS DE DATOS ORIENTACIONES (TEMA Nº 7)
 TEMA Nº 7 DISTRIBUCIONES CONTINUAS DE PROBABILIDAD OBJETIVOS DE APRENDIZAJE: Conocer las características de la distribución normal como distribución de probabilidad de una variable y la aproximación de
TEMA Nº 7 DISTRIBUCIONES CONTINUAS DE PROBABILIDAD OBJETIVOS DE APRENDIZAJE: Conocer las características de la distribución normal como distribución de probabilidad de una variable y la aproximación de
Cuál es el campo de estudio de la prueba de hipótesis?
 ESTIMACIÓN Establecer generalizaciones acerca de una población a partir de una muestra es el campo de estudio de la inferencia estadística. La inferencia estadística se divide en estimación y prueba de
ESTIMACIÓN Establecer generalizaciones acerca de una población a partir de una muestra es el campo de estudio de la inferencia estadística. La inferencia estadística se divide en estimación y prueba de
1. Precio de las obligaciones 2. Rentabilidad al vencimiento 3. El precio de las acciones: Modelo de descuento de dividendos
 Tema 7 VALORACION DE ACCIONES Y BONOS. Precio de las obligaciones. Rentabilidad al vencimiento 3. El precio de las acciones: Modelo de descuento de dividendos Obligaciones Cuando los gobiernos o las empresas
Tema 7 VALORACION DE ACCIONES Y BONOS. Precio de las obligaciones. Rentabilidad al vencimiento 3. El precio de las acciones: Modelo de descuento de dividendos Obligaciones Cuando los gobiernos o las empresas
Más sobre las series geométricas. 1. Derivación de series geométricas elementales
 Semana - Clase 2 4/0/0 Tema : Series Más sobre las series geométricas Las series infinitas se encuentran entre las más poderosas herramientas que se introducen en un curso de cálculo elemental. Son un
Semana - Clase 2 4/0/0 Tema : Series Más sobre las series geométricas Las series infinitas se encuentran entre las más poderosas herramientas que se introducen en un curso de cálculo elemental. Son un
Matemáticas Financieras. Sesión 3 Intereses
 Matemáticas Financieras Sesión 3 Intereses Contextualización de la Sesión 3 En esta sesión iniciaremos con una nueva unidad. Comenzaremos con el interés simple, es muy importante dominar éste tema ya que
Matemáticas Financieras Sesión 3 Intereses Contextualización de la Sesión 3 En esta sesión iniciaremos con una nueva unidad. Comenzaremos con el interés simple, es muy importante dominar éste tema ya que
Lección 5. Punto flotante
 Lección 5. Punto flotante MIGUEL ANGEL UH ZAPATA 1 Análisis Numérico I Facultad de Matemáticas, UADY Agosto 2014 1 Centro de Investigación en Matemáticas, Unidad Mérida En esta lección aprenderemos lo
Lección 5. Punto flotante MIGUEL ANGEL UH ZAPATA 1 Análisis Numérico I Facultad de Matemáticas, UADY Agosto 2014 1 Centro de Investigación en Matemáticas, Unidad Mérida En esta lección aprenderemos lo
Objetivos. 1. Variable Aleatoria y Función de Probabilidad. Tema 4: Variables aleatorias discretas Denición de Variable aleatoria
 Tema 4: Variables aleatorias discretas Objetivos Dominar el uso de las funciones asociadas a una variable aleatoria discreta para calcular probabilidades. Conocer el signicado y saber calcular la esperanza
Tema 4: Variables aleatorias discretas Objetivos Dominar el uso de las funciones asociadas a una variable aleatoria discreta para calcular probabilidades. Conocer el signicado y saber calcular la esperanza
La descomposición del crecimiento económico: Una aplicación a la economía andaluza
 La descomposición del crecimiento económico: Una aplicación a la economía andaluza José L. Torres (Universidad de Málaga) Analistas Económicos de Andalucía Documento de Análisis 6/2010 Resumen: La contabilidad
La descomposición del crecimiento económico: Una aplicación a la economía andaluza José L. Torres (Universidad de Málaga) Analistas Económicos de Andalucía Documento de Análisis 6/2010 Resumen: La contabilidad
RESUMEN DE ALGUNOS CONCEPTOS ESTADÍSTICOS ELEMENTALES Y NOTACIÓN EMPLEADA EN EL CURSO
 RESUMEN DE ALGUNOS CONCEPTOS ESTADÍSTICOS ELEMENTALES Y NOTACIÓN EMPLEADA EN EL CURSO 1 rojo 1 2 3 4 5 6 Supongamos que tenemos dos dados, uno rojo y otro verde, cada uno de los cuales toma valores entre
RESUMEN DE ALGUNOS CONCEPTOS ESTADÍSTICOS ELEMENTALES Y NOTACIÓN EMPLEADA EN EL CURSO 1 rojo 1 2 3 4 5 6 Supongamos que tenemos dos dados, uno rojo y otro verde, cada uno de los cuales toma valores entre
Caso 105. Tamaño de muestra y potencia de una prueba. Diseño de experimentos. Jesús López Fidalgo
 Caso 105. Tamaño de muestra y potencia de una prueba. Diseño de experimentos. Jesús López Fidalgo Caso Práctico El objetivo de este ejercicio es analizar diferentes tipos de pruebas estadísticas en las
Caso 105. Tamaño de muestra y potencia de una prueba. Diseño de experimentos. Jesús López Fidalgo Caso Práctico El objetivo de este ejercicio es analizar diferentes tipos de pruebas estadísticas en las
UNIVERSIDAD NACIONAL MAYOR DE SAN MARCOS FACULTAD DE CIENCIAS CONTABLES ESCUELA ACADÉMICO PROFESIONAL DE GESTIÓN TRIBUTARIA SÍLABO
 ESCUELA ACADÉMICO PROFESIONAL DE GESTIÓN TRIBUTARIA SÍLABO I. INFORMACIÓN GENERAL Asignatura : FINANZAS CORPORATIVAS Ciclo de Estudios : Sétimo Código del Curso : 112735 Carácter : Obligatorio Pre Requisito
ESCUELA ACADÉMICO PROFESIONAL DE GESTIÓN TRIBUTARIA SÍLABO I. INFORMACIÓN GENERAL Asignatura : FINANZAS CORPORATIVAS Ciclo de Estudios : Sétimo Código del Curso : 112735 Carácter : Obligatorio Pre Requisito
Tema 7: Derivada de una función
 Tema 7: Derivada de una función Antes de dar la definición de derivada de una función en un punto, vamos a introducir dos ejemplos o motivaciones iniciales que nos van a dar la medida de la importancia
Tema 7: Derivada de una función Antes de dar la definición de derivada de una función en un punto, vamos a introducir dos ejemplos o motivaciones iniciales que nos van a dar la medida de la importancia
ANEXO 1. CONCEPTOS BÁSICOS. Este anexo contiene información que complementa el entendimiento de la tesis presentada.
 ANEXO 1. CONCEPTOS BÁSICOS Este anexo contiene información que complementa el entendimiento de la tesis presentada. Aquí se exponen técnicas de cálculo que son utilizados en los procedimientos de los modelos
ANEXO 1. CONCEPTOS BÁSICOS Este anexo contiene información que complementa el entendimiento de la tesis presentada. Aquí se exponen técnicas de cálculo que son utilizados en los procedimientos de los modelos
Estimación de la evolución de proyectos en el ámbito de la producción industrial mediante la parametrización de la curva S del coste acumulado
 Estimación de la evolución de proyectos en el ámbito de la producción industrial mediante la parametrización de la curva S del coste acumulado Contenido Qué vamos a ver? Introducción Antecedentes Objetivos
Estimación de la evolución de proyectos en el ámbito de la producción industrial mediante la parametrización de la curva S del coste acumulado Contenido Qué vamos a ver? Introducción Antecedentes Objetivos
CALCULO DE INCERTIDUMBRE DE LAS MEDICIONES DE ENSAYOS
 Gestor de Calidad Página: 1 de 5 1. Propósito Establecer una guía para el cálculo de la incertidumbre asociada a las mediciones de los ensayos que se realizan en el. Este procedimiento ha sido preparado
Gestor de Calidad Página: 1 de 5 1. Propósito Establecer una guía para el cálculo de la incertidumbre asociada a las mediciones de los ensayos que se realizan en el. Este procedimiento ha sido preparado
Gobierno de La Rioja MATEMÁTICAS CONTENIDOS
 CONTENIDOS MATEMÁTICAS 1.- Números reales Distintas ampliaciones de los conjuntos numéricos: números enteros, números racionales y números reales. Representaciones de los números racionales. Forma fraccionaria.
CONTENIDOS MATEMÁTICAS 1.- Números reales Distintas ampliaciones de los conjuntos numéricos: números enteros, números racionales y números reales. Representaciones de los números racionales. Forma fraccionaria.
Ajustes por funciones exponenciales (malthusiana) y sigmoidales (logística y gompertziana)
 Fundamentos de Biología Aplicada I. Curso 009 010. Ajustes por funciones exponenciales malthusiana y sigmoidales logística y gompertziana El objetivo es aproximar una colección de datos obtenidos a partir
Fundamentos de Biología Aplicada I. Curso 009 010. Ajustes por funciones exponenciales malthusiana y sigmoidales logística y gompertziana El objetivo es aproximar una colección de datos obtenidos a partir
Derivadas de orden superior
 Tema 6 Derivadas de orden superior 6 Polinomios de Taylor Nuestro objetivo es aproimar una función dada mediante funciones polinómicas Resulta conveniente estudiar las funciones polinómicas con más detenimiento
Tema 6 Derivadas de orden superior 6 Polinomios de Taylor Nuestro objetivo es aproimar una función dada mediante funciones polinómicas Resulta conveniente estudiar las funciones polinómicas con más detenimiento
TEST DE RAZONAMIENTO NUMÉRICO. Consejos generales
 TEST DE RAZONAMIENTO NUMÉRICO Consejos generales 1 I. INTRODUCCIÓN En lo relativo a los cálculos de porcentajes, es fundamental tener en cuenta que los porcentajes, en realidad, son referencias abstractas,
TEST DE RAZONAMIENTO NUMÉRICO Consejos generales 1 I. INTRODUCCIÓN En lo relativo a los cálculos de porcentajes, es fundamental tener en cuenta que los porcentajes, en realidad, son referencias abstractas,
Autor: Mariano Morettini Profesor Adjunto
 UNIVERSIDAD NACIONAL DE MAR DEL PLATA FACULTAD DE CIENCIAS ECONOMICAS Y SOCIALES APROXIMACIONES DE DISTRIBUCIONES DE PROBABILIDAD: ENFOQUE EMPÍRICO Carrera: Licenciatura en Economía Cátedra: Estadística
UNIVERSIDAD NACIONAL DE MAR DEL PLATA FACULTAD DE CIENCIAS ECONOMICAS Y SOCIALES APROXIMACIONES DE DISTRIBUCIONES DE PROBABILIDAD: ENFOQUE EMPÍRICO Carrera: Licenciatura en Economía Cátedra: Estadística
Posgrado de Especialización en Administración de Organizaciones Financieras. Unidad 4 ESTRUCTURA TEMPORAL DE LOS TIPOS DE INTERES (ETTI)
 Unidad 4 ESTRUCTURA TEMPORAL DE LOS TIPOS DE INTERES (ETTI) ETTI La estructura temporal de los tipos de interés es el conjunto de tasas de interés vigentes en el mercado financiero, según el plazo de vencimiento
Unidad 4 ESTRUCTURA TEMPORAL DE LOS TIPOS DE INTERES (ETTI) ETTI La estructura temporal de los tipos de interés es el conjunto de tasas de interés vigentes en el mercado financiero, según el plazo de vencimiento
Inferencia. Mauricio Olivares. 19 de junio de 2015 ITAM
 Inferencia Mauricio Olivares ITAM 19 de junio de 2015 Recuerda de nuestra clase anterior que m(x) = α + βx. Recuerda de nuestra clase anterior que m(x) = α + βx. Esta es una relación poblacional, no hay
Inferencia Mauricio Olivares ITAM 19 de junio de 2015 Recuerda de nuestra clase anterior que m(x) = α + βx. Recuerda de nuestra clase anterior que m(x) = α + βx. Esta es una relación poblacional, no hay
Ranking de Gestoras de Fondos de Pensiones en España
 Ranking de Gestoras de Fondos de Pensiones en España 199-21 Pablo Fernández Profesor del IESE Titular de la Cátedra PricewaterhouseCoopers de Corporate Finance e-mail: fernandezpa@iese.edu Javier Aguirreamalloa
Ranking de Gestoras de Fondos de Pensiones en España 199-21 Pablo Fernández Profesor del IESE Titular de la Cátedra PricewaterhouseCoopers de Corporate Finance e-mail: fernandezpa@iese.edu Javier Aguirreamalloa
Valoración de empresas a partir del EVA, BE y CVA 1
 Valoración de empresas a partir del EVA, BE y CVA 1 (Economic Value Added, Beneficio Económico y Cash Value Added) Por Pablo Fernández En este trabajo se estudia una serie de parámetros utilizados en la
Valoración de empresas a partir del EVA, BE y CVA 1 (Economic Value Added, Beneficio Económico y Cash Value Added) Por Pablo Fernández En este trabajo se estudia una serie de parámetros utilizados en la
CÁLCULO DE DERIVADAS
 TEMA 4 CÁLCULO DE DERIVADAS Contenidos Criterios de Evaluación 1. Función derivada.. Derivadas sucesivas. 3. Derivadas elementales. 4. Álgebra de derivadas. 5. La Regla de la Cadena. 6. Continuidad y derivabilidad.
TEMA 4 CÁLCULO DE DERIVADAS Contenidos Criterios de Evaluación 1. Función derivada.. Derivadas sucesivas. 3. Derivadas elementales. 4. Álgebra de derivadas. 5. La Regla de la Cadena. 6. Continuidad y derivabilidad.
[5.1] Cómo estudiar este tema? [5.5] Modelos de rentas más usuales. [5.6] Operaciones de constitución de un capital
![[5.1] Cómo estudiar este tema? [5.5] Modelos de rentas más usuales. [5.6] Operaciones de constitución de un capital [5.1] Cómo estudiar este tema? [5.5] Modelos de rentas más usuales. [5.6] Operaciones de constitución de un capital](/thumbs/50/26100534.jpg) Rentas financieras [5.1] Cómo estudiar este tema? [5.2] Concepto de renta [5.3] Clasificación de una renta [5.4] Valor de una renta [5.5] Modelos de rentas más usuales [5.6] Operaciones de constitución
Rentas financieras [5.1] Cómo estudiar este tema? [5.2] Concepto de renta [5.3] Clasificación de una renta [5.4] Valor de una renta [5.5] Modelos de rentas más usuales [5.6] Operaciones de constitución
ECONOMETRÍA II Prof.: Begoña Álvarez TEMA 1 INTRODUCCIÓN. Estimación por máxima verosimilitud y conceptos de teoría asintótica
 ECONOMETRÍA II Prof.: Begoña Álvarez 2007-2008 TEMA 1 INTRODUCCIÓN Estimación por máxima verosimilitud y conceptos de teoría asintótica 1. ESTIMACIÓN POR MÁXIMA VEROSIMILITUD (MAXIMUM LIKELIHOOD) La estimación
ECONOMETRÍA II Prof.: Begoña Álvarez 2007-2008 TEMA 1 INTRODUCCIÓN Estimación por máxima verosimilitud y conceptos de teoría asintótica 1. ESTIMACIÓN POR MÁXIMA VEROSIMILITUD (MAXIMUM LIKELIHOOD) La estimación
Estadística. Grado en Relaciones Laborales y Recursos Humanos. Tema 6 Estadística poblacional.
 Estadística. Grado en Relaciones Laborales y Recursos Humanos Tema 6 Estadística poblacional. Fenómenos demográficos 1 Variable estadística edad a la que ocurre un suceso Los fenómenos demográficos que
Estadística. Grado en Relaciones Laborales y Recursos Humanos Tema 6 Estadística poblacional. Fenómenos demográficos 1 Variable estadística edad a la que ocurre un suceso Los fenómenos demográficos que
Tema 8. Las inversiones y su selección. La rentabilidad de las inversiones
 Tema 8. Las inversiones y su selección. La rentabilidad de las inversiones - Tipos de inversiones - Variables fundamentales que definen un plan de inversión - Rentabilidad esperada y requerida. - Riesgo
Tema 8. Las inversiones y su selección. La rentabilidad de las inversiones - Tipos de inversiones - Variables fundamentales que definen un plan de inversión - Rentabilidad esperada y requerida. - Riesgo
Tema 7. Variables Aleatorias Continuas
 Presentación y Objetivos. Tema 7. Variables Aleatorias Continuas En este tema se propone el estudio de las variables aleatorias continuas más importantes, desde la más simple incrementando el grado de
Presentación y Objetivos. Tema 7. Variables Aleatorias Continuas En este tema se propone el estudio de las variables aleatorias continuas más importantes, desde la más simple incrementando el grado de
Unidad IV. La sucesión de sumas parciales asociada a una sucesión está definida para cada como la suma de la sucesión desde hasta :
 Unidad IV Series. 4.1 Definición de seria. Una serie es la generalización de la noción de suma a los términos de una sucesión infinita. Informalmente, es el resultado de sumar los términos: a 1 + a 2 +
Unidad IV Series. 4.1 Definición de seria. Una serie es la generalización de la noción de suma a los términos de una sucesión infinita. Informalmente, es el resultado de sumar los términos: a 1 + a 2 +
Sistema de Capitalización Continua MATEMÁTICA FINANCIERA. Derivación del factor de capitalización continua
 Sistema de MATEMÁTICA FINANCIERA SISTEMA DE CAPITALIZACIÓN CONTINUA Luis Alcalá UNSL Segundo Cuatrimeste 06 La TEA equivalente a una tasa nominal fija, aumenta a medida que aumentamos la frecuencia de
Sistema de MATEMÁTICA FINANCIERA SISTEMA DE CAPITALIZACIÓN CONTINUA Luis Alcalá UNSL Segundo Cuatrimeste 06 La TEA equivalente a una tasa nominal fija, aumenta a medida que aumentamos la frecuencia de
Las Matemáticas para la Gestión del Riesgo en Carteras Financieras. Carteras compuestas por dos activos con correlaciones estadísticas arbitrarias
 Las Matemáticas para la Gestión del Riesgo en Carteras Financieras Carteras compuestas por dos activos con correlaciones estadísticas arbitrarias Apellidos, nombre Departamento Centro Cortés López, Juan
Las Matemáticas para la Gestión del Riesgo en Carteras Financieras Carteras compuestas por dos activos con correlaciones estadísticas arbitrarias Apellidos, nombre Departamento Centro Cortés López, Juan
Técnicas numéricas para las Ecuaciones diferenciales de primer orden: Método de Euler
 Lección 6 Técnicas numéricas para las Ecuaciones diferenciales de primer orden: Método de Euler 61 Introducción a los métodos numéricos En este capítulo y en los anteriores estamos estudiado algunas técnicas
Lección 6 Técnicas numéricas para las Ecuaciones diferenciales de primer orden: Método de Euler 61 Introducción a los métodos numéricos En este capítulo y en los anteriores estamos estudiado algunas técnicas
Tema 8. Análisis de dos variables Ejercicios resueltos 1
 Tema 8. Análisis de dos variables Ejercicios resueltos 1 Ejercicio resuelto 8.1 La siguiente tabla muestra la distribución del gasto mensual en libros y el gasto mensual en audiovisual en euros en los
Tema 8. Análisis de dos variables Ejercicios resueltos 1 Ejercicio resuelto 8.1 La siguiente tabla muestra la distribución del gasto mensual en libros y el gasto mensual en audiovisual en euros en los
