Estructura y geometría cristalina
|
|
|
- Enrique Morales Bustos
- hace 6 años
- Vistas:
Transcripción
1 Principales estructuras cristalinas. redes de Bravais empaquetamientos HCP / FCC / BCC Direcciones y planos cristalográficos Índices de Miller Aplicación n a análisis de estructuras cristalográficas sencillas Difracción de rayos X Fórmula de Bragg Difractogramas de polvo Análisis de estructuras cúbicas Laboratorio de Simulación de Materiales no Metálicos 1
2 Lo que hay que saber calcular en MatII: fracción de empaquetamiento atómico densidades (volumétrica, superficial, lineal) huecos disponibles y su tamaño dados índices, identificar direcciones y planos, y viceversa asignar clase cristalográfica a un material calcular distancias entre planos de una forma aplicar Ley de Bragg para identificar las estructuras más sencillas Muy importante Laboratorio de Simulación de Materiales no Metálicos 2
3 El cristal (la estructura cristalina) está formada por RED + BASE se coloca una base en TODOS Y CADA UNO de los puntos de la red RED + BASE Muy importante CRISTAL Laboratorio de Simulación de Materiales no Metálicos 3
4 Redes de Bravais; ; tres definiciones equivalentes: un conjunto infinito enumerable de puntos que tiene exactamente el mismo aspecto cuando se observa desde cualquiera de ellos. el conjunto de todos los puntos con vectores de posición n que satisfacen: R = na 1 1+ n2a2+ n3a3 donde a1, a2, a3 n, n, n son tres enteros. son tres vectores cualesquiera no coplanarios y un conjunto infinito enumerable de vectores, no todos coplanarios, cerrado bajo las operaciones de adición n y sustracción n de vectores. Nota: en estas definiciones, la red se considera tanto como un conjunto de puntos, como un conjunto de traslaciones o como un conjunto de vectores. En la práctica no suele haber duda de a cuál de éstas alternativas nos referimos. Laboratorio de Simulación de Materiales no Metálicos 4
5 a, a, a los vectores Estructura y geometría cristalina se denominan vectores primitivos y se dice que generan la red. a 3 a 2 a 1 los vectores primitivos no son únicos hay un número n infinito de posibles vectores primitivos: Laboratorio de Simulación de Materiales no Metálicos 5
6 Número de coordinación de la red es el número n de puntos de la red más m s próximos a un punto cualquiera de la red Celda unitaria primitiva: : la porción n del espacio que, cuando se translada con todos los vectores de la red, cubre ( tesela( tesela ) ) el espacio sin dejar vacíos y sin solaparse con otras copias de ella misma. hay infinitas posibilidades de elegir una celda unitaria primitiva para una red de Bravais dada. Laboratorio de Simulación de Materiales no Metálicos 6
7 una celda unitaria primitiva contiene exactamente un punto de red una celda unitaria (no primitiva) o celda unitaria convencional es una porción n del espacio que lo tesela completamente al ser transladada por un subconjunto de los vectores de red. suele ser más m s grande que la celda unitaria primitiva y tener la misma simetría a que la red de Bravais. Celda primitiva de Wigner-Seitz es una celda primitiva que posee la simetría a completa (es decir, todos los elementos de simetría) de la red de Bravais correspondiente. La celda primitiva de Wigner-Seitz de un punto de red se define como: el conjunto de puntos del espacio que están más próximos al punto de red en cuestión que a cualquier otro. Laboratorio de Simulación de Materiales no Metálicos 7
8 red de Bravais (2D) bisectrices P celdas primitivas de Wigner-Seitz los puntos dentro de esta región están más cerca de P que de cualquier otro punto de la red Laboratorio de Simulación de Materiales no Metálicos 8
9 El grupo (completo) de simetría de una estructura (cristalina, mat. compuesto, etc.) es un conjunto de operaciones geométricas (translación, n, rotación, reflexión, inversión) n) respecto a las que es invariante y que contiene exclusivamente: translaciones por vectores de la red operaciones que dejan un punto de la red fijo operaciones construidas por aplicación sucesiva de operaciones de los dos tipos anteriores. El grupo espacial de una estructura es el subgrupo que contiene sólo las translaciones. El grupo puntual de una estructura es el subgrupo que contiene sólo las operaciones que dejan un punto fijo (rotaciones, inversiones y reflexiones, + combinaciones de éstas). Laboratorio de Simulación de Materiales no Metálicos 9
10 Estas operaciones que dejan un punto fijo son: rotaciones por un múltiplo de 2π/n alrededor de un eje gira un punto o vector de red 2π/n alrededor de un eje reflexión en un plano refleja un punto o vector de red en un plano inversión (o reflexión en un punto) cambia de signo las tres coordenadas de un vector de red rotación-reflexión gira y a continuación refleja en un plano perpendicular al eje de giro rotación-inversión gira y a continuación invierte un punto o vector (reflexión o inversión en un punto contenido en el eje de rotación) Laboratorio de Simulación de Materiales no Metálicos 10
11 Un elemento de simetría (en sentido cristalográfico) es el lugar geométrico de los puntos que permanecen invariantes por la correspondiente operación n del grupo puntual: si una estructura (clase) es simétrica respecto a inversión en un punto, este punto (centro de inversión) es un elemento de simetría. si una estructura (clase) es simétrica respecto a un giro de 2π/2, el eje de esta rotación (eje binario) es un elemento de simetría. si una estructura (clase) es simétrica respecto a una reflexión en un plano, este plano de reflexión es un elemento de simetría. Importante: no debe ser confundido con un elemento del grupo (puntual) de simetría (en sentido de teoría a de grupos): un elemento de simetría a (cristalográfico) p.ej. un eje ternario, puede generar varios elementos del grupo puntual de simetría a de la clase correspondiente. Los estereogramas de la Tabla I son un modo compacto y muy eficiente ente de enumerar los elementos de simetría a (cristalográficos) de cada una de las 32 clases. Laboratorio de Simulación de Materiales no Metálicos 11
12 Si consideramos las operaciones del grupo espacial, obtenemos las 14 redes de Bravais Las 14 redes de Bravais (en 3D) se pueden clasificar en siete sistemas cristalográficos cada uno de los siete grupos puntuales da lugar a varias (entre 1 y 4) redes de Bravais cúbico: 3 tetragonal: 2 ortorrómbico: 4 monoclínico: 2 triclínico: 1 romboédrico (o trigonal): 1 hexagonal: 1 TOTAL 14 P I F P I P P C F I P C P Laboratorio de Simulación de Materiales no Metálicos 12
13 Si consideramos el grupo puntual se obtienen las 32 clases puntuales cristalográficas o simplemente clases cristalográficas Por último, si además s consideramos el grupo espacial, se obtienen los 230 grupos espaciales cristalográficos ficos: Red de Bravais Estructuras cristalográficas (base de simetría esférica) (base de simetría arbitraria; restringe la simetría de la red) Nº de grupos puntuales: 7 32 ( los 7 sistemas cristalográficos ) ( los 32 grupos puntuales cristalográficos ) Nº de grupos espaciales: ( las 14 redes de Bravais ) ( los 230 grupos espaciales ) Nota: los cristalógrafos a veces defienden la existencia de sólo 6 sistemas cristalográficos (ver nota del traductor al pie de la pág.46). Desde el punto de vista de los grupos puntuales de las redes de Bravais no hay duda alguna sobre el número de sistemas cristalográficos: 7. Para más detalle, puede consultarse W. Borchard-Ott, Kristallographie, 6ª edición, Springer (2002) Laboratorio de Simulación de Materiales no Metálicos 13
14 Es esencial saber identificar los elementos de simetría a de un cristal, de un material compuesto, de un material orientado, etc. muy importante Laboratorio de Simulación de Materiales no Metálicos 14
15 Las clases cristalográficas y sus elementos de simetría Laboratorio de Simulación de Materiales no Metálicos 15
16 En MatII empleamos el términot simétrico como invariante respecto a a (interpretación n habitual en física): f p.ej. una estructura cristalina es simétrica respecto a un giro de 90º si, al girarla 90º,, no es posible distinguir la estructura resultante de la original Laboratorio de Simulación de Materiales no Metálicos 16
17 La simetría a (invarianza( invarianza) ) es un principio físico f extraordinariamente potente. Es más m s fundamental que las leyes de conservación: n: invarianza de las leyes físicas respecto a traslación en el tiempo: implica conservación de energía. invarianza de las leyes físicas respecto a traslación en el espacio: implica conservación de cantidad de movimiento. invarianza de las leyes físicas respecto a rotación: implica conservación de momento angular. etc... Laboratorio de Simulación de Materiales no Metálicos 17
18 En MatII: la simetría a geométrica determina en gran medida la existencia o ausencia de propiedades físicas y por tanto las posibilidades de utilización n de los materiales los materiales pueden tener ciertas propiedades sólo si su estructura molecular, morfología a o su estructura macroscópica cumplen ciertos requisitos de simetría (o de falta de simetría, como en el caso de los efectos piezoeléctricos directo e inverso) para propiedades tensoriales el número n de componentes (o coeficientes) de la propiedad que son independientes,, está determinado por la simetría del cristal / material Laboratorio de Simulación de Materiales no Metálicos 18
19 Identificación de la clase cristalográfica Para identificar a qué sistema y a qué clase pertenece un material cristalino, orientado, compuesto, etc., en general: 1. determinar el sistema: bien a la vista de las dimensiones y ángulos de la celda básica o unidad equivalente. o bien con ayuda de la tabla de elementos de simetría característicos (Tabla III) 2. es importante colocar la celda básica o el cristal en los ejes en la posición convencional o estándar. 3. determinar la clase con ayuda de la tabla de representaciones estereográficas, (Tabla I) con ayuda de la Tabla II Laboratorio de Simulación de Materiales no Metálicos 19
20 Ejes en sistemas cristalográficos Orientación convencional (estándar) de los ejes cristalográficos: x β a O γ c c α z b y a b c α β γ x, y, z a lo largo de las aristas de la celda (en general no son perpendiculares entre sí, no son cartesianos). en los sistemas hexagonal y trigonal se puede introducir un cuarto eje u coplanario con x e y de modo que x, y y u forman 120º (ejes de Miller- Bravais), y son siempre perpendiculares entre sí (cartesianos) y forman un triedro a derechas La orientación convencional (estándar) de los ejes x, y, z en los diferentes sistemas cristalográficos es: i) triclínico: ii) monoclínico: Oy paralelo a eje de simetría binario; a b c α = γ = 90º β iii) ortorrómbico: Ox, Oy, Oz paralelos a los tres ejes de simetría binarios; iv) tetragonal: Oz paralelo al eje de simetría cuaternario; a = b c α = β = γ = a b c α = β = γ = v) cúbico: Ox, Oy, Oz paralelos a las aristas del cubo cuyas diagonales son los ejes de simetría ternarios; vi) trigonal: Oz paralelo al eje de simetría ternario; vii) hexagonal: Oz paralelo al eje de simetría senario; a = b = c α = β = γ = 90º 90º a = b c α = β = 90º, γ = 120º a = b c α = β = 90º, γ = 120º 90º Laboratorio de Simulación de Materiales no Metálicos 20
21 Ejes en sistemas cristalográficos Orientación convencional (estándar) de los ejes cartesianos, y : i) monoclínico: paralelo a Oy ii) tetragonal, trigonal y hexagonal : paralelo a Oz; paralelo a Ox iii) ortorrómbico y cúbico: paralelo a Ox; paralelo a Oy; paralelo a Oz iv) clases límite: paralelo a Oz y ambos coincidentes con un eje de orden Laboratorio de Simulación de Materiales no Metálicos 21
22 Ejes en sistemas cristalográficos IMPORTANTE: EN DOS CASOS, EL TEXTO NO DEFINE CON CLARIDAD LAS CELDAS O LAS ORIENTACIONES CONVENCIONALES DE LOS EJES. 60º 120º 60º z c a = b c α = β = 90º, γ = 120º Los puntos de red de la celda del sistema hexagonal son los vértices de un prisma recto cuya base es un rombo; NO es un hexágono x a Orientación convencional correcta en el sistema monoclínico (Int. Union of Crystallography) β γ α b y Laboratorio de Simulación de Materiales no Metálicos 22
23 En MatII,, los cálculos c se deben llevar a cabo SIEMPRE en un sistema cartesiano Bien en el definido en la transp. anterior O bien en otro, rotado respecto al anterior, pero NUNCA en los ejes cristalográficos x, y, z (salvo que coincidan con los, y ) Laboratorio de Simulación de Materiales no Metálicos 23
24 Elementos de simetría Para los 7 sistemas cristalográficos, las 32 clases cristalográficas se especifican enumerando los elementos de simetría más característicos, cada elemento se describe por medio de un símbolo o notación Internacional estándar 1. Centro de simetría a o de inversión: cristal o material invariante cuando se invierten (inversión) los signos de las tres coordenadas x 1 -x 1, x 2 -x 2, x 3 -x 3 Eje de rotación n n-arion ario: cristal o material invariante cuando se realiza un giro de 2π/n radianes. Eje de rotación- inversión n n-arion ario: cristal o material invariante cuando se realiza un giro de 2π/n radianes seguido de una inversión. Elemento de simetría Centro de simetría Plano especular Eje de rotación monario Eje de rotación binario Eje de rotación ternario Eje de rotación cuaternario Eje de rotación senario Eje de inversión monario centro de simetría Eje de inversión binario Eje de inversión ternario 3 más centro de simetría Eje de inversión cuaternario (incluye un eje binario) Eje de inversión senario m al eje binario Símbolo en el estereograma sin símbolo línea gruesa o círculo máximo en línea gruesa 3 más m al eje ternario sin símbolo sin símbolo igual que para m Símbolo Internacional 1 La notación empleada es la más extendida (Internacional) debida a Mauguin y Hermann (Cotton, F. A. Chemical Applications of Group Theory, 3rd ed. New York: Wiley, p. 379, 1990). Aún se encuentran en algunos textos los Laboratorio de Simulación de Materiales no Metálicos símbolos de Schönflies, más antiguos y menos utilizados m ( m ) ( 3/ m )
25 Estereograma En las tablas siguientes 1, los elementos de simetría de cada clase están representados por medio de estereogramas 2,3 en los que también aparecen los ejes convencionales (x, y, z) y (x 1, x 2, x 3 ). El origen (punto invariante) del grupo puntual está en el origen de una esfera de referencia. Las orientaciones de los elementos de simetría están determinadas por sus intersecciones con la superficie de la esfera de referencia cada diagrama representa la proyección del hemisferio superior sobre el plano ecuatorial usando el polo inferior como foco de la proyección: 1 Nye, J.F. Physical Properties of Crystals, Oxford Science Publications (1995) 2 Borchard-Ott, W., Kristallographie, 6ª edición, Springer (2002) 3 Los símbolos de las clases centrosimétricas están recuadrados Laboratorio de Simulación de Materiales no Metálicos 25
26 En las siguientes tablas, las clases centrosimétricas tricas van recuadradas Las clases de cada sistema cristalográfico son los subgrupos propios del grupo (que es el de mayor simetría a y aparece en último lugar en la Tabla I) y es la clase holoédrica u holoedro) Laboratorio de Simulación de Materiales no Metálicos 26
27 El orden de la clase (subgrupo) ) es el número n de elementos de ese grupo o subgrupo Cristales/materiales altamente simétricos pertenecen a clases de orden alto ( ( con muchos elementos de simetría,, p.ej. la m3m es de orden 48, es decir, su grupo puntual contiene 48 elementos) El orden de las clases no holoédricas puede ser la mitad (clase hemiédrica drica) ) o la cuarta parta (clase tetartoédrica drica) ) del orden del holoedro Laboratorio de Simulación de Materiales no Metálicos 27
28 Elementos de simetría de las 32 clases (Tabla I) TRICLÍNICO TETRAGONAL orden 1 orden 2 MONOCLÍNICO orden 4 orden 4 orden 2 orden 2 orden 4 orden 8 orden 8 ORTORRÓMBICO orden 4 orden 4 orden 8 orden 8 orden 8 orden 16 Laboratorio de Simulación de Materiales no Metálicos 28
29 Elementos de simetría de las 32 clases TRIGONAL HEXAGONAL TETRAGONAL orden 6 orden 6 orden 3 orden 6 orden 12 orden 12 orden 6 orden 6 orden 12 orden 12 orden 12 orden 24 Laboratorio de Simulación de Materiales no Metálicos 29
30 Elementos de simetría de las 32 clases CÚBICO orden 12 orden 24 orden 24 orden 24 orden 48 Laboratorio de Simulación de Materiales no Metálicos 30
31 Elementos de simetría de las 32 clases (Tabla II) Finalmente, las siguientes tablas visualizan las simetrías de cada clase por medio de prismas cuyas caras has sido coloreadas de manera que pertenecen a, y son representativas de la clase correspondiente. 1 1 Ashcroft, N.W., Mermin, N.D., Solid State Physics, Brooks & Cole (1976) Laboratorio de Simulación de Materiales no Metálicos 31
32 Elementos de simetría característicos (Tabla III) Para poder deducir rápidamente a cuál de los 7 sistemas cristalográficos (no a cuál de las 32 clases cristalográficas) pertenece un material compuesto o un material orientado, se identifica cuáles de los siguientes elementos de simetría característicos de cada sistema posee el material: Sistema cristalográfico cúbico Elementos de simetría a característicos cuatro hexagonal tetragonal un un o un o un trigonal ortorrómbico monoclínico un ( ojo!, tres o tres es cúbico) ( ojo!, un m al eje ternario, es decir, 3/ m 6, es hexagonal) y/o m en tres direcciones ortogonales y/o m en una dirección triclínico sólo 1 o 1 Laboratorio de Simulación de Materiales no Metálicos 32
33 Ejemplo Elementos de la clase mmm (grupo de máxima simetría dentro del sistema ortorrómbico): la identidad ( no hacer nada al cristal es siempre miembro del grupo) tres ejes de simetría de rotación binarios tres planos de simetría especular centro de inversión o simetría Total: =8 Esta clase posee 8 elementos (cristalográficos) de simetría; cada uno de ellos genera sólo un elemento del grupo puntual y por tanto su orden es también 8. Es la clase holoédrica u holoedro del sistema ortorrómbico Laboratorio de Simulación de Materiales no Metálicos 33
34 Grupos límite de simetría Finalmente, existen materiales HOMOGENEOS cuya estructura presenta simetría a no cristalográfica (grupos límite l o de Curie, típicamente contienen un eje de orden ), y no son monocristales. Ejemplo: un piezoeléctrico PZT, es policristalino, pero al fabricarlo, se le aplica una polarización n permanente en una dirección n predeterminada. Sus módulos piezoeléctricos tienen una estructura de simetría a no cristalográfica Ejemplo: una fibra textil de PET, se estira durante la fabricación; su módulo m elástico en dirección n longitudinal es muy elevado. Su tensor de rigidez elástica tiene una estructura de simetría a no cristalográfica Laboratorio de Simulación de Materiales no Metálicos 34
35 Grupos límite de simetría (Tabla IV) En Mat II consideramos los 7 grupos de Curie: (un eje de orden infinito) levógiro L o dextrógiro R a izquierdas o a derechas m (un eje de orden infinito, más infinitos planos especulares que contienen el eje) / m (un eje de orden infinito, más un plano especular perpendicular al eje) 2 (un eje de orden infinito, más infinitos ejes binarios perpendiculares al eje de orden infinito) levógiro L o dextrógiro R a izquierdas o a derechas R L R L estas figuras representativas pertenecen a las clases y poseen los elementos de simetría característicos de las clases Laboratorio de Simulación de Materiales no Metálicos 35
36 Grupos límite de simetría (Tabla IV) (un eje de orden infinito, más infinitos ejes de orden infinito perpendiculares al primer eje) levógiro L o dextrógiro R a izquierdas o a derechas / mm (un eje de orden infinito, más infinitos planos especulares que contienen el eje, más un plano especular perpendicular al eje) m (un eje de orden infinito, más infinitos planos especulares que contienen el eje, más infinitos ejes de orden infinito perpendiculares al primer eje, isótropo ) R L Laboratorio de Simulación de Materiales no Metálicos 36
37 Muy importante: Hacer el ejercicio 09_02_01 entero Laboratorio de Simulación de Materiales no Metálicos 37
38 Principales estructuras cristalinas. empaquetamientos de átomos = esferas hexagonal compacto o HCP (hexagonal closed packing) cúbico centrado en las caras o FCC (face centered cubic) cúbico centrado en el cuerpo o BCC (body centered cubic) son especialmente importantes en metales, semicond. y cerámicas HCP y FCC son los empaquetamientos más compactos posibles de esferas iguales (con 12 esferas tangentes a una dada) BCC FCC HCP Laboratorio de Simulación de Materiales no Metálicos 38
39 Principales estructuras cristalinas. FCC y BCC son redes de Bravais. BCC NO es compacta, pero Sí es red de Bravais. HCP NO es red de Bravais, pero SÍ es compacta. FCC SÍ es compacta y Sí es red de Bravais. HCP y FCC son en cierto sentido muy similares: pueden construirse como apilamientos de capas compactas bidimensionales (con 6 esferas tangentes a una dada en el plano) Laboratorio de Simulación de Materiales no Metálicos 39
40 Laboratorio de Simulación de Materiales no Metálicos 40
41 Principales estructuras cristalinas. HCP y FCC difieren en la secuencia (orden) de apilamiento: A-B-A-B-... conduce a HCP A A B Laboratorio de Simulación de Materiales no Metálicos 41
42 Principales estructuras cristalinas. HCP y FCC difieren en la secuencia (orden) de apilamiento: A-B-C-A-B-C-... conduce a FCC A C B Laboratorio de Simulación de Materiales no Metálicos 42
43 Representadas de este modo se ve que HCP y FCC están construidas apilando capas compactas 2D Este es el modo más m s natural de mirar la estructura HCP Sin embargo, no se aprecia a primera vista el aspecto cúbico de la estructura FCC Para ver la FCC claramente, hay que rotar los planos de esferas compacto de manera que su normal apunte en la dirección <111> (forma iguales ángulos con los tres semiejes positivos) Laboratorio de Simulación de Materiales no Metálicos 43
44 HCP y FCC son las estructuras compactas más m s sencillas Existen estructuras más m s complicadas, Se obtienen p.ej.. variando la secuencia: se repite A-B-C-B (llamada hc o también 4H ) a través de defectos alternancia aleatoria (el Co es 90% HCP y 10% FCC) En las estructuras HCP y FCC, las esferas definen o dejan libres huecos,, que pueden ser de dos tipos: tetraédricos octaédricos Muy importante Laboratorio de Simulación de Materiales no Metálicos 44
45 Huecos tetraédricos de las estructuras FCC y HCP: en azul: en verde: átomos de las estructuras FCC y HCP huecos tetraédricos de las estructuras FCC y HCP FCC HCP Laboratorio de Simulación de Materiales no Metálicos 45
46 Huecos octaédricos de las estructuras FCC y HCP: en azul: en amarillo: átomos de las redes FCC y HCP huecos octaédricos de las redes FCC y HCP FCC HCP Laboratorio de Simulación de Materiales no Metálicos 46
47 Localización n de los huecos octaédricos y tetraédricos en torno a una esfera en empaquetamientos compactos: FCC HCP Laboratorio de Simulación de Materiales no Metálicos 47
48 Los huecos son muy importantes porque un gran número n de compuestos inorgánicos nicos ( ( mat. cerámicos) forman estructuras en las que: los aniones (grandes, típicamente oxígeno, azufre) ocupan los sitios de una red FCC o HCP los cationes (pequeños, típicamente metales, aunque a veces pueden ser también aniones) ocupan algunos o todos los huecos intersticiales Laboratorio de Simulación de Materiales no Metálicos 48
49 NaCl (Na ocupa todos los huecos octaédricos) ZnS (Zn ocupa la mitad de los huecos tetraédricos, los T + ) FCC Li 3 Bi (Li ocupa todos los huecos tetraédricos y octaédricos) CaF 2 (F - ocupa todos los huecos tetraédricos) Laboratorio de Simulación de Materiales no Metálicos 49
50 Especialmente importantes en los materiales cerámicos, en particular: en los silicatos y silicoaluminatos (>75% del mercado de mat. cerámicos) el oxígeno define estructuras compactas el silicio y el aluminio ocupan huecos tetraédricos y octaédrico Ver capítulo 8 Laboratorio de Simulación de Materiales no Metálicos 50
51 Posiciones y direcciones cristalográficas Para especificar posiciones atómicas se usa (x,y,z) medidas en unidades de distancia a lo largo de los ejes Para especificar direcciones se usan componentes (como si fuera un vector, pero con componentes enteras lo más pequeñas posibles sin comas signos negativos: barra sobre la componente direcciones equivalentes: idéntica secuencia de átomos y distancias 113 direcciones equivalentes forman un tipo 100 Laboratorio de Simulación de Materiales no Metálicos 51
52 Planos cristalográficos Para especificar planos cristalográficos se usan los índices de Miller: para el plano cristalográfico deseado más s cercano al origen se determinan las intersecciones con los ejes se calculan los inversos se multiplican por el denominador mayor signo negativo: barra sobre la componente (110) conjunto de planos equivalentes: forma { 110} Laboratorio de Simulación de Materiales no Metálicos 52
53 Planos cristalográficos hexagonales en el hexagonal se usan cuatro índices ( hkil) uno de los tres primeros (generalmente el tercero, por convención) es superfluo (es siempre ) pero hace manifiesta la simetría hexagonal, que de otro modo es menos evidente Para direcciones se procede análogamente i= h k Los índices de Miller resultan especialmente útiles en el análisis de estructuras cristalinas por difracción n (rayos X, neutrones) Laboratorio de Simulación de Materiales no Metálicos 53
54 La definición n cristalográfica de los índices de Miller parece arbitraria a primera vista. En análisis de estructuras por rayos X y en física f de estado sólido s se ve inmediatamente la justificación n de esta definición. n. La definición n operativa de los índices de Miller: son las componentes del vector normal (de la red recíproca) más m s corto perpendicular al plano que se considera. Esta definicion obliga sin embargo a introducir la red recíproca, innecesaria en Materiales II. Por eso el libro y la asignatura siguen la definición n cristalográfica, aunque parezca arbitraria. Laboratorio de Simulación de Materiales no Metálicos 54
55 La difractografía y la NMR son las dos herramientas básicas b para elucidar estructuras ordenadas (cristalinas, coloidales, semiconductores, virus) difractograma del NaCl difractograma de la mioglobina difractograma de una dispersión coloidal reconstrucción 3D de un ribosoma Laboratorio de Simulación de Materiales no Metálicos 55
56 La reflexión n de radiación n X en cristales requiere interferencia constructiva: el camino extra debe ser un múltiplo entero de la longitud de onda: 2dsinθ = nλ Condición de Bragg (existe una formulación alternativa debida a von Laue, basada en la red recíproca) Laboratorio de Simulación de Materiales no Metálicos 56
57 La reflexión n de radiación n X en cristales requiere interferencia constructiva: Cada forma de planos producirá un reflejo para un valor determinado del ángulo de incidencia (para un valor fijo de n; la reflexión más intensa se obtiene para orden n=1; en MatII consideraremos siempre n=1) 2d sinθ = nλ Así se obtiene un difractograma de (mono)cristal: hkl { hkl} 2θ 111 2θ 010 Laboratorio de Simulación de Materiales no Metálicos 57
58 En el método del difractograma de polvo se realiza cuando no es posible obtener un monocristal de suficiente tamaño. Una muestra en polvo es una colección n de muchos monocristales orientados al azar (en todas las posibles orientaciones) Se obtiene un difractograma de monocristal,, rotado en torno al eje definido por el rayo X incidente De cada mancha (punto) se obtiene ahora un círculoc 2θ Laboratorio de Simulación de Materiales no Metálicos 58
59 Finalmente, se lee la densidad óptica (el ennegrecimiento) de la película (o el número de fotones recibidos en una CCD) en función n del radio (->( > del ángulo) intensidad (fotones / s) difractrograma de polvo 2θ Laboratorio de Simulación de Materiales no Metálicos 59
60 Existe una tercera alternativa (Método( de Laue) ) en la cual no se gira el cristal sino que se varía a la longitud de onda de la radiación n X incidente. Resumiendo: para buscar reflejos (cuando se cumple la condición n de Bragg) se pueden seguir tres métodos: m Método de Laue: muestra fija, longitud de onda variable Método del (mono)cristal: se gira la muestra, longitud de onda fija Método del difractograma de polvo: se gira la muestra (muchos cristales diminutos), longitud de onda. La fórmula f que aprendemos a continuación n es válida v para cualquier reflejo obtenido por cualquiera de los tres métodosm Los tres métodos m proporcionan mucha más m s información n (cómo extraerla del difractograma,, se sale de los límites l de la asignatura) Laboratorio de Simulación de Materiales no Metálicos 60
61 { hkl} La distancia entre planos de una forma está dada por: d hkl = a h + k + l Luego los picos del difractograma aparecerán n para todos aquéllos ángulos que satisfagan: a 2 sinθ = h + k + l nλ De donde se puede determinar muy fácilmente f la constante de red y algunos detalles cristalográficos, y con más m s trabajo (FFT 3D) toda la información n cristalográfica Laboratorio de Simulación de Materiales no Metálicos 61
2.2 Simetría en los sólidos cristalinos
 2.2 Simetría en los sólidos cristalinos Observación: Distribución de las caras en los cristales Sentido de proporción y equilibrio geométrico Simetría externa de los cristales permite: - Placer estético
2.2 Simetría en los sólidos cristalinos Observación: Distribución de las caras en los cristales Sentido de proporción y equilibrio geométrico Simetría externa de los cristales permite: - Placer estético
Contenido. 5. Estructura cristalina. Omar De la Peña-Seaman IFUAP Física del Estado Sólido Maestría (Física) 1/51 51
 Contenido 5. Estructura cristalina 1 / Omar De la Peña-Seaman IFUAP Física del Estado Sólido Maestría (Física) 1/51 51 Contenido: Tema 05 5. Estructura cristalina 5.1 Arreglo periódico de átomos: bases,
Contenido 5. Estructura cristalina 1 / Omar De la Peña-Seaman IFUAP Física del Estado Sólido Maestría (Física) 1/51 51 Contenido: Tema 05 5. Estructura cristalina 5.1 Arreglo periódico de átomos: bases,
Física del Estado Sólido REDES CRISTALINAS. Dr. Andrés Ozols. Facultad de Ingeniería Universidad de Buenos Aires. Dr. A. Ozols 1
 Física del Estado Sólido REDES CRISTALINAS Dr. Andrés Ozols Facultad de Ingeniería Universidad de Buenos Aires 2009 Dr. A. Ozols 1 ÁTOMOS EN SÓLIDOS Dr. A. Ozols 2 ORDEN CRISTALINO y FORMA René Just Hauy
Física del Estado Sólido REDES CRISTALINAS Dr. Andrés Ozols Facultad de Ingeniería Universidad de Buenos Aires 2009 Dr. A. Ozols 1 ÁTOMOS EN SÓLIDOS Dr. A. Ozols 2 ORDEN CRISTALINO y FORMA René Just Hauy
Diagrama de correlación de enlaces moleculares Antienlace : rojo 1s similar a 2s
 Redes Cristalinas Ciencia de Materiales Ing. en Mecatrónica Otoño 2009 Lilia Meza Montes-IFUAP Diagrama de correlación de enlaces moleculares Antienlace : rojo 1s similar a 2s Sólidos cristalinos y amorfos
Redes Cristalinas Ciencia de Materiales Ing. en Mecatrónica Otoño 2009 Lilia Meza Montes-IFUAP Diagrama de correlación de enlaces moleculares Antienlace : rojo 1s similar a 2s Sólidos cristalinos y amorfos
Capítulo 2 La estructura de los sólidos cristalinos
 Capítulo 2 La estructura de los sólidos cristalinos TEMA 2: La estructura de los sólidos cristalinos 1. Los enlaces interatómicos 2. La estructura cristalina 3. Estructuras de empaquetamiento compacto
Capítulo 2 La estructura de los sólidos cristalinos TEMA 2: La estructura de los sólidos cristalinos 1. Los enlaces interatómicos 2. La estructura cristalina 3. Estructuras de empaquetamiento compacto
Siete sistemas y catorce retículos
 ESTRUCTURA CRISTALINA - PERFECCION Siete sistemas y catorce retículos Celda unitaria c a b Constantes reticulares o parámetros reticulares Longitud de los bordes Ángulos entre los ejes cristalográficos
ESTRUCTURA CRISTALINA - PERFECCION Siete sistemas y catorce retículos Celda unitaria c a b Constantes reticulares o parámetros reticulares Longitud de los bordes Ángulos entre los ejes cristalográficos
CRISTALOGRAFIA. Es un sólido compuesto de átomos, iones o moléculas ordenados de una cierta forma y que se repite en tres dimensiones.
 CRISTALOGRAFIA CRISTAL SÓLIDO MONOCRISTALINO SÓLIDO POLICRISTALINO Es un sólido compuesto de átomos, iones o moléculas ordenados de una cierta forma y que se repite en tres dimensiones. Región donde el
CRISTALOGRAFIA CRISTAL SÓLIDO MONOCRISTALINO SÓLIDO POLICRISTALINO Es un sólido compuesto de átomos, iones o moléculas ordenados de una cierta forma y que se repite en tres dimensiones. Región donde el
Estructura cristalina: Índices de Miller. Y en términos de grado de compacidad? Volumen de átomos= Volumen de la celda= ( ) 3
 1 Cuántos átomos hay en una celda unidad? Vértices 1/8 Caras 1/2 Número total de átomos en la celda unidad: 8 en los vértices: 8 x 1/8 = 1 6 en las caras: 6 x 1/2 = 3 Total: 4 átomos Y en términos de grado
1 Cuántos átomos hay en una celda unidad? Vértices 1/8 Caras 1/2 Número total de átomos en la celda unidad: 8 en los vértices: 8 x 1/8 = 1 6 en las caras: 6 x 1/2 = 3 Total: 4 átomos Y en términos de grado
CONDUCTIVIDAD ELÉCTRICA I E
 CONDUCTVDAD LÉCTRCA La conductividad eléctrica de una substancia se define como la relación entre la intensidad de corriente eléctrica producida y el campo eléctrico que la produce: = el campo eléctrico
CONDUCTVDAD LÉCTRCA La conductividad eléctrica de una substancia se define como la relación entre la intensidad de corriente eléctrica producida y el campo eléctrico que la produce: = el campo eléctrico
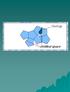 Caso de varios vectores primitivos de un mismo arreglo. Base o Motivo: Átomo o conjunto de átomos que se asocian con un punto de la malla Malla o Lattice: Es un arreglo infinito de puntos en el espacio,
Caso de varios vectores primitivos de un mismo arreglo. Base o Motivo: Átomo o conjunto de átomos que se asocian con un punto de la malla Malla o Lattice: Es un arreglo infinito de puntos en el espacio,
UNIDAD 1: LA MATERIA CRISTALINA
 UNIDAD 1: LA MATERIA CRISTALINA CONCEPTOS MATERIA CRISTALINA: Aquella cuyas partículas están perfectamente ordenadas en el espacio, ocupando posiciones fijas y a distancias regulares unas de otras, formando
UNIDAD 1: LA MATERIA CRISTALINA CONCEPTOS MATERIA CRISTALINA: Aquella cuyas partículas están perfectamente ordenadas en el espacio, ocupando posiciones fijas y a distancias regulares unas de otras, formando
Generalidades del Estado Sólido
 Universidad de Antioquia Instituto de Física Primer Taller de Estado Sólido, CNF-422 Este taller tiene como objetivo que el estudiante haga un recorrido por los diferentes conceptos para preparar el primer
Universidad de Antioquia Instituto de Física Primer Taller de Estado Sólido, CNF-422 Este taller tiene como objetivo que el estudiante haga un recorrido por los diferentes conceptos para preparar el primer
02_01_02 NOTACIÓN DE VOIGT, ESTRUCTURA DE PROPIEDADES, PROPIEDADES EN UNA DIRECCIÓN
 0_0_0 NOTACIÓN DE VOIGT, ESTRUCTURA DE PROPIEDADES, PROPIEDADES EN UNA DIRECCIÓN Laboratorio de Simulación de Materiales no Metálicos Notación de Voigt La notación de Voigt es en general aplicable a cualquiera
0_0_0 NOTACIÓN DE VOIGT, ESTRUCTURA DE PROPIEDADES, PROPIEDADES EN UNA DIRECCIÓN Laboratorio de Simulación de Materiales no Metálicos Notación de Voigt La notación de Voigt es en general aplicable a cualquiera
Estructura de los Sólidos
 Estructura de los Sólidos Estructura Cristalina OBJETIVOS a) Definir sólidos cristalinos y amorfos b) Definir estructura cristalina c) Describir las diferentes estructuras cristalinas d) Utilizar índices
Estructura de los Sólidos Estructura Cristalina OBJETIVOS a) Definir sólidos cristalinos y amorfos b) Definir estructura cristalina c) Describir las diferentes estructuras cristalinas d) Utilizar índices
GEOMETRÍA DE LOS CRISTALES I
 CAPÍTULO 4 GEOMETRÍA DE LOS CRISTALES I 4.1 REDES Conjuntos de puntos imaginarios que tienen una relación fija en el espacio constituyendo un armazón sobre el cual el cristal se construye. En la Figura
CAPÍTULO 4 GEOMETRÍA DE LOS CRISTALES I 4.1 REDES Conjuntos de puntos imaginarios que tienen una relación fija en el espacio constituyendo un armazón sobre el cual el cristal se construye. En la Figura
Capítulo 2 La estructura de los sólidos cristalinos
 Capítulo 2 La estructura de los sólidos cristalinos TEMA 2: La estructura de los sólidos cristalinos 1. Los enlaces interatómicos 2. La estructura cristalina 3. Estructuras cristalinas compactas 4. Direcciones
Capítulo 2 La estructura de los sólidos cristalinos TEMA 2: La estructura de los sólidos cristalinos 1. Los enlaces interatómicos 2. La estructura cristalina 3. Estructuras cristalinas compactas 4. Direcciones
TITULACIÓN DE FORMACIÓN CONTINUA BONIFICADA EXPEDIDA POR EL INSTITUTO EUROPEO DE ESTUDIOS EMPRESARIALES
 Técnico Profesional en Cristaloquímica de Materiales TITULACIÓN DE FORMACIÓN CONTINUA BONIFICADA EXPEDIDA POR EL INSTITUTO EUROPEO DE ESTUDIOS EMPRESARIALES Técnico Profesional en Cristaloquímica de Materiales
Técnico Profesional en Cristaloquímica de Materiales TITULACIÓN DE FORMACIÓN CONTINUA BONIFICADA EXPEDIDA POR EL INSTITUTO EUROPEO DE ESTUDIOS EMPRESARIALES Técnico Profesional en Cristaloquímica de Materiales
SÓLIDOS INORGÁNICOS. Tema 6. FUNDAMENTOS
 SÓLIDOS INORGÁNICOS Tema 6. Fundamentos Tema 7. Sólidos metálicos Tema 8. Sólidos iónicos Tema 9. Sólidos covalentes Tema 10. Sólidos moleculares Tema 11. Defectos y no-estequiometría Tema 12. Propiedades
SÓLIDOS INORGÁNICOS Tema 6. Fundamentos Tema 7. Sólidos metálicos Tema 8. Sólidos iónicos Tema 9. Sólidos covalentes Tema 10. Sólidos moleculares Tema 11. Defectos y no-estequiometría Tema 12. Propiedades
DIFRACCIÓN DE RAYOS X
 Física del Estado Sólido DIFRACCIÓN DE RAYOS X Dr. Andrés Ozols n n k k d cosθ =d.n Θ d Θ k k d cos θ = d.n Facultad de Ingeniería Universidad de Buenos Aires 2009 TEMARIO Objetivo Naturaleza de los rayos
Física del Estado Sólido DIFRACCIÓN DE RAYOS X Dr. Andrés Ozols n n k k d cosθ =d.n Θ d Θ k k d cos θ = d.n Facultad de Ingeniería Universidad de Buenos Aires 2009 TEMARIO Objetivo Naturaleza de los rayos
Empaquetamiento compacto
 Empaquetamiento compacto Energía y empaquetamiento No denso, empaquetamiento aleatorio Energy Distancia del enlace energía de enlace Denso, empaquetamiento ordenado Energy distancia del enlace r Energía
Empaquetamiento compacto Energía y empaquetamiento No denso, empaquetamiento aleatorio Energy Distancia del enlace energía de enlace Denso, empaquetamiento ordenado Energy distancia del enlace r Energía
LABORATORIO DE ESTADO SÓLIDO Y SEMICONDUCTORES 1.1. PRÁCTICA N o 1 REDES DE BRAVAIS Y ESTRUCTURAS CRISTALINAS
 LABORATORIO DE ESTADO SÓLIDO Y SEMICONDUCTORES 1.1 PRÁCTICA N o 1 REDES DE BRAVAIS Y ESTRUCTURAS CRISTALINAS 1. INTRODUCCIÓN 1.1 Red de Bravais y celda primitiva unidad Uno de los conceptos fundamentales
LABORATORIO DE ESTADO SÓLIDO Y SEMICONDUCTORES 1.1 PRÁCTICA N o 1 REDES DE BRAVAIS Y ESTRUCTURAS CRISTALINAS 1. INTRODUCCIÓN 1.1 Red de Bravais y celda primitiva unidad Uno de los conceptos fundamentales
ESTRUCTURAS DE LOS SÓLIDOS CRISTALINOS
 ESTRUCTURAS DE LOS SÓLIDOS CRISTALINOS REDES ESPACIALES Y CELDAS UNIDAD La importancia en la ingeniería de la estructura física de los materiales sólidos depende principalmente de la disposición de los
ESTRUCTURAS DE LOS SÓLIDOS CRISTALINOS REDES ESPACIALES Y CELDAS UNIDAD La importancia en la ingeniería de la estructura física de los materiales sólidos depende principalmente de la disposición de los
1.-La Cristalografía. 2.-Simetría
 1.-La Cristalografía La Cristalografía es la ciencia que se ocupa de los sólidos cristalinos y describe su estructura interna, es decir, como están distribuidos los átomos en su interior. También estudia
1.-La Cristalografía La Cristalografía es la ciencia que se ocupa de los sólidos cristalinos y describe su estructura interna, es decir, como están distribuidos los átomos en su interior. También estudia
Qué es la textura de un policristal? Introducción a la textura: Conceptos básicos
 Qué es la textura de un policristal? Introducción a la textura: Conceptos básicos (la textura cristaloráfica, como yo lo entiendo) Gaspar Gónzález-Doncel CENIM, C.S.I.C. ggd@cenim.csic.es Esquema a seguir
Qué es la textura de un policristal? Introducción a la textura: Conceptos básicos (la textura cristaloráfica, como yo lo entiendo) Gaspar Gónzález-Doncel CENIM, C.S.I.C. ggd@cenim.csic.es Esquema a seguir
Síntesis y Caracterización Estructural de los Materiales Ángel Carmelo Prieto Colorado
 Síntesis y Caracterización Estructural de los Materiales Ángel Carmelo Prieto Colorado Física de la Materia Condensada, Cristalografía y Mineralogía. Facultad de Ciencias. Universidad de Valladolid. Estructura
Síntesis y Caracterización Estructural de los Materiales Ángel Carmelo Prieto Colorado Física de la Materia Condensada, Cristalografía y Mineralogía. Facultad de Ciencias. Universidad de Valladolid. Estructura
NIVELACIÓN MATEMÁTICA 2 AÑO Contenidos: Transformaciones Isométricas Prof. Juan Schuchhardt
 1 Contenidos: Transformaciones Isométricas Prof. Juan Schuchhardt Introducción: Una transformación de una figura geométrica indica que, de alguna manera, ella es alterada o sometida a algún cambio. En
1 Contenidos: Transformaciones Isométricas Prof. Juan Schuchhardt Introducción: Una transformación de una figura geométrica indica que, de alguna manera, ella es alterada o sometida a algún cambio. En
Expresión matricial de las operaciones de simetría
 Epresión matricial de las operaciones de simetría Cada una de las operaciones de simetría se puede describir como una transformación de ejes de coordenadas, de tal manera que las coordenadas de la imagen
Epresión matricial de las operaciones de simetría Cada una de las operaciones de simetría se puede describir como una transformación de ejes de coordenadas, de tal manera que las coordenadas de la imagen
LA CIRCUNFERENCIA. La circunferencia es la sección producida por un plano perpendicular al eje.
 LA CIRCUNFERENCIA La circunferencia es la sección producida por un plano perpendicular al eje. β = 90º La circunferencia es un caso particular de elipse. Se llama circunferencia al lugar geométrico de
LA CIRCUNFERENCIA La circunferencia es la sección producida por un plano perpendicular al eje. β = 90º La circunferencia es un caso particular de elipse. Se llama circunferencia al lugar geométrico de
3. La estructura de sólidos cristalinos 3.1 Conceptos fundamentales 3.2 Celda unitaria 3.3 Redes de Bravias 3.4 Estructuras cristalinas 3.
 Contenido 3. La estructura de sólidos cristalinos 3.1 Conceptos fundamentales 3.2 Celda unitaria 3.3 Redes de Bravias 3.4 Estructuras cristalinas 3.5 Volumen y densidad 3.6 Direcciones y planos cristalográficos
Contenido 3. La estructura de sólidos cristalinos 3.1 Conceptos fundamentales 3.2 Celda unitaria 3.3 Redes de Bravias 3.4 Estructuras cristalinas 3.5 Volumen y densidad 3.6 Direcciones y planos cristalográficos
LABORATORIO DE ESTADO SÓLIDO Y SEMICONDUCTORES 1.1. PRÁCTICA N o 1 REDES DE BRAVAIS Y ESTRUCTURAS CRISTALINAS
 LABORATORIO DE ESTADO SÓLIDO Y SEMICONDUCTORES 1.1 PRÁCTICA N o 1 REDES DE BRAVAIS Y ESTRUCTURAS CRISTALINAS 1. INTRODUCCIÓN 1.1 Red de Bravais y celda primitiva unidad Uno de los conceptos fundamentales
LABORATORIO DE ESTADO SÓLIDO Y SEMICONDUCTORES 1.1 PRÁCTICA N o 1 REDES DE BRAVAIS Y ESTRUCTURAS CRISTALINAS 1. INTRODUCCIÓN 1.1 Red de Bravais y celda primitiva unidad Uno de los conceptos fundamentales
Puntos y Vectores. 16 de Marzo de 2012
 Geometría en Puntos y Vectores Universidad Autónoma Metropolitana Unidad Iztapalapa 16 de Marzo de 2012 Introducción En Geometría analítica plana las relaciones y las propiedades geométricas se expresan
Geometría en Puntos y Vectores Universidad Autónoma Metropolitana Unidad Iztapalapa 16 de Marzo de 2012 Introducción En Geometría analítica plana las relaciones y las propiedades geométricas se expresan
CRISTALES, RED Y MOTIVO. Figuras y ejercicios. (Figuras del texto de C. Kittel, Introducción a la Física del Estado Sólido)
 CRISTALES, RED Y MOTIVO. Figuras y ejercicios. (Figuras del texto de C. Kittel, Introducción a la Física del Estado Sólido) 1. Introducción a Cristales Fig. 1 Estas ilustraciones corresponden a un Tratado
CRISTALES, RED Y MOTIVO. Figuras y ejercicios. (Figuras del texto de C. Kittel, Introducción a la Física del Estado Sólido) 1. Introducción a Cristales Fig. 1 Estas ilustraciones corresponden a un Tratado
MODIFICACIÓN DE LAS PROPIEDADES DE LOS METALES CONTENIDOS
 MODIFICACIÓN DE LAS PROPIEDADES DE LOS METALES CONTENIDOS Generalidades Estructura interna de los metales. Defectos en la estructura cristalina Soluciones sólidas Mecanismos de endurecimiento de los metales
MODIFICACIÓN DE LAS PROPIEDADES DE LOS METALES CONTENIDOS Generalidades Estructura interna de los metales. Defectos en la estructura cristalina Soluciones sólidas Mecanismos de endurecimiento de los metales
TEMA 8 ESTRUCTURA CRISTALINA
 Tema 8. Estructura cristalina 1 TEMA 8 ESTRUCTURA CRISTALINA Los sólidos pueden clasificarse: 1.- Por su ordenación: 1a. Sólidos amorfos: tienen una estructura desordenada. Sus átomos o moléculas se colocan
Tema 8. Estructura cristalina 1 TEMA 8 ESTRUCTURA CRISTALINA Los sólidos pueden clasificarse: 1.- Por su ordenación: 1a. Sólidos amorfos: tienen una estructura desordenada. Sus átomos o moléculas se colocan
Difracción de rayos X. Química Analítica Inorgánica Tecnólogo Minero
 Difracción de rayos X Química Analítica Inorgánica Tecnólogo Minero Por qué estudiar difracción de rayos X? Composición Difracción üfenómeno característico de las ondas üdesviación de éstas al encontrar
Difracción de rayos X Química Analítica Inorgánica Tecnólogo Minero Por qué estudiar difracción de rayos X? Composición Difracción üfenómeno característico de las ondas üdesviación de éstas al encontrar
Estructuras Cristalinas. Julio Alberto Aguilar Schafer
 Estructuras Cristalinas Julio Alberto Aguilar Schafer Modelo del estado líquido los metales Modelo del paso del estado líquido al estado sólido de los metales Equilibrio líquido-vapor Presión de vapor
Estructuras Cristalinas Julio Alberto Aguilar Schafer Modelo del estado líquido los metales Modelo del paso del estado líquido al estado sólido de los metales Equilibrio líquido-vapor Presión de vapor
Álgebra y Geometría Analítica I - LF 2016 Práctica 1: Algunos elementos de la Geometría Analítica
 Álgebra y Geometría Analítica I - LF 2016 Práctica 1: Algunos elementos de la Geometría Analítica 1. a) Marcar en un eje los puntos a(1);b( 2) y c(4). b) Hallar los puntos simétricos respecto al origen
Álgebra y Geometría Analítica I - LF 2016 Práctica 1: Algunos elementos de la Geometría Analítica 1. a) Marcar en un eje los puntos a(1);b( 2) y c(4). b) Hallar los puntos simétricos respecto al origen
GRUPOS PUNTUALES. 4.- Si un plano de simetría contiene un eje de orden n, existen n planos que contienen el eje. formando entre ellos ángulos de
 GRUPOS PUNTUALES Existen algunas relaciones entre elementos de simetría que pueden ser útiles a la hora de deducir cuales son los conjuntos de estos que forman grupo. 1.- Todos los elementos de simetría
GRUPOS PUNTUALES Existen algunas relaciones entre elementos de simetría que pueden ser útiles a la hora de deducir cuales son los conjuntos de estos que forman grupo. 1.- Todos los elementos de simetría
2 Transformaciones en 3D
 2 Transformaciones en 3D La manera más fácil de conseguir las transformaciones básicas (traslación, rotación, escalación, en general las transformaciones afines) es utilizando matrices de transformación.
2 Transformaciones en 3D La manera más fácil de conseguir las transformaciones básicas (traslación, rotación, escalación, en general las transformaciones afines) es utilizando matrices de transformación.
Estructura Interna de los Materiales
 TEMA III Estructura Interna de los Materiales LECCIÓN 3 Estructura Cristalina y Amorfa 1 3.1 ESTADOS DE LA MATERIA Ciencia y Tecnología de los Materiales La materia puede presentarse en tres estados: gaseoso,
TEMA III Estructura Interna de los Materiales LECCIÓN 3 Estructura Cristalina y Amorfa 1 3.1 ESTADOS DE LA MATERIA Ciencia y Tecnología de los Materiales La materia puede presentarse en tres estados: gaseoso,
Identidad Eje de simetría de orden n
 1 Teoría de grupos aplicada a la simetría 1.1 Operaciones de simetría 1.2 Grupos puntuales de simetría 1.3 Tablas de caracteres 1.4 Representaciones de simetría 1.1 Operaciones de simetría metría molecular.
1 Teoría de grupos aplicada a la simetría 1.1 Operaciones de simetría 1.2 Grupos puntuales de simetría 1.3 Tablas de caracteres 1.4 Representaciones de simetría 1.1 Operaciones de simetría metría molecular.
TECTOSILICATOS INTRODUCCIÓN GRUPO DE LA SILICE ESTRUCTURAS POLIMORFISMO. Magdalena Rodas
 TECTOSILICATOS INTRODUCCIÓN GRUPO DE LA SILICE ESTRUCTURAS POLIMORFISMO Magdalena Rodas TECTOSILICATOS Grupo de la sílice (SiO 2 ) Grupo de los feldespatos (Si 3 Al O 8 ) -1 Grupo de los feldespatóides
TECTOSILICATOS INTRODUCCIÓN GRUPO DE LA SILICE ESTRUCTURAS POLIMORFISMO Magdalena Rodas TECTOSILICATOS Grupo de la sílice (SiO 2 ) Grupo de los feldespatos (Si 3 Al O 8 ) -1 Grupo de los feldespatóides
Programa de Acceso Inclusivo, Equidad y Permanencia. PAIEP, Universidad de Santiago
 Guía de vectores. Vectores En matemática, un vector es una herramienta geométrica utilizada para representar una magnitud física definida en un sistema de referencia que se caracteriza por tener módulo
Guía de vectores. Vectores En matemática, un vector es una herramienta geométrica utilizada para representar una magnitud física definida en un sistema de referencia que se caracteriza por tener módulo
Espacios vectoriales. Vectores del espacio.
 Espacios vectoriales. Vectores del espacio. Consideremos un paralelepípedo de bases ABCD y EFGH, siendo A(1,1,1), B(2,1,1), C(2,4,1) y E(1,2,7). Halla: a) el área de una de las bases; b) el volumen del
Espacios vectoriales. Vectores del espacio. Consideremos un paralelepípedo de bases ABCD y EFGH, siendo A(1,1,1), B(2,1,1), C(2,4,1) y E(1,2,7). Halla: a) el área de una de las bases; b) el volumen del
1.2. Celdas Unitarias Parámetros Reticulares
 Capítulo 2 Organización Atómica 1.2. Celdas Unitarias Parámetros Reticulares 1.2.1. Celdas Unitarias La estructura atómica influye en la forma en que los átomos se unen entre sí; esto además nos ayuda
Capítulo 2 Organización Atómica 1.2. Celdas Unitarias Parámetros Reticulares 1.2.1. Celdas Unitarias La estructura atómica influye en la forma en que los átomos se unen entre sí; esto además nos ayuda
EJERCICIOS DE SELECTIVIDAD DE GEOMETRIA
 EJERCICIOS DE SELECTIVIDAD DE GEOMETRIA 2003 (4) Ejercicio 1. Considera los vectores u = (1,1,1), v = (2,2,a) y w = (2,0,0), (a) [1'25 puntos] Halla los valores de a para que los vectores u, v y w sean
EJERCICIOS DE SELECTIVIDAD DE GEOMETRIA 2003 (4) Ejercicio 1. Considera los vectores u = (1,1,1), v = (2,2,a) y w = (2,0,0), (a) [1'25 puntos] Halla los valores de a para que los vectores u, v y w sean
Simetría molecular. Facultad de Química, UNAM. Prof. Jesús Hernández Trujillo. Simetría molecular/jht p. 1/3
 Simetría molecular/jt p. 1/3 Simetría molecular Prof. Jesús ernández Trujillo Facultad de Química, UNAM Simetría molecular/jt p. 2/3 Contenido La noción de simetría Simetría molecular Operaciones de simetría
Simetría molecular/jt p. 1/3 Simetría molecular Prof. Jesús ernández Trujillo Facultad de Química, UNAM Simetría molecular/jt p. 2/3 Contenido La noción de simetría Simetría molecular Operaciones de simetría
Bases Matemáticas para la Educación Primaria. Guía de Estudio. Tema 5: Transformaciones geométricas planas. Orientación espacial
 Bases Matemáticas para la Educación Primaria Guía de Estudio Tema 5: Transformaciones geométricas planas. Orientación espacial 1 Transformaciones geométricas 2 ISOMETRÍAS EN LIBROS DE PRIMARIA Cuáles de
Bases Matemáticas para la Educación Primaria Guía de Estudio Tema 5: Transformaciones geométricas planas. Orientación espacial 1 Transformaciones geométricas 2 ISOMETRÍAS EN LIBROS DE PRIMARIA Cuáles de
Cónicas. Clasificación.
 Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Estructura Atómica y Cristalina. Departamento de Tecnología IES San José
 1. INTRODUCCIÓN. Las propiedades y comportamiento de los materiales dependen, principalmente de su constitución y de su estructura. Por ello estudiaremos la disposición geométrica de los átomos y las interacciones
1. INTRODUCCIÓN. Las propiedades y comportamiento de los materiales dependen, principalmente de su constitución y de su estructura. Por ello estudiaremos la disposición geométrica de los átomos y las interacciones
Geometría. 2 (el " " representa el producto vectorial)? En caso afirmativo, justifíquese. En caso contrario, póngase un ejemplo que lo confirme.
 Geometría 1 (Junio-96 Dados los vectores a,b y c tales que a, b 1 y c 4 y a b c, calcular la siguiente suma de productos escalares: a b b c a c (Sol: -1 (Junio-96 Señalar si las siguientes afirmaciones
Geometría 1 (Junio-96 Dados los vectores a,b y c tales que a, b 1 y c 4 y a b c, calcular la siguiente suma de productos escalares: a b b c a c (Sol: -1 (Junio-96 Señalar si las siguientes afirmaciones
Sistemas de Coordenadas
 C.U. UAEM Valle de Teotihuacán Licenciatura en Ingeniería en Computación Sistemas de Coordenadas Unidad de Aprendizaje: Fundamentos de Robótica Unidad de competencia V Elaborado por: M. en I. José Francisco
C.U. UAEM Valle de Teotihuacán Licenciatura en Ingeniería en Computación Sistemas de Coordenadas Unidad de Aprendizaje: Fundamentos de Robótica Unidad de competencia V Elaborado por: M. en I. José Francisco
APUNTES DE FÍSICA I Profesor: José Fernando Pinto Parra UNIDAD 2 ÁLGEBRA VECTORIAL
 Vectores y escalares. REPÚBLICA BOLIVARIANA DE VENEZUELA APUNTES DE FÍSICA I Profesor: José Fernando Pinto Parra UNIDAD 2 ÁLGEBRA VECTORIAL Las magnitudes escalares son aquellas magnitudes físicas que
Vectores y escalares. REPÚBLICA BOLIVARIANA DE VENEZUELA APUNTES DE FÍSICA I Profesor: José Fernando Pinto Parra UNIDAD 2 ÁLGEBRA VECTORIAL Las magnitudes escalares son aquellas magnitudes físicas que
Vectores. b) Hallar la magnitud de cada uno de los vectores P Q, QRy P R. c) Encontrar el vector fijo equivalente a QP.
 Wilson Herrera 1 Vectores 1. Dados los puntos P (1, 2), Q( 2, 2) y R(1, 6): a) Representarlos en el plano XOY. b) Hallar la magnitud de cada uno de los vectores P Q, QRy P R. c) Encontrar el vector fijo
Wilson Herrera 1 Vectores 1. Dados los puntos P (1, 2), Q( 2, 2) y R(1, 6): a) Representarlos en el plano XOY. b) Hallar la magnitud de cada uno de los vectores P Q, QRy P R. c) Encontrar el vector fijo
Master en Análisis Forense
 Master en Análisis Forense Evidencias físicas Métodos Cristalográficos de Caracterización en AF Tema 3.- Difracción de Rayos X Dr. José Luis Pizarro Dpto. Mineralogía y Petrología Fac. Ciencia y Tecnología
Master en Análisis Forense Evidencias físicas Métodos Cristalográficos de Caracterización en AF Tema 3.- Difracción de Rayos X Dr. José Luis Pizarro Dpto. Mineralogía y Petrología Fac. Ciencia y Tecnología
Problemas de exámenes de Geometría
 1 Problemas de exámenes de Geometría 1. Consideramos los planos π 1 : X = P+λ 1 u 1 +λ 2 u 2 y π 2 : X = Q+µ 1 v 1 +µ 2 v 2. Cuál de las siguientes afirmaciones es incorrecta? a) Si π 1 π 2 Ø, entonces
1 Problemas de exámenes de Geometría 1. Consideramos los planos π 1 : X = P+λ 1 u 1 +λ 2 u 2 y π 2 : X = Q+µ 1 v 1 +µ 2 v 2. Cuál de las siguientes afirmaciones es incorrecta? a) Si π 1 π 2 Ø, entonces
Determinación de los índices de Miller de planos en cristales de Cu y GaP
 Determinación de los índices de Miller de planos en cristales de Cu y GaP Grupo 2 Franchino Viñas, S. A. Hernández Maiztegui, F. f ranchsebs@yahoo.com.ar f ranx22182@hotmail.com Muglia, J. Panelo, M. Salazar
Determinación de los índices de Miller de planos en cristales de Cu y GaP Grupo 2 Franchino Viñas, S. A. Hernández Maiztegui, F. f ranchsebs@yahoo.com.ar f ranx22182@hotmail.com Muglia, J. Panelo, M. Salazar
15/04/2011. Cristales metálicos. Estructuras Cristalinas más usuales de Metales Puros (y de sus soluciones sólidas)
 15/04/2011 Estructuras Cristalinas más usuales de Metales Puros (y de sus soluciones sólidas) Reglas generales Para un cristal al equilibrio químico, los átomos se ordenarán en forma regular y compacta,
15/04/2011 Estructuras Cristalinas más usuales de Metales Puros (y de sus soluciones sólidas) Reglas generales Para un cristal al equilibrio químico, los átomos se ordenarán en forma regular y compacta,
TEMA 11.- VECTORES EN EL ESPACIO
 TEMA 11.- VECTORES EN EL ESPACIO 1.- INTRODUCCIÓN Un vector fijo AB del espacio (también lo era en el plano) es un segmento orientado que tiene su origen en un punto A y su extremo en otro punto B. Estos
TEMA 11.- VECTORES EN EL ESPACIO 1.- INTRODUCCIÓN Un vector fijo AB del espacio (también lo era en el plano) es un segmento orientado que tiene su origen en un punto A y su extremo en otro punto B. Estos
Sistema óptico: sistema a través del cual puede pasar la luz y que separa dos medios de distinto índice de refracción Sistemas centrados
 Óptica geométrica. Formación de imágenes en espejos y lentes. La longitud de onda de la luz suele ser muy peueña en comparación con el tamaño de obstáculos o aberturas ue se encuentra a su paso. Esto permite
Óptica geométrica. Formación de imágenes en espejos y lentes. La longitud de onda de la luz suele ser muy peueña en comparación con el tamaño de obstáculos o aberturas ue se encuentra a su paso. Esto permite
Sólidos Arreglos y celdas unitarias. Ramón L. Hernández Castillo Enero 2012
 Sólidos Arreglos y celdas unitarias Ramón L. Hernández Castillo Enero 2012 Importancia de estudiar los sólidos cristalinos La mayoría de los compuestos inorgánicos son sólidos Casi todos los elementos
Sólidos Arreglos y celdas unitarias Ramón L. Hernández Castillo Enero 2012 Importancia de estudiar los sólidos cristalinos La mayoría de los compuestos inorgánicos son sólidos Casi todos los elementos
Introducción a la Física del Estado Sólido
 Semana 1. Estructura cristalina. Definición de arreglos periódicos. Tipos de redes. Clasificación de simetrías. Índices de planos cristalinos. Ejemplos de estructuras cristalinas simples. Cristales no
Semana 1. Estructura cristalina. Definición de arreglos periódicos. Tipos de redes. Clasificación de simetrías. Índices de planos cristalinos. Ejemplos de estructuras cristalinas simples. Cristales no
20. TRANSFORMACIONES Y MOVIMIENTOS
 20. TRANSFORMACIONES Y MOVIMIENTOS Los movimientos y las transformaciones son modificaciones aplicadas a los elementos del plano puntos, rectas, figuras_ con el fin de cambiar su posición o para convertirlos
20. TRANSFORMACIONES Y MOVIMIENTOS Los movimientos y las transformaciones son modificaciones aplicadas a los elementos del plano puntos, rectas, figuras_ con el fin de cambiar su posición o para convertirlos
Colegio Internacional Torrequebrada. Departamento de Matemáticas
 Geometría. Problema 1: Calcula la distancia del punto P(1, 1, 1) a la recta Problema 2: Dadas las rectas, se pide: a) Analiza su posición relativa. b) Halla la ecuación general del plano π que contiene
Geometría. Problema 1: Calcula la distancia del punto P(1, 1, 1) a la recta Problema 2: Dadas las rectas, se pide: a) Analiza su posición relativa. b) Halla la ecuación general del plano π que contiene
IMPERFECCIONES EN SÓLIDOSS
 IMPERFECCIONES EN SÓLIDOSS UN ORDENAMIENTO PERFECTO DE LOS ÁTOMOS EN LOS MATERIALES CRISTALINOS SOLAMENTE PUEDE OCURRIR A UNA TEMPERATURA DE 0 K. TAL SÓLIDO IDEAL NO EXISTE: TODOS TIENEN GRAN NÚMERO DE
IMPERFECCIONES EN SÓLIDOSS UN ORDENAMIENTO PERFECTO DE LOS ÁTOMOS EN LOS MATERIALES CRISTALINOS SOLAMENTE PUEDE OCURRIR A UNA TEMPERATURA DE 0 K. TAL SÓLIDO IDEAL NO EXISTE: TODOS TIENEN GRAN NÚMERO DE
Translaciones, giros, simetrías.
 Translaciones, giros, simetrías. Transformaciones geométricas Transformación geométrica es una aplicación del plano en el plano tal que a cada punto de un plano le hace corresponder otro punto del mismo
Translaciones, giros, simetrías. Transformaciones geométricas Transformación geométrica es una aplicación del plano en el plano tal que a cada punto de un plano le hace corresponder otro punto del mismo
Interpretación de Diagramas de Difracción
 Interpretación de Diagramas de Difracción Teoría: Ley de Bragg Para interpretar los diagramas de difracción se requiere una teoría. W.H. Bragg y su hijo fueron pioneros en el tema y desarrollaron una sencilla
Interpretación de Diagramas de Difracción Teoría: Ley de Bragg Para interpretar los diagramas de difracción se requiere una teoría. W.H. Bragg y su hijo fueron pioneros en el tema y desarrollaron una sencilla
Física del estado sólido
 Física del estado sólido Propiedades de cristales nálisis estructural mediante rayos X LD ojas de Física P7... Método de Laue: estudio de la estructura cristalina de los monocristales Objetivos del experimento
Física del estado sólido Propiedades de cristales nálisis estructural mediante rayos X LD ojas de Física P7... Método de Laue: estudio de la estructura cristalina de los monocristales Objetivos del experimento
UNIDAD DE APRENDIZAJE II
 UNIDAD DE APRENDIZAJE II Saberes procedimentales 1. Emplea de manera sistemática conceptos algebraicos, geométricos, trigonométricos y de geometría analítica. 2. Relaciona una ecuación algebraica con a
UNIDAD DE APRENDIZAJE II Saberes procedimentales 1. Emplea de manera sistemática conceptos algebraicos, geométricos, trigonométricos y de geometría analítica. 2. Relaciona una ecuación algebraica con a
ÓPTICA GEOMÉTRICA 1. Conceptos básicos. 2. Espejos planos. 3. Espejos esféricos. 4. Dioptrios. 5. Lentes delgadas. 6. La visión.
 ÓPTICA GEOMÉTRICA 1. Conceptos básicos. 2. Espejos planos. 3. Espejos esféricos. 4. Dioptrios. 5. Lentes delgadas. 6. La visión. Física 2º bachillerato Óptica geométrica 1 ÓPTICA GEOMÉTRICA La óptica geométrica
ÓPTICA GEOMÉTRICA 1. Conceptos básicos. 2. Espejos planos. 3. Espejos esféricos. 4. Dioptrios. 5. Lentes delgadas. 6. La visión. Física 2º bachillerato Óptica geométrica 1 ÓPTICA GEOMÉTRICA La óptica geométrica
Capítulo 25. Rayos X
 Capítulo 25 Rayos X 1 Generación y absorción de rayos X La frecuencia máxima de rayos X producidos por una diferencia de potencial V vale: ν max = e V h Para que un fotón de rayos X se pueda desintegrar
Capítulo 25 Rayos X 1 Generación y absorción de rayos X La frecuencia máxima de rayos X producidos por una diferencia de potencial V vale: ν max = e V h Para que un fotón de rayos X se pueda desintegrar
Fundamentos de óptica fotorrefractiva
 Fundamentos de óptica fotorrefractiva Prof. M.L. Calvo 11 y 12 de abril de 2011 ECUACIÓN DE ONDAS EN MEDIOS ANISÓTROPOS Y NO LINEALES El vector desplazamiento eléctrico cumple en estos medios: (, ) = ε
Fundamentos de óptica fotorrefractiva Prof. M.L. Calvo 11 y 12 de abril de 2011 ECUACIÓN DE ONDAS EN MEDIOS ANISÓTROPOS Y NO LINEALES El vector desplazamiento eléctrico cumple en estos medios: (, ) = ε
FORMACIÓN DE IMÁGENES EN ESPEJOS
 FORMACIÓN DE IMÁGENES EN ESPEJOS La reflexión que producen los objetos depende de las características de los cuerpos, de esta forma existen dos tipos de reflexiones a saber: 1.- Reflexión especular o regular.
FORMACIÓN DE IMÁGENES EN ESPEJOS La reflexión que producen los objetos depende de las características de los cuerpos, de esta forma existen dos tipos de reflexiones a saber: 1.- Reflexión especular o regular.
ÁLGEBRA Y GEOMETRÍA ANALÍTICA PRIMER CUATRIMESTRE 2014 EL PLANO
 ÁLGEBRA Y GEOMETRÍA ANALÍTICA PRIMER CUATRIMESTRE 04 GUIA DE ESTUDIO: EL PLANO Esta guía tiene la intención de ayudarte en el aprendizaje de los contenidos desarrollados en el material de estudio El plano
ÁLGEBRA Y GEOMETRÍA ANALÍTICA PRIMER CUATRIMESTRE 04 GUIA DE ESTUDIO: EL PLANO Esta guía tiene la intención de ayudarte en el aprendizaje de los contenidos desarrollados en el material de estudio El plano
Breve introducción al grupo de Rubik
 Breve introducción al grupo de Rubik. Introducción El cubo de Rubik es un puzle secuencial en tres dimensiones caracterizado por 26 piezas: 6 centros, 2 aristas (numeradas de A a L) y 8 vértices (numerados
Breve introducción al grupo de Rubik. Introducción El cubo de Rubik es un puzle secuencial en tres dimensiones caracterizado por 26 piezas: 6 centros, 2 aristas (numeradas de A a L) y 8 vértices (numerados
UNIDAD 3. MODIFICACIÓN DE LAS PROPIEDADES DE LOS METALES
 UNIDAD 3. MODIFICACIÓN DE LAS PROPIEDADES DE LOS METALES 1. GENERALIDADES... Pág. 49 2. ESTRUCTURA INTERNA DE LOS METALES... Pág. 49 2.1. Estructuras cristalinas... Pág. 49 2.2. Estructura cristalina cúbica
UNIDAD 3. MODIFICACIÓN DE LAS PROPIEDADES DE LOS METALES 1. GENERALIDADES... Pág. 49 2. ESTRUCTURA INTERNA DE LOS METALES... Pág. 49 2.1. Estructuras cristalinas... Pág. 49 2.2. Estructura cristalina cúbica
Materia Condensada. Sistemas Complejos.
 Materia Condensada. Sistemas Complejos http://www.fisica.unlp.edu.ar/magnet/fisicamcsc.htm Sistemas Complejos (Física de no-equilibrio): Complejidad intrínseca (fundamental) aplicaciones dificultades derivaciones
Materia Condensada. Sistemas Complejos http://www.fisica.unlp.edu.ar/magnet/fisicamcsc.htm Sistemas Complejos (Física de no-equilibrio): Complejidad intrínseca (fundamental) aplicaciones dificultades derivaciones
. Halla los valores de α en cada uno de los siguientes casos: a) (1 punto) u r, v
 EJERCICIOS BLOQUE III: GEOMETRÍA (04-M;Jun-A-4) Considera la recta r que pasa por los puntos A (,0, ) y (,,0 ) a) ( punto) Halla la ecuación de la recta s paralela a r que pasa por C (,,) b) (5 puntos)
EJERCICIOS BLOQUE III: GEOMETRÍA (04-M;Jun-A-4) Considera la recta r que pasa por los puntos A (,0, ) y (,,0 ) a) ( punto) Halla la ecuación de la recta s paralela a r que pasa por C (,,) b) (5 puntos)
3. Propagación n de la luz en los medios no conductores. Leyes de la reflexión y de la refracción
 3. Propagación n de la luz en los medios no conductores. Leyes de la reflexión y de la refracción 1 3. Propagación de la luz en los medios no conductores. Leyes de la reflexión y de la refracción. 2 Índice
3. Propagación n de la luz en los medios no conductores. Leyes de la reflexión y de la refracción 1 3. Propagación de la luz en los medios no conductores. Leyes de la reflexión y de la refracción. 2 Índice
5. LA LUZ EN LOS MEDIOS ANISÓTROPOS: CUÁDRICAS REPRESENTATIVAS
 5. LA LUZ EN LOS MEDIOS ANISÓTROPOS: CUÁDRICAS REPRESENTATIVAS 5.1. Algunas consideraciones previas La teoría electromagnética de la luz surgió como consecuencia de los trabajos previos de Faraday (1799-1867)
5. LA LUZ EN LOS MEDIOS ANISÓTROPOS: CUÁDRICAS REPRESENTATIVAS 5.1. Algunas consideraciones previas La teoría electromagnética de la luz surgió como consecuencia de los trabajos previos de Faraday (1799-1867)
Función lineal y cuadrática. Curvas de primer y segundo grado.
 Tema 5 Función lineal y cuadrática. Curvas de primer y segundo grado. 5.0.1 Ecuaciones en dos variables. Una linea del plano es el conjunto de puntos (x, y), cuyas coordenadas satisfacen la ecuación F
Tema 5 Función lineal y cuadrática. Curvas de primer y segundo grado. 5.0.1 Ecuaciones en dos variables. Una linea del plano es el conjunto de puntos (x, y), cuyas coordenadas satisfacen la ecuación F
EJERCICIOS BLOQUE III: GEOMETRÍA
 EJERCICIOS BLOQUE III: GEOMETRÍA (05-M4;Jun-B-4) Sea el plano π x + y z + 8 a) (5 puntos) Calcula el punto, P simétrico del punto (,,5 ) b) ( punto) Calcula la recta r, simétrica de la recta plano π P
EJERCICIOS BLOQUE III: GEOMETRÍA (05-M4;Jun-B-4) Sea el plano π x + y z + 8 a) (5 puntos) Calcula el punto, P simétrico del punto (,,5 ) b) ( punto) Calcula la recta r, simétrica de la recta plano π P
TEMA 8. GEOMETRÍA ANALÍTICA.
 TEMA 8. GEOMETRÍA ANALÍTICA. 8..- El plano. Definimos el plano euclideo como el conjunto de puntos ( x, y) R. Así, cada punto del plano posee dos coordenadas. Para representar puntos del plano utilizaremos
TEMA 8. GEOMETRÍA ANALÍTICA. 8..- El plano. Definimos el plano euclideo como el conjunto de puntos ( x, y) R. Así, cada punto del plano posee dos coordenadas. Para representar puntos del plano utilizaremos
Lugar Geométrico. Se llama lugar geométrico a un conjunto de puntos que cumplen una determinada propiedad. Mediatriz
 1 Lugar Geométrico Se llama lugar geométrico a un conjunto de puntos que cumplen una determinada propiedad. Mediatriz Mediatriz de un segmento es el lugar geométrico de los puntos del plano que equidistan
1 Lugar Geométrico Se llama lugar geométrico a un conjunto de puntos que cumplen una determinada propiedad. Mediatriz Mediatriz de un segmento es el lugar geométrico de los puntos del plano que equidistan
QUÍMICA INORGÁNICA AVANZADA INTRODUCCIÓN A LA SIMETRÍA MOLECULAR
 QUÍMICA INORGÁNICA AVANZADA INTRODUCCIÓN A LA SIMETRÍA MOLECULAR Simetría - Desde la antigüedad se ha apreciado la relación entre la simetría de un objeto y su atractivo estético - En matemática tiene
QUÍMICA INORGÁNICA AVANZADA INTRODUCCIÓN A LA SIMETRÍA MOLECULAR Simetría - Desde la antigüedad se ha apreciado la relación entre la simetría de un objeto y su atractivo estético - En matemática tiene
EJERCICIOS DE GEOMETRÍA
 1) Sean las rectas EJERCICIOS DE GEOMETRÍA x 2y 6z 1 r : x y 0 x y 1 s: z 2 a a) Determinar la posición relativa de r y s según los valores de a. b) Calcular la distancia entre las rectas r y s cuando
1) Sean las rectas EJERCICIOS DE GEOMETRÍA x 2y 6z 1 r : x y 0 x y 1 s: z 2 a a) Determinar la posición relativa de r y s según los valores de a. b) Calcular la distancia entre las rectas r y s cuando
Número de matrícula: Las soluciones aparecerán en AulaWeb dentro de los dos días hábiles siguientes a la finalización de la prueba.
 Ing. Industrial / Ing. Químico / Materiales II convocatoria septiembre 8 Nombre: Número de matrícula: sólo una respuesta es correcta las respuestas incorrectas no restan puntos usar por favor bolígrafo,
Ing. Industrial / Ing. Químico / Materiales II convocatoria septiembre 8 Nombre: Número de matrícula: sólo una respuesta es correcta las respuestas incorrectas no restan puntos usar por favor bolígrafo,
Estructuras Cristalinas más usuales de Metales Puros (y de sus soluciones sólidas) Cristales metálicos
 Estructuras Cristalinas más usuales de Metales Puros (y de sus soluciones sólidas) Reglas generales Para un cristal al equilibrio químico, los átomos se ordenarán en forma regular y compacta, de manera
Estructuras Cristalinas más usuales de Metales Puros (y de sus soluciones sólidas) Reglas generales Para un cristal al equilibrio químico, los átomos se ordenarán en forma regular y compacta, de manera
ESTRUCTURAS CRISTALINAS (P2)
 ESTRUCTURAS CRISTALINAS (P2) Objetivos - Visualización de estructuras de sólidos mediante el uso de modelos - Estudio de redes cristalinas basadas en ordenamientos de esferas de igual tamaño - Identificación
ESTRUCTURAS CRISTALINAS (P2) Objetivos - Visualización de estructuras de sólidos mediante el uso de modelos - Estudio de redes cristalinas basadas en ordenamientos de esferas de igual tamaño - Identificación
Tema 4. Cristaloquímica. Descripción estructural y
 Tema 4. Cristaloquímica. Descripción estructural y estructuras tipos Qué objetivos tiene la Cristaloquímica? Las fases cristalinas son componentes esenciales de los materiales, y especificamente de los
Tema 4. Cristaloquímica. Descripción estructural y estructuras tipos Qué objetivos tiene la Cristaloquímica? Las fases cristalinas son componentes esenciales de los materiales, y especificamente de los
La difracción de rayos X y la densidad electrónica. El fenómeno de difracción
 La difracción de rayos X y la densidad electrónica El fenómeno de difracción Rafael Moreno Esparza Facultad de Química UNAM 2007 viernes, 13 marzo 2009 El fenómeno de difracción 1 Rayos X vs NMR Rayos
La difracción de rayos X y la densidad electrónica El fenómeno de difracción Rafael Moreno Esparza Facultad de Química UNAM 2007 viernes, 13 marzo 2009 El fenómeno de difracción 1 Rayos X vs NMR Rayos
Módulo 3. Introducción a la cristalografía
 Módulo 3. Introducción a la cristalografía Poliedros cristalográficos recortables Un método muy recomendable para estudiar la forma y simetría de los cristales consiste en construir poliedros recortables.
Módulo 3. Introducción a la cristalografía Poliedros cristalográficos recortables Un método muy recomendable para estudiar la forma y simetría de los cristales consiste en construir poliedros recortables.
Bloque 2. Geometría. 3. La recta. 1. Definición de recta
 Bloque 2. Geometría 3. La recta 1. Definición de recta Para representar puntos en un plano (superficie de dos dimensiones) utilizamos dos rectas graduadas y perpendiculares, cuyo corte es el punto 0 de
Bloque 2. Geometría 3. La recta 1. Definición de recta Para representar puntos en un plano (superficie de dos dimensiones) utilizamos dos rectas graduadas y perpendiculares, cuyo corte es el punto 0 de
Problemas Tema 7 Enunciados de problemas ampliación Temas 5 y 6
 página 1/13 Problemas Tema 7 Enunciados de problemas ampliación Temas 5 y 6 Hoja 1 1. Dado el segmento de extremos A( 7,3) y B(5,11), halla la ecuación de su mediatriz. 2. Halla la distancia del punto
página 1/13 Problemas Tema 7 Enunciados de problemas ampliación Temas 5 y 6 Hoja 1 1. Dado el segmento de extremos A( 7,3) y B(5,11), halla la ecuación de su mediatriz. 2. Halla la distancia del punto
Unidad 5: Geometría analítica del plano.
 Geometría analítica del plano 1 Unidad 5: Geometría analítica del plano. 1.- Vectores. Operaciones con vectores. Un vector fijo es un segmento entre dos puntos, A y B del plano, al que se le da una orientación
Geometría analítica del plano 1 Unidad 5: Geometría analítica del plano. 1.- Vectores. Operaciones con vectores. Un vector fijo es un segmento entre dos puntos, A y B del plano, al que se le da una orientación
Seminario 4: Óptica Geométrica
 Seminario 4: Óptica Geométrica Fabián Andrés Torres Ruiz Departamento de Física,, Chile 7 de Abril de 2007. Problemas. (Problema 5, capitulo 36,Física, Raymond A. Serway, V2, cuarta edición) Un espejo
Seminario 4: Óptica Geométrica Fabián Andrés Torres Ruiz Departamento de Física,, Chile 7 de Abril de 2007. Problemas. (Problema 5, capitulo 36,Física, Raymond A. Serway, V2, cuarta edición) Un espejo
Defectos cristalinos. Introducción a la Ciencia de Materiales. M. Bizarro
 Defectos cristalinos Monocristal Cuando el arreglo de un sólido cristalino es perfecto o se extiende completamente a lo largo del sólido sin interrupción, se dice que es un monocristal. Todas las celdas
Defectos cristalinos Monocristal Cuando el arreglo de un sólido cristalino es perfecto o se extiende completamente a lo largo del sólido sin interrupción, se dice que es un monocristal. Todas las celdas
Universidad de Murcia
 Universidad de Murcia CRISTALOGRAFÍA Control MURCIA 2011 2012 Francisco Cánovas Picón Índice Índice.............................................. 2 1. Problema 1.......................................
Universidad de Murcia CRISTALOGRAFÍA Control MURCIA 2011 2012 Francisco Cánovas Picón Índice Índice.............................................. 2 1. Problema 1.......................................
Si se pueden obtener las imágenes de x por simple sustitución.
 TEMA 0: REPASO DE FUNCIONES FUNCIONES: TIPOS DE FUNCIONES Funciones algebraicas En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción,
TEMA 0: REPASO DE FUNCIONES FUNCIONES: TIPOS DE FUNCIONES Funciones algebraicas En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción,

 ᒬ 01) En el triángulo ABC de la figura AD = BD;
ᒬ 01) En el triángulo ABC de la figura AD = BD;