Análisis de significados personales e institucionales sobre prácticas de divisibilidad en el marco del enfoque ontosemiótico
|
|
|
- Francisco José Quintero Franco
- hace 6 años
- Vistas:
Transcripción
1 Análisis de significados personales e institucionales sobre prácticas de divisibilidad en el marco del enfoque ontosemiótico Analysis of personal and institutional meanings on divisibility practices within the framework of the onto-semiotic approach Silvia C. Etchegaray Universidad Nacional de Río Cuarto-República Argentina Resumen En este trabajo aplicamos la noción de configuración ontosemiótica, en su doble versión, institucional y personal para analizarla actividad matemática implicada en la resolución de un problema de divisibilidad. Esto supone describir tanto las prácticas matemáticas, objetos y procesos implicados en la resolución experta o esperada del problema (configuración epistémica) como en las producciones de un grupo de estudiantes, ingresantes a la universidad (configuraciones cognitivas). La puesta en funcionamiento de estas herramientas posee, en este trabajo, un doble propósito. Por un lado, caracterizar qué tipo de conocimiento tienen disponibles los estudiantes del profesorado en matemática al egresar de la escuela secundaria en torno a saberes elementales de la divisibilidad, y por el otro, lograr la sistematización de un proceso de investigación contextualizado en la propia institución formadora con el objetivo de que se convierta en fuente de estudio y reflexión para los estudiantes avanzados del profesorado en Matemática. Palabras claves: Significados institucionales, significados personales, divisibilidad, formación de profesores. Abstract In this paper, we apply the notion of onto-semiotic configuration, both in the institutional and personal facets to analyze the mathematical activity involved in solving a divisibility problem. This application involves describing the mathematical practices, objects and processes involved in the practices carried out in the expert resolution of the problem (epistemic configuration) and in the personal productions by a group of students, who are starting in the university (cognitive configurations). We implement these tools with a double purpose. On the one hand, we characterize the kind of mathematics knowledge available by the teachers when they graduate from secondary school around elementary divisibility, and on the other hand, we intend to achieve the systematization of a research process, contextualized in the educational institution with the aim that it becomes a source of study and reflection for advanced students teachers of mathematics. Keywords: Institutional meanings, personal meanings, divisibility, teacher education 1. Introducción En este trabajo vamos a problematizar ciertos saberes matemáticos, específicamente correspondientes a la teoría de la divisibilidad, que imparten en el primer año del Profesorado en Matemática que se dicta en la Universidad Nacional de Río Cuarto (UNRC) (Argentina), usando herramientas conceptuales y metodológicas del Enfoque ontosemiótico del conocimiento y la instrucción matemáticos (EOS) (Godino, 2002;Godino, Batanero y Font, 2007) y que configuran distintos modelos epistemológicos, cognitivos e instruccionales. Etchegaray, S. C. (2017). Análisis de significados personales e institucionales sobre prácticas de divisibilidad en el marco del enfoque ontosemiótico. En J. M. Contreras, P. Arteaga, G. R. Cañadas, M. M. Gea, B. Giacomone y M. M. López-Martín (Eds.), Actas del Segundo Congreso International Virtual sobre el Enfoque Ontosemiótico del Conocimiento y la Instrucción Matemáticos. Disponible en, enfoqueontosemiotico.ugr.es/civeos.html
2 2 Análisis de significados personales e institucionales sobre prácticas de divisibilidad en el marco del enfoque ontosemiótico Estas herramientas están siendo estudiadas y aplicadas en algunos espacios curriculares correspondientes a nuestro programa de formación de profesores de matemáticas al considerarlas útiles para la reflexión y análisis del diseño, implementación y evaluación de los conocimientos matemáticos puestos en juego por los estudiantes en sistemas de prácticas correspondientes a distintas áreas de la Matemática. Comenzamos este artículo planteando una de tales situaciones-problema que vamos a utilizar para contextualizar las herramientas de análisis didáctico elaboradas en el marco del EOS. Se aplicarán aquí con el doble propósito de caracterizar qué tipo de conocimiento tienen disponibles los estudiantes del profesorado en matemática al egresar de la escuela secundaria en torno a saberes elementales de la divisibilidad. Así mismo, se aplicarán para lograr la sistematización de un proceso de investigación contextualizado en nuestra propia institución formadora para que se convierta en fuente de estudio y reflexión para los estudiantes de Matemática que estén cursando el último año de estudio. Creemos que es importante mencionar que estamos implicados tanto en la formación matemática del futuro profesor de matemática, así como en su formación en didáctica de las matemáticas, por lo que planificar nuevas actividades formativas en las cuales se articulen la formación matemática y la formación didáctica en torno a un problema de investigación didáctico-matemático 1 nos resulta de gran interés y utilidad A continuación, en este trabajo, describimos los niveles de análisis de los procesos de estudio que tendremos en cuenta y las herramientas teóricas que propone el EOS para su realización. Las ponemos a funcionar a través del análisis ontosemiótico de prácticas expertas y de prácticas de estudiantes ingresantes ante la resolución de un problema, como ya anticipáramos, contextualizado en el ámbito de la teoría de la divisibilidad. Por último, finalizamos este artículo con algunas conclusiones referentes al problema de investigación estudiado y algunas reflexiones referidas a la relevancia de este tipo de estudios en la formación inicial de profesores. 2. Una situación problema como contexto de reflexión didáctico-matemático En esta sección describimos brevemente la primera situación problema seleccionada que pone a funcionar nociones elementales de Divisibilidad y que se presentó para su resolución a futuros profesores de matemática en el primer año de la carrera. Más específicamente en dicha situación-problema intervienen determinados significados del máximo común divisor (M.C.D) y exige de ciertos procesos cognitivos que permiten evaluar contenidos aritméticos elementales que traen los estudiantes del secundario, lo que se logra desvelar haciendo funcionar herramientas de análisis didáctico correspondientes al EOS en el marco de una problemática profesional local. Tal situación fue seleccionada, como un tipo de situación que relaciona 2 de los modelos del significado global de máximo común divisor, denominados en el estudio epistémico 1 En este caso el foco de nuestro problema de investigación se centra en cómo evaluar los conocimientos disponibles de los ingresantes al profesorado en matemática en torno a saberes elementales de divisibilidad.
3 Silvia C. Etchegaray 3 realizado por Etchegaray, Colombo y Peparelli (2005) como pre-aritmético y aritmético 2 respectivamente. Situación-problema 3 Un camino une en el plano los puntos (0;0) y (120;84). Los tramos que lo componen son horizontales o verticales, todos de igual longitud, y todos tienen sus extremos en puntos de coordenadas enteras. a) Obtener al menos tres recorridos distintos, siempre que fuera posible. b) Habrá alguna forma de que se realice el camino con la mínima cantidad de tramos? c) La regla obtenida, será válida para algún otro par de números? Este problema fue presentado para su resolución a 21 estudiantes de primer año del Profesorado de matemática de la UNRC en el marco de la asignatura Matemática Discreta. Vale mencionar que no se realizaron momentos de aprendizajes previos de los contenidos básicos de divisibilidad que intervienen en dicho problema, justamente para recuperar de la forma más genuina posible los significados personales de los alumnos que se inician en la universidad, es decir, aquellos conocimientos disponibles en el área de la Aritmética, como consecuencia de lo aprendido en la escuela secundaria Simultáneamente, alumnos del último año del profesorado llevan a cabo la denominada resolución experta de la situación. Se adjunta, en el anexo 1, una síntesis de las diferentes resoluciones esperadas, con el objetivo de disponerlas para su posterior análisis. En los dos siguientes apartados (3 y 4) se explicarán y efectuarán los diferentes niveles de análisis didácticos realizados, tanto a las dos resoluciones expertas (o resoluciones esperadas) llevadas a cabo por los estudiantes del último año, como a las respuestas de los estudiantes de primer año. 3. Niveles del análisis didáctico Dentro del marco del EOS se pueden llevar a cabo distintos niveles de análisis (Godino, Font y Wilhelmi, 2007; Font, Planas y Godino; 2010) de los sistemas de prácticas que genera la resolución experta de estas situaciones problemas, o las resoluciones de alumnos, que en este caso están cursando su primer año de estudio. El EOS propone que el investigador realice cinco niveles de análisis aplicables a un proceso de estudio matemático, los cuales constituyen una ampliación progresiva de la capacidad de análisis de dichos procesos de estudio matemático. En este trabajo desarrollaremos los dos primeros niveles de análisis didácticos propuestos, agregándole un primer momento de estudio y reflexión con los estudiantes del último año de estudio, en tanto hacedores de las denominadas resoluciones expertas. Consideramos que se torna necesario incorporar en la descripción de este trabajo, este momento especial de estudio ya que se puede entender como el momento de explicación de la producción matemática realizada por el novel experto, en este caso el estudiante de 2 En el modelo pre-aritmético se consideran los problemas de cálculo del MCD entre dos números enteros dados, mientras que en el modelo aritmético los problemas que se resuelven permiten determinar resultados aritméticos a partir de propiedades del MCD. En la publicación citada se especifican las diferencias de todos los elementos de significado que caracterizan cada uno de los modelos. 3 Tomada de Becker, Pietrocola y Sanchez (2001, p. 27); aquí se presenta como problema introductorio para el aprendizaje del máximo común divisor.
4 4 Análisis de significados personales e institucionales sobre prácticas de divisibilidad en el marco del enfoque ontosemiótico cuarto año del profesorado, al comunicar al docente formador lo que ha pensado, registrado, y reflexionado desde el punto de vista matemático sobre la situación problema seleccionada. Este momento se caracteriza por movilizar un modo de hacer y de decir por parte de los estudiantes del último año de estudio que permitan explicitar lo implícito de las clásicas y muy naturalizadas prácticas matemáticas que resuelven la situación. En otras palabras, este momento tiene como objetivo esencial que se abandone el rol de informante que normalmente poseen todos los sujetos en formación para convertirse en proponentes (Brousseau, 1998)ya que estamos convencidos que el futuro profesor necesita reflexionar sobre su práctica matemática, fundamentar sus decisiones didáctico-matemáticas, en otras palabras desnaturalizar los órdenes preestablecidos como consecuencia de una clásica formación disciplinar. Creemos que hacer explícito lo que implícitamente regula la actividad matemática personal es un proceso necesario de incentivar por quienes estamos a cargo de la formación de profesores y de alto carácter formativo profesional. El momento siguiente corresponde al desarrollo del nivel reconocido por el EOS como el primer nivel de análisis didáctico ya que está ligado a los sistemas de prácticas efectivamente realizados y describe los objetos matemáticos intervinientes y emergentes. En este nivel de análisis y en este trabajo particular la configuración epistémica y la configuración cognitiva son las herramientas metodológicas que se utilizan del EOS, (Godino, 2002) las cuales permiten poner al descubierto la red de relaciones aritméticas entre los elementos primarios de significado, producidos tanto por la resolución experta de estas situaciones problemas (lo esperado en este caso por los estudiantes avanzados) como la de los alumnos de primer año del profesorado (lo declarado). Se aplica a la planificación y a la implementación de un proceso de estudio matemático y pretende estudiar las prácticas matemáticas planificadas y realizadas en dicho proceso. Además, permite descomponer el proceso de estudio en una secuencia de episodios y, para cada uno de ellos, describir las prácticas realizadas siguiendo su curso temporal. En nuestro caso particular dicho procesos se descompuso en tres episodios, uno para cada inciso que se plantea en el problema seleccionado para estudiar en este artículo. En un nuevo momento de análisis, reconocido por el EOS como el segundo nivel de análisis, nos centramos en identificar Procesos matemáticos y potenciales conflictos semióticos. En toda práctica se identifica un sujeto agente (institución o persona) y un medio en el que dicha práctica se realiza (que puede contener otros sujetos u objetos). Puesto que el sujeto agente realiza una secuencia de acciones orientadas a la resolución de un tipo de situacionesproblema es necesario considerar también los objetos, procesos y significados matemáticos involucrados. Este nivel de análisis se centra en los objetos y, sobre todo, en los procesos que intervienen en la realización de las prácticas, y también en los que emergen de ellas. La finalidad es describir la complejidad ontosemiótica de las prácticas matemáticas como factor explicativo de los conflictos semióticos que se producen en su realización. 4. Aplicación de los dos niveles de análisis a la situación-problema de la sección Primer nivel de análisis: sistemas de prácticas y objetos matemáticos Este nivel de análisis se basa en la aplicación de las nociones de práctica matemática ligada a la solución de un tipo de problemas, objetos emergentes (e intervinientes), significados sistémicos institucionales y personales. Estas nociones están desarrolladas en Godino y
5 Silvia C. Etchegaray 5 Batanero (1994), ampliadas en Godino, Batanero y Font (2007) y precisadas en Godino y Font (2007a). La puesta en funcionamiento de estas herramientas conceptuales nos permite en la búsqueda del significado institucional de referencia, formular nuevas cuestiones como las siguientes en torno a la situación-problema y nos ayudan a sistematizar la reflexión guiada (Godino y Batanero, 2009) sobre las prácticas matemáticas desplegadas por los estudiantes avanzados en sus roles de expertos. Qué problemáticas y prácticas se prevén y se realizan en la situación analizada? Cómo se secuencian? La situación propuesta lleva a que emerjan, a partir de cada inciso, tres objetos matemáticos ontológicamente diferentes. En el primero se prevé la formulación de una proposición que refiere a casos particulares, en el segundo la emergencia de una noción como la de divisor común mayor entre dos números especiales y la formulación de una proposición que refiere a un particular tipo, mientras que el tercer inciso plantea la necesidad de describir una técnica general, lo que nos habilita a desarrollar tres configuraciones diferentes. La posible representación gráfica de los recorridos solicitados en el primer inciso, y sobre un mismo sistema de coordenadas, permite visualizar la dependencia de la longitud de los tramos respectos a ambas coordenadas y de identificar la presencia de invariantes, así como justificar la necesidad de que los tramos tengan longitud igual al mayor de los divisores comunes, dado lo que se solicita en el inciso 2. Sin embargo, este sistema de prácticas operativas y discursivas no se reduce a la realización de cálculos y/o gráficos matemáticos particulares, sino que hay que seleccionar cuál o cuáles de las propiedades que lo caracterizan será útil para responder a una problemática general, pero en un ejemplo particular y, finalmente, generalizar todos los elementos que pueden variar en la situación. Por tanto, se transita con esta situación por las diversas fases de un proceso de construcción de un objeto matemático (en este caso el MCD) entendido como un modelo. El problema se puede usar como situación de contextualización y de emergencia de objetos elementales que estructuran la Teoría de la Divisibilidad en el nivel de educación secundaria (divisor, mayor divisor común, cálculo del MCD), y también como aplicación de dichos conocimientos para el nivel superior. Además, dado que la situación requiere en su tercer inciso una doble generalización (de los números que componen el par ordenado: (a, b) objeto interviniente y de la longitud de los tramos: M.C.D objeto emergente) es necesario que los estudiantes produzcan matemática basculando entre dos modelos el pre-aritmético y el aritmético (Etchegaray, Colombo y Peparelli, 2005). Qué objetos (lenguajes, problemas, propiedades, conceptos, procedimientos y argumentos) intervienen en las prácticas? Cuáles son previos y cuáles emergentes? En este artículo describiremos sólo la tercera configuración (como síntesis y ejemplo del análisis realizado a la situación-problema presentada), que sintetiza y operativiza, en tanto marco de referencia institucional, las dos resoluciones expertas del tercer inciso del problema, presentadas en el anexo 1. Vale observar que como en la configuración epistémica se trata de atrapar sintéticamente las relaciones que el experto (en este caso los estudiantes de cuarto año) prevén al tratar de resolver la situación, se ha decidido presentar el análisis de
6 6 Análisis de significados personales e institucionales sobre prácticas de divisibilidad en el marco del enfoque ontosemiótico cada elemento de significado en forma tabular (Tabla 1), diferenciando cada resolución con las abreviaturas R.1 y R.2 respectivamente, como así también, los objetos previos o intervinientes diferenciándolos de los emergentes correspondientes. El problema en este caso es: La regla obtenida en la situación anterior, será válida para algún otro par de números? Tabla 1. Configuración epistémica de las resoluciones expertas (R.1 y R.2) Conceptos Definiciones Objeto Previos o intervinientes R.1 y R.2: divisor R.1: divisor común de dos números Emergente R.1 y R.2: Divisor común mayor (concepto emergente del procedimiento realizado en el inciso anterior) Procedimientos Intervinientes R.1 y R.2: Transformación/evolución de la situación-problema al siguiente enunciado: Unir en el plano los puntos (0;0) y (a;b), a,b ϵz, con la mínima cantidad de tramos horizontales y verticales, todos de igual longitud y sus extremos deben ser coordenadas enteras R.1: Búsqueda de divisores comunes dea y b. R.1: Detección del mayor divisor común de a y b, llámese c R.2: Generalización de la técnica usada para el cálculo de MCD usada en el primer inciso y que lo llamaremos c, entre cualquier par de números, a y b. Significado Dados dos números enteros a y b, a es divisor de b (a b) sí y sólo sí Ǝ kϵz: b=a.k. Se dirá que un número es divisor común de dos enteros si divide a cada uno de ellos, o es divisor de cada uno de ellos. Dados a y b números enteros, el mayor de sus divisores comunes se llama divisor común mayor (dcm) de a y b. Argumentos La pregunta: La regla es válida para algún otro par de números? solicita trabajar con un razonamiento análogo a los problemas anteriores, pero ya no con ciertos números sino con cualesquiera dos números enteros a y b. Independientemente del orden de ejecución de los movimientos, se debe avanzar a lugares hacia la derecha a través de puntos de coordenadas enteras y en todos los tramos la misma longitud, por lo tanto, la longitud de cada tramo debe ser un número entero divisor de a. Se realiza el mismo razonamiento para los movimientos verticales, luego la longitud de cada tramo del recorrido debe ser un divisor común de a y b Además, para que el camino se realice con la mínima cantidad de tramos se debe tomar la longitud más grande que sea posible, es decir, considerar el mayor valor posible de los divisores comunes de a y b, llamado c Además, para que el camino se realice con la mínima cantidad de tramos se debe tomar la longitud determinada por el MCD. llamado c
7 Silvia C. Etchegaray 7 Propiedades Proposiciones Objeto R.1 y R.2: Puesta a funcionar: c a y c b ƎrϵZ: a=c.r y ƎsϵZ: b=c.s y c es mayor que cualquier otro número que también divida al a y al b. Emergente: Dados a y b dos números enteros cualesquiera siempre se puede hallar un camino que una los puntos del plano (0;0) y (a;b) con la mínima cantidad de tramos Significado Hace referencia a que el valor que se busca debe ser un divisor común a ambos números y ser el mayor que cumple con esa doble relación. R.1: Basta buscar los divisores comunes entre a y b y elegir el más grande. R.2: Una vez hallada la técnica, se puede afirmar este enunciado que es la respuesta al problema Segundo nivel de análisis: procesos matemáticos y potenciales conflictos semióticos Como se sabe, este nuevo nivel de análisis aporta información sobre la complejidad ontosemiótica de la actividad matemática desplegada, y por tanto, desvela posibles explicaciones sobre los conflictos semióticos que se pueden producir en su desarrollo. Se basa en la aplicación de la noción de proceso matemático y la tipología de procesos elaborada teniendo en cuenta los tipos de objetos primarios y secundarios (dualidades o atributos contextuales). Estas nociones están desarrolladas en Godino (2002) y precisadas en Godino y Font (2007b). La aplicación de estas herramientas permite formular, entre otras, las cuestiones siguientes relacionadas a los tres incisos de la situación problema en la que se contextualiza este proceso de estudio. Qué procesos y objetos matemáticos son activados en las prácticas matemáticas y didáctico-matemáticas de referencia realizadas por los estudiantes avanzados? En la red de relaciones que conforma el sistema de prácticas que se desarrolla como respuesta al primer inciso del problema detectamos: Procesos de materialización idealización (dualidad ostensivo no ostensivo): - La longitud de los tramos es un objeto ostensivo que evoca el objeto no ostensivo divisor común. - El gráfico de las coordenadas es un objeto ostensivo que evoca el objeto no ostensivo proposición emergente : un recorrido especial con los tramos iguales, también especiales. Procesos de descomposición reificación (dualidad elemental/unitario-sistémico): - Las nuevas propiedades emergentes ligadas a cada recorrido, deberían ser tratadas como un sistema; sin embargo, es necesario utilizarlas como objetos unitarios cuando son aplicadas a la solución de las nuevas cuestiones que a continuación se plantean en el problema (por ejemplo, los problemas del camino con la mínima cantidad de tramos o con algún par de números). En otras palabras, se exige la aplicación de estos procesos actuando dialécticamente en los tres incisos del problema.
8 8 Análisis de significados personales e institucionales sobre prácticas de divisibilidad en el marco del enfoque ontosemiótico En la práctica matemática experta correspondiente al segundo inciso, detectamos: Procesos de materialización idealización (dualidad ostensivo no ostensivo): - La longitud mayor de los tramos es un objeto ostensivo que evoca el objeto no ostensivo divisor común mayor. Finalmente, utilizando la tercera configuración epistémica (que se desplegó en la sección anterior), identificamos: Procesos de particularización generalización (dualidad ejemplar tipo): - Este problema con el tercer inciso exige transitar un proceso de generalización al actuar en forma dual el ejemplo como un particular y a su vez, como un tipo de ejemplo cuando se tiene que pensar sobre cualquier otro par de números. Procesos de materialización idealización (dualidad ostensivo no ostensivo): - La regla que se logra obtener como válida es el objeto ostensivo que evoca el no ostensivo divisor común mayor cuando éste funciona como respuesta general al problema. Se debe materializar mediante una regla el objeto ideal que cumple con las exigencias del problema, a saber: un número que sea el mayor divisor común a ambas coordenadas del punto de llegada. Por último, reconocimos Procesos de representación significación (dualidad expresión contenido)que se consideran densos en la trama de configuraciones epistémicas y procesos matemáticos que se ponen en juego en la resolución del problema, y pueden ser motivo de potenciales conflictos semióticos. Por ello ante la pregunta, Qué conflictos (a priori) pueden tener los estudiantes para la realización de las prácticas matemáticas asociadas a la situación problema con sus tres consignas comenzamos sistematizando en la Tabla 2 los diferentes elementos lingüísticos, diferenciando para cada resolución (R.1 y R.2), objetos y significados de uso de esos objetos. Esta descripción nos permitió prever los siguientes conflictos semióticos: En las prácticas del primer episodio: Reconocer la relación (diferencia y semejanzas) entre tramos y recorrido. Además de comprender que los tramos serán todos iguales requiere reconocer que su longitud es un número entero que sea divisor de 120 y 84 conjuntamente. En el segundo episodio: Reconocer que la mínima cantidad de tramos se obtiene considerando el divisor común más grande (relación opuesta). Y entender que la relación entre longitud de los tramos y cantidad de tramos, exige saber cuántos tramos hay de acuerdo a las longitudes, para luego comparar y quedarse con la menor cantidad. Por último, en la tercera cuestión que plantea el último inciso identificamos que interpretar (otorgar un significado) a la frase: algún otro par de números del enunciado del problema, a partir de reconocer lo que sucede con el 120 y 84, exige identificar la propiedad invariante del objeto que había funcionado como solución en el inciso anterior.
9 Silvia C. Etchegaray 9 Tabla 2. Elementos lingüísticos en las resoluciones expertas R.1 y R.2 Objetos Intervinientes: Tramos horizontales o verticales, todos de igual longitud. Tres recorridos distintos. a b Camino con la mínima cantidad de tramos. Algún otro par de números. Regla obtenida. Emergentes: R. 1: Gráfico con distintas longitudes de los tramos R.2: Gráfico con igual longitud de tramos) MCD (120, 84)=12 Significados R. 1 Divisores comunes entre 120 y 84. R. 2MCD entre 120 y 84 calculado con alguna técnica. R. 1 Tres divisores comunes distintos. R. 2 Divisor común más grande, generando tres disposiciones diferentes de los tramos. R.1 y R.2: ƎkϵZ: b=a.k R. 1 y R. 2 Divisor común más grande. R. 1 y R. 2 (a, b) con a y b enteros. R. 1 y R. 2 Encontrar el divisor común más grande para dos números cualesquiera. Representación de los tres recorridos correspondientes a tres divisores comunes distintos. Representación de los tres recorridos que difieren por la disposición de los tramos, y cuyas longitudes son el divisor común más grande. R. 1 De todos los divisores comunes es el más grande. R. 2 Resultado del producto de primos comunes con el menor exponente. Es por esto que transformar la situación inicial particular a la proposición siguiente: unir en el plano los puntos (0;0) y (a;b), a,b Z, con la mínima cantidad de tramos horizontales y verticales, todos de igual longitud y sus extremos deben ser coordenadas enteras, que es la que otorga la respuesta experta al problema, exige transitar no sólo por un camino de traducción de números a letras sino por un proceso de generalización basado en la reflexión de un caso particular como un ejemplo tipo. Dicho proceso necesita hacer explícita la propiedad pre-aritmética del máximo común divisor que recuperan Etchegaray, Colombo y Peparelli (2005), es decir, comprender al máximo común divisor como una relación de orden total en N, entre los divisores comunes. Incluso en las configuraciones lo denotamos como dcm, divisor común mayor, ya que esta notación representa con mayor claridad el significado del procedimiento realizado, que es el que le otorga al objeto en cuestión su significado contextual. Una vez evaluada la idoneidad de esta situación problema para levantar el significado del objeto, máximo común divisor, basculando entre dos modelos diferentes, a saber, prearitmético, y aritmético, es necesario preguntarnos por el alcance de los significados personales que la misma pone al descubierto en alumnos de primer año del profesorado en matemática en la UNRC. Esto es debido al interrogante general que regula el estudio planteado, qué tipo de conocimiento tienen disponibles los estudiantes del profesorado en matemática, al egresar de la escuela secundaria, en torno a saberes elementales de la divisibilidad? Cabe volver a mencionar que este trabajo particular solo intenta compartir un
10 10 Análisis de significados personales e institucionales sobre prácticas de divisibilidad en el marco del enfoque ontosemiótico análisis de significados institucionales y personales correspondiente a sólo uno de los problemas seleccionados para avanzar en la investigación propuesta. 5. Continuación del recorrido de investigación: inicios de análisis de significados personales La situación problema presentada para su resolución a los alumnos de primer año del Profesorado de Matemática de la Universidad Nacional de Río Cuarto, en el marco de la asignatura Matemática Discreta, con un total de 21 alumnos, generó sendas producciones personales que son las que se analizan con los estudiantes avanzados de la carrera. Se llevaron a cabo con los citados futuros profesores, cuatro momentos de actividad didáctico-matemática tomando siempre como referencia herramientas conceptuales y metodológicas del EOS. El primer momento constó de una identificación de las prácticas matemáticas realizadas por los estudiantes de primer año, a partir de las resoluciones efectivas realizadas a la situación problemática. Se puede entender como un primer nivel de análisis somero y descriptivo acerca de estas prácticas, en el cual se visibilizaron distintos usos y funcionamientos por parte de los alumnos ingresantes, de los elementos de significados (objetos intervinientes y emergentes) que conforman el significado situacional del MCD, objeto de indagación de esta investigación. En un segundo momento se realizó una categorización de tales prácticas personales basándonos en una de las dualidades identificadas que atraviesa en su totalidad la situaciónproblema y que claramente se manifiesta como una problemática en las resoluciones efectivas, la elemental/unitario sistémico, sostenida por los procesos de descomposición y de reificación. Esta categorización tiene el propósito de seleccionar sistemas de prácticas especiales para continuar con un análisis más profundo de las mismas y, así, desvelar cómo una herramienta de análisis didáctico sirve para desnaturalizar relaciones y hacer visibles diferencias en la actividad matemática desarrollada entre una variedad de prácticas personales En un tercer momento se describe la red de relaciones que intervienen en las resoluciones elegidas de acuerdo a la categorización realizada en el momento anterior, mediante la construcción de sus respectivas configuraciones cognitivas. Dada la posibilidad de extensión de este trabajo, se recurre en el siguiente sub-apartado a ejemplos concretos de este tipo de respuestas que permitieron efectuar la categorización mencionada comunicando una síntesis del análisis realizado. El cuarto y último momento está caracterizado por contrastar el análisis epistémico llevado a cabo en las secciones 2 y 3 con el análisis cognitivo, actual. Ello, con el propósito de enriquecer o refutar las cuestiones / aspectos /hipótesis planteadas en el significado institucional esperado que se había construido con los estudiantes avanzados, a través de sus resoluciones expertas.
11 Silvia C. Etchegaray Segundo y tercer momento En el análisis de las resoluciones de los estudiantes de primer año de Matemática se observó un aspecto que consideramos muy positivo: sobre un total de 21 alumnos, todos (excepto 2 estudiantes) pudieron plantear algún abordaje a los tres incisos del problema e intentar avanzar en sus resoluciones. La categorización de las prácticas personales se sustenta en que los objetos matemáticos intervinientes y emergentes en dichas prácticas, según el juego de lenguaje generado en el contexto del problema, pueden ser considerados desde la dualidad elemental sistémico, dualidad reconocida por el EOS. Teniendo en cuenta además el proceso de descomposición reificación que la sostiene, y que por ende tensiona esta dualidad, se categorizaron dichos sistemas de prácticas en tres grupos. A saber: un primer grupo caracterizado por un tipo de práctica en la cual prevalece en su totalidad una perspectiva elemental, un segundo grupo en el cual prevalece desde el comienzo de la situación una perspectiva sistémica y un tercer grupo integrado por prácticas que transitan/basculan de una perspectiva a otra. Se adjuntan en el anexo 2 ejemplos de producciones de cada grupo considerado y a continuación se realiza una síntesis del análisis llevado a cabo para cada grupo de producciones Síntesis del análisis al primer grupo En el primer grupo, caracterizado como se anticipó por una preponderancia de su perspectiva elemental (o unitaria) sobre lo que exige desarrollar la situación, las expresiones cantidad de tramos, igual longitud de los tramos, entre otras, se ponen en juego de manera transparente; como si se tratara de entidades unitarias (o elementales) y no se observa la estrecha relación y diferencia entre ambos. El argumento que sustenta estas prácticas es del tipo inductivo, explorando con aquellos números que dividan a 120 y 84; esto está regulado por un lenguaje más cotidiano, coloquial, casi sin abreviaturas ni símbolos. En este grupo, pasar a la segunda tarea (inciso 2) la cual requiere de comparar aquellos números que encontraron comunes a 120 y 84 para establecer aquel que es mayor y por ende la cantidad de tramos del recorrido sea menor, es realizada como un ejemplo más. En estas resoluciones predomina la exploración mediante el gráfico de sistemas de coordenadas con diferentes colores los recorridos, indagando cuáles son aquellos divisores de 120 y 84 para que los tramos tengan la misma longitud en todo el recorrido. En general, los tres recorridos se establecen cambiando el divisor, es decir la longitud de los tramos, y no tanto disponiendo de modos distintos los tramos. En otras palabras, todas las acciones realizadas están reguladas principalmente por el proceso de descomposición, no logrando que se ponga a funcionar la reificación de los elementos trabajados, lo que impide lograr una perspectiva sistémica del objeto máximo común divisor Síntesis del análisis al segundo grupo En el segundo grupo se puede observar que prevalece una mirada sistémica del problema desde su abordaje. En efecto, se consideran desde el inicio a los números 120 y 84 como un sistema, a la cantidad tramos y la longitud de los mismos como entidades compuestas que
12 12 Análisis de significados personales e institucionales sobre prácticas de divisibilidad en el marco del enfoque ontosemiótico refieren a múltiplo, divisor y divisor común mayor, y que entre estos objetos matemáticos hay siempre una determinada relación. En estos sistemas de prácticas predomina la técnica de factorización de números primos de 120 y 84 para hallar el objeto que da solución al problema. Aquí la técnica utilizada les asegura que el MCD es el divisor común mayor de dos números, pero no se hace visible ninguna otra relación de este número con los divisores comunes. No hay argumentación aclaratoria de las propiedades aritméticas que posee el número 12 en este caso. Esta práctica matemática está regulada por un lenguaje más resumido y más simbólico. En este grupo, pasar del inciso primero al siguiente no requiere, en cuanto a procedimiento y argumento, de gran dificultad pues ya lo han hallado antes al número que funciona como divisor común que es el 12 y lo han identificado como el objeto que soluciona la situación en su conjunto. Se debería analizar con los estudiantes si el argumento que sustenta el procedimiento de la técnica aporta información acerca de que ese número es o no el correcto que realiza la mínima cantidad de tramos. La técnica de factorización que utilizaron pareciera que les da la seguridad de lo que pide el problema y por ende naturalizan todo argumento para justificar su proceder. En general, en este tipo de prácticas, los tres recorridos poseen todos los tramos de longitud 12 pero cambiando la posición de los tramos. Al prevalecer la técnica de factorización, el lenguaje gráfico deja de ser una herramienta útil para explorar cuál es la longitud de los tramos, sino que es sólo un medio para expresar los distintos recorridos obtenidos de combinar de diversas maneras los tramos horizontales y verticales y que además no es siempre utilizado. En otras palabras, el proceso dialéctico de descomposición-reificación es puesto a funcionar desde el comienzo por estos estudiantes, más allá de que valdría profundizar sobre las prácticas argumentativas respecto al uso dado a cada técnica y/o a cada definición utilizada, lo que permitiría hacer más visible el significado personal otorgado al objeto que se problematiza con esta situación-problema Síntesis del análisis al tercer grupo Por último, se logró identificar un grupo formado por aquellas prácticas que no se ubican plenamente ni en una perspectiva esencialmente elemental (o unitaria) ni en la sistémica, sino que hay una cierta composición de ambas, o más bien transitan de una perspectiva a la otra. Esto es así pues el abordaje del problema (inciso a) se caracteriza por la aplicación de una clara perspectiva elemental de la situación y es recién en el segundo inciso que logran reconocer las propiedades que regulan al objeto específico (el dcm) para resolverla y lograr así mediante un proceso de reificación identificar la relación conjunta que exige comprender que es el divisor común mayor, el objeto aritmético que da solución a la situación. El tercer inciso que requiere por parte de los estudiantes que resuelven un doble proceso de generalización pueden realizarlo mediante la argumentación referida a la generalización del objeto interviniente. No logran explicitar cómo obtendrían ese divisor común necesario, o sea la generalización del objeto emergente.
13 Silvia C. Etchegaray Primeras conclusiones sobre el problema de investigación planteado Este análisis sobre significados personales realizado a prácticas matemáticas personales en torno a este problema de divisibilidad, que fuera resuelto sin ninguna intervención docente, nos permiten hacer visible ciertos puntos clave para una posterior gestión docente que intente hacer reflexionar sobre el alcance y limitaciones del significado aritmético del MCD en la primera asignatura de la carrera del profesorado. Indudablemente el inciso 2 de esta situación problema elegida para analizar, es el que funciona como punto de inflexión para que emerja el necesario doble proceso de generalización que exige la construcción de la regla general que solicita esta situación y que conforma el alcance del significado aritmético del MCD (Etchegaray, Colombo, Peparelli, 2005). Justamente la última categorización expuesta (la compuesta: entre lo elemental y lo sistémico) podría ser considerada como el material de discusión colectiva en una clase posterior de Matemática Discreta 4. En efecto, explicitar la red de relaciones que le permitieron a este/esos/ alumno/s alternar entre una mirada elemental o unitaria y una perspectiva sistémica puede ayudar a evolucionar, tanto la exclusiva perspectiva elemental que no había permitido generalizar ambos objetos (ni el interviniente, ni el emergente), como hacer explícita las propiedades aritméticas que caracterizan el objeto emergente en las prácticas reguladas por una total perspectiva sistémica, las que se naturalizaron totalmente, tal como se puede observar en las segundas producciones que se anexan. En otras palabras, hacer avanzar al conjunto de la clase desde sus propias producciones, con una gestión sostenida esencialmente por la intencionalidad docente que se visibiliza en el análisis de las resoluciones esperadas (sección 3). 7. Reflexiones finales El análisis de las tres tareas (los tres incisos de la situación-problema) sobre las que se organizaron las correspondientes configuraciones epistémicas y cognitivas, a nivel de prácticas operativas y discursivas y de procesos duales relativos al contexto institucional seleccionado, tal como lo exponen Godino, Font y Wihelmi (2008), es un paso previo necesario para la elaboración de instrumentos de evaluación de los aprendizajes. El modelo epistémico y cognitivo que caracteriza al "enfoque ontosemiótico" del conocimiento matemático y que intenta ponerse a funcionar en dos niveles, en este trabajo, proporciona herramientas de análisis que permiten planificar clases e instrumentos de evaluación con validez ecológica, esto es, adaptadas al contexto, a los conocimientos disponibles de los estudiantes y a las intencionalidades docentes. Por último, consideramos importante introducir en la formación inicial de profesores espacios que creen las condiciones necesarias para la construcción, por parte de los estudiantes avanzados, de significados institucionales que, funcionando como marcos referenciales, permitan otorgar sentido a herramientas conceptuales tales como las configuraciones ontosemióticas y los análisis de procesos. Estas herramientas con muy útiles para mejorar su práctica profesional y la cual no es homologable a ninguna técnica para 4 Asignatura que, como ya se anticipara, es en la que se implementó este estudio y que corresponde al primer año del profesorado en Matemática de la UNRC.
14 14 Análisis de significados personales e institucionales sobre prácticas de divisibilidad en el marco del enfoque ontosemiótico enseñar. Tales prácticas formativas conjugan y relacionan dialécticamente conocimiento matemático y conocimiento didáctico, en su faceta epistémica. Referencias Becker, M. E., Pietrocola, N. y Sanchez, C., (2001) Aritmética. Buenos Aires: Red Olímpica. Brousseau,G. (1998).La theorie des situations didactiques. Grenoble: La PenséeSauvage. Etchegaray, S., Colombo, S. y Peparelli, S. (2005). Configuraciones epistémicas asociadas a la noción de máximo común divisor.en A. Contreras, L. Ordóñez y C. Batanero (Eds.), Actas delprimer Congreso Internacional sobre Aplicaciones y Desarrollos de la Teoría de las Funciones Semióticas(pp ). Universidad de Jaén. Font, V., Planas, N. y Godino, J. D. (2010). Modelo para el análisis didáctico en educación matemática. Infancia y Aprendizaje, 33(2), Godino, J. D. (2002). Un enfoque ontológico y semiótico de la cognición matemática. Recherches en Didactiques des Mathématiques, 22 (2/3), Godino, J. D. y Batanero, C. (1994). Significado institucional y personal de los objetos matemáticos. Recherches en Didactique des Mathématiques, 14 (3), Godino, J. D. Batanero, C. y Font, V. (2007). The ontosemiotic approach to research in mathematics education.zdm.the International Journal on Mathematics Education, 39 (1-2), Godino, J. D. y Batanero, C. (2009). Formación de profesores de matemáticas basada en la reflexión guiada sobre la práctica. Conferencia Invitada al VI CIBEM, Puerto Montt (Chile).Disponible en, Godino, J. D. y Font, V. (2007a). Algunos desarrollos de la teoría de los significadossistémicos. Disponible en, Godino, J. D. y Font, V. (2007b). Algunos desarrollos y aplicaciones de la teoría de las funciones semióticas. Disponible en, Godino, J. D., Font, V. y Wilhelmi, M. R. (2008) Análisis didáctico de procesos de estudio matemático basado en el enfoque ontosemiótico. Publicaciones, 38, Anexo 1: Resoluciones esperadas Resolución experta R.1 Inciso a) Buscar los divisores comunes entre 120 y 84 para asegurarnos que los tramos sean de igual longitud. Con cada divisor común hallar la cantidad de tramos verticales y horizontales para unir los puntos (0; 0) y (120; 84) con un recorrido. Inciso b) Elegir el divisor común más grande entre 120 y 84 para encontrar el camino con la mínima cantidad de tramos, porque al considerar el divisor común más grande la longitud del tramo es la mayor posible y por lo tanto se forma el recorrido con la menor cantidad posible. Inciso c) Buscar los divisores comunes entre a y b y elegir el más grande, que lo llamaremos c, análogamente a lo realizado antes. Resolución experta R.2
15 Silvia C. Etchegaray 15 Inciso a) Calcular el MCD entre 120 y 84 con alguna técnica (factorización en primos, división entera, u otra) y construir los tres recorridos solicitados con la misma longitud de los tramos, pero disponiéndolos distintos. Inciso b) Si, cualquiera de las del inciso a) Inciso c) Generalizar la técnica de cálculo de MCD que llamaremos c y que haya sido usada en el inciso a) para cualquier par de números a y b. Anexo 2 1) Respuestas del inciso c)correspondientes al grupo 1 (perspectiva elemental)
16 16 Análisis de significados personales e institucionales sobre prácticas de divisibilidad en el marco del enfoque ontosemiótico 2) Respuesta a toda la situación-problema correspondiente al grupo 2 (perspectiva sistémica) 3) Respuesta correspondiente al grupo 3 (perspectiva que bascula entre lo elemental y lo sistémico)
EL TRABAJO DE COMPETENCIAS PROFESIONALES EN EL AULA
 EL TRABAJO DE COMPETENCIAS PROFESIONALES EN EL AULA 5º. Taller de Competencias Profesionales Ingrid Gamboa Octubre 2010 OBJETIVO DEL TALLER Realimentar los conceptos y definiciones del enfoque curricular
EL TRABAJO DE COMPETENCIAS PROFESIONALES EN EL AULA 5º. Taller de Competencias Profesionales Ingrid Gamboa Octubre 2010 OBJETIVO DEL TALLER Realimentar los conceptos y definiciones del enfoque curricular
UNIDAD 12: ESTADISTICA. OBJETIVOS
 UNIDAD 12: ESTADISTICA. OBJETIVOS Conocer y manejar los términos básicos del lenguaje de la estadística descriptiva elemental. Conocer y manejar distintas técnicas de organización de datos estadísticos
UNIDAD 12: ESTADISTICA. OBJETIVOS Conocer y manejar los términos básicos del lenguaje de la estadística descriptiva elemental. Conocer y manejar distintas técnicas de organización de datos estadísticos
LOS SIGNIFICADOS EN LA DIDÁCTICA DE LA ESTADÍSTICA *
 Teresita E. Terán Graciela Molina Liliana Cuciarelli Liliana Severino Irma Rosa Norberto Martín César Mignoni Instituto de Investigaciones Teóricas y Aplicadas, Escuela de Estadística LOS SIGNIFICADOS
Teresita E. Terán Graciela Molina Liliana Cuciarelli Liliana Severino Irma Rosa Norberto Martín César Mignoni Instituto de Investigaciones Teóricas y Aplicadas, Escuela de Estadística LOS SIGNIFICADOS
CONTENIDOS MÍNIMOS BLOQUE 2. NÚMEROS
 CONTENIDOS Y CRITERIOS DE EVALUACIÓN DE MATEMÁTICAS 1º DE ESO. Bloque 1: Contenidos Comunes Este bloque de contenidos será desarrollado junto con los otros bloques a lo largo de todas y cada una de las
CONTENIDOS Y CRITERIOS DE EVALUACIÓN DE MATEMÁTICAS 1º DE ESO. Bloque 1: Contenidos Comunes Este bloque de contenidos será desarrollado junto con los otros bloques a lo largo de todas y cada una de las
3.º ESO. Matemáticas orientadas a las enseñanzas aplicadas
 3.º ESO. Matemáticas orientadas a las enseñanzas aplicadas BLOQUE DE APRENDIZAJE I: PROCESOS, MÉTODOS Y ACTITUDES EN MATEMÁTICAS 1. Identificar, formular y resolver problemas numéricos, geométricos, funcionales
3.º ESO. Matemáticas orientadas a las enseñanzas aplicadas BLOQUE DE APRENDIZAJE I: PROCESOS, MÉTODOS Y ACTITUDES EN MATEMÁTICAS 1. Identificar, formular y resolver problemas numéricos, geométricos, funcionales
Ampliación de las funciones docentes:
 Ampliación de las funciones docentes: resignificación del currículum y atención a la diversidad gestión institucional interacción con el mundo del trabajo diseño e implementación de situaciones de enseñanza-aprendizaje
Ampliación de las funciones docentes: resignificación del currículum y atención a la diversidad gestión institucional interacción con el mundo del trabajo diseño e implementación de situaciones de enseñanza-aprendizaje
Planificación didáctica de MATEMÁTICAS 3º E.S.O.
 Planificación didáctica de MATEMÁTICAS 3º E.S.O. (Orientadas a las enseñanzas aplicadas) Julio de 2016 Rev.: 0 Índice 1.- INTRODUCCIÓN... 1 2.- BLOQUE I. PROCESOS, MÉTODOS Y ACTITUDES EN MATEMÁTICAS...
Planificación didáctica de MATEMÁTICAS 3º E.S.O. (Orientadas a las enseñanzas aplicadas) Julio de 2016 Rev.: 0 Índice 1.- INTRODUCCIÓN... 1 2.- BLOQUE I. PROCESOS, MÉTODOS Y ACTITUDES EN MATEMÁTICAS...
PLANIFICACIÓN DE LA UNIDAD DIDÁCTICA 4. TÍTULO DE LA UNIDAD La energía mecánica y sus aplicaciones en la vida diaria
 Grado: quinto Área: Ciencia, Tecnología y Ambiente PLANIFICACIÓN DE LA UNIDAD DIDÁCTICA 4 TÍTULO DE LA UNIDAD La energía mecánica y sus aplicaciones en la vida diaria SITUACIÓN SIGNIFICATIVA Para mover
Grado: quinto Área: Ciencia, Tecnología y Ambiente PLANIFICACIÓN DE LA UNIDAD DIDÁCTICA 4 TÍTULO DE LA UNIDAD La energía mecánica y sus aplicaciones en la vida diaria SITUACIÓN SIGNIFICATIVA Para mover
Las pruebas SABER, un ejercicio de lectura
 Las pruebas SABER, un ejercicio de lectura Martha Jeaneth Castillo Ballén Lingüista y literata, con especialización en educación y estudios de maestría en Literatura Hispanoamericana. Hace parte del equipo
Las pruebas SABER, un ejercicio de lectura Martha Jeaneth Castillo Ballén Lingüista y literata, con especialización en educación y estudios de maestría en Literatura Hispanoamericana. Hace parte del equipo
TEMA. Resolución de problemas. [2.1] Cómo estudiar este tema? [2.2] Definición de problema. [2.3] Tipología de problema
![TEMA. Resolución de problemas. [2.1] Cómo estudiar este tema? [2.2] Definición de problema. [2.3] Tipología de problema TEMA. Resolución de problemas. [2.1] Cómo estudiar este tema? [2.2] Definición de problema. [2.3] Tipología de problema](/thumbs/53/31448552.jpg) Resolución de problemas [2.1] Cómo estudiar este tema? [2.2] Definición de problema [2.3] Tipología de problema [2.4] Pensamiento formal y pensamiento concreto [2.5] Cómo mejorar el planteamiento de los
Resolución de problemas [2.1] Cómo estudiar este tema? [2.2] Definición de problema [2.3] Tipología de problema [2.4] Pensamiento formal y pensamiento concreto [2.5] Cómo mejorar el planteamiento de los
Secretaría General ELEMENTOS Y CARACTERÍSTICAS DEL PROGRAMA DE ESTUDIOS
 Secretaría General ELEMENTOS Y CARACTERÍSTICAS DE ESTUDIOS ELEMENTOS Y CARACTERÍSTICAS DE ESTUDIOS Junio, 2014 ELEMENTOS Portada Son los datos de identificación del programa de estudios. Incluye: Logos
Secretaría General ELEMENTOS Y CARACTERÍSTICAS DE ESTUDIOS ELEMENTOS Y CARACTERÍSTICAS DE ESTUDIOS Junio, 2014 ELEMENTOS Portada Son los datos de identificación del programa de estudios. Incluye: Logos
Matemáticas UNIDAD 5 CONSIDERACIONES METODOLÓGICAS. Material de apoyo para el docente. Preparado por: Héctor Muñoz
 CONSIDERACIONES METODOLÓGICAS Material de apoyo para el docente UNIDAD 5 Preparado por: Héctor Muñoz Diseño Gráfico por: www.genesisgrafica.cl LA RELACIÓN DE PROPORCIONALIDAD 1. DESCRIPCIÓN GENERAL DE
CONSIDERACIONES METODOLÓGICAS Material de apoyo para el docente UNIDAD 5 Preparado por: Héctor Muñoz Diseño Gráfico por: www.genesisgrafica.cl LA RELACIÓN DE PROPORCIONALIDAD 1. DESCRIPCIÓN GENERAL DE
Secretaría General ELEMENTOS Y CARACTERÍSTICAS DEL PROGRAMA DE ESTUDIOS
 Secretaría General ELEMENTOS Y CARACTERÍSTICAS DE ESTUDIOS Junio, 2014 Portada ELEMENTOS Y CARACTERÍSTICAS DE ESTUDIOS Son los datos de identificación del programa de estudios. Incluye: Logos institucionales
Secretaría General ELEMENTOS Y CARACTERÍSTICAS DE ESTUDIOS Junio, 2014 Portada ELEMENTOS Y CARACTERÍSTICAS DE ESTUDIOS Son los datos de identificación del programa de estudios. Incluye: Logos institucionales
Teorías del aprendizaje
 Teorías del aprendizaje TEORÍAS DEL APRENDIZAJE 1 Sesión No. 7 Nombre: El cognitivismo: Aplicación en la educación Contextualización Sabías que las teorías cognitivas tienen un amplio campo de aplicación
Teorías del aprendizaje TEORÍAS DEL APRENDIZAJE 1 Sesión No. 7 Nombre: El cognitivismo: Aplicación en la educación Contextualización Sabías que las teorías cognitivas tienen un amplio campo de aplicación
Bases Matemáticas para la Educación Primaria. Guía de Estudio. Tema 3: Números racionales. Parte I: Fracciones y razones Números racionales
 Bases Matemáticas para la Educación Primaria Guía de Estudio Tema 3: Números racionales Parte I: Fracciones y razones Números racionales 1 Situación introductoria ANÁLISIS DE CONOCIMIENTOS PUESTOS EN JUEGO
Bases Matemáticas para la Educación Primaria Guía de Estudio Tema 3: Números racionales Parte I: Fracciones y razones Números racionales 1 Situación introductoria ANÁLISIS DE CONOCIMIENTOS PUESTOS EN JUEGO
13. Utilizar la fórmula del término general y de la suma de n términos consecutivos
 Contenidos mínimos 3º ESO. 1. Contenidos. Bloque I: Aritmética y álgebra. 1. Utilizar las reglas de jerarquía de paréntesis y operaciones, para efectuar cálculos con números racionales, expresados en forma
Contenidos mínimos 3º ESO. 1. Contenidos. Bloque I: Aritmética y álgebra. 1. Utilizar las reglas de jerarquía de paréntesis y operaciones, para efectuar cálculos con números racionales, expresados en forma
UNIDAD 6: ECUACIONES OBJETIVOS
 UNIDAD 6: ECUACIONES Conocer los conceptos de ecuación, así como la terminología asociada. Identificar y clasificar los distintos tipos de ecuaciones polinómicas en función de su grado y número de incógnitas.
UNIDAD 6: ECUACIONES Conocer los conceptos de ecuación, así como la terminología asociada. Identificar y clasificar los distintos tipos de ecuaciones polinómicas en función de su grado y número de incógnitas.
A continuación se presenta la información de la altura promedio para el año de 1998 en Holanda de hombres y mujeres jóvenes.
 M150: Creciendo A) Presentación del problema LOS JOVENES CRECEN MAS ALTO A continuación se presenta la altura promedio para el año de 1998 en Holanda de hombres y mujeres jóvenes. B) Preguntas del problema
M150: Creciendo A) Presentación del problema LOS JOVENES CRECEN MAS ALTO A continuación se presenta la altura promedio para el año de 1998 en Holanda de hombres y mujeres jóvenes. B) Preguntas del problema
DISEÑO METODOLÓGICO. SEMINARIO TALLER DIRIGIDO POR: CLAUDIA ZAPATA FERREIRA, MSc. University of Buffalo
 DISEÑO METODOLÓGICO hfghfghghdfghfgh CÓMO ESCOGER EL MEJOR DISEÑO? SEMINARIO TALLER DIRIGIDO POR: CLAUDIA ZAPATA FERREIRA, MSc. University of Buffalo DISEÑO METODOLÓGICO También denominada material y métodos
DISEÑO METODOLÓGICO hfghfghghdfghfgh CÓMO ESCOGER EL MEJOR DISEÑO? SEMINARIO TALLER DIRIGIDO POR: CLAUDIA ZAPATA FERREIRA, MSc. University of Buffalo DISEÑO METODOLÓGICO También denominada material y métodos
Objetivos. Criterios de evaluación. Contenidos. Actitudes. Conceptos. Procedimientos
 P R O G R A M A C I Ó N D E L A U N I D A D Objetivos 1 Identificar relaciones de divisibilidad entre números naturales y reconocer si un número es múltiplo o divisor de otro número dado. 2 Utilizar los
P R O G R A M A C I Ó N D E L A U N I D A D Objetivos 1 Identificar relaciones de divisibilidad entre números naturales y reconocer si un número es múltiplo o divisor de otro número dado. 2 Utilizar los
Teoría de Números. Divisibilidad. Olimpiada de Matemáticas en Tamaulipas
 Teoría de Números Divisibilidad Olimpiada de Matemáticas en Tamaulipas 1. Introducción Divisibilidad es una herramienta de la aritmética que nos permite conocer un poco más la naturaleza de un número,
Teoría de Números Divisibilidad Olimpiada de Matemáticas en Tamaulipas 1. Introducción Divisibilidad es una herramienta de la aritmética que nos permite conocer un poco más la naturaleza de un número,
Dirección electrónica:
 Nombre: Juan Manuel Villegas Banda Función: Maestro frente a grupo. Escuela: Secundaria General Lucio Blanco. Asignatura: Matemáticas. Municipio: Playas de Rosarito. Tema: Introducción al lenguaje algebraico.
Nombre: Juan Manuel Villegas Banda Función: Maestro frente a grupo. Escuela: Secundaria General Lucio Blanco. Asignatura: Matemáticas. Municipio: Playas de Rosarito. Tema: Introducción al lenguaje algebraico.
Estándares de evaluación en la materia de MATEMÁTICAS de 1º de ESO. Curso 2016/2017.
 Estándares de evaluación en la materia de MATEMÁTICAS de 1º de ESO. Curso 2016/2017. Bloque 1. Procesos, métodos y actitudes en matemáticas. Los criterios correspondientes a este bloque son los marcador
Estándares de evaluación en la materia de MATEMÁTICAS de 1º de ESO. Curso 2016/2017. Bloque 1. Procesos, métodos y actitudes en matemáticas. Los criterios correspondientes a este bloque son los marcador
Capítulo 4. Lógica matemática. Continuar
 Capítulo 4. Lógica matemática Continuar Introducción La lógica estudia la forma del razonamiento, es una disciplina que por medio de reglas y técnicas determina si un teorema es falso o verdadero, además
Capítulo 4. Lógica matemática Continuar Introducción La lógica estudia la forma del razonamiento, es una disciplina que por medio de reglas y técnicas determina si un teorema es falso o verdadero, además
UNIDAD 1: NÚMEROS NATURALES OBJETIVOS
 UNIDAD 1: NÚMEROS NATURALES Realizar las operaciones con números naturales (suma, resta, multiplicación y división) y operaciones combinadas de las anteriores. Diferenciar entre división exacta y entera,
UNIDAD 1: NÚMEROS NATURALES Realizar las operaciones con números naturales (suma, resta, multiplicación y división) y operaciones combinadas de las anteriores. Diferenciar entre división exacta y entera,
MÉTODO SINGAPUR. Para la enseñanza de Matemáticas
 MÉTODO SINGAPUR Para la enseñanza de Matemáticas ÍNDICE Introducción El marco del currículo Conceptos Habilidades Procesos Metacognición Actitudes Más Información INTRODUCCIÓN El método Singapur es una
MÉTODO SINGAPUR Para la enseñanza de Matemáticas ÍNDICE Introducción El marco del currículo Conceptos Habilidades Procesos Metacognición Actitudes Más Información INTRODUCCIÓN El método Singapur es una
Monografía. Por sus raíces griegas ( mono, uno, y graphos, estudio), se refiere al estudio de un
 Monografía Definición Por sus raíces griegas ( mono, uno, y graphos, estudio), se refiere al estudio de un tema específico. En una extensión regular de 30 a 50 cuartillas, aborda un asunto que ha sido
Monografía Definición Por sus raíces griegas ( mono, uno, y graphos, estudio), se refiere al estudio de un tema específico. En una extensión regular de 30 a 50 cuartillas, aborda un asunto que ha sido
35 Están en capacidad de resolver problemas que
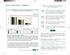 Meta: Matemática Grado 9 8 7 6 ES DE LOGRO EN MATEMÁTICA 8 8 8 8 8 55 5 52 49 52 7 6 7 4 6 ES DE LOGRO Sólo 6 de cada estudiantes de grado º en el Meta alcanzan el nivel esperado de calidad en la matemática
Meta: Matemática Grado 9 8 7 6 ES DE LOGRO EN MATEMÁTICA 8 8 8 8 8 55 5 52 49 52 7 6 7 4 6 ES DE LOGRO Sólo 6 de cada estudiantes de grado º en el Meta alcanzan el nivel esperado de calidad en la matemática
Bloque 1. Contenidos comunes. (Total: 3 sesiones)
 4º E.S.O. OPCIÓN A 1.1.1 Contenidos 1.1.1.1 Bloque 1. Contenidos comunes. (Total: 3 sesiones) Planificación y utilización de procesos de razonamiento y estrategias de resolución de problemas, tales como
4º E.S.O. OPCIÓN A 1.1.1 Contenidos 1.1.1.1 Bloque 1. Contenidos comunes. (Total: 3 sesiones) Planificación y utilización de procesos de razonamiento y estrategias de resolución de problemas, tales como
OBJETIVOS DE APRENDIZAJE Y LAS HABILIDADES
 OBJETIVOS DE APRENDIZAJE Y LAS HABILIDADES OBJETIVOS Analizar críticamente la formulación de objetivos de aprendizaje y sus componentes. Ensayar la formulación de objetivos de aprendizaje en un sector
OBJETIVOS DE APRENDIZAJE Y LAS HABILIDADES OBJETIVOS Analizar críticamente la formulación de objetivos de aprendizaje y sus componentes. Ensayar la formulación de objetivos de aprendizaje en un sector
Matemáticas UNIDAD 3 CONSIDERACIONES METODOLÓGICAS. Material de apoyo para el docente. Preparado por: Héctor Muñoz
 CONSIDERACIONES METODOLÓGICAS Material de apoyo para el docente UNIDAD 3 Preparado por: Héctor Muñoz Diseño Gráfico por: www.genesisgrafica.cl MÚLTIPLOS Y DIVISORES DE NÚMEROS NATURALES 1. DESCRIPCIÓN
CONSIDERACIONES METODOLÓGICAS Material de apoyo para el docente UNIDAD 3 Preparado por: Héctor Muñoz Diseño Gráfico por: www.genesisgrafica.cl MÚLTIPLOS Y DIVISORES DE NÚMEROS NATURALES 1. DESCRIPCIÓN
ESCUELA NORMAL SUPERIOR PÚBLICA DEL ESTADO DE HIDALGO LICENCIATURA EN EDUCACIÓN SECUNDARIA MODALIDAD MIXTA CURSO ESCOLAR NOVENO SEMESTRE
 GOBIERNO DEL ESTADO DE HIDALGO SECRETARÍA DE EDUCACIÓN PÚBLICA DE HIDALGO SUBSECRETARÍA DE EDUCACIÓN BÁSICA Y NORMAL DEPARTAMENTO DE EDUCACIÓN NORMAL ESCUELA NORMAL SUPERIOR PÚBLICA DEL ESTADO DE HIDALGO
GOBIERNO DEL ESTADO DE HIDALGO SECRETARÍA DE EDUCACIÓN PÚBLICA DE HIDALGO SUBSECRETARÍA DE EDUCACIÓN BÁSICA Y NORMAL DEPARTAMENTO DE EDUCACIÓN NORMAL ESCUELA NORMAL SUPERIOR PÚBLICA DEL ESTADO DE HIDALGO
Estas decisiones dependen fundamentalmente de las finalidades y objetivos priorizados.
 Como organizar y secuenciar los contenidos Seleccionar por un lado las temáticas o ideas en función de las organizar los contenidos y, por el otro, secuenciarlos, es decir, distribuirlos en el tiempo.
Como organizar y secuenciar los contenidos Seleccionar por un lado las temáticas o ideas en función de las organizar los contenidos y, por el otro, secuenciarlos, es decir, distribuirlos en el tiempo.
2. CONOCIMIENTO Actividad por la cual se adquiere certeza de la realidad, de la existencia del entorno, con características comprobadas.
 1 1. CONOCER Proceso intelectual por el cual se establece relación entre quien conoce (actor) y el objeto conocido (realidad). 2. CONOCIMIENTO Actividad por la cual se adquiere certeza de la realidad,
1 1. CONOCER Proceso intelectual por el cual se establece relación entre quien conoce (actor) y el objeto conocido (realidad). 2. CONOCIMIENTO Actividad por la cual se adquiere certeza de la realidad,
COLEGIO HELVETIA PROGRAMA DE MATEMÁTICAS GRADO ONCE
 COLEGIO HELVETIA PROGRAMA DE MATEMÁTICAS GRADO ONCE 201-2015 OBJETIVO GENERAL: Entender las bases conceptuales de función, el problema del infinito, así como sus aplicaciones a otras áreas del conocimiento
COLEGIO HELVETIA PROGRAMA DE MATEMÁTICAS GRADO ONCE 201-2015 OBJETIVO GENERAL: Entender las bases conceptuales de función, el problema del infinito, así como sus aplicaciones a otras áreas del conocimiento
Plan de Estudios Articulación de la Educación Básica
 Plan de Estudios 2011 Articulación de la Educación Básica Campos de Formación. Lenguaje y comunicación. Desarrolla competencias comunicativas y de lectura en los estudiantes a partir del trabajo con los
Plan de Estudios 2011 Articulación de la Educación Básica Campos de Formación. Lenguaje y comunicación. Desarrolla competencias comunicativas y de lectura en los estudiantes a partir del trabajo con los
Los conocimientos previos de los alumnos: una base necesaria para la enseñanza y el aprendizaje
 Los conocimientos previos de los alumnos: una base necesaria para la enseñanza y el aprendizaje Guía para el Análisis e Implementación Introducción El propósito de esta cápsula es propiciar la reflexión
Los conocimientos previos de los alumnos: una base necesaria para la enseñanza y el aprendizaje Guía para el Análisis e Implementación Introducción El propósito de esta cápsula es propiciar la reflexión
REALIZAR CÁLCULOS EXACTOS Y APROXIMADOS
 REALIZAR CÁLCULOS EXACTOS Y APROXIMADOS 2do Grado Universidad de La Punta Consideraciones Generales: Las actividades que proponemos a continuación tienen como objetivo construir un repertorio de sumas
REALIZAR CÁLCULOS EXACTOS Y APROXIMADOS 2do Grado Universidad de La Punta Consideraciones Generales: Las actividades que proponemos a continuación tienen como objetivo construir un repertorio de sumas
BLOQUE I: GEOMETRÍA PLANA Y FIGURAS GEOMÉTRICAS. Ecuaciones y sistemas. 2 (20 horas) Funciones y gráficas. 2 (20 horas) Estadística y probabilidad
 PROGRAMACIÓN DIDÁCTICA Materia IV Período FBPI Tramo II Ámbito Científico-Tecnológico Bloque I Geometría plana y figuras geométricas Créditos 3 (30 horas) Bloque II Créditos Ecuaciones y sistemas 2 (20
PROGRAMACIÓN DIDÁCTICA Materia IV Período FBPI Tramo II Ámbito Científico-Tecnológico Bloque I Geometría plana y figuras geométricas Créditos 3 (30 horas) Bloque II Créditos Ecuaciones y sistemas 2 (20
GUÍA DE TRABAJO DE GRADO MAESTRÍA EN GERENCIA DE LA INNOVACIÓN EMPRESARIAL
 GUÍA DE TRABAJO DE GRADO MAESTRÍA EN GERENCIA DE LA INNOVACIÓN EMPRESARIAL La presente guía pretende sentar las bases para la homogeneización del formato de todos los trabajos presentados por el alumnado
GUÍA DE TRABAJO DE GRADO MAESTRÍA EN GERENCIA DE LA INNOVACIÓN EMPRESARIAL La presente guía pretende sentar las bases para la homogeneización del formato de todos los trabajos presentados por el alumnado
GUIA PARA LA ELABORACIÓN DE PROYECTO DE INVESTIGACIÓN
 GUIA PARA LA ELABORACIÓN DE PROYECTO DE INVESTIGACIÓN Esta guía es una referencia útil para los aspirantes a la Maestría en Antropología Social que proporciona los elementos para la elaboración de una
GUIA PARA LA ELABORACIÓN DE PROYECTO DE INVESTIGACIÓN Esta guía es una referencia útil para los aspirantes a la Maestría en Antropología Social que proporciona los elementos para la elaboración de una
Taller: Planificación con Matriz de Marco Lógico. Vólker Gutiérrez Aravena Presidente Cultura Mapocho
 Taller: Planificación con Matriz de Marco Lógico Vólker Gutiérrez Aravena Presidente Cultura Mapocho Elementos centrales de la Planificación Estratégica Qué es? Una poderosa herramienta de diagnóstico,
Taller: Planificación con Matriz de Marco Lógico Vólker Gutiérrez Aravena Presidente Cultura Mapocho Elementos centrales de la Planificación Estratégica Qué es? Una poderosa herramienta de diagnóstico,
Que los estudiantes posean las habilidades de aprendizaje que les permitan continuar estudiando de
 Denominación de la materia 1.8. Implementación y gestión de la innovación TIC en instituciones educativas Duración y ubicación temporal dentro del plan de estudios Itinerario especialización. Segundo semestre
Denominación de la materia 1.8. Implementación y gestión de la innovación TIC en instituciones educativas Duración y ubicación temporal dentro del plan de estudios Itinerario especialización. Segundo semestre
Criterios de Evaluación MÍNIMOS
 s 2º ESO / 2ºPAB Concreción : CE.1 Utilizar números enteros, fracciones, decimales y porcentajes sencillos, sus operaciones y propiedades, para recoger, transformar e intercambiar información y resolver
s 2º ESO / 2ºPAB Concreción : CE.1 Utilizar números enteros, fracciones, decimales y porcentajes sencillos, sus operaciones y propiedades, para recoger, transformar e intercambiar información y resolver
INTRODUCCIÓN A LA TEORÍA ECONÓMICA
 DE LA ASIGNATURA: INTRODUCCIÓN A LA TEORÍA ECONÓMICA GRADO EN ECONOMÍA Y GRADO EN ADMINISTRACIÓN Y DIRECCIÓN DE EMPRESAS 1. Datos Descriptivos de la Asignatura: Nombre: Introducción a la Teoría Económica
DE LA ASIGNATURA: INTRODUCCIÓN A LA TEORÍA ECONÓMICA GRADO EN ECONOMÍA Y GRADO EN ADMINISTRACIÓN Y DIRECCIÓN DE EMPRESAS 1. Datos Descriptivos de la Asignatura: Nombre: Introducción a la Teoría Económica
Este libro recoge los aportes de las participaciones
 Este libro recoge los aportes de las participaciones en el II Foro Internacional de Educación Superior en Entornos virtuales: perspectivas teóricas y metodológicas, realizado el 6 y 7 de noviembre de 2008
Este libro recoge los aportes de las participaciones en el II Foro Internacional de Educación Superior en Entornos virtuales: perspectivas teóricas y metodológicas, realizado el 6 y 7 de noviembre de 2008
RELACIÓN ENTRE LA INVESTIGACIÓN EDUCATIVA Y LA FORMACIÓN DOCENTE
 RELACIÓN ENTRE LA INVESTIGACIÓN EDUCATIVA Y LA FORMACIÓN DOCENTE Ricardo R. Fabián Espinoza FACENA (UNNE). ISFD Dr. Juan Pujol. Corrientes (Argentina) rrfespinoza@gmail.com RESUMEN En este trabajo se intenta
RELACIÓN ENTRE LA INVESTIGACIÓN EDUCATIVA Y LA FORMACIÓN DOCENTE Ricardo R. Fabián Espinoza FACENA (UNNE). ISFD Dr. Juan Pujol. Corrientes (Argentina) rrfespinoza@gmail.com RESUMEN En este trabajo se intenta
PLAN DE TRABAJO. Después de concluir las actividades correspondientes a esta etapa del curso, el participante será capaz de:
 PLAN DE TRABAJO generales Después de concluir las actividades correspondientes a esta etapa del curso, el participante será capaz de: - Elaborar un plan de aprendizaje para una unidad didáctica. - Planear
PLAN DE TRABAJO generales Después de concluir las actividades correspondientes a esta etapa del curso, el participante será capaz de: - Elaborar un plan de aprendizaje para una unidad didáctica. - Planear
Duración: 2 horas pedagógicas
 PLANIFICACIÓN DE LA SESIÓN DE APRENDIZAJE Grado: Cuarto I. TÍTULO DE LA SESIÓN Duración: 2 horas pedagógicas Conociendo las medidas de localización UNIDAD 4 NÚMERO DE SESIÓN 12/14 II. APRENDIZAJES ESPERADOS
PLANIFICACIÓN DE LA SESIÓN DE APRENDIZAJE Grado: Cuarto I. TÍTULO DE LA SESIÓN Duración: 2 horas pedagógicas Conociendo las medidas de localización UNIDAD 4 NÚMERO DE SESIÓN 12/14 II. APRENDIZAJES ESPERADOS
CREATIVIDAD E INNOVACION.
 CREATIVIDAD E INNOVACION. DESARROLLO 1. Introducción Dentro de las diferentes acciones que se están desarrollando dentro del Proyecto CLEAR, una de las prácticas habituales está siendo la realización de
CREATIVIDAD E INNOVACION. DESARROLLO 1. Introducción Dentro de las diferentes acciones que se están desarrollando dentro del Proyecto CLEAR, una de las prácticas habituales está siendo la realización de
Denominación de la materia. N créditos ECTS = 18 carácter = MIXTA ADMINISTRACIÓN Y GESTIÓN
 Denominación de la materia ADMINISTRACIÓN Y GESTIÓN N créditos ECTS = 18 carácter = MIXTA Ubicación dentro del plan de estudios y duración La materia está formada por 3 asignaturas de 6 créditos ECTS cada
Denominación de la materia ADMINISTRACIÓN Y GESTIÓN N créditos ECTS = 18 carácter = MIXTA Ubicación dentro del plan de estudios y duración La materia está formada por 3 asignaturas de 6 créditos ECTS cada
I. CONSIDERACIONES GENERALES
 MATRIZ DE ESPECIFICACIONES DE LA PRUEBA NACIONAL DE SUFICIENCIA EN COMPRENSIÓN DE TEXTOS Y RAZONAMIENTO LÓGICO MATEMÁTICO PARA LA INCORPORACIÓN AL COLEGIO MAYOR SECUNDARIO PRESIDENTE DEL PERÚ I. CONSIDERACIONES
MATRIZ DE ESPECIFICACIONES DE LA PRUEBA NACIONAL DE SUFICIENCIA EN COMPRENSIÓN DE TEXTOS Y RAZONAMIENTO LÓGICO MATEMÁTICO PARA LA INCORPORACIÓN AL COLEGIO MAYOR SECUNDARIO PRESIDENTE DEL PERÚ I. CONSIDERACIONES
Dirección de Educación Secundaria
 Dirección de Educación Secundaria Taller macrorregional de fortalecimiento de capacidades pedagógicas para especialistas Taller de planificación curricular Diseño y elaboración de sesiones de aprendizaje
Dirección de Educación Secundaria Taller macrorregional de fortalecimiento de capacidades pedagógicas para especialistas Taller de planificación curricular Diseño y elaboración de sesiones de aprendizaje
Bloque temático Marketing turístico Curso Segundo. Tipos asignatura Obligatoria Créditos 6 cr. ECTS Horas de trabajo autónomo
 PLAN DOCENTE Código- Asignatura 062111 Investigación de mercados Bloque temático Marketing turístico Curso Segundo Tipos asignatura Obligatoria Créditos 6 cr. ECTS Horas presenciales 60 horas Horas de
PLAN DOCENTE Código- Asignatura 062111 Investigación de mercados Bloque temático Marketing turístico Curso Segundo Tipos asignatura Obligatoria Créditos 6 cr. ECTS Horas presenciales 60 horas Horas de
II. COMO REALIZAR EL ANÁLISIS DE LAS PRUEBAS
 II. COMO REALIZAR EL ANÁLISIS DE LAS PRUEBAS Tal como se anotó al comienzo de este documento, a lo largo de la historia de la evaluación masiva en Colombia, han evolucionado tanto los fundamentos disciplinares
II. COMO REALIZAR EL ANÁLISIS DE LAS PRUEBAS Tal como se anotó al comienzo de este documento, a lo largo de la historia de la evaluación masiva en Colombia, han evolucionado tanto los fundamentos disciplinares
Estándares de Contenido y Desempeño, Estándares de Ejecución y Niveles de Logro Marcado* MATEMÁTICA
 Estándares de Contenido y Desempeño, Estándares de Ejecución y Niveles de Logro Marcado* MATEMÁTICA * Se distinguen con negrita en el texto. ESTÁNDAR DE CONTENIDO Y DESEMPEÑO Nº 1 Conocer la estructura
Estándares de Contenido y Desempeño, Estándares de Ejecución y Niveles de Logro Marcado* MATEMÁTICA * Se distinguen con negrita en el texto. ESTÁNDAR DE CONTENIDO Y DESEMPEÑO Nº 1 Conocer la estructura
UNIVERSIDAD ABIERTA PARA ADULTOS UAPA ESCUELA DE POSTGRADO MAESTRÍA EN CIENCIAS DE LA EDUCACIÓN MENCIÓN GESTION DE CENTROS EDUCATIVOS
 UNIVERSIDAD ABIERTA PARA ADULTOS UAPA ESCUELA DE POSTGRADO MAESTRÍA EN CIENCIAS DE LA EDUCACIÓN MENCIÓN GESTION DE CENTROS EDUCATIVOS PROGRAMA DE LA ASIGNATURA METODOLOGÍA DE LA INVESTIGACIÓN EDUCATIVA
UNIVERSIDAD ABIERTA PARA ADULTOS UAPA ESCUELA DE POSTGRADO MAESTRÍA EN CIENCIAS DE LA EDUCACIÓN MENCIÓN GESTION DE CENTROS EDUCATIVOS PROGRAMA DE LA ASIGNATURA METODOLOGÍA DE LA INVESTIGACIÓN EDUCATIVA
DIPLOMADO EN GERENCIA DE PROYECTOS CON ÉNFASIS EN PMI
 FACULTAD DE ADMINISTRACIÓN DIPLOMADO EN GERENCIA DE PROYECTOS CON ÉNFASIS EN PMI PRESENTACIÓN El Diplomado está diseñado para que los participantes se comprometan en un proceso de intercambio de conocimiento
FACULTAD DE ADMINISTRACIÓN DIPLOMADO EN GERENCIA DE PROYECTOS CON ÉNFASIS EN PMI PRESENTACIÓN El Diplomado está diseñado para que los participantes se comprometan en un proceso de intercambio de conocimiento
JORNALIZACIÓN POR ASIGNATURA Y UNIDAD
 JORNALIZACIÓN POR ASIGNATURA Y UNIDAD GRADO:SECCIÓN: RESPONSABLE: FECHA: DIAS Y SEMANAS LABORALES POR AÑO MESES E F M A M J J A S O N TOTAL SEMANAS 1 4 3 4 4 4 5 4 4 5 2 40 DIAS 5 20 15 20 20 20 25 20
JORNALIZACIÓN POR ASIGNATURA Y UNIDAD GRADO:SECCIÓN: RESPONSABLE: FECHA: DIAS Y SEMANAS LABORALES POR AÑO MESES E F M A M J J A S O N TOTAL SEMANAS 1 4 3 4 4 4 5 4 4 5 2 40 DIAS 5 20 15 20 20 20 25 20
CAPITULO IV ANÁLISIS, INTERPRETACIÓN Y COMPROBACIÓN DE
 CAPITULO IV ANÁLISIS, INTERPRETACIÓN Y COMPROBACIÓN DE RESULTADOS 4.1 TABULACIÓN DE DATOS N PREGUNTA ALTERNATIVAS SI NO A VECES TOTAL 1 Considera que la normativa de los programas del Plan 2021 favorecen
CAPITULO IV ANÁLISIS, INTERPRETACIÓN Y COMPROBACIÓN DE RESULTADOS 4.1 TABULACIÓN DE DATOS N PREGUNTA ALTERNATIVAS SI NO A VECES TOTAL 1 Considera que la normativa de los programas del Plan 2021 favorecen
Proceso de Investigación y Modelo Integral
 Proceso de Investigación y Modelo Integral Metodología de la Investigación 1 Temas Definición de Investigación Investigación Cuantitativa Investigación Cualitativa Modelo Integral Modelo de dos etapas.
Proceso de Investigación y Modelo Integral Metodología de la Investigación 1 Temas Definición de Investigación Investigación Cuantitativa Investigación Cualitativa Modelo Integral Modelo de dos etapas.
PENDIENTES DE MATEMÁTICAS DE 3º ESO (CURSO )
 PENDIENTES DE MATEMÁTICAS DE 3º ESO (CURSO 2015-2016) CRITERIOS E INDICADORES Se detallan a continuación los criterios de evaluación junto con sus indicadores de contenidos asociados. Criterio 1: Identificar
PENDIENTES DE MATEMÁTICAS DE 3º ESO (CURSO 2015-2016) CRITERIOS E INDICADORES Se detallan a continuación los criterios de evaluación junto con sus indicadores de contenidos asociados. Criterio 1: Identificar
1. El concepto de número natural. 2. Adición y sustracción de números naturales. 3. Multiplicación y división de números naturales.
 ESTRUCTURA CONCEPTUAL DEL AREA DE: EJES ARTICULADORES Y PRODUCTIVOS DEL AREA CONOCIMIENTOS REPÚBLICA DE COLOMBIA DEPARTAMENTO DE CÓRDOBA MUNICIPIO DE VALENCIA INSTITUCIÓN EDUCATIVA CATALINO GULFO RESOLUCIÓN
ESTRUCTURA CONCEPTUAL DEL AREA DE: EJES ARTICULADORES Y PRODUCTIVOS DEL AREA CONOCIMIENTOS REPÚBLICA DE COLOMBIA DEPARTAMENTO DE CÓRDOBA MUNICIPIO DE VALENCIA INSTITUCIÓN EDUCATIVA CATALINO GULFO RESOLUCIÓN
Formulario para presentar Proyecto: Impresoras 3D. Guía general para la presentación del proyecto
 Formulario para presentar Proyecto: Impresoras 3D Guía general para la presentación del proyecto INFORMACIÓN DEL PROYECTO Nombre del proyecto Institución Dirección Localidad Departamento Nombre del Director/a
Formulario para presentar Proyecto: Impresoras 3D Guía general para la presentación del proyecto INFORMACIÓN DEL PROYECTO Nombre del proyecto Institución Dirección Localidad Departamento Nombre del Director/a
Guía docente Título superior de diseño
 Dirección Xeral de Educación, Formación Profesional e Innovación Educativa EEASSD DO SISTEMA EDUCATIVO DE GALICIA Guía docente Título superior de diseño Especialidad: DISEÑO DE INTERIORES Asignatura: PROYECTOS
Dirección Xeral de Educación, Formación Profesional e Innovación Educativa EEASSD DO SISTEMA EDUCATIVO DE GALICIA Guía docente Título superior de diseño Especialidad: DISEÑO DE INTERIORES Asignatura: PROYECTOS
Lectura: LA MAGÍA DE LOS NÚMEROS PRIMOS
 Lectura: LA MAGÍA DE LOS NÚMEROS PRIMOS Consideraciones didácticas y soluciones Los números primos, y todo lo que a partir de ahí comienza en torno a la divisibilidad, constituyen un tema de formación
Lectura: LA MAGÍA DE LOS NÚMEROS PRIMOS Consideraciones didácticas y soluciones Los números primos, y todo lo que a partir de ahí comienza en torno a la divisibilidad, constituyen un tema de formación
Los números naturales
 1. Identificación Nivel: Primario Área: Matemática Grado: Sexto SC. 1: Resumen: En esta Unidad Didáctica se identifican, se leen y se escriben los. Se utilizan los en la solución de problemas de la vida
1. Identificación Nivel: Primario Área: Matemática Grado: Sexto SC. 1: Resumen: En esta Unidad Didáctica se identifican, se leen y se escriben los. Se utilizan los en la solución de problemas de la vida
INVESTIGACIÓN EVALUATIVA. Elena Ramos Cristina Alonso Noelia Moyano Esmeralda Olmo Natalia Gómez
 INVESTIGACIÓN EVALUATIVA Elena Ramos Cristina Alonso Noelia Moyano Esmeralda Olmo Natalia Gómez Teoría de la evaluación EVALUACIÓN: Proceso de recogida de información orientado a la emisión de juicios
INVESTIGACIÓN EVALUATIVA Elena Ramos Cristina Alonso Noelia Moyano Esmeralda Olmo Natalia Gómez Teoría de la evaluación EVALUACIÓN: Proceso de recogida de información orientado a la emisión de juicios
Teorías del aprendizaje
 Teorías del aprendizaje TEORÍAS DEL APRENDIZAJE 1 Sesión No. 5 Nombre: El conductismo: Teorías conductistas y educación Contextualización Cuáles son las aplicaciones que las teorías conductistas tienen
Teorías del aprendizaje TEORÍAS DEL APRENDIZAJE 1 Sesión No. 5 Nombre: El conductismo: Teorías conductistas y educación Contextualización Cuáles son las aplicaciones que las teorías conductistas tienen
DESARROLLANDO EL PENSAMIENTO GEOMÉTRICO.
 DESARROLLANDO EL PENSAMIENTO GEOMÉTRICO. I. OBJETIVO GENERAL: Fortalecer los conocimientos disciplinares y desarrollar habilidades matemáticas necesarias para gestionar procesos de aprendizaje relacionados
DESARROLLANDO EL PENSAMIENTO GEOMÉTRICO. I. OBJETIVO GENERAL: Fortalecer los conocimientos disciplinares y desarrollar habilidades matemáticas necesarias para gestionar procesos de aprendizaje relacionados
MICROSOFT PROJECT 2010
 MICROSOFT PROJECT 2010 METODOLOGÍA DE LOS CURSOS Cursos interactivos sobre materias especializadas en los que el alumno avanza de forma guiada bajo una concepción learning by doing (aprender haciendo).
MICROSOFT PROJECT 2010 METODOLOGÍA DE LOS CURSOS Cursos interactivos sobre materias especializadas en los que el alumno avanza de forma guiada bajo una concepción learning by doing (aprender haciendo).
CURSO: DISEÑO DE ESTRATEGIAS DIDÁCTICAS INNOVADORAS EN PLATAFORMAS E-LEARNING ELEMENTOS PARA LA ELABORACIÓN DE ESTRATEGIAS DIDÁCTICAS
 CURSO: DISEÑO DE ESTRATEGIAS DIDÁCTICAS INNOVADORAS EN PLATAFORMAS E-LEARNING ELEMENTOS PARA LA ELABORACIÓN DE ESTRATEGIAS DIDÁCTICAS Yolanda Campos Campos CONTEXTO APARTADO Participantes Quiénes? Describe
CURSO: DISEÑO DE ESTRATEGIAS DIDÁCTICAS INNOVADORAS EN PLATAFORMAS E-LEARNING ELEMENTOS PARA LA ELABORACIÓN DE ESTRATEGIAS DIDÁCTICAS Yolanda Campos Campos CONTEXTO APARTADO Participantes Quiénes? Describe
UNIVERSIDAD NACIONAL AGRARIA LA MOLINA VICERRECTORADO ACADÉMICO
 UNIVERSIDAD NACIONAL AGRARIA LA MOLINA VICERRECTORADO ACADÉMICO SÍLABO POR COMPETENCIAS A. ANTECEDENTES Mediante la Resolución Rectoral N 591-2004-UNALM se crea la Unidad de Calidad y Acreditación Universitaria
UNIVERSIDAD NACIONAL AGRARIA LA MOLINA VICERRECTORADO ACADÉMICO SÍLABO POR COMPETENCIAS A. ANTECEDENTES Mediante la Resolución Rectoral N 591-2004-UNALM se crea la Unidad de Calidad y Acreditación Universitaria
UNIDAD 8: SUCESIONES Y SERIES
 UNIDAD 8: SUCESIONES Y SERIES Llegamos a la última unidad de la asignatura correspondiente a Sucesiones y Series, recuerde mantener la motivación hasta el final, el tema que vamos a tratar aquí es de especial
UNIDAD 8: SUCESIONES Y SERIES Llegamos a la última unidad de la asignatura correspondiente a Sucesiones y Series, recuerde mantener la motivación hasta el final, el tema que vamos a tratar aquí es de especial
Cuaderno de Actividades graduadas. Guía para el/la docente Primero Básico
 Cuaderno de Actividades graduadas Matemáticas Guía para el/la docente Primero Básico Cuaderno de Actividades graduadas Matemáticas Guía para el/la docente Primero Básico Unidad de Educación Básica División
Cuaderno de Actividades graduadas Matemáticas Guía para el/la docente Primero Básico Cuaderno de Actividades graduadas Matemáticas Guía para el/la docente Primero Básico Unidad de Educación Básica División
DERIVADA DE LA FUNCIONES BÁSICAS TANGENTE, COTANGENTE, SECANTE Y COSECANTE
 DERIVADA DE LA FUNCIONES BÁSICAS TANGENTE, COTANGENTE, SECANTE Y COSECANTE Sugerencias para quien imparte el curso: En esta sección de la propuesta didáctica se parte de plantear un problema de optimización
DERIVADA DE LA FUNCIONES BÁSICAS TANGENTE, COTANGENTE, SECANTE Y COSECANTE Sugerencias para quien imparte el curso: En esta sección de la propuesta didáctica se parte de plantear un problema de optimización
TEMA Nº Desarrollo curricular. 2. Elaboración del currículum EL MODELO DE CARTAS DESCRIPTIVAS A. DEFINICIONES
 TEMA Nº 8 EL MODELO DE CARTAS DESCRIPTIVAS 1. Desarrollo curricular Definiciones propias El currículum es el plan que norma y conduce el proceso de enseñanza y aprendizaje en una institución educativa.
TEMA Nº 8 EL MODELO DE CARTAS DESCRIPTIVAS 1. Desarrollo curricular Definiciones propias El currículum es el plan que norma y conduce el proceso de enseñanza y aprendizaje en una institución educativa.
EXPRESIONES ALGEBRAICAS EXPRESIONES ALGEBRAICAS Y POLINOMIOS
 EXPRESIONES ALGEBRAICAS Trabajar en álgebra consiste en manejar relaciones numéricas en las que una o más cantidades son desconocidas. Estas cantidades se llaman VARIABLES, INCÓGNITAS o INDETERMINADAS
EXPRESIONES ALGEBRAICAS Trabajar en álgebra consiste en manejar relaciones numéricas en las que una o más cantidades son desconocidas. Estas cantidades se llaman VARIABLES, INCÓGNITAS o INDETERMINADAS
INGENIERIA CIVIL. Tercera Reunión General del Proyecto Tuning América Latina: innovación educativa y social Santiago de Chile del 2 al 4 de mayo 2012
 INGENIERIA CIVIL Tercera Reunión General del Proyecto Tuning América Latina: innovación educativa y social Santiago de Chile del 2 al 4 de mayo 2012 RESULTADO 7 Estrategias comunes para la medición del
INGENIERIA CIVIL Tercera Reunión General del Proyecto Tuning América Latina: innovación educativa y social Santiago de Chile del 2 al 4 de mayo 2012 RESULTADO 7 Estrategias comunes para la medición del
GUÍAS. Módulo Enseñar SABER PRO
 GUÍAS Módulo Enseñar SABER PRO 2014-2 Módulo Enseñar Este módulo involucra competencias relacionadas con la comprensión, la formulación y el uso de la didáctica de las disciplinas con el propósito de favorecer
GUÍAS Módulo Enseñar SABER PRO 2014-2 Módulo Enseñar Este módulo involucra competencias relacionadas con la comprensión, la formulación y el uso de la didáctica de las disciplinas con el propósito de favorecer
RESUMEN METODOLOGÍA DE SISTEMATIZACIÓN. Propuesta UICN -Mesoamérica
 RESUMEN METODOLOGÍA DE SISTEMATIZACIÓN Propuesta UICN -Mesoamérica APROVECHEMOS NUESTRAS EXPERIENCIAS Es una guía con pasos a seguir. No es la única, pero es la que nuestra organización utiliza. Ayuda
RESUMEN METODOLOGÍA DE SISTEMATIZACIÓN Propuesta UICN -Mesoamérica APROVECHEMOS NUESTRAS EXPERIENCIAS Es una guía con pasos a seguir. No es la única, pero es la que nuestra organización utiliza. Ayuda
PROFESORADO DE EDUCACIÓN INICIAL
 INSTITUTO PARROQUIAL NUESTRA SEÑORA DEL ROSARIO 5-PT NIVEL SUPERIOR Fray Luis Beltrán 192 - Tel/Fax 0261-4941414 E-mail: nsrosario@nttec.com.ar LAVALLE - MENDOZA PROFESORADO DE EDUCACIÓN INICIAL CICLO
INSTITUTO PARROQUIAL NUESTRA SEÑORA DEL ROSARIO 5-PT NIVEL SUPERIOR Fray Luis Beltrán 192 - Tel/Fax 0261-4941414 E-mail: nsrosario@nttec.com.ar LAVALLE - MENDOZA PROFESORADO DE EDUCACIÓN INICIAL CICLO
Al finalizar el semestre y dada una situación real o hipotética, el estudiante estará en capacidad de:
 FACULTAD DE CIENCIAS ADMINISTRATIVAS Y ECONÓMICAS DEPARTAMENTO DE MERCADEO Y NEGOCIOS INTERNACIONALES Código-Materia: 03195 Negocios Internacionales Programa Semestre: Administración de Empresas, Semestre
FACULTAD DE CIENCIAS ADMINISTRATIVAS Y ECONÓMICAS DEPARTAMENTO DE MERCADEO Y NEGOCIOS INTERNACIONALES Código-Materia: 03195 Negocios Internacionales Programa Semestre: Administración de Empresas, Semestre
Vicerrectorado de Tecnologías de la Información e Innovación Docente Programa de Desarrollo del Personal Docente e Investigador
 Plan de Desarrollo: Competencia comunicativa oral: Estrategias explicativas y argumentativas PRESENTACIÓN En el contexto del de la Universidad de Cádiz y con el fin de facilitar y mejorar el desarrollo
Plan de Desarrollo: Competencia comunicativa oral: Estrategias explicativas y argumentativas PRESENTACIÓN En el contexto del de la Universidad de Cádiz y con el fin de facilitar y mejorar el desarrollo
UNIVERSIDAD AUTONOMA DE TLAXCALA
 UNIVERSIDAD AUTONOMA DE TLAXCALA INTERACCION HUMANO COMPUTADORA MA. MARGARITA LABASTIDA ROLDAN EVALUACIONES DE LA USABILIDAD Inspección consistente. Listas de comprobación. Análisis de sistemas existentes.
UNIVERSIDAD AUTONOMA DE TLAXCALA INTERACCION HUMANO COMPUTADORA MA. MARGARITA LABASTIDA ROLDAN EVALUACIONES DE LA USABILIDAD Inspección consistente. Listas de comprobación. Análisis de sistemas existentes.
LECTURA 01: LA ESTADÍSTICA. TÉRMINOS DE ESTADÍSTICA. RECOLECCIÓN DE DATOS TEMA 1: LA ESTADISTICA: DEFINICION Y CLASIFICACION
 LECTURA 01: LA ESTADÍSTICA. TÉRMINOS DE ESTADÍSTICA. RECOLECCIÓN DE DATOS TEMA 1: LA ESTADISTICA: DEFINICION Y CLASIFICACION 1. DEFINICION La estadística es una ciencia que proporciona un conjunto métodos
LECTURA 01: LA ESTADÍSTICA. TÉRMINOS DE ESTADÍSTICA. RECOLECCIÓN DE DATOS TEMA 1: LA ESTADISTICA: DEFINICION Y CLASIFICACION 1. DEFINICION La estadística es una ciencia que proporciona un conjunto métodos
UNIDAD DIDACTICA. Esta unidad es el punto de partida para la correcta asimilación de las posteriores unidades didácticas del módulo.
 UNIDAD DIDACTICA TÍTULO: INTRODUCCIÓN A LA PROGRAMACIÓN. INTRODUCCIÓN E IMPORTANCIA: La importancia de esta unidad didáctica estriba en la familiarización del alumno con la metodología requerida para la
UNIDAD DIDACTICA TÍTULO: INTRODUCCIÓN A LA PROGRAMACIÓN. INTRODUCCIÓN E IMPORTANCIA: La importancia de esta unidad didáctica estriba en la familiarización del alumno con la metodología requerida para la
Distribución anual de saberes de Matemática para Segundo Ciclo según NAP CUARTO GRADO 1 TRIMESTRE. En relación con el número y las operaciones:
 CUARTO GRADO 1 TRIMESTRE Números Naturales * El reconocimiento y uso de los números naturales, de la organización del sistema decimal de numeración y la explicitación de sus características, en situaciones
CUARTO GRADO 1 TRIMESTRE Números Naturales * El reconocimiento y uso de los números naturales, de la organización del sistema decimal de numeración y la explicitación de sus características, en situaciones
DISEÑO CURRICULAR DE LA ESCUELA SECUNDARIA DE LA UNL TÍTULO: BACHILLER EN CIENCIAS SOCIALES Y HUMANIDADES
 DISEÑO CURRICULAR DE LA ESCUELA SECUNDARIA DE LA UNL TÍTULO: BACHILLER EN CIENCIAS SOCIALES Y HUMANIDADES Características Generales de la Escuela Secundaria de la UNL La escuela brinda una propuesta educativa
DISEÑO CURRICULAR DE LA ESCUELA SECUNDARIA DE LA UNL TÍTULO: BACHILLER EN CIENCIAS SOCIALES Y HUMANIDADES Características Generales de la Escuela Secundaria de la UNL La escuela brinda una propuesta educativa
CAPÍTULO III 3. METODOLOGÍA Y DISEÑO 3.1 DISEÑO DE LA INVESTIGACIÓN
 CAPÍTULO III 3. METODOLOGÍA Y DISEÑO 3.1 DISEÑO DE LA INVESTIGACIÓN Esta investigación tiene un enfoque cualitativo porque ha utilizado información de naturaleza descriptiva en los resultados obtenidos
CAPÍTULO III 3. METODOLOGÍA Y DISEÑO 3.1 DISEÑO DE LA INVESTIGACIÓN Esta investigación tiene un enfoque cualitativo porque ha utilizado información de naturaleza descriptiva en los resultados obtenidos
Compartir Saberes. Guía para maestro. Función Afín. Guía realizada por Bella Peralta Profesional en Matemáticas.
 Guía para maestro Guía realizada por Bella Peralta Profesional en Matemáticas La función afín es estudiada de diversas formas en las matemáticas escolares, además de profundizar en algunos aspectos de
Guía para maestro Guía realizada por Bella Peralta Profesional en Matemáticas La función afín es estudiada de diversas formas en las matemáticas escolares, además de profundizar en algunos aspectos de
Acompañar al docente. Instrumentos para el asesoramiento
 Acompañar al docente Instrumentos para el asesoramiento Instrumentos para el asesoramiento Instrumentos para la observación de clases y producciones Existen numerosos instrumentos de observación y análisis
Acompañar al docente Instrumentos para el asesoramiento Instrumentos para el asesoramiento Instrumentos para la observación de clases y producciones Existen numerosos instrumentos de observación y análisis
Máster Universitario en Dirección de Empresas MBA. Programa de la Asignatura: Estrategia Competitiva y Gestión del Cambio
 Máster Universitario en Dirección de Empresas MBA Programa de la Asignatura: Estrategia Competitiva y Gestión del Cambio Curso 2014-2015 1. PRINCIPALES HABILIDADES Y COMPETENCIAS QUE DESARROLLA LA MATERIA
Máster Universitario en Dirección de Empresas MBA Programa de la Asignatura: Estrategia Competitiva y Gestión del Cambio Curso 2014-2015 1. PRINCIPALES HABILIDADES Y COMPETENCIAS QUE DESARROLLA LA MATERIA
Cómo estudiar más y mejor? Autoras: MsC. Haydee Leal García. MsC. Sol Angel Galdós Sotolongo. Investigadoras del ICCP
 Cómo estudiar más y mejor? Autoras: MsC. Haydee Leal García. MsC. Sol Angel Galdós Sotolongo. Investigadoras del ICCP Objetivo: Ofrecer algunas recomendaciones y sugerencias para realizar el estudio con
Cómo estudiar más y mejor? Autoras: MsC. Haydee Leal García. MsC. Sol Angel Galdós Sotolongo. Investigadoras del ICCP Objetivo: Ofrecer algunas recomendaciones y sugerencias para realizar el estudio con
MODELO DIDÁCTICO PLANIFICACIÓN POR COMPETENCIAS A TRAVÉS DE CUADRANTES
 MODELO DIDÁCTICO PLANIFICACIÓN POR COMPETENCIAS A TRAVÉS DE S PROPÓSITO Interpretar la estructura metodológica de la Planificación a través de cuadrantes didácticos para su aplicación eficaz en el proceso
MODELO DIDÁCTICO PLANIFICACIÓN POR COMPETENCIAS A TRAVÉS DE S PROPÓSITO Interpretar la estructura metodológica de la Planificación a través de cuadrantes didácticos para su aplicación eficaz en el proceso
NOMBRE DEL CURSO: CALCULO DIFERENCIAL CÓDIGO UNIDAD ACADÉMICA NIVEL ACADÉMICO CICLOS DE FORMACIÓN FACULTAD INGENIERIA TÉCNICO PROFESIONAL
 I. INFORMACIÓN GENERAL NOMBRE DEL CURSO: CALCULO DIFERENCIAL CÓDIGO 190102 UNIDAD ACADÉMICA NIVEL ACADÉMICO CICLOS DE FORMACIÓN FACULTAD INGENIERIA TÉCNICO PROFESIONAL PROGRAMA DEPARTAMENTO CIENCIAS BASICAS
I. INFORMACIÓN GENERAL NOMBRE DEL CURSO: CALCULO DIFERENCIAL CÓDIGO 190102 UNIDAD ACADÉMICA NIVEL ACADÉMICO CICLOS DE FORMACIÓN FACULTAD INGENIERIA TÉCNICO PROFESIONAL PROGRAMA DEPARTAMENTO CIENCIAS BASICAS
Tema II:Evaluación de los entornos virtuales CÓMO EVALUAR EL E-LEARNING?
 Especialidad en Tecnología Educativa Módulo VI Evaluación del aprendizaje en los entornos virtuales Tema II:Evaluación de los entornos virtuales INSTRUCTOR Dra. María Teresa Pantoja Sánchez Lic. Comp.
Especialidad en Tecnología Educativa Módulo VI Evaluación del aprendizaje en los entornos virtuales Tema II:Evaluación de los entornos virtuales INSTRUCTOR Dra. María Teresa Pantoja Sánchez Lic. Comp.
Diseño Instruccional Paso 2 Paso 5
 TAREAS DE LA VIDA REAL EN EL CONTEXTO PROFESIONAL, CLASES DE TAREAS, OBJETIVOS DE DESEMPEÑO Y EVALUACIÓN DEL DESEMPEÑO Diseño Instruccional Paso 2 Paso 5 acet Proyecto AULA - enero de 2011 2 Paso 2 Tareas,
TAREAS DE LA VIDA REAL EN EL CONTEXTO PROFESIONAL, CLASES DE TAREAS, OBJETIVOS DE DESEMPEÑO Y EVALUACIÓN DEL DESEMPEÑO Diseño Instruccional Paso 2 Paso 5 acet Proyecto AULA - enero de 2011 2 Paso 2 Tareas,
Pautas para la Elaboración de la Programación Didáctica
 REPÚBLICA BOLIVARIANA DE VENEZUELA MINISTERIO DE EDUCACIÓN SUPERIOR UNIVERSIDAD IBEROAMERICANA DEL DEPORTE VICE-RECTORADO ACADÉMICO Pautas para la Elaboración de la Programación Didáctica Julio, 2008 La
REPÚBLICA BOLIVARIANA DE VENEZUELA MINISTERIO DE EDUCACIÓN SUPERIOR UNIVERSIDAD IBEROAMERICANA DEL DEPORTE VICE-RECTORADO ACADÉMICO Pautas para la Elaboración de la Programación Didáctica Julio, 2008 La
UNIDAD 7. SISTEMA MÉTRICO DECIMAL
 UNIDAD 7. SISTEMA MÉTRICO DECIMAL Reconocer la necesidad de medir, apreciar la utilidad de los instrumentos de medida y conocer los más importantes. Definir el metro como la unidad principal de longitud,
UNIDAD 7. SISTEMA MÉTRICO DECIMAL Reconocer la necesidad de medir, apreciar la utilidad de los instrumentos de medida y conocer los más importantes. Definir el metro como la unidad principal de longitud,
