Elementos de lógica de predicados *
|
|
|
- Lucas Maestre Rey
- hace 6 años
- Vistas:
Transcripción
1 Elementos de lógica de predicados * 1. Lenguaje Definimos un lenguaje L para la lógica de predicados de primer orden como el par A, F, donde A representa el alfabeto o conjunto de signos de L y F el conjunto de oraciones o fórmulas (expresiones bien formadas) de L. A su vez A es el conjunto unión de los siguientes conjuntos: 1. {,,,,, }, constantes lógicas (también denominado de los sincategoremas lógicos), llamadas negador, disyuntor, conjuntor, implicador, cuantificador universal y cuantificador existencial, respectivamente; 2. Un conjunto de signos categoremáticos o léxico, integrado por un número infinito enumerable de variables individuales, un número infinito enumerable de variables proposicionales y un número infinito enumerable de letras predicativas de aridad 1, 2,.... x, y, z y estas mismas letras con los subíndices necesarios representan variables individuales; p, q, r, y ellas mismas con subíndices, son variables proposicionales 1, mientras que P n, Q n, R n, y ellas mismas con los subíndices necesarios, son letras predicativas de aridad n 1 (el índice superior, que indica la aridad o número de huecos de argumento, puede omitirse si no es motivo de ambigüedad en cada contexto). 3. Eventualmente, A se puede extender mediante un conjunto enumerable de constantes individuales o parámetros, ( a, b, c, y ellas mismas con los subíndices necesarios). Asimismo con signos de función o functores de aridad n 1 (f n, g n, h n, y ellas mismas con los subíndices necesarios). Igualmente se puede introducir el predicado diádico =. 4. Un conjunto de signos auxiliares, como (, ), [, ], etc. F es el más pequeño conjunto que verifica lo siguiente: 1. si p es una letra proposicional, entonces p F (p es una fórmula). Si P k es una letra predicativa k-ádica, k 1, y t 1,..., t k son k signos individuales (es una ocurrencia de dicho número de signos, puede, por tanto, haber repetición), entonces P k t 1...t k F (es decir, P k t 1...t k es una fórmula); * Secciones 1 y 2 extraídas de A. Nepomuceno, Curso práctico de lógica, Sevilla, Kronos, Lo más habitual es presentar lenguajes formales de primer orden que no contienen variables proposicionales, llamándose variables exclusivamente a las individuales; para evitar confusiones, cuando hablemos de variables sin más especificación, nos estaremos refiriendo a las individuales. Para el estudio de la lógica proposicional se definiría un lenguaje formal específico cuyo léxico estaría integrado por variables proposicionales, careciendo de otras variables, signos predicativos, etc. 1
2 2. si α, β F (si α y β son fórmulas) y x es una variable individual, entonces α, α β, α β, α β, xα, xα F (es decir, α, α β, α β, α β, xα y xα son fórmulas). Nótese que si el lenguaje contiene identidad, que se suele representar como =, dados dos términos t 1 y t 2, las expresiones = t 1 t 2 y = t 1 t 2 son fórmulas, aunque es más frecuente escribir t 1 = t 2 y t 1 = t 2 (o bien t 1 t 2 ), respectivamente. Otras nociones resultan de utilidad en nuestro estudio. Destacamos las siguientes: Una fórmula atómica es aquélla en la cual no aparece ningún signo lógico; una variable proposicional o una letra predicativa de aridad n 1 seguida de n ocurrencias de signos individuales, son fórmulas atómicas. Una fórmula elemental o literal es una fórmula atómica o una fórmula atómica precedida del negador. Si α es una fórmula atómica se dice que es un literal positivo, mientras que α es un literal negativo y cada uno es complementario del otro. El grado de una fórmula (o grado de complejidad) es el número de ocurrencias de signos lógicos en dicha fórmula. La fórmula ((p q) (r (p s))) tiene grado 4, ocurriendo en ella dos veces el conjuntor y dos veces el disyuntor. Dada la fórmula α, mediante G(α) nos referimos al grado de α: si α es artómica, entonces G(α) = 0, si α es β,entonces G(α) = G(β) + 1, si α es β γ,o β γ, o β γ, entonces G(α) = G(β) + G(γ) + 1, si α es xβ o xβ, entonces G(α) = G(β) + 1. Dada una fórmula α, cualquier fórmula, según la definición dada, que forme parte de la construcción de α, incluida ella misma, se denomina subfórmula de α. Ejemplo: la fórmula 2 x((p x) ( y(rxy)) (P y)) consta de las siguientes subfórmulas: P y, P x, Rxy, yrxy, yrxy P y, y, por último, P x yrxy P y, x(p x yrxy P y). Llamamos alcance de (una ocurrencia de) un signo lógico en una fórmula α a la(s) subfórmula(s) de α de menor grado que se ve(n) afectada(s) por dicha ocurrencia del signo lógico. En el ejemplo precedente, Rxy es el alcance de (es un signo lógico monádico), mientras que Rxy y P y constituyen las dos subfórmulas que caen bajo el alcance de (signo lógico diádico), P x y yrxy P y caen bajo el alcance de (de carácter diádico) y P x yrxy P y es el alcance de (signo lógico monádico). 2 Para mayor facilidad escribiremos x(p x yrxy P y), como es habitual en la literatura lógica; se suprimen paréntesis supérfluos cuando el alcance de los signos está bien delimitado. La noción de alcance se establece a continuación. 2
3 Signo principal de una fórmula es el signo cuyo alcance es de mayor grado. En el ejemplo anterior, el signo principal es. Las ocurrencias de las variables en un fórmula puede ser libres o ligadas. Una ocurrencia libre es aquélla que no cae bajo el alcance de un cuantificador que la tiene como sufijo; si una ocurrencia no es libre, entonces es ligada. Ejemplo: en yrxy P y la ocurrencia de la x es libre, mientras que la variable y ocurre dos veces, la primera ocurrencia es ligada y la segunda libre; por otra parte, y ocurre ligada respecto de x en yrxy, puesto que x cae bajo el alcance de un cuantificador ( ) que tiene a y como sufijo. Las constantes siempre ocurren libres, ya que nunca serán sufijos de un cuantificador aunque pueden estar bajo el alcance de un cuantificador, que tendrá cierta variable como sufijo. Una fórmula con variables libres se dice que es abierta. Una fórmula que no es abierta (no contiene variables libres) es una fórmula cerrada o sentencia. Llamamos términos a las variables individuales y a los parámetros. Si el lenguaje formal consta de functores, entonces el conjunto T de los términos se define como el más pequeño que verifica: si x es una variable, entonces x T, si b es un parámetro, entonces b T, si g n es un functor n-ádico y t 1,..., t n T (puede haber repetición), entonces g n (t 1,..., t n ) T, para cada n 1. En un lenguaje con functores, dados, por ejemplo, el signo predicativo diádico R y el functor triádico g, con los términos t 1, t 2, t 3, tendremos que Rt 2 t 1, Rg(t 3, g(t 1, t 1, t 3 ), t 2 )t 2, etc., son fórmulas. Por otra parte, los functores permiten formalizar determinadas expresiones de frecuente uso en el lenguaje ordinario: la madre de María es alta se puede formalizar como P g(m), donde P representa el predicado...es alta, g la función la madre de... y m a María. Si se cuenta con la identidad, la expresión la madre de María es Ana, será g(m) = a, donde a es el nombre de Ana. La sustitución de una variable x por un término t en una fórmula β, que se representa por β(t/x) se establece según las cláusulas: si x no ocurre, o no ocurre libre, en β, entonces β(t/x) es β; si t no está libre respecto de x en β, entonces β(t/x) es β; en otro caso, β(t/x) es la fórmula resultante de reemplazar en β cada ocurrencia libre de x por t. 2. Semántica Para estudiar la semántica de L introducimos algunas nociones necesarias. Una interpretación de L, también denominada L-estructura (estructura interpretativa para L, del mismo tipo que L) M es el par D, I, donde D es un dominio no vacío, denominado dominio de la interpretación (dominio de la L-estructura) o universo de discurso, mientras que I es la función interpretación definida con dominio en parte del vocabulario de L y rango en D y en predicados y relaciones (en su caso, también funciones) definidos en D, de la manera siguiente: 1. Para cada parámetro b de L, I(b) D, 3
4 2. Para cada signo predicativo n-ádico P, n 1, I(P ) D n ; lo cual es lo mismo que afirmar que I(P ) P(D n ) [Nótese que si P es monádico, D 1 = D y, por tanto, I(P ) D]. 3. Si f es un signo funcional n-ádico, n 1, I(f) : D n D; es decir, I(f) es una función n-ádica definida con dominio en D n y rango en D Si el lenguaje contiene identidad =, ésta se interpreta de la siguiente manera: I(=) = { b, c D 2 : b = c}, es decir, como el conjunto de pares de individuos del universo de discurso, tales que son idénticos. Dada M = D, I, a cada sentencia α de L podemos asignar un elemento del conjunto {0, 1}, lo que representamos mediante M(α); es decir, para cada sentencia α L, M(α) {0, 1}. Ello se establece recursivamente: 1. si α es una letra proposicional, entonces M(α) = 0, o bien M(α) = 1 4, 2. en otro caso, si α es atómica: a) de la forma P b (P es un signo predicativo monádico, b es un parámetro), entonces M(α) = 1 syss I(b) I(P ); b) de la forma P b 1 b 2...b n (P es un signo predicativo n-ádico, para n 2, y b i es una ocurrencia de un parámetro para i = 1, 2,...n), entonces M(α) = 1 syss I(b 1 ), I(b 2 ),..., I(b n ) I(P ). En el caso de sentencias de identidad como b 1 = b 2, es decir, I(b 1 ) = I(b 2 ). 3. si α es β, M(α) = 1 syss M(β) = 0, M(b 1 = b 2 ) = 1 syss I(b 1 ), I(b 2 ) I(=), 4. si α es β γ, M(α) = 1 syss M(β) = 1 ó M(γ) = 1, 5. si α es β γ, M(α) = 1 syss M(β) = 1 y M(γ) = 1, 6. si α es β γ, M(α) = 1 syss M(β) = 0 ó M(γ) = 1, 7. si α es xβ, M(α) = 1 syss M (β(b/x)) = 1, para al menos una L-estructura M que coincide con M excepto, a lo sumo, en el valor del parámetro b (libre respecto de x en β) para la función interpretación correspondiente (podría ser, pues I (b) I(b), pero ésta sería, a lo sumo, la única diferencia entre M y M; para abreviar, en lo sucesivo, indicaremos esta circunstancia como M = M), b 3 Véanse las nociones de función, dominio, etc. estudiadas más arriba, en el apartado correspondiente a teoría de conjuntos. 4 La asignación de un valor de tal conjunto bimembre a una variable proposicional se haría arbitrariamente. Si L carece de variables proposicionales (como se indicó, es lo más habitual), entonces se omite esta cláusula. Cuando se interpreta un lenguaje formal proposicional no se establecen las restantes cláusulas. 4
5 8. si α es xβ, M(α) = 1 syss M (β(b/x)) = 1, para toda L-estructura M = b M. A veces se presentan las nociones semánticas considerando asignaciones de valores a las variables; en tal caso, dada una L-estructura M = D, I, hemos de tener en cuenta asignaciones σ tales que para cada variable x, σ(x) D; el valor semántico de cada término t, dada una asignación σ, se representa como t M,σ y se define: 1. si t es una variable, entonces t M,σ = σ(t), si t es un parámetro, entonces t M,σ = I(t), 2. si t es un functor o un signo predicativo de determinada aridad, entonces t M,σ = I(t). Ahora, para cada asignación σ y una fórmula atómica α de la forma P t 1...t n no tiene por qué ser una sentencia, M σ (α) = 1 el valor de α para la L-estructura M y la asignación σ syss se verifica que t M,σ 1,..., t M,σ n P M,σ = I(P ), y así sucesivamente. Con relación a : si α es xβ, M σ (α) = 1 syss M σ (β) = 1, para toda σ (de manera análoga para ). No obstante, y para mayor facilidad, continuaremos estudiando las nociones semánticas centrándonos en el primer formato propuesto. Dada una sentencia cualquiera, para cada L-estructura, podemos, a partir de la evaluación de su signo lógico principal y del valor de sus componentes, determinar el valor para la L- estructura. En definitiva, si la sentencia es compleja, mediante evaluación de sus signos lógicos podemos determinar si para una L-estructura dada vale 0 ó 1. Decimos que una L-estructura M satisface o es un modelo de una sentencia α syss M(α) = 1. Mediante M = α indicamos que M satisface α, equivalentemente, M es un modelo de α (ahora se pueden evaluar los signos lógicos teniendo en cuenta esta definición: M = β syss no es el caso que M = β, y así sucesivamente tómese como ejercicio ). Una sentencia α L es satisfactible (satisfacible, o consistente) syss existe una L-estructura M tal que M = α, o, lo que es lo mismo, syss M(α) = 1. Mediante Sat α indicamos que α es satisfacible. Una sentencia es no satisfactible (no satisfacible, insatisfactible, o inconsistente) syss no existe ninguna L-estructura que la satisfaga. Si una L-estructura satisface a todas y cada una de las sentencias de un conjunto dado, decimos que dicha L-estructura satisface simultáneamente (o simplemente satisface, para abreviar) o es un modelo de tal conjunto; también podemos decir que tal conjunto es simultáneamente satisfactible (o simplemente satisfactible o consistente). Si M satisface al conjunto de sentencias Γ, podemos expresar esta circunstancia como M = Γ. Una sentencia α L es válida en un dominio D syss si toda L-estructura M, cuyo universo de discurso sea D, satisface α; es decir, si toda L-estructura definible a partir de D (todo modelo definible a partir de D) satisface α. Una sentencia α L es universalmente válida syss toda L-estructura la satisface. También podemos decir que α es universalmente válida syss si es válida en todo dominio no vacío. Una noción semántica de importancia capital es la de consecuencia lógica. Dado un conjunto de sentencias Γ L y una sentencia β L, decimos que β es consecuencia lógica de Γ, en símbolos Γ = β, syss toda L-estructura que satisface Γ, satisface β. Nótese que si una sentencia α es universalmente válida, entonces es consecuencia lógica de cualquier conjunto Γ de sentencias, incluso cuando Γ =, pues cualquier L-estructura que satisfaga a Γ, también satisface α ( Todas satisfacen α!). Para indicar que α es universalmente válida anotamos = α. Si no es el caso que Γ = α, decimos que α es semánticamente independiente de Γ; basta para ello que exista al menos una L-estructura que satisfaciendo Γ no satisfaga α. 5
6 El siguiente es un teorema semántico (cuya demostración es un interesante ejercicio): Dados un conjunto Γ de sentencias y las sentencias α y β, Γ {α} = β si y sólo si Γ = α β. Asimismo, si Γ = {γ 1, γ 2,..., γ n }, entonces Γ = α syss [con n 1 parejas de paréntesis], syss = γ 1 (γ 2... (γ n α)...) = γ 1 γ 2... γ n α. Por otra parte, Γ = β syss Γ {β} es inconsistente. 3. Tablas semánticas A las reglas propias de las tablas semánticas en lógica proposicional, añadimos las dos siguientes: 1. regla γ: xϕ ϕ(b 1 /x) ϕ(b 2 /x)... ϕ(b n /x) xϕ ϕ(b 1 /x) ϕ(b 2 /x)... ϕ(b n /x) b 1,..., b n son todas las constantes que ocurren en sentencias de la rama, n 1 (si no ocurre ninguna, entonces n = 1); la nueva parte de la rama es Φ + ϕ(b 1 /x) ϕ(b n /x) (ϕ(b i /x) es una sentencia-γ, para todo i n) 2. regla δ: xϕ ϕ(b/x) xϕ ϕ(b/x) donde b es una nueva constante que no ocurría en ninguna sentencia de la rama; la nueva parte de la rama es Φ + ϕ(b/x) y ésta es una sentencia-δ. 4. Deducción natural Además de las reglas usadas en lógica proposicional, consideramos las siguientes. [RESTRICCIÓN: Aunque no sea necesario esta condición en muchas reglas, asumiremos que en todos los casos el dominio es no vacío. NOTACIÓN: En lo que sigue asumimos la siguiente notación: a es una constante individual, x e y son variables individuales, ϕ(x) y ϕ(y) son fórmulas cualesquiera en las que, respectivamente, ocurren libre x e y, mientras que α, β y ω son fórmulas cualquiera; por su parte, ϕ[α] es una fórmula cualquiera de la que α es una subfórmula y ϕ[β int α] es el resultado de intercambiar en ϕ[α] una o más ocurrencias de la fórmula α por las correspondientes ocurrencias de β.] 6
7 4.1. Reglas básicas Generalizador ϕ(a) ϕ(a) E I ( ) (*) Esta regla se puede aplicar sólo si se cumple además la condición crítica de que a no ocurra en ninguna premisa y en ninguna hipótesis auxiliar no cancelada de las que dependa ϕ(a) (obviamente, dado que la sustitución de la constante por la variable debe ser uniforme, tampoco debe ocurrir en ). Particularizador ϕ(a). ψ ψ E (**) ϕ(a) I (**) Esta regla se puede aplicar sólo si se cumple además la condición crítica de que a no ocurra en ψ, en así como en ninguna premisa y en ninguna hipótesis auxiliar no cancelada de las que dependa ψ Reglas derivadas Descenso cuantificacional Desc Mutación de variable del generalizador yϕ(y) MV ( ) Mutación de variable del particularizador yϕ(y) MV ( ) (*) Regla válida sólo si y no ocurre libre en ϕ(x). 7
8 Definición del generalizador Definición del particularizador Negación del generalizador Negación del particularizador x ϕ(x) x ϕ(x) x ϕ(x) x ϕ(x) Def Def Neg Neg Ejercicios Demostrar usando tablas semánticas y deducción natural. 1. y(p y x(rx Qxy)) x(rx y(p y Qxy)) 2. x(p x yqxy), x( yqxy zrxyz), z Rxyz xp x 3. x(rx Qx), x(p x Qx) x(p x Rx) 4. x y(rx (P y Hy)), xy(rx P y) xp x xhx 5. x(p x Qx), xrx, x(rx Qx) x P x 6. x(rx Qx), x(p x Qx) x(p x Rx) 7. x(p x Qx) xqx 8. x( y(f y Rxy) y(p y Rxy)), xy(p y Rxy) xy(f y Rxy) 9. x(p x Qx), x(p x Rx) x(rx Qx) 10. x(p x Qx), x(p x Rx) x(rx Qx) 11. x(p x Qx) x( Qx P x) 12. x(p x Qx Rx), x(p x Qx Sx) x(p x Sx Rx) 13. x(p x Qx), x(rx Sx), x( Sx Qx) x(p x Rx) 14. x(p x Qx) ( xp x xqx) 15. x(p x Qx y(qy Rxy)) x(p x Qx Rxx) 8
Lógica de primer orden: Repaso y notación
 Lógica de primer orden: Repaso y notación IIC3263 IIC3263 Lógica de primer orden: Repaso y notación 1 / 29 Lógica de primer orden: Vocabulario Una fórmula en lógica de primer orden está definida sobre
Lógica de primer orden: Repaso y notación IIC3263 IIC3263 Lógica de primer orden: Repaso y notación 1 / 29 Lógica de primer orden: Vocabulario Una fórmula en lógica de primer orden está definida sobre
Teorema de incompletitud de Gödel
 Teorema de incompletitud de Gödel Theorem (Gödel) Th(N) es una teoría indecidible. IIC2213 Teorías 79 / 109 Teorema de incompletitud de Gödel Theorem (Gödel) Th(N) es una teoría indecidible. Corolario
Teorema de incompletitud de Gödel Theorem (Gödel) Th(N) es una teoría indecidible. IIC2213 Teorías 79 / 109 Teorema de incompletitud de Gödel Theorem (Gödel) Th(N) es una teoría indecidible. Corolario
Lógica Proposicional Lenguaje Proposicional Implicación semántica
 Capítulo 1 Lógica Proposicional 1.1. Lenguaje Proposicional Un lenguaje proposicional consta de los siguientes símbolos: las proposicones atómicas, también llamados enunciados atómicos o simplemente variables
Capítulo 1 Lógica Proposicional 1.1. Lenguaje Proposicional Un lenguaje proposicional consta de los siguientes símbolos: las proposicones atómicas, también llamados enunciados atómicos o simplemente variables
Capítulo 2 El Método de Resolución
 Capítulo 2 El Método de Resolución En este capítulo se realiza una descripción general del método de resolución, dado que el programa de razonamiento automático OTTER lo utiliza y prueba a través de refutación.
Capítulo 2 El Método de Resolución En este capítulo se realiza una descripción general del método de resolución, dado que el programa de razonamiento automático OTTER lo utiliza y prueba a través de refutación.
Lógica de Primer Orden
 Lógica de Primer Orden IIC2213 IIC2213 Lógica de Primer Orden 1 / 60 Lógica de primer orden Dos de los objetivos de la lógica proposicional: Poder modelar el proceso de razonamiento. Poder formalizar la
Lógica de Primer Orden IIC2213 IIC2213 Lógica de Primer Orden 1 / 60 Lógica de primer orden Dos de los objetivos de la lógica proposicional: Poder modelar el proceso de razonamiento. Poder formalizar la
Programación II Sesión 2: Especificación de problemas
 Programación II Sesión 2: Especificación de problemas Diego R. Llanos Ferraris UNED, Centro Asociado de Palencia Nota: Estos apuntes son la guía utilizada por el Profesor Tutor para impartir el seminario
Programación II Sesión 2: Especificación de problemas Diego R. Llanos Ferraris UNED, Centro Asociado de Palencia Nota: Estos apuntes son la guía utilizada por el Profesor Tutor para impartir el seminario
Tema 1: Sintaxis y Semántica de la Lógica Proposicional
 Tema 1: Sintaxis y Semántica de la Lógica Proposicional Dpto. Ciencias de la Computación e Inteligencia Artificial Universidad de Sevilla Lógica y Computabilidad Curso 2010 11 LC, 2010 11 Lógica Proposicional
Tema 1: Sintaxis y Semántica de la Lógica Proposicional Dpto. Ciencias de la Computación e Inteligencia Artificial Universidad de Sevilla Lógica y Computabilidad Curso 2010 11 LC, 2010 11 Lógica Proposicional
Tema 6: Teoría Semántica
 Tema 6: Teoría Semántica Sintáxis Lenguaje de de las las proposiciones Lenguaje de de los los predicados Semántica Valores Valores de de verdad verdad Tablas Tablas de de verdad verdad Tautologías Satisfacibilidad
Tema 6: Teoría Semántica Sintáxis Lenguaje de de las las proposiciones Lenguaje de de los los predicados Semántica Valores Valores de de verdad verdad Tablas Tablas de de verdad verdad Tautologías Satisfacibilidad
Tema 9: Cálculo Deductivo
 Facultad de Informática Grado en Ingeniería Informática Lógica PARTE 2: LÓGICA DE PRIMER ORDEN Tema 9: Cálculo Deductivo Profesor: Javier Bajo jbajo@fi.upm.es Madrid, España 24/10/2012 Introducción a la
Facultad de Informática Grado en Ingeniería Informática Lógica PARTE 2: LÓGICA DE PRIMER ORDEN Tema 9: Cálculo Deductivo Profesor: Javier Bajo jbajo@fi.upm.es Madrid, España 24/10/2012 Introducción a la
Resolución en lógica de primer orden
 Resolución en lógica de primer orden Eduardo Bonelli Departamento de Computación, FCEyN, UBA 15 de mayo, 2006 Clase pasada Repasamos lógica proposicional Introdujimos el método de resolución para lógica
Resolución en lógica de primer orden Eduardo Bonelli Departamento de Computación, FCEyN, UBA 15 de mayo, 2006 Clase pasada Repasamos lógica proposicional Introdujimos el método de resolución para lógica
Lógica de predicados
 Matemática Discreta y Lógica 2 Lógica de predicados 1 Cuantificadores El lenguaje de la lógica proposicional que ya vimos, no es suficiente para representar todo el lenguaje matemático. Por ejemplo, la
Matemática Discreta y Lógica 2 Lógica de predicados 1 Cuantificadores El lenguaje de la lógica proposicional que ya vimos, no es suficiente para representar todo el lenguaje matemático. Por ejemplo, la
LÓGICA DE PREDICADOS 6. LA SEMÁNTICA DE PRIMER ORDEN
 LÓGICA DE PREDICADOS 6. LA SEMÁNTICA DE PRIMER ORDEN Juan Carlos León Universidad de Murcia Esquema del tema 6.1. Noción de interpretación de primer orden 6.2. Las reglas de valoración semántica 1 Lógica
LÓGICA DE PREDICADOS 6. LA SEMÁNTICA DE PRIMER ORDEN Juan Carlos León Universidad de Murcia Esquema del tema 6.1. Noción de interpretación de primer orden 6.2. Las reglas de valoración semántica 1 Lógica
Introducción a la lógica proposicional
 Introducción a la lógica proposicional Fernando Soler Toscano fsoler@us.es 1. Lógica proposicional 1.1. El lenguaje de la lógica proposicional Fórmulas. El lenguaje de la lógica proposicional está compuesto
Introducción a la lógica proposicional Fernando Soler Toscano fsoler@us.es 1. Lógica proposicional 1.1. El lenguaje de la lógica proposicional Fórmulas. El lenguaje de la lógica proposicional está compuesto
Introducción a la Lógica Proposicional Seminario de Matemáticas
 Introducción a la Lógica Proposicional Seminario de Matemáticas Julio Ariel Hurtado Alegría ahurtado@unicauca.edu.co 8 de mayo de 2015 Julio A. Hurtado A. Departamento de Sistemas 1 / 34 Agenda Motivación
Introducción a la Lógica Proposicional Seminario de Matemáticas Julio Ariel Hurtado Alegría ahurtado@unicauca.edu.co 8 de mayo de 2015 Julio A. Hurtado A. Departamento de Sistemas 1 / 34 Agenda Motivación
Lógica de Predicados de Primer Orden
 Lógica de Predicados: Motivación Todo natural es entero y 2 es un natural. Luego 2 es entero. p q r p, q r es claramente un razonamiento válido pero no es posible demostrarlo desde la Lógica Proposicional
Lógica de Predicados: Motivación Todo natural es entero y 2 es un natural. Luego 2 es entero. p q r p, q r es claramente un razonamiento válido pero no es posible demostrarlo desde la Lógica Proposicional
Deducción natural. Teorema de la deducción A B
 Deducción natural La derivación natural hace uso de varias reglas de inferencia. Introduce conectiva Elimina conectiva Nombre Regla Nombre Regla I I I Teorema de la deducción Teorema de la deducción A,B
Deducción natural La derivación natural hace uso de varias reglas de inferencia. Introduce conectiva Elimina conectiva Nombre Regla Nombre Regla I I I Teorema de la deducción Teorema de la deducción A,B
LógicaS Modales. Ricardo Oscar Rodríguez Departamento de Computación, Fac. Ciencias Exactas y Naturales, Universidad de Buenos Aires, Argentina.
 Departamento de Computación, Fac. Ciencias Exactas y Naturales, Universidad de Buenos Aires, Argentina. Segunda Clase. 1er. Cuatrimestre, 2016 Outline 1 Repaso clase anterior Sintáxis Lógicas Modales Autocongruentes
Departamento de Computación, Fac. Ciencias Exactas y Naturales, Universidad de Buenos Aires, Argentina. Segunda Clase. 1er. Cuatrimestre, 2016 Outline 1 Repaso clase anterior Sintáxis Lógicas Modales Autocongruentes
Completitud en Lógica de Predicados
 Completitud en de Predicados Predicados - Completitud 1 Corrección. Significa que las derivaciones expresan una consecuencia lógica. Establece una correspondencia tal que partiendo de nociones sintácticas
Completitud en de Predicados Predicados - Completitud 1 Corrección. Significa que las derivaciones expresan una consecuencia lógica. Establece una correspondencia tal que partiendo de nociones sintácticas
Lógica de predicados 3. Sintaxis. Juan Carlos León Universidad de Murcia
 Lógica de predicados 3. Sintaxis Juan Carlos León Universidad de Murcia Esquema del tema 3.1. Fórmulas bien formadas y funciones proposicionales 3.2. Alcance. Variables libres y ligadas 3.3. Teoremas 3.4.
Lógica de predicados 3. Sintaxis Juan Carlos León Universidad de Murcia Esquema del tema 3.1. Fórmulas bien formadas y funciones proposicionales 3.2. Alcance. Variables libres y ligadas 3.3. Teoremas 3.4.
PALABRA CLAVE Interpretación lógica
 Curso 2009- Bloque II: Teoría a Semántica Tema 5: Conceptos Semánticos Básicos B (Cap-3 3 libro) Tema 6: Técnicas y Métodos M Semánticos para validar argumentos (Cap-3 3 libro) Objetivos Aprender los conceptos
Curso 2009- Bloque II: Teoría a Semántica Tema 5: Conceptos Semánticos Básicos B (Cap-3 3 libro) Tema 6: Técnicas y Métodos M Semánticos para validar argumentos (Cap-3 3 libro) Objetivos Aprender los conceptos
Teoría de Modelos Finitos: Motivación
 Teoría de Modelos Finitos: Motivación IIC3260 IIC3260 Teoría de Modelos Finitos: Motivación 1 / 29 Poder expresivo de una lógica: Caso finito Desde ahora en adelante nos vamos a concentrar en las estructuras
Teoría de Modelos Finitos: Motivación IIC3260 IIC3260 Teoría de Modelos Finitos: Motivación 1 / 29 Poder expresivo de una lógica: Caso finito Desde ahora en adelante nos vamos a concentrar en las estructuras
Lógica de predicados
 Lógica de predicados Cálculo de predicados Hay ciertos argumentos que parecen ser perfectamente lógicos y que no pueden ser especificados usando cálculo proposicional. Ejemplos: Todos los gatos tienen
Lógica de predicados Cálculo de predicados Hay ciertos argumentos que parecen ser perfectamente lógicos y que no pueden ser especificados usando cálculo proposicional. Ejemplos: Todos los gatos tienen
Cálculo de predicados. Lógica de predicados. Cálculo de predicados. Cálculo de predicados 08/06/2011
 Lógica de predicados Hay ciertos argumentos que parecen ser perfectamente lógicos y que no pueden ser especificados usando cálculo proposicional. Ejemplos: Todos los gatos tienen cola Tomás es un gato
Lógica de predicados Hay ciertos argumentos que parecen ser perfectamente lógicos y que no pueden ser especificados usando cálculo proposicional. Ejemplos: Todos los gatos tienen cola Tomás es un gato
Tema 2: Métodos de Deducción para la Lógica Proposicional
 Tema 2: Métodos de Deducción para la Lógica Proposicional Dpto. Ciencias de la Computación Inteligencia Artificial Universidad de Sevilla Lógica y Computabilidad Curso 2010 11 LC, 2010 11 Métodos de Deducción
Tema 2: Métodos de Deducción para la Lógica Proposicional Dpto. Ciencias de la Computación Inteligencia Artificial Universidad de Sevilla Lógica y Computabilidad Curso 2010 11 LC, 2010 11 Métodos de Deducción
Lógica Proposicional IIC1253. IIC1253 Lógica Proposicional 1/64
 Lógica Proposicional IIC1253 IIC1253 Lógica Proposicional 1/64 Inicio de la Lógica Originalmente, la Lógica trataba con argumentos en el lenguaje natural. Ejemplo Es el siguiente argumento válido? Todos
Lógica Proposicional IIC1253 IIC1253 Lógica Proposicional 1/64 Inicio de la Lógica Originalmente, la Lógica trataba con argumentos en el lenguaje natural. Ejemplo Es el siguiente argumento válido? Todos
Lógica de proposiciones
 1 Introducción Lenguaje lógico simbólico más sencillo. Permite representar sentencias simples del lenguaje natural mediante formulas atómicas, cuya composición representa sentencias más complejas: p temperatura
1 Introducción Lenguaje lógico simbólico más sencillo. Permite representar sentencias simples del lenguaje natural mediante formulas atómicas, cuya composición representa sentencias más complejas: p temperatura
L ogica 2 Enrique Casanovas Curso
 Lógica 2 Enrique Casanovas Curso 1999-2000 Índice general 1. Sintaxis 3 2. Semántica 9 3. Consecuencia y equivalencia lógica 18 4. Cálculo deductivo 28 Bibliografía 41 Índice de Materias 42 2 Capítulo
Lógica 2 Enrique Casanovas Curso 1999-2000 Índice general 1. Sintaxis 3 2. Semántica 9 3. Consecuencia y equivalencia lógica 18 4. Cálculo deductivo 28 Bibliografía 41 Índice de Materias 42 2 Capítulo
Clases de complejidad computacional: P y NP
 1er cuatrimestre 2006 La teoría de Se aplica a problemas de decisión, o sea problemas que tienen como respuesta SI o NO (aunque es sencillo ver que sus implicancias pueden extenderse a problemas de optimización).
1er cuatrimestre 2006 La teoría de Se aplica a problemas de decisión, o sea problemas que tienen como respuesta SI o NO (aunque es sencillo ver que sus implicancias pueden extenderse a problemas de optimización).
Tema 1: Conjuntos. Miguel Ángel Olalla Acosta Departamento de Álgebra Universidad de Sevilla. Septiembre de 2017
 Tema 1: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2017 Olalla (Universidad de Sevilla) Tema 1: Conjuntos Septiembre de 2017 1
Tema 1: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2017 Olalla (Universidad de Sevilla) Tema 1: Conjuntos Septiembre de 2017 1
Teorema de Compacidad
 Teorema de Compacidad Seminario de Teoría de Modelos - FCEyN - UBA 1 de septiembre de 2011 Teorema 1 (Compacidad). Una L-teoría T es satisfacible si y solo si todo subconjunto finito de T es satisfacible.
Teorema de Compacidad Seminario de Teoría de Modelos - FCEyN - UBA 1 de septiembre de 2011 Teorema 1 (Compacidad). Una L-teoría T es satisfacible si y solo si todo subconjunto finito de T es satisfacible.
REGLAS Y LEYES LOGICAS
 LOGICA II REGLAS Y LEYES LOGICAS Una regla lógica, o regla de inferencia (deductiva), es una forma válida de razonamiento que es empleada para inferir deductivamente ciertos enunciados a partir de otros.
LOGICA II REGLAS Y LEYES LOGICAS Una regla lógica, o regla de inferencia (deductiva), es una forma válida de razonamiento que es empleada para inferir deductivamente ciertos enunciados a partir de otros.
Tema 10: Conceptos Metalógicos
 Facultad de Informática Grado en Ingeniería Informática Lógica PARTE 2: LÓGICA DE PRIMER ORDEN Tema 10: Conceptos Metalógicos Profesor: Javier Bajo jbajo@fi.upm.es Madrid, España 12/11/2012 Introducción
Facultad de Informática Grado en Ingeniería Informática Lógica PARTE 2: LÓGICA DE PRIMER ORDEN Tema 10: Conceptos Metalógicos Profesor: Javier Bajo jbajo@fi.upm.es Madrid, España 12/11/2012 Introducción
Lógica de Predicados 1!
 Lógica de Predicados 1! rafael ramirez rafael.ramirez@upf.edu 55.316 (Tanger) Porqué Lógica de Predicados! La logica proposicional maneja bien afirmaciones compuestas de no, y, o, si entonces En situaciones
Lógica de Predicados 1! rafael ramirez rafael.ramirez@upf.edu 55.316 (Tanger) Porqué Lógica de Predicados! La logica proposicional maneja bien afirmaciones compuestas de no, y, o, si entonces En situaciones
TABLAS SEMÁNTICAS Y METALÓGICA (EL CASO DE LA LÓGICA DE SEGUNDO ORDEN)
 = CRÍTICA, Revista Hispanoamericana de Filosofía Vol. XXXI, No. 93 (diciembre 1999): 21 47 TABLAS SEMÁNTICAS Y METALÓGICA (EL CASO DE LA LÓGICA DE SEGUNDO ORDEN) ÁNGEL NEPOMUCENO FERNÁNDEZ Departamento
= CRÍTICA, Revista Hispanoamericana de Filosofía Vol. XXXI, No. 93 (diciembre 1999): 21 47 TABLAS SEMÁNTICAS Y METALÓGICA (EL CASO DE LA LÓGICA DE SEGUNDO ORDEN) ÁNGEL NEPOMUCENO FERNÁNDEZ Departamento
Tema 1: Conjuntos. Miguel Ángel Olalla Acosta Departamento de Álgebra Universidad de Sevilla. Septiembre de 2016
 Tema 1: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2016 Olalla (Universidad de Sevilla) Tema 1: Conjuntos Septiembre de 2016 1
Tema 1: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2016 Olalla (Universidad de Sevilla) Tema 1: Conjuntos Septiembre de 2016 1
Sistema Axiomático para el Cálculo Proposicional
 Sistema Axiomático para el Cálculo Proposicional Lógica Matemática José de Jesús Lavalle Martínez 12 de julio de 2011 Resumen Este documento es una traducción de partes de la sección 1.4 AN AXIOM SYSTEM
Sistema Axiomático para el Cálculo Proposicional Lógica Matemática José de Jesús Lavalle Martínez 12 de julio de 2011 Resumen Este documento es una traducción de partes de la sección 1.4 AN AXIOM SYSTEM
Teoría de Modelos. E. Casanovas
 Teoría de Modelos E. Casanovas 1999-2000 Revisado Septiembre 2003 Índice general 1. Preliminares 4 2. Homomorfismos 11 3. Teoremas de Compacidad y Löwenheim-Skolem 15 4. Extensiones elementales 22 5. Teoremas
Teoría de Modelos E. Casanovas 1999-2000 Revisado Septiembre 2003 Índice general 1. Preliminares 4 2. Homomorfismos 11 3. Teoremas de Compacidad y Löwenheim-Skolem 15 4. Extensiones elementales 22 5. Teoremas
1. Resolución en lógica proposicional
 1. Resolución en lógica proposicional 1.1. Introducción 1.1.1. Pseudo-motivación Si tengo una fórmula de proposicional, puedo probar con fuerza bruta todas las valuaciones a ver si es satisfactible? Si
1. Resolución en lógica proposicional 1.1. Introducción 1.1.1. Pseudo-motivación Si tengo una fórmula de proposicional, puedo probar con fuerza bruta todas las valuaciones a ver si es satisfactible? Si
Problemas de Decisión
 Problemas de Decisión La motivación de este capítulo puede estar dado por lo siguiente: Dado un conjunto Σ de fórmulas proposicionales en L(P ), existe un algoritmo general para determinar si Σ = ϕ Qué
Problemas de Decisión La motivación de este capítulo puede estar dado por lo siguiente: Dado un conjunto Σ de fórmulas proposicionales en L(P ), existe un algoritmo general para determinar si Σ = ϕ Qué
Sintaxis y Propiedades. Estructuras
 Sintaxis y Propiedades Predicados 1 Estructuras Def 2.2.1 [estructura] Una estructura es una secuencia ordenada M = tal que: A es un conjunto no vacío, ( Notacion: A =
Sintaxis y Propiedades Predicados 1 Estructuras Def 2.2.1 [estructura] Una estructura es una secuencia ordenada M = tal que: A es un conjunto no vacío, ( Notacion: A =
Tema 5: Teoría de la Demostración en Predicados
 Tema 5: Teoría de la Demostración en Predicados Resumen introducción lógica de predicados Resumen introducción lógica de predicados Conceptos: ahora para lógica de predicados de 1 er orden Estructura deductiva
Tema 5: Teoría de la Demostración en Predicados Resumen introducción lógica de predicados Resumen introducción lógica de predicados Conceptos: ahora para lógica de predicados de 1 er orden Estructura deductiva
Capítulo 2 Conjuntos. 2.1 Introducción. 2.2 Determinación de conjuntos. Definición:
 Capítulo 2 Conjuntos 2.1 Introducción El concepto de conjunto, de singular importancia en la ciencia matemática y objeto de estudio de una de sus disciplinas más recientes, está presente, aunque en forma
Capítulo 2 Conjuntos 2.1 Introducción El concepto de conjunto, de singular importancia en la ciencia matemática y objeto de estudio de una de sus disciplinas más recientes, está presente, aunque en forma
Lenguajes y Gramáticas
 Lenguajes y Gramáticas Teoría de Lenguajes Fernando Naranjo Introduccion Se desarrollan lenguajes de programación basados en el principio de gramática formal. Se crean maquinas cada vez mas sofisticadas
Lenguajes y Gramáticas Teoría de Lenguajes Fernando Naranjo Introduccion Se desarrollan lenguajes de programación basados en el principio de gramática formal. Se crean maquinas cada vez mas sofisticadas
Repaso de Lógica de Primer Orden
 Repaso de Lógica de Primer Orden IIC3260 IIC3260 Repaso de Lógica de Primer Orden 1 / 29 Lógica de primer orden: Vocabulario Una fórmula en lógica de primer orden está definida sobre algunas constantes
Repaso de Lógica de Primer Orden IIC3260 IIC3260 Repaso de Lógica de Primer Orden 1 / 29 Lógica de primer orden: Vocabulario Una fórmula en lógica de primer orden está definida sobre algunas constantes
Lógica. Matemática discreta. Matemática discreta. Lógica
 Lógica Matemática discreta Lógica: rama de las matemáticas instrumento para representar el lenguaje natural proporciona un mecanismo de deducción 2 y de predicados Razonamientos Cálculo proposicional Cálculo
Lógica Matemática discreta Lógica: rama de las matemáticas instrumento para representar el lenguaje natural proporciona un mecanismo de deducción 2 y de predicados Razonamientos Cálculo proposicional Cálculo
Soluciones del examen de Lógica informática (Grupos 1 y 2) del 23 de Septiembre de José A. Alonso Jiménez
 Soluciones del examen de Lógica informática (Grupos 1 y 2) del 23 de Septiembre de 2005 José A. Alonso Jiménez Grupo de Lógica Computacional Dpto. de Ciencias de la Computación e Inteligencia Artificial
Soluciones del examen de Lógica informática (Grupos 1 y 2) del 23 de Septiembre de 2005 José A. Alonso Jiménez Grupo de Lógica Computacional Dpto. de Ciencias de la Computación e Inteligencia Artificial
IIC2213. IIC2213 Teorías 1 / 42
 Teorías IIC2213 IIC2213 Teorías 1 / 42 Qué es una teoría? Una teoría es un cúmulo de información. Debe estar libre de contradicciones. Debe ser cerrada con respecto a lo que se puede deducir de ella. Inicialmente
Teorías IIC2213 IIC2213 Teorías 1 / 42 Qué es una teoría? Una teoría es un cúmulo de información. Debe estar libre de contradicciones. Debe ser cerrada con respecto a lo que se puede deducir de ella. Inicialmente
LÓGICA PROPOSICIONAL 1. LENGUAJE DE LA LÓGICA PROPOSICIONAL 2. SÍMBOLOS LÓGICOS. 1.a. Símbolos formales. Símbolos no lógicos. Símbolos auxiliares
 LÓGICA PROPOSICIONAL 1. LENGUAJE DE LA LÓGICA PROPOSICIONAL Un lenguaje para el ámbito de la lógica se estructura en tres niveles diferentes: símbolos formales, reglas de formación de fórmulas y reglas
LÓGICA PROPOSICIONAL 1. LENGUAJE DE LA LÓGICA PROPOSICIONAL Un lenguaje para el ámbito de la lógica se estructura en tres niveles diferentes: símbolos formales, reglas de formación de fórmulas y reglas
Lógica Matemática, Sistemas Formales, Cláusulas de Horn
 Lógica Matemática, Sistemas Formales, Cláusulas de Horn Lic. José Manuel Alvarado La lógica se ocupa de las argumentaciones válidas. Las argumentaciones ocurren cuando se quiere justificar una proposición
Lógica Matemática, Sistemas Formales, Cláusulas de Horn Lic. José Manuel Alvarado La lógica se ocupa de las argumentaciones válidas. Las argumentaciones ocurren cuando se quiere justificar una proposición
Nuestro objetivo es demostrar que autómata = lógica Qué significa esto? Queremos encontrar una lógica que defina a los lenguajes regulares
 Autómata = Lógica Nuestro objetivo es demostrar que autómata = lógica Qué significa esto? Queremos encontrar una lógica que defina a los lenguajes regulares Pero antes: Vamos a hacer un breve repaso sobre
Autómata = Lógica Nuestro objetivo es demostrar que autómata = lógica Qué significa esto? Queremos encontrar una lógica que defina a los lenguajes regulares Pero antes: Vamos a hacer un breve repaso sobre
Lógica I modelo de examen (curso ) Ejemplo de respuestas
 Lógica I modelo de examen (curso 2007-08) Ejemplo de respuestas 1. Definiciones: - Grado de una fórmula es el número total de conectivas (iguales o distintas) que contiene. - Función de verdad es una función
Lógica I modelo de examen (curso 2007-08) Ejemplo de respuestas 1. Definiciones: - Grado de una fórmula es el número total de conectivas (iguales o distintas) que contiene. - Función de verdad es una función
Lenguajes de Primer Orden. Satisfacibilidad
 Capítulo 2 Lenguajes de Primer Orden. Satisfacibilidad 2.1. Lenguajes de Primer Orden Un lenguaje de primer orden, L, consta de los siguientes símbolos: símbolos de variable: x 1,...,x n,... y a veces
Capítulo 2 Lenguajes de Primer Orden. Satisfacibilidad 2.1. Lenguajes de Primer Orden Un lenguaje de primer orden, L, consta de los siguientes símbolos: símbolos de variable: x 1,...,x n,... y a veces
Matemáticas Discretas Lógica
 Coordinación de Ciencias Computacionales - INAOE Matemáticas Discretas Lógica Cursos Propedéuticos 2010 Ciencias Computacionales INAOE Lógica undamentos de Lógica Cálculo proposicional Cálculo de predicados
Coordinación de Ciencias Computacionales - INAOE Matemáticas Discretas Lógica Cursos Propedéuticos 2010 Ciencias Computacionales INAOE Lógica undamentos de Lógica Cálculo proposicional Cálculo de predicados
Lógica informática ( )
 1 / 45 Lógica informática (2012 13) Tema 7: Sintaxis y semántica de la lógica de primer orden José A. Alonso Jiménez Andrés Cordón Franco María J. Hidalgo Doblado Grupo de Lógica Computacional Departamento
1 / 45 Lógica informática (2012 13) Tema 7: Sintaxis y semántica de la lógica de primer orden José A. Alonso Jiménez Andrés Cordón Franco María J. Hidalgo Doblado Grupo de Lógica Computacional Departamento
Demostración Automática. Tema 2. Procesamiento del conocimiento con la Lógica Matemática
 Demostración Automática de Teoremas Tema 2. Procesamiento del conocimiento con la Lógica Matemática Temas Introducción Sistemas de axiomas Teoría de la demostración. Sistema de Kleene Deducción natural
Demostración Automática de Teoremas Tema 2. Procesamiento del conocimiento con la Lógica Matemática Temas Introducción Sistemas de axiomas Teoría de la demostración. Sistema de Kleene Deducción natural
El lenguaje P. Lógica y Computabilidad ( ) símbolos p. Verano convenciones. Lógica Proposicional - clase 1
 Lógica y Computabilidad Verano 2011 Departamento de Computación - FCEyN - UBA Lógica Proposicional - clase 1 Lenguaje de lógica proposicional, semántica, tautología, consecuencia semántica, conjunto satisfacible,
Lógica y Computabilidad Verano 2011 Departamento de Computación - FCEyN - UBA Lógica Proposicional - clase 1 Lenguaje de lógica proposicional, semántica, tautología, consecuencia semántica, conjunto satisfacible,
Grupos libres. Presentaciones.
 S _ Tema 12.- Grupos libres. Presentaciones. 12.1 Grupos libres. En el grupo Z de los enteros vimos una propiedad (cf. ejemplos.5), que lo caracteriza como grupo libre. Lo enunciamos al modo de una Propiedad
S _ Tema 12.- Grupos libres. Presentaciones. 12.1 Grupos libres. En el grupo Z de los enteros vimos una propiedad (cf. ejemplos.5), que lo caracteriza como grupo libre. Lo enunciamos al modo de una Propiedad
Eliminación de cuantificadores
 Eliminación de cuantificadores Teorema Si una teoría admite eliminación de cuantificadores, y existe un algoritmo que construye ϕ sc a partir de ϕ, entonces es decidible. Cómo se demuestra este teorema?
Eliminación de cuantificadores Teorema Si una teoría admite eliminación de cuantificadores, y existe un algoritmo que construye ϕ sc a partir de ϕ, entonces es decidible. Cómo se demuestra este teorema?
La Lógica Proposicional
 La Lógica Proposicional 1. Las proposiciones y sus tipos. Una proposición es una oración enunciativa, es decir, una oración que afirma o niega algo y que puede ser verdadera o falsa. Las proposiciones
La Lógica Proposicional 1. Las proposiciones y sus tipos. Una proposición es una oración enunciativa, es decir, una oración que afirma o niega algo y que puede ser verdadera o falsa. Las proposiciones
Lógica Proposicional. Del conjunto de hipótesis Γ se deduce α?
 Proposicional Metateoría: Corrección y Completitud Proposicional - 1 Del conjunto de hipótesis Γ se deduce α? Γ = α? -Tablas de verdad - Equivalencia lógicas Existen métodos que siempre responden SI o
Proposicional Metateoría: Corrección y Completitud Proposicional - 1 Del conjunto de hipótesis Γ se deduce α? Γ = α? -Tablas de verdad - Equivalencia lógicas Existen métodos que siempre responden SI o
MLM 1000 - Matemática Discreta
 MLM 1000 - Matemática Discreta L. Dissett Clase 04 Resolución. Lógica de predicados c Luis Dissett V. P.U.C. Chile, 2003 Aspectos administrativos Sobre el tema vacantes: 26 personas solicitaron ingreso
MLM 1000 - Matemática Discreta L. Dissett Clase 04 Resolución. Lógica de predicados c Luis Dissett V. P.U.C. Chile, 2003 Aspectos administrativos Sobre el tema vacantes: 26 personas solicitaron ingreso
Teoremas: Condiciones Necesarias, Condiciones Suficientes y Condiciones Necesarias y Suficientes
 FUNCIONES DE VARIABLE COMPLEJA 1 Teoremas: Condiciones Necesarias, Condiciones Suficientes y Condiciones Necesarias y Suficientes Lógica Matemática Una prioridad que tiene la enseñanza de la matemática
FUNCIONES DE VARIABLE COMPLEJA 1 Teoremas: Condiciones Necesarias, Condiciones Suficientes y Condiciones Necesarias y Suficientes Lógica Matemática Una prioridad que tiene la enseñanza de la matemática
Métodos de Inteligencia Artificial
 Métodos de Inteligencia Artificial L. Enrique Sucar (INAOE) esucar@inaoep.mx ccc.inaoep.mx/esucar Tecnologías de Información UPAEP Contenido Lógica proposicional Lógica de predicados Inferencia en lógica
Métodos de Inteligencia Artificial L. Enrique Sucar (INAOE) esucar@inaoep.mx ccc.inaoep.mx/esucar Tecnologías de Información UPAEP Contenido Lógica proposicional Lógica de predicados Inferencia en lógica
Axiomas del Cálculo de Predicados
 Axiomas del Cálculo de Predicados Si bien el cálculo proposicional nos permitió analizar cierto tipo de razonamientos y resolver acertijos lógicos, su poder expresivo no es suficiente para comprobar la
Axiomas del Cálculo de Predicados Si bien el cálculo proposicional nos permitió analizar cierto tipo de razonamientos y resolver acertijos lógicos, su poder expresivo no es suficiente para comprobar la
Sintaxis LÓGICA COMPUTACIONAL CÁLCULO DE PROPOSICIONES. Funciones boolenas. Semántica
 Proposiciones atómicas y compuestas Sintaxis LÓGICA COMPUTACIONAL CÁLCULO DE PROPOSICIONES Francisco Hernández Quiroz Departamento de Matemáticas Facultad de Ciencias, UNAM E-mail: fhq@cienciasunammx Página
Proposiciones atómicas y compuestas Sintaxis LÓGICA COMPUTACIONAL CÁLCULO DE PROPOSICIONES Francisco Hernández Quiroz Departamento de Matemáticas Facultad de Ciencias, UNAM E-mail: fhq@cienciasunammx Página
Resolución Proposicional
 Resolución Proposicional IIC2213 IIC2213 Resolución Proposicional 1 / 19 Resolución proposicional Sabemos que Σ = ϕ si y sólo si Σ { ϕ} es inconsistente. Cómo verificamos si Σ { ϕ} es inconsistente? El
Resolución Proposicional IIC2213 IIC2213 Resolución Proposicional 1 / 19 Resolución proposicional Sabemos que Σ = ϕ si y sólo si Σ { ϕ} es inconsistente. Cómo verificamos si Σ { ϕ} es inconsistente? El
Lógica Proposicional. Significado de una Fórmula Proposicional
 Proposicional Semántica Semántica Proposicional - Significado de una Fórmula Proposicional El significado de una proposición está dado por su valor de verdad (o sea, si es Verdadera o Falsa) que se obtiene
Proposicional Semántica Semántica Proposicional - Significado de una Fórmula Proposicional El significado de una proposición está dado por su valor de verdad (o sea, si es Verdadera o Falsa) que se obtiene
Contenido. BLOQUE I: PRELIMINARES Tema 2 ALGUNAS NOCIONES DE TEORÍA DE CONJUNTOS, RELACIONES Y FUNCIONES Lógica Grado en Ingeniería Informática
 Contenido BLOQUE I: PRELIMINARES Tema 2 ALGUNAS NOCIONES DE TEORÍA DE CONJUNTOS, RELACIONES Y FUNCIONES Lógica Grado en Ingeniería Informática Alessandra Gallinari URJC Nociones de teoría de conjuntos
Contenido BLOQUE I: PRELIMINARES Tema 2 ALGUNAS NOCIONES DE TEORÍA DE CONJUNTOS, RELACIONES Y FUNCIONES Lógica Grado en Ingeniería Informática Alessandra Gallinari URJC Nociones de teoría de conjuntos
Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias.
 Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias. Dr. Rafael Morones E. Dept. de Matemáticas ITAM August 5, 2002 1 Contenido 1 Preliminares. 3 1.1 Sucesiones...............................
Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias. Dr. Rafael Morones E. Dept. de Matemáticas ITAM August 5, 2002 1 Contenido 1 Preliminares. 3 1.1 Sucesiones...............................
INTRODUCCION A LA INTELIGENCIA ARTIFICIAL MÓDULO 6- CÁLCULO DE PREDICADOS Y LÓGICA DE PRIMER ORDEN
 INTRODUCCION A LA INTELIGENCIA ARTIFICIAL MÓDULO 6- CÁLCULO DE PREDICADOS Y LÓGICA DE PRIMER ORDEN Referencias: Inteligencia Artificial Russell and Norvig Cap.6. Artificial Intellingence Nils Nilsson Ch.4
INTRODUCCION A LA INTELIGENCIA ARTIFICIAL MÓDULO 6- CÁLCULO DE PREDICADOS Y LÓGICA DE PRIMER ORDEN Referencias: Inteligencia Artificial Russell and Norvig Cap.6. Artificial Intellingence Nils Nilsson Ch.4
IIC 2252 - Matemática Discreta
 IIC 2252 - Matemática Discreta L. Dissett Clase 04 Lógica de predicados. Reglas de inferencia en lógica de predicados. Lógica de predicados Definiciones básicas: Un predicado es una afirmación que depende
IIC 2252 - Matemática Discreta L. Dissett Clase 04 Lógica de predicados. Reglas de inferencia en lógica de predicados. Lógica de predicados Definiciones básicas: Un predicado es una afirmación que depende
Lógica Proposicional
 Proposicional Semántica Semántica Proposicional - Significado de una Fórmula Proposicional El significado de una proposición está dado por su valor de verdad (o sea, si es Verdadera o Falsa) que se obtiene
Proposicional Semántica Semántica Proposicional - Significado de una Fórmula Proposicional El significado de una proposición está dado por su valor de verdad (o sea, si es Verdadera o Falsa) que se obtiene
Máquinas de Turing IIC3242. IIC3242 Máquinas de Turing 1 / 42
 Máquinas de Turing IIC3242 IIC3242 Máquinas de Turing 1 / 42 Complejidad Computacional Objetivo: Medir la complejidad computacional de un problema. Vale decir: Medir la cantidad de recursos computacionales
Máquinas de Turing IIC3242 IIC3242 Máquinas de Turing 1 / 42 Complejidad Computacional Objetivo: Medir la complejidad computacional de un problema. Vale decir: Medir la cantidad de recursos computacionales
La trascendencia de e y π
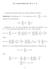 La trascendencia de e y π Comenzamos introduciendo unos convenios útiles de notación: Definición 1 Escribiremos h r = r!, de modo que si fz) = m c r z r C[z], entonces fh) representará fh) = m c r h r
La trascendencia de e y π Comenzamos introduciendo unos convenios útiles de notación: Definición 1 Escribiremos h r = r!, de modo que si fz) = m c r z r C[z], entonces fh) representará fh) = m c r h r
Lógica Proposicional (LP)
 Lógica Proposicional (LP) Proposición Enunciado del que puede afirmarse si es verdadero o falso Oración declarativa Cuáles de las siguientes son proposiciones? ) Pedro es alto. 2) Juan es estudiante. 3)
Lógica Proposicional (LP) Proposición Enunciado del que puede afirmarse si es verdadero o falso Oración declarativa Cuáles de las siguientes son proposiciones? ) Pedro es alto. 2) Juan es estudiante. 3)
Lógica de proposiciones (5)
 Lógica de proposiciones (5) Fundamentos de Informática I I..I. Sistemas (2005-06) César Llamas Bello Universidad de Valladolid 1 Lógica Índice Lógica proposicional ecuacional Lógica: semántica Semántica
Lógica de proposiciones (5) Fundamentos de Informática I I..I. Sistemas (2005-06) César Llamas Bello Universidad de Valladolid 1 Lógica Índice Lógica proposicional ecuacional Lógica: semántica Semántica
Ejercicios de Lógica Proposicional *
 Ejercicios de Lógica Proposicional * FernandoRVelazquezQ@gmail.com Notación. El lenguaje proposicional que hemos definido, aquel que utiliza los cinco conectivos,,, y, se denota como L {,,,, }. Los términos
Ejercicios de Lógica Proposicional * FernandoRVelazquezQ@gmail.com Notación. El lenguaje proposicional que hemos definido, aquel que utiliza los cinco conectivos,,, y, se denota como L {,,,, }. Los términos
Recordatorio Basico de Álgebra para Lógica
 Recordatorio Basico de Álgebra para Lógica Guido Sciavicco 1 Conjuntos Definición 1 Un conjunto es una colleccion, finita o infinita, de elementos. Ejemplo 2 La colleccion de los elementos a, b, c, denotada
Recordatorio Basico de Álgebra para Lógica Guido Sciavicco 1 Conjuntos Definición 1 Un conjunto es una colleccion, finita o infinita, de elementos. Ejemplo 2 La colleccion de los elementos a, b, c, denotada
Tema 2: Teoría de la Demostración
 Tema 2: Teoría de la Demostración Conceptos: Estructura deductiva Teoría de la Demostración Sistemas axiomáticos: Kleene Fórmulas válidas Teorema de la Deducción Introducción a la T. de la Demostración
Tema 2: Teoría de la Demostración Conceptos: Estructura deductiva Teoría de la Demostración Sistemas axiomáticos: Kleene Fórmulas válidas Teorema de la Deducción Introducción a la T. de la Demostración
Lógica I (curso ) - 23 de enero de 2006 (modelo de respuestas)
 Lógica I (curso 2005-06) - 23 de enero de 2006 (modelo de respuestas) 1. Definir un sistema formal... Para definir un sistema formal hay que especificar su lenguaje y su mecanismo deductivo. Llamemos H
Lógica I (curso 2005-06) - 23 de enero de 2006 (modelo de respuestas) 1. Definir un sistema formal... Para definir un sistema formal hay que especificar su lenguaje y su mecanismo deductivo. Llamemos H
CIENCIAS FORMALES CIENCIAS FÁCTICAS
 UNA CLASIFICACIÓN DE LAS CIENCIAS CIENCIAS FORMALES CIENCIAS FÁCTICAS CIENCIAS FORMALES MATEMÁTICA LÓGICA CIENCIAS FÁCTICAS FÍSICA BIOLOGÍA QUÍMICA CIENCIAS SOCIALES OTRAS CIENCIAS FORMALES VOCABULARIO
UNA CLASIFICACIÓN DE LAS CIENCIAS CIENCIAS FORMALES CIENCIAS FÁCTICAS CIENCIAS FORMALES MATEMÁTICA LÓGICA CIENCIAS FÁCTICAS FÍSICA BIOLOGÍA QUÍMICA CIENCIAS SOCIALES OTRAS CIENCIAS FORMALES VOCABULARIO
Tema 4: Lógica de Predicados
 Tema 4: Lógica de Predicados Motivación Todos los hombres son mortales Sócrates es un hombre Luego Sócrates es mortal Propiedades Juan enseña a Pedro Algunos hombres enseñan a Pedro Todos los hombres enseñan
Tema 4: Lógica de Predicados Motivación Todos los hombres son mortales Sócrates es un hombre Luego Sócrates es mortal Propiedades Juan enseña a Pedro Algunos hombres enseñan a Pedro Todos los hombres enseñan
Tema 8: Formas normales.
 Lógica informática Curso 2003 04 Tema 8: Formas normales. Cláusulas José A. Alonso Jiménez Andrés Cordón Franco Dpto. de Ciencias de la Computación e Inteligencia Artificial Universidad de Sevilla LI 2003
Lógica informática Curso 2003 04 Tema 8: Formas normales. Cláusulas José A. Alonso Jiménez Andrés Cordón Franco Dpto. de Ciencias de la Computación e Inteligencia Artificial Universidad de Sevilla LI 2003
El sistema deductivo de Hilbert
 El sistema deductivo de Hilbert IIC2213 IIC2213 El sistema deductivo de Hilbert 1 / 17 Completidad de resolución proposicional Qué tenemos que agregar a nuestro sistema de deducción para que sea completo?
El sistema deductivo de Hilbert IIC2213 IIC2213 El sistema deductivo de Hilbert 1 / 17 Completidad de resolución proposicional Qué tenemos que agregar a nuestro sistema de deducción para que sea completo?
Lógica proposicional. Ivan Olmos Pineda
 Lógica proposicional Ivan Olmos Pineda Introducción Originalmente, la lógica trataba con argumentos en el lenguaje natural es el siguiente argumento válido? Todos los hombres son mortales Sócrates es hombre
Lógica proposicional Ivan Olmos Pineda Introducción Originalmente, la lógica trataba con argumentos en el lenguaje natural es el siguiente argumento válido? Todos los hombres son mortales Sócrates es hombre
INTRODUCCION AL ALGEBRA.
 INTRODUCCION AL ALGEBRA. 3a- RELACIONES. Apuntes de la Cátedra. Alberto Serritella. Colaboraron: Vanesa Bergonzi Cristian Mascetti. Ricardo Galeazzi Edición Previa CECANA CECEJS CET Junín 2010. UNNOBA
INTRODUCCION AL ALGEBRA. 3a- RELACIONES. Apuntes de la Cátedra. Alberto Serritella. Colaboraron: Vanesa Bergonzi Cristian Mascetti. Ricardo Galeazzi Edición Previa CECANA CECEJS CET Junín 2010. UNNOBA
Capítulo 1: Fundamentos: Lógica y Demostraciones Clase 2: Lógica de Predicados y Métodos de Demostración
 Capítulo 1: Fundamentos: Lógica y Demostraciones Clase 2: Lógica de Predicados y Métodos de Demostración Matemática Discreta - CC3101 Profesor: Pablo Barceló P. Barceló Matemática Discreta - Cap. 1: Fundamentos:
Capítulo 1: Fundamentos: Lógica y Demostraciones Clase 2: Lógica de Predicados y Métodos de Demostración Matemática Discreta - CC3101 Profesor: Pablo Barceló P. Barceló Matemática Discreta - Cap. 1: Fundamentos:
2.1. Introducción Lógica: Campo del conocimiento relacionado con el estudio y el análisis de los métodos de razonamiento. El razonamiento lógico es es
 Tema 2. Introducción a la lógica 1. Introducción 2. Lógica de proposiciones 1. Definiciones 2. Sintaxis 3. Semántica Bibliografía Matemática discreta y lógica. Grassman y Tremblay. 1997. Prentice Hall.
Tema 2. Introducción a la lógica 1. Introducción 2. Lógica de proposiciones 1. Definiciones 2. Sintaxis 3. Semántica Bibliografía Matemática discreta y lógica. Grassman y Tremblay. 1997. Prentice Hall.
Introducción a la Lógica Modal
 Introducción a la Lógica Modal Pedro Cabalar Depto. Computación Universidade da Coruña, SPAIN 4 de mayo de 2006. Cabalar ( Depto. Computación Universidade da Coruña, SPAIN Lógica ) Modal 4 de mayo de 2006
Introducción a la Lógica Modal Pedro Cabalar Depto. Computación Universidade da Coruña, SPAIN 4 de mayo de 2006. Cabalar ( Depto. Computación Universidade da Coruña, SPAIN Lógica ) Modal 4 de mayo de 2006
Tema 4: Lógica de Predicados
 Tema 4: Lógica de Predicados Motivación Todos los hombres son mortales Sócrates es un hombre Luego Sócrates es mortal Propiedades Juan enseña a Pedro Algunos hombres enseñan a Pedro Todos los hombres enseñan
Tema 4: Lógica de Predicados Motivación Todos los hombres son mortales Sócrates es un hombre Luego Sócrates es mortal Propiedades Juan enseña a Pedro Algunos hombres enseñan a Pedro Todos los hombres enseñan
LÓGICA FORMAL TEORIAS DE PRIMER ORDEN. Axiomática
 LÓGICA FORMAL TEORIAS DE PRIMER ORDEN Francisco Bueno Pedro López Departamento de Inteligencia Artificial Facultad de Informática Universidad Politécnica de Madrid Teoría de Primer Orden 1 Formalmente,
LÓGICA FORMAL TEORIAS DE PRIMER ORDEN Francisco Bueno Pedro López Departamento de Inteligencia Artificial Facultad de Informática Universidad Politécnica de Madrid Teoría de Primer Orden 1 Formalmente,
ALGEBRA y ALGEBRA LINEAL. Primer Semestre CAPITULO I LOGICA Y CONJUNTOS.
 ALGEBRA y ALGEBRA LINEAL 520142 Primer Semestre CAPITULO I LOGICA Y CONJUNTOS. DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas Universidad de Concepción 1 La lógica es
ALGEBRA y ALGEBRA LINEAL 520142 Primer Semestre CAPITULO I LOGICA Y CONJUNTOS. DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas Universidad de Concepción 1 La lógica es
06 Análisis léxico II
 2 Contenido Alfabetos, símbolos y cadenas Operaciones con cadenas Concatenación de dos cadenas Prefijos y sufijos de una cadena Subcadena y subsecuencia Inversión de una cadena Potencia de una cadena Ejercicios
2 Contenido Alfabetos, símbolos y cadenas Operaciones con cadenas Concatenación de dos cadenas Prefijos y sufijos de una cadena Subcadena y subsecuencia Inversión de una cadena Potencia de una cadena Ejercicios
 El lenguaje formal de la Lógica Qué es un lenguaje formal? Un lenguaje formal, en tanto que lenguaje artificial, está formado por los siguientes elementos básicos: Unos signos primitivos del lenguaje,
El lenguaje formal de la Lógica Qué es un lenguaje formal? Un lenguaje formal, en tanto que lenguaje artificial, está formado por los siguientes elementos básicos: Unos signos primitivos del lenguaje,
Lógica de predicados 1. Lenguaje formal (parte 1)
 Lógica de predicados 1. Lenguaje formal (parte 1) Juan Carlos León Universidad de Murcia Esquema del tema 1.1. Nombres y predicados 1.2. Cuantificadores y variables 1.3. Silogística y lógica de predicados
Lógica de predicados 1. Lenguaje formal (parte 1) Juan Carlos León Universidad de Murcia Esquema del tema 1.1. Nombres y predicados 1.2. Cuantificadores y variables 1.3. Silogística y lógica de predicados
Semántica del Cálculo Proposicional
 Semántica del Cálculo Proposicional Revisiones: Abril y Mayo del 2005 - Abril 2006 Á 1. Valuación como función. Notación: Con Form se identifica al conjunto de todas las fómulas y Var al conjunto de todas
Semántica del Cálculo Proposicional Revisiones: Abril y Mayo del 2005 - Abril 2006 Á 1. Valuación como función. Notación: Con Form se identifica al conjunto de todas las fómulas y Var al conjunto de todas
DETERMINACIÓN DE UN CONJUNTO
 CONJUNTO UNIVERSAL U A Gráficamente, al conjunto universal se lo representa mediante un rectángulo. Cualquier otro conjunto A es representado por una región cerrada, dentro del rectángulo, A este tipo
CONJUNTO UNIVERSAL U A Gráficamente, al conjunto universal se lo representa mediante un rectángulo. Cualquier otro conjunto A es representado por una región cerrada, dentro del rectángulo, A este tipo
Proposicional. Curso Mari Carmen Suárez de Figueroa Baonza
 Semántica Proposicional Curso 2014 2015 Mari Carmen Suárez de Figueroa Baonza mcsuarez@fi.upm.es Contenidos Introducción Interpretación de FBFs proposicionales Validez Satisfacibilidad Validez y Satisfacibilidad
Semántica Proposicional Curso 2014 2015 Mari Carmen Suárez de Figueroa Baonza mcsuarez@fi.upm.es Contenidos Introducción Interpretación de FBFs proposicionales Validez Satisfacibilidad Validez y Satisfacibilidad
Capítulo 8: Sistemas completos de contectivos
 Capítulo 8: Sistemas completos de contectivos por G 3 Agosto 2014 Resumen Un conectivo de aridad n, es una función que asigna un valor de verdad a un conjuntos de n proposiciones ordenadas Mostramos que
Capítulo 8: Sistemas completos de contectivos por G 3 Agosto 2014 Resumen Un conectivo de aridad n, es una función que asigna un valor de verdad a un conjuntos de n proposiciones ordenadas Mostramos que
Sistemas deductivos. Lógica Computacional. Curso 2005/2006. Departamento de Matemática Aplicada Universidad de Málaga
 Sistemas deductivos Lógica Computacional Departamento de Matemática plicada Universidad de Málaga Curso 2005/2006 Contenido 1 Sistema axiomático de Lukasiewicz Sistema proposicional Extensión a predicados
Sistemas deductivos Lógica Computacional Departamento de Matemática plicada Universidad de Málaga Curso 2005/2006 Contenido 1 Sistema axiomático de Lukasiewicz Sistema proposicional Extensión a predicados
