Las ecuaciones de Lagrange se plantean de la forma siguiente: es la matriz jacobiana traspuesta de las restricciones del problema,
|
|
|
- Lucas Salas Cruz
- hace 5 años
- Vistas:
Transcripción
1 . RESOLUCIÓN DE PROBLEMAS ESTÁTICOS. Se aplicará la teoría desarrollada a problemas estáticos concretos, empleando para cada uno de ellos los dos sistemas clásicos de referencia, sistema biapoyado y sistema tangencial, comparando los resultados obtenidos al aplicar una u otra referencia. Dichos problemas estáticos son: viga empotrada con carga en el extremo, viga empotrada con momento en el extremo, viga biapoyada con carga aplicada en el centro y viga biapoyada con momento aplicado en el extremo. Para la resolución genérica de problemas aplicamos las ecuaciones de Lagrange, dependiendo del problema que vayamos a resolver habría que aplicar unas u otras condiciones de contorno para particularizar la resolución del sistema en concreto. Las ecuaciones de Lagrange se plantean de la forma siguiente: d dt L L + C q& q T q L = T U λ = Q e (.1) donde T y U representan respectivamente la energía cinética y potencial del sólido, T C q es la matriz jacobiana traspuesta de las restricciones del problema, λ son los multiplicadores de Lagrange y Q e son las fuerzas generalizadas. Sustituyendo la segunda ecuación representada anteriormente en la primera obenemos: d dt T T q& q U + q + C T q λ = Q e (.) d T T para problemas estáticos, = = dt q& q expresión anterior de la forma: con lo que se simplifica la C T q λ = Q e U q (.) siendo U e q = F la definición de las fuerzas elásticas, luego: 17
2 C λ = Q + F T q e e (.) A continuación se muestra una tabla donde se representan las propiedades físicas de la viga a estudiar. Longitud, L (m) 8 Densidad, ρ ( kg / m ) Área de sección transversal, A ( m ), ,99 1 Momento de inercia, I ( m ) 8,1 1 Masa, m (kg) 1, 615 Módulo de Young, (Pa) 6, E 1 Tabla.1 Estas propiedades se han usado en diversos estudios donde se ha aplicado ANCF, por ello la elección de las mismas para la resolución de los distintos problemas que se plantean a lo largo de este trabajo..1. Viga empotrada con carga vertical en el extremo. F O Fig..1 Basándonos en la resolución genérica del problema, programamos una subrutina empleando el programa Mathemática por el cual resolvemos la posición del elemento. Debido a la no linealidad del sistema de ecuaciones a resolver, utilizamos un método numérico (Newton-Raphson) para obtener la posición de la viga como consecuencia de la aplicación de la carga. Mediante la formulación en coordenadas nodales absolutas se irá discretizando progresivamente la viga, analizando y comparando los resultados obtenidos según discreticemos en uno, dos, tres ó n elementos. 18
3 19 Para el cálculo del problema para más de un elemento hay que introducir las denominadas matrices de conectividad (B) para asegurar la continuidad en toda la viga cuando discretizamos ésta en más de un elemento Discretización en un elemento.. Fig. Para un elemento, la longitud del mismo y de la viga completa coinciden. Las restricciones del problema son 1 = = = e e e. La matriz Jacobiana particularizada para la viga empotrada tiene la forma: (.5) Si el vector de multiplicadores de Lagrange es ( ) 1,, λ λ λ = λ, obtenemos: (.6) F e e e e 1 e e e e = C e = 1 λ λ λ λ C T e
4 Teniendo F el valor de 1 Newton, el vector de fuerzas generalizadas particularizado para este problema es el siguiente: Q e = 1 (.7) A continuación obtendremos las expresiones que definen las fuerzas elásticas del elemento. Para el cálculo de las mismas usamos la función de forma global definida en (.5). Seleccionando el punto O (origen de la viga) como referencia, las componentes de un desplazamiento relativo de un punto arbitrario con respecto a O puede definirse según (.9). Definimos ahora un vector unitario i cuya orientación nos servirá para evaluar los desplazamientos longitudinales y transversales que obtendremos durante el desarrollo de este trabajo. Dependiendo del sistema de referencia donde definamos dicho vector unitario podríamos obtener resultados diferentes, ya que cada problema puede ajustarse mejor a un sistema u otro. Para el problema de la viga empotrada con carga vertical en el extremo, la resistencia de materiales dictamina un desplazamiento de.1 metros en el punto de aplicación de la carga. Sistema biapoyado. Para este sistema, la dirección del vector unitario que define el eje de abscisas es la de una recta que pasa por los dos nodos del elemento, siendo el otro vector perpendicular al anterior. El primero queda definido según las expresiones (.1) y (.11). Las deformaciones longitudinales y transversales de la viga aparecen en (.1). La energía potencial U queda reflejada según (.15), con lo que las fuerzas elásticas se obtendrían derivando la expresión de la energía potencial respecto las coordenadas nodales, quedando reflejado este procedimiento en la ecuación (.16).
5 Sistema tangente. La diferencia respecto al sistema biapoyado radica en la definición del vector i. Para este sistema concreto de coordenadas las componentes del vector unitario de orientación aparecen reflejadas en las expresiones (.1) y (.1). Sistema basado en la energía. Como se explicó en el apartado de este trabajo, el vector unitario i debe de optimizar la energía de deformación del sistema. Una vez obtenido dicho vector unitario se procedería a la obtención de las fuerzas elásticas según la expresión (.16)..1.. Discretización en n elementos. e e e e 1 F Fig.. e e e e ( n + 1) ( n + 1) ( n + 1) 1 ( n + 1) Para más de un elemento hay que introducir el concepto de conectividad entre los mismos para obtener continuidad en la viga. Mediante unas matrices denominadas matrices de conectividad podemos desarrollar perfectamente el problema para más de un elemento sin más que modificar levemente las ecuaciones que definen el sistema. Las matrices de conectividad las denominaremos B n, correspondiendo el subíndice al elemento en concreto al que se refiere, así pues para el ejemplo de dos elementos n podrá tomar los valores 1 y, es decir, tendremos dos matrices; B 1 y B. Dichas matrices tienen una dimensión 8 v, siendo v el número de variables del problema, el cual depende de los elementos en los que hayamos dividido el mismo. Así pues, v = ( n + 1) siendo n el número de 1
6 elementos en los que discreticemos la viga. La construcción de las matrices de continuidad es muy simple siguiendo un patrón que desarrollaremos a continuación. Dichas matrices están compuestas por una submatriz identidad de dimensión 8 8 y el resto de la matriz se rellena de ceros, dependiendo de la posición de la submatriz identidad dentro de la matriz global, tendremos la matriz de continuidad correspondiente a un elemento concreto. Si cada columna de la matriz B n se asocia a una variable del problema, la submatriz identidad quedaría encajonada en las columnas de variables que conformarían el elemento n. B n correspondientes a las Con las matrices de continuidad redefinimos las ecuaciones de movimiento que modelan el problema. De esta forma: C T q λ = B T n Q e n j= 1 T ( B F ( e)) j j (.8) Resolución de los modelos. Sistema de referencia biapoyado Representamos en el siguiente gráfico el desplazamiento vertical en el extremo de la viga en voladizo para cada discretización. Fig..
7 A continuación se representará gráficamente las iteraciones del método de Newton-Raphson necesarias para la resolución del problema aplicado a las n discretizaciones empleadas, así como el tiempo de ejecución del algoritmo. Fig..5 Fig..6
8 Los valores exactos del desplazamiento vertical en el extremo de la viga para cada discretización en los elementos descritos en la gráfica se visualizan en la siguiente tabla de valores, junto con el número de iteraciones y tiempo de ejecución del sistema de ecuaciones resuelto mediante el programa Matlab. elementos Desplazamiento en el extremo iteraciones método de Newton- Raphson Tiempo de ejecución del algoritmo Tabla Tanto en la gráfica como en la tabla puede observarse el salto significativo ocurrido en el momento que evaluamos el desplazamiento vertical para dos elementos tras obtenerse una solución muy aproximada a la exacta al evaluar el problema con uno sólo. A partir de la evaluación para dos elementos, las distintas soluciones tienden a la solución exacta a medida que se aumenta el número de elementos que componen el problema. Llegados a la discretización en ocho elementos, la solución del desplazamiento permanece constante. Puede observarse la variación del número de iteraciones del método de Newton-Raphson que también ocurre cuando discretizamos en dos elementos, necesitándose, junto al cálculo con tres elementos, hasta dos iteraciones más que las necesarias para llegar a la solución exacta.
9 Sistema de referencia tangente Al igual que en el caso biapoyado, se representará a continuación la evolución que sufre el desplazamiento en el extremo de la viga respecto al número de elementos en el se discretiza la misma (Fig..7)..7 Fig. Junto a esta gráfica, se incluyen dos más que nos indican las iteraciones del método de Newton-Raphson respecto a los elementos en los que se divide la viga (Fig..8) y, el tiempo de ejecución del algoritmo para cada discretización (Fig..9). 5
10 Fig..8 Fig..9 En la siguiente tabla se exponen los diferentes resultados expuestos en los gráficos anteriores. 6
11 elementos Desplazamiento en el extremo iteraciones método de Newton- Raphson Tiempo de ejecución del algoritmo Tabla. Al igual que para el sistema biapoyado, para dos elementos se produce un salto significativo en la solución del problema. A diferencia que en el sistema anterior, para el sistema de referencia tangente obtenemos la solución exacta del problema para un solo elemento, sin embargo, para n = Κ se obtienen peores soluciones que en el sistema de referencia biapoyado, donde son necesarias menos iteraciones para llegar a una solución estable que en el caso del sistema de referencia tangente. La variación en el número de iteraciones que se obtienen para dos elementos es más significativa en el caso del sistema tangente que en el biapoyado. Además los tiempos de ejecución totales del algoritmo son sensiblemente mayores para el sistema tangente que para el sistema de referencia biapoyado. 7
12 Sistema de referencia de máxima energía de deformación a flexión La figura.1 representa el desplazamiento en el extremo de la viga respecto al número de elementos en los que se divide la misma aplicando para ello el nuevo sistema de referencia desarrollado. Fig..1 La siguiente figura refleja la evolución de las iteraciones del método de cálculo empleado en cada problema, es decir, para los distintos elementos en los que progresivamente se va dividiendo la viga (Fig..11) 8
13 Fig..11 La siguiente gráfica expone el tiempo necesario que necesita el algoritmo de cálculo para resolver cada problema. Fig..1 9
14 En la siguiente tabla se listan los diferentes valores empleados en la construcción de los diferentes gráficos anteriores. elementos Desplazamiento en el extremo iteraciones método de Newton- Raphson Tiempo de ejecución del algoritmo Tabla. Se puede comprobar como con el sistema de referencia de máxima energía de deformación por flexión se obtienen resultados más exactos que con los sistemas tradicionales. No sólo se alcanza con exactitud la solución analítica del problema, sino que se cumple para n = 1Κ elementos. Además se consigue un número de iteraciones y un tiempo de ejecución del algoritmo más rápido y eficiente que con los sistemas tradicionales de referencia... Viga empotrada con fuerza horizontal aplicada en el extremo. F Fig..1 Se aplicarán los sistemas de referencia definidos para el problema de la viga empotrada con una fuerza horizontal aplicada en el extremo. Las
15 condiciones de contorno de este problema son las mismas que para la viga con carga vertical en el extremo, pero cambian las fuerzas generalizadas que se aplican al problema. De esta manera, dichas fuerzas quedan descritas como: Q e = 1 (.9) En este caso F tiene un valor de 1 N para poder apreciar deformación a lo largo de la viga debido a la gran rigidez que posee la misma en sentido axial. Aplicando la resistencia de materiales a este problema aparecerá una deformación axial de.159 metros a lo largo de la viga. A continuación se resolverá el problema aplicando los distintos sistemas de referencia descritos en este proyecto. Sistema de referencia biapoyado Aplicando el sistema de referencia biapoyado obtendremos un gráfico donde se refleja el desplazamiento axial que sufre la viga respecto a las diferentes discretizaciones en las que se divide el problema. 1
16 Fig..1 La figura.15 representa las iteraciones necesarias realizadas por el método de Newton-Raphson para la obtención de la solución más aproximada a la exacta ó, ella misma, para cada número de iteraciones en los que se ha planteado el problema.
17 Fig..15 A continuación se muestra el tiempo de ejecución del algoritmo a medida que la viga se va discretizando progresivamente. Fig..16
18 La tabla que se muestra a continuación reúne los datos con los que se han construido los gráficos anteriores. elementos Desplazamiento en el extremo iteraciones método de Newton- Raphson Tiempo de ejecución del algoritmo Tabla.5 Para el problema de la viga empotrada con carga horizontal aplicada en el extremo, la elección de un sistema de referencia biapoyado tiene un buen comportamiento ya que, como se puede observar, tomando la viga completa como un único elemento, se alcanza el valor exacto que nos define la resistencia de materiales, con un número de iteraciones pequeño para cada discretización y unos tiempos de ejecución del algoritmo ínfimos. Sistema de referencia tangente Se aplicará el sistema de referencia tangente al problema de la viga empotrada, con carga axial en el extremo libre de la misma. La figura.17 representa la deformación horizontal que sufre la viga respecto a las diversas discretizaciones con los que se resuelve el problema.
19 Fig..17 La gráfica que se muestra a continuación representa las iteraciones del algoritmo de Newton-Raphson necesarias para la resolución del problema de la viga empotrada, para cada una de las diferentes iteraciones planteadas. 5
20 Fig..18 El tiempo necesario que emplea el algoritmo de Newton-Raphson en cada resolución, se encuentra reflejado en la gráfica de la figura.19. Fig..19 6
21 La tabla de valores que se presenta a continuación muestra los datos usado en las representaciones gráficas anteriores. elementos Desplazamiento en el extremo iteraciones método de Newton- Raphson Tiempo de ejecución del algoritmo Tabla.6 Como puede observarse, al comparar tanto las diversas gráficas obtenidas mediante el sistema de referencia biapoyado junto con las obtenidas aplicando el sistema de referencia tangente, así como las tablas.5 y.6, se llega a la conclusión de que es indiferente aplicar cualquiera de los dos sistemas de referencia mencionados anteriormente ya que se llegan a las misma soluciones, tanto en lo referente al desplazamiento en el extremo de la viga, como en el número de iteraciones del algoritmo de cálculo como en el tiempo de ejecución del mismo. Se aplicará a continuación el sistema de referencia de optimización de la energía para de esta manera comparar todos los datos obtenidos. Sistema de referencia de máxima energía de deformación a flexión Se representa a continuación el desplazamiento en el extremo de la viga respecto al número de elementos en los que se va discretizando la viga del problema, aplicando para ello el sistema que optimiza la energía de deformación. 7
22 Fig.. La siguiente figura representa las iteraciones necesarias que ha de realizar el algoritmo de Newton-Raphson para obtener las distintas soluciones para cada número de elementos en los que se discretiza la viga del problema. Fig..1 8
23 A continuación, se muestra el tiempo empleado por el algoritmo de cálculo para la resolución del problema, aplicado a cada una de las discretizaciones realizadas. Fig.. Los datos usados en la construcción de los gráficos anteriores se muestran en la tabla.7. Al comparar dicha tabla con las obtenidas al aplicar los sistemas de referencia biapoyado y tangente se observa como para el problema de la viga empotrada con fuerza horizontal aplicada en el extremo libre es indiferente el uso de cualquier sistema de referencia, ya que con cualquiera se obtienen excelentes resultados. Esto es debido a que en el problema descrito no existe deformación a flexión en la viga, lo que no condiciona los resultados finales dependiendo del sistema de referencia empleado. 9
24 elementos Desplazamiento en el extremo iteraciones método de Newton- Raphson Tiempo de ejecución del algoritmo Tabla.7.. Viga empotrada con momento aplicado en el extremo. M Fig.. Se analiza el problema de la viga en voladizo aplicando un momento en el extremo libre de la misma. Las condiciones iniciales del problema son las mismas para esta configuración que las descritas en el apartado.1, salvo la definición de las fuerzas generalizadas del problema, que para éste quedan descritas como: M Q e = e7 + e 8 (.1) e8 e7
25 donde M = 1 N.m. Para discretizar el problema en n elementos no hay más que aplicar la expresión (.8). Si se aplica la resistencia de materiales a este problema aparecerá una deformación de metros en el extremo de la viga. A continuación se resolverá el problema aplicando los distintos sistemas de referencia descritos en este proyecto. Sistema de referencia biapoyado La siguiente gráfica compara los resultados obtenidos usando el sistema de referencia biapoyado con la solución exacta del problema aplicando la resistencia de materiales. Fig.. Las gráficas.15 y.16 representan respectivamente las iteraciones necesarias del método de Newton-Raphson para la resolución del problema en cada una de las distintas discretizaciones en la que se ha resuelto la viga con momento aplicado en el extremo; así como el tiempo empleado por el algoritmo en la resolución de dicho problema. 1
26 Fig..5 Fig..6 La tabla.8 agrupa los datos con los que se han representado las gráficas de las figuras.,.5 y.6.
27 elementos Desplazamiento en el extremo iteraciones método de Newton- Raphson Tiempo de ejecución del algoritmo Tabla.8 Puede observarse como el sistema de referencia biapoyado proporciona una solución exacta a la analítica, lo que implica una buena elección de sistema de referencia para la resolución del problema. Sistema de referencia tangente A continuación, como se ha hecho en los apartados previos, se analizará el problema de la viga con momento aplicado en el extremo aplicando el sistema de referencia tangente. La figura.7 representa la evolución que sufre el desplazamiento en el extremo de la viga respecto al número de elementos en el se discretiza la misma.
28 Fig..7 Junto a la gráfica anterior, se incluyen dos más que nos indican las iteraciones del método de Newton-Raphson respecto a los elementos en los que se divide la viga (Fig..8) y, el tiempo de ejecución del algoritmo para cada discretización (Fig..9).
29 Fig..8 Fig..9 La tabla.9 reúne los datos con los que se han construido los gráficos anteriores. 5
30 elementos Desplazamiento en el extremo iteraciones método de Newton- Raphson Tiempo de ejecución del algoritmo Tabla.9 Si se observa la gráfica donde quedan representadas las distintas soluciones, dicha representación sigue una evolución muy parecida a la obtenida en el problema de la viga en voladizo con carga en el extremo, es decir, de partir de una solución exacta para un elemento, salta a una solución no exacta con una discretización superior y, progresivamente, a medida que aumenta el número de elementos en los que dividimos la viga la solución va tendiendo a la analítica. Destacar sin embargo que esta variación respecto la solución exacta es muy pequeña como se muestra en la tabla de valores. Tanto el número de iteraciones del algoritmo como los tiempos de ejecución del mismo son muy parecidos para ambos casos, resaltar la alteración en la columna donde aparece el número de iteraciones en los primeros cuatro valores, que engloba el momento en el que el algoritmo vuelve a tender a la solución exacta una vez alcanzada ésta tras evaluar el problema para un elemento. 6
31 Sistema de referencia de máxima energía de deformación a flexión La gráfica siguiente nos muestra el desplazamiento en el extremo de la viga respecto al número de elementos en los que discretizamos el problema usando el sistema de referencia que optimiza la energía. Fig.. La siguiente figura muestra el número de iteraciones necesarias del algoritmo de Newton-Raphson para la resolución del problema según el número de elementos en los que discretizamos el mismo. 7
32 Fig..1 La figura. representa el tiempo de ejecución del algoritmo para cada resolución del problema, es decir, para cada número de elementos en los que se discretiza el mismo. Fig.. 8
33 La tabla de valores que se adjunta a continuación engloba los diferentes datos usados en las representaciones gráficas anteriores, englobadas dentro de la resolución del problema mediante el sistema de referencia de optimización de la energía. elementos Desplazamiento en el extremo iteraciones método de Newton- Raphson Tiempo de ejecución del algoritmo Tabla.1 Como puede observarse en las gráficas y en la tabla de valores adjuntas, el método de cálculo por el cual se maximiza la energía de deformación a flexión proporciona valores exactos a los obtenidos aplicando la resistencia de materiales, en cuanto a desplazamiento en el extremo de la viga se refiere, al igual que cuando se aplica el sistema de referencia biapoyado. Sin embargo, es en el número de iteraciones del método de Newton-Raphson, donde el sistema que optimiza la energía de deformación mejora los resultados obtenidos respecto a cuando se aplica el sistema de referencia biapoyado. Los resultados obtenidos mediante el sistema de referencia tangente son peores que los que se obtienen mediante los sistemas de referencia restantes, ya que en éstos últimos las deformaciones medidas son menores que si se miden en el sistema tangente. 9
34 .. Viga biapoyada con carga aplicada en el centro. F Fig.. La resolución del problema de la viga biapoyada con carga centrada se enfoca de la misma manera que para el problema de la viga empotrada, debiéndose tener en cuenta las condiciones particulares que demanda el primero. Así pues, para el problema de la viga biapoyada con carga en el centro se tendría en el caso de que se discretice la viga usando un solo elemento: C e 1 = 1 1 (.9) obtenemos: Si el vector de multiplicadores de Lagrange es = ( λ, λ λ ) λ, 1, C T e λ1 λ λ = λ (.1) Teniendo F el valor de 1 Newton, el vector de fuerzas generalizadas particularizado para este problema es el siguiente: 5
35 Q e 1 1 = 1 1 (.11) Definidas las condiciones iniciales del problema, debe resolverse el mismo aplicando los distintos sistemas de referencia desarrollados. Para el caso de discretizar el problema en n elementos no hay más que aplicar la expresión (.8). Si se aplica la resistencia de materiales a este problema aparecerá una deformación de 9 metros en el centro de la viga. A continuación se resolverá este problema aplicando los distintos sistemas de referencia descritos. Sistema de referencia biapoyado Aplicando el sistema de referencia biapoyado, se representa el desplazamiento en el centro de la viga respecto el número de elementos en los que dividimos la misma, obteniéndose los resultados visibles en la figura.. 51
36 Fig.. Las dos gráficas que se muestran a continuación representan, respectivamente, las iteraciones del método de cálculo utilizado respecto al número de elementos en los que se divide el problema (Fig..5) y, el tiempo de ejecución del algoritmo de cálculo para cada situación en el que se discretiza la viga (Fig..6). 5
37 Fig..5 Fig..6 Los datos que se enumeran en la siguiente tabla recogen con exactitud los valores obtenidos durante la resolución de la viga biapoyada con carga aplicada en el extremo, usándose el sistema de referencia biapoyado. 5
38 elementos Desplazamiento en el centro de la viga iteraciones método de Newton- Raphson Tiempo de ejecución del algoritmo Tabla.11 Tanto en la gráfica, como en la tabla de resultados para los distintos números de elementos, se observa una evolución de la solución final partiendo de un valor inexacto para n = 1 elemento hasta igualar la solución analítica del problema a medida que aumentamos el número de elementos en los que discretizamos la viga. Cuando n = existe una pequeña variación de la solución que se corrige a medida que se va incrementando el valor de n. No obstante, si se observa con atención la tabla de valores, la variación de la solución es prácticamente despreciable aunque en la representación gráfica parece más importante debido a los márgenes tan estrechos de valores en los que se representa la solución del problema para los distintos números de elementos en los que se discretiza la viga en cuestión. Sistema de referencia tangente Empleándose el sistema de referencia tangente, se resuelve el problema de la viga biapoyada con carga aplicada en el centro de la misma. La figura.7 representa el desplazamiento que sufre la viga respecto a las diferentes discretizaciones que se aplican al problema. 5
39 Fig..7 La gráfica que se muestra a continuación, muestra las iteraciones del método de Newton-Raphson necesarias para la resolución del problema en cada una de las diferentes discretizaciones empleadas. Fig..8 55
40 En la siguiente figura, se muestra el tiempo necesario de ejecución del algoritmo de resolución para cada discretización empleada en el problema. Fig..9 La tabla.1 refleja los diferentes resultados obtenidos en la resolución de la viga biapoyada con carga aplicada en el centro de la misma. elementos Desplazamiento en el centro de la viga Tabla.1 iteraciones método de Newton- Raphson 5 5 Tiempo de ejecución del algoritmo
41 Con el sistema de referencia tangente, al igual que con el sistema biapoyado, existe una evolución de la solución aproximándose ésta a la solución analítica a medida que incrementamos el número de elementos en los que discretizamos la viga del problema. Sin embargo, puede observarse como es necesaria una mayor discretización de la viga para alcanzar la solución exacta respecto a la solución que aparece cuando se aplica el sistema de referencia biapoyado. Además, tanto el número de iteraciones realizadas por el algoritmo de cálculo como los tiempos de ejecución del mismo son mayores aplicando el sistema de referencia tangente que cuando se aplica el sistema biapoyado. Sistema de referencia de máxima energía de deformación a flexión Se aplicará finalmente el método de optimización de la energía, representándose a continuación los diferentes resultados obtenidos. En primer lugar, se muestra la evolución del desplazamiento en el centro de la viga respecto al número de elementos en los que se discretiza el problema. Fig.. 57
42 En segundo lugar, la figura.1 representa las iteraciones del método de Newton-Raphson necesarias para obtener la solución en cada una de las diferentes discretizaciones en las que se divide el problema. Fig..1 En último lugar, se representa el tiempo necesario de ejecución del algoritmo para la resolución del problema de la viga biapoyada para cada una de las discretizaciones que conforman el mismo. 58
43 Fig.. La tabla que se adjunta incorpora los datos empleados en las diferentes gráficas expuestas con anterioridad. En dicha tabla puede apreciarse con exactitud los valores obtenidos para la resolución del problema de la viga biapoyada con carga aplicada en el centro de la barra, usándose el sistema de referencia de optimización de la energía. 59
44 elementos Desplazamiento en el centro de la viga iteraciones método de Newton- Raphson Tiempo de ejecución del algoritmo Tabla.1 Los resultados obtenidos para el sistema de referencia que optimiza la energía son prácticamente exactos a los que se obtienen al aplicar el sistema biapoyado. En este caso, el vector unitario i que maximiza la energía de deformación a flexión coincide con el obtenido en el sistema de referencia biapoyado. No obstante, si se compara el número de iteraciones del algoritmo y los tiempos de ejecución del mismo, se observa que son menores para la configuración que optimiza la energía de deformación respecto a si se toma el sistema de referencia biapoyado. Para el problema de la viga biapoyada con carga aplicada en el centro se obtiene un resultado parecido al desarrollado en el apartado.1 en lo referente a la eficiencia del método utilizado. Con el sistema de referencia de máxima energía de deformación a flexión se obtienen mejores resultados respecto a los sistemas de referencia tradicionales. 6
45 .5. Viga biapoyada con momento aplicado en el extremo. M Fig.. Para este problema concreto, las condiciones iniciales y de contorno coinciden con los desarrollados para la viga biapoyada con carga centrada. Es el vector que define las fuerzas generalizadas del problema lo que cambia respecto al problema descrito en el apartado.. En este caso, el vector Q e se define igual que el que aparece en la expresión (.1), donde también se considera que M = 1 N.m. Evaluando la deformación en el centro de la viga, la resistencia de materiales dictamina un desplazamiento de.76 metros. A continuación se resolverá el problema aplicando los distintos sistemas de referencia descritos en este proyecto. Sistema de referencia biapoyado Se representará a continuación la evolución que sufre el desplazamiento en el centro de la viga respecto al número de elementos en el se discretiza la misma (Fig..). 61
46 Fig.. Junto a la gráfica anterior, se incluyen dos gráficas más que representan las iteraciones del método de Newton-Raphson respecto a los elementos en los que se divide la viga (Fig..5) y, el tiempo de ejecución del algoritmo para cada discretización (Fig..6). Fig..5 6
47 Fig..6 La tabla.1 agrupa los datos obtenidos en la resolución de la viga biapoyada con momento aplicado en el extremo cuando se usa el sistema de referencia biapoyado. elementos Desplazamiento en el centro de la viga iteraciones método de Newton- Raphson Tiempo de ejecución del algoritmo Tabla.1 6
48 Puede observarse como el sistema de referencia biapoyado proporciona una solución exacta a la analítica, lo que implica una buena elección de sistema de referencia para la resolución del problema. A medida que se desarrollen las demás soluciones se podrán comparar dichos resultados con la proporcionada aplicando el sistema biapoyado de referencia en cuestión de iteraciones del algoritmo y tiempos de ejecución del mismo, ya que como puede observarse, se obtienen unos resultados en términos de desplazamiento exactos a la solución analítica. Sistema de referencia tangente A continuación se representa, para el sistema de referencia tangente, el desplazamiento en el centro de la viga respecto al número de elementos en los que se discretiza el problema. Fig..7 Las dos gráficas que se muestran a continuación representan, respectivamente, las iteraciones del método de cálculo utilizado respecto al número de elementos en los que se divide el problema (Fig..8) y, el tiempo de ejecución del algoritmo de cálculo para cada situación en el que se discretiza la viga (Fig..9). 6
49 Fig..8 Fig..9 65
50 Para finalizar, se representa la tabla con los datos exactos expuestos en las gráficas anteriores, dentro de la resolución del problema aplicando el sistema de referencia tangente. elementos Desplazamiento en el centro de la viga iteraciones método de Newton- Raphson Tiempo de ejecución del algoritmo Tabla.15 La aplicación del sistema de referencia tangente aporta unas soluciones muy parecidas a las logradas con la referencia biapoyada, es en el número de iteraciones del algoritmo y en los tiempos de ejecución del mismo donde se puede observar diferencia pero casi despreciable como se ha ido obteniendo durante la resolución de los demás problemas planteados. Sistema de referencia de máxima energía de deformación a flexión La gráfica siguiente nos muestra el desplazamiento en el centro de la viga respecto al número de elementos en los que discretizamos el problema usando el sistema de referencia que optimiza la energía. 66
51 Fig..5 La siguiente figura muestra el número de iteraciones necesarias del algoritmo de Newton-Raphson para la resolución del problema según el número de elementos en los que discretizamos el mismo. Fig
52 La figura.5 representa el tiempo de ejecución del algoritmo para cada resolución del problema, es decir, para cada número de elementos en los que se discretiza el mismo. Fig..5 La tabla de valores que se adjunta a continuación incluye los diferentes datos usados en las representaciones gráficas anteriores, englobadas dentro de la resolución del problema mediante el sistema de referencia de optimización de la energía. 68
53 elementos Desplazamiento en el centro de la viga iteraciones método de Newton- Raphson Tiempo de ejecución del algoritmo Tabla.16 Puede observarse que ante igualdad en el desplazamiento en el centro de la viga, es en el número de iteraciones y en el tiempo de ejecución de las mismas donde este sistema de referencia supera a los restantes. 69
CONCLUSIONES 5. CONCLUSIONES.
 5. CONCLUSIONES. Entre los sistemas de referencia empleados para el cálculo de las fuerzas elásticas, para un elemento finito de dos nodos que utiliza la teoría de Euler- Bernoulli [11], basándose en las
5. CONCLUSIONES. Entre los sistemas de referencia empleados para el cálculo de las fuerzas elásticas, para un elemento finito de dos nodos que utiliza la teoría de Euler- Bernoulli [11], basándose en las
Resistencia de Materiales. Estructuras. Tema 11. Inestabilidad en barras. Pandeo. Barra Empotrada-Empotrada.
 Resistencia de Materiales. Estructuras Tema 11. Inestabilidad en barras. Pandeo Módulo 6 Barra Empotrada-Empotrada. En los módulos anteriores se ha estudiado el caso del pandeo en la barra articulada-articulada,
Resistencia de Materiales. Estructuras Tema 11. Inestabilidad en barras. Pandeo Módulo 6 Barra Empotrada-Empotrada. En los módulos anteriores se ha estudiado el caso del pandeo en la barra articulada-articulada,
2. Modelo Numérico. 2.1 Geometría del modelo
 2. Modelo Numérico 2.1 Geometría del modelo El presente estudio se lleva a cabo mediante la utilización de un código basado en el Método de los Elementos de Contorno (París y Cañas [8]), lo cual hace posible
2. Modelo Numérico 2.1 Geometría del modelo El presente estudio se lleva a cabo mediante la utilización de un código basado en el Método de los Elementos de Contorno (París y Cañas [8]), lo cual hace posible
CAPÍTULO 5. RESUMEN Y CONCLUSIONES
 CAPÍTULO 5 RESUMEN Y CONCLUSIONES En resumen, el proyecto presentado ha consistido en el estudio problema de contacto mediante el software comercial ANSYS. Así mismo, también se ha estudiado la influencia
CAPÍTULO 5 RESUMEN Y CONCLUSIONES En resumen, el proyecto presentado ha consistido en el estudio problema de contacto mediante el software comercial ANSYS. Así mismo, también se ha estudiado la influencia
CFGS CONSTRUCCION METALICA MODULO 246 DISEÑO DE CONSTRUCCIONES METALICAS
 CFGS CONSTRUCCION METALICA MODULO 246 DISEÑO DE CONSTRUCCIONES METALICAS U.T. 5.- FLEXION. 4.1.- Viga. Una viga es una barra recta sometida a fuerzas que actúan perpendicularmente a su eje longitudinal.
CFGS CONSTRUCCION METALICA MODULO 246 DISEÑO DE CONSTRUCCIONES METALICAS U.T. 5.- FLEXION. 4.1.- Viga. Una viga es una barra recta sometida a fuerzas que actúan perpendicularmente a su eje longitudinal.
2 =0 (3.146) Expresando, las componentes del tensor de esfuerzos en coordenadas cartesianas como: 2 ; = 2 2 ; =
 3.7. Función de Airy Cuando las fuerzas de cuerpo b son constantes en un sólido con estado de deformación o esfuerzo plano, el problema elástico se simplifica considerablemente mediante el uso de una función
3.7. Función de Airy Cuando las fuerzas de cuerpo b son constantes en un sólido con estado de deformación o esfuerzo plano, el problema elástico se simplifica considerablemente mediante el uso de una función
EJERCICIOS PROPUESTOS
 EJERCICIOS PROPUESTOS Norberto Marcelo Nigro a,1 Gerardo Franck a,2 a Facultad de Ingenieria y Ciencias Hidricas de la Universidad Nacional del Litoral (FICH-UNL), Ciudad Universitaria, 3000 Santa Fe,
EJERCICIOS PROPUESTOS Norberto Marcelo Nigro a,1 Gerardo Franck a,2 a Facultad de Ingenieria y Ciencias Hidricas de la Universidad Nacional del Litoral (FICH-UNL), Ciudad Universitaria, 3000 Santa Fe,
Resistencia de materiales
 Resistencia de materiales April 3, 009 En ingeniería se denomina viga a un elemento constructivo lineal que trabaja principalmente a exión. La teoría de vigas es una parte de la resistencia de materiales
Resistencia de materiales April 3, 009 En ingeniería se denomina viga a un elemento constructivo lineal que trabaja principalmente a exión. La teoría de vigas es una parte de la resistencia de materiales
Introducción a la Elasticidad y Resistencia de Materiales
 Lección 1 Introducción a la Elasticidad y Resistencia de Materiales Contenidos 1.1. Mecánica del Sólido Rígido y Mecánica del Sólido Deformable............................. 2 1.1.1. Sólido Rígido..........................
Lección 1 Introducción a la Elasticidad y Resistencia de Materiales Contenidos 1.1. Mecánica del Sólido Rígido y Mecánica del Sólido Deformable............................. 2 1.1.1. Sólido Rígido..........................
Deformaciones. Contenidos
 Lección 2 Deformaciones Contenidos 2.1. Concepto de deformación................... 14 2.2. Deformación en el entorno de un punto.......... 15 2.2.1. Vector deformación. Componentes intrínsecas........
Lección 2 Deformaciones Contenidos 2.1. Concepto de deformación................... 14 2.2. Deformación en el entorno de un punto.......... 15 2.2.1. Vector deformación. Componentes intrínsecas........
Capítulo 3 El Método de los Elementos de Contorno y la Formulación Hipersingular.
 Capítulo 3 El Método de los Elementos de Contorno y la Formulación Hipersingular. 3.1. Introducción El Método de los Elementos de Contorno (MEC) se ha implantado firmemente en numerosos campos de la ingeniería
Capítulo 3 El Método de los Elementos de Contorno y la Formulación Hipersingular. 3.1. Introducción El Método de los Elementos de Contorno (MEC) se ha implantado firmemente en numerosos campos de la ingeniería
Ramírez López-Para, P; Loizaga Garmendia, M; López Soto, J
 Ejercicio 2, pag.1 lanteamiento El disco de la figura está soldado a la barra acodada y ésta lo está a su vez a la barra B. El conjunto gira con una velocidad angular ω rad/s y una aceleración angular
Ejercicio 2, pag.1 lanteamiento El disco de la figura está soldado a la barra acodada y ésta lo está a su vez a la barra B. El conjunto gira con una velocidad angular ω rad/s y una aceleración angular
Cálculo de estructuras con SAP2000 ANEXO. MEF vs Matricial.
 Cálculo de estructuras con SAP2000 ANEXO. MEF vs Matricial. Cálculo de Estructuras con SAP2000 ÍNDICE ÍNDICE... 3 1. Fundamento matemático del MEF... 4 1.1. Principio de los trabajos virtulaes.... 7 1.2.
Cálculo de estructuras con SAP2000 ANEXO. MEF vs Matricial. Cálculo de Estructuras con SAP2000 ÍNDICE ÍNDICE... 3 1. Fundamento matemático del MEF... 4 1.1. Principio de los trabajos virtulaes.... 7 1.2.
6 PROTOCOLO DE PRUEBAS
 6 PROTOCOLO DE PRUEBAS 6.1 Introducción Se exponen a continuación los resultados de la puesta a prueba del comportamiento del algoritmo. Para facilitar el proceso de análisis del comportamiento del algoritmo,
6 PROTOCOLO DE PRUEBAS 6.1 Introducción Se exponen a continuación los resultados de la puesta a prueba del comportamiento del algoritmo. Para facilitar el proceso de análisis del comportamiento del algoritmo,
Cinemática del sólido rígido
 Cinemática del sólido rígido Teoría básica para el curso Cinemática del sólido rígido, ejercicios comentados α δ ω B B A A P r B AB A ω α O Ramírez López-Para, Pilar Loizaga Garmendia, Maider López Soto,
Cinemática del sólido rígido Teoría básica para el curso Cinemática del sólido rígido, ejercicios comentados α δ ω B B A A P r B AB A ω α O Ramírez López-Para, Pilar Loizaga Garmendia, Maider López Soto,
CAPÍTULO 1. Ecuaciones de Movimiento del Sistema
 CAPÍTULO 1 Ecuaciones de Movimiento del Sistema El sistema que se construyó y cuyo análisis es del presente capítulo tiene las siguientes constricciones: 1. El carro solo se puede desplazar en la dirección
CAPÍTULO 1 Ecuaciones de Movimiento del Sistema El sistema que se construyó y cuyo análisis es del presente capítulo tiene las siguientes constricciones: 1. El carro solo se puede desplazar en la dirección
02 Elementos finitos para tensión/ compresión axial. Diego Andrés Alvarez Marín Profesor Asistente Universidad Nacional de Colombia Sede Manizales
 02 Elementos finitos para tensión/ compresión axial Diego Andrés Alvarez Marín Profesor Asistente Universidad Nacional de Colombia Sede Manizales 1 El método de los elementos finitos El método de los elementos
02 Elementos finitos para tensión/ compresión axial Diego Andrés Alvarez Marín Profesor Asistente Universidad Nacional de Colombia Sede Manizales 1 El método de los elementos finitos El método de los elementos
Capítulo 1. Introducción Introducción
 Capítulo 1 Introducción 1.1. Introducción La dinámica es la parte de la mecánica que estudia el movimiento de los cuerpos teniendo en cuenta las causas que lo provocan. Esta rama del conocimiento científico
Capítulo 1 Introducción 1.1. Introducción La dinámica es la parte de la mecánica que estudia el movimiento de los cuerpos teniendo en cuenta las causas que lo provocan. Esta rama del conocimiento científico
Deflexión DE vigas. Universidad de Oriente Núcleo de Bolívar Unidad de Estudios Básicos Área de Matemáticas Asignatura: Matemáticas IV
 Universidad de Oriente Núcleo de Bolívar Unidad de Estudios Básicos Área de Matemáticas Asignatura: Matemáticas IV Deflexión DE vigas Profesor: Cristian Castillo Realizado por: Barrios, Yasnahir Campos,
Universidad de Oriente Núcleo de Bolívar Unidad de Estudios Básicos Área de Matemáticas Asignatura: Matemáticas IV Deflexión DE vigas Profesor: Cristian Castillo Realizado por: Barrios, Yasnahir Campos,
2. ANÁLISIS DEL TECHO DE UN AUDITORIO MEDIANTE FEM
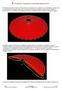 . ANÁLISIS DEL TECHO DE UN AUDITORIO MEDIANTE FEM El Objetivo es analizar el techo en forma de cono con abertura de un auditorio circular de diámetro igual a m, la altura total del cono sería.m, pero a
. ANÁLISIS DEL TECHO DE UN AUDITORIO MEDIANTE FEM El Objetivo es analizar el techo en forma de cono con abertura de un auditorio circular de diámetro igual a m, la altura total del cono sería.m, pero a
II.- CONCEPTOS FUNDAMENTALES DEL ANÁLISIS ESTRUCTURAL
 II.- CONCEPTOS FUNDAMENTALES DEL ANÁLISIS ESTRUCTURAL 2.1.- Introducción Los métodos fundamentales disponibles para el analista estructural son el método de la flexibilidad (o de las fuerzas), y el método
II.- CONCEPTOS FUNDAMENTALES DEL ANÁLISIS ESTRUCTURAL 2.1.- Introducción Los métodos fundamentales disponibles para el analista estructural son el método de la flexibilidad (o de las fuerzas), y el método
1. ANALISIS DE UN RESERVORIO CIRCULAR MEDIANTE FEM
 . ANALISIS DE UN RESERVORIO CIRCULAR MEDIANTE FEM Analizar la pared de un reservorio circular de radio interior m, espesor de la pared.m, altura de la pared desde la losa de fondo m. Considerar solamente
. ANALISIS DE UN RESERVORIO CIRCULAR MEDIANTE FEM Analizar la pared de un reservorio circular de radio interior m, espesor de la pared.m, altura de la pared desde la losa de fondo m. Considerar solamente
ELASTICIDAD POR FLEXIÓN: UNA EXPERIENCIA DE LABORATORIO ADAPTABLE A LOS DISTINTOS NIVELES EDUCATIVOS
 III Taller Iberoamericano de Enseñanza sobre Educación en Ciencia e Ingeniería de Materiales (TIECIM 0) EASTICIDAD POR FEXIÓN: UNA EXPERIENCIA DE ABORATORIO ADAPTABE A OS DISTINTOS NIVEES EDUCATIVOS T.
III Taller Iberoamericano de Enseñanza sobre Educación en Ciencia e Ingeniería de Materiales (TIECIM 0) EASTICIDAD POR FEXIÓN: UNA EXPERIENCIA DE ABORATORIO ADAPTABE A OS DISTINTOS NIVEES EDUCATIVOS T.
Anexo II: Ejemplo de Simulación de un Caso Bidimensional
 ANEXO II: Ejemplo de Simulación de un Caso Bidimensional (Estudio de la Corriente de Salida del Rótor y Comparación de los Resultados Obtenidos Simulando el Difusor de Forma Aislada) Para estudiar la interacción
ANEXO II: Ejemplo de Simulación de un Caso Bidimensional (Estudio de la Corriente de Salida del Rótor y Comparación de los Resultados Obtenidos Simulando el Difusor de Forma Aislada) Para estudiar la interacción
MECÁNICA TÉCNICA TEMA XVIII
 MECÁNICA TÉCNICA TEMA XVIII 1.- Vigas de eje recto En el tema XI se definieron y estudiaron las vigas de alma llena, también se vio que estas vigas las podemos representar por medio de sus ejes que son
MECÁNICA TÉCNICA TEMA XVIII 1.- Vigas de eje recto En el tema XI se definieron y estudiaron las vigas de alma llena, también se vio que estas vigas las podemos representar por medio de sus ejes que son
Prob 2. A Una pieza plana de acero se encuentra sometida al estado tensional homogéneo dado por:
 PRÁCTICAS DE ELASTICIDAD AÑO ACADÉMICO 2012-201 Prob 1. El estado tensional de un punto de un sólido elástico se indica en la Figura donde las tensiones se epresan en MPa. Se pide: a. Calcular el vector
PRÁCTICAS DE ELASTICIDAD AÑO ACADÉMICO 2012-201 Prob 1. El estado tensional de un punto de un sólido elástico se indica en la Figura donde las tensiones se epresan en MPa. Se pide: a. Calcular el vector
Derivación de funciones de varias variables.
 Derivación de funciones de varias variables. En este apartado se presentan los conceptos básicos que aparecen en la derivación de funciones de varias variables. La idea es establecer un método para estudiar
Derivación de funciones de varias variables. En este apartado se presentan los conceptos básicos que aparecen en la derivación de funciones de varias variables. La idea es establecer un método para estudiar
Cálculo de un laminado arbitrario
 Máster Universitario en Ingeniería de las Estructuras, Cimentaciones y Materiales UNIVERSIDAD POLITÉCNICA DE MADRID MATERIALES COMPUESTOS ESTRUCTURALES Cálculo de un laminado arbitrario CURSO 2009-2010
Máster Universitario en Ingeniería de las Estructuras, Cimentaciones y Materiales UNIVERSIDAD POLITÉCNICA DE MADRID MATERIALES COMPUESTOS ESTRUCTURALES Cálculo de un laminado arbitrario CURSO 2009-2010
El Principio de los Desplazamientos Virtuales (PDV)
 El Principio de los Desplazamientos Virtuales (PDV) Apellidos, nombre Basset Salom, uisa (lbasset@mes.upv.es) Departamento Centro Mecánica de Medios Continuos y Teoría de Estructuras Escuela Técnica Superior
El Principio de los Desplazamientos Virtuales (PDV) Apellidos, nombre Basset Salom, uisa (lbasset@mes.upv.es) Departamento Centro Mecánica de Medios Continuos y Teoría de Estructuras Escuela Técnica Superior
Unidad 5: Geometría analítica del plano.
 Geometría analítica del plano 1 Unidad 5: Geometría analítica del plano. 1.- Vectores. Operaciones con vectores. Un vector fijo es un segmento entre dos puntos, A y B del plano, al que se le da una orientación
Geometría analítica del plano 1 Unidad 5: Geometría analítica del plano. 1.- Vectores. Operaciones con vectores. Un vector fijo es un segmento entre dos puntos, A y B del plano, al que se le da una orientación
El esfuerzo axil. Contenidos
 Lección 8 El esfuerzo axil Contenidos 8.1. Distribución de tensiones normales estáticamente equivalentes a esfuerzos axiles.................. 104 8.2. Deformaciones elásticas y desplazamientos debidos
Lección 8 El esfuerzo axil Contenidos 8.1. Distribución de tensiones normales estáticamente equivalentes a esfuerzos axiles.................. 104 8.2. Deformaciones elásticas y desplazamientos debidos
1) Determinar qué elección de h asegurará, a priori, que la solución numérica del P.C.: con el método de diferencias centrales, existe y es única.
 I. Resolución numérica de Problemas de Contorno en E.D.O.: Métodos en diferencias finitas 1) Determinar qué elección de h asegurará, a priori, que la solución numérica del P.C.: y (x) + 4 sen x y (x) 4
I. Resolución numérica de Problemas de Contorno en E.D.O.: Métodos en diferencias finitas 1) Determinar qué elección de h asegurará, a priori, que la solución numérica del P.C.: y (x) + 4 sen x y (x) 4
Examen de Análisis Matemático. a) (1 punto) Calcula las derivadas de las siguientes funciones: (1 + 3x) 1 2
 Curso º Bachillerato 16/05/017 Ejercicio 1 a) (1 punto) Calcula las derivadas de las siguientes funciones: f() = 1+3 ; g() = ln(1 5) + e7 b) (1 punto) Estudia la derivabilidad de la función dada por: a)
Curso º Bachillerato 16/05/017 Ejercicio 1 a) (1 punto) Calcula las derivadas de las siguientes funciones: f() = 1+3 ; g() = ln(1 5) + e7 b) (1 punto) Estudia la derivabilidad de la función dada por: a)
Acústica y vibraciones mecánicas
 Sistemas de un grado de libertar libre Ecuación de movimiento de un sistema masa-resorte Considerando el sistema de la figura y por la aplicación dela segunda ley de Newton o principio de conservación
Sistemas de un grado de libertar libre Ecuación de movimiento de un sistema masa-resorte Considerando el sistema de la figura y por la aplicación dela segunda ley de Newton o principio de conservación
Capítulo VI. Diferenciabilidad de funciones de varias variables
 Capítulo VI Diferenciabilidad de funciones de varias variables La definición de diferenciabilidad para funciones el cociente no tiene sentido, puesto que no está definido, porque el cociente entre el vector
Capítulo VI Diferenciabilidad de funciones de varias variables La definición de diferenciabilidad para funciones el cociente no tiene sentido, puesto que no está definido, porque el cociente entre el vector
IX. Vibración de sistemas continuos
 Objetivos:. Determinar expresiones para la energía cinética y potencial de sistemas continuos: barras y vigas.. Emplear métodos variacionales para deducir la ecuación de unidimensional: barras (axial)
Objetivos:. Determinar expresiones para la energía cinética y potencial de sistemas continuos: barras y vigas.. Emplear métodos variacionales para deducir la ecuación de unidimensional: barras (axial)
Capítulo 5. Resultados
 45 Capítulo 5 Resultados En este capítulo se muestran los resultados obtenido en el estudio de dos configuraciones. El primer apartado de este capítulo Análisis del factor de forma entre dos rectángulos
45 Capítulo 5 Resultados En este capítulo se muestran los resultados obtenido en el estudio de dos configuraciones. El primer apartado de este capítulo Análisis del factor de forma entre dos rectángulos
Materiales II 07_09_01.mcd
 Materiales II 07_09_0.mcd Los elastómeros son materiales poliméricos orgánicos que presentan elasticidad no lineal. Es posible demostrar que su módulo elástico o de Young es, en primera aproximación, independientemente
Materiales II 07_09_0.mcd Los elastómeros son materiales poliméricos orgánicos que presentan elasticidad no lineal. Es posible demostrar que su módulo elástico o de Young es, en primera aproximación, independientemente
El modelo de elementos finitos consta de 32 elementos LINE2 de 1D con 2 nodos por elemento:
 ACTUALIZACIÓN DE UN MODELO NUMÉRICO DE LA PASARELA DE LA CARTUJA A PARTIR DE DATOS EXPERIMENTALES 4. MODELO DE ELEMENTOS FINITOS 4.1. MODELO 1-D 4.1.1. INTRODUCCIÓN El modelo de elementos finitos consta
ACTUALIZACIÓN DE UN MODELO NUMÉRICO DE LA PASARELA DE LA CARTUJA A PARTIR DE DATOS EXPERIMENTALES 4. MODELO DE ELEMENTOS FINITOS 4.1. MODELO 1-D 4.1.1. INTRODUCCIÓN El modelo de elementos finitos consta
Análisis Estructural El Método de las Rigideces DC
 Análisis Estructural Matricial Aunque tanto el método de flexibilidades (fuerzas) como el de rigideces (desplazamientos) se pueden expresar de manera matricial, el método de las rigideces es mucho más
Análisis Estructural Matricial Aunque tanto el método de flexibilidades (fuerzas) como el de rigideces (desplazamientos) se pueden expresar de manera matricial, el método de las rigideces es mucho más
TEMA 4: PROBLEMAS RESUELTOS DE DEFORMACIÓN ANGULAR
 Problemas eformación ngular T : PROLS RSULTOS ORÓN NGULR.. plicando el método de la deformación angular obtener el diagrama de momentos flectores y dibujar aproximadamente la deformada de la estructura
Problemas eformación ngular T : PROLS RSULTOS ORÓN NGULR.. plicando el método de la deformación angular obtener el diagrama de momentos flectores y dibujar aproximadamente la deformada de la estructura
1. EJEMPLO Enunciado. 1.2 Convenciones generales
 . EJEMPLO. Referencia: "MATLAB Guide to Finite Elements, An Interactive Approach" Autor: P.I kattan Página del libro en que se encuentra el ejemplo:. Enunciado Considere la placa del gráfico somedo a las
. EJEMPLO. Referencia: "MATLAB Guide to Finite Elements, An Interactive Approach" Autor: P.I kattan Página del libro en que se encuentra el ejemplo:. Enunciado Considere la placa del gráfico somedo a las
MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II. CURSO 2008/2009. PRUEBA ESCRITA DEL BLOQUE DE ÁLGEBRA. 9 de diciembre de 2008.
 IES Salduba MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II CURSO 008/009 PRUEBA ESCRITA DEL BLOQUE DE ÁLGEBRA 9 de diciembre de 008 Bloque I Unidades y Sistemas de ecuaciones lineales Matrices Ejercicio
IES Salduba MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II CURSO 008/009 PRUEBA ESCRITA DEL BLOQUE DE ÁLGEBRA 9 de diciembre de 008 Bloque I Unidades y Sistemas de ecuaciones lineales Matrices Ejercicio
Examen de TEORIA DE MAQUINAS Diciembre 12 Nombre...
 Examen de TEORIA DE MAQUINAS Diciembre 12 Nombre... El mecanismo de la figura es un cuadrilátero articulado manivela-balancín. La distancia entre los puntos fijos A y D es 4L/ 3. En la mitad del balancín
Examen de TEORIA DE MAQUINAS Diciembre 12 Nombre... El mecanismo de la figura es un cuadrilátero articulado manivela-balancín. La distancia entre los puntos fijos A y D es 4L/ 3. En la mitad del balancín
UNIVERSIDAD NACIONAL DE EDUCACIÓN A DISTANCIA
 UNIVERSIDAD NACIONAL DE EDUCACIÓN A DISTANCIA NOMBRE.............................................. APELLIDOS........................................... CALLE................................................
UNIVERSIDAD NACIONAL DE EDUCACIÓN A DISTANCIA NOMBRE.............................................. APELLIDOS........................................... CALLE................................................
MATEMÁTICAS: PAU 2015 JUNIO CASTILLA Y LEÓN
 MATEMÁTICAS: PAU 05 JUNIO CASTILLA Y LEÓN Opción A Ejercicio A m + 0 0 Dada la matriz A = ( 3 m + ), se pide: 0 m a) Hallar los valores de m para que la matriz A 0 tenga inversa. ( 5 puntos) La condición
MATEMÁTICAS: PAU 05 JUNIO CASTILLA Y LEÓN Opción A Ejercicio A m + 0 0 Dada la matriz A = ( 3 m + ), se pide: 0 m a) Hallar los valores de m para que la matriz A 0 tenga inversa. ( 5 puntos) La condición
ANALISIS DE IMPACTO LATERAL DE CHASIS JAULA DE VEHICULO UNIPERSONAL DE TRES RUEDAS
 Facultad de Ingeniería - UNLP ANALISIS DE IMPACTO LATERAL DE CHASIS JAULA DE VEHICULO UNIPERSONAL DE TRES RUEDAS Menghini, Matías UID GEMA, Departamento de Aeronáutica, Facultad de Ingeniería de La Plata
Facultad de Ingeniería - UNLP ANALISIS DE IMPACTO LATERAL DE CHASIS JAULA DE VEHICULO UNIPERSONAL DE TRES RUEDAS Menghini, Matías UID GEMA, Departamento de Aeronáutica, Facultad de Ingeniería de La Plata
Deflexiones de vigas y marcos
 Deflexiones de vigas y marcos Cuando se carga una estructura, sus elementos esforzados se deforman. Cuando esto ocurre, la estructura cambia de forma y sus puntos se desplazan. Aunque estas deflexiones
Deflexiones de vigas y marcos Cuando se carga una estructura, sus elementos esforzados se deforman. Cuando esto ocurre, la estructura cambia de forma y sus puntos se desplazan. Aunque estas deflexiones
Introducción al cálculo numérico. Método de Euler
 Capíítullo T1 Introducción al cálculo numérico. Método de Euler En la figura 1.1 se muestra una masa sometida a la aceleración de la gravedad soportada por un muelle un amortiguador viscoso colocados en
Capíítullo T1 Introducción al cálculo numérico. Método de Euler En la figura 1.1 se muestra una masa sometida a la aceleración de la gravedad soportada por un muelle un amortiguador viscoso colocados en
Examen de TEORIA DE MAQUINAS Diciembre 12 Nombre...
 Examen de TEORIA DE MAQUINAS Diciembre 12 Nombre... El mecanismo de la figura es un cuadrilátero articulado manivela-balancín. La distancia entre los puntos fijos A y D es 4L/ 3. En la mitad del balancín
Examen de TEORIA DE MAQUINAS Diciembre 12 Nombre... El mecanismo de la figura es un cuadrilátero articulado manivela-balancín. La distancia entre los puntos fijos A y D es 4L/ 3. En la mitad del balancín
MDOF. Dinámica Estructural Aplicada II C 2012 UCA
 MDOF Dinámica Estructural Aplicada II C 2012 UCA Desde el punto de vista dinámico, interesan los grados de libertad en los que se generan fuerzas generalizadas de inercia significativas; es decir, fuerzas
MDOF Dinámica Estructural Aplicada II C 2012 UCA Desde el punto de vista dinámico, interesan los grados de libertad en los que se generan fuerzas generalizadas de inercia significativas; es decir, fuerzas
f x = 0 f y = 6 kp=cm 3 f z = 17 kp=cm 3
 Relación de problemas: Elasticidad lineal 1. Una barra de sección rectangular con anchura 100 mm, fondo 50 mm y longitud 2 m se somete a una tracción de 50 Tm; la barra sufre un alargamiento de 1 mm y
Relación de problemas: Elasticidad lineal 1. Una barra de sección rectangular con anchura 100 mm, fondo 50 mm y longitud 2 m se somete a una tracción de 50 Tm; la barra sufre un alargamiento de 1 mm y
5. FORMULACIÓN DEL PROBLEMA DE SISTEMAS
 5. FORMULACIÓN DEL PROBLEMA DE SISTEMAS MULTICUERPO Para definir completamente el sistema multicuerpo del modelo se comienza por describir los parámetros antropométricos utilizados para la implementación
5. FORMULACIÓN DEL PROBLEMA DE SISTEMAS MULTICUERPO Para definir completamente el sistema multicuerpo del modelo se comienza por describir los parámetros antropométricos utilizados para la implementación
Momento angular de una partícula. Momento angular de un sólido rígido
 Momento angular de una partícula Se define momento angular de una partícula respecto de del punto O, como el producto vectorial del vector posición r por el vector momento lineal mv L=r mv Momento angular
Momento angular de una partícula Se define momento angular de una partícula respecto de del punto O, como el producto vectorial del vector posición r por el vector momento lineal mv L=r mv Momento angular
La aplicación de separación de voz separalab
 Capítulo 4 La aplicación de separación de voz separalab 4.1 Introducción Este capítulo del proyecto está dedicado exclusivamente al aspecto práctico de la realización del mismo. Presentaremos varias simulaciones
Capítulo 4 La aplicación de separación de voz separalab 4.1 Introducción Este capítulo del proyecto está dedicado exclusivamente al aspecto práctico de la realización del mismo. Presentaremos varias simulaciones
Dinámica del Sólido Rígido
 Dinámica del Sólido Rígido El presente documento de clase sobre dinámica del solido rígido está basado en los contenidos volcados en la excelente página web del curso de Física I del Prof. Javier Junquera
Dinámica del Sólido Rígido El presente documento de clase sobre dinámica del solido rígido está basado en los contenidos volcados en la excelente página web del curso de Física I del Prof. Javier Junquera
Tema 7: Geometría Analítica. Rectas.
 Tema 7: Geometría Analítica. Rectas. En este tema nos centraremos en estudiar la geometría en el plano, así como los elementos que en este aparecen como son los puntos, segmentos, vectores y rectas. Estudiaremos
Tema 7: Geometría Analítica. Rectas. En este tema nos centraremos en estudiar la geometría en el plano, así como los elementos que en este aparecen como son los puntos, segmentos, vectores y rectas. Estudiaremos
Derivadas Parciales (parte 2)
 40 Derivadas Parciales (parte 2) Ejercicio: Si donde y. Determinar Solución: Consideraremos ahora la situación en la que, pero cada una de las variables e es función de dos variables y. En este caso tiene
40 Derivadas Parciales (parte 2) Ejercicio: Si donde y. Determinar Solución: Consideraremos ahora la situación en la que, pero cada una de las variables e es función de dos variables y. En este caso tiene
La recta en el plano.
 1 CONOCIMIENTOS PREVIOS. 1 La recta en el plano. 1. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Intervalos y sus definiciones básicas. Representación
1 CONOCIMIENTOS PREVIOS. 1 La recta en el plano. 1. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Intervalos y sus definiciones básicas. Representación
Facultad de Ingeniería. Escuela de Ingeniería Civil. Proyectos de Estructuras de Concreto. Modelos de Shell y Membrana
 Facultad de Ingeniería. Escuela de Ingeniería Civil. Proyectos de Estructuras de Concreto. MODELADO EN SAP DE CARGAS DISTRIBUIDAS SOBRE VIGAS Modelos de Shell y Membrana Profesor: Gutiérrez, Arnaldo Integrantes:
Facultad de Ingeniería. Escuela de Ingeniería Civil. Proyectos de Estructuras de Concreto. MODELADO EN SAP DE CARGAS DISTRIBUIDAS SOBRE VIGAS Modelos de Shell y Membrana Profesor: Gutiérrez, Arnaldo Integrantes:
Práctica 4 Límites, continuidad y derivación
 Práctica 4 Límites, continuidad y derivación En esta práctica utilizaremos el programa Mathematica para estudiar límites, continuidad y derivabilidad de funciones reales de variable real, así como algunas
Práctica 4 Límites, continuidad y derivación En esta práctica utilizaremos el programa Mathematica para estudiar límites, continuidad y derivabilidad de funciones reales de variable real, así como algunas
RESISTENCIA DE MATERIALES I INGENIERÍA CIVIL MECÁNICA ESFUERZOS COMBINADOS
 RESISTENCIA DE MATERIALES I INGENIERÍA CIVIL MECÁNICA FLEXION Y AXIAL 2013 roberto.ortega.a@usach.cl RESISTENCIA DE MATERIALES I ICM FLEXION Y AXIAL 2013 roberto.ortega.a@usach.cl RESISTENCIA DE MATERIALES
RESISTENCIA DE MATERIALES I INGENIERÍA CIVIL MECÁNICA FLEXION Y AXIAL 2013 roberto.ortega.a@usach.cl RESISTENCIA DE MATERIALES I ICM FLEXION Y AXIAL 2013 roberto.ortega.a@usach.cl RESISTENCIA DE MATERIALES
Ecuaciones diferenciales de Equilibrio
 Ecuaciones diferenciales de Equilibrio 28 de marzo de 2006 1. Elasticidad en una dimensión 1.1. Esfuerzo σ y carga lineal b(x) Para examinar un cuerpo desde el contínuo, que es la primera hipótesis (a),
Ecuaciones diferenciales de Equilibrio 28 de marzo de 2006 1. Elasticidad en una dimensión 1.1. Esfuerzo σ y carga lineal b(x) Para examinar un cuerpo desde el contínuo, que es la primera hipótesis (a),
Nombre de la Asignatura Matemáticas III( ) INFORMACIÓN GENERAL Escuela. Departamento Unidad de Estudios Básicos
 Código 008-2814 UNIVERSIDAD DE ORIENTE INFORMACIÓN GENERAL Escuela Departamento Unidad de Estudios Básicos Ciencias Horas Semanales 06 Horas Teóricas 03 Pre-requisitos 008-1824 Total Horas Semestre 96
Código 008-2814 UNIVERSIDAD DE ORIENTE INFORMACIÓN GENERAL Escuela Departamento Unidad de Estudios Básicos Ciencias Horas Semanales 06 Horas Teóricas 03 Pre-requisitos 008-1824 Total Horas Semestre 96
6. Aplicación a un Modelo 2D de una Estructura Jacket
 6. Aplicación a un Modelo 2D de una Estructura Jacket 6.1 Introducción En este capítulo tratamos de calcular una estructura offshore de un proyecto real mediante la aplicación del procedimiento de cálculo
6. Aplicación a un Modelo 2D de una Estructura Jacket 6.1 Introducción En este capítulo tratamos de calcular una estructura offshore de un proyecto real mediante la aplicación del procedimiento de cálculo
Física Ondas 10/11/06
 Física Ondas 10/11/06 I.E.S. Elviña DEPARTAMENTO DE FÍSICA E QUÍMICA Nombre Problemas [5 Ptos.] 1. Para el proyectil de la figura, calcula: (a) El vector velocidad con que se incrusta en el suelo. [1]
Física Ondas 10/11/06 I.E.S. Elviña DEPARTAMENTO DE FÍSICA E QUÍMICA Nombre Problemas [5 Ptos.] 1. Para el proyectil de la figura, calcula: (a) El vector velocidad con que se incrusta en el suelo. [1]
PROPUESTA SIMPLIFICADA PARA ENCONTRAR LA MATRIZ DE RIGIDEZ DE UN PÓRTICO DE HORMIGÓN.
 PROPUESTA SIMPLIFICADA PARA ENCONTRAR LA MATRIZ DE RIGIDEZ DE UN PÓRTICO DE HORMIGÓN. INTRODUCCIÓN. A continuación se presenta un método simplificado para encontrar la matriz de rigidez de un pórtico constitutivo
PROPUESTA SIMPLIFICADA PARA ENCONTRAR LA MATRIZ DE RIGIDEZ DE UN PÓRTICO DE HORMIGÓN. INTRODUCCIÓN. A continuación se presenta un método simplificado para encontrar la matriz de rigidez de un pórtico constitutivo
2014 RESISTENCIA DE MATERIALES I ICM RESISTENCIA DE MATERIALES I INGENIERÍA CIVIL MECÁNICA ESFUERZOS COMBINADOS
 RESISTENCIA DE MATERIALES I INGENIERÍA CIVIL MECÁNICA FLEXION Y AXIAL 2014 roberto.ortega.a@usach.cl RESISTENCIA DE MATERIALES I ICM FLEXION Y AXIAL 2014 roberto.ortega.a@usach.cl RESISTENCIA DE MATERIALES
RESISTENCIA DE MATERIALES I INGENIERÍA CIVIL MECÁNICA FLEXION Y AXIAL 2014 roberto.ortega.a@usach.cl RESISTENCIA DE MATERIALES I ICM FLEXION Y AXIAL 2014 roberto.ortega.a@usach.cl RESISTENCIA DE MATERIALES
CARGAS CRÍTICAS DE PANDEO DE COLUMNAS FISURADAS
 UNIVERSIDAD CARLOS III DE MADRID ESCUELA POLITÉCNICA SUPERIOR DEPARTAMENTO DE MECÁNICA DE MEDIOS CONTINUOS Y TEORÍA DE ESTRUCTURAS CARGAS CRÍTICAS DE PANDEO DE COLUMNAS FISURADAS TRABAJO FIN DE GRADO GRADO
UNIVERSIDAD CARLOS III DE MADRID ESCUELA POLITÉCNICA SUPERIOR DEPARTAMENTO DE MECÁNICA DE MEDIOS CONTINUOS Y TEORÍA DE ESTRUCTURAS CARGAS CRÍTICAS DE PANDEO DE COLUMNAS FISURADAS TRABAJO FIN DE GRADO GRADO
Sensibilidad de posición de la plataforma móvil respecto de las longitudes de las bielas en un manipulador paralelo tipo 6-RUS
 Sensibilidad de posición de la plataforma móvil respecto de las longitudes de las bielas en un manipulador paralelo tipo 6-RUS J Aginaga García, I Zabalza Villava, JJ Gil Soto Universidad Pública de Navarra,
Sensibilidad de posición de la plataforma móvil respecto de las longitudes de las bielas en un manipulador paralelo tipo 6-RUS J Aginaga García, I Zabalza Villava, JJ Gil Soto Universidad Pública de Navarra,
Diseño óptimo de estructuras. p. 1/30. mecánicas bajo incertidumbre en las cargas
 Diseño óptimo de estructuras mecánicas bajo incertidumbre en las cargas Felipe Alvarez y Miguel Carrasco II Encuentro Núcleo Científico Milenio Sistemas Complejos de Ingeniería Universidad de Chile 15-16
Diseño óptimo de estructuras mecánicas bajo incertidumbre en las cargas Felipe Alvarez y Miguel Carrasco II Encuentro Núcleo Científico Milenio Sistemas Complejos de Ingeniería Universidad de Chile 15-16
VI. Sistemas de dos grados de libertad
 Objetivos: 1. Describir que es un sistema de dos grados de.. Deducir las ecuaciones diferenciales de movimiento para un sistema de dos grados de masa-resorte-amortiguador, con amortiguamiento viscoso y
Objetivos: 1. Describir que es un sistema de dos grados de.. Deducir las ecuaciones diferenciales de movimiento para un sistema de dos grados de masa-resorte-amortiguador, con amortiguamiento viscoso y
Capítulo 1. Ejemplos numéricos Introducción
 Capítulo 1 Ejemplos numéricos 1.1. Introducción En este capítulo vamos a comprobar la bondad de la formulación desarrollada. Para ello resolveremos dos problemas de prueba que incorporan las dificultades
Capítulo 1 Ejemplos numéricos 1.1. Introducción En este capítulo vamos a comprobar la bondad de la formulación desarrollada. Para ello resolveremos dos problemas de prueba que incorporan las dificultades
CAPÍTULO 2 OBTENCION DE LOS PARAMETROS GENERALES PARA UNA SOLA CAPA DE MATERIAL COMPUESTO SOMETIDA A TENSIÓN
 CAPÍTULO 2 OBTENCION DE LOS PARAMETROS GENERALES PARA UNA SOLA CAPA DE MATERIAL COMPUESTO SOMETIDA A TENSIÓN 2.1 Introducción 2.1.1 Clasificación de los materiales compuestos. Las características de los
CAPÍTULO 2 OBTENCION DE LOS PARAMETROS GENERALES PARA UNA SOLA CAPA DE MATERIAL COMPUESTO SOMETIDA A TENSIÓN 2.1 Introducción 2.1.1 Clasificación de los materiales compuestos. Las características de los
Anexo III: Definición del Mecanismo.
 Anexo III: Definición del Mecanismo. Pag. AIII-1 ÍNDICE III.1 Introducción III.2 Parámetros de las Distintas Estaciones III.3 Dimensiones del Sistema piñón-cremallera III.3.1 Piñón III.3.2 Cremallera AIII-3
Anexo III: Definición del Mecanismo. Pag. AIII-1 ÍNDICE III.1 Introducción III.2 Parámetros de las Distintas Estaciones III.3 Dimensiones del Sistema piñón-cremallera III.3.1 Piñón III.3.2 Cremallera AIII-3
5.1 Análisis de sensibilidad para dos conicidades de las ruedas
 Capitulo 5 Resultados En este capítulo se realiza un análisis de sensibilidad de los autovalores del modelo con respecto al cambio en ciertas variables del mismo. Se han comparado los autovalores obtenidos
Capitulo 5 Resultados En este capítulo se realiza un análisis de sensibilidad de los autovalores del modelo con respecto al cambio en ciertas variables del mismo. Se han comparado los autovalores obtenidos
4 Métodos analíticos para el cálculo de tensiones y deformaciones plásticas
 +3Δ =3 = 3( Δ) Ec. 3.10 Ahora bien, como una vez iniciada la plastificación debe cumplirse el criterio de Von Mises debido a la condición de consistencia, se tiene: = =0 = 3( Δ) 3( Δ) = 0 Ec. 3.11 Qué
+3Δ =3 = 3( Δ) Ec. 3.10 Ahora bien, como una vez iniciada la plastificación debe cumplirse el criterio de Von Mises debido a la condición de consistencia, se tiene: = =0 = 3( Δ) 3( Δ) = 0 Ec. 3.11 Qué
Estructuras de Edificación: Tema 21 - El método del equilibrio en estructuras de nudos rígidos.
 Estructuras de Edificación: Tema 21 - El método del equilibrio en estructuras de nudos rígidos. David Herrero Pérez Departamento de Estructuras y Construcción Universidad Politécnica de Cartagena Grado
Estructuras de Edificación: Tema 21 - El método del equilibrio en estructuras de nudos rígidos. David Herrero Pérez Departamento de Estructuras y Construcción Universidad Politécnica de Cartagena Grado
COMPORTAMIENTO DINÁMICO DE TORRES DE PROCESO CON FONDO CÓNICO
 COMPORTAMIENTO DINÁMICO DE TORRES DE PROCESO CON FONDO CÓNICO Carlos Cortés Salas y Héctor A. Sánchez Sánchez * Instituto Mexicano del Petróleo *Sección de Estudios de Posgrado e Investigación ESIA - IPN
COMPORTAMIENTO DINÁMICO DE TORRES DE PROCESO CON FONDO CÓNICO Carlos Cortés Salas y Héctor A. Sánchez Sánchez * Instituto Mexicano del Petróleo *Sección de Estudios de Posgrado e Investigación ESIA - IPN
Soluciones de los ejercicios del primer examen parcial
 Matemáticas III (GIC, curso 2015 2016) Soluciones de los ejercicios del primer examen parcial EJERCICIO 1. Determina en qué ecuación se transforma la ecuación en derivadas parciales z yy + 3z xy + 2z xx
Matemáticas III (GIC, curso 2015 2016) Soluciones de los ejercicios del primer examen parcial EJERCICIO 1. Determina en qué ecuación se transforma la ecuación en derivadas parciales z yy + 3z xy + 2z xx
TEMA: MOVIMIENTO ARMÓNICO SIMPLE
 TEMA: MOVIMIENTO ARMÓNICO SIMPLE C-J-04 a) Al colgar una masa en el extremo de un muelle en posición vertical, éste se desplaza 5 cm; de qué magnitudes del sistema depende la relación entre dicho desplazamiento
TEMA: MOVIMIENTO ARMÓNICO SIMPLE C-J-04 a) Al colgar una masa en el extremo de un muelle en posición vertical, éste se desplaza 5 cm; de qué magnitudes del sistema depende la relación entre dicho desplazamiento
Introducción a las Estructuras
 Introducción a las Estructuras Capítulo nueve: Pandeo DOS 6. Método omega. General. Este método simplificado utiliza un coeficiente de seguridad establecido en tablas y determina las cargas y tensiones
Introducción a las Estructuras Capítulo nueve: Pandeo DOS 6. Método omega. General. Este método simplificado utiliza un coeficiente de seguridad establecido en tablas y determina las cargas y tensiones
Un i d a d 5. d i fe r e n C i a L es d e o r d e n s U pe r i o r. Objetivos. Al inalizar la unidad, el alumno:
 Un i d a d 5 má x i m o s, mínimos y d i fe r e n C i a L es d e o r d e n s U pe r i o r Objetivos Al inalizar la unidad, el alumno: Identificará los puntos críticos, máximos y mínimos absolutos y relativos
Un i d a d 5 má x i m o s, mínimos y d i fe r e n C i a L es d e o r d e n s U pe r i o r Objetivos Al inalizar la unidad, el alumno: Identificará los puntos críticos, máximos y mínimos absolutos y relativos
Ejercicio 1 del modelo 2 de la opción A de sobrantes de Solución
 Ejercicio 1 del modelo 2 de la opción A de sobrantes de 2001 Sea f: R R la función dada por f(x) = 8 x 2. (a) [1 punto] Esboza la gráfica y halla los extremos relativos de f (dónde se alcanzan y cuáles
Ejercicio 1 del modelo 2 de la opción A de sobrantes de 2001 Sea f: R R la función dada por f(x) = 8 x 2. (a) [1 punto] Esboza la gráfica y halla los extremos relativos de f (dónde se alcanzan y cuáles
A continuación se presentan algunos ejercicios resueltos, paso a paso, extraídos del libro Aplicaciones Físicas de la Integral Definida:
 A continuación se presentan algunos ejercicios resueltos, paso a paso, etraídos del libro : EJEMPLO Sea R la región definida por (, ) R = /. Se tiene una placa con la forma de la región R sumergida verticalmente
A continuación se presentan algunos ejercicios resueltos, paso a paso, etraídos del libro : EJEMPLO Sea R la región definida por (, ) R = /. Se tiene una placa con la forma de la región R sumergida verticalmente
Ejercicios de optimización sin restricciones
 Ejercicios de optimización sin restricciones Programación Matemática Licenciatura en Ciencias y Técnicas Estadísticas Curso 5/6 Indica la dirección que el método de Newton (sin modificaciones calcularía
Ejercicios de optimización sin restricciones Programación Matemática Licenciatura en Ciencias y Técnicas Estadísticas Curso 5/6 Indica la dirección que el método de Newton (sin modificaciones calcularía
TRABAJO DE ELEMENTOS DE MÁQUINAS Y VIBRACIONES 3º INGENIERÍA INDUSTRIAL
 Trabajo 1: Dinámica de un sistema motor-volante de inercia-masa de un vehículo dinámico del sistema de la figura. Las variables que definen la posición del mecanismo serán las coordenadas indicadas en
Trabajo 1: Dinámica de un sistema motor-volante de inercia-masa de un vehículo dinámico del sistema de la figura. Las variables que definen la posición del mecanismo serán las coordenadas indicadas en
EJERCICIO 17. Si definimos una nueva base ortonormal (,
 EJERCICIO 17 a) Por la hipótesis de linealidad de la elasticidad clásica, el estado de deformación que buscamos es la suma de los dos estados de deformación superpuestos, uno de ellos uniaxial y el otro
EJERCICIO 17 a) Por la hipótesis de linealidad de la elasticidad clásica, el estado de deformación que buscamos es la suma de los dos estados de deformación superpuestos, uno de ellos uniaxial y el otro
UNIDAD DE APRENDIZAJE IV
 UNIDAD DE APRENDIZAJE IV Saberes procedimentales Emplea de manera sistemática conceptos algebraicos, geométricos, trigonométricos y de geometría analítica. Relaciona la ecuación de segundo grado en dos
UNIDAD DE APRENDIZAJE IV Saberes procedimentales Emplea de manera sistemática conceptos algebraicos, geométricos, trigonométricos y de geometría analítica. Relaciona la ecuación de segundo grado en dos
IES Fco Ayala de Granada Septiembre de 2011 (Septiembre Modelo 2) Solución Germán-Jesús Rubio Luna
 IES Fco Ayala de Granada Septiembre de 0 (Septiembre Modelo ) Germán-Jesús Rubio Luna UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO 00-0. MATEMÁTICAS II Opción A Ejercicio opción A,
IES Fco Ayala de Granada Septiembre de 0 (Septiembre Modelo ) Germán-Jesús Rubio Luna UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO 00-0. MATEMÁTICAS II Opción A Ejercicio opción A,
CAPÍTULO IV. 4. Desarrollo, descripción y manual de usuario de la paquetería para el análisis
 CAPÍTULO IV 4. Desarrollo, descripción y manual de usuario de la paquetería para el análisis matricial de armaduras 4.1 Desarrollo de la paquetería Como se mencionó en el primer capítulo, este proyecto
CAPÍTULO IV 4. Desarrollo, descripción y manual de usuario de la paquetería para el análisis matricial de armaduras 4.1 Desarrollo de la paquetería Como se mencionó en el primer capítulo, este proyecto
UNIVERSIDAD DIEGO PORTALES. FACULTAD DE INGENIERIA. INSTITUTO DE CIENCIAS BASICAS.
 UNIVERSIDAD DIEGO PORTALES. FACULTAD DE INGENIERIA. INSTITUTO DE CIENCIAS BASICAS. Cálculo III, Examen Final. Semestre Primavera 1 Tiempo: 11 min. Problema 1 [1,5 puntos] La curvatura de una trayectoria
UNIVERSIDAD DIEGO PORTALES. FACULTAD DE INGENIERIA. INSTITUTO DE CIENCIAS BASICAS. Cálculo III, Examen Final. Semestre Primavera 1 Tiempo: 11 min. Problema 1 [1,5 puntos] La curvatura de una trayectoria
EJERCICIOS REPASO 2ª EVALUACIÓN
 MATRICES Y DETERMINANTES 1.) Sean las matrices: EJERCICIOS REPASO 2ª EVALUACIÓN a) Encuentre el valor o valores de x de forma que b) Igualmente para que c) Determine x para que 2.) Dadas las matrices:
MATRICES Y DETERMINANTES 1.) Sean las matrices: EJERCICIOS REPASO 2ª EVALUACIÓN a) Encuentre el valor o valores de x de forma que b) Igualmente para que c) Determine x para que 2.) Dadas las matrices:
Estructuras de Edificación: Tema 18 - Estructuras articuladas. Cálculo de desplazamientos.
 Estructuras de Edificación: Tema 18 - Estructuras articuladas. Cálculo de desplazamientos. David Herrero Pérez Departamento de Estructuras y Construcción Universidad Politécnica de Cartagena Grado en Ingeniería
Estructuras de Edificación: Tema 18 - Estructuras articuladas. Cálculo de desplazamientos. David Herrero Pérez Departamento de Estructuras y Construcción Universidad Politécnica de Cartagena Grado en Ingeniería
Modelo 4 de Sobrantes de 2004
 Ejercicio n de la opción A del modelo 4 de 24 9 Considera la integral definida I d + [ 5 puntos] Epresa la anterior integral definida aplicando el cambio de variables + t. [ punto] Calcula I. I d + Cambio
Ejercicio n de la opción A del modelo 4 de 24 9 Considera la integral definida I d + [ 5 puntos] Epresa la anterior integral definida aplicando el cambio de variables + t. [ punto] Calcula I. I d + Cambio
Análisis cinemático de estructuras planas
 Análisis cinemático de estructuras planas Apellidos, nombre Basset Salom, Luisa (lbasset@mes.upv.es) Departamento Centro Mecánica de Medios Continuos y Teoría de Estructuras Escuela Técnica Superior de
Análisis cinemático de estructuras planas Apellidos, nombre Basset Salom, Luisa (lbasset@mes.upv.es) Departamento Centro Mecánica de Medios Continuos y Teoría de Estructuras Escuela Técnica Superior de
Representación en el espacio de estado. Sistemas Control Embebidos e Instrumentación Electrónica UNIVERSIDAD EAFIT
 Representación en el espacio de estado Representación en espacio de estado Control clásico El modelado y control de sistemas basado en la transformada de Laplace, es un enfoque muy sencillo y de fácil
Representación en el espacio de estado Representación en espacio de estado Control clásico El modelado y control de sistemas basado en la transformada de Laplace, es un enfoque muy sencillo y de fácil
Recta de mejor ajuste por el método de los Mínimos Cuadrados
 Apéndice A Recta de mejor ajuste por el método de los Mínimos Cuadrados En este apéndice se detallará el cálculo de los parámetros de la recta de mejor ajuste (o de regresión) a un conjunto de puntos por
Apéndice A Recta de mejor ajuste por el método de los Mínimos Cuadrados En este apéndice se detallará el cálculo de los parámetros de la recta de mejor ajuste (o de regresión) a un conjunto de puntos por
