Teoría de la Computabilidad
|
|
|
- Ángela Juárez Sevilla
- hace 5 años
- Vistas:
Transcripción
1 Teoría de la Computabilidad Santiago Figueira Departamento de Computación, FCEyN, UBA Primer cuatrimestre
2 Contenido clase 0 - Repaso de la parte de Computabilidad de LyC: p. 3 clase 1 - Funciones Primitivas recursivas, iteración, esqueleto de funciones primitivas recursivas, recursión anidada en varias variables: p. 27 clase 2 - Halting problem, Reducibilidades one-one y many one, Teorema de Rice, Teorema de Isomorfismo de Myhill, cilindros: p. 49 clase 3 - Conjuntos 1-completos, conjuntos productivos y creativos: p. 66 clase 4 - Reducibilidad tt, cómputos con oráculo, principio del uso: p. 79 clase 5 - Teorema del Salto, Lema del Límite, grados Turing: p. 94 clase 6 - Jerarquía Aritmética, Teorema de Post, Conjuntos Σ n-completos: p. 109 clase 7 - Problema de Post, Conjuntos simples: p. 127 clase 8 - Conjuntos hipersimples, funciones computablemente mayoradas: p. 139 clase 9 - Conjuntos bajos, solución al problema de Post: p. 148 clase 10 (opcional) - Aleatoriedad y Computabilidad: p
3 Teoría de la Computabilidad Clase 0 Repaso de la parte de Computabilidad de LyC 3
4 Organización de la materia 3 puntos para Licenciatura en Computación, 3 puntos para Doctorado en Computación correlativa: LyC Lunes de 13 a 17 en aula 11 del pab. I Evaluación: seguramente un parcial y un trabajo final. 4
5 Bibliografía En orden de importancia Robert I. Soare, Recursively Enumberable Sets and Degrees: A Study of Computable Functions and Computably Generated Sets (Perspectives in Mathematical Logic), Springer, Hartley Rogers, Theory of Recursive Functions and Effective Computability, The MIT Press, Piergiorgio Odifreddi, Classical Recursion Theory, Vol. 1 (Studies in Logic and the Foundations of Mathematics, Vol. 125), North Holland, Piergiorgio Odifreddi, Classical Recursion Theory, Vol. 2 (Studies in Logic and the Foundations of Mathematics, Vol. 143), North Holland, Martin Davis, Ron Sigal, Elaine Weyuker, Computability, Complexity and Languages, fundamentals of theoretical computer science, Elsevier,
6 Composición y recursión primitiva Definición Sea f : N k N y g 1,..., g k : N n N. h : N n N se obtiene a partir de f y g 1,..., g k por composición si h(x 1,..., x n ) = f (g 1 (x 1,..., x n ),..., g k (x 1,..., x n )) Definición h : N n+1 N se obtiene de g : N n+2 N y f : N n N por recursión primitiva si h(x 1,..., x n, 0) = f (x 1,..., x n ) h(x 1,..., x n, t + 1) = g(t, x 1,..., x n, h(x 1,..., x n, t)) 6
7 Funciones primitivas recursivas P 1 Funciones iniciales O(x) = 0 S(x) = x + 1 I n i (x 1,..., x n ) = x i para todo n 1 y i {1,..., n} Definición La clase P 1 de funciones primitivas recursivas es la clase de funciones más chica: conteniendo las funciones iniciales cerrada por composición cerrada por recursión primitiva 7
8 Ejemplos de funciones en P 1 funciones aritméticas básicas: suma, resta, producto, potencia conectivos booleanos:,, (verdadero se interpreta como 1 y falso como 0) predicados aritméticos básicos: =, definición por casos: si g 1,..., g m, h P 1 y p 1,..., p m P 1 son predicados mutuamente excluyentes entonces también está en P 1 la función g 1 ( x) si p 1 ( x). f ( x) = g m ( x) si p m ( x) h( x) si no sumatorias y productorias: si f P 1 entonces también están en P 1 las funciones y y g(y, x) = f (t, x) y h(y, x) = f (t, x) t=0 t=0 8
9 Ejemplos de funciones en P 1 cuantificadores acotados: si p P 1 es un predicado entonces también están en P 1 : ( t) y p(t, x) y ( t) y p(t, x) minimización acotada: si p P 1 es un predicado entonces también está en P 1 la función mínimo t y tal que si existe tal t p(t, x) es verdadero mín p(t, x) = t y y + 1 si no codificación y decodificación de k-uplas: x 1,..., x k π i (z) codificación y decodificación de secuencias: [x 1,..., x n ] z[i] 9
10 Recursión course-of-value Teorema P 1 está cerrada por recursión course-of-value en donde la definición de f ( x, y + 1) involucra no solo el último valor f ( x, y) sino también cualquier número (quizá todos) los valores (f ( x, z)) z y. Más formalmente, si definimos la función de historia ˆf ( x, y) = [f ( x, 0),..., f ( x, y)], tenemos que si g, h P 1 entonces también está en P 1 la función f definida como: f ( x, 0) = g( x) f ( x, y + 1) = h( x, y, ˆf ( x, y)) 10
11 Recursión simultánea Teorema P 1 está cerrada por recursión simultánea en donde un número finito de funciones f 1,..., f n se definen simultáneamente y la definición de f m ( x, y + 1) puede involucrar no solo f m ( x, y) sino también cualquier número (quizá todos) los valores (f i ( x, y)) 1 i n. 11
12 Funciones parciales Una función parcial es simplemente una función que puede indefinirse en algunos (quizá todos) sus argumentos. Una función parcial es total si se define para todos sus argumentos. Las funciones primitivas recursivas son totales. Solo trabajamos con funciones N k N. Notamos f ( x) cuando f está definida en x f ( x) cuando f está indefinida en x El dominio de una función es conjunto de argumentos en el que la función se define: dom f = { x : f ( x) }. Si f y g son funciones parciales, por f ( x) = g( x) nos referimos a [f ( x) g( x) ] [f ( x) g( x) f ( x) = g( x) ]. }{{}}{{} N N 12
13 Máquinas de Turing q Se compone de : una cinta dividida en celdas infinita en ambas direcciones cada celda contiene un símbolo de un alfabeto dado Σ. Σ L, R / Σ representa el blanco en una celda L y R son símbolos reservados (representarán acciones que puede realizar la cabeza) una cabeza lee y escribe un símbolo a la vez se mueve una posición a la izquierda o una posición a la derecha una tabla finita de instrucciones dice qué hacer en cada paso 13
14 Tabla de instrucciones Σ es el alfabeto. L, R / Σ, Σ. Q es el conjunto finito de estados A = Σ {L, R} es el conjunto de acciones un símbolo s Σ se interpreta como escribir s en la posición actual L se interpreta como mover la cabeza una posición hacia la izquierda R se interpreta como mover la cabeza una posición hacia la derecha Una tabla de instrucciones T es un subconjunto (finito) de La tupla se interpreta como Q Σ A Q (q, s, a, q ) T Si la máquina está en el estado q leyendo en la cinta el símbolo s, entonces realiza la acción a y pasa al estado q 14
15 Máquinas de Turing Una máquina de Turing es una tupla donde (Σ, Q, T, q 0, q f ) Σ (finito) es el conjunto símbolos (L, R / Σ, Σ) Q (finito) es el conjunto de estados tiene dos estados distinguidos: q 0 Q es el estado inicial q f Q es el estado final T Q Σ Σ {L, R} Q es la tabla de instrucciones va a ser finita porque Σ y Q lo son cuando no hay restricciones sobre T decimos que M es una máquina de Turing no determinísitca cuando no hay dos instrucciones en T que empiezan con las mismas primeras dos coordenadas, decimos que M es una máquina de Turing determinísitca Si no decimos nada, es una máquina de Turing determinística. 15
16 Representación de números y tuplas en la cinta Fijamos Σ = {, 1}. representaremos a los números naturales en unario (con palotes). el número x N se representa como x = }{{} x+1 representamos a las tuplas (x 1,..., x n ) como lista de (representaciones de) los x i separados por blanco la tupla (x1,..., x n ) se representa como x 1 x 2 x n 16
17 Funciones parciales computables Una función (parcial) f : N n N es parcial computable si existe una máquina de Turing determinística M = (Σ, Q, T, q 0, q f ) con Σ = {, 1} tal que cuando empieza en la configuración inicial... x 1 x 2... x n... (con los enteros x i representados en unario y nada más en la cinta de entrada salvo la representación de la entrada): si f (x 1,..., x n ) entonces siguiendo sus instrucciones en T llega a una configuración final de la forma... f (x 1,..., x n )... q f (quizá algo más en la cinta) si f (x 1,..., x n ) entonces nunca termina en el estado q f. Una función es computable si es parcial computable y total. 17 q 0
18 Enumeración de las máquinas de Turing Habiendo fijado Σ, q 0, q f, cada máquina de Turing puede ser identificada por su tabla de instrucciones. Una tabla de instrucciones es un conjunto finito de 4-uplas. Cada tabla de instrucciones (i.e. cada máquina) puede ser codificado de manera efectiva por un número. Definición M e es la máquina de Turing con tabla de instrucciones con código e. ϕ (n) e es la función parcial de n variables computada por la máquina M e. Abreviamos ϕ (1) = ϕ. Notación: ϕ e es la e-ésima función parcial computable e es el índice o código o número de Gödel de ϕ e. 18
19 Teoremas de Forma Normal y de Enumeración Teorema (Forma Normal) Existe un predicado T (e, x, t) y una función U(y) primitivos recursivos tal que ϕ e (x) = U(mín T (e, x, t)). t Teorema (Enumeración, existencia de máquina universal) Para cada n 1 hay una función parcial computable de n + 1 variables, ϕ (n+1) z n, tal que ϕ z (n+1) n (e, x 1,..., x n ) = ϕ (n) e (x 1,..., x n ). 19
20 Teorema del Parámetro (TP) Teorema Para cada m, n 1 existe una función primitiva recursiva 1-1 s m n de m + 1 variables tal que para todo y 1,..., y m, z 1,..., z n N, ϕ s m n (x,y 1,...,y m)(z 1,..., z n ) = ϕ x (y 1,..., y m, z 1,..., z n ). 20
21 Teorema de la Recursión (TR) Teorema Para cualquier función computable f existe un n N (llamado punto fijo de f ) tal que ϕ n = ϕ f (n). Teorema (Recursión con parámetros) Para cualquier función computable f : N 2 N existe una función computable n : N N tal que ϕ n(y) = ϕ f (n(y),y). Demostración. Definir d computable tal que { ϕ ϕ d(x,y) (z) = ϕx (x,y)(z) si ϕ x (x, y) si no Sea v tal que ϕ v (x, y) = f (d(x, y), y). Definir n(y) = d(v, y). ϕ n(y) = ϕ d(v,y) = ϕ ϕv (v,y) = ϕ f (d(v,y),y) = ϕ f (n(y),y). 21
22 Conjuntos, secuencias, cadenas Cuando hablamos de un conjunto de naturales A pensamos siempre en la función característica de ese conjunto. { 1 si x A A(x) = 0 si no Así, un conjunto puede ser computable o primitivo recursivo. A puede ser visto también como una secuencia infinita de 0s y 1s: A(0) A(1) A(2) A(3) A(4) A(5) {0, 1} Los primeros n bits de A (visto como tira de 0s y 1s) es A n = A(0) A(1)... A(n 1) Las cadenas finitas de 0s y 1s pueden ser vistas como conjuntos finitos. 22
23 Ejecución de a pasos Definición Notamos ϕ e,s (x) = y si x, y, e < s e y es la salida de la máquina con código e ejecutada por < s pasos. si tal y existe, decimos que ϕ e,s (x) converge (ϕ e,s (x) ). en caso contrario decimos que ϕ e,s (x) diverge (ϕ e,s (x) ). Teorema Los siguientes conjuntos son computables: { e, x, s : ϕ e,s (x) } { e, x, y, s : ϕ e,s (x) = y} 23
24 Conjuntos computablemente enumerables Definición Un conjunto A N es comptuablemente enumerable (c.e.) si A es el dominio de alguna función parcial computable. El e-ésimo conjunto c.e. se denota W e = dom ϕ e = {x : ϕ e (x) } = {x : ( t) T (e, x, t)} W e,s = dom ϕ e,s (por convención si x W e,s entonces x, e < s). Teorema A es computable sii A y A son c.e. Teorema Si f es parcial computable y A es c.e. entonces f 1 (A) es c.e. 24
25 Caracterizaciones de los conjuntos c.e. Teorema Si A, son equivalentes: 1. A es r.e. 2. A es el rango de una función primitiva recursiva 3. A es el rango de una función computable 4. A es el rango de una función parcial computable 25
26 Una función computable que no es primitiva recursiva Se pueden enumerar las funciones primitivas recursivas de 1 variable: ψ 1, ψ 2,... Teorema (Enumeración de funciones primitivas recursivas) Hay una función f computable de 2 variables tal que f (e, x) = ψ e (x). Analicemos g : N N definida como g(x) = f (x, x). claramente g es computable porque f lo es. supongamos que g P 1 entonces h(x) = g(x) + 1 = f (x, x) + 1 P1 existe un e tal que ψ e = h tenemos f (e, x) = h(x) = f (x, x) + 1 e está fijo pero x es variable instanciando x = e llegamos a un absurdo por qué esto no funciona para funciones parciales computables en vez de primitivas recursivas? 26
27 Teoría de la Computabilidad Clase 1 Funciones Primitivas recursivas, iteración, esqueleto de funciones primitivas recursivas, recursión anidada en varias variables 27
28 Composición y recursión primitiva Definición Sea f : N k N y g 1,..., g k : N n N. h : N n N se obtiene a partir de f y g 1,..., g k por composición si h(x 1,..., x n ) = f (g 1 (x 1,..., x n ),..., g k (x 1,..., x n )) Definición h : N n+1 N se obtiene de g : N n+2 N y f : N n N por recursión primitiva si h(x 1,..., x n, 0) = f (x 1,..., x n ) h(x 1,..., x n, t + 1) = g(t, x 1,..., x n, h(x 1,..., x n, t)) 28
29 Funciones primitivas recursivas P 1 Funciones iniciales O(x) = 0 S(x) = x + 1 I n i (x 1,..., x n ) = x i para todo n 1 y i {1,..., n} Definición La clase P 1 de funciones primitivas recursivas es la clase de funciones más chica: conteniendo las funciones iniciales cerrada por composición cerrada por recursión primitiva 29
30 Recursión anidada en una variable Definición f se define a partir de g 1,..., g n por recursión anidada en una variable si f ( x, 0) = g( x) f ( x, y) = h( x, y) donde h( x, y) es un término numérico construido por números naturales n las variables x e y las funciones g 1,..., g m el símbolo f los valores de f usados en la definición de f ( x, y) son de la forma f ( t, s) donde s tiene un valor numérico < y Teorema P 1 está cerrada por recursión anidada en una variable. 30
31 Caracterización alternativa de P 1 Definición Una función f se define por iteración a partir de t si f (x, n) = t (n) (x) donde t (n) denota el resultado de n aplicaciones sucesivas de t (por convención t (0) (x) = x). Teorema La clase de funciones primitivas recursivas es la clase más chica: conteniendo las funciones iniciales y funciones de codificación y decodificación de pares cerrada por composición cerrada por iteración 31
32 Caracterización alternativa de P 1 (demo) Sea C la clase más chica de funciones que satisfacen las condiciones del teorema. C P 1 Las funciones de codificación y decodificación son primitivas recursivas. La iteración f (x, n) = t (n) (x) es un caso especial de recursión primitiva: f (x, 0) = x f (x, n + 1) = t(f (x, n)) P 1 C Hay que ver que C es cerrada por recursión primitiva. Observar que C tiene cod./decod. de pares y composición, por lo tanto tiene cod./decod. de n-uplas para cualquier n fijo. Sean g, h C y sea f definida como f ( x, 0) = g( x) f ( x, y + 1) = h( x, y, f ( x, y)) Basta ver que esta función está en C: s( x, n) = x, n, f ( x, n) 32
33 La función s( x, 0) = x, 0, f ( x, 0) = x, 0, g( x) está en C porque g y están en C. Podemos transformar en s( x, n) = x, n, f ( x, n) }{{} z s( x, n + 1) = x, n + 1, f ( x, n + 1) = x, n + 1, h( x, n, f ( x, n) ) }{{} z con esta función, que también está en C: t( x, n, z) = x, n + 1, h( x, n, z). Como C está cerrada por iteración, está en C esta función: s( x, n) = t (n) (s( x, 0)). 33
34 La familia de funciones (h n ) n N Sea h 0 (x) = x + 1 y h n+1 (x) = h n (x) (x) Proposición x h n (x). Demostración. Por inducción en n. Para n = 0 es trivial. Para n + 1, suponer ( z) z h n (z). Es fácil probar por inducción en m que x h n (m) (x). En particular x h n (x) (x) = h n+1 (x). 34
35 Propiedades de (h n ) n N Proposición Si n m y x > 0 entonces h n (x) h m (x). Demostración. Basta probar ( x > 0) h n (x) h n+1 (x) = h n (x) (x). Basta probar h n (z) h n (m) (z) por inducción en m > 0. Para m = 1 es trivial. Para m + 1, h n (z) h n (m) (z) por HI h n (h n (m) (z)) por Proposición de pág. 34 = h n (m+1) (z) 35
36 Propiedades de (h n ) n N Proposición Si x y entonces h n (x) h n (y). Demostración. Por inducción en n. Para n = 0 es trivial. Para n + 1, h n+1 (x) = h n (x) (x) h n (y) (x) por Proposición de pág. 34 (y x veces) h n (y) (y) por HI (y veces) = h n+1 (y). 36
37 Propiedades de (h n ) n N Proposición h 1 (x) = 2x. Demostración. Basta probar h (m) 0 (x) = x + m por inducción en m. Para m = 0 es trivial. Para m + 1, h (m+1) 0 (x) = h 0 (h (m) 0 (x)) = h 0 (x + m) por HI = (x + m) + 1 porque h 0 (z) = z + 1 = x + (m + 1). 37
38 Propiedades de (h n ) n N Proposición h 2 (x) = x 2 x. Demostración. Basta probar h (m) 1 (x) = x 2 m por inducción en m. Para m = 0 es trivial. Para m + 1, h (m+1) 1 (x) = h 1 (h (m) 1 (x)) = h 1 (x 2 m ) por HI = (x 2 m ) 2 porque h 1 (z) = 2z = x 2 m+1 38
39 Todas las h n son primitivas recursivas Teorema Para cada n, h n es primitiva recursiva. Demostración. Obvio, pues la función sucesor está en P 1 y P 1 está cerrada por iteración. 39
40 Cada función primitiva recursiva es dominada por alguna h n Teorema Para cada f primitiva recursiva, hay un n tal que f ( x) h n ( x) para casi todo x. Demostración. Por inducción en la caracterización alternativa de P 1 (pág. 31). Veamos que: las funciones iniciales y las funciones de codificación y decodificación lo cumplen si h, g 1,..., g m lo cumplen, f ( x) = h(g 1 ( x),..., g m ( x)) también lo cumple si t lo cumple, f (x, y) = t (y) (x) también lo cumple. 40
41 Cada función primitiva recursiva es dominada por alguna h n Funciones iniciales, codificación y decodificación O(x) = 0 está dominada por h 0 S(x) = x + 1 está dominada por h 0 I n i (x 1,..., x n ) = x i está dominada por h 0 porque I n i (x 1,..., x n ) j x j h 0 j x j x, y = 2 x (y + 1) 1 está dominada por h 2 porque h 2 (x + y) = (x + y) 2 x+y 2 x (y + 1) 1 para casi todo x, y. π 1 (x), π 2 (x) x, dominadas por h 0 (x) 41
42 Cada función primitiva recursiva es dominada por alguna h n Composición Supongamos que f ( x) = h(g 1 ( x),..., g m ( x)) y por HI tenemos que para un n 2 suficientemente grande (usar Proposición de pág. 35), g i ( x) h n ( x) para casi todo x y h( y) h n ( y) para casi todo y. f ( x) = h(g 1 ( x),..., g m ( x)) h n ( 1 i m g i( x)) por HI sobre h h n ( 1 i m h n( x)) por HI sobre g i y Prop. pág. 36 = h n (m h n ( x)) h n (h 2 (h n ( x))) si m x y porque h 2 (z) = z 2 z h n (h n (h n ( x))) por n 2 y Props. págs. 35 y 36 = h n (3) ( x) h ( x) n ( x) si 3 x y Prop. pág. 34 = h n+1 ( x) 42
43 Cada función primitiva recursiva es dominada por alguna h n Iteración Supongamos que f (x, y) = t (y) (x) y por HI para algún n, t(x) h n (x) para casi todo x. f (x, y) = t (y) (x) n (x) por HI y veces y Prop. pág. 36 h n (x+y) (x + y) por Props. págs. 34 y 36 = h n+1 (x + y) h (y) 43
44 La función diagonal domina a cualquier primitiva recursiva Teorema La función diagonal d(x) = h x (x) domina toda función primitiva recursiva N N. Demostración. Sea f una función primitiva recursiva. Existe n tal que para casi todo x, f (x) h n (x) h x (x) si x > n y por Prop. de pág. 35 = d(x) Entonces para casi todo x, f (x) d(x). Corolario d no es primitiva recursiva. Demostración. Si lo fuera, d(x) + 1 también lo sería. Por teorema anterior, para casi todo x tenemos d(x) + 1 d(x). Absurdo. 44
45 Recursión anidada en n variables Sea lex el orden lexicográfico de N n. Definición f se define a partir de g 1,..., g n por recursión anidada en n variables si f ( x, 0) = g( x) ( 0 N n ) f ( x, y) = h( x, y) ( y N n, y 0) donde h( x, y) es un término numérico construido por números naturales las variables x e y las funciones g 1,..., g m el símbolo f los valores de f usados en la definición de f ( x, y) son de la forma f ( t, s) donde s N n tiene un valor numérico < lex y. 45
46 Funciones n-primitivas recursivas P n Definición La clase P n de funciones n-primitivas recursivas es la clase de funciones más chica: conteniendo las funciones iniciales cerrada por composición cerrada por recursión anidada en a lo sumo n variables 46
47 P 1 no está cerrado por recursión anidada en 2 variables Teorema P 1 P 2. Demostración. Las funciones (h n ) n N se pueden describir así: h 0 (x) = x + 1 h n (0) (x) = x h n (z+1) (x) = h n (h n (z) h n+1 (x) = h n (x) (x) Se pueden ver como una única función h(n, z, x) = h (z) n (x) (x)) definidas por recursión anidada en las variables n y z (pensar h n como h (1) n ): h(n, 0, x) = x h(n + 1, 1, x) = h(n, x, x) h(0, 1, x) = x + 1 h(n, z + 1, x) = h(n, 1, h(n, z, x)) Si h fuese primitiva recursiva, también lo sería d(x) = h x (x) = h(x, 1, x) y esto contradice el Teorema de pág
48 Jerarquía de funciones n-recursivas El resultado anterior se puede generalizar. Teorema Para todo n, P n P n+1. 48
49 Teoría de la Computabilidad Clase 2 Halting problem, Reducibilidades one-one y many one, Teorema de Rice, Teorema de Isomorfismo de Myhill, cilindros 49
50 K, el Halting Problem Definición K = {x : ϕ x (x) } = {x : x W x }. Teorema K es c.e. Demostración. g(x) = ϕ x (x) es una función parcial computable. K = dom g. Teorema K es no es computable. Demostración. Si K fuera computable, entonces esta función también lo sería: { ϕ x (x) + 1 si x K f (x) = 0 si no Pero f ϕ x para todo x. Absurdo. 50
51 K 0, otro Halting Problem Definición K 0 := { x, y : ϕ x (y) } Proposición K 0 es c.e. Demostración. g( x, y ) = ϕ x (y) es una función parcial computable. K 0 = dom g. Corolario K 0 es no es computable. Demostración. x K sii x, x K 0. Si K 0 fuera computable, también lo sería K. 51
52 Reducibilidades many-one y one-one La demostración del corolario anterior sugiere un método indirecto para demostrar resultados de indecidibilidad de nuevos conjuntos: reducir K a esos conjuntos. Definición A es many-one reducible a B (A m B) si hay una función computable f tal que x A sii f (x) B. A es one-one reducible a B (A 1 B) si A m B vía una función 1-1 (i.e. inyectiva) Informalmente, A m B si A es a lo sumo tan difícil como B. Conociendo B puedo computar A. Para todo x, haciendo una sola pregunta a B, decido si x A o x / A. La pregunta es: f (x) B? 52
53 Propiedades de 1 y m Proposición 1 y m son reflexivas y transitivas. Demostración. Ejercicio. Proposición 1. A 1 B A m B 2. A 1 B A 1 B 3. A m B A m B 4. Si A m B y B computable, entonces A es computable 5. Si A m B y B c.e., entonces A es c.e. Demostración 1,2,3. Ejercicio. 53
54 4. Si A m B y B computable, entonces A es computable: Supongamos que f es computable tal que x A sii f (x) B. Como B es computable, la función característica de A, definida como A(x) = B(f (x)) también lo es. 5. Si A m B y B c.e., entonces A es c.e.: Supongamos A m B vía f. Sea R computable tal que Entonces x B sii ( y) R(x, y). x A sii f (x) B sii ( y) computable {}}{ R(f (x), y). 54
55 Más propiedades de 1 y m Proposición 1. Existen A, B incomparables con respecto a m (A m B y B m A) 2. Existen A, B no computables e incomparables con respecto a m Demostración. 1. m N y N m. 2. Considerar K y K. K es c.e. pero K no es c.e. Por teorema anterior (5) K m K. Por teorema anterior (3) K m K. Corolario A m B A m B. Demostración. Tomar A = B = K. 55
56 Grados m y grados 1 Definición A m B si A m B y B m A A 1 B si A 1 B y B 1 A deg 1 (A) = {B : B 1 A} es el grado 1 de A deg m (A) = {B : B m A} es el grado m de A 56
57 Semiretículo superior (upper semilattice) Un semiretículo superior L = (L,, ) es un conjunto parcialmente ordenado tal que cada par de elementos tiene un least upper bound (lub). c L es un lub de a, b L si: a c b c si d L verifica a d y b d entonces c d Al lub de a y b también se lo llama supremo o join. Si a y b son elementos de L entonces a b denota el lub de a y b. 57
58 m forma un semiretículo superior Definición A B = {2x : x A} {2x + 1 : x B}. Proposición El orden de m forma un semiretículo superior sobre deg m. Es decir, cualesquiera dos grados m tienen un lub. Demostración. Veamos que deg m (A B) es el lub de deg m (A) y deg m (B) en el orden m. A m A B vía λx.2x B m A B vía λx.2x + 1 supongamos C tal que A m C vía f y B m C vía g. Entonces A B m C vía h definida como h(2x) = f (x) h(2x + 1) = g(x) 58
59 Más conjuntos indecidibles Teorema K 1 Tot := {x : ϕ x es una función total} Demostración. Definir la función parcial computable { 1 si x K g(x, y) = sino Por el Teorema del Parámetro, existe una función 1-1 computable f tal que ϕ f (x) (y) = g(x, y). x K ϕ f (x) = λy.1 f (x) Tot x / K ϕ f (x) = λy. f (x) / Tot Entonces x K sii f (x) Tot. 59
60 Teorema de Rice Definición A N es un conjunto de índices si para todo x, y, si x A y ϕ x = ϕ y entonces y A. Teorema (Rice) Si A es un conjunto de índices no trivial (i.e. A, N) entonces A no es computable. Demostración. Sea b tal que ( x) ϕ b (x). Supongamos que b A y probemos que K 1 A (del mismo modo, si b A entonces K 1 A). Como A, sea a A. Como A es un conjunto de índices, ϕ a ϕ b. Por el TR, sea f una función computable 1-1 tal que { ϕ a (y) si x K ϕ f (x) (y) = si no x K ϕ f (x) = ϕ a f (x) A x K ϕ f (x) = ϕ b f (x) A 60
61 Permutaciones computables Definición Una permutación computable es una función N N computable biyectiva. Una propiedad es computablemente invariante si es invariante bajo cualquier permutación computable. Ejemplos de propiedades computablemente invariantes: A es c.e. #A = n A es computable Ejemplos de propiedades no computablemente invariantes: 2 A A contiene solo números pares A es un conjunto de índices Definición A es computablemente isomorfo a B (A B) si hay una permutación computable p tal que A = p(b). Es decir, x A sii p(x) B. 61
62 Teorema de Isomorfismo de Myhill Teorema A B sii A 1 B. Demostración Trivial. Sea A 1 B vía f y B 1 A vía g. Definimos permutación computable h por etapas. h = s h s. h 0 =. Cada h s es finita, 1-1, y cumple x A sii h s (x) B para x dom h s Paso 1: f (0) = 2 h1 (0) = 2 Paso 2: g(0) = 1 h 1 2 (0) = 1 o sea h 2(1) = 0 Paso 3: h3 (1) ya está definido: h 3 (1) = h 2 (1) = 0 Paso 4: g(1) = 4 h 1 4 (1) = 4 Paso 5: f (2) = 1 f (4) = 3 h5 (2) = f h 1 1 f (1) = 3 62
63 Formalizamos la demostración de Supongamos definida h s y definamos h s+1 de esta manera: si s + 1 = 2x + 1, definir h s+1 (x). Si h s (x) está definido, no hacer nada. Si no, enumerar {f (x), f (hs 1 f (x)),..., f (hs 1 f ) n (x),... } hasta encontrar el primer y / rg h s. Definir h s+1 (x) = y. Observar que h s+1 es finita, 1-1 y x A sii y B. si s + 1 = 2x + 2, definir h 1 (x) de forma similar, cambiando f g hs hs 1 dom hs rg h s Vamos a clasificar conjuntos módulo permutaciones computable (lo mismo pasa en algebra: clasifica estructuras módulo isomorfismo). 63
64 Cilindros Definición A es un cilindro si A B N para algún B. Teorema 1. A 1 A N 2. A N m A (por lo tanto A m A N) 3. A es un cilindro sii ( B) [B m A B 1 A] 4. A m B sii A N 1 B N Demostración 1. Ejercicio. 2. Ejercicio. 64
65 3. A es un cilindro sii ( B) [B m A B 1 A]: Sea A C N y supongamos que B m A. Entonces B m C vía alguna función computable f. Sea g(x) = f (x), x. g es 1-1 x B sii g(x) C N Entonces B 1 C N 1 A. De 2 sabemos que A N m A. Por hipótesis, A N 1 A. De 1 sabemos A 1 A N. Luego A 1 A N. Por Teorema de Isomorfismo, A A N, de modo que A es un cilindro. 4. A m B sii A N 1 B N: Supongamos A m B. Entonces A N m A m B 1 B N. Luego A N m B N. Por 3 (y porque B N es trivialmente un cilindro), A N 1 B N. Supongamos que A N 1 B N. Tenemos A 1 A N 1 B N m B. 65
66 Teoría de la Computabilidad Clase 3 Conjuntos 1-completos, conjuntos productivos y creativos 66
67 Conjuntos 1-completos Definición Un conjunto c.e. A es r-completo (r {1, m}) si W e r A para todo e. Recordar Proposición K 0 es 1-completo. Demostración. x W e sii e, x K 0. K 0 := { x, y : ϕ x (y) }. Como K es c.e., tenemos K 1 K 0 (esto ya lo habíamos probado por otro lado antes). 67
68 K 1 K 0 Ya vimos K 1 K 0. Proposición K 0 1 K. Demostración. Misma idea que demostración de K 1 Tot funciona. Definir la función parcial computable { 1 si x K 0 g(x, z) = sino Por el Teorema del Parámetro, existe una función 1-1 computable f tal que ϕ f (x) (z) = g(x, z). x K 0 ϕ f (x) = λz.1 f (x) K x / K 0 ϕ f (x) = λz. f (x) / K Entonces x K 0 sii f (x) K. 68
69 K, K 0 y K 1 son 1-completos Definición K 1 := {x : W x }. Proposición K 1 K 1. Demostración. Ejercicio. Como K 1 es c.e. y K 0 es 1-completo, K 1 1 K 0. Ya habíamos visto K 1 K 0 y K 1 K 1. Entonces K 1 K 0 1 K 1 Corolario K, K 0 y K 1 son 1-completos. 69
70 Conjuntos productivos y creativos Una forma de ver que K no es c.e. es el hecho de que dado el índice de un conjunto W c.e. incluido en K uno puede obtener un número que está en K pero no en W : Definición W x K x K \ W x. Un conjunto P es productivo si existe una función parcial computable ψ, llamada función productiva para P, tal que ( x)[w x P [ψ(x) ψ(x) P \ W x ]]. Un conjunto C es creativo si es c.e. y C es productivo. Por ejemplo, K es creativo vía la identidad ψ(x) = x. Idea: un conjunto C es creativo si es efectivamente no computable: para cualquier candidato W x para C, ψ(x) es un contraejemplo efectivo. 70
71 Conjuntos productivos Proposición Cualquier conjunto productivo es productivo vía una función total. Demostración. Sea P productivo vía ψ. Por el TP, sea g computable tal que { 1 si ψ(x) ϕ x (y) ϕ g(x) (y) = si no Entonces W g(x) = { W x si ψ(x) si no Definir q(x) como ψ(x) o ψ(g(x)), la que converja primero. W x P ψ(x) W g(x) = W x P es productivo vía q q es total: ψ(x) q(x) ψ(x) Wg(x) = P ψ(g(x)) q(x) 71
72 Conjuntos productivos Proposición Cualquier conjunto productivo es productivo vía una función 1-1 total. Demostración Sea P productivo vía q total. Veamos cómo convertir q en p 1-1. Sea h computable tal que { 1 si ϕ x (y) y = q(x) ϕ h(x) (y) = si no Tenemos W h(x) = W x {q(x)}. Observar que W x P W h(x) P ( n) W h (n) (x) P y W h (n) (x) = W x {q(x), qh(x),..., qh (n 1) (x)} 72
73 Transformamos q total en p total y 1-1. Definimos p(0), p(1),... en ese orden. Definir p(0) = q(0). Para x > 0, computar p(x) así: enumerar {q(x), qh(x), qh (2) (x),... } hasta que ocurre alguno de estos dos casos: 1. algún qh (n) (x) / {p(0),..., p(x 1)}. Definir p(x) = qh (n) (x). supongamos W x P. Como W h (n) (x) P entonces p(x) = qh (n) (x) P \ W h (n) (x) P \ W x 2. existe m < n tal que qh (m) (x) = qh (n) (x) Veamos que Wx P: Supongamos W x P W x P (mismo argumento de arriba) ( k) qh (k) (x) P \ W h (k) (x) En particular, qh (n) (x) P \ W h (x). (n) Pero qh (m) (x) W h (n) (x) por definición. Absurdo. Entonces da lo mismo cómo definir p(x). Basta con que sea un número adecuado para que p no deje de ser 1-1. Por ejemplo, p(x) = mín{y : y / {p(0),..., p(x 1)}}. 73
74 Conjuntos Productivos Teorema Si P es productivo entonces 1. P no es c.e. 2. P contiene un conjunto c.e. infinito W 3. si P m A entonces A es productivo Demostración 1. Inmediato (ejercicio). 2. Sea P productivo vía p total y 1-1. Sea W n =. Por TP sea h 1-1 tal que W h(x) = W x {p(x)}. Definir W = {p(n), ph(n), ph (2) (n),... } W es c.e. W es infinito porque p y h son 1-1 W P porque P es productivo vía p (ver observación p. 72) 74
75 3. Sea P m A vía f. Sea P productivo vía p total. Sea g computable tal que { 0 si f (y) W x ϕ g(x) (y) = si no Tenemos W g(x) = f 1 (W x ) = {y : f (y) W x } Veamos que A es productivo vía fpg: W x A f 1 (W x ) f 1 (A) como x P f (x) A, entonces f 1 (A) P entonces Wg(x) P luego pg(x) P \ Wg(x) veamos que fpg(x) A \ Wx : pg(x) P fpg(x) A pg(x) / W g(x) fpg(x) / W x 75
76 Productivo implica 1 K Teorema Si P es productivo entonces K 1 P. Demostración. Sea P productivo vía p total y 1-1. Por TP definir f computable tal que { {p(x)} si y K W f (x,y) = si no Por TR con parámetros, existe una función computable n 1-1 tal que { {pn(y)} si y K W n(y) = W f (n(y),y) = si no y K W n(y) = {pn(y)} W n(y) P pn(y) P y K W n(y) = W n(y) P pn(y) P Entonces K 1 P vía λy.pn(y). 76
77 Creativo implica 1-completo Corolario Si C es creativo, entonces C es 1-completo. Demostración. C es c.e. y C es productivo. Entonces por teorema anterior K 1 C. Entonces K 1 C. Como K es 1-completo, C es 1-completo. 77
78 Equivalencias Corolario Los siguientes son equivalentes: 1. P es productivo 2. K 1 P 3. K m P Demostración. 1 2 sale de teorema de pág es trivial. 3 1 sale del hecho de que K es productivo y teorema de pág. 74. Corolario Los siguientes son equivalentes: 1. C es creativo 2. C es 1-completo 3. C es m-completo 78
79 Teoría de la Computabilidad Clase 4 Reducibilidad tt, cómputos con oráculo, principio del uso 79
80 Tablas de verdad Definición Una tabla de verdad k-aria es una función {0, 1} k {0, 1}. Un par x, α, x N k y α una tabla de verdad k-aria es una tt-condición Una tt-condición (x 1,..., x n ), α es satisfecha por A si α(a(x 1 ),..., A(x k )) = 1. Por ejemplo, α = (n, m), α es satisfecha por A sii n A y m A Las tablas de verdad son objetos finitos. Las tt-condiciones también. Suponemos una codificación de las tt-condiciones con N. 80
81 Reducibilidad tabla de verdad (truth table) Sabemos que K, K y K K están en clases m distintas. Pero intuitivamente son interreducibles. Definición A es truth table reducible a B (A tt B) si hay una función computable f tal que para todo x x A sii la tt-condición (codificada por) f (x) es satisfecha por B Por ejemplo, para todo A: A tt A vía la función f (x) que codifica la tt-condición x, α, donde α(0) = 1, α(1) = 0. A tt A A vía la función f (x) que codifica la tt-condición 2x + 1, α, donde α(0) = 0, α(1) = 1. A A tt A vía f (2x) = x, α, donde α(0) = 0, α(1) = 1; f (2x + 1) = x, α, donde α(0) = 1, α(1) = 0. 81
82 Propiedades de tt Definición A tt B si A tt B y B tt A. Definición Un conjunto c.e. A es tt-completo si W e tt A para todo e. Teorema 1. A m B A tt B 2. A tt A (por lo tanto A tt A) 3. tt forma un semiretículo superior 4. Si A tt B y B computable, entonces A es computable 5. Si A es computable entonces ( B) A tt B Demostración. Ejercicio. 82
83 tt tampoco alcanza Consideremos C = {x : ϕ x (x) y la tt-condición ϕ x (x) es satisfecha por K} Intuitivamente C es reducible a K, es decir pero... Proposición C tt K. C intuitivamente K, Demostración. Supongamos C tt K. Entonces C tt K vía ϕ e total. e C sii ϕ e (e) es satisfecho por K porque C tt K sii e C por definición de C 83
84 Máquinas de Turing una cinta dividida en celdas infinita en ambas direcciones cada celda contiene un símbolo de un alfabeto dado Σ. Σ L, R / Σ representa el blanco en una celda L y R son símbolos reservados (representarán acciones que puede realizar la cabeza) una cabeza lee y escribe un símbolo a la vez se mueve una posición a la izquierda o una posición a la derecha una tabla finita de instrucciones dice qué hacer en cada paso 84
85 Máquinas de Turing Una máquina de Turing (determinística) es una tupla donde (Σ, Q, δ, q 0, q f ) Σ (finito) es el conjunto símbolos (Fijamos Σ = {, 1}) Q (finito) es el conjunto de estados tiene dos estados distinguidos: q 0 Q es el estado inicial q f Q es el estado final δ : Q Σ Q Σ {R, L} es la tabla de instrucciones o programa va a ser finita porque Σ y Q lo son δ(q, s) = (q, s, d) se interpreta como Si la máquina está en el estado q leyendo en la cinta el símbolo s, entonces escribe s sobre s, se mueve hacia la izquierda si d = L o derecha si d = R, y pasa al estado q 85
86 Máquinas de Turing con oráculo Es una Máquina de Turing con una cinta adicional que es solo de lectura. la nueva cinta se llama cinta oracular (fijamos Σ = {, 0, 1}) la vieja cinta se llama cinta de trabajo y funciona igual que antes (fijamos Σ = {, 1}) La nueva tabla de instrucciones o programa de una máquina de Turing oracular es una función δ : Q Σ Σ Q Σ {R, L} δ(q, s, x) = (q, s, d) se interpreta como Si la máquina está en el estado q leyendo en la cinta el símbolo s y en la cinta oracular está el símbolo x, entonces escribe s sobre s en la cinta de trabajo, pasa al estado q y se mueve hacia la izquierda si d = L o derecha si d = R en ambas cintas 86
87 Enumeración de máquinas con oráculo Igual que antes, los programas se pueden enumerar: Φ e es el e-ésimo programa, o la e-ésima máquina de Turing oracular. Φ e necesita dos entradas una entrada finita x 1,..., x n para la cinta de trabajo una entrada posiblemente infinita A N para la cinta oracular Se suele escribir Φ A e (x 1,..., x n ) para referirse a la e-ésima máquina de Turing oracular con oráculo A y entrada x 1,..., x n. 87
88 Configuración inicial Se codifica la entrada x 1,..., x n como antes (sobre alfabeto Σ = {, 1}) el oráculo A como una lista de ceros y unos A(0), A(1), A(2)... (sobre alfabeto Σ = {, 0, 1}). Como siempre { 1 si n A A(n) = 0 si no La configuración inicial es esta:... x 1 x 2... x n... q 0... A(0) A(1) A(2) A(3)... (con los números x i representados en unario) 88
89 Cómputos relativos a oráculos Definición Una función parcial f es Turing computable en A (o A-computable), notado f T A, si existe un programa e tal que es decir: f (x 1,..., x n ) = Φ A e (x 1,..., x n ), si f (x 1,..., x n ) entonces Φ A e (x 1,..., x n ), partiendo de la configuración inicial y siguiendo sus instrucciones, llega a una configuración final de la forma... f (x 1,..., x n )... q f (quizá algo más en la cinta de trabajo; recordar que la cinta oracular es solo de lectura y se mueve a la par de la cinta de trabajo) si f (x 1,..., x n ) entonces Φ A e (x 1,..., x n ) nunca llega al estado final. 89
90 El uso En cualquier cómputo Φ A e (x 1,..., x n ) la máquina e solo mira una cantidad finta de elementos del oráculo. Sea y + 1 el máximo número de celdas no consultadas durante ese cómputo. Decimos que los elementos z y son usados en el cómputo. Definición Notamos Φ A e,s(x) = y para x, y, e < s, s > 0, si Φ A e (x) = y en < s pasos y usando solo números z < s del oráculo. Notamos Φ A e,s(x) para x, y, e < s, s > 0, si Φ A e,s(x) = y para algún y. El uso u(a, e, x, s) se define como 1+el máximo número usado u(a, e, x, s) = en el cómputo Φ A si Φ A e,s(x) e,s(x) 0 si no Para σ {0, 1}, notamos Φ σ e,s(x) = y, si Φ A e,s(x) = y para algún A σ, y solo elementos menores a σ son usados en este último cómputo. 90
91 Propiedades del uso Si Φ A e,s(x) = y entonces x, y, e < s y u(a, e, x, s) s Φ σ e,s(x) = y donde σ = A u(a, e, x, s) ( t s) [Φ A e,t(x) = y u(a, e, x, s) = u(a, e, x, t)] Habíamos definido u(a, e, x, s). Definición u(a, e, x) es u(a, e, x) = { u(a, e, x, s) si Φ A e,s(x) para algún s si no 91
92 El principio del uso (use principle) Teorema 1. Φ A e (x) = y ( s)( σ A) Φ σ e,s(x) = y 2. Φ σ e,s(x) = y ( t s)( τ σ) Φ τ e,t(x) = y 3. Φ σ e (x) = y ( A σ) Φ A e (x) = y Corolario Si Φ A e,s(x) = y y B u = A u entonces Φ B e,s(x) = y, donde u = u(a, e, x, s). 92
93 Propiedades de Φ A e y Φ σ e Teorema 1. { e, σ, x, s : Φ σ e,s(x) } es computable 2. { e, σ, x : Φ σ e (x) } es c.e. Teorema Son funciones parciales A-computables: 1. λe, s, x.φ A e,s(x) (esta no es total) { 1 si Φ A 2. λe, s, x. e,s(x) (esta es total) 0 si no 93
94 Teoría de la Computabilidad Clase 5 Teorema del Salto, Lema del Límite, grados Turing 94
95 Relativizaciones de resultados conocidos Teorema (Teorema del Parámetro Relativizado - TPR) Para cada m, n 1 existe una función primitiva recursiva 1-1 s m n de m + 1 variables tal que para todo A N y para todo y 1,..., y m, z 1,..., z n N, Φ A s m n (x,y 1,...,y m) (z 1,..., z n ) = Φ A x (y 1,..., y m, z 1,..., z n ) Teorema (Teorema de la Recursión Relativizado - TRR) Para cualquier función A-computable f : N 2 N existe una función computable n tal que Φ A n(y) = ΦA f (n(y),y). Es más, la definición de n no depende de A. Es decir, si f (x, y) = Φ A e (x, y) entonces n se puede definir uniformemente en e. 95
96 Conjuntos A-computables, A-c.e. y Σ A 1 Definición W A e = dom Φ A e W A e,s = dom Φ A e,s W σ e = dom Φ σ e W σ e,s = dom Φ σ e,s Definición B es computable en A (o A-computable), notado B T A, si B = Φ A e para algún e. notamos A T B cuando A T B y B T A notamos A <T B cuando A T B y B T A notamos degt (A) = {B : B T A} B es c.e. en A (o A-c.e. ) si B = We A para algún e B es de la forma Σ A 1 (abreviado B ΣA 1 ) cuando B = {x : ( y) R A (x, y)} para algún predicado A-computable R A. 96
97 Convención Definimos Φ A e,s de modo que Φ A e,s(x) x, e < s Si B es A-c.e., entonces B = dom Φ A e para algún e. Tenemos una A-enumeración natural de B. En general se la nota (B s ) s N y está definida como B s = dom Φ A e,s {0,..., s 1}. En realidad, B s abrevia una función A-computable b : N N tal que b(s) = codificación de B s usando N B s satisface para todo x, B(x) = ĺım s ( n)( s) B n = B s n B s (x) 97
98 Equivalencias entre A-c.e. y Σ A 1 Teorema Son equivalentes: 1. B es A-c.e. 2. B es Σ A 1 3. B = o B es el rango de alguna función A-computable Demostración 1 2 Sea B = dom Φ A e entonces B = {x : ( s) Φ A e,s(x) }. Recordar que { 1 si Φ A λe, s, x. e,s(x) 0 si no es A-computable. 98
99 2 3 Sea b B y sea B = {x : ( y) R A (x, y)}. Supongamos R A es (n + 1)-ario. Definimos la función A-computable { x si R A (x, y 1,..., y n ) f ( x, y 1,..., y n ) = b si no veamos que x B ( z) f (z) = x: x B ( y) R A (x, y) f ( x, y ) = x veamos que ( z) f (z) B: Sea z = x, y. R A (x, y) f (z) = b B R A (x, y) x B. Luego f (z) = f ( x, y ) = x B 3 1 Sea e tal que Φ A e (N) = B. Definir la función parcial { 0 si ( x, s) Φ A f (y) = e,s(x) = y si no f es parcial A-computable y dom f = B. 99
100 Relativizaciones de resultados anteriores Teorema Si B es A-computable entonces B también. Teorema Si B es A-computable entonces B es A-c.e. Teorema (Complementación) Si B y B son A-c.e. entonces B es A-computable. 100
101 El salto Recordar que Se pueden relativizar K = {x : ϕ x (x) } = {x : x W x } K 0 = { x, y : ϕ x (y) } K A = {x : Φ A x (x) } = {x : x W A x } K A 0 = { x, y : Φ A x (y) } Definición El salto (jump) de A, notado A, se define como A = K A = {x : Φ A x (x) } = {x : x W A x } A (n) es el n-esimo salto de A. Se define como A (0) = A y A (n+1) = (A (n) ). Observar que = K. Teorema K A 1 K A 0 101
102 El Teorema del Salto (TS) Teorema 1. A es A-c.e. 2. A T A 3. B es A-c.e. sii B 1 A 4. si A es B-c.e. y B T C entonces A es C-c.e. 5. B T A sii B 1 A 6. si B T A entonces B 1 A 7. A es B-c.e. sii A es B-c.e. 102
103 Demostración del Teorema del Salto 1. A es A-c.e.: La función parcial f (x) = Φ A x (x) es A-computable y dom f = A. Entonces A es A-c.e. 2. A T A: Supongamos que A es A-computable. Entonces A es A-c.e. Luego existe e tal que W A e = A = {x : x / W A x }. Entonces e We A sii e / We A. Absurdo. 3. B es A-c.e. sii B 1 A : Existe e tal que B = We A = dom Φ A e. Entonces x B sii Φ A e (x) sii x, e K0 A. Como λx. x, e es 1-1, entonces B 1 K0 A. Además, K 0 A 1 K A = A. Supongamos f computable tal que x B sii f (x) A. Entonces x B sii Φ A f (x)(f (x)). La función parcial λx.φ A f (x)(f (x)) es A-computable, entonces su dominio (que es B) es A-c.e. 103
104 Demostración del Teorema del Salto 4. si A es B-c.e. y B T C entonces A es C-c.e.: Por Teorema pág. 97, si A, A es el rango de una función f tal que f T B. Como B T C entonces f T C. Luego A es el rango de una función C-computable. 5. B T A sii B 1 A : Por TS1 B es B-c.e. Como B T A, por TS4, B es A-c.e. Por TS3, B 1 A. B, B 1 A (ejercicio). Por TS3 B y B son A-c.e. Por Teorema de Complementación (pág. 101), B T A. 6. si B T A entonces B 1 A : Directo de TS5. 7. A es B-c.e. sii A es B-c.e. Directo de TS4. 104
105 Lema del ĺımite Teorema Para toda función total f, f T A sii hay una función A-computable g de dos variables tal que f (x) = ĺım s g(x, s). Demostración Supongamos que f = Φ A e. Por TS1 A es A-c.e. Sea (A s) s N una enumeración A-computable de A. Definir: { Φ A s e,s(x) si Φ A s e,s(x) g(x, s) = 0 si no Claramente g T A. Sea t suficientemente grande tal que ( z t) [Φ A t z e,t (x) A t z = A z] Entonces para todo s t tenemos Φ A s z e,s (x) = Φ A s z e (x) = Φ A z e (x) = Φ A e (x) = f (x) Luego ĺım s g(x, s) = f (x). 105
106 Sup. f (x) = ĺım s g(x, s) para g A-computable. Definir A x = {s : ( t) [s t g(x, t) g(x, t + 1)]} A x es finito porque existe el ĺımite ĺım s g(x, s) s / A x ( t s) g(x, t) = g(x, t + 1) g(x, s) = f (x) B = { s, x : s A x } = {z : ( t) [π 1 (z) t g(π 2 (z), t) g(π 2 (z), t + 1)]} es claramente Σ A 1, luego A-c.e., luego B T A (TS). La siguiente función es B-computable: m(x) = mín{s : s / A x } = mín{s : s, x / B}. Entonces g(x, m(x)) = f (x). Como g T A T A y m T B T A entonces f A. 106
107 Grados Turing Recordar que deg T (A) = {B : A T A} Si a es un grado Turing, a = deg T (A ) para A a. Sabemos que a > T a a es c.e. en a Sea 0 (n) = deg T ( (n) ). Entonces tenemos una jerarquía de grados 0 < T 0 < T 0 < T
108 Ejemplos 0 = deg T ( ) = {B : B es computable} 0 = deg T ( ) = deg T (K) = deg T (K 0 ) = deg T (K 1 ) 0 = deg T ( ) = deg T (Tot) = deg T (Fin) 0 = deg T ( ) = deg T (Cof) = deg T (Rec) = deg T (Ext) donde Tot := {x : W x = N} = {x : Φ x es total} Fin := {x : W x es finito} Cof := {x : W x es cofinito} Rec := {x : W x es computable} Ext := {x : Φ x es extendible a una función total computable} 108
109 Teoría de la Computabilidad Clase 6 Jerarquía Aritmética, Teorema de Post, Conjuntos Σ n -completos 109
110 Conjuntos Σ n y Π n Definición Un conjunto B es Σ 0 o Π 0 sii B es computable Para n 1, un conjunto B es Σ n (notado B Σ n ) sii existe una relación computable R(x, y 1,..., y n ) tal que x B sii ( y 1 )( y 2 )( y 3 )... (Qy n ) }{{} n 1 alternancias donde Q = si n es par y Q = si n es impar. R(x, y 1,..., y n ) Para n 1, un conjunto B es Π n (notado B Π n ) sii existe una relación computable R(x, y 1,..., y n ) tal que x B sii ( y 1 )( y 2 )( y 3 )... (Qy n ) }{{} n 1 alternancias donde Q = si n es par y Q = si n es impar. R(x, y 1,..., y n ) B es n (notado B n ) sii B Σ n Π n. 110
111 Relaciones y fórmulas Σ n y Π n Definición Una relación R N k es Σ n (Π n ) si es Σ n (Π n ) el conjunto { r 1,..., r k : (r 1,..., r k ) R} Una fórmula ϕ(x 1,..., x n ) con variables libres x 1,..., x n es Σ n (Π n ) si es Σ n (Π n ) la relación Por ejemplo, {(a 1,..., a n ) : N = ϕ(a 1,..., a n )} R N 3 es Σ 2 si existe una relación R computable tal que (x, y, z) R sii ( u)( v) R (x, y, z, u, v). si R es computable, es Π 3 la siguiente fórmula: ( x)( y)( z) R(x, y, z, w) 111
112 Propiedades de Σ n y Π n Teorema 1. A Σ n A Π n 2. A Σ n (Π n ) ( m > n) A Σ m Π m 3. A, B Σ n (Π n ) A B, A B Σ n (Π n ) 4. R Σ n n > 0 A = {x : ( y) R(x, y)} A Σ n 4. R Π n n > 0 A = {x : ( y) R(x, y)} A Π n 5. B m A A Σ n (Π n ) B Σ n (Π n ) 6. Si R Σ n (Π n ) entonces están en Σ n (Π n ): A = { x, y : ( z < y) R(x, y, z)} B = { x, y : ( z < y) R(x, y, z)} 112
113 1. A Σ n A Π n : Si A = {x : ( y 1 )( y 2 )( x 3 )... R(x, y 1,..., y n )} entonces A = {x : ( y 1 )( y 2 )( y 3 )... R(x, y 1,..., y n )} 2. A Σ n (Π n ) ( m > n) A Σ m Π m : Observar que ( x 1 )( x 2 )( x 3 )... (Qx n ) R(x, x 1,..., x n ) sii ( x 0 )( x 1 )( x 2 )( x 3 )... (Qx n ) R(x, x 1,..., x n ) }{{} R (x,x 0,x 1,...,x n) sii ( x 1 )( x 2 )( x 3 )... (Qx n )( Qx n+1 ) R(x, x 1,..., x n ) }{{} R (x,x 1,...,x n,x n+1 ) donde Q = si Q = y viceversa. Lo mismo para fórmulas Π n. 113
114 3. A, B Σ n (Π n ) A B, A B Σ n (Π n ): Supongamos Entonces x A sii ( y 1 )( y 2 )... R(x, y) x B sii ( z 1 )( z 2 )... S(x, z) x A B sii ( y 1 )( y 2 )... R(x, y) ( z 1 )( z 2 )... S(x, z) sii sii ( y 1 )( z 1 )( y 2 )( z 2 )... R(x, y) S(x, z) ( u 1 )( u 2 )... R(x, π 1 (u 1 ), π 1 (u 2 ),... ) S(x, π 2 (u 1 ), π 2 (u 2 ),... ) El mismo truco para A B y para Π n. 114
115 4. R Σ n n > 0 A = {x : ( y) R(x, y)} A Σ n Supongamos Entonces (x, y) R sii ( z 1 )( z 2 )... R (x, y, z 1, z 2,... ). x A sii ( y) R(x, y) sii ( y)( z 1 )( z 2 )... R (x, y, z 1, z 2,... ) sii ( u)( z 2 )... R (x, π 1 (u), π 1 (u), z 2,... ) 4. R Π n n > 0 A = {x : ( y) R(x, y)} A Π n Análogo a B m A A Σ n (Π n ) B Σ n (Π n ) Sea A = {x : ( y 1 )( y 2 )... R(x, y)} y sea B m A via f. Entonces B = {x : ( y 1 )( y 2 )... R(f (x), y) } }{{} computable Lo mismo para el caso Π n. 115
116 6. Si R Σ n (Π n ) entonces están en Σ n (Π n ): A = { x, y : ( z < y) R(x, y, z)} B = { x, y : ( z < y) R(x, y, z)} Por inducción en n. Si n = 0, A y B son computables. Sea n > 0 y supongamos cierta la propiedad para todo < n. Supongamos R Σ n. Por 4, B Σ n. Existe S Π n 1 tal que Entonces R(x, y, z) sii ( u) S(x, y, z, u). x, y A sii ( z < y) R(x, y, z) sii ( z < y)( u) S(x, y, z, u) sii donde σ se interpreta como una y-upla. Por HI ( σ)( z < y) S(x, y, z, π z (σ)) { x, y, σ : ( z < y) S(x, y, z, π z (σ))} Π n 1. Entonces A Σ n. El caso R Π n es análogo. 116
117 Ejemplos Proposición Fin Σ 2. Demostración. x Fin sii W x es finito sii Proposición Cof Σ 3. Fin := {x : W x es finito} Cof := {x : W x es cofinito} ( s)( t) [t > s Demostración. x Cof sii W x es finito sii computable {}}{ W x,s = W x,t ] ( y)( z) [z > y z W x ] sii ( y)( z)( s) [z > y computable {}}{ z W x,s ] 117
118 Conjuntos Σ n y Π n -completos y Teorema de Post (TP) Definición Un conjunto A es Σ n -completo (Π n -completo) si A Σ n (Π n ) y B 1 A para todo B Σ n (Π n ). Teorema (Post) Para todo n 0: 1. B Σ n+1 sii B es c.e. en algún conjunto Π n sii B es c.e. en algún conjunto Σ n 2. (n) es Σ n -completo, para n > 0 3. B Σ n+1 sii B es c.e. en (n) 4. B n+1 sii B T (n) 118
119 1. B Σ n+1 sii B es c.e. en algún conjunto Π n sii B es c.e. en algún conjunto Σ n : Habíamos visto que B es C-c.e. sii B es C-c.e. (TS 7). El último sii sale de ahí. Veamos el primer sii : Sea B Σ n+1. Entonces existe R Π n tal que x B sii ( y) R(x, y) Entonces B es Σ R 1 y por lo tanto B es R-c.e. Supongamos que B es C-c.e. para C Π n. Entonces existe un e tal que x B sii x We C sii ( s)( σ) [σ C x We,s σ ] }{{} computable Basta ver que σ C es Σ n+1 σ C sii ( i < σ ) [σ(i) = C(i)] sii ( i < σ ) [[σ(i) = 1 i C] [σ(i) = 0 i / C]] }{{}}{{} Π n Σ n Sabemos Π n, Σ n Σ n+1 y que Σ n+1 Σ n+1 Σ n+1. Como el externo está acotado, C Σ n
120 2. (n) es Σ n -completo, para n > 0: Por inducción en n. Es claro que vale para n = 1. Supongamos (n) es Σ n -completo. B Σ n+1 sii B es c.e. en algún C Σ n por TP1 sii B es c.e. en (n) por HI, C 1 (n) sii B 1 (n+1) por TS3 3. B Σ n+1 sii B es c.e. en (n) : B Σ n+1 sii B es c.e. en algún conjunto Σ n por TP1 sii B es c.e. en (n) por TP2 4. B n+1 sii B T (n) : B n+1 sii B, B Σ n+1 sii B, B son c.e. en (n) por TP3 sii B T (n) 120
121 Jerarquía estricta Sabemos Π n, Σ n m<n Σ m Π m Π n, Σ n n Corolario Si n > 0 entonces n Π n, Σ n. Demostración. (n) Σ n. Supongamos que (n) n. Por TP4 (n) T (n 1) y esto contradice TS2. Entonces (n) Σ n \ n. Análogamente (n) Π n \ n. 121
122 Ejemplo Proposición Fin es Σ 2 -completo. Demostración. Ya vimos que Fin Σ 2. Sea A Σ 2 y veamos A 1 Fin. Por definición x A sii ( y)( z) R(x, y, z). Por el Teorema del Parámetro, existe f computable 1-1 tal que { 0 si ( y u) ( z) R(x, y, z) ϕ f (x) (u) = si no Tenemos si x A entonces existe y tal que no es cierto ( z) R(x, y, z). Luego, no es cierto ( y u) ( z) R(x, y, z) para u y. Entonces W f (x) es finito, o sea f (x) Fin. x A W f (x) = N f (x) / Fin 122
Sumatorias y productorias (desde 0) Lógica y Computabilidad. Sumatorias y productorias (desde 1)
 Lógica y Computabilidad Verano 2011 Departamento de Computación - FCEyN - UBA Computabilidad - clase 3 Sumatorias y productorias, cuantificadores acotados, minimización acotada, codificación de pares y
Lógica y Computabilidad Verano 2011 Departamento de Computación - FCEyN - UBA Computabilidad - clase 3 Sumatorias y productorias, cuantificadores acotados, minimización acotada, codificación de pares y
Lenguaje de programación S (Davis/Sigal/Weyuker) Lógica y Computabilidad. Ejemplo 1. Ejemplo 2
 Lógica y Computabilidad Verano 2011 Departamento de Computación - FCEyN - UBA Computabilidad - clase 4 Lenguaje S, estado, descripción instantánea, cómputo, funciones parciales computables, minimización
Lógica y Computabilidad Verano 2011 Departamento de Computación - FCEyN - UBA Computabilidad - clase 4 Lenguaje S, estado, descripción instantánea, cómputo, funciones parciales computables, minimización
Tipos de datos en S. Lógica y Computabilidad. Codificación de variables y etiquetas de S. Codificación de programas en S
 Tipos de datos en S Lógica y Computabilidad Verano 2011 Departamento de Computación - FCEyN - UBA Computabilidad - clase 5 Codificación de programas, Halting problem, diagonalización, tesis de Church,
Tipos de datos en S Lógica y Computabilidad Verano 2011 Departamento de Computación - FCEyN - UBA Computabilidad - clase 5 Codificación de programas, Halting problem, diagonalización, tesis de Church,
Lógica y Computabilidad
 Lógica y Computabilidad Santiago Figueira Departamento de Computación, FCEyN, UBA verano 2015 1 Contenido - Computabilidad 1. Introducción, máquinas de Turing, funciones parciales, funciones Turing computables,
Lógica y Computabilidad Santiago Figueira Departamento de Computación, FCEyN, UBA verano 2015 1 Contenido - Computabilidad 1. Introducción, máquinas de Turing, funciones parciales, funciones Turing computables,
1. Programas y funciones computables
 Computabilidad 1 Índice 1. Programas y funciones computables 3 1.1. El lenguaje S........................................... 3 1.2. Programas de S......................................... 3 1.3. Macros...............................................
Computabilidad 1 Índice 1. Programas y funciones computables 3 1.1. El lenguaje S........................................... 3 1.2. Programas de S......................................... 3 1.3. Macros...............................................
Resumen de aritmética de Peano
 Resumen de aritmética de Peano UDELAR/FING/IMERL 16 de febrero de 2017 1. Fundamentos de la Aritmética de Peano. Axioma 1.1. Existe un conjunto al que denotamos N, un elemento 0 N y una función s : N N
Resumen de aritmética de Peano UDELAR/FING/IMERL 16 de febrero de 2017 1. Fundamentos de la Aritmética de Peano. Axioma 1.1. Existe un conjunto al que denotamos N, un elemento 0 N y una función s : N N
Tema 5: Programas Universales
 Tema 5: Programas Universales Dpto. Ciencias de la Computación e Inteligencia Artificial Universidad de Sevilla Lógica y Computabilidad Curso 2006 07 LC, 2006 07 Programas universales 5.1 Procedimientos
Tema 5: Programas Universales Dpto. Ciencias de la Computación e Inteligencia Artificial Universidad de Sevilla Lógica y Computabilidad Curso 2006 07 LC, 2006 07 Programas universales 5.1 Procedimientos
a partir de otras funciones. Entonces C es la menor clase de funciones que contiene a las funciones básicas y es cerrada por los p. d.
 Tema 3: Funciones Primitivas Recursivas Caracterización de clases de funciones: Maneras básicas de definir una clase de funciones C: Descriptiva: C satisface ciertas propiedades. (Ejemplo: la clase GCOMP)
Tema 3: Funciones Primitivas Recursivas Caracterización de clases de funciones: Maneras básicas de definir una clase de funciones C: Descriptiva: C satisface ciertas propiedades. (Ejemplo: la clase GCOMP)
Conjuntos c.e., co-c.e. y otras yerbas
 1/19 Conjuntos c.e., co-c.e. y otras yerbas Conjuntos c.e., co-c.e. y otras yerbas Ariel Bendersky Febrero 2018 2/19 Conjuntos c.e., co-c.e. y otras yerbas Conjuntos y función característica - Mini repaso
1/19 Conjuntos c.e., co-c.e. y otras yerbas Conjuntos c.e., co-c.e. y otras yerbas Ariel Bendersky Febrero 2018 2/19 Conjuntos c.e., co-c.e. y otras yerbas Conjuntos y función característica - Mini repaso
Teorema de Compacidad
 Teorema de Compacidad Seminario de Teoría de Modelos - FCEyN - UBA 1 de septiembre de 2011 Teorema 1 (Compacidad). Una L-teoría T es satisfacible si y solo si todo subconjunto finito de T es satisfacible.
Teorema de Compacidad Seminario de Teoría de Modelos - FCEyN - UBA 1 de septiembre de 2011 Teorema 1 (Compacidad). Una L-teoría T es satisfacible si y solo si todo subconjunto finito de T es satisfacible.
Tema 5: Funciones recursivas
 Tema 5: Funciones recursivas Dpto. Ciencias de la Computación e Inteligencia Artificial Universidad de Sevilla Lógica y Computabilidad Curso 2005 06 LC, 2005 06 Funciones Recursivas 5.1 Procedimientos
Tema 5: Funciones recursivas Dpto. Ciencias de la Computación e Inteligencia Artificial Universidad de Sevilla Lógica y Computabilidad Curso 2005 06 LC, 2005 06 Funciones Recursivas 5.1 Procedimientos
1. Conjuntos y funciones
 Centro de Matemática Facultad de Ciencias Universidad de la República Introducción a la Topología Curso 2016 PRACTICO 1: CONJUNTOS. 1 1. Conjuntos y funciones Ejercicio 1. Si I es un conjunto y A α es
Centro de Matemática Facultad de Ciencias Universidad de la República Introducción a la Topología Curso 2016 PRACTICO 1: CONJUNTOS. 1 1. Conjuntos y funciones Ejercicio 1. Si I es un conjunto y A α es
sup si A no es acotado.
 Capítulo 5 Teoría de Baire 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y la
Capítulo 5 Teoría de Baire 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y la
Terminaremos el capítulo con una breve referencia a la teoría de cardinales.
 TEMA 5. CARDINALES 241 Tema 5. Cardinales Terminaremos el capítulo con una breve referencia a la teoría de cardinales. Definición A.5.1. Diremos que el conjunto X tiene el mismo cardinal que el conjunto
TEMA 5. CARDINALES 241 Tema 5. Cardinales Terminaremos el capítulo con una breve referencia a la teoría de cardinales. Definición A.5.1. Diremos que el conjunto X tiene el mismo cardinal que el conjunto
Entscheidungsproblem I TEORÍA DE LA COMPUTACIÓN MÁQUINAS DE TURING Y DECIDIBILIDAD. Máquinas de Turing (TM) Procedimiento efectivo
 Entscheidungsproblem I TEORÍA DE LA COMPUTACIÓN MÁQUINAS DE TURING Y DECIDIBILIDAD Francisco Hernández Quiroz Departamento de Matemáticas Facultad de Ciencias, UNAM E-mail: fhq@ciencias.unam.mx Página
Entscheidungsproblem I TEORÍA DE LA COMPUTACIÓN MÁQUINAS DE TURING Y DECIDIBILIDAD Francisco Hernández Quiroz Departamento de Matemáticas Facultad de Ciencias, UNAM E-mail: fhq@ciencias.unam.mx Página
Introducción a la complejidad computacional
 Introducción a la complejidad computacional definida sobre anillos arbitrarios 18 de junio de 2016 Fuente: http://www.utmmcss.com/ Por qué otro modelo? Continuo vs discreto. Intuición interiorizada del
Introducción a la complejidad computacional definida sobre anillos arbitrarios 18 de junio de 2016 Fuente: http://www.utmmcss.com/ Por qué otro modelo? Continuo vs discreto. Intuición interiorizada del
Entscheidungsproblem I LENGUAJES RECURSIVAMENTE ENUMERABLES MÁQUINAS DE TURING. DECIDIBILIDAD. Máquinas de Turing (TM) Procedimiento efectivo
 Entscheidungsproblem I LENGUAJES RECURSIVAMENTE ENUMERABLES MÁQUINAS DE TURING. DECIDIBILIDAD Francisco Hernández Quiroz Departamento de Matemáticas Facultad de Ciencias, UNAM E-mail: fhq@ciencias.unam.mx
Entscheidungsproblem I LENGUAJES RECURSIVAMENTE ENUMERABLES MÁQUINAS DE TURING. DECIDIBILIDAD Francisco Hernández Quiroz Departamento de Matemáticas Facultad de Ciencias, UNAM E-mail: fhq@ciencias.unam.mx
Teorema de incompletitud de Gödel
 Teorema de incompletitud de Gödel Theorem (Gödel) Th(N) es una teoría indecidible. IIC2213 Teorías 79 / 109 Teorema de incompletitud de Gödel Theorem (Gödel) Th(N) es una teoría indecidible. Corolario
Teorema de incompletitud de Gödel Theorem (Gödel) Th(N) es una teoría indecidible. IIC2213 Teorías 79 / 109 Teorema de incompletitud de Gödel Theorem (Gödel) Th(N) es una teoría indecidible. Corolario
Lenguajes de primer orden. Lógica y Computabilidad. símbolos lógicos y auxiliares: x ( ) Segundo cuatrimestre 2011
 Lenguajes de primer orden Lógica y Computabilidad Segundo cuatrimestre 2011 Departamento de Computación - FCEyN - UBA Lógica de Primer Orden - clase 1 Lenguaje de lógica de primer orden, términos, fórmulas,
Lenguajes de primer orden Lógica y Computabilidad Segundo cuatrimestre 2011 Departamento de Computación - FCEyN - UBA Lógica de Primer Orden - clase 1 Lenguaje de lógica de primer orden, términos, fórmulas,
El lenguaje P. Lógica y Computabilidad ( ) símbolos p. Verano convenciones. Lógica Proposicional - clase 1
 Lógica y Computabilidad Verano 2011 Departamento de Computación - FCEyN - UBA Lógica Proposicional - clase 1 Lenguaje de lógica proposicional, semántica, tautología, consecuencia semántica, conjunto satisfacible,
Lógica y Computabilidad Verano 2011 Departamento de Computación - FCEyN - UBA Lógica Proposicional - clase 1 Lenguaje de lógica proposicional, semántica, tautología, consecuencia semántica, conjunto satisfacible,
Clase práctica 8: Funciones Primitivas Recursivas
 Clase práctica 8: Funciones Primitivas Recursivas Laski (inspirado en Facundo Carreiro y Hernán Czemerinski) Primer Cuatrimestre 2014 1 Repaso de la teórica Para probar que una función es primitiva recursiva
Clase práctica 8: Funciones Primitivas Recursivas Laski (inspirado en Facundo Carreiro y Hernán Czemerinski) Primer Cuatrimestre 2014 1 Repaso de la teórica Para probar que una función es primitiva recursiva
1. Conjuntos y funciones
 PRACTICO 1: CONJUNTOS. 1. Conjuntos y funciones Es útil saber de memoria las siguientes propiedades de conjuntos y funciones. Tanto como saber las tablas. Ejercicio 1. Si I es un conjunto y A α es un conjunto
PRACTICO 1: CONJUNTOS. 1. Conjuntos y funciones Es útil saber de memoria las siguientes propiedades de conjuntos y funciones. Tanto como saber las tablas. Ejercicio 1. Si I es un conjunto y A α es un conjunto
diám A = x,y A d(x,y) si A es acotado si A no es acotado. {d(x,y) : x,y A}
 Capítulo 6 Teoría de Baire 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y la
Capítulo 6 Teoría de Baire 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y la
Universidad Central de Venezuela Facultad de Ciencias Escuela de Computación. Lecturas en Ciencias de la Computación ISSN
 Universidad Central de Venezuela Facultad de Ciencias Escuela de Computación Lecturas en Ciencias de la Computación ISSN 1316-6239 Relaciones Prof. Luis Manuel Hernández R. ND 2006-02 Centro de Cálculo
Universidad Central de Venezuela Facultad de Ciencias Escuela de Computación Lecturas en Ciencias de la Computación ISSN 1316-6239 Relaciones Prof. Luis Manuel Hernández R. ND 2006-02 Centro de Cálculo
Conjuntos, relaciones y funciones Susana Puddu
 Susana Puddu 1. Repaso sobre la teoría de conjuntos. Denotaremos por IN al conjunto de los números naturales y por ZZ al de los enteros. Dados dos conjuntos A y B decimos que A está contenido en B o también
Susana Puddu 1. Repaso sobre la teoría de conjuntos. Denotaremos por IN al conjunto de los números naturales y por ZZ al de los enteros. Dados dos conjuntos A y B decimos que A está contenido en B o también
sup si A no es acotado.
 Capítulo 6 Espacios completos 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y
Capítulo 6 Espacios completos 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y
Ejercicios resueltos. Computación. Tema 4
 Ejercicios resueltos. omputación. Tema 4 Ejercicio.-Sea P un programa GOT O tal que #(P ) = 16. a) uántas instrucciones tiene P? b) Dar todas las instrucciones de P. c) Generalizar el resultado anterior
Ejercicios resueltos. omputación. Tema 4 Ejercicio.-Sea P un programa GOT O tal que #(P ) = 16. a) uántas instrucciones tiene P? b) Dar todas las instrucciones de P. c) Generalizar el resultado anterior
Capítulo V: CONJUNTOS RECURSIVAMENTE ENUMERABLES
 Capítulo V: CONJUNTOS RECURSIVAMENTE ENUMERABLES Mario de J. Pérez Jiménez Grupo de investigación en Computación Natural Dpto. Ciencias de la Computación e Inteligencia Artificial Universidad de Sevilla
Capítulo V: CONJUNTOS RECURSIVAMENTE ENUMERABLES Mario de J. Pérez Jiménez Grupo de investigación en Computación Natural Dpto. Ciencias de la Computación e Inteligencia Artificial Universidad de Sevilla
Derivada de la función compuesta. Regla de la cadena
 Derivada de la función compuesta. Regla de la cadena Cuando en las matemáticas de bachillerato se introduce el concepto de derivada, su significado y su interpretación geométrica, se pasa al cálculo de
Derivada de la función compuesta. Regla de la cadena Cuando en las matemáticas de bachillerato se introduce el concepto de derivada, su significado y su interpretación geométrica, se pasa al cálculo de
Pauta 11 : Conjuntos Infinitos
 MA1101-5 Introducción al Álgebra Profesor: Mauricio Telias Auxiliar: Arturo Merino P1. [Varios de numerabilidad] a) Considere el conjunto Pauta 11 : Conjuntos Infinitos 2 de junio del 2017 C = {..., 16,
MA1101-5 Introducción al Álgebra Profesor: Mauricio Telias Auxiliar: Arturo Merino P1. [Varios de numerabilidad] a) Considere el conjunto Pauta 11 : Conjuntos Infinitos 2 de junio del 2017 C = {..., 16,
Introducción a la indecidibilidad
 Introducción a la indecidibilidad José M. empere Departamento de istemas Informáticos y Computación Universidad Politécnica de Valencia Lenguajes y problemas Un problema será considerado cualquier cuestión
Introducción a la indecidibilidad José M. empere Departamento de istemas Informáticos y Computación Universidad Politécnica de Valencia Lenguajes y problemas Un problema será considerado cualquier cuestión
Estructuras Discretas. Conjuntos. Conjuntos & Funciones. Especificación de Conjuntos.
 Estructuras Discretas Conjuntos Conjuntos & Funciones Claudio Lobos clobos@inf.utfsm.cl niversidad Técnica Federico Santa María Estructuras Discretas INF 152 Definición: conjunto n conjunto es una colección
Estructuras Discretas Conjuntos Conjuntos & Funciones Claudio Lobos clobos@inf.utfsm.cl niversidad Técnica Federico Santa María Estructuras Discretas INF 152 Definición: conjunto n conjunto es una colección
Tema 5: Procedimientos para obtener funciones computables
 Tema 5: Procedimientos para obtener funciones computables Dpto. Ciencias de la Computación e Inteligencia Artificial Universidad de Sevilla Lógica y Computabilidad Curso 2010 11 LC, 2010 11 Procedimientos
Tema 5: Procedimientos para obtener funciones computables Dpto. Ciencias de la Computación e Inteligencia Artificial Universidad de Sevilla Lógica y Computabilidad Curso 2010 11 LC, 2010 11 Procedimientos
COMPACIDAD Y COMPLETITUD: DOS TEOREMAS CLÁSICOS DE LA TEORÍA DE MODELOS
 COMPACIDAD Y COMPLETITUD: DOS TEOREMAS CLÁSICOS DE LA TEORÍA DE MODELOS JOEL TORRES DEL VALLE 1 1 Universidad Cartagena Resumen. Se presentan dos teoremas clásicos de la Teoría de Modelos: Teorema de La
COMPACIDAD Y COMPLETITUD: DOS TEOREMAS CLÁSICOS DE LA TEORÍA DE MODELOS JOEL TORRES DEL VALLE 1 1 Universidad Cartagena Resumen. Se presentan dos teoremas clásicos de la Teoría de Modelos: Teorema de La
Integración de Funciones Reales
 Capítulo 20 Integración de Funciones Reales Nos proponemos estudiar en este capítulo las propiedades fundamentales del operador integral. n particular, extenderemos aquí al caso de funciones medibles con
Capítulo 20 Integración de Funciones Reales Nos proponemos estudiar en este capítulo las propiedades fundamentales del operador integral. n particular, extenderemos aquí al caso de funciones medibles con
Resumen ANÁLISIS LÓGICO INDUCCIÓN Y RECURSIÓN. Conjuntos inductivos. Definiciones circulares
 Resumen ANÁLISIS LÓGICO INDUCCIÓN Y RECURSIÓN Francisco Hernández Quiroz Departamento de Matemáticas Facultad de Ciencias, UNAM E-mail: fhq@ciencias.unam.mx Página Web: www.matematicas.unam.mx/fhq En este
Resumen ANÁLISIS LÓGICO INDUCCIÓN Y RECURSIÓN Francisco Hernández Quiroz Departamento de Matemáticas Facultad de Ciencias, UNAM E-mail: fhq@ciencias.unam.mx Página Web: www.matematicas.unam.mx/fhq En este
Lógica Proposicional
 Lógica y Computabilidad Julián Dabbah (sobre clases de María Emilia Descotte y Laski) 6 de octubre de 2017 Repaso Sintaxis Variables / símbolos proposicionales (PROP): p, p', p,... (los notamos p, q, r...,
Lógica y Computabilidad Julián Dabbah (sobre clases de María Emilia Descotte y Laski) 6 de octubre de 2017 Repaso Sintaxis Variables / símbolos proposicionales (PROP): p, p', p,... (los notamos p, q, r...,
Teoría de la Dimensión
 Capítulo II Teoría de la Dimensión En este capítulo introduciremos una de las propiedades más importantes que tienen los espacios vectoriales: la dimensión. Dos son los modos posibles de llegar a la noción
Capítulo II Teoría de la Dimensión En este capítulo introduciremos una de las propiedades más importantes que tienen los espacios vectoriales: la dimensión. Dos son los modos posibles de llegar a la noción
Números naturales y recursividad
 Números naturales y recursividad Rafael F. Isaacs G. * Fecha: 12 de abril de 2004 Números naturales Cuál es el primer conjunto de números que estudiamos desde la escuela primaria? Se sabe que los números
Números naturales y recursividad Rafael F. Isaacs G. * Fecha: 12 de abril de 2004 Números naturales Cuál es el primer conjunto de números que estudiamos desde la escuela primaria? Se sabe que los números
Es claro que es una relación de equivalencia. Para ver que tener la misma cardinalidad y la cardinalidad están bien definidas queremos ver que
 Capítulo II Cardinalidad Finita II.1. Cardinalidad Definimos I n para n N como I n = {k N : 1 k n}. En particular I 0 =, puesto que 0 < 1. Esto es equivalente a la definición recursiva { si n = 0 I n =
Capítulo II Cardinalidad Finita II.1. Cardinalidad Definimos I n para n N como I n = {k N : 1 k n}. En particular I 0 =, puesto que 0 < 1. Esto es equivalente a la definición recursiva { si n = 0 I n =
Clases de complejidad computacional: P y NP
 1er cuatrimestre 2006 La teoría de Se aplica a problemas de decisión, o sea problemas que tienen como respuesta SI o NO (aunque es sencillo ver que sus implicancias pueden extenderse a problemas de optimización).
1er cuatrimestre 2006 La teoría de Se aplica a problemas de decisión, o sea problemas que tienen como respuesta SI o NO (aunque es sencillo ver que sus implicancias pueden extenderse a problemas de optimización).
Conjuntos computables y Teorema de Rice
 Lógica y Computabilidad Julián Dabbah (Robado de una clase de Franco Frizzo basada en una clase de María Emilia Descotte) 20 de septiembre de 2017 Repaso Conjuntos computables La función característica
Lógica y Computabilidad Julián Dabbah (Robado de una clase de Franco Frizzo basada en una clase de María Emilia Descotte) 20 de septiembre de 2017 Repaso Conjuntos computables La función característica
2. El Teorema del Valor Medio
 2.24 45 2. El Teorema del Valor Medio Comenzaremos esta sección recordando dos versiones del teorema del valor medido para funciones de 1-variable y por tanto ya conocidas: 2.22 Sea f : [a, b] R R una
2.24 45 2. El Teorema del Valor Medio Comenzaremos esta sección recordando dos versiones del teorema del valor medido para funciones de 1-variable y por tanto ya conocidas: 2.22 Sea f : [a, b] R R una
La lógica de segundo orden: Sintaxis
 La lógica de segundo orden: Sintaxis Dado: Vocabulario L Definición La lógica de segundo orden (LSO) sobre L es definida como la extensión de LPO que incluye las siguientes reglas: Si t 1,..., t k son
La lógica de segundo orden: Sintaxis Dado: Vocabulario L Definición La lógica de segundo orden (LSO) sobre L es definida como la extensión de LPO que incluye las siguientes reglas: Si t 1,..., t k son
Máquinas de Turing. 18 de junio de 2015
 Máquinas de Turing 18 de junio de 2015 1. Introducción Hasta ahora hemos visto clases de lenguajes relativamente simples. Lo que vamos a ver ahora es preguntarnos qué lenguajes pueden definirse por cualquier
Máquinas de Turing 18 de junio de 2015 1. Introducción Hasta ahora hemos visto clases de lenguajes relativamente simples. Lo que vamos a ver ahora es preguntarnos qué lenguajes pueden definirse por cualquier
Tema 1: Conjuntos. Miguel Ángel Olalla Acosta Departamento de Álgebra Universidad de Sevilla. Septiembre de 2018
 Tema 1: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2018 Olalla (Universidad de Sevilla) Tema 1: Conjuntos Septiembre de 2018 1
Tema 1: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2018 Olalla (Universidad de Sevilla) Tema 1: Conjuntos Septiembre de 2018 1
ÁLGEBRA LINEAL I NOTAS DE CLASE UNIDAD 2
 ÁLGEBRA LINEAL I NOTAS DE CLASE UNIDAD 2 Abstract Estas notas conciernen al álgebra de matrices y serán actualizadas conforme el material se cubre Las notas no son substituto de la clase pues solo contienen
ÁLGEBRA LINEAL I NOTAS DE CLASE UNIDAD 2 Abstract Estas notas conciernen al álgebra de matrices y serán actualizadas conforme el material se cubre Las notas no son substituto de la clase pues solo contienen
Conjuntos finitos y conjuntos numerables
 Tema 3 Conjuntos finitos y conjuntos numerables En este tema vamos a usar los números naturales para contar los elementos de un conjunto, o dicho con mayor precisión, para definir los conjuntos finitos
Tema 3 Conjuntos finitos y conjuntos numerables En este tema vamos a usar los números naturales para contar los elementos de un conjunto, o dicho con mayor precisión, para definir los conjuntos finitos
Sucesiones. Una sucesión de números reales es una tira, o una lista, de nḿeros reales que generalmente denotamos como
 Universidad de la República Facultad de Ingeniería IMERL Sucesiones Curso Cálculo 1 2008 Una sucesión de números reales es una tira, o una lista, de nḿeros reales que generalmente denotamos como a 1, a
Universidad de la República Facultad de Ingeniería IMERL Sucesiones Curso Cálculo 1 2008 Una sucesión de números reales es una tira, o una lista, de nḿeros reales que generalmente denotamos como a 1, a
Teorías. Una teoría acerca de una base de conocimiento Σ contendrá no sólo a Σ sino que a todo lo que se puede deducir de Σ.
 Teorías Qué es una teoría? Ya hemos usado antes la noción de base de conocimiento Este concepto se refiere a un conocimiento, representado a través de axiomas. Una teoría acerca de una base de conocimiento
Teorías Qué es una teoría? Ya hemos usado antes la noción de base de conocimiento Este concepto se refiere a un conocimiento, representado a través de axiomas. Una teoría acerca de una base de conocimiento
Continuidad y Continuidad Uniforme. Aplicaciones lineales continuas.
 Continuidad y Continuidad Uniforme. Aplicaciones lineales continuas. Beatriz Porras 1 Límites Las definiciones de ĺımite de funciones de varias variables son similares a las de los ĺımites de funciones
Continuidad y Continuidad Uniforme. Aplicaciones lineales continuas. Beatriz Porras 1 Límites Las definiciones de ĺımite de funciones de varias variables son similares a las de los ĺımites de funciones
Entscheidungsproblem I LENGUAJES RECURSIVAMENTE ENUMERABLES MÁQUINAS DE TURING. DECIDIBILIDAD OTROS MODELOS COMPUTACIONALES. Máquinas de Turing (TM)
 Entscheidungsproblem I LENGUAJES RECURSIVAMENTE ENUMERABLES MÁQUINAS DE TURING. DECIDIBILIDAD OTROS MODELOS COMPUTACIONALES Francisco Hernández Quiroz Departamento de Matemáticas Facultad de Ciencias,
Entscheidungsproblem I LENGUAJES RECURSIVAMENTE ENUMERABLES MÁQUINAS DE TURING. DECIDIBILIDAD OTROS MODELOS COMPUTACIONALES Francisco Hernández Quiroz Departamento de Matemáticas Facultad de Ciencias,
Clase Práctica 1 - Inducción estructural, conectivos adecuados y consecuencia - Viernes 23 de marzo de 2012
 Lógica y Computabilidad Primer Cuatrimestre 2012 Clase Práctica 1 - Inducción estructural, conectivos adecuados y consecuencia - Viernes 23 de marzo de 2012 Definición 1. Notaremos con Form al conjunto
Lógica y Computabilidad Primer Cuatrimestre 2012 Clase Práctica 1 - Inducción estructural, conectivos adecuados y consecuencia - Viernes 23 de marzo de 2012 Definición 1. Notaremos con Form al conjunto
Descomposición de dos Anillos de Funciones Continuas
 Miscelánea Matemática 38 (2003) 65 75 SMM Descomposición de dos Anillos de Funciones Continuas Rogelio Fernández-Alonso Departamento de Matemáticas Universidad Autónoma Metropolitana-I 09340 México, D.F.
Miscelánea Matemática 38 (2003) 65 75 SMM Descomposición de dos Anillos de Funciones Continuas Rogelio Fernández-Alonso Departamento de Matemáticas Universidad Autónoma Metropolitana-I 09340 México, D.F.
8.1. Extensiones algebraicas. Grado.
 1 Tema 8.-. Extensiones algebraicas. Cuerpos de descomposición. Elemento primitivo. 8.1. Extensiones algebraicas. Grado. Si k es un subcuerpo de K, diremos que K es una extensión de k, que notaremos K
1 Tema 8.-. Extensiones algebraicas. Cuerpos de descomposición. Elemento primitivo. 8.1. Extensiones algebraicas. Grado. Si k es un subcuerpo de K, diremos que K es una extensión de k, que notaremos K
Teoremas de Taylor. Capítulo 7
 Capítulo 7 Teoremas de Taylor Una vez más nos disponemos a extender a las funciones de varias variables resultados ya conocidos para funciones de una variable, los teoremas de aproximación de Taylor. Por
Capítulo 7 Teoremas de Taylor Una vez más nos disponemos a extender a las funciones de varias variables resultados ya conocidos para funciones de una variable, los teoremas de aproximación de Taylor. Por
Tema 1: Conjuntos. Miguel Ángel Olalla Acosta Departamento de Álgebra Universidad de Sevilla. Septiembre de 2017
 Tema 1: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2017 Olalla (Universidad de Sevilla) Tema 1: Conjuntos Septiembre de 2017 1
Tema 1: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2017 Olalla (Universidad de Sevilla) Tema 1: Conjuntos Septiembre de 2017 1
CARACTERIZACIONES DE LA COMPLETITUD DE R
 CARACTERIZACIONES DE LA COMPLETITUD DE R 1 Definición 1. Diremos que un cuerpo ordenado K es arquimediano si lím n n que decir que N, visto como subconjunto de K, no está acotado en K. = 0 en K. Esto es
CARACTERIZACIONES DE LA COMPLETITUD DE R 1 Definición 1. Diremos que un cuerpo ordenado K es arquimediano si lím n n que decir que N, visto como subconjunto de K, no está acotado en K. = 0 en K. Esto es
Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias.
 Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias. Dr. Rafael Morones E. Dept. de Matemáticas ITAM August 5, 2002 1 Contenido 1 Preliminares. 3 1.1 Sucesiones...............................
Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias. Dr. Rafael Morones E. Dept. de Matemáticas ITAM August 5, 2002 1 Contenido 1 Preliminares. 3 1.1 Sucesiones...............................
Principio de acotación uniforme
 Capítulo 4 Principio de acotación uniforme 4.1. Introducción. Teorema de Baire En este último capítulo vamos a establecer una serie de resultados sobre aplicaciones lineales y continuas entre espacios
Capítulo 4 Principio de acotación uniforme 4.1. Introducción. Teorema de Baire En este último capítulo vamos a establecer una serie de resultados sobre aplicaciones lineales y continuas entre espacios
Teoremas de Convergencia
 Capítulo 24 Teoremas de Convergencia El teorema de la convergencia monótona (Lema 21.3) establece ciertas condiciones sobre una sucesión de funciones medibles para que se puedan permutar los símbolos y
Capítulo 24 Teoremas de Convergencia El teorema de la convergencia monótona (Lema 21.3) establece ciertas condiciones sobre una sucesión de funciones medibles para que se puedan permutar los símbolos y
Capítulo 4: Polinomios
 Capítulo 4: Polinomios Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Diciembre de 2015 Olalla (Universidad de Sevilla) Capítulo 4: Polinomios Diciembre de
Capítulo 4: Polinomios Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Diciembre de 2015 Olalla (Universidad de Sevilla) Capítulo 4: Polinomios Diciembre de
Fundamentos de Ciencias de la Computación
 Fundamentos de Ciencias de la Computación Clase 16: Problema de Primer Cuatrimestre de 2005 Departamento de Cs. e Ing. de la Computación Universidad Nacional del Sur Bahía Blanca, Argentina Un problema
Fundamentos de Ciencias de la Computación Clase 16: Problema de Primer Cuatrimestre de 2005 Departamento de Cs. e Ing. de la Computación Universidad Nacional del Sur Bahía Blanca, Argentina Un problema
Problemas de Decisión
 Problemas de Decisión La motivación de este capítulo puede estar dado por lo siguiente: Dado un conjunto Σ de fórmulas proposicionales en L(P ), existe un algoritmo general para determinar si Σ = ϕ Qué
Problemas de Decisión La motivación de este capítulo puede estar dado por lo siguiente: Dado un conjunto Σ de fórmulas proposicionales en L(P ), existe un algoritmo general para determinar si Σ = ϕ Qué
11.1. Funciones uniformemente continuas
 Lección 11 Continuidad uniforme Completando el análisis de los principales teoremas que conocemos sobre continuidad de funciones reales de variable real, estudiamos ahora la versión general para espacios
Lección 11 Continuidad uniforme Completando el análisis de los principales teoremas que conocemos sobre continuidad de funciones reales de variable real, estudiamos ahora la versión general para espacios
Inducción Matemática Conjuntos Funciones. Matemática Discreta. Agustín G. Bonifacio UNSL. Repaso de Inducción, Conjuntos y Funciones
 UNSL Repaso de Inducción, y Inducción Matemática (Sección 1.7 del libro) Supongamos que queremos demostrar enunciados del siguiente tipo: P(n) : La suma de los primeros n números naturales es n(n+1)
UNSL Repaso de Inducción, y Inducción Matemática (Sección 1.7 del libro) Supongamos que queremos demostrar enunciados del siguiente tipo: P(n) : La suma de los primeros n números naturales es n(n+1)
La clase de hoy. 22 de abril de 2017
 La clase de hoy 22 de abril de 2017 1. Satisfacibilidad 1.1. Vamos a extender ahora nuestra noción de verdad bajo una interpretación de enunciados a fórmulas. Por supuesto, el tema es cómo interpretar
La clase de hoy 22 de abril de 2017 1. Satisfacibilidad 1.1. Vamos a extender ahora nuestra noción de verdad bajo una interpretación de enunciados a fórmulas. Por supuesto, el tema es cómo interpretar
Álgebra II Primer Cuatrimestre 2016
 Álgebra II Primer Cuatrimestre 2016 Práctica 1: Grupos - Primera parte Notaciones usuales Z n D n H = {±1, ±i, ±j, ±k} Enteros módulo n Grupo diedral de orden 2n Grupo de cuaterniones Definiciones y ejemplos
Álgebra II Primer Cuatrimestre 2016 Práctica 1: Grupos - Primera parte Notaciones usuales Z n D n H = {±1, ±i, ±j, ±k} Enteros módulo n Grupo diedral de orden 2n Grupo de cuaterniones Definiciones y ejemplos
La trascendencia de e y π
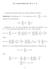 La trascendencia de e y π Comenzamos introduciendo unos convenios útiles de notación: Definición 1 Escribiremos h r = r!, de modo que si fz) = m c r z r C[z], entonces fh) representará fh) = m c r h r
La trascendencia de e y π Comenzamos introduciendo unos convenios útiles de notación: Definición 1 Escribiremos h r = r!, de modo que si fz) = m c r z r C[z], entonces fh) representará fh) = m c r h r
Lógica y Computabilidad Capítulo 3
 Dpto. CCIA, Universidad de Sevilla 19 Lógica y Computabilidad. 2004 05 Capítulo 3 Capítulo 3 Funciones Recursivas 3.1. La clase de las funciones recursivas Comenzaremos presentando tres procedimientos
Dpto. CCIA, Universidad de Sevilla 19 Lógica y Computabilidad. 2004 05 Capítulo 3 Capítulo 3 Funciones Recursivas 3.1. La clase de las funciones recursivas Comenzaremos presentando tres procedimientos
Espacios conexos. 6.1 Conexos
 Capítulo 6 Espacios conexos 6.1 Conexos Definición 6.1.1 (Conjuntos separados). Dado un espacio topológico (X, τ) y dos subconjuntos A, B X, diremos que A y B están separados si A B = A B = Es evidente
Capítulo 6 Espacios conexos 6.1 Conexos Definición 6.1.1 (Conjuntos separados). Dado un espacio topológico (X, τ) y dos subconjuntos A, B X, diremos que A y B están separados si A B = A B = Es evidente
Cálculo infinitesimal Grado en Matemáticas Curso 20014/15 Clave de soluciones n o 6. Derivadas de orden superior
 Cálculo infinitesimal Grado en Matemáticas Curso 2004/5 Clave de soluciones n o 6 Derivadas de orden superior 70. Hallar los polinomios de Taylor del grado indicado y en el punto indicado para las siguientes
Cálculo infinitesimal Grado en Matemáticas Curso 2004/5 Clave de soluciones n o 6 Derivadas de orden superior 70. Hallar los polinomios de Taylor del grado indicado y en el punto indicado para las siguientes
Teorema de Lagrange. En esta sección demostramos algunos hechos básicos sobre grupos, que se pueden deducir de la definición
 Teorema de Lagrange Capítulo 3 3.1 Introducción En este capítulo estudiaremos uno de los teoremas más importantes de toda la teoría de grupos como lo es el Teorema de Lagrange. Daremos en primer lugar
Teorema de Lagrange Capítulo 3 3.1 Introducción En este capítulo estudiaremos uno de los teoremas más importantes de toda la teoría de grupos como lo es el Teorema de Lagrange. Daremos en primer lugar
Funciones de Variable Real
 Tema 1 Funciones de Variable Real 1.1. La Recta Real Los números reales se pueden ordenar como los puntos de una recta. Los enteros positivos {1, 2, 3, 4,...} que surgen al contar, se llaman números naturales
Tema 1 Funciones de Variable Real 1.1. La Recta Real Los números reales se pueden ordenar como los puntos de una recta. Los enteros positivos {1, 2, 3, 4,...} que surgen al contar, se llaman números naturales
Capítulo IV: FUNCIONES RECURSIVAS
 Capítulo IV: FUNCIONES RECURSIVAS IV.2: FUNCIONES PRIMITIVAS RECURSIVAS Mario de J. Pérez Jiménez Grupo de investigación en Computación Natural Dpto. Ciencias de la Computación e Inteligencia Artificial
Capítulo IV: FUNCIONES RECURSIVAS IV.2: FUNCIONES PRIMITIVAS RECURSIVAS Mario de J. Pérez Jiménez Grupo de investigación en Computación Natural Dpto. Ciencias de la Computación e Inteligencia Artificial
F-ESPACIOS. 1.- Introducción
 F-ESPACIOS 1.- Introducción Recordemos que un subconjunto A de un espacio topológico X se llama diseminado o raro (nowhere dense en ingés) si A=. Un subconjunto que se pueda escribir como unión numerable
F-ESPACIOS 1.- Introducción Recordemos que un subconjunto A de un espacio topológico X se llama diseminado o raro (nowhere dense en ingés) si A=. Un subconjunto que se pueda escribir como unión numerable
Conjuntos finitos y conjuntos numerables
 Tema 3 Conjuntos finitos y conjuntos numerables En este tema vamos a usar los números naturales para contar los elementos de un conjunto, o dicho con mayor precisión, para definir los conjuntos finitos
Tema 3 Conjuntos finitos y conjuntos numerables En este tema vamos a usar los números naturales para contar los elementos de un conjunto, o dicho con mayor precisión, para definir los conjuntos finitos
Sucesiones y Series Sucesiones
 Capítulo 6 Sucesiones y Series 6.. Sucesiones En particular estudiaremos las sucesiones de números reales, es decir, las que verifican la siguiente definición. Definición 6... Llamaremos sucesión a la
Capítulo 6 Sucesiones y Series 6.. Sucesiones En particular estudiaremos las sucesiones de números reales, es decir, las que verifican la siguiente definición. Definición 6... Llamaremos sucesión a la
EJERCICIOS RESUELTOS. NÚMEROS Y FUNCIONES. CONTINUIDAD Y LÍMITE FUNCIONAL.
 EJERCICIOS RESUELTOS. NÚMEROS Y FUNCIONES. CONTINUIDAD Y LÍMITE FUNCIONAL. 1. Estúdiese la continuidad de la función f : R R, definida por f (x) = xe(1/x) si x = 0, f (0) = 1.. Sea f : R R continua, mayorada
EJERCICIOS RESUELTOS. NÚMEROS Y FUNCIONES. CONTINUIDAD Y LÍMITE FUNCIONAL. 1. Estúdiese la continuidad de la función f : R R, definida por f (x) = xe(1/x) si x = 0, f (0) = 1.. Sea f : R R continua, mayorada
Tema 1: Conjuntos. Miguel Ángel Olalla Acosta Departamento de Álgebra Universidad de Sevilla. Septiembre de 2016
 Tema 1: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2016 Olalla (Universidad de Sevilla) Tema 1: Conjuntos Septiembre de 2016 1
Tema 1: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2016 Olalla (Universidad de Sevilla) Tema 1: Conjuntos Septiembre de 2016 1
MÁQUINAS DE TURING CIENCIAS DE LA COMPUTACION I 2009
 MÁQUINAS DE TURING Las máquinas de Turing, así como los AF y los AP se utilizan para aceptar cadenas de un lenguaje definidas sobre un alfabeto A. El modelo básico de máquina de Turing, tiene un mecanismo
MÁQUINAS DE TURING Las máquinas de Turing, así como los AF y los AP se utilizan para aceptar cadenas de un lenguaje definidas sobre un alfabeto A. El modelo básico de máquina de Turing, tiene un mecanismo
Computabilidad y Lenguajes Formales: Teoría de la Computabilidad: Decidibilidad
 300CIG007 Computabilidad y Lenguajes Formales: Teoría de la Computabilidad: Decidibilidad Pontificia Universidad Javeriana Cali Ingenieria de Sistemas y Computación Prof. Gloria Inés Alvarez V. Lo indecidible
300CIG007 Computabilidad y Lenguajes Formales: Teoría de la Computabilidad: Decidibilidad Pontificia Universidad Javeriana Cali Ingenieria de Sistemas y Computación Prof. Gloria Inés Alvarez V. Lo indecidible
Tema 1: Fundamentos.
 Tema 1: Fundamentos. 1. Nociones básicas de la Teoría de Conjuntos. Definición. Un conjunto es una colección de objetos. A los objetos de un conjunto se les llama elementos del conjunto. Se denominará
Tema 1: Fundamentos. 1. Nociones básicas de la Teoría de Conjuntos. Definición. Un conjunto es una colección de objetos. A los objetos de un conjunto se les llama elementos del conjunto. Se denominará
Divisibilidad en Z. Apéndice A. A.0 Subgrupos de Z
 Apéndice A Divisibilidad en Z Todo número compuesto es medido por algún número primo. Todo número o bien es número primo o es medido por algún número primo. Euclides, Elementos, Libro VII Cualquier número
Apéndice A Divisibilidad en Z Todo número compuesto es medido por algún número primo. Todo número o bien es número primo o es medido por algún número primo. Euclides, Elementos, Libro VII Cualquier número
ALGEBRA y ALGEBRA LINEAL. Primer Semestre CAPITULO I LOGICA Y CONJUNTOS.
 ALGEBRA y ALGEBRA LINEAL 520142 Primer Semestre CAPITULO I LOGICA Y CONJUNTOS. DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas Universidad de Concepción 1 La lógica es
ALGEBRA y ALGEBRA LINEAL 520142 Primer Semestre CAPITULO I LOGICA Y CONJUNTOS. DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas Universidad de Concepción 1 La lógica es
Sucesiones y series de funciones
 Sucesiones y series de funciones Renato Álvarez Nodarse Departamento de Análisis Matemático Facultad de Matemáticas. Universidad de Sevilla http://euler.us.es/ renato/ 8 de octubre de 2012 Sucesiones y
Sucesiones y series de funciones Renato Álvarez Nodarse Departamento de Análisis Matemático Facultad de Matemáticas. Universidad de Sevilla http://euler.us.es/ renato/ 8 de octubre de 2012 Sucesiones y
Funciones primtivas recursivas y clases PRC (parte I)
 Funciones primtivas recursivas y clases PRC (parte I) Hernán Czemerinski Miércoles 2 de febrero de 2011 Definición 1. Llamamos funciones iniciales a n(x) = 0 s(x) = x + 1 u n i (x 1,..., x n ) = x i con
Funciones primtivas recursivas y clases PRC (parte I) Hernán Czemerinski Miércoles 2 de febrero de 2011 Definición 1. Llamamos funciones iniciales a n(x) = 0 s(x) = x + 1 u n i (x 1,..., x n ) = x i con
ÁLGEBRA (Ciencias) año 2014 PRÁCTICA N 4. ELEMENTOS DE TEORÍA DE CONJUNTOS: nociones básicas
 ÁLGEBRA (Ciencias) año 2014 PRÁCTICA N 4 ELEMENTOS DE TEORÍA DE CONJUNTOS: nociones básicas 1. Decir, justificando adecuadamente, si las siguientes afirmaciones son verdaderas o falsas: (a) { } (b) { }
ÁLGEBRA (Ciencias) año 2014 PRÁCTICA N 4 ELEMENTOS DE TEORÍA DE CONJUNTOS: nociones básicas 1. Decir, justificando adecuadamente, si las siguientes afirmaciones son verdaderas o falsas: (a) { } (b) { }
Conjuntos Abiertos y Cerrados
 Conjuntos Abiertos y Cerrados 1. (a) En la prueba de que la intersección de una colección finita de conjuntos abiertos es un conjunto abierto, dónde se uso la hipótesis de que la colección es finita? 2.
Conjuntos Abiertos y Cerrados 1. (a) En la prueba de que la intersección de una colección finita de conjuntos abiertos es un conjunto abierto, dónde se uso la hipótesis de que la colección es finita? 2.
Ejercicios resueltos. Computación. Tema 3
 Ejercicios resueltos. Computación. Tema 3 Ejercicio.- Sea f : N 3 N y g 1 : N N, g 2 : N 2 N y g 3 : N 3 N. a) En los siguientes casos, expresar f como composición de funciones de la misma aridad. 1. f(x,
Ejercicios resueltos. Computación. Tema 3 Ejercicio.- Sea f : N 3 N y g 1 : N N, g 2 : N 2 N y g 3 : N 3 N. a) En los siguientes casos, expresar f como composición de funciones de la misma aridad. 1. f(x,
Continuidad y monotonía
 Tema 14 Continuidad y monotonía Generalizando lo que se hizo en su momento para sucesiones, definiremos la monotonía de una función, en forma bien fácil de adivinar. Probaremos entonces dos resultados
Tema 14 Continuidad y monotonía Generalizando lo que se hizo en su momento para sucesiones, definiremos la monotonía de una función, en forma bien fácil de adivinar. Probaremos entonces dos resultados
Matemática computable
 Conjuntos computables - Combinatoria - Álgebra Antonio Montalbán. U. de Chicago Coloquio Uruguayo de Matemática. Diciembre, 2009 Conjuntos computables - Combinatoria - Álgebra 1 Conjuntos computables 2
Conjuntos computables - Combinatoria - Álgebra Antonio Montalbán. U. de Chicago Coloquio Uruguayo de Matemática. Diciembre, 2009 Conjuntos computables - Combinatoria - Álgebra 1 Conjuntos computables 2
Estructuras algebraicas. Departamento de Álgebra. Apuntes de teoría
 ESTRUCTURAS ALGEBRAICAS GRADO EN MATEMÁTICAS. CURSO 2015/2016 Apuntes de teoría Tema 1: Grupos y subgrupos. 1.1. Introducción Definición 1.1. Un grupo es un par (G, ), donde G es un conjunto no vacío,
ESTRUCTURAS ALGEBRAICAS GRADO EN MATEMÁTICAS. CURSO 2015/2016 Apuntes de teoría Tema 1: Grupos y subgrupos. 1.1. Introducción Definición 1.1. Un grupo es un par (G, ), donde G es un conjunto no vacío,
Teoría de la Computabilidad
 MT para computar funciones Teoría de la Computabilidad Módulo 9: Máquinas de Turing para Computar Funciones Extensiones de las Máquinas de Turing Departamento de Cs. e Ing. de la Computación Universidad
MT para computar funciones Teoría de la Computabilidad Módulo 9: Máquinas de Turing para Computar Funciones Extensiones de las Máquinas de Turing Departamento de Cs. e Ing. de la Computación Universidad
LÓGICA FORMAL TEORIAS DE PRIMER ORDEN. Sintaxis y semántica
 LÓGICA FORMAL TEORIAS DE PRIMER ORDEN Sintaxis y semántica Pedro López Departamento de Inteligencia Artificial Facultad de Informática Universidad Politécnica de Madrid Lenguajes de primer orden 1 La lógica
LÓGICA FORMAL TEORIAS DE PRIMER ORDEN Sintaxis y semántica Pedro López Departamento de Inteligencia Artificial Facultad de Informática Universidad Politécnica de Madrid Lenguajes de primer orden 1 La lógica
Ejercicios resueltos. Teoría de la Computabilidad. Tema 3
 Ejercicios resueltos. Teoría de la Computabilidad. Tema 3 Ejercicio.- Sea f : N 3 N y g 1 : N N, g 2 : N 2 N y g 3 : N 3 N. a) En los siguientes casos, expresar f como composición de funciones de la misma
Ejercicios resueltos. Teoría de la Computabilidad. Tema 3 Ejercicio.- Sea f : N 3 N y g 1 : N N, g 2 : N 2 N y g 3 : N 3 N. a) En los siguientes casos, expresar f como composición de funciones de la misma
Capítulo 3: El anillo de los números enteros
 Capítulo 3: El anillo de los números enteros Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Noviembre de 2016 Olalla (Universidad de Sevilla) El anillo de
Capítulo 3: El anillo de los números enteros Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Noviembre de 2016 Olalla (Universidad de Sevilla) El anillo de
Espacios topológicos. 3.1 Espacio topológico
 Capítulo 3 Espacios topológicos 3.1 Espacio topológico Definición 3.1.1. Un espacio topológico es un par (X, τ), donde X es un conjunto, y τ es una familia de subconjuntos de X que verifica las siguientes
Capítulo 3 Espacios topológicos 3.1 Espacio topológico Definición 3.1.1. Un espacio topológico es un par (X, τ), donde X es un conjunto, y τ es una familia de subconjuntos de X que verifica las siguientes
